| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A142 | |
| Number of page(s) | 15 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202346854 | |
| Published online | 13 February 2024 | |
Detecting stellar activity cycles in p-mode travel times
Proof of concept using SOHO/VIRGO solar observations
1
Max-Planck-Institut für Sonnensystemforschung, Göttingen, Germany
e-mail: vasilyev@mps.mpg.de
2
Institut für Astrophysik, Georg-August-Universität Göttingen, Göttingen, Germany
3
Center for Space Science, NYUAD Institute, New York University Abu Dhabi, Abu Dhabi, UAE
Received:
9
May
2023
Accepted:
17
November
2023
Context. The 11 yr solar cycle is known to affect the global modes of solar acoustic oscillations. In particular, p mode frequencies increase with solar activity.
Aims. We propose a new method to detect the solar cycle from the p-mode autocorrelation function, and we validate this method using VIRGO/SPM photometric time series from solar cycles 23 and 24.
Methods. The p-mode autocorrelation function shows multiple wavepackets separated by time lags of ∼123 min. Using a one-parameter fitting method (from local helioseismology), we measure the seismic travel times from each wavepacket up to skip number 40.
Results. We find that the travel-time variations due to the solar cycle strongly depend on the skip number, with the strongest signature in odd skips from 17 to 31. Taking the noise covariance into account, the travel-time perturbations can be averaged over all skip numbers to enhance the signal-to-noise ratio.
Conclusions. This method is robust to noise, simpler to implement than peak bagging in the frequency domain, and is promising for asteroseismology. We estimate that the activity cycle of a Sun-like star should be detectable with this new method in Kepler-like observations down to a visual magnitude of mK ∼ 11. However, for fainter stars, activity cycles are easier to detect in the photometric variability on rotational timescales.
Key words: asteroseismology / Sun: activity / Sun: helioseismology / stars: activity
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open access funding provided by Max Planck Society.
1. Introduction
In the case of the Sun, magnetic activity follows an 11 yr cycle, which is seen in many observables on the solar surface and in the atmosphere. This cycle is prominent in the variations of the sunspot number and the sunspot area, which are used as the standard proxies of solar activity. In the chromosphere, solar active regions lead to increased emission, which is most evident in the core of the CaII H&K lines (e.g., White et al. 1998). Activity cycles on Sun-like stars produce both long-term spectral and photometric variations detected with ground-based spectroscopic (see e.g., Mount Wilson Observatory HK Project, Wilson 1978; Duncan et al. 1991; Baliunas et al. 1995) and photometric observations (see e.g., Radick et al. 2018). High-precision space photometry made it possible to find evidence for activity cycles in thousands of stars (Reinhold et al. 2017).
Methods of helio- and asteroseismology provide an independent way to study magnetic activity. The sunspot cycle is known to affect solar p modes, as seen in the variations of their frequencies (see e.g., Woodard & Noyes 1985; Fossat et al. 1987; Jiménez-Reyes et al. 1998; Chaplin et al. 2003; Salabert et al. 2004; Howe et al. 2018), line widths, amplitudes (see e.g., Pallé et al. 1990; Anguera Gubau et al. 1992; Salabert et al. 2007), and energy supply rates (Kiefer & Broomhall 2021). Mode frequencies and line widths increase with activity, and mode amplitudes decrease (see e.g., Basu 2016, for a review). In particular, the large frequency separation is affected (Broomhall et al. 2011). Modes with higher frequencies are more affected, from which we deduce that magnetic perturbations act on the modes in the surface layers (Libbrecht & Woodard 1990). Santos et al. (2016) find that sunspots contribute around 30% of the frequency shifts of low-degree p modes. A contribution from solar activity at high latitudes is not excluded (Moreno-Insertis & Solanki 2000).
The first detection of activity using stellar p modes was reported for the F5V CoRoT star HD49933 by García et al. (2010). A modulation of the mode frequencies and amplitudes over 120 days was detected, with higher frequencies corresponding to smaller amplitudes. In addition, frequency shifts are larger at higher frequencies, indicating a near-surface effect (Salabert et al. 2011). Using Kepler high-cadence (1 min) data, Salabert et al. (2018) and Santos et al. (2019) extended this analysis to a larger sample of Sun-like stars. Frequency shifts decrease with stellar age and surface rotation period and correlate with effective temperature.
Measuring the frequency shifts of individual modes – which are often much lower than 1 μHz – is very challenging, especially at low signal-to-noise ratios. Palle et al. (1989) proposed to use a cross-correlation technique to measure a mean frequency shift over all modes in the power spectrum. Régulo et al. (2016) and Kiefer et al. (2017) applied the cross-correlation method to analyze Kepler stars. In more than half the stars, periodic variations of the mean frequency shifts were accompanied by variations in other activity proxies, such as the photometric activity (Santos et al. 2018).
Fitting oscillation power spectra is a delicate enterprise that requires many parameters: several parameters for each mode and parameters for the background noise. Here, we propose to extract seismic information from the autocovariance of the intensity time series, I, over a segment of the data of length T:
The function C displays a series of wavepackets that are nearly regularly spaced in time, each associated with a particular arrival time (or skip number). For each skip number, we extract a single parameter: the travel-time perturbation between C and the smooth reference Cref. This one-parameter fit – first developed in time – distance helioseismology (Gizon & Birch 2002) – has been shown to be very robust to noise Gizon & Birch (2004) and is very easy to implement (Sect. 2.2.2). It has become a standard method in this field and has been used, for example, to infer the Sun’s meridional flow (Gizon et al. 2020).
For each wavepacket, the travel-time perturbation τ is extracted from C(t) by cross-correlation with a sliding reference Cref(t − τ). The function Cref is an estimate of the expectation value of C, obtained from a model or from an average over many realizations of C. Because the function C is noisy, the travel-time perturbation measured by cross-correlation with Cref is also noisy. To handle this problem, the idea is to replace C by the smooth function Cϵ = ϵC + (1 − ϵ)Cref, where ϵ is small. The travel-time perturbation ϵτ can now unambiguously be measured from Cϵ by comparison with the sliding reference Cref. Formally, this procedure can be summarized as follows:
The limit ϵ → 0 ensures that the above calculation is meaningful irrespective of the level of noise in C. For the sth wavepacket, we have
where the integral is over a time interval wins centered on the sth wavepacket. The minimization can be carried out analytically to obtain
where the function Ws is smooth and depends only on Cref and its first derivative 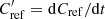 ; see Gizon & Birch (2004) and Sect. 2. This definition of travel time, Eq. (4), is extremely robust to noise and is straightforward to compute. Furthermore, the travel-time perturbation is linear in the perturbation to the autocorrelation function. This property ensures a simple connection between travel-time measurements and perturbations to the stellar model. Using travel-time kernels that describe the sensitivity of the measurements to localized changes in the solar interior (e.g., Gizon & Birch 2002; Gizon et al. 2017; Fournier et al. 2018), we can interpret the seismic data by solving a linear inverse problem. In addition, this definition of travel time enables us to model the noise covariance matrix (Gizon & Birch 2004; Fournier et al. 2014).
; see Gizon & Birch (2004) and Sect. 2. This definition of travel time, Eq. (4), is extremely robust to noise and is straightforward to compute. Furthermore, the travel-time perturbation is linear in the perturbation to the autocorrelation function. This property ensures a simple connection between travel-time measurements and perturbations to the stellar model. Using travel-time kernels that describe the sensitivity of the measurements to localized changes in the solar interior (e.g., Gizon & Birch 2002; Gizon et al. 2017; Fournier et al. 2018), we can interpret the seismic data by solving a linear inverse problem. In addition, this definition of travel time enables us to model the noise covariance matrix (Gizon & Birch 2004; Fournier et al. 2014).
The paper is organized as follows. In Sect. 2, we present the VIRGO/SPM data that cover the last two solar cycles and we describe the data analysis. In Sect. 3, we measure the solar seismic travel times over segments of the data (T = 90 days) and show that the travel times change with the solar cycle. The implications of our findings for the detection of activity cycles on other stars are discussed in Sect. 4.
2. Method
2.1. Observations
We use Sun-as-a-star observations from the VIRGO experiment on board the Solar and Heliospheric Observatory (SOHO). The VIRGO/SPM instrument is a three-channel full-beam Sun photometer (Fröhlich et al. 1995, 1997). It measures solar brightness variations in the continuum through three filters that are centered on wavelengths 402 nm (blue), 500 nm (green), and 862 nm (red) with a temporal cadence of δt = 1 min. The bandwidth of each filter is 5 nm. The response functions of the three channels are located near the base of the solar photosphere, within ±10 km of the τ500 nm = 1 surface (see Fligge et al. 1998, for details). The blue and green channels are more sensitive to the lower part of the solar atmosphere, the red channel to higher layers (Jiménez et al. 2005).
The VIRGO/SPM1 instrument has been observing the Sun continuously since January 1996, except for two long gaps. In the summer of 1998, a gap of about 100 days was due to a rotation maneuver of the spacecraft that went wrong. The second gap of about one month occurred in January 1999 as a result of spacecraft problems. In addition, 5–8% of the data are not usable depending on the channel (e.g., Jiménez et al. 2002). The data that we use here cover 22 yr from 23 January 1996 to 26 June 2018 (solar cycles 23 and 24). The data are detrended and gaps are filled using linear interpolation. Two segments of the data are selected in Fig. 1 to display the temporal variations on the rotation timescale and on the p-mode oscillation timescale.
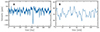 |
Fig. 1. One-year (A) and two-hour (B) segments of VIRGO/SPM brightness data (red channel). In both plots, the origin of time is 28 March 2014. |
2.2. Data analysis
2.2.1. Autocovariance function
Let us consider the intensity, I(t), measured in one of the VIRGO channels at time cadence δt. We split the time series into M time intervals of equal duration T = (2K + 1)δt, specified through an integer K. For example, for K = 64 800 we have T = 90 days. The central time of each segment of the data is
where t00 is a reference start time and Δt is the sampling (e.g., 2 months). These segments may overlap. Nonoverlapping contiguous segments have Δt = T. In each segment of the data, time is conveniently specified by two indices, i and k:
with 0 ≤ i ≤ M − 1 and −K ≤ k ≤ K. Over each time segment, we define the time series {Ii} such that
Figure 2 summarizes the notations.
 |
Fig. 2. Schematics showing how the data segments {Ii} are constructed from the original time series of the observed intensity. |
To each segment of the data, we apply a Fourier transform:
where ωj = jΔω is the frequency and Δω = 2π/T is the frequency resolution. The autocovariance function is given by
where kδt is the correlation time lag.
Figure 3A shows the autocovariance functions calculated for time series in the red, green, and blue VIRGO/SPM channels covering the same T = 90 day segment in 2018 from 28 March to 26 June. The p modes are clearly seen near time lags 250 min and 500 min (the wavepackets with s = 2 and s = 4). At zero time lag, the autocovariance function has a sharp peak with a width of ∼20 min due to the solar granulation. This granulation peak at zero time lag is well reproduced in Fig. 3B using a numerical simulation of solar magnetoconvection simulations in a small Cartesian box (Beeck et al. 2013).
 |
Fig. 3. Autocovariance functions of intensity time series. (A) Autocovariance function of the VIRGO/SPM data (T = 90 d). The red, green, and blue curves correspond to the three channels. (B) Autocovariance of MURaM solar convection simulations (T = 15 h). (C) Autocovariance function for the p-mode data computed for a segment of VIRGO data with T = 90 days (red channel). (D) Reference autocovariance function obtained by averaging over M = 91 consecutive segments covering 22 yr. The first seven wavepackets are labeled s = 1 through 7. The curves in panels C and D are computed from filtered time series (Gaussian filter centered on 3 mHz with a full width of 2 mHz). (E) Zoom onto wavepacket s = 4 and width of the temporal window function f4(t). |
To focus on the p modes, we filter the data by multiplying with a Gaussian filter F(ωj) centered at 3 mHz with a full width of 2 mHz:
where kδt is the correlation time lag. We separately filter the positive and negative frequency domains using a Gaussian filter with a full width at half maximum (FWHM) of 2 mHz centered on about 3 mHz and −3 mHz, respectively. In Fig. 3C, we show the autocovariance function computed with the filtered data collected over 90 days.
Next, we construct a reference autocovariance function by averaging Ci over all the time intervals:
In Fig. 3D, we show the reference autocovariance function computed by averaging over M = 91 segments of data covering 22 yr in total. In the time-lag range from 0 to 3.5 days, there are about 40 p-mode wave packets. To each wave packet, we assign an index s equal to the number of skips that waves forming the given wave packet have before coming back to the original point. We denote the total number of wave packets used in the analysis as Nskips. The first wave packet, denoted s = 1, arrives with a time lag of 1/Δν, where Δν is the large frequency separation:
where c(r) is the sound speed profile and R⊙ the solar radius. During this time, waves travel from the surface to their lower turning points and are partially reflected back to the surface. Due to the very small amplitude of this wave packet, we exclude it from the further analysis. The waves that are not reflected back travel further, cross the Sun, reach the surface, get reflected, and travel back. They arrive with a time lag of ≈240 min, and we denote them wave packet s = 2. With an increase in the number of skips, the penetration depth of p-modes decreases, and depending on the perturbations of the solar structure, p-modes can travel faster or slower. In the autocovariance function, this causes a negative or positive time lag of the wave packet relative to the wave packet with the same skip number in the reference autocovariance.
2.2.2. Travel-time measurements
We use the definition for the travel time introduced by Gizon & Birch (2004). For a given p-mode wave packet s, it is a time lag that minimizes the difference between the measured autocovariance Ci and the reference autocovariance Cref:
where ti is defined in Eq. (5), and Ws(kδt) is the weight for the sth wave packet:
where fs(t) is the window function to isolate the sth wave packet, and 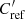 is the time derivative of the reference autocovariance function (computed in Fourier space). By construction, the window function is only nonzero in a time-lag interval around the wave packet s. In Fig. 3E, we show the measured and the reference autocovariance for the wave packet s = 4, and the window function used to isolate it. Following the above approach, we measure travel times for Nskip = 40 wave packets with skips from s = 2 to 41.
is the time derivative of the reference autocovariance function (computed in Fourier space). By construction, the window function is only nonzero in a time-lag interval around the wave packet s. In Fig. 3E, we show the measured and the reference autocovariance for the wave packet s = 4, and the window function used to isolate it. Following the above approach, we measure travel times for Nskip = 40 wave packets with skips from s = 2 to 41.
3. Results
3.1. Solar-cycle variations in the travel times
In Fig. 4, we show the travel times τs as functions of ti for the years 1996–2018 and for each skip number s ≤ 41. A modulation due to the 11 yr solar cycle is seen, except for skips s = 3 and 5. Near cycle maximum, the travel times are shorter (negative τs), while they are longer near cycle minimum. The relative variations in travel time induced by the solar cycle depend on the skip number and on the cycle number (23 or 24). For example, the imprint of the sunspot cycle is very easy to see in the travel-time variations for the odd skips from 15 to 35. On the contrary, the cycle is difficult to see in the variations of skips 3, 5, 7, 9, 24, 26, 28, and 41. The noise in the travel times clearly depends on the skip number. For example, skips 3, 39, and 41 are particularly noisy.
 |
Fig. 4. Measured travel times τs(ti) for all wavepackets with s ≤ 41. The red curves show the filtered data τs, smooth(ti) according to Eq. (15). The value of s is written in the top left corner of each plot. The data analyzed here are from VIRGO/SPM (red channel) divided into non-overlapping segments of T = Δt = 90 days in length (see Fig. 2). |
We now wish to measure the amplitude of the variations due to the solar cycle and its uncertainty in each of the time series τs shown in Fig. 4. For each skip number s, we estimate the signal by applying a low-pass filter to the data, such that only periods longer than 1.5 yr remain. This threshold also lets through the quasi-biennial variations (e.g., Bazilevskaya et al. 2014). To filter the data, we use a sixth-order Butterworth filter H6(ω, ωc) = (1 + (ω/ωc)12)−1 with a cut-off frequency of ωc = 2π/(1.5 yr):
where ωq = 2πq/(MΔt) and 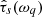 is the Fourier transform of the travel times. For Fig. 4, we have M = 91 and Δt = 90 days. The noise in the travel times can be estimated by computing the standard deviation of the residuals:
is the Fourier transform of the travel times. For Fig. 4, we have M = 91 and Δt = 90 days. The noise in the travel times can be estimated by computing the standard deviation of the residuals:
with
We define the times tSSN_max and tSSN_min to correspond to the solar cycle maximum in November 2001 and the cycle minimum in December 2008. Next, we define the travel-time difference:
By construction, we expect As > 0 when the variations in travel times are dominated by the solar cycle perturbations. For example, in Figs. 5A and B the variations of τ19(ti) are very clearly anti-correlated with the sunspot number. Figures 5C and D show the residual high-frequency noise in the travel times and how the travel times are filtered for estimation of A19.
 |
Fig. 5. Comparison between the sunspot number (SSN) smoothed over 13 months (A) and seismic travel times, τs, for skip number s = 19 (B) measured in the red VIRGO/SPM channel data. Vertical dashed lines indicate cycle maximum and minimum. The red line represents the filtered data, τs, smooth(t), which we use to measure the amplitude of the travel-time variations due to the solar cycle As (black arrow). (C) Residuals between τs and τs, smooth. (D) Power spectrum of τs, normalized to the power of the 11-yr harmonic. A Butterworth filter (red line) is used to extract τs, smooth(t). |
According to the definition of As, its variance is given by
where σs is given by Eq. (16). Then, for each skip s, we define the ratio between the signal due to the solar cycle and the noise level as
In Figs. 6A and B, we show As, 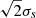 , and S/Ns for skip numbers s = 2 to 41. We find that they strongly depend on skip number s. Surprisingly, the highest signal-to-noise ratios (S/Ns > 3) are for odd skip numbers from s = 15 to 35. Skip numbers s = 3, 5, 7, 24 and 26 are very noisy (S/Ns < 0.5).
, and S/Ns for skip numbers s = 2 to 41. We find that they strongly depend on skip number s. Surprisingly, the highest signal-to-noise ratios (S/Ns > 3) are for odd skip numbers from s = 15 to 35. Skip numbers s = 3, 5, 7, 24 and 26 are very noisy (S/Ns < 0.5).
 |
Fig. 6. Detectability of the solar cycle in individual skip travel times. (A) Amplitudes of travel-time variations due to the solar cycle, As, versus skip number s (see Eq. (18)), with error bars of |
3.2. Noise correlations in travel times
The noise covariance matrix for τs is given by
where s and s′ belong to {2, 3, …Nskip + 1}. The noise correlation matrix is then Rss′ = Λss′/σsσs′. Figures 6C–E show cuts through the matrices Λ and R. As mentioned in the previous section, the variance of the noise depends strongly on the value and parity (odd or even) of s (Fig. 6C). At a fixed s′, the noise covariance Λss′ and the noise correlation Rss′ depend strongly on the skip number s. For example, for s′ = 19, the correlation is large and positive (Rs, 19 > 0.6) for odd skips from s = 15 to 23 and for even skips from s = 32 to 40, but the correlation is negative for even skips from s = 12 to 22 (Figs. 6D and E).
3.3. Travel-time averages and signal-to-noise ratio
Here, we construct a linear combination of the travel times that takes the noise correlations into account in order to reduce the overall noise and detect the solar activity cycle with the highest S/N. Minimizing the variance of the noise can be achieved (1) by transforming the travel times to statistical orthogonality and (2) by applying a straight average (see, e.g., Kessy et al. 2018). To construct a new set of statistically independent travel-time measurements, we apply the standard transformation
where 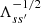 is the whitening matrix. By construction, the covariance matrix of the whitened data is the identity matrix:
is the whitening matrix. By construction, the covariance matrix of the whitened data is the identity matrix:
Next, we compute a straight average of the whitened time series over skips to obtain the average travel time:
Equations (22) and (24) can be combined into one formula:
The average signal and noise components are
The standard deviation of the average noise is
Given these average quantities, the solar activity cycle amplitude becomes
with variance
and
Figure 7 shows the measured averaged travel time 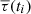 , the average signal
, the average signal 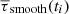 , and the noise level
, and the noise level 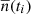 , all obtained after averaging over Nskip = 40 skips. The improvement in the S/N as a function of skip number is plotted in Fig. 8. We find that the S/N increases steadily with Nskip until Nskip ≈ 20, and then reaches a plateau. The maximum S/N is approximately 8.
, all obtained after averaging over Nskip = 40 skips. The improvement in the S/N as a function of skip number is plotted in Fig. 8. We find that the S/N increases steadily with Nskip until Nskip ≈ 20, and then reaches a plateau. The maximum S/N is approximately 8.
 |
Fig. 7. Average seismic travel time. (A) Measured average travel time |
 |
Fig. 8. Detectability of the solar cycle in the average VIRGO travel times. (A) Cycle amplitude |
The weights αs lead to an average travel time, which has the highest S/N. If, instead, we were to chose weights proportional to 1/σs or 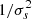 , the S/N of the average travel time would be significantly lower, as illustrated in Fig. 9.
, the S/N of the average travel time would be significantly lower, as illustrated in Fig. 9.
 |
Fig. 9. Signal-to-noise ratio associated with different averages of the seismic travel times versus maximum skip number Nskip used in the average. For all Nskip, the weights αs used in the average (blue) provide a S/N that is higher than the weights proportional to 1/σs (orange) and |
4. Discussion
4.1. Comparison of seismic travel times with other activity proxies
We use the frequency shifts of 60 low-degree modes with l ≤ 3 that were measured by Howe et al. (2017), 2018) from the Birmingham Solar Oscillations Network (BiSON) data between 23 January 1996 and 31 December 2016. The individual mode frequency shifts were measured for overlapping segments of T = 365 days in length with a sampling time of Δt = 91.25 days (only one-quarter of the data points are statistically independent). The average frequency shifts, weighted by mode inertia, are denoted by ⟨δν⟩ and are plotted in Fig. 10E. In order to directly compare the BiSON frequency shifts to the seismic travel times and the photometric variability, we divided the VIRGO data into the same overlapping segments (T = 365 days and Δt = 91.25 days). From these data segments, we obtain the average travel time 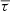 with Nskip = 40 and the photometric rms.
with Nskip = 40 and the photometric rms.
 |
Fig. 10. Solar cycle variations in the seismic average mode frequency shift from Howe et al. (2017) (A), the seismic average travel time (B) and photometric variability (C). The orange curve connects the data points. The data analyzed here was divided into overlapping time segments of T = 1 yr in length and mid-points separated by Δt = 91.25 d. (D, E) Power spectra of the activity observables shown in panels A–C. All power spectra are normalized to the power at frequency 1/(9 yr). The abscissa shows the period in the left panel and the frequency in the right panel. |
Figures 10A–C display all three data sets: the average frequency shifts, the average travel times, and the photometric rms values. Variations over the 11 yr solar cycle are clearly seen in all three datasets. The variations of the average frequency shifts and travel times are more closely related to each other than each one of them is to the rms data. This last point is also seen when comparing the three power spectra (Figs. 10D, E). In particular, the rms data have significant power near periods of 3.8 yr and 2.7 yr (with a gap near 3.2 yr), while the seismic data have a smoother distribution of power for periods above 3.2 yr. The noise level for periods below ∼2 yr is similar in all three data sets.
Figure 11 shows the photometric variability and seismic travel times of the Sun using nonoverlapping segments of T = 90 days in length. We notice that the photometric variability time series shows pronounced spikes in July 2000 and October 2003 during Cycle 23, which can be attributed to the transit of large active regions. At the end of the month of October 2003, the increase in photometric variability was particularly notable, reaching almost 500 ppm due to the combined contributions of two large sunspot groups (NOAA 10488 and NOAA 10486) that shared the same longitude in the rotating frame (see Fig. 11, the top left panel). This is consistent with the simulations of Işık et al. (2020), which show that longitudinal nests of active regions may amplify the brightness variations on other Sun-like stars compared to the Sun. Moreover, Pojoga & Cudnik (2002) reported that a significant fraction of all solar active regions belong to longitudinal clusters on the surface, providing a possible explanation for the larger photometric variability observed during solar maximum than the seismic variability (Fig. 11). Indeed, unlike photometric variability, the seismic waves are not sensitive to the longitudinal distribution of magnetic activity but sense a longitudinal average.
 |
Fig. 11. Comparison between photometric variability and travel-time perturbations. Bottom left panel: photometric variability computed from nonoverlapping time segments of T = 90 days in duration. The three arrows correspond to three particular times in July 2000, September 2001, and October 2003. The strong spike in the data in October 2003 is due to the transit of two large active regions (top left panel). Top right panel: seismic travel times computed for the same 90 day time segments. As above, the three arrows point to July 2000, September 2001, and October 2003. Bottom right panel: scatter plot between photometric variability and seismic travel times. The correlation coefficient between these datasets is R = 0.74. |
Figure 12 shows the correspondence between the photometric variability, mode frequency shifts, and seismic travel times. To reduce random noise, we used overlapping time segments of T = 1 yr in length. As anticipated, the two seismic measurements are highly correlated (R = 0.98), although they are not identical. We marked three dates on the plot, which correspond to the same active phase of Cycle 23 as in Fig. 11. Two of these dates correspond to local maxima in the photometric variability, and the middle date corresponds to a maximum for the seismic data (both frequency shift and travel time). The photometric variability exhibits a distinctive double-peak pattern in both Cycles 23 and 24, with the two peaks separated by approximately 3 yr. The seismic data also display local maxima, but the variations are smoother and considerably different from the photometric variability observed during Cycle 23. In particular, the seismic data show a peak in September 2001, which has no counterpart in the photometric variability. We also note that during the rising and declining phases of Cycle 23, the relationship between photometric variability and travel times shows hysteresis.
 |
Fig. 12. Comparison between photometric variability, p-mode frequency shifts, and seismic travel times. The data analyzed here were divided into overlapping segments of T = 365 days in length with a sampling time of 91.25 days. The three arrows correspond to July 2000, September 2001, and October 2003, as in Fig. 11. The bottom right panel shows the scatter plot between travel times and mode frequencies. The center-right panel shows the scatter plot between travel times and photometric variability. In the left bottom panel, the gray line shows smoothed sunspot number. |
As demonstrated in the lower-left panel of Fig. 12, the p-mode frequency variations are found to be well-correlated with the number of sunspots (gray curve) during cycles 23 and 24 (see also, e.g., Jain et al. 2012). However, the photometric variability does not exhibit a strong correlation with sunspot number, suggesting that seismic data and photometric variability are independent diagnostics of solar activity. Combining these two independent measures may provide useful insights into the number and spatial distribution of active regions on the surface.
Several activity proxies, including the sunspot numbers and areas, the 10.7 cm radio flux, and the coronal index, exhibit variations on timescales ranging from 0.6 to 4 yr, in addition to the well-known 11 yr cycle (for a review, see Bazilevskaya et al. 2014). The origin of these variations remains unclear. Of particular interest is the quasi-biennial variation observed in the p-mode frequency shifts, which is also evident in the sunspot numbers and areas, the 10.7 cm radio flux, and the coronal index (Broomhall & Nakariakov 2015). To isolate the quasi-biennial variations from the three datasets, we apply a Gaussian filter centered around the period of 2.5 yr with a width of 1 yr (see Fig. 13). The correlation coefficient between the filtered travel times (−τ) and the p-mode frequency shifts is found to be significant at 0.88. However, over the period of 1996 – 2018, the correlation between the seismic data and the photometric variability is close to zero. This is consistent with previous work by Broomhall et al. (2009), who also observed differences in the phase between the seismic data and the 10.7 cm flux.
 |
Fig. 13. Quasi-biennial variations in |
4.2. Prospects for detecting stellar activity cycles
In this section, we discuss the prospects for applying our method to the analysis of short cadence stellar observations. Here, we only consider distant stars with a magnetic cycle like that of the Sun and with a rotation axis perpendicular to the line of sight. Different geometrical and magnetic configurations (see, e.g., Gizon 2002; Papini & Gizon 2019) are beyond the scope of this study.
In order to simulate broadband photometric data for a Sun-like star, we use the VIRGO/PMO6 total solar irradiance data and introduce random noise to emulate additional shot noise. The PMO6 data span from February 1996 to October 2018 with a temporal cadence of 1 min. We introduce noise such that the S/N is Kepler-like for stars of given magnitudes, from mK = 8 to 13. Figure 14 shows example simulations (segments of duration 1 yr and 2 h) for stars with magnitudes of mK = 8, 10, and 12. The monthly brightness variations are caused by transits of active regions (faculae and sunspots) that are visible to at least mK = 12. On short timescales, the p-mode oscillations are clearly visible up to a magnitude of mK ≈ 10.
 |
Fig. 14. Comparison between the solar VIRGO/SPM observations and simulated Sun-as-a-Kepler-star data. Example one-year time series of (A) VIRGO/SPM observations and (B–D) simulated Sun-as-a-Kepler-star data for stars of different visual magnitudes. (E–H) p-mode power spectra near 3 mHz. The values in the upper-right corners give the power ratios between the height of the (l = 0) peak at 3.097 mHz and the noise background. (I–L) Filtered data in the p-mode frequency range 1–5 mHz. |
We cut the light curves into 90 day nonintersecting segments and measure the p-mode travel times for the first 40 skips. We then compute the average:
and, for the sake of simplicity, we define the noise with respect to this average:
Using the noise covariance matrix
we average the travel times over Nskip:
with
We then extract the “stellar cycle” from the average travel time by fitting a simple cosine function,
where a, Pcyc, and t0 are parameters.
We estimate the photometric variability of each data segment by calculating the rms of the flux. In order to determine the amplitude of the activity cycle, we fit a cosine function as described previously. Figures 15A–F show the activity cycle observed in seismic travel times (left panels) and photometric variability (right panels) for apparent magnitudes of mK = 8, 10, and 12. The activity cycle is detected using both methods for mK = 8 and 10, but not for mK = 12, where shot noise is too high for seismic measurements.
 |
Fig. 15. Detectability of the solar cycle in the average travel times in a case of Sun-as-a-Kepler-star observations. (A, C, E) Simulated travel times for distant solar analogs obtained by adding photon noise to the VIRGO observations. The apparent Kepler magnitude mK is indicated on each panel. (B, D, F) Photometric variability (rms) from the same simulated time series. (G–I) Cycle parameters extracted from fits to the travel times (orange curves in panels A, C, E), |
To identify the limiting visual magnitude at which the activity cycle is detectable, we define S/N for each magnitude as:
where 𝔼[a] is the expectation value of the cycle amplitude and σa the associated noise level, both obtained from 20 independent realizations of photometric noise (see Fig. 15I). In Fig. 15J, we find that S/N ∼ 1.5 for mK = 12. A clean cycle detection is achieved for mK = 11, where S/N ≈ 8. For mK = 11, the other two parameters (Pcyc, t0) are also determined to be approximately 8 months and 6 months, respectively, with high precision. We therefore conclude that the seismic travel-time method is a valuable tool for detecting activity cycles in Sun-like stars.
4.3. The case of HD 173701
In order to further illustrate this point, we examine the bright star HD 173701 (KIC 8006161) observed by the Kepler mission, with a magnitude of mK = 7.4. Previous studies by Kiefer et al. (2017) and Salabert et al. (2018) reported strong activity variations in the p-mode frequency shifts during the years 2010–2014 (see Fig. 16A). Additionally, Karoff et al. (2018) used spectroscopic measurements of the chromospheric emission from multiple epochs spanning from 1979 to 2015 and determined that the star has an activity cycle with a period of 7.4 yr; during the Kepler observations, it was in the rising phase of this cycle (see their Fig. 5).
 |
Fig. 16. Variability of the Kepler star HD 173701 (KIC 8006161) as inferred from (A) p-mode frequency shifts by Salabert et al. (2018), (B) average seismic travel-time shift from our work and (C) photometric variability. The vertical errors bars correspond to ±1 standard deviations. The horizontal error bars represent the observation duration for each measurement (90 days). |
Here, we analyze the star HD 173701 using the methods discussed above and compare with the results from Salabert et al. (2018). We divided the data collected by Kepler into segments of T = 90 days in length with an overlap of 45 days. In each segment, we measured the travel times and computed the photometric variability. The seismic activity variations inferred from the travel-time measurements and photometric variability are shown in Fig. 16. Our measurements (Fig. 16B) and those of Salabert et al. (2018; Fig. 16A) show similar temporal variations over the period of Kepler days from 250 to 1150 (see Figs. 16A and B). This includes minima of activity at ∼500 and 800 days, a local maximum of activity at 750 days, as well as a rising phase from 800 to 1100 days. Beyond approximately 1150 days, the two datasets are noticably different: while the Salabert et al. (2018) data show an increase in activity, our data reach a plateau. In Fig. 16C, we show the evolution of the photometric variability, which differs from the seismic data, except for a common minimum of activity at 500 days. We conclude that the two seismic methods give comparable results with similar error bars, while the photometric variability provides an independent diagnostic of stellar activity (as in the case of the Sun).
5. Conclusion
In this work, we describe a new method specifically designed to detect temporal changes in seismic data due to stellar activity, which is simpler than fitting the frequency splittings (cf. Gizon 2002; Chaplin et al. 2003; Benomar et al. 2023). Our method works for the Sun and for the bright Kepler star HD 173701. We measured multiple-skip travel times using a cross-correlation technique originally developed in local helioseismology. Surprisingly, we find that the signature of the solar cycle is strongest in odd skips from 17 to 31 (i.e., at time lags in the range of 35–64 h).
However, we note that the present method focuses only on the asphericity measurements and does not provide any information on other important stellar parameters, such as stellar rotation rate or inclination angle. Thus, in its current form, our method is no substitute for the peak bagging method. Despite this limitation, we expect the method to be useful for analyzing the seismic data from stars to be observed by the upcoming PLATO mission (Rauer et al. 2016).
The VIRGO/SPM datasets are available at http://irfu.cea.fr/dap/Phocea/Vie_des_labos/Ast/ast_visu.php?id_ast=3581
Acknowledgments
L.G. provided the basic idea, V.V. performed the data analysis, and the authors wrote the paper together. We thank Rachel Howe for providing the solar p-mode frequency shifts, Wolfgang Finsterle for the calibrated VIRGO/PMO6 observations, and Damien Fournier for suggesting the whitening transformation. L.G. acknowledges useful discussions with Othman Benomar. V.V. and L.G. received funding from the Max Planck Society under the grant “Preparation for PLATO Science” and from the German Aerospace Center under the grants “PLATO Data Center” (50OO1501 and 50OP1902). This work was supported in part by the ERC Synergy Grant WHOLE SUN 810218 to L.G. The VIRGO instrument onboard SOHO is a cooperative effort of scientists, engineers, and technicians to whom we are indebted. SOHO is a project of international collaboration between ESA and NASA. We used the open-source codes MATPLOTLIB (Hunter 2007), NUMPY (Harris et al. 2020), and SCIPY (Virtanen et al. 2020).
References
- Anguera Gubau, M., Pallé, P. L., Perez Hernandez, F., Régulo, C., & Roca Cortés, T. 1992, A&A, 255, 363 [NASA ADS] [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [Google Scholar]
- Basu, S. 2016, Liv. Rev. Sol. Phys., 13, 2 [Google Scholar]
- Bazilevskaya, G., Broomhall, A. M., Elsworth, Y., & Nakariakov, V. M. 2014, Space Sci. Rev., 186, 359 [CrossRef] [Google Scholar]
- Beeck, B., Cameron, R. H., Reiners, A., & Schüssler, M. 2013, A&A, 558, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benomar, O., Takata, M., Bazot, M., et al. 2023, A&A, 680, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Broomhall, A. M., & Nakariakov, V. M. 2015, Sol. Phys., 290, 3095 [NASA ADS] [CrossRef] [Google Scholar]
- Broomhall, A. M., Chaplin, W. J., Elsworth, Y., Fletcher, S. T., & New, R. 2009, ApJ, 700, L162 [NASA ADS] [CrossRef] [Google Scholar]
- Broomhall, A. M., Chaplin, W. J., Elsworth, Y., & New, R. 2011, MNRAS, 413, 2978 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., Elsworth, Y., Isaak, G. R., et al. 2003, MNRAS, 343, 343 [CrossRef] [Google Scholar]
- Duncan, D. K., Vaughan, A. H., Wilson, O. C., et al. 1991, ApJS, 76, 383 [Google Scholar]
- Fligge, M., Solanki, S. K., Unruh, Y. C., Froehlich, C., & Wehrli, C. 1998, A&A, 335, 709 [NASA ADS] [Google Scholar]
- Fossat, E., Gelly, B., Grec, G., & Pomerantz, M. 1987, A&A, 177, L47 [NASA ADS] [Google Scholar]
- Fournier, D., Gizon, L., Hohage, T., & Birch, A. C. 2014, A&A, 567, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fournier, D., Hanson, C. S., Gizon, L., & Barucq, H. 2018, A&A, 616, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fröhlich, C., Romero, J., Roth, H., et al. 1995, Sol. Phys., 162, 101 [Google Scholar]
- Fröhlich, C., Crommelynck, D. A., Wehrli, C., et al. 1997, Sol. Phys., 175, 267 [CrossRef] [Google Scholar]
- García, R. A., Mathur, S., Salabert, D., et al. 2010, Science, 329, 1032 [Google Scholar]
- Gizon, L. 2002, Astron. Nachr., 323, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Gizon, L., & Birch, A. C. 2002, ApJ, 571, 966 [Google Scholar]
- Gizon, L., & Birch, A. C. 2004, ApJ, 614, 472 [Google Scholar]
- Gizon, L., Barucq, H., Duruflé, M., et al. 2017, A&A, 600, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gizon, L., Cameron, R. H., Pourabdian, M., et al. 2020, Science, 368, 1469 [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, R., Davies, G. R., Chaplin, W. J., et al. 2017, MNRAS, 470, 1935 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, R., Chaplin, W. J., Davies, G. R., et al. 2018, MNRAS, 480, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Işık, E., Shapiro, A. I., Solanki, S. K., & Krivova, N. A. 2020, ApJ, 901, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Jain, R., Tripathy, S. C., Watson, F. T., et al. 2012, A&A, 545, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiménez, A., Roca Cortés, T., & Jiménez-Reyes, S. J. 2002, Sol. Phys., 209, 247 [CrossRef] [Google Scholar]
- Jiménez, A., Jiménez-Reyes, S. J., & García, R. A. 2005, ApJ, 623, 1215 [CrossRef] [Google Scholar]
- Jiménez-Reyes, S. J., Régulo, C., Pallé, P. L., & Roca Cortés, T. 1998, A&A, 329, 1119 [NASA ADS] [Google Scholar]
- Karoff, C., Metcalfe, T. S., Santos, Â. R. G., et al. 2018, ApJ, 852, 46 [Google Scholar]
- Kessy, A., Lewin, A., & Strimmer, K. 2018, Am. Stat., 72, 309 [CrossRef] [Google Scholar]
- Kiefer, R., & Broomhall, A.-M. 2021, MNRAS, 500, 3095 [Google Scholar]
- Kiefer, R., Schad, A., Davies, G., & Roth, M. 2017, A&A, 598, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Libbrecht, K. G., & Woodard, M. F. 1990, Nature, 345, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno-Insertis, F., & Solanki, S. K. 2000, MNRAS, 313, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Palle, P. L., Regulo, C., & Roca Cortes, T. 1989, A&A, 224, 253 [NASA ADS] [Google Scholar]
- Pallé, P. L., Régulo, C., & Roca Cortés, T. 1990, in Progress of Seismology of the Sun and Stars, eds. Y. Osaki, & H. Shibahashi (Berlin, Heidelberg: Springer, Berlin Heidelberg), 129 [CrossRef] [Google Scholar]
- Papini, E., & Gizon, L. 2019, Front. Astron. Space Sci., 6, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Pojoga, S., & Cudnik, B. 2002, Sol. Phys., 208, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Radick, R. R., Lockwood, G. W., Henry, G. W., Hall, J. C., & Pevtsov, A. A. 2018, ApJ, 855, 75 [Google Scholar]
- Rauer, H., Aerts, C., Cabrera, J., & PLATO Team 2016, Astron. Nachr., 337, 961 [Google Scholar]
- Régulo, C., García, R. A., & Ballot, J. 2016, A&A, 589, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reinhold, T., Cameron, R. H., & Gizon, L. 2017, A&A, 603, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salabert, D., Fossat, E., Gelly, B., et al. 2004, A&A, 413, 1135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salabert, D., Chaplin, W. J., Elsworth, Y., New, R., & Verner, G. A. 2007, A&A, 463, 1181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salabert, D., Régulo, C., Ballot, J., García, R. A., & Mathur, S. 2011, A&A, 530, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salabert, D., Régulo, C., Pérez Hernández, F., & García, R. A. 2018, A&A, 611, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, A. R. G., Cunha, M. S., Avelino, P. P., Chaplin, W. J., & Campante, T. L. 2016, MNRAS, 461, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, A. R. G., Campante, T. L., Chaplin, W. J., et al. 2018, ApJS, 237, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, A. R. G., Campante, T. L., Chaplin, W. J., et al. 2019, ApJ, 883, 65 [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- White, O. R., Livingston, W. C., Keil, S. L., & Henry, T. W. 1998, in Synoptic Solar Physics, eds. K. S. Balasubramaniam, J. Harvey, & D. Rabin, ASP Conf. Ser., 140, 293 [NASA ADS] [Google Scholar]
- Wilson, O. C. 1978, ApJ, 226, 379 [Google Scholar]
- Woodard, M. F., & Noyes, R. W. 1985, Nature, 318, 449 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. One-year (A) and two-hour (B) segments of VIRGO/SPM brightness data (red channel). In both plots, the origin of time is 28 March 2014. |
| In the text | |
 |
Fig. 2. Schematics showing how the data segments {Ii} are constructed from the original time series of the observed intensity. |
| In the text | |
 |
Fig. 3. Autocovariance functions of intensity time series. (A) Autocovariance function of the VIRGO/SPM data (T = 90 d). The red, green, and blue curves correspond to the three channels. (B) Autocovariance of MURaM solar convection simulations (T = 15 h). (C) Autocovariance function for the p-mode data computed for a segment of VIRGO data with T = 90 days (red channel). (D) Reference autocovariance function obtained by averaging over M = 91 consecutive segments covering 22 yr. The first seven wavepackets are labeled s = 1 through 7. The curves in panels C and D are computed from filtered time series (Gaussian filter centered on 3 mHz with a full width of 2 mHz). (E) Zoom onto wavepacket s = 4 and width of the temporal window function f4(t). |
| In the text | |
 |
Fig. 4. Measured travel times τs(ti) for all wavepackets with s ≤ 41. The red curves show the filtered data τs, smooth(ti) according to Eq. (15). The value of s is written in the top left corner of each plot. The data analyzed here are from VIRGO/SPM (red channel) divided into non-overlapping segments of T = Δt = 90 days in length (see Fig. 2). |
| In the text | |
 |
Fig. 5. Comparison between the sunspot number (SSN) smoothed over 13 months (A) and seismic travel times, τs, for skip number s = 19 (B) measured in the red VIRGO/SPM channel data. Vertical dashed lines indicate cycle maximum and minimum. The red line represents the filtered data, τs, smooth(t), which we use to measure the amplitude of the travel-time variations due to the solar cycle As (black arrow). (C) Residuals between τs and τs, smooth. (D) Power spectrum of τs, normalized to the power of the 11-yr harmonic. A Butterworth filter (red line) is used to extract τs, smooth(t). |
| In the text | |
 |
Fig. 6. Detectability of the solar cycle in individual skip travel times. (A) Amplitudes of travel-time variations due to the solar cycle, As, versus skip number s (see Eq. (18)), with error bars of |
| In the text | |
 |
Fig. 7. Average seismic travel time. (A) Measured average travel time |
| In the text | |
 |
Fig. 8. Detectability of the solar cycle in the average VIRGO travel times. (A) Cycle amplitude |
| In the text | |
 |
Fig. 9. Signal-to-noise ratio associated with different averages of the seismic travel times versus maximum skip number Nskip used in the average. For all Nskip, the weights αs used in the average (blue) provide a S/N that is higher than the weights proportional to 1/σs (orange) and |
| In the text | |
 |
Fig. 10. Solar cycle variations in the seismic average mode frequency shift from Howe et al. (2017) (A), the seismic average travel time (B) and photometric variability (C). The orange curve connects the data points. The data analyzed here was divided into overlapping time segments of T = 1 yr in length and mid-points separated by Δt = 91.25 d. (D, E) Power spectra of the activity observables shown in panels A–C. All power spectra are normalized to the power at frequency 1/(9 yr). The abscissa shows the period in the left panel and the frequency in the right panel. |
| In the text | |
 |
Fig. 11. Comparison between photometric variability and travel-time perturbations. Bottom left panel: photometric variability computed from nonoverlapping time segments of T = 90 days in duration. The three arrows correspond to three particular times in July 2000, September 2001, and October 2003. The strong spike in the data in October 2003 is due to the transit of two large active regions (top left panel). Top right panel: seismic travel times computed for the same 90 day time segments. As above, the three arrows point to July 2000, September 2001, and October 2003. Bottom right panel: scatter plot between photometric variability and seismic travel times. The correlation coefficient between these datasets is R = 0.74. |
| In the text | |
 |
Fig. 12. Comparison between photometric variability, p-mode frequency shifts, and seismic travel times. The data analyzed here were divided into overlapping segments of T = 365 days in length with a sampling time of 91.25 days. The three arrows correspond to July 2000, September 2001, and October 2003, as in Fig. 11. The bottom right panel shows the scatter plot between travel times and mode frequencies. The center-right panel shows the scatter plot between travel times and photometric variability. In the left bottom panel, the gray line shows smoothed sunspot number. |
| In the text | |
 |
Fig. 13. Quasi-biennial variations in |
| In the text | |
 |
Fig. 14. Comparison between the solar VIRGO/SPM observations and simulated Sun-as-a-Kepler-star data. Example one-year time series of (A) VIRGO/SPM observations and (B–D) simulated Sun-as-a-Kepler-star data for stars of different visual magnitudes. (E–H) p-mode power spectra near 3 mHz. The values in the upper-right corners give the power ratios between the height of the (l = 0) peak at 3.097 mHz and the noise background. (I–L) Filtered data in the p-mode frequency range 1–5 mHz. |
| In the text | |
 |
Fig. 15. Detectability of the solar cycle in the average travel times in a case of Sun-as-a-Kepler-star observations. (A, C, E) Simulated travel times for distant solar analogs obtained by adding photon noise to the VIRGO observations. The apparent Kepler magnitude mK is indicated on each panel. (B, D, F) Photometric variability (rms) from the same simulated time series. (G–I) Cycle parameters extracted from fits to the travel times (orange curves in panels A, C, E), |
| In the text | |
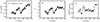 |
Fig. 16. Variability of the Kepler star HD 173701 (KIC 8006161) as inferred from (A) p-mode frequency shifts by Salabert et al. (2018), (B) average seismic travel-time shift from our work and (C) photometric variability. The vertical errors bars correspond to ±1 standard deviations. The horizontal error bars represent the observation duration for each measurement (90 days). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



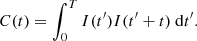

![$$ \begin{aligned} \tau _s = \lim _{\epsilon \rightarrow 0} \mathop {\mathrm{argmin} }_{t^{\prime }} \int _{\text{ win}_s} \left[ \epsilon C(t)+ (1-\epsilon ) C_{\rm ref}(t) - C_{\rm ref}(t-\epsilon t^{\prime }) \right]^2 \mathrm{d}t, \end{aligned} $$](/articles/aa/full_html/2024/02/aa46854-23/aa46854-23-eq3.gif)
![$$ \begin{aligned} \tau _s = \int W_s(t) \left[ C(t) - C_{\rm ref}(t) \right] \mathrm{d}t, \end{aligned} $$](/articles/aa/full_html/2024/02/aa46854-23/aa46854-23-eq4.gif)
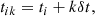
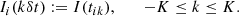
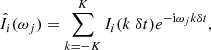
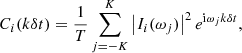
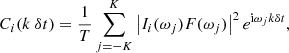
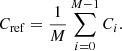
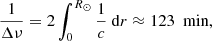
![$$ \begin{aligned} \tau _s(t_i) = \delta t \sum _{k} W_s(k\ \delta t) \left[ C_i(k\ \delta t) - C_\mathrm{ref} (k\ \delta t) \right], \end{aligned} $$](/articles/aa/full_html/2024/02/aa46854-23/aa46854-23-eq14.gif)
![$$ \begin{aligned} W_s (t) = -\frac{ f_s( t) \, C^\prime _\mathrm{ref} ( t) }{\delta t \sum _k f_s(k\ \delta t) [C^\prime _\mathrm{ref} (k\ \delta t)]^2}, \end{aligned} $$](/articles/aa/full_html/2024/02/aa46854-23/aa46854-23-eq15.gif)
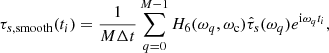
![$$ \begin{aligned} \sigma _s = \sqrt{\frac{1}{M-1} \sum _{i=0}^{M-1} \Big [n_s(t_i)\Big ]^2} ,\end{aligned} $$](/articles/aa/full_html/2024/02/aa46854-23/aa46854-23-eq19.gif)
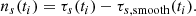
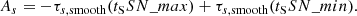
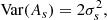
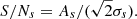
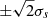
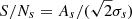
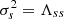
![$$ \begin{aligned} \Lambda _{ss^{\prime }} = \mathbb{E} [ n_s n_{s^{\prime }} ] \simeq \frac{1}{M-1} \sum _{i=0}^{M-1} n_s(t_i) n_{s^{\prime }}(t_i), \end{aligned} $$](/articles/aa/full_html/2024/02/aa46854-23/aa46854-23-eq28.gif)
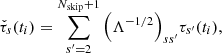
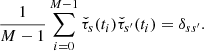
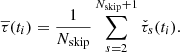
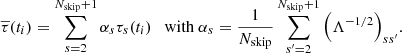
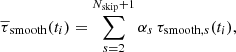
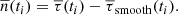
![$$ \begin{aligned} \overline{\sigma } = \sqrt{\frac{1}{M-1} \sum _{i=0}^{M-1} \Big [\overline{n} (t_i)\Big ]^2}. \end{aligned} $$](/articles/aa/full_html/2024/02/aa46854-23/aa46854-23-eq36.gif)
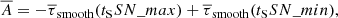
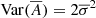
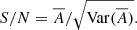
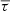
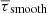
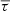
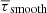
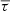
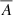
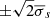
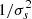
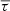
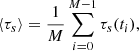
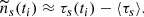
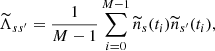
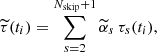
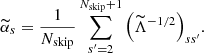
![$$ \begin{aligned} \widetilde{\tau }_{\mathrm{fit} } (t) = - a \cos \left[ 2\pi (t - t_{0}) / P_\mathrm{cyc} \right], \end{aligned} $$](/articles/aa/full_html/2024/02/aa46854-23/aa46854-23-eq59.gif)
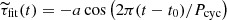
![$$ \begin{aligned} S/N (m_K) = \frac{\mathbb{E} [a(m_K)] }{ \sigma _a (m_K)} , \end{aligned} $$](/articles/aa/full_html/2024/02/aa46854-23/aa46854-23-eq61.gif)