| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 18 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202347325 | |
| Published online | 15 December 2023 | |
2D chemical evolution models
II. Effects of multiple spiral arm patterns on O, Eu, Fe, and Ba abundance gradients
1
INAF Osservatorio Astronomico di Trieste, Via G.B. Tiepolo 11, 34131 Trieste, Italy
e-mail: emanuele.spitoni@inaf.it
2
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, Bd de l’Observatoire, CS 34229, 06304 Nice cedex 4, France
3
Dipartimento di Fisica, Sezione di Astronomia, Università di Trieste, Via G.B. Tiepolo 11, 34143 Trieste, Italy
4
INFN Sezione di Trieste, Via Valerio 2, 34134 Trieste, Italy
5
Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
6
Osservatorio Astrofisico di Torino, Istituto Nazionale di Astrofisica (INAF), 10025 Pino Torinese, Italy
Received:
30
June
2023
Accepted:
17
October
2023
Context. According to observations and numerical simulations, the Milky Way could exhibit several spiral-arm modes of various pattern speeds, with the slower patterns located at larger galactocentric distances.
Aims. Our aim is to quantify the effects of the spiral arms on the azimuthal variations in the chemical abundances of oxygen and iron and for the first time of neutron-capture elements (europium and barium) in the Galactic disc. We assume a model based on multiple spiral-arm modes with different pattern speeds. The resulting model is an updated version of previous 2D chemical evolution models.
Methods. We apply new analytical prescriptions for the spiral arms in a 2D Galactic disc chemical evolution model, exploring the possibility that the spiral structure is formed by the overlap of chunks with different pattern speeds and spatial extent.
Results. The predicted azimuthal variations in abundance gradients are dependent on the considered chemical element. Elements synthesised on short timescales (i.e. oxygen and europium in this study) exhibit larger abundance fluctuations. Moreover, for progenitors with short lifetimes, the chemical elements returned to the ISM perfectly trace the star formation perturbed by the passage of the spiral arms. The map of the star formation rate (SFR) predicted by our chemical evolution model with multiple patterns of spiral arms presents arcs and arms compatible with those revealed by multiple tracers (young upper-main sequence stars, Cepheids, and the distribution of stars with low radial actions). Finally, our model predictions are in good agreement with the azimuthal variations that emerged from the analysis of Gaia DR3 GSP-Spec [M/H] abundance ratios, if at most recent times the pattern speeds match the Galactic rotational curve at all radii.
Conclusions. We provide an updated version of a 2D chemical evolution model capable of tracing the azimuthal density variations created by the presence of multiple spiral patterns. We show that elements synthesised on short timescales exhibit larger abundance fluctuations.
Key words: Galaxy: disk / Galaxy: abundances / Galaxy: formation / Galaxy: evolution / Galaxy: kinematics and dynamics / ISM: abundances
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Significant azimuthal variations in the abundance gradients of external galaxies have been found in various contemporary observational studies. Sánchez et al. (2015) and Sánchez-Menguiano et al. (2016) extensively examined the chemical inhomogeneities of the external galaxy NGC 6754 using the Multi Unit Spectroscopic Explorer (MUSE) and concluded that the azimuthal variations in oxygen abundance are more prominent in the external regions of the galaxy. Using MUSE, Vogt et al. (2017) conducted a study of the galaxy HCG 91c and found that enrichment of the interstellar medium (ISM) occurs primarily along spiral structures and less efficiently across them. Li et al. (2013) detected azimuthal variations in the oxygen abundance in the external galaxy M101. Ho et al. (2017), analysing the galaxy NGC 1365, observed systematic azimuthal variations of approximately 0.2 dex over a wide range of radial distances, with a peak at the two spiral arms.
Investigations of azimuthal inhomogeneities of chemical abundances have also been carried out in the Milky Way system. Balser et al. (2011, 2015) and Wenger et al. (2019) studied the oxygen abundances of HII regions and found that the slopes of the gradients differed by a factor of two across their three Galactic azimuth angle bins. Additionally, significant local iron abundance inhomogeneities have been observed using Galactic Cepheids (Pedicelli et al. 2009; Genovali et al. 2014). More recently, Kovtyukh et al. (2022) analysed Cepheids from high-resolution spectra obtained by the Milky WAy Galaxy wIth SALT speCtroscopy project (MAGIC, Kniazev et al. 2019), to find that abundance asymmetries are particularly pronounced in the inner Galaxy and outer disc, where they reach approximately 0.2 dex, aligning with similar discoveries in nearby spiral galaxies.
Poggio et al. (2022), using Gaia DR3 General Stellar Parametrizer Spectroscopy (GSP-Spec, Gaia Collaboration 2022, 2023; Recio-Blanco et al. 2023) showed statistically significant bumps on top of the observed radial metallicity gradients, with amplitudes of up to 0.05–0.1 dex. These results suggest that the assumption of a linear radial decrease is not applicable to this sample. The strong correlation between the spiral structure of the Galaxy and the observed chemical pattern in the younger sample suggests that the former could be responsible for the detected chemical inhomogeneities. The signature of the spiral arms is more prominent in younger stars and progressively disappears in cooler (and older) giants.
Several theoretical studies explored the nature and origin of such azimuthal variations in the abundance gradients. Khoperskov et al. (2018) focused on the formation of azimuthal metallicity variations in the discs of spiral galaxies, specifically in the absence of initial radial metallicity gradients. The findings indicate that the azimuthal variations in the average metallicity of stars across a spiral galaxy are not solely a result of the reshaping of an initial radial metallicity gradient through radial migration. Instead, such variations naturally emerge in stellar discs that initially possess only a negative vertical metallicity gradient. Khoperskov et al. (2023) studied the influence of radial gas motions on the ISM metallicity near the spiral arms in the presence of an existing radial metallicity gradient, finding that the gas metallicity displays a dispersion of approximately 0.04–0.06 dex at a specific distance from the Galactic centre.
Spitoni et al. (2019a, hereafter ES19) presented one of the first 2D chemical evolution models capable of tracing azimuthal variations. These authors showed that the main effect of considering density fluctuations from the chemo-dynamical model by Minchev et al. (2013) for the Galaxy is to create azimuthal variations of approximately 0.1 dex. Additionally, these variations are particularly noticeable in the outer regions of the Milky Way, in agreement with recent findings from observations of external galaxies (Sánchez et al. 2015; Sánchez-Menguiano et al. 2016).
Later, with their chemical evolution model in the presence of spiral arms, Mollá et al. (2019) predicted azimuthal oxygen abundance patterns for the last 2 Gyr of evolution, finding these predictions to be in reasonable agreement with recent observations obtained with VLT/MUSE for NGC 6754. In ES19, the amplitude of the azimuthal variation was shown to increase with galactocentric distance when the density fluctuation proposed by Minchev et al. (2013) is considered; as a consequence, different modes with multiple spiral-arm patterns coexist. If different modes combine linearly, we could approximate a realistic galactic disc by adding several spiral sets with different pattern speeds, as seen in observations (e.g. Meidt et al. 2009) and simulations (e.g. Masset & Tagger 1997; Quillen et al. 2011; Minchev et al. 2012). These patterns can be slow, and shifted towards the outer radii, as observed in studies such as Minchev & Quillen (2006) and Quillen et al. (2011). It is important to point out that the material spiral arms propagating near the co-rotation at all galactic radii have been described by a number of recent numerical works, with different interpretations (see Grand et al. 2012; Comparetta & Quillen 2012; D’Onghia et al. 2013; Hunt et al. 2019).
To ensure a comprehensive perspective, it is important to emphasise that there is no agreement in the literature regarding the presence of various spiral-arm modes exhibiting multiple pattern speeds. Some authors claim that the spiral arms rotate like a rigid body with a single pattern speed (Lin & Shu 1964, 1966), while others suggest that the arms are stochastically produced by local gravitational amplification in a differentially rotating disc by a process called “swing amplification” (Goldreich & Lynden-Bell 1965; Julian & Toomre 1966). It is also important to note that the morphology of the spiral structure in our Galaxy is highly debated, and no clear consensus has been reached, notwithstanding numerous efforts towards the mapping of its large-scale structure (Georgelin & Georgelin 1976; Levine et al. 2006; Hou et al. 2009; Hou & Han 2014; Reid et al. 2014, 2019).
In light of the above considerations, in this article, we want to extend the work of ES19 – which focused on the effects of the spiral arm on the chemical enrichment of the Galactic thin disc – by considering for the first time structures characterised by multiple pattern speeds for different chemical elements, such as oxygen, iron, barium, and europium. Within this work, the terminology “thin and thick discs” refers to the low- and high-[α/Fe] sequences in the [α/Fe]–[Fe/H] plane. By defining the thin and thick discs based on morphology rather than chemical composition, a combination of stars from both the low- and high-[α/Fe] sequences is identified, leading to a reciprocal identification as well (Minchev et al. 2015; Martig et al. 2016). Making this distinction is of utmost importance in order to prevent any confusion. As in ES19, we trace the chemical evolution of the thin disc component, specifically the low-α population. We assume that the oldest stars within this low-α component have ages of approximately 11 Gyr, which is consistent with asteroseismic age estimations (Silva Aguirre et al. 2018; Spitoni et al. 2019b).
Our paper is organised as follows: in Sect. 2, we summarise the chemical evolution model of ES19 in the presence of single pattern spiral arms. In Sect. 3, we present the methodology adopted in this paper to include – in the chemical evolution model – the density perturbations originated by spiral arms with multiple patterns. In Sect. 4, the adopted nucleosynthesis prescriptions are reported. In Sect. 5, we present our results and in Sect. 6 we compare our results with Gaia DR3 observational data. Finally, we draw conclusions and propose future perspectives in Sect. 7.
2. The chemical evolution model of ES19 with single spiral patterns
Here, we provide some details of the 2D chemical evolution model presented by ES19. In particular, in Sect. 2.1 we recall the main assumption in this model regarding the gas accretion history and the adopted inside-out prescriptions of the Milky Way disc, and in Sect. 2.2 we present how the density fluctuations created by single-mode spiral arms have been included in the chemical evolution model of ES19.
2.1. The gas accretion and inside-out prescriptions for the low-α disc
The Galactic thin disc is assumed to be formed by accretion of gas with pristine chemical composition (Matteucci & Francois 1989) and the associated infall rate for a generic element i, at the time t, and galactocentric distance R (with no azimuthal dependence) is:
where 𝒳i is the mass abundance of the element i of the infall gas (which is assumed to be primordial here), while the quantity τD(R) is the timescale of gas accretion. The coefficient a(R) is constrained by imposing a fit to the observed current total surface mass density ΣD profile. We impose that the Galactic surface gas density of the disc at the beginning of the simulation (i.e. evolutionary time t = 0 Gyr) is negligible. The observed present-day total disc surface mass density in the solar neighbourhood is Σ⊙ = 54 M⊙ pc−2 (see Chiappini et al. 2001; Romano et al. 2010; Vincenzo et al. 2017; Palicio et al. 2023a) and its variation with the function of the galactocentric distance reads:
where tG is the present time and RD is the disc scale length, which is assumed to be 3.5 kpc. As suggested first by Matteucci & Francois (1989) and then by Chiappini et al. (2001), an important ingredient in reproducing the observed radial abundance gradients along the Galactic disc is the inside-out formation of the disc; that is, the timescale τD(R) increases with Galactic radius, assuming the following linear relation:
The “inside-out” growth of the Galactic thin disc has also been found in most zoom-in dynamical simulations in the cosmological context (Kobayashi & Nakasato 2011; Brook et al. 2012; Bird et al. 2013; Martig et al. 2014; Vincenzo & Kobayashi 2020). We adopt the Scalo (1986) initial stellar mass function (IMF), which is assumed to be constant in time and space.
2.2. Including the effects of the density perturbations from a single spiral mode
Spitoni et al. (2019a) presented a new 2D chemical evolution model designed to trace the azimuthal variations of the abundance gradients along the disc, in particular showing the effects of spiral arm structures. The model divides the disc into concentric shells of 1 kpc in width in the radial direction. Each annular region is composed of 36 zones, each of 10° in width. These latter authors showed the effects of spiral arms on chemical evolution, considering variations of the star formation rate (SFR) along the different regions produced by density perturbations, with these latter being driven by the analytical spiral arms described by Cox & Gómez (2002). In particular, Spitoni et al. (2019a) analysed the effects of a spiral arm structure characterised by a single mode, that is, a constant angular velocity pattern throughout the spiral structure.
Here, we briefly summarise the main model assumptions. The expression for the change in the total mass density perturbation caused by spiral arms – given in an inertial reference frame that does not rotate with the Galactic disc – is
The quantity χ(R, tG) represents the present-day amplitude of the spiral density and can be expressed as:
where RS is the radial scale-length of the drop-off in density amplitude of the arms, and Σ0 is the surface arm density at fiducial radius R0. In Eq. (4), the quantity M(γ) is the modulation function for the “concentrated arms” presented by Cox & Gómez (2002) and can be written as:
where γ stands for
In Eq. (7), m refers to the multiplicity (e.g. the number of spiral arms), α is the pitch angle1, Ωs is the angular velocity of the pattern, and ϕp(R0) is the coordinate ϕ computed at t = 0 Gyr and R0. As underlined in ES19, an important feature of such a perturbation is that its average density at a fixed galactocentric distance R and time t is zero.
In the ES19 model, spiral arm overdensities are included in the chemical evolution as perturbations of the Kennicutt (1998) SFR law (with the exponent k fixed to 1.5) through the following equation:
where ν is the star formation efficiency and δS is an adimensional perturbation and is defined as:
where tG is the present-day evolutionary time and we assume that the ratio χ(R, t)/ΣD(R, t) is constant in time. More details and proprieties of the above-introduced expressions can be found in ES19.
3. Modeling multiple spiral patterns
Here, we extend the analysis of ES19 considering the presence of multiple spiral patterns and tracing their effects on the chemical evolution of diverse elements synthesised on different time-scales, namely oxygen, iron, europium, and barium. We consider multi-pattern spiral arm structures in the chemical evolution models, as suggested by Minchev (2016), in order to test the possibility that the spiral structure is composed of many overlapping spatially limited clumps with different velocity patterns. Analogously to Eq. (4), the expression for the time evolution of the density perturbation created by multi-pattern spiral arms is:
where N is the total number of spiral clumps and the MMS, j (γj) term is the new modulation function defined for the jth spiral mode clump associated with the angular velocity Ωs, j and can be expressed as follows:
where the value of the indicator function 𝟙 delimits the radial extension of the considered spiral arm mode enclosed between the galactocentric distances Rj, min and Rj, max, and is equal to one if the argument is within the radial interval, and zero otherwise.
Imposing that the ratio χ(R, t)/ΣD(R, t) is constant in time, the adimensional perturbation δS defined in Sect. 2.2 becomes:
As for the dimensional quantity introduced by ES19 (Eq. (9)), the new perturbation defined in Eq. (12) also has the important feature, in that its average value at a fixed galactocentric distance R and time t is
This prescription overcomes the overly simplified approach of ES19, and takes into account the more complex behaviour already predicted by N-body simulations (Quillen et al. 2011; Minchev et al. 2012; Sellwood & Carlberg 2014), and external galaxies (Elmegreen et al. 1992; Rix & Zaritsky 1995; Meidt et al. 2009), where multiple spiral patterns have been found.
While ES19 explored this scenario by modelling individual spiral patterns, each with a different angular velocity, in this study we present a more self-consistent approach, considering simultaneously different pattern speeds and limited spatial extensions (as expected from observations and simulation) and using the same chemical evolution model for the Galactic disc.
Following the same approach as Minchev (2016), in Fig. 1 we show the spiral pattern speeds Ωs, j(R) of a spiral structure with multiplicity m = 2 composed of three chunks moving at different pattern speeds Ωs, j(R) (Model A in Table 1). The jth spiral structure is confined in the region R ∈ [Rj, min, Rj, max]. As in ES19, the disc rotational velocity Ωd(R) has been extracted from the simulation by Roca-Fàbrega et al. (2014).
 |
Fig. 1. Spiral pattern speeds Ωs, 1(R), Ωs, 2(R), and Ωs, 3(R) of the multiple spiral modes moving at different pattern speeds (Model A in Table 1) are indicated by the three coloured horizontal lines. Inner and outer spiral structures (moving with the above-mentioned pattern speeds) are also indicated by the thicker purple, blue, and green lines, respectively. The disc angular velocity Ωd(R) computed by Roca-Fàbrega et al. (2014) is indicated with the dotted line. The 2:1 and 4:1 outer and inner Lindblad resonances (OLR and ILR) occur along the solid and dashed black curves, respectively. We compute resonances as Ωp2(R) = Ωd(R)±κ/2 and Ωp4(R) = Ωd(R)±κ/4, respectively, where κ is the local radial epicyclic frequency. The long vertical dashed lines show the positions of the co-rotation radii assuming the three different ΩS values. |
Properties of the three spiral-arm structures with different pattern speeds for the considered models.
We compute the 2:1 and 4:1 outer and inner Lindblad resonances (OLR and ILR) as Ωp2(R) = Ωd(R)±κ/2 and Ωp4(R) = Ωd(R)±κ/4, respectively, where κ is the local radial epicyclic frequency. The velocity of the central spiral structure is fixed at the value Ωs, 2 = 20 km s−1 kpc−1, which is consistent with the Roca-Fàbrega et al. (2014) model. A similar value was first estimated by moving groups in the U-V plane by Quillen & Minchev (2005, Ω = 18.1 ± 0.8 km s−1 kpc−1). It is interesting to note that one of the co-rotational radii is located at 8.75 kpc, hence close to the solar galactocentric distance (R, Z)⊙ = (8.249, 0.0208) kpc (GRAVITY Collaboration 2021; Bennett & Bovy 2019). We stress that recent observations show higher spiral speed values in the solar neighbourhood. For instance, Dias et al. (2019) find a pattern speed of 28.2 km s−1 kpc−1 and Quillen et al. (2018) of 29 km s−1 kpc−1 at 8 kpc. Nevertheless, for consistency with the results presented in ES19, we prefer to retain both the velocity disc and the co-rotation estimated in the vicinity of the Solar System (Ωs2) by Roca-Fàbrega et al. (2014).
As shown in ES19, the most significant effect of the spiral arms should take place at the co-rotation resonance, where the chemical evolution should go much faster because of the lack of the relative gas–spiral motions and the more efficient metal mixing. Moreover, it is widely established that discrete spiral waves in stellar discs can exist between their main resonances (ILR-OLR). As second-order resonances (i.e. 4:1 for a two-armed spiral) can also be quite important, as shown in Minchev (2016), and give rise to square orbits in the frame moving with the spiral pattern, we highlight them in Fig. 1.
We stress that Castro-Ginard et al. (2021) and Quillen et al. (2018) also find evidence for transient spiral arms, showing that different segments exhibit varying pattern speeds. In this article, we refer to spiral structures as suggested by Minchev (2016) and Hilmi et al. (2020, see their Sect. 5.4), with velocity patterns rescaled to the rotational curve of Roca-Fàbrega et al. (2014). Importantly, it should be noted that the methodology introduced in this work is versatile in nature and can be expanded to analyse any generic velocity configuration within the spiral arms and disc.
In Fig. 2, we report different snapshots of the temporal evolution of the modulation function 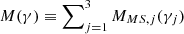 introduced in Eq. (11) for Model A (see Table 1 for other parameter values). At the initial time, all the spiral chunks perfectly trace a spiral arm structure with multiplicity m = 2. However, as time goes by, different arc-shaped substructures become increasingly prominent in the modulation function map because of the different pattern speeds. It is possible to appreciate that as the number of arcs increases, the amplitude of M(γ) decreases. The strength of the perturbation is maximum when we recover the m = 2 spiral arm configuration after 350 Myr of evolution.
introduced in Eq. (11) for Model A (see Table 1 for other parameter values). At the initial time, all the spiral chunks perfectly trace a spiral arm structure with multiplicity m = 2. However, as time goes by, different arc-shaped substructures become increasingly prominent in the modulation function map because of the different pattern speeds. It is possible to appreciate that as the number of arcs increases, the amplitude of M(γ) decreases. The strength of the perturbation is maximum when we recover the m = 2 spiral arm configuration after 350 Myr of evolution.
 |
Fig. 2. Different snapshots of the temporal evolution of the new modulation function |
4. Nucleosynthesis prescriptions
As mentioned in Sect. 1, the main purpose of this work is to show the results of the azimuthal variations of abundance gradients for oxygen, iron, europium, and barium. In this section, we provide the nucleosynthesis prescriptions for these elements.
4.1. Oxygen and iron
As done in a number of chemical evolution models in the past (e.g. Spitoni et al. 2019b, 2022, 2023; Vincenzo et al. 2019), we adopt the nucleosynthesis prescriptions by François et al. (2004) for oxygen and iron; these latter authors selected the best sets of yields required to best fit the data (we refer the reader to their work for details related to the observational data). In particular, for Type II SNe yields, these authors found that the Woosley & Weaver (1995) values correspond to the best fit of the data. This occurs because no modifications are required for iron yields, as computed for solar chemical composition, whereas the best results for oxygen are given by yields computed as functions of metallicity. The theoretical yields by Iwamoto et al. (1999) are adopted for the Type SNeIa, while the prescription for single low-intermediate stellar mass is by van den Hoek & Groenewegen (1997).
Although the prescriptions of François et al. (2004) still provide reliable yields for several elements, we must be cautious about oxygen. Several results have shown that rotation can affect the oxygen nucleosynthesis in massive stars (Meynet & Maeder 2002), and therefore the chemical evolution therein (Cescutti & Chiappini 2010), in particular at low metallicity. However, this does not affect our results because the data considered in this project are relatively metal rich. Moreover, we are mostly interested in differential effects rather than absolute values. This set of yields has been widely used in the literature (Cescutti et al. 2007, 2022; Mott et al. 2013; Spitoni et al. 2022, 2023; Palla et al. 2022) and has been found to reproduce the main features of the solar neighbourhood.
4.2. Europium and barium
A neutron star merger (NSM) is considered a fundamental production site for the Eu in our analysis. Matteucci et al. (2014) and Cescutti et al. (2015) considered the realisation probability of double neutron star systems belonging to massive stars that will eventually merge, or simply the fraction of such events (αNSM).
These authors adopted a value of 2 × 10−6 M⊙ for Eu yields. This is consistent with the range of yields suggested by Korobkin et al. (2012), who propose that NSM can produce from 10−7 to 10−5 M⊙ of Eu per event. Moreover, Matteucci et al. (2014) and Cescutti et al. (2015) assumed that a fixed fraction of massive stars in the 10 − 30 M⊙ range are NSM progenitors. To match the present rate of NSM in the Galaxy (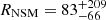 Myr−1; Kalogera et al. 2004), we set the parameter αNSM to 0.05. The recent observation of the event GW170817 appears to support this rate (Matteucci 2021; Molero et al. 2021a).
Myr−1; Kalogera et al. 2004), we set the parameter αNSM to 0.05. The recent observation of the event GW170817 appears to support this rate (Matteucci 2021; Molero et al. 2021a).
We set a fixed time delay of 1 Myr for the coalescence of two neutron stars, which is consistent with the assumptions of Matteucci et al. (2014) and Cescutti et al. (2015). We note that this model assumes that all neutron star binaries have the same coalescence time, but a more realistic approach would consider a distribution function of such timescales, similar to the explosion time distribution for SNIa (see Simonetti et al. 2019 and Molero et al. 2021b). In the present work, we do not consider the stochasticity of the r-process events. Given the fixed and short delay time considered, the scenario is also compatible with other sources of r-process material such as MRD SNe (Winteler et al. 2012; Nishimura et al. 2015) and collapsars (Siegel et al. 2019). We adopted the yields of Cristallo et al. (2009, 2011) for nucleosynthesis by the s-process in low-mass AGB stars (1.3–3 M⊙), meaning that in this work they play a role in the production of barium in particular. The yields from non-rotating stars were used in our analysis, but they tend to overestimate the production of s-process elements at solar abundance. In contrast, the yields from rotating AGB stars produce insufficient neutron-capture elements. To address this issue, and taking inspiration from Rizzuti et al. (2019), we divided the non-rotating yields by a factor of 2 in order to reproduce the observed data at solar metallicity. The s-process contribution from rotating massive stars has also been considered incorporating the yields by Frischknecht et al. (2016), as specified in Table 3 of Rizzuti et al. (2019). We recall that Cescutti et al. (2013, 2015) and Cescutti & Chiappini (2014) first considered s-process contribution from rotating massive star using the nucleosynthesis prescriptions proposed by Frischknecht et al. (2012),
5. Results
In this section, we present the results of the effect of multiple spiral arm patterns on the chemical evolution of oxygen, iron, europium, and barium in the Galactic thin disc. In Sect. 5.1, we consider the spiral arm pattern speeds as shown in Fig. 1 (Model A in Table 1). In Sect. 5.2, we report results for Models A1, A2, and A3, where the three spiral structures are considered separately (e.g. three arms, each with its own pattern speed) in different runs of the Galactic chemical evolution model (see Table 1 for further details). In Sect. 5.3, we discuss the effects of different angular velocities for the most external spiral structure (Ωs, 3; Models B1 and B2). In Sect. 5.4, we introduce additional complexities to the spiral arm models presented so far, considering spiral arms with different pattern speeds and modes. Finally, in Sect. 5.5, we investigate the hypothesis that, in recent times, all galactocentric distances are co-rotational radii, which means that the spiral arms have been, at least relatively recently, rotating at the same angular velocity as the Galactic disc. Indeed, several recent numerical studies have highlighted the possibility that material spiral arms propagate close to co-rotation at various radii throughout the galaxy (see Grand et al. 2012; Comparetta & Quillen 2012; Hunt et al. 2019).
All the model results presented in this paper adopt the prescriptions of the spiral arm analytical model of Cox & Gómez (2002), which were also applied by ES19: the drop-off in density amplitude of the arms is fixed at a radial scale length of RS = 7 kpc, and the pitch angle is assumed to be constant in time and fixed at the value of α = 15°. The surface arm density, Σ0, is set to 20 M⊙ pc−2 (we refer the reader to ES19 for a description of the motivation behind this value) at the fiducial radius of R0 = 8 kpc, and we also assume that ϕp(R0) = 0°. It is worth mentioning that, as in ES19, we follow the chemical evolution of the thin disc component, and we assume that the oldest stars are associated with ages of ∼11 Gyr, which is in agreement with asteroseismic age estimates (Silva Aguirre et al. 2018).
5.1. Multi-pattern spiral arm structure: Model A
Figure 3 shows the predicted 2D map of the SFR projected onto the Galactic disc by Model A after 11 Gyr of Galactic disc evolution (present-day). Although the considered spiral arms have multiplicity m = 2, the signatures of multiple arcs and substructures originated by different velocity patterns are well visible in the regions with enhanced star formation. In the upper panel of Fig. 4, the position of the spiral arms in the Galaxy as mapped by the overdensities of upper-main sequence (UMS) stars of Poggio et al. (2021) is overplotted on the present-day SFR predicted by Model A (the same as Fig. 3). In this plot, we report the stellar overdensities as defined by Eq. (1) of Poggio et al. (2021) for positive density contrast values.
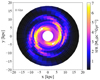 |
Fig. 3. Galactic disc SFR resulting from Model A after 11 Gyr of evolution projected onto the Galactic plane after the start of disc formation (see Table 1 and text for model details). The colour-coding indicates the SFR values in units of M⊙ pc−2 Gyr−1. |
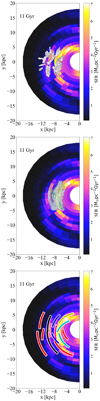 |
Fig. 4. Zoom-in view of 2D map of the SFR resulting from Model A after 11 Gyr of the evolution of Fig. 3 compared with some tracers of spiral arms or arcs present in literature. Upper panel: overdensities in the distribution of UMS stars of the Poggio et al. (2018) sample with Gaia EDR3 astrometry (Gaia Collaboration 2021a) as presented by Poggio et al. (2021). We report only positive values of stellar overdensities as defined by Eq. (1) of Poggio et al. (2021). Middle panel: distribution of the median of the radial action JR of Gaia DR3 stars (see text for more details) on the Galactic Plane (|Zmax|< 0.5 kpc and R < 10 kpc) as computed by Palicio et al. (2023b) and here only reporting the star with JR < 0.01 R⊙ V⊙ (green shaded area). Lower panel: solid lines represent the segments of spiral arms traced by Cepheids of Lemasle et al. (2022) in which the colour coding is the one adopted by Palicio et al. (2023b). |
In the middle panel, we show the map of the median of the radial action JR on the Galactic plane (|Zmax| < 0.5 kpc and R < 10 kpc) as computed by Palicio et al. (2023b) for Gaia DR3 stars with full kinematic information only for bins with JR < 0.01 R⊙ V⊙, which trace the innermost region of the Scutum-Sagittarius spiral arms. For stars in the disc, JR can be interpreted as a parameter that quantifies oscillation in the radial direction, with JR = 0 for circular orbits. We refer the reader to Appendix B of Palicio et al. (2023b) for a detailed explanation of how the radial action JR has been computed.
Finally, in the lower panel, the solid lines represent the segments of spiral arms traced by Cepheids in Lemasle et al. (2022). We note that there is good agreement between the above-mentioned spiral-arm tracers and the location of the predicted enhanced star formation regions driven by the passage of the multi-pattern spiral arm of Model A. In Fig. 5, we note that the present-day SFR profiles predicted by Model A at different azimuthal coordinates throughout the Galactic disc are in agreement with the visible-band observations presented by Kennicutt & Evans (2012) and Stahler & Palla (2004, supernova remnants (SNRs), pulsars, and HII regions), and Green (2014, SNRs).
 |
Fig. 5. Present-day radial SFR profile predicted by Model A for different azimuthal coordinates (coloured lines). In both panels, the shaded light-blue area denotes the range of maximum and minimum SFR values at various galactocentric distances. Upper panel: predicted SFRs are compared with the visible-band observations presented in Guesten & Mezger (1982) and rescaled by Kennicutt & Evans (2012) to the total SFR of 1.9 M⊙ yr−1 provided by Chomiuk & Povich (2011), as indicated by the black solid line. Lower panel: red diamonds with error bars are observational data for the star formation profile from SNRs, pulsars, and HII regions normalised to the solar vicinity value (SFR/SFR⊙) from Stahler & Palla (2004). The dark-blue solid line represents the analytical fit of the SNR compilation by Green (2014) as reported in Palla et al. (2020) and Spitoni et al. (2021). The model predictions for different azimuths SFRϕ are divided by their respective solar vicinity SFR⊙, ϕ values. |
Figure 6 shows the present-day abundance gradients for O, Eu, Fe, and Ba predicted by Model A after 11 Gyr of evolution for different azimuthal coordinates. It is important to stress that, as already found by Cescutti et al. (2007) and more recently by Molero et al. (2023), the predicted gradient for barium is almost flat or is slightly decreasing in the innermost Galactic regions.
 |
Fig. 6. Present-day oxygen (upper left panel), europium (upper right panel), iron (lower left panel), and barium (lower right panel) abundance gradients for different azimuths as predicted by Model A (see Table 1 for model details). In each panel, the coloured dashed vertical lines indicate the location of the co-rotation radii for the three spiral structures characterised by different pattern speeds. Model predictions are compared with Cepheids data provided by Kovtyukh et al. (2022) and Luck & Lambert (2011) for oxygen and europium, and by Genovali et al. (2014) for iron and by Luck (2018) for barium. The data trends (black dashed lines) are computed by calculating the running median in bins of 0.5 kpc, with a 40% overlap, and a minimum number of stars per bin of two for O, Fe, and Eu, and one for Ba; this lower minimum for Ba is chosen because of the low number of measurements in the sample. The shaded regions on the plot represent the standard deviation of these trends. For the sake of visualisation, we focus on the abundance range [–0.5, 0.6] dex, excluding stars with [Ba/H] > 0.6 dex. |
As already underlined in the analysis of the azimuthal variation of oxygen in ES19, the more significant variations are located close to the co-rotation. We note that as the co-rotation is shifted towards the outer Galactic regions, variations become more enhanced. This is in agreement with the results of ES19, where the density perturbation extracted by the chemo-dynamical model of Minchev et al. (2013) was included. In addition, we note that in this case, significant variations have also been found in chemical abundances in the outer Galactic regions.
Spitoni et al. (2019a) stressed that the chemical enrichment process at the co-rotation is expected to be more efficient because of the absence of relative gas–spiral motions. The co-rotation radius experiences a higher SFR because of the increased gas overdensity, which persists for a longer duration. This leads to the formation of more massive stars and the ejection of more metals into the local ISM. To illustrate this, in Fig. 7, we show he excess chemical abundances with respect to the azimuthal average.
 |
Fig. 7. Present-day residual azimuthal variations in oxygen, europium, iron, and barium abundance, respectively computed at different galactocentric distances for the multiple spiral structure of Model A in Table 1. The coloured solid lines indicate the variations at the co-rotation radii for the three spiral structures characterised by different pattern speeds with the same colour-coding as the dashed vertical lines of Fig. 6. |
With this model, we can make predictions as to the azimuthal variations originating from spiral arm structures for different chemical elements. From Fig. 6, it is clear that azimuthal variations depend on the studied chemical element: elements produced on short timescales (i.e. oxygen almost totally synthesised in Type II SNe and europium in NSM and via r-processes) show the largest variations. As the progenitors in these cases have short lifetimes, the chemical elements returned to the ISM perfectly trace the SFR fluctuations created by the mass overdensities in the spiral arms. This results in a pronounced variation of the abundance gradients compared with other elements ejected into the ISM after an important time delay. For example, the bulk of iron is produced by Type Ia SNe and the timescale for returning it to the ISM depends on the assumed SN progenitor model and the associate delay-time distribution (Greggio 2005; Matteucci et al. 2009; Palicio et al. 2023a). The typical timescale for Fe enrichment in the Milky Way solar neighbourhood is around 1–1.5 Gyr (Matteucci et al. 2009). From Fig. 6, we note that a larger spread in chemical abundances is also present in the Cepheid data for elements produced in short timescales (oxygen and europium) compared to iron, which is in agreement with our model predictions. For barium, there are insufficient stellar abundances available to make any firm conclusions.
In our approach, we neglect dynamical processes that could affect the gas distribution in the co-rotations. For instance, Barros et al. (2021) studied both hydrodynamic analytical solutions and simulations, and pointed out that the interaction of the gaseous matter of the disc with the spiral perturbation should produce a flow of gas that establishes at the co-rotation region. In particular, an inward flow of gas to the inner regions of the Galaxy and an outward flow to the outer regions are present at the co-rotation circle, from which the flows diverge. As a natural consequence of this dynamic process, a ring-shaped void of gas should form at the co-rotation radius. Nonetheless, Lépine et al. (2017) showed that the Local Arm is an outcome of the spiral co-rotation resonance, which traps arm tracers and the Sun inside it. This latter finding supports the scenario where some mass should cluster inside the co-rotation zones, thereby contributing to increased density in these regions. In conclusion, two processes with opposite effects (gas depletion and clustering) seem to coexist, and it is still not clear which is the dominant one.
In our model, the lack of relative velocity between disc and spiral structures is the main cause of the pronounced azimuthal abundance variation at the co-rotation. As shown in Fig. 8, we see significant dips in gas distribution at the three co-rotational radii. However, these declines align exclusively with positive variations in chemical abundance (see Fig. 9). In light of the dynamical results mentioned by Barros et al. (2021), our findings must be considered as an upper limit on the azimuthal variations originated by spiral arms. On the other hand, it is important to point out that in the chemodynamical simulations of the Milky Way-like spiral galaxies, as presented by Khoperskov et al. (2023), there is no evidence of any annular void region in the gas distribution (see their Fig. 2), which Barros et al. (2021) suggest would be a signature of the presence of co-rotation.
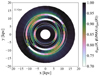 |
Fig. 8. Galactic disc surface gas density distribution resulting from Model A after 11 Gyr of evolution normalised to the maximum values at different galactocentric distances. We also use white edges to highlight the annular regions where three co-rotational radii are situated. |
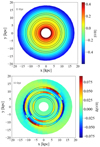 |
Fig. 9. Oxygen abundance distribution in the Galactic disc resulting from Model A after 11 Gyr of evolution and projected onto the Galactic plane after the start of disc formation (see Table 1 and text for model details). Upper panel: [O/H] values. Lower panel: distribution of residual azimuthal variations Δ [O/H] in oxygen. In each panel, we also highlight the annular regions where the three co-rotational radii are situated using black edges. |
Scarano & Lépine (2013), analysing external galaxies, claimed that the presence of a step in metallicity and the change of slope of the gradient at this radius are due to co-rotation. However, it is important to underline that a change in the slope in the abundance gradient can be the result of other chemo-dynamical processes, such as the inside-out formation scenario, or a variable star formation efficiency or IMF throughout the Galactic disc (see Matteucci 2021 for a review).
In Fig. 10, we show the temporal evolution of the oxygen abundance gradients after 3, 5, 9, and 11 Gyr of evolution. At early times, the azimuthal variations are more prominent, as already pointed out by ES19.
 |
Fig. 10. Temporal evolution of the oxygen abundance gradient after 3, 5, and 11 Gyr of thin disc evolution for different azimuth coordinates as predicted by Model A. The colour code is the same as in Fig. 6. |
As the oxygen abundance increases (i.e. closer to the “saturation” level of the chemical enrichment), the chemical variations due to perturbations of the SFR become smaller. In addition, the Galactic chemical evolution is a cumulative process in time. In early times, the stronger spiral structure induces azimuthal variations, which are later washed out by phase mixing. Hence, we provide an important prediction for the high-redshift galaxies with spiral arms that will be analysed in future works, especially thanks to James Webb Space Telescope (JWST) discoveries. Indeed, Fudamoto et al. (2022), analysing the initial image captured by JWST of SMACS J0723.3-7327, highlighted the presence of two extremely red spiral galaxies, likely at cosmic noon (1 < z < 3).
5.2. Single-pattern spiral arms (Models A1, A2, and A3)
Recent investigations pointed out that it is very likely that the Milky Way possesses multiple modes with different patterns, with slower patterns situated towards outer radii (Minchev & Quillen 2006; Quillen et al. 2011). ES19 only presented the effects of spiral arms with single patterns in a chemical evolution model (e.g. considering diverse velocities solely in different Galactic models). In order to be in agreement with the observations of external galaxies (Sánchez et al. 2015), and with the results obtained using the fluctuations from the chemodynamical model of Minchev et al. (2013), ES19 assumed that the modes with different patterns combine linearly, and that their total effects on abundance azimuthal variations respond linearly to the different modes considered. We confirmed this hypothesis by verifying that the sum of residual azimuthal variations predicted for Models A1, A2, and A3 (i.e. models where the three chunks of spiral arms are considered separately; see Table 1) is almost identical to that of Model A:
We conclude that, in our approach, we do not find any amplifications of the azimuthal variation in the zones where the different chunks of spiral arms are connected and spatially overlap.
5.3. Varying the pattern velocity for the external spiral structure: Models B1 and B2
Models B1 and B2 (see Table 1) have the same pattern speeds, Ωs, 1 and Ωs, 2, as Model A, and the two innermost spiral structures have the same radial extension, but for the external clump, diverse velocities have been tested to quantify the effects of different external co-rotational radii. In Model B1, the velocity of the outermost spiral chunk is Ωs, 3 = 17 km s−1 kpc−1 (i.e. the co-rotation is located at 10.25 kpc from the Galactic centre). On the other hand, in Model B2 we impose that Ωs, 3 = 13 km s−1 kpc−1 (i.e. a co-rotation located at 13.30 kpc).
In Table 2, we report the maximum residual azimuthal variations Δmax [X/H] for oxygen, europium, iron, and barium predicted by models B1 and B2 at the respective co-rotations of the outermost spiral chunk, which is characterised by an angular velocity of Ωs, 3. We confirm that the lower the velocity Ωs, 3, the more prominent the amplitudes of the azimuthal variations, as already discussed in previous sections and in ES19. It is evident that a difference in the pattern speed of ΔΩs, 3 = 4 km s−1 kpc−1 in the most external spiral mode leads to a shift of roughly 3 kpc in the co-rotation radius, and has substantial effects on the chemical evolution of the Galactic disc.
Maximum azimuthal residual variations Δmax [X/H] for oxygen, europium, iron, and barium predicted by models B1 and B2 at the respective co-rotations of the outermost spiral chunk (characterised by angular velocity Ωs, 3 and the co-rotation radius R3, cor.).
5.4. Spiral arms with different pattern speeds and modes
In this section, we introduce additional complexities to the spiral arm models presented so far, with the aim being to examine the influence of multiple patterns and different modes on the chemical evolution of the thin disc. We extracted the pattern speeds from the power spectrogram of the m = 1, 2, 3, and 4 Fourier components constructed by Hilmi et al. (2020). To this end, we used a time window of 350 Myr for their Model 1. This model is based on the high-resolution hydrodynamical simulations of MW-sized galaxies from the NIHAO-UHD project of Buck et al. (2020; galaxy g2.79e12).
In Fig. 11, we present the velocity patterns for various modes extracted by Hilmi et al. (2020) and scaled to the circular velocity determined by Roca-Fàbrega et al. (2014). In analogy with Eq. (10), the expression for the time-evolution of the density perturbation created by the different speeds and modes of Fig. 11 can be written as
 |
Fig. 11. As in Fig. 1, but for spiral modes extracted from the spectrogram analysis of Model1 by Hilmi et al. (2020), which was based on the Buck et al. (2020) cosmological simulation. Different multiplicities are shown in each panel, as indicated. In each panel, the disc angular velocity Ωd(R) is indicated with the dotted line. In the two upper panels (with modes m = 2 and m = 4), we also show the resonances Ωp2(R) = Ωd(R)±κ/2 and Ωp4(R) = Ωd(R)±κ/4, which are indicated with solid and dashed black curves, respectively. In the lower two panels, the solid and dashed black lines were computed as Ωp1(R) = Ωd(R)±κ and Ωp3(R) = Ωd(R)±κ/3. |
where Nm is the number of spiral clumps associated with the mode m. The coefficients Am are set by adopting the power spectrograms from Fig. 11 of Hilmi et al. (2020) in order to redistribute the spiral density perturbation across different modes (A1 = 0.1, A2 = 0.4, A3 = 0.1 and A4 = 0.4). In Fig. 12, we display the residual azimuthal variations in oxygen, europium, iron, and barium abundance at the present day, calculated at distances of 4, 6, and 9 kpc.
 |
Fig. 12. Present-day residual azimuthal variations in oxygen, europium, iron, and barium abundance, respectively, computed at 4, 6, and 9 kpc for Model1 by Hilmi et al. (2020), as introduced in Sect. 5.4, where the spiral structure is characterised by multiple modes of different multiplicity from 1 to 4. |
It is worth highlighting the presence of additional wiggles in the azimuthal variations compared to the results of Model A (see Fig. 7, where the single mode m = 2 was imposed), which arise from the coexistence and interplay of different modes. However, the amplitude of the azimuthal variation at 9 kpc remains roughly the same. Therefore, in the subsequent section, we employ Model A as our reference model for further investigations.
5.5. Extending the co-rotation to all galactocentric distances (Models A+C1, A+C2, A+C3)
The results of the chemical evolution models presented so far are based on evidence that the Milky Way can contain multiple patterns, with slower patterns situated towards outer radii (Minchev & Quillen 2006; Quillen et al. 2011). Furthermore, in other dynamical works (Grand et al. 2012; Hunt et al. 2019), co-rotating arms can be found at all radii in transient spiral arm structures.
The occurrence of temporary spiral structure results in phase mixing, leading to the formation of ridges and arches in the nearby kinematics observed in the Gaia data (Gaia Collaboration 2023, 2021b; Ramos et al. 2018; Palicio et al. 2023b). By incorporating a bar with various pattern speeds, Grand et al. (2012) and Hunt et al. (2019) successfully generated a model with a reasonably accurate resemblance to observations. In addition, in the pure N-body simulation of Grand et al. (2012) of a barred galaxy, the spiral arms are transient features whose pattern speeds decline with radius, meaning that the pattern speed closely matches the rotation of star particles.
To mimic the above-mentioned scenarios, we impose that at recent evolutionary times, the pattern speeds Ωs, j match the rotational curve at all radii; that is, the condition Ωs, j(R) = Ωd(R) is extended to all galactocentric distances for each of the spiral chunks of Model A. As indicated in Table 1, we applied this condition for the last 100 Myr (Model A+C1), 300 Myr (Model A+C2), and 1 Gyr (Model A+C3) of Galactic chemical evolution, respectively.
Figures 13 and 14 present the abundance gradients and the residual azimuthal variations predicted by these three new models. As expected, the amplitudes for the considered chemical elements are amplified compared with Model A, especially at different galactocentric distances from that of the co-rotations of Model A, as visible in Fig. 13 for Models A+C1 and A+C2. The longer the condition for the transient spiral arm is met, the larger the amplitude of the azimuthal variation. Indeed, as discussed in previous sections, the condition Ωs, j(R) = Ωd(R) imposes that, at fixed galactocentric distance R and azimuthal coordinate ϕ, the perturbation term δMS (introduced in Eq. (12)) in the SFR does not vary over time. Hence, the chemical fluctuation should be amplified. The extreme case of Model A+C3 with the condition Ωs, j(R) = Ωd(R) in the last 1 Gyr should be considered as a test (see last rows in Figs. 13 and 14). For instance, for oxygen, the maximum amplitude at 12 kpc is Δmax[O/H] ∼ 0.37 dex, whereas for Model A it is Δmax[O/H] ∼ 0.17 dex, which means an increase by a factor of 2.18.
 |
Fig. 13. Comparison of azimuthal variations in abundance gradients for oxygen, europium, iron, and barium predicted by Model A (first row) with models where the condition of transient spiral have been considered. Model A+C1 is reported in the second row, where the condition Ωs, j(R) = Ωd(R) is valid for all Galactic radii (co-rotation extended at all distances) during the last 100 Myr of Galactic evolution; Model A+C2 is shown in the third row, where the above-mentioned condition is only met for the last 300 Myr; and Model A+C3 is shown in the last row, where this condition is met for 1 Gyr. The colour convention of the lines is the same as in Fig. 6. The vertical lines indicate the corotations of Model A. |
 |
Fig. 14. As in Fig. 7, but also for Model A+C1 (second row), Model A+C2 (third row), and Model A+C3 (last row), respectively. |
5.6. Tightly wound spiral structures
The work of Quillen et al. (2018) and Laporte et al. (2019) suggested that tightly wound spiral structures should be considered based on the modelling of phase-space structure found in the second Gaia data release (Gaia Collaboration 2018). A smaller pitch angle gives rise to a more tightly wound spiral structure. Reshetnikov et al. (2023) studied the pitch angles of spiral arms in galaxies within the Hubble Space Telescope COSMOS field. Analysing a sample of 102 face-on galaxies with a two-armed pattern, these authors found a decreasing trend in the pitch angle value from a redshift range of z = 1 to z = 0. However, in this study, we do not test the effects of a decreasing pitch angle in time on the chemical evolution of the Galactic disc. As already pointed out by ES19, the amplitude of the azimuthal variation in the abundance gradients is not dependent on the pitch angle. As highlighted by Fig. 18 of ES19, small pitch angles solely reduce the phase difference of the abundance variation between different radii.
6. Gaia DR3 data
Gaia DR3 Gaia Collaboration (2022, 2023) and Recio-Blanco et al. (2023) have brought about a true and unprecedented revolution in all-sky spectroscopy. With about 5.6 million stars, the Gaia DR3 General Stellar Parametrizer – Spectroscopy (GSP-Spec, Recio-Blanco et al. 2023) all-sky catalogue is the largest compilation of stellar chemo-physical parameters to date and the first one composed of space data without the issues of biased samples, which hamper observations from Earth. In Gaia Collaboration (2023), the high quality GSP-Spec chemical abundances for α-elements and Fe have been used to provide important constraints in the field of Galactic archaeology. Spitoni et al. (2023) presented updated chemical evolution models for the evolution of the thick and thin discs constrained by α-elements in the solar vicinity. The interaction with the Sagittarius dwarf galaxy could explain the observed feature in the abundance ratios. Galactic archaeology for the heavy elements was presented by Contursi et al. (2023) analysing the GSP-Spec cerium, and the comparison with Spitoni et al. (2023) model predictions was presented. In Sect. 6.1, we compare our model predictions with the azimuthal variations found in the metallicity distribution of Poggio et al. (2022), whereas in Sect. 6.2 we compare them with the GSP-Spec [M/H] abundance ratios of Cepheids.
6.1. Comparison with Poggio et al. (2022)
Poggio et al. (2022) exploited Gaia DR3 data, providing a map of inhomogeneities in the Milky Way disc [M/H] abundances, which extends to approximately 4 kpc from the solar position. This was achieved by studying various samples of bright giant stars, which were selected based on their effective temperatures and surface gravities using the GSP-Spec module. The “Sample A” composed by these authors, which is made up of hotter (and younger) stars, exhibits significant inhomogeneities, which manifest as three (or possibly four) metal-rich elongated features that correspond to the positions of the spiral arms in the Galactic disc. In Fig. 15, we compare the present-day residual azimuthal variation Δ[Fe/H] predicted by Models A, A+C1, A+C2, and A+C3 with the Δ[M/H] of the Poggio et al. (2022) Sample A because they should better trace the present-day ISM inhomogeneities predicted by our models. We recall that in GSP-Spec, [M/H] values follow the [Fe/H] abundance with a tight correlation. For this reason, in the following plots, we compare [Fe/H] ratios predicted by our models with Gaia DR3 [M/H] abundance ratios.
 |
Fig. 15. Present-day residual azimuthal variations in iron computed at different galactocentric distances for the multiple spiral structures of Models A, A+C1, A+C1, and A+C3, compared with the metallicity variation found by Poggio et al. (2022) when analysing GSP-Spec abundances of Gaia DR3 (Gaia Collaboration 2023). Horizontal lines with the same colour indicate the 10th and 90th percentiles of the metallicity variation as computed by Poggio et al. (2022) at different galactocentric distances. In each panel, the shaded grey area indicates the region spanned by Poggio et al. (2022) data. In the zoom-in plot associated with the fourth panel, we report the Poggio et al. (2022) data, indicating the median metallicity for Sample A as a function of Galactic azimuth for different galactocentric distances (after the median metallicity of the stars for each ring has been subtracted). |
We note that the amplitude of the variations predicted by Model A is smaller than that displayed by Sample A of Poggio et al. (2022) in the interval between the 10th and 90th percentiles. It is also important to stress that in the Poggio et al. (2022) data, there is not a strong dependence of the amplitude on the radius, in contrast with our Model A results. Furthermore, in the range of galactocentric distances of Fig. 15, Model A shows a maximum amplitude of azimuthal fluctuation near the co-rotation radius of the second spiral chunk (Ωs, 2 = 20 km s−1 kpc−1) and almost negligible azimuthal variation is found at 7 kpc.
However, the agreement is quite good with Models A+C1 and A+C2, where for the last 100 Myr and 300 Myr of evolution, respectively, we impose the transient spiral arm condition (i.e. Ωs, j(R) = ΩD(R)). On the other hand, Model A+C3 produces much larger azimuthal variations than the observed ones. In Fig. 16, we show that the present-day SFR profile throughout the Galactic disc for Model A+C2 is in agreement with observations. Compared to Fig. 5, in this case, we see that slightly higher peaks of SF are predicted in the Galactic region enclosed between 9 and 12 kpc.
6.2. Comparison with Gaia DR3 GSP-Spec Cepheids
Ripepi et al. (2023) presented the Gaia DR3 catalogue of Cepheids of all types, which was obtained through the analysis carried out with the Specific Object Study (SOS) Cep&RRL pipeline. In Fig. 17, we show the abundance gradient of Gaia DR3 Cepheids in the Galactic disc with calibrated GSP-Spec metallicity [M/H] as suggested by Recio-Blanco et al. (2023). We impose that the fluxNoise flag of Table 2 of Recio-Blanco et al. (2023) be set equal to 0 (best quality data). The Gaia source “IDs” of the Cepheid sources are those identified in Gaia DR3 (Ripepi et al. 2023). We computed the galactocentric distances by adopting the Sun’s galactocentric position (R, Z)⊙ = (8.249, 0.0208) kpc (GRAVITY Collaboration 2021; Bennett & Bovy 2019), the high-precision astrometric parameters from Gaia EDR3 (Gaia Collaboration 2021a), and additional information provided by Gaia DR3 for the radial velocities (Katz et al. 2023; Gaia Collaboration 2022).
 |
Fig. 17. Present-day iron abundance gradient predicted by Models A, A+C1, A+C2, and A+C3 at different azimuthal coordinates. In each panel, the shaded light-blue area denotes the range of maximum and minimum Fe abundance values at various distances from the centre of the galaxy spanned by the models. The Cepheids data collected by Genovali et al. (2014) and the GSP-Spec [M/H] for Gaia DR3 sources within the sample of Cepheids presented by Ripepi et al. (2023) are reported with empty and full light-red dots, respectively. The average abundance values and relative errors – when dividing these two data sets into six radial bins – are shown by black and red pentagons, respectively. |
In Fig. 17, we note that the abundance gradient emerging from GSP-Spec metallicities is in good agreement with that of Genovali et al. (2014). The larger spread in the GSP-Spec metallicity is due to the higher mean uncertainties (∼0.15 dex) compared to those computed with high-resolution spectroscopy in Genovali et al. (2014, ∼0.08 dex). In the same plots, we also highlight the abundance variation in [Fe/H] predicted by Models A, A+C1, A+C2, and A+C3. We note that the only model that can partially account for the spread in Gaia data and in Genovali et al. (2014) is Model A+C3. We recall that this last case should be considered extreme, where the condition Ωs, j(R) = Ωd(R) is extended to all galactocentric distances for 1 Gyr. In conclusion, we believe that the observed spread in the abundance gradient is only partially explainable through spiral arms and other dynamical processes should be taken into account.
7. Conclusions and future perspectives
In this paper, we present an updated version of the 2D chemical evolution model for the Galactic disc presented by Spitoni et al. (2019a), considering the density fluctuation created by multiple patterns in the spiral arms. We carried out a detailed study of their effects on the abundance gradients of oxygen, iron, barium, and europium. In particular, for the predicted [Fe/H], we also show a comparison with the recent GSP-Spec [M/H] abundances (Gaia Collaboration 2023; Poggio et al. 2022). Our main results can be summarised as follows:
-
We find that azimuthal variations are dependent on the considered chemical element. Elements synthesised on short timescales (i.e. oxygen and europium in this study) exhibit larger abundance fluctuations. Moreover, having progenitors with short lifetimes, the chemical elements restored to the ISM perfectly trace the SFR perturbed by the passage of spiral arms. This results in important azimuthal variations of the abundance gradient compared with other elements ejected into the ISM after a significant delay (i.e. iron and barium).
-
The 2D map of the projected SFR onto the Galactic disc (in the presence of spiral arms with multiple patterns predicted by Model A, see Table 1) shown arcs and arms compatible with tracers of spiral arms (young UMR stars, Cepheids, distribution of stars with low radial actions).
-
Spitoni et al. (2019a), from their study of single-pattern spiral arms, find that the largest fluctuations in the azimuthal abundance gradients are found near the co-rotation radius, where the relative velocity with respect to the disc is close to zero. Larger azimuthal variations are associated with the most external spiral clumps, where the associated co-rotation radius is placed at larger galactocentric distances.
-
Assuming that the modes with different patterns combine linearly, we show that the total effects of the different modes on abundance azimuthal variations also respond linearly to the different modes considered.
-
Imposing that the pattern speeds match the Galactic rotational curve at all radii in the last 100 Myr of evolution leads to amplification of the azimuthal variation.
-
The predicted azimuthal variation is consistent with the variation in metallicity found by Poggio et al. (2022) based on Gaia DR3, that is, if transient spiral arms are assumed at recent evolution times (during the last ≃300 Myr).
In the future, we plan to explore the scenario where the spiral pattern winds up at Ωd = Ω(R)−κ/2 (where κ is the epicyclic frequency), as proposed by Bland-Hawthorn & Tepper-García (2021). Hunt et al. (2019) highlighted the intricate challenge of separating the impacts of the bar and the spiral structure. Hence, in future work, we plan to also include variations produced by the Galactic bar (e.g. Palicio et al. 2018, 2020). In Barbillon et al. (in prep.), we would like to extend the analysis of Poggio et al. (2022) to other GSP-Spec chemical elements (i.e. total α, Mg, Ca, Si, and Ti) and compare the findings with our models. We also plan to consider stellar migration as an additional dynamical process in our model. Indeed, several cosmological works highlighted the importance of stellar migration in the azimuthal variation of abundance gradients in the vicinity of spiral arms (Grand et al. 2012, 2014, 2016; Sánchez-Menguiano et al. 2016). It is also our intention to study the effects of spiral arms on the Galactic chemical evolution of short-lived radionuclides, such as 26Al and 50Fe, using the same model and nucleosynthesis prescriptions as in Vasini et al. (2022, 2023). Because these elements are tracers of star formation, we expect to find a signature of the passage of spiral structures on their present-day distribution (Siegert et al. 2023). Finally, we plan to use our chemical evolution model to test the effects of gas flows at the co-rotation, as highlighted in Barros et al. (2021).
Acknowledgments
The authors thank the anonymous referee for various suggestions that improved the paper. We thank P. De Laverny, S. Khoperskov and M. Sormani for useful discussions. E. Spitoni and A. Recio-Blanco received funding from the European Union’s Horizon 2020 research and innovation program under SPACE-H2020 grant agreement number 101004214 (EXPLORE project). This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement N. 101063193. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. I. Minchev acknowledges support by the Deutsche Forschungsgemeinschaft under the grant MI 2009/2-1. P. A. Palicio acknowledges the financial support from the Centre national d’études spatiales (CNES). This work was partially supported by the European Union (ChETEC-INFRA, project no. 101008324). F. Matteucci and A. Vasini thank I.N.A.F. for the 1.05.12.06.05 Theory Grant – Galactic archaeology with radioactive and stable nuclei.
References
- Balser, D. S., Rood, R. T., Bania, T. M., & Anderson, L. D. 2011, ApJ, 738, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Balser, D. S., Wenger, T. V., Anderson, L. D., & Bania, T. M. 2015, ApJ, 806, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Barros, D. A., Pérez-Villegas, A., Michtchenko, T. A., & Lépine, J. R. D. 2021, Front. Astron. Space Sci., 8, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, M., & Bovy, J. 2019, MNRAS, 482, 1417 [NASA ADS] [CrossRef] [Google Scholar]
- Bird, J. C., Kazantzidis, S., Weinberg, D. H., et al. 2013, ApJ, 773, 43 [Google Scholar]
- Bland-Hawthorn, J., & Tepper-García, T. 2021, MNRAS, 504, 3168 [CrossRef] [Google Scholar]
- Brook, C. B., Stinson, G. S., Gibson, B. K., et al. 2012, MNRAS, 426, 690 [Google Scholar]
- Buck, T., Obreja, A., Macciò, A. V., et al. 2020, MNRAS, 491, 3461 [Google Scholar]
- Castro-Ginard, A., McMillan, P. J., Luri, X., et al. 2021, A&A, 652, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., & Chiappini, C. 2010, A&A, 515, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., & Chiappini, C. 2014, A&A, 565, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., Matteucci, F., François, P., & Chiappini, C. 2007, A&A, 462, 943 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., Chiappini, C., Hirschi, R., Meynet, G., & Frischknecht, U. 2013, A&A, 553, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., Romano, D., Matteucci, F., Chiappini, C., & Hirschi, R. 2015, A&A, 577, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., Bonifacio, P., Caffau, E., et al. 2022, A&A, 668, A168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Chomiuk, L., & Povich, M. S. 2011, AJ, 142, 197 [Google Scholar]
- Comparetta, J., & Quillen, A. C. 2012, ArXiv e-prints [arXiv:1207.5753] [Google Scholar]
- Contursi, G., de Laverny, P., Recio-Blanco, A., et al. 2023, A&A, 670, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, D. P., & Gómez, G. C. 2002, ApJS, 142, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Straniero, O., Gallino, R., et al. 2009, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Piersanti, L., Straniero, O., et al. 2011, ApJS, 197, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Dias, W. S., Monteiro, H., Lépine, J. R. D., & Barros, D. A. 2019, MNRAS, 486, 5726 [NASA ADS] [CrossRef] [Google Scholar]
- D’Onghia, E., Vogelsberger, M., & Hernquist, L. 2013, ApJ, 766, 34 [Google Scholar]
- Elmegreen, B. G., Elmegreen, D. M., & Montenegro, L. 1992, ApJS, 79, 37 [NASA ADS] [CrossRef] [Google Scholar]
- François, P., Matteucci, F., Cayrel, R., et al. 2004, A&A, 421, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frischknecht, U., Hirschi, R., & Thielemann, F. K. 2012, A&A, 538, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frischknecht, U., Hirschi, R., Pignatari, M., et al. 2016, MNRAS, 456, 1803 [Google Scholar]
- Fudamoto, Y., Inoue, A. K., & Sugahara, Y. 2022, ApJ, 938, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Katz, D., et al.) 2018, A&A, 616, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021a, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Antoja, T., et al.) 2021b, A&A, 649, A8 [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2022, A&A, 674, A22 [Google Scholar]
- Gaia Collaboration (Recio-Blanco, A., et al.) 2023, A&A, 674, A38 [CrossRef] [EDP Sciences] [Google Scholar]
- Genovali, K., Lemasle, B., Bono, G., et al. 2014, A&A, 566, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgelin, Y. M., & Georgelin, Y. P. 1976, A&A, 49, 57 [NASA ADS] [Google Scholar]
- Goldreich, P., & Lynden-Bell, D. 1965, MNRAS, 130, 125 [Google Scholar]
- Grand, R. J. J., Kawata, D., & Cropper, M. 2012, MNRAS, 421, 1529 [CrossRef] [Google Scholar]
- Grand, R. J. J., Kawata, D., & Cropper, M. 2014, MNRAS, 439, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Grand, R. J. J., Springel, V., Kawata, D., et al. 2016, MNRAS, 460, L94 [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2021, A&A, 654, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, D. A. 2014, in Supernova Environmental Impacts, eds. A. Ray, & R. A. McCray, IAU Symp., 296, 188 [NASA ADS] [Google Scholar]
- Greggio, L. 2005, A&A, 441, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guesten, R., & Mezger, P. G. 1982, Vistas Astron., 26, 159 [Google Scholar]
- Hilmi, T., Minchev, I., Buck, T., et al. 2020, MNRAS, 497, 933 [Google Scholar]
- Ho, I. T., Seibert, M., Meidt, S. E., et al. 2017, ApJ, 846, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Hou, L. G., & Han, J. L. 2014, A&A, 569, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hou, L. G., Han, J. L., & Shi, W. B. 2009, A&A, 499, 473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, J. A. S., Bub, M. W., Bovy, J., et al. 2019, MNRAS, 490, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Julian, W. H., & Toomre, A. 1966, ApJ, 146, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Kalogera, V., Kim, C., Lorimer, D. R., et al. 2004, ApJ, 601, L179 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, D., Sartoretti, P., Guerrier, A., et al. 2023, A&A, 674, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennicutt, R. C., Jr. 1998, ApJ, 498, 541 [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Khoperskov, S., Di Matteo, P., Haywood, M., & Combes, F. 2018, A&A, 611, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S., Sivkova, E., Saburova, A., et al. 2023, A&A, 671, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kniazev, A. Y., Usenko, I. A., Kovtyukh, V. V., & Berdnikov, L. N. 2019, Astrophys. Bull., 74, 208 [CrossRef] [Google Scholar]
- Kobayashi, C., & Nakasato, N. 2011, ApJ, 729, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Korobkin, O., Rosswog, S., Arcones, A., & Winteler, C. 2012, MNRAS, 426, 1940 [NASA ADS] [CrossRef] [Google Scholar]
- Kovtyukh, V., Lemasle, B., Bono, G., et al. 2022, MNRAS, 510, 1894 [Google Scholar]
- Laporte, C. F. P., Johnston, K. V., & Tzanidakis, A. 2019, MNRAS, 483, 1427 [Google Scholar]
- Lemasle, B., Lala, H. N., Kovtyukh, V., et al. 2022, A&A, 668, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lépine, J. R. D., Michtchenko, T. A., Barros, D. A., & Vieira, R. S. S. 2017, ApJ, 843, 48 [CrossRef] [Google Scholar]
- Levine, E. S., Blitz, L., & Heiles, C. 2006, Science, 312, 1773 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y., Bresolin, F., & Kennicutt, R. C., Jr. 2013, ApJ, 766, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, C. C., & Shu, F. H. 1964, ApJ, 140, 646 [Google Scholar]
- Lin, C. C., & Shu, F. H. 1966, Proc. Natl. Acad. Sci., 55, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E. 2018, AJ, 156, 171 [Google Scholar]
- Luck, R. E., & Lambert, D. L. 2011, AJ, 142, 136 [Google Scholar]
- Martig, M., Minchev, I., & Flynn, C. 2014, MNRAS, 442, 2474 [CrossRef] [Google Scholar]
- Martig, M., Fouesneau, M., Rix, H.-W., et al. 2016, MNRAS, 456, 3655 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F., & Tagger, M. 1997, A&A, 322, 442 [NASA ADS] [Google Scholar]
- Matteucci, F. 2021, A&ARv, 29, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [Google Scholar]
- Matteucci, F., Spitoni, E., Recchi, S., & Valiante, R. 2009, A&A, 501, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matteucci, F., Romano, D., Arcones, A., Korobkin, O., & Rosswog, S. 2014, MNRAS, 438, 2177 [Google Scholar]
- Meidt, S. E., Rand, R. J., & Merrifield, M. R. 2009, ApJ, 702, 277 [Google Scholar]
- Meynet, G., & Maeder, A. 2002, A&A, 390, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I. 2016, Astron. Nachr., 337, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., & Quillen, A. C. 2006, MNRAS, 368, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012, A&A, 548, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2013, A&A, 558, A9 [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Martig, M., Streich, D., et al. 2015, ApJ, 804, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Molero, M., Romano, D., Reichert, M., et al. 2021a, MNRAS, 505, 2913 [NASA ADS] [CrossRef] [Google Scholar]
- Molero, M., Simonetti, P., Matteucci, F., & della Valle, M., 2021b, MNRAS, 500, 1071 [Google Scholar]
- Molero, M., Magrini, L., Matteucci, F., et al. 2023, MNRAS, 523, 2974 [NASA ADS] [CrossRef] [Google Scholar]
- Mollá, M., Wekesa, S., Cavichia, O., et al. 2019, MNRAS, 490, 665 [CrossRef] [Google Scholar]
- Mott, A., Spitoni, E., & Matteucci, F. 2013, MNRAS, 435, 2918 [Google Scholar]
- Nishimura, N., Takiwaki, T., & Thielemann, F.-K. 2015, ApJ, 810, 109 [Google Scholar]
- Palicio, P. A., Martinez-Valpuesta, I., Allende Prieto, C., et al. 2018, MNRAS, 478, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Palicio, P. A., Martinez-Valpuesta, I., Allende Prieto, C., & Dalla Vecchia, C. 2020, A&A, 634, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palicio, P. A., Spitoni, E., Recio-Blanco, A., et al. 2023a, A&A, 678, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palicio, P. A., Recio-Blanco, A., Poggio, E., et al. 2023b, A&A, 670, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palla, M., Matteucci, F., Spitoni, E., Vincenzo, F., & Grisoni, V. 2020, MNRAS, 498, 1710 [Google Scholar]
- Palla, M., Santos-Peral, P., Recio-Blanco, A., & Matteucci, F. 2022, A&A, 663, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pedicelli, S., Bono, G., Lemasle, B., et al. 2009, A&A, 504, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poggio, E., Drimmel, R., Lattanzi, M. G., et al. 2018, MNRAS, 481, L21 [Google Scholar]
- Poggio, E., Drimmel, R., Cantat-Gaudin, T., et al. 2021, A&A, 651, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poggio, E., Recio-Blanco, A., Palicio, P. A., et al. 2022, A&A, 666, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quillen, A. C., & Minchev, I. 2005, AJ, 130, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Quillen, A. C., Dougherty, J., Bagley, M. B., Minchev, I., & Comparetta, J. 2011, MNRAS, 417, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Quillen, A. C., Carrillo, I., Anders, F., et al. 2018, MNRAS, 480, 3132 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos, P., Antoja, T., & Figueras, F. 2018, A&A, 619, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Recio-Blanco, A., de Laverny, P., Palicio, P. A., et al. 2023, A&A, 674, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2019, ApJ, 885, 131 [Google Scholar]
- Reshetnikov, V. P., Marchuk, A. A., Chugunov, I. V., Usachev, P. A., & Mosenkov, A. V. 2023, Astron. Lett., 48, 644 [Google Scholar]
- Ripepi, V., Clementini, G., Molinaro, R., et al. 2023, A&A, 674, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rix, H.-W., & Zaritsky, D. 1995, ApJ, 447, 82 [Google Scholar]
- Rizzuti, F., Cescutti, G., Matteucci, F., et al. 2019, MNRAS, 489, 5244 [NASA ADS] [Google Scholar]
- Roca-Fàbrega, S., Antoja, T., Figueras, F., et al. 2014, MNRAS, 440, 1950 [CrossRef] [Google Scholar]
- Romano, D., Karakas, A. I., Tosi, M., & Matteucci, F. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., Galbany, L., Pérez, E., et al. 2015, A&A, 573, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Menguiano, L., Sánchez, S. F., Pérez, I., et al. 2016, A&A, 587, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scalo, J. M. 1986, Fund. Cosmic Phys., 11, 1 [NASA ADS] [EDP Sciences] [Google Scholar]
- Scarano, S., & Lépine, J. R. D. 2013, MNRAS, 428, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Carlberg, R. G. 2014, ApJ, 785, 137 [CrossRef] [Google Scholar]
- Siegel, D. M., Barnes, J., & Metzger, B. D. 2019, Nature, 569, 241 [Google Scholar]
- Siegert, T., Pleintinger, M. M. M., Diehl, R., et al. 2023, A&A, 672, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silva Aguirre, V., Bojsen-Hansen, M., Slumstrup, D., et al. 2018, MNRAS, 475, 5487 [NASA ADS] [Google Scholar]
- Simonetti, P., Matteucci, F., Greggio, L., & Cescutti, G. 2019, MNRAS, 486, 2896 [NASA ADS] [CrossRef] [Google Scholar]
- Spitoni, E., Cescutti, G., Minchev, I., et al. 2019a, A&A, 628, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Silva Aguirre, V., Matteucci, F., Calura, F., & Grisoni, V. 2019b, A&A, 623, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Verma, K., Silva Aguirre, V., et al. 2021, A&A, 647, A73 [EDP Sciences] [Google Scholar]
- Spitoni, E., Aguirre Børsen-Koch, V., Verma, K., & Stokholm, A. 2022, A&A, 663, A174 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Recio-Blanco, A., de Laverny, P., et al. 2023, A&A, 670, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stahler, S. W., & Palla, F. 2004, The Formation of Stars (Wiley-VCH), 865 [Google Scholar]
- van den Hoek, L. B., & Groenewegen, M. A. T. 1997, A&AS, 123, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasini, A., Matteucci, F., & Spitoni, E. 2022, MNRAS, 517, 4256 [NASA ADS] [CrossRef] [Google Scholar]
- Vasini, A., Matteucci, F., Spitoni, E., & Siegert, T. 2023, MNRAS, 523, 1153 [NASA ADS] [CrossRef] [Google Scholar]
- Vincenzo, F., & Kobayashi, C. 2020, MNRAS, 496, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Vincenzo, F., Matteucci, F., & Spitoni, E. 2017, MNRAS, 466, 2939 [CrossRef] [Google Scholar]
- Vincenzo, F., Spitoni, E., Calura, F., et al. 2019, MNRAS, 487, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, F. P. A., Pérez, E., Dopita, M. A., Verdes-Montenegro, L., & Borthakur, S. 2017, A&A, 601, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wenger, T. V., Balser, D. S., Anderson, L. D., & Bania, T. M. 2019, ApJ, 887, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Winteler, C., Käppeli, R., Perego, A., et al. 2012, ApJ, 750, L22 [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [Google Scholar]
All Tables
Properties of the three spiral-arm structures with different pattern speeds for the considered models.
Maximum azimuthal residual variations Δmax [X/H] for oxygen, europium, iron, and barium predicted by models B1 and B2 at the respective co-rotations of the outermost spiral chunk (characterised by angular velocity Ωs, 3 and the co-rotation radius R3, cor.).
All Figures
 |
Fig. 1. Spiral pattern speeds Ωs, 1(R), Ωs, 2(R), and Ωs, 3(R) of the multiple spiral modes moving at different pattern speeds (Model A in Table 1) are indicated by the three coloured horizontal lines. Inner and outer spiral structures (moving with the above-mentioned pattern speeds) are also indicated by the thicker purple, blue, and green lines, respectively. The disc angular velocity Ωd(R) computed by Roca-Fàbrega et al. (2014) is indicated with the dotted line. The 2:1 and 4:1 outer and inner Lindblad resonances (OLR and ILR) occur along the solid and dashed black curves, respectively. We compute resonances as Ωp2(R) = Ωd(R)±κ/2 and Ωp4(R) = Ωd(R)±κ/4, respectively, where κ is the local radial epicyclic frequency. The long vertical dashed lines show the positions of the co-rotation radii assuming the three different ΩS values. |
| In the text | |
 |
Fig. 2. Different snapshots of the temporal evolution of the new modulation function |
| In the text | |
 |
Fig. 3. Galactic disc SFR resulting from Model A after 11 Gyr of evolution projected onto the Galactic plane after the start of disc formation (see Table 1 and text for model details). The colour-coding indicates the SFR values in units of M⊙ pc−2 Gyr−1. |
| In the text | |
 |
Fig. 4. Zoom-in view of 2D map of the SFR resulting from Model A after 11 Gyr of the evolution of Fig. 3 compared with some tracers of spiral arms or arcs present in literature. Upper panel: overdensities in the distribution of UMS stars of the Poggio et al. (2018) sample with Gaia EDR3 astrometry (Gaia Collaboration 2021a) as presented by Poggio et al. (2021). We report only positive values of stellar overdensities as defined by Eq. (1) of Poggio et al. (2021). Middle panel: distribution of the median of the radial action JR of Gaia DR3 stars (see text for more details) on the Galactic Plane (|Zmax|< 0.5 kpc and R < 10 kpc) as computed by Palicio et al. (2023b) and here only reporting the star with JR < 0.01 R⊙ V⊙ (green shaded area). Lower panel: solid lines represent the segments of spiral arms traced by Cepheids of Lemasle et al. (2022) in which the colour coding is the one adopted by Palicio et al. (2023b). |
| In the text | |
 |
Fig. 5. Present-day radial SFR profile predicted by Model A for different azimuthal coordinates (coloured lines). In both panels, the shaded light-blue area denotes the range of maximum and minimum SFR values at various galactocentric distances. Upper panel: predicted SFRs are compared with the visible-band observations presented in Guesten & Mezger (1982) and rescaled by Kennicutt & Evans (2012) to the total SFR of 1.9 M⊙ yr−1 provided by Chomiuk & Povich (2011), as indicated by the black solid line. Lower panel: red diamonds with error bars are observational data for the star formation profile from SNRs, pulsars, and HII regions normalised to the solar vicinity value (SFR/SFR⊙) from Stahler & Palla (2004). The dark-blue solid line represents the analytical fit of the SNR compilation by Green (2014) as reported in Palla et al. (2020) and Spitoni et al. (2021). The model predictions for different azimuths SFRϕ are divided by their respective solar vicinity SFR⊙, ϕ values. |
| In the text | |
 |
Fig. 6. Present-day oxygen (upper left panel), europium (upper right panel), iron (lower left panel), and barium (lower right panel) abundance gradients for different azimuths as predicted by Model A (see Table 1 for model details). In each panel, the coloured dashed vertical lines indicate the location of the co-rotation radii for the three spiral structures characterised by different pattern speeds. Model predictions are compared with Cepheids data provided by Kovtyukh et al. (2022) and Luck & Lambert (2011) for oxygen and europium, and by Genovali et al. (2014) for iron and by Luck (2018) for barium. The data trends (black dashed lines) are computed by calculating the running median in bins of 0.5 kpc, with a 40% overlap, and a minimum number of stars per bin of two for O, Fe, and Eu, and one for Ba; this lower minimum for Ba is chosen because of the low number of measurements in the sample. The shaded regions on the plot represent the standard deviation of these trends. For the sake of visualisation, we focus on the abundance range [–0.5, 0.6] dex, excluding stars with [Ba/H] > 0.6 dex. |
| In the text | |
 |
Fig. 7. Present-day residual azimuthal variations in oxygen, europium, iron, and barium abundance, respectively computed at different galactocentric distances for the multiple spiral structure of Model A in Table 1. The coloured solid lines indicate the variations at the co-rotation radii for the three spiral structures characterised by different pattern speeds with the same colour-coding as the dashed vertical lines of Fig. 6. |
| In the text | |
 |
Fig. 8. Galactic disc surface gas density distribution resulting from Model A after 11 Gyr of evolution normalised to the maximum values at different galactocentric distances. We also use white edges to highlight the annular regions where three co-rotational radii are situated. |
| In the text | |
 |
Fig. 9. Oxygen abundance distribution in the Galactic disc resulting from Model A after 11 Gyr of evolution and projected onto the Galactic plane after the start of disc formation (see Table 1 and text for model details). Upper panel: [O/H] values. Lower panel: distribution of residual azimuthal variations Δ [O/H] in oxygen. In each panel, we also highlight the annular regions where the three co-rotational radii are situated using black edges. |
| In the text | |
 |
Fig. 10. Temporal evolution of the oxygen abundance gradient after 3, 5, and 11 Gyr of thin disc evolution for different azimuth coordinates as predicted by Model A. The colour code is the same as in Fig. 6. |
| In the text | |
 |
Fig. 11. As in Fig. 1, but for spiral modes extracted from the spectrogram analysis of Model1 by Hilmi et al. (2020), which was based on the Buck et al. (2020) cosmological simulation. Different multiplicities are shown in each panel, as indicated. In each panel, the disc angular velocity Ωd(R) is indicated with the dotted line. In the two upper panels (with modes m = 2 and m = 4), we also show the resonances Ωp2(R) = Ωd(R)±κ/2 and Ωp4(R) = Ωd(R)±κ/4, which are indicated with solid and dashed black curves, respectively. In the lower two panels, the solid and dashed black lines were computed as Ωp1(R) = Ωd(R)±κ and Ωp3(R) = Ωd(R)±κ/3. |
| In the text | |
 |
Fig. 12. Present-day residual azimuthal variations in oxygen, europium, iron, and barium abundance, respectively, computed at 4, 6, and 9 kpc for Model1 by Hilmi et al. (2020), as introduced in Sect. 5.4, where the spiral structure is characterised by multiple modes of different multiplicity from 1 to 4. |
| In the text | |
 |
Fig. 13. Comparison of azimuthal variations in abundance gradients for oxygen, europium, iron, and barium predicted by Model A (first row) with models where the condition of transient spiral have been considered. Model A+C1 is reported in the second row, where the condition Ωs, j(R) = Ωd(R) is valid for all Galactic radii (co-rotation extended at all distances) during the last 100 Myr of Galactic evolution; Model A+C2 is shown in the third row, where the above-mentioned condition is only met for the last 300 Myr; and Model A+C3 is shown in the last row, where this condition is met for 1 Gyr. The colour convention of the lines is the same as in Fig. 6. The vertical lines indicate the corotations of Model A. |
| In the text | |
 |
Fig. 14. As in Fig. 7, but also for Model A+C1 (second row), Model A+C2 (third row), and Model A+C3 (last row), respectively. |
| In the text | |
 |
Fig. 15. Present-day residual azimuthal variations in iron computed at different galactocentric distances for the multiple spiral structures of Models A, A+C1, A+C1, and A+C3, compared with the metallicity variation found by Poggio et al. (2022) when analysing GSP-Spec abundances of Gaia DR3 (Gaia Collaboration 2023). Horizontal lines with the same colour indicate the 10th and 90th percentiles of the metallicity variation as computed by Poggio et al. (2022) at different galactocentric distances. In each panel, the shaded grey area indicates the region spanned by Poggio et al. (2022) data. In the zoom-in plot associated with the fourth panel, we report the Poggio et al. (2022) data, indicating the median metallicity for Sample A as a function of Galactic azimuth for different galactocentric distances (after the median metallicity of the stars for each ring has been subtracted). |
| In the text | |
 |
Fig. 16. As in Fig. 5, but for the Model A+C2. |
| In the text | |
 |
Fig. 17. Present-day iron abundance gradient predicted by Models A, A+C1, A+C2, and A+C3 at different azimuthal coordinates. In each panel, the shaded light-blue area denotes the range of maximum and minimum Fe abundance values at various distances from the centre of the galaxy spanned by the models. The Cepheids data collected by Genovali et al. (2014) and the GSP-Spec [M/H] for Gaia DR3 sources within the sample of Cepheids presented by Ripepi et al. (2023) are reported with empty and full light-red dots, respectively. The average abundance values and relative errors – when dividing these two data sets into six radial bins – are shown by black and red pentagons, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



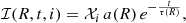
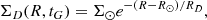
![$$ \begin{aligned} \tau _{D}(R) = 1.033 \cdot R \, [\text{ kpc}] - 1.27 \, [\text{ Gyr}]. \end{aligned} $$](/articles/aa/full_html/2023/12/aa47325-23/aa47325-23-eq3.gif)
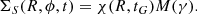
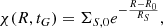
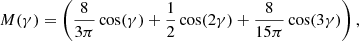
![$$ \begin{aligned} \gamma (R,\phi ,t)= m\left[\phi +\Omega _{s} t -\phi _p(R_0) -\frac{\ln (R/R_0)}{\tan (\alpha )}\right]\cdot \end{aligned} $$](/articles/aa/full_html/2023/12/aa47325-23/aa47325-23-eq7.gif)
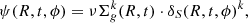
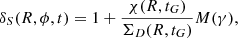
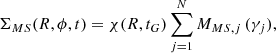
![$$ \begin{aligned} M_{MS, j} \,(\gamma _j) \equiv M_j(\gamma _j)\cdot \mathbb{1} {\left[R_{j,\,\mathrm {min}},\ R_{j,\, \mathrm {max}}\right]}, \end{aligned} $$](/articles/aa/full_html/2023/12/aa47325-23/aa47325-23-eq11.gif)
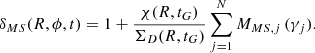
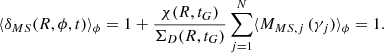
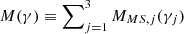
![$$ \begin{aligned} \Delta \mathrm{[O/H]}_{\mathrm{A}} \simeq \Delta \mathrm{[O/H]}_{\mathrm{A1}}+\Delta \mathrm{[O/H]}_{\mathrm{A2}}+\Delta \mathrm{[O/H]}_{\mathrm{A3}}. \end{aligned} $$](/articles/aa/full_html/2023/12/aa47325-23/aa47325-23-eq17.gif)