| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A162 | |
| Number of page(s) | 16 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202347101 | |
| Published online | 20 October 2023 | |
Three-temperature radiation hydrodynamics with PLUTO
Tests and applications in the context of protoplanetary disks
Max Planck Institut für Astronomie,
Königstuhl 17,
Heidelberg
69117, Germany
e-mail: muley@mpia.de
Received:
5
June
2023
Accepted:
3
August
2023
In circumstellar disks around T Tauri stars, visible and near-infrared stellar irradiation is intercepted by dust at the disk’s optical surface and reprocessed into thermal infrared. It subsequently undergoes radiative diffusion through the optically thick bulk of the disk. The gas component, overwhelmingly dominated by mass but contributing little to the opacity, is heated primarily by gas-grain collisions. However, in hydrodynamical simulations, typical models for this heating process (local isothermality, β-cooling, and two-temperature radiation hydrodynamics) incorporate simplifying assumptions that limit their ranges of validity. To build on these methods, we developed a “three-temperature” numerical scheme, which self-consistently models energy exchange between gas, dust, and radiation, as a part of the PLUTO radiation-hydrodynamics code. With a range of test problems in 0D, 1D, 2D, and 3D, we demonstrate the efficacy of our method and make the case for its applicability across a wide range of problems in disk physics, including hydrodynamic instabilities and disk-planet interactions.
Key words: radiative transfer / hydrodynamics / protoplanetary disks / methods: numerical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open Access funding provided by Max Planck Society.
1 Introduction
Protoplanetary disks, the rotationally-supported excess from the star-formation process, consist primarily of hydrogen and helium gas, with trace molecular species. Despite its preponderance by mass, this gas component has a low frequency-integrated opacity, making direct radiative heating and cooling inefficient. The disk’s energy exchange with the radiation field is instead mediated by the dust component, typically taken to constitute just 1% of its total mass. Chiang & Goldreich (1997) studied this process semi-analytically, finding that incident stellar radiation – which peaks in the visible and near-infrared for classical T Tauri stars – creates a superheated dust layer at a disk’s radial τr = 1 surface. This layer reprocesses the radiation into the thermal infrared, half of which dissipates into interstellar space and half of which radiatively diffuses through dust grains in the optically thick disk midplane. The surrounding gas is then thermally coupled to the dust temperature structure via collisions. In turn, the density structure of the gas and, consequently, that of the entrained dust that sets the τr = 1 surface, adapts to maintain hydrostatic equilibrium.
By far, the most detailed models of protoplanetary disk thermal structure come from physical-chemical codes (e.g., Woitke et al. 2009; Bruderer et al. 2012; Bruderer 2013; Calahan et al. 2021), followed by standalone, multiwavelength radiative transfer codes (e.g., Dullemond et al. 2012; Whitney et al. 2013). However, the computational expense of these numerical algorithms, along with their implicit assumption that disks are static on timescales relevant to thermal physics, makes them intractable to include in dynamical problems. Hydrodynamical simulations must therefore use various parametrizations, of which the “locally isothermal” assumption, whereby the temperature in each grid cell is fixed to its initial value, has been historically important for its simplicity and ease of interpretation. However, more recently, simulations of hydrodynamic instabilities and the anticyclonic vortices they generate (Malygin et al. 2017; Pierens & Lin 2018; Tarczay-Nehéz et al. 2020; Manger et al. 2021; Huang & Yu 2022), gaps and rings (Miranda & Rafikov 2019; Ziampras et al. 2020), spiral arms (Miranda & Rafikov 2020a,b), and circumplanetary disks (Fung et al. 2019) have revealed that the choice of disk thermodynamics prescription has a substantial influence on their morphology and behavior. The quality of disk observations continues to improve (e.g. Keppler et al. 2018; Ren et al. 2018; Teague et al. 2019; Pinte et al. 2022) and meaningfully interpreting them requires a more accurate, self-consistent treatment of disk heating and cooling in hydrodynamic models.
To this end, numerical radiation hydrodynamics (RHD) is promising. For computational efficiency, these simulations generally use the “grey approximation” in which radiation energy densities, fluxes, and material opacities are averaged over frequency. One widely used method in the study of protoplanetary disks (e.g., Klahr & Kley 2006; Kley et al. 2009; Bitsch et al. 2013; Flock et al. 2013; Binkert et al. 2023) is flux-limited diffusion (FLD; Levermore & Pomraning 1981), in which the radiative flux, Fr, is proportional to the gradient of radiation energy density Er, subject to a limiter that ensures the system satisfies the speed-of-light limit, |Fr| ≤ cEr. Although FLD works well in optically thick regions, its definition of flux is limited in the thin limit, making it unable to produce anisotropic features in the radiation field such as beams or shadows. The M1 approximation (Levermore 1984) handles these issues with a separate evolution equation for flux. M1 can accurately reproduce both the optically thick diffusion and optically thin free-streaming limits, but has limitations in situations where free-streaming beams cross one another.
Differentiating between dust and gas temperatures is a comparatively recent development in RHD simulations. The star-formation simulations of Bate & Keto (2015), as well as the thermochemical disk simulations of Wang & Goodman (2017), Wang et al. (2019) and Hu et al. (2023), use equilibrium prescriptions to compute dust temperature. By contrast, Pavlyuchenkov & Zhilkin (2013), Pavlyuchenkov et al. (2015), and Vorobyov et al. (2020) use iterative Newton-Raphson schemes to self-consistently compute energy exchange between gas, dust, and radiation, while using FLD for radiation transport.
In what follows, we present our own three-temperature scheme, implemented within the PLUTO hydrodynamics code (Mignone et al. 2007). To compute the energy exchange, we use Newton-Raphson iterations (albeit with differences from the aforementioned works) and to transport radiation, we use the M1 scheme already developed for PLUTO (Melon Fuksman & Mignone 2019; Melon Fuksman et al. 2021) to handle both the optically thick and thin regimes in protoplanetary disks. Section 2 describes our numerical method. Section 3 details our code tests: the first two (0D matter-radiation coupling and 1D Ensman shock tube) have known reference solutions and demonstrate basic function, while the latter two (2D self-shadowing and 3D disk-planet interaction) illustrate applications to realistic disks. Section 4 provides a summation of our work and discusses possible future areas of research.
2 Method
2.1 Basic equations
We developed a strategy to solve the equations of radiation hydrodynamics, including a secondary dust fluid. We made the simplifying assumptions that dust grains are kinetically well-coupled to the gas (Stokes number St ≪ 1) and that they have negligible inertia (globally constant dust-to-gas ratio of fd ≪ 1), in other words, both evolve with the same velocity field and the dust has no momentum:
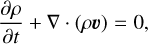 (1a)
(1a)
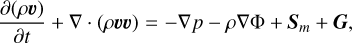 (1b)
(1b)
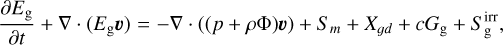 (1c)
(1c)
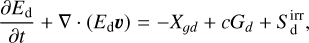 (1d)
(1d)
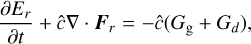 (1e)
(1e)
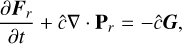 (1f)
(1f)
where p, υ, p represent the gas density, pressure, and velocity respectively. Also, ρd is the dust density, while fd is the dust-to-gas ratio, Φ is the gravitational potential, and {Eg, Ed, Er} are the total energy densities for gas, dust, and radiation respectively. Then, c is the speed of light, while the ĉ term is a “reduced speed of light” (Gnedin & Abel 2001) which enables longer timesteps, but must nevertheless exceed all hydrodynamic velocities relevant to the problem (Skinner & Ostriker 2013).
We assume that the gas follows an ideal equation of state:
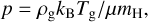 (2)
(2)
where kB is the Boltzmann constant, Tg the gas temperature, µ the mean molecular weight, and mH the mass of a hydrogen atom. The adiabatic index γ = ∂ In p/∂ In ρ is a constant, implying an internal (thermal) energy density:
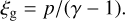 (3)
(3)
Because we do not consider the kinetic energy of dust in this work, the internal energy of dust, ξd, is equal to its total energy Ed. For consistency of notation in what follows, we additionally define a symbol ξr = Er.
Dust and gas exchange internal energy collisionally via the term
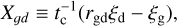 (4)
(4)
where tc is the thermal relaxation time and rgd = kB/µmHfdcd(γ − 1) is the ratio of heat capacity per unit volume between gas and dust. Also, cd is the specific heat capacity of dust. We compute the gas cooling time, tc, as a function of the dust-gas stopping time, ts, in the Epstein regime (Burke & Hollenbach 1983; Speedie et al. 2022):
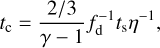 (5)
(5)
where η is an order-unity “accommodation coefficient,” which we ignore going forward. The corresponding dust cooling time is given by:
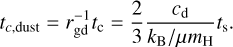 (6)
(6)
In a realistic disk, the stopping time is computed by averaging over a grain-size distribution, which we describe as part of Sect. 3.3. The usual two-temperature radiation hydrodynamics represents the limit where tc → 0.
Net radiative heating and cooling is given for the gas by
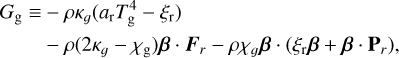 (7a)
(7a)
Similarly, the attenuation of radiative flux by gas is given by
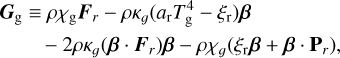 (7c)
(7c)
involving absorption opacities κ, total (absorption plus scattering) opacities χ, temperatures T, the radiation constant, ar = 4σSB/c, and the radiation pressure tensor Pr. Typically, κ is computed as a Planck average over frequency, while χ is computed as a Rosseland average. We define G = GG + Gd; because our current implementation assumes dust follows the gas and has negligible inertia, it is this total G that gets added to the gas momentum equation and integrated during the hydrodynamic step.
Each of the expressions in Eq. (7) can be divided into a β-independent and β-dependent part, G = Gw + G′ (β). The G′ (β) parts arise from a Lorentz transformation of the radiation-interaction terms from the fluid’s comoving frame to the observer’s frame, truncated in the mildly relativistic regime (Skinner & Ostriker 2013; Melon Fuksman & Mignone 2019). In protoplanetary disks, β ≪ 11, so these terms are small and can be integrated explicitly.
The radiation pressure tensor Pr(Er, Fr) is evaluated according to the Ml closure (Levermore 1984), which accurately reproduces the free-streaming and diffusion limits:
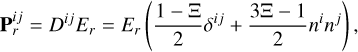 (8)
(8)
where n = Fr/||Fr||, w = ||Fr||/Er, and δij is the Kronecker delta.
Here, 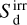 and
and 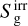 represent radiation emitted directly by the star, which has a higher frequency spectrum than the dust-emitted radiation represented by Er; the source terms are computed (e.g., via ray tracing) at every hydrodynamic timestep, rather than being evolved dynamically as Er and Fr are. Then, Sm and Sm represent the energy and momentum source terms, respectively, such as the thermal conductivity and viscosity that are already implemented into PLUTO and integrated during the hydrodynamic step.
represent radiation emitted directly by the star, which has a higher frequency spectrum than the dust-emitted radiation represented by Er; the source terms are computed (e.g., via ray tracing) at every hydrodynamic timestep, rather than being evolved dynamically as Er and Fr are. Then, Sm and Sm represent the energy and momentum source terms, respectively, such as the thermal conductivity and viscosity that are already implemented into PLUTO and integrated during the hydrodynamic step.
2.2 Conservation laws
With the reduced speed of light approximation, and ignoring non-ideal source terms other than Gg, Gd, Gg, Gd, Xgd, our system conserves the following modified total energy and momentum:
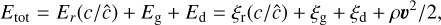 (10)
(10)
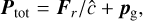 (11)
(11)
which are reduced to the standard definitions when c = ĉ. As mentioned earlier, Skinner & Ostriker (2013) verified that this modification does not impact the dynamics of the system, provided that ĉ is much larger than hydrodynamic velocities characteristic of the system.
2.3 Operator splitting and timestepping
We solve the dusty radiation-hydrodynamic (Eq. (1)) using a Strang split, sandwiching a full step of the hydrodynamic terms Δt between two half-steps Δt/2 of the radiative terms. In quasi-conservative form:
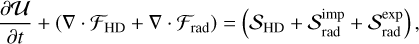 (12a)
(12a)
where 𝒰 is a vector of conserved variables, 𝒮 are source terms, and ℱ are advective fluxes:
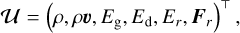 (12b)
(12b)
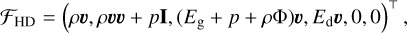 (12c)
(12c)
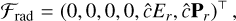 (12d)
(12d)
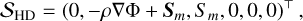 (12e)
(12e)
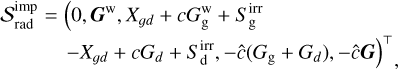 (12f)
(12f)
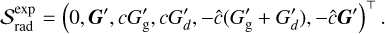 (12g)
(12g)
The overall timestep duration Δt is set by applying the Courant criterion to the hydrodynamical signal speeds υHD. But because ĉ ≫ υHD, the radiation half-steps Δt/2 must be further divided into substeps of duration Δtrad to ensure that the radiation subsystem meets its own Courant criterion. The integration of these substeps can take place through one of two implicit-explicit (IMEX) methods, either IMEX1 (Melon Fuksman & Mignone 2019)
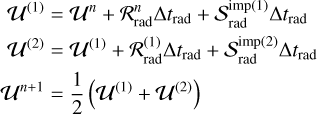 (13)
(13)
or IMEX-SSP2(2,2,2), in which the explicit part is strong stability-preserving (SSP):
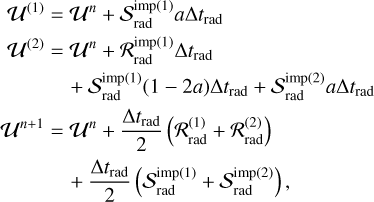 (14)
(14)
both of which are analogous to a second-order Runge-Kutta method (Pareschi & Russo 2005). In the above, ℛrad is a shorthand for 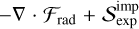 and
and  . ℛrad operators are integrated explicitly. However, the
. ℛrad operators are integrated explicitly. However, the 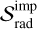 operators, incorporating stiff terms such as opacity and gas-grain collision with characteristic timescales potentially much shorter than advective timescales, are integrated implicitly and are in general functions of trad.
operators, incorporating stiff terms such as opacity and gas-grain collision with characteristic timescales potentially much shorter than advective timescales, are integrated implicitly and are in general functions of trad.
In what follows, we concern ourselves with solving the implicit source terms. The explicit, advective radiative terms ℱrad, encompassing the transport of radiation energy density by radiative flux, ĉFr, and of radiative flux by the radiation pressure tensor, ĉPr, are updated using a Godunov scheme and Riemann solver, as described in Melon Fuksman & Mignone (2019).
2.4 Momentum source terms
We update the radiative flux using a first-order implicit step as follows:
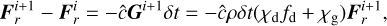 (15)
(15)
where δt equals Δtrad times the appropriate order-unity pre-factor for the implicit steps of Eqs. (13) and (14), This can be solved analytically, by rearrangement. The resulting change in fluid momentum,
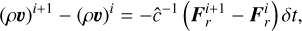 (16)
(16)
can then be found in a straightforward way by conservation.
From the final momenta, we can obtain the change in kinetic energy for gas
![$K_g^{i + 1} - K_g^i = {{\left[ {{{\left( {{\bf{p}}_g^{i + 1}} \right)}^2} - {{\left( {{\bf{p}}_g^i} \right)}^2}} \right]} \mathord{\left/ {\vphantom {{\left[ {{{\left( {{\bf{p}}_g^{i + 1}} \right)}^2} - {{\left( {{\bf{p}}_g^i} \right)}^2}} \right]} {2\rho }}} \right. \kern-\nulldelimiterspace} {2\rho }},$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq36.png) (17)
(17)
in which we make use of the fact that ρ is unchanged during a radiation timestep.
When the total dust and gas opacities χ values are constant, the above equations must only be solved once. In general, however, they can be functions of temperature and density and so, they must be solved before every iteration of the energy source terms. We describe them in the following section.
2.5 Energy source terms
The exchange of internal energies ξ between dust, gas, and radiation, is updated as follows:
![$\matrix{ {\xi _{\rm{d}}^{i + 1} - \xi _{\rm{d}}^i = - {{\left( {t_{\rm{c}}^{i + 1}} \right)}^{ - 1}}\left[ {{r_{{\rm{gd}}}}\xi _{\rm{d}}^{i + 1} - \xi _{\rm{g}}^{i + 1}} \right]\delta t} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - {{\left( {T_{\rm{d}}^{i + 1}} \right)}^{ - 1}}\left[ {{a_r}{{\left( {T_{\rm{g}}^{i + 1}} \right)}^4} - \xi _{\rm{r}}^{i + 1}} \right]\delta t} \hfill \cr } ,$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq37.png) (18a)
(18a)
![$\matrix{ {\xi _{\rm{g}}^{i + 1} - \xi _{\rm{g}}^i = - {{\left( {t_{\rm{c}}^{i + 1}} \right)}^{ - 1}}\left[ {{r_{{\rm{gd}}}}\xi _{\rm{d}}^{i + 1} - \xi _{\rm{g}}^{i + 1}} \right]\delta t} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - {{\left( {T_{\rm{g}}^{i + 1}} \right)}^{ - 1}}\left[ {{a_r}{{\left( {T_{\rm{g}}^{i + 1}} \right)}^4} - \xi _{\rm{r}}^{i + 1}} \right]\delta t} \hfill \cr } ,$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq38.png) (18b)
(18b)
with the dust temperature, Td = ξg/(ρcdfd), and the gas temperature, Tg = ξg/(ρkB/µ). To simplify notation, we have introduced the symbols Td = (cρκdfd) (the timescale required for light to travel one mean free path through dust) and Tg = (cρκg)−1 (the same, for gas); the relevant absorption opacities, κ, and cooling times, tc, are generally functions of temperature and density. Then, δt indicates the length of an implicit partial step, which is Δtrad in the case of IMEX1 (Eq. (13)) and aΔtrad or (1 – 2a)Δtrad, depending on the specific partial step, in the case of IMEX-SSP2(2,2,2) (Eq. (14)).
The i superscripts indicate quantities at the beginning of the implicit partial step, while those with i + 1 indicate those at the end. 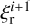 is not computed directly in the above system, but is given by conservation of energy, modified to account for the reduced speed of light and the irradiation source terms
is not computed directly in the above system, but is given by conservation of energy, modified to account for the reduced speed of light and the irradiation source terms 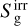 and
and 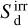 :
:
![$\matrix{ {\xi _{\rm{r}}^{i + 1} - \xi _{\rm{r}}^i = - \left( {{{\hat c} \mathord{\left/ {\vphantom {{\hat c} c}} \right. \kern-\nulldelimiterspace} c}} \right)\left[ {\left( {\xi _{\rm{d}}^{i + 1} - \xi _{\rm{d}}^i} \right) + \left( {\xi _{\rm{g}}^{i + 1} - \xi _{\rm{g}}^i} \right)} \right]\delta t} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - {{\left( {{{\hat c} \mathord{\left/ {\vphantom {{\hat c} c}} \right. \kern-\nulldelimiterspace} c}} \right)}^{ - 1}}\left( {S_{\rm{g}}^{{\rm{irr}}} + S_{\rm{d}}^{{\rm{irr}}}} \right)\delta t.} \hfill \cr } ,$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq42.png) (18c)
(18c)
We insert 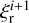 from Eq. (18c) into Eqs. (18a) and (18b) and solve the system using a multidimensional Newton’s method (detailed in Appendix A). All equations operate on cell-averaged quantities. We note that the values of the stellar irradiation source term,
from Eq. (18c) into Eqs. (18a) and (18b) and solve the system using a multidimensional Newton’s method (detailed in Appendix A). All equations operate on cell-averaged quantities. We note that the values of the stellar irradiation source term, 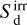 , are updated, by ray-tracing, only at the start of each overall timestep, Δt, even though their contribution to the energy density is added during each radiation substep. For the tests presented here, we set
, are updated, by ray-tracing, only at the start of each overall timestep, Δt, even though their contribution to the energy density is added during each radiation substep. For the tests presented here, we set 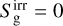 , but we foresee it being useful in the future to model photoelectric or line heating in the upper disk (Dullemond et al. 2007).
, but we foresee it being useful in the future to model photoelectric or line heating in the upper disk (Dullemond et al. 2007).
Our implementation has the advantage of conserving total modified energy to machine precision, and converging within a small number of iterations (typically ≲5–10 in disk-planet interaction simulations, even with temperature- and density-dependent cooling times). Moreover, it accommodates temperature change that is rapid compared to Δtrad, making it useful in nonequilibrium cases such as accretion shocks, subject to constraints set by the reduced speed of light approximation.
3 Tests
To verify the accuracy of our scheme and demonstrate its applicability to protoplanetary disks, we ran test problems in 0D, 1D, 2D, and 3D. For the tests we present, we used third-order Runge-Kutta (RK3) timestepping with third-order weighted essentially non-oscillatory (WeNO3) reconstruction (Yamaleev & Carpenter 2009) and a Harten-Lax-van Leer-Contact (HLLC) Riemann solver for both the gas and radiation. The sole exception is our 2D disk self-shadowing test, in which large contrasts in temperature, density, and velocity emerge in high, close-in regions of the disk. As such, for this problem, we opt for second-order Runge-Kutta (RK2) time integration and piecewise linear method (PLM) spatial reconstruction with a van Leer flux limiter.
3.1 0D test: Radiation-matter coupling
For our first set of tests, we considered a zero-dimensional (0D) setup probing only the local evolution of gas, dust, and radiation temperatures. We turned off the hydrodynamic equations and radiation advective terms and set irradiation source terms and radiative flux to zero to isolate the effects of radiation-matter coupling. In this case, we can express the evolution of internal energies concisely in terms of ξ = (ξd, ξg)⊤ as:
![${{\partial {\bf{\xi }}} \over {\partial t}} = \left[ {{\bf{C\xi }}} \right] + \left[ {{{\bf{A}}_{{\rm{tot}}}} + {\bf{A\xi }} + {\bf{Q}}\left( {\bf{\xi }} \right)} \right],$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq46.png) (19)
(19)
where A includes linear absorption terms, C the collisional terms, Atot the constant absorption terms, and Q the nonlinear emission terms:
![${\bf{C}} = \left[ {\matrix{ { - t_{\rm{c}}^{ - 1}{r_{{\rm{gd}}}}\, + t_{\rm{c}}^{ - 1}} \hfill \cr { + t_{\rm{c}}^{ - 1}{r_{{\rm{gd}}}}\, - t_{\rm{c}}^{ - 1}} \hfill \cr } } \right],$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq47.png) (20a)
(20a)
![${\bf{A}} = {{\hat c} \over c}\left[ {\matrix{ { - T_{\rm{d}}^{ - 1}\, - T_{\rm{d}}^{ - 1}} \hfill \cr { - T_{\rm{g}}^{ - 1}\, - T_{\rm{g}}^{ - 1}} \hfill \cr } } \right],$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq48.png) (20b)
(20b)
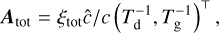 (20c)
(20c)
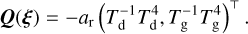 (20d)
(20d)
For our setup, we used a gas density of ρg = 7.78 × 10−18 g cm−3 with a dust-to-gas ratio of fd = 10−2 and stopping time ts = 10−9t0, where t0 = 8 days is the code unit for time. We used a fixed opacity of κd = 3.9 cm2 g−1 and ĉ = c. At t = 0, we set Tg = 101 K, Tg = 102 K, and Tr = 103 K. The specific heat capacity of the gas, cg, is defined by its mean molecular weight, µ = 1, and adiabatic index of γ = 7/5; we set the dust specific heat capacity, cd, equal to that of the gas. By analogy with the determination of Stokes number St = ts Ω of quasi-Keplerian disks, we can compute a characteristic timescale for this system, tcross = lcross /υcross, where lcross and υcoss are the length and velocity scales of interest. In this case, we chose a lcross = (κdƒdρg)−1 = 3.38 × 1018cm (the mean free path of the system) and a υcross = (kB Tg/µmp)1/2 = 287 m s−1. This yields a result of tcross = 3.6 × 106 y or ts/tcross = 5.87 × 10−18.
The system should relax to an equilibrium state in which dust, gas, and radiation have equivalent effective temperatures, specifically, ξd = ξg/rgd = cgρg(ξr/ar)1/4. Furthermore, in several special cases, it has analytical solutions against which our numerical scheme can be tested. For instance, when collisional energy exchange between gas and dust happens much faster than absorption, the system has a solution in terms of matrix exponentials:
![${\bf{\xi }}\left( t \right) \approx \exp \left[ {{\bf{C}}t} \right]{{\bf{\xi }}_0}.$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq51.png) (21)
(21)
Given our simulation parameters, we find that Eq. (21) is a good description of the temperature evolution at early times. We plot its predictions for Tg and Td as black and red lines respectively in Fig. 1. On timescales of t > tc/(1 + rgd) ≈ ts, such a system reaches a quasi-steady state where ξd = ξg/rgd – in other words, the temperatures of dust and gas become equal.
By contrast, when the absorption and emission terms dominate over collisions, and additionally the system is radiation-energy dominated throughout its evolution (i.e., (c/ĉ)ξr ≡ (ξtot − ξd − ξg) ≫ ξg + ξd), ĉ drops out of the equations and we get:
![${\partial \over {\partial t}}\left[ {\matrix{ {{\xi _{\rm{d}}}} \cr {{\xi _{\rm{g}}}} \cr } } \right] \approx \left[ {\matrix{ {T_{\rm{d}}^{ - 1}\left( {{\xi _{{\rm{r,0}}}} - {a_{\rm{r}}}{{\left( {{{{\xi _{\rm{d}}}} \mathord{\left/ {\vphantom {{{\xi _{\rm{d}}}} {\rho {f_{\rm{d}}}{c_{\rm{d}}}}}} \right. \kern-\nulldelimiterspace} {\rho {f_{\rm{d}}}{c_{\rm{d}}}}}} \right)}^4}} \right)} \cr {T_{\rm{g}}^{ - 1}\left( {{\xi _{{\rm{r,0}}}} - {a_{\rm{r}}}{{\left( {{{{\xi _{\rm{g}}}} \mathord{\left/ {\vphantom {{{\xi _{\rm{g}}}} {\rho {c_{\rm{g}}}}}} \right. \kern-\nulldelimiterspace} {\rho {c_{\rm{g}}}}}} \right)}^4}} \right)} \cr } } \right].$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq52.png) (22)
(22)
Each component of Eq. (22) is identical to the form found in Eq. (69) and Fig. 5 of Melon Fuksman & Mignone (2019). This yields an implicit analytic relation that can be inverted by root-finding:
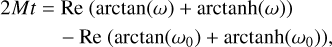 (23)
(23)
where 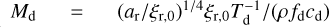 ,
, 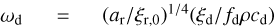 , and ωd,0 = ωd(t = 0); Mg and ωg are likewise obtained and ξr is assumed to be constant throughout the evolution of the system.
, and ωd,0 = ωd(t = 0); Mg and ωg are likewise obtained and ξr is assumed to be constant throughout the evolution of the system.
When the collision timescale is much shorter than the absorption-emission timescale, but the dust and gas are already in collisional equilibrium, we can obtain yet another special case by summing the two rows of Eq. (22):
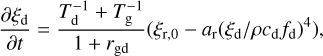 (24)
(24)
where we constrain ξd = ξg /rgd. The solution to Eq. (24) is also offered in the form of Eq. (23), with 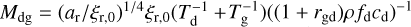 and ωdg = (ar/ξr,0)1/4(ξd/ρfdcd).
and ωdg = (ar/ξr,0)1/4(ξd/ρfdcd).
We plot Eq. (24) as a purple curve in Fig. 1. Our scheme accurately handles the regime where the dust and gas temperatures are well-coupled, showing that it is effective at reproducing the “two-temperature” limit of typical radiation-hydrodynamics simulations.
 |
Fig. 1 0D test of our three-temperature scheme, for which we set the dust-gas stopping time ts = 10−9t0 = 8 × 10−9 d and the opacity κd = 3.9 cm2g−1. Pluses indicate numerical results, while solid lines indicate analytical solutions taken from Eqs. (21) (red, black) and (24) (purple). Because the system is dominated by radiation energy, the radiation temperature (blue) is nearly constant throughout the system’s evolution. |
3.2 1D test: Subcritical dusty radiative shock
Having verified that our scheme accurately reproduces three-temperature static thermal coupling, we seek to study its performance in a a dynamical setting. To this end, we ran a modified version of the 1D subcritical radiative shock in Ensman (1994), a standard test for radiation-hydrodynamic codes (see e.g., Sect. 4.1 of Melon Fuksman et al. 2021, and references therein) incorporating sharp transitions in temperature and opacity.
In this setup, our domain spans the interval [0,7 × 1010 cm]. The initial gas density is ρg = 7.78 × 10−10 g cm−3, with a dust-to-gas ratio fd = 10−2. Dust, gas, and radiation temperatures are all initialized in equilibrium, Tr = Tg = Td = 10 K; γ = 7/5, µ = 1, and cd = cg are the same as in the 0D case. The dust absorption opacity is set such that the inverse mean free path of radiation through dust, 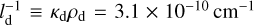 , with dust scattering opacity of χd − κd, and a gas total opacity of χg, both assumed to be zero. To form the shock, given our otherwise equilibrium initial conditions, we set an initial gas velocity υx = −6 km s−1 and imposed a reflective condition on the left boundary. We fiducially chose a reduced speed of light ĉ = 10−3 c and a spatial resolution Nx = 1200 cells. These figures give results that are consistent with those of our tests (not shown) at ĉ = c, and both higher and lower resolutions.
, with dust scattering opacity of χd − κd, and a gas total opacity of χg, both assumed to be zero. To form the shock, given our otherwise equilibrium initial conditions, we set an initial gas velocity υx = −6 km s−1 and imposed a reflective condition on the left boundary. We fiducially chose a reduced speed of light ĉ = 10−3 c and a spatial resolution Nx = 1200 cells. These figures give results that are consistent with those of our tests (not shown) at ĉ = c, and both higher and lower resolutions.
We tested stopping times, ts = {10−7,10−4,10−1 }t0, where we again used t0 = 8 d as the code unit for time. For this problem, we define the characteristic timescale using ld as our length scale and υx as the velocity scale, yielding tcross = 7.78 × 10−2t0 and ts/tcross = 1.28 × {10−5,10−2,101}. The last case is included to demonstrate the properties of our code when dust and gas have weak thermal coupling, although the long ts/ tcross would also allow for relative motion between dust and gas, which we did not model.
In Fig. 2, we plot temperature snapshots at t = 0. 054t0 = 3.75 × 104 s for all stopping times, selecting Nx = 1200 as our fiducial resolution. For ts = 10−1, the gas temperature is that of a standard hydrodynamic shock. In the pre-shock region, dust and gas are essentially in equilibrium; in the post-shock region, by contrast, the dust heats at a rate 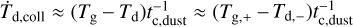 , where minuses and pluses denote pre- and post-shock quantities, respectively. Deeper in the post-shock region, this trend breaks down, as radiative cooling (which scales as
, where minuses and pluses denote pre- and post-shock quantities, respectively. Deeper in the post-shock region, this trend breaks down, as radiative cooling (which scales as 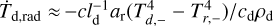 ) becomes sufficient to counteract the effects of collisional heating.
) becomes sufficient to counteract the effects of collisional heating.
In the ts = 10−4t0 case, the cooling time, tc,dust, is short and Td increases rapidly immediately after encountering the shock. Because the collisional heating rate is faster than for ts = 10−1t0, the radiative cooling rate, and thus the maximum post-shock dust temperature, must be correspondingly higher. In the pre-shock region, this process is inverted: radiation propagating from the shock front heats the dust above its initial preshock value and, via collisions, the gas. For the strongly coupled case, with ts = 10−7t0, dust and gas are in collisional equilibrium, and we recover the two-temperature results of Melon Fuksman et al. (2021). Because the Courant-limited radiation timestep Δtrad ≈ Δx/ĉ is much longer than our dust coupling time, this result demonstrates the efficacy of our IMEX scheme in the stiff regime.
In these 1D simulations, changes in the radiation field are driven by collisional heating of the dust, and ultimately by the rightward motion of the shock front in a process that s much slower than radiation propagation or absorption and emission. In this regime, we can drop the time derivative terms in Eq. (1f) and take the nonrelativistic limit of:
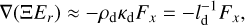 (25)
(25)
where the [I] parameter is defined in Eq. (9) as a function of the “reduced flux” w. Adding a sign to this reduced flux wx = Fx/Er = ±w and rearranging terms, we get:
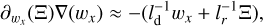 (26)
(26)
where 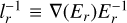 is the relative rate of change in the radiation field. In other words, variations in the radiation field on length scales shorter (longer) than some critical scale ldΞ|wx|−1 drive (damp) the flux.
is the relative rate of change in the radiation field. In other words, variations in the radiation field on length scales shorter (longer) than some critical scale ldΞ|wx|−1 drive (damp) the flux.
This is clearly visible in Fig. 2: in the ts = 10−1t0 case, the relatively moderate gradient in radiation energy means that the transition from the wx ≈ 0 diffusion regime to the wx ≈ 1 free-streaming regime occurs smoothly over the post-shocked region. For s ≳ 5 × 105 km, radiation from the shock front is sufficiently extincted, so the radiation field is dominated by the flat 10 K background; accordingly, |lr| → ∞ and wx damps to zero.
By contrast, the ts = 10−7t0 case has a flat radiation field for much of the post-shock region, but a sharper one in the immediate vicinity of the shock, creating an abrupt transition between the diffusion and free-streaming regimes. Because the post-shock radiation field is stronger in this case, it propagates to a greater optical depth before decaying into the flat Tr = 10 K background, so the wx damping seen in the ts = 10−1t0 simulation is not visible in the plotted region. The ts = 10−1t0 case represents an intermediate case between these two extremes.
 |
Fig. 2 Temperature profiles in the dusty radiative shock test at t = 0.054t0 = 3.75 × 104 sec, for a variety of stopping times. For ts = 10−1, the gas temperature is that of a standard hydrodynamic shock, with only weak losses to dust and radiation; for ts = 10−7, Td, and Tg have come into equilibrium, and they (along with wx and Tr) match the results of the two-temperature radiative shock tests in Sect. 4.1 of (Melon Fuksman et al. 2021). We note that the signed “reduced flux” of wx = Fx/Er is denoted as f in their work. |
3.3 2D test: Self-shadowing instability
The self-shadowing or thermal wave instability (SSI; see e.g., D’Alessio et al. 1999; Dullemond 2000; Watanabe & Lin 2008; Flock et al. 2020; Wu & Lithwick 2021) has been proposed as a planet-free means of generating gaps and rings in circumstellar disks. The SSI begins with a disk in initial radiative and (vertical) hydrostatic equilibrium. A small perturbation to the disk’s radial τr = 1 surface would create slightly raised regions that absorb more stellar irradiation, and lowered, obscured regions, which absorb less. To maintain hydrostatic equilibrium, the raised regions would increase in scale height (and thus absorb even more starlight), while the lowered ones would decrease in scale height and absorb even less.
The SSI is readily reproduced in 1+1D simulations that parametrize the vertical extent of a disk (e.g., Ueda et al. 2021). It can also be generated (e.g., Ueda et al. 2019) by an iterative procedure that first uses radiative transfer to obtain a disk’s temperature profile, given its density structure; assuming hydrostatic equilibrium, this profile is then used to recompute the density structure for the next iteration.
However, Melon Fuksman & Klahr (2022) found that this picture breaks down with additional physics: in their two-temperature radiation hydrodynamics simulations, the SSI bumps do not grow from noise and then they decay rapidly, even when artificially introduced via the aforementioned iterative procedure. They explain their results by arguing that the erosion of perturbations at the τr = 1 surface, caused by in-plane radiation transport and the hydrostatic adaptation of the gas in the upper disk, occurs on timescales that are much shorter than the classical vertical radiative heating timescale of the disk (Hubeny 1990; Zhu et al. 2015; Zhang & Zhu 2020), as in:
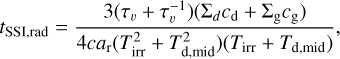 (27)
(27)
where 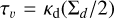 is the vertical optical depth of the disk to the midplane in thermal infrared, Σd and Σg are the dust and gas surface densities, Tirr is the equilibrium temperature of the stellar irradiation field in the optically thin region of the disk, and Td,mid is the dust midplane temperature. Physically, this means that bumps at the optical surface decay long before they can impact the temperature at the disk surface.
is the vertical optical depth of the disk to the midplane in thermal infrared, Σd and Σg are the dust and gas surface densities, Tirr is the equilibrium temperature of the stellar irradiation field in the optically thin region of the disk, and Td,mid is the dust midplane temperature. Physically, this means that bumps at the optical surface decay long before they can impact the temperature at the disk surface.
A nonzero coupling time between gas and dust temperatures would allow for a temperature perturbation at the τr = 1 surface to establish itself in the underlying disk column by propagating only through the dust; this is a much faster process than that implied via Eq. (27), in which the gas and dust are heated together. The subsequent adaptation of the gas’s vertical structure to this already-established background would conform better to the assumptions of iterative methods which have been successful in reproducing the SSI. Moreover, such a coupling time would delay the response of the perturbed τr = 1 gas to in-plane radiation transport, limiting the radial diffusion of SSI bumps. We emphasize that nothing about this prediction accounts for the effects of nonzero coupling times between dust and gas velocities on the evolution of the SSI. We defer this topic to a future work.
In the context of protoplanetary disks, a realistic coupling time may be found by computing ts with the Epstein drag law (see e.g., Barranco et al. 2018; Speedie et al. 2022; Melon Fuksman et al. 2023) as follows:
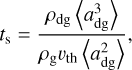 (28)
(28)
where ρdg is the bulk density of each dust grain and 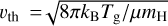 is the gas thermal velocity. A quantity in angle brackets 〈g(adg)〉 represents the integral of that quantity over the (normalized) grain size distribution n(a):
is the gas thermal velocity. A quantity in angle brackets 〈g(adg)〉 represents the integral of that quantity over the (normalized) grain size distribution n(a):
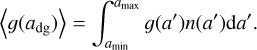 (29)
(29)
For our three-temperature tests of the SSI, we used the setup dg3t100 from Melon Fuksman & Klahr (2022), generated with the aforementioned iterative procedure, as the basis for our initial conditions. We employ a reduced speed of light of ĉ = 10−3 c; our tests at ĉ′ = 5ĉ = 5 × 10−3 c (not shown) yielded converged results. The gas follows an ideal equation of state, with an adiabatic index of γ = 1.41 and a mean molecular weight of µ = 2.3. We assumed a total dust fraction of 1%, of which 10% by mass (fd = 10−3) are taken to be small grains relevant to the gas’s thermal evolution. These grains were taken to consist of 62.5% silicate and 37.5% graphite, with a bulk density of ρgr = 2.5 g cm−3 and a specific heat capacity of cd = 0.7 Jg−1 K−1; their sizes follow a classical MRN (Mathis et al. 1977) distribution, n(a) ∝ a−3.5, with amin = 5 nm and amax = 250 nm2.
From these grain properties, we computed a temperature-dependent, frequency-integrated dust opacity, κd(Td), based on the tabulated frequency-dependent figures by Krieger & Wolf (2020, 2022) as well as ts. We additionally bracketed the dust stopping time to lie within [10−10/2π, 101 /2π] years and took Tg → max(Tg, 10 K) for the purpose of computing υth. We assumed a classical T Tauri star with M* = 1 M⊙, R* = 2.0865 R⊙, and T* = 4000 K, to compute the dust irradiation source term, Sd, as well as the gravitational potential:
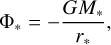 (30)
(30)
where r* ≡ ‖x − x‖ is the distance between the star and a given point in the domain. We plot the resulting initial condition, as well as relevant contours for radial optical depth, τr, and gas cooling parameter, 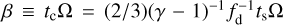 , shown in the upper panel of Fig. 3. We emphasize that our yß-cooling parameter reflects only gas-grain collisions; because we self-consistently modeled the radiative transfer, we did not incorporate assumptions about time or length scales for radiative diffusion or optically thin cooling, as in some previous works (e.g., Bae et al. 2021).
, shown in the upper panel of Fig. 3. We emphasize that our yß-cooling parameter reflects only gas-grain collisions; because we self-consistently modeled the radiative transfer, we did not incorporate assumptions about time or length scales for radiative diffusion or optically thin cooling, as in some previous works (e.g., Bae et al. 2021).
We ran our SSI simulation in 2D axisymmetric polar coordinates, with radial limits at r = [0.4,100] au and polar limits at θ = π/2 + [−0.23,0.23]. This domain was spanned by {Nr, Nθ} = {512,170} grid cells, logarithmically spaced in the radial direction and uniformly spaced in polar angle. At the boundaries, all fields were set equal to those in dg3t0.1, the fiducial smooth hydrostatic setup in Melon Fuksman & Klahr (2022). We also included a damping zone in the region {r < rdamp,in} ∪ {p < 0}, where rdamp,in = 0.5 au and p ≡ −|θ − π/2| + 0.12 + 0.13(r/au). In this zone, we enforced Td = Tg, while relaxing ρ and υ to their smooth hydrostatic values on a timescale of:
![${t_{{\rm{damp}}}} = 0.1{\rm{\Omega }}{\left( r \right)^{ - 1}}{\cos ^2}\left[ {{\pi \mathord{\left/ {\vphantom {\pi {2\left( {{{1 + p} \mathord{\left/ {\vphantom {{1 + p} {{p_ + }}}} \right. \kern-\nulldelimiterspace} {{p_ + }}}} \right)}}} \right. \kern-\nulldelimiterspace} {2\left( {{{1 + p} \mathord{\left/ {\vphantom {{1 + p} {{p_ + }}}} \right. \kern-\nulldelimiterspace} {{p_ + }}}} \right)}}} \right],$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq71.png) (31a)
(31a)
in the region where s < 0, and
![${t_{{\rm{damp}}}} = 0.1{\rm{\Omega }}{\left( r \right)^{ - 1}}{\cos ^{ - 2}}\left[ {{\pi \mathord{\left/ {\vphantom {\pi {2\left( {{{r - {r_{{\rm{in}}}}} \over {{r_{{\rm{damp,in}}}} - {r_{{\rm{in}}}}}}} \right)}}} \right. \kern-\nulldelimiterspace} {2\left( {{{r - {r_{{\rm{in}}}}} \over {{r_{{\rm{damp,in}}}} - {r_{{\rm{in}}}}}}} \right)}}} \right],$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq72.png) (31b)
(31b)
elsewhere in the damping zone; we have tested alternative damping prescriptions and found no substantive change to our results. For comparison with the two-temperature regime, we also ran a simulation with a fixed global stopping time of ts = (2π)−1 × 10−10 yr, but otherwise identical.
In Fig. 4, we plot Td and Tg from our realistic three-temperature simulation, as well as the matter temperature, Tref, in the two-temperature reference simulation, at t = {0, 1, 10, 100} y. In the reference simulation, the initial scale-height perturbations at the τr = 1 surface dissipate rapidly and are almost completely absent by t = 10 y, reproducing the results of the equivalent two-temperature runs in Melon Fuksman & Klahr (2022). Our three-temperature realistic simulation, in which ß ≈ 1 at the τr = 1 surface, shows a similar evolution, as Tg still evolves too fast to achieve the smooth, columnar hydrostatic adaptation obtained in 1+1D and iterative approaches that reproduce the SSI. To better understand this temperature evolution, we plot in Fig. 5 the time evolution of Td, Tg, and Tref – normalized by the final, relaxed reference temperature Trelax, in a fiducial disk column at r = 2 au.
By t = 102 yr, the temperature profile within the τr = 1 surface of the realistic simulation has largely reached the same smooth equilibrium as in the reference. The slow-cooling disk atmosphere in the realistic case, heated by waves emitted by the disk’s initial relaxation and reflecting off the boundaries, is too low in density and optical depth to substantively alter this picture. It remains an open question as to what extent three-temperature methods can sustain the SSI. In this regard, our numerical experiments with a dust-gas coupling time artificially increased by 100× (described in Appendix B) show some promise, allowing SSI waves to survive and propagate inward for roughly ~102 yr before decaying.
 |
Fig. 3 Initial Td = Tg for our 2D self-shadowing test Sect. (3.3), based on dg3t100 from Melon Fuksman & Klahr (2022), shown above, and the same for our 3D planet-driven spiral test Sect. (3.4), based on dg3t0.1, shown below. We overplot the contours for the radial optical depth, τr, in red (computed using opacities Planck-averaged over the stellar spectrum) and cooling parameter of β = tcΩ. Our calculations of these quantities assume an MRN distribution of small silicon-graphite grains and a 1M⊕ classical T Tauri star as the source of light and gravity. In the lower plot, a white dot indicates the position of the embedded 1 MJ planet, while grey shading covers the region outside the r = [8,100] au boundaries of our 3D simulation. |
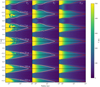 |
Fig. 4 2D temperature profiles from our SSI tests. The Tg (left) and Td (middle) columns come from our simulations with realistic ts, whereas Tref (right) is from our reference simulations with ts = (2π)−1 × 10−10 yr. For ease of interpretation, we overplot β = 1 (white) and τ = 1 (red) surfaces. The reference disk relaxes rapidly to a smooth hydrostatic configuration; the bulk of the realistic disk does so as well, although differences persist in the slowly-cooling disk atmosphere. |
 |
Fig. 5 Time evolution of Td (top), Tg (center), and Tref (bottom) in a disk column at the fiducial r = 2 au, as compared to the final, relaxed state of Tref. As in Fig. 4, we plot the τr = 1 optical surface in red and the ß = 1 cooling surface in white. Tref, as well as Td and Tg, rapidly relax to a smooth equilibrium disk inside the ß = 1 surface. Sound waves in the upper atmosphere, excited by the initial relaxation of the disk, are visible in Tg due to the slow cooling rate at high altitude. |
3.4 3D test: Planet-driven spirals
In recent years, high-resolution observations in NIR (e.g., Benisty et al. 2015; Wagner et al. 2019; Xie et al. 2021) and in various molecular lines (e.g., Teague et al. 2019; Wölfer et al. 2021) have revealed spiral structures in circumstellar disks. It is hypothesized that some fraction of these are driven by embedded, planetary-mass companions (Goldreich & Tremaine 1978, 1979, 1980; Goodman & Rafikov 2001).
Early simulations of these spirals (e.g., Kley 1999) often used 2D, vertically averaged setups, with a locally isothermal equation of state. Subsequent advances in computational power made it feasible to run disk-planet interaction simulations in full 3D (e.g., Fung & Dong 2015; Dong et al. 2016), relax the assumption of local isothermality (Zhu et al. 2015), and implement realistic vertical temperature structures (Juhász & Rosotti 2018); these, in turn, have enabled meaningful comparisons of simulated spirals to observations in dust (Dong & Fung 2017) and gas (Muley et al. 2021). More recently, Bae et al. (2021) used a parametrized cooling prescription to include the effects of matter-radiation interaction and gas-grain collisions. In what follows, we build on these previous works by modeling spirals with self-consistent, three-temperature radiation hydrodynamics.
For this test, we use the relaxed hydrostatic setup dg3t0.1 from Melon Fuksman & Klahr (2022) as a starting point. The dust properties, stellar parameters, and cooling prescription are the same as those in Sect. 3.3, and we plot our initial condition, as well as the resulting contours for ß and τr, in the lower panel of Fig. 3. For this test, we assumed ĉ = 10−4c. Our simulation was run in 3D spherical coordinates, with radial boundaries at r = [8,100] au, polar boundaries at θ = π/2 + [−0.27,0.27], and azimuthal boundaries at ϕ = [0,2π]; this simulation box is covered by {Nr, Nθ, Nϕ} = {234,54,583} cells, logarithmic in radius and uniform in azimuthal and polar angle. All fields are fixed to their initial values at the radial and azimuthal boundaries, and periodic at the azimuthal boundary.
In addition to the star and its gravitational potential, Φ*, our simulation includes a q ≡ Mp/M* = 10−3 planet (Mp ≈ 1.05MJ), fixed on a circular Keplerian orbit with semimajor axis ap = 20 au; at this radius, our temperature profile implies a disk aspect ratio (h/r)p = 0.057 and a qth = 5.5 times the thermal mass. The planetary potential is given, following Klahr & Kley (2006), by
![${{\rm{\Phi }}_p} = - {{G{M_p}} \over {{r_p}}}\left\{ {\matrix{ 1 & {{\rm{if}}\,\,{r_p} \ge {r_s}} \cr {\left( {{{\left[ {{{{r_p}} \mathord{\left/ {\vphantom {{{r_p}} {{r_s}}}} \right. \kern-\nulldelimiterspace} {{r_s}}}} \right]}^4} - 2{{\left[ {{{{r_p}} \mathord{\left/ {\vphantom {{{r_p}} {{r_s}}}} \right. \kern-\nulldelimiterspace} {{r_s}}}} \right]}^3} + 2\left[ {{{{r_p}} \mathord{\left/ {\vphantom {{{r_p}} {{r_s}}}} \right. \kern-\nulldelimiterspace} {{r_s}}}} \right]} \right)} & {{\rm{if}}\,\,{{\rm{r}}_p} < {r_s}} \cr } ,} \right.$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq73.png) (32)
(32)
where rp ≡ ‖x − xp‖ is the distance between the planet and a point in our domain, and rs is the smoothing length, implemented to avoid a singularity in the potential. In our simulations, we set rs = rH/2.
To avoid unphysically shocking the disk at early times, we introduced this companion at ti = 1 yr and grew it from zero to its final mass over the following tgrow = 10 yr. We solved our equations in the planet’s co-rotating frame, fixing its azimuthal coordinate as ϕp = π/4. In this frame, the pattern speed of the spiral, and consequently of the non-axisymmetric radiation field, is zero; deviations would be on the order of cs ≈ 10−6c ≈ 10−2ĉ. Numerical tests at ĉ′ = 2 × 10−5 = ĉ/5, not shown here, yield a well-converged spiral amplitude. To prevent the growth of large-scale disk instabilities such as the Rossby wave instability (RWI; Lovelace & Romanova 2014), we included a kinematic viscosity 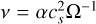 , where α = 0.001 is the Shakura & Sunyaev (1973) viscosity parameter. As in Sect. 3.3, we ran a three-temperature realistic simulation, as well as an otherwise-identical reference simulation with ts = (2π)−1 × 10−10 yr.
, where α = 0.001 is the Shakura & Sunyaev (1973) viscosity parameter. As in Sect. 3.3, we ran a three-temperature realistic simulation, as well as an otherwise-identical reference simulation with ts = (2π)−1 × 10−10 yr.
To keep the focus on the spirals, we analyzed the snapshot at tcut = 500 yr, before our super-thermal planet has had the chance to carve a gap in the disk. In Fig. 6, we present the gas densities in our three-temperature realistic (ρgas) and two-temperature reference (ρref) simulations, taken at r = 30 au and θ = {0,0.15,0.2}. At θ = 0, the primary and secondary Lindblad spirals are visible in both ρgas and ρref, and agree to within several percent. This is expected because the three-temperature mid-plane value ß ≲ 10−2 and reference simulation global value ß ≲ 10−11 are both much shorter than the spiral-crossing timescale, βsprial ≈ (h/r)|1 − Ωp/Ω30|−1 (Sturm et al. 2020), where Ω30 is the Keplerian frequency at 30 au. In the upper disk, the realistic ß ≈ 1 exceeds /ßspiral, while the reference ß remains unchanged. Due to this difference in the thermal physics, the density structures become discrepant at the ~20% level, with Lindblad spirals being more sharply defined in ρref than in ρgas.
In Fig. 7, we plot temperatures at the same cuts studied in Fig. 6. In the midplane of our three-temperature simulation, strong dust-gas coupling ensures that Td and Tg are equal. At θ = 0.15, dust-gas coupling is somewhat weaker, with a ß ≈ 10−1 ≈ ßspiral, and differences between Td and Tg are visible throughout the azimuthal extent of our cut. High in the disk atmosphere, at θ = 0.2, the normalized cooling time is ß ≈ 1, much longer than the spiral-crossing timescale for gas. Here, we observe a spiral feature in Tg with an amplitude ~10%, which is comparable to that found the ß = 1, Mp = 400 M⊕ spiral simulation in Muley et al. (2021), but is not visible in Td or Tref.
At θ = 0, we observe a slight temperature dip centered at ϕ = ϕp = π/4, while at θ = 0.15 and θ = 0.2, we find a temperature bump at the same azimuthal position. This is ultimately caused by the gravitational influence of the planet, which lowers the τr = 1 surface overhead and thus changes the illumination of material in the radial band ϕ ≈ ϕp, r ≳ rp. Such a feature was also observed in the Monte Carlo radiative transfer post-processing of Muley et al. (2021)’s hydrodynamical simulations.
To provide a more visual understanding of these results, we present 2D polar cuts of Td, Tg, and Tref at θ = 0.0 and θ = 0.2 in Fig. 8. We find, as in our 1D quantitative plots, that the morphology of Tref largely agrees with that of Td, despite substantial differences in ß between and within each simulation, while Tg and Td only agree with one another when ß < ßspiral. We interpret this to imply that Td is set by the very short timescales for the dust's collisional energy exchange 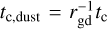 (following Eq. (6)) and for radiative cooling, either vertically or in-plane (Miranda & Rafikov 2020a; Ziampras et al. 2020). How Tg, in turn, reacts to the dust depends on the much longer local gas cooling time tc = ß/Ω. This a result that could affect the observational signatures disk-planet interaction produces in gas and dust. We note, in addition, a slight discrepancy between the background Tdust and Tref, with the latter being systematically lower throughout the disk; this is because spirals are more vertically extended in the two-temperature limit, and so cast stronger shadows throughout the disk. We intend to investigate these issues further in a future study.
(following Eq. (6)) and for radiative cooling, either vertically or in-plane (Miranda & Rafikov 2020a; Ziampras et al. 2020). How Tg, in turn, reacts to the dust depends on the much longer local gas cooling time tc = ß/Ω. This a result that could affect the observational signatures disk-planet interaction produces in gas and dust. We note, in addition, a slight discrepancy between the background Tdust and Tref, with the latter being systematically lower throughout the disk; this is because spirals are more vertically extended in the two-temperature limit, and so cast stronger shadows throughout the disk. We intend to investigate these issues further in a future study.
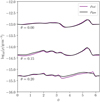 |
Fig. 6 Density values for our three-temperature realistic (ρgas) and reference (ρref) simulations, taken at the indicated θ values at a fixed r = 30 au. Densities largely agree to within a few percent between both models, but the discrepancy rises to ~20% at the τr = 1 surface, causing a mild impact on the temperature structure below. |
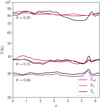 |
Fig. 7 Temperatures in our three-temperature realistic (Tgas, Tdust) and reference (Tref) simulations, taken at the same cuts as in Fig. 6. In the midplane, where coupling times are short, Tgas = Tdust, but in the disk atmosphere, where coupling is weaker, there is a noticeable (~10%) discrepancy between the two: Tdust reflects the stellar irradiation field, while Tgas is driven by the PdV work done by the planetary spiral. |
 |
Fig. 8 Relative difference between the temperature at tcut = 500 yr and the initial profile, in polar cuts at θ = 0.0 and θ = 0.2. The morphology of Td and Tg agree in the midplane, but diverge at higher altitude, while the morphology of Td and Tref agree everywhere. In each panel, we indicate the Hill sphere of the planet with a small solid grey circle, and our cuts in Figs. 6 and 7 with a large dotted grey circle. |
4 Conclusion
We have developed an implicit-explicit (IMEX) numerical scheme for the PLUTO hydrodynamics code to self-consistently model energy exchange between gas, dust, and radiation. The implicit substep, consisting of nonrelativistic matter-radiation interaction source terms, is solved iteratively with a multidimensional Newton-Raphson method, whereas the explicit substep, consisting of radiation transport and relativistic interaction source terms, is solved using a Godunov scheme, following Melon Fuksman & Mignone (2019). Because this explicit part is Courant-limited, we use the reduced speed of light approximation, as implemented by Melon Fuksman et al. (2021), to improve computational efficiency. This gives physically reasonable results, so long as the reduced speed of light ĉ is much higher than all other relevant velocities in the problem.
In our 0D matter-radiation coupling test, we demonstrate the ability of our scheme to reproduce the “two-temperature” regime of traditional radiation hydrodynamics, where dust and gas are well-coupled. For the 1D Ensman (1994) shock tube test, we relax this assumption and investigate the behavior of gas, dust, and radiation temperatures in different coupling regimes. Our subsequent tests illustrate the applicability of three-temperature radiation hydrodynamics to active problems in circumstellar disk research, including realistic opacities and dust-gas coupling times computed from local temperature and density. Our 2D test shows that the self-shadowing instability, which arises in 1+1D time-dependent models with parametrized disk scale height, as well as 2D iterative techniques that alternate the calculation of radiative and hydrostatic equilibrium, decays rapidly in the two-temperature limit; this is also the case with realistic three-temperature coupling times, in line with previous expectations (Melon Fuksman & Klahr 2022). However, an increased cooling time (Appendix B) allows for dust temperatures in most of the disk column to rapidly adapt to stellar irradiation before the gas can react, which better satisfies the key assumptions of the aforementioned iterative and 1D hydrostatic methods, and so allows SSI-type scale-height perturbations to survive for somewhat longer before decaying. In our 3D spiral simulations, dust temperatures are remarkably consistent between the two- and three-temperature regimes, but gas temperatures disagree in the upper atmosphere. This is a result that carries certain implications for observations of spirals in gas tracers such as 12CO. Future potential applications of our three-temperature scheme include studies of circumplanetary disk accretion shocks, planetary gap opening, photoevaporation, and hydrodynamic or MHD instabilities such as the vertical shear instability, among many others.
Our scheme makes the simplifications that dust and gas move at the same velocity, and that dust inertia is negligible (St ≡ tsΩ ≪ 1, ƒd ≪ 1). While these are reasonable assumptions for the sub-µm grains that supply most of a disk’s total opacity and set its overall thermal structure, they are invalid for the millimeter grains that concentrate at pressure maxima and produce much of its continuum emission. Including such grains would require accounting for multispecies momentum transfer including back-reaction from the gas (using schemes such as those detailed in e.g., Benítez-Llambay et al. 2019; Huang & Bai 2022) and thermal coupling. While such a method would be immensely helpful in interpreting continuum observations of gaps, rings, and spirals, it would be computationally demanding and require extensive testing beyond the scope of this work.
With the MRN distribution, 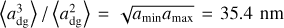 , and dust fraction
, and dust fraction 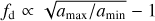 . With these relations, it can be shown that the gas cooling time tc (Eq. (5)) converges to a fixed limiting value as long as amax ≫ amįn. Physically, this means that collisional energy exchange is dominated by the smallest grains.
. With these relations, it can be shown that the gas cooling time tc (Eq. (5)) converges to a fixed limiting value as long as amax ≫ amįn. Physically, this means that collisional energy exchange is dominated by the smallest grains.
Acknowledgements
We thank Remo Burn, Cornelis Dullemond, Mario Flock, Thomas Henning, Carolin Kimmig, Giancarlo Mattia, Thomas Rometsch, and Prakruti Sudarshan for useful discussions. We are also grateful to the anonymous referee, whose report helped improve the quality of this paper. All numerical simulations were performed on the Cobra cluster of the Max Planck Society and the Vera Cluster of the Max Planck Institut für Astronomie, both hosted by the Max Planck Computing and Data Facility (MPCDF) in Garching bei München. The research of J.D.M.F. and H.K. is supported by the German Science Foundation (DFG) under the priority program SPP 1992: “Exoplanet Diversity” under contract KL 1469/16-1/2.
Appendix A Newton-Raphson iterations
We rearrange Equations 18a and 18b as a vector of quantities 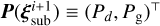 , where
, where 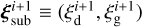 . Thus we obtain:
. Thus we obtain:
![$\matrix{ {{P_d} = \xi _{\rm{d}}^i - \xi _{\rm{d}}^{i + 1} - {{\left( {t_{\rm{c}}^{i + 1}} \right)}^{ - 1}}\left[ {{r_{{\rm{gd}}}}\xi _{\rm{d}}^{i + 1} - \xi _{\rm{g}}^{i + 1}} \right]\delta t} \hfill \cr {\,\,\,\,\,\, - c\rho \kappa _{\rm{d}}^{i + 1}{f_{\rm{d}}}\left[ {{a_{\rm{r}}}{{\left( {T_{\rm{d}}^{i + 1}} \right)}^4} - \xi _{\rm{r}}^{i + 1}} \right]\delta t + S{\,_d}\delta t} \hfill \cr } ,$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq80.png) (A.1)
(A.1)
![$\matrix{ {{P_{\rm{g}}} = \xi _{\rm{g}}^i - \xi _{\rm{g}}^{i + 1} + {{\left( {t_{\rm{c}}^{i + 1}} \right)}^{ - 1}}\left[ {{r_{{\rm{gd}}}}\xi _{\rm{d}}^{i + 1} - \xi _{\rm{g}}^{i + 1}} \right]\delta t} \hfill \cr {\,\,\,\,\,\,\, - c\rho \kappa _{\rm{g}}^{i + 1}\left[ {{a_{\rm{r}}}{{\left( {T_{\rm{g}}^{i + 1}} \right)}^4} - \xi _{\rm{r}}^{i + 1}} \right]\delta t + S{\,_{\rm{g}}}\delta t} \hfill \cr } ,$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq81.png) (A.2)
(A.2)
Using Newton's method, we attempt to find a vector ξi+1,*, such that P(ξi+1,*) = 0 to within some small tolerance α. The relevant Jacobian matrix J(ξi+1) ≡ ∂P/∂ξi+l is:
![${\bf{J}}\left( {{\bf{\xi }}_{{\rm{sub}}}^{i + 1}} \right) = \left[ {\matrix{ {{{\partial {P_d}} \mathord{\left/ {\vphantom {{\partial {P_d}} {\partial \xi _{\rm{d}}^{i + 1}}}} \right. \kern-\nulldelimiterspace} {\partial \xi _{\rm{d}}^{i + 1}}}} \hfill & {{{\partial {P_d}} \mathord{\left/ {\vphantom {{\partial {P_d}} {\partial \xi _{\rm{g}}^{i + 1}}}} \right. \kern-\nulldelimiterspace} {\partial \xi _{\rm{g}}^{i + 1}}}} \hfill \cr {{{\partial {P_{\rm{g}}}} \mathord{\left/ {\vphantom {{\partial {P_{\rm{g}}}} {\partial \xi _{\rm{d}}^{i + 1}}}} \right. \kern-\nulldelimiterspace} {\partial \xi _{\rm{d}}^{i + 1}}}} \hfill & {{{\partial {P_g}} \mathord{\left/ {\vphantom {{\partial {P_g}} {\partial \xi _{\rm{g}}^{i + 1}}}} \right. \kern-\nulldelimiterspace} {\partial \xi _{\rm{g}}^{i + 1}}}} \hfill \cr } } \right],$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq83.png) (A.4)
(A.4)
![${{\partial {P_d}} \mathord{\left/ {\vphantom {{\partial {P_d}} {\partial \xi _{\rm{d}}^{i + 1}}}} \right. \kern-\nulldelimiterspace} {\partial \xi _{\rm{d}}^{i + 1}}} = - \left( {1 + {{{r_{{\rm{gd}}}}\delta t} \mathord{\left/ {\vphantom {{{r_{{\rm{gd}}}}\delta t} {t_{\rm{c}}^{i + 1}}}} \right. \kern-\nulldelimiterspace} {t_{\rm{c}}^{i + 1}}}} \right) - c\rho \kappa _{\rm{d}}^{i + 1}{f_{\rm{d}}}\delta t\left[ {{{4{a_{\rm{r}}}\left( {T_{\rm{d}}^{i + 1}} \right)} \mathord{\left/ {\vphantom {{4{a_{\rm{r}}}\left( {T_{\rm{d}}^{i + 1}} \right)} {\rho {f_{\rm{d}}}{c_{\rm{d}}}}}} \right. \kern-\nulldelimiterspace} {\rho {f_{\rm{d}}}{c_{\rm{d}}}}} + {{\hat c} \mathord{\left/ {\vphantom {{\hat c} c}} \right. \kern-\nulldelimiterspace} c}} \right],$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq84.png) (A.5)
(A.5)
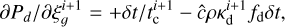 (A.6)
(A.6)
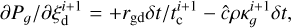 (A.7)
(A.7)
![${{\partial {P_g}} \mathord{\left/ {\vphantom {{\partial {P_g}} {\partial \xi _{\rm{g}}^{i + 1} = \left( {1 + {{\delta t} \mathord{\left/ {\vphantom {{\delta t} {t_{\rm{c}}^{i + 1}}}} \right. \kern-\nulldelimiterspace} {t_{\rm{c}}^{i + 1}}}} \right) - c\rho \kappa _g^{i + 1}\delta t}}} \right. \kern-\nulldelimiterspace} {\partial \xi _{\rm{g}}^{i + 1} = \left( {1 + {{\delta t} \mathord{\left/ {\vphantom {{\delta t} {t_{\rm{c}}^{i + 1}}}} \right. \kern-\nulldelimiterspace} {t_{\rm{c}}^{i + 1}}}} \right) - c\rho \kappa _g^{i + 1}\delta t}}\left[ {{{4{a_{\rm{r}}}{{\left( {T_{\rm{g}}^{i + 1}} \right)}^3}} \mathord{\left/ {\vphantom {{4{a_{\rm{r}}}{{\left( {T_{\rm{g}}^{i + 1}} \right)}^3}} {{{\rho {c_g} + \hat c} \mathord{\left/ {\vphantom {{\rho {c_g} + \hat c} c}} \right. \kern-\nulldelimiterspace} c}}}} \right. \kern-\nulldelimiterspace} {{{\rho {c_g} + \hat c} \mathord{\left/ {\vphantom {{\rho {c_g} + \hat c} c}} \right. \kern-\nulldelimiterspace} c}}}} \right].$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq87.png) (A.8)
(A.8)
![${\bf{J}}\left( {{\bf{\xi }}_n^{i + 1}} \right)\left[ {{\bf{\xi }}_{n + 1}^{i + 1} - {\bf{\xi }}_n^{i + 1}} \right] = - {{\bf{P}}_n},$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq88.png) (A.9)
(A.9)
where n is an iteration index, in contrast to the timestep index i.
Appendix B Self-shadowing instability with long coupling times
Our investigation in Section 3.3 found that, just as in the two-temperature case, our “realistic” three-temperature disk with self-consistently evaluated dust-gas coupling times cannot sustain the self-shadowing instability (SSI). This result, however, leaves open the question of whether there is any circumstance under which three-temperature dynamics could favor the survival of the SSI. To study this possibility, we ran a simulation with dust-gas coupling times 100× larger than those in the realistic run in Section 3.3. To facilitate comparison with our previous results, we hold all other simulation parameters (including, crucially, the dust opacity prescription and dust-to-gas ratio) fixed. Formally, solving for ts in Equation 5, this would imply a Stokes number St ≈ 0.06 for grains at the τr = 1 surface, which can be expected to experience vertical drift. However, we emphasize that this 100×-cooling setup is artificial, and is designed to approximate and long relaxation times that arise in disk upper atmospheres in detailed calculations of grain growth, settling, and depletion (see e.g., Bae et al. 2021, for one such scenario). The dust populations arising from these calculations are, by construction, in steady state, and do not experience net vertical drift.
 |
Fig. B.1 Plot similar to our Figure 5, but with Td and Tg taken from our simulation with cooling times artificially raised by a factor of 100. There are clear vertical patterns in the dust and gas temperature profiles, corresponding to inward-traveling perturbations at the τr = 1 surface characteristic of the SSI. |
In Figure B.1, we plot the time evolution of Td, Tg, and Tref normalized by the final, relaxed reference temperature Trelax in a fiducial disk column at r = 2 au. In the two-temperature reference simulation, the initialized self-shadowing perturbations rapidly decay (as already evident from Figure 4), but in the three-temperature 100× realistic simulation, they survive for some time, as evidenced by the vertical bands in Td and Tg between t = 101 − 102 y.
At the leading edge of a self-shadowing scale-height perturbation, the flaring angle of the τr = 1 is high and intercepts more direct stellar irradiation. Although Td reflects this change immediately, the fact that ß ≫ 1 in this disk region means that the response of Tg (and the consequent vertical expansion of the gas column to seek hydrostatic equilibrium) is significantly slower. As the gas column puffs up, it creates a new leading edge immediately to its interior; when this edge puffs up in turn, it blocks stellar irradiation from reaching the original column, causing it to cool and shrink. In this fashion, self-shadowing waves can propagate inward towards the star purely through vertical motions of the fluid elements. This mechanism would not operate when dust and gas are well-coupled; in that regime, both components would have a common temperature, and would respond to surface perturbations via layered radiative diffusion. The long timescale for this diffusion (given very roughly by Equation 27) means that surface perturbations would decay before having an effect deep in the disk (Melon Fuksman & Klahr 2022).
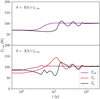 |
Fig. B.2 Quantitative time evolution of Td and Tg from the 100×-realistic simulation, and Tref in the reference simulation, at r = 2 au, both in the midplane (θ = 0, above) and three scale heights above it (θ ≈ 0.088, below). As qualitatively shown in Figure B.1, Tref reaches a smooth equilibrium, whereas Td and Tg exhibit damped oscillations due to the passage of self-shadowing waves. See text for more details. |
For a more quantitative view, we present in Figure B.2 the time evolution of Td, Tg, and Tref at r = 2 au and θ = π/2 + {0.0,0.088} (the latter θ corresponding to three scale heights above the midplane). At both altitudes, Tref relaxes almost immediately to its hydrostatic equilibrium value, where it remains for the rest of the simulation. The evolution of Td and Tg is more complex. High in the disk, the dust temperature rises interior to self-shadowing bumps, and drops exterior to them; with some delay due to gas cooling parameters ß ≈ 1, we see that Td relaxes toward Tg and the interior and exterior gas columns adapt to the new hydrostatic equilibrium. The net result, as mentioned earlier and in line with typical expectations for the SSI, is the apparent inward propagation of self-shadowing bumps. The changes these bumps make to the disk’s illumination profile impact the midplane temperature, albeit with some delay and attenuation due to radiative diffusion.
In Figure B.3, we present snapshots of the full long-coupling disk at selected times. Puffed-up disk columns heated above the background temperature, a hallmark signature of self-shadowing waves, are clearly visible here. They are captured n Figures B.1 and B.2 as they travel inward through r = 2 au. By t = 250 y, however, the long-cooling disk has largely relaxed to the same smooth equilibrium as the reference disk. Differences persist in the very slowly-cooling disk atmosphere, as well as in the r ≲ 1 au region in the immediate vicinity of our fixed inner radial boundary.
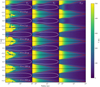 |
Fig. B.3 Evolution of the SSI with a dust-gas coupling time 100× longer than in the self-consistent setup presented in 3.3. An inward-propagating SSI bump is clearly visible. At t = 250 y, the disk has largely relaxed to the same configuration as in the reference simulation. Differences do persist, however, outside the ß = 1 surface and near the inner boundary. |
References
- Bae, J., Teague, R., & Zhu, Z. 2021, ApJ, 912, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Barranco, J. A., Pei, S., & Marcus, P. S. 2018, ApJ, 869, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R., & Keto, E. R. 2015, MNRAS, 449, 2643 [NASA ADS] [CrossRef] [Google Scholar]
- Benisty, M., Juhasz, A., Boccaletti, A., et al. 2015, A & A, 578, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benítez-Llambay, P., Krapp, L., & Pessah, M. E. 2019, ApJS, 241, 25 [Google Scholar]
- Binkert, F., Szulágyi, J., & Birnstiel, T. 2023, MNRAS, 525, 4299 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., Crida, A., Morbidelli, A., Kley, W., & Dobbs-Dixon, I. 2013, A & A, 549, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruderer, S. 2013, A & A, 559, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruderer, S., van Dishoeck, E. F., Doty, S. D., & Herczeg, G. J. 2012, A & A, 541, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burke, J. R., & Hollenbach, D. J. 1983, ApJ, 265, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Calahan, J. K., Bergin, E. A., Zhang, K., et al. 2021, ApJS, 257, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [Google Scholar]
- D'Alessio, P., Cantó, J., Hartmann, L., Calvet, N., & Lizano, S. 1999, ApJ, 511, 896 [CrossRef] [Google Scholar]
- Dong, R., & Fung, J. 2017, ApJ, 835, 38 [Google Scholar]
- Dong, R., Fung, J., & Chiang, E. 2016, ApJ, 826, 75 [Google Scholar]
- Dullemond, C. P. 2000, A & A, 361, L17 [NASA ADS] [Google Scholar]
- Dullemond, C. P., Hollenbach, D., Kamp, I., & D'Alessio, P. 2007, in Protostarsand Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 555 [Google Scholar]
- Dullemond, C. P., Juhasz, A., Pohl, A., et al. 2012, Astrophysics Source Code Library [record ascl:1202.015] [Google Scholar]
- Ensman, L. 1994, ApJ, 424, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Flock, M., Fromang, S., González, M., & Commerçon, B. 2013, A & A, 560, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flock, M., Turner, N. J., Nelson, R. P., et al. 2020, ApJ, 897, 155 [Google Scholar]
- Fung, J., & Dong, R. 2015, ApJ, 815, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Fung, J., Zhu, Z., & Chiang, E. 2019, ApJ, 887, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, N. Y., & Abel, T. 2001, New Astron., 6, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1978, ApJ, 222, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1979, ApJ, 233, 857 [Google Scholar]
- Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [Google Scholar]
- Goodman, J., & Rafikov, R. R. 2001, ApJ, 552, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, X., Li, Z.-Y., Wang, L., Zhu, Z., & Bae, J. 2023, MNRAS, 523, 4883 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, P., & Bai, X.-N. 2022, ApJS, 262, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, S., & Yu, C. 2022, MNRAS, 514, 1733 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I. 1990, ApJ, 351, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Juhász, A., & Rosotti, G. P. 2018, MNRAS, 474, L32 [Google Scholar]
- Keppler, M., Benisty, M., Müller, A., et al. 2018, A & A, 617, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klahr, H., & Kley, W. 2006, A & A, 445, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W. 1999, MNRAS, 303, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., Bitsch, B., & Klahr, H. 2009, A & A, 506, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krieger, A., & Wolf, S. 2020, A & A, 635, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krieger, A., & Wolf, S. 2022, A & A, 662, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levermore, C. D. 1984, J. Quant. Spec. Radiat. Transf., 31, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Levermore, C. D., & Pomraning, G. C. 1981, ApJ, 248, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Lovelace, R. V. E., & Romanova, M. M. 2014, Fluid Dyn. Res., 46, 041401 [NASA ADS] [CrossRef] [Google Scholar]
- Malygin, M. G., Klahr, H., Semenov, D., Henning, T., & Dullemond, C. P. 2017, A & A, 605, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manger, N., Pfeil, T., & Klahr, H. 2021, MNRAS, 508, 5402 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [Google Scholar]
- Melon Fuksman, J. D., & Klahr, H. 2022, ApJ, 936, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Melon Fuksman, J. D., & Mignone, A. 2019, ApJS, 242, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Melon Fuksman, J. D., Klahr, H., Flock, M., & Mignone, A. 2021, ApJ, 906, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Melon Fuksman, J. D., Flock, M., & Klahr, H. 2023, A & A, submitted [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Miranda, R., & Rafikov, R. R. 2019, ApJ, 878, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Miranda, R., & Rafikov, R. R. 2020a, ApJ, 904, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Miranda, R., & Rafikov, R. R. 2020b, ApJ, 892, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Muley, D., Dong, R., & Fung, J. 2021, AJ, 162, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Pareschi, L., & Russo, G. 2005, J. Sci. Comput., 25, 129 [MathSciNet] [Google Scholar]
- Pavlyuchenkov, Y. N., & Zhilkin, A. G. 2013, Astron. Rep., 57, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlyuchenkov, Y. N., Zhilkin, A. G., Vorobyov, E. I., & Fateeva, A. M. 2015, Astron. Rep., 59, 133 [CrossRef] [Google Scholar]
- Pierens, A., & Lin, M.-K. 2018, MNRAS, 479, 4878 [NASA ADS] [Google Scholar]
- Pinte, C., Teague, R., Flaherty, K., et al. 2022, arXiv e-prints [arXiv:2203.09528] [Google Scholar]
- Ren, B., Dong, R., Esposito, T. M., et al. 2018, ApJ, 857, L9 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A & A, 24, 337 [NASA ADS] [Google Scholar]
- Skinner, M. A., & Ostriker, E. C. 2013, ApJS, 206, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Speedie, J., Booth, R. A., & Dong, R. 2022, ApJ, 930, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Sturm, J. A., Rosotti, G. P., & Dominik, C. 2020, A & A, 643, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tarczay-Nehéz, D., Regály, Z., & Vorobyov, E. 2020, MNRAS, 493, 3014 [CrossRef] [Google Scholar]
- Teague, R., Bae, J., Huang, J., & Bergin, E. A. 2019, ApJ, 884, L56 [Google Scholar]
- Ueda, T., Flock, M., & Okuzumi, S. 2019, ApJ, 871, 10 [Google Scholar]
- Ueda, T., Flock, M., & Birnstiel, T. 2021, ApJ, 914, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., Matsukoba, R., Omukai, K., & Guedel, M. 2020, A & A, 638, A102 [CrossRef] [EDP Sciences] [Google Scholar]
- Wagner, K., Stone, J. M., Spalding, E., et al. 2019, ApJ, 882, 20 [Google Scholar]
- Wang, L., & Goodman, J. 2017, ApJ, 847, 11 [Google Scholar]
- Wang, L., Bai, X.-N., & Goodman, J. 2019, ApJ, 874, 90 [Google Scholar]
- Watanabe, S.-I., & Lin, D. N. C. 2008, ApJ, 672, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Whitney, B. A., Robitaille, T. P., Bjorkman, J. E., et al. 2013, ApJS, 207, 30 [Google Scholar]
- Woitke, P., Kamp, I., & Thi, W. F. 2009, A & A, 501, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wölfer, L., Facchini, S., Kurtovic, N. T., et al. 2021, A & A, 648, A19 [CrossRef] [EDP Sciences] [Google Scholar]
- Wu, Y., & Lithwick, Y. 2021, ApJ, 923, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Xie, C., Ren, B., Dong, R., et al. 2021, ApJ, 906, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Yamaleev, N. K., & Carpenter, M. H. 2009, J. Comput. Phys., 228, 3025 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, S., & Zhu, Z. 2020, MNRAS, 493, 2287 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Dong, R., Stone, J. M., & Rafikov, R. R. 2015, ApJ, 813, 88 [Google Scholar]
- Ziampras, A., Kley, W., & Dullemond, C. P. 2020, A & A, 637, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 0D test of our three-temperature scheme, for which we set the dust-gas stopping time ts = 10−9t0 = 8 × 10−9 d and the opacity κd = 3.9 cm2g−1. Pluses indicate numerical results, while solid lines indicate analytical solutions taken from Eqs. (21) (red, black) and (24) (purple). Because the system is dominated by radiation energy, the radiation temperature (blue) is nearly constant throughout the system’s evolution. |
| In the text | |
 |
Fig. 2 Temperature profiles in the dusty radiative shock test at t = 0.054t0 = 3.75 × 104 sec, for a variety of stopping times. For ts = 10−1, the gas temperature is that of a standard hydrodynamic shock, with only weak losses to dust and radiation; for ts = 10−7, Td, and Tg have come into equilibrium, and they (along with wx and Tr) match the results of the two-temperature radiative shock tests in Sect. 4.1 of (Melon Fuksman et al. 2021). We note that the signed “reduced flux” of wx = Fx/Er is denoted as f in their work. |
| In the text | |
 |
Fig. 3 Initial Td = Tg for our 2D self-shadowing test Sect. (3.3), based on dg3t100 from Melon Fuksman & Klahr (2022), shown above, and the same for our 3D planet-driven spiral test Sect. (3.4), based on dg3t0.1, shown below. We overplot the contours for the radial optical depth, τr, in red (computed using opacities Planck-averaged over the stellar spectrum) and cooling parameter of β = tcΩ. Our calculations of these quantities assume an MRN distribution of small silicon-graphite grains and a 1M⊕ classical T Tauri star as the source of light and gravity. In the lower plot, a white dot indicates the position of the embedded 1 MJ planet, while grey shading covers the region outside the r = [8,100] au boundaries of our 3D simulation. |
| In the text | |
 |
Fig. 4 2D temperature profiles from our SSI tests. The Tg (left) and Td (middle) columns come from our simulations with realistic ts, whereas Tref (right) is from our reference simulations with ts = (2π)−1 × 10−10 yr. For ease of interpretation, we overplot β = 1 (white) and τ = 1 (red) surfaces. The reference disk relaxes rapidly to a smooth hydrostatic configuration; the bulk of the realistic disk does so as well, although differences persist in the slowly-cooling disk atmosphere. |
| In the text | |
 |
Fig. 5 Time evolution of Td (top), Tg (center), and Tref (bottom) in a disk column at the fiducial r = 2 au, as compared to the final, relaxed state of Tref. As in Fig. 4, we plot the τr = 1 optical surface in red and the ß = 1 cooling surface in white. Tref, as well as Td and Tg, rapidly relax to a smooth equilibrium disk inside the ß = 1 surface. Sound waves in the upper atmosphere, excited by the initial relaxation of the disk, are visible in Tg due to the slow cooling rate at high altitude. |
| In the text | |
 |
Fig. 6 Density values for our three-temperature realistic (ρgas) and reference (ρref) simulations, taken at the indicated θ values at a fixed r = 30 au. Densities largely agree to within a few percent between both models, but the discrepancy rises to ~20% at the τr = 1 surface, causing a mild impact on the temperature structure below. |
| In the text | |
 |
Fig. 7 Temperatures in our three-temperature realistic (Tgas, Tdust) and reference (Tref) simulations, taken at the same cuts as in Fig. 6. In the midplane, where coupling times are short, Tgas = Tdust, but in the disk atmosphere, where coupling is weaker, there is a noticeable (~10%) discrepancy between the two: Tdust reflects the stellar irradiation field, while Tgas is driven by the PdV work done by the planetary spiral. |
| In the text | |
 |
Fig. 8 Relative difference between the temperature at tcut = 500 yr and the initial profile, in polar cuts at θ = 0.0 and θ = 0.2. The morphology of Td and Tg agree in the midplane, but diverge at higher altitude, while the morphology of Td and Tref agree everywhere. In each panel, we indicate the Hill sphere of the planet with a small solid grey circle, and our cuts in Figs. 6 and 7 with a large dotted grey circle. |
| In the text | |
 |
Fig. B.1 Plot similar to our Figure 5, but with Td and Tg taken from our simulation with cooling times artificially raised by a factor of 100. There are clear vertical patterns in the dust and gas temperature profiles, corresponding to inward-traveling perturbations at the τr = 1 surface characteristic of the SSI. |
| In the text | |
 |
Fig. B.2 Quantitative time evolution of Td and Tg from the 100×-realistic simulation, and Tref in the reference simulation, at r = 2 au, both in the midplane (θ = 0, above) and three scale heights above it (θ ≈ 0.088, below). As qualitatively shown in Figure B.1, Tref reaches a smooth equilibrium, whereas Td and Tg exhibit damped oscillations due to the passage of self-shadowing waves. See text for more details. |
| In the text | |
 |
Fig. B.3 Evolution of the SSI with a dust-gas coupling time 100× longer than in the self-consistent setup presented in 3.3. An inward-propagating SSI bump is clearly visible. At t = 250 y, the disk has largely relaxed to the same configuration as in the reference simulation. Differences do persist, however, outside the ß = 1 surface and near the inner boundary. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



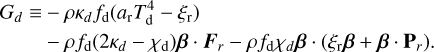
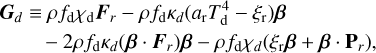
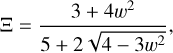
![$\xi _{\rm{r}}^{i + 1} = \xi _{\rm{r}}^i - {{\hat c} \over c}\left[ {\left( {\xi _{\rm{d}}^{i + 1} - \xi _{\rm{d}}^i} \right) + \left( {\xi _{\rm{g}}^{i + 1} - \xi _{\rm{g}}^i} \right)} \right].$](/articles/aa/full_html/2023/10/aa47101-23/aa47101-23-eq82.png)