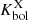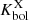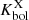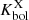| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A201 | |
| Number of page(s) | 22 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202346795 | |
| Published online | 24 October 2023 | |
HYPerluminous quasars at the Epoch of ReionizatION (HYPERION): A new regime for the X-ray nuclear properties of the first quasars
1
INAF – Osservatorio Astronomico di Roma, Via di Frascati 33, 00078 Monte Porzio Catone, Italy
e-mail: luca.zappacosta@inaf.it
2
INAF – Osservatorio Astronomico di Trieste, Via G. Tiepolo 11, 34143 Trieste, Italy
3
IFPU – Institute for Fundamental Physics of the Universe, Via Beirut 2, 34151 Trieste, Italy
4
Dipartimento di Matematica e Fisica, Università Roma Tre, Via della Vasca Navale 84, 00146 Roma, Italy
5
INFN, Sezione Roma1, Dipartimento di Fisica, Università di Roma La Sapienza, Piazzale Aldo Moro 2, 00185 Roma, Italy
6
Dipartimento di Fisica e Astronomia ‘Augusto Righi’, Università degli Studi di Bologna, Via P. Gobetti, 93/2, 40129 Bologna, Italy
7
INAF-Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Piero Gobetti, 93/3, 40129 Bologna, Italy
8
Institut d’Astrophysique de Paris, Sorbonne Université, CNRS, UMR 7095, 98 bis bd Arago, 75014 Paris, France
9
Dipartimento di Fisica, Sezione di Astronomia, Università di Trieste, Via Tiepolo 11, 34143 Trieste, Italy
10
Centre for Extragalactic Astronomy, Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
11
Center for Astrophysics – Harvard & Smithsonian, Cambridge, MA 02138, USA
12
INFN – Sezione di Roma “Tor Vergata”, Via della Ricerca Scientifica 1, 00133 Roma, Italy
13
Space Science Data Center, SSDC, ASI, Via del Politecnico snc, 00133 Roma, Italy
14
Centro de Astrobiología (CAB), CSIC-INTA, Camino Bajo del Castillo s/n, ESAC campus, 28692 Villanueva de la Cañada, Spain
15
NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
16
Scuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy
17
INAF–Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
18
European Space Agency, ESTEC, Keplerlaan 1, 2201 AZ, Noordwijk, The Netherlands
19
ASI – Agenzia Spaziale Italiana, Via del Politecnico snc, 00133 Roma, Italy
20
Dipartimento di Fisica, Università di Roma “Tor Vergata”, Via della Ricerca Scientifica 1, 00133 Roma, Italy
21
Department of Astronomy, University of Maryland, College Park, MD 20742, USA
22
INAF – Istituto di Astrofisica Spaziale e Fisica Cosmica Milano, Via A. Corti 12, 20133 Milano, Italy
23
INFN-National Institute for Nuclear Physics, Via Valerio 2, 34127 Trieste, Italy
24
DiSAT, Università degli Studi dell’Insubria, Via Valleggio 11, 22100 Como, Italy
25
INFN, Sezione di Milano-Bicocca, Piazza della Scienza 3, 20126 Milano, Italy
26
INAF, Osservatorio Astronomico di Brera, Via E. Bianchi 46, 23807 Merate, Italy
27
Cavendish Laboratory, University of Cambridge, 19 J. J. Thomson Ave., Cambridge CB3 0HE, UK
28
Kavli Institute for Cosmology, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
29
Department of Physics & Astronomy, University College London, Gower Street, London WC1E 6BT, UK
30
Dipartimento di Fisica, Università di Roma La Sapienza, Piazzale Aldo Moro 2, 00185 Roma, Italy
31
Sapienza School for Advanced Studies, Viale Regina Elena 291, 00161 Roma, Italy
Received:
2
May
2023
Accepted:
5
July
2023
The existence of luminous quasars (QSOs) at the epoch of reionization (EoR; i.e., z > 6) powered by well-grown supermassive black holes (SMBHs) with masses ≳109 M⊙ challenges models of early SMBH formation and growth. To shed light on the nature of these sources, we started a multiwavelength program based on a sample of 18 HYPerluminous quasars at the Epoch of ReionizatION (HYPERION). These are the luminous QSOs whose SMBHs must have had the most rapid mass growth during the first gigayear of the Universe and therefore acquired the largest mass at their respective epochs. In this paper, we present the HYPERION sample and report results from the first year of the planned three years of observations of the 2.4 Ms XMM-Newton Multi-Year Heritage program on which HYPERION is based. The goal of this program is to accurately characterise the X-ray nuclear properties of QSOs at the EoR. Through a joint X-ray spectral analysis of ten sources, covering the rest-frame ∼2 − 50 keV energy range, we report a steep average photon index (Γ ≈ 2.4 ± 0.1). No absorption is required at levels of 1021 − 1022 cm−2. The measured average Γ is inconsistent at ≥4σ level with the canonical value (Γ = 1.8 − 2) measured in QSOs at z < 6. Such a steep spectral slope is also significantly steeper than that reported in lower-z analog QSOs with similar luminosity or accretion rate, suggesting genuine redshift evolution. Alternatively, we can interpret this result as suggesting the presence of a very low energy cutoff Ecut ≈ 20 keV on a standard Γ = 1.9 power-law, the likes of which is rarely reported at lower z. We also report mild indications that, on average, HYPERION QSOs show higher levels of coronal soft X-rays at 2 keV compared to the accretion disk UV at 2500 Å than expected for lower-z AGN in the high-luminosity regime. We speculate that either a redshift-dependent coupling between the X-ray corona and accretion disk or intrinsically different coronal properties account for the steepness of the X-ray spectral slope, especially in the presence of powerful winds. The reported steep slopes, if confirmed in lower-luminosity regimes, may have an important impact on the design of next-generation X-ray facilities and future surveys designed to investigate the early Universe.
Key words: X-rays: galaxies / galaxies: active / galaxies: high-redshift / galaxies: nuclei / quasars: general / quasars: supermassive black holes
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Almost 300 spectroscopically confirmed quasars (QSOs) have been reported to date at z ≈ 6 − 7.6 (Fan et al. 2023, and references therein) during the epoch of reionization (EoR). These objects are powered by supermassive black holes (SMBHs) with masses (MBH) from ∼108 M⊙ to ∼1010 M⊙ shining with high bolometric luminosities (Lbol) in the range of 1046 − 1048 erg s−1 (∼1013 − 1015 L⊙) close to the Eddington luminosity limit (LEdd), that is, with Eddington ratios λEdd = Lbol/LEdd ≳ 0.2 (e.g., Willott et al. 2010; Mazzucchelli et al. 2017; Shen et al. 2019).
The mere existence of MBH as large as ∼109 M⊙ at EoR poses serious challenges to theoretical models designed to explain how these systems formed in less than 1 Gyr (Volonteri 2010; Johnson & Haardt 2016). High-z SMBH progenitors formed at z ≈ 20 − 30 (e.g., Valiante et al. 2016) would require seed BHs masses of at least ∼1000 − 10 000 M⊙ continuously growing at the Eddington rate for ∼0.5 − 0.8 Gyr (assuming a standard radiative efficiency of ϵ = 0.1) in order to reach the typical MBH reported by the SMBHs powering z > 6 − 7 quasars (see e.g., Wu et al. 2015; Bañados et al. 2018b; Yang et al. 2020; Wang et al. 2021b). This is challenging as it requires the uninterrupted availability of ∼109 M⊙ of gas throughout the ∼1 billion years of growth (Johnson & Bromm 2007; Milosavljević et al. 2009). A continuous feeding at the observed λEdd < 1 would instead imply an initial seed mass of > 104 M⊙ for the large majority of currently discovered z > 6 QSOs.
Theoretical studies (see Inayoshi et al. 2020; Lusso et al. 2023, for recent reviews) indeed suggest that z > 6 SMBHs must have formed from very large initial masses (i.e., the so-called heavy seeds of 104 − 106 M⊙), growing at Eddington-limited gas-accretion rates (e.g., Volonteri 2010; Valiante et al. 2016). Alternatively, they may have grown efficiently from lower mass BHs (∼100 M⊙; light seeds), remnants of Population III stars, through a series of short and intermittent super-Eddington accretion phases (e.g., Volonteri et al. 2015; Pezzulli et al. 2016). However, the viability of these two channels of SMBH formation is still unclear (Johnson & Haardt 2016). BHs may also grow through coalescence with other BHs during galaxy mergers in the framework of the hierarchical structure formation scenario (Volonteri et al. 2003; Tanaka & Haiman 2009). The merger timescale of a binary BH is highly uncertain, but is likely to be long (up to a few tens of Gyr) especially at high redshift (e.g., Biava et al. 2019; Souza Lima et al. 2020).
The fundamental challenges posed by these sources have prompted a massive effort in following-up the hyperluminous (Lbol > 1047 erg s−1) quasars at near-infrared (NIR; UV/optical rest-frame) and far-infrared/submillimeter (FIR/submm) wavelengths with the largest and most sensitive observatories and with the best facilities available to date (e.g., Willott et al. 2010; Wang et al. 2013; Venemans et al. 2016, 2017; Mazzucchelli et al. 2017; Reed et al. 2017; Feruglio et al. 2018; Shen et al. 2019; Onoue et al. 2019; Fan et al. 2019; Schindler et al. 2020; Yang et al. 2021; Farina et al. 2022; Walter et al. 2022; Bischetti et al. 2022). In the X-rays, despite similar dedicated observational efforts (e.g., Brandt et al. 2002; Farrah et al. 2004; Moretti et al. 2014; Page et al. 2014; Gallerani et al. 2017; Ai et al. 2017; Nanni et al. 2018; Bañados et al. 2018a; Pons et al. 2019; Salvestrini et al. 2019; Connor et al. 2020; Wang et al. 2021a; Vito et al. 2021, 2022; Yang et al. 2022; Wolf et al. 2023), our knowledge of the properties of z > 6 quasars has been limited by the sensitivity and efficiency of current X-ray observatories and a lack of all-sky X-ray surveys. Despite this, a few mostly marginal indications of different nuclear and host properties – compared to lower-z QSO analogs – have been reported. These indications involve: (1) hints of X-ray photon index steepening (Vito et al. 2019; Wang et al. 2021a); (2) faster and/or more frequent nuclear winds (Meyer et al. 2019; Schindler et al. 2020; Yang et al. 2021; Bischetti et al. 2022); (3) and excessive MBH compared to host-galaxy dynamical mass with respect to the local scaling relation (e.g., Pensabene et al. 2020; Neeleman et al. 2021; Farina et al. 2022; Tripodi et al. 2023). Given the challenging nature of massive z > 6 QSOs, it is tempting to ascribe all those properties to their peculiar SMBH mass-assembly history. However, further confirmation is needed on firmer statistical grounds, and their interpretation requires careful evaluation. Indeed, an observational selection solely based on interesting, peculiar, bright sources; the availability of a restricted set of good-quality data; or the lack of a uniform, physically motivated sample selection may lead to a biased interpretation of these results.
The importance of an X-ray characterization of QSOs at EoR lies in the fact that the X-ray emission carries nearly instantaneous information on the innermost accreting regions of the AGN. Indeed, a fraction of the thermal UV emission radiated by the accretion disk is reprocessed (i.e., Compton up-scattered) in the X-rays (e.g., Haardt & Maraschi 1993) by a compact, inner (i.e., 10–20 gravitational radii; e.g., De Marco et al. 2013; MacLeod et al. 2015; Chartas et al. 2016; Kara et al. 2016), optically thin region, the hot corona. Such radiation has a power-law spectral shape and a typical photon index of Γ = 1.8 − 2 slope. The latter is constant up to z ∼ 5 (Piconcelli et al. 2005; Vignali et al. 2005; Shemmer et al. 2008; Just et al. 2007; Zappacosta et al. 2018), falling off at high energies with an exponential cutoff at > 100 keV (e.g., Dadina 2008; Vasudevan et al. 2013; Malizia et al. 2014; Ricci et al. 2018) depending on the physical properties of the corona (Fabian et al. 2015, 2017). The photon index has been proposed as a possible indicator of the AGN accretion rate as parameterized by the Eddington ratio λEdd, that is, the mass-normalized bolometric luminosity (e.g., Shemmer et al. 2008; Brightman et al. 2013; Trakhtenbrot et al. 2017; Liu et al. 2021; but see Laurenti et al. 2022 and Kamraj et al. 2022). A tight anti-correlation has long been reported between the accretion disk monochromatic UV luminosity at 2500 Å (L2500 Å) and the optical-to-X-ray spectral index (αOX), parametrizing the relative contributions of the accretion disk UV (L2500 Å) and corona X-ray (2 keV; L2 keV) radiative outputs (e.g., Avni & Tananbaum 1982; Vignali et al. 2003; Steffen et al. 2006; Lusso & Risaliti 2016; Martocchia et al. 2017; Timlin et al. 2020). The physical properties and the relative geometrical configuration of the accretion disk-corona system therefore play a crucial role in shaping the αOX and Γ relations (e.g., Kubota & Done 2018). Validation of the αOX–L2500 Å relation at very high redshifts may allow us to extend and improve cosmology studies (Risaliti & Lusso 2019) up to those early epochs.
Apart from marginal indications of steeper Γ in the stacked or joint spectral fitting analysis of z > 6 QSOs, past X-ray studies found no other, convincing signs of evolutionary properties. However, these studies suffered from (i) limited constraining power due to low X-ray count statistics (< 10 − 15 net-counts), preventing proper spectral analysis on a source-by-source basis, and (ii) a small number of sources with reliable spectral data quality (Nanni et al. 2017, 2018; Ai et al. 2017; Gallerani et al. 2017; Vito et al. 2019; Pons et al. 2020; Wang et al. 2021a; Medvedev et al. 2021; Wolf et al. 2023; Connor et al. 2020).
In this paper, we present (1) a new sample of z > 6 QSOs selected with a physically motivated criterion to include the titans among z > 6 QSOs: that is, those powered by SMBHs that appear to have undergone the fastest BH growth compared to other coeval sources; (2) a XMM-Newton Multi-Year Heritage X-ray program on this sample designed to begin the first systematic X-ray spectroscopic exploration of QSOs at EoR; and (3) the results of the first year of the XMM-Newton program. In Sect. 2, we present our QSO sample and the XMM-Newton Multi-Year Heritage X-ray program. The reduction of the X-ray data from the first year of the Heritage program and X-ray photometry is described in Sect. 3. The X-ray spectral analysis is reported in Sect. 4. Our results are presented and discussed in Sects. 5 and 6, respectively, and we present our conclusions in Sect. 7.
Throughout the paper, we adopt a ΛCDM cosmology with H0 = 70 km s−1 Mpc−1, ΩM = 0.27, and ΩΛ = 0.73. Errors are reported at 1σ level with upper limits quoted at 90% confidence level.
2. The HYPERION sample and the XMM-Newton Heritage program
The HYPERION sample is defined by the selection of all the z > 6 hyperluminous QSOs (Lbol ≥ 1047 erg s−1) known up to 2020 that required an initial seed BH mass of 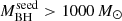 accreting via continuous exponential growth at the Eddington rate to form the measured SMBH mass. The selection was performed on the 46 unlensed radio-quiet hyperluminous z > 6 QSOs known with published SMBH masses at the end of 2020 (i.e., Willott et al. 2010; De Rosa et al. 2011; Mazzucchelli et al. 2017; Wu et al. 2015; Bañados et al. 2018b; Shao et al. 2017; Reed et al. 2019; Wang et al. 2018; Pons et al. 2019; Chehade et al. 2018; Shen et al. 2019; Yang et al. 2020; Wang et al. 2020; Eilers et al. 2020; Andika et al. 2020; Onoue et al. 2019; Matsuoka et al. 2019). The selection criterion of the HYPERION QSOs is reported in Fig. 1 as the red curve. The curves represent the time-dependent exponential mass growth – modeled as
accreting via continuous exponential growth at the Eddington rate to form the measured SMBH mass. The selection was performed on the 46 unlensed radio-quiet hyperluminous z > 6 QSOs known with published SMBH masses at the end of 2020 (i.e., Willott et al. 2010; De Rosa et al. 2011; Mazzucchelli et al. 2017; Wu et al. 2015; Bañados et al. 2018b; Shao et al. 2017; Reed et al. 2019; Wang et al. 2018; Pons et al. 2019; Chehade et al. 2018; Shen et al. 2019; Yang et al. 2020; Wang et al. 2020; Eilers et al. 2020; Andika et al. 2020; Onoue et al. 2019; Matsuoka et al. 2019). The selection criterion of the HYPERION QSOs is reported in Fig. 1 as the red curve. The curves represent the time-dependent exponential mass growth – modeled as 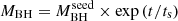 with an e-folding time of
with an e-folding time of 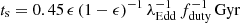 – of seed BHs of different masses (labeled in Fig. 1) formed at z = 20 (Valiante et al. 2016), assuming continuous accretion at the Eddington rate, that is, λEdd = 1, radiative efficiency of ϵ = 0.1, and an active phase duty cycle of fduty = 1. This sample therefore includes the “titans” among QSOs, that is, those powered by the SMBH with the largest mass assembly over the first gigayear of the Universe.
– of seed BHs of different masses (labeled in Fig. 1) formed at z = 20 (Valiante et al. 2016), assuming continuous accretion at the Eddington rate, that is, λEdd = 1, radiative efficiency of ϵ = 0.1, and an active phase duty cycle of fduty = 1. This sample therefore includes the “titans” among QSOs, that is, those powered by the SMBH with the largest mass assembly over the first gigayear of the Universe.
 |
Fig. 1. Selection and properties of the HYPERION sample. Left: SMBH mass as a function of redshift. All the reported points (diamonds and stars) are the subsample of 46 hyperluminous (Lbol > 1047 erg s−1) quasars with known SMBH masses reported at the end of 2020. The final selected 18 sources are reported as red stars. The curves represent the exponential growth of seed BHs of different masses (labeled) formed at z = 20, assuming continuous accretion (fduty = 1) at the Eddington rate (λEdd = 1; see Sect. 2). The red curve, corresponding to a growing seed of 1000 M⊙, was used to select the HYPERION sample. Right: distribution of the HYPERION sample in the MBH vs. Lbol plane (red stars) along with the distribution of the 83 z > 6 quasars with available MBH. All MBH are based on single-epoch MgII virial estimator and Lbol is from bolometric correction from the literature as of 2020. MBH and Lbol were consistently recomputed for all sources assuming the same ΛCDM cosmology and adopting the mass calibration from Vestergaard & Osmer (2009) and a bolometric correction of 5.15 to the 3000 Å luminosity from Richards et al. (2006). Dashed lines report the location of sources emitting a fixed fraction of LEdd. The contours report the location of the lower redshift (z = 0.7 − 1.9) SDSS-DR7 quasars from Shen et al. (2011) with MgII-derived masses. |
We note that this selection criterion is a convenient way to statistically select the sample of QSOs powered by SMBHs that experienced the most rapid growth during their formation history. This selection is physically motivated as it allows us to identify these sources through a reference curve, starting at a specific 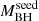 , for the continuous Eddington-limited mass growth. Under this assumption, the
, for the continuous Eddington-limited mass growth. Under this assumption, the 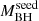 reported in Table 1 and required by each SMBH to grow its mass has to be considered solely as a proxy for the mass growth rate experienced by each SMBH and not necessarily as a physically meaningful quantity.
reported in Table 1 and required by each SMBH to grow its mass has to be considered solely as a proxy for the mass growth rate experienced by each SMBH and not necessarily as a physically meaningful quantity.
HYPERION QSO sample, ordered by decreasing redshift, and its general properties.
All HYPERION QSOs were discovered through an optical to mid-infrared (MIR) selection and benefit from extensive high-quality multi-band photometric and spectroscopic coverage from rest-frame UV (i.e., observed NIR band) to submm/mm bands. By definition, NIR spectroscopic data for all the HYPERION QSOs are available from spectrographs operating at either of the following observatories: Very Large Telescope (VLT), Magellan, Gemini, or Keck. From these data, we derived MgII-based single-epoch virial masses and bolometric luminosities from 3000 Å bolometric correction (e.g., Wu et al. 2015; Mazzucchelli et al. 2017; Bañados et al. 2018b; Reed et al. 2019; Shen et al. 2019). Similarly, photometric data in the NIR and submm/mm bands, are available at different levels of quality (e.g., Tripodi et al. 2023; Feruglio et al. 2023; Saccheo et al., in prep.).
We obtained MBH employing the MgII virial mass estimator by Vestergaard & Osmer (2009) which employs the full width at half maximum (FWHM) of the MgII line and the 3000 Å continuum luminosity. We also computed Lbol via the 3000 Å bolometric correction from Richards et al. (2006). We note that this choice of virial mass estimator makes our selection conservative and therefore robust, because among the MgII virial mass estimators, the one from Vestergaard & Osmer (2009) tends to give the lowest SMBH mass estimates (see e.g., Farina et al. 2022) and therefore the lowest 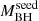 . Furthermore, the average E(B − V) estimated through a spectral energy distribution (SED) analysis for the HYPERION QSOs is < 0.01 (Saccheo et al., in prep.) and therefore the mass estimates are not affected by spectral reddening. The right panel of Fig. 1 shows the distribution of the HYPERION QSOs in the MBH vs. Lbol plane along with the distribution of the 83 z > 6 QSOs with estimated masses known by the end of 2020. The HYPERION QSOs distributed in the redshift range z ≈ 6 − 7.5 (mean z ∼ 6.7) have an average log(Lbol/erg s−1) ≈ 47.3 and span a mass range ≈109 − 1010 M⊙ leading to λEdd = 0.3 − 2.6. We note that the uncertainties on virial mass estimates are dominated by systematic uncertainties reaching 0.3–0.5 dex (e.g., Shen & Liu 2012). There is a certain amount of variation in the estimated masses: if we employ the Shen et al. (2011) MgII-based mass estimator for our selection, which typically gives high MBH estimates (Farina et al. 2022), we obtain 0.2 dex higher SMBH masses, implying λEdd smaller by ∼40% and
. Furthermore, the average E(B − V) estimated through a spectral energy distribution (SED) analysis for the HYPERION QSOs is < 0.01 (Saccheo et al., in prep.) and therefore the mass estimates are not affected by spectral reddening. The right panel of Fig. 1 shows the distribution of the HYPERION QSOs in the MBH vs. Lbol plane along with the distribution of the 83 z > 6 QSOs with estimated masses known by the end of 2020. The HYPERION QSOs distributed in the redshift range z ≈ 6 − 7.5 (mean z ∼ 6.7) have an average log(Lbol/erg s−1) ≈ 47.3 and span a mass range ≈109 − 1010 M⊙ leading to λEdd = 0.3 − 2.6. We note that the uncertainties on virial mass estimates are dominated by systematic uncertainties reaching 0.3–0.5 dex (e.g., Shen & Liu 2012). There is a certain amount of variation in the estimated masses: if we employ the Shen et al. (2011) MgII-based mass estimator for our selection, which typically gives high MBH estimates (Farina et al. 2022), we obtain 0.2 dex higher SMBH masses, implying λEdd smaller by ∼40% and 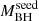 larger by a factor 1.6.
larger by a factor 1.6.
Table 1 lists the 18 selected QSOs in the HYPERION sample along with their celestial coordinates, MgII-based redshifts, Lbol, MBH, Eddington ratio (λEdd), required 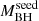 , and L2500 Å obtained through interpolation of photometric points (Saccheo et al., in prep.). All these quantities were re-evaluated by uniformly adopting a ΛCDM cosmology with ΩM = 0.27 and ΩΛ = 0.73. Hereafter, we refer to the single QSOs with abbreviated names; these are reported in Table 1, as “J” plus the digits of their RA.
, and L2500 Å obtained through interpolation of photometric points (Saccheo et al., in prep.). All these quantities were re-evaluated by uniformly adopting a ΛCDM cosmology with ΩM = 0.27 and ΩΛ = 0.73. Hereafter, we refer to the single QSOs with abbreviated names; these are reported in Table 1, as “J” plus the digits of their RA.
For two HYPERION QSOs (J0224 and J0100), good-quality archive X-ray data from XMM-Newton are already available and their spectral analysis was presented by Pons et al. (2019) and Ai et al. (2017). For the remaining HYPERION QSOs, we have an ongoing 2.4 Ms XMM-Newton Multi-Year Heritage program (PI L. Zappacosta; Proposal ID 088499) – approved in December 2020 with a three-year time span – designed to collect unprecedented high-quality X-ray data for such a large sample of QSOs at EoR. Specifically, the HYPERION XMM-Newton Multi-Year Heritage program (hereafter XMM-HYPERION) is collecting, for the first time, X-ray data for seven sources and is improving the data quality for nine previously observed sources for which the X-ray data available are of limited quality (either leading to nondetections or to mainly 10–15 net-count detections; e.g., Vito et al. 2019; Pons et al. 2019; Connor et al. 2020). The aim of XMM-HYPERION is to achieve the high-quality data standard obtained for the unlensed QSOs J0224 and J0100 (i.e., at least 100 net counts from pn+MOS1+MOS2 data in the 0.5–10 keV band) for all QSOs in the sample. This would ensure a ∼10% accuracy level (1σ) characterization of X-ray spectral properties, namely the photon index of the power-law and the unabsorbed 2–10 keV luminosity (L2 − 10) on these sources.
3. Data reduction and photometry
In this work, we report data from the first year of observations of the XMM-HYPERION program. In addition, we also present a re-analysis of the two archival HYPERION sources J0224 and J0100 for consistency. In total, we present ∼0.94 Ms of new data on ten sources, which increases to ∼1.04 Ms when accounting for the observations of the two archival sources. Table 2 presents details of the considered observations. XMM-HYPERION observations are already complete for only one of the considered targets, namely J1342, with two exposures. Observations of the remaining targets in this subsample will be completed over the following two years of the XMM-HYPERION program with at least one further exposure. The exact schedule of the exposures is flexible and may vary depending on the flux state of each target measured on their first exposure.
Journal of the observations of the HYPERION targets from the XMM-HYPERION (upper part of the table) and archive (lower part of the table).
The XMM-Newton data were processed with SAS v19.1.0. Following the standard procedures outlined in the XMM-Newton science threads, we used the epicproc package to create newly calibrated event files. We produced high-energy light curves for the EPIC pn and MOS detectors in the energy ranges 10–12 keV and > 10 keV, respectively. We visually inspected these light curves for the presence of high background flares. Following the recommendations presented in the most updated calibration technical notes1, we identified the good time intervals by removing the part of the pn observations affected by rates higher than 0.4 cts s−1 (∼0.41 cts s−1 for J011). As for the MOS1 and MOS2 exposures, we adopted thresholds in the range 0.12–0.17 cts s−1 and 0.18-0.22 cts s−1, respectively. We determined that, for the pn, only one observation (J0244) had ∼20% of the exposure affected by high background periods. All other sources had their observation impacted by ∼40%−50%. Regarding the MOS exposures, we calculated a percentage of time affected by high backgrounds in the range ∼8%−27% and ∼6%−19% for MOS1 and MOS2, respectively. In Table 2 we report nominal and cleaned exposures for each observation.
We first identified the point-like sources across the field of view. We created 0.5–2 keV energy band pn images and ran the task edetect_chain on these by setting a detection maximum likelihood (DETML2) threshold DETML = 6. This blind search also produced the detection of all the QSO targets, with the exception of J011, J0020, and J231.6 (but see below for J0020). We verified the target detection, accounting for the source position prior and performing forced aperture photometry on the QSO positions. We extracted the source counts on circular regions of 20 arcsec in radius (corresponding to ∼80% of the on-axis PSF encircled energy fraction at 1.5 keV) centered on the QSO optical position (see Table 1), except for the cases of J0244 and J0020, which had a nearby source (28 arcsec and 17 arcsec distant), for which we adopted smaller apertures of 15 arcsec and 12 arcsec radius (∼65%−70% of the PSF encircled energy fraction), respectively. The background counts were extracted for the MOS cameras on circular apertures of 2.5–3.4 arcmin in radius centered on the QSO position. For the pn camera, we adopted rectangular regions positioned around the target, rotated roughly with the same detector position angle and with long and short sides in the range 3.6–3.9 arcmin and 1.9–2.7 arcmin, respectively. The background count extraction was performed excluding detector circular regions of 40 arcsec in radius centered on (1) the contaminant point sources previously identified on the 0.5–2 keV pn image, (2) other sources reported on both MOS cameras, and (3) the target QSOs. For the bright sources, we excluded larger regions of 50 arcsec in radius. Figure 2 shows the adopted extraction regions on the 0.5–2 keV images of the three XMM-Newton cameras for the first observation of J1342 (J1342_1; see Table 2). Images and adopted extraction regions for the second observation of J1342 (J1342_2) and other sources are reported in Appendix A.1.
 |
Fig. 2. EPIC 0.5–2 keV pn, MOS1, and MOS2 camera images for the first J1342 observation reported in Table 2 of the XMM-HYPERION program presented in this work. All the images are smoothed by a Gaussian kernel of 3 pixels in radius for better visualization. Source and background regions adopted for photometric and spectral extractions are reported in red and black, respectively. Dashed circular regions indicate areas excluded from the background extraction. Images for the second J1342 exposure (J1342_2) and other XMM-HYPERION QSOs presented in this work are reported in Appendix A.1. |
We computed the ≥99% confidence level source detection by calculating the no-source binomial probability and estimated net counts (with uncertainties) on the 0.5–2 keV (soft band), 2–10 keV (hard band), and 0.5–10 keV (full band) images of the three XMM-Newton cameras (see Weisskopf et al. 2007; Vito et al. 2019). We considered as detections the sources with a no-source binomial probability ≤1% on either the pn detector or on both the MOS detectors in at least one band. Table 3 reports the measured source counts with uncertainties. All the targets resulted in detections, with the exception of J011 and J231.6 (J0020 is detected in this case), which is in broad agreement with the results of the source-detection search performed across the field. For the sources J083.8 and J029, this is the first reported X-ray detection.
Source net counts from fixed-aperture photometry on the EPIC detectors in the soft, hard, and full energy bands.
For the undetected sources, we calculated pn upper limits on fluxes, luminosities, and on αOX3. These are reported in Table 4 along with the spectral measurements for the detected sources (see Sect. 4). Specifically, we estimated the total counts in the soft and hard band by correcting the fixed aperture photometry of 20 arcsec radius reported in Table 3 and accounting for ∼80% of the 1.5 keV total encircled energy fraction. We estimated the fluxes using the X-ray spectral fitting package XSPEC (Arnaud 1996) assuming the spectral response files extracted at the source position and adopting a power-law model with both Γ = 2 and Γ = 2.4 (i.e., the average Γ from a joint spectral analysis of the detected sources; see Sect. 4.2 for details) absorbed by the Galactic column density. The latter is taken from the HI4PI survey (HI4PI Collaboration 2016) as the weighted average at the position of each source within a radius of 0.1 deg. We then estimated the unabsorbed 2–10 keV and 2 keV luminosities with XSPEC by assuming the same absorbed power-law spectral model.
Best-fit parameters from the X-ray spectral analysis.
4. Spectral analysis
In the following, we report the spectral analysis performed for all the detected sources in Table 3.
4.1. Single source analysis
The source and background spectral extractions were performed on the same regions adopted for the count extractions. Given the low counts of the sources and the background dominated regime, we evaluated the best spectral binning scheme before performing the spectral analysis. We simulated different input spectra and evaluated the accuracy of each binning scheme in recovering the input power-law parameters. We tried the following binning schemes: minimum 1, 3, 5, 10 counts per bin and the optimal Kaastra & Bleeker (2016, KB hereafter) grouping. We verified that the KB binning4, which provides the optimal binning for data and model accounting for the source spectral shape, the variable spectral resolution, and the average photon energy in each bin, is the best scheme for recovering unbiased estimates of the parameters, and is also insensitive to the energy over which the spectral analysis is performed. We use the KB scheme for the following spectral analysis. See Appendix B for a detailed description of the simulations.
The spectral analysis was performed with XSPEC v12.11.1. We performed the modelings by using the Cash statistics with direct background subtraction (W-stat in XSPEC; Cash 1979; Wachter et al. 1979).
Given the Type 1 nature of these sources, their high redshift, and the low number of counts in the spectra, we adopted a simple power-law model – that is, assuming no intrinsic NH for the QSOs – modified by the absorption by the Galaxy interstellar medium (adopting HI4PI Collaboration 2016, maps), parameterized by a tbabs model in XSPEC. We jointly modeled the three EPIC camera spectra. Given the low-counts regime, we neglect intercalibration shifts between the detectors after checking that they are consistent with unity within the uncertainties. We performed the fits for only the ten detected sources and carried out the analysis in the energy range 0.3–7 keV (corresponding to rest-frame energies from ∼2 to ∼50 keV) by leaving Γ and the normalization free to vary.
The best-fit parameters are reported in Table 4 where the uncertainty on the fluxes and luminosities is computed by freezing Γ at its best-fit value. Spectra and best-fit models for the XMM-HYPERION targets are reported in Fig. 3. This is the first X-ray spectral analysis reported for the sources J083.8 and J029. Other detected sources were previously observed and analyzed with data of lower quality, either with Chandra and/or XMM-Newton. A comparison with previous analyses is reported in Appendix C. Given the background-dominated regime, we verified that changing the spectral analysis energy range to progressively lower or higher observed energies (i.e., 2, 5, or 10 keV) does not significantly impact our results, with values being always less than 10% from the best-fit Γ and well within the 1σ uncertainties quoted in Table 4.
 |
Fig. 3. XMM-Newton pn (black), MOS1 (red), and MOS2 (green) 0.3–7 keV spectra and best-fit models (stepped continuous thick lines) for the ten detected HYPERION QSOs presented in this paper. Spectra were further rebinned for visual purposes and are reported at their rest-frame energy. Residuals are shown as data minus best-fit model in the bottom panels. For the source J1342, blue, cyan, and magenta represent the second data set. |
4.2. Average spectral slope
To obtain a measure of the average spectral slope from this HYPERION subsample, we performed a joint modeling from all the ten detected sources. Each QSO dataset, except J0100, contributes to the joint fit with pn+MOS1+MOS2 0.3–7 keV net counts in the range ∼50 − 140. In the case of J0100, which has more than 300 pn+MOS net counts, we selected three “chunks” (chunks1, chunks2, and chunks3) of observations representative of the average pn and MOS net counts gathered from the other datasets, that is, with ∼50 ± 20 and ∼40 ± 15 net counts for pn and MOS1+MOS2 detectors, respectively. In order to ensure a random sampling of the observation, the three chunks were selected by adopting a nonoverlapping count-rate selection of the high-energy light curves used for the high-background screening5. We performed a joint pn+MOS1+MOS2 spectral analysis of each chunk and verified that with the simple power-law modeling modified by the Galactic absorption, the Γ and the 2–10 keV and 2 keV X-ray luminosities are consistent with those reported for the entire dataset (see Table 4).
We performed the joint modeling of the ten QSOs exploiting the 11 datasets (including the two observations of J1342) three times, each analysis including one of the three chunks of the J0100 observation. In total, we modeled a total of about 900 net counts of spectral data (0.3–7 keV) of which approximately 500 and 400 net counts are from pn and MOS detectors, respectively. We adopted a simple power-law model absorbed by Galactic interstellar medium, with Γ linked across all the datasets. We included and tied the cross-calibration constants for each detector. We left the linked Γ and the normalizations for each source free to vary. A fit to these data resulted in best-fit values of 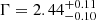 (including chunk1 of J0100; W-stat/d.o.f. = 1922.8/1730), Γ = 2.40 ± 0.11 (including chunk2; W-stat/d.o.f. = 1934.2/1730), and
(including chunk1 of J0100; W-stat/d.o.f. = 1922.8/1730), Γ = 2.40 ± 0.11 (including chunk2; W-stat/d.o.f. = 1934.2/1730), and 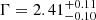 (including chunk3; W-stat/d.o.f. = 1944.0/1730).
(including chunk3; W-stat/d.o.f. = 1944.0/1730).
We verified the stability of the results as a function of the energy range and find that the best-fit value changes within the range Γ = 2.39 − 2.46 with no trend as a function of energy. Errors on Γ increase from 0.10 to 0.13 by restricting the band interval. We also removed the datasets with the highest number of net counts (142 total net counts; J0244) and lowest net counts (47 and 52 total net counts; J036.5 and J0020, respectively), obtaining substantially unaffected best-fit Γ values (Γ = 2.37 − 2.42).
Given the good spectral quality (large number of counts) reached in the joint analysis, we also tried to include an intrinsic absorption term to estimate the average hydrogen column density in QSO at EoR. The absorber may be associated with local absorption in the vicinity of the QSO, or with material further out in dense patches of the intergalactic medium. We obtain best-fit NH ranging from 2.1 × 1021 cm−2 to 3.7 × 1022 cm−2 and a corresponding, slightly steeper Γ in the range 2.42–2.62. However, the NH are highly uncertain and consistent with no absorption at ∼1.2 − 1.3σ level. Therefore, we conclude that mild absorption (NH ≈ 1021 − 1022 cm−2) is not required in HYPERION QSOs.
Finally, we performed a fit in the same rest-frame energy range for each source. The common energy range is defined as 0.3 keV * (1 + zmax)−7 keV * (1 + zmin)≈2.6 − 49 keV, where zmin and zmax are the highest and lowest redshift covered by the HYPERION sample considered in this work. We obtained Γ ranging from 2.37 to 2.47, with uncertainties of the order of 0.11–0.13.
We also tried a power-law model with a high-energy cutoff (Ecut) under the hypothesis that the steepening of the spectrum is due to the cutoff close to or within the relatively high rest-frame energies covered by the spectral data. By setting Γ in the range of canonical values 1.8–2.0, we obtain an energy cutoff Ecut in the range 14 − 25 keV in all cases. Specifically, the best-fit Ecut values for the assumed Γ = 1.9 are all in the range ∼17 − 19 keV. Indeed, we obtain 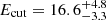 keV for J0100 chunk1,
keV for J0100 chunk1, 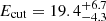 keV for chunk2, and
keV for chunk2, and 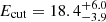 keV for chunk3. All the fits are statistically indistinguishable from the simple power-law case, having |ΔW-stat|≲2.
keV for chunk3. All the fits are statistically indistinguishable from the simple power-law case, having |ΔW-stat|≲2.
We note that in our joint and single source analysis, we neglected contributions from a Compton reflection component due to the coronal X-rays inverse Compton-scattered by the surrounding matter. Typically, QSOs show low or virtually no reflection (e.g., Vignali et al. 1999; Reeves & Turner 2000; Page et al. 2005; Zappacosta et al. 2018). A non-negligible Compton reflection contribution in the HYPERION QSOs would result in even steeper Γ for their power-law continuum.
5. Results
In the following, we compare the X-ray properties inferred from our analysis of the HYPERION spectra with those reported for other z ≤ 6 sources, especially QSOs that are analogous in terms of luminosity and λEdd, in order to assess possible differences linked to radiative output or accretion rate – as parameterized by the λEdd – or to the SMBH mass-accretion history stage of the SMBH, adopting 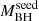 as a proxy.
as a proxy.
5.1. The steepness of the X-ray spectrum
The Γ measured for each HYPERION QSO is on average very steep. Figure 4 shows the distribution of Γ as a function of λEdd for our HYPERION QSOs and other AGN and QSOs. Recent relations measured for a local sample of low-luminosity AGN involving these two quantities are reported to aid with the interpretation of the plot (Trakhtenbrot et al. 2017; Liu et al. 2021). HYPERION sources show the steepest values on average, the large majority exhibiting Γ ≥ 2.3. Other z > 6 QSOs with good-quality data (i.e., > 30 net counts) not included in HYPERION (i.e., which failed the 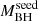 selection criterion) from Vito et al. (2019) show flatter Γ values. Other λEdd-analog QSO samples at lower redshift, that is, the hyperluminous WISSH z = 2 − 3 QSOs from Zappacosta et al. (2020) and the high-λEdd nearby (z < 1) QSOs from Laurenti et al. (2022, hereafter L22), have noticeably flatter Γ (although with large scatter), in agreement with the canonical Γ = 1.8 − 2 values. The reported relations predict Γ ≈ 1.9 − 2.1 at the average HYPERION λEdd. The average Γ for HYPERION QSOs from the joint spectral analysis is inconsistent with the relations at > 3σ level.
selection criterion) from Vito et al. (2019) show flatter Γ values. Other λEdd-analog QSO samples at lower redshift, that is, the hyperluminous WISSH z = 2 − 3 QSOs from Zappacosta et al. (2020) and the high-λEdd nearby (z < 1) QSOs from Laurenti et al. (2022, hereafter L22), have noticeably flatter Γ (although with large scatter), in agreement with the canonical Γ = 1.8 − 2 values. The reported relations predict Γ ≈ 1.9 − 2.1 at the average HYPERION λEdd. The average Γ for HYPERION QSOs from the joint spectral analysis is inconsistent with the relations at > 3σ level.
 |
Fig. 4. Γ vs. λEdd for a compilation of local or high-λEdd AGN and high-redshift luminous QSOs. Red stars are the HYPERION QSOs presented in this work. Green four-pointed stars are other z > 6 QSOs detected with ≳30 net counts from the X-ray spectral analysis performed by Vito et al. (2019) and not included in the HYPERION sample. Quasars at Cosmic Noon (z = 2 − 4) are reported as purple triangles (the WISSH QSOs from Zappacosta et al. 2020), empty cyan circles (Shemmer et al. 2006a, 2008), and pink diamonds (Nardini et al. 2019; Trefoloni et al. 2023). Local high-λEdd QSOs (Laurenti et al. 2022) and local AGN including Narrow Line Seyfert 1 (NLSy1s) galaxies (Liu et al. 2021) are shown as blue squares and yellow circles, respectively. Reported are also the most recent relations from a linear fit to the local AGN (i.e., Trakhtenbrot et al. 2017; Liu et al. 2021). The uncertainties on λEdd from QSOs with MBH estimated using a single-epoch virial mass estimator are dominated by systematic uncertainties and can be as high as 0.5 dex. The statistical uncertainty on λEdd for the local AGN (Liu et al. 2021) whose masses are estimated via reverberation mapping is 0.1 dex and 0.2 dex for the sub-Eddington and super-Eddington sources, respectively. |
In the Γ vs. z plot reported in Fig. 5, we show our joint analysis Γ value compared with the results of other, independent joint analyses of z ≳ 6 QSOs (Nanni et al. 2017; Vito et al. 2019; Wang et al. 2021a). Thanks to the combination of a sizable number of detected sources and the higher quality data gathered by the first year of XMM-HYPERION, the uncertainty in our average joint value is smaller by a factor 2–3.
 |
Fig. 5. Distribution of the average Γ as a function of redshift. The plot includes data from joint spectral analysis or average values from samples of QSOs. In particular, starred data are from joint spectral analysis of samples of z > 6 QSOs. The black star with a central red circle, the green four-pointed star, the magenta six-pointed star, and the three-pointed star are HYPERION QSOs, and the samples of Vito et al. (2019), Wang et al. (2021a), and Nanni et al. (2017), respectively. The empty squares, diamond, and circle are averages from the stacked spectral analyses of luminous and hyperluminous QSOs from Just et al. (2007), Vignali et al. (2005), and Shemmer et al. (2006b), respectively. The empty triangle represents the average Γ from the PG quasars (Piconcelli et al. 2005). Blue squares are high-λEdd local QSOs (Laurenti et al. 2022) and purple triangles are hyperluminous high-λEdd WISSH QSOs (Zappacosta et al. 2020). Pink diamonds are z ∼ 3 luminous blue quasars from Nardini et al. (2019). Vertical error bars report 1σ uncertainties on Γ while horizontal error bars indicate the redshift range covered by the QSO sample considered in each dataset. |
We also report in the plot previous joint spectral analysis Γ values from other luminous QSO samples at 1 < z < 6 (Vignali et al. 2005; Shemmer et al. 2006a; Just et al. 2007), and the average values for the WISSH QSOs from Zappacosta et al. (2020), for the local PG QSOs (Piconcelli et al. 2005) and the high-λEdd L22 QSOs. These are samples of analogous sources in terms of Lbol and/or λEdd. All z < 6 results from these analogous sources show consistency with Γ = 1.8 − 2. The average Γ from all the considered z < 6 QSO samples is Γz < 6 = 1.91 ± 0.04.
HYPERION QSOs have a Γ value that is inconsistent with Γ = 2 at > 4σ. The same inconsistency level holds with the Γ reported for z < 6 sources of similar Lbol or λEdd. In particular, Γ for HYPERION is inconsistent at ∼4.8σ level with Γz < 6. For the WISSH QSO sample analyzed by Zappacosta et al. (2020), we also measured the average Γ obtained by performing the spectral fits from 2 keV, that is, the same rest-frame low-energy bound probed for the HYPERION QSOs. We obtained an average of Γ = 1.93 ± 0.08, which is consistent with the average value of Γ = 1.84 ± 0.07 inferred from the full band (i.e., from 0.2–0.3 keV observed frame low-energy bound, corresponding to 0.6–0.9 keV rest-frame) spectral modelings. This further indicates that the steepness of the HYPERION Γ values does not depend on the probed rest-frame energy range. Consistency between the HYPERION Γ value and those from past works analyzing z > 6 samples is reported at the 1 − 2σ level. This is due to the large uncertainties reported in past z > 6 QSO analyses.
All of the above comparisons suggest that the Γ of HYPERION QSOs is steeper regardless of the luminosity or accretion rate of the QSOs and therefore that it is due to an evolutionary effect. Given the selection criteria used to build the HYPERION QSO sample, this evolutionary effect is possibly linked to the particularly fast SMBH mass growth history of these sources.
In order to test this hypothesis, we divided the ten HYPERION QSOs into two samples of equal size according to their SMBH growth history and therefore based on their required 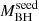 . Specifically, we selected: (i) a high
. Specifically, we selected: (i) a high 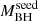 sample (i.e.,
sample (i.e., 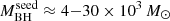 ; including J1342, J1120, J0100, J0020, and J036.5) and (ii) a low
; including J1342, J1120, J0100, J0020, and J036.5) and (ii) a low 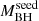 sample (i.e.,
sample (i.e., 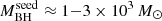 ; including J0244, J0224, J0050, J083.8, and J029). X-ray data for each sample include an approximately equal number of pn+MOS1+MOS2 counts, with 410 and 495 net counts for the high-
; including J0244, J0224, J0050, J083.8, and J029). X-ray data for each sample include an approximately equal number of pn+MOS1+MOS2 counts, with 410 and 495 net counts for the high-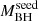 and low-
and low-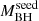 samples, respectively. We performed a joint spectral analysis for each sample. For the high-
samples, respectively. We performed a joint spectral analysis for each sample. For the high-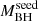 sample, we obtained Γ = 2.64 − 2.7 (depending to the J0100 chunk used), with an uncertainty of ∼0.16, and for the low-
sample, we obtained Γ = 2.64 − 2.7 (depending to the J0100 chunk used), with an uncertainty of ∼0.16, and for the low-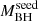 sample, we obtained Γ = 2.21 ± 0.13, a difference that is significant at the 2.1 − 2.4σ level. The average redshift of each sample is 6.86 and 6.37 for the high-
sample, we obtained Γ = 2.21 ± 0.13, a difference that is significant at the 2.1 − 2.4σ level. The average redshift of each sample is 6.86 and 6.37 for the high-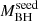 and low-
and low-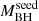 samples, respectively. Therefore, the Γ difference could also be due to a redshift (i.e., temporal) dependence. Indeed, redshift and
samples, respectively. Therefore, the Γ difference could also be due to a redshift (i.e., temporal) dependence. Indeed, redshift and 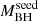 in this sample correlate with a Spearman rank correlation coefficient of ∼0.8. This is probably due to Malmquist bias, as the virial mass estimators are luminosity dependent. To explore the redshift dependence we performed joint analyses of the five lowest-redshift QSOs and five highest-redshift QSOs (z = 6.29 and z = 6.94, respectively) obtaining Γ = 2.21 − 2.29 (± ∼ 0.14) and
in this sample correlate with a Spearman rank correlation coefficient of ∼0.8. This is probably due to Malmquist bias, as the virial mass estimators are luminosity dependent. To explore the redshift dependence we performed joint analyses of the five lowest-redshift QSOs and five highest-redshift QSOs (z = 6.29 and z = 6.94, respectively) obtaining Γ = 2.21 − 2.29 (± ∼ 0.14) and 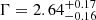 , respectively, and confirming the increasing Γ trend with redshift. However, this Γ steepening, if confirmed, is happening in ∼108 years, which is a very short period of time for any likely redshift-dependent mechanism to act on cosmological timescales. We therefore support the hypothesis that the steepening (if confirmed by additional data) is dependent on
, respectively, and confirming the increasing Γ trend with redshift. However, this Γ steepening, if confirmed, is happening in ∼108 years, which is a very short period of time for any likely redshift-dependent mechanism to act on cosmological timescales. We therefore support the hypothesis that the steepening (if confirmed by additional data) is dependent on 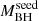 and therefore on the rapid mass growth of the SMBH.
and therefore on the rapid mass growth of the SMBH.
A steep spectrum can also be mimicked by a power law with canonical Γ = 1.9 and a high-energy cutoff at relatively low energies. Our data are not able to discriminate between a simple power law and a cutoff power-law model, and therefore we can rule out neither possibility. Figure 6 shows the distribution of energy cutoff Ecut as a function of L2 − 10. The HYPERION QSOs considered in this work are compared to z < 0.5 lower-luminosity AGN and to z = 2 − 4 hyperluminous lensed QSOs (Lanzuisi et al. 2019; Bertola et al. 2022) as well as to local super-Eddington accreting AGN from Tortosa et al. (2023). The HYPERION value of Ecut is at extremely low energies and, although consistent with a few measurements for low-luminosity AGN, is inconsistent with the few measurements for QSOs at similar L2 − 10. Furthermore, this measured Ecut is far from the forbidden area in which runaway electron–positron pair production would act as a thermostat, lowering the temperature of the corona and therefore Ecut (see Svensson 1984; Stern et al. 1995). The extent of the forbidden region is dependent on MBH and is calculated from Fabian et al. (2015) assuming a slab geometry for the corona (we do not show the less extended and therefore less conservative regions for a corona with a hemisphere geometry).
 |
Fig. 6. Distribution of Ecut as a function of L2 − 10. Light blue and orange filled circles are estimates from a compilation of local AGN (Bertola et al. 2022, and references therein) and z ≈ 2 − 4 QSOs (Lanzuisi et al. 2019; Bertola et al. 2022). Purple circles are from local super Eddington accreting AGN from Tortosa et al. (2023). Hollow magenta circles are binned averages estimated by Ricci et al. (2018) for a large sample of local AGN from the BAT AGN Spectroscopic Survey (BASS). The HYPERION average Ecut measurement (assuming Γ = 1.9) from our joint analysis is reported as a black star with an inner red circle. Green regions are the forbidden regions (for a slab corona model) due to runaway electron–positron pair production (see Svensson 1984) for log(MBH/M⊙) = 8.5 and log(MBH/M⊙) = 9.5. |
Ricci et al. (2018) found a statistically significant anti-correlation between Ecut and λEdd for a sample of local AGN from the BASS survey (Koss et al. 2017) and up to λEdd ≈ 0.4. An extrapolation of this relation to the average λEdd = 0.8 (or λEdd = 0.5 if adopting the mass estimator from Shen et al. 2011) of the HYPERION subsample studied in this work indicates values as low as 100 keV (i.e., accounting for the uncertainty given by the median absolute deviation of this relation). Our Ecut is inconsistent at > 3σ level with the trend of this relation (i.e., the 3σ upper bound is ∼60 keV).
5.2. Comparing the X-ray contribution to the UV/bolometric radiative output
We also compared the behavior of the X-ray coronal luminosity of the HYPERION QSOs to the bolometric radiative output. The bolometric correction 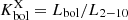 has a somewhat flat trend at Seyfert-like luminosities progressively increasing toward higher luminosity sources (e.g., Marconi et al. 2004; Lusso et al. 2012; Duras et al. 2020). The left panel of Fig. 7 shows the bolometric correction
has a somewhat flat trend at Seyfert-like luminosities progressively increasing toward higher luminosity sources (e.g., Marconi et al. 2004; Lusso et al. 2012; Duras et al. 2020). The left panel of Fig. 7 shows the bolometric correction 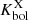 as a function of Lbol. The HYPERION QSOs are in agreement with the trend delineated by other data (except the nearby optically selected high-λEdd QSO from L22) and described by the relation of Duras et al. (2020). Despite this, the locations of the HYPERION QSOs in the
as a function of Lbol. The HYPERION QSOs are in agreement with the trend delineated by other data (except the nearby optically selected high-λEdd QSO from L22) and described by the relation of Duras et al. (2020). Despite this, the locations of the HYPERION QSOs in the 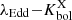 plane as reported in the right panel of Fig. 7 appear to be in disagreement with the trend reported by Duras et al. (2020). This disagreement is shared by all QSO samples and highlights the lack of a clear dependence between
plane as reported in the right panel of Fig. 7 appear to be in disagreement with the trend reported by Duras et al. (2020). This disagreement is shared by all QSO samples and highlights the lack of a clear dependence between 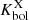 and λEdd. This is mainly due by the steep Lbol dependence of
and λEdd. This is mainly due by the steep Lbol dependence of 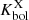 at high-luminosity regimes6. This is not well sampled by Duras et al. (2020) and is dominated by the bulk of the low-luminosity, highly accreting AGN population.
at high-luminosity regimes6. This is not well sampled by Duras et al. (2020) and is dominated by the bulk of the low-luminosity, highly accreting AGN population.
 |
Fig. 7. X-ray bolometric correction ( |
We now investigate the αOX parametrizing the slope between the monochromatic luminosities at 2 keV and 2500 Å and defined as αOX = log(L2 keV/L2500 Å)/log(ν2 keV/ν2500 Å). Figure 8 reports αOX vs. L2500 Å for several AGN samples spanning more than four decades in L2500 Å along with best-fit relations from Lusso & Risaliti (2016) and Martocchia et al. (2017). Unlike other hyperluminous or high-λEdd QSOs exhibiting, on average, a weaker X-ray emission compared to the UV one, the HYPERION QSOs exhibit, on average, slightly higher 2 keV luminosities, which almost systematically exceed expectations based on the αOX vs. L2500 Å relation, with no sources exhibiting the X-ray weakness typically shown by a consistent fraction of sources in the WISSH and L22 samples. Indeed, at the mean log L2500 Å, the Lusso & Risaliti (2016) relation, providing the more accurate parameterization of the bulk of the AGN population, predicts αOX = −1.69, while the average for the detected HYPERION QSOs is 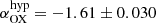 . This translates to an average
. This translates to an average 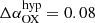 . We computed the distribution of the ΔαOX values for HYPERION and the Lusso & Risaliti (2016) QSOs detected with a signal-to-noise ratio (S/N) > 5 (see Fig. 9) and performed a Kolmogorov–Smirnov test on the detected data to check the difference between the two datasets. The two distributions differ mildly, with a null-hypothesis probability of Pnull = 0.0576. We further verified this disagreement by performing 10 000 random draws of ΔαOX in subsamples of ten sources (i.e., the same size as the detected HYPERION QSO sample reported in this work) from the Lusso & Risaliti (2016) sample. We verified that their average ΔαOX does not exceed that shown by the HYPERION QSOs for 98.4% of the time, and therefore that the disagreement of our sources is not strong. This result is also slightly at variance with the αOX previously estimated for z > 6 QSOs by other works (Vito et al. 2019; Wang et al. 2021a). This is mainly due to the fact that these latter assumed a Γ = 2 to derive L2 keV. Therefore, we can partly explain this mild difference between distributions as being due to a combination of steep Γ and unchanged integrated L2 − 10, (i.e., in line with the values expected by the
. We computed the distribution of the ΔαOX values for HYPERION and the Lusso & Risaliti (2016) QSOs detected with a signal-to-noise ratio (S/N) > 5 (see Fig. 9) and performed a Kolmogorov–Smirnov test on the detected data to check the difference between the two datasets. The two distributions differ mildly, with a null-hypothesis probability of Pnull = 0.0576. We further verified this disagreement by performing 10 000 random draws of ΔαOX in subsamples of ten sources (i.e., the same size as the detected HYPERION QSO sample reported in this work) from the Lusso & Risaliti (2016) sample. We verified that their average ΔαOX does not exceed that shown by the HYPERION QSOs for 98.4% of the time, and therefore that the disagreement of our sources is not strong. This result is also slightly at variance with the αOX previously estimated for z > 6 QSOs by other works (Vito et al. 2019; Wang et al. 2021a). This is mainly due to the fact that these latter assumed a Γ = 2 to derive L2 keV. Therefore, we can partly explain this mild difference between distributions as being due to a combination of steep Γ and unchanged integrated L2 − 10, (i.e., in line with the values expected by the 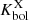 vs. Lbol relation). Indeed, at fixed L2 − 10 and a change in Γ slope from 2 to 2.4 increases L2 keV by a factor of ∼1.3 and hence αOX by ∼0.11, in agreement with
vs. Lbol relation). Indeed, at fixed L2 − 10 and a change in Γ slope from 2 to 2.4 increases L2 keV by a factor of ∼1.3 and hence αOX by ∼0.11, in agreement with 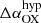 .
.
 |
Fig. 8. αOX vs. L2500 Å for a compilation of AGN catalogs. Symbols refer to the AGN samples as in Fig. 4, except for the green dots, which are detected AGN with S/N > 5 from Lusso & Risaliti (2016). Upper limits for the HYPERION QSOs are estimated assuming a power law with fixed Γ = 2.4 (see Sect. 3 and Table 4). The dashed line is the linear fit from Martocchia et al. (2017) while the solid line refers to the best-fit relation from Lusso & Risaliti (2016) and for the subsample with S/N > 5, E(B − V)≥0.1, and 1.6 ≤ Γ1 − 5 ≤ 2.8, with Γ1 − 5 being the photon index estimated between the luminosities at 1 keV and 5 keV. Light blue crosses and asterisks present the values predicted by the QSOSED model (Kubota & Done 2018) assuming average HYPERION parameters and spin a = 0 and a = 1, respectively. These values are reported from top-left to bottom-right from log ṁ = −1 to log ṁ = 0.2 in steps of Δlog ṁ = 0.2. |
 |
Fig. 9. Normalized distributions of the ΔαOX relative to the relation from Lusso & Risaliti (2016; see Fig. 8) for HYPERION QSOs (red filled histogram) and the AGN detected with S/N > 5 from Lusso & Risaliti (2016; dashed hollow histogram). The gray region marks the position of the X-ray-weak sources. |
Assuming a best-fit power-law model with a high-energy cutoff and canonical Γ = 1.9 would result in an average αOX = −1.65 ± 0.071, which is somewhat softer and is more in line with the αOX vs. L2500 Å relations, with a ΔαOX = 0.042.
We note that in this high luminosity regime, there is a clear contrast between the HYPERION QSOs and the QSOs at Cosmic Noon (z = 2 − 4). Indeed, the latter QSOs are characterized by flatter slopes (on average Γ ≈ 1.85), translating to a smaller αOX than those shown by the former QSOs by ∼0.2. Furthermore, a fraction corresponding to ∼30% of the WISSH QSOs and the luminous blue QSOs at z = 3 analyzed by Zappacosta et al. (2020) and Nardini et al. (2019) are characterized by intrinsic X-ray weakness further lowering their average αOX values.
6. Probing a new regime in the nuclear properties of QSOs at EOR
The measured X-ray properties of HYPERION QSOs clearly differ from those of their analogs in terms of luminosity and λEdd at lower z. Steep X-ray spectral slopes (regardless of whether they are due to steep Γ or to a low-energy onset of the power-law cutoff) as measured here are previously unreported among the QSO population. Such slopes are more typical of lower MBH (< 106 M⊙) highly accreting low-luminosity AGN, such as the NLSy1 galaxies (e.g., Miniutti et al. 2009; Ludlam et al. 2015). The steep Γ measured for the HYPERION QSOs are also confirmation of the results reported for single but peculiar z > 6 sources such as the very bright radio-loud (Medvedev et al. 2021) or narrow-line quasars (Wolf et al. 2023) for which Γ = 2.5 ± 0.2 (90% errors) and 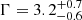 have been obtained. It is possible that the steepness derives from a different geometry of the accretion disk or corona system, a different coupling between the accretion disk and the corona, or from peculiar coronal properties.
have been obtained. It is possible that the steepness derives from a different geometry of the accretion disk or corona system, a different coupling between the accretion disk and the corona, or from peculiar coronal properties.
Kubota & Done (2018) present a framework of a radially stratified accretion disk with a standard outer disk, an inner warm Comptonizing region, and an innermost hot corona region, adopting a truncated disk geometry with the corona dissipating power in the inner hot accretion flow (see Fig. 2 in Kubota & Done 2018). By imposing a fixed 0.02LEdd fractional dissipation from the hot flow in their model, these authors are able to obtain an increasing hard X-ray Γ dependence on the Eddington-normalized accretion rate (ṁ = Ṁ/ṀEdd, where Ṁ is the mass accretion rate and ṀEdd = LEdd/c2). The relation found by Kubota & Done (2018) is somewhat steeper than the most recent Γ vs. λEdd relations reported in Fig. 4. Their model is however in broad agreement with the measured αOX vs. L2500 Å relations. In Fig. 8, we show the prediction of their QSOSED model (a simplified variant of their model with assumptions tuned for QSOs) for a nonrotating (i.e., spin parameter a = 0) and maximally rotating (a = 0.998) SMBH, for different log ṁ from −1 to 0.2 and adopting the average log(MBH/M⊙) = 9.43 value for the HYPERION QSOs. For each log ṁ step, we normalized the model to the HYPERION average L2 − 10 = 1.7 × 1045 erg s−1.
The αOX predicted by QSOSED for nonrotating SMBHs is consistent with the αOX measured for the HYPERION QSOs. A maximally spinning SMBH case disagrees with the data predicting flatter αOX. The preference for the null spin case therefore suggests a scenario of chaotic SMBH accretion flows rather than a more regular secular flow of accretion from the galaxy disk, which would instead lead to a conservation of the angular momentum. Figure 10 shows the Γ vs. αOX plot for the joint Γ and average αOX values of the HYPERION QSOs compared to the QSOSED model predictions. Predicted values are in good agreement with the QSO data, suggesting, for the HYPERION QSOs, an average log ṁ ≈ −0.4 (which is close to the average Γ and αOX for the sample analyzed here) for the nonspinning BH case.
 |
Fig. 10. Γ vs. αOX for HYPERION QSOs compared to the QSOSED model prediction. Red stars are single HYPERION QSOs, while the black star with central red circle shows the average αOX and joint best-fit Γ for the detected HYPERION QSOs. Light blue crosses and asterisks are the model predictions (for a = 0 and a ≈ 1, respectively) whose labels report the log ṁ value. |
In Sect. 5.1 we report a marginal indication that Γ is further steepening at higher redshifts and/or for the sources requiring the highest 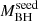 for their SMBH formation. In the framework of the Kubota & Done (2018) model, and in general, taking the anticorrelation trend of Γ vs. λEdd as a reference, a redshift dependence would translate to a higher accretion rate, meaning that the highest redshift sources are still accreting, on average, at high ṁ compared to the low-redshift ones with measured flatter Γ. The most likely
for their SMBH formation. In the framework of the Kubota & Done (2018) model, and in general, taking the anticorrelation trend of Γ vs. λEdd as a reference, a redshift dependence would translate to a higher accretion rate, meaning that the highest redshift sources are still accreting, on average, at high ṁ compared to the low-redshift ones with measured flatter Γ. The most likely 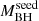 subsample division case points to a scenario in which the SMBHs with the fastest mass-accretion history are still highly accreting compared to those that had slower accretion pathways, and would probably result, on average, in even more massive SMBHs in the future.
subsample division case points to a scenario in which the SMBHs with the fastest mass-accretion history are still highly accreting compared to those that had slower accretion pathways, and would probably result, on average, in even more massive SMBHs in the future.
6.1. The origin of the steep X-ray spectral slopes
We can also parameterize the steep spectral slope with a power law with canonical Γ = 1.9 and a low high-energy cutoff. We measured Ecut ≈ 20 keV, which is very low compared to the currently measured values reported in Fig. 6, but is well constrained as it falls within the rest-frame energy band. We are not able to discriminate between a simple power-law model and one with the addition of a low-energy cutoff. In this regard, it is worth mentioning that the high-quality spectrum (i.e., 1400 net counts at 0.2–10 keV) analyzed by Medvedev et al. (2021) for the z = 6.18 radio-loud QSO CFHQS J142952+544717 does not show any signature of such a low-energy cutoff, providing a lower limit at 30–50 keV, according to the different model parameterization (although a possible X-ray jet component may impact the cutoff detectability). As our result applies to a well-defined population of QSOs, it is worth discussing the possibility that a low-energy cutoff could also have led to the reported steep spectral slopes. Interestingly, a few local, highly accreting Seyfert 1 galaxies with low energy cutoff similar (i.e., 20–30 keV) to those measured in HYPERION QSOs have already been reported (Vasudevan et al. 2013; Kamraj et al. 2018).
These values correspond to coronal temperatures as low as ∼7 − 10 keV. There are a number of possibilities that could account for such low-temperature coronae. These involve either an interaction (coupling) between a highly accreting accretion disk and the corona or peculiar physical states of the corona. In super-Eddington sources, such as NLSy1s, the strong, soft disk radiation field is capable of effectively increasing the Compton cooling of the corona, leading to a steep spectrum with a low-energy cutoff (Pounds et al. 1995). Recent JWST observations support the hypothesis of super-Eddington accreting AGNs in the early Universe (z > 8; e.g., Larson et al. 2023; Maiolino et al. 2023). In this case, we can expect similar X-ray nuclear properties for them (i.e., steep photon index and/or relatively low-energy cutoff).
Radiatively driven winds launched from the accretion disk of highly accreting SMBHs can provide an alternative explanation for the steep spectral slopes. If these winds have mass-ejection rates larger than the disk mass accretion rates, it is possible that they carry away matter from the innermost disk regions at a rate higher than the mass-accretion rate, effectively causing the truncation of the disk well before the innermost stable orbit. This would force the corona to be irradiated and hence Compton-cooled by softer seed photons (Laor & Davis 2014; Kara et al. 2017). A recent result reported by Bischetti et al. (2022) based on the XQR-30 sample (D’Odorico et al. 2023) of bright z ∼ 6 QSOs shows a very high fraction of broad absorption-line (BAL) winds, that is, a factor 2.4 larger than in low-z QSOs, with velocities up to 17% the speed of light. This may lend support to this scenario, also accounting for a redshift evolution (see also Bischetti et al. 2023). So far, only two HYPERION QSOs have been reported to host a BAL (i.e., J0038 and J231.6, Wang et al. 2018; Bischetti et al. 2022). This indicates a BAL fraction of 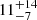 % – where the uncertainties account for Poisson statistics – to be compared with the
% – where the uncertainties account for Poisson statistics – to be compared with the 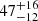 % reported in the XQR-30 sample. Assuming a 47% BAL fraction, the probability of having only two BALs in a sample of 18 QSOs (as in HYPERION) by chance is 0.2%. However, we note that homogeneous high-quality spectroscopic datasets (i.e., S/N ≳ 15, R ∼ 6000) for all HYPERION QSOs are not available. Therefore, a dedicated study to compare the occurrence of BALs in the HYPERION and XQR-30 samples at the same sensitivity level is currently not possible. In any case, a nondetection of a large BAL fraction is not necessarily an indication of a lack of nuclear winds. CIV emission line blueshifts (relative to MgII) have been measured for a large part of the HYPERION QSOs in several works, indicating fast broad-line winds of up to 5000 − 6000 km s−1 (e.g., Mazzucchelli et al. 2017; Meyer et al. 2019; Shen et al. 2019; Schindler et al. 2020; Yang et al. 2021).
% reported in the XQR-30 sample. Assuming a 47% BAL fraction, the probability of having only two BALs in a sample of 18 QSOs (as in HYPERION) by chance is 0.2%. However, we note that homogeneous high-quality spectroscopic datasets (i.e., S/N ≳ 15, R ∼ 6000) for all HYPERION QSOs are not available. Therefore, a dedicated study to compare the occurrence of BALs in the HYPERION and XQR-30 samples at the same sensitivity level is currently not possible. In any case, a nondetection of a large BAL fraction is not necessarily an indication of a lack of nuclear winds. CIV emission line blueshifts (relative to MgII) have been measured for a large part of the HYPERION QSOs in several works, indicating fast broad-line winds of up to 5000 − 6000 km s−1 (e.g., Mazzucchelli et al. 2017; Meyer et al. 2019; Shen et al. 2019; Schindler et al. 2020; Yang et al. 2021).
A similar disk-truncation scenario may also occur if the inner disk regions are impacted by tidal disruption-like events (TDEs), which increase the accretion rate of the inner regions as a consequence of fast angular momentum removal of the perturbed accreting material by bound debris streams (Chan et al. 2019) as recently suggested for the reported changing-look event in the low-luminosity local AGN 1ES 1927+654 (Ricci et al. 2020; Masterson et al. 2022). Such events, which in the most extreme cases may lead to destruction of the corona as the magnetic field pattern powering the corona is suppressed, are expected to show a X-ray softer-when-brighter behavior (Sobolewska & Papadakis 2009). This cannot be explored with this dataset given the large uncertainties in Γ for each source. Nevertheless, it is interesting to note that in the re-brightening phase of 1ES 1927+654, the X-ray spectrum appears very soft (i.e., with a steep Γ ≳ 3) like some of our QSOs and with an additionally low Ecut < 20 keV. In order for this scenario to be applicable to our z > 6 QSOs, these events need to be frequently recurring, so that statistically the sources are caught on average with a soft spectrum. Optimistic TDE rates for 109 − 1010 M⊙ SMBHs are in the range of ∼5 × 10−6 − 10−5 yr−1 (Stone & Metzger 2016). This implies a TDE event every 1 − 2 × 105 yr. Chan et al. (2019) speculates that it will take at most decades before the disk and therefore the corona return to an unperturbed state. This timescale is orders of magnitudes shorter than the TDE timescale and makes this scenario unfeasible.
Alternatively, peculiar corona properties may result in lower temperatures. In high-optical-depth coronae, disk seed photons may undergo multiple scatterings before leaving the corona, effectively lowering its temperature (Tortosa et al. 2017). Finally, in hybrid coronae models (Zdziarski et al. 1993; Fabian et al. 2017) in which thermal and nonthermal particles coexist in a highly magnetized plasma, the heating and cooling processes are faster than the electron cooling time by inverse Compton. In this case, even a small fraction of nonthermal electrons with MeV energies can cause intense runaway electron–positron pair-production. The cooled pairs may redistribute their energy to the thermal particles afterward, thereby lowering the temperature of the corona. Although attractive, for these scenarios, a redshift dependence is still not easy to justify.
Finally, an interesting scenario may couple the presence of optically thick coronae to the occurrence of nuclear winds which, as we already discussed, may provide a justification for a z > 6 redshift dependence in sources characterized by Eddington or super-Eddington accretion flows (Kawanaka & Mineshige 2021). In these sources, the radiation-driven wind can act as a low-temperature, optically thick corona, where the optical depth is larger for winds with a higher mass-outflow rate. This gives rise to progressively softer (steeper) spectra. If this is indeed the existing scenario, then this could be an indication that these sources are accreting at super critical rates, that is, much higher than those implied by λEdd.
6.2. Implications for the z > 6 AGN population and its detectability in the X-rays
Our result represents one of the most significant differences reported so far between QSOs at EoR and those at lower redshifts. Given the sample selection, in principle this result should only be valid for those QSOs where the central SMBH underwent a fast mass-growth history. This includes the recently discovered z ≈ 8 − 10 JWST AGN (Larson et al. 2023; Maiolino et al. 2023; Bogdan et al. 2023), which would require 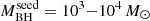 (in Fig. 1, left) and are therefore expected to have experienced fast mass growth. The mild indication (at the 2σ level) of an increasing Γ with increasing
(in Fig. 1, left) and are therefore expected to have experienced fast mass growth. The mild indication (at the 2σ level) of an increasing Γ with increasing 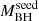 , if confirmed, could imply a flattening of Γ for QSOs requiring a less extreme
, if confirmed, could imply a flattening of Γ for QSOs requiring a less extreme 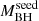 and mass growth. This would reconcile the X-ray properties of the less extreme HYPERION QSOs with those reported for normal lower-z QSOs. However, both the real fraction of sources with low
and mass growth. This would reconcile the X-ray properties of the less extreme HYPERION QSOs with those reported for normal lower-z QSOs. However, both the real fraction of sources with low 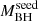 and the presence of a relation between Γ and
and the presence of a relation between Γ and 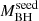 are still open issues. We cannot therefore exclude that our results may apply to the entire z > 6 QSO or AGN population. If this is the case, this may have an important impact on the source detectability in future X-ray surveys and on our capabilities to study and understand nuclear accretion mechanisms at EoR.
are still open issues. We cannot therefore exclude that our results may apply to the entire z > 6 QSO or AGN population. If this is the case, this may have an important impact on the source detectability in future X-ray surveys and on our capabilities to study and understand nuclear accretion mechanisms at EoR.
Indeed, the predicted 0.5–2 keV and 2–10 keV fluxes for sources with a given 0.5–10 keV luminosity are a factor of ∼1.9 and ∼4.1 fainter when assuming a power-law with Γ = 2.4 instead of a canonical Γ = 1.9 value. Alternatively, assuming a power law with an Ecut at 20 keV and Γ = 1.9 at the average redshift of the HYPERION sample, namely z = 6.7, these factors change to ∼1.3 and ∼4.2, respectively. In this case, at higher redshifts (e.g., z = 8), the detection would be even harder as the factors would increase to ∼1.4 and ∼5.3, respectively.
This issue must be considered when defining the sensitivity capabilities and the design of next-generation X-ray observatories (e.g., ATHENA, Lynx, AXIS), especially those designed to observe the highest-redshift Universe that we are currently probing with JWST. This is a fundamental step in extending our current understanding of the yet-undiscovered AGN population of which the QSOs we are currently studying may represent just a small portion. Indeed, recent JWST observations suggest that previously known high-redshift star-forming galaxies may harbor an AGN in their nucleus (Cameron et al. 2023; Maiolino et al. 2023; Übler et al. 2023). The disclosure of these previously “hidden” AGN may have a role in explaining the high-UV luminosity density of luminous galaxies (Trinca et al., in prep.) observed at z ≳ 8 (Donnan et al. 2023; Harikane et al. 2023; Bouwens et al. 2023).
7. Conclusions and future prospects
In this paper, we present the HYPERION sample of QSOs at the EoR selected for their fast SMBH growth history. Indeed, HYPERION QSOs are powered by SMBHs that would descend from seeds of  at z = 20 if accreting continuously at the Eddington rate. The sample consists of 18 QSOs at redshifts z ≈ 6 − 7.5 (mean z ∼ 6.7) with an average luminosity of Lbol ≈ 1047.3 erg s−1 and MBH ≈ 109 − 1010 M⊙. HYPERION builds on a 2.4 Ms XMM-Newton Multi-Year Heritage program (three years) designed to accurately characterize, for the first time on a statistically sound sample, the X-ray nuclear properties of QSOs at the EoR. In this paper, we report the spectral analysis of the first year of XMM-Newton observations of HYPERION. We analyzed XMM-Newton observations of 12 HYPERION QSOs for a total exposure of ∼1 Ms. New XMM-HYPERION observations for ten sources are presented in this paper. These include the first X-ray detection and spectral analysis ever reported for two sources (J083.8 and J029). All but 2 of the 12 QSOs were detected, with J231.6 and J011 undetected. Our main findings can be summarized as follows:
at z = 20 if accreting continuously at the Eddington rate. The sample consists of 18 QSOs at redshifts z ≈ 6 − 7.5 (mean z ∼ 6.7) with an average luminosity of Lbol ≈ 1047.3 erg s−1 and MBH ≈ 109 − 1010 M⊙. HYPERION builds on a 2.4 Ms XMM-Newton Multi-Year Heritage program (three years) designed to accurately characterize, for the first time on a statistically sound sample, the X-ray nuclear properties of QSOs at the EoR. In this paper, we report the spectral analysis of the first year of XMM-Newton observations of HYPERION. We analyzed XMM-Newton observations of 12 HYPERION QSOs for a total exposure of ∼1 Ms. New XMM-HYPERION observations for ten sources are presented in this paper. These include the first X-ray detection and spectral analysis ever reported for two sources (J083.8 and J029). All but 2 of the 12 QSOs were detected, with J231.6 and J011 undetected. Our main findings can be summarized as follows:
-
The X-ray spectral analysis on individual sources using simple power-law models on spectra with 50–140 net counts (pn+MOS, 0.3–7 keV) resulted in a wide range of Γ ≈ 1.9 − 3, with the large majority of sources (80%) exhibiting steep Γ ≳ 2.1.
-
A power-law joint spectral analysis of the ten detected sources resulted in an average Γ ≈ 2.4 ± 0.1. Moderate absorption (i.e., ∼1021 − 1022 cm−2) is not required. The steep Γ value rules out, for the first time (at the ∼4σ level), a canonical Γ = 2 and the average Γ reported in z < 6 QSOs of similar luminosity or λEdd. This implies that the steepness of the X-ray spectrum in HYPERION QSOs is an evolutionary signature of the HYPERION QSOs regardless of the QSO radiative output or SMBH accretion rate.
-
A joint spectral analysis with a Γ = 1.9 power law and a high-energy cutoff model resulted in a very low-energy Ecut ∼ 20 keV. This value is unreported at such high luminosities and redshifts. Future XMM-HYPERION data, will enable us to establish if this cutoff power law model is a better statistical representation of the true spectrum of these QSOs with respect to the simple power-law model.
-
The X-ray bolometric correction is in line with the trend reported for the bulk of AGN at high-luminosity regimes. However, we find that the optical-to-X-ray spectral index αOX (and ΔαOX) is slightly higher than the αOX vs. L2500 Å relations reported for large AGN samples. This is a consequence of the HYPERION QSOs steep X-ray spectral slopes.
We interpret the steep spectral slopes as an indication of cool coronae originating either from (i) the interaction with the soft radiation field of the accretion disk or (ii) the peculiar properties of the X-ray corona itself. In the first case, the disk is supposed to be highly accreting or truncated in the inner regions, possibly by nuclear winds with a high mass-outflow rate. Alternatively, enhanced cooling may be due to multiple scattering in high-optical-depth coronae, or to highly energetic nonthermal electrons cooling and interacting with thermal electrons in hybrid coronae models.
We think that the inner disk truncation scenario, with truncation due to disk winds with a high mass flux, offers a robust explanation of the Γ redshift evolution, as this latter relies on redshift-dependent results found for nuclear winds; other scenarios cannot explain this redshift evolution.
The XMM-HYPERION program presented here constitutes a remarkable leap forward in the nuclear characterization of QSOs at the EoR. More XMM-Newton data will soon be available. These will strengthen our findings and extend them to the entire HYPERION sample. This will allow us to assess the rate at which Γ steepens as a function of redshift or the mass growth history (adopting  as a proxy). Broad-band UV/X-ray physical models for the continuum from the accretion disk and corona system will be applied to these data in conjunction with quasi-simultaneous UV rest-frame data, which we are progressively collecting during the three years of the XMM-HYPERION program. Our data will enable us to shed light on the coupling between X-ray and broad-line properties. Furthermore, with submm/mm data, we will be able to investigate the impact of the QSO X-ray radiation field affecting the excitation of the molecular medium, which can be constrained by targeting high-J transitions of the CO molecule rotational ladder.
as a proxy). Broad-band UV/X-ray physical models for the continuum from the accretion disk and corona system will be applied to these data in conjunction with quasi-simultaneous UV rest-frame data, which we are progressively collecting during the three years of the XMM-HYPERION program. Our data will enable us to shed light on the coupling between X-ray and broad-line properties. Furthermore, with submm/mm data, we will be able to investigate the impact of the QSO X-ray radiation field affecting the excitation of the molecular medium, which can be constrained by targeting high-J transitions of the CO molecule rotational ladder.
If the nuclear properties reported here for the HYPERION QSOs are confirmed as being typical of the whole QSO population at the EoR, the distinctive steep spectral slopes obtained from our analysis will have an important impact on the source detectability in future X-ray surveys. In particular, the soft and hard band fluxes for sources of a given luminosity will be approximately two and four times fainter, respectively, than expected for a power law with a canonical, flatter spectral index. The hard band fluxes will be even fainter at higher redshifts if the true spectral model consists in a standard Γ = 1.9 power law with a low-energy (∼20 keV) cutoff. Accounting for this will have an impact on the design and capabilities of the future X-ray flagship observatories that are being built to probe nuclear accretion in the early Universe.
XMM-SOC-CAL-TN-0018 which is available at https://xmmweb.esac.esa.int/docs/documents/CAL-TN-0018.pdf
For this particular binning, we used the FTOOLS (http://heasarc.gsfc.nasa.gov/ftools) command ftgrouppha with grouptype option “opt”.
Acknowledgments
We thank the anonymous referee for the constructive comments which helped clarify several aspects of the paper. The analysis and results presented in this work are based on observations obtained with XMM-Newton an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA. We thank the XMM-Newton Science Operation Centre and Norbert Schartel for their help, prompt support and advise for the scheduling and optimisation of the XMM-HYPERION program. The authors acknowledge financial support from the Bando Ricerca Fondamentale INAF 2022 Large Grant “Toward an holistic view of the Titans: multi-band observations of z > 6 QSOs powered by greedy supermassive black-holes”. L.Z. and F.T. acknowledge support from INAF “Progetti di Ricerca di Rilevante Interesse Nazionale” (PRIN), Bando 2019 “Piercing through the clouds: a multiwavelength study of obscured accretion in nearby supermassive black holes”. G.M. was partly supported by grant n. PID2020-115325GB-C31 funded by MCIN/AEI/10.13039/501100011033. C.D. acknowledges support from the STFC consolidated grant ST/T000244/1. We thank Stefano Bianchi, Ciro Pinto and Luigi Stella for useful discussions.
References
- Ai, Y., Fabian, A. C., Fan, X., et al. 2017, MNRAS, 470, 1587 [NASA ADS] [CrossRef] [Google Scholar]
- Andika, I. T., Jahnke, K., Onoue, M., et al. 2020, ApJ, 903, 34 [Google Scholar]
- Arnaud, K. A. 1996, ASP Conf. Ser., 101, 17 [Google Scholar]
- Avni, Y., & Tananbaum, H. 1982, ApJ, 262, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Bañados, E., Connor, T., Stern, D., et al. 2018a, ApJ, 856, L25 [Google Scholar]
- Bañados, E., Venemans, B. P., Mazzucchelli, C., et al. 2018b, Nature, 553, 473 [Google Scholar]
- Bertola, E., Vignali, C., Lanzuisi, G., et al. 2022, A&A, 662, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biava, N., Colpi, M., Capelo, P. R., et al. 2019, MNRAS, 487, 4985 [Google Scholar]
- Bischetti, M., Feruglio, C., D’Odorico, V., et al. 2022, Nature, 605, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Bischetti, M., Fiore, F., Feruglio, C., et al. 2023, ApJ, 952, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdan, A., Goulding, A., Natarajan, P., et al. 2023, ArXiv e-prints [arXiv:2305.15458] [Google Scholar]
- Bouwens, R., Illingworth, G., Oesch, P., et al. 2023, MNRAS, 523, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, W. N., Schneider, D. P., Fan, X., et al. 2002, ApJ, 569, L5 [Google Scholar]
- Brightman, M., Silverman, J. D., Mainieri, V., et al. 2013, MNRAS, 433, 2485 [Google Scholar]
- Cameron, A. J., Katz, H., Rey, M. P., & Saxena, A. 2023, MNRAS, 523, 3516 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [Google Scholar]
- Chan, C.-H., Piran, T., Krolik, J. H., & Saban, D. 2019, ApJ, 881, 113 [Google Scholar]
- Chartas, G., Rhea, C., Kochanek, C., et al. 2016, Astron. Nachr., 337, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Chehade, B., Carnall, A. C., Shanks, T., et al. 2018, MNRAS, 478, 1649 [Google Scholar]
- Connor, T., Bañados, E., Mazzucchelli, C., et al. 2020, ApJ, 900, 189 [Google Scholar]
- Dadina, M. 2008, A&A, 485, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Marco, B., Ponti, G., Cappi, M., et al. 2013, MNRAS, 431, 2441 [Google Scholar]
- De Rosa, G., Decarli, R., Walter, F., et al. 2011, ApJ, 739, 56 [NASA ADS] [CrossRef] [Google Scholar]
- D’Odorico, V., Bañados, E., Becker, G. D., et al. 2023, MNRAS, 523, 1399 [CrossRef] [Google Scholar]
- Donnan, C. T., McLeod, D. J., Dunlop, J. S., et al. 2023, MNRAS, 518, 6011 [Google Scholar]
- Duras, F., Bongiorno, A., Ricci, F., et al. 2020, A&A, 636, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eilers, A.-C., Hennawi, J. F., Decarli, R., et al. 2020, ApJ, 900, 37 [Google Scholar]
- Fabian, A. C., Lohfink, A., Kara, E., et al. 2015, MNRAS, 451, 4375 [Google Scholar]
- Fabian, A. C., Lohfink, A., Belmont, R., Malzac, J., & Coppi, P. 2017, MNRAS, 467, 2566 [Google Scholar]
- Fan, X., Wang, F., Yang, J., et al. 2019, ApJ, 870, L11 [Google Scholar]
- Fan, X., Bañados, E., & Simcoe, R. A. 2023, ARA&A, 61, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Farina, E. P., Schindler, J.-T., Walter, F., et al. 2022, ApJ, 941, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Farrah, D., Priddey, R., Wilman, R., Haehnelt, M., & McMahon, R. 2004, ApJ, 611, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Feruglio, C., Fiore, F., Carniani, S., et al. 2018, A&A, 619, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feruglio, C., Maio, U., Tripodi, R., et al. 2023, ApJ, 954, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Gallerani, S., Zappacosta, L., Orofino, M. C., et al. 2017, MNRAS, 467, 3590 [Google Scholar]
- Haardt, F., & Maraschi, L. 1993, ApJ, 413, 507 [Google Scholar]
- Harikane, Y., Nakajima, K., Ouchi, M., et al. 2023, ApJ, submitted [arXiv:2304.06658] [Google Scholar]
- HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inayoshi, K., Visbal, E., & Haiman, Z. 2020, ARA&A, 58, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. L., & Bromm, V. 2007, MNRAS, 374, 1557 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. L., & Haardt, F. 2016, PASA, 33, e007 [NASA ADS] [CrossRef] [Google Scholar]
- Just, D. W., Brandt, W. N., Shemmer, O., et al. 2007, ApJ, 665, 1004 [Google Scholar]
- Kaastra, J. S., & Bleeker, J. A. M. 2016, A&A, 587, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamraj, N., Harrison, F. A., Baloković, M., Lohfink, A., & Brightman, M. 2018, ApJ, 866, 124 [CrossRef] [Google Scholar]
- Kamraj, N., Brightman, M., Harrison, F. A., et al. 2022, ApJ, 927, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Kara, E., Alston, W. N., Fabian, A. C., et al. 2016, MNRAS, 462, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Kara, E., García, J. A., Lohfink, A., et al. 2017, MNRAS, 468, 3489 [NASA ADS] [CrossRef] [Google Scholar]
- Kawanaka, N., & Mineshige, S. 2021, PASJ, 73, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Koss, M., Trakhtenbrot, B., Ricci, C., et al. 2017, ApJ, 850, 74 [Google Scholar]
- Kubota, A., & Done, C. 2018, MNRAS, 480, 1247 [Google Scholar]
- Lanzuisi, G., Gilli, R., Cappi, M., et al. 2019, ApJ, 875, L20 [Google Scholar]
- Laor, A., & Davis, S. W. 2014, MNRAS, 438, 3024 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. L., Finkelstein, S. L., Kocevski, D. D., et al. 2023, ApJ, 953, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Laurenti, M., Piconcelli, E., Zappacosta, L., et al. 2022, A&A, 657, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, H., Luo, B., Brandt, W. N., et al. 2021, ApJ, 910, 103 [Google Scholar]
- Ludlam, R. M., Cackett, E. M., Gültekin, K., et al. 2015, MNRAS, 447, 2112 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E., & Risaliti, G. 2016, ApJ, 819, 154 [Google Scholar]
- Lusso, E., Comastri, A., Vignali, C., et al. 2010, A&A, 512, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lusso, E., Comastri, A., Simmons, B. D., et al. 2012, MNRAS, 425, 623 [Google Scholar]
- Lusso, E., Valiante, R., & Vito, F. 2023, in Handbook of X-ray and Gamma-ray Astrophysics, eds. Cosimo Bambi, & Andrea Santangelo (Springer), 122 [Google Scholar]
- MacLeod, C. L., Morgan, C. W., Mosquera, A., et al. 2015, ApJ, 806, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Scholtz, J., Witstok, J., et al. 2023, ArXiv e-prints [arXiv:2305.12492] [Google Scholar]
- Malizia, A., Molina, M., Bassani, L., et al. 2014, ApJ, 782, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169 [Google Scholar]
- Martocchia, S., Piconcelli, E., Zappacosta, L., et al. 2017, A&A, 608, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masterson, M., Kara, E., Ricci, C., et al. 2022, ApJ, 934, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuoka, Y., Onoue, M., Kashikawa, N., et al. 2019, ApJ, 872, L2 [Google Scholar]
- Mazzucchelli, C., Bañados, E., Venemans, B. P., et al. 2017, ApJ, 849, 91 [Google Scholar]
- Medvedev, P., Gilfanov, M., Sazonov, S., Schartel, N., & Sunyaev, R. 2021, MNRAS, 504, 576 [CrossRef] [Google Scholar]
- Meyer, R. A., Bosman, S. E. I., & Ellis, R. S. 2019, MNRAS, 487, 3305 [Google Scholar]
- Milosavljević, M., Bromm, V., Couch, S. M., & Oh, S. P. 2009, ApJ, 698, 766 [CrossRef] [Google Scholar]
- Miniutti, G., Ponti, G., Greene, J. E., et al. 2009, MNRAS, 394, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Moretti, A., Ballo, L., Braito, V., et al. 2014, A&A, 563, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortlock, D. J., Warren, S. J., Venemans, B. P., et al. 2011, Nature, 474, 616 [Google Scholar]
- Nanni, R., Vignali, C., Gilli, R., Moretti, A., & Brandt, W. N. 2017, A&A, 603, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nanni, R., Gilli, R., Vignali, C., et al. 2018, A&A, 614, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardini, E., Lusso, E., Risaliti, G., et al. 2019, A&A, 632, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neeleman, M., Novak, M., Venemans, B. P., et al. 2021, ApJ, 911, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Onoue, M., Kashikawa, N., Matsuoka, Y., et al. 2019, ApJ, 880, 77 [Google Scholar]
- Page, K. L., Reeves, J. N., O’Brien, P. T., & Turner, M. J. L. 2005, MNRAS, 364, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Page, M. J., Simpson, C., Mortlock, D. J., et al. 2014, MNRAS, 440, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Pensabene, A., Carniani, S., Perna, M., et al. 2020, A&A, 637, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pezzulli, E., Valiante, R., & Schneider, R. 2016, MNRAS, 458, 3047 [NASA ADS] [CrossRef] [Google Scholar]
- Piconcelli, E., Jimenez-Bailón, E., Guainazzi, M., et al. 2005, A&A, 432, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pons, E., McMahon, R. G., Simcoe, R. A., et al. 2019, MNRAS, 484, 5142 [NASA ADS] [CrossRef] [Google Scholar]
- Pons, E., McMahon, R. G., Banerji, M., & Reed, S. L. 2020, MNRAS, 491, 3884 [Google Scholar]
- Pounds, K. A., Done, C., & Osborne, J. P. 1995, MNRAS, 277, L5 [NASA ADS] [Google Scholar]
- Reed, S. L., McMahon, R. G., Martini, P., et al. 2017, MNRAS, 468, 4702 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, S. L., Banerji, M., Becker, G. D., et al. 2019, MNRAS, 487, 1874 [Google Scholar]
- Reeves, J. N., & Turner, M. J. L. 2000, MNRAS, 316, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Ho, L. C., Fabian, A. C., et al. 2018, MNRAS, 480, 1819 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Kara, E., Loewenstein, M., et al. 2020, ApJ, 898, L1 [Google Scholar]
- Richards, G. T., Lacy, M., Storrie-Lombardi, L. J., et al. 2006, ApJS, 166, 470 [Google Scholar]
- Risaliti, G., & Lusso, E. 2019, Nat. Astron., 3, 272 [Google Scholar]
- Salvestrini, F., Risaliti, G., Bisogni, S., Lusso, E., & Vignali, C. 2019, A&A, 631, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schindler, J.-T., Farina, E. P., Bañados, E., et al. 2020, ApJ, 905, 51 [Google Scholar]
- Shao, Y., Wang, R., Jones, G. C., et al. 2017, ApJ, 845, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Shemmer, O., Brandt, W. N., Netzer, H., Maiolino, R., & Kaspi, S. 2006a, ApJ, 646, L29 [Google Scholar]
- Shemmer, O., Brandt, W. N., Schneider, D. P., et al. 2006b, ApJ, 644, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Shemmer, O., Brandt, W. N., Netzer, H., Maiolino, R., & Kaspi, S. 2008, ApJ, 682, 81 [Google Scholar]
- Shen, Y., & Liu, X. 2012, ApJ, 753, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [Google Scholar]
- Shen, Y., Wu, J., Jiang, L., et al. 2019, ApJ, 873, 35 [Google Scholar]
- Sobolewska, M. A., & Papadakis, I. E. 2009, MNRAS, 399, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Souza Lima, R., Mayer, L., Capelo, P. R., Bortolas, E., & Quinn, T. R. 2020, ApJ, 899, 126 [Google Scholar]
- Steffen, A. T., Strateva, I., Brandt, W. N., et al. 2006, AJ, 131, 2826 [Google Scholar]
- Stern, B. E., Poutanen, J., Svensson, R., Sikora, M., & Begelman, M. C. 1995, ApJ, 449, L13 [NASA ADS] [Google Scholar]
- Stone, N. C., & Metzger, B. D. 2016, MNRAS, 455, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Svensson, R. 1984, MNRAS, 209, 175 [CrossRef] [Google Scholar]
- Tanaka, T., & Haiman, Z. 2009, ApJ, 696, 1798 [NASA ADS] [CrossRef] [Google Scholar]
- Timlin, J. D., Brandt, W. N., Ni, Q., et al. 2020, MNRAS, 492, 719 [Google Scholar]
- Tortosa, A., Marinucci, A., Matt, G., et al. 2017, MNRAS, 466, 4193 [NASA ADS] [Google Scholar]
- Tortosa, A., Ricci, C., Ho, L. C., et al. 2023, MNRAS, 519, 6267 [NASA ADS] [CrossRef] [Google Scholar]
- Trakhtenbrot, B., Ricci, C., Koss, M. J., et al. 2017, MNRAS, 470, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Trefoloni, B., Lusso, E., Nardini, E., et al. 2023, A&A, 677, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tripodi, R., Feruglio, C., Kemper, F., et al. 2023, ApJ, 946, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Übler, H., Maiolino, R., Curtis-Lake, E., et al. 2023, A&A, 677, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valiante, R., Schneider, R., Volonteri, M., & Omukai, K. 2016, MNRAS, 457, 3356 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., Brandt, W. N., Mushotzky, R. F., et al. 2013, ApJ, 763, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Venemans, B. P., Walter, F., Zschaechner, L., et al. 2016, ApJ, 816, 37 [Google Scholar]
- Venemans, B. P., Walter, F., Decarli, R., et al. 2017, ApJ, 845, 154 [Google Scholar]
- Vestergaard, M., & Osmer, P. S. 2009, ApJ, 699, 800 [Google Scholar]
- Vignali, C., Comastri, A., Cappi, M., et al. 1999, ApJ, 516, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Vignali, C., Brandt, W. N., & Schneider, D. P. 2003, AJ, 125, 433 [Google Scholar]
- Vignali, C., Brandt, W. N., Schneider, D. P., & Kaspi, S. 2005, AJ, 129, 2519 [NASA ADS] [CrossRef] [Google Scholar]
- Vito, F., Brandt, W. N., Bauer, F. E., et al. 2019, A&A, 630, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vito, F., Brandt, W. N., Ricci, F., et al. 2021, A&A, 649, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vito, F., Mignoli, M., Gilli, R., et al. 2022, A&A, 663, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Volonteri, M. 2010, A&ARv, 18, 279 [Google Scholar]
- Volonteri, M., Haardt, F., & Madau, P. 2003, ApJ, 582, 559 [Google Scholar]
- Volonteri, M., Silk, J., & Dubus, G. 2015, ApJ, 804, 148 [Google Scholar]
- Wachter, K., Leach, R., & Kellogg, E. 1979, ApJ, 230, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F., Neeleman, M., Decarli, R., et al. 2022, ApJ, 927, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, F., Yang, J., Fan, X., et al. 2018, ApJ, 869, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, F., Davies, F. B., Yang, J., et al. 2020, ApJ, 896, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, F., Fan, X., Yang, J., et al. 2021a, ApJ, 908, 53 [Google Scholar]
- Wang, F., Yang, J., Fan, X., et al. 2021b, ApJ, 907, L1 [Google Scholar]
- Wang, R., Wagg, J., Carilli, C. L., et al. 2013, ApJ, 773, 44 [Google Scholar]
- Weisskopf, M. C., Wu, K., Trimble, V., et al. 2007, ApJ, 657, 1026 [Google Scholar]
- Willott, C. J., Albert, L., Arzoumanian, D., et al. 2010, AJ, 140, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, J., Nandra, K., Salvato, M., et al. 2023, A&A, 669, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wu, X.-B., Wang, F., Fan, X., et al. 2015, Nature, 518, 512 [Google Scholar]
- Yang, J., Wang, F., Fan, X., et al. 2020, ApJ, 897, L14 [Google Scholar]
- Yang, J., Wang, F., Fan, X., et al. 2021, ApJ, 923, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, J., Fan, X., Wang, F., et al. 2022, ApJ, 924, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Zappacosta, L., Comastri, A., Civano, F., et al. 2018, ApJ, 854, 33 [Google Scholar]
- Zappacosta, L., Piconcelli, E., Giustini, M., et al. 2020, A&A, 635, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zdziarski, A. A., Lightman, A. P., & Maciolek-Niedzwiecki, A. 1993, ApJ, 414, L93 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: XMM-Newton EPIC detectors images of the XMM-HYPERION QSOs in the 0.5-2 keV
We present here pn, MOS1, and MOS2 0.5-2 keV images of the observations reported in Table 2. For each detector, we report source and background region files adopted for photometry and spectral extraction. The figure for exposure J1342_1, that is, the first observation of J1342 is reported in Fig. 2.
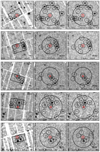 |
Fig. A.1. EPIC 0.5-2 keV pn, MOS1, and MOS2 camera images for sources of the XMM-HYPERION program presented in this work (J1342_1 is reported in Fig. 2). All the images are smoothed by a Gaussian kernel of 3 pixels in radius for better visualization. Source and background counts and spectral extraction regions are reported in red and black, respectively. Dashed circular regions indicate areas excluded by the background extraction. |
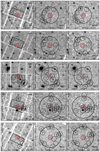 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
Appendix B: Optimal spectral binning for spectra with low counts
In order to evaluate the optimal binning for our spectra, we simulated spectra for steep and flat Γ and evaluated the accuracy (i.e., the difference between input and best-fit simulated value in units of the input value) in recovering the input Γ and L2 − 10 values. We take the spectra in our sample with 60-70 net counts (pn+MOS, 0.3-10 keV) as a reference. Specifically, for the steep and flat Γ, we adopted the input best-fit values reported in Table 4 for J029 and J0050, respectively. We therefore simulated a set of 10000 spectra for each Γ case, evaluating the following binning schemes: unbinned, binned at minimum 1, 3, 5, and 10 counts, and the optimal sampling from Kaastra & Bleeker (2016), hereafter called KB. For each binning scheme, we also evaluated the energy range dependence in the following intervals 0.3-2 keV, 0.3-5 keV, 0.3-7 keV, and 0.3-10 keV. In general, we found that the binning scheme plays a negligible role in the accuracy of our results, especially compared to the size of our statistical errors (i.e., the scatter of the distribution of the best-fit values), which are always almost a factor of a few up to 1-2 orders of magnitude larger at all energy intervals probed. Therefore, possible systematic uncertainties in the fitting process are in general compensated by the larger statistical uncertainties. Figure B.1 shows the accuracy in recovering the average Γ and L2 − 10 as a function of binning and energy range. In general, unbinned results are very inaccurate, especially in energy intervals including background-dominated upper energy bounds (i.e., > 2 keV), and can bias the recovered values by more than 10%. On average, going to larger bins improves the accuracy of the parameter estimation to subpercent or percent levels for flat or steep input Γ, respectively, and to the level of a few percent in case of L2 − 10. The KB binning scheme consistently recovers more accurate results (i.e., by at least a factor of 2-3) at all energies, regardless of the input Γ (showing larger accuracies for flat Γ).
 |
Fig. B.1. Accuracy, as a function of the binning scheme and energy range, in recovering the input Γ and L2 − 10 through a set of 10000 spectral simulations. |
Appendix C: Comparison with previous analysis of the XMM-HYPERION detected source
In this section, we compare our best-fit Γ and L2 − 10 reported in Table 4 with previous analyses carried out on the same sources with archived observations.
J1342. A 45 ks Chandra observation of J1342 was analyzed by Bañados et al. (2018a) and Vito et al. (2019). The source was detected with ∼14 net counts (0.5-7 keV). These authors attempted a basic spectral analysis with a power-law model with Galactic absorption, obtaining similar results. Vito et al. (2019) found 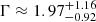 and
and 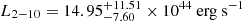 (errors at 90% level). These values are consistent at ≲ 1 σ level with ours.
(errors at 90% level). These values are consistent at ≲ 1 σ level with ours.
J1120. A ∼340 ks XMM-Newton observation divided in three exposures was analyzed by several authors (Page et al. 2014; Moretti et al. 2014; Nanni et al. 2017; Vito et al. 2019). The observation was found to be heavily contaminated by background flares (∼50% in pn). The last analysis by Vito et al. (2019) obtained 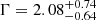 and
and 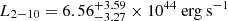 (errors at 90% level). The Γ is consistent at an ∼1σ level with our value. The luminosity L2 − 10 is inconsistent at the ∼4.5σ level. Hence, the source appears to have increased its luminosity by a factor of ∼4.
(errors at 90% level). The Γ is consistent at an ∼1σ level with our value. The luminosity L2 − 10 is inconsistent at the ∼4.5σ level. Hence, the source appears to have increased its luminosity by a factor of ∼4.
J0020. A 25 ks XMM-Newton observation was analyzed by Pons et al. (2020). According to the authors, the source was undetected with a L2−10 < 4.76 × 1045 erg s−1 upper limit. Their estimate is consistent with our luminosity value.
J0244. A 17 ks XMM-Newton observation was analyzed by Pons et al. (2020). According to the authors, the source was undetected with a L2−10 < 4.37 × 1045 erg s−1 upper limit. Their estimate is consistent with our luminosity value.
J036.5. A 25 ks Chandra observation was analyzed by Vito et al. (2019). The source was detected with 5.5 net counts. These authors attempted a spectral analysis obtaining a 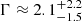 and L2−10 < 20.53 × 1044 erg s−1. A ∼17 ks XMM-Newton observation was also analyzed by Pons et al. (2020). These authors did not detect the source and only obtained a very high upper limit on the luminosity of L2−10 < 17.62 × 1045 erg s−1. All measurements are consistent with our best-fit values.
and L2−10 < 20.53 × 1044 erg s−1. A ∼17 ks XMM-Newton observation was also analyzed by Pons et al. (2020). These authors did not detect the source and only obtained a very high upper limit on the luminosity of L2−10 < 17.62 × 1045 erg s−1. All measurements are consistent with our best-fit values.
J0050. A 34 ks Chandra observation was analyzed by Vito et al. (2019). The source was detected with 7.4 net counts. These authors attempted a spectral analysis obtaining a 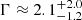 and
and 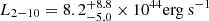 . Their values are consistent with ours at < 1σ level.
. Their values are consistent with ours at < 1σ level.
J0224. For this source, only a 26 ks XMM-Newton is available in the archive. This is the observation we analyze in this work. A previous analysis of this observation was carried out by Pons et al. (2020). These latter authors obtained 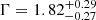 and L2−10 = 2.92 ± 0.43 × 1045 erg s−1. These values are consistent at < 1.2σ level with ours.
and L2−10 = 2.92 ± 0.43 × 1045 erg s−1. These values are consistent at < 1.2σ level with ours.
J0100. For this source, a 15 ks Chandra observation and a ∼65 ks XMM-Newton observation are archived. We analyzed the longer XMM-Newton observation, which provides a factor of > 20 more net counts than the Chandra one. The XMM-Newton observation was analyzed by Ai et al. (2017) and by Vito et al. (2019). The latter authors obtained 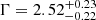 and
and 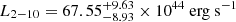 (errors at 90% level). These values are consistent with our analysis. Their Γ is consistent at the level of < 1σ, while the luminosity is consistent at the ∼1.5σ level.
(errors at 90% level). These values are consistent with our analysis. Their Γ is consistent at the level of < 1σ, while the luminosity is consistent at the ∼1.5σ level.
All Tables
HYPERION QSO sample, ordered by decreasing redshift, and its general properties.
Journal of the observations of the HYPERION targets from the XMM-HYPERION (upper part of the table) and archive (lower part of the table).
Source net counts from fixed-aperture photometry on the EPIC detectors in the soft, hard, and full energy bands.
All Figures
 |
Fig. 1. Selection and properties of the HYPERION sample. Left: SMBH mass as a function of redshift. All the reported points (diamonds and stars) are the subsample of 46 hyperluminous (Lbol > 1047 erg s−1) quasars with known SMBH masses reported at the end of 2020. The final selected 18 sources are reported as red stars. The curves represent the exponential growth of seed BHs of different masses (labeled) formed at z = 20, assuming continuous accretion (fduty = 1) at the Eddington rate (λEdd = 1; see Sect. 2). The red curve, corresponding to a growing seed of 1000 M⊙, was used to select the HYPERION sample. Right: distribution of the HYPERION sample in the MBH vs. Lbol plane (red stars) along with the distribution of the 83 z > 6 quasars with available MBH. All MBH are based on single-epoch MgII virial estimator and Lbol is from bolometric correction from the literature as of 2020. MBH and Lbol were consistently recomputed for all sources assuming the same ΛCDM cosmology and adopting the mass calibration from Vestergaard & Osmer (2009) and a bolometric correction of 5.15 to the 3000 Å luminosity from Richards et al. (2006). Dashed lines report the location of sources emitting a fixed fraction of LEdd. The contours report the location of the lower redshift (z = 0.7 − 1.9) SDSS-DR7 quasars from Shen et al. (2011) with MgII-derived masses. |
| In the text | |
 |
Fig. 2. EPIC 0.5–2 keV pn, MOS1, and MOS2 camera images for the first J1342 observation reported in Table 2 of the XMM-HYPERION program presented in this work. All the images are smoothed by a Gaussian kernel of 3 pixels in radius for better visualization. Source and background regions adopted for photometric and spectral extractions are reported in red and black, respectively. Dashed circular regions indicate areas excluded from the background extraction. Images for the second J1342 exposure (J1342_2) and other XMM-HYPERION QSOs presented in this work are reported in Appendix A.1. |
| In the text | |
 |
Fig. 3. XMM-Newton pn (black), MOS1 (red), and MOS2 (green) 0.3–7 keV spectra and best-fit models (stepped continuous thick lines) for the ten detected HYPERION QSOs presented in this paper. Spectra were further rebinned for visual purposes and are reported at their rest-frame energy. Residuals are shown as data minus best-fit model in the bottom panels. For the source J1342, blue, cyan, and magenta represent the second data set. |
| In the text | |
 |
Fig. 4. Γ vs. λEdd for a compilation of local or high-λEdd AGN and high-redshift luminous QSOs. Red stars are the HYPERION QSOs presented in this work. Green four-pointed stars are other z > 6 QSOs detected with ≳30 net counts from the X-ray spectral analysis performed by Vito et al. (2019) and not included in the HYPERION sample. Quasars at Cosmic Noon (z = 2 − 4) are reported as purple triangles (the WISSH QSOs from Zappacosta et al. 2020), empty cyan circles (Shemmer et al. 2006a, 2008), and pink diamonds (Nardini et al. 2019; Trefoloni et al. 2023). Local high-λEdd QSOs (Laurenti et al. 2022) and local AGN including Narrow Line Seyfert 1 (NLSy1s) galaxies (Liu et al. 2021) are shown as blue squares and yellow circles, respectively. Reported are also the most recent relations from a linear fit to the local AGN (i.e., Trakhtenbrot et al. 2017; Liu et al. 2021). The uncertainties on λEdd from QSOs with MBH estimated using a single-epoch virial mass estimator are dominated by systematic uncertainties and can be as high as 0.5 dex. The statistical uncertainty on λEdd for the local AGN (Liu et al. 2021) whose masses are estimated via reverberation mapping is 0.1 dex and 0.2 dex for the sub-Eddington and super-Eddington sources, respectively. |
| In the text | |
 |
Fig. 5. Distribution of the average Γ as a function of redshift. The plot includes data from joint spectral analysis or average values from samples of QSOs. In particular, starred data are from joint spectral analysis of samples of z > 6 QSOs. The black star with a central red circle, the green four-pointed star, the magenta six-pointed star, and the three-pointed star are HYPERION QSOs, and the samples of Vito et al. (2019), Wang et al. (2021a), and Nanni et al. (2017), respectively. The empty squares, diamond, and circle are averages from the stacked spectral analyses of luminous and hyperluminous QSOs from Just et al. (2007), Vignali et al. (2005), and Shemmer et al. (2006b), respectively. The empty triangle represents the average Γ from the PG quasars (Piconcelli et al. 2005). Blue squares are high-λEdd local QSOs (Laurenti et al. 2022) and purple triangles are hyperluminous high-λEdd WISSH QSOs (Zappacosta et al. 2020). Pink diamonds are z ∼ 3 luminous blue quasars from Nardini et al. (2019). Vertical error bars report 1σ uncertainties on Γ while horizontal error bars indicate the redshift range covered by the QSO sample considered in each dataset. |
| In the text | |
 |
Fig. 6. Distribution of Ecut as a function of L2 − 10. Light blue and orange filled circles are estimates from a compilation of local AGN (Bertola et al. 2022, and references therein) and z ≈ 2 − 4 QSOs (Lanzuisi et al. 2019; Bertola et al. 2022). Purple circles are from local super Eddington accreting AGN from Tortosa et al. (2023). Hollow magenta circles are binned averages estimated by Ricci et al. (2018) for a large sample of local AGN from the BAT AGN Spectroscopic Survey (BASS). The HYPERION average Ecut measurement (assuming Γ = 1.9) from our joint analysis is reported as a black star with an inner red circle. Green regions are the forbidden regions (for a slab corona model) due to runaway electron–positron pair production (see Svensson 1984) for log(MBH/M⊙) = 8.5 and log(MBH/M⊙) = 9.5. |
| In the text | |
 |
Fig. 7. X-ray bolometric correction ( |
| In the text | |
 |
Fig. 8. αOX vs. L2500 Å for a compilation of AGN catalogs. Symbols refer to the AGN samples as in Fig. 4, except for the green dots, which are detected AGN with S/N > 5 from Lusso & Risaliti (2016). Upper limits for the HYPERION QSOs are estimated assuming a power law with fixed Γ = 2.4 (see Sect. 3 and Table 4). The dashed line is the linear fit from Martocchia et al. (2017) while the solid line refers to the best-fit relation from Lusso & Risaliti (2016) and for the subsample with S/N > 5, E(B − V)≥0.1, and 1.6 ≤ Γ1 − 5 ≤ 2.8, with Γ1 − 5 being the photon index estimated between the luminosities at 1 keV and 5 keV. Light blue crosses and asterisks present the values predicted by the QSOSED model (Kubota & Done 2018) assuming average HYPERION parameters and spin a = 0 and a = 1, respectively. These values are reported from top-left to bottom-right from log ṁ = −1 to log ṁ = 0.2 in steps of Δlog ṁ = 0.2. |
| In the text | |
 |
Fig. 9. Normalized distributions of the ΔαOX relative to the relation from Lusso & Risaliti (2016; see Fig. 8) for HYPERION QSOs (red filled histogram) and the AGN detected with S/N > 5 from Lusso & Risaliti (2016; dashed hollow histogram). The gray region marks the position of the X-ray-weak sources. |
| In the text | |
 |
Fig. 10. Γ vs. αOX for HYPERION QSOs compared to the QSOSED model prediction. Red stars are single HYPERION QSOs, while the black star with central red circle shows the average αOX and joint best-fit Γ for the detected HYPERION QSOs. Light blue crosses and asterisks are the model predictions (for a = 0 and a ≈ 1, respectively) whose labels report the log ṁ value. |
| In the text | |
 |
Fig. A.1. EPIC 0.5-2 keV pn, MOS1, and MOS2 camera images for sources of the XMM-HYPERION program presented in this work (J1342_1 is reported in Fig. 2). All the images are smoothed by a Gaussian kernel of 3 pixels in radius for better visualization. Source and background counts and spectral extraction regions are reported in red and black, respectively. Dashed circular regions indicate areas excluded by the background extraction. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. B.1. Accuracy, as a function of the binning scheme and energy range, in recovering the input Γ and L2 − 10 through a set of 10000 spectral simulations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.