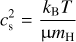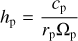| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202346607 | |
| Published online | 07 September 2023 | |
Constraining the gas distribution in the PDS 70 disc as a method to assess the effect of planet-disc interactions
1
Kapteyn Astronomical Institute, University of Groningen,
PO Box 800,
9700
AV Groningen,
The Netherlands
e-mail: bportilla@astro.rug.nl
2
Dipartimento di Fisica, Università degli Studi di Milano,
Via Celoria 16,
20133
Milano,
Italy
3
Leiden Observatory, Leiden University,
PO Box 9513,
2300
RA Leiden,
The Netherlands
4
University Observatory, Faculty of Physics, Ludwig-Maximilians-Universität München,
Scheinerstr. 1,
81679
Munich,
Germany
5
Center for Astrophysics, Harvard & Smithsonian,
60 Garden St.,
Cambridge, MA
02138,
USA
6
European Southern Observatory,
Karl-Schwarzschild-Str. 2,
85748
Garching,
Germany
7
Max-Planck-Institut für Extraterrestrische Physik,
Geissenbachstrasse 1,
85748
Garching,
Germany
8
Department of Astronomy, University of Florida,
Gainesville, FL
32611-2055,
USA
9
Univ. Grenoble Alpes, CNRS, IPAG,
38000
Grenoble,
France
10
Department of Earth, Atmospheric, and Planetary Sciences, Massachusetts Institute of Technology,
77 Massachusetts avenue, 54-918,
Cambridge, MA
02139,
USA
Received:
3
April
2023
Accepted:
26
June
2023
Context. Embedded planets are potentially the cause of substructures, such as gaps and cavities, observed in the continuum images of several protoplanetary discs. Likewise, gas distribution is expected to change in the presence of one or several planets, and the effect can be detected with current observational facilities. Thus, the properties of the substructures observed in the continuum as well as in line emission encode information about the presence of planets in a system and how they interact with the natal disc. The pre-transitional disc around the star PDS 70 is the first case of two young planets being imaged within a dust-depleted gap that was likely carved by the planets themselves.
Aims. We aim to determine the spatial distribution of the gas and dust components in the PDS 70 disc. The axisymmetric substructures observed in the resulting profiles are interpreted in the context of planet-disc interactions.
Methods. We developed a thermo-chemical forward model for an axisymmetric disc to explain a subset of the Atacama Large Millimeter/Submillimeter Array (ALMA) band 6 observations of three CO isotopologues plus the continuum towards PDS 70. The model accounts for the continuum radiative transfer, steady-state chemistry, and gas thermal balance in a self-consistent way and produces synthetic observables via ray tracing.
Results. We demonstrate that the combination of a homogeneous dust size distribution across the disc and relatively low values of viscosity (α ≲ 5 × 10−3) can explain the band 6 continuum observations. For the gas phase, analysis of the synthetic observables points to a gas density peak value of ~0.1 g cm−2 located at 75 au and a minimum of ~10−3 g cm−2 at 20 au. The location of the minimum matches the semi-major axis of the innermost planet PDS 70 b. Combining the gas and dust distributions, the model results in a variable gas-to-dust ratio profile throughout the disc that spans two orders of magnitude within the first 130 au and shows a step gradient towards the outer disc, which is consistent with the presence of a pressure maxima driven by planet-disc interactions. Particularly, the mean gas-to-dust ratio within the dust gap between 16 and 41 au is found to be ~630. We find a gas density drop factor of ~19 at the location of the planet PDS 70 c with respect to the peak gas density at 75 au. Combining this value with results from the literature on the hydrodynamics of planet-disc interactions, we find this gas gap depth to be consistent with independent planet mass estimates from infrared observations. Our findings point towards gas stirring processes taking place in the common gap due to the gravitational perturbation of the two planets.
Conclusions. The distribution of gas and dust in the PDS 70 disc can be constrained by forward modelling the spatially resolved observations from high-resolution and high-sensitivity instruments like ALMA. This information is a key piece in the qualitative and quantitative interpretation of the observable signatures of planet-disc interactions.
Key words: methods: numerical / planets and satellites: formation / protoplanetary disks / stars: individual: PDS 70 / submillimeter: planetary systems / planet-disk interactions
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The accepted explanation for the origin of giant planets points to a formation process that takes place in the midplane of discs made of gas and dust around young stellar objects. In consequence, a planet’s properties are expected to be regulated, at least to a first order, by the amount and the properties of the material comprising the disc. Therefore, it is logical to think of a two-sided relationship where the properties of the planet and the disc are determined by each other. Observing young planets in the embedded phase is thus a crucial step in understanding how their properties link to those of the disc.
The observability of planets embedded in the natal proto-planetary disc was elusive until recently due to the observational limitations to image planets close to a host star. Typical working angles achieved with the Hubble Space Telescope are close to ~1 arc sec, whereas ground-based telescopes lack the sensitivity needed to spot faint structures. Several attempts to observe embedded protoplanets have covered a broad region of the spectrum, from short (visual and near infrared) to long (submillimetre) wavelengths (Benisty et al. 2022). In the short wavelength regime, particularly at visual wavelengths, accretion signatures can be observed. When the star is actively accreting, the inflow of gas from the outer disc has to make its way to the inner disc, and along this journey, part of it can be accreted by the planets, resulting in accretion signatures like Ha emission (e.g. Natta et al. 2004; Szulágyi & Ercolano 2020). Searches for those signatures have been carried out with scarce success within the solar neighbourhood (Zurlo et al. 2020). At near-infrared wavelengths, the high continuum optical depth prevents planets from being directly imaged; hence, gaps and cavities are suitable places to search for protoplanets due to their relatively low extinction (Paardekooper & Mellema 2004; Espaillat et al. 2014). Recent advances in differential imaging techniques have not only allowed for the identification of disc substructures but have also led to the detection of young planets since they emit thermal emission in the near infrared (see Benisty et al. 2022 for a recent review). At submillimetre wavelengths, spatially resolved gas kinematics is another way to detect embedded planets (see Pinte et al. 2022 for a review). The presence of a planet can induce deviations from a Keplerian profile in the isovelocity curves of the gas component. The extent of the deviation is proportional to the mass of the planet causing the distortion, and it can be detected with interferometric facilities such as the Atacama Large Millimetre/Submillimetre Array (ALMA). Based on this idea, two planets with a mass a few times that of Jupiter have been proposed to explain the perturbations in the velocity field and substructures observed in HD 163296 (Pinte et al. 2018; Teague et al. 2018) and in HD 97048 (Pinte et al. 2019). In both cases, the location of the planets would lie beyond 100 au; this reflects a limitation of the gas kinematic method due to ALMA not being able to probe the gas kinematics inside ~10 au.
Recent advances in high spatial resolution and high contrast optical and near-infrared imaging of discs have allowed for the discovery of two protoplanets in the cavity of a pre-transitional disc: PDS 70 b and c (Keppler et al. 2018; Haffert et al. 2019). Infrared spectroscopy of these planets alongside analysis of their astrometric data constrained their masses down to a few times that of Jupiter and suggest a 2:1 resonant orbital configuration (Müller et al. 2018; Wang et al. 2021). Observations in Ha showed that the planets are accreting circumstellar material at a relatively low rate of ~10−2-10−1 MJup Myr−1 (Haffert et al. 2019; Hashimoto et al. 2020), indicative of a post-runaway growth scenario. This also suggests that there is still gas flowing through the dust-depleted cavity. In a recent ALMA campaign, Facchini et al. (2021) identified emission from 12 molecular species in the PDS 70 circumstellar disc, including three CO isotopologues, H2CO, and small hydrocarbons. They found that most of the emission comes from the outer disc, while the region within the orbit of the innermost planet displays only 12CO and HCO+ emission.
There have been several attempts to determine the mass of the two protoplanets in the PDS 70 disc. This is particularly challenging for planet c because of its closeness to the outer dust ring and the presence of a circumplanetary disc, as both act as sources of contamination. For planet b, Hashimoto et al. (2020) inferred a value of 12 MJup when analysing the properties of the Ha line. Keppler et al. (2018), Müller et al. (2018), Mesa et al. (2019), Wang et al. (2020) found values between 1 and 17 MJup using near-infrared spectroscopy. Finally, Bae et al. (2019), Wang et al. (2021) placed an upper limit of 10 MJup via orbital stability considerations. A possible way to ameliorate these uncertainties is by using detailed thermo-chemical models that are able to translate multiple observational constraints into physical properties (such as density distributions) that encode information about a planet’s mass.
Hydrodynamical simulations have shown that the presence of one or several massive protoplanets can partially deplete a disc of its primordial material through accretion and/or transfer of angular momentum in the form of spiral density waves (Paardekooper et al. 2022). For the single-planet case, Kanagawa et al. (2015) found a scaling relation between the level of gas depletion in the cavity and the mass of the planet. This relation also depends on the disc’s properties, particularly on the scale height and the disc’s viscosity. Duffell & Dong (2015) performed a similar study, including up to three planets in the simulations. They found that when planets are massive enough, their spheres of influence are consequently larger and favour gap merging. Once this regime has been reached, the mutual gravitational perturbation amongst the planets stirs the gas inside the common gap, making it shallower. This implies that in order to get the same level of gas depletion created by a single planet of a given mass, a system with multiple planets would require them to be more massive. With these simulations being computationally demanding, Duffell & Dong (2015) explored only a limited subset of the parameter space. In particular, their work is restricted to equal-mass planets in a 2:1 orbital com-mensurability within a disc characterised by a Shakura-Sunyaev a parameter of 10−2. In conclusion, simulations suggest that the level of gas depletion in a cavity carved out by one or several planets encodes information about their mass.
All of the above suggests that a robust constraint on the spatial distribution of gas and dust can provide information about the intricate connection amongst planets and discs. In this work, we retrieve the gas and dust distribution in the PDS 70 disc and analyse the inferred substructures in the context of planet-disc interactions. We use a subset of the ALMA gas observations from Facchini et al. (2021) imaged at high spatial resolution, gas and dust radiative transfer forward modelling, and semi-analytic results from hydrodynamical simulations. In Sect. 2, we describe the observations, the tools, and the methods we used to develop the thermo-chemical model. In Sect. 3, we compare the synthetic observables to the observations, and we present the radial dependence of the gas-to-dust ratio and quantify the amount of gas in the cavity. In Sect. 4, we apply the derived radial profiles to compute the level of gas depletion in the gap. We use this information to estimate a characteristic value for the mass of the planets and to qualitatively assess the stirring of gas produced by them. We also discuss the main caveats of our approach in this section. Our conclusions are listed in Sect. 5.
2 Methods
2.1 Observational data
We worked with ALMA band 6 observations taken as part of the programme #2019.1.01619.S (PI: S. Facchini). The instrument configuration was targeted to detect spatially resolved emission from molecular lines at 0.1 arcsec resolution covering the frequency range 217.194-233.955 GHz. A total of 16 transitions were detected from 12 different molecular species, including isotopologues. In particular, we used the imaged set for C18O J = 2–1, 13CO J = 2–1, and 12CO J = 2–1 presented in Law et al. (2023) with a beam full width half maximum of ~0.15 arcsec (17 au) and an rms noise level of ~1.0 mJy beam−1 estimated on the mean value of the spectrum. A full description of the observations and the data reduction process is presented in Facchini et al. (2021) and Law et al. (2023).
Parameters of the thermo-chemical model.
2.2 Radiative transfer simulations: from the continuum to gas-phase models
The two-dimensional model for the continuum presented in Portilla-Revelo et al. (2022) was taken as a starting point to develop a thermo-chemical model for the source. That model reproduces the ALMA observation at 855 µm and the VLT/SPHERE observation in polarised-scattered light at 1.25 µm.
The model for the dust emission was developed in the three-dimensional version of the continuum radiative transfer code MCMax3D (Min et al. 2009)1. To translate it into the thermo-chemical code ProDiMo (Woitke et al. 2009, 2016; Kamp et al. 2010; Thi et al. 2011)2, we kept the properties of the dust disc constant as given in Table 1. The protoplanetary disc was simulated as a two-zone object with a boundary at 41 au that delimits the transition from the gap’s outer edge to the outer disc in the continuum. Both zones are populated with dust grains made of carbon and silicates in percentages by volume of 19.2 and 60.8%, respectively, and with a fraction of vacuum accounting for 20% of the grain volume. The 2D dust mass density distribution was mapped from the spherical grid of MCMax3D onto the cylindrical grid of ProDiMo in order to subsequently derive the column density per grain size by integrating the mass density over the vertical coordinate. The cylindrical grid has 120 radial and 100 vertical points logarithmically spaced. Figure A.1 shows the total dust surface density as well as some values for selected grain sizes. The dust column density was used to define the limits of the dust gap, which we assumed extended from 16 au to 41 au. This profile also set an upper limit of 10−5 g cm−2 to the dust column density inside the gap, indicating a drop by a factor of 2500 with respect to the outer disc. The dust model is limited by the ALMA continuum sensitivity at 855 µm, which explains why it is radially extended only up to 130 au.
In ProDiMo, the Shakura-Sunyaev α parameter (Shakura & Sunyaev 1973) mimics dust settling according to Dubrulle et al. (1995). In essence, the a value sets a different scale height to each bin size in the dust distribution. Each dust scale height is proportional to the gas pressure scale height, and the proportionality constant varies inversely with the grain size. Portilla-Revelo et al. (2022) used a value of α ~ 10−2 across the disc, which is equal to the value fixed in the simulations by Duffell & Dong (2015) and consistent with the upper limit explored by Kanagawa et al. (2015). However, recent numerical studies on the viscous evolution of discs (Delage et al. 2022) as well as empirical evidence (Rosotti 2023) support values of a lower than a few times 10−3. To make a compromise between these two scenarios, we adopted a constant value of α = 5 × 10−3 in both zones in this work. This is within the range of the existing constraints presented in Rosotti (2023) for other discs. A lower turbulence enhances dust settling, which in turn lowers the submillimetre flux, especially from the outer disc, where most of the dust mass resides. Therefore, to compensate for a lower submillimetre flux, we homogenised the dust size distribution across both zones to be in the range of 0.001 µm to 3 mm. This modification decreases the dust opacity of the inner disc compared to that in Portilla-Revelo et al. (2022), allowing more photons to reach the outer disc, which increases the heating and boosts the submillimetre flux. A final fine-tuning to the surface density profile was required to reproduce the ALMA continuum image at 855 µm and the polarised-scattered image at 1.25 µm. This change produced a disc dust mass of 3.5 × 10−5 M⊙, which is 22% less than the mass estimated in Portilla-Revelo et al. (2022). Both profiles are compared in Fig. A.2. A comparison of the midplane dust temperature for both models is shown in Fig. A.3.
For the gas component, we used a parameterised structure for the vertical distribution. We assumed a Gaussian vertical profile:
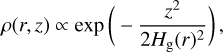 (1)
(1)
where the parametrised gas scale height is
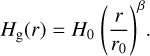 (2)
(2)
Here, H0 is the reference scale height at r0, and β is the flaring exponent.
For completeness, the full set of model parameters and their values are summarised in Table 1. With the parameterised structure of the gas disc and the dust column density, ProDiMo calculates the continuum radiative transfer and iterates the model over the heating-cooling balance and the chemistry in the disc. For the chemistry, we used a reduced chemical network with 100 species and 1286 reactions (Kamp et al. 2017). In our model, CO isotopologue chemistry is not included, and consequently the effects of isotope-selective photodissociation of CO are not simulated. The ratios for 12CO/13CO and 12CO/C18O were taken from Henkel et al. (1994). In the line radiative transfer step, we simulated the following transitions: C18O J = 2–1, 13CO J = 2–1, and 12CO J = 2–1.
Properties of the observational data used in this work as presented in Law et al. (2023).
2.3 Post-processing of the model and comparison to the observation
The simulated CO data cubes were post-processed as follows. First, we used CASA version 6.4 (McMullin et al. 2007) to convolve the cube with a Gaussian beam. The size and orientation of the resolution element passed to the convolve2d task to match the observation can be found in Table 2 for each transition. Then, we used the imcontsub task to subtract the continuum signal from each channel in the convolved cube. One-third of the total number of channels were assumed to be line-free and were used to fit a zero-order polynomial to estimate the continuum level. Finally, we used the task immoments to collapse the cube and create the moment zero map for each transition. In this step, we used all the continuum-subtracted channels in the cube without any sigma clip on the pixel values along the spectral axis.
The azimuthally averaged radial profile of the moment zero map was obtained using the GoFish package (Teague 2019). In this step, we adopted an inclination of i = 51.7° for the disc with respect to the plane of sky and a position angle of 160.4° measured east-of-north (Keppler et al. 2019). The moment zero map was binned radially with a spacing of θmaj /4, where θmaj is the major axis of the resolution element of the observation. The resulting radial profiles of the synthetic moment zero maps were overlaid to the observations, and the goodness of the model was determined by visual inspection.
2.4 Modelling optically thin lines
This section introduces the method we used to reproduce observed integrated intensities from optically thin emitters. The method is based on an iterative procedure where the initial guess is provided by a simple semi-analytic model that connects the optically thin emission from an adequate tracer with the total gas column density.
First, we needed to determine a suitable optically thin tracer. From the solution of the radiative transfer equation with no background sources, the ratio of the integrated intensities for 13CO and C18O would be equal to the ratio of the respective optical depths if both of the isotopologues were optically thin. We assumed that the optical depth ratio is equal to the respective isotopologue ratio in the local interstellar medium (ISM) of 7.3 ± 0.7 (Wilson & Rood 1994). Then, we expected the integrated intensities to scale roughly as 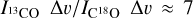 . However, the observed profiles suggest that there are regions in the disc where this ratio is close to three, which is too low to be consistent with the uncertainties in the isotopologue ratio measurement. This suggested that the 13CO emission is moderately optically thick, and accordingly, we assumed C18O to be a suitable proxy for optically thin emission.
. However, the observed profiles suggest that there are regions in the disc where this ratio is close to three, which is too low to be consistent with the uncertainties in the isotopologue ratio measurement. This suggested that the 13CO emission is moderately optically thick, and accordingly, we assumed C18O to be a suitable proxy for optically thin emission.
The intensity emitted by a plane-parallel slab of optically thin material can be related to the population of emitters in the upper excited state Ni via
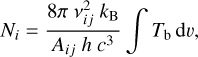 (3)
(3)
where vij and Aij are the frequency and the spontaneous emission coefficient of the transition i → j, kB and h are the Boltzmann and Planck constants, c is the speed of light, and Tb is the brightness temperature integrated in intervals of velocity dυ. Therefore, for optically thin C18O J = 2–1, the observed brightness temperature can be linked to the abundance of C18O molecules in the upper state. Additionally, if local thermodynamic equilibrium (LTE) holds, the level population of the excited state can be written explicitly in terms of the total abundance of C18O via the partition function. Equation (3) can be finally expressed in terms of the C18O surface density ΣC18O as
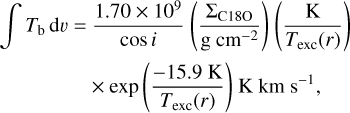 (4)
(4)
where cos i is a correction factor that accounts for the inclination of the source with respect to the plane of sky. For simplicity, the position-dependent excitation temperature Texc(r) was assumed to be equal to the dust temperature at the corresponding midplane location (see Fig. A.3).
By combining the semi-analytic model given by Eq. (4) with the observed azimuthally averaged profile of the moment zero map for C18O J = 2–1, we obtained an initial approximation of the column density distribution of C18o molecules. To estimate the total gas column density from the C18O distribution, we had to make a series of assumptions about the isotopologue abundance with respect to that of H2. As we are only interested in getting an initial approximation of the gas distribution, we adopted the local interstellar medium value for the ratio 12CO/C18O ≈ 560 (Wilson & Rood 1994) alongside a canonical 12CO/H2 ≈ 10−4 (Dickman 1978). The resulting semi-analytic profile for the total gas distribution is shown in Fig. A.4, and we note that it already points to the presence of a gas-depleted gap.
We used this initial gas distribution to run a first thermo-chemical ProDiMo model (i.e. solving for the continuum radiative transfer, heating-cooling balance, and chemistry), which was post-processed following the steps described in Sect. 2.3. Although the synthetic observables retrieved from the first run do not explain the observations satisfactorily, the semi-analytic approach is still useful because it does not require expensive exploration of the parameter space that defines the gas column density. Nonetheless, the semi-analytic approach ignores complexities such as any cumulative effect on the heating-cooling balance and on the chemistry that could arise from the column of material built up in the radial direction, which is consistently modelled in a full thermo-chemical simulation.
Subsequently, we modified the gas distribution using the following iterative procedure. After running the first thermo-chemical model using the semi-analytic initial gas distribution, we divided the radial profile of the synthetic moment zero map for C18O J = 2–1 by the observed one at each location where observational information is available. These ratios are point-by-point correction factors that inform the model about where in the disc gas mass has to be added or removed. We then multiplied point-by-point the gas profile of the initial simulation by the correction factors and used the resulting profile as an input for a second thermo-chemical run. We iterated over the same procedure until the relative difference between the modelled and observed profiles for C18O J = 2–1 was less than 10%. During the iterations, the dust column density was kept fixed, and only the gas column density was varied. Finally, we used the same gas profile to obtain synthetic observables for 13CO J = 2–1 and 12CO J = 2–1.
3 Results
3.1 Benchmark for the continuum model
To verify the translation of the MCMax3D disc setup into the ProDiMo 2D setup, we ran the ProDiMo model using the same constant gas-to-dust ratio of 100 from Portilla-Revelo et al. (2022). We simulated the continuum ALMA observation at 855 µm and the spectral energy distribution. The ray-traced image was convolved with a Gaussian beam of size 67 × 50 mas (~ 8 × 6 au) and a position angle of 61. 5°, as in Isella et al. (2019). A comparison to the observed data set is presented in Fig. 1. Both results are in good agreement with the observations, which demonstrates that the implementation of the MCMax3D model into ProDiMo was correctly done.
We note that some fundamental differences exist between MCMax3D and ProDiMo. An important one is the treatment of the scattering. While MCMax3D uses a full treatment of the scattering phase function, ProDiMo only models isotropic scattering. Despite this fact, the difference in the synthetic observables for the continuum is negligible.
3.2 Gas column density and gas-to-dust ratio profiles in the PDS 70 disc
After five iterations, the procedure outlined in Sect. 2.4 yielded a relative error of less than 10% with respect to the intensity profile of the C18O J = 2–1 observation. The fifth iteration is then the best representative model. The comparison between the observed and modelled profiles for both optically thin and thick tracers is shown in Fig. 2. Although the gas column density is inferred based only on C18O, it also does a passable job of reproducing the 13CO J = 2–1 and 12CO J = 2–1 data.
The final gas column density and gas-to-dust ratio profiles are shown in Fig. 3. The value of the gas-to-dust ratio ranges from ten in the region beyond the cavity’s outer edge (r ≳ 40 au) to almost 1000 in the cavity. The lower value of the gas-to-dust ratio can be explained by the accumulation of dust caused by the existence of a pressure bump at the gap’s outer edge. Therefore, our approach naturally points towards the expected consequence of the long-range interaction between the planets and the outer disc: the emergence of a pressure bump where dust can accumulate and grow (Pinilla et al. 2012). The higher value is driven by the low dust column density in the cavity that is expected from the observations in the continuum and their modelling.
There is a clear modulation of the gas-to-dust profile that follows the shape of the dust column density. The gas-to-dust ratio shows strong gradients where the dust density reaches a minimum value in the dust gap and at r ~110 au. The constant value of 10−5 g cm−2 for the dust column density in the outermost disc (see Fig. 3) is also set by the ALMA observation, which traces mostly (sub)millimetre-sized grains. Observations of these outer regions at shorter wavelengths are required to constrain the (sub)micron-sized population. We emphasise that, by construction, the limit of applicability of our model is 130 au.
3.3 Estimating the gas mass inside the dust gap
The amount of gas inside the dust gap 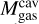 can be readily estimated by integrating the gas column density over the radial extension of the dust cavity from 16 to 41 au and over the entire azimuth. For an axisymmetric disc, the gas mass relates to the column density via
can be readily estimated by integrating the gas column density over the radial extension of the dust cavity from 16 to 41 au and over the entire azimuth. For an axisymmetric disc, the gas mass relates to the column density via
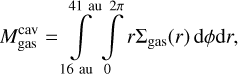 (5)
(5)
which yields 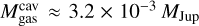 . If we repeat this procedure for the dust component, we obtain
. If we repeat this procedure for the dust component, we obtain 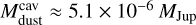 . Therefore, we found an average gas-to-dust ratio of ~630 within the limits of the dust gap. For the inner disc extending from 0.04 au to 16 au, the retrieved value for the gas mass is 7.6 × 10−4 Mjup and 7.9 × 10−5 Mjup for the dust mass, implying a gas-to-dust ratio of ~10. These quantities for the inner disc must be taken with caution due to the limited spatial resolution of our data set.
. Therefore, we found an average gas-to-dust ratio of ~630 within the limits of the dust gap. For the inner disc extending from 0.04 au to 16 au, the retrieved value for the gas mass is 7.6 × 10−4 Mjup and 7.9 × 10−5 Mjup for the dust mass, implying a gas-to-dust ratio of ~10. These quantities for the inner disc must be taken with caution due to the limited spatial resolution of our data set.
The total gas mass of the best representative model is >3.0 × 10−4M⊙ (inside 130 au). The radial extent of the gas disc in PDS 70 is expected to go well beyond what is traced by the (sub)millimetre dust. Thus, we interpret this value as a lower limit.
 |
Fig. 1 Synthetic observables for the continuum compared to data. Left: predicted spectral energy distribution (black and red curves) and photometry towards PDS 70 (blue dots). The photometric data were taken from Gregorio-Hetem et al. (1992), Cutri et al. (2003), Hashimoto et al. (2012), and Keppler et al. (2019). The value at 855 µm (Keppler et al. 2019) is from integrating the brightness distribution over an elliptical aperture of the projected radius 130 au. Right: azimuthally averaged radial profiles from the ALMA continuum observation at 855 µm and from the modelled images ray traced at the same wavelength. The shaded area indicates the resolution element of the continuum observation of 0.067 arcsec. |
 |
Fig. 2 Azimuthally averaged profiles for the integrated intensity of C18O J= 2–1 (left), 13CO J=2–1 (middle), and 12CO J = 2–1 (right). The solid lines are the modelled profiles, and the blue dots are the ALMA observations. Vertical dashed lines indicate the limits of the dust gap. The shaded area indicates the resolution element of the C18O J = 2–1 observation of 0.16 arcsec. |
4 Discussion
4.1 Linking gas depletion to planet masses
Models of planet formation predict the opening of a gap in the gas distribution by planets of mass >15 M⊕. For a disc hosting a single gap-carving planet, the mass of the planet Mp correlates with the depth of the gap. Kanagawa et al. (2015) showed that this relation is given by
![$ {{{M_{\rm{p}}}} \over {{M_*}}} = {\left[ {25\,\,\left( {{1 \over {{{{{\rm{\Sigma }}_{\rm{p}}}} \mathord{\left/ {\vphantom {{{{\rm{\Sigma }}_{\rm{p}}}} {{{\rm{\Sigma }}_{\rm{0}}}}}} \right. \kern-\nulldelimiterspace} {{{\rm{\Sigma }}_{\rm{0}}}}}}} - 1} \right)\,h_{\rm{p}}^5\,\alpha } \right]^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}, $](/articles/aa/full_html/2023/09/aa46607-23/aa46607-23-eq10.png) (6)
(6)
where ΣP and Σ0 are gas column densities measured at the bottom of the cavity and at the gap’s edge, respectively. Their ratio represents the level of gas depletion in the cavity. Equation (6) also depends on the scale height and turbulence strength measured by the Shakura-Sunyaev α parameter (Shakura & Sunyaev 1973). For fixed values of the scale height and turbulence parameter, it is clear that
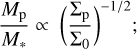 (7)
(7)
the mass of a planet scales with the inverse of the square root of the gas depletion it causes.
For the multiple-planet case, Duffell & Dong (2015) provided a set of closed fitting formulas relating the level of gas depletion to the planet mass (see Eq. (14) in that paper). Planets were assumed to have the same mass and to move on circular orbits under the effect of the combined gravitational potential of the star and the other planets. They were located in a 2:1 mean motion resonance with one another. The star was at rest and unperturbed by the planets. The disc was assumed to be globally isothermal, with a constant sound speed that satisfies a scale height value of 0.05 at the location of the outermost planet. The functional form of the fitting formula depends on how the mass of the planet is related to a critical value of the planet-to-star mass ratio (qcrit)> which is readily derived from the gap merging criterion (i.e. from the commensurability of the minimum separation between the two planets to the radial extent of their spheres of influence). Using the best fit orbital solution for PDS 70 b and c from Wang et al. (2021), we found qcrit = 0.002. Particularly for planet-to-stellar mass ratio values ≳2.2 × qcrit, the scaling law from Duffell & Dong (2015) takes the form
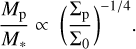 (8)
(8)
From the scaling relations given by Eqs. (7) and (8), we saw that in order to explain the same level of gas depletion, a disc with multiple planets would require those planets to be more massive than the single-planet counterpart.
Following the theoretical results by Duffell & Dong (2015) and Kanagawa et al. (2015), we used the results in Fig. 3 to estimate the degree of gas depletion in the gap of the PDS 70 disc. The location of the gap edge for the gas distribution was assumed to match that of the peak value, and therefore we adopted Σ0 = 0.13 g cm−2 at r = 75 au. The minimum occurs at 20.4 au and has a value of Σmin = 3.3 × 10−3 g cm−2. Interestingly, the location of the minimum matches the best fit solution for the semi-major axis of PDS 70 b found by Wang et al. (2021). These values imply a gas density drop by a factor of ~39 at 20 au. To be consistent with the prescription in Duffell & Dong (2015) for the multiple-planet case, the gas depletion must be redefined with respect to the value measured at the location of the outermost planet. The semi-major axis of planet c is ac = 34.3 au (Wang et al. 2021), and at that radius, the gas surface density is Σp = 7.0 × 10−3 g cm−2. Therefore, the level of gas depletion is
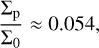 (9)
(9)
which is equivalent to a density drop factor of ~ 19 at ac = 34 au.
We directly compared Eq. (9) with Eq. (14) from Duffell & Dong (2015), which is the fitting formula connecting the gas depletion with the planet mass. The result is shown in Fig. 4 where the horizontal line intersects the theoretical curve at a planet mass of 4 MJup. We stress that the planet mass derived through this method is degenerate by construction because the underlying hydrodynamical models assumed equal-mass planets. Accordingly, we constrained the mass of each planet to be roughly 4 Mjup. For comparison, we overlayed the mass estimates of the two planets given by Wang et al. (2021), which were obtained via analysis of near-infrared data. The respective shaded areas indicate the 68% confidence interval in their mass determination. In conclusion, the value that we predict for the mass of each planet in the PDS 70 disc via analysis of submil-limetre data is in good agreement with literature values based on infrared techniques3.
Although our 4 MJup estimate is close to the mean value for PDS 70 b, according to Wang et al. (2021), it is more towards the lower side for PDS 70 c. For the latter case, special considerations have to be made to account for obscuration effects of the circumplanetary disc (CPD) and, to a lesser degree, of the circumstellar outer disc. As for the CPD effect, we can crudely approximate the fraction of the planet mass that the CPD would represent. In Portilla-Revelo et al. (2022), we estimated the CPD dust mass to be ~0.1 M⊕. Assuming a gas-to-dust ratio of 100 for the CPD, its total mass would account for nearly 1% of the estimated planet mass. Therefore, although our method is agnostic to the presence of a CPD, we do not expect this characteristic to impact our results.
Although Duffell & Dong (2015) fixed the values of the turbulence strength and the pressure scale height in their simulations, we expect the mass estimation in the multi-planet case to depend on those parameters as well, just as in Kanagawa et al. (2015) for the single-planet case (see Eq. (6)). Due to the forward modelling approach implemented in this work, we cannot provide a full statistical account of the uncertainties associated to each parameter in the thermo-chemical model. Instead, in the following subsections, we investigate the robustness of our mass estimate based on some key parameters. This is not intended to be an exhaustive exploration of the whole range of values those quantities can adopt, and instead it is limited to a series of physically motivated scenarios.
 |
Fig. 3 Gas and dust densities inferred from the best representative model. Top: predicted gas and dust surface densities in gram per square centimetre (g cm−2) versus distance to the star. Bottom: gas-to-dust ratio. The shaded area indicates the resolution element of the C18O J = 2–1 observation of 0.16 arcsec. The vertical lines indicate the location of the planets. |
 |
Fig. 4 Value of the gas depletion inferred from our model (grey line) overlaid to the scaling relation from Duffell & Dong (2015) (black line). The two curves intersect at ~4MJup. The dashed lines and shaded areas indicate the mean value and the 68% confidence interval for the mass of PDS 70 b and c given by Wang et al. (2021). |
4.1.1 The effect of dust filtration on the pressure scale height
Simulations in Duffell & Dong (2015) and Kanagawa et al. (2015) did not account for particle filtration at the outer edge of the cavity. In other words, they assumed that the dust grains, even the millimetre-sized ones, follow the same radial distribution as the sub-micrometre grains and the gas particles. As dust is the main source of opacity at visual and infrared wavelengths, the way it is distributed can alter the thermal structure of the disc and its gas physics. Many theoretical studies have suggested that the gas and dust distributions can largely deviate from each other when substructures such as gaps opened by planets are present (Rice et al. 2006). This phenomenon might be in operation in PDS 70, as suggested by the hydrodynamical simulations from Bae et al. (2019) where only sub-micron sized grains were observed to populate the inner disc after 0.6 Myr. A similar scenario is supported by the spectral energy distribution fitting and scattered-light modelling of the same source in Portilla-Revelo et al. (2022). However, as demonstrated in Sect. 3.1, the multiple degeneracies amongst the parameters of a forward model leave room to explain the same observables with a homogeneous dust size distribution. In principle, the scenario of a disc with segregated grains can be conciliated with the non-segregated case by claiming efficient grain growth in the inner disc, but inferring the presence of this process in PDS 70 would require a dedicated modelling that includes the appropriate physics.
Instead, we estimated the effect that dust filtration could have on our derived planet masses. Dust filtration alters the opacity properties in the inner zone. For a fixed dust column density, an inner disc (r ≲ 16 au) populated with grains of maximum size amax ~ 100 µm is expected to have a higher visual and infrared opacity than the outer disc where amax ~ 3 mm. This affects the thermal structure of the disc and in turn impacts the scale height via the gas temperature. This will affect the planet mass estimate according to Eq. (6).
Assuming LTE conditions and that the gas and dust temperatures are equal, which is a good approximation in the midplane where the planets reside, it is easy to make a semi-analytical study of the impact of dust filtration on the planet mass estimate. To achieve this goal, we first computed the dust temperature for the two size distributions we are interested in. Assuming a balance between stellar heating and blackbody radiation cooling, the dust equilibrium temperature Td is given by the solution to the implicit equation
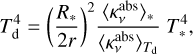 (10)
(10)
where R* and T* are the stellar radius and effective temperature, r is the distance from the planet to the star, and the absorption opacities 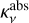 are averaged over the stellar spectrum in the numerator and over the blackbody spectrum in the denominator. We solved Eq. (10) for two values of the maximum grain size in the inner zone, amax = 100 µm and amax = 3 mm, which respectively represent two scenarios, that is, when filtration is present at the gap’s edge and when it is not. The calculation yielded Td,100 µm/Td,3 mm = 1.2. Finally, we assumed that the mass in the multiple-planet case also scales as
are averaged over the stellar spectrum in the numerator and over the blackbody spectrum in the denominator. We solved Eq. (10) for two values of the maximum grain size in the inner zone, amax = 100 µm and amax = 3 mm, which respectively represent two scenarios, that is, when filtration is present at the gap’s edge and when it is not. The calculation yielded Td,100 µm/Td,3 mm = 1.2. Finally, we assumed that the mass in the multiple-planet case also scales as 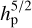 , as in the single-planet case (Eq. (6)). Due to the square root dependence of the sound speed on the temperature4, this difference of 20% in temperature translates into a difference of just 10% in the sound speed. Accordingly, the relative difference on the scale heights should be of the order of 10% as well. Finally, assuming that all the parameters but the scale height in Eq. (6) remain constant, we expected a difference of 26% in the planet mass. This brought our initial estimate of 4 MJup up to 5 MJup.
, as in the single-planet case (Eq. (6)). Due to the square root dependence of the sound speed on the temperature4, this difference of 20% in temperature translates into a difference of just 10% in the sound speed. Accordingly, the relative difference on the scale heights should be of the order of 10% as well. Finally, assuming that all the parameters but the scale height in Eq. (6) remain constant, we expected a difference of 26% in the planet mass. This brought our initial estimate of 4 MJup up to 5 MJup.
4.1.2 Dependence on α and Σ0
From Eq. (6), it follows that the planet mass depends on both the Shakura-Sunyaev a parameter and the unperturbed Σ0 density to the one-half power (to the one-fourth power in the multiple-planet case). The values of those parameters are model dependent and in principle correlated and so are their uncertainties. However, that correlation is not trivial to establish because of the several intricacies amongst the heating and cooling mechanisms and the chemical processes that in the end determine the shape of the gas density. The simplest method to circumvent this problem is to work on an alternative forward model that uses a different value of α to derive a new best fit gas density profile.
Building on the dust model in Portilla-Revelo et al. (2022) that used α = 2 × 10−2 and amax = 100 µm, and α = 10−2 and amax = 3 mm, in the inner and outer zones respectively, we constructed an alternative model for the gas that reproduces the C18O J = 2–1 observation. The retrieved density profile shows a peak value of 0.17 g cm−2 at 76 au, while the density at the location of PDS 70 c is 7.4 × 10−3 g cm−2. These values are very similar to those presented in Sect. 4.1 for the best fit model, and therefore, following Duffell & Dong (2015) for the multiple-planet case, the planet masses are expected to be similar too.
Conversely, for the single-planet case, we expected from Eq. (6) a planet twice as massive due to the factor of four in the ratio of α parameters in both models. However, the alternative model also predicts a hotter midplane, which is in part explained by the higher continuum opacity of the inner zone. In fact, the representative model in Sect. 2.4 predicts Tgas = 16 K for the gas temperature at the location of PDS 70 c, whereas the alternative model has Tgas = 21 K. Introducing these dependencies into Eq. (6), we found that the planet mass increases to 9 MJuP, a factor of 2.4 difference from the mass estimate. This high value still falls within the predicted mass of PDS 70 c but is beyond that of planet b.
Although these experiments help quantify the impact of α on the mass estimate, they do not break the degeneracy between the two quantities, which is a more fundamental issue that should be addressed with an expanded parameter space exploration in the hydrodynamical simulations. We also note that the α parameters used in the hydrodynamical models and in ProDiMo act in different ways, driving gas flows and determining vertical settling of dust grains, respectively. The viscosity responsible for these two phenomena might not have the same physical origin. In the future, the two modelling approaches should be directly coupled to improve the method. Additionally, our forward modelling suggests that α = 5 × 10−3, but this by no means implies that we can rule out lower values. An enhanced settling could bring Σ0 to lower values such that the depletion level coincides with the plateau between qcrit and 2.2 × qcrit seen in Fig. 4 where the mass is entirely unconstrained. Therefore, an independent measurement of a in PDS 70 is needed and should be the aim of a future work.
The results presented in this section show that although they strongly depend on the model, for reasonable choices in the disc’s parameters, our approach is capable of constraining the mass of embedded planets within a factor of a few of what is inferred from direct observation. Since those parameters are dictated by a dedicated modelling of multiple observables, they are likely to be refined as new observations come along. We demonstrated in this work that such an approach has the potential to naturally reduce the uncertainties in the mass estimation of young protoplanets, especially in cases where direct observations prove impossible.
4.2 Gas stirring in the gap of PDS 70
An upper limit for the level of gas depletion can be obtained by applying Eq. (6) to the lowest value of the combined planet mass that is consistent with the VLTI/GRAVITY measurements (Wang et al. 2021). We assumed this lowest value equals the arithmetic mean of the values at the lower end in the 68% credible intervals in Wang et al. (2021). This is 2.5 MJup. Solving Eq. (6) for the level of gas depletion, we found the upper limit to be5 9.0 × 10−3, which is a factor of six lower than our estimate given in Eq. (9) (we note that this factor will only increase if we pick the mean planet masses or those at the upper end of the interval). To conciliate the two values, we would have to assume a lower combined mass, but this would be inconsistent with the constraints imposed by the infrared data. Another way to bring these factors close to each other is by invoking gas stirring due to the perturbative effect that each planet exerts on the gas in the common gap. In fact, Fig. 3 in Duffell & Dong (2015) predicts that gas stirring due to two or more planets can naturally explain gas gaps being shallower by at least a factor of ten compared to the gap depths expected in the single-planet case.
We stress again that this analysis depends strongly on the ability of our model to capture the actual physical state of the disc. In that case, our results support the idea that gas stirring processes are at play in the planet-hosting gap in the PDS 70 disc.
4.3 Modelling optically thick lines
The abundance of12 CO is almost two orders of magnitude larger than the less common and moderately optically thick isotopo-logue 13CO. Hence, we assumed the former to be optically thick. Unlike the thin case, optically thick emission is mainly driven by temperature.
We performed two tests in order to assess the performance of the model in reproducing optically thick emission. First, we can compare our results to the line flux emitted by the disc within the first 130 au. This region is delimited by the red dashed ellipse in Fig. A.6. The model predicts an integrated value of 3624 mJy km s−1 for 12CO J = 2–1. This is close to the observed value of 3545 mJy km s−1. For 13CO J = 2–1, we obtained a value of 1355 mJy km s−1, which is again in good agreement with the observed value of 1331 mJy km s−1.
As a second test, we analysed the spatially resolved intensities. The right panel in Fig. 2 shows a comparison of the simulated 12CO to its observational counterpart. The maximum deviation from the observation occurs within the limits of the dust gap, especially near the outer edge, whereas the fits seem passable outside the gap. This suggests that although several parameters can be tweaked to alleviate the discrepancy, we should focus our attention on those that are expected to have a local effect in the gas temperature. Analysis of the heating mechanisms contributing to the gas temperature showed that inside the gap, for values of z/r ~ 0.1, heating by H2 formation on dust is the leading heating mechanism, followed by dust thermal accommodation. Both of these heating mechanisms are proportional to the dust density. Therefore, we modified the dust distribution, keeping constant the gas density and exploring the impact on the 12CO emission. We artificially increased the dust mass contained between 27 and 60 au by a factor of ~30% by deforming the column density using a Gaussian function with a standard deviation of 9 au within those limits (Fig. 5). We ran the thermo-chemical model on top of this dust profile, and the radial profile predicted for the 12CO emission is shown in Fig. 6. As expected, the higher column density near the gap’s outer edge has a localised effect on the 12CO intensity that now agrees better with the observation. The modified dust density guarantees that the fit to the other observables is not severely undermined.
In fact, the left panel of Fig. 6 shows the radial profiles of the 12CO J = 2– 1 moment zero maps from the best representative model and from a similar model that used the modified dust surface density of Fig. 5. The predicted intensities differ only in the region where the dust density was increased, and the maximum difference is 30%. For 13CO and C18O, the relative deviations are minor and as low as 4% for the C18O case (Fig. 6, right panel). We demonstrate with this experiment that there is a subset of the parameter space that can be tweaked to bring the optically thick emission closer to the observation while keeping the gas density and the level of turbulence unchanged. It also shows that these modifications of the temperature structure will not substantially change our main conclusions driven by the analysis of optically thin emission.
Modifying the dust profile is by no means the only way to improve the fit to thick lines. In recent papers, it has been shown for other discs that gas cavities are smaller than the dust counterpart and that the temperatures in the cavities tend to increase (see e.g. Wölfer et al. 2023; Leemker et al. 2022). If the same applies to PDS 70, these effects combined can bring the12 CO profiles into closer agreement with the observations without requiring modification of the dust distribution.
Polycyclic aromatic hydrocarbons (PAHs) might have an influence in setting the gas temperature within gaps and cavities (Leemker et al. 2022). For example, Calahan et al. (2021) found for HD 163296 that the PAHs have a significant contribution to the gas heating only in the layers where gas and dust temperatures decouple. Given the lack of constraints on the PAH abundance in T Tauri discs (Geers et al. 2006), we did not perform a detailed exploration for this parameter, and we used a fixed abundance of 1% of the ISM value.
The thermal accommodation coefficient that regulates the energy exchange rate in inelastic collisions between gas and dust particles (Burke & Hollenbach 1983) and can take any value between zero and one was not explored in detail, and we used a fixed value of 0.2. However, it is clear that a single value for this quantity will be insufficient if the dust properties change throughout the disc.
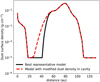 |
Fig. 5 Dust column density profiles of the PDS 70 disc (solid line, same as in Fig. 3) and a similar disc with 30% extra dust mass between 27 and 60 au. |
4.4 Emitting surfaces
The fact that molecular line emission originates well above the midplane sets important constraints on the modelling, mainly when dealing with optically thick transitions. From the ProDiMo models, it is straightforward to extract information about where in the disc radiation from a certain molecular species is being emitted. We define here the line emitting region as the area from which the 15–85% percentile of the radiation is being emitted along the radial and vertical directions. The comparison between the area of emission to the emitting surface observation-ally derived can be used as another proof of the robustness of the model.
Law et al. (2023) derive line emitting surfaces for several molecules in PDS 70. We used the parameters of the best fit solution for the emitting surfaces in that paper and compare them with the line emitting regions for 13CO and 12CO predicted by the model (see Fig. 7). In both cases, the emitting area is below the critical density threshold for 12CO J = 2–1 given by the white curve, justifying the use of LTE excitation.
In general, there is good agreement between the area of emis-sion and the emitting surface from the observation inside 100 au. However, at larger distances, the model tends to overpredict the height of emission of 13CO, while it underpredicts that of 12CO. An extension of the model to larger semi-major axes is needed to study the behaviour of the emitting regions in the outskirts of the disc.
4.5 Variations in the C/O ratio
The abundance of CO has been shown to be correlated to the C/O ratio, with high C/O ratios implying lower CO abundances (Bergin et al. 2016). When combining high-resolution ALMA observations and dedicated thermo-chemical models for the AS 209, HD 163296, and MWC 480 discs, Bosman et al. (2021) showed that a high C/O ratio (>2) and a strong depletion of small dust grains are needed to reproduce the measured peak values of the C2H column densities.
Our best representative model uses a canonical solar C/O ratio of 0.457 that is assumed to be constant across the disc. To estimate the effect that a potentially higher C/O ratio would have on our synthetic observables, we decreased the elemental abundance of oxygen such that the C/O ratio goes up to ~1.1. We used this value to make sure the chemistry switches into the regime of carbon chemistry (i.e. the CO formation locks up all oxygen). We ran a simulation where the rest of the parameters were kept constant, and the results are shown in Fig. A.5. We found that the quality of the fit to the brightness profiles is not severely diminished and an additional fine-tuning to the total gas distribution seems unnecessary. On the basis of this simple experiment, we do not expect substantial changes in the synthetic CO observables due to the C/O ratio being slightly above one.
5 Conclusions
We studied the gas distribution of the PDS 70 disc using radiative transfer modelling of dust and line emission with a special focus on the dust-depleted gap where the two planets, PDS 70 b and c, reside. We used a subset of the chemical inventory from Facchini et al. (2021) to develop a thermo-chemical model that explains ALMA band 6 observations of C18O J = 2–1, 13CO J = 2–1, and 12CO J = 2–1. The continuum emission at 855 µm and the photometry towards the source were also reproduced. The modelling results were used to characterise the spatial distribution of gas and dust in the disc, and the results are interpreted in the light of the theory of planet-disc interaction. Our main conclusions are as follows:
We find a position-dependent gas-to-dust ratio profile with values ranging from ~ 10 to 1000 across the first 130 au in the disc. The profile depicts a sharp transition from the gap to the outer disc. This is consistent with the existence of a pressure maxima outside the orbit of the planets originated by the dynamical interaction between the planets and the outer disc.
The model suggests a gas mass of 3.2 × 10−3 MJup within the dust-depleted gap where the two planets reside. Combined with the dust mass constrained from the modelling of the continuum emission, the spatially averaged gas-to-dust ratio in the gap is approximately 630.
Combining the level of gas depletion in the gap with the results of the hydrodynamical models by Duffell & Dong (2015), we estimate a mass value of 4 MJup for each of the two planets detected in the gap of the PDS 70 disc. This value is consistent with independent constraints based on infrared spectroscopy. We emphasise that the mass derived in this work is equal for the two planets since this is an inherited limitation from the underlying hydrodynamical model. Although the planet masses estimated here depend on the model parameters, especially on the turbulence strength, we demonstrate that, for reasonable choices in the parameters, the values of the planet masses are robust within a factor of a few of what is inferred from direct observation. This work demonstrates the power of using a multi-wavelength and synergistic approach to characterise planets in the embedded phase.
Based on the best representative model, we find a level of gas depletion that is lower by a factor of six with respect to the value expected from the action of a single planet. This could be a result of the gas stirring produced in the gap from the combined gravitational effect of the two planets.
We estimate that 85% of the 12CO J = 2–1 and 13CO J = 2–1 emission originating in the outer disc (r > 60 au) comes from of z > 6 au and z > 3 au above the midplane, respectively.
In this work, we demonstrated the capabilities of forward thermo-chemical modelling coupled with well-established results from hydrodynamical models to exploit a relatively new parameter space of planet formation theories: direct observations of young planets embedded in their progenitor disc. As new cases of study emerge, multi-wavelength and multi-phase observations at high resolutions and sensitivities will be essential. This motivates both the development of new and the refinement of existing models that can help characterise not only the natal disc but also the nascent planets.
 |
Fig. 6 Effect of a localised variation of the dust distribution on line emission. Top left: Azimuthal profiles of the 12CO J=2–1 integrated maps from two models with slightly different dust distributions between 27 au and 60 au. The blue dots are the observations. The shaded area indicates the region where the dust mass was artificially increased by 30% to boost heating by dust thermal accommodation. Bottom left: relative difference of modelled intensities with respect to the best representative model for the 12CO J = 2–1 case. Right: relative difference of integrated intensities for the 13CO J = 2–1 and C18O J = 2–1 cases. |
 |
Fig. 7 Emitting regions from which 15–85% of the 13CO J = 2–1 (grey solid box) and 12CO J = 2–1 (black solid box) radiation is emitted. Dotted lines indicate the emitting region in the vertical direction only. The grey and black crosses are mapped from the fitting functions to the respective emitting surfaces derived in Law et al. (2023). The white curve is the 1.5 × 104 cm−3 contour for the critical density of the 12CO J = 2–1 transition with H2 as the collision partner. The colour map is the gas density. |
Acknowledgements
We thank the anonymous referee for a constructive report and for suggesting the analysis that inspired Sect. 4.2. We thank prof. Paul Duffell for a prompt response to our inquiry on the definition of the gas depletion in the gap. This work is partly supported by the Netherlands Research School for Astronomy (NOVA). S.F. is funded by the European Union under the European Union’s Horizon Europe Research & Innovation Programme 101076613 (UNVEIL). C.H.R. acknowledges the support of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Research Unit “Transition discs” – 325594231. This research was supported by the Excellence Cluster ORIGINS which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311. C.H.R. is grateful for support from the Max Planck Society. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (PROTOPLANETS, grant agreement No. ∼101002188).
Appendix A Physical structure of the modelled protoplanetary disc around PDS 70
 |
Fig. A.1 Dust surface density profiles for selected grain sizes (dashed lines) and the total profile resulting from adding up the density contained in each dust size bin (continuous line). |
 |
Fig. A.2 Comparison of the dust surface density used in this work with that in Portilla-Revelo et al. (2022). |
 |
Fig. A.3 Dust midplane equilibrium temperature compared to that in Portilla-Revelo et al. (2022). |
 |
Fig. A.4 Comparison of the initial gas density obtained from the semi-analytic model (Eq.4) and the final profile of the best representative model. |
 |
Fig. A.5 Azimuthally averaged profiles for C18O J = 2 – 1 (left), 13CO J = 2 – 1 (middle), and 12CO J = 2 – 1 (right) moment zero maps. The modelled curves are the results from two models with different C/O ratios in the disc. The black solid lines were retrieved from the best representative model that uses C/O = 0.457, and the red dashed lines represent simulations with C/O = 1.097. The vertical dashed lines indicate the limits of the dust gap. |
 |
Fig. A.6 Moment zero maps for C18O J = 2 – 1 (top), 13CO J = 2 – 1 (middle), and 12CO J = 2 – 1 (bottom). The left column contains the observations, and the right column contains the models. The dashed ellipse indicates a semi-major axis of 130 au, which is the limit of applicability of our model. An orbital inclination of 51.7° was assumed, the same as for the continuum. |
References
- Bae, J., Zhu, Z., Baruteau, C., et al. 2019, ApJ, 884, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Benisty, M., Dominik, C., Follette, K., et al. 2022, arXiv e-prints [arXiv:2203.09991] [Google Scholar]
- Bergin, E. A., Du, F., Cleeves, L. I., et al. 2016, ApJ, 831, 101 [Google Scholar]
- Bosman, A. D., Alarcón, F., Bergin, E. A., et al. 2021, ApJS, 257, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Burke, J. R., & Hollenbach, D. J. 1983, ApJ, 265, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Calahan, J. K., Bergin, E. A., Zhang, K., et al. 2021, ApJS, 257, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Delage, T. N., Okuzumi, S., Flock, M., Pinilla, P., & Dzyurkevich, N. 2022, A&A, 658, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dickman, R. L. 1978, ApJS, 37, 407 [CrossRef] [Google Scholar]
- Dubrulle, B., Morfill, G., & Sterzik, M. 1995, Icarus, 114, 237 [Google Scholar]
- Duffell, P. C., & Dong, R. 2015, ApJ, 802, 42 [Google Scholar]
- Espaillat, C., Muzerolle, J., Najita, J., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 497 [Google Scholar]
- Facchini, S., Teague, R., Bae, J., et al. 2021, AJ, 162, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Geers, V. C., Augereau, J. C., Pontoppidan, K. M., et al. 2006, A&A, 459, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gregorio-Hetem, J., Lepine, J. R. D., Quast, G. R., Torres, C. A. O., & de La Reza, R. 1992, AJ, 103, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Gullbring, E., Hartmann, L., Briceño, C., & Calvet, N. 1998, ApJ, 492, 323 [Google Scholar]
- Haffert, S. Y., Bohn, A. J., de Boer, J., et al. 2019, Nat. Astron., 3, 749 [Google Scholar]
- Hashimoto, J., Dong, R., Kudo, T., et al. 2012, ApJ, 758, L19 [Google Scholar]
- Hashimoto, J., Aoyama, Y., Konishi, M., et al. 2020, AJ, 159, 222 [Google Scholar]
- Henkel, C., Wilson, T. L., Langer, N., Chin, Y. N., & Mauersberger, R. 1994, in The Structure and Content of Molecular Clouds, eds. T. L. Wilson, & K. J. Johnston (Berlin: Springer), 439, 72 [Google Scholar]
- Isella, A., Benisty, M., Teague, R., et al. 2019, ApJ, 879, L25 [Google Scholar]
- Kamp, I., Tilling, I., Woitke, P., Thi, W. F., & Hogerheijde, M. 2010, A&A, 510, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamp, I., Thi, W. F., Woitke, P., et al. 2017, A&A, 607, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kanagawa, K. D., Muto, T., Tanaka, H., et al. 2015, ApJ, 806, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Keppler, M., Benisty, M., Müller, A., et al. 2018, A&A, 617, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keppler, M., Teague, R., Bae, J., et al. 2019, A&A, 625, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Law, C. J., Benisty, M., Facchini, S., et al. 2023, ApJ, submitted [Google Scholar]
- Leemker, M., Booth, A. S., van Dishoeck, E. F., et al. 2022, A&A, 663, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, ASP Conf. Ser., 376, 127 [Google Scholar]
- Mesa, D., Keppler, M., Cantalloube, F., et al. 2019, A&A, 632, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Min, M., Dullemond, C. P., Dominik, C., de Koter, A., & Hovenier, J. W. 2009, A&A, 497, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, A., Keppler, M., Henning, T., et al. 2018, A&A, 617, L2 [Google Scholar]
- Natta, A., Testi, L., Muzerolle, J., et al. 2004, A&A, 424, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S. J., & Mellema, G. 2004, A&A, 425, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., Dong, R., Duffell, P., et al. 2022, ArXiv e-prints [arXiv:2203.09595] [Google Scholar]
- Pinilla, P., Birnstiel, T., Ricci, L., et al. 2012, A&A, 538, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Price, D. J., Ménard, F., et al. 2018, ApJ, 860, L13 [Google Scholar]
- Pinte, C., van der Plas, G., Ménard, F., et al. 2019, Nat. Astron., 3, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Pinte, C., Teague, R., Flaherty, K., et al. 2022, arXiv e-prints [arXiv:2203.09528] [Google Scholar]
- Portilla-Revelo, B., Kamp, I., Rab, C., et al. 2022, A&A, 658, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, W. K. M., Armitage, P. J., Wood, K., & Lodato, G. 2006, MNRAS, 373, 1619 [Google Scholar]
- Rosotti, G. P. 2023, New A Rev., 96, 101674 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Szulágyi, J., & Ercolano, B. 2020, ApJ, 902, 126 [CrossRef] [Google Scholar]
- Teague, R. 2019, J. Open Source Softw., 4, 1632 [NASA ADS] [CrossRef] [Google Scholar]
- Teague, R., Bae, J., Bergin, E. A., Birnstiel, T., & Foreman-Mackey, D. 2018, ApJ, 860, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Thanathibodee, T., Molina, B., Calvet, N., et al. 2020, ApJ, 892, 81 [Google Scholar]
- Thi, W. F., Woitke, P., & Kamp, I. 2011, MNRAS, 412, 711 [Google Scholar]
- Wang, J. J., Ginzburg, S., Ren, B., et al. 2020, AJ, 159, 263 [Google Scholar]
- Wang, J. J., Vigan, A., Lacour, S., et al. 2021, AJ, 161, 148 [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [Google Scholar]
- Woitke, P., Kamp, I., & Thi, W. F. 2009, A&A, 501, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., Min, M., Pinte, C., et al. 2016, A&A, 586, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wölfer, L., Facchini, S., van der Marel, N., et al. 2023, A&A, 670, A154 [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, H., Herczeg, G. J., Linsky, J. L., et al. 2012, ApJ, 744, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Zurlo, A., Cugno, G., Montesinos, M., et al. 2020, A&A, 633, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
ProDiMo is a radiation thermo-chemical code that solves for the continuum radiative transfer (using a discrete ordinate method instead of a Monte Carlo approach), the gas heating-cooling balance, and the chemical abundances. The code assumes a two-dimensional geometry implemented on a cylindrical grid. In this work, we used ProDiMo version ebd47ddf. The code can be found at https://prodimo.iwf.oeaw.ac.at/
Planetary masses found in Wang et al. (2021) are 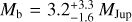 and
and 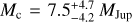 The superscript and subscript values represent the 68% credible interval.
The superscript and subscript values represent the 68% credible interval.
All Tables
Properties of the observational data used in this work as presented in Law et al. (2023).
All Figures
 |
Fig. 1 Synthetic observables for the continuum compared to data. Left: predicted spectral energy distribution (black and red curves) and photometry towards PDS 70 (blue dots). The photometric data were taken from Gregorio-Hetem et al. (1992), Cutri et al. (2003), Hashimoto et al. (2012), and Keppler et al. (2019). The value at 855 µm (Keppler et al. 2019) is from integrating the brightness distribution over an elliptical aperture of the projected radius 130 au. Right: azimuthally averaged radial profiles from the ALMA continuum observation at 855 µm and from the modelled images ray traced at the same wavelength. The shaded area indicates the resolution element of the continuum observation of 0.067 arcsec. |
| In the text | |
 |
Fig. 2 Azimuthally averaged profiles for the integrated intensity of C18O J= 2–1 (left), 13CO J=2–1 (middle), and 12CO J = 2–1 (right). The solid lines are the modelled profiles, and the blue dots are the ALMA observations. Vertical dashed lines indicate the limits of the dust gap. The shaded area indicates the resolution element of the C18O J = 2–1 observation of 0.16 arcsec. |
| In the text | |
 |
Fig. 3 Gas and dust densities inferred from the best representative model. Top: predicted gas and dust surface densities in gram per square centimetre (g cm−2) versus distance to the star. Bottom: gas-to-dust ratio. The shaded area indicates the resolution element of the C18O J = 2–1 observation of 0.16 arcsec. The vertical lines indicate the location of the planets. |
| In the text | |
 |
Fig. 4 Value of the gas depletion inferred from our model (grey line) overlaid to the scaling relation from Duffell & Dong (2015) (black line). The two curves intersect at ~4MJup. The dashed lines and shaded areas indicate the mean value and the 68% confidence interval for the mass of PDS 70 b and c given by Wang et al. (2021). |
| In the text | |
 |
Fig. 5 Dust column density profiles of the PDS 70 disc (solid line, same as in Fig. 3) and a similar disc with 30% extra dust mass between 27 and 60 au. |
| In the text | |
 |
Fig. 6 Effect of a localised variation of the dust distribution on line emission. Top left: Azimuthal profiles of the 12CO J=2–1 integrated maps from two models with slightly different dust distributions between 27 au and 60 au. The blue dots are the observations. The shaded area indicates the region where the dust mass was artificially increased by 30% to boost heating by dust thermal accommodation. Bottom left: relative difference of modelled intensities with respect to the best representative model for the 12CO J = 2–1 case. Right: relative difference of integrated intensities for the 13CO J = 2–1 and C18O J = 2–1 cases. |
| In the text | |
 |
Fig. 7 Emitting regions from which 15–85% of the 13CO J = 2–1 (grey solid box) and 12CO J = 2–1 (black solid box) radiation is emitted. Dotted lines indicate the emitting region in the vertical direction only. The grey and black crosses are mapped from the fitting functions to the respective emitting surfaces derived in Law et al. (2023). The white curve is the 1.5 × 104 cm−3 contour for the critical density of the 12CO J = 2–1 transition with H2 as the collision partner. The colour map is the gas density. |
| In the text | |
 |
Fig. A.1 Dust surface density profiles for selected grain sizes (dashed lines) and the total profile resulting from adding up the density contained in each dust size bin (continuous line). |
| In the text | |
 |
Fig. A.2 Comparison of the dust surface density used in this work with that in Portilla-Revelo et al. (2022). |
| In the text | |
 |
Fig. A.3 Dust midplane equilibrium temperature compared to that in Portilla-Revelo et al. (2022). |
| In the text | |
 |
Fig. A.4 Comparison of the initial gas density obtained from the semi-analytic model (Eq.4) and the final profile of the best representative model. |
| In the text | |
 |
Fig. A.5 Azimuthally averaged profiles for C18O J = 2 – 1 (left), 13CO J = 2 – 1 (middle), and 12CO J = 2 – 1 (right) moment zero maps. The modelled curves are the results from two models with different C/O ratios in the disc. The black solid lines were retrieved from the best representative model that uses C/O = 0.457, and the red dashed lines represent simulations with C/O = 1.097. The vertical dashed lines indicate the limits of the dust gap. |
| In the text | |
 |
Fig. A.6 Moment zero maps for C18O J = 2 – 1 (top), 13CO J = 2 – 1 (middle), and 12CO J = 2 – 1 (bottom). The left column contains the observations, and the right column contains the models. The dashed ellipse indicates a semi-major axis of 130 au, which is the limit of applicability of our model. An orbital inclination of 51.7° was assumed, the same as for the continuum. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.