| Issue |
A&A
Volume 675, July 2023
|
|
|---|---|---|
| Article Number | A184 | |
| Number of page(s) | 26 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202245827 | |
| Published online | 21 July 2023 | |
The quest for Magrathea planets
I. Formation of second-generation exoplanets around double white dwarfs
1
Sapienza – University of Rome, Physics department,
Piazzale Aldo Moro 5,
00185
Rome, Italy
e-mail: ledda.1350727@studenti.uniroma1.it
2
Instituto de Astrofísica de Andalucía, CSIC,
Glorieta de la Astronomía s/n,
18008
Granada, Spain
3
INAF – Osservatorio Astrofisico di Torino,
via Osservatorio 20,
10025
Pino Torinese, Italy
4
INAF – IAPS,
Via Fosso del Cavaliere 100,
00133
Rome, Italy
Received:
30
December
2022
Accepted:
5
April
2023
Context. The formation of planets around binary stars is the subject of ongoing investigations focusing on the early stages of stellar life. The evolution of binaries that become double white dwarfs (DWDs), however, can cause the ejection of high amounts of dust and gas. This material can give rise to circumbinary discs and become the cradle of new planets, yet no studies to date have focused on the formation of circumbinary planets around DWDs. These binaries will be the main sources of gravitational waves (GWs) detectable by the Laser Interferometer Space Antenna (LISA) mission from the European Space Agency (ESA), opening the possibility to detect circumbinary planets around short-period DWDs everywhere in the Milky Way and in the Large Magellanic Cloud via the modulation of their GW signal.
Aims. We investigated the formation process and characteristics (e.g. formation times, masses, and final locations) of Magrathea planets within circumbinary discs around detached DWDs, paying particular attention to the formation of gas giant (GG) planets.
Methods. We simulated multiple planet formation tracks to explore how the planetary formation processes typical of pre-main sequence (pre-MS) discs are affected by the disc environments surrounding DWDs. We investigate the mass and orbital evolution of planetary seeds growing first through pebble accretion, then by gas accretion. Our growth tracks account for both the disc accretion rate onto the central binary and the disc photoevaporation rate caused by stellar irradiation.
Results. We present both planetary formation tracks taking place in steady-state discs, and formation tracks taking place in discs evolving as a function of time. Our simulations show that planetary formation should be common in circumbinary discs around DWDs, but the formation of GG planets can be hindered by the temperatures of the disc and the rapid disc depletion.
Conclusions. Our results show that planetary formation in circumbinary discs around DWDs can be possible. In particular, the extreme planetary formation environment implies three significant results: (i) the accretion rate and the metallicity of the disc should be high in order to form sub-stellar objects with masses up to ~31 MJ, this is achieved only if planet formation starts soon after the onset of the disc and if first-generation seeds are present in the disc; (ii) seeds formed within 0.1 Myr, or within 1 Myr, of the onset of the disc can only produce sub-Neptunian (SN) planets and Neptunian (N) planets, unless the disc accommodates first-generation seeds with mass 10 M⊕; (iii) most of the planets are finally located within 1 au of the disc centre, while they are still undergoing the gas accretion phase.
Key words: planets and satellites: formation / protoplanetary disks / binaries: close / white dwarfs
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
To date, most of the 5235 confirmed1 exoplanets have been found orbiting single stars. However, a consistent fraction (~4% as of May 20222) orbits stellar binaries. All planets that form within protoplanetary discs surrounding pre-main sequence (pre-MS) stars (no matter their multiplicity) are usually referred to as first-generation planets. However, both theory and observations show that discs surrounding binaries can also appear at later times as a consequence of stellar evolution processes (i.e. when one of the components of the central binary has already left the main sequence MS; e.g. Kashi & Soker 2011; Menu et al. 2015; Hardy et al. 2016; Van Winckel 2018; Oomen et al. 2018; and references therein). This disc, formed in the post asymptotic giant branch (post-AGB) phase of one of the stellar components, is called a second-generation disc. Any planet forming in such an environment is commonly referred to as a second-generation planet (Perets 2010).
In this paper we focus on second-generation discs around double white dwarf (DWD) systems. The evolutionary stages leading to the formation of DWDs are still uncertain. The overall picture emerging from current studies is that the DWD progenitors experience at least two mass transfer phases, occurring when one of the stars becomes a giant or a sub-giant, through various processes that depend on the initial stellar masses and binary separation. In the case of an unstable mass transfer, the donor star (i.e. the one that is evolving) shares its atmosphere with the companion, fully enveloping it in the common envelope (CE) phase (e.g. Paczynski 1976; Ivanova et al. 2013). At the end of this phase, when the shared envelope is ejected, the fraction of its mass that does not reach the escape velocity remains bound to the central binary, eventually forming a second-generation circumbinary disc (Kashi & Soker 2011).
When a post-common envelope (post-CE) disc forms, there is the possibility for it to be the cradle of second-generation planets, whose mass could reach several Jovian masses (Schleicher & Dreizler 2014). A work by Zorotovic & Schreiber (2013) found that many eclipsing post-common envelope binaries (PCEBs) display eclipse timing variations that could be attributed to circumbinary sub-stellar bodies. Should the latter indeed prove to be of planetary nature, these authors suggest that it is unlikely that the planets formed when both components of the system were MS stars. Rather, they may have formed following the CE stage and the creation of a second-generation disc. The system of NN Serpentis provides an illustrative example of this process. NN Serpentis consists of a white dwarf (WD) of 0.535 M⊙ and a red dwarf of 0.111 M⊙ (Mustill et al. 2013), and several studies agree in suggesting a second-generation nature of its two circumbinary gas giant (GG) planets3 (Zorotovic & Schreiber 2013; Mustill et al. 2013; Schleicher & Dreizler 2014; Völschow et al. 2014; Hardy et al. 2016).
Recently Kluska et al. (2022) suggested the possible presence of planets around post-AGB binaries. These systems are thought to have experienced a fast CE phase caused by the evolution of an asymptotic giant branch (AGB) star (i.e. the progenitor of a WD). This mass transfer phase produces a circumbinary disc similar to that observed around young stars. However, ~12% of the sample of post-AGB stars considered by Kluska et al. (2022) show the presence of transition discs (i.e. discs having large inner dust cavities). Such cavities have been interpreted by the authors as being caused (i) by the presence of a first-generation GG that survived the mass transfer phase or (ii) by the formation of a second-generation GG after the mass transfer. In the first case a variation in the local pressure gradient of the disc, caused by the presence of a surviving planet, could prevent the inward flux of dust from reaching the inner disc regions, favouring the formation of a second-generation planet in disc regions outside the first-generation planet's orbital radius. Both cases (i) and (ii) suggest that the second-generation planet should form within ~1 Myr, depending on the disc mass, on the gas accretion rate onto the binary, and on the initial temperature of the AGB star (Oomen et al. 2019). Given that the post-common-envelope age of the NN Serpentis system is ~1 Myr, the same concept is applicable to its planets, which should have formed within the age of the system, should they be planets of second generation.
Accounting for planets in evolved stellar binary systems, we know that no Magrathea4 planet (i.e. a circumbinary planet orbiting a DWD) has been detected yet (Danielski et al. 2019), nor has one been detected in a binary system whose components have both evolved, apart from the planet around PSR B1620-26AB (where the binary is composed by a WD and a pulsar). This planetary system is believed to be the result of a stellar encounter, hence shaped by a very different evolution than a typical isolated circumbinary system (Sigurdsson et al. 2003). Nonetheless, circumbinary planets around evolved binaries are expected to exist, either as first-generation planets surviving one or more CEs (Kostov et al. 2016; Columba et al. 2023) or by forming directly in circumbinary second-generation discs, as previously discussed.
To date, no dedicated study has been performed on the formation of second-generation planets around DWDs. However, due to the similarities that discs around evolved binaries share with their pre-MS counterparts (Perets 2010 and references therein), it is reasonable to expect that the processes that regulate the growth of planets in pre-MS discs can also occur in second-generation discs. As the evolution of circumbinary discs around evolved binaries is still uncertain, in this study we adopt the well-studied framework developed for the evolution of pre-MS discs (Lynden-Bell & Pringle 1974; Hartmann et al. 1998). Pre-MS discs are expected to viscously evolve such that while the mass of the disc flows inward, the angular momentum flows outward (i.e. the disc gets depleted because of accretion onto the central object while increasing its extension).
The circumbinary discs we consider here are formed by the CE material that remains bound to the inner binary (i.e. coming from the envelope of the secondary giant evolving star). In the particular case of a DWD, after the second CE we are left with a newborn WD and an older cooler WD. The temperature of a young WD can be very high (more than ~ 104 K), and decreases over time down to the order of 103 K (Mestel 1952). This can result in a disc with initially high overall temperatures, such that the condensation temperatures of both dust and ices are reached at larger orbital radii than in pre-MS discs. In turn, this implies that the growing solid core of a planet, which starts its formation in the outer regions of the disc, can have a smaller feeding zone as it migrates towards the inner hotter regions of the disc. Moreover, the irradiation of the central object onto the disc causes photoevaporation of the gas particles of the disc over time, which, together with the accretion onto the binary, contributes to the disc depletion rate, and thus to the disc lifetime. In order for the formation of a giant planet to compensate for such limiting processes, the accretion of solids onto the initial planetary core should be highly efficient.
In this manuscript we explore the scenario of planetary formation occurring in second-generation discs (i.e. the formation processes in circumbinary discs around detached DWDs). Short-period (less than ~2 h) DWDs are expected to be the most common sources of gravitational waves (GWs) in the observational band of the Laser Interferometer Space Antenna mission (LISA, Amaro-Seoane et al. 2017, 2023; Korol et al. 2017). Recent studies have opened up the possibility for giant exoplanets to be found around these binaries through the detection of the modulation the planet causes in the GW signal produced by the DWD itself (Tamanini & Danielski 2019; Danielski et al. 2019; Danielski & Tamanini 2020). For this, we focus our studies on the formation of giant exoplanets. This sets our work in the broader context of the studies for the development of the planetary detection science case of the LISA mission. Such a development includes the LISA detection prospects of sub-stellar objects (SSOs) orbiting DWDs through Bayesian analysis by Katz et al. (2022); the modelling of the long-term evolution of circumbinary systems hosting a giant planet, from MS until the DWD stage by Columba et al. (2023); and the determination of the LISA detection efficiency by Danielski et al. (in prep.).
The paper is organised as follows. In Sect. 2 we describe the planet-forming environment (i.e. the specific DWD systems and circumbinary disc models we adopt for our simulations), together with the planetary formation processes. In Sect. 3 we present our results, which consist of growth tracks in steady-state discs (usually referred to as analytical formation tracks), and growth tracks and migration tracks in time-evolving discs. These tracks allow us to test the kind of planets that can form and their formation times as a function of the free parameters of the problem. Finally, we discuss the results in Sect. 4 and draw conclusions in Sect. 5.
Stellar masses, periods P, and eccentricity e of the analysed DWDs at the end of the second CE, and respective progenitors.
2 Methods and models
The planet-forming environment we consider in this work (i.e. a second-generation disc around a DWD) is characterised by a parameter space usually not available in MS systems. Therefore, it can offer an important test bed for the planet formation theories currently used for first-generation discs. In this section we describe both the DWD systems and the circumbinary disc model we used.
2.1 The planet-forming environment: the central DWD
In order to explore differences and similarities among the formation processes in post-AGB and pre-MS discs, we tested four DWD systems. The parameters of each DWD system are reported in Table 1, together with the values of their progenitors’ parameters. The systems span a different range of masses and periods to account for a variety of circumbinary discs in term of total mass and disc cavity radius (see Sect. 2.2). The evolutionary history of these systems has been simulated using the binary population synthesis code SEBA5, originally developed by Portegies Zwart & Verbunt (1996) and later adapted for DWDs by Nelemans et al. (2001) and Toonen et al. (2012).
The system DWD1 is the main system we used for our simulations, as it is expected to represent a typical DWD system (Korol et al. 2017), whose subsequent evolution is such that planet formation has enough time to occur. After the second CE the DWD2 binary has a period of 0.43 h, which, accounting for the binary mass and circular orbit, will produce a GW frequency of wGW = 8.11 mHz falling within the frequency range of the LISA band (0.1 mHz-1 Hz). This system will merge in 9 Myr and for this reason we selected two more systems, DWD3 and DWD4, from the LISA DWD population, meaning that, when placed within the Milky Way’s history context, their orbits have shrunk enough for them to be detectable by LISA (Korol et al. 2017, 2019; Amaro-Seoane et al. 2023). These two systems were selected with a longer merging time (Table 1) to make sure we account for enough time for planetary formation before any other binary evolution happen in the system (i.e. contact or mass transfer) with final merging in single WD or supernova Ia. In either case, further evolutionary steps could (i) lead to a non-binary object, or (ii) preclude any detection with LISA, which is the reason why we excluded it from our study.
We use the exploration of the planet formation potential of the system DWD1 as our illustrative case study, while for the remaining systems we exclusively focus on the growth tracks in discs evolving as a function of time as they provide the more realistic information. We note that even for eccentric progenitors, the orbits of all binary circularise throughout evolution; as a consequence all our disc models are based on circular stellar orbits. Moreover, the binaries have very small periods, such that the gravity field can be considered as the central one, and such that their perturbations are effective only over a very short distance from the barycentre. SeBa simulations provided the temperature of the secondary star (i.e. the youngest WD), Teff 2, immediately after the CE, together with the type of WD formed (i.e. He WDs for all the systems analysed). For our simulations we set the initial temperature, at t0 = 0, to the SeBa Teff 2 values. However, we accounted for the variation in the WD temperature after the second CE. In particular, we chose two more temperature values within 1 Myr from the end of the CE (i.e. 0.1 and 1 Myr). These temperatures were measured using the synthetic evolutionary sequences for helium atmospheres6, whose high temperature models were developed by Bédard et al. (2020) and include non-local thermodynamic equilibrium (non-LTE) effects. The reason for which we accounted for a variation in the stellar temperature is to explore different types of disc environments (see Sect. 2.2).
2.2 The second-generation circumbinary disc model
As mentioned above, the disc model is linked to the type of DWD formation through the CE phase, and the disc mass depends on the binary system characteristics and its evolution. In principle, circumbinary discs can form after both the first and the second CEs. However, as the disc's fate across the first CE is unclear and its lifetime is highly dependent on the lag of time between the evolution out of MS of both stars, we focus here on the disc formed after the second CE.
To date, no discs have been detected around DWDs; however, simulations have shown the formation of a central cavity in circumbinary discs due to the binary torque arising from the non-axisymmetric part of the binary potential (Rafikov 2016, and references therein). The cavity radius is usually found to be about 2ab, where ab is the binary separation (Artymowicz et al. 1991; Artymowicz & Lubow 1994; MacFadyen & Milosavljevic 2008; Rafikov 2016 and references therein), so for our simulations we adopted rin = 2ab as the inner disc radius. The external radius observed for circumbinary discs around evolved stars is usually found between a few dozen au to 500 au (Rafikov 2016; Izzard & Jermyn 2018). Because of this, and due to the lack of observational constraints related to the systems studied in this work, we adopted a representative set of values for the characteristic external radius, rc, of our disc: 50, 100, and 150 au. Because of the viscous spreading of the gas during the disc evolution, these discs are expected to expand to radii of 200, 400, and 600 au, respectively (Lynden-Bell & Pringle 1974; Hartmann et al. 1998). The first value of rc, 50 au, corresponds to the possible extension of the disc that gave rise to our Solar System (Kretke et al. 2012); the third value, 150 au, represents the extension of the wide disc observed around the A-type star HD 163296 (Isella et al. 2016); the second value, 100 au, is intermediate between the other two.
Given that no studies exist about planetary formation around DWDs, nor studies about circumbinary discs around DWDs, we assume that the disc behaves like passively irradiated circumstellar discs (Chiang & Goldreich 1997). We adopt the surface density and temperature profiles by Schleicher & Dreizler (2014). The density profile is described by
where n is the power-law index, which we set to 1, and where Σ0 is the surface density at rc. The temperature profile of the disc is described by two equations: one representative of the inner region where the disc heating is dominated by irradiation, and one for the outer region where irradiation from the stars is negligible.
In the inner disc region where the stellar irradiation is the dominant mechanism, we can find the temperature profile of the disc by equating the fluxes emitted and absorbed by the disc (Schleicher & Dreizler 2014):
In Eq. (2), Tb is defined by
where Teq is the equilibrium temperature of an irradiated object placed at a distance rin from the DWD. The equilibrium temperature is computed considering the total luminosity of the DWD (i.e. the sum of the luminosity of the WDs of the system). Each stellar luminosity was derived by treating the emitted WDs energy as black-body radiation and by using the WD parameters of radius and effective temperature (see Table 1) obtained by the SeBa simulations (see Sect. 2.1). Instead, the term Teff 2 accounts for the initial temperature of the gas once ejected from the star, which we assume matches that of the youngest white dwarf. The variable t0 is the starting time of planetary formation, which we chose to be 10τc, 0.1 Myr, and 1 Myr (see Sect. 2.3). The parameter Tc represents the cooling time of the disc with respect to the initially high post-CE temperatures of the gas. Details about this parameter will be discussed in Sect. 2.3.
The parameter θ is the grazing angle with respect to which the star radiation strikes the disc, and is defined as (Chiang & Goldreich 1997)
where H = cs/Ω is the disc scale height, cs the speed of sound, Ω the Keplerian angular velocity, and H/r the disc aspect ratio. The second term in Eq. (4) makes Eq. (2) steeper, causing it to reach lower temperatures as r increases. In this work we follow Schleicher & Dreizler (2014) and neglect the second term in Eq. (4). This choice implies a slightly higher overall disc temperature as r increases, but considerably simplifies the disc and planetary evolution calculations. The higher temperatures of the disc reduce the radial range available for the seeds to reach the isolation mass as dust and ices in the disc will be in solid form at larger radii from the stars (Lodders 2003). Therefore, by neglecting the second term in Eq. (4), we obtain lower planetary masses than using Eq. (4) with the second term, and consequently a conservative estimate of the planet-forming potential around the DWDs.
Equation (2) can therefore be written as
where ζ = 3/4. By using Eq. (5), the speed of sound in the irradiated region can be expressed as
where cs1 is the sound speed at 1 au, µ is the mean molecular weight (in units of mp), and kB and mp are the Boltzmann constant and the proton mass, respectively.
In the outer disc region where irradiation is negligible, following Schleicher & Dreizler (2014) we consider disc fragmentation as the main heating source. From the Toomre stability criterion, as the Toomre parameter Q = csΩ/πGΣ approaches unity, disc fragmentation occurs, and turbulence and shocks may compensate for the disc cooling in the outer regions of the disc (Schleicher & Dreizler 2014). At the stage of fragmentation (Q ~ 1), we can estimate the speed of sound as
where Σ and Ω are the surface density and the angular velocity of the disc, respectively. By equating Eq. (7) with 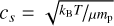 , we obtain the temperature profile in the outer regions of the disc,
, we obtain the temperature profile in the outer regions of the disc,
where mp is the proton mass, kB is the Boltzmann constant, and G is the gravitational constant.
In Fig. 1 we show the temperature profiles for the circumbinary discs surrounding each of the DWD systems under study (see Table 1). The profiles are estimated when the youngest WD is just born. The negative slope of the curves is due to Eq. (5), while the positive slope, when present, is due to Eq. (8); the change in slope identifies the orbital distance where the dominant heating process changes. Since the disc structure depends on the evolution of the system during the last CE (i.e. rin = 2ab), the values of rin are different for each system. Since planet formation in the outer turbulent disc regions is governed by different physical processes than the pebble accretion scenario we consider in this study, we focus only on the inner irradiated region. The turning points between the two temperature regimes in Fig. 1 therefore give the outer boundaries of the planet-forming regions we investigate.
 |
Fig. 1 Temperature profiles of the circumbinary discs surrounding the DWD systems (see legend). The profiles are estimated at t0 = 10τc (see Table 1 for details about the systems) for a disc with rc = 50 au. |
2.3 Accretion and photoevaporation rates of the disc
The lifetime of protoplanetary discs around pre-MS stars is set by their gas accretion rate on the central star and by their photoevaporation by stellar irradiation. Both processes act to remove mass from circumstellar discs, limiting the duration of the planetary formation process. Since the temporal evolution of discs around evolved stars, and DWD in particular, is poorly known, we fill the gaps in our understanding and work by analogy with pre-MS discs.
Around 95% of pre-MS stars within the spectral type interval K0-M5 stop accreting material from their circumstellar discs before 5 Myr, reaching an accretion rate of ≈10−11 M⊙ yr−1 (Fedele et al. 2010). We consequently set the upper limit of the disc lifetime and the planetary formation process to be 5 Myr. Also by analogy, the planetary formation process in pre-MS discs is known to start within the first 1 Myr of the disc life (Scott 2007; Manara et al. 2018 ; Mulders et al. 2021 ; Lichtenberg et al. 2022; Bernabò et al. 2022), so we consider three representative starting times in our analysis: 10τc, 0.1 Myr, and 1 Myr. These initial times t0 account for the time needed to assemble the Moon-sized planetary seeds at the beginning of the simulations (see Sect. 3) and span the range revealed by the meteorites formation times (Scott 2007; Lichtenberg et al. 2022).
Each of these values of t0 implies a different scenario for the formation of the planetary seeds and is associated with a different temperature and luminosity of the youngest WD as it cools over time (see Sect. 2.1). The scenario with t0 = 10 τc assumes that the planet formation process starts as soon as the gas in the second-generation disc cools down to allow the condensation of dust. The scenario with t0 = 0.1 Myr assumes that the planetary seed requires about 105 yr to assemble, compatible with the fastest formation timescales from meteorites (Scott 2007; Lichtenberg et al. 2022). Finally, the scenario with t0 = 1 Myr is consistent with the formation timescale of massive planets suggested by the collisional dust regeneration process in circumstellar discs (Bernabò et al. 2022).
The parameter τc used to time the first scenario is the characteristic cooling time of the disc and is defined as τc = C · Pd, where C = 0.01 and Pd is the orbital period of the disc at rc (Nelson et al. 2000; Woitke 2015; Rabago & Zhu 2021). The adoption of t0 = 10 τc (see Sect. 2.2) means that we consider a disc whose gas has cooled down significantly with respect to the initial post-CE phase, but still retains some of its initial thermal budget while having undergone negligible physical evolution, as τc ~ 1% of Pd (i.e. the dynamical time of the disc). Moreover, 10 τc < 246 yr throughout all our simulations, meaning that this time is negligible both with respect to the cooling time of the youngest WD and with respect to the pebble accretion rates. Consequently, we associate with Teff 2 the temperatures indicated in Table 1 when t0 = 10 τc.
Following Hartmann et al. (1998) we describe the accretion rate of our disc by
where Ṁg(t0) = −2πrcug(rc)Σ0 is the accretion rate at t = t0, with ug(rc) the inward radial velocity of the gas at rc and Σ0 the density at rc (see Sect. 2.4.1). The parameter δ represents the power-law index of the viscosity ν. Specifically, ν = αcsH ∝ r3/1r−ζ = rδ, where α characterises the efficiency of angular momentum transfer in the disc (Shakura & Sunyaev 1973). For our disc, δ = 3/2 − ζ = 0.75. The parameter ts is the viscous timescale of the disc
with rc the characteristic disc size and vc = v(rc) (Johansen et al. 2019).
In their recent study of giant planet formation, Tanaka et al. (2020) consider photoevaporation rates between 10−9 and 10−8 Myr. Given that our central object is a binary composed of two WDs, we adopted one of their highest values: Ṁw = 10−8 M⊕ yr−1.
In Fig. 2 we show as an example the accretion rate Ṁg and the photoevaporation rate Ṁw of the disc surrounding the system DWD1. In each panel we show one track for each adopted starting time value (t0 = 10τc and t0 = 0.1, 1 Myr). Each panel is associated with a different value of rc. In particular, rc = 50, 100, 150 au from top panel to bottom panel, respectively (i.e. the density of the represented discs decreases from top panel to bottom panel). Therefore, in each individual panel, every accretion rate track is associated with the same value of rc. As the time increases, the accretion rate decreases (see Eq. (9)). The later the planetary formation starts, the closer Ṁg(t0) is to Ṁw. By decreasing t0, the disc becomes colder as the youngest WD cools significantly over time lowering the disc equilibrium temperature (i.e. the second term of Eq. (3) decreases). Consequently, both the radial speed of the gas and Ṁg(t0) decrease. In our exploratory study, however, once we set t0 (i.e. Teff 2), the temperature profile of the disc does not change throughout the simulation. As we discuss in Sect. 2.4.2, the difference between Ṁg and Ṁw determines whether a planet can undergo runaway gas accretion or not. Specifically, circumbinary discs characterised by Ṁg − Ṁw = 0 cannot form GGs.
2.4 Planetary formation processes
It is reasonable to expect that the same processes that regulate the growth of planets in circumstellar protoplanetary discs can also occur in second-generation circumbinary discs. Our core formation models start from a seed mass of 0.01 Ṁ⊕, based on theoretical (Chambers 2010; Johansen & Lambrechts 2017) and observational constraints (e.g. Scott 2007; Brasser 2013; Lammer et al. 2021). We account for the formation time of the starting seed with the different starting times of our simulations, which are also linked to the temperature evolution of the younger WD (see Sect. 2.1).
The core accretion phase is described through the pebble accretion scenario (Johansen et al. 2019). The gas accretion phase is described following Tanaka et al. (2020). We consider both a gas contraction phase, starting at the end of pebble accretion, and the subsequent runaway gas accretion.
 |
Fig. 2 Gas accretion rates (Ṁg) and photoevaporation rate (Ṁw) of the disc surrounding the system DWD1. The accretion rates start at 10τc, 0.1 Myr, and 1 Myr after the birth of the youngest WD (see legend in each panel), which has a temperature of 75 000, 45 650, and 33 950 K, respectively. From top panel to bottom panel rc = 50, 100, 150 au, respectively. |
2.4.1 Pebble accretion
In the following we consider the accretion of solids onto our seeds as described by the faster pebble accretion regime (i.e. the 2D Hill regime; Lambrechts & Johansen 2012). The accretion of pebbles by a protoplanetary core can follow different regimes, namely drift accretion (or Bondi accretion) and Hill accretion regimes. Both regimes are characterised by the protoplanet having a specific radius of influence (Bondi radius and Hill radius, respectively), which in turn determines how effective the protoplanet is in deviating and accreting a pebble embedded in the gas flux of the disc. The transition between drift regime and Hill regime occurs at 0.001–0.01 M⊕ (Lambrechts & Johansen 2012, 2014; Johansen & Lambrechts 2017). When the mass of the protoplanet is low and its Hill radius is smaller than the scale height of the pebbles, accretion through the Hill regime occurs in a 3D way. If the Hill radius is larger than the scale height of the pebbles, accretion through Hill regime occurs in a 2D way (Bitsch et al. 2015, and references therein). As the protoplanet cannot accrete pebbles from outside its Hill radius, 2D Hill accretion is faster than 3D Hill accretion (Lambrechts & Johansen 2012, 2014). Starting from a seed mass of 0.01 M⊕, we account for the initial 3D Hill accretion phase through the starting time t0.
The pebble accretion rate is
where M is the mass of the growing planet; Σp is the pebble surface density of the disc; rH = [M/(3Mb)]1/3r is the Hill radius of the protoplanet, with Mb the total mass of the binary; and St is the Stokes number of the pebbles, which is proportional to the pebbles size.
Following Johansen et al. (2019), we consider accretion of millimetre-sized pebbles (St ≪ 1). The radial velocities of the inward gas and pebbles can be defined respectively as
where Δv ≈ vK is the relative velocity between the pebble and the core, with vK the Keplerian velocity at orbital radius r (Lambrechts & Johansen 2012). Coupling Eqs. (12) with the formula of inward gas and pebble fluxes
we can express the ratio of the pebble to gas surface densities Σp/Σg as
In the last equation, χ = −∂ ln P/∂ ln r = n + ζ/2 + 3/2 and ξ = Ṁp/Ṁg. Following Johansen et al. (2019), we set St ~ α, which implies (i) approximately the same radial speed for gas and pebbles (i.e. the same depletion time for both components), which in turn results in ξ approximately equal to the metallicity of the disc7, and (ii) pebbles whose dimensions are consistent with observations of millimetre- to centimetre-sized pebbles in protoplanetary discs over a wide range of ages (Pérez et al. 2012; Huang et al. 2018). In particular, we set S t ~ 0.01.
As the temperature of the disc increases with decreasing orbital distance from the central stars, inward drifting pebbles will lose growing fractions of their mass due to the sublimation of their composing materials (Lodders 2003). As a result, as the growing planet migrates towards the disc inner regions, a lower mass of pebbles becomes available to support its growth, and pebble accretion eventually stops. The planet migration towards the inner regions of the disc is caused by the torque between the surrounding disc material and the planet itself. This migration mechanism, which is called Type I migration, is defined by
where Mb is the total mass of the binary and kmig = 2(1.36 + 0.62β + 0.43ζ) (D'Angelo & Lubow 2010; Johansen et al. 2019).
Dividing Eqs. (11) by (15), we obtain the equation for pebble accretion in a steady-state disc:
The solution of the previous equation is
where M0 and r0 are the initial mass and position of the seed. Equation (16) provides the growth tracks in steady-state disc for pebble accretion in our results. The time-dependent pebble accretion phase is instead described by Eq. (11), which can also be expressed as
The last equation clearly shows that ξ and Ṁg are important parameters for an efficient pebble accretion phase to occur. In particular, as Ṁg decreases over time, the sooner pebble accretion starts, the higher its rate is, and the quicker the planetary mass grows. On the other hand, discs surrounding young DWDs are characterised by temperatures up to 104 K. This results in more inflated discs (i.e. into higher H/r; see Eqs. (5)–(6)), with condensation lines shifted towards larger orbital radii. This aspect is important because pebble accretion stops once the mass of the planet reaches the isolation mass. As the protoplanet mass grows, its gravitational influence on the surrounding material grows as well. The local gas density is perturbed such that the pressure gradient out of the planet-forming region tends to zero, stopping the drift of pebbles towards the protoplanet. In parallel, the planet perturbs the pressure gradient inside its orbital location and creates a dust trap that commoves with the planet while it migrates inwards. As a result, the planet is prevented from accreting the pebbles that reside inside its orbit. Considering typical orders of magnitude of H/r ~ 10−2, α ~ 10−3−10−4 and cs ~ 102 m s−1, we have up ≈ 0 if the pressure gradient, and thus Δν, tends to zero (see Eqs. (12)) (Lambrechts & Johansen 2014). We estimate the isolation mass as (Lambrechts et al. 2014; Bitsch et al. 2018; Johansen et al. 2019)
We replaced the exponent and the normalisation of the term in H/r from Johansen et al. (2019) consistently with our temperature profile power low index (i.e. ζ = 3/4). Our ζ value also implies that in our case is H/r ~ r1/8. The higher H/r, the higher the isolation mass, and the harder it can be for the planet to reach the gas accretion phase. The parameter α3 = 10−3 is a constant and αν = 10−4 is the turbulent viscosity parameter (Johansen et al. 2019). Once the pebble isolation mass is reached, the gas accretion phase of planetary formation can start.
2.4.2 Gas accretion
During the pebble accretion phase, gas accumulates in the Hill sphere of the planet. However, the energy deposited in the gas by the flux of pebbles prevents it from collapsing because of the planet’s gravity. As a result, the planet accumulates an inflated gaseous envelope. Once pebble accretion is halted, the thermal energy provided by pebbles ceases. The gas pressure in the envelope prevents it from quickly collapsing onto the planet, but the envelope starts a slow contraction phase while more gas is accreted. When the planet reaches a mass Mcrit ~ 2Miso (i.e. when the mass of the envelope becomes roughly the same as the mass of the rocky core), the pressure of the gas is not able to counteract gravity, and a runaway gas accretion phase starts (D’Angelo & Lubow 2010, and references therein; Johansen et al. 2019; D’Angelo et al. 2021).
During the gas contraction phase the gas component of the planet-forming region is slowly depleted due to the accreting planet. This causes a variation in the torque between the gas in the planet-forming region and the planet itself, which in turn affects the migration rate of the planet. Following Johansen et al. (2019) and Tanaka et al. (2020), we adopt Type I migration for the planet during gas contraction, and Type II migration for the planet during runaway gas accretion. In particular, following Tanaka et al. (2020) we adopt a new accurate formulation for Type II migration, where the torque exerted on the planet is proportional to the gas surface density inside the gap because the planet mainly interacts with the gas at its bottom (Kanagawa et al. 2018; Tanaka et al. 2020). In this case the Type II migration rate is described by
where Σgap is the surface density of the gap carved by the growing planet. The gap surface density can be expressed as
where Σout is the unperturbed surface density of the planet-forming region (Kanagawa et al. 2018).
The formalism used to describe the gas contraction phase and the runaway gas accretion phase is reported as follows.
Gas contraction: The envelope contraction occurs on a Kelvin–Helmholtz timescale, whose duration depends on the ratio of the mass of the gaseous envelope to that of the planetary core, and on the envelope opacity (Tanaka et al. (2020), and references therein). This timescale can be expressed as
where k is the envelope opacity, which we set to 0.05 cm2/g (Tanaka et al. 2020). The gas contraction rate can be determined by the ratio of the mass of the planet to Eq. (22), such that
The ratio of Eqs. (23) to (15) leads to the formula for the gas contraction phase in a steady-state disc:
Runaway gas accretion: Once the planet reaches Mcrit, the runaway gas accretion phase starts. For more details of this process, we refer to the work of Tanaka et al. (2020). The runaway gas accretion rate is
where now Σgap ∝ Ṁg − Ṁw = ΔṀgw. When the latter term is 0, the gas accretion rate of the disc Ṁg cannot compensate for the gas loss due to the photoevaporation rate Ṁw, and the planet-forming region is not replenished by the gas flux. This halts runway gas accretion and planet migration (Tanaka et al. 2020).
Dividing Eqs. (25) by (20) we have the equation for runaway gas accretion in a steady-state disc
3 Results
In this section we present the growth tracks in a steady-state disc (or time-independent tracks) and growth tracks in a time-evolving disc (or time-dependent tracks) for the model of a circumbinary disc described in Sect. 2.2, following the formalism introduced in Sect. 2.
The time-independent tracks show the growth of the planets neglecting the time evolution of the disc, which means that the planets produced are not affected for example by the decrease over time in the accretion rate of the disc onto the binary. Therefore, such tracks represent the maximum planet-forming potential of the disc. On the other hand, the time-dependent tracks are affected both by the accretion rate and the photoevaporation rate of the disc. The simulations follow the evolution of seeds with initial masses of 0.01 M⊙ placed at different starting radial distances from the central binary. We make different assumptions for the origin of these seeds depending on the starting time of planet formation (i.e. t0 = 10τc, 0.1 Myr and 1 Myr). When t0 = 10τc, we assume the seeds have a first-generation nature, meaning that they formed before the CE that originated the discs we study in this work. When t0 ≥ 0.1 Myr we assume the seeds formed within t0 in the second-generation disc (see Sect. 2.3).
The number of seeds in the simulations depends on the extension of the radial region between rin and the orbital radius outside of which planet formation occurs through disc instability (i.e. due to the collapse of self gravitating clumps of gas originated by disc gravitational instabilities). Specifically, we do not consider the region of the disc where Eq. (8) holds as it represents a planet formation channel governed by different physical processes (e.g. Helled et al. 2014) than those we consider in this work. As a result, the spatial region sampled by both kinds of formation tracks always stops before the transition radius between Eqs. (8) and (5). The disc temperature profile is always described by Eq. (5) in the sampled region. The spatial region for planetary formation is further reduced during the pebble accretion phase as solids experience almost complete sublimation in disc regions where T > 1200 K (Lodders 2003). If a planet has a mass M < Miso at r ≤ rt, with rt the radial coordinate where T = 1200 K, its growth stops and it never reaches Miso.
Free parameters used in the simulations for the DWD1 system.
3.1 Exploring formation within a post-CE disc around the system DWD1
In our first analysis we study planet formation around the system DWD1 in two steps, first by analysing the steady-state disc and then the time-evolving disc. The set of parameters we consider in our analysis is summarised in Table 1.
Following Schleicher & Dreizler (2014), the mass that remains bound to the binary after the last CE is ≥10% of the envelope of the last-evolving star (Kashi & Soker 2011; Passy et al. 2012; Schleicher & Dreizler 2014 and references therein). For the DWD1 system we compute Mbound = 0.26 M⊙. We assume this to be also the total mass of the circumbinary disc: Md = Mbound = 0.26 M⊙.
We explore planet formation as a function of the disc metallicity ξ (i.e. the pebble-to-gas ratio; see Sect. 2.4.1), the disc characteristic radius rc, and the effective temperature Teff 2 of the youngest WD. The gas surface density values at rc (i.e. Σ0) are 150, 38, and 17 g/cm2 for rc = 50, 100, 150 au, respectively.
3.1.1 Parameters adopted and definition of planetary classes
We derive the disc metallicity ξ from the stellar value. We choose three typical stellar values: a solar type one (Z = 0.014) and two higher values that fall in the metallicity range of planet-hosting stars (Z = 0.021 and Z = 0.028). This means we consider cases with metallicity values 1× solar, 1.5× solar, and 2× solar. To account for the condensation gradients created in the disc by its temperature profile, and the resulting incomplete condensation of the heavy elements (dust and pebbles; Turrini et al. 2021, 2022), we set the disc metallicities ξ to be 70% of the adopted stellar values (i.e. ξ = 0.7 Z; see Table 2). The values of Teff 2 when t0 > 0 have been estimated by interpolation of the cooling tracks described in Sect. 2.1.
We classify the simulated planets and their representative mass ranges as follows.
Sub-Neptunes (SNs, 1 < M/M⊕< 9): These planets complete the gas contraction phase, but do not undergo runaway gas accretion. The mass of these planets is equally composed of gas and solids, but, depending on their final orbit and atmospheric irradiation, they could lose most if not all of their primary atmospheres. In the first scenario they could evolve into mini-Neptunes, while in the second into super-Earths.
Neptunians (Ns, 9 < M/M⊕ < 40): The mass of these planets is also equally composed of gas and solids, but they are usually originated by seeds starting their evolution in the outer regions of the disc. Therefore they can reach higher isolation masses (i.e. higher critical masses). However, they do not undergo runaway gas accretion.
Gas Giants (GGs, 40 < M/M⊕< 10 000): These planets undergo runaway gas accretion and their mass is dominated by gas.
 |
Fig. 3 Planetary growth tracks for DWD1 disc model with rc = 150 au and Teff.2 = 75 000 K. From top to bottom: ξ = 0.01, 0.015, 0.02. Left panels: time-independent growth tracks. The vertical dot-dashed line indicates the radial coordinate rt, where T = 1200 K. The dashed line represents the isolation mass profile for the given disc model (Eq. (19)). Right panels: time-dependent growth tracks. Starting from t0, the tracks reach Miso when they change slope (e.g. leftmost track at ~170 000 yr). |
3.1.2 Planetary formation in the circumbinary disc aroud DWD1 : steady-state disc case
The tracks described in this section implicitly assume a stationary disc structure lasting for as long as needed for the planets to form. As such, they provide an indication of the maximum planet-forming potential of the disc, but not of the real planet population it can produce during its lifetime.
The shape of these time-independent tracks is mainly affected by the radial position where the planet reaches Miso and Mcrit, and by the transition radius rt where the disc temperature is 1200 K. However, although the temperatures of the disc surrounding DWD1 can reach up to ~16 000 K (see Fig. 1), rt < 0.5 au (vertical dot-dashed line) for every simulation. Moreover, such high temperatures imply pebble accretion rates (see Eq. (16) and Fig. 2) that are high enough to compensate for the high isolation masses (see Eq. (19)). Therefore, every seed reaches the isolation mass, whatever the value of ξ and rc.
The left panels of Fig. 3 show the time-independent tracks for a disc with rc = 150 au, and Teff 2 = 75 000 K. The metallicity ξ is 0.01 (top panel), 0.015 (middle panel), and 0.02 (bottom panel). The dashed line represents the isolation mass profile of the disc. Therefore, the part of each track under the dashed line represents the pebble accretion phase; the part of each track above the dashed line represents the gas accretion phase. Every seed reaches the isolation mass before the sublimation line at ~0.38 au. However, the lowest isolation masses are not able to reach the critical mass and do not undergo runaway gas accretion (e.g. Fig. 3, top left panel).
If instead the seeds are initially located farther away from rin, they can accrete pebbles across a larger distance, reaching higher isolation masses than seeds closer to rin. Consequently, their gas contraction phase is fast (see Eq. (22)) and they trigger runaway gas accretion. An increase in ξ speeds up the pebble accretion phase (see Eq. (16)) for every seed. From the top left to the bottom left panel of Fig. 3, we can see some of the seeds located closer to rin reaching the isolation mass and eventually runaway gas accretion. The seeds located farther outreach higher isolation masses and consequently higher final masses at the end of the runaway gas accretion.
It is important to note that the results shown in Fig. 3 do not account for the temporal dimension; therefore, they represents the maximum planet-forming potential of that particular disc model. If we account for the temporal dimension, the results are the right panels of Fig. 3, which we describe in the next section.
3.1.3 The time-evolving disc case
The time-dependent tracks include both mass growth tracks and migration tracks as a function of time in discs where Ṁg decays over time. Therefore, they provide realistic information about the different masses, final positions, and formation times of the planets. Once t0 is fixed, the corresponding temperature of the stars and the temperature profile of the circumbinary disc are held constant throughout the entire simulation. In the time-dependent tracks the difference between Ṁg and Ṁw (i.e. the photoevaporation rate) is crucial: the closer to 0 is ΔṀgw (see Sect. 2.4.2), the smaller the amount of gas supplied to the planet-forming region during the runaway gas accretion phase (see Eq. (25)).
The planet-forming potential of the DWD1 disc emerging from the time-dependent tracks (Fig. 3, right panels) depicts a different picture from the time-independent tracks we previously discussed (Fig. 3 left panels). The growth tracks in each of the right panels can be read left to right. The leftmost track is related to the seed initially located at r0 = 1 au; the rightmost track is related to the seed initially located closer to rc. The disc region we are sampling is the one where Eq. (5) holds (see Sect. 2.2 and Fig. 1). The fast-growing part of the tracks represents the gas accretion phase, while the part of track below gas accretion is the pebble accretion phase. Between the two, the gas contraction is represented by a path that becomes steeper for higher isolation masses. As an illustrative example, the leftmost track in the right panel with ξ = 0.015 almost does not increase in mass after reaching the isolation mass, which is ~4 M⊕. On the other hand, in the same panel, isolation masses higher than ~10 M⊕ are characterised by fast gas contraction followed by runaway gas accretion once Mcrit ~ 2Miso is reached.
The tracks represented in Fig. 3 start at t0 = 10τc (from top to bottom, t0 = 35, 100, 150 yr; see Sect. 2.3); therefore, the accretion rate of the disc is the highest possible (see Fig. 2). However, even when ξ = 0.02 the leftmost tracks do not undergo runaway gas accretion. This is due to the migration of the seeds, whose initial positions are the closest to rin, and to their isolation masses, which are the lowest available for the seeds (see dashed lines in the left panels of Fig. 3). The combination of these two factors implies a slow gas contraction phase combined with a migration rate higher than during pebble accretion (see Eqs. (15) and (23)), which eventually lead the planets to rin. For the same reason, there are two tracks that interrupt runaway gas accretion in the right panels with ξ = 0.01, 0.015. When runaway gas accretion starts, the closer ΔṀgw is to 0, the smaller the amount of gas supplied to the planet-forming region, and the lower the mass the planet can reach. Despite the high accretion rate of the disc, when ξ = 0.01 or 0.015, the planets are already close to rin when the gas accretion phase starts.
Given that the isolation mass, and therefore the critical mass, increase with the radius of the disc, it takes more time for the seeds starting farther away from the binary stars to end pebble accretion and trigger gas accretion. When t0 = 10τc and rc = 150 au, the rightmost tracks in Fig. 3 start runaway gas accretion always after ~0.7 Myr, when the gas accretion rate has already decreased by ~35% with respect to its initial value (see Fig. 2, bottom panel). They therefore experience a lower runaway gas accretion rate with respect to planets that started their evolution closer to the stars (e.g. at 50 au). This effect becomes more marked with decreasing ξ (i.e. with decreasing pebble accretion rate). Consequently, the mass range of the GGs in the right panels of Fig. 3 narrows with increasing ξ.
When rc = 50 or 100 au, the number of SN and N planets increases with respect to that of GGs, as the highest isolation masses cannot be reached. However, all planets reach higher masses with decreasing rc (i.e. with increasing disc density) as the total disc mass is fixed (see Sect. 3.1). The reduced number of GGs is due to the smaller extensions of the discs, which limit the size of the regions where seeds could eventually form GGs as we saw previously.
In Fig. 4 we show the case of the disc model with parameters rc = 100 au, ξ = 0.01, and Teff 2 = 75 000 K. The top right panel shows the evolution of the orbital radii of the planets, where the topmost tracks are related to planets initially located farther from r∈. The pebble accretion phase is mostly represented by the initially horizontal part of the tracks. Due to the high temperatures of the disc, the isolation masses are high. When a planet is close to its isolation mass, its orbital track quickly deviates from the constant path, and the following gas contraction phase eventually leads the planet to rin. The farther the initial position of the seeds, the higher the isolation masses they can reach, and the timescale of their gas contraction phase decreases. Therefore, the gas contraction phase in such orbital tracks is apparently vertical. The runaway gas accretion phase, which occurs with Type II migration, can be identified by a significant slow down in the planet migration, which halts if the GG reaches its final mass before the disc lifetime.
By comparing the top right panel with the top left panel in the same figure, we can see that the migration rate increases proportionally to the mass of the planet. This can possibly lead the planets to rin before they complete the gas accretion phase. Two tracks in the top left panel of Fig. 4 reach rin at ~0.38 and ~0.82 Myr during runaway gas accretion, as we can see from the top right panel. The top right panel also shows that the later the runaway gas accretion starts, the closer the accretion rate of the disc is to the photoevaporation rate (bottom right panel of the same figure). Therefore, the planet-forming region is depleted faster and the planet stops migrating and increasing its mass.
The bottom left panel of Fig. 4 shows the masses and radii of the top left and top right panel on the y-axis and the x-axis, respectively. That is, the bottom left panel is analogous to the time-independent tracks (e.g. left panels of Fig. 3), but it is made of time-dependent masses and radii. Therefore, it shows the actual planet-forming potential of the disc model adopted for that tracks.
When t0 = 10τc the planetary formation is boosted by the residual heat of the post-CE phase (see Eq. (3)). Therefore, ΔṀgw and the isolation masses are the highest possible, which in turn facilitates the formation of GGs or Ns of high mass (see Sect. 3.1.5). On the contrary, when t0 = 0.1 or 1 Myr, the ΔṀgw is close to 0 already from the beginning of the simulations (see Fig. 2). Even if a planet reaches an isolation mass higher than ~10 M⊕, runaway gas accretion cannot be triggered. Therefore, no GGs form in these cases and the disc can only produce SNs and Ns. In particular, when t0 = 1 Myr, the accretion rate is so low that the disc mostly forms SNs, and only a few Ns when rc = 150 au (see Fig. 2, bottom panel, and Fig. 5).
 |
Fig. 4 Time-dependent growth tracks (top left) and orbital tracks (top right) for the disc model with rc, ξ, Teff 2 indicated at the top of the panels (DWD1 system). The bottom left panel shows the same tracks as the top left and top right panels, but with the mass on the y-axis and the orbital radius on the x-axis. The bottom right panel shows the accretion rate of the disc described by the adopted parameters (Σ0 = 37.53 g cm−2). In the top right panel, the dot-dashed line corresponds to the orbital radius where T = 1200 K. The apparently vertical lines corresponds to the gas contraction phase (see Sect. 3.1.3). The fractions of track before and after the ‘vertical’ section correspond to the pebble accretion and the runaway gas accretion phase, respectively. |
3.1.4 Timing of planetary formation and orbital evolution
We now draw the global picture and discuss the implications of the characteristic formation times of the planets born from the circumbinary disc surrounding DWD1. For each adopted value of t0 we report the results in three sets of tables: Tables 3, A.1, and A.2. Every set is composed of three sub-tables, one for each value of rc. Each sub-table has three rows corresponding to different values of ξ, and seven columns. From left to right, the columns show the formation time of the first planet (Δt1); if a GG exists, the formation time of the first GG (Δtg); the percentage of SNs, Ns, and GGs formed with respect to the total number of planets (nF); the percentage of planets whose final positions are within rin and 1 au (i.e. within A1), within 1 and 4 au (i.e. within Δ14), and between 4 au and rc (i.e. within Δ4). We focus on the orbital interval within 4 au as it is associated with the range of orbital periods where the LISA mission can detect giant planets within its nominal mission lifetime (Danielski et al. 2019). We consider as planets all the seeds that have reached at least 0.1 M⊕ (Sinukoff et al. 2013), which is the mass of Mars.
When t0 = 10τc, the effective temperature of the youngest hottest WD is Teff 2 = 75 000 K, and the disc is the hottest possible. The accretion rate is also the highest possible, and in this case we obtained GGs for each value of rc. However, a few GGs do not complete runaway gas accretion as they reach the inner radius of the disc (e.g. Fig. 4). The formation time of such GGs coincides with their crossing times of the disc, which span from 0.15 to 0.8 Myr (see Table 3). The GGs left complete runaway gas accretion within at least 2 Myr, whatever the extension of the disc and the value of ξ.
Due to the high accretion rate of the disc every seed can reach the isolation mass and start gas contraction. Consequently, the first planets formed are always SNs, and they formed very quickly (between 0.03 and 0.1 Myr in seven cases out of nine). However, given that such SNs grew up from seeds initially located close to 1 au, they spent most of their evolution within 1 au. Moreover, it took at least 2 Myr for the farther seeds to complete runaway gas accretion. Therefore, in every case most, if not all, the evolution of the planets end within 1 au from the centre of the disc (see Table 3). Only the case with rc = 150 au shows between 26% and 37% of planets within 1 and 4 au, and they are all GGs.
When t0 = 0.1 Myr, ΔṀgw decreases significantly with respect to the previous case (e.g. Fig. 2); therefore, no GGs are formed. However, the accretion rate is high enough to allow a quick formation of the first planets (SNs), which is still within 0.035 and 0.1 Myr in almost all cases (see Table A.1). However, as no planet starts the runaway gas accretion and transitions to the slower Type II migration, every planet formed in this case ends its evolution within 1 au of the disc centre.
Finally, after 1 Myr, when Teff 2 = 33 950 K and the disc is the coolest one, the disc can only form SNs, which complete their growth process between 0.15 and 0.35 Myr. Since these planets form early and rapidly migrate due Type I migration, all planets end their evolution within 1 au from the centre of the disc.
 |
Fig. 5 Time-dependent growth tracks of the planets formed by the circumbinary disc surrounding DWD1 when planetary formation starts at t0 = 0.1 Myr (top panel) and t0 = 1 Myr (bottom panel). |
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD1 when t0 = 10τc.
3.1.5 Planetary formation efficiency of the adopted disc models
The mass range and percentage of planets produced by the adopted disc models for system DWD1 can be summarised as follows.
t0 = 10τc (Teff 2 = 75 000 K): As ΔṀgw is the largest possible (e.g. Fig. 2), we obtain GGs in almost every case, apart from the two models with rc = 50 au, ξ = 0.01 and 0.015, where most of the planets are Ns (see Table 3). However, the latter class of planets forms in every case, and their mass range is 8.5–26 Μ⊕ (0.027–0.082 MJ). The GGs that grew from seeds closer to rin only complete their evolution in the case rc = 50 au, and their mass is within 4500–10000 Μ⊕ (14.15–31.45 MJ). This is due to the higher disc density when rc = 50 au. In the other cases (rc = 100, 150 au), where the disc extension is larger, new seeds are able to begin runaway gas accretion, even if a fraction of them do not complete it. The mass range is therefore wider than the case rc = 50 au: 100–8800 Μ⊕ (0.31–27.68 MJ). Given the higher percentage of Ns and GGs with increasing rc (see Table 3), the percentage of SNs decreases from 33% (rc = 50 au, ξ = 0.01) to 5% (rc = 150 au, ξ = 0.02), and their total mass range is between 3.5 and 8 Μ⊕.
t0 = 0.1 Myr (Τeff 2 = 45 700 K). In this case most of the planets are SNs for every choice of the adopted parameters (see Table A.1). The discs form no GGs and only a limited number of Ns. Their mass range is within 9–17 Μ⊕ (0.03–0.05 MJ). This outcome, and the consequent high percentage of SNs, is due to the decreased disc accretion rate, which is not able to support a fast pebble accretion phase in most of the cases. Moreover, the isolation mass profile of the disc includes smaller masses with respect to t0 < 0.1 Myr, where the disc temperatures are the highest (see Eq. (19)). Therefore, the seeds cannot reach high isolation masses and the gas contraction phase is slow (see Eq. (22)). The mass range of these SNs is 2–2.9 Μ⊕.
t0 = 1 Myr (Teff 2 = 33 950 K). As the temperatures of the disc are the lowest possible, this case is a more extreme version of the one at t0 = 0.1 Myr. The planets formed in this case are all SNs, apart from the models rc = 150 au, ξ = 0.015, 0.02 (see Table A.2). In these cases the farther seeds become Ns and their mass range is 9–13 M⊕ (0.030.04 MJ). The masses of SNs are between 2–2.6 M⊕.
Scenarios including high Ṁw produce a smaller number of GGs with lower masses and a larger population of Ns than with a lower Ṁw. The new Ns are planets that reached the critical mass, but could not undergo runaway gas accretion due to ΔṀgw ≈ 0. On the other hand, a low value of Ṁw can facilitate the formation of GGs at any time, as their planet-forming region would be supplied mass for a longer time through Ṁg. Therefore, by using one of the highest values of Ṁw from the study of Tanaka et al. (2020) we obtained conservative results. If we consider Ṁw = 10−7 M⊙ yr−1, which is the highest value considered by Tanaka et al. (2020), the model that produced the GGs with the highest masses (i.e. the disc surrounding the DWD1 system at t0 = 10τc with parameters ξ = 0.02, rc = 50 au) produces less massive GGs (see top panel and bottom panel of Fig. 6, respectively).
3.2 Planetary formation around LISA-observable DWDs
As previously discussed, the GW signal of the compact systems DWD2, DWD3, and DWD4 can be detected by the LISA space mission. Therefore, the formation of planets within their post-CE circumbinary discs is the subject of this section. In particular, we explore the similarities and discrepancies among the class of planets formed, and among the timescales needed for their formation. In the following, we only analyse the time-dependent planetary formation tracks. The values used for the free parameters rc and ξ are listed in Table 2, and the stellar parameters in Table 1.
 |
Fig. 6 Time-dependent growth tracks starting at t0 = 10τc for the circumbinary disc of DWD1 with parameters rc = 50 au, ξ = 0.02 (top panel), considering a constant photoevaporation rate of Ṁw = 10−7 M⊙ yr−1. The accretion rate and photoevaporation rate are shown in the bottom panel. In this case ΔṀgw (see Sect. 2.4.2) is smaller than in the top panel of Fig. 2. The masses of the GGs are shown in the top panel, which are lower than those indicated in Sect. 3.1.5. |
3.2.1 The DWD2 case
The DWD2 system has a circumbinary disc with mass Md = 0.09 M⊙ and Σ0 = 51, 13, 6 g cm−2 for rc = 50, 100, 150 au, respectively. The three main temperatures along the cooling track of the youngest WD are Teff 2 = 58 400, 32 000, 25 000 K at t0 = 10τc, 0.1 Myr, and 1 Myr, respectively. The results of the simulations are shown in Tables A.3–A.5.
Figure 1 shows that the circumbinary disc of the DWD2 system is the coldest we consider at t0 = 10τc. Consequently, even in the most favourable case (i.e. t0 = 10τc and Teff 2 = 58 400 K), the planets formed in the disc have low masses and are mostly SNs.
The case t0 = 10τc is the only one that produces all kinds of planets (see Sect. 3.1.1), and in particular, it is the only case that produces Ns and GGs. The latter are produced only when rc = 100 au and ξ = 0.02, with a mass within 130–160 M⊕ (0.41−0.5 MJ). The disc with rc = 150 au does not form GGs (see Table A.3). In this disc seeds initially located farther away from the stars could reach higher isolation mass, and thus experience a quick gas contraction phase and trigger runaway gas accretion. However, ΔṀgw = 0 (see Sect. 2.4.2) before runaway gas accretion is triggered; therefore, the Ns reach the critical mass, but the depleted planet-forming region is not replenished by Ṁg and the Ns cannot accrete more gas. When rc = 150 au the masses of Ns are among the highest of every simulation (between 16 and 28 M⊕; i.e. 0.05–0.09 MJ). Overall, Ns reach masses between 9 and 28 M⊕ (0.03–0.09 MJ). The rest of the planets are SNs, with masses in the range 2−2.8 M⊕.
Given that the accretion rate is low from the beginning of every simulation, when t0 = 0.1 or 1 Myr, the discs form only SNs (i.e. planet formation has limited efficiency). Therefore, regardless of t0, all the planets produced end their evolution within 1 au and the formation times are shorter than 0.1 Myr only when rc = 50 au (see Tables A.3-A.5). Otherwise, it can take up to 0.45 Myr to form a SN, when the disc density and ξ are the lowest, and t0 = 1 Myr (see Table A.5). When t0 = 0.1 or 1 Myr the mass range of the SNs is 1.2–8.5 M⊕.
3.2.2 The DWD3 case
The circumbinary disc surrounding the DWD3 system has mass Md = 0.25 M⊙ and Σ0 = 143, 34, 16 g cm−2 for rc = 50, 100, 150 au, respectively. We simulated the planetary formation tracks considering the three different temperatures Teff 2 = 52 000, 32 200, 24 900 K corresponding to t0 = 0, 0.1,1 Myr, respectively. The results of the simulations are shown in Tables A.6–A.8.
This disc is more massive and dense than the DWD2 case, and it is similar but colder than the one surrounding the DWD1 system. At t0 = 10 τc we have a great diversity of planets. When rc = 50 au, despite its high density the disc can form Ns only when ξ = 0.02. This is due firstly to the accretion rate, which is three times lower than that of the disc surrounding the DWD1 system with the same parameters, and secondly to the temperature of the disc, which is globally lower than the DWD1 case (see Fig. 1). Consequently, the isolation masses the seeds can reach are lower and they cannot complete the gas contraction phase (i.e. the disc forms only SNs and Ns) (see Table A.6). When rc = 100 or 150 au, more space is available for the seeds to reach higher isolation masses, and the disc forms GGs within a mass range 880–4700 M⊕ (2.77–14.78 MJ). The lower upper boundary to the masses of the GGs is a consequence of the lower Ṁg, which suppresses the growth of the planet sooner than for the DWD1 case (see Eq. (25)). Moreover, the generally less efficient pebble accretion (i.e. lower Ṁg, see Eq. (18)) slows down the planetary growth, and the GGs are formed later than 2.5 Myr, apart from the model rc = 150 au, ξ = 0.015, where a GG reached rin before completing the runaway gas accretion (see Table A.6).
For all three rc values the disc forms Ns, whose masses are the highest for rc = 100 and 150 au. Globally, their mass range is 9–23 M⊕ (0.03–0.07 MJ). The rest of the planets are SNs with masses 2.6–8.5 M⊕ that form within 0.15 Myr (see Table A.8). When t0 ≥ 0.1 Myr the disc forms only SNs with masses in the range 1.8–8 M⊕ and whose formation times are between 0.04 and 0.13 Myr. The only exception is the case t0 = 0.1 Myr, rc = 150 au, ξ = 0.02. As previously mentioned, the temperatures of the disc surrounding DWD3 are lower than the DWD1 case; therefore, without the boost of heat provided by the post-CE phase, the pebble accretion phase is less efficient and the isolation masses are lower. This has two consequences. Firstly, even if the disc produces Ns in one case, their mass is not higher than 10 M⊕ (0.03 MJ); secondly, all the planets, whatever the t0, end their evolution within 1 au (see Tables A.6–A.8).
3.2.3 The DWD4 case
In the DWD4 system (Table 1), the disc formed after the last CE phase has Md = 0.087 M⊙ and Σ0 = 50, 12, 6 g cm−2 for rc = 50, 100, 150 au, respectively. The three main temperatures along the cooling track of the youngest WD, Teff 2 = 50 100, 32 200, and 24 900 K at t0 = 10τc, 0.1, and 1 Myr, respectively. The results of the simulations are shown in Tables A.9–A.11.
Although the temperature profile is similar to that of the DWD3 disc (see Fig. 1), the DWD4 disc produces GGs only for two sets of initial conditions (t0 = 10τc, rc = 100 au, ξ = 0.015, 0.02), and their masses are among the lowest produced by all four systems considered in this work. The DWD4 system is surrounded by the least dense of all the discs yet explored, but the region where Eq. (5) holds can be larger than that of the disc surrounding the DWD3 system (see Fig. 1). Therefore, the type of planets and the planetary masses it produces are between the DWD3 case (similar disc temperatures, which allows the formation of GGs) and the DWD2 case (similar extensions of the irradiated disc region, which allows the formation of Ns with masses higher than those of DWD3).
When t0 = 10τc the disc forms only one small GG of ~40 M⊕ (0.12 MJ) when rc = 100 au. This is also true for half of the GGs produced in the case left (ξ = 0.02), whose masses are not higher than 90 M⊕ (0.28 MJ). These planets started runaway gas accretion, but this occurred when ΔṀgw = 0, and therefore their growth stopped quickly. The rest of the GGs produced have masses between 140 and 380 M⊕ (0.44–1.19 MJ). No GG can form after 1 Myr as a consequence of the low accretion rates, which soon stops supplying gas to the planet-forming region. Therefore the planet-forming region quickly loose its gas and (i) the planets have no more gas to accrete soon after reaching the critical mass, and (ii) they stop migrating because no more gas is present in the planet-forming region. Consequently, in four cases out of five a fraction of these GGs end their evolution within 1 and 4 au (see Table A.9). The rest of the GGs, together with the other planets produced by the disc, end their evolution within 1 au.
When t0 = 10τc the disc also forms SNs and Ns, whose masses are within the ranges 2.4–8.5 M⊕ and 9–40 M⊕ (0.03–0.12 MJ), respectively. Due to the lower accretion rate with respect to the rest of the systems (i.e. the lower disc density), they form between 0.06 and 0.4 Myr. When t0 ≥ 0.1 Myr, the discs produce Ns in three cases out of nine (see Tables A.10 and A.11), and their masses are higher than those produced in the DWD3 system despite the lower density of the disc of DWD4. As previously mentioned, this is due to the larger extension of the irradiated region of the disc8. DWD4 can host seeds initially located farther away than those in the DWD3 discs, which allows them to reach slightly higher isolation masses. The planets continue evolving along gas contraction until they reach rin, and their final mass ranges between 9 and 17 M⊕ (0.03–0.05 MJ). The rest of the planets are SNs with masses within 1.6–8.5 M⊕, and they form within 0.07 and 0.33 Myr, and therefore more slowly than those of the disc surrounding DWD3 at t0 = 10τc as the latter is characterised by an higher accretion rate.
When t0 = 1 Myr, despite the lower accretion rate of the disc, the disc produces Ns when rc = 150 au, ξ = 0.2. The reason is the same that justifies the formation of Ns when t0 = 0.1 Myr. The Ns produced in this case have masses in the range 9.2–10.2 M⊕ (0.029–0.032 MJ). The rest of the planets are SNs with masses in the range 1.5–8.2 M⊕, which are formed within 0.3 and 0.65 Myr. Apart from the set of parameters at t0 = 10τc discussed above, every disc model at any t0 forms planets that end their evolution within 1 au.
3.3 Planet formation with first-generation Neptunian planets
In the previous sections we assumed the seeds used to start the planet formation processes formed within 0.1 and 1 Myr after the formation of the circumbinary discs (see Sect. 3). When t0 = 10τc, we assumed the seeds to be Moon-sized first-generation bodies. In this section we expand the previous analysis by considering first-generation seeds with mass M0 = 10 M⊕ (0.031 MJ). In other words, we analyse what second-generation planets can form if the discs contain first-generation Neptunian planets that survive the evolution of the binary systems under study, and focus on whether GGs can form.
When t0 = 0.1 Myr the only systems forming GGs are DWD1 and DWD4. In particular, the disc surrounding DWD1 forms GGs when rc = 150 au and ξ = 0.015, 0.02, and their mass range is 1500–2300 M⊕ (4.72–7.23 MJ). Given that in this case M0 is larger, the seeds can start the runaway gas accretion phase when ΔṀgw is higher than zero (see Fig. 2, bottom panel). The same considerations made when M0 = 0.01 M⊕ holds even in this case (see Sects. 3.1.3, 3.1.4, 3.1.5), given that the disc properties did not change. Therefore, although in this case Ṁg ≃ 2.7Ṁw, when rc = 150 au the extension of the disc surrounding DWD1 is enough to provide a favourable environment for the formation of GGs from seeds with M0 = 10 M⊕. Such GGs are formed within 2.6 Myr. The Ns planets formed have masses within the range 11.2–30 M⊕ (0.03–0.09 MJ), whatever the extension of the disc, and they are formed within 0.01 and 0.07 Myr. Given the mass of the seeds, their migration rates are high since the beginning of the simulations. Therefore all planets end their evolution within 1 au from the centre of the disc, whatever the set of parameters adopted for the discs.
The discs surrounding the system DWD4 have the lowest densities among all the discs we considered (see Sect. 3.2.3). Nevertheless DWD4 forms GGs for the disc parameters rc = 100 au, ξ = 0.015, 0.02. As in the case M0 = 0.01 M⊕, although the disc surrounding the DWD3 system has similar temperatures to (see Fig. 1) and higher densities than those surrounding the DWD4 system (see Sect. 3.2.2), the latter produces discs where the irradiated region is more extended. Therefore, when t0 = 0.1 Myr, DWD3 does not form GGs even when M0 = 10 M⊕. However, because of the low accretion rate, the GGs produced by DWD4 have low masses: within 62 and 75 M⊕ (0.19–0.23 MJ). They are formed within 0.4 Myr and their evolution ends within 1 au.
Interestingly, when rc = 150 au, the DWD4 system could form GGs as well, but the planets reach the critical mass after ΔṀgw = 0, so that the planet-forming region is depleted and runaway gas accretion cannot start. This occurs whatever the value of ξ, and it is due to the same reason that produced the GGs for rc = 100 au. As the growth of the Ns is halted by the absence of gas in the planet-forming region (i.e. by ΔṀgw = 0), they stop migrating before reaching rin, as GGs would. Therefore, ~19% of the Ns end their evolution within 1 and 4 au. Finally, they form within 0.26 and 0.28 Myr and reach masses the range 27–37 M⊕ (0.08–0.12 MJ). The Ns left are within 1 au and form within 0.01 and 0.05 Myr with masses lower than 18.5 M⊕ (0.06 MJ).
A similar configuration of Ns (i.e. Ns reaching the critical mass without triggering runaway gas accretion) also occurs for the DWD2 system. The latter is the second lowest density disc, but it has also the second largest planet-forming area (see Fig. 1).
Therefore, the planets it forms when M0 = 10 M⊕ are similar to those formed by the disc surrounding the DWD3 system. However, due to the extended planet-forming area, the disc surrounding the DWD3 system with parameters rc = 150 au and ξ = 0.02 forms three planets whose growth is halted by the planet-forming region being depleted during the formation process. That is, ΔṀgw = 0 and no more gas can be accreted by the planets. Such planets reach masses between 26.5 and 28.5 M⊕ (0.083–0.089 MJ), and they are formed within 0.08 and 0.1 Myr. The rest of the Ns formed by the discs surrounding DWD2 system are within 11.2–25 M⊕ (0.03–0.08 MJ) and formed within 0.01 and 0.11 Myr. The final locations of all Ns are within 1 au.
When t0 = 1 Myr, despite the higher seed mass, no discs form GGs. This is due to ΔṀgw ≈ 0 since the beginning of the simulations. The Ns formed have masses in the range 10.8–27.6 M⊕ (0.03–0.09 MJ) and their final locations are within 1 au. They are formed within 0.01 Myr and 0.35 Myr. The disc surrounding the DWD3 system forms the smallest Ns, while the one surrounding DWD4 forms the Ns with the highest masses. In particular, the circumbinary disc of DWD4 with parameters rc = 150 au, ξ = 0.015, 0.02 forms Ns reaching the critical mass. This occurred also for the circumbinary discs of DWD4 with the same parameters when t0 = 0.1 Myr. However, in this case such Ns are all finally located within 1 au, as are the Ns which do not reach Mcrit. That is, in this case the larger extension of the planet-forming area of the disc with respect to other systems (i.e. the irradiated area) is not sufficient to halt migration before 1 au. The critical masses reached are within the range 26–29.9 M⊕ (0.08û0.09 MJ).
4 Discussion
In this work we studied the planet formation process in second-generation circumbinary discs around DWD systems. We assumed initial seeds of mass 0.01 Me and studied their evolution for different starting times, t0, of planet formation and for different disc models (Table 2). Depending on the value of t0, we assumed the seeds to be either of first-generation origin (t0 = 10τc) or to form directly in the second-generation disc (t0 = 0.1, 1 Myr). A representation of the percentages of planets formed by our disc models is shown in Fig. 7. We also tested our discs with seeds of mass 10 M⊕ when t0 = 0.1, 1 Myr, assuming they are first-generation bodies that never underwent the runaway gas accretion process.
The gas accretion rate Ṁg and the photoevaporation rate Ṁw have a crucial role in determining the final planetary masses. If the planetary formation starts too late after the formation of the last WD of the system, the initial value Ṁg(t0) might be very close to Ṁw. This hinders the pebble accretion phase (see Eq. (18)), and could inhibit the formation of GGs because of the reduced mass supplied to their planet-forming regions (i.e. ΔṀgw ≈ 0; see Eq. (25)). In particular, an increase in Ṁw by an order of magnitude reduced the masses of the GGs of the case t0 = 10τc, rc = 50 au, and ξ = 0.02 from 10 000 M⊕ (31.45 MJ) to ~4200 M⊕ (13.21 MJ) (see Sect. 3.1.5). This disc forms the GGs with the highest masses when Ṁw = 10−8 M⊙ yr−1. This particular scenario suggests that the presence of GGs of low mass or Ns around a DWD can be useful to constrain the photoevaporation rate of the disc that produced them.
The different accretion rates from system to system are strictly related to the temperature profile and to the density of the disc. Shorter and denser discs allow for a faster pebble accretion, but the initial seeds would be closer to the disc inner edge. Therefore, they can only reach the lowest isolation masses possible (e.g. left panels of Fig. 3), and consequently their gas contraction phase is slow (see Eq. (22)). Moreover, during the fast pebble accretion phase the Type I migration rate quickly increases as well, leading most of the planets to the inner radius of the disc, rin. Consequently, planetary formation ends mostly because the planets do not have more space to grow, and not because they reach their critical masses. In this case, most of the planets formed are SNs, and a smaller fraction are Ns. In particular, the coldest discs (i.e. when t0 = 1 Myr) can only form SNs.
The only deviation from this scenario occurs in the presence of first-generation seeds of mass 10 M⊕, which we used to test the planet-forming potential of the discs when the accretion rate is the lowest (i.e. t0 = 0.1, 1 Myr; e.g. Fig. 2). In these cases the initial mass is already higher than or equal to the isolation mass. Therefore, the planets have more space to grow before reaching rin, eventually reaching the critical mass, Mcrit. However, the accretion rate when t0 = 0.1, 1 Myr is low and the planet-forming region is already depleted of gas when the planets reach Mcrit. Therefore, the planets stop migrating towards the disc inner edge and this halts their growth. This is also one of the two mechanisms that allow planets to be located farther than 1 au at the end of their evolution. The other mechanism is due to the planets reaching their maximum mass at the end of runaway gas accretion (Tanaka et al. 2020). Once the runaway gas accretion starts, lower values of ΔṀgw lead to faster depletion of the planet-forming region, again halting the migration, and lower final masses of the GGs. The GGs with the highest masses form when ΔṀgw is the largest and the disc extension is the shortest, but they reach their final location, within 1 au, in ~2 Myr or more. If the disc extension is the largest, the GGs have lower masses, but it is more likely for them to stop migrating before 1 au.
Another important aspect is related to the specific formation channel we adopted. In our study we only considered the region of the disc heated by the radiation of the central system (i.e. the region of the disc where Eq. (5) holds). This choice excluded the outer part of our disc models, but depending on the binary configuration after the last CE, the external excluded part has a different extension. In particular, planets can have more space to grow in discs with a larger irradiated region. Therefore, seeds located farther away have a greater chance to trigger the gas accretion phase with respect to discs with shorter irradiated regions. Thanks to this possibility, if two discs have similar temperature profiles, the one with lower density, such as DWD4, could form planets of higher masses than discs with higher density, such as DWD3 (e.g. when rc = 150 au and t0 = 0.1 Myr, the planet-forming area of DWD3 has an extension of ~50 au, that of DWD4 has an extension of ~100 au). However, this occurs when the discs are the coldest (i.e. t0 = 0.1, 1 Myr), independently of whether M0 = 0.01 M⊕ and M0 = 10 M⊕. When temperatures are the highest possible (i.e. t0 = 10τc), DWD3 can compensate for the shorter planet-forming area and forms planets with higher masses than the disc of DWD4. As shown in Fig. 1, another system with a large planet-forming area is DWD2. However, the disc temperatures are the lowest among all the discs, independently of the starting time of planet formation. Therefore, such discs form mostly SNs and low mass Ns.
It is important to note that when the temperatures of the disc are higher than those considered here, the isolation mass profile of the disc shifts towards higher masses. This allows for faster gas contraction phases and faster GGs formation once Miso is reached. On the other hand, given that Miso/Ṁg(t0) ∝ T2, no seed could reach the isolation mass if the temperatures of the disc are too high. The only possibility to form GGs (or even Ns) in this case would be to increase the extension of the disc, which would provide the seeds with more space to grow, or to increase ξ, which would accelerate the pebble accretion phase.
A last general finding is that high values of ξ reduce the formation time of planetary cores. The most favourable environments for the formation of GGs are discs around stars with metallicity higher than solar metallicity that incorporate first-generation planetary material. Moreover, such GGs could be located farther from the inner radius of the disc, as a high disc metallicity would speed up the transition between the faster Type I migration regime and the slower Type II migration regime. However, the farthest GGs can only be found in discs with an extension larger than rc = 100 au as in more compact discs the seeds cannot reach isolation masses high enough to start runaway gas accretion quickly (see Eq. (23)).
The systems and disc models we studied confirm that it could be possible to form second-generation GGs within ~2 Myr. However, the formation of these planets requires the presence of first-generation bodies of mass of at least 0.01 M⊕. In particular, if the discs are hot and dense, GGs can form in discs with extensions between 50 and 150 au (e.g. in our systems DWD1 and DWD3). Otherwise, the planet-forming area of the disc should be as large as possible in order to compensate for low density and/or low temperatures (e.g. in our systems DWD2 and DWD4). However, if the disc is too large (i.e. rc = 150 au), its density can be too low and can suppress the advantage for the farthest seeds to have more space to grow.
The disc models considered in this study have demonstrated that it is easier to form second-generation Ns and SNs than second-generation GGs; in other words, our second-generation circumbinary discs can form planets either after 0.1 or 1 Myr from their formation. The low temperatures of the discs, especially in combination with high metallicities, allow every seed to reach the isolation mass and partially follow the gas contraction phase. However, it is unlikely that these planets stop migrating before reaching the inner radius of the disc. It is more likely for this to occur for seeds with mass M0 = 10 M⊕. In this case, the sooner planetary formation starts, the higher the possibility to form GGs. However, due to the low accretion rates when t0 = 0.1, 1 Myr, runaway gas accretion stops soon after its onset.
When considering the DWDs detectable by the LISA mission, DWD2, DWD3, and DWD4 (see Table 1), the systems host giant planets whose masses range from ~0.13 MJ to ~15 MJ when we consider all disc temperature, metallicity, and extension combinations (see Fig. 8). Aside from the planetary mass, the other parameter relevant for the detection is the orbital separation from the central binary. Following the results by Danielski et al. (2019), giant planets with masses higher than 0.27 MJ and separations smaller than ~4 au could be detected. In our analysis, immediately after the onset of the disc at t0 = 10τc, all three systems are capable of producing GG planets whose semimajor axes fall within 4 au (Tables A.3, A.6, A.9 and Figs. 9, 10). In particular, DWD3 is the LISA system whose environment can produce GGs with the highest masses (see Fig. 11). These planets are located within 1 au, and their masses fall in the range M = 2.77–14.78 MJ (see Fig. 8, third column). These characteristics make DWD3 the best system among those analysed for producing second-generation planets that could be detected by LISA. However, here we do not account for the distance of the systems from Earth, on which the amplitude of the monochromatic GWs depend (Korol et al. 2020). Furthermore, while DWD2 has a binary separation that produces a GW signal within the LISA band, DWD3 and DWD4 will need to further shrink their orbits for their GWs to be detectable by LISA. For this the above planetary detectability considerations are meant to be indicative, based on previous analysis (Danielski et al. 2019; Katz et al. 2022). A focused Bayesian analysis on the detection significance of these systems will be performed in future studies.
 |
Fig. 7 Distribution of planets among DWD systems adopted in this work. From left to right, for each DWD system the pie charts show the distribution of SNs, Ns, and GGs. From top to bottom, the distribution of planets among the systems are shown at the different values of t0 adopted for our simulations: 10τc, 0.1 Myr, and 1 Myr. The bottom right and the middle right charts show that no system forms GGs when t0 = 0.1, 1 Myr (see Appendix A). |
 |
Fig. 8 Mass distribution of the planets formed by the DWD systems analysed in this work. All histograms are normalised with respect to the total number of planets formed in each case, and the Y-axis are plotted in log scale. From left to right, the histograms show the mass distribution for each DWD system. From top to bottom, the first three rows of histograms show the distribution as a function of the values of t0 adopted for our simulations (i.e. 10τc, 0.1 Myr, and 1 Myr, respectively). These histograms show only the mass distribution of SNs (blue bins) and Ns (red bins). The histograms in the bottom row show only the distributions of GGs for each system at t0 = 10τc as GGs only form in this case. |
 |
Fig. 9 Distributions of final positions of planets formed at t0 = 10τc by the DWD systems adopted in this work. All the histograms have Y-axis in log scale and each bin is normalised with respect to the total number of planets formed by each system. The largest histograms show the distribution of the final positions of all the planets for each DWD system. Each of these histograms has two smaller overlapping histograms showing the final positions of Ns and GGs. When t0 = 0.1, 1 Myr, all planets (which consists only of SNs and Ns) migrate towards the inner radius of the disc, rin (see Appendix A). Therefore, the related histograms would only show one bin around the rin value of the discs. |
 |
Fig. 10 Final position distribution of the GGs formed at t0 = 10τc by each DWD system analysed in this work. Each bar is normalised with respect to the total number of planets formed by each DWD system, and the Y-axis is in log scale. The final positions are distributed among the radial intervals rin − 1 au (blue bars), 1–4 au (orange bars), and 4 au − rc (yellow bars) (see Appendix A). |
5 Conclusions
The results of this study argue that second-generation circumbinary discs around DWDs are capable of forming second-generation Magrathea planets. However, the possibility that the formation of the planets with the highest masses (i.e. GGs), occurs exclusively in second-generation discs appears unfavoured. Rather, these planets are most likely originated by first-generation bodies whose growth process has been restarted by the disc of stellar material produced by the binary evolution. Even if our models do not form GGs at t0 ≥ 0.1 Myr, this does not exclude that they could form in second-generation discs as we restricted our analysis only to the region of the disc mainly heated by stellar radiation without exploring the scenario where these planets form by disc instability.
Our results point towards a key role of the accretion rate of the disc, which in the adopted treatment depends mainly on the disc temperature and density profiles as we focus on a fixed viscosity value following Johansen et al. (2019). However, viscosity plays a similar role to density and temperature in affecting the disc accretion rate and the planet formation tracks, especially in the early stages of the disc lifetime. In particular, when planet formation starts, the higher the accretion rate is with respect to the photoevaporation rate of the disc, the easier it is for the planets to reach the critical mass. Moreover, the higher the disc metallicity, the faster the pebble accretion, meaning that the seeds can reach the isolation mass more quickly. A combination of high accretion rate and metallicity defines the best environment for planet formation, and in particular for the formation of giant planets.
In general, our disc models are characterised by steep isolation mass profiles. The latter facilitates the formation of SN and N planets, which are the most common planets. On the other hand, the steepness of the isolation mass profile hinders the outer seeds from reaching the isolation mass. When they reach it and they complete their gas contraction phase, the accretion rate of the disc is already too low with respect to the photoevaporation rate, and the planet-forming region quickly runs out of gas.
Most of the second-generation planets we found reach the inner regions of the disc (within 1 au from the inner edge of the disc) while they are still undergoing the gas accretion phase. Therefore, they should be observed close to the binary system. In particular, planets formed from first-generation seeds can reach the critical mass more easily if the planet formation starts soon after the onset of the disc and the disc metallicity and density are high. In this case they could be found within 1 and 4 au.
The GGs formed by our systems reached very high masses for some of the parameters we used for our discs. However, considering the global population of GGs for each system, it is less likely to find planets with masses within ~ 1000–2500 M⊕ (~3.14–7.86 MJ) than with masses within 2500–7500 M⊕ (~7.86–23.59 MJ) and 40–640 M⊕ (0.12–2.01 MJ). In particular, the best scenario for LISA mission observations (i.e. the DWD3 system) shows that ~78.57% of GGs have masses higher than 0.27 MJ, and all of them reach a final location within 1 au. Among the systems that can be observed by LISA, DWD4 is the only one forming GGs whose final locations are within 1 and 4 au. In particular, 50% of such GGs are finally located within 1 au and 50% are located within 1 and 4 au. Moreover, ~44.44% of them have masses higher than 0.27 MJ.
The analysis presented here serves as the first step towards addressing planetary formation at the end of binary evolution, when both stars begin their cooling-down process. This work is set within a more comprehensive analysis both to study the orbital stability of the newly formed planetary systems (Nigioni et al., in prep.) and to account for the potential presence of first-generation planets (or planetesimals) within the second-generation disc throughout specific long-term evolution modelling (Columba et al. 2023). These theoretical developments will allow us to further deepen our knowledge of the events occurring in the final stages of a circumbinary system, and to have an improved vision on the occurrence rates of Magrathea exoplanets detectable with LISA.
 |
Fig. 11 Distributions of mass and final position of the GGs formed at t0 = 10τc by each system analysed in this work. The X-axis and the Y-axis of each of the 3D histograms show the radial position and the mass of the planets, respectively. The X-axis values increase from right to left. The number of planets in each 3D bin is normalised with respect to the total number of planets formed by each system. Following the vertical colour bar on the right of each histogram, the pale yellow bins include the largest amount of GGs, and the dark-blue bins include the smallest amount of GGs. |
Acknowledgements
The authors thank Jacques Kluska and Valeriya Korol for the helpful discussions. D.T. acknowledges the support of the Italian National Institute of Astrophysics (INAF) through the INAF Main Stream project “Ariel and the astrochemical link between circumstellar discs and planets” (CUP: C54I19000700005) and of the Italian Space Agency (ASI) through the ASI-INAF agreement no. 2021-5-HH.0. C.D. acknowledges financial support from the grant CEX2021-001131-S funded by MCIN/AEI/ 10.13039/501100011033 and the Group project Ref. PID2019-110689RB-I00/AEI/10.13039/501100011033.
Appendix A Tables of results
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD1 when t0 = 0.1 Myr.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD1 when t0 = 1 Myr.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD2 when t0 = 10τc.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD2 when t0 = 0.1 Myr.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD2 when t0 = 1 Myr.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD3 when t0 = 10τc.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD3 when t0 = 0.1 Myr.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD3 when t0 = 1 Myr.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD4 when t0 = 10τc.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD4 when t0 = 0.1 Myr.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD4 when t0 = 1 Myr.
References
- Adams, D. 1979, The Hitchhiker’s Guide to the Galaxy (Australia: Pan Books) [Google Scholar]
- Amaro-Seoane, P., Andrews, J., Arca Sedda, M., et al. 2023, Liv. Rev. Relativ., 26, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Amaro-Seoane, P., Audley, H., Babak, S., et al. 2017, arXiv e-prints [arXiv:1702.00786] [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [Google Scholar]
- Artymowicz, P., Clarke, C. J., Lubow, S. H., & Pringle, J. E. 1991, ApJ, 370, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Bédard, A., Bergeron, P., Brassard, P., & Fontaine, G. 2020, ApJ, 901, 93 [Google Scholar]
- Bernabò, L. M., Turrini, D., Testi, L., Marzari, F., & Polychroni, D. 2022, ApJ, 927, L22 [CrossRef] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Morbidelli, A., Johansen, A., et al. 2018, A&A, 612, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brasser, R. 2013, Space Sci. Rev., 174, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E. 2010, ApJ, 724, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [Google Scholar]
- Columba, G., Danielski, C., Dorozsmai, A., & Toonen, S. 2023, A&A, 675, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Angelo, G., & Lubow, S. H. 2010, ApJ, 724, 730 [Google Scholar]
- D’Angelo, G., Weidenschilling, S. J., Lissauer, J. J., & Bodenheimer, P. 2021, Icarus, 355, 114087 [CrossRef] [Google Scholar]
- Danielski, C., & Tamanini, N. 2020, Int. J. Mod. Phys. D, 29, 2043007 [NASA ADS] [CrossRef] [Google Scholar]
- Danielski, C., Korol, V., Tamanini, N., & Rossi, E. M. 2019, A&A, 632, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fedele, D., van den Ancker, M. E., Henning, T., Jayawardhana, R., & Oliveira, J. M. 2010, A&A, 510, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hardy, A., Schreiber, M. R., Parsons, S. G., et al. 2016, MNRAS, 459, 4518 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [Google Scholar]
- Helled, R., Bodenheimer, P., Podolak, M., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 643 [Google Scholar]
- Huang, J., Andrews, S. M., Cleeves, L. I., et al. 2018, ApJ, 852, 122 [Google Scholar]
- Isella, A., Guidi, G., Testi, L., et al. 2016, Phys. Rev. Lett., 117, 251101 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
- Izzard, R., & Jermyn, A. 2018, Galaxies, 6, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., & Lambrechts, M. 2017, Ann. Rev. Earth Planet. Sci., 45, 359 [Google Scholar]
- Johansen, A., Ida, S., & Brasser, R. 2019, A&A, 622, A202 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kanagawa, K. D., Tanaka, H., & Szuszkiewicz, E. 2018, ApJ, 861, 140 [Google Scholar]
- Kashi, A., & Soker, N. 2011, MNRAS, 417, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, M. L., Danielski, C., Karnesis, N., et al. 2022, MNRAS, 517, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Kluska, J., Van Winckel, H., Coppée, Q., et al. 2022, A&A, 658, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korol, V., Rossi, E. M., Groot, P. J., et al. 2017, MNRAS, 470, 1894 [NASA ADS] [CrossRef] [Google Scholar]
- Korol, V., Rossi, E. M., & Barausse, E. 2019, MNRAS, 483, 5518 [NASA ADS] [CrossRef] [Google Scholar]
- Korol, V., Toonen, S., Klein, A., et al. 2020, A&A, 638, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kostov, V. B., Moore, K., Tamayo, D., Jayawardhana, R., & Rinehart, S. A. 2016, ApJ, 832, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Kretke, K. A., Levison, H. F., Buie, M. W., & Morbidelli, A. 2012, AJ, 143, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lammer, H., Brasser, R., Johansen, A., Scherf, M., & Leitzinger, M. 2021, Space Sci. Rev., 217, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Lichtenberg, T., Schaefer, L. K., Nakajima, M., & Fischer, R. A. 2022, ArXive-prints [arXiv:2203.10023] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [Google Scholar]
- MacFadyen, A. I., & Milosavljević, M. 2008, ApJ, 672, 83 [Google Scholar]
- Manara, C. F., Morbidelli, A., & Guillot, T. 2018, A&A, 618, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Menu, J., van Boekel, R., Henning, T., et al. 2015, A&A, 581, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mestel, L. 1952, MNRAS, 112, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Mulders, G. D., Pascucci, I., Ciesla, F. J., & Fernandes, R. B. 2021, ApJ, 920, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Mustill, A. J., Marshall, J. P., Villaver, E., et al. 2013, MNRAS, 436, 2515 [NASA ADS] [CrossRef] [Google Scholar]
- Nelemans, G., Yungelson, L. R., Portegies Zwart, S. F., & Verbunt, F. 2001, A&A, 365, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelson, A. F., Benz, W., & Ruzmaikina, T. V. 2000, ApJ, 529, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Oomen, G.-M., Van Winckel, H., Pols, O., et al. 2018, A&A, 620, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oomen, G.-M., Van Winckel, H., Pols, O., & Nelemans, G. 2019, A&A, 629, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paczynski, B. 1976, IAU Symp., 73, 75 [NASA ADS] [Google Scholar]
- Passy, J.-C., De Marco, O., Fryer, C. L., et al. 2012, ApJ, 744, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Perets, H. B. 2010, ArXiv e-prints [arXiv:1001.0581] [Google Scholar]
- Pérez, L. M., Carpenter, J. M., Chandler, C. J., et al. 2012, ApJ, 760, L17 [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., & Verbunt, F. 1996, A&A, 309, 179 [NASA ADS] [Google Scholar]
- Pulley, D., Sharp, I. D., Mallett, J., & von Harrach, S. 2022, MNRAS, 514, 5725 [NASA ADS] [CrossRef] [Google Scholar]
- Rabago, I., & Zhu, Z. 2021, MNRAS, 502, 5325 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2016, ApJ, 830, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. R. G., & Dreizler, S. 2014, A&A, 563, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarz, R., Funk, B., Zechner, R., & Bazsó, Á. 2016, MNRAS, 460, 3598 [Google Scholar]
- Scott, E. R. D. 2007, Ann. Rev. Earth Planet. Sci., 35, 577 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Sigurdsson, S., Richer, H. B., Hansen, B. M., Stairs, I. H., & Thorsett, S. E. 2003, Science, 301, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Sinukoff, E., Fulton, B., Scuderi, L., & Gaidos, E. 2013, Space Sci. Rev., 180, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Tamanini, N., & Danielski, C. 2019, Nat. Astron., 3, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., Murase, K., & Tanigawa, T. 2020, ApJ, 891, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Toonen, S., Nelemans, G., & Portegies Zwart, S. 2012, A&A, 546, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turrini, D., Schisano, E., Fonte, S., et al. 2021, ApJ, 909, 40 [Google Scholar]
- Turrini, D., Codella, C., Danielski, C., et al. 2022, Exp. Astron., 53, 225 [CrossRef] [Google Scholar]
- Van Winckel, H. 2018, arXiv e-prints [arXiv:1809.00871] [Google Scholar]
- Völschow, M., Banerjee, R., & Hessman, F. V. 2014, A&A, 562, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P. 2015, Eur. Phys. J. Web Conf., 102, 00011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorotovic, M., & Schreiber, M. R. 2013, A&A, 549, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Catalogue of exoplanets in binary star systems, maintained by R. Schwarz (Schwarz et al. 2016).
It is important to mention that a recent study (Pulley et al. 2022) raised the necessity of a refinement of the models used to describe the eclipse time variations (ETVs) observed for NN Ser. Without this refinement the models fail to predict ETVs more than a year into the future. This does not exclude, however, the presence of circumbinary planets; rather the authors suggest the importance of deepening other mechanisms affecting ETVs (e.g. magnetic effects associated with the secondary of the binary system).
From the book ‘The Hitchhiker’s Guide to the Galaxy’ (Adams 1979). Magrathea is a planet orbiting a binary star burning with ‘white fire’, which we conveniently interpreted to be two white dwarfs, given that they emit white light instead of yellow, like our Sun in the visible band.
The software package simulates the evolution of single and binary stars from the zero age main sequence (ZAMS) up to and including remnant phases, and it can be found at https://github.com/ amusecode/SeBa
All Tables
Stellar masses, periods P, and eccentricity e of the analysed DWDs at the end of the second CE, and respective progenitors.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD1 when t0 = 10τc.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD1 when t0 = 0.1 Myr.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD1 when t0 = 1 Myr.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD2 when t0 = 10τc.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD2 when t0 = 0.1 Myr.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD2 when t0 = 1 Myr.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD3 when t0 = 10τc.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD3 when t0 = 0.1 Myr.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD3 when t0 = 1 Myr.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD4 when t0 = 10τc.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD4 when t0 = 0.1 Myr.
Formation times, fraction, and positions of the planets produced by the circumbinary disc of DWD4 when t0 = 1 Myr.
All Figures
 |
Fig. 1 Temperature profiles of the circumbinary discs surrounding the DWD systems (see legend). The profiles are estimated at t0 = 10τc (see Table 1 for details about the systems) for a disc with rc = 50 au. |
| In the text | |
 |
Fig. 2 Gas accretion rates (Ṁg) and photoevaporation rate (Ṁw) of the disc surrounding the system DWD1. The accretion rates start at 10τc, 0.1 Myr, and 1 Myr after the birth of the youngest WD (see legend in each panel), which has a temperature of 75 000, 45 650, and 33 950 K, respectively. From top panel to bottom panel rc = 50, 100, 150 au, respectively. |
| In the text | |
 |
Fig. 3 Planetary growth tracks for DWD1 disc model with rc = 150 au and Teff.2 = 75 000 K. From top to bottom: ξ = 0.01, 0.015, 0.02. Left panels: time-independent growth tracks. The vertical dot-dashed line indicates the radial coordinate rt, where T = 1200 K. The dashed line represents the isolation mass profile for the given disc model (Eq. (19)). Right panels: time-dependent growth tracks. Starting from t0, the tracks reach Miso when they change slope (e.g. leftmost track at ~170 000 yr). |
| In the text | |
 |
Fig. 4 Time-dependent growth tracks (top left) and orbital tracks (top right) for the disc model with rc, ξ, Teff 2 indicated at the top of the panels (DWD1 system). The bottom left panel shows the same tracks as the top left and top right panels, but with the mass on the y-axis and the orbital radius on the x-axis. The bottom right panel shows the accretion rate of the disc described by the adopted parameters (Σ0 = 37.53 g cm−2). In the top right panel, the dot-dashed line corresponds to the orbital radius where T = 1200 K. The apparently vertical lines corresponds to the gas contraction phase (see Sect. 3.1.3). The fractions of track before and after the ‘vertical’ section correspond to the pebble accretion and the runaway gas accretion phase, respectively. |
| In the text | |
 |
Fig. 5 Time-dependent growth tracks of the planets formed by the circumbinary disc surrounding DWD1 when planetary formation starts at t0 = 0.1 Myr (top panel) and t0 = 1 Myr (bottom panel). |
| In the text | |
 |
Fig. 6 Time-dependent growth tracks starting at t0 = 10τc for the circumbinary disc of DWD1 with parameters rc = 50 au, ξ = 0.02 (top panel), considering a constant photoevaporation rate of Ṁw = 10−7 M⊙ yr−1. The accretion rate and photoevaporation rate are shown in the bottom panel. In this case ΔṀgw (see Sect. 2.4.2) is smaller than in the top panel of Fig. 2. The masses of the GGs are shown in the top panel, which are lower than those indicated in Sect. 3.1.5. |
| In the text | |
 |
Fig. 7 Distribution of planets among DWD systems adopted in this work. From left to right, for each DWD system the pie charts show the distribution of SNs, Ns, and GGs. From top to bottom, the distribution of planets among the systems are shown at the different values of t0 adopted for our simulations: 10τc, 0.1 Myr, and 1 Myr. The bottom right and the middle right charts show that no system forms GGs when t0 = 0.1, 1 Myr (see Appendix A). |
| In the text | |
 |
Fig. 8 Mass distribution of the planets formed by the DWD systems analysed in this work. All histograms are normalised with respect to the total number of planets formed in each case, and the Y-axis are plotted in log scale. From left to right, the histograms show the mass distribution for each DWD system. From top to bottom, the first three rows of histograms show the distribution as a function of the values of t0 adopted for our simulations (i.e. 10τc, 0.1 Myr, and 1 Myr, respectively). These histograms show only the mass distribution of SNs (blue bins) and Ns (red bins). The histograms in the bottom row show only the distributions of GGs for each system at t0 = 10τc as GGs only form in this case. |
| In the text | |
 |
Fig. 9 Distributions of final positions of planets formed at t0 = 10τc by the DWD systems adopted in this work. All the histograms have Y-axis in log scale and each bin is normalised with respect to the total number of planets formed by each system. The largest histograms show the distribution of the final positions of all the planets for each DWD system. Each of these histograms has two smaller overlapping histograms showing the final positions of Ns and GGs. When t0 = 0.1, 1 Myr, all planets (which consists only of SNs and Ns) migrate towards the inner radius of the disc, rin (see Appendix A). Therefore, the related histograms would only show one bin around the rin value of the discs. |
| In the text | |
 |
Fig. 10 Final position distribution of the GGs formed at t0 = 10τc by each DWD system analysed in this work. Each bar is normalised with respect to the total number of planets formed by each DWD system, and the Y-axis is in log scale. The final positions are distributed among the radial intervals rin − 1 au (blue bars), 1–4 au (orange bars), and 4 au − rc (yellow bars) (see Appendix A). |
| In the text | |
 |
Fig. 11 Distributions of mass and final position of the GGs formed at t0 = 10τc by each system analysed in this work. The X-axis and the Y-axis of each of the 3D histograms show the radial position and the mass of the planets, respectively. The X-axis values increase from right to left. The number of planets in each 3D bin is normalised with respect to the total number of planets formed by each system. Following the vertical colour bar on the right of each histogram, the pale yellow bins include the largest amount of GGs, and the dark-blue bins include the smallest amount of GGs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



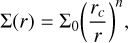
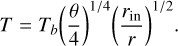
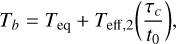
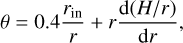
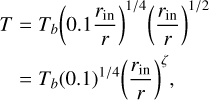
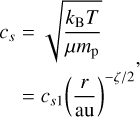
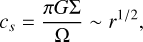
![$T = {{2{m_{\rm{p}}}} \over {{k_{\rm{B}}}}}{\left[ {{{\pi G{\rm{\Sigma }}\left( r \right)} \over {\rm{\Omega }}}} \right]^2} \sim r,$](/articles/aa/full_html/2023/07/aa45827-22/aa45827-22-eq11.png)
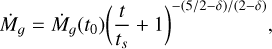
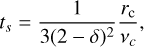
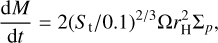
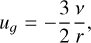
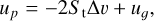
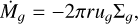
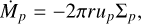
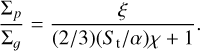
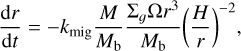
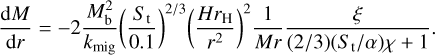
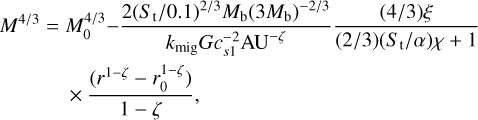
![$\matrix{ {{{{\rm{d}}M} \over {{\rm{d}}t}} = 2{{\left( {{{{S_{\rm{t}}}} \over {0.1}}} \right)}^{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}{{G{M_{\rm{b}}}} \over {{{\left( {3{M_{\rm{b}}}} \right)}^{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}}}} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times {{\xi {{\dot M}_g}\left( t \right)} \over {2\pi c_{s1}^2\left[ {\chi {S_{\rm{t}}} + \left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}} \right)\alpha } \right]{\rm{A}}{{\rm{U}}^\zeta }}}{M^{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}{r^{\zeta - 1}}.} \hfill \cr } $](/articles/aa/full_html/2023/07/aa45827-22/aa45827-22-eq23.png)
![${M_{{\rm{iso}}}} = 20{M_ \oplus }{\left[ {{{{H \mathord{\left/ {\vphantom {H r}} \right. \kern-\nulldelimiterspace} r}} \over {{{\left( {{H \mathord{\left/ {\vphantom {H r}} \right. \kern-\nulldelimiterspace} r}} \right)}_{5{\rm{au}}}}}}} \right]^6}\left[ {0.34{{\left( {{{\log {\alpha _3}} \over {\log {\alpha _\upsilon }}}} \right)}^4} + 0.66} \right]\left( {1 - {{2.5 - \chi } \over 6}} \right).$](/articles/aa/full_html/2023/07/aa45827-22/aa45827-22-eq24.png)
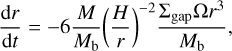
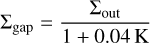
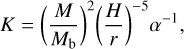
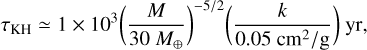
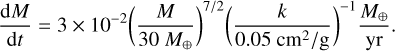
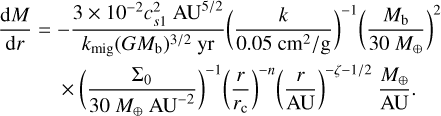
![$\matrix{ {{{{\rm{d}}M} \over {{\rm{d}}t}} = \left[ {0.29\,{{\left( {{M \over {{M_{\rm{b}}}}}} \right)}^{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-\nulldelimiterspace} 3}}}{{\left( {{H \over r}} \right)}^{ - 2}}{\rm{\Omega }}{r^2}} \right]\sum\nolimits_{{\rm{gap}}} {} } \hfill \cr {\,\,\,\,\,\,\,\,\,\, = D\sum\nolimits_{{\rm{gap}}} {} ,} \hfill \cr } $](/articles/aa/full_html/2023/07/aa45827-22/aa45827-22-eq31.png)