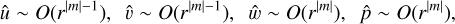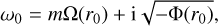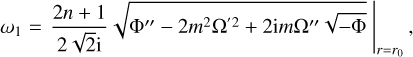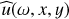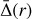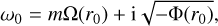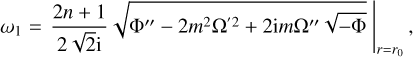| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 20 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202243586 | |
| Published online | 26 April 2023 | |
How tidal waves interact with convective vortices in rapidly rotating planets and stars
1
AIM, CEA, CNRS, Université Paris-Saclay, Université Paris Cité,
Orme des Merisiers Bât 709,
91191
Gif-sur-Yvette Cedex, France
2
Institute for Theoretical Astroparticle Physics, Karlsruhe Institute of Technology (KIT),
Campus North, Bldg. 401, Postfach 3640
76021
Karlsruhe, Germany
3
Centre for Fluid and Complex Systems, Coventry University,
Priory Street,
Coventry
CV1 5FB,
UK
e-mail: junho.park@coventry.ac.uk
4
Department of Engineering Sciences and Applied Mathematics, Northwestern University,
2145 Sheridan Road,
Evanston IL
60208,
USA
5
CIERA, Northwestern University,
1800 Sherman Ave,
Evanston IL
60201, USA
6
Department of Applied Mathematics, School of Mathematics, University of Leeds,
Woodhouse Lane,
Leeds,
LS2 9JT,
UK
Received:
18
March
2022
Accepted:
6
March
2023
Context. The dissipation of tidal inertial waves in planetary and stellar convective regions is one of the key mechanisms that drive the evolution of star–planet and planet–moon systems. This dissipation is particularly efficient for young low-mass stars and gaseous giant planets, which are rapid rotators. In this context, the interaction between tidal inertial waves and turbulent convective flows must be modelled in a realistic and robust way. In the state-of-the-art simulations, the friction applied by convection on tidal waves is commonly modeled as an effective eddy viscosity. This approach may be valid when the characteristic length scales of convective eddies are smaller than those of the tidal waves. However, it becomes highly questionable in the case where tidal waves interact with potentially stable large-scale vortices such as those observed at the poles of Jupiter and Saturn. The large-scale vortices are potentially triggered by convection in rapidly-rotating bodies in which the Coriolis acceleration forms the flow in columnar vortical structures along the direction of the rotation axis.
Aims. We investigate the complex interactions between a tidal inertial wave and a columnar convective vortex.
Methods. We used a quasi-geostrophic semi-analytical model of a convective columnar vortex, which is validated by numerical simulations. First, we carried out linear stability analysis using both numerical and asymptotic Wentzel–Kramers–Brillouin–Jeffreys (WKBJ) methods. We then conducted linear numerical simulations of the interactions between a convective columnar vortex and an incoming tidal inertial wave.
Results. The vortex we consider is found to be centrifugally stable in the range –Ωp ≤ Ω0 ≤ 3.62Ωp and unstable outside this range, where Ω0 is the local rotation rate of the vortex at its center and Ωp is the global planetary (stellar) rotation rate. From the linear stability analysis, we find that this vortex is prone to centrifugal instability with perturbations with azimuthal wavenumbers m = {0,1, 2}, which potentially correspond to eccentricity, obliquity, and asynchronous tides, respectively. The modes with m > 2 are found to be neutral or stable. The WKBJ analysis provides analytic expressions of the dispersion relations for neutral and unstable modes when the axial (vertical) wavenumber is sufficiently large. We verify that in the unstable regime, an incoming tidal inertial wave triggers the growth of the most unstable mode of the vortex. This would lead to turbulent dissipation. For stable convective columns, the wave-vortex interaction leads to the mixing of momentum for tidal inertial waves while it creates a low-velocity region around the vortex core and a new wave-like perturbation in the form of a progressive wave radiating in the far field. The emission of this secondary wave is the strongest when the wavelength of the incoming wave is close to the characteristic size (radius) of the vortex. Incoming tidal waves can also experience complex angular momentum exchanges locally at critical layers of stable vortices.
Conclusions. The interaction between tidal inertial waves and large-scale coherent convective vortices in rapidly-rotating planets (stars) leads to turbulent dissipation in the unstable regime and complex behaviors such as mixing of momentum and radiation of new waves in the far field or wave-vortex angular momentum exchanges in the stable regime. These phenomena cannot be modeled using a simple effective eddy viscosity.
Key words: hydrodynamics / convection / instabilities / waves / planet-star interactions / planets and satellites: dynamical evolution and stability
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Tidal star–planet and planet–moon interactions are one of the key physical mechanisms that drive the evolution of planetary systems (e.g., Laskar et al. 2012; Ahuir et al. 2021; Lainey et al. 2020). In the case of stars, as well as fluid (gaseous or liquid) planetary layers, the tidal force triggers several flows. On the one hand, the tidal potential induces a large-scale nonwave-like flow associated with tidal deformation (e.g., Zahn 1966a; Remus et al. 2012; Ogilvie 2013). On the other hand, as this flow is not a complete solution of the hydrodynamical equations, the nonwave-like flow is completed by tidal waves, the so-called dynamical tide (Zahn 1975; Ogilvie & Lin 2004). The kinetic and potential energies of these flows are then dissipated through different friction mechanisms, such as turbulent friction in convective layers and heat diffusion in stably stratified regions (e.g., Ogilvie 2014; Mathis 2019). In this framework, the rate of tidal dissipation in stellar and planetary convective regions has broad consequences for the evolution of star–planet and planet–moon systems. In the case of star-planet systems, the dissipation of tidal inertial waves – which have the Coriolis acceleration as a restoring force – in the convective envelope of low-mass stars during their pre-main sequence leads to a strong outward(inward) migration if the planet is above(inside) the corotation orbit (e.g., Bolmont & Mathis 2016). This shapes the orbital distribution of short-period gaseous exoplanets (e.g., Benbakoura et al. 2019; Barker 2020; Ahuir et al. 2021). The efficiency of this tidal friction is due to the rapid rotation of low-mass stars during this evolutionary stage (e.g., Gallet & Bouvier 2013, 2015); it leads to an efficient excitation of tidal inertial waves. In addition, regarding our Solar System, our understanding of the tidal evolution of the Jupiter and Saturn systems has been revolutionized. Both planets are the seat of a tidal dissipation stronger by one or several orders of magnitude than previous predictions based on scenarios for the formation of their moons (Goldreich & Soter 1966). This strong dissipation is necessary to explain their rapid orbital migration, which was discovered thanks to high-precision astrometric measurements (Lainey et al. 2009, 2012, 2017, 2020). As in the case of rapidly rotating young stars, the dissipation of tidal inertial waves propagating in the convective regions of Jupiter and Saturn – which are also fast rotators – has been proposed as one of the possible mechanisms to explain the observed strong dissipation (Ogilvie & Lin 2004; Wu 2005; Goodman & Lackner 2009; Lainey et al. 2020). However, this leads us to two fundamental questions. Firstly, we do understand the nature of the interaction between tidal flows and turbulent convective flows, or how they are dissipated. And secondly, the role of rapid rotation in these processes remains to be explored.
The interaction between tidal and turbulent convective flows is one of the most challenging and debated topics in the theory of stellar and fluid planetary tides. The first proposed modelings all adopted the vision of convective small-scale eddies acting on tidal flows, which have the largest characteristic length scales. This led Zahn (1966b, 1989), and Goldreich & Keeley (1977) to use the theory of mixing length to derive an effective eddy viscosity which is applied to the large-scale nonwave-like or equilibrium tide (e.g., Zahn 1966b; Barker 2020) and to tidal inertial waves (Wu 2005). There has been a longstanding debate as to the dependence of this eddy viscosity on the ratio between the tidal period (PT) and the convective characteristic turnover time (Pc, Goodman & Oh 1997; Penev et al. 2007; Ogilvie & Lesur 2012). The most recent state-of-the-art simulations (Duguid et al. 2020b,a; Vidal & Barker 2020b,a) favor the Goldreich & Keeley (1977) proposition, with a scaling proportional to (PT/Pc)2 for high values of the tidal frequency but with a more complex behavior at intermediate values. Recently, Terquem (2021) proposed a more refined formalism leading to promising results (Terquem & Martin 2021) but these authors are challenged by the findings of direct numerical simulations (Barker & Astoul 2021) Notably, these studies do not take into account the action of rotation on turbulent convective flows.
An initial attempt to study the effects of rotation in this context was made by Mathis et al. (2016), who used mixing length theory for rotating convective flows (Stevenson 1979; Augustson & Mathis 2019), and their findings were supported by direct numerical simulations (Barker et al. 2014; Currie et al. 2020). This theory allows us to derive characteristic convec-tive velocity and length scales that take into account the action of the Coriolis acceleration on convective flows. The Coriolis acceleration decreases the efficiency of the heat transport, leading to a decrease in the effective turbulent eddy viscosity acting on tidal flows. At the same time, there have been breakthroughs in our understanding of rapidly rotating convective flows in stars and planets thanks to global nonlinear numerical simulations and the space missions JUNO and Cassini, which explored Jupiter and Saturn, respectively. First, stable vortices were discovered at the poles of Jupiter and Saturn (e.g., Adriani et al. 2018; Godfrey 1988; Sánchez-Lavega et al. 2006; Dyudina et al. 2008; Fletcher et al. 2018). Their formation can result from deep-seated rapidly rotating convection (Yadav et al. 2020; Garcia et al. 2020; Cai et al. 2021). At the same time, Julien et al. (2012) and Hindman et al. (2020) provide a systematic classification of convective flows as a function of rotation rate. These studies revealed that columnar convective turbulent structures are aligned along the rotation axis direction. This alignment results from the Taylor-Proudman constraint imposed by the Coriolis acceleration on convective flows. In the presence of a companion, this leads to configurations where tidal inertial waves propagate in turbulent, rapidly-rotating convective flows with structured columnar vortices. In this complex configuration, convective eddies can be of a greater scale than those assumed in the mixing-length approach and it becomes necessary to study their complex interactions with tidal inertial waves.
In this article, we explore this process by studying the propagation of a monochromatic (tidal) inertial wave through a columnar turbulent convective vortex. In Sect. 2, we formulate the equations needed to understand the wave–vortex interaction problem. In this framework, we propose a semi-analytical model for the convective Taylor columnar vortex and describe the regime where centrifugal instability occurs. We formulate the equations for the stability analysis and linear evolution of perturbations for a tidally forced inertial wave interacting with the vortex. In Sect. 3, we study the stability of the convective column based on numerical stability computation and compare with asymptotic results from a detailed WKBJ analysis reported in the Appendix. In the unstable regime, we verify that an incoming radial tidal wave can, with other motions, trigger the most unstable mode. This may lead to turbulence. In Sect. 4, we conduct numerical simulations to investigate how a tidal inertial wave interacts with a stable convective column in the linear regime. In Sect. 5, we propose possible scenarios of the nonlinear interactions between convective vortices and tidally forced inertial waves. Finally, conclusions, discussions, and perspectives are provided in Sect. 6.
2 Mathematical formulation for the interactions between a convective Taylor column and inertial modes
2.1 Governing equations
To understand how a convective Taylor column interacts with (tidal) inertial waves (Fig. 1), we first investigate an intrinsic property of the convective structure: stability. The stability analysis allows us to examine how a convective column would respond to external forcing and when intense instability would occur because of its interaction with specific perturbations such as linear eigenmodes of basic states or the optimal perturbation represented as the sum of the eigenmodes (Schmid & Henningson 2001; Antkowiak 2005). In a local framework rotating with an angular speed Ωp, which is the global planetary (stellar) rotation rate, we consider the continuity and momentum equations:
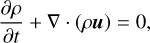 (1)
(1)
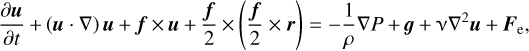 (2)
(2)
where ρ is the density, u is the velocity vector, f is the Coriolis vector, where f = f êz = 2Ωpêz, r is the position vector, P is the pressure, g is the gravity vector, ν is the kinematic viscosity, ∇ is the vector differential operator, and Fe is the vector of external (tidal) forcing. We assume an incompressibility condition by considering the density ρ as a constant and decompose the pressure P into P = P0 + p, where P0 satisfies the hydrostatic balance with the centrifugal acceleration taken into account as
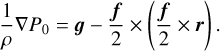 (3)
(3)
Under these assumptions, Eqs. (1) and (2) reduce to
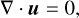 (4)
(4)
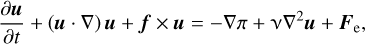 (5)
(5)
where π = p/ρ is the normalized pressure.
Our study considers a local polar traditional f-plane centered around the rotation axis of the planet or star, where the rotation vector and the gravity are aligned, with an associated cylindrical coordinate system (r, θ, z). In this case, we have the following set of equations for the velocity u = (u,v,w), the normalized pressure π, and the forcing Fe = (Fu, Fv, Fw):
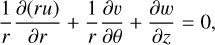 (6)
(6)
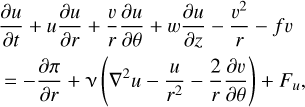 (7)
(7)
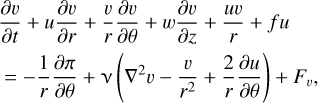 (8)
(8)
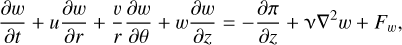 (9)
(9)
where the vertical component of the Coriolis acceleration vanishes. Being in the polar traditional f-plane allows us to treat a case where the equations for (tidal) inertial waves propagating within a vortex with a radial structure are separable.
While the vortex has a polar nature here, the inertial waves can also propagate in a Cartesian, planar manner, as depicted in the schematic in Fig. 1 (left panel) of the wave–vortex interaction in the Cartesian coordinate system. To analyze this planar wave propagation, we need to consider the set of equations for the velocity u = (ux, uy,w) in Cartesian coordinates (x, y, z) on the traditional f-plane as follows:
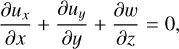 (10)
(10)
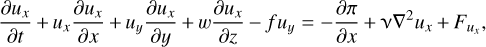 (11)
(11)
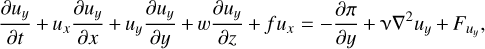 (12)
(12)
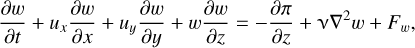 (13)
(13)
where the following relations among the horizontal velocity components are satisfied:
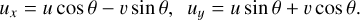 (14)
(14)
This traditional polar study constitutes the first necessary step toward understanding the complex wave–vortex interaction. For example, it is relevant to the study of interactions between tidal inertial waves and large polar vortices such as those observed in giant planets. However, one should keep in mind that, in a more general case away from the poles (e.g., a case with the nontradi-tional f-plane approximation applicable at a general colatitude; see e.g., Park et al. 2021), the propagation equation for inertial waves is no longer separable (Gerkema & Shrira 2005). This would lead to a more complex situation, where 2D inertial wave attractors (e.g., Maas 2001; Rieutord et al. 2001) are interacting with a vertical vortex (Duran-Matute et al. 2013; Boury et al. 2021, see also Fig. 1 right panel). We first focus here on the already complex polar problem, while the fully 2D problem will be studied in the future.
 |
Fig. 1 Schematics of the tidal wave-vortex interaction. Left panel: schematic of the interaction between a tidal inertial wave and a single convective Taylor column in the f -plane. We introduce the cylindrical coordinates (r, θ, z). Right panel: schematic of a meridian cut of a planet or star showing propagation of a tidal inertial wave (blue lines) in a convective envelope and its interaction with a single Taylor column. |
 |
Fig. 2 Proflies of base vorticity ζ(r, black in panel a) and base angular velocity Ω(r, black in panel b) and their first (blue) and second (red) derivatives for the current model (17, solid lines) and the model (16) from Grooms et al. (2010, dashed lines). Panel c: profiles of the Rayleigh discriminant Φ(r) for Ω/f = −1 (black), Ω0/f = 0.5 (blue) and Ω0/f = 2 (red). |
2.2 Convective Taylor column
2.2.1 Basics of rapidly rotating flows
Convection plays a fundamental role in stars and planets. Rotation fundamentally modifies the behavior of convection through the action of the Coriolis acceleration (e.g., Davidson 2013) and changes the equilibrium structure of the body because of the centrifugal force (e.g., Wang et al. 2016). This impacts the interactions and energy exchanges with (gravito-)inertial (tidal) waves (Mathis et al. 2014; Augustson et al. 2020).
In rotating convection, one of the fundamental flows that appear even in very turbulent regimes are columnar structures that result from the interaction between buoyancy-driven convection and the Coriolis acceleration. Rapid rotation tends to cause those structures to align with the rotation axis of the body. Indeed, in an inviscid adiabatic fluid, a steady-state solution obeys the Taylor-Proudman theorem, whereby the fluid velocity becomes invariant along the rotation vector (e.g., Davidson 2013). However, the entropy gradient is, in general, slightly nona-diabatic with a density gradient leading to quasigeostrophic flow in rapidly rotating systems with net heat flux. Such flows can be modeled using asymptotic methods if the scale separation along the direction of the rotation axis and the orthogonal direction is large enough. These dynamically rich nonlinear systems have been studied in great detail (Veronis 1959; Gough et al. 1975; Julien et al. 1998). Their solutions involve the formation of columnar flow structures in both laminar and turbulent regimes in numerical and experimental settings (Stellmach et al. 2014; Aurnou et al. 2015; Cheng et al. 2015). Exact analytical solutions validated on numerical simulations can be found as well (Grooms et al. 2010; Grooms 2015). These solutions are separable; some having a fixed horizontal structure and some having a varying vertical one, and have been discussed by Julien et al. (1998, 2012), Sprague et al. (2006), Grooms et al. (2010), and Grooms (2015). The equations for the vertical structure can be condensed into a nonlinear boundary value problem. This provides a robust analytical description of the structure of the flow with which we investigate their stability and interactions with incoming tidal inertial waves.
2.2.2 Semi-analytical quasigeostrophic models
Simulations of quasigeostrophic convective flows provide guidance as to the model coherent structures that may exist in rapidly rotating planets and stars. These simulations range from near the onset of instability to the most turbulent states that can be reached thanks to supercomputers, which are still far from the real planetary and stellar regimes. One characteristic that appears to bridge laminar and the most turbulent simulations is the formation of large-scale vortical structures that span the vertical domain. In the laminar regime, these vortices are long lived (even persistent) and only weakly interact with each other. In turbulent simulations, they are formed by the advec-tion of small-scale vortices into domain-spanning larger-scale structures, representing an inverse cascade of energy into the largest-scale vortex that can be intermittent. An analogy can be made between many of the features of the turbulent and the laminar structures, under the assumption that they weakly interact with each other.
Analytical solutions for such laminar and turbulent structures were derived by Grooms et al. (2010) and Grooms (2015), respectively. These are solutions to a nonlinear eigenvalue problem that arises from a simplification of the full quasigeostrophic equations. First, it is assumed that nonlinear horizontal interactions between the columnar structures are weak while passive advec-tion is still allowed. In this regard, each columnar structure is assumed to be axisymmetric and time-independent, meaning that there is no horizontal self-interaction, which affects the structure by itself along its temporal evolution. The equations resulting from these assumptions are Eqs. (9) and (10) in Grooms et al. (2010). One solution of these equations is of the separable form for the poloidal velocity potential 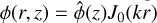 , and yields the vertical component of the vorticity ζ(z, r) = −∂zϕ with J0(kr) the zeroth-order Bessel function with a radial wavenumber k. This Bessel function solution is chosen over the better-fitting Hankel function solution examined in Grooms et al. (2010) because the latter diverges for r → 0 (we refer the reader to Abramowitz & Stegun 1972, for the properties of these functions). However, as stated in Grooms et al. (2010), the radial function must be truncated. We choose to do this exponentially so that an infinite radial domain may be studied when looking at the interaction with an incoming tidal inertial wave. Moreover, the vertical structure is taken to be far from the bounding surfaces so that it can be locally approximated as a constant with
, and yields the vertical component of the vorticity ζ(z, r) = −∂zϕ with J0(kr) the zeroth-order Bessel function with a radial wavenumber k. This Bessel function solution is chosen over the better-fitting Hankel function solution examined in Grooms et al. (2010) because the latter diverges for r → 0 (we refer the reader to Abramowitz & Stegun 1972, for the properties of these functions). However, as stated in Grooms et al. (2010), the radial function must be truncated. We choose to do this exponentially so that an infinite radial domain may be studied when looking at the interaction with an incoming tidal inertial wave. Moreover, the vertical structure is taken to be far from the bounding surfaces so that it can be locally approximated as a constant with 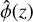 = constant. In this case, we can define the local vorticity of the fluid such that:
= constant. In this case, we can define the local vorticity of the fluid such that:
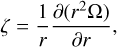 (15)
(15)
where Ω is the local angular velocity. A comparison of the approximate solution employed here (solid lines) with the solution derived in Grooms et al. (2010; dashed lines) is shown in Fig. 2, where the divergence of the Hankel function can be seen as the radius approaches zero but the oscillations are damped, requiring the exponential damping of the Bessel function. More specifically, the radial profile of the vorticity ζ(r) in terms of the Hankel function is
![$ \zeta \left( r \right) \sim {\mathop{\rm Re}\nolimits} \left[ {{\rm{H}}_0^{\left( 1 \right)}\left( {{k_{\rm{H}}}r} \right)} \right], $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq18.png) (16)
(16)
where Re denotes the real part, 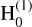 denotes the Hankel function of the first kind at the zeroth order, and kH = 1.34exp(0.153i)/R0 with R0 the reference radial length scale of the structure. In contrast, the local angular velocity profile used here is instead
denotes the Hankel function of the first kind at the zeroth order, and kH = 1.34exp(0.153i)/R0 with R0 the reference radial length scale of the structure. In contrast, the local angular velocity profile used here is instead
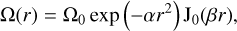 (17)
(17)
where Ω0 is the local angular velocity of the convective column at r = 0, and α and β are constants 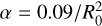 and β = 0.76/R0, which are chosen to minimize the error between the vorticity (16) proposed by Grooms et al. (2010) and our model. As shown in Figs. 2a,b, the two profiles (16) and (17) match fairly well and there is no singularity at r = 0 for the second derivative of the angular velocity (17) or the second derivative of the vortic-ity. Throughout the paper, we use the angular velocity profile given in Eq. (17) to derive analytic expressions for the dispersion relations, which are crucial for understanding the interaction between a convective column and tidally forced inertial waves.
and β = 0.76/R0, which are chosen to minimize the error between the vorticity (16) proposed by Grooms et al. (2010) and our model. As shown in Figs. 2a,b, the two profiles (16) and (17) match fairly well and there is no singularity at r = 0 for the second derivative of the angular velocity (17) or the second derivative of the vortic-ity. Throughout the paper, we use the angular velocity profile given in Eq. (17) to derive analytic expressions for the dispersion relations, which are crucial for understanding the interaction between a convective column and tidally forced inertial waves.
2.2.3 Conditions for the centrifugal instability
Hydrodynamics theories on vortices and their instability have been well established, and they are easily applicable to understand the stability of general convective Taylor columns. In rotating fluids, columnar convective structures are prone to centrifugal instability, which occurs due to an imbalance between the centrifugal acceleration and pressure gradient in the radial direction. The centrifugal instability can be predicted using the Rayleigh’s criterion, which was initially proposed by Rayleigh (1917) for an inviscid rotating flow with angular velocity Ω(r), and was then generalized by Kloosterziel & van Heijst (1991) for rotating flows on the traditional f-plane. The criterion states that an inviscid vortex on the f -plane can become centrifu-gally unstable if there exists a region where the Rayleigh’s discriminant Φ(r) becomes negative, that is,
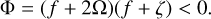 (18)
(18)
The necessary and sufficient conditions for the centrifugal instability were originally derived for axisymmetric perturbations with m = 0 (Synge 1933), but the follow-up study by Billant & Gallaire (2005) extended the criterion for general perturbations with m ≥ 0 by deriving the dispersion relation using the Wentzel–Kramers–Brillouin–Jeffreys (WKBJ) approximation. The Rayleigh’s criterion (18) is also applicable for the centrifugal instability of vortices in rotating and stratified fluids (Park & Billant 2013a) and for the inertial instability of shear flows in rotating and stratified fluids (Arobone & Sarkar 2012; Park et al. 2020).
For the convective column with the angular velocity profile (17), examples of Φ(r) normalized by f2 are shown in Fig. 2c for different values of the ratio Ω0/f. For instance, for Ω0 = −f or Ω0 = 2f, there are regions where Φ(r) becomes negative, and therefore the convective column can become centrifugally unstable to incoming perturbations such as tidal inertial waves. At Ω0 = 0.5f, Φ(r) is always positive for all r and so it is cen-trifugally stable. In this regime, incoming tidal inertial waves will interact with stable vortices and this interaction can promote new radiating waves. This configuration is investigated in detail in Sect. 4.
Figure 3 displays the sign of Φ in the parameter space (r/R0, Ω0/f). We see that there are regions of negative Φ for Ω0 < −0.5 f and Ω0 > 1.81 f. In terms of the global planetary rotation rate Ωp, we can divide the regime of Ω0 into two regimes, as
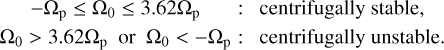 (19)
(19)
 |
Fig. 3 Sign of the Rayleigh discriminant Φ(r) in the parameter space (r/R0, Ω0/f) where black regions indicate Φ < 0 and white regions indicate Φ ≥ 0. Upper and lower dashed lines represent the upper limit (Ω0/f = 1.81) and the lower limit (Ω0/f = −0.5) that bound the cen-trifugally stable region. |
2.3 Linear stability equations
While the regime (19) identifies where the base flow is centrifu-gally stable or unstable, we need to perform the linear stability analysis to quantitatively compute the growth rate of the centrifugal instability. To our knowledge, this is the first time that this analysis is performed in the case of the model ofquasi-geostrophic columnar convective vortex, such that studied here.
In the cylindrical coordinate system presented in Fig. 1 (right panel), we consider perturbations subject to the base velocity U = (0, rΩ(r), 0) and pressure Π as follows:
 (20)
(20)
where ú = (ú, ύ, ẃ) is the velocity perturbation and 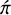 is the normalised pressure perturbation. When these perturbations are infinitesimal, we obtain from Eqs. (6)–(9) the following linearized equations
is the normalised pressure perturbation. When these perturbations are infinitesimal, we obtain from Eqs. (6)–(9) the following linearized equations
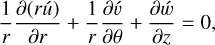 (21)
(21)
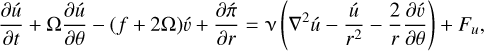 (22)
(22)
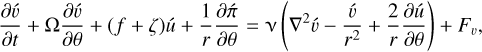 (23)
(23)
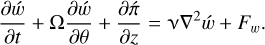 (24)
(24)
First, we examine the intrinsic stability of the convective Taylor column by considering no external tidal forcing (i.e., Fe = 0). This problem is closely related to the case with free waves in a sheared region (Astoul et al. 2021), where the inertial wave enters and perturbs the base shear flow. The response of the base flow to (tidal) inertial waves strongly depends on its stability. Therefore, it is crucial to investigate the stability beforehand to understand the wave–vortex interaction. In the stability analysis, we apply the formulation of the normal mode to perturbations as follows:
![$ \left( {\matrix{ {u'} \cr {\upsilon '} \cr {w'} \cr {\pi '} \cr } } \right) = \left( {\matrix{ {\hat u\left( r \right)} \cr {\hat \upsilon \left( r \right)} \cr {\hat w\left( r \right)} \cr {\hat p\left( r \right)} \cr } } \right)\exp \left[ {{\rm{i}}\left( {{k_z}z + m\theta - \omega t} \right)} \right] + {\rm{c}}{\rm{.c}}{\rm{.,}} $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq30.png) (25)
(25)
where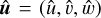 and
and 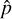 are the mode shapes of velocity and pressure, kz is the vertical wavenumber, m is the azimuthal wavenumber, c.c. denotes the complex conjugate, and ω = ωr + iωi is the complex frequency where the real part ωr denotes the frequency and the imaginary part ωi denotes the temporal growth rate, respectively. The use of the normal mode leads to the following linear stability equations:
are the mode shapes of velocity and pressure, kz is the vertical wavenumber, m is the azimuthal wavenumber, c.c. denotes the complex conjugate, and ω = ωr + iωi is the complex frequency where the real part ωr denotes the frequency and the imaginary part ωi denotes the temporal growth rate, respectively. The use of the normal mode leads to the following linear stability equations:
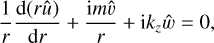 (26)
(26)
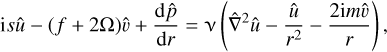 (27)
(27)
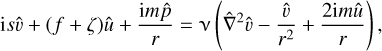 (28)
(28)
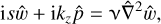 (29)
(29)
where s = −ω + mΩ is the Doppler-shifted frequency and 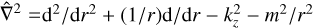 is the Laplacian operator. Due to the symmetry: ω(m, kz) = ω(m, −kz) = −ω*/(−m, −kz), (Park & Billant 2013a) where* denotes the complex conjugate, and we consider hereafter only the non-negative wavenumbers (m ≥ 0 and kz ≥ 0). The linear stability Eqs. (26)–(29) can be solved numerically with the following simplified eigenvalue problem:
is the Laplacian operator. Due to the symmetry: ω(m, kz) = ω(m, −kz) = −ω*/(−m, −kz), (Park & Billant 2013a) where* denotes the complex conjugate, and we consider hereafter only the non-negative wavenumbers (m ≥ 0 and kz ≥ 0). The linear stability Eqs. (26)–(29) can be solved numerically with the following simplified eigenvalue problem:
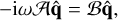 (30)
(30)
where 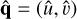 and 𝒜 and ℬ are the operator matrices as
and 𝒜 and ℬ are the operator matrices as
![$ {\cal A} = \left[ {\matrix{ {{{\cal A}_{11}}} & {{{\cal A}_{12}}} \cr {{{\cal A}_{21}}} & {{{\cal A}_{22}}} \cr } } \right],\,\,\,{\cal B}\left[ {\matrix{ {{{\cal B}_{11}}} & {{{\cal B}_{12}}} \cr {{{\cal B}_{21}}} & {{{\cal B}_{22}}} \cr } } \right] $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq40.png) (31)
(31)
where
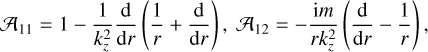 (32)
(32)
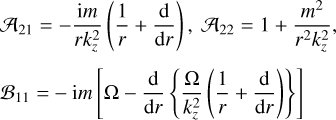 (33)
(33)
![$ \matrix{ {{{\cal B}_{11}} = - {\rm{i}}m\left[ {\left. {{\rm{\Omega }} - {{\rm{d}} \over {k_z^2}}\left( {{1 \over r} + {{\rm{d}} \over {{\rm{d}}r}}} \right)} \right\}} \right]} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\, + v\,\left[ {{{\hat \nabla }^2} - {1 \over {{r^2}}} - {1 \over {k_z^2}}{{\rm{d}} \over {{\rm{d}}r}}\left\{ {{{\hat \nabla }^2}\left( {{1 \over r} + {{\rm{d}} \over {{\rm{d}}r}}} \right)} \right\}} \right],} \hfill \cr } $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq43.png) (34)
(34)
![$ {{\cal B}_{12}} = \left( {f + 2{\rm{\Omega }}} \right) - {{{m^2}} \over {k_z^2}}{{\rm{d}} \over {{\rm{d}}r}}\left( {{{\rm{\Omega }} \over r}} \right) - {\rm{i}}m\nu \left[ {{2 \over {{r^2}}} + {1 \over {k_z^2}}{{\rm{d}} \over {{\rm{d}}r}}\left\{ {{{\hat \nabla }^2}\left( {{1 \over r}} \right)} \right\}} \right], $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq44.png) (35)
(35)
![$ {{\cal B}_{21}} = - \left( {f + \zeta } \right) - {{{m^2}} \over {rk_z^2}}\left( {{1 \over r} + {{\rm{d}} \over {{\rm{d}}r}}} \right) + {{{\rm{i}}mv} \over r}\left[ {{2 \over 1} - {1 \over {k_z^2}}{{\hat \nabla }^2}\left( {{1 \over r} + {{\rm{d}} \over {{\rm{d}}r}}} \right)} \right], $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq45.png) (36)
(36)
![$ {{\cal B}_{22}} = - {\rm{i}}mv{\rm{\Omega }}\left( {1 + {{{m^2}} \over {{r^2}k_z^2}}} \right) + v\left[ {{{\hat \nabla }^2} - {1 \over {{r^2}}} + {{{m^2}} \over {rk_z^2}}{{\hat \nabla }^2}\left( {{1 \over r}} \right)} \right]. $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq46.png) (37)
(37)
In this eigenvalue problem, we use the Chebyshev spectral method for a discretization with collocation points in the radial direction (Antkowiak 2005; Park 2012) to obtain a complete eigenvalue spectrum from the eigenvalue problem (30).
In the inviscid limit v = 0, Eqs. (26)–(29) can be further simplified into a single second-order ordinary differential equation for û :
![$ \matrix{ {{{{{\rm{d}}^{\rm{2}}}\hat u} \over {{\rm{d}}{r^2}}} + \left( {{1 \over r} - {{Q'} \over Q}} \right){{{\rm{d}}\hat u} \over {{\rm{d}}r}}} \hfill \cr {\,\,\,\,\,\,\,\,\, + \left[ { - k_z^k{\rm{\Delta }} - {{{m^2}} \over {{r^2}}} - {{mrQ} \over s}{{\left( {{{f + \zeta } \over {{r^2}Q}}} \right)}^\prime } + Q{{\left( {{1 \over {rQ}}} \right)}^\prime }} \right]\hat u = 0,} \hfill \cr } $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq47.png) (38)
(38)
where prime denotes the radial derivative, and Q and Δ are the functions defined as
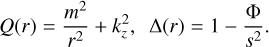 (39)
(39)
In solving the second-order ODE (38), we consider the boundary conditions in the two limits r → ∞ and r → 0 with analytic asymptotic solutions. For instance, we can find an asymptotic solution for (38) in the limit r → ∞ as
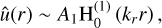 (40)
(40)
where A1 is the constant amplitude, 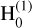 is the Hankel function of the first kind, and kr is the radial wavenumber of the solution in the far field defined as
is the Hankel function of the first kind, and kr is the radial wavenumber of the solution in the far field defined as
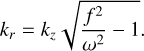 (41)
(41)
The solution (40) in the limit r → ∞ behaves asymptotically as an inertial wave solution with an exponential decay if |f | > |ω|, while the solution is evanescent if |f| < |ω|. For the solution around the center r = 0, we apply the Taylor expansion on (26)–(29) to have the following asymptotic solutions:
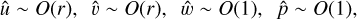 (42)
(42)
if |m| ≥ 1 (see also, Saffman 1992).
3 Stability of the convective column
In this section, we focus on analyzing the stability of the convective column model (17), which is prone to centrifugal instability. The stability analysis is the first step toward understanding how a convective Taylor column responds to external perturbations. Using numerical and asymptotic methods, we compute the dispersion relation (i.e., the expression of the growth rate and frequency in terms of the wavenumbers) of the modes of the convective column. Such analyses can identify the most unstable mode – which is most likely to be observed in the interaction process between the convective column and inertial waves – and its characteristic temporal and length scales. In this section, we consider the inviscid case where v = 0. This allows us to perform an asymptotic analysis with the WKBJ method for the centrifugal instability in the large-kz limit. Here, we present the stability analysis results for our convective column model and the asymptotic expressions of the dispersion relations for neutral and unstable modes. The details of the WKBJ method are presented in Appendix A. We also note that the viscosity stabilizes modes of the convective column, but the dynamics of unstable or stable modes are not expected to change significantly in the presence of the viscosity, which is weak in the interiors of stars and giant planets. The linear evolution of neutral or unstable modes is discussed below.
 |
Fig. 4 Eigenvalue spectra for an unstable case at Ω0/f = 3 and kzR0 = 10 for (a) m = 0, (b) m = 1, and (c) m = 2. Different numbers of the Chebyshev collocation points Ncheb are tested for convergence. |
3.1 Results of the linear stability analysis
Figure 4 displays spectra of the eigenvalues ω = ωr + 1ωi at Ω0/f = 3 and kzRo = 10 for various azimuthal wavenumbers m. The m = {0, 1, 2} modes correspond to the eccentricity, obliquity, and asynchronous tides, respectively. It is particularly interesting to see how dynamical tides with m > 0 can potentially destabilize a convective column leading to turbulence and dissipation. For the axisymmetric case (m = 0), eigenvalues are symmetrically distributed with respect to the origin and we have neutral modes with the zero growth rate (i.e., ωi = 0) in the frequency range |ωr/f < 6, and both stable and unstable modes with the zero frequency (i.e., ωr = 0) in the growth-rate range |ωi/f| < 1. These eigenvalues are numerically well converged at a relatively low resolution Ncheb = 100. In Fig. 4b, we see that eigenvalues for m = 1 are no longer symmetric with respect to the line ωr = 0 and we have neutral modes in the frequency range −4 < ωr/f < 8.5 and both stable and unstable modes in the growth-rate range |ωr/f| < 0.85 with a nonzero frequency ωr/ f ≠ 0. While some of these modes are well converged at a resolution of Ncheb ≥ 200, some modes with a nonzero growth rate in the frequency range −0.2 < ωr/f < 0.8 are not well converged even at a high resolution Ncheb = 400. We verified that these unconverged modes possess singular points (e.g., the critical layers at which the incident wave exchanges its angular momentum with the convective column) and much higher resolutions are required to resolve these modes correctly (see also the numerical treatment by Astoul et al. 2021). In this paper, we do not investigate the dynamics of these singular modes but focus on converged modes that have a high frequency or growth rate. The spectral characteristics for m = 2 shown in Fig. 4c are similar to those for m = 1, but we only observed two unstable modes that are numerically converged at Ncheb = 400. For the parameters Ω0/f = 3 and kzR0 = 10 considered in Fig. 4, we find that the growth rate of the most unstable mode decreases with m and no unstable mode is observed after m > 3.
Figure 5 displays the mode shape û(r) of the most unstable modes and the first neutral modes with the highest frequency for various azimuthal wavenumbers m, which are picked up in the eigenvalue spectra in Fig. 4. We also plot the gray-shaded area to demonstrate where the Rayleigh discriminant Φ(r) is negative. The unstable modes have an oscillatory shape inside the region Φ < 0, while they are evanescent such that they increase exponentially from r = 0 and decrease exponentially as r → ∞. It is also found that the number of zero crossings for the unstable modes increases with m. The neutral modes, on the other hand, have different features; for instance, they have a peak around r ≃ 0.5 below the region Φ < 0 and decrease exponentially as r → ∞. From these solution behaviors, we can expect that the wavelike behavior is observed in the region Φ < 0 when it is centrifugally unstable. According to the definition by Le Dizès & Lacaze (2005), a mode that has a wavelike behavior far from the core r = 0 is called the ring mode, while a mode with the wavelike behavior around r = 0 is called the core mode. Therefore, we can distinguish that the unstable modes in Fig. 5a are the ring mode while the neutral modes in Fig. 5b are the core mode.
Figure 6 shows how eigenvalues change with the vertical wavenumber kz for neutral and unstable modes at Ω0/f = 3. For the neutral modes, there are countless branches depending on the number of zero-crossings, but we only display the first four upper branches in Figs. 6a,b that have the highest frequencies and the four lower branches with the lowest frequencies. In Fig. 6a, we see that the frequency of the upper branches begins at ωr = mΩ0 at kz = 0, and increases with kz and reaches an asymptote as kz → ∞. The asymptotic behaviors in the limit kz → ∞ can be understood by applying the Wentzel–Krammers– Brillouin–Jeffreys (WKBJ) approximation (Fröman & Fröman 1965). Referring the readers to Appendix for detailed technical details of the intermediate steps, here we provide the final analytic expressions of the dispersion relation for neutral and unstable modes obtained using the WKBJ approximation. For upper branches, we find the expressions of the dispersion relation for the neutral modes in the form of the Taylor expansion with 1 /kz as
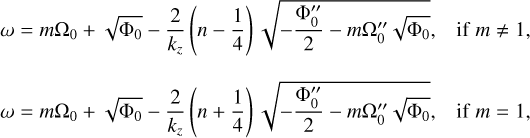 (44)
(44)
where n denotes the branch number and the subscript 0 implies that the variables are evaluated at r = 0. We see good agreement between the numerical results and asymptotic predictions on the frequency of the upper branches, especially as kz → 0. The frequency of the lower branches, on the other hand, decreases as kz increases and reaches an asymptote as kz → ∞. From the WKBJ analysis, we find the analytical expressions of the dispersion relation for the lower branches as
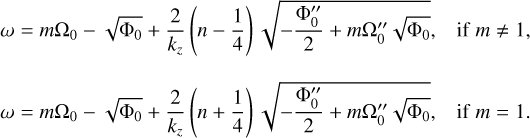 (45)
(45)
Good agreement is also obtained between the numerical and asymptotic results for the lower branches, as shown in Fig. 6b.
In Figs. 6c,d, we plot the frequency ωr and growth rate ωi of the most unstable mode versus kz. The axisymmetric mode (m = 0) has zero frequency and its growth rate ωi increases with kz. The frequency and growth rate of nonaxisymmetric modes (m ≥ 1 ) increase with kz and approach their asymptotes as kz → ∞. From the WKBJ analysis, we find the following Taylor expansion of the complex frequency ω:
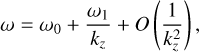 (46)
(46)
and r0 is a double turning point where the radial derivative of 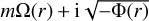 becomes zero (for more details, see Appendix and Billant & Gallaire 2005). It is clearly shown in Figs. 6c,d that the numerical and asymptotic results are in good agreement. We verified numerically that there is no longer instability for higher azimuthal wavenumber m ≥ 3 for the convective column with the angular velocity profile given in Eq. (17). Furthermore, we find an instability at kz = 0 only for m = 2. This zero-vertical-wavenumber instability is reminiscent of the vortex shear instability reported for other vortex profiles (see e.g., Billant & Gallaire 2005).
becomes zero (for more details, see Appendix and Billant & Gallaire 2005). It is clearly shown in Figs. 6c,d that the numerical and asymptotic results are in good agreement. We verified numerically that there is no longer instability for higher azimuthal wavenumber m ≥ 3 for the convective column with the angular velocity profile given in Eq. (17). Furthermore, we find an instability at kz = 0 only for m = 2. This zero-vertical-wavenumber instability is reminiscent of the vortex shear instability reported for other vortex profiles (see e.g., Billant & Gallaire 2005).
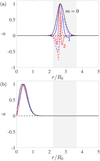 |
Fig. 5 Real (solid) and imaginary (dashed) parts of (a) the most unstable mode and (b) the first neutral mode with the highest frequency at Ω0/f = 3 and kzR0 = 10 for different azimuthal wavenumbers: m = 0 (black), m = 1 (blue), and m = 2 (red). The gray-shaded region shows where the Rayleigh discriminant Φ is negative. |
 |
Fig. 6 Frequency ωr as a function of the vertical wavenumber kz of the neutral modes for the four upper branches (panel a) and the four lower branches (panel b) at Ω0/f = 3 for m = 0 (black), m = 1 (blue), and m = 2 (red). Frequency ωr (panel c) and growth rate ωi (panel d), respectively, versus vertical wavenumber kz for the most unstable mode at Ω0/f = 3 for m = 0 (black), m = 1 (blue), and m = 2 (red). For all panels, solid lines are numerical results and dashed lines denote the WKBJ predictions for panel a: Eq. (44), panel b: Eq. (45) for m = 0, 1 (core mode) and (A.22) for m = 2 (ring mode), and panels c and d: Eq. (46). |
 |
Fig. 7 Spatiotemporal diagrams in the space (r, t) for inertial waves entering from r/R0 = 20 at the forcing frequency ωf = 0.3, m = 1, kzR0 = 5, ν = 0 for an unstable column with Ω0/f = 3 (panel a) and a stable column with Ω0/f = 0.5 (panel b). Panel c displays the time evolution of wave energy E(t) for the unstable case (a, black solid line) and stable case (b, black dashed line). The blue line denotes the energy growth C exp(2ωit) with a constant C chosen for comparison with the unstable case. |
3.2 Linear evolution of unstable modes
In addition to the stability analysis, we also investigate how inertial waves entering from the far field interact with a convective column. To understand the interaction, the first step is to perform linear simulations with a tidally forced inertial wave incoming from the far field. Considering the cylindrical coordinates, the mathematical formulation is similar to that of the stability analysis when the following ansatz is considered:
![$ \left( {\matrix{ {u'} \cr {\upsilon '} \cr {w'} \cr {\pi '} \cr } } \right) = \left( {\matrix{ {\tilde u\left( {r,t} \right)} \cr {\tilde \upsilon \left( {r,t} \right)} \cr {\tilde w\left( {r,t} \right)} \cr {\tilde p\left( {r,t} \right)} \cr } } \right)\exp \left[ {{\rm{i}}\left( {{k_z}z + m\theta } \right)} \right] + {\rm{c}}{\rm{.c}}{\rm{.,}} $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq60.png) (49)
(49)
where 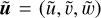 and
and  are the time-dependent mode shapes of velocity and normalised pressure. Applying the ansatz (49) to Eqs. (21)–(24) leads to the following linear time-evolution equation
are the time-dependent mode shapes of velocity and normalised pressure. Applying the ansatz (49) to Eqs. (21)–(24) leads to the following linear time-evolution equation
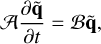 (50)
(50)
where 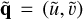 and 𝒜 and ℬ are the same operator matrices as in the eigenvalue problem (30). To impose the boundary conditions around the center r = 0, we consider the conditions (42)–(43) and use the proper differentiation matrices to match the boundary conditions (for details, we refer to Antkowiak 2005). To impose the boundary conditions in the far field, we consider the time-periodic solution as
and 𝒜 and ℬ are the same operator matrices as in the eigenvalue problem (30). To impose the boundary conditions around the center r = 0, we consider the conditions (42)–(43) and use the proper differentiation matrices to match the boundary conditions (for details, we refer to Antkowiak 2005). To impose the boundary conditions in the far field, we consider the time-periodic solution as
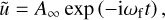 (51)
(51)
where A∞ is the constant amplitude and wf is the forcing frequency. For the time-marching of Eq. (50), we use the implicit Euler method. While the stability analysis uses the Chebyshev spectral method for discretization in the radial direction r to facilitate the imposition of boundary conditions (Park 2012), we use the 4th-order finite difference method for the radial discretization to have a uniform spacing. This allows us to have more collocation points in the far field and thus we can properly resolve the incoming inertial waves.
Panels a and b of Fig. 7 display the spatiotemporal diagrams of the real part of the radial velocity Re [ũr(r, t)] as the inertial wave is forced at r = 20R0 with the amplitude = 10−6, frequency wf = 0.3f, wavenumbers (kzRo, m) = (5, 1) for two base flows: unstable and stable convective columns with Ω0 = 3f and Ω0 = 0.5f, respectively. On the one hand, the unstable case in Fig. 7a shows that the tidally forced wave propagates inwards in the radial direction. This incoming cylindrical wave has a characteristic whereby the front has a longer wavelength and a smaller amplitude than the rear part. Although the front of the wave has a very small amplitude, it can still trigger the most unstable mode, which grows the fastest in time. If the nonlinearity is taken into account in this unstable case, a strong interaction with the convective column can be induced and turbulence can be triggered as a consequence. On the other hand, we see in Fig. 7b for the stable case that the tidally forced inertial wave propagates inwards but there is no sign of the strong interaction between the wave and the convective column. At a much later time ft > 140, we verified that indeed no unstable mode is triggered for the stable case.
To quantify the difference between the two regimes, we define the energy of perturbations:
![$ E\left( t \right) = \int_0^\infty {\left[ {{{\left| {{{\tilde u}_r}} \right|}^2} + {{\left| {{{\tilde u}_\theta }} \right|}^2} + {{\left| {{{\tilde u}_z}} \right|}^2}} \right]r{\rm{d}}r.} $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq66.png) (52)
(52)
Figure 7c clearly shows that the perturbation energy for the unstable case increases significantly after ft > 120 and grows exponentially in time, while the energy for the tidal inertial wave interacting with the stable convective column does not increase significantly in time. We find that the sudden increase in the perturbation energy for the unstable case corresponds to the emergence of the most unstable mode with the growth rate wi,max This is verified by comparing the slope of the two curves: the unstable perturbation growth shown with a black solid line and the exponential growth exp(2wi,max)t of the most unstable mode shown as a blue line. In comparing these two cases, we must consider the exponent 2wi,max, which can be easily obtained by putting ũr(r, t) = ûr exp(−iωt) into the energy Eq. (52). It is not shown here but we also verified that a similar appearance of the unstable mode occurs when the incoming inertial waves with different forcing frequencies are considered for unstable convective columns.
These results are coherent with what is expected from the stability analysis. Once the instability occurs and triggers turbulence, the vortex will be destroyed and turbulent dissipation will follow as a consequence (see e.g., the work by Pizzi et al. 2022, for the case of the precession instability-driven turbulence). It is important here to underline that the trigger of unstable modes is not necessarily from tidal inertial waves but any low-amplitude noise is likely to cause the instability leading to turbulence. Especially for the case where the tidal period scaled as |ωf|−1 is larger than the characteristic time of the instability scaled as |ωf|−1 (i.e., the case where |ωf| < |ωi|), one can expect the instability to develop quickly before the incoming tidal wave starts to interact with the vortex, and therefore other types of low-amplitude perturbations would be the main trigger of the vortex instability. A more important configuration is the one where tidal inertial waves interact with stable convective vortices such as the numerous ones observed for instance at the surface of giant planets. Whether or not stable vortices would interact with the tidal waves is less well understood. The current case only considers cylindrical inertial waves propagating in the radial direction. However, we must also study the general case where a large-scale stable vortex in planets or stars interacts with an incoming tidally forced wave that goes through the center of the vortex as depicted in Fig. 1 (left panel). To understand this regime, in the following section we examine the interaction between a stable vortex and a tidal inertial wave in the Cartesian coordinate system.
4 Interaction between a planar inertial wave and a stable convective column
In the previous section, we examine the interaction between the convective vortex and inertial wave, both of which are of a cylindrical nature. A problem that draws more attention from astrophysicists working on tidal interaction and inertial-wave propagation (see e.g., André et al. 2017, 2019) is how the tidally forced inertial wave interacts with complex fluid flow structures. In the case of convective vortices, this motivates us to consider inertial waves propagating in a plane and going through the vortex as described in Fig. 1 (left panel). To investigate this, we formulate the problem in the Cartesian coordinate system and conduct two-dimensional linear simulations. This allows us to examine the vortex interaction with any incoming tidal waves, and we are not necessarily restricted to the 1D cylindrical waves as in the previous section. A similar configuration was considered by Mclntyre (2019) who analytically examined the wave-vortex interaction by considering a vortex, which has an irrotational velocity field outside the vortex core, and a wave traveling through the vortex center.
We reformulate the base flow by considering the base velocity in the Cartesian coordinates as U = (Ux, Uy, 0) where Ux(x, y) = rΩ sin θ = −Ωy and Uy(x, y) = rΩ cos θ = Ωx are the base velocity in the x- and y-directions, respectively. Subject to this base flow, we obtain the linearized equations for perturbation velocity ú = (úx, úy, ẃ) and pressure 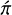 as follows:
as follows:
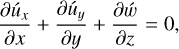 (53)
(53)
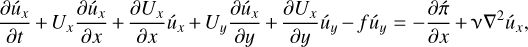 (54)
(54)
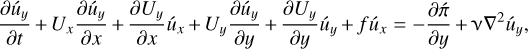 (55)
(55)
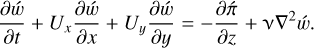 (56)
(56)
As the base flow U(x, y) is homogeneous only in the z-direction, we consider the following ansatz for the perturbation in Cartesian coordinates:
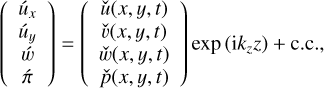 (57)
(57)
where 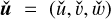 and
and 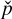 are the two-dimensional time-dependent mode shapes of velocity and normalised pressure, respectively. Applying the ansatz (57) to the linearized Eqs. (53)–(56) leads to the following equations:
are the two-dimensional time-dependent mode shapes of velocity and normalised pressure, respectively. Applying the ansatz (57) to the linearized Eqs. (53)–(56) leads to the following equations:
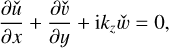 (58)
(58)
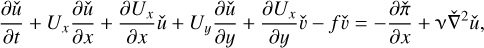 (59)
(59)
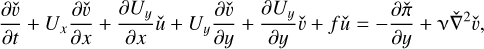 (60)
(60)
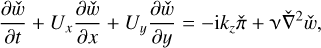 (61)
(61)
where 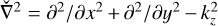 . In an operator form, the above equations can be expressed as
. In an operator form, the above equations can be expressed as
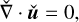 (62)
(62)
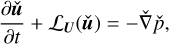 (63)
(63)
where ℒU denotes the linear operator applied to ǔ.
To solve the two-dimensional linearized perturbation Eqs. (58)–(61) and compute 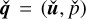 using numerical simulations, we use the fractional-step method for time marching and the Fourier spectral method for spatial discretization in the x– and y– coordinates to impose periodic boundary conditions. In the simulations, we consider the initial condition in which an inertial wave is propagating in the horizontal direction x by imposing ky = 0 (see e.g. Fig. 8 upper left panel). There is no loss of generality in considering the inertial wave with ky = 0 as convective columns have a cylindrical geometry.
using numerical simulations, we use the fractional-step method for time marching and the Fourier spectral method for spatial discretization in the x– and y– coordinates to impose periodic boundary conditions. In the simulations, we consider the initial condition in which an inertial wave is propagating in the horizontal direction x by imposing ky = 0 (see e.g. Fig. 8 upper left panel). There is no loss of generality in considering the inertial wave with ky = 0 as convective columns have a cylindrical geometry.
The inertial-wave solution 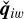 can be obtained by considering the zero base flow U = 0 in the Eqs. (58)–(61) leading to the following equations:
can be obtained by considering the zero base flow U = 0 in the Eqs. (58)–(61) leading to the following equations:
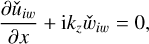 (64)
(64)
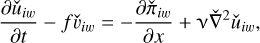 (65)
(65)
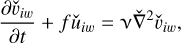 (66)
(66)
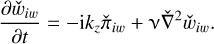 (67)
(67)
By considering the ansatz
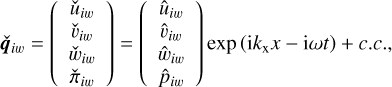 (68)
(68)
we obtain the following dispersion relation for the inertial wave:
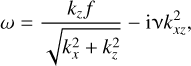 (69)
(69)
where 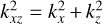 , and the corresponding polarization relations as follows:
, and the corresponding polarization relations as follows:
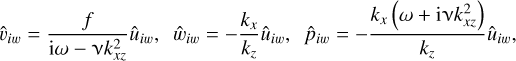 (70)
(70)
which are the classical solutions for viscous inertial waves when ky = 0. We note that the above inertial-wave solution 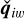 is not a stationary solution of the Eqs. (58)–(61) as U ≠ 0 in the equations, and therefore the perturbation
is not a stationary solution of the Eqs. (58)–(61) as U ≠ 0 in the equations, and therefore the perturbation  evolves in time as it interacts with the convective vortex.
evolves in time as it interacts with the convective vortex.
Figure 8 shows an example of the temporal evolution of perturbation interacting with a stable convective column at Ω0/f= 1 . For indication of the vortex center, we use dashed lines to mark a radius r = 3.16R0 at which the first zero-crossing of the angular velocity (i.e., Ω(r) = 0) occurs. As the simulations consider linear equations, the wave–vortex interaction is one way, that is, inertial waves are affected by convective columns but not vice versa. We clearly see that the perturbation velocity ft of the inertial wave is mixed by the vortex in the early stages of the simulation.The mixing of momentum at this stage is likely due to the advection term 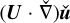 as the perturbation is advected by the rotating base flow. This mixing process by advection is similar to sweeping (e.g., Clark di Leoni et al. 2014; Campagne et al. 2015), which occurs when the waves are advected by large-scale flows. However, we note that there is a difference from the sweeping process, in that the wave-vortex interaction creates the low-velocity ring region around the vortex core as the mixing continues. Inside the ring region, a confined perturbation with an azimuthal wavenumber m = 1 appears as a result of the interaction. More interestingly, in the far field away from the vortex core, the interaction promotes radiation of a progressive wave. Although we impose the inertial wave in a planar, Cartesian way, it is noteworthy that the new radiating progressive wave is of a cylindrical nature. These dynamical behaviors, namely mixing and radiation of a wavelike mode, are also observed for other wavenumber sets when either a long-wavelength, fast-moving wave (e.g., kzR0 = 1, kxR0 = 0.25 and phase speed cx = Re(w/(f kxR0)) = 3.88) or a short-wavelength, slow-moving wave (e.g., kzR0 = 1, kxR0 = 2, cx = 0.22) interact with stable convective columns. We also note that such a new radiating wave is not observed for the cases with 1D cylindrical incoming waves studied in Sect. 3. These waves cannot penetrate the vortex center r = 0 due to the boundary conditions (A.9) while the 2D planar incoming waves are not restricted by any boundary conditions and overlap the vortex core, a situation where a wave scattering (Stone 2000) similar to what we see in Fig. 8 or a wave-induced mean force (McIntyre 2019) can be generated.
as the perturbation is advected by the rotating base flow. This mixing process by advection is similar to sweeping (e.g., Clark di Leoni et al. 2014; Campagne et al. 2015), which occurs when the waves are advected by large-scale flows. However, we note that there is a difference from the sweeping process, in that the wave-vortex interaction creates the low-velocity ring region around the vortex core as the mixing continues. Inside the ring region, a confined perturbation with an azimuthal wavenumber m = 1 appears as a result of the interaction. More interestingly, in the far field away from the vortex core, the interaction promotes radiation of a progressive wave. Although we impose the inertial wave in a planar, Cartesian way, it is noteworthy that the new radiating progressive wave is of a cylindrical nature. These dynamical behaviors, namely mixing and radiation of a wavelike mode, are also observed for other wavenumber sets when either a long-wavelength, fast-moving wave (e.g., kzR0 = 1, kxR0 = 0.25 and phase speed cx = Re(w/(f kxR0)) = 3.88) or a short-wavelength, slow-moving wave (e.g., kzR0 = 1, kxR0 = 2, cx = 0.22) interact with stable convective columns. We also note that such a new radiating wave is not observed for the cases with 1D cylindrical incoming waves studied in Sect. 3. These waves cannot penetrate the vortex center r = 0 due to the boundary conditions (A.9) while the 2D planar incoming waves are not restricted by any boundary conditions and overlap the vortex core, a situation where a wave scattering (Stone 2000) similar to what we see in Fig. 8 or a wave-induced mean force (McIntyre 2019) can be generated.
The appearance of this radiating mode is also well captured in spatiotemporal diagrams computed by extracting the velocity component ǔ at x = 0 as shown in Fig. 9. For the case in panel (a) with (kxR0, kzR0) = (0.25, 1), where the inertial wave has a long wavelength in the x-direction and fast phase speed cx = 3.88, we clearly see the low-velocity ring region around y/R0 ≃ ±2.7 and the structure of the radiating mode, that is, a perturbation confined within the low-velocity ring region and a radiating progressive wave in the far field. For the case in panel (b), with a larger kxR0 = 1 (the same case in Fig. 8), the interference between the imposed inertial wave and new radiating mode is more apparent. The shape of the perturbation inside the ring region is also more irregular and it seems that the perturbation has a higher azimuthal wavenumber than the mode in panel (a). A similar tendency, that is, strong mixing and radiation, is observed as kx is further increased to kxR0 = 2 as shown in Fig. 9c.
The generation mechanism of radiating modes (denoted by the subscript «rm» in the following) can be understood mathematically by considering another perturbation, 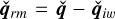 , which satisfies the following equations:
, which satisfies the following equations:
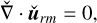 (71)
(71)
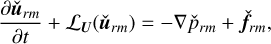 (72)
(72)
where 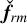 is the forcing term induced by the interaction between the convective column and inertial wave as
is the forcing term induced by the interaction between the convective column and inertial wave as
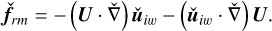 (73)
(73)
These equations are obtained by substituting 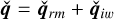 into the linearized perturbation equations (58)–(61) and subtracting the inertial-wave Eqs. (64)–(67). The interaction term
into the linearized perturbation equations (58)–(61) and subtracting the inertial-wave Eqs. (64)–(67). The interaction term 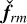 forces the linear system (yf72) with a characteristic frequency ω from the dispersion relation of the incoming inertial wave (69). A stable convective column has neutral or stable modes with frequencies close to ω, and therefore the forcing can trigger these modes by resonance and new radiating modes appear as the sum of these modes due to the forcing
forces the linear system (yf72) with a characteristic frequency ω from the dispersion relation of the incoming inertial wave (69). A stable convective column has neutral or stable modes with frequencies close to ω, and therefore the forcing can trigger these modes by resonance and new radiating modes appear as the sum of these modes due to the forcing 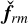 triggered by the vortex-wave interaction. An example of a radiating mode forced by this interaction is displayed in Fig. 10a, which clearly shows the structure of cylindrical radiation. If we apply the 2D Fourier transform to the velocity field ǔ(x, y, t) in the spatial directions x and y at a given time t, we can obtain, as shown in Fig. 10b, the wave amplitude ûrm(kx, ky, t) in the wavenumber space (kx, ky) where
triggered by the vortex-wave interaction. An example of a radiating mode forced by this interaction is displayed in Fig. 10a, which clearly shows the structure of cylindrical radiation. If we apply the 2D Fourier transform to the velocity field ǔ(x, y, t) in the spatial directions x and y at a given time t, we can obtain, as shown in Fig. 10b, the wave amplitude ûrm(kx, ky, t) in the wavenumber space (kx, ky) where
![$ {\hat u_{rm}}\left( {{k_x},{k_y},t} \right) = \int_{ - \infty }^\infty {\int_{ - \infty }^\infty {{{\hat u}_{rm}}\left( {x,y,t} \right)\exp \left[ { - {\rm{i}}\left( {{k_x}x + {k_y}y} \right)} \right]{\rm{d}}x{\rm{d}}y} } . $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq105.png) (74)
(74)
The largest amplitude is obtained at (kxRo, kyRo) = (1, 0), which corresponds to the wavenumber set of the initially imposed inertial wave. We note that other wavenumber components also have amplitudes comparable to this largest one, especially around the circle (kxRo)2 + (kyRo)2 = 1 where most of the energy of the radiating mode appears to lie. This implies that the inertial wave-vortex interaction leads to the energy transfer from the Cartesian wavenumber components kx and ky into the cylindrical wavenumber component 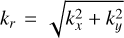 The nature of the planar wave therefore becomes cylindrical as a consequence. In Fig. 10c, we also plot the frequency spectrum
The nature of the planar wave therefore becomes cylindrical as a consequence. In Fig. 10c, we also plot the frequency spectrum 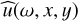 for the points at x = 0 with different y by applying the Fourier transform to ǔ as
for the points at x = 0 with different y by applying the Fourier transform to ǔ as
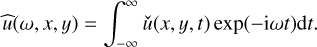 (75)
(75)
We clearly see that the frequency spectra reach their maximum peaks around the frequency 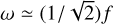 , which corresponds to the real part of the inertial-wave frequency wiw from Eq. (69). This confirms our above statement that the inertial wave triggers stable vortex modes with frequencies close to wiw and the radiating mode appears as the sum of these modes.
, which corresponds to the real part of the inertial-wave frequency wiw from Eq. (69). This confirms our above statement that the inertial wave triggers stable vortex modes with frequencies close to wiw and the radiating mode appears as the sum of these modes.
It is not shown here but we also verified the excitation of radiating modes by an interaction between inertial waves and unstable convective columns. However, for unstable con-vective columns, their most unstable modes eventually become dominant as observed in the previous section on the interaction between unstable convective columns and cylindrical, tidally forced incoming waves and they lead to the destruction of the vortex.
By multiplying the Eq. (72) with 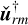 (where † denotes the complex conjugate) and averaging it over the domain where x ϵ [−Lx, Lx] and y ϵ [−Ly, Ly], we obtain the following equation for the perturbation energy of a radiating mode:
(where † denotes the complex conjugate) and averaging it over the domain where x ϵ [−Lx, Lx] and y ϵ [−Ly, Ly], we obtain the following equation for the perturbation energy of a radiating mode:
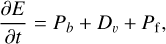 (76)
(76)
where E is the perturbation kinetic energy of the radiating mode, Pb is the energy contribution from the direct interaction between the convective column and the mode, Dv denotes the energy loss by viscous dissipation, and Pf is the energy production by the forcing induced by the interaction between the convec-tive column and the inertial wave, all of which are defined as follows:
![$\matrix{ {E = {1 \over 2}\int_{ - {L_x}}^{{L_x}} {\int_{ - {L_y}}^{{L_y}} {\left( {{{\left| {{{\hat u}_{rm}}} \right|}^2} + {{\left| {{{\hat \upsilon }_{rm}}} \right|}^2} + {{\left| {{{\hat w}_{rm}}} \right|}^2}} \right){\rm{d}}y{\rm{d}}x,} } } \hfill \cr {{P_b} = - \int_{ - {L_x}}^{{L_x}} {\int_{ - {L_y}}^{{L_y}} {\left( {{{\partial {U_x}} \over {\partial x}}{{\left| {{{\hat u}_{rm}}} \right|}^2} + {{\partial {U_x}} \over {\partial y}}\hat u_{rm}^\dag {{\hat u}_{rm}}} \right.} } } \hfill \cr {\left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {{\partial {U_y}} \over {\partial y}}{{\left| {{{\hat \upsilon }_{rm}}} \right|}^2}} \right){\rm{d}}y{\rm{d}}x,} \hfill \cr {{D_\upsilon } = - \nu \int_{ - {L_x}}^{{L_x}} {\int_{ - {L_y}}^{{L_y}} {\left[ {{{\left| {{{\partial {{\hat u}_{rm}}} \over {\partial x}}} \right|}^2} + {{\left| {{{\partial {{\hat u}_{rm}}} \over {\partial y}}} \right|}^2} + {{\left| {{{\partial {{\hat \upsilon }_{rm}}} \over {\partial x}}} \right|}^2} + {{\left| {{{\partial {{\hat \upsilon }_{rm}}} \over {\partial y}}} \right|}^2}} \right.} } } \hfill \cr {\left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {{\left| {{{\partial {{\hat w}_{rm}}} \over {\partial x}}} \right|}^2} + {{\left| {{{\partial {{\hat w}_{rm}}} \over {\partial y}}} \right|}^2} + k_z^2\left( {{{\left| {{{\hat u}_{rm}}} \right|}^2} + {{\left| {{{\hat \upsilon }_{rm}}} \right|}^2} + {{\left| {{{\hat w}_{rm}}} \right|}^2}} \right)} \right]{\rm{d}}y{\rm{d}}x,} \hfill \cr {{P_{\rm{f}}} = - \int_{ - {L_x}}^{{L_x}} {\int_{ - {L_y}}^{{L_y}} {{\bf{\hat u}}_{rm}^\dag } \cdot \left[ {\left( {{\bf{U}} \cdot \hat \nabla } \right){\bf{\hat u}}{ & _{iw}} + \left( {{{{\bf{\hat u}}}_{iw}} \cdot \hat \nabla } \right){\bf{U}}} \right]} \,\,{\rm{d}}y{\rm{d}}x.} \hfill \cr }$](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq112.png) (77)
(77)
Figure 11 shows examples of how perturbation energies of different radiating modes change over time. Panel a shows the kinetic energy E normalized by Eiw (0), the kinetic energy of the inertial wave Eiw at t = 0, for comparison between cases with different wavenumbers kx and kz. This normalization allows us a quantitative comparison among different inertial waves by considering the same wave energy as an input. For the cases at kz = 1, we find that the energy of new radiating modes increases largely as a result of the wave–vortex interaction when the imposed iner-tial waves have the wavenumber kxR0 ~ O(1), the case where the wavelength scale is of the same order as the vortex radius R0. These new radiating modes achieve more than 20% of the input inertial–wave energy. The number is non-negligible and therefore highlights the importance of the role of inertial wave– vortex interaction in creating potential extra turbulent dissipation in fast-rotating planets or stars. It is also noteworthy that the new radiating modes gain less energy if the imposed inertial waves have a longer wavelength (e.g., kxR0 = 0.125) or a shorter wavelength (e.g., kxR0 = 10) than the vortex length scale R0. For the case with (kxR0, kzR0) = (1, 1), we plot different energy-rate contributions in panel (b), namely Pb, Dv, and Pf, and we compare with the time rate of perturbation energy ∂E/∂t.
As expected, the viscous dissipation Dv is always negative. Therefore, it contributes to the decrease in E. However, its magnitude is small compared to other contribution terms. The term Pb indicating the transfer of momentum between the radiating mode and the convective column is oscillatory around zero. The term Pf, on the other hand, is always positive for the case with kxR0 = 1 , and therefore the main contribution to the perturbation energy production comes from Pf, the energy injection by the forcing induced by the inertial wave–vortex interaction. It is not shown here but we also verified that the forcing term Pf is the main source of energy of the new radiating mode for other cases with different wavenumbers.
In summary, we verified that the interaction between stable convective columns and planar incoming inertial waves promotes the mixing of momentum around the vortex centre, creates low–velocity ring regions, and triggers a new wave-like perturbation radiating in the far field with a frequency close to the characteristic frequency of the primary inertial wave. The energy of this secondary radiating mode is sourced mainly from the inertial wave–vortex interaction and the amount of energy from the perturbation is a non-negligible fraction of the input iner-tial wave energy, especially when the length scale of the inertial wave is comparable to that of the vortex radius. This implies that the convective column can act as an additional source of energy to create more efficient turbulent dissipation by generating the secondary radiating mode.
 |
Fig. 8 Time evolution of the perturbation velocity ŭ(x, y) illustrating the interaction between an inertial wave with (kxR0, kzR0) = (1, 1) and a stable vortex with Ω0/f = 1 at |
 |
Fig. 9. Spatiotemporal diagrams of ǔ in the space (t, y) extracted at x = 0 for the wavenumber sets (kxR0, kzR0): (a), (0.25, 1); (b), (1, 1); and (c), (2, 1). |
 |
Fig. 10 Perturbation velocity ǔrm(x, y) of the radiating mode extracted at ft = 40 for the case in Fig. 8 (panel a). Panel b displays the corresponding wave amplitude |û(kx, ky, t) in the wavenumber space (kx, ky) at ft = 40. Panel c displays the frequency spectrums |
 |
Fig. 11 Perturbation energy E(t) for the radiating modes created by incoming inertial waves with various wavenumber sets (kxR0, kzR0; panel a). The energy is normalized by the initial inertial-wave energy Eiw(t = 0) for comparison among different cases. Panel b displays the time rates for perturbation energy ∂E/∂t (solid), base shear contribution Pb (dashed), viscous dissipation Dv (dotted), and power injected by the incoming inertial wave–vortex interaction Pf (dash-dot) for the case with (kxR0, kzR0) = (1, 1). The energy rates are normalized by fEiw(0) for nondimensionalization. |
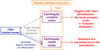 |
Fig. 12 Schematic diagram of possible interactions between tidal iner-tial waves and convective columnar vortices. |
5 Towards a complete nonlinear picture
When nonlinear effects are taken into account in the wave–vortex interaction, interesting behaviors are expected. In the unstable regime, where vortices are intrinsically unstable, tidal waves, as in any other disturbance (depending on the relative timescales, as discussed in Sect. 3.2), can destabilize them leading to fully turbulent states where energy is dissipated at small scales. From the current study, it is not clear which type of perturbation will most effectively yield turbulence. Nonlinear simulations can address this question and help us to understand the evolution of an unstable convective vortex along its nonlinear interaction with perturbation such as tidal waves or noise. Then, convection or the nonlinear interactions between incoming tidal inertial waves and the vortex (Duran-Matute et al. 2013; Boury et al. 2021) can trigger new columnar vortices, which can potentially be unstable or not. In the unstable case, this can potentially lead to a cycle of creation and destruction of vortices, which was indeed observed by Barker & Lithwick (2013) in their study of the dynamics of the tidal elliptic instability in rotating flows. In the stable case, it is interesting to note that tidal inertial waves can transfer the momentum they carry to the vortex at critical layers as identified in Appendix B but also extract energy from the vortex via an over-reflection or transmission mechanism. These complex behaviors, which we summarize in Fig. 12, allow us to point out that the modeling of the interactions between tides and rotating convection using effective turbulent friction cannot be applied to describe the interactions between tidal inertial waves and coherent convective vortices in the general case.
The results obtained with the convective column model proposed by Grooms et al. (2010) can also be applied to other vortices triggered by rotating double-diffusive convection (Moll & Garaud 2017) or by the nonlinear interactions of tidal inertial waves (Astoul & Barker 2022). The inertial wave–vortex interaction is also crucial in other configurations. For instance, a recent study by Pizzi et al. (2022) investigates the interaction in the presence of precession turbulence. These authors consider a base precessional shear flow that is subject to an instability called the precessional instability (Kerswell 1993). The instability triggers turbulence and such a turbulent precessional flow contains vortices as 2D structures and inertial waves as 3D structures. Pizzi et al. (2022) found that the 3D inertial wave becomes stronger as the precession increases and the nonlinear wave–vortex interaction contributes to turbulent dissipation more efficiently. They also reported a cyclic behavior of the flow where vortices appear and disappear as a result of the nonlinear interactions (as in Barker & Lithwick 2013, and de Vries et al., in prep., for the case of nonlinear evolution of the tidal elliptic instability). These findings increased our motivation to carry out a future study of the nonlinear interaction between tidally forced inertial waves and convective columns to better understand the contribution of the wave–vortex interaction to turbulent dissipation along the evolution of rapidly rotating planets and stars.
6 Conclusion and discussion
In this paper, we investigate how tidally forced inertial waves interact with a convective columnar vortex in rapidly rotating planets and stars. In Sect. 2, we present our study of the con-vective column; we used a semi-analytical model proposed by Grooms et al. (2010), and adapted the model without any mathematical singularity around the column center r = 0 to allow us to make a complete theoretical stability analysis. We find that the convective columnar vortex (17) is centrifugally stable when −Ωp < Ω0 < 3.62Ωp (Ωp and Ω0 being the global planetary (stellar) rotation and the rotation of the flow at the center of the vortex, respectively) and unstable otherwise.
As the stability is closely linked to the dynamics of the tidal wave–vortex interaction, we studied centrifugally unstable modes and neutral modes in great detail using linear stability analysis (Sect. 3). We find that the convective column is unstable to axisymmetric m = 0 perturbations (which can be induced by eccentricity tides) and weakly nonaxisymmetric perturbations with azimuthal wavenumbers m = {1, 2} (which correspond to obliquity and asynchronous tides, respectively). The WKBJ analysis detailed in the Appendix allows us to derive thoroughly explicit expressions of the maximum growth rate at a given ratio Ω0/Ωp for unstable modes and the frequency of neutral modes. We subsequently present linear simulations of the interaction between convective columns and tidally forced radial incoming inertial waves. We verified that such an interaction triggers the most unstable mode of an unstable convective column.
In Sect. 4, we present a study of the interactions between stable convective vortices and tidal inertial waves. We provide key results by conducting linear simulations of tidally forced incoming planar inertial waves interacting with a stable vortex. We observe that the wave–vortex interaction leads to the mixing of momentum and the creation of low-velocity regions around the vortex core. The interaction promotes efficient radiation of a new wave-like perturbation in the case where the wavelength of the incoming wave is close to the characteristic vortex length. This secondary wave can be regarded as the sum of neutral or stable modes of the vortex and frequencies close to the characteristic frequency of the primary inertial wave. As the amplitude of the secondary wave is non-negligible compared to that of the primary wave, it constitutes a supplementary potential source of dissipation. Finally, angular momentum exchanges can occur at critical layers.
As identified in Sect. 5, it will be crucial in the near future to understand the role of the nonlinearities. Moreover, it will be necessary to go beyond the simplified traditional polar f-plane approximation. In particular, the 2D nonseparable dynamics of tidal inertial wave attractors should be treated. Finally, if the external convective regions of gaseous giant planets are not the seat of the magnetic field generation through dynamo action, this cannot be the case for low-mass stars, and in this latter case, magnetic fields should therefore be taken into account (e.g., Barker & Lithwick 2014; Lin & Ogilvie 2018; Astoul et al. 2019).
Acknowledgements
The authors thank the referee for her/his comments, which have allowed us to improve our manuscript. The authors acknowledge support from the European Research Council through ERC grant SPIRE 647383 and from GOLF and PLATO CNES grants at the Department of Astrophysics of CEA. J. Park acknowledges support from the Royal Astronomical Society and Office of Astronomy for Development through the RAS-OAD astro4dev grant and from the Engineering and Physical Sciences Research Council (EPSRC) through the EPSRC mathematical sciences small grant (EP/W019558/1). A. Astoul acknowledges support from the Science and Technology Facilities Council (STFC) grant ST/S000275/1, as well as the Leverhulme Trust for early career grant.
Appendix A WKBJ approximation for large vertical wavenumber kz
Previous studies revealed that the centrifugal instability of rotating flows reaches its maximum growth rate as kz → ∞ in the inviscid limit (Billant & Gallaire 2005, 2013; Park & Billant 2013a; Park et al. 2017). We also see in Sect. 3 that eigenvalues of the convective Taylor column demonstrate asymptotic behaviors in the large-kz limit. To understand these behaviors and derive analytic expressions of the dispersion relation, we adopt the WKBJ approximation for large kz by applying it to û as
![$ \hat u\left( r \right)\~\exp \left[ {{1 \over }\sum\limits_{n = 0}^\infty {{^n}{S_n}\left( r \right)} } \right], $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq115.png) (A.1)
(A.1)
where ϵ is a small parameter to be defined. Applying (A.1) to the second-order ODE (38), we find
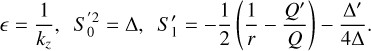 (A.2)
(A.2)
The leading-order term S0, where 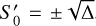 , determines the exponential behavior of the solution, and it depends on the sign of Δ. For instance, if Δ > 0, we express û as an evanescent solution:
, determines the exponential behavior of the solution, and it depends on the sign of Δ. For instance, if Δ > 0, we express û as an evanescent solution:
![$ \hat u = {{{Q^{{\textstyle{1 \over 2}}}}} \over {{r^{{\textstyle{1 \over 2}}}}{\Delta ^{{\textstyle{1 \over 2}}}}}}\left[ {{A_1}\exp \left( {{k_z}\int_r {\sqrt {\Delta \left( t \right){\rm{dt}}} } } \right) + {A_2}\exp \left( { - {k_z}\int_r {\sqrt {\Delta \left( t \right){\rm{dt}}} } } \right)} \right], $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq118.png) (A.3)
(A.3)
or as a wavelike solution if Δ < 0:
![$ \matrix{ \hfill {\hat u = {{{Q^{{\textstyle{1 \over 2}}}}} \over {{r^{{\textstyle{1 \over 2}}}}{{\left( { - \Delta } \right)}^{{\textstyle{1 \over 2}}}}}}\left[ {{B_1}\exp \left( {{\rm{i}}{k_z}\int_r {\sqrt { - \Delta \left( t \right)} {\rm{dt}}} } \right)} \right.} \cr \hfill {\left. { + {B_2}\exp \left( { - {\rm{i}}{k_z}\int_r {\sqrt { - \Delta \left( t \right)} {\rm{dt}}} } \right)} \right].} \cr } $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq119.png) (A.4)
(A.4)
To more easily comprehend the sign of Δ(r) = 1 − Φ/ (−ω + mΩ)2, it is convenient to define the radial epicyclic frequencies ω±(r):
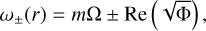 (A.5)
(A.5)
(see also, Le Dizès & Lacaze 2005; Le Dizès 2008; Park & Billant 2013b). We also define the critical frequency wc and radius rc at which the Doppler-shifted frequency s vanishes:
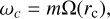 (A.6)
(A.6)
(i.e., the frequency and radius at which the corotation resonance occurs in the inviscid case; see e.g., Astoul et al. 2021). In Fig. A.1a, we plot ω± and ωc for Ω0/f = 3 and m = 1. The epicyclic frequencies ω± depend on m and Ω0, and their behavior can be upside-down for anticyclonic cases with Ω0/f < 0 (see e.g., Fig. A.1b for Ω0/f = −2). The gray-shaded area between ω+ and ω− shows the region where the solution is wave-like (i.e., Δ < 0), while the white area denotes the region where the solution is evanescent (i.e., Δ > 0). This implies that, for a given frequency ω, the WKBJ solution is wavelike if ω lies in the range ω− < ω < ω+ while the solution is evanescent if ω > ω+ or ω < ω−. The crossings of ωr = ω± indicate where Δ(r) is zero (see also, Park 2012). This implies that they indicate the location of the turning point rt where Δ(rt) = 0 and where solution behavior changes from wave-like to evanescent, or vice versa. Fig. A.1 also shows the typical frequencies of the neutral modes in the upper and lower branches (cases I, II, IV, and V) and unstable modes (case III). If the frequency ω lies in the range ωc(0) < ω < ω+(0), as in case I, we have one turning point rt and the solution is wave-like in the range 0 < r < rt while it is evanescent outside the turning point r > rt. At this frequency, we can construct an eigenfunction as the exponentially decaying solution for r > rt while waves are trapped between the turning point rt and r = 0 (see also, Le Dizès & Lacaze 2005). For the cases II and V where the frequency lies in the range ω−(0) < ω < ωc(0), we can construct the eigenfunction in the same way. For case IV, the frequency ωr crosses ω+, implying that there are two turning points. Between the two turning points, the solution is wave-like, while it is evanescent elsewhere. This configuration corresponds to the ring mode. Case III of the unstable mode is different; first, it has a frequency in the range 0 < ω < ωc(0), implying that there is a critical point rc where ωc(rc) = 0. The unstable mode also has a positive growth rate, ωi > 0, and therefore Δ is no longer real but complex on the real r-axis. Division of the WKBJ solutions into wavelike and evanescent solutions around the turning point rt is therefore not applicable on the real r-axis and we need to investigate the solution behavior of the unstable mode in the complex plane.
 |
Fig. A.1 Epicyclic frequencies ω± (solid lines) and critical frequency ωc (dashed line) for m = 1 and (a) Ω0/f = 3 and (b) Ω0/f = −2. The gray area denotes the region where the solution is wave-like (i.e., Δ < 0), while the white area is the evanescent region (i.e., Δ > 0). Dotted lines represent frequencies ωr for neutral modes in the upper (cases I and IV) and lower (cases II and V) branches, and for unstable modes (case III). |
In the following subsections, we present the detailed derivation of the dispersion relations of the frequency for the upper and lower branches of the neutral modes (cases I, II, IV, and V) using the epicyclic frequencies. And for case III, we use the analysis in the complex plane used by Billant & Gallaire (2005) to derive the frequency and growth rate of the unstable modes.
Appendix A.1 Dispersion relations for neutral modes
We first investigate the dispersion relations of the neutral modes that have a real frequency ω. In Fig. A.1, we display possible frequencies where we can construct the neutral mode. For instance, in case I, where the frequency lies in the range max(ωc)< ωr < max(ω+) we have one turning point rt and the solution is evanescent outside rt :
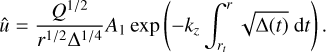 (A.7)
(A.7)
In order to impose the decaying boundary condition as r → ∞, A2 = 0 is imposed in Eq. (A.3). In addition, by considering the connection around the turning point rt (see also, Olver 1974; Bil-lant & Gallaire 2005; Le Dizès & Lacaze 2005), we obtain the wave-like solution in the range 0 < r < rt as
![$ \matrix{ {\hat u = {{{A_1}} \over 2}{{{Q^{1/2}}} \over {{r^{1/2}}{{\left( { - \Delta } \right)}^{1/4}}}}\left[ {{\rm{exp}}\left( {{\rm{i}}{k_z}\int_r^{{r_t}} {\sqrt { - \Delta \left( t \right)} } \,\,{\rm{d}}t - i{\pi \over 4}} \right)} \right.} \cr {\left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \exp \left( { - {\rm{i}}{k_z}\int_r^{{r_t}} {\sqrt { - \Delta \left( t \right)} } \,\,{\rm{d}}t + {\rm{i}}{\pi \over 4}} \right)} \right].} \cr } $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq123.png) (A.8)
(A.8)
This mode is the core mode because the wave is confined between the core r = 0 and the turning point rt (Le Dizès & Lacaze 2005). Depending on the azimuthal wavenumber m, we impose the boundary condition at the center r = 0 as
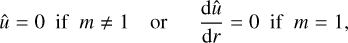 (A.9)
(A.9)
based on the asymptotic relations (42) and (43), (see also, Saffman 1992). Imposing such conditions to (A.8) leads to the following quantization relations at leading order:
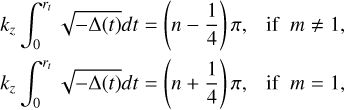 (A.10)
(A.10)
where n is an integer indicating the mode number. We see that the right-hand-side terms are always finite, and therefore the integrals on the left-hand side should converge to zero as kz → ∞. This implies that the turning point migrates to the center r = 0 in this limit; this allows us to expand all the functions around r = 0:
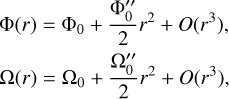 (A.11)
(A.11)
where the subscript 0 represents the fact that the functions are evaluated in r = 0. Applying the expansions (A.11) to the quantization relations (A.10), we can also expand the frequency in the power of kz as
 (A.12)
(A.12)
After having inserted the expansion (A.12) into the quantization conditions (A.10), we find the frequency for upper branches as
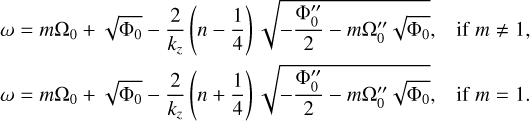 (A.13)
(A.13)
From Fig. 6a, we see that there is good agreement between the asymptotic dispersion relation (A.13) and the numerical solutions, especially for large kz. We note that ω1 is negative for the upper branches; therefore, the frequency ω increases with kz and asymptotes to 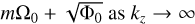 .
.
The quantization relations (A.10) can be similarly applied for lower branches for other core-mode cases II and V in Fig. A.1 where the frequency ω now meets the epicyclic frequency ω−. In this case, we find the frequency expansion as follows:
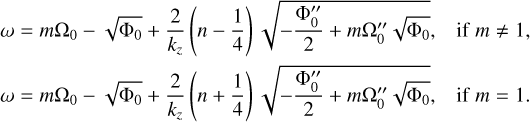 (A.14)
(A.14)
For the lower branches, ω1 is now positive, and the frequency ω decreases and asymptotes to 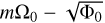 as kz increases. We see in Fig. 6b that the asymptotic dispersion relations (45) agree well with numerical results for the lower-branch frequency.
as kz increases. We see in Fig. 6b that the asymptotic dispersion relations (45) agree well with numerical results for the lower-branch frequency.
On the other hand, we also have a mode called the ring mode (Le Dizès & Lacaze 2005) where the wavelike solution is confined between the two turning points rt2 and rt2 where rt1 < rt2 (see e.g., the case IV in Fig. A.1b). In this case, the wavelike solution (A.8) is connected around rt1 by the evanescent solution in the range 0 < r < rt1 :
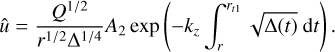 (A.15)
(A.15)
Matching the solutions (A.8) and (A.15) leads to the following quantization condition:
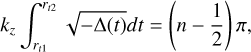 (A.16)
(A.16)
(see also, Billant & Gallaire 2005). As kz increases, these turning points migrate towards the point rmax + at which ω+ is the maximum and the derivative of ω+ is zero:
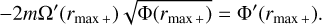 (A.17)
(A.17)
Such a behavior around rmax + leads to the following expression for the frequency:
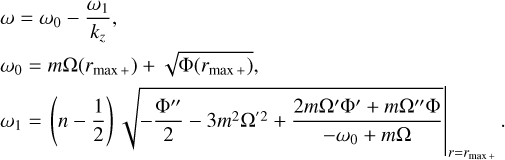 (A.18)
(A.18)
The ring mode in the upper branches can be constructed when ω+(0) < ω+(rmax +), i.e.,
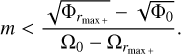 (A.19)
(A.19)
We find numerically that this inequality corresponds to −1.2 < Ω0/f < 0 for m = 0, −2.8 < Ω0/f < 0 for m = 1, and Ω0/f < 0 for m ≥ 2.
For lower branches, we can have the same quantization condition as in Eq. (A. 16) when ω−(0) > ω−(rmin -) where
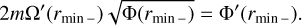 (A.20)
(A.20)
The inequality ω−(0) > ω−(rmin -) is equivalent to
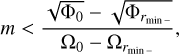 (A.21)
(A.21)
and it corresponds to −1.2 < Ω0/f < 0 for m = 0, −0.8 < Ω0/f < 0 for m = 1, Ω0/f > −0.6 for m = 2, and Ω0/f > 0 for m ≥ 3. We also have the frequency expression evaluated at rmin - for the ring mode in the lower branches as follows:
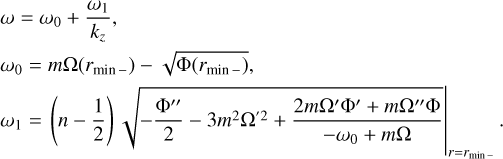 (A.22)
(A.22)
We also checked that the asymptotic frequencies (A.18) and (A.22) are in good agreement with numerical results.
Appendix A.2 Dispersion relations for unstable modes
For a general azimuthal wavenumber m and complex frequency ω, the function Δ(r) is complex on the real r-axis and the turning points rt where Δ(rt) = 0 are in the complex plane. Figure A.2 shows locations of the turning points in the complex plane for m = 2 and Ω0/f = 3 when the eigenfrequency ω = 0.778 + 0.45i at kzR0 = 30 from the numerical computation is considered. Due to the oscillatory behaviors of the Bessel function J0 of the angular velocity profile (17) as |r| → ∞ for | arg(r)| < π/2 (see also, Abramowitz & Stegun 1972), there are many turning points in the complex plane. But while other turning points are far from the real r-axis, the two turning points rt1 and rt2 are somewhat close to the real r-axis and they will influence the WKBJ solution effectively. To better understand the exponential behavior of the WKBJ solution, we also draw in Fig. A.2 the Stokes lines defined as
 (A.23)
(A.23)
(see also, Olver 1974; Billant & Gallaire 2005). The Stokes lines emanate from the turning points and they delimit the regions of the WKBJ solutions in the same behavior. The points 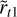 and
and  , where the Stokes lines cross the real r-axis, also delimit the solutions on the real r-axis. By the definition (A.23), the WKBJ solutions on the Stokes line between the two turning points are wave-like. Furthermore, it is noticeable that a Stokes line emanating from rt1 shows a spiral pattern around the critical point rc, as Δ is singular.
, where the Stokes lines cross the real r-axis, also delimit the solutions on the real r-axis. By the definition (A.23), the WKBJ solutions on the Stokes line between the two turning points are wave-like. Furthermore, it is noticeable that a Stokes line emanating from rt1 shows a spiral pattern around the critical point rc, as Δ is singular.
 |
Fig. A.2 An example of the Stokes lines network for ω = 0.778 + 0.46i at m = 2, kzR0 = 30, and Ω0/f = 3 (panel a). Black solid lines denote the Stokes lines, short lines indicate the direction where Re(Δ) remains constant, and a blue-dashed line denotes the progressive path. Panel b shows he integral versus the real part of r along the progressive path in (a). |
The Stokes line network in the complex plane in Fig. A.2 is very similar to that of the Carton & McWilliams vortex studied in Billant & Gallaire (2005). We follow their approach by considering the WKBJ solution that decreases exponentially from r = rt1 in the range 0 < r < rt1 :
![$ \hat u = {C_1}{{{Q^{1/2}}} \over {{r^{1/2}}{\Delta ^{1/4}}}}\exp \left[ { - {k_z}\int_r^{{r_{t1}}} {\sqrt {\Delta \left( t \right)} } \,\,{\rm{d}}t} \right]. $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq144.png) (A.24)
(A.24)
This solutions matches with the wavelike solution in the range rt1 < r rt2:
![$ \hat u = 2{C_1}{{{Q^{1/2}}} \over {{r^{1/2}}{{\left( { - \Delta } \right)}^{1/4}}}}\sin \left[ {{k_z}\int_{{r_{t1}}}^r {\sqrt { - \Delta \left( t \right)} } \,\,{\rm{d}}t + {\pi \over 4}} \right]. $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq145.png) (A.25)
(A.25)
Furthermore, we have the evanescent solution after the turning point rt2:
![$ \matrix{ {\hat u = {{{Q^{1/2}}} \over {{r^{1/2}}{\Delta ^{1/4}}}}\left[ {{D_1}\exp \left( { - {k_z}\int_{{r_{t2}}}^r {\sqrt {\Delta \left( t \right)} \,\,{\rm{d}}t} } \right)} \right.} \cr {\left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {D_2}\exp \left( {{k_z}\int_{{r_{t2}}}^r {\sqrt {\Delta \left( t \right)} \,\,{\rm{d}}t} } \right)} \right].} \cr } $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq146.png) (A.26)
(A.26)
We note that for r > rt2, there are many turning points in the complex plane as a result of the oscillatory behavior of the vortex profile in Eq. (17). These turning points, like rt3 in Fig. A.2, are far from the real axis. With this characteristic, we can avoid the multiple-turning-point analysis by choosing a proper progressive path (Le Dizès & Lacaze 2005). More precisely, the idea is to check whether the integral 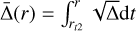 is holomorphic (i.e., complex differentiable) and Re
is holomorphic (i.e., complex differentiable) and Re 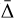 ) is monotonic along the progressive path. As we can see in Fig. A.2b, the integral
) is monotonic along the progressive path. As we can see in Fig. A.2b, the integral 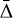 is monotonically decreasing along the progressive path displayed in Fig. A.2a. This implies that we can keep the WKBJ solution (A.26) along the progressive path as r → ∞, and can therefore impose D2 = 0 to apply the exponentially decreasing boundary condition.
is monotonically decreasing along the progressive path displayed in Fig. A.2a. This implies that we can keep the WKBJ solution (A.26) along the progressive path as r → ∞, and can therefore impose D2 = 0 to apply the exponentially decreasing boundary condition.
 |
Fig. A.3 Real and imaginary parts of the double turning point r0 versus Ω0/f for different azimuthal wavenumbers: m = 0 (black), m = 1 (blue) and m = 2 (red; panels a and b). Gray-shaded areas represent the centrifugally stable regime. Panel c displays the movement of the double turning point r0 in the complex plane as m changes for Ω0/f= 5 (black) and Ω0/f= −2 (blue). |
By connecting the solution (A.25) and the solution (A.26) with D2 = 0 at r = rt2 , we obtain the following quantization condition:
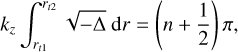 (A.27)
(A.27)
where n is the mode number. This is identical to the quantization condition obtained by Billant & Gallaire (2005). We see from Eq. (A.27) that Im 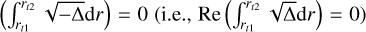 , and this implies that the two turning points should be connected by the Stokes lines as seen in Fig. A.2. Also, it is important to note that the right-hand side of Eq. (A.27) is always finite while the integral on the left-hand side should become zero as kz → ∞ This implies that rt1 and rt2 should collapse to a point as kz → ∞. From this information, Billant & Gallaire (2005) considered a double turning point r0 between the two turning points (see also Fig. A.2), where the radial derivative of
, and this implies that the two turning points should be connected by the Stokes lines as seen in Fig. A.2. Also, it is important to note that the right-hand side of Eq. (A.27) is always finite while the integral on the left-hand side should become zero as kz → ∞ This implies that rt1 and rt2 should collapse to a point as kz → ∞. From this information, Billant & Gallaire (2005) considered a double turning point r0 between the two turning points (see also Fig. A.2), where the radial derivative of 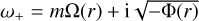 becomes zero, i.e.,
becomes zero, i.e.,
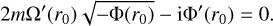 (A.28)
(A.28)
In Fig. A.3, we show how the location of the double turning point r0 changes in the complex plane for both cyclonic and anti-cyclonic cases for various azimuthal wavenumbers. For cyclonic cases Ω0/f > 0, r0 departs from the real axis at m = 0 and lies in the upper complex plane (Im (r0) > 0) for m > 0, while it lies in the lower complex plane (Im (r0) < 0) for anticyclonic cases Ω0/f < 0. For both cases, we find that the double turning point r0 disappears for m ≤ 3.
Once the location of r0 is known, we can apply the Taylor expansion around r0 in the limit kz → ∞ to derive the following dispersion relation as
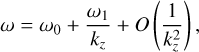 (A.29)
(A.29)
(see also, Billant & Gallaire 2005). In Fig. 6(c,d), we see that the WKBJ prediction (46) is in good agreement with numerical results for the most unstable eigenvalues (i.e., n = 1) for various azimuthal wavenumbers m.
Appendix B Note on the critical layers
There is a certain range of frequency where neutral, stable, or even unstable modes can possess a critical layer at r = rc where s = 0. In the inviscid limit ν = 0, the critical radius rc is a pole of the function Ā and therefore the second-order ordinary differential equation Eq. (38) becomes singular. This can also be seen from the WKBJ solutions such that the divergence of Δ leads to the divergence of the leading-order term of the WKBJ solution (A.4). Therefore, a dedicated analysis of Eq. (38) in the vicinity of rc must be performed. As r goes to rc, Eq. (38) can be approximated at leading order as
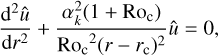 (B.1)
(B.1)
where Roc is the shear Rossby number and αk is the ratio of vertical to azimuthal wavenumbers defined as:
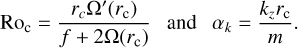 (B.2)
(B.2)
We note that Eq. (B.1) is analogous to the differential equation for inertial waves close to a corotation resonance when using a cylindrical differential rotation profile in a local shear box model in Cartesian coordinates (see in particular Sect. 3.4 of Astoul et al. 2021, when the box is at the south pole of a spherical shell). As introduced in Astoul et al. (2021) or Alvan et al. (2013) for internal gravity waves approaching a corotation resonance, we define a new parameter ℛ appearing in Eq. (B.1) as
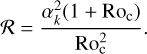 (B.3)
(B.3)
Applying the Frobenius series to solve the equation (B.1) leads to the following solutions at leading order:
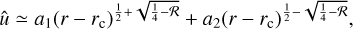 (B.4)
(B.4)
if ℛ < 1/4 where a1 and a2 are constants, or
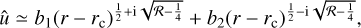 (B.5)
(B.5)
if ℛ > 1/4 where b1 and b2 are constants.
The solutions (B.5) in the regime ℛ > 1/4 can experience a strong attenuation as it crosses r = rc. For instance, if we consider the analytic continuity of Eq. (B.5) for r > rc by taking the lower half in the complex plane1, we obtain the solution for r < rc as
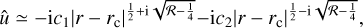 (B.6)
(B.6)
where 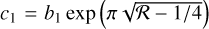 and
and 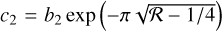 are the amplitudes of the solution for r < rc related to the amplitudes of the solution for r < rc. To determine in which directions the waves propagate from the corotation, we introduce the wave action flux 𝒜, which is an invariant quantity along the radius r in the inviscid limit. This quantity is conserved in the whole domain except at corotation, and is therefore a useful tool with which to determine the direction of the wave-energy propagation and quantify the angular momentum flux exchanges between the waves and the mean flow (e.g., Grimshaw 1975, 1979; Andrews & McIntyre 1978, in the context of inertial gravity waves). In the cylindrical coordinates, this invariant can be derived as
are the amplitudes of the solution for r < rc related to the amplitudes of the solution for r < rc. To determine in which directions the waves propagate from the corotation, we introduce the wave action flux 𝒜, which is an invariant quantity along the radius r in the inviscid limit. This quantity is conserved in the whole domain except at corotation, and is therefore a useful tool with which to determine the direction of the wave-energy propagation and quantify the angular momentum flux exchanges between the waves and the mean flow (e.g., Grimshaw 1975, 1979; Andrews & McIntyre 1978, in the context of inertial gravity waves). In the cylindrical coordinates, this invariant can be derived as
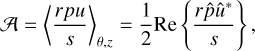 (B.7)
(B.7)
where 〈·〉θ,z denotes the average in the z- and θ-directions and Re the real part. By taking a linear combination of the momentum equations (26), (28), and (29) in the inviscid limit, one can get an expression for the pressure:
![$ \hat p = - {\rm{i}}{{s\hat u' + \hat u/r\left[ {s - m\left( {f + \zeta } \right)} \right]} \over Q}. $](/articles/aa/full_html/2023/05/aa43586-22/aa43586-22-eq167.png) (B.8)
(B.8)
Its substitution into the wave action flux Eq. (B.7) yields
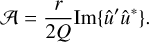 (B.9)
(B.9)
Injecting the solutions Eqs. (B.5) and (B.6) into Eq. (B.9) leads to the following wave-action flux above and below the corotation:
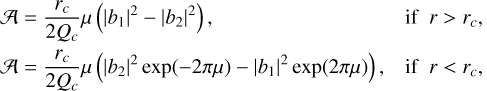 (B.10)
(B.10)
where 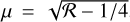 , provided again that
, provided again that 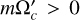 . In this framework, the direction of wave propagation in the region r > rc is given by the sign of s𝒜 as this quantity is related to the group velocity (e.g., Grimshaw 1975; Bretherton & Garrett 1968). From Eq. (B.10) and given that
. In this framework, the direction of wave propagation in the region r > rc is given by the sign of s𝒜 as this quantity is related to the group velocity (e.g., Grimshaw 1975; Bretherton & Garrett 1968). From Eq. (B.10) and given that 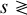 0 for
0 for 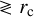 , the first wave of amplitude |b1| is traveling outwards because s𝒜 > 0 (for both r > rc and r < rc), while the second wave of amplitude |b2| is traveling inwards because s𝒜 < 0. This implies that both waves are attenuated as their wave action fluxes are reduced by a factor of exp(−2πµ) after they move through the corotation, as similarly reported by Astoul et al. (2021) for inertial waves in a shear box model with cylindrical differential rotation when ℛ > 1/4. In the regime ℛ ≤ 1/4, the wave action flux analysis cannot determine the wave direction unambiguously and therefore a further numerical analysis is required as was carried out by these latter authors. Depending on the boundary conditions and other internal properties, such as wave frequency, wavenumbers, or the shear Rossby number, the inertial waves may experience either damping, over-reflection, or over-transmission. The latter can ultimately lead to shear instability if the waves interfere constructively and sustain their growth as successive over-reflection (or over-transmission) of the waves occurs (Lindzen 1988; Harnik & Heifetz 2007; Astoul & Barker 2022).
, the first wave of amplitude |b1| is traveling outwards because s𝒜 > 0 (for both r > rc and r < rc), while the second wave of amplitude |b2| is traveling inwards because s𝒜 < 0. This implies that both waves are attenuated as their wave action fluxes are reduced by a factor of exp(−2πµ) after they move through the corotation, as similarly reported by Astoul et al. (2021) for inertial waves in a shear box model with cylindrical differential rotation when ℛ > 1/4. In the regime ℛ ≤ 1/4, the wave action flux analysis cannot determine the wave direction unambiguously and therefore a further numerical analysis is required as was carried out by these latter authors. Depending on the boundary conditions and other internal properties, such as wave frequency, wavenumbers, or the shear Rossby number, the inertial waves may experience either damping, over-reflection, or over-transmission. The latter can ultimately lead to shear instability if the waves interfere constructively and sustain their growth as successive over-reflection (or over-transmission) of the waves occurs (Lindzen 1988; Harnik & Heifetz 2007; Astoul & Barker 2022).
References
- Abramowitz, M., & Stegun, I. A. 1972, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (Dover Publications) [Google Scholar]
- Adriani, A., Mura, A., Orton, G., et al. 2018, Nature, 555, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Ahuir, J., Strugarek, A., Brun, A. S., & Mathis, S. 2021, A&A, 650, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alvan, L., Mathis, S., & Decressin, T. 2013, A&A, 553, A86 [CrossRef] [EDP Sciences] [Google Scholar]
- André, Q., Barker, A. J., & Mathis, S. 2017, A&A, 605, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, Q., Mathis, S., & Barker, A. J. 2019, A&A, 626, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrews, D. G., & McIntyre, M. E. 1978, J. Fluid Mech., 89, 647 [Google Scholar]
- Antkowiak, A. 2005, PhD thesis, Université Paul Sabatier de Toulouse, France [Google Scholar]
- Arobone, E., & Sarkar, S. 2012, J. Fluid Mech., 703, 29 [Google Scholar]
- Astoul, A., & Barker, A. J. 2022, MNRAS, 516, 2913 [NASA ADS] [CrossRef] [Google Scholar]
- Astoul, A., Mathis, S., Baruteau, C., et al. 2019, A&A, 631, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astoul, A., Park, J., Mathis, S., Baruteau, C., & Gallet, F. 2021, A&A, 647, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Augustson, K. C., & Mathis, S. 2019, ApJ, 874, 83 [Google Scholar]
- Augustson, K. C., Mathis, S., & Astoul, A. 2020, ApJ, 903, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Aurnou, J. M., Calkins, M. A., Cheng, J. S., et al. 2015, Phys. Earth Planet. Interiors, 246, 52 [CrossRef] [Google Scholar]
- Barker, A. J. 2020, MNRAS, 498, 2270 [Google Scholar]
- Barker, A. J., & Astoul, A. A. V. 2021, MNRAS, 506, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Barker, A. J., & Lithwick, Y. 2013, MNRAS, 435, 3614 [CrossRef] [Google Scholar]
- Barker, A. J., & Lithwick, Y. 2014, MNRAS, 437, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Barker, A. J., Dempsey, A. M., & Lithwick, Y. 2014, ApJ, 791, 13 [Google Scholar]
- Benbakoura, M., Réville, V., Brun, A. S., Le Poncin-Lafitte, C., & Mathis, S. 2019, A&A, 621, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Billant, P., & Gallaire, F. 2005, J. Fluid Mech., 542, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Billant, P., & Gallaire, F. 2013, J. Fluid Mech., 734, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Bolmont, E., & Mathis, S. 2016, Celest. Mech. Dyn. Astron., 126, 275 [Google Scholar]
- Booker, J. R., & Bretherton, F. P. 1967, J. Fluid Mech., 27, 513 [Google Scholar]
- Boury, S., Sibgatullin, I., Ermanyuk, E., et al. 2021, J. Fluid Mech., 926, A12 [NASA ADS] [CrossRef] [Google Scholar]
- Bretherton, F. P., & Garrett, C. J. R. 1968, Proc. Roy. Soc. Lond. A, 302, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Cai, T., Chan, K. L., & Mayr, H. G. 2021, Planet. Sci. J., 2, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Campagne, A., Gallet, B., Moisy, F., & Cortet, P.-P. 2015, Phys. Rev. E, 91, 043016 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, J. S., Stellmach, S., Ribeiro, A., et al. 2015, Geophys. J. Int., 201, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Clark di Leoni, P., Cobelli, P. J., Mininni, P. D., Dmitruk, P., & Matthaeus, W. H. 2014, Phys. Fluids, 26, 035106 [Google Scholar]
- Currie, L. K., Barker, A. J., Lithwick, Y., & Browning, M. K. 2020, MNRAS, 493, 5233 [CrossRef] [Google Scholar]
- Davidson, P. A. 2013, Turbulence in Rotating, Stratified, and Electrically Conducting Fluids (Cambridge University Press) [CrossRef] [Google Scholar]
- Duguid, C. D., Barker, A. J., & Jones, C. A. 2020a, MNRAS, 497, 3400 [Google Scholar]
- Duguid, C. D., Barker, A. J., & Jones, C. A. 2020b, MNRAS, 491, 923 [Google Scholar]
- Duran-Matute, M., Flór, J.-B., Godeferd, F. S., & Jause-Labert, C. 2013, Phys. Rev. E, 87, 041001 [NASA ADS] [CrossRef] [Google Scholar]
- Dyudina, U. A., Ingersoll, A. P., Ewald, S. P., et al. 2008, Science, 319, 1801 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L. N., Orton, G. S., Sinclair, J. A., et al. 2018, Nat. Commun., 9, 3564 [NASA ADS] [CrossRef] [Google Scholar]
- Fröman, N., & Fröman, P. O. 1965, JWKB Approximation – Contributions to the Theory (North-Holland Publishing Company) [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallet, F., & Bouvier, J. 2015, A&A, 577, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia, F., Chambers, F. R. N., & Watts, A. L. 2020, MNRAS, 499, 4698 [NASA ADS] [CrossRef] [Google Scholar]
- Gerkema, T., & Shrira, V. I. 2005, J. Fluid Mech., 529, 195 [Google Scholar]
- Godfrey, D. A. 1988, Icarus, 76, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Keeley, D. A. 1977, ApJ, 211, 934 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Soter, S. 1966, Icarus, 5, 375 [Google Scholar]
- Goodman, J., & Lackner, C. 2009, ApJ, 696, 2054 [Google Scholar]
- Goodman, J., & Oh, S. P. 1997, ApJ, 486, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Gough, D. O., Spiegel, E. A., & Toomre, J. 1975, J. Fluid Mech., 68, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Grimshaw, R. 1979, Geophys. Astrophys. Fluid Dyn., 14, 303 [Google Scholar]
- Grimshaw, R. H. J. 1975, J. Fluid Mech., 70, 287 [Google Scholar]
- Grooms, I. 2015, Geophys. Astrophys. Fluid Dyn., 109, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Grooms, I., Julien, K., Weiss, J. B., & Knobloch, E. 2010, Phys. Rev. Lett., 104, 224501 [NASA ADS] [CrossRef] [Google Scholar]
- Harnik, N., & Heifetz, E. 2007, J. Atmos. Sci., 64, 2238 [NASA ADS] [CrossRef] [Google Scholar]
- Hindman, B. W., Featherstone, N. A., & Julien, K. 2020, ApJ, 898, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Julien, K., Knobloch, E., & Werne, J. 1998, Theor. Comput. Fluid Dyn., 11, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Julien, K., Rubio, A. M., Grooms, I., & Knobloch, E. 2012, Geophys. Astrophys. Fluid Dyn., 106, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Kerswell, R. R. 1993, Geophys. Astrophys. Fluid Dyn., 72, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Kloosterziel, R. C., & van Heijst, G. J. F. 1991, J. Fluid Mech., 223, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lainey, V., Arlot, J.-E., Karatekin, Ö., & van Hoolst, T. 2009, Nature, 459, 957 [Google Scholar]
- Lainey, V., Karatekin, Ö., Desmars, J., et al. 2012, ApJ, 752, 14 [Google Scholar]
- Lainey, V., Jacobson, R. A., Tajeddine, R., et al. 2017, Icarus, 281, 286 [Google Scholar]
- Lainey, V., Casajus, L. G., Fuller, J., et al. 2020, Nat. Astron., 4, 1053 [Google Scholar]
- Laskar, J., Boué, G., & Correia, A. C. M. 2012, A&A, 538, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Dizès, S. 2008, J. Fluid Mech., 597, 283 [CrossRef] [Google Scholar]
- Le Dizès, S., & Lacaze, L. 2005, J. Fluid Mech., 542, 69 [CrossRef] [Google Scholar]
- Lin, Y., & Ogilvie, G. I. 2018, MNRAS, 474, 1644 [Google Scholar]
- Lindzen, R. S. 1988, Pure Appl. Geophys., 126, 103 [Google Scholar]
- Maas, L. R. M. 2001, J. Fluid Mech., 437, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, S. 2019, in EAS Publications Series, 82, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Neiner, C., & Tran Minh, N. 2014, A&A, 565, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Auclair-Desrotour, P., Guenel, M., Gallet, F., & Le Poncin-Lafitte, C. 2016, A&A, 592, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McIntyre, M. E. 2019, J. Fluid Mech., 881, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Miles, J. W. 1961, J. Fluid Mech., 10, 496 [Google Scholar]
- Moll, R., & Garaud, P. 2017, ApJ, 834, 44 [Google Scholar]
- Ogilvie, G. I. 2013, MNRAS, 429, 613 [Google Scholar]
- Ogilvie, G. I. 2014, ARA&A, 52, 171 [Google Scholar]
- Ogilvie, G. I., & Lesur, G. 2012, MNRAS, 422, 1975 [Google Scholar]
- Ogilvie, G. I., & Lin, D. N. C. 2004, ApJ, 610, 477 [Google Scholar]
- Olver, F. W. J. 1974, Asymptotics and Special Functions (Academic Press - Elsevier Inc. and all) [Google Scholar]
- Park, J. 2012, PhD thesis, Ecole Polytechnique, France [Google Scholar]
- Park, J., & Billant, P. 2013a, Phys. Fluids, 25, 086601 [NASA ADS] [CrossRef] [Google Scholar]
- Park, J., & Billant, P. 2013b, J. Fluid Mech., 725, 262 [Google Scholar]
- Park, J., Billant, P., & Baik, J.-J. 2017, J. Fluid Mech., 822, 80 [Google Scholar]
- Park, J., Prat, V., & Mathis, S. 2020, A&A, 635, A133 [EDP Sciences] [Google Scholar]
- Park, J., Prat, V., Mathis, S., & Bugnet, L. 2021, A&A, 646, A64 [EDP Sciences] [Google Scholar]
- Penev, K., Sasselov, D., Robinson, F., & Demarque, P. 2007, ApJ, 655, 1166 [Google Scholar]
- Pizzi, F., Mamatsashvli, G., Barker, A. J., Giesecke, A., & Stefani, F. 2022, Phys. Fluids, 34, 125135 [NASA ADS] [CrossRef] [Google Scholar]
- Rayleigh, O. 1917, Proc. Roy. Soc. Lond. A, 93, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Remus, F., Mathis, S., & Zahn, J. P. 2012, A&A, 544, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M., Georgeot, B., & Valdettaro, L. 2001, J. Fluid Mech., 435, 103 [Google Scholar]
- Saffman, P. G. 1992, Vortex Dynamics (Cambridge University Press) [Google Scholar]
- Sánchez-Lavega, A., Hueso, R., Pérez-Hoyos, S., & Rojas, J. F. 2006, Icarus, 184, 524 [CrossRef] [Google Scholar]
- Schmid, P., & Henningson, D. S. 2001, Stability and Transition in Shear Flows (New York: Springer-Verlag) [Google Scholar]
- Sprague, M., Julien, K., Knobloch, E., & Werne, J. 2006, J. Fluid Mech., 551, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Stellmach, S., Lischper, M., Julien, K., et al. 2014, Phys. Rev. Lett., 113, 254501 [NASA ADS] [CrossRef] [Google Scholar]
- Stevenson, D. J. 1979, Geophys. Astrophys. Fluid Dyn., 12, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, M. 2000, Phys. Rev. B, 61, 11780 [NASA ADS] [CrossRef] [Google Scholar]
- Synge, J. L. 1933, Trans. R. Soc. Can., 27, 1 [Google Scholar]
- Terquem, C. 2021, MNRAS, 503, 5789 [NASA ADS] [CrossRef] [Google Scholar]
- Terquem, C., & Martin, S. 2021, MNRAS, 507, 4165 [CrossRef] [Google Scholar]
- Veronis, G. 1959, J. Fluid Mech., 5, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal, J., & Barker, A. J. 2020a, MNRAS, 497, 4472 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal, J., & Barker, A. J. 2020b, ApJ, 888, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., Miesch, M. S., & Liang, C. 2016, ApJ, 830, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y. 2005, ApJ, 635, 688 [Google Scholar]
- Yadav, R. K., Heimpel, M., & Bloxham, J. 2020, Sci. Adv., 6, eabb9298 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J. P. 1966a, Ann. Astrophys., 29, 313 [NASA ADS] [Google Scholar]
- Zahn, J. P. 1966b, Ann. Astrophys., 29, 489 [NASA ADS] [Google Scholar]
- Zahn, J. P. 1975, A&A, 41, 329 [NASA ADS] [Google Scholar]
- Zahn, J. P. 1989, A&A, 220, 112 [Google Scholar]
because 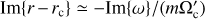 provided that
provided that 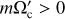 , and with the radiation condition Im{ω} > 0 where Im features the imaginary part (Miles 1961; Booker & Bretherton 1967; Astoul et al. 2021, for a more detailed description of the mathematical analysis about the connection of solutions).
, and with the radiation condition Im{ω} > 0 where Im features the imaginary part (Miles 1961; Booker & Bretherton 1967; Astoul et al. 2021, for a more detailed description of the mathematical analysis about the connection of solutions).
All Figures
 |
Fig. 1 Schematics of the tidal wave-vortex interaction. Left panel: schematic of the interaction between a tidal inertial wave and a single convective Taylor column in the f -plane. We introduce the cylindrical coordinates (r, θ, z). Right panel: schematic of a meridian cut of a planet or star showing propagation of a tidal inertial wave (blue lines) in a convective envelope and its interaction with a single Taylor column. |
| In the text | |
 |
Fig. 2 Proflies of base vorticity ζ(r, black in panel a) and base angular velocity Ω(r, black in panel b) and their first (blue) and second (red) derivatives for the current model (17, solid lines) and the model (16) from Grooms et al. (2010, dashed lines). Panel c: profiles of the Rayleigh discriminant Φ(r) for Ω/f = −1 (black), Ω0/f = 0.5 (blue) and Ω0/f = 2 (red). |
| In the text | |
 |
Fig. 3 Sign of the Rayleigh discriminant Φ(r) in the parameter space (r/R0, Ω0/f) where black regions indicate Φ < 0 and white regions indicate Φ ≥ 0. Upper and lower dashed lines represent the upper limit (Ω0/f = 1.81) and the lower limit (Ω0/f = −0.5) that bound the cen-trifugally stable region. |
| In the text | |
 |
Fig. 4 Eigenvalue spectra for an unstable case at Ω0/f = 3 and kzR0 = 10 for (a) m = 0, (b) m = 1, and (c) m = 2. Different numbers of the Chebyshev collocation points Ncheb are tested for convergence. |
| In the text | |
 |
Fig. 5 Real (solid) and imaginary (dashed) parts of (a) the most unstable mode and (b) the first neutral mode with the highest frequency at Ω0/f = 3 and kzR0 = 10 for different azimuthal wavenumbers: m = 0 (black), m = 1 (blue), and m = 2 (red). The gray-shaded region shows where the Rayleigh discriminant Φ is negative. |
| In the text | |
 |
Fig. 6 Frequency ωr as a function of the vertical wavenumber kz of the neutral modes for the four upper branches (panel a) and the four lower branches (panel b) at Ω0/f = 3 for m = 0 (black), m = 1 (blue), and m = 2 (red). Frequency ωr (panel c) and growth rate ωi (panel d), respectively, versus vertical wavenumber kz for the most unstable mode at Ω0/f = 3 for m = 0 (black), m = 1 (blue), and m = 2 (red). For all panels, solid lines are numerical results and dashed lines denote the WKBJ predictions for panel a: Eq. (44), panel b: Eq. (45) for m = 0, 1 (core mode) and (A.22) for m = 2 (ring mode), and panels c and d: Eq. (46). |
| In the text | |
 |
Fig. 7 Spatiotemporal diagrams in the space (r, t) for inertial waves entering from r/R0 = 20 at the forcing frequency ωf = 0.3, m = 1, kzR0 = 5, ν = 0 for an unstable column with Ω0/f = 3 (panel a) and a stable column with Ω0/f = 0.5 (panel b). Panel c displays the time evolution of wave energy E(t) for the unstable case (a, black solid line) and stable case (b, black dashed line). The blue line denotes the energy growth C exp(2ωit) with a constant C chosen for comparison with the unstable case. |
| In the text | |
 |
Fig. 8 Time evolution of the perturbation velocity ŭ(x, y) illustrating the interaction between an inertial wave with (kxR0, kzR0) = (1, 1) and a stable vortex with Ω0/f = 1 at |
| In the text | |
 |
Fig. 9. Spatiotemporal diagrams of ǔ in the space (t, y) extracted at x = 0 for the wavenumber sets (kxR0, kzR0): (a), (0.25, 1); (b), (1, 1); and (c), (2, 1). |
| In the text | |
 |
Fig. 10 Perturbation velocity ǔrm(x, y) of the radiating mode extracted at ft = 40 for the case in Fig. 8 (panel a). Panel b displays the corresponding wave amplitude |û(kx, ky, t) in the wavenumber space (kx, ky) at ft = 40. Panel c displays the frequency spectrums |
| In the text | |
 |
Fig. 11 Perturbation energy E(t) for the radiating modes created by incoming inertial waves with various wavenumber sets (kxR0, kzR0; panel a). The energy is normalized by the initial inertial-wave energy Eiw(t = 0) for comparison among different cases. Panel b displays the time rates for perturbation energy ∂E/∂t (solid), base shear contribution Pb (dashed), viscous dissipation Dv (dotted), and power injected by the incoming inertial wave–vortex interaction Pf (dash-dot) for the case with (kxR0, kzR0) = (1, 1). The energy rates are normalized by fEiw(0) for nondimensionalization. |
| In the text | |
 |
Fig. 12 Schematic diagram of possible interactions between tidal iner-tial waves and convective columnar vortices. |
| In the text | |
 |
Fig. A.1 Epicyclic frequencies ω± (solid lines) and critical frequency ωc (dashed line) for m = 1 and (a) Ω0/f = 3 and (b) Ω0/f = −2. The gray area denotes the region where the solution is wave-like (i.e., Δ < 0), while the white area is the evanescent region (i.e., Δ > 0). Dotted lines represent frequencies ωr for neutral modes in the upper (cases I and IV) and lower (cases II and V) branches, and for unstable modes (case III). |
| In the text | |
 |
Fig. A.2 An example of the Stokes lines network for ω = 0.778 + 0.46i at m = 2, kzR0 = 30, and Ω0/f = 3 (panel a). Black solid lines denote the Stokes lines, short lines indicate the direction where Re(Δ) remains constant, and a blue-dashed line denotes the progressive path. Panel b shows he integral versus the real part of r along the progressive path in (a). |
| In the text | |
 |
Fig. A.3 Real and imaginary parts of the double turning point r0 versus Ω0/f for different azimuthal wavenumbers: m = 0 (black), m = 1 (blue) and m = 2 (red; panels a and b). Gray-shaded areas represent the centrifugally stable regime. Panel c displays the movement of the double turning point r0 in the complex plane as m changes for Ω0/f= 5 (black) and Ω0/f= −2 (blue). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.