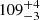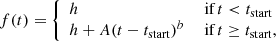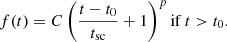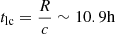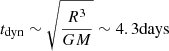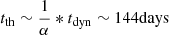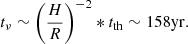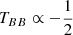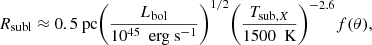| Issue |
A&A
Volume 672, April 2023
|
|
|---|---|---|
| Article Number | A167 | |
| Number of page(s) | 25 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202245078 | |
| Published online | 19 April 2023 | |
Discovery of the luminous X-ray ignition eRASSt J234402.9−352640
I. Tidal disruption event or a rapid increase in accretion in an active galactic nucleus?⋆
1
Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
e-mail: dhoman@aip.de
2
Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, ul. Bartycka 18, 00-716 Warszawa, Poland
3
University of California, San Diego, Center for Astrophysics and Space Sciences, MC 0424, La Jolla, CA 92093-0424, USA
4
Department of Physics, Washington University in St. Louis, One Brookings Drive, St. Louis, MO 63130, USA
5
Dr. Karl Remeis-Observatory & ECAP, Friedrich-Alexander-Universität Erlangen-Nürnberg, Sternwartstr. 7, 96049 Bamberg, Germany
6
Lehrstuhl für Astronomie, Universität Würzburg, Emil-Fischer-Straße 31, 97074 Würzburg, Germany
7
Wayne State University, Department of Physics & Astronomy, 666 W. Hancock St, Detroit, MI 48201, USA
8
Max-Planck-Institut für extraterrestrische Physik, Gießenbachstraße, 85748 Garching, Germany
9
South African Astronomical Observatory, PO Box 9 Observatory, Cape Town 7935, South Africa
10
Department of Astronomy, University of Cape Town, Private Bag X3, Rondebosch 7701, South Africa
11
Department of Physics, University of the Free State, PO Box 339 Bloemfontein 9300, South Africa
12
Department of Physics and Astronomy, University of Padova, Via F. Marzolo 8, 35131 Padova, Italy
13
Las Campanas Observatory – Carnegie Institution for Science, Colina el Pino, Casilla 601, La Serena, Chile
14
Astrophysics Science Division, NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
15
Astronomical Observatory, University of Warsaw, Al. Ujazdowskie 4, 00-478 Warsaw, Poland
16
Graduate School of Science and Engineering, Saitama University, 255 Shimo-Okubo, Sakura-ku, Saitama City, Saitama 338-8570, Japan
17
Center for Astrophysics, Harvard & Smithsonian, 60 Garden St, Cambridge, MA 02138, USA
Received:
28
September
2022
Accepted:
8
February
2023
In November 2020, a new, bright object, eRASSt J234402.9−352640, was discovered in the second all-sky survey of SRG/eROSITA. The object brightened by a factor of at least 150 in 0.2–2.0 keV flux compared to an upper limit found six months previous, reaching an observed peak of 1.76−0.24+0.03 × 10−11 erg cm−2 s−1. The X-ray ignition is associated with a galaxy at z = 0.10, making the peak luminosity log10(L0.2−2 keV/[erg s−1]) = 44.7 ± 0.1. Around the time of the rise in X-ray flux, the nucleus of the galaxy brightened by approximately 3 mag. in optical photometry, after correcting for the host contribution. We present X-ray follow-up data from Swift, XMM-Newton, and NICER, which reveal a very soft spectrum as well as strong 0.2–2.0 keV flux variability on multiple timescales. Optical spectra taken in the weeks after the ignition event show a blue continuum with broad, asymmetric Balmer emission lines, and high-ionisation ([OIII]λλ4959,5007) and low-ionisation ([NII]λ6585, [SII]λλ6716,6731) narrow emission lines. Following the peak in the optical light curve, the X-ray, UV, and optical photometry all show a rapid decline. The X-ray light curve shows a decrease in luminosity of ∼0.45 over 33 days and the UV shows a drop of ∼0.35 over the same period. eRASSt J234402.9−352640 also shows a brightening in the mid-infrared, likely powered by a dust echo of the luminous ignition. We find no evidence in Fermi-LAT γ-ray data for jet-like emission. The event displays characteristics of a tidal disruption event (TDE) as well as of an active galactic nucleus (AGN), complicating the classification of this transient. Based on the softness of the X-ray spectrum, the presence of high-ionisation optical emission lines, and the likely infrared echo, we find that a TDE within a turned-off AGN best matches our observations.
Key words: X-rays: individuals: eRASSt J234402.9−352640 / accretion, accretion disks / galaxies: active
Full Table 4 is only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/672/A167
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
All massive galaxies are thought to harbour a supermassive black hole (SMBH) at their centre (Sołtan 1982). A SMBH can power strong emission through accretion of surrounding matter, both on long timescales and in shorter-lived outbursts. Active galactic nuclei (AGN) represent the more continuous form of accretion and have a strong impact on the evolution of their host galaxies through various feedback mechanisms (e.g. Kormendy & Ho 2013; Heckman & Best 2014). Variability is inherent to AGN emission, across the electromagnetic spectrum and on all timescales. X-ray observations show that between 1% and 4% of local galaxies host an AGN (e.g. Haggard et al. 2010; Birchall et al. 2022). It is likely that active accretion is intermittent over a galaxy’s lifetime; however, AGN duty cycles lack strong observational constraints (Novak et al. 2011; Schawinski et al. 2015; Shen 2021). Stochastic (i.e. aperiodic) optical continuum variability in AGN has been found to be of the order of 10–20% of the flux on a timescale of months (e.g. Kelly et al. 2009; MacLeod et al. 2013), increasing to 2–3 times the flux on a timescale of years (e.g. Uttley et al. 2003; Breedt et al. 2009, 2010). More extreme variability has also been observed, including large outbursts in both X-ray and optical emission (e.g. Brandt et al. 1995; Shappee et al. 2014; Trakhtenbrot et al. 2019a). In recent years, studies of large samples of AGN have revealed that optical variability up to 1 mag is not uncommon and can be found in up to 50% of AGN on a timescale of a decade (Lawrence et al. 2016; Rumbaugh et al. 2018; Graham et al. 2020). Whether strong variability is the extreme end of ‘regular’ AGN variability, or is representative of a different type of process, such as a change in accretion mode, is still an open question (e.g. Ruan et al. 2019).
An inherently more short-term SMBH accretion event is caused by the tidal disruption of a star followed by the subsequent fallback and accretion of the debris, referred to as a tidal disruption event (TDE; Rees 1988; Phinney 1989). These events were initially predicted to be observed as large-amplitude, ultra-soft X-ray flares originating from galactic nuclei (Rees 1988). The first such candidates were observed in the Röntgensatellit (ROSAT; Truemper 1992) All-Sky survey (e.g. Bade et al. 1996; Grupe et al. 1999; Komossa & Bade 1999; Komossa & Greiner 1999; Greiner et al. 2000; Donley et al. 2002). In recent years, the majority of TDE candidates have been found through optical surveys (e.g. van Velzen et al. 2011, 2021; Gezari et al. 2017; Hung et al. 2017). Optically selected TDEs are characterised by light curves that show a rapid rise in brightness followed by a relatively smooth decay. Follow-up optical spectroscopy of TDE candidates generally reveals transient, blue continua (blackbody temperatures ∼104 K), and in some cases broad emission lines (e.g. Balmer, He II, and/or Bowen lines; Charalampopoulos et al. 2022, and references therein). As the number of TDE candidates has grown, it has become increasingly clear that these systems show a broad range of observed behaviours, such as the presence or absence of optical emission lines (Leloudas et al. 2019; van Velzen et al. 2021), the presence or absence of radio emission (Alexander et al. 2020), the presence or absence of X-ray emission (Holoien et al. 2016; Auchettl et al. 2018), as well as differing rates of decay in the post-peak phase (van Velzen et al. 2021), and a candidate with a double-peaked optical light curve (Malyali et al. 2021; Chen et al. 2022).
Due to the broad phenomenological range in both AGN variability and TDEs, distinguishing these different classes of events has proven difficult in many cases (Merloni et al. 2015; Auchettl et al. 2018). Fundamentally, they both represent a rapid change in the accretion rate, ‘powering up’ the central engine, although the precise accretion processes could differ among TDEs (for a recent review, see Gezari 2021). In recent years, a number of studies have been published concerning strong, ‘flaring’ ignitions in AGN, associating them with either extreme AGN variability (e.g. Gezari et al. 2017; Yan et al. 2019; Trakhtenbrot et al. 2019b; Frederick et al. 2021) or with a TDE (e.g. van Velzen et al. 2016a; Blanchard et al. 2017; Liu et al. 2020; Brightman et al. 2021). A combination of AGN-like and TDE-like features in other objects has led to their identification as transient events within AGN (Ricci et al. 2020; Holoien et al. 2022), or has made a definitive classification impossible without additional data (e.g. Neustadt et al. 2020; Malyali et al. 2021; Hinkle et al. 2022).
The Extended ROentgen Survey with an Imaging Telescope Array (eROSITA; Predehl et al. 2021), aboard the Spectrum Roentgen/Gamma (SRG) spacecraft (Sunyaev et al. 2021), has greatly expanded the search for transients in the X-ray sky. A number of new TDE candidates have already been detected by SRG/eROSITA (Sazonov et al. 2021; Malyali et al. 2021). In this paper, we report on the initial discovery and multi-wavelength follow-up of eRASSt J234402.9−352640 (hereafter J234402), which was detected in the second eROSITA all-sky survey. A significant increase in the flux from the same source measured by Gaia on 2020-10-14 was reported by Hodgkin et al. (2020) in TNS Astronomical Transient Report (#85552). In this paper we present our initial findings and conclusions, as we pursue ongoing follow-up of this object. The data and results presented here pertain to the period up to February 2021, when further observations of the object had to be paused due to Sun block. We will present the results of the resumed, post-Sun-block observations in follow-up work (Malyali et al., in prep.).
The paper is structured as follows. In Sect. 2 we present our X-ray observations. In Sect. 3 we describe our datasets in other wavebands: Sect. 3.1 covers the available UV, optical, and IR photometry; Sect. 3.2 provides an overview of our optical spectroscopic follow-up; in Sect. 3.3 we describe our analysis of Fermi-LAT γ-ray data. We discuss our results in Sect. 4, within the context of extreme AGN variability and a TDE. We summarise our conclusions in Sect. 5. Throughout this paper, we assume a flat cosmology with H0 = 70 km s−1 Mpc−1, ΩM = 0.3, and ΩΛ = 0.7 (Hinshaw et al. 2013). In this cosmology, 1″ corresponds to 1.8 kpc at the redshift of eRASSt J234402−352640 (z = 0.10; light travel time 1.3 Gyr), where the associated luminosity distance is 460 Mpc. All uncertainties represent a 1σ (68.3% for a single parameter) confidence interval unless stated otherwise.
2. X-ray observations and analysis
Following detection by eROSITA, X-ray-follow-up observations of J234402 took place between November 2020 and January 2021, after which the object was positioned too close to the Sun for follow-up. The follow-up comprised a Swift monitoring programme, an XMM-Newton pointing, and an extended NICER observation covering 18 days. The combined dataset is presented in Fig. 1. For the analysis in this paper, we use the following parameters and measurements unless otherwise stated: a Galactic total (H I + H2) hydrogen column density NH = 1.2 × 1020 cm−2 (Willingale et al. 2013), the cosmic abundances of Wilms et al. (2000), and the photoelectric absorption cross sections provided by Verner et al. (1996).
 |
Fig. 1. Overview of X-ray data collected on J234402. The light curve starts from the detection of the ignition event with eROSITA in November 2020. The 3σ upper limit of the eRASS1 scan in May 2020 was 1.1 × 10−13 erg cm−2 s−1 (log10(LX/[erg s−1]) = 41.8). The flux evolution over time is significant, showing both an overall decrease and large fluctuations on shorter timescales. To illustrate the magnitude of the variability on the shortest timescales, the light curves of individual eRASS2 scans and for the XMM-Newton EPIC-pn data, binned to 500s, are included in insets. The vertical extent of the grey boxes around the eROSITA and XMM-Newton markers shows the size of the y-axes of the insets within the larger plot. In the inset of the eROSITA light curve the horizontal axis marks the time in ks since MJD 59181.75, and in the inset of the XMM-Newton light curve it marks the time in ks since MJD 59205.44. On the right vertical axis we show the log10(LX/[erg s−1]) values associated with the observed flux. To calculate these values, we made use of the best-fit model (2BB, Sect. 2.2). |
We checked the Second ROSAT Source Catalogue (2RXS; Boller et al. 2016) for a counterpart that could have been found between June 1990 and July 1991 during the ROSAT All-Sky Survey. No point source is detected within a 15 arcmin radius of J234402. The average flux upper limit for inclusion in 2RXS is estimated by Boller et al. (2016) to be approximately 10−13 erg cm−2 s−1 in the 0.1–2.0 keV band. For a redshift of 0.10 and an assumed photon index of 2.0, we find an upper limit of L0.1 − 2keV ∼ 2 × 1042 erg s−1 for the ROSAT epoch. The limit on the absorbed luminosity indicates there was no strong X-ray emission – which would have been indicative of an AGN – at the time of the ROSAT survey. No serendipitous archival observations of the target were found for XMM-Newton, Swift, or Chandra.
2.1. SRG/eROSITA
The X-ray ignition in J234402 was detected by eROSITA through a comparison of sources detected in the first and second eROSITA All-Sky Survey (eRASS1 and eRASS2). The eROSITA position of the event is RA, Dec = 23:44:02.9, −35:26:39.4 (J2000) with a total uncertainty of 1.0 arcsec, where we have included a 0.6 arcsec systematic uncertainty. We identified a point source at a distance of 2.2 arcsec with coordinates RA, Dec = 23:44:02.9, −35:26:41.6 in the Gaia eDR3 catalogue (Gaia Collaboration 2021) as the optical counterpart. The eROSITA data presented in this paper were reduced using eSASSusers_211214 (Brunner et al. 2022) and we made use of HEASOFT v6.28 (XSPEC 12.11.1).
The object was not detected in eRASS1 (24–25 May 2020), with a 3σ sensitivity limit of f3σ, 0.2 − 2 keV = 1.1 × 10−13 erg cm−2 s−1. However, in eRASS2 (27–29 November 2020) the source was discovered with a 0.2–2 keV flux of 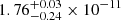 erg cm−2 s−1. The eROSITA fluxes are listed in Table 1, which provides an overview of all X-ray fluxes measured in our follow-up programme. A single eRASS epoch comprises multiple scans that each last approximately 40 s, covering the same sky position at intervals of 4 h. As the satellite was affected by a technical issue, there are only three individual scans for which we could extract flux data within the eRASS2 epoch. The values for the individual scans are shown in Table 2. The eRASS2 fluxes show remarkable variability, dropping by ∼1/3 over 4 hours between the first and second scan, with a 4σ significance for this change.
erg cm−2 s−1. The eROSITA fluxes are listed in Table 1, which provides an overview of all X-ray fluxes measured in our follow-up programme. A single eRASS epoch comprises multiple scans that each last approximately 40 s, covering the same sky position at intervals of 4 h. As the satellite was affected by a technical issue, there are only three individual scans for which we could extract flux data within the eRASS2 epoch. The values for the individual scans are shown in Table 2. The eRASS2 fluxes show remarkable variability, dropping by ∼1/3 over 4 hours between the first and second scan, with a 4σ significance for this change.
Overview of the X-ray fluxes measured for J234402.
Fluxes for individual scans of eRASS2 epoch.
The combined spectrum for the eRASS2 observation is shown in Fig. 2. The spectrum is soft, with most counts below 0.5 keV. We fitted the eRASS2 spectrum with a range of models and find that a model consisting of two blackbodies modified by Galactic absorption (TBABS*(ZBBODY+ZBBODY)) provides the best fit, with χ2/d.o.f. = 140.7/108. The blackbody temperatures in this fit are 100 ± 5 eV and 38 ± 4 eV. The best-fit model is included in Fig. 2.
 |
Fig. 2. Binned eROSITA spectrum of J234402. The spectrum for the eRASS2 observation (28–29 November 2020) is very soft, a characteristic confirmed in all our X-ray observations. Included in red (solid line) is the best-fit model, consisting of two redshifted black bodies (dotted lines), corrected for Galactic absorption. |
2.2. XMM-Newton
The XMM-Newton observation of J234402 took place on 22 December 2020 (MJD 59203), with an exposure of 14 ks. The data were reduced with the SAS package (18.0.0) and HEASOFT (v6.24) using the standard settings for point sources. Small window mode was used and pile-up does not affect the observations. We created a standard source and background spectrum for each of pn, MOS1, and MOS2. We found total good time intervals of 8.1 ks (∼34 000 pn net counts). The spectra were grouped with a minimum binning of 20 counts per bin. For the pn, we extracted single (pattern 0) and double (patterns 1–4) spectra separately (hereafter pn0 and pn14), as the double-events spectrum has calibration issues below 0.4 keV due to the use of small window mode.
No significant detection above 1.2 keV was made in any camera. We therefore extracted the spectra in the range 0.2–1.2 keV for pn0, MOS1, and MOS2, and in 0.4–1.2 keV for pn14. The counts show significant variability, dropping by a factor of two over ∼3 h. We quantify the variability using the fractional rms variability amplitude (Vaughan et al. 2003), and find Fvar = 20.2 ± 0.9%. Although the X-ray flux changed significantly over the course of the XMM-Newton exposure, we do not detect any significant changes in the X-ray spectrum over this same period.
We tested a range of X-ray spectral models using the nested sampling package MULTINEST v.3.10 (Skilling 2004; Feroz et al. 2009) via the Bayesian X-ray Analysis and PyMultinest packages for XSPEC (BXA, version 3.31, using Xspec version 12.10.1; Buchner et al. 2014). We used default arguments for MULTINEST (400 live points and a sampling efficiency of 0.8), and assumed uniform or log-normal initial prior distributions. We used the 5th and 95th percentiles of the posterior distribution for Bayesian fits. We report Bayesian evidence Z, to compare goodness of fit between models1.
Multiple one-component models yield poor fits, but reveal both the extreme softness of the spectrum and its strong convex spectral curvature. Physically motivated models based on disk emission, such as DISKPBB and COMPTT achieve reasonable results, provided the seed photon temperature and (for COMPTT) the electron temperature is of the order of 50–100 eV. The overall best-fitting model is the purely phenomenological log-parabola (ZLOGPAR). The best-fitting physically motivated model is a double blackbody (ZBBODY+ZBBODY, 2BB), with kBT1 = 53 ± 2 eV and 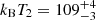 eV. We also tested for the presence of ionised absorption, by making use of the WARMABS model. Combinations WARMABS*ZBBODY and WARMABS*POWERLAW resulted in poor fits, as the absorption could not account for the spectral curvature. Combinations of WARMABS with well-fitting models such as ZLOGPAR resulted in a negligible improvement in goodness of fit. More complex models including Comptonised components also yield acceptable fits, with temperatures in the same order of magnitude as 2BB. An overview of our fitting results is shown in Table A.1.
eV. We also tested for the presence of ionised absorption, by making use of the WARMABS model. Combinations WARMABS*ZBBODY and WARMABS*POWERLAW resulted in poor fits, as the absorption could not account for the spectral curvature. Combinations of WARMABS with well-fitting models such as ZLOGPAR resulted in a negligible improvement in goodness of fit. More complex models including Comptonised components also yield acceptable fits, with temperatures in the same order of magnitude as 2BB. An overview of our fitting results is shown in Table A.1.
Based on our fitting results, it is not clear if one- or two-component models are generally preferred. However, the spectral data seem to lack an obvious ‘inflection’ point indicating distinct emission components, and all of the two-component fits have components blending slowly into each other. Of the models based on physical parameters, we find that the 2BB model provides the best fit in relation to the number of free parameters. We therefore adopt 2BB as our optimal model. An unfolded model spectrum for our dual-blackbody model is plotted in Fig. 3. The 0.2–2.0 keV model flux for the full observation is 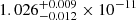 erg cm−2 s−1 in our best-fit model (1LOGPAR). Using 2BB we find a very similar value.
erg cm−2 s−1 in our best-fit model (1LOGPAR). Using 2BB we find a very similar value.
 |
Fig. 3. Unfolded model spectrum from XMM-Newton. The spectrum was unfolded using the best-fit dual blackbody model (2BB), with blackbody temperatures of 53 ± 2 eV and |
2.3. Swift-XRT
The Neil Gehrels Swift Observatory (Gehrels et al. 2004) observed J234402 on five occasions (PI A. Malyali): 20 and 27 December 2020, followed by 6, 18, and 22 January 2021 (MJDs 59203, 59210, 59220, 59232, and 59236). Each exposure lasted approximately 1 ks. We present spectral data from the X-ray Telescope (XRT) and photometry data from the Ultraviolet/Optical Telescope (UVOT; the UV data are described in Sect. 3.1.4). All XRT observations used Photon Counting mode. Event files were calibrated using XRTPIPELINE in HEASOFT v.6.28 and the latest calibration files. Source spectra were extracted from a circular region of radius 20 pixels (47″). Backgrounds were extracted from annular regions with inner and outer radii 30 and 36 pixels (70″ and 84″), which were selected to be free from background sources. We used the latest response matrix in the calibration database. Ancillary response files were generated using XRTMKARF.
We fitted the Swift-XRT spectra in the range 0.2–2.0 keV using XSPEC, making use of Cash statistics, due to the relatively low photon count. The spectra were re-binned to a minimum of 15 counts per bin. We fitted a single power-law, a single blackbody, and a dual blackbody (2BB). For 2BB we kept the temperatures and the ratio of the normalisations frozen at the best-fit values of the XMM-Newton EPIC-pn fit. Untying the normalisations yielded a negligible improvement in goodness of fit. For the single-power-law and single-blackbody fits to the observation of MJD 59232 the low number of counts required us to freeze the values Γ and kBT, respectively, to the average values from the fits to the other four XRT spectra. The derived fluxes are included in Table 1, and a full overview of the results of the model fits is presented in Table A.2. The XRT data do not allow us to significantly prefer one model over another. For consistency, we derived the 0.2–2.0 keV Swift-XRT fluxes using the best-fit 2BB model.
2.4. NICER
J234402 was observed with NICER in the period covering 5 January 2021 to 22 January 2021 (MJD 58853–58870). Due to high levels of optical loading, the final good time intervals where the background could be reliably subtracted cover the period 6 to 11 January (MJD 58854–58859, see Appendix A.3 for further discussion). We made use of the NICER reduction pipeline to produce the standard RMF, ARF, and background files. We fitted the NICER data using XSPEC v12.12.0, which is part of HEASOFT v6.28. The data have been re-binned to a minimum of 25 counts per bin and we use χ2-statistics. The spectra were fit in the 0.3–2 keV energy range.
2.4.1. NICER light curve
The counts light curve for the energy band 0.3–2 keV is presented in Fig. 4. The source clearly shows strong variability on a timescale of days. We find Fvar = 55.4 ± 0.5%. Although the light curve shows a pattern of repeated ups and downs, we would caution against an interpretation as a (quasi-)periodic oscillation based on these data alone. There is extensive literature on the appearance of temporary sinusoid-like signals in data generated by stochastic red noise processes, as well as mistaken claims of detection of periodic signals (for a discussion, see e.g. Press 1978; Vaughan et al. 2016). We note that we do not exclude the possibility of a periodic signal in the NICER data, but stress that the current sampling and duration do not allow for a claim of detection, especially given that such a claim would be based on observing a very small number of putative cycles.
 |
Fig. 4. NICER light curve and hardness ratio of J234402. Top: 0.3–2 keV NICER light curve. The light curve shows significant variability on a timescale of days. The sharp turns up and down are consistent with the rapid variability observed in the XMM-Newton and eROSITA data. The dashed line indicates the cut-off between the low-state and high-state intervals at 3.78 counts s−1, as discussed in Sect. 2.4.2. Bottom: hardness ratio (HR) in NICER light curve. We define the HR using the 0.3–0.5 keV and the 0.5–2 keV count rates (R0.3 − 0.5 and R0.5 − 2, respectively), as defined in the text. We detect no significant change over time. |
2.4.2. NICER spectra
Single-model fits prove to be poor matches to the NICER data. A single blackbody results in χ2/d.o.f. = 644.6/136 and a single power-law in χ2/d.o.f. = 1643.5/136. Similarly, a double-power-law proves a very bad fit, with strong residuals in both the high- and low-energy ranges. A moderately good fit is achieved with a combination of a blackbody and a power-law, with χ2/d.o.f. = 179.3/134. However, the best fit is found with 2BB, which results in χ2/d.o.f. = 144.2/134, with blackbody temperatures of kBT1 = 105 ± 3 eV and kBT2 = 59 ± 1 eV. This best-fit model and the spectral data are shown in Fig. 5. Using 2BB, we find the highest flux in the 0.2–2.0 keV light curve to be 1.10 × 10−11 erg cm−2 s−1.
 |
Fig. 5. Spectrum from NICER for the cumulative observation time. The best-fit double-blackbody model (2BB) is shown in red, with the two blackbody components shown as dashed black and blue lines. The residuals of our best-fit model are shown in the bottom panel. |
To investigate whether the strong changes in count rate over time correlate with spectral changes, we first considered whether there is any evolution in the spectral hardness ratio (HR) over time. We defined the HR using the 0.3–0.5 keV count rate (L) and the 0.5–2 keV count rate (H) as (L–H)/(L+H). Epochs with a count rate below zero were excluded from this calculation. We find no significant evolution in the HR over time. Next, we split the combined NICER data up and compare the spectra for the different subsections. Fitting results are shown in Table 3. The first split is by time: we divide the integrating period in two at MJD 59222.80, such that each sub-spectrum has approximately the same number of counts, and we extract the spectrum for the first and the second half. Fitting both spectra with our 2BB model (only redshifts and Galactic NH frozen), we find no significant differences in the fitting parameters. Secondly, we split our data into periods of high and low count rate. We define the ‘high state’ as those periods where the count rate in the 0.3–1 keV range is greater than 3.78 ct s−1 and the ‘low state’ as the periods where the count rate is below this value. We find a slightly higher temperature for one of the blackbodies in the high count spectrum; however, the difference is less than 2σ.
Fitting parameters and goodness-of-fit values for X-ray spectral fits to subsets of NICER data.
Stronger evidence for spectral changes was found when we fixed the BB-temperatures to the values found for the XMM-Newton spectrum and only let the normalisations vary: the fit for the high-state NICER data is considerably better than for the low-state data. Comparing the goodness-of-fit for the models with BB-temperatures fixed to the XMM-Newton values with the NICER best-fit models (for the high and low state, respectively), we find Δχ2 = 23.54 for the high-state data and Δχ2 = 57.02 for the low state. We note that although the XMM-Newton data correspond to a significantly higher flux level than the average of the NICER data, the flux level around the peaks in the NICER emission is comparable to the XMM-Newton level (Fig. 1). Next, we compared the high-state and low-state spectra by freezing the value of the BB-temperatures to those in the low-state best-fit model and fitting this model to the high state data. We find a value of Δχ2 = 70.76, compared to the high-state best fit, a significant difference. The changes in X-ray luminosity therefore appear tied to spectral changes. This agrees with the trend visible in the Swift XRT data (Table A.2), which show higher kBTBB for higher flux levels.
3. Follow-Up at other wavelengths
3.1. Photometry
We present an optical photometric dataset that combines publicly available data and follow-up observations obtained by our team. These data allow us to study the optical evolution of J234402 at high cadence. Optical imaging shows that the ignition is in the northern part of a group of four galaxies (see Fig. B.3). In the following sections we discuss the different datasets making up our photometric data. We correct all our photometry for Galactic reddening using the extinction curve from Fitzpatrick (1999) and AV = 0.0386, which we base on the dust map and filter-band corrections provided by Schlafly & Finkbeiner (2011)2. Our combined optical light curve is shown in the lower panel of Fig. 6 and we present our optical dataset in tabular form in Table 4. All data are reported in AB magnitudes (Oke 1974).
 |
Fig. 6. Optical and infrared photometric data on J234402 over the past five years. The top panel show the NEOWISE-R data for the W1 and W2 infrared bands and the bottom panel shows the optical light curve based on a combination of public survey data and follow-up observations obtained by our team. All measurements have been corrected for Galactic extinction. The optical light curve shows a relatively quiescent state interrupted by a sharp flare, followed by a plateau and subsequent decay. The data are not host subtracted. The downward arrows represent 3σ upper limits in the ATLAS dataset. All data include statistical uncertainties. For most points on our dataset, the statistical uncertainties are too small to be visible in this plot. |
Overview of the optical photometric data obtained for J234402.
3.1.1. Public optical surveys
We obtained publicly available photometric data from the ATLAS survey. The ATLAS data were taken with filters cyan (420–650 nm) and orange (560–820 nm) and were extracted by running forced photometry on the available reduced images (Tonry et al. 2018; Smith et al. 2020). Observations with S/N < 3 do not provide a reliable magnitude and are represented as 3σ upper limits. We made use of ATLAS difference photometry, in which the pre-ignition flux (dominated by the host galaxy) has been subtracted. As the o and c filters are not included in the filter-specific de-reddening corrections presented by Schlafly & Finkbeiner (2011), we made our own estimate of the attenuation for these filters. We simulated a reddened signal, based on a flat spectrum, and convolved this with the filter transmission curves. We took the ratios of the original (non-attenuated) and reddened signals as an approximation of the flux lost to absorption. The corrections applied to the o and c magnitudes in our dataset are 0.027 and 0.039 mag, respectively. To improve the signal-to-noise, the ATLAS light curvewere re-binned to combine data from single nights, using a weighted average to find the flux and errors. We subsequently converted to magnitudes.
For the Gaia data (Gaia Collaboration 2016), we extracted the G-band magnitudes from the Gaia Alerts web server3. The G-band functions as a white light filter (∼300–1100 nm). To create the G-band light curve, photometric measurements are averaged over the period in which Gaia’s FOV transits the object, following Gaia’s scanning pattern. The photometry made available on the alerts server is based on a preliminary calibration. Using the same procedure as for the ATLAS filters, we find a reddening correction of 0.03 for the GaiaG-band.
The Gaia and ATLAS light curves show that the ignition in November 2020 is a clear break with the level of output in the preceding years. However, both light curves show a low level of variability (< 0.3 mag) prior to the ignition, which warrants closer inspection. Of particular interest in the ATLAS light curve are the apparent peaks around MJD 58700 and 58840. We used the unbinned ATLAS data to investigate whether any (near-)contemporaneous ATLAS and Gaia data show a similarity in trend around these peaks. There is no clear similarity in the light curves around these times, or indeed elsewhere in the light curve. We therefore investigate the likelihood that the pre-ignition changes are dominated by observational uncertainties.
In the case of the ATLAS data, we take into account that the observations were made with relatively small, terrestrial telescopes and that variable seeing will therefore lead to changes in the contribution of the host galaxy to the reported magnitudes for the nucleus. The amplitude of the peaks in the ATLAS light curve lies within the range of the seemingly random scatter. Using the ATLAS difference photometry, the two features mentioned above do not appear significant. The Gaia G-band measurements are based on PSF photometry (Evans et al. 2018) and as the observations are not affected by seeing, we expect that changes in host contribution are not a significant contribution to the observed scatter. However, an investigation of DR2 photometry (Evans et al. 2018; Arenou et al. 2018) found that spurious outliers caused by nearby sources, as well as by problems with background calibration, are likely to be included in Gaia’s epoch photometry. These uncertainties are a particular concern for fainter sources (G > 17). This means that based on our dataset we cannot make a conclusive statement about the presence of low-level variability prior to the ignition.
3.1.2. New optical follow-up
J234402 was monitored with the 0.4m PROMPT6 telescope, operated as part of Skynet (an introduction to this network is provided in Martin et al. 2019), using Johnson B and R filters. These observations provided nine additional epochs to the light curve. The images were reduced in the standard manner (bias correction, flat-fielding) and the fluxes were extracted using 3 arcsec apertures, using 20–25 arcsec annuli to establish the background.
3.1.3. XMM-Newton Optical Monitor
The XMM-Newton Optical Monitor (OM) observed J234402 with five exposures, simultaneous with the X-ray observation. Each observation was made both in image and fast mode, using the UVM2 filter (effective wavelength 231 nm). The first two exposures were 1200 s each; the final three were 2500 s each. We reduced the data using OMICHAIN and OMFCHAIN, which are part of XMM_SAS. These routines perform flat-fielding, source detection, and aperture photometry for each individual exposure. They also combine all images into a mosaiced image and perform source detection and aperture photometry on the mosaiced image. The resulting values are corrected for detector dead time.
We verified that the source was detected in each exposure, confirmed that the source was not too close to the edge of the window in fast mode, and established that there were no obvious imaging artefacts in any image mode exposure. We find that the mean UVM2 OM count rate is 1.65 ct s−1, which corresponds to a flux density of 4.23 × 10−15 erg cm−2 s−1 Å−1 and a magnitude of 16.07. To explore variability down to timescales of 800 s, we made use of the fast mode data. The optical variability is significantly less than the variability of J234402 in X-rays (see Fig. A.1). We find Fvar of < 1.0% and 20.2 ± 0.9%, for optical and X-rays, respectively.
3.1.4. Swift-UVOT
We observed J234402 with UVOT in four filters in each of the five Swift observations: U, UVW1, UVM2, and UVW2 (central wavelengths 3465, 2600, 2246, and 1928 Å, respectively). Aperture photometry was performed using the ASI SSDC’s Multi-Mission Interactive Archive online tool4. Using this tool we derive aperture-corrected, background-subtracted, and Galactic extinction-corrected flux densities. Source extraction was performed using UVOTDETECT and CALDB version 20201026. We extracted source counts from a radius of 5 arcsec around the target and the background from an annulus with inner and outer radii of 27.5 and 35 arcsec, respectively. AB magnitudes were calculated using the zero points from Breeveld et al. (2011). We corrected for potential instrumental variability using two standard stars in the FOV (see Appendix B.1.2 for further details). The corrected magnitudes and flux densities are listed in Table 5.
Swift-UVOT magnitudes for J234402.
The UV brightness in all filters drops over the course of our monitoring, in line with the decreasing X-ray flux. At the time of the first Swift observation, the optical fluxes were also in decline. Over the course of the Swift observations, covering approximately 33 days, the UV fluxes decrease by an average of ∼0.35. The decrease in flux was more pronounced in the X-rays as the 0.2–2 keV flux dropped ∼0.45 over the same period. The UV fluxes have not been corrected for the contribution from the host galaxy; however, we expect this contribution to be stable on a timescale of weeks. In all five observations, the UVOT magnitudes are considerably higher than the archival UV values we find in the Revised Catalogue of GALEX UV Sources (Bianchi et al. 2017). In the NUV and FUV bands, with effective wavelengths of 1516 Å and 2267 Å, the source was observed in 2005 as part of the all-sky imaging survey at 19.94 ± 0.07 and 20.83 ± 0.16 mag, respectively. This is consistent with the archival limits we find in the X-rays and optical bands: J234402 was significantly less luminous in the years prior to the ignition event.
3.1.5. WISE
We obtain infrared photometry from the NEOWISE-R mission (Wright et al. 2010; Mainzer et al. 2014), using the NASA IRSA archives. The WISE bands W1 and W2 are centred on 3.368 and 4.618 microns, respectively. We use the fluxes generated by the automated forced photometry pipeline. WISE clearly resolves the northern and southern sources. Coordinate matching for the NEOWISE-R extraction was limited to a 5 arcsec radius. The fluxes are binned to ∼180 days, to match the satellite’s scanning pattern, and converted to magnitudes. We applied a sigma-clip to the flux measurements in each bin to remove a small number of clearly erroneous flux entries, after which we calculated the error-weighted mean flux. The resulting magnitudes are included in the top panel of Fig. 6.
The WISE light curves show a distinct brightening, by approximately 0.3 magnitude in W1 and W2, around the time of the ignition event. We investigated the significance of this change by calculating the standard deviation of the fluxes prior to the ignition event and comparing this value to the size of the increase. We find that the standard deviation is 68.8 ± 19.6 for the W1 band and 57.1 ± 20.1 for the W2 band. The fluxes are in raw counts, following background subtraction, and we used a bootstrap Monte Carlo method to estimate the uncertainties. Compared to the average flux over the pre-ignition period, the flux increased by 280 counts and 131 counts around the time of ignition for W1 and W2, respectively, representing changes by 4.1σ and 2.3σ. We therefore believe that the increase in infrared flux is not associated with the ‘normal’ stochastic variability exhibited by J234402 prior to the ignition event, but rather that the increase in IR is connected to the increases in X-ray, UV, and the optical.
3.1.6. Light curve properties
We made use of the ATLAS difference photometry to find the time of peak and to constrain the slope of the rise. As the pre-ignition flux has been subtracted, we consider the difference photometry to represent the flux of the brightened nucleus only. A detailed view of the host-corrected ATLAS data around the time of the ignition is shown in Fig. 7. We mark three distinct phases in the light curve: (I) the sudden turnover from the quiescent state into a sharp rise; (II) a temporary flattening in the brightening, lasting approximately 30 days, followed by a renewed increase in flux leading to the peak output; (III) decay after the peak, lasting until the period of Sun block. We fitted the data in the three phases separately and derived key parameters that describe the early evolution of J234402’s light curve.
 |
Fig. 7. Evolution of optical output in ATLAS o-band and c-band filters. The data are ATLAS differential photometry and the view focuses on the time around the ignition event. All data points include statistical errors. We distinguish three phases in the first months of the ignition event’s light curve: a sharp initial rise, a temporary levelling off & re-brightening, and decay. The demarcations between the phases are shown as grey vertical lines. We compare the data in these three phases with simple power-law models (Eqs. (1) and (2)). The initial rise is fit to the o-band data only and the result is shown in dashed green, with 1σ error margins shown as shaded regions. We include the best-fit rising power-law in phase II (dashed black) primarily to guide the eye, as the light curve data proved to sparse for a well-constrained fit. For the decay period, we separately fit the o-band and the c-band data, and results are shown as the red (dotted) and blue (dot-dashed) lines, respectively. |
First we established the point of turnover, where the initial rise halts temporarily. As the sampling of the c-band data is too sparse over this period, we performed this fit for the o-band data only. We fitted the flux data with a parabola, matching the rapid rise, quick turnover, and the apparent temporary decrease in flux. As the halt in the brightening is quite brief, we fitted our parabola in a relatively narrow range, similar to the procedure in for example Holoien et al. (2022) and Hinkle et al. (2022), fitting between MJD 59111 and 59129. We estimated the error on our fit using a Monte Carlo method. We created 104 iterations of our light curve, where the flux in each bin was shifted by a random value drawn from a Gaussian distribution with σ equal to the measurement uncertainty of the flux. We fitted each of these iterations and took the median values to be our best-fit parameters. We took the 16th and 84th percentiles of the parameter distributions as the uncertainties. Using this method we find tpeak, 1 = MJD 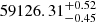 . This first ‘peak’ is marked with the left grey, vertical line in Fig. 7. It forms the delineation between Phase I and Phase II.
. This first ‘peak’ is marked with the left grey, vertical line in Fig. 7. It forms the delineation between Phase I and Phase II.
Next, we fitted the early-time rise of the light curve using all o-band data up to tpeak, 1. We modelled the flux as constant prior to the ignition at tstart and as a power law afterwards:
where t is in days and the free parameters in our least-squares fit are the constant level h, the normalisation A, and the power-law index b. The uncertainties were estimated in the same manner as we did for tpeak, 1. We find 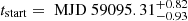 ,
, 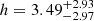 μJy,
μJy, 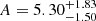 μJy, and the power-law index
μJy, and the power-law index 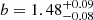 . The best fit is shown in green (dashed) in Fig. 7, as well as the 16th and 84th-percentile uncertainties, indicated by the shaded regions. Comparing tpeak, 1 with tstart, we find a total rise time of
. The best fit is shown in green (dashed) in Fig. 7, as well as the 16th and 84th-percentile uncertainties, indicated by the shaded regions. Comparing tpeak, 1 with tstart, we find a total rise time of 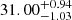 days. The rise period is within the range of values found for various nuclear transients: the TDE ASASSN-19bt (41.2 ± 0.5 days ; Holoien et al. 2019), the TDE ASASSN-19dj (∼27 days; Hinkle et al. 2021), the TDE AT2019qiz (30.6 days; Nicholl et al. 2020), and the ambiguous nuclear transient ASASSN-20hx (∼29 days; Hinkle et al. 2022). The power-law index b is lower than a quadratic rise, which was found for ASASSN-19bt and ASASSN-19dj.
days. The rise period is within the range of values found for various nuclear transients: the TDE ASASSN-19bt (41.2 ± 0.5 days ; Holoien et al. 2019), the TDE ASASSN-19dj (∼27 days; Hinkle et al. 2021), the TDE AT2019qiz (30.6 days; Nicholl et al. 2020), and the ambiguous nuclear transient ASASSN-20hx (∼29 days; Hinkle et al. 2022). The power-law index b is lower than a quadratic rise, which was found for ASASSN-19bt and ASASSN-19dj.
To estimate the time of the main peak in the light curve we again fitted a parabola, this time in the range MJD 59127–59191. We find tpeak, 2 = MJD 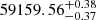 . This value is used as the peak time in Fig. 7. The o-band light curve between tpeak, 1 and tpeak, 2, Phase II in our schema, shows a plateau, followed by a rise to the main peak. We fitted the data with the function defined in Eq. (1) and find a shallower increase, with
. This value is used as the peak time in Fig. 7. The o-band light curve between tpeak, 1 and tpeak, 2, Phase II in our schema, shows a plateau, followed by a rise to the main peak. We fitted the data with the function defined in Eq. (1) and find a shallower increase, with 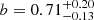 (the black dashed line in Fig. 7).
(the black dashed line in Fig. 7).
Finally, we fitted the decay in Phase III. While the light curve of a TDE is canonically expected to decline post-peak according to a t−5/3 power-law profile (i.e. in the fallback-dominated regime; Rees 1988; Phinney 1989), the observed values are known to have a wide range. We used the following model based on the decay model used by van Velzen et al. (2021):
We separately fitted the decay function to the o-band and the c-band data. We fixed t0 to tpeak, 2 and allowed the other parameters to vary freely. For the o-band, we find time-scaling factor 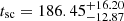 days, normalisation
days, normalisation 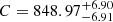 μJy, and power-law exponent
μJy, and power-law exponent 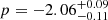 . The c-band fluxes appear to have a slightly steeper decay, as we find
. The c-band fluxes appear to have a slightly steeper decay, as we find 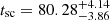 days,
days, 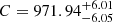 μJy, and
μJy, and 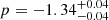 . Although the exponent is less negative for the bluer photometry band, tsc is significantly smaller. As tsc pushes the start of the decay period back in time, a large value of tsc represents a shallower decay. We note that the freedom in setting both tsc and p means that our function can be used to model a wide range of light curves that show any form of decay over time.
. Although the exponent is less negative for the bluer photometry band, tsc is significantly smaller. As tsc pushes the start of the decay period back in time, a large value of tsc represents a shallower decay. We note that the freedom in setting both tsc and p means that our function can be used to model a wide range of light curves that show any form of decay over time.
3.2. Spectroscopy
3.2.1. Overview of observations
We obtained several long-slit spectra of the optical counterpart of J234402 as well as of the three close-by southern sources. No archival spectroscopic observations exist of J234402 prior to the outburst, although a 2dFGRS (Colless et al. 2003) was taken of the blend of the southern sources (Appendix B).
Our new observations were made from the beginning of December 2020 until the Sun-block period (January 2021). The spectra were taken using the IMACS Short-Camera (Dressler et al. 2011) mounted on the 6.5m Baade Magellan telescope located at Las Campanas Observatory, the Robert Stobie Spectrograph (RSS; Burgh et al. 2003; Kobulnicky et al. 2003) mounted on the 10m South African Large Telescope (SALT; Buckley et al. 2006), and the FORS2 instrument (Appenzeller et al. 1998) mounted on the 8.2m Very Large Telescope Array’s UT1 at Cerro Paranal. An overview of the observations is listed in Table 6. All four observations covered J234402, and the Baade and SALT observations together covered the three southern sources. Our spectra of J234402 are shown in Fig. 8. The spectra were taken over a relatively brief interval (17 days), prior to Sun block and we observe no significant spectral changes over this period. We note, however, that in our follow-up after the Sun-block period, we do observe considerable spectral evolution, thus strengthening the case for the association of the X-ray flare with the optical outburst. We will discuss these later spectra in a follow-up paper.
 |
Fig. 8. Optical spectra of J234402. The data are from our follow-up campaign with Baade (Magellan), VLT, and SALT. The spectra show a blue continuum as well as strong broad and narrow emission lines. The broad lines show a distinct asymmetry, with a blue wing. The spectra have been scaled using the P6 photometry and are presented here with a flux offset for clarity. Several important emission lines are marked with dashed lines. Spectral regions affected by telluric absorption have been indicated by grey bands. The inset shows a close-up of Hβ for the two spectra separated by the largest time span (17 days), as well as the difference between the spectra. The fitted host+continuum components have been subtracted from the spectra in the inset and they were normalised using the [OIII]λ5007 line fluxes. Over the period of follow-up presented here, the object shows no significant spectral evolution. |
Overview of our optical spectroscopic observations of J234402.
The IMACS and RSS observations were taken at non-parallactic angles, to cover the southern sources. As both SALT and Baade make use of an Atmospheric Dispersion Corrector, the non-parallactic observations had no impact on the observed spectral shapes. Using the same parameters as for our photometry, all spectra were corrected for Galactic extinction. We scaled the absolute flux level of the spectra using contemporary photometry. For the spectrum taken on 23 December with SALT, we have R-band photometry from P6 taken on the same night. We scale the SALT spectrum so that the derived R-band flux matches that of our photometry. Subsequently we fitted the narrow [OIII]λλ4959,5007 lines in all four spectra (using a single Gaussian for each line). We scaled the other three spectra to the photometry-scaled SALT spectrum, by matching the integrated flux of the [OIII] lines.
3.2.2. Spectroscopic analysis
The spectra of J234402 show a blue optical continuum and strong, asymmetric Balmer emission lines. To analyse the spectra, we performed a least-squares fit to the data, making use of the lmfit package5. The fitting process was iterative: the first step was to fit a model consisting of a power-law continuum, an FeII template, and a host-galaxy template to the data. The FeII-template is the empirical (1 Zw I-based) template presented in Bruhweiler & Verner (2008). For the host template we made use of a spectrum produced from the stellar population synthesis models of Bruzual & Charlot (2003), using a model of 11.5 Gy and 0.05 solar metallicity. The strength of the host contribution was established in the fit to the Baade spectrum, after which this parameter was fixed in the fitting of the other three spectra. The second step was to fit the residuals of the continuum+FeII+host fit with Gaussians, to approximate the emission line profiles. The fitting results for the Baade spectrum of J234402, the first spectrum taken after the eROSITA detection, are shown in Fig. 9. We list the average fitting parameters in Table 7.
 |
Fig. 9. Our fitting procedure for the optical spectra. The procedure is illustrated for the spectrum taken with the Baade telescope on MJD 59195. (a) Continuum fit. The continuum is fit with a function consisting of a single power law (red dotted), an FeII-emission template (black), and a host-galaxy template (green). The residuals for all fits are shown underneath their respective plots. (b) Fit of continuum-subtracted spectrum around Hβ. The combined fit consists of five Gaussian profiles, two for the narrow [OIII] (black dotted) lines and a narrow (green dashed), broad (blue dot-dashed), and very broad (black dashed) component for Hβ. (c) Fit of continuum-subtracted spectrum around Hα. The combined fit for this region consists of six Gaussians: two for the narrow [NII] lines, two for the narrow [SII] lines (dotted black), and three for the Hα emission, with the same colours as the components used to fit Hβ. |
Results of fitting the optical spectra of J234402.
The slope of the continuum power law (fλ ∝ λ−α) is ∼2.5, a value typical of luminous AGN (e.g. Vanden Berk et al. 2001). There is no indication of a strong FeII contribution to the spectrum, and we detect no individual FeII emission lines. The FORS2 spectrum has features below 4000 Å however these are most likely not physical (see Appendix B for a detailed discussion). To fit the regions around Hα and Hβ, we made use of a locally fitted continuum. The fitting regions are 6100–7000 Å and 4600–5200 Å, for Hα and Hβ, respectively. To account for the strong asymmetry in the lines, we used three Gaussian components (narrow, broad, and very broad). We find that both Hα and Hβ include a strong, very-broad component, which is offset to the blue compared to the two narrower components (Fig. 9). In both Balmer lines, the broadest component is quite distinct from its narrower counterparts. The very-broad components have full widths at half maximum (FWHM) of ∼5000 km s−1, significantly wider than the broad components. The offsets between the centres of the broad line components and the narrow line components are 52.4 ± 1.3 Å and 12.6 ± 1.3 Å for Hα and Hβ, respectively. If we associate this Doppler shift with an inflow or outflow, the associated radial flow speeds would be of the order of 1000 km s−1.
The Balmer decrement, f(Hα)/f(Hβ), for the very broad components is ∼1.4, which remarkably is below the expected recombination value of approximately 3. We checked the impact of our fitting method on these results by refitting Hβ in our highest S/N spectrum (Baade), but limiting the flux in the very broad component to 1/3*f(HαVB). This resulted in an acceptable fit, where the broad-line model component compensates for the lowered very-broad component. However, in this case the Balmer decrement for the broad component drops below 3. In fact, we find that the Balmer decrement calculated using the sum of the broad and very broad Gaussians remains approximately constant at 2.1, under various constraints. As the continuum subtraction is of considerable importance in estimating the line fluxes, we experimented with various fits to the local continuum around the lines, but find no acceptable solutions that would result in a Balmer decrement ≥3. We therefore conclude that this unusual flux ratio is intrinsic to the spectrum of J234402, although its origin remains unclear. Interestingly, Li et al. (2022) find a low value of the Balmer decrement immediately following the flare in 1ES 1927+654, as low as ∼1, which increases to > 3 on a timescale of hundreds of days. We will continue to monitor the evolution of this anomalous line ratio in J234402, to investigate whether it is related to the rapid changes in the BLR.
Two Helium lines are visible in the residuals of our spectral fitting (Fig. 9). He I λ5876 is clearly detected: it is mixed with an absorption feature, which we associate with the Na I D1 and D2 doublet (λλ5889.9, 5895.9). Due to this blend of features we did not fit the line profile for He I λ5876. We do note that there is no visible change in this line among our spectra. He II λ4686 is only detected as a narrow emission line. This is somewhat surprising, as the strong soft X-ray emission could be expected to be associated with a strong ionising continuum, powering strong broad He II emission. A significant mismatch among line strengths, although unusual, has been detected in AGN samples (Ferland et al. 2020), in individual highly variable AGN over time (e.g. Homan et al. 2023), and among TDEs (van Velzen et al. 2021). We calculated an upper limit on the total He II flux by summing the flux in the continuum-subtracted spectrum (this therefore includes any narrow line emission) and find 1.4 erg cm−2 s−1. This results in an upper limit of 2% for the flux ratio He II λ4686/Hβ.
We used the line parameters of J234402 to create a diagnostic diagram following Baldwin et al. (1981; BPT). In Fig. 10, we present the diagrams for [OIII]λ5007/Hβ compared to [NII]λ6584/Hα and [SII]λ6717/Hα. The flux ratios for J234402 fall within the AGN classification of the diagram. As [OI]λ6100 lies within a telluric absorption region, we cannot provide a reliable estimate using this line. We only used the narrow-line fluxes from our spectral decomposition. In Fig. 10, we include individual results from each of our spectra in order to highlight the uncertainties involved. The line ratios show the relative strength of the high-ionisation [OIII] lines, which likely require an AGN to power them. Based on consideration of the light-travel-time to the narrow-line region, we can therefore say that the SMBH in J234402 was likely actively accreting for extended periods within the last millennia.
 |
Fig. 10. Line flux diagnostic diagrams (Baldwin et al. 1981) for J234402. The classification curves are from Kewley et al. (2006). The location of each of the J234402 spectra is indicated with a red star. The two subplots show the ratio [OIII]λ5007/Hβ (a) plotted against [NII]λ6584/Hα and (b) plotted against [SII]λ6717/Hα. The shaded regions represent the line flux ratios of ∼100 000 SDSS galaxies (restricted to 0.05 < z < 0.15), using the fluxes made available in the MPA-JHU data release (http://wwwmpa.mpa-garching.mpg.de/SDSS/DR7/). Darker shades of grey mean a higher number density of objects. For the Balmer lines of J234402, the fluxes were calculated using only the narrow components of the line decomposition (Fig. 9). The narrow lines are formed at a kpc-scale distance from the central source and therefore represent a past accretion state. The line diagnostics suggest that the nucleus of J234402 was active for an extended period within the last ∼103 yr. The inset in the bottom left of each plot shows the mean of the formal uncertainties associated with the J234402 spectral fits. |
3.3. Fermi-LAT
To search for possible γ-ray emission related to the formation of a jet during the ignition event, we used data from the Fermi Large Area Telescope (LAT). Fermi-LAT continuously monitors the sky in an energy range from 30 MeV up to more than 300 GeV (Atwood et al. 2009). For the data analysis, we used the recent Pass 8 data, including the post-launch instrument response function, P8R3_SOURCE_V2, together with the ScienceTools version 1.2.23 and fermipy version 0.20.0. We selected photons with energies between 100 MeV and 300 GeV and located within a region of interest (ROI) of 10° centred on the eROSITA coordinates. We excluded photons that entered the LAT with a zenith angle > 90°. We evaluated the γ-ray data during two time ranges, which approximately represent the pre-ignition and post-ignition period for J234402. We define pre-ignition as the period from eRASS 1 (24 May 2020) to the Gaia transient alert (14 October 2020) and post-ignition as the period from the Gaia alert to 31 January 2021, the start of the Sun-block period.
The data were modelled using a maximum likelihood analysis. The significance of each modelled γ-ray signal within the ROI is given by the test statistic value TS = 2Δlog(ℒ), (Mattox et al. 1996). The TS value can be roughly translated into a significance as 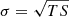 . Our model consists of known γ-ray sources from the Fermi-LAT Fourth source catalogue (4FGL; Abdollahi et al. 2020) within 15° of the ignition coordinates, the Galactic diffuse model gll_iem_v07, and the model for the isotropic diffusion emission iso_P8R3_SOURCE_V2_v1. The closest 4FGL source has a distance of 2.8° to the coordinates of the transient; hence no known γ-ray source can be associated with J234402.
. Our model consists of known γ-ray sources from the Fermi-LAT Fourth source catalogue (4FGL; Abdollahi et al. 2020) within 15° of the ignition coordinates, the Galactic diffuse model gll_iem_v07, and the model for the isotropic diffusion emission iso_P8R3_SOURCE_V2_v1. The closest 4FGL source has a distance of 2.8° to the coordinates of the transient; hence no known γ-ray source can be associated with J234402.
We next attempted to establish the presence of a point source that is not included in the catalogue, by adding it at the counterpart coordinates to our model. We assumed a power-law spectrum with a photon index of 2. After the first fit, we excluded all sources from the model that have TS < 4 (σ < 2) or TS = nan. We kept the galactic and isotropic diffuse models free, as well as all parameters and normalisations for sources within 3°. For both the pre-ignition and post-ignition periods, we find no significant detection at the location of J234402. For the pre-ignition period, we find a 2σ upper limit6 of 2.17 × 10−9 photons cm−2 s−1 (1.6 × 10−12 erg cm−2 s−1), and for the post-ignition period, a 2σ upper limit of 1.8 × 10−8 photons cm−2 s−1 (6.3 × 10−12 erg cm−2 s−1). We note that the slightly lower upper limit for the pre-ignition period can be explained by the longer time range included in the analysis (∼5 months vs. 3.5 months), and does not necessarily imply a higher γ-ray flux.
4. Discussion
J234402 is a strong extragalactic ignition event with observed changes in X-rays, UV, optical emission, and IR. We aim to place J234402 in the context of the broad range of AGN variability and of TDEs and other transient objects. In Fig. 11, we show the optical spectrum of J234402 taken 35 days after the optical peak along with representative spectra from several other classes of objects, namely, changing-look AGN7, TDEs8, and a hydrogen-rich SN8. Based on the strong X-ray emission, a supernova appears to be an unlikely explanation; however, the optical spectrum alone does not provide sufficient information to distinguish between the AGN and the TDE scenario.
 |
Fig. 11. Spectrum of J234402 compared with spectra of several classes of objects. The optical spectrum of J234402 (black) is shown together with spectra from several other classes of objects that show extreme outbursts: TDEs (green), supernovae (blue), and changing-look AGN (red). The emission lines marked in red (dashed) are those more typically associated with AGN and the emission lines marked in blue (dotted), are those that are prominent in both AGN and TDEs. The narrow-line features of J234402 are more typical of an AGN; however, the broad-line features agree with both a TDE and an AGN interpretation. The included TDE spectra belong to the TDE–H+He AT2019dsg (z = 0.051, spectrum 34 days after discovery, Nicholl et al. 2019), the TDE–H AT2018hyz (z = 0.046, spectrum 6 days after discovery, Dong et al. 2018), and the TDE–H+He AT2018dyb (z = 0.018, spectrum 34 days after peak emission, Leloudas et al. 2019). The SN spectrum belongs to the H-rich SLSN II SN2013hx (z = 0.125, spectrum 55 days after detection, Inserra et al. 2018). The two changing-look AGN spectra both represent the relative high state of the objects: SDSSJ111536.57+054449.7 (z = 0.090, first reported by Yan et al. 2019) and SDSSJ102152.34+464515.6 (z = 0.204, first reported by MacLeod et al. 2016). All spectra have been corrected for redshift, the flux densities have been normalised for the purpose of comparison, and we have removed features that were obviously associated with atmospheric absorption. No correction was made for the host galaxy contribution. |
Distinguishing between the two scenarios can be difficult as the observational characteristics can be ambiguous (e.g. Drake et al. 2011; Merloni et al. 2015; Neustadt et al. 2020; Hinkle et al. 2021).
4.1. J234402 and AGN ignitions
4.1.1. Physical parameters
Under the assumption that the outburst in J234402 is caused by variability in an AGN, we can make estimates of some key properties of the system. To do so, we made use of relations between the broad line emitting region (BLR) and the continuum emission, which are well established for AGN. Based on our fit to the continuum and the established redshift of 0.10, we find a continuum luminosity at 5100 Å of λLλ ∼ 7.1 × 1043 erg s−1. Using the bolometric correction, log(Lbol) = 4.89 + 0.91×log(λLλ), (cf. Runnoe et al. 2012), we find a value for the current isotropic bolometric luminosity of Lbol ∼ 6.2 × 1044 erg s−1. We note that this estimate carries considerable uncertainty, as the bolometric corrections were derived for a broad population of AGN and do not necessarily translate to an extremely variable object such as J234402.
We can compare the current Lbol with an estimate of the bolometric luminosity based on narrow the [OIII]λ5007 line. As the size of the narrow line region precludes any large variations in the timescale of the ignition event, L[OIII] provides an indicator of the luminosity state ∼103 years prior to the ignition event. Using the bolometric correction of Stern & Laor (2012), we find 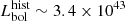 erg s−1. Based on narrow-line diagnostics (Fig. 10), we associate the accretion phase that powered the [OIII] emission with AGN activity. As
erg s−1. Based on narrow-line diagnostics (Fig. 10), we associate the accretion phase that powered the [OIII] emission with AGN activity. As 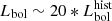 , the nucleus is currently significantly brighter than during this historic AGN phase.
, the nucleus is currently significantly brighter than during this historic AGN phase.
We can further compare the results of our optical fitting with values typical of AGN. The power-law continuum that is visible in the optical spectrum is somewhat steeper than the theoretical prediction for a thin accretion disk (with slope α = −2.52 ± 0.01). The theoretically predicted slope, α = −2.33, has been found in difference spectra (Kokubo et al. 2014; MacLeod et al. 2016) of variable AGN, although averaged AGN spectra show a shallower slope of −1.54 (Vanden Berk et al. 2001). Based on the L5100 to LHα scaling relationship established in Greene & Ho (2005), our measured value of L5100 would correspond to LHα = 3.5 × 1042 erg s−1. This is significantly higher than the line luminosities we find in J234402 for which LHα = 3.7 × 1041 erg s−1, for the combined very-broad and broad-line components. The discrepancy suggests that the BLR is not as fully formed as it is in stably accreting AGN.
The tight scaling relationship between λL5100 and the light-travel distance to the line-forming region in AGN (RBLR; e.g. Peterson et al. 2004; Bentz et al. 2009, 2013) allows us to make an estimate of RBLR. Using the scaling parameters established by Bentz et al. (2009) for Hβ (their K = 1.554 & α = 0.546), we find RBLR, Hβ = 29.7 light days. Combining this radius with FWHM(Hβ), we are able to estimate a virial mass for the central black hole. For the combination of the broad and very broad Gaussian components, the FWHM(Hβ) = 3321 km s−1. Adopting a virial factor f = 1 (cf. Peterson et al. 2004) we find MBH ∼ 107.8 M⊙. Using the scaling relation established by Vestergaard & Peterson (2006), we find a similar MBH ∼ 107.9 M⊙. The associated Eddington luminosity, LEdd, for this mass is 8.0 × 1045 erg s−1. Finally, combining the various derived properties, we find an Eddington ratio of λEdd ≡ Lbol/LEdd ∼ 0.08. As the bolometric correction assumes isotropic emission, a condition likely not fulfilled in the case of strong outflows, this value could represent a lower limit for λEdd. We note that this method is based on the assumption of a virialised BLR, a condition possibly not met in J234402. Therefore, we emphasise that this mass estimate needs to be interpreted with caution. This is also evident in the choice of virial factor f. f is dependent on both the orientation and the physical configuration of the BLR, which are unknown for J234402. Using the value f = 4.3 (cf. Grier et al. 2013), we find MBH ∼ 108.4 M⊙, a significant difference from the previous estimate.
The mass estimate calibrated to an AGN sample can be compared with mass estimates based on different methods, to provide additional constraints. The black-hole mass in galaxies is known to correlate with the infrared luminosity of the galactic bulge (Marconi & Hunt 2003). We make use of the updated correlation between MBH and K-band magnitude provided in Graham (2007): log(MBH/M⊙) = −0.37(MK + 24)+8.29. In the 2MASS catalogue, the northern and southern sources are detected as separate objects, and we find mK = 14.38 for J234402 (observed in 1998). We assume that at the time of measurement, the AGN contribution to the K-band flux is negligible. As the galaxy is not resolved, the 2MASS value represents an upper limit on the bulge luminosity and therefore on MBH. Using the 2MASS value, we find MBH < 108.3 M⊙. In a different approach, we use the width of [OIII]λ5007 as an estimate of the bulge stellar-velocity dispersion σ*, to apply the established MBH − σ* relation (following e.g. Nelson 2000). This method assumes that the physical extent of the narrow-line-forming region is such that the velocity dispersion of the [OIII]-emitting gas is set by the gravitational potential of the bulge, making σ[OIII] a good approximation of σ* (cf., Xiao et al. 2011, in galaxies with low MBH). Based on the Baade observation, we find σ[OIII] = 169 km s−1. In optical spectra, line broadening will always be a combination of instrumental and intrinsic broadening (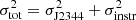 ). To account for the strength of the instrumental effect for the [OIII]λ5007 line, we measured the instrumental broadening using the arc-lamp frame of the Baade observation. We find that the instrumental contribution to the line width is ∼1%, whcih will be of negligible influence on the estimates black-hole mass. Using the scaling relation from Tundo et al. (2007), we find MBH ∼ 107.9 M⊙. The three methods of estimating the mass of the SMBH therefore provide consistent results, if we choose the lower value for the virial factor.
). To account for the strength of the instrumental effect for the [OIII]λ5007 line, we measured the instrumental broadening using the arc-lamp frame of the Baade observation. We find that the instrumental contribution to the line width is ∼1%, whcih will be of negligible influence on the estimates black-hole mass. Using the scaling relation from Tundo et al. (2007), we find MBH ∼ 107.9 M⊙. The three methods of estimating the mass of the SMBH therefore provide consistent results, if we choose the lower value for the virial factor.
4.1.2. Extreme X-ray variability in AGN
Large amplitude X-ray brightening has been observed in the AGN NGC 2617 (Shappee et al. 2014), XMMSL1 J061927.1-655311 (Saxton et al. 2014), HE 1136–2304 (Parker et al. 2016), iPTF 16bco (Gezari et al. 2017), NGC 1566 (Parker et al. 2019; Oknyansky et al. 2020), 1ES 1927+654 (Trakhtenbrot et al. 2019a; Ricci et al. 2020, 2021), SDSS J155258+273728 (Ai et al. 2020), and AT2019pev (Yu et al. 2022). In all of these objects, the X-ray brightening was accompanied by rapid optical and UV flux increases (where UV observations were available). In most objects, the X-ray brightening was accompanied by the appearance of broad Balmer emission lines in the optical spectrum. However, broad emission lines in HE 1136–2304 had disappeared post-brightening, compared to an archival spectrum taken 11 years earlier. The order of magnitude increase in 0.3–10 keV flux in UGC 2332 (Wang et al. 2020) was matched by a change in optical spectrum from type 2 to type 1.8 (i.e. appearance of broad Hα), reversing a transition from 1.5 to 2 in the previous decades.
The persistence of the new, brighter state and any emission lines differs from object to object – in NGC 2617, the persistence of UV emission years later suggests a long-lasting change of accretion state (Oknyansky et al. 2017), whereas in NGC 1566 and 1ES 1927+654, the flux faded over months–years. When sufficiently sampled, the shapes of the light curves therefore provide some distinguishing power between AGN and TDEs. However, the most important distinguishing characteristic for all these objects is the hardness of the X-ray spectrum. In all events discussed above, the X-ray spectrum had a power-law component with Γ ≲ 2, thus firmly identifying an AGN contribution to the emission. Noda et al. (2016) found that in the Seyfert 1.5 NGC 3516, there is in fact a positive correlation between B-band flaring and the strength of the Γ ∼ 1.7 power-law component in the 2–45 keV spectrum. The very soft spectrum of J234402 therefore stands out.
4.1.3. Soft X-ray ignitions in AGN
The nearby galaxy NGC 3599 (Esquej et al. 2007) brightened in X-rays by a factor of 150 between 1993 and 2003 and showed a particularly soft spectrum (Γ ∼ 3 for a fit with a single power law). The bright state lasted at least 18 months and was followed by a decline lasting several years. Based on the timescales involved, Saxton et al. (2014) concluded a fast-rising TDE is unlikely, making AGN variability based on a disk instability (see below) the more likely cause. IC 3599 (Brandt et al. 1995; Komossa & Bade 1999) has shown X-ray outbursts in 1990 and 2010, which have been interpreted both as repeated partial tidal stripping of a star (Campana et al. 2015) and intrinsic AGN variability (Grupe et al. 2015). The ROSAT spectrum of the first outburst was notably soft (Γ ∼ 4.8), although the Swift-XRT spectra of the second outburst indicate that a fit with a power law+blackbody (with power-law index Γ ∼ 2.6) is perhaps more suitable. This harder-when-fainter behaviour, typical of AGN, is not observed in J234402, although our continuing observations will allow us to confirm this.
These soft X-ray ignitions differ from J234402 in several key aspects: (1) they are shorter lived, (2) they are associated with smaller SMBHs (typically MBH ∼ 105 − 6 M⊙ with the exception of NGC 3599, which has MBH ∼ 108 M⊙ and an evolution over months–years), and (3) all objects for which optical spectroscopy is available lack strong broad emission lines in their optical spectra.
4.1.4. Timescales
To qualify the nature of the accretion process, the timescales of the changes provide some of the most helpful constraints. Although one can define many model-dependent timescales for accretion flows, they generally fall into a few broad categories: the light crossing timescale (tlc), the dynamical or orbital timescale (tdyn), the thermal timescale (tth) related to cooling or heating of the disk, and the viscous timescale (tν) at which large changes can propagate through the disk through viscosity. For the standard thin-disk model and using the parametrisation provided in Stern et al. (2018), we can determine the aforementioned timescales in J234402. We use MBH = 107.9 M⊙, set the viscosity parameter to α = 0.03 and the ratio between the disk scale height and the radius (H/R) to 0.05 (these values for α and H/R are typical for a geometrically thin disk). As the best-constrained timescales for J234402 are based on optical data, we evaluate the theoretical timescales at 100 rg – this represents the typical size of the inner optically emitting region9. With these considerations, we find the following estimates for the timescales relevant for accretion flows:
We can compare these values with the observed evolution in J234402. The rapid rise time (Phase I) is ∼30 days and the total time to peak (Phase I+II) is ∼60 days. The decay timescale is of course not well constrained by the current dataset (this will be covered in our Paper II); however, we can use tsc (Eq. (2) in Sect. 3.1.6) as a first estimate. tsc is ∼80 days for the ATLAS c-band data and ∼186 days for the o-band data. These values best match our estimates for the timescale tth, although for the rise time the dynamical timescale is also a good match.
The defining timescale for the standard thin accretion disk is the viscous timescale; however, it has been found that many forms of AGN variability operate on timescales too small to match this description (see e.g. Lawrence 2018). Several instabilities that operate on tth have been proposed to explain extreme changes in AGN accretion rates (see e.g. the discussion in Stern et al. 2018), which could reasonably explain the outburst in J234402.
One possible mechanism for speeding up large changes is the Lightman-Eardley (LE) disk instability (Lightman & Eardley 1974) in combination with a truncated accretion disk. In this scenario, the disk is truncated at a given inner radius, resulting in an inner region that slowly (∼tν) fills with material until the LE instability triggers a rapid (∼tth) ignition and heating of the disk that produces a soft, thermal X-ray flare. The inner region is then drained once more as the inner disk is accreted, resulting in the decay phase in the light curve. Saxton et al. (2015) find that such a process is a possible explanation for the variability observed in NGC 3599. The decay timescale in this scenario is constrained to be greater than tdyn, but also to be smaller than the rise timescale. The first condition is easily matched by J234402; however, the second condition does not appear to hold. Although the optical brightening in J234402 matches a thermal timescale for the system, the relatively slow decay implies that an LE instability cannot fully explain the observed behaviour.
4.2. J234402 and TDEs
4.2.1. Comparing physical parameters
Following the criteria on X-ray behaviour set out in Auchettl et al. (2018), J234402 is a good TDE candidate, as the spectrum is very soft and shows limited spectral evolution in the first months following the flare. A soft X-ray spectrum best fit with a blackbody model is common in TDEs (Gezari 2021). The rest-frame luminosity of L0.2 − 2keV = 1044.9 erg s−1, which is derived from the eRASS2 observation, is quite high for a non-jetted TDE (Sect. 3.3). The luminosity function derived by Auchettl et al. (2018) sharply cuts off around 1044 erg s−1. The estimated SMBH mass of 107.9 M⊙ is quite near the Hills mass (Hills 1975) of a non-spinning BH with MBH = 108 M⊙, which is the theoretical limit for a tidal disruption of a star outside the black hole’s event horizon. However, black-hole spin could allow for black holes with masses greater than the Hills mass to produce very luminous TDEs (Leloudas et al. 2016; Mummery & Balbus 2020). The X-ray light curve (Fig. 1) shows a clear decay, albeit not strictly monotonic. Short-term X-ray variability in TDEs is a known phenomenon (e.g. Wevers et al. 2019; van Velzen et al. 2021). J234402 would therefore be an unusually bright but not an unusually variable TDE candidate.
The ratio of the [OIII]λ5007 to 0.2–2 keV X-ray luminosity for J234402 is approximately 104.1. This is significantly larger that the L0.3 − 20 keV/L[OIII] ratio of 102.0 found for local type 1 AGN (Heckman et al. 2005), but is consistent with the values found for TDE candidates (Sazonov et al. 2021). This result is in agreement with the large discrepancy that we find between 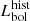 derived from [OIII] and the current Lbol (based on the optical spectrum, see Sect. 4.1): the current luminosity significantly surpasses the luminosity associated with any previous AGN activity.
derived from [OIII] and the current Lbol (based on the optical spectrum, see Sect. 4.1): the current luminosity significantly surpasses the luminosity associated with any previous AGN activity.
Under the assumption that the optical continuum flux is driven by blackbody emission, we estimate the blackbody temperature (TBB) and bolometric luminosity from the optical spectra (see Fig. B.4) and derive the blackbody radius (RBB). Using the average values from the four spectra, we find log(TBB/[K]) = 4.1 and log(RBB/[cm]) = 15.5. Figure 12 shows a comparison of our values with those derived for the TDE sample presented in van Velzen et al. (2021). J234402 appears on the larger and cooler ends of the ranges of values. However, we note that the values for J234402 are based on observations taken ∼25 days after the peak, whereas the other measurements are around tpeak. J234402 may have had more time to expand and cool. Interpreting the optical emission from J234402 as a blackbody therefore appears consistent with the results from other TDEs. We find Lbol, BB = 1.7 × 1044 erg s−1, in approximate agreement with the result from Sect. 4.1. To calculate the ratio between the luminosity based on the optical data, Lbol, BB, and the soft X-ray luminosity, we make use of the XMM-Newton data as the observation periods nearly coincide. We find Lbol, BB/LX ≈ 0.7, which is on the low end for most TDEs (compared with Fig. 10 in van Velzen et al. 2021).
 |
Fig. 12. Derived blackbody temperatures and blackbody radii of several TDEs compared to those of J234402. TDE-H and THD-He refer to TDEs with only hydrogen or only helium lines in their spectrum, respectively (see Sect. 4.2 for further detail). The dashed grey lines show the expected log |
4.2.2. Optical evolution
The optical identification of TDEs has mostly been based on large photometric surveys (van Velzen et al. 2021; Gezari 2021, refs). The timescale of the rapid rise in J234402 (Phase I, before the plateau) of ∼30 days fits within the observed range of rise times for TDEs. We find that the rise time in the sample of van Velzen et al. (2021) varies from ∼2 to 32 days. J234402 is therefore at the long end of this range. The temporary halt in the flux increase (Phase II) is unusual in the light curves of TDEs, lacking a clear equivalent in observed objects. The optical decline exhibits a power-law-like slope that is consistent with TDEs (Gezari 2021).
The spectroscopic presentation of optically selected TDEs shows a broad distribution in the strength of H and He lines. Generally, TDEs can be classified into objects that develop broad Hα and Hβ lines (TDE-H), those that develop Balmer lines as well as broad He II λ4686 (TDE-H+He), and those that only show broad He features (TDE-He; Arcavi et al. 2014; Leloudas et al. 2016; van Velzen et al. 2021). Using this classification system, J234402 would fall into the TDE-H category. Bowen fluorescence, which has been associated with the TDE AT2019qiz (Nicholl et al. 2020) and the nuclear transient AT2017bgt (Trakhtenbrot et al. 2019a), is not apparent in J234402 (N III λ4640 is in range for our spectroscopy).
One of the most distinctive features of J234402’s spectrum is the strongly asymmetric line profile of the Balmer lines. The FWHM of the broadest components is ∼103 km s−1, which is of the same order of magnitude as the transient and blueshifted broad emission features detected in the TDEs AT2019qiz (Hα; Nicholl et al. 2020) and PS1-10jh (He II λ4686; Gezari et al. 2015). In both cases, the offset of the broad components is associated with an outflow, even matching outflow signatures in radio observations in AT2019qiz.
Coronal emission lines, such as [ArXIV]λ4414, [FeIX]λ5304, [FeVII]λ6088, have been associated with TDEs (Komossa et al. 2008; Wang et al. 2012) as well as variable AGN (Brandt et al. 1995; Grupe et al. 1995). In a subset of extreme coronal line emitters, the coronal emission has been accompanied by the presence of strong Balmer emission lines (Wang et al. 2012). Given the strength of the X-ray emission is J234402, we investigated the possibility of a similar combination of these emission features in our optical spectra. We find no evidence of coronal line emission. The lack of any coronal lines, or indeed of lower-ionisation FeII emission features, could indicate that the available gas is relatively metal-poor. Alternatively, the lines will take more time to develop.
4.3. IR evolution
The observed increase in the IR light curve, associated with the X-ray and optical outburst (Sect. 3.1.5), provides additional information about the circumnuclear environment. One possibility is that the IR emission is part of the same outburst as the optical flare. As we estimate the mass of SMBH to be rather high, it is feasible that the outer reaches of the accretion disk have a sufficiently low effective temperature to emit significantly in the IR. In this case the increased emission is the result of a heating up of an existing accretion disk, as the effect of the accretion-rate increase in the inner disk travels outwards. A different interpretation is that the IR emission is the result of reprocessing of UV and optical emission by dust, which is commonly seen in AGN (for a review, see e.g. Netzer 2015) and has also been observed in a small number of TDEs (van Velzen et al. 2016b; Jiang et al. 2017, 2021). Under this assumption, we can estimate a minimum response timescale for the circumnuclear dust to the outburst. The interval between tstart, the beginning of the optical ignition event, and the most recent WISE epoch is approximately 68 days. If we further assume that the reprocessing of incoming radiation by the dust is immediate, we can relate this maximum response time to a light-travel distance from the central engine of 1.8 × 1017 cm (0.06 pc). We can compare this distance to the mean sublimation radius (cf. Barvainis 1987; Netzer 2015) within which the incident UV flux is strong enough to destroy dust grains by photodissociation:
where Tsub, X is the sublimation temperature for different types of dust grains, typically 1800 K for carbonaceous grains and 1500 K for silicate grains (Netzer 2015), and the angular term f(θ) defines the anisotropy of the nuclear emission. Using our estimate for Lbol of 6.2 × 1044 erg s−1, Tsub, Si, and f(θ) = 1, we find a sublimation radius of 1.2 × 1018 cm (0.39 pc), much larger than the light-travel distance. A refinement of this approach would be to take into account the physical distribution of the dust: if the observed response originates in dust that is located along our line of sight to the nucleus, the light travel time could be longer than in the rough estimate given above. In fact, the profile of the IR light curve in the months–years following the outburst can help track the distribution of the dust, based on varying response times. We will investigate this evolution in follow-up work.
In a sample of 23 optically selected TDEs, Jiang et al. (2021) found that most TDEs showed no response in the IR emission, except for those that appeared to occur within AGN. A possible interpretation for this correlation is that the covering factor of dusty regions in inactive galaxies is too small for any detectable reprocessing by dust to occur. A significant accretion rate may be necessary to support a thick, dusty structure (van Velzen et al. 2016a). IR echos from TDEs in AGN have also been observed in radio-selected TDEs (e.g. Mattila et al. 2018). The W1–W2 colour in J234402 around the time of peak is 0.26, which can be associated with a blackbody temperature ∼2600 K. During the last observation before the ignition event, W1–W2 = 0.35, which corresponds to a temperature of ∼2100 K. It therefore appears that the brightening is associated with an increase in the dust temperature. A change in dust temperature has been associated with TDEs showing IR dust echos (van Velzen et al. 2011; Jiang et al. 2017), whereas three changing-look AGN that were selected based on changes in their WISE magnitudes (Stern et al. 2018; Ross et al. 2018) showed no significant temperature changes, on a timescale of years.
4.4. A TDE in an AGN
Several characteristics of J234402 best match a TDE, in particular the soft X-ray spectrum and the onset of a rapid decay. However, the optical spectrum indicates the presence of an AGN. In recent years, more objects with a mix of AGN and TDE qualities have been observed, presenting a challenge to classification. AT2017bgt (Trakhtenbrot et al. 2019b) and ASASSN-18jd (Neustadt et al. 2020) both exhibited strong increases in the optical, hard X-ray spectra, and combinations of spectral features observed in AGN (narrow [OIII]) and in TDEs (e.g. Bowen fluorescence of NIIIλ4640). The longevity of the new spectral features (> 1 year) indicates these may be a new type of transient (Trakhtenbrot et al. 2019b). The transient ASASSN-17jz (Holoien et al. 2022) was classified as a possible SN IIn outburst that may have occurred in or near the accretion disk of an existing, low-luminosity AGN and may have triggered an increase in the accretion rate. Like J234402, the object has a soft X-ray spectrum (Γ ∼ 3.4), strong Balmer lines in its optical spectra, and no evidence of Bowen fluorescence. A very broad (∼6000 km s−1) Hβ component faded on a timescale of years. We inspected the NEOWISE-R observations for ASASSN-17jz and found that a sharp rise and subsequent decay are clearly visible in the IR light curve, coincident with the ignition event. This could present an additional similarity to J234402 and is consistent with the notion that a pre-existing disk is a requirement for a strong IR echo.
There are several reports of possible TDEs occurring within objects classified as AGN, including ASASSN-14li (van Velzen et al. 2016a), PS16dtm (Blanchard et al. 2017), 1ES 1927+654 (Trakhtenbrot et al. 2019a; Ricci et al. 2020, 2021), and SDSS J022700.77-042020.6 (Liu et al. 2020). The behaviours of these objects are quite diverse. The optical light curves of 1ES 1927+654 and SDSS J0227-0420 are similar to that of J234402; however, PS16dtm reaches a plateau in the light curve that lasts several months. Both PS16dtm and 1ES 1927+654 dimmed in X-rays following the optical ignition, due to the disappearance of the power-law component in the spectrum, though in the case of 1ES 1927+654, the X-rays and the power-law component recover on a timescale of months. The decay of the X-ray light curve in ASASSN-14li is also slower than observed in J234402. The optical spectra of 1ES 1927+654 show a combination of narrow [OIII] lines and strong broad Balmer lines. The Balmer lines in 1ES 1927+654 appeared on a timescale of months (this is not constrained for J234402, but the presence of strong Balmer lines ∼70 days after tpeak matches this timeline). In contrast, PS16dtm shows little spectral evolution, except the development of a complex of FeII lines, which is not observed in J234402. A possible explanation for this difference is that PS16dtm was classified as a Narrow-Line Sy1, characterised by a low MBH and strong Iron emission, in contrast to the high MBH of J234402. We therefore do not find a clear equivalent to J234402 among other ambiguous transients, although ASASSN-17jz shares some significant characteristics.
Summarising, we can say that the soft X-ray spectrum and rapid onset of the decay observed at all wavelengths indicate that J234402 was likely powered by a TDE. The relative strength of the high-ionisation [OIII] lines, compared to the [NII] and [SII] lines, in the optical spectra in J234402 indicate the (historical) presence of an AGN. The non-detection in ROSAT and the lack of any clear power-law component in our new X-ray spectra indicate that J234402’s AGN phase was likely in the past. However, the possible low-level variability in the optical light curve, visible in the ATLAS data, means we cannot exclude the possibility that the SMBH in J234402 was still actively accreting at a low level in the years directly prior to the ignition. Together this paints a scenario in which a TDE occurred in an environment that was shaped by AGN activity.
For TDEs that occur in AGN, the accretion process powering the emission can be significantly more complex than in ‘secular’ TDEs, owing to the interaction between the stellar debris with the pre-existing disk (Chan et al. 2019). The different kinematic components we detect in the broad Balmer lines are indicative of a rapidly evolving system, with the broadest (i.e., the innermost) components providing strong evidence of an outflow. We speculate that the apparent stratification in the BLR is affected by the AGN environment of the TDE – fast-orbiting clouds close to the central engine are generated in the event itself, whereas the outer BLR could be caused by irradiation of a pre-existing structure.
5. Conclusion and outlook
We have presented the results of the eROSITA detection and subsequent multi-wavelength follow-up of a significant extragalactic X-ray ignition in J234402, in which the 0.2–2 keV flux increased by at least a factor of 150 in the six-month interval between eROSITA scans. The spectrum is very soft and best fit with a dual blackbody (T ∼ 106 K). The X-ray flux shows strong variability on timescales from hours to days. These short-term fluctuations occur within a trend of overall decline in the two months following the detection. Optical photometry shows that prior to the X-ray detection, the emission from J234402 showed a rapid rise of ∼3 mag on a timescale of weeks, which is followed by a plateau and decline in the following months. This decline is matched in the UV. Our follow-up optical spectroscopy shows that the source has a blue continuum and strong, broad Balmer emission lines, as well as narrow high-ionisation [OIII] lines. We do not observe any optical spectral evolution over the course of our follow-up. The IR emission shows an increase that is correlated with the optical flare.
Based on the optical spectra and using AGN scaling relations, we derive a bolometric luminosity of 6.1 × 1044 erg s−1 and a black hole mass of 107.9 M⊙. The ignition event has characteristics in agreement with both a TDE and an AGN; however, the soft X-ray spectrum and the onset of a rapid decline in the light curve lead us to identify J234402 as a likely TDE within a low-luminosity or turned-off AGN. The strength of the high-ionisation narrow lines, as evident in the BPT diagnostic, suggests that J234402 was in an AGN phase as recent as a few millennia ago. We have limited our discussion to the data before January 2021 when J234402 went into Sun block. Our data cover the rise and peak of the X-ray and optical light curves. To confirm our interpretation of the accretion event, we will make use of further follow-up data, which we are currently gathering.
We expect that our continued observations will allow us to better constrain the interaction between the ignition event and the surrounding nuclear medium. Photometric monitoring will enable us to find the decay timescale and to search for any deviations from the monotonic decay in the UV and optical that is expected for TDEs. We expect the X-ray variability to diminish over time, as we associate it with the transient emission originating from the interaction of the accreting stellar debris and the disk. Using the decay light curve, we will also be able to put constraints on the properties of the stellar progenitor of the TDE. By tracking the evolution of the broad emission lines, we will be able to see if the distinct kinematic structures we identified will evolve differently, or if a shared origin in a single outflow is a more likely scenario. Finally, if the IR response is caused by a dust echo, we expect the emission to brighten further before also diminishing. The analysis of the combined data, including the period after Sun block and new radio observations, is underway and will be the topic of follow-up papers.
Z is defined following Buchner et al. (2014), Sect. 5.2.
Retrieved from https://irsa.ipac.caltech.edu/applications/DUST/
Spectrum for J111536 made publicly available by Yan et al. (2019).
Depending on the contribution of reprocessed X-ray and UV radiation to the optical output (see e.g. Noda et al. 2016, for a discussion on this topic).
Acknowledgments
The authors thank the anonymous reviewer for their insightful and constructive suggestions. DH acknowledges support from DLR grant FKZ 50 OR 2003. MK is supported by DFG grant KR 3338/4-1. AM, TS, and SK acknowledge full or partial support from Polish Narodowym Centrum Nauki grants 2016/23/B/ST9/03123, 2018/31/G/ST9/03224, and 2019/35/B/ST9/03944. AG was funded by the German Science Foundation (DFG grant number KR 3338/4-1). MG is supported by the EU Horizon 2020 research and innovation programme under grant agreement No 101004719. The authors wish to express their thanks to J. Wilms and A. Schwope for their contributions to many useful discussions. This work is based on data from eROSITA, the soft X-ray instrument aboard SRG, a joint Russian-German science mission supported by the Russian Space Agency (Roskosmos), in the interests of the Russian Academy of Sciences represented by its Space Research Institute (IKI), and the Deutsches Zentrum für Luft- und Raumfahrt (DLR). The SRG spacecraft was built by Lavochkin Association (NPOL) and its subcontractors, and is operated by NPOL with support from the Max Planck Institute for Extraterrestrial Physics (MPE). The development and construction of the eROSITA X-ray instrument was led by MPE, with contributions from the Dr. Karl Remeis Observatory Bamberg & ECAP (FAU Erlangen-Nuernberg), the University of Hamburg Observatory, the Leibniz Institute for Astrophysics Potsdam (AIP), and the Institute for Astronomy and Astrophysics of the University of Tübingen, with the support of DLR and the Max Planck Society. The Argelander Institute for Astronomy of the University of Bonn and the Ludwig Maximilians Universität Munich also participated in the science preparation for eROSITA. This work was supported in part by NASA through the NICER mission and the Astrophysics Explorers Program. NICER data used in this work were gathered under a Guest Observer (GO) approved programme and NICER DDT time augmented the GO-approved time significantly. We acknowledge the use of public data from the Swift data archive (ObsIDs: 13946001, 13946002, 13946004-006). This work is based on observations obtained with XMM-Newton (ObsID: 0862770101), an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA. The ROSAT Project was supported by the Bundesministerium für Bildung und Forschung (BMBH/DLR) and the Max-Planck-Gesellschaft. This research has made use of the NASA/IPAC Infrared Science Archive, which is funded by the National Aeronautics and Space Administration and operated by the California Institute of Technology The Fermi LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of the LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l’Énergie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation, the Swedish Research Council and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the Centre National d’Etudes Spatiales in France. This work performed in part under DOE Contract DE-AC02- 76SF00515. This work has made use of data from the Asteroid Terrestrial-impact Last Alert System (ATLAS) project. The Asteroid Terrestrial-impact Last Alert System (ATLAS) project is primarily funded to search for near earth asteroids through NASA grants NN12AR55G, 80NSSC18K0284, and 80NSSC18K1575; byproducts of the NEO search include images and catalogs from the survey area. This work was partially funded by Kepler/K2 grant J1944/80NSSC19K0112 and HST GO-15889, and STFC grants ST/T000198/1 and ST/S006109/1. The ATLAS science products have been made possible through the contributions of the University of Hawaii Institute for Astronomy, the Queen’s University Belfast, the Space Telescope Science Institute, the South African Astronomical Observatory, and The Millennium Institute of Astrophysics (MAS), Chile. We acknowledge ESA Gaia, DPAC and the Photometric Science Alerts Team (http://gsaweb.ast.cam.ac.uk/alerts). This paper includes data gathered with the 6.5 meter Magellan Telescopes located at Las Campanas Observatory, Chile. Parts of this work are based on observations made with ESO telescopes at La Silla Paranal Observatory under ESO programme 105.20UT.001. Some of the observations reported in this paper were obtained with the Southern African Large Telescope (SALT) under program 2020-2-MLT-008 (PI: A. Markowitz). Polish participation in SALT is funded by grant No. MNiSW DIR/WK/2016/07. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. The Digitized Sky Surveys were produced at the Space Telescope Science Institute under U.S. Government grant NAG W-2166. The images of these surveys are based on photographic data obtained using the Oschin Schmidt Telescope on Palomar Mountain and the UK Schmidt Telescope. The plates were processed into the present compressed digital form with the permission of these institutions. The UK Schmidt Telescope was operated by the Royal Observatory Edinburgh, with funding from the UK Science and Engineering Research Council (later the UK Particle Physics and Astronomy Research Council), until 1988 June, and thereafter by the Anglo-Australian Observatory. The blue plates of the southern Sky Atlas and its Equatorial Extension (together known as the SERC-J), as well as the Equatorial Red (ER), and the Second Epoch [red] Survey (SES) were all taken with the UK Schmidt.
References
- Abdollahi, S., Acero, F., Ackermann, M., et al. 2020, ApJS, 247, 33 [Google Scholar]
- Ai, Y., Dou, L., Yang, C., et al. 2020, ApJ, 890, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, K. D., van Velzen, S., Horesh, A., & Zauderer, B. A. 2020, Space Sci. Rev., 216, 81 [CrossRef] [Google Scholar]
- Appenzeller, I., Fricke, K., Fürtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] [Google Scholar]
- Arcavi, I., Gal-Yam, A., Sullivan, M., et al. 2014, ApJ, 793, 38 [Google Scholar]
- Arenou, F., Luri, X., Babusiaux, C., et al. 2018, A&A, 616, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [CrossRef] [Google Scholar]
- Auchettl, K., Ramirez-Ruiz, E., & Guillochon, J. 2018, ApJ, 852, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Bade, N., Komossa, S., & Dahlem, M. 1996, A&A, 309, L35 [NASA ADS] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [Google Scholar]
- Barvainis, R. 1987, ApJ, 320, 537 [Google Scholar]
- Bentz, M. C., Peterson, B. M., Netzer, H., Pogge, R. W., & Vestergaard, M. 2009, ApJ, 697, 160 [Google Scholar]
- Bentz, M. C., Denney, K. D., Grier, C. J., et al. 2013, ApJ, 767, 149 [Google Scholar]
- Bianchi, L., Shiao, B., & Thilker, D. 2017, ApJS, 230, 24 [Google Scholar]
- Birchall, K. L., Watson, M. G., Aird, J., & Starling, R. L. C. 2022, MNRAS, 510, 4556 [NASA ADS] [CrossRef] [Google Scholar]
- Blanchard, P. K., Nicholl, M., Berger, E., et al. 2017, ApJ, 843, 106 [Google Scholar]
- Boller, T., Freyberg, M. J., Trümper, J., et al. 2016, A&A, 588, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandt, W. N., Pounds, K. A., & Fink, H. 1995, MNRAS, 273, L47 [Google Scholar]
- Breedt, E., Arévalo, P., McHardy, I. M., et al. 2009, MNRAS, 394, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Breedt, E., McHardy, I. M., Arévalo, P., et al. 2010, MNRAS, 403, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Breeveld, A. A., Landsman, W., Holland, S. T., et al. 2011, Am. Inst. Phys. Conf. Ser., 1358, 373 [NASA ADS] [Google Scholar]
- Brightman, M., Ward, C., Stern, D., et al. 2021, ApJ, 909, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Bruhweiler, F., & Verner, E. 2008, ApJ, 675, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Brunner, H., Liu, T., Lamer, G., et al. 2022, A&A, 661, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buckley, D. A. H., Swart, G. P., & Meiring, J. G. 2006, SPIE Conf. Ser., 6267, 62670Z [Google Scholar]
- Burgh, E. B., Nordsieck, K. H., Kobulnicky, H. A., et al. 2003, SPIE Conf. Ser., 4841, 1463 [NASA ADS] [Google Scholar]
- Campana, S., Mainetti, D., Colpi, M., et al. 2015, A&A, 581, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chan, C.-H., Piran, T., Krolik, J. H., & Saban, D. 2019, ApJ, 881, 113 [Google Scholar]
- Charalampopoulos, P., Leloudas, G., Malesani, D. B., et al. 2022, A&A, 659, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, J.-H., Dou, L.-M., & Shen, R.-F. 2022, ApJ, 928, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M., Peterson, B. A., Jackson, C., et al. 2003, [arXiv:astro-ph/0306581] [Google Scholar]
- Dong, S., Bose, S., Chen, P., et al. 2018, ATel, 12198, 1 [NASA ADS] [Google Scholar]
- Donley, J. L., Brandt, W. N., Eracleous, M., & Boller, T. 2002, AJ, 124, 1308 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, A. J., Djorgovski, S. G., Mahabal, A., et al. 2011, ApJ, 735, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Bigelow, B., Hare, T., et al. 2011, PASP, 123, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Esquej, P., Saxton, R. D., Freyberg, M. J., et al. 2007, A&A, 462, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, D. W., Riello, M., De Angeli, F., et al. 2018, A&A, 616, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferland, G. J., Done, C., Jin, C., Landt, H., & Ward, M. J. 2020, MNRAS, 494, 5917 [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [Google Scholar]
- Frederick, S., Gezari, S., Graham, M. J., et al. 2021, ApJ, 920, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [Google Scholar]
- Gezari, S. 2021, ARA&A, 59, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Gezari, S., Chornock, R., Lawrence, A., et al. 2015, ApJ, 815, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Gezari, S., Hung, T., Cenko, S. B., et al. 2017, ApJ, 835, 144 [Google Scholar]
- Graham, A. W. 2007, MNRAS, 379, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, M. J., Ross, N. P., Stern, D., et al. 2020, MNRAS, 491, 4925 [NASA ADS] [Google Scholar]
- Greene, J. E., & Ho, L. C. 2005, ApJ, 630, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Schwarz, R., Zharikov, S., & Orio, M. 2000, A&A, 362, L25 [NASA ADS] [Google Scholar]
- Grier, C. J., Martini, P., Watson, L. C., et al. 2013, ApJ, 773, 90 [CrossRef] [Google Scholar]
- Grupe, D., Beuermann, K., Mannheim, K., et al. 1995, A&A, 299, L5 [NASA ADS] [Google Scholar]
- Grupe, D., Thomas, H. C., & Leighly, K. M. 1999, A&A, 350, L31 [NASA ADS] [Google Scholar]
- Grupe, D., Komossa, S., & Saxton, R. 2015, ApJ, 803, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Haggard, D., Green, P. J., Anderson, S. F., et al. 2010, ApJ, 723, 1447 [NASA ADS] [CrossRef] [Google Scholar]
- Hambly, N. C., Irwin, M. J., & MacGillivray, H. T. 2001, MNRAS, 326, 1295 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., & Best, P. N. 2014, ARA&A, 52, 589 [Google Scholar]
- Heckman, T. M., Ptak, A., Hornschemeier, A., & Kauffmann, G. 2005, ApJ, 634, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G. 1975, Nature, 254, 295 [Google Scholar]
- Hinkle, J. T., Holoien, T. W. S., Auchettl, K., et al. 2021, MNRAS, 500, 1673 [Google Scholar]
- Hinkle, J. T., Holoien, T. W. S., Shappee, B. J., et al. 2022, ApJ, 930, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Hinshaw, G., Larson, D., Komatsu, E., et al. 2013, ApJS, 208, 19 [Google Scholar]
- Hodgkin, S. T., Breedt, E., Delgado, A., et al. 2020, Transient Name Server Discovery Report, 2020–3112, 1 [Google Scholar]
- Holoien, T. W. S., Kochanek, C. S., Prieto, J. L., et al. 2016, MNRAS, 455, 2918 [NASA ADS] [CrossRef] [Google Scholar]
- Holoien, T. W. S., Vallely, P. J., Auchettl, K., et al. 2019, ApJ, 883, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Holoien, T. W. S., Neustadt, J. M. M., Vallely, P. J., et al. 2022, ApJ, 933, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D., Lawrence, A., Ward, M., et al. 2023, MNRAS, 519, 1745 [Google Scholar]
- Hung, T., Gezari, S., Blagorodnova, N., et al. 2017, ApJ, 842, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Inserra, C., Smartt, S. J., Gall, E. E. E., et al. 2018, MNRAS, 475, 1046 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, N., Wang, T., Yan, L., et al. 2017, ApJ, 850, 63 [Google Scholar]
- Jiang, N., Wang, T., Hu, X., et al. 2021, ApJ, 911, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, B. C., Bechtold, J., & Siemiginowska, A. 2009, ApJ, 698, 895 [Google Scholar]
- Kewley, L. J., Groves, B., Kauffmann, G., & Heckman, T. 2006, MNRAS, 372, 961 [Google Scholar]
- Kobulnicky, H. A., Nordsieck, K. H., Burgh, E. B., et al. 2003, SPIE Conf. Ser., 4841, 1634 [NASA ADS] [Google Scholar]
- Kokubo, M., Morokuma, T., Minezaki, T., et al. 2014, ApJ, 783, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Komossa, S., & Bade, N. 1999, A&A, 343, 775 [NASA ADS] [Google Scholar]
- Komossa, S., & Greiner, J. 1999, A&A, 349, L45 [NASA ADS] [Google Scholar]
- Komossa, S., Zhou, H., Wang, T., et al. 2008, ApJ, 678, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
- Lawrence, A. 2018, Nat. Astron., 2, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Lawrence, A., Bruce, A. G., MacLeod, C., et al. 2016, MNRAS, 463, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Leloudas, G., Fraser, M., Stone, N. C., et al. 2016, Nat. Astron., 1, 0002 [Google Scholar]
- Leloudas, G., Dai, L., Arcavi, I., et al. 2019, ApJ, 887, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Li, R., Ho, L. C., Ricci, C., et al. 2022, ApJ, 933, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lightman, A. P., & Eardley, D. M. 1974, ApJ, 187, L1 [Google Scholar]
- Liu, Z., Li, D., Liu, H.-Y., et al. 2020, ApJ, 894, 93 [Google Scholar]
- MacLeod, M., Ramirez-Ruiz, E., Grady, S., & Guillochon, J. 2013, ApJ, 777, 133 [NASA ADS] [CrossRef] [Google Scholar]
- MacLeod, C. L., Ross, N. P., Lawrence, A., et al. 2016, MNRAS, 457, 389 [Google Scholar]
- Mainzer, A., Bauer, J., Cutri, R. M., et al. 2014, ApJ, 792, 30 [Google Scholar]
- Malyali, A., Rau, A., Merloni, A., et al. 2021, A&A, 647, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marconi, A., & Hunt, L. K. 2003, ApJ, 589, L21 [Google Scholar]
- Martin, J. R., Reichart, D. E., Dutton, D. A., et al. 2019, ApJS, 240, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Mattila, S., Pérez-Torres, M., Efstathiou, A., et al. 2018, Science, 361, 482 [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [Google Scholar]
- Merloni, A., Dwelly, T., Salvato, M., et al. 2015, MNRAS, 452, 69 [Google Scholar]
- Mummery, A., & Balbus, S. A. 2020, MNRAS, 497, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, C. H. 2000, ApJ, 544, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H. 2015, ARA&A, 53, 365 [Google Scholar]
- Neustadt, J. M. M., Holoien, T. W. S., Kochanek, C. S., et al. 2020, MNRAS, 494, 2538 [CrossRef] [Google Scholar]
- Nicholl, M., Short, P., Angus, C., et al. 2019, ATel, 12752, 1 [NASA ADS] [Google Scholar]
- Nicholl, M., Wevers, T., Oates, S. R., et al. 2020, MNRAS, 499, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Noda, H., Minezaki, T., Watanabe, M., et al. 2016, ApJ, 828, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Novak, G. S., Ostriker, J. P., & Ciotti, L. 2011, ApJ, 737, 26 [Google Scholar]
- Oke, J. B. 1974, ApJS, 27, 21 [Google Scholar]
- Oknyansky, V. L., Gaskell, C. M., Huseynov, N. A., et al. 2017, MNRAS, 467, 1496 [NASA ADS] [Google Scholar]
- Oknyansky, V. L., Winkler, H., Tsygankov, S. S., et al. 2020, MNRAS, 498, 718 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, M. L., Komossa, S., Kollatschny, W., et al. 2016, MNRAS, 461, 1927 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, M. L., Schartel, N., Grupe, D., et al. 2019, MNRAS, 483, L88 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [Google Scholar]
- Phinney, E. S. 1989, Nature, 340, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Predehl, P., Andritschke, R., Arefiev, V., et al. 2021, A&A, 647, A1 [EDP Sciences] [Google Scholar]
- Press, W. H. 1978, Comments Astrophys., 7, 103 [NASA ADS] [Google Scholar]
- Rees, M. J. 1988, Nature, 333, 523 [Google Scholar]
- Remillard, R. A., Loewenstein, M., Steiner, J. F., et al. 2022, AJ, 163, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Kara, E., Loewenstein, M., et al. 2020, ApJ, 898, L1 [Google Scholar]
- Ricci, C., Loewenstein, M., Kara, E., et al. 2021, ApJS, 255, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, N. P., Ford, K. E. S., Graham, M., et al. 2018, MNRAS, 480, 4468 [Google Scholar]
- Ruan, J. J., Anderson, S. F., Eracleous, M., et al. 2019, ApJ, 883, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Rumbaugh, N., Shen, Y., Morganson, E., et al. 2018, ApJ, 854, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Runnoe, J. C., Brotherton, M. S., & Shang, Z. 2012, MNRAS, 422, 478 [Google Scholar]
- Saxton, R. D., Read, A. M., Komossa, S., et al. 2014, A&A, 572, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saxton, R. D., Motta, S. E., Komossa, S., & Read, A. M. 2015, MNRAS, 454, 2798 [NASA ADS] [CrossRef] [Google Scholar]
- Sazonov, S., Gilfanov, M., Medvedev, P., et al. 2021, MNRAS, 508, 3820 [NASA ADS] [CrossRef] [Google Scholar]
- Schawinski, K., Koss, M., Berney, S., & Sartori, L. F. 2015, MNRAS, 451, 2517 [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Shappee, B. J., Prieto, J. L., Grupe, D., et al. 2014, ApJ, 788, 48 [Google Scholar]
- Shen, Y. 2021, ApJ, 921, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Skilling, J. 2004, Am. Inst. Phys. Conf. Ser., 735, 395 [NASA ADS] [Google Scholar]
- Smith, K. W., Smartt, S. J., Young, D. R., et al. 2020, PASP, 132, 085002 [Google Scholar]
- Sołtan, A. 1982, MNRAS, 200, 115 [CrossRef] [Google Scholar]
- Stern, J., & Laor, A. 2012, MNRAS, 426, 2703 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, D., McKernan, B., Graham, M. J., et al. 2018, ApJ, 864, 27 [Google Scholar]
- Sunyaev, R., Arefiev, V., Babyshkin, V., et al. 2021, A&A, 656, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J. L., Denneau, L., Heinze, A. N., et al. 2018, PASP, 130, 064505 [Google Scholar]
- Trakhtenbrot, B., Arcavi, I., MacLeod, C. L., et al. 2019a, ApJ, 883, 94 [Google Scholar]
- Trakhtenbrot, B., Arcavi, I., Ricci, C., et al. 2019b, Nat. Astron., 3, 242 [Google Scholar]
- Truemper, J. 1992, QJRAS, 33, 165 [NASA ADS] [Google Scholar]
- Tundo, E., Bernardi, M., Hyde, J. B., Sheth, R. K., & Pizzella, A. 2007, ApJ, 663, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Uttley, P., Edelson, R., McHardy, I. M., Peterson, B. M., & Markowitz, A. 2003, ApJ, 584, L53 [NASA ADS] [CrossRef] [Google Scholar]
- van Velzen, S., Farrar, G. R., Gezari, S., et al. 2011, ApJ, 741, 73 [Google Scholar]
- van Velzen, S., Anderson, G. E., Stone, N. C., et al. 2016a, Science, 351, 62 [NASA ADS] [CrossRef] [Google Scholar]
- van Velzen, S., Mendez, A. J., Krolik, J. H., & Gorjian, V. 2016b, ApJ, 829, 19 [NASA ADS] [CrossRef] [Google Scholar]
- van Velzen, S., Gezari, S., Hammerstein, E., et al. 2021, ApJ, 908, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Vanden Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [Google Scholar]
- Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003, MNRAS, 345, 1271 [Google Scholar]
- Vaughan, S., Uttley, P., Markowitz, A. G., et al. 2016, MNRAS, 461, 3145 [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [Google Scholar]
- Vestergaard, M., & Peterson, B. M. 2006, ApJ, 641, 689 [Google Scholar]
- Wang, T.-G., Zhou, H.-Y., Komossa, S., et al. 2012, ApJ, 749, 115 [Google Scholar]
- Wang, J., Xu, D. W., & Wei, J. Y. 2020, ApJ, 901, 1 [Google Scholar]
- Wevers, T., Pasham, D. R., van Velzen, S., et al. 2019, MNRAS, 488, 4816 [Google Scholar]
- Willingale, R., Starling, R. L. C., Beardmore, A. P., Tanvir, N. R., & O’Brien, P. T. 2013, MNRAS, 431, 394 [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
- Xiao, T., Barth, A. J., Greene, J. E., et al. 2011, ApJ, 739, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, L., Wang, T., Jiang, N., et al. 2019, ApJ, 874, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Z., Kochanek, C. S., Mathur, S., et al. 2022, MNRAS, 515, 5198 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Szanecki, M., Poutanen, J., Gierliński, M., & Biernacki, P. 2020, MNRAS, 492, 5234 [NASA ADS] [CrossRef] [Google Scholar]
- Życki, P. T., Done, C., & Smith, D. A. 1999, MNRAS, 309, 561 [Google Scholar]
Appendix A: X-ray observations
A.1. XMM-Newton analysis
Figure A.1 shows the combined X-ray and UV counts data of the XMM-Newton observation. We test a range of spectral models in XSPEC (version 12.11.1d) using χ2 statistics. In parallel, we test the same models using the nested sampling algorithm MULTINEST v.3.10 (Skilling 2004; Feroz et al. 2009) via the Bayesian X-ray Analysis and PyMultinest packages for XSPEC (BXA, version 3.31, using Xspec version 12.10.1; Buchner et al. 2014, see section 2.2) Both methods yield highly similar results in terms of model goodness of fit. In addition we find that for the majority of model parameters, best-fit values and 90% confidence level uncertainties obtained using both methods are consistent. We therefore included only the Bayesian evidence in the discussion in Section 2.2; however, we present a full overview of our fitting results in Table A.1.
 |
Fig. A.1. XMM-Newton count rate light curves for EPIC pn 0.2–2.0 keV (500 s bins; blue) and for Optical Monitor UVM2 fast mode (800 s bins; orange). MET refers to Mission Elapsed Time, and the MET zeropoint used for the x-axis corresponds to 10:33:53 on 23 December 2020. Both datasets are plotted in counts per second. Whereas the X-ray emission is clearly strongly variable over the duration of the observation, the optical light curve shows no significant variability on this timescale. |
Overview of the best-fitting models to the XMM-Newton data.
For the XMM-Newton data we use 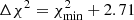 for the least-squares fitting, which corresponds to a 90% confidence level for one parameter when errors are symmetric. We use the 5th and 95th percentiles of the posterior distribution for Bayesian fits.
for the least-squares fitting, which corresponds to a 90% confidence level for one parameter when errors are symmetric. We use the 5th and 95th percentiles of the posterior distribution for Bayesian fits.
A.2. Swift-XRT analysis
For the Swift-XRT observations we tested several models in XSPEC using Cash statistics (Section 2.3). We tested a single power-law, a single blackbody, and a double blackbody (2BB), the summary results of which are included in Table 1. We present a full overview of the results of our fitting of the Swift-XRT spectra in Table A.2.
Swift-XRT spectral fitting results.
A.3. NICER reductions and analysis
To maximise the observing time before the Sun-block period, the observations were pushed as close as possible to the instrumental limits of NICER. These limits are set by a maximum X-ray contamination by optical loading. As the effect of the optical loading was larger than expected, a significant fraction of the data unfortunately needed to be rejected, particularly close to the Sun-block period. The final good time intervals (GTIs) cover the period 6 to 11 January (MJD 58854–58859) and represent a combined exposure time of 18.5 ks.
Observations are separated into time intervals (TIs) with exposures between 30-60 sec for filtering, and a background spectrum is constructed for each TI using the 3C50 background estimator. Absolute count rates from 50 Focal Plane Modules (FPMs) are used, excluding noisy detectors 14 and 34. Two indicators of optical loading are chosen to filter the dataset: residual background and undershoot rate. The first, based on signal in an energy band that has negligible source contribution, follows the level 3 filtering guidelines standardised in Remillard et al. (2022). This filtering process excludes TIs in which 3C50 underestimates the background due to elevated levels of optical loading (0.2–0.3 keV) or the high energy particle background (13–15 keV), indicating an unreliable source spectrum for the TI. Periods of underestimated optical loading are identified as those intervals where the background-subtracted count rate in the 0.2–0.3 keV band is greater than 2 photons per second. For periods with count rates below this limit, the optical loading was found to be sufficiently low to be able to accurately model the background for all energy bands. For periods with a 0.2–0.3 keV count rate above the limit, the optical loading proved too strong to accurately model the background at energies above 0.3 keV, and these periods were therefore excluded from our GTIs.
Second, TIs affected by optical loading at energies above 0.3 keV are screened out using the detector undershoot rate. This is an instrumental parameter that counts detector resets due to the accumulation of electrons in the equipment freed by incident optical photons (Remillard et al. 2022). Optical loading and the associated undershoot rates are highest at low Sun angles, reaching a maximum of 300-400 counts s−1 closest to the Sun-block period. For TIs with an undershoot rate above 150 counts s−1, a correlated relationship between undershoot rate and count rate in the 0.3–2 keV source sensitivity band is observed. This indicates that in-band count rates are significantly contaminated by optical loading when the undershoot rate is greater than 150 counts s−1, even when the contribution from optical loading is modelled appropriately in the 0.2-0.3 keV band. Because 3C50 currently lacks the capability to model the effect of extreme levels of optical loading at energies above 0.3 keV, we excluded observations with an undershoot rate > 150 counts s−1 from our GTIs.
For periods where both background residuals and undershoot rate are below their respective limits, the optical loading was found to be sufficiently low to be able to accurately model the background for all energy bands. We subsequently use the NICER reduction pipeline to produce the standard RMF and ARF. We fit the NICER data using XSPEC v12.12.0, which is part of HEASOFT v6.28. The data have been re-binned to a minimum of 25 counts per bin, and we use χ2-statistics.
The NICER spectrum of J234402 shows soft emission. As the count rate above 1.2 keV is relatively low, we experimented with different fitting ranges to assess the impact of the presence of noise in this energy range. Performing all fits described above in the energy ranges 0.3–2.0 keV and 0.3–1.2 keV, we find that 2BB (Section 2.2) is the best-fitting model in both cases, with no significant impact on the goodness-of-fit. In fact, the only significant impact we find is that the power-law+blackbody proves a slightly better model in the 0.3–1.2 keV range with χ2/dof increasing from 179.3/134 (in the 0.3–2.0 keV range) to 103.6/84 (in the 0.3–1.2 keV range). We interpret this to mean that the power-law component, evidently a poor fit to our data, is better constrained when using the broader energy range due to the lack of signal above 1.2 keV. We therefore chose to use the 0.3–2.0 keV range for fitting the NICER data, as it provides the best constraints for our models, while avoiding the background-dominated energy range above 2 keV. The model fitting results quoted for NICER have all been derived in the 0.3–2.0 keV range.
To calculate the NICER fluxes included in Figure 1, we scaled the 0.3–2.0 count rate using a 0.2–2.0 keV flux based on our best-fit 2BB model, which was fit to the combined NICER data. Although there is some spectral variability, we find that the effect of the spectral changes on the count-to-flux scaling is negligible.
Appendix B: UV and optical observations
B.1. Photometry
In Figure B.1 we show a close-up of our photometric light curve (not host-corrected) in combination with our UV and X-ray data. The figure also shows the epochs for our optical spectroscopy.
 |
Fig. B.1. The optical, UV, and X-ray light curves around the time of ignition. Fluxes and magnitudes are corrected for Galactic absorption. Top: The X-ray light curve, consisting of the eROSITA, XMM-Newton, Swift-XRT, and NICER data. Bottom: Light curves for ATLAS c and o, Gaia g, Swift-UVOT, and PROMPT6 R data. These data are not host subtracted. The data are plotted in time relative to the point of the first peak in the o-band light curve (see Section 3.1.6). The dashed vertical lines represent the epochs for our optical spectroscopy. The optical data show a sharp increase over approximately 3 weeks, followed by a sharp turnover, a further bump visible in the o and c bands, and subsequent decline. The decline in optical brightness is matched in the UV and X-ray data. |
B.1.1. POSS2 photometry
J234402 was observed with the UK Schmidt telescope in the POSS2 B band in 1985 (MJD 46267) and the POSS2 R band in 1997 (MJD 50691). The blend of the three southern sources was identified as a single target for the 2dFGRS (Colless et al. 2003). The extraction of the POSS2 photographic flux values is complex, as it depends on the responses of the emulsion + filter combinations used in the POSS2 observations. We make use of the magnitudes calculated for the SuperCOSMOS Survey (Hambly et al. 2001). In the POSS2-R image, magnitudes were extracted for both the northern target and the blended group of southern targets. However, for the POSS2-B imaging, a magnitude is only available for the combined flux from the cluster consisting of all four objects.
To estimate the impact of the blending in the POSS2-B image, we downloaded the reduced image from the MAST DSS server. We use Astropy (Astropy Collaboration 2013, 2018) routines to create a background map for the image, automatically detect sources in the background-subtracted data, and separate these sources where possible. The routine successfully separates J234402 from the blend of the three southern sources. We find that approximately 40% of the combined flux is associated with J234402. Adjusting the SuperCOSMOS magnitude by this fraction, we find that the POSS2-B magnitude for J234402 is 18.2 and POSS2-R magnitude is 16.9. Hambly et al. (2001) quote the average accuracy of the POSS photometry as within 0.3 mag. We note that since the POSS2 photometric system differs from that of our more recent observations, a direct comparison is difficult. However, these data remain valuable as a constraint on the longer term evolution of J234402.
B.1.2. Swift-UVOT photometry
We test for the contribution of instrumental variability to the flux changes among observations. We correct the UVOT flux measurements by calibrating to two stars in the UVOT field of view (source IDs 2311717768560445056 and 2311905170869138560, referred to here as S5056 and S8560, respectively). We illustrate this method in Figure B.2. For the U, W1, and W2 filters, we calculate the average flux for the standard stars. In each filter, we calculate the difference between the observed and the average flux per epoch. We assume that these deviations are not intrinsic to the sources, bur rather are instrumental, and we adjust the magnitudes for J234422 accordingly. For M2, we have insufficient epochs with a good detection of the reference stars, so we cannot correct the flux in this filter. This is also the reason that we cannot apply this method to the XMM-Newton OM-UVM2 data to correct for inter-mission uncertainties. The uncorrected and corrected magnitudes are included in Figure B.2, to show the size of the correction.
 |
Fig. B.2. Example of adjusting Swift-UVOT fluxes, for the U-band. The magnitudes of two standard stars are shown in the top two panels (the magnitude of the first standard star could not be extracted for the fourth epoch). We assume the flux of these objects to be constant over the time covered by the Swift observations. We calculate the difference with the mean flux (indicated by the dashed line) for the observed flux in each epoch and adjust the magnitudes for J234402 accordingly. The bottom panel shows the uncorrected (grey) and corrected (open) magnitudes for the U-band observations of J234402. |
B.2. Optical spectroscopy
B.2.1. Location of the ignition event
Our follow-up optical spectroscopy shows that the northern galaxy (in the group of four) has a strong blue continuum, as well as broad Balmer emission lines. Spectra for the southern objects in the group resemble those of quiescent galaxies. This agrees with the eROSITA and Gaia localisations of the brightening X-ray and optical sources, to identify the northern galaxy as the location of the ignition event. Spectra for all four objects are shown in Figure B.3. The three southern objects are at approximately the same redshift as the bluer northern source with z ranging from 0.099 to 0.101. The match in redshift indicates the four objects are likely in physical proximity and form a small group. Using the angular separation between objects A and D, approximately 9", as a rough estimate for the maximum extent of the group, we find a transverse proper distance of approximately 18 kpc.
 |
Fig. B.3. Counterpart and environment of J234402. Left: The optical counterpart of J234402. The yellow star represents the X-ray position and the yellow circle indicates the 1.0" (1σ radius) positional uncertainty of the eROSITA detection. This image was taken as an acquisition exposure with the Baade telescope using a white filter during our spectroscopic follow-up campaign. The source area includes four targets (labelled A–D), which were found to be at the same redshift. The Northern object, labelled A, is associated with the significant X-ray-flux increase detected by eROSITA, as well as with the significant optical outburst seen with Gaia (TNS#85552). Right: Overview of the spectra taken for the four objects that make up the galaxy group containing J234402. The labels A through D correspond to the objects in the image on the left. Object A is J234402. The spectra are plotted at their observed wavelengths, and the positions of several spectral lines, at z = 0.100 are shown in each plot. The plots illustrate the clear difference in spectral classification among the objects — object A shows an AGN-like spectrum, whereas the other three objects appear to be quiescent galaxies. The flux scale is arbitrary, and we note that the spectrum for object D has not been flux-calibrated. Spectra for A, B, and C are from the Baade (Magellan) observation. The spectrum for D is from the SALT observation of MJD 59206 (23 December). |
B.2.2. The FORS2 spectrum
The FORS2 spectrum shows several distinct features at wavelengths lower than 4000 Å(Figure 8). The absence of these features in the near-contemporaneous SALT spectrum (23 Dec.) led us to further investigate the ‘bumps’ in the FORS2 spectrum. We checked the flux calibration by comparing the flux-scaled spectrum of the standard star (HZ4) with the tabled archival data for that star. We found that in the wavelength range below 4000 Å the flux-calibrated spectrum is overestimated in a pattern that matches the ‘bumps’ seen in the spectrum of J234402. The discrepancy between the flux-scaled, observed spectrum and the tabled data in this region of the spectrum is as large as 10%, compared to < 3% in the rest of the spectrum.
B.2.3. Fitting a blackbody temperature
We illustrate our fitting procedure for a blackbody spectrum to the optical spectrum, in Figure B.4. The procedure is similar to that described in Section 3.2.2. We include a host-galaxy template and a blackbody spectrum. The parameters of the host-galaxy template are fixed to the values found for the Baade spectrum. We let the blackbody temperature and a normalisation parameter vary freely.
 |
Fig. B.4. Illustration of our fitting procedure for optical spectra with blackbody+host model. The example spectrum was taken with the Baade telescope on MJD 59195. The top panel shows the data and model, and the bottom panel shows the residuals. The fitting model consists of the Planck function (green) and a template for the emission from the host galaxy (black). The best-fit model (red) is defined by log(Tbb/[K]) = 4.10 and results in a bolometric luminosity log(Lbb/[erg s−1]) = 44.3. |
All Tables
Fitting parameters and goodness-of-fit values for X-ray spectral fits to subsets of NICER data.
All Figures
 |
Fig. 1. Overview of X-ray data collected on J234402. The light curve starts from the detection of the ignition event with eROSITA in November 2020. The 3σ upper limit of the eRASS1 scan in May 2020 was 1.1 × 10−13 erg cm−2 s−1 (log10(LX/[erg s−1]) = 41.8). The flux evolution over time is significant, showing both an overall decrease and large fluctuations on shorter timescales. To illustrate the magnitude of the variability on the shortest timescales, the light curves of individual eRASS2 scans and for the XMM-Newton EPIC-pn data, binned to 500s, are included in insets. The vertical extent of the grey boxes around the eROSITA and XMM-Newton markers shows the size of the y-axes of the insets within the larger plot. In the inset of the eROSITA light curve the horizontal axis marks the time in ks since MJD 59181.75, and in the inset of the XMM-Newton light curve it marks the time in ks since MJD 59205.44. On the right vertical axis we show the log10(LX/[erg s−1]) values associated with the observed flux. To calculate these values, we made use of the best-fit model (2BB, Sect. 2.2). |
| In the text | |
 |
Fig. 2. Binned eROSITA spectrum of J234402. The spectrum for the eRASS2 observation (28–29 November 2020) is very soft, a characteristic confirmed in all our X-ray observations. Included in red (solid line) is the best-fit model, consisting of two redshifted black bodies (dotted lines), corrected for Galactic absorption. |
| In the text | |
 |
Fig. 3. Unfolded model spectrum from XMM-Newton. The spectrum was unfolded using the best-fit dual blackbody model (2BB), with blackbody temperatures of 53 ± 2 eV and |
| In the text | |
 |
Fig. 4. NICER light curve and hardness ratio of J234402. Top: 0.3–2 keV NICER light curve. The light curve shows significant variability on a timescale of days. The sharp turns up and down are consistent with the rapid variability observed in the XMM-Newton and eROSITA data. The dashed line indicates the cut-off between the low-state and high-state intervals at 3.78 counts s−1, as discussed in Sect. 2.4.2. Bottom: hardness ratio (HR) in NICER light curve. We define the HR using the 0.3–0.5 keV and the 0.5–2 keV count rates (R0.3 − 0.5 and R0.5 − 2, respectively), as defined in the text. We detect no significant change over time. |
| In the text | |
 |
Fig. 5. Spectrum from NICER for the cumulative observation time. The best-fit double-blackbody model (2BB) is shown in red, with the two blackbody components shown as dashed black and blue lines. The residuals of our best-fit model are shown in the bottom panel. |
| In the text | |
 |
Fig. 6. Optical and infrared photometric data on J234402 over the past five years. The top panel show the NEOWISE-R data for the W1 and W2 infrared bands and the bottom panel shows the optical light curve based on a combination of public survey data and follow-up observations obtained by our team. All measurements have been corrected for Galactic extinction. The optical light curve shows a relatively quiescent state interrupted by a sharp flare, followed by a plateau and subsequent decay. The data are not host subtracted. The downward arrows represent 3σ upper limits in the ATLAS dataset. All data include statistical uncertainties. For most points on our dataset, the statistical uncertainties are too small to be visible in this plot. |
| In the text | |
 |
Fig. 7. Evolution of optical output in ATLAS o-band and c-band filters. The data are ATLAS differential photometry and the view focuses on the time around the ignition event. All data points include statistical errors. We distinguish three phases in the first months of the ignition event’s light curve: a sharp initial rise, a temporary levelling off & re-brightening, and decay. The demarcations between the phases are shown as grey vertical lines. We compare the data in these three phases with simple power-law models (Eqs. (1) and (2)). The initial rise is fit to the o-band data only and the result is shown in dashed green, with 1σ error margins shown as shaded regions. We include the best-fit rising power-law in phase II (dashed black) primarily to guide the eye, as the light curve data proved to sparse for a well-constrained fit. For the decay period, we separately fit the o-band and the c-band data, and results are shown as the red (dotted) and blue (dot-dashed) lines, respectively. |
| In the text | |
 |
Fig. 8. Optical spectra of J234402. The data are from our follow-up campaign with Baade (Magellan), VLT, and SALT. The spectra show a blue continuum as well as strong broad and narrow emission lines. The broad lines show a distinct asymmetry, with a blue wing. The spectra have been scaled using the P6 photometry and are presented here with a flux offset for clarity. Several important emission lines are marked with dashed lines. Spectral regions affected by telluric absorption have been indicated by grey bands. The inset shows a close-up of Hβ for the two spectra separated by the largest time span (17 days), as well as the difference between the spectra. The fitted host+continuum components have been subtracted from the spectra in the inset and they were normalised using the [OIII]λ5007 line fluxes. Over the period of follow-up presented here, the object shows no significant spectral evolution. |
| In the text | |
 |
Fig. 9. Our fitting procedure for the optical spectra. The procedure is illustrated for the spectrum taken with the Baade telescope on MJD 59195. (a) Continuum fit. The continuum is fit with a function consisting of a single power law (red dotted), an FeII-emission template (black), and a host-galaxy template (green). The residuals for all fits are shown underneath their respective plots. (b) Fit of continuum-subtracted spectrum around Hβ. The combined fit consists of five Gaussian profiles, two for the narrow [OIII] (black dotted) lines and a narrow (green dashed), broad (blue dot-dashed), and very broad (black dashed) component for Hβ. (c) Fit of continuum-subtracted spectrum around Hα. The combined fit for this region consists of six Gaussians: two for the narrow [NII] lines, two for the narrow [SII] lines (dotted black), and three for the Hα emission, with the same colours as the components used to fit Hβ. |
| In the text | |
 |
Fig. 10. Line flux diagnostic diagrams (Baldwin et al. 1981) for J234402. The classification curves are from Kewley et al. (2006). The location of each of the J234402 spectra is indicated with a red star. The two subplots show the ratio [OIII]λ5007/Hβ (a) plotted against [NII]λ6584/Hα and (b) plotted against [SII]λ6717/Hα. The shaded regions represent the line flux ratios of ∼100 000 SDSS galaxies (restricted to 0.05 < z < 0.15), using the fluxes made available in the MPA-JHU data release (http://wwwmpa.mpa-garching.mpg.de/SDSS/DR7/). Darker shades of grey mean a higher number density of objects. For the Balmer lines of J234402, the fluxes were calculated using only the narrow components of the line decomposition (Fig. 9). The narrow lines are formed at a kpc-scale distance from the central source and therefore represent a past accretion state. The line diagnostics suggest that the nucleus of J234402 was active for an extended period within the last ∼103 yr. The inset in the bottom left of each plot shows the mean of the formal uncertainties associated with the J234402 spectral fits. |
| In the text | |
 |
Fig. 11. Spectrum of J234402 compared with spectra of several classes of objects. The optical spectrum of J234402 (black) is shown together with spectra from several other classes of objects that show extreme outbursts: TDEs (green), supernovae (blue), and changing-look AGN (red). The emission lines marked in red (dashed) are those more typically associated with AGN and the emission lines marked in blue (dotted), are those that are prominent in both AGN and TDEs. The narrow-line features of J234402 are more typical of an AGN; however, the broad-line features agree with both a TDE and an AGN interpretation. The included TDE spectra belong to the TDE–H+He AT2019dsg (z = 0.051, spectrum 34 days after discovery, Nicholl et al. 2019), the TDE–H AT2018hyz (z = 0.046, spectrum 6 days after discovery, Dong et al. 2018), and the TDE–H+He AT2018dyb (z = 0.018, spectrum 34 days after peak emission, Leloudas et al. 2019). The SN spectrum belongs to the H-rich SLSN II SN2013hx (z = 0.125, spectrum 55 days after detection, Inserra et al. 2018). The two changing-look AGN spectra both represent the relative high state of the objects: SDSSJ111536.57+054449.7 (z = 0.090, first reported by Yan et al. 2019) and SDSSJ102152.34+464515.6 (z = 0.204, first reported by MacLeod et al. 2016). All spectra have been corrected for redshift, the flux densities have been normalised for the purpose of comparison, and we have removed features that were obviously associated with atmospheric absorption. No correction was made for the host galaxy contribution. |
| In the text | |
 |
Fig. 12. Derived blackbody temperatures and blackbody radii of several TDEs compared to those of J234402. TDE-H and THD-He refer to TDEs with only hydrogen or only helium lines in their spectrum, respectively (see Sect. 4.2 for further detail). The dashed grey lines show the expected log |
| In the text | |
 |
Fig. A.1. XMM-Newton count rate light curves for EPIC pn 0.2–2.0 keV (500 s bins; blue) and for Optical Monitor UVM2 fast mode (800 s bins; orange). MET refers to Mission Elapsed Time, and the MET zeropoint used for the x-axis corresponds to 10:33:53 on 23 December 2020. Both datasets are plotted in counts per second. Whereas the X-ray emission is clearly strongly variable over the duration of the observation, the optical light curve shows no significant variability on this timescale. |
| In the text | |
 |
Fig. B.1. The optical, UV, and X-ray light curves around the time of ignition. Fluxes and magnitudes are corrected for Galactic absorption. Top: The X-ray light curve, consisting of the eROSITA, XMM-Newton, Swift-XRT, and NICER data. Bottom: Light curves for ATLAS c and o, Gaia g, Swift-UVOT, and PROMPT6 R data. These data are not host subtracted. The data are plotted in time relative to the point of the first peak in the o-band light curve (see Section 3.1.6). The dashed vertical lines represent the epochs for our optical spectroscopy. The optical data show a sharp increase over approximately 3 weeks, followed by a sharp turnover, a further bump visible in the o and c bands, and subsequent decline. The decline in optical brightness is matched in the UV and X-ray data. |
| In the text | |
 |
Fig. B.2. Example of adjusting Swift-UVOT fluxes, for the U-band. The magnitudes of two standard stars are shown in the top two panels (the magnitude of the first standard star could not be extracted for the fourth epoch). We assume the flux of these objects to be constant over the time covered by the Swift observations. We calculate the difference with the mean flux (indicated by the dashed line) for the observed flux in each epoch and adjust the magnitudes for J234402 accordingly. The bottom panel shows the uncorrected (grey) and corrected (open) magnitudes for the U-band observations of J234402. |
| In the text | |
 |
Fig. B.3. Counterpart and environment of J234402. Left: The optical counterpart of J234402. The yellow star represents the X-ray position and the yellow circle indicates the 1.0" (1σ radius) positional uncertainty of the eROSITA detection. This image was taken as an acquisition exposure with the Baade telescope using a white filter during our spectroscopic follow-up campaign. The source area includes four targets (labelled A–D), which were found to be at the same redshift. The Northern object, labelled A, is associated with the significant X-ray-flux increase detected by eROSITA, as well as with the significant optical outburst seen with Gaia (TNS#85552). Right: Overview of the spectra taken for the four objects that make up the galaxy group containing J234402. The labels A through D correspond to the objects in the image on the left. Object A is J234402. The spectra are plotted at their observed wavelengths, and the positions of several spectral lines, at z = 0.100 are shown in each plot. The plots illustrate the clear difference in spectral classification among the objects — object A shows an AGN-like spectrum, whereas the other three objects appear to be quiescent galaxies. The flux scale is arbitrary, and we note that the spectrum for object D has not been flux-calibrated. Spectra for A, B, and C are from the Baade (Magellan) observation. The spectrum for D is from the SALT observation of MJD 59206 (23 December). |
| In the text | |
 |
Fig. B.4. Illustration of our fitting procedure for optical spectra with blackbody+host model. The example spectrum was taken with the Baade telescope on MJD 59195. The top panel shows the data and model, and the bottom panel shows the residuals. The fitting model consists of the Planck function (green) and a template for the emission from the host galaxy (black). The best-fit model (red) is defined by log(Tbb/[K]) = 4.10 and results in a bolometric luminosity log(Lbb/[erg s−1]) = 44.3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.