EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 671 (March 2023) A&A, 671 (2023) A139 Full HTML
Open Access
Issue
A&A
Volume 671, March 2023
Article Number A139
Number of page(s) 24
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202244980
Published online 16 March 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The interior structure and evolution of a star are largely determined by its mass and chemical composition at formation. Precise and accurate observational constraints on these fundamental physical quantities are required for the validation, calibration, and improvement of theoretical models of the interior structure and evolution of stars. Despite being much more complex than single stars, binary star systems are a treasure trove for testing stellar structure and evolution models and helping us understand how these might be improved. In the case of eclipsing binaries (EBs) where both components are detected spectroscopically, it is possible to measure their masses and radii with high precision and accuracy using only orbital mechanics and geometry. Detached systems are particularly valuable as they are expected to evolve as single stars without alteration of their evolution via mass transfer episodes.

The role of precise empirical mass measurements is difficult to overstate for validating and calibrating modern and sophisticated stellar models. Herrero et al. (1992) presented a study of 25 luminous Galactic OB-type stars and reported a discrepancy between the masses inferred from their spectra (via wind theory) and those predicted by evolutionary models. The authors termed the effect the ‘mass discrepancy’ and emphasised the difficulty in attributing it to either of the two theories involved (wind and stellar evolution). Since then, many attempts have been made to diagnose the cause of the mass discrepancy in intermediate- to high-mass stars.

Given the high precision and accuracy that detached eclipsing binaries (dEBs) that are double-lined spectroscopic binaries (SB2) allow us to achieve in measurements of mass and surface gravity (e.g., Torres et al. 2010), these objects are important for studying the mass discrepancy. Burkholder et al. (1997) studied seven early-type spectroscopic binaries with masses below 15 M⊙ and reported a good agreement between masses inferred from binary dynamics and those estimated with evolutionary models in all cases where the stars are non-interacting. Guinan et al. (2000) and Pavlovski et al. (2009) presented independent studies of the high-mass SB2 dEB V380 Cyg and reported a substantial mass discrepancy for the evolved primary component, in the sense that its dynamical mass is too low compared to the predictions of standard stellar models. Whereas Guinan et al. (2000) showed that the discrepancy could be resolved by introducing extra near-core mixing in the form of convective core overshooting, Pavlovski et al. (2009) found that rotationally induced mixing in models was insufficient to explain the mass discrepancy. Indeed, Tkachenko et al. (2014b) demonstrated that only the combined effects of rotation and convective core overshooting can account for the mass discrepancy observed in V380 Cyg.

Recently, Massey et al. (2012), Morrell et al. (2014), Mahy et al. (2015), and Pavlovski et al. (2018) reported systematic discrepancies between the Keplerian and evolutionary masses of stars less massive than 30 M⊙. Mahy et al. (2020b) find a good agreement between the spectroscopic and dynamical masses for 26 early-type binary components, whereas their evolutionary masses appear to be systematically overestimated. These results hint towards models of interior structure and evolution being the primary cause of the mass discrepancy. Tkachenko et al. (2020) and Johnston (2021) demonstrate that the problem cannot be attributed to differences in observation and analysis methods between research groups, and instead show that the mass discrepancy progressively increases with the evolutionary stage of the star. In particular, the authors find that higher convective core masses were required in models of stellar structure and evolution for stars that are born with a convective core. The effects of excess core mass can be efficiently mimicked with an enhanced mixing in the near-core regions, irrespective of the true cause(s) of the mixing.

Connecting the treatment of interior mixing in stellar evolution models and the mass discrepancy requires extra observational constraints. Surface chemical composition measurements are ideal because chemical abundance patterns are expected to be substantially altered by various mechanisms of interior mixing and chemical element transport in stars. For example, Heap et al. (2006) found surface nitrogen enrichment in 80% of their sample stars and speculated on the role of rotation in causing this phenomenon. Overall, these observational findings are in good agreement with predictions from rotating stellar evolution models for high-mass stars (Meynet & Maeder 2000; Maeder & Meynet 2000; Heger et al. 2000; Heger & Langer 2000; Langer 2012), with the caveat that the observed nitrogen enrichments (Heap et al. 2006) are larger than those predicted by the models.

Hunter et al. (2008, 2009) studied a large sample of intermediate- to high-mass stars in the Magellanic Clouds. Some of their findings corroborate the theory of rotationally induced mixing, while others contradict it (e.g., rapidly and slowly rotating stars without and with substantial surface nitrogen enrichment, respectively). Slowly rotating, nitrogen-enriched stars were also found by Markova et al. (2018), who suggested that inadequacies of the models in these particular cases might be related to the efficiency of rotational mixing. At the same time, Pavlovski et al. (2018) presented a detailed study of the surface chemical compositions in several high-mass SB2 dEBs and find no dependence of the abundances of carbon (C), nitrogen (N), and oxygen (O) on either the projected rotational velocity (v sin i) or surface gravity (log g) of the star.

Whilst changes in the photospheric CNO abundances of high-mass B-type single stars have been found (Przybilla et al. 2010; Nieva & Przybilla 2012; Maeder et al. 2014; Cazorla et al. 2017a,b; Markova et al. 2018), the role of rotationally induced mixing in the formation of these chemical abundance patterns remains poorly quantified. At the same time, Aerts et al. (2014) demonstrated that neither v sin i nor the rotational frequency of a star has significant predictive power for the surface N abundance. Instead, this abundance correlates strongly with the effective temperature (Teff) of the star and the frequency of its dominant acoustic oscillation mode. Furthermore, Rogers et al. (2013) showed that internal gravity waves (IGWs) excited at the convective–radiative boundary near the core in high-mass stars are efficient in transporting angular momentum and chemicals on short timescales and over large distances. Pedersen et al. (2018) demonstrate that the IGW-driven functional form of the interior mixing profile is a good candidate to simultaneously explain the observed properties of gravity-mode oscillations and surface abundances in B-type stars.

Double-lined dEBs are at the forefront of efforts to resolve deficiencies in theoretical stellar models. The masses and radii of the component stars can be measured precisely and independently of models, and the requirement for the stars to have the same age and initial chemical composition at formation provides an additional stringent constraint on theoretical models. Moreover, measured masses and radii give a precise surface gravity that can be used to break the degeneracy between Teff and log g in spectral analysis, boosting the accuracy of measurements of the surface chemical compositions of the stars. The DEBCat1 catalogue of dEBs (Southworth et al. 2015) currently lists approximately 300 examples with precisely measured masses and radii, but only a small fraction of high-mass systems have useful constraints on their photospheric chemical abundances (Serenelli et al. 2021). In this study, we aim to enlarge the sample of high-mass SB2 dEBs with accurately determined surface chemical abundance patterns. In Sects. 2 and 3 we present the sample and high-quality spectroscopic data used in this study. Section 4 covers the determination of the spectroscopic orbits of the stars, Sects. 5 and 6 the inference of their atmospheric parameters and chemical abundances, and Sect. 7 the light curve analysis. The chemical compositions, ages, and distances to the binary stars analysed are compared in Sect. 8 to the properties of their parent clusters. We finish with a discussion (Sect. 9) and conclusions (Sect. 10). It is important to state that the various analyses presented in this work were performed iteratively to ensure internal consistency in the derived results.

2. Sample

We selected four main-sequence (MS) dEBs for study, based on the masses of the components, their membership of open clusters or associations, and on their visibility during the telescope time we were allocated. Basic information on these targets is given in Table 1. All eight stars have a spectral type of late-O or early-B and a surface gravity between 3.7 and 4.2 dex, so are in a relatively early evolutionary phase. All systems except V573 Car reside in eccentric orbits. All are confirmed members of open clusters, although we did not impose any additional constraints on their ages and/or chemical compositions from the cluster membership. All of our targets except GL Car were included in the homogeneous sample of Tkachenko et al. (2020).

Table 1.

Basic characteristics of the binary systems studied in this work.

V1034 Sco is located in the core of the open cluster NGC 6231, which in turn is near the centre of the Sco OB1 association. A detailed spectroscopic and X-ray study was presented by Sana et al. (2003). Light curves have been presented and analysed by Sana et al. (2005) and Bouzid et al. (2005). The most recent analysis is that published by Rosu et al. (2022b), who determined physical properties of the components and measured apsidal motion from our and other archival spectra, retrieved from the European Southern Observatory (ESO) archive, and all available light curves, including TESS.

GL Car is a dEB studied by the Copenhagen Group (Giménez & Clausen 1986) using uvby photometry. The system shows a significant orbital eccentricity (e = 0.157) and fast apsidal motion with U = 25.20 ± 0.02 yr (Giménez & Garcia-Pelayo 1983; Giménez & Clausen 1986; Wolf et al. 2008). We know of no previous time-series spectroscopy of the system, so the current work provides the first measurements of its physical properties.

V573 Car is one of the brightest stars in very young open cluster Trumpler 16, although its membership is disputed (Kaltcheva & Georgiev 1993). Its spectroscopic binary nature was found by Walborn (1982), and the discovery of eclipses was made by Freyhammer et al. (2001) during a study of the nearby massive binary system η Carinae. Freyhammer et al. (2001) obtained extensive uvby photometry and, combined with radial velocities (RVs) from Levato et al. (1991), determined the physical properties of the system.

V346 Cen contains early B-type components in an orbit with a significant eccentricity (Houk & Cowley 1975). Apsidal motion is present with a period of U = 306 ± 4 yr (Giménez et al. 1986a; Drobek et al. 2013). High-quality light curves in the Strömgren uvby system were obtained and analysed by the Copenhagen group (Giménez et al. 1986a,b). The only full spectroscopic dataset for this system is our own High Accuracy Radial velocity Planet Searcher (HARPS) data, available through the ESO archive, and which were already analysed by Mayer et al. (2016).

3. Observations

3.1. Spectroscopy

The spectra presented in this work were all taken in one observing run2 over the nights 2–7 April 2009 using the HARPS cross-dispersed échelle spectrograph (Mayor et al. 2003) at the 3.6 m telescope at ESO La Silla. HARPS achieves extreme RV precision due to a high mechanical stability, being fed by two optical fibres, sited in a vacuum chamber, and calibrated by a Th-Ar emission lamp. We operated HARPS in the high-efficiency EGGS mode, which has a resolving power of R = 80 000, and used the second fibre to obtain the sky background during each observation. Each spectrum consists of 72 orders incident on two CCDs, covering 3780–6900 Å with a gap at 5304–5337 Å between the CCDs.

We reduced the spectra using semi-automatic Image Reduction and Analysis Facility (IRAF)3 scripts. Reduction of the spectra included the standard steps: bias subtraction, flat-field correction, spectral order localisation, extraction, and wavelength calibration. Normalisation of extracted spectral orders was performed by fitting ninth-order polynomial functions to selected continuum points in the blaze function. Since the Balmer lines cover up to three consecutive spectral orders, these were normalised by interpolating the blaze functions from adjacent orders as described by Kolbas et al. (2015). The HARPS blaze functions are very stable so the normalisation and merging of even these difficult orders produced very satisfactory results.

3.2. Photometry

Our analysis below originally relied on published ground-based light curves, as will be discussed in Sect. 7. In the course of this work, additional data became available from the NASA Transiting Exoplanet Survey Satellite (TESS), a space-based mission that has observed most of the celestial sphere in sectors of 27.4 d duration (Ricker et al. 2015). The TESS datasets used in the current study are shown in Fig. 1. Additional data are shown in Fig. A.1, and may be useful in future for period or apsidal motion studies. These reduced photometric data are given in Table A.1 (at the CDS).

thumbnail Fig. 1.

Light curves used in the current study from our reduction of data from the TESS satellite. They have been normalised to zero magnitude for display purposes.

TESS observed V1034 Sco in sectors 12 (1800 s cadence) and 39 (600 s cadence). We extracted the light curves using custom aperture masks. V1034 Sco is in a crowded field and the TESS pixels subtend a large angle (21″) so the light curves contain a significant amount of third light. Our analysis was based on sector 39 due to the better temporal sampling.

V346 Cen was observed using TESS in sectors 10 and 11 (1800 s cadence), and 37 and 38 (600 s cadence). The light curves available for download from MAST4 (The Barbara A. Mikulski Archive for Space Telescopes) are very affected by the field crowding but are nevertheless much better than the ground-based data for this object. We based our analysis on the data from sectors 37 and 38.

TESS observed V573 Car in sectors 10, 36 and 37. Because this object is very close to the extremely bright η Car binary system, the standard data products from TESS (Jenkins et al. 2016) are unreliable. We therefore extracted photometry from the halo of V573 Car by making a careful customised pixel selection for the aperture mask, with the aim to maximise the collected flux of V573 Car compared to the flux of η Car. The resulting light curves are of relatively low quality and suffer from a large and varying amount of third light, so we did not use these in our analysis. We note that V573 Car was just outside the field of view of TESS during sector 11 but we were still able to extract a light curve using halo photometry.

GL Car was observed by TESS in sectors 10 and 11 (1800 s cadence), and 37 (600 s cadence). The light curves available on MAST have eclipses that are too deep so we again extracted our own photometry from the TESS full-frame images using custom aperture masks.

4. Spectroscopic orbits

The spectra of binary systems containing high-mass stars are difficult to analyse for several reasons. First, the v sin i values are typically large, smearing out the spectral lines and causing the lines from the two components to blend together even around the phases of maximum RV difference. Second, there are relatively few spectral lines that are strong enough to provide useful RV information. We therefore determined the spectroscopic orbits of the stars using the method of spectral disentangling (SPD). This method was introduced by Simon & Sturm (1994) in wavelength space and by Hadrava (1995) in Fourier space. It represents the observed composite spectra of a binary system as a sum of the individual spectra of the two stars shifted in RV according to their orbital motion. Thanks to SPD, it is possible to quantitatively analyse time-series spectra of SB2 systems even when line blending is strong (Hensberge et al. 2000; Pavlovski & Hensberge 2005). We note that no template spectra are needed for SPD, thus avoiding any biases due to template mismatch (Hensberge et al. 2007).

We used the FDBINARY5 code (Ilijic et al. 2004) to perform SPD in Fourier space using fast Fourier transform. For each object we analysed all spectra simultaneously to determine the disentangled spectra of the two stars and their spectroscopic orbital parameters. We fitted directly for the orbital parameters, without the intermediate step of calculating RVs. The orbital parameters were the orbital period, P, time of periastron passage, Tperi, eccentricity, e, argument of periastron, ω, and velocity semi-amplitudes, KA and KB. The orbital periods were held fixed as they are well determined from previous analyses. The orbital solutions are given in Table 2 in which the mass ratio (q = KA/KB) is also given.

Table 2.

Parameters of the spectroscopic orbits for the four targets determined by SPD.

We also disentangled individual short segments of spectra in order to concentrate on spectral lines of interest, avoid interstellar lines, and achieve reasonable computation times. The Balmer lines were not used in the determination of the spectroscopic orbits because they are much wider than the changes in RV of the stars over an orbital cycle. The best fits were obtained using the downhill simplex algorithm (Press et al. 1992). We found 100 runs with 1000 iterations each to be sufficient to ensure the global minimum was found whilst keeping the required computation time manageable. Convergence was achieved quickly because of the high quality of the HARPS spectra and the availability of preliminary orbital parameters from the literature. Uncertainties in the results were obtained using 10 000 bootstrapping simulations (Pavlovski et al. 2018). Figure 2 is a visualisation of the spectroscopic orbits of the four targets and the phase distribution of our spectra.

thumbnail Fig. 2.

Visualisation of the spectroscopic orbits of our targets. The best-fitting orbits are shown with black lines. The RVs of the stars at the times of observation are shown with red symbols for the primary component and blue symbols for the secondary component. Note that these are not measured RVs, and hence the uncertainties in RVs are not assigned to individual symbols, because we calculated orbital parameters directly from all observed spectra for each system (see Sect. 4).

4.1. V1034 Sco

V1034 Sco has been found to have a small eccentricity (Hill et al. 1974; Levato & Morrell 1983). We were able to measure precise velocity amplitudes for the components (Table 2) that highlight the low mass ratio of the system.

Our results are in good agreement with those from Sana et al. (2003, 2005) and agree within the error bars with those from Rosu et al. (2022b). We conclude that the RV semi-amplitudes of the components of V1034 Sco are now well determined since the accuracy achieved is about 0.2% for the primary and 0.4% for the secondary. The argument of periastron is quite uncertain due to the small eccentricity, and is much better determined from the photometric analysis in Sect. 7.

4.2. GL Car

To the best of our knowledge, our spectroscopic orbit for GL Car is the first one published. The mass ratio is in fairly good agreement with the photometric value of q = 0.943 ± 0.009 found by Giménez & Clausen (1986). We fixed the eccentricity to a value of 0.146, which is precisely known from analyses of its apsidal motion (Wolf et al. 2008). We fitted for the argument of periastron, which is well determined when the eccentricity is fixed.

4.3. V537 Car

This is the only binary system with a circular orbit in our sample. The HARPS spectra densely cover both quadratures. We also obtained spectra during the primary and secondary minimum, but did not use these in our analysis because the eclipses are not total.

A spectroscopic orbit for V573 Car has previously been published by Freyhammer et al. (2001) but based on only two newly obtained spectra and eight spectra taken from Levato & Malaroda (1982). The velocity amplitudes measured by these authors are quite uncertain but agree with ours to within the error bars.

4.4. V346 Cen

V346 Cen has a significant eccentricity of e = 0.289 ± 0.006. Our HARPS spectra have good phase coverage and SPD quickly converged to a stable solution (Table 2). Our results are in reasonable agreement with the only previous spectroscopic analysis of this system (Mayer et al. 2016), as expected because they used the same spectra.

However, the velocity amplitudes we measured are both 1.5 km s−1 lower than those of Mayer et al. (2016). We attribute this to differences in the methods employed in the two analyses. In particular, Mayer et al. (2016) employed cross-correlation (Zucker & Mazeh 1994) to determine RVs, using as templates the disentangled spectra themselves. This approach is mathematically incorrect and extensive numerical experiments have shown that it is not reliable (Ilijic et al. 2001); SPD has instead been shown to be the best approach to determining spectroscopic orbits (Southworth & Clausen 2007). Our approach yields masses that are smaller by 0.26 M⊙ and 0.11 M⊙ than those found by Mayer et al. (2016) for the primary and secondary component of the system, respectively, which is larger than the quoted uncertainties.

5. Atmospheric parameters

For determination of the atmospheric parameters and individual abundances of C, N, O, Mg and Si, we employed a hybrid non-local thermodynamic equilibrium (NLTE) approach as described in detail in Nieva & Przybilla (2007, 2012). A hybrid NLTE approach means that the modelling combines hydrostatic, plane-parallel, and line-blanketed model atmospheres in local thermodynamic equilibrium (LTE) with line formation calculated in NLTE. We used the ATLAS9 code (Kurucz 1979; Castelli & Kurucz 2003) for the calculations of model atmospheres. Then emergent fluxes and line profiles were calculated with the codes DETAIL and SURFACE (Giddings 1980; Butler & Giddings 1985). In DETAIL the coupled radiative transfer and statistical equilibrium equations are solved, while SURFACE was used for the calculations of NLTE synthetic spectra. The following model atoms were used in these calculations: H I (Przybilla & Butler 2004), HeI/II (Przybilla 2005), CII/III (Nieva & Przybilla 2006), N II (Przybilla & Butler 2001), OI/II (Becker & Butler 1988; Przybilla et al. 2000), Mg II (Przybilla et al. 2001), and SiII/III/IV (Becker & Butler 1990).

We used the disentangled spectra generated in the previous section to determine the Teff, v sin i, and microturbulent velocity (ξt) for each of the eight stars in our sample. This process was greatly helped by the availability of log g values from the measured masses and radii (see Sect. 7) so our analysis was performed iteratively. The disentangled spectra were still in the common continuum of the binary system so needed to be re-normalised to the continuum of the individual component stars. This was done iteratively alongside the light curve analysis, to arrive at light ratios that were consistent between the two types of the analysis (Ilijic et al. 2004; Pavlovski & Hensberge 2005).

The exception to the process above was GL Car, for which the light curve solutions suffered from a degeneracy that caused the light ratio to be highly uncertain. We therefore fitted the disentangled spectra to obtain the Teff, v sin i and log g values and the light ratio directly, using the approach of Tamajo et al. (2011) and Kolbas et al. (2015). After iteration with the light curve solution, log g was fixed for the final measurements of the remaining parameters. We have found that such spectroscopically determined light ratios can be competitive with those from light curve analysis (Pavlovski et al. 2009, 2018, 2022).

Since we are dealing with late-O, and early-B type stars, the helium ionisation balance (He I/He II) is a sensitive indicator of Teff. Our spectra cover a broad spectral range and thus allowed us to use a large number of lines: 4009, 4026, 4388, 4437, 4471, 4713, 4921, 5015, 5047, 5875, and 6678 Å for He I and 4200, 4541, 4686, and 5411 Å for He II. Once a first set of parameters was obtained, we made the light ratio a free parameter to check its reliability. As a further check we also fitted the Hδ, Hγ and Hβ lines, during which we excluded wavelengths affected by interstellar absorption (specifically the red wing of Hβ). We did not base our Teff measurements on the Balmer lines because their large width makes them susceptible to errors due to continuum normalisation.

The He line strengths also depend on ξt, which for hot stars can be obtained by minimising the scatter in the O abundances. We started with the assumptions of solar He abundance and ξt = 2 km s−1, and subsequently relaxed each of them before re-fitting. Convergence was fast, taking either one or two iterations for all eight stars. Once this was achieved, we repeated our optimal fitting of the disentangled spectra described above. The results of this process are given in Table 3. In Fig. 3 the quality of fits for some He lines is shown. Below we compare our results to published determinations for each system, except for GL Car for which there is no other analysis based on modern spectroscopy.

thumbnail Fig. 3.

Fits to the He I 4388 Å and He II 4541 Å lines. The ionisation balance of He I and He II was used in the determination of Teff for the stars. The blue data are the disentangled spectra and the red lines the best fits. The upper row is for the primary stars, and the lower row is for the secondary stars. The lower signal-to-noise ratio (S/N) for the secondary components arises because they are fainter than the primary components. The absence of He II 4541 Å absorption in V1034 Sco B and V346 Cen B is obvious and indicates that Teff < 23 000 K.

Table 3.

Atmospheric parameters derived from optimal fitting of disentangled spectra of the components to a grid of NLTE spectra.

5.1. V1034 Sco

In the most recent study, Rosu et al. (2022b) analysed disentangled spectra of the components obtained from the HARPS spectra obtained in our observing run, and available at the ESO archive. The Teff they derived are within 1σ uncertainty of our results. This is encouraging, especially as Rosu et al. (2022b) used a different NLTE spectrum synthesis code to us.

Rosu et al. (2022b) also fitted for surface gravity, using the wings of the Balmer and some He I lines, whereas we prefer the surface gravities determined with a high precision from the masses and radii. The two analyses agree to within 2σ, but the uncertainties of the values from Rosu et al. (2022b) are much larger (±0.10 dex) than our own (±0.01 dex).

5.2. V573 Car

Freyhammer et al. (2001) studied V573 Car using two high-resolution spectra from the Fibre-fed Optical Echelle Spectrograph (FEROS) spectrograph, taken near opposite quadratures. They fitted the spectra with NLTE synthetic spectra for the He I, He II, Hδ, and Hγ lines. The helium lines of the components are not completely resolved at quadrature due to the high v sin i, and the Balmer lines are not resolved.

The agreement between their and our Teff measurements is well within the 1σ error bars for component A, but only within 2σ for component B. We attribute this to the very small number of spectra available to Freyhammer et al. (2001) compared to our own extensive dataset. We also find that fitting disentangled spectra is superior to fitting individual observed spectra because it avoids problems with blending of lines from the two stars. Moreover, disentangled spectra have a higher S/N than individual observed spectra.

5.3. V346 Cen

The atmospheric parameters for both components of V346 Cen were determined by Mayer et al. (2016) from the same set of the HARPS spectra as we used. In their analysis, Mayer et al. (2016) used optimal fitting of disentangled spectra in similar manner as we did, for fixed surface gravities and microturbulent velocities (fixed to ξt = 2 km s−1) and using a grid of synthetic spectra from Lanz & Hubeny (2007). They found a large discrepancy for the secondary: their spectroscopic analysis gave 20 991 ± 190 K and their light curve analysis gave 25 376 ± 18 K. The former value is in much better agreement with our result (Table 3), and the complete absence of the He II lines demands Teff < 23 000 K (based on a detailed examination of theoretical spectra for the He II 4686 Å line). Mayer et al. (2016) did not discuss the He II lines in the secondary’s spectrum at all. They also gave unrealistically small uncertainties for Teff: ±25 K for the primary, ±190 K for the secondary from spectroscopy, and ±18 K for the secondary from the light curve analysis. Such low uncertainties are typical for formal errors of the fitting algorithms, but are unrealistic.

6. Abundance analysis

With the Teff, ξt and v sin i from Sect. 5, and log g from the masses and radii of the stars (Sect. 7), we have all the quantities needed for determining surface abundances. We calculated model atmospheres for the Teff and log g values of the components with the ATLAS9 code. Then a grid of synthetic spectra was calculated in NLTE with DETAIL, and SURFACE. The following species were considered: C, N, O, Mg, and Si. Spectra for a broad range of elemental abundances were calculated, spanning ±0.05 dex in steps of 0.05 dex, around the ‘present-day cosmic abundances’ determined in Nieva & Przybilla (2012) (log ϵ(C) = 8.25, log ϵ(N) = 7.69, log ϵ(O) = 8.71, log ϵ(Mg) = 7.56, and log ϵ(Si) = 8.45). These were broadened by the instrumental broadening, and a rotational kernel. The microturbulent velocity was taken into account in the line profile calculations with SURFACE as determined from minimising the scatter in the O abundances and given in Table 3. Abundances were determined by minimising the residuals (χ2 criterion) between the re-normalised disentangled spectrum and the synthetic spectrum. In the re-normalisation of the disentangled spectra to their individual continuum, the light ratio obtained in the light curve analysis (Sect. 7) was used, except for GL Car where the spectroscopically determined light ratio was employed.

The number of lines available for the abundance determination of a particular element varies due primarily to Teff. For the Teff range covered by our target stars, the spectral lines of CNO are quite varied. The most numerous spectral lines are for O, which is why we used them to determine ξt. The spectral lines of C are the least numerous, and the broad wavelength coverage of HARPS spectra is of vital importance. We show examples of the disentangled and synthetic spectra in Figs. 4–7 for selected CNO lines.

thumbnail Fig. 4.

Example of fits to N lines for our target stars. In this case, the N II 3995 Å line is shown for V1034 Sco (primary star on the left, secondary star on the right). The blue lines show the re-normalised disentangled spectra of the stars. The red lines show synthetic spectra from our pre-calculated grid for three different abundances (labelled in the bottom-right corner in each panel).

thumbnail Fig. 5.

Same as Fig. 4 but for O lines in the components of GL Car. The complex blend of O II lines at 4941 and 4943 and the O II line at 4955 Å are shown.

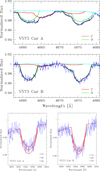thumbnail Fig. 6.

Same as Fig. 4 but for lines in the components of V573 Car. The upper two panels show O II lines at 4661, 4673, and 4676 Å (green lines), which are blended with C II lines at 4659, 4663, 4665, and 4673 Å (red lines). The calculated synthetic spectrum is shown using a black line. The lower two panels show the N II 3995 Å lines.

thumbnail Fig. 7.

Same as Fig. 4 but for V346 Cen. The upper two panels show the C II lines at 5133–5151 Å, and the bottom two panels show the N II 4630.5 Å line for the two components.

The results for all five elements are given in Table 4, as well as the indices [N/C] and [N/O]. Uncertainties were calculated including the standard deviation of the mean for available spectral lines, and the uncertainty due to uncertainties in Teff and ξt. Uncertainty in the abundances due to uncertainties in the surface gravity are negligible since log g is determined to high precision from the masses and radii.

Table 4.

Abundances determined for the stars in our sample of binary systems.

A fairly good agreement between the abundances in both components of the same binary system is seen from examination of Table 4. The most notable difference is for the abundance of magnesium (Mg), which in three cases (V1034 Sco, V573 Car, and V346 Cen) is modestly larger than the uncertainties. The Mg abundances are inferred from a single line, Mg II 4481 Å, so their uncertainties are larger than for other species. For other elements, the observed abundance differences are mostly below 0.1 dex, well within the 1σ uncertainty interval. Apart from Mg, the largest deviations are for the C abundance in V346 Cen (log ϵ(C)A − log ϵ(C)B = −0.20 ± 0.08 dex), the N abundance in V573 Car (−0.13 ± 0.12), and the O abundance in V346 Cen (−0.10 ± 0.08). V346 Cen A has the lowest C abundance among the eight stars, with log ϵ(C) = 8.13 ± 0.05, almost 0.20 dex less than the mean C abundance. Contrary to this, the N abundance for the same star is normal. It is also worth noting that V346 Cen A is the most evolved in our sample of eight OB stars.

Figure 8 compares individual CNO abundances determined for the eight stars in this work to our previous abundance measurements in high-mass binaries. The new determinations are shown in solid blue circles, whilst our previous results are represented with open blue circles. Our previous determinations are for 17 high-mass stars in nine binary systems: V578 Mon (Pavlovski & Hensberge 2005; Garcia et al. 2014; Pavlovski et al. 2018), V453 Cyg (Pavlovski & Southworth 2009; Pavlovski et al. 2018), V380 Cyg (Pavlovski et al. 2009; Tkachenko et al. 2014b), σ Sco (Tkachenko et al. 2014a), α Vir (Tkachenko et al. 2016), CW Cep (Johnston et al. 2019), AH Cep (Pavlovski et al. 2018), V478 Cyg (Pavlovski et al. 2018), and the primary component in V621 Per (Southworth et al., in prep.). There are no discernable systematics between the new and previous sample. This is expected because we are consistently using the same reduction and analysis tools, so the 25 stars (in 13 binary systems) represent a homogeneous sample. In the last three rows of Table 4 the mean values for abundances in the present sample, in OB binaries studied previously by us, and the ‘present cosmic abundance standard’ – an abundance pattern evaluated for B-type stars by Nieva & Przybilla (2012) – are given for comparison. As already mentioned, both our samples are in perfect agreement and there are no outliers. However, it can be seen that the CNO abundances for OB stars in binary systems are below the cosmic abundance standard, with very few exceptions. Nieva & Przybilla (2012) determined elemental abundances for sample of sharp-lined early B-type stars, enabling a very high accuracy. This was not an option for our work because our sample stars are all in short-period binary and systems so are either moderate or fast rotators. Thus, the spectral lines are usually broad and overlapping, making the choice of suitable spectral lines for abundance determination more limited, and thus affecting the accuracy of the results.

thumbnail Fig. 8.

Individual abundances of carbon (left), nitrogen (middle), and oxygen (right) as a function of surface gravity. The stars in the present sample are indicated with filled blue circles, while stars taken from our previous studies are shown with open blue circles. The surface gravity (obtained from the binary solution) is used as a proxy for stellar evolution. Solid red lines show theoretical evolutionary tracks for a 15 M⊙ star and three values of the initial rotational velocity, Ω/Ωcrit = 0.1, 0.3, and 0.5 (Georgy et al. 2013). The cosmic standard abundance values of Nieva & Przybilla (2012) are indicated with horizontal dashed lines.

Figure 8 presents a comparison of the inferred CNO abundances with theoretical evolutionary tracks of a 15 M⊙ star computed for three values of the initial rotational velocity Ω/Ωcrit = 0.1, 0.3 and 0.5 (Georgy et al. 2013). In their model calculations Georgy et al. (2013) used the following initial abundances: log ϵ(C) = 8.28, log ϵ(N) = 8.67, log ϵ(O) = 8.55. The values for the abundances of C and N are in fair agreement with our present and previous findings (cf., Table 5, but differ by 0.15 dex for the O abundance. Therefore, we empirically ‘corrected’ the initial O abundance in the theoretical models, and shift the O abundance upwards in Fig. 8, and accordingly for [N/O] in Fig. 9.

thumbnail Fig. 9.

Same as Fig. 8 but for the [N/C] and [N/O] abundance indices.

Table 5.

Comparison of abundances determined for targets in the present work to those of their parent clusters.

One can see that the models predict significant depletion and enhancement of C and N, respectively, as the rotation rate of the star increases, while only a marginal depletion is predicted for O. Moreover, these abundance trends are substantial at the start of the MS evolution already. However, the individual abundances of CNO elements measured by us do not follow the relations predicted by the models: instead we observe a scatter of values around or slightly below the cosmic standard abundance values of Nieva & Przybilla (2012).

Furthermore, the N to C abundance ratio index [N/C] is a sensitive probe of the stellar evolution model predictions, as can be seen in Fig. 9. The models suggest a noticeable increase in the surface N abundance with respect to the abundance of C (top panel) and O (bottom panel) as the rotation rate of the star Ω/Ωcrit increases. Similar to the individual elemental abundances discussed above, we do not observe the increase in the [N/C] and [N/O] indices as the surface gravity of the star decreases. Moreover, the bulk of our abundance measurements cluster around the mean [N/C] and [N/O] values found by Nieva & Przybilla (2012) in the solar neighbourhood, with the spread being significantly smaller than one would expect if the abundance ratios were altered substantially by the effect of stellar rotation.

No previous abundance determinations are available for any of the binary systems analysed in this work. However, we can check our results against published abundances for the open clusters our sample are members of. Photospheric abundances for B-type stars in the open cluster NGC 6231 were determined by Kilian et al. (1994) and Mathys et al. (2002). Results from these studies are compared to our results for V1034 Sco in Table 5. The parent clusters for the other three systems have not (yet) been subject to a chemical composition study, but the open cluster NGC 3293 (which is part of young association Car OB1 Turner et al. 1980) is well studied. Hunter et al. (2009) determined abundances from 50 B-type stars, while in a recent publication Morel et al. (2022) examined a large sample of about 150 B-type stars in the framework of the Gaia-ESO Survey. Since the dEBs V573 Car and GL Car belongs to the Car OB1 association, we use NGC 3293 as a proxy for the abundance pattern in Car OB1. It is interesting that the massive sample of B-type stars analysed in Morel et al. (2022), with a spread in v sin i values, show a pattern of under-abundances compared to the standard solar abundances (Asplund et al. 2009), in accordance with our general abundance pattern.

7. Light curve analysis

We assembled the available light curves of the four targets in this work and modelled them using a consistent approach in order to determine their physical properties. The light curves were fitted using the Wilson–Devinney (WD) code (Wilson & Devinney 1971; Wilson 1979), which implements Roche geometry to determine the shapes of the stars and thus the brightness of binary systems as a function of orbital phase. We used the 2004 version of the WD code, driven with the JKTWD wrapper (Southworth et al. 2011).

For each system we performed a series of tests to determine the best approach to modelling it with JKTWD. Once we had arrived at the preferred solution, we performed further tests to determine the range of plausible solutions and thus the uncertainties in the fitted parameters. This step was taken because we have consistently found that the formal error bars calculated by the WD code underestimate the true uncertainty of the fitted parameters (Pavlovski & Southworth 2009; Pavlovski et al. 2009, 2018; Southworth et al. 2020), as indicated in the user guide to the code (Wilson & Van Hamme 2004).

Unless otherwise specified we used Mode 0 in the WD code, which is for detached binary systems where the light contributions for each star are fitted individually, simple reflection, and the logarithmic limb darkening (LD) law. We fitted for the potentials and light contributions of the two stars, the orbital inclination and a phase shift with respect to the adopted orbital ephemeris. The mass ratio was fixed at the spectroscopic value, bolometric albedos were set to 1.0, synchronous rotation was assumed, and the gravity brightening exponents were set to 1.0. A circular orbit was assumed for V573 Car but the possibility of an eccentric orbit was checked. The input LD coefficients were obtained by bilinear interpolation in the tables of van Hamme (1993).

For the purposes of determining the uncertainties in the fitted parameters, we ran a series of alternative solutions for differing choice of WD code mode of operation, choice of numerical resolution, treatment of reflection, choice of LD law, whether the LD coefficients were fixed or fitted, treatment of third light, variation of the mass ratio within the uncertainties, and the possibility of orbital eccentricity (for V573 Car). We also considered the effects of albedo, rotational velocity and gravity brightening, by fixing them at different values and also attempting to fit for them directly.

The net result of this process was a default solution for each system, accompanied by a measurement of how much each fitted parameter changed between this default solution and each of the alternative solutions. These changes were then added in quadrature to arrive at a final robust uncertainty value for each fitted parameter. The results for all four systems are summarised in Table 6. The fractional radii are volume-equivalent values obtained from the LC flavour of the WD code.

Table 6.

Summary of the parameters for the WD2004 solutions of the light curves of the systems.

7.1. V1034 Sco

Two photometric datasets of V1034 Sco have been published. Bouzid et al. (2005) presented light curves taken in the Strömgren uvby filters, with 409, 645, 1058 and 1036 data points, respectively. Sana et al. (2005) obtained light curves in two narrow-band filters, designated λ4685 and λ6051, containing 112 and 138 data points, respectively. For our exploratory solutions we used the Sana et al. (2005) data as the Bouzid et al. (2005) data are not available.

In the course of this work a new light curve became available from sector 39 of the TESS satellite (see Sect. 3). As the TESS data are of much higher quality than the other photometry, we based our final results for V1034 Sco on these data. Before doing so, we performed a preliminary fit with JKTEBOP (Southworth 2013) to obtain an orbital ephemeris then phase-binned these data down to 500 bins to decrease the computation time. Our final solution is for an eccentric orbit, including third light, and the logarithmic LD law and the linear LD coefficient fitted for each star and passband. The main contributors to the uncertainty in the fractional radii are the treatment of albedo and gravity darkening. Uncertainties arising from the choice of numerical resolution, WD program mode, rotation rate and LD were all significantly smaller and therefore contributed negligibly when all uncertainties for each parameter were added in quadrature. The parameters and their uncertainties are given in Table 6, and the best fits are shown in Fig. 10.

thumbnail Fig. 10.

Light curves and best WD models for V1034 Sco. The differential magnitudes are plotted vs. orbital phase and are colour-coded according to the central wavelengths of the passbands. The source and passband of each light curve is labelled. The residuals of the fit are shown at the base of the figure. Offsets have been applied between the light curves and residuals for clarity.

7.2. GL Car

Light curves of GL Car in the Strömgren uvby system were obtained by Giménez et al. (1985) using the 0.5 m Strömgren Automated Telescope at ESO La Silla. They comprise 526 observations through each filter, 234 in the 1982 observing season and 308 in the 1983 season. These data were analysed by Giménez & Clausen (1986) using the WINK code (Wood 1971). The observations were obtained in electronic form from the archive of J. V. Clausen and used in the current work to obtain a preliminary solution. We found values and uncertainties for the fitted parameters in good agreement with those from Giménez & Clausen (1986).

Subsequent to our analysis of the uvby data a new light curve of GL Car became available from TESS. We phase-binned this and modelled it using WD, fitting for an eccentric orbit and third light. The rotation rates (F1 and F2) were set to the ratios of the measured rotational velocities (Table 3) and the synchronous values, determined iteratively. Unlike the uvby data, the TESS light curve shows a strong correlation between the light ratio and the amount of third light. We therefore applied the light ratio from our spectroscopic analysis. Because there is no mechanism to explicitly apply a spectroscopic light ratio in WD2004 we propagated the light ratio from our spectral interval (which corresponds closely to the Johnson B band) to the Strömgren uvby bands (see Southworth 2010) using ATLAS9 theoretical spectra (Castelli et al. 1997) and passband response functions from Maíz Apellániz (2006). We forced WD2004 to match them by fixing the HLUM parameters at the appropriate values. Including this constraint greatly improved the reliability of the results.

We find precise fractional radii for GL Car once our spectroscopic light ratio is included (Table 6). The uncertainties are dominated by those from this light ratio, but are still below 1% and a factor of three smaller than those from the uvby data alone. They also agree well with the less precise results from Giménez & Clausen (1986). The fitted orbital eccentricity is in excellent agreement with that from its apsidal motion (e = 0.1459 ± 0.0015 from Wolf et al. 2008). The orbital phase of secondary eclipse has changed a lot between the uvby and TESS datasets, and the different morphology of the light curve is obvious (see Fig. 11).

thumbnail Fig. 11.

Light curves and best WD models for GL Car. Other comments are the same as for Fig. 10.

7.3. V573 Car

V573 Car was studied by Freyhammer et al. (2001) using the Dutch 0.9 m telescope at ESO La Silla. A total of 1910 observations were obtained through the Strömgren filters: 763 in y, 513 in b, 350 in v, and 284 in u. We fitted all four light curves simultaneously, using the ephemeris from Freyhammer et al. (2001). We assumed a circular orbit in most cases, but did run a fit with e and ω free to check if this led to a better fit to the data (it did not). We also assumed no third light, after attempts to fit for it had a negligible effect on the results and also led to a slightly negative value for this parameter. The best fit is shown in Fig. 12.

thumbnail Fig. 12.

Light curves and best WD models for V573 Car. Other comments are the same as for Fig. 10.

The fitted parameters were the potentials of the two stars, the orbital inclination, a phase shift, and the light contributions of the two stars in each passband. To avoid very small values for the light contributions we re-normalised each light curve to be at approximately zero relative magnitude at quadrature. We adopted the linear LD law as it gave results very similar to those for the logarithmic and square-root laws; attempts to fit for the LD coefficients led to unphysical solutions. The rotational velocities of the stars were held to the synchronous values.

We found that the solution of the light curves is degenerate in that significantly different values of the ratio of the radii or the light contributions of the stars led to almost indistinguishable fits. This was also found by Freyhammer et al. (2001), who constrained their solution using a light ratio measured from their spectra. We took the same approach.

For our final result (Table 6) we give the solution for fitting all four light curves simultaneously, constrained by the spectroscopic light ratio. The uncertainties in the parameters include contributions from the uncertainty in the spectroscopic light ratio, the effect of a change of 5% in the rotation velocities of the stars, and the treatment of albedo and gravity darkening. Other sources of uncertainty (see above) were checked and found to be negligible. We were able to measure the fractional radii of the stars to precisions of 0.8% (star A) and 1.1% (star B); the main contribution to these uncertainties is the spectroscopic light ratio (for star A) and the treatment of gravity darkening (for star B). The values we find are in reasonable agreement with those from Freyhammer et al. (2001), but our uncertainties are slightly larger.

7.4. V346 Cen

Extensive photometry in the Strömgren uvby system was obtained by Giménez et al. (1986b), comprising 1056 observations made simultaneously through all four filters using the Strömgren Automated Telescope (Grønbech et al. 1976). These data have been analysed by Giménez et al. (1986a) using the WINK model, and by Mayer et al. (2016) using the PHOEBE code. The two studies agree on the values of the fractional radii to within the uncertainties quoted by Giménez et al. (1986a) but not the uncertainties quoted by Mayer et al. (2016). We therefore performed our own analysis of these data in order to assess robust error bars and check the level of agreement with the previous studies.

Our WD code model for the uvby data provided a good fit to the observations (Fig. 13) but required ω to be fixed at a suitable value to avoid the fit diverging to unphysical solutions. We set the rotation rates to 2.49 and 2.70 based on the rotational velocities of the stars measured from the disentangled spectra. The logarithmic LD law was adopted, although the other two laws gave almost identical results. Third light was fixed at zero because attempts to fit for it returned a small negative value that was consistent with zero. Our results were in excellent agreement with those of Giménez et al. (1986b).

thumbnail Fig. 13.

Light curves and best WD models for V346 Cen. Other comments are the same as for Fig. 10.

After this work had been performed, light curves from sectors 37 and 38 of the TESS satellite became available. These are of much higher quality so we used them for our final analysis. We performed a preliminary fit with JKTEBOP to obtain an orbital ephemeris then phase-binned them into 500 bins to make the computations faster. Our approach was the same as for the uvby data except that we were able to fit for ω and also needed to fit for third light due to significant contamination of the TESS light curve. We found the best fit to the TESS data to be highly stable against changes in mass ratio, rotation rate, treatment of LD, albedo, gravity darkening and numerical grid size. We had to fix the LD coefficients as they diverged to unphysical values when we attempted to fit for them.

The final parameters and uncertainties of the fit are given in Table 6. The fits are shown in Fig. 13, and two things are worth highlighting. First, the morphology of the light curve has changed between the uvby and TESS epochs due to apsidal motion. The phase of secondary eclipse has changed and it is no longer annular – the primary eclipse has become a transit instead. Second, the TESS data show a clear pulsation signature. This affected the quality of our solution and was probably why we were unable to fit for LD coefficients. The pulsation almost certainly arises from the EB itself and not from the contaminating light, because they are commensurate with the orbital period (see Fig. A.2). V346 Cen is therefore another high-mass EB showing pulsations (Southworth & Bowman 2022). Because our light curve solution did not account for pulsations, we conservatively doubled the uncertainties in the measured fractional radii.

Following the binary analysis, an analysis of the residual light curve (hereafter called the pulsation light curve) revealed the presence of tidally excited pulsations, as illustrated in Fig. 14. To measure this tidally induced variability, we fitted sine waves, corresponding to the 20 lowest-order orbital harmonic frequencies, to the out-of-eclipse part of the pulsation light curve. Fitted orbital harmonics were accepted when the signal-to-noise ratio S/N ≥ 4.0, where S/N was calculated as the ratio of the amplitude of the fitted sine wave, and the average signal amplitude of the Lomb–Scargle periodogram (Scargle 1982) in a 1 d−1 window around the considered frequency. Finally, the measured amplitudes, phases and orbital harmonic frequencies were optimised simultaneously by non-linearly fitting them to the pulsation light curve. Their values are listed in Table 7.

thumbnail Fig. 14.

Tidally excited pulsations of V346 Cen. Top: observed light curve of V346 Cen for sectors 37 and 38, phase-folded with the binary orbital period. The eclipses are indicated by the grey bands. Middle: pulsation light curve of V346 Cen for sectors 37 and 38, phase-folded with the binary orbital period. Data points taken during the eclipses again lie within the grey bands. Bottom: Lomb–Scargle periodogram, calculated for the out-of-eclipse data points of the pulsation light curve for sectors 37 and 38. The vertical dashed lines indicate harmonics of the orbital frequency.

Table 7.

Values of the amplitudes, A, frequencies, ν, phases, ϕ, and signal-to-noise ratios, S/N, of the orbital harmonics, calculated for the out-of-eclipse data points in the pulsation light curve of V346 Cen.

From these results, we determined that the tidally induced pulsation corresponds to the ninth orbital harmonic, in agreement with what is shown in Fig. 14. The physical origin of the other measured orbital harmonics is less clear. While they may also partially correspond to tidally induced pulsations, this could not be confirmed. At least part of it is likely caused by the non-sinusoidal nature and orbital-phase-dependent amplitude modulations of the ninth orbital harmonic signal. Moreover, as shown in the middle panel of Fig. 14, this pulsation has a minimum during the primary eclipse and a maximum during the secondary eclipse, which indicates that it belongs to the primary component.

Finally, after the significant tidally excited variability was removed from the pulsation light curve, we evaluated the residuals. As illustrated in Fig. 15, the remaining data exhibit signatures of stochastic low-frequency variability, as has been reported in the literature for other high-mass stars (e.g., Bowman et al. 2019, 2020).

thumbnail Fig. 15.

Stochastic low-frequency variability of V346 Cen. Top: part of the (out-of-eclipse) residual light curve of V346 Cen, after fitting the orbital harmonics. Bottom: Lomb–Scargle periodogram, calculated for the out-of-eclipse data points of the residual light curve for sectors 37 and 38.

7.5. Physical properties

We determined the physical properties of the systems using the results from the spectroscopic and photometric analyses outlined above. For this we used the velocity amplitudes, Teff values, e and ω from the spectroscopic analysis, and the fractional radii and orbital inclination from the photometric analysis. To perform the calculations we used the JKTABSDIM code (Southworth et al. 2005), which propagates the error bar from each input parameter using a perturbation analysis. We used a version of JKTABSDIM modified to use the International Astronomical Union (IAU) system of nominal solar values (Prša et al. 2016) plus the National Institute of Standards and Technology (NIST) 2018 values for the Newtonian gravitational constant and the Stefan–Boltzmann constant. The results of this analysis are given in Table 8.

Table 8.

Physical properties measured for the four systems analysed in this work.

Distances have been derived using the measured radii and Teff of the stars, apparent magnitudes of the system in the Johnson-Cousins UBVRI and the Two Micron All-Sky Survey (2MASS) JHKs bands, and the theoretical bolometric corrections tabulated by Girardi et al. (2002). We adjusted the interstellar extinction E(B − V) to obtain consistent distances in the optical and infrared passbands. These results are given in Table 8 alongside the Gaia Early Data Release 3 (EDR3) parallaxes (Gaia Collaboration 2016, 2021) and the distance from simple inversion of the parallax. We see agreement within the error bars, the most discrepant (1.6σ) being for V573 Car. Very similar conclusions are drawn if we use the geometric or photo-geometric distances from Bailer-Jones et al. (2021). We conclude that our results for all four targets are independently verified by the Gaia parallaxes.

8. The parent clusters

Knowledge of the properties of stars in dEBs allows the determination of their distance. Moreover, a comparison of the properties of dEBs to stellar evolutionary models constrains their age. The age of stars in our sample, except for GL Car, were determined from isochrone fitting in Tkachenko et al. (2020) for two cases: (i) as a single star and (ii) as a binary where the two components have the same age. Three different interior structures were assumed in these calculations, and hence in Table 9 we give lower and upper limits for the age. The distances to the binary systems in our sample are given in Table 8.

Table 9.

Distances and ages for the binary systems in the present sample compared to those of the parent clusters.

8.1. V1034 Sco and NGC 6231

The distance to V1034 Sco was evaluated by Sana et al. (2005) who found 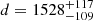d = 1528 − 109 + 117 $ d = 1528^{+117}_{-109} $ pc, which is within 1σ of the distance we calculated. The light curve solution in Bouzid et al. (2005) suffers from an ambiguity in setting the primary’s Teff so the authors calculated the distance for both cases. The larger one is exactly the same as those reported by Sana et al. (2005), and the shorter one is 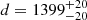d = 1399 − 20 + 20 $ d = 1399^{+20}_{-20} $ pc. Mayer et al. (2008) determined the distance to another dEB in this cluster, V1007 Sco, as 1622 pc (no uncertainty given), which is somewhat larger than the other distance estimates mentioned here.

The open cluster NGC 6231 belongs to the star-formation complex Sco OB1 (Perry et al. 1991). The cluster is the oldest and most massive in Sco OB1 (Damiani et al. 2016). The ages of the cluster members have been estimated to be between 2 and 8 Myr (Sung et al. 2013; Damiani et al. 2016; Kuhn et al. 2017), with OB stars being an older population in the cluster. The cluster is rich in spectroscopic binaries: García & Mermilliod (2001) listed about 30 systems, 16 of which are certain. Mayer et al. (2008) did an exhaustive search of the cluster members, and listed ten EBs. The most recent distance determinations to NGC 6231 are based on Gaia parallaxes. Kuhn et al. (2019) quoted 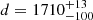d = 1710 − 100 + 13 $ d = 1710^{+13}_{-100} $ pc using Gaia Data Release 2, while Banyard et al. (2022) found the median geometric and photo-geometric distances for their sample of about 60 stars in the cluster using Gaia EDR3 parallaxes to be 1579 and 1576 pc, respectively.

Rosu et al. (2022b) determined the age of V1034 Sco to be τ = 6.8 ± 1.4 Myr, in perfect agreement with the result of Tkachenko et al. (2020). Three other binary systems that are members of this cluster were studied: HD 152248 (Rosu et al. 2020), HD 152219 (Rosu et al. 2022b), and HD 152218 (Rosu et al. 2022a). Their ages were determined from the apsidal motion rate and range from 5 to 9.5 Myr.

8.2. GL Car and NGC 3572/Collinder 240

Giménez & Clausen (1986) found a distance to GL Car of d = 2100 pc. They did not give an uncertainty but quoted an error of 100 pc due to bolometric corrections and interstellar reddening. This distance is smaller than our result and that from the Gaia Data Release 3 (DR3) parallax. Giménez & Clausen (1986) extensively discussed possible physical relationships to the open clusters in the vicinity of GL Car, which is in a region crowded with young open clusters and in the direction of the Sagittarius-Carina spiral arm.

Membership of GL Car in NGC 3572 was proposed by Sahade & Berón Dàvila (1963). Giménez & Clausen (1986) rejected this association due to the shorter distance to the dEB than the cluster, and because NGC 3572 is a compact cluster with a radius of 5′ and GL Car is at an angular distance of 40′. It was recognised that the open cluster NGC 3572 consists of two overlapping clusters, one at 2.3 kpc and one at 3.0 kpc (Clariá 1976). The nearer cluster is also considered by Clariá (1976) to be the probable nucleus of a scattered group of OB stars located in the vicinity, identified as Collinder 240 and an extension of Car OB2. This is a region in which the line of sight is tangential to the molecular cloud ridge in the Carina Arm, and is projected on a rather small area in the sky. It shows as a region with a higher concentration of OB stars, but with a radial extension of several kiloparsecs.

The age of GL Car was determined to be τ = 2.0 ± 0.5 Myr (Giménez & Clausen 1986). This is compatible with age determinations for Collinder 240, τ ∼ 1 Myr, and Car OB2, τ = 4 Myr (Garcia 1994).

8.3. V573 Car and Trumpler 16

Freyhammer et al. (2001) determined a distance to V573 Car of d = 2600 ± 120 pc, and an age of τ = 1.5 ± 1.0 Myr. Their distance determination is within 1σ of ours. Also, the very young age is confirmed with extensive isochrone fitting to different stellar interior structure models in Tkachenko et al. (2020), as summarised in Table 9.

V573 Car is situated near the centre of the open cluster Trumpler 16, close to η Carinae, the brightest star in the cluster, and one of the most intriguing objects in the Galaxy. The cluster itself, with its neighbouring clusters, Trumpler 14, and Trumpler 15, forms a chain of rich clusters in the prominent Carina star-forming complex, a conspicuous part of the Carina-Vela spiral arm. The whole region is recognised as the young association Carina OB1, which also includes NGC 3293 and several small open clusters, the H II region and prominent nebula NGC 3372 powered by η Car (Smith 2006; Wright 2020). Pre-Gaia distance estimates relied mostly on multi-colour photometry, and gave distances in the range 2.2–2.9 kpc and young ages in the range 1–3 Myr (Hur et al. 2012). Using Gaia EDR3 Shull et al. (2021), Maíz Apellániz et al. (2022) and Göppl & Preibisch (2022) found distances to the cluster Trumpler 16 at the lower end of the range: 2.32 ± 0.12, 2.38 ± 0.20 and 2.36 ± 0.05 kpc, respectively, all within 1σ of our determination.

8.4. V346 Cen and Stock 14

The distance and age of V346 Cen were also determined by Giménez et al. (1986b), which allows a direct comparison with our results. Giménez et al. (1986b) determined the distance d = 2.38 ± 0.18 kpc, which is within 1σ of our determination. The age of the binary system they found, 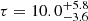τ = 10 . 0 − 3.6 + 5.8 $ \tau = 10.0^{+5.8}_{-3.6} $ Myr, also agrees well with our result, τ = 10.7–16.0 Myr (Table 9).

Stock 14, the parent cluster of V346 Cen, is described as a loose but clearly defined open cluster (Moffat & Vogt 1975; Eichendorf & Reipurth 1979). The most recent deep UBV photometry of Stock 14 was obtained by Drobek et al. (2013) primarily in a search for new variable stars. Their photometry allowed the determination of the distance and an estimate of the age for Stock 14, 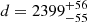d = 2399 − 55 + 56 $ d = 2399^{+56}_{-55} $ pc, and τ = 20 ± 10 Myr. The authors confirmed the cluster membership of V346 Cen. Re-evaluation of the photometric distance and age of Stock 14 by Paunzen & Netopil (2006) also favoured a shorter distance than previous determinations. They obtained a distance of d = 2439 ± 326 pc, and an age of τ = 10 ± 2 Myr, in fine agreement with the extensive photometric study by Drobek et al. (2013) as well as our results for V346 Cen.

9. Discussion

The results of the analyses above are summarised in Table 4 for elemental abundances and Table 8 for fundamental stellar quantities. The stars in the present work cover a range of mass (8.4–17.1 M⊙), radius (4.1–8.3 R⊙), Teff (22 500–32 200 K), surface gravity (3.7–4.2 dex) and v sin i (90–185 km s−1) and are all unevolved MS stars from late-O to early-B spectral types. We have achieved a high accuracy in the fundamental stellar properties, with uncertainties in mass of 0.6–2.0%, radius of 0.8–1.7%, and log g of 0.009–0.021 dex. Having a precise log g allows us to avoid its degeneracy with Teff in spectral analysis, resulting in uncertainties of 1.7–2.5% in Teff. Since Teff and log g are the principal quantities for specifying a model atmosphere, precise values are a prerequisite in measuring chemical abundances to a high precision. We now discuss the implications of our results for two subjects: evolutionary models for high-mass stars, and chemical evolution in high-mass binaries.

Studies of chemical abundances in high-mass stars mostly concentrate on more advanced evolutionary stages, so it is difficult to perform a quantitative comparison between our results and those published elsewhere. Martins et al. (2017) presented a study of six short-period binary systems. Of them, two are contact or over-contact systems and so will have abundances altered by mass transfer: one (DH Cep) has component stars considerably more massive than our sample (38 M⊙ and 33 M⊙), though the remaining three (Y Cyg, AH Cep, and V478 Cyg) are suitable for the comparison. Of these, AH Cep and V478 Cyg were analysed in our previous work (Pavlovski et al. 2018) so a direct comparison is possible. Two studies agreed to within 2σ uncertainties in the [N/C] and [N/O], but only because of the large uncertainties quoted by Martins et al. (2017). It is hard to trace the reason for this, but it may be related to the large uncertainties in the atmospheric parameters in their study.

Results of a comprehensive analysis of a large sample of binary and/or multiple stars in the Tarantula Nebula have recently been published (Almeida et al. 2017; Mahy et al. 2020b,a) based on medium-resolution (R = 6400) spectra from VLT/FLAMES/GIRAFFE covering 3964–4567 Å. A total of 51 SB1 and SB2 systems were studied, of which 13 are eclipsing. The atmospheric parameters were determined using NLTE methods, and He, C and N abundances derived. The objects studied fall into five different groups: (1) long-period systems (P > 20 d) with well-detached components; (2) eccentric short-period (P < 10 d) detached binaries; (3) circular-orbit short-period (P < 10 d) binaries with strong tidal effects; (4) semi-detached systems; and (5) contact systems. No N enrichment was found for binaries in the first two groups, despite the components having v sin i values of 50–250 km s−1. This finding is in disagreement with evolutionary models with rotationally induced mixing (Maeder & Meynet 2000; Heger & Langer 2000; Heger et al. 2000). Furthermore, a large N abundance was found for apparently slowly rotating stars in binaries. This agrees with initial findings by Hunter et al. (2007, 2008, 2009) who detected three distinctive groups in a diagram of [N/H] vs. v sin i for single OB stars (sometimes dubbed the ‘Hunter diagram’): (1) stars showing N enrichment with v sin i; (2) rapidly rotating stars with no sign of N enrichment; and (3) stars with low v sin i and excessive N abundance.

In the third group of binaries from Mahy et al. (2020b), N enrichment was found for the fast rotators. This is a group of stars in which the strongest influence of tidal forces on rotationally induced mixing is expected, following theoretical calculations by de Mink et al. (2009). By far the largest N enhancement was found for stars with almost the lowest v sin i in this group (∼50 km s−1), just as in the case of findings for stars in the first two groups. Mahy et al. (2020b) concluded that stars in detached binaries (groups 1–3) are evolving as single stars. A lack of a clear relationship between N abundance and v sin i is in conflict with theoretical models and makes it hard to understand the effect of rotationally induced turbulent mixing in stellar interiors.

A very recent comprehensive spectroscopic analysis of a large set of B-type stars in the young open cluster NGC 3293 (Morel et al. 2022) also corroborates these results: in the sample of almost 150 B-type stars, the majority of which have high v sin i, apparently no star with excess N abundance was detected. Only two stars are found with mild N enhancement, and these stars have a low v sin i. A lack of N enhancement in fast-rotating B stars, and conversely, further evidence for N enhancement in low-v sin i B stars, is in clear contradiction with theoretical evolutionary models that incorporate rotationally induced mixing.

A state-of-the-art statistical analysis was carried out by Aerts et al. (2014) to identify possible mechanism(s) that could explain the distribution of stars in the Hunter diagram. The authors collected a statistically significant sample of well-studied Galactic single B stars for which seven observables were available (surface N abundance, rotational frequency, magnetic field strength, and the amplitude and frequency of their dominant acoustic and gravity modes of oscillation). A multivariate analysis indicated that the Teff and the frequency of the dominant acoustic oscillation mode have the most predictive power of the surface N abundance, whereas the rotational frequency of the star does not have any predictive power at all. Up to now, no follow-up studies have been undertaken to investigate these unexpected results.

Strong support for rotationally induced mixing has come from detailed abundance study for early B-type stars by Przybilla et al. (2008) and Nieva & Przybilla (2012). The authors selected 20 early-B stars with a low v sin i to allow a high precision in determination of the atmospheric parameters and chemical abundances. Przybilla et al. (2010) confirmed an observationally tight correlation in the plot of abundance ratios N/C versus N/O, with a slope predicted via nuclear reactions in the CNO process. The targets had a broad evolutionary range, from dwarfs to supergiants, and their CNO abundances followed predictions of the nuclear reaction theory.

From our current and previous (see Sect. 6) studies, we have a sample of 13 dEBs, for which 25 components have measured CNO abundances. We compared these to a sample of high-mass stars published in Przybilla et al. (2010) and Nieva & Przybilla (2012) in the logarithmic N/C vs. N/O diagram (left panel in Fig. 16). This is a powerful diagnostic tool in which the slope between [N/C] and [N/O] represents changes in CNO abundances due to nuclear reactions as deriveind Przybilla et al. (2010). It is striking that the two samples cover the same mass range (8–20 M⊙) but do not fully overlap in the diagram. For binary components there is a cut-off at [N/C] ∼ −0.4 dex and [N/O] ∼ −0.8 dex and they cluster around values close to solar ([N/C]⊙ = −0.52 dex and [N/O]⊙ = −1.00 dex), but a slope can be seen. The targets in the current work strengthen our previous conclusion that properties of interior mixing in binary stars are different from and might be less efficient than in single high-mass stars (Pavlovski et al. 2018).

thumbnail Fig. 16.

Observed CNO abundances for binary and single high-mass stars compared to theoretical evolutionary models. Left panel: abundances of the CNO elements for high-mass stars in a diagram of [N/C] index versus [N/O] index. Stars in binary systems (Sect. 6) are represented by solid blue circles. For comparison, abundance determinations for single early-B type stars (Nieva & Przybilla 2012) are represented by green circles. Single stars obey a trend indicated by an analytical approximation to the nuclear reactions path for the CNO cycle derived in Przybilla et al. (2010) and Maeder et al. (2014). The slope in this diagram indicates a gradual enhancement of N at the expense of C. A slight decrease in the O abundance is also predicted. Whilst the single and binary stars span almost identical mass and Teff ranges, and are all MS stars, it is clear they do not share the same distribution (see Sect. 9). Right panel: Observed [N/C] index for 25 high-mass stars in binaries (solid blue circles) compared to single B-type stars (solid green circles; Nieva & Przybilla 2012) as a function of surface gravity. Solid red lines in the right panel show theoretical evolutionary tracks for a 15 M⊙ star and five values of the initial rotational velocity, Ω/Ωcrit = 0.1, 0.3, 0.5, 0.7, and 0.9 (Georgy et al. 2013). Striking differences between single stars and stars in binary systems are discussed in Sect. 9.

This striking effect is also clearly seen in the diagram of [N/C] versus log g (Fig. 16). Theoretical evolutionary tracks are presented for a 15 M⊙ star and five values of the initial rotational velocity Ω/Ωcrit = 0.1, 0.3, 0.5, 0.7, and 0.9 (Georgy et al. 2013). The overall spread in [N/C] could be interpreted as due to evolutionary changes or (very) high initial rotational velocities. However, only single stars from the sample of (Nieva & Przybilla 2012) tend to be consistent with the large [N/C] ratio predicted by the models for large initial rotational velocity values of Ω/Ωcrit ⪆ 0.5 and [N/C] ⪆ −0.4 dex. The main issue with the interpretation of the observed distribution in the context of the rotationally induced mixing alone is the generally low projected rotational velocity values (v sin i < 30 km s−1) found by Nieva & Przybilla (2012) for about half of their sample stars. For the effect of rotational mixing being alone responsible for the observed [N/C] and [N/O] abundance ratios, one would require the majority of apparently slow rotators in the sample of Nieva & Przybilla (2012) to be stars that are seen pole-on. This is a highly improbable scenario, so we conclude that the CNO abundances and their ratios observed in single high-mass stars are altered by multiple processes rather than just a single mechanism of rotational mixing. For example, high-mass stars are know to possess magnetic fields, stellar winds, and pulsations. To this (strong) tidal effects in close high-mass binary systems should be added. All these mechanisms, in one way or another, are expected to impact the efficiency of internal mixing, and hence the surface chemical composition.

However, the comparison between these two sets of empirical data, one with single high-mass stars and the other with high-mass stars in binary systems, is not straightforward. First and foremost, the sets differ in their distributions of v sin i. The set of single stars were deliberately selected to be sharp-lined stars, so contains a mix of intrinsically slowly rotating stars and ones with small inclinations and thus small sin i terms. The set of binary stars, on the other hand, contains objects whose equatorial rotational velocities are accurately known, assuming their rotational and orbital axes have been aligned during formation or by tidal effects. Furthermore, even though the v sin i distribution could be statistically corrected to intrinsic rotational velocities for single stars, there is a substantial difference in the rotational history between single and binary stars that one cannot easily account for. Evolution of stellar rotational velocity from its initial value at the zero-age MS, and its subsequent changes in the course of stellar evolution due primarily to changes in radius, is substantially different due to tidal effects. This is particularly important for short-period systems whose rotation is synchronised with and thus governed by their orbital period. Nevertheless, the non-detection of substantial changes in the CNO abundances of stars in binaries contradicts the predictions of single-star rotational evolutionary models. For the sample of Przybilla et al. (2010) and Nieva & Przybilla (2012), that is to say, a single high-mass stars with low observed v sin i, the possibility remains that they agree with the theoretical predictions.

Tidal forces in binary and/or multiple systems affect the geometry of the orbits and the shape and spin of the components (Mazeh et al. 2008). In order of increasing timescale, the stellar spin axes are aligned first, then their rotation is synchronised, and finally the orbit is circularised. Later evolution is dominated by mass transfer due to the increase in the sizes of the component stars. Our hypothesis that tidal effects suppress the efficiency of rotational mixing is not supported by theoretical calculations (de Mink et al. 2013), which predict precisely the opposite: that short-period circularised binary systems should experience rotationally induced turbulent mixing in stellar interiors.

In looking for possible mechanisms that diminish turbulent mixing in the components of binary systems, Koenigsberger et al. (2021) examined differential rotation in asynchronous binary systems. If the components in a binary system are not yet in synchronous rotation, tidally induced and time-variable differential rotation could develop. The calculations by Koenigsberger et al. (2021) clearly show the role of asynchronism: the induced rotation structure and its temporal variability depend on the degree of departure from synchronism. The authors further speculated that, in this context, slowly rotating asynchronous binaries could have more efficient mixing than the more rapidly rotating but tidally locked systems. This shows that processes triggered by asynchronous rotation in binary systems cannot be ignored, and that a comparison between samples of single and binary stars should be done with particular care, even when the latter are in a detached configuration. We note that 12 of the 14 binaries in our sample have eccentric orbits but that most of the component stars rotate synchronously.

10. Conclusion

Despite their astrophysical importance, high-precision fundamental stellar quantities (mass, radius, and Teff) have been determined for only a few high-mass stars in binary systems in our Galaxy (Southworth et al. 2015). Even fewer have surface chemical composition measurements (Serenelli et al. 2021). With the present work we add four more binary systems to this list: V1034 Sco, V346 Cen, GL Car, and V573 Car, which contain stars of masses from 8.4 to 17.1 M⊙. Most of these stars are young, with only two in the second half of their MS evolution.

We have presented high-quality HARPS spectra that we analysed using SPD to determine the spectroscopic orbits and individual spectra of the component stars. These in turn were analysed using an NLTE approach. We have modelled the available light curves for our systems, comprising uvby photometry in all cases and TESS photometry in three cases, to determine their photometric parameters. Combining these analyses, we have determined high-precision masses, radii, surface gravities, Teff values, v sin i values, and C, N, O, Mg, and Si abundances for all eight stars in the four binary systems. Of particular interest are the CNO abundances since these elements are involved in core hydrogen burning through the CNO cycle. During a star’s evolution, its N abundance increases and its C abundance decreases. Rotationally induced mixing of stellar material, or some other mixing processes, could bring nuclear-processed material from the stellar core to the surface. Therefore, the [N/C] ratio is a sensitive probe of interior mixing processes during the MS evolutionary stage.

The CNO abundances determined in this work corroborate our previous findings (Pavlovski et al. 2018), that interior mixing is different in binary stars compared to single stars. A tight correlation of [N/C] with [N/O] versus the predicted evolutionary changes has been found for single early B-type stars (Przybilla et al. 2010; Nieva & Przybilla 2012), whereas binary systems in our sample show much less variation in both [N/C] and [N/O]. However, care is needed when comparing them with single stars due to the differences in rotational velocity between these types of objects. It remains true that the binary sample does not reproduce the results found for a sample of single low-v sin i B-type stars.

On other hand, recent spectroscopic analysis of large samples of high-mass stars in binaries (Mahy et al. 2020a) and single B-type stars in the young open cluster NGC 3293 (Morel et al. 2022) apparently confirmed the lack of substantial changes in CNO abundances for high-v sin i stars (i.e., for intrinsically fast-rotating stars).

We speculate that proximity effects in binary systems somehow suppress the mixing of chemical elements and/or the transport of chemical elements from the interior to the surface. However, firmer conclusions will need a substantial expansion of the binary stars sample and an extension to more massive and hotter stars, and/or wider long-period binary systems.

2

ESO proposal 083.D-0040(A), PI J. Southworth.

3

IRAF is distributed by the National Optical Astronomy Observatory, which are operated by the Association of the Universities for Research in Astronomy, Inc., under cooperative agreement with the NSF.

Acknowledgments

Careful reading of the manuscript and useful suggestions provided by the referee are acknowledged. We are indebted to Keith Butler and Norbert Przybilla for kindly sharing their codes, and the model atoms used in the present work. KP and ET were initially supported by the Croatian Science Foundation through research grant IP-2014-09-8656. The research leading to these results has (partially) received funding from the KU Leuven Research Council (grant C16/18/005: PARADISE) and from the BELgian federal Science Policy Office (BELSPO) through PRODEX grant PLATO. TVR gratefully acknowledges support from the Research Foundation Flanders (FWO) under grant agreement number 12ZB620N.

References

  1. Aerts, C., Molenberghs, G., Kenward, M. G., & Neiner, C. 2014, ApJ, 781, 88 [Google Scholar]
  2. Almeida, L. A., Sana, H., Taylor, W., et al. 2017, A&A, 598, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
  5. Banyard, G., Sana, H., Mahy, L., et al. 2022, A&A, 658, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Becker, S. R., & Butler, K. 1988, A&A, 201, 232 [NASA ADS] [Google Scholar]
  7. Becker, S. R., & Butler, K. 1990, A&A, 235, 326 [NASA ADS] [Google Scholar]
  8. Bouzid, M. Y., Sterken, C., & Pribulla, T. 2005, A&A, 437, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bowman, D. M., Aerts, C., Johnston, C., et al. 2019, A&A, 621, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bowman, D. M., Burssens, S., Simón-Díaz, S., et al. 2020, A&A, 640, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Burkholder, V., Massey, P., & Morrell, N. 1997, ApJ, 490, 328 [NASA ADS] [CrossRef] [Google Scholar]
  12. Butler, K., & Giddings, J. 1985, Newsletter of Analysis of Astronomical Spectra, No. 9 (London: University College London) [Google Scholar]
  13. Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, 210, A20 [Google Scholar]
  14. Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997, A&A, 318, 841 [NASA ADS] [Google Scholar]
  15. Cazorla, C., Morel, T., Nazé, Y., et al. 2017a, A&A, 603, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Cazorla, C., Nazé, Y., Morel, T., et al. 2017b, A&A, 604, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Clariá, J. J. 1976, AJ, 81, 155 [CrossRef] [Google Scholar]
  18. Damiani, F., Micela, G., & Sciortino, S. 2016, A&A, 596, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. de Mink, S. E., Cantiello, M., Langer, N., et al. 2009, A&A, 497, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [Google Scholar]
  21. Drobek, D., Pigulski, A., Shobbrook, R. R., & Narwid, A. 2013, Acta Astron., 63, 339 [NASA ADS] [Google Scholar]
  22. Eichendorf, W., & Reipurth, B. 1979, A&A, 77, 227 [NASA ADS] [Google Scholar]
  23. Freyhammer, L. M., Clausen, J. V., Arentoft, T., & Sterken, C. 2001, A&A, 369, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Garcia, B. 1994, ApJ, 436, 705 [NASA ADS] [CrossRef] [Google Scholar]
  27. García, B., & Mermilliod, J. C. 2001, A&A, 368, 122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Garcia, E. V., Stassun, K. G., Pavlovski, K., et al. 2014, AJ, 148, 39 [NASA ADS] [CrossRef] [Google Scholar]
  29. Georgy, C., Ekström, S., Granada, A., et al. 2013, A&A, 553, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Giddings, J. R. 1980, PhD Thesis, University College London, UK [Google Scholar]
  31. Giménez, A., & Clausen, J. V. 1986, A&A, 161, 275 [NASA ADS] [Google Scholar]
  32. Giménez, A., & Garcia-Pelayo, J. M. 1983, Ap&SS, 92, 203 [NASA ADS] [CrossRef] [Google Scholar]
  33. Giménez, A., Clausen, J. V., Helt, B. E., & Vaz, L. P. R. 1985, A&AS, 62, 179 [Google Scholar]
  34. Giménez, A., Clausen, J. V., & Andersen, J. 1986a, A&A, 160, 310 [Google Scholar]
  35. Giménez, A., Clausen, J. V., Helt, B. E., & Vaz, L. P. R. 1986b, A&AS, 66, 45 [NASA ADS] [Google Scholar]
  36. Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Göppl, C., & Preibisch, T. 2022, A&A, 660, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Grønbech, B., Olsen, E. H., & Strömgren, B. 1976, A&AS, 26, 155 [NASA ADS] [Google Scholar]
  39. Guinan, E. F., Ribas, I., Fitzpatrick, E. L., et al. 2000, ApJ, 544, 409 [NASA ADS] [CrossRef] [Google Scholar]
  40. Hadrava, P. 1995, A&AS, 114, 393 [NASA ADS] [Google Scholar]
  41. Heap, S. R., Lanz, T., & Hubeny, I. 2006, ApJ, 638, 409 [Google Scholar]
  42. Heger, A., & Langer, N. 2000, ApJ, 544, 1016 [CrossRef] [Google Scholar]
  43. Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
  44. Hensberge, H., & Pavlovski, K. 2007, in Binary Stars as Critical Tools and Tests in Contemporary Astrophysics, eds. W. I. Hartkopf, P. Harmanec, & E. F. Guinan, 240, 136 [NASA ADS] [Google Scholar]
  45. Hensberge, H., Pavlovski, K., & Verschueren, W. 2000, A&A, 358, 553 [NASA ADS] [Google Scholar]
  46. Herrero, A., Kudritzki, R. P., Vilchez, J. M., et al. 1992, A&A, 261, 209 [NASA ADS] [Google Scholar]
  47. Hill, G., Crawford, D. L., & Barnes, J. V. 1974, AJ, 79, 1271 [Google Scholar]
  48. Houk, N., & Cowley, A. P. 1975, University of Michigan Catalogue of two-dimensional spectral types for the HD Stars, I. Declinations -90.0 to -53.0, (Ann Arbor: University of Michigan) [Google Scholar]
  49. Hunter, I., Dufton, P. L., Smartt, S. J., et al. 2007, A&A, 466, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Hunter, I., Brott, I., Lennon, D. J., et al. 2008, ApJ, 676, L29 [NASA ADS] [CrossRef] [Google Scholar]
  51. Hunter, I., Brott, I., Langer, N., et al. 2009, A&A, 496, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Hur, H., Sung, H., & Bessell, M. S. 2012, AJ, 143, 41 [NASA ADS] [CrossRef] [Google Scholar]
  53. Ilijic, S., Hensberge, H., & Pavlovski, K. 2001, in Astrotomography, Indirect Imaging Methods in Observational Astronomy, eds. H. M. J. Boffin, D. Steeghs, & J. Cuypers, LNP, 573, 269 [NASA ADS] [CrossRef] [Google Scholar]
  54. Ilijic, S., Hensberge, H., Pavlovski, K., & Freyhammer, L. M. 2004, in Spectroscopically and Spatially Resolving the Components of the Close Binary Stars, eds. R. W. Hilditch, H. Hensberge, & K. Pavlovski, ASP Conf. Ser., 318, 111 [Google Scholar]
  55. Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, SPIE Conf. Ser., 9913, 99133E [Google Scholar]
  56. Johnston, C. 2021, A&A, 655, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Johnston, C., Pavlovski, K., & Tkachenko, A. 2019, A&A, 628, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Kaltcheva, N. T., & Georgiev, L. N. 1993, MNRAS, 261, 847 [NASA ADS] [CrossRef] [Google Scholar]
  59. Kilian, J., Montenbruck, O., & Nissen, P. E. 1994, A&A, 284, 437 [NASA ADS] [Google Scholar]
  60. Koenigsberger, G., Moreno, E., & Langer, N. 2021, A&A, 653, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Kolbas, V., Pavlovski, K., Southworth, J., et al. 2015, MNRAS, 451, 4150 [NASA ADS] [CrossRef] [Google Scholar]
  62. Kuhn, M. A., Getman, K. V., Feigelson, E. D., et al. 2017, AJ, 154, 214 [NASA ADS] [CrossRef] [Google Scholar]
  63. Kuhn, M. A., Hillenbrand, L. A., Sills, A., Feigelson, E. D., & Getman, K. V. 2019, ApJ, 870, 32 [CrossRef] [Google Scholar]
  64. Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
  65. Langer, N. 2012, ARA&A, 50, 107 [CrossRef] [Google Scholar]
  66. Lanz, T., & Hubeny, I. 2007, ApJS, 169, 83 [CrossRef] [Google Scholar]
  67. Levato, H., & Malaroda, S. 1982, PASP, 94, 807 [NASA ADS] [CrossRef] [Google Scholar]
  68. Levato, H., & Morrell, N. 1983, ApJ, 23, 183 [Google Scholar]
  69. Levato, H., Malaroda, S., Morrell, N., Garcia, B., & Hernandez, C. 1991, ApJS, 75, 869 [NASA ADS] [CrossRef] [Google Scholar]
  70. Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [Google Scholar]
  71. Maeder, A., Przybilla, N., Nieva, M.-F., et al. 2014, A&A, 565, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Mahy, L., Rauw, G., De Becker, M., Eenens, P., & Flores, C. A. 2015, A&A, 577, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Mahy, L., Almeida, L. A., Sana, H., et al. 2020a, A&A, 634, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Mahy, L., Sana, H., Abdul-Masih, M., et al. 2020b, A&A, 634, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Maíz Apellániz, J. 2006, AJ, 131, 1184 [CrossRef] [Google Scholar]
  76. Maíz Apellániz, J., Barbá, R. H., Fernández Aranda, R., et al. 2022, A&A, 657, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Markova, N., Puls, J., & Langer, N. 2018, A&A, 613, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Martins, F., Mahy, L., & Hervé, A. 2017, A&A, 607, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Massey, P., Morrell, N. I., Neugent, K. F., et al. 2012, ApJ, 748, 96 [NASA ADS] [CrossRef] [Google Scholar]
  80. Mathys, G., Andrievsky, S. M., Barbuy, B., Cunha, K., & Korotin, S. A. 2002, A&A, 387, 890 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Mayer, P., Harmanec, P., Nesslinger, S., et al. 2008, A&A, 481, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Mayer, P., Harmanec, P., Wolf, M., et al. 2016, A&A, 591, A129 [EDP Sciences] [Google Scholar]
  83. Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
  84. Mazeh, T. 2008, in EAS Publications Series, eds. M. J. Goupil, & J. P. Zahn, 29, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS] [Google Scholar]
  86. Moffat, A. F. J., & Vogt, N. 1975, A&AS, 20, 125 [NASA ADS] [Google Scholar]
  87. Morel, T., Blazère, A., Semaan, T., et al. 2022, A&A, 665, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Morrell, N. I., Massey, P., Neugent, K. F., Penny, L. R., & Gies, D. R. 2014, ApJ, 789, 139 [NASA ADS] [CrossRef] [Google Scholar]
  89. Nieva, M. F., & Przybilla, N. 2006, ApJ, 639, L39 [NASA ADS] [CrossRef] [Google Scholar]
  90. Nieva, M. F., & Przybilla, N. 2007, A&A, 467, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Nieva, M. F., & Przybilla, N. 2012, A&A, 539, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Paunzen, E., & Netopil, M. 2006, MNRAS, 371, 1641 [NASA ADS] [CrossRef] [Google Scholar]
  93. Pavlovski, K., & Hensberge, H. 2005, A&A, 439, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Pavlovski, K., & Southworth, J. 2009, MNRAS, 394, 1519 [NASA ADS] [CrossRef] [Google Scholar]
  95. Pavlovski, K., Tamajo, E., Koubský, P., et al. 2009, MNRAS, 400, 791 [NASA ADS] [CrossRef] [Google Scholar]
  96. Pavlovski, K., Southworth, J., & Tamajo, E. 2018, MNRAS, 481, 3129 [NASA ADS] [Google Scholar]
  97. Pavlovski, K., Hummel, C. A., Tkachenko, A., et al. 2022, A&A, 658, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Pedersen, M. G., Aerts, C., Pápics, P. I., & Rogers, T. M. 2018, A&A, 614, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Perry, C. L., Hill, G., & Christodoulou, D. M. 1991, A&AS, 90, 195 [NASA ADS] [Google Scholar]
  100. Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in FORTRAN. The Art of Scientific Computing, 2nd edn. (Cambridge: Cambridge University Press) [Google Scholar]
  101. Prša, A., Harmanec, P., Torres, G., et al. 2016, AJ, 152, 41 [Google Scholar]
  102. Przybilla, N. 2005, A&A, 443, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Przybilla, N., & Butler, K. 2001, A&A, 379, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Przybilla, N., & Butler, K. 2004, ApJ, 609, 1181 [NASA ADS] [CrossRef] [Google Scholar]
  105. Przybilla, N., Butler, K., Becker, S. R., Kudritzki, R. P., & Venn, K. A. 2000, A&A, 359, 1085 [NASA ADS] [Google Scholar]
  106. Przybilla, N., Butler, K., Becker, S. R., & Kudritzki, R. P. 2001, A&A, 369, 1009 [CrossRef] [EDP Sciences] [Google Scholar]
  107. Przybilla, N., Nieva, M.-F., & Butler, K. 2008, ApJ, 688, L103 [CrossRef] [Google Scholar]
  108. Przybilla, N., Firnstein, M., Nieva, M. F., Meynet, G., & Maeder, A. 2010, A&A, 517, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
  110. Rogers, T. M., Lin, D. N. C., McElwaine, J. N., & Lau, H. H. B. 2013, ApJ, 772, 21 [NASA ADS] [CrossRef] [Google Scholar]
  111. Rosu, S., Rauw, G., Conroy, K. E., et al. 2020, A&A, 635, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Rosu, S., Rauw, G., Farnir, M., Dupret, M. A., & Noels, A. 2022a, A&A, 660, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  113. Rosu, S., Rauw, G., Nazé, Y., Gosset, E., & Sterken, C. 2022b, A&A, 664, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  114. Sahade, J., & Berón Dàvila, F. 1963, Ann. d’Astrophys., 26, 153 [Google Scholar]
  115. Sana, H., Hensberge, H., Rauw, G., & Gosset, E. 2003, A&A, 405, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  116. Sana, H., Antokhina, E., Royer, P., et al. 2005, A&A, 441, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
  118. Serenelli, A., Weiss, A., Aerts, C., et al. 2021, A&A Rev., 29, 4 [NASA ADS] [CrossRef] [Google Scholar]
  119. Shull, J. M., Darling, J., & Danforth, C. W. 2021, ApJ, 914, 18 [NASA ADS] [CrossRef] [Google Scholar]
  120. Simon, K. P., & Sturm, E. 1994, A&A, 281, 286 [NASA ADS] [Google Scholar]
  121. Smith, N. 2006, MNRAS, 367, 763 [Google Scholar]
  122. Southworth, J. 2010, MNRAS, 408, 1689 [Google Scholar]
  123. Southworth, J. 2013, A&A, 557, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  124. Southworth, J. 2015, in Living Together: Planets, Host Stars and Binaries, eds. S. M. Rucinski, G. Torres, & M. Zejda, 496, ASP Conf. Ser., 164 [Google Scholar]
  125. Southworth, J., & Bowman, D. M. 2022, MNRAS, 513, 3191 [CrossRef] [Google Scholar]
  126. Southworth, J., & Clausen, J. V. 2007, A&A, 461, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Southworth, J., Maxted, P. F. L., & Smalley, B. 2005, A&A, 429, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  128. Southworth, J., Zima, W., Aerts, C., et al. 2011, MNRAS, 414, 2413 [NASA ADS] [CrossRef] [Google Scholar]
  129. Southworth, J., Bowman, D. M., Tkachenko, A., & Pavlovski, K. 2020, MNRAS, 497, L19 [Google Scholar]
  130. Sung, H., Sana, H., & Bessell, M. S. 2013, AJ, 145, 37 [NASA ADS] [CrossRef] [Google Scholar]
  131. Tamajo, E., Pavlovski, K., & Southworth, J. 2011, A&A, 526, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  132. Tkachenko, A., Aerts, C., Pavlovski, K., et al. 2014a, MNRAS, 442, 616 [Google Scholar]
  133. Tkachenko, A., Degroote, P., Aerts, C., et al. 2014b, MNRAS, 438, 3093 [Google Scholar]
  134. Tkachenko, A., Matthews, J. M., Aerts, C., et al. 2016, MNRAS, 458, 1964 [NASA ADS] [CrossRef] [Google Scholar]
  135. Tkachenko, A., Pavlovski, K., Johnston, C., et al. 2020, A&A, 637, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  136. Torres, G., Andersen, J., & Giménez, A. 2010, A&A Rev., 18, 67 [Google Scholar]
  137. Turner, D. G., Grieve, G. R., Herbst, W., & Harris, W. E. 1980, AJ, 85, 1193 [NASA ADS] [CrossRef] [Google Scholar]
  138. van Hamme, W. 1993, AJ, 106, 2096 [Google Scholar]
  139. Walborn, N. R. 1982, ApJS, 48, 145 [NASA ADS] [CrossRef] [Google Scholar]
  140. Wilson, R. E. 1979, ApJ, 234, 1054 [Google Scholar]
  141. Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [Google Scholar]
  142. Wilson, R. E., & Van Hamme, W. 2004, Computing Binary Star Observables (Wilson-Devinney Program User Guide), Available at ftp://ftp.astro.ufl.edu/pub/wilson [Google Scholar]
  143. Wolf, M., Zejda, M., & de Villiers, S. N. 2008, MNRAS, 388, 1836 [Google Scholar]
  144. Wood, D. B. 1971, AJ, 76, 701 [NASA ADS] [CrossRef] [Google Scholar]
  145. Wright, N. J. 2020, New Astron. Rev., 90, 101549 [CrossRef] [Google Scholar]
  146. Zucker, S., & Mazeh, T. 1994, ApJ, 420, 806 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Additional plots

thumbnail Fig. A.1.

Light curves of our target stars, from our own reduction of data from the TESS satellite, that were not included in the work in this paper but could useful for studies of the period changes and apsidal motion. The reduced photometric data are given in Table A.1, which is only available in electronic form at the CDS (see footnote at the first page).

thumbnail Fig. A.2.

Light curve of V346 Cen from the TESS satellite, plotted versus orbital phase but with a small magnitude offset linearly dependent on time to shift successive cycles upwards in the figure. The earliest points are coloured red, and the latest points are coloured blue. The repetition of the pulsation signature with orbital phase is easy to see.

thumbnail Fig. A.3.

Portions of the disentangled spectra of the stars (labelled) studied in this work.

All Tables

Table 1.

Basic characteristics of the binary systems studied in this work.

In the text
Table 2.

Parameters of the spectroscopic orbits for the four targets determined by SPD.

In the text
Table 3.

Atmospheric parameters derived from optimal fitting of disentangled spectra of the components to a grid of NLTE spectra.

In the text
Table 4.

Abundances determined for the stars in our sample of binary systems.

In the text
Table 5.

Comparison of abundances determined for targets in the present work to those of their parent clusters.

In the text
Table 6.

Summary of the parameters for the WD2004 solutions of the light curves of the systems.

In the text
Table 7.

Values of the amplitudes, A, frequencies, ν, phases, ϕ, and signal-to-noise ratios, S/N, of the orbital harmonics, calculated for the out-of-eclipse data points in the pulsation light curve of V346 Cen.

In the text
Table 8.

Physical properties measured for the four systems analysed in this work.

In the text
Table 9.

Distances and ages for the binary systems in the present sample compared to those of the parent clusters.

In the text

All Figures

thumbnail Fig. 1.

Light curves used in the current study from our reduction of data from the TESS satellite. They have been normalised to zero magnitude for display purposes.
In the text
thumbnail Fig. 2.

Visualisation of the spectroscopic orbits of our targets. The best-fitting orbits are shown with black lines. The RVs of the stars at the times of observation are shown with red symbols for the primary component and blue symbols for the secondary component. Note that these are not measured RVs, and hence the uncertainties in RVs are not assigned to individual symbols, because we calculated orbital parameters directly from all observed spectra for each system (see Sect. 4).
In the text
thumbnail Fig. 3.

Fits to the He I 4388 Å and He II 4541 Å lines. The ionisation balance of He I and He II was used in the determination of Teff for the stars. The blue data are the disentangled spectra and the red lines the best fits. The upper row is for the primary stars, and the lower row is for the secondary stars. The lower signal-to-noise ratio (S/N) for the secondary components arises because they are fainter than the primary components. The absence of He II 4541 Å absorption in V1034 Sco B and V346 Cen B is obvious and indicates that Teff < 23 000 K.
In the text
thumbnail Fig. 4.

Example of fits to N lines for our target stars. In this case, the N II 3995 Å line is shown for V1034 Sco (primary star on the left, secondary star on the right). The blue lines show the re-normalised disentangled spectra of the stars. The red lines show synthetic spectra from our pre-calculated grid for three different abundances (labelled in the bottom-right corner in each panel).
In the text
thumbnail Fig. 5.

Same as Fig. 4 but for O lines in the components of GL Car. The complex blend of O II lines at 4941 and 4943 and the O II line at 4955 Å are shown.
In the text
thumbnail Fig. 6.

Same as Fig. 4 but for lines in the components of V573 Car. The upper two panels show O II lines at 4661, 4673, and 4676 Å (green lines), which are blended with C II lines at 4659, 4663, 4665, and 4673 Å (red lines). The calculated synthetic spectrum is shown using a black line. The lower two panels show the N II 3995 Å lines.
In the text
thumbnail Fig. 7.

Same as Fig. 4 but for V346 Cen. The upper two panels show the C II lines at 5133–5151 Å, and the bottom two panels show the N II 4630.5 Å line for the two components.
In the text
thumbnail Fig. 8.

Individual abundances of carbon (left), nitrogen (middle), and oxygen (right) as a function of surface gravity. The stars in the present sample are indicated with filled blue circles, while stars taken from our previous studies are shown with open blue circles. The surface gravity (obtained from the binary solution) is used as a proxy for stellar evolution. Solid red lines show theoretical evolutionary tracks for a 15 M⊙ star and three values of the initial rotational velocity, Ω/Ωcrit = 0.1, 0.3, and 0.5 (Georgy et al. 2013). The cosmic standard abundance values of Nieva & Przybilla (2012) are indicated with horizontal dashed lines.
In the text
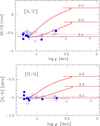thumbnail Fig. 9.

Same as Fig. 8 but for the [N/C] and [N/O] abundance indices.
In the text
thumbnail Fig. 10.

Light curves and best WD models for V1034 Sco. The differential magnitudes are plotted vs. orbital phase and are colour-coded according to the central wavelengths of the passbands. The source and passband of each light curve is labelled. The residuals of the fit are shown at the base of the figure. Offsets have been applied between the light curves and residuals for clarity.
In the text
thumbnail Fig. 11.

Light curves and best WD models for GL Car. Other comments are the same as for Fig. 10.
In the text
thumbnail Fig. 12.

Light curves and best WD models for V573 Car. Other comments are the same as for Fig. 10.
In the text
thumbnail Fig. 13.

Light curves and best WD models for V346 Cen. Other comments are the same as for Fig. 10.
In the text
thumbnail Fig. 14.

Tidally excited pulsations of V346 Cen. Top: observed light curve of V346 Cen for sectors 37 and 38, phase-folded with the binary orbital period. The eclipses are indicated by the grey bands. Middle: pulsation light curve of V346 Cen for sectors 37 and 38, phase-folded with the binary orbital period. Data points taken during the eclipses again lie within the grey bands. Bottom: Lomb–Scargle periodogram, calculated for the out-of-eclipse data points of the pulsation light curve for sectors 37 and 38. The vertical dashed lines indicate harmonics of the orbital frequency.
In the text
thumbnail Fig. 15.

Stochastic low-frequency variability of V346 Cen. Top: part of the (out-of-eclipse) residual light curve of V346 Cen, after fitting the orbital harmonics. Bottom: Lomb–Scargle periodogram, calculated for the out-of-eclipse data points of the residual light curve for sectors 37 and 38.
In the text
thumbnail Fig. 16.

Observed CNO abundances for binary and single high-mass stars compared to theoretical evolutionary models. Left panel: abundances of the CNO elements for high-mass stars in a diagram of [N/C] index versus [N/O] index. Stars in binary systems (Sect. 6) are represented by solid blue circles. For comparison, abundance determinations for single early-B type stars (Nieva & Przybilla 2012) are represented by green circles. Single stars obey a trend indicated by an analytical approximation to the nuclear reactions path for the CNO cycle derived in Przybilla et al. (2010) and Maeder et al. (2014). The slope in this diagram indicates a gradual enhancement of N at the expense of C. A slight decrease in the O abundance is also predicted. Whilst the single and binary stars span almost identical mass and Teff ranges, and are all MS stars, it is clear they do not share the same distribution (see Sect. 9). Right panel: Observed [N/C] index for 25 high-mass stars in binaries (solid blue circles) compared to single B-type stars (solid green circles; Nieva & Przybilla 2012) as a function of surface gravity. Solid red lines in the right panel show theoretical evolutionary tracks for a 15 M⊙ star and five values of the initial rotational velocity, Ω/Ωcrit = 0.1, 0.3, 0.5, 0.7, and 0.9 (Georgy et al. 2013). Striking differences between single stars and stars in binary systems are discussed in Sect. 9.
In the text
thumbnail Fig. A.1.

Light curves of our target stars, from our own reduction of data from the TESS satellite, that were not included in the work in this paper but could useful for studies of the period changes and apsidal motion. The reduced photometric data are given in Table A.1, which is only available in electronic form at the CDS (see footnote at the first page).
In the text
thumbnail Fig. A.2.

Light curve of V346 Cen from the TESS satellite, plotted versus orbital phase but with a small magnitude offset linearly dependent on time to shift successive cycles upwards in the figure. The earliest points are coloured red, and the latest points are coloured blue. The repetition of the pulsation signature with orbital phase is easy to see.
In the text
thumbnail Fig. A.3.

Portions of the disentangled spectra of the stars (labelled) studied in this work.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.