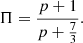| Issue |
A&A
Volume 669, January 2023
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 16 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202243564 | |
| Published online | 10 January 2023 | |
INTEGRAL study of MAXI J1535−571, MAXI J1820+070, and MAXI J1348 − 630 outbursts
I. Detection and polarization properties of the high-energy emission
1
Sorbonne Université, CNRS/IN2P3, Laboratoire de Physique Nucléaire et de Hautes Énergies, LPNHE, 4 place Jussieu, 75005 Paris, France
e-mail: cangemi@apc.in2p3.fr
2
Université Paris-Cité, AstroParticules et Cosmologie, APC, 10 rue Alice Domon et Léonie Duquet, 75013 Paris, France
3
Université Paris-Saclay, Université Paris-Cité, CEA, CNRS, AIM, 91191 Gif-surYvette, France
4
INAF-Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate, Italy
5
European Space Agency (ESA), European Space Research and Technology Centre (ESTEC), Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
6
Institut de Planétologie et d’Astrophysique de Grenoble, Université de Grenoble-Alpes, 38000 Grenoble, France
7
Dr. Karl Remeis-Sternwarte and Erlangen Centre for Astroparticle Physics, Friedrich-Alexander Universitát Erlangen-Nürnberg, Sternwartstr. 7, 96049 Bamberg, Germany
Received:
16
March
2022
Accepted:
15
October
2022
In black hole X-ray binaries, a nonthermal high-energy component is sometimes detected at energies above 200 keV. The origin of this high-energy component is debated and distinct spectral modelizations can lead to different interpretations. High-energy polarimetry measurements with the INTErnational Gamma-Ray Astrophysics Laboratory (INTEGRAL) enable new diagnostics on the physics responsible for the MeV spectral component in black hole X-ray binaries. In this work, we aim to investigate the high-energy behavior of three bright sources discovered by the Monitor of All-sky X-ray Image: MAXI J1535−571, MAXI J1820+070, and MAXI J1348−630. We took advantage of their brightness to investigate their soft γ-ray (0.1–2 MeV) properties with INTEGRAL. We used both spectral and polarimetric approaches to probe their high-energy emission with the aim of bringing new constraints on the MeV emission in black hole X-ray binaries. We first studied the spectral characteristics of the sources in the 3–2000 keV range using JEM-X, IBIS, and SPI, with a semi-phenomenological description of the data. We then used IBIS as a Compton telescope in order to evaluate the polarization properties of the sources above 300 keV. A high-energy component was detected during the hard-intermediate state and soft-intermediate state of MAXI J1535−571, the low-hard state of MAXI J1820+070, and the low-hard state of MAXI J1348−630. The components detected in MAXI J1820+070 and MAXI J1348 − 630 were polarized with a polarization fraction of 26 ± 9° and > 56% in the 300–1000 keV range, respectively. With no polarization information for MAXI J1535−571, the component detected could either come from the jets or the corona. In the case of MAXI J1820+070, the extrapolation of the synchrotron spectrum measured in the infrared indicates that the component is likely due to a nonthermal distribution of electrons from a hybrid corona. For MAXI J1348−630, the high fraction of polarization points toward a jets origin; however, we cannot formally conclude this without any infrared data giving information on the optically thin part of the synchrotron spectrum.
Key words: black hole physics / acceleration of particles / polarization / radiation mechanisms: non-thermal / X-rays: binaries
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Black hole X-ray binaries are transient systems that can transit through various spectral states during their outburst. The two main states are denoted as the low-hard state (LHS) and the high-soft state (HSS; see Remillard & McClintock 2006; Belloni 2010, for a precise definition of spectral states). The LHS corresponds to the rising phase of the outburst; its 1–200 keV spectrum can be well described by a power law with a photon index of Γ ∼ 1.5 with an exponential cutoff usually around 100 keV. This component is usually interpreted as the emission from Compton scattering of disk photons by electrons from a hot plasma called the “corona”. These sources are also sites of ejections of material at relativistic speeds, and sources of strong disk winds. The discovery of jets led to these sources being names “microquasars” (Mirabel et al. 1992). A small extension, steady “compact” jet is observed in the LHS, and has been resolved in a few sources: Cygnus X–1, GRS 1915+105, and more recently, MAXI J1348–630 (e.g., Stirling et al. 2001; Fuchs et al. 2003; Carotenuto et al. 2021). Transitions from the harder to the softer states are accompanied by transient, discrete, and large-scale ejections (e.g., Fender et al. 1999; Hannikainen et al. 1999; Mirabel et al. 1998; Corbel et al. 2001; Rodriguez et al. 2008a), and no jet seems to persist in the HSS (although see Rushton et al. 2012 and Zdziarski et al. 2020 for the case of Cygnus X-1). The X-ray flux in the HSS is dominated by the photon disk emission peaking at ∼1 keV. This component is associated with a continuum usually described with a power law with a photon index Γ > 2.5 and whose origin is still not yet understood.
In several sources, observations made at higher energies (> 200 keV) have revealed the presence of a high-energy nonthermal component extending up to 1 MeV (Grove et al. 1998; Cadolle Bel et al. 2006; Laurent et al. 2011; Rodriguez et al. 2015; Cangemi et al. 2021a). The origin of this high-energy emission is still not well understood and (at least) two scenarios have been invoked to explain its origin. In the first scenario, this component is the extension of the Synchrotron spectrum from the basis of the jets (Markoff et al. 2005; Laurent et al. 2011; Jourdain et al. 2014; Rodriguez et al. 2015; Kantzas et al. 2021). The alternative explanation suggests that this component arises from a nonthermal distribution of electrons in a hybrid thermal and nonthermal corona (e.g., Del Santo et al. 2013; Romero et al. 2014; Cangemi et al. 2021a,b). In the case of the high-mass Black Hole Binary (BHB), Cygnus X-1, Cangemi et al. (2021a) have suggested that the high-energy tails, seen both in the HSS and LHS, have different origins: in the HSS, a hybrid corona is favored, while the jet would be at the origin of the LHS high-energy tail.
Polarization measurements of the high-energy emission from BHBs is probably the best way to disentangle between these different scenarios, as we expect distinct polarization properties between Compton and synchrotron emission. The INTErnational Gamma-Ray Astrophysics Laboratory (INTEGRAL) has already brought important insights into polarization measurements thanks to the design of the SPectrometer on board on INTEGRAL (SPI, Vedrenne et al. 2003) and the Imager on Board on INTEGRAL Satellite (IBIS; Ubertini et al. 2003), which can be used as a Compton telescope with its two layers plane (the INTEGRAL Soft Gamma-Ray Imager (ISGRI) and the Pixellated Imaging Cesium Iodide Telescope, (PICsIT)). Indeed, the high polarization degree of the > 400 keV Cygnus X-1 high-energy tail detected both with IBIS and SPI (Laurent et al. 2011; Jourdain et al. 2012) has shown to be compatible with the emission of the compact jet in the LHS of this source (Rodriguez et al. 2015). Cygnus X − 1 is currently the only source for which polarization measurements have been able to constrain the origin of the high-energy component. It is therefore important to look at other sources in order to probe the origin of this component and try to obtain a more general understanding of the ∼MeV emission in microquasars.
MAXI J1535−571, MAXI J1820+070, and MAXI J1348 − 630 are X-ray transients that were discovered by the Monitor of All-Sky X-ray Image (MAXI) on board on the International Space Station (Matsuoka et al. 2009) during their outburst in September 2017 (Negoro et al. 2017), March 2018 (Kawamuro et al. 2018), and January 2019 (Yatabe et al. 2019), respectively. The three outbursts were then followed by INTEGRAL (e.g., Lepingwell et al. 2018; Bozzo et al. 2018; Cangemi et al. 2019a,b), and all three sources were particularly bright and reached a maximum flux of a few Crabs. Not many other sources have previously reached such a brightness, and therefore polarization studies using short accumulation (i.e., a few days) of data led to totally unconstrained results. Even for Cygnus X-1, the detection of polarized emission required the accumulation of Ms of data over large intervals of time.
Bright radio emission associated with a flat radio spectrum (Russell et al. 2017) and strong emission in the infrared band (Dinçer 2017; Vincentelli et al. 2021) led to the identification of MAXI J1535−571 as a BHB. Recent broadband spectroscopy with AstroSat enabled an estimation of the black hole mass of ∼10.3 M⊙ (Sridhar et al. 2019). The source displays strong X-ray variability, including low-frequency quasi-periodic oscillations (QPOs, Stiele & Kong 2018; Huang et al. 2018; Stevens et al. 2018; Bhargava et al. 2019; Sreehari et al. 2019). MAXI J1820+070 is an X-ray binary harbouring a black hole of mass ∼8.5 M⊙, accreting from a companion star of ∼0.4 M⊙ (Torres et al. 2019, 2020). The intense brightness of the system has triggered multiple multiwavelength observing campaigns (e.g., Bright et al. 2020; Trushkin et al. 2018; Tetarenko et al. 2021; Hoang et al. 2019) and the source was the center of many studies.
MAXI J1348 − 630 is also a BHB with a black hole of mass ∼11 M⊙ (Lamer et al. 2021) and the source is located at ∼3.3 kpc, according to the measurement of Lamer et al. (2021) with SRG/eROSITA and XMM-Newton observations. The source also shows strong X-ray variability and QPOs were observed during the transition from LHS to HSS transition (Belloni et al. 2020). The source also shows an interesting behavior when looking at is radio and X-ray correlation, which infers the relation between the emission from the compact jets and the inner accretion flow (Corbel et al. 2013). The correlation displays two different tracks referred as the “standard” and the “outliers” tracks. Usually, a source follows one of the tracks during its outburst, but Carotenuto et al. (2021) have shown that in the case of MAXI J1348−630, the source follows the outliers track during the first part of the outburst before joining the standard track. Table 1 summarizes all the known parameters for the three sources.
Summary of the known parameters for the three studied sources.
In this study, we present the evolution of the outbursts of these three different sources as observed by INTEGRAL. We make use of its unique capabilities in order to probe the main properties over the full 3–1000 keV range covered by the observatory. We also present polarization measurements of the high-energy component when significant emission is detected above 300 keV. The description of the observations and the data reduction methods are reported in Sect. 2. Section 3 is dedicated to the phenomenological spectral analysis. We then present the results from our polarization measurements with the Compton mode above 300 keV for the three sources in Sect. 4. The results are finally discussed in Sect. 5.
2. Data reduction
2.1. Spectral extraction: INTEGRAL/JEM-X
We only used data from JEM-X unit 1. The data were reduced with the OFF-LINE SCIENTIFIC ANALYSIS (OSA) version 11.1 software. We followed the standard steps described in the JEM-X user manual1. Spectra were extracted for each SCience Window2 (scw hereafter) where the source as automatically detected by the software at the image creation and fitting step. Spectra were then computed over 32 logarithmic spectral channels from ∼3 to ∼34 keV using the standard binning definition. Individual spectra for each period were then combined with the OSAspe_pick tool according to the classification scheme described in Sect. 2.4. The appropriate ancillary response files (arfs) were produced during the spectral extraction and were combined with spe_pick, while the redistribution matrix file (rmf) was rebinned from the instrument characteristic standard rmf with j_rebin_rmf. We addded a 3% systematic error on all spectral channels for each of the stacked spectra, as recommended in the JEM-X user manual. For our spectral analysis, we considered the spectra from 3 to 20 keV.
2.2. Spectral extraction: INTEGRAL/IBIS/ISGRI
Data from the INTEGRAL/IBIS upper detector ISGRI were also reduced with the OSA 11.1 software. We used the standard procedure described in the IBIS manual3. For each scw, we created the sky model and reconstructed the sky image and the source count rates by deconvolving the shadowgrams projected onto the detector plane. For the three sources, spectra were extracted using 60 logarithmically spaced channels between 20 keV and 1000 keV. Response matrixes were automatically generated running the OSA 11.1 spectral extraction. We then used the spe_pick tool to create stacked spectra for each different outburst periods (see Sect. 2.4). 2% of systematics were added to each stacked spectra, as indicated in the IBIS user manual.
2.3. Spectral extraction INTEGRAL/SPI
We followed a similar procedure already applied in the case of Cygnus X-3 (Cangemi et al. 2021b). To summarize, we used the SPI DATA ANALYSIS INTERFACE (SPIDAI) to reduce SPI data. During the outburst of MAXI J1348−630, SPI was in annealing from MJD 58501 to MJD 58522 (INTEGRAL revolutions 2047–2054), and therefore we did not have available SPI data during the LHS and the IMS, but we extracted the SPI spectrum in the HSS. We respectively created a sky model containing MAXI J1535−571, MAXI J1820+070, and MAXI J1348−630, and we set their variability to 5 scws. We then created the background model by setting the variability timescale of the normalization of the background pattern to 5 scws. Sometimes, solar flares, radiation belt entries, and other nonthermal incidents can lead to unreliable results. Therefore, we removed scws for which the reconstructed count compared to the detector counts gave a poor χ2 (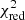 > 1.5), in order to avoid these effects. This selection reduced the total number of scws by ∼10%. The shadowgrams were then deconvolved to obtain the source flux, and spectra were extracted between 20 keV and 2000 keV using 27 logarithmically spaced channels. For each spectrum, we applied a correcting factor of 1/0.85 above 400 keV in order to take into account a change efficiency above this threshold (Roques & Jourdain 2019).
> 1.5), in order to avoid these effects. This selection reduced the total number of scws by ∼10%. The shadowgrams were then deconvolved to obtain the source flux, and spectra were extracted between 20 keV and 2000 keV using 27 logarithmically spaced channels. For each spectrum, we applied a correcting factor of 1/0.85 above 400 keV in order to take into account a change efficiency above this threshold (Roques & Jourdain 2019).
2.4. Data selection and period definition
We considered scw between MJD 58004–58019 (09/08/2017–09/23/2017), 58193–58249 (03/16/2018–05/11/2018), and 58512–58541 (01/29/2019–02/27/2019), respectively corresponding to the outburst of MAXI J1535−571, MAXI J1820+070, and MAXI J1348−630, where the sources are less than 10° off axis. Figure 1 shows the INTEGRAL/ISGRI light curves between 30 keV and 50 keV, along with the MAXI/GSC monitoring, in order to show the INTEGRAL observations in the long-term context of the whole outburst.
 |
Fig. 1. MAXI/GSC 2–20 keV (in black) and INTEGRAL/IBIS 30–50 keV (colored dots) light curves of MAXI J1535 − 571 (top panel), MAXI J1820+070 (middle panel), and MAXI J1348 − 630 (bottom panel). The left and the right y-axes indicate the count rate for MAXI/GSC and INTEGRAL/IBIS, respectively. Definitions of the different periods and the corresponding colors are described in Sect. 2.4. The count rates for 1 Crab are indicated with the pink and blue dotted lines for MAXI/GSC and INTEGRAL/IBIS, respectively. |
For the three sources, we performed a purely phenomenological fit for each scw, in the 3–300 keV energy range using JEM-X unit 1 and ISGRI, in order to separate the three datasets into different periods according to their spectral shapes and properties. The fits were performed using XSPEC (Arnaud 1996); we used a cutoff power-law model (CUTOFFPL) and added the emission from a disk (DISKBB) when needed. We also multiplied the model with a constant (CONSTANT), allowing us to take into account calibration issues between the instruments and the differences in total exposure between the instruments4. Constants were let free, whereas other parameters were tied between instruments.
In summary, we used CONSTANT*CUTOFFPL or CONSTANT*(CUTOFFPL + DISKBB) when high residuals were observed at low energy. Because of the low exposure of the individual spectra, we did not use absorption here, the aim being to roughly describe the shape of the spectra in order to separate the different periods of the outbursts. We then extracted the values of the photon index, the exponential cutof,f and the disk temperature. The evolution of these different parameters are shown in Fig. 2 for the three sources.
 |
Fig. 2. Temporal evolution of the different spectral parameters extracted from our phenomenological spectral fitting for MAXI J1535 − 571 (left panel), MAXI J1820+070 (middle panel), and MAXI J1348 − 630 (right panel). Definitions of the different periods and their corresponding colors are described in Sect. 2.4. |
For MAXI J1535−571, based on the value of the photon index, which transits from ∼1.9 to ∼2.3 from MJD 58004 to MJD 58016, we divided our datasets into two periods: the first one from MJD 58004 to MJD 58012, and the second one after MJD 58016. The two periods are shown in green and orange in Fig. 1. This subdivision is consistent with the epochs defined in Russell et al. (2020), where they find that the source was in a hard-intermediate state (HIMS) state from MJD 58008 to 58016 before its transition into a soft-intermediate state (SIMS) at MJD 58017. Therefore, we named our two periods according to this classification.
Concerning MAXI J1820+070, the values of the photon index and the exponential cutoff are consistent with typical values observed in an LHS during all the INTEGRAL observations. We thus define a unique period for the characterization of this outburst. The unique period is shown in blue in Fig. 1. This is consistent with the different epochs defined in Buisson et al. (2019), where they show that the source starts its transition into the HSS around MJD 58306, after our observations.
The study of the MAXI J1348 − 630 spectral evolution shows two changes in the spectral shape. The first change occurs around MJD 58517, where we observe an increase in the photon index from ∼1.6 to 2.3 and an increase in the cutoff energy from 50 keV to above the detection threshold. We define these two periods as the LHS (in blue of Fig. 1) and the intermediate state (IMS, in yellow on Fig. 1). Here we are not able to identify the different flavors (HIMS and SIMS) of the IMS. The observations from the last period, after MJD 58539, show a higher photon index value ∼2.3 associated with a high-energy exponential cutoff, not constrained in the majority of our observations (see the lower limits on Fig. 2). Belloni et al. (2020) found a similar state classification when analysing data from NICER. Figure 1 shows the LHS, IMS, and HSS periods in blue, yellow and pink, respectively.
The broadband INTEGRAL spectra are shown on Fig. 3. The different state spectra are plotted with different colors using the same color code as in Fig. 1.
 |
Fig. 3. Stacked spectra extracted from JEM-X, ISGRI, and SPI for MAXI J1535 − 571 (left panel), MAXI J1820+070 (middle panel), and MAXI J1348 − 630 (right panel). The different colors indicate the different epochs considered using the same color code as in Fig. 1. |
3. State-dependent spectral analysis
3.1. Methodology
According to the state classification described in Sect. 2.4, we have different stacked spectra for different periods of the three outbursts. In order to assess the potential presence of a high-energy tail in a state-resolved way, we followed the same methodology described in Cangemi et al. (2021a,b). This methodology is divided in two steps: we first analyzed the data from 3 to 100 keV with a reflected (REFLECT, Magdziarz & Zdziarski 1995) thermal Comptonization continuum (NTHCOMP, Zdziarski et al. 1996). We also added the iron line at 6.4 keV with a Gaussian (GAUSSIAN). Although the reflection is not needed in the individual spectra, it is needed in the stacked spectra in order to obtain a statistically good fit. We chose this Comptonization model rather than another because the MAXI J1820+070 spectrum is better fitted with this model than with other thermal Comptonization models we have tested (e.g., COMPTT). This model has also been used by Shidatsu et al. (2019) to fit MAXI/GSC and Swift/BAT data of MAXI J1820+070. For the sake of consistency, we also used NTHCOMP for MAXI J1535 − 571 and MAXI J1348−630. We further added the absorption by the interstellar medium (TBABS, Wilms et al. 2000) using ANGR solar abundances (Anders & Ebihara 1982). The model was written CONSTANT*TBABS*(REFLECT(NTHCOMP) + GAUSSIAN) in XSPEC. We added the emission from a disk (DISKBB, Mitsuda et al. 1984) when needed. In this case, the model became CONSTANT*TBABS*(REFLECT(NTHCOMP) + DISKBB + GAUSSIAN). We let the energy of the iron line vary between 6.2 keV to 6.5 keV, whereas its width was allowed to vary between 0.2 keV and 0.5 keV. Once we obtained a satisfactory fit, we added the data above 100 keV, let the parameters vary freely, and searched for the presence of residuals at high energy. In the cases of large residuals observed above 300 keV, we added a power-law component (CONSTANT*TBABS*(REFLECT(NTHCOMP) + GAUSSIAN + POWERLAW) or CONSTANT*TBABS*(REFLECT(NTHCOMP) + DISKBB + GAUSSIAN + POWERLAW) to the model and investigated the significance of this component by performing an F-test. We used an inclination of i = 67° (Miller et al. 2018), 63° (Torres et al. 2019), and 28° (Anczarski et al. 2020) for the reflection components for MAXI J1535−571, MAXI J1820+070, and MAXI J1348−630, respectively. The reflection fraction was allowed to vary between 0 < Ω/2π< 2.
The best-fit parameters obtained in the 3–2000 keV band are reported in Table 2 and the corresponding spectral fits for each source in the different states are shown in Fig. 4. If the addition of a disk was necessary to fit the data, we indicate “yes” in the row called “Disk”. Rows “Flux” and “Fluxpo” respectively refer to the flux given by the total model and the flux that comes from an additional power-law component in the 300–1000 keV range.
 |
Fig. 4. Best-fit models obtained from our phenomenological fittings of the 3–2000 keV for MAXI J1535 − 571 (top panel), MAXI J1820+070 (middle panel), and MAXI J1348 − 630 (bottom panel). Different colors indicate different epochs using the same color code as in Fig. 1. JEM-X, ISGRI, and SPI data are represented in blue, red, and yellow, respectively. Residuals for each period are plotted separately at the bottom of the corresponding spectrum. Different model components are shown with different line styles: Comptonized continuum (dashed), disk (dotted-dashed), additional power law (densely dotted), gaussian (dotted). |
Parameters obtained for our phenomenological fitting for each source and each period.
3.2. Results
3.2.1. MAXI J1535−571
During the HIMS, the seed-photon energy is unconstrained, and we thus fixed its value to 0.3 keV according to, for example, Sridhar et al. (2019), Tao et al. (2018). The value for the density column nH ∼3.3 × 1022 cm−2 is consistent with the value measured by Sridhar et al. (2019; Astrosat) but it is slightly lower than the value obtained by Xu et al. (2018; NuSTAR). This difference can arise by the use of slightly different epochs of observations between the different analyses. Moreover, Xu et al. (2018) attribute their high value (nH ∼ 8 × 1022 cm−2) to the inclusion of the thermal disk in their modeling. The electron temperature of kT ∼ 52 keV we obtain is consistent with results from Sridhar et al. (2019) and Tao et al. (2018). We find a photon index of the Comptonized continuum rather soft Γth ∼ 2.38, slighly higher that found in the different modelizations of Sridhar et al. (2019) and a reflection fraction of Ω2π ∼ 1.1. During the SIMS, we observed residuals below ∼10 keV and we added a disk to model the corresponding spectra. The disk temperature is tied to the photon seed temperature of NTHCOMP. We find kT0 ∼ 1.24 keV, in agreement with the value obtained by Tao et al. (2018). The other parameters were roughly the same as in the SIMS, except for Γth ∼ 2.52 for which we observe a slight increase. Our best fit gives a lower limit of > 1.8 for the reflection fraction. We have tested other reflection models such as RELXILL, which also give a similarly large reflection fraction. In their study, Miller et al. (2018) tested different reflection models, including RELXILL and RELLINE, and also obtained a large reflection fraction. Following these authors, such a large value is compatible with an X-ray source very close to the black hole, the large reflection then being due to the strong expected light bending. Our results agree with their best fit parameters. We do not enter into more details about the reflection component here since it is not the main subject of this paper.
Interestingly, we need an additional power-law component for both states in order to model the spectra above 300 keV. For the HIMS, inclusion of the power law improves 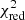 from 155.95/93 d.o.f. to
from 155.95/93 d.o.f. to 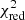 = 112.45/91 d.o.f.; for the SIMS, it is improved from
= 112.45/91 d.o.f.; for the SIMS, it is improved from 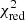 = 292.30/94 d.o.f. to
= 292.30/94 d.o.f. to 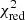 = 133.88/92 d.o.f.
= 133.88/92 d.o.f.
The photon index Γ0of this power law is consistent between the two periods, and we find Γ0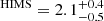 and Γ0
and Γ0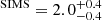 . We observe that the flux > 300 keV is dominated by this additional component. In order to assess the existence of this power-law component, we also tried to fit the data using solely a power law instead of the thermal Comptonization model. In this case, the data was poorly represented (
. We observe that the flux > 300 keV is dominated by this additional component. In order to assess the existence of this power-law component, we also tried to fit the data using solely a power law instead of the thermal Comptonization model. In this case, the data was poorly represented (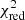 HIMS = 490.53/94 d.o.f. and
HIMS = 490.53/94 d.o.f. and 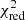 SIMS = 210.15/95 d.o.f.), and we observed strong residuals in the 30–50 keV range, clearly indicating the presence of a cutoff in this energy range.
SIMS = 210.15/95 d.o.f.), and we observed strong residuals in the 30–50 keV range, clearly indicating the presence of a cutoff in this energy range.
3.2.2. MAXI J1820+070
In MAXI J1820+070, the value of the density column was unconstrained, and thus we fixed it according to the value nH = 1.4 × 1021 obtained by Kajava et al. (2019). We find a Comptonized continuum rather hard with a photon index of Γth ∼ 1.61 and an electron energy kT ∼ 57 keV. Our value for the electron energy is higher compared to the value found by Zdziarski et al. (2021), kT ∼ 12 keV, using the data above 20 keV from ISGRI and SPI and the 3–80 keV data from NuSTAR. However, they use a modified version of COMPPS5 as their thermal description of the continuum and this could explain the difference compared to our study. The value we find for the electron temperature is also roughly consistent with the work of Chakraborty et al. (2020) and Buisson et al. (2019), who combined NuSTAR and Astrosat data. They both used a two coronal component model and found kT ∼ 38 keV when tying the two corona temperature components. We did not add a disk component to the model and we fixed the photon seed energy to kT0 = 0.2 keV (e.g., Wang et al. 2020; Dziełak et al. 2021). We find a reflection fraction Ω/2π > 1.
When adding the data above 300 keV, the addition of a power law to the model strongly improved the goodness of the fit (from 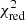 = 367.23/77 d.o.f. to
= 367.23/77 d.o.f. to 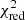 = 88.68/75 d.o.f.). We observe that the > 300 keV is largely dominated by the emission from this high-energy component (82% of the 300–1000 keV flux).
= 88.68/75 d.o.f.). We observe that the > 300 keV is largely dominated by the emission from this high-energy component (82% of the 300–1000 keV flux).
3.2.3. MAXI J1348−630
The parameter nHwas unconstrained, and we fixed its value to nH = 8.6 × 1021 cm−2 (Tominaga et al. 2020). Parameters found in the LHS are very close to those found during the outburst of MAXI J1820+070. We obtained a photon index Γth ∼ 1.69 and an electron energy kT ∼ 44 keV. It is mentioned that a black body component is present in the LHS (e.g., Tominaga et al. 2020; Chakraborty et al. 2020; Zhang et al. 2021) with a temperature of ∼0.5 keV. At such a temperature, the flux of the disk could contribute > 3 keV, and therefore we added a DISKBB component in our model. The normalization of this component was fixed to 12000, the value found by Chakraborty et al. (2020). Strong residuals are observed at high energies when fitting solely with CONST*(REFLECT(NTHCOMP) + GAUSS). The addition of a power-law component improved 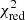 from 112.42/70 d.o.f. to 62.56/68 d.o.f. We find a photon index of Γ0 = 2.0 and measure a reflection fraction of ∼0.8.
from 112.42/70 d.o.f. to 62.56/68 d.o.f. We find a photon index of Γ0 = 2.0 and measure a reflection fraction of ∼0.8.
We also used a disk to model the IMS and the HSS. As for the states of MAXI J1535−571, the flux at low energy is dominated by the disk emission. The photon disk energy is slightly higher during the IMS than during the HSS. Using NICER and Astrosat, Zhang et al. (2021) and Jithesh et al. (2021) found a consistent value analysing data from different observations made during the HSS. However, Zhang et al. (2021) observed a higher value of Γth(∼3.3) than that observed during both periods corresponding to our HIMS and SIMS. It should be noted that we also modelled those two periods with a simple reflected power law and a disk (REFLECT(POWERLAW) + DISKBB + GAUSSIAN). In this case, we did not find a satisfactory fit for the IMS (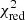 Int = 248.13/75), but the HSS can be well described by this purely phenomenological model and parameters are consistent with the previous modelization.
Int = 248.13/75), but the HSS can be well described by this purely phenomenological model and parameters are consistent with the previous modelization.
4. Polarization with the Compton mode
4.1. Principle of the Compton mode
Thanks to its two layer detectors, ISGRI at the top and the (PICsIT, Labanti et al. 2002) at the bottom, IBIS can be used as a Compton polarimeter. This concept relies on the cross section dσ, which represents the probability for a polarized photon with an energy E1 to enter in interaction with an electron from the detector (e.g., Evans & Beiser 1956):
where E2 is the energy of the scattered photon in the solid angle dΩ, θc is the scatter angle, r0 is the electron radius, and ϕ is the azimuthal angle of the scattered photon with respect to the polarization direction (see e.g., Fig. 1 of Forot et al. 2007). Using the relation between E1 and E2,
we note that for a fixed scattered angle, the cross section will be maximal for ϕ = π/2 + kπ with k ∈ Z. This creates an asymmetry in the number of detected photons by PICsIT. We can evaluate the detected photon distribution on the PICsIT detector with respect to the azimuth ϕ:
where C is the mean count rate. Then we can deduce the polarization angle PA = ϕ0 − π/2 and the polarization fraction Π:
where a100 represents the amplitude of a 100% polarized source (Suffert et al. 1959). The value of a100 depends on several factors, such as the detector dimension, the detection threshold, and the level of noise. In the case of IBIS, we simulated the emission from a monochromatic source, for which we applied the same treatment as for a real source. The resulting modulation was used to deduce the value of a100 for this energy. We then weighted this value by the source spectrum and obtained the value of a100 for the desired energy band. It is usually around 0.2–0.3, depending on the considered energy band (Laurent et al. 2011; Rodriguez et al. 2015). Figure A.1 shows the evolution of a100 as a function of the energy.
In order to measure N(ϕ), we needed to select the simple Compton events, namely those for which photons interact only once in ISGRI and once in PICsIT. “Spurious events” were removed according to the method described in Forot et al. (2007). Photons were accumulated in six different angle ranges of 30° each. In order to improve the signal-to-noise ratio in each channel, we took advantage of the π symmetry of the differential cross section described by Eq. (1) since, for example, the first channel contains photons with an azimuth 0° < ϕ < 30° and photons with an azimuth 180° < ϕ < 210°. Shadowgrams were formed for each channel angle chosen by the user, then deconvolved, and the count rates were extracted.
The uncertainty on N(ϕ) was dominated by statistical fluctuations, since our observations were background dominated. Therefore, confidence intervals for ϕ0 and a0 were not derived by a N(ϕ) fit to the data, but were obtained with a Bayesian approach following the work of Forot et al. (2008), and described in Vaillancourt (2006) and Weisskopf et al. (2006). In this computation, we supposed that all real polarization angles and fractions have a uniform probability distribution (Quinn 2012; Maier et al. 2014), and that the real polarization angle and fraction were ϕ0 and a0. We then needed the probability density distribution of measuring a and ϕ from Npt-independent data points in N(ϕ) during a period π, which is given by (Vaillancourt 2006; Forot et al. 2008; Maier et al. 2014) :
where σC is the uncertainty of C. Uncertainties of a and ϕ could then be deduced by integrating dP(a, ϕ) with respect to the other dimension. We emphasize that this probability is a conditional probability and was calculated by supposing that the emission was indeed polarized.
There are also several systematics uncertainties that arise from measurements of polarization with a Compton telescope using a coded mask. The non-axisymmetric geometry of the detectors and the systematics due to the analysis process were studied in detail in Forot et al. (2008). We also study the modulation from the background by selecting events from detector pixels hidden from the source by opaque mask elements, for scws of MAXI J1820+070. We find a modulation of 5% for the different energy bands used in the analysis. All these systematic uncertainties are taken into account in the derivation of the polarization constraints measured in this paper.
4.2. Results
Figure 5 shows polarigrams in the 300–1000 keV band for the different periods of the three sources, following the same color code as in Fig. 1. Figures A.3 and A.4 show polarigrams in the 300–1000 keV and 400–1000 keV bands, respectively. Polarigrams are fitted with a constant (dashed gray line) and the sinusoid function described in Eq. (3), shown by the colored line. During the LHS periods of MAXI J1820+070 and MAXI J1348−630, we also show in Fig. 6 the integrated probability function described by Eq. (5) as a function of the polarization angle ϕ and the polarization fraction Π. Other probability density functions are shown on Fig. A.2. Table 3 summarizes the different parameters we measured for the three sources and for three different energy bands: 300–400 keV, 400–1000 keV, and 300–1000 keV. We indicate the total effective exposure time, the signal-to-noise ratio, the a100 value, the 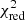 obtained by fitting N(ϕ) by a constant (C) or by the sinusoid function (S) described by equation (3), the polarization angle PA, and the polarization fraction Π. It should be noted that we used a range of 0–180° for our fitting. Uncertainties represent an interval confidence of 67%. The last column indicates whether polarization is detected (✓) or not (×). We considered that polarization was detected by validating two conditions: (1) we needed a signal-to-noise ratio higher than 12 to obtain reliable results, with this value being based on empirical results on the Crab (Laurent et al. 2016); and (2) the probability, punpola, of measuring modulation, knowing that the source is unpolarized, was < 1%. All punpola are shown in Table 3 (only for polarigrams where the signal-to-noise ratio was higher than 12).
obtained by fitting N(ϕ) by a constant (C) or by the sinusoid function (S) described by equation (3), the polarization angle PA, and the polarization fraction Π. It should be noted that we used a range of 0–180° for our fitting. Uncertainties represent an interval confidence of 67%. The last column indicates whether polarization is detected (✓) or not (×). We considered that polarization was detected by validating two conditions: (1) we needed a signal-to-noise ratio higher than 12 to obtain reliable results, with this value being based on empirical results on the Crab (Laurent et al. 2016); and (2) the probability, punpola, of measuring modulation, knowing that the source is unpolarized, was < 1%. All punpola are shown in Table 3 (only for polarigrams where the signal-to-noise ratio was higher than 12).
 |
Fig. 5. Polarigrams of the three sources obtained in the 300–1000 keV energy band range. |
Parameters obtained for our polarization analysis using the Compton mode.
We did not detect polarization for MAXI J1535−571. Indeed, for both states and for the three energy bands, the signal-to-noise ratio was too poor and no modulation was detected.
The diagnosis is different for MAXI J1820+070. Indeed, for the three considered energy bands, polarigrams show clear deviation from a constant that poorly represents the data.
We find a much better description of the data with the sine function (Eq. (3)). In the three energy bands, we calculated the probability given by Eq. (5) using the values of a and ϕ we find in our best fit. Figure 6 (left) shows the contour plot we obtained in the 300–1000 keV bands; polarization was detected with an interval confidence higher than 99%, and we find a polarization angle and a polarization fraction consistent with PA ∼ 110° and Π ∼ 25% in the three energy bands.
 |
Fig. 6. Probability density described by Eq. (5) as a function of the polarization angle and the polarization fraction calculated for MAXI J1820+070 (left) and MAXI J1348 − 630 in the LHS (right). |
Concerning MAXI J1348−630, polarigrams extracted from the IMS and HSS periods have a poor signal-to-noise ratio. On the other hand, polarigrams from the LHS period have a sufficient signal-to-noise ratio to probe the presence of a modulation. We find that polarigrams are poorly described by a constant and punpol < 1% in the different energy bands. We then calculated the probability (Eq. (5)) to measure the polarization angle PA and a polarization fraction Π. The contour plot is shown in Fig. 6 (right). We find lower limits for the polarization fraction of 49%, 70%, and 56% with a polarization angle of ∼160°, ∼180° , and ∼180° for the 300–400 keV, 300–1000 keV, and 300–1000 keV bands, respectively.
5. Discussion and interpretation
5.1. Summary of the results
5.1.1. MAXI J1535−571
We separate the data into two intervals corresponding to a HIMS and a SIMS, which respectively matched epochs defined in Russell et al. (2020). In both periods, the source spectra were rather soft and characterized by a photon index 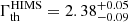 and
and 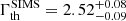 . The low-energy emission started to be dominated by the accretion disk during the SIMS period and its energy temperature peaked at kT0
. The low-energy emission started to be dominated by the accretion disk during the SIMS period and its energy temperature peaked at kT0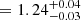 keV, which is a typical value usually observed in soft states of BHBs (e.g., Remillard & McClintock 2006). The energy from the corona electrons was not well defined in both states with a value greater than 50 keV.
keV, which is a typical value usually observed in soft states of BHBs (e.g., Remillard & McClintock 2006). The energy from the corona electrons was not well defined in both states with a value greater than 50 keV.
We detected an additional component above the Comptonization bump during both states. This high-energy component is described by a power law with a photon index of 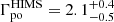 and
and 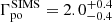 .
.
Using the Compton mode, we did not detect polarization in either state. We remark, however, that the source flux above 300 keV was quite low (see Table 2), resulting in a poor signal-to-noise ratio for our polarization measurements. The non-detection is compatible with this empirical minimum value to obtain a trustworthy detection of signal. Therefore, we cannot conclude, for MAXI J1535−571, if the lack of polarization detection at high energy is intrinsically characteristic of the source or if it is an observational issue.
5.1.2. MAXI J1820+070
MAXI J1820+070 is the brightest of the three sources observed in the ISGRI 30–50 keV range. The source was observed during its LHS (e.g., Buisson et al. 2019). The spectrum is characterized by a hard photon index Γth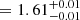 and corona electron energy of
and corona electron energy of 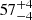 keV. An additional power-law component clearly improves the fit and we find a photon index of Γ0
keV. An additional power-law component clearly improves the fit and we find a photon index of Γ0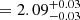 . This component strongly dominates the spectrum above 300 keV with a flux of 4.6 × 10−9 erg s−1 cm−2.
. This component strongly dominates the spectrum above 300 keV with a flux of 4.6 × 10−9 erg s−1 cm−2.
Polarigrams extracted in the 300–400 keV, 400–1000 keV, and 300–1000 keV bands show a strong modulation of the signal and we measured a 300–1000 keV polarization fraction of Π = 26 ± 9 and a polarization angle PA = 110 ± 11° (see Table 3 for the energy-dependent results). Errors are given in a 67% confidence range.
5.1.3. MAXI J1348−630
We followed the evolution of the source during its outburst and identified three different periods corresponding to three different states of the source: LHS, IMS, and HSS. During its LHS, we found a photon index of Γth = 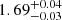 and an electron energy kT
and an electron energy kT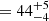 keV. We detected an additional power-law component with a photon index of Γ0
keV. We detected an additional power-law component with a photon index of Γ0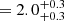 .
.
While a high-energy tail is clearly present in the LHS, no high-energy component was detected in either of the softer states. Consistently polarization can be probed only in the LHS, and we indeed detected the same polarization angle PA = 180 ± 10° for the 400–1000 keV and 300–1000 keV bands. This value is not strictly consistent with the value of PA = 160 ± 9° that we measured in the 300–400 keV band, but it is consistent at 90% confidence (PA = 160 ± 30°). This slight discrepancy could arise from some contribution of the Comptonized continuum, as the 300–400 keV range is not purely described by the additional power law. We measured a high polarization fraction for the three energy bands with a lower limit of > 70% for the 400–1000 keV band. The other energy bands allow lower polarization fractions: Π300−400 keV > 49% and Π300−1000 keV > 56%.
5.2. Origin of the high-energy emission
We detected a power-law tail in addition to the standard Comptonisation component during the HIMS and SIMS of MAXI J1535−571, the LHS of MAXI J1820+070, and during the LHS of MAXI J1348−630. This component was strongly present at the beginning of the outburst when the global spectral shape was hard, and its strength decayed as the outburst evolved to softer states. There are two obvious possibilities for the “apparent” absence of high-energy tails in softer states. Either 1) the emission genuinely vanishes; 2) the high-energy emission falls below detection threshold.
Case 1) implies that the medium responsible for the high-energy component disappears in the softer states. One obvious candidate is the compact jet, which is known to be quenched in the HSS (e.g., Fender et al. 1999), and it was claimed that it emitted in the 400–2000 keV range in Cygnus X-1 (Laurent et al. 2011; Jourdain et al. 2012; Rodriguez et al. 2015). Since ejections of coronae state transitions have been proposed in other sources (e.g., Rodriguez et al. 2008a,b), the corona would also be a good candidate. Case 2) implies an evolution of the high-energy component parameters (at least its flux), which also leads to at least two interpretations: 2a) same medium with evolving properties, for example, in Cygnus X-3 the tail seems unrelated to the jet’s behavior, and is well explained by a hybrid corona in all states (Cangemi et al. 2021b); and 2b) different emitting media, as observed in Cygnus X-1 (Cangemi et al. 2021a). In the case of Cygnus X-1, we note that the jet’s origin in both states could also be a possibility (Zdziarski et al. 2020).
Polarization is an additional diagnostic to constrain the origin of the tail. The synchrotron spectrum of a population of N electrons with an energy between E and E + dE, and with an electron index p, dN(E)∝E−pdE, can be approximated by a power law, P(E)∝E−α. The spectral index α and the electron index p are tied by the equation α = (p − 1)/2 (Rybicki & Lightman 1986), and α can also be related to the photon index Γ : α = Γ − 1. In a very ordered magnetic field, the polarization fraction of a polarized emission expected in the optically thin regime of the synchrotron spectrum, is (Rybicki & Lightman 1986):
In the case of MAXI J1348−630, the value of the photon index during the LHS, Γ0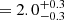 , leads to a polarization fraction of
, leads to a polarization fraction of 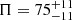 %, which is consistent with the polarization fraction observed in the three energy bands considered. Therefore, the observed emission could arise from the synchrotron emission from the jet’s base in a very ordered magnetic field. Besides, synchrotron emission from compact radio jets has been observed during the LHS of MAXI J1348 − 630 (e.g., Russell et al. 2020; Carotenuto et al. 2021).
%, which is consistent with the polarization fraction observed in the three energy bands considered. Therefore, the observed emission could arise from the synchrotron emission from the jet’s base in a very ordered magnetic field. Besides, synchrotron emission from compact radio jets has been observed during the LHS of MAXI J1348 − 630 (e.g., Russell et al. 2020; Carotenuto et al. 2021).
While the upper limit (or non-detection) in the case of MAXI J1535 − 571 does not allow us to conclude about the origin of the high-energy component, the case of MAXI J1820+070 is quite interesting. The rather low level of polarization (compared to MAXI J1348 − 630 and Cygnus X-1) may indicate various possibilities. Here the measured value of the photon index Γ0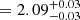 leads to a polarization fraction of 75 ± 2%, which is not consistent with the polarization fraction we measured. This could indicate either that: (1) the magnetic field is disrupted by some mechanism and/or different jet zones emits polarized radiation with different angles; or (2) there is another origin than the jets for the polarized emission.
leads to a polarization fraction of 75 ± 2%, which is not consistent with the polarization fraction we measured. This could indicate either that: (1) the magnetic field is disrupted by some mechanism and/or different jet zones emits polarized radiation with different angles; or (2) there is another origin than the jets for the polarized emission.
5.3. Spectral energy distribution basic analysis
While a precise spectral modelization with physical models is beyond the scope of this paper, we can apply a simple approach using spectral energy distribution to verify the jet hypothesis. Here, the goal is to investigate whether the optically thin part of the synchrotron spectrum from the jet is consistent with our measured high-energy component. Therefore, we need the information on the synchrotron break frequency of the jet’s spectrum, as well as the spectral index of the optically thin part. Then, we can extrapolate the synchrotron spectrum up to 1 MeV and check the consistency with the hard X-rays.
5.3.1. MAXI J1535−571
Figure 7 shows different datasets from Russell et al. (2020) in the HIMS (green) and in the SIMS (orange). The gray line indicates the energy of the synchrotron break, whereas the green line is the optically thin part of the synchrotron spectrum obtained by Russell et al. (2020; α = 0.83 ± 0.09, where α is the spectral index of the optically thin part of the synchrotron spectrum), extrapolated up to 1000 keV. We also show the spectra extracted in this work and their associated measured power laws. The box in the top right corner of the figure is an enlarged view from 100 keV to 1000 keV. We observe that the extrapolation of the optically thin spectrum is consistent, within the error bars, with the power law in the HIMS. This could point toward a jet’s origin of the high-energy component in this state. However, the uncertainties are large at high energy high energies, and without polarization measurements, we cannot exclude a hybrid corona origin. Concerning the SIMS, Russell et al. (2020) show that the radio emission is quenched in this state. Therefore, the nonthermal component > 200 keV in this state could come from another region from the jet that still radiates in the X-ray or has another origin.
 |
Fig. 7. MAXI J1535 − 571 spectra using observational data from Russell et al. (2020) and this work. HIMS and SIMS data are represented in green and orange, respectively. The measured additional high-energy components are indicated with dotted lines. Their 90% uncertainties interval range is represented by the colored area. The purple dotted line is the extrapolation of the optically thin synchrotron spectrum from Russell et al. (2020) with α = 0.83 ± 0.09. |
5.3.2. MAXI J1820+070
The dotted green line in Fig. 8 shows the extrapolation of the optically thin synchrotron spectrum measured with simulatenous (12 April 2018) X-Shooter data (green dots Rodi et al. 2021). The X-ray spectrum from this work is shown with blue dots, whereas the dotted blue line shows our measured power law. Here, the IR optically thin spectrum is not consistent with the high-energy component that we measured. This result clearly excludes a pure synchrotron jet’s origin for the additional component and favors a hybrid corona origin as proposed by Zdziarski et al. (2021). Regarding our polarization measurements, a polarization fraction of 26 ± 9% is also consistent with a hybrid corona origin (Beheshtipour et al. 2017).
 |
Fig. 8. MAXI J1820+070 spectrum using observational data from Rodi et al. (2021) and this work. The measured additional high-energy component is indicated by the blue dotted line. The green dotted line is the extrapolation of the optically thin synchrotron spectrum from Rodi et al. (2021). |
5.3.3. MAXI J1348−630
No infrared data have been published on MAXI J1348 − 630 so far. Therefore, we do not have information on the synchrotron cutoff. However, we tried to investigate the consistency of the high-energy emission detected with synchrotron emission from the jets assuming a spectral index −0.5 < α < 0.8, a flux 40 < F < 300 mJy at the synchrotron cutoff energy 1.5 × 1015 Hz. Figure 9 shows the resulting broadband spectrum. We also plot the optically thick part of the synchrotron spectrum as measured by Carotenuto et al. (2021) with ATCA at MJD 58514.01.
 |
Fig. 9. Broadband spectrum of MAXI J1348−630. The light-blue line is the spectrum as measured by Carotenuto et al. (2021). The green zone corresponds to our synchrotron thin spectrum hypothesis (see the text). The insert plot focuses on the 1–1000 keV range. The different colors indicate the resulting power law for different normalization values of the DISKBB. |
As we added a disk to model the spectrum (see Sect. 3), we investigated the impact of the black body disk normalization value on the power-law normalization and photon index values. We let the normalization parameter of DISKBB vary from 1 × 104 to 2 × 104, which is the upper limit obtained by Chakraborty et al. (2020). The resulting power laws from the fit are shown in different colors in Fig. 9 and the insert is an enlarged view from 1 keV to 1000 keV. The normalization of the black body disk has a strong impact on the power-law properties and we note that for normalization higher than ∼15 000, the power-law component is consistent with the purple zone, and therefore with the synchrotron scenario. However, although the high polarization fraction is also consistent with synchrotron emission, our synchrotron hypothesis also strongly depends on the energy of the synchrotron break, and we cannot formally conclude a synchrotron origin without any precise measurement of the optically thin part of the synchrotron spectrum.
6. Summary and conclusion
In this work, we used the INTEGRAL unique capabilities to investigate the high-energy properties of three sources: MAXI J1535−571, MAXI J1820+070, and MAXI J1348 − 630 during their outburst. For each outburst, we divided the data into different state periods based on their spectral characteristics. Thanks to the combination of JEM-X, ISGRI, and SPI data, we created stacked spectra in the 3–2000 keV band range for each of these states. We then used a simple phenomenological spectral approach in order to investigate the behavior of the sources at high energy and to search for an additional high-energy component.
We used the Compton mode of INTEGRAL/IBIS to study polarization properties and we find that the 300–1000 keV emission from the LHS of MAXI J1820+070 and MAXI J1348 − 630 are polarized.
We extrapolated the optically thin part observed in the IR of the synchrotron spectrum to investigate the potential origin of the high-energy component detected in these sources. In the HIMS of MAXI J1535−571, the synchrotron spectrum is consistent with the detected high-energy component. However, we could not measure polarization in this source, and therefore we cannot exclude a hybrid corona origin. For MAXI J1820+070, the extrapolation of the synchrotron spectrum is not consistent with the extension measured in the X-rays. Therefore, the nonthermal component could arise from a nonthermal distribution of electron electrons from the corona. The polarization fraction that we measured is also consistent with this scenario. In the case of the high-energy component detected in the LHS of MAXI J1348−630, the high polarization fraction we measured is consistent with synchrotron emission in a very ordered magnetic field. However, we prefer not to make any conclusions on the origin of the high-energy component without any clear information on the optically thin part of the synchrotron spectrum.
Acknowledgments
J.R., P.L. P.-O.P and C.G. acknowledge partial funding from the French Space Agency (CNES). J.R. and P.-O.P acknowledge partial fundings from the French Programme National des Hautes Energies (PNHE). T.M.B. acknowledges financial contribution from the agreement ASI-INAF n. 2017-14-H.0 and from PRIN INAF 2019 n.15. Based on observations with INTEGRAL, an ESA project with instruments and science data centre funded by ESA member states (especially the PI countries: Denmark, France, Germany, Italy, Switzerland, Spain) and with the participation of Russia and the USA.
References
- Anczarski, J., Neilsen, J., Remillard, R., et al. 2020, in AAS Meeting Abstracts, 235 [Google Scholar]
- Anders, E., & Ebihara, M. 1982, Meteoritics, 17, 180 [NASA ADS] [Google Scholar]
- Arnaud, K. A. 1996, ASP Conf. Ser., 101, 17 [Google Scholar]
- Atri, P., Miller-Jones, J. C. A., Bahramian, A., et al. 2020, MNRAS, 493, L81 [CrossRef] [Google Scholar]
- Beheshtipour, B., Krawczynski, H., & Malzac, J. 2017, ApJ, 850, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Belloni, T. M. 2010, in States and Transitions in Black Hole Binaries, (Springer), 794, 53 [NASA ADS] [Google Scholar]
- Belloni, T. M., Zhang, L., Kylafis, N. D., Reig, P., & Altamirano, D. 2020, MNRAS, 496, 4366 [NASA ADS] [CrossRef] [Google Scholar]
- Bhargava, Y., Belloni, T., Bhattacharya, D., & Misra, R. 2019, MNRAS, 488, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Bozzo, E., Savchenko, V., Ferrigno, C., et al. 2018, ATel, 11478, 1 [NASA ADS] [Google Scholar]
- Bright, J. S., Fender, R. P., Motta, S. E., et al. 2020, Nat. Astron., 4, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Buisson, D. J. K., Fabian, A. C., Barret, D., et al. 2019, MNRAS, 490, 1350 [NASA ADS] [CrossRef] [Google Scholar]
- Cadolle Bel, M., Sizun, P., Goldwurm, A., et al. 2006, A&A, 446, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cangemi, F., Belloni, T., & Rodriguez, J. 2019a, ATel, 12471, 1 [NASA ADS] [Google Scholar]
- Cangemi, F., Rodriguez, J., Belloni, T., Clavel, M., & Grinberg, V. 2019b, ATel, 12457, 1 [NASA ADS] [Google Scholar]
- Cangemi, F., Beuchert, T., Siegert, T., et al. 2021a, A&A, 650, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cangemi, F., Rodriguez, J., Grinberg, V., et al. 2021b, A&A, 645, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carotenuto, F., Corbel, S., Tremou, E., et al. 2021, MNRAS, 504, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Chakraborty, S., Navale, N., Ratheesh, A., & Bhattacharyya, S. 2020, MNRAS, 498, 5873 [NASA ADS] [CrossRef] [Google Scholar]
- Chauhan, J., Miller-Jones, J. C. A., Anderson, G. E., et al. 2019, MNRAS, 488, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Corbel, S., Kaaret, P., Jain, R. K., et al. 2001, ApJ, 554, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Corbel, S., Coriat, M., Brocksopp, C., et al. 2013, MNRAS, 428, 2500 [Google Scholar]
- Del Santo, M., Malzac, J., Belmont, R., Bouchet, L., & De Cesare, G. 2013, MNRAS, 430, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Dinçer, T. 2017, ATel, 10716, 1 [Google Scholar]
- Dziełak, M. A., De Marco, B., & Zdziarski, A. A. 2021, MNRAS, 506, 2020 [Google Scholar]
- Evans, R. D., & Beiser, A. 1956, Phys. Today, 9, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Fender, R., Corbel, S., Tzioumis, T., et al. 1999, ApJ, 519, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Forot, M., Laurent, P., Lebrun, F., & Limousin, O. 2007, ApJ, 668, 1259 [NASA ADS] [CrossRef] [Google Scholar]
- Forot, M., Laurent, P., Grenier, I. A., Gouiffès, C., & Lebrun, F. 2008, ApJ, 688, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Fuchs, Y., Rodriguez, J., Mirabel, I. F., et al. 2003, A&A, 409, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grove, J. E., Johnson, W. N., Kroeger, R. A., et al. 1998, ApJ, 500, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Hannikainen, C. D., Hunstead, W. R., Durouchoux, P., et al. 1999, Astrophys. Lett. Commun., 38, 237 [NASA ADS] [Google Scholar]
- Hoang, J., Molina, E., Lopez, M., et al. 2019, Int. Cosmic Ray Conf., 36, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Y., Qu, J. L., Zhang, S. N., et al. 2018, ApJ, 866, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Jithesh, V., Misra, R., Maqbool, B., & Mall, G. 2021, MNRAS, 505, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Jourdain, E., Roques, J. P., Chauvin, M., & Clark, D. J. 2012, ApJ, 761, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Jourdain, E., Roques, J. P., & Chauvin, M. 2014, ApJ, 789, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Kajava, J. J. E., Motta, S. E., Sanna, A., et al. 2019, MNRAS, 488, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Kantzas, D., Markoff, S., Beuchert, T., et al. 2021, MNRAS, 500, 2112 [Google Scholar]
- Kawamuro, T., Negoro, H., Yoneyama, T., et al. 2018, ATel, 11399, 1 [Google Scholar]
- Labanti, C., Di Cocco, G., Malaguti, G., et al. 2002, Nucl. Instrum. Methods Phys. Res. A, 477, 561 [CrossRef] [Google Scholar]
- Lamer, G., Schwope, A. D., Predehl, P., et al. 2021, A&A, 647, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laurent, P., Rodriguez, J., Wilms, J., et al. 2011, Science, 332, 438 [Google Scholar]
- Laurent, P., Gouiffes, C., Rodriguez, J., & Chambouleyron, V. 2016, in 11th INTEGRAL Conference Gamma-Ray Astrophysics in Multi-Wavelength Perspective, 22 [Google Scholar]
- Lepingwell, V. A., Bazzano, A., Bird, A. J., et al. 2018, ATel, 11884, 1 [NASA ADS] [Google Scholar]
- Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [Google Scholar]
- Maier, D., Tenzer, C., & Santangelo, A. 2014, PASP, 126, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Markoff, S., Nowak, M. A., & Wilms, J. 2005, ApJ, 635, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuoka, M., Kawasaki, K., Ueno, S., et al. 2009, PASJ, 61, 999 [Google Scholar]
- Miller, J. M., Gendreau, K., Ludlam, R. M., et al. 2018, ApJ, 860, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Mirabel, I. F., Rodriguez, L. F., Cordier, B., Paul, J., & Lebrun, F. 1992, Nature, 358, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Mirabel, I. F., Dhawan, V., Chaty, S., et al. 1998, A&A, 330, L9 [NASA ADS] [Google Scholar]
- Mitsuda, K., Inoue, H., Koyama, K., et al. 1984, PASJ, 36, 741 [NASA ADS] [Google Scholar]
- Negoro, H., Ishikawa, M., Ueno, S., et al. 2017, ATel, 10699, 1 [NASA ADS] [Google Scholar]
- Quinn, J. L. 2012, A&A, 538, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [Google Scholar]
- Rodi, J., Tramacere, A., Onori, F., et al. 2021, ApJ, 910, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, J., Hannikainen, D. C., Shaw, S. E., et al. 2008a, ApJ, 675, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, J., Shaw, S. E., Hannikainen, D. C., et al. 2008b, ApJ, 675, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, J., Grinberg, V., Laurent, P., et al. 2015, ApJ, 807, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, G. E., Vieyro, F. L., & Chaty, S. 2014, A&A, 562, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roques, J.-P., & Jourdain, E. 2019, ApJ, 870, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Rushton, A., Miller-Jones, J. C. A., Campana, R., et al. 2012, MNRAS, 419, 3194 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, T. D., Miller-Jones, J. C. A., Sivakoff, G. R., Tetarenko, A. J., & Jacpot Xrb Collaboration 2017, ATel, 10711, 1 [NASA ADS] [Google Scholar]
- Russell, T. D., Lucchini, M., Tetarenko, A. J., et al. 2020, MNRAS, 498, 5772 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1986, Radiative Processes in Astrophysics (Wiley-VCH) [Google Scholar]
- Shidatsu, M., Nakahira, S., Murata, K. L., et al. 2019, ApJ, 874, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Sreehari, H., Ravishankar, B. T., Iyer, N., et al. 2019, MNRAS, 487, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Sridhar, N., Bhattacharyya, S., Chandra, S., & Antia, H. M. 2019, MNRAS, 487, 4221 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, A. L., Uttley, P., Altamirano, D., et al. 2018, ApJ, 865, L15 [Google Scholar]
- Stiele, H., & Kong, A. K. H. 2018, ApJ, 868, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Stirling, A. M., Spencer, R. E., de la Force, C. J., et al. 2001, MNRAS, 327, 1273 [Google Scholar]
- Suffert, M., Endt, P. M., & Hoogenboom, A. M. 1959, Physica, 25, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Tao, L., Chen, Y., Güngör, C., et al. 2018, MNRAS, 480, 4443 [NASA ADS] [CrossRef] [Google Scholar]
- Tetarenko, A. J., Casella, P., Miller-Jones, J. C. A., et al. 2021, MNRAS, 504, 3862 [NASA ADS] [CrossRef] [Google Scholar]
- Tominaga, M., Nakahira, S., Shidatsu, M., et al. 2020, ApJ, 899, L20 [Google Scholar]
- Torres, M. A. P., Casares, J., Jiménez-Ibarra, F., et al. 2019, ApJ, 882, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, M. A. P., Casares, J., Jiménez-Ibarra, F., et al. 2020, ApJ, 893, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Trushkin, S. A., Nizhelskij, N. A., Tsybulev, P. G., & Erkenov, A. 2018, ATel, 11539, 1 [NASA ADS] [Google Scholar]
- Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [CrossRef] [EDP Sciences] [Google Scholar]
- Vaillancourt, J. E. 2006, PASP, 118, 1340 [Google Scholar]
- Vedrenne, G., Roques, J. P., Schönfelder, V., et al. 2003, A&A, 411, L63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vincentelli, F. M., Casella, P., Russell, D. M., et al. 2021, MNRAS, 503, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y., Ji, L., Zhang, S. N., et al. 2020, ApJ, 896, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. C., Elsner, R. F., Hanna, D., et al. 2006, ArXiv e-prints, [arXiv:astro-ph/0611483] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
- Xu, Y., Harrison, F. A., García, J. A., et al. 2018, ApJ, 852, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Yatabe, F., Negoro, H., Nakajima, M., et al. 2019, ATel, 12425, 1 [NASA ADS] [Google Scholar]
- Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Shapopi, J. N. S., & Pooley, G. G. 2020, ApJ, 894, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Jourdain, E., Lubiński, P., et al. 2021, ApJ, 914, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, L., Altamirano, D., Uttley, P., et al. 2021, MNRAS, 505, 3823 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional figures
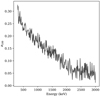 |
Fig. A.1. Evolution of the modulation parameter a100 as a function of the energy. |
 |
Fig. A.2. Probability density described by Eq. (5) as a function of the polarization angle and the polarization fraction calculated for MAXI J1820+070 (top) and MAXI J1348 − 630 (bottom) in the LHS for different energy bands. |
 |
Fig. A.3. Polarigrams of the three sources obtained in the 300–400 keV energy band range. |
 |
Fig. A.4. Polarigrams of the three sources obtained in the 400–1000 keV energy band range. |
All Tables
Parameters obtained for our phenomenological fitting for each source and each period.
All Figures
 |
Fig. 1. MAXI/GSC 2–20 keV (in black) and INTEGRAL/IBIS 30–50 keV (colored dots) light curves of MAXI J1535 − 571 (top panel), MAXI J1820+070 (middle panel), and MAXI J1348 − 630 (bottom panel). The left and the right y-axes indicate the count rate for MAXI/GSC and INTEGRAL/IBIS, respectively. Definitions of the different periods and the corresponding colors are described in Sect. 2.4. The count rates for 1 Crab are indicated with the pink and blue dotted lines for MAXI/GSC and INTEGRAL/IBIS, respectively. |
| In the text | |
 |
Fig. 2. Temporal evolution of the different spectral parameters extracted from our phenomenological spectral fitting for MAXI J1535 − 571 (left panel), MAXI J1820+070 (middle panel), and MAXI J1348 − 630 (right panel). Definitions of the different periods and their corresponding colors are described in Sect. 2.4. |
| In the text | |
 |
Fig. 3. Stacked spectra extracted from JEM-X, ISGRI, and SPI for MAXI J1535 − 571 (left panel), MAXI J1820+070 (middle panel), and MAXI J1348 − 630 (right panel). The different colors indicate the different epochs considered using the same color code as in Fig. 1. |
| In the text | |
 |
Fig. 4. Best-fit models obtained from our phenomenological fittings of the 3–2000 keV for MAXI J1535 − 571 (top panel), MAXI J1820+070 (middle panel), and MAXI J1348 − 630 (bottom panel). Different colors indicate different epochs using the same color code as in Fig. 1. JEM-X, ISGRI, and SPI data are represented in blue, red, and yellow, respectively. Residuals for each period are plotted separately at the bottom of the corresponding spectrum. Different model components are shown with different line styles: Comptonized continuum (dashed), disk (dotted-dashed), additional power law (densely dotted), gaussian (dotted). |
| In the text | |
 |
Fig. 5. Polarigrams of the three sources obtained in the 300–1000 keV energy band range. |
| In the text | |
 |
Fig. 6. Probability density described by Eq. (5) as a function of the polarization angle and the polarization fraction calculated for MAXI J1820+070 (left) and MAXI J1348 − 630 in the LHS (right). |
| In the text | |
 |
Fig. 7. MAXI J1535 − 571 spectra using observational data from Russell et al. (2020) and this work. HIMS and SIMS data are represented in green and orange, respectively. The measured additional high-energy components are indicated with dotted lines. Their 90% uncertainties interval range is represented by the colored area. The purple dotted line is the extrapolation of the optically thin synchrotron spectrum from Russell et al. (2020) with α = 0.83 ± 0.09. |
| In the text | |
 |
Fig. 8. MAXI J1820+070 spectrum using observational data from Rodi et al. (2021) and this work. The measured additional high-energy component is indicated by the blue dotted line. The green dotted line is the extrapolation of the optically thin synchrotron spectrum from Rodi et al. (2021). |
| In the text | |
 |
Fig. 9. Broadband spectrum of MAXI J1348−630. The light-blue line is the spectrum as measured by Carotenuto et al. (2021). The green zone corresponds to our synchrotron thin spectrum hypothesis (see the text). The insert plot focuses on the 1–1000 keV range. The different colors indicate the resulting power law for different normalization values of the DISKBB. |
| In the text | |
 |
Fig. A.1. Evolution of the modulation parameter a100 as a function of the energy. |
| In the text | |
 |
Fig. A.2. Probability density described by Eq. (5) as a function of the polarization angle and the polarization fraction calculated for MAXI J1820+070 (top) and MAXI J1348 − 630 (bottom) in the LHS for different energy bands. |
| In the text | |
 |
Fig. A.3. Polarigrams of the three sources obtained in the 300–400 keV energy band range. |
| In the text | |
 |
Fig. A.4. Polarigrams of the three sources obtained in the 400–1000 keV energy band range. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



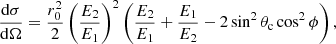
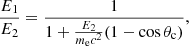
![$$ \begin{aligned} N(\phi ) = C[1 + a_\mathrm{0} \cos (2(\phi -\phi _\mathrm{0} ))], \end{aligned} $$](/articles/aa/full_html/2023/01/aa43564-22/aa43564-22-eq70.gif)
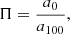
![$$ \begin{aligned}&\mathrm{d} P(a, \phi ) = \frac{N_\mathrm{pt} C^2}{\pi \sigma _\mathrm{C} ^2} \exp \Bigg [-\frac{N_\mathrm{pt} C^2}{2\sigma _\mathrm{C} ^2} \Bigg . [a^2+a_\mathrm{0} ^2 - 2aa_\mathrm{0} \cos (2\phi - 2\phi _\mathrm{0} )] \Bigg . \Bigg ]\, a \, \mathrm{d} a \, \mathrm{d} \phi , \end{aligned} $$](/articles/aa/full_html/2023/01/aa43564-22/aa43564-22-eq72.gif)