| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A171 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202243414 | |
| Published online | 29 August 2022 | |
FAUST
V. Hot methanol in the [BHB2007] 11 protobinary system; hot corino versus shock origin
1
IRAP, Université de Toulouse, CNRS, UPS, CNES,
31400
Toulouse, France
e-mail: cvastel@irap.omp.eu
2
Max-Planck-Institut für extraterrestrische Physik,
Gießenbachstraße 1,
85748
Garching, Germany
3
Université Grenoble Alpes, CNRS, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG),
38000
Grenoble, France
4
Centro de Astrobiologia (CSIC-INTA),
Ctra. de Torrejon a Ajalvir, km 4,
28850
Torrejon de Ardoz, Spain
5
Graduate School of Informatics and Engineering, The University of Electro-Communications,
Chofu, Tokyo
182-8585, Japan
6
INAF – Osservatorio Astrofisico di Arcetri,
Largo E. Fermi 5,
50125,
Florence, Italy
7
National Radio Astronomy Observatory,
PO Box O,
Socorro, NM
87801, USA
8
European Southern Observatory,
Karl-Schwarzschild Str. 2,
85748
Garching bei München, Germany
9
RIKEN Cluster for Pioneering Research,
2-1, Hirosawa, Wako-shi,
Saitama
351-0198, Japan
10
Department of Physics, The University of Tokyo,
7-3-1, Hongo, Bunkyo-ku,
Tokyo
113-0033, Japan
11
Research Center for the Early Universe, The University of Tokyo,
7-3-1, Hongo, Bunkyo-ku,
Tokyo
113-0033, Japan
12
Institut de Radioastronomie Millimétrique,
38406
Saint-Martin d’Hères, France
13
Department of Astronomy, The University of Tokyo,
7-3-1 Hongo, Bunkyo-ku,
Tokyo
113-0033, Japan
14
Department of Chemistry, Biology, and Biotechnology, The University of Perugia,
Via Elce di Sotto 8,
06123
Perugia, Italy
15
Astrochemistry Laboratory,
Code 691, NASA Goddard Space Flight Center, 8800 Greenbelt Road,
Greenbelt, MD
20771, USA
16
Cergy Paris Université, Sorbonne Université, Observatoire de Paris, PSL University, CNRS, LERMA,
95000,
Cergy, France
17
Instituto de Radioastronomía y Astrofísica, Universidad Nacional Autόnoma de México,
A.P. 3-72 (Xangari),
8701
Morelia, Mexico
18
Department of Astronomy, Xiamen University,
Zengcuo’an West Road,
Xiamen
361005, PR China
19
National Astronomical Observatory of Japan,
Osawa 2-21-1, Mitaka-shi,
Tokyo
181-8588, Japan
20
NRC Herzberg Astronomy and Astrophysics,
5071 West Saanich Road,
Victoria,
BC V9E 2E7, Canada
21
Department of Physics and Astronomy, University of Victoria,
Victoria, BC
V8P 5C2, Canada
22
Komaba Institute for Science, The University of Tokyo,
3-8-1 Komaba, Meguro,
Tokyo
153-8902, Japan
23
Center for Frontier Science, Chiba University,
1-33 Yayoi-cho, Inage-ku,
Chiba
263-8522, Japan
24
Department of Chemistry, University of Virginia,
McCormick Road,
PO Box 400319,
Charlottesville, VA,
22904, USA
25
Department of Physics and Astronomy, Rice University,
6100 Main Street, MS-108,
Houston, TX
77005, USA
26
Instituto de Astronomía, Universidad Nacional Autόnoma de México, Ciudad Universitaria,
A.P. 70-264,
Cuidad de México
04510, Mexico
27
Institute of Low Temperature Science, Hokkaido University,
N19W8, Kita-ku, Sapporo,
Hokkaido
060-0819, Japan
28
Departament de Química, Universitat Autònoma de Barcelona,
08193
Bellaterra, Spain
29
Steward Observatory,
933 N Cherry Ave.,
Tucson, AZ
85721, USA
30
Leiden Observatory, Leiden University,
PO Box 9513,
2300 RA
Leiden, The Netherlands
31
Department of Physics and Astronomy, University College London,
Gower Street,
London
WC1E 6BT, UK
32
Materials Science and Engineering, College of Engineering, Shibaura Institute of Technology,
3-7-5 Toyosu, Koto-ku,
Tokyo
135-8548, Japan
33
Departament de Física Quàntica i Astrofísica, Institut de Ciències del Cosmos, Universitat de Barcelona (IEEC-UB),
Martí Franquès, 1,
08028
Barcelona, Catalunya, Spain
34
Astronomical Institute, Graduate School of Science, Tohoku University,
6-3 Aoba, Aramaki, Aoba-ku, Sendai,
Miyagi
980-8578, Japan
Received:
24
February
2022
Accepted:
17
June
2022
Aims. Methanol is a ubiquitous species commonly found in the molecular interstellar medium. It is also a crucial seed species for the build-up of chemical complexity in star forming regions. Thus, understanding how its abundance evolves during the star formation process and whether it enriches the emerging planetary system is of paramount importance.
Methods. We used new data from the ALMA Large Program FAUST (Fifty AU STudy of the chemistry in the disc/envelope system of solar protostars) to study the methanol line emission towards the [BHB2007] 11 protobinary system (sources A and B), where a complex structure of filaments connecting the two sources with a larger circumbinary disc has previously been detected.
Results. Twelve methanol lines have been detected with upper energies in the [45–537] K range along with one 13CH3OH transition and one methyl formate (CH3OCHO) line blended with one of the methanol transitions. The methanol emission is compact (FWHM ~ 0.5″) and encompasses both protostars, which are separated by only 0.2″ (28 au). In addition, the overall methanol line emission presents three velocity components, which are not spatially resolved by our observations. Nonetheless, a detailed analysis of the spatial origin of these three components suggests that they are associated with three different spatial regions, with two of them close to 11B and the third one associated with 11A. A radiative transfer analysis of the methanol lines gives a kinetic temperature of [100–140] K, an H2 volume density of 106–107 cm−3 and column density of a few 1018 cm−2 in all three components with a source size of ~0.15″. Thus, this hot and dense gas is highly enriched in methanol with an abundance as high as 10−5. Using previous continuum data, we show that dust opacity can potentially completely absorb the methanol line emission from the two binary objects.
Conclusions. Although we cannot firmly exclude other possibilities, we suggest that the detected hot methanol is resulting from the shocked gas from the incoming filaments streaming towards [BHB2007] 11A and B, respectively. Higher spatial resolution observations are necessary to confirm this hypothesis.
Key words: astrochemistry / radiative transfer / techniques: interferometric / line: identification / ISM: abundances / ISM: molecules
© C. Vastel et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
The rich chemistry observed in solar-type protostars is triggered at earlier stages of the protostellar evolution (e.g. Ceccarelli et al. 2007; Caselli & Ceccarelli 2012). Methanol (CH3OH) is a key ingredient in the enhancement of this chemical complexity from prestellar cores to protoplanetary discs (Vastel et al. 2014; Bizzocchi et al. 2014; Maret et al. 2005; Walsh et al. 2016; Spezzano et al. 2020, 2022; Punanova et al. 2022). It is the seed from which interstellar complex organic molecules (iCOMs: Ceccarelli et al. 2017) sprout (e.g. Charnley et al. 1992; Garrod et al. 2008; Balucani et al. 2015; Taquet et al. 2016; Aikawa et al. 2020; Jin & Garrod 2020). They have been detected towards prestellar cores (Bacmann et al. 2012; Vastel et al. 2014; Jiménez-Serra et al. 2016, 2021; Scibelli & Shirley 2020), where their presence in the gas has been explained by non-thermal desorption processes such as photodesorption from UV photons (Bertin et al. 2016), chemical desorption (Minissale et al. 2016), sputtering caused by a gentle shock (Flower & Pineau des Forets 1995), or cosmic-ray induced chemistry (Shingledecker et al. 2018; Wakelam et al. 2021) and the reactive desorption of methanol followed by gas-phase reactions (Vasyunin et al. 2017). iCOMs have also been found at a later stage: the Class 0/I protostars (André et al. 1993). Here, the central protostar is embedded in a dense envelope as the parental dense core undergoes gravitational collapse. The iCOMs are observed in the lukewarm region where the dust temperature is between the CO and H2O sublimation temperatures (~30–100 K (e.g. Jaber et al. 2014) and in the compact hot corino region where the dust temperatures are higher than ~ 100 K and densities are larger than ~107 cm−3 (e.g. Ceccarelli et al. 2000b; Cazaux et al. 2003; Bottinelli et al. 2004; Jørgensen et al. 2016; Yang et al. 2021; Chahine et al. 2022). Finally, iCOMs are also detected in protoplanetary discs (Öberg et al. 2015, 2021; Favre et al. 2018; Lee et al. 2019).
The gas phase is therefore chemically enriched in iCOMs, due to either direct release from dust mantles or gas phase formation from simpler molecules released from the mantles. Two possibly distinct classes of solar Class 0/I protostars have been found: the hot corinos (Ceccarelli et al. 2007) and the warm carbon chain chemistry sources (WCCC: Sakai & Yamamoto 2013), although intermediate situations are also possible (e.g. Yang et al. 2021). An intermediate (hybrid) source was also found by Oya et al. (2017).
Since the chemical composition of the planetary systems depends on the chemical evolution starting from the earliest phases of the protostar formation, it is crucial to understand how the molecular complexity is transferred from the large-scale envelope (a few thousand au) to the small-scale structures of the protostellar system and how it is maintained in the inner disc system (≤50 au).
In this context, the ALMA (Atacama Large Millimeter/submillimeter Array) Large Program FAUST (Fifty AU STudy of the chemistry in the disc/envelope system of Solar-like protostars)1 is designed to survey the chemical composition of a sample of 13 Class 0/I protostars on a scale of about 50–1000 au (all sources have a distance lower than 250 pc). The description of the project is reported in Codella et al. (2021). The selected sources represent the protostellar chemical diversity observed at large scales and have been observed in three frequency setups chosen to study both continuum and line emission from specific molecules: 85.0–89.0 GHz, 97.0–101.0 GHz, 214.0–219.0 GHz, 229.0–234.0 GHz, 242.5–247.5 GHz, and 257.5–262.5 GHz. The FAUST survey provides a uniform sample in terms of frequency setting, angular resolution, and sensitivity. We report the first results obtained towards the [BHB2007] 11 Class 0/I protostar system focused on the most simple iCOM, methanol.
2 The [BHB2007] 11 protobinary system
The [BHB2007] 11 source was originally identified as a single object in the Barnard 59 (B59) molecular cloud, which is located at a distance of 163 ± 5 pc (Gaia second data release: Dzib et al. 2018). B59 hosts a proto-cluster of low-mass young stellar objects (YSOs) at different evolutionary stages as first shown by Onishi et al. (1999) using the 1–0 transition of 12CO, 13CO, and C18O with the NANTEN telescope with a 2.7′ beam. Following this, the proto-cluster was extensively observed in infrared bands (Brooke et al. 2007; Forbrich et al. 2009; Covey et al. 2010; Román-Zúñiga et al. 2010; Sandell et al. 2021), ammonia (NH3) emission (Rathborne et al. 2008; Redaelli et al. 2017), and X-rays (Forbrich et al. 2010). The protostellar nature of the youngest and most embedded member of the cluster, [BHB2007] 11 was confirmed by several studies reporting bipolar outflows (Riaz et al. 2009; Duarte-Cabral et al. 2012), hints of dynamical infall (Hara et al. 2013; Alves et al. 2017), and a spectral energy distribution (SED) consistent with a Class 0/I protostar with bright far-infrared emission and Lbol ~ 4.4 L⊙ (Sandell et al. 2021).
Alves et al. (2017) used ALMA in its extended configuration to observe the dust continuum emission at 1.3 mm and molecular transitions of CO, C18O and H2CO lines (angular resolution of 0.22″). The dust distribution reveals an ~180 au disc surrounded by a fainter, elongated structure tracing the inner component of the core envelope. The spectral line data reveal a bipolar outflow launched at the edge of the inner disc at a radial distance of 90-130 au from the central source. The disc is rotationally supported, with Keplerian rotation revealed by H2CO lines (Alves et al. 2017, 2019). At much higher angular resolution (~0.04″), Alves et al. (2019) uncovered a young binary protostar system embedded in circumstellar discs that have radii of 2–3 au. The protostars are named [BHB2007] 11A (hereafter 11A) for the northern source (α (2000) = 17h11m23.097s, δ (2000) = −27°24′32.85″) and [BHB2007] 11B (hereafter 11B) for the southern source (α (2000) = 17h11m23.09s, δ (2000) = −27°24′33″). These systems are surrounded by a complex filamentary structure (the so-called streamers) connecting to the larger circumbinary disc. We note that streamers have recently been seen in other more evolved objects (Alves et al. 2020) and modelled as mostly free-falling (Pineda et al. 2020; see Pineda et al. 2022, for a review). The binary mass ratio is ≳1, since the 11A disc is slightly more massive (of the order of a Jupiter mass) than the 11B disc and the system has a projected separation of 28 au (~0.2″). Source 11B is located between high-velocity components of the CO emission (VLSR < −1.5 km s−1 and VLSR > 9 km s−1), which is interpreted as enhanced gas accretion towards 11B from the circumbinary disc. Both protostars are accreting from their individual circumstellar discs as inferred from centimetric continuum emission observed from both sources. The radio data are consistent with free-free emission from ionised jets launched by the disc-star system (Alves et al. 2019). The dynamical mass of the protobinary system has been estimated as an upper limit from the Keplerian model of the H2CO data with a value of 2.25 ± 0.13 M⊙.
In this paper, we report high-J methanol emission (45 K< Eup < 537 K ) from [BHB2007] 11 obtained in the framework of the FAUST collaboration observed in a ~0.4″ beam. These data unveil the hot corino nature of the source seen over multiple velocity components. From these data, we derive the hot gas properties (column density and temperature) for each velocity component.
3 Observations
[BHB2007] 11 was observed with ALMA (FAUST Large Program 2018.1.01205.L) with two frequency setups in Band 6 (setups 1 and 2) and one frequency setup in Band 3 (setup 3). The data exploited here were acquired between 2018 and 2020 using the 12-m and 7-m arrays for setups 1 and 2, and the 12-m array for setup 3. The baseline length in the configurations of the 12-m array for setups 1 and 2 (C43-4 and C43-1) ranges from 15 m to 1.3 km, and the baseline length in the configuration of the 7-m array ranges from 8.9 m to 48.9 m. For setup 3, the baseline length in the configurations of the 12-m array (C43-6 and C43-3) ranges from 15 m to 3 km. The observations were centred at α (2000) = 17h11m23.125s, δ (2000) = −27°24′32.87″. J2056-4714 and J1427-4206 were used as bandpass calibrators for setup 2 (12-m array), and J1700-2610 was used as phase calibrator and flux calibrator. J1427-4206 and J2056-4714 were used as bandpass calibrator and flux calibrator for setup 1 (12-m array), and J1700-2610 was used as phase calibrator.
The data were reduced in the Common Astronomy Software Applications package (CASA) version 5.6.1 (McMullin et al. 2007) using a modified version of the ALMA calibration pipeline and an additional in-house calibration routine to correct for the system temperature and spectral line data normalisation2. Self-calibration was carried out using carefully-selected, line-free continuum channels for each configuration. The complex gain corrections derived from the self-calibration were then applied to all channels in the data, and the continuum model derived from the self-calibration was then subtracted from the data to produce continuum-subtracted line data. A self-calibration technique was also used to align both amplitudes and phases across the multiple configurations to correct for any remaining offsets in the flux density scales and to correct for systematic position offsets that may be caused by either source proper motion or other system issues.
For each setup, iterative-phase self-calibration with a very long solution interval was then used for the position alignment across multiple configurations. In addition, amplitude offsets between datasets needed to be corrected. To do this, a model derived from a very deeply cleaned and masked image was used to obtain amplitude corrections per execution block. The dynamic range of the resulting self-calibrated image was improved by a factor of three for setup 1, without reduction in the peak flux density of the source. Figure 1 shows an amplitude versus uv-distance plot of the data from the different configurations before and after this amplitude alignment for setup 1 in the continuum spectral window (least noisy). The data were averaged per baseline across the entire dataset. The improvement in the dynamic range was less significant for setup 2 (around 10%), because for setup 2, the amplitude scale of the 12-m array (TM 1 and TM 2) was much better aligned coming out of the calibration pipeline and per-configuration self-calibration process than they were for setup 1.
The resulting continuum-subtracted line cube was made using a Briggs robust parameter of 0.5, and we obtained a synthesised beam with a 0.44″ × 0.37″ position angle (PA) = −82° at 261.687 GHz, and a 0.41″ × 0.39″ PA = 47° at 218 GHz. We estimate an overall systematic uncertainty of 10% for each dataset. The observed spectral windows (also called spw) are centred on the frequencies listed in Table 1. The bandwidth is 59 MHz for 12 m (62 MHz for 7-m), except for the continuum window with a 1.875 GHz (2 GHz for 7-m) bandwidth. Spectral line imaging was performed with the CASA3 package, while the data analysis was performed using the IR AM/GILDAS4 package as well as the CASSIS5 package.
 |
Fig. 1 Amplitude versus uv-distance plots before (top) and after (below) self-calibration. |
Observed spectral windows in the observed FAUST data.
4 Line identification
The line identification was performed using the CASSIS software that connects to the JPL and CDMS databases. This is a standalone software, written in Java, freely delivered to the community to help with visualising, analysing and modelling observations from ground or space-based observatories. CASSIS has been developed at IRAP since 2005 and is part of the OVGSO6 data centre that is aimed at promoting the Virtual Observatory (VO) technology. CASSIS displays any spectrum (ASCII, FITS, or GILDAS/CLASS format or the result from the query to any Simple Spectral Access Protocol (SSAP) VO or EPN-TAP7 VO service from IVOA8 registries) and identifies atomic and molecular species through its link to the databases such as CDMS (Müller et al. 2005) or JPL (Pickett et al. 1998) via an SQLite database, or via a direct access to VAMDC9 for any available spectroscopic database.
The systemic velocity of [BHB2007] 11 is Vlsr = 3.6 km s−1 with respect to the local standard of rest (Onishi et al. 1999). We identified and detected twelve methanol transitions in the observed spectral windows of the three spectral setups (dust peak emission) and only one 13CH3OH transition (234 GHz but not at 94.4 GHz where the rms reached 0.9 K). No deuterated counterparts such as CH2DOH at 261.7 GHz have been detected. We list, in Table 2, the spectroscopic parameters of the detected transitions using the CDMS database. The spectral resolutions are also quoted as δV (km s−1) for each detected transition. The methanol transitions cover a broad range in energy from Eup ~ 45 to 537 K.
Spectroscopic parameters of the methanol transitions (using the CDMS database) detected towards [BHB2007] 11 and results from the Gaussian fits.
5 Results
5.1 Dust emission
Figure 2 shows the dust continuum maps obtained in the three setups (ACA+12 m combined). The dust distribution is consistent with the previous maps of Alves et al. (2017), showing bright emission from the circumbinary disc (inclined ~56° with respect to the line of sight) at the centre of the elongated envelope emission. The apparent misalignment between the envelope major axis and the disc major axis suggests a warped disc. This is consistent with the velocity structure previously revealed by H2CO lines, where low upper energy level (Eup) transitions trace envelope rotation and infall, misaligned with the disc rotation seen in high-Eup transitions (Alves et al. 2017, 2018). At the present resolution, the proto-binary system reported by Alves et al. (2019) is not resolved; however, faint extended emission oriented north-west-south-east is detected (at a 3σ level) in the ~1-mm bands (setups 1 and 2) beyond the envelope. The radial profile of the continuum emission, taken from increasing elliptical annuli oriented at a position angle of 167° east of north (the orientation of the inner envelope), is displayed in Fig. 3. The contribution from the disc is distinguishable from the fainter structure that surrounds it, as the disc brightness is well represented by a Gaussian distribution whose wings do not encompass the extended emission.
With the continuum data aligned in position across the three FAUST setups, we reconstructed the continuum maps with a common clean beam of 0.35″. We then computed the SED from a linear fit (in log-log scale) over the fluxes observed in the three setups (Fig. 4). We note that the flux density (and error) used to construct the SED are derived from 2D Gaussian fits over the disc emission, where the emission is centrally peaked, while the envelope flux is derived from a contour excluding the disc.10 Table 3 reports the peak flux and flux density for the circumbinary disc, for which we find a spectral index of 3.0 ± 0.1. The same index is reported by Alves et al. (2019), whose observations cover ALMA Bands 3, 6, and 7. In contrast, the dust emission from the inner envelope has a spectral index of 3.4 ± 0. 2, which is slightly lower than the canonical value of the interstellar medium (ISM; αISM = 3.7, Testi et al. 2014), implying that the grains in the envelope are potentially mildly larger than in the ISM (≲10 μm, Agurto-Gangas et al. 2019).
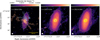 |
Fig. 2 Dust continuum maps obtained in each setup. The rms noise level is 50 μJy beam−1 for Band 3 observations (setup 3, left panel), 90 μJy beam−1 for setup 1 in Band 6 (middle panel), and 70 μJy beam−1 for setup 2 in Band 6 (right panel). The intensity contour levels in the left panel are −5, 5, 10, 30, 50, 70, and 90 × the noise level, while the intensity contours in the middle and right panels are −5, 5, and 50 and from 100 to 1000 (in steps of 100) × 70 μJy beam−1 the noise level in setup 2. The colour scale at the top is the same for all panels. The red dots indicate the positions of 11A (north) and 11B (south) as reported by Alves et al. (2019). The sources are not resolved with the present resolution. The left panel also shows the integrated intensity contours from CO (2 → 1) emission from the bipolar outflow powered by [BHB2007] 11 (Alves et al. 2017). The synthesised beam is displayed in the bottom left corner of each panel (0.36″ × 0.34″, 0.39″ × 0.33″ and 0.42″ × 0.29″ for setups 3, 1, and 2, respectively). |
 |
Fig. 3 Radial profile of dust continuum emission at 252 GHz (setup 2) towards [BHB2007] 11. The profile is centred on the continuum peak. The red line shows a Gaussian fit to the disc’s brightness distribution. The dashed line indicates the synthesised beam size. The grey line shows the rms noise level of the continuum emission. |
 |
Fig. 4 Spectral energy distribution determined for the dust emission within the circumbinary disc (α = 3.0, black line) and in the envelope (α = 3.4, dotted dashed line). The flux densities for the disc and envelope are indicated as filled circles and open triangles, respectively. The errors are dominated by the uncertainty in the flux calibration, which is assumed to be ~10%. The dashed line shows the SED determined from the free-free (centimetric) emission detected with the Very Large Array (Alves et al. 2019). |
Peak flux and flux density for the circumbinary disc.
5.2 Molecular emission
Figure 5 shows the moment 0 maps (in Jy beam km s−1) of the CH3OH high spectral resolution lines at 218, 244, and 262 GHz using the 12-m array. These three transitions are the only ones observed at high spectral resolution (0.1–0.2 km s−1). The contours start at 4σ at every 10σ for 218.440 and 243.916 GHz and every 3σ at 261.704 GHz. The ellipse in the bottom left corner represents the ALMA synthesised beam. The emission is compact (less than 1″) and centred at the same location, which means that, in this region, the gas is co-existent, from the low energy transition to the higher energy transition. The beam encompasses both 11A and 11B, separated by 0.2″, which therefore cannot be resolved. The other transitions where the spectral resolution is lower (0.6–1.2 km s−1) also show a centred compact emission.
It is obvious from Fig. 5 that all methanol transitions do not necessarily trace the same extended structure. The 218 GHz and 244 GHz transitions, which have an upper energy of 45 K and 50 K, respectively, are tracing a more extended region (around 1″) compared to the highest energy levels at 540 K for the 246.074 GHz transition tracing a seemingly more compact region (around 0.5″).
 |
Fig. 5 Moment 0 map of the high spectral resolution methanol transitions at 218.440 GHz (Eu = 45.46 K), 243.916 GHz (Eu = 49.66 K), and 261.704 GHz (Eu = 359.77 K). Contours start at 4σ at every 10σ for 218.440 and 243.916 GHz, and every 3σ at 261.704 GHz. The ellipse in the bottom left corner represents the ALMA synthesised beam. Both sources A and B identified by Alves et al. (2019) are indicated by white filled circles. |
5.2.1 CH3OH line identification
We extracted the average spectrum over the region above 4σ in the integrated intensity map for each molecular transition (either in Jy beam−1 or in Kelvins) into the CASSIS software and the high spectral resolution transitions are presented in Fig. 6, while the lower spectral resolution transitions of methanol are presented in Figs. 7 and 8. From these figures we can clearly distinguish three components, which are visible at −2 km s−1, 2.8 km s−1 and 9.9 km s−1. Table 2 shows the results of the best-fit adjustment using the Levenberg–Marquardt fitting within CASSIS using a large number of iterations (Tmb in Kelvins, FWHM and VLSR in km s−1).
The maximum recoverable scale of the 12-m-array data is 9″–11″. Since the CH3OH emission is compact and its size is less than 3″, the missing flux in the 12-m-array data is negligible. In fact, we confirmed that the flux of the data combined with the 7-m- and 12-m-array data (maximum recoverable scale: 16″–19″) is comparable with that of the 12-m-array data (see Fig. 9 for the 243.916 GHz transition). We therefore only used the 12-m-array data in the following.
Figure 10 shows the velocity field (moment 1) of the two extreme (in upper energy values), high spectral resolution methanol transitions at −50 K (243.916 GHz) and −350 K (261.704 GHz) upper energy levels (Eup). The velocity structure ranges from −5 to 15 km s−1 in both low and high transitions, and it has a northwest-southeast gradient centred on the 11B source at the systemic velocity of the source. Although we cannot resolve the protostars in these maps, this could indicate that the methanol maps are more sensitive to the kinematics of the southern source.
Due to the molecular complexity of this source, we explored the line blending from other species. The CH3OH transition at 261.704 GHz is indeed clearly blended, as shown in Fig. 6, with the 21(7,14)–20(7,13) E transition of methyl formate (CH3OCHO) at 261715.5180 MHz. Figure 11 shows the methyl formate transition with the three components at −2 km s−1, 2.8 km s−1 , and 9.9 km s−1 indicated as thin dashed lines. It is clear that the −2 km s−1 methanol transition is blended with the 9.9 km s−1 transition of methyl formate. A subsequent analysis of the iCOMs detected in our [BHB2007] 11 FAUST data will be published at a later time.
Within CASA (imfit command), we fitted a 2D Gaussian to the integrated intensity maps of the three high spectral resolution transitions, taking into account the three velocity components. At 243.916 GHz, the image component size (deconvolved from beam) for (i) the 9.9 km s−1 velocity component (channel 195) is 0.27″ × 0.23″ (major axis FWHM × minor axis FWHM), (ii) the −2 km s−1 (channel 274) is 0.27″ × 0.16″ (major axis FWHM × minor axis FWHM), and (iii) the 2.8 km s−1 (channel 242) is 0.53″ × 0.36″ (major axis FWHM × minor axis FWHM). The 218.440 GHz transition gives similar results, and the 261.704GHz non-blended components at +9.9 and 2.8 km s−1 tend towards a point-source deconvolved source size. Therefore, the two extreme velocity components seem slightly more compact than the 2.8 kms-1.
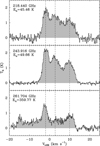 |
Fig. 6 Tb (K) spectra for the high spectral resolution Methanol transitions at 218.440, 243.916, and 261.704 GHz. The dashed lines correspond to the results of the best-fit Gaussian at −2 km s−1, 2.8 km s−1, and 9.9 km s−1. The −2 km s−1 component of the 261.704 GHz transition is blended with a transition of methyl formate (see text). |
 |
Fig. 7 Spectra (in mJy beam−1) for the low spectral resolution Methanol transitions. The dashed lines correspond to the results of the bestfit Gaussian of the high spectral resolution transitions at −2 km s−1, 2.8 km s−1, and 9.9 km s−1. |
5.2.2 13CH3OH line identification
Only one transition of the 13C methanol isotopologue has been detected at 234GHz with Eup = 48K, and it presents the same characteristics as methanol and methyl formate with three components, as shown in Fig. 12. In Table 2, we present the results from the best-fit Gaussian adjustments for this transition. Figure 13 shows that the integrated line intensity is much noisier than the other methanol moment 0 maps but is still compact and centred on the same position.
6 Modelling of the methanol and dust emission
We first performed a local thermodynamic equilibrium (LTE) analysis to estimate the excitation temperature and column density for our methanol transitions. To achieve that, we defined a polygon extracted from the average spectrum over a region above 4σ in the integrated intensity map of the 218.440 GHz methanol transition. This polygon was then used to extract the average spectrum for each methanol transition. We then performed a best-fit of the three components and obtained a rotational-diagram (RD) analysis followed by a non-LTE analysis to estimate the H2 volume density, the column density, kinetic temperature, and size of the source. The integrated line intensities used in the following are presented in Table 4.
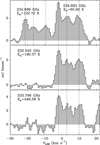 |
Fig. 8 Spectra (in mJy beam−1) for the low spectral resolution methanol transitions in the 234 GHz spectral windows. The dashed lines correspond to the results of the Gaussian components obtained from each of the high spectral resolution transitions at −2 km s−1, 2.8 km s−1, and 9.9 km s−1. |
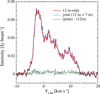 |
Fig. 9 Difference between the 12-m-only data and the joint data for the A-CH3OH transition at 243.916 GHz. |
6.1 LTE rotational-diagram analysis
For a molecule in LTE, all excitation temperatures are the same, and the population of each level is given by
where Q is the partition function, k is the Boltzmann constant, Trot is the rotational temperature (in Kelvins), gu is the statistical weight in the upper level, Eu/k is the energy of the upper level (in Kelvins), Nu is the column density in the upper level, and Ntot is the column density of the species. We can rewrite this equation to obtain
A rotational diagram can be useful to determine whether the emission is optically thick or thin, whether the level populations are described by LTE, and to determine what temperature describes the population distribution in the event that LTE applies (Goldsmith & Langer 1999). Equation (2) can be written in terms of the observed integrated area W when the lines are optically thin:
where h is the Planck constant, Aul is the Einstein coefficient (s−1) between level up and level low, v is the frequency for each observed transition, and c is the celerity of light. The error bars should be taken into account for the order 1 polynomial fit in order to obtain a reliable value for the uncertainty on the rotational temperature as well as the total column density. From the CASSIS Line Analysis module, the user can fit the lines and produce a detailed .rotd file with the integrated area and rms values for each transition. The user is required to give a value for the instrumental calibration uncertainty. The uncertainty (∆W) of the integrated area is computed though the following formula:
where cal is the calibration value (%), W is the integrated area (in K km s−1), rms is the noise around the selected species (in K), FWHM is the full width at half maximum (km s−1), and δV is the bin size (in km s−1). Therefore, the plotted uncertainties are simply
From the fitted straight line (y = ax + b), the slope a is related to the rotational excitation temperature as Trot = −1/a. Then ∆Trot = ∆a/a2. The intercept b is related to the total column density as Ntot = Q(Trot) × eb. Therefore, ∆Ntot = Q(Trot) × ∆b × eb.
The RD analysis is presented in Fig. 14 along with the resulting column densities and excitation (also called rotational) temperature. All the transitions are shown, although the blended transition of the 261.7 GHz methanol transition at −2 km s−1 is not used in the fit. A large dispersion can be seen in the figures. The low energy transitions are also tracing the more extended and colder envelope compared to the higher energy transitions. Removing the transitions with an upper energy under 150 K does not change the results because of the wide dispersion in these points.
The estimated parameters for the three components are similar. At −2 km s−1: N = (1.0 ± 0.4)1016 cm−2, Trot = (167 ± 31)K. At 2.8 km s−1: N = (1.1 ± 0.3)1016cm−2, Trot = (152 ± 16) K. At 9.9 km s−1: N = (1.2 ± 0.4)1016cm−2, Trot = (165 ± 27) K. The column densities are the beam-averaged and the lines are predicted to be optically thin.
 |
Fig. 10 Velocity field determined from methanol transitions at low and high energy levels. The contours indicate the continuum intensity levels from the high spatial resolution observations of Alves et al. (2019). The compact emission contours arise from the circumstellar discs around each protostar of the binary system: 11A (northern component) and 11B (southern component). The dashed line in the left panel shows the direction of the cut used to produce the position-velocity diagram displayed in Fig. 17. The cut position angle is 140° and its width is 0.5″, encompassing both protostars. |
 |
Fig. 11 Spectra at VLSR = 3.6 km s−1 of the [BHB2007] 11 source showing the E-CH3OCHO 21(7,14)-20(7,13) transition at 261.715 GHz blended with the CH3OH transition at 261.704GHz. The dashed lines correspond to the results of the best-fit Gaussian components obtained from the high spectral resolution methanol transitions at −2 km s−1, 2.8 km s−1, and 9.9 km s−1 for the methyl formate transition. |
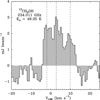 |
Fig. 12 Spectrum (in mJ beam−1) of only detected transition of 13 CH3 OH at 234 GHz. The dashed lines correspond to the results of the best-fit Gaussian components obtained from the high spectral resolution transitions at −2 km s−1, 2.8 km s−1, and 9.9 km s−1. |
 |
Fig. 13 Moment 0 map of 13CH3OH transition at 234 GHz. Contours start at 4σ at every 2σ. The ellipse in the bottom left corner represents the ALMA synthesised beam. Both sources 11A and 11B identified by Alves et al. (2019) are indicated as white filled circles. |
Integrated intensities used for the LTE and non-LTE analysis, extracted over a region above 4σ in the integrated intensity map of the 218.440 GHz methanol transition.
6.2 Non-LTE LVG analysis
In order to better take into account the possible non-LTE effects, we modelled the methanol line emission via the large velocity gradient (LVG) code, grelvg, developed by Ceccarelli et al. (2003). We used the collisional coefficients with para-H2 computed by Rabli & Flower (2010) between 10 and 200 K for the first 256 levels and provided by the BASECOL database (Dubernet et al. 2012, 2013). We therefore used the methanol transitions up to J = 15 for the non-LTE analysis. We assumed an A-/E-CH3OH ratio equal to 1 and a 12C/13C ratio equal to 68 (e.g. Milam et al. 2005). To compute the line escape probability as a function of the line optical depth, we adopted a spherical geometry and a line width equal to 3.2 km s−1 for the −2 km s−1 component, 6 km s−1 for the 2.8 km s−1 component, and 5 km s−1 for the 9.9 km s−1 component, following the observations.
We ran a large grid of models (~ 10 000) to cover the χ2 surface in the parameter’s space: the total (A- plus E-) methanol column density N(CH3OH) from 1 × 1013 to 2 × 1018 cm−2, the
H2 density nH2 from 1 × 105 to 1 × 109 cm−3, and the temperature T from 15 to 200 K. We then simultaneously fitted the measured 12C and 13C -A- and 12C E- line intensities extracted from the 4σ polygon of the 218.440 GHz methanol transition by comparing them with those predicted by the model, leaving N(CH3OH), nH2 and T. Since the line emission is unresolved with our spatial resolution, we also left the emitting size θs as a free parameter. We performed this same procedure for the three velocity components separately.
With regard to the component at −2 km s−1, we obtained a good fit (reduced ; χ2 = 1.2 for 5 degrees of freedom) for all lines with the following values: N(A+E CH3OH) = (1.4 ± 0.6) × 1018 cm−2, T = (110 ± 10) K, 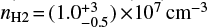 and θs = (0.15″ ± 0.10″). Figure 15 reports the minimum ; χ2, with respect to the temperature T and density nH2, as a function of the methanol column density N(CH3OH-A). The same figure also shows the temperature-density ;χ2 contour plot at the best-fit N(CH3OH) (note that the x-axis reports N(CH3OH)/2). Finally, the third panel of Fig. 15 shows the observed/predicted line intensity ratio as a function of the line upper level energy Eup. The 12C lines are predicted to be from moderately (the 234.69 GHz line has the smallest value, τ = 0.64) to heavily (the 243.91 GHz line has the largest value, τ ~ 12) optically thick, while the 13C line is optically thin (τ = 0.25).
and θs = (0.15″ ± 0.10″). Figure 15 reports the minimum ; χ2, with respect to the temperature T and density nH2, as a function of the methanol column density N(CH3OH-A). The same figure also shows the temperature-density ;χ2 contour plot at the best-fit N(CH3OH) (note that the x-axis reports N(CH3OH)/2). Finally, the third panel of Fig. 15 shows the observed/predicted line intensity ratio as a function of the line upper level energy Eup. The 12C lines are predicted to be from moderately (the 234.69 GHz line has the smallest value, τ = 0.64) to heavily (the 243.91 GHz line has the largest value, τ ~ 12) optically thick, while the 13C line is optically thin (τ = 0.25).
Concerning the component at +9.9 km s−1, the best fit (reduced ; χ2 = 1.9) gives values very similar to those obtained for the −2 km s−1 component, namely N(CH3OH) = (3.0 ± 0.8) × 1018 cm−2, T = (130 ± 10) K, nH2 = (2.5 ± 2.2) × 107 cm−3 and θs = (0.12″ ± 0.10″).
Finally, with regard to the component at +2.8 km s−1, the best fit (reduced; χ2 = 2.7) gives the following values: N(CH3OH) = (4.0 ± 1.0) × 1018 cm−2, T = (130 ± 10) K, nH2 = (2.0 ± 0.5) × 106 cm−3 and θs = (0.13″ ± 0.10″).
We now give a summary of the non-LTE analysis The three velocity components trace gas with similar characteristics: hot (with a temperature around 110-130K), dense (with a H2 density of 2–20 × 106 cm−3), enriched in methanol (with a methanol column density [1–5] × 1018 cm−2), and relatively compact (0.12″–0.15″). Table 5 lists the results of the analysis for the three components. Assuming that the emission in each velocity component originates from a spherically symmetric region, one can estimate the approximate H2 column density (~2 × 1023 cm−2) and then the methanol abundance, whose value is very high, ~10−5.
Compared to the results of the LTE RD analysis (see Sect. 6.1), the non-LTE analysis predicts slightly lower gas temperatures and much higher methanol column densities, by about two orders of magnitude. These differences are due to two major effects. First, the column densities calculated with the RD are beam-averaged, whilst the LVG analysis, where the emitting size is derived, shows that the methanol emission is relatively compact. This explains the large difference between the two estimates. Second, the RD in Fig. 14 show a clear scatter of the points around the best-fit straight line, which indicates optically thick lines and/or non-LTE effects. They both lead to a misleading evaluation of the gas temperature (and, to a lesser extent, methanol column density). Finally, even though the source size and the optical depths of the lines can be corrected a posteriori (using the rotational diagram analysis), non-LTE effects (e.g. sub-thermally populated lines), if present, cannot be corrected unless a non-LTE analysis is performed. In summary, in the RD analysis, all of the above mentioned effects lead to an underestimation of the methanol column density and incorrect gas temperature.
 |
Fig. 14 Rotational diagrams of the detected methanol lines for the −2 km s−1 (top panel), 2.8 km s−1 (middle panel), and 9.9 km s−1 (bottom panel) components, respectively. |
 |
Fig. 15 Results from the non-LTE analysis. Upper panel: results from the χ2 minimisation for the −2 km s−1 component simultaneously fitting the A and E forms with a ratio equal to unity and the 13C E methanol transition with a ratio of 68. The minimum therefore has to be multiplied by two to obtain the A+E forms of methanol. Middle panel: density and temperature range obtained for the best-fit methanol column density of 2 × (7 × 1017) cm−2 and source size of 0.15″. Bottom panel: observed integrated intensities versus modelled ones as a function of the upper energy level value with respect to the lowest value. These are 7.9 K for E methanol (red filled circles) and 0 K for A methanol (red filled stars). The 13C E methanol is represented as a red filled triangle. |
6.3 Dust opacity towards the binary system objects, 11A and 11B
As described in Sect. 2, [BHB2007] 11 is a binary system where the two objects (11A and 11B) are embedded in their respective circumstellar discs (Alves et al. 2019). The discs are both detected in the continuum at 0.94cm with the Karl G. Jansky Very Large Array (JVLA) and at 1.3 mm with ALMA. Following the findings of De Simone et al. (2020) that the dust in front of the hot corino of NGC1333 IRAS4A1 completely absorbs its methanol lines in the millimeter wavelengths, here we aim to estimate the possible absorption of the methanol emission specifically related to the compact disc scales around each of the sources 11A and 11B. Within this scope, we used the dust continuum observations by Alves et al. (2019) at 225 GHz, who found a flux density F225 equal to 5.2 ± 0.53 mJy towards 11A and 5.62 ± 0.45 mJy towards 11B. The deconvolved sizes are 7.3(±1.3) × 5.4(±1.1) au2 and 4.9(±1.1) × 3.7(±1.0) au2 for 11A and 11B, respectively. Thus, the 225 GHz continuum emission is more compact in 11B than 11A, despite having a similar flux density.
We can constrain the dust optical depth τν and temperature towards each of the two sources using the following equation:
where Bν(Td) is the Planck function, which depends on the dust temperature, Td, and Ωs is the source solid angle, derived from the continuum observations. The source solid angle is defined as ~A/d2, where A is the source’s emitting area (derived from the source’s size) and d2 is the distance to the sources. The dust optical depth can be estimated by inverting Eq. (6) as follows:
Finally, using Eq. (7), we can estimate the possible dust absorption coefficient using the following equation:
As we do not know the dust temperature, Td, of the sources, we derived the dust optical depth for temperatures ranging between 100 and 500 K with steps of 10 K from 100 K to 200 K, and by steps of 20 K from 200 to 500 K, following the method described in Bouvier et al. (2021). The observed 225 GHz flux provides a lower limit to Td. Specifically, the condition Fv/Ωs ≤ Bv(Td) implies Td ≥ 130 K in 11A and Td ≥ 300 K in 11B (as it is more compact). Then, for each dust temperature, we can derive the dust opacity at 225 GHz, reported in Fig. 16. The figure shows that τν is well constrained in the two sources, except around the minimum Td for each of them, where the error bars become very large. Specifically, in 11A, τν varies from 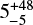 at Td ~ 130 K to
at Td ~ 130 K to 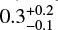 at Td = 500 K; in 11B, τν varies from
at Td = 500 K; in 11B, τν varies from 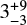 at Td ~ 300 K to
at Td ~ 300 K to 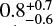 at Td = 500 K. The dust opacities tend to be optically thick, and taking the largest dust optical depths gives τν ≤ 53 and τν ≤ 12 in 11A and 11B, respectively. Therefore, the possible methanol lines from the hot corinos associated with 11A and 11B, if they exist, can be completely attenuated by the foreground dust.
at Td = 500 K. The dust opacities tend to be optically thick, and taking the largest dust optical depths gives τν ≤ 53 and τν ≤ 12 in 11A and 11B, respectively. Therefore, the possible methanol lines from the hot corinos associated with 11A and 11B, if they exist, can be completely attenuated by the foreground dust.
Results from the non-LTE analysis.
7 Origin of the observed methanol components
In the following, we discuss the possible origin of the three velocity components detected in our methanol spectra. In order to better understand this point, we created a position-velocity (PV) diagram for the methanol transition at 243.916 GHz (Eup ~ 50 K) displayed in Fig. 17. The PV plot is produced from a cut oriented parallel to the velocity gradient observed in the moment 1 map of the methanol emission (Fig. 10), whose PA is 140° east of north. The cut width is 0.5″, the value of which is comparable to the angular resolution of the FAUST data and encompasses both core 11A and core 11B, separated by only 0.2″. Unlike the H2CO PV plot, which shows a smooth Keplerian profile over the velocity range (Alves et al. 2019), a fragmented profile is clearly seen in the methanol PV plot. The three substructures correspond to the three velocity components observed in the methanol spectra (a similar distribution is observed at the higher Eup transition).
Although we cannot locate the methanol emission with respect to the binary system due to our limited angular resolution, we notice that blueshifted and redshifted emission in the high velocity channels where the S/N is larger than 5 (−4.89 km s−1 in blue and 13.3 km s−1 in red) tends to be aligned with source 11B (Fig. 18, left panel), alike the high-velocity components of the CO emission shown by Alves et al. (2019). The methanol emission at velocity channels near the systemic velocity of the source (−3.6 km s−1) also tends to peak near 11A. The three methanol components appear in a compact configuration that is compatible with the compact methanol seen in the moment 0 maps (Fig. 5).
It is clear from Figs. 6,7, and 8 that the three velocity components are not completely spectrally independent and that they are affected by the fact that they blend into one another. In Fig. 19, we present the integrated intensity and velocity field maps from the 243 GHz methanol transition for the three velocity components in the [−7−0] km s−1 range for the −2 km s−1 component, the [0–6] km s−1 range for the 2.8 km s−1 component, and the [616] km s−1 range for the 9.9 km s−1 component. The three positions are clearly identified in the moment 0 maps: the 2.8 km s−1 component in between [BHB2007] 11A and [BHB2007] 11B, while the −2 and 9.9 km s−1 are located north-west and southeast of [BHB2007] 11B. There is no clear evidence of a velocity structure in these two velocity ranges, which points to the conclusion of the results from a compact shock emission (see Sect. 7.3). The 2.8 km s−1 seems to be more sensitive to the disc rotation (as in the H2CO centroid map in Alves et al. 2019), and that could explain the gradient that is seen more clearly than in the other two components. Also, Fig. 18 (right panel) must be analysed with caution as the overlap of velocity ranges from one component to another can mislead us into concluding that we have an elongated structure for the methanol emission. We added coloured borders to identify the three velocity components observed in our methanol observations in this figure. However, higher spatial resolution observations of methanol are necessary to determine the velocity structure of methanol accurately.
Since the emission in each velocity channel is compact and centrally peaked, we performed 2D Gaussian fits on the emission in each channel to obtain the position of their intensity peak. The accuracy on the relative position is given by Θ/(2 × S/N), where Θ is the synthesised beam size and S/N is the signal-to-noise ratio of the peak with respect to the map noise (Condon 1997; Condon et al. 1998). Thus, the uncertainty in the position is inversely proportional to the S/N in each velocity channel. Centroid fitting to the compact molecular emission yields astrometry with precisions better than those of the spatial resolution in the case of a high S/N. For this calculation, we only considered intensity peaks brighter than five times its Gaussian fit error and a S/N larger than 10.0 (which corresponds to a position accuracy better than 0.02″). The right panel of Fig. 18 shows the 2D Gaussian centroid map with the location of each methanol emission peak (black circle) as a function of velocity. The velocity components satisfying the conditions above span from −4.1 to 12.7km s−1.
It is noticeable that the methanol emission with velocities between 0 and 8 km s−1 tends to lie in the region in between sources 11A and 11B, while the gas with velocities <0 km s−1 and >8 km s−1 seems to approach source B, as is also seen in the CO (2-1) observations presented in Alves et al. (2017, 2020). Their analyses show an increasing velocity towards 11B that seems to indicate acceleration of infalling gas from the circumbinary disc onto 11B. This can be shown on the right side of Fig. 18, where we also mark the CO emission as circles with green borders and the methanol emission as circles with black borders. The CO emission observed by Alves et al. (2017) and shown in the left panel of our Fig. 2 primarily traces large-scale outflowing gas emission, launched from a distance of ~100 au from the disc centre and propagating perpendicularly to the envelope major axis. However, velocity components faster than the outflows are detected within the circumbinary disc at only a few au. These high-velocity CO components reach up to 15 km s−1, and the blueshifted and redshifted velocities (Vlsr < −1.5 km s−1 and VLsr > 9 km s−1, respectively) are centred on and aligned with 11B, the higher velocities being closest to the position of the protostar. We note that no high velocity components are seen near [BHB2007] 11A. The increasing velocity towards [BHB2007] 11B indicates acceleration of infalling gas from the circumbinary disc onto [BHB2007] 11B.
From our methanol analysis, an increasing velocity is not as clear as in CO, possibly due to our lower spatial resolution, but also due to the fact that the three velocity components identified in our methanol spectra are partially overlapping. The information provided by the PV diagram and centroid maps give constraints on the origin of the three velocity components, which is described in the following sub-section.
 |
Fig. 16 Dust optical depth, τv, at 225 GHz as function of the dust temperature, Td, derived from the observations of Alves et al. (2019) and following the method described in Bouvier et al. (2021). The lines show τv as derived from Eq. (7). The errors are calculated using the error propagation method described in Appendix C.2. of Bouvier et al. (2021) and include the calibration uncertainty of 15% (Alves et al. 2019) and the source size uncertainty. The left and right panels refer to 11A and 11B, respectively. |
 |
Fig. 17 PV diagram obtained from the CH3OH emission at 243.916 GHz. The PA and width of the PV cut is indicated in the figure. We note that the direction of the cut used to produce the position-velocity diagram is shown in Fig. 10 as a grey dashed line. The three velocity components observed in the methanol spectra are also indicated. |
7.1 The −2.0 and +9.9 km s−1 components
Based on the arguments above, these two velocity components are likely associated with the gas streaming towards 11B. The most extreme components, −5 km s−1 and 13 km s−1, are consistent with the high-velocity components observed in CO lines distributed along the filaments and confined within the circumbinary disc (see also higher spatial resolution observations by Alves et al. 2019, and their Fig. 2 and S2). These components exceed the Keplerian velocities observed in the H2CO maps of Alves et al. (2019; −3 km s−1 ≲ vKep ≲ 12 km s1), and are distributed around 11B. Our non-LTE analysis of the methanol lines indicates that this gas is very warm (100-140 K), dense (−107 cm−3) and very enriched in methanol (abundance w.r.t H2 ~ 10−5). We discuss the physical origin of gaseous methanol later in this section.
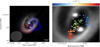 |
Fig. 18 Analysis of the origin of the observed methanol components. Left panel: methanol intensity contours at 243.916 GHz plotted over the dust continuum map of Alves et al. (2019). The contours show the methanol emission at extreme velocity channels detected at a 3σ level (1er = 1.8 mJy beam−1). The blue and red contours correspond to emission at the −4.89 kms−1 and 13.3 kms−1 velocity channels, respectively. White contours show emission (from a 20σ level) from velocity channels near the systemic velocity of the source (2.91 km s−1). The synthesised beam of the methanol (FAUST) data is shown in the lower left corner. Right panel: position of intensity peaks (circles) from the 2D Gaussian fit in each velocity channels separated by ~0.15 km s−1. Colour code for the edges of the circle: red for the 9.9 km s−1 methanol component, green for the 2.8 km s−1 methanol component, and blue for the −2 km s−1 methanol component, while the CO (2–1) high-velocity components are in cyan. The circle size is defined by the uncertainty on the absolute position of the emission peak in each velocity component (largest circle has ~0.02″). |
 |
Fig. 19 Moment 0 and moment 1 maps for the 51,4–41,3 transition of A-CH3OH. Top: integrated intensity maps of the high spectral resolution methanol transition at 243.916 GHz (Eu = 49.66 K) for the three components ([−7−0] km s−1 for the −2 km s−1 component, [0–6] km s−1 for the 2.8 km s−1 component, and [6-16] km s−1 for the 9.9 km s−1 component). Contours start at 4σ at every 4σ. The ellipse in the bottom left corner represents the ALMA synthesised beam. Both sources A and B identified by Alves et al. (2019) are indicated as white filled circles. Bottom: velocity field maps of the high spectral resolution methanol transition at 243.916 GHz (Eu = 49.66 K) for the three components. |
7.2 The +2.8 km s−1 component
This component seems to be associated with 11A when considering the arguments based on the velocity field, PV diagram, and centroid maps above. This gas is also warm (120–140 K), dense (−2 × 106 cm−3), and very enriched in methanol (abundance with respect to H2 ~ 10−5), which would point to a similar origin of the methanol emission of the other two components. Moreover, the H2CO (Eup ~ 70 K) observations of Alves et al. (2019), taken at comparable spectral resolution but a factor ~2 better angular resolution, show relatively warm gas associated with 11A. In fact, the emission observed in the velocity range of 2.55.0 km s−1 is spatially coincident with 11A, which is consistent with our findings (see Fig. S3 in Alves et al. 2019). This component is close to the systemic velocity of 3.6 km s−1 and could be (partially) tracing the Keplerian motion of the disc (similar to H2CO), and so a velocity gradient is expected and identified in Fig. 19 (middle figure, bottom panel). Nevertheless, due to the limited angular resolution of our maps, we should not completely discard that this velocity component has some contribution from 11B or from gas located in between sources.
7.3 Origin of the gaseous methanol: Shock versus thermal desorption
Methanol is known to have a very low abundance ≤10−8 in cold objects (e.g. Friberg et al. 1988; Nagy et al. 2019), while its abundance is high (10−7–105) in hot cores/corinos (e.g. Gibb et al. 2000; Cazaux et al. 2003) and molecular outflow shocks (e.g. Bachiller et al. 1995; Codella et al. 2020). It is commonly accepted that methanol is indeed synthesised on the grain surfaces (e.g. Watanabe & Kouchi 2002; Rimola et al. 2014) during the cold prestellar phase and released from the grain mantles into the gas phase by thermal and non-thermal processes. Hot cores/corinos are therefore the results of thermal processes (e.g. Maret et al. 2005; Taquet et al. 2016), while molecular outflow triggers non-thermal desorption via shocks (e.g. Caselli et al. 1997; Jiménez-Serra et al. 2008).
The temperature derived from the non-LTE analysis of the methanol lines tells us that the gas is hot and dense. The latter would also imply that the dust and gas are thermally coupled (e.g. Goldsmith 2001) and, hence, the dust is also warm enough for methanol to be thermally desorbed, based on the recent estimates of the methanol binding energy by Ferrero et al. (2020). These authors found the CO binding energy ranges between −4400 and −6500 K, which would correspond to a dust sublimation temperature of about 80 to 120 K, assuming that the grain mantles have been warmed up for −104 yr11. Of course, it is possible that methanol is trapped in the water-rich ices, so the sublimation temperature could be dominated by the co-desorption of methanol with water. Again based on Ferrero et al. (2020), this would happen at about 110 K, namely in between the dust sublimation temperature of a pure methanol ice.
The first question to answer is whether the measured temperature, 110-130 K (Sect. 6.2), is compatible with the warming of the dust from the two sources or if it necessitates a non-thermal mechanism. To this end, we can estimate the approximate dust temperature of a dust grain heated by a source at a distance of r. When the dust is optically thin, the dust temperature profile heated by a central source can be approximated by the following equation (Ceccarelli et al. 2000a):
Considering that the two sources 11A and 11B have a total bolometric luminosity of 4.4 L⊙ (Sandell et al. 2021) and that the distance between them is 28 au (0.2″), the dust temperature would be ~93 K. As already stated in Sect. 6.3, the dust is optically thick, therefore the dust temperature should be above ~93 K. This means that all the dust in between 11A and 11B could be warm enough for the methanol to sublimate, within the uncertainties discussed above on the frozen methanol sublimation temperature. A fortiori, if 11A and 11B host one or two hot corinos, the observed methanol could just originate from them. However, the above analysis on the location of the gas (Sects. 7.1 and 7.2) and the dust optical depth towards 11A and 11B (Sect. 6.3) is not in favour of the hypothesis that the observed hot methanol originates in the 11A or 11B cores, therefore invalidating their hot corino nature.
Alternatively, the observed methanol could be the result of the sputtering of the grain mantles in shocks (e.g. Caselli et al. 1997; Jiménez-Serra et al. 2008; De Simone et al. 2020; Codella et al. 2020) created by the streaming of the gas towards 11A and 11B and impacting the quiescent gas of the circumbinary envelope/disc or, possibly, the two circumstellar discs. The mass contained in the shocked gas traced by methanol would then be about 10−6 M⊙, namely a very minor fraction of the dynamical mass (~2.2 M⊙) or even the mass of the larger circumbinary disc (~0.08 M⊙, Alves et al. 2019).
The gas kinematics in a binary system is expected to be more complex compared to a simple protostar formation, with accretion shocks and structures that are related to the transition from the circumbinary material to the circumstellar discs (Matsumoto et al. 2019). Alves et al. (2019) computed a mass accretion rate from the circumbinary disc into the circumstellar disc of −1.1 × 10−5 M⊙ yr−1, which is also consistent with other Class 0/I protostars. Also, the infall motion, traced by the highvelocity CO, is perfectly consistent with the dynamical mass of the system. A similar situation to that of [BHB2007] 11 is seen in the young binary system IRAS16293 A, where some molecular tracers such as HNCO, NH2CHO, and t-HCOOH coincide with the location of the dust sub-structures detected in the continuum emission, away from the the two binaries (Maureira et al. 2020). Also, the CH3OH emission and the HCOOCH3 molecular emission detected by Oya et al. (2016) likely originate in the ring-like region with a radius of 50 au surrounding the protostar, based on their kinematic structures (Oya & Yamamoto 2020), with temperatures rising to more than 300 K. The evidence presented here (dust opacity, compactness of the three components, centroid analysis) point to the hypothesis of a shocked region due to the large-scale streaming material feeding the proto-binary system (see Fig. 18). However, since the beam of our observations is relatively large with respect to the supposed shock structures, this hypothesis will need to be confirmed by future high-angular-resolution observations.
8 Conclusions
We analysed the emission of methanol measured towards the Class 0/I protostar system [BHB2007] 11 and obtained within the ALMA FAUST large programme. The Band 3 and Band 6 continuum images show that the dust continuum emission is faint and extends beyond the northwest-southeast envelope previously detected by Alves et al. (2019). A series of methanol transitions are detected towards this source and reveal the presence of hot methanol gas arising from three different velocity components centred at VLSR = −2, 2.8 and 9.9 km s−1. The overall emission of hot methanol peaks at the location of the circumbinary disc. The moment 1 maps of the methanol emission show a velocity gradient with the blueshifted gas located towards the northwest and the redshifted gas peaking towards the southeast, consistent with the gas kinematics previously detected in H2CO (Alves et al. 2019). Non-LTE analysis shows that the methanol emission is compact (~0.15″), the gas is hot (100–140 K) and dense (2 × 106–2 × 107 cm−3), and the inferred methanol column densities are of approximately 1018 cm−2. Although the binary systems, [BHB2007] 11A and [BHB2007] 11B, cannot be resolved in the FAUST images, the 2D Gaussian centroid map of the hot methanol line at 243.916GHz shows that this emission arises from the region associated with [BHB2007] 11A and north-west and south-east of [BHB2007] 11B. This could be due to the fact that the dust emission is very optically thick towards the hot corinos and/or the hot methanol gas is associated with shocked gas within an accretion streamer falling onto source [BHB2007] 11B. This idea is supported by the fact that the methanol emission is compact, located near to sources [BHB2007] 11A and B, within the infalling CO gas detected at extreme velocities <−1.5 km s−1 and >9 km s−1. However, higher angular-resolution observations are needed to conclude one of these two possibilities.
Acknowledgements
This project has received funding within the European Union’s Horizon 2020 research and innovation program from the European Research Council (ERC) for the project The Dawn of Organic Chemistry (DOC), grant agreement no. 741002, and from the Marie Sklodowska-Curie for the project Astro-Chemical Origins (ACO), grant agreement no. 811312. I.J.-S. has received partial support from the Spanish State Research Agency (project number PID2019-105552RB-C41). D.J. is supported by NRC Canada and by an NSERC Discovery Grant. S.Y. thanks the support by Grant-in-Aids from Ministry of Education, Culture, Sports, Science, and Technologies of Japan (18H05222). This paper makes use of the following ALMA data: ADS/JAO.ALMA#2018.1.01205.L. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
References
- Agurto-Gangas, C., Pineda, J. E., Szűcs, L., et al. 2019, A&A, 623, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aikawa, Y., Furuya, K., Yamamoto, S., & Sakai, N. 2020, ApJ, 897, 110 [Google Scholar]
- Alves, F. O., Girart, J. M., Caselli, P., et al. 2017, A&A, 603, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alves, F. O., Girart, J. M., Padovani, M., et al. 2018, A&A, 616, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alves, F. O., Caselli, P., Girart, J.M., et al. 2019, Science, 366, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Alves, F. O., Cleeves, L. I., Girart, J. M., et al. 2020, ApJ, 904, L6 [NASA ADS] [CrossRef] [Google Scholar]
- André, P., Ward-Thompson, D., & Barsony, M. 1993, ApJ, 406, 122 [Google Scholar]
- Bachiller, R., Liechti, S., Walmsley, C. M., & Colomer, F. 1995, A&A, 295, L51 [NASA ADS] [Google Scholar]
- Bacmann, A., Taquet, V., Faure, A., Kahane, C., & Ceccarelli, C. 2012, A&A, 541, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balucani, N., Ceccarelli, C., & Taquet, V. 2015, MNRAS, 449, L16 [Google Scholar]
- Bertin, M., Romanzin, C., Doronin, M., et al. 2016, ApJ, 817, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Bizzocchi, L., Caselli, P., Spezzano, S., & Leonardo, E. 2014, A&A, 569, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bottinelli, S., Ceccarelli, C., Lefloch, B., et al. 2004, ApJ, 615, 354 [Google Scholar]
- Bouvier, M., López-Sepulcre, A., Ceccarelli, C., et al. 2021, A&A, 653, A117 [CrossRef] [EDP Sciences] [Google Scholar]
- Brooke, T. Y., Huard, T.L., Bourke, T.L., et al. 2007, ApJ, 655, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., & Ceccarelli, C. 2012, A&ARv, 20, 56 [Google Scholar]
- Caselli, P., Hartquist, T. W., & Havnes, O. 1997, A&A, 322, 296 [NASA ADS] [Google Scholar]
- Cazaux, S., Tielens, A. G. G. M., Ceccarelli, C., et al. 2003, ApJ, 593, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Ceccarelli, C., Castets, A., Caux, E., et al. 2000a, A&A, 355, 1129 [NASA ADS] [Google Scholar]
- Ceccarelli, C., Loinard, L., Castets, A., Faure, A., & Lefloch, B. 2000b, A&A, 362, 1122 [Google Scholar]
- Ceccarelli, C., Maret, S., Tielens, A. G. G. M., Castets, A., & Caux, E. 2003, A&A, 410, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceccarelli, C., Caselli, P., Herbst, E., Tielens, A. G. G. M., & Caux, E. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil, 47 [Google Scholar]
- Ceccarelli, C., Caselli, P., Fontani, F., et al. 2017, ApJ, 850, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Chahine, L., López-Sepulcre, A., Neri, R., et al. 2022, A&A, 657, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charnley, S. B., Tielens, A. G. G. M., & Millar, T. J. 1992, ApJ, 399, L71 [Google Scholar]
- Codella, C., Ceccarelli, C., Bianchi, E., et al. 2020, A&A, 635, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Codella, C., Ceccarelli, C., Chandler, C., et al. 2021, Front. Astron. Space Sci., 8, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1997, PASP, 109, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [Google Scholar]
- Covey, K. R., Lada, C. J., Román-Zúñiga, C., et al. 2010, ApJ, 722, 971 [NASA ADS] [CrossRef] [Google Scholar]
- De Simone, M., Ceccarelli, C., Codella, C., et al. 2020, ApJ, 896, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Duarte-Cabral, A., Chrysostomou, A., Peretto, N., et al. 2012, A&A, 543, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubernet, M., Nenadovic, L., & Doronin, N. 2012, in Astronomical Society of the Pacific Conference Series, Astronomical Data Analysis Software and Systems XXI, eds. P. Ballester, D. Egret, & N. P. F. Lorente, 461, 335 [NASA ADS] [Google Scholar]
- Dubernet, M. L., Alexander, M. H., Ba, Y. A., et al. 2013, A&A, 553, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dzib, S. A., Loinard, L., Ortiz-León, G. N., Rodríguez, L. F., & Galli, P. A. B. 2018, ApJ, 867, 151 [Google Scholar]
- Favre, C., Fedele, D., Semenov, D., et al. 2018, ApJ, 862, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrero, S., Zamirri, L., Ceccarelli, C., et al. 2020, ApJ, 904, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., & Pineau des Forets, G. 1995, MNRAS, 275, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Forbrich, J., Lada, C. J., Muench, A. A., Alves, J., & Lombardi, M. 2009, ApJ, 704, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Forbrich, J., Posselt, B., Covey, K. R., & Lada, C. J. 2010, ApJ, 719, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Friberg, P., Madden, S.C., Hjalmarson, A., & Irvine, W.M. 1988, A&A, 195, 281 [NASA ADS] [Google Scholar]
- Garrod, R. T., Widicus Weaver, S. L., & Herbst, E. 2008, ApJ, 682, 283 [Google Scholar]
- Gibb, E., Nummelin, A., Irvine, W. M., Whittet, D. C. B., & Bergman, P. 2000, ApJ, 545, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F. 2001, ApJ, 557, 736 [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [Google Scholar]
- Hara, C., Shimajiri, Y., Tsukagoshi, T., et al. 2013, ApJ, 771, 128 [CrossRef] [Google Scholar]
- Jaber, A. A., Ceccarelli, C., Kahane, C., & Caux, E. 2014, ApJ, 791, 29 [Google Scholar]
- Jiménez-Serra, I., Caselli, P., Martín-Pintado, J., & Hartquist, T. W. 2008, A&A, 482, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiménez-Serra, I., Vasyunin, A. I., Caselli, P., et al. 2016, ApJ, 830, L6 [Google Scholar]
- Jiménez-Serra, I., Vasyunin, A. I., Spezzano, S., et al. 2021, ApJ, 917, 44 [CrossRef] [Google Scholar]
- Jin, M., & Garrod, R. T. 2020, ApJS, 249, 26 [Google Scholar]
- Jørgensen, J. K., van der Wiel, M.H.D., Coutens, A., et al. 2016, A&A, 595, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, C.-F., Codella, C., Li, Z.-Y., & Liu, S.-Y. 2019, ApJ, 876, 63 [Google Scholar]
- Maret, S., Ceccarelli, C., Tielens, A. G. G. M., et al. 2005, A&A, 442, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsumoto, T., Saigo, K., & Takakuwa, S. 2019, ApJ, 871, 36 [CrossRef] [Google Scholar]
- Maureira, M. J., Pineda, J. E., Segura-Cox, D. M., et al. 2020, ApJ, 897, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Milam, S. N., Savage, C., Brewster, M. A., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [Google Scholar]
- Minissale, M., Dulieu, F., Cazaux, S., & Hocuk, S. 2016, A&A, 585, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [Google Scholar]
- Nagy, Z., Spezzano, S., Caselli, P., et al. 2019, A&A, 630, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., Guzmán, V. V., Furuya, K., et al. 2015, Nature, 520, 198 [Google Scholar]
- Öberg, K. I., Guzmán, V. V., Walsh, C., et al. 2021, ApJS, 257, 1 [CrossRef] [Google Scholar]
- Onishi, T., Kawamura, A., Abe, R., et al. 1999, PASJ, 51, 871 [Google Scholar]
- Oya, Y., & Yamamoto, S. 2020, ApJ, 904, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Oya, Y., Sakai, N., López-Sepulcre, A., et al. 2016, ApJ, 824, 88 [Google Scholar]
- Oya, Y., Sakai, N., Watanabe, Y., et al. 2017, ApJ, 837, 174 [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spec. Radiat. Transf., 60, 883 [Google Scholar]
- Pineda, J. E., Segura-Cox, D., Caselli, P., et al. 2020, Nat. Astron., 4, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Pineda, J., Arzoumanian, D., André, P., et al. 2022, in Protostars and Planets VII [arXiv:2205.03935] [Google Scholar]
- Punanova, A., Vasyunin, A., Caselli, P., et al. 2022, ApJ, 927, 213 [CrossRef] [Google Scholar]
- Rabli, D., & Flower, D. R. 2010, MNRAS, 406, 95 [Google Scholar]
- Rathborne, J. M., Lada, C. J., Muench, A. A., Alves, J. F., & Lombardi, M. 2008, ApJS, 174, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Redaelli, E., Alves, F. O., Caselli, P., et al. 2017, ApJ, 850, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Riaz, B., Martín, E. L., Bouy, H., & Tata, R. 2009, ApJ, 700, 1541 [NASA ADS] [CrossRef] [Google Scholar]
- Rimola, A., Taquet, V., Ugliengo, P., Balucani, N., & Ceccarelli, C. 2014, A&A, 572, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Román-Zúñiga, C. G., Alves, J. F., Lada, C. J., & Lombardi, M. 2010, ApJ, 725, 2232 [Google Scholar]
- Sakai, N., & Yamamoto, S. 2013, Chem. Rev., 113, 8981 [Google Scholar]
- Sandell, G., Reipurth, B., Vacca, W. D., & Bajaj, N. S. 2021, ApJ, 920, 7 [Google Scholar]
- Scibelli, S., & Shirley, Y. 2020, ApJ, 891, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Shingledecker, C. N., Tennis, J., Le Gal, R., & Herbst, E. 2018, ApJ, 861, 20 [Google Scholar]
- Spezzano, S., Caselli, P., Pineda, J. E., et al. 2020, A&A, 643, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spezzano, S., Fuente, A., Caselli, P., et al. 2022, A&A, 657, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taquet, V., Wirström, E. S., & Charnley, S. B. 2016, ApJ, 821, 46 [Google Scholar]
- Testi, L., Birnstiel, T., Ricci, L., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R.S. Klessen, C.P. Dullemond, & T. Henning, 339 [Google Scholar]
- Vastel, C., Ceccarelli, C., Lefloch, B., & Bachiller, R. 2014, ApJ, 795, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Vasyunin, A. I., Caselli, P., Dulieu, F., & Jiménez-Serra, I. 2017, ApJ, 842, 33 [Google Scholar]
- Wakelam, V., Dartois, E., Chabot, M., et al. 2021, A&A, 652, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walsh, C., Loomis, R. A., Öberg, K. I., et al. 2016, ApJ, 823, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, N., & Kouchi, A. 2002, ApJ, 571, L173 [Google Scholar]
- Yang, Y.-L., Sakai, N., Zhang, Y., et al. 2021, ApJ, 910, 20 [Google Scholar]
The circumbinary disc emission over which the SED was computed is determined as the first closed contour around it (i.e. not encompassing the extended N-S emission): 15, 120, and 230 times the rms noise of the beam-matched maps in setups 3, 1, and 2, respectively. The SED for the envelope uses the integrated flux higher than five times the rms noise but lower than the contours listed above (i.e. it excludes the circumbinary disc).
All Tables
Spectroscopic parameters of the methanol transitions (using the CDMS database) detected towards [BHB2007] 11 and results from the Gaussian fits.
Integrated intensities used for the LTE and non-LTE analysis, extracted over a region above 4σ in the integrated intensity map of the 218.440 GHz methanol transition.
All Figures
 |
Fig. 1 Amplitude versus uv-distance plots before (top) and after (below) self-calibration. |
| In the text | |
 |
Fig. 2 Dust continuum maps obtained in each setup. The rms noise level is 50 μJy beam−1 for Band 3 observations (setup 3, left panel), 90 μJy beam−1 for setup 1 in Band 6 (middle panel), and 70 μJy beam−1 for setup 2 in Band 6 (right panel). The intensity contour levels in the left panel are −5, 5, 10, 30, 50, 70, and 90 × the noise level, while the intensity contours in the middle and right panels are −5, 5, and 50 and from 100 to 1000 (in steps of 100) × 70 μJy beam−1 the noise level in setup 2. The colour scale at the top is the same for all panels. The red dots indicate the positions of 11A (north) and 11B (south) as reported by Alves et al. (2019). The sources are not resolved with the present resolution. The left panel also shows the integrated intensity contours from CO (2 → 1) emission from the bipolar outflow powered by [BHB2007] 11 (Alves et al. 2017). The synthesised beam is displayed in the bottom left corner of each panel (0.36″ × 0.34″, 0.39″ × 0.33″ and 0.42″ × 0.29″ for setups 3, 1, and 2, respectively). |
| In the text | |
 |
Fig. 3 Radial profile of dust continuum emission at 252 GHz (setup 2) towards [BHB2007] 11. The profile is centred on the continuum peak. The red line shows a Gaussian fit to the disc’s brightness distribution. The dashed line indicates the synthesised beam size. The grey line shows the rms noise level of the continuum emission. |
| In the text | |
 |
Fig. 4 Spectral energy distribution determined for the dust emission within the circumbinary disc (α = 3.0, black line) and in the envelope (α = 3.4, dotted dashed line). The flux densities for the disc and envelope are indicated as filled circles and open triangles, respectively. The errors are dominated by the uncertainty in the flux calibration, which is assumed to be ~10%. The dashed line shows the SED determined from the free-free (centimetric) emission detected with the Very Large Array (Alves et al. 2019). |
| In the text | |
 |
Fig. 5 Moment 0 map of the high spectral resolution methanol transitions at 218.440 GHz (Eu = 45.46 K), 243.916 GHz (Eu = 49.66 K), and 261.704 GHz (Eu = 359.77 K). Contours start at 4σ at every 10σ for 218.440 and 243.916 GHz, and every 3σ at 261.704 GHz. The ellipse in the bottom left corner represents the ALMA synthesised beam. Both sources A and B identified by Alves et al. (2019) are indicated by white filled circles. |
| In the text | |
 |
Fig. 6 Tb (K) spectra for the high spectral resolution Methanol transitions at 218.440, 243.916, and 261.704 GHz. The dashed lines correspond to the results of the best-fit Gaussian at −2 km s−1, 2.8 km s−1, and 9.9 km s−1. The −2 km s−1 component of the 261.704 GHz transition is blended with a transition of methyl formate (see text). |
| In the text | |
 |
Fig. 7 Spectra (in mJy beam−1) for the low spectral resolution Methanol transitions. The dashed lines correspond to the results of the bestfit Gaussian of the high spectral resolution transitions at −2 km s−1, 2.8 km s−1, and 9.9 km s−1. |
| In the text | |
 |
Fig. 8 Spectra (in mJy beam−1) for the low spectral resolution methanol transitions in the 234 GHz spectral windows. The dashed lines correspond to the results of the Gaussian components obtained from each of the high spectral resolution transitions at −2 km s−1, 2.8 km s−1, and 9.9 km s−1. |
| In the text | |
 |
Fig. 9 Difference between the 12-m-only data and the joint data for the A-CH3OH transition at 243.916 GHz. |
| In the text | |
 |
Fig. 10 Velocity field determined from methanol transitions at low and high energy levels. The contours indicate the continuum intensity levels from the high spatial resolution observations of Alves et al. (2019). The compact emission contours arise from the circumstellar discs around each protostar of the binary system: 11A (northern component) and 11B (southern component). The dashed line in the left panel shows the direction of the cut used to produce the position-velocity diagram displayed in Fig. 17. The cut position angle is 140° and its width is 0.5″, encompassing both protostars. |
| In the text | |
 |
Fig. 11 Spectra at VLSR = 3.6 km s−1 of the [BHB2007] 11 source showing the E-CH3OCHO 21(7,14)-20(7,13) transition at 261.715 GHz blended with the CH3OH transition at 261.704GHz. The dashed lines correspond to the results of the best-fit Gaussian components obtained from the high spectral resolution methanol transitions at −2 km s−1, 2.8 km s−1, and 9.9 km s−1 for the methyl formate transition. |
| In the text | |
 |
Fig. 12 Spectrum (in mJ beam−1) of only detected transition of 13 CH3 OH at 234 GHz. The dashed lines correspond to the results of the best-fit Gaussian components obtained from the high spectral resolution transitions at −2 km s−1, 2.8 km s−1, and 9.9 km s−1. |
| In the text | |
 |
Fig. 13 Moment 0 map of 13CH3OH transition at 234 GHz. Contours start at 4σ at every 2σ. The ellipse in the bottom left corner represents the ALMA synthesised beam. Both sources 11A and 11B identified by Alves et al. (2019) are indicated as white filled circles. |
| In the text | |
 |
Fig. 14 Rotational diagrams of the detected methanol lines for the −2 km s−1 (top panel), 2.8 km s−1 (middle panel), and 9.9 km s−1 (bottom panel) components, respectively. |
| In the text | |
 |
Fig. 15 Results from the non-LTE analysis. Upper panel: results from the χ2 minimisation for the −2 km s−1 component simultaneously fitting the A and E forms with a ratio equal to unity and the 13C E methanol transition with a ratio of 68. The minimum therefore has to be multiplied by two to obtain the A+E forms of methanol. Middle panel: density and temperature range obtained for the best-fit methanol column density of 2 × (7 × 1017) cm−2 and source size of 0.15″. Bottom panel: observed integrated intensities versus modelled ones as a function of the upper energy level value with respect to the lowest value. These are 7.9 K for E methanol (red filled circles) and 0 K for A methanol (red filled stars). The 13C E methanol is represented as a red filled triangle. |
| In the text | |
 |
Fig. 16 Dust optical depth, τv, at 225 GHz as function of the dust temperature, Td, derived from the observations of Alves et al. (2019) and following the method described in Bouvier et al. (2021). The lines show τv as derived from Eq. (7). The errors are calculated using the error propagation method described in Appendix C.2. of Bouvier et al. (2021) and include the calibration uncertainty of 15% (Alves et al. 2019) and the source size uncertainty. The left and right panels refer to 11A and 11B, respectively. |
| In the text | |
 |
Fig. 17 PV diagram obtained from the CH3OH emission at 243.916 GHz. The PA and width of the PV cut is indicated in the figure. We note that the direction of the cut used to produce the position-velocity diagram is shown in Fig. 10 as a grey dashed line. The three velocity components observed in the methanol spectra are also indicated. |
| In the text | |
 |
Fig. 18 Analysis of the origin of the observed methanol components. Left panel: methanol intensity contours at 243.916 GHz plotted over the dust continuum map of Alves et al. (2019). The contours show the methanol emission at extreme velocity channels detected at a 3σ level (1er = 1.8 mJy beam−1). The blue and red contours correspond to emission at the −4.89 kms−1 and 13.3 kms−1 velocity channels, respectively. White contours show emission (from a 20σ level) from velocity channels near the systemic velocity of the source (2.91 km s−1). The synthesised beam of the methanol (FAUST) data is shown in the lower left corner. Right panel: position of intensity peaks (circles) from the 2D Gaussian fit in each velocity channels separated by ~0.15 km s−1. Colour code for the edges of the circle: red for the 9.9 km s−1 methanol component, green for the 2.8 km s−1 methanol component, and blue for the −2 km s−1 methanol component, while the CO (2–1) high-velocity components are in cyan. The circle size is defined by the uncertainty on the absolute position of the emission peak in each velocity component (largest circle has ~0.02″). |
| In the text | |
 |
Fig. 19 Moment 0 and moment 1 maps for the 51,4–41,3 transition of A-CH3OH. Top: integrated intensity maps of the high spectral resolution methanol transition at 243.916 GHz (Eu = 49.66 K) for the three components ([−7−0] km s−1 for the −2 km s−1 component, [0–6] km s−1 for the 2.8 km s−1 component, and [6-16] km s−1 for the 9.9 km s−1 component). Contours start at 4σ at every 4σ. The ellipse in the bottom left corner represents the ALMA synthesised beam. Both sources A and B identified by Alves et al. (2019) are indicated as white filled circles. Bottom: velocity field maps of the high spectral resolution methanol transition at 243.916 GHz (Eu = 49.66 K) for the three components. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



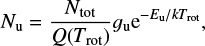
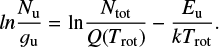
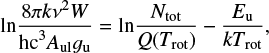
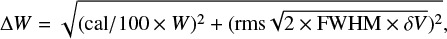
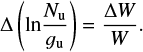
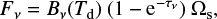
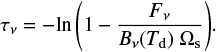
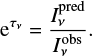
![${T_{\rm{d}}}\left[ {\rm{K}} \right] = 75{\left[ {{{{L_*}} \over {27{L_ \odot }}}} \right]^{0.25}}{\left[ {{r \over {150\,{\rm{au}}}}} \right]^{ - 0.5}}.$](/articles/aa/full_html/2022/08/aa43414-22/aa43414-22-eq16.png)