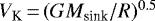| Issue |
A&A
Volume 658, February 2022
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 21 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202037479 | |
| Published online | 31 January 2022 | |
Discs and outflows in the early phases of massive star formation: Influence of magnetic fields and ambipolar diffusion
1
Univ Lyon, Ens de Lyon, Univ Lyon1, CNRS, Centre de Recherche Astrophysique de Lyon UMR5574,
69007
Lyon,
France
e-mail: benoit.commercon@ens-lyon.fr
2
Université de Paris and Université Paris-Saclay, CEA, CNRS, AIM,
91190
Gif-sur-Yvette, France
3
Université de Paris, CNRS, Astroparticule et Cosmologie,
75013
Paris, France
4
Université Paris-Saclay and Université de Paris, CEA, CNRS, AIM,
91190
Gif-sur-Yvette, France
5
Data Management and Software Centre, European Spallation Source ERIC,
Ole Maaløes Vej 3,
2200
Copenhagen, Denmark
Received:
10
January
2020
Accepted:
17
September
2021
Context. Massive star formation remains one of the most challenging problems in astrophysics, as illustrated by the fundamental issues of the radiative pressure barrier and the initial fragmentation. The wide variety of physical processes involved, in particular the protostellar radiative feedback, increase the complexity of massive star formation in comparison with its low-mass counterpart.
Aims. We aim to study the details of mass accretion and ejection in the vicinity of massive star forming cores using high-resolution (5 au) three-dimensional numerical simulations. We investigated the mechanisms at the origin of outflows (radiative force versus magnetic acceleration). We characterised the properties of the disc forming around massive protostars depending on the physics included: hydrodynamics, magnetic fields, and ambipolar diffusion.
Methods. We used state-of-the-art three-dimensional adaptive-mesh-refinement models of massive dense core collapse, which integrate the equations of (resistive) grey radiation magnetohydrodynamics, and include sink particle evolution. For the first time, we include both protostellar radiative feedback via pre-main-sequence evolutionary tracks and magnetic ambipolar diffusion. To determine the role of magnetic fields and ambipolar diffusion play in the formation of outflows and discs, we studied three different cases: a purely hydrodynamical run, a magnetised simulation under the ideal approximation (perfect coupling), and a calculation with ambipolar diffusion (resistive case). In the most micro-physically complex model (resistive MHD), we also investigated the effect the initial amplitude of both magnetic field and solid body rotation have on the final properties of the massive protostellar system. We used simple criteria to identify the outflow and disc material and follow their evolution as the central star accretes mass up to 20 M⊙ in most of our models. The radiative, magnetic, and hydrodynamical properties of the outflows and discs are quantitatively measured and cross-compared between models.
Results. Massive stars form in all our models, together with outflows and discs. The outflow is completely different when magnetic fields are introduced, so magneto-centrifugal processes are the main driver of the outflow up to stellar masses of 20 M⊙. Then, the disc properties heavily depend on the physics included. In particular, the disc formed in the ideal and resistive runs show opposite properties in terms of plasma beta; that is, the ratio of thermal-to-magnetic pressures and of magnetic field topology. While the disc in the ideal case is dominated by the magnetic pressure and the toroidal magnetic fields, the one formed in the resistive runs is dominated by the thermal pressure and essentially has a vertical magnetic field in the inner regions (R < 100−200 au).
Conclusions. We find that magnetic processes dominate the early evolution of massive protostellar systems (M⋆ < 20 M⊙) and shapes the accretion and ejection as well as the disc formation. Ambipolar diffusion is mainly at work at disc scales and regulates its properties. We predict magnetic field’s topology within the disc and outflows, as well as disc masses and radii to be compared with observations. Lastly, our finding for the outflow and disc properties are reminiscent of the low-mass star formation framework, suggesting that accretion and ejection in young massive and low-mass protostars are regulated by the same physical processes in the early stages.
Key words: hydrodynamics / magnetohydrodynamics (MHD) / radiative transfer / stars: formation / methods: numerical / stars: massive
© B. Commerçon et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Massive stars dominate the energy input in the interstellar medium from birth to death. As such, their formation mechanism needs to be better understood in order to put constraints on their impact on star formation and galaxy evolution as a whole. It is currently accepted that massive stars form in giant molecular clouds, which exhibit turbulent motions and magnetic fields (e.g. Tan et al. 2014; Motte et al. 2018). However, the mechanisms by which massive stars achieve their mass in these giant, turbulent, and magnetised complexes remain poorly constrained. In particular, two major issues make it difficult to assemble a large reservoir of mass within a single massive star: the radiative pressure barrier and the initial fragmentation. Thanks to the formidable increase of observational capabilities, it is now possible to probe massive star forming regions with an unprecedented angular resolution corresponding to sub-50 au scales (e.g. Beuther et al. 2019; Maud et al. 2019). In parallel, heavy numerical developments are undertaken in order to accurately describe the physics of star formation in numerical models (see Teyssier & Commerçon 2019, for a recent review).
A number of observational studies focus on the fragmentation of massive cores, which are thought to be the progenitors of massive stars (e.g. Bontemps et al. 2010; Palau et al. 2013; Zhang et al. 2015; Fontani et al. 2016; Csengeri et al. 2017; Figueira et al. 2018; Sanhueza et al. 2019; Sanna et al. 2019a). There is no clear consensus on which physical process regulates the fragmentation level. There is, however, a trend in which massive dense cores are not as fragmented as expected (Wang et al. 2014; Csengeri et al. 2017; Nony et al. 2018) and magnetic fields have an important role in fragmentation (Li et al. 2015; Dall’Olio et al. 2019). Using state-of-the-art multi-dimensional and multi-physics numerical models, it has also been demonstrated that magnetic fields, radiative transfer, and turbulence all play role in setting the fragmentation level of massive star forming regions (Hennebelle et al. 2011; Commerçon et al. 2011b; Myers et al. 2013; Fontani et al. 2018). It is worth noting that both radiative feedback and magnetic fields can be very efficient in preventing massive dense cores from fragmenting heavily (Commerçon et al. 2011b; Myers et al. 2013).
At core scales, important efforts have been made to investigate the mechanisms which regulate mass accretion and ejection in the vicinity of massive star forming regions. There is growing evidence that massive stars form in a similar way to low-mass stars (e.g. Zhang et al. 2019a; Beltrán et al. 2014; Tan et al. 2016) and that discs and outflows are formed in the early stages (Duarte-Cabral et al. 2013; Tan et al. 2016; Yang et al. 2018; Zhang et al. 2019a). In addition, an increasing number of studies report the detection of an hourglass magnetic field at massive core scales (Girart et al. 2009; Qiu et al. 2014; Ching et al. 2016; Beltrán et al. 2019). In particular, Qiu et al. (2014) estimated a magnetic field strength of ~ 1.1 mG, resulting in a mass-to-magnetic flux ratio of 1.4 times the critical value. A milliGauss magnetic field amplitude is consistent with estimates in other massive star forming regions (e.g. Girart et al. 2013; Dall’Olio et al. 2019; Beltrán et al. 2019). Last but not least, Girart et al. (2009) and Qiu et al. (2014) concluded that their observations are consistent with magnetic braking; that is, a magnetically regulated collapse.
The first direct observation of a disc around a young massive protostar was reported in Kraus et al. (2010), where they find evidence in IRAS 13481-6124 of a very compact disc (< 20 au) at the late stages; that is, after the main accretion phase. However, direct evidence of discs in young, deeply embedded sources is expected to be weak because of confusion with the surrounding envelope (Cesaroni et al. 2017). Girart et al. (2017, 2018) presented sub-arcsecond angular resolution observations with the Sub-millimetre Array (SMA) and the Atacama Large Millimetre Array (ALMA) interferometers of the B0-type protostar GGD27 MM1, which is powering the HH80-81 radio jet. Their observations clearly resolve a disc oriented perpendicularly to the radio jet, with a radius of about 300 au. Beuther et al. (2019) presented a sub-50 au scales observation of the hot core region G351.77-0.54 with ALMA. They did not report the presence of a large (R > 1000 au) disc. Additional, spatially resolved compact discs have also been reported in recent literature (Fernández-López et al. 2016; Motogi et al. 2019). Multi-dimensional numerical simulations have also investigated disc formation and evolution in massive dense core collapse, either in the hydrodynamical case (e.g. Yorke & Sonnhalter 2002; Klassen et al. 2016; Kuiper & Hosokawa 2018) or in the ideal magneto-hydrodynamics (MHD) case (e.g. Banerjee et al. 2006; Seifried et al. 2013; Myers et al. 2013; Gray et al. 2018). Pure hydrodynamical and ideal MHD models represent the two extreme limits of the coupling between the gas and magnetic fields. It is true that non-ideal coupling effects such as the Ohmic diffusion, the Hall effect, and the ambipolar diffusion are at play in the physical conditions typical of protostellar collapse (e.g. Marchand et al. 2016). Contrary to low-mass star formation (e.g Masson et al. 2016; Hennebelle et al. 2020b), the effect of non-ideal MHD has not been investigated extensively in the massive star formation framework (however, see Matsushita et al. 2017; Kölligan & Kuiper 2018).
In low-mass protostars, it is now accepted that the observed bipolar outflows and jets are launched via magneto-centrifugal processes (Frank et al. 2014; Li et al. 2014). Recently, Ching et al. (2016) reported SMA observations towards NGC 1333 IRAS 4A of CO polarisation and find evidence of helical magnetic fields in the outflow. Outflows and jets are also observed in high-mass star forming regions (Shepherd & Churchwell 1996; Zhang et al. 2001; Beuther et al. 2002; Duarte-Cabral et al. 2013; Maud et al. 2015; McLeod et al. 2018). There is observational evidence that these outflows and jets are linked with magnetic fields. First, synchrotron emission has been associated with jets in observations of massive protostellar sources (Carrasco-González et al. 2010; Beltrán et al. 2016; Sanna et al. 2019b; Zhang et al. 2019b). Second, observations of an alignment between outflows and the magnetic field direction inferred from spectral-line linear polarisation have also been reported in massive star forming regions (Cortes et al. 2006; Beuther et al. 2010; Girart et al. 2013). Importantly, in the high-mass regime, the protostellar luminosity becomes high enough to balance the gravity and prevent further accretion: the radiative pressure barrier. Multi-dimensional numerical models have shown that the radiative force may indeed accelerate the gas and also generate bipolar outflows that channel radiation to escape and allow accretion through the disc (Yorke & Sonnhalter 2002; Kuiper et al. 2012; Klassen et al. 2016) or via radiative Rayleigh-Taylor instabilities (Krumholz et al. 2007; Rosen et al. 2016). Using sub-grid models, Kuiper et al. (2015) included both the radiative feedback and protostellar outflow from massive stars and showed that protostellar outflows help to form more massive stars. Seifried et al. (2012) used ideal MHD and Matsushita et al. (2017) used resistive MHD to perform 3D collapse simulations of magnetised massive dense cores and reported outflow formation self-consistently driven by magneto centrifugal processes, but they neglected protostellar radiative feedback. There is no study to date that explores the combined effect of magnetic fields and protostellar radiative feedback on the launching of outflows in massive protostellar systems.
The aim of this paper is to lay the foundations of the combined effects of protostellar radiative feedback and of magnetic fields in the formation of the star-disc-outflow system in massive collapsing dense cores. This work is part of a more general framework of numericalexperiments, in which we increase, step-by-step, the complexity of the physics included. As is now widely done in the low-mass regime, we introduced resistive effects through ambipolar diffusion in order to take into account the non-perfect coupling of gas with magnetic fields. We also integrated the effect of protostellar radiative feedback using sub-grid pre-main-sequence (PMS) evolutionary tracks to compute the protostellar luminosity. We used 3D dynamical models of massive dense core protostellar collapse, gradually introducing more realistic physical processes (magnetic fields and ambipolar diffusion). In this study, we used a grey approximation for the protostellar irradiation, which is known to underestimate the radiative acceleration (e.g. Kuiper et al. 2010; Mignon-Risse et al. 2020). In Mignon-Risse et al. (2020), we presented a hybrid method built over the grey irradiation scheme that demonstrates good performance when estimating the radiative acceleration. First results, focusing on the interplay between turbulence, ambipolar diffusion, and accurate stellar irradiation are presented in a related study (Mignon-Risse et al. 2021b,a).
The paper is organised as follows. In Sect. 2, we detail our numerical method, setup, and initial conditions. We present our results in Sect. 3, giving particular focus to the outflows and disc properties. Section 4 is devoted to highlighting the role of ambipolar diffusion in the disc formation process and comparing with observational and other numerical works. We also discuss the limits of our work and propose possible future directions for study in Sect. 4. Section 5 concludes our work.
2 Methods and initial conditions
2.1 Radiation magneto-hydrodynamics model
Our numerical model integrates the equation of radiation-magneto-hydrodynamics (RMHD) and includes radiative protostellar feedback. In the following, we detail our numerical tool. We used the adaptive-mesh-refinement (AMR) code RAMSES (Teyssier 2002), which is based on a finite-volume, second-order Godunov scheme and a constrained transport algorithm for ideal magnetohydrodynamics (Fromang et al. 2006; Teyssier et al. 2006). The non-ideal MHD solver, including the effect of ambipolar diffusion and Ohmic diffusion as corrections of the electromagnetic force (EMF) at the cell edges is presented in Masson et al. (2012). In this study, we accounted only for the ambipolar diffusion in the non-ideal MHD runs. In addition, we used the radiation-hydrodynamics (RHD) solver presented in a series of papers (Commerçon et al. 2011a, 2014; González et al. 2015), which integrates the equation of RHD in the flux-limited diffusion approximation (FLD, e.g. Minerbo 1978; Levermore & Pomraning 1981). The full RMHD equations with all the radiative quantities estimated in the co-moving frame and under the grey approximation (radiative quantities are integrated over the entire frequency spectrum) read as follows:
![\begin{equation*} \begin{array}{llll} \partial_t \rho + \nabla\cdot \left[\rho\textbf{u} \right] &\,{=}\,0, \\ \partial_t \rho \textbf{u} + \nabla \cdot\left[\rho \textbf{u}\otimes \textbf{u} + P \mathbb{I} \right]&\,{=}\,- \lambda\nabla E_{\textrm{r}} +\textbf{F}_{\textrm{L}} -\rho\nabla\phi,\\ \partial_t E_{\textrm{T}} + \nabla\cdot \left[\textbf{u}\left(E_{\textrm{T}} + P + \frac{B^2}{2} \right) \right.& \\ \hspace{30pt}\left.-\left(\textbf{u}\cdot\textbf{B}\right)\textbf{B}-\textbf{E}_{\textrm{AD}}\,{\times}\,\textbf{B}\right] &\,{=}\, - \mathbb{P}_{\textrm{r}}\nabla:\textbf{u} - \lambda \textbf{u} \nabla E_{\textrm{r}} \\ & \hspace{9pt} + \nabla \cdot\left(\frac{c\lambda}{\rho \kappa_{\textrm{R}}} \nabla E_{\textrm{r}}\right)+L_{\star}\\&\hspace{9pt} -\rho\textbf{u}\cdot\nabla\phi, \\ \partial_t E_{\textrm{r}} + \nabla\cdot \left[\textbf{u}E_{\textrm{r}}\right] &\,{=}\, - \mathbb{P}_{\textrm{r}}\nabla:\textbf{u} + \nabla \cdot\left(\frac{c\lambda}{\rho \kappa_{\textrm{R}}} \nabla E_{\textrm{r}}\right) \\ & \hspace{9pt} + \kappa_{\textrm{P}}\rho c(a_{\textrm{R}}T^4 - E_{\textrm{r}})\\ &\hspace{9pt} +L_{\star},\\ \partial_t \textbf{B} - \nabla\,{\times}\,\left[\textbf{u}\,{\times}\,\textbf{B} +\textbf{E}_{\textrm{AD}}\right]&\,{=}\,0,\\ \nabla\cdot\textbf{B}&\,{=}\,0,\\ \Delta\phi &\,{=}\,4\pi G \rho, \end{array} \end{equation*}](/articles/aa/full_html/2022/02/aa37479-20/aa37479-20-eq1.png) (1)
(1)
where ρ is the material density, u is the velocity, P is the thermal pressure, λ is the radiative flux limiter, Er is the radiative energy, FL = (∇ × B) × B is the Lorentz force, ϕ is the gravitational potential, ET the total energy ET = ρϵ + 1∕2ρu2 + 1∕2B2 + Er (ϵ is the gas internal specific energy), B is the magnetic field, EAD is the ambipolar EMF, κP is the Planck mean opacity, κR is the Rosseland mean opacity, 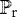 is the radiation pressure, L⋆ the luminosity source (i.e. protostar luminosity), and T is the gas temperature. The system is closed using the perfect gas relation, P = ρkBT∕(μgasmH), with μgas the gas mean molecular weight.
is the radiation pressure, L⋆ the luminosity source (i.e. protostar luminosity), and T is the gas temperature. The system is closed using the perfect gas relation, P = ρkBT∕(μgasmH), with μgas the gas mean molecular weight.
The ambipolar EMF is given by
![\begin{equation*} \textbf{E}_{\textrm{AD}}\,{=}\,\frac{\eta_{\textrm{AD}}}{B^2}\left[\left(\nabla\,{\times}\,\textbf{B}\right) \,{\times}\, \textbf{B} \right] \,{\times}\, \textbf{B}, \end{equation*}](/articles/aa/full_html/2022/02/aa37479-20/aa37479-20-eq3.png) (2)
(2)
where ηAD is the ambipolar diffusion resistivity, calculated as a function of the density, temperature, and magnetic field amplitude. We used the abundances from the equilibrium chemistry code described in Marchand et al. (2016), which depends on the density and temperature. As noted by Shu (1992) and Masson et al. (2012), the ambipolar diffusion, that is, the neutral-ion friction, results in a heat source term in the gas internal energy equation:
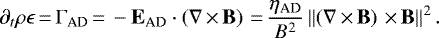 (3)
(3)
For the radiative transfer, we used the grey Rosseland and Planck opacities tabulated in Vaytet et al. (2013), who compiled the dust opacityfrom Semenov et al. (2003), the molecular gas opacity form Ferguson et al. (2005), and the atomic gas opacity from Badnell et al. (2005).
2.2 Initial conditions
Our initial conditions are similar to the ones found in previous works focusing on isolated massive star formation (e.g. Krumholz et al. 2009; Kuiper et al. 2010; Klassen et al. 2016). We considered 100 M⊙ spherical dense cores with a uniform temperature of 20 K. The initial density profile is centrally condensed and follows 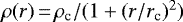 , where the central density is ρc ~ 7.7 × 10−18 g cm−3 (corresponding to a freefall time of 24 kyr) and the density contrast between the centre and the border of the core equals 100. The extent of the central plateau is rc = 0.02 pc and the initial core radius is r0 = 0.2 pc. We used an ideal gas equation of state, with the mean molecular weight μgas = 2.31 and the specific heat ratio γ = 5∕3. This corresponds to a ratio of thermal to gravitational energies of 6%. We imposed an initial solid-body rotation along the x-axis with angular frequency (respective ratio of rotational-to-gravitational energies β) Ωs ≈ 9.5 × 10−15 Hz (β ≈ 0.01, slow rotation), and Ωf ≈ 2.1 × 10−14 Hz (β ≈ 0.05, fast rotation). We deliberately chose a low angular velocity to foster on the star-disc-outflow system formation without undergoing heavy fragmentation in the process. We did not apply any initial perturbation in the different RMHD variables.
, where the central density is ρc ~ 7.7 × 10−18 g cm−3 (corresponding to a freefall time of 24 kyr) and the density contrast between the centre and the border of the core equals 100. The extent of the central plateau is rc = 0.02 pc and the initial core radius is r0 = 0.2 pc. We used an ideal gas equation of state, with the mean molecular weight μgas = 2.31 and the specific heat ratio γ = 5∕3. This corresponds to a ratio of thermal to gravitational energies of 6%. We imposed an initial solid-body rotation along the x-axis with angular frequency (respective ratio of rotational-to-gravitational energies β) Ωs ≈ 9.5 × 10−15 Hz (β ≈ 0.01, slow rotation), and Ωf ≈ 2.1 × 10−14 Hz (β ≈ 0.05, fast rotation). We deliberately chose a low angular velocity to foster on the star-disc-outflow system formation without undergoing heavy fragmentation in the process. We did not apply any initial perturbation in the different RMHD variables.
The magnetic field is initially aligned with the rotation axis and is uniform through the cloud. Its strength is given by the mass-to-flux parameter μ, which represents the ratio between the mass-to-flux calculated at the border of the core 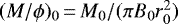 and the critical mass-to-flux ratio
and the critical mass-to-flux ratio 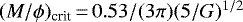 (Mouschovias & Spitzer 1976). This choice of initial magnetic configuration makes the mass-to-flux ratio μ not uniform with radius, scaling as μ ~ 1∕R, up to a value μc of 10 times the initial one in the central plateau region, which represents a relatively weak magnetisation (e.g. μc = 50 for μ = 5).
(Mouschovias & Spitzer 1976). This choice of initial magnetic configuration makes the mass-to-flux ratio μ not uniform with radius, scaling as μ ~ 1∕R, up to a value μc of 10 times the initial one in the central plateau region, which represents a relatively weak magnetisation (e.g. μc = 50 for μ = 5).
2.3 Numerical resolution and sink particles
The simulation box is four times larger than the initial core radius (~ 0.8 pc). The coarser grid resolution is 643, and we allowed for nine additional levels of refinement, which gives a minimum resolution of Δxmin = 5 au. The grid was refined using a Jeans length criterion with at least ten points per Jeans length. We used periodic boundary conditions1.
We used sink particles to describe the dynamics of the collapse below the maximum resolution. We employed the publiclyavailable implementation of sink particles in the RAMSES code (Bleuler & Teyssier 2014), with some modifications in the checks performed for their creation. We used the clump finder algorithm of Bleuler & Teyssier (2014) for the sink creation site identification, but we did not apply their virial check. Instead, we performed two alternative checks that are used in other popular implementations of sink particles (e.g. Bate et al. 1995; Federrath et al. 2010): the bound state check, that is, the total energy in the clump is negative (Epot + Ekin + Etherm + Emag + Erad < 0); and the Jeans instability check, that is, the mass inside the clump should exceed the local Jeans mass (Epot + 2Etherm < 0). We exploited a threshold density of 1010 cm−3 for the clump identification.
The accretion radius racc was set to 4Δxmin ~ 20 au, and we imposed that the sink accretion volume sit at the maximum level of refinement. We did not allow sink particle creation if the density peak of the clump finder algorithm fell within the sink accretion radius of another sink. The sink particles with mass < 1 M⊙ were evolved using the particle-mesh Cloud-in-Cell method of RAMSES (Teyssier 2002), while the trajectory of sink particles more massive than 1 M⊙ were computed using direct force summation (both for the gas-sink and the sink-sink interactions Bleuler & Teyssier 2014).
For the sink accretion, we used the threshold accretion scheme (Federrath et al. 2010; Bleuler & Teyssier 2014). We scanned the cells whose centre lies within racc and checked for Jeans unstable gas by computing the Jeans density in each cell ρsink. The mass accreted by the sink particles from the cell was set to
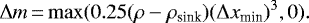 (4)
(4)
It is not clear at this stage whether sink particles should accrete angular momentum or not. The subsequent evolution of the angular momentum transport inside the sink accretion radius cannot be followed in our models. We thus assume another sub-grid prescription for angular momentum. We define facc,mom as the fraction of angular momentum accreted by the sink. If facc,mom = 1, all the angular momentum is accreted by the sink particle. On the contrary, all the angular momentum stays on the grid cell for facc,mom = 0. We chose facc,mom = 1 as the fiducial value in this study, and we present a comparison between these two extreme cases in Appendix B. Last but not least, magnetic fields are not accreted with the gas by the sink particle.
Last, we forced sink merging when two sinks sit in a common accretion volume, without any additional check other than the proximity criterion. This aggressive merging procedure favours the formation of more massive stars.
2.4 Sub-grid model for radiative feedback
The protostellar luminosity sources L⋆ are associated with the evolution of the sink particles. We used the PMS evolution models of Kuiper & Yorke (2013) to compute the protostellar properties (luminosity, radius). The PMS tracks were obtained with the STELLAR evolution code (Bodenheimer et al. 2007; Yorke & Bodenheimer 2008) and tabulated as a function of the stellar mass and the mass accretion rate.
We assume that each sink particle represents a single protostar, and that all the mass accreted by the sink particle goes into the stellar content (most favourable case for the radiative feedback), i.e. Msink = M⋆. In this work, we only include the effect of the protostellar internal luminosity and we neglect the accretion luminosity. This choice is matter of debate of course, but since we are interested in the regime where the stellar mass becomes larger than 8 M⊙, it is fair to include only the internal luminosity that dominates in this mass range (e.g. Hosokawa & Omukai 2009). We discuss this limitation in Sect. 4.5 and postpone the exploration of the accretion luminosity influence to future studies. In order to obtain the internal luminosity from the PMS track tables, we did not account for the instantaneous accretion rate, but we used the mean accretion rate defined as Ṁmean = M⋆∕t⋆, where M⋆ and t⋆ are the mass and the age of the protostar. Kuiper & Yorke (2013) showed that using the mean accretion rate instead of the instantaneous one provides a reasonable estimate of the protostar’s influence on their environment. The energy input L⋆ Δt is then spread uniformly over the sink accretion volume at each finer level timestep. We tested the use of weighting functions for the energy input as in Krumholz et al. (2007), and we found no significant differences in the results compared with the uniform input.
2.5 Disc and outflow identification
In this paper, we focus on the results after the first sink particle creation. We identify the disc and outflow regions given the global flow properties and the mass and position of the sink particles. We observe in the simulations that sink particles can move back and forth around the centre of mass of the star-disc-outflow system (~ 10 au). These little oscillations cause problems when estimating the velocity in the frame of the sink particles. We therefore neglected the sink velocityin our analysis. For the disc identification, we computed the angular momentum vector direction within a sphere of 100 au around the sink particle position. Then, we estimated the velocity of the gas in the cylindrical coordinate system where the z-axis is aligned along the angular momentum vector. We applied the criteria derived in Joos et al. (2012) to select the cells that constitute the rotationally supported disc. We briefly recall the criteria: the density verifies n > 109 cm−3; the gas is rotationally supported, vϕ > fthresvr; the gas is close to hydrostatic equilibrium, vϕ > fthresvz; the rotation support is larger than the thermal support, 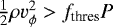 .
.
We used fthres = 2. We note that we did not use the connectivity criterion of Joos et al. (2012), since we find from experience that it does not affect the mass of disc (and thus the radius in which most of the mass is contained). The disc radius is computed as the radius at which 90% of the disc mass is contained. We then identified the outflow region as follows: we computed the radial velocity relative to the sink particle position and accounted for the cells with positive radial velocity vr larger than the escape velocity 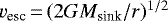 , where r is the distance between the cell and the sink particle position.
, where r is the distance between the cell and the sink particle position.
2.6 Simulation parameters
The five models we present in the main part of this paper are summarised in Table 1. Our fiducial run (MU5AD) includes magnetic fields with a moderate intensity (μ = 5) and ambipolar diffusion, as well as a slow initial rotation. We then compare this fiducial case with the results obtained with a hydrodynamical model (HYDRO), a magnetised model with ideal MHD (MU5I), a strongly magnetised (μ = 2) model with ambipolar diffusion (MU2AD), and a magnetised model with ambipolar diffusion and a fast initial rotation (MU5ADf). The HYDRO model (without magnetic fields) is very similar to what has been done in previous studies (e.g. Krumholz et al. 2009; Klassen et al. 2016) and served as a reference model to compare with the literature.
In Appendix A, we also present a numerical convergence study based on our fiducial model. In Appendix B we give a comparison of our fiducial model with a sub-grid accretion scheme in which all the angular momentum of the gas accreted is transferred to the sink particle facc,mom = 1.
Summary of the simulation parameters (the star labels of our fiducial model).
3 Results
3.1 Overview
Table 1 reports the time of formation of the first sink particle, t0, at which we renormalised the time evolution afterwards. Given our strongly peaked initial density profile and low initial rotation level, all times t0 are very close together and close to the initial central density free-fall time. Figure 1 shows edge-on and face-up density maps of the five runs listed in Table 1 at two different times, when the mass of the central sink particle is 5 M⊙ and 10 M⊙.
At the beginning of the simulations, the gas collapses toward the centre, until the creation of a sink particle. Around the sink, a rotating disc builds up in the plane perpendicular to the initial solid-body rotation x-axis in all models. The largest discs are formed in the HYDRO and MU5ADf runs. The density in the disc mid-plane is also largest in the MU5I and MU5ADf runs at late times. Outflows are generated in all the magnetised models and propagate along the rotation axis. The largest outflow velocities are found in the runs with ambipolar diffusion where we report maximum velocities of 25–30 km s−1 on 5000 au scales (for a sink mass of Msink = 10 M⊙). We observe that none of our models exhibit strong fragmentation, and only the HYDRO model shows secondary sink formation, but these secondary sinks are rapidly merged with the central one.
Figure 2 displays histograms of density-temperature and density-magnetic field for the five runs when the central sink mass is 10 M⊙. All the temperature-density plots look similar, with a central temperature > 1000 K. One can notice that in the ideal-MHD run, the magnetic field amplitude increases up to value larger than 1 G at high densities as the gas is collapsing as a consequence of the flux-frozen approximation. On the contrary, in all the runs with non-ideal MHD, the magnetic fields stop amplifying at high density. This is due to the strong ambipolar diffusion in the central regions of the collapsing cores. It then reaches a maximum value < 1 G with a plateau visible in the B-ρ histograms. This result is essentially similar to the one observed in the low-mass star formation regime (Masson et al. 2016; Hennebelle et al. 2020b) as well as in similar experiments with initial turbulence (Mignon-Risse et al. 2021b). Importantly, the efficient ambipolar diffusion makes it possible to redistribute magnetic fields in the low-density medium. The region with densities of less than 10−15 g cm−3, that is, the inner envelop, exhibits larger magnetisation in the models with ambipolar diffusion than in the ideal MHD case. In addition, we observe high temperature (≃1000 K) and low density (≃10−18 g cm−3) regions in the runs with ambipolar diffusion. This corresponds to material within the outflow, close to the protostars (< 1000 au), where the current is strong. As a consequence, the heating by ambipolar diffusion (see Eq. (3)) is strong in these regions.
3.2 Mass evolution
Table 2 reports the mass of the sink, disc and outflow in the five runs at two different times, when the sink mass equals 5 and 10 M⊙. First, the sink mass-accretion rate is lowest for the MU5ADf run, but all sink accretion rates are similar within a factor less than 4. For the outflow, the mass ejection rate is the highest in the resistive runs and negligible inthe HYDRO case. Interestingly, the outflow in the ideal MHD case MU5I stalls at about 1 M⊙. In the resistive runs, the mass ejection rate also correlates well with the sink accretion rate, within less than a factor 3. A significant fraction of the mass (>25% in comparison with the accreted mass onto the sink particle) is thus expelled in the resistive runs. On the contrary, the disc grows faster in mass in the HYDRO case.
Figure 3 shows the mass evolution as a function of time of the different components (sink, disc, and outflow) for the HYDRO, MU5I, MU2I, MU5AD, and MU5ADf models. At first glance, we clearly observe a difference between the HYDRO case and the magnetised ones. The HYDRO run shows the largest sink and disc mass growth and forms an outflow with a negligible mass (we do not report it in Table 2). In addition, the late evolution of the HYDRO central sink mass shows accretion burst events, which are due to mergers with secondary sink particles. The least accreting sink is formed in the MU5ADf. Interestingly, this corresponds to the magnetised model with the largest massgrowth of the disc and of the outflow. Then, the resistive runs have outflows of mass larger than 1 M⊙, with the largest outflow rate measured in the models with a weak initial magnetic field (μ = 5). The outflowin the ideal MHD case MU5I stops being fed and vanishes after about 30 kyr (Msink ≃ 10 M⊙), before it starts again when the sink particle has a mass > 15 M⊙.
From the runs with ambipolar diffusion, we see on one hand that the time evolution of the sink and disc mass is more dependent on the initial rotation level than on the initial magnetisation. On the other hand, the outflow mass is more dependent on the initial magnetisation. We also do not report any strong universal correlation between the outflow mass and the total mass of the sink and the disc.
Overall,while the sink mass in all models and outflow mass in the resistive ones only steadily increase as a function of time, the disc mass is not increasing as fast. On the contrary, it shows accretion and ejection phases with time, indicating that the material accreted by the disc is transiting through it to be either ejected or accreted by the sink particle.
Figure 4 shows the evolution of the internal luminosity given by the PMS evolution sub-grid model. First, the luminosity for a given protostellar mass is very similar in all models. This is due to the fact that we do not keep track of the temporal history in the protostellar evolution, so that all models fall on a similar track. Nevertheless, since the accretion rate onto the protostar varies between the models, the time evolution shows variations of about one order ofmagnitude at an age of 50 kyr, where the HYDRO (respectively MU5ADf) run exhibits the fastest (respectively slowest) increase. We thus expect the effect of the protostellar radiation to be delayed in the magnetised models.
We should at this point clarify that the mass evolution of the star-disc-outflow system is barely affected by the formation of secondary sink particles. Only the HYDRO run forms secondary sink particles. The first secondary sink is formed in the rotation plane (i.e. in the disc) at a distance of 100 au from the first sink, which mass is about 16.5 M⊙. It reaches a mass of about 0.7 M⊙ before being merged with the central one in less than 1 kyr, when their accretion radii overlap. In total, ten secondary sinks were also formed in the disc plane at distances of <500 au. Nine sink particles quickly merged with the most massive one, migrating inward through the disc in < 10 kyr. The maximum mass of the secondary sink particles before merging is 2.5 M⊙. We note that a small sink particle, of mass ≃ 0.01 M⊙ is ejected from the disc. However, given the tiny mass of the latter, we did not consider it for further analysis. Only one secondary sink survives, and forms binary system with the primary one, with separation ≃ 460 au and masses of 26.8 and 6.8 M⊙ at the end of the simulation t = t0 + 69 kyr.
 |
Fig. 1 Density maps in the plane of the disc and perpendicular to it for the models HYDRO (top), MU5I (second line), MU2AD (third line), MU5AD (fourth line), and MU5ADf (bottom). Two different times are represented: M⋆ = 5 M⊙ (left) and M⋆ = 10 M⊙ (right). The mass M⋆ gives the total mass converted into sink particles at each snapshot. The arrows represent the velocity vectors in the plane. |
 |
Fig. 2 Density-temperature (top panels) and density-magnetic field amplitude (bottom panels) histograms for the models HYDRO, MU5I, MU2AD, MU5AD, and MU5ADf (from left to right) when the central sink mass is 10 M⊙. The colour-coding indicates the mass. |
Summary of the different component masses.
 |
Fig. 3 Mass evolution of the sink (top left), disc (top right), and outflow (bottom left) as a function of time after sink creation, and of the outflow as a function of the total disc+sink mass (bottom right). |
 |
Fig. 4 Evolution of protostellar internal luminosity as a function of the protostellar mass (left) and of the time after sink formation (right). |
3.3 Outflows
In this section, we examine the properties of the outflows, as well as the physical mechanisms responsible of the launching. First, we look at the global morphology of the outflows. Then, we study their physical properties.
3.3.1 Morphology
All models have outflows. The weakest outflow is found in the HYDRO model as shown in Fig. 3. The left panel of Fig. 5 shows a volume rendering of the outflowing gas in this case when the sink mass is 20 M⊙ and the outflow mass is ≃ 0.01 M⊙. The outflow is made of radiative bubbles, as observed in previous works by different authors (e.g. Krumholz et al. 2009; Klassen et al. 2016). Indeed, in the HYDRO case, there is no other force than the one provided by the protostellar luminosity that can accelerate the gas against gravitational pull. We note that these bubbles are fragmented by episodic ejections that result from the development of non-axisymmetric features in the rotating region. Since we do not account for the accretion luminosity in our sub-grid radiative feedback module, the episodic events are essentially due to the infalling gas dynamic. Interestingly, the outflow extends more in the radial direction (about 2000 au) than in the vertical one (about 1000 au maximum). By measuring the different components of the gravitational acceleration, it turns out that it is highest in the vertical direction since the disc mass contributes significantly to the gravitational potential. As a consequence, the radiative acceleration, which is essentially isotropic close to the protostar, isthe most efficient in the regions of low gravitational acceleration (the radial direction). In addition, the radiation escapes most favourably in the low optical depth envelope, that is, just above the disc plane. The anisotropic expansion of the radiative bubbles is thus a consequence of the anisotropic accretion flow on the star-disc system.
The right panel of Fig. 5 shows the outflow in the fiducial MU5AD case when the sink mass is 15 M⊙ and the outflow mass is about 6 M⊙. The morphology is completely different than in the HYDRO case with an outflow extending up to 80 000 au in the vertical direction with a maximum velocity more than three times higher. The introduction of the magnetic field drastically changes the outflow morphology.
 |
Fig. 5 Volume rendering of the outflow in the HYDRO run at the end of the simulation (left) and in the MU5AD run when the sink mass is 15 M⊙ (right). The colour-coding represents the radial velocity and is given in km s−1. In the left panel (HYDRO), the region represents a box of ≃40003 au, while the vertical extent is of about 75 000 au in the right panel (MU5AD run). |
3.3.2 Outflow origin
The morphology of the outflows we report above suggests that different mechanisms are at play. In the HYDRO case, as previously mentioned, there is no doubt that the outflow material is accelerated by the radiative force. We note that the outflow appears about 40 kyr after the sink formation, when the sink mass is almost 20 M⊙. The outflow hardly develops and remains with a limited extent of about 1000 au in the vertical direction.
Figure 6 shows maps of the density and of the force ratio in the outflows for the MU5AD run when the sink mass is 5 M⊙ (top) and 15 M⊙ (bottom). The outflow remains similar in shape, although it gets broader with time. In the entire outflow region, the Lorentz force dominates the gravitational one by more than one order of magnitude. Closer to the sink particle up to a distance of 2000 au, the radiative force also dominates over the gravitational one, the extent of this region increasing with the stellar mass. The radiative and Lorentz forces thus both contribute to the outflow launching. When comparing the Lorentz and radiative forces (right column), the Lorentz force clearly dominates the force balance everywhere and is thus the main contributor to the acceleration of the outflowing gas. The outflow in the MU5AD case is thus of magnetic origin. We nevertheless note that caution should be taken since the grey approximation underestimates the magnitude of the radiative force, the latter being larger if one accounts for frequency-dependent irradiation (e.g. Kuiper et al. 2010; Mignon-Risse et al. 2020). We discuss this limitation in Sect. 4.5.
At a stellar mass of 15 M⊙, the radiative acceleration is greater than the gravitational one to a larger extent in the MU5AD case than in the HYDRO case. This is due to the low-density cavity created by the magnetic outflow in the vertical direction, which facilitates the radiation escape in a low optical depth region. In the HYDRO case, the density is too high because of the collapsing envelope, and the radiation cannot accelerate the gas sufficiently to escape.
Figure 7 illustrates the magnetically driven origin of the outflow in the MU5AD run when the sink mass is 15 M⊙. The Alfvén velocity and magnetic field topology are shown in the left panels, and plasma β = P∕Pmag and velocity in the right panels. The toroidal component of the magnetic field clearly dominates in the outflow region, which is characteristic of self-collimated magnetically driven outflow. Correspondingly, the outflow region is dominated by the magnetic pressure with β <1. We observe the same features in the other runs with ambipolar diffusion (MU2AD, and MU5ADf) throughout their evolution after the launching of the outflow. A detailed analysis on the different MHD mechanisms at play in outflow launching (magnetic pressure versus magneto-centrifugal acceleration) goes beyond the scope of the present study. We invite the reader to refer to Mignon-Risse et al. (2021a) for a dedicated study on the outflow acceleration in similar models including ambipolar diffusion and turbulence.
In the ideal MHD MU5I run, we already noted in Sect. 3.2 that the outflow almost disappears when the sink mass is 10 M⊙. The outflow mass starts decreasing at mass ≃ 4 M⊙. Before this, the outflow is very similar to the one in the ambipolar diffusion case, except that the magnetic field amplitude is larger in thecentral region because of the magnetic field amplification resulting from the ideal MHD approximation. We also note that in this case, the outflow is launched at the same time that the sink particle forms, and as a consequencethe outflow is broader and has a larger extent compared to the ambipolar diffusion runs. At a mass > 4 M⊙, the PMS luminosity strongly increases (L > 103L⊙), as can be noted from Fig. 4, which causes a significant increase of the thermal pressure in the sink particle vicinity. This large thermal pressure variation, combined with the large magnetic pressure resulting form the ideal MHD approximation, results in a destabilisation of the central region and in a kick of the central sink particle as observed, for instance, in numerical works reporting interchange instability (e.g. Zhao et al. 2011). As a consequence, the magnetic structure of the outflow base is disrupted and the MHD driving of the outflow stops. This behaviour is not observed in the runs with ambipolar diffusion, since the magnetic field amplification is prevented in the central regions (see Fig. 2). In addition, the material at the outflow base is preheated by the friction provided by the strong ambipolar diffusion heating. We note that the outflow restarts in the MU5I run when the central sink mass exceeds 15 M⊙. As can be seen from Fig. 3, the outflow mass loading is very efficient at this stage in the MU5I model. Indeed, both the radiative and the Lorentz force accelerations are much larger than at earlier times and participate in the launching of the outflow.
To summarise, the outflow formation and evolution completely change when magnetic fields are introduced in the models. We note that ambipolar diffusion stabilises the outflow driving at early stages when the sink mass is less than 20 M⊙. A more detailed analysis of the outflow launching and structure is provided in the follow-up study, Mignon-Risse et al. (2021a).
 |
Fig. 6 Density and force balance in the outflows for the MU5AD run when the sink mass is 5 M⊙ (top) and 15 M⊙ (bottom). Left panels: density cuts in the xz-plane within the outflow. Three other panels: maps of the ratios between the gravitational, the Lorentz, and the radiative forces. The colour maps are in logarithmic scale and the force ratio colour map is limited to the range [−1, 1] for plot readability, but its value can exceed these values. The bottom row is zoomed in the inner 10 000 au region. |
 |
Fig. 7 Magnetic field topology and plasma β = P∕Pmag in the xz-plane in the MU5AD run, when the sink mass is 15 M⊙. Left panels: amplitude of the Alfvén velocity (blue colours) and the segments show the magnetic fields direction in the xz-plane. The colour-coding represents the ratio between the toroidal component of the magnetic fields over the total magnetic fields. Yellow-to-white segments exhibit strong toroidal fields with Bϕ ∕B > 0.3. Right panels: maps of the plasma β = P∕Pmag with velocity vectors overplotted. The red regions are dominated by the thermal pressure, while the blue ones are dominated by the magnetic pressure. |
 |
Fig. 8 Density maps perpendicular to the disc plane (top) and in the disc plane (bottom) when the sink mass is ≈ 10 M⊙ for the runs HYDRO, MU5I, MU2AD, MU5AD, and MU5ADf, from left to right. The vectors indicate the gas velocity. Only the material of the disc is plotted. |
3.4 Properties of the disc
3.4.1 Disc size
Figure 8 shows density maps of the disc material in the equatorial plane and in the perpendicular direction in the HYDRO, MU5I, MU2AD, MU5AD, and MU5ADf runs when the sink mass is 10 M⊙. The disc formed in the HYDRO run has a radius of about 170 au and a mass of 7.2 M⊙. The disc develops spiral arms which are a sign of instability, but the disc does not fragment. In the MU5I run, the disc is more extended with a radius of about 220 au and a mass of 3.5 M⊙. The disc is also puffier, with a vertical height of about 100 au. The disc does not develop strong spiral arms in this case, and it does not experience fragmentation. The discs formed in the MU5AD and MU2AD runs are very similar. First, they are much smaller, with a radius below 100 au (98 and 73 au, respectively), and less massive (3.3 and 2.4 M⊙, respectively). Interestingly, the disc radius is smaller in the MU5AD run than in the MU5I one, whereas we would expect the ideal MHD framework to provide a more efficient magnetic braking as it is widely observed in low-mass star formation (see below). Last, the disc in the MU5ADf case is the largest one, but its material remains at a low density compared to the HYDRO case. It exhibits a spiral arm at large radii, but it does not fragment.
Figure 9 shows the time evolution of the disc radius for the same models as in Fig. 8. The MU5AD and MU2AD runs show a very similar time evolution for the disc size, increasing slowly with time. The disc radius in the HYDRO case increases the most, to reach about 800 au at the end of the simulation. The disc exhibits periods of expansion and contraction of a few thousand years while globally expanding. This succession of expansion and contraction events is due to the apparition of prominent spiral arms (see below). In the MU5ADf case, the disc increases rapidly and is largest when the sink mass is 10 M⊙. As previously noted, even if the disc is large in radius, its density is low at large radii and its mass is comparable to the one in run MU5AD. The disc in the MU5I run stops increasing at about 200 au at time 30 kyr. It shrinks after 30 kyr, which roughly corresponds to the time when the destabilisation of the central part due to high magnetic and thermal pressure is the strongest (the MHD outflow stops being driven).
We now focus on a puzzling observation: the disc radius in the MU5I model is larger than the one in the MU5AD, whereas one would expect ideal MHD to enhance magnetic braking and prevent disc formation (for the low mass star case, see Hennebelle & Fromang 2008). Firstly, we stress that given our initial conditions, the magnetisation corresponds to a weak field case (μc = 50 for the MU5 runs). It is thus expected with such low magnetisation that discs form even in the ideal MHD limit (Commerçon et al. 2010; Seifried et al. 2012). Initially, for sink mass < 5 M⊙, we note that the discs are comparable in size whatever the MHD framework. Then, the disc is larger in the MU5I case and is only a factor less than 2 larger than the MU5AD case, with a maximum difference around 30 kyr. Secondly, we compare the efficiency of the magnetic braking in the envelope for the four magnetised models. We measured that magnetic braking is (1) the main angular momentum transport mechanism in the envelope, and (2) of the same order of magnitude in all models (not shown here for readability). The surrounding of the disc is highly ionised so that magnetic braking is efficient in the envelope even in the resistive case (for the low mass case, see Lee et al. 2021). The magnetic field amplitude measured in Fig. 2 is indeed of the same order in the envelope close to the disc in all models (density close to 10−15 g cm−3). Instead, we find that the amount of angular momentum carried out by the outflow material varies a lot if ambipolar diffusion is taken into account. Figure 10 shows the evolution of the angular momentum contained in the disc and in the outflow as a function of the central sink particle mass. The MU5ADf exhibits the highest angular momentum since it is the model with a higher initial rotation level. The disc angular momentum in the three other models is similar within less than one order of magnitude. On the contrary, the outflow carries angular momentum very differently depending on the MHD approximation. In the resistive case, the angular momentum in the outflow increases continuously with the central mass. In the MU5I case, the amount of angular momentum follows what we previously observed for the outflow driving. It first increases as soon as the outflow is launched, but it then decreases when the sink mass exceeds ≃ 8 M⊙. It starts increasing again at central masses > 15 M⊙ when the outflow is driven again. In addition, if we focus on the ratio between the outflow and the disc angular momentum, we see that it is smallest for MU5I. As the outflow is driven mainly on disc scales, it indicates that the outflow is less efficient extracting angular momentum from the disc in the MU5I case. Since the magnetic braking on the envelope is similar in all models, the angular momentum left in the disc is largest in the MU5I case, and this explains why the disc grows faster in this case. Last, we also note that the disc is more diluted in the MU5I case, while the mass is similar (for time less than 40 kyr). As a consequence, the disc grows.
 |
Fig. 9 Time evolution of disc radius for the HYDRO, MU5I, MU2AD, MU5AD, and MU5ADf runs. The symbols on the curves show the time at which the sink mass is 10 M⊙. |
 |
Fig. 10 Evolution of angular momentum contained in the disc (solid line) and in the outflow (dashed) in the magnetised models MU5I, MU2AD, MU5AD, and MU5ADf. The symbols on the curves show the time at which the sink mass is 10 M⊙. |
3.4.2 Disc stability
We already noted that the discs experience gravitational instability and spiral arm formation. A useful parameter to quantify the stability of the rotationally supported disc is the Toomre parameter (Toomre 1964), defined as
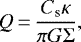 (5)
(5)
where Cs is the gas sound speed, Σ is the disc surface density (in g cm−2), and κ is the epicyclic frequency. For Keplerian discs, the epicyclic frequency κ is equal to the angular velocity Ω, defined as Ω = vKepl∕Rdisc, with 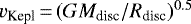 . In the next paragraphs and in Fig. 14, we show that the Keplerian rotation is a good approximation in the disc.
. In the next paragraphs and in Fig. 14, we show that the Keplerian rotation is a good approximation in the disc.
We compute the Toomre parameter locally in the rotation plane as Q(y, z) by averaging (mass-weighted) the sound speed and the angular velocity over the disc height as follows (assuming the rotation axis is the x-axis):
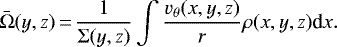 (6)
(6)
Figure 11 shows maps of the Toomre parameter Q in the rotation plane for the disc material when the central sink particle mass is 10 M⊙. The most unstable disc is found in the HYDRO case, with almost all the disc material exhibiting Q < 1. On the contrary, the disc in MU5I is stable everywhere. The extra support provided by magnetic fields makes the disc puffy, and the density is thus lower, as seen in Fig. 8. In the resistive runs, we see that the disc is stable in the outer part, while it is unstable in the inner part. The unstable regions correspond to the one where the temperature and plasma beta are the highest. Interestingly, we find that the size of the unstable region is very similar between all the resistive runs and is about 100 au. We advise caution with regard to the size of the unstable region in the disc since its absolute value can be affected by our choice to neglect the accretion luminosity and of the isotropic FLD irradiation (e.g. Mignon-Risse et al. 2020).
We note that we do not take into account the Alfvén velocity in the Toomre parameter estimate as in Kim & Ostriker (2001) or Vaytet et al. (2018). The disc in the cases with ambipolar diffusion or without magnetic fields are dominated by the thermal pressure, so we can neglect the magnetic support. On the contrary, we may nevertheless underestimate the Toomre parameter in the MU5I model where the Alfvén speed is found to be slightly higher than the sound speed (see Fig. 14). This would, however, not change our results since the disc in MU5I is already the most unstable.
3.4.3 Properties of the magnetised discs
In this section, we focus on the properties of the disc formed in the magnetised models. In particular, we discuss the fundamental differences between the ideal MHD and the resistive runs. Figure 12 shows the plasma β in the disc and close envelope when the sink mass is 10 M⊙ for the runs MU5I and MU5AD. In the ideal MHD run, all the disc region exhibits β <1; that is, it isdominated by the magnetic pressure. On the contrary, the disc in the MU5AD run shows β ≫ 1 in the inner disc region; that is, it is dominated by the thermal pressure by more than two orders of magnitude. The magnetic pressure is thus negligible when the disc evolves at early times if ambipolar diffusion is active. We note that similar results are found in thelow-mass star formation regime (Masson et al. 2016; Lam et al. 2019; Hennebelle et al. 2020b), with discs in the resistive models dominated by the thermal pressure. These results have been further confirmed in Mignon-Risse et al. (2021b), where we run similar models with ambipolar diffusion but account for initial turbulence and using a better irradiation scheme.
Figure 13 shows the mean density, the Toomre parameter, and the density-averaged plasma β radial profiles within the disc. We take the arithmetic mean weighted by the density as a function of the radius, averaging over azimuths and height. The density profiles are broadly similar in the models with ambipolar diffusion, with a trend of increasing density withtime in the models with slow rotation (MU2AD and MU5AD). The density profile is shallower in the MU5ADf run, the disc being more massive and also more extended. In the MU5I run, the disc inner density is lower than in the resistive runs, which is a consequence of the extra support provided by the toroidal magnetic pressure that lifts the gas in the vertical direction. We also note that the vertical column density is also lowest in the MU5I at radii < 100 au. The corresponding plasma β shows essentially opposite features between ideal and resistive MHD. In the resistive runs, the inner parts of the disc have β >1, as already mentioned. Interestingly, the largest β is found in the fast rotation model MU5ADf, probably a consequence of the smaller accretion rate of the sink and the disc which allows more time for ambipolar diffusion to operate before reaching 10 M⊙ (see Table 2). In the MU5I case, the disc is dominated by magnetic pressure for sink mass < 20 M⊙. The Toomre parameter also shows opposite behaviour. It is larger than 1 at all radii in the MU5I run. In the resistive runs, it is less than unity in the inner region of the disc and larger than unity in the external parts. The size of the unstable region tends to increase with time, in particular in the MU5AD case.
We now investigate the properties of the velocity and magnetic fields in the disc. To quantify the relative importance of ambipolar diffusion over other dynamical effects, we define the Elsasser number for ambipolar diffusion Am as the ratio between the rotation time Ω−1 and the ion-neutral collision time 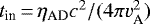 :
:
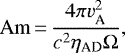 (7)
(7)
where Ω is the Keplerian rotation frequency.
Figure 14 represents the radial profiles within the disc of the mean velocities and magnetic field components for the MU5I, MU5AD, and MU5ADf runs. In addition, we show the mean Elsasser number profile in the magnetic component plots of the resistive runs (right axes). The averaging is done the same way as in Fig. 13. In all the models, the velocity is dominated by the azimuthal component, which matches the Keplerian velocity very well throughout the disc. The radial and vertical components are negligible. As expected, the β >1 (respectively < 1) regions exhibit Alfvén velocities smaller (respectively larger) than the sound speed. The magnetic field topology in the MU5I is clearly dominated by the toroidal component at all masses. On the contrary, the vertical component dominates in the inner part of the disc in the resistive runs. This result is in agreement with what we find in previous work in the context of a low-mass star (Masson et al. 2016; Hennebelle et al. 2016, 2020b) in the regions where ambipolar diffusion is very efficient at decoupling the gas from the magnetic fields. In the external parts of the disc, however, the toroidal component dominates. These regions correspond roughly to an Elsasser number Am > 1, meaning that ambipolar diffusion is not the dominant process in the external parts of the disc. One can define two disc radii here: the centrifugally supported structure, as defined in Sect. 2.5, and the radii at which ambipolar diffusion is not the dominant process, that is, where the magnetic fields start being wrapped up by rotational motions.
Figure 15 shows the distribution of the Toomre parameter as a function of the Elsasser number in the disc for the MU5AD run when the sink mass is 15 M⊙. We see a good correlation between the increasing Toomre parameter and the Elsasser number. In particular, most of the disc material that is Toomre-unstable exhibits Am < 1. On the contrary, the stable regions of the disc are mostly not dominated by ambipolar diffusion.
To summarise, we find that the magnetic field topology and amplitude change dramatically when resistive MHD is considered compared tothe ideal MHD case. Importantly, the inner region of the discs in the resistive models are gravitationally unstable and dominated by the thermal pressure and by resistive effects, with an essentially vertical magnetic field and an Elsasser number Am < 1. The outer parts of the disc are gravitationally stable and exhibit a toroidal magnetic field with a large magnetic pressure dominating over the thermal one (β > 1), and Am > 1.
 |
Fig. 11 Maps of Toomre parameter Q in the rotation plane when the sink mass is ≈10 M⊙ for the runs HYDRO, MU5I, MU2AD, MU5AD, and MU5ADf, from left to right. Only the disc material is used to compute the Toomre parameter as explained in the main text. The colour map indicates the logarithm of Q, with blue (respectively red) indicating Q < 1 (respectivelyQ > 1) regions. |
 |
Fig. 12 Plasma β for MU5I (left) and MU5AD (right) runs at the same times as in Fig. 8. Top (bottom) row: edge-on (face on) cut. Scales of β are logarithmic. |
 |
Fig. 13 Mean radial profiles of density (top), Toomre parameter (bottom, dotted line), and plasma β (bottom, solid line) at different times for the MU5I, MU2AD, MU5AD, and MU5ADf runs, from left to right. |
4 Discussion
In this section, we first discuss the mechanisms that regulate the disc formation and early evolution in the resistive runs. Then, we compare ourfindings to previous work in both the low- and high-mass star formation regime and detail the limits of our current study and numerical framework.
4.1 Is the disc size regulated by ambipolar diffusion?
The disc properties we have reported so far are dependent on the physics included and the initial level of rotation. While analytically estimating the centrifugal radius in the hydrodynamic case is straightforward, it becomes more heavily physics-dependent when magnetic fields are taken into account because of magnetic braking and magnetic diffusion processes. Hennebelle et al. (2016) propose a semi-analytical model to estimate the size of the disc in the case of a flow dominated by ambipolar diffusion.
The disc radius inferred by Hennebelle et al. (2016) corresponds to the radius at which the ambipolar diffusion starts to take over all other dynamical processes (induction, rotation, and freefall). It reads
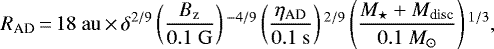 (8)
(8)
where Bz and ηAD are the vertical magnetic field amplitude and the ambipolar resistivity evaluated at the disc radius. The parameter δ corresponds to a normalisation parameter with respect to the singular isothermal sphere profile (SIS, Shu 1977). In Fig. 13, we estimate a difference between the measured density profiles and the SIS of roughly two orders of magnitude. Since the rotation and the magnetic pressure also participate in the establishment of the density profile (e.g. Hennebelle et al. 2004), we assume that δ is of the order of a few. For the sake of simplicity, we take δ = 1 hereafter since the dependency of the analytic estimate scales as δ2∕9.
Figure 16 shows the evolution of the ratio of the disc radii measured in the MU2AD, MU5AD, and MU5ADf runs over the analytical prediction computed following Eq. (8). The agreement is within less than a factor of 2 for the slow rotation models, while it increases up to a factor larger than 3 in the fast rotating MU5ADf run at masses larger than 8 M⊙. Indeed, the disc part in which the Elsasser number Am > 1 in the MU5ADf run is much larger than the one in the MU5AD one. At radii > 100−200 au, the rotation time becomes longer than the ion-neutral collision time (Am > 1), meaning that the magnetic fields and the neutral are well coupled (through the collisions with ions) and a toroidal component is efficiently generated by the differential rotation. We show in Fig. 14 that the toroidal magnetic field component strongly dominates over a large fraction of the disc in the MU5ADf run for sink masses > 5 M⊙. In the outer disc, the Alfvén velocity is also comparable to the sound speed, which indicates the importance of the toroidal magnetic pressure support. Equation (8) is valid in the region where ambipolar diffusion is efficient in preserving the generation of toroidal magnetic fields by the differential rotation. Clearly, the analytical estimate does not apply in the outer regions of the disc at late time, but rather on the inner part dominated by ambipolar diffusion.
Ambipolar diffusion thus obviously regulates the disc formation and early evolution, but then as the disc grows, the ambipolar diffusion becomes negligible in the outer parts. This being said, the plasma β remains of the order of unity, meaning that the generation of toroidal field by differential rotation remains limited compared to the ideal MHD case where the toroidal fields dominate over more than one order of magnitude.
 |
Fig. 14 Mean radial profiles of the velocities and magnetic field components for the MU5I (first two rows), MU5AD (rows 3 and 4), and MU5ADf (rows 5 and 6). The time (and sink mass) increases from left to right. In the velocity plots, we represent the radial velocity Vr (thick red line), azimuthal velocity Vϕ (thick green), vertical velocity Vz (thick blue), Alfvén velocity VA (dashed blue), sound speed Cs (green cross), and Keplerian velocity |
4.2 Characteristics of the star-disc-outflow system and observational prediction
In this section, we summarise the characteristic features we observed in our models, depending on the physics included. We restricted our analysis to the period that we covered in this study, prior to a stellar mass of 20 M⊙.
First, in the hydrodynamical case, we observed that the disc is the largest, the most massive, and the most gravitationally unstable. A very weak outflow is formed (height of a few 100s au), in which the gas is accelerated by the radiative force. This picturedoes not change qualitatively if we account for a more realistic irradiation scheme, thanks to which the radiative outflow can expand further away as a consequence of a larger radiative acceleration (Mignon-Risse et al. 2020).
Second, in all our magnetised models, a system made of a star, a disc, and an outflow is formed. For stellar mass M⋆ < 20 M⊙, the outflow has a mass of 2–10 M⊙ and can extend up to a few tens of thousands of au. The outflow is essentially made of gas accelerated by magnetic processes and is self-collimated by magnetic fields. The magnetic field in the outflow is thus essentially toroidal. The fact that both the ideal and resistive cases share the same properties for the early evolution of the outflow lead us to think that the outflow is generated in the upper layersof the disc, where ionisation is high.
For the disc, one should distinguish the ideal run from the resistive runs that exhibit opposite features. On the one hand, in the ideal case, the disc is puffy, supported by the magnetic pressure, and gravitationally stable. The magnetic field is essentially toroidal throughout the disc. On the other hand, the disc in the resistive runs is thinner and supported mostly by the thermal pressure. One can distinguish two parts in the disc: the inner region, which is gravitationally unstable where ambipolar diffusion is dominant and the magnetic field is vertical, and the outer disc, which is gravitationally stable and where ambipolar diffusion is negligible and the magnetic field is mostly toroidal.
These characteristic features can then help us to determine the important physical processes at play in the vicinity of massive star forming region. If a collimated outflow is observed in objects less massive than 20 M⊙, then we predict that the outflow would be accelerated by magnetic processes. Models neglecting magnetic fields are unable to launch extended collimated outflows for this mass range. Second, the size of the disc can help us to determine the importance of magnetic fields. We expect a larger disc to form in the hydrodynamical case. Nevertheless, here we discuss factors of approximately 2. In order to have a clearer distinction, polarised emission observations of the disc should help first to state the presence of magnetic field, and second the importance of resistive effect (presence of a vertical field).
It is worth noting that the plasma, beta, and magnetic topology are key quantities that govern the subsequent evolution of the disc (e.g. Fromang et al. 2007; Flock et al. 2011; Béthune et al. 2017). Our models can help to put constraints on the initial conditions for further studies looking at the evolution of the protostellar disc as it is widely done for low-mass stars.
A step forward would be to provide synthetic observations of dust emission and polarisation from our models, but this goes beyond the scope of this paper. In Sect. 4.4, we provide a brief qualitative comparison between our models and recent observations.
 |
Fig. 15 Histogram of the Toomre parameter Q as a function of the Elsasser number Am in the disc for the MU5AD model when the sink mass is 15 M⊙. The Toomre parameter is computed as explained in the main text, as a function of the position (r, θ) in the rotation plane. For each position, the Elsasser number is averaged over the disc height. The colour coding indicates the column density. The vertical (resp. horizontal) line shows the Am = 1 (resp. Q = 1). |
 |
Fig. 16 Ratio of disc radius measured in the models with ambipolar diffusion (MU2AD in green, MU5AD in blue, and MU5ADf inyellow) and the analytical prediction of Hennebelle et al. (2016) as a function of the total sink and disc mass. |
4.3 Comparison with previous work
Multi-dimensional simulations of massive stars including hydrodynamics and radiative transfer have been performed for about twenty years. Yorke & Sonnhalter (2002) presented 2D axisymmetric calculations of the collapse of slowly rotating massive cores of mass ranging from 30 to 120 M⊙ and compare the results obtained with a grey irradiation to the ones obtained with a frequency-dependent model. They accounted for the internal luminosity of the forming protostars, as well as the accretion luminosity (total luminosity). They show that the final mass of the protostar can be increased by a factor of 2 when accounting for multi-frequency radiative transfer (42.9 M⊙ against 22.9 M⊙). They showed that massive stars can be formed via accretion through a disc. The anisotropy of the radiative flux due to this disc is called the flashlight effect and is enhanced with the effects of frequency-dependent radiation transfer. Kuiper et al. (2011, 2012) extended this work using 3D models with a hybrid method to treat the frequency-dependent irradiation coming from the central star. They confirm the importance of the frequency-dependent irradiation as well as the flashlight effect, which helps to form massive stars via disc accretion. In addition, they show that the expanding cavity is radiation-pressure-dominated and remains stable over time, which is consistent with our results in the hydrodynamical case, although we used a grey irradiation.
Krumholz et al. (2007) performed 3D AMR RHD simulations of the collapse of 100–200 M⊙ turbulent massive cores accounting for the total luminosity of the forming protostars with a grey radiative transfer. They find that radiative feedback has a dramatic impact on the dynamics of the collapsing clouds by heating the gas and preventing it from strongly fragmenting. They report the formation of unstable discs of size ≈ 500 au around the massive protostars that are able to channel mass inward very rapidly due to large-scale gravitational instability. Krumholz et al. (2009) later showed that the cavities driven by the radiative pressure may be unstable to radiative Rayleigh-Taylor instability (RTI), which helps to channel the gas onto the massive protostars through filaments that self-shield against radiation. Rosen et al. (2016) extended this work using a frequency-dependent irradiation scheme and confirmed the development of RTI. Our results in the hydrodynamical case do not exhibit RTI development. In a companion work, Mignon-Risse et al. (2020) show that the radiative outflow cavity is stable, because the gas velocity through the interface of the cavity is large enough to prevent the development of RT instabilities if one accounts for a more accurate irradiation scheme. We note that our results are consistent with those of Klassen et al. (2016), who presented 3D AMR RHD simulations with a hybrid radiative transfer solver. They find stable bubbles expanding through radiation pressure, as well as large protostellar discs that grow rapidly and become Toomre unstable. The disc does not fragment but forms spiral arms and channels material onto the star at an accretion rate of a few 10−4 M⊙ yr−1 in the case of a 100 M⊙ core.
Nevertheless, the picture of the outflow launching and disc formation change dramatically when magnetic fields are taken into account. The disc is more stable and the magnetic outflow develops much earlier than the radiative one. The magnetic outflows develop quickly; that is, before radiation dominates the acceleration, on a scale of tens of thousands of au, and it is well collimated. The magnetic outflow thus creates a channel in which the intense radiation of the forming protostars radiation will efficiently escape. This result was indeed anticipated in models accounting for sub-grid protostellar outflow models on top of the protostellar irradiation, where radiation can escape easily in the outflow channel (e.g. Krumholz et al. 2005; Cunningham et al. 2011; Kuiper et al. 2015). The theoretical framework for the development of the radiative Rayleigh-Taylor instability in the presence of magnetic fields is at present missing from the literature. In addition, weshould point out that our results remain limited to the very early stages, when the central mass is < 20 M⊙. Additional work, pushing time integration towards higher masses should be carried out in order to properly address the development of the RTI.
Cunningham et al. (2011) presented similar AMR simulations to Krumholz et al. (2007) but included the feedback effects of protostellar outflows using a sub-grid model, on top of the protostellar radiative heating and radiation pressure exerted on the infalling gas. They showed that the protostellar radiation focused in the direction of protostellar outflow cavities is sufficient to prevent the formation of radiation pressure-supported circumstellar gas bubbles. Kuiper et al. (2015) presented 2D axisymmetric simulations including both the radiative feedback and protostellar outflow from massive stars via sub-grid models. They show that the kinematic feedback is predominant at early times, whereas the radiative acceleration becomes significant at later times. The outflows open a cavity extending to the core edge in which the radiation escapes. The outflows extend the flashlight effect from the disc scale to the core scale and help to form more massive stars. Overall, we confirm these results, but the outflows we reported in this study are self-consistently launched by magnetic processes.
To evaluate the effect of magnetic fields, Seifried et al. (2011, 2012) presented 3D MHD simulations of collapsing 100 M⊙ cores in the ideal MHD approximation and neglecting the protostellar radiative feedback. They found that for weak magnetic fields (μ > 10), well-defined Keplerian discs with sizes of a few 100 au are formed, whereas their formation is suppressed for strong magnetic fields (μ < 10) due to a very efficient magnetic braking. At first sight, this result seems contradictory to our finding in the MU5I run. We explain this by the large central mass-to-flux ratio used in our models (μc = 50 for MU5 models), while they set up a non-uniform magnetic field with a larger amplitude in the centre than ours (> 500 G versus ≃ 70 μG). The accretion rates they observed are of the order of a few 10−4 M⊙ yr−1. The outflows observed in their simulations are launched by magneto-centrifugal acceleration, which are initially poorly collimated and are then better collimated over time due to the development of fast jets. On the disc scales, Myers et al. (2013) performed 3D AMR ideal MHD simulations of collapsing turbulent and magnetised 300 M⊙ massive cores, with a maximum resolution of 10 au. They include radiative transfer with a grey FLD approximation, as well as radiative protostellar feedback. They report the formation of Keplerian discs, with a radius of 40 au when the sink mass is 3.5 M⊙. In the MU5I model, we measured a disc size of ≃75 au at the same sink mass, which is fairly similar given all the differences between the numerical setup of Myers et al. (2013) and our own. Interestingly, they reported the presence of episodic outflows of velocities ≃ 10 km s−1, which become stronger once the sink mass is larger than 20 M⊙. The outflow velocity, as well as the episodic feature, are very consistent with our findings in the MU5I model. Altogether, our results using the ideal MHD approximation compare well with the literature. This strengthens the importance of resistive effects on the early evolution of discs and outflows in young massive protostars.
Matsushita et al. (2017) studied 3D collapse using resistive MHD (Ohmic resistivity) and a barotropic equation of state to mimic the thermal behaviour of the collapsing gas. For strong magnetic fields, they find that magnetically driven massive outflows are launched, whereas they are subdued or absent for weak magnetic fields. In addition, in the weakly magnetised case, they show that fragmentation occurs and prevents the formation of massive star. The outflows they report have a wide opening angle at the disc scale and a collimated structure at large scales, similarly to what we present in this study. Kölligan & Kuiper (2018) presented 2D axisymmetric simulations of the collapse of 100 M⊙ dense cores using Ohmic diffusion and an isothermal equation of state. They had a higher resolution than ours (Δx = 0.09 au, sink cell size of 1 au) and integrated up to a central sink mass >50 M⊙. They report disc and outflow formation, in a similar qualitative picture to the one presented in the resistive runs of this study. The disc size they report is larger than ours (>1000 au), but given the differences in numerical methods (dimensionality, grid) and physics included (Ohmic versus ambipolar diffusion), it is not clear what the main reason for this difference is. Further comparison work is required. For the outflow, Kölligan & Kuiper (2018) reported the formation of a magneto-centrifugally launched, highly collimated central jet and a slow, wide-angle magnetic-pressure-driven tower flow. The latter component is launched in the outer disc and dominates the angular momentum transport, similarly to what we find in Fig. 10. We note that we do not retrieve the high-velocity jet component reported by Kölligan & Kuiper (2018) in our results, which is certainly due to our limited numerical resolution that does not allow us to reach a high rotation velocity. Indeed, the ejection velocity is linked to the (Keplerian) rotation velocity in the standard theory of outflow launching (e.g. Spruit 1996). While we did not investigate the exact origin of the magnetic outflow (magnetic tower or magneto-centrifugal acceleration), we confirm that even in the presence of radiative feedback, the development of magnetised outflows is ubiquitous, as first demonstrated by Banerjee et al. (2006). We refer readers to Mignon-Risse et al. (2021a) for a comprehensive study of the outflows in similar models. For the disc, our results confirm that disc can form, even in the ideal MHD regime. We are the first to study its structure in detail depending on the physics taken into account (magnetic field topology, plasma beta). In particular, we demonstrate that the results of low-mass models can be extended to higher mass and that resistive effect change completely the properties of the disc (aspect ratio, stability). Further work is needed, as for instance the inclusion of the two other resistive effects, the Ohmic diffusion and the Hall effect, which are found to influence disc formation in the low-mass regime (e.g. Tsukamoto et al. 2015; Vaytet et al. 2018; Marchand et al. 2019; Zhao et al. 2020).
Our centrally condensed initial conditions, which are similar to those used in other works (Krumholz et al. 2009; Seifried et al. 2011; Mignon-Risse et al. 2021b), do not favour fragmentation. Our results regarding fragmentation are thus strongly biased by this choice, and only disc fragmentation is expected to occur. The fragmentation we report in this study is consistent with previous studies. In the HYDRO run, a binary system is formed from disc fragmentation with most of the mass going in the primary fragment, similarly to what has been reported in Krumholz et al. (2007). In the ideal MHD case, we did not report fragmentation because of the extra support provided by magnetic fields. This result is consistent with that of Seifried et al. (2011) for a strong field case. For the resistive runs, the discs are gravitationally unstable in the inner regions but do not fragment. Similar results are reported in Matsushita et al. (2017) and Mignon-Risse et al. (2021b) in the aligned case. We note that Mignon-Risse et al. (2021b) report disc fragmentation in the case where initial turbulence is super-Alfvénic. Regarding fragmentation, further time integration is also required in order to investigate the disc stability evolution as the central star becomes more massive.
Last, we did not take into account turbulence or misalignment in our initial setup, whereas numerical experiments in the literature have proven that they affect the magnetic braking efficiency and enable the formation of Keplerian discs (e.g. Hennebelle & Ciardi 2009; Santos-Lima et al. 2012; Joos et al. 2012, 2013; Seifried et al. 2013). In Mignon-Risse et al. (2021b,a), we present an extension of the present models with ambipolar diffusion, where we include turbulence in the initial setup, as well as a more accurate scheme for stellar irradiation based on Mignon-Risse et al. (2020). We show that the disc properties remain unchanged because ambipolar diffusion dominates in the inner disc. Regarding fragmentation, sub-Alfvénic models of Mignon-Risse et al. (2021b) do not fragment as the ones in the present study do, but super-Alfvénic models lead to disc fragmentation and binary formation. Interestingly, the properties of the discs surrounding each star in the binary system remain very similar to what we report here. Regarding outflows, Mignon-Risse et al. (2021a) showed that the outflow remains magnetically driven at early stages in sub-sonic models, even if the contribution of the radiative acceleration increases thanks to the hybrid irradiation scheme that better addresses stellar photons. We note, however, that the outflow launching is strongly perturbed in the case of initial supersonic turbulence.
4.4 Comparison with observations
Massive star formation regions are usually observed at distances greater than 1 kpc, which limits the resolution of such observations. Very few disc candidates in young, massive star forming regions have thus been reported in the literature (for a review, see Beltrán & de Wit 2016; Rosen et al. 2020). We review a few of them in the following section and compare with our results.
Ahmadi et al. (2018) studied the fragmentation and kinematics of the high-mass star forming region W3(H2O) and found indications for possible disc fragmentation on 1000 AU scales. In all our model, we do not report such a wide fragmenting disc. The most favourable case to compare with this work would be the HYDRO case because of the large disc radius, but it does not reproduce the observed highly collimated and massive (10 M⊙) outflows reported by Zapata et al. (2011) in W3(H2O). We must stress, however, that our initial conditions were not chosen to be favourable to disc fragmentation because of the low initial rotation level. The influence of initial turbulence should also be investigated for that purpose.
More recently, Motogi et al. (2019) reported ALMA observation of a young high-mass protostellar object (10 M⊙, no ultra-compact HII region), accreting at about 10−3 M⊙ yr−1, of which the characteristics are very consistent with the early evolutionary scenario of a low-mass protostar. From dust continuum emission, they report a disc mass of 2−7 M⊙ and a disc size of 250 au, which is associated with a lower limit of 0.4 for the Toomre parameter. Altogether, this observation is very consistent with our models including ambipolar diffusion, though their estimated protostellar age (104 yr) is relatively shorter.
Patel et al. (2005) found a rotating disc-like structure of mass 1–8 M⊙ and size 330 au in Cepheus A HW2 centred on a massive 15 M⊙ protostar. Fernández-López et al. (2016) reported polarised emission observations from this disc-like structure and found an indication of either a uniform magnetic field threading the disc (polarised emission) or of grain growth up to a few tens of μm in size within a few 104 yr (scattering). They exclude the possibility of polarised emission coming from a toroidal field. On top of this, Vlemmings et al. (2006) measured magnetic field strengths in the HW2 disc area ranging from 100 to 600 mG. Overall, this object is again very consistent with the models integrating ambipolar diffusion we present here: a moderate magnetisation at the disc border (10–100 mG) and a rather uniform vertical field in the inner disc, contrasting with the stronger magnetisation and the toroidal field found in the ideal MHD case.
Last, a couple of recent observations report Keplerian motions associated with compact sources (discs?) in young massive protostars thanks to the ALMA interferometer. Maud et al. (2019) presented observations of the G17.64+0.16 young massive protostar (≃ 45 M⊙) that revealed a disc of size ≃120 au associated with Keplerian rotation. Similarly, Ginsburg et al. (2018) reported Keplerian rotation and a disc size of 50 au around the Orion SrCI source (≃ 15 M⊙). These observations are consistent with the disc size we report in the MU2AD and MU5AD runs. Johnston et al. (2015, 2020) report near-Keplerian rotation associated with a disc size of 1000 au in the massive protostar AFGL4176mm1. The disc exhibits sub-structures (possibly spiral arm), and its stability analysis shows that it is gravitationally unstable. Only the HYDRO run in our models can lead to such a large disc radius. However, Mignon-Risse et al. (2021b) showed that if initial supersonic and super-Alfvénic turbulence are considered, such large rotating and unstable structures can form in magnetised models with ambipolar diffusion (see their Fig. 8).
This qualitative comparison remains highly biased towards high-resolution observations of massive star disc candidates, which allows us to directly probe and resolve the disc scales in order to compare with our models. A more careful and quantitative analysis, including synthetic observations for a side-by-side comparison, is clearly required but this goes beyond the scope of the current paper.
4.5 Limits of the model and future work
We identified two types of limits that may affect the generalisation of our conclusions. The first comes from the numerical methods we used, and the second is about the initial conditions and parameter space exploration.
First, we used an aggressive merging scheme for the sink particles, meaning that every sink particle that enters the accretion radius of another, more massive one is immediately merged. We purposely chose to merge all the overlapping sink in order to favour mass accretion and the formation of massive stellar sources. We reported the formation of secondary sink particles in the HYDRO run, but most secondary ones were merged with the central one within a few hundred years, and the mass of the accreted secondary sink particles remained small compared to the central one (more than a factor of 10 in mass). The HYDRO run ended in a binary system and a secondary sink of mass ≃ 0.01 M⊙ was ejected from the disc. In all magnetised models, the system ended in a single star without secondary sink formation. The second limitation comes from the grey FLD irradiation scheme we used. It has been shown in the literature that averaging over frequencies and using only the zeroth moment of the radiative transfer equation can underestimate the radiative force by two orders of magnitude (e.g. Kuiper et al. 2012). Besides this, the isotropic FLD irradiation scheme is also expected to have an effect on thedisc radial temperature profile, which might then affect the disc stability. In a recent methodological paper, Mignon-Risse et al. (2020) proposed an improvement of the irradiation scheme using the M1 moment models to handle stellar irradiation (Rosdahl et al. 2013; Rosdahl & Teyssier 2015). We note that the recent work of Mignon-Risse et al. (2021b,a) investigate the effect of a better irradiation scheme combined with ambipolar diffusion and initial turbulence. They confirm our results qualitatively, in particular on the relative importance of the magnetic versus radiative accelerations up to M⋆ ≃ 20 M⊙, and on the magnetic properties of the discs.
Third, we did not explore the influence of the fraction of the incident kinetic energy radiated away, that is, the accretion luminosity. This choice was motivated by the large uncertainties that remain in order to propose a coherent model to set the accretion luminosity. Recent radiation-(magneto)hydrodynamic simulations of protostellar core formation indicate that the accretion shock onto the protostar at the early stages is a subcritical radiative shock, meaning that all the incident kinetic energy is transferred to the protostar and not radiated away Vaytet et al. (2013, 2018); Bhandare et al. (2020). This result applies for the very early stages of protostellar core formation, and the extrapolation of this properties to PMS evolution is very uncertain. Baraffe et al. (2009) computed PMS evolution of young low-mass protostars (up to 1 M⊙) and showed that an evolution including the effects of episodic accretion at the stellar scale can explain the observed luminosity spread in H-R diagrams of star forming regions, provided that the accretion is cold, meaning that a significant fraction of the accretion energy is radiated away. These results need to be extended to massive young protostars, however. Moreover, Hennebelle et al. (2020a) show that including the instantaneous full accretion luminosity provides strong heating so that the measured sink mass function in a numerical experiment becomes top-heavy and is not in agreement with the observed stellar initial mass function. Last, the internal luminosity from the massive young protostar is expected to exceed the accretion luminosity for M⋆ ⋧ 8 M⊙ (e.g. Hosokawa & Omukai 2009), which is the regime we target in this study. Given the large uncertainties, we do not consider any accretion luminosity here and postpone the exploration of its influence in future studies. In addition, further work should include a detailed study on the way to properly account for the energy radiated away down to protostellar scales, but this goes far beyond the scope of the present study.
Then, we only explore a narrow range of initial conditions: aligned rotator (magnetic fields and rotation axis are parallel) and only two magnetisation and rotation levels. It has been shown in the context of low-mass star formation that misalignment and turbulence greatly affects the formation of a protostellar disc (Hennebelle & Ciardi 2009; Joos et al. 2012, 2013; Santos-Lima et al. 2012; Masson et al. 2016). Besides this, the initial density profile may also drastically affect the fragmentation of the collapsing massive cores (Girichidis et al. 2011; Lee & Hennebelle 2018). The parameter space exploration will be performed in future works in order to test the resilience of our findings on the mechanisms governing the accretion and ejection processes in young massive stellar objects.
Last, we assume that dust and gas are both dynamically and thermally perfectly coupled. It has recently been shown in numerical simulation work that dust and gas may decouple dynamically in collapsing dense cores with efficient dust enrichment for grains larger than 10 μm (Bate & Lorén-Aguilar 2017; Lebreuilly et al. 2019). There is also growing observational evidence of large grains in the vicinity of collapsing cores, both in the low- and high-mass regimes (Fernández-López et al. 2016; Sadavoy et al. 2018; Galametz et al. 2019; Valdivia et al. 2019). In addition, dust is the main opacity source, so protostellar irradiation primarily couples with the dust and then the gas via the drag. Furthermore, Hoang (2021) recently suggested that the effects of grain rotational disruption by radiative torques in young massive protostars can lead to the destruction of micron dust grains, which results in a reduction of radiation pressure opacity. Last but not least, dust growth is expected to quantitatively change the non-ideal MHD resistivities, which may also amplify the effect of ambipolar diffusion, for instance (Zhao et al. 2016; Guillet et al. 2020). Future studies following the differential dynamics of the dust and gas mixture, coupled with magnetic fields evolution and radiation transport, are naturally the next step forward.
5 Conclusion
We present a first suite of 3D numerical simulations integrating the combined effect of protostellar evolution and ambipolar diffusion in the context of the early evolution of massive protostars (up M⋆ ≃ 20 M⊙). We compared the effect of magnetic fields with respect to a pure hydrodynamical case. Then, we explored the impact of the physics (ideal versus non-ideal MHD) and of the initial conditions (magnetisation and rotation level) on the formation of the star-disc-outflow system.
First, we find that the magnetised models differ dramatically from the hydrodynamical one, with different mass-accretion rates and particularly mass-ejection rates. A disc is formed in all our models, but again with quantitative differences on the mass and radius between hydrodynamical and MHD models. More importantly, the magnetic properties of the disc formed in the non-ideal MHD framework are opposite to an ideal MHD. While the latter case exhibits strong toroidal fields throughout the disc, with plasma β <1, the non-ideal MHD inner discs are dominated by the thermal pressure (β > 1). In addition,these discs are threaded by a vertical field in their inner parts (≤ 100−200 au) and generate a toroidal field in the outer parts via differential rotation. Correspondingly, the inner regions of the disc in the resistive runs are gravitationally unstable and dominated by resistive effects, while the outer parts are gravitationally stable and more coupled to the magnetic field’s evolution. This result, as well as the disc radius, can be tested in future high angular resolution observations. It also puts well-defined constraints on the initial conditions for the subsequent evolution of (protoplanetary?) discs around massive stars.
Second, we find that the accretion-ejection is regulated by the formation of discs and magnetised outflows that dominate mass ejection in the early stages. Our results confirm that when outflows are self-consistently launched, the well-studied flashlight effect (outflows create a channel for the radiation to escape at large distances) still holds.
Magnetic fields and ambipolar diffusion dramatically affect mass accretion and ejection and disc formation in the early stages of massive star formation. Our analysis of the accretion and ejection mechanisms at play in young massive protostars are a scaled-up version of the one occurring within low-mass protostars. The exploration of the initial parameter space deserves further study in order to test the robustness of the accretion and ejection magnetically regulated scenario, in particular in the presence of initial turbulence. The effect of a more accurate irradiation scheme, as well as the differential dynamics of dust and gas, should be investigated in the near future. Moreover, our results remain limited to the early stages of (very) massive star formation, and further works need to be carried out for stellar mass > 20 M⊙.
Acknowledgements
We thank Ugo Lebreuilly and Rolf Kuiper for useful discussion. We thank Rolf Kuiper for kindly sharing the PMS evolution tracks. We acknowledge financial support from “Programme National de Physique Stellaire” (PNPS) of CNRS/INSU, CEA and CNES, France. N.V. gratefully acknowledges support from the European Commission through the Horizon 2020 Marie Skłodowska-Curie Actions Individual Fellowship 2014 programme (Grant Agreement no. 659706). This work was granted access to the HPC resources of CINES (Occigen) under the allocation 2018-047247 made by GENCI. In addition, we thank the Département d’Astrophysique, IRFU, CEA Saclay, and the Laboratoire Astrophysique Instrumentation Modélisation, France, for granting us access to the supercomputer IRFUCOAST-ALFVEN where the groundwork with many test calculations were performed. Figures 1, 2, 7, 8, 9, 12, and B.2 were created using the OSIRIS (https://bitbucket.org/nvaytet/osiris) visualization package for RAMSES. Figure 5 was created using the VisIt (https://wci.llnl.gov/simulation/computer-codes/visit) software.
Appendix A Resolution convergence
In this section, we discuss the influence of the spatial resolution on our results. We ran three new models similar to MU5AD but changed the maximum level of refinement ℓmax of the AMR grid. MU5AD has a ℓmax = 15 corresponding to a finest resolution of 5 au. We ran simulations with ℓmax = 13, ℓmax = 14, and ℓmax = 16, corresponding to the finest resolution of 20 au, 10 au, and 2.5 au, respectively. The sink accretion radius varies with resolution and equals four times the finest resolution. Due to the computational cost, the simulation with ℓmax = 16 cannot be run until long times and has only reached a sink mass of 7 M⊙.
Figure A.1 shows the evolution of the sink, disc, and outflow for these four runs. The sink mass as a function of the sink age (upper left panel) appears to be independent of the resolution. Concerning the disc, its mass increases with time in all models but the lowest resolution one: ℓmax = 13. The global trendis an increasing disc mass with increasing resolution. As for the outflow, its mass increases in time for each simulation, but its growth rate is faster at coarser resolutions (opposite behaviour to that of the disc mass). Interestingly, we measured outflow velocities that increase with the resolution. This further confirms the magnetic origin of the outflow, which velocity scales with the rotation velocity at its base. The fiducial value used in this paper (ℓmax = 15, 5 au) seemsnot to be converged quantitatively for the disc and outflow mass. However, the finest resolution for all the runs are computationally out of reach, and the qualitative results are similar whatever the resolution. We therefore think that our qualitative conclusions remain valid.
 |
Fig. A.1 Mass evolution of the sink (top-left), disc (top-right), and outflow (bottom-left) as a function of time after sink creation, and of the outflow as a function of the total disc+sink mass (bottom-right). The different colour scales for different maximum levels of refinement ℓmax and resolution are as follows: 20 au (black), 10 au (red), 5 au (green), and 2.5 au (blue). |
Appendix B Dependence on the angular momentum sub-grid model
In this section, we discuss the influence of the angular momentum accretion in the sink algorithm on our results. In our fiducial model, MU5AD, all the angular momentum of the gas is accreted onto the sink. We ran a new model where the angular momentum is not accreted.
Figure B.1 shows the mass evolution of the different components (sink, outflow, and disc) in the two simulations. The sink mass grows faster when the angular momentum is accreted. Indeed, in that case, the gas around the sink particle lowers its angular momentum and then falls more easily on the sink. On the contrary, the rotationally supported disc is favoured in the case where the angular momentum is not removed. For the same reason, the outflow, as it is generated by magnetic processes, is also more massive and stronger with no angular momentum accreted. This can also be seen in Fig. B.2, which shows the density maps in the disc plane and perpendicular to it when the sink has a mass of 10 M⊙. The morphologies are very similar, even if the disc is larger when angular momentum is not accreted.
 |
Fig. B.1 Mass evolution as a function of the sink age (left panel) or the total mass (right panel) for the models with (red) or without (black) the angular momentum accreted. |
 |
Fig. B.2 Density maps in the plane of the disc and perpendicular to it for the model with no angular momentum accreted (top) and with all the angular momentum accreted (fiducial model MU5AD, bottom). |
References
- Ahmadi, A., Beuther, H., Mottram, J. C., et al. 2018, A&A, 618, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Badnell, N. R., Bautista, M. A., Butler, K., et al. 2005, MNRAS, 360, 458 [Google Scholar]
- Banerjee, R., Pudritz, R. E., & Anderson, D. W. 2006, MNRAS, 373, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., & Gallardo, J. 2009, ApJ, 702, 27 [Google Scholar]
- Bate, M. R., & Lorén-Aguilar, P. 2017, MNRAS, 465, 1089 [Google Scholar]
- Bate, M. R., Bonnell, I. A., & Price, N. M. 1995, MNRAS, 277, 362 [Google Scholar]
- Beltrán, M. T., & de Wit, W. J. 2016, A&ARv, 24, 6 [Google Scholar]
- Beltrán, M. T., Sánchez-Monge, Á., Cesaroni, R., et al. 2014, A&A, 571, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beltrán, M. T., Cesaroni, R., Moscadelli, L., et al. 2016, A&A, 593, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beltrán, M. T., Padovani, M., Girart, J. M., et al. 2019, A&A, 630, A54 [Google Scholar]
- Béthune, W., Lesur, G., & Ferreira, J. 2017, A&A, 600, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Schilke, P., Sridharan, T. K., et al. 2002, A&A, 383, 892 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Vlemmings, W. H. T., Rao, R., & van der Tak, F. F. S. 2010, ApJ, 724, L113 [Google Scholar]
- Beuther, H., Ahmadi, A., Mottram, J. C., et al. 2019, A&A, 621, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhandare, A., Kuiper, R., Henning, T., et al. 2020, A&A, 638, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bleuler, A., & Teyssier, R. 2014, MNRAS, 445, 4015 [Google Scholar]
- Bodenheimer, P., Laughlin, G. P., Rózyczka, M., & Yorke, H. W., eds. 2007, Numerical Methods in Astrophysics: an Introduction (New York: Taylor & Francis) [Google Scholar]
- Bontemps, S., Motte, F., Csengeri, T., & Schneider, N. 2010, A&A, 524, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrasco-González, C., Rodríguez, L. F., Anglada, G., et al. 2010, Science, 330, 1209 [CrossRef] [Google Scholar]
- Cesaroni, R., Sánchez-Monge, Á., Beltrán, M. T., et al. 2017, A&A, 602, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ching, T.-C., Lai, S.-P., Zhang, Q., et al. 2016, ApJ, 819, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Commerçon, B., Hennebelle, P., Audit, E., Chabrier, G., & Teyssier, R. 2010, A&A, 510, L3+ [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Commerçon, B., Teyssier, R., Audit, E., Hennebelle, P., & Chabrier, G. 2011a, A&A, 529, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Commerçon, B., Hennebelle, P., & Henning, T. 2011b, ApJ, 742, L9 [CrossRef] [Google Scholar]
- Commerçon, B., Debout, V., & Teyssier, R. 2014, A&A, 563, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortes, P. C., Crutcher, R. M., & Matthews, B. C. 2006, ApJ, 650, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Csengeri, T., Bontemps, S., Wyrowski, F., et al. 2017, A&A, 600, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cunningham, A. J., Klein, R. I., Krumholz, M. R., & McKee, C. F. 2011, ApJ, 740, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Dall’Olio, D., Vlemmings, W. H. T., Persson, M. V., et al. 2019, A&A, 626, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duarte-Cabral, A., Bontemps, S., Motte, F., et al. 2013, A&A, 558, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Federrath, C., Banerjee, R., Clark, P. C., & Klessen, R. S. 2010, ApJ, 713, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [Google Scholar]
- Fernández-López, M., Stephens, I. W., Girart, J. M., et al. 2016, ApJ, 832, 200 [CrossRef] [Google Scholar]
- Figueira, M., Bronfman, L., Zavagno, A., et al. 2018, A&A, 616, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flock, M., Dzyurkevich, N., Klahr, H., Turner, N. J., & Henning, T. 2011, ApJ, 735, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Fontani, F., Commerçon, B., Giannetti, A., et al. 2016, A&A, 593, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontani, F., Commerçon, B., Giannetti, A., et al. 2018, A&A, 615, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frank, A., Ray, T. P., Cabrit, S., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 451 [Google Scholar]
- Fromang, S., Hennebelle, P., & Teyssier, R. 2006, A&A, 457, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromang, S., Papaloizou, J., Lesur, G., & Heinemann, T. 2007, A&A, 476, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galametz, M., Maury, A. J., Valdivia, V., et al. 2019, A&A, 632, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginsburg, A., Bally, J., Goddi, C., Plambeck, R., & Wright, M. 2018, ApJ, 860, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Girart, J. M., Beltrán, M. T., Zhang, Q., Rao, R., & Estalella, R. 2009, Science, 324, 1408 [NASA ADS] [CrossRef] [Google Scholar]
- Girart, J. M., Frau, P., Zhang, Q., et al. 2013, ApJ, 772, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Girart, J. M., Estalella, R., Fernández-López, M., et al. 2017, ApJ, 847, 58 [CrossRef] [Google Scholar]
- Girart, J. M., Fernández-López, M., Li, Z. Y., et al. 2018, ApJ, 856, L27 [CrossRef] [Google Scholar]
- Girichidis, P., Federrath, C., Banerjee, R., & Klessen, R. S. 2011, MNRAS, 413, 2741 [Google Scholar]
- González, M., Vaytet, N., Commerçon, B., & Masson, J. 2015, A&A, 578, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, W. J., McKee, C. F., & Klein, R. I. 2018, MNRAS, 473, 2124 [NASA ADS] [CrossRef] [Google Scholar]
- Guillet, V., Hennebelle, P., Pineau des Forêts, G., et al. 2020, A&A, 643, A17 [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Ciardi, A. 2009, A&A, 32, 29 [Google Scholar]
- Hennebelle, P., & Fromang, S. 2008, A&A, 24, 9 [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., Whitworth, A. P., Cha, S. H., & Goodwin, S. P. 2004, MNRAS, 348, 687 [CrossRef] [Google Scholar]
- Hennebelle, P., Commerçon, B., Joos, M., et al. 2011, A&A, 528, A72 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., Commerçon, B., Chabrier, G., & Marchand, P. 2016, ApJ, 830, L8 [Google Scholar]
- Hennebelle, P., Commerçon, B., Lee, Y.-N., & Chabrier, G. 2020a, ApJ, 904, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., Commerçon, B., Lee, Y.-N., & Charnoz, S. 2020b, A&A, 635, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoang, T. 2021, ApJ, 921, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Hosokawa, T., & Omukai, K. 2009, ApJ, 691, 823 [Google Scholar]
- Johnston, K. G., Robitaille, T. P., Beuther, H., et al. 2015, ApJ, 813, L19 [Google Scholar]
- Johnston, K. G., Hoare, M. G., Beuther, H., et al. 2020, A&A, 634, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joos, M., Hennebelle, P., & Ciardi, A. 2012, A&A, 543, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joos, M., Hennebelle, P., Ciardi, A., & Fromang, S. 2013, A&A, 554, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, W.-T., & Ostriker, E. C. 2001, ApJ, 559, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Klassen, M., Pudritz, R. E., Kuiper, R., Peters, T., & Banerjee, R. 2016, ApJ, 823, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Kölligan, A., & Kuiper, R. 2018, A&A, 620, A182 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, S., Hofmann, K.-H., Menten, K. M., et al. 2010, Nature, 466, 339 [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Klein, R. I. 2005, ApJ, 618, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Klein, R. I., & McKee, C. F. 2007, ApJ, 656, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Klein, R. I., McKee, C. F., Offner, S. S. R., & Cunningham, A. J. 2009, Science, 323, 754 [Google Scholar]
- Kuiper, R., & Hosokawa, T. 2018, A&A, 616, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuiper, R., & Yorke, H. W. 2013, ApJ, 772, 61 [Google Scholar]
- Kuiper, R., Klahr, H., Dullemond, C., Kley, W., & Henning, T. 2010, A&A, 511, A81+ [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuiper, R., Klahr, H., Beuther, H., & Henning, T. 2011, ApJ, 732, 20 [CrossRef] [Google Scholar]
- Kuiper, R., Klahr, H., Beuther, H., & Henning, T. 2012, A&A, 537, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuiper, R., Yorke, H. W., & Turner, N. J. 2015, ApJ, 800, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Lam, K. H., Li, Z.-Y., Chen, C.-Y., Tomida, K., & Zhao, B. 2019, MNRAS, 489, 5326 [Google Scholar]
- Lebreuilly, U., Commerçon, B., & Laibe, G. 2019, A&A, 626, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, Y.-N., & Hennebelle, P. 2018, A&A, 611, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, Y.-N., Charnoz, S., & Hennebelle, P. 2021, A&A, 648, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levermore, C. D., & Pomraning, G. C. 1981, ApJ, 248, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z. Y., Banerjee, R., Pudritz, R. E., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 173 [Google Scholar]
- Li, H.-B., Yuen, K. H., Otto, F., et al. 2015, Nature, 520, 518 [Google Scholar]
- Marchand, P., Masson, J., Chabrier, G., et al. 2016, A&A, 592, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchand, P., Tomida, K., Commerçon, B., & Chabrier, G. 2019, A&A, 631, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masson, J., Teyssier, R., Mulet-Marquis, C., Hennebelle, P., & Chabrier, G. 2012, ApJS, 201, 24 [Google Scholar]
- Masson, J., Chabrier, G., Hennebelle, P., Vaytet, N., & Commerçon, B. 2016, A&A, 587, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsushita, Y., Machida, M. N., Sakurai, Y., & Hosokawa, T. 2017, MNRAS, 470, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Maud, L. T., Moore, T. J. T., Lumsden, S. L., et al. 2015, MNRAS, 453, 645 [Google Scholar]
- Maud, L. T., Cesaroni, R., Kumar, M. S. N., et al. 2019, A&A, 627, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLeod, A. F., Reiter, M., Kuiper, R., Klaassen, P. D., & Evans, C. J. 2018, Nature, 554, 334 [CrossRef] [Google Scholar]
- Mignon-Risse, R., González, M., Commerçon, B., & Rosdahl, J. 2020, A&A, 635, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignon-Risse, R., González, M., & Commerçon, B. 2021a, A&A, 656, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignon-Risse, R., González, M., Commerçon, B., & Rosdahl, J. 2021b, A&A, 652, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minerbo, G. N. 1978, J. Quant. Spectr. Rad. Transf., 20, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Motogi, K., Hirota, T., Machida, M. N., et al. 2019, ApJ, 877, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Bontemps, S., & Louvet, F. 2018, ARA&A, 56, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Mouschovias, T. C., & Spitzer, Jr. L. 1976, ApJ, 210, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, A. T., McKee, C. F., Cunningham, A. J., Klein, R. I., & Krumholz, M. R. 2013, ApJ, 766, 97 [Google Scholar]
- Nony, T., Louvet, F., Motte, F., et al. 2018, A&A, 618, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palau, A., Fuente, A., Girart, J. M., et al. 2013, ApJ, 762, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, N. A., Curiel, S., Sridharan, T. K., et al. 2005, Nature, 437, 109 [CrossRef] [Google Scholar]
- Qiu, K., Zhang, Q., Menten, K. M., et al. 2014, ApJ, 794, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Rosdahl, J., & Teyssier, R. 2015, MNRAS, 449, 4380 [Google Scholar]
- Rosdahl, J., Blaizot, J., Aubert, D., Stranex, T., & Teyssier, R. 2013, MNRAS, 436, 2188 [Google Scholar]
- Rosen, A. L., Krumholz, M. R., McKee, C. F., & Klein, R. I. 2016, MNRAS, 463, 2553 [NASA ADS] [CrossRef] [Google Scholar]
- Rosen, A. L., Offner, S. S. R., Sadavoy, S. I., et al. 2020, Space Sci. Rev., 216, 62 [Google Scholar]
- Sadavoy, S. I., Myers, P. C., Stephens, I. W., et al. 2018, ApJ, 859, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Sanhueza, P., Contreras, Y., Wu, B., et al. 2019, ApJ, 886, 102 [Google Scholar]
- Sanna, A., Kölligan, A., Moscadelli, L., et al. 2019a, A&A, 623, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanna, A., Moscadelli, L., Goddi, C., et al. 2019b, A&A, 623, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos-Lima, R., de Gouveia Dal Pino, E. M., Lazarian, A., 2012, ApJ, 747, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Seifried, D., Banerjee, R., Klessen, R. S., Duffin, D., & Pudritz, R. E. 2011, MNRAS, 417, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Seifried, D., Pudritz, R. E., Banerjee, R., Duffin, D., & Klessen, R. S. 2012, MNRAS, 422, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Seifried, D., Banerjee, R., Pudritz, R. E., & Klessen, R. S. 2013, MNRAS, 432, 3320 [NASA ADS] [CrossRef] [Google Scholar]
- Semenov, D., Henning, T., Helling, C., Ilgner, M., & Sedlmayr, E. 2003, A&A, 410, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shepherd, D. S., & Churchwell, E. 1996, ApJ, 457, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [Google Scholar]
- Shu, F. H. 1992, The Physics of Astrophysics: Gas Dynamics (USA: University Science Books), 2 [Google Scholar]
- Spruit, H. C. 1996, ASI Ser. C, 477, 249 [NASA ADS] [Google Scholar]
- Tan, J. C., Beltrán, M. T., Caselli, P., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 149 [Google Scholar]
- Tan, J. C., Kong, S., Zhang, Y., et al. 2016, ApJ, 821, L3 [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teyssier, R., & Commerçon, B. 2019, Front. Astron. Space Sci., 6, 51 [CrossRef] [Google Scholar]
- Teyssier, R., Fromang, S., & Dormy, E. 2006, J. Comput. Phys., 218, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [Google Scholar]
- Tsukamoto, Y., Iwasaki, K., Okuzumi, S., Machida, M. N., & Inutsuka, S. 2015, ApJ, 810, L26 [Google Scholar]
- Valdivia, V., Maury, A., Brauer, R., et al. 2019, MNRAS, 488, 4897 [NASA ADS] [CrossRef] [Google Scholar]
- Vaytet, N., Chabrier, G., Audit, E., et al. 2013, A&A, 557, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaytet, N., Commerçon, B., Masson, J., González, M., & Chabrier, G. 2018, A&A, 615, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vlemmings, W. H. T., Diamond, P. J., van Langevelde, H. J., & Torrelles, J. M. 2006, A&A, 448, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, K., Zhang, Q., Testi, L., et al. 2014, MNRAS, 439, 3275 [Google Scholar]
- Yang, A. Y., Thompson, M. A., Urquhart, J. S., & Tian, W. W. 2018, ApJS, 235, 3 [Google Scholar]
- Yorke, H. W., & Bodenheimer, P. 2008, ASP Conf. Ser., 387, 189 [Google Scholar]
- Yorke, H. W., & Sonnhalter, C. 2002, ApJ, 569, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Zapata, L. A., Rodríguez-Garza, C., Rodríguez, L. F., Girart, J. M., & Chen, H.-R. 2011, ApJ, 740, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q., Hunter, T. R., Brand, J., et al. 2001, ApJ, 552, L167 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q., Wang, K., Lu, X., & Jiménez-Serra, I. 2015, ApJ, 804, 141 [Google Scholar]
- Zhang, Y., Tan, J. C., Sakai, N., et al. 2019a, ApJ, 873, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Tanaka, K. E. I., Rosero, V., et al. 2019b, ApJ, 886, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, B., Li, Z.-Y., Nakamura, F., Krasnopolsky, R., & Shang, H. 2011, ApJ, 742, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, B., Caselli, P., Li, Z.-Y., et al. 2016, MNRAS, 460, 2050 [Google Scholar]
- Zhao, B., Caselli, P., Li, Z.-Y., et al. 2020, MNRAS, 492, 3375 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Density maps in the plane of the disc and perpendicular to it for the models HYDRO (top), MU5I (second line), MU2AD (third line), MU5AD (fourth line), and MU5ADf (bottom). Two different times are represented: M⋆ = 5 M⊙ (left) and M⋆ = 10 M⊙ (right). The mass M⋆ gives the total mass converted into sink particles at each snapshot. The arrows represent the velocity vectors in the plane. |
| In the text | |
 |
Fig. 2 Density-temperature (top panels) and density-magnetic field amplitude (bottom panels) histograms for the models HYDRO, MU5I, MU2AD, MU5AD, and MU5ADf (from left to right) when the central sink mass is 10 M⊙. The colour-coding indicates the mass. |
| In the text | |
 |
Fig. 3 Mass evolution of the sink (top left), disc (top right), and outflow (bottom left) as a function of time after sink creation, and of the outflow as a function of the total disc+sink mass (bottom right). |
| In the text | |
 |
Fig. 4 Evolution of protostellar internal luminosity as a function of the protostellar mass (left) and of the time after sink formation (right). |
| In the text | |
 |
Fig. 5 Volume rendering of the outflow in the HYDRO run at the end of the simulation (left) and in the MU5AD run when the sink mass is 15 M⊙ (right). The colour-coding represents the radial velocity and is given in km s−1. In the left panel (HYDRO), the region represents a box of ≃40003 au, while the vertical extent is of about 75 000 au in the right panel (MU5AD run). |
| In the text | |
 |
Fig. 6 Density and force balance in the outflows for the MU5AD run when the sink mass is 5 M⊙ (top) and 15 M⊙ (bottom). Left panels: density cuts in the xz-plane within the outflow. Three other panels: maps of the ratios between the gravitational, the Lorentz, and the radiative forces. The colour maps are in logarithmic scale and the force ratio colour map is limited to the range [−1, 1] for plot readability, but its value can exceed these values. The bottom row is zoomed in the inner 10 000 au region. |
| In the text | |
 |
Fig. 7 Magnetic field topology and plasma β = P∕Pmag in the xz-plane in the MU5AD run, when the sink mass is 15 M⊙. Left panels: amplitude of the Alfvén velocity (blue colours) and the segments show the magnetic fields direction in the xz-plane. The colour-coding represents the ratio between the toroidal component of the magnetic fields over the total magnetic fields. Yellow-to-white segments exhibit strong toroidal fields with Bϕ ∕B > 0.3. Right panels: maps of the plasma β = P∕Pmag with velocity vectors overplotted. The red regions are dominated by the thermal pressure, while the blue ones are dominated by the magnetic pressure. |
| In the text | |
 |
Fig. 8 Density maps perpendicular to the disc plane (top) and in the disc plane (bottom) when the sink mass is ≈ 10 M⊙ for the runs HYDRO, MU5I, MU2AD, MU5AD, and MU5ADf, from left to right. The vectors indicate the gas velocity. Only the material of the disc is plotted. |
| In the text | |
 |
Fig. 9 Time evolution of disc radius for the HYDRO, MU5I, MU2AD, MU5AD, and MU5ADf runs. The symbols on the curves show the time at which the sink mass is 10 M⊙. |
| In the text | |
 |
Fig. 10 Evolution of angular momentum contained in the disc (solid line) and in the outflow (dashed) in the magnetised models MU5I, MU2AD, MU5AD, and MU5ADf. The symbols on the curves show the time at which the sink mass is 10 M⊙. |
| In the text | |
 |
Fig. 11 Maps of Toomre parameter Q in the rotation plane when the sink mass is ≈10 M⊙ for the runs HYDRO, MU5I, MU2AD, MU5AD, and MU5ADf, from left to right. Only the disc material is used to compute the Toomre parameter as explained in the main text. The colour map indicates the logarithm of Q, with blue (respectively red) indicating Q < 1 (respectivelyQ > 1) regions. |
| In the text | |
 |
Fig. 12 Plasma β for MU5I (left) and MU5AD (right) runs at the same times as in Fig. 8. Top (bottom) row: edge-on (face on) cut. Scales of β are logarithmic. |
| In the text | |
 |
Fig. 13 Mean radial profiles of density (top), Toomre parameter (bottom, dotted line), and plasma β (bottom, solid line) at different times for the MU5I, MU2AD, MU5AD, and MU5ADf runs, from left to right. |
| In the text | |
 |
Fig. 14 Mean radial profiles of the velocities and magnetic field components for the MU5I (first two rows), MU5AD (rows 3 and 4), and MU5ADf (rows 5 and 6). The time (and sink mass) increases from left to right. In the velocity plots, we represent the radial velocity Vr (thick red line), azimuthal velocity Vϕ (thick green), vertical velocity Vz (thick blue), Alfvén velocity VA (dashed blue), sound speed Cs (green cross), and Keplerian velocity |
| In the text | |
 |
Fig. 15 Histogram of the Toomre parameter Q as a function of the Elsasser number Am in the disc for the MU5AD model when the sink mass is 15 M⊙. The Toomre parameter is computed as explained in the main text, as a function of the position (r, θ) in the rotation plane. For each position, the Elsasser number is averaged over the disc height. The colour coding indicates the column density. The vertical (resp. horizontal) line shows the Am = 1 (resp. Q = 1). |
| In the text | |
 |
Fig. 16 Ratio of disc radius measured in the models with ambipolar diffusion (MU2AD in green, MU5AD in blue, and MU5ADf inyellow) and the analytical prediction of Hennebelle et al. (2016) as a function of the total sink and disc mass. |
| In the text | |
 |
Fig. A.1 Mass evolution of the sink (top-left), disc (top-right), and outflow (bottom-left) as a function of time after sink creation, and of the outflow as a function of the total disc+sink mass (bottom-right). The different colour scales for different maximum levels of refinement ℓmax and resolution are as follows: 20 au (black), 10 au (red), 5 au (green), and 2.5 au (blue). |
| In the text | |
 |
Fig. B.1 Mass evolution as a function of the sink age (left panel) or the total mass (right panel) for the models with (red) or without (black) the angular momentum accreted. |
| In the text | |
 |
Fig. B.2 Density maps in the plane of the disc and perpendicular to it for the model with no angular momentum accreted (top) and with all the angular momentum accreted (fiducial model MU5AD, bottom). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.