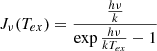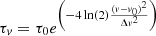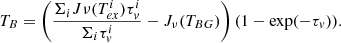| Issue |
A&A
Volume 654, October 2021
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202141233 | |
| Published online | 11 October 2021 | |
The distribution and origin of C2H in NGC 253 from ALCHEMI
1
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: holdship@strw.leidenuniv.nl
2
Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK
3
European Southern Observatory, Alonso de Córdova, 3107, Vitacura, Santiago 763-0355, Chile
4
Joint ALMA Observatory, Alonso de Córdova, 3107, Vitacura, Santiago 763-0355, Chile
5
National Astronomical Observatory of Japan, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
6
Institute of Astronomy and Astrophysics, Academia Sinica, 11F of AS/NTU Astronomy-Mathematics Building, No. 1, Sec. 4, Roosevelt Rd, Taipei 10617, Taiwan
7
Department of Astronomy, School of Science, The Graduate University for Advanced Studies (SOKENDAI), 2-21-1 Osawa, Mitaka, Tokyo 181-1855, Japan
8
National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA 22903-2475, USA
9
Department of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory, 43992 Onsala, Sweden
10
Department of Physics, Faculty of Science and Technology, Keio University, 3-14-1 Hiyoshi, Yokohama, Kanagawa 223–8522, Japan
11
Institute of Astronomy, Graduate School of Science, The University of Tokyo, 2-21-1 Osawa, Mitaka, Tokyo 181-0015, Japan
12
Institute of Space Sciences (ICE, CSIC), Campus UAB, Carrer de Magrans, 08193 Barcelona, Spain
13
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
14
Observatorio Astronómico Nacional (OAN-IGN), Observatorio de Madrid, Alfonso XII, 3, 28014 Madrid, Spain
15
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
16
Centro de Astrobiología (CSIC-INTA), Ctra. de Ajalvir Km. 4, Torrejón de Ardoz, 28850 Madrid, Spain
17
INAF-Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Florence, Italy
18
Astron. Dept., Faculty of Science, King Abdulaziz University, PO Box 80203, Jeddah 21589, Saudi Arabia
19
New Mexico Institute of Mining and Technology, 801 Leroy Place, Socorro, NM 87801, USA
20
National Radio Astronomy Observatory, PO Box O, 1003 Lopezville Road, Socorro, NM 87801, USA
Received:
1
May
2021
Accepted:
8
July
2021
Context. Observations of chemical species can provide insights into the physical conditions of the emitting gas however it is important to understand how their abundances and excitation vary within different heating environments. C2H is a molecule typically found in PDR regions of our own Galaxy but there is evidence to suggest it also traces other regions undergoing energetic processing in extragalactic environments.
Aims. As part of the ALCHEMI ALMA large program, we map the emission of C2H in the central molecular zone of the nearby starburst galaxy NGC 253 at 1.6″ (28 pc) resolution and characterize it to understand its chemical origins.
Methods. We used spectral modeling of the N = 1−0 through N = 4−3 rotational transitions of C2H to derive the C2H column densities towards the dense clouds in NGC 253. We then use chemical modeling, including photodissociation region (PDR), dense cloud, and shock models to investigate the chemical processes and physical conditions that are producing the molecular emission.
Results. We find high C2H column densities of ∼1015 cm−2 detected towards the dense regions of NGC 253. We further find that these column densities cannot be reproduced if it is assumed that the emission arises from the PDR regions at the edge of the clouds. Instead, we find that the C2H abundance remains high even in the high visual extinction interior of these clouds and that this is most likely caused by a high cosmic-ray ionization rate.
Key words: galaxies: individual: NGC 253 / astrochemistry / submillimeter: galaxies / radiative transfer
© ESO 2021
1. Introduction
Observations of chemical species provide a wealth of information about the physical conditions of astrophysical objects. However, in order to get the most information from a particular observation, it is important to understand the chemistry and excitation of molecules and related atomic species under different conditions. Whether the species under study is a classical dense gas tracer like CS (e.g., van der Tak et al. 2000) or more characteristic of photon-dominated regions (PDRs) such as C+, many of the most useful tracers are those whose relationships to physical parameters of interest are well understood.
Within the Milky Way, ethynyl (C2H) is a typical photodissociation region (PDR) tracer as its chemistry is strongly linked to C+ (Meier & Turner 2005). It is observed at low fractional abundances (∼10−10) in dense clouds (Wootten et al. 1980; Watt et al. 1988) and enhanced to ∼10−8 in low density gas (Turner et al. 1999; Lucas & Liszt 2000), where UV photons can penetrate and ionize C which is a key reactant in a chain of reactions that form C2H. Whilst C2H is also abundant in these environments in extragalactic objects (e.g., Aladro et al. 2011, 2015), there is an indication that it may be tracing more than just PDR regions in those extragalactic environments (García-Burillo et al. 2017).
A previous work focused on the Seyfert galaxy NGC 1068 (García-Burillo et al. 2017) indicated that C2H could be a tracer of the interface between high energy outflows and the ambient gas in a galaxy. The starburst ring of this galaxy showed a typical C2H abundance (∼10−8) similar to that found in diffuse clouds in Galactic environments. However, a larger, more extended component of gas had an abundance of ∼10−6 in the region between the molecular disk and ionized gas outflow. Chemical modeling efforts showed this larger abundance was only consistent with the short, early stages of models where some energetic process such as high cosmic ray ionization or shocks enhanced the C2H abundance. It was theorized in that work that the interface between an outflow and ambient gas would create an environment where unprocessed gas would continually be replenished and subjected to energetic processing. This could create a pseudo-steady state where the C2H abundance is stable at the high value found in the early stages of simple shock models.
It is possible therefore that C2H is a good tracer of molecular gas that is undergoing energetic processing and, more specifically, of the interface between active galactic nuclei (AGN) driven outflows and their environment. This would make it a useful tool for extragalactic observations. However, this must be tested against other galaxies. Moreover, only one multiplet of C2H was observed towards NGC 1068 and so additional transitions must be observed to assess excitation conditions and thus give a clearer picture.
NGC 253 is a prototypical starburst galaxy that hosts several large (∼30 pc), dense (∼105 cm−3) clouds which are well studied (e.g., Sakamoto et al. 2011; Leroy et al. 2018). Though similar in size to giant molecular clouds (GMCs) in the Milky Way, they are orders of magnitude more massive and have higher velocity dispersions (Leroy et al. 2015). NGC 253 was the chosen target of the ALCHEMI ALMA large program (Martín et al. 2021), which aimed at obtaining the most complete extragalactic molecular inventory in the central molecular zone of a starburst galaxy at a spatial resolution of tens of parsecs. NGC 253 also has a starburst driven outflow which can be observed at X-ray wavelengths (Dahlem et al. 1998) and in molecular emission (Bolatto et al. 2013; Krieger et al. 2019). This outflow may lead to a chemical environment similar to the AGN driven outflow of NGC 1068.
In summary, NGC 253 presents an interesting test case for the scenario proposed and modeled for NGC 1068. The star-forming regions of NGC 253 should present C2H emission similar to that found in the starburst ring of NGC 1068. More importantly, if enhanced C2H abundances are observed along the outflow then the chemical origin must be due to some commonality between the outflows from both galaxies. Alternatively, if enhanced abundances are not observed, this would indicate a different chemical composition between starburst-driven outflows and AGN-driven outflows.
To investigate this, images of multiple transitions of C2H in the central molecular zone (CMZ) of NGC 253, as well as calculations of the column density and fractional abundance are presented. In Sect. 2, the observations and ALCHEMI large program are described. In Sect. 3, the C2H emission distribution and column densities are discussed. In Sect. 4, average fractional abundances are interpreted through chemical models.
2. Observations and image processing
2.1. Observations
The analysis presented in this article makes use of the data collected by the ALMA ALCHEMI large program, which is an unbiased spectral survey of NGC 253 covering the full ALMA spectral bands 3 through 7. The ALCHEMI program and all observational details are described extensively in Martín et al. (2021). A summary of ALCHEMI survey details pertinent to the C2H data presented in this article is given here.
NGC 253 was observed toward a nominal phase center of α = 00h47m33.26s, δ = −25° 17′17.7″ (ICRS). Observations were configured to cover a common rectangular area of 50″ × 20″ with a position angle of 65° (East of North). The spectral configuration for the ALCHEMI Survey of NGC 253 was configured with 47 receiver tunings; each comprising four 1.875 GHz spectral windows. All tunings were imaged to a shared beam size of  and the maximum recoverable scale was 15″1. At a distance of 3.5 Mpc (Rekola et al. 2005), these correspond to linear scales of 28 and 250 pc, respectively. Within the ALCHEMI frequency coverage, four multiplets of C2H transitions namely N = 1−0, 2−1, 3−2, and 4−3 were observed. This includes 39 hyperfine transitions across ALMA bands 3, 5, 6, and 7 and these are listed in Table 1.
and the maximum recoverable scale was 15″1. At a distance of 3.5 Mpc (Rekola et al. 2005), these correspond to linear scales of 28 and 250 pc, respectively. Within the ALCHEMI frequency coverage, four multiplets of C2H transitions namely N = 1−0, 2−1, 3−2, and 4−3 were observed. This includes 39 hyperfine transitions across ALMA bands 3, 5, 6, and 7 and these are listed in Table 1.
C2H transitions covered by the ALCHEMI large program’s observations taken from JPL (Pickett 1998).
The datacubes used in this work have been made available as part of the public release of the ALCHEMI data. The FITS files associated with the B3a, B5d, B6g, and B7o science goals were used for this work each covering a single multiplet from N = 1−0 to N = 4−3.
2.2. Data processing
We loaded and processed the FITS files using Astropy and Spectral Cube (Astropy Collaboration 2013, 2018). Standard routines from those packages were then used to produce moment 0 maps. The velocity ranges for those maps are given in Table 2 and were chosen so that they contain all the C2H lines but excluded any strong lines from other species that may contaminate the maps. This was informed by local thermodynamic equilibrium (LTE) modeling of the ALCHEMI project’s ALMA compact array data of the region (Martín et al. 2021) that provided both the velocity ranges that would cover all expected C2H emission and the line intensities of possible contaminating lines. Only the N = 3−2 transition was likely to be contaminated and, as a result, we chose a velocity interval that excluded a hyperfine component with frequency 261.834 GHz in order to remove the 76 − 65 line of SO. The spectral modeling performed in this work (Sect. 3.3) predicted negligible emission from the omitted C2H line and verified that the chosen velocity ranges contained all other C2H emission.
Velocity limits used to produce the moment 0 maps for each C2H multiplet.
We also extracted spectra using Spectral Cube and used the package’s unit conversion to convert the extracted spectra to units of Kelvin. We estimated the noise value for any given spectrum from the mean difference between the median value and all channels lower than the median. This is effectively taking the variance whilst excluding channels above the average as they are “contaminated” by signal. Where the spectra were extracted from multiple pixels, such as in the GMCs (Sect. 3.1), a median stack of the individual pixel spectra was taken.
2.3. Spectral modeling
C2H is a molecule with hyperfine structure that, together with the broad velocity distributions in the data, produces spectra with large numbers of blended lines. Furthermore, the complex dynamic situation in NGC 253 gives rise to multiple, blended emitting components (Krieger et al. 2020). As such, a spectral model is required to disentangle the emission.
In this work, we used SpectralRadex2 to model the spectra. This is a Python package that creates model spectra from RADEX using a formalism described in Appendix A. Briefly, it contains a wrapper to run RADEX (van der Tak et al. 2007) in order to obtain the excitation temperature and the optical depth at the line centre of every modeled transition. The package then produces model spectra by assuming that each transition follows a Gaussian line profile described by the central velocity and FWHM. It has been benchmarked against the RADEX based spectral model in CASSIS3 (Vastel et al. 2015) for a wide variety of test cases and each best fit presented in this work has been replicated in CASSIS. Collisional rates between C2H and ortho and para H2 were used (Dagdigian 2018) to produce the RADEX outputs assuming an ortho to para ratio of 3:1. These cover a temperature range of 10−300 K and were taken from the LAMDA database4 (Schöier et al. 2005).
3. Results
3.1. Distribution of C2H
In Fig. 1, the integrated emission of each observed group of C2H hyperfine transitions is shown. Each group of transitions follows broadly the same distribution with the N = 2−1 group being the brightest. Most strikingly, the majority of the C2H emission does not appear to follow the full extent of the outflow traced in CO by Krieger et al. (2019). The N = 1−0 emission traces the SW streamer which has been observed in CO (Walter et al. 2017) (see Fig. 2) but the outflow is otherwise not apparent.
 |
Fig. 1. Integrated emission maps of C2H in NGC 253. The beam size for all panels is 1.6″ and is shown in the bottom left panel. Since the beam size is shared, the wider spatial distribution of the N = 1−0 emission is not caused by a beam size effect. Contours at the 3, 5, 10, 20 and 50σ level are drawn in black. The noise levels in order of increasing N are 1.4, 8.5, 2.0 and 1.6 K km s−1. Each ellipse shows the position and size of the Gaussian fits to the four individual clumps described in Sect. 3.1. The numbers indicate the position of the GMCs in Leroy et al. (2015). |
 |
Fig. 2. Integrated emission map of the C2H N = 1−0 multiplet as in Fig. 1 but showing the full extent of the emission. Contours are shown at the 3, 5, 10, 20 and 50σ levels for noise level of σ = 1.5 K km s−1. Black squares indicate the positions sampled for spectra in Fig. 3. |
The majority of the emission arises from five clumps that are therefore the focus of this work. The position of each clump corresponds to one of the giant molecular clouds (GMCs) identified in Leroy et al. (2015) and so their numbering system is adopted. However, it should be noted that, at higher resolution, GMC 4, 5 and 6 have been resolved into smaller structures and consist of several dense objects that are blended in larger beams (Ando et al. 2017; Mangum et al. 2019).
The positions of the clumps were first approximately identified by eye and then five 2D dimensional Gaussian distributions were fit to the N = 2−1 moment 0 map using those positions as initial guesses for the central coordinates. The sizes and central positions of the Gaussians were then simultaneously adjusted to minimize the discrepancy between their sum and the moment 0 map. This allowed the positions and sizes of the five clumps to be fit, taking into account the overlap between them. These five objects are the brightest GMCs in the region when observed in both the continuum and the CO 2−1 transition (Sakamoto et al. 2011).
In order to approximate an angular size for the GMCs, the FWHM of a symmetric Gaussian with the same solid angle as the fitted 2D Gaussian was calculated. This was taken to be the convolved size of the source in the beam (ΩS * B). From this, the filling factor can be calculated as
which is a simple substitution of ΩS * B into the more standard 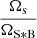 (Martín et al. 2019) where ΩB is the solid angle of the beam. These filling factors were used to correct the intensity of all spectra extracted from the GMCs in this work. The positions of the GMCs, their convolved angular sizes and the filling factors are given in Table 3.
(Martín et al. 2019) where ΩB is the solid angle of the beam. These filling factors were used to correct the intensity of all spectra extracted from the GMCs in this work. The positions of the GMCs, their convolved angular sizes and the filling factors are given in Table 3.
Details of the GMCs observed in C2H and studied in this work including co-ordinates, convolved size and beam filling factor.
Whilst most emission is confined to the GMCs, there is also extended emission over the CMZ. In Fig. 1, it is clear the emission above the 3σ level generally extends far past the GMCs, covering the CMZ region traced by other molecules (Sakamoto et al. 2011). The CMZ emission is strongest and has the largest extent in the N = 1−0 emission. All beam sizes are 1.6″ so the wider spatial distribution of the N = 1−0 emission is not a beam size effect. Therefore, there must be a gas component present that is sufficiently different in nature to the GMCs to excite N = 1−0 emission more strongly than the others. Figure 2 shows the extent of this emission which is referred to as the extended emission going forward.
3.2. Characterizing the extended emission
The focus of this work is on the C2H emission from the GMCs. However, one would expect some contribution from the extended emission to any spectra extracted from the GMC positions because the map in Fig. 2 shows the CMZ surrounds the GMCs. Moreover, preliminary modeling work showed that the N = 1−0 and N = 4−3 lines could not be simultaneously fit by a single component in any spectrum.
In order to attempt to reduce the degeneracy inherent in fitting multiple gas components to a spectrum, the extended emission was characterized first to obtain constraints on possible values that could be used in the GMC fit. In Fig. 3, spectra from random positions throughout the extended region are shown. They have been resampled to common frequency bins and median stacked without velocity shifting. The positions from which they were extracted are indicated by black squares in Fig. 2.
 |
Fig. 3. Median stack of all spectra sampled from the extended region of the CMZ. The median is shown as a line and the shaded region gives the 95% confidence interval on this value. The black squares in Fig. 2 indicate the positions from which spectra were extracted for this composite spectrum. The black lines indicate the positions of the C2H components in each N transition, Doppler shifted by 255 km s−1, the LSR velocity of NGC 253. |
These spectra are not directly analysed and are meant only to show the general trend of the extended emission from the CMZ. They are strongest in the N = 1−0 transition and become successively weaker at higher N, with the 2−1 line being anomalously weak. This same trend can be seen in the moment 0 maps. Thus the properties of the CMZ gas can be constrained by demanding the emission predicted by radiative transfer model follows this trend.
A large grid of RADEX models was run in which the gas density, column density and gas temperature were varied. The trialled ranges of these variables are given in Table 4. The parameter space that would be appropriate for the extended emission was then found by utilising two simple constraints. First, all models where the peak N = 1−0 emission was less than 0.03 K were rejected because this would be less than three times the rms noise in the CMZ spectra. Second, any model where the N = 1−0 emission was not the strongest of the four detected lines was also rejected as the N = 1−0 lines are the brightest part of the extended emission. The parameter values of the remaining models define a parameter space that would be appropriate for the extended emission.
RADEX parameters used to constrain the gas properties of the extended emission component.
Table 4 gives the parameter ranges that conformed to the above constraints. This is also illustrated in Fig. 4 where the points indicate a set of parameters that match our constraints. From this figure, relationships between the variables can be seen. Given the weak constraints from the data used for this procedure, the parameters are not well constrained. In particular, the column density is essentially unconstrained as the relative strengths of lines is all that was used rather than the absolute values.
 |
Fig. 4. Model parameters that fit constraints from the extended emission of the CMZ. Each point represents the parameters of a model where the N = 1−0 line was the strongest line and was above noise. |
However, the constraints on the gas properties are important. The gas must be at a low density between 3.5 × 103 cm−3 and 1.7 × 104 cm−3. It must also be warm as all models that fit our loose constraints have a gas temperature > 50 K. This is similar to the PDR regions in which C2H is observed in our own Galaxy (Pilleri et al. 2013; Cuadrado et al. 2015). Further, these limits can be used to inform the GMC modeling in Sect. 3.3, breaking the degeneracy inherent in fitting multiple gas components to a single spectrum.
3.3. Characterizing the GMCs
In order to model the GMC spectra, two gas components were used for each GMC. The first was limited to the constrained range of parameters given in Table 4 to allow for the extended emission contributing to the spectra. The second component simply had to have a larger density than the extended emission and represents the component from the GMC itself.
The fits were performed via a Bayesian inference procedure in which emcee (Foreman-Mackey et al. 2013) was used to evaluate the posterior distribution of the parameters assuming flat priors and a Gaussian likelihood. The error on each channel was taken to be the spectral noise and an absolute calibration uncertainty of 15% (see Martín et al. 2021 for details) of the channel intensity added in quadrature. Thus the reported most likely values are equivalent to those found through χ2 minimization but the reported uncertainties are based on the probability distribution of the parameters given the measured spectra.
One special case was GMC 5 for which the best fit is shown in Fig. 5. This GMC very clearly has two distinct velocity components, possibly due to the fact that GMC 5 actually comprises at least four clumps with varying gas velocities (Ando et al. 2017). Despite this known substructure, we chose to fit the two velocity components that are apparent in the data; one with a central velocity of less than 200 km s−1 and one with a velocity larger than 200 km s−1. Since the CMZ contaminates both, we further add two low density components. This gives a total of four components: one low density and one high density for each velocity range.
 |
Fig. 5. Best fit model for GMC 5. The black trace shows the measured spectra with error bars. The histograms show the spectral model components in colour and their total in grey. The legend gives the central velocity (V0) and linewidth (ΔV) of each component. The two blue components are the low density CMZ contribution and the others are the high density GMC components. |
The spectra fits in Fig. 5 and Appendix B show that the assumption that the extended emission is contaminating the GMC spectra are justified. The results of the fitting in these figures show the N = 1−0 line is dominated by the extended emission component as expect from the fact the extended emission is brightest in this component.
The focus of this work is on the GMC emission and so only the values of the high density component are reported in the following sections. The parameters describing the extended components are therefore treated as nuisance parameters and are simply marginalized over. As a result, the reported uncertainty on the GMC component parameters contains the uncertainty from the degeneracy inherent in fitting multiple components.
3.3.1. C2H abundance
The inferred properties of the GMCs, excluding the extended emission, are presented in Table 5. For each GMC, the single best fit value of each parameter is presented along with the interval containing 67% of the probability density of the marginalized posterior distribution of that parameter. This can be thought of as a 1σ interval. The RADEX derived column density of C2H is fairly uniform across the GMCs, each having a best fit value in the range 1015 − 1016 cm−2.
Parameter estimates with 1σ range from the spectral model fitting to each GMC.
However, if the total H2 column density of the cloud is considered, the C2H abundances are more varied. Using the H2 column density measured from the continuum by Mangum et al. (2019) towards each GMC and assuming the H2 and C2H trace the same gas, we calculate the C2H fractional abundances which are given in Table 6. These vary in the range 3.6 × 10−10 − 1.7 × 10−8.
Most likely fractional abundance of C2H and likely bounds.
3.3.2. Gas properties
In general the temperature of the gas is poorly constrained by our C2H data, with the marginalized posteriors for the temperature being approximately flat in the range 50−300 K. This is to be expected given that the highest upper state energy of the detected transitions is 41.9 K and thus we should not be sensitive to changes in temperature much above this value. Mangum et al. (2019) also found temperatures > 50 K on scales similar to the GMCs using measurements of H2CO emission.
On the other hand, the gas densities are relatively well constrained and consistent with other measurements in the region. At ∼105 cm−3, the gas density is similar to the high end of the range found using dust masses from Sakamoto et al. (2011) and the values measured at higher resolution by Leroy et al. (2018) also from dust.
4. The origin of C2H in the NGC 253 GMCs
In the previous section, column densities were derived for each GMC, excluding the extended emission. In this section, those column densities and the corresponding fractional abundances are used to constrain chemical models to investigate the origin of C2H in these clouds.
4.1. PDR chemistry
C2H is ubiquitous in galactic PDRs (Lucas & Liszt 2000) and so we explore the possibility that the observed emission arises from the low Av outer edges of the GMCs. Therefore, a grid of PDR models was run using UCL_PDR5 (Bell et al. 2006; Priestley et al. 2017), a code that has been extensively benchmarked (Röllig et al. 2007). In these models, a 1D cloud of gas in equilibrium was considered with a variety of physical parameters given in Table 7 assuming a uniform density. The model iteratively solves the temperature and chemistry considering a variety of heating and cooling processes as well as 215 chemical species interacting through ∼2900 reactions until an equilibrium is reached.
Parameters varied for PDR chemical model.
The model produces fractional abundances as a function of distance into the GMC or, equivalently, visual extinction. Therefore, the species’ column densities can also be calculated by limiting the model to the maximal H2 column density measured towards the region and integrating the C2H density over that range.
The fractional abundance of C2H as a function of depth in these models is given in Fig. 6. The key result is that whilst many models reach C2H abundances compatible with those measured in NGC 253 at low Av, none are capable of explaining the observed column density of ∼1015 cm−2 if a uniform medium is assumed. In fact, assuming a maximum H2 column density of 2.2 × 1024 cm−2 (the largest measured by Mangum et al. 2019 towards one of the GMCs discussed here), the largest possible C2H column density from a model with the canonical Milky Way cosmic-ray ionization rate of ζ0 = 1.3 × 10−17 s−1 is 6 × 1013 cm−2. This is over an order of magnitude too low to match any GMC.
 |
Fig. 6. Fractional abundance as a function of depth into the cloud from PDR modeling and observations. The depth into the cloud is given as the equivalent visual extinction. The black dots are numbered according to the GMC they represent and error bars show the observed abundance towards that GMC, their position on the x-axis is arbitrary and does not represent the cloud sizes. The lines show UCL_PDR models with different parameters. The shaded band covers the abundance range of all GMC measurements. In the low cosmic-ray ionization rate models (left), the abundance decreases with distance into the cloud so the total column density is less than the observed column density despite the high abundances reached at low Av. |
This is because the abundance reduces with depth into the cloud so only the outer edges contribute to the column. One solution to this would be to invoke clumpiness. However, for PDR chemistry to be responsible for the observed C2H emission, the average Av would need to be less than 2 mag despite the fact the column density in these clouds would give an Av > 500 mag.
If, on the other hand, an enhanced cosmic-ray ionization rate is introduced, the model abundances of C2H become enhanced and constant with respect to Av. This enhancement is due to the high ionization rate creating an environment where the ionization fraction is high, much like a PDR, even in high Av regions of the model. In the models, C2H is produced primarily through the chain,
-
C+ + CH2 → C2H+ + H
-
H2 + C2H+ → C2
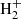 + H
+ H -
C2
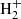 + e− → C2H + H
+ e− → C2H + H
regardless of whether C+ is produced through photochemistry or cosmic ray ionization. For a rate of 1000 ζ0, many models give a C2H abundance of ∼10−8 regardless of depth into the cloud. This produces column densities in line with those observed. Therefore, ruling out the possibility that the GMCs are so clumpy that the average visual extinction is less than 2 mag, it can be concluded that the C2H emission observed in NGC 253 does not primarily originate from the PDR regions in the clouds. If that is the case, the C2H emission must come from within the clouds where some process maintains the C2H abundance at high visual extinctions and this is explored in the following sections.
4.2. Dense cloud chemistry
Given the likelihood that C2H emission observed towards the GMCs in NGC 253 comes from within those clouds rather than the UV irradiated skin, it becomes appropriate to model the chemistry with a dense cloud model where photo-processes are assumed to be negligible. UCLCHEM6, a gas-grain chemical code (Holdship et al. 2017) was used for this purpose.
It is assumed that since the extinction of UV photons is the only depth dependent process, the entire interior of a GMC can be modeled as a single point with an Av that is sufficiently high to make all UV processes negligible. Therefore, a grid of single point models was run with an Av of 10 mag which is sufficient to reduce the local UV field in the model to zero. This grid covered a range of gas densities, temperatures, and cosmic-ray ionization rates to represent different GMC conditions which are given in Table 8.
Parameters varied for dark cloud chemical model.
Each GMC model used initial abundances that were generated by a model that started from purely atomic gas with solar elemental abundances (Asplund et al. 2009) with silicon depleted to 1% of its solar value. The initial density was nH2 = 102 cm−3 and the density then increased according to a freefall collapse model to the required density of the GMC model. This provided realistic initial abundances for a GMC that has formed from diffuse gas without assuming values which the chemical network may not be able to produce. Each model was run for 5 Myr so that the abundance over time and the steady-state value could be analysed.
The model results in Fig. 7 show that equilibrium values are quickly reached. Note that at t = 0 yr, the model is already at the post-collapse density. In fact, in many cases, the C2H abundance becomes constant after as few as 104 years. Further, within the limits of the grid, the steady state abundance of C2H is typically not strongly affected by the gas temperature. In fact, as long as the abundance of C2H is sufficiently high to match the observations, the temperature only creates a small variance as shown by the shaded region around each line in the plot. Instead, the combination of the gas density and cosmic-ray ionization rate sets the abundance.
 |
Fig. 7. Fractional abundance of C2H as a function of time in the UCLCHEM models. Each line shows the median value of the abundance for a given cosmic-ray ionization rate as temperature is varied and the shaded regions show the minimum and maximum abundances over that temperature variation. The cosmic-ray ionization rate is given as a multiple of ζ0 = 1.3 × 10−17 s−1 and a sample of the lines are given in the legend. The grey shaded area shows the observed range. |
If it is assumed the abundances reach steady state, the cosmic-ray ionization rate required to obtain the measured C2H abundances appears to have a log-log relationship to the density. This is to be expected given that higher densities tend to decrease the total ionization fraction in the models and so a higher cosmic-ray ionization rate is needed to maintain the PDR-like chemistry that produces C2H. Thus, using the estimates of the gas density from Sect. 3.3.2, it may be possible to constrain the ionization rate. Figure 8 shows the steady state abundance of C2H as a function of the gas density and cosmic-ray ionization rate. Overplotted are points representing each GMC, showing the range of densities found in Sect. 3.3.2 and the cosmic-ray ionization rate range that gives model abundances within the measured limits for that GMC.
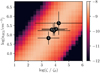 |
Fig. 8. Steady state C2H abundance shown in colour scale as a function of gas density and cosmic-ray ionization rate in units of ζ0 = 1.3 × 10−17 s−1. The values given are a median over different gas temperatures. Each point represents a GMC with the vertical lines showing the upper and lower limits on the density for that cloud. The horizontal lines span the cosmic-ray ionization rate values that give abundances within the measured range for those density values. GMC 7 does not appear on this diagram as no model produces a large enough abundance of C2H to match even its observed lower-limit. |
GMC 7 presents a problem as no model produces a large enough abundance of C2H to match even the lower limit for that GMC and hence it is missing from Fig. 8. However, there is a lot of uncertainty in both the derived fractional abundance and the chemical model. The H2 column density used to convert to abundance was derived using an assumed dust temperature and dust to gas ratio as well as assuming optically thin dust emission. If the resulting column density was underestimated by even a factor of 2, the abundance can be fit. If we further consider uncertainties such as the initial elemental abundance of carbon in the chemical model, a discrepancy of this magnitude is unsurprising.
The poor fit of GMC 7 and the fact that the cosmic-ray ionization rate can only be constrained to within a few orders of magnitude for the other GMCs indicates that this analysis should only be considered qualitatively. The fits show that the cosmic ray ionization rate is likely to be high in these regions but the specific values are very uncertain. Each GMC has a lower limit on the cosmic-ray ionization rate of 1500 ζ0 except for the high velocity component of GMC 5 where the density is poorly constrained and so ζ can be as low as 100 ζ0. Overall, we can conclude that the observed C2H emission could arise from the chemistry of a cosmic ray dominated region where the cosmic-ray ionization rate must be much higher than standard but cannot constrain it to within an order of magnitude.
4.3. Shock chemistry
Whilst the previous section indicates cosmic rays may be the main driver of the chemistry producing C2H, it should be noted that other possibilities exist. Most importantly, the model effectively treats cosmic rays as ionization events that are not reduced by the gas column density and so other sources of ionization such as the strong X-ray irradiation in the region (Strickland et al. 2002) could be at work instead. It is also possible that physical processes such as shocks not included in the previous models could cause an enhanced abundance of C2H.
The dense cloud modeling shows that simply heating the gas or increasing the density cannot produce enough C2H. This is illustrated in Fig. 7 where the shaded regions show little variation in abundances as the temperature varies between 50 and 300 K and in Fig. 8 which shows the C2H abundance actually decreases with increasing density for a given cosmic ray ionization rate. However, more complex physical processes could be at work. A natural possibility is turbulence which would affect the chemistry through shocks as low velocity shocks have previously been found to dominate the heating in the region (Martín et al. 2006). These shocks would tend to heat and compress the gas as well as remove material from the grains. Furthermore, in NGC 1068 it was found one possible cause of the high C2H abundances was in fact shocks (Aladro et al. 2013; García-Burillo et al. 2017).
To explore this, we run a simple grid of shock models using UCLCHEM’s shock module based on the C-shock parametrization of Jiménez-Serra et al. (2008). We vary the shock velocity from 5 to 40 km s−1, to trial a range of velocities over which the shock treatment is applicable. We apply these shocks to gas with pre-shock densities between 104 and 106 cm−3 with initial abundances taken from a collapse model as described in Sect. 4.2. We vary the pre-shock gas temperature from 10 to 50 K and cosmic-ray ionization rate between 1 and 10 ζ0 to separate the effects of shocks and high ionization rates. These parameter ranges are summarized in Table 9.
Parameters varied for shock chemical models.
In almost every model, the pre-shock C2H abundance was an order of magnitude too low to match observations and the passage of a shock permanently reduced the C2H abundance, meaning most shocks could not reproduce observations. However, a small subset of shock models with a density of 104 cm−3 and a shock velocity greater than 20 km s−1, had C2H abundances that were enhanced briefly by the shock passage. In each of these models, there is a short period of ∼105 years where the C2H abundance is enhanced to the levels observed in NGC 253 (see Fig. 9).
 |
Fig. 9. Fractional abundance of CCH through time for a 20 km s−1 shock propagating through gas with a pre-shock density of 104 cm−3 plotted in black, temperature through the shock plotted in red. The range of observed C2H abundances is shown in grey. |
Naturally, a single simple shock model is difficult to apply to a large cloud that is possibly experiencing multiple small shocks due to turbulent internal motion. However, taking an average over the shock structure, the model abundances of this subset of shock models are all within the lower and upper bounds on the C2H abundance for at least one GMC as given in Table 7. Therefore, if one argues that shocks are so ubiquitous in these GMCs that almost all of the gas is constantly in a state of having just been shocked (within 105 years) then the overall average C2H abundance will be within our observational constraints.
However, there are several aspects of the GMCs that indicate the required shock conditions are not met in these objects. Our models indicate shocks with a velocity greater than 20 km s−1 are necessary but previous work has suggested shocks (< 20 km s−1) are common in the region (García-Burillo et al. 2000; Martín et al. 2006). Moreover, the post shock density in these models is only 5 × 104 cm−3 and the gas densities in the GMCs are larger. This is vital as models with higher pre-shock gas densities do not reproduce the observed abundances. Finally, it is unlikely that all of the gas in the GMCs is shocked repeatedly on a timescale of 105 years but averaging over longer times in the shock model produces abundances that are lower than those observed.
To summarize, a subset of shock models could potentially reproduce the abundances of C2H observed in these clouds and therefore cannot be ruled out. However, the conditions required do not match those measured for the GMCs and the gas would have to be almost constantly undergoing a shock. Therefore, we consider it unlikely in comparison to the wide range of cosmic ray dominated models that fit the measured abundances.
4.4. Relationship to other sources
In the Milky Way, it is typical to observe C2H with abundances similar to those measured for NGC 253 in PDRs. However, it is clear from the modeling done in this work that it cannot be the case that C2H in NGC 253 arises entirely from PDRs. The observed column densities are far too high and another process must be at play.
In this work, we have proposed that a large degree of ionization, likely from cosmic rays, is responsible for the C2H abundance or, less likely, ubiquitous shocks in the GMC. This is similar to the molecular cloud G+0.693−0.027 which has a C2H abundance of 4 × 10−8 (Bizzocchi et al. 2020). The cosmic ray ionization rate is expected to be several orders of magnitude higher than the standard Milky Way value at the Galactic centre. However, the chemistry in the cloud is also thought to be shock dominated (Requena-Torres et al. 2006).
A comparison to NGC 1068 is also of interest. In that galaxy, the C2H emission was observed towards both the starburst ring and along the AGN driven outflow. However, only the N = 1−0 transition was observed by García-Burillo et al. (2017) and so the column density could not be well constrained. Assuming temperatures around 50 K and LTE, a fractional abundance of C2H similar to that measured here for NGC 253 can be recovered for the starburst ring. However, a true comparison of the star forming regions in these galaxies would require higher N transitions of C2H to be observed toward NGC 1068 as the majority of emission from the GMCs in NGC 253 was found in those lines.
C2H was also detected in NGC 1068 at higher abundances in the range 10−7 to 10−6 around the AGN driven outflow. A variety of physical factors including high UV fields, high cosmic-ray ionization rates and shocks could all produce this abundance for a very short time according to chemical modeling work in García-Burillo et al. (2017). As a result, the authors conclude the high abundances are maintained by a dynamic environment around the outflow in which gas is constantly resupplied to the interface between the outflow and its surroundings. As a result, a pseudo-steady state is reached where the gas is well fit by the early stages of their chemical models. Whilst this picture makes sense for an outflow interface, it does not apply to the GMCs observed in NGC 253 which are much more static.
Thus, we are tracing fundamentally different gas in each galaxy with C2H. This is evidenced by the fact the majority of the C2H emission does not appear to follow the outflow of NGC 253 as traced in CO by Krieger et al. (2019). In fact, only the N = 1−0 line traces the base of the outflow as found in previous work (Meier et al. 2015) unlike in NGC 1068 where is traces a large extend of the outflow (García-Burillo et al. 2017). This lack of outflow emission indicates that the energetic processing producing the high abundance of C2H in NGC 1068’s AGN driven outflow is not present in NGC 253’s starburst driven outflow. NGC 253 appears to represent a third class of C2H rich gas in which an ionizing process such as cosmic ray ionization maintains an ion dominated chemistry and therefore enhanced abundances of C2H well into dark regions. It is clearly distinguishable from the outflow case by its lower C2H abundance and coincidence with dense gas but differentiated from PDR emission by its high column density.
5. Conclusions
The emission of the N = 1−0 to N = 4−3 rotational transitions of C2H in NGC 253 was imaged with ALMA at a resolution of 28 pc (1.6″). Most of the C2H emission traces the dense gas of the brightest GMCs that have been previously studied in the CMZ of NGC 253. However, the emission from the N = 1−0 transition also traces diffuse gas in the CMZ itself. C2H does not appear to follow the galaxy’s starburst driven outflow.
Spectral modeling was used to infer the gas properties of the GMCs. The temperatures were found to be > 50 K and the gas densities varied from 105 cm−3 to 106 cm−3. These values are in line with those previously measured in the GMCs. The column density of C2H was also constrained to be in the range 1015 − 1016 cm−2 which corresponds to fractional abundances ∼10−9.
Chemical modeling showed that despite being enhanced in PDRs, the C2H emission in these GMCs could not entirely arise from the photon dominated outer regions of these dense clouds but must instead come from within the clouds. C2H in these GMCs most likely arises from gas where the ionization fraction is kept high by some ionizing process such as cosmic rays. Alternatively, ubiquitous shocks could be responsible for the measured C2H abundance but this would require the entire gas to be shocked on such a short timescale that this is unlikely.
If a high cosmic-ray ionization rate is responsible for the C2H abundance, the ionization rate in each GMC is constrained to within a few orders of magnitude only. The values for each GMC vary from 103 to 106ζ0. A more sensitive probe of the cosmic-ray ionization rate should be utilized in these regions to confirm the presence of a high ionization rate and better constrain its value.
The maximum recoverable scale corresponds to the size of the largest structure that can be observed with a given array configuration of an interferometer. In practice, it can be estimated as λ/Bmin, where λ is the wavelength and Bmin is the length of the shortest projected baseline during the observations. (See also https://almascience.nrao.edu/documents-and-tools/cycle8/alma-technical-handbook/view.)
Acknowledgments
We thank the anonymous referee for their report which led to the improvement of this manuscript. JH and SV are funded by the European Research Council (ERC) Advanced Grant MOPPEX 833460.vii VMR and LC are funded by the Comunidad de Madrid through the Atracción de Talento Investigador (Doctores con experiencia) Grant (COOL: Cosmic Origins Of Life; 2019-T1/TIC-15379). This paper makes use of the following ALMA data: ADS/JAO.ALMA#2017.1.00161.L and ADS/JAO.ALMA#2018.1.00162.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ.
References
- Aladro, R., Martín, S., Martín-Pintado, J., et al. 2011, A&A, 535, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aladro, R., Viti, S., Bayet, E., et al. 2013, A&A, 549, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aladro, R., Martín, S., Riquelme, D., et al. 2015, A&A, 579, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ando, R., Nakanishi, K., Kohno, K., et al. 2017, ApJ, 849, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bell, T. A., Hartquist, T., Viti, S., & Williams, D. A. 2006, A&A, 459, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bizzocchi, L., Prudenzano, D., Rivilla, V. M., et al. 2020, A&A, 640, A98 [EDP Sciences] [Google Scholar]
- Bolatto, A. D., Warren, S. R., Leroy, A. K., et al. 2013, Nature, 499, 450 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cuadrado, S., Goicoechea, J. R., Pilleri, P., et al. 2015, A&A, 575, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dagdigian, P. J. 2018, MNRAS, 479, 3227 [Google Scholar]
- Dahlem, M., Weaver, K. A., & Heckman, T. M. 1998, ApJS, 118, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- García-Burillo, S., Martín-Pintado, J., Fuente, A., & Neri, R. 2000, A&A, 355, 499 [NASA ADS] [Google Scholar]
- García-Burillo, S., Viti, S., Combes, F., et al. 2017, A&A, 608, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holdship, J., Viti, S., Jiménez-Serra, I., Makrymallis, A., & Priestley, F. 2017, AJ, 154, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Hsieh, T. H., Lai, S. P., Belloche, A., Wyrowski, F., & Hung, C. L. 2015, ApJ, 802, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Caselli, P., Martín-Pintado, J., & Hartquist, T. 2008, A&A, 482, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krieger, N., Bolatto, A. D., Walter, F., et al. 2019, ApJ, 881, 43 [CrossRef] [Google Scholar]
- Krieger, N., Bolatto, A. D., Leroy, A. K., et al. 2020, ApJ, 897, 176 [Google Scholar]
- Leroy, A. K., Bolatto, A. D., Ostriker, E. C., et al. 2015, ApJ, 801, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Bolatto, A. D., Ostriker, E. C., et al. 2018, ApJ, 869, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Lucas, R., & Liszt, H. S. 2000, A&A, 358, 1069 [NASA ADS] [Google Scholar]
- Mangum, J. G., Ginsburg, A. G., Henkel, C., et al. 2019, ApJ, 871, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Martín, S., Mauersberger, R., Martín-Pintado, J., Henkel, C., & García-Burillo, S. 2006, ApJS, 164, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Martín, S., Martín-Pintado, J., Blanco-Sánchez, C., et al. 2019, A&A, 631, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martín, S., Mangum, J. G., & Harada, N. 2021, A&A, submitted, https://doi.org/10.1051/0004-6361/202141567 [Google Scholar]
- Meier, D. S., & Turner, J. L. 2005, ApJ, 618, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Meier, D. S., Walter, F., Bolatto, A. D., et al. 2015, ApJ, 801, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M. 1998, Appl. Opt., 24, 2235 [NASA ADS] [Google Scholar]
- Pilleri, P., Treviño-Morales, S., Fuente, A., et al. 2013, A&A, 554, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Priestley, F., Barlow, M. J., & Viti, S. 2017, MNRAS, 472, 4444 [NASA ADS] [CrossRef] [Google Scholar]
- Rekola, R., Richer, M. G., McCall, M. L., et al. 2005, MNRAS, 361, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Requena-Torres, M. A., Martín-Pintado, J., Rodríguez-Franco, A., et al. 2006, A&A, 455, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röllig, M., Abel, N. P., Bell, T. A., et al. 2007, A&A, 467, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakamoto, K., Mao, R. Q., Matsushita, S., et al. 2011, ApJ, 735, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strickland, D. K., Heckman, T. M., Weaver, K. A., Hoopes, C. G., & Dahlem, M. 2002, ApJ, 568, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, B. E., Terzieva, R., & Herbst, E. 1999, ApJ, 518, 699 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., van Dishoeck, E. F., Evans, N. J., II, & Blake, G. A. 2000, ApJ, 537, 283 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vastel, C., Bottinelli, S., Caux, E., Glorian, J. M., & Boiziot, M. 2015, in SF2A-2015: Proceedings of the Annual Meeting of the French Society of Astronomy and Astrophysics, eds. F. Martins, S. Boissier, V. Buat, L. Cambrésy, & P. Petit, 313 [Google Scholar]
- Walter, F., Bolatto, A. D., Leroy, A. K., et al. 2017, ApJ, 835, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Watt, G. D., White, G. J., Millar, T. J., & van Ardenne, A. 1988, A&A, 195, 257 [NASA ADS] [Google Scholar]
- Wootten, A., Bozyan, E. P., Garrett, D. B., Loren, R. B., & Snell, R. L. 1980, ApJ, 239, 844 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: SpectralRadex
A.1. Package description
SpectralRadex7 is a Python module that was created in the process of this work and is now generally available through github8 and Pypi. As such it is described here in detail.
The module comprises two parts: a wrapper for RADEX (van der Tak et al. 2007) and a spectral modeling library. Whilst many packages exist for the former purpose, most either compile the original RADEX source code including Fortran 77 COMMON blocks using numpy’s F2PY or create an interface for calling the compiled RADEX binary. The former has less I/O overhead and should be preferred but the use of COMMON blocks means no copies of the program can be run simultaneously and is therefore problematic for multiprocessing. SpectralRadex solves this issue by rewriting the RADEX source code, updating it to modern Fortran standards and dropping common blocks in favour of Fortran modules before compiling with F2PY.
For the latter purpose, SpectralRadex makes use of RADEX to produce non-LTE spectra from RADEX inputs, a set of frequencies at which to evaluate the intensities and the velocity by which all lines should be shifted. The formalism for this is detailed below and borrows heavily from CASSIS (Vastel et al. 2015).
A.2. Spectral modeling Formalism
In order to calculate the emission from a single molecular transition as a function of frequency, the excitation temperature and the optical depth are required. The brightness temperature is given by,
where Jv is the radiation temperature, Tex is the excitation temperature, TBG is the background temperature, and τv is the optical depth as a function of velocity. The radiation temperature is simply,
where ν is the frequency, h is Planck’s constant and k is Boltzmann’s constant. The optical depth, can then be calculated by converting frequency to equivalent velocity shift using the rest frequency of the transition and then assuming a Gaussian line profile
where τ0 is the optical depth at line centre, v0 is the velocity shift of the emission, and Δv is the FWHM of the line. Thus all that is required is to calculate Tex and τ0 for a given transition and set of physical parameters.
This can be achieved through the use of RADEX. For a given set of physical parameters RADEX will provide the optical depth at line centre for every transition and the excitation temperature that gives the correct brightness temperature at line centre. Thus, a non-LTE spectrum can be generated by taking these quantities from an appropriate RADEX model. In the high density limit, this tends to the LTE solution but at lower densities it can deviate significantly.
In SpectralRadex, TB is calculated as a function of frequency for each line and then combined to give the overall spectrum of the molecule. Where lines overlap, SpectralRadex follows Hsieh et al. (2015) and uses an opacity weighted radiation temperature:
Appendix B: The other fits
In this section, the best fit models for each of the GMC spectra are shown except for GMC 5 which is shown in Figure 5. Figure B.1 shows GMC7, Figure B.2 shows GMC 6 and Figure B.3 shows the best fit to GMC 4.
 |
Fig. B.1. Measured spectrum from GMC 7 in black with error bars. Model spectra generated from most likely values for GMC 7 as filled histograms. The blue component shows the low density extended emission, the red shows the high density GMC emission, and the grey shows the complete model. |
 |
Fig. B.2. Similar to Figure B.1 for GMC 6. |
 |
Fig. B.3. Similar to Figure B.1 for GMC 4. |
 |
Fig. B.4. Similar to Figure B.1 for GMC 3. |
All Tables
C2H transitions covered by the ALCHEMI large program’s observations taken from JPL (Pickett 1998).
Details of the GMCs observed in C2H and studied in this work including co-ordinates, convolved size and beam filling factor.
RADEX parameters used to constrain the gas properties of the extended emission component.
All Figures
 |
Fig. 1. Integrated emission maps of C2H in NGC 253. The beam size for all panels is 1.6″ and is shown in the bottom left panel. Since the beam size is shared, the wider spatial distribution of the N = 1−0 emission is not caused by a beam size effect. Contours at the 3, 5, 10, 20 and 50σ level are drawn in black. The noise levels in order of increasing N are 1.4, 8.5, 2.0 and 1.6 K km s−1. Each ellipse shows the position and size of the Gaussian fits to the four individual clumps described in Sect. 3.1. The numbers indicate the position of the GMCs in Leroy et al. (2015). |
| In the text | |
 |
Fig. 2. Integrated emission map of the C2H N = 1−0 multiplet as in Fig. 1 but showing the full extent of the emission. Contours are shown at the 3, 5, 10, 20 and 50σ levels for noise level of σ = 1.5 K km s−1. Black squares indicate the positions sampled for spectra in Fig. 3. |
| In the text | |
 |
Fig. 3. Median stack of all spectra sampled from the extended region of the CMZ. The median is shown as a line and the shaded region gives the 95% confidence interval on this value. The black squares in Fig. 2 indicate the positions from which spectra were extracted for this composite spectrum. The black lines indicate the positions of the C2H components in each N transition, Doppler shifted by 255 km s−1, the LSR velocity of NGC 253. |
| In the text | |
 |
Fig. 4. Model parameters that fit constraints from the extended emission of the CMZ. Each point represents the parameters of a model where the N = 1−0 line was the strongest line and was above noise. |
| In the text | |
 |
Fig. 5. Best fit model for GMC 5. The black trace shows the measured spectra with error bars. The histograms show the spectral model components in colour and their total in grey. The legend gives the central velocity (V0) and linewidth (ΔV) of each component. The two blue components are the low density CMZ contribution and the others are the high density GMC components. |
| In the text | |
 |
Fig. 6. Fractional abundance as a function of depth into the cloud from PDR modeling and observations. The depth into the cloud is given as the equivalent visual extinction. The black dots are numbered according to the GMC they represent and error bars show the observed abundance towards that GMC, their position on the x-axis is arbitrary and does not represent the cloud sizes. The lines show UCL_PDR models with different parameters. The shaded band covers the abundance range of all GMC measurements. In the low cosmic-ray ionization rate models (left), the abundance decreases with distance into the cloud so the total column density is less than the observed column density despite the high abundances reached at low Av. |
| In the text | |
 |
Fig. 7. Fractional abundance of C2H as a function of time in the UCLCHEM models. Each line shows the median value of the abundance for a given cosmic-ray ionization rate as temperature is varied and the shaded regions show the minimum and maximum abundances over that temperature variation. The cosmic-ray ionization rate is given as a multiple of ζ0 = 1.3 × 10−17 s−1 and a sample of the lines are given in the legend. The grey shaded area shows the observed range. |
| In the text | |
 |
Fig. 8. Steady state C2H abundance shown in colour scale as a function of gas density and cosmic-ray ionization rate in units of ζ0 = 1.3 × 10−17 s−1. The values given are a median over different gas temperatures. Each point represents a GMC with the vertical lines showing the upper and lower limits on the density for that cloud. The horizontal lines span the cosmic-ray ionization rate values that give abundances within the measured range for those density values. GMC 7 does not appear on this diagram as no model produces a large enough abundance of C2H to match even its observed lower-limit. |
| In the text | |
 |
Fig. 9. Fractional abundance of CCH through time for a 20 km s−1 shock propagating through gas with a pre-shock density of 104 cm−3 plotted in black, temperature through the shock plotted in red. The range of observed C2H abundances is shown in grey. |
| In the text | |
 |
Fig. B.1. Measured spectrum from GMC 7 in black with error bars. Model spectra generated from most likely values for GMC 7 as filled histograms. The blue component shows the low density extended emission, the red shows the high density GMC emission, and the grey shows the complete model. |
| In the text | |
 |
Fig. B.2. Similar to Figure B.1 for GMC 6. |
| In the text | |
 |
Fig. B.3. Similar to Figure B.1 for GMC 4. |
| In the text | |
 |
Fig. B.4. Similar to Figure B.1 for GMC 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



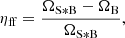
) \end{aligned} $$](/articles/aa/full_html/2021/10/aa41233-21/aa41233-21-eq6.gif)