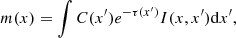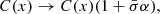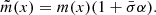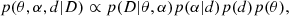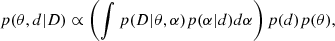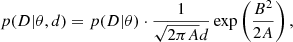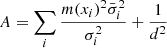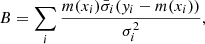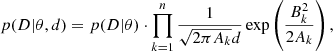| Issue |
A&A
Volume 651, July 2021
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202140501 | |
| Published online | 20 July 2021 | |
Sharpening quasar absorption lines with ESPRESSO⋆
Temperature of warm gas at z ∼ 2, constraints on the Mg isotopic ratio, and structure of cold gas at z ∼ 0.5
1
Institut d’Astrophysique de Paris, CNRS-SU, UMR 7095, 98bis bd Arago, 75014 Paris, France
e-mail: noterdaeme@iap.fr
2
Ioffe Institute, Politekhnicheskaya 26, 194021 Saint Petersburg, Russia
3
European Southern Observatory, Alonso de Córdova 3107, Vitacura, Casilla 19001, Santiago 19, Chile
4
Direction Générale de l’Aviation Civile, CRNA Nord, 9 rue de Champagne, 91200 Athis-Mons, France
5
Departamento de Astronomía, Universidad de Chile, Casilla 36-D, Santiago, Chile
6
Department of Astronomy, University of Geneva, Chemin Pegasi 51, 1290 Versoix, Switzerland
Received:
5
February
2021
Accepted:
2
May
2021
Aims. We aim to study several key physical properties of quasar absorption-line systems that are subtly encoded in their absorption profiles and have not yet been thoroughly investigated or constrained.
Methods. We analysed a high-resolution (R = 140 000) spectrum of the bright quasar HE 0001−2340 (zem = 2.26) obtained with ESPRESSO, which was recently installed at the Very Large Telescope. We analysed three systems at z = 0.45, z = 1.65, and z = 2.19 using multiple-component Voigt-profile fitting. We also compared our spectrum with those obtained with VLT/UVES, covering a total period of 17 years.
Results. We disentangle turbulent and thermal broadening in many components spread over about 400 km s−1 in the z ≈ 2.19 sub-damped Lyman-α system. We derive an average temperature of 16 000 ± 1300 K, which is about twice the canonical value of the warm neutral medium in the Galactic interstellar medium (ISM). A comparison with other high-z, low-metallicity absorbers reveals an anti-correlation between gas temperature and total H I column density. Although requiring confirmation, this could be the first observational evidence of a thermal decrease with galactocentric distance; in other words, we may be witnessing a thermal transition between the circumgalactic medium and the cooler ISM. We revisit the Mg isotopic ratios at z = 0.45 and z = 1.65 and constrain them to be ξ = (26Mg + 25Mg)/24Mg < 0.6 and < 1.4 in these two systems, respectively. These values are consistent with the standard solar ratio; that is, we do not confirm strong enhancement of heavy isotopes previously inferred from UVES data. Finally, we confirm the partial coverage of the quasar emission-line region by a Fe I-bearing cloud in the z = 0.45 system and present evidence for velocity substructure of the gas that has Doppler parameters of the order of only ∼0.3 km s−1. This agrees well with the low kinetic temperature of T ∼ 100 K inferred from modelling of the gas physical conditions.
Conslusions. This work demonstrates the unique insight provided by high-fidelity, high-resolution optical spectrographs on large telescopes when used to investigate the thermal state of the gas in and around galaxies as well as its spatial and velocity structure on small scales, and to constrain the associated stellar nucleosynthetic history.
Key words: quasars: absorption lines / quasars: individual: HE 0001−2340
© P. Noterdaeme et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The advent of high-resolution spectrographs on 8–10 m class telescopes, in particular the High Resolution Echelle Spectrometer (HIRES, Vogt et al. 1994) on the Keck telescope followed by the Ultraviolet and Visual Echelle Spectrograph (UVES, Dekker et al. 2000) on the Very Large Telescope (VLT), has played a crucial role in the exploration of the distant Universe in absorption towards quasars and Gamma-ray burst afterglows. These spectrographs have enormously increased not only the number and variety of absorption-line systems observed at high spectral resolution but also the amount of information that can be extracted from them. High-resolution spectroscopy can be used to investigate the diffuse gas in greater detail, in particular its chemical enrichment (e.g., Prochaska et al. 2007; Petitjean et al. 2008; Vladilo et al. 2018; De Cia et al. 2018; Péroux & Howk 2020, among many others) and kinematics (Prochaska & Wolfe 1997; Ledoux et al. 2006), as well as its physical state and the prevailing physical conditions (e.g., Srianand et al. 2005; Vreeswijk et al. 2007; Neeleman et al. 2015; Noterdaeme et al. 2017; Balashev et al. 2017).
Over the years, the astrophysical community has learnt to decode the wealth of information available in the absorption spectra, with other applications on a wide range of topics, such as the possible space–time variation of fundamental constants (e.g., Milaković et al. 2021 and references therein), constraints on the sizes of the background source emission-line regions (Balashev et al. 2011; Bergeron & Boissé 2017), measurements of the cosmic microwave background temperature at high-z (Noterdaeme et al. 2011), measurements of the primordial abundance of deuterium (e.g., Cooke et al. 2014), and so on. Many of these studies, which rely on analysing fine details in the spectra, have reached a point where progress is mostly limited by the quality of the data. With a resolution of up to several times that of other spectrographs, together with an exquisite wavelength calibration, the Echelle SPectrograph for Rocky Exoplanets and Stable Spectroscopic Observations (ESPRESSO, Pepe et al. 2021) on the Very Large Telescope (VLT) has the potential to reveal a new level of detail. By getting closer to the intrinsic line widths, which are in general well below the resolution element of other spectrographs, ESPRESSO opens up the possibility to investigate the structure of cold gas with very narrow lines, to break the degeneracy between macroscopic (turbulent) and microscopic (thermal) motions in gaseous clouds, and to investigate the contribution of different isotopes to a given absorption line, among other applications.
This paper deals with three different and independent topics that all take advantage of the same ESPRESSO spectrum: that of the quasar HE 0001−2340. We therefore chose a less standard paper structure. After describing the observations and data reduction in Sect. 2 and the systems present along the line-of-sight in Sect. 3, the subsequent sections deal with the temperature of the diffuse gas at z = 2.2 (Sect. 4), the Mg isotopic ratio at z = 0.45 and z = 1.65 (Sect. 5), and the structure of the cold gas at z = 0.45 (Sect. 6), which we briefly introduce at the beginning of each section. We summarise our results in Sect. 7.
2. Observations and data reduction
The observations of HE 0001−2340 (V = 16.7, zem = 2.28) were carried out in service mode during the nights of November 9, 12, and 28, 2018, using ESPRESSO in single UT mode at the Melipal Unit Telescope #3. Located at the incoherent combined Coudé focus of the VLT, ESPRESSO is a highly stabilised, thermally controlled échelle spectrograph fed by two fibres, one for the target and the other for simultaneous reference calibration. We recorded the sky light in Fibre B for a proper sky subtraction. We used the high-resolution (HR) mode of the instrument leading to a median resolving power of 139 000 as measured from emission lines in ThAr calibration frames. The fibre aperture on sky in this mode is  . Ambient conditions while observing were good with a typical seeing of
. Ambient conditions while observing were good with a typical seeing of  , at an average airmass of 1.13, and clear sky. Once inside the spectrograph, the light from the two fibres is dispersed by an échelle grating and the spectral orders are split up into a Blue (379–525 nm) and a Red (525–788 nm) channel. The corresponding spectra are recorded on separate charge coupling devices whose pixels were binned two by one in the spatial direction. This provides a spatial sampling of 4.5 pixels per slice, and similar sampling in the dispersion direction.
, at an average airmass of 1.13, and clear sky. Once inside the spectrograph, the light from the two fibres is dispersed by an échelle grating and the spectral orders are split up into a Blue (379–525 nm) and a Red (525–788 nm) channel. The corresponding spectra are recorded on separate charge coupling devices whose pixels were binned two by one in the spatial direction. This provides a spatial sampling of 4.5 pixels per slice, and similar sampling in the dispersion direction.
The data were reduced using the ESO Reflex workflow of the ESPRESSO Data Reduction System (DRS) version 2.0.0 publicly released by ESO. After bias, dark, and inter-order background subtraction, an optimal extraction of the 2D spectral orders is performed using master flat-fields as order profiles. During this process, dead, hot, and saturated pixels are masked out and cosmic-ray hits are rejected. After flat-fielding and de-blazing, the 2D spectra were wavelength-calibrated using the combination of ThAr and Fabry-Pérot light sources. The sky spectrum was extracted from Fibre B and subtracted from the science frames. The latter were then rebinned and merged into 1D data products with associated error and quality maps. Flux calibration was performed using estimated absolute efficiencies and atmospheric extinction curves. Each exposure was corrected for atmospheric absorption features by fitting a synthetic transmission spectrum to the Red-arm spectra using the public code molecfit (Smette et al. 2015; Kausch et al. 2015). Individual exposures were then combined with a drizzling-like approach using the espda_coadd_spec recipe of the Data Analysis System (DAS) v1.0.3 after conversion of the wavelength scales to helio-vacuum. The resolving power adopted for each of the final Blue and Red-arm spectra is given in Table 1, and is about 5% higher (resp. lower) in the Red (resp. the blue) compared to the overall median value. The average signal-to-noise ratio per pixel is about S/N ∼ 25 in the Blue and S/N ∼ 45 in the Red.
Observational data.
As we complement ESPRESSO with UVES data to investigate the possible time-variation of absorption lines in Sect. 6, we provide a log of all these observations in Table 1. Details on the UVES data are presented by D’Odorico (2007), Agafonova et al. (2011), and Bergeron & Boissé (2017). The S/N per pixel of the UVES spectra are around 90, 65, and 60 at 420 nm for the combined 2001, 2009, and 2017 spectra, respectively1.
3. Systems along the line of sight to HE 0001−2340
Capitalising on the high quality of our ESPRESSO spectrum, we performed a systematic identification of absorption-line systems covered by the observations. Firstly, we visually identified the most obvious absorption systems based on the easily recognisable doublets Mg IIλλ2796,2803 and C IVλλ1548, 1550 and marked absorption features from other species at the same redshift. We then scanned the full spectrum visually, identifying the remaining absorption features until no unidentified features remained. This procedure was done independently by two team members (PN and GD) and re-checked by a third member (CL). We made our best effort to identify even weak features that may be helpful for studies other than the one presented here. We used both the combined 1D spectrum and the individual exposures to ascertain the astrophysical nature of features versus possible telluric residuals, which are shifted differently when applying the heliocentric correction.
In total, we identify no less than 12 absorption systems with redshifts ranging between z = 0 and the quasar emission redshift, zem = 2.26. These are summarised in Table 2 together with the detected transition lines.
Absorption lines identified in the ESPRESSO spectrum of HE 0001−2340.
4. Kinetic temperatures of the gas at z = 2.2
Thermal balance in neutral gas leads to an equation of state with two stable phases under an external pressure (Field et al. 1969): a warm and diffuse phase (also known as the warm neutral medium; WNM) with temperatures of the order of 104 K, and a cold, denser phase (the cold neutral medium; CNM) with T ∼ 100 K. Below some minimal pressure, the gas is mostly a WNM while it is predominantly a CNM above some maximal pressure. Between these two pressure limits, the gas is a mixture of both warm and cold phases (e.g., Wolfire et al. 2003). This is generally the case in typical galactic discs. Other, more unstable phases also complete this picture (e.g., Salpeter 1976), but in the following we stick to a canonical two-phase description for simplicity.
The temperature and phase mixing of the neutral gas have been investigated locally using H I 21-cm emission/absorption data (e.g., Heiles & Troland 2003) but this technique is still inapplicable to the distant Universe. At high redshift, the neutral gas is currently only detectable through damped Lyman-α absorption imprinted on the spectra of bright background sources.
The small incidence rate of 21-cm absorption (e.g., Kanekar et al. 2014) and molecular hydrogen (e.g., Ledoux et al. 2003; Noterdaeme et al. 2008; Jorgenson et al. 2014; Balashev & Noterdaeme 2018) – both sensitive probes of cold gas – as well as more indirect constraints from the fine-structure excitation of C II and Si II (Neeleman et al. 2015) show that most damped Lyman-α systems (DLAs) probe the WNM (see also Krogager & Noterdaeme 2020 for estimations of intrinsic statistics, i.e. corrected for selection effects). While the temperature of the CNM is well constrained from the excitation of the low rotational levels of H2 (see, e.g., Ledoux et al. 2002; Noterdaeme et al. 2007; Balashev et al. 2019, among other studies), the temperature of the WNM at high redshift is generally assumed to be around the canonical, local value (8000 K). This was used to derive the CNM fraction from the observed harmonic mean of the 21-cm spin temperature (e.g., Srianand et al. 2012). Direct measurements of the WNM temperature are difficult to obtain and essentially rely on determining the thermal broadening of the lines resulting from the Maxwell–Boltzmann distribution of gas particle velocities. However, as macroscopic motions are also present, the observed Doppler broadening (b) is the quadratic sum of thermal and turbulent broadening: 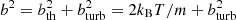 , where T is the gas temperature, m the mass of the species, and kB the Boltzmann constant. Disentangling thermal from turbulent broadening therefore requires observations of several species with different masses within the same clouds, but this also depends on precise measurements of total b which are hard to obtain even at relatively high S/N and spectral resolution (Carswell et al. 2012).
, where T is the gas temperature, m the mass of the species, and kB the Boltzmann constant. Disentangling thermal from turbulent broadening therefore requires observations of several species with different masses within the same clouds, but this also depends on precise measurements of total b which are hard to obtain even at relatively high S/N and spectral resolution (Carswell et al. 2012).
4.1. Thermal broadening
The availability of ESPRESSO is an excellent opportunity to disentangle turbulent and thermal broadening (Lee et al. 2021) over the full extent of absorption-line profiles, in particular when light species are well constrained. In the case of the DLA at z = 2.187 towards HE 0001−2340, the C II and O I absorption-line complexes exhibit unsaturated components that make the measurement easier to perform. Richter et al. (2005) already performed a detailed analysis of this system using UVES data. We therefore do not wish to redo a complete study of this system but rather focus on disentangling thermal from turbulent broadening. For our analysis, we used the VPFIT software package v12.3 (Carswell & Webb 2014).
As a starting point, we used the velocity structure inferred by Richter et al. (2005) as a first guess in the fitting process and we have adopted their component labelling for an easier comparison. We do not see evidence for component F, which is rejected by VPFIT, while at the higher resolution of ESPRESSO the modelling of component A requires splitting into three subcomponents, that we denote A1, A2, and A3 in this paper (see Table B.1).
We performed the fit allowing for a mixture of turbulent and thermal broadening in each component. The best-fit results are shown in Fig. 1 and the corresponding parameter values are listed in Table B.1. For most components (namely 12 out of 17), the degeneracy between turbulent and thermal broadening is easily broken and we obtain good constraints on bturb and T. We note that, for component D, thermal broadening dominates over turbulence and the fit is essentially consistent with bturb = 0 km s−1. However, several components (i.e. C, G, H, M, and N) have poorer constraints and their fit is consistent with turbulent broadening alone (i.e. the 1σ temperature range encompasses T = 0 K) and therefore in this case we instead report upper limits on the temperature. The weakest components (G and N) are very close to the noise level, meaning that even the total Doppler parameter values are almost unconstrained, which leads to loose constraints on the temperature that are of little practical use, if any.
 |
Fig. 1. Multi-component Voigt-profile fitting of metal lines in the sub-DLA at z = 2.187. The normalised ESPRESSO spectrum is shown in black, with the best-fit synthetic spectrum overlaid in red. The blue dashed curve corresponds to the synthetic spectrum computed using the best-fit parameters obtained by Richter et al. (2005) from the analysis of UVES data. We note that their component A here splits into three subcomponents that we call A1, A2, and A3 in Table B.1 and their component F at v ∼ −150 km s−1 appears to be spurious as seen from C IIλ1334. |
To further test the robustness of the decomposition into thermal and turbulent contributions, we also fitted the data using independent (total) b-parameters for each species and derived bturb and T a posteriori from the relation between the total Doppler parameter squared and the inverse of the mass of each species as done by Carswell et al. (2012) for example.
Although the errors on the Doppler parameters evaluated independently for each species in each component become large, the increase of b-values with decreasing mass of the species, following the relation b ∝ m−0.5, is very well determined. Such a measurement was possible for 14 components, which we show in Fig. A.1. One advantage of this method is that any departure from the linear relation for a given species would help identify an issue with the data or the fitting process, or could in principle mean that the species do not all pertain to the same gas. A comparison between turbulent Doppler parameters and temperatures obtained with each of the two methods is shown in Fig. 2. Unsurprisingly, the results from the two methods are very much consistent with each other, which supports the convenient (and standard) assumption of co-spatiality, and allows us to use turbulent plus thermal broadening for each velocity component while fitting (i.e. method 1). This also permits the use of fewer free parameters while the total reduced 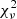 remains unchanged. In the following, we therefore use the values derived from method 1, i.e. with a physically motivated link between Doppler parameters of different species, but the results remain unchanged if values from method 2 are used instead.
remains unchanged. In the following, we therefore use the values derived from method 1, i.e. with a physically motivated link between Doppler parameters of different species, but the results remain unchanged if values from method 2 are used instead.
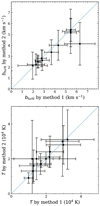 |
Fig. 2. Comparison of the turbulent component of the Doppler parameter (top) and the temperature (bottom) derived from two different methods (1: using bturb and T as free parameters for all species of a given component; 2: fitting total b-values for each species and deriving bturb and T a posteriori from the variation of b with the inverse of the species mass). Blue dotted lines show the one-to-one relation. |
We measure temperatures in the range 9000 − 32 000 K (see Fig. 3) with a dispersion of about 6300 K, which is of the same order as the 1σ uncertainty on individual temperature measurements. These values are indeed consistent within uncertainties with a single temperature for all of the velocity components of the system, with weighted mean ⟨T⟩ = 16 000 ± 1300 K (unweighted ⟨T⟩ = 20 000 K, excluding upper limits only). This temperature is twice as high as the canonical value of 8000 K generally assumed for the Galactic interstellar medium (ISM; Wolfire et al. 2003).
 |
Fig. 3. Kinetic temperatures determined in various components along the line profile of the sub-DLA at zabs = 2.187 (zero of the velocity scale). The dashed blue line and shaded area correspond to the weighted mean and associated error ⟨T⟩ = 16 000 ± 1300 K. The dotted lines show one standard deviation around this mean. |
4.2. Comparison with other measurements at z > 2
To investigate whether the higher-than-canonical temperature measured here is inherent to one system or is more generally seen in high-z DLAs, a sample of DLA temperature measurements must be compiled. To our knowledge, no systematic study of this type has ever been performed. One possibility is to use deuterium, which is the second lightest species after hydrogen and whose ∼105 times smaller abundance enables the observation of unsaturated DI lines.
Little attention has yet been paid to this possibility (but see Noterdaeme et al. 2012) mainly because the focus has so far been been on measuring the primordial D/H ratio (e.g., Cooke et al. 2018) where the measurement of the temperature is only a byproduct. We therefore searched the literature for additional temperature measurements, in particular in DI-related publications which are easy to identify. When the temperatures were not explicitly given (for the systems towards Q0913+072 and J1558-0031), we derived them from the provided b-values (Pettini et al. 2008; O’Meara et al. 2006). Because of the proximity between DI and H I lines (Δv = −81.6 km s−1), and because the systems were generally selected to be metal poor (so that the gas is less processed and the D/H ratio is close to primordial), these measurements concern only one or a few components at the blue edge of the profiles. We also included the measurement of Dutta et al. (2014) who emphasised the importance of taking into account thermal broadening to discuss the abundance of carbon in metal-poor DLAs2.
The compiled temperature measurements are summarised in Table 3. All systems are DLAs or sub-DLAs, with the exception of the absorber at z = 2.504 towards Q 1009+2956 (Burles & Tytler 1998) which is a Lyman-limit system (LLS) in which most of the gas is likely ionised. Figure 4 reveals an anti-correlation between the kinetic temperature and the total H I column density of the systems, with a Pearson correlation coefficient of r = −0.78 and a probability of this anti-correlation being pure coincidence of p = 1.6 × 10−3. A linear decrease of about 3500 K per decade of N(H I) provides a reasonable description of the data over the full range of N(H I). To test whether the anti-correlation is driven by the only LLS, which also has the highest temperature in our sample, we repeated the exercise without that data point and obtained r = −0.63, with a probability that this is due to coincidence of still only about 3%. In this case, the decrease in temperature with increasing N(H I) is even steeper with 5000 K per N(H I)-dex.
 |
Fig. 4. Kinetic temperatures derived from Doppler broadening in various absorption-line systems as a function of the total H I column densities of these systems. Empty circles correspond to measurements obtained thanks to the presence of deuterium (typically in one or a few close components) while filled squares correspond to average measurements in complex systems made possible by high-resolution spectroscopy. Grey triangles represent measurements in individual components of the DLA towards HE 0001−2340 (Fig. 3). The data exhibit an anti-correlation with a Pearson coefficient of r = −0.78 and a probability that this is pure coincidence of p = 0.16%. The solid blue (respectively red) line corresponds to an unweighted linear fit including (resp. excluding) the lowest N(H I) value towards Q 1009+2956. |
Kinetic temperatures in various systems determined from thermal broadening of the lines.
4.3. The anti-correlation between T and overall N(H I)
The decrease in kinetic temperature with increasing N(H I) appears to be real but the physical reason behind it is not immediately clear. Importantly, temperatures are measured locally, generally in a few components, while the measured H I column density corresponds to the total value throughout the absorber. This indicates that while the kinetic temperatures are likely determined by conditions belonging to individual clouds (e.g., the strength of the UV field, ionisation fraction, and gas metallicity), it also shows some dependence on larger scales. The metallicities are low in our sample, and the systems may therefore correspond to gas located far away from star-forming regions so that the UV flux is dominated by the metagalactic background (e.g., Khaire & Srianand 2019) and hence is similar for all systems. In that case, the observed T–N(H I) anti-correlation could be connected to the known anti-correlation between H I column density and impact parameter (e.g., Krogager et al. 2017). One possibility is that, the lower the H I column density, the greater the distance from the galaxy, and the greater the mixing with shock-heated ionised gas in the halo. Alternatively, the typically low N(H I) values in our sample may enhance photo-ionisation heating and more generally alter thermal balance, which is sensitive to the ionisation fraction of the medium. Unfortunately, we cannot discriminate between these explanations. Further measurements of kinetic temperatures over a wide range of environments (ideally with simultaneous constraints on impact parameters) and physical conditions are needed to understand the observed T–N(H I) anti-correlation.
The dependence between a local (temperature) and a global property (total N(H I)) demands further investigation with quantitative modelling of the thermal state of the gas. In addition to confirming the observed T − N(H I) anti-correlation, it will be interesting to investigate its dispersion at any given column density. One could naively expect that the dispersion is larger at higher column density —not only from one system to another but also amongst components in a given system— owing to varying conditions when the gas closer to or within galaxies is probed. In turn, at large galactocentric distances, conditions may vary more smoothly. Another possibility is to investigate how the temperatures are related to metallicity and kinematics, as simulations suggest that outflowing gas has both higher metallicities and temperatures. Deriving kinetic temperatures in a large sample of systems through high-resolution spectroscopy may therefore provide new, valuable information that could improve our understanding of the thermal state of the neutral phase in the circumgalactic medium at high redshift.
5. Constraints on the isotopic Mg ratio
Constraining the relative abundances of magnesium isotopes is a powerful probe of star-formation processes over cosmological timescales because the main contributors to 24Mg are massive stars while the other two stable isotopes (25Mg and 26Mg) come mostly from intermediate-mass stars (Vangioni & Olive 2019). Agafonova et al. (2011) used a UVES spectrum of HE 0001−2340 to obtain the first measurement of the Mg isotopic ratio at cosmological distances, and derived a strong overabundance of heavy isotopes. The higher resolution achieved with ESPRESSO, better sampling, and the exquisite wavelength calibration allow us to revisit this measurement, in spite of the lower S/N per pixel in our spectrum. In the following, we test two methods to measure this ratio.
The first method corresponds to that used by Agafonova et al. (2011) and is based on the apparent velocity shift of Mg II lines. Indeed, for a given transition, the absorption line wavelengths from different isotopes are very similar, resulting in the observation of a single line. However, the apparent central rest-frame wavelengths of the lines depend on the isotopic ratio, meaning that comparing their apparent velocity shift with respect to other species can in principle constrain this ratio at any redshift (Levshakov et al. 2009).
The second method relies on a direct fit, explicitly including the transitions from the three isotopes into the Voigt-profile model, assuming no intrinsic shift with respect to other species. This direct fit is possible because the isotopic wavelength separation is comparable to the ESPRESSO resolution element.
5.1. Isotopic ratio from apparent velocity shifts
In Fig. 5, we show the Voigt-profile fit to the Ca II, Ca I, Fe I, Mg II, and Mg I lines detected in the narrow component at z = 0.45206. The redshifts of calcium and iron lines were tied together and taken as a reference with which to compare the apparent velocities of the Mg IIλλ2796,2803 doublet and the Mg Iλ2852 lines. The magnesium lines were fitted using a single component and the composite wavelengths from Murphy & Berengut (2014), λ0 = 2796.35379, 2803.530982 (Mg II) and 2852.962797 (Mg I), which correspond to weighted wavelengths with solar relative isotopic abundances 78.99:10:11.01 (24Mg : 25Mg : 26Mg). From this, we obtained an apparent velocity shift of +0.03 ± 0.12 km s−1 and +0.53 ± 0.32 km s−1 for Mg II and Mg I, respectively. While the positive shift of Mg I indicates in principle an abundance of heavy isotopes of less than solar, this is only marginally significant (1.6σ) and based on a single and weak absorption line. From Fig. 5, it also appears that assuming a smaller velocity shift (−0.17 km s−1 from Agafonova et al. 2011) also provides a good fit, without noticeable structure in the residuals. Hence, we do not consider this line in the following. In any case, the sensitivity of the Mg I line to the isotopic ratio is even smaller than for Mg II.
 |
Fig. 5. Single Voigt profile fit to the cold, narrow component at z = 0.45206 (ESPRESSO data: black with grey error bars, synthetic spectrum: red). Residuals (in units of standard deviation) are shown in the subpanel above each line panel. The zero of the velocity scale is taken at the velocity of the iron and calcium lines. The redshifts of the magnesium lines were left to vary independently from the other lines and are displayed as short red tick marks. The blue profiles and the corresponding blue tick marks and residuals correspond to the apparent velocity shift (−0.47 and −0.17 km s−1 from Mg II and Mg I respectively) measured by Agafonova et al. (2011) from UVES data. |
In turn, the velocity shift for Mg II is better constrained, but our measured value, Δv(Mg II) = +0.03 ± 0.12 km s−1, is in tension (> 3σ) with the velocity shift, Δv(Mg II) = −0.44 ± 0.05 km s−1, obtained by Agafonova et al. (2011)3. This is clearly seen in Fig. 5, where assuming this latter value introduces a shift with respect to the ESPRESSO data, which is mostly noticeable as an s-shaped structure in the Mg IIλ2796 residuals.
To test the significance of our measurement and the conversion from velocity shift to isotopic ratio, we generated artificial spectra featuring the Mg II absorption doublet with an input total column density of N(Mg II) = 1012 cm−2 to mimic the line observed here and varying isotopic ratio ξ = (25Mg+26Mg)/24Mg, assuming r = 26Mg/25Mg = r⊙ ≈ 1. We convolved these spectra with the appropriate instrumental profile, used the same wavelength binning, and added Gaussian noise (with S/N = 20, as in our data). For each ξ value, we generated 100 artificial spectra that we fitted using the same procedure. The results of this exercise are shown in Fig. 6. The average obtained for 100 artificial spectra (dark blue line in Fig. 6) agrees very well with the values obtained for a noiseless spectrum (pink line in the same figure), showing that the finite S/N of the data does not introduce any systematic bias. Considering the Mg II values only, the measured velocity shift of +0.03 ± 0.12 km s−1 translates to 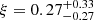 (using the mean of 100 spectra with S/N = 20). The 68.3% interval on the measured velocities in the artificial noisy data assuming this central ξ-value is ≈0.1 km s−1. This is in agreement with the formal 1σ uncertainty from fitting the real data, and is even slightly smaller. Indeed, the latter uncertainty takes into account the uncertainty on the anchor redshift from the other lines in the error budget.
(using the mean of 100 spectra with S/N = 20). The 68.3% interval on the measured velocities in the artificial noisy data assuming this central ξ-value is ≈0.1 km s−1. This is in agreement with the formal 1σ uncertainty from fitting the real data, and is even slightly smaller. Indeed, the latter uncertainty takes into account the uncertainty on the anchor redshift from the other lines in the error budget.
 |
Fig. 6. Velocity shift (with respect to lines with the standard isotopic ratio) as a function of ξ = (25Mg + 26Mg)/24Mg assuming r = 26Mg/25Mg = 1 for mock ESPRESSO data. The solid blue line corresponds to the mean value for 100 mock spectra for each input ξ value, and the dark and light-blue regions represent the regions containing 68.3% and 95.5% of the values, respectively. The pink line corresponds to a noiseless mock spectrum. The observed velocity shift and associated 1σ uncertainty for the system at z = 0.45206 are shown as orange horizontal solid and dotted lines, respectively. |
5.2. Explicitly including the isotopes in the absorption model
Next, we tried the second, more direct method, explicitly including the three isotopes in the Voigt profile model and assuming no intrinsic shift with respect to other species. We derived the best-fitting χ2 values for a range of assumed isotopic abundance ratio, following a standard method as described by Lampton et al. (1976). In practice, we tied together the redshift of all species shown in Fig. 5 and assumed fixed isotopic ratio, while letting the total column densities and the Doppler parameters free. However, we assumed r = 26Mg/25Mg = 1 as previously. The Δχ2 as a function of ξ are shown in Fig. 7. The minimum value is reached for ξ = 0.25 (this best fit is shown in Fig. 8) and the associated 68.3% confidence range using this single parameter is given by Δχ2 = 1. We then obtain 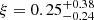 , nicely confirming the value and confidence region obtained from the apparent velocity shift method.
, nicely confirming the value and confidence region obtained from the apparent velocity shift method.
 |
Fig. 7.
|
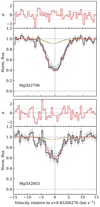 |
Fig. 8. Synthetic Mg II absorption profiles for the system at z = 0.452 (red line) corresponding to the best fit (ξ = 0.25, assuming r = 1) including 24Mg II, 25Mg II, and 26Mg II lines (dashed-blue, dashed-orange, and dashed-green, respectively) overlaid on the ESPRESSO data (black with grey error bars). The top panels show the residuals. |
5.3. The system at z = 1.65
Agafonova et al. (2011) also obtained constraints for components in the systems at z = 1.58 and z = 1.65 from the same data along the same line of sight. For the system at z = 1.58, modelling the absorption profile of the subsystem that they considered requires several components. In addition, the Mg II lines are saturated and partially affected by telluric absorption. Therefore, we did not attempt to get a constraint on the Mg isotopic ratio for this system. For the simpler, single-component system at z = 1.65, we obtain Δv = −0.08 ± 0.27 km s−1 (Mg II) and Δv = −0.23 ± 0.35 km s−1 (Mg I), which are surprisingly consistent with the values reported by Agafonova et al. (−0.08 ± 0.20 and −0.28 ± 0.44, respectively) and again consistent with no velocity shift (see Fig. 9). Using the variation of χ2 as a function of the assumed ξ as described above, we derive a 68.3% confidence interval of ξ = 0.09 − 1.36 with the best fit-value at ξ = 0.42, see Fig. 10.
 |
Fig. 9. Fit to the metal lines at z = 1.65. The long dashed line (zero of the velocity scale) corresponds to the redshift of Fe II and Si II, while the short ticks mark the centroids of the Mg II and Mg I lines. The velocity shifts seen here are indistinguishable from those measured from UVES data by Agafonova et al. (2011) for this system. |
5.4. No evidence for strong enhancement of heavy isotopes
Before concluding, we note that while our single component Voigt-profile fits provide a very good representation of the data for both systems, they may not capture any possible hidden velocity structure. Indeed, as we show in the following section, substructure is likely present in the cold, Fe I-bearing gas. Even in the presence of substructures, a strong enhancement of heavy isotopes remains unlikely. Indeed, the presence of a velocity component in the red wing of the main profile could in principle compensate for the velocity shift induced by heavy isotopes, but it would require an ad hoc combination of velocity and strength. Furthermore, such a peculiar situation should be the case for both systems studied here. On the other hand, the presence of an additional component in the blue wing of the profile could mimic the presence of 25Mg and 26Mg when their actual abundance is close to zero. While we do not see any evidence for such a component in the profile of other species, the obtained constraints should conservatively be considered upper limits, that is, ξ < 0.6 and ξ < 1.4 for the systems at z = 0.45 and 1.65, respectively. We note that the obtained uncertainties on the ξ values already allowed for zero abundance of heavy isotopes anyway.
Another issue concerns our assumption of r = 26Mg/25Mg = 1 ≈ r⊙. This is more difficult to address as allowing for a free value of r would introduce more degeneracy which is hard to investigate with the S/N reached in our current data. In addition, these two heavy isotopes are expected to arise from stars of similar mass, and so their relative abundance is not expected to vary significantly. With the exquisite wavelength calibration of ESPRESSO, it is possible to investigate this issue, provided much higher S/N is obtained.
In conclusion, we do not confirm the strong enhancement of heavy Mg isotopes in either of the two systems considered here. The apparent shift observed in the UVES data is therefore unlikely to be due to a space-time variation of the fine-structure constant α (Murphy et al. 2008) or to strong enhancement of heavy Mg isotopes, but is instead due to subtle wavelength distortions in the UVES data that have been revealed and investigated in a number of works aiming at precision spectroscopy (Rahmani et al. 2013; Whitmore & Murphy 2015; Dumont & Webb 2017).
6. Structure of the cold-gas absorber at z = 0.452
D’Odorico (2007) first identified the z = 0.45206 absorption system and detected the neutral species Fe I, SiI, and Ca I, which are rarely found in quasar absorption systems. By modelling the physical conditions in this system, Jones et al. (2010) constrained the temperature to be T < 100 K and the density to be in the range 100 − 1000 cm−3. Given the relatively small column densities inferred from their model (N(H I) in the range 1018.5 − 20.8 cm−2), this suggests a small longitudinal size. For N(H I) = 1019.6 cm−2 and a density of 300 cm−3, the size is l∥ ∼ 0.04 pc.
It is therefore reasonable to expect a similarly small transverse extent as well. A small transverse size of the cloud can in principle lead to several interesting effects. First, if at a given wavelength, the size of the background source becomes comparable to that of the absorbing cloud, then the former may no longer be considered a point source. This leads to partial coverage (e.g., Balashev et al. 2011). Indeed, Bergeron & Boissé (2017) found a partial coverage effect for the Fe Iλ2719Å line that is by chance located on top of the Lyα emission line from the quasar. However, this Fe I line is blended with Lyα absorption, which complicates the analysis. Second, the presence of structures within the cloud may in principle lead to time variations of the line profiles as the exact location of the line of sight with respect to the absorbing gas may vary due to relative motions of the absorber and/or observer with respect to the background source (Boissé et al. 2015). However, the line of sight drifts are expected to be at best of the order of a few 10−3 pc over 10 years. This means that time variation of the profiles is expected only if significant structures are present at such extremely small scales.
In order to constrain the transverse spatial and line-of-sight velocity structure of the absorber, we used our ESPRESSO spectrum together with UVES spectra obtained previously in 2001, 2009, and 2017, hence covering a time interval of 17 years. Unfortunately, the strongest Fe I transitions at 2484 and 2523 Å are not covered by the ESPRESSO spectrum. Notwithstanding, they are covered by all UVES spectra that have bluer coverage. As many Fe I lines are weak, we took into account the uncertainty in continuum construction when fitting these lines. The fitting method is described in Appendix A.
Following previous UVES studies, we first fitted the Fe I lines with a single-component Voigt-profile. We used combined spectra obtained for each set of observations. In other words, we used four different spectra: three from UVES taken in 2001, 2009, and 2017 and our new ESPRESSO spectrum. To fit the absorption lines for each spectra we adopted the average resolution powers of 55 000, 65 000, and 60 000 for 2001, 2009, and 2017 UVES spectra, respectively. For the ESPRESSO spectrum, we used different resolutions for the blue and red channels, as provided in Table 1. Nevertheless, we were not able to obtain a simultaneously satisfactory fit of the ESPRESSO + UVES data taken altogether. Considering each spectrum independently, we find differences in the derived Fe I parameters between epochs, the most noticeable difference being in the Doppler parameter, which we find to be significantly higher in the ESPRESSO spectrum (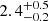 km s−1) than suggested by any of the UVES spectra (∼0.6 km s−1) with a typical uncertainty of less than 0.1 km s−14. The inconsistency between the one-component models fitted to the ESPRESSO and UVES data independently is shown in Fig. 11. While it is tempting to attribute this to time variation of the line profiles, such an interpretation is suspicious in light of the fact that we did not see any significant changes between UVES 2001 and 2017, and the difference appears only in the new ESPRESSO spectrum. Therefore, it is more likely that the difference is actually due to an inappropriate model of the velocity profile. Indeed, one can see from Fig. 11 that the observed Fe Iλ3021Å and 3720Å line profiles for ESPRESSO and UVES have about the same width when the resolution of the two instruments differs by a factor of 2.5. This strongly suggests the presence of more than one component.
km s−1) than suggested by any of the UVES spectra (∼0.6 km s−1) with a typical uncertainty of less than 0.1 km s−14. The inconsistency between the one-component models fitted to the ESPRESSO and UVES data independently is shown in Fig. 11. While it is tempting to attribute this to time variation of the line profiles, such an interpretation is suspicious in light of the fact that we did not see any significant changes between UVES 2001 and 2017, and the difference appears only in the new ESPRESSO spectrum. Therefore, it is more likely that the difference is actually due to an inappropriate model of the velocity profile. Indeed, one can see from Fig. 11 that the observed Fe Iλ3021Å and 3720Å line profiles for ESPRESSO and UVES have about the same width when the resolution of the two instruments differs by a factor of 2.5. This strongly suggests the presence of more than one component.
 |
Fig. 11. Fit to the Fe I absorption lines with one-component model. From top to bottom, the black line corresponds to the data obtained with UVES 2009 and ESPRESSO 2018 (Fe Iλ2484Å line is missed in ESPRESSO spectrum), the red and blue profiles are the one-component models constrained respectively from UVES and ESPRESSO data only. |
Fitting the Fe I lines with a two-component model solves the issue (see Fig. 12). The whole set of UVES and ESPRESSO data is now well fitted with the same set of parameters, which is given in Table 4. Remarkably, we find Doppler parameters of only b ∼ 0.3 km s−1. Assuming thermal broadening only, this corresponds to a kinetic temperature T ∼ 300 K. As turbulent motions can also contribute to the line broadening, the actual temperature must be lower than this value, in agreement with the T ∼ 100 K derived from modelling the physical conditions in the gas.
 |
Fig. 12. Fit to the Fe I absorption lines with a two-component model. From top to bottom, the black line corresponds to the data obtained with UVES (2001, 2009 and 2017) and ESPRESSO (2018). The fit profiles are represented using a 0.68 central percentile interval of their own distributions sampled from the obtained posterior probability distribution of the fitting parameters. Red and green areas correspond to the total profile and contribution of each component, respectively. Residuals are shown above each panel. |
Results from fitting UVES and ESPRESSO altogether.
To take into account the possible partial coverage in Fe Iλ2719Å line, we considered a modified line profile with simple partial covering model (see e.g., Ganguly et al. 1999), where the covering factor is an independent and free parameter during the fit. We confirm the partial coverage of the Ly-α emission by the cold, Fe I-bearing gas with Cf ≈ 0.4 − 0.6, assuming the same covering factor for both Fe I components and for all exposures. Alternatively, fitting the spectra with independent covering factor for each exposure, we obtain a gradual increase of the covering factor, Cf, with time from 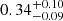 in 2001 (consistent with values obtained by Bergeron & Boissé 2017) to
in 2001 (consistent with values obtained by Bergeron & Boissé 2017) to 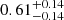 in 2018 (see Fig. 13), although this is not highly statistically significant given the relatively high uncertainties on individual values.
in 2018 (see Fig. 13), although this is not highly statistically significant given the relatively high uncertainties on individual values.
 |
Fig. 13. Fit to the region around Fe Iλ2719 Å line at z = 0.452. From top to bottom, the black line corresponds to the data obtained with UVES in 2001, 2009, and 2017 and ESPRESSO in 2018. The fit profiles are presented in the same manner as in Fig. 12. The horizontal dashed line and grey stripe show 1 − Cf and its uncertainty, respectively. The constrained value of Cf for each spectrum is given in the bottom-left of each panel. |
The continuum emission accounts for about 30% of the total observed flux at the position of Ly-α and is more likely fully covered by the Fe I-absorbing cloud, as we do not see any evidence for partial coverage at other wavelengths. This is also expected because the accretion disc responsible for the UV continuum emission is expected to have a size of at most ∼10−3 pc. The time-variation of Cf, if confirmed, would suggest that the covering fraction of the Ly-α emission line flux increases from 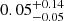 to
to 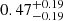 between 2001 and 2018 (see Eq. (4) of Bergeron & Boissé 2017). As the ratio of the continuum to Ly-α emission line flux does not vary significantly (less than 20% over the same period), this indicates that the possible time-variation of Cf is likely attributed to the relative motion of the Fe I-bearing cloud with respect to the line of sight. It also means that a large fraction of Ly-α photons arise from a region smaller in projection than the Fe I-bearing cloud. In other words, at least half of the Ly-α photons with velocities corresponding to the position of the Fe Iλ2719Å line are produced in the very nuclear region of the quasar. It would be interesting to continue monitoring this system to see if the covering fraction continues to increase, setting an upper limit to the amount of photons arising from (or scattered by) gas in more extended regions around the quasar nucleus.
between 2001 and 2018 (see Eq. (4) of Bergeron & Boissé 2017). As the ratio of the continuum to Ly-α emission line flux does not vary significantly (less than 20% over the same period), this indicates that the possible time-variation of Cf is likely attributed to the relative motion of the Fe I-bearing cloud with respect to the line of sight. It also means that a large fraction of Ly-α photons arise from a region smaller in projection than the Fe I-bearing cloud. In other words, at least half of the Ly-α photons with velocities corresponding to the position of the Fe Iλ2719Å line are produced in the very nuclear region of the quasar. It would be interesting to continue monitoring this system to see if the covering fraction continues to increase, setting an upper limit to the amount of photons arising from (or scattered by) gas in more extended regions around the quasar nucleus.
This work shows that resolving the velocity structure along the line of sight is a crucial step towards a physical interpretation of the data. This includes the investigation of possible variations of the line profiles (e.g., covering factors) due to the transverse motion of the cloud with respect to the line of sight.
7. Summary
We present an analysis of a very high-resolution spectrum (R ≳ 130 000) of the quasar HE 0001−2340 obtained using the new VLT/ESPRESSO spectrograph. Our observations cover the range 380 − 788 nm with exquisite spectral fidelity and wavelength-calibration accuracy. These characteristics allow us to investigate the velocity profiles of several absorption systems with unprecedented precision.
We disentangled the thermal and turbulent broadening in individual components of the metal absorption-line complex (spread over about 400 km s−1) associated with a low-metallicity sub-DLA at z = 2.187. We infer temperatures of ∼16 000 K, which is twice the canonical Galactic WNM value. By compiling temperature measurements in other low-metallicity high-z systems, we reveal an anti-correlation between the kinetic temperature in individual velocity components and the total H I column density integrated over the profile. Interestingly, the systems have metallicities, H I column densities, and temperatures in-between those found in the warm neutral ISM of galaxy discs and those seen in the intergalactic medium. We are therefore possibly witnessing gas cooling in the circumgalactic medium in a transition region between intergalactic medium and ISM. This finding opens up exciting prospects to further investigate the thermal state of the gas around galaxies using high-resolution spectroscopy.
The high spectral resolution and wavelength accuracy allowed us to constrain the Mg isotopic ratio at z = 0.45 and z = 1.65, which we find to be consistent with the solar value. Apparent strong enhancement of heavy Mg isotopes previously reported in the literature for these systems were hence likely due to distortion in the UVES wavelength scale. This also shows that ESPRESSO is well suited for such isotopic measurements in various absorption systems, opening up a new way to place constraints on the stellar nucleosynthetic history over cosmic time (see also Welsh et al. 2020).
Finally, we confirm partial coverage of the background source at Ly-α (quasar rest-frame) wavelengths by the Fe I absorption system at zabs = 0.45. In other words, the background source can no longer be considered an infinitely narrow beam; about half of the quasar photons at these wavelengths do not pass through the absorber. Thanks to the combined analysis of UVES and ESPRESSO data, we were also able to reveal velocity substructure within the Fe I-bearing gas that presents two components with Doppler parameters of only b ∼ 0.3 km s−1, confirming the low kinetic temperature obtained from modelling of the gas physical conditions.
Our results are mostly S/N-limited, meaning that more stringent constraints could be obtained by the addition of further exposures. Our work highlights several important science cases that can be addressed from single-object high-resolution spectroscopy with large telescopes. These will certainly become routinely addressed with future ground-based instruments such as HIRES on the E-ELT (Marconi et al. 2021), G-CLEF on the GMT (Szentgyorgyi et al. 2016), and HROS on the TMT (Froning et al. 2006), as well as Pollux on the LUVOIR space telescope (Bouret et al. 2018).
We note that the four spectra (ESPRESSO, UVES-2001, UVES-2009 and UVES-2017) will be jointly analysed in Sect. 6, but are not combined altogether.
Milaković et al. (2021) recently used the HARPS spectrograph and derived gas temperatures as byproducts in a study of the possible cosmic-time variation of the fine-structure constant. As the redshift (zabs = 1.1) and metallicity (log Z/Z⊙ = −0.22) of this system are different from the rest of our sample, we do not include it in our analysis. We note however that the corresponding mean temperature (9100 ± 1100 K) would perfectly match the anti-correlation discussed here.
Acknowledgments
We thank the anonymous referee for detailed and constructive comments. We thank Michael Murphy for discussions on the Mg II wavelengths and isotopic-ratio measurements, and Peter Shternin for discussions on Bayesian hierarchical modelling. We acknowledge support from the French Agence Nationale de la Recherche under ANR grant 17-CE31-0011-01/project “HIH2” (PI Noterdaeme). S. B. and K. T. are partially supported by RFRB grant 18-52-15021 and the Foundation for the Advancement of Theoretical Physics and Mathematics “BASIS”. C. L. thanks ESO for support during a Research Period. G. D. thanks IAP for hospitality when this work was initiated. S. L. was funded by project FONDECYT 1191232.
References
- Agafonova, I. I., Molaro, P., Levshakov, S. A., & Hou, J. L. 2011, A&A, 529, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balashev, S. A., & Noterdaeme, P. 2018, MNRAS, 478, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Balashev, S. A., Petitjean, P., Ivanchik, A. V., et al. 2011, MNRAS, 418, 357 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Balashev, S. A., Zavarygin, E. O., Ivanchik, A. V., Telikova, K. N., & Varshalovich, D. A. 2016, MNRAS, 458, 2188 [CrossRef] [Google Scholar]
- Balashev, S. A., Noterdaeme, P., Rahmani, H., et al. 2017, MNRAS, 470, 2890 [NASA ADS] [CrossRef] [Google Scholar]
- Balashev, S. A., Klimenko, V. V., Noterdaeme, P., et al. 2019, MNRAS, 490, 2668 [CrossRef] [Google Scholar]
- Bergeron, J., & Boissé, P. 2017, A&A, 604, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boissé, P., Bergeron, J., Prochaska, J. X., Péroux, C., & York, D. G. 2015, A&A, 581, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouret, J. C., Neiner, C., Gómez de Castro, A. I., et al. 2018, in Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray, eds. J. W. A. den Herder, S. Nikzad, K. Nakazawa, SPIE Conf. Ser., 10699, 106993B [Google Scholar]
- Burles, S., & Tytler, D. 1998, ApJ, 507, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Carswell, R. F., & Webb, J. K. 2014, VPFIT: Voigt profile fitting program [Google Scholar]
- Carswell, R. F., Becker, G. D., Jorgenson, R. A., Murphy, M. T., & Wolfe, A. M. 2012, MNRAS, 422, 1700 [NASA ADS] [CrossRef] [Google Scholar]
- Cooke, R. J., Pettini, M., Jorgenson, R. A., Murphy, M. T., & Steidel, C. C. 2014, ApJ, 781, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Cooke, R. J., Pettini, M., & Steidel, C. C. 2018, ApJ, 855, 102 [NASA ADS] [CrossRef] [Google Scholar]
- De Cia, A., Ledoux, C., Petitjean, P., & Savaglio, S. 2018, A&A, 611, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, in Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye, & A. F. Moorwood, Proc. SPIE, 4008, 534 [CrossRef] [Google Scholar]
- D’Odorico, V. 2007, A&A, 470, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumont, V., & Webb, J. K. 2017, MNRAS, 468, 1568 [Google Scholar]
- Dutta, R., Srianand, R., Rahmani, H., et al. 2014, MNRAS, 440, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Field, G. B., Goldsmith, D. W., & Habing, H. J. 1969, ApJ, 155, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Froning, C., Osterman, S., Beasley, M., Green, J., & Beland, S. 2006, in SPIE Conf. Ser., eds. I. S. McLean, & M. Iye, 6269, 62691V [Google Scholar]
- Ganguly, R., Eracleous, M., Charlton, J. C., & Churchill, C. W. 1999, AJ, 117, 2594 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., & Troland, T. H. 2003, ApJ, 586, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, T. M., Misawa, T., Charlton, J. C., Mshar, A. C., & Ferland, G. J. 2010, ApJ, 715, 1497 [NASA ADS] [CrossRef] [Google Scholar]
- Jorgenson, R. A., Murphy, M. T., Thompson, R., & Carswell, R. F. 2014, MNRAS, 443, 2783 [NASA ADS] [CrossRef] [Google Scholar]
- Kanekar, N., Prochaska, J. X., Smette, A., et al. 2014, MNRAS, 438, 2131 [NASA ADS] [CrossRef] [Google Scholar]
- Kausch, W., Noll, S., Smette, A., et al. 2015, A&A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khaire, V., & Srianand, R. 2019, MNRAS, 484, 4174 [CrossRef] [Google Scholar]
- Krogager, J.-K., & Noterdaeme, P. 2020, A&A, 644, L6 [CrossRef] [EDP Sciences] [Google Scholar]
- Krogager, J. K., Møller, P., Fynbo, J. P. U., & Noterdaeme, P. 2017, MNRAS, 469, 2959 [NASA ADS] [CrossRef] [Google Scholar]
- Lampton, M., Margon, B., & Bowyer, S. 1976, ApJ, 208, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Ledoux, C., Srianand, R., & Petitjean, P. 2002, A&A, 392, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ledoux, C., Petitjean, P., & Srianand, R. 2003, MNRAS, 346, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Ledoux, C., Petitjean, P., Fynbo, J. P. U., Møller, P., & Srianand, R. 2006, A&A, 457, 71 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Lee, C.-C., Webb, J. K., Carswell, R. F., & Milakovic, D. 2021, MNRAS, 504, 787 [CrossRef] [Google Scholar]
- Levshakov, S. A., Agafonova, I. I., Molaro, P., Reimers, D., & Hou, J. L. 2009, A&A, 507, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marconi, A., Abreu, M., Adibekyan, V., et al. 2021, Messenger, 182, 27 [Google Scholar]
- Milaković, D., Lee, C.-C., Carswell, R. F., et al. 2021, MNRAS, 500, 1 [CrossRef] [Google Scholar]
- Murphy, M. T., & Berengut, J. C. 2014, MNRAS, 438, 388 [Google Scholar]
- Murphy, M. T., Webb, J. K., & Flambaum, V. V. 2008, MNRAS, 384, 1053 [NASA ADS] [CrossRef] [Google Scholar]
- Neeleman, M., Prochaska, J. X., & Wolfe, A. M. 2015, ApJ, 800, 7 [CrossRef] [Google Scholar]
- Noterdaeme, P., Petitjean, P., Srianand, R., Ledoux, C., & Le Petit, F. 2007, A&A, 469, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Ledoux, C., Petitjean, P., & Srianand, R. 2008, A&A, 481, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Petitjean, P., Srianand, R., Ledoux, C., & López, S. 2011, A&A, 526, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., López, S., Dumont, V., et al. 2012, A&A, 542, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Krogager, J.-K., Balashev, S., et al. 2017, A&A, 597, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Meara, J. M., Tytler, D., Kirkman, D., et al. 2001, ApJ, 552, 718 [NASA ADS] [CrossRef] [Google Scholar]
- O’Meara, J. M., Burles, S., Prochaska, J. X., et al. 2006, ApJ, 649, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Cristiani, S., Rebolo, R., et al. 2021, A&A, 645, A96 [CrossRef] [EDP Sciences] [Google Scholar]
- Péroux, C., & Howk, J. C. 2020, ARA&A, 58, 363 [CrossRef] [Google Scholar]
- Petitjean, P., Ledoux, C., & Srianand, R. 2008, A&A, 480, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pettini, M., & Cooke, R. 2012, MNRAS, 425, 2477 [CrossRef] [Google Scholar]
- Pettini, M., Zych, B. J., Murphy, M. T., Lewis, A., & Steidel, C. C. 2008, MNRAS, 391, 1499 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Prochaska, J. X., & Wolfe, A. M. 1997, ApJ, 487, 73 [CrossRef] [Google Scholar]
- Prochaska, J. X., Wolfe, A. M., Howk, J. C., et al. 2007, ApJS, 171, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Rahmani, H., Wendt, M., Srianand, R., et al. 2013, MNRAS, 435, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Richter, P., Ledoux, C., Petitjean, P., & Bergeron, J. 2005, A&A, 440, 819 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1976, ApJ, 206, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Srianand, R., Petitjean, P., Ledoux, C., Ferland, G., & Shaw, G. 2005, MNRAS, 362, 549 [CrossRef] [Google Scholar]
- Srianand, R., Gupta, N., Petitjean, P., et al. 2012, MNRAS, 421, 651 [NASA ADS] [Google Scholar]
- Szentgyorgyi, A., Baldwin, D., Barnes, S., et al. 2016, in Ground-based and Airborne Instrumentation for Astronomy VI, eds. C. J. Evans, L. Simard, H. Takami, et al., SPIE Conf. Ser., 9908, 990822 [Google Scholar]
- Vangioni, E., & Olive, K. A. 2019, MNRAS, 484, 3561 [CrossRef] [Google Scholar]
- Vladilo, G., Gioannini, L., Matteucci, F., & Palla, M. 2018, ApJ, 868, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, S. S., Allen, S. L., Bigelow, B. C., et al. 1994, in Instrumentation in Astronomy VIII, eds. D. L. Crawford, E. R. Craine, et al., SPIE Conf. Ser., 2198, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Vreeswijk, P. M., Ledoux, C., Smette, A., et al. 2007, A&A, 468, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Welsh, L., Cooke, R., Fumagalli, M., & Pettini, M. 2020, MNRAS, 494, 1411 [CrossRef] [Google Scholar]
- Whitmore, J. B., & Murphy, M. T. 2015, MNRAS, 447, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003, ApJ, 587, 278 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Hierarchical Bayesian modelling of the Fe I absorber
We describe here the method used to fit the Fe I absorption lines with Voigt profiles in Sect. 6. As most of the Fe I lines are weak, we were forced to take into account continuum placement uncertainties. To do this rigorously, we used a hierarchical Bayesian approach. In a standard Bayesian approach, the distribution of the model parameters is given by
where p(θ) is a prior on the model parameters (denoted by θ) and D stands for observed data. The likelihood function p(D|θ) under the assumption of Gaussian distribution of the pixel uncertainties can be written as
where xi, yi, and σi are the wavelength, flux, and uncertainty in the ith pixel of the spectrum, respectively. Evidently D ≡ (xi, yi, σi). The model profile, m, is usually specified for absorption lines as
where τ(x) is an optical depth describing the profiles of absorption lines, I(x, x′) is the instrument function, and C(x) denotes the unabsorbed continuum of the background source. When the background source is a quasar, the continuum does not have a simple shape. In addition, the spectra are generally not flux-calibrated, and the presence of absorption lines unrelated to the absorption system in question affects the apparent continuum. Therefore, the unabsorbed quasar continuum is usually determined by interpolating the observed spectrum using regions unaffected by absorption, as determined by visual inspection. B-spline functions are frequently used to this end. This works well for relatively strong absorption lines and does not introduce significant biases on the inferred absorption model parameters. However, for weak absorption lines, the subjectivity of continuum placement can have stronger consequences.
To take this uncertainty into account, we propose the following extension of the Bayesian model. For simplicity, let us first describe a single absorption line. The observed spectrum is subject to random statistical noise, resulting in the dispersion of spectral pixels, around some smooth envelope. In the model situation, this dispersion corresponds to the value of the pixel uncertainties, that is, to the spectral quality. Hence the dispersion of the continuum placement (the difference between the constructed and true continuum) is expected to be proportional to 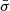 – a mean pixel uncertainty within some wavelength range in the vicinity of the line. Therefore, it is natural to describe the continuum displacement in the units of
– a mean pixel uncertainty within some wavelength range in the vicinity of the line. Therefore, it is natural to describe the continuum displacement in the units of 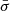 . This is particularly useful for the modelling of multiple absorption lines in distinct wavelength ranges, with different spectral quality. In the first approximation, the effect of continuum placement uncertainty can be addressed by changing the continuum following
. This is particularly useful for the modelling of multiple absorption lines in distinct wavelength ranges, with different spectral quality. In the first approximation, the effect of continuum placement uncertainty can be addressed by changing the continuum following
where α is a parameter specifying the continuum displacement in units of 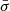 . Therefore, a model profile
. Therefore, a model profile 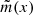 that takes into account continuum uncertainty can be expressed as
that takes into account continuum uncertainty can be expressed as
One can in principle use α as a nuisance parameter during the fit and constrain absorption model parameters jointly with α. However, the result is that an improper choice of the continuum model may bias the absorption model parameters. Additionally, in cases of multiple absorption lines, each line (or line region if some lines are blended) should have its own α. This may lead to an undesired significant increase in the number of model parameters. This can be circumvented by using a hierarchical Bayesian approach.
We assume that α follows some distribution p(α|d) described by some parameter d. This corresponds to the sampling of the continuum placement, i.e. we mimic the situation where different people obtain independent continuum placement. The posterior distribution of the parameters can then be written as
where θ is the set of the model parameters describing only the absorption profile, and p(d) is a prior on d. As we are not interested in the distribution of α, we can marginalise over this parameter
which means that the integral in the bracket is a modified likelihood function, p(D|θ, d).
Considering that p(D|θ, α) is described by Eq. (A.2) with replacement Eq. (A.5), and assuming that p(α|d) is a Gaussian function with zero mean and dispersion d, we can take an integral over α in analytical form, which gives
where
where 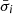 is the mean dispersion within the spectral region around pixel i.
is the mean dispersion within the spectral region around pixel i.
In case of several continuum regions (when fitting multiple lines), this formalism can be applied to the set of (α1, …, αn) describing piece-wise correction to the continuum. In that case, we have a product of p(αk|dk) in Eqs. (A.6) and (A.7) (with marginalisation over each αk). To minimise the number of parameters it is reasonable to assume that all p(αk|dk) have the same shape with d1 = ⋯ = dn ≡ d, that is, we are left with only one parameter d that is used to describe the sampling of the continuum uncertainty. In that case we obtain a similar likelihood function
where Ak and Bk are expressed by similar expressions to those in Eqs. (A.9) and (A.10) with the exception that the sums are taken over the pixels corresponding to kth interval of the continuum correction.
Following this approach, we fitted the Fe I lines at z = 0.45 towards HE 0001−2340. We assume flat priors on the z, b, log N and covering fraction Cf. For continuum placement uncertainties we used one hyper-parameter, h, which as presented above, describes the dispersion of the continuum displacements distribution (we assumed it to be a Gaussian) in units of median pixel uncertainties in ∼1 Å-wide region around each of the considered lines. We used a prior on h to be Gaussian with 1.0 mean and dispersion 0.2. The posterior probability function of the parameters was sampled using an affine-invariant Monte-Carlo Markov Chain sampler.
 |
Fig. A.1. Temperature and turbulent broadening parameter determinations using independent Doppler parameters for each species (i.e. method 2) in various components. For the weakest component (C, G and N), the uncertainties are too large to provide meaningful constraints. Black points and error bars represent the square of the total Doppler parameter b measured for various species (Fe II, S II Si II, Al II, O I and C II) as a function of the inverse of their mass. The blue line and shaded area represent the linear fit to the data and 1σ confidence band. |
Appendix B: Additional table
Results from Voigt-profile fitting of metal species associated to the DLA at z = 2.187.
All Tables
Kinetic temperatures in various systems determined from thermal broadening of the lines.
Results from Voigt-profile fitting of metal species associated to the DLA at z = 2.187.
All Figures
 |
Fig. 1. Multi-component Voigt-profile fitting of metal lines in the sub-DLA at z = 2.187. The normalised ESPRESSO spectrum is shown in black, with the best-fit synthetic spectrum overlaid in red. The blue dashed curve corresponds to the synthetic spectrum computed using the best-fit parameters obtained by Richter et al. (2005) from the analysis of UVES data. We note that their component A here splits into three subcomponents that we call A1, A2, and A3 in Table B.1 and their component F at v ∼ −150 km s−1 appears to be spurious as seen from C IIλ1334. |
| In the text | |
 |
Fig. 2. Comparison of the turbulent component of the Doppler parameter (top) and the temperature (bottom) derived from two different methods (1: using bturb and T as free parameters for all species of a given component; 2: fitting total b-values for each species and deriving bturb and T a posteriori from the variation of b with the inverse of the species mass). Blue dotted lines show the one-to-one relation. |
| In the text | |
 |
Fig. 3. Kinetic temperatures determined in various components along the line profile of the sub-DLA at zabs = 2.187 (zero of the velocity scale). The dashed blue line and shaded area correspond to the weighted mean and associated error ⟨T⟩ = 16 000 ± 1300 K. The dotted lines show one standard deviation around this mean. |
| In the text | |
 |
Fig. 4. Kinetic temperatures derived from Doppler broadening in various absorption-line systems as a function of the total H I column densities of these systems. Empty circles correspond to measurements obtained thanks to the presence of deuterium (typically in one or a few close components) while filled squares correspond to average measurements in complex systems made possible by high-resolution spectroscopy. Grey triangles represent measurements in individual components of the DLA towards HE 0001−2340 (Fig. 3). The data exhibit an anti-correlation with a Pearson coefficient of r = −0.78 and a probability that this is pure coincidence of p = 0.16%. The solid blue (respectively red) line corresponds to an unweighted linear fit including (resp. excluding) the lowest N(H I) value towards Q 1009+2956. |
| In the text | |
 |
Fig. 5. Single Voigt profile fit to the cold, narrow component at z = 0.45206 (ESPRESSO data: black with grey error bars, synthetic spectrum: red). Residuals (in units of standard deviation) are shown in the subpanel above each line panel. The zero of the velocity scale is taken at the velocity of the iron and calcium lines. The redshifts of the magnesium lines were left to vary independently from the other lines and are displayed as short red tick marks. The blue profiles and the corresponding blue tick marks and residuals correspond to the apparent velocity shift (−0.47 and −0.17 km s−1 from Mg II and Mg I respectively) measured by Agafonova et al. (2011) from UVES data. |
| In the text | |
 |
Fig. 6. Velocity shift (with respect to lines with the standard isotopic ratio) as a function of ξ = (25Mg + 26Mg)/24Mg assuming r = 26Mg/25Mg = 1 for mock ESPRESSO data. The solid blue line corresponds to the mean value for 100 mock spectra for each input ξ value, and the dark and light-blue regions represent the regions containing 68.3% and 95.5% of the values, respectively. The pink line corresponds to a noiseless mock spectrum. The observed velocity shift and associated 1σ uncertainty for the system at z = 0.45206 are shown as orange horizontal solid and dotted lines, respectively. |
| In the text | |
 |
Fig. 7.
|
| In the text | |
 |
Fig. 8. Synthetic Mg II absorption profiles for the system at z = 0.452 (red line) corresponding to the best fit (ξ = 0.25, assuming r = 1) including 24Mg II, 25Mg II, and 26Mg II lines (dashed-blue, dashed-orange, and dashed-green, respectively) overlaid on the ESPRESSO data (black with grey error bars). The top panels show the residuals. |
| In the text | |
 |
Fig. 9. Fit to the metal lines at z = 1.65. The long dashed line (zero of the velocity scale) corresponds to the redshift of Fe II and Si II, while the short ticks mark the centroids of the Mg II and Mg I lines. The velocity shifts seen here are indistinguishable from those measured from UVES data by Agafonova et al. (2011) for this system. |
| In the text | |
 |
Fig. 10. Same as Fig. 7 for the system at z = 1.65. |
| In the text | |
 |
Fig. 11. Fit to the Fe I absorption lines with one-component model. From top to bottom, the black line corresponds to the data obtained with UVES 2009 and ESPRESSO 2018 (Fe Iλ2484Å line is missed in ESPRESSO spectrum), the red and blue profiles are the one-component models constrained respectively from UVES and ESPRESSO data only. |
| In the text | |
 |
Fig. 12. Fit to the Fe I absorption lines with a two-component model. From top to bottom, the black line corresponds to the data obtained with UVES (2001, 2009 and 2017) and ESPRESSO (2018). The fit profiles are represented using a 0.68 central percentile interval of their own distributions sampled from the obtained posterior probability distribution of the fitting parameters. Red and green areas correspond to the total profile and contribution of each component, respectively. Residuals are shown above each panel. |
| In the text | |
 |
Fig. 13. Fit to the region around Fe Iλ2719 Å line at z = 0.452. From top to bottom, the black line corresponds to the data obtained with UVES in 2001, 2009, and 2017 and ESPRESSO in 2018. The fit profiles are presented in the same manner as in Fig. 12. The horizontal dashed line and grey stripe show 1 − Cf and its uncertainty, respectively. The constrained value of Cf for each spectrum is given in the bottom-left of each panel. |
| In the text | |
 |
Fig. A.1. Temperature and turbulent broadening parameter determinations using independent Doppler parameters for each species (i.e. method 2) in various components. For the weakest component (C, G and N), the uncertainties are too large to provide meaningful constraints. Black points and error bars represent the square of the total Doppler parameter b measured for various species (Fe II, S II Si II, Al II, O I and C II) as a function of the inverse of their mass. The blue line and shaded area represent the linear fit to the data and 1σ confidence band. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



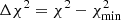
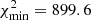
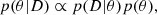
![$$ \begin{aligned} p(D|\theta ) \propto \prod \limits _{i}\exp \left[-\frac{1}{2}\left(\frac{m(x_i) - { y}_i}{\sigma _i}\right)^2\right], \end{aligned} $$](/articles/aa/full_html/2021/07/aa40501-21/aa40501-21-eq34.gif)