EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 650 (June 2021) A&A, 650 (2021) A194 Full HTML
Free Access
Issue
A&A
Volume 650, June 2021
Article Number A194
Number of page(s) 25
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/202140751
Published online 29 June 2021

© ESO 2021

1 Introduction

The data obtained by the Gaia mission (Gaia Collaboration 2016) have triggered an on-going revolution in our understanding of stellar and Galactic astrophysics (see e.g. Brown 2021). Gaia is delivering astrometry and photometry for more than 109 stars. To complement Gaia, with radial velocities and chemical abundances, several large stellar spectroscopic surveys have started or are being planned.

Stellar characterisation is essential, for example, for tracing the timeline of processes driving the formation and evolution of the Milky Way. Stellar chemical abundances and ages are powerful complements to kinematic and dynamic properties in studies of the stellar populations (e.g. Freeman & Bland-Hawthorn 2002). Nevertheless, it is common to observe a large dispersion in the values of stellar parameters and abundances when comparing literature results or the performance of different analysis methods applied to the same spectra (Lebzelter et al. 2012; Hinkel et al. 2014, 2016; Smiljanic et al. 2014; Jofré et al. 2017; Brucalassi et al. 2021). This outcome is a consequence of the complexity of the task. Various astrophysical parameters must be derived from limited information carried by the, mostly incomplete, stellar data (e.g. spectra, photometric magnitudes, and parallax measurements). The data themselves are affected by random noise and systematic uncertainties. Moreover, the interpretation of the stellar data depends on the use of auxiliary models and data (e.g. for atomic transitions), which have their own limitations (see, e.g. Amarsi et al. 2018; Barklem 2016; Blanco-Cuaresma 2019; Bonifacio et al. 2018, for different aspects of these problems).

Ideally, to characterise a star, one would directly measure its most fundamental parameters: the luminosity (L) or, in practice, the bolometric flux (FBOL) and distance; the radius (R); and the mass (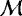M$\mathcal{M}$). From these parameters, it is possible to compute values of effective temperature (Teff) and surface gravity (log g). In reality,extracting fundamental parameters from direct measurements is only possible in a restricted number of cases (Torres et al. 2010; Bohlin et al. 2014; Hekker 2020; Serenelli et al. 2021). Therefore, Teff and log g values are mostly obtained from indirect, model-dependent methods (see e.g. Smalley 2005).

The spectroscopic method using Fe lines is a frequently used technique to simultaneously derive Teff, log g, and metallicity ([Fe/H]1). One approach, which is usually referred to as the equivalent width (EW) method, relies on measuring EWs to constrain the parameters using the excitation and ionisation equilibrium of Fe lines (e.g. Magrini et al. 2013; Sousa 2014; Tabernero et al. 2019). The equilibria of Fe lines can also be used via the direct fitting of the lines with synthetic spectra (see, e.g. the codes described by Blanco-Cuaresma et al. 2014; Sbordone et al. 2014). An alternative is the so-called spectrum synthesis method, where large sections of the observed spectrum are compared to synthetic theoretical spectra in search for the best fitting one (e.g. Worley et al. 2016; Piskunov & Valenti 2017; Gavel et al. 2019).

Spectroscopic methods are often avoided when deriving Teff in metal-poor stars ([Fe/H] ≤−1 dex) in order to prevent biased results. Instead, the InfraRed Flux Method (IRFM, Blackwell & Shallis 1977; Blackwell et al. 1979, 1980) is preferred (see Meléndez & Ramírez 2004; Meléndez et al. 2006). Effective temperatures derived with the IRFM are usually considered robust and much less susceptible to the model limitations that affect spectroscopic methods, such as granulation effects or departures from the local thermodynamic equilibrium (so-called non-LTE effects). Nevertheless, the method is still affected by uncertainties in the reddening and inconsistencies in the absolute flux calibration (see e.g. González Hernández & Bonifacio 2009; Casagrande et al. 2010, and references therein).

Thanks to the increased sensitivity of instruments such as the Precision Astronomical Visible Observations (PAVO) beam combiner (Ireland et al. 2008) in the Center for High Angular Resolution Astronomy (CHARA) interferometric array (ten Brummelaar et al. 2005), angular diameters of nearby dwarfs and subgiants can now be measured, delivering data for a quasi-direct2 Teff determination with an accuracy within 100 K (e.g. Bazot et al. 2011; White et al. 2013; Karovicova et al. 2018, 2020). This enables the establishment of a standard Teff scale that can be used to evaluate the accuracy of model-dependent techniques.

On the base of this interferometric Teff scale, Balmer line profiles synthesised using three-dimensional (3D), non-LTE model atmospheres were recently found to accurately reproduce the observed profiles (Amarsi et al. 2018; Giribaldi et al. 2019). This important result restored confidence on a method frequently applied to avoid biases related to degeneracy among the atmospheric parameters since the shape of the wings of the Balmer lines essentially only depends on Teff (e.g. Cayrel et al. 1985; Cayrel de Strobel 1985; Fuhrmann et al. 1994; Fuhrmann 1998; Mishenina & Kovtyukh 2001, among many others). Despite its potential for providing accurate Teff values, to date, only a few works have made use of Balmer lines computed with 3D non-LTE models (Amarsi et al. 2019; Nordlander et al. 2019; Hanke et al. 2020). This is most likely the case because of complications related to the normalisation of wide profiles in modern echelle spectra.

The accurate calibration of stellar parameters has become imperative in the current era of large spectroscopic surveys (Jofré et al. 2019). On-going and future projects, such as Gaia-ESO (Gilmore et al. 2012; Randich et al. 2013), GALactic Archaeology with HERMES (GALAH, De Silva et al. 2015), Large sky Area Multi-Object fibre Spectroscopic Telescope (LAMOST, Cui et al. 2012), Maunakea Spectroscopic Explorer (MSE, The MSE Science Team et al. 2019), 4-metre Multi-Object Spectroscopic Telescope (4MOST, de Jong et al. 2019), Milky Way Mapper (MWM, Kollmeier et al. 2017), will together obtain spectra for more than 107 stars. The analysis of this amount of data requires innovative methodologies for instance given by codes, such as The Cannon (Ness et al. 2015), StarNet (Fabbro et al. 2018), and The Payne (Ting et al. 2019), or those explored by several other authors (e.g. Kassounian et al. 2019; Leung & Bovy 2019; Guiglion et al. 2020; Wang et al. 2020). Some of these methods depend on training samples of stars that have well-derived, accurate parameters. A lack of accuracy can result in systematic problems of the training sample propagating to the new analysis (see e.g. the trend between Teff and [Fe/H] of stars in the Praesepe cluster displayed in Fig. 11 of Wheeler et al. 2020).

Stars with good-quality interferometric Teff have been compiled into a sample called the Gaia benchmark stars (GBS henceforth, Heiter et al. 2015; Jofré et al. 2014, 2018). This sample includes, in addition, a few stars for which Teff values were inferred by colour calibrations based on interferometric measurements or, alternatively, by using the IRFM. The uncertainties of the interferometric Teff values is of 1% or better. The uncertainties of the Teff values based on calibrations can be slightly higher, with typical values between 80 and 100 K; but they are still useful for accuracy diagnostics. The log g values of the GBS are based on masses determined using stellar evolution models. For dwarfs and subgiants, typical uncertainties in log g are also of the order of 1% or better(≤0.04 dex).

Apart from the GBS, several samples of calibrating stars, with accurate masses, have become available thanks to recent advances in asteroseismology (Valentini et al. 2016, 2017; Serenelli et al. 2017; Pinsonneault et al. 2018; Worley et al. 2020). Stars in eclipsing binaries are an additional option for use as calibrators. Masses and radii of the components can be measured with very high accuracy (e.g. Hełminiak et al. 2019; Ratajczak et al. 2021), with the possibility of using these measurements to derive effective temperatures of a high quality (Miller et al. 2020). There is, however, still a strong need of larger samples of calibrators, in particular to improve the coverage of the parameter space towards low metallicities (e.g. Hawkins et al. 2016; Valentini et al. 2019).

In this work, we introduce the TITANS3 reference stars, a selection of metal-poor stars for which we provide accurate and precise parameters and abundances and it is intended to serve for the calibration of spectroscopic analysis methods. In this first publication, we focus on providing values of Teff and log g for dwarf and subgiant stars with Teff within 5500–6600 K and log g within 3.7–4.6 dex. The metallicity range of this sample lies between −1.0 and −3.1 dex. We did not impose a lower limit in metallicity; this was rather set by the availability of the spectra required to apply our methodology. Effective temperatures were determined fitting Hα line profiles. The Hα line becomes progressively weaker and less useful for our method as Teff decreases. This limit of usability sets at about ~4500 K for giants and ~5000 K for dwarfs. However, once again, for the current sample of TITANS, the lower limit in the Teff range was set by the availability of good-quality spectra. As we discuss later in the paper, the Hα profiles of metal-poor stars are significantly sensitive to log g, which we inferred using Gaia parallaxes from the Early Data Release 3 (EDR3, Gaia Collaboration 2021). Therefore, the atmospheric parameters in this sample owe their fine accuracy to the Gaia mission. This is the reason why we call these stars TITANS.

The paper is organised as follows. The sample and the observational data are described in Sect. 2. The determination of atmospheric parameters and the accuracy of the results are discussed in Sects. 3 and 4, respectively. In Sect. 5, we separate the stars into different Galactic substructures. Finally, our results are summarised in Sect. 6.

2 Sample selection and observational data

2.1 Selection of the TITANS sample

The main source of sample stars was the work of Casagrande et al. (2010). Additional candidates were assembled from Ryan et al. (1996), Gehren et al. (2006), Reddy & Lambert (2008), Nissen & Schuster (2010), and Beers et al. (2017). The stars were included in the preliminary sample if their previously determined atmospheric parameters were as follows: Teff ≥ 5000 K, [Fe/H] ≤−0.9 dex, and log g   ≥ 3.5 dex.

We then restricted the sample to stars with spectra obtained with the Ultraviolet and Visual Echelle Spectrograph (UVES, Dekker et al. 2000) that were publicly available in the data archive4 of the European Southern Observatory (ESO). The spectra had to encompass the Hα line at 6562.797 Å, have a resolution higher than R = 40 000, and a signal-to-noise ratio (S/N) higher than 100. We made use of the processed, single-exposure UVES spectra. Data reduction was conducted with the ESO UVES pipeline (Ballester et al. 2000).

During the analysis, several of the spectra that we collected were found to present distortions related to spectral order merging. For this first work, we did not attempt to re-reduce those spectra, but we simply removed them from the working data set. This resulted in a substantial decrease in the original sample, as for many stars all their available spectra ended up being excluded. We plan to come back to these spectra in later stages of the project. For other stars, only one or two spectra remained. The final sample is given in Table 1, which includes Teff with its quoted uncertainties, log g values, [Fe/H] values, and their corresponding sources in the literature. The distribution of the stars in the Kiel diagram is presented inFig. 1, the parameters displayed are those derived in this work (Table 2). We note that for the star HD 160617, which had all UVES spectra excluded from the analysis, we instead analysed high-quality spectra obtained with the High Accuracy Radial velocity Planet Searcher (HARPS, Mayor et al. 2003) spectrograph, as we already had these spectra at hand for a different purpose.

2.2 Comparison sample of Gaia benchmarks

The GBS sample was used in our analysis to test the accuracy of the methods. Stars with [Fe/H] > 1 dex were also included for testing purposes. We included all GBS that have HARPS and/or UVES spectra with R > 40 000 and S∕N > 100, and without signs of order merging defects. Most of the selected data have indeed S∕N ~ 200. For one star, τ Cet, we also used three UVES spectra that have S∕N ~ 50. The final list of selected Gaia benchmark stars is as follows: β Hyi, τ Cet, ϵ For, δ Eri, β Vir, η Boo, α Cen A, 18 Sco, Sun5, β Gem, ξ Hya, HD 107328, ϵ Vir, HD 140283, HD 84937, HD 22879, HD 49933, HD 298986, HD 106038, HD 201891, and HD 102200.

Table 1

Atmospheric parameters of the TITANS in the literature.

2.3 Additional data processing

The spectra were Doppler corrected to the rest-frame wavelength scale with the iSpec software framework (Blanco-Cuaresma et al. 2014) using a pre-computed synthetic solar spectrum available within iSpec as a template (namely, Synth.Sun.300_1100nm). When the corrections are applied, iSpec also transforms the Doppler-shifts of the observational spectra from wavelength units to velocity units. These values are later used to compute heliocentric velocities as described in the next section. According to the software documentation, the template spectrum was generated by the code SPECTRUM (Gray & Corbally 1994) using a MARCS model (Gustafsson et al. 2008), the default VALD (Kupka et al. 2011) line list, and the parameters Teff = 5777 K, log g = 4.44, [Fe/H] = 0.00, microturbulence velocity (vmic) = 1.07 km s−1, and macroturbulence (vmac) = 4.19 km s−1 with R ~ 300 000.

iSpec was also used to normalise the spectra for the metallicity determination. The routine used for the global normalisation within iSpecwas configured to minimise errors, avoiding flux counts above the unity that are clearly not related to the spectral noise for example. Every normalised spectrum was visually inspected in the regions around the Fe lines that were selected for the metallicity analysis.

Separately, we corrected a duplicated set of spectra using the IRAF6 task dopcor. This set was usedfor the Hα profile fitting, which was performed outside iSpec. Normalisation and fitting Hα profiles is a specific procedure, described in detail in Giribaldi et al. (2019) and briefly explained in Sect. 3.1 below.

thumbnail Fig. 1

Distribution of the TITANS in the Kiel diagram. The stellar parameters used in the plot are those displayed in Table 2. The Gaia benchmark stars with [Fe/H] < −0.8 dex are identified with bold contours. Isochrones corresponding to the age and [Fe/H] of each benchmark star are plotted.

2.4 Kinematics and orbits

We computed Galactic velocities and orbits for the sample stars to be able to investigate their membership in different substructures of the Galaxy. For that, we used coordinates, proper motions, and parallaxes from Gaia EDR3 (Lindegren et al. 2021b). All parallax values had relative errors, σϖ∕ϖ, better than 20%. We thus used a simple parallax inversion to compute the stellar distances (see Bailer-Jones 2015; Luri et al. 2018). We applied corrections to parallax biases discussed in Lindegren et al. (2021a) only to the stars for which the biases were found significant. These are BPS CS 22166-030 and UCAC2 20056019, and their corrections are + 0.05 and + 0.06 mas, respectively.However, they still induced negligible changes in the derived values of log g and Teff. These are approximately −0.03 dex and +15 K on each parameter, respectively. For simplicity, for the remaining stars, the biases were ignored as their effect on the parameters would be even smaller.

Heliocentric radial velocities were derived by means of Astropy routines (Astropy Collaboration 2013, 2018), using the Doppler corrections computed as described in Sect. 2.3. The heliocentric radial velocities (vhelio) of the TITANS are listed in Table 4. We also computed the orbits for the GBS using Gaia EDR3 and their vhelio values. The orbits of the stars were integrated for a total of 15 Gyr, using the programme galpy (Bovy 2015) with the gravitational potential of McMillan (2017). A Monte Carlo method with 100 random samples was used to estimate the uncertainties in the orbital parameters. From these calculations, we extracted quantities such as the orbital energy, the orbital angular momentum, and the orbital actions.

3 Atmospheric parameters

The atmospheric parameters were determined combining Hα profile fitting, spectral synthesis of neutral and ionised iron lines, and the fitting of isochrones in two auto-consistent loop series. Each of these three techniques was used to derive Teff, [Fe/H], and log g, respectively, while keeping the other atmospheric parameters fixed. As the starting values (priors) we used those in Table 1. The series of steps in the analysis can be summarised as follows.

First, we ran a Teff–[Fe/H] loop series that starts by determining Teff from the Hα line fitting, keeping the prior values of log g and [Fe/H] fixed. Then, [Fe/H] was derived through the fitting of the observed Fe lines with synthetic spectra computed with the new value of Teff together with the prior value of log g. As the Hα profile is not sensitive to [Fe/H] in the metal-poor regime, consistency between Teff and [Fe/H] was accomplished by the end of the first loop in all cases.

Second, we ran a Teff –log g loop series that starts by determining log g using theoretical isochrones, adopting the Teff and [Fe/H] values computed in the first loop series. The newly derived log g value substituted the prior for the next iteration that rederived Teff. The loop series continued until consistency was reached between Teff and log g. In most cases, it was enough to run this loop series twice.

Finally, as the last step, the Teff and log g values derived in the second loop were fixed to derive the ultimate [Fe/H] value. The conclusive atmospheric parameters of the TITANS are given in Table 2. The table also incorporates the metal-poor GBS (with [Fe/H] < −0.8 dex), as for many of them our new parameters are more accurate than the estimates previously available. Element abundances for the TITANS and the metal-poor GBS will be discussed in subsequent works in this series. Deriving accurate Teff values from Hα fitting in metal-poor stars is more challenging than in metal-rich stars because of the degeneracy between Teff and log g that becomes relevant. In Fig. 2, we show an error flow diagram that illustrates the impact of one given parameter on the other parameters calculated in the next steps of the loop series. This shows how each step of the analysis progressively removes parameter offsets. It can be seen that large variations in metallicity induce only small changes in Teff at the beginning of the loops. These changes become progressively negligible as the loops are completed. On the other hand, changes in log g still induce small variations in Teff at the end of the first Teff –log g loop. This explains why a second Teff –log g loop was usually needed. The methods used to constrain each parameter are described in more detail below.

Table 2

Fundamental parameters and metallicities of the TITANS.

3.1 Effective temperature

The most important development with respect to the methodology used in Giribaldi et al. (2019) is the adoption of a new grid of hydrodynamic 3D non-LTEHα profiles, synthesised with the codes provided by Amarsi et al. (2018). The grid covers the following dimensions: Teff from 4000 to 7000 K (in steps of 100 K), log g from 1.0 to 5.0 dex (in steps of 0.1 dex), and [Fe/H] from −4.0 to +1.0 dex (in steps of 0.5 dex). The projected rotational velocity (vsin i) and the Gaussian instrumental profile (v broad) were fixed to default values of 1.85 and 1.0 km s−1, respectively. In any case, their contributions to the broadening of the Hα wings are negligible.

The normalisation-fitting procedure used to derive Teff from Hα profiles is described in detail in Sects. 3 and 4 of Giribaldi et al. (2019). Briefly, normalisation and fitting are parts of one iterative procedure in which visual compatibility between the observed and synthetic profiles, along the wavelength axis, is required. In this way, we can adjust the procedure to correct for profile distortions induced by the continuum normalisation.

The first and last steps of this procedure are exemplified in Figs. 3 and 4 for the case of a HARPS spectrum of HD 84937, one of the GBS. In the first normalisation, the observed profile is seen to be slightly shallower than the synthetic one in the external regions. Normalisation errors become more evident in the outer regions of the wings because the profile sensitivity to the temperature vanishes as the wavelength approaches the continuum. The Hα profile fits7 of the TITANS, from which Teff was determined, are compiled in Fig. A.1

The fitting of the Hα profile was done using masks that select regions without metallic or telluric lines. The line core (at least within ± 1.8 Å from λ6562.797 Å) was systematically masked out because in this region the photospheric models depart from the observational profiles as the contribution of the chromosphere progressively increases as λ approaches the line centre (e.g. Leenaarts et al. 2012). The choice of the masks varies because additional fitting regions become available for hotter and/or more metal-poor stars. For each observed profile, the fitting was done per pixel inside the regions selected by each mask. In other words, for each pixel of the observed spectrum, we searched forthe synthetic profile that has the closest value of normalised flux. This results in a distribution of Teff values, obtained from the analysis of each pixel. Such distributions are depicted in the bottom panels of Figs. 3 and 4. From these distributions, we obtain an estimate of the best Teff value, and of its error, by means of a Gaussian fit. This approach was demonstrated to be efficient at minimising the contribution of pixels contaminated by unexpected weak telluric or metallic lines in the temperature budget. Any contaminated pixel would have a lowerflux beyond what would be caused by the noise pattern. These pixels are then associated to higher temperatures that make the histograms depart from a normal distribution on its right tail. Hence, the fitting of a Gaussian profile to the temperaturedistribution tends to clip the contribution of contaminated pixels. An example of this performance can be observed in Figs. 3 and 4, where the contaminated pixels are located at ~ 6569.5 Å.

When possible, for each star, several observed Hα line profiles were used to derive separate estimates of Teff. This helps to clip outliers related to distorted wing profiles. The final best estimate of Teff was then computed with a weighted mean of the values obtained from each individual spectrum after applying a 2σ clipping. The weights are given by the square inverse of the 1σ errors of the Teff from each fit. For the stars that only have one good spectrum available (HE 0926-0508, Ross 453, Ross 892, UCAC2 20056019, and Wolf 1492), in order to improve the robustness of the estimated Teff and of its uncertainty, we performed a simple Bayesian analysis. We used a normal distribution prior over a Monte Carlo sampling of the histograms with 106 points. The reported values were set to fall inside a confidence interval of 95%.

thumbnail Fig. 2

Error flow diagram up to the beginning of the second loop. Each box displays, for each technique, the magnitude of the changes in a certain parameter induced by the variations given for the parameters in the previous box.

3.2 Metallicity, micro and macroturbulence

Metallicity was determined by fitting synthetic spectra using iSpec to run the 1D LTE radiative transfer code Turbospectrum (Plez 2012). MARCS model atmospheres (Gustafsson et al. 2008), computed under LTE, were used. The procedure was performed in two steps. In the first step, we relied on the statistical power of many lines to constrain vmic and vmac. In the second step, we refined the Fe lines selection and used only the best ones to constrain the metallicity.

For the first step, we adopted a selection of transitions based on the Gaia-ESO line list (Heiter et al. 2015, 2021) which is provided inside iSpec8 and we combined it with the Fe II line list of Meléndez & Barbuy (2009). We chose a total of 35 Fe I and Fe II lines that were visually found to be well shaped and not extremely blended in two high-quality spectra of HD 140283 and HD 84937. Following Blanco-Cuaresma (2019), we always fixed vsin i to the value used in that work for the Sun, that is vsin i⊙ = 1.6 km s−1, and we let only vmic and vmac vary freely. As discussed in Blanco-Cuaresma (2019) and elsewhere (e.g. dos Santos et al. 2016), the effects of vsin i and vmac are difficult to disentangle from the spectral analysis only. By fixing a value for vsin i we can, by direct line fitting, find the optimal combination of parameters that is needed to reproduce the broadening of the lines. We discuss tests regarding the degeneracy between these parameters in more detail in the second paper of the series, where we plan to present chemical abundances for the TITANS (Giribaldi & Smiljanic, in prep.).

For the second step, we adopted the selection of good Fe I lines of metal-poor dwarfs from Jofré et al. (2014) and, separately, selected isolated Fe II lines from Meléndez & Barbuy (2009). Thus, two sets of [Fe/H] values were derived, one from the neutral lines and another from the ionised lines. With the broadening fixed to the parameters determined in the first step, only the Fe abundance was allowed to vary to fit each line. The best estimate of [Fe/H] was determined by the average of the individual line abundances, applying a 2σ-clipping. For stars with more than one spectrum under analysis, the final metallicity was computed by the weighted mean of the metallicities obtained from the analysis of each spectrum. This procedure was validated by recovering the [Fe/H] values (under LTE) for the three metal-poor GBS HD 140283, HD 84937, and HD 22879, as given in Table 3 of Jofré et al. (2015), to better than ± 0.05 dex (when using the Fe I lines). We did not attempt to rederive metallicities for the metal-rich GBS, as our focus is on metal-poor stars and analysing the remaining GBS would require a different selection of Fe lines.

Metallicity values from neutral and ionised lines for the TITANS are listed in Table 2. Both sets of [Fe/H] are compatible; the mean difference is zero and the σ dispersion is ± 0.05 dex. Further, there is no correlation of the [Fe/H] difference with Teff, [Fe/H], and log g. According to the analysis of Amarsi et al. (2016) on HD 84937 and HD 140283, hydrodynamical 3D non-LTE models shift the 1D LTE abundances from Fe II lines by+0.1 dex, on average, with larger corrections for the Fe I lines. Because of this, we adopted [Fe II/H] for the Teff (Hα) determination, although without any offset correction. The impact of this decision on the Teff error budget is discussed in Sect. 3.4. We postpone a more detailed discussion about the metallicities, and possible systematic corrections, for the second paper in the series (Giribaldi & Smiljanic, in prep.).

thumbnail Fig. 3

First normalisation-fitting for HD 84937 with HARPS. The spectrum is segmented in pieces of 20 Å to facilitate the visualisation of the details. The original spectrum is plotted in grey, and the black line is the spectrum degraded to facilitate the comparison with the synthetic profile shown in red. The shades are the fitting masks. Bottom panel: Gaussian fitto the histogram of temperatures related to the wavelength bins within the windows represented by the shades.
thumbnail Fig. 4

Last normalisation-fitting for HD 84937 with HARPS. The elements in the plots are the same as in Fig. 3.

3.3 Surface gravity

Surface gravity, log giso, was determined from theoretical isochrones with the Python code q2 (qoyllur-quipu)9 developed by Ramírez et al. (2014). It makes use of Yonsei-Yale isochrones (Kim et al. 2002; Yi et al. 2003) and requires parallax, V magnitude, Teff, [Fe/H], and their respective uncertainties as inputs. The code computes a probability distribution of the stellar mass using a frequentist approach. Furthermore, q2 also provides the associated stellar 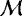M$\mathcal{M}$, R, and age as outputs. They were compiled along with the atmospheric parameters in Table 2.

Parallaxes from the Gaia EDR3 catalogue were used. The V magnitudes were mostly retrieved from the SIMBAD database or, when not available, from Casagrande et al. (2010) or from the HIPPARCOS catalogue (Perryman et al. 1997). The V magnitudes were corrected from extinction using reddening values, E(B − V), computed with the online tool Stilism10 (Capitanio et al. 2017) and adopting the relation AV = 3.1 × E(B − V). When the stellar distance (estimated here as the inverse of the parallax) exceeds the limits of Stilism, the E(B − V) was alternatively computed using the Infrared Science Archive online tool11. This tool provides estimates of Galactic dust extinction based on Schlafly & Finkbeiner (2011). To these reddening values, which represent the total for a line of sight, we applied the corrections given by Beers et al. (2002). The V magnitudes and reddening values that were used are also listed in Table 2.

To calculate the log g value in the first of the Teff –log g loop series, we assumed 0.2 dex and 0.05 mag as the uncertainties of [Fe/H] and V (as needed by the code q2). We also added 20 K to the internal uncertainty of Teff, to account possible additional uncertainties through the loops. Once the error analysis described in Sect. 3.4 was finished, we recomputed log giso and its uncertainty using the correct value determined with Eq. (1).

3.4 Uncertainty analysis

The total uncertainty of the Teff value is given by the following: δ(Teff)2 = δTeff−model2+δTeff−fit2+δTeff−inst2+δTeff−log g2+δTeff−[Fe/H]2,\begin{equation*}\centering \delta(T_{\mathrm{eff}})^{2}\,{=}\,\delta_{T_{\mathrm{eff}}-\mathrm{model}}^{2} &#x002B; \delta_{T_{\mathrm{eff}}-\mathrm{fit}}^{2} &#x002B; \delta_{T_{\mathrm{eff}}-\mathrm{inst}}^{2} &#x002B; \delta_{T_{\mathrm{eff}}-\mathrm{log}\;g}^{2} &#x002B; \delta_{T_{\mathrm{eff}}-\mathrm{[Fe/H]}}^{2} ,\end{equation*}(1)

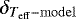where δTeff−model$\delta_{T_{\mathrm{eff}}-\mathrm{model}}$ is the uncertainty of the model profile, 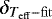δTeff−fit$\delta_{T_{\mathrm{eff}}-\mathrm{fit}}$ is the uncertainty of the fittingprocedure, 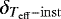δTeff−inst$\delta_{T_{\mathrm{eff}}-\mathrm{inst}}$ is the uncertainty induced by any instrument residual pattern, 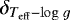δTeff−log g$\delta_{T_{\mathrm{eff}}-\mathrm{log}\;g}$ is the uncertainty related to the interdependence between Teff and log g, and δTeff−[Fe/H]$\delta_{T_{\mathrm{eff}}-\mathrm{[Fe/H]}}$ is the uncertainty related to the interdependence between Teff and [Fe/H].

Based on a comparison with the accurate scale defined by the GBS (see Sect. 4), we estimated a typical 1σ value for 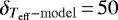δTeff−model = 50$\delta_{T_{\mathrm{eff}}-\mathrm{model}}\,{=}\,50$ K at the metal-poor regime. The uncertainty in the fitting procedure, 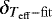δTeff−fit$\delta_{T_{\mathrm{eff}}-\mathrm{fit}}$, is related to the S/N of each spectrum. Since the normalisation and fitting are part of one single procedure, this value also includes the error in locating the continuum. When only one spectrum is available, 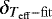δTeff−fit$\delta_{T_{\mathrm{eff}}-\mathrm{fit}}$ is given by the 1σ dispersion of the Gaussian fit of its temperature histogram (details are given in Sect. 3.1). When more spectra are available for one given star, 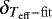δTeff−fit$\delta_{T_{\mathrm{eff}}-\mathrm{fit}}$ is given by the 1σ dispersion of the mean temperatures associated with the analysis of each spectrum. For the TITANS, 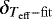δTeff−fit$\delta_{T_{\mathrm{eff}}-\mathrm{fit}}$ values are between 3 and 38 K with a typical value of 15 ± 9 K. As the uncertainty caused by instrument residual patterns, 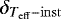δTeff−inst$\delta_{T_{\mathrm{eff}}-\mathrm{inst}}$, we adopted the standard deviation of the comparison made in the consistency analysis reported in Sect. 4.1. This analysis compares Teff values derived from high-quality spectra obtained with the HARPS and UVES instruments for the same stars. We estimated 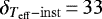δTeff−inst = 33$\delta_{T_{\mathrm{eff}}-\mathrm{inst}}\,{=}\,33$ K.

To map the interdependence between Teff and log g, we used the grid Hα profiles with [Fe/H] = −2 dex. We assumed that their behaviour can act as a conservative proxy for the whole metallicity range. The impact that a variation in log g has in Teff progressively decreases for higher [Fe/H] and remains nearly constant for lower values of metallicity.

We proceeded as follows. First, we introduced artificial Poisson noise equivalent to S∕N = 250 to the synthetic line profiles. Then, we performed the profile fitting analysis using the very sensitive wavelength regions located between 2.5 and 7 Å to the blue and red sides of the Hα core 6562.797 Å. The fittings were performed assuming, as input, log g, which are values that are different by ±0.1 dex than the correct value. In this way, we can map the influence on Teff of a given Δlog g.

Figure 5 shows the distribution of ΔTeff obtained in this exercise as function of Teff and log g. These plots correspond to the negative variation in log g, which induces positive temperature variations. However, we observed that ΔTeff behaves almost symmetrically. We excluded from the analysis the data with Teff and log g combinations of little physical meaning, that is, Teff > 6500 K and log g > 4.5 dex.

The figure shows that ΔTeff mostly remains below 40 K, except for a few profiles with Teff > 6300 K, and for one profile with log g = 3.7 dex and Teff = 6000 K. Such high variations correspond to simulated profiles that are highly asymmetric. From the plots in Fig. 5, we conclude that a variation of Δlog g = ± 0.1 dex creates an effect of ΔTeff ≈∓35 K.

The average Gaia EDR3 parallax precision for the stars in this work is of ± 0.02 mas. The log g values computed by isochrone fitting then have a precision of about 0.03 dex, with input temperatures of ± 50 K precision. With a log g uncertainty of this magnitude, and the Δlog g and ΔTeff relation determined above, we estimated that the temperatures computed in the end of the last loop will be affected by 0.03 × ΔTeff/Δlog g 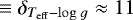≡δTeff−log g≈11$\equiv \delta_{T_{\mathrm{eff}}-\mathrm{log}\;g} \approx 11$ K.

We followed the same reasoning to map the Teff–[Fe/H] interdependence. We found that the impact of [Fe/H] offsets are eliminated through the first loop when the Hα profile fitting and the Fe lines fitting are performed. The typical uncertainty in [Fe/H] is of ± 0.05 dex on average. This includes the effect of a typical Teff error of ± 60 K, a typical log g error of ± 0.05 dex, and a line-by-line fitting error of ±0.01 dex. This line-by-line fitting error is the typical scatter obtained from lines measured across multiple spectra of the same star. A variation of ± 0.05 dex in [Fe/H] has an impact of only a few Kelvin, in extreme cases, on Teff (Hα). Thus, we assume δTeff−[Fe/H] = 0$\delta_{T_{\mathrm{eff}}-\mathrm{[Fe/H]}}\,{=}\,0$ K. In Sect. 3.2, we have briefly mentioned that the [Fe/H] values from ionised Fe lines might need a 3D non-LTE correction of about + 0.1 dex. Such a change in [Fe/H] induces a typical Teff variation of − 5 K for a metal-poor turn-off star, such as HD 84937, or even smaller for a metal-poor subgiant, such as HD 140283. The largest variations of up to −20 K are seen in models with parameter combinations that have little physical meaning, that is those with Teff > 6500 K and log g > 4.5 dex. Therefore, we conclude that any offset in Teff caused by our use of 1D LTE [Fe/H] values is of the order of + 5 K.

The average of the total uncertainty of the Teff values is thus determined to be of ±60 K. We remark that in Table 2 we give Teff errors that do not include 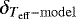δTeff−model$\delta_{T_{\mathrm{eff}}-\mathrm{model}}$ when Eq. (1) is applied. In the table, we preferred to include what we consider to be the internal errors (i.e. the precision) of the method. The 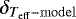δTeff−model$\delta_{T_{\mathrm{eff}}-\mathrm{model}}$ component of the total error is, instead, related to the method accuracy or trueness.

thumbnail Fig. 5

Temperature difference between our best value and the one that is recovered by assuming an offset of − 0.1 dex in log g. The difference is shown as function of log g (top panel) and of the model temperature (bottom panel). In the top panel, cases for 5400, 6400, and 6600 K are highlighted as the lines in blue, green, and yellow, respectively. In the bottom panel, cases for 3.8, 4.1, and 4.5 dex are highlighted as the lines in blue, green, and yellow, respectively.

4 Accuracy of the parameter scale

4.1 Consistency between HARPS and UVES spectra

It is shown in Giribaldi et al. (2019) that HARPS spectra present negligible variation in the instrumental residual patterns with time. The authors then conclude that such spectra are fully suitable for Hα profile temperature diagnostics. Instead, in this work, we mostly rely on UVES spectra as these allowed a bigger sample of metal-poor stars to be built. It is thus important for us to establish that consistent results can be obtained irrespective of whether our analysis method is applied to HARPS or UVES spectra.

Analysing a broad line, such as Hα, in echelle data is challenging because the line spans several spectral orders which need to be correctly merged. Although the flat-fielding procedure eliminates most of the instrumental patterns, the shape of the extracted spectrum may remain convoluted with subtle residuals (see for instance Škoda et al. 2008). These residuals can manifest as small incompatibilities between observed and synthetic Hα profiles, causing offsets in the derived temperature values.

For this comparison, we employed six GBS stars for which we could retrieve good-quality HARPS and UVES spectra (see Table 3). The results are shown in Fig. 6. The average of the differences is close to the perfect agreement at + 9 K. This shows that, collectively, the temperatures obtained from both sets of spectra are compatible. The dispersion of 33 K is very good, considering that spectra of low S/N were included for τ Cet.

The eight HARPS spectra of τ Cet that we used have S∕N  > 500. This excellent spectral quality permitted the derivation of temperatures with individual fitting errors of about ± 30 K. On the other hand, among the four UVES spectra of this star, only one is of good quality, with S∕N = 282. For it, we derived a Teff with an offset of − 22 K. The remaining three spectra haveS∕N ~ 50. Looking at the fits to the profiles of τ Cet in Appendix A, it can be seen that the individual fitting errors of the low quality spectra are ± 150, ± 134, and ± 133 K. This suggests that S/N is responsible for the realatively poorer agreement for this star as seen in Fig. 6.

The temperature values for HD 140283 also present a relatively large dispersion, which seems connected to the S/N as well. Its spectra have S∕N = 108, 139, 145, 273, and 386; whereas, for example, all the spectra of 18 Sco exceed S∕N = 200. For the UVES spectrum of HD 140283 with best S/N, we obtain a difference of only 24 K in comparison to the temperature obtained from its HARPS spectrum. This allows us to conclude that, when using UVES spectra without obvious distortions and of good S/N, temperature offsets induced by residual instrumental patterns are negligible. It is thus possible to obtain accurate Teff values from the analysis UVES spectra, which are compatible with the values obtained from the analysis of HARPS spectra, whose accuracy, in turn, is demonstrated in Giribaldi et al. (2019).

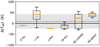thumbnail Fig. 6

Temperatures derived from UVES spectra relative to the average temperatures derived from HARPS data for each of the GBS labelled in the plot. Grey symbols represent the individual values from multiple spectra. The box-bars extend from the lower to upper quartiles, with an orange line representing the median. The whiskers show the complete range of the values. The dashed line indicates the average difference, + 9 K, and the shaded area encloses the standard deviation of ±33 K.

4.2 Comparison with the Gaia benchmark stars

Having established that the Teff values derived from the analysis of UVES and HARPS spectra are compatible with each other, we now present a more extensive accuracy test of the methodology applied to a larger number of GBS. The derived parameter values are listed in Table 3 along with the type and number of spectra used for the determinations as well as the reference parameters. The table also indicates the method by which the reference Teff values were derived, and it is divided, ranking the most direct method on the top to the less direct one on the bottom. We refer the reader to the original sources in the table notes for detailed information about the methods. Missing values in the log giso column are due to the lack of Gaia parallax measurements for the corresponding stars. For the metal-rich GBS, we did not rederive the [Fe/H] values, but instead fixed the value to the reference ones from Jofré et al. (2014).

We did not include the star HD 122563, although it has one HARPS spectrum of high S/N and without obvious order merging distortions because we did not find a synthetic profile in the grid that reproduces the very asymmetric shape of its observational profile. This was the only spectrum for a star of its type (i.e. a very metal-poor giant) that we tried to analyse. The reasons for this discrepancy are unclear and uncovering the explanation is beyond the scope of this paper. Possibilities include artefacts in the spectrum, some stellar peculiarity, and problems in the modelling of this type of giant. HD 175305 is another benchmark that was not included in the comparison because it lacks HARPS or UVES spectra.

The fits to the Hα profile of each benchmark are shown in Fig. A.2. Our Teff values are compared to the reference ones in Fig. 7. The individual values agree with each other within their 3σ uncertainties for all stars, and within 2σ dispersions, except for β Hyi and HD 102200 which slightly exceed the 2σ limits by a few Kelvin. No significant correlation is seen between the Teff differences and any of the atmospheric parameters. We can thus conclude that our methodology provides unbiased results of Teff for stars in a large range of parameters, also including giants. It is our plan to extend the TITANS sample with giants in forthcoming papers of the series. The dispersion of the Teff differences, of about ±50 K, seems to bedominated by the uncertainty of the GBS scale, which is of the same order, ± 61 K on average. We decided to adopt the ±50 K dispersion as the 1σ uncertainty associated with the accuracy of the Teff measurements that are possible with the current model of Hα lines. This quantity is used as 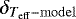δTeff−model$\delta_{T_{\mathrm{eff}}-\mathrm{model}}$ in Eq. (1). We stress that this is likely an upper-bound estimate that mostly reflects the uncertainty of the GBS Teff values used as reference. The accuracy limit can be better constrained in case a sample of accurate standards with Teff of superb precision (i.e. σ(Teff) ± 20 K, at most) becomes available. This would permit the proper mapping of the accuracy of the Hα models across the parameter space.

In the metal-poor regime, only HD 140283 has a reference Teff value based on a measurement of its angular diameter (θ) (Karovicova et al. 2020). For HD 84937, the reference value of Teff was derived from θ–colour relations (Kervella et al. 2004). For the remaining GBS, HD 298986, HD 102200, HD 106038, and HD 201891, reference Teff values were those derived using the IRFM by Hawkins et al. (2016). These Teff values are in the same scale of the IRFM implementation from Casagrande et al. (2010) and were shown to agree with the Teff derived using the θ–colour relations of Kervella et al. (2004) to within 100 K. The fact that we derived compatible temperatures in the metal-poor regime, where the reference scale is shared between IRFM and interferometry, provides confidence on the accuracy of the Hα-based Teff scale. The temperatures we derived for HD 140283 and HD 84937 are also compatible with those derived by Amarsi et al. (2018). For the Sun, the authors find a slightly cooler value of 5721 ± 26 K caused by small normalisation distortion of the solar profile that they used (Wallace et al. 2011). This distortion is discussed in Giribaldi et al. (2019).

A comparison between our log g values and the reference ones for the GBS is presented in Fig. 8. The plot suggests an increased dispersion affecting exactly the metal-poor dwarfs. It happens, however, that the reference log g values of the GBS were computed with parallaxes from the new reduction of HIPPARCOS data (van Leeuwen 2007), with the only exception of HD 140283 whose reference log g was derived with a parallax value from Gaia DR2. We derived log giso with improved parallax values from Gaia EDR3. Thus, for a fair comparison, we recomputed our log giso values, adopting the older parallaxes instead. As expected, we obtain a better agreement with the reference log g and the large scatter disappears (see Fig. 8). Given the improved precision of the Gaia parallaxes, we consider that our new log giso determination, available in Table 3, supersedes the original log g reference values of the metal-poor GBS. We are thus confident to have employed a method that achieves very good accuracy in the determination of log g.

We note that the log g reference values for τ Cet and ϵ For were not included in Table 3 because they were evaluated to be uncertain in Heiter et al. (2015), hence they are not recommended for calibration or validation purposes. These values are 4.49 ± 0.02 dex and 3.52 ± 0.08 dex for each star, respectively, as displayed in Table 10 in that paper. Our log giso values in Table 3 are actually compatible with these determinations.

Table 3

Atmospheric parameters and Galactic membership for the sample of Gaia benchmark stars.

thumbnail Fig. 7

For the GBS of Table 3, difference between Teff(Hα) and the reference Teff as function of the reference Teff, [Fe/H], and log g from the top to the bottom, respectively. The red lines are linear regressions, and the shaded areas indicate 1σ and 2σ dispersions.
thumbnail Fig. 8

For the GBS of Table 3, difference between log giso and reference log g as functionof the reference value. The labels identify the metal-poor GBS. The circles represent the values for which log giso was derived using the Gaia parallaxes. The dashes represent the values for which log giso was derived using the same (HIPPARCOS) parallaxes that were used to derive the reference log g from Jofré et al. (2018).

4.3 Comparison with IRFM temperatures

A comparison with Teff values derived using the IRFM is an important step in validating our temperature scale. The IRFM is the only technique that can offer a nearly model-independent determination of Teff for distant stars because interferometric measurements are not feasible for them. The accuracy of the IRFM has been discussed and progressively improved in several works (e.g. Alonso et al. 1996; Ramírez & Meléndez 2005; González Hernández & Bonifacio 2009; Casagrande et al. 2010). A comparison against Teff values based on interferometric data by Casagrande et al. (2014) suggests that a typical 1% can be achieved by the direct application of IRFM. New colour–Teff relations, for use with Gaia photometry, have recently been implemented by Casagrande et al. (2020), not only for dwarfs and subgiants but also for giants.

The comparison with the IRFM Teff values is shown in Fig. 9. The figure includes 35 stars (80% of our sample) for which IRFM Teff were extracted from Casagrande et al. (2010, Table 8); they are compiled in Table 1 and noted by the code Ca10. These are the original values directly derived by the technique, and not by colour–Teff relations, thus the [Fe/H] determination has a negligible influence on them. A small correlation, above the 1σ errors, is only observed with log g (bottom panel of Fig. 9). The trend with log g is mainly driven by five stars with log g > 4.4 dex, all of them with cooler temperatures inferred from Hα, and one starwith log g < 3.8, which had a hotter Hα-based Teff.

The five stars with log g > 4.4 are HD 34328, BD+29 2091, HD 126681, HD 193901, and LP 831-70. Except for the last, they are all located within 100 pc. Thus, uncertainties in the photometric magnitudes caused by interstellar extinction are likely not the source of the differences. For two of them, HD 126681 and LP 831-70, we used V magnitudes that are larger by 0.2 mag with respect to those used to derive the IRFM Teff. This difference indeed increases log g by 0.05 dex, resulting in a decrease of 20 K in Teff(Hα). This essentially removes the discrepancies, leaving differences of − 13 and − 9 K for the two stars, respectively. Of the other three stars, we note that BD+29 2091 lacks R and I magnitudes,which are needed to compute bolometric corrections for the IRFM implementation. The use of V alone gives less precise results (Casagrande et al. 2006, Sect. 7). We believe this can likely explain part of the − 95 K difference observed between our values and the IRFM Teff values. We could not find similar issues for the remaining two stars, HD 34328 and HD 193901, which present temperature differences of − 59 and − 67 K. These differences, however, are still consistent with the total uncertainty that we estimated for our Teff determination.

At the low extreme of log g, the star BPS CS22166-030 is a particular case, presenting the largest temperature difference (216 K). About 100 K of this difference can be explained by the more precise Gaia parallax, which results in a log g that is smaller by 0.24 dex than the value used in the IRFM determination. Further, as BD+29 2091, this star lacks R and I magnitudes, which increases the uncertainty of its IRFM Teff. We could not find any collective change in all the parameters required for the isochrone fitting (Teff, [Fe/H], V, and parallax) which, within their 3σ uncertainties, would conciliate our log g and Teff(Hα) values with the literature values. We consider our values more robust, as they are supported by the Gaia parallax measurements.

Three of the TITANS, CD − 71 1234, G24 − 3, and HE 0926 − 0508, were analysed by Casagrande et al. (2020) where the values 6605 ± 77 K, 6668 ± 74 K, and 6458 ± 75 K were derived for each one, respectively. Our Teff(Hα) values almost exactly match the new IRFM Teff for the last two stars. For the first one, our Teff(Hα) is −173 K cooler; however, it agrees with the original IRFM Teff of 6408 ± 69 K.

Doppler shifts in the spectra of spectroscopic binaries are a possible source of error in the Hα fitting, as they can cause an additional enhancement of the line. We searched for known binary systems in the catalogue of Kervella et al. (2019). Their method is based on detecting anomalies in the long-term proper motion of stars in common between the Gaia DR2 (Gaia Collaboration 2018) and HIPPARCOS catalogues. This is the case of HD 116064, identified as a double-lined spectroscopic binary (Smith et al. 1998), for which we find a moderately large temperature difference of 127 K (Teff(Hα) being hotter). In fact, this star has the most imprecise parallax of the sample, 14.40 ± 0.14 mas, which affects the accuracy of log giso, and therefore the accuracy of Teff(Hα). Another binary in this sample is CD − 48 2445 (Hansen et al. 2017), for which the temperature difference is 92 K, again with the Teff(Hα) hotter than the one inferred with the IRFM. These stars are flagged in Table 2. We conclude that unrecognised binarity can be a source of additional scatter in the Teff comparison. Its general influence in this sample, however, must be small, as the comparison shows a zero offset and a dispersion of ~ 65 K, which is very close to the total Teff error that we estimated.

thumbnail Fig. 9

For the TITANS, the difference between temperatures derived by Hα fitting and those by the IRFM, as a function of Teff, [Fe/H], and log g from topto bottom, respectively. The red lines are linear regressions, and the shaded areas indicate 1σ and 2σ dispersions. The same vertical scale is used as in Fig. 7.

5 Galactic substructure membership

With the advent of Gaia, it became possible to study the kinematic and dynamical properties of large stellar samples, and thus to unfold the merger history of the Milky Way. This development has lead to the recent discovery of major halo substructures such as Gaia Enceladus or Gaia Sausage (Helmi et al. 2018; Belokurov et al. 2018) and Sequoia (Myeong et al. 2019; Barbá et al. 2019), among other suggestions (e.g. Koppelman et al. 2019; Limberg et al. 2021, and references therein). At least the major structures among these new discoveries are thought to be the result of early merger events and, thus, to come from smaller galaxies or stellar systems with different chemical evolution histories, when compared to the in situ Galactic halo.

We decided to investigate whether our sample of metal-poor reference stars includes any candidate member of these stellar structures. Such stars, having accurate stellar atmospheric parameters, can be used for the determination of high-quality chemical abundances.This development can pave the way for the accurate chemical characterisation of the stellar systems that merged with the Milky Way. We used the orbital parameters of the TITANS and the GBS, computed as described in Sect. 2.4, to classify the stars adopting the criteria defined by Massari et al. (2019, criterion I henceforth) and Myeong et al. (2019, criterion II henceforth). We considered both criteria since, currently, there is no consensus on the boundaries that enclose the Sequoia and the Gaia-Enceladus remnant stars. These criteria, involving orbital energy, angular momentum, and orbital actions, are shown as boxes in the panels of Fig. 10.

As can be noted, the two criteria do not always agree on which stars can be associated with each structure. Itis possible that chemical abundances could help to disentangle the structures. We will report on chemo-dynamic analysis of stellar properties performed with that aim elsewhere (da Silva et al., in prep.). Using criterion I, several TITANS become candidate members of Gaia-Enceladus. Only the stars BD + 24 1676, HE 0926-0508, and LP 815 − 43 are classified as within Gaia-Enceladus by both criteria. Stars BD+26 2621, HD 59392, and BD+02 4651 are classified as within Gaia-Enceladus by the criterion of Massari et al. (2019), but as within Sequoia by the criterion of Myeong et al. (2019). Both criteria classify star HD 34328 as a Sequoia member. Star Wolf 1492 is part of Sequoia by criterion I, but not by criterion II. The stars Ross 453 and HD 132475 are classified within Sequoia by criterion II, but remain unclassified by criterion I. Finally, CD − 33 3337 is a possible Helmi stream candidate member, as is one of the GBS, HD 298986 (Myeong et al. 2019 does not provide criteria for the Helmi streams). From the metal-poor GBS, HD 140283 and HD 84937 belong to the Gaia-Enceladus, and HD 298986 belongs to the Helmi streams by criterion I. HD 106038, is classified as a member of Gaia-Enceladus by criterion I, but as a member of Sequoia by criterion II. This information is summarised in Table 4.

thumbnail Fig. 10

Top: Lindblad diagram – total orbital binding energy as a function of the angular momentum component in the direction of the Galactic north pole. The colours show the Massari et al. (2019) criteria to identifySequoia (the red box and red symbols), Gaia Enceladus (the blue box and blue symbols), and Helmi streams (orange symbols). Unclassified stars are shown in grey. The Sun is shown as the yellow ⊙ symbol. The TITANS are shown as stars and the GBS as crosses. Bottom: action space map – difference of action in the z and r directions by the action in the ϕ direction, all divided by total action (see Fig. 9 in Myeong et al. 2019). The blue box shows the limits for the Gaia-Enceladus merger and the red box shows the limits for Sequoia, according to the Myeong et al. (2019) criteria. The symbols and colours for the stars are the same as in the top panel.

6 Conclusions

In response to the current demand of reference stars for all-sky-surveys, we introduced the TITANS: a selection of metal-poor stars with accurate parameters intended as calibration objects for spectroscopic analysis. In this first paper, we provide Teff and log g values for dwarf and subgiants. We estimated the typical 1σ accuracy of the Teff values to be of the order of 50 K, while the average precision is of ~40 K. The accuracy and precision of log g remains within 0.04 dex.

The atmospheric parameters presented here are model-dependent, inasmuch as the Teff values depend on computations of synthetic Hα profiles and the log g values depend on stellar evolution models. Therefore, we scrutinised the methodology against the Gaia benchmark stars. The reference Teff of the benchmarks were inferred either quasi-directly, by interferometric measurements, or by photometric calibrations based on interferometric measurements or, in last instance, by the IRFM, which is almost model-independent.

The reliability of the TITANS’ parameters, presented in Table 2, thus stands on the ability of our methodology to recover the reference parameters of the Gaia benchmarks. The prime result, in this regard, is showcased in the comparison of Fig. 7. We did not find significant correlations or offsets with respect to any atmospheric parameter. This allowed us to conclude that the method permits the derivation of accurate Teff values within the whole parameter space analysed here. From this comparison, we determined the accuracy of the 3D non-LTE Hα model used to derive Teff to be 50 K. We note that this value is unavoidably tied to, and perhaps dominated by, the uncertainties of the reference Teff scale, the average value of which is 60 K. Thus, this is likely the main source of the dispersion in the plots. Similarly, we found that our method recovers values of surface gravity that are very close to the standard ones, when the same parallaxes are used (Fig. 8).

A direct comparison with Teff values obtained using the IRFM for the TITANS confirms the results above (Fig. 9). A weak correlation of the temperature differences was found only with respect to log g. Nevertheless, we have shown this to be partially explained by photometric or parallax uncertainties, affecting the IRFM analysis. Still, the differences are small and of the same magnitude of the uncertainties of both sets of temperatures. The important conclusion then is that Teff scales based on interferometry, on the IRFM, and on 3D non-LTE Hα models are consistent to within 1%. This conclusion is valid not only for metal-rich stars (as shown in Giribaldi et al. 2019), but also for metal-poor stars (as demonstrated here).

From the perspective of precision spectroscopy, the series of consistent analysis loops, as implemented here, is an efficient methodology to eliminate biases due to the inter-dependence between the atmospheric parameters. There were two keys for the success of our methodology. The first one was the state-of-the-art of the Hα models based on 3D non-LTE atmospheric models (Amarsi et al. 2018). The second one was the availability of parallax measurements of a superb quality provided by the Gaia mission (Gaia Collaboration 2021). Both were important since, for metal-poor stars, the fine tuning of Teff from Hα fitting requires accurate log g values, which could only be obtained via the accurate and precise parallaxes. Finally, we remark that the TITANS are a reliable new sample to be used as templates for calibrating spectroscopic techniques, in the analysis of large star samples, and/or the application of strictly differential spectroscopic methods as done, for example, by Reggiani et al. (2016, 2017) for metal-poor stars and by Yong et al. (2013) for stellar clusters.

Table 4

Membership classification of the TITANS.

Acknowledgements

The authors acknowledge the anonymous referee for the careful reading of the manuscript and the constructive criticism that has helped us to improve the presentation of the results. R.E.G., A.R.S., and R.S. acknowledge support by the National Science Centre, Poland, through project 2018/31/B/ST9/01469. REG acknowledges Ana Giribaldi and Margarita Santamaría for the initial support of this work. D.C. acknowledges partial support by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) – Finace code 001. This work is based on observations collected at the European Southern Observatory under ESO programmes: 67.D-0439(A), 095.D-0504(A), 093.D-0095(A), 68.B-0475(A), 074.B-0639(A), 65.L-0507(A), 076.B-0133(A), 077.D-0299(A), 68.D-0094(A), 71.B-0529(A), 67.D-0086(A), 077.B-0507(A), 70.D-0474(A), 072.B-0585(A), 076.A-0463(A), 086.D-0871(A), 090.B-0605(A), 67.D-0554(A), 188.B-3002(H), 188.B-3002(B), 266.D-5655(A), 072.C-0513(B), 075.D-0760(A), 096.C-0053(A), 081.C-0802(C), 082.C-0427(A), 086.C-0145(A), 072.C-0488(E), 073.D-0590(A), 081.D-0531(A), 183.C-0972(A), 183.D-0729(A), 080.D-0347(A), 078.C-0233(B), 082.B-0610(A), 085.C-0063(A), 190.C-0027(A), 192.C-0852(A), 196.C-0042(E), 295.C-5031(A), 60.A-9036(A), 60.A-9700(G), 082.B-0610(A), 086.C-0284(A), 086.C-0448(A), 289.D-5015(A), 60.A-9036(A). Use was made of the Simbad database, operated at the CDS, Strasbourg, France, and of NASA’s Astrophysics Data System Bibliographic Services. This research has made use of the services of the ESO Science Archive Facility. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This work made use of TOPCAT (Taylor 2005). This research made use of Astropy (http://www.astropy.org), a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018). This work presents results from the European Space Agency (ESA) space mission Gaia. Gaia data are being processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular the institutions participating in the Gaia MultiLateral Agreement (MLA). The Gaia mission website is https://www.cosmos.esa.int/gaia. The Gaia archive website is https://archives.esac.esa.int/gaia.

Appendix A Profile fits

thumbnail Fig. A.1

Profile fits of the TITANS labeled in the plots. The elements in the plots are the same as in Fig. 3.
thumbnail Fig. A.2

Profile fits of the Gaia benchmark stars labeled in the plots. The elements in the plots are the same as in Fig. 3.

References

  1. Alonso, A., Arribas, S., & Martinez-Roger, C. 1996, A&AS, 117, 227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Amarsi, A. M., Lind, K., Asplund, M., Barklem, P. S., & Collet, R. 2016, MNRAS, 463, 1518 [Google Scholar]
  3. Amarsi, A. M., Nordlander, T., Barklem, P. S., et al. 2018, A&A, 615, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Amarsi, A. M., Nissen, P. E., Asplund, M., Lind, K., & Barklem, P. S. 2019, A&A, 622, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
  7. Bailer-Jones, C. A. L. 2015, PASP, 127, 994 [NASA ADS] [CrossRef] [Google Scholar]
  8. Ballester, P., Modigliani, A., Boitquin, O., et al. 2000, The Messenger, 101, 31 [NASA ADS] [Google Scholar]
  9. Barbá, R. H., Minniti, D., Geisler, D., et al. 2019, ApJ, 870, L24 [NASA ADS] [CrossRef] [Google Scholar]
  10. Barklem, P. S. 2016, A&ARv, 24, 9 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bazot, M., Ireland, M. J., Huber, D., et al. 2011, A&A, 526, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Beers, T. C., Drilling, J. S., Rossi, S., et al. 2002, AJ, 124, 931 [CrossRef] [Google Scholar]
  13. Beers, T. C., Placco, V. M., Carollo, D., et al. 2017, ApJ, 835, 81 [NASA ADS] [CrossRef] [Google Scholar]
  14. Belokurov, V., Erkal, D., Evans, N. W., Koposov, S. E., & Deason, A. J. 2018, MNRAS, 478, 611 [Google Scholar]
  15. Blackwell, D. E., & Shallis, M. J. 1977, MNRAS, 180, 177 [NASA ADS] [CrossRef] [Google Scholar]
  16. Blackwell, D. E., Shallis, M. J., & Selby, M. J. 1979, MNRAS, 188, 847 [NASA ADS] [CrossRef] [Google Scholar]
  17. Blackwell, D. E., Petford, A. D., & Shallis, M. J. 1980, A&A, 82, 249 [NASA ADS] [Google Scholar]
  18. Blanco-Cuaresma, S. 2019, MNRAS, 486, 2075 [Google Scholar]
  19. Blanco-Cuaresma, S., Soubiran, C., Heiter, U., & Jofré, P. 2014, A&A, 569, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Bohlin, R. C., Gordon, K. D., & Tremblay, P. E. 2014, PASP, 126, 711 [NASA ADS] [Google Scholar]
  21. Bonifacio, P., Caffau, E., Ludwig, H. G., et al. 2018, A&A, 611, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Bovy, J. 2015, ApJS, 216, 29 [Google Scholar]
  23. Brown, A. G. A. 2021, ARA&A, submitted [arXiv:2102.11712] [Google Scholar]
  24. Brucalassi, A., Tsantaki, M., Magrini, L., et al. 2021, Exp. Astron., in press [arXiv:2101.02242] [Google Scholar]
  25. Capitanio, L., Lallement, R., Vergely, J. L., Elyajouri, M., & Monreal-Ibero, A. 2017, A&A, 606, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Casagrande, L., Portinari, L., & Flynn, C. 2006, MNRAS, 373, 13 [NASA ADS] [CrossRef] [Google Scholar]
  27. Casagrande, L., Portinari, L., Glass, I. S., et al. 2014, MNRAS, 439, 2060 [Google Scholar]
  28. Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Casagrande, L., Lin, J., Rains, A. D., et al. 2020, MNRAS, submitted [arXiv:2011.02517] [Google Scholar]
  30. Cayrel de Strobel, G. 1985, in Calibration of Fundamental Stellar Quantities, eds. D. S. Hayes, L. E. Pasinetti, & A. G. D. Philip, 111, 137 [Google Scholar]
  31. Cayrel, R., Cayrel de Strobel, G., & Campbell, B. 1985, A&A, 146, 249 [NASA ADS] [Google Scholar]
  32. Cui, X.-Q., Zhao, Y.-H., Chu, Y.-Q., et al. 2012, Res. Astron. Astrophys., 12, 1197 [NASA ADS] [CrossRef] [Google Scholar]
  33. Davis, J., Tango, W. J., & Booth, A. J. 2000, MNRAS, 318, 387 [Google Scholar]
  34. de Jong, R. S., Agertz, O., Berbel, A. A., et al. 2019, The Messenger, 175, 3 [NASA ADS] [Google Scholar]
  35. De Silva, G. M., Freeman, K. C., Bland-Hawthorn, J., et al. 2015, MNRAS, 449, 2604 [Google Scholar]
  36. Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 4008, Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye, & A. F. Moorwood, 534–545 [Google Scholar]
  37. dos Santos, L. A., Meléndez, J., do Nascimento, J.-D., et al. 2016, A&A, 592, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Fabbro, S., Venn, K. A., O’Briain, T., et al. 2018, MNRAS, 475, 2978 [Google Scholar]
  39. Freeman, K., & Bland-Hawthorn, J. 2002, ARA&A, 40, 487 [Google Scholar]
  40. Fuhrmann, K. 1998, A&A, 338, 161 [NASA ADS] [Google Scholar]
  41. Fuhrmann, K., Axer, M., & Gehren, T. 1994, A&A, 285, 585 [NASA ADS] [Google Scholar]
  42. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Gaia Collaboration (Brown, A. G. A. et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Gavel, A., Gruyters, P., Heiter, U., et al. 2019, A&A, 629, A74 [CrossRef] [EDP Sciences] [Google Scholar]
  46. Gehren, T., Shi, J. R., Zhang, H. W., Zhao, G., & Korn, A. J. 2006, A&A, 451, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Gaia-ESO Public Spectroscopic Survey [Google Scholar]
  48. Giribaldi, R. E., Ubaldo-Melo, M. L., Porto de Mello, G. F., et al. 2019, A&A, 624, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. González Hernández, J. I., & Bonifacio, P. 2009, A&A, 497, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Gray, R. O., & Corbally, C. J. 1994, AJ, 107, 742 [Google Scholar]
  51. Guiglion, G., Matijevič, G., Queiroz, A. B. A., et al. 2020, A&A, 644, A168 [EDP Sciences] [Google Scholar]
  52. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Hanke, M., Hansen, C. J., Ludwig, H.-G., et al. 2020, A&A, 635, A104 [CrossRef] [EDP Sciences] [Google Scholar]
  54. Hansen, C. J., Jofré, P., Koch, A., McWilliam, A., & Sneden, C. S. 2017, A&A, 598, A54 [EDP Sciences] [Google Scholar]
  55. Hawkins, K., Jofré, P., Heiter, U., et al. 2016, A&A, 592, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Heiter, U., Jofré, P., Gustafsson, B., et al. 2015, A&A, 582, 49 [Google Scholar]
  57. Heiter, U., Lind, K., Asplund, M., et al. 2015, Phys. Scr, 90, 054010 [CrossRef] [Google Scholar]
  58. Heiter, U., Lind, K., Bergemann, M., et al. 2021, A&A, 645, A106 [EDP Sciences] [Google Scholar]
  59. Hekker, S. 2020, Frontiers in Astronomy and Space Sciences, 7, 3 [Google Scholar]
  60. Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [NASA ADS] [CrossRef] [Google Scholar]
  61. Hełminiak, K. G., Konacki, M., Maehara, H., et al. 2019, MNRAS, 484, 451 [CrossRef] [Google Scholar]
  62. Hinkel, N. R., Timmes, F. X., Young, P. A., Pagano, M. D., & Turnbull, M. C. 2014, AJ, 148, 54 [Google Scholar]
  63. Hinkel, N. R., Young, P. A., Pagano, M. D., et al. 2016, ApJS, 226, 4 [Google Scholar]
  64. Ireland, M. J., Mérand, A., ten Brummelaar, T. A., et al. 2008, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 7013, Optical and Infrared Interferometry, eds. M. Schöller, W. C. Danchi, & F. Delplancke, 701324 [Google Scholar]
  65. Jofré, P., Heiter, U., Soubiran, C., et al. 2014, A&A, 564, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Jofré, E., Petrucci, R., Saffe, C., et al. 2015, A&A, 574, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Jofré, P., Heiter, U., Worley, C. C., et al. 2017, A&A, 601, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Jofré, P., Heiter, U., Tucci Maia, M., et al. 2018, Res. Notes Am. Astron. Soc., 2, 152 [NASA ADS] [CrossRef] [Google Scholar]
  69. Jofré, P., Heiter, U., & Soubiran, C. 2019, ARA&A, 57, 571 [Google Scholar]
  70. Karovicova, I., White, T. R., Nordlander, T., et al. 2018, MNRAS, 475, L81 [Google Scholar]
  71. Karovicova, I., White, T. R., Nordlander, T., et al. 2020, A&A, 640, A25 [CrossRef] [EDP Sciences] [Google Scholar]
  72. Kassounian, S., Gebran, M., Paletou, F., & Watson, V. 2019, Open Astron., 28, 68 [Google Scholar]
  73. Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004, A&A, 426, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Kervella, P., Arenou, F., Mignard, F., & Thévenin, F. 2019, A&A, 623, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Kim, Y.-C., Demarque, P., Yi, S. K., & Alexander, D. R. 2002, ApJS, 143, 499 [Google Scholar]
  76. Kollmeier, J. A., Zasowski, G., Rix, H.-W., et al. 2017, ArXiv e-prints, [arXiv:1711.03234] [Google Scholar]
  77. Koppelman, H. H., Helmi, A., Massari, D., Price-Whelan, A. M., & Starkenburg, T. K. 2019, A&A, 631, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Kupka, F., Dubernet, M. L., & VAMDC Collaboration 2011, Baltic Astron., 20, 503 [Google Scholar]
  79. Lebzelter, T., Heiter, U., Abia, C., et al. 2012, A&A, 547, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Leenaarts, J., Carlsson, M., & Rouppe van der Voort, L. 2012, ApJ, 749, 136 [Google Scholar]
  81. Leung, H. W., & Bovy, J. 2019, MNRAS, 483, 3255 [NASA ADS] [Google Scholar]
  82. Limberg, G., Rossi, S., Beers, T. C., et al. 2021, ApJ, 907, 10 [Google Scholar]
  83. Lindegren, L., Bastian, U., Biermann, M., et al. 2021a, A&A, 649, A4 [EDP Sciences] [Google Scholar]
  84. Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021b, A&A, 649, A2 [EDP Sciences] [Google Scholar]
  85. Luri, X., Brown, A. G. A., Sarro, L. M., et al. 2018, A&A, 616, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Magrini, L., Randich, S., Friel, E., et al. 2013, A&A, 558, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Massari, D., Koppelman, H. H., & Helmi, A. 2019, A&A, 630, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
  89. McMillan, P. J. 2017, MNRAS, 465, 76 [Google Scholar]
  90. Meléndez, J.,& Ramírez, I. 2004, ApJ, 615, L33 [Google Scholar]
  91. Meléndez, J., Shchukina, N. G., Vasiljeva, I. E., & Ramírez, I. 2006, ApJ, 642, 1082 [Google Scholar]
  92. Meléndez, J.,& Barbuy, B. 2009, A&A, 497, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Miller, N. J., Maxted, P. F. L., & Smalley, B. 2020, MNRAS, 497, 2899 [Google Scholar]
  94. Mishenina, T. V., & Kovtyukh, V. V. 2001, A&A, 370, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Myeong, G. C., Vasiliev, E., Iorio, G., Evans, N. W., & Belokurov, V. 2019, MNRAS, 488, 1235 [Google Scholar]
  96. Ness, M., Hogg, D. W., Rix, H. W., Ho, A. Y. Q., & Zasowski, G. 2015, ApJ, 808, 16 [Google Scholar]
  97. Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Nordlander, T., Bessell, M. S., Da Costa, G. S., et al. 2019, MNRAS, 488, L109 [Google Scholar]
  99. Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [Google Scholar]
  100. Pinsonneault, M. H., Elsworth, Y. P., Tayar, J., et al. 2018, ApJS, 239, 32 [Google Scholar]
  101. Piskunov, N., & Valenti, J. A. 2017, A&A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Plez, B. 2012, Turbospectrum: Code for spectral synthesis [Google Scholar]
  103. Ramírez, I., & Meléndez, J. 2005, ApJ, 626, 446 [Google Scholar]
  104. Ramírez, I., Meléndez, J., & Asplund, M. 2014, A&A, 561, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  105. Randich, S., Gilmore, G., & Gaia-ESO Consortium 2013, Msngr, 154, 47 [Google Scholar]
  106. Ratajczak, M., Pawłaszek, R. K., Hełminiak, K. G., et al. 2021, MNRAS, 500, 4972 [Google Scholar]
  107. Reddy, B. E., & Lambert, D. L. 2008, MNRAS, 391, 95 [Google Scholar]
  108. Reggiani, H., Meléndez, J., Kobayashi, C., Karakas, A., & Placco, V. 2017, A&A, 608, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Reggiani, H., Meléndez, J., Yong, D., Ramírez, I., & Asplund, M. 2016, A&A, 586, A67 [EDP Sciences] [Google Scholar]
  110. Ryan, S. G., Norris, J. E., & Beers, T. C. 1996, ApJ, 471, 254 [Google Scholar]
  111. Sbordone, L., Caffau, E., Bonifacio, P., & Duffau, S. 2014, A&A, 564, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
  113. Serenelli, A., Johnson, J., Huber, D., et al. 2017, ApJS, 233, 23 [Google Scholar]
  114. Serenelli, A., Weiss, A., Aerts, C., et al. 2021, A&ARv, 29, 4 [Google Scholar]
  115. Škoda, P., Šurlan, B., & Tomić, S. 2008, in Proc. SPIE, 7014, Ground-based and Airborne Instrumentation for Astronomy II, 70145X [Google Scholar]
  116. Smalley, B. 2005, Mem. Soc. Astron. Ital. Suppl., 8, 130 [Google Scholar]
  117. Smiljanic, R., Korn, A. J., Bergemann, M., et al. 2014, A&A, 570, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  118. Smith, V. V., Lambert, D. L., & Nissen, P. E. 1998, ApJ, 506, 405 [Google Scholar]
  119. Sousa, S. G. 2014, ARES + MOOG: A Practical Overview of an Equivalent Width (EW) Method to Derive Stellar Parameters (Springer International Publishing), 297 [Google Scholar]
  120. Tabernero, H. M., Marfil, E., Montes, D., & González Hernández J. I. 2019, A&A, 628, A131 [CrossRef] [EDP Sciences] [Google Scholar]
  121. Taylor, M. B. 2005, in Astronomical Society of the Pacific Conference Series, 347, Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, 29 [Google Scholar]
  122. ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [Google Scholar]
  123. The MSE Science Team, (Babusiaux, C., et al.) 2019, ArXiv e-prints, [arXiv:1904.04907] [Google Scholar]
  124. Ting, Y.-S., Conroy, C., Rix, H.-W., & Cargile, P. 2019, ApJ, 879, 69 [Google Scholar]
  125. Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
  126. Valentini, M., Chiappini, C., Miglio, A., et al. 2016, Astron. Nachr., 337, 970 [Google Scholar]
  127. Valentini, M., Chiappini, C., Davies, G. R., et al. 2017, A&A, 600, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  128. Valentini, M., Chiappini, C., Bossini, D., et al. 2019, A&A, 627, A173 [CrossRef] [EDP Sciences] [Google Scholar]
  129. van Leeuwen F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  130. Wallace, L., Hinkle, K. H., Livingston, W. C., & Davis, S. P. 2011, ApJS, 195, 6 [NASA ADS] [CrossRef] [Google Scholar]
  131. Wang, R., Luo, A. L., Chen, J.-J., et al. 2020, ApJ, 891, 23 [Google Scholar]
  132. Wheeler, A., Ness, M., Buder, S., et al. 2020, ApJ, 898, 58 [Google Scholar]
  133. White, T. R., Huber, D., Maestro, V., et al. 2013, MNRAS, 433, 1262 [Google Scholar]
  134. Worley, C. C., de Laverny, P., Recio-Blanco, A., Hill, V., & Bijaoui, A. 2016, A&A, 591, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  135. Worley, C. C., Jofré, P., Rendle, B., et al. 2020, A&A, 643, A83 [CrossRef] [EDP Sciences] [Google Scholar]
  136. Yi, S. K., Kim, Y.-C., & Demarque, P. 2003, ApJS, 144, 259 [Google Scholar]
  137. Yong, D., Meléndez, J., Grundahl, F., et al. 2013, MNRAS, 434, 3542 [NASA ADS] [CrossRef] [Google Scholar]
1

[A/B] = log(N(A)N(B))Star−log(N(A)N(B))Sun$ \log{\left(\frac{N(\text{A})}{N(\text{B})} \right)_{\text{Star}}} - \log{\left(\frac{N(\text{A})}{N(\text{B})} \right)_{\text{Sun}}} $, where N denotes the number abundance of a given element.

2

Strictly speaking, Teff values based on interferometric measurements carry a marginal dependence on model atmospheres because of the need for limb-darkening corrections to estimate the angular diameters (Davis et al. 2000).

3

In Greek mythology, the TITANS are the offsprings of Gaia.

5

For the Sun we used the normalised HARPS spectra of Giribaldi et al. (2019).

6

IRAF is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation: http://ast.noao.edu/data/software

7

To improve the visibility of the plots, we chose to display only the right wing of the line.

8

The selection ‘turbospectrum_synth_good_for_params_all’.

All Tables

Table 1

Atmospheric parameters of the TITANS in the literature.

In the text
Table 2

Fundamental parameters and metallicities of the TITANS.

In the text
Table 3

Atmospheric parameters and Galactic membership for the sample of Gaia benchmark stars.

In the text
Table 4

Membership classification of the TITANS.

In the text

All Figures

thumbnail Fig. 1

Distribution of the TITANS in the Kiel diagram. The stellar parameters used in the plot are those displayed in Table 2. The Gaia benchmark stars with [Fe/H] < −0.8 dex are identified with bold contours. Isochrones corresponding to the age and [Fe/H] of each benchmark star are plotted.
In the text
thumbnail Fig. 2

Error flow diagram up to the beginning of the second loop. Each box displays, for each technique, the magnitude of the changes in a certain parameter induced by the variations given for the parameters in the previous box.
In the text
thumbnail Fig. 3

First normalisation-fitting for HD 84937 with HARPS. The spectrum is segmented in pieces of 20 Å to facilitate the visualisation of the details. The original spectrum is plotted in grey, and the black line is the spectrum degraded to facilitate the comparison with the synthetic profile shown in red. The shades are the fitting masks. Bottom panel: Gaussian fitto the histogram of temperatures related to the wavelength bins within the windows represented by the shades.
In the text
thumbnail Fig. 4

Last normalisation-fitting for HD 84937 with HARPS. The elements in the plots are the same as in Fig. 3.
In the text
thumbnail Fig. 5

Temperature difference between our best value and the one that is recovered by assuming an offset of − 0.1 dex in log g. The difference is shown as function of log g (top panel) and of the model temperature (bottom panel). In the top panel, cases for 5400, 6400, and 6600 K are highlighted as the lines in blue, green, and yellow, respectively. In the bottom panel, cases for 3.8, 4.1, and 4.5 dex are highlighted as the lines in blue, green, and yellow, respectively.
In the text
thumbnail Fig. 6

Temperatures derived from UVES spectra relative to the average temperatures derived from HARPS data for each of the GBS labelled in the plot. Grey symbols represent the individual values from multiple spectra. The box-bars extend from the lower to upper quartiles, with an orange line representing the median. The whiskers show the complete range of the values. The dashed line indicates the average difference, + 9 K, and the shaded area encloses the standard deviation of ±33 K.
In the text
thumbnail Fig. 7

For the GBS of Table 3, difference between Teff(Hα) and the reference Teff as function of the reference Teff, [Fe/H], and log g from the top to the bottom, respectively. The red lines are linear regressions, and the shaded areas indicate 1σ and 2σ dispersions.
In the text
thumbnail Fig. 8

For the GBS of Table 3, difference between log giso and reference log g as functionof the reference value. The labels identify the metal-poor GBS. The circles represent the values for which log giso was derived using the Gaia parallaxes. The dashes represent the values for which log giso was derived using the same (HIPPARCOS) parallaxes that were used to derive the reference log g from Jofré et al. (2018).
In the text
thumbnail Fig. 9

For the TITANS, the difference between temperatures derived by Hα fitting and those by the IRFM, as a function of Teff, [Fe/H], and log g from topto bottom, respectively. The red lines are linear regressions, and the shaded areas indicate 1σ and 2σ dispersions. The same vertical scale is used as in Fig. 7.
In the text
thumbnail Fig. 10

Top: Lindblad diagram – total orbital binding energy as a function of the angular momentum component in the direction of the Galactic north pole. The colours show the Massari et al. (2019) criteria to identifySequoia (the red box and red symbols), Gaia Enceladus (the blue box and blue symbols), and Helmi streams (orange symbols). Unclassified stars are shown in grey. The Sun is shown as the yellow ⊙ symbol. The TITANS are shown as stars and the GBS as crosses. Bottom: action space map – difference of action in the z and r directions by the action in the ϕ direction, all divided by total action (see Fig. 9 in Myeong et al. 2019). The blue box shows the limits for the Gaia-Enceladus merger and the red box shows the limits for Sequoia, according to the Myeong et al. (2019) criteria. The symbols and colours for the stars are the same as in the top panel.
In the text
thumbnail Fig. A.1

Profile fits of the TITANS labeled in the plots. The elements in the plots are the same as in Fig. 3.
In the text
thumbnail Fig. A.2

Profile fits of the Gaia benchmark stars labeled in the plots. The elements in the plots are the same as in Fig. 3.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.