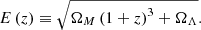| Issue |
A&A
Volume 650, June 2021
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 25 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202039156 | |
| Published online | 08 June 2021 | |
J-PLUS: The star formation main sequence and rate density at d ≲ 75 Mpc
1
Centro de Estudios de Física del Cosmos de Aragón, Plaza San Juan 1, 44001 Teruel, Spain
e-mail: gvilellarojo@gmail.com
2
Centro de Estudios de Física del Cosmos de Aragón, Unidad Asociada al CSIC, Plaza San Juan 1, 44001 Teruel, Spain
3
Instituto de Astronomia, Geofísica e Ciências Atmosféricas, Universidade de São Paulo, 05508-090 São Paulo, Brazil
4
Departamento de Física Teórica y del Cosmos, Universidad de Granada, 18071 Granada, Spain
5
IAA-CSIC, Glorieta de la Astronomía s/n, 18008 Granada, Spain
6
Departamento de Física de la Tierra y Astrofísica, Universidad Complutense de Madrid, 28040 Madrid, Spain
7
IPARCOS, Facultad de CC Físicas, Universidad Complutense de Madrid, 28040 Madrid, Spain
8
Department of Physics, Lancaster University, Lancaster LA1 4YB, UK
9
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
10
Observatório Nacional, Rua General José Cristino, 77 – Bairro Imperial de São Cristóvão, 20921-400 Rio de Janeiro, Brazil
11
Donostia International Physics Centre (DIPC), Paseo Manuel de Lardizabal 4, 20018 Donostia-San Sebastián, Spain
12
IKERBASQUE, Basque Foundation for Science, 48013 Bilbao, Spain
13
University of Michigan, Department of Astronomy, 1085 South University Ave., Ann Arbor, MI 48109, USA
14
University of Alabama, Department of Physics and Astronomy, Gallalee Hall, Tuscaloosa, AL 35401, USA
Received:
11
August
2020
Accepted:
7
January
2021
Aims. Our goal is to estimate the star formation main sequence (SFMS) and the star formation rate density (SFRD) at z ≤ 0.017 (d ≲ 75 Mpc) using the Javalambre Photometric Local Universe Survey (J-PLUS) first data release, that probes 897.4 deg2 with twelve optical bands.
Methods. We extract the Hα emission flux of 805 local galaxies from the J-PLUS filter J0660, being the continuum level estimated with the other eleven J-PLUS bands, and the dust attenuation and nitrogen contamination corrected with empirical relations. Stellar masses (M⋆), Hα luminosities (LHα), and star formation rates (SFRs) were estimated by accounting for parameters covariances. Our sample comprises 689 blue galaxies and 67 red galaxies, classified in the (u − g) vs. (g − z) color–color diagram, plus 49 AGN.
Results. The SFMS is explored at log M⋆ ≳ 8 and it is clearly defined by the blue galaxies, with the red galaxies located below them. The SFMS is described as log SFR = 0.83log M⋆ − 8.44. We find a good agreement with previous estimations of the SFMS, especially those based on integral field spectroscopy. The Hα luminosity function of the AGN-free sample is well described by a Schechter function with log LHα∗ = 41.34, log ϕ* = −2.43, and α = −1.25. Our measurements provide a lower characteristic luminosity than several previous studies in the literature.
Conclusions. The derived star formation rate density at d ≲ 75 Mpc is log ρSFR = −2.10 ± 0.11, with red galaxies accounting for 15% of the SFRD. Our value is lower than previous estimations at similar redshift, and provides a local reference for evolutionary studies regarding the star formation history of the Universe.
Key words: galaxies: general / galaxies: evolution / galaxies: fundamental parameters / galaxies: star formation / galaxies: luminosity function / mass function
© ESO 2021
1. Introduction
The star formation rate (SFR) of a galaxy accounts for the mass of gas that is transformed into stars per unit time. It is common to use units of solar masses M⊙ per year to describe it. Through the observation and understanding of stellar population properties, one can unveil the history of a galaxy, and get better insight into its current state. To better comprehend the formation and evolution of galaxies, we aim to relate the SFR to other galaxy properties, such as its total stellar mass M⋆, morphology, environment, gas content, or nuclear activity. By doing so, we look for those parameters that might play a major role in the rate at which galaxies form stars.
Since the pioneering study of Gallego et al. (1995), where the star formation rate density (SFRD) in the local Universe is measured, a large amount of studies have traced the SFRD evolution with redshift up to z ∼ 8 (e.g., Lilly et al. 1996; Hopkins & Beacom 2006; Cucciati et al. 2012; Sobral et al. 2013; Madau & Dickinson 2014; Novak et al. 2017; Maniyar et al. 2018; Driver et al. 2018, and references therein). The current consensus is that the SFRD increases with look-back time to z ∼ 2 − 3, then decreases towards cosmic dawn.
More recently, and in addition to the SFRD, the fundamental relation between the SFR and the stellar mass, often called star formation main sequence (SFMS, Brinchmann et al. 2004; Noeske et al. 2007) was introduced, and is now well established and supported by observations, showing correlation with other properties such as galaxy morphology (see González Delgado et al. 2016, and references therein). The linear relation in logarithmic scale between these two basic galaxy properties has been analyzed at z = 0 − 6, suggesting a slope a in the range 0.5 ≲ a ≲ 1, and an evolving normalization b that mirrors the SFRD behavior (e.g., Whitaker et al. 2012; Speagle et al. 2014; Salmon et al. 2015; Lee et al. 2015; Tomczak et al. 2016; Santini et al. 2017; Popesso et al. 2019a; Leslie et al. 2020, and references therein).
In this framework, it is clear that a robust anchorage of these magnitudes and relations at z ∼ 0 is needed to set the current star formation properties of the Universe, and to provide a local reference for evolutionary studies.
To analyze the SFR at a given cosmological epoch, a proxy for the star formation activity and a representative sample of galaxies are both needed. In the first case, we look for consequences of star formation processes, and we refer to these as SFR indicators. These can be classified in two main families. The first one is based on the direct consequences of the SFR; the main indicator of this family is the ultraviolet (UV) light emitted by young, short-lived, O and B stars. These stars have short life spans (30 Myr, Calzetti 2013), and are the most straightforward tracer of the SFR. However, this indicator suffers from two major drawbacks. The first one is dust attenuation in the star-forming region. Photons trying to escape it will interact with dust grains, causing a loss of the UV radiation that we receive. The other one is the Earth’s atmosphere, which shields us from the UV radiation.
The second big family of SFR tracers are indirect. In this family, we include the dust-processed light, which is emitted by dust grains heated by the UV radiation, and the recombination lines that appear on top of the stellar continuum spectral energy distribution (SED) of the star-forming regions. Among these recombination lines, we have the Hα line. This emission occurs when an electron in a hydrogen atom is ionized by the UV field of the young, massive stars, and then returns back to the fundamental state. During this process, the electron may transit from the 3rd to the 2nd energy level, emitting as a consequence a photon with rest-frame wavelength 6562.8 Å. We refer to this transition as the Hα line, as it is the least energetic of all the transitions that end in the 2nd energy level (i.e., the Balmer series).
To build a representative sample of galaxies and derive the global SFR in a cosmological epoch, there are also different, complementary approaches. On the one hand, spectroscopic observations are those that provide the most accurate measurements of emission or absorption line fluxes. This is at the cost of large samples, or aperture corrections. While integral field spectroscopic (IFS) surveys are an excellent choice to overcome the spatial coverage limitation, galaxies require a target pre-selection. Single-fiber spectroscopy, despite being suitable to gather information of many galaxies in the same observing time, requires aperture corrections that dilute spatial information.
On the other hand, photometric studies that count with well adapted narrow-band filters are able to retrieve the largest samples, with no need for aperture correction. This is at the cost of much lower spectral precision, that is translated into a loss in precision when measuring emission-line fluxes. However, in the investigation of properties of galaxies in the nearby Universe, a statistically meaningful sample is crucial. Cosmic variance may introduce biases that cannot be compensated for target pre-selection. To understand the properties of galaxies around ours, a blind, homogeneous study is the best tool. In this regard, the Javalambre Photometric Local Universe Survey (J-PLUS1, Cenarro et al. 2019) becomes ideal. By blindly surveying the Northern sky with twelve optical filters (seven narrow and five broad band), it gathers information about stars, galaxies, and objects in the Solar System. In particular, the J-PLUS filter J0660, of 14 nm width, is centered at rest-frame Hα emission and it is able to trace the SFR up to a distance of d ∼ 75 Mpc (z ≤ 0.017).
In this Paper, we analyze the J-PLUS first data release (DR1) to derive the SFMS and SFRD at z ∼ 0. Additionally, we compute the stellar mass function and Hα luminosity function in our sample. This work, in combination with the forthcoming paper of Logroño-Garcìa (in prep.), are the culmination of two previous studies: the first is Vilella-Rojo et al. (2015, hereafter VR15), in which we present the best method to extract the Hα flux using J-PLUS synthetic data, including corrections for dust attenuation and [N II] contamination. In the second paper, Logroño-García et al. (2019), the methodology presented in VR15 is tested using real J-PLUS data and common star-forming regions observed spectroscopically by the Sloan Digital Sky Survey (SDSS, York et al. 2000) and the Calar Alto Legacy Integral Field Area (CALIFA, Sánchez et al. 2012) survey. The comparison between the spectroscopic Hα flux and the one derived from J-PLUS data reveals that the photometric measurement is not biased and presents a minimum uncertainty of 20%.
This paper is organized as follows: in Sect. 2, we explain how we select our sample of nearby galaxies (z ≤ 0.017, or d ≲ 75 Mpc under the assumed cosmology) and the measurement of their distances, stellar masses, Hα luminosities, and SFRs. We analyze this data to obtain the SFMS and SFRD in the local universe in Sect. 3. In Sect. 4, we present a discussion of our findings in the context of the current literature, and a summary of the main results is provided in Sect. 5.
This paper makes use of the AB system (Oke & Gunn 1983) of magnitudes, a Salpeter (1955) initial mass function (IMF), and a flat Universe cosmology with Ωm = 0.3, ΩΛ = 0.7, and h = 0.7.
2. Data and sample of local emission-line galaxies
In this section, we describe how we retrieved Hα emitters within our searching interval in redshift (z ≤ 0.017). First, we summarize the main characteristics of J-PLUS and its first data release in Sect. 2.1. Then, we explain the criteria for a source to be considered a local galaxy at z ≤ 0.017 (Sect. 2.2). We assign distances, Hα luminosities, stellar masses, and star formation rates to J-PLUS local emitters in Sect. 2.3. Finally, we show how galaxies distribute within this parameter space in Sect. 2.4.
2.1. J-PLUS photometric data
J-PLUS is an imaging survey project intending to cover a fraction of the Northern sky from the Observatorio Astrofísico de Javalambre (OAJ2, Cenarro et al. 2014) using an 83-cm diameter telescope (JAST/T80) equipped with a 9.2k × 9.2k pixel camera (T80Cam, Marin-Franch et al. 2015) providing a 2 deg2 field of view. The system is equipped with a set of twelve, purpose designed, photometric filters, the five SDSS (ugriz) filters and seven medium or narrow-band filters primary designed to classify stars. They are placed on key stellar features covering around the 4000 Å break region (J0378, J0395, J0410, J0430), the magnesium doublet (J0515) and the calcium triplet (J0861), plus the filter on the Hα line (J0660). Thus, J-PLUS covers the whole optical wavelength range, enabling different kind of studies in stellar astrophysics (Bonatto et al. 2019; Whitten et al. 2019; Solano et al. 2019), galaxies at several redshift ranges (Logroño-García et al. 2019; San Roman et al. 2019; Nogueira-Cavalcante et al. 2019) or in clusters (Molino et al. 2019; Jiménez-Teja et al. 2019), and extreme Lyman-α emitters at z > 2 (Spinoso et al. 2020).
The first J-PLUS data set was released in July 2018. The J-PLUS DR13 includes photometric information for 511 pointings that cover an area of 897.4 deg2 after correcting for overlapping areas and masking optical artifacts. The catalogs, publicly accessible at the J-PLUS website, contains ∼13.4 million objects detected in r band using SExtractor (Bertin & Arnouts 1996) with mr ≤ 21 mag. The photometry in the twelve J-PLUS bands was performed with the SExtractor dual mode feature. Details on the reduction and calibration processes can be found in Cenarro et al. (2019) and López-Sanjuan et al. (2019a).
2.2. Definition of the local sample
2.2.1. Initial selection of spectroscopic sources
We started from the general J-PLUS catalogs and retrieved all the detected sources with an apparent AUTO magnitude mr ≤ 18 and high-quality flags in the surveyed area. This excluded sources that are at the edge of the images, near to a bright star, or affected by optical artifacts. To get rid of stars, we applied the stellarity parameter4 derived by López-Sanjuan et al. (2019b) and imposed total_prob_star < 0.5. This is a Bayesian classification that takes into account the morphological features of a source, and a priori information from the Gaia DR2 parallaxes (Gaia Collaboration 2018).
This initial selection has several benefits. It provides a completeness higher than 95% for stellar masses larger than 109 M⊙, and a surface brightness limit of μr ∼ 24 mag arcsec−2 for nearby, well resolved galaxies (Sects. 2.4.1 and 3.2). It also introduces a cut in the number of faint emitters at higher redshift that would contaminate our sample ([O III] + Hβ at z ∼ 0.33, or [O II] at z ∼ 0.77; see Izquierdo-Villalba et al. 2019); and finally, it covers a well defined, non pre-selected area to compute volume densities.
The initial selection yielded 109 815 sources. We cross-correlated these sources with other databases, named NED5, Simbad6 (Wenger et al. 2000), and SDSS, to assign a spectroscopic redshift (zspec) to them. After cleaning from duplicates and merging regions of unique, large galaxies wrongly classified by SExtractor as individual sources, we ended with 684 galaxies at 0.001 < zspec ≤ 0.017. A representative example is shown in the upper panels of Fig. 1.
 |
Fig. 1. Illustrative examples of the J-PLUS DR1 sample of local galaxies, presenting sources 26216-6250 (RA = 227.1397, Dec = 52.2960; UGC 9741 at zspec = 0.0083) and 26266-6298 (RA = 231.1995, Dec = 55.1277; there is no spectroscopic redshift for this source in the analyzed databases, see Sect. 2.2.2). The sky location of the sources is marked with a bullet in the left and central panels, and the white ellipse marks the three effective radii contour for the sources. Left panels: color composite of the galaxies, obtained from the gri J-PLUS images. Central panels: J0660 emission in units of σem, the dispersion of the pixels in the image (Sect. 2.3.1), as scaled in the color bar. This emission image has been obtained by applying the 3F methodology in VR15 to the r, J0660, and i J-PLUS images. Several star-forming knots are apparent. Right panels: J-PLUS twelve-band photometry (the SED) of those pixels with J0660 emission larger than σem (Sect. 2.3.1) and inside three effective radii. Squares show the five SDSS-like filters (ugriz), and circles the seven medium- and narrow-band filters (J0378, J0395, J0410, J0430, J0515, J0660, and J0861). The flux in J0660, J0515, and J0378 is raised with respect to the continuum level due to the Hα + [N II], [O III], and [O II] emission, respectively. The derived physical properties of the galaxies (Sects. 2.3.2 and 2.3.4) are labeled in the panels. |
At this stage, the completeness of the zspec sample is unknown and a large fraction of local galaxies with mr ≤ 18 but without spectroscopic information could be hidden in J-PLUS data. To deal with this issue, we searched for high-confidence Hα emitters without zspec.
2.2.2. Selection of local galaxies with excess in J0660
The Hα emission of local galaxies is traced by the J-PLUS J0660 filter up to z = 0.017. In combination with the emission of [N II], it causes the flux inside J0660 to be above the expected continuum. It is precisely this feature that we were looking for.
For each source passing the initial magnitude (mr ≤ 18) and quality selection (Sect. 2.2.1), we queried the ISO_GAUSS magnitudes in the r, J0660, and i filters, along with their respective photometric errors. The ISO_GAUSS magnitudes in the J-PLUS database were estimated as the usual ISO magnitudes in SExtractor over images convolved with a Gaussian kernel of 1.5 arcsec. This reduces the differences due to the point spread function (PSF) variations among passbands with a well defined kernel.
To these fluxes, we applied the equations of the three filters (3F) method, as described in VR15. This algorithm is similar to the classical color – narrowband magnitude diagram that has been widely used in the literature (e.g., Bunker et al. 1995), but instead of relying in a 0-color for non-emitters, it assumes a featureless linear continuum for the line in the wavelength range of the emission. In our case, we relied on r and i to trace the continuum inside J0660. This was done using a Monte-Carlo approach, in which the flux inside the three aforementioned bands were perturbed within their respective error j times, and in each iteration we retrieved an inference of the excess inside J0660, which we refer to as FJ0660, j. We did this 3000 times. In the end, we computed the median of all the FJ0660, j, which we refer to as ⟨F⟩, and considered a source to have a significant J0660 excess if
where NMAD denotes the normalized median absolute deviation (Hampel 1974). A total of 3426 objects with J0660 excess were selected.
Within these sources, some of them are contaminants without Hα emission. The assumption of a linear continuum without features produces that some non-emitting astrophysical objects exhibit a J0660 excess unrelated with star formation. To discern the nature of the selected sources, we analyzed them in a color–color diagram. After inspected all the available combinations, we chose the J-PLUS colors (J0515 − r) and (g − i) as the best ones to discriminate between different objects (Fig. 2).
 |
Fig. 2. (J0515 − r) vs. (g − i) color–color diagram from ISO_GAUSS magnitudes of mr ≤ 18 sources with significant J0660 excess. Left panel: sources with no spectroscopic redshift in SDSS. Right panel: J0660 emitters, with spectroscopic redshift in SDSS. Cyan dots represent sources within our redshift of interest, while red dots are sources with higher redshift. The three regions defined to isolate low-z galaxies (R1), blended stars (R2), and high-z galaxies (R3) are labeled in the panel. |
Three main populations were found in this color–color diagram. There is a concentration of sources at (g − i)∼1.5 and (J0515 − r)∼0.6, a sequence of sources extending bluewards down to (g − i)∼0.5 and (J0515 − r)∼0.2, and a set of redder sources with (J0515 − r)≳0.8. We inspected the properties of these three populations, finding that they are dominated by different astrophysical sources. In this study, J-PLUS photometry was complemented with the available spectroscopic information. We found that the redder population is mainly composed by double (physically or in projection) stars that were detected as an unique, extended source by SExtractor. The SED of these red stars has a local maximum at J0660 in the J-PLUS filter system, being selected as objects with J0660 excess (upper panel in Fig. 3). The main concentration of sources comprises early-type galaxies dominated by old stellar populations and located at z ∼ 0.1. As in the previous case, this galaxy population exhibits a J0660 excess on its SED (bottom panel in Fig. 3). Finally, the genuine Hα emitting galaxies of interest are located in the bluest population.
 |
Fig. 3. Representative example of a source in the region R2 (upper panel) and the region R3 (bottom panel) of the (J0515 − r) vs. (g − i) color–color diagram. In both panels, the J-PLUS ISO_GAUSS photometry of the source in shown, with symbols as in the right panels of Fig. 1. A color composite of the sources, obtained from the gri J-PLUS images, is presented in the insets. |
From the analysis above, we defined three regions in the (J0515 − r) vs. (g − i) diagram. The region R1 (1540 sources) aims to isolate the desired Hα emitters; region R2 (351 sources) is mostly populated by double stars; finally, region R3 (1535 sources) selects z ∼ 0.1 galaxies. The definition of region R1 was based on completeness, and it includes all the 466 sources with J0660 excess and 0.001 < zspec ≤ 0.017. As consequence, a large contamination of galaxies at higher redshift is also present, with 485 sources having zspec > 0.017 (Fig. 2). Thus, there are 589 sources in region R1 without spectroscopic information that can be located at low or high redshift.
We visually checked those sources, and classified them as low-redshift or high-redshift (z > 0.017) galaxies. We looked for characteristic SED features of low-redshift galaxies, such as the [O III] emission traced by the J0515 filter at 0.007 < z ≤ 0.017 (bottom right panel in Fig. 1), the [O II] emission traced by the J0378 filter (top right panel in Fig. 1), and a clear blue overall color at λ ≳ 4500 Å (Fig. 1). These properties contrast with the typical red colors and the lack of other emission features displayed by the interlopers (Fig. 3). We summarize the result of this exercise in Table 1. We selected 158 local emitters without spectroscopic information, and an illustrative example is presented in the bottom panels of Fig. 1.
Redshift classification of the S/N ≥ 3 emitters in J0660 that lie within the region R1 inside the (J0515 − r) vs. (g − i) color–color diagram.
As a summary, we gathered a sample of 842 nearby galaxies, out of which 684 have spectroscopic redshift information. From these, 466 present a 3σ excess in J0660 and 218 have lower emission significance. The remaining 158 galaxies that complete the sample do not have spectroscopic redshift information but have a significant excess in J0660. The next step was to derive the physical properties of these galaxies.
2.3. Physical properties of the local sample
We describe in this section the extraction of the J-PLUS photometry of the 842 local galaxies in our sample (Sect. 2.3.1), and the estimation from these information of their Hα flux (FHα, Sect. 2.3.2), distance (d, Sect. 2.3.3), Hα luminosity (LHα), stellar mass M⋆, and SFR (Sect. 2.3.4).
2.3.1. J-PLUS photometry of local emitters
Here, we detail the measurement of the photometric flux in the twelve J-PLUS filters for the galaxies in our sample with the final goal of providing the best possible estimation of their Hα flux, as described in Sect. 2.3.2.
We started by isolating galaxies in the twelve J-PLUS images. For this, we use ten effective radii as estimated by SExtractor, creating a cropped image from the original J-PLUS data. These images were homogenized to a common PSF in advance, as described in Logroño-García et al. (2019). We run again SExtractor on the r-band image with a configuration optimized for large galaxies, obtaining the final structural parameters of the source (i.e., effective radius and the elliptical Kron aperture).
Then, a emission flux image was computed. We used the r and i images to define a linear continuum for each pixel, subtracting it from the observed J0660 image. The targeted Hα + [N II] emission is also included in the r filter, so we used the equations described in VR15 to deal with this effect7.
For each galaxy emission image, we computed the pixel flux histogram. This histogram resembles a Gaussian distribution, which is described by an average flux, μem ∼ 0, and a dispersion, σem. We note that the emission image encloses an area that extends up to ten effective radii of the galaxy, making the number of emitting pixels small compared to the whole number of pixels of the image. In addition, the dispersion σem was estimated from the 16 to 84 percentiles of the distribution, minimizing the impact of the emission pixels located in the positive tail. We estimated that the contribution of the emission pixels is therefore negligible when measuring the background flux. At this stage, we can classify any pixel in the emission image according to its signal in terms of σem (middle panels in Fig. 1).
Now, for each galaxy in the sample, we combined the flux of all the pixels that have an emission flux larger than N times the dispersion σem with the following process:
-
We selected a confidence level N.
-
All pixels with emission flux larger than Nσem and within three effective radii were tagged.
-
The tagged pixels were selected in each of the twelve J-PLUS images.
-
The signal in these pixels was added, creating a flux and an observed magnitude, in a given J-PLUS band.
-
The fluxes and magnitudes were de-reddened from Milky Way extinction using the color excess from Bayestar178 (Green et al. 2018) at galaxy position and the extinction coefficients reported in Whitten et al. (2019).
In the end, eleven photometric catalogs were derived, where the confidence level N belongs to the interval [−5,5] with unity steps. We refer to these as pix{pm}N catalogs, where N refers to the positive (p) or negative (m) confidence level N used to extract the photometry. It is important to remark that, even though these catalogs are created using the pixels that fulfill an emission criteria, the pixm5 catalog de facto contains the total apparent fluxes and magnitudes of each galaxy in each J-PLUS band. We note that each pix{mp}N photometry provide different information about the analyzed galaxies and their star formation properties, and we benefit of this extra spatial information along the paper.
The pix{mp}N catalogs were used to derive the physical properties of the 842 local galaxies in our sample, as described in the next sections.
2.3.2. Estimation of the Hα emission flux
First, we measured the Hα emission flux of each galaxy, FHα. To do so, we used the SED-fitting methodology that is fully described in VR15, along with the statistical dust and [N II] corrections estimated in the same work. This methodology relies on the full SED of the galaxy to estimate the continuum level at the J0660 filter, including Hα stellar absorption, so the twelve J-PLUS fluxes were used in the process. For completeness, we did this for each pix{pm}N catalog.
We remind here the empirical dust and [N II] corrections that we used. We estimated the color excess of the selected emitting area as
With this, the relation between the observed emission flux obtained from the SED-fitting routine, Fobs, and the intrinsic, dust-free flux comprising the Hα and [N II] emission, ![$ F_{\mathrm{H}\alpha+\mathrm{[{\mathrm{N}\,\textsc{ii}}]}} $](/articles/aa/full_html/2021/06/aa39156-20/aa39156-20-eq4.gif) , is given by
, is given by
where k′ is a polynomial that depends on wavelength and the selective-to-total excess ratio RV. We estimate k′ = 3.33 from the Calzetti et al. (2000) parametrization for RV = 4.05. This corrects the internal extinction of the analysed source, and the Milky Way extinction was accounted for in the estimation of the pix{pm}N catalogs.
Once we have corrected the Hα+ [N II] emission from dust reddening, we removed the [N II] contribution. To this aim, we used the following empirical relation derived by VR15:
The procedure above was observationally validated in Logroño-García et al. (2019) using the J-PLUS early data release (EDR). We selected a sample of 46 star-forming regions that had been observed with CALIFA or SDSS, but also with J-PLUS. With this we made sure that we had an spectroscopic measurement of the Hα flux to compare with the photometric measurement. We conclude that our methodology provides an unbiased FHα with a minimum uncertainty of 20%, that is included in the final error budget together with the statistical error in the measurement. We further test the Hα flux measurements in Sect. 4.1.
We were not able to extract an Hα flux for 37 galaxies in the local sample with the above procedure. There are low surface brightness galaxies with a low pixel-by-pixel significance in the emission. The final sample of local Hα emitters used hereafter comprises 805 galaxies.
2.3.3. Computing distances to local galaxies
In this section, we explain how we computed the distance to the galaxies in our sample. This is important to describe it in detail because the distance was used both in the calculation of the stellar mass and the Hα luminosity (Sect. 2.3.4). This introduces a correlation between these two parameters that has to be accounted for. Additionally, it is well known that redshifts (either photometric or spectroscopic) may be strongly affected by peculiar velocities in the local Universe and are thus a degraded proxy for the cosmological distance.
We started by dividing the sample of 805 local Hα emitters in three sub-samples, according to the information that we have to infer a distance9:
-
Sample G0: Galaxies with neither redshift-independent distance nor spectroscopic redshift. There are 158 galaxies in this category (20% of the total sample).
-
Sample G1: Galaxies without a redshift-independent measurement of the distance, but with a measured spectroscopic redshift. There are 487 galaxies in this situation (60% of the total sample).
-
Sample G2: Galaxies with a redshift-independent measurement of the distance. Distances were retrieved from the NED data base, and obtained with different methods, such as the Tully–Fischer relation, or the tip of the red giant branch. They account for the remaining 160 galaxies (20% of the total sample). All of them also have a spectroscopic redshift.
We obtained the distance modulus (m − M) for galaxies in Sample G2 from the NED. The distance to these galaxies was determined by the associated distance to the median (m − M), in the case that more than one value was provided in the NED. If just one value of (m − M) is available, we used it. In the same way, we also computed distance errors. We explain how we assigned errors to these distances, noted δd, in Appendix A.
Galaxies in Sample G1 have a redshift-derived distance. This redshift is not fully coupled to the Hubble flow, meaning that peculiar velocities introduce an uncertainty to the luminosity distance derived from zspec. To test the impact of peculiar velocities in the distances derived from spectroscopic redshifts, we used the redshift-independent information in Sample G2.
We found that the ratio between the distances estimated from the Hubble flow (dz) and those estimated from redshift-independent methods (dL) in Sample G2 is well described by a Gaussian with median 0.97 and dispersion 0.20 (Fig. 4). To find the best peculiar velocity that describes the observed relation for Sample G2 galaxies, we generated a set of 5000 synthetic galaxies distributed up to z = 0.017 according to a volume prior. To each of these galaxies, for which we know the real distance and the Hubble flow redshift, we added a term of peculiar velocity drawn from a Gaussian distribution, with σ = vpeculiar. We then re-computed the luminosity distance that we would have obtained if we had used this perturbed zspec to measure it. We did this for several vpeculiar, and we found that vpeculiar = 750 km s−1 generates a distribution of relative errors in distance that reproduces well the observed one with Sample G2 galaxies, as shown in Fig. 4. This component includes the typical peculiar velocity of the local galaxies and the mean uncertainty on the redshift-independent distances. It must be interpreted therefore as a formal minimum error in the comparison between redshift-dependent and independent distances. Moreover, the assumed value of vpeculiar = 750 km s−1 does not have a significant impact in the main scientific results of this work, as shown in Appendix B, where we repeat all the analysis carried out in further sections with different vpeculiar to assess the impact of this assumption.
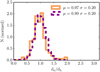 |
Fig. 4. Histogram of the ratio between the redshift-derived (dz) and the redshift-independent (dL) luminosity distance for galaxies in Sample G2 (orange histogram). The purple histogram represents the same, but for a sample of simulated galaxies distributed according to a volume prior and with a spectroscopic redshift that has been perturbed with a peculiar velocity term of vpeculiar = 750 km s−1. |
The result above also provides a limiting distance, dlim, at which errors in the current methods to obtain a redshift-independent distance are larger than the floor uncertainty imposed by vpeculiar in the zspec distances. Hence, we imposed a cut in dlim = 60 Mpc. Galaxies in Sample G2 with a distance measurement larger than 60 Mpc will be assigned a distance according to their spectroscopic redshift, disregarding the redshift-independent measurement. In Appendix B, we show that changing this criterion does not significantly affect the results of this paper.
The detailed analysis above justifies the distance assignment that is described in the next section.
2.3.4. Stellar masses, Hα luminosity, and SFR: The Monte-Carlo routine
We now explain the Monte-Carlo routine that we used to assign an Hα luminosity (hence, a SFR) and a M⋆ to the galaxies in our sample. This routine consists of perturbing the Hα fluxes, and the distances, within their error bars. These two perturbations lead to a different value of LHα, SFR, and M⋆ in each iteration. To start with, Hα fluxes were always perturbed with a noise component drawn from a Gaussian distribution with σ its error. Distances were perturbed within their errors depending on the information that we have. We used the following recipe:
-
Sample G0: Galaxies with no distance information:
-
In each iteration, we assigned a random distance according to a volume prior.
-
-
Sample G1: Galaxies that do not have a z-independent measurement of the distance, but with a zspec:
-
Sample G2: Galaxies that have a collection of redshift-independent measurements of the distance:
-
If their median distance is smaller than 60 Mpc, we used both the distance and the uncertainty from the redshift-independent methods.
-
We perturbed the distance with a random error drawn from a Gaussian distribution with μ = 0 and σ = δd Mpc. In case the final distance is negative, we took the absolute value.
-
If their median distance is larger than 60 Mpc, we proceeded in the same way that with galaxies of Sample G1.
-
To compute the stellar mass of the galaxies, expressed in Solar mass units, we used the mass-to-light vs. color relation (MLCR) for star-forming galaxies described in the work by López-Sanjuan et al. (2019c). This relation is based on the observed (i.e., dust-attenuated) g − i color and we scaled it to a Salpeter IMF:
where Mi is the absolute magnitude of the galaxy in the i band. In this case, we did not perturb the apparent g and i magnitudes, as their error is negligible. However, by changing the distance, we were changing Mi. Finally, and to account for the intrinsic dispersion of this relation, we included an extra perturbation, drawn from a Gaussian distribution with σ = 0.07 dex (López-Sanjuan et al. 2019c). We favoured the estimation of the stellar mass from a MLCR over a SED-fitting technique because both approaches provide similar accuracy (e.g., Taylor et al. 2011) and to minimize the correlation between the derived Hα fluxes, based on SED-fitting, and the stellar masses.
We computed the Hα luminosity as
and the star formation rate as
where the Kennicutt (1998) relation between Hα luminosity and SFR for a Salpeter (1955) IMF and case B recombination is assumed, and C(q, T) is a statistical correction that accounts for the missing Hα flux on inclined systems. This correction depends on the minor-to-major axis ratio of the galaxy, q, and its morphological type, T. The inclination correction is unity for 60% of the galaxies in the sample and has a median value of C = 1.22 for the remaining 40%, with a maximum correction of C = 1.78. The details about the estimation of this inclination correction are in the forthcoming paper by Logroño-Garcìa (in prep.), where the morphology of the local sample is derived and studied.
We repeated the process above n = 5000 times. In the end, for each galaxy, we had a collection of n values for the distance, M⋆, LHα, and SFR. The median of these values were used as our measurements in the rest of the paper, while the uncertainties were computed as the NMAD of the n values of each parameter. We also computed the typical values for the covariance and the correlations, to find that the average correlation factor between M⋆ and the SFR is ∼0.75. These correlations were used in the statistical analysis of the sample.
We derived stellar masses, Hα luminosities, and SFRs for each pix{pm}N catalog. In the following, stellar masses refers to pixm5 (total) photometry, and LHα and SFR to pixp1 photometry. We found that the latter are similar to the global ones from pixm5 but with a higher signal-to-noise ratio.
2.4. General properties of the sample
2.4.1. Global distributions
In this section, we characterize the sample of 805 local Hα emitters. Distributions of mr, redshift, Hα flux, and the relation between LHα and redshift are plotted in Fig. 5.
 |
Fig. 5. General properties of the J-PLUS DR1 local sample at z ≤ 0.017. Upper left panel: distribution in the r-band apparent magnitude. The three sub-samples with different distance information are labeled in the panel (see Sect. 2.3.3, for details). Upper right panel: distribution in Hα flux. Lower left panel: redshift distribution of those galaxies in the sample with zspec. Lower right panel: Hα luminosity vs. redshift for those galaxies in the sample with zspec. The solid line marks the luminosity for a galaxy with log FHα = −13.2 as reference. |
It is worth noting that galaxies in Sample G0 appear to be the faintest in mr magnitude and Hα flux, and their distribution in fluxes does not resemble the distribution of fluxes that combines Sample G1 and Sample G2. This can be due to two possibilities, either these galaxies are all particularly far (with a limit of 73 Mpc), but have bright luminosities, or these galaxies are intrinsically less luminous and are spread all over our volume in a regular way.
To assess this problem, we recursively moved these galaxies through our volume, keeping the flux, but assigning the same distance to all of them and computing the luminosity distribution of these Sample G0 galaxies as if all of them were at this distance. By doing this we found that, in order to reproduce the luminosity distribution of the rest of the sources with known distances, all galaxies in Sample G0 should be at ∼80 Mpc, which means that we should not see an excess in the J0660 filter. This leads us to believe that these galaxies are indeed properly classified as low-redshift galaxies, but with faint Hα luminosities.
Finally, we present in Fig. 6 the relation between stellar mass and ⟨μr⟩, defined as the mean r-band surface brightness within three effective radii. We found a limiting surface brightness of ⟨μr⟩∼24.0 mag arcsec−2, in agreement with the limit of the general J-PLUS catalog (Cenarro et al. 2019). The larger apparent size of the local sample with respect to the general galaxy population in J-PLUS makes the mr ≤ 18 selection equivalent in terms of surface brightness to the mr ∼ 21 limiting magnitude for the general population, minimizing the bias against low surface brightness galaxies. The trend between stellar mass and ⟨μr⟩ that appears in Fig. 6 suggests that the J-PLUS local sample is complete in stellar mass for log M⋆ ≳ 9 galaxies. This is confirmed in Sect. 3.2, where the stellar mass function of the sample is derived and analyzed.
 |
Fig. 6. Mean r-band surface brightness within three effective radii, ⟨μr⟩, as a function of the stellar mass for the local sample of Hα emitters. The color scale shows the apparent magnitude of the sources. The hatched area marks a surface brightness larger than 24 mag arcsec−2. The vertical dotted line marks a stellar mass of log M⋆ = 9. |
2.4.2. Active galactic nuclei
The J-PLUS filter set does not allow us to discern active galactic nuclei (AGN) using known tools such as the BPT diagram (Baldwin et al. 1981). To cope with this, we check the NED for information regarding the nuclear activity of our sources. From now on, we remove sources with any kind of nuclear activity from our study. After removing 49 AGN from the 805 sources in our catalog, a total of 756 galaxies remain.
2.4.3. Color properties of the sample
To provide further insights into the nature of our emitters, we study them in a (u − g) vs. (g − z) color–color diagram. After revising the resulting diagrams with the available pix{pm}N photometries, we used the pixp3 catalog. We recall that the photometry in this catalog contains information of the pixels with high emission flux. Hence, it encapsulates the information on the average properties of the star-forming regions. In contrast, if we use the pixm5 catalog, we obtain the total colors of the galaxy. We compare the (u − g) vs. (g − z) obtained with both pixp3 and pixm5 catalogs in Fig. 7.
 |
Fig. 7. (u − g) vs. (g − z) color–color diagram of our local galaxy sample computed from pixels with signal-to-noise higher than 3 (pixp3; left panel) and higher than −5 (i.e., total colors, labeled as pixm5; right panel) in the Hα detection images. The colored contours show the density of sources to highlight the presence of local maxima. The dotted lines in the left panel mark our selection for the Red sample (red area), the Blue sample being the complementary set (blue area). The upper- and right-side normalized histograms are the density projections in (g − z) and (u − g), respectively. The red and blue shaded histograms in both panels mark the Red and Blue samples selected with pixp3 colors. |
Interestingly, we found that the pixp3 photometry unveils two different populations that are not clearly discernible if the total color of the galaxy, as traced by pixm5, is used. The separation between both populations increases as we move from pixm5 to pixp5 catalogue. However, not all sources have emission pixels above 5σem, and the colors are therefore not available. The pixp3 catalog provides the optimum compromise between a clean separation of populations and minimum loss of sources that lack high-significance emission, providing a broadband color measurement for most of the sample.
We separated the two populations by imposing a selection criteria on pixp3 colors:
-
Blue sample: Galaxies with (u − g) ≤ 1.6 ∪ (g − z) ≤ 1.15.
-
Red sample: Galaxies with (u − g) > 1.6 ∩ (g − z) > 1.15.
The 28 galaxies without available pixp3 colors were assigned to the Blue sample. In the end, we selected 689 galaxies in the Blue sample and 67 galaxies in the Red sample. We call Full sample the combination of the Blue and Red samples (756 galaxies). As we will demonstrate, the star formation properties of these two populations are remarkably different.
2.5. Sample characterization: conclusions
In this section, we have explained the routine to retrieve low-z Hα emitters, extract their J-PLUS photometry, and estimate their Hα flux. This yielded a catalog of 805 bona fide galaxies. Then, we explained how we computed distances, and their uncertainties, to these galaxies. With this, we have presented the Monte-Carlo routine to obtain the Hα luminosity, SFR, and M⋆. This allowed to perform a basic characterization of the main physical properties of these galaxies. In the end, after removing AGN, our final catalog contains 756 galaxies, 689 in the Blue sample and 67 in the Red sample, which will be used in the following sections. The catalog with the information of the galaxies in the Full sample is publicly available in the J-PLUS webpage10. The study of the morphological properties of this sample is beyond the scope of the present work and it is addressed in the forthcoming paper by Logroño-Garcìa (in prep.).
3. Star formation in the local Universe
In this section, we present the main scientific results of this paper. These are: the star formation main sequence (Sect. 3.1), the two projections of this relation, i.e., the stellar mass function (SMF, Sect. 3.2) and the Hα luminosity function (HαLF, Sect. 3.3), and the star formation rate density at d ≲ 75 Mpc (Sect. 3.4).
3.1. Star formation main sequence
In the upper left panel of Fig. 8, we present the relation between SFR and stellar mass for the Full sample. Both the SFR and M⋆, as well as their errors, had been computed with the routine that is described in Sect. 2.3. We found that a main trend appears, spanning from log M⋆ ∼ 7.5 up to log M⋆ ∼ 11. This main trend is accompanied by a secondary, parallel sequence, with lower SFR that appears at log M⋆ ∼ 9.5 up to log M⋆ ∼ 11. Between these two sequences, there is an underpopulated gap. We highlight the impact of the correlated errors in the observed relation. The dispersion of the points is largely smaller than the computed uncertainties if both variables are assumed independent. However, the ∼0.75 correlation between stellar mass and SFR, mainly driven by the shared distance, roughly moves the data along the observed relation and the dispersion is therefore dominated by the intrinsic variance in the properties of the galaxy sample, and not by the uncertainties in the measurements.
 |
Fig. 8. Star formation rate vs. stellar mass in the J-PLUS DR1 sample at d ≲ 75 Mpc. Upper left panel: relation for the Full sample (756 galaxies, bullets). The error bars provide the semi-major and semi-minor axis of the error ellipse, highlighting the covariance in the variables. The green dots mark the 49 AGN in the sample; these are shown here only with illustrative purposes, and are not taken into account when computing the main results of this work. Upper right panel: relation for the Full sample. The color of the points reflects the (u − g)pixp3 color of the galaxy, as scaled in the inner bar. Bottom left panel: relation for the Blue sample (689 galaxies). Bottom right panel: relation for the Red sample (67 galaxies). The solid line in both bottom panels is the best-fitting linear relation to the SFMS defined by the Blue sample. |
To provide more insight into the nature of the two observed sequences, we studied the (u − g) color of the sources, computed using the pixp3 catalog, in the upper right panel of Fig. 8. We found a clear gradient in color that is coupled to the gradient in stellar mass, being the most massive galaxies the reddest ones. At a fixed stellar mass of log M⋆ ∼ 10.5, the average color of galaxies in the primary sequence is (u − g)∼1.25, and in the secondary sequence is (u − g)∼1.80. This suggests a link between the two observed sequences with the Blue and Red samples defined in Sect. 2.4.3.
We found indeed that the Blue sample defines the canonical star formation main sequence (bottom left panel in Fig. 8). The characterization of the SFMS is presented in the next section. We also found that the secondary sequence is populated by the Red sample (bottom right panel in Fig. 8). This suggests a different origin for the star formation in these systems, as we will discuss latter.
3.1.1. Fitting the star formation main sequence
We fitted the SFMS defined by the Blue sample while we explored the parameter space in the Monte-Carlo routine (Sect. 2.3). Each time we perturbed the SFRs and stellar masses, we fitted a linear relation to the resulting distribution. The form of the equation that we fitted is the following:
The fitting was done using emcee (Foreman-Mackey et al. 2013), a Markov chain Monte-Carlo (MCMC) code. We used a set of 20 walkers, 500 steps, and a burn-in phase of 300 steps. In each iteration of the Monte-Carlo process, we saved 100 random values of a and b that the emcee walkers have sampled during the sampling phase. We emphasize that the fitting is not error-weighted. Instead, we fitted the linear relation using the resulting distribution of points after having been perturbed.
When the Monte-Carlo routine ends, we had 5 × 105 sampling points for each parameter, which we used to model the probability distribution function (PDF) of a and b, and the correlation between these two parameters. We present here the median and the NMAD values of the PDFs for a and b, which are used as error bars. The best-fitting parameters are:
The best-fitting SFMS is presented in the bottom panels of Fig. 8. We will put our results in the context of previous findings in Sect. 4.2. The dispersion of the data with respect to the best-fitting line, σ(SFR−SFRfit), is 0.25 dex, comparable with previous work (∼0.3 dex, Whitaker et al. 2012; Ilbert et al. 2015; Popesso et al. 2019b). To conclude, the best – fitting values for the SFMS if the Red sample is included are a = 0.73 ± 0.05 and b = −7.6 ± 0.50. As expected, the slope becomes flatter due to the presence of galaxies with low star formation rate at the high-mass end of the relation.
3.1.2. Ionization source in red galaxies
We found that the Red sample defines a lower SFR sequence with respect to the canonical SFMS traced by the Blue sample. One can argue that the Hα ionization source in these systems is not related with star-forming processes, and that AGN or post-AGB stars could account for the needed UV radiation field.
First, we had removed known AGN from our sample (Sect. 2.4.2), minimizing their possible impact. Second, the typical Hα equivalent width (EW) of diffuse gas ionized by post-AGB stars is EW ≤ 3 Å (Cid Fernandes et al. 2011; Kehrig et al. 2012; Gomes et al. 2016). The instrumental setup from J-PLUS impose an EW limit of 12 Å (VR15), so the Hα measurements are expected to be insensitive to post-AGB ionization.
The sequence of post-AGB ionized galaxies selected with Hα EW ≤ 3 Å is studied in detail by Cano-Díaz et al. (2019) using IFS data from the Mapping Nearby Galaxies at Apache Point Observatory (MaNGA, Bundy et al. 2015) survey. They find a clear sequence in the SFR vs. stellar mass space with a = 1.09, b = −13.0, and a dispersion of 0.18 dex. The near-unity slope is interpreted by the authors as a direct consequence of post-AGB stars being the main ionizing source, with the available UV flux scaling with the stellar mass of the galaxy. We checked that our Red sample is more than 3σ (0.6 dex) above the post-AGB ionization sequence in Cano-Díaz et al. (2019), reinforcing the star formation origin of our observed Hα flux. This is also supported by the derived stellar mass function of the Red sample (Sect. 3.2).
As a final remark, the star-forming and post-AGB ionized sources produce also two different populations in the spatially-resolved SFMS (e.g., Hsieh et al. 2017; Cano-Díaz et al. 2019). The J-PLUS DR1 sample analyzed in this paper is well suited for spatially-resolved studies, providing extra clues about the origin of the measured Hα flux. This issue will be addressed in a future work.
We conclude that the origin of the Hα flux observed in the Red sample is compatible with star formation, and therefore we will include it in the estimation of the Hα luminosity function (Sect. 3.3) and the star formation rate density (Sect. 3.4).
3.2. Stellar mass function
We now study the two main projections of the SFMS along its axis. These are: the Hα luminosity function, and the stellar mass function. The first one describes the number of sources that emit a given Hα luminosity, per unit volume, and per unit luminosity. The second one describes the number of sources with a given stellar mass, per unit volume and unit mass. The estimations from our data are tabulated in Appendix D.
To estimate the SMF, we used the stellar masses computed during the Monte-Carlo routine described in Sect. 2.3 and assumed a cosmological volume estimated from the unmasked area of 897.4 deg2 surveyed by J-PLUS DR1 coupled with a maximum probed distance of 75 Mpc. The reported errors only account for Poisson uncertainties in the counts.
The stellar mass function of the Blue and Red samples are presented in Fig. 9, and the data are provided in Table D.1. We found that the Red sample dominates at masses higher than log M⋆ ∼ 10.5, with the Blue sample being larger in number density below this mass. The maximum of the Blue sample SMF is reached at log M⋆ ∼ 8.9, then the number density decreases towards lower stellar masses.
 |
Fig. 9. Upper panel: stellar mass function for the Blue sample (blue dots) and the Red sample (red dots). Blue and Red solid lines represent the SMF for blue and red galaxies respectively, taken from Baldry et al. (2012). White diamonds and black circles represent the SMF of spectroscopic Hα emitters in GAMA, taken from Gunawardhana et al. (2015). Dashed blue and red lines represent the GAMA blue and red SMF from Baldry et al. (2012), but multiplied by the Blue sample incompleteness, presented in the lower panel. An extra 0.35 factor is also applied to the red SMF from Baldry et al. (2012) to match the observed fraction of red galaxies with spectroscopic Hα emission from Gunawardhana et al. (2015). Bottom panel: stellar mass completeness estimated form the comparison between GAMA blue galaxies and Blue sample SMF (cyan solid line). The purple line is the best-fitting Sigmoid function to the completeness, whose parameters are labeled in the panel. |
To interpret our results, we compared the SMF from J-PLUS with the SMF reported by Baldry et al. (2012) at z < 0.06 in the GAlaxy and Mass Assembly (GAMA, Driver et al. 2011) survey, both for red and blue galaxies as defined by the observed dichotomy in the GAMA (u − g) vs. Mr color–absolute magnitude diagram. We also included the SMF derived by Gunawardhana et al. (2015) in GAMA for spectroscopic star-forming Hα emitters, both red and blue (Fig. 9). We find that the SMF of the Blue sample is remarkably similar to blue SMFs from GAMA, both the general and the star-forming population. This suggests that our sample is probing a representative volume of the local Universe, and that the observed maximum in the stellar mass function reflects our completeness in the selection of blue, star-forming galaxies.
Given the good agreement between the J-PLUS and the GAMA SMFs, we used the Baldry et al. (2012) results to estimate the completeness of our sample. To do so, we divided the observed number counts inside each mass bin of our incomplete mass function by the predicted values from the Baldry et al. (2012) fitting. We found that the resulting distribution is well described by a Sigmoid function (bottom panel in Fig. 9),
where ℳ is the logarithm of the stellar mass at which the sample is 50% complete. We find ℳ = 8.48 and κ = 0.21, meaning that our sample is more than 50% complete in stellar mass at log M⋆ ≳ 8.5 and more than 95% complete at log M⋆ ≳ 9. This completeness is in agreement with the expectations from the surface brightness analysis presented in Fig. 6. Later, we use this relation to infer the Hα luminosity function weighting the number of sources by their incompleteness in stellar mass (Sect. 3.3.1).
The shape of the Red sample is also similar to the red SMF reported by Baldry et al. (2012) but with a difference in the normalization. We qualitatively matched both SMFs by multiplying the red SMF in Baldry et al. (2012) by a factor of 0.35 (Fig. 9). Moreover, the SMF of the Red sample closely resembles the Gunawardhana et al. (2015) results for red star-forming, Hα emitters. The shape and scale agreement with the spectroscopic Hα emitters from Gunawardhana et al. (2015) further supports the star-forming origin of the Hα emission for the Red sample, as already discussed in Sect. 3.1.2. In addition to the results from GAMA, Sobral et al. (2011) also find a significant population of red galaxies with Hα emission at z = 0.84. Our findings expand those in Sobral et al. (2011) and Gunawardhana et al. (2015) to the local volume.
Disentangling the physical origin of the Red sample is beyond of the scope of the present paper, and we explore the morphological properties of the Red and Blue samples in the companion paper by Logroño-Garcìa (in prep.) to get more clues on this regard.
3.3. Hα luminosity function in the local Universe
In this section, we present the star-forming Hα luminosity function derived from J-PLUS DR1 data at d ≲ 75 Mpc. We applied two different weighted schemes to account for volume and flux incompleteness, one based on the stellar mass function (Sect. 3.3.1) and the other on the Vint/Vmax technique (Sect. 3.3.2).
3.3.1. Mass-weighted Hα luminosity function
Like in previous sections, we used a Monte-Carlo approach to infer the mass-weighted HαLF. In this case, the root of the procedure remains the same than in Sect. 2.3. The main addition to the process is that, in each iteration of the Monte-Carlo sampling, and after computing the stellar masses of each galaxy, we fitted a Sigmoid function to the comparison between the resulting stellar mass distribution and the GAMA stellar mass function (Sect. 3.2). This fitting was used as a completeness proxy for that iteration of the process, and with it we computed a mass weight for each galaxy. These weights were used to create the mass-weighted distribution of Hα luminosities. We note that the mass weight can be used as a proxy for the Hα luminosity incompleteness because of the SFMS, that closely relate both quantities.
We present the J-PLUS HαLF at d ≲ 75 Mpc in the right panel of Fig. 10, and the data are provided in Table D.2. We proved luminosities of log LHα ≳ 39.5. We compute it for the Blue sample and the Full sample. Even if we find that the star formation properties of the Red and Blue sample are different, in both cases we are probing the current star formation in the source (Sects. 3.1.2 and 3.2). As expected from the results in Sect. 3.1, the Blue sample dominates the star-forming population at the faint end, and the Red sample increases the density of star-forming galaxies at the bright end.
 |
Fig. 10. Hα luminosity functions estimated from J-PLUS DR1 at z ≤ 0.017. Left panel: HαLF estimated by the Vint/Vmax technique from the Full sample (green dots), accompanied with the best-fitting Schechter distribution to these data (green line). The black line in this plot uses the same data, but a different weighting technique based on the Stellar Mass Function. Right panel: empty dots are the HαLF estimated using only the Blue sample, together with the best-fitting Schechter distribution to these data, once weighted by their stellar mass (blue line). For comparison we show the best Schechter fitting using the mass-weighted Full sample (black line, in common with left panel black line). We see that neither the weighting criteria nor the sample have a major impact on the best-fitting distribution. However, the mass-weighted samples allow us to explore 0.5 dex the faint-end slope of the distribution. |
We fitted the observed HαLFs with a Schechter (1976) distribution. This is expressed as
where ![$ L_{\mathrm{H}\alpha}^{*}\,\mathrm{[erg\,s^{-1}]} $](/articles/aa/full_html/2021/06/aa39156-20/aa39156-20-eq16.gif) , ϕ* [Mpc−3], and α are the parameters that define the distribution.
, ϕ* [Mpc−3], and α are the parameters that define the distribution.
This fitting was performed with emcee, using a sample of 20 walkers, 2000 sampling steps, and a burn-in phase of 1000 steps. We did this 600 times, and each time we stored 1000 sampling points. In the end, we had 600 000 sampling points to draw the PDF of each parameter in the Schechter distribution. The approach that we have described is convenient to take into account the potential degeneracy between the parameters. The resulting best-fitting parameters for the Full sample are:
We compare our values with previous work in the literature in Sect. 4.3.
3.3.2. Vint/Vmax Hα luminosity function
We re-computed the HαLF from a different approach, and we compare the results to the previous one. In this approach, we did not use the stellar masses to asses the incompleteness of a galaxy, and we used instead the classical Vint/Vmax technique described in Schmidt (1968) and Huchra & Sargent (1973). We explain the idea behind this correction in detail in Appendix C.
As a summary, for a given limiting Hα flux, the Vint/Vmax technique accounts for the larger volume probed by the more luminous galaxies, that can be observed to larger distances. This effect is coupled with the completeness in the Hα detection flux, that decreases the number of sources at faint fluxes. The stellar mass weight presented in Sect. 3.2 and applied in the previous section is intended to account for both effects, and we test here this assumption.
We found that the distribution in Hα flux has a plateau that starts around log FHα ∼ −13 (Fig. 5). For fainter emission fluxes, we are not able to recover all the sources. We set the limiting flux for the Vint/Vmax analysis in 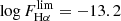 and varied it in the Monte-Carlo runs by ±0.1 dex and ±0.2 dex, so that in the end, the distribution had been fitted 250 times for each of the 5 different values of
and varied it in the Monte-Carlo runs by ±0.1 dex and ±0.2 dex, so that in the end, the distribution had been fitted 250 times for each of the 5 different values of 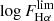 . To fit the Schechter distributions, we used the same emcee walkers and steps. This time, we ended up with 1 250 000 sampling points to describe the final best-fitting parameters, and their uncertainties.
. To fit the Schechter distributions, we used the same emcee walkers and steps. This time, we ended up with 1 250 000 sampling points to describe the final best-fitting parameters, and their uncertainties.
The derived HαLF for the Full sample is presented in the left panel of Fig. 10, together with the mass-weighted results in the previous section. We found an excellent agreement between both methodologies down to log LHα ∼ 40. The mass-weighted LF reach 0.5 dex fainter luminosities than the Vint/Vmax LF because of the completeness scheme used, that in addition to volume effects also include information about Hα flux incompleteness. Therefore, fluxes below 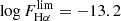 are used and fainter luminosities reached. As a reference, the average number of galaxies analyzed in the Vint/Vmax case is 325, that increases to 720 in the mass-weighted case.
are used and fainter luminosities reached. As a reference, the average number of galaxies analyzed in the Vint/Vmax case is 325, that increases to 720 in the mass-weighted case.
We conclude that the mass-weighted results in previous section are similar with the well established Vint/Vmax technique, but reaching 0.5 dex fainter luminosities.
3.3.3. Impact of AGN on the Hα luminosity function
The HαLFs presented in previous sections only refers to star-forming galaxies. However, we could include in this observable the Hα emission coming from galaxies targeted as AGN. In this case, the HαLF did not account for the origin of the Hα photons, being independent of the astrophysical process that causes them. Including 49 AGN in the analysis (Sect. 2.4.2), the robustness of the two methods would still hold, while our resulting best-fitting parameters in the mass-weighted case would have changed by +0.03 dex in 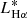 , +0.05 dex in ϕ*, and +0.04 in α. These changes are always compatible with the star-forming HαLF at 1σ level.
, +0.05 dex in ϕ*, and +0.04 in α. These changes are always compatible with the star-forming HαLF at 1σ level.
3.4. Star formation rate density
In this section, we aim to infer the value of the star formation rate density at d ≲ 75 Mpc. We defined the SFRD as
where ℒHα is the luminosity-weighted integral of the star-forming, mass-weighted HαLF estimated in Sect. 3.3.1,
where Γ is the Gamma function. We integrated down to zero to facilitate the computation and because the estimated α value implies a small contribution to the total density from the lower luminosities. As an example, integrating down to log LHα = 39.5 or 37 decreases the final density by 0.020 or 0.002 dex, respectively. In the end, we obtain
The retrieved error includes the statistical uncertainty (±0.04 dex) and the impact of cosmic variance (±0.10 dex), as detailed in the next section. We find that 15% (0.05 dex) of the SFRD is located in the Red sample. This is a significant contribution to the current star formation rate. We discuss this result and the relation with previous determinations in Sect. 4.4.
We now study the impact of cosmic variance in the determination of ρSFR. The cosmic or sample variance (CV) is the excess variance with respect to a Poissonian process that emerges from the clustered nature of galaxies (e.g., Somerville et al. 2004; Moster et al. 2011). The smaller the probed volume, the larger the impact of cosmic variance is, and measurements can significantly depart for the desired median value in the Universe. The volume at z ≤ 0.017 that is explored with the 897.4 deg2 of J-PLUS DR1 accounts for 34757.7 Mpc3. This is a relative small volume in a cosmological context, so the cosmic variance should impact our results.
The cosmic variance at a given luminosity is estimated as
where σdm is the cosmic variance of the underlying dark matter distribution that is common to any galaxy, and B (L) is the galaxy bias of the targeted population (Somerville et al. 2004; Moster et al. 2011; Robertson 2010; López-Sanjuan et al. 2015). In addition, the cosmic variance imprints a large correlation between galaxies of different luminosities, leading to significant off-diagonal terms in the covariance matrix (Σ) of the luminosity function (Smith 2012). Formally,
where ΣP accounts for the Poissonian uncertainties and
The correlation between different luminosities due to the cosmic variance is typically 0.4 − 0.8 (Smith 2012; López-Sanjuan et al. 2017; Kawinwanichakij et al. 2020). We decided to not include the cosmic variance in the analysis of the HαLF in Sect. 3.3 because the luminosity-dependent bias of Hα emitters in the local Universe is currently unknown to our best knowledge, and a proper cosmic variance analysis is therefore unfeasible.
The luminosity-weighted integral in Eq. (18) simplifies the problem, and the SFRD cosmic variance becomes equivalent to
where
is the number- and luminosity-weighted effective bias of the population under study. Because the peak of the Hα luminosity density occurs at 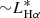 (Gunawardhana et al. 2013), the cosmic variance at this luminosity is a good proxy for the cosmic variance of the SFRD.
(Gunawardhana et al. 2013), the cosmic variance at this luminosity is a good proxy for the cosmic variance of the SFRD.
Following the reasoning above, we used the empirical prescription in Driver & Robotham (2010) as a proxy to estimate the impact of the cosmic variance in our determination of the SFRD, because it is based on 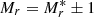 magnitude galaxies with mr ≲ 18 at z < 0.1. The cosmic variance is mainly driven by the probed cosmological volume, but the survey geometry also plays a relevant role. Assuming a squared, contiguous area, we estimated a 48% (0.17 dex) cosmic variance in J-PLUS DR1, while the addition of 511 independent square fields of 2 deg2 provides a 6% (0.02 dex) cosmic variance. These are two extreme values, and the actual J-PLUS footprint has several, large contiguous areas, with a fraction of scattered fields (see Cenarro et al. 2019). To better estimate the cosmic variance in our study, we split the J-PLUS DR1 area in a series of contiguous, nearly independent pieces, and estimated the cosmic variance in each one after accounting by their geometry. Then, we combined them under independence assumption following Moster et al. (2011). With this, we reached a 25% (0.10 dex) uncertainty introduced by cosmic variance for the J-PLUS DR1 at z ≤ 0.017.
magnitude galaxies with mr ≲ 18 at z < 0.1. The cosmic variance is mainly driven by the probed cosmological volume, but the survey geometry also plays a relevant role. Assuming a squared, contiguous area, we estimated a 48% (0.17 dex) cosmic variance in J-PLUS DR1, while the addition of 511 independent square fields of 2 deg2 provides a 6% (0.02 dex) cosmic variance. These are two extreme values, and the actual J-PLUS footprint has several, large contiguous areas, with a fraction of scattered fields (see Cenarro et al. 2019). To better estimate the cosmic variance in our study, we split the J-PLUS DR1 area in a series of contiguous, nearly independent pieces, and estimated the cosmic variance in each one after accounting by their geometry. Then, we combined them under independence assumption following Moster et al. (2011). With this, we reached a 25% (0.10 dex) uncertainty introduced by cosmic variance for the J-PLUS DR1 at z ≤ 0.017.
Compared with the statistical error of 0.04 dex, the cosmic variance is the leading source of uncertainty in our SFRD measurement.
4. Discussion
In the following sections, we compare our results about star formation in the local Universe with previous work in the literature. This will put our estimations in context, and permits the evaluation of possible systematic uncertainties in our measurements.
4.1. Systematic errors on Hα flux estimation
We start the discussion by looking at our Hα measurements. The extraction of Hα flux from J-PLUS photometry, including [N II] removal and dust de-reddening, is extensively tested in VR15 with synthetic data and in Logroño-García et al. (2019) with J-PLUS early data. The conclusion reached by these studies is that we are able to measure FHα without bias and with a minimum error of 20%, mainly driven by the statistical dust and [N II] corrections.
We expanded the analysis in the above papers with two extra tests. First, we repeated the study in Logroño-García et al. (2019) with the extended data provided by J-PLUS DR1. That added 99 new comparison regions with SDSS spectroscopic measurements. The total number of spectroscopic regions analyzed was 125 from SDSS and 20 from CALIFA. The obtained results mirrors the initial findings by Logroño-García et al. (2019), and we refer the reader to this work for extra information.
Second, we studied the distribution of Hα extinction, AHα, as a function of stellar mass (see Garn & Best 2010) in the Full sample, as shown in Fig. 11. This analysis was motivated by the large discrepancy in the median extinctions reported by Gallego et al. (1995), Nakamura et al. (2004), and Duarte Puertas et al. (2017); AHα ∼ 0.85, when compared with the median extinction in our sample, AHα ∼ 0.15. We find that our data closely follows the expected extinction vs. stellar mass relation estimated by Duarte Puertas et al. (2017) using aperture-corrected SDSS spectroscopic data (see also Gilbank et al. 2010; Garn & Best 2010), and that the apparent discrepancy in AHα is just a reflection of the lower stellar masses probed by our sample. This result strengths the statistical dust correction presented in VR15.
 |
Fig. 11. Relation between Hα extinction, AHα, and stellar mass in the Full sample. The red contours depict the 1, 2, and 3σ density of sources in SDSS spectroscopic data presented by Duarte Puertas et al. (2017). |
We conclude that the initial results from VR15 and Logroño-García et al. (2019) about the reliability and accuracy of the J-PLUS estimation of Hα fluxes have been reinforced with the analysis presented in this section.
4.2. Star formation main sequence
We compare here the estimation of the Blue sample SFMS with prior determinations in literature. The number of studies regarding the SFMS at low redshift (z ≲ 0.1) is large, and we present the comparisons with spectroscopic work based on Hα as SFR tracer in Fig. 12. The comparison with studies based on Hα imaging is presented in Fig. 13. The main characteristics of each study are summarized in Table 2. For this comparison, stellar masses and SFRs were converted to a Salpeter (1955) IMF.
 |
Fig. 12. Star-formation main sequence in J-PLUS (bullets and cyan line) and in previous work in the literature. The source papers are labeled in the panels and summarized in Table. 2. The draw lines cover the stellar mass range spanned by each study. |
Compilation of local (z < 0.1) SFMS based on Hα as star formation tracer.
We also accounted for the time evolution in the normalization of the SFMS down to our median redshift, z = 0.012, following the (1 + z)3.21 evolution found by Popesso et al. (2019a). We denoted such evolution as Δbz, and the assumed values are reported in Table 2. The use of other suggested evolution for the SFMS (i.e., Speagle et al. 2014) does not alter the conclusions in this section.
We focus first on spectroscopic studies from SDSS, GAMA, CALIFA, and MaNGA surveys. On the one hand, regardless of the study we compare with, there is strong consistency between our slope, a = 0.83, and prior determinations of this value, well constrained between a ∼ 0.7 and a ∼ 0.9. This robustness is also pointed out in the study by Cano-Díaz et al. (2016). On the other hand, the normalization factor shows more variance. In particular, this is the main source of discrepancy between our work and some previous fiber-based spectroscopic surveys. We consider that the most probable explanation for this difference is the aperture corrections.
Our image-based measurements, as well as most IFS surveys, do not require aperture corrections to obtain the total Hα flux of a galaxy. Those measurements based on fibers or long-slit spectroscopy demand an aperture correction to account for the missing Hα flux outside the available aperture (e.g., Brinchmann et al. 2004). The comparison of our SFMS with those derived with CALIFA (Cano-Díaz et al. 2016; Catalán-Torrecilla et al. 2017) and MaNGA (Belfiore et al. 2017; Cano-Díaz et al. 2019; Sánchez et al. 2019) data is satisfactory, while some of the fiber-based measurements from SDSS provide larger SFRs than expected by our measurements even after accounting for time evolution (Elbaz et al. 2007; Zahid et al. 2012; Lara-López et al. 2013). We note that the average redshift from IFS studies (z ∼ 0.02 − 0.03) is closer to our probed volume than those based on fiber spectroscopy (z ∼ 0.07). The studies of Renzini & Peng (2015) and Duarte Puertas et al. (2017) are also based on SDSS fiber measurements, and are in much better agreement with our results. We highlight the work of Duarte Puertas et al. (2017), that uses an improved aperture correction based on CALIFA data (Iglesias-Páramo et al. 2016) to recover the total flux from SDSS fiber spectroscopy. The excellent agreement with our SFMS supports their aperture correction.
We continue the discussion by comparing our results with the Hα imaging estimations from Gavazzi et al. (2013) and Gavazzi et al. (2015), as presented in Fig. 13. They are based on Hα3 survey data, and we use their g and i magnitudes when possible to estimate the stellar mass of the galaxies following Eq. (6). For a detailed explanation about Hα3 observations and Hα flux determinations, we refer the reader to Gavazzi et al. (2012). We find an excellent agreement with these studies, covering J-PLUS and Hα3 the same parameter space. It is apparent on the left panel in Fig. 13 that the Red sample population is also present in the Hα3 data, which is HI-selected from the HI Arecibo legacy fast ALFA (ALFALFA, Giovanelli et al. 2005) survey, so a prevalence of gas-rich, star-forming galaxies is expected. This supports that the Hα emission in the Red sample has a star-forming origin, as discussed in Sect. 3.1.2. We also note that the results from Gavazzi et al. (2015) on the right panel in Fig. 13 suggests a bending in the high-mass end (log M⋆ ≳ 10) of the SFMS. Such bending have been studied in several works (Lee et al. 2015; Popesso et al. 2019b), and it produces a lower slope (a ∼ 0.4) at the high-mass end than on less massive samples (a ∼ 0.8). The high-mass bending is also appreciable in our data when the Full sample is analyzed, but it is not apparent from the Blue sample alone. This implies that the Red sample composed by lower SFR galaxies has a measurable impact in the SFMS at the high-mass end. We also found that the result from Popesso et al. (2019b), estimated at log M⋆ ≥ 10, provides similar SFRs in the shared mass range despite the large difference in the slope between both studies (a = 0.83 vs. a = 0.34), warning about the direct comparison between the SFMS parameters obtained from the fitting to the data. Finally, we analyse the morphological properties of the Red sample in the forthcoming paper by Logroño-Garcìa (in prep.) to get further clues on this regard.
 |
Fig. 13. Star formation rate vs. stellar mass in the J-PLUS DR1 Full sample (bullets) in comparison with previous work based on Hα imaging. Left panel: results from Hα3 data in the Local Supercluster area (circles, Gavazzi et al. 2013), and for LSB galaxies at z ≤ 0.017 (triangles, McGaugh et al. 2017). Right panel: median log SFR as a function of stellar mass in the Local Supercluster and the Coma cluster derived by Gavazzi et al. (2015). The red solid line marks the median log SFR estimated from the Full sample. |
The data from McGaugh et al. (2017) probes the low surface brightness (LSB) regime. Interestingly, the LSB galaxies studied by McGaugh et al. (2017) cover the low SFR region of our SFMS. This suggests that our sample is not biased against LSB systems, reinforcing the surface brightness analysis presented in Sect. 2.4.1.
Finally, in Fig. 14, we compare our observational SFMS in the local Universe with the expectations from the cosmological hydro-dynamical simulations Illustris (Sparre et al. 2015) and IllustrisTNG (Donnari et al. 2019). These simulations probe galaxies with stellar masses larger than log M⋆ ≳ 9. We find an excellent agreement with the latest IllustrisTNG expectations. The predictions from the original Illustris suite over-predict the SFR at log M⋆ ≳ 10, as reported by Donnari et al. (2019), and are in agreement with our observations at lower stellar masses.
 |
Fig. 14. Star formation main sequence in J-PLUS (bullets and blue line) compared with the expectations from the cosmological hydro-dynamical simulations Illustris (Sparre et al. 2015, green line) and IllustrisTNG (Donnari et al. 2019, orange line). |
As summary, the comparison with previous SFMS estimations presented in this section support our results. We highlight the good agreement with IFS surveys and with the Hα imaging work of Gavazzi et al. (2013) and Gavazzi et al. (2015). The comparison of the stellar mass function in our sample with the local estimation from GAMA (Baldry et al. 2012) is detailed in Sect. 3.2, so we move to the Hα luminosity function in the next section.
4.3. Hα luminosity function
We compare now our HαLF with previous determinations. This is shown in Fig. 15, where we plot the data of each study transformed to our assumed cosmology. The Schechter parameters provided by some studies are listed in Table 3. For this comparison, we use the mass-weighted HαLF derived from the Full sample.
 |
Fig. 15. Hα luminosity function in J-PLUS DR1 at z ≤ 0.017 (black dashed line) and previous estimations from the literature at z ≤ 0.1. The source papers and their legends are labeled in the corresponding panels. |
Compilation of the Schechter parameters for local (z < 0.1) Hα luminosity functions.
The first comparison is with the work by Gunawardhana et al. (2013). We find that our distribution lies below their data. Given that their effective redshift is larger than ours (z ∼ 0.08), the samples are not directly comparable, as some time evolution is expected. In such case, their estimation can be assumed as an upper limit to our local determination. The same argument is valid for the values measured at the faint end (log LHα ≲ 40) by Ly et al. (2007).
We compare now our results with the studies by Gallego et al. (1995), based on the UCM Survey (Zamorano et al. 1994), and Nakamura et al. (2004), based on SDSS. Both studies are based on spectroscopic measurements of the Hα flux. We see in Table 3 that their best-fitting parameters show better consistency within them than with ours. On the one hand, we find our value of 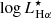 to be below theirs; on the other hand, our measurement of log ϕ⋆ is above. This behavior is expected due to the strong correlation that is found between both parameters.
to be below theirs; on the other hand, our measurement of log ϕ⋆ is above. This behavior is expected due to the strong correlation that is found between both parameters.
Being both studies spectroscopic in origin, they require aperture corrections to account for the Hα flux in the outer regions of the galaxy. The good agreement that we find with IFS surveys, as shown in Sect. 4.2, implies that our measurements are not biased on this regard. Other potential source of discrepancy is dust correction. The typical dust attenuation found by Gallego et al. (1995) and Nakamura et al. (2004) is AHα ∼ 0.85, significantly larger than the median extinction in our sample, AHα ∼ 0.15. However, we have shown in Sect. 4.1 that the estimated Hα attenuation in our sample follows the mass-to-extinction relation by Duarte Puertas et al. (2017) in SDSS. Thus, we believe that our dust correction is appropriate.
We move to the study from James et al. (2008), that estimate the HαLF in a d ≲ 40 Mpc sample using narrow-band imaging from the Hα galaxy survey (HαGS, James et al. 2004). The authors use the relation between B-band luminosity and SFR from HαGS to weight the B-band luminosity function in the local volume, obtaining the HαLF. They do not provide a Schechter fit to their data, shown in the bottom right panel at Fig. 15. Their values present an excellent agreement with our results within the common luminosity range, except for their highest luminosity point at log LHα = 42.1 with log Φ = −3.3. We note that to reach this number density in our surveyed volume, only two extra galaxies would be needed in our sample.
We find the strongest disagreement with the works by Westra et al. (2010) and Pérez-González et al. (2003). Despite the determination by Westra et al. (2010) is drawn from a sample that covers a similar redshift range to the one of Gunawardhana et al. (2013), in their case the HαLF lies significantly below our distribution at log LHα ≲ 41. However, it is worth noting that their work is based in observations of only 4 deg2, which points at cosmic variance as the main source of disagreement.
Conversely, the work by Pérez-González et al. (2003) presents the most discrepant value of 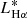 when compared to ours and also a deficit of log LHα ∼ 40 galaxies by 0.5 dex is noticeable. In their work, Pérez-González et al. (2003) use a sample of 79 galaxies drawn from a parent sample of 191 UCM Survey galaxies. The Hα fluxes of these galaxies are measured using narrow-band imaging, so no aperture correction is needed. However, we note that some of their galaxies present Hα luminosities that we do not find in our volume (log LHα ≥ 42, and even ≥42.5). In their study, they emphasize that the UCM Survey galaxies present enhanced star formation when compared with normal, quiescent spiral galaxies. Hence, part of the discrepancies with Pérez-González et al. (2003) and Gallego et al. (1995) could be attributed to the target pre-selection with objective prism spectroscopy (Zamorano et al. 1994).
when compared to ours and also a deficit of log LHα ∼ 40 galaxies by 0.5 dex is noticeable. In their work, Pérez-González et al. (2003) use a sample of 79 galaxies drawn from a parent sample of 191 UCM Survey galaxies. The Hα fluxes of these galaxies are measured using narrow-band imaging, so no aperture correction is needed. However, we note that some of their galaxies present Hα luminosities that we do not find in our volume (log LHα ≥ 42, and even ≥42.5). In their study, they emphasize that the UCM Survey galaxies present enhanced star formation when compared with normal, quiescent spiral galaxies. Hence, part of the discrepancies with Pérez-González et al. (2003) and Gallego et al. (1995) could be attributed to the target pre-selection with objective prism spectroscopy (Zamorano et al. 1994).
The HαLF comparison performed in this section reveals tension with previous estimations in the literature. The origin of such discrepancies is not fully understood. The main discrepant feature is our lower 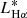 by ∼0.5 dex. This is caused by the lack of high-luminosity (i.e., high star-forming) galaxies in our sample. On top of the possible impact of cosmic evolution and target pre-selection in other studies, our probed cosmological volume could be not large enough to find the most extreme, sparse Hα emitters. As a reference, the cosmic volume covered by Gallego et al. (1995) is a factor of ten larger than ours. This factor increases to 85 in the case of Nakamura et al. (2004) and Gunawardhana et al. (2013). However, we can not discard that such extreme emitters are indeed absent at d ≲ 75 Mpc, suggesting a low star-formation rate environment for the Local Group.
by ∼0.5 dex. This is caused by the lack of high-luminosity (i.e., high star-forming) galaxies in our sample. On top of the possible impact of cosmic evolution and target pre-selection in other studies, our probed cosmological volume could be not large enough to find the most extreme, sparse Hα emitters. As a reference, the cosmic volume covered by Gallego et al. (1995) is a factor of ten larger than ours. This factor increases to 85 in the case of Nakamura et al. (2004) and Gunawardhana et al. (2013). However, we can not discard that such extreme emitters are indeed absent at d ≲ 75 Mpc, suggesting a low star-formation rate environment for the Local Group.
Irrespective of the evident discrepancies pointed out, the good agreement with the estimated SFMS from IFS and Hα imaging surveys (Sect. 4.2), and with the stellar mass function derived by Baldry et al. (2012) in the GAMA survey (Sect. 3.2), suggest that our data are representative of the star-forming population at d ≲ 75 Mpc.
4.4. Star formation rate density
In Sect. 3.4, we present our determination of the SFRD, obtained by integrating the HαLF. In Fig. 16, we present our measurement in the context of previous local determinations, as summarized in Table 4. We focus on studies based on Hα as SFR tracer, supplemented with the recent SED-fitting results from González Delgado et al. (2016), Driver et al. (2018), and Sánchez et al. (2019).
 |
Fig. 16. Star formation rate density at z ≤ 0.1. The blue dot shows the value from the local sample in J-PLUS DR1. The measurements (symbols) and the evolution parametrizations (lines) from the literature are depicted in the legend. |
Compilation of star formation rate densities at z ≤ 0.1.
We found that our measured log ρSFR = −2.10 ± 0.11 is at the lower envelope of previous estimations at z ≤ 0.1.
We start by comparing the J-PLUS DR1 value with the estimations from different SFRD evolution models (lines in Fig. 16). The functions from Hopkins & Beacom (2006), Madau & Dickinson (2014), Khostovan et al. (2015), and Davies et al. (2016) yield log ρSFR ∼ −1.85, while the functions from Fardal et al. (2007) and Sobral et al. (2013) provide log ρSFR ∼ −2.05. Our measurement is in agreement with the latter, and it is ∼0.25 dex below the former. Regarding individual observations, the values at z ≳ 0.05, that cluster at log ρSFR ∼ −1.8, can be reconciled within the expected evolution derived using the parametrization in Fardal et al. (2007).
Interestingly, the comparison with some of the most local values at z ≲ 0.05 can not be explained neither by cosmic evolution nor uncertainties in the measurements. The result from James et al. (2008) at d ≲ 40 Mpc is ∼0.4 dex larger than our value, log ρSFR ∈ [ − 1.80, −1.64]. The authors weights the observed B-band luminosity function by the SFR-to-luminosity ratio derived from a sub-sample of galaxies with Hα imaging, being their confidence interval lead by dust extinction uncertainties. They also replicate the process with a SDSS sample of blue galaxies, finding a smaller value at a larger effective redshift (log ρSFR = −1.89 at z ∼ 0.04). As we already discussed in Sect. 4.3, the HαLFs in both works are similar in the range log LHα ∈ [39.5, 41.6], with a higher number density in James et al. (2008) above log LHα > 41.6. Without making any assumptions for the analytical distribution of their HαLF, we estimated that this excess could account for ∼0.1 dex, moving their lower limit in SFRD to ρSFR ∼ −1.90, still at ∼2σ of the J-PLUS estimation.
The results from Hanish et al. (2006), Van Sistine et al. (2016) and Audcent-Ross et al. (2018) suggests log ρSFR ∼ −1.75, that is 0.3 dex larger than our value. These studies follow a similar approach to estimate the SFRD: starting for a sample of HI-selected galaxies, a sub-sample is followed with Hα imaging to estimate the relation between SFR and HI mass. Then, they integrate the HI mass function weighted with the previous SFR–HI mass relation to compute the SFRD. After carefully revising the data in Van Sistine et al. (2016), we find a significant density of galaxies with log SFR > 0.7 (their Fig. 13) that are not present in our sample. We argue that the relation between SFR and HI mass from J-PLUS data could be less step than in Van Sistine et al. (2016), mitigating the retrieved discrepancy. This is supported by the good agreement with Gavazzi et al. (2013) and Gavazzi et al. (2015) presented in Sect. 4.2, as their sample is HI-selected from ALFALFA as well. A detailed study of the SFR vs. HI mass relation is beyond the scope of the present paper, and we plan to address this issue in a future work.
The higher value found by Pérez-González et al. (2003) is explained by their larger 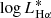 when compared with our measurements. We refer to reader to Sect. 4.3 for a detailed discussion.
when compared with our measurements. We refer to reader to Sect. 4.3 for a detailed discussion.
Finally, we highlight the agreement with the recent study of González Delgado et al. (2016) based on the SED-fitting analysis of CALIFA galaxies, that provides log ρSFR = −1.98 at z = 0.02. The understanding of the reasons behind the current tension between our local measurement and those at similar redshift will benefit of the estimation of the Hα-based SFRD from IFS surveys such as CALIFA and MaNGA, a missing piece of information to our best knowledge.
Regarding the ∼15% contribution of the Red sample to the total SFRD in the local Universe, other studies in the literature also point out the significant contribution of red and morphological early-type galaxies to the star-forming population at low redshift (e.g., Gunawardhana et al. 2015; López Fernández et al. 2018; Sánchez et al. 2019). We will analyze the morphology of the Blue and Red samples in the forthcoming paper by Logroño-Garcìa (in prep.).
We conclude that the star formation rate density from J-PLUS DR1 at d ≲ 75 Mpc favors the SFRD evolution proposed by Fardal et al. (2007) and Sobral et al. (2013). Further studies in the local Universe are needed to better understand the current discrepancies and provide a robust anchoring point for evolutionary studies.
5. Summary and conclusions
In this paper, we have used J-PLUS DR1 to obtain a representative collection of 805 Hα-emitting galaxies located at z ≤ 0.017 (d ≲ 75 Mpc). We have used this sample to study the star formation main sequence, and its two projections: the Hα luminosity function and the stellar mass function. With this information, we have determined the star formation rate density in the local Universe. The most relevant aspects and results of this work are:
-
The local sample comprises 49 AGN, 689 blue galaxies, and 67 red galaxies. The color classification was performed in the (u − g) vs. (g − z) color–color diagram, where our sample exhibits a bimodal distribution, computed from those pixels in J-PLUS images with signal-to-noise larger than three in Hα emission.
-
The star formation main sequence is clearly defined by the blue galaxies, with the red galaxies located below them. The SFMS is described as log SFR = 0.83log M⋆ − 8.44. We find a good agreement with previous SFMSs in the literature, specially those based on integral field spectroscopy.
-
The stellar mass function of our blue galaxies closely resembles the one from blue galaxies in the GAMA survey, while our red galaxies follows a downgraded version by a factor of 0.35 of the red stellar mass function presented in GAMA. This implies that our local sample is 95% complete for log M⋆ > 9 galaxies.
-
The Hα luminosity function is well described by a Schechter function with
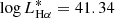 , log ϕ* = −2.43, and α = −1.25. We find a lower characteristic luminosity that several previous work in the literature.
, log ϕ* = −2.43, and α = −1.25. We find a lower characteristic luminosity that several previous work in the literature. -
The star formation rate density at d ≲ 75 Mpc is log ρSFR = −2.10 ± 0.11 for a Salpeter IMF. The red galaxies account for 15% of the local SFRD. This value favors the evolutionary fittings presented in Fardal et al. (2007) and Sobral et al. (2013).
We have computed these results in a consistent way, including in each step all the uncertainties, and accounting for the potential correlation between parameters.
The results presented along this paper show a good agreement with previous findings regarding the SFMS. However, the comparison of the HαLF reveals a lower 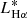 . We argue that this can be a real effect, being the local volume devoid of highly star-forming galaxies, or a sampling bias, being our surveyed volume unable to trace the sparse, high-luminosity population. Finally, our SFRD measurement is lower than most values at the same redshift. Further work is needed to understand the discrepancies and provide a robust anchoring point in the local Universe for evolutionary studies.
. We argue that this can be a real effect, being the local volume devoid of highly star-forming galaxies, or a sampling bias, being our surveyed volume unable to trace the sparse, high-luminosity population. Finally, our SFRD measurement is lower than most values at the same redshift. Further work is needed to understand the discrepancies and provide a robust anchoring point in the local Universe for evolutionary studies.
The analysis in this paper makes use of J-PLUS DR1 data. The covered area will be double in the future second data release, providing a test for the cosmic variance hypothesis about the lack of high-star forming systems in the current sample. This will be also possible with other large-area photometric surveys with narrow-band filters. We highlight the Census of the local Universe (CLU; Cook et al. 2019) survey, covering ∼26 700 deg2 down to m ∼ 19 with four filters of 8 nm width to explore Hα at z ≤ 0.047; and the Javalambre Physics of the Accelerating Universe Astrophysical Survey (J-PAS11, Benítez et al. 2014; Bonoli et al. 2020), that will cover ∼8500 deg2 down to m ∼ 22.5 with 56 filters of 14 nm width to study Hα emission at z ≲ 0.4. The combination of area and depth from J-PLUS and these surveys will provide important clues about the evolution of the SFRD in the last 2 Gyr of the Universe.
Acknowledgments
Based on observations made with the JAST/T80 telescope for J-PLUS project at the Observatorio Astrofísico de Javalambre in Teruel, a Spanish Infraestructura Cientifico-Técnica Singular (ICTS) owned, managed and operated by the Centro de Estudios de Física del Cosmos de Aragón (CEFCA). Data has been processed and provided by CEFCA’s Unit of Processing and Archiving Data (UPAD). Funding for the J-PLUS Project has been provided by the Governments of Spain and Aragón through the Fondo de Inversiones de Teruel; the Aragón Government through the Research Groups E96, E103, and E16_17R; the Spanish Ministry of Science, Innovation and Universities (MCIU/AEI/FEDER, UE) with grants PGC2018-097585-B-C21 and PGC2018-097585-B-C22; the Spanish Ministry of Economy and Competitiveness (MINECO) under AYA2015-66211-C2-1-P, AYA2015-66211-C2-2, AYA2012-30789, and ICTS-2009-14; and European FEDER funding (FCDD10-4E-867, FCDD13-4E-2685). The Brazilian agencies FINEP, FAPESP, and the National Observatory of Brazil have also contributed to this project. We thank the comments and suggestions of the referee, that improved the manuscript and the quality of the results. G.V.R. wants to thank A. and K. Gavin O’Shaughnessy for the language corrections. J.M.V. acknowledges financial support from the State Agency for Research of the Spanish MCIU through the “Center of Excellence Severo Ochoa” award to the Instituto de Astrofísica de Andalucía (SEV-2017-0709), and grant AYA2016-79724-C4-4P. R.A.D. acknowledges support from the Conselho Nacional de Desenvolvimento Científico e Tecnolágico – CNPq through BP grant 308105/2018-4, and the Financiadora de Estudos e Projetos – FINEP grants REF. 1217/13 – 01.13.0279.00 and REF 0859/10 – 01.10.0663.00 for hardware support for the J-PLUS project through the National Observatory of Brazil. We thank the help of Prof. G. Gavazzi in the analysis and understanding of Hα3 data. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013), and Matplotlib, a 2D graphics package used for Python for publication-quality image generation across user interfaces and operating systems (Hunter 2007). Some of the data sets discussed in the manuscript were recovered with WebPlotDigitizer (https://automeris.io/WebPlotDigitizer/index.html), a free software developed to facilitate easy and accurate data extraction from a variety of plot types.
References
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Audcent-Ross, F. M., Meurer, G. R., Wong, O. I., et al. 2018, MNRAS, 480, 119 [Google Scholar]
- Baldry, I. K., Driver, S. P., Loveday, J., et al. 2012, MNRAS, 421, 621 [NASA ADS] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belfiore, F., Maiolino, R., Tremonti, C., et al. 2017, MNRAS, 469, 151 [Google Scholar]
- Belfiore, F., Maiolino, R., Bundy, K., et al. 2018, MNRAS, 477, 3014 [Google Scholar]
- Benítez, N., Dupke, R., Moles, M., et al. 2014, ArXiv e-prints [arXiv:1403.5237] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonatto, C., Chies-Santos, A. L., Coelho, P. R. T., et al. 2019, A&A, 622, A179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonoli, S., Marín-Franch, A., Varela, J., et al. 2020, A&A, submitted [arXiv:2007.01910] [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bothwell, M. S., Kenicutt, R. C., Johnson, B. D., et al. 2011, MNRAS, 415, 1815 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Bershady, M. A., Law, D. R., et al. 2015, ApJ, 798, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Bunker, A. J., Warren, S. J., Hewett, P. C., & Clements, D. L. 1995, MNRAS, 273, 513 [Google Scholar]
- Calzetti, D. 2013, in Star Formation Rate Indicators eds. J. Knapen, & J. H. Falcón-Barroso, 419 [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cano-Díaz, M., Sánchez, S. F., Zibetti, S., et al. 2016, ApJ, 821, L26 [Google Scholar]
- Cano-Díaz, M., Ávila-Reese, V., Sánchez, S. F., et al. 2019, MNRAS, 488, 3929 [Google Scholar]
- Catalán-Torrecilla, C., Gil de Paz, A., Castillo-Morales, A., et al. 2017, ApJ, 848, 87 [Google Scholar]
- Cenarro, A. J., Moles, M., Marín-Franch, A., et al. 2014, Proc. SPIE, 9149, 91491I [Google Scholar]
- Cenarro, A. J., Moles, M., Cristóbal-Hornillos, D., et al. 2019, A&A, 622, A176 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cid Fernandes, R., Stasińska, G., Mateus, A., & Vale Asari, N. 2011, MNRAS, 413, 1687 [Google Scholar]
- Cook, D. O., Kasliwal, M. M., Van Sistine, A., et al. 2019, ApJ, 880, 7 [Google Scholar]
- Cucciati, O., Tresse, L., Ilbert, O., et al. 2012, A&A, 539, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davies, L. J. M., Driver, S. P., Robotham, A. S. G., et al. 2016, MNRAS, 461, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Donnari, M., Pillepich, A., Nelson, D., et al. 2019, MNRAS, 485, 4817 [Google Scholar]
- Driver, S. P., & Robotham, A. S. G. 2010, MNRAS, 407, 2131 [NASA ADS] [CrossRef] [Google Scholar]
- Driver, S. P., Hill, D. T., Kelvin, L. S., et al. 2011, MNRAS, 413, 971 [Google Scholar]
- Driver, S. P., Andrews, S. K., da Cunha, E., et al. 2018, MNRAS, 475, 2891 [NASA ADS] [CrossRef] [Google Scholar]
- Duarte Puertas, S., Vilchez, J. M., Iglesias-Páramo, J., et al. 2017, A&A, 599, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Efstathiou, G., Ellis, R. S., & Peterson, B. A. 1988, MNRAS, 232, 431 [Google Scholar]
- Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fardal, M. A., Katz, N., Weinberg, D. H., & Davé, R. 2007, MNRAS, 379, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallego, J., Zamorano, J., Aragon-Salamanca, A., & Rego, M. 1995, ApJ, 455, L1 [Google Scholar]
- Garn, T., & Best, P. N. 2010, MNRAS, 409, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., Fumagalli, M., Galardo, V., et al. 2012, A&A, 545, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, G., Fumagalli, M., Fossati, M., et al. 2013, A&A, 553, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, G., Consolandi, G., Dotti, M., et al. 2015, A&A, 580, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilbank, D. G., Baldry, I. K., Balogh, M. L., Glazebrook, K., & Bower, R. G. 2010, MNRAS, 405, 2594 [NASA ADS] [Google Scholar]
- Giovanelli, R., Haynes, M. P., Kent, B. R., et al. 2005, AJ, 130, 2598 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes, J. M., Papaderos, P., Kehrig, C., et al. 2016, A&A, 588, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González Delgado, R. M., Cid Fernandes, R., Pérez, E., et al. 2016, A&A, 590, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, G. M., Schlafly, E. F., Finkbeiner, D., et al. 2018, MNRAS, 478, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Gunawardhana, M. L. P., Hopkins, A. M., Bland-Hawthorn, J., et al. 2013, MNRAS, 433, 2764 [NASA ADS] [CrossRef] [Google Scholar]
- Gunawardhana, M. L. P., Hopkins, A. M., Taylor, E. N., et al. 2015, MNRAS, 447, 875 [Google Scholar]
- Hampel, F. R. 1974, J. Am. Stat. Assoc., 69, 383 [Google Scholar]
- Hanish, D. J., Meurer, G. R., Ferguson, H. C., et al. 2006, ApJ, 649, 150 [Google Scholar]
- Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [Google Scholar]
- Hsieh, B. C., Lin, L., Lin, J. H., et al. 2017, ApJ, 851, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J., & Sargent, W. L. W. 1973, ApJ, 186, 433 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias-Páramo, J., Vílchez, J. M., Rosales-Ortega, F. F., et al. 2016, ApJ, 826, 71 [Google Scholar]
- Ilbert, O., Arnouts, S., Le Floc’h, E., et al. 2015, A&A, 579, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izquierdo-Villalba, D., Angulo, R. E., Orsi, A., et al. 2019, A&A, 631, A82 [CrossRef] [EDP Sciences] [Google Scholar]
- James, P. A., Shane, N. S., Beckman, J. E., et al. 2004, A&A, 414, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- James, P. A., Knapen, J. H., Shane, N. S., Baldry, I. K., & de Jong, R. S. 2008, A&A, 482, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiménez-Teja, Y., Dupke, R. A., Lopes de Oliveira, R., et al. 2019, A&A, 622, A183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kawinwanichakij, L., Papovich, C., Ciardullo, R., et al. 2020, ApJ, 892, 7 [Google Scholar]
- Kehrig, C., Monreal-Ibero, A., Papaderos, P., et al. 2012, A&A, 540, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennicutt, R. C., Jr 1998, ARA&A, 36, 189 [Google Scholar]
- Khostovan, A. A., Sobral, D., Mobasher, B., et al. 2015, MNRAS, 452, 3948 [NASA ADS] [CrossRef] [Google Scholar]
- Lara-López, M. A., Hopkins, A. M., López-Sánchez, A. R., et al. 2013, MNRAS, 434, 451 [Google Scholar]
- Lee, N., Sanders, D. B., Casey, C. M., et al. 2015, ApJ, 801, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Leslie, S. K., Schinnerer, E., Liu, D., et al. 2020, ApJ, 899, 58 [Google Scholar]
- Lilly, S. J., Le Fevre, O., Hammer, F., & Crampton, D. 1996, ApJ, 460, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Logroño-García, R., Vilella-Rojo, G., López-Sanjuan, C., et al. 2019, A&A, 622, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López Fernández, R., González Delgado, R. M., Pérez, E., et al. 2018, A&A, 615, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Cenarro, A. J., Hernández-Monteagudo, C., et al. 2015, A&A, 582, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Tempel, E., Benítez, N., et al. 2017, A&A, 599, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Varela, J., Cristóbal-Hornillos, D., et al. 2019a, A&A, 631, A119 [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Vázquez Ramió, H., Varela, J., et al. 2019b, A&A, 622, A177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Díaz-García, L. A., Cenarro, A. J., et al. 2019c, A&A, 622, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ly, C., Malkan, M. A., Kashikawa, N., et al. 2007, ApJ, 657, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Ly, C., Lee, J. C., Dale, D. A., et al. 2011, ApJ, 726, 109 [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Maniyar, A. S., Béthermin, M., & Lagache, G. 2018, A&A, 614, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marin-Franch, A., Taylor, K., Cenarro, J., Cristobal-Hornillos, D., & Moles, M. 2015, IAU Gen. Assemb., 29, 2257381 [Google Scholar]
- McGaugh, S. S., Schombert, J. M., & Lelli, F. 2017, ApJ, 851, 22 [Google Scholar]
- Molino, A., Costa-Duarte, M. V., Mendes de Oliveira, C., et al. 2019, A&A, 622, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moster, B. P., Somerville, R. S., Newman, J. A., & Rix, H.-W. 2011, ApJ, 731, 113 [Google Scholar]
- Nakamura, O., Fukugita, M., Brinkmann, J., & Schneider, D. P. 2004, AJ, 127, 2511 [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [Google Scholar]
- Nogueira-Cavalcante, J. P., Dupke, R., Coelho, P., et al. 2019, A&A, 630, A88 [EDP Sciences] [Google Scholar]
- Novak, M., Smolčić, V., Delhaize, J., et al. 2017, A&A, 602, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-González, P. G., Zamorano, J., Gallego, J., Aragón-Salamanca, A., & Gil de Paz, A. 2003, ApJ, 591, 827 [Google Scholar]
- Popesso, P., Morselli, L., Concas, A., et al. 2019a, MNRAS, 490, 5285 [Google Scholar]
- Popesso, P., Concas, A., Morselli, L., et al. 2019b, MNRAS, 483, 3213 [Google Scholar]
- Renzini, A., & Peng, Y.-J. 2015, ApJ, 801, L29 [Google Scholar]
- Robertson, B. E. 2010, ApJ, 716, L229 [CrossRef] [Google Scholar]
- Salmon, B., Papovich, C., Finkelstein, S. L., et al. 2015, ApJ, 799, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- San Roman, I., Sánchez-Blázquez, P., Cenarro, A. J., et al. 2019, A&A, 622, A181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Marino, R. A., et al. 2012, A&A, 546, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., Avila-Reese, V., Rodríguez-Puebla, A., et al. 2019, MNRAS, 482, 1557 [Google Scholar]
- Santini, P., Fontana, A., Castellano, M., et al. 2017, ApJ, 847, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Schmidt, M. 1968, ApJ, 151, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. E. 2012, MNRAS, 426, 531 [Google Scholar]
- Sobral, D., Best, P. N., Smail, I., et al. 2011, MNRAS, 411, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Smail, I., Best, P. N., et al. 2013, MNRAS, 428, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Solano, E., Martín, E. L., Caballero, J. A., et al. 2019, A&A, 627, A29 [EDP Sciences] [Google Scholar]
- Somerville, R. S., Lee, K., Ferguson, H. C., et al. 2004, ApJ, 600, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Sparre, M., Hayward, C. C., Springel, V., et al. 2015, MNRAS, 447, 3548 [Google Scholar]
- Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Spinoso, D., Orsi, A., López-Sanjuan, C., et al. 2020, A&A, 643, A149 [EDP Sciences] [Google Scholar]
- Taylor, E. N., Hopkins, A. M., Baldry, I. K., et al. 2011, MNRAS, 418, 1587 [NASA ADS] [CrossRef] [Google Scholar]
- Tomczak, A. R., Quadri, R. F., Tran, K.-V. H., et al. 2016, ApJ, 817, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS] [Google Scholar]
- Van Sistine, A., Salzer, J. J., Sugden, A., et al. 2016, ApJ, 824, 25 [Google Scholar]
- Vilella-Rojo, G., Viironen, K., López-Sanjuan, C., et al. 2015, A&A, 580, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Westra, E., Geller, M. J., Kurtz, M. J., Fabricant, D. G., & Dell’Antonio, I. 2010, ApJ, 708, 534 [Google Scholar]
- Whitaker, K. E., van Dokkum, P. G., Brammer, G., & Franx, M. 2012, ApJ, 754, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Whitten, D. D., Placco, V. M., Beers, T. C., et al. 2019, A&A, 622, A182 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
- Zahid, H. J., Dima, G. I., Kewley, L. J., Erb, D. K., & Davé, R. 2012, ApJ, 757, 54 [Google Scholar]
- Zamorano, J., Rego, M., Gallego, J. G., et al. 1994, ApJ, 95, 387 [Google Scholar]
Appendix A: Estimation of redshift-independent distances
The purpose of this appendix is to explain how we assign uncertainties to redshift-independent distances. These uncertainties are the ones that we use in the Monte-Carlo sampling process, leading to the values of Hα luminosity and stellar masses upon which we derive all the results.
As we mentioned in Sect. 2.3.3, we first check the NED for redshift-independent distances. In the NED, these are given by the distance modulus, (m − M). In the case that a galaxy has multiple determinations of (m − M), we compile all of them, and their corresponding uncertainties, ϵ(m−M). Most of these are obtained using the Tully–Fischer relation (Tully & Fisher 1977), but a small percentage of them use other indicators, such as the tip of the Red Giant Branch, Cepheid variables, or Type Ia Super Novae.
After gathering the information from NED, each galaxy may have a different number of (m−M) measurements. Thus, for eachgalaxy we compute three statistics:
-
the median (m − M), which we refer to as ⟨(m−M)⟩,
-
the standard deviation of all the (m − M) values, referred to as σ(m−M),
-
the median uncertainty ϵ(m − M), which we refer to as ⟨ϵ(m−M)⟩.
To assign a final uncertainty to a distance measurement, we combine both the standard deviation and the median uncertainty, such that
We do this because the typical uncertainty in (m−M) is significantly larger than the standard deviation of a collection of (m−M) measurements. By compiling around 400 measurements from the NED12 we find that, regardless of the distance modulus, the median uncertainty converges to a value of δ(m−M) = 0.42.
Now, to convert distance moduli (m−M) to luminosity distances, dL, we use:
An expression for the error in distance computed with the distance moduli is obtained using the standard procedure of error propagation in Eq. (A.2), which leads to:
This means that the relative error budget of the distance obtained with this method is around a 20%:
In the end, we use ⟨(m−M)⟩ and Eq. (A.2) to compute the redshift-independent luminosity distance, and δ(m−M) and Eq. (A.3) to compute its uncertainty.
Appendix B: Impact of the distance algorithm in the results
In Sect. 2.3.3, we explain the algorithm that we use to assign distances and their uncertainties to our sample of galaxies. In this Appendix, we want to quantify the impact of the algorithm that we use, when compared to other possible choices for the distance.
B.1. Definition of the distance Runs
For this approach, we analyzed the exact same data in several different ways, that we will refer to as Runs. Some aspects are common to all the runs. These are:
-
All the Runs consist of 300 realizations to sample the parameter space following a Monte-Carlo approach.
-
In each of them, Hα fluxes are always perturbed with a random component drawn from a Gaussian distribution with σ = δFHα.
-
In all Runs, galaxies from Sample G0 (no information of the distance whatsoever) are assigned a random distance according to a volume prior.
-
Sample G1 galaxies are assigned a distance according to their spectroscopic redshift. This is perturbed with a term of peculiar velocity v′ that is drawn from a Gaussian distribution with μ = 0 and σ = vpeculiar, so each galaxy is perturbed with a different v′.
-
Galaxies with a redshift-independent distance, and below a certain distance limit (which we refer to as dlim in this section), are assigned their redshift-independent distance if d < dlim, and are perturbed with a term of noise that is drawn from a Gaussian distribution, with μ = 0 and σ = δd. The way we compute the uncertainty is explained in Appendix A.
-
Galaxies with a redshift-independent distance, but with d > dlim, are assigned a distance using their spectroscopic redshift, and perturbed like it is described in Step 4.
The main difference between each run is the way we assign distances to galaxies, and their uncertainties. We summarize the properties of each run in Table B.1, and briefly describe the motivation of each set of simulations.
Summary of the properties of each Run.
Run 0: This is the reference run, with which we obtain the values reported in the paper. We use vpeculiar = 750 km s−1 and dlim = 60 Mpc. The choice of these fiducial values is justified in Sect. 2.3.3.
Run 1, Run 2, Run 3, and Run 4: As can be seen in Table B.1, these set of Runs have all in common dlim = 0 Mpc, which means that we never use the redshift-independent distances. All galaxies are assigned a distance according to their spectroscopic redshift. The only difference between them is the vpeculiar that we use. In the case of Run 1, we do not perturb distances at all, except for those that do not have either a redshift-independent measurement or a spectroscopic redshift, which are assigned a random distance each iteration. This will help us asses the importance of our assumption of vpeculiar.
Run 7, Run 8, Run 9, and Run 10: Contrarily to the case of Runs 1, 2, 3, and 4, in these Runs we set dlim = ∞ Mpc, which means that whenever a galaxy has a redshift-independent distance, we use it regardless of the distance. These set of Runs provide insights into the impact of using distances imposing any cut in dlim, disregarding the fact that at some point errors in redshift-independent distances can dominate over redshift-derived ones and introduce extra uncertainty.
Run 5 and Run 6: These runs are the middle point between the two other cases, slightly closer to the set up for Run 0.
Non-tested combinations: There are combinations that have not been tested as they lack physical sense, or would only provide redundant information. For instance, we have not considered the cases where vpeculiar = 0 km s−1 and dlim = 40 Mpc or dlim = 60 Mpc. If we are going to assign errors to the sample with redshift-independent distance it had no point to not add errors to redshift-derived distances. On the other hand, if vpeculiar ≥ 1000 km s−1, the uncertainty that is introduced dominates over the error associated to redshift-independent distances. Hence, it has no sense to add a noise budget that is more likely to dominate over another source of uncertainty that is better constrained.
B.2. Results
We now compare the outcome of each run with the others to understand the impact of each assumption. We plot the values of 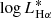 , α, log ϕ*, and log ρSFR in Fig. B.1, and present them in Table B.2.
, α, log ϕ*, and log ρSFR in Fig. B.1, and present them in Table B.2.
 |
Fig. B.1. Summary of the best-fitting parameters for the Mass-weighted, Full sample, Hα LFs, and SFMS, as a function of the Run. For the properties of each Run, see Table B.2. |
Impact of the distance assignment on the main parameters derived along this paper.
We find that our algorithm to assign distances does not have a major impact on the values of the Schechter distribution, or on its integral. All of the eleven Runs are in good agreement, and their dispersion is well constrained by the error bars of each estimation.
If we consider the two extreme cases, which are Runs 1 and 10, we find that they are not the most dissimilar. In fact, the most discrepant values appear when we compare Runs 1 and 4, which both belong to the set of Runs that never use redshift-independent distances. We see that the assumptions in vpeculiar are the ones that affect more the results, while the mixed methods (i.e., Runs 0, 5, and 6) retrieve almost the same results for each parameter, being their discrepancies insignificant compared to their error bars.
B.3. Impact of the distance assignment
In this appendix, we have studied the impact of our assumptions when assigning distances to galaxies. To do so, we have performed eleven different measurements, changing each time the value of the two free parameters that we considered in our model: these are the distance when redshift-based distances have smaller uncertainty than redshift independent measurements (dlim) and the peculiar velocity field from which we draw a perturbation for the spectroscopic redshifts, vpeculiar.
We find that all the values that we obtain are in good agreement within each other, leading us to conclude that our method to retrieve distances is not having a large impact in the results that have been presented in this paper.
Appendix C: Vint/Vmax correction
In Sect. 3.3, we have computed the HαLF using two different approaches: using the stellar mass function as a proxy for incompleteness, and assuming a correction based on the volume that we observe given our limit in Hα flux. In this Appendix we provide more insight into this correction, which is usually referred to as Vint/Vmax.
The core idea of this correction is to compensate for the Malmquist bias, which appears when one selects objects of fixed apparent magnitude (or, to put it in other words, with a cut in flux). The volume containing the more distant, intrinsically luminous objects is larger than the occupied by the nearer, intrinsically fainter ones. However, the most distant volume is poorly surveyed due to the fact that intrinsically fainter objects at large distances will have fluxes below our limiting flux. The Vint/Vmax technique aims to correct this effect in a way in which one does not require any a priori information, except the assumption that any sufficiently large sub-volume in your survey will be populated by objects with the same luminosity distribution. This is the weakest point of the method (see Efstathiou et al. 1988, for a detailed discussion on corrections). This technique is used in many studies to correct luminosity functions at different redshifts (Gallego et al. 1995; Pérez-González et al. 2003; James et al. 2008; Ly et al. 2011; Bothwell et al. 2011). Basically:
where L1 and L2 are the edges of the luminosity bin for which we want to compute the completeness, ΔL = L2 − L1, G(L) is a function defined as G(L) ≡ max[L1, Flim4πd2(z)], z1 = 0.001, and z2 is the maximum redshift were we would be able to detect a galaxy with luminosity L2 giving our limiting flux. More formally, and assuming a flat ΛCDM Universe (i.e., Ωk = 0):
where DH ≡ c/H0, and
Finally, the completeness for each luminosity bin is estimated as Vint/Vmax, where Vmax is the maximum available volume and it is estimated with G(L) = L1 and z2 = 0.017 in Eq. (C.1).
This correction is illustrated in Fig. C.1. It provides the fraction of volume that we can trace given a limiting flux, at each redshift. Decreasing the limiting flux to fainter values (i.e., going deeper in flux) would shift the solid curve of limiting luminosity along the Y axis towards fainter luminosities. Hence, a given luminosity bin would trace a larger volume.
 |
Fig. C.1. Luminosity associated to the limiting flux at each redshift. Solid curve: it represents the maximum luminosity that we are expected to see at each redshift. Yellow filled area: volume traced by all the galaxies that have a luminosity with a given luminosity bin, enclosed between L1 and L2 (horizontal solid lines). We refer to this volume as Vint Diagonally filled area: Total volume that would be traced without any limit in the minimum luminosity that we could observe. We refer to this as Vmax. |
Appendix D: Hα luminosity and stellar mass functions
In this appendix, we provide the numerical values of the stellar mass function for the Blue and Red samples computed in Sect. 3.2, Table D.1, and the mass-weighted Hα luminosity function computed form the Full sample in Sect. 3.3, Table D.2.
Mass function, divided into Blue and Red sample, expressed in Salpeter (1955) IMF. Corresponds with values in Fig. 9.
Mass-weighted, Full sample, Hα luminosity function.
All Tables
Redshift classification of the S/N ≥ 3 emitters in J0660 that lie within the region R1 inside the (J0515 − r) vs. (g − i) color–color diagram.
Compilation of the Schechter parameters for local (z < 0.1) Hα luminosity functions.
Impact of the distance assignment on the main parameters derived along this paper.
Mass function, divided into Blue and Red sample, expressed in Salpeter (1955) IMF. Corresponds with values in Fig. 9.
All Figures
 |
Fig. 1. Illustrative examples of the J-PLUS DR1 sample of local galaxies, presenting sources 26216-6250 (RA = 227.1397, Dec = 52.2960; UGC 9741 at zspec = 0.0083) and 26266-6298 (RA = 231.1995, Dec = 55.1277; there is no spectroscopic redshift for this source in the analyzed databases, see Sect. 2.2.2). The sky location of the sources is marked with a bullet in the left and central panels, and the white ellipse marks the three effective radii contour for the sources. Left panels: color composite of the galaxies, obtained from the gri J-PLUS images. Central panels: J0660 emission in units of σem, the dispersion of the pixels in the image (Sect. 2.3.1), as scaled in the color bar. This emission image has been obtained by applying the 3F methodology in VR15 to the r, J0660, and i J-PLUS images. Several star-forming knots are apparent. Right panels: J-PLUS twelve-band photometry (the SED) of those pixels with J0660 emission larger than σem (Sect. 2.3.1) and inside three effective radii. Squares show the five SDSS-like filters (ugriz), and circles the seven medium- and narrow-band filters (J0378, J0395, J0410, J0430, J0515, J0660, and J0861). The flux in J0660, J0515, and J0378 is raised with respect to the continuum level due to the Hα + [N II], [O III], and [O II] emission, respectively. The derived physical properties of the galaxies (Sects. 2.3.2 and 2.3.4) are labeled in the panels. |
| In the text | |
 |
Fig. 2. (J0515 − r) vs. (g − i) color–color diagram from ISO_GAUSS magnitudes of mr ≤ 18 sources with significant J0660 excess. Left panel: sources with no spectroscopic redshift in SDSS. Right panel: J0660 emitters, with spectroscopic redshift in SDSS. Cyan dots represent sources within our redshift of interest, while red dots are sources with higher redshift. The three regions defined to isolate low-z galaxies (R1), blended stars (R2), and high-z galaxies (R3) are labeled in the panel. |
| In the text | |
 |
Fig. 3. Representative example of a source in the region R2 (upper panel) and the region R3 (bottom panel) of the (J0515 − r) vs. (g − i) color–color diagram. In both panels, the J-PLUS ISO_GAUSS photometry of the source in shown, with symbols as in the right panels of Fig. 1. A color composite of the sources, obtained from the gri J-PLUS images, is presented in the insets. |
| In the text | |
 |
Fig. 4. Histogram of the ratio between the redshift-derived (dz) and the redshift-independent (dL) luminosity distance for galaxies in Sample G2 (orange histogram). The purple histogram represents the same, but for a sample of simulated galaxies distributed according to a volume prior and with a spectroscopic redshift that has been perturbed with a peculiar velocity term of vpeculiar = 750 km s−1. |
| In the text | |
 |
Fig. 5. General properties of the J-PLUS DR1 local sample at z ≤ 0.017. Upper left panel: distribution in the r-band apparent magnitude. The three sub-samples with different distance information are labeled in the panel (see Sect. 2.3.3, for details). Upper right panel: distribution in Hα flux. Lower left panel: redshift distribution of those galaxies in the sample with zspec. Lower right panel: Hα luminosity vs. redshift for those galaxies in the sample with zspec. The solid line marks the luminosity for a galaxy with log FHα = −13.2 as reference. |
| In the text | |
 |
Fig. 6. Mean r-band surface brightness within three effective radii, ⟨μr⟩, as a function of the stellar mass for the local sample of Hα emitters. The color scale shows the apparent magnitude of the sources. The hatched area marks a surface brightness larger than 24 mag arcsec−2. The vertical dotted line marks a stellar mass of log M⋆ = 9. |
| In the text | |
 |
Fig. 7. (u − g) vs. (g − z) color–color diagram of our local galaxy sample computed from pixels with signal-to-noise higher than 3 (pixp3; left panel) and higher than −5 (i.e., total colors, labeled as pixm5; right panel) in the Hα detection images. The colored contours show the density of sources to highlight the presence of local maxima. The dotted lines in the left panel mark our selection for the Red sample (red area), the Blue sample being the complementary set (blue area). The upper- and right-side normalized histograms are the density projections in (g − z) and (u − g), respectively. The red and blue shaded histograms in both panels mark the Red and Blue samples selected with pixp3 colors. |
| In the text | |
 |
Fig. 8. Star formation rate vs. stellar mass in the J-PLUS DR1 sample at d ≲ 75 Mpc. Upper left panel: relation for the Full sample (756 galaxies, bullets). The error bars provide the semi-major and semi-minor axis of the error ellipse, highlighting the covariance in the variables. The green dots mark the 49 AGN in the sample; these are shown here only with illustrative purposes, and are not taken into account when computing the main results of this work. Upper right panel: relation for the Full sample. The color of the points reflects the (u − g)pixp3 color of the galaxy, as scaled in the inner bar. Bottom left panel: relation for the Blue sample (689 galaxies). Bottom right panel: relation for the Red sample (67 galaxies). The solid line in both bottom panels is the best-fitting linear relation to the SFMS defined by the Blue sample. |
| In the text | |
 |
Fig. 9. Upper panel: stellar mass function for the Blue sample (blue dots) and the Red sample (red dots). Blue and Red solid lines represent the SMF for blue and red galaxies respectively, taken from Baldry et al. (2012). White diamonds and black circles represent the SMF of spectroscopic Hα emitters in GAMA, taken from Gunawardhana et al. (2015). Dashed blue and red lines represent the GAMA blue and red SMF from Baldry et al. (2012), but multiplied by the Blue sample incompleteness, presented in the lower panel. An extra 0.35 factor is also applied to the red SMF from Baldry et al. (2012) to match the observed fraction of red galaxies with spectroscopic Hα emission from Gunawardhana et al. (2015). Bottom panel: stellar mass completeness estimated form the comparison between GAMA blue galaxies and Blue sample SMF (cyan solid line). The purple line is the best-fitting Sigmoid function to the completeness, whose parameters are labeled in the panel. |
| In the text | |
 |
Fig. 10. Hα luminosity functions estimated from J-PLUS DR1 at z ≤ 0.017. Left panel: HαLF estimated by the Vint/Vmax technique from the Full sample (green dots), accompanied with the best-fitting Schechter distribution to these data (green line). The black line in this plot uses the same data, but a different weighting technique based on the Stellar Mass Function. Right panel: empty dots are the HαLF estimated using only the Blue sample, together with the best-fitting Schechter distribution to these data, once weighted by their stellar mass (blue line). For comparison we show the best Schechter fitting using the mass-weighted Full sample (black line, in common with left panel black line). We see that neither the weighting criteria nor the sample have a major impact on the best-fitting distribution. However, the mass-weighted samples allow us to explore 0.5 dex the faint-end slope of the distribution. |
| In the text | |
 |
Fig. 11. Relation between Hα extinction, AHα, and stellar mass in the Full sample. The red contours depict the 1, 2, and 3σ density of sources in SDSS spectroscopic data presented by Duarte Puertas et al. (2017). |
| In the text | |
 |
Fig. 12. Star-formation main sequence in J-PLUS (bullets and cyan line) and in previous work in the literature. The source papers are labeled in the panels and summarized in Table. 2. The draw lines cover the stellar mass range spanned by each study. |
| In the text | |
 |
Fig. 13. Star formation rate vs. stellar mass in the J-PLUS DR1 Full sample (bullets) in comparison with previous work based on Hα imaging. Left panel: results from Hα3 data in the Local Supercluster area (circles, Gavazzi et al. 2013), and for LSB galaxies at z ≤ 0.017 (triangles, McGaugh et al. 2017). Right panel: median log SFR as a function of stellar mass in the Local Supercluster and the Coma cluster derived by Gavazzi et al. (2015). The red solid line marks the median log SFR estimated from the Full sample. |
| In the text | |
 |
Fig. 14. Star formation main sequence in J-PLUS (bullets and blue line) compared with the expectations from the cosmological hydro-dynamical simulations Illustris (Sparre et al. 2015, green line) and IllustrisTNG (Donnari et al. 2019, orange line). |
| In the text | |
 |
Fig. 15. Hα luminosity function in J-PLUS DR1 at z ≤ 0.017 (black dashed line) and previous estimations from the literature at z ≤ 0.1. The source papers and their legends are labeled in the corresponding panels. |
| In the text | |
 |
Fig. 16. Star formation rate density at z ≤ 0.1. The blue dot shows the value from the local sample in J-PLUS DR1. The measurements (symbols) and the evolution parametrizations (lines) from the literature are depicted in the legend. |
| In the text | |
 |
Fig. B.1. Summary of the best-fitting parameters for the Mass-weighted, Full sample, Hα LFs, and SFMS, as a function of the Run. For the properties of each Run, see Table B.2. |
| In the text | |
 |
Fig. C.1. Luminosity associated to the limiting flux at each redshift. Solid curve: it represents the maximum luminosity that we are expected to see at each redshift. Yellow filled area: volume traced by all the galaxies that have a luminosity with a given luminosity bin, enclosed between L1 and L2 (horizontal solid lines). We refer to this volume as Vint Diagonally filled area: Total volume that would be traced without any limit in the minimum luminosity that we could observe. We refer to this as Vmax. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



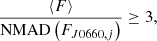
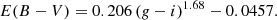
![$$ \begin{aligned} F_{\mathrm{H} \alpha +\mathrm [{\text{ N}}{\small {{\text{ II}}}}] } = F_{\rm obs} 10^{0.4\,E(B-V)\,k\prime }\quad \mathrm{[erg\,s^{-1}\,cm^{-2}]}, \end{aligned} $$](/articles/aa/full_html/2021/06/aa39156-20/aa39156-20-eq5.gif)
![$$ \begin{aligned} \log F_{\mathrm{H} \alpha } = {\left\{ \begin{array}{ll} 0.989\log (F_{\mathrm{H} \alpha +\mathrm [{\text{ N}}{\small {{\text{ II}}}}] } )-0.193,&\text{ if} g-i \le 0.5, \\ 0.954\log (F_{\mathrm{H} \alpha +\mathrm [{\text{ N}}{\small {{\text{ II}}}}] } )-0.753,&\text{ if} g-i > 0.5. \end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2021/06/aa39156-20/aa39156-20-eq6.gif)
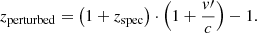
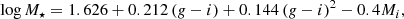
![$$ \begin{aligned} L_{\mathrm{H} \alpha } = 4\pi d^2\,C(q, T)\,F_{\mathrm{H}\alpha }\quad \mathrm{[erg\,s^{-1}]}, \end{aligned} $$](/articles/aa/full_html/2021/06/aa39156-20/aa39156-20-eq9.gif)
![$$ \begin{aligned} \mathrm{SFR} = 7.9\cdot 10^{-42}\,L_{\mathrm{H} \alpha }\quad [M_{\odot }\,\mathrm{yr}^{-1}], \end{aligned} $$](/articles/aa/full_html/2021/06/aa39156-20/aa39156-20-eq10.gif)
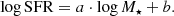
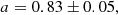
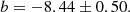
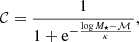
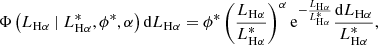
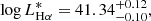
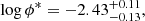
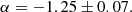
![$$ \begin{aligned} \rho _{\mathrm{SFR} } = 7.9\times 10^{-42} \mathcal{L} _{\mathrm{H}\alpha }\quad [M_{\odot }\,\mathrm yr^{-1}\,Mpc^{-3}] , \end{aligned} $$](/articles/aa/full_html/2021/06/aa39156-20/aa39156-20-eq24.gif)
![$$ \begin{aligned} \mathcal{L} _{\mathrm{H} \alpha } = \int _{0}^{\infty }\!\!\!\Phi \left( L_{\mathrm{H} \alpha } \right) L_{\mathrm{H} \alpha } \mathrm{d}L_{\mathrm{H} \alpha } = \phi ^* L_{\rm {H}\alpha }^* \Gamma (\alpha + 2)\,\quad \mathrm [erg\,s^{-1}\,Mpc^{-3}] , \end{aligned} $$](/articles/aa/full_html/2021/06/aa39156-20/aa39156-20-eq25.gif)
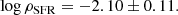
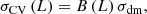
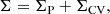
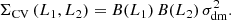
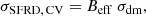
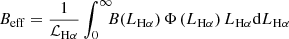
![$$ \begin{aligned} \delta \left(m-M\right) = \sqrt{ \langle \epsilon \left( m-M \right)\rangle ^{2} + \left[ \sigma \left( m-M \right)\right]^{2} } . \end{aligned} $$](/articles/aa/full_html/2021/06/aa39156-20/aa39156-20-eq46.gif)
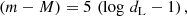
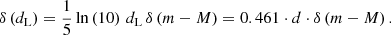
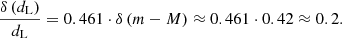
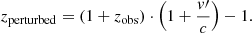
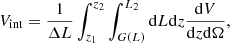
![$$ \begin{aligned} \frac{\mathrm{d}V}{\mathrm{d}z\mathrm{d}\Omega } = D_{H}^{3} \frac{1 }{ E\left(z\right)} \left[ \int _{0}^{z\prime } \frac{\mathrm{d}z\prime }{E\left(z\prime \right)} \right], \end{aligned} $$](/articles/aa/full_html/2021/06/aa39156-20/aa39156-20-eq121.gif)