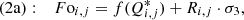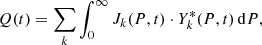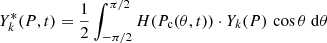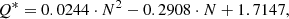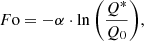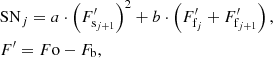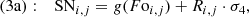| Issue |
A&A
Volume 649, May 2021
|
|
|---|---|---|
| Article Number | A141 | |
| Number of page(s) | 13 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202140711 | |
| Published online | 28 May 2021 | |
Solar cyclic activity over the last millennium reconstructed from annual 14C data⋆
1
Space Physics and Astronomy Research Unit and Sodankylä Geophysical Observatory, University of Oulu, Oulu, Finland
e-mail: Ilya.Usoskin@oulu.fi
2
Max Planck Institute for Solar System Research, Justus-Von-Liebig-Weg 3, 37077 Göttingen, Germany
3
Ioffe Physical-Technical Institute, St. Petersburg, Russia
4
Laboratory of Ion Beam Physics, ETH-Zürich, Zürich, Switzerland
5
Institute of Environmental Physics, Heidelberg University, Heidelberg, Germany
6
School of Space Research, Kyung Hee University, Yongin, Gyeonggi-Do 446 701, Republic of Korea
Received:
3
March
2021
Accepted:
27
March
2021
Aims. The 11-year solar cycle (Schwabe cycle) is the dominant pattern of solar magnetic activity reflecting the oscillatory dynamo mechanism in the Sun’s convection zone. Solar cycles have been directly observed since 1700, while indirect proxy data suggest their existence over a much longer period of time, but generally without resolving individual cycles and their continuity. Here we reconstruct individual solar cycles for the last millennium using recently obtained 14C data and state-of-the-art models.
Methods. Starting with the 14C production rate determined from the so far most precise measurements of radiocarbon content in tree rings, solar activity was reconstructed in the following three physics-based steps: (1) correction of the 14C production rate for the changing geomagnetic field; (2) computation of the open solar magnetic flux; and (3) conversion into sunspot numbers outside of grand minima. All known uncertainties, including both measurement and model uncertainties, were straightforwardly accounted for by a Monte-Carlo method.
Results. Cyclic solar activity is reconstructed for the period 971–1900 (85 individual cycles) along with its uncertainties. This more than doubles the number of solar cycles known from direct solar observations. We found that the lengths and strengths of well-defined cycles outside grand minima are consistent with those obtained from the direct sunspot observations after 1750. The validity of the Waldmeier rule (cycles with fast-rising phase tend to be stronger) is confirmed at a highly significant level. Solar activity is found to be in a deep grand minimum when the activity is mostly below the sunspot formation threshold for about 250 years. Therefore, although considerable cyclic variability in 14C is seen even during grand minima, individual solar cycles can hardly be reliably resolved therein. Three potential solar particle events, ca. 994, 1052, and 1279 AD, are shown to occur around the maximum phases of solar cycles.
Conclusions. A new approximately 1000-year-long solar activity reconstruction, in the form of annual (pseudo) sunspot numbers with the full assessment of all known uncertainties, is presented based on new high-precision Δ14C measurements and state-of-the-art models, more than doubling the number of individually resolved solar cycles. This forms a solid basis for new, more detailed studies of solar variability.
Key words: Sun: activity / sunspots
Tabular data of the reconstructed activity are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/649/A141
© ESO 2021
1. Introduction
Cyclic variability with a period of about 11 years (Schwabe cycle) is the dominant pattern of solar magnetic activity (Hathaway 2015) reflecting the oscillating dynamo mechanism in the solar convection zone (Charbonneau 2020). However, the 11-year cycle is far from a perfect sine-wave and varies both in magnitude and length on a longer timescale (Usoskin 2017). Historically, the most common and the longest index of solar magnetic activity has been the synthetic sunspot number (SN) based on direct solar observations by a cohort of astronomers worldwide since 1610 (Vaquero et al. 2016). Although the SN series is somewhat uncertain before ca. 1900 (Clette et al. 2014), it clearly depicts the dominance of the Schwabe cyclicity and its variability.
The overall level of solar activity and its secular variability over the last ten millennia has been reconstructed from decadaly resolved cosmogenic radioisotopes 14C and 10Be (Solanki et al. 2004; Usoskin et al. 2004, 2016; Vonmoos et al. 2006; Delaygue & Bard 2011; Steinhilber et al. 2012; Wu et al. 2018b), but the 11-year cycle cannot be resolved from these data sets. Still, the existence of the 11-year solar cycle before 1610 can be found from cosmogenic radioisotopes for some periods (e.g., Miyake et al. 2013b; Güttler et al. 2013; Muscheler et al. 2016) with special emphasis on the 11-year cycle during grand minima (Beer et al. 1998; Miyahara et al. 2004; Moriya et al. 2019; Fogtmann-Schulz et al. 2019, 2020). The existence of climate cyclicity with an appropriate period was also found in fossil data for previous epochs (e.g., Luthardt & Rößler 2017; Li et al. 2018). However, the continuity of the 11-year cyclicity was not proven as most of those studies were based on spectral analyses of the data (e.g., Eastoe et al. 2019), showing spectral peaks in the range of 10–12 years, but they did not resolve individual solar cycles. Therefore, until recently, we only knew about individual solar cycles for the last 410 years since 1610, including a ≈70-year spotless period of the Maunder minimum.
A major breakthrough has been made by Brehm et al. (2021) who measured annually-resolved Δ14C in tree rings for the last millennium since the mid-tenth century, with unprecedented accuracy. This data set reveals continuous solar cycles for the last millennium, at least outside of the grand solar minima, and it displays three abrupt enhancements potentially associated with solar particle events (SPEs): one known event in 994 AD (Miyake et al. 2013a) and two new ones in 1052 and 1279 AD. Brehm et al. (2021) provide an estimate of the solar modulation potential ϕ, which characterises the flux intensity of galactic cosmic rays, but whose physical interpretation is unclear (Caballero-Lopez & Moraal 2004; Usoskin et al. 2005; Herbst et al. 2010; Asvestari et al. 2017a). It is not straightforward to convert ϕ into quantities useful for Sun-Earth relations, such as solar magnetic flux or solar irradiance.
Here we provide, for the first time, a physics-based quantitative reconstruction of solar magnetic activity since 971 AD at a cadence that allows individual solar cycles to be resolved. Provided quantities are open solar magnetic flux (OSF, henceforth denoted as Fo) and the SN (at least for the times outside deep grand minima). Within the grand minima, we provide solar activity in the form of pseudo-SNs, as described below. The reconstruction includes a sequence of model steps, each based on the up-to-date knowledge of the physical processes involved and the related uncertainties. We emphasise that the reconstruction does not involve any freely tunable ad hoc parameters or normalisation since all model parameters were determined independently of this reconstruction.
2. Data
The series of the production rate of radiocarbon (denoted as Q henceforth) data for 971–1900 with uncertainties was obtained from Brehm et al. (2021) who computed it from the measured annual Δ14C measurements with a pseudo-monthly resolution applying the most recent carbon-cycle box model (Büntgen et al. 2018) and correcting for the Suess effect (dilution of atmospheric concentration of 14C because of the fossil fuel burning since the late 19th century). It is consistent with the earlier decadal 14C production rate (Roth & Joos 2013), but it resolves individual solar cycles. This data set contains several short 1-year interpolations corresponding to gaps in the raw Δ14C data set (1203, 1277, 1304, 1309, 1312, 1578, 1645, 1702, and 1715) and one longer gap (6 years between 1043 and 1048). The solar cycle corresponding to the latter gap is marked as unreliable. During the analysed period, an extreme solar event occurred at ca. 994 (Mekhaldi et al. 2015; Miyake et al. 2013a) that may distort the 14C production. The effect of this event was removed by subtracting the modelled production of ΔQ = 3.9 at cm−2 s−1 (Mekhaldi et al. 2015) spread over the years 992, 993, and 994 as 1, 1.9, and 1 at cm−2 s−1, respectively, before further analysis. Similarly we removed the potential events of 1052 considered as a 0.65 × 994 AD event, starting in 1051, and 1279, considered as a 0.8 × 994 AD event, starting in 1279 (see Brehm et al. 2021). However, since the exact strength of these events is not well-known yet, we mark the corresponding cycles as not well-defined. The effect of removing these events is shown in Sect. 3.5. Because of the high level of noise in the Q-series, it was slightly smoothed (Savitzky-Golay filter of order three and frame length nine) before further processing. This Q-series is shown in Fig. 1.
 |
Fig. 1. 14C production rate Q (black curve) with 1σ uncertainties, obtained from Brehm et al. (2021), used here after corrections for the 994, 1052, and 1279 AD events and smoothing (see Sect. 2). The green RJ13 curve depicts Q from Roth & Joos (2013). |
3. The method
The method of sunspot activity reconstruction consists of three consecutive steps,
each was performed 10 000 times in a Monte-Carlo (MC) procedure as described below. Henceforth, the index i denotes the number of the realisation and j is the year within the time series (j = 1 corresponds to 971 AD).
3.1. Step (1): Reducing Q to the modern geomagnetic field
To remove the effect of the variable geomagnetic shielding, we reduced the production rate Q, obtained by Brehm et al. (2021), to Q* corresponding to that for the reference geomagnetic field with the fixed dipole moment M0. The following sub-steps were used:
First (step 1a), one out of the four archeomagnetic models, namely U16 (Usoskin et al. 2016), COV (Hellio & Gillet 2018), pfm9k.1b (Nilsson et al. 2014), or SHA (Pavón-Carrasco et al. 2014), was randomly chosen for each realisation i. These models (shown in Fig. 2) were selected to represent the diversity of the main groups working in paleo- and archeo-magnetic reconstructions, and they cover the full range of uncertainties of archaeomagnetic models for the last millennium. As the reference geomagnetic field, we have considered recent IGRF (IGRF model – Thébault et al. 2015) conditions with the dipole moment M0 = 7.75⋅1022 A m2, corresponding to the time when cosmic-ray spectra were directly measured in space (see Step 3).
 |
Fig. 2. Time variability of the virtual axial dipole moment (VADM) as presented in archeomagnetic models considered here, U16 (Usoskin et al. 2016), COV-ARCH (Hellio & Gillet 2018), pfm9k.1b (Nilsson et al. 2014), and SHA (Pavón-Carrasco et al. 2014). |
The reduction (step 1b) to the reference field M0 was performed using computations based on the Galactic cosmic-ray (GCR) spectra directly measured during the last decade (see Sect. 3.2.1 for more details). Using the measured spectra as input, we computed (using the production model by Poluianov et al. 2016) expected values of Q(M) for different values of the geomagnetic dipole moment M. The relation between Q(M) and Q* corresponding to the modern geomagnetic field is shown in Fig. 3, which covers a modulation range of Q corresponding to a full solar cycle. One can see that the relation is almost perfectly linear. Thus, Q-values at time t at which the dipole moment is M(t) can be converted into the production rate at the modern value M0 = 7.75 ⋅ 1022 A m2, as Q*(t) = h(QM(t)), where h is an appropriate linear relation as shown in Fig. 3. The production rate Q* reduced to the modern M0 is shown in Fig. 4.
 |
Fig. 3. Dependence between Q-values computed for different geomagnetic dipole moments M, as denoted in the legend in units of ⋅1022 A m2 and Q* at the modern-day value of M0 = 7.75⋅1022 A m2. GCR spectra directly measured by AMS for May 2011 through May 2017 (see Sect. 3.2.1) were used when calculating Q-values. |
 |
Fig. 4. Radiocarbon production rate Q* reduced to the modern geomagnetic shielding (M0 = 7.75 1022 A m2) with 1σQ* errors. |
3.2. Step (2): Open flux
This step includes conversion of the 14C production rate Q* (reduced to the reference conditions) to the open solar magnetic flux Fo:
where f is a functional relating Q* to Fo (see Eq. (6)), Ri, j is a normally distributed random number with zero mean and unity standard deviation, and σ3 is the uncertainty of the conversion (see below). The method used here to reconstruct the open solar flux (OSF) Fo from Q* is described below. In contrast to earlier works, it is based on direct cosmic-ray measurements over the last decades.
3.2.1. Use of direct space-era data
All previous models of cosmogenic isotope production were based on theoretically modelled GCR spectra, often parameterised by the so-called force-field model (Caballero-Lopez & Moraal 2004; Usoskin et al. 2005), which, however, has an intrinsic uncertainty related to the local interstellar spectrum of GCR (Herbst et al. 2010; Asvestari et al. 2017a). Since the spectrum of GCR beyond the Earth’s atmosphere and magnetosphere was unverifiable until recently, the associated model uncertainty was present in all previous computations based on the force-field approximation (e.g., Masarik & Beer 2009). This introduced uncertainties in the level of the OSF (or other solar activity indices), sometimes leading to blind ad hoc ‘calibrations’ of the models.
Recently, the situation has been dramatically improved when the space-borne Alpha Magnetic Spectrometer experiment (AMS – see Aguilar et al. 2018) provided direct measurements of GCR energy spectra above the atmosphere over a large part of solar cycle 24 from May 2011 through May 2017, with a 27-day time resolution. Not only protons, but also heavier cosmic-ray species were measured, up to iron and nickel, thus providing, for the first time, direct data on GCR spectra and its variability over a solar cycle. The AMS instrument is installed onboard the International Space Station at a low orbit and spends most of the time inside the magnetosphere. However, thanks to the inclined (≈52°) orbit, it also receives low-energy cosmic rays (rigidity down to 1 GV and energy 400 and 200 MeV nuc−1 for protons and heavier nuclei, respectively) over high-latitude parts of the orbit. This makes it possible to obtain directly measured spectra of GCR (> 1 GV), leading to the ultimate verification and, if needed, the calibration of the 14C production model. The contribution of even lower-energy (< 1 GV rigidity) GCR particles to 14C production is very small (≈0.5%, Asvestari et al. 2017a), because it is limited to the small-area polar regions, while the yield function grows rapidly with energy. Accordingly, we accounted for that part of the GCR spectrum not measured directly by AMS by extrapolating it with a best-fit force-field approximation below 1 GV. The uncertainties related to this extrapolation are negligible (< 0.1%).
The globally averaged production rate of a cosmogenic isotope in the Earth’s atmosphere at time t can be calculated as
where the summation is over the type k of cosmic-ray particles (protons, helium, etc.), Jk(P, t) is the rigidity (momentum over charge) spectrum of cosmic-ray particles of type k near Earth, but outside the atmosphere and magnetosphere,
is the globally averaged yield function of the isotope production by cosmic-ray particles of type k with rigidity P, Pc is the local geomagnetic cutoff rigidity (e.g., Elsasser et al. 1956; Usoskin et al. 2010) at a given geomagnetic latitude θ and time t, H(x) is the Heaviside step function, and Yk(P) is the yield function of the isotope production (Kovaltsov et al. 2012; Poluianov et al. 2016). As the global yield function 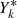 of 14C, we used the one (Asvestari et al. 2017a) based on a recent computation by Poluianov et al. (2016), energy and rigidity spectra Jk of cosmic rays were taken as measured by the AMS experiment during 2011–2017, and the corresponding values of Q* were calculated. Thus computed values of Q* are shown in Fig. 5 against count rates of a standard polar neutron monitor (NM), viz. Oulu NM data record available online1. The relation between them is very tight and can be parameterised as
of 14C, we used the one (Asvestari et al. 2017a) based on a recent computation by Poluianov et al. (2016), energy and rigidity spectra Jk of cosmic rays were taken as measured by the AMS experiment during 2011–2017, and the corresponding values of Q* were calculated. Thus computed values of Q* are shown in Fig. 5 against count rates of a standard polar neutron monitor (NM), viz. Oulu NM data record available online1. The relation between them is very tight and can be parameterised as
 |
Fig. 5. Scatter plot of the 14C global production rate Q*, computed based on the AMS-02 data for the period 2011–2017, and a polar NM64 (Oulu) neutron monitor count rate for the same period, with the dot-dashed red line depicting the dependence (Eq. (5)). |
where Q* is the global 14C production rate in at cm−2 s−1 for the modern epoch (M0) and N is the count rate of a polar sea-level NM in the Hz/counter.
3.2.2. Extension towards 1957–2019
Using Eq. (5) and the polar NM record, we have extended the expected annual Q* series backwards to 1957. These values are plotted in Fig. 6 against OSF Fo as assessed from in situ space-borne data applying the kinematic correction since 1963 (Lockwood et al. 2009; Owens et al. 2017), extended to recent years according to Owens (personal communication, 2019) and based on geomagnetic indices (Lockwood & Owens 2014). The values are highly significantly correlated (the Pearson’s correlation coefficient r = −0.86 ± 0.03 and p-value < 10−6), but the scatter is large, especially during the years between 1968 and 1980 (see Fig. 7) likely because of the poor quality of in situ solar wind data.
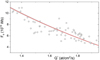 |
Fig. 6. Scatter plot of the annual solar open magnetic flux Fo (Lockwood et al. 2009; Owens et al. 2017) against the 14C production rate Q* estimated from NMs (see Fig. 5). The red curve depicts the best-fit dependence (Eq. (6)). |
 |
Fig. 7. Panel A: evolution of annual open solar flux: Fo(O17) based on in situ measurements (Owens et al. 2017) and Fo* reconstructed here based on relations (5) and (6). Panel B: difference between them dF = Fo − Fo(O17). Panel C: histogram of the occurrence of dF values with the best-fit Gaussian (mean 0.1 ⋅ 1014 Wb and σ = 0.9 ⋅ 1014 Wb). |
3.2.3. Expected relations between Q and Fo
Based on basic physical principles, a dependence between the isotope production rate and OSF is expected to be nearly exponential, Q* = Q0 ⋅ exp( − Fo/α), which leads to
where Q0 = 2.5 at cm−2 s−1 is the production rate in the absence of solar modulation (Poluianov et al. 2016), viz. by the local interstellar spectrum (Fo = 0). The value of α = (17.2 ± 0.2)⋅1014 Wb was found as the least-squares best fit to the data points shown in Fig. 6.
Figure 7 shows a comparison between the OSF, derived from space-borne measurements Fo(O17) (Lockwood et al. 2009; Owens et al. 2017) and Fo calculated here from NM data using Eqs. (5) and (6), as well as the difference between them (panel B). One can see that the cycles are reproduced quite well, both in the mean level and in the amplitude. The two OSF series agree reasonably well, with the mean difference being 0.1 and the standard deviation 0.9 (both in units of 1014 Wb). These deviations directly enter the uncertainty of the Fo reconstruction from Q, and we considered σ3 = 0.9 ⋅ 1014 Wb in Eq. (2). It is very important that the low level of the current cycle 24 (2010–2018) is reproduced correctly, suggesting that the secular variability is also captured by the model.
3.2.4. Reconstruction of Fo
In the next step, we applied the relation (2) to the Q* over the whole time series, keeping in mind the found uncertainty of σFo = 0.9 ⋅ 1014 Wb and a possible systematic bias of 0.1 ⋅ 1014 Wb. OSF Fo reconstructed in this way is shown in Fig. 8, with panel A depicting the whole time series and panel B displaying a blow-up of the period since 1700. For comparison, several other OSF reconstructions are shown, including the Fo determined from space-based measurements for the last decades as discussed in Sect. 3.2.1, and two reconstructions (Wu et al. 2018a) using the method entering the SATIRE-T model (Vieira & Solanki 2010; Krivova et al. 2010), but based on the following two different sunspot series: ISN (v.2) available at SILSO (Clette & Lefèvre 2016), and GSN (Hoyt & Schatten 1998). We note that these two sunspot series serve as the conservative upper and lower bounds for the uncertainties of different sunspot series (Usoskin 2017). Before ca. the 1880s, the reconstruction lied mainly between the two coloured curves, being closer to the ISN-based one during the 18th century. It is important to note, however, that the model underlying the red and blue dashed curves in Fig. 8 provides Fo that is too low during extended periods of particularly low activity, such as grand minima, because of the limitation of the earlier OSF models.
 |
Fig. 8. Evolution of the reconstructed annual Fo. The mean curve (black) and 1σ uncertainties (grey shaded area) were computed by 10 000 MC realisations (see text). The green curve represents the smoothed (22-yr SSA) variability. The mean level of 2.5 ⋅ 1014 Wb defines the grand minima when solar magnetic activity drops below the sunspot formation threshold. Other reconstructions are shown for comparison: that of Wu et al. (2018a, W18) based on the SATIRE-T model applied to ISN (v.2); the same SATIRE-T model but applied to the GSN (W18(GSN)), as well as the OSF reconstructed from space-based measurements (Owens et al. 2017, – O17). Panel B: zoom to the period after 1700. The data are available at the CDS. |
3.3. Step (3): Conversion of Fo into a SN
The OSF Fo can be estimated from the SN using a semi-empirical model (e.g., Solanki et al. 2002; Vieira & Solanki 2010), which also enters the SATIRE-T model (Krivova et al. 2010; Wu et al. 2018a) used for solar irradiance reconstruction. It is based on solving a set of linear differential equations with several sources, considering a source term describing the emergence of active regions (ARs) and ephemeral regions (ERs) at the solar surface and their decay. The latter includes the transfer of flux from ARs and ERs into slowly and rapidly evolving components of the OSF. This model has recently been extended, improved, and updated to take into account more recent observations of the number distribution of magnetic features with different levels of magnetic flux (Krivova et al. 2021). Instead of just ERs, it also includes the flux emerging in the form of internetwork fields, combining the two under the term small-scale emergences (SSEs). All emerging magnetic bipoles are described by a single power-law distribution, which allows for a non-zero emergent flux even when there are no sunspots. Thus, in contrast to the earlier SATIRE-T model, the new model returns a non-zero Fo during grand minima, consistent with observational findings that it was of the order of 2⋅1014 Wb and varied cyclicly during the MM (Beer et al. 1998; Owens et al. 2012; Asvestari et al. 2017b).
However, the inversion of the model (viz. Fo → SN) is not possible analytically. We therefore took the following alternative path, using a semi-empirical approach based on a statistical inversion of the forward model.
One shortcoming of the employed forward model is that it relies on sunspots to determine the strength of OSF. Therefore, at least the forward model cannot handle fluctuations well in the level of solar activity if this occurs at levels too low to produce sunspots. The clear variation in the production of cosmogenic isotopes (both 10Be and 14C) during grand minima (Beer et al. 1998; Asvestari et al. 2017b; Brehm et al. 2021) suggest, however, that variations in solar activity do take place at such times which are reflected in the number of sunspots only to a small extent (Vaquero et al. 2015). In the context of the inverted model used here, such variations formally translate into variations in the SN, although there were in reality hardly any sunspots on the solar disc at that time (Usoskin et al. 2015; Vaquero et al. 2015). To counter this, we introduced a threshold of Fb = 2.5 ⋅ 1014 Wb, which corresponds to zero sunspots (see Eq. (7)). We consider that solar cycles with Fo < 2.5 ⋅ 1014 Wb in the smoothed OSF series correspond to grand minima and cannot be robustly defined. This means that at times when the green curve in Fig. 8 drops below the horizontal dashed line, we consider the variation in solar activity reconstructed by the model not to be dominantly caused by sunspots. Rather, such fluctuations are then considered to be mainly due to changes in the number of non-spot magnetic features on the solar surface, such as small-scale magnetic elements (e.g., Solanki 1993), forming a network and plage. Such activity cycles dominated by non-spot variations have been marked by a dashed line in Fig. 12 and by italics in Table 1, listing all the cycles.
Solar activity cycles as reconstructed here from annually resolved 14C.
3.3.1. Statistical inversion
First, we composed a synthetic series of annual SNs based on the ISN (v.2) (Clette & Lefèvre 2016) since 1700 and a scaled GSN (Hoyt & Schatten 1998) for the period 1610–1699. The latter is needed since the ISN does not cover the Maunder minimum, and we want to include this low-activity period. This series is shown in Fig. 9 as the thin black curve.
 |
Fig. 9. Synthetic SN series, composed of ISN (v.2) after 1700 and GSN before that (black curve), and its ‘reconstruction’ after the chain SN → Fo → SN’ (red curve). |
This series was split into 36 individual cycles between consecutive minima of 13-month smoothed SN and about 11-yr intervals during the Maunder minimum. We produced 1000 synthetic SN-series, formed by randomly permuting these 36 solar cycles and computing the corresponding 1000 OSF series using the equations applied in the SATIRE-T model. Thus, we have 1000 sets of the annual ‘input’ SN series and the corresponding ‘output’ OSF series.
Next, we searched for a relation that inverts the input and the output, viz. Fo → SN, using an empirical approach. Because of the presence of distinct slow secular (Lockwood et al. 1999), which is dependent on the previous history (see Solanki et al. 2000), and oscillating 11-year components in the OSF, we first decomposed each Fo synthetic series into slow, Fs, and oscillating fast Ff = Fo − Fs components. SN of the year j reconstructed from Fo was calculated as
where F′s and F′f are the slow and fast components (both expressed in units of 1014 Wb), obtained as the first component of the singular spectral analysis (SSA, cutoff period of 5 years) of the F′ series and the residual, respectively, and parameters are a = 2.4 ± 0.05, b = 11.5 ± 0.1, and Fb = 2.2 ⋅ 1014 Wb. The mean root mean square (RMS) over the 1000 series was found to be 7.8 in SN units for this set of parameters. The use of other filters does not notably alter the final result, but it leads to larger error bars (RMS 10–13). Thus, the model uncertainty of this step conversion was set as σ4 = 8.
3.3.2. Testing the inversion
An example of the inversion for the reference series is shown as the red curve in Fig. 9. One can see that all cycles are correctly reproduced in shape and their overall level (the mean difference is 1.9), but with a slightly reduced amplitude (maxima are lower and minima are higher), the Pearson’s correlation coefficient is 0.963 and the rms = 15. The Maunder minimum is reproduced very well.
We tested the inversion method (Eq. (7)) using the OSF reconstruction based on in situ data by Owens et al. (2017) (see the blue curve Fo(O17) in Fig. 7). The obtained SNs are shown in Fig. 10 along with the ISN (v.2.0). One can see that the agreement is good (mean difference d = 0.3, Pearson’s correlation coefficient 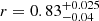 , and rms = 35), except for the period from 1963–1982, which was characterised by earlier, quite uncertain magnetic-field in situ data, so that they disagree with the cosmic-ray data (Fig. 7). When the OSF computed from the cosmic-ray data (Sect. 3.2.1) is used, the agrement between the ‘reconstructed’ (blue curve) and the actual SNs improves significantly (d = −0.03,
, and rms = 35), except for the period from 1963–1982, which was characterised by earlier, quite uncertain magnetic-field in situ data, so that they disagree with the cosmic-ray data (Fig. 7). When the OSF computed from the cosmic-ray data (Sect. 3.2.1) is used, the agrement between the ‘reconstructed’ (blue curve) and the actual SNs improves significantly (d = −0.03, 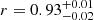 , and rms = 26). Thus, we can conclude that the method provides a good way to reconstruct the SN from OSF data.
, and rms = 26). Thus, we can conclude that the method provides a good way to reconstruct the SN from OSF data.
 |
Fig. 10. SNs, computed using Eq. (7) from the Fo data for the instrumental era (see Fig. 7) reconstructed by Owens et al. (2017, O17) and from NM data, along with the ISN (v.2). |
3.4. Solar-activity reconstruction
The SN reconstruction was performed with 10 000 random realisations, each going through steps 1–3 and applying independent random numbers as described above in formulas (1) and (2). The SN (in the units of ISN v.2), at least for times when solar activity is characterised by a sunspot cycle, such as during recent decades, is computed as
where the functional g is defined by Eq. (7).
From 10 000 thus obtained SN series, we computed the mean series ⟨SN(t)⟩ and its standard deviation σSN(t), which are considered as the final mean reconstruction and its 1σ uncertainties. The final SN series is provided as a table at the CDS and shown in Figs. 11B and 12 with 1σ uncertainties and in comparison with other direct or indirect series. It is gratifying that individual solar cycles are clearly resolved outside of the grand minima. Figure 11A depicts a smoothed (15-yr first SSA component) SN-series with the corresponding uncertainties, in comparison with similarly smoothed ISN and GSN series as well as decadal 14C INTCAL-based reconstructions by Usoskin et al. (2016) and a multi-proxy based one by Wu et al. (2018b) (all series were properly scaled to match the ISN v.2 scale). The agreement with previous cosmogenic-proxy reconstructions, including those of U16 (Usoskin et al. 2016) and W18 (Wu et al. 2018b), is very good (see Sect. 4.1.3).
 |
Fig. 11. Time evolution of the reconstructed SNs (black curve with ±1σ grey-shaded uncertainties) in comparison with other direct and indirect SN series. Panel B: final annual reconstruction, and Panel C: its zoom for the period after 1700. Panel A: smoothed (15-yr first SSA component) annual series in comparison with other similarly smoothed or decadal series. These series are as follows: ISN (v.2, SILSO), GSN* (Hoyt & Schatten 1998), C17* (Chatzistergos et al. 2017), as well as two recent reconstructions based on 14C – U16* (Usoskin et al. 2016) and W18* (Wu et al. 2018b) (the asterisk indicates that the series is scaled up by a factor of 1.667 to match the ISN v.2 definition). Blue arrows denote grand minima of solar activity: Oort (OM), Wolf (WM), Spörer(SM), Maunder (MM), and Dalton (DM) minima. The data are available at the CDS. |
 |
Fig. 12. Same as Fig. 11, but split into three subsequent time intervals of 310 years each. Cycles, which are not well defined during the grand minima (see Sect. 3.3), are indicated with the dashed line. |
Formally negative mean SN-values appear for about 250 years; about 80 of them are negative beyond the 1σ-uncertainty and only six remain negative at the 2σ level (Fig. 12). Thus, formally negative SN-values are statistically consistent with zero. For further analysis, we kept the negative values since replacing them with zeros would distort the overall level.
We note that while the uncertainties are large (mean 68 % uncertainty is about 34 in SN units), they are largely systematic (related to the model uncertainties). Thus they do not affect the temporal evolution, and only the level of activity can be impacted. An important advantage of the employed data is that their quality (and thus the SN reconstruction) is stable during the entire period.
3.5. The effect of the 994, 1052, and 1279 AD events
One confirmed peak of additional 14C production in 994 AD (Miyake et al. 2013a) and possible peaks in 1052 and 1279 AD (Brehm et al. 2021) are known during the analysed period. Since they are likely of non-GCR origin and thus can distort the cyclic evolution of the reconstructed solar activity, we removed them from the original Q series as described in Sect. 2. The effect of the removal of the 994 AD event is shown in Fig. 13A. If the event is not corrected, a full solar cycle is ‘swallowed up’ (a bump in the 14C production is interpreted as very weak solar activity), while a formal (no ad hoc tuning) correction of the effect restores a nearly perfect cycle with the maximum in 994 AD. Thus, the event of 994 is found to take place at the early declining phase of a strong solar cycle.
 |
Fig. 13. Evolution of the reconstructed SNs (blue curve with ±1σ grey-shaded uncertainties) for the periods around the corrected events: 994 AD (panel A), 1052 AD (panel B), and 1279 (panel C). The red curve depicts SNs if no correction is applied. Red arrows indicate the time of the events. |
The effect of the removal of the potential event in 1052 is shown in Fig. 13B. The correction fully restores the cyclic shape otherwise swallowed up by the event. The restored cycle has its maximum in 1053, thus the 1052 event took place near the maximum of a moderate cycle during the Oort grand minimum.
The effect of the removal of the event of 1279 is shown in Fig. 13C, but it also affects the reconstructed OSF. Again, this correction restores the cyclic shape. As can be seen from Fig. 13C, this event likely occurred around the maximum phase of a moderate cycle.
In conclusion, the new annual data set makes it possible to correctly reconstruct the overall level and phases of individual cycles of solar activity. Because of uncertainties related to the event removal, we mark the related cycles as non highly reliable. The reconstructed SN cycles are analysed in Sect. 4.
4. Solar activity cycles
We analysed the annual solar-activity series since 971 AD and identified individual solar cycles as presented in Table 1. A quality flag q was ascribed to each cycle so that it uses values from 0 to 5 as follows: 0 – the cycle cannot be reliably identified (29 such cycles were found); 1 – the cycle is greatly distorted, at least one of its ends cannot be defined (seven cycles); 2 – the cycle can be approximately identified, but either its shape or level is distorted (14 cycles); 3 – a reasonably defined cycle (ten cycles); 4 – a well-defined cycle with a somewhat unclear amplitude (19 cycles); 5 – a clear cycle in both shape and amplitude (six cycles). The series contains 85 full cycles (971–1900) with a mean cycle length of 10.8 years (see Sect. 4.2).
4.1. Activity levels
4.1.1. Distribution of activity levels
The distribution of the cycle-averaged SNs is shown in Fig. 14A, where two clearly separated modes can be observed: the grand-minimum mode with ⟨SN⟩ < 20 (well fitted with a Gaussian with the mean m = 1 and σ = 8), and a normal mode with m = 48 and σ = 31. The clear separation of the modes confirms the earlier finding that grand minima form a special mode of solar activity, as discovered by Usoskin et al. (2014) using the INTCAL data for the last three millennia. The distribution of ⟨SN⟩ for the well-defined (q ≥ 4) cycles can be fitted with a single-mode Gaussian distribution (m = 49, σ = 36).
 |
Fig. 14. Distribution of cycle-averaged ⟨SN⟩ SNs along with fitted bimodal Gaussians. Panel A: SNs reconstructed here for 971–1900 (85 full cycles). The two curves are as follows: grand-minimum mode (magenta dashed line, mean m = 1, σ = 8) and normal mode (red dashed line m = 48, σ = 31). Orange bars correspond to the well-defined cycle q ≥ 4 (m = 49, σ = 36, 25 cycles). Panel B: ISN (v.2) SNs for 1750–2019 (24 full cycles), including two modes: a normal one (m = 64, σ = 16) and a grand-maximum one (m = 107, σ = 13). |
For comparison, the distribution of the cycle-averaged ⟨SN⟩ for the direct SN series (ISN v.2, 1750–2019) is shown in Fig. 14B. Although the statistics is low (24 full cycles), two distinct modes can be found: a normal one (m = 63 and σ = 16) and the grand-maximum one (m = 107, σ = 13).
It is important that the distributions of the normal-mode activity, centred at about 50 ⟨SN⟩, cannot be distinguished in a statistical sense (p-value 0.07) for the direct SN observations and the reconstructed one. For the period of direct overlap between the series (1750–1900), the mean reconstructed ⟨SN⟩ value is 62 ± 10, while it is 77 ± 8 for the ISN (v.2) series, implying that the difference is systematic, but insignificant (p = 0.24). A grand-minimum mode is clear in SN reconstructed here for the last millennium (≈50% of time), but absent in the ISN series, where only a short and shallow Dalton minimum is present. On the other hand, the ISN data set contains the modern grand maximum in the second half of the 20th century, while no grand maxima are found for the period 970–l900. A few high cycles can be seen in the reconstructed SN, ca. 990, 1200, 1370, and 1790, but the modern grand maximum is unique in the combination of both the level and length over the last millennium, in agreement with earlier findings (e.g., Usoskin et al. 2003, 2007; Solanki et al. 2004). The very high cycles at the beginning of the series may be related to the not-yet-relaxed carbon-cycle model.
4.1.2. Grand minima
The last millennium was not very typical in solar activity as it covers the low phase of the Halstatt cycle with five grand solar minima (Oort, Wolf, Spörer, Maunder and Dalton – see Fig. 11A), with a total duration of about 430 years (Usoskin et al. 2016; Brehm et al. 2021). Thus, the Sun spent nearly half of the last millennium in the grand minimum mode, while the average fraction is about 17% for a 10 000-year period (Usoskin et al. 2007; Inceoglu et al. 2015). Out of these 430 years, about 220 years can be identified as deep-minimum phases when the level of activity drops very low, below the sunspot formation threshold Fo < 2.5 ⋅ 1014 Wb to the following: 1300–1330 (Wolf minimum), 1410–1540 (Spörer minimum), and 1650–1710 (Maunder minimum), as marked in Table 1.
The reconstructed mean level of solar activity during the major grand minima is consistent with a SN of zero within the error bars (Fig. 11A) for the Wolf, Spörer, and Maunder minima, but it is of the order of 10 for the shorter and shallower Oort and Dalton minima, which is in agreement with the direct SN data during the Dalton minimum.
Shapes of individual cycles are poorly defined (quality flag q is low) during the deep phases of the major minima. To check the robustness of the cycle assessment, we performed the following test. We produced 1000 synthetic noise-based series of Q14C with the statistical distribution (mean 2 and σ = 0.22, both in units of at g−1 cm−2), corresponding to those (Brehm et al. 2021) of the actual data set during the Spörer minimum (1400–1550). The synthetic series was processed further by applying the same method as described in Sect. 3, viz. identically to the main reconstruction. One such realisation of the SN reconstructed from purely noisy series is shown in Fig. 15A as the red curve, along with the main SN reconstruction for the period of the Spörer minimum. It exhibits a seemingly oscillating pattern with a typical length of 3–20 years and an amplitude of 10–20 in SN, some of these oscillations are comparable to the cycles reconstructed from the real data. For each of these 1000 noise-based reconstructions, we computed the fast Fourier transform (FFT, amplitude) spectrum, and then took the upper 95th percentile of them, as shown by the red dotted line in Fig. 15B. One can see that the spectrum is nearly flat, with the amplitude being 5–7 in SN. The FFT spectrum of the final reconstructed SN series, based on the real data, for the period of 1400–1550 is shown in black and contains peaks around 8.5, 11, and 13 years. These peaks are significantly higher than the 95% confidence level. The peak at about 9 years is consistent with a result for the Maunder minimum (Vaquero et al. 2015) based on a sunspot observation.
 |
Fig. 15. Reconstructed solar activity around the Spörer minimum. Panel A: the black curve with grey-shaded error bars represents the main reconstruction and is identical to that in Fig. 12, while the red curve depicts a reconstruction based on one realisation of the simulated noise series (see text). Panel B: FFT spectrum (amplitude) of the main SN reconstruction (shown in panel A) for the period 1400–1550, while the red dotted line depicts the upper 95th percentile of the FFT spectra of 1000 noise-based reconstructions for the same period (see text). Panel C: same as panel B, but for OSF. |
Therefore, we conclude that while the presence of the Schwabe cycle during the Spörer minimum is statistically significant, individual cycles are not robustly defined. Accordingly, we mark all cycles inside the deep grand minima as unreliable (quality flag q = 0) and exclude them from the cycle length analysis. A similar pattern can be observed in the OSF evolution during a grand minimum (Fig. 15C).
Cycles outside the grand minima are defined fairly reliably. However, there are several distorted or merged cycles, including ca. 1100, 1360, 1560, and 1720 (see Table 1), which occurred shortly after the transition from a grand minimum to normal activity. This may be related to the fact that the relation between the heliospheric modulation of cosmic rays and solar magnetic activity can be inverted during grand minima, as shown observationally for the Maunder minimum (Beer et al. 1998; Usoskin et al. 2001) and as proposed theoretically (Owens et al. 2012).
The level of the reconstructed activity is very low, it is below the sunspot-formation threshold during the Maunder minimum, which is in agreement with all other data sets (Vaquero et al. 2015; Usoskin et al. 2015). It is interesting that, according to the new reconstruction, the deep phase of the Maunder minimum extended until about ca. 1710, which is in agreement with earlier results (Eddy 1976; Usoskin et al. 2015; Vaquero & Trigo 2015) but in contradiction with the formal ISN data series (Fig. 11C).
4.1.3. Comparison with direct SN series
A comparison of the SN reconstructed here with other series based on direct sunspot observations is shown in Fig. 11. All series were reduced to the ISN (v.2) definition. The lower-bound is represented by the GSN (Hoyt & Schatten 1998), which yields the lowest SNs among all of the series, while ISN (v.2) (Clette & Lefèvre 2016) forms the upper bound.
Figure 11A presents a comparison of smoothed (15-yr first SSA component) series. The reconstructed activity lies between the two bounds for the period of 1750–1900. It is closer to the GSN series in the 19th century, while being close to ISN (v.2) in the second half of the 18th century. ISN (v.2) falls > 1σ above the reconstructed data around 1830–1870, ca. 1810, and before 1730, while GSN lies > 1σ below the reconstructed series between ca. 1730 and 1780. Thus, the reconstructed SN is consistent with both ISN and GSN being somewhat close to the GSN one. The reconstructed SN goes quite low around 1900, which is probably related to the somewhat uncertain Suess-effect correction.
Figure 11C focuses on the last three centuries. One can see that we correctly reconstructed most individual solar cycles, at least in the sense of times of their maxima and minima, which agree within ±2 years with those in the actual SNs. Exceptions are the periods ca. 1840, when an extra cycle appeared to distort the neighbouring cycles; ca. 1725, when a long, possibly merged cycle appeared; and ca. 1770, when a cycle was distorted by a sudden drop. The former two distortions may be related to a transition between grand-minimum (Dalton and Maunder minima, respectively) and normal modes of activity, as discussed above, while the latter one is related to a strong jump in 14C production. Thus, out of the 18 cycles during the period 1700–1900, 15 were reproduced correctly and three are distorted, but the total number of cycles is preserved.
Magnitudes of the cycles vary: While some reconstructed cycles cover the full extent of the directly measured sunspot cycles which drop to close to zero near activity minima (see ca. 1860), some have a small magnitude, such as ca. 1790. Consequently, the reconstructed series tends to underestimate the true amplitude of the SN series at such times. However, as is visible from Fig. 11A, the mean level is preserved.
The SN series obtained here does not follow any single SN series in the literature, but it shows elements of different ones, being closer to one at some times and another at other times. The mean differences between the cycle-averaged SN values reconstructed here and those based on direct solar observations (all series were reduced to the ISN v.2 definition) for the 19th century are as follows: 15 ± 3.2 for ISN (v.2), implying a significant systematic difference (ISN v.2 is systematically higher); −4.8 ± 3.3 for GSN, implying that it is systematically lower; and 2.9 ± 3.8 for the series by Chatzistergos et al. (2017), implying their mutual consistency. We conclude that the method correctly reconstructs the mean level as well as minimum and maximum dates of individual cycles, but the exact magnitudes of some sunspot cycles may be distorted.
4.2. Cycle lengths
The wavelet power spectrum of the reconstructed sunspot activity is shown in Fig. 16A with ‘ridges’ (local maxima of the spectrum for each year) shown as black dots. The reconstructed series was extended to cover the 20th century with the ISN (v.2) series.
 |
Fig. 16. Panel A: wavelet power spectrum (Morlet basis, k = 6) of the reconstructed SN series, extended by ISN (v.2) after 1900. The white curve bounds the cone of influence (COI) where the spectrum is unreliable because of the proximity to the edges of the series. Black dots denote local maxima of the power (> 104) in the period bands 7–16, 75–140, and 180–250 years. The horizontal dashed line marks the location of the 11-year period. Panel B: cycle length (minimum-to-minimum) as a function of time (assigned to the cycle maximum year) for resolvable (q > 0, 56 cycles) reconstructed cycles (open dots) and for well-defined cycles (q ≥ 4, 25 cycles, filled circles). Red stars are the cycle lengths, rounded to the nearest integer (to be reduced to the annual resolution), in the ISN (v.2) series (http://www.sidc.be/silso/cyclesminmax) for 1750–2019. The dashed line represents the mean cycle length of 11 years over the ISN series. The grey shading denotes grand minima of solar activity. Panel C: comparison between the smoothed cycle-length evolution. The smooth red curve is the three-point running mean of the individual cycle lengths (q > 0). The light blue WV curve is the wavelet-defined period (identical to the upper black curve in panel A). |
One can see the dominant ≈11-year Schwabe quasi-periodicity visible as the yellow-red ribbon at 8–16 years with several breaks corresponding to grand minima (Oort, Wolf, Spörer, and Maunder minima), when the reconstructed cycles have a low amplitude and are not reliable. It was proposed earlier that the typical length of the Schwabe cycle tends to increase before and during grand minima (e.g., Fligge et al. 1999; Miyahara et al. 2006a), as based on poorer statistics. We confirm this pattern for the Maunder and Dalton minima, but not for other minima (see Fig. 16).
Another pronounced periodicity corresponds to the Suess and de Vries cycle of about 210 years, which appears very stable without any significant fluctuation. The 210-year periodicity manifests itself mostly as the recurrence of grand minima within a cluster (Usoskin et al. 2007, 2016). The so-called Gleissberg or centennial cycle is visible as a broad pattern at about 120 years, extending to shorter periods during 1700–1800, and not being very stable, which is in agreement with earlier findings (e.g., Ogurtsov et al. 2002).
A shortcoming of the wavelet analysis is that it yields an estimate of the general variability of the periods and does not provide information on individual cycles. Using dates of the solar cycle minima (Table 1), one can analyse lengths of individual solar cycles as shown in Fig. 16B for all resolvable cycles (q > 0, open circles), well-defined cycles (q ≥ 4, filled circles), and the directly observed cycles (red stars). The length of individual resolvable cycles (q > 0) generally agrees (red versus light blue curves in Fig. 16C) with the wavelet-based definition after a three-point smoothing of the former, which roughly corresponds to the wavelet package extension. This confirms that our minimum-to-minimum cycle length definition is robust, since the wavelet-based definition considers the full variability within the wavelet package, and not only minima or maxima.
The distribution of the cycle lengths is shown in Fig. 17 along with the following fitted normal distributions: 10.8 ± 1.9 years for 56 resolvable cycles with q > 0 (grey bars), 10.8 ± 1.4 years for well-defined cycles (q ≥ 4, 25 cycles, blue bars), and 11.0 ± 1.1 years for the ISN (23 cycles, orange bars). We tested the hypothesis of the equality of the cycle length distributions using the z-score test. All three distributions (outside of the grand minima) cannot be considered different at any reasonable significance level. Thus, we conclude that the cycle-length distribution of the reconstructed cycles outside deep grand minima is statistically consistent with that for the directly observed solar cycles after 1750.
 |
Fig. 17. Distribution of cycle lengths for all resolvable cycles with q > 0 (grey bars), well-defined cycles (q ≥ 4, blue), and ISN (v.2) series (http://www.sidc.be/silso/cyclesminmax) for 1750–2019. Dashed lines represent the fitted normal distributions. |
4.3. Waldmeier rule
The Waldmeier rule states that cycles with a faster rising SN are stronger. This rule is based on a statistically significant correlation between the length of the rising phase and the peak height of the cycles (Hathaway 2015; Usoskin et al. 2021). Since the amplitude of the cycle SNmax is not well determined here, we considered a more robust quantity of the cycle-averaged SN ⟨SN⟩ from Table 1. The relation between the length of the scending phase Tas = Ymax − Ymin (in years) and ⟨SN⟩ for all 85 cycles appears insignificant (Pearson linear correlation coefficient r≈0). However, when only well-defined cycles (quality flag q ≥ 4) are considered, the Waldmeier rule appears highly significant (r = -0.58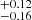 , p-value=0.001, N = 25) as
, p-value=0.001, N = 25) as
⟨SN⟩=(−26 ± 16)⋅Tas + (197 ± 90).
The Waldmeier rule for the direct SN series defined in the same way (i.e. the cycle-mean SN versus the length of the ascending phase rounded to an integer) yields the following relations:
⟨SN⟩ = (−14.5 ± 7)⋅Tas + (150 ± 35)
(r = −0.67 ± 0.15, p < 0.001) for ISN (v.2) and
⟨SN⟩ = (−12.8 ± 9)⋅Tas + (137 ± 45)
(r = −0.53 ± 0.15, p = 0.005) for GSN.
Thus, we confirm that the Waldmeier rule is also valid on the millennial-scale, at least in the sense of the cycle-average SN rather than cycle-peak SN, which is poorly defined in the reconstructed SN time series.
5. Summary and conclusions
A new quantitative reconstruction of annually resolved solar activity, in the form of SNs (at least outside grand minima) with a full uncertainty assessment, is presented for the period 971–1900. For the first time, individual solar cycles are presented for the whole of the last millennium, more than doubling the existing statistics of solar cycles. Overall, 85 solar cycles have been reconstructed (the mean length 10.8 ± 1.9 years), of which 25 cycles are well-resolved (the mean cycle length 10.8 ± 1.4 years), ten cycles are reasonably defined, 21 are poorly defined, and 29 cycles cannot be reliably identified. The unresolvable cycles correspond to the deep-minimum phase of solar activity during grand minima. The periods of low activity were abnormally frequent (about 40% of the time) during the last millennium, covering a cluster of four grand minima (Usoskin et al. 2016). The new reconstruction agrees well, within the uncertainties, with the estimates of the SNs based on direct telescopic observations during the 18th and 19th centuries, in both the mean level and the mean cycle length. This greatly increases the number of known solar cycles, from 36 cycles known for the period between 1610–2019, including 24 well-defined ones after 1755, eight poorly resolved and four unresolvable cycles around the Maunder minimum, to 96 cycles (971–2019) including 50 well- and reasonably defined cycles, 17 poorly defined cycles, and 29 individually unresolvable cycles for the last millennium.
The grand minima form a separate mode of solar activity with solar activity dropping below the sunspot formation threshold during their deepest phases. The deepest grand minima were the Spörer minimum with the deep phase covering 1410–1540, the Maunder minimum (1650–1710), and the Wolf minimum (1300–1330), while the shorter Oort and Dalton minima did not drop to such a deep level (cf. Brehm et al. 2021). A cyclic variation in solar activity was found even during the deep phases of the grand minima, agreeing with and extending earlier results (Beer et al. 1998; Miyahara et al. 2006b; Miyake et al. 2013b), but their significance is low since their magnitude is less than a 1σ uncertainty. However, the variation in solar activity at such times was at a level that it produced none or, at the most, a few sunspots.
The new data confirm that the Maunder minimum extended until at least 1710, which is in agreement with other data sets, but in contradiction to the ISN series. It is found that in the record constructed from 14C data, distorted cycles appear at the transition phase between grand minima and normal activity, allowing for the possibility that the relation between solar activity and heliospheric modulation of cosmic rays may be different for the two modes (e.g., Owens et al. 2012). Alternatively, at the end of a grand minimum, the solar dynamo may behave in ways not treated properly by the model used here to reconstruct SN.
Three sudden increases in 14C production, in 994, 1052, and 1279 AD, were removed from the initial data set before the reconstruction. The fact that this step restores cyclic solar variability nearly perfectly around these dates supports our method of treating these events. The event of 994 AD, the second-largest SPE known to date, took place at the early declining phase of a moderately strong solar cycle; the event of 1052 AD corresponded to the maximum phase of a moderate solar cycle; the event of 1279 AD took place at the maximum phase of a moderate solar cycle, but the phase may be affected by the removal procedure. The validity of the empirical Waldmeier rule (cycles with a faster ascending phase tend to be stronger, viz. have a greater mean SN) is confirmed at a significant statistical level for well-defined cycles (quality flag q ≥ 4), but it is blurred out when all cycles are considered.
The new, first quantitative SN reconstruction at the annual timescale with full uncertainties, building on the important work of Brehm et al. (2021) and making use of a significantly improved reconstruction technique, opens up new avenues in solar and solar-terrestrial studies with implications for the solar dynamo (specifically the transition between grand-minimum and normal activity modes), reconstructions of solar irradiance, etc.
The results presented here represent a big step forward compared with earlier reconstructions of solar activity, which, with few exceptions (Stuiver & Braziunas 1993; Miyahara et al. 2004; Fogtmann-Schulz et al. 2017), have only provided decadal resolution over the last millennium or longer (e.g., Usoskin et al. 2003; Solanki et al. 2004; Vonmoos et al. 2006; Steinhilber et al. 2012; Wu et al. 2018b). The record of individually resolved solar cycles has been nearly tripled (doubled for well-resolved cycles), providing a basis for more precise solar and solar-terrestrial studies extending now over the whole last millennium.
Acknowledgments
This work was partly supported by the Academy of Finland (Projects ESPERA no. 321882).
References
- Aguilar, M., Ali Cavasonza, L., Alpat, B., et al. 2018, Phys. Rev. Lett., 121, 051101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Asvestari, E., Gil, A., Kovaltsov, G. A., & Usoskin, I. G. 2017a, J. Geophys. Res. (Space Phys.), 122, 9790 [Google Scholar]
- Asvestari, E., Usoskin, I. G., Kovaltsov, G. A., et al. 2017b, MNRAS, 467, 1608 [NASA ADS] [Google Scholar]
- Beer, J., Tobias, S., & Weiss, N. 1998, Sol. Phys., 181, 237 [Google Scholar]
- Brehm, N., Bayliss, A., Christl, M., et al. 2021, Nat. Geosci., 14, 10 [Google Scholar]
- Büntgen, U., Wacker, L., Galvan, J., et al. 2018, Nat. Commun., 9, 3605 [Google Scholar]
- Caballero-Lopez, R., & Moraal, H. 2004, J. Geophys. Res., 109, A01101 [Google Scholar]
- Charbonneau, P. 2020, Liv. Rev. Sol. Phys., 17, 4 [Google Scholar]
- Chatzistergos, T., Usoskin, I. G., Kovaltsov, G. A., Krivova, N. A., & Solanki, S. K. 2017, A&A, 602, A69 [CrossRef] [EDP Sciences] [Google Scholar]
- Clette, F., & Lefèvre, L. 2016, Sol. Phys., 291, 2629 [Google Scholar]
- Clette, F., Svalgaard, L., Vaquero, J., & Cliver, E. 2014, Space Sci. Rev., 186, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Delaygue, G., & Bard, E. 2011, Clim. Dyn., 36, 2201 [Google Scholar]
- Eastoe, C., Tucek, C., & Touchan, R. 2019, Radiocarbon, 61, 661 [Google Scholar]
- Eddy, J. 1976, Science, 192, 1189 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Elsasser, W., Nay, E., & Winkler, J. 1956, Nature, 178, 1226 [NASA ADS] [CrossRef] [Google Scholar]
- Fligge, M., Solanki, S. K., & Beer, J. 1999, A&A, 346, 313 [NASA ADS] [Google Scholar]
- Fogtmann-Schulz, A., Østbø, S. M., Nielsen, S. G. B., et al. 2017, Geophys. Res. Lett., 44, 8621 [NASA ADS] [CrossRef] [Google Scholar]
- Fogtmann-Schulz, A., Kudsk, S. G. K., Trant, P. L. K., et al. 2019, Geophys. Res. Lett., 46, 8617 [Google Scholar]
- Fogtmann-Schulz, A., Baittinger, C., Karoff, C., Olsen, J., & Knudsen, M. 2020, Radiocarbon, 1, [Google Scholar]
- Güttler, D., Wacker, L., Kromer, B., Friedrich, M., & Synal, H. A. 2013, Nucl. Instrum. Methods Phys. Res. B, 294, 459 [Google Scholar]
- Hathaway, D. H. 2015, Liv. Rev. Sol. Phys., 12, 4 [Google Scholar]
- Hellio, G., & Gillet, N. 2018, Geophys. J. Intern., 214, 1585 [Google Scholar]
- Herbst, K., Kopp, A., Heber, B., et al. 2010, J. Geophys. Res., 115, D00I20 [Google Scholar]
- Hoyt, D. V., & Schatten, K. H. 1998, Sol. Phys., 179, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Inceoglu, F., Simoniello, R., Knudsen, V. F., et al. 2015, A&A, 577, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovaltsov, G., Mishev, A., & Usoskin, I. 2012, Earth Planet. Sci. Lett., 337, 114 [Google Scholar]
- Krivova, N. A., Vieira, L. E. A., & Solanki, S. K. 2010, J. Geophys. Res., 115, A12112 [NASA ADS] [CrossRef] [Google Scholar]
- Krivova, N., Solanki, S., Hofer, B., et al. 2021, A&A, in press, https://doi.org/10.1051/0004-6361/202140504 [Google Scholar]
- Li, P., Tang, D., Shi, X., et al. 2018, Precambrian Res., 315, 75 [Google Scholar]
- Lockwood, M., & Owens, M. J. 2014, J. Geophys. Res., 119, 5193 [Google Scholar]
- Lockwood, M., Stamper, R., & Wild, M. N. 1999, Nature, 399, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, M., Owens, M., & Rouillard, A. P. 2009, J. Geophys. Res. (Space Phys.), 114, A11104 [Google Scholar]
- Luthardt, L., & Rößler, R. 2017, Geology, 45, 279 [Google Scholar]
- Masarik, J., & Beer, J. 2009, J. Geophys. Res., 114, D11103 [Google Scholar]
- Mekhaldi, F., Muscheler, R., Adolphi, F., et al. 2015, Nat. Commun., 6, 8611 [NASA ADS] [CrossRef] [Google Scholar]
- Miyahara, H., Masuda, K., Muraki, Y., et al. 2004, Sol. Phys., 224, 317 [Google Scholar]
- Miyahara, H., Masuda, K., Muraki, Y., Kitagawa, H., & Nakamura, T. 2006a, J. Geophys. Res., 111, A03103 [NASA ADS] [CrossRef] [Google Scholar]
- Miyahara, H., Sokoloff, D., & Usoskin, I. 2006b, in Solar Terrestrial (ST), eds. W. H. Ip, & M. Duldig (Singapore; Hackensack, USA: World Scientific), Adv. Geosci., 2, 1 [Google Scholar]
- Miyake, F., Masuda, K., & Nakamura, T. 2013a, J. Geophys. Res., 118, 7483 [Google Scholar]
- Miyake, F., Masuda, K., & Nakamura, T. 2013b, Nat. Commun., 4, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Moriya, T., Miyahara, H., Ohyama, M., et al. 2019, Radiocarbon, 61, 1749 [Google Scholar]
- Muscheler, R., Adolphi, F., Herbst, K., & Nilsson, A. 2016, Sol. Phys., 291, 3025 [Google Scholar]
- Nilsson, A., Holme, R., Korte, M., Suttie, N., & Hill, M. 2014, Geophys. J. Int., 198, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Ogurtsov, M., Nagovitsyn, Y., Kocharov, G., & Jungner, H. 2002, Sol. Phys., 211, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Owens, M. J., Usoskin, I., & Lockwood, M. 2012, Geophys. Res. Lett., 39, L19102 [Google Scholar]
- Owens, M. J., Lockwood, M., Riley, P., & Linker, J. 2017, J. Geophys. Res. (Space Phys.), 122, 10980 [Google Scholar]
- Pavón-Carrasco, F. J., Osete, M. L., Torta, J. M., & De Santis, A. 2014, Earth Planet. Sci. Lett., 388, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Poluianov, S., Kovaltsov, G. A., Mishev, A. L., & Usoskin, I. G. 2016, J. Geophys. Res. (Atmos.), 121, 8125 [Google Scholar]
- Roth, R., & Joos, F. 2013, Clim. Past, 9, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. 1993, Space Sci. Rev., 63, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S., Schüssler, M., & Fligge, M. 2000, Nature, 408, 445 [Google Scholar]
- Solanki, S., Schüssler, M., & Fligge, M. 2002, A&A, 383, 706 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solanki, S. K., Usoskin, I. G., Kromer, B., Schüssler, M., & Beer, J. 2004, Nature, 431, 1084 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Steinhilber, F., Abreu, J., Beer, J., et al. 2012, Proc. Nat. Acad. Sci. USA, 109, 5967 [Google Scholar]
- Stuiver, M., & Braziunas, T. F. 1993, Holocene, 3, 289 [Google Scholar]
- Thébault, E., Finlay, C. C., Beggan, C. D., et al. 2015, Earth Planets Space, 67, 79 [CrossRef] [Google Scholar]
- Usoskin, I. G. 2017, Liv. Rev. Sol. Phys., 14, 3 [Google Scholar]
- Usoskin, I. G., Mursula, K., & Kovaltsov, G. A. 2001, J. Geophys. Res., 106, 16039 [Google Scholar]
- Usoskin, I. G., Solanki, S. K., Schüssler, M., Mursula, K., & Alanko, K. 2003, Phys. Rev. Lett., 91, 211101 [Google Scholar]
- Usoskin, I., Mursula, K., Solanki, S., Schüssler, M., & Alanko, K. 2004, A&A, 413, 745 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Usoskin, I. G., Alanko-Huotari, K., Kovaltsov, G. A., & Mursula, K. 2005, J. Geophys. Res., 110, A12108 [NASA ADS] [CrossRef] [Google Scholar]
- Usoskin, I. G., Solanki, S. K., & Kovaltsov, G. A. 2007, A&A, 471, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Usoskin, I. G., Mironova, I. A., Korte, M., & Kovaltsov, G. A. 2010, J. Atmos. Sol.-Terr. Phys., 72, 19 [Google Scholar]
- Usoskin, I. G., Hulot, G., Gallet, Y., et al. 2014, A&A, 562, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Usoskin, I. G., Arlt, R., Asvestari, E., et al. 2015, A&A, 581, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Usoskin, I. G., Gallet, Y., Lopes, F., Kovaltsov, G. A., & Hulot, G. 2016, A&A, 587, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Usoskin, I., Kovaltsov, G., & Kiviaho, W. 2021, Sol. Phys., 296, 13 [Google Scholar]
- Vaquero, J. M., & Trigo, R. M. 2015, New Ast., 34, 120 [Google Scholar]
- Vaquero, J. M., Kovaltsov, G. A., Usoskin, I. G., Carrasco, V. M. S., & Gallego, M. C. 2015, A&A, 577, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaquero, J., Svalgaard, L., Carrasco, V., et al. 2016, Sol. Phys., 291, 3061 [Google Scholar]
- Vieira, L. E. A., & Solanki, S. K. 2010, A&A, 509, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vonmoos, M., Beer, J., & Muscheler, R. 2006, J. Geophys. Res., 111, A10105 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, C. J., Usoskin, I. G., Krivova, N., et al. 2018a, A&A, 615, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wu, C.-J., Krivova, N. A., Solanki, S. K., & Usoskin, I. G. 2018b, A&A, 620, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. 14C production rate Q (black curve) with 1σ uncertainties, obtained from Brehm et al. (2021), used here after corrections for the 994, 1052, and 1279 AD events and smoothing (see Sect. 2). The green RJ13 curve depicts Q from Roth & Joos (2013). |
| In the text | |
 |
Fig. 2. Time variability of the virtual axial dipole moment (VADM) as presented in archeomagnetic models considered here, U16 (Usoskin et al. 2016), COV-ARCH (Hellio & Gillet 2018), pfm9k.1b (Nilsson et al. 2014), and SHA (Pavón-Carrasco et al. 2014). |
| In the text | |
 |
Fig. 3. Dependence between Q-values computed for different geomagnetic dipole moments M, as denoted in the legend in units of ⋅1022 A m2 and Q* at the modern-day value of M0 = 7.75⋅1022 A m2. GCR spectra directly measured by AMS for May 2011 through May 2017 (see Sect. 3.2.1) were used when calculating Q-values. |
| In the text | |
 |
Fig. 4. Radiocarbon production rate Q* reduced to the modern geomagnetic shielding (M0 = 7.75 1022 A m2) with 1σQ* errors. |
| In the text | |
 |
Fig. 5. Scatter plot of the 14C global production rate Q*, computed based on the AMS-02 data for the period 2011–2017, and a polar NM64 (Oulu) neutron monitor count rate for the same period, with the dot-dashed red line depicting the dependence (Eq. (5)). |
| In the text | |
 |
Fig. 6. Scatter plot of the annual solar open magnetic flux Fo (Lockwood et al. 2009; Owens et al. 2017) against the 14C production rate Q* estimated from NMs (see Fig. 5). The red curve depicts the best-fit dependence (Eq. (6)). |
| In the text | |
 |
Fig. 7. Panel A: evolution of annual open solar flux: Fo(O17) based on in situ measurements (Owens et al. 2017) and Fo* reconstructed here based on relations (5) and (6). Panel B: difference between them dF = Fo − Fo(O17). Panel C: histogram of the occurrence of dF values with the best-fit Gaussian (mean 0.1 ⋅ 1014 Wb and σ = 0.9 ⋅ 1014 Wb). |
| In the text | |
 |
Fig. 8. Evolution of the reconstructed annual Fo. The mean curve (black) and 1σ uncertainties (grey shaded area) were computed by 10 000 MC realisations (see text). The green curve represents the smoothed (22-yr SSA) variability. The mean level of 2.5 ⋅ 1014 Wb defines the grand minima when solar magnetic activity drops below the sunspot formation threshold. Other reconstructions are shown for comparison: that of Wu et al. (2018a, W18) based on the SATIRE-T model applied to ISN (v.2); the same SATIRE-T model but applied to the GSN (W18(GSN)), as well as the OSF reconstructed from space-based measurements (Owens et al. 2017, – O17). Panel B: zoom to the period after 1700. The data are available at the CDS. |
| In the text | |
 |
Fig. 9. Synthetic SN series, composed of ISN (v.2) after 1700 and GSN before that (black curve), and its ‘reconstruction’ after the chain SN → Fo → SN’ (red curve). |
| In the text | |
 |
Fig. 10. SNs, computed using Eq. (7) from the Fo data for the instrumental era (see Fig. 7) reconstructed by Owens et al. (2017, O17) and from NM data, along with the ISN (v.2). |
| In the text | |
 |
Fig. 11. Time evolution of the reconstructed SNs (black curve with ±1σ grey-shaded uncertainties) in comparison with other direct and indirect SN series. Panel B: final annual reconstruction, and Panel C: its zoom for the period after 1700. Panel A: smoothed (15-yr first SSA component) annual series in comparison with other similarly smoothed or decadal series. These series are as follows: ISN (v.2, SILSO), GSN* (Hoyt & Schatten 1998), C17* (Chatzistergos et al. 2017), as well as two recent reconstructions based on 14C – U16* (Usoskin et al. 2016) and W18* (Wu et al. 2018b) (the asterisk indicates that the series is scaled up by a factor of 1.667 to match the ISN v.2 definition). Blue arrows denote grand minima of solar activity: Oort (OM), Wolf (WM), Spörer(SM), Maunder (MM), and Dalton (DM) minima. The data are available at the CDS. |
| In the text | |
 |
Fig. 12. Same as Fig. 11, but split into three subsequent time intervals of 310 years each. Cycles, which are not well defined during the grand minima (see Sect. 3.3), are indicated with the dashed line. |
| In the text | |
 |
Fig. 13. Evolution of the reconstructed SNs (blue curve with ±1σ grey-shaded uncertainties) for the periods around the corrected events: 994 AD (panel A), 1052 AD (panel B), and 1279 (panel C). The red curve depicts SNs if no correction is applied. Red arrows indicate the time of the events. |
| In the text | |
 |
Fig. 14. Distribution of cycle-averaged ⟨SN⟩ SNs along with fitted bimodal Gaussians. Panel A: SNs reconstructed here for 971–1900 (85 full cycles). The two curves are as follows: grand-minimum mode (magenta dashed line, mean m = 1, σ = 8) and normal mode (red dashed line m = 48, σ = 31). Orange bars correspond to the well-defined cycle q ≥ 4 (m = 49, σ = 36, 25 cycles). Panel B: ISN (v.2) SNs for 1750–2019 (24 full cycles), including two modes: a normal one (m = 64, σ = 16) and a grand-maximum one (m = 107, σ = 13). |
| In the text | |
 |
Fig. 15. Reconstructed solar activity around the Spörer minimum. Panel A: the black curve with grey-shaded error bars represents the main reconstruction and is identical to that in Fig. 12, while the red curve depicts a reconstruction based on one realisation of the simulated noise series (see text). Panel B: FFT spectrum (amplitude) of the main SN reconstruction (shown in panel A) for the period 1400–1550, while the red dotted line depicts the upper 95th percentile of the FFT spectra of 1000 noise-based reconstructions for the same period (see text). Panel C: same as panel B, but for OSF. |
| In the text | |
 |
Fig. 16. Panel A: wavelet power spectrum (Morlet basis, k = 6) of the reconstructed SN series, extended by ISN (v.2) after 1900. The white curve bounds the cone of influence (COI) where the spectrum is unreliable because of the proximity to the edges of the series. Black dots denote local maxima of the power (> 104) in the period bands 7–16, 75–140, and 180–250 years. The horizontal dashed line marks the location of the 11-year period. Panel B: cycle length (minimum-to-minimum) as a function of time (assigned to the cycle maximum year) for resolvable (q > 0, 56 cycles) reconstructed cycles (open dots) and for well-defined cycles (q ≥ 4, 25 cycles, filled circles). Red stars are the cycle lengths, rounded to the nearest integer (to be reduced to the annual resolution), in the ISN (v.2) series (http://www.sidc.be/silso/cyclesminmax) for 1750–2019. The dashed line represents the mean cycle length of 11 years over the ISN series. The grey shading denotes grand minima of solar activity. Panel C: comparison between the smoothed cycle-length evolution. The smooth red curve is the three-point running mean of the individual cycle lengths (q > 0). The light blue WV curve is the wavelet-defined period (identical to the upper black curve in panel A). |
| In the text | |
 |
Fig. 17. Distribution of cycle lengths for all resolvable cycles with q > 0 (grey bars), well-defined cycles (q ≥ 4, blue), and ISN (v.2) series (http://www.sidc.be/silso/cyclesminmax) for 1750–2019. Dashed lines represent the fitted normal distributions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



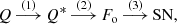
![$$ \begin{aligned}&(1\mathrm{a}) :\qquad \quad M_{i,j} = M_j^{(k_i)},\,\,\, k_i=r_{[1-4]} \nonumber \\&(1\mathrm{b}) :\qquad \quad Q_{i,j}(M_{i,j}) \rightarrow Q^*_{i,j}(M_0). \end{aligned} $$](/articles/aa/full_html/2021/05/aa40711-21/aa40711-21-eq2.gif)