| Issue |
A&A
Volume 647, March 2021
|
|
|---|---|---|
| Article Number | A69 | |
| Number of page(s) | 25 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202039613 | |
| Published online | 11 March 2021 | |
Understanding the evolution and dust formation of carbon stars in the Large Magellanic Cloud via the JWST
1
Dipartimento di Matematica e Fisica, Università degli Studi Roma Tre, Via della Vasca Navale 84, 00100 Roma, Italy
e-mail: ester.marini@uniroma3.it
2
INAF, Observatory of Rome, Via Frascati 33, 00077 Monte Porzio Catone (RM), Italy
3
Instituto de Astrofísica de Canarias (IAC), 38200 La Laguna, Tenerife, Spain
4
Departamento de Astrofísica, Universidad de La Laguna (ULL), 38206 La Laguna, Tenerife, Spain
5
Koninklijke Sterrenwacht van België, Ringlaan 3, 1180 Brussels, Belgium
6
Nordita, KTH Royal Institute of Technology and Stockholm University, Roslagstullsbacken 23, 106 91 Stockholm, Sweden
7
Department of Physics and Astronomy, Macquarie University, Sydney, NSW 2109, Australia
8
Dipartimento di Fisica e Astronomia ‘Galileo Galilei’, Univ. di Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
Received:
7
October
2020
Accepted:
20
December
2020
Context. Carbon stars have been, and still are, extensively studied. Given their complex internal structure and their peculiar chemical composition, they are living laboratories in which we can test stellar structure and evolution theories of evolved stars. Furthermore, they are the most relevant dust manufacturers, thus playing a crucial role in the evolution of galaxies.
Aims. We aim to study the dust mineralogy of the circumstellar envelope of carbon stars in the Large Magellanic Cloud (LMC) to achieve a better understanding of the dust formation process in the outflow of these objects. We intend to investigate the expected distribution of carbon stars in the observational planes built with the filters of the Mid-Infrared Instrument (MIRI) mounted onboard the James Webb Space Telescope (JWST) to select the best planes allowing an exhaustive characterisation of the stars.
Methods. We compared the synthetic spectral energy distributions, obtained by modelling asymptotic giant branch stars and the dust formation process in the wind, with the spectra of carbon stars in the LMC, taken with the Infrared Spectrograph onboard the Spitzer Space Telescope. From the detailed comparison between synthetic modelling and observation we characterise the individual sources and derive the detailed mineralogy of the dust in the circumstellar envelope.
Results. The sample of stars considered here is composed of stars of diverse mass, formation epoch, degree of obscuration, and metallicity. We find that precipitation of MgS on SiC seeds is common to all non-metal-poor carbon stars. Solid carbon is the dominant dust component, with percentages above 80% in all cases; a percentage between 10% and 20% of carbon dust is under the form of graphite, the remaining being amorphous carbon. Regarding the observational planes based on the MIRI filters, the colour-magnitude ([F770W]–[F1800W], [F1800W]) plane allows the best understanding of the degree of obscuration of the stars, while the ([F1800W]–[F2550W], [F1800W]) diagram allows better discrimination among stars of different metallicities.
Key words: stars: AGB and post-AGB / stars: abundances / stars: evolution / stars: winds / outflows
© ESO 2021
1. Introduction
Asymptotic giant branch (AGB) stars are important dust manufacturers in the Universe. Contrary to early studies, which suggest a dominant role of supernovae, it is now generally recognised that the contribution of AGB stars to dust production in the Universe cannot be neglected, even in early epochs (Valiante et al. 2009, 2017). Consequently, the knowledge of the AGB phase and the modality with which these stars form dust are important to investigate the physics of the interstellar medium and more generally the galaxy evolution, considering the critical role played by dust in influencing the star formation process (Hollenbach & Salpeter 1971; Mathis 1990; Draine 2003; Gong et al. 2017).
In recent years, we have witnessed significant steps forward in the description of the AGB phase, with the implementation of the description of dust formation in the winds departing from the photosphere of the central star (Ventura et al. 2012, 2014; Nanni et al. 2013, 2014; Dell’Agli et al. 2019). These models have been successfully applied to study the evolved stellar populations of the Magellanic Clouds (Dell’Agli et al. 2014a, 2015a,b; Nanni et al. 2016, 2018, 2019a) and other galaxies in the Local Group (Dell’Agli et al. 2016, 2018, 2019). Further fields of application include the modelling of dust evolution in the Milky Way (Ginolfi et al. 2018), in local and high-redshift galaxies (Schneider et al. 2014; Nanni et al. 2020a), and in the Universe (Gioannini et al. 2017).
In the near future, studies aimed at improving our understanding of dust production in the envelope of AGB stars will benefit from the launch of the JWST, which will allow an unprecedented exploration of the evolved stellar populations in the Local Universe. The large aperture (6.5 m) and the sub-arsecond spatial resolution will allow the study of resolved dusty stellar populations at moderate and large distances, up to ∼4 Mpc (Jones et al. 2017). The JWST will provide spectroscopy in the 5 − 28.5 μm range (Bouchet et al. 2015), thus offering a unique opportunity to study the evolution of AGB stars and the dust formation process in their expanding wind, in a large variety of environments. The full exploitation of the JWST potentialities will allow the characterisation of the evolved stellar populations observed in the galaxies of the Local Group, and possibly beyond, provided that we know how AGB stars evolve in the observational planes built with the JWST filters.
A first step in this direction was achieved by Jones et al. (2017), who considered the Spitzer spectroscopic data obtained with the Infrared Spectrograph (IRS) instrument of ∼1000 objects in the Magellanic Clouds and obtained the magnitudes in the various MIRI filters via convolution with the corresponding transmission curves. The aim of this work is to set reliable classification schemes to disentangle different classes of objects. Regarding the evolved stellar populations (AGB and RSG stars), the analysis by Jones et al. (2017) was based on existing libraries of spectra, spanning a wide range of photospheric parameters and dust composition.
In this context, we recently launched a research project aimed at exploring how the JWST space mission will allow the characterisation of the evolved stellar populations of galaxies. We based our investigation on the IRS data of LMC stars, because only a detailed analysis of the spectral energy distribution (SED) allows an accurate understanding of the dust composition in the circumstellar envelope. An example of this approach is reported in the work by Jones et al. (2014), which was aimed at deriving the amount of alumina dust in the wind of oxygen-rich stars in the LMC.
Differently from Jones et al. (2017), we used evolutionary sequences of AGB stars that include the description of dust production, making it possible to predict the SED evolution, which consists of a sequence of synthetic spectra, each representing a specific evolutionary stage of the AGB phase. In Marini et al. (2020), we studied the sample of M-type AGB stars in the LMC. By comparing IRS and synthetic SED, we characterised the individual sources and we investigated the obscuration sequences of oxygen-rich AGB stars in the planes built with the JWST filters.
Here, we extend the analysis of Marini et al. (2020) to the C-rich star sample in the LMC. This step is important in the general context of dust production by stars in galaxies, because the overall dust production rate from AGB sources is dominated by carbonaceous species in the Magellanic Clouds (Schneider et al. 2014; Nanni et al. 2018, 2019a,b), and even more so in metal-poor environments (Cioni & Habing 2003; Boyer et al. 2013). For these reasons, carbon stars have been extensively investigated, both in terms of the capability of carbon dust to drive an AGB wind (Mattsson et al. 2010; Mattsson & Höfner 2011; Bladh et al. 2019; Sandin & Mattsson 2020) and in studies aimed at constraining the physical parameters and the dynamical properties of the winds of individual carbon stars (Rau et al. 2017, 2019; Brunner et al. 2018; Maercker et al. 2018).
To date, the most exhaustive studies focused on the carbon star population of the LMC (based on the results from AGB+dust modelling) are those by Dell’Agli et al. (2015a) and Nanni et al. (2019a). The former used results from the InfraRed Array Camera (IRAC) and the Multi-band Imaging Photometer (MIPS) photometry to characterise the stars according to their position in the observational planes. Nanni et al. (2019a) considered different observations in the infrared and optical data from Gaia, and they derived important trends connecting mass-loss rate, dust production rate, and dust-to-gas ratio of the stars with the infrared colours, which were properly taken as indicators of the degree of obscuration.
This work, similarly to those of Dell’Agli et al. (2015a) and Nanni et al. (2019a), is based on results from stellar evolution and dust formation modelling, calculated specifically for the present study, with the evolutionary sequences extended to the beginning of the post-AGB phase. However, following the same approach as in Marini et al. (2020), we mostly focus on the results from IRS spectroscopy to reach a better understanding of dust formation in the wind of carbon stars. Furthermore, we analyse the results whilst taking the JWST into consideration, in order to provide the scientific community with the appropriate tools to analyse the carbon star populations of galaxies.
The present investigation was developed on two levels. We first derived the luminosities and the optical depths of the individual sources by comparing the IRS and the synthetic SEDs, the latter being obtained by the modelling of the AGB evolution and of the dust formation process. These estimates are rather robust, because the extinction of carbon stars is mostly due to solid carbon particles and is substantially independent of the presence of other dust species. This step allows the characterisation of the stars considered in terms of mass, formation epoch, and chemical composition of the progenitors.
After the identification of the sources, we focused on dust mineralogy to determine the percentages of the different dust species in the circumstellar envelope. This requires a detailed analysis of the IRS SED, considering that the morphology of the different spectral features is extremely sensitive to the type and the quantity of the dust grains formed in the stellar wind. Our aim is to improve our knowledge of the dynamical and chemical structure of the wind of carbon stars, to shed new light on the dust formation process, to understand the conditions that lead to the formation of specific dust compounds: this information will prove crucial to the characterisation of the carbon star samples in galaxies different from the Magellanic Clouds, which will be observed by the JWST.
In this investigation we focused on the distribution of the stars in the observational planes built with the MIRI filters, because the IRS spectra cover the 5 − 37 μm spectral region. Our goal was to select the planes that allow the best characterisation of the sources observed and to identify those planes where the bifurcation of the various sequences can be associated with some peculiar properties of the star; for example the presence of specific dust particles or the metallicity.
The paper is organised as follows: in Sect. 2, we present the sample of stars used for the analysis; the numerical codes used to calculate the evolutionary sequences to model dust formation and to build the synthetic spectra are described in Sect. 3; the evolution and the dust formation mechanism in the models used are discussed in Sect. 4; in Sect. 5, we present the characterisation of the sources observed, whereas in Sect. 6 we address the determination of the dust mineralogy and the information obtained regarding the structure of the winds; the expected distribution of carbon stars in the observational planes built with the MIRI filters is discussed in Sect. 7.
2. The selected sample
In this paper, we use the LMC sample of 147 C-rich AGB spectra from the SAGE-Spec database at the NASA/IPAC Infrared Science Archive, which was reduced by Jones et al. (2017) using the method discussed in Kemper et al. (2010). This database includes all staring-mode observations with the Spitzer IRS taken in the area of the sky covered by the SAGE survey (Meixner et al. 2006), which covers the LMC entirely. Jones et al. (2017) classified the sources of the sample by using the decision tree classification method by Woods et al. (2011): the primary criterion for the classification was the Spitzer spectrum itself, but it also relied on the additional information provided by the SED, the estimate of the bolometric luminosity, and supplementary information from the literature. C-rich AGB stars, in particular, are usually identified by molecular absorption features, particularly C2H2 (acetylene) at 7.5 and 13.7 μm, and by the dust features at 11.3 μm and 30 μm.
To study the expected distribution of the stars in the observational planes built with the magnitudes in the MIRI filters, we used the mid-IR magnitudes ([F770W], [F1000W], [F1130W], [F1280W], [F1500W], [F1800W], [F2100W], [F2550W]) calculated by Jones et al. (2017), who integrated the IRS spectra of each source over the MIRI spectral response. In some cases, the IRS data do not match IRAC and MIPS photometry, which could be an effect of variability, considering that IRS, IRAC, and MIPS data were collected in different epochs. To this end, we used the criterion proposed by Groenewegen & Sloan (2018) stating that variability can account for a difference of up to 20% between the fluxes derived from the analysis of the IRS SED and those found via the IRAC and MIPS magnitudes. In these cases, we left the MIRI magnitudes found by Jones et al. (2017) unchanged. In the cases where the difference is above 20%, we scaled the IRS spectra to match the corresponding IRAC and MIPS photometry, and we recalculated the corresponding MIRI magnitudes via convolution over the MIRI transmission curves.
The majority of these objects cover the 5 − 37 μm range of the low-resolution modules of the IRS, so the fluxes for the F560W filter are not available. For 27 of these objects, the spectral coverage by the Spitzer-IRS is limited to the 5 − 14 μm range, therefore the mid-IR photometry beyond this wavelength is not available: we thus excluded them from our analysis. In addition, a paucity of sources show a steep rise starting from ∼20 μm and no decline up to the end of the spectra. We believe that these peculiar SEDs are affected by nearby background emission, as also stated by Gładkowski et al. (2019), and for this reason were not considered in the analysed sample.
3. Physical and numerical input
3.1. Stellar evolution modelling
The evolutionary sequences were calculated by means of the ATON code for stellar evolution (Ventura et al. 1998). An exhaustive description of the numerical details of the code and the most recent updates can be found in Ventura et al. (2013).
3.1.1. The chemical composition
Most of the analysis is based on models of metallicity Z = 0.008, helium mass fraction Y = 0.26, and a mixture taken from Grevesse & Sauval (1998) with α−enhancement [α/Fe] = +0.2. This is the same chemical composition used in Ventura et al. (2014); we preferred to recalculate the evolutionary sequences from the beginning in order to follow the very final phases in detail, which, as we see in the following sections, are those with the largest degree of obscuration and that can account for the presence of the objects with the largest infrared emission.
The models not undergoing the helium flash were evolved from the pre-main sequence until the almost total consumption of the envelope. Low-mass models (M ≤ 2 M⊙) experiencing the helium flash were evolved from the horizontal branch, starting from the core mass and surface chemical composition calculated up to the tip of the red giant branch (RGB). For the objects whose SED suggests a metal-poor composition, we used Z = 0.001 and Z = 0.002 tracks with initial helium Y = 0.25 and [α/Fe] = +0.4 mixture from Grevesse & Sauval (1998). Finally, models of metallicity Z = 0.004, Y = 0.26, [α/Fe] = +0.2 were also considered. The Z = 0.001, Z = 0.002 and Z = 0.004 models were taken from Ventura et al. (2014).
3.1.2. Convection
The temperature gradient within regions unstable to convection was calculated via the full spectrum of turbulence (FST) model (Canuto & Mazzitelli 1991). The overshooting of convective eddies within radiatively stable regions is modelled by assuming that the velocity of convective elements decays exponentially beyond the neutrality point, fixed via the Schwartzschild criterion. The e-folding distance of the velocity decays during the core burning phases (hydrogen and helium) and during the AGB phase is taken as 0.02HP and 0.002HP, respectively. The latter values reflect the calibrations discussed, respectively, in Ventura et al. (1998, 2014).
3.1.3. Mass loss
The mass-loss rates during the phases when the star is oxygen-rich were determined via the Blöcker (1995) treatment, with the parameter entering the formula of Blöcker (1995) set to η = 0.02; this choice follows the calibration given in Ventura et al. (2000). For carbon stars, we used the mass-loss description from the Berlin group (Wachter et al. 2002, 2008).
3.1.4. Opacities
The radiative opacities are calculated according to the OPAL release, in the version documented by Iglesias & Rogers (1996). The molecular opacities in the low-temperature regime (T < 104 K) are calculated with the AESOPUS tool (Marigo & Aringer 2009). The opacities are constructed self-consistently by following the changes in the chemical composition of the envelope, which include, in particular, the individual abundances of carbon, nitrogen, and oxygen.
3.2. Dust production
The interpretation of the IR spectra of obscured carbon stars requires the knowledge of the dust present in the circumstellar envelope, namely the density; the radial distribution; and the percentages of the different dust species formed. To this aim, we modelled the formation and growth of dust particles in the wind of AGB stars according to the schematisation proposed by the Heidelberg group (Ferrarotti & Gail 2006), similarly to previous works by our team (Ventura et al. 2012, 2014, 2015, 2016), which was used in a series of papers by the Padua group (Nanni et al. 2013, 2014, 2016, 2018, 2020b; Nanni 2019). The interested reader can find all the relevant equations in Ventura et al. (2012). Here, we provide a brief description of the methodology used.
In the present framework, dust particles are assumed to form and grow in the wind, which expands isotropically from the photosphere of the star. Each dust species starts to form at the so-called condensation point, where the growth rate exceeds the vaporisation rate; the latter is dependent on the thermodynamic properties of the solid compounds, mainly on the formation enthalpies of the solid compounds and of the gaseous molecules involved in the formation reaction (Ferrarotti & Gail 2006).
The dynamics of the wind is described by the momentum equation, where the acceleration is determined by the competition between gravity and radiation pressure acting on the newly formed dust grains. The coupling between grain growth and wind dynamics is given by the extinction coefficients, describing the absorption and scattering of the radiation by dust particles. The evolution with time of dust grains is determined by the difference between the growth and the vaporisation rate. The former is given by the gas molecules hitting the already formed grains, and the latter is related to the vapour pressure of gaseous molecules over the solid compounds.
In the basic configuration, we assume that the dust species formed in the winds of carbon stars are silicon carbide (SiC) and amorphous carbon (C). This assumption is suitable for determining the main properties of the wind, and namely the terminal velocity and the degree of obscuration, which we quantify via the optical depth at the wavelength λ = 10 μm, τ10. For the detailed interpretation of the SED of the various sources, we also account for the formation of graphite and of MgS; for the latter species, we consider either the possibility that it forms as individual species or that MgS mantles form on SiC cores (Zhukovska et al. 2008). The extinction coefficients were found by using the optical constants from Zubko et al. (1996; amorphous carbon), Pegourie (1988; SiC), Begemann et al. (1994; MgS), and Draine & Lee (1984; graphite). The optical constants of SiC+MgS compounds were calculated on the basis of the method described in Zhukovska et al. (2008).
The modelling of dust formation, as described above, allows the determination of the asymptotic velocity of the gas particles, the size reached by the grains of the various species, and the optical depth. Furthermore, this computation provides an estimate of the surface fraction of gaseous silicon, carbon and magnesium condensed into dust (see Eqs. (20)–(23) and (34)–(35) in Ferrarotti & Gail 2006) and the dust production rate for each dust species, which depends on the gas mass-loss rate, the surface mass fractions of the aforementioned chemical elements, and the fraction of the latter species condensed into dust (see Sect. 5.2 in Ferrarotti & Gail 2006).
3.3. Spectral energy distribution
The interpretation of the IRS SEDs demands the computation for each stellar mass of a sequence of theoretical SEDs. These correspond to the evolutionary stages of carbon stars and to the dust formed in the circumstellar envelope, modelled according to the methods described earlier in this section.
To characterise the individual AGB sources and derive the mass and formation epoch of the progenitor stars, we confront the IRS data with the sequences of synthetic spectra obtained for each model star, which represent the evolution of the SED of the star during the AGB phase. To build these sequences, we first select a few points along the evolutionary track, distributed among the various interpulse phases. Typically, we select one evolutionary stage corresponding to the largest luminosity during the interpulse, before the ignition of the following thermal pulse (TP). Towards the final evolutionary phases, when the mass-loss rate rises and a significant fraction of the envelope is lost during a single interpulse, we select one or two additional points in order to follow in more detail the variation of the stellar properties as mass is lost from the envelope. For completeness, we also consider a couple of stages following the extinction of each TP, when the contribution of the CNO burning shell accounts for 10% and 30% of the overall energy release of the star. Based on the physical parameters attained by the star during these phases, particularly luminosity, effective temperature, current mass, mass-loss rate, and surface chemical composition, we model dust formation. This allows the determination of the amount of dust formed, the dust mineralogy, the size of the dust particles, and τ10.
The last step consists of the calculation of the synthetic SED, which is done by means of the code DUSTY (Nenkova et al. 1999). As input radiation, we used the SED found by interpolation in effective temperature, surface gravity, and C/O ratios among the COMARCS model atmospheres (Aringer et al. 2009) of the appropriate metallicity.
4. Carbon stars: Evolution and dust production
The carbon star stage is reached as a consequence of repeated third dredge-up (TDU) episodes, which take place during the AGB phase after the occurrence of TPs. During these events, the surface convective layer penetrates inwards, down to regions of the star previously exposed to helium burning nucleosynthesis (Iben 1974, 1975; Lattanzio 1987, 1993; Boothroyd & Sackmann 1988). The consequence of TDU is the transportation of carbon nuclei synthesised via 3α reactions to the surface regions, which become more and more enriched in carbon: once the number of C nuclei overcomes the number of O, the star becomes a C-star.
Stars of masses below ∼1 M⊙ do not become C-stars. This threshold mass decreases slightly with metallicity, because lower Z stars, owing to the smaller amount of oxygen, reach the C/O> 1 condition (Karakas 2014) more easily. For the Z = 0.008 models used in the present work, we find that the minimum mass required to attain the C-star stage is 1.25 M⊙1.
The mass range of carbon stars is also limited from above, because stars with CO cores of mass above ∼0.8 M⊙ (Ventura et al. 2013) experience hot bottom burning (HBB), consisting of the activation of a series of p-capture reactions at the base of the external envelope, which favour the destruction of the surface carbon. In this investigation, we find that the aforementioned limit in the core mass translates into a threshold initial mass of 3.3 M⊙.
It is not excluded that stars of higher mass go through evolutionary phases, during which they are C-stars. This may occur either during the initial AGB stages, before HBB is activated, or at the very end of the AGB life, when HBB is turned off and the occurrence of a few TDU events might increase the C/O ratio above unity (Frost et al. 1998). However, while we take this into account for the interpretation of a few outliers in the sample that we analysed, in the following sub-section we focus our attention on the stars with initial mass M ≤ 3.3 M⊙, because only these objects are expected to reach a significant degree of obscuration and to provide a non-negligible contribution to the dust enrichment of the interstellar medium during the C-star phase.
4.1. The behaviour of 2 M⊙ stars
To more clearly illustrate the key aspects of the evolution of these objects, in Fig. 1 we show the variation with time of luminosity, effective temperature, surface C/O, and mass-loss rate of a star of initial mass 2 M⊙. The figure refers to the evolutionary phases between the beginning of the TP phase (from which the times on the abscissa are counted) and the almost complete ejection of the external mantle.
 |
Fig. 1. Evolution as a function of time (counted from the beginning of the TP phase) of the luminosity (top-left panel), effective temperature (top, right), surface C/O (bottom, left) and mass-loss rate (bottom, right) of a model of initial mass 2 M⊙ and metallicity Z = 0.008. |
The 2 M⊙ model shown in Fig. 1 experiences 14 TPs. The C-star stage is reached after nine TPs: the duration of the C-star phase is ∼6 × 105 Myr, which corresponds to ∼25% of the AGB life (2.4 Myr). The relatively short duration of the C-star phase is a common property of carbon stars (Karakas 2014). It is related to the transition from M- to C-star and the aforementioned increase in the mass-loss rate (Ventura & Marigo 2009, 2010), which renders the remaining part of the AGB lifetime shorter. This effect can be seen in the right panels of Fig. 1, where we note that the effective temperature drops by ∼1000 K during the last four interpulse phases, while at the same time the mass-loss rate increases by almost two orders of magnitude, up to Ṁ ∼ 10−4 M⊙ yr−1.
During the interpulse periods of the C-star phase, we find that the luminosity of the star is constant within ∼20%, spanning the 6500 < L/L⊙ < 7500 L⊙ range. These phases account for 90% of the total AGB lifetime. As is clear from Fig. 1, the luminosity drops to ∼2000 − 3000 L⊙ after each TP, before the CNO activity is fully restored.
The almost constant luminosity characterising the quiescent CNO burning evolution is partly explained by the previously mentioned short relative duration of the C-star phase, during which the stars experience only a few TPs. An additional reason is that after the C-star stage is reached, the TDU experienced becomes deeper and deeper, which prevents a significant growth of the core mass, and hence of the luminosity. The small variation of the luminosity of the star during the C-star phase, combined with the fact that stars of different masses evolve at different luminosities, opens the way to use it as a mass indicator, which is important to identify the progenitors of the stars.
To discuss dust production in the 2 M⊙ star, in the top-left panel of Fig. 2 we present the variation of the dust production rate (DPR), that being the amount of dust produced by the star in a given evolutionary phase, expressed in units of M⊙ yr−1. In the top-right panel of Fig. 2, the DPR is shown as a function of the current mass of the star, to have an idea of the dust yields expected.
 |
Fig. 2. Top panels: variation of the dust production rate as a function of time (left) and of the current mass of the star (right) during the AGB evolution of the model of initial mass 2 M⊙ and metallicity Z = 0.008 presented in Fig. 1. The individual contributions from silicates, solid carbon, and silicon carbide are shown. Bottom panels: variation of the expected SED during four different stages (indicated with the arrows in the top-right panel) when considering only solid carbon and SiC (left), and when graphite and MgS are also considered (right). In these examples, the number density of the seeds of amorphous carbon dust relative to hydrogen is assumed 10−13, whereas the density of the seeds of the other dust species are scaled with respect to amorphous carbon according to the percentages given in the two panels. |
During the first part of the AGB evolution, when the star is oxygen-rich, the dust formed is under the form of alumina dust and silicates. Alumina dust forms in a more internal region of the envelope, at a distance of ∼2 stellar radii (R*) from the photosphere of the star, whereas the condensation region of silicates is more external, at a distance of 5 − 10 R* from the stellar surface (Dell’Agli 2012; Dell’Agli et al. 2014b). The extinction properties of the circumstellar envelope are mostly related to silicates, because alumina dust forms in small quantities and is extremely transparent to the radiation. During most of the O-rich phase, dust production is negligible, because the mass-loss rate is extremely low and the effective temperatures are close to 4000 K (see Fig. 1): both these conditions prevent significant dust formation in the wind.
During the final part of the AGB evolution, the dust formed is made up of carbonaceous dust, which is mostly SiC and solid carbon (Ventura et al. 2012). The latter species generally forms in higher quantities, with the exception of the first interpulse phase after the achievement of the C-star stage, during which the carbon excess is smaller than, or of the same order of magnitude of the silicon abundance. This is shown in the top panels of Fig. 2, where we see that the SiC contribution to the DPR is higher than that of solid carbon during the phases immediately following the achievement of the C-star stage. The overall degree of obscuration of the star is almost entirely determined by solid carbon dust; this is not only due to the fact that this is generally the most abundant dust species, but, more importantly, to the larger extinction coefficients of solid carbon compared to SiC (see Fig. 10 in Ferrarotti & Gail 2002).
Upon inspection of Fig. 2, we see that the DPR during the interpulse phase increases by 2–3 orders of magnitude when the transition from O-rich to carbon star occurs. This behaviour, common to all the stars that eventually become carbon stars, is due to two reasons: (a) the rate of mass loss is much higher during the C-star phase (see bottom-left panel of Fig. 1), which favours dust production, owing to the higher densities of the wind (see Eq. (14) in Ferrarotti & Gail 2001); and (b) the formation of carbon dust is favoured compared to silicates, because the surface carbon excess with respect to oxygen is significantly higher than the density of gaseous silicon, which is the key quantity to determine the formation of silicates during the O-rich phases.
Because of the mass lost during the C-star phase, most of the dust produced by the stars that eventually reach the C-star stage is made up of carbon dust (Ferrarotti & Gail 2006; Nanni et al. 2013; Ventura et al. 2014), despite the fact that the C-star lifetime is usually shorter than the initial phase, during which the star is oxygen rich.
Understanding the dust formation process is extremely important when it comes to predicting the variation of the SED of these objects, as they evolve through the AGB. This step is crucial when a detailed comparison with the observations is required. In the bottom-left panel of Fig. 2, we show the synthetic SED of the 2 M⊙ star, corresponding to the three evolutionary stages, indicated with arrows in the top-right panel. We note that the luminosity of the star is unchanged within 200 L⊙, among the three cases; thus, the significant difference in the flux distribution is entirely due to the IR emission, which becomes larger and larger as the dust production rate increases.
In this particular case, we see that the peak of the SED gradually shifts from ∼3 μm to ∼12 μm. We note the emission feature related to SiC, at 11.3 μm, which turns into absorption when the circumstellar envelope, becomes extremely thick.
4.2. Formation and evolution of carbon stars: The role of the stellar mass
The behaviour of C-stars is sensitive to the mass of the progenitor. Higher mass stars are brighter, because their core mass is larger. Furthermore, the higher the initial mass of the star, the higher the mass in the envelope at the beginning of the TP-AGB phase; this reflects into a higher number of TDU events, and, for a given TDU efficiency, into a more efficient surface carbon enrichment and a higher dust production rate.
A summary of the main physical and chemical properties of the models used in the present analysis are given in Table 1, where for each mass we report the evolutionary time, the duration of the TP-AGB and the carbon-star phase, the luminosity range during the C-star phase, the final surface carbon-to-oxygen ratio, and the highest dust production rate and optical depth reached. The latter two quantities are attained towards the late AGB phases, before the general contraction, which marks the beginning of the post-AGB evolution.
Main properties of the Z = 0.008 models discussed in the text.
Figure 3 displays the evolution of stars with masses within the 1.25 − 3.3 M⊙ range that reach the surface C/O> 1 condition and evolve as carbon stars for the remaining part of their evolution. In the same figure, we also report the tracks corresponding to the 3.5 M⊙ star, which evolves as a carbon star during a small fraction of the AGB phase, before HBB causes the drop in the surface carbon, and of the 5 M⊙ star of metallicity Z = 0.001, which becomes a C-star in the final part of the AGB evolution, after HBB is turned off.
 |
Fig. 3. Variation of luminosity (top-left panel), carbon excess C−O (top-right, see text for the definition), dust production rate (bottom-left) and τ10 (bottom-right) of the AGB models used in the present work. The evolutions are shown with respect to the current mass of the star on the abscissa. The different lines connect a few points selected during the evolution trough the C-star phase. Open points refer to the evolution of a 5 M⊙ star of metallicity Z = 0.001 |
The top-right panel of Fig. 3 shows the carbon excess, C−O, defined as the difference between the surface number densities of carbon and oxygen nuclei, normalised to the density of hydrogen: C−O = 12 + log[(n(C) − n(O))/n(H)]. This quantity is relevant to understanding how much carbon dust forms (Mattsson et al. 2008; Bladh et al. 2019). In 1.25 − 1.5 M⊙ stars, we find that C−O is slightly below 8; on the other hand, 3 M⊙ stars reach C−O ∼ 9 during the very final AGB phases. In the 3.3 M⊙ case, the final carbon excess is smaller than in lower mass stars, because the final TDU episodes are so efficient and deep that some oxygen enrichment of the envelope occurs. The overproduction of oxygen in carbon stars is consistent with the study of the chemistry of carbon-rich planetary nebulae by García-Hernández et al. (2016). In the 3.5 M⊙ star C−O< 7.7, because the ignition of HBB prevents further increase in the surface carbon and eventually makes the star O-rich. The same upper limit approximately holds for the 5 M⊙, Z = 0.001 model, as the accumulation of carbon in the surface regions begins only during the final AGB phases, after HBB is turned off.
The evolution of the DPR, shown in the bottom-left panel of Fig. 3, reflects the trend with the initial mass followed by the carbon excess. The higher availability of the surface carbon affects dust formation in two ways: (a) stars with a higher carbon mass fraction are more expanded, and their effective temperatures are cooler, which favours dust production; and (b) the higher the percentage of gaseous carbon, the larger the number of molecules available to condense into solid carbon grains. M ≥ 2.5 M⊙ stars attain DPRs above 10−6 M⊙ yr−1 during the final phases, whereas in the M < 2 M⊙ counterparts DPR is below 10−7 M⊙ yr−1. The 2 M⊙ case discussed in the previous section follows an intermediate behaviour, with a maximum DPR of the order of 4 × 10−7 M⊙ yr−1.
The formation of dust is associated with the shift of the SED to IR wavelengths, owing to scattering and absorption of photon by dust grains in the circumstellar envelope, which becomes more and more opaque in relation to the electromagnetic radiation, with the consequent increase in τ10 (the evolution of which is shown in the bottom-right panel of Fig. 3). According to the present modelling, we find that the largest optical depths, τ10 ∼ 5, are attained by 3 M⊙ stars; on the other hand, low-mass stars with an initial mass ∼1.5 M⊙ reach τ10 ∼ 1 during the final AGB phases. Based on these arguments, Dell’Agli et al. (2015a) suggested that the most obscured stars in the LMC, identified in the colour-colour plane obtained with the IRAC filters, are the progeny of 2.5 − 3 M⊙ stars, formed during the burst in the star formation rate of the LMC, which occurred ∼300 − 600 Myr ago (Harris & Zaritsky 2009).
4.3. Uncertainties in AGB and dust production modelling
The results regarding the characterisation of carbon stars are partly affected by some uncertainties, which are related to AGB modelling and to the description of dust formation. Before entering the discussion on the interpretation of the individual sources, we believe it is important to present a summary of the impact of these uncertainties on the conclusions reached.
As outlined in Sects. 4.1 and 4.2, the quantity of dust that carbon stars form depends on the amount of 12C transported by TDU from the internal regions to the convective envelope. This is extremely sensitive to the treatment of the convective borders (Herwig 2000, 2005; Karakas & Lattanzio 2014). However, this does not represent a serious issue in the present context, because the carbon star population of the LMC has been traditionally used as a living laboratory to test the efficiency of TDU. Among others, we mention the works by Groenewegen & de Jong (1993), Marigo et al. (1999), Karakas et al. (2002), and Kamath et al. (2012), who provided robust calibrations of the extent of TDU for stars of different masses. Thorough investigations aimed at calibrating mass loss, TDU efficiency, and dust properties of AGB stars in the Magellanic Clouds were recently presented in Pastorelli et al. (2019, 2020).
Among the physical quantities relevant to the evolution through the AGB, shown in Fig. 1, mass loss is the most poorly known. This is a delicate point, because the description of mass loss determines the rate at which the mass of the envelope is expelled into the interstellar medium, the duration of the AGB phase, and thus the amount of carbon that is gradually accumulated in the surface regions via TDU (Ventura & D’Antona 2005a).
Several evolutionary codes adopt the classic period, such as the mass-loss-rate relation by Vassiliadis & Wood (1993), both for O-rich and carbon stars (Cristallo et al. 2009; Karakas & Lattanzio 2014). Some research teams have based the mass-loss modelling of carbon stars on the theoretical radiation-hydrodynamical models published by the Berlin group (Wachter et al. 2002, 2008), which considered dust production in C-rich winds and the effects of radiation pressure on the carbonaceous dust particles formed in the circumstellar envelope (Weiss & Ferguson 2009; Ventura et al. 2018). The formulae by Wachter et al. (2002, 2008) do not include any dependence on the carbon excess with respect to oxygen, which should affect the amount of dust formed in the wind of the stars (Mattsson 2008; Mattsson et al. 2010; Eriksson et al. 2014; Bladh et al. 2019).
The treatment of mass loss affects the description of the dust formation process, because the density of the wind is directly proportional to Ṁ. In optically thin environments, we expect the calculated optical depth to show some level of sensitivity to Ṁ. On the other hand, compensation occurs in the optically thick case. This is because the formation of more dust in the regions just above the condensation zone triggers a higher acceleration of the wind, which decreases the density of the gas, thus inhibiting further dust formation. In these cases, the description of mass loss affects the topography of the wind, but the effect on the global amount of dust formed, hence on the optical depth along the observation line, is modest.
The description of the stellar wind and of the dust formation process used in the present investigation is characterised by uncertainties, the most relevant being the effects of pulsations, the poor knowledge of the sticking coefficients, and of the density of seed nuclei upon which the dust grains grow. The primary effect of large amplitude pulsations is the formation of several shock fronts, which are moving outwards and potentially able to project dense matter to cool regions of the envelope, which is in turn suitable for the condensation of gas molecules into dust (Bowen 1988; Bertschinger & Chevalier 1985; Fleischer et al. 1992). The inclusion of the effects of shocks is beyond current computational capabilities; furthermore, these calculations would be extremely time consuming in the present case, because the system of moments and radiative transfer equations commonly used to model the atmosphere should be applied to all the models in which the AGB evolution is split (usually between ∼50 000 and ∼100 000), according to the criteria followed to choose the time steps. On the other hand, what we obtain by use of the stationary wind modelling is the average amount of dust formed in the outflow.
The role of the sticking coefficients of the different dust species is extensively discussed in Ferrarotti & Gail (2001, 2002, 2006). In the present context, the key point is how the choice of the coefficients affects the formation of solid carbon, which is the species that gives the dominant contribution to the optical depth. Generally speaking, we find that changes in the sticking coefficients can alter the dust density gradient from the carbon dust condensation zone, but the effects on the size reached by carbon grains and on the overall dust formed is of a percentage much smaller than the change in αC.
One of the most relevant open points connected with the dust formation in the wind of AGB stars is the nature and the density of seed nuclei. These impact the density of the dust grains, the fraction f of the gas condensed into dust, and the overall scattering coefficient, which is proportional to f (Ferrarotti & Gail 2001). In the present computations, following Ferrarotti & Gail (2006), we adopted nd = 10−13 for all the dust species considered. However, other choices are possible; for example, Nanni et al. (2013) proposed scaling the number density of the seeds of carbon dust with C−O.
The choice of nd translates into the size of the grains formed: a higher nd for a given dust species implies higher condensation fractions of the relevant gaseous molecules, which decrease the growth rate 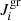 , thus leading to the formation of smaller sized particles. If we focus attention on carbon grains to determine the degree of obscuration of the star at a given evolutionary stage, we find that the choice of nd reflects the size reached by the carbon grains, but it only has a small effect on the value of τ10. Therefore, in the interpretation of the IRS spectra, which is addressed in the following sections, we safely rely on the highest values of τ10 reported in Table 1.
, thus leading to the formation of smaller sized particles. If we focus attention on carbon grains to determine the degree of obscuration of the star at a given evolutionary stage, we find that the choice of nd reflects the size reached by the carbon grains, but it only has a small effect on the value of τ10. Therefore, in the interpretation of the IRS spectra, which is addressed in the following sections, we safely rely on the highest values of τ10 reported in Table 1.
On the other hand, we cannot rule out that different dust species have different nd. This would not affect τ10, but it would change the relative distribution of the different particles, which would in turn translate into significant alterations in the SED. As an example, in the bottom panels of Fig. 2 we show how the SED of the star is modified if small percentages of graphite and MgS are added to SiC and C.
A description of the wind of carbon stars with such a high predictive power is currently unavailable. In the following, we characterise the individual stars based on our expectations regarding the evolution of the luminosity and the optical depth in stars of various masses and during different evolutionary phases. Moreover, we used the observations as a guide to understand which dust species form and in what percentages.
5. The characterisation of carbon stars in the LMC
To understand the distribution of carbon stars and the obscuration sequences in the observational planes (colour-colour and colour-magnitude diagrams obtained with the JWST filters), we need to characterise the individual sources. To this aim, we first confront the IRS data of each star belonging to the sample described in Sect. 2 with the sequence of synthetic SEDs, which represent the evolution of the spectrum of each model star, built as described in Sect. 3. The identification of the synthetic SED that best reproduces the IRS spectrum leads to a robust derivation of the luminosity and of the optical depth of each source, which are essential ingredients to deduce the mass of the progenitors (see Table 1) and the current AGB phase through which they are evolving. The results are reported in Table 2, which gives the derived values of L, τ10, and dust mineralogy for each source investigated.
Interpretation of the sample carbon stars analysed in the present work.
A few examples of this analysis are shown in Fig. 4, in which we report the interpretation of the SED of stars of various L and τ10. The main deviations of the synthetic SED from the observed spectrum are in relation to the C2H2 molecular bands in the regions 6.6 − 8.5 μm (centred at ∼7.5 μm) and 13.5 − 13.9 μm (Matsuura et al. 2006) and the CO+C3 band in the region 5.0 − 6.2 μm (Jørgensen et al. 2000). The properties of these features have been widely analysed in the past (e.g. Sloan et al. 2016 and references therein), but unfortunately they are poorly (or not at all) reproduced by model atmospheres available in the literature, owing to scarce knowledge of the opacities of such molecules. The ∼7.5 μm feature affects the flux in the 6 − 9 μm spectral region, the effect becoming smaller and smaller as τ10 increases, eventually vanishing for τ10 > 1. On the other hand the C2H2 ∼ 13.7 μm feature, which affects the emission in the 12 − 16 μm domain, is present in the spectra of carbon stars characterised by different τ10, even in those with very large infrared emission. The CO+C3 band is the most tricky to handle in the present analysis, because it is spread across a spectral region only partially covered by IRS, which poses some problems in the extrapolation of the flux in the optical and near-IR domains. For the stars where this ambiguity is most relevant, we considered the combination of the IRS data with results from photometry, following an approach similar to that of Groenewegen & Sloan (2018). Fortunately, the analysis of the most obscured stars is not affected by the CO+C3 band, as the SED peaks at longer wavelengths.
 |
Fig. 4. Comparison between the IRS (black lines) and the synthetic (red) spectra of a few sources in the LMC sample of carbon stars, with various luminosities and degrees of obscuration. The values of luminosities and τ10 reported in each panel are those allowing the best fit, corresponding to the red lines. The cyan lines indicate the synthetic SED entering the carbon condensation zone, resulting from the absorption of the radiation from the photosphere by SiC particles in the innermost region of the circumstellar envelope. |
The result of the interpretation of the observations of the stars in the sample analysed here is shown in Fig. 5, where we report the distribution of the individual sources on the τ10 versus luminosity plane. The tracks corresponding to the evolution of the AGB stars discussed in Sect. 4.2 are overimposed on the points indicating the stars in the sample discussed here. The green squares in Fig. 5 indicate stars with luminosities below 7500 L⊙: these are the oldest objects in the sample, descending from stars of initial mass below 2 M⊙, and they were formed in epochs earlier than 1 Gyr ago. The red triangles indicate objects younger than 1 Gyr, descending from stars of initial mass above 2 M⊙. In particular, those with luminosities above 104 L⊙ are interpreted as the progeny of stars of initial mass 2.5 − 3.3 M⊙, formed during the peak in the star formation history of the LMC, between 300 and 600 Myr ago (Harris & Zaritsky 2009). Magenta crosses refer to bright stars, with luminosities above 20 000 L⊙.
 |
Fig. 5. Luminosities and optical depths derived for the stars in the sample analysed in the present work. Green squares and red triangles indicate the progeny of M < 2 M⊙ stars and the higher mass counterpart, respectively; orange asterisks refer to stars with luminosities below 5000 L⊙; magenta crosses indicate stars brighter than 20 000 L⊙; blue diamonds indicate extremely obscured objects, which were taken from Gruendl et al. (2008) and the source SSID 9; and the stars indicated with open diamonds are SSID 125 and SSID 190. The black lines and points in the figure refer to the evolution of the same models shown in Fig. 3, and the initial masses are indicated next to the corresponding track. Magenta stars indicate the results obtained by artificially increasing the mass-loss rate of the stars of initial masses 1.1 M⊙, 2.5 M⊙, 3 M⊙, after reaching the C-star stage, according to the discussion in Sect. 5.3. |
The distribution of the stars in Fig. 5 is determined by the mass distribution of the progenitors (luminosity) and the amount of carbon accumulated in the surface regions, which affects the dust formation in the outflow, and thus the optical depth. The stars on the right side of the diagram are those producing dust at higher rates. We find that the gas-to-dust ratio, Ψ, decreases when moving to higher τ10, ranging from Ψ ∼ 700, for the stars with little dust, to Ψ ∼ 100, for the most obscured sources. These results are fully consistent with those obtained by Nanni et al. (2019a), who correctly warned against assuming a constant Ψ when fitting the observed SED. The gas and dust mass-loss rates also increase with τ10, until reaching Ṁ ∼ 1.5 × 10−4 M⊙ yr−1 and DPR ∼10−6 M⊙ yr−1. In the τ10 < 1 domain, the Ṁ and DPR values derived here are consistent with Nanni et al. (2019a), whereas for the stars with the largest degree of obscuration, the present results are similar to those of Gullieuszik et al. (2012).
The tracks reported in Fig. 5 nicely reproduce the distribution of the sources on the plane, with the exception of a few groups of stars, for which the derivation of the main physical and evolutionary properties is not straightforward. In particular, we refer to: (a) the stars with luminosities below 5000 L⊙, indicated with orange asterisks, which are too faint when compared to the evolutionary tracks; and (b) the stars in the right of the figure, at τ10 > 3, indicated with blue diamonds, of which the degree of obscuration is in excess of the theoretical expectations (see the largest τ10 values expected for stars of a different mass and luminosity, reported in Table 1). We discuss the stars outlined in points (a) and (b) and the bright stars indicated with magenta crosses separately.
5.1. Stars in the post-thermal pulse phase
The sources SSID 3, SSID 66, SSID 103, and SSID 141 are characterised by luminosities below 5000 L⊙. The IRS spectrum of the latter star, with our best-fit interpretation, is shown in the left panel of Fig. 6. These energy fluxes are at odds with the results shown in the top-left panel of Fig. 3 and in Fig. 5. Both of these report the luminosities of the stars during the sequence of interpulse phases, during which the CNO burning activity is fully recovered after the temporary extinction caused by the ignition of the thermal pulse. On the other hand, the re-ignition of the CNO shell after the TP is extinguished is not immediate, thus the luminosity undergoes a series of periodic variations, with temporary dips in conjunction with the ignition of TPs. The right panel of Fig. 6 shows the variation with time of the luminosity of the stars of initial mass 1.5, 2, 2.5 M⊙, during the C-star phase. We see that at the ignition of each TP, L drops below 3000 L⊙, and then increases as CNO burning is gradually re-activated. The rise of the luminosity following each TP is slow enough that the possibility of observing stars in such low-luminosity phases is statistically non-negligible. This holds particularly for the lowest mass stars considered.
 |
Fig. 6. Left: IRS SED of source SSID 141, compared with our interpretation based on synthetic modelling. Right: AGB evolution with time of the luminosity of 1.5, 2, 2.5 M⊙ stars; the O-rich phase was omitted for readability. The sequence of the 2.5 M⊙ was artificially shifted by 1 Myr for readability. The grey shaded region indicates the luminosity range of the low-luminosity stars SSID 3, SSID 66, SSID 103, and SSID 141. |
As a result of our findings, we propose that the low-luminosity stars identified in the IRS sample are carbon stars that have recently experienced a TP and are evolving through a phase in which the H-burning shell has not fully recovered its efficiency. This interpretation is consistent with the small degree of obscuration that we derived for these stars, because during these evolutionary phases the stars assume a compact configuration, which prevents the formation of large quantities of dust.
5.2. A signature of hot bottom burning?
The sources indicated with magenta crosses in Fig. 5 (SSID 4109, 4451, 4540, 4776) are characterised by luminosities above 20 000 L⊙, which is significantly higher than the other stars in the sample and above the upper limit expected for carbon stars (∼17 000 L⊙). These are given in Sect. 4.2. These luminosities indicate that the cores of these stars are more massive than their counterparts discussed in Sect. 4.2, meaning they are higher mass progenitors.
The mass threshold given in Sect. 4.2 was based on the fact that higher mass stars experience HBB, which destroys the surface carbon, thus preventing the stars from becoming carbon stars. Indeed, stars within a narrow mass range, clustering around 3.5 M⊙, experience a series of TDU events before HBB is activated. These stars reach the C-star stage and evolve as carbon stars for a few TPs, until the beginning of HBB.
An example of this behaviour is shown in the right panel of Fig. 7, reporting the evolution of a 3.5 M⊙ model, in terms of the surface C/O and of the luminosity. The effects of TDU can be seen in the rise of C/O after each TP, whereas HBB causes a drop in C/O after each TDU event. In this specific case, HBB starts after 12 TPs and the stars evolve as C-star during four interpulse phases, before the surface C/O drops below unity. The ignition of HBB is accompanied by the fast rise in the luminosity of the star, which increases from ∼17 000 L⊙ to above 20 000 L⊙. During the C-star phase, we find L ∼ 25 000 L⊙, which is in agreement with the luminosities derived for SSID 4109 and 4451.
 |
Fig. 7. IRS and best-fit SED for sources SSID 4451 (left panel) and SSID 4109 (middle). Right: evolution with time (counted since the beginning of the TP-AGB phase) of luminosity (black) and surface C/O (red track, scale on the right) of a 3.5 M⊙ star. The grey shaded area indicates the phase during which the star is carbon-rich. |
We propose that these two sources descend from 3.5 − 4 M⊙ progenitors, formed ∼250 Myr ago, which have reached the C-star phase and are currently experiencing HBB at the base of the envelope. According to this interpretation, they are evolving through the C-star phase, before becoming oxygen-rich again. If this understanding is correct, these stars are characterised by a surface C/O slightly above unity and they are enriched in lithium, because the time elapsed since the start of HBB is not sufficient to destroy the surface 3He, which allows the Cameron & Fowler (1971) mechanism to operate. These sources would be examples of the lithium-rich carbon stars that Ventura et al. (1999) proposed as independent distance indicators, based on the robust estimate of the luminosities at which we expect this mechanism to occur. We rule out the possibility that the progenitors are higher mass stars formed more recently, because stars of an initial mass above 4 M⊙ experience HBB from the early AGB phases, thus the formation of C-stars is inhibited.
The scenario invoked to explain the IRS spectrum of SSID 4109 and 4451 could potentially also work for SSID 4776. However, the SED of the latter star is peculiar, since we find no evidence of the 11.3 μm SiC feature and of the 30 μm bump: this suggests that the dust is composed exclusively of solid carbon. The situation regarding SSID 4540, of which the SED is shown in the left panel of Fig. 8, is even more tricky, because the estimated luminosity of 32 000 L⊙ is higher than the largest luminosity attained by the 3.5 M⊙ model shown in the right panel of Fig. 7. The large luminosity and the SiC- and MgS-free dust mineralogy lead us to consider the alternative possibility that the progenitors of SSID 4540 and SSID 4776 are metal-poor massive AGB stars. For most of the AGB lifetime, these stars experience vigorous HBB at the base of the external mantle, which causes the depletion of the surface carbon, and, unlike their higher metallicity counterparts, a strong reduction of the surface oxygen. During the final AGB phases, when HBB is turned off by the loss of the external envelope, the very low amount of residual oxygen in the external regions allows a few TDU episodes to turn the stars into C-stars. This is shown in the right panel of Fig. 8, where the evolution of the luminosity and of the surface C/O of a 5 M⊙, Z = 0.001 model is reported. The luminosities at which this transition occurs are in the 25 000 − 35 000 L⊙ range, which is consistent with the estimation for SSID 4540 and SSID 4776.
 |
Fig. 8. Left: IRS SED of source SSID 4540, compared with our interpretation, based on synthetic modelling. Right: AGB evolution with time of the luminosity (black line, scale on the left) and of the surface C/O ratio (red line, scale on the right) of a 5 M⊙ model with metallicity Z = 0.001. The grey shaded area indicates the evolutionary phase during which the star evolves as a carbon star. |
If this is interpretation is correct, these stars share their origin with the O-rich objects in the LMC, which Marini et al. (2019) identified as metal-poor stars. Here, the significant destruction of the surface oxygen, caused by HBB, means that the dust in their surroundings is dominated by solid iron grains. According to this hypothesis, SSID 4540 and SSID 4776 are currently evolving through the stages immediately following those of the stars studied by Marini et al. (2019), after they become a C-stars. They would be the youngest object in the sample studied here, with an age of ∼100 Myr. An important difference with respect to the origin invoked for SSID 4109 and 4451 is the surface chemical composition, which should exhibit an extremely poor oxygen content and no evidence of lithium.
These stars are not expected to produce great quantities of dust, because the carbon excess with respect to oxygen is low, given the effects of HBB experienced during the earlier evolution. This is consistent with the small optical depths, τ10 = 0.06 − 0.08, deduced from the analysis of the SED, and with the shape of the IRS spectrum (see left panel of Fig. 8), which shows no significant IR emission.
5.3. Extreme carbon stars
The existence of LMC stars with extremely red mid-IR colours was first discussed by Gruendl et al. (2008), who used IRAC and MIPS photometry and IRS follow-up to identify seven objects as extreme carbon stars. Gruendl et al. (2008) underlined the peculiarities of these sources, especially the derived mass loss rates, which the authors claim to span the (5 × 10−5 − 2 × 10−4) M⊙ yr−1 range, significantly higher than those deduced for carbon stars, when radiative transfer modelling is used to reproduce their photometric properties (van Loon et al. 1999).
In Fig. 5, the stars discussed by Gruendl et al. (2008), on the right side of the τ10 − L plane, are indicated with blue diamonds. We use the same symbol to identify SSID 9, which we also consider extreme, as it lies in the same region of the diagram populated by the Gruendl et al. (2008) sources. Figure 9 shows the IRS spectra of four of these stars, with the parameters required to reproduce the details of the observed SED. In all cases, with SSID 4299 being the only exception, a clear SiC absorption feature is visible, indicating an extremely thick dusty region. We note that the interpretation of the spectra of these objects is not affected by the presence of the molecular bands discussed in the first part of this section. The sources SSID 125 and SSID 190, belonging to the Gruendl et al. (2008) sample, are indicated in Fig. 5 with open blue diamonds; these stars are extremely red and show a peculiar SED, peaking at wavelengths λ > 20 μm. An example is shown in Fig. 10.
 |
Fig. 9. SED fitting of four of the extremely red objects studied by Gruendl et al. (2008). |
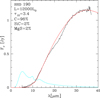 |
Fig. 10. IRS (black) and synthetic (red) spectra of the source SSID 190. |
The possible nature of the extreme stars by Gruendl et al. (2008) was discussed by Sloan et al. (2016) and Groenewegen & Sloan (2018), who stressed the difficulty in fitting the data of these stars, particularly in the context of modelling dust formation in radial outflows, departing from the surface of single carbon stars. An interesting overview of the critical issues faced when modelling stars with a very large infrared excess is found in Nanni et al. (2019a), which explored the role of the mass-loss rate, carbon excess, optical constants of solid carbon dust.
We confirm here that the interpretation of these objects, based on the standard modelling so far used to describe the other stars analysed, is extremely hard. The results presented in Figs. 5 and 9 outline that the optical depths required to reproduce the observations, which span the 3 < τ10 < 7 range, are significantly higher than the majority of the largest τ10 expected on the basis of theoretical modelling, reported in Table 1. Indeed, the synthetic SEDs shown in the four panels of Fig. 9 and the parameters corresponding to these stars reported in Table 2 were obtained by artificially increasing the optical depth of the most obscured model, taken from the points of the evolutionary sequences used to characterise all the other stars in the sample.
The top-right panel of Fig. 3 shows that optical depths τ10 ∼ 5 are reached during the latest AGB phases of 2 − 3 M⊙ stars. These largely obscured models might partly explain, as far as the degree of obscuration is concerned, the SSID 4299 and SSID 4781 data (see bottom-right panel of Fig. 9), which are the brightest sources in this group, for which we estimate a luminosity around 10 000 L⊙. However, there is no way to account for the observations of the fainter objects, particularly those with estimated luminosities in the L < 6000 L⊙ range: these energy fluxes indicate M ∼ 1.1 − 1.5 M⊙ progenitors, which are not expected to evolve to such extreme τ10, owing to the relatively low carbon excess reached (see Fig. 3).
We cannot rule out that the stationary wind model used in the present investigation to model dust formation might underestimate the amount of dust formed in the wind of AGB stars. As discussed in Sect. 4.3, the present model neglects the effects of pulsations and the pulsation-induced shocks, which might drive dense gas clouds into external regions of the outflow, where dust condensation would be favoured by the cool temperatures. Furthermore, we do not account for gas-to-dust drift here, which might affect the structure of the wind and cause higher dust yields. Sandin & Mattsson (2020) recently performed unique state-of-the-art simulations of C-star wind formation, confirming that drift is significant at low mass-loss rates and becomes less and less so as the rate goes up. This means we cannot firmly conclude that the dust yields should be significantly higher without replicating the stellar evolution modelling and including a correction for drift. The effect on the integrated DPR depends on the evolution of the mass-loss rate, which in turn depends on how the stellar parameters and carbon excess evolve. A further critical point related to the analysis presented here, discussed in Sect. 4.3, is that the mass-loss rate, described according to Wachter et al. (2002), is independent of the carbon excess.
Despite the above uncertainties, we believe that there is no room to obtain τ10 values significantly higher than those reported in Table 1. This is definitively impossible in the case of M < 2 M⊙ stars, for the reasons given above. For what attains the stars of masses above 2 M⊙, the large values of τ10 reached are mainly caused by the high mass-loss rates experienced during the latest AGB phases, which are slightly below ∼2 × 10−4 M⊙ yr−1. We consider these rates as upper limits, because their calculation is based on the description by Wachter et al. (2002, 2008), which might overestimate the true mass-loss rates (Bladh et al. 2019).
A possible reason for the discrepancy between the τ10 obtained by modelling and the degree of obscuration derived from the analysis of the spectra is that the winds are significantly denser than predicted by the theoretical modelling, suggesting that dust is formed at higher rates than predicted by stellar evolution calculations. We reconsidered the C-star phase of the models presented in Sect. 4, and artificially increased the mass-loss rate to be used in the modelling of dust formation, until obtaining the values of τ10 required to fit the IRS spectra. We found consistency with mass loss rates of the order of Ṁ ∼ 5 × 10−4 M⊙ yr−1. It goes without saying that these calculations are based on the assumption that the outflow is radially symmetric, which might be not the case for these peculiar objects; yet we consider this exercise as a tool to infer a reliable estimate of the order of magnitude of the mass-loss rate of the star, which is required in order to produce wind densities compatible with the observations.
Sloan et al. (2016) and Groenewegen & Sloan (2018) hinted at the possibility that the extreme carbon stars are part of binary systems. Dell’Agli et al. (2020) proposed that these carbon stars, with a low-mass companion, have recently filled the Roche lobe. Figure 11 shows the AGB variation with time of the radius and the surface C/O of stars of different initial masses. We see that in all cases the stars undergo a phase of rapid expansion soon after they become carbon stars. The fast increase in the stellar radius enhances the probability that the Roche lobe is overfilled, launching a phase of strong mass loss, which we artificially imposed starting from the corresponding evolutionary points, indicated with green arrows in Fig. 11. As previously discussed, use of Ṁ = 5 × 10−4 M⊙ yr−1 leads to efficient formation of dust, in high enough quantities to reconcile the optical depth of the envelope with the degree of obscuration indicated by the observations. As shown in Fig. 5, the results obtained, indicated with magenta stars, are in significant agreement with the τ10 and luminosity values of the extreme stars derived from the analysis of the IRS spectra. For SSID 125 and SSID 190, Dell’Agli et al. (2020) proposed a slightly different interpretation, based on the cool dust temperature required to fit the IRS spectra, of the order of ∼350 K, which might indicate that the dust layer is moving away from the system; this is also consistent with the derived optical depths, τ10 ∼ 2 − 3, among the lowest in the extreme star sub-sample, which might be due to the decrease in the gas densities, caused by the expansion. These findings possibly suggest that these systems have recently moved away from the AGB and have entered the post-AGB phase; this understanding would be consistent with the interpretation proposed by Groenewegen & Sloan (2018).
 |
Fig. 11. Evolution of radius (black lines, scale on the left) and surface C/O ratio (red, scale on the right) during the AGB phase of stars of initial masses 1.1 M⊙ (left panel), 2.5 M⊙ (middle), and 3 M⊙ (right). The thin, blue horizontal lines indicate the C=O condition, whereas the green arrows indicate the phase of rapid expansion of the star, as a consequence of the surface carbon enrichment. |
In all cases, the interpretation based on the fact that these stars are evolving through, or have recently crossed, a common envelope phase is consistent with the relatively small fraction of solid carbon dust, in most cases below 80%, because the fast loss of the external envelope prevents the accumulation of large quantities of carbon in the surface regions.
If this understanding is correct, these stars would produce dust at rates in excess of 10−6 M⊙ yr−1, which would make them extraordinarily efficient dust manufacturers. The entire DPR of galaxies would be dominated by a paucity of these systems.
6. The winds of carbon stars: What we learn from IRS spectra
In Sect. 5, we discuss the fact that the luminosity and the optical depth of the individual sources can be safely derived by comparing the observed spectrum with the synthetic SED, calculated on the basis of a basic wind model, which assumes that the dust is composed only of carbon and SiC.
On the other hand, we know that other dust species form in the winds of carbon stars; furthermore, it is possible that not all the solid carbon forms in the amorphous state, but that a fraction of it might be in other aggregates, such as graphite. The comprehension of the details of the dust formation process requires knowledge of the mineralogy of the dust formed, for which we must determine the abundances of the different species considered, or, equivalently, the individual contributions to the overall cross-section. This ambitious task requires the interpretation of the whole SED, including the details of the features and the slopes of the stellar spectra, in the whole wavelength interval covered by IRS.
This step is important for two reasons: (a) the derivation of the details of the composition of dust will provide precious information on the structure of the winds of carbon stars and on the efficiency of the formation process of the various dust species; and (b) the interpretation of the observations from JWST requires knowledge of the dust species in the circumstellar envelope, since most of the mid-IR JWST filters cover spectral regions partly or fully overlapped with the aforementioned features (see bottom panels of Fig. 2).
The search for the parameters allowing the best fit of the SED of the individual sources was done by eye for each star. We did not use any automatic procedure, despite this being less time consuming, because in the present context the priority is the correct reproduction of the whole SED. We now discuss the dust species other than solid carbon and how their presence reflects onto the SED in detail.
6.1. Silicon carbide
Silicon carbide is by far the second most abundant species after carbon. The presence of SiC dust was used by several authors (Groenewegen et al. 2007, 2009; Groenewegen & Sloan 2018; Srinivasan et al. 2009, 2010) to reproduce the spectra of carbon stars, based on the observation of the well-distinguished SiC feature, centred at 11.3 μm. This can be seen in the synthetic SED reported in the bottom panels of Fig. 2 and in the IRS spectra shown in Fig. 4. As discussed in Sect. 4.1, SiC is the most stable species; therefore, to build the synthetic SED we assumed that the radiation from the photosphere of the star is first reprocessed by an internal SiC layer, then by a more external dusty shell, where SiC grains cohabit with carbon particles and other species. While we may safely assume that SiC grains are the only solid particles formed in the internal part of the outflow, in the more external regions of the circumstellar envelope the presence of SiC could be associated with the formation of MgS (Zhukovska et al. 2008). Indeed, we discuss in the following section, SiC is cited as a substrate for MgS precipitation, due to the obvious similarities of structure and bonding properties of SiC and MgS.
6.2. MgS
The spectrum of several carbon stars is characterised by a wide bump in the spectral region around the 25 − 30 μm region, which can be seen in the bottom panels of Fig. 4. The presence of such a band was detected in the observations of carbon stars in the Milky Way (Hony et al. 2002; Volk et al. 2002) and in the Magellanic Clouds (Zijlstra et al. 2006). Goebel & Moseley (1985) first proposed that this feature can be associated with MgS, because the latter compound has a feature in the same spectral region. The various possibilities proposed so far to explain the 30 μm bump were discussed in the recent review by Volk et al. (2020). Here, we base our work on the analysis of Sloan et al. (2014), who concluded that MgS is the best candidate to account for this spectroscopic evidence.
A significant step forward in the modelling of MgS production in the circumstellar envelope of carbon stars was done by Zhukovska et al. (2008), who included the growth of MgS grains in the description of the stellar wind. In the paper by Zhukovska et al. (2008), it is shown that the formation of pure MgS dust cannot account for the observed feature, because the formation of MgS is expected to take place at temperatures ∼900 K, after the wind has been accelerated by the formation of carbon dust, and the density has dropped to values too small to allow a significant growth of MgS particles. We did some tests after including the formation of MgS in the set of equations used here and confirmed the results by Zhukovska et al. (2008); the largest size reached by MgS grains is below 0.01 μm, which corresponds to cross-sections far too small to account for the observed feature.
To model the MgS feature, we considered the idea proposed by Zhukovska et al. (2008), that the growth of MgS occurs via precipitation on SiC grains. This choice opens the possibility of forming bigger grains, because the SiC particles formed in the internal regions enter the MgS condensation zone sized from 0.03 − 0.07 μm (Nanni et al. 2013; Ventura et al. 2014). We find that precipitation of MgS on these already formed SiC grains would further increase the dimension of these particles by ∼0.02 μm, if we assume that the deposition begins from the point where the pure MgS dust would start to form. This result is consistent with the analysis by Zhukovska et al. (2008).
To better understand how the presence of SiC+MgS dust affects the SED of carbon stars, we calculated a series of synthetic SEDs, where the condensation point and the percentage contribution of this compound were allowed to vary within reasonable ranges. The detailed fit of the MgS feature in the SED allows the determination of the percentage of the SiC+MgS particles with respect to the total dust formed, and of the fractional width of the MgS mantle with respect to the total dimension of the SiC+MgS grains. The latter quantity is related to the condensation point, as a larger mantle is formed when the condensation zone is more internal. An example of this kind of analysis is shown in Fig. 12, where the effects of changing the percentage of SiC+MgS dust and of the size of the MgS mantle are indicated.
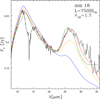 |
Fig. 12. IRS spectrum of SSID 18 (black line) compared with synthetic SEDs, corresponding to the same luminosity and τ10, and different percentages of SiC+MgS and of the relative width of the MgS mantle (aman) on top of SiC core. The various lines correspond to the following: red (our best-fit model), with SiC+MgS = 9% and aman = 0.05 μm; green, with SiC+MgS = 35% and aman = 0.02 μm; blue, with SiC+MgS = 9% and aman = 0.02 μm; and orange, with SiC+MgS = 6% and aman = 0.05 μm. |
We find that in the majority of the sources analysed, the fraction of MgS+SiC particles is around 5%, of the same order of pure SiC grains. The detailed fit of the morphology of the 25 − 30 μm feature demands that the width of the MgS mantle account for 30 − 40% of the overall size of the SiC+MgS grains, which is consistent with assuming that precipitation of MgS onto SiC cores begins in a more internal region of the outflow than found for pure MgS dust. A few examples of stars with SED characterised by SiC and MgS features are shown in Fig. 13.
 |
Fig. 13. IRS spectra of sources SSID 4197 (top-left panel), SSID 4783 (top-right), SSID 4002 (bottom-left), and SSID 4692 (bottom-right), with the best-fit models obtained with the luminosities, optical depths, and dust mineralogy indicated in the individual panels |
The conclusions we draw for the present analysis are that around 50% of the SiC particles formed in the internal regions of the circumstellar envelope act as seeds for the deposition of MgS. This is consistent with the study of the 30 μm feature in carbon stars published in Messenger et al. (2013), who found a tight correlation between the 11.3 μm and the 30 μm features in the spectra of Galactic carbon stars, concluding that the carriers of these features are strongly related to each other. SiC and SiC+MgS dust make up around 10% of the total dust, this result being substantially independent of the degree of obscuration of the star. Furthermore, the formation of SiC+MgS particles takes place in the same region of the circumstellar envelope where solid carbon condensation occurs.
6.3. Graphite
While it is generally recognised that carbon dust is the primary source of extinction in the envelope of carbon stars, the debate is still open regarding the possibility that the dominant species is under the form of amorphous carbon or graphite. The discovery of pre-solar graphite grains from meteorites (Zinner 2008; Xu et al. 2016) indicates that the graphite contribution must be non-negligible. Based on results from radiative transfer modelling, Speck et al. (2009) suggested that graphite is the dominant dust species instead of amorphous carbon. On the other hand, Andersen et al. (2003) argued that the absence of the narrow band at 11.52 μm in most observed spectra, and the fact that the slope of infrared graphite spectra follows λ−2, imply that graphite formation in AGB winds is unlikely. Generally speaking, the physical conditions in AGB atmospheres seem to favour amorphous carbon dust, since graphite formation requires temperatures that significantly limit the growth interval in a typical C-star.
The stationary wind model adopted here allows the determination of the growth rate of carbon dust and the calculation of the extinction related to carbon grains; however, we cannot derive any indication on whether the carbon particles formed are under the form of amorphous carbon or graphite. We chose to derive the relative contribution from amorphous carbon and graphite by looking for the best fit of the SED of carbon stars in the sample examined here. The approach we followed was to first derive the luminosity, optical depth, and percentages of SiC and MgS according to the method so far discussed; and then to assume a variable percentage of graphite with respect to carbon until we reached full consistency with the observed SED.
An example of the analysis done is shown in Fig. 14, where we show the interpretation of the SED of the source SSID 4722, of which the spectrum exhibits a fairly large level of infrared emission, with τ10 slightly below unity. Changing the fraction of graphite with respect to the total of carbon dust (hence amorphous carbon + graphite) does not significantly alter the morphology of the SED in the wavelength region close to the emission peak (in the example shown in Fig. 14), but it has a strong effect on the λ > 20 μm domain, which is lifted by the presence of graphite.
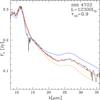 |
Fig. 14. IRS spectrum of SSID 4722 compared with synthetic SED, differing for the percentage of graphite. The different lines refer to the following percentages: 0% (orange), 15% (red), 30% (blue). |
Other results, for which a non-negligible fraction of graphite was required to reproduce the observed SED of the stars in the λ > 20 μm spectral region, can be seen in Fig. 15. The figure shows the comparison between the IRS and the synthetic spectra, for stars of various luminosities and τ10.
 |
Fig. 15. IRS spectra of sources SSID 4794 (top-left panel), SSID 4238 (top-right panel), SSID 4589 (bottom-left panel), and SSID 4150 (bottom-right panel), with the best-fit models obtained with the luminosities, optical depths, and dust mineralogy indicated in the individual panels. |
From the analysis of the sources examined, we deduce that amorphous carbon is the dominant dust component. Graphite is formed in the circumstellar envelope of τ10 > 0.1 stars. The percentage of graphite grows with τ10 and ranges from a few percent to ∼20%.
7. The JWST observational planes
It is extremely important to understand how carbon stars are expected to distribute on the observational planes that will be built with the mid-IR filters of the MIRI camera. This will be crucial to interpreting the data collected by JWST and selecting the combination of filters allowing the best determination of the degree of obscuration and the mineralogy of the stars, along with the identification of the progenitors, in terms of the formation epoch and chemical composition.
In Sect. 6, we discuss the spectral features in the SED of carbon stars, the most important being the 11.3 μm feature and the bump at ∼30 μm. These spectral features can also be seen in the synthetic spectra shown in Fig. 2 (the 30 μm feature is not present in the left panel, because in these simulations only amorphous carbon and SiC were considered).
We outline that the dust species responsible for the presence of these features do not provide any significant contribution to the overall degree of obscuration of the star, which is mainly given by absorption by solid carbon grains. On the other hand, the reprocessing of the radiation by SiC and MgS particles affects the morphology of the SED in regions of the spectrum that fall inside the transmission curves of the majority of the MIRI filters. As is clear in Figs. 2 and 4, the MIRI filters covered by the IRS spectral range and falling in a wavelength interval substantially clear of features associated with dust are F770W, F1000W, and F1800W.
The filter F770W is affected by the molecular band centred at 7.5 μm, which becomes less and less deep as the degree of obscuration increases, and it has no relevance in the spectra of the stars with the greatest IR emission. This behaviour can be seen, for example, in the sequence of spectra in Fig. 4, where we note the few incidences of this feature in the interpretation of the spectrum of the most obscured source SSID 18 (shown in the bottom-right panel). According to the present analysis, we find that in the τ10 > 1 domain the acetylene 7.5 μm feature is not relevant in the determination of the main properties of the stars, whereas the impact on the analysis of the poorly obscured objects can be safely managed by introducing a correction factor to account for the depression of the flux in that spectral region. We return to this point shortly.
The wavelength interval covered by F1000W is only partially overlapped with the SiC feature, provided that the latter is very prominent. We see later that this does not affect the general colour-τ10 trend, while, on the other hand, the use of this filter allows us to retrieve information concerning the metallicity of the stars.
The spectral region covered by the transmission curve of F1800W (see bottom panels in Fig. 2) is not affected by molecular or dust features. This suggests that we should use the F1800W flux in the interpretation of the SED of carbon stars. The only point to take into account is that the reprocessing of the radiation by MgS and graphite particles makes the SED flatter in the 12 − 20 μm region, which reflects a higher F1800W flux. This is clear from the comparison between the synthetic SED shown in the bottom-left and bottom-right panels of Fig. 2. The F1800W fluxes based on synthetic models where the presence of MgS and graphite dust is neglected are slightly underestimated.
Based on these arguments, we consider the colour-magnitude ([F770W]–[F1800W], [F1800W]) and ([F1000W]–[F1800W], [F1800W]) planes as the most suitable to study the obscuration sequences of carbon stars, where the characterisation of the individual objects is fairly independent of the details of the dust mineralogy and scarcely affected by the details of the morphology of the most relevant spectral features.
The left panel of Fig. 16 shows the distribution of the sample of carbon stars described in Sect. 2 on the ([F770W]–[F1800W], [F1800W]) plane. The sources within the sub-sample that we analysed in detail in the present investigation are shown with different symbols. In the figure, we show the tracks corresponding to the sequences of synthetic SED of Z = 0.008 stars of initial mass 1.5 M⊙ (black squares) and 3 M⊙ (black triangles) as solid lines. These were calculated by assuming a dust composition made up only of solid carbon and SiC. The dashed lines indicate the tracks of the same stars, recalculated to account for the presence of SiC+MgS and graphite grains, in quantities consistent with the discussion in Sect. 6. The dashed lines connecting the blue squares and red triangles refer to the evolution of 1.5 M⊙ and 2.5 M⊙ stars of metallicity Z = 0.002, taken as a representative of a metal-poor population. In this case, we do not show the corresponding tracks that consider SiC and MgS, because little formation of these species is expected in the wind of metal-poor stars.
 |
Fig. 16. Left: stars in sample described in Sect. 2 are shown in the colour-magnitude ([F770W]–[F1800W], [F1800W]) plane. The same symbols as those in Fig. 5 were adopted. Black squares and triangles indicate the expected evolution of stars of metallicity Z = 0.008 and initial masses 1.5 M⊙ and 3 M⊙, respectively. Dashed lines refer to the expected evolution of 1.5 M⊙ and 3 M⊙ stars, when the presence of Sic+MgS and graphite grains are considered in the computation of the synthetic SED. The blue squares and red triangles, connected with dotted tracks, refer to the evolution of Z = 0.002 stars of initial masses 1.5 M⊙ and 2.5 M⊙, respectively. Magenta pentagons indicate the tracks of 1.1 M⊙, 2.5 M⊙, and 3 M⊙ (from fainter to brighter) models, obtained by artificially increasing the mass loss rate after the jump in the stellar radius caused by the increase in the surface carbon, according to the discussion in Sect. 5.3. Right: distribution of stars in the colour-magnitude ([F1000W]-[F1800W], [F1800W]) plane. |
The evolutionary tracks provide a nice fit of the observations, with the exception of the stars discussed in Sect. 5.3. For the latter objects, we followed the indications given in Sect. 5.3, meaning we modelled dust production by assuming a higher mass-loss rate since the phase during which the stars experience a fast expansion, owing to the carbon enrichment of the surface regions. The results obtained, shown with magenta stars on the plane, are in fair agreement with the colour and magnitudes of the extreme stars.
The ∼0.2 mag colour shift between the synthetic and the observed colours of the bluest stars in the sample, characterised by little dust in the circumstellar envelope, is connected with the absorption C2H2 feature at 7.5 μm, as discussed earlier in this section. This is the correction to be applied to the synthetic ([F770W]–[F1800W]) colour of carbon stars with little dust in the circumstellar envelope.
The stars on this colour-magnitude plane define a well-distinguished obscuration sequence, spanning the 0 < [F770W]−[F1800W] < 4.5 colour range, and the 3.5 < [F1800W] < 8.5. ([F770W]−[F1800W]) magnitude interval is a reliable indicator of the degree of obscuration of the stars. We find a tight correlation between this colour and the optical depth, which extends from [F770W]−[F1800W]∼0.5, τ10 ∼ 0.1, and the objects with the largest infrared emission, with [F770W]−[F1800W]∼4.5 and τ10 ∼ 7. Roughly, we have:
For a given ([F770W]−[F1800W]), the observed distribution exhibits a ∼1 mag spread in [F1800W], which is due to differences in the luminosity of the stars covering the 5000 − 17 000 L⊙ range (see Fig. 5). The position on the plane is connected with the formation epoch of the sources, the stars formed more recently being in the upper part of the diagram.
The bright sources discussed in Sect. 5.2, which we associate either with stars currently experiencing HBB or to metal-poor, massive AGB stars during the late AGB phases, make a sort of upper envelope of the distribution of the stars on this plane. The tracks based on models that consider SiC+MgS and graphite are slightly redder than those that take into account only solid carbon and SiC. This difference, which is visible only for the most obscured stars, is related to the increase in the F1800W flux, consistently with the discussion at the beginning of the present section.
The tracks corresponding to metal-poor stars are bluer than the Z = 0.008 tracks. This difference is visible only for the stars characterised by optical depths τ10 > 0.1, whereas they are substantially overlapped in the low τ10 domain. This is explained by the lower rate of dust formation in metal-poor stars, which is related to the absence of SiC and to the higher effective temperatures and inhibits the formation of great quantities of dust (Ventura et al. 2014). The scarcity of stars in the region of the plane covered by the metal-poor, 2.5 M⊙ track indicates that the lacking formation of metal-poor stars occurred in the LMC in the last Gyr, which is in agreement with the studies on the star formation in the LMC (Harris & Zaritsky 2009).
The distribution of the sample stars in the colour-magnitude ([F1000W]−[F1800W], [F1800W]) plane is shown in the right panel of Fig. 16, with the same evolutionary tracks reported in the left panel. The trend traced by the observations is similar to the one in the ([F770W]−[F1800W], [F1800W]) diagram, with the difference being that the colour range is in this case ∼2.5 mag wide. As expected, ([F770W]−[F1800W]) is more sensitive to τ10 in comparison to ([F1000W]−[F1800W]). The relationship between ([F1000W]−[F1800W]) and τ10 can be approximated by
In the lower-left side of the plane, populated by stars with little dust, the low-metallicity tracks are bluer than their Z = 0.008 counterparts: this is connected with the SiC feature, present in the SED of Z = 0.008 objects and absent in that of metal-poor stars, which causes a slight lift of the F1000W flux. We note that the metal-poor tracks are overlapped on the observations, suggesting that a significant fraction of stars with little or no dust in the circumstellar envelope belong to a low-metallicity population. We return to this point later in this section.
Figure 17 shows the distribution of the stars in the colour-colour ([F770W]−[F1800W], [F770W]−[F1130W]) plane. The same tracks as those in Fig. 16 are shown.
 |
Fig. 17. Left: position of stars in the sample presented in Sect. 2 in the colour-colour ([F770W]−[F1800W], [F770W]−[F1130W]) plane. The symbols for the stars and the evolutionary tracks are the same as in Fig. 16. Right: zoom of the same plane shown in the left panel, to outline the bifurcation between stars of different metallicity. |
The obscuration pattern traced by the sample stars is clear in this plane, and it can be roughly approximated by a straight line, with 0.5 slope. Generally speaking, ([F770W]−[F1130W]) gets redder and redder as τ10 increases. For τ10 < 1, this trend is mostly due to the presence of the SiC feature in the SED, which increases the flux in the 11.3 μm region (see the blue and red lines in the bottom panels of Fig. 2). For higher τ10, the increase in ([F770W]−[F1130W]) is related to the shift of the SED towards the mid-IR part of the spectral range, the peak being at wavelengths λ > 10 μm (see the green line in the bottom panels of Fig. 2).
The tracks of metal-poor models are below those of the more metal-rich stars because the F1130W flux is smaller, owing to the low quantity (or absence) of SiC in the circumstellar envelope. The difference between the Z = 0.002 and Z = 0.008 tracks are negligible at large τ10, because under those conditions the SiC feature becomes less prominent, and the SED shifts to longer wavelengths.
The evolutionary tracks in this plane reproduce the extension of the trend traced by the stars in the sample. The extreme stars are again an exception on this side, their colours being reproduced only by invoking higher mass-loss rates and according to the discussion in Sect. 5.3. In the region of the plane at [F770W]−[F1130W] < 0.8, there is an offset between the Z = 0.008 tracks and the observations, even when the correction for the presence of MgS+SiC and graphite is considered. The Z = 0.002 tracks are in much better agreement with the observational evidence in this region of the colour-colour plane, which is populated by stars with little dust in their surroundings, with τ10 < 0.5. Most of these stars descend from low-mass progenitors with an initial mass below ∼1.5 M⊙ and formed in epochs older than 2 Gyr. In the spectrum of the majority of these stars, there is no evidence for the SiC feature, which is the reason why their position is better reproduced by Z = 0.002 models. While we cannot rule out that some unknown mechanism inhibits the formation of SiC particles under particular circumstances, the most plausible explanation for this result is that the low-mass stars with little degree of obscuration in the sample discussed in Sect. 2 are mostly metal-poor stars; this is consistent with the age-metallicity relationship of the LMC, studied in Harris & Zaritsky (2009), and with the study by Dell’Agli et al. (2015a), who claimed the presence of a significant fraction of low-metallicity objects in the LMC stars descending from M < 2 M⊙ progenitors. The right panel of Fig. 17 shows a zoom of the colour-colour plane in the 0 < [F770W]−[F1800W] < 2 region. Here, we note a clear dichotomy in the distribution of the stars, which we interpret as a metallicity spread. The stars painted in pink, with no SiC, correspond to the metal-poor population, whereas the green counterparts represent the more metal-rich stellar component. This spread vanishes for 0 < [F770W]−[F1800W] < 1.5, because metal-poor stars are not expected to evolve to such red colours.
We now turn our attention to the colour-magnitude ([F1800W]−[F2550W], [F1800W]) diagram, shown in Fig. 18, with the same symbols used in Figs. 16 and 17. In this plane, as expected, the use of the tracks that consider the formation of SiC+MgS is mandatory, because the transmission curve of the F2550W filter is entirely overlapped with the 30 μm bump. The significant discrepancy between the tracks calculated with or without SiC+MgS can be understood by confronting the synthetic SEDs shown in the bottom panels of Fig. 2. In the higher τ10 cases, the SEDs are most noticeably different, particularly in the F2550W flux. This is despite the fact that the assumed MgS percentage is only 5% of the total dust. We see in Fig. 18 that the tracks that consider MgS are in much better agreement with the observations and are overlapped with most of the stars with F1800W < 6.
 |
Fig. 18. Position of stars in the sample presented in Sect. 2 in the colour-magnitude ([F1800W]−[F2550W], [F1800W]) plane. The symbols for the stars and the evolutionary tracks are the same as in Fig. 16. |
The colour range of the sample stars in the ([F1800W]−[F2550W], [F1800W]) plane is ∼1 mag. This is significantly smaller than in the ([F770W]−[F1800W], [F1800W]) plane (see Fig. 16), where the colour difference between the stars with no dust and the most obscured ones is ∼4 mag. This difference is explained by the saturation of ([F1800W]−[F2550W]) for τ10 > 3, because the SED becomes approximately horizontal in the λ > 20 μm domain.
The low-metallicity tracks shown in Fig. 18 define an approximately vertical trend, which is because there is no 30 μm bump in the spectra of these stars and the slope in the 15 − 30 μm spectral region is practically unchanged. The latter point is linked to the fact that low-metallicity stars are not expected to evolve at τ10 > 1. We note that the Z = 0.002 tracks nicely reproduce the position of the stars with [F1800W]−[F2550W]∼0.1 − 0.2 and 4 < [F1800W] < 6. These sources are the same as those located in the [F770W]−[F1130W] < 0.8 region in the colour-colour plane shown in Fig. 17, which we identify as low-metallicity stars. This conclusion is further reinforced by the present analysis, suggesting a criterion to disentangle stars of different chemical compositions in the ([F1800W]−[F2550W], [F1800W]) diagram.
Recent studies focused on the distributions of evolved stars in the observational planes built with the MIRI filters were published by Jones et al. (2017) and Kraemer et al. (2017), and a similar discussion is also given in Groenewegen & Sloan (2018). Kraemer et al. (2017) investigated various colour-colour planes, in order to study how the sequences of carbon-rich and oxygen-rich AGBs, young stellar objects, and red super giants can be clearly separated. Unfortunately, a clear comparison with the present analysis is not straightforward, because no colour-magnitude plane is considered, and in all the planes proposed by Kraemer et al. (2017) the F560W flux is used; whereas we ruled out this filter, as the IRS spectra used here do not allow a reliable estimate of [F560W].
Jones et al. (2017) presented an exhaustive analysis on how different classes of objects will populate the observational planes, outlining that the planes allowing the best disentangling of the various types of objects are based on the combination of F1000W and F2100W MIRI filters. This is indeed a valid criterion to separate evolved stars from other objects, but significant overlapping of O-rich and C-rich AGB and RSG stars prevents us from using this filter combination to study the C-star population, which is the primary goal of the present work. We find that use of F1800W allows a better analysis of the C-star population than F2100W, as the latter is influenced by the 25 − 30 μm bump. Jones et al. (2017) showed that the plane where carbon stars are most easily identified is the colour-magnitude ([F1500W]−[F2100W], [F1500W]) diagram. Use of this plane makes it possible to definitively disentangle carbon stars with low and moderate infrared excess from the other classes of objects, whereas those with the largest degree of obscuration are overlapped with O-rich AGBs and red supergiants. Here, we decided to avoid using F1500W, because, as discussed in Sect. 5, it is affected by the C2H2 band centred in the 13.5 − 13.9 μm spectral region.
A wider exploration of the JWST potentialities was presented in Groenewegen & Sloan (2018). The advantage of the latter work over Kraemer et al. (2017), Jones et al. (2017), and the present investigation is the wider spectral region considered, which is not limited to the wavelengths covered by MIRI. In Groenewegen & Sloan (2018), it is shown that the C-star sequence is expected to spread over a large magnitude interval in the ([F150W]−[F360W], [F360W]) plane, with the C-star band being substantially separated from other objects. Regarding the mid-IR domain, Groenewegen & Sloan (2018) proposed the colour–colour ([F770W]−[F1800W], [F560W]−[F770W]) plane to distinguish carbon stars from oxygen-rich AGBs. Interestingly, Groenewegen & Sloan (2018) suggested using the F560W, F770W, and F1800W filters to study obscured AGBs, which are among those recommended here, with the exception of F560W, for the reasons given above.
8. Conclusions
We studied a sample of carbon stars in the LMC, for which the mid-IR SED was obtained by means of the IRS spectrograph onboard Spitzer. To characterise the sources in this sample, we calculated stellar models evolved through the AGB phase, until the almost complete ejection of the external convective envelope. For each stellar mass, we first modelled dust formation in the outflow to determine the amount and the mineralogy of the dust formed during various evolutionary phases. These results, combined with the main stellar parameters derived from stellar evolution modelling, were the ingredients used to determine a sequence of synthetic SEDs, which allowed us to describe how the SED of these stars changes as they evolve through the AGB.
The comparison between the IRS spectra and the synthetic SEDs leads to a reliable determination of the optical depth and the luminosity of the individual sources, which in turn can be used to deduce the mass and formation epoch of the progenitors and to provide an estimate of the amount of carbon accumulated in the surface regions via repeated TDU episodes. The majority of the sources analysed has luminosities in the 5000 − 17 000 L⊙ range and optical depths of τ10 < 3, which is in agreement with the results from carbon star modelling. Approximately half of the stars examined descend from M < 2 M⊙ progenitors older than 1 Gyr, and the remaining half are composed of younger objects formed no later than 1 Gyr ago and are the progeny of M > 2 M⊙ stars.
The sample discussed in the present work includes a paucity of objects with luminosities below 5000 L⊙, which we interpret as stars that have not yet fully resumed CNO burning after having experienced a TP, and four very bright stars with L > 20 000 L⊙, which we suggest descend either from ∼3.5 M⊙ stars currently experiencing HBB or from metal-poor ∼5 M⊙ stars evolving through the latest AGB phases. We also find a group of extremely red stars, which is difficult to explain within the context of the obscuration path followed by single carbon stars. We believe that they belong to binary systems in which a common envelope phase caused a significant increase in the mass-loss rate. This enhanced dust formation in the outflow, and two of these objects have likely left the AGB and are moving to the post-AGB phase.
The detailed comparison between the IRS data and the synthetic spectra allows us to fix important properties of the dynamics and the dust composition of the stellar wind. Most of the observed SEDs show a prominent bump in the 25 − 30 μm spectral region, of which the origin is still debated. Our results confirm previous claims that MgS alone cannot account for the observational evidence, because the grains of this dust species form in an external region of the outflow where the growth rate is so low that the amount of MgS formed is negligible. Conversely, when assuming that MgS forms by precipitation on pre-existing SiC grains, we find a nice agreement with the observations, provided that the width of the MgS mantle is within 20 − 40% of the SiC core. This suggests that precipitation of MgS begins in a region of the outflow more internal than the zone where pure MgS forms: approximately in the same region where condensation of gaseous carbon into solid particles takes place.
With regard to the JWST perspective, we propose the colour-magnitude ([F770W]−[F1800W], [F1800W]) and ([F1000W]−[F1800W], [F1800W]) diagrams as the planes where the obscuration sequences of carbon stars of different masses can be more clearly distinguished. The former plane allows a better determination of the optical depth, given the strong sensitivity of the [F770W]−[F1800W] colour to τ10; on the other hand, in the latter plane the evolutionary tracks are more sensitive to the metallicity, which allows the disentangling of stars of different chemical compositions. Poignant information can also be deduced through the analysis of the distribution of the stars in the ([F1800W]−[F2550W], [F1800W]) plane. [F1800W]−[F2550W] is not particularly sensitive to the optical depth; on the other hand, the position of the stars in this diagram critically depends on the presence of the 30 μm bump, which, if we assume to be due to MgS, renders this colour extremely sensitive to the metallicity. Furthermore, this is the plane where the stars on leave from the AGB can be more clearly separated from the remaining carbon star population.
This lower limit refers to the mass at the beginning of the AGB phase, under the hypothesis that no mass loss occurred during the previous evolutionary phases. Should mass loss during the RGB be considered, the threshold mass under which no carbon stars form would be ∼1.4 M⊙. This is slightly lower than the lower limit for the formation of Galactic carbon stars found by Marigo et al. (2020), a result consistent with the lower metallicity of LMC stars compared to the Milky Way.
Acknowledgments
DAGH acknowledges support from the State Research Agency (AEI) of the Spanish Ministry of Science, Innovation and Universities (MCIU) and the European Regional Development Fund (FEDER) under grant AYA2017-88254-P. DK acknowledges the support of the Australian Research Council (ARC) Decra grant (95213534). EM is indebted to the anonymous referee for the detailed and careful reading of the manuscript, which helped to improve significantly the quality of this work.
References
- Andersen, A. C., Höfner, S., & Gautschy-Loidl, R. 2003, A&A, 400, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aringer, B., Girardi, L., Nowotny, W., Marigo, P., & Lederer, M. T. 2009, A&A, 503, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Begemann, B., Dorschner, J., Henning, T., et al. 1994, ApJ, 423, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertola, F., Bressan, A., Burstein, D., et al. 1995, ApJ, 438, 680 [CrossRef] [Google Scholar]
- Bertschinger, E., & Chevalier, R. A. 1985, ApJ, 167, 190 [Google Scholar]
- Bladh, S., Eriksson, K., Marigo, P., Liljegren, S., & Aringer, B. 2019, A&A, 623, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blöcker, T. 1995, A&A, 297, 727 [NASA ADS] [Google Scholar]
- Blöcker, T., & Schöenberner, D. 1991, A&A, 244, L43 [Google Scholar]
- Boothroyd, A. I., & Sackmann, I.-J. 1988, ApJ, 328, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchet, P., García-Marín, M., Lagage, P.-O., et al. 2015, PASP, 127, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Bowen, G. H. 1988, ApJ, 329, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Boyer, M. L., Girardi, L., Marigo, P., et al. 2013, ApJ, 774, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Brunner, M., Maercker, M., Mecina, M., Khouri, T., & Kerschbaum, F. 2018, A&A, 614, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cameron, A. G. W., & Fowler, W. A. 1971, ApJ, 164, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M. C., & Mazzitelli, I. 1991, ApJ, 370, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Y. Q., Zhao, G., Zhao, J. K., et al. 2019, AJ, 158, 249 [CrossRef] [Google Scholar]
- Cioni, M.-R. L., & Habing, H. J. 2003, A&A, 402, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, J. P. 1980, Theory of Stellar Pulsation (Princeton: Princeton University Press), 165 [CrossRef] [Google Scholar]
- Cox, A. N., & Stewart, J. N. 1969, Acad. Nauk. Sci. Inf., 15, 1 [Google Scholar]
- Cristallo, S., Straniero, O., Gallino, R., et al. 2009, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Piersanti, L., Straniero, O., et al. 2011, ApJS, 197, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Straniero, O., Piersanti, L., et al. 2015, ApJS, 219, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Agli, F. 2012, Master Thesis, University of Rome, Italy [Google Scholar]
- Dell’Agli, F., Ventura, P., Garcia Hernandez, D. A., et al. 2014a, MNRAS, 442, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Agli, F., García-Hernández, D. A., Rossi, C., et al. 2014b, MNRAS, 441, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Agli, F., Ventura, P., Schneider, R., et al. 2015a, MNRAS, 447, 2992 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Agli, F., García-Hernández, D. A., Ventura, P., et al. 2015b, MNRAS, 454, 4235 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Agli, F., Di Criscienzo, M., Boyer, M. L., et al. 2016, MNRAS, 460, 4230 [CrossRef] [Google Scholar]
- Dell’Agli, F., Di Criscienzo, M., Ventura, P., et al. 2018, MNRAS, 479, 5035 [Google Scholar]
- Dell’Agli, F., Di Criscienzo, M., García-Hernández, D. A., et al. 2019, MNRAS, 482, 4733 [CrossRef] [Google Scholar]
- Dell’Agli, F., Marini, E., D’Antona, F., et al. 2020, MNRASL, 499, 1531 [Google Scholar]
- D’Ercole, A., Vesperini, E., D’Antona, F., et al. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Di Criscienzo, M., Dell’Agli, F., Ventura, P., et al. 2013, MNRAS, 433, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Di Criscienzo, M., Ventura, P., García-Hernández, D. A., et al. 2016, MNRAS, 462, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ApJ, 598, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Ek, M., Hunt, A. C., Lugaro, M., et al. 2019, Nat. Astron., 4, 273 [CrossRef] [Google Scholar]
- Eriksson, K., Nowotny, W., Höfner, S., et al. 2014, A&A, 566, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrarotti, A. S., & Gail, H.-P. 2001, A&A, 371, 133 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Ferrarotti, A. S., & Gail, H.-P. 2002, A&A, 382, 256 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrarotti, A. S., & Gail, H.-P. 2006, A&A, 447, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fleischer, A. J., Gauger, A., & Sedlmayr, E. 1992, A&A, 266, 339 [Google Scholar]
- Frost, C. A., Cannon, R. C., Lattanzio, J. C., et al. 1998, A&A, 332, L17 [Google Scholar]
- Garcia-Berro, E., & Iben, I. 1994, ApJ, 434, 306 [Google Scholar]
- García-Hernández, D. A., Ventura, P., Delgado-Inglada, G., et al. 2016, MNRAS, 458, L118 [NASA ADS] [CrossRef] [Google Scholar]
- Ginolfi, M., Graziani, L., Schneider, R., et al. 2018, MNRAS, 473, 4538 [NASA ADS] [CrossRef] [Google Scholar]
- Gioannini, L., Matteucci, F., & Calura, F. 2017, MNRAS, 471, 4615 [NASA ADS] [CrossRef] [Google Scholar]
- Gładkowski, M., Szczerba, R., Sloan, G. C., et al. 2019, A&A, 626, A92 [EDP Sciences] [Google Scholar]
- Goebel, J. H., & Moseley, S. H. 1985, ApJ, 290, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Gong, M., Ostriker, E. C., & Wolfire, M. G. 2017, ApJ, 843, 38 [CrossRef] [Google Scholar]
- Gruendl, R. A., Chu, Y.-H., Seale, J. P., et al. 2008, ApJ, 688, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space sci. Rev., 85, 161 [Google Scholar]
- Groenewegen, M. A. T., & de Jong, T. 1993, A&A, 267, 410 [NASA ADS] [Google Scholar]
- Groenewegen, M. A. T., & Sloan, G. C. 2018, A&A, 609, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T., Wood, P. R., Sloan, G. C., et al. 2007, MNRAS, 376, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T., Sloan, G. C., Soszynski, I., & Petersen, E. A. 2009, A&A, 506, 1277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gullieuszik, M., Groenewegen, M. A. T., Cioni, M.-R. L., et al. 2012, A&A, 537, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanner, M. 1988, Infrared Observations of Comets Halley and Wilson and Properties of the Grains [Google Scholar]
- Harris, J., & Zaritsky, D. 2009, AJ, 138, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
- Herwig, F. 2005, ARA&A, 43, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D., & Salpeter, E. E. 1971, ApJ, 163, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Hony, S., Waters, L. B. F. M., & Tielens, A. G. G. M. 2002, A&A, 390, 533 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iben, I., Jr 1974, ARA&A, 12, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I. 1975, ApJ, 196, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Johansson, J., Thomas, D., & Maraston, C. 2012, MNRAS, 421, 1908 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, O. C., Kemper, F., Srinivasan, S., et al. 2014, MNRAS, 440, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, O. C., Meixner, M., Justtanont, K., & Glasse, A. 2017, ApJ, 841, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, U. G., Hron, J., & Loidl, R. 2000, A&A, 356, 253 [NASA ADS] [Google Scholar]
- Kamath, D., Karakas, A. I., & Wood, P. R. 2012, ApJ, 746, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I. 2010, MNRAS, 403, 1413 [Google Scholar]
- Karakas, A. I. 2014, MNRAS, 445, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I., & Lattanzio, J. C. 2014, PASA, 31, e030 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I., & Lugaro, M. 2016, ApJ, 825, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I., Lattanzio, J. C., & Pols, O. R. 2002, PASA, 19, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I., Lugaro, M., Carlos, M., et al. 2018, MNRAS, 477, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, D., Nagashima, C., Nagayama, T., et al. 2007, PASJ, 59, 615 [NASA ADS] [Google Scholar]
- Kemper, F., Woods, P. M., Antoniou, V., et al. 2010, PASP, 122, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Kraemer, K. E., Sloan, G. C., Wood, P. R., et al. 2017, ApJ, 834, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Kubryk, M., Prantzos, N., & Athanassoula, E. 2015, A&A, 580, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laor, A., & Draine, B. T. 1993, ApJ, 402, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Lattanzio, J. C. 1987, ApJ, 313, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Lattanzio, J. C. 1993, Planetary Nebulae, 235 [Google Scholar]
- Lewis, K. M., Lugaro, M., Gibson, B. K., et al. 2013, ApJ, 768, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., Tagliente, G., Karakas, A. I., et al. 2014, ApJ, 780, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., Karakas, A. I., Pető, M., et al. 2018, Geochim. Cosmochim. Acta, 221, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Maercker, M., Khouri, T., De Beck, E., et al. 2018, A&A, 620, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P. 2002, A&A, 387, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., & Aringer, B. 2009, A&A, 508, 1538 [Google Scholar]
- Marigo, P., Girardi, L., & Bressan, A. 1999, A&A, 344, 123 [NASA ADS] [Google Scholar]
- Marigo, P., Cummings, J. D., Curtis, J. L., et al. 2020, Nat. Astron., 4, 1102 [CrossRef] [Google Scholar]
- Marini, E., Dell’Agli, F., Di Criscienzo, M., et al. 2019, ApJ, 871, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Marini, E., Dell’Agli, F., Di Criscienzo, M., et al. 2020, MNRAS, 340, 485 [Google Scholar]
- Mathis, J. S. 1990, ARA&A, 28, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuura, M., Wood, P. R., Sloan, G. C., et al. 2006, MNRAS, 371, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F. 2012, Chemical Evolution of Galaxies (Berlin Heidelberg: Springer-Verlag) [Google Scholar]
- Mattsson, L. 2008, On the Winds of Carbon Stars and the Origin of Carbon: A Theoretical Study (Ph.D. Dissertation). Acta Universitatis Upsaliensis, Uppsala, Retrieved from http://urn.kb.se/resolve?urn=urn:nbn:se:uu:diva-99593 [Google Scholar]
- Mattsson, L., & Höfner, S. 2011, A&A, 533, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattsson, L., Wahlin, R., Höfner, S., et al. 2008, A&A, 484, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattsson, L., Wahlin, R., & Höfner, S. 2010, A&A, 509, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattsson, L., Wahlin, R., & Höfner, S. 2012, A&A, 546, C1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meixner, M., Gordon, K. D., Indebetouw, R., et al. 2006, AJ, 132, 2268 [NASA ADS] [CrossRef] [Google Scholar]
- Messenger, S. J., Speck, A., & Volk, K. 2013, ApJ, 764, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2013, A&A, 558, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nanni, A. 2019, MNRAS, 482, 4726 [NASA ADS] [CrossRef] [Google Scholar]
- Nanni, A., Bressan, A., Marigo, P., et al. 2013, MNRAS, 434, 2390 [NASA ADS] [CrossRef] [Google Scholar]
- Nanni, A., Bressan, A., Marigo, P., et al. 2014, MNRAS, 438, 2328 [NASA ADS] [CrossRef] [Google Scholar]
- Nanni, A., Marigo, P., Groenewegen, M. A. T., et al. 2016, MNRAS, 462, 1215 [NASA ADS] [CrossRef] [Google Scholar]
- Nanni, A., Marigo, P., Girardi, L., et al. 2018, MNRAS, 473, 5492 [NASA ADS] [CrossRef] [Google Scholar]
- Nanni, A., Groenewegen, M. A. T., Aringer, B., et al. 2019a, MNRAS, 487, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Nanni, A., Groenewegen, M. A. T., Aringer, B., et al. 2019b, IAU Symp., 478 [Google Scholar]
- Nanni, A., Burgarella, D., Theulé, P., et al. 2020a, A&A, 641, A168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nanni, A., Marigo, P., & Groenewegen, M. A. T. 2020b, IAU General Assembly, 405 [Google Scholar]
- Nenkova, M., Ivezic, Z., & Elitzur, M. 1999, Thermal Emission Spectroscopyand Analysis of Dust, Disks, and Regoliths, 20 [Google Scholar]
- Paczyński, B. 1970, Acta Astron., 20, 287 [Google Scholar]
- Pastorelli, G., Marigo, P., Girardi, L., et al. 2019, MNRAS, 485, 5666 [Google Scholar]
- Pastorelli, G., Marigo, P., Girardi, L., et al. 2020, MNRAS, 498, 3283 [Google Scholar]
- Pegourie, B. 1988, A&A, 194, 335 [NASA ADS] [Google Scholar]
- Rau, G., Hron, J., Paladini, C., et al. 2017, A&A, 600, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rau, G., Ohnaka, K., Wittkowski, M., Airapetian, V., & Carpenter, K. 2019, ApJ, 882, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Renzini, A., & Voli, M. 1981, A&A, 500, 221 [Google Scholar]
- Rieke, G. H., Wright, G. S., Böker, T., et al. 2015, PASP, 127, 584 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Matteucci, F., Ventura, P., et al. 2001, A&A, 374, 646 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, D., Karakas, A. I., Tosi, M., et al. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, D., Matteucci, F., Zhang, Z.-Y., et al. 2017, MNRAS, 470, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Matteucci, F., Zhang, Z.-Y., et al. 2019, MNRAS, 490, 2838 [NASA ADS] [CrossRef] [Google Scholar]
- Sackmann, I.-J., & Boothroyd, A. I. 1992, ApJL, 392, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Sandin, C., & Mattsson, L. 2020, MNRAS, 499, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, R., Valiante, R., Ventura, P., et al. 2014, MNRAS, 442, 1440 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, R., Hunt, L., & Valiante, R. 2016, MNRAS, 457, 1842 [NASA ADS] [CrossRef] [Google Scholar]
- Schultheis, M., Rich, R. M., Origlia, L., et al. 2019, A&A, 627, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sharp, C. M., & Huebner, W. F. 1990, ApJS, 72, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L. 2007, A&A, 476, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sloan, G. C., Lagadec, E., Zijlstra, A. A., et al. 2014, ApJ, 791, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Sloan, G. C., Kraemer, K. E., McDonald, I., et al. 2016, ApJ, 826, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Speck, A. K., Corman, A. B., Wakeman, K., et al. 2009, ApJ, 691, 1202 [NASA ADS] [CrossRef] [Google Scholar]
- Spitoni, E., Romano, D., Matteucci, F., et al. 2015, ApJ, 802, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Srinivasan, S., Meixner, M., Leitherer, C., et al. 2009, AJ, 137, 4810 [NASA ADS] [CrossRef] [Google Scholar]
- Srinivasan, S., Sargent, B. A., Matsuura, M., et al. 2010, AJ, 137, 4810 [Google Scholar]
- Srinivasan, S., Sargent, B. A., & Meixner, M. 2011, A&A, 532, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Srinivasan, S., Boyer, M. L., Kemper, F., et al. 2016, MNRAS, 457, 2814 [NASA ADS] [CrossRef] [Google Scholar]
- Thorsbro, B., Ryde, N., Rich, R. M., et al. 2020, ApJ, 894, 26 [CrossRef] [Google Scholar]
- Valiante, R., Schneider, R., Bianchi, S., et al. 2009, MNRAS, 397, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Valiante, R., Gioannini, L., Schneider, R., et al. 2017, Mem. Soc. Astron. It., 88, 420 [NASA ADS] [Google Scholar]
- van Loon, J. T., Groenewegen, M. A. T., de Koter, A., et al. 1999, A&A, 351, 559 [NASA ADS] [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [Google Scholar]
- Ventura, P. 2010, Light Elements in the Universe, 147 [Google Scholar]
- Ventura, P., & D’Antona, F. 2005a, A&A, 439, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventura, P., & D’Antona, F. 2005b, A&A, 431, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventura, P., & Marigo, P. 2009, MNRAS, 399, L54 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., & Marigo, P. 2010, MNRAS, 408, 2476 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Zeppieri, A., Mazzitelli, I., & D’Antona, F. 1998, A&A, 334, 953 [Google Scholar]
- Ventura, P., D’Antona, F., & Mazzitelli, I. 1999, ApJ, 524, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., D’Antona, F., & Mazzitelli, I. 2000, A&A, 363, 605 [Google Scholar]
- Ventura, P., D’Antona, F., Mazzitelli, I., et al. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Di Criscienzo, M., Schneider, R., et al. 2012, MNRAS, 420, 1442 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Di Criscienzo, M., Carini, R., & D’Antona, F. 2013, MNRAS, 431, 3642 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Dell’Agli, F., Schneider, R., et al. 2014, MNRAS, 439, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Karakas, A. I., Dell’Agli, F., et al. 2015, MNRAS, 450, 3181 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Karakas, A. I., Dell’Agli, F., et al. 2016, MNRAS, 457, 1456 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Karakas, A., Dell’Agli, F., García-Hernández, D. A., & Guzman-Ramirez, L. 2018, MNRAS, 475, 2282 [NASA ADS] [Google Scholar]
- Volk, K., Kwok, S., Hrivnak, B. J., et al. 2002, ApJ, 567, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Volk, K., Sloan, G. C., & Kraemer, K. E. 2020, Ap&SS, 365, 88 [Google Scholar]
- Wachter, A., Schröder, K. P., Winters, J. M., Arndt, T. U., & Sedlmayr, E. 2002, A&A, 384, 452 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wachter, A., Winters, J. M., Schröder, K. P., & Sedlmayr, E. 2008, A&A, 486, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weiss, A., & Ferguson, J. W. 2009, A&A, 508, 1343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wegg, C., Rojas-Arriagada, A., Schultheis, M., et al. 2019, A&A, 632, A121 [CrossRef] [EDP Sciences] [Google Scholar]
- Winters, J. M., Le Bertre, T., Jeong, K. S., Helling, C., & Sedlmayr, E. 2000, A&A, 361, 641 [NASA ADS] [Google Scholar]
- Woods, P. M., Oliveira, J. M., Kemper, F., et al. 2011, MNRAS, 411, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y., Lin, Y., Zhang, J., et al. 2016, ApJ, 825, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Harris, J., Thompson, I. B., et al. 2004, AJ, 128, 1606 [NASA ADS] [CrossRef] [Google Scholar]
- Zhukovska, S., Gail, H.-P., & Trieloff, M. 2008, A&A, 479, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zijlstra, A. A., Matsuura, M., Wood, P. R., et al. 2006, MNRAS, 370, 1961 [NASA ADS] [CrossRef] [Google Scholar]
- Zinner, E. 2008, Org. Matter Space, 251, 341 [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., et al. 1996, MNRAS, 282, 132 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Evolution as a function of time (counted from the beginning of the TP phase) of the luminosity (top-left panel), effective temperature (top, right), surface C/O (bottom, left) and mass-loss rate (bottom, right) of a model of initial mass 2 M⊙ and metallicity Z = 0.008. |
| In the text | |
 |
Fig. 2. Top panels: variation of the dust production rate as a function of time (left) and of the current mass of the star (right) during the AGB evolution of the model of initial mass 2 M⊙ and metallicity Z = 0.008 presented in Fig. 1. The individual contributions from silicates, solid carbon, and silicon carbide are shown. Bottom panels: variation of the expected SED during four different stages (indicated with the arrows in the top-right panel) when considering only solid carbon and SiC (left), and when graphite and MgS are also considered (right). In these examples, the number density of the seeds of amorphous carbon dust relative to hydrogen is assumed 10−13, whereas the density of the seeds of the other dust species are scaled with respect to amorphous carbon according to the percentages given in the two panels. |
| In the text | |
 |
Fig. 3. Variation of luminosity (top-left panel), carbon excess C−O (top-right, see text for the definition), dust production rate (bottom-left) and τ10 (bottom-right) of the AGB models used in the present work. The evolutions are shown with respect to the current mass of the star on the abscissa. The different lines connect a few points selected during the evolution trough the C-star phase. Open points refer to the evolution of a 5 M⊙ star of metallicity Z = 0.001 |
| In the text | |
 |
Fig. 4. Comparison between the IRS (black lines) and the synthetic (red) spectra of a few sources in the LMC sample of carbon stars, with various luminosities and degrees of obscuration. The values of luminosities and τ10 reported in each panel are those allowing the best fit, corresponding to the red lines. The cyan lines indicate the synthetic SED entering the carbon condensation zone, resulting from the absorption of the radiation from the photosphere by SiC particles in the innermost region of the circumstellar envelope. |
| In the text | |
 |
Fig. 5. Luminosities and optical depths derived for the stars in the sample analysed in the present work. Green squares and red triangles indicate the progeny of M < 2 M⊙ stars and the higher mass counterpart, respectively; orange asterisks refer to stars with luminosities below 5000 L⊙; magenta crosses indicate stars brighter than 20 000 L⊙; blue diamonds indicate extremely obscured objects, which were taken from Gruendl et al. (2008) and the source SSID 9; and the stars indicated with open diamonds are SSID 125 and SSID 190. The black lines and points in the figure refer to the evolution of the same models shown in Fig. 3, and the initial masses are indicated next to the corresponding track. Magenta stars indicate the results obtained by artificially increasing the mass-loss rate of the stars of initial masses 1.1 M⊙, 2.5 M⊙, 3 M⊙, after reaching the C-star stage, according to the discussion in Sect. 5.3. |
| In the text | |
 |
Fig. 6. Left: IRS SED of source SSID 141, compared with our interpretation based on synthetic modelling. Right: AGB evolution with time of the luminosity of 1.5, 2, 2.5 M⊙ stars; the O-rich phase was omitted for readability. The sequence of the 2.5 M⊙ was artificially shifted by 1 Myr for readability. The grey shaded region indicates the luminosity range of the low-luminosity stars SSID 3, SSID 66, SSID 103, and SSID 141. |
| In the text | |
 |
Fig. 7. IRS and best-fit SED for sources SSID 4451 (left panel) and SSID 4109 (middle). Right: evolution with time (counted since the beginning of the TP-AGB phase) of luminosity (black) and surface C/O (red track, scale on the right) of a 3.5 M⊙ star. The grey shaded area indicates the phase during which the star is carbon-rich. |
| In the text | |
 |
Fig. 8. Left: IRS SED of source SSID 4540, compared with our interpretation, based on synthetic modelling. Right: AGB evolution with time of the luminosity (black line, scale on the left) and of the surface C/O ratio (red line, scale on the right) of a 5 M⊙ model with metallicity Z = 0.001. The grey shaded area indicates the evolutionary phase during which the star evolves as a carbon star. |
| In the text | |
 |
Fig. 9. SED fitting of four of the extremely red objects studied by Gruendl et al. (2008). |
| In the text | |
 |
Fig. 10. IRS (black) and synthetic (red) spectra of the source SSID 190. |
| In the text | |
 |
Fig. 11. Evolution of radius (black lines, scale on the left) and surface C/O ratio (red, scale on the right) during the AGB phase of stars of initial masses 1.1 M⊙ (left panel), 2.5 M⊙ (middle), and 3 M⊙ (right). The thin, blue horizontal lines indicate the C=O condition, whereas the green arrows indicate the phase of rapid expansion of the star, as a consequence of the surface carbon enrichment. |
| In the text | |
 |
Fig. 12. IRS spectrum of SSID 18 (black line) compared with synthetic SEDs, corresponding to the same luminosity and τ10, and different percentages of SiC+MgS and of the relative width of the MgS mantle (aman) on top of SiC core. The various lines correspond to the following: red (our best-fit model), with SiC+MgS = 9% and aman = 0.05 μm; green, with SiC+MgS = 35% and aman = 0.02 μm; blue, with SiC+MgS = 9% and aman = 0.02 μm; and orange, with SiC+MgS = 6% and aman = 0.05 μm. |
| In the text | |
 |
Fig. 13. IRS spectra of sources SSID 4197 (top-left panel), SSID 4783 (top-right), SSID 4002 (bottom-left), and SSID 4692 (bottom-right), with the best-fit models obtained with the luminosities, optical depths, and dust mineralogy indicated in the individual panels |
| In the text | |
 |
Fig. 14. IRS spectrum of SSID 4722 compared with synthetic SED, differing for the percentage of graphite. The different lines refer to the following percentages: 0% (orange), 15% (red), 30% (blue). |
| In the text | |
 |
Fig. 15. IRS spectra of sources SSID 4794 (top-left panel), SSID 4238 (top-right panel), SSID 4589 (bottom-left panel), and SSID 4150 (bottom-right panel), with the best-fit models obtained with the luminosities, optical depths, and dust mineralogy indicated in the individual panels. |
| In the text | |
 |
Fig. 16. Left: stars in sample described in Sect. 2 are shown in the colour-magnitude ([F770W]–[F1800W], [F1800W]) plane. The same symbols as those in Fig. 5 were adopted. Black squares and triangles indicate the expected evolution of stars of metallicity Z = 0.008 and initial masses 1.5 M⊙ and 3 M⊙, respectively. Dashed lines refer to the expected evolution of 1.5 M⊙ and 3 M⊙ stars, when the presence of Sic+MgS and graphite grains are considered in the computation of the synthetic SED. The blue squares and red triangles, connected with dotted tracks, refer to the evolution of Z = 0.002 stars of initial masses 1.5 M⊙ and 2.5 M⊙, respectively. Magenta pentagons indicate the tracks of 1.1 M⊙, 2.5 M⊙, and 3 M⊙ (from fainter to brighter) models, obtained by artificially increasing the mass loss rate after the jump in the stellar radius caused by the increase in the surface carbon, according to the discussion in Sect. 5.3. Right: distribution of stars in the colour-magnitude ([F1000W]-[F1800W], [F1800W]) plane. |
| In the text | |
 |
Fig. 17. Left: position of stars in the sample presented in Sect. 2 in the colour-colour ([F770W]−[F1800W], [F770W]−[F1130W]) plane. The symbols for the stars and the evolutionary tracks are the same as in Fig. 16. Right: zoom of the same plane shown in the left panel, to outline the bifurcation between stars of different metallicity. |
| In the text | |
 |
Fig. 18. Position of stars in the sample presented in Sect. 2 in the colour-magnitude ([F1800W]−[F2550W], [F1800W]) plane. The symbols for the stars and the evolutionary tracks are the same as in Fig. 16. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned}&\log \tau _{10} \sim -0.1\times ([F770W]-[F1800W])^2\nonumber \\&\quad + 0.9\times ([F770W]-[F1800W]) -1.2. \end{aligned} $$](/articles/aa/full_html/2021/03/aa39613-20/aa39613-20-eq2.gif)
![$$ \begin{aligned}&\log \tau _{10} \sim -0.2\times ([F1000W]-[F1800W])^2 \nonumber \\&\quad + 1.13\times ([F1000W]-[F1800W]) -0.75. \end{aligned} $$](/articles/aa/full_html/2021/03/aa39613-20/aa39613-20-eq3.gif)