EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 645 (January 2021) A&A, 645 (2021) A53 Full HTML
Free Access
Issue
A&A
Volume 645, January 2021
Article Number A53
Number of page(s) 23
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202038113
Published online 08 January 2021

© ESO 2021

1 Introduction

Aldehyde molecules, which contain a functional group CHO, play an important role in the formation of complex organic molecules (COMs, molecules containing six or more atoms with at least one carbon, Herbst & van Dishoeck 2009). The two-carbon to three-carbon chain aldehydes are generally found in the cold dense regions of star formation as well as in the innermost warm region of protostellar envelope, the hot core. In particular, propenal (C2 H3CHO), also called acrolein, is considered as a prebiotic species due to its formation after the decomposition of sugars (Moldoveanu 2010; Bermúdez et al. 2013)and its role in the synthesis of amino acids via Strecker-type reactions (Strecker 1850, 1854) as tested in laboratory studies (e.g. van Trump & Miller 1972; Shibasaki et al. 2008; Grefenstette 2017). On the other hand, on the primordial Earth, C2 H3CHO is one of a few species that readily reacts with nucleobases of the ribonucleic acid (RNA, Nelsestuen 1980), which makes it a possible sink for the nucleobases and an important hindrance to the start of the RNA world (e.g. Gargaud et al. 2007; Neish et al. 2010). Propynal (HCCCHO), C2 H3CHO and propanal (C2 H5CHO) are suspected to be linked through their formation on ice surfaces by successive hydrogenation (e.g. Hudson & Moore 1999). C2 H3CHO and C2 H5CHO were first detected in the interstellar medium toward the Galactic Center source Sgr B2(N) (Hollis et al. 2004; Requena-Torres et al. 2008), while HCCCHO was first detected towards the dark cloud TMC–1 (Irvine et al. 1988; Turner 1991).

Three-carbon-chain molecules have also been observed in the ISM and are, in general, more abundant towards protostars characterised by warm carbon-chain chemistry (WCCC), such as L1527 (Sakai et al. 2008), and cold dense clouds. For example, propylene (C3 H6) was detected for the first time towards TMC-1 (Marcelino et al. 2007). It has so far never been reported in warmer environments, where COMs are found with high abundances, such as hot cores/corinos, contrary to methyl acetylene (CH3 CCH) already found with high abundances in such objects (e.g. van Dishoeck et al. 1995; Cazaux et al. 2003).

In this paper we report detections of C2 H3CHO and C3 H6 towards the low-mass Class 0 protostellar binary IRAS 16293–2422 (IRAS 16293 hereafter). This source, located in the ρ Ophiuchus cloud complex at a distance of 144 ± 7 pc (Zucker et al. 2019), is well-known as a reference in astrochemistry because of its molecule-rich envelope and the presence of numerous bright emission lines at millimetre wavelengths (for example, van Dishoeck et al. 1995; Cazaux et al. 2003; Caux et al. 2011). The high sensitivity and the high angular resolution of the Atacama Large (sub)Millimeter Array (ALMA) allowed many new detections around solar-type protostars and in the interstellar medium. Using ALMA observations of the Protostellar Interferometric Line Survey (PILS, Jørgensen et al. 2016), some of these new detections of COMs, such as deuterated formamide (NHDCHO and NH2 CDO) and isocyanic acid (HNCO) by Coutens et al. (2016), methyl chloride (CH3 Cl, Fayolle et al. 2017), methyl isocyanate (CH3NCO, Ligterink et al. 2017), cyanamide (NH2CN, Coutens et al. 2018a), methyl isocyanide (CH3NC, Calcutt et al. 2018a), and nitrous acid (HONO, Coutens et al. 2019) have been reported towards this protostellar binary. C2 H5CHO (Lykke et al. 2017) and CH3CCH (Calcutt et al. 2019) are also detected in the embedded hot corino towards the “B component” (IRAS 16293B) of this source. This demonstrates the possibility of finding the unsaturated precursors of C2 H5CHO and provide new constraints on the formation of these species in low-mass protostellar environments. It also suggests the need to develop models to describe these three-carbon species (C3 -species hereafter) using laboratory measurements and theoretical calculations both for the gas phase and grain surfaces (Loison et al. 2014, 2017; Hickson et al. 2016a; Qasim et al. 2019).

This paper is organised as follows: Sect. 2 describes the observations and the spectroscopic data used in this study. The results and the analysis are presented in Sect. 3. These results are then compared to a chemical model which is described in Sect. 4. Finally, the comparison between the results and the model are discussed in Sect. 5 and the conclusions summarised in Sect. 6.

2 Observations

Observations at 1.3 and 0.8 mm wavelength, carried out with ALMA, corresponding to Band 6 and 7, respectively, towards IRAS 16293 were used in this study. The pointing centre, located between the two protostars of the binary system at αJ2000 = 16h32m22. s72; δJ2000 = −24°28′34′′.3, was the same for all the observations. The species that are the main focus of this study are the C3 -species C2 H3CHO and C3 H6, as well as the chemically related species HCCCHO, C2 H5CHO, propanol (n-C3H7OH) and its isoconformer (i-C3 H7OH), tricarbon monoxide (C3O), C3 H8, and glyoxal (cis-HC(O)CHO). Note that the most abundant conformer of HC(O)CHO, trans-HC(O)CHO, has no dipole moment and does not display any pure rotational transitions, thus it cannot be detected at millimetre wavelengths.

2.1 Band 6 observations

The ALMA-Band 6 data are a combination of PILS observations in Cycle 1 (project-id: 2012.1.00712.S, PI: Jørgensen, J. K.) and Cycle 4 observations taken from Taquet et al. (2018; project-id: 2016.1.01150.S, PI: Taquet, V.). The observations cover a total of ~5.5 GHz spread between 221.7 and 250.7 GHz with a frequency resolution of 0.122 MHz, corresponding to a velocity resolution of ~0.16 km s−1. The two datasets have been treated the same way and were restored with the same 0′′. 5 circular beam as in Band 7. The continuum subtraction and the data calibration are detailed in Jørgensen et al. (2016) and Taquet et al. (2018), for Cycle 1 and Cycle 4 observations, respectively. Calibration uncertainties are better than 5% and the sensitivity reached is 1 –10 mJy beam−1 per channel, depending on the observations.

2.2 Band 7 observations

The Band 7 data are taken from the PILS observations (project-id: 2013.1.00278.S, PI: Jørgensen, J. K.) and cover the full range of 329 to 363 GHz at a frequency resolution of 0.244 MHz, which corresponds to ~0.2 km s−1 in this frequency range, and were restored with a circular beam of 0′′. 5. The continuum subtraction and the data reduction are described in Jørgensen et al. (2016). The sensitivity reaches down to 7–10 mJy beam−1 per channel and the relative calibration uncertainty across the band is ~5%. Table 1 summarises the details of the spectral windows used in this study.

2.3 Spectroscopic data

The spectroscopic data used to identify C2 H3CHO transitions are taken from the Cologne Database for Molecular Spectroscopy (CDMS, Müller et al. 2001, 2005). The CDMS entry is based on Daly et al. (2015) with additional data from Winnewisser et al. (1975); Cherniak & Costain (1966). The dipole moment was determined by Blom et al. (1984).

The C3 H6 rotational transitions are taken from its CDMS entry, based on Craig et al. (2016) with numerous additional transition frequencies from Hirota (1966), Pearson et al. (1994) and Wlodarczak et al. (1994). The dipole moment was measured by Lide & Mann (1957). The spectroscopic entry includes the transitions of A and E torsional substate conformers, which arise from the methyl internal rotation splitting.

Five spectroscopic conformers of n-C3H7OH exist, distinguished by the orientation of their methyl and OH groups. Ga-n-C3H7OH is the lowestvibrational ground state conformer. The CDMS entry used in this study is largely based on Kisiel et al. (2010), with interactions with other conformers studied by Kahn & Bruice (2005) and additional data from Maeda et al. (2006a); White (1975). The entry only takes the Ga- conformer into account. The correction factor corresponding to the contribution of the other conformers is 2.75 at Tex = 100 K.

The CDMS entries for the two conformers gauche, the energetically lowest, and anti of i-C3 H7OH are based on Maeda et al. (2006b); Ulenikov et al. (1991); Hirota (1979). Rotation-tunneling interactions between theconformers are incorporated in the Hamiltonian using the formulation described in Christen & Müller (2003). Unlike the n-C3H7OH entry, the i-C3 H7OH partition function already includes the contribution of gauche and anti conformers.

Spectroscopic data of HCCCHO were taken from its CDMS entry, which is based on McKellar et al. (2008) with additional data from Costain & Morton (1959) and Winnewisser (1973). The dipole moment was measured by Brown & Godfrey (1984).

C3O spectroscopic data are found in the CDMS. The entry is based on the work of Bizzocchi et al. (2008), where they used previous studies and measurements (Klebsch et al. 1985; Tang et al. 1985; Brown et al. 1983). The dipole moment is reported in the last cited work. The entry does not take the contribution of the torsional/vibrational excited state into account.

C3 H8 spectroscopic data are taken from the Jet Propulsion Laboratory database (JPL, Pickett et al. 1998). The JPL entry is based on Drouin et al. (2006), which is a compilation of extensive own data and data taken from Lide (1960), and Bestmann et al. (1985a,b). The partition function includes contributions from the first vibrational and torsional excited states. The dipole moment is reported in Lide (1960).

cis-HC(O)CHO is higher in energy by 1555 ± 48 cm−1 or 2237 ± 69 K than trans-HC(O)CHO, however, the latter has no dipole moment thus does not display any rotational transitions. The spectroscopic data are taken from its CDMS entry which is based on the study of Hübner et al. (1997), which also includes the measurement of the dipole moment. Due to the enthalpy difference between cis and trans conformers, the population fraction of cis-HC(O)CHO is 1.9 × 10−10 at 100 K. The abundance derived from the molecular emission of this conformer has to be divided by this factor to retrieve the total abundance of HC(O)CHO.

The main spectroscopic parameters of the different species analysed in this study are summarised in Table C.1.

Table 1

Observations towards IRAS 16293B used in this study.

3 Observational results

For this study we follow the majority of the previous PILS papers and focus on an offset position by 0′′. 5 in the South-West direction from the most compact source of the binary system, IRAS 16293B (e.g. Jørgensen et al. 2016; Calcutt et al. 2018b; Ligterink et al. 2017). The spectrum at this position shows narrow lines and is less affected by the strong absorption arising from the continuum emission. At this position the molecular lines have a full width at half-maximum (FWHM) of ~1 km s−1 and a velocity peak position (vlsr) of ~ 2.5−2.8 km s−1.

3.1 C3-species lines

A total of 12 unblended lines of C2 H3CHO have been identified across Bands 6 and 7, with an intensity higher than 3σ–with σ calculated as the root mean square (RMS) of the noise spectrum. 38 other lines that match in terms of frequency were found in the range of the observations. However, they show significant blending with other species. All the lines predicted by the local thermodynamic equilibrium (LTE) model are present in the observations. The upper-level energies of the detected transitions lie between 158 and 401 K, which provide constraints on the excitation temperature. Among these transitions, those at frequencies of 225.192, 330.550 and 336.473 GHz have been used in the fit even though they seem to be slightly blended with other species. All these transitions are listed in Table E.1. C2 H3CHO has been searched for towards IRAS 16293A as well, however, no lines above 3σ were found, presumably due to the larger linewidth (~3 km s−1), and thus the more severe blending, compared to IRAS 16293B.

For C3 H6, 21 unblended lines were found in the different frequency ranges of the observations. The upper-level energies of the detected transitions lie between 84 and 264 K. 34 lines above 3σ are present in the spectrum, but they are significantly blended with other species, thus they were discarded from the fit. The transition at 349.153 GHz, with an upper-level energy of 355 K, was used in the fit to better assess the excitation temperature, even though the intensity of the line is lower than 3σ. All these transitions are listed in Table F.1. The same lines were found to be completely blended towards IRAS 16293A.

Figure 1 shows the integrated line emission of C2 H3CHO and C3 H6. The spatial extent of their emission is marginally resolved and located in the hot corino region, consistently with the other O-bearing COMs detected in the same dataset (e.g. Jørgensen et al. 2016; Lykke et al. 2017; Calcutt et al. 2018b).

HCCCHO, n-C3H7OH and i-C3 H7OH, as well as C3O and cis-HC(O)CHO were searched for in the data, however, no line above 1σ was found.

3.2 Column densities

The identification of C2 H3CHO and C3 H6 has been confirmed by modelling the molecular emission under the LTE assumption and comparing the spectrum extracted at an offset position from the continuum peak position of IRAS 16293B. The model has been used in Manigand et al. (2020), where more substantial details can be found. This synthetic spectrum considers the gas as a homogeneous slab under LTE conditions and uses the optically thin molecular lines to fit the observed spectrum and to estimate the column density, the rotational temperature, the peak velocity shift, the FWHM and the source size, which is fixed to 0′′. 5, based on the previous PILS studies.

We run a grid of models in column densities from 1013 to 1017 cm−2 and for excitation temperatures ranging from 50 to 300 K in steps of 25 K. The peak velocity shift and FWHM were set to 2.7 and 0.8 km s−1, respectively, for C2 H3CHO and 2.5 and 0.8 km s−1, respectively, for C3 H6, after a visual inspection of the alignment of the observed lines and the model. The best model was estimated through a χ2 minimisation, with a modified weighting factor as detailed in Manigand et al. (2020). The modified weighting factor favours the under-estimation of the intensity of the modelled spectrum, which reflects possible unexpected blending effects with other species. A correction factor was applied to the derived column density to take into account the continuum contribution as detailed, for example, in Jørgensen et al. (2018) and Calcutt et al. (2018b). The relative uncertainty of the column density and the rotational temperature is 20%.

The best agreement between the data and the model for C2 H3CHO was found at an excitation temperature of 125 ± 25 K and a column density of 3.4 ± 0.7 × 1014 cm−2. All the lines used in the fit are shown in Fig. 2. The lower intensity of the lines in Band 7 compared to those in Band 6 emphasises the relatively low rotational temperature derived from the model.

The rotational temperature and column density of C3 H6 was found to be 75 ± 15 K and 4.2 ± 0.8 × 1016 cm−2, respectively. All the brightest lines in Band 6 are marginally optically thick for the best fit physical conditions. Nevertheless, the optically thick line at 235.272 GHz shows very good agreement with the observed line, which consolidates the unusually low value of 75 K found for the rotational temperature towards the IRAS 16293B hot corino region. The C3 H6 lines used to assess the column density and the rotational temperature are shown in Fig. 3.

The majority of C3 H6 transitions are split into A and E torsional sub-states due to the CH3–group in the molecule. This kind of split is common to most of the species having the CH3 group, such as CH3OH or CH3OCHO. For C3 H6, the intensities of the lines at 340.827, 347.774 and 351.738 GHz, corresponding to E-transitions, are overestimated by the LTE model. The A-transitions that have the same quantum numbers, in particular the same upper-level energies and Einstein’s coefficients, are in good agreement with the model. This overestimation of the E-transitions alone may suggestthat the spin weight ratio between the transitions arising from A and E substates is not equal to unity.

To test this hypothesis, we added the spin weight of the E-transitions with respect to the A-transitions in the LTE model and assessed this ratio, given the best fit found for the excitation temperature, velocity shift and FWHM. This spin weight factor gE/A is multiplied to the upper state degeneracy of the E-transitions. The best fit was found at the same column density, i.e. 4.2 ± 0.8 × 1016 cm−2, and a spin weight ratio of gE/A = 0.6 ± 0.1. Figure 4 shows the LTE model, including the discrepancy of the E-transitions with respect to the A-transitions. This difference between the A- and E-transitions could reflect an abundance asymmetry between the different conformers, due to low temperature at the moment of their formation, for example. Similar E/A ratios were observed towards dark clouds (Friberg et al. 1988), cold prestellar clumps (Menten et al. 1988) and more recently towards young stellar objects (Wirström et al. 2011). Nevertheless, in this study, there are still too few isolated transitions to be able to rule out any bias from the spectroscopic data that could explain this asymmetric E/A spin ratio.

For the sake of the chemical modelling comparison, the upper limits on the column density were derived for HCCCHO, C3 H7OH, C3 O, C3 H8, and cis-HC(O)CHO. These upper limits correspond to the column density reached in the model when the most intense lines reached 3σ at ~100 K, which is the average excitation temperature of C2 H3CHO and C3 H6. The upper limit of cis-HC(O)CHO leads to an upper limit of the total amount of HC(O)CHO of < 2.6 × 1023 cm−2 in the gas phase, which does not provide any real constraint on this molecule. Table 2 summarises the column densities and rotational temperatures of the newly detected species towards source B. Previous detections of chemically related species, namely acetaldehyde (CH3CHO), acetone (CH3COCH3), ethyl methyl ether (C2 H5OCH3), C2 H5CHO and CH3CCH, reported from the same dataset by Lykke et al. (2017) and Calcutt et al. (2019), are also indicated in the table and have been used for a comparison with the chemical model. Qasim et al. (2019) already reported a column density upper limit for Ga-n-C3H7OH of < 1.2 × 1015 cm−2 at 300 K and < 7.4 × 1014 cm−2 at 125 K, using the Band 6 dataset of Taquet et al. (2018). Given their same dataset and the correction factor to include the contribution of the other conformers, this estimate is consistent with the results presented here. In the following, we consider the more conservative column density upper limit of < 3.0 × 1015 cm−2.

thumbnail Fig. 1

Integrated intensity maps of the line emission for C3H6 and C2 H3CHO, summed over ± 0.5 MHz. The locations of IRAS 16293B continuum peak and the offset position are marked by the black star and plus sign, respectively. The blue contours start at 4σ and increase by steps of 4σ, where σ is 5 mJy beam−1 km s−1 for the integrated intensity. A representative beam of 0′′.5 is shown in the lower right corner of each panel.

4 The chemical model

In this section, we compare the abundance, and the upper limits, derived from the observations towards IRAS 16293B with a physico-chemical model of a typical low-mass forming star. The core of the simulation uses the Nautilus code (Ruaud et al. 2016), a 3-phase (gas, dust ice surfaces and dust ice mantle) time-dependent chemical model. The chemical study presented here is very similar, in terms of realisation, chemical code and astronomical source, to the studies of Andron et al. (2018) and Coutens et al. (2019). The majority of the differences resides in the extended chemical network used here.

The following subsections present the physical model that describes the evolution of physical conditions of the dust and gas during the simulation, the chemical network that computes the abundance variation caused by the reactions included in the network andthe results obtained from the simulations.

thumbnail Fig. 2

Identified lines of C2H3CHO: the synthetic spectrum, in red, is plotted along with the offset position spectrum towards IRAS 16293B. The straight dashed black line represents the detection limit at the intensity of 3σ. The upper-level energy of the transition is noted in the upper left corner of each panel. The reference spectrum in blue takes the previous species reported in PILS into account (Jørgensen et al. 2016, 2018; Lykke et al. 2017; Coutens et al. 2016; Ligterink et al. 2017; Persson et al. 2018; Calcutt et al. 2018a; Drozdovskaya et al. 2018; Manigand et al. 2019).
thumbnail Fig. 3

Identified lines of C3H6: the synthetic spectrum, in red, is plotted along with the offset position spectrum towards IRAS 16293B. The dashed lines correspond to optically thick lines. The straight dashed black line represents the detection limit at the intensity of 3σ. The upper-level energy of the transition is noted in the upper left corner of each panel. The torsional state “E” or “A” of each transition is noted in green on the spectra. The reference spectrum in blue takes the previous species reported in PILS into account (see Fig. 2 and references therein).

4.1 Physical model

Two successive evolutionary stages of a low-mass protostar are simulated: a uniform and constant stage, corresponding to the pre-stellar phase, or the cold-core phase, followed by an evolving stage during which the density and the temperature at the centre of the cloud increases while the envelope is collapsing towards the centre until breaking the hydrostatic equilibrium to form the protostar, i.e. the collapse phase.

The cold-core phase consists of a homogeneous and static cloud at a temperature of 10 K for both gas and dust, a gas density of 2 × 104 cm−3, a visual extinction of 4.5 mag, a cosmic-ray ionisation rate of 1.3 × 10−17 s−1, and a standard external UV field of 1 G0. The collapsephase is the same as used by Aikawa et al. (2008, 2012), Wakelam et al. (2014), Andron et al. (2018), and Coutens et al. (2019). The physical structure used in their study was derived from a 1D radiative hydrodynamical model (Masunaga & Inutsuka 2000), starting from the infall of the cold core, until the collapse stage of the first hydrostatic core, triggered by the dissociation of H2 by collisions. While the physical structure evolves with time, several parcels of gas are tracked in time and position and their physical properties are traced throughout the collapse. Each parcel ends up at a different radius at the end of the simulation, which allows the evolution of the distribution of the molecular compounds included in the chemical network to be followed. In this study, the chosen parcel of gas starts the collapse at a radius of >104 au, where it stays for the major part of the collapse and ends-up at a radius of 15 au (see Fig. 5 in Aikawa et al. 2008), where the gas reaches a temperature of ~ 265 K and a density of 4 × 108 cm−3. Figure A.1 shows the evolution of the physical conditions of the targeted parcel of dust and gas. The parcel spends only the last couple of hundred years at a temperature higher than 100 K at a radius <130 au.

thumbnail Fig. 4

Identified lines of C3H6 synthetic spectrum, in red, including the E/A spin weight ratio of 0.6 ± 0.1 are plotted along with the offset position spectrum towards IRAS 16293B. The dashed lines correspond to optically thick lines. The straight dashed black line represents the detection limit at the intensity of 3σ. The upper-level energy of the transition is noted in the upper left corner of each panel. The torsional state “E” or “A” of each transition is noted in green on the spectra. The reference spectrum in blue takes into account the previous species reported in PILS (see Fig. 2 and reference therein).
Table 2

Column densities of detected species and upper limits of non-detection towards the offset position from IRAS 16293B.

Table 3

Initial abundances used in the chemical model.

4.2 Chemical network

The chemical network includes the kida.uva.2014 gas-grain-phases network as a base (Wakelam et al. 2012, 2015 with updates from Ruaud et al. 2015; Hincelin et al. 2015; Loison et al. 2016, 2017; Hickson et al. 2015, 2016b; Wakelam et al. 2017; Vidal et al. 2017). The initial abundances used in the simulations are listed in Table 3.

Despite the inclusion of dozens of new species, hundred of new reactions, and the inclusion of hundreds of theoretical calculations to determine reaction barriers, there are still large uncertainties on branching ratios due to the lack of experimental studies and the difficulty of determining these branching ratios theoretically. Besides, the diffusion energies of radicals on surfaces are not well-known, which again leads to great uncertainties in determining which reactions becomes the most important when the temperaturerises. More details on the upgrades made to the chemical network can be found in Appendix B.1.

The chemical model distinguishes the ice surface and the ice mantle during the computation of the chemical reactions and the interaction processes between the different phases. For the comparison with the observations, the ice surface and ice mantle are considered as a single phase. We consequently summed the ice surface and ice mantle abundances to get the total ice abundances. The species in the solid phase are annotated with “s-” in front of their names.

To discuss the formation and destruction paths of the different species, the abundances relative to H2 have been used in the comparison. This representation is convenient for discussing the evolution of the abundances with the modification of the density and the temperature along with the collapse of the protostellar envelope. The H2 column density can be derived from the dust continuum radiation, assuming a dust size and an opacity distributions. However, the high continuum absorption seen towards IRAS 16293B in the PILS observations suggests that the dust emission is optically thick. Jørgensen et al. (2016) estimated the lower limit of >1.2 × 1025 cm−2 for the H2 column density. Therefore, we chose to use the abundances relative to CH3OH when comparing the final state of the simulation to the observational results. The abundances derived from the observationsare taken from Jørgensen et al. (2016, 2018), Lykke et al. (2017), Manigand et al. (2020) and this study.

4.3 Simulation runs

Different reactions have been considered to reproduce the observations similarly to what has been done in other studies (e.g. Coutens et al. 2018b). Among the important reactions investigated in this paper, the gas-phase formation reaction involving OH is crucial in the formation of C3O from the consumption of C3 and has been studied by Loison et al. (2017): 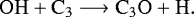OH+C 3 → C 3 O+H. \begin{equation*}\mathrm{OH &#x002B; C_3} \longrightarrow \mathrm{C_3O &#x002B; H}. \end{equation*}(1)

The surface production pathways are marginally contributing to the formation of C3 O radicals present on the ice surfaces, during the pre-stellar phase. The major destructive path of C3 occurs through the gas-phase reaction: 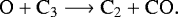O+C 3 → C 2 +CO. \begin{equation*}\mathrm{O &#x002B; C_3} \longrightarrow \mathrm{C_2 &#x002B; CO}. \end{equation*}(2)

This reaction is thought to play an important role in the abundance of C3 Hx, C3 O, and C2 HxCHO species (Hickson et al. 2015). The radical-radical addition reactions on grain surfaces are marginally contributing to the final abundances of these complex species.

To investigate the chemical network involved in the formation of C3 -species, we run several simulations, depending on the tested chemical branch:

– A1: this simulation is the fiducial model, with which the other models can be compared. The common COMs, such as CH3OCH3 and CH3OCHO, are mainly formed on grain surfaces but gas-phase formation pathways are also included, except for CH2(OH)CHO, (CH2OH)2 and CH3OCH2OH. The hydroxyl radical OH contributes only to the formation of C3 O and HCCCHO in the gas phase. A reaction rate of 1.0 × 10−12 cm3 molecule−1 s−1 is considered for the gas-phase reaction (2).

– B1: the hydrogenation of HC(O)CHO, based on Chuang et al. (2016), has been added to the grain surface reaction network: s-HC(O)CHO+2 s-H→ s-CH 2 (OH)CHO s-CH 2 (OH)CHO+2 s-H→s- ( CH 2 OH) 2 . \begin{align*}&\mathrm{\text{s-}HC(O)CHO &#x002B; 2\ \text{s-}H} \longrightarrow \mathrm{\text{s-}CH_2(OH)CHO}\\ &\mathrm{\text{s-}CH_2(OH)CHO &#x002B; 2\ \text{s-}H} \longrightarrow \mathrm{\text{s-}(CH_2OH)_2}. \end{align*}

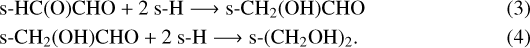
In addition, we have included the hydrogenation of CH3OCHO, forming CH3OCH2OH, to the network: 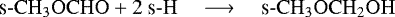s-CH 3 OCHO+2 s-H →  s-CH 3 OCH 2 OH \begin{equation*}\mathrm{\text{s-}CH_3OCHO &#x002B; 2\ \text{s-}H} \quad \longrightarrow \quad \mathrm{\text{s-}CH_3OCH_2OH} \end{equation*}(5)

based on thehydrogenation of CH2(OH)CHO (reaction (3)).

– C1: this run uses the same reaction network as the fiducial run A1. In this case, the pre-stellar phase lasts longer than the other runs, i.e. 3 × 106 yr instead of 1 × 106 yr, which gives the cold chemistry more time to proceed.

– D1: inorder to evaluate the contribution rate of the radical-radical addition on the grain surface to the abundance of HCCCHO, C2 H3CHO and C2 H5CHO, the following reactions have been removed from the network: s-HCO+ s-C 2 H 3 → s-C 2 H 3 CHO → s-C 2 H 4 +s-CO \begin{eqnarray*}\mathrm{\text{s-}HCO} &#x002B; \mathrm{\text{s-}C_2H_3} &\longrightarrow & \mathrm{\text{s-}C_2H_3CHO} \\ &\longrightarrow & \mathrm{\text{s-}C_2H_4 &#x002B; \text{s-}CO} \end{eqnarray*} s-HCO+ s-C 2 H 5 → s-C 2 H 5 CHO → s-C 2 H 6 +s-CO. \begin{eqnarray*}\mathrm{\text{s-}HCO} &#x002B; \mathrm{\text{s-}C_2H_5} &\longrightarrow & \mathrm{\text{s-}C_2H_5CHO} \\ &\longrightarrow & \mathrm{\text{s-}C_2H_6 &#x002B; \text{s-}CO}. \end{eqnarray*}

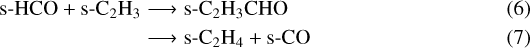
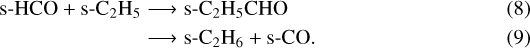
The addition reaction of HCO and C2H on grains is not contributing to the formation of HCCCHO in our chemical network because the amount of available C2 H on the ice surfaces is limited by the very high activation barrier of the hydrogen abstraction of C2 H2 (>56 000 K, Zhou et al. 2008).

– E1: this run takes into account the hydrogenation of HC(O)CHO and CH3OCHO, as it is for run B1, and the activation energies for hydrogenation and abstraction reactions of H2 CO, CH3OH, C2 H2, C2 H4, C2 H6, C2 H3CHO, and C2 H5CHO, taken from the recent laboratory study of Qasim et al. (2019) about propanal and propanol formation on ice surfaces from CO, and the references therein (Andersson et al. 2011; Goumans & Kästner 2011; Kobayashi et al. 2017; Song & Kästner 2017; Álvarez-Barcia et al. 2018; Zaverkin et al. 2018). The activation energies taken from Qasim et al. (2019) are, in general, lower than those used in the simulation runs A1 to D1.

– A2 toE2: these runs are similar to the runs A1 to E1, but with a lower reaction rate of 10−16 cm3 s−1 for reaction (2).

The list of the reactions added, extrapolated or removed in each run, with the associated branching ratios and reaction rates, is presented in Appendix B.2. The formation enthalpies of the intermediate species that intervene in the new hydrogenation paths on grain surfaces are taken from Goldsmith et al. (2012).

4.4 Modelling results

The evolution of the abundances during the collapse phase of the run A1 is shown in Fig. 5. For the COMs formed in a hot corino region, most of the molecules targeted are produced on grain surfaces and are released in the gas-phase when the temperature reaches the desorption temperature, between 80 and 130 K depending on the species.

This production scheme leads to a jump of several orders of magnitude in gas-phase abundances of the species around such temperatures. Concerning the C3-species, the jump ingas-phase abundances is smaller which indicates significant gas-phase production route contributions. These gas-phase contributions seem higher for the most unsaturated species, such as HCCCHO, C3 and C3 O. At the end of the simulation, all the formed molecules are in the gas phase.

Figure 6 summarises the gas-phase abundances relative to CH3OH of the C3 -species that are under investigation in this study and a few other COMs, such as CH3OCHO, CH2(OH)CHO, (CH2OH)2, CH3OCH2OH, C2 H5OH, CH3COCH3, and C2 H5OCH3, at the end of the collapse phase for every simulation. Because of the assumptions from the physical model compared to the actual physical structure of IRAS 16293B, which is still not perfectly known, an abundance difference of less than one order of magnitude is considered as an agreement between the simulation and the observations.

thumbnail Fig. 5

Time evolution of abundances in the gas phase (solid lines) and on the grain surface (dotted) of several species during the collapse phase of the A1 run. The time axis is reversed to better visualise the abundances evolution. Both panels show the results of the same simulation but with a different selection of species, with their name annotated following the colour code of the curves.

4.4.1 C3-species

The abundances of C3–species, that are CH3CCH, C3 H6, C3 H8, HCCCHO, C2 H3CHO, and C2 H5CHO, are correlated to those of their precursors, C3 and C3O. As C3 is efficiently produced and is not a very reactive species in the gas phase, s-CH3CCH and s-C3 H6 are quite abundant in the solid phase. The comparison between the runs A1–E1 and A2–E2 shows that most of the C3 -species are sensitive to a decrease in the reaction rate of the C3 destruction reaction (2). As the reaction rate decreases, there is more C3 available to form C3-species, thus their abundances increase. The increase in the abundances is more pronounced for the more saturated species.

The abundances of the C3-species at the end of the simulation run C1 are significantly different from those at the end of the fiducial run. The longer time spent at very low temperatures during the prestellar phase pushes the hydrogenation reactions to produce more saturated C3 -species by consuming the unsaturated precursors. This is particularly shown by the lower abundances of C3 O and HCCCHO contrasting the higher abundances of C2 H3CHO and C2 H5CHO.

The ice-surface formation pathways of C2 H3CHO and C2 H5CHO, through reactions (6) and (8), are deactivated in the simulation run D1. The final abundances show a decrease compared tothe simulation where the molecules are produced through ice-surface reactions, among others. The updated activation energies, taken from the study of Qasim et al. (2019) and tested in the simulation E1, do not change the final abundances of the C3 -species significantly.

The C3 H7OH species is a particular case as there is an alternative production pathway apart from successive hydrogenation of C3 O, mostly the O + C3 H8 reaction. The slight overestimate for C3 H7OH may be due to an overestimate of the s-OH + s-C3 H7 recombination branching ratio versus the disproportionation, that is the exchange reaction of one H atom from one radical to the other: 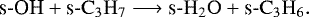s-OH+ s-C 3 H 7 → s-H 2 O+ s-C 3 H 6 . \begin{equation*} \text{s-OH} &#x002B; \text{s-}\mathrm{C_3H_7} \longrightarrow \text{s-}\mathrm{H_2O} &#x002B; \text{s-}\mathrm{C_3H_6}. \end{equation*}(10)

Its isomer C2 H5OCH3, however, is well reproduced by the models, despite the fact that there is only the formation pathway through radical-radical addition that are implemented in the chemical network (see Table B.1). The variation of the final abundance of C2 H5OCH3 is very similar to that of C2 H5OH which suggests that they share the same type of formation reactions on ice surfaces, assuming that the major formation pathways of C2 H5OH effectively take place on ice surfaces as well.

4.4.2 COMs hydrogenation

Concerning the species formed through radical-radical addition, the slight to large overestimation or underestimation of the calculated abundances when considering the fiducial run A1 likely reflects the uncertainties of the association channel branching ratios compared to the disproportionation channel.

The underestimation of (CH2OH)2 is unexpected considering the large amount of s-CH2OH as well as the large branching ratio used for the reaction s-CH2OH + s-CH2OH → s-(CH2OH)2, that is 50%, in the fiducial chemical network. Despite the approximate agreement between the simulations and the observations for CH3OCHO and CH2(OH)CHO, these two species are over-produced by the radical-radical additions whereas (CH2OH)2 and CH3OCH2OH, which are only produced by radical-radical additions on grain surfaces, are both under-produced.

The run B1 includes the hydrogenation formation pathways on grain surfaces of HC(O)CHO and CH3OCHO. These reactions lead to the consumption of the unsaturated species and the production of saturated ones. The agreement of this run with observations is better than for the fiducial chemical network in terms of abundances of CH2(OH)CHO, (CH2OH)2, CH3OCHO, and CH3OCH2OH, suggesting that hydrogenation reactions play an important role in formation of such COMs in hot corino regions. The hydrogenation of CH3OCHO has been recently studied in laboratory by Krim et al. (2018). They reported a calculated energy barrier of 32.7 kJ mol−1 for the ice-surface reaction s-H + s-CH3OCHO and concluded that this pathway did not seem to contribute to the formation of CH3OCH2OH. The experimental result of Krim et al. mainly shows that this reaction is slower than the s-H + s-H2CO → s-CH3O reaction but does notcompletely exclude its role in interstellar ice conditions. In our simulation, we include this reaction with a barrier equal to 3000 K (25 kJ mol−1) as average between the value calculated in this work, the value calculated by Krim et al., and the value calculated by Álvarez-Barcia et al. (2018), i.e. 4960 K (41.2 kJ mol−1). This reaction, like all H reactions with barriers, is partly allowed by the tunnel effect.

The reaction s-HCO + s-HCO has been suggested to produce s-HC(O)CHO (Fedoseev et al. 2015; Chuang et al. 2016) to explain the formation of CH2(OH)CHO and (CH2OH)2 in experimental surface hydrogenation of CO molecules. HC(O)CHO production through s-HCO + s-HCO reaction is also achieved by Simons et al. (2020) using density functional theory (DFT, Scuseria & Staroverov 2005) calculations in a model in which the surface molecules were not explicitly taken into account. Additionally, the recent experimental work of Butscher et al. (2017) indicates that the reaction of two HCO radicals on ice surfaces does not lead to HC(O)CHO but rather to H2 CO and CO. Considering the conflicting results from different studies, it is difficult to estimate the proportion of HC(O)CHO produced by the s-HCO + s-HCO reaction. In this study, we consider a branching ratio of 5% for HC(O)CHO formation through the s-HCO + s-HCO reaction. This leads to a significant production of HC(O)CHO due to the great abundance of HCO on the grains, which is around 1% of the CH3OH (see Fig. 6). The comparison with the observations is delicate because the most stable isomer of HC(O)CHO, the trans- one, has no dipole moment and the population fraction of cis-HC(O)CHO is equal to 1.9 × 10−10 at 100 K, considering that the thermal equilibrium is reached, and is not detected in the observations.

The updated activation energies from Qasim et al. (2019) of abstraction reactions of CH3OH and H2 CO affect the final abundances of the COMs that are predominantly formed through radical-radical addition reactions. In particular, the lower final abundance of (CH2OH)2 in run E1 compared to B1 is affected by the newly implemented abstraction reaction of CH3OH which produces CH3O radicals.

thumbnail Fig. 6

Final abundances reached at the end of each simulation run for the targeted species. The dashed blue line shows the observed abundance of the species towards IRAS 16293B. The error bars and the blue area correspond to one half order of magnitude confidence limit, thus a 1σ-difference between observations and simulations corresponds to one order of magnitude. The dashed blue region represents the abundance values that are consistent with the corresponding upper limit. The abundance scale of C3 O is lower than the other plots. The abundance upper limit of HC(O)CHO is < 2.6 × 104 relative to CH3OH, therefore, there is no observational constraint on the abundance of HC(O)CHO. The abundance upper limit of C3 H7OH is the sum of n-C3H7OH and i-C3H7OH abundance upper limits.

5 Discussion

In most of the models, C3 reaches a high abundance in the gas phase, due to its low reactivity. This leads to a high abundance of s-C3 in solid phase, which results in high abundances of all the C3-species in the gas phase, especially CH3CCH, C3 O, and HCCCHO, which are much more abundant than observed. A better agreement to the observations can be found when the rate constant for the O +C3→C2 + CO gas-phase reaction is set to 1 × 10−12 cm3 s−1, assuming a lower activation barrier than in the theoretical work of Woon & Herbst (1996).

The agreement for CH3CCH, C3 H6, C2 H3CHO, and C2 H5CHO is rather good between the fiducial run A1 and the observations for IRAS 16293. However, this leads to an underestimation of CH3CCH and C3 H6 abundances in the case of dense molecular clouds, the agreement being notably less good with observations of TMC-1 (Marcelino et al. 2007; Markwick et al. 2002) as shown by Hickson et al. (2016a). Alternatively, the abundances of C3 O and HCCCHO are in good agreement with the observations for dense clouds (Herbst et al. 1984; Irvine et al. 1988; Ohishi & Kaifu 1998; Loison et al. 2016), but they are overproduced for IRAS 16293B. The overproduction of C3 O and HCCCHO for the case of IRAS 16293B may be due to under-represented consumption pathways of these species through ice-surface reactions and demonstrates that laboratory studies in this area are required.

The duration of the prestellar phase has a significant impact on the COM abundances at the end of the simulation. A longer time spent in the prestellar phase enhances the impact of efficient reactions at cold temperature (10 K) on the final abundance. This effect is presumably due to the ongoing hydrogenation at cold temperature, and the addition of nearby radicals, with a non-efficientthermal diffusion on the ice surfaces at a such temperature. The agreement with the observations for C3 H6 and C3 H8 is particularly better with a longer prestellar phase in the simulation. The impact on the abundance of C2 H3CHO and C2 H5CHO is less important in comparison with the observations.

Concerning the other COMs, a longer prestellar phase leads to a better match of the simulated and observed abundances, in particular for (CH2OH)2. The absence of strong outflows from IRAS 16293 B has been suggested as due to this protostar being the less evolved source compared to its companion (van der Wiel et al. 2019), which shows at least two major outflows (Yeh et al. 2008; Kristensen et al. 2013; Girart et al. 2014). The abundance ratio of vinyl cyanide (C2 H3CN) and ethyl cyanide (C2 H5CN) observed by Calcutt et al. (2018b) suggests that the warm-up timescale was shorter for IRAS 16293A, the more luminous binary component, or it has a higher accretion rate compared to IRAS 16293B. Another scenario could be that IRAS 16293A started to collapse earlier than IRAS 16293B. This delay of the beginning of the collapse of each protostar of a binary system could be the result of the fragmentation of the parent cloud when the first protostar started to form. This scenario is in agreement with the dynamical modelling study of Kuffmeier et al. (2019), in which the CO-rich bridge structure between the two protostars has been interpreted as a product of the multiple system dynamics and could be a remnant of the parent cloud fragmentation.

The agreement with the observations of the abundance ratios of unsaturated species over saturated ones between the three C2 HxCHO species is associated with an overall overproduction of these species during the prestellar phase. This overproduction suggests that the common precursors C3, and then C3 O, are also overproduced. The over-abundance of C3 and C3O could be a result of an underestimation of the consumption of these species by a lack of reactions in the chemical network. The largest carbon-chain species taken into account in the chemical network are C5 Hx in linear forms, and a few benzene-like molecules, such as C6 H5CN, associated to their recent detection in the ISM reported in the study of McGuire et al. (2018). The larger poly-aromatic hydrocarbons (PAH), which are expected to be abundant in space (Puget & Leger 1989), are not included in the calculation. This limitation in the size of carbon-chain species might be the origin of the over-production, or underconsumption, of the small carbon-chain species, which are the building blocks of these PAHs at cold temperatures as suggested by the recent studies of Joblin & Cernicharo (2018) and Kaiser et al. (2015).

6 Conclusion

This study presents the observations and the chemical modelling of C3 -species around the Class 0 protostar IRAS 16293B. Using ALMA observations from the PILS survey, the molecular emission is analysed by comparing the spectrum to LTE models to determine the excitation temperatures and column densities of these species. Then, the abundances relative to CH3OH are compared to the three-phase chemical model Nautilus to investigate the different formation pathways of such molecules under the typical physical conditions of the hot corino region. Different models were tested, each one focusing on a single aspect of the chemical network. The key findings are summarised in the following:

  • 1.

    We report the first detection of C2H3CHO and C3H6 towards the protostar IRAS 16293B. Their emission has an excitation temperature of 125 and 75 K, respectively, and their column densities are found to be 3.4 ± 0.7 × 1014 and 4.2 ± 0.8 × 1016 cm−2, respectively. These molecules were not detected towards the other member of the binary system. For C3H6, the E-transitions were found to exhibit a lower intensity with respect to the A-transitions, leading to a ratio of the E-transitions over A-transitions emitting molecules, being 0.6 ± 0.1 in terms of column densities. The column density upper limits of several chemically related species, that are HCCCHO, C3H7OH, C3O, HC(O)CHO, and C3H8, are also reported to provide constraints on the chemical simulations.

  • 2.

    Most of the simulations reproduce the abundances observed towards IRAS 16293B within an order of magnitude. The final abundances of the different simulations are sensitive to the duration of the prestellar phase, especially when the successive hydrogenation reactions play an important role in the formation of more saturated species. This seems to be the case for CH3CCH, HC(O)CHO and CH3OCHO which form C3H6, C3H8, CH2(OH)CHO, (CH2OH)2 and CH3OCH2OH. The longer the cloud spends at low temperatures, the more abundant the saturated species, and the more depleted the precursors.

  • 3.

    On ice surfaces, the successive hydrogenation reactions of C3O, forming HCCCHO, C2H3CHO, and C2H5CHO, and the radical-radical additions of HCO and C2H3 or C2H5 equally contribute to the amount of C3-species observed in the hot corino of IRAS 16293B.

  • 4.

    A high gas-phase reaction rate of 1 × 10−12 cm3 s−1 for the gas-phase reaction C3 + O →C2 + CO is necessary to fit the final abundances of C3-species detected in the observations. The very efficient production of C3 and C3O, along with the overall overproduction of C3-species, suggests that consumption pathways of C3 species are missing in the chemical network. These chemical routes could be related to the production and growth of PAHs at cold temperatures, which are not included in the present chemical model.

Most of the models reproduce the abundances of the C3 -species towards IRAS 16293B, which emphasises the contribution of the grain-surfaces production pathways under the hot corino physical conditions. Besides, the formation of these species on grain surfaces suggests that they can be incorporated into the protostellar disk as the protostar evolves into a Class I protostar and contribute to the formation of prebiotic molecules. Deeper observations of Class I protostellar disks and the detection of more complex species towards Class I objects are necessary to clearly stateon the presence of these molecular species in such objects. Finally, the overproduction of unsaturated C3 -species, in general, suggests the lack of longer carbon-chain molecules formation pathways on grain surfaces and in gas phase and indicate the need of laboratory and theoretical studies of such reactions.

Acknowledgements

The authors thank the referee for useful comments that improved the quality of this manuscript. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2012.1.00712.S, ADS/JAO.ALMA# 2013.1.00278.S, and ADS/JAO.ALMA#2016.1.01150.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. The group of JKJ acknowledges support from the H2020 European Research Council (ERC) (grant agreement No 646908) through ERC Consolidator Grant “S4F”. Research at Centre for Star and Planet Formation is funded by the Danish National Research Foundation. A.C. acknowledges financial support from the Agence Nationale de la Recherche (grant ANR-19-ERC7-0001-01). S.F.W. acknowledges financial support by the Swiss National Science Foundation (SNSF) Eccellenza Professorial Fellowship PCEFP2_181150. MND and BMK acknowledge the Swiss National Science Foundation (SNSF) Ambizione grant 180079. MND also acknowledges the Center for Space and Habitability (CSH) Fellowship, and the IAU Gruber Foundation Fellowship. This research has made use of NASA’s Astrophysics Data System and VizierR catalogue access tool, CDS, Strasbourg, France (Ochsenbein et al. 2000), as well as community-developed core Python packages for astronomy and scientific computing including Astropy (Astropy Collaboration 2013), Scipy (Jones et al. 2001), Numpy (van der Walt et al. 2011) and Matplotlib (Hunter 2007).

Appendix A Physical model evolution

Figure A.1 shows the evolution of the density, the temperature, the extinction coefficient and the infall velocity of the gas during the collapse phase.

thumbnail Fig. A.1

Evolution of the density, dust temperature, visual extinction and infall velocity across the envelope during the simulation. The time is indicated at several positions on the curves, with t = 0 yr set to the end of the collapse phase in the simulation.

Appendix B Chemical network

B.1 Upgrades from the NAUTILUS public version

The chemical network used here is limited to a skeleton up to five atoms of carbons for linear chains, including oxygen nitrogen and sulfur-bearing, neutral and ionic compounds. Besides, benzene, benzonitrile (C6 H5CN) and ethylbenzene (C6 H5C2H) are also included with their ions. Special care has been taken with end-of-chain processing, which is an important source of error for finite models that want to account for infinite chemistry. In principle, there is no limit for the formation of very large molecules, that are then associated to a very large dilution and thus an abundance of large molecules in most cases very small by bottom-up chemistry. In other words, the limitations are imposed by the extent of the chemical network and the formation of molecules up to five carbons in their structure ensures a proper representation of the production of smaller molecules, such as the C3 -species. Even though there are some notable changes in the gas-phase chemistry (new reactions, update of rate constants and branching ratios according to new measurements and theoretical calculations), the most important changes were made for the grain-surfaces chemistry. The chemistry will be detailed in future articles, thus we only present major changes that concern the species discussed in this work.

We have started to homogenise the chemistry on grains completing the possible reactions for the most abundant species on grains. First, we systematically supplemented the hydrogenation reactions through s-H and s-H2 reactions, which are critical because they are favoured by the completion between diffusion and reaction through tunnelling. To estimate the probabilities of the tunnelling effect, we systematically consider a barrier width of 1 Angstrom and we calculate the height of the reaction barriers in the gas phase using the density functional theory (DFT, Scuseria & Staroverov 2005) with the functional M06-2X and the AVTZ basis (Zhao & Truhlar 2008); we have calculated 240 barrier heights for s-H and s-H2 reactions. The reactions with s-H2 lead to quick consumption of s-CN, s-OH, s-NH2, s-C, s-CH, s-CH2, s-C2, s-C2 H, s-C2 H3 as long as there is a lot of s-H2 on grains. Reactions of these species with s-H2 are exothermic and are enhanced by tunnelling effect when an activation barrier exists. For some low exothermic reactions, such as s-CH2 + s-H2, s-C2 H3 + s-H2, and s-NH2 + s-H2, a barrier of 1 Angstrom undoubtedly overestimates the tunnelling effect. However, considering the very high abundance of s-H2, this should not be critical in the end, at least as long as there is a lot of s-H2 on grains, although more accurate tunnelling treatment would be desirable in the future. We have also modified the Nautilus code to better take into account the tunnelling effect for reactions involving hydrogen atom transfer between heavy species. For example, the O + C3H8 → OH + C3H7 → C3H7OH ∕ C3H6 + H2O reaction is now an efficient source of propanol production through tunnelling of the first step followed by reaction between s-OH and s-C3 H7 radicals which are supposed to stay close enough on the grains to react. We also consider diffusion by tunneling for all species, with a diffusion barrier width of 2.5 Angstrom according to Ásgeirsson et al. (2017) and a diffusion barrier height equal to 0.6 of the binding energy. The width of the diffusion barrier is not critical as long as it is greater than 2 Angstrom but limits the reactivity through tunnelling for reactions with a high barrier (>5000 K).

We have therefore introduced a large number of reactions involving s-HCO, s-CH3, s-CH3O, s-CH2OH, s-NH, s-HS and to a lesser extent s-H2NO, s-HNOH, s-H2CN, s-HCNH, s-CH3NH, s-CH2NH2, s-HOCO, s-H2NS, s-HNSH, s-C2 H3, s-C2 H5, s-C3 Hx = 0−3,5,7 and a few others. For s-CN, s-OH, s-C, s-CH, s-C2, and s-C2H we considera limited number of reactions as these species react with s-H2. For s-NH2 and s-CH2 we consider a relatively large number of reactions even if they can react with H2 due to their potential role at high temperatures (>20 K) where s-H2 is low and where their abundance is not negligible due to photodissociation of s-NH3 and s-CH4. Of all the possible reactions, those between radicals play an important role in the formation of COMs. As noted already by Garrod (2013), the reaction between two radicals can either lead to a single molecule or to H atom exchange, called disproportionation, for example s- HCO + s-HCO →s-HC(O)CHO or s- H2CO + s-CO, respectively. The branching ratios are in general poorly known even in the gas phase. Most models favor, when they consider these reactions, formation of the single molecule or use statistical ratios (Garrod 2013). However, when branching ratio determinations exist in the gas phase, it leads to almost exclusively disproportionation except for reactions with CH3 for which single molecule production is important (Baggott et al. 1987). Moreover, the branching ratios are likely to be significantly different between the gas and grain processes. A recent experimental work (Butscher et al. 2017) suggested that the reaction of two s-HCO radicals on ice surfaces does not lead to HC(O)CHO but rather to s-H2CO and s-CO. Additionally, Enrique-Romero et al. (2016) found that the interaction between s-HCO and s-CH3 with water ice (through cluster water ice approximation) imposes an initial geometry leading to the formation of s-CH4 and s-CO through Eley-Rideal reactive mechanism, hindering the formation of s-CH3CHO at least at low temperatures (~10 K). However, a revision of the model (Enrique-Romero et al. 2020) suggests the possibility to still form s-CH3CHO through reaction of s-CH3 and s-HCO. s-CH3CHO molecules are likely produced at temperatures where s-HCO and s-CH3 acquire some mobility. In our network, for reactions involving s-CH3 we always consider a non-negligible branching ratio for the formation of a single molecule deduced from gas-phase measurements. For the radical reactions we largely favour the disproportionation channel except when it is the only effective way to produce some observed species such as CH3OCHO, which is produced by s-CH3O + s-HCO on ice surfaces. For the barrier-less addition reactions on unsaturated radicals, such as H + H2 CCCN, we consider addition on several sites due to non-localised radical character of the lonely electron (H2 C = C∙–C≡N ↔ H2C = C = C = N∙) with branching ratios deduced from Mulliken atomic spin density given by theoretical calculations. This leads to nitrile (R–CN) and imine (R = NH) production (Krim et al. 2019), but only low alcohol production in the case of s-H reaction through H atom addition on unsaturated aldehyde radicals (Krim et al. 2018).

Table B.1

Branching ratios of radical addition reactions.

Table B.2

Hydrogenation reactions of CH(O)CHO from Chuang et al. (2016) and CH3OCHO on grain surfaces.

The systematic inclusion of reactions between radicals leads to the formation of a very large number of species on grains. We have not systematically completed the chemistry of all the new species, this would lead to an almost infinite number of reactions and species. In a first approach we focused on the most abundant species. For some, but not all of them, we have included the corresponding desorption mechanisms and gas phase chemistry. They are namely C2 H5CN, C3 H3CN, HCOCN, C2 H3CHO, C2 H5CHO, HC(O)CHO, CH3COOH, CH2(OH)CHO and (CH2OH)2. At the same time, the gas chemistry of CH3OCH3, CH3COCH3, C2 H5OH and C6 H6 was fully incorporated in the network. Branching ratios used for radicals recombination in this work are summarised in Table B.1. s-n-C3H7OH is not included in the network by simplification as neither n-C3H7OH nor i-C3 H7OH have been firmly detected.

B.2 Discussed reactions

This section presents the list of involved reactions in each run of the chemical simulation. Table B.2 shows the hydrogenation reactions of HC(O)CHO (Chuang et al. 2016) and CH3OCHO on grain surfaces. The branching ratios have been assumed to be 50% for all the intermediate species. The high reactivity of these species should prevent them from having the time to leave the surface before reacting with another hydrogen atom. Thus, the chemical and physical desorption processes are included in the network only for the more stable species HC(O)CHO, CH2(OH)CHO and (CH2OH)2. Formation enthalpies of the intermediate species are taken from Goldsmith et al. (2012). Energy barriers of hydrogenation reactions of HC(O)CHO, CH2(OH)CHO and CH3OCHO are based on studies of Colberg & Friedrichs (2006), Álvarez-Barcia et al. (2018), Krim et al. (2018) and our calculations. The reactions s-HCO + s-C2H3 and s-HCO + s-C2H5 that are removed in the runs D1 and D2 are shown in Table B.1.

Appendix C Main spectroscopic parameters

The main spectroscopic parameters of the species analysed in this paper are shown in Table C.1. It includes the database, the tag number, the dipole moment | | μ | | $\left| \left| \vec{\mu}\right| \right|$, the principle axis rotational parameters A, B and C, and the references.

Appendix D Final abundances of the simulation runs

This appendix section presents the results of the simulations runs for all the relevant species of this study. Table D.1 shows the final abundances of the runs while Figs. D.1–D.10 represent the abundance evolution during each simulation run for the studied species.

Table C.1

Main spectroscopic parameters of the analysed species.

Table D.1

Species abundances, relative to CH3OH, at the end of the collapse phase for all the runs.

thumbnail Fig. D.1

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run A1. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
thumbnail Fig. D.2

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run A2. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
thumbnail Fig. D.3

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run B1. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
thumbnail Fig. D.4

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run B2. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
thumbnail Fig. D.5

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run C1. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
thumbnail Fig. D.6

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run C2. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
thumbnail Fig. D.7

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run D1. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
thumbnail Fig. D.8

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run D2. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
thumbnail Fig. D.9

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run E1. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
thumbnail Fig. D.10

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run E2. The time axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.

Appendix E C2H3CHO line list

This section lists, in Table E.1, the C2 H3CHO transitions corresponding to the lines having an intensity above 3σ in the observations. The firmly detected transitions, which are optically thin and unblended in the conditions of the best fit, are annotated with the letter “Y”.

Table E.1

Line list of the observed C2H3CHO transitions above 3σ.

Appendix F C3H6 line list

This section lists, in Table F.1, the C3 H6 transitions corresponding to the lines having an intensity above 3σ in the observations. The firmly detected transitions, which are optically thin and unblended in the conditions of the best fit, are annotated with the letter “Y”.

Table F.1

Line list of the observed C3H6 transitions above 3σ.

References

  1. Aikawa, Y., Wakelam, V., Garrod, R. T., & Herbst, E. 2008, ApJ, 674, 984 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aikawa, Y., Wakelam, V., Hersant, F., Garrod, R. T., & Herbst, E. 2012, ApJ, 760, 40 [NASA ADS] [CrossRef] [Google Scholar]
  3. Álvarez-Barcia, S., Russ, P., Kästner, J., & Lamberts, T. 2018, MNRAS, 479, 2007 [NASA ADS] [CrossRef] [Google Scholar]
  4. Andersson, S., Goumans, T. P. M., & Arnaldsson, A. 2011, Chem. Phys. Lett., 513, 31 [NASA ADS] [CrossRef] [Google Scholar]
  5. Andron, I., Gratier, P., Majumdar, L., et al. 2018, MNRAS, 481, 5651 [NASA ADS] [CrossRef] [Google Scholar]
  6. Ásgeirsson, V., Jónsson, H., & Wikfeldt, K. T. 2017, J. Phys. Chem. C, 121, 1648 [CrossRef] [Google Scholar]
  7. Astropy Collaboration (Robitaille, T P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Baggott, J. E., Frey, H. M., Lightfoot, P. D., & Walsh, R. 1987, J. Phys. Chem. 91, 3386 [CrossRef] [Google Scholar]
  9. Bermúdez, C., Peña, I., Cabezas, C., Daly, A. M., & Alonso, J. L. 2013, Chem. Phys. Chem., 14, 893 [CrossRef] [Google Scholar]
  10. Bestmann, G., Lalowski, W., & Dreizler, H. 1985a, Zeitschrift Naturforschung Teil A, 40, 271 [CrossRef] [Google Scholar]
  11. Bestmann, G., Dreizler, H., Vacherand, J. M., et al. 1985b, Zeitschrift Naturforschung Teil A, 40, 508 [CrossRef] [Google Scholar]
  12. Bizzocchi, L., Degli Esposti, C., & Dore, L. 2008, A&A, 492, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Blom, C. E., Grassi, G., & Bauder, A. 1984, J. Am. Chem. Soc., 106, 7427 [CrossRef] [Google Scholar]
  14. Brown, R. D., & Godfrey, P. D. 1984, Aust. J. Chem., 37, 1951 [CrossRef] [Google Scholar]
  15. Brown, R. D., Eastwood, F. W., Elmes, P. S., & Godfrey, P. D. 1983, J. Am. Chem. Soc., 105, 6496 [CrossRef] [Google Scholar]
  16. Butscher, T., Duvernay, F., Rimola, A., Segado-Centellas, M., & Chiavassa, T. 2017, Phys. Chem. Chem. Phys., 19, 2857 [CrossRef] [Google Scholar]
  17. Calcutt, H., Fiechter, M. R., Willis, E. R., et al. 2018a, A&A, 617, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Calcutt, H., Jørgensen, J. K., Müller, H. S. P., et al. 2018b, A&A, 616, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Calcutt, H., Willis, E. R., Jørgensen, J. K., et al. 2019, A&A, 631, A137 [CrossRef] [EDP Sciences] [Google Scholar]
  20. Caux, E., Kahane, C., Castets, A., et al. 2011, A&A, 532, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Cazaux, S., Tielens, A. G. G. M., Ceccarelli, C., et al. 2003, ApJ, 593, L51 [NASA ADS] [CrossRef] [Google Scholar]
  22. Cherniak, E. A., & Costain, C. C. 1966, J. Chem. Phys., 45, 104 [CrossRef] [Google Scholar]
  23. Christen, D., & Müller, H. S. P. 2003, Phys. Chem. Chem. Phys., 5, 3600 [CrossRef] [Google Scholar]
  24. Chuang, K. J., Fedoseev, G., Ioppolo, S., van Dishoeck, E. F., & Linnartz, H. 2016, MNRAS, 455, 1702 [Google Scholar]
  25. Colberg, M., & Friedrichs, G. 2006, J. Phys. Chem. A, 110, 160 [CrossRef] [Google Scholar]
  26. Costain, C. C., & Morton, J. R. 1959, J. Chem. Phys., 31, 389 [NASA ADS] [CrossRef] [Google Scholar]
  27. Coutens, A., Jørgensen, J. K., van der Wiel, M. H. D., et al. 2016, A&A, 590, 1 [Google Scholar]
  28. Coutens, A., Willis, E. R., Garrod, R. T., et al. 2018a, A&A, 612, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Coutens, A., Viti, S., Rawlings, J. M. C., et al. 2018b, MNRAS, 475, 2016 [NASA ADS] [CrossRef] [Google Scholar]
  30. Coutens, A., Ligterink, N. F. W., Loison, J. C., et al. 2019, A&A, 623, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Craig, N. C., Groner, P., Conrad, A. R., Gurusinghe, R., & Tubergen, M. J. 2016, J. Mol. Spectr., 328, 1 [CrossRef] [Google Scholar]
  32. Daly, A. M., Bermúdez, C., Kolesniková, L., & Alonso, J. L. 2015, ApJS, 218, 30 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  33. Drouin, B. J., Pearson, J. C., Walters, A., & Lattanzi, V. 2006, J. Mol. Spectr., 240, 227 [NASA ADS] [CrossRef] [Google Scholar]
  34. Drozdovskaya, M. N., van Dishoeck, E. F., Jørgensen, J. K., et al. 2018, MNRAS, 476, 4949 [NASA ADS] [CrossRef] [Google Scholar]
  35. Enrique-Romero, J., Rimola, A., Ceccarelli, C., & Balucani, N. 2016, MNRAS, 459, L6 [NASA ADS] [CrossRef] [Google Scholar]
  36. Enrique-Romero, J., Álvarez-Barcia, S., Kolb, F. J., et al. 2020, MNRAS, 493, 2523 [CrossRef] [Google Scholar]
  37. Fayolle, E. C., Öberg, K. I., Jørgensen, J. K., et al. 2017, Nat. Astron., 1, 703 [NASA ADS] [CrossRef] [Google Scholar]
  38. Fedoseev, G., Cuppen, H. M., Ioppolo, S., Lamberts, T., & Linnartz, H. 2015, MNRAS, 448, 1288 [NASA ADS] [CrossRef] [Google Scholar]
  39. Friberg, P., Madden, S. C., Hjalmarson, A., & Irvine, W. M. 1988, A&A, 195, 281 [Google Scholar]
  40. Gargaud, M., Amils, R., Cernicharo, J., et al. 2007, Encyclopedia of Astrobiology (Berlin: Springer-Verlag) [Google Scholar]
  41. Garrod, R. T. 2013, ApJ, 778, 158 [NASA ADS] [CrossRef] [Google Scholar]
  42. Girart, J. M., Estalella, R., Palau, A., Torrelles, J. M., & Rao, R. 2014, ApJ, 780, L11 [NASA ADS] [CrossRef] [Google Scholar]
  43. Goldsmith, C. F., Magoon, G. R., & Green, W. H. 2012, J. Phys. Chem. A, 116, 9033 [CrossRef] [Google Scholar]
  44. Goumans, T. P. M., & Kästner, J. 2011, J. Phys. Chem. A, 115, 10767 [CrossRef] [Google Scholar]
  45. Grefenstette, N. M. 2017, PhD thesis, University College London, UK [Google Scholar]
  46. Herbst, E., & van Dishoeck, E. F. 2009, ARA&A, 47, 427 [NASA ADS] [CrossRef] [Google Scholar]
  47. Herbst, E., Smith, D., & Adams, N. G. 1984, A&A, 138, L13 [NASA ADS] [Google Scholar]
  48. Hickson, K. M., Loison, J.-C., Bourgalais, J., et al. 2015, ApJ, 812, 107 [CrossRef] [Google Scholar]
  49. Hickson, K. M., Wakelam, V., & Loison, J.-C. 2016a, Mol. Astrophys., 3, 1 [NASA ADS] [CrossRef] [Google Scholar]
  50. Hickson, K. M., Loison, J.-C., Nuñez-Reyes, D., & Méreau, R. 2016b, J. Phys. Chem. Lett., 7, 3641 [CrossRef] [Google Scholar]
  51. Hincelin, U., Chang, Q., & Herbst, E. 2015, A&A, 574, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Hirota, E. 1966, J. Chem. Phys., 45, 1984 [CrossRef] [Google Scholar]
  53. Hirota, E. 1979, J. Chem. Phys., 83, 1457 [CrossRef] [Google Scholar]
  54. Hollis, J. M., Jewell, P. R., Lovas, F. J., Remijan, A., & Møllendal, H. 2004, ApJ, 610, L21 [NASA ADS] [CrossRef] [Google Scholar]
  55. Hübner, H., Leeser, A., Burkert, A., Ramsay, D. A., & Hüttner, W. 1997, J. Mol. Spectr., 184, 221 [CrossRef] [Google Scholar]
  56. Hudson, R. L., & Moore, M. H. 1999, Icarus, 140, 451 [NASA ADS] [CrossRef] [Google Scholar]
  57. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
  58. Irvine, W. M., Brown, R. D., Cragg, D. M., et al. 1988, ApJ, 335, L89 [NASA ADS] [CrossRef] [Google Scholar]
  59. Joblin, C., & Cernicharo, J. 2018, Science, 359, 156 [CrossRef] [Google Scholar]
  60. Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open source scientific tools for Python, [Online; accessed January 7, 2021] [Google Scholar]
  61. Jørgensen, J. K., van der Wiel, M. H. D., Coutens, A., et al. 2016, A&A, 595, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Jørgensen, J. K., Müller, H. S. P., Calcutt, H., et al. 2018, A&A, 620, A170 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Kahn, K., & Bruice, T. C. 2005, Chem. Phys. Chem., 6, 487 [Google Scholar]
  64. Kaiser, R. I., Parker, D. S. N., & Mebel, A. M. 2015, Ann. Rev. Phys. Chem., 66, 43 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  65. Kisiel, Z., Dorosh, O., Maeda, A., et al. 2010, Phys. Chem. Chem. Phys., 12, 8329 [CrossRef] [Google Scholar]
  66. Klebsch, W., Bester, M., Yamada, K. M. T., Winnewisser, G., & Joentgen, W. 1985, A&A, 152, L12 [Google Scholar]
  67. Kobayashi, H., Hidaka, H., Lamberts, T., et al. 2017, ApJ, 837, 155 [NASA ADS] [CrossRef] [Google Scholar]
  68. Krim, L., Jonusas, M., Guillemin, J.-C., Yáñez, M., & Lamsabhi, A. M. 2018, Phys. Chem. Chem. Phys., 20, 19971 [NASA ADS] [CrossRef] [Google Scholar]
  69. Krim, L., Guillemin, J.-C., & Woon, D. E. 2019, MNRAS, 485, 5210 [CrossRef] [Google Scholar]
  70. Kristensen, L. E., Klaassen, P. D., Mottram, J. C., Schmalzl, M., & Hogerheijde, M. R. 2013, A&A, 549, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Kuffmeier, M., Calcutt, H., & Kristensen, L. E. 2019, A&A, 628, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Lide, D. R. Jr. 1960, J. Chem. Phys., 33, 1514 [CrossRef] [Google Scholar]
  73. Lide, D. R. Jr. & Mann, D. E. 1957, J. Chem. Phys., 27, 868 [CrossRef] [Google Scholar]
  74. Ligterink, N. F. W., Coutens, A., Kofman, V., et al. 2017, MNRAS, 469, 2219 [NASA ADS] [CrossRef] [Google Scholar]
  75. Loison, J.-C., Wakelam, V., Hickson, K. M., Bergeat, A., & Mereau, R. 2014, MNRAS, 437, 930 [NASA ADS] [CrossRef] [Google Scholar]
  76. Loison, J.-C., Agúndez, M., Marcelino, N., et al. 2016, MNRAS, 456, 4101 [Google Scholar]
  77. Loison, J.-C., Agúndez, M., Wakelam, V., et al. 2017, MNRAS, 470, 4075 [NASA ADS] [CrossRef] [Google Scholar]
  78. Lykke, J. M., Coutens, A., Jørgensen, J. K., et al. 2017, A&A, 597, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Maeda, A., DeLucia, F. C., Herbst, E., et al. 2006a, ApJS, 162, 428 [NASA ADS] [CrossRef] [Google Scholar]
  80. Maeda, A., Medvedev, I. R., De Lucia, F. C., & Herbst, E. 2006b, ApJS, 166, 650 [NASA ADS] [CrossRef] [Google Scholar]
  81. Manigand, S., Calcutt, H., Jørgensen, J. K., et al. 2019, A&A, 623, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Manigand, S., Jørgensen, J. K., Calcutt, H., et al. 2020, A&A, 635, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Marcelino, N., Cernicharo, J., Agúndez, M., et al. 2007, ApJ, 665, L127 [NASA ADS] [CrossRef] [Google Scholar]
  84. Markwick, A. J., Millar, T. J., & Charnley, S. B. 2002, A&A, 381, 560 [CrossRef] [EDP Sciences] [Google Scholar]
  85. Masunaga, H.,& Inutsuka, S.-i. 2000, ApJ, 536, 406 [CrossRef] [Google Scholar]
  86. McGuire, B. A., Burkhardt, A. M., Kalenskii, S., et al. 2018, Science, 359, 202 [Google Scholar]
  87. McKellar, A. R. W., Watson, J. K. G., Chu, L.-K., & Lee, Y.-P. 2008, J. Mol. Spectr., 252, 230 [NASA ADS] [CrossRef] [Google Scholar]
  88. Menten, K. M., Walmsley, C. M., Henkel, C., & Wilson, T. L. 1988, A&A, 198, 253 [NASA ADS] [Google Scholar]
  89. Moldoveanu, S. 2010, Pyrolysis of Organic Molecules: Applications to Health and Environmental Issues (Amsterdam: Elsevier), 28 [Google Scholar]
  90. Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
  92. Neish, C. D., Somogyi, Á., & Smith, M. A. 2010, Astrobiology, 10, 337 [CrossRef] [Google Scholar]
  93. Nelsestuen, G. L. 1980, J. Mol. Evol., 15, 59 [CrossRef] [Google Scholar]
  94. Ochsenbein, F., Bauer, P., & Marcout, J. 2000, A&AS, 143, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Ohishi, M., & Kaifu, N. 1998, Faraday Discussions, 109, 205 [NASA ADS] [CrossRef] [Google Scholar]
  96. Pearson, J. C., Sastry, K. V. L. N., Herbst, E., & Delucia, F. C. 1994, J. Mol. Spectr., 166, 120 [CrossRef] [Google Scholar]
  97. Persson, M. V., Jørgensen, J. K., Müller, H. S. P., et al. 2018, A&A, 610, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Transf., 60, 883 [Google Scholar]
  99. Puget, J. L., & Leger, A. 1989, ARA&A, 27, 161 [NASA ADS] [CrossRef] [Google Scholar]
  100. Qasim, D., Fedoseev, G., Chuang, K. J., et al. 2019, A&A, 627, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  101. Requena-Torres, M. A., Martín-Pintado, J., Martín, S., & Morris, M. R. 2008, ApJ, 672, 352 [NASA ADS] [CrossRef] [Google Scholar]
  102. Ruaud, M., Loison, J. C., Hickson, K. M., et al. 2015, MNRAS, 447, 4004 [NASA ADS] [CrossRef] [Google Scholar]
  103. Ruaud, M., Wakelam, V., & Hersant, F. 2016, MNRAS, 459, 3756 [NASA ADS] [CrossRef] [Google Scholar]
  104. Sakai, N., Sakai, T., Hirota, T., & Yamamoto, S. 2008, ApJ, 672, 371 [NASA ADS] [CrossRef] [Google Scholar]
  105. Scuseria, G. E., & Staroverov, V. N. 2005, in Theory and Applications of Computational Chemistry, eds. C. E. Dykstra, G. Frenking, K. S. Kim, & G. E. Scuseria (Amsterdam: Elsevier), 669 [CrossRef] [Google Scholar]
  106. Shibasaki, M., Kanai, M., & Mita, T. 2008, The Catalytic Asymmetric Strecker Reaction (American Cancer Society) (Hoboken, NJ: John Wiley), 1 [Google Scholar]
  107. Simons, M. A. J., Lamberts, T., & Cuppen, H. M. 2020, A&A, 634, A52 [CrossRef] [EDP Sciences] [Google Scholar]
  108. Song, L., & Kästner, J. 2017, ApJ, 850, 118 [NASA ADS] [CrossRef] [Google Scholar]
  109. Strecker, A. 1850, Justus Liebigs Annalen der Chemie, 75, 27 [CrossRef] [Google Scholar]
  110. Strecker, A. 1854, Justus Liebigs Annalen der Chemie, 91, 349 [CrossRef] [Google Scholar]
  111. Tang, T. B., Inokuchi, H., Saito, S., Yamada, C., & Hirota, E. 1985, Chem. Phys. Lett., 116, 83 [NASA ADS] [CrossRef] [Google Scholar]
  112. Taquet, V., van Dishoeck, E. F., Swayne, M., et al. 2018, A&A, 618, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  113. Turner, B. E. 1991, ApJS, 76, 617 [NASA ADS] [CrossRef] [Google Scholar]
  114. Ulenikov, O. N., Malikova, A. B., Qagar, C. O., et al. 1991, J. Mol. Spectr., 145, 262 [CrossRef] [Google Scholar]
  115. van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
  116. van der Wiel, M. H. D., Jacobsen, S. K., Jørgensen, J. K., et al. 2019, A&A, 626, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. van Trump, J. E., & Miller, S. L. 1972, Science, 178, 859 [CrossRef] [Google Scholar]
  118. van Dishoeck, E. F., Blake, G. A., Jansen, D. J., & Groesbeck, T. D. 1995, ApJ, 447, 760 [NASA ADS] [CrossRef] [Google Scholar]
  119. Vidal, T. H. G., Loison, J.-C., Jaziri, A. Y., et al. 2017, MNRAS, 469, 435 [NASA ADS] [CrossRef] [Google Scholar]
  120. Wakelam, V., Herbst, E., Loison, J. C., et al. 2012, ApJS, 199, 21 [NASA ADS] [CrossRef] [Google Scholar]
  121. Wakelam, V., Vastel, C., Aikawa, Y., et al. 2014, MNRAS, 445, 2854 [NASA ADS] [CrossRef] [Google Scholar]
  122. Wakelam, V., Loison, J. C., Herbst, E., et al. 2015, ApJS, 217, 20 [NASA ADS] [CrossRef] [Google Scholar]
  123. Wakelam, V., Loison, J. C., Mereau, R., & Ruaud, M. 2017, Mol. Astrophys., 6, 22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  124. White, W. F. 1975, Microwave spectra of some volatile organic compounds, Technical report [Google Scholar]
  125. Winnewisser, G. 1973, J. Mol. Spectr., 46, 16 [NASA ADS] [CrossRef] [Google Scholar]
  126. Winnewisser, M., Winnewisser, G., Honda, T., & Hirota, E. 1975, Zeitschrift Naturforschung Teil A, 30, 1001 [CrossRef] [Google Scholar]
  127. Wirström, E. S., Geppert, W. D., Hjalmarson, Å., et al. 2011, A&A, 533, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  128. Wlodarczak, G., Demaison, J., Heineking, N., & Csaszar, A. G. 1994, J. Mol. Spectr., 167, 239 [CrossRef] [Google Scholar]
  129. Woon, D. E., & Herbst, E. 1996, ApJ, 465, 795 [NASA ADS] [CrossRef] [Google Scholar]
  130. Yeh, S. C. C., Hirano, N., Bourke, T. L., et al. 2008, ApJ, 675, 454 [NASA ADS] [CrossRef] [Google Scholar]
  131. Zaverkin, V., Lamberts, T., Markmeyer, M. N., & Kästner, J. 2018, A&A, 617, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  132. Zhao, Y., & Truhlar, D. G. 2008, Theor. Chem. Acc., 120, 215 [CrossRef] [Google Scholar]
  133. Zhou, L., Kaiser, R. I., Gao, L. G., et al. 2008, ApJ, 686, 1493 [NASA ADS] [CrossRef] [Google Scholar]
  134. Zucker, C., Speagle, J. S., Schlafly, E. F., et al. 2019, ApJ, 879, 125 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Observations towards IRAS 16293B used in this study.

In the text
Table 2

Column densities of detected species and upper limits of non-detection towards the offset position from IRAS 16293B.

In the text
Table 3

Initial abundances used in the chemical model.

In the text
Table B.1

Branching ratios of radical addition reactions.

In the text
Table B.2

Hydrogenation reactions of CH(O)CHO from Chuang et al. (2016) and CH3OCHO on grain surfaces.

In the text
Table C.1

Main spectroscopic parameters of the analysed species.

In the text
Table D.1

Species abundances, relative to CH3OH, at the end of the collapse phase for all the runs.

In the text
Table E.1

Line list of the observed C2H3CHO transitions above 3σ.

In the text
Table F.1

Line list of the observed C3H6 transitions above 3σ.

In the text

All Figures

thumbnail Fig. 1

Integrated intensity maps of the line emission for C3H6 and C2 H3CHO, summed over ± 0.5 MHz. The locations of IRAS 16293B continuum peak and the offset position are marked by the black star and plus sign, respectively. The blue contours start at 4σ and increase by steps of 4σ, where σ is 5 mJy beam−1 km s−1 for the integrated intensity. A representative beam of 0′′.5 is shown in the lower right corner of each panel.
In the text
thumbnail Fig. 2

Identified lines of C2H3CHO: the synthetic spectrum, in red, is plotted along with the offset position spectrum towards IRAS 16293B. The straight dashed black line represents the detection limit at the intensity of 3σ. The upper-level energy of the transition is noted in the upper left corner of each panel. The reference spectrum in blue takes the previous species reported in PILS into account (Jørgensen et al. 2016, 2018; Lykke et al. 2017; Coutens et al. 2016; Ligterink et al. 2017; Persson et al. 2018; Calcutt et al. 2018a; Drozdovskaya et al. 2018; Manigand et al. 2019).
In the text
thumbnail Fig. 3

Identified lines of C3H6: the synthetic spectrum, in red, is plotted along with the offset position spectrum towards IRAS 16293B. The dashed lines correspond to optically thick lines. The straight dashed black line represents the detection limit at the intensity of 3σ. The upper-level energy of the transition is noted in the upper left corner of each panel. The torsional state “E” or “A” of each transition is noted in green on the spectra. The reference spectrum in blue takes the previous species reported in PILS into account (see Fig. 2 and references therein).
In the text
thumbnail Fig. 4

Identified lines of C3H6 synthetic spectrum, in red, including the E/A spin weight ratio of 0.6 ± 0.1 are plotted along with the offset position spectrum towards IRAS 16293B. The dashed lines correspond to optically thick lines. The straight dashed black line represents the detection limit at the intensity of 3σ. The upper-level energy of the transition is noted in the upper left corner of each panel. The torsional state “E” or “A” of each transition is noted in green on the spectra. The reference spectrum in blue takes into account the previous species reported in PILS (see Fig. 2 and reference therein).
In the text
thumbnail Fig. 5

Time evolution of abundances in the gas phase (solid lines) and on the grain surface (dotted) of several species during the collapse phase of the A1 run. The time axis is reversed to better visualise the abundances evolution. Both panels show the results of the same simulation but with a different selection of species, with their name annotated following the colour code of the curves.
In the text
thumbnail Fig. 6

Final abundances reached at the end of each simulation run for the targeted species. The dashed blue line shows the observed abundance of the species towards IRAS 16293B. The error bars and the blue area correspond to one half order of magnitude confidence limit, thus a 1σ-difference between observations and simulations corresponds to one order of magnitude. The dashed blue region represents the abundance values that are consistent with the corresponding upper limit. The abundance scale of C3 O is lower than the other plots. The abundance upper limit of HC(O)CHO is < 2.6 × 104 relative to CH3OH, therefore, there is no observational constraint on the abundance of HC(O)CHO. The abundance upper limit of C3 H7OH is the sum of n-C3H7OH and i-C3H7OH abundance upper limits.
In the text
thumbnail Fig. A.1

Evolution of the density, dust temperature, visual extinction and infall velocity across the envelope during the simulation. The time is indicated at several positions on the curves, with t = 0 yr set to the end of the collapse phase in the simulation.
In the text
thumbnail Fig. D.1

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run A1. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
In the text
thumbnail Fig. D.2

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run A2. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
In the text
thumbnail Fig. D.3

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run B1. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
In the text
thumbnail Fig. D.4

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run B2. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
In the text
thumbnail Fig. D.5

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run C1. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
In the text
thumbnail Fig. D.6

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run C2. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
In the text
thumbnail Fig. D.7

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run D1. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
In the text
thumbnail Fig. D.8

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run D2. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
In the text
thumbnail Fig. D.9

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run E1. Thetime axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
In the text
thumbnail Fig. D.10

Evolution of the abundances of three-carbon species during the prestellar and the collapse phase of the simulation run E2. The time axis is reversed to better visualise the abundance evolution. Each color corresponds to a single species, with its abundance in the gas phase and on grain surfaces shown in solid and dotted lines, respectively.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.