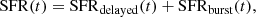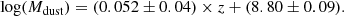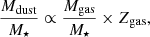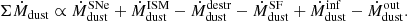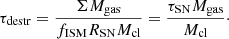EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 644 (December 2020) A&A, 644 (2020) A144 Full HTML
Free Access
Issue
A&A
Volume 644, December 2020
Article Number A144
Number of page(s) 25
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202038405
Published online 14 December 2020

© ESO 2020

1. Introduction

Recent advent of infrared (IR) instruments such are Herschel and ALMA have allowed us to identify long, high-redshift tails (2 <  z <  7) for individual dusty star-forming galaxies (DSFGs, e.g. Weiß et al. 2013; Riechers et al. 2013; Oteo et al. 2017; Zavala et al. 2018; Strandet et al. 2017; Jin et al. 2019; Casey et al. 2019; for comprehensive reviews, see Casey et al. 2014; Hodge & da Cunha 2020). The nature of these sources is critical to our understanding of how massive galaxies assemble and how their large dust reservoirs may have been formed at early cosmic times (e.g. Dwek et al. 2014; Zhukovska et al. 2016; Popping et al. 2017; Aoyama et al. 2019; Nanni et al. 2020). Along with recent progress with regard to increasing the statistics of DSFGs, many observational works have revisited the correlation between the star-formation rate (SFR) and stellar mass (M⋆) in star-forming galaxies, showing that in the vast majority of known DSFGs these two quantities are expected to form a nearly linear relation, namely, the so-called “main sequence” (MS; Brinchmann et al. 2004; Noeske et al. 2007; Elbaz et al. 2010; Daddi et al. 2010; Rodighiero et al. 2011; Sargent et al. 2014; Speagle et al. 2014; Whitaker et al. 2015; Schreiber et al. 2015; Pearson et al. 2018). The prominent positive outliers of this sequence with boosted specific SFR (sSFR = SFR/M⋆) are known as starbursts (SB). A knowledge of the physical properties of these two populations allows us to better understand the heterogeneous characteristics of distant DSFGs with regard to their evolutionary stage within the main-sequence paradigm (e.g. Sargent et al. 2014; Scoville et al. 2017; Silverman et al. 2018).

It is generally believed that multiwavelength observations (e.g. from ultraviolet (UV) to sub-mm) are key to assembling a complete picture of the stellar mass (M⋆) and SFR of dusty galaxies. On one hand, dust affects the spectral energy distributions (SED) of galaxies to the extent that at shorter wavelengths, stellar light is more absorbed by dust and re-emitted in the far-infrared (FIR). On the other hand, along with molecular and atomic lines, dust is one of major coolants of the interstellar medium (ISM) and prevents gas heating up from the general interstellar radiation field, thus playing an important role in the process of star formation (Cuppen et al. 2017). As a consequence, the ratio between the dust and stellar mass (Mdust/M⋆) stands as a key parameter for understanding the physical processes involved in producing the dust, metals, and stars in DSFGs. It has been suggested that Mdust/M⋆ can be a useful marker of the galaxy ISM and survival capacity of dust grains against the multiple destruction processes (Dunne et al. 2011; Rowlands et al. 2014; Tan et al. 2014; Béthermin et al. 2015; Calura et al. 2017; De Vis et al. 2017; Michałowski et al. 2019; Burgarella et al. 2020).

In spite of its importance, the cosmic evolution of Mdust/M⋆ has not yet been fully understood. Linking the cosmic evolution of dust-to-stellar properties in massive galaxies is extremely challenging task due to various reasons, for instance: (1) A proper constraint of dust quantities, such as dust luminosity (LIR) and Mdust, requires exquisite IR SEDs with rich wavelength sampling towards Rayleigh-Jeans (RJ) tail. Until recently, the limited depth of FIR surveys restricts statistical studies of high-z DSFGs either to the most luminous objects (e.g. Riechers et al. 2013; Dowell et al. 2014; Oteo et al. 2018; Donevski et al. 2018; Miller et al. 2018; Pavesi et al. 2018) or strongly lensed galaxies (e.g. Negrello et al. 2010; Wardlow et al. 2014; Strandet et al. 2017; Ciesla et al. 2020); (2) Considering the limiting beam size of single-dish FIR instruments, extensive follow-ups with high spatial resolution are required to better constrain the IR SEDs and redshifts of sources (Cox et al. 2011; Hodge et al. 2013; Simpson et al. 2015, 2020; da Cunha et al. 2015; Miettinen et al. 2015, 2017; Oteo et al. 2017; Dunlop et al. 2017; Fudamoto et al. 2017; Stach et al. 2019; An et al. 2019; Dudzevičiūtė et al. 2020; Gómez-Guijarro et al. 2019); (3) The DSFGs are usually highly dust-obscured, meaning that their continuum emission is very faint at rest-frame UV/optical wavelengths. Due to these reasons, there are still considerable uncertainties in the derived physical properties of DSFGs. Consequently, some vital quantities, such as M⋆, Mdust, or the active galactic nucleus fraction (AGN fraction, fAGN), are poorly constrained, which often prevent us from knowing the position of DSFGs in the SFR–M⋆ plane with respect to the “main sequence”.

To partially overcome those issues, statistical methods based on stacking are often applied to infer the average properties of DSFGs that lie close to the confusion limit (e.g., Schreiber et al. 2015; Béthermin et al. 2015). More recently, a new generation of source extraction methods based on positional, redshift, and SED priors were tested in order to directly resolve individual galaxies from confused IR images (e.g. Pearson et al. 2017; Hurley et al. 2017; Liu et al. 2018). These techniques have enabled observational constraints to be placed on DSFGs, such as scaling between the dust mass and gas mass (Leroy et al. 2011; Magdis et al. 2012; Zahid et al. 2014; Scoville et al. 2017; Tacconi et al. 2018; Liu et al. 2019a) as well as the evolution of dust temperature (Magdis et al. 2012; Béthermin et al. 2015; Liang et al. 2019). Such discoveries have raised important questions about the dust mass content in the early universe, particularly with regard to characterising the observational imprints of the main sources of dust mass production and destruction at high z.

In addition to observational efforts over the last decade, a great deal of attention has been paid to theoretical studies of the formation of DSFGs and their dark matter (DM) halos via the application of different classes of cosmological simulations (Hayward 2013; Narayanan et al. 2015; McKinnon et al. 2017; Davé et al. 2019; Aoyama et al. 2019) or semi-analytic and analytic methods (Lacey et al. 2016; Popping et al. 2017; Imara et al. 2018; Cousin et al. 2019; Vijayan et al. 2019; Lagos et al. 2019; Pantoni et al. 2019). To investigate the evolution of the dust content of high-z DSFGs, the models have made significant progress by replacing the simplified scaling relations with the physical recipes for self-consistent dust formation, growth, and destruction in evolving galaxies (e.g. McKinnon et al. 2017; Aoyama et al. 2019; Hou et al. 2019; Graziani et al. 2020; Davé et al. 2019). While this enables the study of diverse samples of DSFGs from the statistical point of view, the interpretation of the key contributors to their dust-to-stellar mass ratio remains a challenge. The main reason for this is the existing tension between the modelled and the observed high number density of the most massive DSFGs (M⋆ >  1010 M⊙, Mdust >  109 M⊙, McKinnon et al. 2017).

We find that is timely to link the methods described above and inspect the nature of Mdust/M⋆ in a large sample of individually detected high-z DSFGs. There are two main questions we address in this work. The first one deals with how the Mdust/M⋆ evolves with cosmic time and position of the galaxy with respect to the main-sequence. Properly answering to this question requires a careful examination of all observational challenges outlined above.

To this end, we assembled large statistical data set that contains MS and SB DSFGs identified over a wide redshift range in the COSMOS field with ALMA. We complement deep multi-wavelength catalogue with the IR fluxes of the carefully de-blended sources and apply physically motivated SED modelling in order to self-consistently derive physical properties of DSFGs. We study different trends with Mdust/M⋆ for galaxies within and above the MS.

We then address the second question, namely, how the Mdust/M⋆ can be understood within the framework of dusty galaxy formation and evolution. We employ state-of-the-art galaxy models, with the aim in achieving a comprehensive understanding of the nature of rapid dust evolution in our sources.

The paper is organised as follows. In Sect. 2, we describe the data analysed in this work. In Sect. 3, we explain the SED fitting methodology and provide average statistical properties for our sample. In Sect. 4, we present the main results that show how the dust-to-stellar mass ratio of ALMA-detected DSFGs scales with the galaxy redshift, sSFR, and M⋆. We provide the recipe for modelling the observed data based on simple empirical prescriptions. In Sect. 5, we compare our results to different models of galaxy formation and evolution. We discuss the role of compact dusty star-formation on observed Mdust/M⋆ in Sect. 6, while our main conclusions are outlined in Sect. 7. Throughout the paper, we assume a Planck Collaboration XIII (2016) cosmology and Chabrier IMF (Chabrier 2003).

2. Data and sample selection

To build the statistically significant sample of DSFGs suitable for our analysis, we adopted homogeneously calibrated multiwavelength catalogues released by the Herschel Extragalactic Legacy Project (HELP, Małek et al. 2018; Shirley et al. 2019; Oliver et al., in prep.). The HELP catalogues offer observational information across the well-known and well-studied extragalactic fields that were targeted by Herschel. We chose the COSMOS field (Scoville et al. 2007) because of the wealth of multi-wavelength data complementing several hundred galaxies that exist in public ALMA archive. The main advantage of the panchromatic catalogue provided by HELP is its homogeneous calibration and implementation of state-of-the-art source extracting and de-blending tool (XID+, Hurley et al. 2017) that allows us to overcome the confusion limit in FIR observations made with the Herschel telescope.

In order to extract the fluxes beyond the conventional Spitzer and Herschel confusion limit, the MIPS (24 μm), PACS (100, 160 μm), and SPIRE fluxes (250, 350, and 500 μm) are assigned to each source with use of probabilistic de-blending method XID+ (Hurley et al. 2017). The code XID+ de-blends confusion limited maps with use of positional and redshift information from the deepest IRAC priors (up to 23.4 mag at 3.6 μm). In this way, we take the advantage of fluctuations within the confused maps and place strong constraints on the peak of sources’ FIR SEDs, improving upon dust-embedded star formation and identify the main contributors to the flux detected with higher resolution instruments that operate at longer wavelengths (i.e. ALMA). Given the positional prior from the HELP catalogue, we identify counterparts to ALMA detected galaxies, either in Band 6 (1.1 mm, 121 source) or Band 7 (870 μm, 207 sources). We adopt fluxes available within the ALMA archive (A3COSMOS, see Liu et al. 2019b for more details).

For the final galaxy sample, we require source detections with S/N ≥ 3 in at least five photometric bands in the mid-IR-to-FIR/sub-mm range (8 μm <  λ <  1100 μm) and with S/N ≥ 5 in at least ten photometric bands covering the optical-NIR range (0.3 μm <  λ <  8 μm). These requirements are particularly important for achieving the robustness to physical parameters estimated from SED fitting (see e.g. Małek et al. 2018). When multiple measurements are available in similar optical-NIR pass-bands, we take the deepest one to reduce the measurement uncertainties. The optical to NIR data come from Subaru Suprime-Cam (six bands), HSC (Y-band), VISTA (J, H, Ks bands), and IRAC (four bands). We assemble the final list of sources (329 in total), out of which 73 galaxies are known publicly available spectroscopic redshifts (zspec), while the rest have photometric redshifts (zphot) generated using a Bayesian combination approach (the precision of zphot is estimated to be δz/1 + zspec <  0.005, see Duncan et al. 2018 for details). The full redshift distribution extends over a wide range (0.5 <  z <  5.25), as shown in top panel of Fig. 1.

thumbnail Fig. 1.

For all panels inside the grey box: distributions of the physical properties estimated for our DSFGs from the SED fitting with CIGALE. From top left to bottom right: goodness of fit expressed as reduced χ2; galaxy redshift; stellar mass; SFR; IR luminosity; dust mass; and galaxy linear offset from the MS (in log scale). Bottom right panel: linear offset of the galaxy’s observed SFR to the SFR expected from the modelled MS (ΔMS in log scale) as a function of redshift. A border between the sources considered as MS and SB DSFGs is indicated by a horizontal, dashed line.

3. Panchromatic SED modelling of the data

3.1. Tools: CIGALE

We make use of very dense panchromatic data coverage and apply full SED (UV+IR) modelling of our DSFGs. As a main tool, we adopt the newest release of Code Investigating GALaxy Emission (CIGALE; Boquien et al. 20191, Noll et al. 2009), which is a state-of-the-art SED modelling and fitting code that combines UV-optical stellar SED with an IR component. The code entirely conserves the energy between dust absorption in the UV-to-NIR domain and emission in the mid-IR and FIR. It is designed for estimating the wide range of physical parameters by comparing modelled galaxy SEDs to observed ones. For each parameter, CIGALE makes a probability distribution function (PDF) analysis, and the output value is the likelihood-weighted mean of the PDF (and, consequently, the associated error is a likelihood-weighted standard deviation). In this work, we carefully chose the model parameters following some of the most recent prescriptions, which are extensively tested on large multi-band datasets with available deep IR observations and, thus, optimised for a wide range of DSFGs (e.g. Lo Faro et al. 2017; Ciesla et al. 2017; Pearson et al. 2018; Małek et al. 2018; Buat et al. 2019). In the following, we briefly summarise the choice of modules and parameters presented in Table 1.

Table 1.

Parameters used for modelling the SEDs with CIGALE.

3.1.1. Stellar component

To construct the stellar component of our SED model, we use Bruzual & Charlot stellar population synthesis model (Bruzual & Charlot 2003, BC03) together with a Chabrier (2003) IMF. We fix metallicity to the solar value, which is usually seen as a good assumption because the more recent star-forming events are using more metallic gas (Asano et al. 2013). Our assumption is additionally motivated by recent spectroscopy studies of DSFGs in the HUDF field, for which metallicities consistent with solar are inferred at 1 <  z <  3 (Boogaard et al. 2019, see also Nagao et al. 2012; Kriek et al. 2016; De Breuck et al. 2019)2. We adopt the flexible star-formation historiy (SFH), which is composed of a delayed component with an additional burst. The functional form is given as:

SFR ( t ) = SFR delayed ( t ) + SFR burst ( t ) , $$ \begin{aligned} \mathrm{SFR}({t}) = \mathrm{SFR}_{\rm delayed}({t})+\mathrm{SFR}_{\rm burst}({t}), \end{aligned} $$(1)

where SFRdelayed(t) ∝ te−t/τmain, and SFRburst(t) ∝ e−(t − t0)/τburst. Here, τmain represents the e-folding time of the main stellar population, while τmain represents e-folding time of the late starburst. The e-folding time of the two stellar populations (old and young) in the SFH was roughly matched to that of Małek et al. (2018). Our choice of SFH is motivated by the study by Ciesla et al. (2017) (see also Forrest et al. 2018), who investigate how accurate different choices of SFHs are shown to be in reproducing the IR observations with respect to the SFR − M⋆ plane. Ciesla et al. (2017) demonstate that exponentially declining and delayed SFH struggle to model high SFRs in z >  2 DSFGs, while exponentially rising and log-normal SFHs have the ability to reach the highest SFRs, but display some inconsistency with observed data of massive galaxies at intermediate and lower redshifts.

3.1.2. Dust attenuation

In order to model the effects of dust on the integrated spectral properties for the large variety of galaxies, we adopted a double power-law recipe for dust attenuation initially described in Charlot & Fall (2000). The Charlot & Fall (2000) attenuation law (CF00) assumes that birth clouds (BCs) and the ISM each attenuate light according to fixed power-law attenuation curves. The formalism is based on age-dependent attenuation, meaning that differential attenuation between young (age < 107 yr) and old (age > 107 yr) stars is assumed. Both attenuation laws are modelled by a power-law function, with the amount of attenuation quantified by the attenuation in the V band. We chose to keep both power-law slopes (BC and ISM) of the attenuation fixed at −0.7. The parameters we adopt for CF00 are already used for the fitting of a large sample of DSFGs (Małek et al. 2018).

The choice of du+st attenuation laws can significantly impact estimated stellar masses of massive, dusty galaxies, thus our motivation to chose CF00 is strengthened by two recent findings: (a) it has been shown that hydrodynamical galaxy models require the inclusion of a birth cloud component to properly match the observed optical depth-attenuation curve slope relation in galaxies (Trayford et al. 2020, see Salim & Narayanan 2020 for the review); and (b) it has been found that the widely used Calzetti attenuation law (Calzetti et al. 2000) sometimes tends to underestimate M⋆ by 0.3−0.5 dex in massive high-z DSFGs (see discussions in Lo Faro et al. 2017; Williams et al. 2019; Buat et al. 2019).

3.1.3. Dust emission model

In general, Mdust can be estimated either with more simplified methods, such as a single SED template fitting (Schreiber et al. 2018) and modified blackbody (MBB) fitting (Pozzi et al. 2020; Clements et al. 2018), or with more complex and physically motivated dust emission models (Draine & Li 2007; Galliano et al. 2011; Draine et al. 2014; Jones et al. 2017, see Galliano et al. 2018 for an extensive review). We chose to perform the modelling of galaxies’ IR SEDs with the physically motivated, dust emission library of Draine et al. (2014; DL14 hereafter).

The DL14 is a multi-parameter library which describes the interstellar dust as a mixture of carbonaceous and amorphous silicate grains. The grain size distributions are chosen to realistically “mimic” the observed extinction in the Milky Way (MW), the Large Magellanic Cloud (LMC), and the Small Magellanic Cloud (SMC). The properties of dust grains are parametrised by the so-called polycyclic aromatic hydrocarbon (PAH) index (qPAH), defined as the fraction of the dust mass in the form of PAH grains. The IR SEDs are calculated for dust grains heated by starlight for various distributions of intensities. The majority of the dust is heated by a radiation field with constant intensity from the diffuse ISM, while much smaller fraction of dust (defined as a fraction γ) is exposed to starlight with interstellar radiation field (ISRF) intensity in a range comprised between Umin to Umax following a power-law distribution. We sample different Umin, keeping the dust emission slope fixed at β = 2 along with illumination fraction fixed at γ = 0.02 (see Magdis et al. 2012; Małek et al. 2018; Buat et al. 2019). In our modelling, LIR is an integral of a SED over the rest-frame wavelength range of λ = 8−1000 μm, while the dust masses are derived by fitting and normalising the IR photometry to the DL14 library.

It has been shown that modelling of broadband SEDs with physically motivated models increases the robustness of dust mass estimates (e.g. Draine & Li 2007; Berta et al. 2016; Schreiber et al. 2018). It has also been shown that single Tdust MBB fitting tends to significantly underestimate the Mdust by a factor of ∼2 as compared to those derived from physically based libraries (Dale et al. 2012; Magdis et al. 2012; De Vis et al. 2017). The discrepancies in estimated Mdust could be larger for galaxies with colder dust and higher vertical distance to the galaxy MS (Berta et al. 2016). On top of this, the consistency has been found between the dust properties (Mdust and LIR) derived with CIGALE DL14 library to those modelled in hydro simulations where dust is treated with radiative transfer (Smith & Hayward 2018; Trčka et al. 2020).

3.1.4. AGN model

AGN activity is known to be present in DSFGs (Symeonidis et al. 2013; Brown et al. 2019) and can significantly impact derived physical properties, particularly stellar mass (Ciesla et al. 2015; Salim et al. 2016; Leja et al. 2018). Thus, to improve the derived galaxy properties we chose to quantify the contribution of AGNs to the total predicted LIR. We derive the fractional contribution of the AGN, defined as the relative impact of the dusty torus of the AGN to the LIR (“AGN fraction”). We adopt AGN templates presented in Fritz et al. (2006) (see also Feltre et al. 2012). The templates are computed at different lines of sight with respect to the torus equatorial plane and account for both (Type 1 and Type 2) AGN emission, from 0° to 90° respectively. The parameters in the AGN model were matched to those from Ciesla et al. (2015). Due to computational reasons we somewhat reduce the number of input options, and model the two extreme values for inclination angle (0° and 90°).

3.2. Statistical properties of our sample

The next step is to fit the full datasets with the models defined in previous section. Before using our SED-derived quantities for the science analysis, we confirm that fitted SEDs are of a good quality, which is quantified with the reduced value of χ2 <  10 (top left panel of Fig. 2). We additionally assign the modelling option available within CIGALE to produce mock catalogues and then follow the approach implemented by Małek et al. (2018) to ensure that our SED fitting procedure does not introduce significant systematics to our measurements (see Appendix B). We discard from further analysis all objects for which the fAGN from our full SED is higher than 20% (29/329 sources, or 9% of the total sample). We also double-check for additional X-ray-bright AGNs in the COSMOS (Civano et al. 2016) and find none. After this step, the remaining 300 sources are used for our final analysis. The full list of sources and their main properties are presented in Table A.1.

thumbnail Fig. 2.

Observed redshift evolution of Mdust. Individual values are displayed with circles, coloured with corresponding LIR. Binned means are shown with black circles and associated 1σ errors. For comparison, we also show the mean Mdust for a large sample of dusty galaxies up to z ∼ 0.5 (Driver et al. 2018, black inverted triangle). The black dashed and dotted lines are best regression fits from this work and from Dudzevičiūtė et al. (2020), respectively.

In Fig. 2, we show the distribution of SED derived properties, while in Table 2, we tabulate median physical values confronted with similar ALMA studies (da Cunha et al. 2015; Dudzevičiūtė et al. 2020). We infer the high median redshift of z = 2.39 with the corresponding 16−84th percentile range (z = 1.66−3.31). These are also IR luminous, with the median, LIR = 2.93 × 1012 L⊙, and with ∼80% of sources above LIR = 1012 L⊙. The two studies we used for statistical comparison applied the MAGPHYS code (da Cunha et al. 2010) and derived physical parameters fitting the UV-to-sub-mm data of ALMA 870 μm selected galaxies in the ALESS field (da Cunha et al. 2015) and UDS field (Dudzevičiūtė et al. 2020). From Table 2, we see there is a consistency among the studies over SED-derived physical quantities (z, LIR, SFR and Mdust). We note that Dudzevičiūtė et al. (2020) analysed a large statistical sample (707 objects in total) but considered only four photometric bands in the optical-NIR part of SED. A similar criterion is imposed by da Cunha et al. (2015) who analysed 99 sources, out of which 22 have less than four photometric detections in optical-NIR range. It is, thus, likely that inclusion of “optically fainter” sources is responsible for marginally higher median redshifts and broader corresponding ranges inferred for these DSFGs relative to ours.

Table 2.

Statistics of our SED derived physical properties with CIGALE, compared to those from known statistical ALMA studies (da Cunha et al. 2015; Dudzevičiūtė et al. 2020).

To model the position with respect to the MS for each source in our sample, we applied the functional form of the MS defined by Speagle et al. (2014) (their “best-fit”, provided with Eq. (28)). For each object from our final catalogue, we assigned ΔMS defined as an linear offset of galaxy’s observed SFR to the SFR expected from the modelled MS. We assume the galaxy is a starburst if ΔMS ≥ 4 (e.g. Elbaz et al. 2018), while the galaxy having ΔMS ≤ 4 is considered a MS DSFG3. We infer that our sample contains 242 MS DSFGs (81% of the total) and 58 SB DSFGs (19% of the total).

4. Evolution of dust-to-stellar properties over cosmic time

4.1. Evolution of Mdust with redshift

In Fig. 2, we plot the redshift evolution of the Mdust for the full sample of our DSFGs. From the multi-band SED fitting, we find the median of 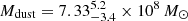M dust = 7 . 33 − 3.4 5.2 × 10 8 M ⊙ $ M_{\mathrm{dust}}=7.33^{5.2}_{-3.4}\times10^{8}\,M_{\odot} $. The relative contribution to the total sample of DSFGs with Mdust >  109 M⊙ is 29%, which places one third of our DSFGs towards the most extreme tail of the dust mass function (DMF). As we see from Table 2, the median Mdust from this work is in consistency with findings from da Cunha et al. (2015) and Dudzevičiūtė et al. (2020). We note that da Cunha et al. (2015) applied slightly different prescription in their dust SED model and explore the grid of SFHs and stellar metallicities in order to derive physical properties of ALMA observed galaxies. This strengthens the conclusion that high Mdust in ALMA detected DSFGs is not an observational artefact due to adopted SED fitting procedure. The inferred Mdust of our DSFGs are in average ∼0.2 dex larger than the values measured through a Herschel stacking analysis of galaxies at z <  2.5 (Santini et al. 2014). A similar difference is seen if we compare it to the median Mdust of a large sample of dusty sources in the local Universe (z <  0.5) detected within the GAMA survey (Driver et al. 2018).

Despite the fact that SFRs of our sources range over almost three orders of magnitude (namely, from 40 M⊙ yr−1 to 1640 M⊙ yr−1), their Mdust exhibits milder variation, on average ∼25% across the observed redshift range. We quantify the observed cosmic evolution of Mdust using a linear regression fit of the form:

log ( M dust ) = ( 0.052 ± 0.04 ) × z + ( 8.80 ± 0.09 ) . $$ \begin{aligned} \log (M_{\rm dust}) = (0.052\pm 0.04)\times z + (8.80\pm 0.09). \end{aligned} $$(2)

The slow rise with redshift is qualitatively consistent with findings from Dudzevičiūtė et al. (2020, namely, their Fig. 11). As pointed out by Dudzevičiūtė et al. (2020), since Mdust is strongly correlated to ALMA 870 μm flux, the broad agreement amongst the different ALMA studies likely reflects the similar flux limits of the single-dish surveys followed-up with ALMA. It has been found that sub-mm flux of extremely luminous DSFGs selected from single dish SCUBA2 camera (at 850 μm) is strongly correlated to redshift (Stach et al. 2019; Simpson et al. 2020). Due to tight connection between dust and gas (young stars are predominantly formed in dense molecular clouds, while dust catalyses transformation from atomic hydrogen into molecular), it has been proposed that steady range of Mdust should correspond to a similarly uniform selection in terms of Mgas (e.g. Swinbank et al. 2014; Simpson et al. 2020).

4.2. Evolution of Mdust − SFR with respect to the MS

In order to achieve a closer insight to the ISM of our DSFGs, we then explore how the dust masses relate to their SFRs. The Mdust and SFR are expected to be correlated in galaxies (da Cunha et al. 2010; Dunne et al. 2011; Bourne et al. 2012; Santini et al. 2014; Rowlands et al. 2014; Kirkpatrick et al. 2017; Aoyama et al. 2019). Such a relationship can naturally be understood due to dust mass being a good tracer of the Mgas in DSFGs (Scoville et al. 2017), while Mgas and SFR are linked through the known Kennicutt–Schmidt relation (KS, Schmidt 1959; Kennicutt 1998; Sargent et al. 2014). However, it is less known whether the expected relation holds with regard to the highest redshifts and higher SFRs.

In Fig. 3, we display how the Mdust relates to SFR. We show the median values of the binned data for the full sample, and for MS and SB DSFGs, separately. We find positive evolutionary trend of SFR with Mdust. which holds for both populations of galaxies, while at the fixed Mdust, SB DSFGs have on average higher SFR than the MS sample. Interestingly, we see that the linear trend between Mdust and SFR starts to flatten towards the upper right part of the diagram. Up to the Mdust ≲ 109 M⊙, the flattening of the relation is mainly caused by MS galaxies. Considering the relation between Mdust and SFR as a consequence of KS law Miettinen et al. (2017) argued that a shallower slope towards higher Mdust could mean that DSFGs deviate from a traditional KS law (see also Santini et al. 2014).

thumbnail Fig. 3.

Observed relation between Mdust and SFR in our DSFGs, shown for the whole sample (binned means, shown as black circles) and divided on SB and MS galaxies (shaded in dark cyan and orange, respectively). The known, empirically based scaling relation between Tdust − SFR − Mdust (Genzel et al. 2015) are overlaid with dashed lines. Different colours correspond to their fixed Tdust, as indicated in the legend. The best fit for local and intermediate redshift ULIRGs (Rowlands et al. 2014) are displayed with dotted and dot-dashed line, respectively.

To better understand this finding, we overlaid our data with the best scaling relations between Mdust and SFR derived by Genzel et al. (2015) and Rowlands et al. (2014). The scaling relations are built upon the approximation that the dust SED can be represented with an average constant Tdust and dust emissivity which is assumed to be β = 1.5. The scaling relations we show in Fig. 3 imply that Mdust and LIR are correlated as L IR / M dust ∝ T dust 4 + β $ L_{\mathrm{IR}}/M_{\mathrm{dust}}\propto T_{\mathrm{dust}}^{4+\beta} $ (Blain et al. 2003). Based on this, we would expect fully linear trend between Mdust and SFR. Our binned data differ from this expectation and can be better described by a (logistic) function that saturates at Mdust ∼ 109 M⊙. Therefore, the sub-linear relation deduced from our sample could also reflect the possible change in ISM conditions (e.g. wide distribution of the radiation field intensities, different optical depths, and source geometry). This is in line with results from studies that have explored the cosmic evolution of interstellar radiation fields and its complex link to galaxy stellar mass (Béthermin et al. 2015; Schreiber et al. 2018) or gas mass (Kirkpatrick et al. 2017; McKinney et al. 2020).

Our DSFGs are probing the highest end of the SFR–Mdust plane, which sparsely overlap with local DSFGs (see da Cunha et al. 2010). This is evidence for extremely efficient and rapid dust formation processes at earlier cosmic epochs (Hjorth et al. 2014; Rowlands et al. 2014; Leśniewska & Michałowski 2019; Dwek et al. 2019). There are several possible explanations why Mdust SFR relation of our DSFGs lie above the locally inferred values. Studying the DSFGs at z ∼ 2, Kirkpatrick et al. (2017) conclude that high-z DSFGs have larger than average molecular gas reservoir than galaxies with similar Mdust at lower redshifts. Other works argued in favor of the much higher efficiency of converting gas into stars. Magdis et al. (2012) demonstrate that dust luminosity emitted per unit of dust mass could also serve as a good indicator of star formation efficiency (SFE = SFR/Mgas ∝ LIR/Mdust). Such an approximation is valid if LIR ∝ SFR ∝ Mgas and under the assumption that ratio between the dust and gas mass (hereafter δDGR) is roughly constant. By examining this formalism, Schreiber et al. (2017) conclude that physical changes in the ISM could be responsible for enhanced SFE, such that most massive galaxies at z <  1 have reduced interstellar radiation fields and correspondingly reduced SFEs.

The cause of the flattening of Mdust-SFR relation is interesting to discuss. From our data, we see that shallower rise is mostly driven by MS DSFGs, while SB DSFGs are more compatible with linear scaling from Genzel et al. (2015). At the first glance, the flattening could be a consequence of our sample being incomplete at a fixed stellar mass. Nevertheless, the similar departure from the linear trend between Mdust and SFR has been found in the complete AzTEC survey of the brightest DSFGs selected as S1.1 mm >  3.5 mJy (Miettinen et al. 2017). Hjorth et al. (2014) investigate simple analytical limiting cases for early dust production, being the first to propose the bending of the SFR–Mdust relation. They postulate that a maximum attainable Mdust is in early starburst phase in which the rapid dust build-up in very massive systems at early cosmic times is the cause of the observed bend-over of the SFR–Mdust relation. However, to reproduce high dust yields, the scenario proposed by Hjorth et al. (2014) imposes extreme dust-formation efficiency by SNe under the galaxy closed-box solution, which is found to be unrepresentative for most of known DSFGs (see e.g. discussion in Pantoni et al. 2019). Therefore, the fact that we see plateau rather than a linear rise of SFR towards the Mdust can be explained if the dust mass build-up is related to additional dust production source, for example, the grain growth in the ejecta and remnant or the ISM. The process is believed to be very fast with a timescale of a few tens of million years (Asano et al. 2013; Hirashita & Nozawa 2017; Popping et al. 2017; Pantoni et al. 2019). In the next section, we closely investigate this possibility through different scaling relations that link dust, gas, and metal content in our DSFGs.

It is also possible that the dust emission in compact DSFGs is affected by opacity effects. As we show in Sect. 6, some of our sources have extreme surface densities of dusty star-formation, which would make the gaseous ISM highly optically thick even in the IR regime (Cortzen et al. 2020). The fact that the SFR−Mdust relation becomes flat for our DSFGs at the high Mdust end further supports this possibility. To check how the opacity assumption affects our results, we use a prescription of a thick dust model from Dowell et al. (2014) and fit the IR SEDs to the sources from the highest dust mass bin (Mdust >  2 × 109 M⊙). We find that use of a thick dust model returns ∼2−3× lower Mdust due to increase in Tdust at a given LIR. This is in line with Cortzen et al. (2020), who studied GN20, known starburst at z = 4, and reported ∼2× discrepancy between the dust masses derived from optically thin and optically thick dust model. However, as pointed by Cortzen et al. (2020), it is difficult to properly quantify these effects because optically thin or thick solutions are heavily degenerate and require independent proxy for Tdust to discriminate between the two. For the sake of consistency, we thus keep our DL14-based Mdust throughout the rest of the paper.

4.3. Evolution of Mdust/M⋆ with respect to the main-sequence

We now explore how various physical quantities of our DSFGs relate to Mdust/M⋆ in MS and SB DSFGs. Our goal here is to use the Mdust/M⋆ as a tool to assess the efficiency of the specific dust production and destruction mechanisms in galaxies. In Fig. 4, we present different evolutionary trends of Mdust/M⋆ for MS and SB DSFGs against the redshift, sSFR, and stellar mass.

thumbnail Fig. 4.

Top panel: Mdust/M⋆ versus redshfit (left) and sSFR (right), of our MS and SB DSFGs. The binned averages and corresponding standard errors for MS and SB subsample are shown as shaded dark cyan and orange area, respectively. The grey, shaded area is the observed trend obtained via stacking analysis by Béthermin et al. (2015). The red star in each panel indicate the median value of most extreme local ULIRGs (da Cunha et al. 2010). Binned values for MS and SB from high-redshift ALMA sample analysed by da Cunha et al. (2015) are shown with triangles and squares, respectively. Also displayed with red symbols are individual detections of the most distant DSFGs at z >  5 (MAMBO-9, Casey et al. 2019; Jin et al. 2019; HFLS3, Riechers et al. 2013; and SPT0311, Strandet et al. 2017). For consistency, we use public data and recalculate Mdust of latter three objects following our method, finding a good agreement with their archival estimates. Right panel: the binned mean values of the full sample are presented with black circles and the results from da Cunha et al. (2015) with filled squares. The error bars represent the dispersion (1σ) associated to the mean. Bottom panel: Mdust/M⋆ versus galaxy stellar mass. Left panel: our estimates compared to those that span the similar stellar mass range. Points are colour-coded in the same way as in the upper plot. Grey circles indicate the local galaxy sample composed of Herschel-detected galaxies (both passive and active) from the Virgo cluster (HRS, Andreani et al. 2018). On the right side, we resolve the overall trend of Mdust/M⋆ vs. M⋆ from this work per different redshift bins and plot the trend with corresponding 1σ uncertainty. Redshift bins are colour-coded as in the legend.

The upper left panel of Fig. 4 illustrates the evolution of the Mdust/M⋆ ratio with redshift. We placed estimated values for MS (SB DSFGs) in 11 (6) redshift bins of 0.3 (0.5). We did not analyse the highest redshift bins (z >  5 for MS and z >  3.5 for SB DSFGs) due to a lack of statistical significance (they contain only two and one objects, respectively). The binned means and their standard errors are shown as cyan and orange regions for MS and SB DSFGs, respectively. The medians of our DSFGs are found to be 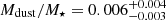M dust / M ⋆ = 0 . 006 − 0.003 + 0.004 $ M_{\mathrm{dust}}/M_{\star}=0.006^{+0.004}_{-0.003} $ for MS DSFGs and 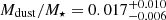M dust / M ⋆ = 0 . 017 − 0.006 + 0.010 $ M_{\mathrm{dust}}/M_{\star}=0.017^{+0.010}_{-0.006} $ for SB DSFGs. We find that for both populations Mdust/M⋆ rises up to the certain redshift (z ∼ 2−2.25) and flattens or bends towards earlier epochs. It is worth noting that no SB DSFGs are observed at z >  4. This can be a consequence of our source selection, but also an indication that SB DSFGs at high-z lie systematically below the central relation for starbursts predicted from KS law (Santini et al. 2014; Béthermin et al. 2015; Silverman et al. 2018; Liu et al. 2019a). Nonetheless, the SB DSFGs typically have 3−4 times higher Mdust/M⋆ as compared to MS DSFGs, regardless of the observed redshift. The variation with redshift amongst the binned values is mild, about 0.3 dex. All these imply that the carefully estimated Mdust/M⋆ can be applied as a useful tool for distinguishing SB and MS dusty galaxies over wide redshift range.

The different evolution of Mdust/M⋆ with redshift for MS and SB DSFGs has already been reported in Béthermin et al. (2015) (see also Tan et al. 2014). They construct the average SED of MS and SB DSFGs detected from the stacking analysis. By deducing the mean intensity of the radiation field, they estimate the Mdust from Draine & Li (2007) dust SEDs. Their result for MS DSFGs is displayed as the grey shaded region in Fig. 4. Considering the MS DSFGs, we can see the similarity between the trends, such that values inferred by Béthermin et al. (2015) suggest an increase in Mdust/M⋆ until z ∼ 1.5, and slight decline towards higher-z’s. This is very similar to the overall evolutionary shape we infer from our data, although average values from Béthermin et al. (2015) are slightly lower than ours, due to the stacking technique they adopted in order to reach lower LIR, thus inferring somewhat lower normalisation for Mdust/M⋆. In any case, our estimates are within 1σ uncertainty from those of Béthermin et al. (2015) over the whole redshift range. The same authors also analyse extreme starbursts (ΔMS >  10), obtaining very steep slope for SB DSFGs at 0 <  z <  2 (see their Fig. 8). To compare observed trends with other studies of individual ALMA galaxies, we bin the data from da Cunha et al. (2015) and select objects as MS and SB DSFGs in the exact same way as for our sample. As evident from Fig. 4, coherence between our data and those from da Cunha et al. (2015) is present over full redshift range. For the sake of clarity, we also show the median value obtained for the sample of the most extreme local ULIRGs (da Cunha et al. 2010), along with some of the most distant individual DSFGs confirmed to date (Riechers et al. 2013; Strandet et al. 2017; Casey et al. 2019). Despite the fact that we yet have to reach the census of observed DSFGs at z >  4−7, it is clear that even the most distant DSFGs have very high Mdust/M⋆, hinting that there could be a wide spread in the dust-to-stellar ratio of star-forming galaxies. Jin et al. (2019) recently showed that some number of the most distant sources with high Mdust/M⋆ could be a rare population of cold starbursts (Tdust <  30 K). They argue in favor of observed cold dust temperatures being a result of either low star-formation efficiency with rapid metal enrichment or evidence for optically thick dust continuum in the FIR (Cortzen et al. 2020).

The top-right panel of Fig. 4 discloses a strong mutual correlation between Mdust/M⋆ and sSFR. This is in agreement to what has been reported in the literature for a different statistical samples of DSFGs (Hunt et al. 2014; Martis et al. 2019) and Lyman Break Galaxies (LBGs, Burgarella et al. 2020). We find that correlation shows a substantial scatter but extends over two orders of magnitude and saturates at the highest sSFR, which is consistent with da Cunha et al. (2015). The scatter could be due to cosmic evolution of the relation between Tdust and M⋆, which is found to be non-monotonic and strongly dependent on galaxy ISM (Kirkpatrick et al. 2017; Imara et al. 2018).

The relation between Mdust/M⋆ and sSFR can be interpreted as age-evolutionary sequence. That said, the difference between objects populating the opposite corners of the Mdust/M⋆−sSFR plane could originate if Mdust grows on timescales faster than M⋆. The important outcome of this interpretation is that DSFGs from the upper-right side of the diagram could be objects dominated by young stellar populations that could have accumulated at early times almost all the dust of a normal “main-sequence” object. These young DSFGs are expected to own large amounts of molecular gas relative to stars which would place them in the uppermost part of the Mdust/M⋆−sSFR diagram, in line with the picture where the sSFRs in more massive DSFGs peak earlier in the Universe than those of less massive objects (Le Floc’h et al. 2005; Behroozi et al. 2013). The subsequent decrease of sSFR is due to exhaustion of their gas reservoirs and reflects the efficiency of dust removal. Such interpretation would be consistent with the scenario proposed by Burgarella et al. (2020), who studied LBGs at z >  5 and found that sources with the youngest stellar populations have the highest sSFRs (see also Calura et al. 2017). We return to this point in Sects. 5.3 and 6.

In the lower panel of Fig. 4, we show Mdust/M⋆ as a function of M⋆. For our sources, we show the median values computed in bins of stellar mass, along with trends inferred for MS and SB DSFGs, separately. We observe a clear anti-correlation between Mdust/M⋆ and M⋆, with the normalisation being higher in SB DSFGs than in MS DSFGs. We confirm that such distinction holds until log(M⋆/M⊙) = 11.2, while above this M⋆ there are no sources considered as starbursts. The anti-correlation of Mdust/M⋆ with M⋆ is known to exists in the locally observed galaxies (Bourne et al. 2012; De Vis et al. 2017; Casasola et al. 2020). We see that our DSFGs tend to have, on average, slightly higher median Mdust/M⋆ per fixed stellar mass than that of the most extreme local ULIRGs (marked with the red star). The difference is much larger and exceeds an order of magnitude if we compare it with locally detected early and late-type galaxies from the Herschel Reference Survey (HRS, Andreani et al. 2018).

We further inspect the evolution of this inverse relation with redshift by dividing the full sample in four redshift bins, as denoted in the lower-right side of Fig. 4. We unveil several interesting features. Firstly, we provide for the first time the strong observational evidence that anti-correlation of Mdust/M⋆ with M⋆, continues up to z ∼ 5 in massive DSFGs. We find a systematic shift towards higher Mdust/M⋆ with increasing redshift. This seems valid at least until M⋆ ∼ 1011 M⊙, after which the difference in normalisation becomes less prominent, coincidental with the stellar mass range that is mostly unpopulated with regard to SB DSFGs. Secondly, there is a tentative evidence for a change of slope of the inverse relation with redshift. Lurking at the lowest redshift bin we see that our data indicate a slight turnover of Mdust/M⋆ at a characteristic M⋆, which is followed by a mild overall change of the amplitude. 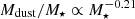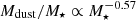Towards higher-z’s the inverse relation becomes steeper, and can be roughly quantified as a simple power law evolving from M dust / M ⋆ ∝ M ⋆ − 0.21 $ M_{\mathrm{dust}}/M_{\star}\propto M^{-0.21}_{\star} $ to M dust / M ⋆ ∝ M ⋆ − 0.57 $ M_{\mathrm{dust}}/M_{\star}\propto M^{-0.57}_{\star} $ at 1.5 <  z <  5. We caution that a less-biased sample of spectroscopically confirmed candidates at z >  3−5 is necessary for supporting this claim.

The observed anti-correlation of Mdust/M⋆ with M⋆ seems a natural reflection of the dust life-cycle: M⋆ grows with time as galaxy evolving, while dust grains (altogether with ISM metals) decrease from the budget being incorporated into the stellar mass. Calura et al. (2017) applied the chemical galaxy model on proto-spheroidal galaxies, suggesting that the observed trend of Mdust/M⋆ with M⋆ is strongly dependent on galaxy star-formation history. They demonstrate that galaxies characterised by prolonged (bursty) star-formation activity, shows a rather flat (steep) behaviour of Mdust/M⋆ with respect to M⋆. They concluded that the observed inverse relation is due to the time evolution of Mdust/M⋆ in the late starburst phase of DSFGs. During this evolutionary phase, M⋆ is still increasing, but the galaxy SFR and the dust production rate decrease resulting in a downhill of Mdust/M⋆ towards the point which characterises the end of star formation.

Imara et al. (2018) developed an analytical solution based on simplified empirical prescriptions and found that the evolution of Mdust/M⋆ with M⋆ can be parametrised as a broken power law, where the breaking point is controlled by δDGR. They highlight that the evolution of galaxy molecular gas mass ratio (defined as μgas = Mgas/M⋆) is crucial in regulating the observed Mdust/M⋆ per fixed M⋆. In this regard, the decreasing trend with higher M⋆ could be due to the deficiency of galaxies with high μgas above the critical stellar mass (M⋆ ≃ 1011 M⊙). Above this value, the gas infall and condensation towards the central regions would become less efficient, while feedback caused by black-holes (BH) would suppress star formation (e.g. Mancuso et al. 2016).

4.4. Modelling the observed evolution of Mdust/M⋆

To better understand what drives the cosmic evolution of Mdust/M⋆, we further modelled our data based on simplified empirical prescriptions. We follow the approach presented in seminal works of Tan et al. (2014) and Béthermin et al. (2015) by rewriting the δDGR as:

M dust M ⋆ ∝ M gas M ⋆ × Z gas , $$ \begin{aligned} \frac{M_{\rm dust}}{M_{\star }}\propto \frac{M_{\rm gas}}{M_{\star }} \times Z_{\rm gas}, \end{aligned} $$(3)

The equation unveils that the evolution of Mdust/M⋆ depends on the evolution of molecular gas mass ratio and gas-phase metallicity4. To solve Eq. (3), we model the redshift evolution of Mgas/M⋆ and Zgas relying on scaling relations from the literature5. In the following, we briefly describe our choice of parameters entering the right side of Eq. (3).

To model the redshift evolution of Mgas/M⋆ we apply the gas scaling relations that are based on IR/sub-mm data. Namely, we consider Eq. (9) from Scoville et al. (2017), Eq. (6) from Tacconi et al. (2018), and Eq. (11) from Liu et al. (2019a). The scaling relations provide empirical recipes for connecting galaxy-integrated properties (Mgas, M⋆, and SFR) in the framework of the star-formation main sequence. These are mostly valid in tracing the molecular mass component. For the relatively high M⋆ of our sample, this is a fair assumption if we consider that rising ISM pressure to high-z would induce a negligible contribution of atomic hydrogen to the total gas mass (Combes 2018; Tacconi et al. 2020). We refer to Scoville et al. (2017), Tacconi et al. (2018), and Liu et al. (2019a) for detailed descriptions and briefly outline the main points below: (1) Scoville et al. (2017) derive Mgas from the optically thin RJ tail of dust emission, assuming that IR SED can be well-described with the constant mass-weighted Tdust, which is assumed to be 25 K; (2) Tacconi et al. (2018) determine Mgas combining three independent methods based on CO line fluxes, FIR SEDs, and single sub-mm flux (1 mm) photometry; (3) Liu et al. (2019a) provide a new functional form for Mgas by re-analysing different systematics and photometric bands’ conversions for a large sample of ∼700 DSFGs detected with ALMA. All methods are based upon investigating statistically significant number of star-forming galaxies whose stellar masses spanning three orders of magnitude at 0 <  z <  4. There are different ways to parametrise Zgas as a function of M⋆ or redshift and SFR, either through the fundamental metallicity relation (FMR; Mannucci et al. 2010, 2011; Curti et al. 2020; Chruslinska & Nelemans 2019), or the mass-metallicity relation (MZR, e.g. Kewley & Ellison 2008; Maiolino et al. 2008; Zahid et al. 2014; Genzel et al. 2015; Hunt et al. 2016).

We applied three different prescriptions known from the literature: (1) the MZR from Hunt et al. (2016), which is based on compiled observations of almost 1000 galaxies observed up to z = 3.7. The Zgas from their sample stretch over two orders of magnitude, while SFRs and stellar masses span five orders of magnitude. They quantify the metalicity as: Zgas = −0.14log(SFR)+0.37log(M⋆)+4.82; (2) The MZR from Genzel et al. (2015, their Eq. (12a)), in which a large sample of galaxies is analysed with either CO line measurements or well-sampled dust SEDs. The galaxies studied by Genzel et al. (2015) span a wide redshift range (0 <  z <  3), and contain a significant fraction of DSFGs. (3) Broken metallicity relation (BMR) proposed by Béthermin et al. (2015), which functions, in principle, like the FMR with a correction of 0.30 × (1.7 − z) dex at z >  1.7.

We then substitute different prescriptions for Zgas and Mgas/M⋆ into Eq. (3). For parameters entering Zgas and Mgas/M⋆, we use our SED derived M⋆, SFR, z, along with ΔMS. By doing this, from Eq. (3), we infer the related cosmic evolution of the Mdust/M⋆. In Fig. 5, we display the modelled evolutionary tracks for MS and SB DSFGs compared to the observed data. We see that up to z ∼ 2−2.5, irrespective of their ΔMS, the observed dust-to-stellar mass evolution can be well-described by any of adopted gas scaling relations, along with the evolution of Zgas derived from Hunt et al. (2016) or Genzel et al. (2015). At z >  2.5, the predictions significantly differ and we find that our data favour the best-fit function from Liu et al. (2019a) and Tacconi et al. (2018), rather than that of Scoville et al. (2017) as it overestimates our values both for MS and SB DSFGs. We also find a larger dispersion of the residuals from the model fits in SB DSFGs than in MS DSFGs, which could imply a wider range of intrinsic physical properties (e.g. Zgas) in our starbursts. Our results for SB DSFGs broadly agree with that of Tan et al. (2014) who fit a compilation of individual starbursts with mildly rising trend of Mdust/M⋆ with redshift, quantified as Mdust/M⋆ ∝ (1 + z)0.51. While we see a broad agreement with Tan et al. (2014) at z ≳ 2, we find that at z ≲ 2 the evolution of Mdust/M⋆ in our SB DSFGs can be best modelled as Mdust/M⋆ ∝ (1 + z)1.13, suggesting much steeper rise.

thumbnail Fig. 5.

From top to bottom: cosmic evolution of Mdust/M⋆ modelled as a combination of gas mass-scaling relations and MZRs. We test the gas scaling relations from Liu et al. (2019a), Tacconi et al. (2018) and Scoville et al. (2017). To model the evolution of gas-phase metallicity, we test different MZRs from Hunt et al. (2016), Genzel et al. (2015), along with the broken fundamental metallicity relation (BMR, Béthermin et al. 2015). The overplotted shaded regions are the same observed data (MS and SB DSFGs) presented in the upper left panel of Fig. 4.

We apply the relation from Liu et al. (2019a) and compute the median Mgas, obtaining Mgas = 9.1 × 1010 M⊙ for MS DSFGs and Mgas = 1.1 × 1011 M⊙ for SB DSFGs. The relation of Scoville et al. (2017) tends to overpredict these values by factor of 1.5−2 relative to Liu et al. (2019a) and Tacconi et al. (2018). Interestingly, the same difference has been reported by Dessauges-Zavadsky et al. (2020), who applied [CII] as a tracer of molecular gas content in a large sample of MS galaxies with a median stellar mass of 109.7 M⊙. The differences between the gas scaling relations have already been investigated in the literature (see discussions in Liu et al. 2019a; Millard et al. 2020). As mentioned in Miettinen et al. (2017), a potential caveat of the Scoville et al. (2017) approach could be assumption of a constant Tdust. The intensity of the radiation field is expected to evolve and, thus, we find that increasing the Tdust (e.g. from 25 to 45 K) the inferred Mgas decreases by a factor of ∼1.3, which would partially explain the offset to our data. An additional reason why the Mdust/M⋆ computed from the Scoville et al. (2017) best-fit overestimates our data could be the way they assign stellar masses to their galaxies. The scaling relation is calibrated based on the ΔMS of IR-bright DSFGs for which SFRs were computed from LIR, but assigned M⋆ were derived separately from optical-NIR SEDs. This approach carries the risk of underestimating M⋆ to those computed from self-consistent SED fitting from UV to sub-mm (Mitchell et al. 2013; Buat et al. 2014). On top of this, the gas scaling relations from Tacconi et al. (2018) and Liu et al. (2019a) account for metalliciity correction, which is not the case for Scoville et al. (2017).

Next, we apply MZR from Genzel et al. (2015) and infer median Zgas expressed as 12 + log(O/H), obtaining 12 + log(O/H) = 8.64 ± 0.05 and 12 + log(O/H) = 8.52 ± 0.09, for MS and SB DSFGs, respectively. These values let us characterise both MS and SB DSFGs as metal-rich objects, since the estimated Zgas are close to solar (12 + log(O/H) = 8.69, Allende Prieto et al. 2001). It is important to stress that the Zgas of high-z SB DSFGs is a topic of active debate (see e.g. discussions in Tan et al. 2014; Liu et al. 2019a; Tacconi et al. 2020). On one hand, optical/near-IR spectroscopy suffers from high dust attenuation and, on the other hand, the statistics of sources that have been spectroscopically studied through fine structure lines with ALMA is still limited (Boogaard et al. 2019). While many studies suggest that at fixed M⋆ objects with higher ΔMS are more gaseous and less metallic, there are recent, opposite claims suggesting super-solar metallicities that imply lower Mgas, but higher SFE and higher δDGR of SB DSFGs, much as in local ULIRGs (Downes & Solomon 1998; Magdis et al. 2012; Puglisi et al. 2017; Silverman et al. 2018; Valentino et al. 2020). For example, using the prescription for Mgas given by Sargent et al. (2014), Béthermin et al. (2015) found that, in order to match the observed Mdust/M⋆, their extreme starbursts require δDGR ≈ 1/50, appropriate for Zgas twice as high as solar (12 + log(O/H) ≈ 9). The fact that modelled curves for SB DSFGs at z >  2.5 are slightly above the data also supports this hypothesis. Our data cannot fully solve this issue, and we caution that our conclusions rely on the assumption that our DSFGs do not deviate strongly from adopted scaling relations. Nevertheless, even with large uncertainties in Zgas, the high Mdust/M⋆ and its very slow decline towards high-z suggest that SB DSFGs were substantially metal abundant even in the distant Universe. This strongly implies the need of rapid metal enrichment in the early star-formation phase. Furthermore, our general conclusion from this modelling exercise is that high Mdust/M⋆ originates from the fact that massive DSFGs are metal-rich. Such rapid metal enrichment at high-z would lead to the solar (or even several times solar) Zgas of very massive, quiescent objects into which these DSFGs might evolve (Man et al., in prep.).

The chemical models that do not include grain growth in the ISM have difficulty matching the dustiest objects under the standard IMF (Dunne et al. 2011; Rowlands et al. 2014; De Vis et al. 2017; Calura et al. 2017). For example, Burgarella et al. (2020) proposed the dust formation scenario, assuming the high dust condensation efficiencies from stellar ejecta and non-standard “top-heavy” IMF, but found the maximum values limited to Mdust/M⋆ ≤ 10−2. Consequently, it would be hard to fully reproduce the significant number of observed DSFGs that populate the top-right corner of Mdust/M⋆−sSFR plane.

It has been postulated that the timing of effective growth of the Mdust growth in the ISM is determined by Zgas (see e.g. Asano et al. 2013). If Zgas in a galaxy exceeds a certain critical value, the grain growth becomes active and the Mdust rapidly increases until metals are depleted from the ISM. This critical value of Zgas is larger for a shorter star-formation timescales, which is well supported by our data, since the typical star-formation timescale (M⋆/SFR) of our DSFGs is less than 1 Gyr, with the median of 8.3 × 108 yr. In addition, 47 sources (15% of the total sample) form their stellar masses at very short timescales of ≲100 Myr. Studying the evolution of galaxies in the SAGE semi-analytical model, Triani et al. (2020) have found that the grain growth starts to dominate overall dust production if 12 + log(O/H) ≳ 8.5 and log(M⋆/M⊙) ≳ 9.2. Here, 84% of our sources fulfil both of these criteria, which implies that the dust grain growth in ISM would be the dominant source of dust production in the vast majority of observed DSFGs. However, to better understand the evolution of Mdust/M⋆ within the framework of dusty galaxy formation, in the next section we inspect models, along with the state-of-the-art cosmological simulations that track the dust life cycle in a self-consistent way.

5. Comparison to the models of dusty galaxy formation and evolution

Theoretical works that aim at investigating the evolution of dust content in galaxies can broadly be separated into analytic and semi-analytical solutions (e.g. Lacey et al. 2010; Gioannini et al. 2017; Popping et al. 2017; Imara et al. 2018; Pantoni et al. 2019; Triani et al. 2020) and hydrodynamical simulations (McKinnon et al. 2017; Aoyama et al. 2018; Hou et al. 2019; Vijayan et al. 2019; Davé et al. 2019). On top of this, there are also phenomenological models (e.g. Cai et al. 2013; Schreiber et al. 2016; Béthermin et al. 2017). The latter group of models are not ab initio, but they could be very useful for complementing our knowledge about specific galaxy population.

5.1. Models

In this work, we consider all three classes of models outlined above. Namely, we analyse the predictions from the: (I) cosmological galaxy formation simulation with self-consistent dust growth and feedback (SIMBA, Davé et al. 2019; II) analytical model of Pantoni et al. (2019); and (III) phenomenological model based on multi-band surveys (Béthermin et al. 2017).

5.1.1. SIMBA cosmological simulation

The cosmological galaxy formation simulation, SIMBA, utilizes mesh-free finite mass hydrodynamics (Hopkins 2015; Davé et al. 2016). We refer the reader to Davé et al. (2019) for extensive description of the simulation and, here, we summarise the most important points. The primary SIMBA simulation has 10243 dark matter particles and 10243 gas elements in a cube of 100 Mpc h−1 side length. The simulation preserves the mass within each fluid element during the evolution, thereby, enabling detailed tracking of gas flows. Star formation is modelled using a molecular H2 gas relation from Schmidt (1959), with the abundance of H2 computed from sub-grid prescription that connects Zgas and gas column density in the local Universe (Krumholz et al. 2012). SIMBA applies fully physically-motivated black-hole growth following the work of Anglés-Alcázar et al. (2017). The novel sub-grid prescriptions for AGN feedback and X-ray feedback are also included. The implementation of dust life cycle is introduced in Li et al. (2019). It is broadly based on the seminal work by Dwek (1998) and its updated version by Popping et al. (2017) and McKinnon et al. (2017).

The net dust production-destruction rate in SIMBA can be generalised as:

Σ M ˙ dust ∝ M ˙ dust SNe + M ˙ dust ISM − M ˙ dust destr − M ˙ dust SF + M ˙ dust inf − M ˙ dust out . $$ \begin{aligned} \Sigma \dot{M}_{\rm dust}\propto \dot{M}_{\rm dust}^\mathrm{SNe}+\dot{M}_{\rm dust}^\mathrm{ISM} - \dot{M}_{\rm dust}^\mathrm{destr}- \dot{M}_{\rm dust}^\mathrm{SF}+ \dot{M}_{\rm dust}^\mathrm{inf}- \dot{M}_{\rm dust}^\mathrm{out}. \end{aligned} $$(4)

The first term on the right side of Eq. (4) describes the dust produced by condensation of a fraction of metals from the ejecta of SNe and asymptotic giant branch (AGB) stars; the second term describes the dust by accretion in the ISM; the third term describes the dust destructed by SNe shock waves; the fourth term is the destruction of dust by astration and stellar feedback; the fifth term is an additional dust production by gas infall; the sixth term describes the expelled dust mass, due to SNe and AGN. The latter two mechanisms are responsible for heating up and removal of gas from the ISM into the DM halo (or even further out).

The full treatment of dust is explained in details by Eqs. (11)−(31) in Davé et al. (2019) and Eqs. (1)−(11) in Li et al. (2019). In general, the dust model makes the explicit assumption that dust can grow only in the dense regions of the ISM. The production of dust by condensation of metals from SNe and AGB ejecta is estimated by Eqs. (4)−(7) in Popping et al. (2017). The dust model within SIMBA does not include contribution from Ia SNe which is opposite to some models that proposed the same condensation efficiency between Type Ia SNe and Type II SNe (Dwek 1998; McKinnon et al. 2017; Popping et al. 2017).

Overall, SIMBA accounts for dust produced from ageing, stellar populations, grain growth, destruction in SN shocks, and the advection and transport of dust in galactic winds. Dust is injected into the ISM as stars evolve off the MS, with Mdust calculated using stellar nucleosynthetic yields and grain condensation efficiencies. The timescale for grain growth through collisions depends on local gas density and temperature, while the timescale for dust destruction through SN sputtering scales inversely with the local SNe rate. The dust grains are assumed to all have the same radius and density (a = 0.1 μm and σ = 2.4 g cm3), respectively (see e.g. Draine et al. 2014). The condensation efficiencies for AGB and core-collapse supernovae (CC SNe) are constant (0.2 and 0.15, respectively). These values are tuned in order to match the observed δGDR − Zgas relation by Rémy-Ruyer et al. (2014).

5.1.2. Pantoni et al. (2019) model

Pantoni et al. (2019, hereafter P19) presented a new set of analytic solutions that self-consistently describes the spatially-averaged time evolution of gas, stellar, metal, and dust content in individual galaxies hosted within a DM halo of a given mass and formation redshift. In particular, the solutions have been applied to the description of high-z DSFGs as the progenitors of local ellipticals. The basic framework is described in P19. It presumes the galaxy as an open (one-zone) system comprising three inter-linked mass components: a reservoir of infalling gas (subject to cooling and condensation), cold star-forming gas (fed by gas infall and depleted by star formation and feedback), and stellar mass (partially restored to the cold phase by stars during their evolution). The corresponding metal and dust enrichment history of the cold gas is self-consistently computed using as input the solutions for the evolution of the mass components. The evolution of Mdust takes into consideration all the relevant physical processes contained in Eq. (4). For exact details about the gas metallicity and dust treatment, see Eqs. (9)−(14) and (33)−(39), respectively, in Pantoni et al. (2019). The main parameters entering the solutions have been set by relying on an in situ evolutionary framework, implying that the star formation in DSFGs at high-z is mainly regulated by internal processes (e.g., Moster et al. 2013; Lapi et al. 2018). Coupling the outcome for individual galaxies with merger rates based on the state-of-the-art numerical simulations, the P19 model show success in reproducing the main statistical relationships followed by high-z DSFGs (e.g., galaxy MS, Mgas, Mdust, etc.) and by their local descendants (e.g., mass-metallicity relation, alpha-enhancement, etc.).

5.1.3. Béthermin et al. (2017) model

The phenomenological model of Béthermin et al. (2017, hereafter B17) relies on the combination of observed dust SED templates of galaxies and IR luminosity functions. The B17 is built on IR/sub-mm data and it is one of few models that are able to simultaneously match the total IR number counts and the evolution of sSFR. The model applies the abundance matching procedure to populate the DM halos of a light cone constructed from the Bolshoi-Planck simulation (Rodríguez-Puebla et al. 2016). The halo catalogues are matched to the observed galaxy stellar mass function (SMF) described by a double Schechter function (Davidzon et al. 2017). Physical properties (SFR, M⋆) are assigned to each object based on the dichotomy model which decomposes bolometric IR-luminosity function with MS and SB dusty galaxies. Furthermore, B17 assume that the scatter on the MS is constant with M⋆ and redshift. The shape of the SEDs is controlled by the galaxy type (MS or SB) and with the mean intensity of the radiation field ⟨U⟩, which couples with the Tdust. Contribution of AGNs and strong lensing are also included following the recipe presented in Béthermin et al. (2012).

5.2. Confronting observed results to models

We now confront our observational findings to the models described above. In order to achieve this goal, we analyse the simulated catalogues. To ensure consistency between observed and simulated data, we impose the same range of modelled M⋆ and sSFR as in our observations (log(M⋆/M⊙) > 10 and log(sSFR/yr−1)>  − 9.5). We note that same IMF (Chabrier 2003) is adopted both in observed and simulated data. We separate modelled galaxies into MS and SB DSFGs following the exact same method we apply over our real data.

We illustrate our findings in Fig. 6, where we show how the Mdust/M⋆ changes as a function of redshift (left panel) and sSFR (right panel). Considering the B17 model, we see that the model predictions are in a good agreement with our data both for MS and SB DSFGs. Despite the fact that B17 is based on averaged observed statistical properties of galaxies and very simplified physical prescriptions, it is successful in matching both the observed evolution of Mdust/M⋆ versus z and sSFR within the 1σ uncertainties. From the left panel, we see that the Mdust/M⋆ modelled for SB DSFGs has a small positive offset of 0.05 dex to our data at the highest redshift bins (z >  3). This indicates that due to our selection criteria, we are likely to miss some rare and prodigious starbursts at high-z. These sources are usually barely detectable even in very deep NIR data and their existence at 3 <  z ≤ 5 has only been confirmed by recent blind ALMA surveys (Williams et al. 2019; Franco et al. 2018; Wang et al. 2019). It is worth noting that in B17 the mean interstellar radiation field ⟨U⟩ steadily evolves in MS DSFGs, but is tuned to be constant in SB DSFGs over 0 <  z <  3. This implies the existence of starbursts that could be slightly colder than MS DSFGs at the same redshift, having very high dust masses (Mdust ≳ 109 M⊙). The latter could be an additional reason why at z ∼ 3 the B17 predicts slightly higher Mdust/M⋆ than in our observations. Nonetheless, the agreement we see between our data and B17 model suggests that our empirical knowledge of how the Mdust/M⋆ evolves within the MS paradigm is moving towards a more comprehensible picture. Such a conclusion is strongly supported by observations of the cosmic evolution of Mgas and sSFR (Liu et al. 2019a).

thumbnail Fig. 6.

Left: redshift evolution of Mdust/M⋆ predicted by different models (see Sect. 5.1). The observed data are overplotted with same colours as in previous figures. The grey, blue, and purple dashed and dotted lines represent predictions for galaxies selected as MS and SB DSFGs from Béthermin et al. (2017), Davé et al. (2019) and Pantoni et al. (2019), respectively. Right: evolution of Mdust/M⋆ as a function of sSFR for the full sample of observed and modelled galaxies. The binned values from this work are shown with black circles with corresponding 1σ vertical error bars. The model predictions are denoted with same colours as in the left panel.

The theoretical predictions of P19 are also broadly consistent with the observed evolution of Mdust/M⋆ with redshift and sSFR, and the overall agreement is valid both for MS and SB DSFGs. One of the major forecasts of P19 is very rapid evolution of Zgas, which attains high values in a quite short timescale (≲108 yr) while being mainly related to in situ processes. Such a rapid evolution becomes particularly important for reproducing the Zgas in z >  3 DSFGs. In P19, the authors predict that Zgas in massive (∼1012 M⊙) DM halos saturates close to slightly super-solar values for the case of standard (Chabrier 2003) IMF. This is an important finding, since many chemical and semi-analytical models propose the use of “top-heavy” IMF as the only solution for assuring very high Mdust and rapid metal enrichment in massive galaxies (e.g. Lacey et al. 2016; Calura et al. 2017). The P19 model also predicts that Mgas increases monotonically up to M⋆ ∼ 1011 M⊙, above which the gas infall and condensation become less efficient causing the subsequent decline in Mgas. This can be a cause of a rapid downfall of Mdust/M⋆ towards the lower sSFR. The good agreement with P19 model provides a strong support to the scenario where significant dust growth in the metal-rich ISM is needed to explain the high Mdust/M⋆.

Compared to the observations of MS DSFGs, the cosmological simulation SIMBA reproduces Mdust/M⋆ well up to z = 1.5, while at z >  1.5 the modelled values are lower but still compatible with the data within 1σ. The modelled Mdust/M⋆ remains as a weakly decreasing function of z, pronounced with an overall change of amplitude by roughly 0.25 dex. This is another success of SIMBA and indicates that the simulation is able capturing the massive dust production (Mdust >  109 M⊙) towards earlier cosmic times, which is hardly reproduced by most of cosmological simulations (see e.g. discussions in McKinnon et al. 2017; Graziani et al. 2020). However, SIMBA is less successful in reproducing the observed Mdust/M⋆ in SB DSFGs and underpredicts this quantity by factor of 3−6 depending on the redshift. The discrepancy between the observed and modelled Mdust/M⋆ towards the higher ΔMS is well-illustrated in the right panel of Fig. 6.

We see that at log(sSFR/yr−1) ≳  − 8.5 the SIMBA predicts much flatter trend with sSFR relative to data, which implies the deficiency of simulated objects with Mdust/M⋆ ≳ 10−2. We find that the relative contribution of sources fulfilling the criterion Mdust/M⋆ >  10−2 is 20% in B17 and only 2% in SIMBA. The underestimation of modelled DSFGs with the highest dust masses (Mdust >  109 M⊙) has already been discussed by Li et al. (2019), who compared simulated dust mass functions from SIMBA and the observed ones at 0 <  z <  2, inferring a ∼2−4 underestimation of model to data. We note that if Mdust and zphot are derived from FIR data only, they could suffer from large uncertainties, and the high-z DMFs are very uncertain constraint on cosmological models. On the contrary, due to the wealth of multiwavelength data coverage and de-blended IR photometry complemented with ALMA observations, estimated Mdust and M⋆ have significantly smaller uncertainties. Therefore, it seems unlikely that our technique led to significant underestimation (overestimation) of derived M⋆ (Mdust). If the latter is true, this could indicate that some model ingredients in SIMBA need to be refined (such as amount of molecular gas relative to stars or dust destruction mechanisms in the sub-grid model).

We note that our sample is incomplete at fixed M⋆, since most of sources were preselected for the purpose of ALMA follow-ups. This would cause difference in galaxy SEDs and starburst fractions as compared to complete samples within the same range of M⋆. We instruct the reader to Liu et al. (2019b) for detailed discussion of ALMA selection biases. Since ALMA Band 6/7 is sensitive to the galaxies with the Tdust colder than that of Herschel at a fixed LIR, we further approximate what would be the Mdust/M⋆ of a mass complete sample of modelled DSFGs. We use the full catalogue based on B17 model which is perfectly suitable for our goal since it is based on 2 deg2 simulation. We relaxed the selection criteria in order to inspect the average Mdust/M⋆ of all unlensed sources with M⋆ >  1010 M⊙ below the detection limit. The “missed” DSFGs peak at z ≈ 3 and they are warmer than ALMA selected sample due to their higher average ⟨U⟩ (thus Tdust). However, the inclusion of these sources does not significantly impact our results since the median Mdust/M⋆ of “missed” objects is found to be 0.004 for MS and 0.008 for SB DSFGs.

5.3. Considering what lies behind the tension between the simulations and observations

In Sect. 4.4, we give a sense of how the Mdust/M⋆ is influenced by different evolutions of molecular gas mass ratio and Zgas. We now turn our attention in investigating the trends with the latter two quantities through modelling. The P19 model predicts the average Zgas, that is, 0.1 dex and 0.02 dex above the solar value for MS and SB DSFGs, respectively. The median Zgas in MS (SB DSFGs) modelled in SIMBA is 0.24 dex (0.22 dex) below the solar. The values are reasonable high for both galaxy populations, but still lower by a factor of ∼1.5 to the medians derived from our data (see Sect. 4.4). This implies that lower Mdust/M⋆ predicted by SIMBA would be partly resulting from lower modelled Zgas.

In order to unveil how the dust, stellar, and molecular gas budget are interlinked in models, we further analyse the simulated δDGR and molecular gas fraction, defined as fgas = Mgas/(Mgas + M⋆). In the upper panel of Fig. 7, we show the fgas as a function of redshift. For our DSFGs, we apply the gas scaling relation of Liu et al. (2019a), inferring the median value of fgas = 0.51 ± 0.12 for the full sample, along with fgas = 0.44 ± 0.09 and fgas = 0.75 ± 0.09 for MS and SB DSFGs, respectively. The observed fgas in SB DSFGs is ∼2−3 times higher than in MS DSFGs, independently of the compared redshift range. Such a clear distinction of fgas in MS and SB DSFGs is in agreement with other studies from the literature (Magdis et al. 2012; Santini et al. 2014; Béthermin et al. 2015; Scoville et al. 2016; Saintonge et al. 2017; Liu et al. 2019a; Simpson et al. 2020).

thumbnail Fig. 7.

Upper panel: cosmic evolution of molecular gas fraction (fgas) in our DSFGs, estimated from the functional form of Liu et al. (2019a) and illustrated with shaded areas. The model predictions for MS and SB DSFGs are overplotted with dashed and dotted lines, respectively. Purple, blue, and grey lines correspond to P19, SIMBA, and B17 respectively. For P19 and SIMBA, the fgas is derived self-consistently, while for B17, we test the same scaling relation we apply in our observations. Lower panel: δDGR as a function of fgas for the full sample of observed and modelled galaxies. Observed mean ratios with corresponding 1σ uncertainty are presented with black circles. The significance of colours that correspond to modelled values is the same as in the upper panel.

We find that the modelled results for fgas are consistent to our estimates for MS DSFGs, with the difference that SIMBA predicts a slower rise of fgas with redshift, as compared to P19 and B17. The models have different success reproducing fgas of SB DSFGs. The B17 and P19 predict continuous increase of fgas, which broadly agrees with our estimates. In considering SIMBA, we see that larger ΔMS is accompanied by only moderate increase of galaxy molecular gas fraction up to z ≃ 2.5 and riches values close to ours only at z ≥ 2.5, where the statistics of modelled starbursts is low. The corresponding median fgas in SB DSFGs modelled by SIMBA is of fgas = 0.45, which is half as much as what our data suggest.

We further investigate how the δDGR scales with fgas. For the full sample of observed DSFGs, we determine the median value of δDGR = 1/148. For MS and SB DSFGs, separately, the medians are δDGR = 1/159 and δDGR = 1/139, respectively. Although the derived values are strongly model dependent, they indicate that MS and SB DSFGs exhibit a slightly different average δDGR (however, see our discussion in Sect. 4.4). The median δDGR in both MS and SB DSFGs agree very well with the calibration by Schreiber et al. (2018), but they are sightly lower than canonical value obtained for local ULIRGs (δDGR = 1/100, Leroy et al. 2011). These points should be borne in mind when applying δDGR for Mgas estimation for high-z DSFGs.

From the bottom panel of Fig. 7 we see that observed δDGR mildly decreases with increasing fgas and flattens at fgas ≳ 0.5. The range of δDGR predicted by B17 and P19 is within 1σ uncertainty with our data, while predictions from SIMBA are consistent at fgas <  0.5, but significantly differ at fgas >  0.5 due to steeper decrease compared to our data. Such a sharp reduction in δDGR translates to relatively low number of DSFGs with Mdust/M⋆ ≳ 0.01 produced in cosmological simulations. By investigating the connection between the δDGR and Zgas in SIMBA, we find that very low δDGR in galaxies from the highest-end of gas fraction is a result of their gas metallicities being lower by a factor of ∼4 relative to solar. The comprehensive treatment of different physical mechanisms that could be responsible for relative shortfall of model predictions, along with numerical limitations, is out of the scope of this paper. In the following we briefly emphasize their importance.

The dust growth timescale is too long. One of the most critical parameters that describes the dust mass growth is the accretion timescale (τacc). It is often modelled as:

τ acc = τ acc , 0 × a − 1 × n H − 1 × T gas − 1 / 2 × Z gas − 1 , $$ \begin{aligned} \tau _{\rm acc} = \tau _{\rm acc,0} \times a^{-1} \times n_{\rm H}^{-1}\times T_{\rm gas}^{-1/2} \times Z_{\rm gas}^{-1}, \end{aligned} $$(5)

where a is a dust grain size which is usually assumed to be spherical with a typical size of ∼0.1 μm (Asano et al. 2013). The nH and Tgas are the number density and temperature of the cold gas phase, and τacc, 0 defines the timing of growth activation. The timescale for dust growth in the ISM changes as a function of gas surface density for different Zgas (see Popping et al. 2017, their Fig. 1). If we apply Mgas of our DSFGs, along with their compact ALMA continuum sizes (see the next section), we infer high median molecular gas surface density of ∼6.7 × 103 M⊙ pc−2. Such a high surface density implies short accretion timescales, on average τacc ∼ 6 × 105 yr. These will be obtained if τacc, 0 <  106 yr which is shorter than what has usually been adopted in cosmological simulations6. The short τacc are proposed by Pantoni et al. (2019), and are also reproduced in very recent semi-analytical models that claim fairly good overall match to the observations (Triani et al. 2020). These are also in line with De Vis et al. (2017), who found that variations in dust growth timescales might help to explain the Mdust deficit at high gas-fractions in their large sample of nearby galaxies. Given the SIMBA’s ∼kpc resolution, a multiphase galaxy ISM cannot be resolved, which prevent us from knowing the exact dependence of the modelled dust content to the gas surface density. As a result, parameters such as the reference τacc are tuned in order to boost the effective gas density. Thereby, it seems likely that use of shorter accretion timescales (equivalent to the increase in dust growth efficiency) in simulations could help partially overcome the shortfall to data.

Dust destruction is too efficient. It is also possible that the dust destruction in simulations is too efficient. The total rate of dust mass destruction is given by Ṁdest ∝ Mdust/τdestr, where dust destruction timescale is usually approximated as (Slavin et al. 2015):

τ destr = Σ M gas f ISM R SN M cl = τ SN M gas M cl · $$ \begin{aligned} \tau _{\rm destr} = \frac{\Sigma M_{\rm gas}}{f_{\rm ISM}R_{\rm SN}M_{\rm cl}} = \frac{\tau _{\rm SN}M_{\rm gas}}{M_{\rm cl}}\cdot \end{aligned} $$(6)

Here ΣMgas is the surface density of molecular gas mass, fISM is the value that accounts for the effects of correlated SNe, RSN is the SNe rate, τSN is the mean interval between supernovae in the Galaxy (the inverse of the rate) and Mcl is the total ISM mass swept-up by a SN event. Here, is important to note that Mcl varies with the ambient gas density and metallicity, and as metals offer an efficient cooling channel in the ISM, higher Zgas would result in a smaller swept mass (see Asano et al. 2013; Hou et al. 2019). Our galaxies are both gas-rich and metal-rich, and by adopting our average values for Mgas and Zgas, we can roughly approximate distraction timescale. Following Slavin et al. (2015), we infer that τdestr is in the range of 0.17 Gyr to 1.87 Gyr, with median of 0.89 Gyr for MS DSFGs, and 0.36 Gyr for SB DSFGs. In fact, the τdestr could increase even more if galaxy magnetic field is stronger at high-z, causing less dust acceleration thus less destruction (Slavin et al. 2015). Therefore, the excess Mdust/M⋆ could point to those systems where the dust survival rate is different at earlier times, as postulated by Dwek et al. (2014). We caution, however, that the main sources which dominate the uncertainties (e.g. SNe rate and the ISM model) are very difficult to determine accurately from observations.

Additional physical mechanisms. The modelled strong anti-correlation of δDGR with fgas could also hint at an overefficient feedback mechanism in cosmological simulations (Hirashita & Nozawa 2017; Aoyama et al. 2018). In this work, we consider a full SIMBA suite that includes both AGN feedback and X-ray heating by black holes. Without these two effects included, we would expect a much weaker anti-correlation between the fgas and M⋆ which would naturally lead to weaker anti-correlation between Mdust/M⋆ and M⋆. This would strongly disagree with our observations (see Fig. 4). On top of this, variations in destruction timescales and efficiencies of ISM dust through SN shocks are also dependent on dust grain size distribution. While most of the simulations discussed in this paper, including SIMBA, adopt same grain physical sizes (a = 0.1 μm), it is postulated that the large fraction of Mdust can survive if grain sizes are larger (Biscaro & Cherchneff 2016; Zhukovska et al. 2016; Aoyama et al. 2019). Finally, the excess ratio between the dust-to-stellar mass could be due to significant Mdust in the large reservoir of metal-enriched circumgalactic gas, as recently observed through ALMA [C II] search on scales of 10−20 kpc (Fujimoto et al. 2019; Ginolfi et al. 2020).

6. Role of compact dusty star-formation in “giants”

To gain an additional insight into the ISM of our DSFGs, we explored the influence of galaxy IR size on Mdust/M⋆. For this purpose, we adopt ALMA dust continuum sizes obtained through homogeneous uv-visibility size analyses with the exponential disk model (n = 1, see Fujimoto et al. 2017 for the detailed description of the procedure). In order to probe the surface densities of dusty star-formation, we follow the approach from Elbaz et al. (2018). Using the SED derived LIR of our sources and their rest-frame IR continuum sizes, we compute the IR luminosity surface density (ΣIR) defined as 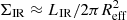Σ IR ≈ L IR / 2 π R eff 2 $ \Sigma_{\mathrm{IR}}\approx{L_{\mathrm{IR}}}/ 2\pi R_{\mathrm{eff}}^{2} $, where Reff is an circularized effective ALMA radius of the source (in kpc).

The median IR size of the full sample is Reff = 1.51 kpc. We find that SB DSFGs are more compact than MS DSFGs (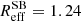 R eff SB = 1.24 $ R_{\mathrm{eff}}^{\mathrm{SB}}=1.24 $ kpc vs. 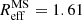R eff MS = 1.61 $ R_{\mathrm{eff}}^{\mathrm{MS}}=1.61 $ kpc respectively). The ΣIR ranges from 3.1 × 1010 − 9.3 × 1012 L⊙ kpc−2, with the median of ΣIR = 6.9 × 1011 L⊙ kpc−2 for the full sample7. The average sizes and ΣIR are typical to those derived for IR-selected DSFGs at z ∼ 2.5 for which the majority of the dusty star formation occurs in a central region (e.g. Simpson et al. 2015; Ikarashi et al. 2015). We find that five of the DSFGs have very high surface densities (ΣIR >  5 × 1012 L⊙ kpc−2). They are suitable candidates for approaching the Eddington limit, which is estimated to be ∼1013 L⊙ kpc−2, based on the balance between the radiation pressure from the star-formation and the self-gravitation (Andrews & Thompson 2011). Such non-AGN candidates for Eddington limited starbursts are known in the literature (e.g. Riechers et al. 2013; Gómez-Guijarro et al. 2018) and it has been proposed that for at least some of them significant dust emission could be excited by an outflow (Oteo et al. 2017).

To further inspect how the galaxy ΣIR impact their dust-to-stellar mass content withing the MS paradigm, we split our full sample in two groups of objects based on their ΣIR. We arbitrarily define “less compact” DSFGs with intermediate surface densities (ΣIR <  1012 L⊙ kpc−2, with 236 objects in total), and “more compact” DSFGs, due to their higher surface densities (ΣIR >  1012 L⊙ kpc−2, with 64 objects in total).

In Fig. 8, we show how the Mdust/M⋆ relates to ΔMS along with galaxy ΣIR. We note that for easier graphical representation of our results, on x-axis we show the galaxy offset to MS in log scale, labelled as ΔMS. From Fig. 8, we see that Mdust/M⋆ tightly relates to ΔMS regardless of the galaxy ΣIR. Within the MS, the objects with intermediate and high ΣIR have almost identical Mdust/M⋆. Above the MS, the Mdust/M⋆ is slightly higher in more compact sources with higher ΣIR8.

thumbnail Fig. 8.

Observed Mdust/M⋆ as a function of a galaxy offset to the MS, defined as ΔMS = log(SFR/SFRMS). Galaxies with intermediate and high ΣIR are denoted with grey and red circles, respectively. The shaded region represents the sequence of MS defined by Speagle et al. (2014) with a 0.5 dex (3 times) scatter. The points that lie outside the grey region represent the SB DSFGs.

The tight relation of Mdust/M⋆ with ΔMS can be interpreted by “in situ” framework which predicts that sources could appear above the MS when caught in an early evolutionary stage. In passing from SB to MS DSFGs one is observing more aged systems and the decrease in Mdust/M⋆ is due to dust being formed on shorter timescales with respect to M⋆. Such interpretation is strengthen by SED derived young, mass-weighted ages of our SB DSFGs, with the median of 409 ± 60 Myr, half as long as in MS DSFGs. We caution that SED derived mass-weighted ages are strongly model-dependent (due to the age-metallicity degeneracy), even though our estimates agree with those reported in the literature (Dudzevičiūtė et al. 2020; Martis et al. 2019).

The link between ΣIR and Mdust/M⋆ less obvious and more challenging to interpret. In the Local Universe, a decrease in size can enhance the efficiency of transforming atomic gas into molecular gas, boosting the Mgas (Larson et al. 2016; Kirkpatrick et al. 2017). Recently, Cochrane et al. (2019) performed detailed study of the spatially-resolved dust continuum emission of simulated DSFGs at z >  1 and found that the most compact dust emission is driven by particularly compact recent star-formation. Distant DSFGs are also expected to have highly turbulent ISM (Scoville et al. 2016). Turbulence can rapidly accelerate the grain growth (Mattsson 2020), which would increase the amount of large dust grains relative to small ones, and produce colder Tdust for a given radiation field. If dust emission is optically thin, this would result in higher Mdust at a given LIR. In our companion paper (Paper II, Donevski et al., in prep.), we will present a detailed analysis of various mechanisms that produce the high dust and gas densities in distant DSFGs.

Future James Webb Space Telescope (JWST) data combined with larger ALMA samples will be of crucial importance for discriminating between different scenarios. The JWST will be able to derive accurate estimates of the AGN contribution to the most massive DSFGs and place important constraints on the gas reservoirs of these sources from various near-IR and mid-IR lines, resulting from a PAH cooling process.

7. Conclusions

We perform a systematic study of the dust-to-stellar mass ratio in 300 massive (M⋆ >  1010 M⊙) DSFGs in the COSMOS field, observed with ALMA over a wide redshift range (0.5 <  z <  5.25). We apply self-consistent, multi-band SED fitting method and explore trends of Mdust/M⋆ with different physical parameters in galaxies within and above the main sequence. We fully evaluate our findings with the models of dusty galaxy formation and evolution. Our main results are summarised as follows:

  • We find that Mdust/M⋆ evolves with the redshift, stellar mass, and specific star formation rate. For both galaxy populations the Mdust/M⋆ rises up to z ∼ 2, steeper in SB than in MS DSFGs, followed by mild decline or flattening at z ≳ 2. We infer the median of 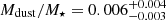M dust / M ⋆ = 0 . 006 − 0.003 + 0.004 $ M_{\mathrm{dust}}/M_{\star}=0.006^{+0.004}_{-0.003} $ and M dust / M ⋆ = 0 . 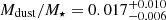017 − 0.006 + 0.010 $ M_{\mathrm{dust}}/M_{\star}=0.017^{+0.010}_{-0.006} $ for MS and SB DSFGs, respectively. Regardless of the observed redshift, the SB DSFGs typically have ∼3 times higher Mdust/M⋆ as compared to MS DSFGs.

  • Contrary to local ULIRGs, the Mdust and SFR in our high-z DSFGs obey a sub-linear trend that exhibits a plateau above the characteristic dust mass (Mdust ≈ 109 M⊙). This implies a possible evolution in terms of the dust properties (e.g. dust opacities).

  • We confirm, for the first time, that the inverse relation between Mdust/M⋆ and the M⋆ holds until z ≈ 5. The normalisation of this inverse relation gradually increases by ∼0.5 dex from z = 1 to z = 5. We interpret the observed trend as an evolutionary transition from earlier to later starburst phases of DSFGs.

  • We model the observed Mdust/M⋆ by applying empirical relations for fgas and MZR. Both MS and SB DSFGs require high, solar-like Zgas in order to match the estimated Mdust/M⋆. The modelled Mdust/M⋆ faithfully represents observed trend in MS DSFGs over the full redshift range. While adopted gas scaling relations anticipate somewhat larger average gas supply in SB than in MS DSFGs (Mgas = 1.03 × 1011 M⊙ vs. Mgas = 8.92 × 1010 M⊙, respectively), at the same time, they slightly overpredict our data for SB DSFGs at z >  2.5. The latter indicates the possibility of super-solar Zgas in some high-z starbursts, pointing towards the need for rapid metal enrichment.

  • We show that Mdust/M⋆ mirrors the increase in molecular gas fraction with the redshift. By linking the gas scaling relation from Liu et al. (2019a) and MZR from Genzel et al. (2015), we infer a median of fgas = 0.44 ± 0.09 for MS DSFGs and fgas = 0.75 ± 0.09 for SB DSFGs.

  • We fully evaluate our findings with different models of dusty galaxy formation. The cosmological simulation SIMBA (Davé et al. 2019) predicts the cosmic evolution of Mdust/M⋆ in MS DSFGs that is consistent within 2σ with our data. SIMBA underpredicts the Mdust/M⋆ in SB DSFGs. This points to the necessity of refining the dust treatment in simulations, for instance, by adding the recipes for dust size distribution or accounting for more rapid metal enrichment in the early starburst phase.

  • The observed Mdust/M⋆ in both MS and SB DSFGs is well-reproduced by the phenomenological model of Béthermin et al. (2017) and the analytic model of Pantoni et al. (2019). The overall agreement with these models has two important implications: (1) existing knowledge about galaxy star-formation MS and the Mdust/M⋆ leans towards the consistently quantitative picture; (2) fast dust growth through accretion in the metal-rich ISM is needed to capture the observed Mdust/M⋆ in high-z DSFGs.

  • We examine the link between Mdust/M⋆ and compact dusty star-formation along the MS paradigm. The observed Mdust/M⋆ in MS DSFGs relates to ΔMS regardless of the galaxy ΣIR, while for SB DSFGs we find an evidence that Mdust/M⋆ is enhanced in systems with higher ΣIR. Further investigation of these objects is crucial for understanding the role of compact dusty star-formation in galaxy evolution.

This work highlights the usefulness of analysing the different trends with Mdust/M⋆ as a diagnostic tool for current and future studies of DSFGs. Firstly, it can be applied to the separation of main-sequence galaxies and starbursts over a wide redshift range. This confirms and complements the conclusions presented in the seminal works of Tan et al. (2014) and Béthermin et al. (2015). Secondly, in combination with the independent molecular gas estimations, Mdust/M⋆ can prove itself to be a powerful probe of the evolutionary phase of massive objects. In a future paper, we will present the direct predictions related to the potential synergy between the next JWST and present (sub)millimeter surveys.

2

Additionally, in the next section, we also compare our results to studies that explore grid of metallicities and star-formation histories.

3

In principle, our results would depend on how well the evolution of the MS with redshift is constrained. In this direction, we also test the MS relation of Schreiber et al. (2015) but find that the choice of adopted MS does not significantly impact the statistics of our MS and SB DSFGs. We thus kept Speagle et al. (2014) relation for an easier comparison with studies that build gas-scaling relations upon the same MS modelling method (see Sect. 4.4).

4

It has been shown that for massive galaxies (M⋆ >  1010 M⊙), it is reasonable to assume 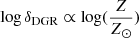log δ DGR ∝ log ( Z Z ⊙ ) $ \log \delta_{\mathrm{DGR}}\propto \log (\frac{Z}{Z_{\odot}}) $ (Leroy et al. 2011; Magdis et al. 2012; Rémy-Ruyer et al. 2014; Schreiber et al. 2018).

5

The associated data can be retrieved at http://doi.org/10.5281/zenodo.4034275

6

For typical values of nH = 103 cm−3 and Tgas ≈ 40−50 K, the τacc, 0 adopted by models is usually 1−20 Myr (see Li et al. 2019; Graziani et al. 2020; Aoyama et al. 2019).

7

The inferred range of ΣIR corresponds to 13−885 M⊙ yr−1 kpc−2 if we convert LIR to dust-obscured SFR through (Kennicutt & Evans 2012) relation for Chabrier IMF.

8

This picture is mostly valid if dusty star-formation is not spread in a series of clumps, which would be tested with higher signal-to-noise (S/N) observations at higher spatial resolution.

Acknowledgments

We are thankful to the anonymous referee for very constructive comments which significantly improved this paper. We would like to acknowledge Veronique Buat, Pauline Vielzeuf, Robert Feldmann, Ciro Pappalardo and Federico Bianchini for useful discussions, comments and/or support. This work has been partially supported by PRIN MIUR 2017 prot. 20173ML3WW002, “Opening the ALMA window on the cosmic evolution of gas, stars and supermassive black holes”. D.D. acknowledge the Dunlap visitor program, at the Dunlap Institute for Astronomy & Astrophysics at the University of Toronto. A.L. acknowledges the MIUR grant “Finanziamento annuale individuale attivitá base di ricerca” and the EU H2020-MSCA-ITN-2019 Project 860744 “BiD4BEST: Big Data applications for Black hole Evolution STudies”. K.M. has been supported by the National Science Centre (UMO-2018/30/E/ST9/00082). D.L. acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 694343). A.M. is supported by a Dunlap Fellowship at the Dunlap Institute for Astronomy & Astrophysics, funded through an endowment established by the David Dunlap family and the University of Toronto. The University of Toronto operates on the traditional land of the Huron-Wendat, the Seneca, and most recently, the Mississaugas of the Credit River; A.M. and D.D. are grateful to have the opportunity to work on this land. S.F. acknowledge support from the European Research Council (ERC) Consolidator Grant funding scheme (project ConTExt, grant No. 648179). The Cosmic Dawn Center is funded by the Danish National Research Foundation under grant No. 140. A.F. acknowledges the support from grant PRIN MIUR 2017 20173ML3WW. This paper make use of following ALMA data: ADS/JAO.ALMA: #2011.0.00064.S, #2011. 0.00097.S, #2011.0.00539.S, #2011.0.00742.S, #2012.1.00076.S, #2012.1.00323.S, #2012.1.00523.S, #2012.1.00536.S, #2012.1.00919.S, #2012.1.00952.S, #2012.1.00978.S, #2013.1.00884.S, #2013.1.00914.S, #2015.1.00137.S, #2015.1.00568.S, #2015.1.00664.S, #2015.1.00704.S, #2015.1.00853.S, #2015.1.00861.S, #2015.1.00862.S, #2015.1.00928.S, #2015.1.01074.S, #2015.1.01590.S, #2015.A.00026.S, #2016.1.00478.S, #2016.1.00624.S, #2016.1.00735.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ.

References

  1. Allende Prieto, C., Lambert, D. L., & Asplund, M. 2001, ApJ, 556, L63 [Google Scholar]
  2. An, F. X., Simpson, J. M., Smail, I., et al. 2019, ApJ, 886, 48 [CrossRef] [Google Scholar]
  3. Andreani, P., Boselli, A., Ciesla, L., et al. 2018, A&A, 617, A33 [CrossRef] [EDP Sciences] [Google Scholar]
  4. Andrews, B. H., & Thompson, T. A. 2011, ApJ, 727, 97 [NASA ADS] [CrossRef] [Google Scholar]
  5. Anglés-Alcázar, D., Davé, R., Faucher-Giguère, C.-A., Özel, F., & Hopkins, P. F. 2017, MNRAS, 464, 2840 [CrossRef] [Google Scholar]
  6. Aoyama, S., Hou, K.-C., Hirashita, H., Nagamine, K., & Shimizu, I. 2018, MNRAS, 478, 4905 [NASA ADS] [CrossRef] [Google Scholar]
  7. Aoyama, S., Hirashita, H., & Nagamine, K. 2019, MNRAS, 482, 2555 [NASA ADS] [CrossRef] [Google Scholar]
  8. Asano, R. S., Takeuchi, T. T., Hirashita, H., & Inoue, A. K. 2013, Earth Planets Space, 65, 213 [NASA ADS] [CrossRef] [Google Scholar]
  9. Behroozi, P. S., Wechsler, R. H., & Conroy, C. 2013, ApJ, 770, 57 [NASA ADS] [CrossRef] [Google Scholar]
  10. Berta, S., Lutz, D., Genzel, R., Förster-Schreiber, N. M., & Tacconi, L. J. 2016, A&A, 587, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Béthermin, M., Daddi, E., Magdis, G., et al. 2012, ApJ, 757, L23 [NASA ADS] [CrossRef] [Google Scholar]
  12. Béthermin, M., Daddi, E., Magdis, G., et al. 2015, A&A, 573, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Béthermin, M., Wu, H.-Y., Lagache, G., et al. 2017, A&A, 607, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Biscaro, C., & Cherchneff, I. 2016, A&A, 589, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Blain, A. W., Barnard, V. E., & Chapman, S. C. 2003, MNRAS, 338, 733 [NASA ADS] [CrossRef] [Google Scholar]
  16. Boogaard, L. A., Decarli, R., González-López, J., et al. 2019, ApJ, 882, 140 [CrossRef] [Google Scholar]
  17. Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Bourne, N., Maddox, S. J., Dunne, L., et al. 2012, MNRAS, 421, 3027 [NASA ADS] [CrossRef] [Google Scholar]
  19. Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
  20. Brown, A., Nayyeri, H., Cooray, A., et al. 2019, ApJ, 871, 87 [CrossRef] [Google Scholar]
  21. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  22. Buat, V., Heinis, S., Boquien, M., et al. 2014, A&A, 561, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Buat, V., Ciesla, L., Boquien, M., Małek, K., & Burgarella, D. 2019, A&A, 632, A79 [CrossRef] [EDP Sciences] [Google Scholar]
  24. Burgarella, D., Nanni, A., Hirashita, H., et al. 2020, A&A, 637, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Cai, Z.-Y., Lapi, A., Xia, J.-Q., et al. 2013, ApJ, 768, 21 [NASA ADS] [CrossRef] [Google Scholar]
  26. Calura, F., Pozzi, F., Cresci, G., et al. 2017, MNRAS, 465, 54 [NASA ADS] [CrossRef] [Google Scholar]
  27. Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
  28. Casasola, V., Bianchi, S., De Vis, P., et al. 2020, A&A, 633, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Casey, C. M., Narayanan, D., & Cooray, A. 2014, Phys. Rep., 541, 45 [Google Scholar]
  30. Casey, C. M., Zavala, J. A., Aravena, M., et al. 2019, ApJ, 887, 55 [Google Scholar]
  31. Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
  32. Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [Google Scholar]
  33. Chruslinska, M., & Nelemans, G. 2019, MNRAS, 488, 5300 [NASA ADS] [Google Scholar]
  34. Ciesla, L., Charmandaris, V., Georgakakis, A., et al. 2015, A&A, 576, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Ciesla, L., Elbaz, D., & Fensch, J. 2017, A&A, 608, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Ciesla, L., Béthermin, M., Daddi, E., et al. 2020, A&A, 635, A27 [CrossRef] [EDP Sciences] [Google Scholar]
  37. Civano, F., Marchesi, S., Comastri, A., et al. 2016, ApJ, 819, 62 [Google Scholar]
  38. Clements, D. L., Pearson, C., Farrah, D., et al. 2018, MNRAS, 475, 2097 [CrossRef] [Google Scholar]
  39. Cochrane, R. K., Hayward, C. C., Anglés-Alcázar, D., et al. 2019, MNRAS, 488, 1779 [NASA ADS] [CrossRef] [Google Scholar]
  40. Combes, F. 2018, A&ARv, 26, 5 [NASA ADS] [CrossRef] [Google Scholar]
  41. Cortzen, I., Magdis, G. E., Valentino, F., et al. 2020, A&A, 634, L14 [EDP Sciences] [Google Scholar]
  42. Cousin, M., Buat, V., Lagache, G., & Bethermin, M. 2019, A&A, 627, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Cox, P., Krips, M., Neri, R., et al. 2011, ApJ, 740, 63 [NASA ADS] [CrossRef] [Google Scholar]
  44. Cuppen, H. M., Walsh, C., Lamberts, T., et al. 2017, Space Sci. Rev., 212, 1 [Google Scholar]
  45. Curti, M., Mannucci, F., Cresci, G., & Maiolino, R. 2020, MNRAS, 491, 944 [NASA ADS] [CrossRef] [Google Scholar]
  46. da Cunha, E., Eminian, C., Charlot, S., & Blaizot, J. 2010, MNRAS, 403, 1894 [NASA ADS] [CrossRef] [Google Scholar]
  47. da Cunha, E., Walter, F., Smail, I. R., et al. 2015, ApJ, 806, 110 [Google Scholar]
  48. Daddi, E., Elbaz, D., Walter, F., et al. 2010, ApJ, 714, L118 [Google Scholar]
  49. Dale, D. A., Aniano, G., Engelbracht, C. W., et al. 2012, ApJ, 745, 95 [NASA ADS] [CrossRef] [Google Scholar]
  50. Davé, R., Thompson, R., & Hopkins, P. F. 2016, MNRAS, 462, 3265 [NASA ADS] [CrossRef] [Google Scholar]
  51. Davé, R., Anglés-Alcázar, D., Narayanan, D., et al. 2019, MNRAS, 486, 2827 [NASA ADS] [CrossRef] [Google Scholar]
  52. Davidzon, I., Ilbert, O., Laigle, C., et al. 2017, A&A, 605, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. De Breuck, C., Weiß, A., Béthermin, M., et al. 2019, A&A, 631, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Dessauges-Zavadsky, M., Ginolfi, M., Pozzi, F., et al. 2020, A&A, 643, A5 [CrossRef] [EDP Sciences] [Google Scholar]
  55. De Vis, P., Gomez, H. L., Schofield, S. P., et al. 2017, MNRAS, 471, 1743 [NASA ADS] [CrossRef] [Google Scholar]
  56. Donevski, D., Buat, V., Boone, F., et al. 2018, A&A, 614, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Dowell, C. D., Conley, A., Glenn, J., et al. 2014, ApJ, 780, 75 [NASA ADS] [CrossRef] [Google Scholar]
  58. Downes, D., & Solomon, P. M. 1998, ApJ, 507, 615 [NASA ADS] [CrossRef] [Google Scholar]
  59. Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
  60. Draine, B. T., Aniano, G., Krause, O., et al. 2014, ApJ, 780, 172 [NASA ADS] [CrossRef] [Google Scholar]
  61. Driver, S. P., Andrews, S. K., da Cunha, E., et al. 2018, MNRAS, 475, 2891 [NASA ADS] [CrossRef] [Google Scholar]
  62. Dudzevičiūtė, U., Smail, I., Swinbank, A. M., et al. 2020, MNRAS, 494, 3828 [Google Scholar]
  63. Duncan, K. J., Jarvis, M. J., Brown, M. J. I., & Röttgering, H. J. A. 2018, MNRAS, 477, 5177 [Google Scholar]
  64. Dunlop, J. S., McLure, R. J., Biggs, A. D., et al. 2017, MNRAS, 466, 861 [Google Scholar]
  65. Dunne, L., Gomez, H. L., da Cunha, E., et al. 2011, MNRAS, 417, 1510 [NASA ADS] [CrossRef] [Google Scholar]
  66. Dwek, E. 1998, ApJ, 501, 643 [NASA ADS] [CrossRef] [Google Scholar]
  67. Dwek, E., Staguhn, J., Arendt, R. G., et al. 2014, ApJ, 788, L30 [NASA ADS] [CrossRef] [Google Scholar]
  68. Dwek, E., Sarangi, A., & Arendt, R. G. 2019, ApJ, 871, L33 [CrossRef] [Google Scholar]
  69. Elbaz, D., Hwang, H. S., Magnelli, B., et al. 2010, A&A, 518, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Elbaz, D., Leiton, R., Nagar, N., et al. 2018, A&A, 616, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Feltre, A., Hatziminaoglou, E., Fritz, J., & Franceschini, A. 2012, MNRAS, 426, 120 [NASA ADS] [CrossRef] [Google Scholar]
  72. Forrest, B., Tran, K.-V. H., Broussard, A., et al. 2018, ApJ, 863, 131 [CrossRef] [Google Scholar]
  73. Franco, M., Elbaz, D., Béthermin, M., et al. 2018, A&A, 620, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Fritz, J., Franceschini, A., & Hatziminaoglou, E. 2006, MNRAS, 366, 767 [Google Scholar]
  75. Fudamoto, Y., Ivison, R. J., Oteo, I., et al. 2017, MNRAS, 472, 2028 [NASA ADS] [CrossRef] [Google Scholar]
  76. Fujimoto, S., Ouchi, M., Shibuya, T., & Nagai, H. 2017, ApJ, 850, 83 [NASA ADS] [CrossRef] [Google Scholar]
  77. Fujimoto, S., Ouchi, M., Ferrara, A., et al. 2019, ApJ, 887, 107 [NASA ADS] [CrossRef] [Google Scholar]
  78. Galliano, F., Hony, S., Bernard, J.-P., et al. 2011, A&A, 536, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Galliano, F., Galametz, M., & Jones, A. P. 2018, ARA&A, 56, 673 [Google Scholar]
  80. Genzel, R., Tacconi, L. J., Lutz, D., et al. 2015, ApJ, 800, 20 [Google Scholar]
  81. Ginolfi, M., Jones, G. C., Béthermin, M., et al. 2020, A&A, 633, A90 [CrossRef] [EDP Sciences] [Google Scholar]
  82. Gioannini, L., Matteucci, F., & Calura, F. 2017, MNRAS, 471, 4615 [NASA ADS] [CrossRef] [Google Scholar]
  83. Gómez-Guijarro, C., Toft, S., Karim, A., et al. 2018, ApJ, 856, 121 [Google Scholar]
  84. Gómez-Guijarro, C., Riechers, D. A., Pavesi, R., et al. 2019, ApJ, 872, 117 [NASA ADS] [CrossRef] [Google Scholar]
  85. Graziani, L., Schneider, R., Ginolfi, M., et al. 2020, MNRAS, 494, 1071 [CrossRef] [Google Scholar]
  86. Hayward, C. C. 2013, MNRAS, 432, L85 [NASA ADS] [CrossRef] [Google Scholar]
  87. Hirashita, H., & Nozawa, T. 2017, Planet. Space Sci., 149, 45 [CrossRef] [Google Scholar]
  88. Hjorth, J., Gall, C., & Michałowski, M. J. 2014, ApJ, 782, L23 [NASA ADS] [CrossRef] [Google Scholar]
  89. Hodge, J. A., & da Cunha, E. 2020, ArXiv e-prints [arXiv:2004.00934] [Google Scholar]
  90. Hodge, J. A., Carilli, C. L., Walter, F., Daddi, E., & Riechers, D. 2013, ApJ, 776, 22 [NASA ADS] [CrossRef] [Google Scholar]
  91. Hopkins, P. F. 2015, MNRAS, 450, 53 [NASA ADS] [CrossRef] [Google Scholar]
  92. Hou, K.-C., Aoyama, S., Hirashita, H., Nagamine, K., & Shimizu, I. 2019, MNRAS, 485, 1727 [NASA ADS] [CrossRef] [Google Scholar]
  93. Hunt, L. K., Palazzi, E., Michałowski, M. J., et al. 2014, A&A, 565, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Hunt, L., Dayal, P., Magrini, L., & Ferrara, A. 2016, MNRAS, 463, 2002 [NASA ADS] [CrossRef] [Google Scholar]
  95. Hurley, P. D., Oliver, S., Betancourt, M., et al. 2017, MNRAS, 464, 885 [NASA ADS] [CrossRef] [Google Scholar]
  96. Ikarashi, S., Ivison, R. J., Caputi, K. I., et al. 2015, ApJ, 810, 133 [NASA ADS] [CrossRef] [Google Scholar]
  97. Imara, N., Loeb, A., Johnson, B. D., Conroy, C., & Behroozi, P. 2018, ApJ, 854, 36 [CrossRef] [Google Scholar]
  98. Jin, S., Daddi, E., Magdis, G. E., et al. 2019, ApJ, 887, 144 [Google Scholar]
  99. Jones, A. P., Köhler, M., Ysard, N., Bocchio, M., & Verstraete, L. 2017, A&A, 602, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Kennicutt, R. C., Jr. 1998, ARA&A, 36, 189 [Google Scholar]
  101. Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
  102. Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [Google Scholar]
  103. Kirkpatrick, A., Pope, A., Sajina, A., et al. 2017, ApJ, 843, 71 [CrossRef] [Google Scholar]
  104. Kriek, M., Conroy, C., van Dokkum, P. G., et al. 2016, Nature, 540, 248 [NASA ADS] [CrossRef] [Google Scholar]
  105. Krumholz, M. R., Dekel, A., & McKee, C. F. 2012, ApJ, 745, 69 [NASA ADS] [CrossRef] [Google Scholar]
  106. Lacey, C. G., Baugh, C. M., Frenk, C. S., et al. 2010, MNRAS, 405, 2 [NASA ADS] [Google Scholar]
  107. Lacey, C. G., Baugh, C. M., Frenk, C. S., et al. 2016, MNRAS, 462, 3854 [NASA ADS] [CrossRef] [Google Scholar]
  108. Lagos, C. D. P., Robotham, A. S. G., Trayford, J. W., et al. 2019, MNRAS, 489, 4196 [CrossRef] [Google Scholar]
  109. Lapi, A., Pantoni, L., Zanisi, L., et al. 2018, ApJ, 857, 22 [NASA ADS] [CrossRef] [Google Scholar]
  110. Larson, K. L., Sanders, D. B., Barnes, J. E., et al. 2016, ApJ, 825, 128 [NASA ADS] [CrossRef] [Google Scholar]
  111. Le Floc’h, E., Papovich, C., Dole, H., et al. 2005, ApJ, 632, 169 [NASA ADS] [CrossRef] [Google Scholar]
  112. Leja, J., Johnson, B. D., Conroy, C., & van Dokkum, P. 2018, ApJ, 854, 62 [NASA ADS] [CrossRef] [Google Scholar]
  113. Leroy, A. K., Bolatto, A., Gordon, K., et al. 2011, ApJ, 737, 12 [Google Scholar]
  114. Leśniewska, A., & Michałowski, M. J. 2019, A&A, 624, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  115. Li, Q., Narayanan, D., & Davé, R. 2019, MNRAS, 490, 1425 [NASA ADS] [CrossRef] [Google Scholar]
  116. Liang, L., Feldmann, R., Kereš, D., et al. 2019, MNRAS, 489, 1397 [NASA ADS] [CrossRef] [Google Scholar]
  117. Liu, D., Daddi, E., Dickinson, M., et al. 2018, ApJ, 853, 172 [Google Scholar]
  118. Liu, D., Schinnerer, E., Groves, B., et al. 2019a, ApJ, 887, 235 [Google Scholar]
  119. Liu, D., Lang, P., Magnelli, B., et al. 2019b, ApJS, 244, 40 [Google Scholar]
  120. Lo Faro, B., Buat, V., Roehlly, Y., et al. 2017, MNRAS, 472, 1372 [NASA ADS] [CrossRef] [Google Scholar]
  121. Magdis, G. E., Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]
  122. Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  123. Małek, K., Buat, V., Roehlly, Y., et al. 2018, A&A, 620, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  124. Mancuso, C., Lapi, A., Shi, J., et al. 2016, ApJ, 823, 128 [NASA ADS] [CrossRef] [Google Scholar]
  125. Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
  126. Mannucci, F., Salvaterra, R., & Campisi, M. A. 2011, MNRAS, 414, 1263 [NASA ADS] [CrossRef] [Google Scholar]
  127. Martis, N. S., Marchesini, D. M., Muzzin, A., et al. 2019, ApJ, 882, 65 [NASA ADS] [CrossRef] [Google Scholar]
  128. Mattsson, L. 2020, MNRAS, 491, 4334 [CrossRef] [Google Scholar]
  129. McKinney, J., Pope, A., Armus, L., et al. 2020, ApJ, 892, 119 [CrossRef] [Google Scholar]
  130. McKinnon, R., Torrey, P., Vogelsberger, M., Hayward, C. C., & Marinacci, F. 2017, MNRAS, 468, 1505 [NASA ADS] [CrossRef] [Google Scholar]
  131. Michałowski, M. J., Hjorth, J., Gall, C., et al. 2019, A&A, 632, A43 [CrossRef] [EDP Sciences] [Google Scholar]
  132. Miettinen, O., Smolčić, V., Novak, M., et al. 2015, A&A, 577, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  133. Miettinen, O., Delvecchio, I., Smolčić, V., et al. 2017, A&A, 606, A17 [CrossRef] [EDP Sciences] [Google Scholar]
  134. Millard, J. S., Eales, S. A., Smith, M. W. L., et al. 2020, MNRAS, 494, 293 [CrossRef] [Google Scholar]
  135. Miller, T. B., Chapman, S. C., Aravena, M., et al. 2018, Nature, 556, 469 [NASA ADS] [CrossRef] [Google Scholar]
  136. Mitchell, P. D., Lacey, C. G., Baugh, C. M., & Cole, S. 2013, MNRAS, 435, 87 [NASA ADS] [CrossRef] [Google Scholar]
  137. Moster, B. P., Naab, T., & White, S. D. M. 2013, MNRAS, 428, 3121 [Google Scholar]
  138. Nagao, T., Maiolino, R., De Breuck, C., et al. 2012, A&A, 542, L34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  139. Nanni, A., Burgarella, D., Theulé, P., Côté, B., & Hirashita, H. 2020, A&A, 641, A168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  140. Narayanan, D., Turk, M., Feldmann, R., et al. 2015, Nature, 525, 496 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  141. Negrello, M., Hopwood, R., De Zotti, G., et al. 2010, Science, 330, 800 [NASA ADS] [CrossRef] [Google Scholar]
  142. Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [Google Scholar]
  143. Noll, S., Burgarella, D., Giovannoli, E., et al. 2009, A&A, 507, 1793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  144. Oteo, I., Ivison, R. J., Negrello, M., et al. 2017, ArXiv e-prints [arXiv:1709.04191] [Google Scholar]
  145. Oteo, I., Ivison, R. J., Dunne, L., et al. 2018, ApJ, 856, 72 [Google Scholar]
  146. Pantoni, L., Lapi, A., Massardi, M., Goswami, S., & Danese, L. 2019, ApJ, 880, 129 [NASA ADS] [CrossRef] [Google Scholar]
  147. Pavesi, R., Riechers, D. A., Sharon, C. E., et al. 2018, ApJ, 861, 43 [NASA ADS] [CrossRef] [Google Scholar]
  148. Pearson, W. J., Wang, L., van der Tak, F. F. S., et al. 2017, A&A, 603, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  149. Pearson, W. J., Wang, L., Hurley, P. D., et al. 2018, A&A, 615, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  150. Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  151. Popping, G., Somerville, R. S., & Galametz, M. 2017, MNRAS, 471, 3152 [NASA ADS] [CrossRef] [Google Scholar]
  152. Pozzi, F., Calura, F., Zamorani, G., et al. 2020, MNRAS, 491, 5073 [CrossRef] [Google Scholar]
  153. Puglisi, A., Daddi, E., Renzini, A., et al. 2017, ApJ, 838, L18 [Google Scholar]
  154. Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2014, A&A, 563, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  155. Riechers, D. A., Bradford, C. M., Clements, D. L., et al. 2013, Nature, 496, 329 [Google Scholar]
  156. Rodighiero, G., Daddi, E., Baronchelli, I., et al. 2011, ApJ, 739, L40 [NASA ADS] [CrossRef] [Google Scholar]
  157. Rodríguez-Puebla, A., Behroozi, P., Primack, J., et al. 2016, MNRAS, 462, 893 [NASA ADS] [CrossRef] [Google Scholar]
  158. Rowlands, K., Dunne, L., Dye, S., et al. 2014, MNRAS, 441, 1017 [NASA ADS] [CrossRef] [Google Scholar]
  159. Saintonge, A., Catinella, B., Tacconi, L. J., et al. 2017, ApJS, 233, 22 [Google Scholar]
  160. Salim, S., & Narayanan, D. 2020, ARA&A, 58, 529 [CrossRef] [Google Scholar]
  161. Salim, S., Lee, J. C., Janowiecki, S., et al. 2016, ApJS, 227, 2 [NASA ADS] [CrossRef] [Google Scholar]
  162. Santini, P., Maiolino, R., Magnelli, B., et al. 2014, A&A, 562, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  163. Sargent, M. T., Daddi, E., Béthermin, M., et al. 2014, ApJ, 793, 19 [NASA ADS] [CrossRef] [Google Scholar]
  164. Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
  165. Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  166. Schreiber, C., Elbaz, D., Pannella, M., et al. 2016, A&A, 589, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  167. Schreiber, C., Pannella, M., Leiton, R., et al. 2017, A&A, 599, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  168. Schreiber, C., Elbaz, D., Pannella, M., et al. 2018, A&A, 609, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  169. Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
  170. Scoville, N., Sheth, K., Aussel, H., et al. 2016, ApJ, 820, 83 [NASA ADS] [CrossRef] [Google Scholar]
  171. Scoville, N., Lee, N., Vanden Bout, P., et al. 2017, ApJ, 837, 150 [NASA ADS] [CrossRef] [Google Scholar]
  172. Shirley, R., Roehlly, Y., Hurley, P. D., et al. 2019, MNRAS, 490, 634 [CrossRef] [Google Scholar]
  173. Silverman, J. D., Rujopakarn, W., Daddi, E., et al. 2018, ApJ, 867, 92 [NASA ADS] [CrossRef] [Google Scholar]
  174. Simpson, J. M., Smail, I., Swinbank, A. M., et al. 2015, ApJ, 807, 128 [NASA ADS] [CrossRef] [Google Scholar]
  175. Simpson, J. M., Smail, I., Dudzevičiūtė, U., et al. 2020, MNRAS, 495, 3409 [CrossRef] [Google Scholar]
  176. Slavin, J. D., Dwek, E., & Jones, A. P. 2015, ApJ, 803, 7 [NASA ADS] [CrossRef] [Google Scholar]
  177. Smith, D. J. B., & Hayward, C. C. 2018, MNRAS, 476, 1705 [CrossRef] [Google Scholar]
  178. Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [NASA ADS] [CrossRef] [Google Scholar]
  179. Stach, S. M., Dudzevičiūtė, U., Smail, I., et al. 2019, MNRAS, 487, 4648 [NASA ADS] [CrossRef] [Google Scholar]
  180. Strandet, M. L., Weiss, A., De Breuck, C., et al. 2017, ApJ, 842, L15 [Google Scholar]
  181. Swinbank, A. M., Simpson, J. M., Smail, I., et al. 2014, MNRAS, 438, 1267 [Google Scholar]
  182. Symeonidis, M., Vaccari, M., Berta, S., et al. 2013, MNRAS, 431, 2317 [NASA ADS] [CrossRef] [Google Scholar]
  183. Tacconi, L. J., Genzel, R., Saintonge, A., et al. 2018, ApJ, 853, 179 [NASA ADS] [CrossRef] [Google Scholar]
  184. Tacconi, L. J., Genzel, R., & Sternberg, A. 2020, ARA&A, 58, 157 [CrossRef] [Google Scholar]
  185. Tan, Q., Daddi, E., Magdis, G., et al. 2014, A&A, 569, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  186. Trayford, J. W., Lagos, C. D. P., Robotham, A. S. G., & Obreschkow, D. 2020, MNRAS, 491, 3937 [CrossRef] [Google Scholar]
  187. Triani, D. P., Sinha, M., Croton, D. J., Pacifici, C., & Dwek, E. 2020, MNRAS, 493, 2490 [CrossRef] [Google Scholar]
  188. Trčka, A., Baes, M., Camps, P., et al. 2020, MNRAS, 494, 2823 [CrossRef] [Google Scholar]
  189. Valentino, F., Daddi, E., Puglisi, A., et al. 2020, A&A, 641, A155 [CrossRef] [EDP Sciences] [Google Scholar]
  190. Vijayan, A. P., Clay, S. J., Thomas, P. A., et al. 2019, MNRAS, 489, 4072 [CrossRef] [Google Scholar]
  191. Wang, T., Schreiber, C., Elbaz, D., et al. 2019, Nature, 572, 211 [Google Scholar]
  192. Wardlow, J. L., Malhotra, S., Zheng, Z., et al. 2014, ApJ, 787, 9 [NASA ADS] [CrossRef] [Google Scholar]
  193. Weiß, A., De Breuck, C., Marrone, D. P., et al. 2013, ApJ, 767, 88 [NASA ADS] [CrossRef] [Google Scholar]
  194. Whitaker, K. E., Franx, M., Bezanson, R., et al. 2015, ApJ, 811, L12 [NASA ADS] [CrossRef] [Google Scholar]
  195. Williams, C. C., Labbe, I., Spilker, J., et al. 2019, ApJ, 884, 154 [CrossRef] [Google Scholar]
  196. Zahid, H. J., Kashino, D., Silverman, J. D., et al. 2014, ApJ, 792, 75 [NASA ADS] [CrossRef] [Google Scholar]
  197. Zavala, J. A., Montaña, A., Hughes, D. H., et al. 2018, Nat. Astron., 2, 56 [NASA ADS] [CrossRef] [Google Scholar]
  198. Zhukovska, S., Dobbs, C., Jenkins, E. B., & Klessen, R. S. 2016, ApJ, 831, 147 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Additional table

Table A.1.

Selected DSFGs and their physical properties.

Appendix B: SED fitting systematics

In order to better evaluate our SED method and explore the eventual biases, we made simulated data set and fit it using the exact same method that we applied to our observed galaxies. The purpose of using simulations is to analyse eventual observational effects on SED fitting results. To achieve this goal, we follow the methods presented in Ciesla et al. (2015) and Małek et al. (2018), who use CIGALE to create mock catalogue of objects for each galaxy for which the physical parameters are known. To build the simulated sample, we adopt the best-fit SED model for each fitted object, which gives one artificial model per galaxy. Input fluxes obtained from the best SEDs are then perturbed, following a Gaussian distribution, with σ corresponding to the observed uncertainty per each photometric band. The fitting of mock galaxies is further performed with the exact same choice of physical models and their input parameters as for our real data.

Figure B.1 illustrates the log difference between the observed physical quantities and the best output parameters of the simulated catalogue. For the stellar mass, dust mass, and IR luminosity, such dispersion is expressed as ΔM⋆, ΔMdust, and ΔLIR, respectively. We find that for all the main physical quantities analysed here, dispersion follows normal distributions with very small offset (≲0.1). Namely, for each physical parameter we find that more than 75% of sources lie within the mean offset of ±0.1. Therefore, we conclude that our SED fitting procedure does not introduce any significant systematics to derived quantities.

thumbnail Fig. B.1.

For each panel: offset between the estimated and simulated value. From top to bottom: stellar mass, dust mass and dust luminosity. The black line and the corresponding shaded region is the best linear regression fit to the parameter offset.

All Tables

Table 1.

Parameters used for modelling the SEDs with CIGALE.

In the text
Table 2.

Statistics of our SED derived physical properties with CIGALE, compared to those from known statistical ALMA studies (da Cunha et al. 2015; Dudzevičiūtė et al. 2020).

In the text
Table A.1.

Selected DSFGs and their physical properties.

In the text

All Figures

thumbnail Fig. 1.

For all panels inside the grey box: distributions of the physical properties estimated for our DSFGs from the SED fitting with CIGALE. From top left to bottom right: goodness of fit expressed as reduced χ2; galaxy redshift; stellar mass; SFR; IR luminosity; dust mass; and galaxy linear offset from the MS (in log scale). Bottom right panel: linear offset of the galaxy’s observed SFR to the SFR expected from the modelled MS (ΔMS in log scale) as a function of redshift. A border between the sources considered as MS and SB DSFGs is indicated by a horizontal, dashed line.
In the text
thumbnail Fig. 2.

Observed redshift evolution of Mdust. Individual values are displayed with circles, coloured with corresponding LIR. Binned means are shown with black circles and associated 1σ errors. For comparison, we also show the mean Mdust for a large sample of dusty galaxies up to z ∼ 0.5 (Driver et al. 2018, black inverted triangle). The black dashed and dotted lines are best regression fits from this work and from Dudzevičiūtė et al. (2020), respectively.
In the text
thumbnail Fig. 3.

Observed relation between Mdust and SFR in our DSFGs, shown for the whole sample (binned means, shown as black circles) and divided on SB and MS galaxies (shaded in dark cyan and orange, respectively). The known, empirically based scaling relation between Tdust − SFR − Mdust (Genzel et al. 2015) are overlaid with dashed lines. Different colours correspond to their fixed Tdust, as indicated in the legend. The best fit for local and intermediate redshift ULIRGs (Rowlands et al. 2014) are displayed with dotted and dot-dashed line, respectively.
In the text
thumbnail Fig. 4.

Top panel: Mdust/M⋆ versus redshfit (left) and sSFR (right), of our MS and SB DSFGs. The binned averages and corresponding standard errors for MS and SB subsample are shown as shaded dark cyan and orange area, respectively. The grey, shaded area is the observed trend obtained via stacking analysis by Béthermin et al. (2015). The red star in each panel indicate the median value of most extreme local ULIRGs (da Cunha et al. 2010). Binned values for MS and SB from high-redshift ALMA sample analysed by da Cunha et al. (2015) are shown with triangles and squares, respectively. Also displayed with red symbols are individual detections of the most distant DSFGs at z >  5 (MAMBO-9, Casey et al. 2019; Jin et al. 2019; HFLS3, Riechers et al. 2013; and SPT0311, Strandet et al. 2017). For consistency, we use public data and recalculate Mdust of latter three objects following our method, finding a good agreement with their archival estimates. Right panel: the binned mean values of the full sample are presented with black circles and the results from da Cunha et al. (2015) with filled squares. The error bars represent the dispersion (1σ) associated to the mean. Bottom panel: Mdust/M⋆ versus galaxy stellar mass. Left panel: our estimates compared to those that span the similar stellar mass range. Points are colour-coded in the same way as in the upper plot. Grey circles indicate the local galaxy sample composed of Herschel-detected galaxies (both passive and active) from the Virgo cluster (HRS, Andreani et al. 2018). On the right side, we resolve the overall trend of Mdust/M⋆ vs. M⋆ from this work per different redshift bins and plot the trend with corresponding 1σ uncertainty. Redshift bins are colour-coded as in the legend.
In the text
thumbnail Fig. 5.

From top to bottom: cosmic evolution of Mdust/M⋆ modelled as a combination of gas mass-scaling relations and MZRs. We test the gas scaling relations from Liu et al. (2019a), Tacconi et al. (2018) and Scoville et al. (2017). To model the evolution of gas-phase metallicity, we test different MZRs from Hunt et al. (2016), Genzel et al. (2015), along with the broken fundamental metallicity relation (BMR, Béthermin et al. 2015). The overplotted shaded regions are the same observed data (MS and SB DSFGs) presented in the upper left panel of Fig. 4.
In the text
thumbnail Fig. 6.

Left: redshift evolution of Mdust/M⋆ predicted by different models (see Sect. 5.1). The observed data are overplotted with same colours as in previous figures. The grey, blue, and purple dashed and dotted lines represent predictions for galaxies selected as MS and SB DSFGs from Béthermin et al. (2017), Davé et al. (2019) and Pantoni et al. (2019), respectively. Right: evolution of Mdust/M⋆ as a function of sSFR for the full sample of observed and modelled galaxies. The binned values from this work are shown with black circles with corresponding 1σ vertical error bars. The model predictions are denoted with same colours as in the left panel.
In the text
thumbnail Fig. 7.

Upper panel: cosmic evolution of molecular gas fraction (fgas) in our DSFGs, estimated from the functional form of Liu et al. (2019a) and illustrated with shaded areas. The model predictions for MS and SB DSFGs are overplotted with dashed and dotted lines, respectively. Purple, blue, and grey lines correspond to P19, SIMBA, and B17 respectively. For P19 and SIMBA, the fgas is derived self-consistently, while for B17, we test the same scaling relation we apply in our observations. Lower panel: δDGR as a function of fgas for the full sample of observed and modelled galaxies. Observed mean ratios with corresponding 1σ uncertainty are presented with black circles. The significance of colours that correspond to modelled values is the same as in the upper panel.
In the text
thumbnail Fig. 8.

Observed Mdust/M⋆ as a function of a galaxy offset to the MS, defined as ΔMS = log(SFR/SFRMS). Galaxies with intermediate and high ΣIR are denoted with grey and red circles, respectively. The shaded region represents the sequence of MS defined by Speagle et al. (2014) with a 0.5 dex (3 times) scatter. The points that lie outside the grey region represent the SB DSFGs.
In the text
thumbnail Fig. B.1.

For each panel: offset between the estimated and simulated value. From top to bottom: stellar mass, dust mass and dust luminosity. The black line and the corresponding shaded region is the best linear regression fit to the parameter offset.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.