| Issue |
A&A
Volume 638, June 2020
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 18 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202037819 | |
| Published online | 19 June 2020 | |
Full 5D characterisation of the Sagittarius stream with Gaia DR2 RR Lyrae⋆
1
Dept. FQA, Institut de Ciències del Cosmos (ICCUB), Universitat de Barcelona (IEEC-UB), Martí Franquès 1, 08028 Barcelona, Spain
e-mail: pramos@fqa.ub.edu
2
Departamento de Astronomía, Instituto de Física, Universidad de la República, Iguá 4225, 11400 Montevideo, Uruguay
3
Kapteyn Astronomical Institute, University of Groningen, Landleven 12, 9747 AD Groningen, The Netherlands
Received:
25
February
2020
Accepted:
23
April
2020
Context. The Sagittarius (Sgr) stream is one of the best tools that we currently have to estimate the mass and shape of our Galaxy. However, assigning membership and obtaining the phase-space distribution of the stars that form the tails of the stream is quite challenging.
Aims. Our goal is to produce a catalogue of the RR Lyrae stars of Sgr and obtain an empiric measurement of the trends along the stream in sky position, distance, and tangential velocity.
Methods. We generated two initial samples from the Gaia DR2 RR Lyrae catalogue: one selecting only the stars within ±20° of the orbital plane of Sagittarius (Strip), and the other resulting from application of the Pole Count Map (nGC3) algorithm. We then used the model-independent, deterministic method developed in this work to remove most of the contamination by detecting and isolating the stream in distance and proper motions.
Results. The output is two empiric catalogues: the Strip sample (higher-completeness, lower-purity) which contains 11 677 stars, and the nGC3 sample (higher-purity, lower-completeness) with 6608 stars. We characterise the changes along the stream in all the available dimensions, namely the five astrometric dimensions plus the metallicity, covering more than 2π rad in the sky, and obtain new estimates for the apocentres and the mean [Fe/H] of the RR Lyrae population. Also, we show the first map of the two components of the tangential velocity thanks to the combination of distances and proper motions. Finally, we detect the bifurcation in the leading arm and report no significant difference between the two branches in terms of metallicity, kinematics, or distance.
Conclusions. We provide the largest sample of RR Lyrae candidates of Sgr, which can be used as input for a spectroscopic follow-up or as a reference for the new generation of models of the stream through the interpolators in distance and velocity that we constructed.
Key words: Galaxy: halo / stars: variables: RR Lyrae / galaxies: dwarf / astrometry
Full Table E.1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/638/A104
© ESO 2020
1. Introduction
The Sagittarius (Sgr) dwarf galaxy (Ibata et al. 1994) is the first detected and most conspicuous relic of an accretion and tidal destruction event in our Galaxy. Since its discovery (Mateo et al. 1996; Totten & Irwin 1998), the stream has been studied extensively using different tracers and techniques in order to map its full extent and various wraps around the Galaxy, which, combined with kinematic information, can be used to understand the dynamics of its tidal disruption and to infer properties of the Galactic dark matter halo (Law & Majewski 2010; Deg & Widrow 2013; Fardal et al. 2019).
Compared to simpler and thinner streams, such as for example GD-1, Pal 5, or Orphan, among dozens now known in our Galaxy (see Grillmair et al. 2016; Mateu et al. 2018; Shipp et al. 2018; Ibata et al. 2019), the Sgr stream has several main characteristics that make it interesting but also challenging to observe and model. The stream is luminous and abundantly populated with stars; it is roughly planar and wraps around the Galaxy at least twice (Martínez-Delgado et al. 2004); and its (observed) debris spans distances from 20 to over 100 kpc (Sesar et al. 2017a). The extended star formation history (de Boer et al. 2015) of its luminous and massive progenitor has produced complex stellar population and metallicity gradients along the stream and, because the debris is all around the sky and spans such a large distance range, it is observationally demanding to trace in a continuous manner. Despite having a high surface brightness and a stellar population that is clearly different from that of the halo, which should in principle facilitate its detection, we still lack a model that can convincingly reproduce the stream. The long-standing problem is the lack of kinematic data and the reproducibility of features such as the bifurcation observed in both tails or the angular separation between apocentres (Belokurov et al. 2006, 2014; Koposov et al. 2012; Navarrete et al. 2017; Gibbons et al. 2016).
One of the key elements needed to properly model the infall of Sgr is the characterisation of the spatial distribution and kinematics of its different populations throughout the sky, in a continuous and homogeneous way. Majewski et al. (2003) made the first all-sky map of the tails using 2MASS M-giants, and were followed by many later studies that obtained radial velocities for red giants, blue horizontal branch stars, and other tracers, usually in small patches along the stream (e.g. Li et al. 2019, and references in Belokurov et al. 2014). Recently, Antoja et al. (2020, hereafter A20), used the precise astrometry of the Gaia second data release (DR2, Gaia Collaboration et al. 2018) to detect the Sgr stream from proper motion alone, without having to select a specific stellar type, and determined for the first time its proper motion along the path of the full stream. However, these latter authors did not obtain distance estimates since the parallaxes at such faint magnitudes provide little information and would require a thorough study of the astrometric systematic errors (global and local). In any case, this would only allow distance estimates out to a few tens of kiloparsecs. Tracers for which photometric distances can be obtained are therefore more useful when studying the stream to its full extent in a comprehensive way.
Before the publication of Gaia DR2, Hernitschek et al. (2017) used PanSTARRS-1 (PS1; Chambers et al. 2016) RR Lyrae stars to measure distances to the Sgr tails and were able to trace both arms, the leading (i.e. the stars that orbit ahead of the progenitor) and the trailing (those that lag behind), all around the sky while characterising its distance and line-of-sight depth. Later, Sesar et al. (2017a) identified new Sgr features at distances over 100 kpc using the same sample. The advantage of using RR Lyrae stars is that they are excellent as standard candles, their photometric distance errors being ∼7% in the optical (Mateu et al. 2012) or as good as ∼3% in the infrared (Sesar et al. 2017b) even without prior knowledge of their metallicity. This is an order of magnitude more precise than the ∼20 − 30% errors that can be achieved with K and M giants (Liu et al. 2014), as these are far more sensitive to metallicity. For these reasons, RR Lyrae have become a standard used in studies of the halo structure (for a review see Table 4 in Mateu & Vivas 2018) and substructure, serving to identify new streams and overdensities (Vivas et al. 2001; Duffau et al. 2006; Sesar et al. 2010; Mateu et al. 2018); to extend and find the connection between seemingly different substructures, like the Orphan and Chenab streams (Koposov et al. 2019); and, combined with Gaia DR2 kinematics, to provide a comprehensive 5D view of the Orphan (Koposov et al. 2019) and Pal 5 streams (Price-Whelan et al. 2019). RR Lyrae, being old (≳10 Gyr) and metal-poor ([Fe/H]≲ − 0.5) stars (Catelan & Smith 2015), are expected to dominate the outskirts of dwarf galaxies (Koleva et al. 2011, and references therein) and are therefore the first to be stripped, tracing the ancient components of a stream and thus contributing to the dynamically oldest wraps.
However, an all-sky view of the kinematics of the Sgr stream with RR Lyrae is still limited because radial velocities are observationally demanding to obtain due to the stars’ pulsations. Currently, these are only available for a few dozen RR Lyrae in selected fields along the Sgr stream (Vivas et al. 2005). In this work, we aim to provide a cohesive 5D view of the distance and proper motions of the Sgr stream using RR Lyrae stars. In Sect. 2 we describe the input catalogue – the RR Lyrae identified as such by the Gaia variability pipelines complemented with the PS1 catalogue. In Sect. 3 we derive distances for these RR Lyrae stars and describe our selection method based on sky coordinates, proper motions, and distances, and use no prior information. In Sect. 4 we present our results providing an entirely empirical characterisation of the stream including for example its proper motion, Galactocentric distance, tangential velocities, and the bifurcation. Finally, we present our conclusions in Sect. 5.
2. RR Lyrae and Gaia sample
The second data release (Gaia Collaboration et al. 2018) of the Gaia mission (Gaia Collaboration et al. 2016) has provided not only positions, magnitudes, and proper motions for more than a billion stars, but also a vast catalogue of variable sources (VC; see Holl et al. 2018). For a detailed description of the detection, classification, and post-processing pipelines we refer the reader to Eyer et al. (2017) and Rimoldini et al. (2019). Among those detected variable sources, there are 140 784 RR Lyrae that have at least 12 good G-band transits which have been validated by the Specific Objects Study (SOS) pipeline (Clementini et al. 2019). We have further increased the number to 228 904 sources by including those classified as RR Lyrae by Holl et al. (2018) and Rimoldini et al. (2019), but not processed by SOS due to the small number of observations available in DR2. We then apply the filter recommended in Rimoldini et al. (2019) to remove obvious contaminants: phot_bp_rp_excess_factor > 2 OR NULL, leaving 175 164 RR Lyrae. Finally, we include 11 318 stars identified as bona fide RR Lyrae in the PS1 catalogue (Sesar et al. 2017b), but not classified as such by the Gaia pipelines. We identify these stars in the DR2 gaia_source table by cross-matching their positions on the sky with a 1″ tolerance, and retrieve their astrometric data.
After removing the stars with no proper motions we obtain a list of 182 495 stars, 122 745 of which have been processed by the SOS pipeline. For some of them, the SOS team has derived photometric metallicities and absorption in the G band. In particular, 39 129 of them have both quantities simultaneously, which we use in Sect. 3.2 to obtain a first measurement of the metallicity distribution along the stream. As stated in Holl et al. (2018), the Gaia catalogue of variable sources is not meant to be complete and we do not expect the completeness to be above 80% when taking only sources with more than 12 field-of-view (FoV) transits (see also Mateu et al., in prep.).
3. Selection of RR Lyrae in the Sagittarius stream
Our aim is to detect the RR Lyrae of the Sgr stream from scratch to produce a characterisation that is as empirical as possible. To do so, we select two sets of initial candidates from the list of stars with proper motions presented in the previous section: the Strip and the nGC3 selections (Sect. 3.1), later pruned to filter out contaminants based on distance (Sect. 3.3) and kinematic information (Sects. 3.4 and 3.5). We use these two different selections since they offer different advantages as we shall see below. In Table 1 we show the number of stars remaining after each selection step.
Number of stars in each sample at each step of the selection process.
3.1. Initial selections: Strip and nGC3
3.1.1. Strip selection. A high-completeness, low-purity sample
A first straightforward list of candidates can be obtained by selecting stars within 20° of the orbital plane defined by the pole (l,b) = (273 8; 13
8; 13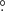 5) from Majewski et al. (2003). This is exactly equivalent to selecting stars with |
5) from Majewski et al. (2003). This is exactly equivalent to selecting stars with |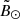 | < 20° in the Sgr coordinate frame1, a spherical heliocentric frame rotated to have the plane of the stream at
| < 20° in the Sgr coordinate frame1, a spherical heliocentric frame rotated to have the plane of the stream at 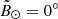 and the Sgr dwarf remnant at
and the Sgr dwarf remnant at 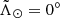 . The resulting selection contains 76 872 RR Lyrae (41% of the full catalogue).
. The resulting selection contains 76 872 RR Lyrae (41% of the full catalogue).
This selection is expected to be highly complete, limited only by the completeness of the input catalogue itself, as no kinematic or additional information (e.g. metallicity) is required. However, precisely because no information other than sky position is used, a large fraction of contaminants is expected, mostly due to the thick disc and halo. This contamination will be reduced significantly after the following selection steps.
3.1.2. nGC3 selection. A low-completeness, high-purity sample
Great circle cell count methods grouped in the xGC3 family (Johnston et al. 1996; Mateu et al. 2011, 2017) are aimed at the detection of groups of stars that populate an orbital plane different from that of the Milky Way disc. In its most basic implementation, this approach relies on the fact that the stars in a stream lie approximately on a plane through the centre of symmetry of the Galactic potential. Geometrically, this implies that the stream is confined to a great circle uniquely defined by the normal vector (pole) of the orbital plane. Therefore, if we grid the sky2 and, for each cell, count the number of stars in a wafer of a certain width perpendicular to it, we should detect an overdensity whenever we align this wafer with the orbital plane of a stream. The result is a pole count map (PCM), which is a density map of the number of stars associated to each pole and, hence, great circle.
The nGC3 method introduced in Abedi et al. (2014) also requires proper motion information in the pole counting. In this method, the velocities of the stars are required to lie in the same great circle as their positions, within a certain tolerance. This helps to clean the sample of contaminant stars that lie in a given great circle band by chance. We cannot take this approach in the heliocentric frame because then the peculiar velocity of the Sun would dominate the PCM. Instead, the nGC3 pole counts are made in the galactocentric reference frame, for which we assume a distance from the Sun to the Galactic Centre (GC) of R⊙ = 8.0 kpc (Camarillo et al. 2018), a velocity of the Sun with respect to the local standard of rest (LSR) [U⊙,V⊙,W⊙] = [11.10, 12.24, 7.25] km s−1 (Schönrich et al. 2010), and VLSR = 240 km s−1 (Reid et al. 2014). Obviously, we also require a distance to each star which implies assuming a metallicity (see Sect. 3.2). We chose as a first value [Fe/H] = − 1.7 dex. We find that the PCM does not change significantly within the range of metallicities typical for RR Lyrae in the halo: −1.5 dex ≤ [Fe/H] ≤ −1.7 dex.
Figure 1 shows the resulting PCM for the RR Lyrae, using a tolerance of 5° for both positional and velocity vectors. The method also returns a list of peaks, that is, local maxima, ordered by the number of counts contained within the corresponding pole. As expected, we observe a peak (label 1) at the centre caused by the disc. The second most dominant peak (label 2) is that produced by the Sgr stream. We also see signatures produced by the Large (label 3) and Small (labels 4 and 5) Magellanic clouds which, being concentrated on the sky, make trails instead of compact overdensities.
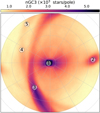 |
Fig. 1. Pole Count Map of the RR Lyrae catalogue described in Sect. 2. The Galactic disc produces the large concentration at (1), while the peaks (3),(4), and (5) are related to the Large and Small Magellanic clouds. The prominent signal on the right, (2), is caused by the Sgr stream. |
The nGC3 selection is made by extracting the RR Lyrae stars associated to the cells, or poles, around peak 2 within the 25th percentile of the maximum counts in that peak. This results in a preliminary list of candidates of 13 004 (7% of the full RR Lyrae catalogue). This sample is expected to be of lower completeness than the Strip selection because the method can introduce correlations between the spatial position and the proper motions and, more importantly, a dependence on the observational errors which can translate into kinematical biases. In particular, the method by construction selects against stars with significant motions perpendicular to the plane of the stream, making it unsuitable for the study of aspects such as velocity dispersion profiles, as we discuss in Sect. 4.6. By contrast, the nGC3 sample is expected to be of higher purity, and therefore better suited for purposes such as the selection of targets for spectroscopic follow-up.
Having a first list of candidates, we next look for trends in distances and proper motions to refine our selection. For the remainder of this section only, to avoid repetition, we use the nGC3 sample to show how our selection methodology works. This sample, by construction, is less contaminated than the Strip sample and allows us to more clearly illustrate the way we separate the candidate stars from the contamination. Wherever important differences with the Strip sample arise they are discussed in the text. The plots corresponding to the Strip selection can be found in Appendix C.
3.2. Distance determination
To determine the distances we begin by using the linear relation for the GaiaG band given in Muraveva et al. (2018):
This relation returns the absolute magnitude of the RR Lyrae star given its metallicity in the Zinn & West (1984, hereafter ZW84) scale. However, we note that the metallicity given by DPAC is calculated from the Fourier parameters of the light curve (Clementini et al. 2019). In particular, in the case of RR Lyrae of type RRab, the metallicity is calibrated with the prescription of Nemec et al. (2013) which, for the range of periods and Fourier parameters of our sample (cf. their Fig. 12), closely matches the Jurcsik & Kovacs (1996) metallicity scale. As noted in Gratton et al. (2004) and Di Fabrizio et al. (2005), there is a systematic difference of +0.3 dex between the metallicities derived from photometry in the Jurcsik & Kovacs (1996) scale and those calculated with spectroscopy3. Therefore, for our particular case, we subtract 0.3 dex from each RRab to convert the metallicities from DPAC into the ZW84 scale. This is not the case for the stars of type RRc, as their metallicity is given in a scale already similar enough to ZW84 (Nemec et al. 2013; Clementini et al. 2019).
Even though we have a way to compute the absolute magnitude for our stars, the metallicity is only available for a small fraction of them (∼35%, see Clementini et al. 2019). Additionally, the Sgr stream presents a gradient in metallicity (e.g. Zhang et al. 2017; Hayes et al. 2020). Our approach is to first test whether there is a metallicity gradient for the RR Lyrae stars with measured metallicity. This is important because it could introduce a distance bias along 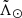 . However, we find that there is not (see below), and we assign an average metallicity to the rest of RR Lyrae.
. However, we find that there is not (see below), and we assign an average metallicity to the rest of RR Lyrae.
To calculate the distances, we use the well-known relation for the apparent magnitude of a star,
for all stars with reported metallicity and absorption in the nGC3 sample. In particular, we choose a sample of 884 stars between 20 kpc and 50 kpc from the Sun, i.e. preferentially selecting stars belonging to the stream (cf. Fig. 4 of Hernitschek et al. 2017), all of which happen to be RRab according to the classification by SOS.
In Fig. 2 we study the dependence of the metallicity on 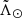 . The gradient we measure is (−1.5±0.4) × 10−3 dex deg−1 and (0.9±3.7) × 10−4 dex deg−1 for the leading and the trailing arms, respectively. While the latter is clearly compatible with zero, the former shows some sign of a gradient. Still, this gradient can be heavily influenced by the contamination, and the variations in metallicity that this would imply (0.15 dex every 100°) are smaller than the typical photometric metallicity precision (∼0.2 dex). Therefore, we recover a mean metallicity
. The gradient we measure is (−1.5±0.4) × 10−3 dex deg−1 and (0.9±3.7) × 10−4 dex deg−1 for the leading and the trailing arms, respectively. While the latter is clearly compatible with zero, the former shows some sign of a gradient. Still, this gradient can be heavily influenced by the contamination, and the variations in metallicity that this would imply (0.15 dex every 100°) are smaller than the typical photometric metallicity precision (∼0.2 dex). Therefore, we recover a mean metallicity ![$ \overline{[\mathrm{Fe}/\mathrm{H}]}_{ZW}=-1.61 $](/articles/aa/full_html/2020/06/aa37819-20/aa37819-20-eq10.gif) dex with no trace of a gradient, in good agreement with previous studies of the RR Lyrae population of Sgr (Cseresnjes 2001). As for the statistical uncertainty on the mean, we find
dex with no trace of a gradient, in good agreement with previous studies of the RR Lyrae population of Sgr (Cseresnjes 2001). As for the statistical uncertainty on the mean, we find ![$ \frac{\sigma_{[\mathrm{Fe}/\mathrm{H}]}}{\sqrt{N}} = 0.02 $](/articles/aa/full_html/2020/06/aa37819-20/aa37819-20-eq11.gif) dex. After repeating the measurement for the Strip sample, we obtain the same result but with a smaller uncertainty (
dex. After repeating the measurement for the Strip sample, we obtain the same result but with a smaller uncertainty (![$ \frac{\sigma_{[\mathrm{Fe}/\mathrm{H}]}}{\sqrt{N}} = 0.01 $](/articles/aa/full_html/2020/06/aa37819-20/aa37819-20-eq12.gif) dex). We re-visit this determination in Sect. 4.4, after having selected a reliable sample of Sgr stars, and we obtain the same value within the uncertainties.
dex). We re-visit this determination in Sect. 4.4, after having selected a reliable sample of Sgr stars, and we obtain the same value within the uncertainties.
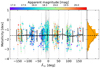 |
Fig. 2. Metallicity dependence on |
Given that there is no significant gradient, we impose the mean metallicity on all the candidate stars. We note that the distribution of apparent magnitude of the RR Lyrae type C is the same as that of the RRab. Assuming that there is no segregation between both types inside the stream, their distance distribution at any given 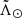 should then be the same. Therefore, we can use the same metallicity for both as long as we apply the same calibration, i.e. Eq. (1).
should then be the same. Therefore, we can use the same metallicity for both as long as we apply the same calibration, i.e. Eq. (1).
In addition, to obtain a distance estimation for each star we need the absorption in the G band. For that, we use the Schlegel et al. (1998) dust maps with the Schlafly & Finkbeiner (2011) re-calibration and the relations that allow us to translate reddening to absorption (Appendix A). Having done that, we apply Eqs. (1) and (2) to the whole list of candidates and propagate the uncertainties in metallicity, apparent magnitude, coefficients of Eq. (1), and absorption4 using the Jacobian of the transformation.
Apart from the statistical uncertainties, we also have a systematic source of uncertainty: our metallicity zero point. As mentioned above, we subtracted 0.3 dex from the metallicities reported by SOS to obtain values in the ZW84 scale. Nevertheless, if that is not the right offset we would be biasing all distances by a fixed proportion:
where ΔZ is the difference between the zero point that we assume and the true one. For instance, having no zero point in reality (ΔZ = +0.3 dex) and having a zero point that is double what we assumed (ΔZ = −0.3 dex), respectively, and for a distance of 25 kpc, we would obtain 23.92 kpc (−4.3%) and 26.13 kpc (+4.5%). We expect the true zero point to be closer to our value and therefore the systematic error to be much smaller than 4%.
3.3. Distance selection
In the top panel of Fig. 3 we present the resulting distribution of distances with 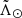 . A conspicuous pattern emerges as a result of selecting sources belonging to the Sgr orbital plane. Nevertheless, there is still a noticeable fraction of contamination even after applying the nGC3 PCM technique: thick disc, halo, and even the Sculptur dwarf Spheroidal at
. A conspicuous pattern emerges as a result of selecting sources belonging to the Sgr orbital plane. Nevertheless, there is still a noticeable fraction of contamination even after applying the nGC3 PCM technique: thick disc, halo, and even the Sculptur dwarf Spheroidal at 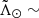 –75° (the latter is easily removed). Continuing with the aim of re-discovering the stream from scratch, we apply a method to select probable members that requires almost no assumptions and that we call Tailored Gaussian Mixture (TGM).
–75° (the latter is easily removed). Continuing with the aim of re-discovering the stream from scratch, we apply a method to select probable members that requires almost no assumptions and that we call Tailored Gaussian Mixture (TGM).
 |
Fig. 3. Distance as a function of |
The idea of the TGM is to select the pattern formed by the Sgr stars with 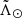 isolating it from both the foreground and the background contamination. For a given bin of
isolating it from both the foreground and the background contamination. For a given bin of 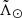 , we process the histogram of heliocentric distances and identify the different components (Sgr and contamination). A Gaussian is then fitted to each component to obtain their widths. The algorithm starts at the dwarf and uses it as an anchor since it is the dominant component at
, we process the histogram of heliocentric distances and identify the different components (Sgr and contamination). A Gaussian is then fitted to each component to obtain their widths. The algorithm starts at the dwarf and uses it as an anchor since it is the dominant component at 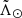 = 0°. The component corresponding to Sgr in the contiguous bins is assigned by finding the one with the highest continuity in heliocentric distance. When none of the components found are close enough to the one in the previous bin, we skip the bin and try with the next one. The details of the method can be found in Appendix B.
= 0°. The component corresponding to Sgr in the contiguous bins is assigned by finding the one with the highest continuity in heliocentric distance. When none of the components found are close enough to the one in the previous bin, we skip the bin and try with the next one. The details of the method can be found in Appendix B.
With this algorithm we obtain a deterministic measurement of the centre of the pattern as well as a first estimation of its depth. The result for the nGC3 sample is shown in the bottom panel of Fig. 3 as error bars located at the centre of each bin in 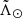 . The vertical extent of the error bars represents the 2σ interval of the dispersion recovered by the fit and the horizontal extent represents the size of the bin (barely visible). We note that using the same metallicity for all the stars increases the contamination because the foreground (thick disc) merges with the signal of the stream. Since the RR Lyrae in the thick disc tend to be more metal rich than those in Sgr, assigning an incorrectly smaller metallicity to these stars translates into larger distances and thus pushes its distribution towards that of the stream, hampering the separation. Finally, by visual inspection we find that in some of the bins the Gaussian fit has not converged to a good solution. The two main causes are (i) too few sources and (ii) the components are too close to be resolved, resulting in an overestimated width. Those few cases (plotted in red in the bottom panel of Fig. 3) have been removed.
. The vertical extent of the error bars represents the 2σ interval of the dispersion recovered by the fit and the horizontal extent represents the size of the bin (barely visible). We note that using the same metallicity for all the stars increases the contamination because the foreground (thick disc) merges with the signal of the stream. Since the RR Lyrae in the thick disc tend to be more metal rich than those in Sgr, assigning an incorrectly smaller metallicity to these stars translates into larger distances and thus pushes its distribution towards that of the stream, hampering the separation. Finally, by visual inspection we find that in some of the bins the Gaussian fit has not converged to a good solution. The two main causes are (i) too few sources and (ii) the components are too close to be resolved, resulting in an overestimated width. Those few cases (plotted in red in the bottom panel of Fig. 3) have been removed.
We finish by creating two splines with the good solutions (green error bars). The first passes through the centres and represents the change in the distance with 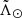 (orange line). We use the second one to trace the changes in depth of the stream and produce a smooth ∼2σ confidence interval, as represented by the shaded orange area. We also show the smoothed median distance predicted by the Law & Majewski (2010, hereafter LM10) model5. These solid (first wrap) and dashed (second wrap) green lines can be seen to follow our orange track in some part of the stream. However, there are important differences which we comment on in Sect. 4. On the other hand, our results are in very good agreement with the recent determination of the pattern of Sgr obtained with RR Lyrae by Hernitschek et al. (2017, see their Fig. 4).
(orange line). We use the second one to trace the changes in depth of the stream and produce a smooth ∼2σ confidence interval, as represented by the shaded orange area. We also show the smoothed median distance predicted by the Law & Majewski (2010, hereafter LM10) model5. These solid (first wrap) and dashed (second wrap) green lines can be seen to follow our orange track in some part of the stream. However, there are important differences which we comment on in Sect. 4. On the other hand, our results are in very good agreement with the recent determination of the pattern of Sgr obtained with RR Lyrae by Hernitschek et al. (2017, see their Fig. 4).
The candidates are selected if they fall inside the orange shaded area, resulting in a set of 7 953 stars (61% of the initial nGC3 sample). In the case of the Strip sample (Fig. C.1) the output of the TGM results in a selection of 18 045 stars (23%). Both samples contain field stars that require additional filters to be discarded, especially at 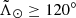 where the Sgr stars get closer to the Sun and merge with the Virgo overdensity (Jurić et al. 2008). In that region we also have the presence of Sgr stars at a distance of ∼90 kpc, which correspond to the apocentre of the trailing arm.
where the Sgr stars get closer to the Sun and merge with the Virgo overdensity (Jurić et al. 2008). In that region we also have the presence of Sgr stars at a distance of ∼90 kpc, which correspond to the apocentre of the trailing arm.
We also include a comparison with a mock catalogue. We query the mock Gaia catalogue by Rybizki et al. (2018) in HEALPix bins of level 4 (∼14 square degrees) along the orbital plane of Sgr selecting 2000 stars for each patch in the sky. We then compute the true distances by simply inverting the true parallaxes and produce the heliocentric distance histograms shown in black on the right of Fig. 3 (normalised to the number of stars in the nGC3 sample). The mock distribution presents a smooth exponential profile with no sign of bumps, in contrast with our data (blue filled histogram). With the mock as a reference, we gain an idea of the contamination that we expect at each portion of the stream, with the parts near pericentre being the most susceptible. This corresponds to the beginning of the trailing tail and the far end of the leading one (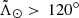 ), this latter being particularly contaminated. After performing our selection (orange histogram at the bottom right panel of Fig. 3) we see that what we have discarded, that is, what we consider contamination (blue line), resembles the mock distribution, except for two details: (i) at short distances, the effect mentioned earlier of using an incorrect metallicity for the thick disc modifies the shape of the distribution and ii) the absolute value of counts at large distances is not the same. The latter could be due either to a problem of normalisation between the thick disc and halo components of the mock or simply to the fact that the parameters of the model do not reproduce the observations accurately enough.
), this latter being particularly contaminated. After performing our selection (orange histogram at the bottom right panel of Fig. 3) we see that what we have discarded, that is, what we consider contamination (blue line), resembles the mock distribution, except for two details: (i) at short distances, the effect mentioned earlier of using an incorrect metallicity for the thick disc modifies the shape of the distribution and ii) the absolute value of counts at large distances is not the same. The latter could be due either to a problem of normalisation between the thick disc and halo components of the mock or simply to the fact that the parameters of the model do not reproduce the observations accurately enough.
3.4. Proper motion selection: right ascension
We continue the selection of RR Lyrae candidates based now on their proper motion trends throughout the Sgr stream. In order to avoid overlap between the different wraps, we take those corresponding to the apocentre of the trailing arm and shift their location by −360°. Therefore, from here onwards the plots reach beyond −180°.
Taking the stars already selected according to their heliocentric distance, we now plot in Fig. 4 the observed proper motion in right ascension as a function of 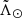 (blue dots). We observe a modulation of the dispersion which is dominated by the correlation between the uncertainty and the distance. This is especially noticeable in the Strip sample (Fig. C.2), where the dispersion near the apocentres is significantly larger. Also, there are at least two clearly identifiable patterns, especially at the beginning of the trailing and the leading arms.
(blue dots). We observe a modulation of the dispersion which is dominated by the correlation between the uncertainty and the distance. This is especially noticeable in the Strip sample (Fig. C.2), where the dispersion near the apocentres is significantly larger. Also, there are at least two clearly identifiable patterns, especially at the beginning of the trailing and the leading arms.
 |
Fig. 4.
|
To understand the effects of the contamination, we resort once more to the mock MW catalogue described in Sect. 3.3. We use the orange area obtained in Sect. 3.2 to filter the particles in the model by distance, add the errors in proper motion provided with the mock catalogue and finally create the 2D histogram shown in the top panel of Fig. 4. As can be seen, it follows quite closely the trail of stars at higher μα*. We note that these mock sources are all labelled as halo stars, except for the small range of 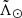 where the stream passes behind the GC, where it is dominated by thick disc stars with a small fraction of thin disc stars.
where the stream passes behind the GC, where it is dominated by thick disc stars with a small fraction of thin disc stars.
As done for the distance, we run our TGM with the parameters listed in Appendix B and skip any bin that contains less than five stars because we have fewer left after the previous selection. The results are shown in the bottom panel of Fig. 4, where we can already see that the prediction of the LM10 model shown in the upper panel (green line) is similar to the trend we detect (see Sect. 4.1 for a discussion on the residuals). Again, after selecting only the stars within the orange shaded area, we are left with 6797 RR Lyrae (52%) stars in the nGC3 sample. In the case of the Strip sample, we find that we cannot recover the same trend beyond 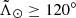 due to the predominance of the contamination. We tried different parameter combinations without any success. Finally, to avoid leaving that region void, we only select stars around the track of the LM10 model beyond
due to the predominance of the contamination. We tried different parameter combinations without any success. Finally, to avoid leaving that region void, we only select stars around the track of the LM10 model beyond 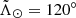 , choosing the ones with −3.5 mas yr−1 ≤ μα* ≤ −0.5 mas yr−1 (orange box in Fig. C.2). This results in a list of 12 583 stars (16%).
, choosing the ones with −3.5 mas yr−1 ≤ μα* ≤ −0.5 mas yr−1 (orange box in Fig. C.2). This results in a list of 12 583 stars (16%).
3.5. Proper motion selection: declination
We apply the TGM now to the proper motion in declination of the remaining stars with the same parameters as in Sect. 3.4 and recover a single component all along the stream, as can be seen in Fig. 5. We note that the halo stars from the mock catalogue present a proper motion that follows that of the Sgr stream closely but not exactly. This is likely due to the fact that μδ is roughly aligned with the motion perpendicular to the stream6, and because the dominant contribution in this direction is the Solar reflex, it is natural that the stream cannot be cleanly separated from the field. In this step, we have therefore performed the equivalent to a two-sigma clipping.
 |
Fig. 5. Same as Fig. 4 but with proper motion in declination. Now we only show the stars selected by distance and μα*. |
After applying these selections we obtain our final list of candidates with 6 608 stars for the nGC3 sample and 11 677 for the Strip. The two catalogues are available as one table at CDS (see Appendix E), with a flag that describes whether the star was selected using one method, the other, or both.
4. Results
Now that we have assembled a reliable list of stars belonging to the Sgr stream, we proceed on to examine its main characteristics. In this section, in contrast with the previous, we focus on the Strip sample because, as we discuss below, the nGC3 presents a kinematical bias induced by the PCM method. The corresponding figures and derived quantities for the nGC3 sample can be found in Appendix D.
4.1. The missing dimensions: proper motions
First, we want to determine the proper motion of the Sgr stream and examine the two samples looking for the presence of any kinematic biases. We do so by comparing the trends in proper motion of our stars with those obtained by A20 and the predictions of LM10. In Fig. 6 (Fig. D.1) we present the proper motions in Galactic coordinates as a function of 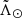 for the Strip (nGC3) sample. The colours of the panels a, μl, and b, μb, as indicated by the colour bars, are the same as in Fig.3a of A20 for ease of comparison. In panel c on the other hand, we show the total proper motion coloured according to the distance derived for each RR Lyrae star. In all three panels, we have added the smooth median obtained from A20 (black) and the predictions of the LM10 model (green). We note that the farthest stars (blue points in panel c have approximately the proper motion that the model predicts for the second wrap, confirming that we are indeed detecting the apocentre of the trailing tail.
for the Strip (nGC3) sample. The colours of the panels a, μl, and b, μb, as indicated by the colour bars, are the same as in Fig.3a of A20 for ease of comparison. In panel c on the other hand, we show the total proper motion coloured according to the distance derived for each RR Lyrae star. In all three panels, we have added the smooth median obtained from A20 (black) and the predictions of the LM10 model (green). We note that the farthest stars (blue points in panel c have approximately the proper motion that the model predicts for the second wrap, confirming that we are indeed detecting the apocentre of the trailing tail.
 |
Fig. 6. Proper motion trends with |
In panel d we plot the difference between the median of our sample and that of A20, both smoothed with a Gaussian filter, and the associated 1σ intervals. While the discrepancy is within 2σ in most parts of the stream, we note that the residuals start to grow again at 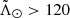 °, which is probably related to the degree of contamination being higher in this region due to our selection (see Sect. 3.4). In the trailing tail, the differences are within 1σ until
°, which is probably related to the degree of contamination being higher in this region due to our selection (see Sect. 3.4). In the trailing tail, the differences are within 1σ until 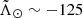 °, at which point the A20 sample becomes heavily affected by the contamination of the disc. Remarkably, A20 find stars in the trailing apocentre amid all the contamination, and the median μtot found by these latter authors is compatible with ours (orange shaded area), even though the only criteria used in their selection was based on proper motions. Overall, the differences are of the order of ∼0.3 mas yr−1 at most, and only with more accurate proper motions will we have the precision needed to decipher whether there is a kinematic separation between the different populations within the stream.
°, at which point the A20 sample becomes heavily affected by the contamination of the disc. Remarkably, A20 find stars in the trailing apocentre amid all the contamination, and the median μtot found by these latter authors is compatible with ours (orange shaded area), even though the only criteria used in their selection was based on proper motions. Overall, the differences are of the order of ∼0.3 mas yr−1 at most, and only with more accurate proper motions will we have the precision needed to decipher whether there is a kinematic separation between the different populations within the stream.
We also examined the residuals against LM10, which we show in panel e. The agreement is within 2σ in the range −150° 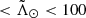 ° and is only broken near the trailing apocentre, which is expected given the differences between the predicted distances and the observed ones (cf. Fig. 3), and beyond L≥120°, the region where we already know that the Strip selection is poor.
° and is only broken near the trailing apocentre, which is expected given the differences between the predicted distances and the observed ones (cf. Fig. 3), and beyond L≥120°, the region where we already know that the Strip selection is poor.
4.2. Galactocentric distance
In Fig. 7, we show a decomposition of the Sgr stream into each of the available dimensions, with the first panel a containing the distribution of the candidate stars in the sky for reference. We begin by analysing the trend in Galactocentric distance with 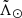 by converting the heliocentric distances derived in Sect. 3.2 with the parameters of the Sun described in Sect. 3.1. We are interested in the distribution of the tidal debris across the Galaxy since this gives us a direct insight into the actual orbit of the progenitor (Binney & Tremaine 2008, but see Sanders & Binney 2013). Additionally, we also want to estimate the location of the apocentres and their angular separation, as these quantities can be used to characterise the stream and compare with independent determinations and models.
by converting the heliocentric distances derived in Sect. 3.2 with the parameters of the Sun described in Sect. 3.1. We are interested in the distribution of the tidal debris across the Galaxy since this gives us a direct insight into the actual orbit of the progenitor (Binney & Tremaine 2008, but see Sanders & Binney 2013). Additionally, we also want to estimate the location of the apocentres and their angular separation, as these quantities can be used to characterise the stream and compare with independent determinations and models.
 |
Fig. 7. Position, distance, and velocity as a function of |
Panel b of Fig. 7 shows the Galactocentric distance distribution of the stars in the Strip sample as a function of 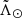 . In orange we show the smoothed median in bins of 5° and its associated 1σ error. The green line corresponds to the prediction by LM10. We notice that the model does not follow our measurements, deferring more than 3σ in most parts of the stream, including the centre of the dwarf. These discrepancies cannot be due to the assumed metallicity zero point. We use Eqs. (1) and (2) to convert the residuals in distance observed in the leading arm into differences in metallicity and we find that there should be a change of ∼1 dex in ∼50° to account for it. This jump is much larger than the uncertainties in metallicity and would have been easily recognisable in Fig. 2. Moreover, the green and orange lines (model and data, respectively) cross at
. In orange we show the smoothed median in bins of 5° and its associated 1σ error. The green line corresponds to the prediction by LM10. We notice that the model does not follow our measurements, deferring more than 3σ in most parts of the stream, including the centre of the dwarf. These discrepancies cannot be due to the assumed metallicity zero point. We use Eqs. (1) and (2) to convert the residuals in distance observed in the leading arm into differences in metallicity and we find that there should be a change of ∼1 dex in ∼50° to account for it. This jump is much larger than the uncertainties in metallicity and would have been easily recognisable in Fig. 2. Moreover, the green and orange lines (model and data, respectively) cross at 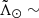 30° and again at
30° and again at 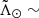 80° implying a change of sign in the residuals. This would also require a shift in the sign of the offset (ΔZ defined in Sect. 3.2) to explain it, which by construction is not possible. Therefore, it is safe to conclude that the deviations from the model are indeed physical. The same applies to the trailing arm, where the discrepancy in metallicity is too large to be artificial. On the other hand, the pattern we find is compatible with the determination made by Hernitschek et al. (2017) although, compared to their work, we do not use any modelling of the halo and, as a result, the trend that we recover is smoother.
80° implying a change of sign in the residuals. This would also require a shift in the sign of the offset (ΔZ defined in Sect. 3.2) to explain it, which by construction is not possible. Therefore, it is safe to conclude that the deviations from the model are indeed physical. The same applies to the trailing arm, where the discrepancy in metallicity is too large to be artificial. On the other hand, the pattern we find is compatible with the determination made by Hernitschek et al. (2017) although, compared to their work, we do not use any modelling of the halo and, as a result, the trend that we recover is smoother.
We tried to calculate the apocentres using the recipe described in Belokurov et al. (2014) and used again in Hernitschek et al. (2017), which consists of describing the apocentres of the debris as a Gaussian profile. We find that fitting a Gaussian to the leading arm does not accurately reproduce our observations and the results are highly dependent on the range of 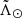 used. Instead, we construct a cubic spline (orange line in Fig. 7b) to smooth the median and obtain a curve that can be evaluated at any point. We then use it to search for the local maximum. Due to the underlying binning, we use half the bin size in
used. Instead, we construct a cubic spline (orange line in Fig. 7b) to smooth the median and obtain a curve that can be evaluated at any point. We then use it to search for the local maximum. Due to the underlying binning, we use half the bin size in 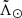 as the uncertainty in the angular position. In distance, we use the error in the median shown as an orange shaded area in Fig. 7b. Applying this strategy to the Strip samples leads to the following values (see Appendix D for the values estimated with nGC3):
as the uncertainty in the angular position. In distance, we use the error in the median shown as an orange shaded area in Fig. 7b. Applying this strategy to the Strip samples leads to the following values (see Appendix D for the values estimated with nGC3):
-
Trailing:
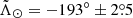 at DGC = (92.48 ± 1.45) kpc,
at DGC = (92.48 ± 1.45) kpc, -
Leading:
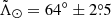 at DGC = (47.73 ± 0.48) kpc,
at DGC = (47.73 ± 0.48) kpc,
with an angular distance between apocentres that implies a differential heliocentric orbital precession of 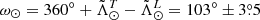 .
.
We only show the statistical uncertainties but we stress again that an incorrect metallicity zero point would bias these estimates. Nevertheless, we expect the difference to be much smaller than 4% in distance (Sect. 3.2). On the other hand, the contribution of the uncertainty in the GC-Sun distance is negligible.
Our determination for the Strip, shown as vertical grey bands across the whole of Fig. 7, has to be compared with the values derived by Belokurov et al. (2014): 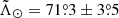 at D = (47.8 ± 0.5) kpc for the leading arm and
at D = (47.8 ± 0.5) kpc for the leading arm and 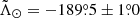 at D = (102.5 ± 2.5) kpc for the trailing arm (
at D = (102.5 ± 2.5) kpc for the trailing arm (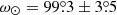 ). We note that there is a ∼3.5σ discrepancy at the far apocentre, which cannot be reconciled by tuning ΔZ without creating tension in the near one. In contrast, the results of Hernitschek et al. (2017) using the RR Lyrae from PS1 are closer to ours:
). We note that there is a ∼3.5σ discrepancy at the far apocentre, which cannot be reconciled by tuning ΔZ without creating tension in the near one. In contrast, the results of Hernitschek et al. (2017) using the RR Lyrae from PS1 are closer to ours: 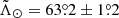 at D = (47.8 ± 0.5) kpc for the leading tail and
at D = (47.8 ± 0.5) kpc for the leading tail and 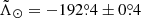 at D = (98.95 ± 1.4) kpc for the trailing tail (
at D = (98.95 ± 1.4) kpc for the trailing tail (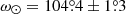 ). Nevertheless, the tension is still present. The major difference is that we have obtained our measurements in a model-independent way and using all the stars in our sample.
). Nevertheless, the tension is still present. The major difference is that we have obtained our measurements in a model-independent way and using all the stars in our sample.
4.3. A peek into the unknown: tangential velocities
Finally, with all five dimensions together (position, proper motion, and distance) we can access an almost unexplored aspect of the stream: the tangential velocity. To do so, we make use of the Python package GALA (Price-Whelan 2017; Price-Whelan et al. 2017) which provides a tool to correct for the solar reflex given the position and velocity of the Sun with respect to the GC. For that, we use the parameters described in Sect. 3. The resulting velocities for the Strip sample are shown in panels c and d of Fig. 7 for the velocity along (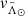 ) and across (
) and across (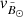 ) the stream, respectively. In contrast with the previous section, here we smooth the median values in bins of 10° in
) the stream, respectively. In contrast with the previous section, here we smooth the median values in bins of 10° in 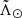 with a Gaussian filter (similar to A20).
with a Gaussian filter (similar to A20).
When looking at the velocity along the 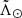 axis (orange line in Fig. 7c) we note the general agreement with the LM10 model (green line). In most of the regions, both trends are compatible within 3σ except for (i) the dwarf itself, where we find that our results are ∼20 km s−1 above the predictions; and ii) beyond
axis (orange line in Fig. 7c) we note the general agreement with the LM10 model (green line). In most of the regions, both trends are compatible within 3σ except for (i) the dwarf itself, where we find that our results are ∼20 km s−1 above the predictions; and ii) beyond 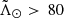 °, where the differences exceed 70 km s−1 at some points. While the latter could be related to the contamination, it would need to bias both the distance by more than 5 kpc and the proper motions by more than 0.3 mas yr−1 to reconcile our observed
°, where the differences exceed 70 km s−1 at some points. While the latter could be related to the contamination, it would need to bias both the distance by more than 5 kpc and the proper motions by more than 0.3 mas yr−1 to reconcile our observed 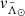 with the model. A more likely scenario is that the orbit of the progenitor in LM10 is not accurately reproducing the observations, which is consistent with our findings of Sect. 4.2 and with the fact that we observe a significantly different tangential velocity for the dwarf.
with the model. A more likely scenario is that the orbit of the progenitor in LM10 is not accurately reproducing the observations, which is consistent with our findings of Sect. 4.2 and with the fact that we observe a significantly different tangential velocity for the dwarf.
The velocity perpendicular to the orbital plane of Sgr is also interesting since it is where the effects of other satellites like the Magellanic Clouds are expected to be more noticeable. This is the case of the Orphan stream, where the misalignment between the velocities of the stars and its orbit have been related to the Large Magellanic Cloud (Erkal et al. 2019). In panel d we show the changes in 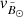 along the stream. We find no significant deviation from zero at the current level of precision but we notice the degeneracy with the velocities used to correct the solar reflex. Hayes et al. (2018) used a sample of Sgr stars to obtained an estimate of the Sun’s velocity with respect to the GC by fitting the observations to the model of LM10. However, ideally we would like to obtain a global fit that can be used to quantify the deviations caused by the satellites and simultaneously estimate the solar parameters. While our sample can indeed be used for that purpose, this analysis is out of the scope of the present work.
along the stream. We find no significant deviation from zero at the current level of precision but we notice the degeneracy with the velocities used to correct the solar reflex. Hayes et al. (2018) used a sample of Sgr stars to obtained an estimate of the Sun’s velocity with respect to the GC by fitting the observations to the model of LM10. However, ideally we would like to obtain a global fit that can be used to quantify the deviations caused by the satellites and simultaneously estimate the solar parameters. While our sample can indeed be used for that purpose, this analysis is out of the scope of the present work.
We can also obtain a measure of the total velocity projected in the sky of the Sgr dwarf that can be used to initialise simulations from the present time, for example. We do so by summing in quadrature both components of velocity for all stars within a cone of 5° around the centre of the Globular Cluster M54 (Bellazzini et al. 2008). Then, the median tangential velocity is V⊥ = 272.56 ± 0.02 km s−1.
Our final output of this part is an interpolator for each component of the velocity for any 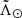 along the stream. Despite the large uncertainties in proper motions, we can still recover a trend that can be used to test future models of Sgr. In Appendix E we explain how to download them, along with the rest of the interpolators used in this work, such as distance, proper motion, and so on.
along the stream. Despite the large uncertainties in proper motions, we can still recover a trend that can be used to test future models of Sgr. In Appendix E we explain how to download them, along with the rest of the interpolators used in this work, such as distance, proper motion, and so on.
4.4. Metallicity
Now that we have a reliable sample of candidates, we can check our initial assumption of a constant metallicity along the arms of Sgr (Sect. 3.2). The fifth panel of Fig. 7 shows the metallicity distribution for the stars for which this parameter has been measured. The error bars correspond to the median, with the associated error, in bins of 30° for both RRab (orange) and RRc (blue) RR Lyrae. The first thing we note is that the median oscillates around the dashed line that represents the mean value calculated in Sect. 3.2, with all stars in the range of distance between 20 kpc and 50 kpc: −1.6 dex.
With this we can already clearly see that there is no appreciable gradient. Nevertheless, we measure it by fitting a line to all RRab stars in the leading (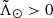 °) and the trailing (
°) and the trailing (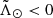 °) arms. By doing so we obtain a slope of (−1.8 ± 0.5) ×10−3 dex deg−1 and (0.3 ± 0.4) × 10−3 dex deg−1 for the leading and trailing arms, respectively. While this could be easily disregarded as unimportant, we note that the current estimates of the metallicity gradient in the tails of Sgr are of the order of 10−3 dex deg−1 (Hayes et al. 2020). Nevertheless, considering the inhomogeneous coverage of the sky of the subsample of stars with metallicity and the possible contribution from contamination, it is hard to trust the variations that we measure. In the worst case scenario, this would cause a difference at the trailing apocentre of ∼0.2 dex, which is of the order of the precision achievable with photometric metallicities. In turn, such a difference would imply that our measurement of the distance obtained in the previous section could be short by ∼3%, that is, that the trailing apocentre could alternatively be at a distance of ∼96 kpc instead of ∼93 kpc. While this effect would bring our estimate closer to the values in the literature7, it is still within its 2σ confidence interval. In summary, we can say that there is no measurable metallicity gradient at the current level of precision offered by the photometric metallicities.
°) arms. By doing so we obtain a slope of (−1.8 ± 0.5) ×10−3 dex deg−1 and (0.3 ± 0.4) × 10−3 dex deg−1 for the leading and trailing arms, respectively. While this could be easily disregarded as unimportant, we note that the current estimates of the metallicity gradient in the tails of Sgr are of the order of 10−3 dex deg−1 (Hayes et al. 2020). Nevertheless, considering the inhomogeneous coverage of the sky of the subsample of stars with metallicity and the possible contribution from contamination, it is hard to trust the variations that we measure. In the worst case scenario, this would cause a difference at the trailing apocentre of ∼0.2 dex, which is of the order of the precision achievable with photometric metallicities. In turn, such a difference would imply that our measurement of the distance obtained in the previous section could be short by ∼3%, that is, that the trailing apocentre could alternatively be at a distance of ∼96 kpc instead of ∼93 kpc. While this effect would bring our estimate closer to the values in the literature7, it is still within its 2σ confidence interval. In summary, we can say that there is no measurable metallicity gradient at the current level of precision offered by the photometric metallicities.
Finally, we show the mean values of metallicity for each type of RR Lyrae star in Table 2 from which we can conclude that the metallicity of this sample is −1.61±0.01 dex.
Metallicity statistics of the nGC3 (Strip) final sample.
4.5. Completeness assessment
Here, we inspect the distribution of the counts along the stream and the overlap between the different samples. The bottom panel of Fig. 7 shows the number of stars of the final Strip sample (blue bars) in 5° bins compared to the counts after the selection based on distance of Sect. 3.3 (orange step). Here, the dashed black line represents the imposed limit of five stars below which we do not compute the median used in panels b, c, and d.
As expected, a significant fraction of the stars fall inside the dwarf itself: 4 730 (40%) in the region 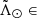 [−10°, 10°]. The rest are spread rather uniformly except for the two parts where the stream crosses behind the MW disc, which are easily identifiable by a sudden drop in the counts. We do observe a larger number of stars in the leading arm compared to the symmetric
[−10°, 10°]. The rest are spread rather uniformly except for the two parts where the stream crosses behind the MW disc, which are easily identifiable by a sudden drop in the counts. We do observe a larger number of stars in the leading arm compared to the symmetric 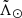 in the trailing arm, which is to be expected near apocentre where the stars in the stream slow down. Nevertheless, as explained in Sect. 3.4, the increase of the proper motion uncertainties near apocentre prevents us from effectively reducing the contamination there. That is why the orange (Strip sample after selecting only based on distance) and blue (final Strip sample) histograms are so close to each other in that region.
in the trailing arm, which is to be expected near apocentre where the stars in the stream slow down. Nevertheless, as explained in Sect. 3.4, the increase of the proper motion uncertainties near apocentre prevents us from effectively reducing the contamination there. That is why the orange (Strip sample after selecting only based on distance) and blue (final Strip sample) histograms are so close to each other in that region.
We also include the counts of the final nGC3 sample as red bars. In this case, the two distributions are similar for 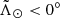 but are more different for the leading arm. The cross-match between both final samples tells us that all but 44 stars in the nGC3 sample are in the Strip sample. Thus, the missing stars in the leading tail are those that cause the difference in total proper motion seen in Fig. 6. Comparing both samples, we note that Cseresnjes (2001) estimated the total amount of RRab stars to be ∼8400. This value is almost exactly halfway between the number of stars in the nGC3 sample and the number in the Strip sample, reinforcing the idea that the former is pure but incomplete and the latter is complete but contaminated.
but are more different for the leading arm. The cross-match between both final samples tells us that all but 44 stars in the nGC3 sample are in the Strip sample. Thus, the missing stars in the leading tail are those that cause the difference in total proper motion seen in Fig. 6. Comparing both samples, we note that Cseresnjes (2001) estimated the total amount of RRab stars to be ∼8400. This value is almost exactly halfway between the number of stars in the nGC3 sample and the number in the Strip sample, reinforcing the idea that the former is pure but incomplete and the latter is complete but contaminated.
Regarding the cross-matched with A20, the first thing that is important to mention is that the sample of A20 contains only 3476 RR Lyrae of the 182 495 from the list presented in Sect. 2. Compared to the Strip sample, the sample used in A20 contains 3233 of the 11 677 selected in this work. If we restrict ourselves to the region where the contamination is lower (−120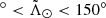 ) then we find that out of the 3145 RR Lyrae in A20, 3033 are among the 10 431 of the Strip sample. This means that the recovery fraction is around 95%. If we now analyse the cross-match between the nGC3 and A20 samples, we see that the sample of A20 contains 2712 stars of the 6608 in the nGC3 sample; 2661 out of 6386 stars if we only consider the low contamination region defined in Sect. 4.5. The resulting recovery fraction is around 80% for the nGC3 sample. Since we obtained these estimates from low-contamination regions, we expect them to be similar to the true completeness but we stress that these percentages apply only to the true members among all the candidates (as if there was no contamination). In any case, the RR Lyrae in A20 that are not in any of our two samples can mostly be found in the dwarf, the tip of the tails (where we know that the contamination in A20 is higher), and, most interestingly, the leading apocentre. However, further investigation of the differences among the samples requires a fine characterisation of the different selection functions and we leave this for a future study. On the other hand, the recovery fraction for the RR Lyrae in A20 is roughly between 30% and 40% (we cannot extrapolate this estimates of completeness to stars with other colours and magnitudes). Nevertheless, expanding the list of A20 would require a good treatment of the contamination and probably the introduction of a model for the halo and thin/thick disc.
) then we find that out of the 3145 RR Lyrae in A20, 3033 are among the 10 431 of the Strip sample. This means that the recovery fraction is around 95%. If we now analyse the cross-match between the nGC3 and A20 samples, we see that the sample of A20 contains 2712 stars of the 6608 in the nGC3 sample; 2661 out of 6386 stars if we only consider the low contamination region defined in Sect. 4.5. The resulting recovery fraction is around 80% for the nGC3 sample. Since we obtained these estimates from low-contamination regions, we expect them to be similar to the true completeness but we stress that these percentages apply only to the true members among all the candidates (as if there was no contamination). In any case, the RR Lyrae in A20 that are not in any of our two samples can mostly be found in the dwarf, the tip of the tails (where we know that the contamination in A20 is higher), and, most interestingly, the leading apocentre. However, further investigation of the differences among the samples requires a fine characterisation of the different selection functions and we leave this for a future study. On the other hand, the recovery fraction for the RR Lyrae in A20 is roughly between 30% and 40% (we cannot extrapolate this estimates of completeness to stars with other colours and magnitudes). Nevertheless, expanding the list of A20 would require a good treatment of the contamination and probably the introduction of a model for the halo and thin/thick disc.
4.6. Velocity dispersion
As mentioned in Gibbons et al. (2014), the stars that escape through the Lagrange points do so with a dispersion in velocity inherited from the dispersion that the stars had at the outskirts of the dwarf, the latter being proportional to the total mass of the infalling satellite. Additionally, the stream can become kinematically heated by the continuous interaction with dark matter subhalos (Johnston et al. 2002). Therefore, learning about the velocity dispersion of the stream allows us to obtain a tighter constraint on the dynamical mass of the progenitor and potentially a test for dark matter models.
In Fig. 8 (Fig. D.2) we show the velocity dispersion profile of 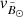 for the Strip (nGC3) sample. We also include the profile of the LM10 model in green (solid line). We have been able to reproduce both curves easily with the LM10 particles by randomly assigning the uncertainties of the observed stars and subsequently applying only the initial selection (Sect. 3.1). The remaining differences between the observed profiles and the ones predicted by the model are mostly due to the fact that we did not apply the whole methodology described in Sects. 3.3–3.5. If we wanted to obtain an estimate of the deviations caused by possible subhalos, it would be necessary to build the selection function of our two samples and accurately model the observational errors.
for the Strip (nGC3) sample. We also include the profile of the LM10 model in green (solid line). We have been able to reproduce both curves easily with the LM10 particles by randomly assigning the uncertainties of the observed stars and subsequently applying only the initial selection (Sect. 3.1). The remaining differences between the observed profiles and the ones predicted by the model are mostly due to the fact that we did not apply the whole methodology described in Sects. 3.3–3.5. If we wanted to obtain an estimate of the deviations caused by possible subhalos, it would be necessary to build the selection function of our two samples and accurately model the observational errors.
 |
Fig. 8. Velocity dispersion profile for |
4.7. The bifurcation
The bifurcation of the Sgr stream was observed for the first time by Belokurov et al. (2006) in the leading tail, and later detected in the trailing arm by Koposov et al. (2012) and Navarrete et al. (2017). This feature can be clearly seen with the M giants and shows the stream splitting into two branches creating a bi-modal distribution of  in some portions of the tails. Although some models have been proposed to explain this feature with only one progenitor, for example Peñarrubia et al. (2010) (but see Peñarrubia et al. 2011), there is no consensus on its cause. Thus, it is important to provide additional observational evidence with different tracers to constrain the range of possibilities.
in some portions of the tails. Although some models have been proposed to explain this feature with only one progenitor, for example Peñarrubia et al. (2010) (but see Peñarrubia et al. 2011), there is no consensus on its cause. Thus, it is important to provide additional observational evidence with different tracers to constrain the range of possibilities.
Figure 9 shows the histogram of 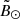 of the final Strip sample for different bins in
of the final Strip sample for different bins in 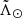 within the range −160
within the range −160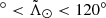 (again, see Appendix D for the equivalent plot for the nGC3 sample). In some portions of the leading arm (top panel) a bi-modal distribution is evident. The strongest signal is in the range 100
(again, see Appendix D for the equivalent plot for the nGC3 sample). In some portions of the leading arm (top panel) a bi-modal distribution is evident. The strongest signal is in the range 100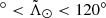 , where the two highest peaks are separated by ∼6°. We note the agreement between our findings and those in Belokurov et al. (2006), where these latter authors report the beginning of the bifurcation at
, where the two highest peaks are separated by ∼6°. We note the agreement between our findings and those in Belokurov et al. (2006), where these latter authors report the beginning of the bifurcation at 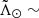 80° and the separation between the two branches growing from ∼7° to ∼10° at
80° and the separation between the two branches growing from ∼7° to ∼10° at 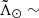 120°. In the trailing arm, there is no appreciable bifurcation. We have increased the bin width to compensate for the lower number of counts, but still we cannot see a significant signal (bottom panel of Fig. 9).
120°. In the trailing arm, there is no appreciable bifurcation. We have increased the bin width to compensate for the lower number of counts, but still we cannot see a significant signal (bottom panel of Fig. 9).
 |
Fig. 9. Histograms of |
To investigate the possible differences between the two branches observed in the leading arm, we compute the weighted means for the distance and proper motions in four bins of 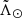 : 90°–100°, 100°–110°, 110°–120°, and 120°–130°. The weight assigned to each star represents the probability of belonging to one branch or the other based on their
: 90°–100°, 100°–110°, 110°–120°, and 120°–130°. The weight assigned to each star represents the probability of belonging to one branch or the other based on their 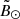 . To obtain these two probability distribution functions, first we create a kernel of
. To obtain these two probability distribution functions, first we create a kernel of 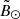 to have a continuous representation of the histogram. We then locate the only two local maxima that the kernel has and associate each one with either branch A (negative
to have a continuous representation of the histogram. We then locate the only two local maxima that the kernel has and associate each one with either branch A (negative 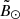 ) or branch B (positive
) or branch B (positive 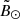 ). After that, we restrict ourselves to ±1.5° of one of the peaks, that is, we only use the values of the kernel near the local maxima, and fit a parabola with which we can obtain a probability at every
). After that, we restrict ourselves to ±1.5° of one of the peaks, that is, we only use the values of the kernel near the local maxima, and fit a parabola with which we can obtain a probability at every 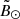 (wherever the parabola returns a negative probability we instead use zero). Finally, we repeat the procedure for the other peak to obtain the second probability distribution. Panels a to d of Fig. 10 show the original histogram of
(wherever the parabola returns a negative probability we instead use zero). Finally, we repeat the procedure for the other peak to obtain the second probability distribution. Panels a to d of Fig. 10 show the original histogram of  at each bin in
at each bin in  (black line) along with the resulting weighted histograms for branches A (blue) and B (orange). Panels e to g contain the corresponding weighted averages and their 1σ uncertainties in heliocentric distance, proper motion in right ascension, and proper motion in declination, respectively. To compute the uncertainty in this estimate, that is, the standard error of the weighted mean (SEM), we used the formalism of Cochran (1977)8. In order to cancel the gradients observed in the previous sections, we subtract the median value obtained from the stars within the bin.
(black line) along with the resulting weighted histograms for branches A (blue) and B (orange). Panels e to g contain the corresponding weighted averages and their 1σ uncertainties in heliocentric distance, proper motion in right ascension, and proper motion in declination, respectively. To compute the uncertainty in this estimate, that is, the standard error of the weighted mean (SEM), we used the formalism of Cochran (1977)8. In order to cancel the gradients observed in the previous sections, we subtract the median value obtained from the stars within the bin.
 |
Fig. 10. Comparison between the bright (A, blue) and faint (B, orange) branches of the bifurcation at different |
The result is that the differences that we measure between the two sides of the bifurcation are always smaller than 2σ. Nevertheless, we note that the orange line in panel (e) is always below the blue one. This can be due to many factors, such as projection effects caused by the stream being a 3D structure, or contamination, since the faint branch (B) is more susceptible than the bright branch (A), or simply because one branch is actually more extincted than the other, which may not be well reproduced with the extinction map that we use. As an example, supposing that the latter is true, we would only need to add < 0.1 mag of extinction to the mean distance of branch A to bring the blue line in panel e down to the orange line.
In contrast with the recent study of Yang et al. (2019), where these latter authors report differences in velocity and metallicity for Blue Horizontal Branch stars in the bifurcation, we conclude that there is no significant separation in either kinematics or distance between the two branches of the leading tail. Furthermore, if the branches were indeed different, their separation should be of the order of < 1.5 kpc and < 0.2 mas −1. We have also looked at the metallicity and find no significant difference, but due to the small number of stars available and the measurement errors, we cannot give any meaningful upper limit. Finally, the fact that we do not observe the bifurcation in the trailing tail could be related either to our selection function or simply to a lack of stars.
5. Conclusions
Gaia has revolutionised the field of Galactic astronomy. With only 22 months of data, the scientific community has already been able to make numerous and quite significant discoveries. Furthermore, DR2 can produce novel results concerning areas that have already been thoroughly examined. The Sgr stream is a good example of this, and in this work, as well as in A20, we wanted to demonstrate what its discovery would have been like in the Gaia era, using only its kinematics.
We have produced two catalogues of probable RR Lyrae members of the Sgr dwarf and stream, starting with the most basic assumptions and exhausting the Gaia outputs to carefully select the list of candidates step by step. The two catalogues are produced by running this trimming process twice, each time from a different starting point. In the first case, we look for stars that are rotating coherently in a plane through the GC and end up with the nGC3 sample: a higher-purity but lower-completeness (≈80%) sample. By demanding that the stars and their velocities do not deviate significantly from the mean orbital plane, we are able to efficiently discard most of the contamination at the cost of introducing kinematical biases. The second time, we select all stars in the sky that are within ±20° from the known mid-plane of the stream. In doing so, we obtain the Strip sample: a higher-completeness (≈95%) but lower-purity sample. In this case, we rely on our data-driven selection schema based on distances and proper motions to get rid of most of the contamination. We have composed a list of 11 721 stars belonging to either the Strip (11 677 stars) or the nGC3 (6 608 stars) sample, and have made this list publicly available.
The main output of this work is the largest sample of RR Lyrae in the Sgr stream to date with both proper motions and distances together. This allows us to study, for the first time, the tangential velocities along the whole stream and provide a reference to compare against. Our results confirm the findings by A20 regarding the proper motion track along the stream. We observe more or less the same trends in proper motion, with differences of less than 0.3 mas yr−1 in most parts of the stream, with the only exception being those regions where either our sample or that of A20 are known to be contaminated. Also, we note that 93% of the RR Lyrae contained in A20 are inside our final sample, confirming that both are detecting the same structure. It will be interesting to compare our work with that of Ibata et al. (2020) in which, as we recently found out, they also provide a list of RR Lyrae obtained with STREAMFINDER (Malhan & Ibata 2018). In doing so, we can produce an independent estimate of the completeness and quantify the possible biases. Of particular interest is the Sagittarius Stream Selected Sample of Bellazzini et al. (2020), composed of the 5385 RR Lyrae from the gaiadr2.vari_rrlyrae catalogue that pass a set of filters requiring that the stars are near the orbital plane of Sgr, rotate with it, and have a 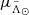 trend compatible with the fit obtained by Ibata et al. (2020). This sample is, by construction, very similar to our nGC3 since it requires that the stars must have their velocity vectors aligned with
trend compatible with the fit obtained by Ibata et al. (2020). This sample is, by construction, very similar to our nGC3 since it requires that the stars must have their velocity vectors aligned with 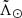 . Nevertheless, apart from having less stars, we note from Fig. 1 of this latter-mentioned publication that there is no specific cut in distance. This means that on the one hand the nearby stars close to the bulge have not been removed, while on the other, features like the fluff (Sesar et al. 2017a) can be better preserved.
. Nevertheless, apart from having less stars, we note from Fig. 1 of this latter-mentioned publication that there is no specific cut in distance. This means that on the one hand the nearby stars close to the bulge have not been removed, while on the other, features like the fluff (Sesar et al. 2017a) can be better preserved.
We compare the evolution of the different observables with 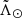 against LM10, the reference model for most studies of Sgr. The residuals in proper motion are within the uncertainties, apart from the known issues discussed in Sect. 4. That is, that the Strip’s mean μα* is not reliable beyond
against LM10, the reference model for most studies of Sgr. The residuals in proper motion are within the uncertainties, apart from the known issues discussed in Sect. 4. That is, that the Strip’s mean μα* is not reliable beyond 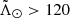 ° and that the nGC3 sample is biased. When comparing the heliocentric distances, we find that the discrepancies are very much significant and not attributable to a gradient in metallicity or an incorrect calibration. Instead, we confirm the results of previous works (e.g. Belokurov et al. 2014; Hernitschek et al. 2017) which already pointed out that the apocentres in LM10 are inaccurate in terms of both
° and that the nGC3 sample is biased. When comparing the heliocentric distances, we find that the discrepancies are very much significant and not attributable to a gradient in metallicity or an incorrect calibration. Instead, we confirm the results of previous works (e.g. Belokurov et al. 2014; Hernitschek et al. 2017) which already pointed out that the apocentres in LM10 are inaccurate in terms of both 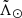 and distance. More recent models are able to reproduce this, such as the one by Fardal et al. (2019), but how well their proper motions perform in light of the new observational constraints that we provide here is yet to be tested. We have also determined new apocentres based on the maximum Galactocentric distance of the tidal debris:
and distance. More recent models are able to reproduce this, such as the one by Fardal et al. (2019), but how well their proper motions perform in light of the new observational constraints that we provide here is yet to be tested. We have also determined new apocentres based on the maximum Galactocentric distance of the tidal debris: 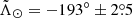 at DGC = (92.48 ± 1.45) kpc for the trailing tail and
at DGC = (92.48 ± 1.45) kpc for the trailing tail and 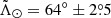 at DGC = (47.73 ± 0.48) kpc for the leading. Our values are in some tension with those determined by Hernitschek et al. (2017) which cannot be explained by an incorrect metallicity zero point, and are most likely related to the fact that we used a completely empirical method to make our estimates.
at DGC = (47.73 ± 0.48) kpc for the leading. Our values are in some tension with those determined by Hernitschek et al. (2017) which cannot be explained by an incorrect metallicity zero point, and are most likely related to the fact that we used a completely empirical method to make our estimates.
With the Strip sample, we have been able to test the tangential velocities predicted by LM10. We find that the predictions agree within uncertainties in the trailing arm but fail to reproduce our observations at the location of the dwarf and at the leading arm. Moreover, we provide a measurement of the total velocity projected in the sky for the progenitor, V⊥ = (274.18 ± 0.02) km s−1. Despite the complexity of our selection process, we can add that the velocity dispersion profiles of the model are also compatible with our observations.
Regarding the metallicity, we do not observe any meaningful gradient with  at the current level of precision and the mean value we recover is −1.6 dex in the ZW84 scale. This is in contrast with other studies where differences are detected for most populations. In particular, Yang et al. (2019) reported a significant difference between the leading and the trailing arm for the Blue Horizontal Branch stars. Even though we use photometric metallicites instead of spectroscopic ones, the former having larger uncertainties, and the hypothetical gradient has to be of the order of 10−3 dex deg−1 at most in absolute value. Such small gradients would cause differences along the stream no larger than ∼0.2 dex, which is similar to the typical precision for the photometric metallicities. However, we notice that the gradients that we have measured, which are compatible with the values obtained by Hayes et al. (2020), would imply that the trailing arm is on average slightly more metal rich than the leading arm, in agreement with previous works (e.g. Yang et al. 2019).
at the current level of precision and the mean value we recover is −1.6 dex in the ZW84 scale. This is in contrast with other studies where differences are detected for most populations. In particular, Yang et al. (2019) reported a significant difference between the leading and the trailing arm for the Blue Horizontal Branch stars. Even though we use photometric metallicites instead of spectroscopic ones, the former having larger uncertainties, and the hypothetical gradient has to be of the order of 10−3 dex deg−1 at most in absolute value. Such small gradients would cause differences along the stream no larger than ∼0.2 dex, which is similar to the typical precision for the photometric metallicities. However, we notice that the gradients that we have measured, which are compatible with the values obtained by Hayes et al. (2020), would imply that the trailing arm is on average slightly more metal rich than the leading arm, in agreement with previous works (e.g. Yang et al. 2019).
The nGC3 sample is a great starting point for a spectroscopic follow-up. Taking advantage of its high purity, the risk of measuring abundances and radial velocities for an off-stream star is minimised. The resulting catalogue would be the most extensive 6D+abundance sample of Sgr RR Lyrae to date, providing a more detailed picture of the metallicity of the stream and probing the full phase-space information for a single tracer.
We also searched for the bifurcation in our data and indeed observe it in both samples. We see a clear signal in the leading arm where it was originally discovered. We observe no significant separation in velocity, distance, or metallicity between the bright and faint branches. Also, we do not detect the bifurcation on the trailing arm where it was found by Koposov et al. (2012), perhaps because of the low number of stars we have in that region or because of the filters in distance and proper motion used to select the members. It will be interesting to obtain follow-up spectroscopic observations of the stars at each branch and study whether or not there is a separation in line of sight velocities as well.
Finally, we provide empiric trends (smoothed medians) in distance, proper motion, and tangential velocities of our final Strip sample (see Appendix E), along with the respective uncertainties. We also give these trends as interpolators that can be evaluated at any  , which can be very helpful when modelling the stream.
, which can be very helpful when modelling the stream.
In this work, we use the convention by Belokurov et al. (2014).
The offset was calculated with respect to the Harris (1996) spectroscopic scale which has almost no shift compared to the ZW84 scale used in this work (Gratton et al. 2004).
Downloaded from http://faculty.virginia.edu/srm4n/Sgr/
The ICRS frame and the Sgr plane defined by Majewski et al. (2003) have similar poles.
Acknowledgments
We thank Bertrand Lemasle for the useful comments and discussions, as well as the whole Gaia team at Barcelona and Groningen. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This project has received funding from the University of Barcelona’s official doctoral program for the development of a R+D+i project under the APIF grant and from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 745617. This work was supported by the MINECO (Spanish Ministry of Economy) through grants ESP2016-80079-C2-1-R (MINECO/FEDER, UE) and ESP2014-55996-C2-1-R (MINECO/FEDER, UE) and MDM-2014-0369 of ICCUB (Unidad de Excelencia “María de Maeztu”). This project has received support from the DGAPA/UNAM PAPIIT program grant IG100319. The work reported on in this publication has been fully or partially supported by COST Action CA18104: MW-Gaia. CM acknowledges support from the ICC University of Barcelona visiting academic grants and thanks the Gaia UB team for hosting her during part of this research. CM also thanks PDU en Ciencias Físicas at CURE (Rocha), for their hospitality.
References
- Abedi, H., Mateu, C., Aguilar, L. A., Figueras, F., & Romero-Gómez, M. 2014, MNRAS, 442, 3627 [NASA ADS] [CrossRef] [Google Scholar]
- Antoja, T., Ramos, P., Mateu, C., et al. 2020, A&A, 635, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellazzini, M., Ibata, R. A., Chapman, S. C., et al. 2008, AJ, 136, 1147 [NASA ADS] [CrossRef] [Google Scholar]
- Bellazzini, M., Ibata, R., Malhan, K., et al. 2020, A&A, 636, A107 [CrossRef] [EDP Sciences] [Google Scholar]
- Belokurov, V., Zucker, D. B., Evans, N. W., et al. 2006, ApJ, 647, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Koposov, S. E., Evans, N. W., et al. 2014, MNRAS, 437, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M., & Murphy, S. 2012, PASP, 124, 140 [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics, Second Edition [Google Scholar]
- Camarillo, T., Mathur, V., Mitchell, T., & Ratra, B. 2018, PASP, 130, 024101 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Catelan, M., & Smith, H. A. 2015, Pulsating Stars (Wiley-VCH) [CrossRef] [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, ArXiv e-prints [arXiv:1612.05560] [Google Scholar]
- Clementini, G., Ripepi, V., Molinaro, R., et al. 2019, A&A, 622, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cochran, W. G. 1977, Sampling Techniques, 3rd edn. (John Wiley) [Google Scholar]
- Cseresnjes, P. 2001, A&A, 375, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Boer, T. J. L., Belokurov, V., & Koposov, S. 2015, MNRAS, 451, 3489 [NASA ADS] [CrossRef] [Google Scholar]
- Deg, N., & Widrow, L. 2013, MNRAS, 428, 912 [NASA ADS] [CrossRef] [Google Scholar]
- Di Fabrizio, L., Clementini, G., Maio, M., et al. 2005, A&A, 430, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duffau, S., Zinn, R., Vivas, A. K., et al. 2006, ApJ, 636, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Erkal, D., Belokurov, V., Laporte, C. F. P., et al. 2019, MNRAS, 487, 2685 [NASA ADS] [CrossRef] [Google Scholar]
- Eyer, L., Mowlavi, N., Evans, D. W., et al. 2017, ArXiv e-prints, unpublished [arXiv:1702.03295] [Google Scholar]
- Fardal, M. A., van der Marel, R. P., Law, D. R., et al. 2019, MNRAS, 483, 4724 [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gibbons, S. L. J., Belokurov, V., & Evans, N. W. 2014, MNRAS, 445, 3788 [NASA ADS] [CrossRef] [Google Scholar]
- Gibbons, S. L. J., Belokurov, V., Erkal, D., & Evans, N. W. 2016, MNRAS, 458, L64 [CrossRef] [Google Scholar]
- Gratton, R. G., Bragaglia, A., Clementini, G., et al. 2004, A&A, 421, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grillmair, C. J., & Carlin, J. L. 2016, Astrophys. Space Sci. Lib., 420, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, C. R., Law, D. R., & Majewski, S. R. 2018, ApJ, 867, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, C. R., Majewski, S. R., Hasselquist, S., et al. 2020, ApJ, 889, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Hernitschek, N., Sesar, B., Rix, H.-W., et al. 2017, ApJ, 850, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Holl, B., Audard, M., Nienartowicz, K., et al. 2018, A&A, 618, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ibata, R. A., Gilmore, G., & Irwin, M. J. 1994, Nature, 370, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Malhan, K., & Martin, N. F. 2019, ApJ, 872, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R., Bellazzini, M., Thomas, G., et al. 2020, ApJ, 891, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, K. V., Hernquist, L., & Bolte, M. 1996, ApJ, 465, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, K. V., Spergel, D. N., & Haydn, C. 2002, ApJ, 570, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Jordi, C., Gebran, M., Carrasco, J. M., et al. 2010, A&A, 523, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jurcsik, J., & Kovacs, G. 1996, A&A, 312, 111 [Google Scholar]
- Jurić, M., Ivezić, Ž., Brooks, A., et al. 2008, ApJ, 673, 864 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Koleva, M., Prugniel, P., De Rijcke, S., & Zeilinger, W. W. 2011, MNRAS, 417, 1643 [NASA ADS] [CrossRef] [Google Scholar]
- Koposov, S. E., Belokurov, V., Evans, N. W., et al. 2012, ApJ, 750, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Koposov, S. E., Belokurov, V., Li, T. S., et al. 2019, MNRAS, 485, 4726 [NASA ADS] [CrossRef] [Google Scholar]
- Law, D. R., & Majewski, S. R. 2010, ApJ, 714, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J., Fellow, L., & Liu, C. 2019, ApJ, 874, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, C., Deng, L.-C., Carlin, J. L., et al. 2014, ApJ, 790, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J., & Weiler, M. 2018, A&A, 619, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Majewski, S. R., Skrutskie, M. F., Weinberg, M. D., & Ostheimer, J. C. 2003, ApJ, 599, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Malhan, K., & Ibata, R. A. 2018, MNRAS, 477, 4063 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Delgado, D., Gómez-Flechoso, M. Á., Aparicio, A., & Carrera, R. 2004, ApJ, 601, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Mateo, M., Mirabal, N., Udalski, A., et al. 1996, ApJ, 458, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Mateu, C., & Vivas, A. K. 2018, MNRAS, 479, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Mateu, C., Bruzual, G., Aguilar, L., et al. 2011, MNRAS, 415, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Mateu, C., Vivas, A. K., Downes, J. J., et al. 2012, MNRAS, 427, 3374 [CrossRef] [Google Scholar]
- Mateu, C., Cooper, A. P., Font, A. S., et al. 2017, MNRAS, 469, 721 [CrossRef] [Google Scholar]
- Mateu, C., Read, J. I., & Kawata, D. 2018, MNRAS, 474, 4112 [NASA ADS] [CrossRef] [Google Scholar]
- Muraveva, T., Delgado, H. E., Clementini, G., Sarro, L. M., & Garofalo, A. 2018, MNRAS, 481, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Navarrete, C., Belokurov, V., Koposov, S. E., et al. 2017, MNRAS, 467,1329 [NASA ADS] [Google Scholar]
- Nemec, J. M., Cohen, J. G., Ripepi, V., et al. 2013, ApJ, 773, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Peñarrubia, J., Belokurov, V., Evans, N. W., et al. 2010, MNRAS, 408, L26 [NASA ADS] [Google Scholar]
- Peñarrubia, J., Zucker, D. B., Irwin, M. J., et al. 2011, ApJ, 727, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Price-Whelan, A. M. 2017, J. Open Source Soft., 2 [Google Scholar]
- Price-Whelan, A., Sipocz, B., Major, S., & Oh, S. 2017, adrn/gala: v0.2.1 [Google Scholar]
- Price-Whelan, A. M., Mateu, C., Iorio, G., et al. 2019, AJ, 158, 223 [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
- Rimoldini, L., Holl, B., Audard, M., et al. 2019, A&A, 625, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rybizki, J., Demleitner, M., Fouesneau, M., et al. 2018, PASP, 130, 074101 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, J. L., & Binney, J. 2013, MNRAS, 433, 1826 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., Binney, J., & Dehnen, W. 2010, MNRAS, 403, 1829 [NASA ADS] [CrossRef] [Google Scholar]
- Sesar, B., Vivas, A. K., Duffau, S., & Ivezić, Ž. 2010, ApJ, 717, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Sesar, B., Hernitschek, N., Dierickx, M. I. P., Fardal, M. A., & Rix, H.-W. 2017a, ApJ, 844, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Sesar, B., Hernitschek, N., Mitrović, S., et al. 2017b, AJ, 153, 204 [Google Scholar]
- Shipp, N., Drlica-Wagner, A., Balbinot, E., et al. 2018, ApJ, 862, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Totten, E. J., & Irwin, M. J. 1998, MNRAS, 294, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Vivas, A. K., Zinn, R., Andrews, P., et al. 2001, ApJ, 554, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Vivas, A. K., Zinn, R., & Gallart, C. 2005, AJ, 129, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Westera, P., Lejeune, T., Buser, R., Cuisinier, F., & Bruzual, G. 2002, A&A, 381, 524 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, C., Xue, X.-X., Li, J., et al. 2019, ApJ, 886, 154 [CrossRef] [Google Scholar]
- Zhang, X., Shi, W. B., Chen, Y. Q., et al. 2017, A&A, 597, A54 [CrossRef] [EDP Sciences] [Google Scholar]
- Zinn, R., & West, M. J. 1984, ApJS, 55, 45 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Reddening to absorption transformations
The reddening maps provided by Schlafly & Finkbeiner (2011) return a value of the colour excess, E(B − V), for each pair of celestial coordinates. To obtain the absorption we then assume a proportionality constant, RV, of 3.1 (Cardelli et al. 1989). However, this yields the absorption in the V-band, AV, and so we still need a conversion to the absorption in the G-band, AG. For that, we use a fitted relationship between the ratio  and the Gaia photometry (see Fig. A.1).
and the Gaia photometry (see Fig. A.1).
 |
Fig. A.1. Fitted relationship between |
The 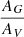 ratio is fitted against the GBP − GRP colour using simulations derived from BaSeL-3.1 (Westera et al. 2002) spectral energy distributions using the same methodology as in Jordi et al. (2010).
ratio is fitted against the GBP − GRP colour using simulations derived from BaSeL-3.1 (Westera et al. 2002) spectral energy distributions using the same methodology as in Jordi et al. (2010).
We used the Gaia passbands derived by Maíz Apellániz & Weiler (2018) as according to the Gaia team9 they are more representative of the Gaia DR2 data. Among the two BP passbands provided in Maíz Apellániz & Weiler (2018) we chose the one that is valid at the faint regime (G > 10.87 mag) which is appropriate for a distant object like the Sgr stream. Nevertheless, only very small differences are present when considering the passband at the bright regime. For the Johnson V passbands, we used the response curve provided by Bessell & Murphy (2012).
To simulate reddened sources in the range 0 < A550 = 11 mag, we use Cardelli et al. (1989) extinction law and RV = 3.1, A550 being the magnitude of the extinction at a wavelength equal to 550 nm.
To achieve a better fitting on 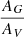 we consider a second-degree dependency with the reddened GBP − GRP colour (the observed one) plus two terms depending on the interstellar absorption in the V passband (AV) as well as a crossed term. The obtained relationship is the following:
we consider a second-degree dependency with the reddened GBP − GRP colour (the observed one) plus two terms depending on the interstellar absorption in the V passband (AV) as well as a crossed term. The obtained relationship is the following:
Appendix B: Tailored Gaussian mixture
Here we explain the TGM algorithm in more detail. We use the particular case of the distance (see Sect. 3.3) to guide the exposition, but the steps are the same for any other quantity that varies as a function of 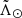 (μα* and μδ). We only tweak the parameters to obtain a better performance for each case: bin size, step size, threshold, maximum separation and kernel bin width.
(μα* and μδ). We only tweak the parameters to obtain a better performance for each case: bin size, step size, threshold, maximum separation and kernel bin width.
First we take all the stars in the range −2.5° 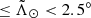 and obtain a Gaussian kernel to the corresponding distance histogram. Having done that, we evaluate the kernel at 100 000 points and apply a peak finder algorithm (scipy.signal.find_peaks) to locate all local maximum. We keep only those whose height are above a certain dimensionless threshold, set arbitrarily so that we can remove the small oscillations appearing on the tails of the distributions due to Poisson noise (0.0075 in this case). The remaining n peaks are then used as centres of n normal probability distributions. Finally, we fit the sum of a constant floor level (free parameter) and n Gaussians for which we set free their widths (σ [kpc]) and amplitudes. For that, we use the Least Square Minimisation algorithm implemented in Scipy and find the σ for each component that better reproduce the kernel. In order to avoid spending too much time at each bin, we limit the number of Gaussians to the four with highest height. Three examples of the fitting process are shown in Fig. B.1.
and obtain a Gaussian kernel to the corresponding distance histogram. Having done that, we evaluate the kernel at 100 000 points and apply a peak finder algorithm (scipy.signal.find_peaks) to locate all local maximum. We keep only those whose height are above a certain dimensionless threshold, set arbitrarily so that we can remove the small oscillations appearing on the tails of the distributions due to Poisson noise (0.0075 in this case). The remaining n peaks are then used as centres of n normal probability distributions. Finally, we fit the sum of a constant floor level (free parameter) and n Gaussians for which we set free their widths (σ [kpc]) and amplitudes. For that, we use the Least Square Minimisation algorithm implemented in Scipy and find the σ for each component that better reproduce the kernel. In order to avoid spending too much time at each bin, we limit the number of Gaussians to the four with highest height. Three examples of the fitting process are shown in Fig. B.1.
 |
Fig. B.1. Example of the TGM applied to the distance distribution at selected bins of |
Given that at 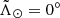 the dominant component is that of the Sgr dwarf, we assign the Gaussian with the largest amplitude to the stream. Subsequently, we simply repeat this strategy every 5° in both directions, negative and positive
the dominant component is that of the Sgr dwarf, we assign the Gaussian with the largest amplitude to the stream. Subsequently, we simply repeat this strategy every 5° in both directions, negative and positive  , but now associating to the stream the component most similar to the previous one. To define which is the most similar we apply the following rule: rank the peaks by height, filter out those that are too far apart, and then chose the first one. In this case, we impose a maximum difference between two consecutive peaks of 10 kpc.
, but now associating to the stream the component most similar to the previous one. To define which is the most similar we apply the following rule: rank the peaks by height, filter out those that are too far apart, and then chose the first one. In this case, we impose a maximum difference between two consecutive peaks of 10 kpc.
This method relies on the separation between the different components at any given  . If they are too close to each other, we need a smaller bin width when creating the kernel to resolve them at the expense of increasing the number of peaks created by simple Poisson noise. On the other hand, if we smooth the kernel too much in an effort to reduce the spurious peaks, the different components can interfere with each other, and therefore we obtain a biased position. Here, we have chosen a value of 0.15 (in the units given by the Scipy function) for both the Strip and the nGC3 samples.
. If they are too close to each other, we need a smaller bin width when creating the kernel to resolve them at the expense of increasing the number of peaks created by simple Poisson noise. On the other hand, if we smooth the kernel too much in an effort to reduce the spurious peaks, the different components can interfere with each other, and therefore we obtain a biased position. Here, we have chosen a value of 0.15 (in the units given by the Scipy function) for both the Strip and the nGC3 samples.
In Sects. 3.4 and 3.5, we applied the same procedure but with the following parameters:
-
Bin size: 2.5°
-
Step size: 5°
-
Bin width: 0.30
-
Threshold: 0.10
-
Separation: 1.5 mas yr−1
As a final remark, it is also worth mentioning that we tried using the common clustering algorithms like DBSCAN, hierarchical DBSCAN or k-means. Nevertheless, most of this methods are based on density and, in our case, the Sgr stream presents significant gradients which result in suboptimal performance. We acknowledge that there could exist a combination of parameters and a coordinate transformation such that a clean separation between the contamination and the stream stars appears but, after some trial and error, we decided to apply the TGM.
Appendix C: Strip sample selection process
Here we show the plots of each state of the filtering process starting from a Strip in the sky around the Sgr orbital plane (see Sect. 3.1). First, we apply the TGM to the heliocentric distance (Fig. C.1) then on the proper motion in right ascension (Fig. C.2) and finally, on the proper motion in declination (Fig. C.3). The number of stars remaining after each step can be found in Table 1.
Appendix D: Summary plots of the nGC3 sample
In this Appendix we discuss the summary plots of the nGC3 sample, similar to what we have done for the Strip sample in Sect. 4.
Figure D.1 contains the tracks in proper motion, equivalent to Fig. 6. With panels a to c it becomes obvious that, in the leading arm, the stars in the nGC3 sample are always on one side of the median predicted by LM10 and the observed by A20. This is confirmed with the residuals, shown in panel d, where we plot the difference between the median of the nGC3 sample and A20 (computed in the same way), along with the 1σ intervals. This figure shows that even though the overall trends are similar, the discrepancy between A20 and the nGC3 sample exceeds 3σ in the leading arm, becoming smaller as  increases. The difference between the nGC3 and the Strip sample in that region is also considerable, at the level of 2σ throughout the range
increases. The difference between the nGC3 and the Strip sample in that region is also considerable, at the level of 2σ throughout the range 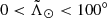 . When compared to the model, additionally to the already mention bias in the leading arm (related to the lack of stars with small total proper motion) we also observe a large discrepancy in proper motions at
. When compared to the model, additionally to the already mention bias in the leading arm (related to the lack of stars with small total proper motion) we also observe a large discrepancy in proper motions at 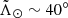 , as well as significant residuals in the trailing arm around
, as well as significant residuals in the trailing arm around 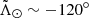 . All together, we suspect that the use of the PCM method has introduced some bias. Indeed, when we apply nGC3 algorithm to the LM10 particles we observe a similar behaviour in the residuals, thus confirming that the nGC3 sample is kinematically biased.
. All together, we suspect that the use of the PCM method has introduced some bias. Indeed, when we apply nGC3 algorithm to the LM10 particles we observe a similar behaviour in the residuals, thus confirming that the nGC3 sample is kinematically biased.
Regarding the trend in Galactocentric distance, we apply the same method described in Sect. 4.2 to this sample and obtain the following apocentres for the tidal debris:
-
Trailing:
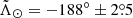 at DGC = (93.22 ± 2.39) kpc
at DGC = (93.22 ± 2.39) kpc -
Leading:
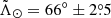 at DGC = (47.34 ± 0.58) kpc.
at DGC = (47.34 ± 0.58) kpc.
The values we obtain for the nGC3 and Strip samples are compatible with one another, but we note that the angular positions in the trailing apocentre differ by one bin (i.e. 5°). Given that the nGC3 sample has few stars in that region, we expect the value inferred from the Strip to be more robust.
We have also calculated the total perpendicular velocity around M54, like we did in Sect. 4.3 for the Strip sample, resulting in a V⊥ of 274.18 ± 0.02 km s−1. The (small) difference between both samples is most likely caused by the larger fraction of contamination present in the Strip sample.
Regarding the metallicity gradients, the difference is also small. In the case of the nGC3 sample, the result is (−2.3 ± 0.7) × 10−3 dex deg−1 in the leading arm and (1.2 ± 0.6) × 10−3 dex deg−1 in the trailing. The velocity dispersion profile, in contrast to the Strip sample, in this case is dominated by the initial selection method: the PCM nGC3 technique. This is illustrated in Fig. D.2 where we show the profile derived from the nGC3 sample (red) along with the prediction of LM10 (solid green) and the result of adding realistic errors in proper motion and applying the PCM to the particles of the model (dotted-dashed line). Finally, regarding the bifurcation discussed in Sect. 4.7, it is also evident in the nGC3 sample as can be seen in Fig. D.3.
Appendix E: Samples and interpolators
Table E.1 contains our final sample after the trimming process detailed in Sect. 3. Along with the source_id and apparent magnitude in the G band, which can be used to identify the star, we also provide the astrometry in three different Celestial coordinates: ICRS, Galactic and Sagittarius (as defined in Sect. 3.1). Additionally, we include the quantities that have been calculated in this work: distance and velocity along (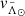 ) and across (
) and across (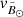 ) the orbit. We have also added the type of star – either RRab, RRc or RRd – according to the SOS team, the PS1 classification and the VC table. Finally, we add two codes that can be used to filter the sources based on, respectively, their source catalogue (SOS, PS1 and/or VC) and our classification (nGC3 and/or Strip). In case of the latter, for instance, the first bit corresponds to the nGC3 sample, being 1 when the star is contained in that sample and 0 otherwise. Similarly for the Strip sample, which is represented by the second bit. As an example, a source with the code “01” on the last column (see caption of Table E.1) has been found on the Strip sample but not on nGC3.
) the orbit. We have also added the type of star – either RRab, RRc or RRd – according to the SOS team, the PS1 classification and the VC table. Finally, we add two codes that can be used to filter the sources based on, respectively, their source catalogue (SOS, PS1 and/or VC) and our classification (nGC3 and/or Strip). In case of the latter, for instance, the first bit corresponds to the nGC3 sample, being 1 when the star is contained in that sample and 0 otherwise. Similarly for the Strip sample, which is represented by the second bit. As an example, a source with the code “01” on the last column (see caption of Table E.1) has been found on the Strip sample but not on nGC3.
First ten rows of the sample of RR Lyrae stars selected with our method as probable members of the Sgr stream and dwarf.
We also provide a series of interpolators that can be used to obtain the values of the heliocentric distance, proper motion in each reference frame (ICRS, Galactic or Sagittarius) and tangential velocities (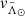 and
and 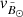 ). The interpolators are given as a table containing the median of the corresponding quantity in bins of
). The interpolators are given as a table containing the median of the corresponding quantity in bins of 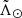 and as a pickled Python function (a stream of bytes that represent said object). In the case of the later, we include instructions for loading them into Python. All this information, and more, can be found online10.
and as a pickled Python function (a stream of bytes that represent said object). In the case of the later, we include instructions for loading them into Python. All this information, and more, can be found online10.
All Tables
First ten rows of the sample of RR Lyrae stars selected with our method as probable members of the Sgr stream and dwarf.
All Figures
 |
Fig. 1. Pole Count Map of the RR Lyrae catalogue described in Sect. 2. The Galactic disc produces the large concentration at (1), while the peaks (3),(4), and (5) are related to the Large and Small Magellanic clouds. The prominent signal on the right, (2), is caused by the Sgr stream. |
| In the text | |
 |
Fig. 2. Metallicity dependence on |
| In the text | |
 |
Fig. 3. Distance as a function of |
| In the text | |
 |
Fig. 4.
|
| In the text | |
 |
Fig. 5. Same as Fig. 4 but with proper motion in declination. Now we only show the stars selected by distance and μα*. |
| In the text | |
 |
Fig. 6. Proper motion trends with |
| In the text | |
 |
Fig. 7. Position, distance, and velocity as a function of |
| In the text | |
 |
Fig. 8. Velocity dispersion profile for |
| In the text | |
 |
Fig. 9. Histograms of |
| In the text | |
 |
Fig. 10. Comparison between the bright (A, blue) and faint (B, orange) branches of the bifurcation at different |
| In the text | |
 |
Fig. A.1. Fitted relationship between |
| In the text | |
 |
Fig. B.1. Example of the TGM applied to the distance distribution at selected bins of |
| In the text | |
 |
Fig. C.1. Same as Fig. 3 for the Strip sample. |
| In the text | |
 |
Fig. C.2. Same as Fig. 4 for the Strip sample. |
| In the text | |
 |
Fig. C.3. Same as Fig. 5 for the Strip sample. |
| In the text | |
 |
Fig. D.1. Same as Fig. 6 for the nGC3 sample. |
| In the text | |
 |
Fig. D.2. Same as Fig. 8 but for the nGC3 sample. |
| In the text | |
 |
Fig. D.3. Same as Fig. 9 for the nGC3 sample. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} M_G = 0.32^{+0.04}_{-0.04}[\mathrm{Fe} /\mathrm{H} ] + 1.11^{+0.06}_{-0.06}. \end{aligned} $$](/articles/aa/full_html/2020/06/aa37819-20/aa37819-20-eq6.gif)
![$$ \begin{aligned} d \,[pc] = 10^{(m_G-M_G-A_G)/5+1}, \end{aligned} $$](/articles/aa/full_html/2020/06/aa37819-20/aa37819-20-eq8.gif)
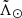
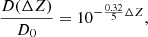
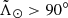
![$ (\mathrm{SEM}_{\mathit{w}})^2 = \frac{n}{(n-1)\sum \omega_i}[\sum\nolimits(\omega_i x_i - \bar{\omega}\bar{x}_{\mathit{w}})^2-2\bar{x}_{\mathit{w}}\sum\nolimits(\omega_i-\bar{\omega})(\omega_i x_i - \bar{\omega}\bar{x}_{\mathit{w}}) + \bar{x}_{\mathit{w}}^2\sum\nolimits(\omega_i-\bar{\omega})^2] $](/articles/aa/full_html/2020/06/aa37819-20/aa37819-20-eq101.gif)