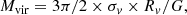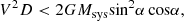| Issue |
A&A
Volume 633, January 2020
|
|
|---|---|---|
| Article Number | A108 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201936466 | |
| Published online | 20 January 2020 | |
The velocity field of the Lyra complex⋆
1
Dipartimento di Fisica dell’Università degli Studi di Trieste – Sezione di Astronomia, Via Tiepolo 11, 34143 Trieste, Italy
2
INAF – Osservatorio Astronomico di Trieste, Via Tiepolo 11, 34143 Trieste, Italy
e-mail: marisa.girardi@inaf.it
3
Fundación Galileo Galilei – INAF (Telescopio Nazionale Galileo), Rambla José Ana Fernández Perez 7, 38712 Breña Baja (La Palma), Canary Islands, Spain
4
Instituto de Astrofísica de Canarias, C/Vía Láctea s/n, 38205 La Laguna (Tenerife), Canary Islands, Spain
5
Departamento de Astrofísica, Univ. de La Laguna, Av. del Astrofísico Francisco Sánchez s/n, 38205 La Laguna, Tenerife, Spain
6
INAF – Osservatorio Astronomico di Brera, Via E. Bianchi 46, 23807 Merate, Italy
7
Dipartimento di Fisica dell’Università Bicocca di Milano, Milano, Italy
8
Department of Astronomy, University of Geneva, ch. d’Ecogia 16, 1290 Versoix, Switzerland
9
INAF – IASF Milano, Via E. Bassini 15, 20133 Milano, Italy
Received:
6
August
2019
Accepted:
10
October
2019
Context. The formation of cosmic structures culminates with the assembly of galaxy clusters, a process that is quite different from cluster to cluster.
Aims. We present the study of the structure and dynamics of the Lyra complex, consisting of the two clusters RXC J1825.3+3026 and CIZA J1824.1+3029, which was very recently studied by using both X-ray and radio data.
Methods. This is the first analysis based on the kinematics of member galaxies. New spectroscopic data for 285 galaxies were acquired at the Italian Telescopio Nazionale Galileo and were used in combination with PanSTARRS photometry. The result of our member selection is a sample of 198 galaxies.
Results. For RXCJ1825 and CIZAJ1824 we report the redshifts, z = 0.0645 and z = 0.0708, the first estimates of velocity dispersion, σv = 995+131−125 km s−1 and σv = 700 ± 50 km s−1, and of dynamical mass, M200 = 1.1 ± 0.4 × 1015 M⊙ and M200 = 4 ± 0.1 × 1014 M⊙. The past assembly of RXCJ1825 is traced by the two dominant galaxies, which are both aligned with the major axis of the galaxy distribution along the east–west direction, and by a minor northeast substructure. We also detect a quite peculiar high velocity field in the southwest region of the Lyra complex. This feature is likely related to a very luminous galaxy, which is characterized by a high velocity. This galaxy is suggested to be the central galaxy of a group that is in interaction with RXCJ1825 according to very recent studies based on X-ray and radio data. The redshift of the whole Lyra complex is z = 0.067. Assuming that the redshift difference between RXCJ1825 and CIZAJ1824 is due to the relative kinematics, the projected distance between the cluster centers is D ∼ 1.3 Mpc and the line–of–sight velocity difference is ∼1750 km s−1. A dynamical analysis of the system shows that the two clusters are likely to be gravitationally bound in a pre-merger phase, and that CIZAJ1824 is moving toward RXCJ1825.
Conclusions. Our results corroborate a picture where the Lyra region is the place of a very complex scenario of cluster assembly.
Key words: galaxies: clusters: individual: RXC J1825.3+3026 / galaxies: clusters: individual: CIZA J1824.1+3029 / galaxies: general / galaxies: kinematics and dynamics
Full Table 1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/633/A108
© ESO 2020
1. Introduction
Clusters of galaxies are the largest gravitationally bound systems in the Universe. According to the Λ cold dark matter (ΛCDM) hierarchical scenario, the formation of a structure progresses in a hierarchical fashion, culminating with the assembly of clusters of galaxies (see Springel et al. 2006 and references therein). Numerical simulations also show that clusters form preferentially through anisotropic accretion along the large-scale structure filaments (e.g., Colberg et al. 1999) and in a significant part through the accretion of galaxy groups, while the merger of two or more several massive entities is a rarer case (e.g., Berrier et al. 2009; McGee et al. 2009). Since the cluster assembly histories show significant variation from cluster to cluster (e.g., Berrier et al. 2009), most observational studies are focused on individual systems.
From the observational side, the trace of the cluster assembly has been studied for a long time through the analysis of substructures based on cluster galaxies (Baier & Ziener 1977; Geller & Beers 1982), X-ray emitting intracluster medium (ICM, Jones & Forman 1999), and more recently on gravitational lensing effects (e.g, Athreya et al. 2002; Dahle et al. 2002). Merging clusters have proved to be fruitful laboratories to study several physical processes. Cluster mergers have been suggested to be the energetic support for radio halos and relics (Tribble 1993; Feretti 1999). The analysis of the merging system named “Bullet cluster” provides strong proof for the existence of dark matter (DM), showing the decoupling of baryonic and DM (Markevitch et al. 2002, 2004). The study of the accretion of groups onto clusters is quite timely in the context of galaxy evolution (e.g., Olave-Rojas et al. 2018 and references therein) since some pre-processing of galaxies in the group environment is expected prior to cluster formation (Zabludoff & Mulchaey 1998).
Optical data are a powerful tool to investigate the presence of structures and the dynamics of cluster mergers (Girardi & Biviano 2002 for a review). Moreover, the photometric and spectroscopic information about cluster galaxies is complementary to the X-ray information since it is well known that galaxies and the ICM react on different timescales during a merger as shown by numerical simulations (e.g., Roettiger et al. 1997; Springel & Farrar 2007). In particular, multi-object spectroscopy observations have allowed for the building of large samples of galaxies with measured redshifts for individual clusters; additionally, they have been proven to be a powerful means to understanding cluster formation, as shown by several dedicated studies (e.g., Girardi et al. 2011, DARC project; Maurogordato et al. 2011, MUSIC project; Owers et al. 2013 using GAMA survey; Balestra et al. 2016, CLASH-VLT project; Golovich et al. 2017, MC2 collaboration).
An ideal candidate in which to study, in detail, how structures grow is the complex of the two clusters RXC J1825.3+3026 (RXCJ1825 hereafter) and CIZA J1824.1+3029 (hereafter CIZAJ1824), hereafter named the Lyra complex. RXCJ1825, also named CIZA J1825.3+3026, was discovered by ROSAT in the X-rays at galactic latitude b = 18.547 deg at z = 0.0645 (Ebeling et al. 2002). This cluster was found to be one of the strongest and spatially resolved sources of the Sunyaev-Zeldovich signal in the Planck all-sky cluster survey (Planck Collaboration VIII 2014). It has been studied as part of the XMM-Newton Cluster Outskirts Project (X-COP, Eckert et al. 2017), which is a very large program based on XMM-Newton X-ray observations (Eckert et al. 2019; Ettori et al. 2019; Ghirardini et al. 2019). In particular, as shown by Fig. 2 from Ghirardini et al. (2019), at about 16′ west, which is slightly WNW of this cluster, there is the smaller cluster CIZAJ1824 that had already been named NPM1G+30.0 and listed by Voges et al. (1999), with redshift z = 0.072 (Kocevski et al. 2007). The recent study of Clavico et al. (2019) shows that whereas CIZAJ1824 is dynamically relaxed, RXCJ1825 is not and shows clear signatures of past and on-going merging. Indeed, the presence of a giant radio halo in RXCJ1825 is likely related to the on-going merging in this system (Botteon et al. 2019).
For these two clusters, no ad hoc optical observations were available at the time we started our study. No dynamical analysis has ever been performed and indeed only one redshift per cluster is known. We were allotted time to perform a spectroscopic survey at the Italian Telescopio Nazionale Galileo (TNG). This study is devoted to the presentation of our analysis of the velocity field of the Lyra complex. The paper is organized as follows. We present the optical data and the cluster catalog in Sect. 2. In Sect. 3 we describe the member selection procedure and global properties of the cluster complex. Section 4 is devoted to the analysis of the structure of the Lyra complex. We report our estimates about the properties of the two individual clusters in Sects. 5 and 6. In Sect. 7 we present our dynamical analysis for the whole complex. We discuss our results in Sect. 8 and present our conclusions in Sect. 9.
Unless otherwise stated, we indicate errors at the 68% confidence level (hereafter c.l.). Throughout this paper, we use H0 = 70 km s−1 Mpc−1 in a flat cosmology with Ω0 = 0.3 and ΩΛ = 0.7. In the adopted cosmology, 1′ corresponds to ∼77.5 kpc at the redshift of the Lyra complex, which is used to fix the Mpc scale of projected distances throughout the paper. All magnitudes are presented in the AB system.
2. Data and galaxy catalog
2.1. New spectroscopic observations
We observed the Lyra field with DOLoRes1 at the Italian Telescopio Galileo (TNG) in June 2018. In particular, we made use of the multi-object spectroscopy (MOS) capabilities of this instrument to observe 12 MOS masks with the LR-B Grism. In total, we observed 12 MOS masks for a total of 390 slits. For nine masks, the total exposure time was 3600 s, and for three masks the exposure time was 5400 s. In February 2019, we took long-slit spectra for another two galaxies (one of them is the bright radio galaxy ID. 039, see Sect. 2.2), and both were observed with an exposure time of 1800 s.
We performed the reduction of the optical spectra with standard IRAF2 tasks and were able to compute redshifts for 256 galaxies by using the cross-correlation method introduced by Tonry & Davis (1979). For another 29 galaxies, we estimated the redshifts by computing the wavelength location of emission lines in their spectra (more details about data reduction can be found in, e.g., Boschin et al. 2013).
In total, our spectroscopic catalog lists 285 galaxies in the field of RXCJ1825. The median value of the cz errors is 114 km s−1. Figure 1 shows the field of the Lyra complex sampled by TNG spectroscopic data.
 |
Fig. 1. Pan-STARRs r-band image of Lyra complex (RXCJ1825+CIZAJ1824 clusters) with superimposed contour levels of XMM X-ray emission taken from Clavico et al. (2019). Circles and squares indicate cluster members and non-members, respectively (see Table 1). Labels indicate galaxies cited in the text. |
We also used the magnitudes g, r, and i available in Pan-STARRS (DR1; Chambers et al. 2016) after correction for Galactic absorption. With the exception of 16 galaxies, g magnitudes are available. Neither r nor i magnitudes are available for four out of the 16 galaxies.
2.2. Galaxy catalog and prominent galaxies
Table 1, which is fully available in electronic form on the CDS website, lists the velocity catalog (see also Fig. 1), indicating the identification number of each galaxy, ID, and membership (Cols. 1 and 2, respectively); right ascension and declination, α and δ (J2000, Col. 3); dereddened r-band Pan-STARRS (DR1) magnitudes, r (Col. 4); and heliocentric radial3 velocities, v = c z⊙ (Col. 5) with errors, Δv (Col. 6). An excerpt from this table is also inserted in this paper. RXCJ1825 hosts two dominant galaxies, the galaxy ID. 226 (r = 14.63, hereafter BCG-E) and the galaxy ID. 186 (r = 15.15, hereafter BCG-W). The centroid of the XMM X-ray emission lies between these two galaxies, and it is much closer to BCG-W than to BCG-E. Hereafter, for the center of RXCJ1825, we adopt the position of the X-ray centroid reported by Clavico et al. (2019), [RA = 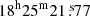 , Dec = +30° 26′25.3″ (J2000.0)]. The two BCGs are shown in Fig. 2.
, Dec = +30° 26′25.3″ (J2000.0)]. The two BCGs are shown in Fig. 2.
Velocity catalog of 285 spectroscopically measured galaxies in field of Lyra complex.
 |
Fig. 2. TNG V-band image of RXCJ1825 region around two brightest galaxies (BCG-E and BCG-W). The color scale units are ADU using a logarithmic display function. |
The companion cluster, CIZAJ1824, hosts a cool core (Clavico et al. 2019) that surrounds the dominant galaxy, the galaxy ID. 030 (r = 14.68, hereafter BCG-CC). As for the center of CIZAJ1824, we adopt the position of its BCG [RA = 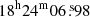 , Dec = +30° 29′30.4″ (J2000.0)].
, Dec = +30° 29′30.4″ (J2000.0)].
In the southwest of the region, the galaxy ID. 050 (r = 15.28, hereafter SG) is at the top of an extended X-ray emission that was detected by Clavico et al. (2019), see also Fig. 1. They suggest that SG was once the central galaxy of a group and is now in an advanced state of disruption after the interaction with RXCJ1825. This scenario explains the excess in the X-ray surface brightness between RXCJ1825 and SG (see Clavico et al. 2019 for details). The position of SG is RA = 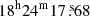 , Dec = +30° 18′15.0″ (J2000.0).
, Dec = +30° 18′15.0″ (J2000.0).
Other interesting galaxies are those with a peculiar radio emission (Botteon et al. 2019). The ID. 139 (r = 15.42), which is located west of the RXCJ1825 center in the direction of CIZAJ1824, has the morphology of a tailed radio galaxy. In the west region of the field that is south of CIZAJ1824, there is another much brighter tailed radio galaxy, which coincides with the optical galaxy ID. 039 (hereafter RG).
3. Member selection and global properties
To select cluster members among the 285 galaxies with redshifts, we applied the 1D adaptive-kernel method (hereafter DEDICA, Pisani 1993), which is very efficient for both medium and high sampled fields (Fadda et al. 1996; Balestra et al. 2016). This method searches for the most significant peaks in the velocity distribution. The Lyra complex is identified with the peak at z ∼ 0.067 and populated by 199 galaxies (in the range 0.055518 ≤ z ≤ 0.079265, see Fig. 3). The non-selected galaxies are all background galaxies.
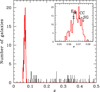 |
Fig. 3. Redshift galaxy distribution. The solid red line histogram refers to the galaxies assigned to the Lyra complex according to the DEDICA reconstruction method. The distribution of the 198 member galaxies with the redshift of prominent galaxies is shown in the inset plot. |
We also rejected the very bright galaxy ID. 225 (r = 15.01) that lies close to the lower limit of our redshift selection. The inspection of our TNG image reveals that it is a huge spiral. In the case that ID. 225 were part of the cluster, this bright galaxy would be the second brightest galaxy in the RXCJ1825 core and even more luminous than BCG-W. However, in the literature, non elliptical BCGs are very rare and in a few of these cases, richer data sets have shown that galaxies belonging to a small foreground group in front of the cluster have been misclassified as BCGs (e.g., Lauer et al. 2014). Indeed, the redshift constraints imposed by the member selection cannot prevent the inclusion of those galaxies with a redshift similar to that of the cluster but really distant (several Mpc) from the cluster in the three-dimensional space. This is shown by the analysis of data of simulated clusters that are projected on a two-dimensional space (e.g., Biviano et al. 2006). Therefore, we assume that the correct interpretation is that ID. 225 is a foreground object at z = 0.056075, lies ∼50 Mpc in front of the cluster complex, and appears projected on the core of RXCJ1825. The final catalog of member galaxies is made up of 198 objects of which 194 have full photometric information as well. By applying the biweight estimator to the 198 members of the complex, we computed a mean redshift of ⟨z⟩ = 0.0674 ± 0.0003, that is, ⟨v⟩ = 20 203 ± 96 km s−1 (Beers et al. 1990, ROSTAT software). We estimated the velocity dispersion of the whole complex, σv, by using the biweight estimator and applying the cosmological correction and the standard correction for velocity errors (Danese et al. 1980). We obtained 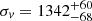 km s−1, where errors are estimated through a bootstrap technique.
km s−1, where errors are estimated through a bootstrap technique.
4. Structure of the Lyra field
4.1. 2D structure
In order to determine the structure of the Lyra complex as projected on the plane of the sky, we applied the 2D adaptive-kernel method (2D-DEDICA, Pisani 1996) to the positions of member galaxies. We detected four peaks with a significance larger than the 99% c.l. and a relative density with respect to the densest peak ρS > 0.3 (see Fig. 4 and Table 2). The most significant and dense peak, RXCJ1825main, indicates the position of the RXCJ1825 cluster. This peak is close to the X-ray centroid. The related isodensity curves of the galaxy distribution design a structure that is elongated in the east–west direction, which is close to the direction traced by the positions of the two BCGs. Northeast of the cluster peak, a minor peak was also detected (RXCJ1825NE). The second significant and dense peak indicates the position of the CIZAJ1824 cluster. The last peak lies between the two clusters (MiddlePeak).
 |
Fig. 4. Spatial distribution on sky and relative isodensity contour map of 198 spectroscopic members of Lyra complex obtained with 2D-DEDICA method. The peaks from east to west are RXCJ1825NE, RXCJ1825main, MiddlePeak, and CIZAJ1824 (see Table 2). The plot is centered on the X-ray centroid of RXCJ1825. The position of the prominent galaxies (BCGs of RXCJ1825, BCG of CIZAJ1824, SG, and RG) are indicated by crosses (blue, red, cyan, and magenta, respectively). The region of RXCJ1825 within 0.5 Mpc is enclosed by the circle for easier comprehension of the projected Mpc size. |
2D substructure from analysis of spectroscopic members.
Our spectroscopic data do not cover the entire cluster field in a uniform way and, in particular, the position of masks might bias the result. To check our results, we used a photometric catalog extracted from the Pan-STARRS survey. We considered non-stellar objects within a radius of ∼20″ from the central point of our spectroscopic observations and we applied the magnitude corrections for the Galactic absorption. We selected likely members on the basis of the r–i versus r color-magnitude relation (CMR), which indicate the locus of member galaxies (e.g., Goto et al. 2002; see Fig. 5). To determine the CMR, we applied the 2σ-clipping fitting procedure to the cluster members: we obtained r–i = 0.950−0.032 × r, based on 132 surviving galaxies. Our fit relation agrees with the results reported in the literature. In fact, the slope of the r–i versus r CMR is about zero (Goto et al. 2002), with values that depend on the analyzed cluster (e.g., between −0.04 and 0. in the sample of Barrena et al. 2012). As for the intercept, our value of r–i = 0.39 for r = 17.5 is very consistent with the value reported for low redshift clusters, r − i ∼ 0.4 for Abell 168 at z ∼ 0.044 and for Abell 1577 at z ∼ 0.14 (Goto et al. 2002, see Figs. 1 and 2 and text). Out of the Pan-STARRS photometric catalog, we considered as likely cluster members the objects lying within 0.07 mag from the CMR, that is about two times the error on the intercept.
 |
Fig. 5. Upper panel: Pan-STARRS r − i vs. r diagram. Small black symbols indicate the galaxies of the photometric catalog, green and magenta symbols indicate member and non-member galaxies of our spectroscopic catalog, large green squares indicate prominent galaxies (BCG-E, BCG-CC, BCG-W, and SG in order of increasing r magnitude). The solid line gives the CMR determined on spectroscopic member galaxies; the dashed lines are drawn at ±0.07 mag from this value and are used to define the photometric members in the Pan-STARRS catalog. Lower panel: same as above, but for Pan-STARRS g − r vs. r diagram. The red solid is drawn at 0.15 mag down to the CMR and is used to discriminate red from blue galaxies. |
Figure 6 shows the contour map for the 450 photometric members that have r ≤ 20, that is ∼4 mag fainter than M*, the characteristic absolute magnitude of the luminosity function of galaxies in clusters. Table 3 lists the significant peaks detected in the same region sampled by our redshift measures. We confirm the results obtained in the spectroscopic sample. RXCJ1825 shows a structure elongated in the east–west direction with a small feature in the northeast. CIZAJ1824 is clearly detected, too. The southwest region of the field is now better sampled and reveals a few structures.
 |
Fig. 6. Spatial distribution on sky and relative isodensity contour map of 450 photometric members with r ≤ 20, obtained with 2D-DEDICA method. The plot is centered on the X-ray centroid of RXCJ1825. The position of prominent galaxies (the BCGs of RXCJ1825, the BCG of CIZAJ1824, SG, and RG) are indicated by crosses (blue, red, cyan, and magenta, respectively). The region of RXCJ1825 within 0.5 Mpc is enclosed by the circle. |
2D substructure from analysis of photometric members.
4.2. 3D structure
The existence of correlations between positions and velocities is a powerful footprint of real substructures. We analyzed the presence of a velocity gradient. We performed a multiple linear regression fit to the observed velocities with respect to the galaxy positions in the plane of the sky computing the coefficient of multiple determination (RC2, NAG Fortran Workstation Handbook 1986). The position angle on the celestial sphere of the velocity gradient is PA = 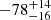 deg (measured counterclockwise from north), meaning higher–velocity galaxies lie in more western regions with the velocity gradient pointing from RXCJ1825 to CIZAJ1824 as expected. We followed Girardi et al. (1996) to asses the significance of this velocity gradient and performed 1000 Monte Carlo simulations by randomly shuffling the galaxy velocities and for each simulation we determined the coefficient of multiple determination RC2. The significance of the velocity gradient is determined as the fraction of times in which the RC2 of the simulated data is smaller than the observed RC2. We found that the velocity gradient is strongly significant at the > 99.9% c.l.
deg (measured counterclockwise from north), meaning higher–velocity galaxies lie in more western regions with the velocity gradient pointing from RXCJ1825 to CIZAJ1824 as expected. We followed Girardi et al. (1996) to asses the significance of this velocity gradient and performed 1000 Monte Carlo simulations by randomly shuffling the galaxy velocities and for each simulation we determined the coefficient of multiple determination RC2. The significance of the velocity gradient is determined as the fraction of times in which the RC2 of the simulated data is smaller than the observed RC2. We found that the velocity gradient is strongly significant at the > 99.9% c.l.
In order to study the velocity field of the cluster complex, we used the statistics and the bubble plot of Dressler & Shectman (1988, hereafter DS-test). For each galaxy, the deviation δ is defined as ![$ \delta_i^2 = [(N_{\mathrm{nn}}+1)/\sigma_{\mathit{v}}^2][(\overline{\mathit{v}_{\mathrm{l}}} - \overline{\mathit{v}})^2+(\sigma_{\mathrm{v,l}} - \sigma_{\mathit{v}})^2] $](/articles/aa/full_html/2020/01/aa36466-19/aa36466-19-eq9.gif) , where the subscript “l” denotes the local quantities computed over the group consisting of the galaxy itself and its Nnn = 10 neighbors. The cumulative deviation of the local kinematical parameters (mean velocity and velocity dispersion) from the global cluster parameters is given by the value Δ, which is the sum of the δi of the individual N galaxies. The significance of Δ, that is how far the system is from dynamical equilibrium, is checked by running 1000 Monte Carlo simulations, which are performed by randomly shuffling the galaxy velocities.
, where the subscript “l” denotes the local quantities computed over the group consisting of the galaxy itself and its Nnn = 10 neighbors. The cumulative deviation of the local kinematical parameters (mean velocity and velocity dispersion) from the global cluster parameters is given by the value Δ, which is the sum of the δi of the individual N galaxies. The significance of Δ, that is how far the system is from dynamical equilibrium, is checked by running 1000 Monte Carlo simulations, which are performed by randomly shuffling the galaxy velocities.
Girardi et al. (1997, 2010) introduced two variations of the DS-test where the contributions of the local mean and dispersion are considered separately. The kinematical indicator based on the local mean proved to be particularly useful. Instead, the kinematical indicator based on the local velocity dispersion requires an elaborate treatment in the presence of very large samples (e.g., Girardi et al. 2015). Following the methodology of Girardi et al. (2010), we used the kinematical indicator based on the deviation of the local mean velocity from the global mean velocity, ![$ \delta_{\mathit{v},i}^2= [(N_{\mathrm{nn}}+1)/\sigma_{\mathit{v}}^2][(\overline{\mathit{v}_{\mathrm{l}}} - \overline{\mathit{v}})^2] $](/articles/aa/full_html/2020/01/aa36466-19/aa36466-19-eq10.gif) . The significance of this test (DSv-test) was determined as it was in the standard DS-test.
. The significance of this test (DSv-test) was determined as it was in the standard DS-test.
Both the DS- and DSv-tests reveal that the Lyra system is not relaxed at the > 99.9% c.l. Figure 7 indicates the presence of RXCJ1825 and CIZAJ1824, which are low and high velocity regions in the velocity field. It also shows that the southwest region is characterized by high velocities that are comparable to those in CIZAJ1824. The intermediate region between RXCJ1825 and CIZAJ1824 is characterized by an even higher velocity region. This suggests that the MiddlePeak is not a structure that connects the two clusters since this structure should be characterized by an intermediate velocity.
 |
Fig. 7. Spatial distribution of 198 members of Lyra complex, each marked with circle. The larger the circle, the larger the deviation δV, i is (the so-called bubble plot). Thin blue and thick red circles show where the value of the local mean velocity is smaller or larger than the global value. The plot is centered on the X-ray centroid of RXCJ1825 and prominent galaxies are indicated for an easier comparison with Fig. 4. |
4.3. Red galaxies
In the local Universe red and/or passive galaxies are known to populate the cluster cores and are used to trace important galaxy systems or structures (e.g., Lubin et al. 2000; Girardi et al. 2015). We used the g–r versus r CMR to separate red and blue spectroscopic members. The fit relation is g–r = 1.334−0.032 × r, based on 116 galaxies. We define blue galaxies as those that are bluer than 0.15 mag with respect to the typical color of red sequence galaxies (see Fig. 5), where the value of 0.15 is about two times the error on the intercept. According to this definition, out of the 194 galaxies with both redshift and magnitude information, 153 and 41 are defined as red and blue galaxies, respectively.
Figure 8 (upper panel) shows the isodensity contours computed for blue and red galaxies separately using the 2D-DEDICA method. The relevant peaks obtained for red galaxies are listed in Table 4. Figure 8 (lower panel) shows the result of the DSv-test. This analysis based on red galaxies generally confirms the results based on all galaxies. According to the DS- and DSv-tests, the presence of substructure is significant at the > 99.9% c.l. and RXCJ1825 and CIZAJ1824 are always detected as low and high velocity regions in the velocity field. The velocity gradient is very significant (> 99.9% c.l.) and points from RXCJ1825 toward CIZAJ1824 (PA = 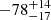 deg), which is in agreement with what was found for all galaxies.
deg), which is in agreement with what was found for all galaxies.
 |
Fig. 8. Upper panel: same as Fig. 4, but with isodensity contours for 41 blue galaxies (in green) and 153 red galaxies (in magenta). Lower panel: same as Fig. 7, but for 153 red galaxies. |
2D substructure from analysis of red spectroscopic members.
The analysis based on red galaxies differs in two respects. A southwest peak is now detected, although just over the threshold of ρS = 0.3 (southwestPeak in Table 4). More interestingly, the MiddlePeak is no longer detected by our 2D-DEDICA analysis and it seems rather related to the presence of blue galaxies (see blue contours in Fig. 8, upper panel). The comparison of Fig. 8 (lower panel) with Fig. 7 shows that the peculiarity of the velocity field in the intermediate region between the two clusters is no longer present. We conclude that the above mentioned detection of a MiddlePeak is due to a few galaxies, maybe a loose group or a filament in the phase of accretion from the field, rather than an important structure that connects the two clusters.
The analysis of the sample of red galaxies confirms that the southwest region of the field is characterized by high velocity galaxies (see Fig. 8, lower panel). We focused our attention on the west region by considering only the 58 red galaxies that belong to the CIZAJ1824 peak and southwestPeak (see Table 4). Using the DS- and DSv-tests, we found no evidence for substructures even when considering a very small number of neighbors (down to Nnn = 5 neighbors), suggesting that CIZAJ1824 and southwestPeak are characterized by very similar kinematical properties. The velocity gradient, which is significant at the 95% c.l., points from the northeast to the southwest (PA = 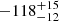 deg, see Fig. 9). These results are somewhat unexpected. In fact, one would expect that the southwest region was populated by galaxies from both of the two clusters, especially by those of the rich RXCJ1825 cluster, and that the southwest region showed an intermediate velocity with a strong gradient pointing from the southwest to CIZAJ1824. We conclude that the Lyra region, and in particular its southwest region, are more complex than expected (see the below section for more information).
deg, see Fig. 9). These results are somewhat unexpected. In fact, one would expect that the southwest region was populated by galaxies from both of the two clusters, especially by those of the rich RXCJ1825 cluster, and that the southwest region showed an intermediate velocity with a strong gradient pointing from the southwest to CIZAJ1824. We conclude that the Lyra region, and in particular its southwest region, are more complex than expected (see the below section for more information).
 |
Fig. 9. Bubble plot for 58 red galaxies belonging to west region (CIZAJ1824 + southwestPeak) where velocity gradient, pointing from low to high velocities, is indicated by small arrow. The spatial distribution of all red galaxies is indicated by small black dots and the related velocity gradient is indicated by the big arrow, pointing from RXCJ1825 to CIZAJ1924. |
4.4. SG and the SW region
To check the peculiarity of the observed velocity field, we performed a simple Monte Carlo simulation to reproduce the position on the sky of galaxies of RXCJ1825 and CIZAJ1824. We used the NFW model for the galaxy distribution and our mass estimates derived in Sect. 6. Figure 10 shows the result of a simulation where we fixed 220 and 80 galaxy points for RXCJ1825 and CIZAJ1824 within the respective R200 radii4, that is a number of galaxies proportional to the respective M200. To be more realistic, we allowed the simulation to fill the whole 2R200 region with galaxies, following the same NFW model for a total number of 327+118 galaxy points. We did not simulate the Gaussian velocity distribution of each cluster, and the galaxy points of RXCJ1825 and CIZAJ1824 are all assumed to have the same velocity of the respective parent cluster (see blue and red points in Fig. 10). The comparison of Fig. 10 with Figs. 7 and 8 (lower panel) show that the simulated field is populated by low velocity galaxy points while the real field is populated by high velocity galaxies. This analysis confirms that the high velocity field detected in the southwest region is very far from what was expected in the context of a system that is only formed by two relaxed clusters.
 |
Fig. 10. Spatial distribution of simulated galaxies of RXCJ1825+CIZAJ1824 system. Blue and red points indicate galaxy points of RXCJ1825 and CIZAJ1824, at low and high velocities, respectively. The black cross indicates the position of SG and the rectangle delimits a region close to SG where the real velocity field is characterized by high velocities (cf. Figs. 7 and 8, lower panel). |
In the southwest region, the brightest galaxy is SG, which is the fifth brightest galaxy of the whole Lyra field analyzed here. In general, the most luminous galaxies in clusters are related to groups as shown when accurate dynamical and/or gravitational lensing analyses are performed (e.g., Girardi et al. 2008 and references therein). SG has a rather high velocity, which is more than 1000 km s−1 higher than that of BCG-CC. In order to detect the galaxies that are related to SG and to minimize possible contamination from the two clusters, we selected galaxies that have velocities that are higher than SG. Figure 11 shows the positions of these galaxies in the sky. Four of these galaxies are close to the center of CIZAJ1824 and might be the high tail of the velocity distribution of its galaxy population. The other three are aligned between SG and RXCJ1825 along a stretched structure.
 |
Fig. 11. Spatial distribution of 198 galaxies of Lyra complex, each marked by circle. The larger the circle, the larger the velocity is. The eight galaxies with a velocity equal to or higher than SG are pointed out by red circles. The position of the prominent galaxies is indicated as well. |
5. Disentangling RXCJ1825 from CIZAJ1824
Our analysis of the 2D galaxy distribution of the Lyra complex detects the two individual clusters well and indicates that RXCJ1825 is more massive than CIZAJ1824 by a factor between two and four. The precise value depends on whether we consider the density of the peaks or the richness of the corresponding samples, and the RXCJ1825main+NE peaks versus the CIZAJ1824 sample or only RXCJ1825main versus CIZAJ1824 (see Tables 2–4).
However, the velocity distribution does not show evidence for the presence of two separated peaks (see Fig. 3, inset) and both the 1D-DEDICA and 1D-KMM methods (Ashman et al. 1994) failed to find a bimodality. Consequently, as for the velocities of the two clusters, we adopt the values of the velocities of the BCGs, as measured from redshift. This is reliable for CIZAJ1824, a very relaxed cluster according to Clavico et al. (2019), for which we measure vBCG − CC = 21215 ± 50 km s−1, and also for RXCJ1825 where the two BCGs have the same velocity within the errors with an average value of vBCG − EW = 19340 ± 67 km s−1.
By analyzing the two samples that correspond to the peaks CIZAJ1824 and RXCJ1825main, which were detected in the 2D-DEDICA analysis of the galaxy distribution, we obtained ⟨v⟩ = 21102 ± 214 km s−1 and ⟨v⟩ = 19618 ± 152 km s−1. This is in agreement within the errors with the measured velocities of the BCGs. For both samples we obtained quite large estimates of velocity dispersion, 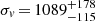 km s−1 and
km s−1 and 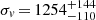 km s−1. However, we expect that each sample may be contaminated by some galaxies that belong to the companion system or other intervening substructures due to the projection effects. We stress the following: first, CIZAJ1824, the poorer cluster, is expected to be the more contaminated one; second, the contamination is expected to be larger among blue galaxies due to the field or the outskirts of the companion cluster; and third, the σv estimator is much less robust than ⟨v⟩, due to the inclusion of interloper galaxies which generally increases the σv estimates.
km s−1. However, we expect that each sample may be contaminated by some galaxies that belong to the companion system or other intervening substructures due to the projection effects. We stress the following: first, CIZAJ1824, the poorer cluster, is expected to be the more contaminated one; second, the contamination is expected to be larger among blue galaxies due to the field or the outskirts of the companion cluster; and third, the σv estimator is much less robust than ⟨v⟩, due to the inclusion of interloper galaxies which generally increases the σv estimates.
In order to disentangle the two systems and obtain reliable estimates for the velocity dispersion, we performed the analysis of the mean velocity profiles and velocity dispersion profiles (e.g., Girardi et al. 2016). The top panel of Fig. 12 shows the complexity of the distribution of galaxies of the Lyra complex in the projected phase-space, that is the rest-frame velocity vrf = (v − ⟨v⟩)/(1 + z) versus the clustercentric radius R. As for the system redshift z (and the related ⟨v⟩=cz), we used that of the full Lyra system, which is assumed to fix the cosmological distance of the system and thus the Mpc scale for R. The following analysis is independent of this assumption. As for the center, the X-ray centroid of RXCJ1825 is assumed.
 |
Fig. 12. Top panel: system rest–frame velocity versus projected clustercentric distance for 198 galaxies in whole cluster complex. The center is the position of the X-ray centroid of RXCJ1825. Blue, green, magenta, and red squares indicate galaxies belonging to the four peaks detected by the 2D-DEDICA method, that is RXCJ1825main, RXCJ1825NE, MiddlePeak, and CIZAJ1824 (see Fig. 4 and Table 2). The two close large circles indicate the two BCGs of RXCJ1825. The other large circle indicates BCG-CC of the CIZAJ1824 cluster. The large square indicates the SG galaxy and the triangle indicates the RG radio-galaxy. Solid and dashed blue curves show the limits due to the escape velocity in RXCJ1825, based on red and all galaxies, respectively (see Sect. 6). Middle and bottom panels: integral profiles of mean velocity and velocity dispersion (only one-σ error bands are shown) which, by definition, converge toward global values of whole complex. Solid and dashed lines refer to red and all galaxy populations. The vertical axes are in units of 103 km s−1. Middle panel: the blue horizontal line indicates the mean velocity of the two BCGs of RXCJ1825. Bottom panel: the blue horizontal line indicates the value of the X-ray temperature of RXCJ1825 estimated by Clavico et al. (2019) and here transformed in σV, assuming βspec = 1 (see Sect. 8). In the three panels the vertical dashed line contains the central region of RXCJ1825 suggested to be uncontaminated by galaxies of the companion cluster or other substructures (see text). |
Figure 12 (middle panel) presents the integral mean velocity profile for all member galaxies and for red galaxies. It is shown that ⟨v⟩ agrees with vBCG − EW in the central region of RXCJ1825 and that the inclusion of more galaxies at larger clustercentric distances causes an increase in the value of the mean velocity, which is likely due to the contamination of galaxies that belong to CIZAJ1824 or other minor substructures. The inspection of the mean velocity profile points out that ⟨v⟩ starts to increase at about 0.4 Mpc, and ⟨v⟩ is already 1-sigma higher than vBCG − EW at 0.5 Mpc. Therefore, we can assume that the contamination is not relevant for R < 0.4 Mpc.
Figure 12 (bottom panel) presents the integral velocity dispersion profile (hereafter VDP) for all member galaxies and for red galaxies. The VDP of relaxed clusters is expected to have a gentle decline down to the global value of the velocity dispersion while the contamination of a companion cluster is producing a sharp increase (e.g., cf. Fig. 2 of Girardi et al. 1998 and Fig. 2 of Girardi et al. 1996). As for RXCJ1825, its VDP sharply declines down to ∼0.15 Mpc, but with large uncertainties, and then increases very slightly in the case of the red galaxies. Since Fig. 12 (top panel) shows that the galaxies of the CIZAJ1824 peak are still far away, we assumed the velocity dispersion that was computed using galaxies within R < 0.4 Mpc to be a reliable estimate of the velocity dispersion of the RXCJ1825 galaxy population. We computed 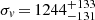 km s−1 using all 62 galaxies and
km s−1 using all 62 galaxies and 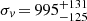 km s−1 using the 49 red galaxies. Since the red population is likely less affected by contamination, we adopted the latter value as the estimate of the velocity dispersion in RXCJ1825 to be more conservative. The minimum point of VDP,
km s−1 using the 49 red galaxies. Since the red population is likely less affected by contamination, we adopted the latter value as the estimate of the velocity dispersion in RXCJ1825 to be more conservative. The minimum point of VDP, 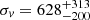 km s−1, is found at R = 0.166 Mpc, which is indeed comparable to the standard size of cluster cores when the galaxy profile is fit with King-like models (see Girardi et al. 1995 and references therein).
km s−1, is found at R = 0.166 Mpc, which is indeed comparable to the standard size of cluster cores when the galaxy profile is fit with King-like models (see Girardi et al. 1995 and references therein).
The results of the same analysis, but for CIZAJ1824, are shown in Fig. 13 where the center is fixed on BCG-CC. Following the above approach, we note that ⟨v⟩ already exhibits a decreasing in the very central regions, thus we suspect that the contamination by RXCJ1825 or other substructures is already important out of ∼0.1 Mpc (0.15 Mpc). The velocity dispersion computed in this small region is 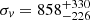 km s−1 (
km s−1 (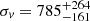 km s−1), based on six (seven) galaxies. However this estimate of σv is not supported by the analysis of the VDP.
km s−1), based on six (seven) galaxies. However this estimate of σv is not supported by the analysis of the VDP.
 |
Fig. 13. Same as Fig. 12, but centered on BCG-CC, adopted center of CIZAJ1824. Dashed red curves in the top panel show the limits due to the escape velocity in CIZAJ1824. Middle panel: the red horizontal line indicates the velocity of BCG-CC. Bottom panel: the red horizontal line indicates the value of the X-ray temperature of CIZAJ1824 estimated by Clavico et al. (2019). In the three panels the vertical dashed line contains the very central region of CIZAJ1824 discussed in the text. |
We resorted to using the method devised by Serna & Gerbal (1996), know as the H-tree method or the Serna-Gerbal method (e.g., Durret et al. 2010; Adami et al. 2018). This method uses a hierarchical clustering analysis to determine the relationship between galaxies according to their relative binding energies. The method assumes by definition that the redshift difference are of kinematical nature. The method also assumes a constant value for the mass-to-light ratio of galaxies and Serna & Gerbal suggested a value comparable to that of the clusters. Out of our catalog of 198 member galaxies, we used the 194 galaxies that have available magnitudes. We considered values of M/Lr = 100, 150, and 200 M⊙/L⊙ as suggested by large statistical studies (e.g., Girardi et al. 2000; Popesso et al. 2005; Proctor et al. 2015). The (gross) results are quite robust independent of the choice of the value of M/Lr. Figure 14 shows the resulting dendogram for M/Lr = 150 M⊙/L⊙, where the total energy appears vertically. At the deepest potential hole there are BCG-E and BCG-W of RXCJ1825. There is no relevant substructure for the most part in the cluster down to a level where a group hosting BCG-CC (hereafter HT2) departs from the main tree, and then a group hosting BCG-E and BCG-W (hereafter HT1), as shown in Fig. 14. The groups HT1 and HT2 are formed of 42 and 19 galaxies, respectively. The mean velocities of HT1 and HT2 are consistent with the mean velocities of the two clusters that were recovered with other methods (see above). The spatial position of the galaxies of HT1 and HT2 are also shown in Fig. 15. A similar result was obtained considering M/Lr = 100 and 200 M⊙/L⊙. We conclude that the two clusters are the only important structures detected in the field.
 |
Fig. 14. Dendogram obtained through Serna & Gerbal algorithm applied to 194 members with available magnitudes (here case is for M/Lr = 150 M⊙/L⊙). The y-axis indicates the binding energy, here in arbitrary units, with the deepest negative energy levels on the bottom. The position of the various galaxies are shown along the x-axis where small labels indicate prominent galaxies. Big labels indicate nodes of the structures discussed in the text. |
Depending on the adopted value of M/Lr, the number of members of HT2 ranges in the 17–19 interval and the value of σv in the 678–743 km s−1 interval. We decided to adopt the average value of σv = 700 ± 50 km s−1, as a reliable estimate of the velocity dispersion of CIZAJ1824 galaxies. As for HT1, the number of members ranges in the 35–49 interval and the value of σv in the 591–766 km s−1 interval. The average value is σv = 650 ± 100 km s−1, which is indeed much smaller than the value we obtained for RXCJ1825 from our VDP analysis, but it agrees with what was measured for the core within ∼0.166 Mpc. We conclude that the HT1 group should be interpreted as the core – plus the galaxies strictly bound to it – of RXCJ1825.
We also applied the Serna & Gerbal method to the sample of red galaxies with the addition of BCG-W. In fact, although BCG-W is slightly bluer than our definition of red galaxies, it is an elliptical galaxy and cannot be neglected in this method where galaxies are weighted with their luminosities. Very reassuringly, the results on this sample of 154 galaxies is comparable to those obtained for the full sample, and the detection of HT1 and HT2 have σv values in the above ranges.
When using all galaxies, the SG galaxy is assigned to the global cluster (in the M/Lr = 200 case) or assigned to a small group of four galaxies (HTSG, in the M/Lr = 100 and 150 M⊙/L⊙ cases). When using red galaxies, the SG galaxy is always assigned to the global cluster. Thus we cannot be confident in the detection of a group related to SG, although we indicate it in Fig. 15 where it appears as a very stretched structure. Finally, the RG galaxy is assigned only in one case to the HT2 group, otherwise it is part of the global cluster or very poor groups at higher energy level.
 |
Fig. 15. Spatial distribution on sky of 194 galaxies of Lyra complex that have available magnitudes. Blue triangles, red squares, and cyan circles indicate galaxies of HT1, HT2, and HTSG as obtained from the Serna & Gerbal method (see Fig. 14). Large black symbols indicate BCGs (circles), SG (square), and RG (triangle). |
Table 5 lists our best estimates for cluster velocity and velocity dispersion, v and σv, for RXCJ1825 and CIZAJ1824, separately. The listed uncertainties are strictly related to the method of analysis.
Properties of RXCJ1825 and CIZAJ1824 clusters.
6. Mass estimates of RXCJ1825 and CIZAJ1824
To compute the mass of the two clusters, we used the values estimated for σv in the previous section (see Table 5) and applied the relation by Munari et al. (2013, their Eq. (1)):
where A1D = 1090 km s−1, the average of the values they proposed, 1/α = 3, and h(z) was computed using the adopted cosmology of this study.
As for RXCJ1825, we estimated a mass M200 = 1.1 ± 0.4 × 1015 M⊙ within R200 = 2.1 ± 0.2 Mpc, where uncertainties of 10% and 30% on R200 and M200 are due to the propagation of the uncertainty on σv. An additional 10% of uncertainty on mass is also added due to the scatter around the theoretical relation. We used the recipe of den Hartog & Katgert (1996) with the assumption of a NFW mass density profile (Navarro et al. 1997; Dolag et al. 2004) to derive the “caustics” from our mass estimate, that is the curves that delimit the region where the rest-frame velocity vrf is smaller than the escape velocity. The plot of the caustics in Fig. 12 (top panel, solid blue curves) suggests that our mass estimate is adequate to describe the position of the RXCJ1825 galaxies in the phase-space. In the same figure, we also plot the caustics derived from the mass M200 = 2.1 × 1015 M⊙ computed using σv = 1244 km s−1 obtained for all galaxies, which give a kind of external envelope. As for CIZAJ1824, we estimated a mass M200 = 3.7 ± 1.1 × 1014 M⊙ within R200 = 1.4 ± 0.1 Mpc; the caustics to verify this mass value are plotted in Fig. 13 (top panel, solid red curves).
7. A bimodal model
If we assume that the two clusters are at the same distance from us, that is their redshift difference is of a kinematic nature, the rest-frame velocity difference between the two cluster is V = Δvrf = Δv/(1 + z) = 1757 km s−1, and the projected distance is D = 1.272 Mpc.
To perform the dynamical analysis of the system, one needs a third observational parameter, the mass of the whole system, Msys. We estimated Msys by adding the mass of the two cluster masses. Since it is known that cluster galaxy density profiles, and likely the DM profiles, extend well out of R200, to 2R200 and beyond (Biviano & Girardi 2003; Rines et al. 2013), the involved global mass of each system may be assumed to be higher by a factor two. The mass of the whole system is then estimated to be in the Msys = 1.5 − 3 × 1015 M⊙ range.
As an alternative estimate of the mass of the whole system, assuming that the system is bound (see below), we computed the mass estimate based on the virial theorem (Limber & Mathews 1960). Following the recipe of Girardi et al. (1998):
where 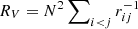 depends on the projected distance rij between any pair of the N galaxies. In principle, this method may overestimate the mass of a system that is bound, but not virialized, by a factor of two. However, numerical simulations show the virial mass estimate to also be quite accurate for superclusters near turnaround (Small et al. 1998). We obtained a mass of Mvir, obs.region = 1.4 × 1015 M⊙ for the sampled region, that is a projected region of ∼2.3 Mpc × 1.5 Mpc. Since this region is much smaller than the R200 region of RXCJ1825, our simple computation confirms that we are looking at a very massive system.
depends on the projected distance rij between any pair of the N galaxies. In principle, this method may overestimate the mass of a system that is bound, but not virialized, by a factor of two. However, numerical simulations show the virial mass estimate to also be quite accurate for superclusters near turnaround (Small et al. 1998). We obtained a mass of Mvir, obs.region = 1.4 × 1015 M⊙ for the sampled region, that is a projected region of ∼2.3 Mpc × 1.5 Mpc. Since this region is much smaller than the R200 region of RXCJ1825, our simple computation confirms that we are looking at a very massive system.
As a third approach and on the assumption that the velocity dispersion might also be an acceptable proxy for the mass before the virialization, we applied the formula of Munari et al. (2013) to the velocity dispersion for the whole Lyra complex, 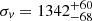 km s−1, and obtained Msys, 200 = 2.6 ± 0.6 × 1015 M⊙, which we interpret as the M200 mass of the cluster that will be formed in the future by the merger of RXCJ1825 and CIZAJ1824. This mass value lies in the 1.5 − 3 × 1015 M⊙ range of the above estimated Msys. Table 6 summarizes the mass values estimated for the whole system.
km s−1, and obtained Msys, 200 = 2.6 ± 0.6 × 1015 M⊙, which we interpret as the M200 mass of the cluster that will be formed in the future by the merger of RXCJ1825 and CIZAJ1824. This mass value lies in the 1.5 − 3 × 1015 M⊙ range of the above estimated Msys. Table 6 summarizes the mass values estimated for the whole system.
Properties of whole system.
To check whether the Lyra system is bound, we computed the two-body Newtonian criterion for gravitational binding that is stated, in terms of the observables, to be
where α is the projection angle between the plane of the sky and the line connecting the centers of the two clumps, and V and D are the velocity difference and the projected distance between the two clusters as mentioned above. Equation (3) is valid in the case of pure radial motion. When adding an orbital component in addition to the radial component, the true formulation is rather V2D < 2GMsyssin2αV cos αR, that is, it allows αV ≠ αR. Assuming Msys = 1.5 × 1015 M⊙, the probability that the system is bound is 31% in the case of radial orbits and 34% in the more general case, following Beers et al. (1982) and Hughes et al. (1995) for the computation. Assuming the more realistic value, Msys = 3 × 1015 M⊙, the probability that the system is bound is 58% and 53% in the two cases.
The above mentioned probabilities are estimated from the solid angles without regard to other constraints. Indeed, redshift surveys of clusters of galaxies limit cluster-cluster peculiar velocities to < 2000 km s−1 (Bahcall et al. 1986) and basic arguments indicate that typical velocities involved in cluster mergers are ∼3000 km s−1 (Sarazin 2002). In fact, the highest values for impact velocity reported in the literature are on the order of 4000 km s−1 and are related to important mergers, very close to the core–core passage (e.g., the bullett cluster of Markevitch et al. 2002; Abell 2744 of Boschin et al. 2006, see also the discussion in Molnar et al. 2013). When one excludes values of α < 15°, which correspond to values of deprojected velocities > 6500 km s−1, the bound probability is enhanced to 78%.
In order to analyze the interaction between the two clusters, we applied the analytical two–body model introduced by Beers et al. (1982) and Gregory & Thompson (1984), following the methodology of Girardi et al. (2008), see Table 7. This model assumes radial orbits for the clumps with no shear or net rotation of the system, as in Eq. (3). Furthermore, the clumps are assumed to start their evolution at time t0 = 0 – here the time zero of the Universe – with separation D0 = 0, and are moving apart or coming together for the first time in their history. We assume that we are seeing the cluster prior to merging at the time t = 12.603 Gyr, the age of the universe at the redshift of the Lyra system. The bimodal model solution gives the total system mass Msys as a function of α. Figure 16 shows the bimodal-model solution in comparison with our estimate of the mass of the system, which is the most uncertain observational parameter, here assumed to be in the 1.5 − 3.0 × 1015 M⊙ range. The present bound outgoing solution (i.e., expanding), BO, is clearly inconsistent with the observed mass. The unbound-outgoing solution, UO, is acceptable but only for a very small range of values of α, that is it is formally quite improbable. Bound ingoing solutions (BI) are quite acceptable and require intermediate values of α, in the range of 30° −70°. Therefore, the geometry of the merger is that CIZAJ1824 is in front of RXCJ1825 and moving toward it. The specific case with α = 50° implies a real distance of 2 Mpc and a real velocity of 2300 km s−1. A distance of 2 Mpc means that the center of CIZAJ1824 is at a distance of ∼R200 from the center of RXCJ1825, and that the two R500-regions of the two clusters are just in touch but not compenetrated (see Table 7).
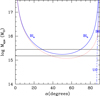 |
Fig. 16. System mass vs. projection angle for bound and unbound solutions (thick solid and thick dashed blue curves, respectively) of two–body model applied to two clusters. Labels BIa and BIb indicate the bound and incoming, i.e., collapsing solutions. Labels BO and UO indicate the bound outgoing, i.e., expanding solutions and unbound outgoing solutions. The horizontal band gives the range of the observational values of the mass system. The thin red dotted curve separates bound and unbound regions according to the Newtonian criterion (above and below the thin dashed curve, respectively). |
Parameters of bimodal model.
We are aware that there are several limitations in characterizing the dynamics when using the bimodal model. The obvious limit is the assumption that the two systems move on a radial orbit. However, basic arguments indicate that typical impact parameters should be small, on the order of 160 kpc (Sarazin 2002). More importantly, the model does not take into account the mass distribution in the two clumps, which starts to be important when their separation is comparable with their size. However, in this specific case, it is likely that the two systems are still far from the core-core passage.
8. Discussion
Here we discuss our results and some points of our analysis. We pay particular attention to the results based on X-ray and radio data (Botteon et al. 2019; Clavico et al. 2019).
8.1. Global dynamics
As for our dynamical analysis of Sect. 7, the analytical two-body model requires that we look at the two clusters before any core-core passage. This assumption is based on the fact that Clavico et al. (2019) find no excess in the X-ray surface brightness profile between RXCJ1825 and CIZAJ1824 and no evidence of a disturbed morphology in the X-ray surface brightness of CIZAJ1824. We also stress the point that our dynamical analysis implicitly assumes that the redshift difference between RXCJ1825 and CIZAJ1824 is due to kinematics, that is both clusters are at the same distance from us. Instead, in the case in which the redshift difference is interpreted as a cosmological distance, the distance between the two clusters is ∼30 Mpc. With the optical data we cannot appreciate this difference, which implies a difference in optical luminosity of ∼20%, in magnitude of ∼0.2 mag, and a non-appreciable difference in color (e.g., Lopes 2007). Indeed, the appearance of BCG-CC on the image is also similar to that of the two RXCJ1825 BCGs. Using the number density of galaxy clusters with masses higher than 4 × 1014 M⊙ (e.g., Eke et al. 1996; Vikhlinin et al. 2009), one expects fewer than 7 × 10−4 clusters as massive as CIZAJ1824 in the sampled volume, thus the casual presence of two unrelated clusters is rather improbable.
8.2. RXCJ1825 and CIZAJ1824
As for RXCJ1825, the two dominant galaxies, BCG-E and BCG-W, have similar magnitudes, Δm12 ∼ 0.5 mag. Also, they are close in the projected position, within ∼0.2 Mpc, and close in the line–of –sight velocity since redshift measures are equal within the uncertainties. The presence of two dominant galaxies in the cluster is generally considered as evidence of a merger in the past since the giant ellipticals observed in the center of the cluster are suspected to be the BCGs of the two previously colliding subclusters. In fact, more and more data can sometimes make the detection of the related subclusters possible (e.g., the case of Coma cluster, Colless & Dunn 1996).
In agreement with the above mentioned scenario, we find that the isodensity contours of the galaxy distribution in the central part of RXCJ1825 is elongated along about the east–west direction. Following Plionis & Basilakos (2002, based on Carter & Metcalfe 1980), we computed the ellipticity (ϵ) and the position angle of the major axis (θ). Using the 49 red galaxies at R < 0.4 Mpc, we obtained 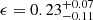 and
and 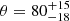 deg. This ENE-WSW direction agrees with the direction joining the two BCGs and the elongation of the X-ray isophotes in the central region (see Fig. 1 and Clavico et al. 2019). This concordance is often found in clusters with evidence of a past merger (e.g., Barrena et al. 2014). Since the two BCGs have the same line–of–sight velocity, their relative motion can only take place in the plane of the sky.
deg. This ENE-WSW direction agrees with the direction joining the two BCGs and the elongation of the X-ray isophotes in the central region (see Fig. 1 and Clavico et al. 2019). This concordance is often found in clusters with evidence of a past merger (e.g., Barrena et al. 2014). Since the two BCGs have the same line–of–sight velocity, their relative motion can only take place in the plane of the sky.
The fact that the two BCGs themselves are strongly elongated may also suggest that the axis connecting the two BCGs lies in the plane of the sky. Moreover, they are both aligned with the cluster. The alignment of dominant galaxies with the parent cluster has been reported by numerous authors (see Joachimi et al. 2015 for a review), but in the literature there is not a particular emphasis on clusters that show two dominant galaxies. Indeed, the second brightest galaxy is found to be very weakly aligned with the first one (e.g., Trevese et al. 1992; Niederste-Ostholt et al. 2010). Two close galaxies are expected to become aligned if they are influenced by the same gravitational forces, or if the galactic cannibalism scenario has a preferred direction. In any case, these mechanisms can also be related to the large scale structure since dominant galaxies are found to be aligned with the neighboring clusters on scales of several tens of Mpc (e.g., West 1994) and the alignment of dominant galaxies is found to be robust against major cluster mergers (Wittman et al. 2019). Therefore, the elongation of the two BCGs and their alignment with the cluster structure are not useful to fix the time when the two BCGs, and the likely related subclusters, joined to form the present cluster.
Clavico et al. (2019) claim that the ICM in the central part of RXCJ1825 is going to relax. The inspection of the TNG image of the two dominant galaxies can add some support to this point; in fact, it suggests that there is extra light in the region between the two BCGs (see Fig. 2). This intracluster light can be taken as evidence that the two galaxies have already interacted, that is the deprojected relative velocity is small and that we are catching RXCJ1825 in a very advanced phase of formation.
Another trace of cluster assembly in RXCJ1825 is the detection of a substructure at ∼0.4 Mpc that is northeast of the center (RXCJ1825NE). It is a poorly dense substructure with no peculiarity in the velocity. It was also detected in the analysis of red galaxies so it might be a small merging group and also the remnant of a more important past merger. Very interestingly, this substructure in the northeast and the SG galaxy discussed below trace the same direction through the cluster center, thus suggesting that NE-SW may be another direction of cluster accretion.
We also report the presence of an overdensity of high velocity galaxies in the region between RXCJ1825 and CIZAJ1824 (MiddlePeak). This overdensity is mostly related to blue galaxies (cf. Figs. 7 and 8 – lower panel), thus suggesting the presence of a few galaxies or a loose group that is just infalling from the field onto the Lyra system.
As for CIZAJ1824, BCG-CC is very luminous with a magnitude value intermediate between those of BCG-E and BCG-W. It is elongated in the north–south direction, slightly NNE-SSW, and is in the same direction as the X-ray isophotes (see Fig. 1). Clavico et al. (2019) report an entropy value of 16.1 ± 0.3 keV cm2 in the central region and one would expect that a BCG surrounded by this low entropy cool core would be characterized by Hα emission (Cavagnolo et al. 2008). Instead, the spectrum of BCG-CC does not show evidence for emission lines, in particular no Hα line is detected (see Fig. 17). Thus CIZAJ1824 is one of the few clusters with low entropy and no Hα emission, which is a rare exception to the much larger trend (see Fig. 1 of Cavagnolo et al. 2008).
 |
Fig. 17. TNG spectrum of BCG-CC where no emission line is present, in particular Hα expected at λ ∼ 7020 angstrom at cluster redshift. |
Our estimates of the velocity dispersion of the RXCJ1825 and CIZAJ1824 galaxy populations are 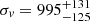 km s−1 and σv = 700 ± 50 km s−1, respectively. For each cluster, σv can be compared with the estimate of the average X-ray temperature, kT = 4.86 ± 0.05 keV and kT = 2.14 ± 0.05 keV (Clavico et al. 2019), by computing the value of
km s−1 and σv = 700 ± 50 km s−1, respectively. For each cluster, σv can be compared with the estimate of the average X-ray temperature, kT = 4.86 ± 0.05 keV and kT = 2.14 ± 0.05 keV (Clavico et al. 2019), by computing the value of 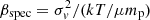 with μ = 0.58 the mean molecular weight and mp the proton mass. We obtained βspec = 1.2 ± 0.3 and βspec = 1.4 ± 0.2 for RXCJ1825 and CIZAJ1824, respectively, that is a two-sigma agreement with βspec = 1, the equipartition of energy per unit mass in galaxies and ICM (see also Figs. 12 and 13, bottom panels).
with μ = 0.58 the mean molecular weight and mp the proton mass. We obtained βspec = 1.2 ± 0.3 and βspec = 1.4 ± 0.2 for RXCJ1825 and CIZAJ1824, respectively, that is a two-sigma agreement with βspec = 1, the equipartition of energy per unit mass in galaxies and ICM (see also Figs. 12 and 13, bottom panels).
RXCJ1825 is found to be a massive cluster, M200 = 1.1 ± 0.4 × 1015 M⊙, and CIZAJ1824 a low mass cluster, M200 = 4 ± 1 × 1014 M⊙. Our M200 mass estimates for RXCJ1825 and CIZAJ1824 are in agreement with those based on X-ray data within uncertainties (M200 = 7 ± 2 × 1014 M⊙ and M200 = 4.2 ± 1.5 × 1014 M⊙, Clavico et al. 2019).
8.3. SG and RG in the SW region
The analysis of Clavico et al. (2019) shows a clear excess of diffuse X-ray emission southwest of RXCJ1825, which is in the same direction of SG. They suggest that this is related to a recent merger where a group, now traced by its central galaxy SG, has interacted with RXCJ1825 and is in an advanced state of disruption. This picture is also well in agreement with the presence of an elongation of the radio halo just in the same direction (Botteon et al. 2019). We find that the southwest region of the velocity field is very peculiar due to its high velocity. The SG galaxy, which is embedded there, is the fifth brightest galaxy of the Lyra field.
It is important to notice that, although the southwest and CIZAJ1824 regions are characterized by similar line–of–sight velocities, the geometry and kinematics are likely to be completely different. Assuming that SG is outgoing from RXCJ1825, SG is behind RXCJ1825 and moving away from it, while CIZAJ1824 is in front of RXCJ1825 and mowing toward it. In looking at Fig. 12, one might doubt that SG is a galaxy that is really bound to RXCJ1825. To better understand the fate of SG, we recomputed the caustics for a toy-model cluster, that is the “future” system formed of RXCJ1825 and CIZAJ1824 where we consider the mass of the whole system Msys. SG lies well inside the caustics, that is SG is likely to be bound to the Lyra system.
As for the search of possible companion galaxies of SG, our redshift data poorly sample the southwest region and we succeeded in detecting a galaxy overdensity close to SG only when applying the 2D-DEDICA analysis to photometric members (see Fig. 6). We need additional redshift data around SG to be more conclusive. However, the fact that we failed to detect a round, dense group of galaxies around SG might not be so unexpected due to the disruption of the group itself. In fact, it is well known that an interaction between two systems can enhance the internal energy of the individual systems, which may react by losing part of their particles (Binney & Tremaine 1987, see chap. 7.2). In fact, from the observational side, there is a plethora of features claimed to be the remnants of past mergers, such as a group that is partially destroyed by ejecting its central galaxy (Colless & Dunn 1996), a plume of outflying galaxies (Flores et al. 2000), and tidal debris that are stripped from the main cluster (Owers et al. 2011). Very likely, the mean velocity of the lost companion galaxies should be about that of the barycenter, in our case that of SG. These lost companions might be the cause of the high velocity excess in the SW region.
Considering galaxies with velocities higher than that of SG, we detect a stretched structure connecting RXCJ1825 to SG (see Fig. 11). However, a very detailed analysis of X-ray data suggests that two of these are just at the beginning of their interaction with the ICM of RXCJ1825 and thus they are likely not part of the same group of SG (see Clavico et al. 2019 for details).
Finally, we discuss RG, the tailed radio-galaxy lying south of CIZAJ1824, which was discovered by Botteon et al. (2019). RG is characterized by a velocity similar to that of BCG-CC and is well bound to the Lyra complex. Due to the presence of the tails we expect that RG is just interacting with the ICM, although it is not clear whether it is interacting with the ICM of CIZAJ1824 or RXCJ1825. Below we discuss two possible alternative scenarios. The direction suggested by the tails points slightly to the west of RXCJ1825 (see Botteon et al. 2019), thus RG might be related to this cluster. In this case, it is in front of RXCJ1825 and moving toward it. Alternatively, the direction in which RG is pointing is not so important and it is moving toward CIZAJ1824 with a partially tangential orbit. Indeed, the RG velocity is so close to the velocity of BCG-CC, which differs for only 230 km s−1 in the rest frame, that the motion of RG is likely to take place primarily in the plane of sky. In this case, the real distance of RG from the CIZAJ1824 center is similar to the projected distance, ∼0.4 Mpc, and thus RG is embedded inside the R500 region of CIZAJ1824. We cannot discriminate between the two scenarios with present data and we suggest to think of RG as a galaxy that is infalling toward the whole Lyra complex.
9. Summary and conclusions
We present the first dynamical analysis of the Lyra complex, consisting of the two clusters of galaxies RXCJ1825 and CIZAJ1824, as based on the kinematics of member galaxies. New spectroscopic data for 285 galaxies were acquired at TNG and the PanSTARRS magnitudes r, g, and i were used. We selected 198 cluster members, which we used for most of our analyses. We list our main results and conclusions below.
Our analysis of the galaxy distribution detects RXCJ1825 and CIZAJ1824 well as individual units, at the distance of ∼16′ and indicates that RXCJ1825 is more populated and more dense of CIZAJ1824, suggesting a mass ratio in the range from 2:1 to 4:1. The redshifts of RXCJ1825 and CIZAJ1824 are z = 0.0645 and z = 0.0708. We report the first estimates of velocity dispersion, 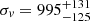 km s−1 and σv = 700 ± 50 km s−1, for RXCJ1825 and CIZAJ1824, respectively. Following the recipe of Munari et al. (2013), our estimates of dynamical mass are M200 = 1.1 ± 0.4 × 1015 M⊙ and M200 = 4 ± 0.1 × 1014 M⊙, with a ≲3 : 1 mass ratio, which is in agreement with the point mentioned above.
km s−1 and σv = 700 ± 50 km s−1, for RXCJ1825 and CIZAJ1824, respectively. Following the recipe of Munari et al. (2013), our estimates of dynamical mass are M200 = 1.1 ± 0.4 × 1015 M⊙ and M200 = 4 ± 0.1 × 1014 M⊙, with a ≲3 : 1 mass ratio, which is in agreement with the point mentioned above.
When assuming that cosmological distance is given by the redshift of the whole Lyra system, z = 0.0674, the line–of–sight velocity difference between RXCJ1825 and CIZAJ1824 is ∼1750 km s−1 and the projected distance is D ∼ 1.3 Mpc. A dynamical analysis indicates that clusters are likely to be gravitationally bound and that CIZAJ1824 lies in front of RXCJ1825 and is moving toward it. The specific case with the projection angle α = 50° leads to collision parameters that are quite reasonable, in particular the R500-regions of the two clusters are just touching but not compenetrated, which is in agreement with the fact that no relevant interaction is detected in the X-ray data (Clavico et al. 2019). The future cluster is expected to be very massive, with a mass value in the 1.5 − 3 × 1015 M⊙ range.
RXCJ1825 is found to not be relaxed and we have evidence that the likely merger related to the two dominant galaxies, a merger in the distant past according to Clavico et al. (2019), lies in the plane of the sky along the east-west, slightly ENE-WSW, direction. The merger is also supported by the detection of a radio halo (Botteon et al. 2019).
The velocity field of the southwest region, where the high velocity and luminous galaxy SG is embedded, is very peculiar because of its high velocity. This high velocity is comparable to that of CIZAJ1824. We show that this is not expected in a model where there are only two clusters. Rather, it suggests the presence of an additional population of high velocity galaxies. This supports the suggestion of Clavico et al. (2019) that SG was the central galaxy of a group, which was just disrupted by its interaction with RXCJ1825. This interaction caused the elongation of X-ray isophotes toward the SW direction, which is the same direction of the extension of the radio halo (Botteon et al. 2019).
Our results show that the Lyra region hosts a very complex galaxy structure, which is currently assembling. This in agreement with the picture delineated from recent radio and X-ray studies (Botteon et al. 2019; Clavico et al. 2019). From the optical side, new improvements can be obtained by collecting redshifts for a larger field in such way as to study RXCJ1825 at least out to its R200 radius, by adding many more redshifts in the southwest region, and by acquiring spectra at higher resolution in such way to obtain detailed spectral features. This would allow us to study the evolution of galaxies in this interesting environment.
Acknowledgments
We thank the referee for useful and constructive comments. We thank Andrea Botteon and Rossella Cassano for useful discussions and the access to their LOFAR radio contours previous than the publication. We thank Barbara Sartoris for an useful cosmological input. M.G. acknowledges financial support from the grant MIUR PRIN 2015 “Cosmology and Fundamental Physics: illuminating the Dark Universe with Euclid” and from the University of Trieste through the program “Finanziamento di Ateneo per progetti di ricerca scientifica – FRA 2018”. This publication is based on observations made on the island of La Palma with the Italian Telescopio Nazionale Galileo (TNG), which is operated by the Fundación Galileo Galilei – INAF (Istituto Nazionale di Astrofisica) and is located in the Spanish Observatorio of the Roque de Los Muchachos of the Instituto de Astrofísica de Canarias. This research has made use of the galaxy catalog of The Pan-STARRS Survey (DR1) and its public science archive. They have been made possible through contributions by the Institute for Astronomy, the University of Hawaii, the Pan-STARRS Project Office, the Max-Planck Society and its participating institutes, the Max Planck Institute for Astronomy, Heidelberg and the Max Planck Institute for Extraterrestrial Physics, Garching, The Johns Hopkins University, Durham University, the University of Edinburgh, the Queen’s University Belfast, the Harvard-Smithsonian Center for Astrophysics, the Las Cumbres Observatory Global Telescope Network Incorporated, the National Central University of Taiwan, the Space Telescope Science Institute, the National Aeronautics and Space Administration under Grant No. NNX08AR22G issued through the Planetary Science Division of the NASA Science Mission Directorate, the National Science Foundation Grant No. AST-1238877, the University of Maryland, Eotvos Lorand University (ELTE), the Los Alamos National Laboratory, and the Gordon and Betty Moore Foundation.
References
- Adami, C., Giles, P., Koulouridis, E., et al. 2018, A&A, 620, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ashman, K. M., Bird, C. M., & Zepf, S. E. 1994, AJ, 108, 2348 [NASA ADS] [CrossRef] [Google Scholar]
- Athreya, R. M., Mellier, Y., van Waerbeke, L., et al. 2002, A&A, 384, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bahcall, N. A., Soneira, R. M., & Burgett, W. S. 1986, ApJ, 311, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Baier, F. W., & Ziener, R. 1977, Astron. Nachr., 298, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Balestra, I., Mercurio, A., Sartoris, B., et al. 2016, ApJS, 224, 33 [Google Scholar]
- Barrena, R., Girardi, M., Boschin, W., & Mardirossian, F. 2012, A&A, 540, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barrena, R., Girardi, M., Boschin, W., De Grandi, S., & Rossetti, M. 2014, MNRAS, 442, 2216 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Geller, M. J., & Huchra, J. P. 1982, ApJ, 257, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Berrier, J. C., Stewart, K. R., Bullock, J. S., et al. 2009, ApJ, 690, 1292 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton: Princeton Univ Press) [Google Scholar]
- Biviano, A., & Girardi, M. 2003, ApJ, 585, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Biviano, A., Murante, G., Borgani, S., et al. 2006, A&A, 456, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boschin, W., Girardi, M., Spolaor, M., & Barrena, R. 2006, A&A, 449, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boschin, W., Girardi, M., & Barrena, R. 2013, MNRAS, 434, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Botteon, A., Cassano, R., Eckert, D., et al. 2019, A&A, 630, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carter, D., & Metcalfe, N. 1980, MNRAS, 191, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Cavagnolo, K. W., Donahue, M., Voit, G. M., & Sun, M. 2008, ApJ, 683, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, arXiv e-prints, [arXiv:1612.05560] [Google Scholar]
- Clavico, S., De Grandi, S., Ghizzardi, S., et al. 2019, A&A, 632, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colberg, J. M., White, S. D. M., Jenkins, A., & Pearce, F. R. 1999, MNRAS, 308, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M., & Dunn, A. M. 1996, ApJ, 458, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Dahle, H., Kaiser, N., Irgens, R. J., Lilje, P. B., & Maddox, S. J. 2002, ApJS, 139, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Danese, L., de Zotti, G., & di Tullio, G. 1980, A&A, 82, 322 [NASA ADS] [Google Scholar]
- den Hartog, R., & Katgert, P. 1996, MNRAS, 279, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., Bartelmann, M., Perrotta, F., et al. 2004, A&A, 416, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dressler, A., & Shectman, S. A. 1988, AJ, 95, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Durret, F., Laganá, T. F., Adami, C., & Bertin, E. 2010, A&A, 517, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ebeling, H., Mullis, C. R., & Tully, R. B. 2002, ApJ, 580, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Eckert, D., Ettori, S., Pointecouteau, E., et al. 2017, Astron. Nachr., 338, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Eckert, D., Ghirardini, V., Ettori, S., et al. 2019, A&A, 621, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eke, V. R., Cole, S., & Frenk, C. S. 1996, MNRAS, 282, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Ghirardini, V., Eckert, D., et al. 2019, A&A, 621, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fadda, D., Girardi, M., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1996, ApJ, 473, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Feretti, L. 1999, in Diffuse Thermal and Relativistic Plasma in Galaxy Clusters, eds. H. Boehringer, L. Feretti, & P. Schuecker, 3 [Google Scholar]
- Flores, R. A., Quintana, H., & Way, M. J. 2000, ApJ, 532, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Geller, M. J., & Beers, T. C. 1982, PASP, 94, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirardini, V., Eckert, D., Ettori, S., et al. 2019, A&A, 621, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, M., & Biviano, A. 2002, in Merging Processes in Galaxy Clusters, eds. L. Feretti, I. M. Gioia, & G. Giovannini, Astrophys. Space Sci. Lib., 272, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Biviano, A., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1995, ApJ, 438, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Fadda, D., Giuricin, G., et al. 1996, ApJ, 457, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Escalera, E., Fadda, D., et al. 1997, ApJ, 482, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Giuricin, G., Mardirossian, F., Mezzetti, M., & Boschin, W. 1998, ApJ, 505, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Borgani, S., Giuricin, G., Mardirossian, F., & Mezzetti, M. 2000, ApJ, 530, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Barrena, R., Boschin, W., & Ellingson, E. 2008, A&A, 491, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, M., Boschin, W., & Barrena, R. 2010, A&A, 517, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, M., Bardelli, S., Barrena, R., et al. 2011, A&A, 536, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, M., Mercurio, A., Balestra, I., et al. 2015, A&A, 579, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, M., Boschin, W., Gastaldello, F., et al. 2016, MNRAS, 456, 2829 [NASA ADS] [CrossRef] [Google Scholar]
- Golovich, N., van Weeren, R. J., Dawson, W. A., Jee, M. J., & Wittman, D. 2017, ApJ, 838, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T., Sekiguchi, M., Nichol, R. C., et al. 2002, AJ, 123, 1807 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, S. A., & Thompson, L. A. 1984, ApJ, 286, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, J. P., Birkinshaw, M., & Huchra, J. P. 1995, ApJ, 448, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Joachimi, B., Cacciato, M., Kitching, T. D., et al. 2015, Space Sci. Rev., 193, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, C., & Forman, W. 1999, ApJ, 511, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Kocevski, D. D., Ebeling, H., Mullis, C. R., & Tully, R. B. 2007, ApJ, 662, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Lauer, T. R., Postman, M., Strauss, M. A., Graves, G. J., & Chisari, N. E. 2014, ApJ, 797, 82 [Google Scholar]
- Limber, D. N., & Mathews, W. G. 1960, ApJ, 132, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Lopes, P. A. A. 2007, MNRAS, 380, 1608 [NASA ADS] [CrossRef] [Google Scholar]
- Lubin, L. M., Brunner, R., Metzger, M. R., Postman, M., & Oke, J. B. 2000, ApJ, 531, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Markevitch, M., Gonzalez, A. H., David, L., et al. 2002, ApJ, 567, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Markevitch, M., Gonzalez, A. H., Clowe, D., et al. 2004, ApJ, 606, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Maurogordato, S., Sauvageot, J. L., Bourdin, H., et al. 2011, A&A, 525, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGee, S. L., Balogh, M. L., Bower, R. G., Font, A. S., & McCarthy, I. G. 2009, MNRAS, 400, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Molnar, S. M., Chiu, I. N. T., Broadhurst, T., & Stadel, J. G. 2013, ApJ, 779, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, E., Biviano, A., Borgani, S., Murante, G., & Fabjan, D. 2013, MNRAS, 430, 2638 [NASA ADS] [CrossRef] [Google Scholar]
- NAG Fortran Workstation Handbook 1986, NAG Fortran Workstation Handbook (Downers Grove, IL: Numerical Algorithms Group) [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Niederste-Ostholt, M., Strauss, M. A., Dong, F., Koester, B. P., & McKay, T. A. 2010, MNRAS, 405, 2023 [NASA ADS] [Google Scholar]
- Olave-Rojas, D., Cerulo, P., Demarco, R., et al. 2018, MNRAS, 479, 2328 [Google Scholar]
- Owers, M. S., Nulsen, P. E. J., & Couch, W. J. 2011, ApJ, 741, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Owers, M. S., Baldry, I. K., Bauer, A. E., et al. 2013, ApJ, 772, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Pisani, A. 1993, MNRAS, 265, 706 [NASA ADS] [Google Scholar]
- Pisani, A. 1996, MNRAS, 278, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VIII. 2014, A&A, 571, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plionis, M., & Basilakos, S. 2002, MNRAS, 329, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Popesso, P., Biviano, A., Böhringer, H., Romaniello, M., & Voges, W. 2005, A&A, 433, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Proctor, R. N., Mendes de Oliveira, C., Azanha, L., Dupke, R., & Overzier, R. 2015, MNRAS, 449, 2345 [NASA ADS] [CrossRef] [Google Scholar]
- Rines, K., Geller, M. J., Diaferio, A., & Kurtz, M. J. 2013, ApJ, 767, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Roettiger, K., Loken, C., & Burns, J. O. 1997, ApJS, 109, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 2002, in Merging Processes in Galaxy Clusters, eds. L. Feretti, I. M. Gioia, & G. Giovannini, Astrophys. Space Sci. Lib., 272, 1 [NASA ADS] [Google Scholar]
- Serna, A., & Gerbal, D. 1996, A&A, 309, 65 [NASA ADS] [Google Scholar]
- Small, T. A., Ma, C.-P., Sargent, W. L. W., & Hamilton, D. 1998, ApJ, 492, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., & Farrar, G. R. 2007, MNRAS, 380, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Frenk, C. S., & White, S. D. M. 2006, Nature, 440, 1137 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tonry, J., & Davis, M. 1979, AJ, 84, 1511 [NASA ADS] [CrossRef] [Google Scholar]
- Trevese, D., Cirimele, G., & Flin, P. 1992, AJ, 104, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Tribble, P. C. 1993, MNRAS, 263, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009, ApJ, 692, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- West, M. J. 1994, MNRAS, 268, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Wittman, D., Foote, D., & Golovich, N. 2019, ApJ, 874, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Zabludoff, A. I., & Mulchaey, J. S. 1998, ApJ, 496, 39 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Velocity catalog of 285 spectroscopically measured galaxies in field of Lyra complex.
All Figures
 |
Fig. 1. Pan-STARRs r-band image of Lyra complex (RXCJ1825+CIZAJ1824 clusters) with superimposed contour levels of XMM X-ray emission taken from Clavico et al. (2019). Circles and squares indicate cluster members and non-members, respectively (see Table 1). Labels indicate galaxies cited in the text. |
| In the text | |
 |
Fig. 2. TNG V-band image of RXCJ1825 region around two brightest galaxies (BCG-E and BCG-W). The color scale units are ADU using a logarithmic display function. |
| In the text | |
 |
Fig. 3. Redshift galaxy distribution. The solid red line histogram refers to the galaxies assigned to the Lyra complex according to the DEDICA reconstruction method. The distribution of the 198 member galaxies with the redshift of prominent galaxies is shown in the inset plot. |
| In the text | |
 |
Fig. 4. Spatial distribution on sky and relative isodensity contour map of 198 spectroscopic members of Lyra complex obtained with 2D-DEDICA method. The peaks from east to west are RXCJ1825NE, RXCJ1825main, MiddlePeak, and CIZAJ1824 (see Table 2). The plot is centered on the X-ray centroid of RXCJ1825. The position of the prominent galaxies (BCGs of RXCJ1825, BCG of CIZAJ1824, SG, and RG) are indicated by crosses (blue, red, cyan, and magenta, respectively). The region of RXCJ1825 within 0.5 Mpc is enclosed by the circle for easier comprehension of the projected Mpc size. |
| In the text | |
 |
Fig. 5. Upper panel: Pan-STARRS r − i vs. r diagram. Small black symbols indicate the galaxies of the photometric catalog, green and magenta symbols indicate member and non-member galaxies of our spectroscopic catalog, large green squares indicate prominent galaxies (BCG-E, BCG-CC, BCG-W, and SG in order of increasing r magnitude). The solid line gives the CMR determined on spectroscopic member galaxies; the dashed lines are drawn at ±0.07 mag from this value and are used to define the photometric members in the Pan-STARRS catalog. Lower panel: same as above, but for Pan-STARRS g − r vs. r diagram. The red solid is drawn at 0.15 mag down to the CMR and is used to discriminate red from blue galaxies. |
| In the text | |
 |
Fig. 6. Spatial distribution on sky and relative isodensity contour map of 450 photometric members with r ≤ 20, obtained with 2D-DEDICA method. The plot is centered on the X-ray centroid of RXCJ1825. The position of prominent galaxies (the BCGs of RXCJ1825, the BCG of CIZAJ1824, SG, and RG) are indicated by crosses (blue, red, cyan, and magenta, respectively). The region of RXCJ1825 within 0.5 Mpc is enclosed by the circle. |
| In the text | |
 |
Fig. 7. Spatial distribution of 198 members of Lyra complex, each marked with circle. The larger the circle, the larger the deviation δV, i is (the so-called bubble plot). Thin blue and thick red circles show where the value of the local mean velocity is smaller or larger than the global value. The plot is centered on the X-ray centroid of RXCJ1825 and prominent galaxies are indicated for an easier comparison with Fig. 4. |
| In the text | |
 |
Fig. 8. Upper panel: same as Fig. 4, but with isodensity contours for 41 blue galaxies (in green) and 153 red galaxies (in magenta). Lower panel: same as Fig. 7, but for 153 red galaxies. |
| In the text | |
 |
Fig. 9. Bubble plot for 58 red galaxies belonging to west region (CIZAJ1824 + southwestPeak) where velocity gradient, pointing from low to high velocities, is indicated by small arrow. The spatial distribution of all red galaxies is indicated by small black dots and the related velocity gradient is indicated by the big arrow, pointing from RXCJ1825 to CIZAJ1924. |
| In the text | |
 |
Fig. 10. Spatial distribution of simulated galaxies of RXCJ1825+CIZAJ1824 system. Blue and red points indicate galaxy points of RXCJ1825 and CIZAJ1824, at low and high velocities, respectively. The black cross indicates the position of SG and the rectangle delimits a region close to SG where the real velocity field is characterized by high velocities (cf. Figs. 7 and 8, lower panel). |
| In the text | |
 |
Fig. 11. Spatial distribution of 198 galaxies of Lyra complex, each marked by circle. The larger the circle, the larger the velocity is. The eight galaxies with a velocity equal to or higher than SG are pointed out by red circles. The position of the prominent galaxies is indicated as well. |
| In the text | |
 |
Fig. 12. Top panel: system rest–frame velocity versus projected clustercentric distance for 198 galaxies in whole cluster complex. The center is the position of the X-ray centroid of RXCJ1825. Blue, green, magenta, and red squares indicate galaxies belonging to the four peaks detected by the 2D-DEDICA method, that is RXCJ1825main, RXCJ1825NE, MiddlePeak, and CIZAJ1824 (see Fig. 4 and Table 2). The two close large circles indicate the two BCGs of RXCJ1825. The other large circle indicates BCG-CC of the CIZAJ1824 cluster. The large square indicates the SG galaxy and the triangle indicates the RG radio-galaxy. Solid and dashed blue curves show the limits due to the escape velocity in RXCJ1825, based on red and all galaxies, respectively (see Sect. 6). Middle and bottom panels: integral profiles of mean velocity and velocity dispersion (only one-σ error bands are shown) which, by definition, converge toward global values of whole complex. Solid and dashed lines refer to red and all galaxy populations. The vertical axes are in units of 103 km s−1. Middle panel: the blue horizontal line indicates the mean velocity of the two BCGs of RXCJ1825. Bottom panel: the blue horizontal line indicates the value of the X-ray temperature of RXCJ1825 estimated by Clavico et al. (2019) and here transformed in σV, assuming βspec = 1 (see Sect. 8). In the three panels the vertical dashed line contains the central region of RXCJ1825 suggested to be uncontaminated by galaxies of the companion cluster or other substructures (see text). |
| In the text | |
 |
Fig. 13. Same as Fig. 12, but centered on BCG-CC, adopted center of CIZAJ1824. Dashed red curves in the top panel show the limits due to the escape velocity in CIZAJ1824. Middle panel: the red horizontal line indicates the velocity of BCG-CC. Bottom panel: the red horizontal line indicates the value of the X-ray temperature of CIZAJ1824 estimated by Clavico et al. (2019). In the three panels the vertical dashed line contains the very central region of CIZAJ1824 discussed in the text. |
| In the text | |
 |
Fig. 14. Dendogram obtained through Serna & Gerbal algorithm applied to 194 members with available magnitudes (here case is for M/Lr = 150 M⊙/L⊙). The y-axis indicates the binding energy, here in arbitrary units, with the deepest negative energy levels on the bottom. The position of the various galaxies are shown along the x-axis where small labels indicate prominent galaxies. Big labels indicate nodes of the structures discussed in the text. |
| In the text | |
 |
Fig. 15. Spatial distribution on sky of 194 galaxies of Lyra complex that have available magnitudes. Blue triangles, red squares, and cyan circles indicate galaxies of HT1, HT2, and HTSG as obtained from the Serna & Gerbal method (see Fig. 14). Large black symbols indicate BCGs (circles), SG (square), and RG (triangle). |
| In the text | |
 |
Fig. 16. System mass vs. projection angle for bound and unbound solutions (thick solid and thick dashed blue curves, respectively) of two–body model applied to two clusters. Labels BIa and BIb indicate the bound and incoming, i.e., collapsing solutions. Labels BO and UO indicate the bound outgoing, i.e., expanding solutions and unbound outgoing solutions. The horizontal band gives the range of the observational values of the mass system. The thin red dotted curve separates bound and unbound regions according to the Newtonian criterion (above and below the thin dashed curve, respectively). |
| In the text | |
 |
Fig. 17. TNG spectrum of BCG-CC where no emission line is present, in particular Hα expected at λ ∼ 7020 angstrom at cluster redshift. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} M_{200}/10^{15}\,{M}_{\odot }=[\sigma _{ v}/A_{\rm 1D}]^{1/\alpha }/h(z), \end{aligned} $$](/articles/aa/full_html/2020/01/aa36466-19/aa36466-19-eq24.gif)