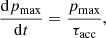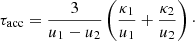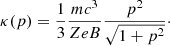| Issue |
A&A
Volume 630, October 2019
|
|
|---|---|---|
| Article Number | A107 | |
| Number of page(s) | 12 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201935940 | |
| Published online | 30 September 2019 | |
Time-dependent galactic winds
II. Effects of boundary variations in the disc and galactic halo
1
Universität Wien, Institut für Astrophysik, Türkenschanzstr. 17, 1180
Wien, Austria
e-mail: ernst.dorfi@univie.ac.at
2
Zentrum für Astronomie und Astrophysik, Technische Universität Berlin, Hardenbergstraße 36, 10623
Berlin, Germany
e-mail: breitschwerdt@astro.physik.tu-berlin.de
Received:
23
May
2019
Accepted:
2
July
2019
Context. Cosmic rays (CRs) are transported out of the galaxy by diffusion and advection due to streaming along magnetic field lines and resonant scattering off self-excited magnetohydrodynamic (MHD) waves. Thus momentum is transferred to the plasma via the frozen-in waves as a mediator assisting the thermal pressure in driving a galactic wind.
Aims. Galactic CRs (GCRs) are accelerated by shock waves generated in supernova remnants (SNRs), and they propagate from the disc into the halo. Therefore CR acceleration in the halo strongly depends on the inner disc boundary conditions.
Methods. We performed hydrodynamical simulations of galactic winds in flux tube geometry appropriate for disc galaxies, describing the CR diffusive-advective transport in a hydrodynamical fashion (by taking appropriate moments of the Fokker-Planck equation) along with the energy exchange with self-generated MHD waves.
Results. Our time-dependent CR hydrodynamic simulations confirm that the evolution of galactic winds with feedback depends on the structure of the galactic halo. In case of a wind-structured halo, the wind breaks down after the last super nova (SN) has exploded.
Conclusions. The mechanism described here offers a natural and elegant solution to explain the power-law distribution of CRs between the “knee” and the “ankle”. The transition will be naturally smooth, because the Galactic CRs accelerated at SN shocks will be “post-accelerated” by shocks generated at the inner boundary and travelling through the halo.
Key words: Galaxy: evolution / ISM: jets and outflows / shock waves / ISM: supernova remnants / cosmic rays
© ESO 2019
1. Introduction
Galactic winds emerging on large scales from galaxies seem to be a ubiquitous phenomenon in the Universe, as has been confirmed by numerous observations (for a recent review see Rupke 2018). For example, it has been argued that at redshifts z ∼ 6‒8 starburst-driven galactic winds can drill channels in the gas distribution in order to allow photon escape and thus contribute to reionization (Sharma et al. 2017). Substantial metal enrichment in low-redshift, circumgalactic halos as well as low-ionization metal absorption lines are also attributed to supernova (SN)-driven galactic wind bubbles (Lochhaas et al. 2018). Moreover, numerical simulations suggest (e.g. Hanasz et al. 2013) that cosmic rays (CRs) can drive large scale winds from high-redshift galaxies. In the past models of photon-driven winds have also been invoked, but as is well known the conversion of photon to gas momentum is low, typically less than 1% (see Dyson & Williams 1997), and high dust opacities would be needed to drive a significant wind (Skinner & Ostriker 2015).
Since in star-forming galaxies similar to the Milky Way there exists a rough energy equipartition between gas, CRs and magnetic fields, feedback processes in the interstellar medium (ISM) also depend on the dynamical action of CRs. To the extent that star formation or the growth of supermassive black holes in galaxies is limited by ISM feedback, CRs can play an active role in this respect (Zweibel 2017).
The realisation of the importance of CR feedback on galaxy evolution and star formation, as well as the back reaction on CR transport itself, has led to a wealth of recent studies (e.g. Thomas & Pfrommer 2019; Amato & Blasi 2018; Girichidis et al. 2018; Mao & Ostriker 2018). In this study we concentrate on regions above so-called superbubbles (SBs), generated by local sequential explosions, and we do not consider the large scale outflows triggered by a global starburst (e.g. Ruszkowski et al. 2017). The explosion energy of repeated SNe is shared between thermal heating, kinetic energy of the expanding bubble, and acceleration of particles to relativistic energies by a first order Fermi mechanism (Krymsky 1977; Axford et al. 1977; Bell 1978a,b; Blandford & Ostriker 1978). The efficiency of CR acceleration in supernova remnants has been analysed with respect to the ambient magnetic field, which breaks the initial symmetry of the bubble and leads to a different acceleration efficiency for the resulting oblique shock (transition from parallel to perpendicular shock between equator and pole for an initially horizontal field). It has been shown (Pais et al. 2018) that the overall efficiency is mainly due to the quasi-parallel part of the shock surface. In hydrodynamic simulations CRs are treated as a relativistic fluid with an adiabatic index γc = 4/3 and are coupled via the magnetic field and its fluctuations to the gaseous component. It has now been observed many times by radio synchrotron emission that CR electrons populate galactic halos, and their transport in a diffusion-advection halo can give useful insight into halo dynamics (Breitschwerdt 1994; Heesen et al. 2018).
The galactic winds treated here are large scale outflows above a local concentration of SN explosions, which drive the flow by the combined action of thermal pressure, CR pressure, and wave pressure of magnetic fluctuations. They provide a crucial mechanism to transport metal-enriched material as well as magnetic fields and CRs into the intergalactic medium (IGM). Thus galactic winds are an important ingredient for the overall evolution of galaxies and their associated ISM, including star formation, due to mass and energy losses. It has been shown that magnetized galactic winds also foster angular momentum loss (Zirakashvili et al. 1996), which can amount to 40% over a lifetime of ten billion years in the case of the Milky Way.
To be more specific, we want to study how locally concentrated outflows are generated. After break-out of the expanding bubble into the galactic halo, the remaining SNe exploding sequentially within the bubble release energy until the reservoir of SN progenitors is exhausted, typically when all stars above 8 M⊙ have exploded (a lower limit of 6 M⊙ is used when taking into account the possibility of electron-capture SNe). Hence, we get a time-dependent boundary between the wind region and the bubble underneath. Such galactic winds are traversed by shock waves and, strictly speaking, the changing inner boundary conditions will allow stationary outflows only in a time-averaged sense. The typical lifetimes of OB-associations of several 106−107 years (Kafatos & McCray 1987) are short compared to the flow times through a galactic wind, and stationary winds require power from several OB-associations due to propagating star formation in the disc. This is in contrast to starbursts with timescales of several 108 years where winds can be mainly driven by the thermal pressure. In contrast, in the case of SB-driven galactic winds, CRs play a vital role in driving the outflow and we also examine the possibility that particle acceleration in shocks propagating down the density gradient in galactic wind flows can boost the particles even to higher energies, in particular if the main site of acceleration is not too far from the galactic disc, as emphasized in Dorfi & Breitschwerdt (2012). Since downstream is the region facing the galactic disc, it is easy for accelerated particles to be convected away from the shock, diffusing towards the disc. The coalescence of repeated shock waves generated by sequential SNe provides a natural environment for such successive re-acceleration events. In this paper we can now closely link the SB evolution to the time-dependent wind structure and explore in detail the re-acceleration site of energetic CRs that are typically less than 15 kpc above the galactic plane.
For further details on the physical equations, assumptions and numerical method we refer to Breitschwerdt et al. (1991) or Dorfi & Breitschwerdt (2012). The main improvement compared to our earlier simulations is due to the time-dependent boundary conditions that closely link the galactic disc parameter to the flux tube properties as outlined in detail in Sect. 2.
A different model for CR acceleration between the “knee” and the “ankle” has been proposed by Völk & Zirakashvili (2004), who use the propagation of compressional waves through the halo generated by the spiral density shock waves in the disc. The pattern speed is different from the Galactic rotation both in the disc and the halo. Therefore magnetic field lines rooted in the dense, low, plasma-beta regions in the disc will slip through weak CR-modified shocks, arising from the collision of Galactic wind flows from regions with higher velocity with those of low velocity gas flows. These so-called slipping interaction regions are assumed to be at a vertical distance of about 20 kpc from the Galactic midplane and should be responsible for the re-acceleration of Galactic CRs to energies up to 1018 eV. While back diffusion of accelerated particles will be much easier than from inwards-facing-galactic-wind termination shock (downstream is away from the disc) at distances more than 100 kpc, we note that in our model (Dorfi & Breitschwerdt 2012) the re-acceleration region is much closer (below 10 kpc) to the disc, with the shocks’ downstream regions pointing towards the Galactic disc.
There are also models that favour acceleration in supernova remnant (SNR) shocks by the first order Fermi mechanism in the disc, arguing for a higher magnetic field strength due to SN explosion into a stellar-wind-compressed ISM (Völk & Biermann 1988) or due to wave growth upstream of the shock as a result of CR streaming (Bell & Lucek 2001). The spectral break beyond the knee has been assigned in the latter case to poor source statistics.
Here we focus on the origin and continuity of the galactic wind flow emanating from the SN and SB sources in the disc, specifically on the time variations of the inner Galactic wind boundary. The paper is structured as follows. In Sect. 2 we describe the physical properties of our model, in particular the evolution of the inner boundary during the galactic wind outflow. In Sect. 3 our results from time-dependent galactic wind simulations for the Milky Way are presented to show how the shock waves generated by the repeated SN explosions coalesce to a single strong shock propagating into the intergalactic space. In particular we emphasize CRs which are accelerated bby these successive shock waves. A discussion and our conclusions close the paper in Sect. 4.
2. Boundaries of galactic wind models
2.1. Kompaneets approximation
As described in Dorfi & Breitschwerdt (2012), the one-dimensional time-dependent treatment of galactic outflows in flux tube geometry requires initial as well as boundary conditions. In this paper we use a simplified description of the evolution of the SB to generate the initial conditions at the bottom of the flux tube, located at z0 = 1 kpc. According to Kompaneets (1960) we calculate an explosion within an exponentially stratified ISM using
where ρ00 = 5 × 10−24 g cm−3 specifies the gas density at the equatorial plane and hz = 80 pc denotes the vertical scale height. We can link the sequence of SN explosions to the evolution of a SB until break out, and adopt the SB properties as initial conditions at the bottom of the galactic wind driven by the gradients of thermal pressure, CR pressure, and Alfvénic wave pressure (e.g. Breitschwerdt et al. 1991). The overall implementation of the SB evolution is sketched in Fig. 1. As suggested in the literature (Maciejewski & Cox 1999; Baumgartner & Breitschwerdt 2013), the volume surrounded by the expanding shock wave is almost indistinguishable from an ellipsoid and can therefore be approximated by
where a and b are the semi-major and semi-minor axes of the rotationally symmetric ellipsoid. At breakout time t0 we kept a(t0) and b(t0) fixed and the lateral extension of the super bubble at this time determines the area of the flux tube at the lower boundary through
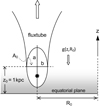 |
Fig. 1. Sketch of the initial configuration adopted for the galactic wind models. The SB is approximated by a Kompaneets solution until break-out, where z0 = 1 kpc fixes the location of the inner boundary conditions of the flux tube. All physical variables depend on time t and on the distance from the Galactic plane z. The gravitational acceleration g(z, R0) also depends on R0, the Galactocentric distance of the flux tube (see text for more details). |
The cross section A(z) of the flux tube is given by
where we adopt zb = 15 kpc as typical scale length for widening the flux tube towards a more spherical geometry. All computations are performed for a Galactocentric distance of R0 = 10 kpc.
This can be estimated as follows. According to Fuchs et al. (2006), the main sequence lifetime of a star can be calculated by τms = τ0(m/M⊙)−β, with τ0 = 1.6 × 108 yr and β = 0.932. If we take ml = 8 M⊙ to be the lowest and mu = 60 M⊙ the highest SN progenitor mass, then the explosion interval is the range of explosion times divided by the number of SN progenitors between ml and mu, N*, that is, 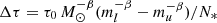 , where N* depends on the richness of the cluster. Thus Δτ ≈ 1.95 × 107 yr/N* = 4.8 × 105 yr for N* = 40. A more detailed calculation taking into account the initial mass function can be found in Breitschwerdt et al. (2016).
, where N* depends on the richness of the cluster. Thus Δτ ≈ 1.95 × 107 yr/N* = 4.8 × 105 yr for N* = 40. A more detailed calculation taking into account the initial mass function can be found in Breitschwerdt et al. (2016).
Each SN explosion releases ESN = 1051 erg, which results in a step-wise increase of the total energy ESB(t) of the SB (see Fig. 2, full line). The thermal energy of the bubble is given by 90% of the total explosion energy and the remaining 10% is used for acceleration of CRs within the SB, meaning ECR(t) = 0.1 ESB(t)
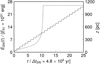 |
Fig. 2. Total energy increase of the repeated SN explosion (solid line) in units of ESN = 1051 erg as a function of time in units ΔtSN = 4.8 × 105 yr, the time between the individual SN explosions. The temporal expansion of the semi-major axis a(t) based on the Kompaneets ellipsoid in units of the explosion interval ΔtSN clearly shows the time t0 = 10.3ΔtSN when the base of the wind expansion is reached at z0 = 1 kpc. |
From Fig. 2 we can infer the evolution of the semi-major axis a(t) (dotted line) of the ellipsoid describing the SB. We see that after t0 = 10.3 ΔtSN = 4.94 × 106 yr the bubble opens rapidly into a galactic wind and we obtain b(t0) = 251 pc and 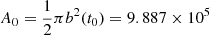 pc2 as starting values for the subsequent time-dependent wind computations (the factor 1/2 arises due to the assumption of a non-constant velocity cross section through A0). The first 13 out of 25 SN explosions are needed to develop this inner structure necessary to initiate the outflow.
pc2 as starting values for the subsequent time-dependent wind computations (the factor 1/2 arises due to the assumption of a non-constant velocity cross section through A0). The first 13 out of 25 SN explosions are needed to develop this inner structure necessary to initiate the outflow.
All general features of these galactic wind models have been described in detail by Dorfi & Breitschwerdt (2012) and without repeating their properties we note that the galactic potential defining g(z, R0) has been calculated according to Miyamoto & Nagai (1975). The physical equations are given by the equation of continuity and the equation of motions containing the pressure gradients of thermal gas, CRs, and Alfvénic waves, and the system is closed by three energy equations for the gas, the CRs, and the waves. The CRs are treated as a relativistic fluid with γc = 4/3 and include a diffusive term with a mean diffusion coefficient 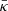 describing the acceleration of particles by a first-order Fermi mechanism (e.g. Drury 1983). All equations are written in flux tube geometry and depend on the distance from the galactic plane z and time t.
describing the acceleration of particles by a first-order Fermi mechanism (e.g. Drury 1983). All equations are written in flux tube geometry and depend on the distance from the galactic plane z and time t.
As mentioned before, the temporal evolution of galactic winds depends not only on the variations at the inner boundary, but also on the initial vertical structure of the medium. Therefore we explore basically two scenarios where the initial background structure corresponds either to a stationary wind (Model W) or the wind is evolving into an almost hydrostatic vertical stratification (Model H). Table 1 summarizes the properties of both initial structures.
Values at the lower boundary of the two initial background models.
The initial background Model W is similar to the stationary reference model of Breitschwerdt et al. (1991) and the time-dependent evolution on timescales larger than 107 years is similar to the simpler models already presented (Dorfi & Breitschwerdt 2012). In those earlier models the pressures at the inner boundary have been increased in one single step by a factor of 10 to study the propagation of a strong shock wave into the galactic wind.
For the initial background Model H we have reduced all pressures by a factor of 10 and hence the outflow velocity is reduced by a factor of 90 compared to Model W. The velocity at the inner boundary in now only u0 = 0.11 km s−1 and u0 ≪ vA (= 69 km s−1). Since the density is kept constant, corresponding to n0 = 1 cm−3, the mass loss is reduced by the same factor of 90 and is therefore negligible. The density of this model drops by almost six orders of magnitude within the inner 50 kpc.
Because by definition all wind models must have non-zero initial velocity, a high-speed tenuous wind with ρ ≃ 10−34 g cm−3 and a velocity on the order of 1000 km s−1 at distances of 300 kpc will always be the result, but with negligible mass loss. However, as seen for example in Figs. 6 and 9, the time-dependent solutions are not influenced by the initial models at such large distances and we can concentrate on flow features close to the galactic plane. For Model H we expect a faster evolution due to larger pressure gradients after the bubble outbreak. The lower gas density in the outer regions will also accelerate the wind evolution because less material close to the galactic disc has to be pushed away by the emerging wind. As seen in Eq. (8), even the case of u0 = 0 can lead to CR losses owing either to streaming with the Alfvén velocity vA or to a diffusive flux with 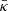 .
.
The outer boundary is located at r = 300 kpc where a simple outflow boundary condition is applied, ∂u/∂z = 0, and all other physical variables are advected outwards. Numerical tests have shown that the wind solutions are not affected when moving the outer boundary from 1000 kpc Dorfi & Breitschwerdt (2012) to the current value of r = 300 kpc. Adopting such a spatially smaller computational domain allows a better resolution of the various flow features.
2.2. Computation of inner boundary values
The total mass within the SB MSB is given through
where ṀSN denotes the mass input from stellar winds and the repeated SN explosions, and ṀGW = A0ρ0u0 denotes the mass loss by the galactic wind. However, since the mass encompassed in the SB shell is on the order of 3 × 104M⊙, it will dominate the ejecta mass by a large factor. After the initial vertical opening of the SB, we set the area A0 of the flux tube to remain constant. Equation (5) also contains the feedback from the galactic wind transporting gas into the galactic halo. The gas density ρ0(t) at the inner boundary of the flux tube can be calculated from the mass balance (Eq. (5)) and volume VSB of the SB,
In analogy, we can calculate the thermal pressure at the boundary of the SB using
where we have assumed γg = 5/3 and ESN, th = 0.9 ESN = 0.9 × 1051 erg throughout all computations. The last term is given by integration of the outflow of hot gas through the surface A0 with velocity u0.
A similar Eq. (7) holds for the CR pressure at the inner boundary of the flux tube but the loss term has to be modified according to
which includes the streaming of CRs with the combined velocity of the gas flow together with the Alfvén speed u0 + vA and the diffusive losses determined by the mean diffusion coefficient 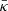 . Assuming a magnetic field of B0 = 10−6 G, we obtain an Alfvén velocity of vA = 69 km s−1. We assume that 10% of the SN explosion energy is converted into CRs, therefore we add Ec = 0.1 ESN at every time interval of ΔtSN = 4.8 × 105 yr.
. Assuming a magnetic field of B0 = 10−6 G, we obtain an Alfvén velocity of vA = 69 km s−1. We assume that 10% of the SN explosion energy is converted into CRs, therefore we add Ec = 0.1 ESN at every time interval of ΔtSN = 4.8 × 105 yr.
The Alfvénic wave pressure Pw, 0 plays, for the initial conditions, only a minor role (compare with Table 1). The temporal evolution at the inner boundary is given by an equation like Eq. (7) and in the case of a wind the inner boundary value is reduced due to
The temporal evolution of all loss terms like ṀGW and ĖGW, as well as the different contributions of advection and diffusion in Eq. (8), are presented in Fig. 7. Again, for more details on the physical system of equation we refer to Breitschwerdt et al. (1991) or Dorfi & Breitschwerdt (2012).
Figure 3 exhibits the temporal change of the gas pressure Pg(t), the CR pressure Pc(t), the mass loss rate Ṁ0(t), and the gas velocity u0(t) at the inner boundary in the time interval up to 8 × 106 years. We set t = 0 at the time when the first eight SNe have opened the SB. All physical variables increase in time and after the last SN added the energy to the SB at t > 6 × 106 yr, we kept all variables fixed except the velocity u0, which has to adapt to the wind solution. In the velocity panel (lower right) we can see how the flow reacts to the change from increasing pressures ∂P/∂t > 0 to a constant pressure by a reduction of the velocity u0(t) after 6 × 106 years. The change of the inner boundary to a constant value generates a rarefaction wave that travels at sound speed in the downstream region of the shocks. Such a non-linear wave reaches the shock wave from behind and reduces its strength (Courant & Friedrichs 1948) therefore coupling the wind solution to the velocity value u0(t) at the inner boundary. Since ρ0 is kept constant, also the mass loss Ṁ0 = A0ρ0u0(t) is influenced by the velocity decrease. This effect also becomes visible on larger temporal scales as plotted in Fig. 4.
 |
Fig. 3. Gas pressure Pg, 0 at the inner boundary (z0 = 1 kpc) of the flux tube for the wind background model Model W (full line) and the almost hydrostatic background Model H (dashed line) as a function of time. After 6 × 106 yr the last SN exploded within the SB and we keep the values of the boundary values fixed. Every ΔtSN = 4.8 × 105 yr and amount of 0.9 ESN = 0.9 × 1051 erg is added to increase Pg, 0. The CR pressure Pc, 0 increases by the usage of 0.1 ESN at every SN explosion. The lower panels exhibit the mass loss by the galactic wind, that is, Ṁ0 = A0ρ0u0 and the velocity at u0. We note that during the phase of repeating SN explosions, Model H generates higher mass loss rates because the winds expand into a more tenuous medium than Model W. |
 |
Fig. 4. Gas pressure Pg, 0 at the inner boundary (z0 = 1 kpc) of the flux tube for Model W (full line) and Model H (dashed line) as a function of time over 108 years. After 6 × 106 yr the last SN exploded and we keep the values of the boundary values fixed, except the velocity u0. Lower panel (right): illustrates how the velocity reacts to the change of the inner boundary from increasing pressures to constant pressures after 6 × 106 years. The lower panels exhibit the mass loss by the galactic wind, that is, Ṁ0 = A0ρ0u0 and the velocity at u0. We note that Model H (dotted line) generates initially higher mass loss rates because the wind expands into a more tenuous medium than Model W (see text for more details). |
The acceleration of CRs by a first-order Fermi process is included by adopting a mean diffusion coefficient of 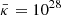 cm2 s−1, which mediates the jumps of Pc, 0 at the inner boundary (Fig. 3, upper right panel). We note that the particle pressure is typically a factor of 10 lower than the gas pressure and we have adopted the different scaling factors for the plots. However, as the flow expands into the intergalactic medium the adiabatic index of the energetic particles of γc = 4/3 is responsible for smaller adiabatic losses compared to the thermal gas (γg = 5/3). The adiabatic index, together with the diffusion of particles that led to mediating gradients, both led to an important contribution on larger scales, as previously described in Breitschwerdt et al. (1993) or Dorfi & Breitschwerdt (2012).
cm2 s−1, which mediates the jumps of Pc, 0 at the inner boundary (Fig. 3, upper right panel). We note that the particle pressure is typically a factor of 10 lower than the gas pressure and we have adopted the different scaling factors for the plots. However, as the flow expands into the intergalactic medium the adiabatic index of the energetic particles of γc = 4/3 is responsible for smaller adiabatic losses compared to the thermal gas (γg = 5/3). The adiabatic index, together with the diffusion of particles that led to mediating gradients, both led to an important contribution on larger scales, as previously described in Breitschwerdt et al. (1993) or Dorfi & Breitschwerdt (2012).
Figure 4 plots the temporal evolution of the boundary conditions over a time interval of 108 years, much longer than the SB evolution of 6 × 106 years. The lower extragalactic density (Model H, dotted line) leads to faster outflows with higher mass loss rates for the first 6.4 × 107 years. A maximum of the mass loss rate Ṁmax = 1.03 × 10−2 M⊙ yr−1 is reached at 3.68 × 107 years.
As the temporal evolution goes on, the initially larger values of the thermal pressure Pg, 0 and the CR pressure Pc, 0 of Model W steadily increase the outflow velocity at the inner boundary u0, which results in a further acceleration of the flow at later times. The stationary outflow at times longer than 108 years is about 20% larger for Model W (full line) than Model H (dotted line). Since the outer boundary is located at 300 kpc the flow time up to this distance is 3.83 × 108 years and 1.03 × 108 years, respectively, which is the minimum needed to establish stationary solutions. The evolution on these large timescales characterized by a common shock wave is similar to the simple models of Dorfi & Breitschwerdt (2012) where from the beginning of a single shock has been initiated.
Comparing the upper panels of Fig. 4, with constant pressures after the last SN explosion (t > 6 × 106 yr), to lower panels (mass loss rate Ṁ0 and inner outflow velocity u0), we can deduce the timescale by which a stationary solution is reached. Model W (full line) is characterized by lower velocities and therefore the time to propagate the constancy of the inner boundary values takes about 108 years, meaning that 108 years are necessary to establish a stationary solution within our computational domain of 300 kpc. As mentioned before, the decrease of the velocity u0 (and mass loss rate Ṁ0) around 18 × 106 yr is caused by a rarefaction wave induced through the change of the inner boundary values. This feature will become even more pronounced in the cases where the feedback between the SB and the wind losses are taken into account (see Sect. 3 and in particular Fig. 9). Model W (dotted line) develops faster and generates less massive winds within large density gradients. These gradients also mediate the rarefaction wave and the change of the inner boundary conditions is less important. Already after about 25 × 106 yr we find almost no further changes in the global outflow structure.
Clearly, the concept of keeping the inner boundary conditions constant after the last SN exploded or neglecting the loss terms is rather artificial, but it is useful to separate and illustrate physical effects occurring in time-dependent galactic outflows. As seen in Sect. 3.2 with corresponding Figs. 5–7, the feedback of the mass and energy loss on the SB already drastically alters the overall wind evolution from the beginning and inhibits the evolution towards asymptotic wind solutions.
 |
Fig. 5. Gas pressure Pg, 0 (upper left panel) at the inner boundary (z0 = 1 kpc) of the flux tube for Model W (full line) and Model H (dashed line) as a function of time including the feedback by galactic wind loss. The CR pressure Pc, 0 (upper panel right) is lower by about a factor of 10 compared to the gas pressure. All boundary values decrease between the SN explosions. After 6 × 106 yr, when the last SN exploded, the boundary values get monotonically smaller, caused by the outflow from the SB. Lower panel (left): exhibits the mass loss by the galactic wind, which reaches a maximum rate around 3.2 × 10−3 M⊙ yr−1 for Model W and 4.1 × 10−3 M⊙ yr−1 for Model H. In both models the maximum outflow velocity u0 (lower panel right) is reached at the last SN explosion. |
 |
Fig. 6. Gas pressure Pg, 0 (upper panel, left) at the inner boundary (z0 = 1 kpc) for Model W (full line) and Model H (dashed line) as seen over a time interval of 108 years for the case when mass and energy losses are included. The CR pressure Pc, 0 (upper panel, right) is about a factor of 10 less than the gas pressure (note the change of scale). The decrease of the mass loss rate Ṁ0 (lower panel, left) occurs already 10 × 106 yr after the SNe have triggered an outflow. After this time the galactic wind changes its nature as inferred from the decreasing values of the outflow velocity u0 (lower panel, right). |
 |
Fig. 7. Energy loss Eth, 0(t) in units of ESN (upper left panel), the CR energy loss contributions due to advection (upper right), the integrated mass loss M0(t) in units of 104 solar masses M⊙ (bottom left), and ECR, adv, 0 and diffusion ECR, diff, 0 in units of ESN (bottom right) as a function of time. |
3. Results
3.1. Mass and energy losses
The inner boundary values of the galactic wind simulations will be influenced by the mass and energy losses of the SB (see Eqs. (5) and (7)) through the area A0 as sketched in Fig. 1. Taking a typical value of 10−3 M⊙ yr−1 we can estimate that over a time interval of 108 years about 105 M⊙ are transported out of the SB. This mass is comparable to the initial total mass of the SB and this mass loss decreases the gas density ρ0(t). The outflow of material becomes easier because less material has to be accelerated out of the galactic potential.
In addition to this density change, the energy losses reduce the thermal pressure as well as the CR pressure to drive the flow. We emphasize that CRs are scattered by the magnetic fluctuations running outwards at the Alfvénic speed vA and therefore the CRs are advected outwards with the combined speed of u0 + vA. The diffusion of particles with a mean diffusion coefficient 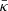 (see e.g. Drury 1983) modifies the CR gradients and adds to the losses of energetic particles as formulated in Eq. (8). The range of this mean diffusion coefficient
(see e.g. Drury 1983) modifies the CR gradients and adds to the losses of energetic particles as formulated in Eq. (8). The range of this mean diffusion coefficient 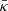 is expected to be in the range between 1028 cm2 s−1 and 1030 cm2 s−1 (e.g. Axford 1981). The acceleration of energetic particles is discussed in more detail in Sect. 3.5.
is expected to be in the range between 1028 cm2 s−1 and 1030 cm2 s−1 (e.g. Axford 1981). The acceleration of energetic particles is discussed in more detail in Sect. 3.5.
Both effects become clearly visible in Figs. 5 and 6 (full lines for Model W, dotted lines for Model H) where the time-dependent inner boundary values of the thermal pressure Pg, 0(t) and the CR pressure Pc, 0(t) are plotted as a function of time. The variations of the gas density ρ0(t) and the velocity u0(t) determine the mass loss Ṁ0(t) streaming through the flux tube. Comparing Fig. 5 to the behaviour of the boundary values without the feedback in Fig. 3 we clearly see the decreasing pressures between the individual SN explosions at every ΔtSN = 4.8 × 105 years. After the last SN at 6 × 106 years all boundary values decrease monotonically. The gas pressures increase until the last SN explodes but the smaller cosmic ray pressures (upper panel, right) are affected by diffusive losses and reach their maximum at 1.44 × 106 years (Model W) and 5.76 × 107 years (Model H), respectively. From the dynamical point of view the CR pressure is less important at the inner boundary and is typically a factor of 10 below the thermal pressure (cf. the different scales in Fig. 5). Since in Model H the large gradients lead to an overall lower background wind density, the bubble more rapidly loses the mass owing to higher mass loss rates (Fig. 5). We find a maximum mass loss rate of 4.1 × 10−3 M⊙ yr−1 (Model H) at time 1.96 × 106 years and 3.2 × 10−3 M⊙ yr−1 at time 2.46 × 106 years (Model W). No stationary solutions can develop and the variations at the inner boundary will terminate the mass and energy loss owing to realistic feedback from the wind.
3.2. Long term evolution
Figure 6 exhibits the change of the inner boundary values if we take into account the mass and energy losses of the SB through a galactic wind. Over the timescale of 108 years, we see that after 107 years the mass loss Ṁ0 ceases (lower panel, left). As already seen in Fig. 5, the inner boundary values of Pg, 0, Pc, 0, Ṁ0, and u0 start to decrease immediately after the last SN explosion and reduce thereby the ability to drive an outflow over longer timescales. The effect of mass and energy losses can be seen by comparing the temporal evolution of the galactic wind without the feedback as plotted in Fig. 4. After less than 25 × 106 yr the outflow has ceased for both models and no more material can be transported outwards into the extragalactic medium. For t > 25 × 106 yr we find almost no more variations of the thermal pressure Pg, 0 ≃ 2 × 10−13 dyn cm−2. The CR pressure Pc, 0 is steadily decreasing after the end of the SN explosions mediated by diffusive losses. We see from the lower panels of Fig. 6 that larger pressures at the inner boundary do not automatically lead to higher mass loss rates, by comparing Model W and Model H. The almost hydrostatic background structure of Model H enables a faster and more massive outflow.
We note that, as opposed to models without feedback, the mass loss of Model H remains higher than Model W during the whole wind evolution, because the solutions have no possibility to develop into a stationary wind. This can be easily seen if one compares the time the flow takes to reach the outer boundary at 300 kpc of about 2.5 107 years with the stationary flow time ∫ dz/u(z), which was found to be approximately 108 years.
The global temporal evolution of such galactic winds can be discussed in the context of Fig. 7, where integrated quantities are plotted over 108 years and in less than 25 × 107 years all integrated quantities reach their final values. According to our initial conditions we put 0.9 × 25ESN as thermal energy and 0.1 × 25ESN as CR energy into our SB located beneath the galactic wind. The upper panels of Fig. 7 plot the integrated loss of thermal energy Eth,0 = ∫Ėth dt as well as the integrated advected CR energy in units of the SN energy of 1051 erg. The removed thermal energies are almost identical for Model W (full lines) and Model H (dashed lines). Since CRs can leave the SB through advection ECR, adv, 0 by a velocity u0 + vA, as well as through a diffusive flux ECR, diff, 0, the left panels of Fig. 7 plot both contributions separately as described in Eq. (8). Comparing these figures we conclude that the diffusive contribution ECR, diff, 0 at the inner boundary remains small compared to the streaming of CRs ECR, adv, 0,
From the integrated mass losses ∫ Ṁ(t) dt as presented in Fig. 7, we get 3.3 × 104 M⊙ for Model W and 2.6 × 104 M⊙ for Model H characterized by the lower initial external density. We find that both models transport almost 25 ESN of thermal energy into the intergalactic medium. Model W (full lines) releases almost the same amount of energetic particles, whereas in Model H (dotted lines) the CRs contribute only an equivalent of about 10 ESN to the extragalactic space.
Taking a typical lateral dimension of b = 251 pc at the outbreak (see Sect. 2.1) and adopting a lower level of 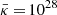 cm2 s−1, we obtain a typical timescale of
cm2 s−1, we obtain a typical timescale of 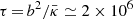 years for the diffusion of energetic particles into the SB. This timescale is short compared to the typical evolution timescale of the galactic wind. We conclude that the CR pressure inside a SB will not decrease under the mean galactic cosmic pressure, assumed to be 10−18 dyn cm−2 for our wind models. This fact explains why in Fig. 7 the integrated values of the CR energy losses by advection ECR, adv, 0 and by diffusion ECR, diff, 0 can reach values comparable to the thermal losses Eth, 0(t). Nevertheless we point out that the main drivers of the flow are the thermal pressure gradients and that CRs play only a minor role in initiating the outflow. From the lower right panel of Fig. 7, where the integrated losses ECR, diff, 0 caused by the diffusion of energetic particles are plotted as a function of time, we infer that the diffusive losses out of the bubble are negligible compared to the flux of CRs ECR, adv, 0 transported out by a galactic wind, and CR gradients are therefore not responsible for driving the outflow. Due to the large mean CR diffusion coefficients of
years for the diffusion of energetic particles into the SB. This timescale is short compared to the typical evolution timescale of the galactic wind. We conclude that the CR pressure inside a SB will not decrease under the mean galactic cosmic pressure, assumed to be 10−18 dyn cm−2 for our wind models. This fact explains why in Fig. 7 the integrated values of the CR energy losses by advection ECR, adv, 0 and by diffusion ECR, diff, 0 can reach values comparable to the thermal losses Eth, 0(t). Nevertheless we point out that the main drivers of the flow are the thermal pressure gradients and that CRs play only a minor role in initiating the outflow. From the lower right panel of Fig. 7, where the integrated losses ECR, diff, 0 caused by the diffusion of energetic particles are plotted as a function of time, we infer that the diffusive losses out of the bubble are negligible compared to the flux of CRs ECR, adv, 0 transported out by a galactic wind, and CR gradients are therefore not responsible for driving the outflow. Due to the large mean CR diffusion coefficients of 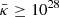 cm2 s−1, only gradients on the order of several kilo parsecs will be affected through diffusive effects. Consequently, at distances beyond 30 kpc CRs become increasingly important to further accelerate the material (see e.g. Fig. 9), provided that reasonably strong coupling to the plasma is ensured.
cm2 s−1, only gradients on the order of several kilo parsecs will be affected through diffusive effects. Consequently, at distances beyond 30 kpc CRs become increasingly important to further accelerate the material (see e.g. Fig. 9), provided that reasonably strong coupling to the plasma is ensured.
3.3. Coalescence of shock waves
The variations of the inner boundary conditions will mainly affect the region above the SB, which in our models is the region above 1 kpc. Every SN explosion generates non-linear waves, which travel into the previously shaped medium. To illustrate these interactions in Fig. 8 we have plotted the location of some shock waves for Model W and Model H triggered by the pressure jump from a SN explosion within the SB. The time axis is given in units of mean explosion interval of ΔtSN = 4.8 × 105 yr. These plots are generated for the original computational data, and an adaptive grid (Dorfi & Drury 1987) with up to 2000 grid points has been used to follow the non-linear evolution of these waves. After each SN explosion a new shock is initiated at the inner boundary located at 1 kpc and the moving grid points concentrate there to resolve the new emerging features. As summarized in Table 2, the developing shocks start with a rather small Mach-number and hence the adaptive grid has to react to very tiny changes of physical variables.
 |
Fig. 8. Coalescence of the first five forward shock waves (full lines) in a time-space diagram for Model W (upper panel) and Model H (lower panel) at the innermost 1.5 kpc. Dotted lines remark the reverse shocks. The time is given in units of the SN explosion interval ΔtSN. The reverse shocks (dotted lines) move at smaller speeds and collide with the forward shock, slowing them down. |
Pressure changes and Mach numbers of the first five shock waves.
From the physical point of view the interactions of these forward and reverse shocks cause rather complicated flow structures even for the case of pure gas dynamics (Courant & Friedrichs 1948). The overtaking of shock waves results in a transmitted shock, reflected in general in a weak rarefaction wave and a contact discontinuity between them. Two head-on colliding shock waves are weakened, retarded, and penetrate each other. Between them they leave a contact discontinuity within an expanding zone of constant pressure and flow velocity. All these structures will emerge on the non-constant background of our initial models. As we use an adaptive grid, the grid points rush towards such interaction zones if new features are generated. In addition the variations at the inner boundary have to be resolved and these grid motions can generate small disturbances in the determination of the shock location seen as kinks in outer shock locations. Owing to all these new structures, the exact location of a particular shock wave on a discrete grid is difficult to determine and the paths plotted in Fig. 8 are computed afterwards and have no influence on the shock propagation itself. We emphasize that we have adopted a conservative numerical scheme. Moreover the later shocks travel almost at sound velocity, M ≃ 1 as seen in Table 2, and their small pressure jumps are therefore difficult to localize.
Table 2 shows that the shock strength decreases as more and more SN explode because the SN energy added to the SB decreases relative to the total energy already deposited within the bubble. The typical Mach numbers are around M ≃ 1 for Model W, where wind from the SB evolves into a background of an earlier wind solution. For Model H starting from an almost hydrostatic background the Mach numbers are slightly higher, especially for the first shock that moves into a static medium, whereas later shocks will propagate into a medium set into motion by previous shock waves, thereby converging towards sound waves with M ≃ 1.
A close inspection of Fig. 8 verifies the aforementioned features of shock interactions. From the inclination of the path of the outermost forward shock we see that the later shock waves are running faster and overtake the earlier shock waves. The head-on collision of a forward shock (full line) with a reverse shock (dotted line) always causes a slowdown of the forward shock, visible as flatter paths. The corresponding reverse shock gets accelerated as seen by steeper paths. The effects of acceleration and deceleration are most pronounced when the Mach number of the respective shocks is high, whereas for weaker (and hence later) shocks the effect is barely visible in Fig. 8. These features are located in the plane part of the flow where we can neglect geometrical effects because the spatial scale of Fig. 8 is limited to 1.5 kpc, small compared to the opening scale of the flux tube zb = 15 kpc.
The action of three pressure gradients resulting from thermal gas, CRs, and Alfvénic waves enhances the complexity of these numerous non-linear wave interactions. The shock waves accelerate energetic particles through a first-order Fermi process and the resulting CR pressure gradients modify the shock structure (e.g. Drury & Völk 1981) by generating a CR precursor through diffusion. This whole zone of interacting non-linear waves propagates outwards along the pressure gradients and gets expanded. Only two shock waves survive and in Table 3 we summarize the evolution of this transitional zone by the typical time and distance after which all waves have been merged. Afterwards the flow structure is dominated by a single outwards-moving strong shock wave followed by a reverse shock that is also advected outwards.
Typical distances, times, and Mach number where the different shock waves merge into a single propagating forward shock.
We emphasize that these shock waves coalesce into a single wave rather close to the galactic plane at radii given in Table 3. As inferred from Fig. 8, the first two shock waves already merge at 1.6 kpc in the case of Model W and at 1.2 kpc for Model H. For Model W the overall merging distance is at zmerge, W = 7 [kpc] corresponding to 1.5 × 107 years and after this event the overall evolution is basically characterized by a single forward shock wave travelling into the intergalactic medium. The case of an almost hydrostatic initial configuration (Model H) leads to a faster shock merging at zmerge, H = 5 [kpc] after 107 years because the steeper gradients accelerate the coalescence of the different shock waves (see also Fig. 8). After the flow features have reached a distance larger than zmerge [kpc] a simpler, single shock approximation is suitable to describe the galactic wind and the results can directly be compared with the previous time-dependent wind models of Dorfi & Breitschwerdt (2012).
The position-time diagram of Fig. 8 illustrates the evolution of the merged forward and reverse shock over the time interval of 108 years. The thin lines correspond to an evolution of the inner bubble without the feedback from galactic wind losses and are plotted mainly as reference to the simpler models in Dorfi & Breitschwerdt (2012). Clearly, the more realistic models with feedback (thick lines) exhibit a similar evolution at small timescales and the difference already becomes pronounced after 107 years. Since the loss term decreases the pressure values at the base of the flux tube, the overall evolution of all waves is characterized by smaller velocities. Again, we can distinguish a merging period of t ≤ 1.5 × 107 years for Model W and t ≤ 1.0 × 107 years for Model H followed by an expansion on larger scales at almost constant shock speeds. The full lines indicate the location of the forward shock, the dashed lines point at the reverse shocks.
In Model W with feedback (lower lines) we find a finite expansion time for the reverse shock, which reaches a maximum spatial dimension of zmax = 5.43 kpc (see also Fig. 9). The region interior to the reverse shock has been depleted and depressurized in such a way that the reverse shock starts to propagate inwards and reaches our inner boundary at 1 kpc after 1.94 × 108 years, where our computation ends. At this time the outer shell is located at a distance of 92 kpc. The forward shock propagates at a speed of us = 490 km s−1.
 |
Fig. 9. Radial structures for Model W up to 120 kpc at three times, 7 × 107, 1.4 × 108, and 2.1 × 108 years, exhibit the shock waves propagating along the flux tube. The upper panels show the different pressure contributions from thermal gas Pg, CRs Pc, and waves Pw (dashed lines). The density and velocity are characterized by the large scale outflow with decreasing inner values. The last model at 2.1 × 108 years presents the reverse shock located around 11 kpc and the inner parts of the flow are directed inwards. |
For Model H the structures can propagate to large distances because the initial model exhibits steeper gradients and less material has to be removed from the flux tube. Moreover the steeper density gradients lead to a higher shock acceleration, as during shock propagation progressively less material has to be compressed by the shock according to the equation of continuity. Again, the models including the wind losses (thick lines) exhibit lower shock speeds, that is, the asymptotic speed of the forward shock decreases from us = 2980 km s−1 to 2770 km s−1. The corresponding values for the reverse shock are subject to larger variations; the speed drops from 980 km s−1 to 390 km s−1. After about 108 years the forward shock has reached our outer boundary located at 300 kpc. In contrast, and as can be seen in Fig. 8, the reverse shock has a lower speed in Model H because it is propagating into an ever-increasing density profile.
3.4. Evolution of spatial structures
The more detailed discussion of the spatial evolution is focused on models including mass and energy losses by the galactic wind. Models without these back reactions are rather similar to those of Dorfi & Breitschwerdt (2012).
In Figs. 9 and 10 we plot the spatial evolution of the galactic winds over more than 108 years for Model W and Model H. The most prominent feature is the forward shock wave running at an asymptotic speed of us = 490 km s−1 down the density gradient within the previous wind structure in Model W, plotted at times 7 × 107, 1.4 × 108, and 2.1 × 108 years. The reverse shock is less important but becomes more visible as it starts to move inwards after about 8 × 107 years. It is interesting to observe that the reverse shock transforms into a so-called termination shock, known from stellar winds, at around 2 × 108 years, when it becomes almost stationary in the Eulerian frame of reference. Once the SB flow at the distance of this shock vanishes, it will move towards the galactic disc, thereby reheating the flow in the inner flux tube, similar to a supernova explosion.
 |
Fig. 10. Radial structures for Model H on the large scale of 300 kpc at times of 3 × 107 yr, 6 × 107 yr, and 9 × 107 yr. Upper panels: different pressure contributions from thermal gas Pg, CRs Pc, and waves Pw (dashed lines). Flow velocites up to 2000 km s−1 are reached and the overall contribution of the reverse shock remains small. |
Comparing the three pressure contributions (upper panels of Figs. 9 and 10), the CR pressure gradients will dominate the flow above 20 kpc. Throughout the whole evolution the increase of CRs in the post-shock region, as well as the precursors in front of the forward shock, exhibit the acceleration of energetic particles in these large scale wind structures. However, due to Mach numbers of M ≃ 3, the overall acceleration efficiency remains so low that the CR pressure is influenced by diffusive losses towards the inner flux tube, which leads to steep gradients (cf. upper right panel). The values at the inner boundary (cf. Fig. 6) show that after 5 × 107 years the CR pressure remains extremely small and the outflow velocity u0 decreases to a few kilometers per second. The spatial scale is roughly given by 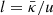 , and with
, and with 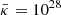 cm2 s−1 and u ≃ 3 km s−1 we obtain l ≃ 10 kpc as also deductible from the plots. The scale reduced by a factor of 10 for the wave pressure Pw (dashed lines, right upper panel) illustrates that the waves are only a minor contribution to drive the flow outwards.
cm2 s−1 and u ≃ 3 km s−1 we obtain l ≃ 10 kpc as also deductible from the plots. The scale reduced by a factor of 10 for the wave pressure Pw (dashed lines, right upper panel) illustrates that the waves are only a minor contribution to drive the flow outwards.
The resulting galactic wind significantly reduces the energy content of the underlying SB (see also Figs. 5 and 6, thick lines) already after the last SN has exploded, at t > 6 × 106 years. At some point the inner part of the flow is no longer supported by the various pressure gradients and starts to fall back for radii smaller than 30 kpc. As mentioned, the CR gradient is the main cause of the reversal of the flow direction. The density structures reveal the propagating forward shock as well as the development of a reverse shock inside 30 kpc when the wind velocity vanishes and the material starts to fall inwards. Clearly, these flow features are more clearly visible in the corresponding velocity plot (lower right panel) and after 108 years we find material falling inwards with negative flow speeds of more than 200 km s−1. We stopped these computations when the reverse shock reached the inner boundary at 2.12 × 108 years.
In contrast to the wind background Model W, the shock waves for Model H with a low halo-like density background travel as fast as us = 2780 km s−1 for the forward shock, and for the reverse shock, 390 km s−1 (see also Fig. 8, thick lines). Figure 10 exhibits the spatial evolution of the galactic wind for Model H on the scale of 300 kpc plotted at three times, t = 3 × 107, 6 × 107, and 9 × 107 years, respectively. Again as seen in all panels, the most prominent feature is the forward shock travelling at an asymptotic speed of us = 2780 km s−1. The reverse shock is located outside of the denser material transported by the galactic wind with velocities of a few 100 km s−1 (cf. lower right panel). In Model H this reverse shock gets advected outwards with a speed of 390 km s−1. In the frame of the contact discontinuity, the reverse shock is moving inwards as also inferred from the growing distance between the two “saw-tooth” features in the velocity (lower right panel). Because of the finite energy deposition by the SNe within the SB and the decreasing pressure support at the inner boundary (cf. Figs. 5 and 6, dashed lines), both shocks get weakened in time as they propagate down the density gradients. As discussed in Dorfi & Breitschwerdt (2012), this expansion phase yields to almost constant shock speeds. We terminate this calculation when the forward shock has reached the outer boundary (300 kpc) after 1.3 × 108 years. At this time the reverse shock is located at 71 kpc. Since we stop the computations at this time, we cannot follow the further evolution of the reverse shock, which at later times will also start to travel inwards.
Although the gas pressure dominates the flow around the inner boundary, the CR pressure provides the major acceleration at larger distances around 30 kpc (upper panels of Fig. 10). The wave pressure (dashed lines) is typically below the particle pressure and therefore less important for these galactic winds. As inferred from Fig. 10, the particles are mainly accelerated at the forward shock, the reverse shock plays only a minor role in the increase of the CR pressure. We emphasize that the presence of the diffusive shock acceleration (DSA) within galactic winds is described by a diffusive term in the energy equation of CRs, which together with γc = 4/3 leads to an overall much smoother pressure structure over our computational domain of 300 kpc, which is about two orders of magnitude in Pc compared to more than 10 orders in thermal pressure Pg. In contrast to Model W (presented in Fig. 9) the lower background densities lead to a merged shock wave with a higher Mach number of M ≃ 10 (cf. Table 3), which enables a more effective particle acceleration. Therefore also the relative diffusive losses into the inner flux tube are smaller because the diffusive length scale of 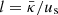 with
with 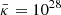 cm2 s−1 and us ≃ 3000 km s−1 is reduced to l ≃ 10 pc, that is, particle diffusion remains a localized phenomenon.
cm2 s−1 and us ≃ 3000 km s−1 is reduced to l ≃ 10 pc, that is, particle diffusion remains a localized phenomenon.
3.5. Acceleration of cosmic rays
As inferred from Figs. 9 and 10, the pressure of the bulk of energetic particles dominates the flow structure above 20 kpc in both cases. Since we use a hydrodynamical description of the CRs, so-called CR hydrodynamics (see e.g. Drury 1983) with γc = 4/3, we have only limited information on the maximum particle energy Emax, reachable during multiple encounters with shock waves triggered by individual SN explosions. This important pressure contribution emerges from particles with lower energies. To obtain an estimate of the individual particle momentum, we can integrate
where the diffusive acceleration timescale τacc is defined through a shock wave with up-stream velocity u1 and down-stream velocity u2. Since we are close to the galactic plane the shock wave remains a plane shock and is given by
Both diffusion coefficients κ1, 2 = κ(p) depend in a Fermi acceleration process on the particle momentum p and can be calculated in the case of fully developed turbulence from the so-called Bohm-limit (Bohm 1949),
An energetic particle can be picked up by successive shock waves and become accelerated to even higher energies. The typical length scale for the energizing particle is given by κ/us; a particle with different energies will experience different compression ratios generated by a changing number of subsequent shock waves (cf. Fig. 8). The spatial size of the shock waves is at least a factor of 102 more extended by changing sizes from a parsec-scale to an almost kiloparsec-scale in galactic winds. The individual waves merge within a few kpc above the galactic plane (see Table 3) and hence we expect only small adiabatic losses compared to acceleration sites located far away in the galactic halo, for example in the outer terminal shock of a galactic wind (Jokipii & Morfill 1987).
We emphasize that a diffusion coefficient on the order of κ ≃ 1028 cm2 s−1 together with a shock speed of us ≃ 3000 km s−1 leads to a typical spatial scale of κ/us ≃ 10 pc; the corresponding acceleration time is on the order of 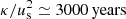 . If the diffusion coefficient reaches a maximum value of κ ≃ 1030 cm2 s−1 (see e.g. Axford 1981) the spatial scale increases to 1 kpc with an acceleration time of 3 × 105 years.
. If the diffusion coefficient reaches a maximum value of κ ≃ 1030 cm2 s−1 (see e.g. Axford 1981) the spatial scale increases to 1 kpc with an acceleration time of 3 × 105 years.
At such large particle energies the diffusion coefficient κ(p) increases linearly with the particle momentum p and scales inversely with the local magnetic field. Hence, during the time before the merging of shock waves tmerge (see Table 3), we expect different particle energies to be exposed to rather different compression ratios and complex flow features.
We concentrate on Model H, which mimics an expansion into a static halo. In Fig. 11 the maximum particle energy Emax is plotted for a particle starting at the “knee” with 1014 eV (solid line), which gets accelerated only by the first leading shock wave propagating into a static galactic halo. When the last SN explodes after 1.2 × 107 years this leading shock wave has travelled a distance of up to 37 kpc. The particle energies result from integrating Eq. (10). As can be seen, the main acceleration region is located below 15 kpc and the first encounter leads to the most important energy increase. Even for z = 20 kpc the adiabatic losses remain small, since according to the adopted flux tube geometry we get a geometrical dilution factor of 1 + (20/15)2 = 2.78 from Eq. (4). The subsequent shock waves (dashed and dashed-dotted lines) can boost the particle to higher energies but the low Mach number around M ≃ 1.2 limits the acceleration efficiency. The horizontal dotted lines indicate that we take particles at 5 kpc and 10 kpc, respectively, to be re-accelerated by subsequent shocks. Since the efficiency decreases with the number of individual shocks, we have considered in Fig. 11 only the first three shock fronts.
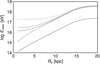 |
Fig. 11. Evolution of the maximum (full line) particle energy Emax in units of [eV] as a function of the shock distance from the galactic plane in units of [kpc] for Model H. The full line corresponds to the first shock (see also Fig. 8), the dashed lines plot particles re-accelerated by the second shock waves, and the dashed-dotted lines exhibit the energy gains due to the third shock wave. |
As mentioned above, an increase of the magnetic field, that is, B0 = 1 μG at the base of our flux tube and/or a different background model leading to faster shocks, will allow particles to reach energies around the “ankle”. As observations of the non-thermal emission of SNRs suggest (see e.g. the case of SN 1006, Ressler et al. 2014) the strength of magnetic fields in the vicinity of a blast wave can significantly be enhanced compared to typical ISM values. Such amplified magnetic fields could also be present in the case of shock waves within a galactic wind triggered by repeated SN explosions, which, as is known, will generate a high level of magnetic turbulence. The physics of such an amplification process together with numerical simulations is discussed for example in Downes & Drury (2014). Adopting these higher field strengths, energetic particles can be accelerated to values up to the “ankle” by a first-order Fermi process in galactic wind shocks.
The total particle energies will also depend on the background medium and clearly an expansion into a halo-like model (cf. Model H) is preferred because an expansion into an existing galactic wind (cf. Model W) leads to slower but more massive winds, which can cease shortly after the last SN exploded. An improvement of the calculations presented here, which is the subject of a future paper, will be the effect of the galactic wind and the associated acceleration of CRs on their energy spectrum, which requires their treatment on the distribution function level.
4. Conclusions
Our simulations bridge the gap between purely steady-state solutions like in Breitschwerdt et al. (1991) and time-dependent galactic winds like in Dorfi & Breitschwerdt (2012), by connecting outflows, which start at a reference level at 1 kpc, to the energy source of a SB beneath them. Therefore we can quantitatively assess the restrictions for steady-state solutions. Since the results we have obtained here show that the outflow breaks down on a timescale of a few 107 years after switch-off of the SN activity, steady-state flows, which are a simplistic approximation to reality, can only exist if the flow time τf is less or comparable to the SB lifetime plus the break-down time of stationarity. This is given by the distance ds of the critical point (saddle point singularity in case of outflow) divided by the information carrying signal (sound) speed cs, that is, τs ∼ dc/cs. The distance ds in turn depends on the mass loss rate or the energy input rate, respectively (see Breitschwerdt et al. 1991) and represents the characteristic length scale of influence, because the flow decouples causally beyond the critical point and will no longer be sustained by pressure gradients from below. Within τs the outflow also drains enough material from the SB so that, again, pressure gradients for steady-state flow cannot be maintained for much longer than a flow time. These constraints are somewhat relaxed by the action of centrifugal forces (Zirakashvili et al. 1996), which are not affected by the SB shutdown.
It has been known for some time that low mass loss rates imply high speed winds and vice versa (for details see Breitschwerdt 1994). High speed winds with low mass loss rates will reach the critical point faster, at lower distances from the disc, and therefore τf will be smaller and steady-state flows are more likely to occur. In contrast massive outflows are sluggish, with low speeds and large timescales for acoustic or magnetosonic waves to travel out to the critical point. The major difference between thermally- and CR-driven galactic winds is that CRs cannot cool, and they do exhibit a larger scale height, |∇Pc/Pc|−1 > |∇Pg/Pg|−1 because γc < γg. Although each outflow has to be evaluated individually, it seems fair to state that SBs with a small stellar content and high gas density will have difficulties in developing steady-state flows, provided that SB break-out occurs at all. In contrast, SBs with a high number of massive stars and a large overpressure with respect to a low density ambient medium can develop fast outflows. The most favourable circumstances for steady-state flows will be in the case of triggered and/or self-propagating star formation, so that channels or cavities that have been created by previous generations of SNe can be maintained over a timescale of ∼108 years or longer.
The role of the bulk of the CRs in the fluid dynamical approximation, coupled by self-excited waves to the plasma, is to provide a softer equation of state, that is, γc = 4/3 for a relativistic fluid, thus being less affected by adiabatic losses, as compared to γg = 5/3 for the thermal plasma. CRs are thereby able to lift off the upper gas layer of the halo at larger distances, and accelerate the flow to higher velocities, thus promoting steady-state flows with low mass loss rates. Interestingly, CR diffusion supports fast winds, as the mass to be lifted off is decreased. Farber et al. (2018) argue that CR decoupling from the neutral or low ionization gas (due to efficient wave damping in low ionization regions), leads to even faster winds because of the increase of the Alfvén speed, particularly near the disc. Therefore, depending on the energy-dependent diffusion coefficient, CRs will always foster a low-mass-loss-rate, magnetized galactic wind in steady-state models as long as MHD scattering waves are present and some coupling to the thermal plasma is present.
The advantage of the model, describing CR-driven galactic winds, presented here, is that it captures the essential physics of the problem while being simple and computationally cheap compared to an ab initio 3D model, because it is intrinsically 1D. To keep the flux tube geometry, we had to treat the evolution of the SB separately. This raises the question of how to connect the SB to the flux tube. Here we have used as a first approach constant density and pressure provided over the timescale of explosions. In a more realistic treatment, we can calculate these variables time dependently. The second simplification, which has to be fixed by hand, is the background into which the emanating wind propagates. While this may be the subject of a parameter study in a future paper, we have treated here two limiting cases, a stationary wind solution and a hydrostatic halo, into which the SB plasma and the CRs propagate. We find that less material located outside the galactic disc (cf. Model H) leads to a higher asymptotic wind speed and to a transport of material further outwards. In essence, these two models should encompass a large variety of realistic scenarios, and they bear all the features, such as complex non-linear wave interactions, which we have discussed here in detail. Independent of which of the two limiting models we choose, it is always found that CR acceleration predominantly occurs in the region where the flux tubes still maintain planar geometry. This limits adiabatic losses and leads to an even simpler description.
Particle energies up to 1018 eV, the so-called ankle, can be reached if the flux tube contains rather dilute gas close to the static limit, because in this case the Mach number of the shocks will be sufficiently high to boost the energy appreciably, as opposed to a smaller relative velocity and hence Mach number if the background medium is expanding away from the galaxy. The individual shocks from repeated SN explosions are imprinted on the galactic wind and merge at distances less than 5 kpc into a single shock wave. This combined shock wave gets accelerated because of the large density and pressure gradients and travels at almost constant speeds to significant distances of a few 100 kpc. The external pressure is communicated to the outflow, leading to the formation of a reverse shock, which starts to travel inwards until tmax = 9.02 × 107 years and reaches a maximum distance of zmax = 5.1 kpc.
In summary, it seems plausible that particles can reach energies up to the ankle at 1018 eV, depending on the diffusion coefficient, which itself is a function of the magnetic field strength. As we have shown, acceleration of energetic particles still occurs sufficiently close to the galactic plane that (i) they do not suffer large adiabatic losses and (ii) they can easily diffuse back to the disc where they are observed. This also explains why CRs below the knee, which are accelerated by disc sources, have a higher degree of isotropy than CRs between the knee and the ankle, which are post-accelerated galactic CRs that are not scattered back from a small diffusion halo of about 1 kpc in z-direction, but from individual local flux tubes, extending several kiloparsecs into the outer halo. The Auger Collaboration (Aab 2017) reports the detection of an anisotropy at the ≥5.2σ-level for light element particles with energies above 8 × 1018 eV. While an extragalactic origin of these ultra-high-energy CRs is favoured, the actual source(s) still remain(s) a mystery. The CRs post-accelerated in the halo, which we have described here, are typically in the energy range 1014−1018 eV, although some contribution to the higher more anisotropic CRs is possible.
Acknowledgments
This publication is supported by the Austrian Science Fund (FWF). DB acknowledges partial support from the Deutsche Forschungsgemeinschaft, DFG, Priority Programme SPP 1573. We thank the referee, Joel Bregman, for his encouragement and suggestions that helped to improve the paper.
References
- Amato, E., & Blasi, P. 2018, AdSpR, 62, 2731 [Google Scholar]
- Axford, W. I. 1981, Proceedings of an International School and Workshop on Plasma Astrophysics, Varenna, ESA SP, 161, 425 [Google Scholar]
- Axford, W. I., Leer, E., & Skadron, G. 1977, Proc. 15th Int. Cosmic Ray Conf. (Plovdiv), 11, 132 [NASA ADS] [Google Scholar]
- Baumgartner, V., & Breitschwerdt, D. 2013, A&A, 557, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, A. R. 1978a, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1978b, MNRAS, 182, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R., & Lucek, S. G. 2001, MNRAS, 321, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D. 1988, in Supernova Remnants and the Interstellar Medium, eds. R. S. Roger, & T. L. Landecker (Cambridge: Cambridge Univ. Press), 309 [Google Scholar]
- Blandford, R. D., & Ostriker, J. P. 1978, ApJ, 221, L29 [Google Scholar]
- Bohm, D. 1949, The Characteristics of Electrical Discharges in Magnetic Fields, 1st edn. (New York: McGraw-Hill) [Google Scholar]
- Bregman, J. N. 1980, ApJ, 236, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Bregman, J. N., Hogg, D. E., & Roberts, M. S. 1992, ApJ, 387, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Breitschwerdt, D. 1994, Habilitation Thesis, University of Heidelberg, 158 [Google Scholar]
- Breitschwerdt, D. 2003, Rev. Mex. Astron. Astrophys., 15, 311 [NASA ADS] [Google Scholar]
- Breitschwerdt, D., & Schmutzler, M. 1994, Nature, 371, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Breitschwerdt, D., & Schmutzler, M. 1999, A&A, 347, 650 [NASA ADS] [Google Scholar]
- Breitschwerdt, D., McKenzie, J. F., & Völk, H. J. 1991, A&A, 245, 79 [NASA ADS] [Google Scholar]
- Breitschwerdt, D., McKenzie, J. F., & Völk, H. J. 1993, A&A, 269, 54 [NASA ADS] [Google Scholar]
- Breitschwerdt, D., Dogiel, V. A., & Völk, H. J. 2002, A&A, 385, 216 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Breitschwerdt, D., Feige, J., Schulreich, M. M., et al. 2016, Nature, 532, 73 [Google Scholar]
- Canizares, C. R., Fabbiano, G., & Trinchieri, G. 1987, ApJ, 312, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Courant, R., & Friedrichs, K. O. 1948, Supersonic Flow and Shock Waves (New York: Springer-Verlag) [Google Scholar]
- Dawson, S., Spinrad, H., Stern, D., et al. 2002, ApJ, 570, 92 [NASA ADS] [CrossRef] [Google Scholar]
- de Avillez, M. 2000, Ap&SS, 272, 22 [NASA ADS] [CrossRef] [Google Scholar]
- de Avillez, M., & Breitschwerdt, D. 2004, A&A, 425, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Avillez, M., & Breitschwerdt, D. 2005, A&A, 436, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Avillez, M., & Breitschwerdt, D. 2007, ApJ, 665, 35 [Google Scholar]
- Dogiel, V. A., Gurevich, A. V., & Zybin, K. P. 1994, A&A, 281, 937 [NASA ADS] [Google Scholar]
- Dorfi, E. A., & Breitschwerdt, D. 2012, A&A, 540, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorfi, E. A., & Drury, L. O’C. 1987, J. Comput. Phys., 69, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Downes, T. P., & Drury, L. O’C. 2014, MNRAS, 444, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L. O’C. 1983, Rep. Progr. Phys., 46, 973 [Google Scholar]
- Drury, L. O’C., & Völk, H. J. 1981, ApJ, 248, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Dyson, J. E., & Williams, D. A. 1997, The Physics of the Interstellar Medium, Chap. 7.1.10 (Bristol: Institute of Physics Publishing) [CrossRef] [Google Scholar]
- Farber, R., Ruszkowski, M., Yang, H.-Y. K., & Zweibel, E. G. 2018, ApJ, 856, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Fuchs, B., Breitschwerdt, D., de Avillez, M. A., Dettbarn, C., & Flynn, C. 2006, MNRAS, 373, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, V. L., & Ptuskin, V. S. 1985, Sov. Sci. Rev. E: Astrophys. Space Phys., 4, 161 [NASA ADS] [Google Scholar]
- Girichidis, P., Naab, T., Hanasz, M., & Walch, S. 2018, MNRAS, 479, 3042 [NASA ADS] [CrossRef] [Google Scholar]
- Gressel, O., Elstner, D., Ziegler, U., & Rüdiger, G. 2018, A&A, 486, L35 [Google Scholar]
- Habe, A., & Ikeuchi, S. 1980, Rep. Progr. Theor. Phys., 64, 1995 [NASA ADS] [CrossRef] [Google Scholar]
- Hanasz, M., Lesch, H., Naab, T., et al. 2013, ApJ, 777, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Hartquist, T. 1983, MNRAS, 203, 117 [NASA ADS] [Google Scholar]
- Heesen, V., Krause, M., Beck, R., et al. 2018, MNRAS, 476, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Ipavich, F. 1975, ApJ, 196, 107 [Google Scholar]
- Jokipii, J. R. 1987, ApJ, 313, 842 [Google Scholar]
- Jokipii, J. R., & Morfill, G. E. 1985, ApJ, 290, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Jokipii, J. R., & Morfill, G. E. 1987, ApJ, 312, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Kafatos, M., & McCray, R. 1987, ApJ, 317, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Kahn, F. D. 1981, in Investigating the Universe, eds. F. D. Kahn, & D. Reidel (Dordrecht: Publishing Company), 1 [Google Scholar]
- Kapferer, W., Ferrari, C., Domainko, W., et al. 2006, A&A, 447, 827 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kikuchi, K., Furusho, T., Ezawa, H., et al. 1999, PASJ, 51, 301 [NASA ADS] [Google Scholar]
- Ko, C. M. 1991, A&A, 242, 85 [NASA ADS] [Google Scholar]
- Kompaneets, A. S. 1960, Sov. Phys. Dokl., 5, 46 [NASA ADS] [Google Scholar]
- Korpi, M. J., Brandenburg, A., Shukurov, A., Tuominen, I., & Nordlund, A. 1999, ApJ, 514, 99 [Google Scholar]
- Krymsky, G. F. 1977, Dokl. Nauk. SSR, 234, 1306 (Engl. Trans. Sov. Phys. Dokl., 23, 327) [NASA ADS] [Google Scholar]
- Kulpa-Dybell, K., Otmianowska-Mazur, K., Kulesza-Żydzik, B., et al. 2011, ApJ, 733, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Kulsrud, R. M., & Pearce, W. D. 1969, ApJ, 156, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Lagage, P. O., & Cesarsky, C. J. 1983, A&A, 125, 249L [NASA ADS] [Google Scholar]
- LeVeque, R. J. 1990, Numerical Methods for Conservation Laws (Basel: Birkhäuser-Verlag) [CrossRef] [Google Scholar]
- Lochhaas, C., Thompson, T. A., Quataert, E., & Weinberg, D. H. 2018, MNRAS, 481, 1873 [NASA ADS] [CrossRef] [Google Scholar]
- Maciejewski, W., & Cox, D. P. 1999, ApJ, 511, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, S. A., & Ostriker, E. C. 2018, ApJ, 854, 89 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F. 1988, in Supernova Remnants and the Interstellar Medium, eds. R. S. Roger, & T. L. Landecker (Cambridge: Cambridge Univ. Press), 205 [Google Scholar]
- McKee, C. F., & Cowie, L. 1977, ApJ, 215, 213 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, J. P. 1977, ApJ, 218, 148 [NASA ADS] [CrossRef] [Google Scholar]
- McKenzie, J. F., & Völk, H. J. 1982, A&A, 116, 191 [NASA ADS] [Google Scholar]
- Miyamoto, M., & Nagai, R. 1975, PASJ, 27, 533 [NASA ADS] [Google Scholar]
- Molendi, S., de Grandi, S., Fusco-Femiano, R., et al. 1999, ApJ, 525, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Normandeau, M., Taylor, A. R., & Dewdney, P. E. 1996, Nature, 380, 687 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pais, M., Pfrommer, C., Ehlert, K., & Pakmor, R. 2018, MNRAS, 478, 5278 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1992, ApJ, 401, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Pierre Auger Collaboration (Aab, A., et al.) 2017, Science, 357, 1266 [NASA ADS] [CrossRef] [Google Scholar]
- Ponman, T. J., Cannon, D. B., & Navarro, J. F. 1999, Nature, 397, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Ptuskin, V. S. 1997, AdSpR, 19, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Ptuskin, V. S., Völk, H. J., Zirakashvili, V. N., & Breitschwerdt, D. 1997, A&A, 321, 434 [NASA ADS] [Google Scholar]
- Ressler, S. M., Katsuda, S., Reynolds, S. P., et al. 2014, ApJ, 790, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Rupke, D. 2018, Galaxies, 6, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Ruszkowski, M., Yang, H.-Y. K., & Zweibel, E. 2017, ApJ, 834, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Sharma, M., Theuns, T., Frenk, C., et al. 2017, MNRAS, 468, 2176 [NASA ADS] [CrossRef] [Google Scholar]
- Skinner, M. A., & Ostriker, E. C. 2015, ApJ, 809, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, T., & Pfrommer, C. 2019, MNRAS, 485, 2977 [NASA ADS] [CrossRef] [Google Scholar]
- Völk, H. J., & Biermann, P. L. 1988, ApJ, 333, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Völk, H. J., & Zirakashvili, V. N. 2004, A&A, 417, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Völk, H. J., Drury, L. O’C., & McKenzie, J. F. 1984, A&A, 130, 19 [NASA ADS] [Google Scholar]
- Zirakashvili, V. N., Breitschwerdt, D., Ptuskin, V. S., & Völk, H. J. 1996, A&A, 311, 113 [NASA ADS] [Google Scholar]
- Zweibel, E. G. 2017, Phys. Plasmas, 24, 055402 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Typical distances, times, and Mach number where the different shock waves merge into a single propagating forward shock.
All Figures
 |
Fig. 1. Sketch of the initial configuration adopted for the galactic wind models. The SB is approximated by a Kompaneets solution until break-out, where z0 = 1 kpc fixes the location of the inner boundary conditions of the flux tube. All physical variables depend on time t and on the distance from the Galactic plane z. The gravitational acceleration g(z, R0) also depends on R0, the Galactocentric distance of the flux tube (see text for more details). |
| In the text | |
 |
Fig. 2. Total energy increase of the repeated SN explosion (solid line) in units of ESN = 1051 erg as a function of time in units ΔtSN = 4.8 × 105 yr, the time between the individual SN explosions. The temporal expansion of the semi-major axis a(t) based on the Kompaneets ellipsoid in units of the explosion interval ΔtSN clearly shows the time t0 = 10.3ΔtSN when the base of the wind expansion is reached at z0 = 1 kpc. |
| In the text | |
 |
Fig. 3. Gas pressure Pg, 0 at the inner boundary (z0 = 1 kpc) of the flux tube for the wind background model Model W (full line) and the almost hydrostatic background Model H (dashed line) as a function of time. After 6 × 106 yr the last SN exploded within the SB and we keep the values of the boundary values fixed. Every ΔtSN = 4.8 × 105 yr and amount of 0.9 ESN = 0.9 × 1051 erg is added to increase Pg, 0. The CR pressure Pc, 0 increases by the usage of 0.1 ESN at every SN explosion. The lower panels exhibit the mass loss by the galactic wind, that is, Ṁ0 = A0ρ0u0 and the velocity at u0. We note that during the phase of repeating SN explosions, Model H generates higher mass loss rates because the winds expand into a more tenuous medium than Model W. |
| In the text | |
 |
Fig. 4. Gas pressure Pg, 0 at the inner boundary (z0 = 1 kpc) of the flux tube for Model W (full line) and Model H (dashed line) as a function of time over 108 years. After 6 × 106 yr the last SN exploded and we keep the values of the boundary values fixed, except the velocity u0. Lower panel (right): illustrates how the velocity reacts to the change of the inner boundary from increasing pressures to constant pressures after 6 × 106 years. The lower panels exhibit the mass loss by the galactic wind, that is, Ṁ0 = A0ρ0u0 and the velocity at u0. We note that Model H (dotted line) generates initially higher mass loss rates because the wind expands into a more tenuous medium than Model W (see text for more details). |
| In the text | |
 |
Fig. 5. Gas pressure Pg, 0 (upper left panel) at the inner boundary (z0 = 1 kpc) of the flux tube for Model W (full line) and Model H (dashed line) as a function of time including the feedback by galactic wind loss. The CR pressure Pc, 0 (upper panel right) is lower by about a factor of 10 compared to the gas pressure. All boundary values decrease between the SN explosions. After 6 × 106 yr, when the last SN exploded, the boundary values get monotonically smaller, caused by the outflow from the SB. Lower panel (left): exhibits the mass loss by the galactic wind, which reaches a maximum rate around 3.2 × 10−3 M⊙ yr−1 for Model W and 4.1 × 10−3 M⊙ yr−1 for Model H. In both models the maximum outflow velocity u0 (lower panel right) is reached at the last SN explosion. |
| In the text | |
 |
Fig. 6. Gas pressure Pg, 0 (upper panel, left) at the inner boundary (z0 = 1 kpc) for Model W (full line) and Model H (dashed line) as seen over a time interval of 108 years for the case when mass and energy losses are included. The CR pressure Pc, 0 (upper panel, right) is about a factor of 10 less than the gas pressure (note the change of scale). The decrease of the mass loss rate Ṁ0 (lower panel, left) occurs already 10 × 106 yr after the SNe have triggered an outflow. After this time the galactic wind changes its nature as inferred from the decreasing values of the outflow velocity u0 (lower panel, right). |
| In the text | |
 |
Fig. 7. Energy loss Eth, 0(t) in units of ESN (upper left panel), the CR energy loss contributions due to advection (upper right), the integrated mass loss M0(t) in units of 104 solar masses M⊙ (bottom left), and ECR, adv, 0 and diffusion ECR, diff, 0 in units of ESN (bottom right) as a function of time. |
| In the text | |
 |
Fig. 8. Coalescence of the first five forward shock waves (full lines) in a time-space diagram for Model W (upper panel) and Model H (lower panel) at the innermost 1.5 kpc. Dotted lines remark the reverse shocks. The time is given in units of the SN explosion interval ΔtSN. The reverse shocks (dotted lines) move at smaller speeds and collide with the forward shock, slowing them down. |
| In the text | |
 |
Fig. 9. Radial structures for Model W up to 120 kpc at three times, 7 × 107, 1.4 × 108, and 2.1 × 108 years, exhibit the shock waves propagating along the flux tube. The upper panels show the different pressure contributions from thermal gas Pg, CRs Pc, and waves Pw (dashed lines). The density and velocity are characterized by the large scale outflow with decreasing inner values. The last model at 2.1 × 108 years presents the reverse shock located around 11 kpc and the inner parts of the flow are directed inwards. |
| In the text | |
 |
Fig. 10. Radial structures for Model H on the large scale of 300 kpc at times of 3 × 107 yr, 6 × 107 yr, and 9 × 107 yr. Upper panels: different pressure contributions from thermal gas Pg, CRs Pc, and waves Pw (dashed lines). Flow velocites up to 2000 km s−1 are reached and the overall contribution of the reverse shock remains small. |
| In the text | |
 |
Fig. 11. Evolution of the maximum (full line) particle energy Emax in units of [eV] as a function of the shock distance from the galactic plane in units of [kpc] for Model H. The full line corresponds to the first shock (see also Fig. 8), the dashed lines plot particles re-accelerated by the second shock waves, and the dashed-dotted lines exhibit the energy gains due to the third shock wave. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



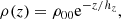
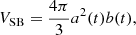
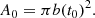
![$$ \begin{aligned} A(z) = A_0\left[ 1 + \left( \frac{z}{z_{\rm b}} \right)^2 \right], \end{aligned} $$](/articles/aa/full_html/2019/10/aa35940-19/aa35940-19-eq4.gif)
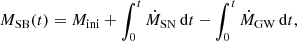
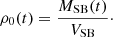
![$$ \begin{aligned} P_{\mathrm{g},0}(t) = \frac{\gamma _{\mathrm{g}} -1}{V_{\mathrm{SB}}} \left[ E_{\rm SB,ini} + \int _0^t \dot{E}_{\rm SN,th}\,\mathrm{d}t - \int _0^t\dot{E}_{\rm GW}\,\mathrm{d}t \right], \end{aligned} $$](/articles/aa/full_html/2019/10/aa35940-19/aa35940-19-eq11.gif)
![$$ \begin{aligned} \dot{E}_{\rm c,GW} = A_0 F_{\mathrm{c},0} = A_0\left[ \frac{\gamma _{\rm c}}{\gamma _{\rm c}-1}({u}_0+{ v}_{\mathrm{A}})P_{\mathrm{c},0} - \left.\frac{\bar{\kappa }}{\gamma _{\rm c}-1}\frac{\partial P_{\mathrm{c}}}{\partial z}\right|_0 \right], \end{aligned} $$](/articles/aa/full_html/2019/10/aa35940-19/aa35940-19-eq12.gif)
![$$ \begin{aligned} \dot{E}_{\rm w,GW} = A_0\left[\frac{\gamma _{\mathrm{w}}}{\gamma _{\mathrm{w}}-1}({u}_0+{ v}_{\mathrm{A}})P_{\mathrm{W},0}\right]. \end{aligned} $$](/articles/aa/full_html/2019/10/aa35940-19/aa35940-19-eq14.gif)