| Issue |
A&A
Volume 630, October 2019
Rosetta mission full comet phase results
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 21 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201833517 | |
| Published online | 20 September 2019 | |
Comparative study of photo-produced ionosphere in the close environment of comets
Department of Physics, Imperial College London,
Prince Consort Road,
London
SW7 2AZ, UK
e-mail: abeth@ic.ac.uk
Received:
28
May
2018
Accepted:
30
October
2018
Context. The Giotto and Rosetta missions gave us the unique opportunity of probing the close environment of cometary ionospheres of 1P/Halley (1P) and 67P/Churyumov-Gerasimenko (67P). The plasma conditions encountered at these two comets were very different from each other, which mainly stem from the different heliocentric distances, which drive photoionization rates, and from the outgassing activities, which drive the neutral densities.
Aims. We asses the relative contribution of different plasma processes that are ongoing in the inner coma: photoionization, transport, photoabsorption, and electron–ion dissociative recombination. The main goal is to identify which processes are at play to then quantitatively assess the ionospheric density.
Methods. We provide a set of analytical formulas to describe the ionospheric number density profile for cometary environments that take into account some of these processes. We discuss the validity of each model in the context of the Rosetta and Giotto missions.
Results. We show that transport is the dominant loss process at large cometocentric distances and low outgassing rates. Chemical plasma loss through e−-ion dissociative recombination matters around 67P near perihelion and at 1P during the Giotto flyby: its effects increase as the heliocentric distance decreases, that is, at higher outgassing activity and higher photoionization frequency. Photoabsorption is of importance for outgassing rates higher than 1028 s−1 and only close to the cometary nucleus, well below the location of both spacecraft. Finally, regardless of the processes we considered, the ion number density profile always follows a 1∕r law at large cometocentric distances.
Key words: comets: general / plasmas / Sun: UV radiation / methods: analytical
© ESO 2019
1 Introduction
The European Space Agency’s Rosetta (Glassmeier et al. 2007) and Giotto (Reinhard 1986) missions gave us the best opportunities of scrutinizing the inner coma and ionosphere of two comets: 1P/Halley (1P) and 67P/Churyumov-Gerasimenko (67P, Churyumov & Gerasimenko 1972). These two comets were probed under very different conditions and at different stages of their orbit. On the one hand, 1P was probed at 0.89 au (to compare with its perihelion at 0.58 au) by the Giotto spacecraft down to 596 km from the comet with a relative velocity of a few tens of kilometers per second over a few hours (Reinhard 1986). On the other hand, Rosetta examined 67P from 3.6 au (August 2014) to perihelion at 1.24 au (August 2015) to 3.8 au at the end of mission (30 September 2016) at a relative velocity of a few meters per second, and with the first in situ plasma measurements down to the surface (Heritier et al. 2017a). A wide variety of plasma conditions have been encountered during the escort phase: an increase in the photoionization by solar extreme ultraviolet (EUV) radiation, as the comet approached the Sun (Heritier et al. 2018), a wide dynamic range in the outgassing rate (Hansen et al. 2016), and a rich diversity and variability in the neutral composition (Le Roy et al. 2015; Gasc et al. 2017).
Based on observations made with the High-Intensity Spectrometer (HIS) on board Giotto, Balsiger et al. (1986) reported the total ion number density for 1P (more specifically, they used the mass-per-charge ratio of 16–19 and 32, masses which are the main contributors to the cometary ion number density as a function of cometocentric distance. They found that from the closest approach (~600 km) to the so-called contact surface (~4600 km), the ion number density profile followed a 1∕r law. This dependence was attributed to the balance between the production by photoionization and the loss by e−-ion dissociative recombination (DR). However, outside this region, farther away, the dependence was different and followed 1∕r2, preceded by a steep increase in plasma density between the two regions. At 67P, during pre-perihelion (February 2015), Edberg et al. (2015) reported a similar dependence in 1∕r of the ion number density for cometocentric distances from a few kilometers up to 250 km. In contrast, Galand et al. (2016) showed that the dependence was attributed to the balance between the production by photoionization and the loss by transport. Similar behaviors were observed at the two comets, but the drivers seemed to be different.
Several analytical and numerical approaches have been proposed to explain the plasma behavior as described above or developed in preparation of these missions. Of these, the most comprehensive numerical models of cometary plasmas were developed by Marconi & Mendis (1983, 1984) and Mendis et al. (1985). This 1D model included the continuity and momentum and energy equations for the electrons and each ion species considered. It includes a broad range of processes, such as the ion-neutral chemistry, photodissociation, photoionization, radiative transfer, dissociative recombination, dust dynamics, and elastic and inelastic collisions. The main feature in the plasma number density profile is a sharp increase at 2.5 ×103 km, which is linked to a steep rise of the electron temperature that in turn lessens the loss through dissociative recombination. This model was designed for Giotto and predated this mission. In comparison, 3D models for 1P for 67P have been proposed as well, such as Rubin et al. (2009, 2014), but at higher spatial resolution (higher than 100 km). In analytical works, Cravens (1987) proposed that the cometary ionosphere below the contact surface is in photochemical equilibrium: photoionization and dissociative recombination balance each other, while loss through transport is neglected. Based on these assumptions, he derived the theoretical size of the so-called diamagnetic cavity, a characteristic magnetic field-free cometary region observed at 1P (Neubauer et al. 1986). More recently, Galand et al. (2016) proposed a model applied to comet 67P at large heliocentric distances during the Rosetta mission; here, photoionization is balanced by transport. Finally, Gombosi (2015) proposed a model including both transport and e− -ion dissociative recombination as loss processes. However, the nucleus was reduced to a point source. These three models are listed in Table 1 with their respective assumptions and applications. None of them includes the attenuation of the solar EUV radiation through the coma. Bhardwaj (2003) assessed the effect of this additional process on the photoionization profile for high outgassing rates, and compared photoionization rates with ionisation rate by photo-e− impact. He did not evaluate the effect of photoabsorption (PA) on electron number density, however.
Figure 1 compares the photoionization rates in the case of cometary expanding coma (colored lines) and in the case of an atmosphere under hydrostatic equilibrium like at Earth (black line). When close to the surface of the nucleus, the rates are always higher for comets (near 1 au) than for the hydrostatic equilibrium case. This is all the more true because the N2 ionization rate is lower than that of water (used in all cases here). Furthermore, the photoionization rates in the two cases do not peak at the same column density or optical depth. One of the purposes of this paper is to shed light on these differences.
We here focus on the total plasma number density and the processes occurring in inner comae and cometary ionospheres, that is, photoionization, photoabsorption, transport, and finally e− -ion dissociative recombination. Ion-neutral chemistry is ignored as it barely affects the total plasma number density; it is sensitive to ion composition only through the dissociative recombination of the terminal ions. However, the most likely terminal ions, including H3O+ and NH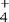 , have dissociative recombination kinetic coefficients on the same order of magnitude (Beth et al. 2016; Heritier et al. 2017b). In Sect. 2 we assess the solar deposition through the coma. In particular, we highlight in Sect. 2.1 the main difference between planetary and cometary ionospheres. In Sect. 2.2 we calculate the effect of the photoabsorption on the solar flux and photoelectron production profile. In Sect. 3 we provide an exhaustive list of analytical formulas for the electron density under different conditions. We introduce new models that are capable of describing the electron density profile of the inner coma for low and intermediate outgassing rates. At the sametime, we link existing models with some of the analytical models we propose. Finally, we compare our results in Sect. 4 with the literature and analytical modeling to highlight the processes and models that are relevant for 1P/Giotto and 67P/Rosetta and discuss additional processes that may be important as well.
, have dissociative recombination kinetic coefficients on the same order of magnitude (Beth et al. 2016; Heritier et al. 2017b). In Sect. 2 we assess the solar deposition through the coma. In particular, we highlight in Sect. 2.1 the main difference between planetary and cometary ionospheres. In Sect. 2.2 we calculate the effect of the photoabsorption on the solar flux and photoelectron production profile. In Sect. 3 we provide an exhaustive list of analytical formulas for the electron density under different conditions. We introduce new models that are capable of describing the electron density profile of the inner coma for low and intermediate outgassing rates. At the sametime, we link existing models with some of the analytical models we propose. Finally, we compare our results in Sect. 4 with the literature and analytical modeling to highlight the processes and models that are relevant for 1P/Giotto and 67P/Rosetta and discuss additional processes that may be important as well.
Analytical formulas for the ion number density profiles for the inner coma present in the literature and provided here.
 |
Fig. 1 Photoelectron production rate at the solar zenith angle 0° as a functionof column density (left y-axis) or optical depth (right y-axis). Two cases are represented: (1) expanding comae: 1P during the Giotto flyby (red solid line) and 67P at two different heliocentric distances (green and blue solid lines, see legend and Table 2), (2) atmospheres in hydrostatic equilibrium like Earth at 1 au (black, solid line). The number density scale height H for the hydrostatic equilibrium case is set to 20 km, and the same photoabsorption cross section is assumed for all three cases. The dotted line corresponds to the production rate below the cometary surface. The circles identify the nucleus surface, and the dotted line corresponds to the hypothetical production rate below. |
Modeling parameters and figures in which they have been used.
2 Solar deposition
2.1 Gravitational effect on the photoelectron production rate
It is well established that the maximum in solar energy deposition at a given wavelength λ, and thus in photoelectron production, occurs at the optical depth τλ = 1 in planetary atmospheres for which the plane-parallel approximation and isothermal hydrostatic equilibrium can be assumed (Chamberlain & Hunten 1987). If the total production of photoelectrons is integrated over the full solar EUV spectrum, we find that the maximum in solar energy deposition has its location at an optical depth of 1 for wavelengths of about 30–35 nm at Earth. This is expected because the strongest solar EUV line is the He II 30.4 nm line.
However, comets are different from planets for the following reasons:
-
They are small bodies, often with a radius of only a few kilometers. The plane-parallel approximation is therefore not appropriate, especially near the surface and the inner coma. Spherical symmetry is usually applied instead.
-
The coma is mainly made of sublimated water, carbon dioxide, and carbon monoxide (Hässig et al. 2015; Gasc et al. 2017), which primarily escape the body. There may be a contribution from the sublimation of dust grains (as at 103P, A’Hearn et al. 2011; 73P, Fougere et al. 2012; and 67P, Fougere et al. 2016) and photodissociation of H2CO into CO, for instance, as inferred at 1P (Eberhardt 1999).
-
The neutral number density n(r) is a function of the cometocentric distance r. It was observed to follow a 1∕r2 dependence at the location of Rosetta from a few kilometers from the surface (e.g., Hässig et al. 2015), which is consistent with the flux conservation at constant velocity and departs from hydrostatic equilibrium. Possible contributions from extended sources on the neutral number density are neglected thereafter in this paper.
-
The neutral gas undergoes an adiabatic expansion (Huebner & Markiewicz 2000; Heritier et al. 2017), which is faster and thus critical close to the surface, and reaches supersonic speeds of about 600–700 m⋅s−1 at a few hundreds of kilometers from the surface.
-
The outgassing rate and the photoionization rate evolve with respect to heliocentric distance, which varies widely along the highly eccentric orbit (Heritier et al. 2018).
Under these conditions, we would expect a different response of the expanding neutral coma to the incoming solar EUV radiation. When we assume a coma with one dominant neutral species, water in our case, the production of electrons at a given wavelength λ is defined as
![\begin{equation*} P_{e^-,\lambda}[r,\chi,Q]=\nu_0(\lambda)n(r) \exp[-\sigma_{\text{abs}}(\lambda)N(r,\chi)],\vspace*{-2pt}\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq2.png) (1)
(1)
where ν0 stands for the unattenuated spectral photoionization frequency, σabs represents the total photoabsorption cross section, and N(r, χ) the upstream column density in the direction of the Sun of the dominant species at the cometocentric distance r and at solar zenith angle χ (see Appendix A and Fig. A.1). The total production of electrons, integrated over all wavelengths, is given by
![\begin{equation*} P_{e^-}[r,\chi,Q]=\int_{\lambda_{\text{min}}}^{\lambda_{\text{th}}} \! I(\infty,\lambda) \sigma_{\text{ion}}(\lambda) n(r) \exp[-\sigma_{\text{abs}}(\lambda)N(r,\chi)]\, \mathrm{d}\lambda,\vspace*{-2pt}\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq3.png) (2)
(2)
where I(∞, λ) stands for the unattenuated incoming solar spectral flux (photons⋅m−3⋅s−1) at the wavelength λ, σion represents the photoionization cross section, λth the ionization threshold wavelength (98.2 nm for water), and λmin the lower bound for integration, usually 0.1 nm, as shorter wavelengths do not significantly contribute to the ionization. The neutral number density is defined as
![\begin{equation*} n[r,Q]=\dfrac{Q}{4\pi U_n r^2}, \vspace*{-2pt}\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq4.png)
where Q stands for the outgassing rate and Un, for the neutral gas outflow velocity. The neutral column density N is given by (Bhardwaj 2003; Beth et al. 2016)
![\[N[r,\chi,Q]=\dfrac{Q}{4\pi U_n r} \dfrac{\chi}{\sin \chi},\]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq5.png)
and the optical depth τλ[r, χ] at the wavelength λ at the cometocentric distance r and the solar zenith angle χ is defined by
![\begin{align*} \tau_{\lambda}[r,\chi,Q]=\sigma_{\text{abs}}(\lambda)N(r,\chi)&=\dfrac{\sigma_{\text{abs}}(\lambda)Q}{4\pi U_n r} \dfrac{\chi}{\sin \chi}\nonumber\\ &=\dfrac{Q}{Q_{c,\lambda}[\chi]}\dfrac{r_c}{r}=\tau_{c,\lambda}[\chi]\dfrac{r_c}{r}, \end{align*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq6.png) (3)
(3)
where rc stands for the cometary radius and τc,λ[χ] = τλ[rc, χ] represents the optical depth at the surface for a given solar zenith angle χ. We introduced a new parameter Qc,λ, which has the dimension of an outgassing rate, as
![\begin{equation*} Q_{c,\lambda}[\chi]=\dfrac{4\pi U_n r_c}{\sigma_{\text{abs}}(\lambda)}\dfrac{\sin\chi}{\chi}=\dfrac{Q}{\tau_{c,\lambda}[\chi]}[s^{-1}].\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq7.png) (4)
(4)
Qc,λ corresponds to the outgassing rate for which the optical depth is 1 at the surface for a given χ and a given λ. Equation (1) becomes
![\begin{align*} P_{e^-,\lambda}[r,\chi,Q]&= \nu_0(\lambda)n(r) \exp\left[-\dfrac{\sigma_{\text{abs}}(\lambda)Q}{4\pi U_n r} \dfrac{\chi}{\sin \chi}\right]\nonumber\\ &=\nu_0(\lambda)n(r) \exp\left[-\tau_{\lambda}(r_c,\chi)\dfrac{r_c}{r}\right]\nonumber\\ &=\nu_0(\lambda)n(r)\exp\left[-\dfrac{Q}{Q_{c,\lambda}[\chi]}\dfrac{r_c}{r}\right]. \end{align*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq8.png) (5)
(5)
At a given wavelength λ, the maximum in electron production rate (Eq. (1)) is located at τλ [r, χ] = 2 in cometary comae, instead of τλ[r, χ] = 1 in planetary atmospheres. A detailed derivation is given in Appendix A for a general case of a number density profile defined as n(r) ∝ r−β, where β = 2 for cometary expanding comae. We also show that planetary isothermal atmospheres in hydrostatic equilibrium correspond to the case of very high β values.
As the number density at comets relies on the outgassing activity, the optical depth is a function of Q and χ; this is the spherical surface at which τλ[r, χ] = 2 moves outward as Q increases and is above the surface for high enough Q. Interestingly, for a fixed outgassing rate, the maximum of ![$P_{e^-,\lambda}[r,\chi]$](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq9.png) , is given by
, is given by
![\begin{multline*} \left(\dfrac{\partial P_{e^-,\lambda}[r,\chi,Q]}{\partial r}\right)_{Q,\lambda,\chi}=0\longrightarrow P_{e^-,\lambda}[r,\chi,Q]_{\text{max}}\\ =\left\{ \begin{array}{cr} \dfrac{\nu_0(\lambda) Q_{c,\lambda}^2}{\pi U_n r^2_c Q}\exp[-2],&\text{if } \tau_{c,\lambda}\geq 2 \text{ (i.e., } Q\geq 2Q_{c,\lambda}),\\\\ \dfrac{\nu_0(\lambda)Q}{4\pi U_n r_c^2}\exp\left[-\dfrac{Q}{Q_{c,\lambda}}\right],&\text{if } \tau_{c,\lambda}<2\text{ (i.e., } Q< 2Q_{c,\lambda}), \end{array} \right. \end{multline*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq10.png) (6)
(6)
However, for a fixed cometocentric distance r′, the maximum of electron production rate at r′ occurs for Q = Qc,λr′∕rc, such that
![\begin{equation*} \left(\dfrac{\partial P_{e^-,\lambda}}{\partial Q}\right)_{r^{\prime},\lambda,\chi}=0\longrightarrow P_{e^-,\lambda}[r^{\prime},\chi,Q]_{\text{max}}=\dfrac{\nu_0(\lambda) Q_{c,\lambda}}{4\pi U_n r_c r^{\prime}}\exp[-1].\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq12.png) (8)
(8)
For a given cometocentric r′, a given photoionization frequency ν0(λ), a given neutral expansion velocity Un, and a given nucleus radius rc, Eq. (8) provides the maximum that the photoelectron production rate can reach when the full range of Q is considered. This bound is reached for Q = Qc,λr′∕rc and is caused by photoabsorption of the solar radiation by the neutral coma.
Figure 2 shows the electron production rate profiles as a function of the outgassing rate in dimensionless units. On the one hand, for optically thin comae or low outgassing activities (i.e., τc,λ< 2 or Q < 2Qc,λ), 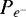 increases monotonically when the cometocentric distance decreases. However, for optically thick comae or high outgassing activities (i.e., τc,λ> 2 or Q > 2Qc,λ), the electron production reaches a maximum at r = (0.5Q∕Qc,λ)rc (i.e., where τλ[r, χ] = 2) and then decreases down to the surface. The maximum reached by
increases monotonically when the cometocentric distance decreases. However, for optically thick comae or high outgassing activities (i.e., τc,λ> 2 or Q > 2Qc,λ), the electron production reaches a maximum at r = (0.5Q∕Qc,λ)rc (i.e., where τλ[r, χ] = 2) and then decreases down to the surface. The maximum reached by 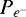 in that case decreases with respect to the outgassing rate Q: as Q increases, the distance r at which τλ [r, χ] = 2 increases, as τλ ∝ Q∕r. For a fixed cometary distance r′, solar zenith angle χ, and photoionization frequency ν0, the maximum in photoelectron production rate occurs at Q = Qc,λr′∕rc such that τλ[r′, χ] = 1 (see Eq. (8) and Fig. 2, solid black line). The highest
in that case decreases with respect to the outgassing rate Q: as Q increases, the distance r at which τλ [r, χ] = 2 increases, as τλ ∝ Q∕r. For a fixed cometary distance r′, solar zenith angle χ, and photoionization frequency ν0, the maximum in photoelectron production rate occurs at Q = Qc,λr′∕rc such that τλ[r′, χ] = 1 (see Eq. (8) and Fig. 2, solid black line). The highest 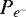 is reached at the surface for Q = Qc,λ. This highlights how critical it is to include photoabsorption: for Q > exp[−1]Qc,λ, a range of cometocentric distances exists for which
is reached at the surface for Q = Qc,λ. This highlights how critical it is to include photoabsorption: for Q > exp[−1]Qc,λ, a range of cometocentric distances exists for which 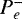 is within the gray area if the photoabsorption is neglected, meaning that
is within the gray area if the photoabsorption is neglected, meaning that 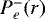 takes forbidden values and is overestimated.
takes forbidden values and is overestimated.
The difference between planetary atmospheres and comae stems from the neutral number and neutral column number densities. Under isothermal hydrostatic equilibrium, the former have a column density proportional to the neutral number density (i.e., τλ [z, χ] = σabs(λ)N[z, χ] ∝ n[z]H, H stands for the scale height, constant regardless of the altitude for isothermal atmosphere). Thus, 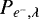 behaves as ∝ τλ exp[−τλ] (Chapman 1931):
behaves as ∝ τλ exp[−τλ] (Chapman 1931):
![\begin{align*} P_{e^-,\lambda,\text{ planets}}[z,\chi]&=\nu_0(\lambda) n(z)\exp\left[-\dfrac{\sigma_{\text{abs}}(\lambda) N(z)}{\cos\chi}\right]\nonumber\\ &=\nu_0(\lambda) n(z)\exp\left[-\dfrac{\sigma_{\text{abs}}(\lambda) n(z)H}{\cos\chi}\right]\nonumber\\ &=\dfrac{\nu_0(\lambda)\cos\chi}{\sigma_{\text{abs}}(\lambda) H}\tau_{\lambda}\exp[-\tau_{\lambda}]. \end{align*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq19.png) (9)
(9)
Unlike the planetary case, for comets τλ[r, χ, Q] = σabsλN[r, χ, Q] ∝ 1∕r ∝ n[r]r, such that ![$P_{e^-,\lambda}\propto\tau^2_{\lambda}\exp[-\tau_{\lambda}]$](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq20.png) :
:
![\begin{align*} P_{e^-, \lambda,\text{ comets}}[r,\chi,Q]&=\nu_0(\lambda) n(r)\exp\left[-\sigma_{\text{abs}}(\lambda) n(r)r\dfrac{\chi}{\sin \chi}\right]\nonumber\\ &=\dfrac{\nu_0(\lambda) \sin \chi}{\sigma_{\text{abs}}(\lambda) r \chi}\tau_{\lambda}\exp[-\tau_{\lambda}]\nonumber\\ &=\dfrac{4 \pi\nu_0(\lambda) U_n}{\sigma_{\text{abs}}^2(\lambda) Q}\dfrac{\sin^2 \chi}{\chi^2}\tau_{\lambda}^2\exp[-\tau_{\lambda}]\nonumber\\ &=\dfrac{\nu_0(\lambda) Q_{c,\lambda}[\chi]}{\sigma_{\text{abs}}(\lambda) Q r_c}\dfrac{\sin \chi}{\chi}\tau^2_{\lambda}\exp[-\tau_{\lambda}],\vspace*{-4pt}\end{align*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq21.png) (10)
(10)
of which the maximum occurs at τ = 2.
Figure 3 shows the photoelectron production rate at comets from a pure water coma for different outgassing rates, scaledto the maximum production rate of the hydrostatic case. This case is derived assuming a constant scale height H ≈ 20 km (typical for the terrestrial lower thermosphere) and the photoionization frequency of water. For an atmosphere in hydrostatic equilibrium, such as at Earth, the maximum photoelectron production occurs at τλ = 1 and χ =0, which corresponds to
![\begin{equation*} P_{e^-,\text{Earth}}(\tau_{\lambda}=1,\chi=0)=\dfrac{\nu^{\text{1~au}}_0(\lambda)}{\sigma_{\text{abs}}(\lambda)H}\exp[-1],\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq22.png) (11)
(11)
independent of the neutral number density. At the surface of Earth, the optical depth in the EUV range is higher than τλ = 105 (out of the boundaries in Fig. 3, which covers the hydrostatic case, τλ ∈ [10−4;102]). For comets, the optical depth τc at the surface is given by Q∕Qc,λ and the photoelectron production rate at surface is given by
![\begin{align*} P_{e^-,\lambda,\text{comets}}(\tau_{\lambda}\,{=}\,\tau_{c,\lambda},\chi\,{=}\,0)&=\left(\!\dfrac{1\,\text{au}}{d_h}\right)^2\dfrac{\nu^{\text{1\ au}}_0(\lambda)}{\sigma_{\text{abs}}(\lambda)r_c}\dfrac{Q}{Q_{c,\lambda}}\exp\left[\! -\dfrac{Q}{Q_{c,\lambda}}\right]\nonumber\\ &=\left(\!\dfrac{1\,\text{au}}{d_h}\right)^2\!\dfrac{H}{r_c}P_{e^-,\text{Earth}}(\tau_{\lambda}\,{=}\,\tau_{c,\lambda},\chi\,{=}\,0),\end{align*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq23.png) (12)
(12)
where dh stands for the heliocentric distance of the comet in au. Equation (12) is represented by the solid black line in Fig. 3 for dh = 1 au. This is the upper bound for which 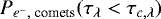 . Beyond it (dark gray region in Fig. 3), the photoelectron production is meaningless as it is below the surface.
. Beyond it (dark gray region in Fig. 3), the photoelectron production is meaningless as it is below the surface.
Figure 3 highlights that there are outgassing rates at which the photoelectron production rate is higher than at Earth. While Earth’s atmosphere is not dominated by water, this statement remains valid. Of the main terrestrial species, N2, O2, and O, only O2 has a photoionization frequency higher than that of H2O (Huebner & Mukherjee 2015). As the terrestrial O2 mixing ratio decreases with altitude in the terrestrial upper atmosphere where the ionosphere is located, we can estimate an upper limit for the total photoionization frequency corrected for a terrestrial composition with an O2 mixing ratio of 0.2 (maximum reached). With a mixing of 80% N2 and 20% O2, the total photoionization frequency is 4.09 × 10−7 s−1 for a quietSun and 1.07 × 10−6 s−1 for an active Sun, to be compared with the photoionization rates of water in the same solar conditions, 4.05 × 10−7 and 1.04 × 10−7 s−1, respectively.
For δ < 1, regardless ofQ, the photoelectron production peak is always located lower down than at Earth in terms of optical depth or column density. For δ > 1, there is a range of Q for which the photoelectron production rate is higher than its maximum value at Earth (i.e., ![$P_{e^-,\text{ comets}}/P_{e^-,\text{ Earth}}[\tau_{\lambda}=1,\chi=0]>1$](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq26.png) in Fig. 3). The extreme values are given by
in Fig. 3). The extreme values are given by
![\begin{align*} Q_{\text{min}}[\delta]&=-W_{0}\left[\dfrac{1}{\delta\exp(1)}\right] Q_c[\chi]\\ Q_{\text{max}}[\delta]&= \left\{ \begin{array}{ll} 4\exp(-1)\delta Q_c[\chi],&\text{if } \delta>\dfrac{\exp[1]}{2},\\\\ -W_{-1}\left[\dfrac{1}{\delta\exp(1)}\right] Q_c[\chi],&\text{if } \dfrac{\exp[1]}{2}>\delta>1, \end{array} \right. \end{align*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq27.png)
where W[x] stands for the Lambert-W function and Qmin[1] = Qmax[1] = Qc,λ[χ]. Conversely, as rc and H are fixed, the constraint on δ can be interpreted in terms of dh:
![\[\delta>1\Longrightarrow\sqrt{\dfrac{H}{r_c}\dfrac{\tan \chi}{\chi}}>\left(\dfrac{d_h}{1\text{ au}}\right)\]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq28.png)
For χ = 0, the necessary but not sufficient condition onthe heliocentric distance dh of the cometis 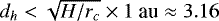 au to have a photoelectron production rate from water higher than at Earth. The additional condition is on Q ∈[Qmin;Qmax]. For instance, at 1 au, Qmin ≈ 7.4 × 1026 s−1 and Qmax ≈ 2.8 × 1029 s−1 (using rc, Un, and σabs in Table 2, last column, and H = 20 km). Furthermore, Fig. 3 shows that for a given heliocentric distance, if close enough to the surface, the production rate at a comet is always higher than in the hydrostatic case for the same column density or optical depth (see also Fig. 1, but corrected for the heliocentric distance).
au to have a photoelectron production rate from water higher than at Earth. The additional condition is on Q ∈[Qmin;Qmax]. For instance, at 1 au, Qmin ≈ 7.4 × 1026 s−1 and Qmax ≈ 2.8 × 1029 s−1 (using rc, Un, and σabs in Table 2, last column, and H = 20 km). Furthermore, Fig. 3 shows that for a given heliocentric distance, if close enough to the surface, the production rate at a comet is always higher than in the hydrostatic case for the same column density or optical depth (see also Fig. 1, but corrected for the heliocentric distance).
 |
Fig. 2 Photoelectron production rate in the coma at the solar terminator (χ = π∕2) in dimensionless units for different outgassing rates as a function of the cometocentric distance in cometary radii. The production decreases monotonically with respect to
r
for Q <2Qc. For Q > 2Qc, the production increases up to the cometocentric distance |
 |
Fig. 3 Photoelectron production rate as a function of the optical depth for different outgassing rates Q at 1 au. For comparison, we have overplotted the profile for an isothermal atmosphere in hydrostatic equilibrium (solid line with circles) with an Earth-like scale height of ~ 20 km made of water vapor (see text). We scaled all profiles with respect to the maximum of the hydrostatic case. The solid black line corresponds to the photoelectron production rate at the surface for any outgassing rate (see Eq. (11)) for a given heliocentric distance (here dh = 1 au). Colored lines are the electron production rates for different outgassing rates: above the surface (solid), and below the surface (dashed). The light gray area corresponds to the region where the photoelectron production rate is higher at comets than for the hydrostatic case. The dark gray region represents values for which the corresponding cometocentric distance would be below the surface. The expanding velocity is set to Un = 600 m⋅s−1. |
2.2 Attenuated solar spectral flux
In this subsection, we assess the photoabsorption of solar EUV radiation by the neutral coma in greater detail. This is one of the processes we study here.
First of all, the coma is assumed to be pure water. Rosetta clearly observed variability in the neutral composition throughout the escort phase with a CO2-dominated coma, especially over the southern hemisphere away from perihelion (Hässig et al. 2015; Hoang et al. 2017; Gasc et al. 2017). This may affect the plasma production by photoionization: CO2 is more efficiently ionized by solar radiation than H2O (i.e., the photoionization cross section is almost twice that of water, Galand et al. 2016). For a given outgassing rate, the plasma production rate is higher between the comet surface and the spacecraft in a CO2-dominated coma than in a H2O-dominated coma, assuming that the spacecraft is at cometocentric distances shorter than the ionization and photodissociation scale lengths of the parent molecules. Moreover, the relative composition influences photoabsorption because the photoabsorption cross sections of CO2 are higher than those of water, and conversely, the CO2 outflow velocity is lower than that of water.
A parameter of interest is Qc,λ[χ], which we defined in Eq. (4). Assessing this parameter requires high spectral photoabsorption resolution cross sections and solar irradiance. The water photoabsorption cross sections are taken from Avakyan et al. (1998) to be between 0.1 and 6.2 nm, and from Chan et al. (1993) between ~6.2 and 98.2 nm (given in eV, 0.5-eV bin), using the ionization efficiency (i.e., σion∕σabs) from Tan et al. (1978), assuming 1 for photons with wavelengths lower than 50 nm (~ 25 eV). The solar flux is based on the Thermosphere Ionosphere Mesosphere Energetics and Dynamics (TIMED) Solar EUV Experiment (SEE; Woods et al. 2005) daily-averaged solar irradiance spectrum given in 1 nm intervals. As the cross sections and the solar EUV flux are not sampled over the same bins, we subdivided them into smaller wavelength bins (typically 0.01 nm wide or less) to take the structure of both into account. The two main sources of uncertainty are the cross sections at short wavelengths (<5 nm) and from the binning of the solar EUV flux (1 nm bin).
The optical depth τλ,c = Q∕Qc,λ gives the efficiency of solar energy deposition at the surface (see Sect. 2.1):
-
if τc,λ < 2, the comais optically thin at the wavelength λ, thus the solar spectral flux around λ is barelyattenuated through the coma;
-
if τc,λ > 2, the comais optically thick at the wavelength λ; the solar flux is efficiently absorbed, at least close to the surface. Moreover, in this case, the maximum solar deposition occurs atthe cometocentric distance r = 0.5τc,λrc = (0.5Q∕Qc,λ[χ])rc (see Eq. (7)).
Figure 4 shows the parameter (r∕rc) at which theoptical depth τλ[r, χ = π∕2] = 2, that is, from Eq. (7): (r∕rc) = 0.5τc,λ = (0.5Q∕Qc,λ[χ]). We also plotthe product between the photon solar spectral flux and the total photoionization cross section for water as a function of λ. For Q < 1028 s−1, the maximum solar energy deposition is below the surface (identified by the dashed black line); in other words, the coma is optically thin ∀λ. For Q = 1029 s−1, the coma starts to be optically thick over the range [15;98.2] nm, with the maximum energy deposition between the surface and 10 rc .
For high outgassing rates (i.e., Q > 1030 s−1), soft X-rays start to be absorbed in the lower part of the coma, near the surface, while radiation at longer wavelengths has been fully absorbed higher up. It should be highlighted that the uncertainties on the photoionization are high at short wavelengths:
-
The spectral range from 0 to 5 nm covers a wide range of energies. This requires a high spectral resolution in photoabsorption cross sections, including near 2.3 nm, where the cross section exhibits a peak that is associated with the emission of two electrons. One of them is a so-called Auger electron. Photons of these energies can indeed ionize electrons of the inner shells (e.g., K or L shells). Then, the hole in the inner shell is filled by an electron from an outer shell with a surplus energy. This energy can be released in two ways: either through X-ray fluorescence (the electron that fills the hole emits an X-ray photon), or through ionizing an electron from the outer shell, which places the atom or molecule in a double-ionized state. Small uncertainties on the photoabsorption cross section lead to large uncertainties on the location of maximum energy deposition, and hence on the vertical structure of the photoelectron production rate.
-
The solar spectral flux used and based on TIMED/SEE is provided over a 1 nm bin and cannot capture the structure of specific solar lines.
One of the main caveats when deriving the electron production profile in Sect. 2.1 is that we have neglected the electron-impact ionization by photoelectrons (and their secondaries). We only included photoionization. However, depending on their initial kinetic energy, which is equal to the photon energy minus the ionization potential, newborn photoelectrons may in their turn ionize neutrals through electron impact. Bhardwaj (2003) provided a quantitative analysis of the ionization by these energetic electrons. Such electrons become the main ionization source of the inner coma for outgassing rates above 1029 s−1. This means that neglecting the effect of photoelectrons as a source of ionization is valid for low Q, typically < 1029 s−1. Finally, an additional source of plasma could be the production of cometary ions through charge exchange between cometary neutrals and the solar wind. However, this process is usually negligible, while the contribution of electron-impact as a source of ionization was found to be significant at large heliocentric distances (Heritier et al. 2018).
We have investigated the validity of our assumption by considering one single value for the photoabsorption cross section and hence the presence of only one main ionization peak. Figure 5 shows the photoelectron production rate from the deposition of the soft X-ray to EUV solar spectral flux at 1 au. Depending on χ and Q, the photoelectron production rate exhibits one, two, and even three distinct peaks above the cometary surface. Each peak is associated with the absorption of a different spectral band. The lower the photoabsorption cross section, the higher the column density of water that is required to efficiently absorb the photons. The main, uppermost peak corresponds to the absorption of photons mainly between 15 and 40 nm, which are dominated by strong solar emission lines: He II (30.4 nm) and several Fe lines from different ionization states. The mean cross section at this maximum is ⟨σabs⟩ = 7.8 × 10−22 m2 . The second corresponds to the energy deposition of soft X-rays (1–10 nm) with a mean cross section ⟨σabs⟩ = 3.8 × 10−23 m2. Finally, the third and least intense peak corresponds to the absorption of harder X-ray photons. Our secondary peak is more pronounced than the peak derived by Bhardwaj (2003). It seems to result from the lower limit of 5 nm used by Bhardwaj (2003), while we extended our calculations for the solar spectral flux down to 0.1 nm. We also used updated cross section values and a higher resolution, as described earlier in this section.
Equation (10) represents the photoelectron production rate as a function of r, χ, and Q. It appears that for a constant outgassing rate Q,
![\begin{equation*} P_{e^-,\lambda}[r,\chi, Q]= \left(\dfrac{\sin \chi}{\chi}\right)^2P_{e^-,\lambda}\left[\dfrac{\sin \chi}{\chi}r,0,Q\right].\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq30.png) (13)
(13)
However, for a constant zenith angle χ,
![\begin{equation*} P_{e^-,\lambda}[r,\chi,Q]=\zeta P_{e^-,\lambda}[\zeta r,\chi,\zeta Q],\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq31.png) (14)
(14)
where ζ is a scaling factor (ζ = 1030∕Q). Combining Eqs. (13) and (14), and the effect of the heliocentric distance dh,
![\begin{align*} &P_{e^-,\lambda}[r,\chi,Q]\nonumber\\ &=P_{e^-,\lambda, 1 \text{ au}}\left[R,0,10^{30}\right]\times\left(\dfrac{10^{30}}{Q}\right)\times\left(\dfrac{\sin \chi}{\chi}\right)^2\times \left(\dfrac{1 \text{ au}}{d_h}\right)^2,&\end{align*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq32.png) (15)
(15)
Based on Fig. 5, it is possible to extend the photoelectron production rate for any r, χ, Q, and dh by applying the scaling relations given by Eqs. (15) and (16). Figure 5 provides ![$P_{e^-,\lambda, 1 \text{ au}}\left[R,0,10^{30}\right]$](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq34.png) . We note that the profile depends on Un (set to 600 m⋅s−1 for Fig. 5) as well. Using a different velocity implies scaling the profile accordingly.
. We note that the profile depends on Un (set to 600 m⋅s−1 for Fig. 5) as well. Using a different velocity implies scaling the profile accordingly.
 |
Fig. 4 Cometocentric distance normalized to rc at which the optical depth τλ[r, χ = π∕2] = 2 for different outgassing rates Q. The dashed line defines the position of the surface. We also plot as a function of λ the product between the solar photon spectral flux I1 au (2015 Aug 15 at 1 au) and the total photoionization cross section σion (black line). The spectral range displayed extends up to 98.2 nm, which is the ionization threshold wavelength of water. The expanding velocity is set to Un = 600 m⋅s−1. |
 |
Fig. 5 Photoelectron production rate as a function of the scaled cometocentric distance R (see text) for a pure water coma. The solar flux is taken from TIMED/SEE on 2015 August 15 at 1 au, with an outgassing rate of Q = 1030 s−1 and at a solar zenith angle of χ = 0. The expanding velocity is set to Un = 600 m⋅s−1. The shape of the production rate remains unchanged for ∀r, Q and χ, although the radial dependency (ordinate) and the amplitude (abscissa) have to be adjusted accordingly (see the relations given by Eqs. (15) and (16)). The location of the surface of 67P (rc = 2 km) has been placed at the corresponding parameter R for different outgassing rates (shown with dashed and dotted horizontal lines for χ = 0 and χ = π∕2, respectively). For each local maximum in photoionization (identified by colored triangles), we plot the corresponding attenuated solar spectral flux at that location in the same color (see inset): the primary peak is driven by the 15–40 nm spectral flux (blue), the secondary peak by the 1–10 nm spectral flux (yellow), and the tertiary peak by the <0.5 nm spectral flux(red). The abscissa in the inset is in log-scale to visualize short wavelengths. |
3 Electron density
In this section, we investigate two mechanisms of interest in the production and loss of cometary ions in the inner coma: the photoionization by EUV solar radiation and the e−-ion dissociative recombination. The former can be strongly attenuated through the coma whereas the latter may at times be more significant than transport. This work is based on analytical solutions of the continuity equation, which is built upon six assumptions:
-
there is no time dependency;
-
the coma is assumed to be spherically symmetric;
-
the ions move radially at constant velocity Ui, which is assumed to be the same as the neutral velocity Un;
-
the solar flux is reduced to one single wavelength (see Sect. 2.2);
-
no ionization processes in addition to photoionization are included; in particular, e−-impact ionization by photoelectrons and their secondaries or by the space environment has been neglected;
-
the e−-ion dissociative recombination rate is assumed to be constant through the coma, that is, the electron temperature is taken to be constant.
The general continuity equation used here is
![\begin{equation*} \dfrac{1}{r^2}\dfrac{\mathrm{d} n_i(r)U_nr^2}{\mathrm{d} r}+{\alpha n_i^2(r)}=\dfrac{\nu_0 Q}{4\pi U_nr^2} \exp\left[-\tau_{c}\dfrac{r_c}{r}\right],\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq35.png) (17)
(17)
where ni stands for the ion or electron number density, ν0 represents the photoionization frequency, Q the total outgassing rate, τc = Q∕Qc the optical depth at the cometary surface, and α the e−-ion dissociative recombination rate. We decided to write the continuity equation in this unusual form, such that the loss terms (transport and e−-ion dissociative recombination) are on the left-hand side, and the production term, here the photoionization, which can be attenuated through the coma, on the right-hand side. Considering a pure water coma and thus a cometary ionosphere solely made of water ions, the e− -ion dissociative recombination rate corresponds to 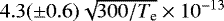 m3⋅s−1 (Rosen et al. 2000) for both ion species. The advantage is that even if there is proton transfer between H2O+ and water which produces H3O+, the recombination rate, and hence the total ion number density, will not change.
m3⋅s−1 (Rosen et al. 2000) for both ion species. The advantage is that even if there is proton transfer between H2O+ and water which produces H3O+, the recombination rate, and hence the total ion number density, will not change.
3.1 Photochemical equilibrium including photoabsorption
In this section, we investigate the ion number density profile under photochemical equilibrium, that is, by neglecting the loss through transport. As we show in Sect. 4, this case applies to very active comets with a high outgassing rate (see Sect. 4.2.1).
3.1.1 Theory
When transport is neglected, the continuity equation is reduced to the balance between the net chemical loss of charges and the ion production rate that is due to solar absorption:
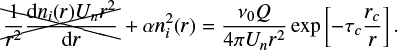 (18)
(18)
Hence, the ion number density profile is given by
![\begin{equation*} {n_i(r)}=\dfrac{U_n}{2\alpha r_c}\sqrt{\dfrac{Q}{Q_0}}\dfrac{r_c}{r} \exp\left[-\dfrac{\tau_{c}}{2}\dfrac{r_c}{r}\right],\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq38.png) (19)
(19)
Q0 has previously been introduced by Gombosi (2015) and may be compared to the outgassing rate Q.
We assumed that the comet is a point source. This lead to significant discrepancies near the surface compared with a full ionospheric model (e.g., see Sect. 3.4) because the plasma number density has to be 0 there. We also neglected additional ionization processes, such as the e− -impact by photoelectrons and their secondaries. For high outgassing rates, these electrons efficiently ionize the neutrals, particularly in the densest part, near the surface (Bhardwaj 2003).
3.1.2 Results
Figure 6 shows the total ion number density that results from photochemical equilibrium and includes photoabsorption of the solar radiation (see Eq. (19)). The dashed line corresponds to photochemical equilibrium in an optically thin coma (no photoabsorption). Close to the surface, the photoabsorption plays a critical role: as not all photons can penetrate deeply into the coma, the plasma production rate exhibits a maximum. Hence, the plasma number density does not monotonically increase all the way down to the surface (as expected for a point-source comet with an optically thin coma). Instead, it exhibits a maximum at r = 0.5τcrc (where the optical depth is 2, see Sect. 2.1), which is above the surface if τc ≥ 2. Thus, the ion number density peaks at the same location as the photoelectron production rate (see Sect. 2.2), as the transport has been neglected and α is constant here. Last but not least, the comet is treated as a point source here; as a result, for the optically thin case (τc = 0, Cravens 1987), the ion plasma density tends toward + ∞ at r = 0, instead of dropping to zero at r = 0 for τc > 0, which is more realistic. At larger cometocentric distances, the ion number density has the same profile regardless of the photoabsorption, as the coma is optically thin to the solar radiation.
3.2 Transport versus photoionization with photoabsorption
In this section, the ion number density profile results from the equilibrium between plasma transport and photoionization, including photoabsorption; the chemical loss through e−-ion dissociative recombination is neglected. This case applies when outgassing is low, that is, the transport timescale is shorter than dissociative recombination timescale (see Sect. 4).
3.2.1 Theory
By neglecting chemical loss, the continuity equation is reduced to
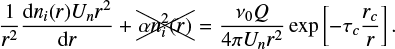 (21)
(21)
The solutionrequires integrating from the surface rc to the position r of the right-hand side, after multiplying both sides by r2. By adequate substitution, we obtain
![\begin{equation*} n_i(r)=\dfrac{\nu_0 Q}{4\pi U^2_n r_c}\dfrac{r_c^2}{r^2}\left(\dfrac{r}{r_c}E_2\left[\dfrac{Q}{Q_c}\dfrac{r_c}{r}\right]-E_2\left[\dfrac{Q}{Q_c}\right]\right),\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq41.png) (22)
(22)
where En is the generalized exponential integral, which is defined by
![\[ E_n[x]=x^{n-1}\int_x^{+\infty}\!\dfrac{\exp[-t]}{t^n}\, \mathrm{d}t=\int_1^{+\infty}\!\dfrac{\exp[-xt]}{t^n}\, \mathrm{d}t \]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq42.png)
![\[nE_{n+1}[x]=\exp[-x]-xE_n[x].\]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq43.png)
Our model takes the finite size rc of the cometinto account. For τc = 0, Eq. (22) is reduced to Eq. (44) given by Vigren & Eriksson (2017), with slight mathematical simplifications (e.g., using the relation E2[x] = exp[−x] − xE1[x]). In addition,the derivation of the number densities for two distinct ion species, H2O+ and H3O+, is given in Appendix B.
 |
Fig. 6 Ion number density profile as a function of the cometary distance (normalized to the cometocentric distance at the surface, rc) for the equilibrium between the attenuated solar flux through the coma (referred to here as different values of the optical depth at the cometary surface) and the e− -ion dissociative recombination rate (see Eq. (19)). The solid black line corresponds to the density profile without photoabsorption and the dashed line to the cometary surface. Increasing τc is similar to increasing the outgassing rate. These profiles depend on neither Un nor α as they have been scaled accordingly. |
3.2.2 Results
Figure 7 shows the location of the total ion number density maximum as a function of the optical depth τc at the cometary surface. We recall that the optical depth is a function of not only the outgassing rate, but also of the solar zenith angle (τc [χ] = τc[0]χ∕sinχ). Thus, for τc [0] ≫ 1, the maximum of the total ion number density depends on χ and the cometary ionosphere has no spherical but a cylindrical symmetry: the maximum in χ of the plasma density peak occurs along the axis between the comet and the Sun. We also assessed the location of the maximum total ion number density in the asymptotic regimes. We found that, for small τc,λ (τc,λ ≪ 1) the maximum is located at 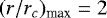 (see Fig. 7, blue line), and for large τc,λ (τc,λ ≫ 1), the maximum is located at
(see Fig. 7, blue line), and for large τc,λ (τc,λ ≫ 1), the maximum is located at 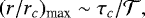 where
where 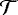 is the solution of
is the solution of ![$2\exp[\mathcal{T}]E_2[\mathcal{T}]=1$](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq47.png) , that is,
, that is, 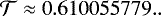 , the optical depth at the maximum (see Fig. 7, red line).
, the optical depth at the maximum (see Fig. 7, red line).
We would like to point out that ni(r) (Eq. (22)) exhibits a lowest upper bound (see the vertical black line in Fig. 8) for increasing outgassing rates. The plasma number density peaks at a constant optical depth for high outgassing rates. This lowest upper bound is given by
![\begin{equation*} n_i[r,\chi]<n_{i,\text{max}}[\chi]=\dfrac{\sin{\chi}}{\chi}\dfrac{\nu_0\mathcal{T}\exp[-\mathcal{T}]}{2\sigma_{\text{abs}}(\lambda) U_n} .\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq49.png) (23)
(23)
In particular, for all χ,
![\begin{equation*} n_i[r,\chi]< 0.1657\dfrac{\nu_0}{\sigma_{\text{abs}}(\lambda) U_n}=2.1\times 10^{11}\dfrac{\nu_0\, [10^{-6}\,\text{s}^{-1}]}{U_n\, [10^3\,\text{m}{\cdot}\text{s}^{-1}]}[\text{m}^{-3}].\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq50.png) (24)
(24)
Even if Q increases, the cometary plasma density for a given photoionization frequency has an upper bound which depends on the solar zenith angle χ. It has to be kept in mind that this limit only takes into account the photoionization rate and not, for instance, additional ionization processes, such as the electron impact by energetic electrons from the space environment. Conversely, cometary observations of higher plasma number densities point out that these additional processes need to be included (e.g., Galand et al. 2016; Heritier et al. 2017). Finally, although the e− -ion dissociative recombination is neglected here, this upper limit remains valid because this additional process is a loss mechanism.
Figure 8 shows the number densities for the total plasma (black), H2O+ (blue), and H3O+ (red). For low outgassing rates, the total ion number density is proportional to Q. As Q increases, the total ion number density then reachesan upper limit ni,max, and its peak shifts outward. Except at very low outgassing rates (Q < 1025 s−1), H3O+ is always the dominant ion species at low cometocentric distances, while farther away, H2O+ becomes dominant. Moreover, we determined the asymptotic profiles for both species: at large cometocentric distances, nH2O+(r) ∽ 1/r whereas nH3O+(r) ∽ log(r)/r2; the latter decreases faster than the former.
Equation (21) is not a first-order differential equation because the right-hand side does not depend on the ion number density. This means that the total ion plasma number density is the integral over wavelength of the solutions, given by Eq. (22), that is,
![\begin{multline*} n_i(r)=\dfrac{Q}{4\pi U^2_n r_c}\dfrac{r_c^2}{r^2}\\ \times \int_{\lambda_{\text{min}}}^{\lambda_{\text{th}}} I(\infty,\lambda)\sigma_{\text{ion}}(\lambda)\left(\dfrac{r}{r_c}E_2\left[\tau_{\lambda}(r_c,\chi)\dfrac{r_c}{r}\right]-E_2\left[\tau_{\lambda}(r_c,\chi)\right]\right)\mathrm{d}\lambda.\end{multline*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq53.png) (25)
(25)
Furthermore, Eq. (25) can be extended and applied to a multi-species coma, with a uniform coma composition in terms of cometocentric distance, considering the outgassing rate, the respective photoabsorption, and photoionization cross sections for each neutral species n. When we assume a neutral composition independent of r, the different neutral species have the same density profile, following ∝ r−2, so that the respective cross section can be replaced by
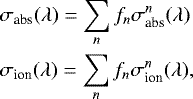
where fn is the volume mixing ratio for the neutral species n.
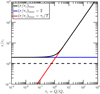 |
Fig. 7 Cometocentric distance normalized to rc at the surface of the maximum ion number density (black solid line) as a function of the optical depth τc at the surface. Two asymptotic profiles are plotted in blue (τc ≪ 1) and red (τc ≫ 1). The dashed line corresponds to the surface of the comet. |
 |
Fig. 8 Total ion (black), H2O+ (blue), and H3O+ (red) ion number density profile at a solar zenith angle of χ = π∕2 and for six different outgassing rates Q: 1025 s−1 (left panel, circles), 1026 s−1 (left panel, dashed line), 1027 s−1 (left panel, pluses), 1025 s−1 (right panel, circles), 1029 s−1 (right panel, dashed line), 1030 s−1 (right panel, pluses). The number densities were scaled accordingly to be plotted as a dimensionless parameter. The vertical line corresponds to the lowest upper bound of the plasma density for χ = π∕2 in dimensionless units, i.e., 0.1657 × 2∕π ≈ 0.1055 (see Eq. (24)). The expanding velocity is set to Un = 600 m⋅s−1. |
3.3 Full ionospheric model in an optically thin coma
In this section, we rigorously assess the effect of the e−-ion dissociative recombination on the plasma number density for an optically thin coma, that is, τc = 0. This situation was encountered at comet 67P at the location of Rosetta near perihelion (Heritier et al. 2018, see Sect. 4.2.2).
3.3.1 Theory
By neglecting photoabsorption, the continuity equation is reduced to
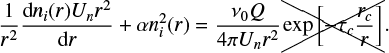 (26)
(26)
Equation (26) is a first-order ordinary differential equation, with the form of a Riccati equation. The derivation of the solution for Eq. (26) is cumbersome and provided in Appendix C. The final solution is given by
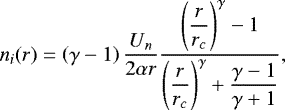 (27)
(27)
where 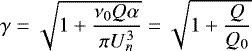 .
.
The location of the maximum is given in Appendix C.
For the case of a point-source-like comet (i.e., rc = 0) or of large cometocentric distances (r ≫ rc), Eq. (27) is reduced to the formula given by Gombosi (2015):
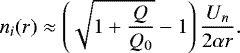 (28)
(28)
We have investigated both asymptotic regimes for Eq. (27) with respect to the outgassing rate Q.
-
At large cometocentric distances or for a point-source-like comet, Eq. (29) becomes
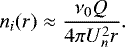 (30)
(30)
The two asymptotic profiles, Eqs. (29) and (31), decrease as 1∕r at large cometocentric distances. However, their respective amplitudes are different: the former is ∝ Q, and the latter is  .
.
 |
Fig. 9 Comparison between the different models (Cravens 1987: red; Galand et al. 2016: blue; Gombosi 2015: circles), and our full model in an optically thin coma (stars) for different values of Q∕Q0 : 0.01 (left), 4 (middle), and 100 (right). These plots are independent of Un: Q∕Q0 is fixed for each plot and the abscissa is scaled. |
3.3.2 Results
Figure 9 shows the comparison between existing models (Cravens 1987; Galand et al. 2016; Gombosi 2015, see also Table 1) and this work. We plot the dimensionless parameter 2αni(r)rc∕Un as a function of r∕rc (see also Sect. 4). The different profiles decrease asymptotically as 1∕r (cf. Eqs. (27)–(29) and (31)), therefore the different profiles are parallel to each other for large cometocentric distances (i.e., r ≫ rc). Near the surface, the lowest upper bound is given by Galand et al. (2016), whereas farther away, this is the profile of Gombosi (2015).
To place this in context, the model of Cravens (1987; see Eq. (31)) was originally developed for 1P. As 1P was close to the Sun during the Giotto flyby (0.89 au), the outgassing rate and the photoionization rate were higher than at 67P so that Q∕Q0 ∝ ν0Q was ≫1. This model is relevant when the transport is neglected against the loss by e− -ion dissociative recombination, in particular for high outgassing rates. However, photoabsorption starts to be significant for Q > 1028 s−1, which is notincluded in this model. In addition, the model cannot take into account the finite size of the comet: ni (rc)≠0. The model of Galand et al. (2016) (see Eq. (29)) was developed for 67P at large heliocentric distances (≥ 3 au) where the comet was not veryactive (Q = 1025–1026 s−1). In this situation, the outward transport of plasma is the dominating net loss process. For this case, Q∕Q0 was ≪ 1. The finite size of the comet is taken into account in this model, which can then be used to estimate the plasma density close to the surface. The model of Gombosi (2015; see Eq. (28)) bridges between the two previous models and their respective operational range (i.e., Q∕Q0 ≪ 1 and Q∕Q0 ≫ 1) such that Eq. (28) is appropriate for an intermediate outgassing rate (Q ~ Q0) as well, but at large cometocentric distances. The comet is reduced to a point source and is not suitable to describe the plasma density close to the surface.
The present work (see Eq. (27)) is an improved version of Gombosi (2015) and Galand et al. (2016) as it is valid for any r and for any Q∕Q0 (as long as photoabsorption does not play a key role). However, none of these models, including ours in this section, take photoabsorption into account. At the location of Giotto and Rosetta, photoabsorption does not significantly affect the total ion number density even during perihelion (see Sect. 4). However, it may affect the ion composition, but this is beyond the scope of this paper.
All previous models agree with or are overestimates of ours. Compared with Cravens (1987) and Galand et al. (2016), both models neglect one of the two loss mechanisms, either transport or the e− -ion dissociative recombination. In comparison with Gombosi (2015), the size of the coma matters. In our case, the plasma cannot be produced below the surface and be transported at larger cometocentric distances, where it contributes to the total plasma number density. However, as the plasma flows at constant velocity, the difference decreases as r increases.
We have performed a quantitative study of the relative error ε at large cometocentric distances for the different assumptions with respect to Eq. (28). Under Cravens (1987) assumptions (Eq. (31)), the relative error is smaller than ε if
![\[\dfrac{Q}{Q_0}>\dfrac{4(\varepsilon+1)^2}{\varepsilon^2(\varepsilon+2)^2}.\]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq63.png)
For instance, assuming a relative error smaller than 10%, Eq. (31) must be used down to Q∕Q0 > 48400∕441 ≈ 110. This has never happened during the Rosetta escort phase, as the coma is dominated by transport. However, it might happen at 1P during the Giotto flyby (see Sect. 4). Under Galand et al. (2016) assumptions (Eq. (30)), the relative error is smaller than ε if
![\[ \dfrac{Q}{Q_0}<4\varepsilon(\varepsilon+1). \]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq64.png)
For instance, when we assume a relative error smaller than 10%, Eq. (30) must be used up to Q∕Q0 < 0.44, which happened at large cometocentric distances during Rosetta escort phase but not during perihelion, as the dissociative recombination becomes a significant loss process (Heritier et al. 2018, see also Sect. 4).
Table 3 summarizes the effect of the different parameters involved in this section and their respective effect on the plasma number density. For instance, α and Un affect both Q∕Q0 and Un ∕2α, a scaling factor of ni(r) (Eq. (27)). The dissociative recombination is a decreasing function of the electron temperature Te .
3.4 Full ionospheric model in the general case
In this section, we take into account the two plasma loss processes, that is, e− -ion dissociative recombination and transport. Furthermore, the photoabsorption of the solar EUV radiation is included. In particular, we assess the effect of the e−-ion dissociative recombination and of photoabsorption on the ion number density.
3.4.1 Theory
The continuity equation is given by Eq. (17). A few substitutions have been introduced in order to simplify it, which are
![\[Y_i=\dfrac{4\pi U_n^2r_c}{\nu_0 Q}n_i(r)\left(\dfrac{r}{r_c}\right)^2,\]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq65.png)
![\[Z=\dfrac{r_c}{r}\longrightarrow\dfrac{\mathrm{d}}{\mathrm{d}r}=-\dfrac{Z^2}{r_c}\dfrac{\mathrm{d}}{\mathrm{d}Z}.\]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq66.png)
Then, Eq. (17) becomes
![\begin{equation*} -\dfrac{\mathrm{d}Y_i}{\mathrm{d}Z}=-\dfrac{1}{4}\dfrac{Q}{Q_0}Y^2_i+\dfrac{1}{Z^2}\exp\left[-\dfrac{Q}{Q_c}Z\right],\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq67.png) (32)
(32)
which has the form of the Riccati equation. Equation (32) can be reduced to a second-order linear differential equation. The function W(Z), defined as
![\[W(Z)=\exp\left[-\dfrac{1}{4}\dfrac{Q}{Q_0}\int\!Y_i(Z)\,\mathrm{d}Z\right],\]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq68.png)
To our knowledge, based on Polyanin & Zaitsev (2017), Eq. (33) does not have an analytical solution. However, we numerically integrated Eq. (32) by applying the explicit Runge-Kutta fourth-order method in order to derive ni (r). This form is not appropriate for Q0 = 0 or for Qc = 0. Moreover, the numerical solutions using Eq. (32) were compared and agree with the analytical solutions given by Eq. (22) when photoabsorption is neglected (i.e., for Q ≪ Qc), given by Eq. (27) when dissociative recombination is neglected (i.e., for Q ≪ Q0) and given by Eq. (30) when both processes are neglected.
 |
Fig. 10 Ion number density as a function of the cometocentric distance normalized to rc for three different outgassing rates: 1026 s−1 (diamond), 1028 s−1 (star), and 1030 s−1 (upward-pointing triangle) for a solar zenith angle χ = π∕2. The colors correspond to different assumptions: PA and DR (yellow), PA and no DR (red), no PA and DR (blue), no PA and no DR (gray). For the e− -ion dissociative recombination, we assumed Te = 150 K. For the photoionization frequency, ν0 = 4.5 × 10−7 s−1 corresponds to the water photoionization frequency at 67P around perihelion to independently assess the effect of the outgassing rate (1.24 au). The expanding velocity is set to Un = 600 m⋅s−1. |
3.4.2 Results
Figure 10 shows the combined effect of the dissociative recombination and the photoabsorption on the ion number density profile. It clearly exhibits a competition between the two mechanisms. On the one hand, the e− -ion dissociative recombination tends to lower the location of the maximum of the ion number density toward the comet. On the other hand, the photoabsorption tends to elevate it outward as it reduces the electron production toward the comet. For outgassing rates below Q = 1028 s−1, no clear difference between the different colored profiles, which are associated with a given Q, is visible, except in the first few kilometers above the surface. However, from Q = 1028 s−1 and above, we clearly see both effects. At Q = 1028 s−1, it is not possible to neglect the photoabsorption in the inner coma below 10 rc, as this may lead to an overestimation by 2 or more orders of magnitude. However, including photoabsorption does not influence ni at large cometocentric distances. The dissociative recombination is relevant from Q = 1028 s−1 and above, similarly to the photoabsorption. This is plausible as Qc [π∕2] and Q0 are both around 1028 s−1 . Unlike the photoabsorption, the dissociative recombination still affects the ion number density at large cometceontric distances, preventing the possibility to neglect it at high outgassing rates.
 |
Fig. 11 Dimensionless parameter 2αni(r)r∕Un (Eq. (27)) as a function of Q∕Q0 (Q0 defined by Eq. (20)). The ion number density ni is derived from Cravens (1987; red solid line, Eq. (31)), Galand et al. (2016; Eq. (29)) assuming r = 1.1 rc (dotted blue line), r = 2 rc (dashed blueline), and r ≫ rc (solid blue line, Eq. (30)), Gombosi (2015) or this work assuming r ≫ rc (black circles, Eq. (28)), and this work assuming r = 1.1 rc (blue upward-pointing triangles, ▴), r = 2 rc (orange downward-pointing triangles, ▾). Photoabsorption is ignored here. Conditions at 1P during the Giotto encounter and at 67P during the Rosetta escort phase are overplotted as gray areas. We provide a broad range of values for 1P as uncertainties remained on the electron temperature and therefore on the e− -ion dissociative recombination rate, which depends on the electron temperature. This last was assumed to be between 150 K (upper bound) and 1000 K (lower bound; see Table 2). For 67P, the dynamic range of Q∕Q0 is primarily driven by the outgassing rate Q, from 1025 (end of mission) to 6 × 1028 s−1(perihelion), and the heliocentric distance, which affects the photoionization frequency. |
4 Discussion
For each of the three cases introduced in Table 2, we review the key processes driving the solar deposition and ionospheric densities in the context. In this section, we review models proposed in the literature, assess their domain of validity in terms of cometocentric distances, and their applicability to comets 1P and 67P.
4.1 Comparison with analytical models in the literature
For three decades now, several analytical models have been proposed to describe the ion number density profile in the inner part of the cometary environment. In particular, this section is dedicated to the comparison of the advantages and disadvantages between some of them, namely models proposed by Cravens (1987), Gombosi (2015), Galand et al. (2016), and in this work.
Figure 11 shows the comparison between previous analytical models (Cravens 1987; Galand et al. 2016; Gombosi 2015) and this work (Eq. (27)). We plot the dimensionless parameter η(r)= 2αni(r)r∕Un (see Sect. 3.3) as a function of Q∕Q0, where Q0 is defined by Eq. (20) (see Sect. 3.1). As the different profiles decrease asymptotically or exactly as 1∕r (cf. Eqs. (27)–(29), (31), and Fig. 9), the parameter η(r) either is or tends at large cometocentric distances toward a constant, which is a function of Q∕Q0 alone (cf. Table 4).
Figure 11 allows visualizing the validity of these three published models in different regimes, that is, for different values of the parameter Q∕Q0. We use Eq. (27) as a fiducial reference model because it takes into account the finite size of the comet, plasma transport, and dissociative recombination, while the other models disregard one of these characteristics or processes. For high outgassing rates, photoabsorption affects the plasma density close to the nucleus. This process is not included in any of the models we compare in this section, but its effect at 1P during the Giotto flyby and at 67P during the Rosetta escort phase is assessed in Sect. 3. We review hereafter the strengths and weaknesses of the three published models (Cravens 1987 in Sect. 4.1.1; Galand et al. 2016 in Sect. 4.1.2; Gombosi 2015 in Sect. 4.1.3) compared with the reference model and assess their domain of validity ignoring here the effect of the photoabsorption.
4.1.1 Cravens (1987)
Cravens (1987), who developed a plasma density model that they applied to high outgassing conditions, assumed a balance between ionization of the coma and chemical plasma loss through e−-ion dissociative recombination. He neglected transport. As a result, the model is expected to be suitable for high outgassing conditions, that is, when chemical plasma loss through e−-ion dissociative recombination dominates transport. We indeed find that the model (Fig. 11, solid red line) agrees with our reference model for high values of Q∕Q0 (Q∕Q0 ≫ 1) and large cometocentric distances: Q∕Q0 > 30 for r ≫ rc (circles) and r = 2rc and for Q∕Q0 > 1000 for r = 1.1rc. The photochemical equilibrium approach applied to Cravens (1987) does not allow taking the size of the nucleus into account. This explains the departure of this model from ours at small cometocentric distances. However, for low outgassing rates (Q∕Q0 < 5), the model from Cravens (1987) considerably overestimates the ion number density by a factor 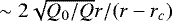 . When Q ≫ Q0 during high outgassing, the plasma density depends on
. When Q ≫ Q0 during high outgassing, the plasma density depends on 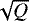 (Eq. (31)). The reason is that the loss term associated with dissociative recombination is quadratic to the ion number density (
(Eq. (31)). The reason is that the loss term associated with dissociative recombination is quadratic to the ion number density (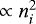 ) and the production term associated with photoionization is ∝ Q. In absence of transport (Q0→0), there is only balance between these two terms, leading to
) and the production term associated with photoionization is ∝ Q. In absence of transport (Q0→0), there is only balance between these two terms, leading to 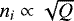 .
.
4.1.2 Galand et al. (2016)
Galand et al. (2016) proposed a plasma density model for application to a low outgassing rate close to the nucleus. This model (Fig. 11, solid dashed and dotted blue lines) agrees with the reference model for low values of Q∕Q0 (Q∕Q0 ≪ 1), regardless of the cometocentric distance. The triangles follow the blue lines for the different cometocentric distances in this regime well. Both models take into account the finite size of the comet. However, for large Q∕Q0, the model proposed by Galand et al. (2016) considerably overestimates the ion number density by a factor 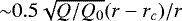 . Interestingly, this factor, when it is on the order of unity, allows identifying the upper cometocentric distance at which the model still remains valid:
. Interestingly, this factor, when it is on the order of unity, allows identifying the upper cometocentric distance at which the model still remains valid:
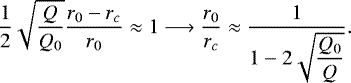 (34)
(34)
This meansthat the model by Galand et al. (2016) is valid either for Q∕Q0 ≲ 4 ∀r, or for Q∕Q0 ≫ 1 with the condition onr ∈ [rc;r0] (Eq. (34)).
Q ≪ Q0 corresponds to the case where the loss through transport dominates the dissociative recombination. As the production term is linear with Q (∝ Q), in absence of plasma loss except through transport (Q0→ + ∞), ni ∝ Q. However, for increasingly higher Q∕Q0, the model from Galand et al. (2016) agrees with the reference model only progressively closer to the comet, where ni is not significant enough for chemical loss to play a key role.
4.1.3 Gombosi (2015)
The model proposed by Gombosi (2015; circles) agrees well with our reference model at any values of Q∕Q0, but only for r ≫ rc or for rc = 0. Table 4 shows that the parameter η(r) is the same for the model from Gombosi (2015) as for ours under these assumptions. However, at finite and low cometocentric distance (e.g., r = 1.1 rc and 2 rc), the model from Gombosi (2015) departs from our reference model for small Q∕Q0, typically lower than 10. This discrepancy is due to the point-source approximation applied by Gombosi (2015).
4.2 Applicability to 1P and 67P
4.2.1 1P
Photoabsorption
In Sect. 3.2 we showed that photoabsorption matters for Q ≥ Qc[χ] (e.g., Qc [0] ≈ 7.9 × 1028 s−1 and Qc [π∕2] ≈ 5.05 × 1028 s−1). Qc [χ] is slightly higher at 1Pthan 67P because the size of the comet is different. At 1P, Krankowsky et al. (1986) reported a total outgassing rate of 6.9 × 1029(±50%) s−1 (see Table 2), including 80% of water. This outgassing rate can be used up to an upper limit, but when we do not correct for the composition, the optical depth at the surface of 1P is ≈8.7 at the subsolar point and ≈13.6 at χ = π∕2. According to Fig. 7, this means that 1P was in the regime where the ion number density peaks at ![$r_{\text{max}}\approx(Q/Q_c[\chi])r_c/\mathcal{T}$](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq76.png) , which corresponds to 78.3 and 123.0 km, respectively.
, which corresponds to 78.3 and 123.0 km, respectively.
As Giotto approximatively flew by 1P at 596 km (≈ 108 rc), the plasma density measured in situ was not significantly sensitive to photoabsorption (see Fig. 12). Moreover, the attenuation by photoabsorption is further damped when dissociative recombination is included. Figure 12 shows a comparison of the plasma density calculated with (no circles) and without (circles) photoabsorption. At a given cometocentric distance, this process affects the ion number density more significantly in absence of dissociative recombination.
Comet 1P was at the limits of our model validity for photoabsorption, as we assumed one plasma density peak driven by solar EUV radiation. For Q = 6.9 × 1029 s−1, a secondary peak in ionization is expected to be present near the nucleus surface (cf. Fig. 5; at 1P, the surface is located at R = 3–8 × 103 km depending on the solar zenith angle near the yellow triangle). When we use the mean photoabsorption cross section that is associated with the secondary peak (i.e., ⟨σabs⟩ = 3.8 × 10−23 m2, see Sect. 2.2), this yields Qc [0] ≈ 1.6 × 1030 s−1, which is close to the outgassing rate at 1P/Halley. We note that Giotto flew by a wide range of solar zenith angles from 0 to χmax ≈ 110°, with the associated value Qc[χmax] ≈ 0.5Qc[0].
 |
Fig. 12 Comparison of the plasma number density profiles with respect to the scaled cometocentric distances between 1P (red, 0.89 au) and 67P (blue, 3.2 au, and green, 1.24 au). The profiles have been generated under different assumptions: including PA and DR (thick solid lines), without PA (circles), and without DR (dotted lines). The dashed line corresponds to the plasma density profile from Cravens (1987) with Te = 1000 K. The black crosses with the error bars are the in situ plasma density measurement by the ion mass spectrometer onboard theGiotto spacecraft at 1P/Halley during the Giotto flyby (Altwegg et al. 1993). The black pluses are in situ plasma density observations by RPC-MIP on board Rosetta at 3.2 au (Galand et al. 2016). |
Dissociative recombination
In Fig. 11 we over-plot the condition encountered at 1P for parameter Q∕Q0 (gray areas). It shows that Q∕Q0 was between≈62 (Te = 1000 K) and 161 (Te = 150 K) during the Giotto flyby. Therefore, transport can be neglected against dissociative recombination. Physically, the ions do not have enough timeto be transported farther away from the comet, they instead quasi-instantly recombine with locally produced electrons. This also provides another underlying assumption here: the ion velocity is close to 0 or is far lower than the neutral velocity, leading to a significant ion-neutral friction that is at the origin, a priori, of the diamagnetic cavity (Cravens 1987; Ip & Axford 1987).
When photoabsorption and dissociative recombination are both included, our results are in good agreement with those of Marconi & Mendis (1984). For similar input parameters (Q ≈ 4.7 × 1029 s−1, 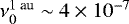 s−1, Un ≈ 600 m⋅s−1, rc ≈ 3 km, and Te ≈ 150 K, not shown here), we obtain a maximum plasma density of 4.6 × 1010 m−3 at r ≈ 46 km and χ = π∕2, to be compared with 1.9 × 1010 m−3 at r ≈ 47 km from Marconi & Mendis (1984). Possible reasons for the discrepancy may be related to photoabsorption effects (e.g., different χ and dust), photoabsorption cross sections combined with different neutral compositions (pure water here compared with 85% H2O, 10% CO2, and 5% N2 from Marconi & Mendis 1984), ion velocity, and electron temperature profiles (constant throughout the coma here, unlike in Marconi & Mendis 1984).
s−1, Un ≈ 600 m⋅s−1, rc ≈ 3 km, and Te ≈ 150 K, not shown here), we obtain a maximum plasma density of 4.6 × 1010 m−3 at r ≈ 46 km and χ = π∕2, to be compared with 1.9 × 1010 m−3 at r ≈ 47 km from Marconi & Mendis (1984). Possible reasons for the discrepancy may be related to photoabsorption effects (e.g., different χ and dust), photoabsorption cross sections combined with different neutral compositions (pure water here compared with 85% H2O, 10% CO2, and 5% N2 from Marconi & Mendis 1984), ion velocity, and electron temperature profiles (constant throughout the coma here, unlike in Marconi & Mendis 1984).
Summary and comparison with observations
When we consider the relevant parameters, namely Qc and Q0, and compare them with the outgassing rate observed at 1P, we find that photoabsorption matters, in particular in the inner coma from the surface to a few hundred kilometers, typically up to 400–500 km, and the e− -ion dissociative recombination is important.
We did not include ionization by photoelectrons in the inner coma. Bhardwaj (2003) quantitatively assessed this effect, and it is significant for outgassing rates higher than 1029 s−1, which is relevant for 1P but not for 67P (Vigren & Galand 2013).
Upon these considerations, to model the inner coma at 1P in a straightforward way, we recommend using Eq. (27) as an analytical model (with a finite size for the nucleus, but without photoabsorption) when the electron number density in the inner coma probed in situ by Giotto is of interest. We further recommend solving the differential equation proposed in Sect. 3.4 for a more refined model (see Fig. 12, green solid line) to be able to assess the electron number density closer to the nucleus.
For further validation, we have compared our modeled electron number density at 1P (solid red line) with observations of plasma density measured during the Giotto flyby near closest approach (black crosses, Altwegg et al. 1993), as shown in Fig. 12. The two sets agree very well.
Equation (31) (Cravens 1987) is reliable as long as it is used to locally assess the ion number density at large cometocentric distances, such as at the location of Giotto. Photoabsorption needs to be included for estimating ni (r) close to the surface, however, and the nucleus size should be considered. Therefore, it is not suitable to derive the diamagnetic cavity size based on an optically thin coma and a point-source comet, as proposed by Cravens (1987). In this derivation, Cravens (1987) balanced the ion-neutral friction (∝ ni(r)nn(r) ~ 1∕r3) with the magnetic pressure (∝ ∂B2∕∂r). He then integrated the friction term with respect to r (Eqs. (9)–(11) in Cravens 1987) in order to obtain B(r). By doing so, most of the magnetic pressure is balanced by the friction close to the source at r = 0, well below the surface.
4.2.2 67P
Photoabsorption
The case study of comet 67P is quite different from that of 1P. Through its two-year escort phase, Rosetta probed comet 67P over a wide range of local outgassing rates, between ~ 1026 and ~ 6 × 1028 s−1 (Hansen et al. 2016), which has to be compared with the parameter Qc [χ] (Eq. (4)). As Rosetta spent most of the time in the terminator plane (i.e., χ = π∕2), Qc [π∕2] = 2Qc[0]∕π ≈ 1.2 × 1028 s−1. Based on the outgassing rate at 67P during the mission, Q was greater than Qc[π∕2] for a short period of time, during July and August 2015, approximately two months near perihelion, between 1.24 and 1.3 au. This represents less than 10% of the escort phase. Outside this period, the photoabsorption does not need to be taken into account, including the inner coma, between the location of Rosetta and the surface. Furthermore, at the location of Rosetta, photoabsorption does not significantly affect the local plasma density even during perihelion as Rosetta was located at cometocentric distances beyond 150 km, which corresponds to r∕rc ≈ 75 (see Fig. 4 in Heritier et al. 2017b, and Fig. 12).
Dissociative recombination
Excluding the uncertainties on the dissociative recombination rate (i.e., on Te), the conditions met at 67P covered a broad range of values for the dimensionless parameter Q∕Q0. As the outgassing rate and the photoionization are coupled with the heliocentric distance, the ratio Q∕Q0 (∝ ν0Q) ranges from ≈1.7 × 10−4 to ≈ 7.2, assuming an electron temperature between 150 and 1000 K. The former provides a safe upper limit: Q∕Q0 is a decreasing function of the electron temperature, and 150 K is on the order of the neutral temperature (Davidsson & Gutiérrez 2005; Tenishev et al. 2008; Heritier et al. 2017b). The lower bound could be even smaller as plasma instruments have reported electron energies of about ~ 10 eV (Eriksson et al. 2017). According to the photoionization frequency throughout the escort phase (Fig. 3 in Heritier et al. 2018) and the outgassing rate, the parameter Q∕Q0 was on the order of the unity and higher for the period 2015 August–November, assuming Te ~ 200 K (Fig. 6 in Heritier et al. 2018). Therefore, the dissociative recombination is not significant except for this period. A detailed and quantitativeanalysis was made in Heritier et al. (2018) throughout the escort phase. They showed that at the location of Rosetta, dissociative recombination affects the plasma density from February 2015 to February 2016 by more than 20%.
Summary
At the location of Rosetta, photoabsorption did not significantly affect the plasma number density. Furthermore, except for a period near perihelion that covers the period from February 2015 to February 2016, the dissociative recombination did not significantly influence the ion number density profile of the inner coma at Rosetta. Hence, away from perihelion, the most appropriate and simplest analytical model remains Eq. (29) (Galand et al. 2016), whereas around perihelion, as 67P approached the Sun, photoionization frequency and outgassing activity both increased: dissociative recombination became more efficient and Q∕Q0 increased to be on theorder of unity, which is considered as an intermediate value. Neither Eq. (29) nor Eq. (31) are appropriate, as the discrepancies from the reference profile given by Eq. (27) are maximum for Q∕Q0 = 4 (see Fig. 11). Furthermore, Eq. (27) ∀r or Eq. (28) for large cometocentric distances should be suitable a priori. However, there are caveats when the analytical models are compared with observations, as discussed in the next paragraph.
Comparison with in situ electron density measurements by Rosetta
Figure 12 shows a comparison between plasma measurements at 67P by the Rosetta Plasma Consortium (RPC)/Mutual Impedance Probe (MIP; Trotignon et al. 2007) at 3.2 au in October 2014 (black pluses, Galand et al. 2016) and modeled plasma density profiles (blue) for the corresponding conditions (see Table 2). We considered a period when ionization was primarily driven by EUV solar radiation, that is, when Rosetta was above the northern summer hemisphere pre-perihelion. Rosetta was close to the nucleus, between 10 (r∕rc ≈ 5) and 20 km (r∕rc ≈ 10), and the outgassing rate was low. Any model including transport agrees well with the observations within the errors of the input parameters. Photoabsorption and dissociative recombination play a negligible role. The plasma density is caused by the balance between transport and photoionization at that time.
At large heliocentric distances, during pre-perihelion over the winter hemisphere and post-perihelion over both hemispheres, a multi-instrument analysis of RPC and ROSINA sensors highlighted that e− -impact is an additional source of ionization (Galand et al. 2016; Heritier et al. 2017, 2018) and has to be considered during periods of low activity. The origin of these ionizing electrons is not well understood yet, but appears to be of external origin (Deca et al. 2017). In addition, plasma measurements down to the surface for the end of mission at 3.8 au showed that the acceleration of the neutral gas in an adiabatic expansion must be taken into account, at least for the first kilometers above the surface (Heritier et al. 2017). At larger cometocentric distances, its effect on the plasma density decreases and is negligible as the neutral gas quickly reaches a steady velocity.
Near perihelion, the main source of ionization is EUV solar radiation, and dissociative recombination can be significant, unlike photoabsorption (Heritier et al. 2018). However, even considering these processes, there are still discrepancies between measured and predicted plasma densities. Henri et al. (2017) have reported in situ plasma observations and the ion-to-neutral ratio for April 2015 to February 2016, which ranged from 1.24 to 2.4 au. Over this period, they found that
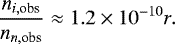 (35)
(35)
As near perihelion, dissociative recombination is significant, but photoabsorption can be neglected, Eq. (28) can be be used to derive ni∕nn. The asymptotic ion-to-neutral ratio is
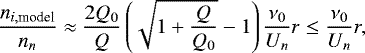 (36)
(36)
where (ν0∕Un)r represents the ratio at large cometocentric distances when only photoionization and transport are included. Even if dissociative recombination is included, with the values provided in Table 2 for 67P at perihelion, we obtain ni ∕nn ≈ 2.6 × 10−10r. It is difficult to perform a thorough, quantitative comparison. Equation (35) covered the time period during which both the heliocentric distance and the outgassing rate varied. The overestimation by our theoretical approach with respect to the observations may be linked to over- or underestimations of several parameters, such as an underestimation of Q (this is unlikely, because we use the highest outgassing rates), an overestimation of ν0, an underestimation of α, meaning an overestimation of Te (which is unlikely, because the assumed Te is already very low), an overestimation of Un (which is unlikely, because it is in the range observed by MIRO, Heritier et al. 2018), and an underestimation of Ui, here assumed to be equal to Un . We address some of these aspects in the following paragraphs.
Overestimation of ν0 near perihelion
Johansson et al. (2017) reported the photo-emission current from EUV solar radiation as measured by the dual LAngmuir Probe (LAP; Eriksson et al. 2007) on board Rosetta. While they agree away from perihelion, the measured and expected photo-emission current at Rosetta apparently differed by a factor up to 2 near perihelion. Thisis correlated with the outgassing activity and the heliocentric distance. Nanograins of ~ 20 nm size could be responsible for attenuating the solar radiation. Consequently, we would expect two effects on the plasma. Firstly, the photoabsorption cross section is expected to increase, depending on the size distribution of the nanograins. Secondly, by decreasing the photoelectron production, the ion number density may be lower than anticipated, yielding a weaker effect of dissociative recombination on the plasma density.
Underestimation of Ui near perihelion
Based on the analyses of the Rosetta Plasma Consortium (RPC, Carr et al. 2007) and on the ROSINA dataset, Vigren et al. (2017) reported ion velocities in the range 2–8 km⋅s−1, which is significantly higher than the neutral velocity or the velocity we assumed here. Assuming such a velocity leads to several corrections in the different analytical formulas we have provided so far in this paper. For Ui ≠ Un and constant, the parameter Q0 changes in Sects. 3.1, 3.3, and 3.4, and should be replaced by
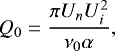 (37)
(37)
where Ui is the ion velocity, which we took to be constant. As Ui is higher than Un, Q∕Q0 is lower than plottedin Fig. 11. This reduces the effect of the dissociative recombination against transport. In addition, the factor Un ∕2α has to be replaced by Ui ∕2α. In Sect. 3.2, the denominator 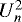 has to be replaced by UnUi, and in Eq. (36), ν0∕Un should be replaced by ν0∕Ui. By increasing the ion velocity, the loss by transport is higher than assumed in this paper, such that we here overestimate the ion number density near perihelion.
has to be replaced by UnUi, and in Eq. (36), ν0∕Un should be replaced by ν0∕Ui. By increasing the ion velocity, the loss by transport is higher than assumed in this paper, such that we here overestimate the ion number density near perihelion.
5 Conclusion
We have assessed key processes that drive the structure of cometary ionospheres for low and intermediate activities. We showed for the first time in Sect. 2 that in cometary ionospheres, the production of photoelectrons peaks where the optical depth is 2, unlike at planetary atmospheres under hydrostatic equilibrium, where it peaks at an optical depth of 1. Moreover, in the limit of outgassing rates lower than 1029 s−1, the mean photoabsorption cross section is constant. In Sect. 3, we provided analytical formulas for the ion number density profile in the inner ionosphere of comets, completing and comparing our results with the literature. In particular, we have assessed the effects, combined or otherwise, of photoabsorption and dissociative recombination in the coma, and assessed their respective contribution to the plasma density in the context of the Giotto and Rosetta missions (Sect. 4). At 1P during the Giotto flyby, dissociative recombination dominated transport, and photoabsorption was significant close to the nucleus. Nevertheless, the latter affected the lower part of the ionosphere, which was not sampled by the Giotto in situ measurements. At 67P, photoabsorption, and away from perihelion, dissociative recombination, do not significantly affect the plasma density at the location of Rosetta. Photochemical equilibrium models as developed for 1P/Halley (e.g., Cravens 1987) are not suitable for application to 67P/Churyumov-Gerasimenko. Plasma transport is always significant in the coma of comet 67P probed by Rosetta.
Acknowledgements
Work at Imperial College London is supported by STFC of UK under grant ST/K001051/1 and ST/N000692/1, ESA under contract No.4000119035/16/ES/JD. We are also grateful to ISSI International Team on the plasma environment of comet 67P after Rosetta, number 402, and the TIMED/SEE team for providing us with the solar flux data set (http://lasp.colorado.edu/see/). We warmly thank an anonymous referee for his/her constructive comments that have helped us improve the manuscript.
Appendix A Optical depth on comets
 |
Fig. A.1 Schematic of the configuration between the Sun (yellow), the comet (black), and a water molecule to determine the column density at a given
(r, χ) in the coma. s
is the abscissa along the line between the molecule and the Sun. s0
is the lower bound of integration (s0 < 0 and χ > π∕2 in the figure as s
increases sunward). rs
is the cometocentric distance for a given s, which is |
In this appendix, we demonstrate analytically that the maximum photoionization rate occurs at τλ = 2, as the neutral number density decreases as ~r−2 (Hässig et al. 2015). However, we first derive a general result assuming a more general profile for neutrals given by
![\begin{equation*} n[r]=n_0(r/r_0)^{-\beta}, \end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq82.png) (A.1)
(A.1)
where r is the cometocentric distance, n0 is the number density at r0, and β > 1. The coma isassumed here to be reduced to one neutral species and to be spherically symmetric.
In order to evaluate the optical depth, the column number density N(r, χ) has to be assessed. This quantity depends on the cometocentric r and on the solar zenith angle χ. The column number density at the point (r, χ) in polar coordinates (χ = 0 is along the Sun–comet line on the dayside), of which the case β = 2 is available in Beth et al. (2016), is given by (see Fig. A.1).
![\begin{align*} N[r,\chi]&=n_0 r_0^{\beta} \int_{s_0=r\cos\chi}^{+\infty} \dfrac{1}{(r^2 \sin^2 \chi + s^2)^{\beta/2}}\, \mathrm{d}s\nonumber\\ &= n_0 r_0^{\beta} (r \sin \chi)^{-\beta}\int_{r\cos\chi}^{+\infty} \left(1 + \dfrac{s^2}{r^2\sin^2\chi} \right) ^{-\beta/2}\, \mathrm{d}s. \end{align*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq83.png) (A.2)
(A.2)
This is valid even if χ > π∕2 (cf. Fig. A.1). By applying the following substitution:
![\[X=\dfrac{s}{r\sin\chi}\text{,}\]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq84.png)
![\[\mathrm{d}X=\dfrac{\mathrm{d}s}{r\sin\chi},\]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq85.png)
The right-hand side is then separable, that is, it is the product between a function of r alone, F(r), and of χ alone, G(χ):
![\[ N[r,\chi]= F[r] G[\chi], \]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq87.png)
where (see Formula 3.249.8, Gradshteyn & Ryzhik 2015)
![\[ C_{\beta}=\!\!\int_{0}^{+\infty}\!\! \left(\!1 + X^2 \right) ^{-\beta/2}\!=\dfrac{2\pi}{2^{\beta}}\dfrac{\Gamma[\beta-1]}{\Gamma\left[\dfrac{\beta}{2}\right]^2}=\dfrac{\sqrt{\pi}}{2}\dfrac{\Gamma\left[\dfrac{\beta-1}{2}\right]}{\Gamma\left[\dfrac{\beta}{2}\right]}=G[\pi/2]. \]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq90.png)
Γ is the gamma function, and 2F1 is the Gauss hypergeometric function. The optical depth τλ at the wavelength λ is given by
![\[\tau_{\lambda}[r,\chi]=\sigma_{\text{abs}}[\lambda] N[r,\chi]\propto r^{-\beta+1}G[\chi],\]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq91.png)
where σabs[λ] stands for the photoabsorption cross-section at the wavelength λ. Under the Beer-Lambert-Bouguer law, the electron production rate, 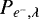 at a given wavelength λ, is
at a given wavelength λ, is
![\begin{equation*} P_{e^{-},\lambda}[r,\chi]=\nu_0 n(r) \exp[-\tau_{\lambda}(r,\chi)],\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq93.png) (A.4)
(A.4)
with ν0 the photoionization rate prior to any absorption. Hence, the maximum of 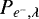 reached at a cometocentric distance rmax for a given χ within the coma fulfills
reached at a cometocentric distance rmax for a given χ within the coma fulfills
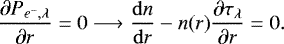 (A.5)
(A.5)
However, from Eq. (A.1),
![\[\dfrac{\mathrm{d} n}{\mathrm{d} r}=-\dfrac{\beta}{r}n(r),\]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq96.png)
and from Eq. (A.3),
![\[\dfrac{\partial \tau_{\lambda}}{\partial r}=\dfrac{1-\beta}{r}\tau_{\lambda}.\]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq97.png)
Hence, Eq. (A.5) implies
![\[\dfrac{\beta}{r}n(r)+\dfrac{1-\beta}{r}\tau_{\lambda}[r,\chi] n(r)=0.\]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq98.png)
This leads to the following expression for the optical depth, τmax,λ, at rmax
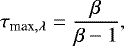 (A.6)
(A.6)
which is independent of χ. If we express 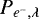 as a function of τλ instead of r, for a given χ we obtain
as a function of τλ instead of r, for a given χ we obtain
![\[ P_{e^{-},\lambda}\propto \tau_{\lambda}^{\frac{\beta}{\beta-1}}\exp[-\tau_{\lambda}]. \]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq101.png)
The maximum occurs at β∕(β − 1), consistent with Eq. (A.6).
For β = 1, the number density is ∝ 1∕r and the column number density is infinite; this leads to an undetermined value of τmax,λ. For comets, β = 2, which yields τmax,λ = 2.
For large β, τλ converges toward 1. This corresponds to what is obtained for an isothermal atmosphere in hydrostatic equilibrium. When we consider that the surface is at r0 (r0 > 0, not a point source) and the altitude z is such tha: z = r − r0, Eq. (A.1) becomes
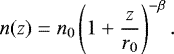 (A.7)
(A.7)
However, the density scale height H is defined as
![\[ H(r)=\dfrac{n(r)}{\left|\dfrac{\mathrm{d}n}{\mathrm{d}r}\right|}=\dfrac{r}{\beta}. \]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq103.png)
Based on Eq. (A.4), this yields H(r) = r∕β. Hence, in the neighborhood of r = r0 and thus of z = 0, Eq. (A.7) becomes
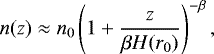 (A.8)
(A.8)
which corresponds to the number density for an isothermal atmosphere in hydrostatic equilibrium.
Appendix B Analytical ion number density profiles of H2O+ and H3O+
To proceed, it is possible to distinguish two water-ion species, H2O+ and H3O+, for a pure water coma. Keeping in mind that the net chemical charge loss (e− -ion dissociative recombination) is ignored, the two main chemistry channels are
and their respective continuity equations read
![\begin{equation*} \dfrac{\mathrm{d} n_{\text{H$_2$O$^+$}}(r)r^2}{\mathrm{d} r}=\dfrac{\nu_0 Q}{4\pi U_n^2} \exp\left[-\tau_c\dfrac{r_c}{r}\right]-\dfrac{k_1Q}{4\pi U_n^2}n_{\text{H$_2$O$^+$}}(r),\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq107.png) (B.1)
(B.1)
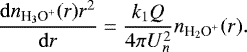 (B.2)
(B.2)
Equation (B.1) is a simple first-order linear differential equation and can be solved analytically:
![\begin{align*} n_{\text{H$_2$O$^+$}}(r)=&\dfrac{\nu_0 Q}{4\pi U^2_n r_c}\dfrac{r_c^2}{r^2}\exp\left[\dfrac{Q}{Q_1}\dfrac{r_c}{r}\right]\nonumber\\ & \times \left\{\dfrac{r}{r_c}E_2\left[\left(\dfrac{Q}{Q_c}+\dfrac{Q}{Q_1}\right)\dfrac{r_c}{r}\right]-E_2\left[\dfrac{Q}{Q_c}+\dfrac{Q}{Q_1}\right]\right\},\end{align*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq109.png) (B.3)
(B.3)
where the parameter Q1 with the dimension of an outgassing rate, is defined as
![\[Q_1={4\pi U^2_nr_c}/{k_1}\approx (2.5-5.6)\sqrt{T}\times~10^{23}\, [\text{s}^{-1}],\]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq110.png)
where Un = 600–900 m⋅s−1, k1 is from Huntress & Pinizzotto (1973), and T is the temperature, in kelvin, of the neutrals supposed to be 150 K. As the total ion number density ni (r) is given by Eq. (22), the number density of H3O+ is obtained from nH3O+(r) = ni(r) − nH2O+(r), yielding
![\begin{eqnarray*} n_{\text{H$_3$O$^+$}}(r)&=&\dfrac{\nu_0 Q}{4\pi U^2_n r_c}\dfrac{r_c^2}{r^2} \nonumber\\ && \times \left\{\dfrac{r}{r_c}\left(E_2\left[\dfrac{Q}{Q_c}\dfrac{r_c}{r}\right]-\exp\left[\dfrac{Q}{Q_1}\dfrac{r_c}{r}\right]E_2\left[\left(\dfrac{Q}{Q_c}+\dfrac{Q}{Q_1}\right)\dfrac{r_c}{r}\right]\right)\right. \nonumber \hspace*{46pt}\left.+\exp\left[\dfrac{Q}{Q_1}\dfrac{r_c}{r}\right]E_2\left[\dfrac{Q}{Q_c}+\dfrac{Q}{Q_1}\right]-E_2\left[\dfrac{Q}{Q_c}\right]\right\} \end{eqnarray*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq112.png) (B.4)
(B.4)
Appendix C Solution for Sect. 3.3
In absence of photoabsorption by the coma, Eq. (17) is reduced to
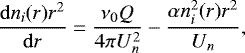 (C.1)
(C.1)
which is a Riccati equation. There is no straightforward solutions for such an equation, and a few manipulations have to be performed to obtain one. The first substitution is
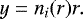 (C.2)
(C.2)
Equation (C.1) becomes
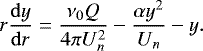 (C.3)
(C.3)
Equation (C.3) is completely separable and can be rewritten as follows:
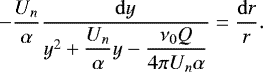 (C.4)
(C.4)
The left-hand side only depends on the variable y, whereas the right-hand side depends only on the variable r. The right-hand side is easy to integrate, unlike the left-hand side. First, we have to perform a partial fraction decomposition and find the roots of the following quadratic polynomial:
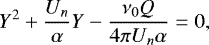 (C.5)
(C.5)
Thus, Eq. (C.4) becomes
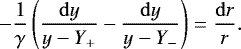 (C.9)
(C.9)
The integration of both sides leads to
![\begin{equation*} -\dfrac{1}{\gamma}\left(\log\left[\left|\dfrac{y-Y_+}{y_0-Y_+}\right|\right]-\log\left[\left|\dfrac{y-Y_-}{y_0-Y_-}\right|\right]\right)=\log\left[\dfrac{r}{r_0}\right] ,\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq123.png) (C.10)
(C.10)
where y0 is the initial value of y at r = r0. By assuming that the plasma number density is 0 at the surface (y0 = y(r0) = y(rc) = 0), we find that
![\begin{equation*} \dfrac{1}{\gamma}\log\left[\left|\dfrac{Y_-(y-Y_+)}{Y_+(y-Y_-)}\right|\right]=\log\left[\dfrac{r_c}{r}\right] ,\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq124.png) (C.11)
(C.11)
Some rearrangements are made to obtain the final expression for y:
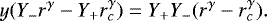 (C.13)
(C.13)
That is, based on Eq. (C.6),
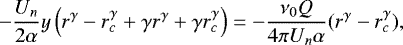 (C.14)
(C.14)
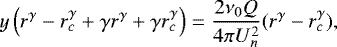 (C.15)
(C.15)
According to the relation between y and ni given by Eq. (C.2), the total ion density is given by
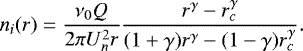 (C.17)
(C.17)
Hence, usingthe previously defined quantity Q0,
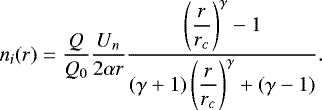 (C.18)
(C.18)
Based on Eqs. (C.7) and (C.18),
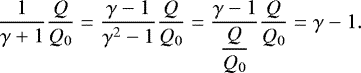 (C.19)
(C.19)
The location of the maximum is
![\[\left(\dfrac{r}{r_c}\right)_{\text{max}}=\sqrt[\gamma]{\dfrac{\gamma^2+1}{\gamma+1}+\dfrac{\gamma}{\gamma+1}\sqrt{\gamma^2+3}},\]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq134.png)
such that 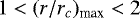 regardless of γ.
regardless of γ.
References
- A’Hearn, M. F., Belton, M. J. S., Delamere, W. A., et al. 2011, Science, 332, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Altwegg, K., Balsiger, H., Geiss, J., et al. 1993, A&A, 279, 260 [NASA ADS] [Google Scholar]
- Avakyan, S. V., Ii’In, R. N., Lavrov, V. M., & Ogurtsov, G. N., eds. 1998, Collision Processes and Excitation of UV Emission from Planetary Atmospheric Gases: A Handbook of Cross Sections (Boca Raton, FL: CRC Press) [Google Scholar]
- Balsiger, H., Altwegg, K., Buhler, F., et al. 1986, Nature, 321, 330 [Google Scholar]
- Beth, A., Altwegg, K., Balsiger, H., et al. 2016, MNRAS, 462, S562 [Google Scholar]
- Bhardwaj, A. 2003, Geophys. Res. Lett., 30, 2244 [NASA ADS] [CrossRef] [Google Scholar]
- Carr, C., Cupido, E., Lee, C. G. Y., et al. 2007, Space Sci. Rev., 128, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Chamberlain, T. P., & Hunten, D. M. 1987, Theory of Planetary Atmospheres: An Introduction to Their Physics and Chemistry, International Geophysics Series (Amsterdam: Elsevier Science) [Google Scholar]
- Chan, W., Cooper, G., & Brion, C. 1993, Chem. Phys., 178, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, S. 1931, Proc. Phys. Soc., 43, 26 [Google Scholar]
- Churyumov, K. I., & Gerasimenko, S. I. 1972, IAU Symp., 45, 27 [NASA ADS] [Google Scholar]
- Cravens, T. E. 1987, Adv. Space Res., 7, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Davidsson, B. J., & Gutiérrez, P. J. 2005, Icarus, 176, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Deca, J., Divin, A., Henri, P., et al. 2017, Phys. Rev. Lett., 118, 205101 [NASA ADS] [CrossRef] [Google Scholar]
- Eberhardt, P. 1999, Space Sci. Rev., 90, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Edberg, N. J. T., Eriksson, A. I., Odelstad, E., et al. 2015, Geophys. Res. Lett., 42, 4263 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksson, A. I., Boström, R., Gill, R., et al. 2007, Space Sci. Rev., 128, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksson, A. I., Engelhardt, I. A. D., André, M., et al. 2017, A&A, 605, A15 [NASA ADS] [EDP Sciences] [Google Scholar]
- Fougere, N., Combi, M., Tenishev, V., et al. 2012, Icarus, 221, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Fougere, N., Altwegg, K., Berthelier, J.-J., et al. 2016, A&A, 588, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galand, M., Héritier, K. L., Odelstad, E., et al. 2016, MNRAS, 462, S331 [CrossRef] [Google Scholar]
- Gasc, S., Altwegg, K., Balsiger, H., et al. 2017, MNRAS, 469, S108 [Google Scholar]
- Glassmeier, K.-H., Boehnhardt, H., Koschny, D., Kührt, E., & Richter, I. 2007, Space Sci. Rev., 128, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gombosi, T. I. 2015, Physics of Cometary Magnetospheres (Washington, DC: American Geophysical Union), 169 [Google Scholar]
- Gradshteyn, I., & Ryzhik, I. 2015, in Table of Integrals, Series, and Products, 8th edn, ed. D. Zwillinger (Boston: Academic Press), 249 [Google Scholar]
- Hansen, K. C., Altwegg, K., Berthelier, J.-J., et al. 2016, MNRAS, 462, S491 [Google Scholar]
- Hässig, M., Altwegg, K., Balsiger, H., et al. 2015, Science, 347, aaa0276 [Google Scholar]
- Henri, P., Vallières, X., Hajra, R., et al. 2017, MNRAS, 469, S372 [Google Scholar]
- Heritier, K. L., Henri, P., Vallières, X., et al. 2017a, MNRAS, 469, S118 [CrossRef] [Google Scholar]
- Heritier, K. L., Altwegg, K., Balsiger, H., et al. 2017b, MNRAS, 469, S427 [Google Scholar]
- Heritier, K., Galand, M., Henri, P., et al. 2018, A&A, 618, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoang, M., Altwegg, K., Balsiger, H., et al. 2017, A&A, 600, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huebner, W., & Markiewicz, W. 2000, Icarus, 148, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Huebner, W., & Mukherjee, J. 2015, Planet. Space Sci., 106, 11 [Google Scholar]
- Huntress, W. T. J., & Pinizzotto, R. F. J. 1973, J. Chem. Phys., 59, 4742 [NASA ADS] [CrossRef] [Google Scholar]
- Ip, W.-H., & Axford, W. I. 1987, Nature, 325, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Johansson, F. L., Odelstad, E., Paulsson, J. J. P., et al. 2017, MNRAS, 469, S626 [NASA ADS] [CrossRef] [Google Scholar]
- Krankowsky, D., Lammerzahl, P., Herrwerth, I., et al. 1986, Nature, 321, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Lamy, P. L., Toth, I., Fernandez, Y. R., & Weaver, H. A. 2004, in Comets II, eds. M.C. Festou, H.U. Keller, & H.A. Weaver (Tucson, AZ: University of Arizona Press), 223 [Google Scholar]
- Le Roy, L., Altwegg, K., Balsiger, H., et al. 2015, A&A, 583, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marconi, M. L., & Mendis, D. A. 1983, ApJ, 273, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, M. L., & Mendis, D. A. 1984, ApJ, 287, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Mendis, D. A., Houpis, H. L. F., & Marconi, M. L. 1985, Fundam. Cosmics Phys., 10, 1 [NASA ADS] [Google Scholar]
- Neubauer, F. M., Glassmeier, K. H., Pohl, M., et al. 1986, Nature, 321, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Polyanin, A., & Zaitsev, V. 2017, Handbook of Ordinary Differential Equations: Exact Solutions, Methods, and Problems (Boca Raton, FL: CRC Press) [CrossRef] [Google Scholar]
- Reinhard, R. 1986, Nature, 321, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Rosen, S., Derkatch, A., Semaniak, J., et al. 2000, Faraday Discuss., 115, 295 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rubin, M., Hansen, K. C., Gombosi, T. I., et al. 2009, Icarus, 199, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, M., Koenders, C., Altwegg, K., et al. 2014, Icarus, 242, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, K., Brion, C., der Leeuw, P. V., & van der Wiel M. 1978, Chem. Phys., 29, 299 [CrossRef] [Google Scholar]
- Tenishev, V., Combi, M., & Davidsson, B. 2008, AJ, 685, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Trotignon, J. G., Michau, J. L., Lagoutte, D., et al. 2007, Space Sci. Rev., 128, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Vigren, E., & Eriksson, A. I. 2017, AJ, 153, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Vigren, E., & Galand, M. 2013, AJ, 772, 33 [Google Scholar]
- Vigren, E., André, M., Edberg, N. J. T., et al. 2017, MNRAS, 469, S142 [CrossRef] [Google Scholar]
- Woods, T. N., Eparvier, F. G., Bailey, S. M., et al. 2005, J. Geophys. Res. Space Phys., 110, A01312 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Analytical formulas for the ion number density profiles for the inner coma present in the literature and provided here.
All Figures
 |
Fig. 1 Photoelectron production rate at the solar zenith angle 0° as a functionof column density (left y-axis) or optical depth (right y-axis). Two cases are represented: (1) expanding comae: 1P during the Giotto flyby (red solid line) and 67P at two different heliocentric distances (green and blue solid lines, see legend and Table 2), (2) atmospheres in hydrostatic equilibrium like Earth at 1 au (black, solid line). The number density scale height H for the hydrostatic equilibrium case is set to 20 km, and the same photoabsorption cross section is assumed for all three cases. The dotted line corresponds to the production rate below the cometary surface. The circles identify the nucleus surface, and the dotted line corresponds to the hypothetical production rate below. |
| In the text | |
 |
Fig. 2 Photoelectron production rate in the coma at the solar terminator (χ = π∕2) in dimensionless units for different outgassing rates as a function of the cometocentric distance in cometary radii. The production decreases monotonically with respect to
r
for Q <2Qc. For Q > 2Qc, the production increases up to the cometocentric distance |
| In the text | |
 |
Fig. 3 Photoelectron production rate as a function of the optical depth for different outgassing rates Q at 1 au. For comparison, we have overplotted the profile for an isothermal atmosphere in hydrostatic equilibrium (solid line with circles) with an Earth-like scale height of ~ 20 km made of water vapor (see text). We scaled all profiles with respect to the maximum of the hydrostatic case. The solid black line corresponds to the photoelectron production rate at the surface for any outgassing rate (see Eq. (11)) for a given heliocentric distance (here dh = 1 au). Colored lines are the electron production rates for different outgassing rates: above the surface (solid), and below the surface (dashed). The light gray area corresponds to the region where the photoelectron production rate is higher at comets than for the hydrostatic case. The dark gray region represents values for which the corresponding cometocentric distance would be below the surface. The expanding velocity is set to Un = 600 m⋅s−1. |
| In the text | |
 |
Fig. 4 Cometocentric distance normalized to rc at which the optical depth τλ[r, χ = π∕2] = 2 for different outgassing rates Q. The dashed line defines the position of the surface. We also plot as a function of λ the product between the solar photon spectral flux I1 au (2015 Aug 15 at 1 au) and the total photoionization cross section σion (black line). The spectral range displayed extends up to 98.2 nm, which is the ionization threshold wavelength of water. The expanding velocity is set to Un = 600 m⋅s−1. |
| In the text | |
 |
Fig. 5 Photoelectron production rate as a function of the scaled cometocentric distance R (see text) for a pure water coma. The solar flux is taken from TIMED/SEE on 2015 August 15 at 1 au, with an outgassing rate of Q = 1030 s−1 and at a solar zenith angle of χ = 0. The expanding velocity is set to Un = 600 m⋅s−1. The shape of the production rate remains unchanged for ∀r, Q and χ, although the radial dependency (ordinate) and the amplitude (abscissa) have to be adjusted accordingly (see the relations given by Eqs. (15) and (16)). The location of the surface of 67P (rc = 2 km) has been placed at the corresponding parameter R for different outgassing rates (shown with dashed and dotted horizontal lines for χ = 0 and χ = π∕2, respectively). For each local maximum in photoionization (identified by colored triangles), we plot the corresponding attenuated solar spectral flux at that location in the same color (see inset): the primary peak is driven by the 15–40 nm spectral flux (blue), the secondary peak by the 1–10 nm spectral flux (yellow), and the tertiary peak by the <0.5 nm spectral flux(red). The abscissa in the inset is in log-scale to visualize short wavelengths. |
| In the text | |
 |
Fig. 6 Ion number density profile as a function of the cometary distance (normalized to the cometocentric distance at the surface, rc) for the equilibrium between the attenuated solar flux through the coma (referred to here as different values of the optical depth at the cometary surface) and the e− -ion dissociative recombination rate (see Eq. (19)). The solid black line corresponds to the density profile without photoabsorption and the dashed line to the cometary surface. Increasing τc is similar to increasing the outgassing rate. These profiles depend on neither Un nor α as they have been scaled accordingly. |
| In the text | |
 |
Fig. 7 Cometocentric distance normalized to rc at the surface of the maximum ion number density (black solid line) as a function of the optical depth τc at the surface. Two asymptotic profiles are plotted in blue (τc ≪ 1) and red (τc ≫ 1). The dashed line corresponds to the surface of the comet. |
| In the text | |
 |
Fig. 8 Total ion (black), H2O+ (blue), and H3O+ (red) ion number density profile at a solar zenith angle of χ = π∕2 and for six different outgassing rates Q: 1025 s−1 (left panel, circles), 1026 s−1 (left panel, dashed line), 1027 s−1 (left panel, pluses), 1025 s−1 (right panel, circles), 1029 s−1 (right panel, dashed line), 1030 s−1 (right panel, pluses). The number densities were scaled accordingly to be plotted as a dimensionless parameter. The vertical line corresponds to the lowest upper bound of the plasma density for χ = π∕2 in dimensionless units, i.e., 0.1657 × 2∕π ≈ 0.1055 (see Eq. (24)). The expanding velocity is set to Un = 600 m⋅s−1. |
| In the text | |
 |
Fig. 9 Comparison between the different models (Cravens 1987: red; Galand et al. 2016: blue; Gombosi 2015: circles), and our full model in an optically thin coma (stars) for different values of Q∕Q0 : 0.01 (left), 4 (middle), and 100 (right). These plots are independent of Un: Q∕Q0 is fixed for each plot and the abscissa is scaled. |
| In the text | |
 |
Fig. 10 Ion number density as a function of the cometocentric distance normalized to rc for three different outgassing rates: 1026 s−1 (diamond), 1028 s−1 (star), and 1030 s−1 (upward-pointing triangle) for a solar zenith angle χ = π∕2. The colors correspond to different assumptions: PA and DR (yellow), PA and no DR (red), no PA and DR (blue), no PA and no DR (gray). For the e− -ion dissociative recombination, we assumed Te = 150 K. For the photoionization frequency, ν0 = 4.5 × 10−7 s−1 corresponds to the water photoionization frequency at 67P around perihelion to independently assess the effect of the outgassing rate (1.24 au). The expanding velocity is set to Un = 600 m⋅s−1. |
| In the text | |
 |
Fig. 11 Dimensionless parameter 2αni(r)r∕Un (Eq. (27)) as a function of Q∕Q0 (Q0 defined by Eq. (20)). The ion number density ni is derived from Cravens (1987; red solid line, Eq. (31)), Galand et al. (2016; Eq. (29)) assuming r = 1.1 rc (dotted blue line), r = 2 rc (dashed blueline), and r ≫ rc (solid blue line, Eq. (30)), Gombosi (2015) or this work assuming r ≫ rc (black circles, Eq. (28)), and this work assuming r = 1.1 rc (blue upward-pointing triangles, ▴), r = 2 rc (orange downward-pointing triangles, ▾). Photoabsorption is ignored here. Conditions at 1P during the Giotto encounter and at 67P during the Rosetta escort phase are overplotted as gray areas. We provide a broad range of values for 1P as uncertainties remained on the electron temperature and therefore on the e− -ion dissociative recombination rate, which depends on the electron temperature. This last was assumed to be between 150 K (upper bound) and 1000 K (lower bound; see Table 2). For 67P, the dynamic range of Q∕Q0 is primarily driven by the outgassing rate Q, from 1025 (end of mission) to 6 × 1028 s−1(perihelion), and the heliocentric distance, which affects the photoionization frequency. |
| In the text | |
 |
Fig. 12 Comparison of the plasma number density profiles with respect to the scaled cometocentric distances between 1P (red, 0.89 au) and 67P (blue, 3.2 au, and green, 1.24 au). The profiles have been generated under different assumptions: including PA and DR (thick solid lines), without PA (circles), and without DR (dotted lines). The dashed line corresponds to the plasma density profile from Cravens (1987) with Te = 1000 K. The black crosses with the error bars are the in situ plasma density measurement by the ion mass spectrometer onboard theGiotto spacecraft at 1P/Halley during the Giotto flyby (Altwegg et al. 1993). The black pluses are in situ plasma density observations by RPC-MIP on board Rosetta at 3.2 au (Galand et al. 2016). |
| In the text | |
 |
Fig. A.1 Schematic of the configuration between the Sun (yellow), the comet (black), and a water molecule to determine the column density at a given
(r, χ) in the coma. s
is the abscissa along the line between the molecule and the Sun. s0
is the lower bound of integration (s0 < 0 and χ > π∕2 in the figure as s
increases sunward). rs
is the cometocentric distance for a given s, which is |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



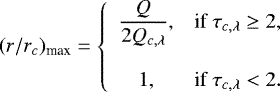
![\[ \delta=\left(\dfrac{1\text{ au}}{d_h}\right)^2\dfrac{H}{r_c}\dfrac{\tan\chi}{\chi}. \]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq25.png)
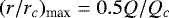
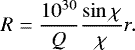
![\begin{equation*} Q_0=\dfrac{\pi U_n^3}{\nu_0\alpha} [\text{s}^{-1}].\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq39.png)
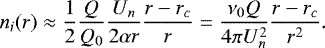
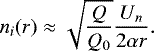
![\begin{equation*} Z^2W^{\prime\prime}(Z)-\dfrac{1}{4}\dfrac{Q}{Q_0}\exp\left[-\dfrac{Q}{Q_c}Z\right]W(Z)=0.\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq69.png)
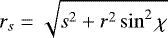
![\begin{equation*} N[r,\chi]=n_0 r_0^{\beta}(r \sin \chi)^{-\beta+1} \int_{1/\tan\chi}^{+\infty} \left(1 + X^2 \right) ^{-\beta/2}\, \mathrm{d}X.\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq86.png)
![\[ F[r]=n[r]r \]](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq88.png)
![\begin{align*} &G[\chi]\\ &\quad\ \ =\sin^{-\beta+1}\! \chi \int_{1/\tan\chi}^{+\infty}\! \left(1 + X^2 \right) ^{-\beta/2}\, \mathrm{d}X\\ &\quad\ \ =\sin^{-\beta+1}\! \chi \int^{\chi}_{0}\! \sin^{\beta-2} \Theta \, \mathrm{d}\Theta\\ &\quad\ \ =\sin^{-\beta+1} \!\chi\, \left\{C_{\beta}-\dfrac{1}{\tan\chi}{}_2F_1\left[\dfrac{1}{2},\dfrac{\beta}{2};\dfrac{3}{2};-\dfrac{1}{\tan^2\chi}\right]\right\}\\ &\quad\ \ =\sin^{-\beta+1} \!\chi\,\left\{C_{\beta}-\cos\chi {}_2F_1\left[\dfrac{1}{2},\dfrac{3-\beta}{2};\dfrac{3}{2};\cos^2\chi\right]\right\}, \end{align*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq89.png)
![\begin{equation*} \lim_{\beta\longrightarrow +\infty}n_0\left(1+\dfrac{z}{\beta H(r_0)}\right)^{-\beta}=n_0\exp\left[-\dfrac{z}{H(r_0)}\right] ,\end{equation*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq105.png)
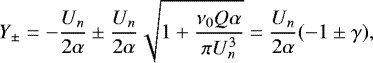
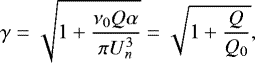
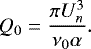
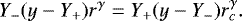
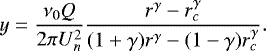
![\begin{align*} n_i(r)&=\dfrac{U_n}{2 \alpha r}(\gamma-1)\dfrac{\left(\dfrac{r}{r_c}\right)^{\gamma}-1}{\left(\dfrac{r}{r_c}\right)^{\gamma}+\dfrac{\gamma-1}{\gamma+1}},\\[9pt] &=\dfrac{U_n}{2 \alpha r}(\gamma-1)\left(1-\dfrac{2\gamma}{\gamma-1}\dfrac{1}{1+\dfrac{\gamma+1}{\gamma-1}\left(\dfrac{r}{r_c}\right)^{\gamma}}\right) .\end{align*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq133.png)
![\begin{align*} &\lim_{\gamma\longrightarrow1}\sqrt[\gamma]{\dfrac{\gamma^2+1}{\gamma+1}+\dfrac{\gamma}{\gamma+1}\sqrt{\gamma^2+3}}=2,\\[9pt] &\lim_{\gamma\longrightarrow+\infty}\sqrt[\gamma]{\dfrac{\gamma^2+1}{\gamma+1}+\dfrac{\gamma}{\gamma+1}\sqrt{\gamma^2+3}}=1, \end{align*}](/articles/aa/full_html/2019/10/aa33517-18/aa33517-18-eq135.png)