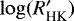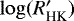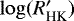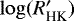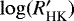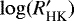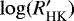| Issue |
A&A
Volume 627, July 2019
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 22 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201935457 | |
| Published online | 28 June 2019 | |
Hot, rocky and warm, puffy super-Earths orbiting TOI-402 (HD 15337)★,★★
1
Astronomy Department of the University of Geneva,
51 chemin des Maillettes,
1290
Versoix,
Switzerland
e-mail: xavier.dumusque@unige.ch
2
Institut of Computational Sciences, University of Zurich,
Winterthurerstrasse 190,
8057
Zurich, Switzerland
3
Harvard-Smithsonian Center for Astrophysics,
60 Garden St,
Cambridge,
MA
02138,
USA
4
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP,
Rua das Estrelas,
4150-762
Porto,
Portugal
5
Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto,
Rua do Campo Alegre,
4169-007
Porto,
Portugal
6
Physikalisches Institut, Universitat Bern,
Silderstrasse 5,
3012
Bern,
Switzerland
7
NASA Ames Research Center,
Moffett Field,
CA
94035, USA
8
Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires,
Buenos Aires,
Argentina
9
CONICET – Universidad de Buenos Aires, Instituto de Astronomía y Física del Espacio (IAFE),
Buenos Aires,
Argentina
10
Department of Physics and Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology,
Cambridge,
MA
02139,
USA
11
NASA Goddard Space Flight Center,
8800 Greenbelt Road,
Greenbelt
MD
20771,
USA
12
School of Physical Sciences, The Open University,
Walton Hall,
Milton Keynes
MK7 6AA,
UK
13
Instituto de Astrofísica de Canarias,
38205
La Laguna,
Tenerife,
Spain
14
Department of Earth, Atmospheric, and Planetary Sciences, Massachusetts Institute of Technology,
Cambridge,
MA
02139,
USA
15
SETI Institute,
Mountain View,
CA
94043,
USA
16
Department of Astrophysical Sciences,
4 Ivy Lane, Princeton University,
Princeton,
NJ
08544,
USA
Received:
13
March
2019
Accepted:
17
April
2019
Context. The Transiting Exoplanet Survey Satellite (TESS) is revolutionising the search for planets orbiting bright and nearby stars. In sectors 3 and 4, TESS observed TOI-402 (TIC-120896927), a bright V = 9.1 K1 dwarf also known as HD 15337, and found two transiting signals with periods of 4.76 and 17.18 days and radii of 1.90 and 2.21 R⊕, respectively. This star was observed prior to the TESS detection as part of the radial-velocity (RV) search for planets using the HARPS spectrometer, and 85 precise RV measurements were obtained before the launch of TESS over a period of 14 yr.
Aims. In this paper, we analyse the HARPS RV measurements in hand to confirm the planetary nature of these two signals.
Methods. HD 15337 happens to present a stellar activity level similar to the Sun, with a magnetic cycle of similar amplitude and RV measurements that are affected by stellar activity. By modelling this stellar activity in the HARPS radial velocities using a linear dependence with the calcium activity index log(RHK′), we are able, with a periodogram approach, to confirm the periods and the planetary nature of TOI-402.01 and TOI-402.02. We then derive robust estimates from the HARPS RVs for the orbital parameters of these two planets by modelling stellar activity with a Gaussian process and using the marginalised posterior probability density functions obtained from our analysis of TESS photometry for the orbital period and time of transit.
Results. By modelling TESS photometry and the stellar host characteristics, we find that TOI-402.01 and TOI-402.02 have periods of 4.75642 ± 0.00021 and 17.1784 ± 0.0016 days and radii of 1.70 ± 0.06 and 2.52 ± 0.11 R⊕ (precision 3.6 and 4.2%), respectively. By analysing the HARPS RV measurements, we find that those planets are both super-Earths with masses of 7.20 ± 0.81 and 8.79 ± 1.68 M⊕ (precision 11.3 and 19.1%), and small eccentricities compatible with zero at 2σ.
Conclusions. Although having rather similar masses, the radii of these two planets are very different, putting them on different sides of the radius gap. By studying the temporal evolution under X-ray and UV (XUV) driven atmospheric escape of the TOI-402 planetary system, we confirm, under the given assumptions, that photo-evaporation is a plausible explanation for this radius difference. Those two planets, being in the same system and therefore being in the same irradiation environment are therefore extremely useful for comparative exoplanetology across the evaporation valley and thus bring constraints on the mechanisms responsible for the radius gap.
Key words: techniques: radial velocities / techniques: spectroscopic / stars: activity / stars: individual: HD 15337 / stars: individual: TOI-402 / stars: individual: TIC-120896927
Table A.1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/627/A43
© ESO 2019
1 Introduction
The Transiting Exoplanet Survey Satellite (TESS, Ricker et al. 2015) is revolutionising the field of exoplanets by detecting such bodies transiting bright and nearby stars. This allows for ground-based spectroscopic follow-up studies to be performed to first confirm those planets and then obtain their densities, which is needed to understand planetary formation. Planets transiting bright stars are also extremely interesting for ground- and space-based follow-up observations aimed at studying their atmospheres by using transmission or emission spectroscopy.
TESS will observe nearly the whole sky in a two-year period, implying that most of the targets observed until now in blind radial-velocity (RV) surveys for exoplanets will be measured (e.g. Π Men, Huang et al. 2018; Gandolfi et al. 2018). This is the case for TOI-402 (TIC ID 120896927), also known as HD 15337, for which a significant number of HARPS observations were obtained. TESS found two transiting candidates orbiting around this star, and the goal of this paper is to confirm them using the publicly available HARPS observations. Note that an independent analysis of the same planetary system using the same data can be found in Gandolfi et al. (2019). The results from this paper are consistent with the analysis performed here.
In Sect. 2, we describe the photometric and spectroscopic observations obtained by TESS and HARPS. In Sect. 3, we analyse those data to confirm the two planets found by TESS and to obtain good constraints on their radius and mass. We finally discuss our results and conclude in Sect. 4.
2 Observations
2.1 TESS photometry
TOI-402 was observed by TESS in two-minute cadence mode during sectors 3 and 4, that is between September 22 and November 15, 2018. The target appeared on camera 2 and CCDs 3 and 4 for sectors 3 and 4, respectively. Nine transits of TOI-402.01 and three of TOI-402.02 were detected in the two sectors, with depths of 406 and 609 ppm with a signal-to-noise-ratio (S/N) of 10.4 and 10.7, respectively1 (Jenkins et al. 2017; Twicken et al. 2018).
In Sect. 3.2, we analyse the data publicly available on MAST2, which were reduced by the Science Processing Operations Center pipeline (Jenkins et al. 2016, 2017; Jenkins 2017). For our transit modelling in Sect. 3.2, we used the raw light curve based on the Pre-search Data Conditioning Simple Aperture Photometry (PDCSAP, Twicken et al. 2010; Smith et al. 2012; Stumpe et al. 2014).
2.2 High-resolution spectroscopy with HARPS
The star HD 15337 was observed with HARPS on the ESO 3.6 m telescope in La Silla, Chile, between December 2003 and September 2017. Those observations were gathered in the framework of the HARPS guaranteed time observation (GTO) and subsequent high-precision large programs (LP) obtained on open time. We note that the GTO and subsequent LP observations lead to the discovery of a large number of super-Earths and Neptunes orbiting nearby solar-type stars (e.g. Lovis et al. 2009; Mayor et al. 2011; Udry et al. 2019).
Out of a total of 87 spectra available on the ESO archive, 85 passed the quality control of the HARPS Data Reduction Software (DRS). The S/N of the spectra at 550 nm ranges between 47 and 142 for a photon-noise RV precision of 0.56 and 1.59 m s−1, respectively. The observations were performed with two different configurations of the HARPS instrument, with circular fibre before June 1, 2015 (BJDUTC = 2 457 174.5), and octagonal fibres after that. This change of optical fibres induced an offset in the RV time-series that depends on the stellar spectral type and is difficult to determine beforehand at the level of meter per second or below (Lo Curto et al. 2015) and therefore, it must be taken into account by adjusting an additional free parameter. In the RV data of HD 15337, the difference between the median of the data before and after June 1, 2015, is 42.4 m s−1. After correcting for this offset, the RV residuals are left with a RV rms of 4.37 m s−1, much higherthan the photon noise uncertainty, pointing towards the presence of extra signals in the data of stellar or planetary origin.
We re-reduced the 85 spectra using the latest and very recent version of the DRS that includes a better wavelength solution owing to the consideration of the CCD stitching (Dumusque et al. 2015; Coffinet et al. 2019) and publish the new extracted RVs and 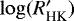 at the CDS. Coffinet et al. (2019) demonstrated that HARPS data derived with this new DRS are of much betterquality. In the case of HD 15337, this new version of the DRS gives very similar results to those from the previous one for the RV data before the change of the fibres (rms of the RV difference 0.3 m s−1); however, the differences are significant for the data gathered after, the rms of the RV difference being 1.6 m s−1. As the data after June 1, 2015, represent 40% of the measurements, using the data derived with this latest version of the DRS has a significant impact on precision.
at the CDS. Coffinet et al. (2019) demonstrated that HARPS data derived with this new DRS are of much betterquality. In the case of HD 15337, this new version of the DRS gives very similar results to those from the previous one for the RV data before the change of the fibres (rms of the RV difference 0.3 m s−1); however, the differences are significant for the data gathered after, the rms of the RV difference being 1.6 m s−1. As the data after June 1, 2015, represent 40% of the measurements, using the data derived with this latest version of the DRS has a significant impact on precision.
We note that all the HARPS publicly available data are currently being re-reduced with this latest version of the DRS at the Astronomy Department of the University of Geneva. Those data will be made available to the community through the Data and Analysis Center for Exoplanets web platform (DACE3).
3 Analysis and results
3.1 Stellar parameters and chemical abundances
The stellar atmospheric parameters (Teff, log g, micro-turbulence and [Fe/H]) and respective error bars were derived using the methodology described in Sousa (2014) and Santos et al. (2013). We make use of the equivalent widths (EWs) of well-selected iron lines. For this relatively cool star we used the appropriate line list presented in Tsantaki et al. (2013). The equivalent widths were measured for the combined HARPS spectrum of TOI-402 using the ARES v2 code4 (Sousa et al. 2007, 2015), and we assume ionisation and excitation equilibrium. The process makes use of a grid of Kurucz model atmospheres (Kurucz 1993) and the radiative-transfer code MOOG (Sneden 1973). As discussed in the references above, this method provides effective temperatures in excellent agreement with values derived using the infra-red flux method (Casagrande et al. 2006, 2010) and which are independent of the derived surface gravity (Torres et al. 2012). The resulting values for Teff, log g, micro-turbulence, and [Fe/H] can be found in Table 1.
Stellar abundances of the elements were also derived using the same tools and models as for stellar parameter determination, as well as using the classical curve-of-growth analysis method assuming local thermodynamic equilibrium.Although the EWs of the spectral lines were automatically measured with ARES, for the elements with fewer than four lines available we performed careful visual inspection of the EW measurements. For the derivation of chemical abundances of refractory elements we closely followed the methods described in Adibekyan et al. (2015). The final abundances derived, which are fully compatible with the ones found in the Hypatia catalogue5 (Hinkel et al. 2014), can be found in Table 1. When comparing the chemical composition with stars of similar atmospheric parameters in the solar neighbourhood (Adibekyan et al. 2012), we find that TOI-402 has typical properties for a thin disc star.
Stellar properties for TOI-402.
3.2 Analysis of TESS photometry
We performed the analysis of the TESS photometry using EXOFASTv2 (Eastman 2017; Eastman et al. 2013) to jointly model the light curve and the host star. We imposed priors on the stellar model generated by Mesa isochrones and stellar tracks (MIST, Dotter 2016; Choi et al. 2016) using the spectral parameters derived in Sect. 3.1, the photometry in the spectral band-passes detailed in Table 1, and the Gaia parallax shown in the same table.
We removed the long-timescale variations due to stellar activity from the TESS light curve of TOI-402 using a moving polynomial, as applied for K2 photometry by Giles et al. (2018). This method consists of fitting a sliding polynomial which at each sliding step fits a large fraction of the light curve (“window”) but only divides this model out of a small section (“step size”). This prevents the method from being sensitive to side effects common with polynomials. In our analysis, we used a third-order polynomial with a step size of 0.1 day and a window size of 5 days. To ensure the result is not jagged, the step size must be significantly smaller than the window size. To preserve the transit depth during this smoothing process, and therefore prevent biasing the final derived planetary radius, we need to perform outlier rejection from the polynomial fit. This is done by doing a 3σ cut of positive outliers and selecting a Xσ cut on negative outliers, where X is chosen so that Xσ is larger than the deepest transit.
When fitting a light curve, EXOFASTv2 uses 31 free parameters. We placed Gaussian priors on Teff, log(g), [Fe/H], and parallax based on our spectral analysis and Gaia results (see Sect. 3.1 and Table 1). We placed loose constraints on the period, epoch, and transit depth to prevent the Monte Carlo Markov chain (MCMC) sampler from entering poor fitting areas of parameter space and left the remaining parameters free. The planet orbits are considered non-eccentric.
For the final MCMC analysis run we used the output values from an initial analysis as starting values. We used a maximum of 50 000 steps and up to 50 independent chains. While running, EXOFASTv2 uses the Gelman-Rubin (GR) statistic (Gelman & Rubin 1992), which compares the within and between chain variances to assess convergence, and Tz, the number of independent draws to assess if the chains have converged. Upon reaching a GR < 1.01 and Tz > 1000 for a sufficient number of draws, EXOFASTv2 considers the chains converged and stops. In our analysis, this was reached after 27 500 steps. To get the final marginalised posterior probability function densities for each parameter, the chains were merged together.
We present the results of the stellar fit in Table 1 and Fig. 1, and the system parameters derived from TESS photometry in Table 2. We note that to test that the smoothing method removinglong-term variation in the light curve due to stellar activity was not perturbing the transit depth of both planets, we ran EXOFASTv2 with and without this smoothing. Both runs gave transit depths that differ by no more than 17 ppm, that is, less than the transit depth uncertainties, implying that the smoothing does not bias the final planetary radius. We also compared the results of analyses with eccentricity fixed at zero and using the value and uncertainties given by the RV analysis as the prior. The results were entirely consistent between the two and therefore we present the results of the analysis with fixed eccentricity.
Comparing our results for the time of transit, orbital period, and transit depth with the values found by the Science Processing Operations Center (SPOC) data validation (DV) analysis6, we find that our values are compatible with the SPOC DV analysis within 1σ for the time of transit and orbital period of both planets. The transit depths of both planets are compatible to within 2σ. Our re-analysis of TESS photometry gives in all cases a better precision than the values found on ExoFOP.
 |
Fig. 1 Left: full PDCSAP light curve from TESS after removing the smoothing model described in Sect. 3.2. The grey points represent the raw measurements, while the blue dots are the same data binned over 10 min. The model showing the best fit to the light curve with two planets corresponding to TOI-402.01 and TOI-402.02 is shown as the black curve. Middle: light curve phase-folded in phase to highlight the transit of TOI-402.01 and the best-fit model. Right: as in the middle plot, but for TOI-402.02. |
Parameters for the TOI-402 planetary system derived from our TESS photometry analysis using EXOFASTv2.
3.3 Stellar rotation and activity
To probe the activity of HD 15337, we analysed the calcium 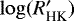 time-series derived from the HARPS data-reduction software. The
time-series derived from the HARPS data-reduction software. The 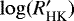 is an observable derived from the S-index, which is itself a measurement of the emission in the core of the Ca II H and K lines normalised to nearby pseudo-continuum (Vaughan et al. 1978). Because the level of those pseudo-continuum is dependant on spectral type, the S-index value cannot be compared between different stars without correcting for the stellar bolometric luminosity, which is performed in the
is an observable derived from the S-index, which is itself a measurement of the emission in the core of the Ca II H and K lines normalised to nearby pseudo-continuum (Vaughan et al. 1978). Because the level of those pseudo-continuum is dependant on spectral type, the S-index value cannot be compared between different stars without correcting for the stellar bolometric luminosity, which is performed in the 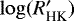 (Noyes et al. 1984). We note that the
(Noyes et al. 1984). We note that the 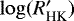 derived from the HARPS pipeline has been calibrated to deliver similar result to those of the band-pass photometer of the Mount-Wilson project (Vaughan et al. 1978).
derived from the HARPS pipeline has been calibrated to deliver similar result to those of the band-pass photometer of the Mount-Wilson project (Vaughan et al. 1978).
As can be seen in the top panel of Fig. 2, HD 15337 presents a magnetic cycle. When fitting a sinusoidal signal to the 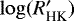 , we find a period of 7 yr, that is, shorter than the solar magnetic cycle. However, we must note that this period is not well constrained. The amplitude of this cycle is comparable to the Sun with
, we find a period of 7 yr, that is, shorter than the solar magnetic cycle. However, we must note that this period is not well constrained. The amplitude of this cycle is comparable to the Sun with 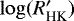 values ranging from −5.0 to −4.85 with a mean value of −4.91. To see if we can detect any activity on the rotational period timescale, we applied a low-pass filter to the
values ranging from −5.0 to −4.85 with a mean value of −4.91. To see if we can detect any activity on the rotational period timescale, we applied a low-pass filter to the 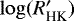 using the algorithm described in Rybicki & Press (1995) and selecting a cutting frequency at 1000 days−1. By removing this long-timescale variation from the raw
using the algorithm described in Rybicki & Press (1995) and selecting a cutting frequency at 1000 days−1. By removing this long-timescale variation from the raw 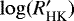 , we obtained the time-series seen in the middle panel of Fig. 2, which we refer to as the high-frequency
, we obtained the time-series seen in the middle panel of Fig. 2, which we refer to as the high-frequency 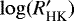 time-series in the rest of the paper. A generalized Lomb-Scargle periodogram (GLS, Zechmeister & Kürster 2009) of this time-series is seen in the bottom of the same figure. A significant peak, with a p-value smaller than 0.01% and a period of 36.55 days, reveals the stellar rotational period of the star (Prot). Using the relation from Mamajek & Hillenbrand (2008) to estimate rotation periods from the colour index B− V and the mean
time-series in the rest of the paper. A generalized Lomb-Scargle periodogram (GLS, Zechmeister & Kürster 2009) of this time-series is seen in the bottom of the same figure. A significant peak, with a p-value smaller than 0.01% and a period of 36.55 days, reveals the stellar rotational period of the star (Prot). Using the relation from Mamajek & Hillenbrand (2008) to estimate rotation periods from the colour index B− V and the mean 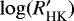 level, we predict a rotation period of 43 ± 5 days, which is compatible with our measurement within 1.5σ. We are therefore confident that 36.55 days is the stellar rotation period measured at the average latitude where active regions are present.
level, we predict a rotation period of 43 ± 5 days, which is compatible with our measurement within 1.5σ. We are therefore confident that 36.55 days is the stellar rotation period measured at the average latitude where active regions are present.
From this analysis of stellar activity, we expect the RVs to be affected on timescales similar to the stellar rotation period, and we also expect a small long-term contribution with an amplitude of ~ 4 m s−1 due to the stellar magnetic cycle (Lovis et al. 2011). We note that the RV signal induced by TOI-402.02 with an orbital period of 17.17 days might be significantly affected by activity as it is close to half the stellar rotation period. Indeed, we know from simulations (e.g. Boisse et al. 2011) and observations that activity signals appear at the stellar rotational period and respective harmonics (Prot, Prot ∕2, Prot ∕3, Prot ∕4).
 |
Fig. 2
|
 |
Fig. 3 Top: fit composed of an offset to account for the change of fibres on June 1, 2015, a second-order polynomial drift, a linear dependence with the low-pass, and the high-frequency |
3.4 Radial-velocity analysis
3.4.1 Preliminary periodogram analysis
To search for the signals of TOI-402.01 and TOI-402.02, the two planet candidates that TESS found orbiting HD 15337, we analysed the HARPS RVs using a periodogram approach. To consider stellar activity and possible long-term drift in the data due to long-period planets or stellar companions, we first fitted a model including a linear dependence with the low-pass filtered 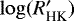 time-series (see Sect. 3.3 and top panel of Fig. 2), the high-frequency
time-series (see Sect. 3.3 and top panel of Fig. 2), the high-frequency 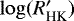 time-series (see Sect. 3.3 and the middle panel of Fig 2), and a second-order polynomial. In addition, we added an offset to adjust the change of HARPS fibres on June 1, 2015. The model that best fits the data using a linear least square can be seen in the top panel of Fig. 3. The middle panel of the same figure shows the GLS periodogram of the RV residuals, which highlight a significant signal corresponding to TOI-402.01 with a p−value of 0.03%, an estimated amplitude of 2.8 m s−1, and a period of 4.76 days, fully compatible with the period found by TESS.
time-series (see Sect. 3.3 and the middle panel of Fig 2), and a second-order polynomial. In addition, we added an offset to adjust the change of HARPS fibres on June 1, 2015. The model that best fits the data using a linear least square can be seen in the top panel of Fig. 3. The middle panel of the same figure shows the GLS periodogram of the RV residuals, which highlight a significant signal corresponding to TOI-402.01 with a p−value of 0.03%, an estimated amplitude of 2.8 m s−1, and a period of 4.76 days, fully compatible with the period found by TESS.
In a second step, we added to the previous model a Keplerian model to account for the signal found at 4.76 days. Beforeperforming a least square on this new model which is non-linear, we require good initial guesses for all the parameters. For the offset, polynomial drift, and linear dependence with activity, we used as initial conditions the best values found in the precedent fit. For the Keplerian model, the period is fixed to the value found in the periodogram, in this case 4.76 days. The eccentricity and mean anomaly are estimated using the amplitude and phase of the signals found at 4.76 days and half of this period, as described in Delisle et al. (2016). The initial guess for the amplitude of the Keplerian signal is obtained by fixing the period, the eccentricity and mean anomaly to the values guessed above and by performing a linear least square on the RV residuals of the previous fit. We then use the scipy.optimize least_squares algorithm to find the best parameters for this new model including the TOI-402.01 Keplerian signal. The GLS periodogram of the RV residuals of this new fit can be found in thebottom panel of Fig. 3. We see in this periodogram the signal of TOI-402.02 with a p-value of 0.47%, an amplitude of 2.2 m s−1, and a period of 17.17 days.
After finding this second signal, we adopted a new model including the original one plus two Keplerian signals. We found the initial conditions for the Keplerian parameters in the same way as described above and performed a new least square minimisation. We show the best-fit model in the top panel of Fig. 4. In the two second-row panels, we show the phase curves for the two Keplerian signals corresponding to TOI-402.01 and TOI-402.02. The two last panels of the same figure show the RV residuals and their corresponding GLS periodogram. It is clear that no other significant signals are found in the data.
Our preliminary modelling of the RVs of HD 15337 reveals the presence of two super-Earths, with masses of 7.1 and 9.1 M⊕, periods of 4.76 and 17.17 days, and eccentricities of 0.10 and 0.21 for TOI-402.01 and 402.02, respectively. The RV residuals after removing our best fit still have a RV rms of 2.17 m s−1, much higher than the precision of the HARPS spectrograph, below 1 m s−1, and the average photon noise RV error of the HD 15337 data, 0.9 m s−1. Therefore, although no significant coherent signal is left in the RV residuals, stellar signal is not fully mitigated. This motivates the use in the following section of a more complex model to account for the correlated noise induced by stellar activity.
We note that we tried to remove from our model the linear dependence with the short-term 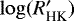 in order to analyse the impact of stellar activity on the derived planetary solutions. The two planets can still be found, although with larger p-values. The stellar rotation period is more significant in the RV residuals of the full model with a p-value of 3.44%. Finally, the eccentricities of TOI-402.01 and 402.02 are larger, 0.29 and 0.42, respectively, which is uncommon for small planets on short-period orbits. This analysis of the RVs of HD 15337, without considering short-term stellar activity, shows that the planetary signals are perturbed by stellar activity, and therefore it should be taken into consideration to obtain robust orbital solutions for TOI-402.01 and TOI-402.02.
in order to analyse the impact of stellar activity on the derived planetary solutions. The two planets can still be found, although with larger p-values. The stellar rotation period is more significant in the RV residuals of the full model with a p-value of 3.44%. Finally, the eccentricities of TOI-402.01 and 402.02 are larger, 0.29 and 0.42, respectively, which is uncommon for small planets on short-period orbits. This analysis of the RVs of HD 15337, without considering short-term stellar activity, shows that the planetary signals are perturbed by stellar activity, and therefore it should be taken into consideration to obtain robust orbital solutions for TOI-402.01 and TOI-402.02.
This preliminary analysis of the RV data of TOI-402 confirms the two planetary candidates detected by TESS. Although the signal for TOI-402.01 is strong and the RV data alone are sufficient to confirm the planet, the second signal at 17.17 days has a p-value of 0.47% and is not at the 0.1% threshold generally required to claim a confident detection. Of course, the a priori knowledge that a 17.17-day transiting signal is found in TESS data validates the planetary nature of this signal.
 |
Fig. 4 Top: best-fit model of our preliminary RV analysis over-plotted on the RV data of HD15337 after removing the instrumental offset due to the change of the fibres on June 1,2015. Second row: phase plot showing the RV signals of TOI-402.01 (left) and TOI-402.02 (right). The best-fit model is shown in black, and the orbital parameters and mass of the detected planets can be found in the title of the two subplots. Third row: RV residuals after fitting our best model. The rms of the residuals of 2.17 m s−1 is significantly higher than the average photon noise error of 0.9 m s−1. Bottom: GLS periodogram of the RV residuals showing no significant signals. Although no signal is seen, the fact that the rms of the residuals is much higher than the photon noise errors indicates that there is still significant activity signal in the residuals. |
3.4.2 Mitigating stellar activity in log(R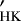 ) using a Gaussian process regression
) using a Gaussian process regression
When RV data are significantly affected by stellar activity, it is common to use either a Gaussian process regression model (GP, e.g. Haywood et al. 2014; Grunblatt et al. 2015; Rajpaul et al. 2015; Faria et al. 2016; Jones et al. 2017; Damasso et al. 2018) or a moving average regression model (e.g. Tuomi & Anglada-Escudé 2013; Tuomi 2014; Feng et al. 2016, 2017) to account for the correlated signal induced by stellar activity. These two techniques have been shown to be the most efficient at mitigating stellar activity while looking for planetary signals (Dumusque et al. 2017).
In this section, we use a GP regression model to account for stellar activity. It is common in the case of good photometry to first train the GP on photometry to obtain good constraints on its hyper-parameters and then to use those constraints as priors for a GP regression model applied to the RV data set. This is possible with Kepler, due to photometric time-series spanning many stellar rotation periods. However, in the case of HD 15337, TESS obtained a photometric time-series spanning a total of only 51 days, representing less than two full rotational periods of the star, estimated to be 36.55 days (see Sect. 3.3). In addition, the TESS photometric time-series in not contemporaneous with the RV measurements and therefore the covariance observed in photometry might be different from the one present in the RV data. We therefore decided to use the 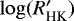 time-series extracted from HARPS spectra. The
time-series extracted from HARPS spectra. The 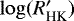 time-series is affected by a long-term magnetic cycle. Here, we want to model with the GP regression only the rotational modulation induced by stellar activity, and therefore we analysed the high-frequency
time-series is affected by a long-term magnetic cycle. Here, we want to model with the GP regression only the rotational modulation induced by stellar activity, and therefore we analysed the high-frequency 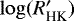 time-series discussed in Sect. 3.3 and shown in the middle panel of Fig. 2.
time-series discussed in Sect. 3.3 and shown in the middle panel of Fig. 2.
For our GP regression, we tested two different kernels. First a simple squared exponential (SE) kernel, which takes into account correlations between points inversely proportional to distance, and a more complex quasi-periodic (QP) kernel which adds a periodic component to it and therefore is often used to model the semi-periodic signals induced by stellar activity that decorrelates with time due to active regions evolving on the surface of a star (e.g. Pont et al. 2013; Haywood et al. 2014; López-Morales et al. 2016; Cloutier et al. 2017; Astudillo-Defru et al. 2017; Bonfils et al. 2018; Díaz et al. 2019). These two kernels result in covariance matrices of the following forms:
![\begin{eqnarray}\mathcal{K}_{ij,\,\textrm{SE}} &=& A_{\log(R^{\prime}_{\mathrm{HK}})}^2\,\exp\left[-\frac{(t_i-t_j)^2}{2\tau^2}\right] + \delta_{ij}\left(\sigma_i^2 + s_{\log(R^{\prime}_{\mathrm{HK}})}^2\right),\\[1.5pt] \mathcal{K}_{ij,\,\textrm{QP}} &=& A_{\log(R^{\prime}_{\mathrm{HK}})}^2\,\exp\left[-\frac{(t_i-t_j)^2}{2\tau^2} - \Gamma^2\,\sin^2\left(\frac{\pi}{P_{\mathrm{rot}}}|t_i - t_j|\right)\right]\\[1.5pt] && + \,\delta_{ij}\left(\sigma_i^2 + s_{\log(R^{\prime}_{\mathrm{HK}})}^2\right), \nonumber \end{eqnarray}](/articles/aa/full_html/2019/07/aa35457-19/aa35457-19-eq20.png)
where 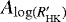 is the amplitude of the GP regression modelling the high-frequency
is the amplitude of the GP regression modelling the high-frequency 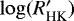 , τ is the de-correlation timescale, Prot is the stellar rotational period, and Γ is the scale of the correlation (e.g. Rasmussen 2006). The last term in both kernels takes into account white noise in the data, which has for variance the sum between the
, τ is the de-correlation timescale, Prot is the stellar rotational period, and Γ is the scale of the correlation (e.g. Rasmussen 2006). The last term in both kernels takes into account white noise in the data, which has for variance the sum between the 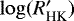 photon noise variance
photon noise variance 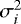 and a parameter
and a parameter 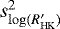 that accounts for additional white noise. In addition to this covariance, a constant will be adjusted to the high-frequency
that accounts for additional white noise. In addition to this covariance, a constant will be adjusted to the high-frequency 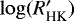 time-series to adjust for the mean.
time-series to adjust for the mean.
We used the george package (Foreman-Mackey 2015) for building the covariance and predicting the GP regression on the 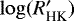 time-series and the emcee package (Foreman-Mackey et al. 2013) for sampling, using the affine invariant MCMC ensemble sampler (Goodman & Weare 2010) and the marginalised posterior probability density functions (PDF) of the model parameters with the goal of maximising a defined likelihood function. In the case of a covariance matrix where elements outside of the diagonal are not null, as is the case here with our GP quasi-periodic kernel, the log-likelihood
time-series and the emcee package (Foreman-Mackey et al. 2013) for sampling, using the affine invariant MCMC ensemble sampler (Goodman & Weare 2010) and the marginalised posterior probability density functions (PDF) of the model parameters with the goal of maximising a defined likelihood function. In the case of a covariance matrix where elements outside of the diagonal are not null, as is the case here with our GP quasi-periodic kernel, the log-likelihood 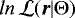 takes the form:
takes the form:
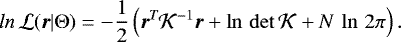 (3)
(3)
In this equation, r is the vector of residuals, in this case the high-frequency 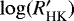 time-series minus the constant parameter to adjust the mean, Θ is a list of allmodel parameters, N is the number of observations, and “det” stands for determinant.
time-series minus the constant parameter to adjust the mean, Θ is a list of allmodel parameters, N is the number of observations, and “det” stands for determinant.
Before performing any analysis, we re-centred the high-frequency 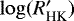 time-series around its mean. We tried first to train the GP regression with either the SE or QP kernels by letting all the parameters free to vary with loose priors, but due to the lack of data and the bad sampling of consecutive stellar rotation periods it was not possible to constrain τ in the case of the SE kernel, and τ, Prot, and Γ in the QP kernel. We therefore decided to fix those parameters.
time-series around its mean. We tried first to train the GP regression with either the SE or QP kernels by letting all the parameters free to vary with loose priors, but due to the lack of data and the bad sampling of consecutive stellar rotation periods it was not possible to constrain τ in the case of the SE kernel, and τ, Prot, and Γ in the QP kernel. We therefore decided to fix those parameters.
By the analysis of activity performed in Sect. 3.3, it is clear that the stellar rotation period is somewhere close to 36.55 days. We therefore fixed Prot to this value. The parameter τ corresponds to the average lifetime of active regions. We first tried to use the relation found in Giles et al. (2017) that uses the scatter in photometry and the stellar effective temperature to estimate the lifetime of spots. With a TESS light-curve rms of 0.49 mmag and a stellar effective temperature of 5131 K, Eq. (8) in Giles et al. (2017) gives a spot lifetime of 24.9 days7, much shorter than the stellar rotation period. This is not expected and could be due to several problems. The relation found in Giles et al. (2017) is calibrated for stars with rotation periods smaller than 20 days, thus more active than HD 15337. In addition, it was based on Kepler photometry, which is performed in a bluer filter than TESS, and therefore should be more affected by stellar activity due to spot contrast increasing towards the blue. On the Sun, the average lifetime of main active regions is about two stellar rotations (Howard 2000). We therefore decided to fix τ at twice Prot, that is, 73.1 days. Finally, we needed to set the value for Γ. Looking at the literature, we found values for Γ of 2.2, 1.2, 2.08, and 2.0 in López-Morales et al. (2016), Cloutier et al. (2017), Damasso & Del Sordo (2017), and Dittmann et al. (2017), respectively. We therefore decided to use a fixed value of 2.0 here as in any case, the exact value of this parameter is not critical.
Before sampling the posterior PDF of both GP models with the kernels described above using the emcee MCMC, we first initialised the different parameters to the values listed in Table 3. We then used the scipy minimize algorithm to obtain an estimate of the maximum a posteriori (MAP) solution for the different parameters. Subsequently, we selected the priors for each parameter as described in Table 3 and performed ten independent MCMC runs starting with the MAP solution, each of them having four times more walkers than the number of parameters, that is, 12 here. For each run, a tiny amount of noise (10−8) was added to the MAP solution before starting sampling. Each run consists of a burn-in phase of 5000 iterations, followed by a production phase of 100 000 iterations. We note that after the burn-in phase, the highest likelihood solution is kept and injected, with a tiny amount of noise (10−8), as initial condition to the production phase.
To check that our MCMC chains properly converged, we used the GR statistic. Within an emcee run, there are 12 chains per parameter, corresponding to the number of selected walkers; however, those chains are not independent as they cross-talk with each other (Goodman & Weare 2010). We therefore compared chains within the ten independent MCMC runs that we performed. For each parameter, the GR statistics is computed for all the chains of walkers 1 up to 12 in the ten independent runs. We therefore get 12 GR statistics values per parameter. In our case, all the GR statistics values were below 1.01, indicating that our chains properly converged. After checking the autocorrelation timescale for each parameter and each walker chain, we kept only one step every 1000 iterations. We then combined for each parameter the chains from all the corresponding walkers and for the ten independent MCMC runs.
In Fig. A.1 we show the correlation between the different marginalised posterior PDFs of the model parameters sampled by our MCMC when using a SE kernel. No significant correlation is observed, and the marginalised posterior PDFs followa well-sampled Gaussian distribution. The marginalised posterior PDFs in the case of the QP kernel are identical. The mean of each marginalised posterior PDF with its 68% uncertainty for both the SE and QP kernels are given in Table 3. As we can see, the results for the SE and QP kernels are fully compatible within errorbars, and therefore in such a case, Occam’s Razor principle tell us that the simpler model should be considered. The SE kernel is therefore favoured, and a likely explanation for that is that the data in hand are not well sampled at the stellar rotation period of the star, which therefore prevents a QP kernel from adding a significant improvement.
The GP regression model using a SE kernel with the mean values listed in Table 3 is over-plotted on the high-frequency 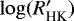 time-series in the top panel of Fig. 5. The two middle panels show the same result, however zoomed-in to better highlight the GP regression during times when a significant amount of data is present. Finally, the residuals are shown in the bottom panel. The
time-series in the top panel of Fig. 5. The two middle panels show the same result, however zoomed-in to better highlight the GP regression during times when a significant amount of data is present. Finally, the residuals are shown in the bottom panel. The 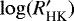 rms decreases from 0.019 in the high-frequency
rms decreases from 0.019 in the high-frequency 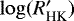 time-series to 0.011 in the
time-series to 0.011 in the 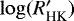 residuals, which demonstrates that our GP regression is able to significantly mitigate stellar activity, even though we had to guess a value for the de-correlation timescale of the SE kernel.
residuals, which demonstrates that our GP regression is able to significantly mitigate stellar activity, even though we had to guess a value for the de-correlation timescale of the SE kernel.
Initial parameters, priors, and best solutions for the models fitted to the 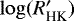 and the RVs.
and the RVs.
 |
Fig. 5 Top: Gaussian process regression over-plotted on the high-frequency |
3.4.3 Gaussian process and Keplerian model fit to the RVs
In the preceding section, we show that a GP regression of the 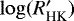 time series using a SE or QP kernel gives equivalent results and therefore a SE kernel should be used to model stellar activity effects as less complex. By making the hypothesis that the covariance due to stellar activity seen in the RVs is similar to the one seen in
time series using a SE or QP kernel gives equivalent results and therefore a SE kernel should be used to model stellar activity effects as less complex. By making the hypothesis that the covariance due to stellar activity seen in the RVs is similar to the one seen in 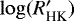 , we use the same de-correlation timescale to model stellar activity in the RV time-series using a GP regression with a SE kernel. Only the amplitude and extra white-noise terms are free to vary and are sampled using an MCMC as the values for those hyper-parameters are different between the
, we use the same de-correlation timescale to model stellar activity in the RV time-series using a GP regression with a SE kernel. Only the amplitude and extra white-noise terms are free to vary and are sampled using an MCMC as the values for those hyper-parameters are different between the 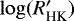 and RV time-series.
and RV time-series.
Based on the preliminary analysis described in Sect. 3.4.1, the model used here to fit the RV data of HD 15337 is composedof two offsets to account for the jump induced in RV by the change of optical fibres on June 1, 2015, a polynomial drift of second order to account for the long-term trend observed in the data, and two Keplerian functions to account for the signal induced by TOI-402.01 and TOI-402.02. This model can be summarised as follows:
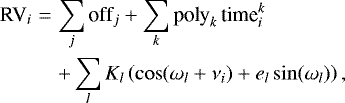 (4)
(4)
where i corresponds to each observation, j = [1, 2] corresponds to different instruments, in this case two for data before and after June 1, 2015, k = [1, 2] for a second-order polynomial, l = [1, 2] for the two planets, Kl, ωl, and el are the amplitude, argument of periapsis, and eccentricity of planet l and νi is the true anomaly. In addition to this model, we use a GP regression with a quasi-periodic kernel to account for the short-term stellar activity present in the RVs. This kernel will be similar to the one described in Eq. (1), with the exception that the amplitude 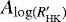 is replaced by ARV and the extra white noise jitter term
is replaced by ARV and the extra white noise jitter term 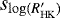 is replaced by sRV. As in Sect. 3.4.2, we sample the marginalised posterior PDFs of the model parameters with an MCMC with the goal of maximising the likelihood function described in Eq. (3). In this equation, r, the vector of residuals, is replaced by the RV times-series minus RVi, our model for the RVs shown in Eq. (4).
is replaced by sRV. As in Sect. 3.4.2, we sample the marginalised posterior PDFs of the model parameters with an MCMC with the goal of maximising the likelihood function described in Eq. (3). In this equation, r, the vector of residuals, is replaced by the RV times-series minus RVi, our model for the RVs shown in Eq. (4).
The offsets and polynomial coefficients are initialised to the best values found during the preliminary RV analysis (see Sect. 3.4.1) and can be found in Table 3. The period, de-correlation timescale, and length scale of the GP regression are fixed due to the small amount and bad sampling of the data (see Sect. 3.4.2) and the GP amplitude is initialised to 2.5 m s−1. The orbital period and time of transit of the two planets are initialised to the values found by the analysisof the TESS light curves performed in Sect. 2.1 and their amplitude, e cosω, and e sin ω are initialised tothe values found during the preliminary RV analysis (see Sect. 3.4.1). We note here that we sample over ecosω and esinω rather than e and ω, as this makes the posterior PDF easier to sample.
Regarding priors, these are summarised in Table 3. We used tight normal priors for the period and time of transit of the two planets based on the results of our transit analysis (see Sect. 3.2) as we do not expect the RV to provide more constraints on those parameters. We also choose a Beta distribution with parameters 0.711 and 2.57 as prior for the eccentricity, as advised by Kipping (2013). All the other priors are chosen uniform.
As explained in details in Sect. 3.4.2, we first searched for the maximum a posteriori (MAP) solution for the different parameters and then performed ten independent MCMC runs starting with the MAP solution using emcee and selecting four times more walkers than the number of parameters, that is, 64 here. Each run consisted of a burn-in phase of 5000 iterations followed by a production phase of 100 000 iterations. We note that after the burn-in phase, the highest likelihood solution is kept and injected with a tiny amount of noise (10−8) as initial condition to the production phase.
To check the convergence of the chains, we used, as in Sect. 3.4.2, the GR statistics over the ten independent MCMC runs. For the 16 parameters and 64 walkers, we thus obtain 1024 GR statistics values that were all below 1.01, therefore implyingthat all our chains converged properly. For each chain, we selected one iteration every 1000 to remove any autocorrelation. For each parameter we then combined the chains from all the corresponding walkers and for the ten independent MCMC runs.
The shape and correlation of the marginalised posterior PDFs of the parameters are shown in Fig. B.1 for the drift, offset polynomial, and GP amplitude parameter and in Figs B.2 and B.3 for the parameters of TOI-402.01 and TOI-402.02, respectively. We observe strong correlations between the offset and the polynomial parameters, however the marginalised posterior PDFs are well sampled. We note that those correlations appear even though we re-centred the time-series around the time of transit8 found by TESS before sampling the posterior PDF. For all the other parameters no strong correlation is observed and the marginalised posterior PDFs are also well sampled. The mean of the marginalised posterior PDF of each parameter is reported in Table 3 with each error being the rms of each marginalised posterior PDF, therefore describing the 68% confidence level of each parameter. Our RV model using those parameters is shown in the top panel of Fig. 6 over-plotted on the data. In the middle and bottom panels of the same figure, we can see the RV residuals and their corresponding GLS periodogram, respectively. As we can see, no significant signal appears in those RV residuals. The strongest signal is at 6.6 days, with a p-value of 3.4% and an estimated amplitude of 0.44 m s−1. The rms of the RV residuals is 1.36 m s−1, much lower than the 2.17 m s−1 obtained with our preliminary RV analysis in Sect. 3.4.1. Using a GP regression with a quasi-periodic kernel therefore much more effectively mitigates stellar activity than using a linear dependence with the high-frequency 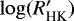 time-series.
time-series.
The marginalised posterior PDFs of the planetary parameters of interest are shown in Fig. 7. All the marginalised posterior PDFs present a Gaussian shape, except for the eccentricity that shows a slight but relatively marginal skewness, and therefore we can confidently select the mean and standard deviation as the best estimate and 68% confident error bar for each planet parameter. Using those means, the planetary signals for TOI-402.01 and 402.02 are shown folded in phase in Fig. 8. The marginalised posterior PDFs for the time of transit and period of both planets are extremely similar to the priors used, as expected, implying that the RV measurements do not constrain those parameters any further. All the other parameters are compatible within 1σ with the preliminary RV analysis performed in Sect. 3.4.1 and shown in Fig. 4. Therefore, even if we consider in this section stellar activity with a better model, which is confirmed by the smaller rms of the RV residuals that we obtain, that is, 1.36 compared to 2.17 m s−1, the impact on the derived planetary parameters is not significant.
To verify that the GP regression fitted here does not significantly absorb the signal of TOI-402.02, we show in Fig. 9 its corresponding periodogram. As expected, the highest signals modelled by the GP regression are found at the stellar rotation period and at longer periods. At 17.17 days, corresponding to the orbital period of TOI-402.02, the GP regression absorbs about 0.13 m s−1. The impact of the GP on the planetary signal of TOI-402.02 is therefore negligible and we can be confident in the orbital parameters derived for this planet.
We note that we also tried to adjust the same model as presented here, this time using a GP regression with a QP kernel whose hyper-parameters were fixed to the values described in the 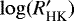 analysis (see Sect. 3.4.2 and top of Table 3). However, like in the
analysis (see Sect. 3.4.2 and top of Table 3). However, like in the 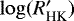 analysis, we obtained values extremely similar to the fit using a SE kernel, well within 1σ. Therefore, we decided in this section to only show the results of the SE kernel as it is a simpler model.
analysis, we obtained values extremely similar to the fit using a SE kernel, well within 1σ. Therefore, we decided in this section to only show the results of the SE kernel as it is a simpler model.
 |
Fig. 6 Top: best-fit model using the mean of all marginalised posterior PDFs obtained by the MCMC sampler over-plotted on the raw RV data of HD 15337 after removing the instrumental offset due to the change of the fibres on June 1, 2015. Middle: RV residuals after removing the best-fit model. The rms of this time-series is 1.36 m s−1. Bottom: GLS periodogram of the RV residuals that does not highlight any significant signals. |
 |
Fig. 7 Marginalised posterior PDFs of the orbital parameters of TOI-402.01 (subscript 1) and TOI-402.02 (subscript 2). The planetary mass posterior PDFs have been derived by considering the orbital inclinations of TOI-402.01 and TOI-402.02 with their respective errors (see Table 2), and the stellar mass with its respective error (see Table 1). The red vertical lines represent the mean value of each distribution. The title of each subplot gives this mean value for each marginalised posterior PDF, in addition to the rms of the distribution giving therefore the 68% confidence interval error. |
 |
Fig. 8 Phase-curves for TOI-402.01 and TOI-402. Top plots: best fitted planetary signal in the RV data after removing the instrument offsets, the second-order polynomial drift, and the GP regression. Bottom plots: RV residuals after removing the planetary signal. |
3.5 Combined photometric and RV analysis
To test if a combined photometric and RV analysis could better constrain the planetary orbital parameters, we performed a combined modelling using EXOFASTv2. Unfortunately, as GP regression is not implemented in EXOFASTv2, this analysis does not model stellar activity.
This combined analysis slightly improves the precision on the orbital period of TOI-402.01 and TOI-402.02 by 16 and 7%, respectively,on the time of transit of TOI-402.01 by 1%, and on the radius of TOI-402.01 by 7%. Also, the eccentricity of both planets slightly decreases to 0.09 instead of 0.17 and 0.19 for TOI-402.01 and TOI-402.02, respectively. However, regarding the planetary masses, the precision becomes worse by 26 and 33%, respectively, due to the fact that stellar activity is not accounted for in this combined analysis. All the values for the different fitted parameters in this combined analysis are well within 1σ of the values found in our analysis of the RVs using as priors the tight constraints given by photometry (see Sect. 3.4.3 and results in Table 3).
From this analysis, we can conclude that the benefit of performing a combined photometric and RV analysis including GP regression would be marginal. We are therefore confident that the mass, radius, and orbital characteristics of TOI-402.01 and TOI-402.02 stated in this paper are robust.
 |
Fig. 9 GLS periodogram of the GP regression showing the RV amplitude in meters per second with respect to the period. The red vertical windows highlight the orbital period of TOI-402.02 and the stellar rotation period. |
4 Discussion
4.1 Interior characterisation
Given the bulk densities, TOI-402.01 is dominated by a rocky composition, while TOI-402.02 must contain volatile layers. We performed an analysis similar to Dorn et al. (2017) to further constrain the planet bulk properties. All the details of the analysis and key figures can be found in Fig. C.1 and Table C.2 summarise posterior distributions of inferred interior parameters for both TOI-402.01 and TOI-402.02. The bulk densities of the two planets are significantly different. In consequence, the interiors of TOI-402.01 have negligible amounts of volatile elements (i.e. water and gas), while there are significant amounts for TOI-402.02.
TOI-402.01 is predominantly rocky (rcore+mantle = 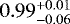 Rp). The mass, radius, and bulk abundances provide information on core size and mantle composition. We note that the bulk abundance constraints do not allow the interiors to match the measured bulk density of ρp = 1.72ρ⊕. This is because the abundance constraints favour Earth-like densities, while the bulk density of TOI-402.01 is higher. In order to better fit the bulk density, we relaxed the constraint on Fe/Si in a separate scenario and thereby allowed for rocky interiors with large core mass fractions (Table C.2). Although this scenario can fit mass and radius, it remains unclear how such iron-rich interiors for massive super-Earths can be formed. We note that the addition of light elements in the core might be crucial to reconcile measured abundance constraints with bulk density. Here, we have assumed pure iron cores for simplicity. Further investigations are required to understand the importance of light core elements for super-Earths.
Rp). The mass, radius, and bulk abundances provide information on core size and mantle composition. We note that the bulk abundance constraints do not allow the interiors to match the measured bulk density of ρp = 1.72ρ⊕. This is because the abundance constraints favour Earth-like densities, while the bulk density of TOI-402.01 is higher. In order to better fit the bulk density, we relaxed the constraint on Fe/Si in a separate scenario and thereby allowed for rocky interiors with large core mass fractions (Table C.2). Although this scenario can fit mass and radius, it remains unclear how such iron-rich interiors for massive super-Earths can be formed. We note that the addition of light elements in the core might be crucial to reconcile measured abundance constraints with bulk density. Here, we have assumed pure iron cores for simplicity. Further investigations are required to understand the importance of light core elements for super-Earths.
TOI-402.02 hosts a thick atmosphere that is likely dominated by primordial H/He. Although, mass and radius are insufficient to determine the composition of the gas envelopes (uncertainties on Zgas are large), considering the evolution of the atmospheres can inform us on the nature of the gas as stellar irradiation drives atmospheric escape and can efficiently erode thin primordial atmospheres of H/He on short time-scales (Dorn & Heng 2018). In consequence, primordial H/He gas can be excluded for atmospheres that are too thin in order to be stable against evaporative loss. Following the work of Dorn & Heng (2018), there is a theoretical minimum threshold thickness for a primordial H/He atmosphere, which corresponds to the amount of gas (in H2) that is lost on a short time-scale (here we use 100 Myr). For TOI-402.01, assuming solar-like X-ray and UV (XUV) flux emitted by the host star, this threshold thickness is 0.12 Rp and thus larger than the inferred thicknesses (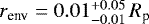 ). Any H/He-dominated layer is therefore excluded for TOI-402.01 and a possible thin atmosphere could be of volcanic origin. In the case of TOI-402.02, the threshold thickness is 0.07 Rp and inferred thicknesses are larger (
). Any H/He-dominated layer is therefore excluded for TOI-402.01 and a possible thin atmosphere could be of volcanic origin. In the case of TOI-402.02, the threshold thickness is 0.07 Rp and inferred thicknesses are larger (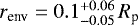 ) which indicates that a primordial H/He layer on TOI-402.02 is likely for this less-irradiated planet.
) which indicates that a primordial H/He layer on TOI-402.02 is likely for this less-irradiated planet.
If TOI-402.01 has indeed an atmosphere, this would be interesting from a theoretical point of view, since outgassing processes are very mass dependent for some tectonic regimes (e.g. stagnant-lid). In the case of stagnant-lid regimes, no massive terrestrial-like atmospheres are expected for planets of ≿8 M⊕ (Noack et al. 2017; Dorn et al. 2018). A massive atmosphere of volcanic origin could only be present if the planet is in a different convection regime, for example with plate tectonics. Whether super-Earths can drive plate tectonics or not is still unclear from the variety of modelling studies (Valencia et al. 2007; Noack & Breuer 2014; Korenaga 2010; Van Heck & Tackley 2011).
4.2 Temporal evolution under XUV-driven atmospheric escape
The estimates in the previous section suggest that TOI-402.01 should havelost a primordial H/He envelope, whereas TOI-402.02 should have kept it. The same conclusion is reached when comparing the location of the planets in the semimajor axis–radius and semimajor axis–mass planes directly with the locus of the evaporation valley as predicted by evaporation models (Owen & Wu 2013; Lopez & Fortney 2013; Jin et al. 2014). In Jin & Mordasini (2018), the authors predict that for solar-like star hosts, Earth-like bulk composition planets less massive than 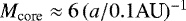 M⊕, which corresponds to
M⊕, which corresponds to 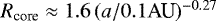 R⊕, loose their entire H/He envelope because of XUV-driven atmospheric escape. For the low-mass close-in planets orbiting TOI-402, the total mass is approximately the same as the (astrophysical) core mass (Lopez & Fortney 2014). Therefore, using the theoretical prediction from Jin & Mordasini (2018), we find that Mcore should be at least ~11.5 M⊕ for TOI-402.01 to keep its H/He envelope, while it should be at least ~5 M⊕ for TOI-402.02. With masses of 7.20 and 8.79 M⊕ for TOI-402.01 and TOI-402.02, respectively, we thus arrive at the conclusion that the inner planet lost its entire H/He envelope, while its outer companion kept a significant part of it. Therefore, these two planets should be found on both sides of the evaporation valley, which is the case given their distinct densities, as discussed above (see also Fig. 11).
R⊕, loose their entire H/He envelope because of XUV-driven atmospheric escape. For the low-mass close-in planets orbiting TOI-402, the total mass is approximately the same as the (astrophysical) core mass (Lopez & Fortney 2014). Therefore, using the theoretical prediction from Jin & Mordasini (2018), we find that Mcore should be at least ~11.5 M⊕ for TOI-402.01 to keep its H/He envelope, while it should be at least ~5 M⊕ for TOI-402.02. With masses of 7.20 and 8.79 M⊕ for TOI-402.01 and TOI-402.02, respectively, we thus arrive at the conclusion that the inner planet lost its entire H/He envelope, while its outer companion kept a significant part of it. Therefore, these two planets should be found on both sides of the evaporation valley, which is the case given their distinct densities, as discussed above (see also Fig. 11).
To directly test the hypothesis that evaporation has shaped the distinct densities of the planets, we have simulated the long-term thermodynamical evolution (cooling, contraction, atmospheric escape) of the two planets. The goal is to understand first whether the observed properties of the planets (like in particular the large density contrast) can indeed be explained by evolution under XUV-driven evaporation, and second to constrain the post formation properties. Similar studies (Lopez & Fortney 2013; Owen & Morton 2016) were conducted in the past for the planets around Kepler-36 (Carter et al. 2012) which also have a large density contrast.
To do so, we simulated the evolution of the planets using the Bern planet evolution model completo21 which was described in Mordasini et al. (2012); Jin et al. (2014); Linder et al. (2019). XUV-driven escape in the radiation-recombination and energy-limited regimes is considered (Murray-Clay et al. 2009). The cores have an Earth-like 2:1 silicate:iron composition described by the polytropic EOS of Seager et al. (2007). The envelope consists of H/He described by the EOS of Saumon et al. (1995). The opacity corresponds to a condensate-free solar-composition gas (Freedman et al. 2014).
Figure 10 shows a simulation that reproduces the observed masses and radii at the observed age of the star. The initial conditions, the final results, and the comparisons to the observed values are given in Table 4. The most important outcome, that is, that TOI-402.01 becomes a bare core and TOI-402.02 keeps H/He, is immediately found without tuning the initial conditions or model parameters away from generic values (i.e. an initial envelope mass of 1 to 10% of the core mass, an efficiency factor of atmospheric escape of about 0.1–0.3, and a saturated XUV luminosity of about 10−3 of the bolometric luminosity).
The only initial condition that requires some fine tuning is the initial (i.e. post-formation) envelope mass of TOI-402.02. The value of 0.3 M⊕ was determined by requiring that the transit radius at 7.5 Gyr correspond to the observed value. This value is on the lower side of what planet-formation models find for a planet with a (core) mass of about 9 M⊕ (e.g. Alibert et al. 2005; Ikoma & Hori 2012; Mordasini 2018), but still well within the range predicted by models explicitly solving the governing internal structure equations (see Mordasini 2018).
For TOI-402.01, the post-formation H/He envelope mass is in contrast not important for the final outcome (one always finds a complete loss of the envelope) and thus remains unconstrained. In the figure, the same value as for TOI-402.02, 0.3 M⊕, was used for simplicity. Choosing for example a much higher initial mass of 1.6 M⊕ (with the same core mass) also leads to a loss of the envelope, but at a later time of about 400 Myr. The reason for this independency is that a higher initial envelope mass means that on one hand, there is more mass to evaporate, but on the other hand, the mean density of the planet is also lower (Lopez & Fortney 2014), which in turn means that the evaporation rate is higher. This drives the system to an outcome that is independent of the post-formation envelope mass.
In the top-left panel of Fig. 10, the radii are initially significantly larger than today. This is mainly due to the high intrinsic luminosity of young planets (Mordasini et al. 2017). The radius of TOI-402.01 is initially larger than that of TOI-402.02, which is a consequence of the identical initial envelope masses and the lower (core) mass of TOI-402.01. The rapid decrease of the radius of TOI-402.01 at the moment when the last bit of H/He is lost (at about 100 Myr) is alsovisible. This significant decrease of the radius on a short timescale gives rise to the existence of the evaporation valley on a population-wide level (Jin et al. 2014). The bottom-left panel shows the corresponding mean densities.
The top-right panel displays the decrease of the H/He envelope mass. We see that the envelope mass of TOI-402.02 today is about 0.08 M⊕, about a third of the initial mass. Most of the escape occurs as expected early on (e.g. Lopez & Fortney 2013), when the stellar XUV luminosity is high, and the planetary radii are large.
The bottom-right panel finally shows the total H/He evaporation rate as a function of time for the two planets. During the saturated phase – assumed to have a duration of 100 Myr (e.g., Tu et al. 2015) – the evaporation rates are high, about 3 × 1011 g s−1 for the outer planet, and even almost 1012 g s−1 for the inner one. The evaporation rate of TOI-402.02 nowadays is predicted to be close to 108 g s−1. For comparison, the escape rate of the warm Neptune-mass planet GJ 3470b was recently measured to be about 1010 g s−1 (Bourrier et al. 2018).
In summary, we conclude that the current-day densities of the planets and in particular the large density contrast between them can be well explained by atmospheric escape of H/He envelopes surrounding Earth-like cores. The same conclusion was already reached for another important system with planets on both side of the valley, Kepler-36 (Lopez & Fortney 2013; Owen & Morton 2016). There is however one interesting difference between Kepler-36 and TOI-402: in Kepler-36, the two planets are at very similar orbital distances (difference of just 11%), but differ clearly in mass (difference of about 80%). This mass difference is the reason that the outer planet around Kepler-36 can keep the H/He.
Here, in TOI-402, the mass difference is in contrast much smaller (only about 20%), but the outer planet resides at a much larger orbital distance (difference of 240%). Here, it is because of this larger orbital distance combined with the negative radial slope of the evaporation valley (Van Eylen et al. 2018) that the outer planet can keep its H/He. The somewhat higher mass of TOI-402.02 alone would in contrast not suffice to prevent complete loss if the planet were to be placed at (or close to) the position of TOI-402.01.
 |
Fig. 10 Temporal evolution of the TOI-402 planets. The panels show as a function of time (a) the transit radius (in Earth radii), (b) the mass of the H/He envelope (in Earth masses), (c) the mean density of the planets, and (d) the XUV-driven hydrodynamic H/He evaporation rate. In the two panels on the left, the horizontal lines show the observed values and the 1-σ error intervals. The yellow region indicates the 1-σ age range of the star, with the vertical grey line showing the nominal age of 7.5 Gyr. |
Initial conditions and results of the evolutionary calculations, and comparison to the observed values.
4.3 Atmospheric characterisation
Although the present atmosphere of TOI-402.02 strongly depends on XUV irradiation history (Vidal-Madjar et al. 2003), our analysis of its past evolution under stellar irradiation shows that it could have survived atmospheric escape and kept a substantial fraction of its primordial volatile envelope, about a third of its total mass (see Fig. 10 and Sect. 4.2). Atmospheric mass loss from TOI-402.02 decreased over time as the host star became less luminous, the planet density increased (making it more difficult for gas to escape), and the radius of its envelope decreased (decreasing the area over which it captures stellar energy). Nonetheless, its atmosphere could still escape today at a moderate rate of about 108 g s−1.
Whether TOI-402.02 is water-rich or hosts a H/He envelope, the composition of its escaping outflow will be dominated by hydrogen atoms. The planet is sufficiently irradiated for water to turn into steam, which would photo-dissociate at high altitudes and sustain a hydrogen-rich upper atmosphere prone to escape (Wu & Chen 1993; Jura 2004). The resulting exosphere could be searched for using transit spectroscopy in the ultraviolet stellar Lyman-α line, which is sensitive to the neutral hydrogen atoms. The neutral fraction of the outflow depends on several processes and properties (photoionization, temperature, planetary density, etc.), but a super-Earth could have upper atmospheresthat are almost completely neutral (Salz et al. 2016). Escape rates of neutral hydrogen on the order of 108 g s−1 from TOI-402.02 could be readily detected in a few transits with the Hubble Space Telescope (see the case of GJ 436b, Bourrier et al. 2016; and HD 97658b, Bourrier et al. 2017, a planet with similar properties and host star to TOI-402.02; see Fig. 11). The main limitation in observing stellar Lyman-α lines resides in their absorption by the interstellar medium. The proximity of TOI-402 (45 pc), combined with its brightness and its stellar type, makes it one of the few stars to host small transiting planets that would allow for Lyman-α transit spectroscopy to be carried out using the Hubble Space Telescope.
The expected signal of water vapour in transmission, for five scale heights and assuming a bond albedo of zero and a mean molecular weight of 20, is around a few parts per million for both TOI-402 planets. This signal is out of reach of present instrumentation, but could be detectable in the near future with the James Webb Space Telescope or future ground-based Extremely Large Telescopes. Searching for the signature of helium in the upper atmosphere of TOI-402.02 could however be done with currentfacilities to disentangle between a water-dominated and a H/He envelope. Helium in the escaping outflow could be detected viaits near-infrared triplet, a new atmospheric tracer (Seager & Sasselov 2000; Oklopčić & Hirata 2018) that can yield deep absorption signatures when observed at high spectral resolution (Allart et al. 2018, 2019; Nortmann et al. 2018; Salz et al. 2018).
 |
Fig. 11 Planetary radius as a function of the stellar irradiation received by the planet (based on Fulton et al. 2017). TOI-402.01 stands just below the radius gap while TOI-402.02 stands above. The GJ 9827 system is added here as it represents, with TOI-402, probably the best system to understand the radius gap through exoplanetology comparison. HD 97658b is also added for a direct comparison with TOI-402.02 as they are supposed to have water-rich composition and, furthermore, a search for photo-dissociation of water has been undertaken on HD 97658b by Bourrier et al. (2017). The data at the origin of this diagram have been extracted from the NASA exoplanet archive (https://exoplanetarchive.ipac.caltech.edu). |
5 Conclusion
We confirm the detection of the two planets transiting TOI-402 found by TESS using HARPS RV measurements. With periods of 4.75642 ± 0.00021 and 17.1784 ± 0.0016 days, radii of 1.70 ± 0.06 and 2.52 ± 0.11 R⊕, and masses of 7.20 ± 0.81 and 8.79 ± 1.68 M⊕, we find that one planet is a hot rocky super-Earth and the other a warm puffy super-Earth. The precision on the planetary radii is 3.6 and 4.2%, respectively. The precision on these planetary masses is 11.3 and 19.1%, including the error in the host stellar mass of 4.9% and in the orbital inclination of 0.4 and 0.06%, respectively. Those values have been derived by re-analysing the TESS photometry using EXOFASTv2, and analysing 85 HARPS public RV measurements. The photometric and spectroscopic analyses were performed separately, however the tight marginalised posterior PDFs for the period and time of transit of TOI-402.01 and TOI-402.02 obtained from photometry were used as priors to the RV analysis. We note that the host star TOI-402 (HD 15337), a K1 dwarf with effective temperature 5131 ± 74 K and logg 4.37 ± 0.13, is a rather low-activity star like the Sun and its RVs are affected by stellar signals at the 2 m s−1 level (see the amplitude of the GP regression in Table 3). We therefore used a GP regression to model stellar activity in the RV time-series.
As we can see in the irradiation-radius diagram shown in Fig. 11, the two planets lie on different sides of the radius gap found at ~1.8 R⊕ (Buchhave et al. 2014; Rogers 2015; Fulton et al. 2017). The origin of this gap is not yet clearly understood (e.g. Lehmer & Catling 2017; Ginzburg et al. 2018). Photo evaporation is likely the main driver (Jin et al. 2014; Owen & Wu 2017; Jin & Mordasini 2018), and the study of the temporal evolution under XUV-driven atmospheric escape of the TOI-402 planetary system performed in this paper confirms this hypothesis (see Sect. 4.2).
With the brightness of the host star (V = 9.09 and J = 7.55), TOI-402 is one of the most amenable systems, with GJ 9827 (Niraula et al. 2017; Rodriguez et al. 2018), to perform comparative exoplanetology across the evaporation valley and thus help us to better understand the radius gap.
Acknowledgements
X.D. is grateful to The Branco Weiss Fellowship–Society in Science for its financial support. This study was based on observations collected at the European Southern Observatory under the GTO program 072.C-0488(E) and Large programs 183.C-0972(A), 192.C-0852(A), 196.C-1006 and 198.C-0836(A). We acknowledge the use of public TESS Alert data from pipelines at the TESS Science Office and at the TESS Science Processing Operations Center. Resources supporting this work were provided by the NASA High-End Computing (HEC) Program through the NASA Advanced Supercomputing (NAS) Division at Ames Research Center for the production of the SPOC data products. We thank the Swiss National Science Foundation (SNSF) and the Geneva University for their continuous support to our planet search programs. This work has been in particular carried out in the framework of the PlanetS National Centre for Competence in Research (NCCR) supported by the SNSF. This publication makes use of the Data & Analysis Center for Exoplanets (DACE), which is a facility based at the University of Geneva (CH) dedicated to extrasolar planets data visualisation, exchange and analysis. DACE is a platform of the PlanetS NCCR, federating the Swiss expertise in Exoplanet research. The DACE platform is available at https://dace.unige.ch. N.S.C., V.A., and S.G.S. were supported by FCT – Fundação para a Ciência e a Tecnologia through national funds and by FEDER through COMPETE2020 – Programa Operacional Competitividade e Internacionalização by these grants: UID/FIS/04434/2013 & POCI-01-0145-FEDER-007672; PTDC/FIS-AST/28953/2017 & POCI-01-0145-FEDER-028953 and PTDC/FIS-AST/32113/2017 & POCI-01-0145-FEDER-032113. S.G.S. acknowledge support from FCT through Investigador FCT contract nr., IF-00028-2014-CP1215-CT0002. V.A. acknowledges support from FCT through Investigador FCT contract IF/00650/2015/CP1273/CT0001. C.M. acknowledges the support from the Swiss National Science Foundation under grant BSSGI0_155816 “PlanetsInTime”. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research has made use of the SIMBAD database operated at CDS, France.
References
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V., Figueira, P., Santos, N. C., et al. 2015, A&A, 583, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alibert, Y., Mordasini, C., Benz, W., & Winisdoerffer, C. 2005, A&A, 434, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allart, R., Bourrier, V., Lovis, C., et al. 2018, Science, 362, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Allart, R., Bourrier, V., Lovis, C., et al. 2019, A&A, 623, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astudillo-Defru, N., Díaz, R. F., Bonfils, X., et al. 2017, A&A, 605, L11 [Google Scholar]
- Boisse, I., Bouchy, F., Hébrard, G., et al. 2011, A&A, 528, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Astudillo-Defru, N., Díaz, R., et al. 2018, A&A, 613, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchet, J., Mazevet, S., Morard, G., Guyot, F., & Musella, R. 2013, Phys. Rev. B, 87, 094102 [NASA ADS] [CrossRef] [Google Scholar]
- Bourrier, V., Lecavelier des Etangs, A., Ehrenreich, D., Tanaka, Y. A., & Vidotto, A. A. 2016, A&A, 591, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourrier, V., Ehrenreich, D., King, G., et al. 2017, A&A, 597, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourrier, V., Lecavelier des Etangs, A., Ehrenreich, D., et al. 2018, A&A, 620, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buchhave, L. A., Bizzarro, M., Latham, D. W., et al. 2014, Nature, 509, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, J. A., Agol, E., Chaplin, W. J., et al. 2012, Science, 337, 556 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Casagrande, L., Portinari, L., & Flynn, C. 2006, MNRAS, 373, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Cloutier, R., Astudillo-Defru, N., Doyon, R., et al. 2017, A&A, 608, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coffinet, A., Lovis, C., Dumusque, X., & Pepe, F. 2019, A&A, in press, DOI: 10.1051/0004-6361/201833272 [Google Scholar]
- Connolly, J. 2009, Geochem., Geophys. Geosyst., 10, Q10014 [Google Scholar]
- Damasso, M., & Del Sordo, F. 2017, A&A, 599, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Damasso, M., Bonomo, A. S., Astudillo-Defru, N., et al. 2018, A&A, 615, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delisle, J.-B., Ségransan, D., Buchschacher, N., & Alesina, F. 2016, A&A, 590, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz, R. F., Delfosse, X., Hobson, M. J., et al. 2019, A&A, 625, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dittmann, J. A., Irwin, J. M., Charbonneau, D., et al. 2017, Nature, 544, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Dorn, C., & Heng, K. 2018, ApJ, 853, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Dorn, C., Khan, A., Heng, K., et al. 2015, A&A, 577, A83 [EDP Sciences] [Google Scholar]
- Dorn, C., Venturini, J., Khan, A., et al. 2017, A&A, 597, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorn, C., Noack, L., & Rozel, A. 2018, A&A, 614, A18 [EDP Sciences] [Google Scholar]
- Dotter, A. 2016, ApJS, 222, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Dumusque, X., Pepe, F., Lovis, C., & Latham, D. W. 2015, ApJ, 808, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Dumusque, X., Borsa, F., Damasso, M., et al. 2017, A&A, 598, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eastman, J. 2017, Astrophysics Source Code Library [record ascl:1710.003] [Google Scholar]
- Eastman, J., Gaudi, B. S., & Agol, E. 2013, PASP, 125, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Faria, J. P., Haywood, R. D., Brewer, B. J., et al. 2016, A&A, 588, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feng, F., Tuomi, M., Jones, H. R. A., Butler, R. P., & Vogt, S. 2016, MNRAS, 461, 2440 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, F., Tuomi, M., & Jones, H. R. A. 2017, A&A, 605, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foreman-Mackey, D. 2015, Astrophysics Source Code Library [record ascl:1511.015] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Freedman, R. S., Lustig-Yaeger, J., Fortney, J. J., et al. 2014, ApJS, 214, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Fulton, B. J., Petigura, E. A., Howard, A. W., et al. 2017, AJ, 154, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Gandolfi, D., Barragán, O., Livingston, J. H., et al. 2018, A&A, 619, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gandolfi, D., Fossati, L., Livingston, J. H., et al. 2019, ApJ, 876, L24 [Google Scholar]
- Gelman, A., & Rubin, D. B. 1992, Stat. Sci., 7, 457 [Google Scholar]
- Giles, H. A. C., Collier Cameron, A., & Haywood, R. D. 2017, MNRAS, 472, 1618 [Google Scholar]
- Giles, H. A. C., Bayliss, D., Espinoza, N., et al. 2018, MNRAS, 475, 1809 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, S., Schlichting, H. E., & Sari, R. 2016, ApJ, 825, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, S., Schlichting, H. E., & Sari, R. 2018, MNRAS, 476, 759 [Google Scholar]
- Goodman, J., & Weare, J. 2010, Comm. App. Math. Comp., 5, 65 [Google Scholar]
- Gordon, S., & McBride, B. J. 1994, Computer program for calculation of complex chemical equilibrium compositions and applications. Part 1: Analysis, NASA RP-1311 [Google Scholar]
- Grunblatt, S. K., Howard, A. W., & Haywood, R. D. 2015, ApJ, 808, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T. 2010, A&A, 520, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, R. D., Collier Cameron, A., Queloz, D., et al. 2014, MNRAS, 443, 2517 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkel, N. R., Timmes, F. X., Young, P. A., Pagano, M. D., & Turnbull, M. C. 2014, AJ, 148, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Houk, N., & Fuentes-Williams, T. H. 1982, BAAS, 14, 615 [NASA ADS] [Google Scholar]
- Howard, R. 2000, Sunspot Evolution, ed. P. Murdin (Bristol: IOP Publishing and London) [Google Scholar]
- Huang, C. X., Burt, J., Vanderburg, A., et al. 2018, ApJ, 868, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Ikoma, M., & Hori, Y. 2012, ApJ, 753, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M. 2017, Kepler Data Processing Handbook: Overview of the Science Operations Center, Tech. rep [Google Scholar]
- Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, Proc. SPIE, 9913, 99133E [Google Scholar]
- Jenkins, J. M., Tenenbaum, P., Seader, S., et al. 2017, Kepler Data Processing Handbook: Transiting Planet Search, Tech. rep [Google Scholar]
- Jin, S., & Mordasini, C. 2018, ApJ, 853, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, S., Mordasini, C., Parmentier, V., et al. 2014, ApJ, 795, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, D. E., Stenning, D. C., Ford, E. B., et al. 2017, ArXiv e-prints [arXiv:1711.01318] [Google Scholar]
- Jura, M. 2004, ApJ, 605, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 434, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Korenaga, J. 2010, ApJ, 725, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1993, SYNTHE spectrum synthesis programs and line data (Cambridge, Mass: Smithsonian Astrophysical Observatory) [Google Scholar]
- Lehmer, O. R., & Catling, D. C. 2017, ApJ, 845, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier des Etangs, A., Pont, F., Vidal-Madjar, A., & Sing, D. 2008, A&A, 481, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Linder, E. F., Mordasini, C., Mollière, P., et al. 2019, A&A, 623, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lo Curto, G., Pepe, F., Avila, G., et al. 2015, The Messenger, 162, 9 [NASA ADS] [Google Scholar]
- Lopez, E. D., & Fortney, J. J. 2013, ApJ, 776, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, E. D., & Fortney, J. J. 2014, ApJ, 792, 1 [NASA ADS] [CrossRef] [Google Scholar]
- López-Morales, M., Haywood, R. D., Coughlin, J. L., et al. 2016, AJ, 152, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Lovis, C., Mayor, M., Bouchy, F., et al. 2009, IAU Symp., 253, 502 [NASA ADS] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, ArXiv e-prints [arXiv:1107.5325] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, ArXiv e-prints [arXiv:1109.2497] [Google Scholar]
- Mordasini, C. 2018, Handbook of Exoplanets, eds., J. A. Belmonte & H. Deeg (Switzerland: Springer International Publishing AG), 143 [Google Scholar]
- Mordasini, C., Alibert, Y., Klahr, H., & Henning, T. 2012, A&A, 547, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Marleau, G.-D., & Mollière, P. 2017, A&A, 608, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murray-Clay, R. A., Chiang, E. I., & Murray, N. 2009, ApJ, 693, 23 [Google Scholar]
- Niraula, P., Redfield, S., Dai, F., et al. 2017, AJ, 154, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Noack, L., & Breuer, D. 2014, Planet. Space Sci., 98, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Noack, L., Rivoldini, A., & Van Hoolst, T. 2017, Phys. Earth Planet. Inter., 269, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Nortmann, L., Pallé, E., Salz, M., et al. 2018, Science, 362, 1388 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Oklopčić, A., & Hirata, C. M. 2018, ApJ, 855, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, J. E., & Morton, T. D. 2016, ApJ, 819, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, J. E., & Wu, Y. 2013, ApJ, 775, 105 [Google Scholar]
- Owen, J. E., & Wu, Y. 2017, ApJ, 847, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Sing, D. K., Gibson, N. P., et al. 2013, MNRAS, 432, 2917 [NASA ADS] [CrossRef] [Google Scholar]
- Rajpaul, V., Aigrain, S., Osborne, M. A., Reece, S., & Roberts, S. 2015, MNRAS, 452, 2269 [NASA ADS] [CrossRef] [Google Scholar]
- Rasmussen, C. E., & Williams, C. K. I. 2006, Gaussian Processes for Machine Learning, 2nd edn., ed. M. Press (Cambridge: MIT Press) [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, J. E., Vanderburg, A., Eastman, J. D., et al. 2018, AJ, 155, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, L. A. 2015, ApJ, 801, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Press, W. H. 1995, Phys. Rev. Lett., 74, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Salz, M., Czesla, S., Schneider, P. C., & Schmitt, J. H. M. M. 2016, A&A, 586, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salz, M., Czesla, S., Schneider, P. C., et al. 2018, A&A, 620, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Sousa, S. G., Mortier, A., et al. 2013, A&A, 556, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saumon, D., Chabrier, G., & van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., & Sasselov, D. D. 2000, ApJ, 537, 916 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., Kuchner, M., Hier-Majumder, C., & Militzer, B. 2007, ApJ, 669, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. C., Stumpe, M. C., Van Cleve, J. E., et al. 2012, PASP, 124, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C. A. 1973, PhD Thesis, The University of Texas at Austin, Austin, USA [Google Scholar]
- Sousa, S. G. 2014, Determination of Atmospheric Parameters of B-, A-, F- and G-Type Stars, eds. Ewa Niemczura, Barry Smalley & Wojtek Pych (Cham: Springer International Publishing), 297 [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A&A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Adibekyan, V., Delgado-Mena, E., & Israelian, G. 2015, A&A, 577, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stassun, K. G., & Torres, G. 2018, ApJ, 862, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Stixrude, L., & Lithgow-Bertelloni, C. 2011, Geophys. J. Int., 184, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Stumpe, M. C., Smith, J. C., Catanzarite, J. H., et al. 2014, PASP, 126, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Fischer, D. A., Sozzetti, A., et al. 2012, ApJ, 757, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Tsantaki, M., Sousa, S. G., Adibekyan, V. Z., et al. 2013, A&A, 555, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tu, L., Johnstone, C. P., Güdel, M., & Lammer, H. 2015, A&A, 577, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tuomi, M. 2014, MNRAS, 440, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Tuomi, M., & Anglada-Escudé, G. 2013, A&A, 556, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Twicken, J. D., Chandrasekaran, H., Jenkins, J. M., et al. 2010, Proc. SPIE, 7740, 77401U [NASA ADS] [CrossRef] [Google Scholar]
- Twicken, J. D., Catanzarite, J. H., Clarke, B. D., et al. 2018, PASP, 130, 064502 [NASA ADS] [CrossRef] [Google Scholar]
- Udry, S., Dumusque, X., Lovis, C., et al. 2019, A&A, 622, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valencia, D., O’connell, R. J., & Sasselov, D. D. 2007, ApJ, 670, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Van Eylen, V., Agentoft, C., Lundkvist, M. S., et al. 2018, MNRAS, 479, 4786 [NASA ADS] [CrossRef] [Google Scholar]
- Van Heck, H.,& Tackley, P. 2011, Earth Planet. Sci., 310, 252 [Google Scholar]
- Vaughan, A. H., Preston, G. W., & Wilson, O. C. 1978, PASP, 90, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Vazan, A., Kovetz, A., Podolak, M., & Helled, R. 2013, MNRAS, 434, 3283 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal-Madjar, A., Lecavelier des Etangs, A., Désert, J.-M., et al. 2003, Nature, 422, 143 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wu, C. Y. R.,& Chen, F. Z. 1993, J. Geophys. Res., 98, 7415 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zinn, J. C., Pinsonneault, M. H., Huber, D., & Stello, D. 2019, ApJ, 878, 136 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A Correlation plots between the marginalised posterior PDFs for our modelling of the high-frequency log(R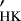 ) time-series
) time-series
 |
Fig. A.1 Correlation between the different marginalised posterior PDFs of the parameters in our modelling of the high-frequency |
Appendix B Correlation plots between the marginalised posterior PDFs for our modelling of the RV time-series
 |
Fig. B.1 Correlation between the different marginalised posterior PDFs of the non-planetary parameters in our modelling of the RV time-series. |
 |
Fig. B.2 Correlation between the different marginalised posterior PDFs of the parameters for planet TOI-402.01. |
 |
Fig. B.3 Correlation between the different marginalised posterior PDFs of the parameters for planet TOI-402.02. |
Appendix C Method for interior characterization
We use the probabilistic analysis of Dorn et al. (2017) for a more detailed interior characterization. The planetary and stellar parameters inferred in this paper are used as input to the our analysis. Our data comprise:
We note that stellar abundances are used as proxies for the planetary bulk composition (Dorn et al. 2015).
Our assumptions for the interior model are similar to those in Dorn et al. (2017, model I) and are summarised in the following. We consider planets being made of iron-rich cores, silicate mantles, layers of water ice and oceans, and an atmosphere. The interior parameters comprise:
-
core size rcore,
-
size of rocky interior rcore+mantle,
-
mantle composition (i.e., Fe/Simantle, Mg/Simantle),
-
mass of water mwater,
-
amount of gas matm,
-
planet intrinsic luminosity Lint,
-
gas metallicity Zgas.
The prior distributions of the interior parameters are stated in Table C.1.
Our interior model uses a self-consistent thermodynamic model from Dorn et al. (2017, model I). For any given set of interior parameters, it allows us to calculate the respective mass, radius, and bulk abundances and compare them to the actual observed data. The thermodynamic model comprises the equation of state (EOS) of iron by Bouchet et al. (2013), the silicate-mantle model by Connolly (2009) to compute equilibrium mineralogy and density profiles given the database of Stixrude & Lithgow-Bertelloni (2011). For the water layers, we follow Vazan et al. (2013) using a quotidian equation of state (QEOS) and above a pressure of 44.3 GPa, we use the tabulated EOS from Seager et al. (2007). We assume an adiabatic temperature profile within core, mantle, and water layers.
For the atmosphere, we solve the equations of hydrostatic equilibrium, mass conservation, and energy transport. For the EOS of elemental compositions of H, He, C, and O, we employ the CEA (Chemical Equilibrium with Applications) package (Gordon & McBride 1994), which performs chemical equilibrium calculations for an arbitrary gaseous mixture, including dissociation and ionization and assuming ideal gas behavior. The envelope metallicity Zenv is the mass fraction of C and O in the envelope, which can range from 0 to 1. An irradiated atmosphere is assumed at the top of the gaseous envelope, for which we assume a semi-gray, analytic, global temperature averaged profile (Guillot 2010). The boundary between theirradiated atmosphere and the envelope is defined where the optical depth in visible wavelength is  (Jin et al. 2014). Within the envelope, the usual Schwarzschild criterion is used to distinguish between convective and radiative layers. The planet radius is defined where the chord optical depth becomes 0.56 (Lecavelier des Etangs et al. 2008).
(Jin et al. 2014). Within the envelope, the usual Schwarzschild criterion is used to distinguish between convective and radiative layers. The planet radius is defined where the chord optical depth becomes 0.56 (Lecavelier des Etangs et al. 2008).
Prior ranges for interior parameters.
Interior parameter estimates with 1σ uncertainties of the marginalised posterior PDFs.
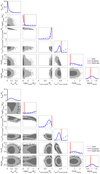 |
Fig. C.1 Two- and one-dimensional marginalised posterior PDFs of interior parameters for TOI-402.01 (upper panel) and TOI-402.02 (lower panel): thickness of atmosphere (denv), water mass (mwater∕Mp), size of rocky interior (rcore+mantle), core size (rcore), and mantle composition (Fe/Simantle and Mg/Simantle). The prior PDFs are shown in dashed (except for denv for which no explicit prior is defined), while the posterior PDFs is shown in solid lines. Earth-like interior values are shown in red for reference. |
The last version of ARES code (ARES v2) can be downloaded at http://www.astro.up.pt/~sousasag/ares
Those values can be found on ExoFOP (https://exofop.ipac.caltech.edu/tess/target.php?id=120896927). We note however that the ExoFOP value for the period of TOI-402.02 is coming from somewhere else as the SPOC DV state 17.18187 ± 0.00304 days and not 17.2148 days. To perform the comparison with our results, we used the results from the SPOC DV analysis.
We note that in Eq. (8) of Giles et al. (2017), the authors use for rms the 2σ range of the rms, therefore twice the conventional rms.
All Tables
Parameters for the TOI-402 planetary system derived from our TESS photometry analysis using EXOFASTv2.
Initial parameters, priors, and best solutions for the models fitted to the 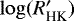 and the RVs.
and the RVs.
Initial conditions and results of the evolutionary calculations, and comparison to the observed values.
Interior parameter estimates with 1σ uncertainties of the marginalised posterior PDFs.
All Figures
 |
Fig. 1 Left: full PDCSAP light curve from TESS after removing the smoothing model described in Sect. 3.2. The grey points represent the raw measurements, while the blue dots are the same data binned over 10 min. The model showing the best fit to the light curve with two planets corresponding to TOI-402.01 and TOI-402.02 is shown as the black curve. Middle: light curve phase-folded in phase to highlight the transit of TOI-402.01 and the best-fit model. Right: as in the middle plot, but for TOI-402.02. |
| In the text | |
 |
Fig. 2
|
| In the text | |
 |
Fig. 3 Top: fit composed of an offset to account for the change of fibres on June 1, 2015, a second-order polynomial drift, a linear dependence with the low-pass, and the high-frequency |
| In the text | |
 |
Fig. 4 Top: best-fit model of our preliminary RV analysis over-plotted on the RV data of HD15337 after removing the instrumental offset due to the change of the fibres on June 1,2015. Second row: phase plot showing the RV signals of TOI-402.01 (left) and TOI-402.02 (right). The best-fit model is shown in black, and the orbital parameters and mass of the detected planets can be found in the title of the two subplots. Third row: RV residuals after fitting our best model. The rms of the residuals of 2.17 m s−1 is significantly higher than the average photon noise error of 0.9 m s−1. Bottom: GLS periodogram of the RV residuals showing no significant signals. Although no signal is seen, the fact that the rms of the residuals is much higher than the photon noise errors indicates that there is still significant activity signal in the residuals. |
| In the text | |
 |
Fig. 5 Top: Gaussian process regression over-plotted on the high-frequency |
| In the text | |
 |
Fig. 6 Top: best-fit model using the mean of all marginalised posterior PDFs obtained by the MCMC sampler over-plotted on the raw RV data of HD 15337 after removing the instrumental offset due to the change of the fibres on June 1, 2015. Middle: RV residuals after removing the best-fit model. The rms of this time-series is 1.36 m s−1. Bottom: GLS periodogram of the RV residuals that does not highlight any significant signals. |
| In the text | |
 |
Fig. 7 Marginalised posterior PDFs of the orbital parameters of TOI-402.01 (subscript 1) and TOI-402.02 (subscript 2). The planetary mass posterior PDFs have been derived by considering the orbital inclinations of TOI-402.01 and TOI-402.02 with their respective errors (see Table 2), and the stellar mass with its respective error (see Table 1). The red vertical lines represent the mean value of each distribution. The title of each subplot gives this mean value for each marginalised posterior PDF, in addition to the rms of the distribution giving therefore the 68% confidence interval error. |
| In the text | |
 |
Fig. 8 Phase-curves for TOI-402.01 and TOI-402. Top plots: best fitted planetary signal in the RV data after removing the instrument offsets, the second-order polynomial drift, and the GP regression. Bottom plots: RV residuals after removing the planetary signal. |
| In the text | |
 |
Fig. 9 GLS periodogram of the GP regression showing the RV amplitude in meters per second with respect to the period. The red vertical windows highlight the orbital period of TOI-402.02 and the stellar rotation period. |
| In the text | |
 |
Fig. 10 Temporal evolution of the TOI-402 planets. The panels show as a function of time (a) the transit radius (in Earth radii), (b) the mass of the H/He envelope (in Earth masses), (c) the mean density of the planets, and (d) the XUV-driven hydrodynamic H/He evaporation rate. In the two panels on the left, the horizontal lines show the observed values and the 1-σ error intervals. The yellow region indicates the 1-σ age range of the star, with the vertical grey line showing the nominal age of 7.5 Gyr. |
| In the text | |
 |
Fig. 11 Planetary radius as a function of the stellar irradiation received by the planet (based on Fulton et al. 2017). TOI-402.01 stands just below the radius gap while TOI-402.02 stands above. The GJ 9827 system is added here as it represents, with TOI-402, probably the best system to understand the radius gap through exoplanetology comparison. HD 97658b is also added for a direct comparison with TOI-402.02 as they are supposed to have water-rich composition and, furthermore, a search for photo-dissociation of water has been undertaken on HD 97658b by Bourrier et al. (2017). The data at the origin of this diagram have been extracted from the NASA exoplanet archive (https://exoplanetarchive.ipac.caltech.edu). |
| In the text | |
 |
Fig. A.1 Correlation between the different marginalised posterior PDFs of the parameters in our modelling of the high-frequency |
| In the text | |
 |
Fig. B.1 Correlation between the different marginalised posterior PDFs of the non-planetary parameters in our modelling of the RV time-series. |
| In the text | |
 |
Fig. B.2 Correlation between the different marginalised posterior PDFs of the parameters for planet TOI-402.01. |
| In the text | |
 |
Fig. B.3 Correlation between the different marginalised posterior PDFs of the parameters for planet TOI-402.02. |
| In the text | |
 |
Fig. C.1 Two- and one-dimensional marginalised posterior PDFs of interior parameters for TOI-402.01 (upper panel) and TOI-402.02 (lower panel): thickness of atmosphere (denv), water mass (mwater∕Mp), size of rocky interior (rcore+mantle), core size (rcore), and mantle composition (Fe/Simantle and Mg/Simantle). The prior PDFs are shown in dashed (except for denv for which no explicit prior is defined), while the posterior PDFs is shown in solid lines. Earth-like interior values are shown in red for reference. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.