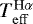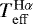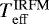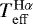| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 22 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201833763 | |
| Published online | 01 April 2019 | |
Accurate effective temperature from Hα profiles★,★★
1
ESO – European Southern Observatory,
Karl-Schwarzchild-Strasse 2,
85748 Garching bei München,
Germany
e-mail: rescateg@eso.org
2
Observatório do Valongo, Universidade Federal de Rio de Janeiro,
Ladeira Pedro Antônio 43,
20.080-090 Rio de Janeiro RJ,
Brazil
e-mail: riano@astro.ufrj.br
3
Zentrum für Astronomie der Universität Heidelberg, Landessternwarte,
Königstuhl 12,
69117 Heidelberg, Germany
4
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas,
4150-762
Porto,
Portugal
5
Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto,
Rua do Campo Alegre 687,
4169-007 Porto, Portugal
6
Departamento de Astronomia do IAG/USP, Universidade de São Paulo, Rua do Matão 1226, Cidade Universitária,
05508-900 São Paulo, SP,
Brazil
Received:
3
July
2018
Accepted:
28
November
2018
Context. The determination of stellar effective temperature (Teff) in F, G, and K stars using Hα profile fitting is a quite remarkable and powerful tool because it does not depend on reddening and is only slightly sensitive to other atmospheric parameters. Nevertheless, this technique is not frequently used because of the complex procedure needed to recover the profile of broad lines in echelle spectra. As a consequence, tests performed on different models have sometimes provided ambiguous results.
Aims. The main aim of this work is to test the ability of the Hα profile fitting technique to derive Teff. We also aim to improve the applicability of this technique to echelle spectra and to test how well 1D + LTE models perform on a variety of F–K stars. We also apply the technique to HARPS spectra and test the reliability and the stability of the HARPS response over several years using the Sun.
Methods. We have developed a normalization method for recovering undistorted Hα profiles and we have first applied it to spectra acquired with the single-order Coudé instrument (resolution R = 45 000) at do Pico dos Dias Observatory to avoid the problem of blaze correction. The continuum location around Hα is optimised using an iterative procedure, where the identification of minute telluric features is performed. A set of spectra was acquired with the MUSICOS echelle spectrograph (R = 40 000) to independently validate the normalization method. The accuracy of the method and of the 1D + LTE model is determined using Coudé/HARPS/MUSICOS spectra of the Sun and Coudé-only spectra of a sample of ten Gaia Benchmark Stars with Teff determined from interferometric measurements. HARPS, Coudé, and MUSICOS spectra are used to determine Teff of 43 sample stars.
Results. We find that a proper choice of spectral windows of fits plus the identification of telluric features allow for a very careful normalization of the spectra and produce reliable Hα profiles. We also find that the most used solar atlases cannot be used as templates for Hα temperature diagnostics without renormalization. The comparison with the Sun shows that Hα profiles from 1D + LTE models underestimate the solar Teff by 28 K. We find the same agreement between Hα and interferometry and between Hα and Infrared Flux Method: a shallow dependency on metallicity according to the relation Teff = TeffHα − 159[Fe/H] + 28 K within the metallicity range − 0.70 to + 0.40 dex. The comparison with the Infrared Flux Method shows a scatter of 59 K dominated by photometric errors (52 K). In order to investigate the origin of this dependency, we analyzed spectra from 3D models and found that they produce hotter temperatures, and that their use largely improves the agreement with the interferometric and Infrared Flux Method measurements. Finally, we find HARPS spectra to be fully suitable for Hα profile temperature diagnostics; they are perfectly compatible with the Coudé spectra, and lead to the same Teff for the Sun as that found when analysing HARPS spectra over a timespan of more than 7 yr.
Key words: line: profiles / techniques: spectroscopic / stars: atmospheres / stars: fundamental parameters / stars: late-type / stars: solar-type
A copy of the spectra is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/624/A10
© ESO 2019
1 Introduction
Effective temperature (Teff) is a fundamental stellar parameter because it defines the physical conditions of the stellar atmosphere and is directly related to the physical properties of the star: mass, radius, and luminosity. Its measurement is essential to determine the evolutionary state of the stars, to perform detailed chemical abundance analyses, and to characterise exoplanets.
Among a variety of model-dependent techniques used to derive Teff in F-, G-, and K-type stars, fitting Balmer lines offers two important advantages: it is not sensitive to reddening and is only very slightly sensitive to other stellar parameters, such as metallicity ([Fe/H]1) and surface gravity (log g; Fuhrmann et al. 1993, 1994; Barklem et al. 2000, 2002). For instance, variations of about 0.1 dex in either of these parameters induce variations of 3 to 35 K in Teff, depending on the metallicity of the star (see Table 4 in Barklem et al. 2002, hereafter BPO02). Thanks to this, the degeneracy between Teff and [Fe/H] when both parameters are simultaneously constrained with the excitation and ionization balance of iron lines (the parameters measured with this technique are referred to as “spectroscopic” hereafter) can be reduced by fixing Teff to subsequently derive the [Fe/H]. Thus, it is possible to distinguish minute differences in chemical abundances, as for example by Porto de Mello et al. (2008) and Ramírez et al. (2011).
In spite of these advantages, the use of Balmer profile fitting remains sporadic for two main reasons: (i) the first concerns the complex normalization of wide line profiles, especially in cross-dispersed echelle spectra due to the instrumental blaze and the fragmentation of the spectrum into multiple orders. (ii) The second concerns the accuracy of the models of Balmer lines, which is not well established, and is partially a consequence of (i). A clear example are the two ranges of Teff derived for the Sun using the model of BPO02 and spectra from different instruments including two versions of the Kitt Peak National Observatory solar atlas Kurucz et al. (1984) and Kurucz (2005; hereafter KPNO1984 and KPNO2005, respectively). A “cool” value of ~5670 K was found by Pereira et al. (2013)2 and Önehag et al. (2014) from KPNO2005 and KPNO1984, respectively, while a “hot” value of ~5730 K was found by BPO02, Ramírez et al. (2011, 2014b) and Cornejo et al. (2012) from other spectra; precise values are listed in Table 2.
The problem of normalizing Hα in echelle spectra has been approached, making use of fibre-fed spectra, whose blaze function has been efficiently removed by the flat-field procedure (e.g. Fuhrmann et al. 1997; Korn et al. 2003, 2006, 2007; Lind et al. 2008; Önehag et al. 2014). Also, a complex normalization method explained by BPO02 (hereafter 2D normalization) has been applied by some authors to remove the blaze (e.g. Fuhrmann et al. 1997; Allende Prieto et al. 2004; Ramírez et al. 2011, 2014b; Matsuno et al. 2017a,b). Briefly, the method consist in interpolating the blaze function for the echelle orders contiguous to that containing Hα.
It is recognised that the introduction of the self-broadening theory of hydrogen atoms by BPO02 constitutes a significant advancement towards the completeness of the physics behind the Balmer-line formation, however the tests on the Sun performed by the authors quoted above indicate that the model, or its application, is not accurate enough. As a consequence, subsequent works concentrated on improving the model by adding more transitions in the self-broadening (Allard et al. 2008; Cayrel et al. 2011), and replacing 1D local thermodynamic equilibrium (LTE) by 3D non-LTE model atmospheres (Barklem 2007; Ludwig et al. 2009a; Pereira et al. 2013; Amarsi et al. 2018) but the solar Teff has not yet been recovered. The large discrepancies in the solar temperatures derived using the same model and different instruments suggest that the treatment of observational spectra is the dominant source of uncertainty; Hα profiles are so sensitive that a minute error in the continuum location may cause significant variation of the derived temperature. The continuum location problem was already identified by BPO02, who also estimated the errors induced by this process in the derived temperature. In this work we aim to minimise these errors by a meticulous analysis of spectra of F, G, and K stars.
We first eliminate instrumental blaze and spectral fragmentation inherent to echelle spectra by using a long-slit single-order spectrograph. The continuum location is then optimised by a normalization-fitting iterative procedure, and is also fine tuned during the process by identifying telluric features that contaminate the spectra.
As a first step of our program of chemical tagging, mainly based in HARPS spectra, we establish a methodology to derive Teff from Hα profiles. Wedetermine the accuracy of the temperature diagnostics with Hα profiles from 1D + LTE model atmospheres and the self-broadening theory of BPO02 (these profiles are referred to as profiles from 1D model atmospheres and their temperatures will be represented by 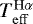 henceforth) by comparing them with the accurate Teff of the Gaia Benchmark Stars derived by interferometry. The method we present is further validated by deriving, for the same stars, compatible Teff values using MUSICOSspectra normalized by the 2D normalization, which is an independent method. Finally, we prove the absence of residual blaze features in HARPS spectra by normalizing them using the same procedure as that used with with Coudé spectra, and obtaining compatible
henceforth) by comparing them with the accurate Teff of the Gaia Benchmark Stars derived by interferometry. The method we present is further validated by deriving, for the same stars, compatible Teff values using MUSICOSspectra normalized by the 2D normalization, which is an independent method. Finally, we prove the absence of residual blaze features in HARPS spectra by normalizing them using the same procedure as that used with with Coudé spectra, and obtaining compatible 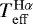 values.
values.
This paper is organized as follows. In Sect. 2, the selection of the sample is described together with the characteristics of the spectroscopic observations. In Sect. 3, we describe the normalization method. In Sect. 4, we describe the fitting procedure. In Sect. 5, we validate the normalization method. The results are presented from Sect. 6 onwards. The accuracy of Hα profiles from 1D models is also determined in Sect. 6. In Sect. 7, 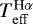 is compared against temperature diagnostics from other frequent techniques. In Sect. 8 we compare our Hα temperature scale with others from the same and different models. In Sect. 9 the effect of replacing 3D by 1D models is tested. In Sect. 10 we test the reliability and stability of HARPS in performing the Hα profile fitting. Finally, in Sect. 11 we summarize our results and conclusions.
is compared against temperature diagnostics from other frequent techniques. In Sect. 8 we compare our Hα temperature scale with others from the same and different models. In Sect. 9 the effect of replacing 3D by 1D models is tested. In Sect. 10 we test the reliability and stability of HARPS in performing the Hα profile fitting. Finally, in Sect. 11 we summarize our results and conclusions.
2 Data
2.1 Sample selection
The sample stars are presented in Table 1. These are 43 F-, G-, and K-type stars including the Sun observed by means of the proxies Ganymede, Ceres, Calisto and Moon. They were selected from the HARPS/ESO archive of reduced and calibrated data, brighter than V = 7 to obtain spectra of good quality with the MUSICOS and Coudé instruments. Thus, three samples of spectra were collected (named according to the spectrograph of acquisition). More stars were observed with Coudé in order to cover as much of the Teff –[Fe/H]–log g parameter space as possible. Therefore, every object in the HARPS and MUSICOS subsamples has associated Coudé spectra. The parameter space covered by the sample stars is presented in Fig. 1. Stellar parameters were extracted from a compilation of catalogues from the literature denoted henceforth as follows: Sousa08: Sousa et al. (2008), Ghezzi10: Ghezzi et al. (2010), Tsantaki13: Tsantaki et al. (2013), Ramirez13: Ramírez et al. (2013), Bensby14: Bensby et al. (2014), Ramirez14a: Ramírez et al. (2014a), Ramirez14b: Ramírez et al. (2014b), Maldonado15: Maldonado et al. (2015), Heiter15: Heiter et al. (2015). In order to compare literature Teff scales with ours, we selected works that derived Teff with three different techniques: excitation and ionization of Fe lines (Sousa08, Ghezzi10, Tsantaki13, Bensby14, Ramirez14a, Ramirez14b, Maldonado15), photometric calibrations based on the Infrared flux method (Ramirez13), and interferometry (Heiter15). Most of the parameters in Table 1 belong to Ramirez13 because our selection started withthis catalogue, which has a large number of stars from HIPPARCOS observable with the southern telescopes.
We added Ceres to the HARPS sample to expand the data in time in order to check the temporal stability of the instrument. The solar proxies analysed are listed in Table 3 together with their date of observation, signal-to-noise ration (S/N), and the temperatures derived in this work. We extracted ten random spectra of the same object per day for several years. The only sixspectra available of 2010/10 were complemented with spectra of the close date 2010/12, and for 2007 and 2009 only the available spectra were used.
Sample stars.
2.2 do Pico dos Dias observations
We used Coudé and MUSICOS in 2016 and 2017. Both spectrographs are fed by the 1.6-m Perkin-Elmer telescope of do Pico dos Dias Observatory (OPD, Brazópolis, Brazil), operated by Laboratório Nacional de Astrof"i"sica (LNA/CNPq). In the Coudé spectrograph the slit width was adjusted to give a two-pixel resolving power R = λ∕Δλ = 45 000. A 1800 l mm−1 diffraction grating was employed in the first order, projecting onto a 13.5 μm, 2048-pixel CCD. The spectral region is centred on the Hα line λ = 6562.797 Å with a spectral coverage of 155 Å.
MUSICOS is a fibre-fed echelle spectrograph (e.g. Baudrand & Bohm 1992; on loan from Pic du Midi Observatorysince 2012) available for the OPD/LNA. We employed the red channel, covering approximately λ5400–8900 Å, comprising about 50 spectral orders, at R ~ 40 000 and 0.05 Å pix−1 dispersion in the Hα wavelength range.
The exposure times were chosen to obtain S/Ns of at least 250 for the faintest stars (V ~ 7) and 300 on average for the other stars.
3 Normalization
The challenge in normalizing Hα profiles arises from the uncertainty of the continuum location, which is estimated defining “continuum windows”. Thus, the success of the normalization resides in the capability of identifying many wide windows that allow the shape of the spectrograph response to be determined.
Frequently, the continuum windows are determined using automatic or semiautomatic procedures, such as the IRAF3 task continuum, selecting the wavelength bins with the highest fluxes by applying clipping. We improve this procedure by iterating on the normalization and fitting processes. In this way the compatibility at the extremes of the wings is checked after every fit. This check is fundamental for consistent temperature measurements because, although the spectrograph response may be well described by a low-order polynomial (as is the case of Coudé), the normalization by interpolation may be highly imprecise close to the line core. This occurs because the continuum regions available to interpolate the polynomial are short compared to the fitted region, and therefore small errors in the outer profile wings trigger larger errors close to the line core where the Hα profile is more sensitive to the temperature. With this method, explained below in detail, we minimise the main source of uncertainty, as demonstrated by the very low dispersion of 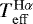 values obtained with many solar spectra in Sects. 6.1 and 10.
values obtained with many solar spectra in Sects. 6.1 and 10.
Normalization is more complex for echelle spectra because of the correction of the blaze and order merging. As discussed by Škoda & Šlechta (2004), distortions in the spectra, such as discontinuities of the orders and ripple-like patterns (see Škoda et al. 2008, Fig. 11), are often produced in slit echelle spectrographs but possibly also in fibre-fed instruments. When this occurs, the spectra are useless and a new reduction from raw data should be applied following the recipe recommended by Škoda et al. (2008). Of course, empirical corrections on the reduced spectra could recover the profiles, but their quality must be verified by recovering the Teff accuracy obtained with non-distorted profiles. On the other hand, spectra with no obvious distortions also need to be tested, because subtle residual blaze features may remain and systematically impact the Teff estimate. Residual blaze features distort the profiles, making them shallower (especially close to the centre of the spectral order), and therefore the distorted spectra mimic profiles of cooler temperatures. In order to investigate this effect in HARPS, the 1D pipeline-reduced HARPS spectra were analysed in the same way as the Coudé spectra were, and the derived 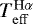 values were compared. The results of this analysis are presented in Sect. 10.
values were compared. The results of this analysis are presented in Sect. 10.
The normalization method applied to Coudé and HARPS is independently validated by deriving 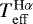 from MUSICOS spectra normalized with the 2D normalization. These results are presented in Sect. 5.
from MUSICOS spectra normalized with the 2D normalization. These results are presented in Sect. 5.
3.1 Normalization of Coudé and HARPS spectra
The normalization is applied by interpolating low-order polynomials with the IRAF task continuum, integrated with the fitting code described in Sect. 4 in an iterative procedure:
- 1.
A first gross normalization is performed neglecting the region 6514–6610 Å in the interpolation. Although the extension of the Hα wings is variable, this region is kept the same for all the sample stars with the purpose of keeping enough room to apply weights in nearby regions to modulate the normalizing curve.
- 2.
The obtained profile is used to fit a precipitable water vapour (PWV) spectrum that will be used to verify the continuum level after every iteration; see Sect. 3.2.
- 3.
The same normalized profile is compared with the grid of synthetic profiles using the fitting code described in Sect. 4 to find the most compatible one.
- 4.
The compatibility between the normalized and synthetic profiles must be visually checked at the “transition regions” (λ < 6536 Å and 6590 Å < λ) in which the continuum turns into line wings. The regions of the line interior are very sensitive to temperature, hence they arepredominant in the fittings. For this reason, if distortions are artificially introduced in the profile during the normalization, they become more evident in the transition regions. This procedure makes our normalizations dependent on the model, but only very weakly, because metallicity and surface gravity (the parameters set beforehand) do not greatly influence the shape of the line, especially in the transition regions. We verified that changes as large as ~ ± 0.3 dex do not significantly modify the shape of the normalized profiles, while larger changes may truncate the procedure. For consistency, HARPS spectra were degraded to the resolution of Coudé in this step (only for this step, not for the fitting procedure); see Fig. 3. Figure A.4 provides examples of transition regions at the red wing of Hα in solar spectra normalized by different authors. In this figure, the fit of the Coudé spectrum of Fig. 2 is compared with fits of KPNO2005 and the solar atlas of Wallace et al. (2011; KPNO2011) to show how this method improves the normalization.
- 5.
Usually the first normalization is deficient; in this case a second one is performed from scratch applying weights to the wings around 6514 and 6610 Å to make the profile deeper or shallower as required to match the flux of the synthetic profile. Subsequently, another fit is applied and the matching check described in step 4 is repeated. The procedure finishes when the observed and synthetic profiles are compatible in the transition regions, as shown in Figs. 2 and 3. An example of the difference between the first gross normalization and the final normalization is shown in Fig. A.6.
3.2 Continuum fine-tune
The solar KPNO2005 atlas and the lines catalogue of Moore et al. (1966) were used to select windows free from metallic lines to check the continuum during the normalization procedure. However, the availability of these windows diminishes progressively in cool and metal-rich stars and because of the presence of telluric lines. Since the humidity at do Pico dos Dias Observatory often exceeded 90% during our observations, the contribution of many minute telluric lines is relevant in the Coudé spectra. To fine-tune the continuum level, as part of the procedure described in Sect. 3.1, we separated telluric features from noise, fitting the observed spectra with synthetic telluric spectra from the PWV library of Moehler et al. (2014)4, as shown in Fig. 4. This library is available at resolutions R = 300 000 and R = 60 000, for the air-masses 1.0, 1.5, 2.0, 2.5, and 3.0 and water content of 0.5, 1.0, 1.5, 2.5, 3.5, 5.0, 7.5, 10.0, and 20.0 mm. The fitting is performed degrading the resolution of the original PWV spectra to match those of the spectrograph used, and selecting the set of PWV spectra with the air-mass closest to that of the observation. Essentially the same results were found as with the Molecfit software package (described in detail in Sect. 4), but the last are more precise.
We quantified the displacement of the continuum due to the presence of telluric features as follows. After normalizing all Coudé spectra, continuum wavelength bins were identified in the solar spectrum of Fig. 2 applying σ-clipping. The fluxes of these wavelength bins were then checked in all other normalized Coudé spectra, and none of them were found to remain as continuum in the whole sample. The colour code of the plot in the figure represents the percentage rate, the windows at [6500.25, 6500.50], [6504.50, 6505.00], [6619.70, 6620.50], [6625.60, 6625.80], [6626.50, 6626.80] Å being the most frequent. Figure 4 shows two cases where two of these windows are affected by the presence of minute telluric lines, and how much the average flux of the five mentioned windows decreases. Analysing all of the sample spectra, we find that when the content of PWV is high, that is, over 5.0 mm, minute telluric features are almost omnipresent and displace the continuum flux by about 0.5%. In our experience, this issue may cause the stellar temperature to be underestimated by between 10 and 30 K. It is however difficult to provide a precise estimate because the flux displacement produced is often not homogeneous, but a distortion of the continuum shape. We stress that no correction is applied during this procedure, only a visual check. The correction is done later, and is explained in Sect. 4.
4 Profiles fitting
This study is based on the grid of synthetic profiles of BPO02 computed using the self-broadening theory developed in Barklem et al. (2000) and the 1D LTE plane-parallel model atmospheres from the MARCS code (Asplund et al. 1997). The atmospheric parameters of the grid are Teff: 4400–7500 K with steps of 100 K, [Fe/H]: − 3.0 to + 0.5 dex with steps of 0.5 dex, log g: 3.4–5.0 dex with steps of 0.5 dex and microturbulence velocity of 1.5 km s−1. In order to derive very precise values of Teff around solar parameters, a more detailed grid from the same theoretical recipe used by Ramírez et al. (2011) is also used here; its parameters are Teff: 5500–6100 K with steps of 10 K, [Fe/H]: − 3.0 to + 0.3 dex with steps of 0.05 dex, log g: 4.2–4.65 dex with steps of 0.05 dex and microturbulence velocity of 1.5 km s−1. The fitting between the observed and synthetic profiles is performed using the “windows of fits” free from metallic lines: [6556.45, 6556.55], [6559.00, 6559.20], [6559.86, 6560.08], [6561.30, 6561.60], [6566.00, 6566.30], [6567.90, 6568.10], [6577.10, 6577.40], and [6589.55, 6589.80]5.
A program in IDL6 was written to perform the fits eliminating the influence of contaminated wavelength bins. It first interpolates the resolution of the grids to 1 K, 0.01 dex, and 0.01 dexin Teff, [Fe/H], and log g. Subsequently, for each wavelength bin, the temperature related to the interpolated synthetic profile with the closest flux value is chosen, with [Fe/H] and log g being fixed beforehand by the user. The most probable temperature and its uncertainty are determined by the median and the robust standard deviation (1.4826 times the median absolute deviation) of the histogram; see e.g. Figs. 2 and 3.
The resolution and sampling of the Coudé spectra allow a total of 26 to 27 wavelength bins inside the windows of fit, enough to perform the fitting procedure described above. In order to optimise 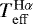 and its error determination when windows of fits are contaminated and to provide a spectral library clean from telluric features, we corrected the normalized Coudé spectra with the Molecfit software package (Smette et al. 2015; Kausch et al. 2015). This software computes the transmission of the Earth’s atmosphere at the time of the observations with the radiative transfer code LBLRTM (Clough et al. 2005), taking into account spectroscopic parameters from the HITRAN database (Rothman et al. 2013) and an atmospheric profile. The atmospheric transmission is fitted to the observed spectrum, and the telluric correction is done dividing the observed spectrum by the atmospheric transmission. We used the average equatorial atmospheric profile, which is the default profile of Molecfit. We chose to fit H2 O (the main absorber in this wavelength region), O2, and O3. The line shape is fitted by a boxcar profile; as starting value for the boxcar FWHM we used 0.36 times the slit width. The wavelength solution of the atmospheric transmission is adjusted with a first-degree polynomial. First, we ran Molecfit automatically on all spectra, avoiding the centre of the Hα line from 6560 to 6566 Å. If the residuals of this first telluric correction were larger than 2% of the continuum, we adapted the starting value of the water abundance and performed a second fit. This telluric correction allowed us to recover with precision the stellar flux inside the contaminated windows of fits in most cases. An example is shown in Fig. 5 where the corrected and non-corrected spectra of HD 2151 are over-plotted.
and its error determination when windows of fits are contaminated and to provide a spectral library clean from telluric features, we corrected the normalized Coudé spectra with the Molecfit software package (Smette et al. 2015; Kausch et al. 2015). This software computes the transmission of the Earth’s atmosphere at the time of the observations with the radiative transfer code LBLRTM (Clough et al. 2005), taking into account spectroscopic parameters from the HITRAN database (Rothman et al. 2013) and an atmospheric profile. The atmospheric transmission is fitted to the observed spectrum, and the telluric correction is done dividing the observed spectrum by the atmospheric transmission. We used the average equatorial atmospheric profile, which is the default profile of Molecfit. We chose to fit H2 O (the main absorber in this wavelength region), O2, and O3. The line shape is fitted by a boxcar profile; as starting value for the boxcar FWHM we used 0.36 times the slit width. The wavelength solution of the atmospheric transmission is adjusted with a first-degree polynomial. First, we ran Molecfit automatically on all spectra, avoiding the centre of the Hα line from 6560 to 6566 Å. If the residuals of this first telluric correction were larger than 2% of the continuum, we adapted the starting value of the water abundance and performed a second fit. This telluric correction allowed us to recover with precision the stellar flux inside the contaminated windows of fits in most cases. An example is shown in Fig. 5 where the corrected and non-corrected spectra of HD 2151 are over-plotted.
The telluric corrected and non-corrected normalized Coudé spectra of the sample stars in Table 1 can be accessed at an online repository7 and at the CDS, or by contacting the first author.
 |
Fig. 2 Coudé Hα profile of one of the solar proxies in Table 3. The red and black lines represent the synthetic and observed profiles. The shaded regions are the windows of fits and the circles represent the continuum bins colour-coded according to their frequency of appearance in all Coudé spectra. The most frequent continuum windows are observed at [6500.25, 6500.50], [6504.50, 6505.00], [6619.70, 6620.50], [6625.60, 6625.80] and [6626.50, 6626.80]. Bottom panel: histogram of temperatures related to the wavelength bins within the windows of fits. A Gaussian is fitted to its median and robust standard deviation. |
 |
Fig. 3 As in Fig. 2 but with a HARPS spectrum of one of the solar proxies from Table 3. The grey line represents the spectrum in its original resolution and the black line represents the spectrum degraded to the resolution of Coudé. Continuum bins in the degraded spectrum are highlighted in green; notice that they mostly match those of Fig. 2. |
 |
Fig. 4 Left panels: fitting of two Coudé spectra (grey line) with synthetic spectra of PWV with concentrations of 7.5 and 5 mm (red and blue lines, respectively) for the same air mass. The circles are the continuum wavelength bins on 1 ± σ(noise). The shades represent 3 of the 5 continuum windows selected in Fig. 2. The arrows point to the windows contaminated by telluric features. Right panels: flux histograms of the spectra on the left panels with the same flux scale. The black horizontal line shows the continuum, and the dashed line is the average flux of the five continuum windows of Fig. 2 and the shades are the spread. |
 |
Fig. 5 Telluric correction and profile fitting of the Coudé spectrum of HD 2151. Left panel:corrected and non-corrected spectra are represented by the black and blue lines, respectively. The windows of fits are represented by the shades, and the arrows point to those windows where the relative flux was perfectly recovered. The red line represents the fitted synthetic profile. Right panel: histogram of temperatures related to the wavelength bins inside the windows of fits. The most probable |
5 Validation of the normalization method
BPO02 found the 2D normalization to be efficient in removing the spectral blaze; the method is described in detail in their paper. It is referred to as 2D normalization because it depends on the two spacial dimensions of the CCD detector. Namely, the normalization curve of the spectral order of interest is found by interpolating the normalization curves of the adjacent orders in the pixel domain.
We validate the normalization method described in Sect. 3.1 used on Coudé and HARPS spectra, deriving 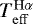 with MUSICOSspectra normalized by the 2D normalization. The comparison in Fig. 6 shows that
with MUSICOSspectra normalized by the 2D normalization. The comparison in Fig. 6 shows that 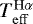 derived with Coudé and MUSICOS are compatible for all stars. We find no trend with respect to the atmospheric parameters, a negligible offset of − 1 K and a low scatter of 25 K. Solar spectra reflected in the Moon and Ganymede were also normalized with this method, from which we derive the average value 5745 ± 16 K (see comparative values in Table 3; the profile fits are shown in Fig. A.2) consistent with the values of
derived with Coudé and MUSICOS are compatible for all stars. We find no trend with respect to the atmospheric parameters, a negligible offset of − 1 K and a low scatter of 25 K. Solar spectra reflected in the Moon and Ganymede were also normalized with this method, from which we derive the average value 5745 ± 16 K (see comparative values in Table 3; the profile fits are shown in Fig. A.2) consistent with the values of 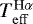 listed in Table 2 derived from Coudé and HARPS spectra.
listed in Table 2 derived from Coudé and HARPS spectra.
6 Accuracy of 1D model atmospheres
6.1 The zero point
We used the six blaze-free Coudé solar spectra listed in Table 3 to determine the accuracy of Hα profiles from 1D model atmospheres for the Sun. The profiles fitted are shown in Fig. A.1. We obtain the average value 5744 ± 7 K. Since we find good agreement between the determinations from Coudé, MUSICOS, and HARPS spectra (Sects. 5 and 10), we determine the zero-point of the model by averaging the inferred Teff values from all solar spectra, resulting in an offset of − 28 ± 1 K with respectto the 5772 K (Prša et al. 2016; Heiter et al. 2015) measured by the Stefan-Boltzmann equation.
Our zero point supports the temperature values initially found by BPO02 with their MUSICOS spectrum and the KPNO1984 atlas, and those found later by Ramírez et al. (2011, 2014b) and Cornejo et al. (2012) with MIKE spectra. On the other hand, it disagrees with any value derived from KPNO solar atlases, including our own determinations. These values are presented in Table 2 and Fig. 7 along with those derived by other authors using enhanced theories from BPO02 onwards.
Figure 7 shows that none of the models recovered the solar Teff, including the most sophisticated ones, such as that by Pereira et al. (2013) based on 3D models and Amarsi et al. (2018) based on 3D models and non-LTE. The plot also shows that the determinations from KPNO spectra are systematically cooler than those from other spectra, except for the first one of BPO02. We also highlight that this determination disagrees with that of Önehag et al. (2014) although they were obtained with the same version of KPNO atlas and the same broadening recipe, which is explained by synthetic profiles computed from different versions of MARCS model atmospheres that use distinct mixing-length parameters.
It is not satisfactory that such dispersion remains for the Sun, our reference star from which spectra of supreme quality are not difficult to obtain. Therefore, in an attempt to identify the origin of the problem, we fitted KPNO atlases with the theoretical profiles of BPO02 (fittings with no further normalization). From these fits, we firstly computed the temperature difference that other models of Hα produce with respect to that of BPO02 for the Sun. These are provided in Table 2. Secondly, we compared these fits with those of Coudé/HARPS/MUSICOS to analyse the quality of their normalizations. The fits are shown in Fig. A.3. They are very precise in the inner profile regions thanks to their high temperature sensitivity and to the high spectral quality in S/N and sampling. However, when the outer regions are scrutinised, evident departures appear; see Fig. A.4. We observed similar departures after the first iteration in our normalization procedure, that is, the custom normalization by polynomial interpolation (see Fig. A.6), the causes of which were explained in Sect. 3.
From KPNO2005 we obtain a value that is cooler than what we obtain with Coudé/HARPS/MUSICOS spectra by 30 K. This atlas version was normalized by polynomial fitting of the observed spectral fluxes, considering also the presence of broad O 3 and ![$[\mathrm{O}_{2}]_{2}$](/articles/aa/full_html/2019/04/aa33763-18/aa33763-18-eq12.png) atmosphericfeatures produced by synthetic spectra. The differences between the temperature values derived by us and the two authors that used profiles from 1D models are entirely explained by the different physics of the models. Hα profiles of Cayrel et al. (2011) were synthesised by ATLAS9, BALMER9 codes (Castelli & Kurucz 2004) and the impact-broadening of Allard et al. (2008) that includes more transitions than the self-broadening of BPO02. The profiles of Pereira et al. (2013) were synthesised also with a slightly different input physics and an updated atmosphere model in comparison to that used in BPO02.
atmosphericfeatures produced by synthetic spectra. The differences between the temperature values derived by us and the two authors that used profiles from 1D models are entirely explained by the different physics of the models. Hα profiles of Cayrel et al. (2011) were synthesised by ATLAS9, BALMER9 codes (Castelli & Kurucz 2004) and the impact-broadening of Allard et al. (2008) that includes more transitions than the self-broadening of BPO02. The profiles of Pereira et al. (2013) were synthesised also with a slightly different input physics and an updated atmosphere model in comparison to that used in BPO02.
From KPNO2011 we obtain a similar value to that obtained with KPNO2005, meaning that the relative flux of both spectra in the innermost regions of the profile agree. On the other hand, significant differences are observed in the outer wings; see Fig. A.4. No information is provided about the normalization method of this atlas, but we suspect that the custom method was applied because we observe significant flux disparities around the continuum regions [6500.25, 6500.50], [6504.50, 6505.00], and [6625.60, 6625.80]; see Fig. A.5. If their flux excess of ~ 0.2% was constant throughout all the wavelength range, this would imply an underestimation of temperature by at least 20 K.
This analysis show that the systematic low temperatures from solar spectra in Table 2 are associated to disparities with the synthetic spectra and/or the continuum, which may indicate minute normalization errors. We show that when a special care is taken in the continuum placement and in fitting the outermost profile regions, consistent results are obtained. These findings are further supported by the agreement with all other 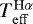 measurements from spectra other than KPNO, as Fig. 7 shows.
measurements from spectra other than KPNO, as Fig. 7 shows.
The temperature differences listed in the last column of Table 2 are computed subtracting the diagnostics by the BPO02 model from those by the Hα models of the authors listed in the first column, both obtained from the same solar spectra listed in the second column. Hence, these differences give the zero points of the Hα models relative to that of BPO02 (−28 ± 1 K), and therefore the two quantities added together give the absolute zero point of the model. Remarkably, we find that the two models using 3D atmospheric models improve the agreement with the actual solar Teff, Amarsi et al. (2018) who also consider non-LTE do reproduce the solar Teff.
 |
Fig. 6 Temperature diagnostics from MUSICOS with respect to those of Coudé vs. atmospheric parameters. [Fe/H] and log g values from Table 1 were used here. The −1 K offset and its 25 K scatter are represented by the dashed lines and the shades, respectively. |
Effective temperature values from solar Hα lines fitted with different models.
 |
Fig. 7 Graphic representation of solar Teff values in Table 2. The horizontal line represents the solar Teff measured by the Stefan-Boltzmann equation. Works that used theoretical models based on 1D atmosphere models are represented by circles, and those that used 3D models are represented by triangles. Grey circles represent works that used the theoretical model of BPO02, and green circles represent works that used a different/enhanced recipe. Works that used KPNO solar atlases are labelled in blue. For them, for comparison purposes, our measurements from corresponding KPNO spectra are included as red crosses in the same line. |
6.2 Accuracy for non-solar stars
Atmospheric parameters of 34 Gaia Benchmark Stars with a wide range of temperature and metallicity were published by Heiter15. Their Teff were derived by measuring angular diameters with interferometry, which is the least model-dependent technique. We acquired Coudé spectra of nine Gaia Benchmark Stars and 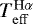 was derived for them using the [Fe/H] and log g values given by the authors. The plot in Fig. 8 shows the comparison of
was derived for them using the [Fe/H] and log g values given by the authors. The plot in Fig. 8 shows the comparison of 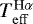 with Teff from interferometry. We find a constant offset of 30 K between the two scales, which confirms the − 28 K zero point found with the solar spectra in Sect. 6.1. No temperature dependence is found with log g but a trend is present with metallicity. The right panel of the figure shows that Hα underestimates Teff by ~100 K at [Fe/H] = − 0.5 dex. In the plots, the temperaturevalues of μ Ara (HD 160691) appear highly discrepant and were ignored to compute the trend. The interferometric Teff of this star is flagged by the authors as not reliable because its angular diameter is not directly measured (see Sect. 3.2). On the other hand, we find its
with Teff from interferometry. We find a constant offset of 30 K between the two scales, which confirms the − 28 K zero point found with the solar spectra in Sect. 6.1. No temperature dependence is found with log g but a trend is present with metallicity. The right panel of the figure shows that Hα underestimates Teff by ~100 K at [Fe/H] = − 0.5 dex. In the plots, the temperaturevalues of μ Ara (HD 160691) appear highly discrepant and were ignored to compute the trend. The interferometric Teff of this star is flagged by the authors as not reliable because its angular diameter is not directly measured (see Sect. 3.2). On the other hand, we find its 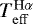 to be consistent with IRFM and all the spectroscopic values in the following sections. The other star for which there is a high level of discrepancy is δ Eri (HD 23249). Discrepancies are also found for this star in the comparison with IRFM in Sect. 7.1. However, its values in the plots of Fig. 8 were not ignored when computing the trends, in order to do an homogeneous comparison with the trends in Fig. 9.
to be consistent with IRFM and all the spectroscopic values in the following sections. The other star for which there is a high level of discrepancy is δ Eri (HD 23249). Discrepancies are also found for this star in the comparison with IRFM in Sect. 7.1. However, its values in the plots of Fig. 8 were not ignored when computing the trends, in order to do an homogeneous comparison with the trends in Fig. 9.
Having determined with high precision the offset of 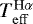 with respect to Teff at solar parameters in the previous section, the
with respect to Teff at solar parameters in the previous section, the 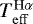 accuracy with respectto [Fe/H] over the metallicity range analysed, is improved from the relation in the plot in the right panel of Fig. 8 to:
accuracy with respectto [Fe/H] over the metallicity range analysed, is improved from the relation in the plot in the right panel of Fig. 8 to:
![\begin{equation*}\mbox{$T_{\mathrm{eff}} = T_{\mathrm{eff}}^{\textrm{H}\alpha}$ $-159(\pm80)$[Fe/H] $+ 28(\pm1)$\,K}\;\;\; (68~\mathrm{K~scatter}) \end{equation*}](/articles/aa/full_html/2019/04/aa33763-18/aa33763-18-eq19.png) (1)
(1)
It is worth mentioning that, since δ Eri has a near-solar metallicity, any possible bias induced by its temperature discrepancy is eliminated by the zero point improvement.
 |
Fig. 8 Left panel: comparison of |
7 Consistency with other Teff scales
We used ten catalogues from the literature to determine the consistency of the Hα profile diagnostics with other techniques. Among them, Sousa08, Ghezzi10, Tsantaki13, Besnby14, Ramirez14a, Ramirez14b, and Maldonado15 determine spectroscopic Teff, while Ramirez13 has Teff derived by photometric calibrations from IRFM.
In this section, as well in Sect. 6.2, 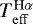 was derived for comparison purposes using log g and [Fe/H] parameters provided by each author as input, so that the comparisons are consistent as far as the stellar parameters are concerned. In the following subsections,
was derived for comparison purposes using log g and [Fe/H] parameters provided by each author as input, so that the comparisons are consistent as far as the stellar parameters are concerned. In the following subsections, 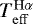 determinations are separately compared with the results obtained with each method.
determinations are separately compared with the results obtained with each method.
7.1 IRFM effective temperatures
The comparison with IRFM is performed with the temperatures of Ramirez13, which were derived by the metallicity-dependent colour–Teff calibrations of Casagrande et al. (2010) using the Johnson-Cousins, 2MASS, Tycho2, and Strömgreen available photometry. To obtain these temperatures, represented by 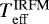 , the authors used a homogeneous set of metallicity values derived from Fe lines, where Teff is not obtained simultaneously with the other parameters but is fixed from photometric calibrations. In this way, both techniques are combined iteratively minimising the Teff–[Fe/H] degeneracy.
, the authors used a homogeneous set of metallicity values derived from Fe lines, where Teff is not obtained simultaneously with the other parameters but is fixed from photometric calibrations. In this way, both techniques are combined iteratively minimising the Teff–[Fe/H] degeneracy.
The plot in Fig. 9 shows the comparison between 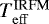 and our Coudé
and our Coudé 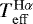 . There is a constant offset of +34 K between the two scales with a 59-K scatter. Their difference shows a trend with metallicity according to the equation displayed in the plot in the middle panel. This trend is almost the same as that found in the comparison with interferometric measurements, asserting the equivalence of the two scales (Casagrande et al. 2014). After applying the relation given by Eq. (1) to
. There is a constant offset of +34 K between the two scales with a 59-K scatter. Their difference shows a trend with metallicity according to the equation displayed in the plot in the middle panel. This trend is almost the same as that found in the comparison with interferometric measurements, asserting the equivalence of the two scales (Casagrande et al. 2014). After applying the relation given by Eq. (1) to 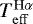 , the trend is indeed fully removed, as shown in the right panel of the figure. The remaining 45-K scatter is close to the average formal errors of
, the trend is indeed fully removed, as shown in the right panel of the figure. The remaining 45-K scatter is close to the average formal errors of 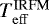 of the stars compared (52 K), which implies that it is dominated by the uncertainties of the colour measurements. Therefore, the contribution of random errors of
of the stars compared (52 K), which implies that it is dominated by the uncertainties of the colour measurements. Therefore, the contribution of random errors of 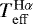 related to the normalization is negligible, supporting the precision of our method.
related to the normalization is negligible, supporting the precision of our method.
 |
Fig. 9 Left and middle panels: as in Fig. 8 but for the |
7.2 Spectroscopic effective temperatures
The need for accurate stellar atmospheric parameters got more attention with the discovery of exoplanets because their characterization depends directly on how accurately and precisely the physical parameters of the host stars are determined. Other studies also require a refined determination of Teff. For example, finding the nature of the connection between stellar metallicity and planetary presence (e.g. Santos et al. 2003; Fischer & Valenti 2005; Sousa et al. 2008; Ghezzi et al. 2010), the detection of diffusion effects in the stellar atmospheres (e.g. Korn et al. 2006, 2007), and the search for chemical signatures of planetary formation (e.g. Meléndez et al. 2009; Ramírez et al. 2009). Some of them deal with a large amount of stars, for which automatic spectroscopic procedures have been developed, that provide results with high internal precision. However, as shown by Ryabchikova et al. (2015) in their Fig. 1, when results from different spectroscopic procedures are compared, significant discrepancies may appear.
In this work we considered for comparison catalogues with small internal errors. Among them Ramirez14a and Ramirez14b are the most precise, with ~10 K, followed by Sousa08, Tsantaki13, and Maldonado15 with ~20 K, then Ghezzi10 and Heiter15 with ~30 K, and Bensby14 with ~70 K. The plots in Fig. 10 show the comparison of our temperature determination from Coudé with those derived by the authors above.
Sousa08, Ghezzi10, and Tsantaki13 all derive Teff assuming LTE and 1D geometry by the Kurucz Atlas 9 (Kurucz 1993) model atmospheres. They used the 2002 version of MOOG (Sneden 1973) and the ARES code for automatic measurement of equivalent widths (Sousa et al. 2007). They differ in the line lists used and in the atomic data adopted. Tsantaki13’s line list is an upgrade of that used by Sousa08 selected with HARPS, where “bad” lines were suppressed to correct Teff overestimation in cooler stars. Both works computed excitation potential values (log gf ) from an inverted solar analysis using equivalent widths measured in solar spectra. The list of Ghezzi10 is short in comparison with those of Sousa08 andTsantaki13, and was selected for the FEROS spectrograph (Kaufer et al. 1999) at lower resolution; they used laboratory log gf values. The comparison with these three works shows a trend with 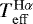 : the larger Teff, the larger the discrepancy. For Ghezzi10, the comparison between our measurements and theirs shows a positive trend with [Fe/H], while for Sousa08 and Tsantaki13 no trend with [Fe/H] is found, but offsets of 48 and 33 K, respectively.
: the larger Teff, the larger the discrepancy. For Ghezzi10, the comparison between our measurements and theirs shows a positive trend with [Fe/H], while for Sousa08 and Tsantaki13 no trend with [Fe/H] is found, but offsets of 48 and 33 K, respectively.
Bensby14 derived Teff considering non-LTE corrections on spectral lines measured manually. The 1D MARCS model atmospheres (Asplund et al. 1997) were used with their own code of convergence of atmospheric parameters. They used a large line list and spectra from different instruments of medium and high resolution, with laboratory log gf values. The comparison of their Teff scale against 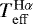 is similar to those of Sousa08 and Tsantaki13. Indeed, Sousa08 find their scale to be compatible to an offset of + 18 K with respect to that of Bensby14 (see Fig. 3 in paper). We find a slightly significant positive trend with [Fe/H].
is similar to those of Sousa08 and Tsantaki13. Indeed, Sousa08 find their scale to be compatible to an offset of + 18 K with respect to that of Bensby14 (see Fig. 3 in paper). We find a slightly significant positive trend with [Fe/H].
Ramirez14a and Ramirez14b used a differential method (Meléndez et al. 2006) with which the atmospheric parameters of high internal precision are obtained. By means of the “q 2 ” package8 both groups of authors used the 2013 version of MOOG and 1D + LTE model-atmosphere grids. They, measured spectral lines manually and used laboratory log gf values. There are two main differences between the procedures of Ramirez14a and Ramirez14b. Firstly, Ramirez14a used the “odfnew” version of Kurucz, while Ramirez14b used the MARCS atmosphere model (Gustafsson et al. 2008). However, according to Ramirez14b the use of different models does not significantly affect the parameters diagnostics because of the differential method applied. Secondly, the stars analysed in both works differ in [Fe/H]: Ramirez14b analysed solar twins while Ramirez14a more metal-rich stars, that is [Fe/H] ≳ 0.2. Thus, Ramirez14b naturally used the Sun as standard for the solar twins, while in Ramirez14a the differential method was applied with respect to every star of the sample. For the Ramirez14b scale of solar twins we find an offset of + 42 ± 13 K with respect to Hα, which agrees with the 28 ± 1 K needed to correct the Hα zero point. For the Ramirez14a scale we find an offset of + 72 ± 17 K. Considering Ramirez14a and Ramirez14b as a unique sample, we find a positive trend with [Fe/H].
Maldonado15 assumed LTE and 1D geometry by the Kurucz Atlas 9 model atmospheres as Sousa08, Ghezzi10, and Tsantaki13, but they used the line list from Grevesse & Sauval (1999) and spectra from several sources including HARPS. For the convergence of the atmospheric parameters they used TGVIT (Takeda et al. 2005). The comparison of their Teff scale against Hα does not show a significant trend, but an offset of +34 K. We found the same offset for IRFM against Hα (Sect. 7.1), which confirms the agreement9 between thisTeff scale and IRFM reported by the authors. On the other hand we find a positive trend with [Fe/H].
The spectroscopic scales analysed in this section show a general agreement with Hα up to ~5700 K and hotter diagnostics for hotter Teff. The trends with [Fe/H] are opposite to what we observe with interferometry and IRFM. After applying the correction relation for metallicity given by Eq. (1) to 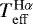 , the Hα scale can beconsidered in the same frame of the interferometry scale, allowing us to study the accuracy of the spectroscopic scales. This is shown in the right panels of Fig. 10, the common pattern shows that spectroscopic temperatures are underestimated by 100–200 K at [Fe/H] = −0.6 dex and overestimated by ~100 K at [Fe/H] = +0.4 dex. The most accurate [Fe/H] range is around the solar value, that is, between −0.3 and +0.1 dex.
, the Hα scale can beconsidered in the same frame of the interferometry scale, allowing us to study the accuracy of the spectroscopic scales. This is shown in the right panels of Fig. 10, the common pattern shows that spectroscopic temperatures are underestimated by 100–200 K at [Fe/H] = −0.6 dex and overestimated by ~100 K at [Fe/H] = +0.4 dex. The most accurate [Fe/H] range is around the solar value, that is, between −0.3 and +0.1 dex.
The relations presented in the plots in Fig. 10 can be used to empirically correct spectroscopic scales. These corrections become important as Teff depart from solar to derive unbiased [Fe/H] values. An example of the impact of the Teff scale on [Fe/H] is provided in Fig. 11. The plots compare the Teff and metallicity scales of Sousa08 and Ramirez13. No offset between both temperature scales appears, but their difference plotted against [Fe/H] replicates the trend obtained in the top-right panel of Fig. 10. The difference between metallicity scales also shows a trend with Teff, associating larger [Fe/H] discrepancies with Teff farther from solar.
 |
Fig. 10 As in Fig. 9 but for spectroscopic Teff. The authors are indicated in the plots in the left panels. In all plots, the black lines represent the perfect agreement and the red lines the trends. When the trends are not significant, the offsets are drawn with dashed red lines. Teff from Ramirez14a (plus symbols) and Ramirez14b (green circles), derived with the same method, are compared in the same plots. |
 |
Fig. 11 Left and middle panels: similar to Fig. 8 but for the |
8 Comparison with other Hα scales
In Sect. 6.1 we determined 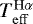 for the Sun andcompared it with other authors that use the same diagnostic. In this section we compare not only zero points but the temperature scales. We again discuss the possible sources of differences between them and how the enhanced models improve the results. The studies cited here have several stars in common with the IRFM catalogue of Ramirez13, but they have only a few or no stars in common with this work. Accordingly, the comparisons are preformed with respect to IRFM as a function of [Fe/H], as done in Sect. 7.1 with our Hα scale; see the plots in Fig. 12 to follow the discussions below.
for the Sun andcompared it with other authors that use the same diagnostic. In this section we compare not only zero points but the temperature scales. We again discuss the possible sources of differences between them and how the enhanced models improve the results. The studies cited here have several stars in common with the IRFM catalogue of Ramirez13, but they have only a few or no stars in common with this work. Accordingly, the comparisons are preformed with respect to IRFM as a function of [Fe/H], as done in Sect. 7.1 with our Hα scale; see the plots in Fig. 12 to follow the discussions below.
BPO02 scale: ten stars are in common with Ramirez13. An analogous plot to that in Fig. 9 shows a similar slope shifted by ~70 K for the metallicity range we analyse. A probable cause for the shift is that the synthetic spectra seem to be predominantly fitted with lower observed fluxes; see for example profiles of HR 22879 and HR 5914 at 6566–6568 Å in Fig. 6 in BPO02. This may be caused by the 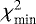 fitting method without sigma clipping applied in low-S/N spectra. For example, Ramirez14b find systematically high
fitting method without sigma clipping applied in low-S/N spectra. For example, Ramirez14b find systematically high 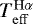 values for larger
values for larger 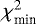 . It should however be mentioned that the results of BPO02 agree with ours in that a trend with metallicity exists. It should be noted that the quality of their spectra and their fitting method were not conceived in order to achieve the high precision that the current study is aiming for.
. It should however be mentioned that the results of BPO02 agree with ours in that a trend with metallicity exists. It should be noted that the quality of their spectra and their fitting method were not conceived in order to achieve the high precision that the current study is aiming for.
Cayrel et al. (2011) scale: the comparison against 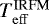 as a function of [Fe/H] shows a slight trend. In the comparison against Teff from interferometry the trend disappears leaving only a flat offset of ~100 K (see green symbols in the plot), as shown by the authors. It appears that the Hα model of Allard et al. (2008) enhances the difference between the model of BPO02 and interferometry close to the solar [Fe/H]. We obtain the same result in Sect. 6.1 for the Sun, that is, the zero point of the model is nearly twice that of BPO02.
as a function of [Fe/H] shows a slight trend. In the comparison against Teff from interferometry the trend disappears leaving only a flat offset of ~100 K (see green symbols in the plot), as shown by the authors. It appears that the Hα model of Allard et al. (2008) enhances the difference between the model of BPO02 and interferometry close to the solar [Fe/H]. We obtain the same result in Sect. 6.1 for the Sun, that is, the zero point of the model is nearly twice that of BPO02.
Ramirez14b scale: precise Teff was derived for 88 solar analogues (i.e. stars that share the same atmospheric parameters with the Sun within an arbitrary narrow range of errors, according to the definition in Porto de Mello et al. 2014) from the photometric calibrations of Casagrande et al. (2010; IFRM), Hα profiles using the model of BPO02, and the spectroscopic technique described in Sect. 7.2. In their Fig. 13, Ramirez14b compare their determinations from Hα with spectroscopy and find, after a zero point correction, a small trend, as we did in Sect. 7.2 comparing our Hα scale with their spectroscopic scale and several others. No comparison is presented against [Fe/H], which is to be expected given that the range of their sample is very narrow, that is, ±0.1 dex around solar metallicity.
Amarsi et al. (2018) scale: spectra of six templates were used to test the model. Two of these stars, the Sun and Procyon, lie within the [Fe/H] range of our sample, while the other four with [Fe/H] between −2.8 and −1.2 dex exceed our range. The comparison with 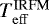 as a function of [Fe/H] shows a trend, but this trend disappears when interferometric Teff is instead compared. The change in slope is mainly given by the interferometric measurement of Procyon, which agrees closely with that from Hα. Accordingly, interferometry perfectly agrees with this Hα scale along the [Fe/H] range of analysis. Further, we also estimated a perfect agreement for the Sun from a differential analysis in Sect. 6.1; the zero point of the model is null.
as a function of [Fe/H] shows a trend, but this trend disappears when interferometric Teff is instead compared. The change in slope is mainly given by the interferometric measurement of Procyon, which agrees closely with that from Hα. Accordingly, interferometry perfectly agrees with this Hα scale along the [Fe/H] range of analysis. Further, we also estimated a perfect agreement for the Sun from a differential analysis in Sect. 6.1; the zero point of the model is null.
Another interesting and fast way of determining Teff from Hα was put forward by Hanke et al. (2018), however, we did not perform a comparison here.
 |
Fig. 12 From left to right panels: analogous comparisons to the middle panel in Fig. 9 for the Hα scales of BPO02, Cayrel et al. (2011), and Amarsi et al. (2018). In all plots, for a quick comparison, the trend with [Fe/H] of Fig. 9 is represented by the dotted line. Green symbols represent interferometric Teff replacing |
9 Hα profiles from 3D models
The previous sections have shown that the comparison of hα diagnostics with the accurate interferometric and IRFM scales shows that the former are relatively robust. The only trend found is a dependence on metallicity in both cases. In order to further investigate such a trend, we have produced and analysed eight Hα profiles from 3D models, with which we expect to understand whether or not the 1D approximation is indeed the main culprit. The eight 3D profiles are from the CIFIST grid of CO5BOLD models (Ludwig et al. 2009b; Freytag et al. 2012), calculated using the spectral synthesis code Linfor3D (version 6.2.2) in LTE approximation. Self-resonance broadening was carried out following BPO02 and Stark broadening was performed in accordance with Griem (1967). We chose the atmospheric parameters of four profiles to bracket a solar model Teff and log g. The four bracketing models were accompanied by four further models of sub-solar metallicity with [Fe/H] = −0.5 dex. The chemical composition follows Grevesse & Sauval (1998) with the exception of the CNO elements which were updated following Asplund (2005). For the metal-depleted models, an α-enhancement of + 0.2 dex was assumed. The variation of the continuum across the Hα profile was modelled by assuming a parabolic dependence of the continuum intensity on wavelength. Doppler shifts stemming from the underlying velocity field were fully taken into account – although they have only a minor effect on the overall profile shape. The final flux profiles were horizontal and temporal averages over typically 20 instants in time, and the centre-to-limb variation of the line was calculated using three limb angles.
To estimate the effects of 3D models on Teff, we analysed the synthetic Hα profiles in the same way as the observed ones. The synthetic profiles were resampled with the same pixel size of HARPS and 0.1% of white noise was added. The fits are shown in Fig. A.7 and the temperatures retrieved from 1D models are compared with their nominal temperatures in Fig. 13 as done in Sect. 6. In this figure, in the plot as a function of [Fe/H], the improvement given by the 3D models (continuous red line) can be estimated from the similarity with which the trend of Fig. 8 (dotted line here, representing interferometric Teff − 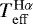 ) is reproduced. The comparison shows that the offset of 1D models is almost reproduced at [Fe/H] = 0 dex, and at [Fe/H] = − 0.5 dex 3D models produce temperatures that tend to be hotter by 0–100 K depending on log g. Hence, temperatures from 3D models are significantly closer to those from interferometry at [Fe/H] = − 0.5 dex, and they show particularly high levels of agreement for low log g values.
) is reproduced. The comparison shows that the offset of 1D models is almost reproduced at [Fe/H] = 0 dex, and at [Fe/H] = − 0.5 dex 3D models produce temperatures that tend to be hotter by 0–100 K depending on log g. Hence, temperatures from 3D models are significantly closer to those from interferometry at [Fe/H] = − 0.5 dex, and they show particularly high levels of agreement for low log g values.
We therefore conclude that the most likely cause for the trend with metallicity, in the parameter space analysed, of our Hα diagnostics with respect to interferometric and IRFM measurements is the use of 1D models. We nonetheless consider theuse of 1D models together with the empirical correction given by Eq. (1) to be an excellent approximation.
 |
Fig. 13 As in Fig. 8 but for 3D models. In the panel on the right, different symbols and colours are used for the two log g values according to the legends. The accuracy of 1D models |
10 Suitability of HARPS
Having shown the suitability of our normalization method with the Coudé spectra, we apply it to HARPS (Mayor et al. 2003). HARPS has been chosen because in order to achieve high radial-velocity precision, the instrument has a very stable field and pupil injection. It is also thermally stable and in vacuum. In addition, the HARPS archive contains plenty of observationsof solar-type stars, including a rich set of solar spectra taken by observing solar system bodies for many years. All these characteristics make HARPS the ideal instrument to investigate the precision of the normalization method that we have developed. The fact that the solar-sibling observations have been repeated for several years allows us to also investigate the stability of this instrument in time, and to determine to the extent to which the HARPS Hα profile has remained constant in time. The test is performed with all solar spectra set out in Table 3, for which 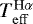 ’s were derived. The plot in the top panel of Fig. 14 visually summarises the results displayed in the table. For each date,
’s were derived. The plot in the top panel of Fig. 14 visually summarises the results displayed in the table. For each date, 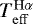 values are represented by plus symbols. Their weighted mean and corresponding spread values are drawn with bars. Next to them, the number of spectra used and their average S/N ratio are noted to show the precision reached when measurements from several spectra are combined. The weighted mean and spread of all measurements are represented by the horizontal line and the shade at 5744 ± 10 K. Evidently, there is no trend with time and the scatter is very low, which confirms the blaze stability of HARPS. This value is in perfect agreement with that of Coudé (see values in Table 2), which implies that not only is the blaze stable but it is also fully removed through the flat-field procedure.
values are represented by plus symbols. Their weighted mean and corresponding spread values are drawn with bars. Next to them, the number of spectra used and their average S/N ratio are noted to show the precision reached when measurements from several spectra are combined. The weighted mean and spread of all measurements are represented by the horizontal line and the shade at 5744 ± 10 K. Evidently, there is no trend with time and the scatter is very low, which confirms the blaze stability of HARPS. This value is in perfect agreement with that of Coudé (see values in Table 2), which implies that not only is the blaze stable but it is also fully removed through the flat-field procedure.
In the bottom panel of Fig. 14 we plot the precision obtained from individual spectra as a function of S/N. It is observed that ~40 K can be obtained from spectra of S/N = 400–500.
Finally, we compare the temperatures derived from HARPS with those derived from Coudé spectra for the other stars in common in our sample. The comparison is shown in Fig. 15 against the three main stellar parameters. It shows an excellent agreement with a negligible offset between the two samples of − 13 ± 34 K with no trends. The temperatures of all stars agree within 1σ errors, with the exception of two (δ Eri and HD 184985) that agree within 2σ.
Solar proxies.
 |
Fig. 14 Top panel: temperatures of the HARPS solar proxies in Table 3 vs. the date upon which spectra were acquired. Daily values are represented by plus symbols and weighted means and errors for each month are drawn in red. The weighted mean and error of all the measurements are represented by the continuous line and the shade on 5744 ± 10 K. Next to the bars, the number of spectra analysed and the mean S/N are noted. Bottom panel: errors of individual measurements in the top panel are plotted vs. S/N. The exponential curve given by the equation in the plot is the best fit to the points. |
11 Summary and conclusions
With the aim of better understanding and minimising the errors that affect Teff measurements from Hα profiles, we developed a new method to normalize the spectra and have tested it extensively. The results are quite consistent, and allow us also to test the accuracy of the temperature diagnostics with Hα profiles from 1D model atmospheres in LTE conditions (Barklem et al. 2002).
The core of this work is the special effort made to recover realistic Hα profiles free from instrumental signatures, namely the blaze function of the echelle spectrographs and those induced by errors of normalization. We eliminated the blaze using the single-order Coudé instrument at do Pico dos Dias Observatory. With it, spectra of 44 F, G, and K stars, including the Sun, with a wide parameter range Teff –[Fe/H]–log g (see Fig. 1) were acquired. We minimised the errors of normalization of Hα profiles by integrating normalization and fit into an iterative procedure, with which we derive precise 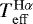 . This procedure additionally uses synthetic spectra of telluric features of PWV to optimise the continuum location. PWV features may be very small and nearly omnipresent around Hα, so they can be easily confused with spectral noise and shift the continuum to lower flux values.
. This procedure additionally uses synthetic spectra of telluric features of PWV to optimise the continuum location. PWV features may be very small and nearly omnipresent around Hα, so they can be easily confused with spectral noise and shift the continuum to lower flux values.
The accuracy of Hα lines from 1D model atmospheres is found to follow the relation 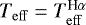 − 159[Fe/H] + 28 K within the metallicity range − 0.70 to + 0.40 dex. This was determined for solar parameters using
− 159[Fe/H] + 28 K within the metallicity range − 0.70 to + 0.40 dex. This was determined for solar parameters using 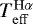 from 57 Coudé/HARPS/MUSICOS solar spectra (Table 3) compared with the reference solar Teff = 5772 K (Prša et al. 2016; Heiter et al. 2015), and for non-solar parameters comparing
from 57 Coudé/HARPS/MUSICOS solar spectra (Table 3) compared with the reference solar Teff = 5772 K (Prša et al. 2016; Heiter et al. 2015), and for non-solar parameters comparing 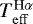 of ten Gaia Benchmark Stars (Heiter et al. 2015) with their Teff from interferometric measurements.
of ten Gaia Benchmark Stars (Heiter et al. 2015) with their Teff from interferometric measurements.
The consistency of our results with Teff scales from IRFM and excitation and ionization equilibrium of Fe lines was also investigated. The comparison with IRFM using the photometric calibrations of Casagrande et al. (2010) shows exactly the same trend as the interferometric one of the Gaia Benchmark Stars (compare Fig. 9 with Fig. 8), asserting the equivalence of the two scales reported by Casagrande et al. (2014). For spectroscopic measurements, the results vary slightly with the authors, but in general they show agreement with Hα up to 5700 K. A trend with metallicity is present and is opposite to that observed with interferometry and IRFM, implying that the spectroscopic scale, in general, underestimates/overestimates Teff by 100 K at [Fe/H] = − 0.6∕+0.4 dex with respectto interferometry and IRFM (see right panels of Fig. 10).
In order to investigate the observed trend with metallicity when comparing our measurements with the interferometric and IRFM ones, we tested 3D model atmospheres. Hα profiles from 3D models produce relatively similar diagnostics to 1D models at solar parameters (we obtain a − 15 K zero point), while at the metal-poor range, [Fe/H] = − 0.5 dex, they almost fully correct 1D model underestimates (see Fig. 13). This therefore indicates that the trend with metallicity is largely due to the use of 1D models. The correction we provide by Eq. (1), however, brings the three scales Hα(1D + LTE), interferometry, and IRFM to the same base.
We further find that the systematic “cool” solar temperature determinations from Hα models in the literature are associated to normalization errors of the different versions of Kitt Peak National Observatory solar atlases. We quantified the impact of the errors in Teff and find that models enhanced by 3D atmosphere geometry (Ludwig et al. 2009a; Freytag et al. 2012; Pereira et al. 2013; Amarsi et al. 2018) do improve the accuracy of 1D models, and that 3D + non-LTE models (Amarsi et al. 2018) lead to a null difference with the solar Teff derived by Stefan-Boltzmann equation.
We tested the suitability of HARPS for the temperature determination with Hα profiles. The tests were performed by analysing spectra of 26 stars in common with the Coudé sample and 47 solar spectra from the period 2007–2015. The solar spectra show consistent results, to better than ± 10 K, demonstrating the stability of the HARPS blaze and the effectiveness of the de-blazing process. The very small offset and scatter (−13 ± 34 K) resulting from the comparison of the stars in common with the Coudé sample confirms that the normalization-fitting integrated method minimises random and systematic errors related to the custom normalization procedure by polynomial interpolation. Hence, when this method is applied, the internal errors of the Hα profile fitting are entirely due to the spectral noise.
Finally, in Table 4 we list the measured 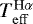 (by combining all measurements from Coudé, HARPS, and MUSICOS spectra) and our best Teff estimate obtained applying the correction for metallicity. The [Fe/H] and log g values used as input for deriving
(by combining all measurements from Coudé, HARPS, and MUSICOS spectra) and our best Teff estimate obtained applying the correction for metallicity. The [Fe/H] and log g values used as input for deriving 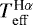 follow the order of preference: Heiter15, Ramirez13, Ramirez14b, Ramirez14a, Maldonado15, Ghezzi10, Sousa08, Tsantaki13, Bensby14.
follow the order of preference: Heiter15, Ramirez13, Ramirez14b, Ramirez14a, Maldonado15, Ghezzi10, Sousa08, Tsantaki13, Bensby14.
 |
Fig. 15 Temperature diagnostics from HARPS respect those of Coudé vs. atmospheric parameters. [Fe/H] and log g values from Table 1 were used here. The −13 K offset and its 34 K scatter are represented by the dashed lines and the shades, respectively. |
Teff of the sample stars.
Acknowledgements
R.E.G. acknowledges a ESO Ph.D. studentship. R.E.G. and M.L.U.M. acknowledge CAPES studentships. G.F.P.M. acknowledges grant 474972/2009-7 from CNPq/Brazil. D.L.O. acknowledges the support from FAPESP (2016/20667-8). S.U. Acknowledges the support of the Fundação para a Ciência e Tecnologia (FCT) through national funds and of the FEDER through COMPETE2020 by these grants UID/FIS/04434/2013 & POCI-01-01-145-FEDER-007672 and PTDC/FIS-AST/1526/2014 & POCI-01-0145-FEDER-016886. H.G.L. acknowledges financial support by the Sonderforschungsbereich SFB 881 “The Milky Way System” (subprojects A4) of the German Research Foundation (DFG). We thank the staff of the OPD/LNA for considerable support in the observing runs needed to complete this project. Use was made of the Simbad database, operated at the CDS, Strasbourg, France, and of NASA Astrophysics Data System Bibliographic Services.
Appendix A Hα profile fits
 |
Fig. A.1 Profile fits of Coudé solar spectra. |
 |
Fig. A.2 Profile fits of MUSICOS solar spectra. |
 |
Fig. A.3 Profile fits of KPNO2005 (top panel), and KPNO2011 (bottom panel) spectra. |
 |
Fig. A.4 From top to bottom panels: transition regions at the red wing in fitted Coudé, KPNO2005, and KPNO2011 spectra. Toppanel: related to the spectrum in Fig. 2, and the two panels below are related to the spectra in Fig. A.3. |
 |
Fig. A.5 For the KPNO2011 atlas, spectral regions that contain the continuum windows [6500.25, 6500.50] and [6504.50, 6505.00] (top panel), and [6619.70, 6620.50], [6625.60,6625.80] and [6626.50, 6626.80] (bottom panel). |
 |
Fig. A.6 Results from the iterative Hα normalization-fitting of one of the two Coudé spectra of 18Sco (HD 146233) following the procedure described in Sect. 3.1. |
 |
Fig. A.7 Fits of 3D profiles (black) with 1D profiles (red). The nominal temperature values of the 3D profiles are noted in the left, while the parameters of the 1D profiles are at the right side. |
References
- Allard, N. F., Kielkopf, J. F., Cayrel, R., & van’t Veer-Menneret, C. 2008, A&A, 480, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allende Prieto, C., Barklem, P. S., Lambert, D. L., & Cunha, K. 2004, A&A, 420, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amarsi, A. M., Nordlander, T., Barklem, P. S., et al. 2018, A&A, 615, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Gustafsson, B., Kiselman, D., & Eriksson, K. 1997, A&A, 318, 521 [NASA ADS] [Google Scholar]
- Barklem, P. S. 2007, A&A, 466, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barklem, P. S., Piskunov, N., & O’Mara, B. J. 2000, A&A, 363, 1091 [NASA ADS] [Google Scholar]
- Barklem, P. S., Stempels, H. C., Allende Prieto, C., et al. 2002, A&A, 385, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baudrand, J., & Bohm, T. 1992, A&A, 259, 711 [NASA ADS] [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Portinari, L., Glass, I. S., et al. 2014, MNRAS, 439, 2060 [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004, ArXiv e-prints [arXiv:astro-ph/0405087] [Google Scholar]
- Cayrel, R., van’t Veer-Menneret, C., Allard, N. F., & Stehlé, C. 2011, A&A, 531, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clough, S. A., Shephard, M. W., Mlawer, E. J., et al. 2005, J. Quant. Spectr. Rad. Transf., 91, 233 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Cornejo, D., Ramirez, I., & Barklem, P. S. 2012, ArXiv e-prints [arXiv:1206.0750] [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Comput. Phys., 231, 919 [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1993, A&A, 271, 451 [NASA ADS] [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1994, A&A, 285, 585 [NASA ADS] [Google Scholar]
- Fuhrmann, K., Pfeiffer, M., Frank, C., Reetz, J., & Gehren, T. 1997, A&A, 323, 909 [NASA ADS] [Google Scholar]
- Ghezzi, L., Cunha, K., Smith, V. V., et al. 2010, ApJ, 720, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1999, A&A, 347, 348 [NASA ADS] [Google Scholar]
- Griem, H. R. 1967, ApJ, 147, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanke, M., Hansen, C. J., Koch, A., & Grebel, E. K. 2018, A&A, 619, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiter, U., Jofré, P., Gustafsson, B., et al. 2015, A&A, 582, A49 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, The Messenger, 95, 8 [Google Scholar]
- Kausch, W., Noll, S., Smette, A., et al. 2015, A&A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korn, A. J., Shi, J., & Gehren, T. 2003, A&A, 407, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korn, A. J., Grundahl, F., Richard, O., et al. 2006, Nature, 442, 657 [Google Scholar]
- Korn, A. J., Grundahl, F., Richard, O., et al. 2007, ApJ, 671, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km/s grid. Kurucz CD-ROM No. 13, Cambridge, MA: Smithsonian Astrophysical Observatory, 13 [Google Scholar]
- Kurucz, R. L. 2005, Mem. Soc. Astron. It. Suppl., 8, 189 [Google Scholar]
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar flux atlas from 296 to 1300 nm (Sunspot, New Mexico: National Solar Observatory) [Google Scholar]
- Lind, K., Korn, A. J., Barklem, P. S., & Grundahl, F. 2008, A&A, 490, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ludwig, H.-G., Behara, N. T., Steffen, M., & Bonifacio, P. 2009a, A&A, 502, L1 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Ludwig, H.-G., Caffau, E., Steffen, M., et al. 2009b, Mem. Soc. Astron. It., 80, 711 [NASA ADS] [Google Scholar]
- Maldonado, J., Eiroa, C., Villaver, E., Montesinos, B., & Mora, A. 2015, A&A, 579, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsuno, T., Aoki, W., Beers, T. C., Lee, Y. S., & Honda, S. 2017a, AJ, 154, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuno, T., Aoki, W., Suda, T., & Li, H. 2017b, PASJ, 69, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Meléndez, J., Dodds-Eden, K., & Robles, J. A. 2006, ApJ, 641, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Asplund, M., Gustafsson, B., & Yong, D. 2009, ApJ, 704, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Moehler, S., Modigliani, A., Freudling, W., et al. 2014, A&A, 568, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moore, C. E., Minnaert, M. G. J., & Houtgast, J. 1966, The solar spectrum 2935 A to 8770 A (Washington: US Government Printing Office) [Google Scholar]
- Önehag, A., Gustafsson, B., & Korn, A. 2014, A&A, 562, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira, T. M. D., Asplund, M., Collet, R., et al. 2013, A&A, 554, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porto de Mello, G. F., Lyra, W., & Keller, G. R. 2008, A&A, 488, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porto de Mello, G. F., da Silva, R., da Silva, L., & de Nader, R. V. 2014, A&A, 563, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prša, A., Harmanec, P., Torres, G., et al. 2016, AJ, 152, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Allende Prieto, C., & Lambert, D. L. 2013, ApJ, 764, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2014a, A&A, 561, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Meléndez, J., Bean, J., et al. 2014b, A&A, 572, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Meléndez, J., Cornejo, D., Roederer, I. U., & Fish, J. R. 2011, ApJ, 740, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L., Gordon, I., Babikov, Y., et al. 2013, J. Quant. Spectr. Rad. Transf., 130, 4 [Google Scholar]
- Ryabchikova, T., Piskunov, N., & Shulyak, D. 2015, in Physics and Evolution of Magnetic and Related Stars, eds. Y. Y. Balega, I. I. Romanyuk, & D. O. Kudryavtsev, ASP Conf. Ser., 494, 308 [NASA ADS] [Google Scholar]
- Santos, N. C., Israelian, G., Mayor, M., Rebolo, R., & Udry, S. 2003, A&A, 398, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Škoda, P., & Šlechta, M. 2004, in IAU Colloq. 193: Variable Stars in the Local Group, eds. D. W. Kurtz, & K. R. Pollard, ASP Conf. Ser., 310, 571 [NASA ADS] [Google Scholar]
- Škoda, P., Šurlan, B., & Tomić, S. 2008, in Ground-based and Airborne Instrumentation for Astronomy II, Proc. SPIE, 7014, 70145X [CrossRef] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sneden, C. A. 1973, Ph.D. Thesis, The University of Texas at Austin [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A&A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Takeda, Y., Ohkubo, M., Sato, B., Kambe, E., & Sadakane, K. 2005, PASJ, 57, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Tsantaki, M., Sousa, S. G., Adibekyan, V. Z., et al. 2013, A&A, 555, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wallace, L., Hinkle, K. H., Livingston, W. C., & Davis, S. P. 2011, ApJS, 195, 6 [NASA ADS] [CrossRef] [Google Scholar]
The Python package “q2” – https://github.com/astroChasqui/q2
Maldonado et al. (2015) find an offset of 41 K, which is not significant considering the ~100 K error bar relative to their IRFM calculations.
All Tables
All Figures
 |
Fig. 1 Parameter space covered by the sample stars. The values are listed in Table 1. |
| In the text | |
 |
Fig. 2 Coudé Hα profile of one of the solar proxies in Table 3. The red and black lines represent the synthetic and observed profiles. The shaded regions are the windows of fits and the circles represent the continuum bins colour-coded according to their frequency of appearance in all Coudé spectra. The most frequent continuum windows are observed at [6500.25, 6500.50], [6504.50, 6505.00], [6619.70, 6620.50], [6625.60, 6625.80] and [6626.50, 6626.80]. Bottom panel: histogram of temperatures related to the wavelength bins within the windows of fits. A Gaussian is fitted to its median and robust standard deviation. |
| In the text | |
 |
Fig. 3 As in Fig. 2 but with a HARPS spectrum of one of the solar proxies from Table 3. The grey line represents the spectrum in its original resolution and the black line represents the spectrum degraded to the resolution of Coudé. Continuum bins in the degraded spectrum are highlighted in green; notice that they mostly match those of Fig. 2. |
| In the text | |
 |
Fig. 4 Left panels: fitting of two Coudé spectra (grey line) with synthetic spectra of PWV with concentrations of 7.5 and 5 mm (red and blue lines, respectively) for the same air mass. The circles are the continuum wavelength bins on 1 ± σ(noise). The shades represent 3 of the 5 continuum windows selected in Fig. 2. The arrows point to the windows contaminated by telluric features. Right panels: flux histograms of the spectra on the left panels with the same flux scale. The black horizontal line shows the continuum, and the dashed line is the average flux of the five continuum windows of Fig. 2 and the shades are the spread. |
| In the text | |
 |
Fig. 5 Telluric correction and profile fitting of the Coudé spectrum of HD 2151. Left panel:corrected and non-corrected spectra are represented by the black and blue lines, respectively. The windows of fits are represented by the shades, and the arrows point to those windows where the relative flux was perfectly recovered. The red line represents the fitted synthetic profile. Right panel: histogram of temperatures related to the wavelength bins inside the windows of fits. The most probable |
| In the text | |
 |
Fig. 6 Temperature diagnostics from MUSICOS with respect to those of Coudé vs. atmospheric parameters. [Fe/H] and log g values from Table 1 were used here. The −1 K offset and its 25 K scatter are represented by the dashed lines and the shades, respectively. |
| In the text | |
 |
Fig. 7 Graphic representation of solar Teff values in Table 2. The horizontal line represents the solar Teff measured by the Stefan-Boltzmann equation. Works that used theoretical models based on 1D atmosphere models are represented by circles, and those that used 3D models are represented by triangles. Grey circles represent works that used the theoretical model of BPO02, and green circles represent works that used a different/enhanced recipe. Works that used KPNO solar atlases are labelled in blue. For them, for comparison purposes, our measurements from corresponding KPNO spectra are included as red crosses in the same line. |
| In the text | |
 |
Fig. 8 Left panel: comparison of |
| In the text | |
 |
Fig. 9 Left and middle panels: as in Fig. 8 but for the |
| In the text | |
 |
Fig. 10 As in Fig. 9 but for spectroscopic Teff. The authors are indicated in the plots in the left panels. In all plots, the black lines represent the perfect agreement and the red lines the trends. When the trends are not significant, the offsets are drawn with dashed red lines. Teff from Ramirez14a (plus symbols) and Ramirez14b (green circles), derived with the same method, are compared in the same plots. |
| In the text | |
 |
Fig. 11 Left and middle panels: similar to Fig. 8 but for the |
| In the text | |
 |
Fig. 12 From left to right panels: analogous comparisons to the middle panel in Fig. 9 for the Hα scales of BPO02, Cayrel et al. (2011), and Amarsi et al. (2018). In all plots, for a quick comparison, the trend with [Fe/H] of Fig. 9 is represented by the dotted line. Green symbols represent interferometric Teff replacing |
| In the text | |
 |
Fig. 13 As in Fig. 8 but for 3D models. In the panel on the right, different symbols and colours are used for the two log g values according to the legends. The accuracy of 1D models |
| In the text | |
 |
Fig. 14 Top panel: temperatures of the HARPS solar proxies in Table 3 vs. the date upon which spectra were acquired. Daily values are represented by plus symbols and weighted means and errors for each month are drawn in red. The weighted mean and error of all the measurements are represented by the continuous line and the shade on 5744 ± 10 K. Next to the bars, the number of spectra analysed and the mean S/N are noted. Bottom panel: errors of individual measurements in the top panel are plotted vs. S/N. The exponential curve given by the equation in the plot is the best fit to the points. |
| In the text | |
 |
Fig. 15 Temperature diagnostics from HARPS respect those of Coudé vs. atmospheric parameters. [Fe/H] and log g values from Table 1 were used here. The −13 K offset and its 34 K scatter are represented by the dashed lines and the shades, respectively. |
| In the text | |
 |
Fig. A.1 Profile fits of Coudé solar spectra. |
| In the text | |
 |
Fig. A.2 Profile fits of MUSICOS solar spectra. |
| In the text | |
 |
Fig. A.3 Profile fits of KPNO2005 (top panel), and KPNO2011 (bottom panel) spectra. |
| In the text | |
 |
Fig. A.4 From top to bottom panels: transition regions at the red wing in fitted Coudé, KPNO2005, and KPNO2011 spectra. Toppanel: related to the spectrum in Fig. 2, and the two panels below are related to the spectra in Fig. A.3. |
| In the text | |
 |
Fig. A.5 For the KPNO2011 atlas, spectral regions that contain the continuum windows [6500.25, 6500.50] and [6504.50, 6505.00] (top panel), and [6619.70, 6620.50], [6625.60,6625.80] and [6626.50, 6626.80] (bottom panel). |
| In the text | |
 |
Fig. A.6 Results from the iterative Hα normalization-fitting of one of the two Coudé spectra of 18Sco (HD 146233) following the procedure described in Sect. 3.1. |
| In the text | |
 |
Fig. A.7 Fits of 3D profiles (black) with 1D profiles (red). The nominal temperature values of the 3D profiles are noted in the left, while the parameters of the 1D profiles are at the right side. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.