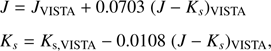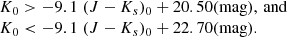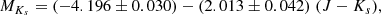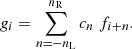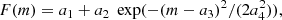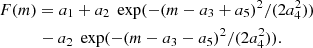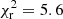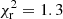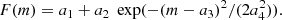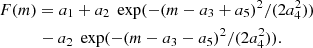| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 26 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833904 | |
| Published online | 29 January 2019 | |
The VMC Survey
XXXIII. The tip of the red giant branch in the Magellanic Clouds⋆
1
Koninklijke Sterrenwacht van België, Ringlaan 3, 1180 Brussels, Belgium
e-mail: martin.groenewegen@oma.be
2
Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
3
Dipartimento di Fisica e Astronomia, Università di Padova, Vicolo dell’Osservatorio 2, 35122 Padova, Italy
4
Department of Physics and Astronomy, Macquarie University, Balaclava Road, Sydney, NSW 2109, Australia
5
Research Centre for Astronomy, Astrophysics and Astrophotonics, Macquarie University, Balaclava Road, Sydney, NSW 2109, Australia
6
International Space Science Institute–Beijing, 1 Nanertiao, Zhongguancun, Hai Dian District, Beijing 100190, PR China
7
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany
8
INAF – Osservatorio Astronomico di Capodimonte, Via Moiariello 16, 80131 Naples, Italy
9
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Piero Gobetti 93/3, 40129 Bologna, Italy
10
Lennard-Jones Laboratories, Keele University, ST5 5BG, UK
Received:
19
July
2018
Accepted:
29
November
2018
In this paper JKs-band data from the VISTA Magellanic Cloud (VMC) survey are used to investigate the tip of the red giant branch (TRGB) as a distance indicator. A linear fit to recent theoretical models is used as the basis for the absolute calibration which reads MKs = −4.196 − 2.013 (J − Ks), valid in the colour range 0.75 < (J − Ks)< 1.3 mag and in the 2MASS system. The observed TRGB is found based on a classical first-order derivative filter and a second-order derivative filter applied to the binned luminosity function using the “sharpened” magnitude that takes the colour term into account. Extensive simulations are carried out to investigate any biases and errors in the derived distance modulus (DM). Based on these simulations criteria are established related to the number of stars per bin in the 0.5 mag range below the TRGB and related to the significance with which the peak in the filter response curve is determined such that the derived distances are unbiased. The DMs based on the second-order derivative filter are found to be more stable and are therefore adopted, although this requires twice as many stars per bin. Given the surface density of TRGB stars in the Magellanic Clouds (MCs), areas of ∼0.5 deg2 in the densest parts to ∼10 deg2 in the outskirts of the MCs need to be considered to obtain accurate and reliable values for the DMs. The TRGB method is applied to specific lines-of-sight where independent distance estimates exist, based on detached eclipsing binaries in the Large and Small Magellanic Clouds (LMC, SMC), classical Cepheids in the LMC, RR Lyrae stars in the SMC, and fields in the SMC where the star formation history (together with reddening and distance) has been derived from deep VMC data. The analysis shows that the theoretical calibration is consistent with the data, that the systematic error on the DM is approximately 0.045 mag (about evenly split between the theoretical calibration and the method), and that random errors of 0.015 mag are achievable. Reddening is an important element in deriving the distance: we derive mean DMs ranging from 18.92 mag (for a typical E(B − V) of 0.15 mag) to 19.07 mag (E(B − V)∼0.04 mag) for the SMC, and ranging from 18.48 mag (E(B − V)∼0.12 mag) to 18.57 mag (E(B − V)∼0.05 mag) for the LMC.
Key words: Magellanic Clouds / stars: distances
© ESO 2019
1. Introduction
The VISTA Magellanic Cloud (VMC) ESO public survey is a photometric survey in the three filters Y, J, and Ks (Cioni et al. 2011) performed with the Visible and Infrared Survey Telescope for Astronomy (VISTA) telescope using the VISTA InfraRed CAMera (VIRCAM) camera (Sutherland et al. 2015). The latter provides a spatial resolution of 0.34″ per pixel and a non-contiguous field-of-view of 1.65° in diameter sampled by 16 detectors. To homogeneously cover the field-of-view it is necessary to fill the gaps between individual detectors using a six-point mosaic. This unit area of VISTA surveys is called a tile and covers 1.77 deg2 of which the central area of 1.475° × 1.017° is covered by at least two of the six pointins in the mosaic.
The VMC survey covers an area of approximately 170 deg2 (110 tiles) of the Magellanic Cloud (MC) system and includes stars as faint as 22 mag in Ks (5σ, Vega mag); see Cioni et al. (2011) for a description of the survey.
The main scientific goals of the VMC survey are to derive the spatially resolved star formation history (SFH) across the Magellanic system (Rubele et al. 2012, 2015, 2018) and to measure its three-dimensional geometry (e.g. Ripepi et al. 2017; Subramanian et al. 2017; Muraveva et al. 2018, see below), which drive, respectively, the depth and the monitoring strategy of the survey. There is much additional science that has been done using VMC data, for example on background galaxies (including quasars), asymptotic giant branch (AGB) stars, planetary nebulae, eclipsing binaries, stellar clusters, variable stars, and the proper motion of the MCs (see Cioni 2016 for some recent science highlights).
The study of the 3D structure of the MCs relies on the use of different stellar distance indicators available in the MCs. The VMC team has addressed this in various papers using the data available, in particular, using Type-II Cepheids (T2Cs; Ripepi et al. 2015, 13 tiles in the Large MC, LMC), Classical Cepheids (CCs; Ripepi et al. 2012, two tiles in the LMC centred on the south ecliptic pole and 30 Doradus; Ripepi et al. 2016, 2017, analysing almost 4800 CCs detected in the OGLE-IV survey across the entire SMC), RR Lyrae (RRL; Muraveva et al. 2018, all 27 tiles in the Small MC, SMC), and the Red Clump (RC; Tatton et al. 2013, one tile centred on 30 Doradus; Subramanian et al. 2017, 13 tiles covering the central part of the SMC).
In this paper we investigate and use yet another distance indicator, the tip of the red giant branch (TRGB), and apply it to VMC data in the MCs. Over the years the TRGB distance has become an important rung of the distance ladder as distances can be routinely obtained with the Hubble Space Telescope (HST) with moderate effort out to ∼10 Mpc (see for example McQuinn et al. 2017 using two orbits of HST) or ∼15 Mpc (see for example Hatt et al. 2018 using six orbits of HST). The Extragalactic Distance Database1 (Jacobs et al. 2009) currently contains 400+ galaxies with TRGB distances.
The classical paper on the subject is Lee et al. (1993) which introduced the method of using an edge-detection algorithm to determine the tip (the TRGB was recognised and used as a distance indicator before, but more in a qualitative way; see references in Lee et al. 1993). Lee et al. (1993) also introduced the classical method of using the I-band for absolute calibration. Later it was recognised that the absolute magnitude in I (or Ks, see later) of the tip is not constant but is a shallow function of metallicity, or, in the observational plane, colour (see Salaris & Girardi 2005 for a theoretical point of view).
Madore et al. (2009) took this into consideration and introduced the idea of “sharpening” the tip by colour-correcting the I-band data before producing the luminosity function. The function marginalized for the tip detection had the form T = I − β ⋅ (V − I), where β is the slope of the tip magnitude as a function of colour, thereby correcting for the metallicity sensitivity of the TRGB.
The TRGB method can also be applied in the near-infrared (NIR), where reddening is lower than in the optical, and TRGB stars are intrinsically brighter, MKs ≈ −6.5 (see later) versus MI ≈ −4.0 mag (see e.g. Serenelli et al. 2017 and references therein).
Cioni et al. (2000) appear to have been the first to investigate the TRGB in the NIR, using I, J, Ks data from the Deep Near Infrared Survey of the Southern Sky (DENIS; Epchtein et al. 1999) for the MCs. They also introduced a new method to detect the tip, based on the second-order derivative of the luminosity function (LF), rather than the traditional Sobel filter (Sobel 1970) which is a first-order derivative filter (see Sect. 4). They found that the TRGB is located at a dereddened magnitude (in the DENIS system) of Ks = 11.94 ± 0.04 (LMC) and 12.58 ± 0.04 mag (SMC). In that paper the distance to the MCs is not actually derived from the TRGB in the infrared, but from the TRGB in bolometric magnitude, calculated from J, Ks, a bolometric correction, and a theoretical calibration. They found distance moduli (DM) of 18.55 ± 0.04 ± 0.08 mag for the LMC and 18.99 ± 0.03 ± 0.08 mag for the SMC (where the two error bars indicate formal and systematic errors, respectively), which imply (in the DENIS system) MKs = −6.61 ± 0.09 mag and MKs = −6.41 ± 0.09 mag for the LMC and SMC, respectively.
Macri et al. (2015) presented the results of the LMC Near-Infrared Synoptic Survey (LMCNISS) covering 18 deg2 down to Ks ∼ 16.5 mag. They found the TRGB to be located at (observed magnitudes, calibrated in the 2MASS system) J = 13.23 ± 0.03, H = 12.35 ± 0.02, and Ks = 12.11 ± 0.01 mag. They used a typical reddening of E(V − I)=0.08 mag (from Haschke et al. 2012a), and the distance to the LMC based on detached eclipsing binaries (dEBs; DM = 18.493 ± 0.048 mag, Pietrzyński et al. 2013) to find MKs = −6.41 ± 0.05 mag. Taking into account the difference in adopted DM, the remaining difference with Cioni et al. (2000) is explained by the difference in the photometric passbands. According to Delmotte et al. (2002), Ks(DENIS) = Ks(2MASS) −(0.14 ± 0.05) mag.
Górski et al. (2016) investigated the TRGB in the MCs using the I-band (from OGLE), J, Ks (from a survey with the InfraRed Survey Facility, IRSF, see Kato et al. 2007, and bolometric magnitudes. They considered 17 fields in the LMC and 5 in the SMC, each 35′ × 35′, selected to have a reddening of E(V − I)< 0.1 mag according to Haschke et al. (2011). They used a kernel of the form [−2, −1, 0, +1, +2] and then calculated the Gaussian-smoothed LF introduced by Sakai et al. (1996) to detect the edge. The mean magnitudes of the measured TRGB in the LMC and SMC are Ks = 12.13 ± 0.04 mag, and 12.91 ± 0.04 mag, respectively, with mean K-band reddening values of 0.05, and 0.02 mag, respectively, in agreement with the estimates above. They appear to assume that the IRSF magnitudes are effectively in the 2MASS system but Kato et al. (2007) indicate differences of 0.01 mag in J and 0.04 mag Ks, and then reach the conclusion that the DM to the LMC and SMC is about 0.2 mag longer than the values based on dEBs (Pietrzyński et al. 2013; Graczyk et al. 2014). For the absolute calibration (see Sect. 3) they used the relation of Valenti et al. (2004) adopting metallicities of [Fe/H] = −0.6 and −1.0 dex for the LMC and the SMC, respectively. In their latest paper Górski et al. (2018) credit this difference of 0.2 mag in DM to population effects and advocate the use of colour-dependent calibration relations rather then metallicity-dependent ones.
The TRGB method in the K-band has been applied to galaxies other than the MCs, namely Fornax (Gullieuszik et al. 2007; Pietrzyński et al. 2009; Whitelock et al. 2009), Carina (Pietrzyński et al. 2009), Sculptor (Menzies et al. 2011), NGC 205 (Jung et al. 2012) and IC 1613 (Chun et al. 2015). The latter two papers use the method introduced by Cioni et al. (2000) to detect the edge using the second-order derivative of the LF2. The TRGB method has been applied to 23 nearby galaxies (≲4 Mpc) by Dalcanton et al. (2012) using the HST F110W and F160W filters. Most recently, Madore et al. (2018) and Hoyt et al. (2018) discuss the TRGB in the JHK band in IC 1613 and the LMC. A more detailed comparison to their work is done in Sect. 3.
In the present paper we apply the TRGB method in the Ks-band across the SMC and LMC using VMC data. In Sect. 2 the selection of the sample is discussed. In Sect. 3 the absolute magnitude of the TRGB in the infrared is discussed, while Sect. 4 discusses the model, which includes a classical (first-order derivative) edge-detection, and an extension and improvement of the second-order derivative method of Cioni et al. (2000).
2. Data overview and sample selection
From the VISTA Science Archive (VSA; Cross et al. 2012) all sources3 brighter than Ks = 15 mag are selected, with a photometric error of < 0.1 mag and a quality bit flag indicating at best minor warnings. This query results in 885 558 sources. There are several magnitudes listed in the source tables. The recommended aperMag3 is taken, which is based on a 2″ aperture in diameter and includes an aperture correction and a saturation correction for the brightest stars (not relevant here). Only likely and probable point sources are selected reducing the number of objects to 851 6584. The sky distribution is shown in Fig. 1. The LMC, the SMC, the two tiles in the Magellanic Stream (MS), and the Magellanic Bridge (MB) are apparent. The small regions missing in the corner of every tile correspond to detector 16 which are excluded by selecting on the quality bit flag5.
 |
Fig. 1. Position on the sky of the selected VMC sources. For clarity only every 40th object is plotted. The LMC, the SMC, the two tiles in the MS, and the MB are apparent. The small regions missing in the corner of every tile correspond to detector 16 which are excluded by enforcing the constraint on ksppErrBits. |
The data are dereddened based on the reddening law of Cardelli et al. (1989) for RV = 3.1 which in the VISTA passbands leads to AJ/AV = 0.283 and AKs/AV = 0.114 (Rubele et al. 2015). The dereddened data are then transformed from the VISTA system to the 2MASS system, which will be the reference photometric system in this paper. Transformation formulae from 2MASS to VISTA are given by González-Fernández et al. (2018) 6 which can be inverted to give:
with the subscript “VISTA” indicating magnitudes in the VISTA system.
Figure 2 shows the colour–magnitude diagram (CMD) for the LMC, SMC, MS and MB. For this figure, a constant E(B − V) of 0.12 (LMC) and 0.075 mag (SMC, MS, MB) are adopted for simplicity, the average of the reddening towards the known dEBs in the LMC and the SMC (see Table 1). The RGB is very well developed in the LMC and the SMC, but there are only a few RGB stars in the MS and MB. The figure also includes lines which are used to select stars for further analysis. The TRGB method is applied to stars with
 |
Fig. 2. Colour–magnitude diagrams of the LMC, SMC, MS, and the MB. For clarity only every 40th (LMC), or 20th (SMC) point is shown, and all points for the MS and MB. The solid lines (see text) indicate the adopted borders to select RGB stars, independent of spatial location (see Eq. (2)). |
TRGB distances to MC fields surrounding dEBs.
These relations are determined by eye to select predominantly RGB stars and minimise AGB/foreground contaminants. As Fig. 2 shows the same relations are effective in making this selection for SMC and LMC alike. When the method outlined below is applied to another stellar system a different set of equations should be determined to take into account differences in DM and colour of the RGB. We note that photometric uncertainties are very small in the VMC data, at Ks = 12, 13, 14 mag, and the typical photometric errors are 1.5, 2.0 and 4.2 millimags, respectively.
The model to detect the TRGB is introduced in Sect. 4, but we first discuss the absolute calibration of the TRGB in the infrared as this also enters into the method.
3. Absolute calibration of the TRGB in the Ks-band
The default calibration for the brightness of the TRGB in the present paper is based on the theoretical calculations of Serenelli et al. (2017) which provide the absolute magnitude in several filters (V and I, J and Ks in the 2MASS system, and HST F110W and F160W filters) based on stellar evolution models, using bolometric corrections to convert luminosity, effective temperature and metallicity to the observational plane. In their Table 1 they provide second-order polynomial fits to MKs for two ranges in (J − Ks). Here we use a subset of their dataset (kindly provided by M. Salaris) to fit a linear equation in the colour range of interest.
Restricting the fit to the colour range 0.75 < (J − Ks)< 1.3 mag to broadly match the colour range of the SMC and LMC TRGBs, model ages older than 4 Gyr (see the discussion in Serenelli et al. 2017), and model ages younger than 14 Gyr, the bi-sector fit is:
with an rms of 0.030 mag (N = 28). The fit is shown as the solid line in Fig. 3. In Sect. 6.3 the sensitivity of the results to this calibration is investigated. An alternative calibration, restricting the colour range to specifically match that of the SMC and LMC TRGBs makes the relation shallower, MKs = ( − 4.331 ± 0.025)−(1.873 ± 0.023) (J − Ks) for 0.82 < (J − Ks)< 1.2 mag with an rms of 0.009 mag (N = 16).
 |
Fig. 3. Calibration of the Ks-band absolute magnitude of the TRGB as a function of (J − Ks) colour, based on the data of Serenelli et al. (2017). The solid line indicates the fit to models in the colour range 0.75 < (J − Ks)< 1.3 mag and ages between 4 and 14 Gyr. Sets of different metallicities are indicated by open triangles ([Fe/H] = −1.49 dex), filled squares ([Fe/H] = −1.27 dex), open circles ([Fe/H] = −0.96 and −0.66 dex), filled triangle ([Fe/H] = −0.35 dex), and open squares ([Fe/H] = −0.25, −0.01 and +0.06 dex). Models outside these criteria are indicated by the small dots. |
When the current paper was near completion Madore et al. (2018) and Hoyt et al. (2018) discussed the absolute calibration of the TRGB in JHK7. They derived the slope from data in IC 1613, and found β = −1.85 ± 0.27, consistent with Serenelli et al. (2017) in general and the specific values from our fits. Using NIR data in the bar of the LMC, adopting the distance to the LMC from the dEBs in Pietrzyński et al. (2013), β = −1.85 from the work on IC 1613, and a low reddening to the LMC of E(B − V)=0.03 ± 0.03 mag, they derived a zero point (ZP) of −6.14 mag (at (J − Ks)=1.0 mag). The error in the ZP they claimed is 0.01 mag (statistical) and 0.06 (systematic), of which 0.02 is due to the uncertainty in the reddening, and 0.05 mag to the adopted LMC distance.
The reddening Hoyt et al. (2018) adopted is quite low, but is also inconsistent with the (mean) reddening towards the dEBs in the LMC, the (mean) distance of which is used to calibrate the ZP. Adopting E(B − V)=0.12 mag (see earlier, and Table 1) their ZP would become −6.17 mag (at (J − Ks)=1.0 mag). This ZP compares to −6.21 and −6.20 mag (at (J − Ks)=1.0 mag) that we derive from the data in Serenelli et al. (2017).
4. Model
The calculations are carried out using a numerical program, which reads in the VMC data. Other inputs are the right ascension (RA) and declination (Dec) of the line-of-sight (los) of interest, the radius, r, of the circle centred on (RA, Dec) to select the data from the VMC input, the adopted reddening E(B − V) for that los, and the adopted width of the bin, w, for the binning of the LF.
The VISTA J, Ks magnitudes are de-reddened and transformed to the 2MASS system as outlined in Sect. 2. If the absolute calibration relation is MKs = α + β ⋅ (J − Ks), the “sharpened” magnitude T = K0 − β ⋅ (J − Ks)0 is constructed with β = −2.013 as standard value following Sect. 3. The error in T is calculated from the propagation of the errors in J, K, and β. We also keep track of (J − Ks)0 and its error. Stars in the region defined by Eq. (2) are selected and the LF in T is constructed using the adopted bin size.
Two edge-detection algorithms are run on the binned LF, based on the first-order and second-order derivative of the LF. The derivatives are calculated using Savitzky-Golay coefficients as implemented in Fortran in “Numerical Recipes” (Press et al. 1992). At a point i the function f is replaced by a linear combination g, of itself and nL “left” and nR “right” neighbouring values:
The Savitzky-Golay coefficients are determined in such a way that the filter fits a polynomial of degree M to the moving window, and then evaluates the derivative of chosen order L. Cioni et al. (2000) performed extensive tests and used M = 2 and nL = nR = 3 for their second-order derivative filter which we adopt here as well8. For the first-order derivative we use M = 1 and nL = nR = 2, resulting in the kernel used by Sakai et al. (1996)9.
The filter response of the LF to the first-order derivative kernel is fitted with a single Gaussian (SG) plus a constant:
where the TRGB magnitude is given by the peak of the Gaussian.
Cioni et al. (2000) also fitted a SG to the response function of the LF to the second-order derivative filter and then applied a correction which depends on the width of the Gaussian fit (see Fig. A2 in Cioni et al. 2000), which can be a few tenths of a magnitude. Here we find (Appendix A) that the response function to the second-order derivative filter can be well fitted by a double Gaussian (DG) of the form:
Compared to the SG it has one additional free parameter, the distance between the positive and negative peaks of the Gaussians, a5, and where the TRGB magnitude is given by the magnitude in between the peaks. For both the SG and DG fits the DM for a given los is then a3 + α.
In Appendix A the numerical details of the method are discussed extensively, including simulations to estimate any biases in the method, the influence of the bin size, and error estimates.
It is found that both the first- and the second-order derivative methods can be applied with negligible bias (a few millimag) if certain criteria are met that concern the significance with which the peak in the response function is detected (SNpk = a2/σa2), the average number of stars per bin (N/bin) in the 0.5 mag below the tip of the RGB, and the error in the magnitude of the peak (σa3) relative to the width of the bin. The second-order derivative method is more stable to noise in the data but needs more stars per bin. Cioni et al. (2000) also prefer the second-order derivative (as mentioned before however, their implementation differs from the current one) over the first-order derivative method.
In the applications discussed below the code is run for a given los for all combinations of 18 radii10 and bin widths11.
The best model is adopted to be the one with the lowest reduced χ2 (χr, min2) that meets the criteria on SNpk, N/bin and a3/w. Below, we also investigate the range in the parameters for models with 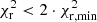 to have an independent estimate of the errors on the derived distances.
to have an independent estimate of the errors on the derived distances.
5. Applications
5.1. TRGB distances towards dEBs in the MCs
In a first application we considered the TRGB in the los towards nine dEBs in the LMC and five in the SMC. In particular for the LMC, the eight systems in Pietrzyński et al. (2013) give a DM to the LMC barycentre of 18.493 ± 0.008 (statistical) ±0.047 (systematic) mag which has become the de-facto value adopted after 2013 for the DM to the LMC in most papers. For the SMC, Graczyk et al. (2014) give a mean DM based on five dEBs of 18.965 ± 0.025 (statistical) ±0.048 (systematic) mag. For comparison, based on a careful, statistical analysis of a large number of recent distance estimates, grouped by main stellar population tracers, de Grijs et al. (2014) and de Grijs & Bono (2015) recommend DMs of 18.49 ± 0.09 to the LMC, and 18.96 ± 0.02 mag (formal errors), with additional systematic uncertainties possibly exceeding 0.15–0.20 mag, for the SMC.
Table 1 lists the identifier, DM and error, and the reddening (the error is given on the second line) given by the references listed in the fourth column. Columns 5–11 contain the results of our analysis: The DM and error, the estimated (J − Ks)0 mag at the TRGB and error (see Appendix A on how they are derived), the radius of the circle used, the bin width, the average number of RGB stars per bin in the 0.5 mag below the TRGB, the significance with which the peak in the response function is detected, and the reduced χ2. The errors quoted are the formal errors.
Figure 4 shows the comparison between the first- and second-order-derivative-based DM and the difference plotted against (J − Ks) colour of the TRGB (left-hand panel), and the comparison of the second-order-derivative-based DM with the published values of the DM for the dEBs.
 |
Fig. 4. Comparison of the TRGB DM based on the first- and second-order derivatives (top panel), and the difference plotted against (J − Ks) colour (middle panel) towards the 14 los containing dEBs. The one-to-one relation is shown in the top panel. In the middle panel in blue are indicated the median of the difference (solid line) and plus-minus the dispersion (taken as 1.48 ⋅ MAD; dashed lines). The bottom panel shows the difference between the second-order-derivative-based TRGB distance and the DM of the dEB systems against colour. The median of the difference (solid line) and plus-minus 1.48 ⋅ MAD (dashed line) are shown as the blue lines. |
Interestingly, an offset between the second- and first-order-derivative-based DM is observed that is not predicted by the simulations. The difference is small (median offset of −0.040, a weighted mean offset of −0.026 mag) and insignificant (the error in this offset is 0.042 mag). It is observed in other applications as well, and we return to this in Sect. 7. The simulations in Appendix A do suggest that the second-order-derivative-based DM is the more reliable and stable of the two methods in reproducing the input DM, and therefore we choose this option in the comparisons to external catalogues. The simulations show that this method requires approximately twice as many stars per magnitude bin than the first-order derivative filter. Inspection of Tables 1, 2 and B.1–B.3 indeed shows that for the best fits, when the resulting areas on the sky are similar for the second- and first-order derivative results, the bin size in the former case is almost always larger than for the latter.
TRGB distances to SMC fields.
The bottom panel of Fig. 4 compares the second-order-derivative-based DM with the published values for the dEBs systems. There is excellent agreement with a difference of 0.009 ± 0.075 mag. There is no trend of the offset with colour. Part of the scatter could be due to the depth along the los. The TRGB distance is based on the RGB stars in a field of ∼0.4 − 2° radius spread along the los while the DM to each dEB is that to a single object.
5.2. TRGB distances towards LMC Cepheids
A second application concerns the TRGB distances towards CCs in the LMC. Inno et al. (2016) presented DM and reddening estimates for 2504 CCs in the LMC, derived by simultaneously fitting V, I, J, H, K and WISE W1 magnitudes (when available) to corresponding period-luminosity (PL)-relations. In the procedure discussed below 16 stars with very negative reddenings (E(B − V)< − 0.07 mag) and 22 stars with very large χ2 (> 600, compared to the median of 20) have been excluded from the sample of Inno et al. (2016).
Some scatter in DM is expected due to the finite width of the instability strips and depth effects. Therefore we average DM and reddening values of Cepheids located close together on the sky in the following way: starting from the first Cepheid in the list12 in Inno et al. (2016) its distance to all neighbours not already marked to belong to another los is calculated. The number, NN, of nearest neighbours is identified (with NN at least 35). If the distance to the NN-th nearest neighbour is less than 0.4° NN is increased by 2, and this is repeated if necessary. The NN Cepheids are marked as belonging to this los, and one proceeds to the next Cepheid in the list. This is repeated until no more Cepheids can be assigned to a los (the distance to the NN-th nearest neighbour should be less than 1.5°). The minimum number of Cepheids and the minimum distance are chosen after some testing, using the results of the dEBs that show that the radius needed for the TRGB to have reliable results is of order 0.45–2° (see Table 1).
In this way, 56 independent los were identified containing 2182 CCs. For each los the median and standard deviation (calculated as 1.48 times the median-absolute-deviation, MAD13) of the DM and reddening were calculated.
The results of the calculations are listed in Table B.1, which lists the identifier (the name of the CC at the centre of each los), the median DM of the CCs in that los, the median of the error in the DM of each CC in that los, the median of the reddening of the CCs in that los (the error, calculated as 1.48 ⋅ MAD of the reddening values around the median, is given on the second line). The radius used to calculate these averages is listed in col. 4. Columns 5–11 in Table B.1 contain the results of our analysis following Table 1. The first line for each object contains the results for the second-order derivative filter response, and the second line those for the first-order derivative filter.
Figure 5 compares the second-r and first-order-derivative-based DM, and a similar observation is made as in the previous section. The difference between the two estimates is −0.029 ± 0.031 mag. The comparison between the second-order-derivative-based TRGB distance and the median DM for the CCs in that los is good with a negligible difference of 0.041 ± 0.070 mag.
 |
Fig. 5. Same as Fig. 4 for 56 los towards CCs in the LMC. Additionally the bottom panel shows the distribution of the DM for the CCs (in black), and the first- (green) and second-order-based-derivative TRGB distance (red), and Gaussian fits to these distributions. For clarity, the green and red histograms have been offset by −0.005 and +0.005 mag from the black one. |
With a large number of los spread across the LMC one can also discuss the distribution of the distances and the mean distance to the LMC. This is illustrated in the bottom-right panel of Fig. 5, which shows histograms of the DM of the 56 los for the CCs (black), the second-order-derivative-based TRGB distance (red), and the first-order-derivative-based TRGB distance (green), and Gaussian fits to these distributions. As the error bar in an individual DM estimate is non-negligible compared with the width of the distribution we also performed Monte Carlo simulations. A new DM for each los was drawn from a Gaussian distributed based on its derived value and error. A new histogram based on these new DM was created and a new Gaussian fit was performed.
For the CCs a median DM of 18.491 mag is found with an error on the mean of 0.005 mag. The σ of the Gaussian distribution is 0.052 mag. For the second-order-based-derivative we find 18.521 ± 0.007, σ = 0.074 mag and for the first-order-based-derivative 18.567 ± 0.006, σ = 0.078 mag. As expected, the value for the CCs is in excellent agreement with the 18.48 ± 0.10 mag (stat. plus syst.) quoted by Inno et al. (2016) for their entire sample.
5.3. TRGB distances towards SMC RR Lyrae stars
No multi-wavelength study similar to Inno et al. (2016) currently exists for Cepheids in the SMC that simultaneously derives reddening and distance (although the VMC team has studied SMC Cepheids, e.g. Ripepi et al. 2017). Towards the SMC we therefore used a similar approach, but using RRL from Muraveva et al. (2018) who studied 2997 fundamental mode RRL from the OGLE-IV survey. They derived the mean Ks-mag from multi-epoch VMC data, and the reddening, E(V − I), from the observed OGLE V, I mean magnitude and the intrinsic (V − I)0 colour, which they took to be a function of V-band pulsation amplitude and pulsation period following Piersimoni et al. (2002). They then adopted (photometric) metallicities available from Skowron et al. (2016) and the period – K band – magnitude – metallicity relation from Muraveva et al. (2015) based on 70 RRL in the LMC and calibrated using the dEB-based LMC distance (Pietrzyński et al. 2013) to derive distances to individual RRL.
The approach described above was used to assign 2686 RRL towards 43 los (21 stars with E(V − I) values of less than −0.1 mag were excluded; the minimum and maximum radii of the circle that defined a los were 0.5 and 1.5° respectively, and a minimum of 50 RRL within a los was imposed). These numbers reflect the higher surface number density of SMC RRL compared to the LMC CCs. For each los the median and standard deviation of the DM and reddening (adopting E(B − V)=E(V − I)/1.22 mag) were calculated.
The results of the calculations are listed in Table B.2. Figure 6 illustrates the results. In this case the difference between the second- and first-order-derivative-based DM is −0.029 ± 0.027 mag. There is a discrepancy between the TRGB and the RRL distances of approximately 0.14 ± 0.06 mag, as illustrated in the lower two panels of Fig. 6. We have carried out Monte Carlo simulations to find that the RRL distance distribution is described by a mean of 18.905 mag with an error in the mean of 0.004 mag, and a width of σ = 0.042 mag. For the second-order-derivative-based TRGB distance this is 19.044 ± 0.003, σ = 0.028 mag. The DM for the RRL is, as expected, in very good agreement with the weighted average of all RRL in Muraveva et al. (2018), namely 18.88 mag with a standard deviation of 0.20 mag. We discuss this difference between the RRL and TRGB distances in Sect. 6.
5.4. TRGB distances towards other SMC fields
Rubele et al. (2018) used VMC data to derive the SFH in the main body and the wing of the SMC. In total they analysed 168 sub-regions covering about 24 square degrees. As part of their method the DM and visual extinction are derived simultaneously with the SFH. Here we use the values based on the analysis of the Ks, (J − Ks) CMD, as they consider these to give the most reliable values for the reddening (we use E(B − V)=AV/3.1 mag).
As before we constructed 17 los towards the SMC using the coordinates of the sub-regions as input and averaging over a number of them (between 5 and 19) to have sufficient statistics to carry out the TRGB analysis. The results are displayed in Fig. 7 and Table 2.
In this case the difference between the second- and first-order-derivative-based DM is −0.052 ± 0.056 mag. The TRGB and the distance derived from the SFH analysis are in excellent agreement, the weighted mean difference being 0.001 ± 0.052 mag. Again we carried out Monte Carlo simulations to find that the distance distribution based on the SFH analysis is described by a mean of 18.95 with an error in the mean of 0.04, and a width of σ = 0.14 mag. For the second-order-derivative-based TRGB distance this is 18.93 ± 0.02, σ = 0.09 mag. The DM from the SFH analysis is, as expected, in very good agreement with the 18.910 ± 0.064 mag given by Rubele et al. (2018) as the DM to the mass-weighted centre of the SMC.
5.5. TRGB distances towards VMC fields
In a final application we used the VMC data themselves to generate los towards SMC, LMC and the MB. The minimum and maximum radii of the circle that defined a los were 0.45 and 2.0°, respectively. A total of 17 los towards the SMC, and 55 towards the LMC were defined. In the direction of the MB three los were placed, spaced at 10° intervals in RA with larger radii of 5–9°.
The reddening was calculated from the procedure used in Sects. 5.2 and 5.3 for LMC and SMC, respectively. The field in the MB closest to the SMC had a E(B − V) value of 0.049 mag determined in this way, while the field in the LMC closest to the MB had a value of 0.043. For the two fields in the MB in between these two pointings a value of 0.045 mag was adopted.
The code was run and the results are listed in Table B.3. Contrary to the previous applications the radius of the area was fixed and the code only considered different bin widths to determine the best fit.
As before Monte Carlo simulations were carried out to find the mean DM of 18.518 ± 0.008 (LMC) and 19.057 ± 0.014 mag (SMC). The simple weighted average of the three fields in the MS is 18.97 ± 0.01 mag; also see Fig. 8 and Sect. 6.4.
 |
Fig. 8. Distribution of DM across the MCs based on the VMC data themselves, with coordinates deprojected relative to RA = 55°, Dec = −73°. The size of the circles is proportional to the area used in calculating the TRGB distance. |
For the SMC we also ran models taking the reddening of the closest SMC subfield from Rubele et al. (2015) (median value over the los of E(B − V)=0.118) instead of that found from the RRL (median value of 0.049) reducing the DM to 18.97 ± 0.07 mag.
6. Discussion
6.1. The internal errors
The errors quoted for the TRGB distances are formal errors as given by the minimisation routine. The fitting routine takes into account the error bars in the luminosity function, as explained in Appendix A. The fact that the reduced χ2 in Tables 1 and B.1, B.2 scatter around unity indicates that this procedure seems to give reliable estimates of the error bars.
As explained in Sect. 4 the best model was assumed to be the one with the lowest reduced χ2 among all models that met certain criteria. As an independent check the scatter in the DM was investigated among the models with a reduced χ2 less than twice the minimum value. If there were five or more such models the dispersion (actually 1.48 ⋅ MAD) around the median was determined and compared with the formal error. This exercise revealed no systematic effects and the errors estimated in such a way are consistent with the formal errors.
6.2. Comparing dEBs and TRGB with Cepheid and RR Lyrae distances
In Sect. 5.1 the TRGB distances are compared with the distances to 14 dEBs. One can also compare the TRGB distances with other independent distance estimates, as we did in Sects. 5.2–5.4. We therefore took an identical approach as in Sects. 5.2 and 5.3 and determined the median DM and reddening value of CCs (in the LMC), and RRL (in the SMC) in the direction of the dEBs. The results are listed in Table 3 which first repeats the DM and reddening derived in the literature for the dEBs and the TRGB distance (based on the second-order derivative method) from Table 1. Columns 5 and 6 give the DM and reddening values based on the CCs and RRL in those fields.
Comparison of distances for the dEBs.
It is evident that the reddening estimates are smaller than adopted in the dEB analysis. In the SMC this is the case for all five objects. Although the differences are within the respective error bars it appears to be a systematic effect. In the LMC this is the case for eight out of nine objects but the differences appear to be smaller on average than for the SMC.
To test the effect of reddening, the TRGB distance was derived using the E(B − V) from col. 6, and the results are listed in col. 7. It is clear that the effect on the DM is roughly inversely proportional to a change in E(B − V). Based on the definition of the sharpened magnitude, the absolute calibration equation (Eq. (3)) and the reddening coefficients one expects a relation ΔDM/ΔE(B − V)= − 1.1.
The overall effect is noticeable however. The weighted mean DM of the nine LMC dEBs is shifted from 18.483 ± 0.006 mag to 18.523 ± 0.005 mag, and that of the five SMC binaries is shifted from 19.023 ± 0.007 mag to 19.051 ± 0.009 mag.
In a similar way we used the data of Rubele et al. and took the sub-region closest to the dEBs in the SMC. The DM and reddening they report are listed in cols. 8 and 9. The reddenings are significantly larger than those used for the dEBs and RRL studies. Column 10 gives the TRGB distance based on these reddenings, and they are significantly shorter on average. The weighted mean DM of the five SMC binaries is 18.920 ± 0.007 mag.
As a final test the reddening of Haschke et al. (2011) was used, taking the value of the closest positional match from their tables. This reddening is listed in col. 11. These reddenings are significantly smaller than those used in the other studies. Column 12 gives the TRGB distance based on these reddenings, and they are significantly longer on average. The weighted mean DM of the nine LMC dEBs is 18.574 ± 0.005 mag, and that of the five SMC binaries is 19.071 ± 0.008 mag.
Regarding the SMC, Marconi et al. (2017) modelled the optical and NIR light curves (JK data from VMC, see Ripepi et al. 2016, corrected for reddening using Haschke et al. 2011) and radial velocity curves of nine fundamental and three first overtone CCs to quote a mean DM of 19.01 mag with 0.08 mag dispersion. The weighted mean value and the error on the mean for this sample are 18.99 mag, and 0.02 mag, respectively.
6.3. The absolute calibration relation
As outlined in Sect. 3 the absolute calibration of the TRGB is a linear relation MK = α + β ⋅ (J − Ks), calibrated using the theoretical calculations by Serenelli et al. (2017). The default relation is based on a linear fit in the colour range 0.75 < (J − Ks)< 1.3 mag and reads MKs = −4.196 − 2.013 (J − Ks) Eq. (3). An alternative fit in a more restricted colour range is MKs = −4.331 − 1.873 (J − Ks) (Sect. 3). At a colour typical for the SMC (J − Ks = 0.95 mag) this relation gives a brighter tip by a negligible amount of 2 millimag; at a colour typical for the LMC (J − Ks = 1.05 mag) this relation gives a fainter tip by 0.01 mag.
Although one therefore expects relatively small differences due to the calibration equation there are differences in (J − Ks) colour over the different los in both galaxies, and therefore all five applications considered in Sect. 5 were re-run with the alternative calibration.
These calculations largely confirm the expectations. The mean distance to the LMC is reduced by 10–15 millimag, while the distance to the SMC increased by 4–9 millimag using the alternative calibration. These differences are of the same order as or smaller than the formal error in the DM for any given los, and are also smaller than the dispersion in the calibrating relation itself.
6.4. Morphology of the MC system
Figure 8 shows the distribution of the DM over the MC system for the los chosen from the VMC data (Sect. 5.5). It is beyond the scope of this paper to discuss the structure of the MC system in detail, but one can notice a gradient across the western part of the LMC, the fields in the Bridge, and the SMC. This is roughly consistent with what other recent papers found; for example Subramanian & Subramaniam (2012) based on RC stars, Ripepi et al. (2017) based on CCs, Muraveva et al. (2018) based on RRL, and Rubele et al. (2018) for the SMC, and the work using RRL and CCs from OGLE-IV for the MC system (Jacyszyn-Dobrzeniecka et al. 2016, 2017). The disadvantage of the TRGB method compared to other methods is that a relatively large area needs to be sampled to obtain a sufficient number of TRGB stars and a high precision for the DM. The number of los that the RRL, CC or RC-based methods can study in the direction of the MCs is an order of magnitude larger.
7. Summary and conclusions
In this paper we discuss the use of the TRGB in the NIR, and apply it to VMC data in the MCs. The basis of our work is the theoretical work by Serenelli et al. (2017) and the relation MKs = −4.196 − 2.013 (J − Ks) we derive for their standard model in the colour range 0.75 < (J − Ks)< 1.3. An alternative calibration in the colour range 0.82 < (J − Ks)< 1.2 is MKs = −4.331 − 1.873 (J − Ks), which gives nearly identical DM to the LMC and SMC. The recent empirical determination of the slope based on data in IC 1613 by Madore et al. (2018) is −1.85 ± 0.27, which is consistent with both relations.
Serenelli et al. (2017) state that the colour transformations introduce larger uncertainties than the differences between the two stellar evolution codes they consider. Their Fig. 9 shows how the absolute K-magnitude depends on the different adopted bolometric corrections. In the range covered by the SMC and LMC ((J − Ks)∼0.95 − 1.05 mag) these differences are small (at the same level as the scatter in the relation judging from their plot), but for (J − Ks)≳1.2 mag they become noticeable. When in the future Gaia data provide reliable and accurate parallaxes, metallicity and reddening estimates for the brightest objects, it may well be possible to select TRGB stars with accurate parallaxes and empirically determine the colour dependence of the calibration relation towards redder colours (higher metallicities).
The scatter in the calibrating relation is 0.030 mag, which we consider as one source of the systematic uncertainty. The methodology is another possible source of uncertainty. The simulations in the Appendix show that criteria related to the number of stars per bin and the significance of detection of the peak of the filter response curve can be defined in such a way as to give unbiased DM to a level of ∼0.005 mag. The second-order derivative filter requires about twice as many stars per bin as the first-order derivative filter to achieve this. The empirical results derived in this paper however show that the DM based on the second- and first-order derivative filters give marginally different results. The weighted mean of the four estimates is −0.033 ± 0.017 mag. We do not have a ready explanation for this. Although depth effects were considered, the modelling of the number density of stars by a Gaussian distribution with different scale lengths is probably too simple, and the first- and second-order derivative filters may behave differently to this. For example, Subramanian et al. (2017) find a bimodal magnitude distribution of RC stars in the eastern part of the SMC, interpreted as a population at a distance of about 12 kpc in front of the main body. To a lesser extent, Subramanian & Subramaniam (2013) found extra-planar features both in front and behind the main disc of the LMC from an analysis of RC stars. In addition, differential reddening along a los and reddening differences across a field-of-view may play a role. At this point we consider this difference in results between the two filters as a measure of a potential systematic uncertainty in the method.
If the condition on the number of stars per bin and the significance of detection of the peak of the filter response curve are met the statistical error in the method is small. Of all the random errors in the DM listed in Tables 1, 2 and B.1, B.2, 50% are 0.015 mag or smaller (91% are less than 0.03 mag).
Therefore, our preferred absolute calibration relation of the TRGB in the Ks-band (in the 2MASS system) in the colour range 0.75 < (J − Ks)0 < 1.3 mag is MKs = −4.196 − 2.013 (J − Ks)0 with a systematic error of 0.045 mag, and where statistical errors of ∼0.015 mag are possible if the criteria on the number of TRGB stars and the quality of the fit are respected.
In practice, the choice of reddening also plays an important role in determining the distance to any stellar system. Table 3 illustrates this for the dEBs. For typical (median) reddenings of ∼0.04 (Haschke et al. 2011), ∼0.06 (based on the RRL study), ∼0.08 (based on the EB studies), and ∼0.15 mag (based on the SFH study), the weighted mean DM of the systems in the SMC is 19.071 ± 0.008, 19.051 ± 0.009, 19.023 ± 0.007, and 18.920 ± 0.007 mag, respectively. Similarly, for the LMC systems, with typical reddenings of ∼0.05 (Haschke et al. 2011), ∼0.10 (based on the CCs study), and ∼0.12 mag (based on the EB studies), the weighted mean DM is 18.574 ± 0.005, 18.523 ± 0.005, and 18.483 ± 0.006 mag, respectively.
Considering the systematic uncertainty quoted above these estimates are consistent within 2σ with the recommended DM of 18.96 ± 0.02 mag (formal error only; de Grijs & Bono 2015. For typical reddening ≲0.08) to the SMC and 18.49 ± 0.09 mag (de Grijs et al. 2014) to the LMC.
Neither paper discusses the correction one needs to apply to the edge magnitude to obtain the true TRGB magnitude when using Cioni et al. (2000)’s original method.
Also see Górski et al. (2018) which appeared when this paper was under review.
The functional call is savgol(SG, nSG, 2, 2, 1, 1) and leads to the kernel [−2, −1, 0, +1, +2]. The call savgol(SG, nSG, 1, 1, 1, 1) would lead to the classical kernel [−1, 0, +1], as first introduced by Lee et al. (1993). Note that Madore & Freedman (1995) use yet another kernel, [−1, −2, 0, +2 +1] to determine the first derivative.
It is acknowledged that the scale height may depend on population, Haschke et al. (2012b) find 2.0 ± 0.4 kpc for RRL [the value used here] and 2.7 ± 0.3 kpc for CCs, and recently even larger values have been reported, for example 4.3 ± 1.0 kpc for RRL in the SMC (Muraveva et al. 2018).
Acknowledgments
This paper is based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO programme 179.B-2003. We thank the CASU and the WFAU in Edinburgh for providing calibrated data products under the support of the Science and Technology Facility Council (STFC) in the UK. Maurizio Salaris (Liverpool John Moores University) is thanked for providing the results from Serenelli et al. (2017) in electronic format. M.-R.C acknowledges support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 682115). This research was supported by the Munich Institute for Astro- and Particle Physics (MIAPP) of the DFG cluster of excellence “Origin and Structure of the Universe”, in connection with the inspiring workshop “The Extragalactic Distance Scale in the Gaia era” organised by Lucas Macri, Rolf Kudritzki, Sherry Suyu, and Wolfgang Gieren. This research has made use of the SIMBAD database and the VizieR catalogue access tool, operated at CDS, Strasbourg, France. The original description of the VizieR service was published in A&AS, 143, 23.
References
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chun, S.-H., Jung, M., Kang, M., Kim, J.-W., & Sohn, Y.-J. 2015, A&A, 578, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cioni, M.-R. L. 2016, The Universe of Digital Sky Surveys, 42, 49 [NASA ADS] [Google Scholar]
- Cioni, M.-R. L., van der Marel, R. P., Loup, C., & Habing, H. J. 2000, A&A, 359, 601 [Google Scholar]
- Cioni, M.-R. L., Clementini, G., Girardi, L., et al. 2011, A&A, 527, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cross, N. J. G., Collins, R. S., Mann, R. G., et al. 2012, A&A, 548, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalcanton, J. J., Williams, B. F., Melbourne, J. L., et al. 2012, ApJS, 198, 6 [NASA ADS] [CrossRef] [Google Scholar]
- de Grijs, R., & Bono, G. 2015, AJ, 149, 179 [NASA ADS] [CrossRef] [Google Scholar]
- de Grijs, R., Wicker, J. E., & Bono, G. 2014, AJ, 147, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Delmotte, N., Loup, C., Egret, D., Cioni, M.-R., & Pierfederici, F. 2002, A&A, 396, 143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elgueta, S. S., Graczyk, D., Gieren, W., et al. 2016, AJ, 152, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Epchtein, N., Deul, E., Derriere, S., et al. 1999, A&A, 349, 236 [NASA ADS] [Google Scholar]
- González-Fernández, C., Hodgkin, S. T., Irwin, M. J., et al. 2018, MNRAS, 474, 5459 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, M., Pietrzyński, G., Gieren, W., et al. 2016, AJ, 151, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, M., Pietrzyński, G., Gieren, W., et al. 2018, AJ, 156, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Graczyk, D., Pietrzyński, G., Thompson, I. B., et al. 2012, ApJ, 750, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Graczyk, D., Pietrzyński, G., Thompson, I. B., et al. 2014, ApJ, 780, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Gullieuszik, M., Held, E. V., Rizzi, L., et al. 2007, A&A, 467, 1025 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haschke, R., Grebel, E. K., & Duffau, S. 2011, AJ, 141, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Haschke, R., Grebel, E. K., & Duffau, S. 2012a, AJ, 144, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Haschke, R., Grebel, E. K., & Duffau, S. 2012b, AJ, 144, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Hatt, D., Freedman, W. L., Madore, B. F., et al. 2018, ApJ, 861, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyt, T. J., Freedman, W. L., Madore, B. F., et al. 2018, ApJ, 858, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Inno, L., Bono, G., Matsunaga, N., et al. 2016, ApJ, 832, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobs, B. A., Rizzi, L., Tully, R. B., et al. 2009, AJ, 138, 332 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jacyszyn-Dobrzeniecka, A. M., Skowron, D. M., Mróz, P., et al. 2016, Acta Astron., 66, 149 [NASA ADS] [Google Scholar]
- Jacyszyn-Dobrzeniecka, A. M., Skowron, D. M., Mróz, P., et al. 2017, Acta Astron., 67, 1 [NASA ADS] [Google Scholar]
- Jung, M. Y., Ko, J., Kim, J.-W., et al. 2012, A&A, 543, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kato, D., Nagashima, C., Nagayama, T., et al. 2007, PASJ, 59, 615 [NASA ADS] [Google Scholar]
- Lee, M. G., Freedman, W. L., & Madore, B. F. 1993, AJ, 106, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Macri, L. M., Ngeow, C.-C., Kanbur, S. M., Mahzooni, S., & Smitka, M. T. 2015, AJ, 149, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Madore, B. F., & Freedman, W. L. 1995, AJ, 109, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Madore, B. F., Mager, V., & Freedman, W. L. 2009, ApJ, 690, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Madore, B. F., Freedman, W. L., Hatt, D., et al. 2018, ApJ, 858, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, M., Molinaro, R., Ripepi, V., et al. 2017, MNRAS, 466, 3206 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, K. B. W., Skillman, E. D., Dolphin, A. E., Berg, D., & Kennicutt, R. 2017, AJ, 154, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Menzies, J. W., Feast, M. W., Whitelock, P. A., & Matsunaga, N. 2011, MNRAS, 414, 3492 [NASA ADS] [CrossRef] [Google Scholar]
- Muraveva, T., Palmer, M., Clementini, G., et al. 2015, ApJ, 807, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Muraveva, T., Subramanian, S., Clementini, G., et al. 2018, MNRAS, 473, 3131 [Google Scholar]
- Piersimoni, A. M., Bono, G., & Ripepi, V. 2002, AJ, 124, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrzyński, G., Górski, M., Gieren, W., et al. 2009, AJ, 138, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrzyński, G., Graczyk, D., Gieren, W., et al. 2013, Nature, 495, 76 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in FORTRAN. The Art of Scientific Computing (Cambridge: Cambridge University Press) [Google Scholar]
- Ripepi, V., Moretti, M. I., Marconi, M., et al. 2012, MNRAS, 424, 1807 [NASA ADS] [CrossRef] [Google Scholar]
- Ripepi, V., Moretti, M. I., Marconi, M., et al. 2015, MNRAS, 446, 3034 [NASA ADS] [CrossRef] [Google Scholar]
- Ripepi, V., Marconi, M., Moretti, M. I., et al. 2016, ApJS, 224, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Ripepi, V., Cioni, M.-R. L., Moretti, M. I., et al. 2017, MNRAS, 472, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Rubele, S., Kerber, L., Girardi, L., et al. 2012, A&A, 537, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rubele, S., Girardi, L., Kerber, L., et al. 2015, MNRAS, 449, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Rubele, S., Pastorelli, G., Girardi, L., et al. 2018, MNRAS, 478, 5017 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, S., Madore, B. F., & Freedman, W. L. 1996, ApJ, 461, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., & Girardi, L. 2005, MNRAS, 357, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Serenelli, A., Weiss, A., Cassisi, S., Salaris, M., & Pietrinferni, A. 2017, A&A, 606, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skowron, D. M., Soszyński, I., Udalski, A., et al. 2016, Acta Astron., 66, 269 [NASA ADS] [Google Scholar]
- Sobel, I. 1970, PhD Thesis, Stanford University [Google Scholar]
- Subramanian, S., & Subramaniam, A. 2012, ApJ, 744, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Subramanian, S., & Subramaniam, A. 2013, A&A, 552, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Subramanian, S., Rubele, S., Sun, N.-C., et al. 2017, MNRAS, 467, 2980 [NASA ADS] [Google Scholar]
- Sutherland, W., Emerson, J., Dalton, G., et al. 2015, A&A, 575, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tatton, B. L., van Loon, J. T., Cioni, M.-R., et al. 2013, A&A, 554, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valenti, E., Ferraro, F. R., & Origlia, L. 2004, MNRAS, 354, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Whitelock, P. A., Menzies, J. W., Feast, M. W., et al. 2009, MNRAS, 394, 795 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Simulations
In this appendix the simulations are described which were used to investigate any biases in the determination of the TRGB.
The simulations are carried out for a galaxy at a distance (D) of 50 kpc, where the TRGB is roughly at K ∼ 12.3 mag. The choice of the simulated galaxy is arbitrary, but some of the magnitude intervals listed below are tuned to this choice. As an illustration the results of the simulations are compared with the analysis of the actual VMC data for the field around the dEB OGLE-LMC-ECL-09660.
The number of stars on the RGB, and the number of AGB and foreground contaminants, are described by a power law, logN ∼ α(m − mo). For the latter, α = −0.05, mo = 10.0 mag for magnitudes between 10.0 and 14.5 mag, roughly corresponding to the brightest AGB stars and the start of the early-AGB in such a galaxy. For the RGB stars the slope is α = +0.3, between mo = K@TRGB= f(J − K) and 15.0 mag. The two slopes are based on a comparison of the K-band luminosity function (LF) with real VMC data. The probability of a star being an AGB or foreground contaminant is fc.
The simulation proceeds as follows. The total number of simulated stars is Nsim. A random number between 0 and 1 is drawn. If this number is < fc, a K-mag is drawn from the LF of AGB and foreground contaminants. Otherwise the star is considered an RGB star. We considered contaminations of fc = 0.01, 0.1, 0.20, 0.38, 0.55, 0.75. For the field around LMC-ECL-09660 fc = 0.20 is appropriate.
In case of an RGB star, a random number is drawn to generate a (J − K)@TRGB according to a Gaussian distribution. Here a mean of 1.0 mag and a dispersion of 0.05 mag are assumed, typical of the LMC (see Fig. A.6).
Assuming an absolute calibration MK = α + β (J − K), with α = −4.196 mag and β = −2.013 (see Sect. 3) the expected K-mag @TRGB in the simulated galaxy, MK + 5log(D)−5, is known, and an RGB K-mag is drawn from the LF mentioned above.
The J magnitude is calculated from the K mag and a (J − K) colour, which is based on the generated (J − K)@TRGB and a mean K − (J − K) relation based on real VMC data (see Fig. A.2).
Gaussian distributed photometric errors in J and K, based on real VMC data of the mean photometric error and dispersion as a function of K, are added to the simulated data
Finally, the depth of the galaxy is simulated, by considering an exponential function ( ∼ exp(−d/H)) along the los. We have considered H = 10 pc (i.e. almost no effect), 800 pc (used in the examples shown here) and 2000 pc, representative for the LMC and SMC, respectively, according to Haschke et al. (2012a,b)14. Finally the T mag is calculated, K − β (J − K).
The advantage of using the T mag is illustrated in Fig. A.1. Assume a Gaussian distribution of the (J − K) colour at the TRGB. Since the absolute K magnitude depends on colour, the theoretical K magnitude at the TRGB is also Gaussian distributed, shown as the black histogram. As discussed above, the RGB LF is sampled assuming a power-law distribution, and the blue histogram indicates the LF of RGB stars. There is no clear cut-off. The blue histogram shows the distribution in T mag, that is K − β (J − K), shifted by the expected mean colour term. The edge is defined much more clearly.
 |
Fig. A.1. For a Gaussian distribution of the (J − K) colours at the TRGB with a width of 0.05 mag, and the relation between MK and (J − K) discussed in the text, the black histogram is the theoretical distribution of the K-mag of stars at the TRGB for a Galaxy at the distance of the LMC. Since the LF is sampled, the actual distribution of all RGB stars in K is the blue histogram. The cut-off is not sharp and samples neither the true brightest RGB stars, nor the peak in the true K-mag distribution. The red histogram shows the simulated distribution in T-mag (shifted by −2.013 < SPSDOUBLEDOLLAR > × the adopted mean (J − K) colour at the TRGB). The cut-off is much sharper. |
 |
Fig. A.2. Simulation (two left-hand panels) and real VMC data around LMC-ECL-09660 (two right-hand panels). In the simulation 20 000 stars are generated. The top panels show a classic K, (J − K) CMD. In the left bottom panel the 18 730 stars are plotted that are within the colour selection box, in the T, (J − K) CMD. The blue solid lines indicate the derived location of the TRGB, and the blue dashed line is the mean T, (J − K) relation derived in the interval from the TRGB to one magnitude fainter, but shown for all magnitudes. |
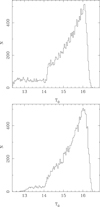 |
Fig. A.3. The T magnitude LF in the simulation (top panel) and in the field around LMC-ECL-09660 (bottom panel). |
 |
Fig. A.4. Results of the simulation. Response to the two filters used, one that derives the second-order derivative (and which is fitted with two Gaussians) in the top panel, and in the bottom panel the classic Sobel-like filter that finds the first-order derivative (and which is fitted with a single Gaussian). The blue line indicates the region used to estimate the rms level in the response function. In the top panel the bin width is 0.037 mag, the peak is detected with a S/N of 12, and there are 152 stars per bin between the TRGB and 0.5 mag fainter in the LF. In the bottom panel these numbers are 0.020 mag, 11, and 82 stars/bin. The derived DM are virtually identical: 18.5009 ± 0.0027 ( |
 |
Fig. A.5. Fit of single and double Gaussians to the filtered LF for LMC-ECL-09660. The blue line indicates the range in magnitude used to estimate the noise level in the LF. |
A bin width (w) is chosen and the binned T mag LF is then analysed using the first- and second-order derivative kernels using Savitzky-Golay coefficients as explained in the main text. The response to the first-order derivative is fitted with a single Gaussian plus a constant (SG),
The response to the second-order derivative is fitted with a double Gaussian plus a constant (DG),
The fitting is done with the Levenberg–Marquardt algorithm (routine mrqmin as implemented in Fortran in Press et al. 1992).
Initial guesses for the parameters are required; the constant a1 is set to zero, the width of the Gaussian a4 is set to the bin width, for the DG the difference between the two Gaussians a5 is set to 1.5 times the bin width, and the location and height of the peak (a3, a2) are obtained from a rough analysis of the LF. An “error” for the derived response function is determined by calculating the rms in a region brighter than the estimated location of the peak, as illustrated in Fig. A.4.
The fit parameters of interest are the mean magnitude and its error (a3, the T magnitude of the TRGB), the significance with which the peak is detected (SNpk = a2/σa2), and the ratio of the error in the mean magnitude compared with the bin width (σa3/w).
Additional parameters are also derived: the number of stars within a 0.5 mag range brighter and fainter than the TRGB (Nbright, Nfaint), from which one can calculate a contamination ratio (Nbright/(Nbright + Nfaint)) and the average number of RGB stars per bin (Nbin = Nfaint/(0.5/bin width)).
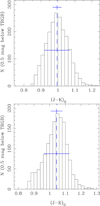 |
Fig. A.6. Top panel: results for the simulation. Bottom panel: results for the field around LMC-ECL-09660. The distribution of (J − K) colour at the TRGB, estimated from the general (J − K)−T relation (the blue line in Fig. A.2) using an 0.5 mag interval below the TRGB is shown. The blue dashed and solid lines (roughly at half the maximum) indicate the mean and Gaussian dispersion, respectively. The narrower blue line above the peak indicates the formal error in the (J − K)@TRGB estimate. In the simulation the input was a Gaussian with mean 1.0 mag, and dispersion 0.05 mag. The analysis of the simulated data gives (J − K)@TRGB of 0.996 ± 0.025 mag, and a dispersion in the distribution of 0.063 mag. |
The (J − K) magnitude at the TRGB is also estimated. Using the data in the one magnitude region below the tip a linear relation between T and (J − K) is determined. From that the (J − K)@TRGB is determined from a3, and its error based on σa3 and the errors in the slope and zero point of the linear fitting relation.
The distribution in (J − K) colour near the TRGB is also determined. In the 0.5 mag region below the tip every ((J − K), T) point is projected onto the mean T − (J − K) relation. This allows to estimate the (J − K) as if this point were at the tip.
Almost 1200 simulations were run for different numbers of simulated stars, bin widths, fractions of AGB contaminants and three values of H. The figures below discuss the bias in DM, calculated as the fitted DM minus the true/input DM. Figures A.7–A.9 are for the second-order derivative filter fitted with the DG, and Figs. A.10–A.12 are for the first-order derivative fitted with the SG.
Shown is the bias as a function of the quantities that are available from the fits: the number of stars per bin, the signal-to-noise ratio (S/N) with with the peak in the response function is derived, the bin width, the fraction of contaminants, the reduced χ2, and the error in the magnitude of the peak compared with the width of the bin.
As expected qualitatively, if the RGB near the tip is well populated and the peak in the response is well determined, the bias is essentially negligible (of order a few millimag), and smaller than the (systematic) errors due to uncertainties in reddening, transformation to the 2MASS system, or the absolute calibration of the TRGB method (see the main text).
The conditions that are used for the real data are a detection of the peak with a SNpk > 5, an average number of stars per bin in the 0.5 mag below the tip of > 85 (second-order derivative), or > 40 (first-order derivative), and a ratio (a3/w) that is small enough (see detailed relations in the captions of Figs. A.8 and A.11).
Table A.1 shows the bias and dispersion for the models that meet these conditions. It shows that the bias and dispersion are ∼6 millimag or less, with the second-order derivative filtering overall showing the tendency for slightly smaller values, for example inspect and compare Figs. A.9 and A.12.
 |
Fig. A.7. Diagnostic plots for the DG-filter. Stars in red have fewer than 85 RGB stars per bin. The bias is defined as (derived DM − true DM). Scale height is coded as follows: H = 10 pc, circles; H = 800 pc, triangles; H = 2000 pc, squares. |
 |
Fig. A.8. Diagnostic plots for the DG-filter. Final selection where red means excluded models with: Number of RGB stars per bin < 85, or S/N of the peak < 5, or bin width > 0.085, or a contamination fraction > 0.38, or an (error / bin width) above the curve, given by y = 0.2778 ⋅ x2 − 1.75 ⋅ x + 1.90, where x = log(N per bin) and y = log (error / bin width). |
 |
Fig. A.9. Diagnostic plots for the DG-filter. Final selection, with all non-red points from Fig. A.8 plotted on a smaller scale (−0.01 to +0.02 mag). Scale height also additionally colour coded (H = 10 pc, black circles; H = 800 pc, green triangles; H = 2000 pc, blue squares). The bottom panel shows the bias divided by the error bar. Larger simulations have only been run for the smallest scale height. |
 |
Fig. A.10. Diagnostic plots for the SG-filter. Stars in red have fewer than 40 RGB stars per bin. |
 |
Fig. A.11. Diagnostic plots for the SG-filter. Final selection where red means excluded models with: Number of RGB stars per bin < 40, or S/N of the peak < 5, or bin width > 0.065, or a contamination fraction > 0.38, or an (error / bin width) above the curve, given by y = 0.3990 ⋅ x2 − 2.445 ⋅ x + 2.869, where x = log(N per bin) and y = log (error/bin width). |
 |
Fig. A.12. Diagnostic plots for the SG-filter. Final selection, with all non-red points from Fig. A.11 plotted on a smaller scale (−0.01 to +0.02 mag). Scale height colour coded as in Fig. A.9. The bottom panel shows the bias divided by the error bar. Larger simulations have only been run for the smallest scale height. |
Median bias and dispersion in DM for models that meet the selection criteria.
Appendix B: Additional tables
TRGB distances to LMC fields surrounding CCs.
TRGB distances to SMC fields surrounding RRLs.
TRGB distances to MC fields.
All Tables
All Figures
 |
Fig. 1. Position on the sky of the selected VMC sources. For clarity only every 40th object is plotted. The LMC, the SMC, the two tiles in the MS, and the MB are apparent. The small regions missing in the corner of every tile correspond to detector 16 which are excluded by enforcing the constraint on ksppErrBits. |
| In the text | |
 |
Fig. 2. Colour–magnitude diagrams of the LMC, SMC, MS, and the MB. For clarity only every 40th (LMC), or 20th (SMC) point is shown, and all points for the MS and MB. The solid lines (see text) indicate the adopted borders to select RGB stars, independent of spatial location (see Eq. (2)). |
| In the text | |
 |
Fig. 3. Calibration of the Ks-band absolute magnitude of the TRGB as a function of (J − Ks) colour, based on the data of Serenelli et al. (2017). The solid line indicates the fit to models in the colour range 0.75 < (J − Ks)< 1.3 mag and ages between 4 and 14 Gyr. Sets of different metallicities are indicated by open triangles ([Fe/H] = −1.49 dex), filled squares ([Fe/H] = −1.27 dex), open circles ([Fe/H] = −0.96 and −0.66 dex), filled triangle ([Fe/H] = −0.35 dex), and open squares ([Fe/H] = −0.25, −0.01 and +0.06 dex). Models outside these criteria are indicated by the small dots. |
| In the text | |
 |
Fig. 4. Comparison of the TRGB DM based on the first- and second-order derivatives (top panel), and the difference plotted against (J − Ks) colour (middle panel) towards the 14 los containing dEBs. The one-to-one relation is shown in the top panel. In the middle panel in blue are indicated the median of the difference (solid line) and plus-minus the dispersion (taken as 1.48 ⋅ MAD; dashed lines). The bottom panel shows the difference between the second-order-derivative-based TRGB distance and the DM of the dEB systems against colour. The median of the difference (solid line) and plus-minus 1.48 ⋅ MAD (dashed line) are shown as the blue lines. |
| In the text | |
 |
Fig. 5. Same as Fig. 4 for 56 los towards CCs in the LMC. Additionally the bottom panel shows the distribution of the DM for the CCs (in black), and the first- (green) and second-order-based-derivative TRGB distance (red), and Gaussian fits to these distributions. For clarity, the green and red histograms have been offset by −0.005 and +0.005 mag from the black one. |
| In the text | |
 |
Fig. 6. Same as Fig. 5 for 43 los towards RRL in the SMC. |
| In the text | |
 |
Fig. 7. As in Fig. 4 but for 17 los towards fields in the SMC. |
| In the text | |
 |
Fig. 8. Distribution of DM across the MCs based on the VMC data themselves, with coordinates deprojected relative to RA = 55°, Dec = −73°. The size of the circles is proportional to the area used in calculating the TRGB distance. |
| In the text | |
 |
Fig. A.1. For a Gaussian distribution of the (J − K) colours at the TRGB with a width of 0.05 mag, and the relation between MK and (J − K) discussed in the text, the black histogram is the theoretical distribution of the K-mag of stars at the TRGB for a Galaxy at the distance of the LMC. Since the LF is sampled, the actual distribution of all RGB stars in K is the blue histogram. The cut-off is not sharp and samples neither the true brightest RGB stars, nor the peak in the true K-mag distribution. The red histogram shows the simulated distribution in T-mag (shifted by −2.013 < SPSDOUBLEDOLLAR > × the adopted mean (J − K) colour at the TRGB). The cut-off is much sharper. |
| In the text | |
 |
Fig. A.2. Simulation (two left-hand panels) and real VMC data around LMC-ECL-09660 (two right-hand panels). In the simulation 20 000 stars are generated. The top panels show a classic K, (J − K) CMD. In the left bottom panel the 18 730 stars are plotted that are within the colour selection box, in the T, (J − K) CMD. The blue solid lines indicate the derived location of the TRGB, and the blue dashed line is the mean T, (J − K) relation derived in the interval from the TRGB to one magnitude fainter, but shown for all magnitudes. |
| In the text | |
 |
Fig. A.3. The T magnitude LF in the simulation (top panel) and in the field around LMC-ECL-09660 (bottom panel). |
| In the text | |
 |
Fig. A.4. Results of the simulation. Response to the two filters used, one that derives the second-order derivative (and which is fitted with two Gaussians) in the top panel, and in the bottom panel the classic Sobel-like filter that finds the first-order derivative (and which is fitted with a single Gaussian). The blue line indicates the region used to estimate the rms level in the response function. In the top panel the bin width is 0.037 mag, the peak is detected with a S/N of 12, and there are 152 stars per bin between the TRGB and 0.5 mag fainter in the LF. In the bottom panel these numbers are 0.020 mag, 11, and 82 stars/bin. The derived DM are virtually identical: 18.5009 ± 0.0027 ( |
| In the text | |
 |
Fig. A.5. Fit of single and double Gaussians to the filtered LF for LMC-ECL-09660. The blue line indicates the range in magnitude used to estimate the noise level in the LF. |
| In the text | |
 |
Fig. A.6. Top panel: results for the simulation. Bottom panel: results for the field around LMC-ECL-09660. The distribution of (J − K) colour at the TRGB, estimated from the general (J − K)−T relation (the blue line in Fig. A.2) using an 0.5 mag interval below the TRGB is shown. The blue dashed and solid lines (roughly at half the maximum) indicate the mean and Gaussian dispersion, respectively. The narrower blue line above the peak indicates the formal error in the (J − K)@TRGB estimate. In the simulation the input was a Gaussian with mean 1.0 mag, and dispersion 0.05 mag. The analysis of the simulated data gives (J − K)@TRGB of 0.996 ± 0.025 mag, and a dispersion in the distribution of 0.063 mag. |
| In the text | |
 |
Fig. A.7. Diagnostic plots for the DG-filter. Stars in red have fewer than 85 RGB stars per bin. The bias is defined as (derived DM − true DM). Scale height is coded as follows: H = 10 pc, circles; H = 800 pc, triangles; H = 2000 pc, squares. |
| In the text | |
 |
Fig. A.8. Diagnostic plots for the DG-filter. Final selection where red means excluded models with: Number of RGB stars per bin < 85, or S/N of the peak < 5, or bin width > 0.085, or a contamination fraction > 0.38, or an (error / bin width) above the curve, given by y = 0.2778 ⋅ x2 − 1.75 ⋅ x + 1.90, where x = log(N per bin) and y = log (error / bin width). |
| In the text | |
 |
Fig. A.9. Diagnostic plots for the DG-filter. Final selection, with all non-red points from Fig. A.8 plotted on a smaller scale (−0.01 to +0.02 mag). Scale height also additionally colour coded (H = 10 pc, black circles; H = 800 pc, green triangles; H = 2000 pc, blue squares). The bottom panel shows the bias divided by the error bar. Larger simulations have only been run for the smallest scale height. |
| In the text | |
 |
Fig. A.10. Diagnostic plots for the SG-filter. Stars in red have fewer than 40 RGB stars per bin. |
| In the text | |
 |
Fig. A.11. Diagnostic plots for the SG-filter. Final selection where red means excluded models with: Number of RGB stars per bin < 40, or S/N of the peak < 5, or bin width > 0.065, or a contamination fraction > 0.38, or an (error / bin width) above the curve, given by y = 0.3990 ⋅ x2 − 2.445 ⋅ x + 2.869, where x = log(N per bin) and y = log (error/bin width). |
| In the text | |
 |
Fig. A.12. Diagnostic plots for the SG-filter. Final selection, with all non-red points from Fig. A.11 plotted on a smaller scale (−0.01 to +0.02 mag). Scale height colour coded as in Fig. A.9. The bottom panel shows the bias divided by the error bar. Larger simulations have only been run for the smallest scale height. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.