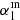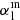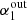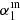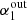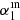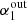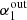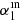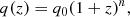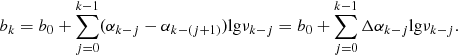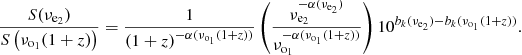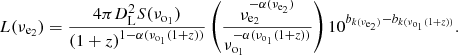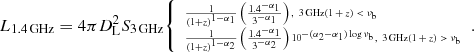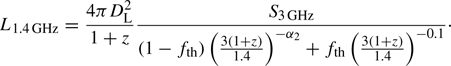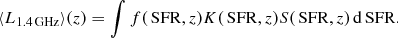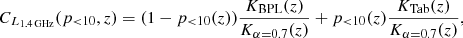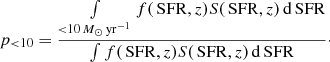| Issue |
A&A
Volume 621, January 2019
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201834002 | |
| Published online | 18 January 2019 | |
The VLA-COSMOS 3 GHz Large Project: Average radio spectral energy distribution of highly star-forming galaxies⋆
1
Department of Physics, Faculty of Science, University of Zagreb, Bijenička cesta 32, 10000 Zagreb, Croatia
e-mail: ktisanic@phy.hr
2
Leiden Observatory, Leiden University, Niels Bohrweg 2, 2333 CA Leiden, The Netherlands
3
MPI for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
4
INAF – Osservatorio di Astrofisica e Scienza dello Spazio, Via Gobetti 93/3, 40129 Bologna, Italy
5
Argelander Institute for Astronomy, University of Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
6
Department of Astronomy, University of Cape Town, Private Bag X3, Rondebosch 7701, South Africa
Received:
1
August
2018
Accepted:
22
November
2018
We construct the average radio spectral energy distribution (SED) of highly star-forming galaxies (HSFGs) up to z ∼ 4. Infrared and radio luminosities are bound by a tight correlation that is defined by the so-called q parameter. This infrared–radio correlation provides the basis for the use of radio luminosity as a star-formation tracer. Recent stacking and survival analysis studies find q to be decreasing with increasing redshift. It was pointed out that a possible cause of the redshift trend could be the computation of rest-frame radio luminosity via a single power-law assumption of the star-forming galaxies’ (SFGs) SED. To test this, we constrained the shape of the radio SED of a sample of HSFGs. To achieve a broad rest-frame frequency range, we combined previously published Very Large Array observations of the COSMOS field at 1.4 GHz and 3 GHz with unpublished Giant Meterwave Radio Telescope (GMRT) observations at 325 MHz and 610 MHz by employing survival analysis to account for non-detections in the GMRT maps. We selected a sample of HSFGs in a broad redshift range (z ∈ [0.3, 4], SFR ≥ 100 M⊙ yr−1) and constructed the average radio SED. By fitting a broken power-law, we find that the spectral index changes from α1 = 0.42 ± 0.06 below a rest-frame frequency of 4.3 GHz to α2 = 0.94 ± 0.06 above 4.3 GHz. Our results are in line with previous low-redshift studies of HSFGs ( SFR > 10 M⊙ yr−1) that show the SED of HSFGs to differ from the SED found for normal SFGs ( SFR < 10 M⊙ yr−1). The difference is mainly in a steeper spectrum around 10 GHz, which could indicate a smaller fraction of thermal free–free emission. Finally, we also discuss the impact of applying this broken power-law SED in place of a simple power-law in K-corrections of HSFGs and a typical radio SED for normal SFGs drawn from the literature. We find that the shape of the radio SED is unlikely to be the root cause of the q − z trend in SFGs.
Key words: galaxies: evolution / galaxies: statistics / radio continuum: galaxies / galaxies: star formation
The table of the cross-matched fluxes is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/621/A139
© ESO 2019
1. Introduction
Star formation rate (SFR) measurements derived from the ultraviolet and optical emission are sensitive to dust (Kennicutt 1998a), and infrared-derived SFRs are easy to understand only in the optically thick case (Kennicutt 1998a; Condon 1992). On the other hand, radio emission in star-forming galaxies (SFGs) below ∼30 GHz is unbiased by dust (Condon 1992). Furthermore, it has been found that the infrared and radio luminosities are bound by a tight correlation over many orders of magnitude (van der Kruit 1971; Helou et al. 1985; Condon 1992). This infrared-radio correlation provides the basis for radio luminosity as a star-formation tracer, as infrared luminosity is linked to the SFR (Kennicutt 1998b). It is defined by the so-called q parameter, defined as q = logLTIR/3.75 THz − log(L1.4 GHz), where LTIR is the total infrared luminosity (8 − 1000 μm) in units of W and L1.4 GHz is the luminosity density at 1.4 GHz in units of W Hz−1. A frequency of 3.75 THz is used to obtain a dimensionless quantity. In the calorimeter model (Voelk 1989), q is expected to be constant over a wide range of magnetic field strengths through electrons that lose their energy because of synchrotron and inverse Compton losses. This produces a tight correlation, even though individual galaxies may show deviations. Theoretical considerations (Murphy 2009) predict q to increase with redshift, mostly because of the synchrotron electrons’ inverse Compton scattering off cosmic microwave background photons. Recent stacking and survival analysis studies find q to be decreasing with increasing redshift (Ivison et al. 2010; Magnelli et al. 2015; Delhaize et al. 2017; Calistro Rivera et al. 2017). Delhaize et al. (2017) pointed out that the computation of rest-frame radio luminosity via a K-correction using only a simple, single power-law assumption of the star-forming galaxies’ spectral energy distribution (SED) might cause such a trend.
The exact shape of the radio SED of star-forming galaxies is usually assumed to be a superposition of the steep synchrotron spectrum, described by a power law, and a ∼10% contribution at 1.4 GHz of a flat free–free spectrum (Condon 1992). These results are supported by observations of nearby galaxies at 3 − 30 Mpc (z ≈ 0.01) with an SFR < 10 M⊙ yr−1 (Tabatabaei et al. 2017).
For (ultra)luminous infrared galaxies ((U)LIRGs, SFR > 10 M⊙ yr−1), observations in the local Universe find their radio SEDs to be steep around 10 GHz, corresponding to a spectrum that shows less flattening above 10 GHz than in galaxies with an SFR < 10 M⊙ yr−1 (Clemens et al. 2008; Leroy et al. 2011; Galvin et al. 2018). Both free–free self-absorption and modifications to the spectrum due to the aging of the electron population would also be present. These processes result in deviations from a simple power-law at low (νrest ≲ 1 GHz) and high (νrest ≳ a few GHz) frequencies that are observationally hard to constrain.
In this paper, we constrain the shape of the average radio spectral energy distribution (SED) of a 1.4 GHz-selected sample ( SFR > 100 M⊙ yr−1) of highly star-forming galaxies (HSFGs) in the ∼0.4 − 10 GHz frequency range within the COSMOS field. To obtain a broad frequency range, we use the fluxes from the 1.4 GHz Very Large Array (VLA)-COSMOS Joint Project (Schinnerer et al. 2010) and the 3 GHz VLA-COSMOS Large Project (Smolčić et al. 2017a,b) and reduce previously unpublished Giant Meterwave Radio Telescope (GMRT) observations at 325 MHz and 610 MHz. We construct the average radio SED by using survival analysis to account for the lower sensitivity of the GMRT maps.
In Sect. 2 we describe the VLA and GMRT datasets used in this paper, in Sect. 3 we describe the galaxy sample of HSFGs, in Sect. 4 we construct the average radio SED for HSFGs and test the applicability of our method. In Sect. 5 we report the average radio spectral indices of HSFGs, while in Sect. 6 we discuss the shape of the radio spectrum of SFGs and the impact on the infrared–radio correlation. In this paper we use the convention for the spectral index Fν ∼ ν−α, where Fν is the flux density and α is the spectral index.
2. Data
To assess the radio spectral energy distribution, we combined catalogs of the COSMOS field at four observer-frame frequencies: 325 MHz and 610 MHz, obtained with the GMRT, and at 1.4 GHz (Schinnerer et al. 2010) and 3 GHz (Smolčić et al. 2017a), obtained by the VLA. Here we briefly describe these VLA (Sect. 2.1 ) and GMRT (Sect. 2.2) data.
2.1. Available VLA data
The VLA COSMOS 3 GHz Large Project map (Smolčić et al. 2017a) was constructed from 384 h of observations of the 2deg2 COSMOS field. Observations were carried out over 192 pointings in the S-band with VLA in A and C antenna configurations. This was a wide-band observation with a total bandwidth of 2084 MHz derived from 16 spectral windows, each 128 MHz wide. The final mosaic reached a median root-mean-square (rms) of 2.3 μJy beam−1 at a resolution of 0.75″. Considering the large bandwidth and the volume of the data, each pointing was imaged separately using the multi-scale multi-frequency synthesis algorithm (Rau & Cornwell 2011; hereafter MSMF) and then combined into a single mosaic. The MSMF algorithm had been found to be optimal for both resolution and image quality in terms of the rms noise and sidelobe contamination (Novak et al. 2015). The 3 GHz catalog has been derived using BLOBCAT (Hales et al. 2012) with a 5σ threshold. In total, 10 830 sources were recovered (67 of which were multi-component sources). For more details, see Smolčić et al. (2017a).
The 1.4 GHz catalog is a joint catalog comprised of the VLA COSMOS 1.4 GHz Large (Schinnerer et al. 2007) and Deep surveys (Schinnerer et al. 2010). The joint catalog was constructed by combining the observations of the central 50′×50′ subregion of the COSMOS field (VLA-COSMOS Deep Project Schinnerer et al. 2010) at a resolution of 2.5″ × 2.5″ and previously published observations of the entire 2deg2 COSMOS field at a resolution of 1.5″ × 1.4″ (VLA-COSMOS Large Project Schinnerer et al. 2007). The average rms in the resulting map was found to be 12 μJy. The large survey consisted of 240 h of observations over 23 pointings spread out over the entire COSMOS field in the L band centered at 1.4 GHz and with a total bandwidth of 37.5 MHz in VLA A configuration and 24 h in the C configuration. Schinnerer et al. (2010) supplemented the 7 central pointings with an additional 8.25 h of observations per pointing using the A configuration and the same L-band configuration. These new measurements were then combined in the uv-plane with the Large Project observations. The joint catalog was constructed by using the SExtractor package (Bertin & Arnouts 1996) and the AIPS task SAD, yielding 2865 sources (Schinnerer et al. 2010).
2.2. GMRT data
The GMRT 325 and 610 MHz data reduction, imaging, cataloging, and testing is described in detail in Appendix A. Here we give a brief overview of the procedure.
The overall data reduction procedure is similar for both observing frequencies. The observations were carried out with 30 antennas with their longest baseline being 25 km. The data were then reduced by using the source peeling and atmospheric modeling pipeline (SPAM, described in detail in Intema et al. 2017). Finally, the source extraction package BLOBCAT was used to extract sources down to 5σ, where σ is the local rms value computed from rms maps produced by the AIPS task RMSD. The values of σ are shown in the visibility functions, presented in top left panels of Figs. A.1 and A.2 for the 325 MHz and 610 MHz rms maps, respectively. The fluxes were corrected for bandwidth-smearing, and resolved sources were identified.
The 325 MHz observations of a single pointing were carried out under the project 07SCB01 (PI: S. Croft; at a reference frequency of 325 MHz and a bandwidth of 32 MHz). The observations lasted for 45 h in total, comprising four observations with a total on-source time of ∼40 h. They were reduced using the SPAM pipeline and imaged at a resolution of 10.8 × 9.5 arcsec2. A primary beam correction was applied to the pointing. We measured a median rms of 97 μJy beam−1 over the ∼2deg2 COSMOS field. In total, 633 sources were identified using BLOBCAT down to 5σ. By employing a peak-over-total flux criterion, we consider 177 of these sources to be resolved.
The 610 MHz observations were carried out at a central frequency of 608 MHz using a bandwidth of 32 MHz. Observations lasting 86 h (spread over eight observations with an average time on source per pointing of ∼4 h) were conducted under the project 11HRK01 (PI: H. R. Klöckner). A total of 19 pointings were observed. The data were reduced using the SPAM pipeline, and imaged at a resolution of 5.6 × 3.9 arcsec2. Following Intema et al. (2017), primary beam correction and the average pointing error corrections were applied to each pointing prior to mosaicing. We measured a median rms of 39 μJy beam−1 in the final mosaic over the ∼2deg2 COSMOS field. BLOBCAT was used to extract 999 sources down to 5σ, 196 of which we consider to be resolved.
3. Sample
To construct a complete and pure sample of star-forming galaxies over a wide range in redshift, we used the criteria described in Smolčić et al. (2017b), which we briefly summarize below. Starting from the VLA COSMOS Large Project 3 GHz Source Catalog, cross-correlated with multi-wavelength counterparts detected in the COSMOS field, we selected the clean star-forming galaxy sample (CSFG), as defined in Smolčić et al. (2017b), and imposed an additional cut of infrared-derived SFRs of SFR > 100 M⊙ yr−1.
Smolčić et al. (2017b) cross-correlated the 3 GHz Source Catalog with multi-wavelength counterparts, drawn from three catalogs: (i) the COSMOS2015 catalog (Laigle et al. 2016), which contains sources detected on a χ2 sum of Y, J, H, Ks and z++ images, (ii) the i-band catalog (Capak et al. 2007), which contains sources detected from a combination of the CFHT i* and Subaru i+ original point spread function (PSF) images, and iii) the IRAC catalog, which contains sources detected in the 3.6 μm band (Sanders et al. 2007). Smolčić et al. (2017b) combined counterparts from the three catalogs to maximize the number of counterparts as the i-band (IRAC) catalog is sensitive to potentially blue (red) sources undetected in the Y, J, H, Ks, z++ stack. Over the inner 1.77 deg2 subarea of the COSMOS field, which excludes all regions affected by saturated or bright sources in the optical to near-infrared bands, and thus contains sources with the best possible photometry, Smolčić et al. (2017b) found 7729 COSMOS2015, 97 i-band, and 209 IRAC counterparts to the 8696 3 GHz sources within this area. The COSMOS2015 and i-band catalogs offer precise photometric redshifts, with a joint precision of σΔz/(1 + z) = 0.01.
The CSFG sample was constructed from the full 3 GHz galaxy sample with COSMOS2015 or i-band counterparts as the cleanest sample of star-forming galaxies by excluding AGN through a combination of criteria, such as X-ray luminosity, mid-infrared (color–color and SED-based) criteria, r+ − NUV colors, and (> 3σ) excess in the distribution of the ratio of 1.4 GHz radio luminosity and IR-based SFRs as a function of redshift (see Sect. 6.4 and Fig. 10 in Smolčić et al. 2017b). To determine the physical properties of the galaxies, a three-component SED-fitting procedure (Delvecchio et al. 2017) was applied using all of the available photometry. The fitting procedure was based on MAGPHYS (da Cunha et al. 2008) and SED3FIT (Berta et al. 2013) to account for the AGN component of the SED. SFRs were computed from the 8 to 1000 μm rest-frame infrared luminosity that was obtained by using the best-fit galaxy template and was then converted into SFR through the Kennicutt (1998a) conversion factor and scaled to a Chabrier (2003) initial mass function. Star formation rates are shown for the entire 3 GHz Large Project catalog and the subset of highly star-forming galaxies ( SFR ≥ 100 M⊙ yr−1) in Fig. 1 as a function of redshift. The figure shows that a cut above 100 M⊙ yr−1 minimizes incompleteness above z ≈ 2, which strongly influences the sample below 100 M⊙ yr−1. To check whether the remaining incompleteness could influence our results, we repeated our analysis of Sect. 5 for the more complete subsample of HSFGs out to z ∼ 2. We find no significant difference in the resulting SED and therefore conclude that the 100 M⊙ yr−1 cut sufficiently reduces incompleteness out to z ∼ 4.
 |
Fig. 1. Star formation rate vs. redshift for the “clean star-forming galaxy sample” (CSFG, black points), as defined by Smolčić et al. (2017b), and described in Sect. 3. Orange points indicate a subset of the CSFG sample that was detected at both 1.4 GHz and 3 GHz. Red points indicate the HSFG sample used here, i.e., the subset of the CSFG sample with an additional cut of the infrared-derived SFR, SFR > 100 M⊙ yr−1. Histograms show the redshift and SFR distributions with the different subsamples colored as in the main figure. For greater clarity, the HSFG sample is marked by filled histograms, and its limits in the main figure are denoted by dotted red lines. |
Finally, we cross-matched the 3 GHz catalog with the above described cuts and the 1.4 GHz joint catalog, to arrive at a sample of 306 galaxies that have two reliably determined fluxes in the rest-frame frequency-flux space. We call the subset of the CSFG sample that is detected at both 1.4 and 3 GHz and has SFR > 100 M⊙ yr−1 the highly star-forming galaxy (HSFG) sample. The 325 MHz and 610 MHz catalogs were then cross-matched with the HSFG sample catalog with a matching radius of 1 beam, leading to 29 and 52 sources in the HSFG sample, respectively. The summary of the number of detections and non-detections in the catalogs used to construct the radio SED of the HSFG sample is provided in Fig. 2.
 |
Fig. 2. Number of detections in GMRT catalogs of sources in the HSFG samples. The gray area represents the sources that are not detected in the GMRT maps, while blue and orange areas represent sources detected at 325 MHz and 610 MHz, respectively. |
In summary, the selected sample is effectively a 1.4 GHz data-selected HSFG ( SFR > 100 M⊙ yr−1). With this dataset, we associated the 3 GHz data, with a much lower rms (∼12 μJy beam−1 and ∼2 μJy beam−1 at 1.4 GHz and 3 GHz, respectively), minimizing potential biases that could arise in the 1.4 − 3 GHz spectral index distribution, given that almost all 1.4 GHz sources (90%, Smolčić et al. 2017a) have counterparts at 3 GHz. In total, the HSFG sample contains 306 galaxies, out of which 9% (29) were detected at 325 MHz and 17% (52) at 610 MHz.
4. Average radio SED
In this section, we describe the method used to construct the radio SED and the models used to analyze it. In Sect. 4.1 we describe how we constructed the radio SED of HSFGs from the GMRT and VLA observations of the COSMOS field while accounting for lower sensitivities of the GMRT maps using survival analysis. In Sects. 4.2 and 4.3 we describe the models of the radio SED and the Monte Carlo simulations that test the applicability of the fitting procedure, respectively.
4.1. Construction of the average radio SED of HSFGs
To construct a typical SED for HSFGs in the COSMOS field, we normalized the spectra of individual galaxies at a particular rest-frame frequency. Considering that the redshifts of sources in our sample vary from 0.3 to 4, we obtain a well-constrained SED from rest-frame frequencies of ∼0.5 GHz to ∼15 GHz.
A complication to this basic idea is that there are very few detections of HSFGs in the 325 and 610 MHz maps. For this reason, we normalized the flux densities at all frequencies based on a linear fit to the 1.4 and 3 GHz spectra. We chose the normalization rest-frame frequency to be the median log-frequency of sources in the HSFG sample at 1.4 GHz and 3 GHz. For the HSFG sample, this frequency is 5.7 GHz. We constrained the 325 and 610 MHz flux densities of non-detections by five times the local rms flux density of their respective maps. The problem is therefore to constrain the spectral index when a significant portion of the data is left-censored, meaning that many of the data points below a rest-frame frequency of 1 GHz, corresponding to observer frame 325 and 610 MHz frequencies, are upper limits. To correctly deal with upper limits, we decided to employ the survival analysis technique described in the following paragraph and illustrated in Fig. 3.
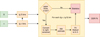 |
Fig. 3. Flowchart of the radio SED fitting procedure described in Sect. 4.1. The input values are source fluxes, S, and rest-frame frequencies, ν. The log fluxes are then binned in log-rest-frame frequency bins. If there are no upper limits in a certain bin, the mean and standard deviation are calculated immediately, and if that is not the case, the log fluxes are converted into a right-censored dataset, and the Kaplan–Meier estimate is calculated. This estimate is then fit to a Weibull distribution, yielding the analytically determined means and standard deviations. The resulting different bins are then treated as data points with errors in both axes and are fit by a particular model by employing the ODR method. |
We combined into a single dataset the normalized fluxes and normalized upper limits of individual galaxies at different rest-frame frequencies. As we have four different observer-frame frequencies, the number of our data points is four times larger than the number of galaxies. To achieve uniform frequency binning, we used 20 bins that were equally separated in log space of the rest-frame frequencies. The number of bins was chosen empirically to achieve a satisfactory number of bins while retaining a sufficient number of data points within each bin for the statistical analysis.
For each bin, i, if there were no upper limits within the bin, we computed the mean of the log rest-frame frequency, νi = 10⟨logνr⟩i, and its standard deviation, σlogνi, along with the mean normalized log flux, ⟨logFν⟩i, and its standard deviation, σlogFi. If there were upper limits within a particular bin, we constructed the Kaplan–Meier estimate of the survival function of fluxes within the bin using the lifelines package1. We did this by converting this left-censored dataset into a right-censored one in accordance with Feigelson & Nelson (1985) as the lifelines package handles right-censored datasets.
We then fit the survival function with the Weibull distribution (Lai et al. 2006). We have found this method to be satisfactory because the Weibull distribution survival function, S(x|λ, k)=e−(x/λ)k, where λ and k are free parameters of the model, can be easily linearized. We estimated ⟨logFν⟩ from k and λ and calculated σlogF as the standard deviation of the Weibull distribution.
Survival analysis assumes that upper limits have the same underlying distribution as the data, and the Kaplan–Meier estimator further assumes that detections and upper limits are mutually independent (Kaplan & Meier 1958). The latter condition is satisfied by normalizing spectra to one frequency, as the normalization redistributes both the data and the upper limits based on the source’s normalization flux. Further tests of this procedure are described in Sect. 4.3 using Monte Carlo simulations of the properties of the HSFG sample.
4.2. SED fitting
Previous studies, listed in Sect. 1, have shown that the shape of the radio SED deviates from a simple power law. As the SED at higher frequencies (ν ≳ 10 GHz) is expected to have a contribution not only by synchrotron, but also by free–free emission, the simplest modification to a simple power-law would be adding a thermal contribution with a flat spectral index of 0.1 (Condon 1992) that would produce a flattening of the SED above 10 GHz:
where νr is the rest-frame frequency, and the parameters of the model are α2, the nonthermal spectral index, b, the normalization constant, νn, the normalization frequency, and f = f(νn), the thermal fraction at νn. In our HSFG sample, however, we observe that the SED flattens below 3 − 4 GHz (see Sect. 5 and figures therein). To account for this, we assumed a broken power-law instead of using only the nonthermal spectral index. Therefore, the full SED would be
where νn is the normalization frequency, νb the break frequency, α1 (α2) the spectral index below (above) νb, and b the normalization constant.
In the HSFG sample, as described in Sect. 6.1, we do not find f to be significantly greater than 0 for νn ∼ 1 GHz. We therefore simplified Eq. (2) to a broken power-law model for the log-normalized flux
In the broken power-law model, the break frequency, νb, can be both a free parameter or fixed to a particular value prior to fitting. The break frequency is derived using the Markov chain Monte Carlo (MCMC) method (implemented using the affine invariant sampler of the emcee package Foreman-Mackey et al. 2013) on the broken power-law fit with the break frequency as a free parameter. By inspecting the distribution of limits and detections, we find that the break frequency should lie above the highest frequency at which the last upper limit occurs. We thereby conclude that the break frequency would not be significantly affected by upper limits.
The MCMC code samples the log-likelihood distribution of parameters, θ = (α1, α2, b, νb),
where the values ⟨logF⟩i and σlogFi and νi are log-flux derived by using survival analysis in each log-frequency bin with the main value of log frequency in each bin being xi. For the sake of simplicity of implementation, we considered only the errors in normalized log flux in the denominator of Eq. (4) when using the MCMC method.
The final fitting of the broken power-law model is performed using the orthogonal distance regression method (hereafter, ODR), which accounts for the errors on both axes. The 1σ confidence interval, σ(νr), is computed as 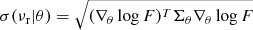 , with Σθ being the covariance matrix of the fit parameters derived using the ODR method and θ being the vector of free parameters of the broken power-law.
, with Σθ being the covariance matrix of the fit parameters derived using the ODR method and θ being the vector of free parameters of the broken power-law.
4.3. Method verification through simulations
Our average SED was derived using survival analysis, where the percentage of upper limits below rest-frame 1 GHz is high. We tested the applicability of the survival analysis by deriving the radio spectral indices for a mock sample of galaxies. The mock samples were generated with preset spectral indices by simulating different properties of the HSFG sample and of the SED shape.
We constructed the mock sample based on the distribution of individual galaxy redshifts, z, a spectral index between 1.4 and 3 GHz, α2, and the log-flux normalization, b, in the real HSFG sample. We have chosen to vary the mean value of the low-frequency spectral index, α1, to achieve different degrees of flattening in the simulations while keeping the number of galaxies in the simulation equal to the number of galaxies in the real sample. In order to simulate the flattening of the spectral index below the break frequency, νb, we assumed a broken power-law with a spectral index of α1 below νb, with the following assumptions: (1) α1 has the same variance as α2 and 2) α1 is uncorrelated with α2, z, and b. Before creating the full mock catalog, we removed the sources in the mock 325 MHz and 610 MHz catalogs with fluxes below 5σ, where σ is the median rms of the respective 325 MHz and 610 MHz COSMOS maps to simulate non-detections.
Overall, by analyzing the input (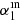 ) and output (
) and output (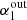 ) spectral index, we find that it is necessary to correct the derived spectral index by 20% (downward) for
) spectral index, we find that it is necessary to correct the derived spectral index by 20% (downward) for 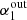 ∼ 0.5 and incrementally smaller correction for higher
∼ 0.5 and incrementally smaller correction for higher 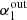 . The simulation suggests that the reason for this is the large number of upper limits occurring for lower spectral indices (i.e., flatter input slopes). The left panel of Fig. 4 shows the dependence of the input spectral index of simulations,
. The simulation suggests that the reason for this is the large number of upper limits occurring for lower spectral indices (i.e., flatter input slopes). The left panel of Fig. 4 shows the dependence of the input spectral index of simulations, 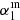 , on the output spectral index of simulations,
, on the output spectral index of simulations, 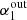 , while the middle panel shows the dependence of the
, while the middle panel shows the dependence of the 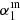 /
/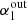 ratio on
ratio on 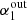 Additionally, we show the behavior of the fraction of limits below 1 GHz as a function of
Additionally, we show the behavior of the fraction of limits below 1 GHz as a function of 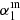 in the right panel of Fig. 4. For
in the right panel of Fig. 4. For 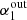 > 1, this correction again rises to 20%. Considering the results presented in the next section, this multiplicative correction is 0.8 ± 0.1 for the real dataset, as indicated by the red points in Fig. 4. Turning the argument around, under the assumption that α1 is normally distributed, the percentage of upper limits below 1 GHz (88%), observed in the real data, indicates α1 ∼ 0.4.
> 1, this correction again rises to 20%. Considering the results presented in the next section, this multiplicative correction is 0.8 ± 0.1 for the real dataset, as indicated by the red points in Fig. 4. Turning the argument around, under the assumption that α1 is normally distributed, the percentage of upper limits below 1 GHz (88%), observed in the real data, indicates α1 ∼ 0.4.
 |
Fig. 4. Results of simulations produced by varying the mean value of the input spectral index α1 (labeled as |
5. Results
Here we present the results of the radio spectral index of the HSFG sample modeled by a broken power-law. In deriving the upper limits, we used the local rms values from the GMRT maps.
The results of this procedure are shown in the left panel of Fig. 5, yielding a break frequency of νb = 4.3 ± 0.6 GHz (derived by the ODR method). Outside the 2σ confidence interval (red ellipses in the left panel of Fig. 5), the distribution starts to diverge from the simple form expected by the fit. Furthermore, the MCMC-derived parameter medians in the left panel of Fig. 5 are not aligned with the ODR-derived means and the covariance ellipses derived by ODR fitting diverge from the σ contours of MCMC parameter estimates. This divergence probably arises because the SED shape is not equally sensitive to the change of every parameter in the model, resulting in deviations in the MCMC method that are more pronounced outside the 2σ confidence interval. Therefore, for the final result, we chose to fix the break frequency to the best-fit value provided by the ODR method and use it to fit the SED with a broken power-law with a fixed break frequency. The break frequency derived in this way is fixed to be νb = 4.3 GHz for all following considerations. We fixed the value of νb to the ODR-derived best-fitting value and not to the MCMC median because of the MCMC behavior outside the 2σ confidence interval. We note that these results using break frequency values in the range from 3 − 6 GHz are not expected to affect the presented results. This is visible from the wide distribution of νb in the lower left plot in the left panel of Fig. 5. As presented in the right panel of Fig. 5, the reduced model behaves according to expectations of a normal distribution.
 |
Fig. 5. Broken power-law parameter estimation based on the MCMC algorithm used in deriving the break frequency. The red lines and ellipses show the results of the corresponding ODR fit, while the black contours show the 1, 2, and 3σ contours of the MCMC samples. Left panel: four-parameter fit with the break frequency treated as a free parameter. Right panel: three-parameter broken power-law fit derived by fixing the break frequency to the best-fit value of νb in the left panel. |
In Fig. 6 we show the average radio SED of HSFGs and the derived broken power-law SED with fixed νb. The percentage of upper limits was 88 ± 2%, which is consistent with α1 ∼ 0.5 in Fig. 4. The spectral index changes from α1 = 0.53 ± 0.04 below νb to α2 = 0.94 ± 0.06 above νb. Considering the correction calculated using simulations in Sect. 4.3, the corrected spectral index is 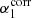 = 0.42 ± 0.06. Some of the models described in Sect. 6.1 can explain this difference, for example, the difference of 0.5 is expected by model (3) assuming continuous injection of electrons (Pacholczyk 1980). Although our data clearly do not follow a simple power-law, we also report the result of the simple power-law fit of 0.67 ± 0.05 to facilitate a quick comparison to the literature.
= 0.42 ± 0.06. Some of the models described in Sect. 6.1 can explain this difference, for example, the difference of 0.5 is expected by model (3) assuming continuous injection of electrons (Pacholczyk 1980). Although our data clearly do not follow a simple power-law, we also report the result of the simple power-law fit of 0.67 ± 0.05 to facilitate a quick comparison to the literature.
 |
Fig. 6. Average SED of the star-forming galaxy sample. Gray data points show individual detections, yellow arrows show upper limits, green circles show means in bins with no upper limits, and magenta circles show mean values derived using survival analysis. The red shaded interval shows the broken power-law fit with its 1σ error confidence interval. The errors derived using survival analysis are the standard deviations of the Weibull distribution that was fit on the Kaplan–Meier survival function. |
In the left and right panels of Fig. 7, we compute mean values of redshift and star-formation rates for different rest-frame frequency bins of our radio SED, respectively. The mean redshifts and SFRs do not vary more than one standard deviation of all the data points (σz = 0.3, σlog SFR = 0.6) below 10 GHz, and there is no clear trend between contiguous frequency bins below this frequency. Only a small fraction of the data points, corresponding to z > 2.3, lie above 10 GHz, and they could not influence the SED fitting procedure significantly. We therefore conclude that our average SED represents the SED of a single population of highly star-forming galaxies (with properties z = 1.7 ± 0.6 and log SFR = 2.4 ± 0.3) over the whole frequency range from 300 MHz to 10 GHz.
 |
Fig. 7. Mean properties of various rest-frame frequency bins in the HSFG radio SED. Shown are the mean redshift (left panel) and log SFR values (right panel) for each bin. Colored circles show the means of detections, while down-pointing arrows show the mean values for non-detections in each redshift bin. The dashed line shows the best-fitting broken power-law SED. |
6. Discussion
In Sect. 6.1 we discuss the shape of the radio SED of star-forming galaxies and alternative, physically motivated fitting strategies. In Sect. 6.2 we discuss the impact of the shape of the radio SED on the infrared-radio correlation.
6.1. Shape of the radio SED
In the left panel of Fig. 8, we overplot the different SEDs from the literature and our broken power-law (BPL). Our results, covering a broad range of redshifts, are in overall agreement with literature SEDs derived for (U)LIRGS in the nearby Universe (z ⪅ 0.1, SFR > 10 M⊙ yr−1) (for galaxies with an SFR in the 50 − 150 M⊙ yr−1 range; Clemens et al. 2008; Leroy et al. 2011). We find disagreement with the typical model of “normal” star-forming galaxies (NSFGs) above ∼10 GHz (Klein et al. 1988; Condon 1992; Tabatabaei et al. 2017), which may be due to the different thermal fractions in normal and highly star-forming galaxies. In the nearby Universe (z < 0.1), the typical SED of NSFGs is described by a simple nonthermal power-law with a spectral index of ∼0.8 and a thermal fraction of 8 − 10% at ∼1 GHz (Klein et al. 1988; Condon & Yin 1990), while studies of HSFGs find a flat spectrum around ∼1 GHz and a steepening spectrum above 10 GHz (Clemens et al. 2008; Leroy et al. 2011).
 |
Fig. 8. Left panel: comparison of the average SED data (magenta points) and our broken power-law fit (magenta lines) with different literature SEDs (Clemens et al. 2008; Leroy et al. 2011) for ULIRGs. For comparison, we show the Condon (1992) model for a normal SFG. Right panel: comparison of the different goodness-of-fit tests for different models. We show the log-likelihood test and the Akaike and Bayesian information criteria. We give the average of these three criteria for reference. |
For our HSFGs with SFR > 100 M⊙ yr−1, we find a relatively flat (α ∼ 0.5) spectral index below ∼4 GHz. This result is in line with previous studies of (U)LIRGs (Clemens et al. 2008; Leroy et al. 2011; Galvin et al. 2018). There are multiple effects that could produce a flattening in the spectrum of galaxies in the radio, but only synchrotron aging and free–free absorption play a role in the 1 − 10 GHz range. Effects like synchrotron self-absorption and the Razin–Tsytovič effect (Razin 1960; Razin 1951), an effect that is due to the refractive index of plasma in the radio, can be ruled out because they are usually found at frequencies below 1 GHz (Deeg et al. 1993). These effects could be even more suppressed, as magnetic fields have been found to be stronger for higher SFRs (Tabatabaei et al. 2017). Furthermore, we do not expect to be able to successfully find evidence for any more complex shape of the SED such as multi-peak behavior of free–free absorption because of the different opacities of different star-forming regions within a galaxy, as any such behavior would be averaged out when constructing an average SED. Tabatabaei et al. (2017) instead pointed out that the nonthermal spectral index (which can be compared to our α1) flattens with increasing SFR density, which gives a possible explanation why this effect is pronounced in our HSFG sample.
Bressan et al. (2002) modeled the radio SEDs of dusty starburst galaxies that initially have SFRs in the range of 100 − 1000 M⊙ yr−1. They concluded that if the SFR changes abruptly, the core-collapse supernova rate will lag behind as a result of the finite lifetimes of stars, leading to a suppressed synchrotron emission in young starbursts. This effect can produce flat spectra below 10 GHz, as the thermal fraction is initially very high. Prouton et al. (2004) analyzed the behavior of the thermal fraction with the age of the starburst for galaxies with an SFRs from 30 to ∼150 M⊙ yr−1. They found that the thermal fraction decreases from the initial value of almost 100% to below 10% at 1.4 GHz within 107.5 yr.
For the HSFGs in the COSMOS field, we find a steep (α ∼ 1) spectrum above 4 GHz that does not exhibit signs of free–free emission. A steep spectral index has also been found by Galvin et al. (2018) (α = 1.06) for galaxies with an SFR in the range of ∼50 − 250 M⊙ yr−1, which they associated with a steeper injection index of the CR distribution. Clemens et al. (2008) found a similar trend (for galaxies with an SFR ∼ 50 − 150 M⊙ yr−1 ) that they tried to explain using the continuous injection model, which can explain differences in spectral indices up to Δα ≈ 0.5.
Since the SED of HSFGs has been found to differ from a simple power-law, we fit the following models often used in literature (e.g., Calzetti et al. 1994; Condon 1992; Clemens et al. 2008; Condon & Ransom 2016; Lisenfeld et al. 2004; Klein et al. 2018) that might explain this behavior:
(1) Mixed model: This model assumes that the power-law synchrotron spectrum with a spectral index α is attenuated by free–free absorption with opacity 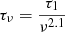 arising from the same region.
arising from the same region.
(2) Foreground screen model: This model assumes that the power-law synchrotron spectrum with a spectral index α is attenuated by free–free absorption with opacity 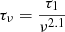 arising from a region that is in our line of sight, but is not cospatial with the emitting region.
arising from a region that is in our line of sight, but is not cospatial with the emitting region.
(3) Synchrotron aging model: In contrast to the previous two models, this model does not take into account free–free absorption of synchrotron radiation initially described by a simple power-law. This model instead explains the shape of the SED by taking into account that the cosmic ray electron population loses energy with time. The model predicts a spectrum that was initially described by an injection index that produces a power-law SED with a spectral index α that gradually steepens above a frequency νb to a spectral index α + Δα due to aging.
(4) Synchrotron self-absorption: The synchrotron self-absorption model has the same form as model 1, with the opacity of the form τν = (ν/νb)−(α + 5/2), where α is the synchrotron spectral index and νb the break frequency.
(5) Lisenfeld et al. (2004) model: In this model, the electrons are propagated through and eventually out of the galactic halo by means of convective winds.
(6) Free–free emission: Models 1–5 can be extended by including an additional contribution of thermal free–free emission, fth, as described by Eq. (2). We consider the following: (6a) Synchrotron aging model with free–free emission, and (6b) Lisenfeld et al. (2004) model with free–free emission.
Among the models listed above, free–free absorption and synchrotron aging models would reproduce flattening at lower frequencies, while models (6a) and (6b) can be used to estimate the contribution of free–free emission to the spectrum. The parameterization of the fitted SEDs and their parameters can be found in Table 1. We find that models (1) and (2), which include free–free absorption, fit the low-frequency data well. They overestimate the measured flux at higher frequencies (by ∼0.1 dex at 10 GHz), however. The synchrotron aging model (3) agrees with the broken power-law at both low and high frequencies. The low-frequency spectral index corresponds to the value typically found in supernova remnants (SNRs) and the Galactic plane in the Milky Way (Green 2014; Klein et al. 2018). We tried to constrain the thermal fraction with the broken power-law model by using Eq. (2), but found a strong degeneracy between parameters fth and α2 and therefore cannot draw meaningful results from this model. This degeneracy is expected for this class of models (Transtrum et al. 2010) and can only be broken by more observations at even higher frequency (> 10 GHz).
Rankings of different fitted models with their parameters.
To compare how well these models explain our dataset, we used the log-likelihood test and the Akaike and Bayesian information criteria (AIC and BIC, respectively). The greatest log likelihood means that the broken power-law is optimal in terms of the fitting. In contrast to the log-likelihood test, AIC and BIC criteria favor models with a smaller number of free parameters, penalizing the models with a higher number of free parameters by higher AIC and BIC values. In the right panel of Fig. 8 we show the ranking in our statistical analyses (log likelihood, AIC, and BIC) for the models in Table 1. The results reported in Table 1 were computed using the ODR method restricted to a 2σ subset of the respective model’s parameter space, derived using the MCMC procedure.
We found that our broken power-law model has the greatest log likelihood and the second lowest AIC and BIC values. The BPL model shares the same average rank of the AIC, BIC, and log-likelihood ranks with model (5) because model (5) has fewer free parameters and is therefore favored by the AIC and BIC values, while it ranks third on the log-likelihood test. As shown in Fig. C.1, the broken power-law model and models (3), (5), (6a), and (6b) describe the average radio SED points sufficiently well. We therefore conclude that we can favor models ranking the lowest on all three tests. In addition to the broken power-law, the highest ranking models are model (5) and its extension that includes free–free emission (model 6b). Additionally, literature models of HSFGs (Clemens et al. 2008; Leroy et al. 2011) score better in all three tests than the standard NSFG model (Condon 1992). This comparison means that HSFGs do not have the same SED shape as the NSFGs. The main difference to the NSFGs is the behavior at higher frequencies, which might be due to a smaller thermal fraction at higher SFR. Since our empirical broken power-law describes our dataset better than simple theoretical models (models 1–3), and different goodness-of-fit criteria sort their preference differently, we conclude that neither simple free–free absorption over the whole sample nor synchrotron aging are the only drivers of the radio SED of HSFGs.
6.2. Infrared–radio correlation
Recent stacking and survival analysis studies (Ivison et al. 2010; Magnelli et al. 2015; Delhaize et al. 2017; Calistro Rivera et al. 2017) have found the infrared–radio correlation (described by the q parameter) to decrease with increasing redshift. Delhaize et al. (2017) mentioned the possibility that the computation of rest-frame radio luminosity via a K-correction using a single power-law assumption of the star-forming galaxies’ SED could produce a redshift-dependent trend.
Here we calculate the infrared–radio correlation by using a K-correction based on our best-fitting broken power-law SED for galaxies with an SFR > 10 M⊙ yr−1 and the combination of thermal and nonthermal emission, following Eq. (2), with a nonthermal spectral index of α = 0.97 and a 10% thermal fraction (Tabatabaei et al. 2017) for SFR < 10 M⊙ yr−1 (described in detail in Appendix B). We adopted a threshold between these two types of SFGs at 10 M⊙ yr−1, considering that our results are consistent with studies of (U)LIRGs (SFR > 10 M⊙ yr−1 Clemens et al. 2008; Leroy et al. 2011). We find that the broken power-law derived luminosity is 20% lower than that derived by assuming a 0.7 spectral index for redshifts below z ∼ 1. We also find that the difference is negligible for sources above z ≳ 2. We constrained the infrared–radio correlation using the same procedure as applied by Delhaize et al. (2017). In the infrared, we used Herschel-detected ≥5σ objects, with the COSMOS2015 (Laigle et al. 2016) 24 μm catalog as priors to minimize blending, while in the radio, we used the Smolčić et al. (2017b) 3 GHz Large Project Counterpart catalog. If an object is undetected in the radio, we estimated its upper q limit as five times the local rms value in the 3 GHz map convolved to a resolution at which its peak flux ceases to change significantly with increased convolution, while we used lower q limits based on upper limits to the infrared luminosity, derived through integration of the best-fit SED. For details, see Delhaize et al. (2017). In short, we used the joint radio- and infrared-detected samples of star-forming galaxies in the COSMOS field, and then used the survival analysis method to find the mean q value for different redshift bins and fit a power law of the form
where q0 is the value of q derived for z = 0 and n is the exponent. Contrary to what would be expected from theory (Murphy 2009), but in line with previous studies (Delhaize et al. 2017; Calistro Rivera et al. 2017), the q value, shown in Fig. 9 and computed taking into account the K-corrections described above, decreases with redshift with n = −0.17 ± 0.02, and q0 = 2.88 ± 0.03. In Fig. 9 we show the q − z trend derived under various SED assumptions, as described above. In all the cases, we find that q decreases with increasing redshift. We therefore conclude that the shape of the radio SED, as assumed here, probably does not explain the q − z trend. For comparison, in Fig. 9, we also show the resulting q − z trend based on a simple power-law fit with α = 0.79 for galaxies with an SFR < 10 M⊙ yr−1 (Tabatabaei et al. 2017). This fit is less complex, but has a lower parameter uncertainty. We find that this simplification does not significantly alter the resulting q − z trend (n = −0.18 ± 0.01 and q0 = 2.89 ± 0.03.).
 |
Fig. 9. Infrared–radio correlation, qTIR, as a function of redshift for galaxies in the Delhaize et al. (2017) joint radio and infrared sample. We used the broken power-law SED from this paper for star-forming galaxies with an SFR > 10 M⊙ yr−1 and the following SED shapes for SFR < 10 M⊙ yr−1 (Tabatabaei et al. 2017): 1) a simple power-law SED with a spectral index of 0.79 (black line, K-correction 1) or a nonthermal spectral index of 0.97, and a 10% thermal fraction at 1 GHz (green line, K-correction 2). We show the Delhaize et al. (2017) relation for reference (magenta line). |
Molnár et al. (2018) have studied the impact of morphology on the evolution of the q parameter (for star-forming galaxies covering a broad SFR range of 1 − 1000 M⊙ yr−1 and in the redshift range of 0.2 − 1.5) and found that spheroid-dominated star-forming galaxies show a steep redshift behavior (n = −0.19 ± 0.02), while disk-dominated galaxies do not (n = −0.04 ± 0.01). They argued that in order for the radio spectral index of spheroid-dominated galaxies to explain the q − z behavior, it would have to decrease with redshift from α = 0.7 at z = 0.8 to α = 0.45 at z = 1.5. To investigate this, we have derived an average radio SED for complete samples of star-forming galaxies based on morphology. To match the selection performed by Molnár et al. (2018), we selected SFGs with an SFR > 20 M⊙ yr−1 to be fairly complete out to a redshift of z = 1.5, with the requirement that we included only galaxies marked as either spheroid- or disk-dominated, based on the classification of Molnár et al. (2018). We show the position in the SFR − z plane of their respective complete subsets in the left panel of Fig. 10 and their respective broken power-law fits in the right panel. Overall, we find that the median MCMC-derived break frequency is 3 GHz and that the differences in the parameters of the broken power-law fit between spheroid (α2 = 0.9 ± 0.3, α1 = 0.5 ± 0.1) and disk-dominated (α2 = 1 ± 0.2, α1 = 0.51 ± 0.09) galaxies are smaller than 1σ. This suggests that a difference in radio-SEDs of these morphologically different galaxies, and thus a potentially different K-correction, is not the cause of the differing trend found by Molnár et al. (2018).
 |
Fig. 10. Left panel: distribution of sources in the SFR − z plane, analogous to Fig. 1. Cyan points and magenta crosses indicate the distributions of disk- and spheroid-dominated subsamples of star-forming galaxies, as defined in Molnár et al. (2018). The 3σ contours of the CSFG sample are shown as black lines, and the orange rectangle marks the edges of the chosen nearly complete disk- and spheroid-dominated samples. Right panel: their respective SEDs. |
7. Summary
We constructed the average radio spectral energy distribution for a 1.4 GHz-selected sample of highly star-forming galaxies with an SFR > 100 M⊙ yr−1 in the COSMOS field. To achieve a broad rest-frame frequency range, we combined previously published VLA observations at 1.4 GHz and 3 GHz with unpublished GMRT observations at 325 MHz and 610 MHz by employing survival analysis to account for non-detections in the GMRT maps caused by their higher rms values. By fitting a broken power-law to the SED, we find the spectral index to change from α1 = 0.42 ± 0.06 below 4.3 GHz to α2 = 0.94 ± 0.06 above 4.3 GHz. Our results are in line with previous low-redshift studies of star-forming galaxies with an SFR > 10 M⊙ yr−1 that show that their SED differs from the one found in normal star-forming galaxies by having a steeper spectral index around 10 GHz, which could imply a smaller thermal fraction than in normal star-forming galaxies.
We further constructed the IR–radio correlation by using our broken power-law SED for galaxies with an SFR > 10 M⊙ yr−1 and an SED based on a steep nonthermal synchrotron spectral index (α = 0.97) and a 10% thermal fraction at 1.4 GHz (Tabatabaei et al. 2017) for galaxies with SFR < 10 M⊙ yr−1. We find that the shape of the radio-SED is probably not the root cause of the redshift trend found by previous studies, as we see a clear trend of the IR–radio correlation decreasing with increasing redshift also when a more sophisticated K-correction is applied to the data.
Acknowledgments
This research was funded by the European Union’s Seventh Frame-work program under grant agreement 337595 (ERC Starting Grant, “CoSMass”). EV acknowledges funding from the DFG grant BE1837/13-1. EV also acknowledges support of the Collaborative Research Center 956, subproject A1 and C4, funded by the Deutsche Forschungsgemeinschaft (DFG). JD acknowledges financial assistance from the South African SKA Project (SKA SA; www.ska.ac.za).
References
- Berta, S., Lutz, D., Santini, P., et al. 2013, A&A, 551, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bondi, M., Ciliegi, P., Zamorani, G., et al. 2003, A&A, 403, 857 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Silva, L., & Granato, G. L. 2002, A&A, 392, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bridle, A. H., & Schwab, F. R. 1999, in Synthesis Imaging in Radio Astronomy II, eds. G. B. Taylor, C. L. Carilli, & R. A. Perley, ASP Conf. Ser., 180, 371 [NASA ADS] [Google Scholar]
- Calistro Rivera, G., Williams, W. L., Hardcastle, M. J., et al. 2017, MNRAS, 469, 3468 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1994, ApJ, 429, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Clemens, M. S., Vega, O., Bressan, A., et al. 2008, A&A, 477, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Condon, J. J. 1992, ARA&A, 30, 575 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Condon, J. J., & Ransom, S. M. 2016, Essential Radio Astronomy (Princeton, NJ: Princeton University Press) [CrossRef] [Google Scholar]
- Condon, J. J., & Yin, Q. F. 1990, ApJ, 357, 97 [NASA ADS] [CrossRef] [Google Scholar]
- da Cunha, E., Charlot, S., & Elbaz, D. 2008, MNRAS, 388, 1595 [NASA ADS] [CrossRef] [Google Scholar]
- Deeg, H.-J., Brinks, E., Duric, N., Klein, U., & Skillman, E. 1993, ApJ, 410, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Delhaize, J., Smolčić, V., Delvecchio, I., et al. 2017, A&A, 602, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delvecchio, I., Smolčić, V., Zamorani, G., et al. 2017, A&A, 602, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feigelson, E. D., & Nelson, P. I. 1985, ApJ, 293, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Galvin, T. J., Seymour, N., Marvil, J., et al. 2018, MNRAS, 474, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Green, D. A. 2014, Bull. Astron. Soc. India, 42, 47 [NASA ADS] [Google Scholar]
- Hales, C. A., Murphy, T., Curran, J. R., et al. 2012, MNRAS, 425, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G., Soifer, B. T., & Rowan-Robinson, M. 1985, ApJ, 298, L7 [Google Scholar]
- Intema, H. T., Jagannathan, P., Mooley, K. P., & Frail, D. A. 2017, A&A, 598, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivison, R. J., Magnelli, B., Ibar, E., et al. 2010, A&A, 518, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaplan, E. L., & Meier, P. 1958, J. Am. Stat. Assoc., 53, 457 [Google Scholar]
- Kennicutt, Jr., R. C. 1998a, ARA&A, 36, 189 [Google Scholar]
- Kennicutt, Jr., R. C. 1998b, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, U., Wielebinski, R., & Morsi, H. W. 1988, A&A, 190, 41 [NASA ADS] [Google Scholar]
- Klein, U., Lisenfeld, U., & Verley, S. 2018, A&A, 611, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lai, C.-D., Murthy, D., & Xie, M. 2006, in Weibull Distributions and Their Applications ed. H. Pham (London: Springer), 63 [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Evans, A. S., Momjian, E., et al. 2011, ApJ, 739, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Lisenfeld, U., Wilding, T. W., Pooley, G. G., & Alexander, P. 2004, MNRAS, 349, 1335 [NASA ADS] [CrossRef] [Google Scholar]
- Magnelli, B., Ivison, R. J., Lutz, D., et al. 2015, A&A, 573, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molnár, D. C., Sargent, M. T., Delhaize, J., et al. 2018, MNRAS, 475, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J. 2009, ApJ, 706, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Novak, M., Smolčić, V., Civano, F., et al. 2015, MNRAS, 447, 1282 [NASA ADS] [CrossRef] [Google Scholar]
- Pacholczyk, A. G. 1980, Radio galaxies. Radiative Transfer, Dynamics, Stability and Evolution of a Synchrotron Plasmon, 239 [Google Scholar]
- Prouton, O. R., Bressan, A., Clemens, M., et al. 2004, A&A, 421, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rau, U., & Cornwell, T. J. 2011, A&A, 532, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Razin, V. A. 1960, IzVUZ, 3, 584 [Google Scholar]
- Razin, V. N. 1951, Vestn. Mosk. Univ., 11, 27 [Google Scholar]
- Sanders, D. B., Salvato, M., Aussel, H., et al. 2007, ApJS, 172, 86 [Google Scholar]
- Schinnerer, E., Sargent, M. T., Bondi, M., et al. 2010, ApJS, 188, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Smolčić, V., Carilli, C. L., et al. 2007, ApJS, 172, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Smolčić, V., Ciliegi, P., Jelić, V., et al. 2014, MNRAS, 443, 2590 [NASA ADS] [CrossRef] [Google Scholar]
- Smolčić, V., Novak, M., Bondi, M., et al. 2017a, A&A, 602, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smolčić, V., Delvecchio, I., Zamorani, G., et al. 2017b, A&A, 602, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smolcic, V., Intema, H., Slaus, B., et al. 2018, A&A, 620, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabatabaei, F. S., Schinnerer, E., Krause, M., et al. 2017, ApJ, 836, 185 [Google Scholar]
- Transtrum, M. K., Machta, B. B., & Sethna, J. P. 2010, Phys. Rev. Lett., 104, 060201 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P. C. 1971, A&A, 15, 110 [NASA ADS] [Google Scholar]
- Voelk, H. J. 1989, A&A, 218, 67 [NASA ADS] [Google Scholar]
Appendix A: GMRT data reduction
Here we describe the calibration, imaging, source extraction, and validation (including all of the corrections applied) of the GMRT 325 and 610 MHz data.
A.1. Observations and imaging
The GMRT observations of the 2 deg2 COSMOS field were conducted using 30 antennas, their longest baseline being 25 km. The channel width of observations was 125 kHz, with a total bandwidth of 32 MHz. The observations were reduced with the source peeling and atmospheric modeling pipeline (SPAM, described in detail in Intema et al. 2017). It accounts for radio interference at low radio frequencies and for direction-dependent effects, such as ionospheric dispersive delay.
 |
Fig. A.1. Top row: left panel: visibility function for the entire 325 MHz map (blue line) and the 2deg2 COSMOS field (orange line). The median rms within the COSMOS field is denoted by the black dashed line. Middle panel: positions of sources detected using blobcat in the 325 MHz map. The blue rectangle denotes the 2deg2 COSMOS field, while the dashed circle shows the pointing half-power radius. Right panel: ratio of total fluxes detected in the 325 MHz map and in the Smolčić et al. (2014) map. The mean and the 1σ interval of the ratio are shown as vertical orange lines. Middle row: left panel: peak-over-total flux ratio, SP/ST, as a function of the distance to the pointing center (d) for the 325 MHz map. Red dots show the medians of SP/ST for different d bins, with 1σ percentiles as error bars. The fitted Bridle & Schwab (1999) is shown by a blue line. The orange points show the skewness for different d bins, while the orange dashed line shows the overall skewness in this dataset. Right panel: total-over-peak flux ratio, ST/SP, as a function of the S/N for the 325 MHz map. The red line shows the fit we used to discern resolved sources. Sources above the red envelope were considered resolved. Bottom row: astrometric offsets of the 325 MHz pointing positions to the 3 GHz catalog. Left panel: two-dimensional distribution of offsets. Dashed blue lines indicate the median offset in right ascension and declination, while the blue shaded region shows the 1, 2, and 3σ covariance ellipses. Middle and right panels: their respective right ascension and declination offset histograms with fitted Gaussians. |
The 325 MHz observations were carried out in a single pointing (see the top middle panel of Fig. A.1) under the project 07SCB01 (PI: S. Croft). The observations were allocated 45 h in total and comprised four observations with an average time per observation of ∼120min and a total time on target of ∼40 h. Data reduction and imaging were performed using the SPAM pipeline, with the final map being imaged at a resolution of 10.8 × 9.5 arcsec2. A primary beam correction was then performed using the parameters from the GMRT manual. The rms as a function of fractional area is shown in the top left panel of Fig. A.1. We find a median rms of 97 μJy beam−1 over the ∼2deg2 COSMOS field, uniformly rising toward the edges of the map.
 |
Fig. A.2. Top row: left panel: visibility function for the entire 610 MHz map (blue line) and the 2deg2 COSMOS field (orange line). The median rms within the COSMOS field is denoted by the black dashed line. Middle panel: positions of sources detected using blobcat in the 610 MHz mosaic. The blue rectangle shows the COSMOS field. Black dashed lines show the areas covered by individual pointings, while the red dashed lines show pointings that were excluded from the analysis. Right panel: peak-over-total flux ratio, SP/ST, as a function of the S/N for the 610 MHz map with sources extracted using blobcat. Red dots show the medians of SP/ST for different S/N bins, with 1σ percentiles as error bars. The red dashed line shows the median SP/ST of all the data points, while the orange dashed lines shows the overall skewness in this dataset. Middle row: left panel: total-over-peak flux ratio, ST/SP, as a function of the S/N for the 610 MHz map after bandwidth smearing correction. The red line shows the fit used to discern resolved sources. Middle and right panels: beam major and minor axes and the beam position angle for the GMRT 610 MHz pointings. The 1σ intervals for the respective beam parameters are shown as colored regions, with dashed lines showing their medians. Bottom row: astrometric offsets of the 610 MHz mosaic positions to the 3 GHz catalog. Left panel: two-dimensional distribution of offsets. Dashed blue lines indicate the median offset in right ascension and declination, and the blue shaded region shows the 1, 2, and 3σ covariance ellipses. Middle and right panels: their respective right ascension and declination offset histograms with fitted Gaussians. |
The 610 MHz observations were carried out over 19 pointings (see the top middle panel of Fig. A.2) under the project 11HRK01 (PI: H. R. Klöckner). The observations were allocated 86 h in total and were spread over eight observations with an average time on source of ∼4 h per pointing. We found that four pointings (labeled 14, 16, 22, and 23) deviated by more than 2σ from the mean beam axes and beam position angles, and these were therefore excluded. The beam properties of the remaining pointings are shown in the middle row of Fig. A.2. After excluding the four pointings, we used one common restoring beam for the remaining pointings. The pointing images were imaged at a common resolution of 5.6 × 3.9 arcsec2. A primary beam correction was then performed on each pointing image before we combined them into one mosaic using the parameters from the GMRT manual, following the procedure outlined in Smolcic et al. (2018). The rms as a function of fractional area is shown in the top left panel of Fig. A.2, yielding a median rms of 39 μJy beam−1 over the 2deg2 COSMOS field.
A summary of the GMRT data reduction statistics can be found in Table 22. Below we describe the source extraction method, reliability tests, and corrections we applied to the catalogs.
Summary of data reduction results of the GMRT maps.
A.2. Source extraction
BLOBCAT (Hales et al. 2012) was used to extract sources down to five times the local rms value (5σ) in each map. The local rms values were taken from the rms map produced by the AIPS task RMSD. We used default BLOBCAT input parameters except for the minimum blob size, which was set to 3 pixels in right ascension and declination, as described in Smolčić et al. (2017a). Even though the imaged pointing extends beyond the COSMOS field, we restricted the catalog and further analysis to the 2 deg2 COSMOS field.
We find 633 source components in the 325 MHz map and 999 source components in the 610 MHz map. After accounting for multicomponent sources and blending, the number of sources in the COSMOS field is 633 (see below for details) in the 325 MHz map, while the number of sources remaining in the 610 MHz map is 986. All of the sources detected by BLOBCAT within the 2 deg2 COSMOS field are shown in the top middle panels of Figs. A.1 and A.2. Below we describe the various tests and corrections performed to generate the final source catalogs.
A.3. Bandwidth smearing
Given the finite bandwidth of the map, a certain amount of bandwidth smearing is expected. To assess the effect of bandwidth smearing on the extracted fluxes, we computed the peak-over-total flux ratio, SP/ST.
For the 325 MHz map, which consists of only one observed pointing, in the middle left panel of Fig. A.1 we show the SP/ST ratio as a function of the distance to the pointing center. Bandwidth smearing reduces the value of peak fluxes compared to the total fluxes with increasing distance to the pointing center (Bridle & Schwab 1999). We binned the data, calculated the median SP/ST, and used the expected functional dependence of the flux ratio and distance to the pointing center in the presence of bandwidth smearing (as explained in detail in Bridle & Schwab 1999) to account for bandwidth smearing of the peak fluxes. We used this relation to correct the peak flux for each source, and we verified that the SP/ST ratio does not depend on distance to the pointing center after the correction. The final total fluxes are consistent with the shallower Smolčić et al. (2014) 324 MHz Catalog (top right panel of Fig. A.1).
In the top right panel of Fig. A.2, we show the peak-over-total flux ratio, SP/ST, as a function of the signal-to-noise ration (S/N) of sources extracted from the 610 MHz mosaic, combined from 19 pointings. We corrected for bandwidth smearing in the 610 MHz mosaic by dividing the peak flux of each source with the median value of the peak-over-total flux distribution.
A.4. Resolved and unresolved sources
In radio maps, ideal unresolved sources with infinitely high S/Ns have peak fluxes in Jy beam−1 equal to their total fluxes because their flux is contained within the area that is covered by the beam. However, because of the noise properties of the map, we expect the ST/SP ratio for unresolved sources to increasingly scatter around unity with decreasing S/N. We thus discerned resolved sources in the 325 MHz map and the 610 MHz mosaic through the following procedure. We first fit the fifth percentile in the total-over-peak ratios that are lower than 1 as a function of the S/N, as the total flux can only be lower than 1 as a result of statistical effects. We did this by fitting all detections with a total flux lower than the peak flux with a relation of the form ST/SP = 1 − a(S/N)b, as is commonly used in the literature (see, e.g., Smolčić et al. 2017a; Bondi et al. 2003). Second, we assumed that the noise is symmetric around unity. We therefore mirrored this envelope around ST/SP = 1 and considered all sources above it resolved.
The best-fit parameters are a = 3.58 and b = −1.13 and a = 1.26 and b = −0.76 for the 325 MHz and 610 MHz catalogs, respectively. Therefore, we consider 177 (196) sources with ST/SP > 1 + 3.58(S/N)−1.13 (ST/SP > 1 + 1.26(S/N)−0.76) to be resolved at 325 MHz (610 MHz), as shown in the middle right (left) panel of Fig. A.1 (Fig. A.2). We set their total fluxes of unresolved sources to the values of their respective peak fluxes. We note that the fraction of resolved sources (see Table 2) is higher in the 610 MHz catalog because the 610 MHz map is 1.3 − 1.8 times more sensitive than the 325 MHz map (derived by assuming spectral indices in the range from 1 to 0.5).
A.5. Multicomponent sources and deblending
If the resolution of the map is good enough, source extraction algorithms start to separate jets, lobes, and star-forming regions of radio sources into separate sources. We therefore need to associate these components with a single source, termed multicomponent. To quantify this effect in our GMRT maps and find multicomponent sources, we made use of the 3 GHz source catalog. This catalog was used because it reaches a much higher depth (it is 4 − 13 times more sensitive than the 325 MHz map and 3 − 7 times more sensitive than the 610 MHz map for spectral indices of 1–0.5) and a higher resolution (0.75″ at 3 GHz vs. ∼10″ at 325 MHz and ∼5.6″ at 610 MHz). If the source has multiple components, that is, components that are not connected by detectable emission, in this higher resolution 3 GHz map (see Smolčić et al. 2017a, for details), it is a good candidate for a multicomponent source in the map of lower resolution. Conversely, we do not expect single-component sources at 3 GHz to appear as multicomponent at lower resolution.
By visually inspecting cutouts of the maps extracted at positions of multicomponent sources in the 3 GHz source catalog, we found components that needed to be combined into one multicomponent source. The method used to detect multicomponent sources was independently verified using the algorithm described in detail in Vardoulaki (2018, in review). This algorithm generated 3 GHz cutouts that were convolved to a 10″ resolution, and we then used them to create masks for the component-finding algorithm. The algorithm searches for positions within the mask and within a radius that is defined by the linear projected size of the source (linear projected sizes are measured by a semi-automatic machine-learning technique and have been verified by eye, Vardoulaki 2018, in prep.). To be consistent with Smolčić et al. (2017a), the total flux was measured after the multicomponent source was identified using the AIPS task TVSTAT after clipping all the pixels below 2σ. This is consistent with the method used for all other radio source catalogs in the COSMOS field (Schinnerer et al. 2007, 2010; Smolčić et al. 2014, 2017a). In the 325 MHz map, we find only 2 components that needed to be combined into 1 multicomponent source, and in the 610 MHz mosaic we find 25 components that needed to be combined into 12 multicomponent sources. As our analysis is based on the 3 GHz source catalog, in the final catalog, we set the position of the multicomponent source in the GMRT catalogs to its respective position in the 3 GHz catalog, its peak flux to −99, and we replaced its total flux by the value derived above and set the multicomponent flag to 1.
We further identified two sources that were blended into one source at 325 MHz. This number of blended sources was expected, based on the analysis of the 3 GHz source catalog (middle right panel of Fig. A.1). We deblend the identified blended source in the 325 MHz map by using BLOBCAT to be consistent with other flux estimates of the catalog. To ensure that BLOBCAT separated the blended source into two sources, we set the fS/N parameter to 5.78. We tested these measured fluxes using the CASA task IMFIT with visually identified masks that separated the two sources. The sum of total fluxes of the two sources derived using BLOBCAT equals the total flux of the blended source. In the final catalog, we replaced the blended source with two entries in the catalog and the BLOBCAT -derived properties of the respective sources.
To summarize, we associated two source components with one source and deblended one source into two separate sources in the 325 MHz catalog. We also associated 25 source components with 12 multicomponent sources in the 610 MHz catalog. The total number of sources in the GMRT catalogs of the COSMOS field is therefore 633 and 986, respectively.
A.6. False-detection rate
As noise in radio-interferometric images is non-Gaussian and source detection is based on a 5σ-base peak detection, we statistically expect that a small percentage of detections might be random noise fluctuations. To assess the false-detection rate, we assumed that the background noise is symmetric around zero and ran BLOBCAT on the inverted maps (i.e., map multiplied by −1), with the same input parameters as in the original maps. Given that sources with negative fluxes are not expected in the radio map, any source extracted from the inverted map can be reliably identified as a false detection. We find 19 “detections” in the inverted 325 MHz map, yielding a false-detection rate of 3% and 13 “detections” in the inverted 610 MHz map, yielding a false-detection rate of 1.3%.
A.7. Astrometry
To test the astrometric accuracy of the data, we show in the bottom row panels of Figs. A.1 and A.2 the offsets of the source positions in the 325 MHz and 610 MHz catalogs, respectively, from those present in the 3 GHz catalog. The mean offsets in right ascension are within one tenth of the beam size of the GMRT maps, which means that the astrometric accuracy is good.
 |
Fig. B.1. Left panel: luminosity at a rest-frame frequency of 1.4 GHz for different redshifts computed using the fiducial value of 1 μJy for (observer frame) 3 GHz flux densities, right panel: correction of 1.4 GHz radio luminosity, CL1.4 GHz computed using the spectral index of α = 0.7 as reference. Solid lines are corrections based on either a broken power-law (red line), derived in Sect. 5 for our HSFG sample, and an SED (black line) of normal star-forming galaxies based on a 0.97 nonthermal spectral index and a 10% thermal fraction (Tabatabaei et al. 2017). The green line shows the SED of NSFGs based on a simple power law (α = 0.79 Tabatabaei et al. 2017). |
A.8. Final catalogs
In the final catalog we report the positions of sources as well as their peak (in Jy beam−1), and total fluxes (in Jy). For the multicomponent sources, the total flux of both components is indicated in one catalog entry. The “Multicomponent” column indicates the presence of more than one component to the source. For resolved sources, the column “Resolved” is set to 1.
Appendix B: K-corrections
Generally, the luminosity at a rest-frame frequency νe2, L(νe2), is connected to the flux measured at the observed frequency νo2, S(νo2), as
where z is the object redshift and the observed frequency is connected to the emitted frequency by νe = νo(1 + z). This relation does not depend explicitly on the shape of the SED, so we have the relation connecting ratios of luminosities at two different frequencies
We can model 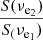 by an SED. Inserting Eq. (B.2) into the first equation, we obtain
by an SED. Inserting Eq. (B.2) into the first equation, we obtain
We can now proceed to find the K-correction for a broken power-law.
B.1. Broken power-law
We assumed that the spectrum is that of a broken power-law with spectral indices α0, α1, and so on, with each new spectral index, αk, beginning above a fixed frequency νk. In this case, the flux for each frequency range k can be expressed as
where bk is the k-th bin normalization constant. Using the fact that the flux needs to be a continuous function of ν, we can roll back bk to the first bin, b0 as
The bin number, k, is easily determined from ν and the list of break frequencies νi, giving functions k(ν) and α(ν). We can repeat this process for each frequency νe1 and νe2, yielding
Finally, we obtain the luminosity as
For the broken power-law with a single break frequency, νe2 = 1.4 GHz and νo1 = 3 GHz, we can express Eq. (B.7) as
Average corrections of luminosity at 1.4 GHz needed if the K-correction was performed by assuming a power-law SED with a spectral index of 0.7.
The left panel of Fig. B.1 shows the luminosity at 1.4 GHz rest-frame derived using various K-corrections. From the right panel of the same figure, we see that luminosities are by up to 26% overestimated compared to the broken power-law for z ≤ 1 if we assume a single spectral index of 0.7.
B.2. K-corrections and thermal fraction
We used the results of Tabatabaei et al. (2017) to derive luminosities of normal star-forming galaxies. They have found that the SED of normal star-forming galaxies has a steep nonthermal spectral index (α2 = 0.97) and a ∼10% thermal fraction at 1.4 GHz. The K-correction in this case is
As discussed in Sect. 6.2, we compared the q − z trends derived using this K-correction and also the K-correction based on the Tabatabaei et al. (2017) simple power-law spectral index of 0.79. In the next section, we derive the average correction of radio luminosity needed for a sample of galaxies consisting of both NSFGs and HSFGs.
B.3. Average K-corrections
To better understand the impact of the different K-corrections on the q − z trend, we also derived corrections of L1.4 GHz for an average 1.4 GHz luminosity by assuming a distribution of fluxes, f( SFR, z), that is dependent on both SFR and z. We started by rewriting Eq. (B.7) for SFGs as L1.4 GHz = K( SFR, z)S3 GHz, where S3 GHz is the observed flux density. As discussed in Sect. 6.2, we used a K-correction, KBPL, based on the broken power-law SED for galaxies with an SFR > 10 M⊙ yr−1 and the Tabatabaei et al. (2017) SED-based K-correction, KTab, for SFR < 10 M⊙ yr−1. The average 1.4 GHz luminosity at redshift z is
We divided this average luminosity by the average luminosity, ⟨L1.4 GHz⟩(z)α, derived by assuming a K-correction, Kα, based on a simple power-law SED with a single spectral index α = 0.7, yielding the correction of L1.4 GHz,
where we have introduced the fraction of sources with an SFR below 10 M⊙ yr−1, p< 10, defined as
 |
Fig. B.2. Average correction of L1.4 GHz for galaxies detected in the radio from the Delhaize et al. (2017) sample. The dashed black line connects corrections in different redshift bins derived by using our broken power-law SED for galaxies with an SFR > 10 M⊙ yr−1, and an SED based on a 0.97 nonthermal spectral index and a 10% thermal fraction (Tabatabaei et al. 2017) for NSFGs ( SFR < 10 M⊙ yr−1). The dashed green line similarly connects points based on the broken power-law for an SFR > 10 M⊙ yr−1 and a simple power-law SED for NSFGs (α = 0.79 Tabatabaei et al. 2017). |
Given the finite number of sources in our sample, this fraction is estimated as the sum of fluxes of all sources within a redshift bin that have an SFR < 10 M⊙ yr−1 divided by the sum of fluxes of all sources within the redshift bin. We see that CL1.4 GHz(p< 10, z) is a linear interpolation between K-corrections derived by assuming a broken power-law SED and the Tabatabaei et al. (2017) SED and can be useful for quickly estimating the impact of using a simple K-correction based on an α = 0.7 power-law SED instead of a more elaborate SED. Average corrections for selected redshifts and p< 10 values can be found in Table B.1. In Fig. B.2 we calculated average corrections for a subset of galaxies from the (Delhaize et al. 2017) sample that were detected in the VLA-COSMOS 3 GHz Counterpart catalog (Smolčić et al. 2017b). The corrections are significant only below z ∼ 1. The fact that the corrections are not needed for higher redshift bins indicates that the shape of the radio SED cannot explain the q − z relationship.
Appendix C: Radio SED of HSFGs with models from Table 1
 |
Fig. C.1. Average radio SED of HSFGs for the models from Sect. 6.1 plotted as in Fig. 6. The red solid lines and shaded intervals represent the best-fitting parameters of Table 1 and confidence intervals, respectively. |
All Tables
Average corrections of luminosity at 1.4 GHz needed if the K-correction was performed by assuming a power-law SED with a spectral index of 0.7.
All Figures
 |
Fig. 1. Star formation rate vs. redshift for the “clean star-forming galaxy sample” (CSFG, black points), as defined by Smolčić et al. (2017b), and described in Sect. 3. Orange points indicate a subset of the CSFG sample that was detected at both 1.4 GHz and 3 GHz. Red points indicate the HSFG sample used here, i.e., the subset of the CSFG sample with an additional cut of the infrared-derived SFR, SFR > 100 M⊙ yr−1. Histograms show the redshift and SFR distributions with the different subsamples colored as in the main figure. For greater clarity, the HSFG sample is marked by filled histograms, and its limits in the main figure are denoted by dotted red lines. |
| In the text | |
 |
Fig. 2. Number of detections in GMRT catalogs of sources in the HSFG samples. The gray area represents the sources that are not detected in the GMRT maps, while blue and orange areas represent sources detected at 325 MHz and 610 MHz, respectively. |
| In the text | |
 |
Fig. 3. Flowchart of the radio SED fitting procedure described in Sect. 4.1. The input values are source fluxes, S, and rest-frame frequencies, ν. The log fluxes are then binned in log-rest-frame frequency bins. If there are no upper limits in a certain bin, the mean and standard deviation are calculated immediately, and if that is not the case, the log fluxes are converted into a right-censored dataset, and the Kaplan–Meier estimate is calculated. This estimate is then fit to a Weibull distribution, yielding the analytically determined means and standard deviations. The resulting different bins are then treated as data points with errors in both axes and are fit by a particular model by employing the ODR method. |
| In the text | |
 |
Fig. 4. Results of simulations produced by varying the mean value of the input spectral index α1 (labeled as |
| In the text | |
 |
Fig. 5. Broken power-law parameter estimation based on the MCMC algorithm used in deriving the break frequency. The red lines and ellipses show the results of the corresponding ODR fit, while the black contours show the 1, 2, and 3σ contours of the MCMC samples. Left panel: four-parameter fit with the break frequency treated as a free parameter. Right panel: three-parameter broken power-law fit derived by fixing the break frequency to the best-fit value of νb in the left panel. |
| In the text | |
 |
Fig. 6. Average SED of the star-forming galaxy sample. Gray data points show individual detections, yellow arrows show upper limits, green circles show means in bins with no upper limits, and magenta circles show mean values derived using survival analysis. The red shaded interval shows the broken power-law fit with its 1σ error confidence interval. The errors derived using survival analysis are the standard deviations of the Weibull distribution that was fit on the Kaplan–Meier survival function. |
| In the text | |
 |
Fig. 7. Mean properties of various rest-frame frequency bins in the HSFG radio SED. Shown are the mean redshift (left panel) and log SFR values (right panel) for each bin. Colored circles show the means of detections, while down-pointing arrows show the mean values for non-detections in each redshift bin. The dashed line shows the best-fitting broken power-law SED. |
| In the text | |
 |
Fig. 8. Left panel: comparison of the average SED data (magenta points) and our broken power-law fit (magenta lines) with different literature SEDs (Clemens et al. 2008; Leroy et al. 2011) for ULIRGs. For comparison, we show the Condon (1992) model for a normal SFG. Right panel: comparison of the different goodness-of-fit tests for different models. We show the log-likelihood test and the Akaike and Bayesian information criteria. We give the average of these three criteria for reference. |
| In the text | |
 |
Fig. 9. Infrared–radio correlation, qTIR, as a function of redshift for galaxies in the Delhaize et al. (2017) joint radio and infrared sample. We used the broken power-law SED from this paper for star-forming galaxies with an SFR > 10 M⊙ yr−1 and the following SED shapes for SFR < 10 M⊙ yr−1 (Tabatabaei et al. 2017): 1) a simple power-law SED with a spectral index of 0.79 (black line, K-correction 1) or a nonthermal spectral index of 0.97, and a 10% thermal fraction at 1 GHz (green line, K-correction 2). We show the Delhaize et al. (2017) relation for reference (magenta line). |
| In the text | |
 |
Fig. 10. Left panel: distribution of sources in the SFR − z plane, analogous to Fig. 1. Cyan points and magenta crosses indicate the distributions of disk- and spheroid-dominated subsamples of star-forming galaxies, as defined in Molnár et al. (2018). The 3σ contours of the CSFG sample are shown as black lines, and the orange rectangle marks the edges of the chosen nearly complete disk- and spheroid-dominated samples. Right panel: their respective SEDs. |
| In the text | |
 |
Fig. A.1. Top row: left panel: visibility function for the entire 325 MHz map (blue line) and the 2deg2 COSMOS field (orange line). The median rms within the COSMOS field is denoted by the black dashed line. Middle panel: positions of sources detected using blobcat in the 325 MHz map. The blue rectangle denotes the 2deg2 COSMOS field, while the dashed circle shows the pointing half-power radius. Right panel: ratio of total fluxes detected in the 325 MHz map and in the Smolčić et al. (2014) map. The mean and the 1σ interval of the ratio are shown as vertical orange lines. Middle row: left panel: peak-over-total flux ratio, SP/ST, as a function of the distance to the pointing center (d) for the 325 MHz map. Red dots show the medians of SP/ST for different d bins, with 1σ percentiles as error bars. The fitted Bridle & Schwab (1999) is shown by a blue line. The orange points show the skewness for different d bins, while the orange dashed line shows the overall skewness in this dataset. Right panel: total-over-peak flux ratio, ST/SP, as a function of the S/N for the 325 MHz map. The red line shows the fit we used to discern resolved sources. Sources above the red envelope were considered resolved. Bottom row: astrometric offsets of the 325 MHz pointing positions to the 3 GHz catalog. Left panel: two-dimensional distribution of offsets. Dashed blue lines indicate the median offset in right ascension and declination, while the blue shaded region shows the 1, 2, and 3σ covariance ellipses. Middle and right panels: their respective right ascension and declination offset histograms with fitted Gaussians. |
| In the text | |
 |
Fig. A.2. Top row: left panel: visibility function for the entire 610 MHz map (blue line) and the 2deg2 COSMOS field (orange line). The median rms within the COSMOS field is denoted by the black dashed line. Middle panel: positions of sources detected using blobcat in the 610 MHz mosaic. The blue rectangle shows the COSMOS field. Black dashed lines show the areas covered by individual pointings, while the red dashed lines show pointings that were excluded from the analysis. Right panel: peak-over-total flux ratio, SP/ST, as a function of the S/N for the 610 MHz map with sources extracted using blobcat. Red dots show the medians of SP/ST for different S/N bins, with 1σ percentiles as error bars. The red dashed line shows the median SP/ST of all the data points, while the orange dashed lines shows the overall skewness in this dataset. Middle row: left panel: total-over-peak flux ratio, ST/SP, as a function of the S/N for the 610 MHz map after bandwidth smearing correction. The red line shows the fit used to discern resolved sources. Middle and right panels: beam major and minor axes and the beam position angle for the GMRT 610 MHz pointings. The 1σ intervals for the respective beam parameters are shown as colored regions, with dashed lines showing their medians. Bottom row: astrometric offsets of the 610 MHz mosaic positions to the 3 GHz catalog. Left panel: two-dimensional distribution of offsets. Dashed blue lines indicate the median offset in right ascension and declination, and the blue shaded region shows the 1, 2, and 3σ covariance ellipses. Middle and right panels: their respective right ascension and declination offset histograms with fitted Gaussians. |
| In the text | |
 |
Fig. B.1. Left panel: luminosity at a rest-frame frequency of 1.4 GHz for different redshifts computed using the fiducial value of 1 μJy for (observer frame) 3 GHz flux densities, right panel: correction of 1.4 GHz radio luminosity, CL1.4 GHz computed using the spectral index of α = 0.7 as reference. Solid lines are corrections based on either a broken power-law (red line), derived in Sect. 5 for our HSFG sample, and an SED (black line) of normal star-forming galaxies based on a 0.97 nonthermal spectral index and a 10% thermal fraction (Tabatabaei et al. 2017). The green line shows the SED of NSFGs based on a simple power law (α = 0.79 Tabatabaei et al. 2017). |
| In the text | |
 |
Fig. B.2. Average correction of L1.4 GHz for galaxies detected in the radio from the Delhaize et al. (2017) sample. The dashed black line connects corrections in different redshift bins derived by using our broken power-law SED for galaxies with an SFR > 10 M⊙ yr−1, and an SED based on a 0.97 nonthermal spectral index and a 10% thermal fraction (Tabatabaei et al. 2017) for NSFGs ( SFR < 10 M⊙ yr−1). The dashed green line similarly connects points based on the broken power-law for an SFR > 10 M⊙ yr−1 and a simple power-law SED for NSFGs (α = 0.79 Tabatabaei et al. 2017). |
| In the text | |
 |
Fig. C.1. Average radio SED of HSFGs for the models from Sect. 6.1 plotted as in Fig. 6. The red solid lines and shaded intervals represent the best-fitting parameters of Table 1 and confidence intervals, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} F\left(\nu _{\rm r}| \begin{matrix}\alpha _2\\ b\\ f\end{matrix}\right) = 10^b\left[\left(\frac{\nu _{\rm r}}{\nu _{\rm n}}\right)^{-\alpha _2} (1-f) + f\left(\frac{\nu _{\rm r}}{\nu _{\rm n}}\right)^{-0.1}\right], \end{aligned} $$](/articles/aa/full_html/2019/01/aa34002-18/aa34002-18-eq1.gif)
![$$ \begin{aligned} F\left(\nu _{\rm r}| \begin{matrix}\alpha _1\\ \alpha _2\\ b\\ f\\ \nu _{\rm b}\end{matrix}\right)= {\left\{ \begin{array}{ll} 10^b\left[\left(\frac{\nu _{\rm r}}{\nu _{\rm n}}\right)^{-\alpha _2} (1-f) + f\left(\frac{\nu _{\rm r}}{\nu _{\rm n}}\right)^{-0.1}\right],&\nu _{\rm r}>\nu _{\rm b}\\ 10^b\left[\left(\frac{\nu _{\rm r}}{\nu _{\rm n}}\right)^{-\alpha _1} (1-f) \left(\frac{\nu _{\rm b}}{\nu _{\rm n}}\right)^{\alpha _1-\alpha _2}+ f\left(\frac{\nu _{\rm r}}{\nu _{\rm n}}\right)^{-0.1}\right],&\nu _{\rm r}<\nu _{\rm b} \end{array}\right.}, \end{aligned} $$](/articles/aa/full_html/2019/01/aa34002-18/aa34002-18-eq2.gif)