Table 1.
Rankings of different fitted models with their parameters.
| Model | Normalized | Ranking | |||
|---|---|---|---|---|---|
| parameters | (normalized) flux density | AIC | BIC | lnL | |
| Broken power-lawa | |||||
| α1 = 0.53 ± 0.04 ( |
Eq. (3) | 2 | 2 | 1 | |
| α2 = 0.94 ± 0.06 | |||||
| Model (1) – mixed modelb | |||||
| α = 0.74 ± 0.06 |
|
6 | 5 | 6 | |
| τ1 = 0.2 ± 0.2 | |||||
| Model (2) – foreground screen modelb | |||||
| α = 0.73 ± 0.06 |
|
6 | 7 | 7 | |
| τ1 = 0.11 ± 0.08 | |||||
| Model (3) – synchrotron aging modelb | |||||
| α = 0.24 ± 0.06 |
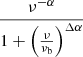 |
4 | 4 | 5 | |
| Δα = 0.55 ± 0.04 | |||||
| Model (4) – synchrotron self-absorption modelc | |||||
| α = 0.70 ± 0.05 |
|
8 | 8 | 8 | |
| νb = 0.76 ± 0.07 GHz | |||||
| Model (5) – (Lisenfeld et al. 2004)b |
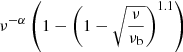 |
1 | 1 | 3 | |
| α = 0.47 ± 0.03 | |||||
| Model (6a) – synchrotron aging+FFEb | |||||
| α = 0.24 ± 0.07 | |||||
| Δα = 0.55 ± 0.04 |
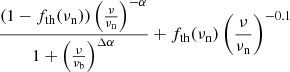 |
7 | 5 | 4 | |
| fth(1 GHz)=0.00 ± 0.02 | |||||
| Model (6b) – Lisenfeld et al. (2004)+FFEb | |||||
| α = 0.50 ± 0.06 |
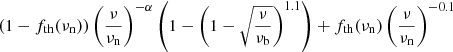 |
3 | 3 | 2 | |
| fth(1 GHz)=0.01 ± 0.027 | |||||
Notes.
For simplicity, we show models without their normalization parameter and indicate the additional contribution of free–free emission with a thermal fraction at 1GHz by “FFE”. We show the rankings based on the Akaike and Bayesian information criteria and the log-likelihood test (lnL).
See Pacholczyk (1980) for details.
See Condon & Ransom (2016) for details.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


