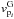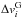| Issue |
A&A
Volume 608, December 2017
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 19 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201628508 | |
| Published online | 12 December 2017 | |
Squeezed between shells? The origin of the Lupus I molecular cloud
II. APEX CO and GASS H i observations⋆,⋆⋆
1 Universitäts-Sternwarte München, Ludwig-Maximilians-Universität, Scheinerstr. 1, 81679 München, Germany
e-mail: bengac@usm.uni-muenchen.de, roccatagliata@arcetri.astro.it
2 INAF–Osservatorio Astrofisico di Arcetri, L.go E. Fermi 5, 50125 Firenze, Italy
3 Max-Planck-Institut für extraterrestrische Physik, Postfach 1312, 85741 Garching, Germany
4 Excellence Cluster Universe, Boltzmannstrasse 2, 85748 Garching, Germany
5 School of Mathematics & Physics, Private Bag 37, University of Tasmania, Hobart 7001, Australia
6 Centre for Astrophysics Research, School of Physics, Astronomy and Mathematics, University of Hertfordshire, College Lane, Hatfield, Hertfordshire AL10 9AB, UK
Received: 14 March 2016
Accepted: 13 October 2017
Context. Lupus I cloud is found between the Upper Scorpius (USco) and Upper Centaurus-Lupus (UCL) subgroups of the Scorpius-Centaurus OB association, where the expanding USco H I shell appears to interact with a bubble currently driven by the winds of the remaining B stars of UCL.
Aims. We investigate whether the Lupus I molecular could have formed in a colliding flow, and in particular, how the kinematics of the cloud might have been influenced by the larger scale gas dynamics.
Methods. We performed APEX 13CO(2–1)and C18O(2–1) line observations of three distinct parts of Lupus I that provide kinematic information on the cloud at high angular and spectral resolution. We compare those results to the atomic hydrogen data from the GASS H i survey and our dust emission results presented in the previous paper. Based on the velocity information, we present a geometric model for the interaction zone between the USco shell and the UCL wind bubble.
Results. We present evidence that the molecular gas of Lupus Iis tightly linked to the atomic material of the USco shell. The CO emission in Lupus Iis found mainly at velocities between vLSR = 3–6 km s-1, which is in the same range as the H i velocities. Thus, the molecular cloud is co-moving with the expanding USco atomic H i shell. The gas in the cloud shows a complex kinematic structure with several line-of-sight components that overlay each other. The nonthermal velocity dispersion is in the transonic regime in all parts of the cloud and could be injected by external compression. Our observations and the derived geometric model agree with a scenario in which Lupus Iis located in the interaction zone between the USco shell and the UCL wind bubble.
Conclusions. The kinematics observations are consistent with a scenario in which the Lupus Icloud formed via shell instabilities. The particular location of Lupus I between USco and UCL suggests that counterpressure from the UCL wind bubble and pre-existing density enhancements, perhaps left over from the gas stream that formed the stellar subgroups, may have played a role in its formation.
Key words: ISM: bubbles / ISM: clouds / ISM: kinematics and dynamics / ISM: structure / ISM: molecules / radio lines: ISM
This publication is based on data acquired with the Atacama Pathfinder Experiment (APEX), which is a collaboration between the Max-Planck-Institut fur Radioastronomie, the European Southern Observatory, and the Onsala Space Observatory.
The 13CO(2–1) and C18O(2–1) spectral cubes are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/608/A102
© ESO, 2017
1. Introduction
Molecular cloud formation is attributed to collisions of large-scale flows in the interstellar medium (ISM) that can be driven by stellar feedback processes such as UV radiation, winds, and supernovae (see review by Dobbs et al. 2014). At the interface of the colliding flows, compression, cooling, and fragmentation of the diffuse atomic medium produces cold sheets and filaments that later may become molecular and self-gravitating. Realizations of this general concept include expanding (super) shells, where an expanding hot bubble collides with the ambient medium (e.g., Krause et al. 2013) and direct collisions of stellar winds (e.g., Calderón et al. 2016).
Such a process might take place between the Upper Scorpius (USco) H i shell and the Upper Centaurus-Lupus (UCL) wind bubble located in the Scorpius-Centaurus OB association (Blaauw 1964; de Zeeuw et al. 1999; Preibisch et al. 2002; Preibisch & Mamajek 2008, Sco-Cen). This is the closest site of recent massive star formation to us at a distance of 110–140 pc only. These shells presumably were created by the feedback of the numerous massive stars in Sco-Cen. In between those two expanding structures there is the Lupus Icloud, which represents a good candidate for which we can study how such a collision process forms and influences new dense clouds in the ISM.
The distance of the Lupus cloud complex is about 140 pc, as discussed in detail by Comerón (2008). Additional details about the region and Lupus Icloud can be found in Gaczkowski et al. (2015, Paper I hereafter).
Molecular line observations of Lupus Iwith different CO isotopes and other high-density tracers have been performed by several groups over the past two decades. Most of these observations have spatial resolutions of several arcminutes, i.e., ~0.1 pc at the distance of Lupus Iof ~140 pc. Tachihara et al. (1996) observed the entire Lupus Icloud in the 13CO (1–0). These authors estimated the cloud mass to be ~1200 M⊙ and discovered the molecular outflow of IRAS source 15398–3359. Hara et al. (1999) have studied 12 cores in Lupus Iin the C18O (1–0) line. The spatial resolution of the NANTEN telescope is 2.7′, while their grid spacing was 2′. These authors derived column densities, temperatures, and sizes for the cores and estimated their total mass to be 152 M⊙. This represents 46% of their total C18O (1–0) emitting gas mass. Vilas-Boas et al. (2000) found 15 condensations in C18O(1–0), and 14 in 13CO(1–0), highlighting the recent star formation activity in Lupus I. A large-scale 12CO(1–0) survey of Lupus Iwas performed by Tachihara et al. (2001). They found a velocity gradient along the long axis of Lupus Ifrom 4 km s-1 in the south to 6 km s-1 in the north. Tothill et al. (2009) analyzed Lupus Iin both CO(4–3)and 13CO(2–1). They found several possible signs of interaction between Lupus Iand the USco H i shell. Benedettini et al. (2012) found eight dense cores in Lupus I using high-density molecular tracers at 3 and 12 mm. They reported the presence of velocity gradients in the cloud and several velocity components along the line of sight. Finally, Benedettini et al. (2015) observed the southern part of the main filament in CS(2–1) and they found several subfilaments in velocity space that correspond to subfilaments they had identified in their Herschel column density maps.
In our dust analysis presented in Paper I we found a double-peaked PDF, which suggests a scenario of external compression of Lupus Ifrom USco and/or UCL. In this work, we follow up on this suggestion and present 13CO(2–1)and C18O(2–1)observations of three distinct regions within the Lupus Icloud with a high angular and spectral resolution of ≈30″ and ≈0.1 km s-1, respectively. We present an analysis of the observational data and a comparison to the available H i data. From those we create a geometrical model for the interaction zone of shell and bubble. We show that the collision scenario is a plausible explanation of the observational data and the creation of Lupus I with other factors likely having played a role as well.
2. Observations and data reduction
2.1. APEX CO observations
The CO line observations of Lupus Iwere performed with the APEX telescope (Güsten et al. 2006) using the APEX-1 receiver of the Swedish Heterodyne Facility Instrument (SHeFI; Vassilev et al. 2008). The observations were carried out on 18 and 20 August 2014 (PI: B. Gaczkowski; Program ID: 093.F-9311(A)). Lupus Iwas observed simultaneously in the 13CO(2–1)(rest frequency 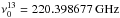 ) and C18O(2–1)(
) and C18O(2–1)(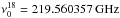 ) line. Three scans across the cloud were performed, as shown in Fig. 1. These were chosen based on our previous dust analysis to obtain representative samples of the conditions along the whole filament. The observing mode was “on-the-fly” and the map parameters for each cut are listed in Table 1. The scanning direction was along the long side of a cut. The velocity resolution of the spectra is Δv = 0.1 km s-1 and the rms noise ranges between ≈0.05–0.1 K for both lines. The perceptible water vapor (PWV) during the observations was between 1.5 and 2 mm. Each cut contains about 620 spectra.
) line. Three scans across the cloud were performed, as shown in Fig. 1. These were chosen based on our previous dust analysis to obtain representative samples of the conditions along the whole filament. The observing mode was “on-the-fly” and the map parameters for each cut are listed in Table 1. The scanning direction was along the long side of a cut. The velocity resolution of the spectra is Δv = 0.1 km s-1 and the rms noise ranges between ≈0.05–0.1 K for both lines. The perceptible water vapor (PWV) during the observations was between 1.5 and 2 mm. Each cut contains about 620 spectra.
The data reduction was carried out with the CLASS package of the IRAM GILDAS software1. The antenna temperature TA was converted into a main-beam temperature Tmb = TA/η, adopting a main-beam efficiency of η = 0.75 for APEX-12. All spectra were baseline subtracted. Finally, for each line and cut, a map (or lmv cube) was produced with the XY_MAP task, which convolves the data with a Gaussian of one-third of the beam. The final angular resolution is 30.1″ and the pixel size is 14.3″.
Details of the molecular line maps obtained for Lupus Iwith APEX-1.
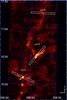 |
Fig. 1 Setup of the APEX-1 13CO(2–1)and C18O(2–1)observations of Lupus I. Along each of the three cuts A, B, and C an on-the-fly map was obtained simultaneously in both lines. The size of each map is indicated with a white box. The background image is the LABOCA continuum map (see Paper I). The Galactic coordinate system is indicated. |
2.2. GASS HI data
The atomic hydrogen data of the entire Sco-Cen region used in our study are part of the second data release of the GASS H I survey (Kalberla et al. 2010). This has a spatial resolution of 16.2′, which corresponds to a length scale of 0.7 pc at the distance of Lupus I. The velocity resolution is 1 km s-1 and the rms noise is 55 mK.
In order to characterize the HI shell around Upper Scorpius (the Upper Scorpius loop) and relate it to the Lupus I cloud, which forms part of the filaments of the shell rim, we fitted an expanding homogeneous spherical shell to the HI data. In addition we used Na I absorption data in the foreground of stars with known distances from Hipparcos measurements, using the same shell model as for the HI data. This follows an analysis approach presented elsewhere (Pöppel et al. 2010; Welsh et al. 2010). The parameters of our expanding-shell model are
-
distance to the center of the shell D0;
-
galactic longitude l0 of the shell center;
-
galactic latitude b0 of the shell center;
-
radius of the inner edge of the shell rin;
-
thickness of the shell Δr;
-
density of hydrogen atoms nH in the shell assumed to be spatially constant;
-
expansion velocity of the shell Vexp;
-
bulk velocity of interstellar medium in the Sco-Cen region V0.
The distance to the shell center D0 was determined from a multiparameter fit to the absorption data, yielding D0 = 138 ± 26 pc. Here, the uncertainties were propagated from the uncertainties in the distance measurements of the stars.
For the fit to the HI data, we transformed this model from 3D Cartesian space (x,y,z) into (l,b,v) space, added the HI Milky Way model of Kalberla et al. (2007) as a large-scale background and optimized model parameters fitting to the HI data by a χ2 minimization. The set of best fitting parameters are:
-
l0 = 347 ± 0.5deg,b0 = 25 ± 0.5deg,rin = (12.3 ± 0.7)deg;
-
Δ r = 2.7 ± 0.3deg,nH = 6 ± 2cm-3,Vexp = (7 ± 1) km s-1;
-
V0 = 8 ± 1 km s-1.
Uncertainties are quoted as 1σ. The total mass of hydrogen in the shell is 11 000 ± 6000 M⊙. This is similar to the value determined by Pöppel et al. (2010) from lower quality data.
The mass determination has additional significant systematic uncertainties, as the shell is not detected on the far side. On the near side, a spherical shape is plausibly seen, but the galactic foreground adds uncertainties.
3. Results
The individual spectra are complex, with a variety of line profiles. The velocity of the emitting gas ranges from vLSR = 3.2 to 6.8 km s-1. The maps were convolved with a Gaussian of two pixels or approximately one beam. All observed spectra can be found in Appendix A in Figs. A.2–A.7. The main 13COemission in cut A is at velocities of vLSR = 5.5–6.2 km s-1 with the highest intensities between 5.9 and 6.1 km s-1. The emission is concentrated at the center of the cut and extends to about 10′ around the center in the channels with highest intensities. Detectable C18Oemission region is limited to about 2′ around the very center of the cut.
The highest intensities of the three cuts are found in cut B. The bulk of the C18Oemission lies at the same velocity range as the 13COemission. It is concentrated on the center of the cut and no emission is found at either edge.
Within cut C several spatially distinct emission regions can be seen in 13COand C18O . In contrast to the other two cuts, the 13COand C18Oemission peaks do not overlap, but are located at opposite ends of the cut. C18Oemission is found at three positions within the cut.
The average 13COand C18Ospectrum was then computed for each cut and these spectra are shown in Fig. 2. The solid lines represent the average 13COspectrum and the dotted lines the average C18Ospectrum multiplied by three. Cut A shows the lowest intensities of all three cuts in both lines. The averaged 13COline is very broad and asymmetric toward velocities lower than the velocity of the peak, i.e., vLSR = 5.75 km s-1. The peak intensity of the 13COline is 1.22 K. The 13COline of cut B is the most narrow and has the highest peak intensity of all three cuts with a value of 4.44 K at vLSR = 5.02 km s-1. For cut C the 13COline also peaks at vLSR = 5.02 km s-1 with a peak intensity of 3.26 K. The averaged C18Olines of cut B and cut C both peak at vLSR = 5.13 km s-1 and have a peak intensity of 1.34 and 0.74 K, respectively.
 |
Fig. 2 Average 13COand C18Ospectra of the three cuts. The integrated intensities (for vLSR = 0–10 km s-1) of the 13COlines are 1.96, 5.69, and 5.55 K km s-1 for cut A, B, and C, respectively. Those of the C18Olines are 1.22, and 0.50 K km s-1 for cut B and cut C, respectively. |
4. Analysis
We first calculated the optical depth, excitation temperature, and column density under the assumption of local thermodynamical equilibrium (LTE). A multi-Gaussian fit determines the different velocity components of the observed spectra. We finally search for a nonthermal contribution to the spectra.
4.1. Local thermodynamical equilibrium density analysis
Spectra with a S/N> 4 were selected to compute optical depth, excitation temperature, and column density. This assures that both lines are clearly detected. For our analysis we assume local thermodynamical equilibrium (LTE) conditions. The excitation temperature Texis equal to the kinetic temperature of the gas and is the same for all transitions and both CO isotopologs. This assumption should hold when the temperature distribution along the line of sight is uniform.
The equations and constants used for the calculations of the excitation temperature and column density in this section can be found in Appendix A.
The H2 column density map calculated from dust emission (see Paper I) showed that almost all of Lupus Ilies below 1 × 1023 cm-2 . Therefore, C18Ois optically thin (Carlhoff et al. 2013). The optical depth of the 13COgas is computed (see, e.g., Myers et al. 1983; Ladd et al. 1998) using the relation 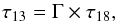 (1)with τ13 = τ(13CO), τ18 = τ(C18O) and Γ = [13CO] / [C18O] is the relative abundance ratio of the given isotopologs. Here we adopt a constant abundance ratio of Γ = 7.3 (Wilson & Rood 1994, local ISM). Then the optical depth τ13 can be approximated by the intensity ratio of the lines
(1)with τ13 = τ(13CO), τ18 = τ(C18O) and Γ = [13CO] / [C18O] is the relative abundance ratio of the given isotopologs. Here we adopt a constant abundance ratio of Γ = 7.3 (Wilson & Rood 1994, local ISM). Then the optical depth τ13 can be approximated by the intensity ratio of the lines 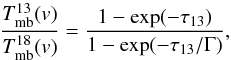 (2)where
(2)where 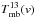 and
and 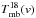 are the main-beam temperature of the corresponding line at velocity channel v. In principle this relation is valid for every velocity channel. Here, we chose
are the main-beam temperature of the corresponding line at velocity channel v. In principle this relation is valid for every velocity channel. Here, we chose 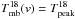 the peak brightness temperature of the C18Oline. Then
the peak brightness temperature of the C18Oline. Then 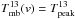 is the corresponding brightness temperature of 13COat the velocity channel of the C18Opeak intensity. The resulting optical depth maps for C18Oare shown in the left panels of Fig. A.1. The optical depth τ18 is in the range 0.3 to 1 for most of the cloud with isolated peaks up to about 1.5.
is the corresponding brightness temperature of 13COat the velocity channel of the C18Opeak intensity. The resulting optical depth maps for C18Oare shown in the left panels of Fig. A.1. The optical depth τ18 is in the range 0.3 to 1 for most of the cloud with isolated peaks up to about 1.5.
 |
Fig. 3 Top left: dust column density map from LABOCA with red contour levels of 0.3, 1, 1.7, 2.3, and 3 × 1022 cm-2 . Integrated C18O(2–1)intensity maps of cut A, B, and C (top rightand bottom figures, respectively). The six boxes into which each cut was divided are shown as well as the contours of the LABOCA 870 μm continuum emission. Levels are from 10–100% of the peak intensity of 1.37 Jy/beam. |
The excitation temperatures are computed using the optically thin C18Oline (Eqs. (A.1) and (A.2) in the Appendix). The resulting Texmaps are shown in the middle panels of Fig. A.1. The mean excitation temperatures for cuts A, B, and C are 16.8, 14.7, and 14.7 K. Our excitation temperatures calculated in our analysis are comparable to previous findings from various CO and molecular observations of Lupus I. With Eq. (A.3) we compute the C18Ocolumn density, and find H2 column density assuming a constant abundance ratio of [C18O] / [H2] = 1.7 × 10-7 (Haworth et al. 2013) for the three column density maps shown in the right panels of Fig. A.1.
The column density distribution (called NH[CO]) has been compared to the total column density obtained from the dust (NH[FIR dust em.] from Paper I).
We fit a Gaussian to the distribution of the ratio between the NH[CO] and NH[FIR dust em.] first considering all the cuts together and then considering each of the three cuts. The distribution peaks at 0.8 with a standard deviation of 0.3. In general, the column density from CO gas emission is found to be lower than the column density from dust emission. Along cut A the ratio between gas and dust column density peaks at 1 with a standard deviation (σ) of 0.7, σ = 0.3 for cut B, while for cut C the peak of the ratio is not clearly identified as the other two cuts.
4.2. Determination of different velocity components and nonthermal motions
In this section we present a detailed analysis of the various CO velocity components. Each cut was divided into six boxes as shown in Fig. 3. The derived position-velocity (PV) diagrams are shown in Fig. 4. Figure 5 shows the average 13CO(top row) and C18Ospectrum (bottom row). Using a multicomponent (up to three) Gaussian fit of the spectra (Figs. A.2 to A.7), we computed the peak position and FWHM for each component of the 13CO(top row) and C18O(see Table 2 for more details).
We conclude from this that a velocity decrease from cut A to cut C is seen. No clear trend is seen in line widths, suggesting a homogeneous level of turbulence.
We then derived the nonthermal velocity dispersion of the gas from the measured line width, subtracting the thermal component. Following the standard assumption that the thermal and non-thermal components are independent (see, e.g., Myers 1983), the nonthermal velocity dispersion σNT is 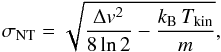 (3)where Δv is the measured line width, kB the Boltzmann constant, Tkin the kinetic gas temperature (here we adopt 10 K), and m the mass of the observed molecule (m13CO = 29 u, mC18O = 30 u). Dividing σNT by the isothermal sound speed cs = 0.19 km s-1 for a 10 K ISM gas, gives a direct measure of nonthermality of the component. For the measured line widths of 13COin the three cuts, this indicator is between 2.0 and 4.5, suggesting that the gas would be supersonic. However, correcting the 13COline width for opacity broadening due to its higher optical depth τ13> 1–2 (Phillips et al. 1979), while C18Oτ18< 1; this yields a lower indicator value of σNT/cs between 0.9 and 1.8. Hence, most of the C18Ogas within the three cuts is in the trans-sonic regime (1 <σNT/cs< 2). Typically, the gas of a quiescent cloud resides in the subsonic regime as found, for example, by Hacar & Tafalla (2011) for L1517. In Lupus Ithis signature of turbulence might have been imprinted on the gas by the large-scale interaction with the H i shell of USco and the wind-blown bubble of UCL.
(3)where Δv is the measured line width, kB the Boltzmann constant, Tkin the kinetic gas temperature (here we adopt 10 K), and m the mass of the observed molecule (m13CO = 29 u, mC18O = 30 u). Dividing σNT by the isothermal sound speed cs = 0.19 km s-1 for a 10 K ISM gas, gives a direct measure of nonthermality of the component. For the measured line widths of 13COin the three cuts, this indicator is between 2.0 and 4.5, suggesting that the gas would be supersonic. However, correcting the 13COline width for opacity broadening due to its higher optical depth τ13> 1–2 (Phillips et al. 1979), while C18Oτ18< 1; this yields a lower indicator value of σNT/cs between 0.9 and 1.8. Hence, most of the C18Ogas within the three cuts is in the trans-sonic regime (1 <σNT/cs< 2). Typically, the gas of a quiescent cloud resides in the subsonic regime as found, for example, by Hacar & Tafalla (2011) for L1517. In Lupus Ithis signature of turbulence might have been imprinted on the gas by the large-scale interaction with the H i shell of USco and the wind-blown bubble of UCL.
 |
Fig. 4 Position-velocity diagrams of cut A, B, and C (from top to bottom) in 13CO(2–1)(left panel) and C18O(2–1)(right panel) along a line through the middle of the cut. The x-axis gives the position along this line. The white arrow in the bottom right corner of the left panels indicates the orientation of the cut in the celestial coordinate frame. The white crosses indicate the velocity of the peak intensity at each x-position. The cutoff is set to 1 K in 13CO(2–1)for all three cuts and 0.5 K in C18O(2–1)for cuts B and C. The C18O(2–1)cutoff for cut A is 0.3 K. All maps have been convolved with a Gaussian of two pixels or approximately one beam. |
5. Comparison between CO and HI
In this section we present a comparison between CO and H i data.
Figure 6 shows for vLSR = 0–8 km s-1 an H i column density map of Lupus I, together with C18O (1–0) emission (Hara et al. 1999) for the same velocity range as the CO emission. Although the peak velocities of HI and CO agree, the H i and CO emission do not spatially agree with each other: the highest H i column density is located at the northwestern end of Lupus I, while in the central and the southern part of Lupus Ithere is less H i emission, roughly by a factor of 1.5. Between b = 15°30′–17° and l = 338°30′–339°30′ the deficit in H i emission around the center-south of Lupus Ihas the form of a little hole. The H i emission, in general, is enhanced at the Galactic west side of Lupus Iand has a deficit on its east side with an average ⟨ NH ⟩ = 5.5 × 1020 cm-2. The atomic to molecular ratio is poorly defined, given the large uncertainties in the these values. Benedettini et al. (2015), for example, reported a ratio of ⟨ NH ⟩ / ⟨ NH2 ⟩ ≈ 1.6 calculated from their Herschel column density maps and the H i data of de Geus (1992).
The particular distribution of CO and H i shows that Lupus Imarks a transition region between the molecular and atomic phase of H i. At those places in the cloud where the atomic hydrogen emission is decreased, the molecular emission is enhanced and vice versa (see Fig. 6). Our analysis shows that the C18Oemission is significantly higher in the center and south of Lupus I. We conclude that the north has not built enough dense molecular material yet to start the star formation process. The lower dust column densities seen there coincide with a higher fraction of atomic material. Correspondingly, C18Oemission is strongest in the central and southern parts of Lupus I where the H i emission has a deficit and active star formation and high CO column densities (N(H2) ≈ 1022 cm-2) can be seen.
 |
Fig. 5 Averaged spectra within the six boxes into which each cut was divided. The top row shows the average 13CO(2–1)spectra; the bottom shows those of C18O(2–1). Each column represents one of the three cuts. The different colors denote the six boxes from 1 to 6. The vertical dashed line marks for orientation vLSR = 6 km s-1 for cut A and vLSR = 5 km s-1 for cuts B and C. |
Heiner et al. (2015) have created synthetic H i and CO observations from a numerical simulation of decaying turbulence in the thermally bistable neutral medium. They found a power-law tail in the column density PDF when molecular clouds formed. This tail, however, only appears in the PDFs of the molecular material and not the H i. Hence, these authors conclude that the molecule formation is directly correlated with gravitational infall. As the dust PDF of the northern part of Lupus I(see Paper I) does not show a power-law tail, the gravitational infall might not yet be strong enough to convert as much atomic material into molecular in the center-south.
 |
Fig. 6 H i column density map calculated from the integrated emission for vLSR = 0–10 km s-1. Black contours show the integrated C18O (1–0) emission observed by Hara et al. (1999). |
6. Geometrical model for the interaction zone
In this section we present a model to check the scenario that Lupus Iis located in the interaction zone of the USco H i shell and the UCL wind bubble.
We constructed a geometrical model with the observer located in the origin of the coordinate system that is a 3D Cartesian Galactic coordinate system with 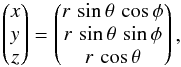 (4)where θ = 90°−b, φ = l, r is the distance, b and l the galactic latitude and longitude, respectively. The x-axis points to the Galactic center. Both H i shell and wind bubble are represented by a sphere. We placed the center of the USco sphere at (l,b) = (347°, + 25°) and a distance of 145 pc. A radius of ~30 pc is the inner shell radius from our H i model fit (details in Kröll 2018) as observations suggest that Lupus Iis located closer to the inner edge of the shell.
(4)where θ = 90°−b, φ = l, r is the distance, b and l the galactic latitude and longitude, respectively. The x-axis points to the Galactic center. Both H i shell and wind bubble are represented by a sphere. We placed the center of the USco sphere at (l,b) = (347°, + 25°) and a distance of 145 pc. A radius of ~30 pc is the inner shell radius from our H i model fit (details in Kröll 2018) as observations suggest that Lupus Iis located closer to the inner edge of the shell.
We estimated the average projected position of the B stars southwest of Lupus Ithat might be responsible for the wind bubble (see Paper I) to be (l,b) = (331°, + 12°). This also agrees with the center of a circle in the ROSAT image enclosing the X-ray emission in this region (cf. Fig. 7 in Paper I). The average distance to the stars of the UCL subgroup is about 5 pc smaller than that to USco (de Zeeuw et al. 1999) and thus we placed the center of our UCL sphere model at 140 pc.
 |
Fig. 7 Geometrical model of the possible interaction zone between the USco H i shell (black sphere) and UCL wind bubble (green sphere). The observer is located in the origin of the coordinate system. The position of Lupus Iis marked by three red asterisks that represent the top, middle, and bottom of the main filament, respectively. The cloud is plotted at three different distances of 150, 140, and 130 pc along the red line, which is the line of sight from us to Lupus I. The black and green solid lines are the line of sight from the observer to the corresponding sphere. The cyan dots indicate those positions on the USco shell that have line-of-sight velocities between 3 and 6 km s-1, i.e., similar to Lupus I(the white gaps are an effect of the grid model used in the calculations). The magenta cross indicates the touch point between the USco and the UCL sphere. The projections are show in the different panels. |
Our UCL wind bubble is thus on the near side of the USco H i shell. Figure 7 shows model in three perspectives at the stage at which the UCL bubble touches the USco sphere. In Fig. 7 all points on the surface of the USco sphere that have a model velocity between 3–6 km s-1are marked in cyan. This represents the CO velocity range we observed in Lupus I. The UCL wind bubble (i.e., the sphere of influence of the massive stars in UCL) interacts with the USco H i shell at positions that have a similar gas velocity to Lupus I.
The Lupus Icloud and the USco H i shell have similar observed velocities and thus it seems reasonable that Lupus Iis expanding with the USco shell.
In our purely geometrical model, which does not accurately reflect the physics and resulting complex morphologies present in the Sco-Cen region, the UCL wind bubble and the USco H i shell nevertheless intersect at velocities consistent with our observations of Lupus I. Therefore, the observational data are in agreement with the idea that Lupus Iis in an interaction zone between the USco H i shell and the UCL wind bubble. Moreover, this model comparison indicates that Lupus Iis expanding with the USco shell and that the cloud is located at the inner edge of the H i shell.
 |
Fig. 8 Left: H i column density map of USco and surroundings of Lupus Icalculated from the integrated emission for vLSR = 0–10 km s-1. The two black circles indicate the inner and outer radius of the USco shell from the model fit. The black and white contours represent the dust emission at 850 μm and the CO(1–0)emission from Planck, respectively. The blue and black labeled dots represent early B-type stars in USco and UCL, respectively. Right: zoom into the region indicated as a dashed black box in the left panel. |
7. Surroundings of Lupus I and interaction with USco and UCL
Figure 8 shows the USco H i shell as observed today. A H i column density map of USco and the surroundings of Lupus Iare shown in the top panel, together with the dust emission at 850 μm and the CO(1–0) emission from Planck, and early B-type stars in USco and UCL. Our model fit to the H i data yields a shell expansion velocity of ~7 km s-1 and a thickness of ~6 pc. The current inner and outer radius is ~30 pc and ~36 pc, respectively ( indicated by the two black circles in Fig. 8). East and west of Lupus Ithere are clear H i voids and the atomic material is concentrated in the same area as the dust. A further zoom on Lupus I(right panel of Fig. 8) reveals a complicated distribution of atomic, molecular, and dust material. Whereas the CO emission is always found in regions of dust emission, there are several areas within the USco shell ridge where there is H i emission but neither dust nor CO are detected. The layering of atomic and molecular material, as can be seen in Lupus I(molecular gas, traced by CO, is surrounded by H i), is also found in some other locations in the shell around Lupus I. In the part of the shell where Lupus Iis located, the molecular gas is found preferably behind the atomic gas, i.e., closer to the inner edge of the shell. However, local turbulence and inhomogeneities apparently lead to complex configurations.
The comparison of our CO to H i data showed that both fall into the same velocity range. If thus Lupus Iis co-moving with the atomic gas in the shell its formation within the shell wall seems plausible. Dawson et al. (2011) found that expanding supershells are capable of sweeping up big amounts of gas from the ISM. Increased density within their walls leads to very short chemical timescales. These authors estimate a transition timescale from atomic to molecular material of ~ 106–107 yr(see also Koyama & Inutsuka 2000; Bergin et al. 2004; Heitsch & Hartmann 2008; Clark et al. 2012). The estimated age of the USco shell is ~5 Myr and hence it should have had sufficient time to accumulate enough atomic gas locally to convert it into molecular gas at the position of Lupus I. From the dust analysis described in Paper I we found that the total cloud (gas + dust) mass of Lupus Iis only ~170 M⊙. This is at least two orders of magnitude lower than the estimated total mass of the USco shell (~104M⊙) as derived from the H i model fit. If the atomic gas was homogeneously distributed within the shell, then at least ~103M⊙ would have been swept up at the current position of Lupus I, which is enough to create a ~100 M⊙ molecular cloud, and is similar to the estimate of the total cloud mass by Tachihara et al. (1996). Furthermore, the analysis of the LABOCA continuum data has revealed many pre- and protostellar cores (see Paper I). This suggests that the formation timescale of the cloud and the onset of star formation should be on the order of even less than 2 Myr, which is still in agreement with the atomic-to-molecular transition timescale. The large-scale magnetic field is perpendicular to the Lupus I filament, i.e., pointing in the direction of the USco shell expansion. This might have favored the accumulation of cold, dense atomic gas along the field lines and promoted fast molecule formation (Matthews et al. 2014; Hartmann et al. 2001; Vázquez-Semadeni et al. 2011).
The slightly supersonic irregular motions we find are in excellent agreement with predictions for clumps formed by the thin shell instability (Vishniac 1983). Three-dimensional simulations explicitly predict such velocities in clumps formed dynamically in expanding supershells (Krause et al. 2013, Fig. 9). We thus have three pieces of evidence: the correspondence between bulk HI and molecular velocities; the spatial anticorrelation between molecular and atomic gas; and the magnitude of the irregular motions, which supports the picture that the Lupus Imolecular cloud has formed dynamically in the expanding USco supershell. Also X-ray observations suggest that the UCL wind bubble might be colliding with the USco H I shell right at the position of Lupus I, squeezing it in between (see Paper I). This wind bubble, probably still additionally pressurized by past supernova activity, might have provided a counterpressure to the expanding USco shell and thus favored this position for an additional compression of the shell material. In this way a new molecular cloud could have been created there and this would explain why there are not more very young star forming clouds, except ρ Ophiucus, which is believed to be pre-existing (e.g., Motte et al. 1998), seen distributed within the wall of the USco shell.
This view is also supported by the column density PDFs of the dust emission (see Paper I) with the double-peak profile over the whole extent of the cloud. Together with the dust column density map this shows that Lupus Iconsists of a dense layer in the center of the filament that is surrounded by much more diffuse material. Simulations have shown that this is consistent with the idea of a two-sided compression through colliding flows (see Matsumoto et al. 2015). Then the molecular cloud is created in a dense and thin sheet that is surrounded by the diffuse material of colliding flows.
This picture does, however, not come without difficulties. A formation of molecular clouds in colliding supershells requires that the shells have the same pressure evolution (Ntormousi et al. 2011). Any pressure difference can lead to cloud ablation and might destroy such clouds within about 106 yr (Krause et al. 2013). Since Lupus I is located between USco and UCL, its position also agrees with the much more extended Sco-CMa stream (Bouy & Alves 2015). It is therefore also possible that pre-existing density enhancements played a role in the formation of Lupus I.
Thompson et al. (2012) detected an increase in star-forming sources at the rim of the shells of HII regions (or IR/Spitzer bubbles). Shells are commonly observed in the Milky Way and other galaxies, but most diffuse shells seen in HI or the infrared do not have obvious triggered star formation. Dense molecular shells and pillars around HII regions often have such triggering (e.g., Elmegreen 2011). Several scenarios attempt to explain star formation associated with expanding shells; these include the scenarios of “collect and collapse” (e.g., Elmegreen & Lada 1977; Whitworth et al. 1994), “radiative driven implosion” (Deharveng et al. 2010), and enhancement of pre-existing density substructures and subsequent “global implosion” (e.g., Palmeirim et al. 2017; Walch et al. 2015). The trans-sonic irregular motion in Lupus I can be explained by the Vishniac thin shell instability. This supports a picture in which clumping and possibly molecular gas formation was going on for a while, but star formation only set in when an external compression, possibly due to a supernova, triggered it. This is also consistent with the double-peaked density PDF in Lupus I and the coeval onset of star formation in the nearby ρ Ophiucus cloud, which could have been triggered by the same event. If the star formation was also related to gradual transformation of gas collected in a shell, then it would be more difficult to understand the sudden and coeval onset of star formation in both Lupus I and ρ Oph. Thus, the data support a more complex, multistage formation process for Lupus I than a simple collect and collapse scenario.
8. Summary and conclusions
In this paper we presented new 13CO(2–1)and C18O(2–1)line observations of Lupus Iwith the APEX telescope at three distinct cuts at different parts of the cloud.
A comparison of our CO data to H i data yielded that the emission of both tracers lies in the same velocity range. Moreover, C18Oemission peaks located in the center-south of Lupus Icoincide with deficits in H i emission, whereas the position of the H i emission peak in the north shows a deficit in C18Oemission. This resembles two different stages in the transition between atomic and molecular material. In the north, a smaller fraction of atomic hydrogen has been converted into molecular hydrogen and subsequently into dense CO. Therefore, this part of the cloud is quiescent. The center-south of the cloud has instead enough molecular material to form stars actively. This could also be a consequence of the lower dust column density in the northern part of Lupus Ibecause a smaller amount of dust particles reduces the formation efficiency of molecular hydrogen and provides less shielding from destructive UV radiation.
A comparison of the large-scale H i, CO and dust emission in the USco shell and in the vicinity of Lupus Irevealed that the molecular gas is always found in regions of dust emission and both of those components are preferentially found behind the outer edge of the atomic shell, i.e., further inward. This is the expected configuration for molecular gas being produced inside the expanding H i shell. The CO velocities of Lupus Iare in the same range as the H i velocities of the USco shell and thus the cloud is co-moving with the shell, which would agree with the formation from the shell material. The timescale of the transition between atomic and molecular gas in such a massive shell with M ≈ 104M⊙ (estimated from our model fit to the H i data) was estimated to be ~106–107 yr. This is consistent with the age of the USco shell (~5 Myr) and the age of the young stellar objects in Lupus I(<2 Myr). The UCL wind bubble on the western side of Lupus Iis colliding with the USco H I shell at the position of Lupus I, thereby squeezing the region in between. Thus, it acted as a counterpressure to the expanding USco shell and favored this position for an additional compression of the shell material. In this way a new molecular cloud was created there. This additional collisional pressure might explain why there are not more very young star-forming clouds seen distributed within the wall of the USco shell. We show with a geometrical model that the observational data are in agreement with this idea. This model also indicates that Lupus Ican be expanding with the USco shell and that the cloud is located at the edge of the inner shell.
We suggest that Lupus Iwas and is strongly affected by large-scale external compression originating from the expansion of the USco H I shell and the UCL wind bubble and that the cloud was formed out of the atomic material swept up by the USco shell and is now expanding with the shell. Pre-existing gas structure and collision with the UCL wind bubble were likely decisive factors that enhanced a local inhomogeneity and density in the USco shell at a position that favored the formation of Lupus I.
Acknowledgments
We would like to thank the referee for his/her constructive comments, which helped to improve this paper. This work was supported by funding from Deutsche Forschungsgemeinschaft under DFG project numbers PR 569/10-1 and PR 569/10-2 in the context of the Priority Program 1573 “Physics of the Interstellar Medium”. Additional support came from funds from the Munich Cluster of Excellence “Origin and Structure of the Universe”. The Herschel spacecraft was designed, built, tested, and launched under a contract to ESA managed by the Herschel/Planck Project team by an industrial consortium under the overall responsibility of the prime contractor Thales Alenia Space (Cannes), and including Astrium (Friedrichshafen) responsible for the payload module and for system testing at spacecraft level, Thales Alenia Space (Turin) responsible for the service module, and Astrium (Toulouse) responsible for the telescope, with in excess of a hundred subcontractors. Based on observations obtained with Planck (http://www.esa.int/Planck), an ESA science mission with instruments and contributions directly funded by ESA Member States, NASA, and Canada. HIPE is a joint development by the Herschel Science Ground Segment Consortium, consisting of ESA, the NASA Herschel Science Center, and the HIFI, PACS, and SPIRE consortia. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. We acknowledge the use of NASA’s SkyView facility (http://skyview.gsfc.nasa.gov) located at NASA Goddard Space Flight Center. M.K. acknowledges support by the Australian Research Council through an Early Career Fellowship, DE130101399.
References
- Benedettini, M., Pezzuto, S., Burton, M. G., et al. 2012, MNRAS, 419, 238 [Google Scholar]
- Benedettini, M., Schisano, E., Pezzuto, S., et al. 2015, MNRAS, 453, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Hartmann, L. W., Raymond, J. C., & Ballesteros-Paredes, J. 2004, ApJ, 612, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Blaauw, A. 1964, in The Galaxy and the Magellanic Clouds, ed. F. J. Kerr, IAU Symp., 20, 50 [Google Scholar]
- Bouy, H., & Alves, J. 2015, A&A, 584, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calderón, D., Ballone, A., Cuadra, J., et al. 2016, MNRAS, 455, 4388 [NASA ADS] [CrossRef] [Google Scholar]
- Carlhoff, P., Nguyen Luong, Q., Schilke, P., et al. 2013, A&A, 560, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clark, P. C., Glover, S. C. O., Klessen, R. S., & Bonnell, I. A. 2012, MNRAS, 424, 2599 [NASA ADS] [CrossRef] [Google Scholar]
- Comerón, F. 2008, Handbook of Star Forming Regions, Vol. II, ed. B. Reipurth, (ASP Monograph Publications), 295 [Google Scholar]
- Dawson, J. R., McClure-Griffiths, N. M., Kawamura, A., et al. 2011, ApJ, 728, 127 [NASA ADS] [CrossRef] [Google Scholar]
- de Geus, E. J. 1992, A&A, 262, 258 [NASA ADS] [Google Scholar]
- de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Deharveng, L., Schuller, F., Anderson, L. D., et al. 2010, A&A, 523, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobbs, C. L., Krumholz, M. R., Ballesteros-Paredes, J., et al. 2014, Protostars and Planets VI (Tucson: University of Arizona Press), 3 [Google Scholar]
- Elmegreen, B. G. 2011, in EAS Pub. Ser. 51, eds. C. Charbonnel, & T. Montmerle, 45 [Google Scholar]
- Elmegreen, B. G., & Lada, C. J. 1977, ApJ, 214, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Gaczkowski, B., Preibisch, T., Stanke, T., et al. 2015, A&A, 584, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., & Tafalla, M. 2011, A&A, 533, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hara, A., Tachihara, K., Mizuno, A., et al. 1999, PASJ, 51, 895 [NASA ADS] [Google Scholar]
- Hartmann, L., Ballesteros-Paredes, J., & Bergin, E. A. 2001, ApJ, 562, 852 [NASA ADS] [CrossRef] [Google Scholar]
- Haworth, T. J., Harries, T. J., Acreman, D. M., & Rundle, D. A. 2013, MNRAS, 431, 3470 [NASA ADS] [CrossRef] [Google Scholar]
- Heiner, J. S., Vázquez-Semadeni, E., & Ballesteros-Paredes, J. 2015, MNRAS, 452, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Heitsch, F., & Hartmann, L. 2008, ApJ, 689, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Dedes, L., Kerp, J., & Haud, U. 2007, A&A, 469, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., McClure-Griffiths, N. M., Pisano, D. J., et al. 2010, A&A, 521, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koyama, H., & Inutsuka, S.-I. 2000, ApJ, 532, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, M., Fierlinger, K., Diehl, R., et al. 2013, A&A, 550, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ladd, E. F., Fuller, G. A., & Deane, J. R. 1998, ApJ, 495, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Mangum, J. G., & Shirley, Y. L. 2015, PASP, 127, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumoto, T., Dobashi, K., & Shimoikura, T. 2015, ApJ, 801, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, T. G., Ade, P. A. R., Angilè, F. E., et al. 2014, ApJ, 784, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Andre, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] [Google Scholar]
- Myers, P. C. 1983, ApJ, 270, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C., Linke, R. A., & Benson, P. J. 1983, ApJ, 264, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Ntormousi, E., Burkert, A., Fierlinger, K., & Heitsch, F. 2011, ApJ, 731, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeirim, P., Zavagno, A., Elia, D., et al. 2017, A&A, 605, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Phillips, T. G., Huggins, P. J., Wannier, P. G., & Scoville, N. Z. 1979, ApJ, 231, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Pöppel, W. G. L., Bajaja, E., Arnal, E. M., & Morras, R. 2010, A&A, 512, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Preibisch, T., & Mamajek, E. 2008, Handbook of Star Forming Regions, Vol. II, ed. B. Reipurth, (ASP Monograph Publications), 235 [Google Scholar]
- Preibisch, T., Brown, A. G. A., Bridges, T., Guenther, E., & Zinnecker, H. 2002, AJ, 124, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Tachihara, K., Dobashi, K., Mizuno, A., Ogawa, H., & Fukui, Y. 1996, PASJ, 48, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Tachihara, K., Toyoda, S., Onishi, T., et al. 2001, PASJ, 53, 1081 [NASA ADS] [Google Scholar]
- Thompson, M. A., Urquhart, J. S., Moore, T. J. T., & Morgan, L. K. 2012, MNRAS, 421, 408 [NASA ADS] [Google Scholar]
- Tothill, N. F. H., Löhr, A., Parshley, S. C., et al. 2009, ApJS, 185, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Vassilev, V., Meledin, D., Lapkin, I., et al. 2008, A&A, 490, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vázquez-Semadeni, E., Banerjee, R., Gómez, G. C., et al. 2011, MNRAS, 414, 2511 [NASA ADS] [CrossRef] [Google Scholar]
- Vilas-Boas, J. W. S., Myers, P. C., & Fuller, G. A. 2000, ApJ, 532, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Vishniac, E. T. 1983, ApJ, 274, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Walch, S., Whitworth, A. P., Bisbas, T. G., Hubber, D. A., & Wünsch, R. 2015, MNRAS, 452, 2794 [NASA ADS] [CrossRef] [Google Scholar]
- Welsh, B. Y., Lallement, R., Vergely, J.-L., & Raimond, S. 2010, A&A, 510, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitworth, A. P., Bhattal, A. S., Chapman, S. J., Disney, M. J., & Turner, J. A. 1994, MNRAS, 268, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L., Rohlfs, K., & Huttemeister, S. 2012, Tools of Radio Astronomy, 5th edn. (Moscow: Fizmatlit) [Google Scholar]
Appendix A: Calculations of gas temperatures and column densities
Appendix A.1: Excitation temperature
The excitation temperature can be calculated via ![\appendix \setcounter{section}{1} \begin{equation} T_\mathrm{ex}(\tau)\,=\,\frac {T^{18}_\nu}{\ln\left\{1+~\left[ \frac{T^{18}_\mathrm{peak}}{T^{18}_\nu}\left(1-\exp(-\taua)\right)^{-1}~+J(T_\mathrm{bg})/T^{18}_\nu \right]^{-1}\right\}} \label{eq:tex} , \end{equation}](/articles/aa/full_html/2017/12/aa28508-16/aa28508-16-eq148.png) (A.1)where
(A.1)where ![\appendix \setcounter{section}{1} \begin{equation} J(T)\equiv\frac{c^2}{2k_{\rm B}\nu^2}\,B_\nu(T)=T_\nu\,[\exp(\rm T_\nu/ T)-1]^{-1} \label{eq:j(t)} , \end{equation}](/articles/aa/full_html/2017/12/aa28508-16/aa28508-16-eq149.png) (A.2)
(A.2)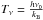 , and Tbg = 2.73 K is the temperature of the cosmic microwave background (CMB). Equations (A.1), (A.2) are derived from the equations given in Wilson et al. (2012).
, and Tbg = 2.73 K is the temperature of the cosmic microwave background (CMB). Equations (A.1), (A.2) are derived from the equations given in Wilson et al. (2012).
Constants of the 13CO(2–1)and C18O(2–1)lines that are needed for the calculations in this section.
Appendix A.2: H2 column density
For the calculation of the column density we used 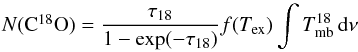 (A.3)from Carlhoff et al. (2013), where the functions f(Tex) and Q(Tex) are defined as
(A.3)from Carlhoff et al. (2013), where the functions f(Tex) and Q(Tex) are defined as ![\appendix \setcounter{section}{1} \begin{equation} f(T_\mathrm{ex})=\frac{3h}{8\pi^3\mu^2}Q(T_\mathrm{ex})\left\{ \left[(J(T_\mathrm{ex})-J(T_\mathrm{bg})\right]\left[1-\exp\left(-\frac{T^{18}_\nu}{T_\mathrm{ex}}\right) \right] \right\}^{-1}, \\ \end{equation}](/articles/aa/full_html/2017/12/aa28508-16/aa28508-16-eq162.png) (A.4)
(A.4)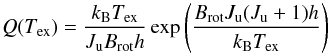 (A.5)with Ju = 2 the upper level of the J = 2 → 1 transition, μ the dipole moment of the molecule, and Brot its rotational constant. The partition function Q(Tex) is approximated for a linear molecule (Mangum & Shirley 2015). The factor τ18/ (1−exp(−τ18)) corrects the integrated intensity for possible opacity broadening of the line (see Goldsmith & Langer 1999). But this effect should be in any case small for the C18Oline because τ18stays below unity in most pixels.
(A.5)with Ju = 2 the upper level of the J = 2 → 1 transition, μ the dipole moment of the molecule, and Brot its rotational constant. The partition function Q(Tex) is approximated for a linear molecule (Mangum & Shirley 2015). The factor τ18/ (1−exp(−τ18)) corrects the integrated intensity for possible opacity broadening of the line (see Goldsmith & Langer 1999). But this effect should be in any case small for the C18Oline because τ18stays below unity in most pixels.
 |
Fig. A.1 Results of the LTE analysis for cut A, B, and C (from top to bottom). The left panel shows the optical depth τ18 , the middle panel the excitation temperature Tex , and the right panel the H2column density. All maps were convolved with a Gaussian of two pixels that corresponds approximatively to the beam size. Pixels within each cut for which the 13CO(2–1)and the C18O(2–1)spectrum had a S/N< 4 are left blank. |
 |
Fig. A.2 Histograms of the average C18O(2–1)spectra of the six boxes across cut A with a bin size of 0.1 km s-1. The black dash-dotted line indicates the 3×rms limit. The values of 3 ×rms and the signal-to-noise ratio S/N are given in the upper right of each plot. The red solid line shows the Gaussian fit to the spectrum. If more than one component was fitted, each of the components is represented by a blue dashed line and the red solid line is their sum. The residuals of the fit are given by the red bars in the small plot below each spectrum. Peak positions vpi and FWHM Δvi of each component in one box are given in the upper left of each plot. A summary of all these values can be found in Table 2, where they are denoted by an upper index G. |
 |
Fig. A.3 Histograms of the average 13CO(2–1)spectra of the six boxes across cut A with a bin size of 0.1 km s-1. The black dash-dotted line indicates the 3 ×rms limit. The values of 3 ×rms and the signal-to-noise ratio S/N are given in the upper right of each plot. The red solid line shows the Gaussian fit to the spectrum. If more than one component was fitted, each of the components is represented by a blue dashed line and the red solid line is their sum. The residuals of the fit are given by the red bars in the small plot below each spectrum. Peak positions vpi and FWHM Δvi of each component in one box are given in the upper left of each plot. A summary of all these values can be found in Table 2, where they are denoted by an upper index G. |
All Tables
Constants of the 13CO(2–1)and C18O(2–1)lines that are needed for the calculations in this section.
All Figures
 |
Fig. 1 Setup of the APEX-1 13CO(2–1)and C18O(2–1)observations of Lupus I. Along each of the three cuts A, B, and C an on-the-fly map was obtained simultaneously in both lines. The size of each map is indicated with a white box. The background image is the LABOCA continuum map (see Paper I). The Galactic coordinate system is indicated. |
| In the text | |
 |
Fig. 2 Average 13COand C18Ospectra of the three cuts. The integrated intensities (for vLSR = 0–10 km s-1) of the 13COlines are 1.96, 5.69, and 5.55 K km s-1 for cut A, B, and C, respectively. Those of the C18Olines are 1.22, and 0.50 K km s-1 for cut B and cut C, respectively. |
| In the text | |
 |
Fig. 3 Top left: dust column density map from LABOCA with red contour levels of 0.3, 1, 1.7, 2.3, and 3 × 1022 cm-2 . Integrated C18O(2–1)intensity maps of cut A, B, and C (top rightand bottom figures, respectively). The six boxes into which each cut was divided are shown as well as the contours of the LABOCA 870 μm continuum emission. Levels are from 10–100% of the peak intensity of 1.37 Jy/beam. |
| In the text | |
 |
Fig. 4 Position-velocity diagrams of cut A, B, and C (from top to bottom) in 13CO(2–1)(left panel) and C18O(2–1)(right panel) along a line through the middle of the cut. The x-axis gives the position along this line. The white arrow in the bottom right corner of the left panels indicates the orientation of the cut in the celestial coordinate frame. The white crosses indicate the velocity of the peak intensity at each x-position. The cutoff is set to 1 K in 13CO(2–1)for all three cuts and 0.5 K in C18O(2–1)for cuts B and C. The C18O(2–1)cutoff for cut A is 0.3 K. All maps have been convolved with a Gaussian of two pixels or approximately one beam. |
| In the text | |
 |
Fig. 5 Averaged spectra within the six boxes into which each cut was divided. The top row shows the average 13CO(2–1)spectra; the bottom shows those of C18O(2–1). Each column represents one of the three cuts. The different colors denote the six boxes from 1 to 6. The vertical dashed line marks for orientation vLSR = 6 km s-1 for cut A and vLSR = 5 km s-1 for cuts B and C. |
| In the text | |
 |
Fig. 6 H i column density map calculated from the integrated emission for vLSR = 0–10 km s-1. Black contours show the integrated C18O (1–0) emission observed by Hara et al. (1999). |
| In the text | |
 |
Fig. 7 Geometrical model of the possible interaction zone between the USco H i shell (black sphere) and UCL wind bubble (green sphere). The observer is located in the origin of the coordinate system. The position of Lupus Iis marked by three red asterisks that represent the top, middle, and bottom of the main filament, respectively. The cloud is plotted at three different distances of 150, 140, and 130 pc along the red line, which is the line of sight from us to Lupus I. The black and green solid lines are the line of sight from the observer to the corresponding sphere. The cyan dots indicate those positions on the USco shell that have line-of-sight velocities between 3 and 6 km s-1, i.e., similar to Lupus I(the white gaps are an effect of the grid model used in the calculations). The magenta cross indicates the touch point between the USco and the UCL sphere. The projections are show in the different panels. |
| In the text | |
 |
Fig. 8 Left: H i column density map of USco and surroundings of Lupus Icalculated from the integrated emission for vLSR = 0–10 km s-1. The two black circles indicate the inner and outer radius of the USco shell from the model fit. The black and white contours represent the dust emission at 850 μm and the CO(1–0)emission from Planck, respectively. The blue and black labeled dots represent early B-type stars in USco and UCL, respectively. Right: zoom into the region indicated as a dashed black box in the left panel. |
| In the text | |
 |
Fig. A.1 Results of the LTE analysis for cut A, B, and C (from top to bottom). The left panel shows the optical depth τ18 , the middle panel the excitation temperature Tex , and the right panel the H2column density. All maps were convolved with a Gaussian of two pixels that corresponds approximatively to the beam size. Pixels within each cut for which the 13CO(2–1)and the C18O(2–1)spectrum had a S/N< 4 are left blank. |
| In the text | |
 |
Fig. A.2 Histograms of the average C18O(2–1)spectra of the six boxes across cut A with a bin size of 0.1 km s-1. The black dash-dotted line indicates the 3×rms limit. The values of 3 ×rms and the signal-to-noise ratio S/N are given in the upper right of each plot. The red solid line shows the Gaussian fit to the spectrum. If more than one component was fitted, each of the components is represented by a blue dashed line and the red solid line is their sum. The residuals of the fit are given by the red bars in the small plot below each spectrum. Peak positions vpi and FWHM Δvi of each component in one box are given in the upper left of each plot. A summary of all these values can be found in Table 2, where they are denoted by an upper index G. |
| In the text | |
 |
Fig. A.3 Histograms of the average 13CO(2–1)spectra of the six boxes across cut A with a bin size of 0.1 km s-1. The black dash-dotted line indicates the 3 ×rms limit. The values of 3 ×rms and the signal-to-noise ratio S/N are given in the upper right of each plot. The red solid line shows the Gaussian fit to the spectrum. If more than one component was fitted, each of the components is represented by a blue dashed line and the red solid line is their sum. The residuals of the fit are given by the red bars in the small plot below each spectrum. Peak positions vpi and FWHM Δvi of each component in one box are given in the upper left of each plot. A summary of all these values can be found in Table 2, where they are denoted by an upper index G. |
| In the text | |
 |
Fig. A.4 Same as Fig. A.2 but for cut B. |
| In the text | |
 |
Fig. A.5 Same as Fig. A.3 but for cut B. |
| In the text | |
 |
Fig. A.6 Same as Fig. A.2 but for cut C. |
| In the text | |
 |
Fig. A.7 Same as Fig. A.3 but for cut C. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.