| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 21 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201527200 | |
| Published online | 11 April 2016 | |
Observational evidence of a slow downfall of star formation efficiency in massive galaxies during the past 10 Gyr
1
Laboratoire AIM-Paris-Saclay, CEA/DSM/Irfu−CNRS−</inline-formula>
Université Paris Diderot, CEA-Saclay,
pt courrier 131,
91191
Gif-sur-Yvette,
France
e-mail:
cschreib@strw.leidenuniv.nl
2
Leiden Observatory, Leiden University,
2300 RA
Leiden, The
Netherlands
3
Institut d’Astrophysique de Paris, UMR 7095, CNRS, UPMC Université
Paris 06, 98bis boulevard
Arago, 75014
Paris,
France
4
University of Crete, Department of Physics,
71003
Heraklion,
Greece
5
Institute for Astronomy, Astrophysics, Space Applications and
Remote Sensing, National Observatory of Athens, 15236
Penteli,
Greece
6
School of Astronomy and Space Sciences, Nanjing
University, 210093
Nanjing, PR
China
7
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD
21218,
USA
8
NASA Postdoctoral Program Fellow, Goddard Space Flight Center,
Code 665, Greenbelt,
MD
20771,
USA
9
Max-Planck-Institut für Extraterrestrische Physik,
Giessenbachstrasse 1,
85748
Garching,
Germany
Received: 16 August 2015
Accepted: 21 January 2016
We study the causes of the reported mass-dependence in the slope of the SFR−M∗ relation, the so-called main sequence of star-forming galaxies, and discuss its implication on the physical processes that shaped the star formation history of massive galaxies over cosmic time. We made use of the near-infrared high-resolution imaging from the Hubble Space Telescope in the CANDELS fields to perform a careful bulge-to-disk decomposition of distant galaxies and measure for the first time the slope of the SFR−Mdisk relation at z = 1. We find that this relation very closely follows the shape of the nominal SFR−M∗ correlation, still with a pronounced flattening at the high-mass end. This clearly excludes, at least at z = 1, the progressive growth of quiescent stellar bulges in star-forming galaxies as the main driver for the change of slope of the main sequence. Then, by stacking the Herschel data available in the CANDELS field, we estimated the gas mass (Mgas = MH i + MH2) and the star formation efficiency (SFE ≡ SFR/Mgas) at different positions on the SFR−M∗ relation. We find that the relatively low SFRs observed in massive galaxies (M∗> 5 × 1010 M⊙) are not caused by a reduced gas content, but by a star formation efficiency that is lower by up to a factor of 3 than in galaxies with lower stellar mass. The trend at the lowest masses is probably linked to the dominance of atomic over molecular gas. We argue that this stellar-mass-dependent SFE can explain the varying slope of the main sequence since z = 1.5, hence over 70% of the Hubble time. The drop in SFE occurs at lower masses in the local Universe (M∗> 2 × 1010 M⊙) and is not present at z = 2. Altogether, this provides evidence for a slow decrease in star formation efficiency in massive main sequence galaxies. The resulting loss of star formation is found to be rising starting from z = 2 to reach a level similar to the mass growth of the quiescent population by z = 1. We finally discuss the possible physical origin of this phenomenon.
Key words: galaxies: evolution / galaxies: bulges / galaxies: star formation / galaxies: statistics / infrared: galaxies
© ESO, 2016
1. Introduction
The observation of a tight relation between the star formation rate (SFR) and the stellar mass (M∗) of galaxies, also called the main sequence of star-forming galaxies (Noeske et al. 2007), at z ≃ 0 (Brinchmann et al. 2004; Elbaz et al. 2007), z ≃ 1 (Noeske et al. 2007; Elbaz et al. 2007), z ≃ 2 (Daddi et al. 2007; Pannella et al. 2009a; Rodighiero et al. 2011; Whitaker et al. 2012), z = 3−4 (Daddi et al. 2009; Magdis et al. 2010; Heinis et al. 2013; Schreiber et al. 2015; Pannella et al. 2015), and even up to z = 7 (e.g., Stark et al. 2009; Bouwens et al. 2012; Stark et al. 2013; González et al. 2014; Steinhardt et al. 2014; Salmon et al. 2015) suggested a new paradigm for galaxy evolution. The tightness of this correlation is inconsistent with the frequent random bursts induced by processes such as major mergers of gas-rich galaxies, and favors more stable, long-lasting episodes of star formation (Noeske et al. 2007).
Most studies focusing on this main sequence have measured the slope (in logarithmic space) of this correlation, and many different values were reported. A thorough compilation was recently published in Speagle et al. (2014), summarizing most measurements obtained so far. In particular, we can distinguish three types of measurements. First, measured slopes close to unity (e.g., Elbaz et al. 2007; Daddi et al. 2007; Pannella et al. 2009a; Peng et al. 2010). Second, slopes shallower than unity, typically 0.8, and as low as 0.6 (e.g., Noeske et al. 2007; Karim et al. 2011; Rodighiero et al. 2011; Bouwens et al. 2012; Steinhardt et al. 2014; Speagle et al. 2014; Pannella et al. 2015). And finally, more recently a third group of studies have advocated a broken power-law shape or continuously varying slopes, where low-mass galaxies are well fit with a slope of unity, and high mass galaxies exhibit much shallower (if not flat) slopes (e.g., Whitaker et al. 2012, 2014; Magnelli et al. 2014; Ilbert et al. 2015; Schreiber et al. 2015; Lee et al. 2015; Gavazzi et al. 2015). This latter, more refined description might explain the diversity of slope measurements that were obtained so far. Indeed, depending on the stellar mass range covered by the sample, which is usually limited, as well as on the chosen redshift window, fitting a single power law will yield different best-fit slopes.
A tempting interpretation of this broken power law is that low-mass galaxies evolve with a unique star formation efficiency, as shown by their universal specific SFR (sSFR ≡ SFR/M∗) (see, e.g., the discussions in Ilbert et al. 2015; Lee et al. 2015). Higher mass galaxies, on the other hand, depart from this universal relation and show a reduced star formation activity, probably gradually declining toward a quiescent state. This picture somewhat contradicts the idea that massive galaxies must quench rapidly (e.g., Peng et al. 2010), a process that often involves violent episodes in the lifetime of the galaxy, such as strong feedback from an active galactic nucleus (AGN; Silk & Rees 1998). Instead, such a slow decline toward the red cloud could be more consistent with less abrupt processes such as radio-mode AGN feedback (Croton et al. 2006; Bower et al. 2006), halo quenching (Gabor & Davé 2012), where the infalling gas is heated up and prevented from forming stars, or morphological quenching (Martig et al. 2009), where the drop in star formation activity is caused by the presence of a massive and dense stellar bulge that increases the differential rotation within the disk and prevents gas from fragmenting.
Summary of the various samples.
Each of these mechanisms directly affects the gas content of the galaxy, either by expelling the gas outside of the galaxy (thereby reducing the gas fraction) or by preventing cooling and fragmentation (thereby reducing the star formation efficiency). Testing these hypotheses implies directly measuring the gas content of galaxies, which formally requires costly spectroscopic campaigns to measure the molecular hydrogen mass through the carbon monoxide (CO) low-J emission lines, and atomic hydrogen (often assumed to be negligible at high redshift) through the 21 cm line. While this has been done extensively at z = 0 (e.g., Walter et al. 2008; Leroy et al. 2009; Saintonge et al. 2011a; Boselli et al. 2014a), so far, only small samples have been observed at z ≥ 1 (e.g., Daddi et al. 2008, 2010a,b; Dannerbauer et al. 2009; Tacconi et al. 2010, 2013), and these are limited to the most massive galaxies at every redshift. To circumvent this observational limitation, an alternative approach has been commonly used in the recent literature (e.g., Magdis et al. 2012; Magnelli et al. 2012b; Santini et al. 2014; Scoville et al. 2014; Béthermin et al. 2015; Genzel et al. 2015), where the gas mass is inferred from the dust mass of a galaxy, assuming, for example, that a fixed fraction of the metals (e.g., ~30%, as discussed in Sect. 4.3) condenses to form dust grains, and with the knowledge of the gas-phase metallicity (see, e.g., Franco & Cox 1986). Measuring dust masses and metallicities is still observationally challenging, but they are available for substantially larger samples. In particular, dust masses can be reliably measured using far-infrared and sub-millimeter photometry, either through individual measurements or stacking of large galaxy samples. At moderate redshifts (z ≤ 1), the Herschel space telescope probes rest-frame wavelengths sufficiently large to accurately constrain the Raleigh-Jeans tail of the dust emission, and can therefore provide good estimations of the dust mass.
One important fact about dust-based gas-mass estimates is that they include by construction the contribution of all phases of hydrogen gas, atomic and molecular. This means in particular that the star formation efficiency that is derived from such measurements probes the depletion of the entire gas reservoir of the galaxy, including the intermediate step of conversion from atomic to molecular hydrogen, and therefore provides a global point of view of the gas consumption. Since the pioneering work of Kennicutt (1998a), this has been the standard measure of the star formation efficiency. It was shown later that the molecular gas is better correlated with the SFR than atomic hydrogen in local spirals (e.g., Wong & Blitz 2002; Bigiel et al. 2008, 2011). While separating the two components in statistically large samples of distant galaxies to study how they relate to the SFR would bring valuable insight on star-formation, this is beyond the scope of the present paper.
Recently, Abramson et al. (2014) put forward another, possibly simpler explanation for the bending of the main sequence. They argued that because of the presence of old stellar bulges within massive galaxies, the total stellar mass becomes a poor proxy for the available gas mass1. The star formation rate is instead expected to correlate with the mass of the disk, since this is where the star-forming gas is located. To support their claim, they used bulge-to-disk decompositions of the observed light profiles of local galaxies in the Sloan Digital Sky Survey (SDSS) and estimated their disk masses. They found indeed that the slope of the main sequence was set back to unity at all masses (at least for M∗> 1010 M⊙) if the disk mass was substituted for the total stellar mass (see, however, Guo et al. 2015, where a different result is obtained using the same data set). Schreiber et al. (2015, hereafter S15) have reported that the high-mass slope of the main sequence decreases gradually with time, departing from unity at z< 2 and reaching the shallowest values in the present (see also Whitaker et al. 2014; Lee et al. 2015; Gavazzi et al. 2015), which seems consistent with the progressive growth of bulges (see also Wuyts et al. 2011; Whitaker et al. 2015 and Tacchella et al. 2015).
The very high angular resolution provided by the Hubble Advanced Camera for Surveys (ACS) imaging enables performing the morphological analysis of the stellar profile of distant galaxies out to z = 1, either through non-parametric approaches (e.g., Abraham et al. 1996; Conselice 2003; Ferguson et al. 2004; Lotz et al. 2004), profile fitting (e.g., Bell et al. 2004; Ravindranath et al. 2004; Barden et al. 2005; McIntosh et al. 2005; Pannella et al. 2006, 2009a; Häussler et al. 2007), or decomposition of this profile into multiple components (e.g., Simard et al. 1999, 2002; Stockton et al. 2008). The advent of the WFC3 camera onboard Hubble has recently allowed studying the rest-frame near-IR (NIR) and optical stellar profiles toward higher redshifts (e.g., van der Wel et al. 2012; Newman et al. 2012; Bruce et al. 2012, 2014; Lang et al. 2014). In particular, Bruce et al. (2012) have performed bulge-to-disk decomposition on the CANDELS H-band imaging in the UDS field, focusing on massive galaxies (M∗> 1011 M⊙) from z = 1 to z = 3, and finding a clear trend of decreasing bulge-to-total ratio (B/T) with redshift. However, Lang et al. (2014) later pushed the analysis down by one order of magnitude in stellar mass in all five CANDELS fields. By fitting stellar-mass maps estimated through fitting the resolved spectral energy distribution (SED), they derived the relation between M∗ and B/T for star-forming and quiescent galaxies and found very little evolution of this relation with redshift. Both these observations are contradictory and would potentially lead to different conclusions when trying to link the bulge mass to the main-sequence bending.
Our goal in this paper is therefore to directly investigate the possible causes for the evolution of the slope. To do so, we analyze a sample of z = 1 galaxies and follow two complementary approaches. On the one hand, we estimate the mass of the disks in each galaxy to determine whether the SFR−Mdisk relation is linear, as found in the local Universe. On the other hand, we estimate the gas masses in our sample and quantify the mass evolution of both the gas fraction (fgas) and the star formation efficiency (SFE) to determine which of these two quantities best correlates with the bending of the main sequence.
Both studies are based on a common sample of z = 1 galaxies drawn from the CANDELS fields (Grogin et al. 2011; Koekemoer et al. 2011), and we also use data from the local Universe (the Herschel Reference Survey) to extend and confirm our results regarding the gas mass measurements. The precise sub-samples used in each study are detailed in Sects. 2.1 and 2.2 for the gas mass study and in Sect. 2.3 for the disk mass study. In Sect. 3 we describe the bulge-to-disk decomposition that we used to measure the stellar mass of the disk, while in Sect. 4 we describe the procedure we employed to measure the gas masses. Our results are then presented in Sect. 5.
In the following, we assume a ΛCDM cosmology with H0 = 70 km s-1 Mpc-1, ΩM = 0.3, ΩΛ = 0.7 and, unless otherwise specified, a Salpeter (1955) initial mass function (IMF) to derive the star formation rates and stellar masses. All magnitudes are quoted in the AB system, such that MAB = 23.9−2.5log 10(Sν [ μJy ]). Finally, the gas masses that we derive include the contribution of helium.
2. Samples and galaxy properties
We here investigate the change of slope in the main sequence from two different angles. Both approaches require different samples that, even if drawn from the same data set, differ noticeably in terms of their stellar mass and star formation rate completeness. For this reason, these samples and their corresponding selections are summarized in Table 1.
On the one hand, we measured the gas content inside main-sequence galaxies to search for a decrease of either the gas fraction or the star formation efficiency. To do so, we used the stacked Herschel SEDs of S15 at z = 1 in the CANDELS fields (see Sect. 2.1) to measure both the SFR and the gas masses. This sample contains all star-forming galaxies at 0.7 <z< 1.3 with M∗ ≥ 3 × 109 M⊙ and is complete both in stellar mass and SFR above this threshold. We complement this analysis with a z = 0 sample of main-sequence galaxies from the Herschel Reference Survey (HRS, see Sect. 2.2), which is volume-limited.
On the other hand, we extracted a subsample of massive galaxies (M∗ ≥ 2 × 1010 M⊙) from our z ~ 1 sample and morphologically decomposed their HST light profile. Of these, we mostly consider the galaxies with an individual IR detection in order to derive robust SFRs for each object, yielding a subsample that is both mass- and SFR-selected. We describe this subsample in Sect. 2.3.
For a description of the fields and the photometry and the method used to measure physical properties such as redshifts, stellar masses, and star formation rates, we refer to the papers where these samples were initially introduced (i.e., S15 and Ciesla et al. 2016).
 |
Fig. 1 Main sequence of star-forming galaxies at different redshifts. Solid circles and fits (solid black line and dotted colored lines) are taken from S15. Statistical error bars are smaller than the symbols. We here focus on a redshift range centered on z = 1, which is highlighted in this plot. There, to illustrate the change of slope of the main sequence, we show as a gray solid line the extrapolation of the low-mass sSFR ≡ SFR /M∗, with a slope of unity. The gray dashed line and the arrow indicate the region of this diagram within which we perform the morphological decomposition of the HST light profiles of z = 1 galaxies (Sect. 2.3). We also show for reference the main sequence as seen in the Herschel Reference Survey at z = 0 (see Ciesla et al. 2016). |
2.1. CANDELS sample for the gas mass measurements at z = 1
For the gas mass measurements at z = 1, we used the stacked Herschel photometry in the CANDELS fields presented in S15. In this work, we showed that the bending of the main-sequence is more pronounced at lower redshifts and is almost absent by z> 2 (see also Fig. 1). To study the origin of this bending, we therefore need to focus on low redshifts, where the bending is most significant. On the other hand, the area covered by the CANDELS fields is relatively small, and consequently we cannot afford to reach too low redshifts of z< 0.5, for instance, without being affected by limited statistics and small volumes. Furthermore, our estimation of the gas mass is based on the dust mass (see Sect. 4.3), and at z> 1.5,Herschel does not probe the Rayleigh-Jeans tail of the dust SED (λrest> 250 μm), which would prevent an accurate determination of the dust mass (Scoville et al. 2014).
For these reasons we chose to base our analysis on galaxies at 0.7 <z< 1.3 and used the same sample as in S15, namely selecting all the galaxies in this redshift window that are classified as UVJ star-forming: 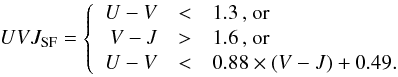 (1)This selection is illustrated below in Fig. 5. As discussed in S15, more than 85% of the Herschel detections are classified as UVJ star-forming. The UVJ selection is therefore an efficient tool to pinpoint star-forming galaxies, even when MIR or FIR detections are lacking. However, it affects the galaxies at high stellar mass more strongly. In particular, between 1011 and 3 × 1011 M⊙, about half of our galaxies are classified as UVJ quiescent. Since the precise definition of Eq. (1) could affect our results, we discuss its effect a posteriori in Appendix C.
(1)This selection is illustrated below in Fig. 5. As discussed in S15, more than 85% of the Herschel detections are classified as UVJ star-forming. The UVJ selection is therefore an efficient tool to pinpoint star-forming galaxies, even when MIR or FIR detections are lacking. However, it affects the galaxies at high stellar mass more strongly. In particular, between 1011 and 3 × 1011 M⊙, about half of our galaxies are classified as UVJ quiescent. Since the precise definition of Eq. (1) could affect our results, we discuss its effect a posteriori in Appendix C.
2.2. HRS sample for the gas mass measurements in the local Universe
For the z = 0 sample, we define the dividing line between “star-forming” and “quiescent” galaxies as follows: 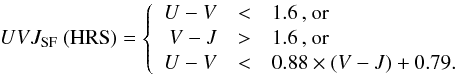 (2)In practice, this is equivalent to making a cut in sSFR> 6 × 10-3 Gyr-1, that is, about one dex below the z = 0 main sequence. Different UVJ dividing lines have been adopted in the literature, reflecting a combination of both zero-point offsets in the photometry and physical evolution of the colors caused by the evolution of the sSFR. For example, Williams et al. (2009) used different UVJ classifications depending on the redshift, with a 0 <z< 0.5 criterion that is different from Eq. (2) by only 0.1 magnitudes, and a 1 <z< 2 criterion identical to our Eq. (1).
(2)In practice, this is equivalent to making a cut in sSFR> 6 × 10-3 Gyr-1, that is, about one dex below the z = 0 main sequence. Different UVJ dividing lines have been adopted in the literature, reflecting a combination of both zero-point offsets in the photometry and physical evolution of the colors caused by the evolution of the sSFR. For example, Williams et al. (2009) used different UVJ classifications depending on the redshift, with a 0 <z< 0.5 criterion that is different from Eq. (2) by only 0.1 magnitudes, and a 1 <z< 2 criterion identical to our Eq. (1).
In the following, we use all the galaxies from the HRS survey that satisfy the UVJ criterion given above, regardless of their morphological type. In practice, the UVJ selection naturally filters out all the early-type galaxies (E-S0-S0/Sa), and about half of the H i-deficient galaxies (as defined in Boselli et al. 2010).
However, it is important to note that although the HRS is a purely K-band selected sample, the volume it spans is relatively small and the HRS is thus subject to cosmic variance. Furthermore, because one of the science goals of the HRS is to study the influence of the environment on the star formation activity, the sample also contains the Virgo cluster, a strong overdensity that encloses 46% of the galaxies in the whole HRS (and 39% of UVJ star-forming galaxies). This is a very biased environment, and although clusters are more common in the local Universe, the HRS is known to be particularly deficient in gas mass, most likely because Virgo is included in the sample (Boselli et al. 2010). To facilitate the comparison with our z = 1 sample described in the previous section, we therefore excluded all the galaxies that belong to Virgo (149 galaxies out of 323) from the HRS. Combined with the UVJ selection, this excludes 80% of the H i-deficient galaxies and yields a final sample of 131 galaxies. We note, however, that our results would be essentially unchanged if we were to keep the Virgo galaxies in our sample.
2.3. CANDELS sample for the morphological decompositions at z = 1
For the morphological analysis, we considered the same redshift window as for the gas mass measurement at z = 1, following the same motivations. In addition, limiting ourselves to z = 1 ensures that the HST H band probes the rest-frame i band, where mass-to-light ratios are weakly varying (e.g., de Jong 1996). However, to obtain reliable morphological decompositions, we need to select galaxies that are sufficiently bright and without strong contamination from neighboring objects. The various steps of the selection described below are illustrated on the stellar mass distribution in Fig. 2.
We thus selected galaxies more massive than 2 × 1010 M⊙, corresponding roughly to an H-band limited sample at these redshifts, with no galaxy fainter than H = 22.5 (see Appendix B where we justify this choice using simulated images). Unfortunately, this stellar mass cut will prevent us from performing the morphological decomposition in the regime where the main sequence is linear, as shown in Fig. 1. However, it is known that disk-dominated galaxies dominate the low-mass galaxy population, both in the local Universe (e.g., Bell et al. 2003) and at higher redshifts (e.g., Pannella et al. 2009a; Lang et al. 2014; Bluck et al. 2014). Therefore we assume in the following that galaxies at M∗< 2 × 1010 M⊙ are disk-dominated, with M∗ ≃ Mdisk, and only consider changes in main-sequence slope above this threshold. We also removed six IRAC power-law AGNs (following Donley et al. 2012).
To prevent systematic effects in the morphological analysis that are due to strong galaxy blending (either due to mergers or chance projections), we also removed from our sample the galaxies that have too close bright neighbors in the H-band image. Therefore, we flagged the galaxies that have at least one companion within 2″ with a total flux that is no less than 10% fainter. This flags out 410 galaxies, and our final “H-sample” consists of 2 439 galaxies (1499 of which are UVJ star-forming according to Eq. (1)).
Then, among these, we also considered the “IR-sample” that consists of star-forming galaxies with a MIR or FIR detection (>5σ), that is, with a reliable SFR estimate coming from Spitzer or Herschel observations. To do so, we first selected star-forming galaxies using the UVJ diagram and Eq. (1). Then, to derive the SFRs, we started from the same IR catalogs as those introduced in S15, but here we additionally revisited the catalogs to solve a problem that can have important consequences for the present study. Briefly, we flagged the Spitzer MIPS detections that are potentially incorrectly associated with their H-band counterparts because of the adopted source extraction procedure. The details of this flagging procedure are described in Appendix A. In total we flagged no more than 5% of the MIPS detections in the catalog as incorrect or uncertain associations. Two thirds of these are UVJ quiescent galaxies and are therefore not part of the IR-sample.
The final IR-sample contains 947 galaxies, and therefore 63% of the star-forming galaxies of the H-sample have a reliable SFR estimation (see Fig. 2). For consistency checks, we performed the morphological detection on the whole H-sample (i.e., including in particular those galaxies that are UVJ quiescent), but only used the IR-sample to derive the slope of the main sequence, meaning that we eventually assembled a sample that is both mass- and SFR-selected. This is not a problem for our purposes. Even though half of the star-forming galaxies close to our stellar mass threshold are not seen in the MIR or FIR, the IR-sample is at least 80% complete for star-forming galaxies above M∗> 5 × 1010 M⊙ (see Fig. 2). Since the change of slope in the main sequence is most pronounced at the massive end, we are able to witness any modification of this slope after the disk mass is substituted to the total stellar mass.
 |
Fig. 2 Stellar mass distribution of the various samples at z = 1 that we consider for the morphological decomposition (Sect. 2.3). Each line corresponds to a step of the selection process, progressively decreasing the number of objects in the sample as in Table 1. The black solid line shows the distribution of our parent sample, containing all the galaxies at 0.7 <z< 1.3 with M∗> 2 × 1010 M⊙ and accurate determination of both redshift and stellar mass. The blue solid line is our H-sample, after removing close pairs and IRAC power-law AGNs from the parent sample. The orange solid line shows galaxies in the H-sample that are classified as UVJ star-forming (Eq. (1)). The red solid line is our IR-sample of galaxies with a MIR or FIR detection. Finally, the dotted line indicates the number of those galaxies for which we can reliably decompose the light profile. |
3. Measuring disk masses in distant galaxies
 |
Fig. 3 Example bulge-to-disk decomposition of an H = 22.2 galaxy from the GOODS-South field, which is among the faintest galaxy in our sample. The first column shows the observed HST WFC3 image of the galaxy, and we also provide its main physical properties in the top left corner. The second column shows the best-fit disk (top) and bulge (bottom) components as extracted by GIM2D. The third column shows the residual of the image after subtracting the bulge (top) and disk (bottom) to visualize the profile of the other component. Finally, the fourth column shows the residual image after both components are subtracted. The best-fit parameters are given in the top right corner. |
In this section we describe the approach we used to determine the disk stellar masses of our z = 1 galaxies. In Sect. 3.1 we detail the morphological decomposition procedure, which tell us how much of the H-band flux was emitted by the bulge and the disk of each galaxy. Then, in Sect. 3.2 we show how we used this light-weighted decomposition to infer the mass-weighted B/T and the disk stellar mass. We also briefly discuss the quality of our decompositions and how they compare to the literature.
3.1. Bulge-to-disk decomposition
To perform the bulge-to-disk decomposition, we followed Pannella et al. (2009b) and used the software GIM2D (Simard et al. 2002) on the HST H-band images (0.06″/pixel resolution). To carry out a proper parametric modeling of the galaxy two-dimensional light distribution, it is of fundamental importance to obtain a careful estimate of the local background level. An extended disk or the low surface brightness wings of a high Sérsic index galaxy can easily mislead the fitting code and hence retrieve an incorrect galaxy model (e.g., Häussler et al. 2007; Pannella et al. 2009a; Barden et al. 2012). To avoid this problem, we ran SExtractor (Bertin & Arnouts 1996) on the public CANDELS H-band images in “cold” mode. This allowed to us to better minimize the artificial source splitting and maximize the number of pixels assigned to each object. Our newly extracted H-band catalog was then cross-matched to the original CANDELS photometric catalog so that every entry was assigned a redshift and stellar mass. Less than 10% of the original sample was not retrieved by our cold source extraction. For the most part, these are blended objects for which a bulge-to-disk decomposition would be both impractical and uncertain, and we did not consider them in the following analysis. For every galaxy, we then extracted a cutout in both the original image and our SExtractor segmentation map, the size of which depends on the actual galaxy angular dimensions. This ensured that GIM2D was able to properly fit for the image background and recover accurate galaxy parametric modeling.
Using these image and segmentation cutouts, we fit a combination of two Sérsic profiles: an exponential disk (n = 1) and a de Vaucouleur profile (n = 4), both convolved with the “hybrid” WFC3 PSFs from van der Wel et al. (2012). An example of this decomposition in given in Fig. 3.
Although the fit settles to physically reasonable solutions in more than 95% of the cases, occasionally, the effective radius of either component converges to zero, meaning that the component is essentially unresolved. In this case, an exponential disk cannot be distinguished from a de Vaucouleur profile, and this unresolved component could be either an AGN, a nuclear starburst, or just the poorly fit core-component of a bulge. Fortunately, such cases were rare, therefore we decided to consider them as poor fits and excluded them from the following analysis.
When defining our sample, we took care to exclude close galaxy pairs that would cause blending problems (see previous section). However, while analyzing the results of the decomposition, we also found that there are a few galaxies that are not even properly deblended in the CANDELS catalogs to begin with, for instance, because the two galaxies are too close to each other and SExtractor considered the pair as a single object. These galaxies cannot be fit with our procedure and typically show large χ2. To filter these catastrophic failures out, we therefore imposed a maximum value of χ2< 2. This also removes remaining catastrophic fit failures and galaxies with too irregular morphologies. This cut excludes 10% of the sample2.
For each galaxy that is properly fit (2081 among the H-sample, 872 among the IR-sample; see dotted line on Fig. 2), we now have an estimation of how the H-band flux is distributed between the disk and the bulge. From this decomposition, we can compute a light-weighted B/T, and we discuss in Sect. 3.2 how to convert this value into a mass-weighted ratio to finally obtain the stellar mass of the disk.
3.2. Estimating the disk mass
 |
Fig. 4 Relation between the total stellar mass (M∗) estimated by fitting the integrated multi-wavelength photometry of the whole galaxy and the measured luminosity from the HST H-band flux (without k-correction) for a sample of disk-dominated (B/T< 0.2, left) and bulge-dominated galaxies (B/T> 0.8, right). Individual galaxies are shown with filled colored circles. The best-fit relation is shown with a straight line, and the dispersion around this relation is shown with light solid lines on each side. The global dispersion is given in the top left corner of each plot and is computed from the median absolute deviation (MAD) using 1.48 × MAD(ΔM∗). |
 |
Fig. 5 Location of galaxies from the H sample with varying mass-weighted B/T on the UVJ diagram (left: B/T< 0.2, middle: 0.2 <B/T< 0.6, right: B/T> 0.6), using the total magnitudes of each galaxy. The dotted line shows the dividing line between the star-forming and quiescent populations defined in Eq. (1). It is clear that both bulge- and disk-dominated galaxies occupy very different regions of the diagram, illustrating the good agreement between the colors and morphology. Intermediate galaxies with roughly equal mass in the disk and bulge (middle panel, ⟨B/T⟩ = 0.4) are spread over the two regions, with a tendency for being preferentially in the quiescent region. |
After the flux of both the bulge and disk are measured, the last step is to measure the stellar mass of the disk. Both components have different mass-to-light ratios because bulges are mostly made of old stars and will typically have higher mass-to-light ratios than the star-forming disks. In practice, since we performed the decomposition in the H band (rest-frame i band at z = 1), the variation in mass-to-light ratio was assumed to be minimal (e.g., de Jong 1996).
To prevent any bias in our results, we nevertheless corrected for this effect. Here we chose to follow an empirical approach where we estimated the average mass-to-light ratio for the bulge components, inferred the bulge masses, and subtracted them from the total stellar masses. The main advantage of this approach is that, although we perform the bulge-to-disk decomposition in a single band, we take advantage of the accurate mass-to-light ratio that was derived by fitting the total photometry of the galaxy, using a large number of photometric bands (S15).
To determine the average mass-to-light ratio of bulges, we built a sample of “pure bulge” galaxies (B/T> 0.8) and compared their 1.6 μm (observer frame) luminosity against the total stellar mass. Since these galaxies are clearly bulge dominated, we neglected the disk mass and assumed that the observed mass-to-light ratio is representative of that of a bulge. The corresponding relation is shown in Fig. 4 (right). We derived the average trend by performing a linear fit to the running median in logarithmic space and obtained 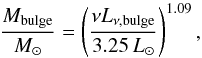 (3)with a constant residual scatter of about 0.1 dex. We then used this relation for all the other galaxies that are not bulge dominated to estimate Mbulge and subtracted this value from M∗ to obtain Mdisk.
(3)with a constant residual scatter of about 0.1 dex. We then used this relation for all the other galaxies that are not bulge dominated to estimate Mbulge and subtracted this value from M∗ to obtain Mdisk.
However, we relied here on the low scatter of the mass-to-light ratio in bulges. It is true that this ratio is less variable in bulges than in star-forming disks (see, e.g., Fig. 4, left) because the latter can display a wider variety of star formation histories. Still, bulges are expected to show some variation of their dust content and metallicity, and this is not be taken into account here. In particular, one possibility we cannot account for is that bulges in composite or disk-dominated galaxies may have different colors than pure bulges. Lastly, another downside of this empirical approach is that because we did not measure the colors of each individual bulge, we cannot flag out the “blue bulges”, which are not bulges, but most likely compact nuclear starbursts. These are supposed to be rare, however, and if anything, this population would end up substantially above the main sequence in the SFR−Mdisk relation and bias the slope toward higher values.
In Fig. 5 we show the location of galaxies on the UVJ diagram that are either disk dominated (B/T< 0.2), intermediate (0.2 <B/T< 0.6), or bulge dominated (B/T> 0.6) according to our mass-weighted bulge-to-total ratios. Reassuringly, the disk-dominated galaxies preferentially populate the UVJ star-forming branch, while the bulge-dominated galaxies pile up in the quiescent cloud, although there is some overlap between the two populations close to the dividing line. Intermediate objects are preferentially located in the quiescent region, but are also widely spread in the tip of the star-forming branch. This illustrates the good agreement between the morphological classification and the properties of the stellar populations, which is the high-redshift equivalent of the Hubble sequence (see also Wuyts et al. 2011).
Lastly, it should be noted that the relations we find between total stellar mass and B/T for UVJ star-forming and quiescent galaxies are consistent with those derived in Lang et al. (2014).
4. Measuring gas masses
In this section, we describe the measurement of dust masses from the FIR to submm photometry, detailed in Sect. 4.1, and then detail the derivation of the associated gas masses in Sects. 4.2 and 4.3.
The conversion from Mdust to Mgas is made using the dust-to-gas ratio, δGDR, which we estimate in this section. This ratio is not universal, and it is known to anticorrelate with the metallicity (e.g., Draine et al. 2007; Leroy et al. 2011; Sandstrom et al. 2013; Rémy-Ruyer et al. 2014). This anticorrelation can be simply understood if a universal fraction fd of all the metals in the ISM are locked into dust grains, while the remaining fraction remains mixed with the gas (e.g., Franco & Cox 1986; Zafar & Watson 2013). With this assumption and a measurement of the dust mass, we only need to know the gas-phase metallicity (Z) to infer the gas mass: 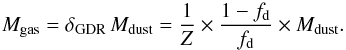 (4)The value of fd can be inferred empirically from observations where both the dust and the gas masses are known. In these cases, the gas mass is usually inferred by adding together 21 cm measurements of the neutral atomic hydrogen and estimates of the molecular hydrogen mass, which are typically obtained from the carbon monoxide (CO) emission lines (since, indeed, molecular hydrogen is extremely hard to observe directly). This latter step implies yet another uncertainty on the conversion factor from CO intensity to molecular gas mass (αCO). To alleviate this problem, Leroy et al. (2011) performed a resolved analysis of local galaxies, jointly inferring the gas-to-dust ratio and αCO from combined dust and H i and CO observations (see also Sandstrom et al. 2013). Assuming that the gas-to-dust ratio remains constant throughout each galaxy, they observed the relation between δGDR and metallicity, and found a dependence that is consistent with Eq. (4). In the present paper, we therefore used their observations to estimate δGDR for all the galaxies in our sample, and therefore Mgas. This approach has been used extensively in recent literature to estimate the gas masses of distant galaxies (e.g., Magdis et al. 2011, 2012; Magnelli et al. 2012a; Santini et al. 2014; Scoville et al. 2014; Béthermin et al. 2015).
(4)The value of fd can be inferred empirically from observations where both the dust and the gas masses are known. In these cases, the gas mass is usually inferred by adding together 21 cm measurements of the neutral atomic hydrogen and estimates of the molecular hydrogen mass, which are typically obtained from the carbon monoxide (CO) emission lines (since, indeed, molecular hydrogen is extremely hard to observe directly). This latter step implies yet another uncertainty on the conversion factor from CO intensity to molecular gas mass (αCO). To alleviate this problem, Leroy et al. (2011) performed a resolved analysis of local galaxies, jointly inferring the gas-to-dust ratio and αCO from combined dust and H i and CO observations (see also Sandstrom et al. 2013). Assuming that the gas-to-dust ratio remains constant throughout each galaxy, they observed the relation between δGDR and metallicity, and found a dependence that is consistent with Eq. (4). In the present paper, we therefore used their observations to estimate δGDR for all the galaxies in our sample, and therefore Mgas. This approach has been used extensively in recent literature to estimate the gas masses of distant galaxies (e.g., Magdis et al. 2011, 2012; Magnelli et al. 2012a; Santini et al. 2014; Scoville et al. 2014; Béthermin et al. 2015).
Since most galaxies in the HRS survey have H i and CO data (at least at the high-mass end), we cross-check in Sect. 4.4 our dust-based gas masses by comparing them against the values obtained more straightforwardly from the H i+CO measurements.
4.1. Dust masses
Average physical properties of the galaxies in the stacked z = 1 sample.
Accurate dust masses can only be derived from FIR measurements down the Rayleigh-Jeans tail of the dust continuum, meaning that at z = 1 we need to measure the observer-frame emission of galaxies at λ ≥ 400 μm. While Herschel does provide deep imaging at 500 μm, the poor angular resolution prevents measuring the 500 μm flux of most galaxies, since finding the correct counterpart to the fluxes measured on these maps is challenging (see, e.g., Shu et al. 2015).
This problem can be avoided by stacking the images, since the contribution from neighboring sources averages out to form a constant background. However, if galaxies tend to be clustered on the sky, the contribution of neighboring sources will not average out to a strictly uniform value and will instead tend to produce more flux toward to the position of the stacked galaxies (see, e.g., Béthermin et al. 2010). This is particularly important for the present study, since the amplitude of this effect will depend on the size of the beam and will therefore preferentially affect the longest wavelengths, which are those that best correlate with the dust mass. In S15 we implemented an empirical correction to remove this flux boosting, which was derived from a set of realistically simulated images. The stacked 500 μm fluxes in the simulation were found to be boosted by 20% on average, and we therefore corrected the observed fluxes by that same amount. After this factor is taken into account, no remaining bias was found in the stacked fluxes3.
 |
Fig. 6 Mean stacked FIR SEDs of star-forming galaxies in our z = 1 sample, split into four mass bins. The broadband photometry (open diamonds) is taken from S15. The fit to the stacked measurements is performed using the dust models of Galliano et al. (2011). It is apparent from this figure that massive galaxies (in red) have a colder dust temperature. This can be clearly seen from the peak wavelength of the best-fit model, or indirectly from the flux ratio S500/S100. |
For our z = 1 sample, we therefore used the stacked SEDs of S15, which are reproduced here in Fig. 6. These SEDs were built by stacking all the UVJ star-forming galaxies in the four CANDELS fields at 0.7 <z< 1.3 and in four bins of stellar mass: log 10(M∗/M⊙) = 9.5 to 10, 10 to 10.5, 10.5 to 11 and 11 to 11.5. As described above, a correction for clustering was also applied.
We then analyzed the stacked FIR photometry with a library of template SEDs built from the amorphous carbon dust model of Galliano et al. (2011). This new library will be presented in a forthcoming paper (Schreiber et al., in prep.) and is introduced to extend the Chary & Elbaz (2001) SED library (hereafter CE01) with the aim to provide a wider and finer-grained range of dust temperatures (or, equivalently, LIR/Mdust) and finer control on the PAH mass-fraction (or, equivalently, IR8 ≡ LIR/L8).
We fit the stacked Herschel photometry with each template of the library, corresponding each to a different value of Tdust (or ⟨U⟩), and picked the one that best fits the observed data. Essentially, there is a direct mapping between the dust temperature and the position of the peak of the FIR emission (i.e., Wein’s law): SEDs peaking at longer wavelengths (which is the case of our highest mass bin) have lower dust temperatures. Then, since each SED in the library is calibrated per unit Mdust, the dust mass is trivially obtained from the normalization of the best-fit template. Here, we allowed the dust temperature to vary between 15 and 50 K, while the PAH mass-fraction is left free to vary between 0 and 1.
The best-fit values we obtain are referenced in Table 2, and the best-fit models are shown in Fig. 6. While our models accurately describe the observed data, we find a systematic offset of the order of 20% in the PACS bands, where the 100 μm and 160 μm fluxes are above and below our model, respectively. No such trend is found for the three SPIRE bands. These offsets could be caused partly by calibration uncertainty (of about 15% for Herschel; Poglitsch et al. 2010; Swinyard et al. 2010), but also by the limited number of free parameters in our dust models4. However, these offsets are small and affect all mass bins in a similar way; they will therefore not impact our results.
For galaxies in the HRS, angular resolution is not a problem, and the Herschel photometry of each galaxy can be obtained and fitted individually without stacking. The dust masses were estimated exactly as for our stacked z = 1 SEDs, fitting the mid- to far-IR SED of the individual HRS galaxies with our template SED library. More detail on the IR photometry and dust properties of these objects is given in Ciesla et al. (2014)5.
As a cross check, we also fit the FIR photometry with the CIGALE SED fitting code, using the Draine & Li (2007) dust SED library. While we recover identical LIR, the Mdust values obtained with the Draine & Li (2007) models are systematically higher by a factor of two compared to our own estimates. Systematic differences in the dust masses are typically found by comparing the results of two different approaches, for instance, comparing the results from the Draine & Li (2007) library against simple modified black bodies (as is shown in Magdis et al. 2012 and Magnelli et al. 2012a), or different chemical compositions of dust grains within the same model (e.g., graphite and silicate versus amorphous carbon grains, as in Galliano et al. 2011; Rémy-Ruyer et al. 2015). The factor of two we observe here is consistent with the value reported by Galliano et al. (2011), who argued that dust masses derived by models using graphite (such as the models of Draine & Li 2007) instead of amorphous carbon grains are overestimated by a factor of 2.6. They also claimed that this overestimation creates a discrepancy with the measured metallicity of the Large Magellanic Cloud by violating the element abundances and therefore advocated to use amorphous carbon grains in dust models instead. Similar conclusions have been drawn for the Milky Way and other nearby galaxies (Compiègne et al. 2011; Jones et al. 2013; Planck Collaboration VIII 2014; Fanciullo et al. 2015).
This emphasizes that without precise knowledge of the detailed chemical composition of the dust, the absolute value of the dust masses should be taken with a grain of salt. Since we are only interested in the relative evolution of the gas mass with stellar mass in this work, this question is of no consequence provided that galaxies of different stellar masses host dust grains of similar chemical composition. The latter is a key assumption of our approach. In the local Universe, the properties and composition of the dust are known to vary, in particular as a function of metallicity (Madden et al. 2006; Wu et al. 2006; O’Halloran et al. 2006; Smith et al. 2007; Draine et al. 2007; Galliano et al. 2008; Ciesla et al. 2014; Rémy-Ruyer et al. 2015). However, since our samples are composed mostly of galaxies with close-to-solar metallicity (at least 0.4 Z⊙ in both our z = 0 and z = 1 samples, see next section), we do not expect our galaxies to exhibit strong variations of their dust composition. In Sect. 4.4, we nevertheless check that this assumption holds by comparing our dust-based gas masses against more direct measurements from H i and CO measurements in the HRS.
4.2. Metallicities
After the dust masses are measured (see previous section), the next step toward the determination of the gas masses is to estimate the metallicity. Since only half of the galaxies in the HRS have individual metallicity measurements (Hughes et al. 2013), and almost none of the galaxies in our z = 1 sample, we need to use empirical recipes to estimate the metallicities. Following recent literature (e.g., Magdis et al. 2012; Santini et al. 2014; Béthermin et al. 2015), we estimated the metallicity from the fundamental metallicity relation (FMR, Mannucci et al. 2010, Eq. (5)) 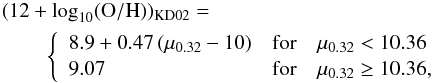 (5)with μ0.32 ≡ log 10(M∗ [ M⊙ ] )−0.32 × log 10(SFR [ M⊙/ yr ]), and where both M∗ and SFR are converted to the Chabrier (2003) IMF (i.e., divided by 1.67 from the Salpeter values, as in Madau & Dickinson 2014). For our z = 1 sample, we used the average stellar mass and SFR obtained in the stacks (see previous section), and for the z = 0 HRS galaxies without metallicity measurement we used their respective M∗ and SFR. We checked that using this prescription or estimating the metallicity from the z = 1 mass-metallicity relation (e.g., Zahid et al. 2011) would not change our conclusions (+ 0.12 dex metallicity shift at z = 1, after accounting for the different calibration6).
(5)with μ0.32 ≡ log 10(M∗ [ M⊙ ] )−0.32 × log 10(SFR [ M⊙/ yr ]), and where both M∗ and SFR are converted to the Chabrier (2003) IMF (i.e., divided by 1.67 from the Salpeter values, as in Madau & Dickinson 2014). For our z = 1 sample, we used the average stellar mass and SFR obtained in the stacks (see previous section), and for the z = 0 HRS galaxies without metallicity measurement we used their respective M∗ and SFR. We checked that using this prescription or estimating the metallicity from the z = 1 mass-metallicity relation (e.g., Zahid et al. 2011) would not change our conclusions (+ 0.12 dex metallicity shift at z = 1, after accounting for the different calibration6).
On the other hand, Kewley & Ellison (2008) showed that substantial systematic differences of metallicity measurements exist, depending both on the available observables used to derive the oxygen abundance and on the calibration that is used. For example, the FMR was derived using the Kewley & Dopita (2002; KD02) calibration, while the metallicities of Magdis et al. (2012) were obtained with the prescription of Pettini & Pagel (2004; PP04). According to Kewley & Ellison (2008), the difference between these two metallicity estimates is roughly constant and equal to about 0.25 dex (at least in the metallicity range considered in this paper), with a scatter of only 0.05 dex: it is only a global shift of the absolute metallicity and will not affect the relative trends. To derive accurate dust-to-gas ratios, it is nevertheless important to ensure that the same metallicity calibration is used consistently in all calculations.
In the following section, we derive a relation between the gas-to-dust ratio and the metallicity, assuming the metallicity is given in the PP04 [N ii] scale. To use this relation, we therefore need to convert the FMR metallicities derived above to this new scale, which we did following the calibration proposed by Kewley & Ellison (2008): 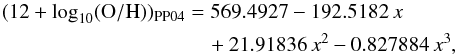 (6)with x ≡ (12 + log 10(O/H))KD02. As written above, in practice for the galaxies we consider in this study these PP04 abundances are systematically lower by 0.3 dex compared to the original KD02 values (this constant shift holds within 0.05 dex for all 12 + log 10(O/H)KD02> 8.5).
(6)with x ≡ (12 + log 10(O/H))KD02. As written above, in practice for the galaxies we consider in this study these PP04 abundances are systematically lower by 0.3 dex compared to the original KD02 values (this constant shift holds within 0.05 dex for all 12 + log 10(O/H)KD02> 8.5).
The measured metallicities of the HRS galaxies are already in this scale and needed no conversion. For HRS galaxies with a metallicity measurement, comparing the latter to the metallicity derived from the FMR, we find a median offset of 0.08 dex and a scatter of 0.1 dex, consistent with the values reported by Mannucci et al. (2010). Since these latter values are low, and to avoid mixing together metallicities that are directly observed and those that are inferred from the FMR, we decided to use the FMR-based metallicities for all galaxies in the HRS. We checked that our results are not affected by this choice. Furthermore, the low scatter we observe in this comparison confirms the accuracy of the FMR in determining metallicities empirically. While the scatter of the FMR could increase toward higher redshifts, it should be noted that our z = 1 stacked measurements are not sensitive to this scatter, since we only considered the average properties of galaxy populations with similar stellar masses, for which the FMR will give an accurate estimate of the average metallicity by construction.
4.3. Gas-to-dust ratios and gas masses
The last step to estimate gas masses is to derive the gas-to-dust ratios. To do so, we employed Eq. (4), which we calibrated using the δGDR measured in a sample of local galaxies by Leroy et al. (2011) (using the revised PP04 metallicities from Magdis et al. 2012) that we multiplied by a factor of 2 to account for systematic differences in the dust mass measurements between the dust model that we used and that of Draine & Li (2007) (see Sect. 4.1). Assuming the linear metallicity dependence of Eq. (4), we find that the δGDR measured by Leroy et al. (2011) are well described by 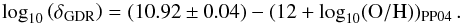 (7)With a solar oxygen abundance of (12 + log 10(O/H))⊙ = 8.73 ± 0.05 (Asplund et al. 2009), this leads to the equivalent expression
(7)With a solar oxygen abundance of (12 + log 10(O/H))⊙ = 8.73 ± 0.05 (Asplund et al. 2009), this leads to the equivalent expression 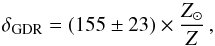 (8)which is consistent with the gas-to-dust ratio of the Milky Way (Mgas/Mdust)MW = 158 (Zubko et al. 2004). Returning to Eq. (4), using a solar metallicity of Z⊙ = 0.0134 (Asplund et al. 2009, assuming an uncertainty of 0.001), we note that this prescription is therefore equivalent to assuming fd = (32 ± 4)%, which is below the maximum value of ~46% allowed by the observed metal depletion of the ISM in the Milky Way7 (e.g., Draine et al. 2007).
(8)which is consistent with the gas-to-dust ratio of the Milky Way (Mgas/Mdust)MW = 158 (Zubko et al. 2004). Returning to Eq. (4), using a solar metallicity of Z⊙ = 0.0134 (Asplund et al. 2009, assuming an uncertainty of 0.001), we note that this prescription is therefore equivalent to assuming fd = (32 ± 4)%, which is below the maximum value of ~46% allowed by the observed metal depletion of the ISM in the Milky Way7 (e.g., Draine et al. 2007).
For our z = 1 sample, Eq. (7) (or Eq. (8)) yields gas-to-dust ratios between 145 and 381 (the precise values we obtain are listed in Table 2), while it ranges from 145 to 488 for the z = 0 HRS galaxies (which cover a wider metallicity range). Using the dust masses we measured in Sect. 4.1, we can infer the total gas mass in each stacked bin at z = 1, and for each HRS galaxy.
4.4. Evaluation of dust-based gas mass estimates
 |
Fig. 7 Left: comparison of two independent estimates of the total (H i + H2) gas masses for the HRS galaxies, either using the dust mass and the metallicity as described in Sect. 4.3 (x axis) or using a more direct measurement from H i+CO spectroscopy (y axis). The black solid line shows the one-to-one relation, while the dotted line gives the best-fit linear trend (slope: 1.03 ± 0.03). Right: difference between these two independent gas mass estimates as a function of stellar mass. The black solid line is the line of perfect agreement, while the dotted line is the best-fit linear trend (slope: 0.01 ± 0.04). |
The procedure described above involves many steps with potential uncertainties and biases. While each of these steps has previously been calibrated in the literature, it remains to check that the overall procedure (which essentially entails estimating gas masses from dust masses, stellar masses and star formation rates) works correctly. We can do so using the exquisite data set from the HRS. Indeed, since a substantial fraction of the galaxies in this sample are covered with H i and CO surveys (Boselli et al. 2014b), we can directly compare our dust-based gas masses against the H i+CO values, assuming a constant αCO = 3.6 M⊙/ (K km/(s pc2)) (Strong et al. 1988) to derive molecular gas masses.
The result is shown in Fig. 7, either comparing the two gas mass estimates directly (left), or as a function of stellar mass (right). The H i+CO gas masses are found to be systematically higher by 30%, and with a scatter of 0.2 dex. The data do not indicate any significant differential trend with stellar mass; we find a potential bias of only (5 ± 14)% between our two extreme mass bins. Since the vast majority (90%) of the M∗> 1010 M⊙ star-forming galaxies are detected in both atomic and molecular surveys, we also performed the analysis of the next sections with these alternative gas mass estimates. We find that our conclusions remain unchanged, save for this global shift of the gas masses by a factor of 1.3, and therefore conclude that our dust-based gas mass estimates in the HRS are robust. Since our z = 1 sample probes a more limited metallicity range (owing to its higher stellar mass cut), we can safely assume that the same conclusion holds for this sample as well.
5. Results
 |
Fig. 8 Upper panel: location of galaxies from the IR-sample with varying B/T on the SFR−M∗ plane, using the stellar mass and star formation rate (IR+UV) of the whole galaxy. On all plots, the vertical dotted line shows our adopted stellar mass cut, the horizontal dotted line is the 90% completeness in SFR, and the solid black line shows the locus of the z = 1 main sequence as observed through stacking in S15, while the solid gray line shows the extrapolation of the low-mass trend assuming a slope of unity, as observed at lower stellar masses (see Fig. 1). In each column, galaxies of different B/T are plotted. In the rightmost panel, we show all galaxies regardless of their B/T. The solid blue lines show the running median of the sample. Lower panel: same as upper panel, but on the SFR−Mdisk plane. |
 |
Fig. 10 Left: relation between the SFE = SFR/Mgas and the stellar mass (M∗) for main-sequence galaxies at z = 1. Colored diamonds show the measured SFEs and M∗ of our stacked sample, the color being associated with the stellar mass as in Fig. 6. The best-fit power law to our measurements, excluding the most massive point, is given with a black solid line (Eq. (9)). Right: gas fraction (fgas ≡ Mgas/ (Mgas + M∗)) as a function of the stellar mass (M∗) for main-sequence galaxies at z = 1. The legend is the same as in the left figure, and here the solid black line gives the value of fgas computed using the best-fit Mgas − M∗ relation, also excluding the most massive point in the fit. The resulting expression of fgas is given in Eq. (10). We also show the measured gas fractions by Magdis et al. (2012) at z = 2 with a dashed gray line and by Santini et al. (2014) at z = 1 with a dot-dashed gray line. |
5.1. SFR–Mdisk relation at z = 1
After measuring the disk masses, we can now examine whether the SFR−Mdisk relation is universal and linear by comparing the slopes of the main sequence using either the total stellar mass M∗ or the disk mass Mdisk. To be able to measure this slope on our whole sample at once and because our redshift window is relatively large, we corrected for the redshift evolution of the main sequence by renormalizing the SFR of each galaxy to a common redshift of z = 1. To do so, we used the redshift evolution measured in S15, taking the trend of low-mass galaxies where the bending of the main sequence is negligible. This correction is typically on the order of 0.05 dex and no more than 0.1 dex.
In Fig. 8 we show the resulting SFR−M∗ (top) and SFR−Mdisk (bottom) relations of our sample. Each panel focuses on a different range of B/T, starting from disk-dominated galaxies on the left, then increasing the contribution of the bulge progressively. In the rightmost panels, we show all galaxies from the IR-sample regardless of their B/T. We show with blue lines the running medians on the measurements in each plot and compare them to the stacked main sequence of S15. In the top rightmost panel, this running median overlaps the stacked relation, which indicates that we are not strongly affected by the SFR selection of our sample. However, we can see from the top leftmost panel that disk-dominated galaxies do not populate a particularly different region of the SFR−M∗ diagram: they cluster around the stacked relation of S15 and follow a sequence of slope 0.67 ± 0.07 (from M∗ = 3 × 1010 to 3 × 1011 M⊙). Even after subtracting the bulge mass, which is by definition very low in these systems, the measured slope is 0.65 ± 0.08, in other words, clearly not unity. For the other galaxies, we do find a trend for some of the lowest sSFR objects to be brought back toward the main sequence by removing the bulge mass, but they constitute a very small fraction of the whole sample (in fact, as can be seen in Fig. 5, a good fraction of the bulge-dominated galaxies are classified as UVJ quiescent) and cannot counterbalance the bending observed in disk-dominated galaxies. In the end, the slope of the SFR−Mdisk relation as measured on the whole sample (bottom-rightmost panel) is 0.60 ± 0.05. Therefore, knowing that the main-sequence slope at M∗< 1010 M⊙ is unity, we do not find that the SFR−Mdisk relation is linear.
In their z = 0 study, Abramson et al. (2014) only considered galaxies with B/T< 0.6, arguing that galaxies above this threshold cannot be fit reliably (we show indeed in Appendix B that disk masses measured in bulge-dominated galaxies are the most uncertain). We therefore tried to reject galaxies with B/T> 0.6 and did not find any significant difference. Most of them do not show any measurable IR emission (83%, compared to 46% for galaxies with B/T< 0.6), and are most likely genuine bulge dominated and quiescent objects.
To ensure that our results are not caused by an uncertain bulge-to-disk decomposition, we show in Fig. 9 that the SFR−M∗ diagram is populated by galaxies of varying effective Sérsic index n (van der Wel et al. 2012, and our own fits in GOODS-North, see Sect. 3.1). While the Sérsic index alone is poorly suited for measuring the disk masses of composite systems, it is a reliable way of identifying disk-dominated galaxies. Indeed, the fit is intrinsically simpler and therefore more stable, and the presence of a significant bulge component will rapidly make the effective Sérsic index depart from 1, the nominal value for pure disks (see, e.g., the Appendix A of Lang et al. 2014). We find that disk-dominated galaxies (n< 1.2) follow a slightly steeper slope of 0.75 ± 0.05, consistent with that found in Salmi et al. (2012) and Whitaker et al. (2015), but this is still not unity. These slope measurements are summarized in Table 3.
5.2. Gas fraction and star formation efficiency at z = 1
We show in Fig. 10 (left) the behavior of the SFE as a function of the stellar mass in our stacked z = 1 sample. These values are also reported in Table 2. From this figure, we see that the SFE of galaxies at M∗< 1011 M⊙ rises steadily with stellar mass, following ![\begin{equation} {\it SFE}\,[1/\Gyr] = \frac{{\it SFR}}{\mgas} = 9.30 \times 10^{-6}\,\left(\frac{\mstar}{\msun}\right)^{0.5}\cdot \label{EQ:sfe} \end{equation}](/articles/aa/full_html/2016/05/aa27200-15/aa27200-15-eq253.png) (9)However, our data point with the highest gas mass, that is, corresponding to the stellar mass of 2 × 1011 M⊙ where the bending of the main sequence is most pronounced, has an SFE that is a factor of 2 lower than that predicted from this scaling law. Our data clearly favor two regimes of SFE: galaxies with low stellar mass follow a universal relation and those with high stellar mass drop below this trend. We note that owing to the uncertainty on the fiducial trend given above, we cannot rule out a weak drop of SFE in the intermediate mass bin, at M∗ ~ 5 × 1010 M⊙ (orange point).
(9)However, our data point with the highest gas mass, that is, corresponding to the stellar mass of 2 × 1011 M⊙ where the bending of the main sequence is most pronounced, has an SFE that is a factor of 2 lower than that predicted from this scaling law. Our data clearly favor two regimes of SFE: galaxies with low stellar mass follow a universal relation and those with high stellar mass drop below this trend. We note that owing to the uncertainty on the fiducial trend given above, we cannot rule out a weak drop of SFE in the intermediate mass bin, at M∗ ~ 5 × 1010 M⊙ (orange point).
Measured slopes of the SFR−X relation, where X is either M∗ or Mdisk.
In contrast, the gas fraction (Fig. 10, right) is found to decrease continuously with stellar mass (similarly to what was found in Magdis et al. 2012 and Santini et al. 2014). This is the expected behavior if the main sequence has a linear (or sublinear) slope, while the SFR−Mgas law (the so-called integrated Schmidt-Kennicutt law) is superlinear with a power-law slope of n> 1 (e.g., Daddi et al. 2010a; Sargent et al. 2014; Santini et al. 2014). Indeed, if SFR ~ M∗ and 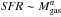 , then
, then 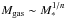 and the gas fraction has to decrease with stellar mass. By fitting the Mgas − M∗ relation for galaxies with M∗< 1011 M⊙, we obtain
and the gas fraction has to decrease with stellar mass. By fitting the Mgas − M∗ relation for galaxies with M∗< 1011 M⊙, we obtain 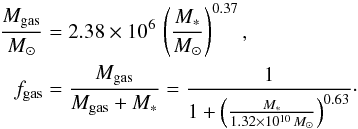 (10)For galaxies with M∗> 3 × 1010 M⊙, we measure a constant value of fgas = 26%, so that galaxies with M∗> 1011 M⊙ have larger gas fractions than expected from the above trend. This can be explained if these galaxies also had lower SFEs in the past, suggesting that we are witnessing a process that acts on long timescales.
(10)For galaxies with M∗> 3 × 1010 M⊙, we measure a constant value of fgas = 26%, so that galaxies with M∗> 1011 M⊙ have larger gas fractions than expected from the above trend. This can be explained if these galaxies also had lower SFEs in the past, suggesting that we are witnessing a process that acts on long timescales.
We also find that the overall decrease of gas fraction cannot be explained solely from the growing mass of the bulges. Indeed, if we substitute the disk mass to the total stellar mass, using the average B/T measured in each mass bin and assuming that galaxies of M∗< 1010 M⊙ are pure disks, the gas fraction in the disk is also found to decrease, albeit with a slightly shallower slope. Similar results are obtained if we use the B/T − M∗ relations of Lang et al. (2014).
It should be noted that the SFE and fgas we measure in high-mass galaxies are consistent with the z = 1 value reported by Béthermin et al. (2015), who applied the same methodology to a single-mass bin around M∗ ~ 1011 M⊙ using galaxies from the larger COSMOS field. On the other hand, similar measurements were performed in Santini et al. (2014), in the same field as Béthermin et al. (2015), finding gas masses lower by about a factor of 3. The discrepancy appears to come from different calibrations of the dust-to-gas ratio and therefore should only result in a systematic shift. However, owing to the shallow depths of the COSMOS survey, Santini et al. (2014) was only able to focus on galaxies more massive than 3 × 1010 M⊙, meaning that they did not probe the linear main-sequence regime (as is illustrated in Fig. 10, right).
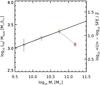 |
Fig. 11 Ratio between the dust mass (Mdust) and the total infrared luminosity (LIR) as a function of the stellar mass for stacked galaxies at z = 1. Colors are the same as in Fig. 10. We overplot a linear fit (in log space) of the first three mass bins with a solid black line. |
Last, to see how the assumptions about metallicity and gas-to-dust ratio affect our result, we show in Fig. 11 the LIR/Mdust ratio, which is a more direct observable. With our adopted dust model, neglecting the contribution of PAHs (we note that they represent only 4% of the total dust mass), the following relation links together this ratio and Tdust, or equivalently, the mass-weighted average intensity of the stellar radiation field ⟨U⟩ to which dust grains are exposed: ![\begin{equation} \frac{\lir}{\mdust} \left[\frac{\lsun}{\msun}\right] = 185 \, \left(\frac{\tdust}{17.5~\kelvin}\right)^{5.54} = 185 \, \mean{U} . \end{equation}](/articles/aa/full_html/2016/05/aa27200-15/aa27200-15-eq273.png) (11)The observed behavior of the LIR/Mdust ratio is very similar to that of the SFE, namely there is a steady rise with stellar mass, and then a sudden drop at M∗> 1011 M⊙. This should not come as a surprise, knowing that our estimated gas-to-dust ratio is at the end a simple power law of the stellar mass (see Sect. 2) and that the SFRs in this sample are largely dominated by the dust-obscured, IR-luminous component. The low-mass slope that we find here is fairly shallow, although we rule out a flat slope (as reported in Magdis et al. 2012) at the 3σ level. Yet, even if we were to adopt such a flat slope as the reference trend, the drop of LIR/Mdust (or SFE) in the highest mass bin would be less pronounced but still significant (4σ).
(11)The observed behavior of the LIR/Mdust ratio is very similar to that of the SFE, namely there is a steady rise with stellar mass, and then a sudden drop at M∗> 1011 M⊙. This should not come as a surprise, knowing that our estimated gas-to-dust ratio is at the end a simple power law of the stellar mass (see Sect. 2) and that the SFRs in this sample are largely dominated by the dust-obscured, IR-luminous component. The low-mass slope that we find here is fairly shallow, although we rule out a flat slope (as reported in Magdis et al. 2012) at the 3σ level. Yet, even if we were to adopt such a flat slope as the reference trend, the drop of LIR/Mdust (or SFE) in the highest mass bin would be less pronounced but still significant (4σ).
5.3. Progressive and mass-dependent decrease of the SFE with time
 |
Fig. 12 Left: relation between the specific SFR (sSFR = SFR/M∗) and the stellar mass (M∗) at various redshifts. Our z = 1 stacked measurements from S15 are shown with empty diamonds, and the average values of the star-forming HRS galaxies are shown with empty circles. The associated error bar is the error on the mean, not the dispersion of the sample. We compare these measurements to the z = 2 values obtained by Magdis et al. (2012) for star-forming BzK galaxies. Right: same as left, but replacing the sSFR by the star formation efficiency (SFE = SFR/Mgas). The diamonds and circles use the gas mass estimated in this paper, while the empty squares come from Magdis et al. (2012) and were computed with the same method. We also show for reference the measurements of Saintonge et al. (2011b) with empty gray circles. Their study only included H2 in Mgas, therefore we rescaled their measurement to include H i assuming Rmol = log 10(MH2/MH i) = 0.425 (log 10(M∗/M⊙)−10.7)−0.387 (Saintonge et al. 2011a, Fig. 9 and Table 4). We also caution that the sample selection in Saintonge et al. (2011b) is different from ours. |
In Fig. 12 (right) we put together our SFR and Mgas measurements at both z = 1 (previous section) and z = 0 using galaxies from the HRS survey to display the evolution of the SFE with stellar mass and redshift. The values in the HRS were obtained by binning galaxies in stellar mass and computing the mean SFE in each bin, since all the HRS star-forming galaxies are individually detected by Herschel and therefore have individual gas masses estimates. These results are compared to that of Magdis et al. (2012), who performed a similar analysis in the GOODS fields, stacking galaxies in different bins of stellar mass from M∗ = 1010 to 3 × 1011 M⊙, but focusing on z = 2BzK galaxies8. The selection effects inherent to the BzK classification are not very well understood, and it is known that this selection tends to affect the shape of the main sequence (Speagle et al. 2014). With this caveat in mind, we proceed to compare these results to our data at z = 0 and z = 1.
We first note that the SFE at various redshifts is systematically different, with higher redshift galaxies showing higher SFEs. This fact is known and is not discussed any further (see, e.g., Genzel et al. 2010; Combes et al. 2013; Tacconi et al. 2013; Santini et al. 2014; Béthermin et al. 2015).
Similarly to our z = 1 sample, the most massive galaxies in the HRS (M∗> 1010 M⊙) are also found to have a reduced SFE, thereby confirming the trend observed in the previous section. However, Magdis et al. (2012) observed a fairly different picture than the one we present here, since their galaxies of all stellar mass are found to lie on the same SFR−Mgas relation, that is, following a universal star formation law.
In fact, this is fully consistent with the observed evolution of the high-mass slope of the main sequence (see, e.g., the comprehensive analysis of Gavazzi et al. 2015), since at z = 2 the SFR−M∗ relation is found to be almost linear (see S15 and Fig. 12, left), indicating that the process that drives this change of slope has not yet taken place. On the other hand, at z = 0 the bending of the main sequence is more pronounced and takes place above a turnover mass that is lower than at z = 1, in agreement with the behavior of the SFE that we observe for the HRS galaxies.
Similar trends of decreasing SFE with stellar mass have been reported in the literature (e.g., Saintonge et al. 2011b; Dessauges-Zavadsky et al. 2015; Mok et al. 2016), although these studies did not mention a turnover of this relation. We argue that this is nevertheless consistent with our result, since these studies could only observe the regime above the z = 0 turnover mass, where the SFE is decreases (see, e.g., Fig. 12 where we overplot the measurements of Saintonge et al. 2011b). Furthermore, it is also likely that this turnover of the SFE−M∗ relation can only be seen if the total gas mass is used, meaning the mass including atomic hydrogen. Indeed, low-mass galaxies typically have lower MH2/MH i ratios (e.g., Saintonge et al. 2011a; Boselli et al. 2014b) and would have substantially higher SFEs if only molecular gas is used (see, e.g., Gardan et al. 2007; Leroy et al. 2008; Gratier et al. 2010; Boselli et al. 2014b).
6. Discussion
6.1. Quantifying the quenching and downfall rates
 |
Fig. 13 Evolution of the mass-weighted quenching and downfall rate densities with redshift. The red curve shows the time derivative of the stellar mass density of UVJ quiescent galaxies, which we assume are produced by a fast-quenching mechanism. The blue curve shows the star formation density that is lost because of the lowered SFE in massive galaxies, which we call the slow-downfall rate. The shaded regions in the background give the uncertainty on both measurements. |
We find that the bending of the main sequence cannot be caused by abnormally low gas fractions, but is instead resulting from a progressive downfall of the star formation efficiency, as shown in Figs. 10 and 12. These observations converge toward a slow downfall of star formation, where massive galaxies gradually decrease their star formation activity while staying on the main sequence (see also Tacchella et al. 2015). While staying on the main sequence, these galaxies become gradually less efficient in their star formation activity instead of abruptly turning off through a fast quenching. Because the SFE decreases with time, these galaxies do not grow too massive by z = 0, as shown in Leja et al. (2015), who simulated the evolution of the observed stellar mass function using a main sequence of varying slope. The decrase in the star formation rate in massive main-sequence galaxies may lead to the death of galaxies if the gas surface density, for example, decreases below the critical density that is necessary to switch on the Schmidt-Kennicutt relation, but our analysis does not allow us to make any firm claim favoring or disfavoring a scenario in which this downfall feeds the red sequence. Instead, we propose here to quantify the downfall rate of this slow process and compare it to the fast-quenching rate associated with the growth of the red sequence.
As shown in Muzzin et al. (2013) and Tomczak et al. (2014), for example, the stellar mass density of UVJ quiescent galaxies increases monotonously with time, illustrating the progressive buildup of the red sequence. The time derivative of this quantity, neglecting stellar mass loss and residual star formation, is a measure of the quenching rate of galaxies (see, e.g., Peng et al. 2010). Here, we make the hypothesis that all the UVJ quiescent galaxies were quenched by a fast process and set 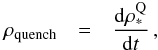 (12)where
(12)where 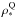 is the stellar mass density of UVJ quiescent galaxies. We parametrize this latter quantity by fitting the redshift evolution reported in the CANDELS fields by Tomczak et al. (2014), accounting for the different choice of IMF:
is the stellar mass density of UVJ quiescent galaxies. We parametrize this latter quantity by fitting the redshift evolution reported in the CANDELS fields by Tomczak et al. (2014), accounting for the different choice of IMF: ![\begin{eqnarray} \rho_{*}^{\rm Q}\,\left[\msun/\Mpc^3\right] &=& (2.6 \pm 0.7) \times 10^8 \exp(-z) \,. \end{eqnarray}](/articles/aa/full_html/2016/05/aa27200-15/aa27200-15-eq286.png) (13)To estimate the downfall rate associated with the slow process that decreases the SFE of massive star-forming galaxies, we compute the difference between the observed SFR density (ρSFR) and the density that would be observed if there was no drop of SFE, therefore if the main sequence had a slope of unity at all stellar masses (
(13)To estimate the downfall rate associated with the slow process that decreases the SFE of massive star-forming galaxies, we compute the difference between the observed SFR density (ρSFR) and the density that would be observed if there was no drop of SFE, therefore if the main sequence had a slope of unity at all stellar masses ( ). This is a measure of the amount of star formation that was lost because of the reduced SFE within the main sequence. We estimate both SFR densities using the stellar mass functions of star-forming galaxies introduced in S15 (that we complement toward z = 0 using the mass function from Baldry et al. 2012) and integrate these mass functions weighted by the SFR. For the observed ρSFR, we use the SFR−M∗ relation given in S15. Defining r ≡ log 10(1 + z) and m ≡ log 10(M∗/ 109 M⊙), this relation reads
). This is a measure of the amount of star formation that was lost because of the reduced SFE within the main sequence. We estimate both SFR densities using the stellar mass functions of star-forming galaxies introduced in S15 (that we complement toward z = 0 using the mass function from Baldry et al. 2012) and integrate these mass functions weighted by the SFR. For the observed ρSFR, we use the SFR−M∗ relation given in S15. Defining r ≡ log 10(1 + z) and m ≡ log 10(M∗/ 109 M⊙), this relation reads ![\begin{eqnarray} \log_{10}(\sfrms [\msun/{\rm yr}]) = m - m_0 + a_0\,r \hspace{2.5cm} \nonumber \\ \hspace{0.9cm} - a_1 \, \big[{\rm max}(0, m - m_1 - a_2\,r)\big]^2\,, \label{EQ:sfrms} \end{eqnarray}](/articles/aa/full_html/2016/05/aa27200-15/aa27200-15-eq291.png) (14)with m0 = 0.5 ± 0.07, a0 = 1.5 ± 0.15, a1 = 0.3 ± 0.08, m1 = 0.36 ± 0.3 and a2 = 2.5 ± 0.6. For
(14)with m0 = 0.5 ± 0.07, a0 = 1.5 ± 0.15, a1 = 0.3 ± 0.08, m1 = 0.36 ± 0.3 and a2 = 2.5 ± 0.6. For  we use this same equation excluding the last term (which is used to describe the bending), that is,
we use this same equation excluding the last term (which is used to describe the bending), that is, ![\begin{eqnarray} \log_{10}(\sfrms^{\rm unity} [\msun/{\rm yr}]) = m - m_0 + a_0\,r. \label{EQ:sfrms_unity} \end{eqnarray}](/articles/aa/full_html/2016/05/aa27200-15/aa27200-15-eq297.png) (15)Since these equations were not calibrated at z< 0.5 in S15, we use the observed main sequence from the HRS galaxies for these redshifts.
(15)Since these equations were not calibrated at z< 0.5 in S15, we use the observed main sequence from the HRS galaxies for these redshifts.
The downfall rate is then defined simply as 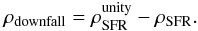 (16)The resulting evolution of both ρquench and ρdownfall is shown in Fig. 13. This figure shows that the fast-quenching mode clearly dominates at all z> 1.5, while the slow downfall rapidly catches up to reach similar rates from z = 1.5 to the present day, that is, over ~70% of the history of the Universe.
(16)The resulting evolution of both ρquench and ρdownfall is shown in Fig. 13. This figure shows that the fast-quenching mode clearly dominates at all z> 1.5, while the slow downfall rapidly catches up to reach similar rates from z = 1.5 to the present day, that is, over ~70% of the history of the Universe.
Two conclusions can be drawn from this observation. First, the fact that both the quenching and downfall rates reach similar values at all z< 1.5 implies that the downfall is a quantitatively important effect that should be considered alongside the growth of the red sequence. Second, it is clear that the two modes act at different epochs in the history of the Universe. While the fast quenching appears to hold a steady rate from z = 4 throughout to the present day, the slow downfall becomes a significant source of SF suppression only at z< 2. This suggests that the buildup of the red sequence and the change of slope in the main sequence are in fact related to two separate physical processes. This is discussed further in the next section.
6.2. Identifying the actors that regulate the SFE and the gas content
We have shown in Sect. 5.1 that the bending of the main sequence remains even if we consider only the stellar mass of the disk, excluding the inert bulges. While it is natural to expect that the specific star formation rate of galaxies could be universal only when computed over the disk rather than total mass of galaxies (as proposed by Abramson et al. 2014) since bulges do not form stars, it would also generate a discrepancy with another concept linked to the main sequence, namely the fact that galaxies are fed by the infall of extragalactic matter, which is in turn proportional to the total mass of galaxies including dark matter (e.g., Dekel et al. 2013): the bulge, even if not forming star, does contribute to the gravitational potential of the galaxy and must therefore provoke additional infall. Hence the fact that our results from Sect. 5.1 refute bulge growth as the actor of the main-sequence bending may not be surprising, and possibly even expected when accounting for the large-scale context of infall. This also echoes the result obtained more recently in the SDSS by Guo et al. (2015), who also found a sublinear slope (i.e., less than unity) for the SFR−M∗ relation of z = 0 pure disk galaxies, which contradicts the results of Abramson et al. (2014).
As discussed in the previous section, we have observed instead in Sect. 5.2 that the star formation efficiency decreases in massive galaxies, leading to a slow downfall of star formation. This suggests the existence of an active process that affects the star formation activity, although the question remains to determine exactly what this process could be. We cannot definitely address this question with the present data alone, but we review in the following the known mechanisms in light of our results.
We may already state that feedback from supernovae is not the favored solution, for it would affect galaxies with a low gravitational potential, and therefore with low stellar masses, more efficiently, which is opposite to our finding. Interestingly, the range in redshift and galaxy mass where the main sequence flattens corresponds to the regime where theory predicts group formation to be most effective, hence suggesting that structure formation or the membership to massive haloes may affect the rate of gas infall and the energetics regulating star formation (disk rotation and turbulence, see, e.g., Hennebelle & Chabrier 2008). Gravitational heating (Birnboim & Dekel 2003; Dekel & Birnboim 2008), that is, the injection of energy into the dark matter halo from gas accretion itself, only depends on the mass of this halo and can therefore also act in isolated galaxies. According to Dekel & Birnboim (2008), this can completely stop star formation in halos more massive than ~6 × 1012 M⊙, corresponding to a typical stellar mass of ~1011 M⊙ at z = 1 (Behroozi et al. 2013). This halo mass is the threshold above which natural cooling cannot counterbalance the energy brought into the halo by accretion. At lower halo masses, typically Mhalo ~ 1012 M⊙ or M∗ ~ 5 × 1010 M⊙, virial shock heating can prevent accretion for about 1 Gyr and eventually lead to a cessation of star formation (see, e.g., Dekel & Birnboim 2006 and the scenario proposed by Tacchella et al. 2015), but another process is then required to prevent rejuvenation. Interestingly, it has been observed that AGN-driven outflows also preferentially act above a similar characteristic stellar mass: more than half of the star-forming galaxies above M∗> 1011 M⊙ show signs of such outflows, while this fraction drops below 20% at M∗< 5 × 1010 M⊙ at both z = 2 and z = 1 (Förster Schreiber et al. 2014; Genzel et al. 2014). While these winds have in principle enough energy to push the gas out of the galaxy, it is likely that they will also affect the distribution of the gas within the galaxy, preventing fragmentation or disrupting molecular clouds. The reason why this would affect the SFE preferentially at z ≤ 1 is unclear, although it might be linked to the fact that z = 2 galaxies are more clumpy and gas-rich and are therefore less affected by the winds (Roos et al. 2015). On the other hand, we cannot rule out the action of the radio-mode AGN feedback, where jets heat the gas in the surroundings of galaxies, which may also be more common in massive galaxies.
Last, another key quantity that is related to the stellar mass is the metallicity. It has been proposed that metallicity might be a main driver of the SFE at small scales, influencing the conversion of prestellar cores into stars through the strength of stellar winds, hence also setting the global SFE of the galaxy (e.g., Dib et al. 2011). Dib et al. (2011) predicted a steady decrease of the molecular SFE = SFR/MH2 with metallicity, which qualitatively matches our observations at high stellar masses. At low stellar masses, the dominance of H i most likely dilutes the effect predicted by Dib et al., which does not affect the conversion of H i into H2. Investigating this path in more detail would require more precise metallicity measurement than we used here.
Over the past years, the emphasis was placed mostly on violent quenching mechanisms to explain the low baryonic fraction per unit dark matter halo mass, switching off the growth of galaxies by supernovae and AGNs at low and high masses, respectively (see, e.g., Silk & Mamon 2012; Behroozi et al. 2013; Behroozi & Silk 2015). We present here evidence that a slow downfall of the star formation efficiency should also be considered as a key mechanism.
7. Conclusions
We addressed here the origin of the change of slope in the main sequence of star-forming galaxies at z< 1.5, where high-mass galaxies exhibit a lower sSFR ≡ SFR/M∗ than would be extrapolated from low-mass galaxies (e.g., Whitaker et al. 2012, 2014; Magnelli et al. 2014; Ilbert et al. 2015; Schreiber et al. 2015; Lee et al. 2015; Gavazzi et al. 2015).
It was reported in the local Universe that the SFR−Mdisk relation is linear, suggesting that it is the bulge that creates most of the change of slope of the main sequence (Abramson et al. 2014). This claim was recently questioned by Guo et al. (2015) at z = 0, who reported that the slope of the SFR−Mdisk relation is in fact sublinear.
We performed the bulge-to-disk decomposition of a sample of ~1000 galaxies at z = 1 in the CANDELS fields with reliable SFRs measured from their mid- to far-IR photometry. We find that similar as for the SFR−M∗ relation, the high-mass slope of the SFR−Mdisk relation remains substantially shallower than unity. A shallow slope like this is also observed among pure disk galaxies, selected either from their decomposed bulge-to-total ratio or from their effective Sérsic index (see also Salmi et al. 2012 for a similar result at z = 1). This implies that a physical mechanism is at play even within the disks of massive galaxies, and that it is uncorrelated to the presence or absence of a bulge.
We then used Herschel stacking to jointly derive the average SFR and dust mass of star-forming galaxies in four bins of stellar mass in the same redshift range. Deriving the gas-phase metallicity from the fundamental metallicity relation, we inferred the total gas mass, assuming that a fixed fraction of the metals are locked into dust, and analyzed the relation between the SFE ≡ SFR/Mgas and the gas fraction in bins of stellar mass. We found that the most massive galaxies with M∗> 2 × 1011 M⊙ show a significantly reduced SFE by about a factor of 2 to 3 when compared to extrapolations from lower stellar masses, while the gas fraction remains constant. We measured gas masses in local galaxies from the Herschel Reference Survey and found a similar behavior, reinforcing this finding. There, the drop of SFE occurs at lower stellar masses, in agreement with the redshift evolution of the slope of the main sequence (see S15).
Combined together, these results point toward the existence of a slow downfall mechanism that affects the SFE of massive star-forming galaxies. We showed that this phenomenon is quantitatively important at z< 1.5 and is very likely disconnected from the fast-quenching phenomenon that builds the red sequence. We argued that both mechanisms should be considered equally when exploring the latest stages of galaxy evolution.
Leads for future research include studying the variation of the SFE above and below the main sequence at fixed stellar mass. We here showed evidence that variations of SFR at high stellar masses are caused by variations in the SFE and not in gas mass. Since we have only been able to probe this through stacking and with relatively uncertain selection effects at z = 1, it would certainly be interesting to confirm these trends for individual objects. This type of analysis can only be accomplished using a statistically complete sample of SFR and dust mass measurements at different stellar masses (ideally with direct metallicity estimates from emission lines). While SFRs and metallicities are currently within our reach, ALMA observations remain the only way to derive individual dust mass measurements for non-starbursting systems. A statistical sample with such measurement can be obtained either through dedicated pointed observations or using a blind continuum survey, which will soon become possible with ALMA.
Regardless of the presence of a bulge, a similar conclusion can be drawn from the absence of a strong correlation between surface densities of stars and gas in nearby galaxies; e.g., Shi et al. (2011).
We did not further select galaxies based on their measured morphological parameters. Abramson et al. (2014) only used face-on galaxies in their z = 0 analysis (axis ratio higher than 0.8), arguing that the decomposition is less reliable for edge-on objects. We could not find any such trend in our simulations (see Appendix B), and we also checked that no systematic trend emerges in the real data when we only used face-on galaxies.
To better constrain the Rayleigh-Jeans tail of the dust emission, we also considered stacking longer wavelength sub-millimeter data from AzTEC or LABOCA, but these are only available for a few fields (AzTEC in GOODS-North and LABOCA in GOODS-South, while both are also covering COSMOS at shallower depth) hence reducing the number of stacked sources significantly. Combined with the fact that at z = 1, the expected flux in these bands is fairly low, we could not detect any significant signal. These upper limits are consistent with the rest of Herschel photometry at the 1 to 2σ level.
We might improve the fit, for example, by adopting overall lower dust temperatures and adding a second component of warm dust, as in da Cunha et al. (2008).
We would reach the same conclusions had we used the dust masses published by Ciesla et al., after correcting them downward by a factor of 2 since these were derived using the Draine & Li (2007) graphite dust model.
It is also worth noting that the FMR could have a redshift dependence, i.e., that Eq. (5) may not hold in the distant Universe (see in particular Troncoso et al. 2014; Tan et al. 2014; Béthermin et al. 2015). However, this is not a problem for the present study since, first, this difference is supposedly a constant shift of the metallicity at all stellar masses, and second, it only takes place at higher redshifts than that probed by our study.
They did stack galaxies at z = 1, but did not separate them in different stellar mass bins. In addition, since the BzK selection only selects star-forming galaxies at z = 2, they had to use another method to discard quiescent galaxies at z = 1. To do so, they used a cut in Sérsic index of n< 1.5 (see e.g., Wuyts et al. 2011, and Fig. 9). Because the associated selection effects are not obvious to determine, we prefer not to consider this data point in the present analysis, although the gas fraction they report is compatible with the one we measure here.
This may sound surprisingly high, but it should be noted that this stacked “SFR” of quiescent galaxies also includes, for a large fraction, some LIR coming from the dust headed by old stars and not actual star formation. Therefore this prescription allows us to take both residual star formation and dust headed by old stars into account at the same time. See also Fumagalli et al. (2014), where this was done in more detail.
By using rest-frame wavelengths that are further apart, this diagram has a larger dynamic range and will separate quiescent and star-forming galaxies more clearly than the UVJ diagram. The downside is that measuring the rest-frame K band is particularly difficult at high redshifts, while the near-UV is hardly accessible at low redshift.
Acknowledgments
We thank the referee, J. Braine, for his comments and suggestions that improved the readability, clarity, and correctness of this paper.
C.S. wants to thank F. Galliano for his input on the dust grain composition and for making his dust model available.
Most of the numerical analysis conducted in this work have been performed using phy++, a free and open source C++ library for fast and robust numerical astrophysics (cschreib.github.io/phypp/).
This work is based on observations taken by the CANDELS Multi-Cycle Treasury Program with the NASA/ESA HST, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555.
This research was supported by the French Agence Nationale de la Recherche (ANR) project ANR-09-BLAN-0224 and by the European Commission through the FP7 SPACE project ASTRODEEP (Ref. No: 312725).
LC benefited from the thales project 383549 that is jointly funded by the European Union and the Greek Government in the framework of the program “Education and lifelong learning”.
T.W. acknowledges support for this work from the National Natural Science Foundation of China under grants No. 11303014.
References
- Abraham, R. G., Tanvir, N. R., Santiago, B. X., et al. 1996, MNRAS, 279, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Abramson, L. E., Kelson, D. D., Dressler, A., et al. 2014, ApJ, 785, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Le Floc’h, E., Chevallard, J., et al. 2013, A&A, 558, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baldry, I. K., Driver, S. P., Loveday, J., et al. 2012, MNRAS, 421, 621 [NASA ADS] [Google Scholar]
- Barden, M., Rix, H., Somerville, R. S., et al. 2005, ApJ, 635, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Barden, M., Häußler, B., Peng, C. Y., McIntosh, D. H., & Guo, Y. 2012, MNRAS, 422, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., & Silk, J. 2015, ApJ, 799, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., & Conroy, C. 2013, ApJ, 770, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., McIntosh, D. H., Barden, M., et al. 2004, ApJ, 600, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Dole, H., Beelen, A., & Aussel, H. 2010, A&A, 512, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Daddi, E., Magdis, G., et al. 2015, A&A, 573, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A. K., Walter, F., et al. 2011, ApJ, 730, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Birnboim, Y., & Dekel, A. 2003, MNRAS, 345, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Bluck, A. F. L., Mendel, J. T., Ellison, S. L., et al. 2014, MNRAS, 441, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Eales, S., Cortese, L., et al. 2010, PASP, 122, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Cortese, L., & Boquien, M. 2014a, A&A, 564, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Cortese, L., Boquien, M., et al. 2014b, A&A, 564, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2012, ApJ, 754, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Bruce, V. A., Dunlop, J. S., Cirasuolo, M., et al. 2012, MNRAS, 427, 1666 [NASA ADS] [CrossRef] [Google Scholar]
- Bruce, V. A., Dunlop, J. S., McLure, R. J., et al. 2014, MNRAS, 444, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chary, R., & Elbaz, D. 2001, ApJ, 556, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Ciesla, L., Boquien, M., Boselli, A., et al. 2014, A&A, 565, A128 [Google Scholar]
- Ciesla, L., Boselli, A., Elbaz, D., et al. 2016, A&A, 585, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Combes, F., García-Burillo, S., Braine, J., et al. 2013, A&A, 550, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Compiègne, M., Verstraete, L., Jones, A., et al. 2011, A&A, 525, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Conselice, C. J. 2003, ApJS, 147, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- da Cunha, E., Charlot, S., & Elbaz, D. 2008, MNRAS, 388, 1595 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dannerbauer, H., Elbaz, D., et al. 2008, ApJ, 673, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dannerbauer, H., Stern, D., et al. 2009, ApJ, 694, 1517 [Google Scholar]
- Daddi, E., Bournaud, F., Walter, F., et al. 2010a, ApJ, 713, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Elbaz, D., Walter, F., et al. 2010b, ApJ, 714, L118 [Google Scholar]
- Dannerbauer, H., Daddi, E., Riechers, D. A., et al. 2009, ApJ, 698, L178 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, R. S. 1996, A&A, 313, 377 [NASA ADS] [Google Scholar]
- Dekel, A., & Birnboim, Y. 2006, MNRAS, 368, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Birnboim, Y. 2008, MNRAS, 383, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., Zolotov, A., Tweed, D., et al. 2013, MNRAS, 435, 999 [NASA ADS] [CrossRef] [Google Scholar]
- Dessauges-Zavadsky, M., Zamojski, M., Schaerer, D., et al. 2015, A&A, 577, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dib, S., Piau, L., Mohanty, S., & Braine, J. 2011, MNRAS, 415, 3439 [NASA ADS] [CrossRef] [Google Scholar]
- Donley, J. L., Koekemoer, A. M., Brusa, M., et al. 2012, ApJ, 748, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fanciullo, L., Guillet, V., Aniano, G., et al. 2015, A&A, 580, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferguson, H. C., Dickinson, M., Giavalisco, M., et al. 2004, ApJ, 600, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Förster Schreiber, N. M., Genzel, R., Newman, S. F., et al. 2014, ApJ, 787, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Franco, J., & Cox, D. P. 1986, PASP, 98, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Fumagalli, M., Labbé, I., Patel, S. G., et al. 2014, ApJ, 796, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Gabor, J. M., & Davé, R. 2012, MNRAS, 427, 1816 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, F., Madden, S. C., Tielens, A. G. G. M., Peeters, E., & Jones, A. P. 2008, ApJ, 679, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, F., Hony, S., Bernard, J., et al. 2011, A&A, 536, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gardan, E., Braine, J., Schuster, K. F., Brouillet, N., & Sievers, A. 2007, A&A, 473, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, G., Consolandi, G., Viscardi, E., et al. 2015, A&A, 576, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genzel, R., Tacconi, L. J., Gracia-Carpio, J., et al. 2010, MNRAS, 407, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Förster Schreiber, N. M., Rosario, D., et al. 2014, ApJ, 796, 7 [Google Scholar]
- Genzel, R., Tacconi, L. J., Lutz, D., et al. 2015, ApJ, 800, 20 [NASA ADS] [CrossRef] [Google Scholar]
- González, V., Bouwens, R., Illingworth, G., et al. 2014, ApJ, 781, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Gratier, P., Braine, J., Rodriguez-Fernandez, N. J., et al. 2010, A&A, 522, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, K., Zheng, X. Z., Wang, T., & Fu, H. 2015, ApJ, 808, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Häussler, B., McIntosh, D. H., Barden, M., et al. 2007, ApJS, 172, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Häussler, B., Bamford, S. P., Vika, M., et al. 2013, MNRAS, 430, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Heinis, S., Buat, V., Béthermin, M., et al. 2013, MNRAS, 429, 1113 [Google Scholar]
- Hennebelle, P., & Chabrier, G. 2008, ApJ, 684, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, T. M., Cortese, L., Boselli, A., Gavazzi, G., & Davies, J. I. 2013, A&A, 550, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Arnouts, S., Le Floc’h, E., et al. 2015, A&A, 579, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P., Fanciullo, L., Köhler, M., et al. 2013, A&A, 558, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karim, A., Schinnerer, E., Martínez-Sansigre, A., et al. 2011, ApJ, 730, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt Robert, C. J., 1998a, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt Robert, C. J., 1998b, ARA&A, 36, 189 [Google Scholar]
- Kewley, L. J., & Dopita, M. A. 2002, ApJS, 142, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Lang, P., Wuyts, S., Somerville, R. S., et al. 2014, ApJ, 788, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, N., Sanders, D. B., Casey, C. M., et al. 2015, ApJ, 801, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Leja, J., van Dokkum, P. G., Franx, M., & Whitaker, K. E. 2015, ApJ, 798, 115 [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Bigiel, F., et al. 2009, AJ, 137, 4670 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Bolatto, A., Gordon, K., et al. 2011, ApJ, 737, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Primack, J., & Madau, P. 2004, AJ, 128, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C., Galliano, F., Jones, A. P., & Sauvage, M. 2006, A&A, 446, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magdis, G. E., Elbaz, D., Daddi, E., et al. 2010, ApJ, 714, 1740 [NASA ADS] [CrossRef] [Google Scholar]
- Magdis, G. E., Daddi, E., Elbaz, D., et al. 2011, ApJ, 740, L15 [Google Scholar]
- Magdis, G. E., Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Magnelli, B., Elbaz, D., Chary, R. R., et al. 2009, A&A, 496, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnelli, B., Lutz, D., Santini, P., et al. 2012a, A&A, 539, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnelli, B., Saintonge, A., Lutz, D., et al. 2012b, A&A, 548, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnelli, B., Lutz, D., Saintonge, A., et al. 2014, A&A, 561, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mancini, C., Renzini, A., Daddi, E., et al. 2015, MNRAS, 450, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Martig, M., Bournaud, F., Teyssier, R., & Dekel, A. 2009, ApJ, 707, 250 [NASA ADS] [CrossRef] [Google Scholar]
- McIntosh, D. H., Bell, E. F., Rix, H., et al. 2005, ApJ, 632, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Mok, A., Wilson, C. D., Golding, J., et al. 2016, MNRAS, 456, 4384 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., Marchesini, D., Stefanon, M., et al. 2013, ApJ, 777, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Ellis, R. S., Bundy, K., & Treu, T. 2012, ApJ, 746, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [Google Scholar]
- O’Halloran, B., Satyapal, S., & Dudik, R. P. 2006, ApJ, 641, 795 [NASA ADS] [CrossRef] [Google Scholar]
- Pannella, M., Hopp, U., Saglia, R. P., et al. 2006, ApJ, 639, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Pannella, M., Carilli, C. L., Daddi, E., et al. 2009a, ApJ, 698, L116 [Google Scholar]
- Pannella, M., Gabasch, A., Goranova, Y., et al. 2009b, ApJ, 701, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Pannella, M., Elbaz, D., Daddi, E., et al. 2015, ApJ, 807, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VIII. 2014, A&A, 571, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ravindranath, S., Ferguson, H. C., Conselice, C., et al. 2004, ApJ, 604, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2014, A&A, 563, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2015, A&A, 582, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renzini, A., & Peng, Y.-J. 2015, ApJ, 801, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Rodighiero, G., Daddi, E., Baronchelli, I., et al. 2011, ApJ, 739, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Roos, O., Juneau, S., Bournaud, F., & Gabor, J. M. 2015, ApJ, 800, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Saintonge, A., Kauffmann, G., Kramer, C., et al. 2011a, MNRAS, 415, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Saintonge, A., Kauffmann, G., Wang, J., et al. 2011b, MNRAS, 415, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Salmi, F., Daddi, E., Elbaz, D., et al. 2012, ApJ, 754, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Salmon, B., Papovich, C., Finkelstein, S. L., et al. 2015, ApJ, 799, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sandstrom, K. M., Leroy, A. K., Walter, F., et al. 2013, ApJ, 777, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Santini, P., Maiolino, R., Magnelli, B., et al. 2014, A&A, 562, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sargent, M. T., Daddi, E., Béthermin, M., et al. 2014, ApJ, 793, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N., Aussel, H., Sheth, K., et al. 2014, ApJ, 783, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, Y., Helou, G., Yan, L., et al. 2011, ApJ, 733, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, X., Elbaz, D., & Bourne, N. 2015, ApJS, 222, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J., & Mamon, G. A. 2012, RA&A, 12, 917 [Google Scholar]
- Silk, J., & Rees, M. J. 1998, A&A, 331, L1 [NASA ADS] [Google Scholar]
- Simard, L., Koo, D. C., Faber, S. M., et al. 1999, ApJ, 519, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Simard, L., Willmer, C. N. A., Vogt, N. P., et al. 2002, ApJS, 142, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. D. T., Draine, B. T., Dale, D. A., et al. 2007, ApJ, 656, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S., Bunker, A., et al. 2009, ApJ, 697, 1493 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Schenker, M. A., Ellis, R., et al. 2013, ApJ, 763, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Steinhardt, C. L., Speagle, J. S., Capak, P., et al. 2014, ApJ, 791, L25 [Google Scholar]
- Stockton, A., McGrath, E., Canalizo, G., Iye, M., & Maihara, T. 2008, ApJ, 672, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Straatman, C. M. S., Labbé, I., Spitler, L. R., et al. 2014, ApJ, 783, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Bloemen, J. B. G. M., Dame, T. M., et al. 1988, A&A, 207, 1 [NASA ADS] [Google Scholar]
- Swinyard, B. M., Ade, P., Baluteau, J., et al. 2010, A&A, 518, L4 [Google Scholar]
- Tacchella, S., Carollo, C. M., Renzini, A., et al. 2015, Science, 348, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
- Tacconi, L. J., Neri, R., Genzel, R., et al. 2013, ApJ, 768, 74 [Google Scholar]
- Tan, Q., Daddi, E., Magdis, G., et al. 2014, A&A, 569, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tomczak, A. R., Quadri, R. F., Tran, K. H., et al. 2014, ApJ, 783, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Troncoso, P., Maiolino, R., Sommariva, V., et al. 2014, A&A, 563, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Wel, A., Bell, E. F., Häussler, B., et al. 2012, ApJS, 203, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F., Brinks, E., de Blok, W. J. G., et al. 2008, AJ, 136, 2563 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., van Dokkum, P. G., Brammer, G., & Franx, M. 2012, ApJ, 754, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Franx, M., Leja, J., et al. 2014, ApJ, 795, 104 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Whitaker, K. E., Franx, M., Bezanson, R., et al. 2015, ApJ, 811, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R. J., Quadri, R. F., Franx, M., van Dokkum, P., & Labbé, I. 2009, ApJ, 691, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, T., & Blitz, L. 2002, ApJ, 569, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Charmandaris, V., Hao, L., et al. 2006, ApJ, 639, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, S., Förster Schreiber, N. M., van der Wel, A., et al. 2011, ApJ, 742, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Zafar, T., & Watson, D. 2013, A&A, 560, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zahid, H. J., Kewley, L. J., & Bresolin, F. 2011, ApJ, 730, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Zubko, V., Dwek, E., & Arendt, R. G. 2004, ApJS, 152, 211 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Cleaning the 24μm catalogs
We focus here on the association of a Spitzer MIPS 24 μm flux to the galaxies in the H-band catalog. The procedure that was used to build the 24 μm flux catalog (see Magnelli et al. 2009) is based on IRAC 3.6 μm position priors: sources are extracted on the 24 μm map (and then, sequentially on the Herschel images) at the position of bright 3.6 μm sources. If two priors are too close to be deblended in the MIPS image, only the brightest 3.6 μm source is kept in the prior list. Because the IRAC bands are good tracers of the stellar mass and because the stellar mass correlates with the star formation rate, this approach is very effective for reliably extracting the vast majority of the MIR and FIR sources. But it will fail in a few rare cases that will be particularly important for our study (see also Mancini et al. 2015). The method is expected to be biased as soon as some objects deviate from the SFR−M∗ correlation. For example, it may occur that a massive, quiescent galaxy lies within a few arcseconds of a star-forming galaxy with lower mass (or slightly higher redshift). The quiescent galaxy, being very massive, is most likely the brightest emitter in the IRAC 3.6 μm image, but it is not expected to shine much in the MIR because it is not forming any stars. The nearby star-forming galaxy, on the other hand, can be fainter in the IRAC image, but will contribute to most, if not all, of the MIR emission. In this situation, the typical outcome is that the star-forming galaxy is removed from the prior list because it has the faintest IRAC flux, while the quiescent galaxy is given all the IR flux. The end result is that we do have in our catalogs a few massive quiescent galaxies with bright 24 μm emission that are obvious mismatches. We emphasize that the problem does not affect the 24 μm fluxes listed in the published catalogs, but rather the association of these fluxes to counterparts in the higher-resolution HST images.
We therefore examined by eye every galaxy of the H sample that was attributed a counterpart in the MIPS image to find this type of problematic cases. To identify quiescent galaxies, we relied on the UVJ classification introduced in the previous section. In total, we find 40 clearly incorrect associations over the four CANDELS fields, based on a combination of the UVJ classification and the presence of a likely star-forming candidate nearby, or by significant off-centering of the MIPS emission. Because this approach is hard to replicate and translate to other surveys, we introduce here a systematic and objective procedure to identify this type of problems that does not require examining every galaxy by eye. It also allows us to further refine the flagging and discard not only galaxies that are clearly incorrect associations, but also those that are uncertain, so that we work with a sample that is as clean as possible.
For each UVJ star-forming galaxy in the H sample, we derived their expected main-sequence star formation rate from their redshift and stellar mass, or in other words, the SFR they would have if they were exactly following the main sequence as defined in S15. From this SFR we subtracted the observed, non-dust-corrected SFRUV and used the Kennicutt (1998b) relation to convert the remaining obscured SFR into LIR. We then used the best-fit IR SEDs of S15 to estimate their 24 μm flux. For UVJ quiescent galaxies, we followed a similar procedure where the total SFR was instead taken from the stacking of UVJ quiescent galaxies, as described in the Appendix of S15. This SFR is typically a factor of ten below the main sequence at all stellar masses9.
Using this procedure, we were able to obtain a rough prediction of the MIR output of all the galaxies in the H-band parent sample. Then, for each galaxy with a 24 μm detection, we estimated the reliability of the MIR association. To do so, we took all the galaxies that 1) lay within 4″ of the detection; 2) have a predicted 24 μm flux that is at least a tenth of that predicted for the detection, and 3) have no measured 24 μm (or below 3σ) in the catalog. We then summed all their fluxes, weighted by the MIPS PSF amplitude at their corresponding distance and divided this sum by the predicted flux of the detection. The resulting value gives an estimate of the fraction of the measured flux that can be contaminated by neighboring sources that were excluded from the prior list.
As expected, the vast majority of the sources in the MIPS catalog are classified as reliable identifications: 80% of them have an estimated contamination of zero. We here only used the individual SFRs of galaxies for which this contamination fraction is below 30%. This criterion recovers 27 of the 40 incorrect associations we identified by eye, the remaining 13 galaxies are either not properly deblended on the HST image or their neighbors have incorrect photometric redshifts and their contamination is underestimated. We therefore also excluded these 13 galaxies from our sample.
We note that this flagging does not apply to the sample we used to make the gas mass measurements (Sect. 4). The gas masses were measured by stacking H-band selected galaxies and therefore do not rely on the 24 μm catalogs.
Appendix B: Reliability of the bulge-to-disk decomposition
To test the reliability and quality of our morphological decomposition, we created a large set of simulated galaxies of known profiles and B/T and tried to measure their properties in the presence of photometric noise. To do so, we used GALFIT (Peng et al. 2002) to model 5000 idealized double Sérsic profiles (n = 1 and n = 4) of varying sizes, axis ratios, position angles, and fluxes, and placed these models on empty regions of the real HST images. We then ran both GALFIT and GIM2D trying to retrieve the input parameters.
We find that the total magnitude of the galaxy is always well recovered, except in the case of some catastrophic failures that happened almost exclusively with GALFIT. Enforcing that the measured total magnitude is close to that chosen in input effectively eliminates most of these poor fits. For the real galaxies, we choose to compare the measured total magnitude to that quoted in the CANDELS catalogs, and discard GALFIT runs for which the difference is more than 0.5 mag.
We also find that the bulge-to-disk decomposition is usually very poor at H> 23 because the measured B/T are either very noisy or systematically biased toward roughly equal partition of the flux. For galaxies brighter than H = 23, we show in Fig. B.1 the comparison between the B/T we inserted into the simulation and those that are recovered by GIM2D. We find that the code is able to identify disk-dominated galaxies with great accuracy, while bulge-dominated galaxies and intermediate systems show a slight systematic underestimation: given the choice, GIM2D will tend to place more flux in the disk component than in the bulge. This effect is small, however, and we checked that our conclusions are not affected if we correct for it by adding 0.05 to the B/T> 0.5. We also observe that the uncertainty on the flux of the disk depends on B/T, with brighter bulges leading to more uncertain disk fluxes. For example, assuming a constant mass-to-light ratio, for Mdisk ≃ 2 × 1010 M⊙, the error on Mdisk is 0.04 dex for B/T ≃ 0, and 0.07 dex for B/T> 0.3. It should be noted that these simulations are only able to capture the ability of the codes to recover what was inserted into the simulated image, that is, idealized profiles with realistic photometric noise and neighbor contamination, but it does not allow us to conclude about the reliability of the decomposition in the case of perturbed, irregular or clumpy galaxies, nor does it hint about actually measuring a disk mass (which is done in Sect. 3.2); it does not contain varying mass-to-light ratios, for example. Therefore the real uncertainties on the measurements are probably larger. Still, even doubled, the errors we estimate here are low enough for our purposes.
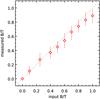 |
Fig. B.1 Comparison between the simulated B/T and that measured by GIM2D for galaxies with H< 22.5. The median measured B/T are shown with empty red diamonds and the error bars give the 16th and 84th percentiles of the distribution. The dotted line in the background gives the expected one-to-one relation. |
The problem of this simulation approach is that we can only test our procedure against idealized galaxy profiles. To ensure that our results are not strongly biased by our decomposition approach, we also ran the same decomposition of the real, observed profiles using GALFIT in parallel. The same images and segmentations were used, the only difference was that we allowed for some small position offset between the bulge and disk. The minimization procedure was also different between both codes, and therefore different results were usually obtained for the same data, providing an estimate of the uncertainty on the decomposition. Since GALFIT requires an initial guess of the fit parameters, we used the single-component morphological parameters measured by van der Wel et al. (2012), who fit a single Sérsic profile to the H-band image of each galaxy in the CANDELS catalogs of GOODS-South, UDS, and COSMOS. We complemented these measurements by running similar fits in GOODS-North. These parameters were used to set the initial size, axis ratio, and position angle of both the disk and bulge components, while the initial flux of each component was set to half the total flux of the galaxy (i.e., an initial B/T = 0.5). We then ran GALFIT, leaving every parameter free, including the position of each component, with a maximum offset between both components of 10 pixels (in practice, the results are essentially the same if we do not allow for such offsets).
We checked that our conclusions are not affected if we only keep the galaxies for which the two codes agree (variation of B/T smaller than 0.15), or if we used only the decomposition provided by GALFIT. In the end, we preferred to used the results provided by GIM2D since this code does not require choosing starting conditions, which are known to influence the final result of GALFIT strongly owing to the presence of local minima in the χ2 (e.g., Lang et al. 2014). We also compared our results against the values obtained by running MegaMorph (Häussler et al. 2013; B. Häussler, priv. comm.). Since MegaMorph does not force the Sérsic index of the bulge component to be equal to nbulge = 4, we only performed the comparison against galaxies that MegaMorph chose to fit with nbulge> 2. We find a scatter in B/T of about 20%, consistent with that found when comparing the results of GALFIT and GIM2D.
Appendix C: Effect of the UVJ selection on the gas mass measurements
 |
Fig. C.1 Same as Fig. 10, but here black diamonds show the measured SFRs and Mgas of our chosen sample, while blue (red) diamonds show the change in these values when we shift the UVJ dividing line toward the star-forming (quiescent) region by 0.1 mag. |
It has been shown that the properties of the SFR−M∗ relation, that is, its slope but also its scatter, are very sensitive to the sample selection (e.g., Speagle et al. 2014). We here used the standard UVJ color−color diagram to isolate quiescent galaxies, and although this selection has been widely used in recent literature (e.g., Whitaker et al. 2012, 2014; Muzzin et al. 2013; Bruce et al. 2014; Lang et al. 2014; Straatman et al. 2014; Pannella et al. 2015), its reliability can still be questioned. While the quiescent and star-forming clouds can be easily identified on this diagram (see, e.g., Fig. 5), there is a non-negligible amount of galaxies in between, populating what is often referred to as the green valley. The dividing line defined by Williams et al. (2009) arbitrarily cuts through this population, and it would be unwise to blindly consider that a green valley galaxy slightly above that line is quiescent and that a similar galaxy slightly below the line is star forming.
One way to circumvent this problem is not to apply any selection of star-forming galaxies in the first place and identify the main sequence as the ridge (or mode) of the galaxy distribution on the SFR−M∗ plane. This was for instance done in Magnelli et al. (2014) and Renzini & Peng (2015). However, this approach is only feasible in samples that are not SFR selected. Building such a sample requires using SFRs that are not fully based on the FIR and that are therefore potentially unreliable (one exception is the deep Hα data of the SDSS, as in Renzini & Peng 2015, but translating this study into the distant Universe is currently beyond our reach). Of course, this is not applicable to stacking analyses either, for which the SFR is only determined a posteriori.
Returning to the UVJ selection, there are two ways our study might be affected by this arbitrary dividing line. On the one hand, the selection may be too strict, and we might discard some galaxies from our sample that are still forming stars at non-negligible rates, but have colors similar to that of quiescent galaxies because of peculiar combination of star formation history and dust content. On the other hand, the selection may be too loose, and our star-forming sample might contain a number of quiescent galaxies. We expect both effects to occur most frequently for the most massive galaxies, where dust is more abundant and where most quiescent galaxies are found. The first alternative can be addressed by considering the position of UVJ quiescent galaxies in the SFR−M∗ plane. There are indeed a few genuinely star-forming galaxies that are classified as UVJ quiescent. However, these galaxies tend to have systematically lower star formation rates than UVJ star-forming galaxies. Therefore, including these mistakenly identified galaxies in our sample would most likely flatten the main sequence even more. The second alternative is probably more worrisome, as the drop of the SFE we observe in massive galaxies might be created by quiescent galaxies polluting our sample. One interesting observation to make out of Fig. 8 (and that can be made more quantitatively by studying the distribution of SFR around the median value Ilbert et al. 2015; Schreiber et al. 2015) is that the mode of the SFR distribution at a given stellar mass (approximated here by the running median) coincides with the average value obtained from the stacked measurements. This means that although our sample is SFR-selected, the number of galaxies below our SFR detection limit is small enough that their effect on the average trend is marginal. For galaxies more massive than 5 × 1010 M⊙, where the bending of the sequence is most pronounced, 79% of the UVJ star-forming galaxies are detected in the FIR. Therefore, the contamination of genuinely quiescent galaxies of the UVJ star-forming sample in this stellar mass range must be reasonably small (i.e., a maximum of 20%).
Nevertheless, in an attempt to quantify how our results are influenced by the choice of the UVJ dividing line, we replicated our SFE measurements by stacking two different additional samples that were built by slightly shifting the UVJ dividing line by ±0.1 magnitude. The resulting SFE and fgas are shown in Fig. C.1. As can be seen from this figure, moving the dividing line further into the quiescent cloud (red points) or further into the star-forming cloud (blue points) does not affect fgas in any statistically significant way. In both cases, we still observe a drop of SFE, although the amplitude of this drop does vary, in this case mostly because of a change of SFR.
This can be put in perspective with the work of Arnouts et al. (2013), who found that the sSFR of a galaxy can be inferred from its position on the NrK diagram, which is conceptually similar to the UVJ diagram10, with an sSFR that continuously increases as a function of the distance to the dividing line. According to Arnouts et al. (2013), using a stricter UVJ selection should bias our sample toward galaxies with a higher sSFR, hence, at fixed mass, with a higher SFR, which is what we observe for the most massive bin. In this context, the fact that the gas mass does not change substantially is particularly interesting, and it is another hint that the mechanism responsible for the bending of the main sequence, whatever it is, mostly affects the SFE and not the gas supply.
All Tables
All Figures
 |
Fig. 1 Main sequence of star-forming galaxies at different redshifts. Solid circles and fits (solid black line and dotted colored lines) are taken from S15. Statistical error bars are smaller than the symbols. We here focus on a redshift range centered on z = 1, which is highlighted in this plot. There, to illustrate the change of slope of the main sequence, we show as a gray solid line the extrapolation of the low-mass sSFR ≡ SFR /M∗, with a slope of unity. The gray dashed line and the arrow indicate the region of this diagram within which we perform the morphological decomposition of the HST light profiles of z = 1 galaxies (Sect. 2.3). We also show for reference the main sequence as seen in the Herschel Reference Survey at z = 0 (see Ciesla et al. 2016). |
| In the text | |
 |
Fig. 2 Stellar mass distribution of the various samples at z = 1 that we consider for the morphological decomposition (Sect. 2.3). Each line corresponds to a step of the selection process, progressively decreasing the number of objects in the sample as in Table 1. The black solid line shows the distribution of our parent sample, containing all the galaxies at 0.7 <z< 1.3 with M∗> 2 × 1010 M⊙ and accurate determination of both redshift and stellar mass. The blue solid line is our H-sample, after removing close pairs and IRAC power-law AGNs from the parent sample. The orange solid line shows galaxies in the H-sample that are classified as UVJ star-forming (Eq. (1)). The red solid line is our IR-sample of galaxies with a MIR or FIR detection. Finally, the dotted line indicates the number of those galaxies for which we can reliably decompose the light profile. |
| In the text | |
 |
Fig. 3 Example bulge-to-disk decomposition of an H = 22.2 galaxy from the GOODS-South field, which is among the faintest galaxy in our sample. The first column shows the observed HST WFC3 image of the galaxy, and we also provide its main physical properties in the top left corner. The second column shows the best-fit disk (top) and bulge (bottom) components as extracted by GIM2D. The third column shows the residual of the image after subtracting the bulge (top) and disk (bottom) to visualize the profile of the other component. Finally, the fourth column shows the residual image after both components are subtracted. The best-fit parameters are given in the top right corner. |
| In the text | |
 |
Fig. 4 Relation between the total stellar mass (M∗) estimated by fitting the integrated multi-wavelength photometry of the whole galaxy and the measured luminosity from the HST H-band flux (without k-correction) for a sample of disk-dominated (B/T< 0.2, left) and bulge-dominated galaxies (B/T> 0.8, right). Individual galaxies are shown with filled colored circles. The best-fit relation is shown with a straight line, and the dispersion around this relation is shown with light solid lines on each side. The global dispersion is given in the top left corner of each plot and is computed from the median absolute deviation (MAD) using 1.48 × MAD(ΔM∗). |
| In the text | |
 |
Fig. 5 Location of galaxies from the H sample with varying mass-weighted B/T on the UVJ diagram (left: B/T< 0.2, middle: 0.2 <B/T< 0.6, right: B/T> 0.6), using the total magnitudes of each galaxy. The dotted line shows the dividing line between the star-forming and quiescent populations defined in Eq. (1). It is clear that both bulge- and disk-dominated galaxies occupy very different regions of the diagram, illustrating the good agreement between the colors and morphology. Intermediate galaxies with roughly equal mass in the disk and bulge (middle panel, ⟨B/T⟩ = 0.4) are spread over the two regions, with a tendency for being preferentially in the quiescent region. |
| In the text | |
 |
Fig. 6 Mean stacked FIR SEDs of star-forming galaxies in our z = 1 sample, split into four mass bins. The broadband photometry (open diamonds) is taken from S15. The fit to the stacked measurements is performed using the dust models of Galliano et al. (2011). It is apparent from this figure that massive galaxies (in red) have a colder dust temperature. This can be clearly seen from the peak wavelength of the best-fit model, or indirectly from the flux ratio S500/S100. |
| In the text | |
 |
Fig. 7 Left: comparison of two independent estimates of the total (H i + H2) gas masses for the HRS galaxies, either using the dust mass and the metallicity as described in Sect. 4.3 (x axis) or using a more direct measurement from H i+CO spectroscopy (y axis). The black solid line shows the one-to-one relation, while the dotted line gives the best-fit linear trend (slope: 1.03 ± 0.03). Right: difference between these two independent gas mass estimates as a function of stellar mass. The black solid line is the line of perfect agreement, while the dotted line is the best-fit linear trend (slope: 0.01 ± 0.04). |
| In the text | |
 |
Fig. 8 Upper panel: location of galaxies from the IR-sample with varying B/T on the SFR−M∗ plane, using the stellar mass and star formation rate (IR+UV) of the whole galaxy. On all plots, the vertical dotted line shows our adopted stellar mass cut, the horizontal dotted line is the 90% completeness in SFR, and the solid black line shows the locus of the z = 1 main sequence as observed through stacking in S15, while the solid gray line shows the extrapolation of the low-mass trend assuming a slope of unity, as observed at lower stellar masses (see Fig. 1). In each column, galaxies of different B/T are plotted. In the rightmost panel, we show all galaxies regardless of their B/T. The solid blue lines show the running median of the sample. Lower panel: same as upper panel, but on the SFR−Mdisk plane. |
| In the text | |
 |
Fig. 9 Same as the upper panel of Fig. 8, but this time varying the Sérsic index n. |
| In the text | |
 |
Fig. 10 Left: relation between the SFE = SFR/Mgas and the stellar mass (M∗) for main-sequence galaxies at z = 1. Colored diamonds show the measured SFEs and M∗ of our stacked sample, the color being associated with the stellar mass as in Fig. 6. The best-fit power law to our measurements, excluding the most massive point, is given with a black solid line (Eq. (9)). Right: gas fraction (fgas ≡ Mgas/ (Mgas + M∗)) as a function of the stellar mass (M∗) for main-sequence galaxies at z = 1. The legend is the same as in the left figure, and here the solid black line gives the value of fgas computed using the best-fit Mgas − M∗ relation, also excluding the most massive point in the fit. The resulting expression of fgas is given in Eq. (10). We also show the measured gas fractions by Magdis et al. (2012) at z = 2 with a dashed gray line and by Santini et al. (2014) at z = 1 with a dot-dashed gray line. |
| In the text | |
 |
Fig. 11 Ratio between the dust mass (Mdust) and the total infrared luminosity (LIR) as a function of the stellar mass for stacked galaxies at z = 1. Colors are the same as in Fig. 10. We overplot a linear fit (in log space) of the first three mass bins with a solid black line. |
| In the text | |
 |
Fig. 12 Left: relation between the specific SFR (sSFR = SFR/M∗) and the stellar mass (M∗) at various redshifts. Our z = 1 stacked measurements from S15 are shown with empty diamonds, and the average values of the star-forming HRS galaxies are shown with empty circles. The associated error bar is the error on the mean, not the dispersion of the sample. We compare these measurements to the z = 2 values obtained by Magdis et al. (2012) for star-forming BzK galaxies. Right: same as left, but replacing the sSFR by the star formation efficiency (SFE = SFR/Mgas). The diamonds and circles use the gas mass estimated in this paper, while the empty squares come from Magdis et al. (2012) and were computed with the same method. We also show for reference the measurements of Saintonge et al. (2011b) with empty gray circles. Their study only included H2 in Mgas, therefore we rescaled their measurement to include H i assuming Rmol = log 10(MH2/MH i) = 0.425 (log 10(M∗/M⊙)−10.7)−0.387 (Saintonge et al. 2011a, Fig. 9 and Table 4). We also caution that the sample selection in Saintonge et al. (2011b) is different from ours. |
| In the text | |
 |
Fig. 13 Evolution of the mass-weighted quenching and downfall rate densities with redshift. The red curve shows the time derivative of the stellar mass density of UVJ quiescent galaxies, which we assume are produced by a fast-quenching mechanism. The blue curve shows the star formation density that is lost because of the lowered SFE in massive galaxies, which we call the slow-downfall rate. The shaded regions in the background give the uncertainty on both measurements. |
| In the text | |
 |
Fig. B.1 Comparison between the simulated B/T and that measured by GIM2D for galaxies with H< 22.5. The median measured B/T are shown with empty red diamonds and the error bars give the 16th and 84th percentiles of the distribution. The dotted line in the background gives the expected one-to-one relation. |
| In the text | |
 |
Fig. C.1 Same as Fig. 10, but here black diamonds show the measured SFRs and Mgas of our chosen sample, while blue (red) diamonds show the change in these values when we shift the UVJ dividing line toward the star-forming (quiescent) region by 0.1 mag. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


