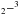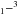| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 26 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321171 | |
| Published online | 06 November 2013 | |
Survival of molecular gas in cavities of transition disks⋆
I. CO
Max-Planck-Institut für Extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching, Germany
e-mail: simonbruderer@gmail.com
Received: 26 January 2013
Accepted: 26 July 2013
Context. Planet formation is closely related to the structure and dispersal of protoplanetary disks. A certain class of disks, called transition disks, exhibit cavities in dust images at scales of up to a few 10s of AU. The formation mechanism of the cavities is still unclear. The gas content of such cavities can be spatially resolved for the first time using the Atacama Large Millimeter/submillimeter Array (ALMA).
Aims. We develop a new series of models to simulate the physical conditions and chemical abundances of the gas in cavities to address the question whether the gas is primarily atomic or molecular inside the dust free cavities exposed to intense UV radiation. Molecular/atomic line emission by carbon monoxide (CO), its isotopologues (13CO, C18O, C17O, and 13C18O) and related species ([C i], [C ii], and [O i]) is predicted for comparison with ALMA and the Herschel Space Observatory.
Methods. We use a thermo-chemical model, which calculates the radiative transfer both in lines and the continuum, and solves for the chemical abundances and gas temperature. The model is based on our previous work, but includes several improvements. We study the dependence of CO abundances and lines on several parameters such as gas mass in the cavity, disk mass and luminosity of the star.
Results. The gas can remain in molecular form down to very low amounts of gas in the cavity (~1% of MEarth). Shielding of the stellar radiation by a dusty inner disk (“pre-transition disk”) allows CO to survive down to lower gas masses in the cavity. The column densities of H2 and CO in the cavity scale almost linearly with the amount of gas in the cavity down to the mass where photodissociation becomes important. The main parameter for the CO emission from cavity is the gas mass. Other parameters such as the outer disk mass, bolometric luminosity, shape of the stellar spectrum or PAH abundance are less important. Since the CO pure rotational lines readily become optically thick, the CO isotopologues need to be observed in order to quantitatively determine the amount of gas in the cavity. Determining gas masses in the cavity from atomic lines ([C i], [C ii], and [O i]) is challenging.
Conclusions. A wide range of gas masses in the cavity of transition disks (~4 orders of magnitude) can be probed using combined observations of CO isotopologue lines with ALMA. Measuring the gas mass in the cavity will ultimately help to distinguish between different cavity formation theories.
Key words: protoplanetary disks / stars: formation / astrochemistry / methods: numerical / radiative transfer
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Planets form in accretion disks around young stars. A detailed understanding of the evolution and dissipation of protoplanetary disks is thus crucial to constrain theories of planet formation (see Armitage 2011, for a recent review). An important stage of the evolution is the phase of gas dispersal which sets an end to the formation of (gas giant) planets. While early gas-rich protoplanetary disks around classical T Tauri stars and late, gas-poor debris disks have been studied in detail (Wyatt 2008; Williams & Cieza 2011 for recent reviews), the transitional phase between these two stages remains enigmatic.
The so-called transition disks with ongoing evolution in their dust and/or gas structure have so far mostly been studied by their continuum emission. Their spectral energy distributions (SEDs; e.g., Strom et al. 1989; Skrutskie et al. 1990; Calvet et al. 2002, 2005; D’Alessio et al. 2005; Espaillat et al. 2007, 2008; Merín et al. 2010; Currie & Sicilia-Aguilar 2011; Cieza et al. 2012; Romero et al. 2012) have strong excess over the stellar photosphere at >20 μm, but no or little excess at shorter wavelengths. This was interpreted with an absence of small and warm dust from the inner part of the disk, with hole sizes from ~5 to ~50 AU. Direct mapping with submillimeter interferometry (Dutrey et al. 2008; Brown et al. 2008, 2009; Andrews et al. 2011, hereafter A11; and Mathews et al. 2012) directly reveal the larger of these dust holes. A subclass of transition disks1 shows evidence of warm optically thick dust near the star in their SED (e.g., Brown et al. 2007; Espaillat et al. 2010), indicative of a dust gap rather than a dust hole.
In contrast, the gas content of transition disks has received much less attention and has been focused largely on Hα studies probing the ionized gas accreting onto the star (e.g., Cieza et al. 2010, 2012; Romero et al. 2012; Espaillat et al. 2012). Little is known about the neutral gas inside dust cavities and it is not even clear how to trace it. Can molecules actually survive inside dust cavities? In the absence of small dust grains, the molecules are not protected from the intense stellar UV radiation by dust shielding. Moreover, the formation of the most basic molecule, H2, is limited in the absence of small dust grains. Nevertheless, pioneering observations at near-IR wavelengths have detected rovibrational emission of CO at 4.7 μm in some sources indicating the presence of hot molecular gas inside their dust cavities (Salyk et al. 2007, 2009, 2011; Pontoppidan et al. 2008; Brittain et al. 2007; Brown et al. 2012). In a few cases, spectrally and spatially resolved lines allow kinematic modeling and point to different inner radii of the CO emission and the dust cavity (Pontoppidan et al. 2008; Brown et al. 2012). However, these lines only trace hot gas (≳300 K) in which the vibrational levels are excited and they cannot be used to constrain the total amount of gas, thought to be at lower temperatures (≲few 100 K). Millimeter/submillimeter observations of pure rotational lines of CO are much better suited to constrain the gas mass in the cavity, but have so far been plagued by (too) low angular resolution and sensitivity of current (sub)millimeter interferometers (e.g. Dutrey et al. 2008; Lyo et al. 2011).
The Atacama Large Millimeter/submillimeter Array (ALMA2) allows the cold gas in cavities of transition disks to be studied for the first time (Casassus et al. 2013; van der Marel et al. 2013). Low-J CO lines observed by ALMA at high angular resolution have several advantages over the near-IR lines. The millimeter lines have low critical densities and are thus in local thermal equilibrium (LTE) which makes the excitation calculation simple. The level energies are low so the bulk of the mass, where near-IR lines are not excited, can be probed. Due to their long wavelengths, the lines are less prone to dust absorption than near/mid-IR lines as e.g. the rovibrational lines of CO at 4.7 μm or the optical [OI] 6300 Å line (e.g., Acke & van den Ancker 2006). Isotopologues of CO can be observed, which allows a wide range of column densities to be measured if the lines of the main isotopologue are optically thick. If gas is present in the cavity, but the conditions do not allow the formation of CO, carbon is likely in the form of neutral (C) or ionized atomic carbon (C+) and oxygen as neutral O. Neutral carbon has lines at submillimeter wavelengths ([C i] 3P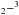 P1 at 370 μm/809 GHz, and [C i] 3P
P1 at 370 μm/809 GHz, and [C i] 3P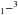 P0 at 609 μm/492 GHz) and can thus also be observed by ALMA. Ionized carbon has the fine structure line [C ii] 2P
P0 at 609 μm/492 GHz) and can thus also be observed by ALMA. Ionized carbon has the fine structure line [C ii] 2P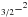 P1/2 at 158 μm and neutral oxygen [O i] 3P
P1/2 at 158 μm and neutral oxygen [O i] 3P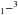 P2 at 63 μm and [O i] 3P
P2 at 63 μm and [O i] 3P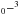 P1 at 145 μm which can be observed by the Herschel Space Observatory.
P1 at 145 μm which can be observed by the Herschel Space Observatory.
Even if the millimeter lines of CO are detected, however, the observed emission cannot be directly translated into a gas mass since it is unclear a priori to what extent the gas is largely molecular or atomic, i.e., whether the molecules can actually survive the strong UV radiation inside the dust free cavity. To determine the amount of gas that is present inside a dust cavity from observations, the physical and chemical structure of the gas needs to be modeled. We present here a set of thermo-chemical models to explore under which conditions molecules like CO are indeed present inside dust cavities and can be used to trace the gas mass. This, in turn, is relevant to constrain different mechanisms that have been proposed for the dust cavity formation.
Modeling gas line emission from protoplanetary disks is a complex task, because the line emission depends on various parameters (e.g. abundance, gas temperature, collision partner density, velocity structure, ...). A comprehensive model should thus calculate these physical and chemical parameters self-consistently for the whole disk structure. Thermo-chemical models of protoplanetary disks solve the problem in a similar way as classical PDR models (e.g. Tielens & Hollenbach 1985): using the local UV radiation field, a chemical network simulation calculates the abundance of various atoms and molecules. The abundances feed into the calculation of heating and cooling rates to obtain the gas temperature. Since the chemical network simulation depends on the gas temperature, the problem needs to be solved iteratively. Various thermo-chemical models of protoplanetary disks have been presented in the past (e.g. Kamp & van Zadelhoff 2001; Glassgold et al. 2004; Gorti & Hollenbach 2004; Jonkheid et al. 2004; Nomura & Millar 2005; Aikawa & Nomura 2006; Woitke et al. 2009; Woods & Willacy 2009; Ercolano et al. 2009; Bruderer et al. 2012). With the exception of Jonkheid et al. (2006), who modeled the molecular emission of one particular transition disk, most modeling effort focused on younger, gas rich disks rather than transition disks. Cleeves et al. (2011) have also modeled a transition disk, but they focus on the outer disk and assume the cavity to be gas free.
In this work, we use our thermo-chemical model, which was presented together with benchmark tests in Bruderer et al. (2012), to calculate a grid of transition disk models. The goal of this work is to predict observables (e.g. line fluxes or images) of a transition disk with a given amount of dust/gas inside the cavity. We thus choose to use a simple approach which is based on a parameterized density structure. This structure was found by A11 to simultaneously fit the SED, submillimeter images and visibilities of twelve transition disks. Besides being based on observational foundations, another advantage of this approach is that one can relate the amount gas in a generic way to predicted/observed line emission, without referring to one particular dust removal scenario. We put the initial focus on carbon monoxide (CO), atomic carbon (C, C+) and oxygen (O) and will discuss other species later. In an extension to this work, we plan to couple our model to the dust evolution models by Birnstiel et al. (2010, 2011, 2012b) and Pinilla et al. (2012b), in order to study the grain growth and planetary clearing scenario in more detail.
The paper is organized as follows: in Sect. 2 we summarize the model used in this work and explain the free parameters. The parameters chosen and caveats of the work are discussed next. The following sections present the model results: we first show the physical structure (e.g. density, temperature) of one representative model in Sect. 3. The abundance structure of CO, H2, C and C+ depending on the key parameters are then discussed in Sect. 4. In Sect. 5 we discuss the CO pure rotational line emission and line opacity effects. The implications of our models to use rotational lines of CO and its isotopologues as tracers of the gas mass in the gap are discussed in Sect. 6. The paper ends with a conclusion section.
2. Model
We use the radiative transfer, chemistry and thermal-balance model introduced by Bruderer et al. (2012, hereafter BR12). For the current application, we have implemented several improvements and minor changes, which are described in Appendix A. Details of the model and results of benchmark tests are reported in BR12, however a brief outline is given here.
Starting from an input density structure, the model solves the continuum radiative transfer problem using a 3D Monte-Carlo method to obtain the dust temperature and local radiation field for UV to millimeter wavelengths. Non-isotropic scattering is accounted for. In a next step, a chemical network simulation is used to obtain the chemical composition. The reaction network is based on a subset of the UMIST 06 network (Woodall et al. 2007) and consists of ~110 species and ~1500 reactions. Freeze-out, thermal and non-thermal evaporation and some basic grain-surface reactions of species hydrogenating on the grain surface (e.g. g:O → g:OH → g:H2O, see Visser et al. 2011) are included as well as formation of H2 and CH+ on the surface of PAHs (Jonkheid et al. 2006). Photodissociation rates are obtained using the molecular cross-section (van Dishoeck et al. 20063) and the far-ultraviolet (FUV) intensity from the continuum transfer calculation, so that the effect of different central stars can be investigated. X-ray ionization and the effect of hot (vibrationally excited) H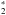 are also accounted for.
are also accounted for.
The chemical abundances are then used as input for a non-LTE excitation calculation of the main cooling atoms and molecules (e.g. O, C+, CO, ...). An escape probability method is used and pumping by the dust continuum is accounted for. Molecular data for collisions and radiative rates are mainly taken from the LAMDA database (Schöier et al. 2005). The gas temperature is obtained from the balance between heating processes (e.g. photoelectric heating on PAHs or small grains) and cooling processes (e.g. by line radiation or gas-grain collisions) similar to classical PDR models (e.g. Tielens & Hollenbach 1985; Sternberg & Dalgarno 1989; Kaufman et al. 1999; Meijerink & Spaans 2005). Since the chemical composition and the molecular excitation depend on the gas temperature, the problem has to be solved iteratively. Once a solution is found, spectral image cubes are derived using a raytracer.
2.1. Parameters of the model
2.1.1. Density structure
The density structure used for our models follows the simple parametric prescription proposed by A11. The structure is motivated by a simple viscous accretion disk model with the viscosity not changing with time and spatially distributed as ν ∝ Rγ (Lynden-Bell & Pringle 1974; Hartmann et al. 1998). Dust and gas are significantly depleted in an inner cavity. A11 use the density structure to perform a simultaneous SED, submillimeter image and visibility fitting and find good agreement for all of the twelve studied transition disks. They note that several parameters are degenerate and also depend on the assumed dust properties. Direct observational constraints on the radial or vertical structure of the gas are difficult to obtain (e.g. Brown et al. 2012). We thus restrict our work to a study of the dependence on certain parameters. In the following, we refer to dust as a small <cm size population of dust grains which contribute considerably to the opacity at UV to millimeter wavelengths.
Figure 1 shows the surface density and vertical structure used in our work. The surface density (Fig. 1a) follows ![\begin{equation} \Sigma_{\rm gas} = \Sigma_{\rm c} \left( \frac{R}{R_{\rm c}} \right)^{-\gamma} \exp\left[- \left( \frac{R}{R_{\rm c}} \right)^{2-\gamma} \right]\cdot \end{equation}](/articles/aa/full_html/2013/11/aa21171-13/aa21171-13-eq29.png) (1)In the outer disk R > Rcav a gas-to-dust ratio Δgas/dust = Σgas/Σdust is used. For
(1)In the outer disk R > Rcav a gas-to-dust ratio Δgas/dust = Σgas/Σdust is used. For 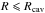 , the gas surface density is lowered by a factor of δgas with respect to the outer disk and by δdust for the dust. This remaining dust is required to reproduce the near-IR excess observed toward a class of transition disks (Brown et al. 2007; Espaillat et al. 2010; A11). Within the dust sublimation radius
, the gas surface density is lowered by a factor of δgas with respect to the outer disk and by δdust for the dust. This remaining dust is required to reproduce the near-IR excess observed toward a class of transition disks (Brown et al. 2007; Espaillat et al. 2010; A11). Within the dust sublimation radius 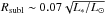 AU (assuming a dust sublimation temperature of ~1500 K; Dullemond et al. 2001), both dust and gas surface density are set to zero. Between the
AU (assuming a dust sublimation temperature of ~1500 K; Dullemond et al. 2001), both dust and gas surface density are set to zero. Between the 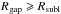 and Rcav, dust is assumed to be absent. In this paper, we refer to the cavity as the region inside Rcav and the gap as the region between Rgap and Rcav.
and Rcav, dust is assumed to be absent. In this paper, we refer to the cavity as the region inside Rcav and the gap as the region between Rgap and Rcav.
 |
Fig. 1 Schematic view of the physical structure used in this work and definition of the main parameters. a) Surface density structure. b) Vertical density structure. |
The vertical distribution of densities (Fig. 1b) follows a Gaussian with scale height angle h = hc(R/Rc)ψ. The physical scale height in units of distance is thus H ~ Rh. A11 employed an increased scale height close to the sublimation radius (Rsubl) and the wall of the outer disk (at Rcav) to mimic “puffed-up” structures. However, due to the missing angular resolution of the observations, the inner rim structure is not well constrained and there is a degeneracy between the height of the inner rim and the amount of dust in the inner disk (δdust). Since the main effect of a dusty inner disk is to shield the gap and outer disk from direct stellar irradiation, we only vary δdust and do not increase the scale height.
Dust settling is implemented considering two different populations of grains (small 0.005 − 1 μm and large 0.005 − 1000 μm) following the approach by D’Alessio et al. (2006). The scale height for the small population is set to h, while the scale height of the larger population to χh with χ < 1. The fraction of surface density distributed to the small and large population is Σdust(1 − f) and Σdustf, respectively. For the outer disk (R > Rcav), the dust densities thus read ![\begin{eqnarray} \rho_{\rm dust, small} &=& \frac{(1-f) \, \Sigma_{\rm dust}}{\sqrt{2 \pi} \, R h} \, \exp\left[-\frac{1}{2} \left( \frac{\pi/2 - \theta}{h} \right)^2 \right] \ \ {\rm and}\\ \rho_{\rm dust, large} &=& \frac{ f \, \Sigma_{\rm dust}}{\sqrt{2 \pi} \, R \chi h} \, \exp\left[-\frac{1}{2} \left( \frac{\pi/2 - \theta}{ \chi h} \right)^2 \right] \ . \end{eqnarray}](/articles/aa/full_html/2013/11/aa21171-13/aa21171-13-eq49.png)
2.1.2. Dust and PAH opacities
Dust opacities for a standard ISM dust composition following Weingartner & Draine (2001) are used, consistent with A11. The mass extinction coefficients are calculated using Mie theory with the miex code (Wolf & Voshchinnikov 2004) and optical constants by Draine (2003) for graphite and Weingartner & Draine (2001) for silicates. Figure 2 shows the absorption and scattering opacities for the large grain population (0.005 μm−1 mm) and the small grain population (0.005 − 1 μm). They are consistent with A11.
The PAH opacities presented in Fig. 2 are given for an ISM abundance and all PAHs assumed to be neutral and in C100H25. The ISM PAH-to-dust mass ratio is 5% (Draine & Li 2007) corresponding to a C100H25 abundance of 4 × 10-7 relative to hydrogen. The PAH opacities are calculated from Li & Draine (2001) and Draine & Li (2007) using the routines by Visser et al. (2007). In our model, PAHs are mainly important as additional absorbers of UV/optical photons, to heat the gas through the photoelectric effect, and to provide an additional path for H2 formation (through hydrogenated PAHs). For UV/optical wavelengths, the model PAH opacities for neutral and ionized PAHs are the same. As we make no attempt to model the infrared features of PAHs (see Visser et al. 2007; Geers et al. 2006), the choice of purely neutral PAHs does not affect our results. We use large PAHs with 100 carbon atoms, since smaller PAHs are predicted to be photodissociated by the strong UV field close to a star (Visser et al. 2007). We assume that PAHs are well mixed with the gas and their density thus scales with the total gas density. PAHs are absent in regions with FUV radiation stronger than 106 times the interstellar radiation field following the results by Visser et al. (2007). We note that observational evidence of PAHs toward several transition disks exist (Brown et al. 2007; Merín et al. 2010) and in one case, PAHs have been imaged to be inside the dust cavity (Geers et al. 2007).
 |
Fig. 2 Dust and PAH opacities. Absorption (κ) and scattering (σ) mass coefficients are given by solid and dashed lines, respectively. |
2.1.3. Other parameters
The elemental composition with respect to the total hydrogen abundance is chosen following Bruderer et al. (2012). We assume about one third of the carbon to be volatile, thus not bound in refractory material (Table 1).
The input stellar spectrum is taken to be a black-body of either 6000 or 10 000 K, in order to study the effect of different amounts of FUV (6−13.6 eV) photons relative to the bolometric luminosity (as for example in T Tauri or Herbig AeBe stars). The fraction of FUV photons fFUV = LFUV/Lbol is 3 × 10-4 (for 6000 K) and 7 × 10-2 (for 10 000 K). The input stellar X-ray spectrum is assumed to be a thermal spectrum of 7 × 107 K within 1−100 keV. The cosmic-ray ionization rate is taken to be 5 × 10-17 s-1. The isotropic interstellar radiation field in the UV (Draine 1978; Draine & Bertoldi 1996) and the cosmic microwave background are also accounted for.
The calculation is carried out on a grid with 100 cells in radial and 80 cells in vertical direction. In vertical direction, the cells are arranged following the scale height at a given radius. In order to properly resolve the inner regions of the inner and outer disk, 50 points are distributed radially in the inner and outer disk each (Fig. 4c).
2.2. Choice of parameters: a grid of models
Since the goal of our study is to understand the physics and chemistry of the gas in the inner dust hole of transition disks rather than reproducing individual objects, we run a grid of models that covers the range of dust structures found by A11. The assumed parameters are summarized in Table 1.
The distribution of gas is not constrained by A11. We assume the gas profile to follow the total dust profile scaled by a factor. In the outer disk, we set the gas-to-dust ratio to Δgas/dust = 100. Within the gap, the gas is scaled by a constant factor of δgas = 10-6 to 1 relative to the density in the outer disk. This is the principal parameter that is varied.
The surface density power-law index is fixed to γ = 1 following A11. We also fix Σc but vary Rc in order to cover the observed surface density profiles (Fig. 3).
We run models both with an inner dusty disk present or absent. Therefore, the dust depletion factor δdust (Fig. 1) is set to δdust = 10-5 or δdust = 10-10. The higher value is about the median found by A11 and yields an optically thick dusty inner disk at UV to optical wavelengths, which can shield the gap from the stellar radiation. The lower value yields an optically thin dusty inner disk. The remaining amount of dust in these models is negligible and an even lower δdust would not change the results. If present, the dusty inner disk extends from the dust sublimation radius to a radius of Rgap = 10 AU. Since the main effect of an inner dusty disk is the shielding of the stellar radiation, which already takes place in the inner wall of the inner disk, models with much smaller gap radii, e.g. Rgap = 1 AU, give very similar results (see Appendix C).
Between a radius of 10 AU and 45 AU, a gap without dust is present. We chose the size of the gap to be relatively large in order to study the physics and chemistry in the gap up to larger radii, which can be probed with current observational facilities. We however note, that the trends found for the 45 AU radius gap also apply to smaller cavity sizes (Appendix C). In the vertical direction, we assume a scale height angle hc = 0.06 rad and a flaring index ψ = 0.2 which is the average of A11. The dust-settling parameters f and χ are fixed to the values by A11.
 |
Fig. 3 Surface density profiles of the observed transition disks (black lines; Andrews et al. 2011) compared to the model surface density profiles used in this work (red lines). Dotted lines indicate regions within the gap. The red and black dots show (Rc,Σc/e). |
The luminosity of the star is assumed to be 1, 3 or 10 L⊙. The X-ray luminosity is taken to be either 1027 or 1030 erg s-1. The higher value corresponds to the X-ray luminosities found toward the disks discussed in A11 (0.5 − 3 × 1030 erg s-1). The lower value yields results both in the chemistry and temperature that are close to X-rays being completely absent.
Parameters of the transition disk models.
2.2.1. Gas and dust masses
The gas- and dust-masses of the outer disk, the gap and inner disk are summarized in Table 2. Models with δgas ≤ 10-1 always have the bulk of the total mass in the outer disk rather than the cavity (gap and inner disk). The amount of 1 Jupiter mass (9.5 × 10-4 M⊙) within the gap is reached for δgas = 3 × 10-1,8 × 10-2, and 3 × 10-2 (for Rc = 25 AU, 50 AU or 100 AU). One Saturn mass (2.9 × 10-4 M⊙) is accordingly reached for δgas = 8 × 10-2,2 × 10-2, and 9 × 10-3.
Gas- and dust-masses of the different models in M⊙.
2.3. Caveats
A number of caveats apply to the models presented here: As discussed in Bruderer et al. (2012), the calculated gas temperature is prone to large uncertainty. A comparison of PDR models run for a density/FUV intensity combination corresponding to the outer disk has revealed a scatter of a factor of a few in gas temperature (Röllig et al. 2007). High-temperature tracers such as ro-vibrational lines (e.g. of CO) or high-J CO lines are more affected by this uncertainty than lower temperature lines (e.g. low-J lines of CO) which form deeper in the disk.
From the comparison of different PDR models and the uncertainty analysis of the chemical network (Vasyunin et al. 2008), we estimate the typical uncertainty of the low-J CO line intensities modeled in this work to be about a factor of two. Since the dynamic range of CO intensities considered here is several orders of magnitude, these uncertainties do not affect our conclusions.
The analytical density structure of our models is a simplification and does not account for the hydrostatic equilibrium of the gas or dust temperature. One of the main effects of the hydrostatic equilibrium is a “puffed-up” inner rim. However, it is unclear at what point such a structure would become unstable and being blown away as a wind. Furthermore, Min et al. (2009) find that the calculation of the vertical structure can lead to density waves propagating on the surface of the disk. In order to resolve these two issues, the structure calculation should be coupled with a hydrodynamical simulation which is beyond the scope of this study and computationally very challenging. Also, the physical mechanism leading to the formation of the dust hole needs to be understood in order to run a more complete simulation.
The dust size distribution and composition is not well constrained from observations and the assumed power-law distributions are only an approximation. In future studies, we plan to incorporate the results of dust evolutionary models (Birnstiel et al. 2010).
Our models are solved for steady-state conditions. While the chemical time-scales are usually short, mixing in vertical or radial direction could smooth out transitions (e.g. Ilgner & Nelson 2006; Heinzeller et al. 2011; Semenov & Wiebe 2011). Abundances of CO isotopologues are approximated by scaling the abundance of the main isotopologue. The CO and H2 photodissociation rate and the C ionization rate are calculated with self- and mutual-shielding factors in a 1+1D way. The accuracy of this treatment has been verified in van Zadelhoff et al. (2003) and Visser et al. (2009).
3. Physical structure
In this section, we discuss the physical structure (density, gas/dust-temperature, ...) of one representative model. For the representative model, we choose Rc = 50 AU, Teff = 10 000 K, Lbol = 10 L⊙, and a X-ray luminosity of LX = 1030 erg s-1 (Table 1).
Figure 4 shows the physical structure of the representative model with δgas = 10-2 and a dusty inner disk present (δdust = 10-5). The different subfigures are given in the (log (r),r/z)-space, so that horizontal lines correspond to a constant height (r/z) and thus to direct rays from a position in the disk to the star. We apply a density cut-off at 105 cm-3, since the column density above it is small and does not contribute to the emission.
 |
Fig. 4 Physical conditions in a representative model (Table 1) with δgas = 10-2 and δdust = 10-5 (dusty inner disk present). Only regions with a gas density larger than 105 cm-3 are shown. The contour lines on the panels match to the lines on the color bars. The panels provide a) gas density structure; b) gas/dust mass ratio; c) calculation grid; d) FUV radiation field; e) visual extinction; f) abundance of PAHs; g) dust temperature; h) gas temperature; i) ratio of gas to dust temperature; j) H2 abundance; k) CO abundance; and l) O abundance. |
The density given in Fig. 4a shows a sharp drop at the cavity radius of 45 AU, due to the scaling of the inner disk density with δgas. The density in the midplane of the inner disk at r < 1 AU is up to 1014 cm-3 even for δgas = 10-2 (label a1). In the gap, the midplane density reaches 109 − 1011 cm-3 (label a2). In the outer disk, the density cuts off to larger radii due to the exponential decrease of the surface density profile (label a3). In the midplane of the outer disk, densities of ~1010 cm-3 are reached. The gas-to-dust ratio in the inner disk (Fig. 4b, label b1) is with 105 a factor of δdust/δgas = 1000 larger compared to the outer disk (100, label b2). The gas-to-dust ratio is not defined in the gap, due to the absence of dust.
The strength of the UV field in units of the interstellar radiation field G0 is given in Fig. 4d. Here, G0 = 1 refers to the interstellar radiation field defined as in Draine (1978) ~2.7 × 10-3 erg s-1 cm-2 with photon-energies Eγ between 6 eV and 13.6 eV. In the inner, upper disk, very high UV strengths of G0 ≳ 109 are reached (label d1), while the inner midplane is shielded from UV radiation (G0 < 1, label d2). In the gap, both shielding by the dusty inner disk and the PAH opacity contribute to the attenuation of the FUV radiation (label d3). In the outer disk, also external radiation from the interstellar radiation field contributes to the FUV field (label d4).
The UV extinction, measured in AV, is given in Fig. 4f. Following BR12, we calculate the extinction from the ratio of the attenuated to the only geometrically diluted flux, τFUV = −ln(Fattenuated/Funattenuated), where F is integrated over the FUV spectrum. In the inner disk, AV = 1 is reached even in the innermost part (label e1). The decrease of height with distance of the AV = 3 surface inside the gap (label e2) indicates that some of the UV radiation is scattered by the small dust of the inner disk into the gap. PAHs do not contribute to the scattering, as their scattering-cross section is small (Fig. 2).
The abundance of PAHs with respect to the ISM abundance is given in Fig. 4f. In the inner, upper disk, PAHs are photodissociated due to the intense UV radiation from the star (label f1). The small dust in the dusty inner disk is able to shield the UV radiation sufficiently to have PAHs surviving (label f2). In absence of a dusty inner disk, PAHs could only survive at radii ≳20 AU (label f3), where geometrical dilution decreases the intensity of the stellar UV radiation sufficiently. The presence of a dusty inner disk has thus influence on the gas in the gap, as it allows PAHs to survive to smaller radii. PAHs affect the gas in the gap through FUV attenuation, the chemistry (H2 formation on PAHs) and gas heating through the photoelectric effect.
The dust temperature Tdust is presented in Fig. 4g. It is only defined in the inner and the outer disk, where dust is present. In the inner upper disk (label g1), the dust heats up to the sublimation temperature of ~1500 K. At the edge of the region where PAHs are present, the additional opacity in the UV leads to additional dust heating, which is seen in the inner disk (label g2). In the midplane of the inner disk, dust temperatures between 100 K and 300 K are found (label g3). The bulk of the outer disk is at dust temperatures between 30 and 100 K (label g4). Dust temperatures are below 30 K only in the outer disk, close to the midplane (label g5).
3.1. Gas temperature
The gas temperature Tgas and the ratio of gas to dust temperature (Tgas/Tdust) are presented in Figs. 4h and 4i, respectively. The latter ratio is only defined in regions where the dust temperature is defined as well.
In the upper atmosphere of the inner disk, gas temperature up to several 1000 K are reached (label h1). In this part of the disk, the main heating mechanism is either coulomb heating through X-rays or collisional de-excitation of Fe ii which is pumped by optical/UV stellar radiation. This back-heating by Fe ii has also been found to be an important heating agent in other models (see Woitke et al. 2009). The main cooling in this region is either through O i or Lyα emission. Moving deeper into the disk (label h2), the H2 abundance is considerable and collisional de-excitation of UV pumped H2 is an important heating mechanism.
Moving to the upper atmosphere at larger radii ≳10 AU, both optical/UV back-heating by atoms and X-ray heating get less effective (label h3) and the gas temperature decreases. Further out, the gas temperature in the upper atmosphere increases again at the radius where PAHs can survive (label h4). Since the PAHs also increase the H2 abundance, through formation of H2 on their surface, heating by UV pumped H2 becomes important. Both at h3 and h4, atomic lines (O i, C ii, Si ii) dominate the cooling. The upper atmosphere of the outer disk (label h7) is heated to several 1000 K by photoelectric heating on PAHs and small grains and also UV pumped H2.
In the midplane of the disk, the gas temperature is generally lower than in the upper atmosphere. In the midplane of the inner and outer disk, Tgas/Tdust is close to 1 (labels i2, i4). For comparison, Tgas/Tdust in the upper atmosphere is a few in the inner disk (label i1) and ~50 in the outer disk (labels i3). In the midplane of the inner disk, at distances R < 1 AU, molecules (CO, H2O) act as heating agents through the pumping by the strong IR radiation field. In this region gas-grain cooling is important despite the high gas-to-dust ratio. Further out (r ≳ 2 AU), the IR radiation field is weaker and the molecules cool, while gas-grain collisions heat the gas. Cosmic-ray heating then also becomes important. In the midplane of the gap (label h5, h6), heating by PAHs and small grains is balanced with molecular and atomic cooling (CO, 13CO and [O i]) . The gas temperature in the gap is still mostly above 100 K, except in the shadow behind the inner disk (label h6). In the gap, dust is absent and neither gas-grain-heating nor -cooling takes part. In the midplane of the outer disk, the gas-grain collisions are again present and gas and dust are well coupled (Tgas/Tdust ~ 1, label i4).
4. Survival of molecules in the cavity
The abundance of H2 and CO for three models with different amounts of gas in the cavity is shown in Fig. 5. The models have δgas = 1,10-4, and 10-6 and a dusty inner disk present. All other parameters are set to the values of the reference model (Table 1).
H 2
 |
Fig. 5 H2 and CO abundance in the representative model (Table 1) with different gas content in the cavity (δgas = 1,10-4 and 10-6) and a dusty inner disk present (δdust = 10-5). Only regions with gas density larger than 105 cm-3 are shown. Upper panels: CO abundance. Lower panels: H2 abundance. |
Molecular hydrogen (H2) in the model with δgas = 1 is photodissociated to fractional abundances below 10-6 in the upper atmosphere of the inner disk (label a1 in Fig. 5). Going deeper into the disk, self-shielding reduces the photodissociation and below a plateau with fractional abundance of 10-4 − 10-2 (label a2), hydrogen is fully in molecular form (label a3). The edge of the dust free gap at r = 10 AU is not seen in the H2 abundance (label a4). This is because H2 can not only form on dust grains, but also through the reaction H− + H → H2 + e−, if this reaction can compete with the (quick) photodetachment of H−. H− is produced by electron attachment of atomic hydrogen. Outside the radius of PAH photodestruction (label a5), hydrogen is fully molecular, because of H2 formation on PAHs. The outer disk is molecular up to large heights, because H2 forms efficiently on dust grains present in the outer disk. We conclude, that for the formation of H2, and to start the chemistry of other species (e.g. CO), either dust or PAHs need to be present to form H2 on the surface or conditions need to allow H2 formation through H + H−.
Under what conditions is H2 formation through H− efficient? Since photodetachment of H− is very rapid, the reaction of H− with H needs to compete with it. The photodetachment rate of H− is ~2 × 10-7 G0nH− cm-3 s-1 for an unshielded 10 000 K blackbody spectrum. The reaction of H− with H on the other hand runs at 1.3 × 10-9nHnH− cm-3 s-1 (Woodall et al. 2007). At the inner edge of the gap (r = 10 AU), the midplane density of the representative model is ~1013δgas cm-3 and the unshielded FUV field corresponds to G0 ~ 3 × 106. Thus, for δgas > 5 × 10-5, the density is high enough for H2 production to be more important than photodetachment. Is the overall rate of H2 formation also considerable? The electron-attachement rate of hydrogen (H + e− → H− + γ) is low, ~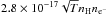 . Assuming all carbon being photoionized (ne− ~ 10-4nH) we can estimate the H2 formation rate under the assumption that all H− is eventually turned into H2. The H2 formation rate then is ~
. Assuming all carbon being photoionized (ne− ~ 10-4nH) we can estimate the H2 formation rate under the assumption that all H− is eventually turned into H2. The H2 formation rate then is ~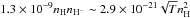 cm-3 s-1. For comparison the H2 formation rate on dust grains is ~
cm-3 s-1. For comparison the H2 formation rate on dust grains is ~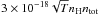 cm-3 s-1, assuming sticking/accommodation coefficients of 1 (an upper limit) and a gas-to-dust ratio of 100. Formation on dust grains is thus a factor of 1000 more efficient. However, even in this model with dusty inner disk present, the gas-to-dust ratio in the inner disk can be much higher than 100 with values of 107 reached (for δgas = 1 and δdust = 10-5) and H2 formation through H− more efficient than on the remaining small amount of dust. We conclude that H2 formation through H− can become more important than formation on dust under the special conditions of high density, high electron abundance, and a high gas-to-dust ratio.
cm-3 s-1, assuming sticking/accommodation coefficients of 1 (an upper limit) and a gas-to-dust ratio of 100. Formation on dust grains is thus a factor of 1000 more efficient. However, even in this model with dusty inner disk present, the gas-to-dust ratio in the inner disk can be much higher than 100 with values of 107 reached (for δgas = 1 and δdust = 10-5) and H2 formation through H− more efficient than on the remaining small amount of dust. We conclude that H2 formation through H− can become more important than formation on dust under the special conditions of high density, high electron abundance, and a high gas-to-dust ratio.
We now study the effect of lowering the gas mass in the cavity (decreasing δgas). Lowering δgas from 1 has different effects on our model. First, the gas density at a given point inside the cavity is scaled down by a factor δgas. Second, since we assume PAHs to be mixed with the gas, the PAH density is also lowered so the FUV radiation can penetrate deeper into the disk. The importance of PAHs to the FUV shielding is understood by their contribution to the opacity shown in Fig. 2. In the models discussed here, the PAH abundance is a factor of 10 lower, but the gas-to-dust ratio a factor of 105δgas higher, so the PAHs dominate the FUV opacity in the dusty inner disk for δgas ≳ 10-4.
The effect of stronger local FUV irradiation due to less shielding by PAHs is seen in the model with δgas = 10-4. The H/H2 transition moves down (label b1) and due to the reduced density, the region outside the PAH photodestruction radius extending to larger height (label a5) is not found in this model (label b2). The steeper gradient of the H/H2 transition in this model is explained by a thermo-chemical feedback loop: models with lower δgas form H2 deeper in the disk where less FUV radiation penetrates. The heating is thus less efficient and the gas temperature lower at the H/H2 transition. Conversely, models with higher δgas have higher temperatures at the H/H2 transition and the H2 formation rate is suppressed by the higher temperature.
The effect of a decreased density on the H2 abundance can be roughly understood by the fact that gas formation rates scale as n2, while photodissociation rates only scale with the density n. Assuming a simplistic H/H2 chemistry, only considering H2 formation with rate coefficient F and H2 photodissociation with rate coefficient DG0, the rate equations for the H2 abundance reads ṅH2 = Fn(n − 2nH2) − DG0nH2. Defining α = nF/(DG0), the H2 density in steady state is 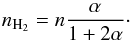 (4)Consequently, the fractional abundance of H2 (nH2/n) scales about linearly with α ∝ n/G0 until it settles off at 1/2 for high values of α.
(4)Consequently, the fractional abundance of H2 (nH2/n) scales about linearly with α ∝ n/G0 until it settles off at 1/2 for high values of α.
Decreasing δgas further to δgas = 10-6 results in the presence of H2 within the cavity only in a geometrically thin layer close to midplane (label c1). In the gap (label c2), hydrogen is not in full molecular form anymore, but still reaches appreciable fractional abundances of ~10-2 − 0.1.
In the outer disk, the amount of H2 does not differ between the three models with different δgas, because the upper layers of the outer disk, where H2 photodissociation proceeds, is posed to direct irradiation by the star independent of δgas. Lowering δgas however allows direct irradiation of the outer disk wall to regions closer to the midplane. Thus, photodissociation can proceed along the wall.
CO
The chemistry of carbon monoxide (CO) is more complex compared to H2. In this section we concentrate on CO, the chemistry of C and C+ will be discussed in more detail in Sect. 4.2. First looking at the model with δgas = 1, we find CO like H2 to be photodissociated in the upper atmosphere (label d1). In this region, carbon is mainly in the form of C+. Moving deeper into the disk, a thin layer of neutral carbon connects to the zone where carbon is fully bound in CO (label d2). For this particular model, the C+/C/CO transition is at larger heights in the atmosphere compared to the H/H2 transitions. This is because, contrary to H2, CO is formed more quickly at higher temperatures through CH+. As soon as a certain level of H2 is available in a high temperature region, C+ reacts with H2 to CH+. This reaction has a high energy barrier (4640 K), but hot (vibrationally excited) H can help to overcome this barrier. The CH+ is then converted by reactions with O to CO+ and with H2 to HCO+ which recombines to CO (Jonkheid et al. 2007). Moving outward to larger radii, the CO abundance increases at the edge of the PAH destruction radius (label d3), because additional H2 (label a5) leads to more efficient CO formation and a decreased photodissociation rate, due to mutual CO-H2 shielding. In the outer, upper disk, a “warm finger” (label d4) of CO is found, where CO formation is again initiated by CH+ (see e.g. BR12).
can help to overcome this barrier. The CH+ is then converted by reactions with O to CO+ and with H2 to HCO+ which recombines to CO (Jonkheid et al. 2007). Moving outward to larger radii, the CO abundance increases at the edge of the PAH destruction radius (label d3), because additional H2 (label a5) leads to more efficient CO formation and a decreased photodissociation rate, due to mutual CO-H2 shielding. In the outer, upper disk, a “warm finger” (label d4) of CO is found, where CO formation is again initiated by CH+ (see e.g. BR12).
Close to the midplane of the model with δgas = 1, carbon is not always in the form of CO, unlike hydrogen in H2. In the inner disk (label d5), the reaction of O with H2 to OH followed by OH + H2 to water drives all oxygen into water. Both reactions have considerable activation barriers and only proceed at temperatures ≳250 K. Since the midplane is well shielded from UV radiation, photodissociation of OH and water are not efficient. In this region, carbon is bound into methane (CH4), due to the absence of free oxygen to form CO. Further out in the midplane, the temperature is insufficient for OH and H2O formation and carbon is in CO. In the outer part of the dusty inner disk (label d6), the density/temperature combination allows freeze out of water. Thus, oxygen is locked-up in ices and carbon is again bound in CH4. In the midplane of the gap, no dust for freeze out is available and carbon remains in CO. Moving to the outer disk (label d7), dust is again present and binds oxygen into the ice and the CO abundance in the midplane is low even though dust temperatures are too high for CO freeze-out.
Lower amounts of gas in the cavity (δgas < 1) affect CO in a similar way as H2. The C+/CO transition shifts to lower heights in the disk. The model with δgas = 10-4 does not form additional CO in the upper disk at the PAH destruction radius (label d3), because no additional H2 is found at that position (label b2). In the midplane of this model, the regions with decreased CO abundance (labels d5 and d6) are absent. This is because the lower density and subsequently lower shielding by PAHs leads to less efficient formation of OH/H2O and more photodissociation in the inner part of the inner disk (label d5). In the outer part of the inner disk, freeze out is less efficient and photodesorption/photodissociation runs more quickly (label d6). Thus, oxygen is not locked in water or water ice anymore and carbon remains in CO. By decreasing δgas, the outer water ice reservoir first disappears before the inner gas phase water vanishes (see Fig. 4k with δgas = 10-2).
For δgas = 10-6, CO is still present within the cavity, but the C+/CO transition has moved further down. In the gap, the abundance of CO is now slightly below the abundance of volatile carbon, i.e. not all carbon is bound in CO. The outer disk does not show differences in the CO abundance between models with different δgas, for the same reasons as discussed for H2 in the previous paragraph.
In summary, we find that H2 and CO can still survive for δgas = 10-6, corresponding to only 0.004 MEarth inside the gap, because they are both very robust against photodissociation, through self- and mutual-shielding. This low value can be better understood by turning it into a column density. Distributing 0.004 MEarth homogeneously over the gap (r = 10 − 45 AU) yields a total column density of 3 × 1019 cm-2. For H2 or CO self-shielding to become active, a column of order 1015 cm-2 is sufficient (Draine & Bertoldi 1996, Visser et al. 2009). In addition, the dust in the inner disk provides an attenuation AV ≳ 5 and is thus able to shield direct FUV radiation even if PAHs are absent. Thus, the survival of H2 and CO even for this low amount of gas in the gap seems plausible. The presence of the molecules does however not necessarily mean that their emission is strong enough for a detection (see Sect. 5).
4.1. The effect of a dusty inner disk on molecular gas
The previous sections have shown that the attenuation of stellar FUV radiation is key for the survival of molecules in the cavity. This raises the question if molecules can still survive, if no FUV shielding by a dusty inner disk is provided. In Fig. 6, the abundance of H2 and CO of a model with an optically thick dusty inner disk (δdust = 10-5) is compared to one without (δdust = 10-10). Note that there is still an inner gas disk in the model without dusty inner disk (Fig. 1). The representative model (Table 1) with δgas = 10-4 is shown.
 |
Fig. 6 H2 and CO abundance of a representative model (Table 1) with dusty inner disk (δdust = 10-5) compared to a model without dusty inner disk (δdust = 10-10). Both models have δgas = 10-4. Upper panels: H2 abundance. Lower panels: CO abundance. |
The differences in the abundance structure of H2 and CO between the model with and without dusty inner disk are evident. The model without dusty inner disk has H2 and CO present only in a geometrically thin layer close to the midplane (labels b1 and d1), while the model with dusty inner disk present has a H/H2 and C+/CO transition at considerable height in the disk (labels a1 and c1). The lower abundance of CO and H2 in the model without dusty inner disk are explained by the missing FUV absorption of the dust. This leads to stronger FUV irradiation of the gap and subsequently, PAHs can only survive outside the radius where geometrical dilution decreases the stellar radiation sufficiently. This is around r ~ 20 AU and can be seen by an enhanced H2 and CO abundance (labels b2 and d2). The midplane gas temperature at radii <20 AU, where no PAHs survive, is nevertheless high (several 1000 K). This is because no gas-grain coupling can cool the gas, while the strong continuum radiation field turns lines into heating agents (Sect. 3.1). The warm temperatures explain why a thin layer of gas close to the midplane forms CO at abundances ~10-4, while the H2 abundance does not exceed 10-4. The remaining H2 at radii <20 AU is formed through H− + H → H2 + e− (Sect. 4), because neither dust grains nor PAHs are present.
Models with more gas in the cavity (δgas > 10-4) and no dusty inner disk present have more gas in H2 and CO (not depicted). For δgas = 1, the C+/CO transition is at similar heights compared to the model with a dusty inner disk present, because of “warm” CO formation through C+ + H2. The two regions where carbon is in the form of methane (Fig. 5d, label d5 and d6) do however not exist because of the missing FUV attenuation. The H2 abundance of this model is also similar to the model with dusty inner disk. However, within a few AU, the FUV radiation is too strong for formation via H− and the H2 abundance is decreased. This is a result of the surface density profile Σ ~ r-1 while the geometrical dilution of FUV radiation ~r-2.
The presence of an optically thick dusty inner disk which shields the gas from direct stellar irradiation is thus crucial for molecules to survive in the gap. In absence of dust and PAHs, other chemical mechanisms like the formation of H2 through H− can still start a chemistry and lead to the presence of molecules. Key for the existence of molecules is a way for the formation of H2. Once an appreciable level of H2 (fractional abundances ≳10-4) is reached, CO can also form.
4.2. Atomic carbon
Figure 7 shows the abundance of C and C+ in models with δgas = 10-6 (dusty inner disk present) and δgas = 10-4,10-6 (no dusty inner disk present). The other parameters are set to to the reference model (Table 1).
 |
Fig. 7 C and C+ abundance of the representative models (Table 1) with δgas = 10-6 and no dusty inner disk (δdust = 10-10) or δgas = 10-4,10-6 with dusty inner disk (δdust = 10-5). Upper panels: C+ abundance. Lower panels: C abundance. |
In the model without dusty inner disk and δgas = 10-4, carbon in the gap is mostly atomic and ionized (label a1). Neutral carbon is only abundant close to the midplane with a fractional abundance ~10-6 (label c1). There, also some CO is present (Fig. 6, label d1) and C is produced by CO photodissociation. Additional C is produced by the photodissociation of CH or the reaction CH + H → C + H2. CH originates from the recombination or photodissociation of CH2, CH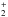 , or CH
, or CH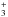 . These molecules form starting with the reaction of C+ with H2 to CH+. Outside the radius of PAH photodestruction (label c2), neutral carbon is more abundant, because of FUV shielding by PAHs and charge exchange with ionized carbon (PAH0 + C+ → PAH+ + C, see BR12). The abundance structure and chemistry of carbon in the outer disk is similar to BR12 and will not be discussed here.
. These molecules form starting with the reaction of C+ with H2 to CH+. Outside the radius of PAH photodestruction (label c2), neutral carbon is more abundant, because of FUV shielding by PAHs and charge exchange with ionized carbon (PAH0 + C+ → PAH+ + C, see BR12). The abundance structure and chemistry of carbon in the outer disk is similar to BR12 and will not be discussed here.
The model with dusty inner disk present and δgas = 10-4 also has carbon in the upper atmosphere in C+. Below this zone, neutral carbon C reaches high abundances of up to ~10-4 in a layer which gets wider to larger distances (label e1). It extends down to the midplane in the gap (label e2). While C is mainly produced by CO and CH photodissociation at heights in the disk, also charge exchange of C+ with PAHs becomes important deeper in the atmosphere. Decreasing the amount of gas in the cavity (smaller δgas) shifts the C+/CO transition down. Subsequently, also the C layer is found closer to the midplane. The model with dusty inner disk and δgas = 10-6 only has a thin layer of neutral carbon C close to the midplane.
5. Molecular line emission
In this section, the molecular line emission of pure rotational lines of CO, observable by ALMA, is discussed. We first show vertical column densities, then study the line formation including opacity effects and finally synthetic images. Equations to convert between different intensity units are provided in Appendix B. The analysis of the atomic fine structure lines ([C i], [C ii], and [O i]) are presented in Sect. 6.3.
5.1. Column densities
A first impression about the expected observables (images and intensities) can be obtained from column densities, since optically thin lines have intensities proportional to the column densities. In Fig. 8, we present vertical column densities of H2, CO, neutral carbon C and ionized carbon C+. The figure gives both representative models (Table 1) with dusty inner disk (δdust = 10-5; solid lines) or without dusty inner disk (δdust = 10-10; dashed lines) and different amounts of gas in the cavity (δgas = 10-6 − 1).
 |
Fig. 8 Vertical column densities of the representative models (Table 1) a) H2; b) CO; c) neutral carbon, and d) ionized carbon. Different colors shows models with different values of δgas. Solid lines represent models with a dusty inner disk present (δdust = 10-5) and the dashed lines models without dusty inner disk (δdust = 10-10). |
The H2 column density of the model with dusty inner disk present (Fig. 8a, solid line) follows the surface density profile for the model with δgas = 1. In the cavity, the column density scales linearly with δgas down to δgas ~ 10-4. Below this value, the signature of H2 photodissociation can be seen by the column density decreasing quicker than the scaling with the amount of gas (δgas). The effect of photodissociation is first seen at the inner edge of the disk, because of strong irradiation and the dust free gap, and corresponds to the absence of H2 formation on dust. The models without dusty inner disk (Fig. 8a, dashed line) show a different column density pattern and dependence on δgas. For δgas = 1 and 10-1, not all hydrogen is in H2 at radii ≲3 AU (Sect. 4.1). Outside this radius, the column density is very similar to the models with dusty inner disk present. For lower δgas, the amount of H2 decreases quickly with δgas, because H2 formation through H− gets inefficient. The H2 column of the model with δgas = 10-3 in the inner 20 AU is two orders of magnitude lower compared to the model with dusty inner disk. Outside 20 AU, the column density is similar to the model with dusty inner disk due to the presence of PAHs. Differences in H2 column density between models with and without dusty inner disk become larger for lower values of δgas. In the outer disk, the H2 column density of all models is equal, independent of δgas and the presence of a dusty inner disk.
 |
Fig. 9 Continuum subtracted integrated line intensity as function of the radius for CO 3 − 2 and its isotopologues. The figure shows intensities derived from the representative models (Table 1). The vertical gray lines at 28 AU and 100 AU indicate the radii and which the intensities are provided in Figs. 12 and 15. |
The CO column density of the model with dusty inner disk (Fig. 8b, solid line) does not follow the surface density profile. Two dips relative to the surface density profile (at r < 1 AU and 2 < r < 10 AU) are due to carbon being bound in methane (Sect. 4). The drop in the CO column at 45 AU is for the same reason. The CO column density only follows the surface density profile outside 200 AU. The dips at r < 10 AU are small in the model with δgas = 10-1 and the model with δgas = 10-2 has only the inner most dip (r < 1 AU) present, as water does not freeze out anymore at 2 < r < 10 AU. Models with lower δgas have a more smooth column density profile, which approximately scales with δgas. As for H2, only models with δgas = 10-5 and 10-6 show the signature of photodissociation. The column density pattern of the model without dusty inner disk is similar to that with inner disk for δgas > 10-4, except that dips in the column density are missing. Below this value, CO is however dissociated more quickly compared to the model with dusty inner disk. As for H2, we find again that the CO column in the outer disk is very similar for all models.
The C and C+ columns are given in Figs. 8c and 8d. Both species show a trend of decreasing column density with δgas. This is however much less pronounced than for CO and H2. For example the C+ column density of the models with dusty inner disk does only vary by about 3 orders of magnitude, while the column density of CO for the same series of models varies by more than 7 orders of magnitude. Approximately the same amount of variation in column density is found for C+ (models without dusty inner disk) and C (models with inner disk). C shows larger variations in models without dusty inner disk, because for δgas = 10-6, all carbon within the cavity can be ionized. The smaller variation in the C and C+ column density compared to H2 and CO results from the fact that these species exist in a transition layer on top of the midplane, which is found at different heights in the disk for different δgas, but still has similar column densities. The column densities of C and C+ in the outer disk are comparable for all models.
We conclude that the column densities of H2 and CO within the cavity scale almost linearly with δgas down to a value of δgas, where photodissociation becomes important. The column densities of C and C+ on the other hand do not scale in this linear fashion.
5.2. Line intensities and opacity effects
The CO rotational lines get optically thick above a certain column density and thus do not directly trace the gas mass in the gap or cavity anymore. An advantage of the CO rotational lines is that rare isotopologues (13CO, C18O, C17O, 13C18O, and 13C17O) can be observed. The isotopologue lines have lower optical depth, due to their lower abundance and thus remain optically thin up to larger gas masses. In this section, we study the integrated intensities and opacity effects on the example of CO J = 3 − 2 and isotopologues. We discuss the representative model (Table 1) with dusty inner disk present (δdust = 10-5). Since 13C17O is mostly below the detection limit and C18O has a similar isotopologue ratio to C17O, we mostly omit those two isotopologues in the following sections, but include them in the relevant figures.
In Fig. 9, the velocity integrated and continuum subtracted intensities depending on the radius are presented for a face-on disk. The gas mass in the cavity is varied with δgas = 10-6 − 1. The main isotopologue (12CO) integrated intensity in the center of the gap (28 AU) decreases only by a factor of ~ 4 from δgas = 1 to δgas = 10-3, due to the high optical depth of this line. For δgas < 10-4, the line is optically thin and the integrated intensity scales almost linearly with the column density and thus δgas (previous section). The lines of the rare isotopologues have lower optical depth and they show a linear dependence of integrated intensity with δgas in the center of the gap (28 AU) already for δgas ≲ 10-1 (C17O), δgas ≲ 10-2 (13CO). 13C18O does not get optically thick and scales linearly with δgas in the gap. The rare isotopologue lines thus directly trace the column density and gas mass in the cavity already for much higher values of δgas compared to 12CO.
 |
Fig. 10 Surface of τ = 1 and line opacities of CO 3 − 2 and isotopologues for the representative model (Table 1) with δgas = 10-2 and a dusty inner disk present (δdust = 10-5). The vertical gray line at 28 AU shows the center of the gap. Upper panel: line center opacity depending on the radius. Lower panel: position of the τ = 1 surface for different radii. |
What is the optical depth of the lines? In Fig. 10a, the total line center opacity (τ = τline + τdust) depending on the radius is shown for a face-on disk with δgas = 10-2. The line center opacities approximately scale with the column density and thus δgas. The dust opacity peaks in the outer disk, at the edge of the cavity (R = 45 AU), with τdust ~ 0.8. Again looking at the center of the gap (28 AU), we find 12CO line center opacities of a few 100. Using the scaling with δgas, we thus confirm that the line gets optically thin at δgas ~ 10-4. Similarly, we see that C17O reaches line center opacities of order 10 for δgas = 1. 13C18O remains optically thin even for δgas = 1.
The reason why optically thick lines still slightly increase with δgas is, that the line can broaden or get optically thick higher in the disk, thus tracing warmer regions (van Zadelhoff et al. 2001; Dartois et al. 2003). What heights of the disk are traced by the CO lines? A simple way to answer this question is to look at the position, where τ = 1 is reached in vertical direction (BR12). In Fig. 10b the height of the τ = 1 surface is presented. The τ = 1 surface of 12CO is at considerably larger height compared to other isotopologues at all radii. Within the cavity, it is at approximately constant height, but it has a much larger height in the outer disk. The 13CO τ = 1 surface shows similar features however, deeper in the disk. The rare isotopologues C18O and C17O do not reach τ = 1 at all radii and have their τ = 1 surface close to the midplane or even on the far side of the disk. 13C18O does not get optically thick. We conclude, that the main isotopologue line traces the warm upper atmosphere, while the rare isotopologues lines trace layers at lower heights in the disk or the whole column density, if they are optically thin.
In conclusion, line opacity effects are key for the understanding of the CO emission and their use as mass tracers. While the main isotopologue line is optically thick down to low gas mass in the cavity, the rare isotopologues can remain optically thin. Provided that their lines can be detected, combined observations of isotopologue lines thus allow us to directly trace a wide range of gas masses.
5.3. Images
As an example of line images derived from the models, Fig. 11 presents (unconvolved) images of the  CO 3 − 2 integrated intensities derived from the series of models studied in the previous section. Compared are models with δgas = 1,10-2,10-3 and 10-4 of both the series of models with or without dusty inner disk present. The distance is assumed to be 100 pc and the inclination is set to 30°. Intensities below 10 K km s-1 are cut off, approximately corresponding to the detection limit of ALMA (see next section). See Figs. 19 and 20 for the 12CO 3 − 2 line and isotopologues (13CO, C17O, and 13C18O) comparing δgas = 10-3 − 1, either with or without dusty inner disk.
CO 3 − 2 integrated intensities derived from the series of models studied in the previous section. Compared are models with δgas = 1,10-2,10-3 and 10-4 of both the series of models with or without dusty inner disk present. The distance is assumed to be 100 pc and the inclination is set to 30°. Intensities below 10 K km s-1 are cut off, approximately corresponding to the detection limit of ALMA (see next section). See Figs. 19 and 20 for the 12CO 3 − 2 line and isotopologues (13CO, C17O, and 13C18O) comparing δgas = 10-3 − 1, either with or without dusty inner disk.
 |
Fig. 11 Images of the integrated intensity (in K km s-1) of 12CO 3 − 2 from the series of representative models (Table 1). Models with δgas = 1,10-2,10-3 and 10-4 are shown. The inclination i = 30° and the black dashed lines show the size of the gap (10 < r < 45 AU). Red dashed lines show the radius where PAHs can survive in absence of UV shielding by a dusty inner disk (Sect. 3). Upper panels: models with a dusty inner disk present (δdust = 10-5). Lower panels: models without an inner disk (δdust = 10-10). |
The integrated intensities of CO and isotopologues in the cavity generally decreases with δgas. As discussed in the previous sections, this decrease is more pronounced toward lower δgas (<10-3) which reflects the photodissociation of CO.
In some of the images, the warm upper edge of the outer disk wall can be seen. If the gas in the cavity is optically thick, only the edge pointed toward us can be seen (e.g. Fig. 11, images with δgas = 10-2). For an optically thin cavity also the edge of the far side is visible (e.g. Fig. 11, images with δgas = 10-4).
Models with or without a dusty inner disk look similar for 12CO and δgas = 1. For lower δgas and also the rare isotopologues, two mechanism acting in different directions are at work: gas temperatures of models without inner disk are higher compared to those with inner disk (Sect. 4.1), but in models without inner disk, the effect of photodissociation decreases the CO column density already for higher δgas (Sect. 5.1). Models without inner disk thus have higher integrated intensities in the cavity, as long as the CO column density is similar to models with inner disk. For the main isotopologue this is the case for δgas down to 10-3 (Fig. 11). For δgas = 10-4, however, the integrated intensity of the model without dusty inner disk is weaker, in agreement with the expectation from the CO column density (Fig. 8). The rare isotopologues show the same effects, but their intensity starts dropping at higher δgas, due to lower optical depth. Differences between models with and without dusty inner disk increase to lower gas masses in the cavity.
6. Discussion
The gas mass in the gap of transition disks is a crucial parameter for theories of planet formation and measuring this parameter thus key. On the other hand, different mechanism for the formation of dust gaps would result in different amounts of gas in the gap. Thus, knowledge of the gas mass can also help to distinguish between different dust gap formation mechanism. The models presented in the previous section can be used to derive a variety of parameters, we however focus on the use of CO lines, observed at high angular resolution by ALMA, as tracers of the gas mass in the cavity. We also discuss, if the gas mass in the cavity can be derived from lower angular resolution observations or from atomic fine structure lines ([C i], [C ii],[O i]).
6.1. Predictions for ALMA: CO
In order to detect low amounts of gas, a good sensitivity is crucial. In the following sections we refer to the ALMA band 7 (CO 3 − 2) detection limit as the line sensitivity for a 5σ detection in 1 h on-source observation. Using the ALMA time sensitivity calculator4, assuming typical weather conditions (3rd octile), dual polarization and the use of 50 12 m antennas, the RMS noise in each 0.25 km s-1 channel is 3 mJy (345 GHz), corresponding to a surface brightness of 3.1 K for a resolution of 0.1′′. For a firm 5σ detection within 1 h on-source observation and a beam small enough to resolve a typical cavity, an integrated intensity of order ~7.7 K km s-1 is thus necessary (assuming an intrinsic line-width of order 1 km s-1).
6.1.1. Tracing the gas mass in the cavity
What is the range of gas masses in the cavity that can be constrained with ALMA observations of CO rotational lines? Figure 12 shows the integrated intensities of 12CO 3 − 2 and isotopologues in the center of the cavity (at r = 28 AU) and the outer disk (at r = 100 AU). Models with- and without dusty inner disk and for different values of δgas are given. The integrated intensities at 100 AU of models with different δgas are very similar (≲20%).
 |
Fig. 12 Integrated intensities of CO 3 − 2 and isotopologues at the center of the gap (r = 28 AU) and in the outer disk (r = 100 AU). The ALMA detection limit for a 5σ detection after 1 h on-source observation with a 0.1′′ beam (see Sect. 6) is given by the vertical dashed black line. Upper panels: models with a dusty inner disk (δdust = 10-5). Lower panels: models without inner disk (δdust = 10-10). |
For a detection limit of order 7.7 K km s-1, 12CO 3 − 2 can be detected in the gap down to δgas = 3 × 10-5 in the case of a model with dusty inner disk. This corresponds to a gas mass in the gap of 3.6 × 10-7 M⊙ or 0.2 MEarth (Table 2). For models without dusty inner disk, the detection limit in gas mass is about an order of magnitude higher (δgas = 3 × 10-4) and corresponds to 2 MEarth. For both series of models with and without dusty inner disk, the 12CO integrated intensity in the gap stays within a factor of a few for high values of δgas, where the line is optically thick. The main isotopologue 12CO line is optically thick for δgas > 10-4 (with dusty inner disk) or δgas > 10-3 (no dusty inner disk). The rare isotopologues get only optically thick for higher values of δgas, with for example 13CO being optically thick for δgas ≳ 10-2 (Sect. 5.2). Above δgas = 10-1, even C17O gets optically thick, but in this mass range, 13C18O is optically thin and above the detection limit. For a disk with δgas = 1, 13C18O can be detected on a 20σ level after 1 h on-source integration.
We conclude that combined observations of different isotopologues are key and will allow us to directly trace a wide range of masses from a full disk with δgas = 1 down to the detection limit of the main isotopologue at values of δgas ~ (0.3 − 3) × 10-4 which are 3.5 − 4.5 orders of magnitude lower in mass. Differences between models with or without dusty inner disk are smaller for higher gas masses, because the lines are optically thick in the cavity and increase to lower masses, where the lines get optically thin.
The same analysis for 12CO 6 − 5 (691 GHz) and isotopologues shows very similar results and is not reported here. The flux sensitivity of ALMA band 9 for the same conditions5 is with 40 mJy a factor of 13 higher, leading to a 5σ detection limit in a 0.1′′ beam after an 1 h on-source of 26 K km s-1. Since the CO 6 − 5 integrated intensities are similar (<50% difference in brightness temperature) compared to CO 3 − 2, the CO 3 − 2 line is more suitable to trace lower amounts of gas. For transition disks with a small cavity radius, the factor of 2 smaller beam of CO 6 − 5 may be required, though.
The gas temperature in the cavity is a few 100 K (Sect. 3) which is high enough to excite the first vibrational levels of CO at Eu ≳ 3100 K to some extent. However, due to the combination of high critical density (~1014 cm-3) and high upper level energy of the rovibrational transitions, they are more sensitive to excitation conditions (density and gas temperature) compared to pure rotational lines. In particular the IR lines depend very much on the gas temperature which is known to be uncertain in thermo-chemical models. In addition, if some dust still remains in the gap, the near infrared lines are more prone to dust extinction than the submillimeter lines. We conclude that submillimeter lines are more suited to trace the gas mass in the cavity.
6.1.2. The need for high resolution interferometry
Since the gas temperature and column densities generally increase to smaller radii, the intensity increases to smaller radii (Fig. 9). This raises the question, if low-resolution (single-dish) observations are sufficient to the trace the gas in the inner disk, due to the potentially higher intensity from gas inside the cavity?
To answer this question, Fig. 13 shows the beam convolved integrated intensities of 12CO 3 − 2 and C18O 3 − 2 for different beam sizes. The disk is face on and has a dusty inner disk present. Other isotopologues show the same features and are thus not given. Beam sizes with FWHM larger than a few 100 AU (a few arcseconds at 100 pc) thus result in integrated intensities within a factor of a few, because the emission of the optically thick lines is quickly dominated by the much larger area from the outer disk and optically thin lines by the larger mass from the outer disk. Single-dish observations are thus clearly insufficient to draw constraints on the gas mass in the cavity.
What resolution is necessary to constrain the gas mass in the cavity? Figure 14 shows images of the model with dusty inner disk present (δdust = 10-5) and δgas = 10-4 convolved to different beam sizes (FWHM 0.05′′, 0.1′′, 0.15′′ and 0.2′′). The minimum integrated intensity inside the gap differs between the beams. Only in the case of the two smallest beams (0.05′′ and 0.1′′), the integrated intensity drops to a value <10 K km s-1 found in the unconvolved image (Fig. 11). Due to the strong intensity gradients of gap to inner disk and gap to outer disk, a small beam size is crucial to derive correct gas masses. For models without strong gradients at the edge of the gap, this issue is less severe (e.g. 12CO 3 − 2 with dusty inner disk and δgas > 10-4). We conclude that a beam size of a fraction of the gap is crucial to derive the gas mass.
6.1.3. Dependence on parameters
How do the CO integrated intensities in the gap depend on the other parameters of the grid of models, such as the disk mass (parameterized by Rc), the bolometric luminosity (Lbol), the stellar spectrum (Teff), and the PAH abundance? In Fig. 15 the 12CO 3 − 2 and C18O 3 − 2 integrated intensities at the center of the gap and the outer disk are shown. One of the parameter (Rc,Lbol,Teff, or the PAH abundance) is varied, while the others are set to the value of the representative model (Table 1). The dependence of the other isotopologues is similar and thus not shown. Since the X-ray spectrum is not found to be an important parameter for the CO integrated intensity in the gap, it is discussed in Appendix D.
 |
Fig. 13 Beam convolved integrated intensities of CO 3 − 2 for different beam sizes. The representative model with a dusty inner disk present is shown. The disk is face on. Left panel: 12CO 3 − 2. Right panel: C18O 3 − 2. |
Increasing Rc from 50 AU to 100 AU leads to a factor of 2.5 larger gas mass in the cavity (gap and inner disk) for a given δgas (Table 2). Conversely, Rc = 25 AU yields a factor of 2.8 lower gas mass compared to Rc = 50. For δgas ≳ 10-3, the integrated intensity of 12CO in the gap agrees to within a factor of <2 between models with different Rc. This results from line opacity effects in combination with similar temperatures at the height in the disk, which is probed by this line. Below δgas = 10-3, the integrated intensity of 12CO from models with lower disk mass drop in intensity at higher values of δgas, compared to those with lower disk mass. The drop scales about linear with the disk mass and thus similar values of the gas mass in the cavity can be detected. This reflects that the density structure in the cavity in more massive models with a lower value of δgas is similar to models with less mass, but higher δgas (Fig. 3). The C18O integrated intensity shows similar features as 12CO. However, the C18O integrated intensity of models with different Rc are only similar for δgas ≳ 10-2, where C18O is optically thick.
Higher bolometric luminosities lead to higher gas and dust temperatures. This is seen in the increased 12CO integrated intensity for higher Lbol and δgas > 10-4. In this mass range, the 12CO line is optically thick. Likewise, C18O shows the same dependence for δgas > 10-2. Below δgas = 10-2, the C18O lines become optically thin and trace the column density. Due to increased photodissociation for higher Lbol, the CO column density generally decreases with Lbol. Below δgas = 10-4, the dependence of CO column density with Lbol is more complex, as the integrated intensity of 12CO shows. In this range of δgas, additional CO formation due to higher gas temperatures can affect the total column density.
A harder spectrum of the star (higher Teff) has different effects on the chemistry and heating/cooling. This is discussed in detail in BR12 in the context of high-J CO lines. Here, a harder spectrum with more CO/H2 dissociating photons and also more heating (e.g. through the photoelectric effect) leads to higher 12CO intensities in the gap, if the line is optically thick (δgas > 10-4). For lower values of δgas, a harder spectrum leads to more photodissociation and thus lower 12CO intensities. Since the C18O line forms deeper in the atmosphere (Sect. 5.2), the effect of the increased gas temperature in the upper atmosphere is not seen. When C18O is optically thin (δgas < 10-2), the decreased integrated intensity for higher Teff is also a result of the increased photodissociation.
PAHs affect the CO integrated intensity in the gap through a combination of chemical effects (e.g. formation of H2 on their surface), heating by the photoelectric effect and absorption of FUV radiation. Lower PAH abundances lead to less H2 formation and heating, but also less FUV absorption. Thus, CO forms deeper in the disk. Since CO is an important coolant in the gap (Sect. 3.1), the gas temperature at the top layer where CO forms is slightly higher. For high values of δgas, where the 12CO or C18O are optically thick and trace this top layer, lower PAH abundances thus lead to higher integrated intensities in the gap. On the other hand, for low values of δgas, where the lines are optically thin, the additional photodissociation due to less FUV shielding by PAHs and less efficient H2 formation leads to lower amounts of CO and thus lower integrated intensities.
We conclude that the main parameter for the low-J CO integrated line intensity is the amount of gas within the cavity (δgas). Other parameters change the gas mass at which CO drops below the detection limit by only a factor of up to a few.
6.2. Predictions for ALMA: C
 |
Fig. 14 Beam convolved images of the integrated intensity (in K km s-1) of 12CO 3 − 2 from a representative model (Table 1) with dusty inner disk present and δgas = 10-4 (Sect. 4). The inclination is i = 30° and the images are convolved to a Gaussian beam with FWHM 0.05′′, 0.1′′, 0.15′′ and 0.2′′. The black dashed lines indicate the size of the gap (r = 10 − 45 AU). |
Neutral carbon lines are other potential tracers of gas in cavities (Sect. 4.2). However, neutral carbon is in a layer between the ionized carbon in the upper atmosphere and molecular gas (CO) closer to the midplane and has similar column densities for different δgas (Fig. 8c). Thus, the [C i] lines observable by ALMA are not expected to be very sensitive on the gas mass. Figure 16 shows the intensity in the gap and the outer disk depending on δgas for the representative models (Table 1) with or without dusty inner disk.
The two carbon lines indeed do not change considerably with δgas for δgas ≥ 10-4 (models with dusty inner disk) and δgas ≥ 10-3 (models without dusty inner disk). The intensities are much lower compared to CO and at higher frequency, which are more difficult to observe. The ALMA time sensitivity estimator for the same settings as above, shows that for the same detection limit, about a factor of 10 longer integration time is needed. Even this sensitivity is only marginal sufficient to detected [C i] at the necessary angular resolution. We conclude that [C i] observation are less suited to measure the amount of gas in cavities of transition disks.
6.3. Tracing transition disks with Herschel: C+?
The fine structure line of ionized carbon ([C ii] 2P P1/2 at 158 μm) cannot be studied from the ground. The Herschel Space Observatory (Pilbratt et al. 2010) has observed the line toward different transition disks with the PACS instrument (Poglitsch et al. 2010) and velocity resolved with the HIFI instrument (de Graauw et al. 2010). Due to the better sensitivity of PACS compared to HIFI, most observations have been carried out spectrally unresolved with PACS and we focus here on integrated intensities. The angular resolution of Herschel at 158 μm is ~11′′, corresponding to ~1000 AU at 100 pc. Cavities can thus only be detected indirectly, if the emission from the cavity is much stronger compared to the outer disk and dominates the unresolved flux.
P1/2 at 158 μm) cannot be studied from the ground. The Herschel Space Observatory (Pilbratt et al. 2010) has observed the line toward different transition disks with the PACS instrument (Poglitsch et al. 2010) and velocity resolved with the HIFI instrument (de Graauw et al. 2010). Due to the better sensitivity of PACS compared to HIFI, most observations have been carried out spectrally unresolved with PACS and we focus here on integrated intensities. The angular resolution of Herschel at 158 μm is ~11′′, corresponding to ~1000 AU at 100 pc. Cavities can thus only be detected indirectly, if the emission from the cavity is much stronger compared to the outer disk and dominates the unresolved flux.
 |
Fig. 15 Integrated intensities of 12CO 3 − 2 (solid lines) and C18O 3 − 2 (dashed lines) at the center of the gap (r = 28 AU) and in the outer disk (r = 100 AU). The panels show the intensities for variations of one parameter (Rc, Lbol, Teff and the PAH abundance). If not varied, the parameters are set to the values of the representative models (Table 1: Rc = 50 AU, Lbol = 10 L⊙, Teff = 10 000 K and a PAH abundance of 10% the ISM abundance). |
 |
Fig. 16 Integrated intensities of [C i] 3P |
 |
Fig. 17 Beam convolved integrated intensities of [C ii] 2P |
 |
Fig. 18 Beam convolved integrated intensities of [O i] 3P1 − 3P2 at 63 μm and 3P0 − 3P1 at 145 μm and for different beam sizes. The disk is face on and has a dusty inner disk present. |
 |
Fig. 19 Images of the integrated intensity (in K km s-1) of CO isotopologues (12CO, 13CO, C17O, and 13C18O) from the series of representative models (Table 1) with dusty inner disk present (δdust = 10-5). Models with δgas = 1,10-1,10-2 and 10-3 are shown. The inclination i = 30° and the black dashed lines show the size of the gap (10 < r < 45 AU). The C18O images look similar to the C17O images and thus not shown. 1st row: 12CO 3 − 2. 2nd row: 13CO 3 − 2. 3rd row: C17O 3 − 2. 4th row: 13C18O 3 − 2. |
 |
Fig. 20 Images of the integrated intensity (in K km s-1) of CO isotopologues (12CO, 13CO, C17O, and 13C18O) from the series of representative models (Table 1) without dusty inner disk (δdust = 10-10). Models with δgas = 1,10-1,10-2 and 10-3 are shown. The inclination i = 30° and the black dashed lines show the size of the gap (10 < r < 45 AU). The C18O images look similar to the C17O images and thus not shown. 1st row: 12CO 3 − 2. 2nd row: 13CO 3 − 2. 3rd row: C17O 3 − 2. 4th row: 13C18O 3 − 2. |
Figure 17 shows the integrated intensity of [C ii] for different beam sizes. The representative models (Table 1) including a dusty inner disk present are shown. Similar to the equivalent figure for CO (Fig. 13), a large increase in integrated intensity with δgas is found for small beam sizes compared to the size of the cavity. If the beam size is much larger and a substantial fraction of the intensity is due to the outer disk, the integrated intensity depends little on δgas (less than a factor of 3). The increase is larger for models with δgas = 10-1 and 1, but models with lower values of δgas agree to within ~50% at beam sizes much larger than the cavity. Good knowledge about the outer radius of the disk would be required to draw conclusions at this level and we conclude that only for high amounts of gas in the cavity, some of the spatially unresolved [C ii] emission can be due to emission from within the cavity.
For completeness, the two neutral oxygen fine structure lines at 63 μm and 145 μm observed by the PACS instrument onboard Herschel are also discussed. Compared to the lines of CO, [C i] and [C ii] studied before, the [O i] lines have a higher upper level energy of 228 K and 327 K, respectively (compared to <100 K). The oxygen emission is thus more centrally peaked (see BR12) and the cavity contribution to spatially unresolved observations should be larger compared to [C ii]. Figure 18 shows the [O i] integrated intensities in different beams. For beams corresponding to FHWM larger than a few 100 AU, the increase in intensity for the models with δgas = 10-1 and 1 is indeed larger compared with [C ii] (up to about a factor 6). Models with lower δgas however still agree to within a factor of 2−3 and measuring gas masses in the cavity using [O i] lines is challenging as well.
6.4. Implications
The previous sections have shown that combined observations of CO rotational lines and isotopologues allow us to directly trace a wide range of gas masses in the cavity corresponding to a full gas disk (δgas = 1) down to δgas ~ (0.3 − 3) × 10-4. Even lower values of δgas may be traced with observations longer than 1 h on-source.
How can this range of gas masses help to distinguish between different dust gap formation mechanism? Clearing of the gap by a single Jupiter mass planet reduces the gas mass in the gap by a factor of 10−1000 (δgas = 10-1 − 10-3), depending on the viscosity. A more massive 9 MJupiter planet leads to δgas ~ 10-2 − 10-3 (Pinilla et al. 2012a). Photoevaporation (e.g. Bally & Scoville 1982; Hollenbach et al. 1994; Clarke et al. 2001; Alexander et al. 2006; Ercolano et al. 2008; Gorti & Hollenbach 2009) has short processing time-scales and once its effect sets in, would quickly lead to a gas free cavity. Pure grain-growth on the other hand (e.g. Dullemond & Dominik 2005; Birnstiel et al. 2012a) should not alter the gas structure much (δgas ~ 1).
Thus, high gas masses (δgas ≳ 10-1) point to gap clearing by a less massive planet (≲1 MJupiter) or pure grain-growth. Resolved submillimeter dust images may help to distinguish between the two scenarios, because clearing by a planet results in a gap, while grain growth leads to a hole empty of submm grains. We note however, that models of pure grain growth are unable to explain the gap formation alone (Birnstiel et al. 2012a). Intermediate values of δgas, with δgas < 10-1, point to planet-disk interaction. In this mass regime, knowledge of the gas mass in the gap is of special interest, as it sets constraints for further planet formation or the dynamics of the planets. To estimate the planetary mass, additional constrains on the viscosity may help to break the degeneracy between reduction of the gas mass in the gap and viscosity (Mulders et al. 2013). Low gas masses in the gap (δgas < 3 × 10-5) on the other hand are hard to achieve with planet clearing, even in the case of multiple systems (Dodson-Robinson & Salyk 2011; Zhu et al. 2011). Such low masses thus point to photoevaporation, possibly in combination with planet clearing (Rosotti et al. 2013). We conclude that measuring the gas mass in the cavity alone is not sufficient to distinguish between different gap formation mechanism or to constrain details of the mechanism at work. It can however exclude some mechanisms and help to confirm or discard constraints by other tracers (e.g. continuum images or the SED). In a forthcoming paper, we plan to couple the present model with a model for dust evolution (Birnstiel et al. 2010, 2011, 2012b) which will allow us to study the combined use of lines and the continuum in order to better constrain the gap formation mechanism.
7. Conclusions and outlook
In this work, we have applied a new type of thermo-chemical models on transition disks to study the survival of simple molecules (H2 and CO) in the dust free gap of these disks for a range of parameters. Predictions for ALMA are derived and observation strategies to trace the amount of gas in the cavity are discussed. While the focus of the work is on high-resolution observations that can trace the cavity spatially resolved, we also discuss the possibility to trace the gas mass in the cavity using spatially unresolved Herschel observations.
Our main conclusions are
-
1.
CO and H2 can survive the intense stellar UV radiation in gaps of transition disks down to gas masses in the gap corresponding to a fraction of the Earth mass (~0.004 MEarth). Important for the survival of CO and H2 is self- and mutual-shielding and alternative H2 formation routes. Alternative H2 formation routes are formation on PAHs or through H−, which can both proceed in gas depleted of dust (Sect. 4).
-
2.
The main parameter for the CO emission from the cavity is the gas mass in the cavity. The integrated intensity of optically thin CO isotopologue lines scales linearly with gas mass down to the mass where photodissociation gets important. Other parameters such as the outer disk mass, bolometric luminosity, shape of the stellar spectrum or PAH abundance are less important (Sects. 5.1, 6.1.1, 6.1.3).
-
3.
The lines of the main isotopologue 12CO are optically thick for δgas > 10-4, where δgas is the scaling of the gas mass in the cavity relative to a full gas disk. The rare isotopologues are already optically thin for δgas ≲ 10-1 (C17O), δgas ≲ 10-2 (C18O and 13CO). 13C18O remains optically thin for δgas = 1, and is still detectable for high gas masses (Sects. 5.2, 6.1.1).
-
4.
Combined observations of CO isotopologues (12CO, 13CO, C18O, C17O, 13C18O) allow us to directly trace a wide range of gas masses in the cavity between a full gas disk (δgas = 1) down to the detection limit of 12CO at δgas ~ (0.3−3) × 10-4. With the ALMA sensitivity we will be able to routinely trace gas masses in the cavity of transition disk in nearby star forming regions down to a fraction of the Earth mass (~0.2 MEarth). This value is reached with a 5σ detection after a 1 h on-source observation, thus lower masses can be traced with longer observations (Sect. 6.1.1).
-
5.
The presence of a dusty inner disk (“pre-transition disk′′), which shields the gap from direct stellar irradiation, allows CO and H2 to survive in the gap down to lower gas masses corresponding to δgas ~ 10-6. In the absence of a dusty inner disk, the molecules can only survive for δgas ≳ 10-4 (Sect. 4.1). Differences in abundance and derived intensities between models with and without inner disk increase at lower values of δgas (Sects. 5.1, 6.1.1).
-
6.
High resolution observations with beam size corresponding to a fraction of the gap size are crucial to determine the amount of gas in the cavity (Sect. 6.1.2).
-
7.
Observations of atomic fine structure lines of carbon ([C i] and [C ii]) and oxygen ([O i]) are less suited to measure the amount of gas in the cavity compared to low-J lines of CO (Sects. 4.2, 5.1, 6.2, and 6.3).
In extension to this work, which presents a parameter study, we will compare model results with ALMA observations (van der Marel et al. 2013, Bruderer et al., in prep.) and also study the emission of other molecular tracers (e.g. of HCO+ or CN).
Online material
Appendix A: Improvements and changes of the model compared to Bruderer et al. (2012)
Appendix A.1: Continuum radiative transfer
The 3D Monte-Carlo radiative transfer method implemented in the model consists of two stages (see Bruderer et al. 2012, Appendices A.1 and A.2). In the first stage, the dust temperature is obtained using a method combining the algorithm by Bjorkman & Wood (2001) and Lucy (1999). In order to improve the accuracy of the dust temperature in very optically thick midplanes and to speed up the calculation, we have replaced the modified random walk (MRW) approach (Min et al. 2009; Robitaille 2010) by the solution of the diffusion equation. Following a suggestion by Pinte et al. (2009), photon packages are mirrored back from very optically thick regions in the midplane where opacities at the peak wavelength of the star are τ > 1000. At this depth in the disk, the radiation field is close to isotropic and the mean intensity is similar to a black body of the local radiation field. Thus, the diffusion approximation may be employed. After all photon packages have been propagated, the dust temperature in the midplane is obtained from the solution of the diffusion equation 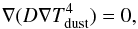 (A.1)where D is the diffusion constant D = 1/(3ρκR(Tdust)), with the Rosseland mean mass extinction coefficient κR(Tdust). The diffusion equation is also used for cells with low photon statistics (see Min et al. 2009).
(A.1)where D is the diffusion constant D = 1/(3ρκR(Tdust)), with the Rosseland mean mass extinction coefficient κR(Tdust). The diffusion equation is also used for cells with low photon statistics (see Min et al. 2009).
To verify the changes made in the code, we have re-run the benchmark tests suggested in Pinte et al. (2009) (see Fig. A.3 in Bruderer et al. 2012). As an example, Fig. A.1 shows a comparison of the midplane dust temperature obtained with our updated code and MCFost (Pinte et al. 2006). The model with isotropic scattering and a midplane opacity of τ = 105 is shown. We find very good agreement with deviations comparable to those between other codes tested in the benchmark study. The main improvement to Bruderer et al. (2012) is the reduced calculation time combined with a better accuracy in regions of high opacity or low photon statistics, like regions shielded by a very opaque inner rim.
 |
Fig. A.1 Disk midplane dust temperature for the disk benchmark problem proposed in Pinte et al. (2009) (τ = 105). The result obtained from our code is given in the red dashed line, the results by MCFost (Pinte et al. 2006) in black. |
The second stage of the Monte-Carlo method calculates mean intensities (Bruderer et al. 2012, Appendix A.2). This part has only been used for FUV wavelengths before. We have updated the code to calculate mean intensities of the entire spectrum from UV to radio wavelengths. We typically use about 60 wavelength bins. The updated code also accounts for photons emitted by the dust. The fraction of photon packages emitted by the protostar, the dust and the interstellar radiation field or cosmic microwave background is chosen according to their relative contribution to the luminosity at one wavelength (e.g. Pinte et al. 2006; Harries 2011).
 |
Fig. A.2 Comparison of the model fluxes between the current model and the representative model of HD 100546 in Bruderer et al. (2012). |
The accuracy of the mean intensity calculated in the second stage can be verified by checking the consistency with the dust temperature obtained in the first stage. We compare the energy balance 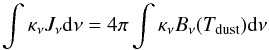 (A.2)using the dust temperature Tdust from the first stage and the mean intensity Jν from the second stage and find agreement to within a few percent. The advantage of splitting the calculation in two stages is that the photons propagating in the first stage mainly sample the peak wavelength of the local radiation field to obtain an accurate dust temperature, while the photons in the second stage are distributed equally between the wavelengths to obtain a well sampled radiation field at all wavelengths. This is important for photodissociation, chemistry, and excitation.
(A.2)using the dust temperature Tdust from the first stage and the mean intensity Jν from the second stage and find agreement to within a few percent. The advantage of splitting the calculation in two stages is that the photons propagating in the first stage mainly sample the peak wavelength of the local radiation field to obtain an accurate dust temperature, while the photons in the second stage are distributed equally between the wavelengths to obtain a well sampled radiation field at all wavelengths. This is important for photodissociation, chemistry, and excitation.
Appendix A.2: Molecular excitation
The main difference between Bruderer et al. (2012) and the present model is the non-LTE calculation of the molecular/atomic excitation. In order to simplify the calculation, we chose to compute the molecular excitation in a 1+1D approach only accounting for the vertical and radial direction to obtain the escape probabilities. The rate coefficient for transitions between level i and j (Eq. (A.17) in Bruderer et al. 2012) is 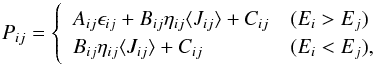 (A.3)with the collisional rate coefficients Cij, the Einstein A and B-coefficients Aij and Bij, respectively and the level energy Ei. The continuum mean intensity ⟨ Jij ⟩ is taken from the Monte-Carlo radiative transfer calculation. The escape probabilities in vertical direction ϵij and radial direction ηij are obtained from (e.g. Avrett & Hummer 1965),
(A.3)with the collisional rate coefficients Cij, the Einstein A and B-coefficients Aij and Bij, respectively and the level energy Ei. The continuum mean intensity ⟨ Jij ⟩ is taken from the Monte-Carlo radiative transfer calculation. The escape probabilities in vertical direction ϵij and radial direction ηij are obtained from (e.g. Avrett & Hummer 1965), 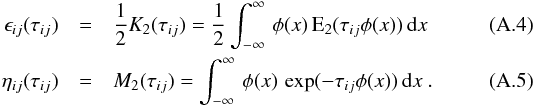 with τij, the line center opacity in vertical or radial direction, respectively. The line profile is taken to be a Doppler line profile function
with τij, the line center opacity in vertical or radial direction, respectively. The line profile is taken to be a Doppler line profile function 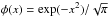 and E2(x) is the second exponential integral. The expression for ϵij corresponds to the escape probability of a slab, averaged over angle and line profile and the expression for ηij to the escape probability averaged over the line profile. In order to quickly evaluate the integrals in the above expressions, they are implemented using a Padé-approximation which is accurate to better than 0.1% for the whole opacity range used in the models.
and E2(x) is the second exponential integral. The expression for ϵij corresponds to the escape probability of a slab, averaged over angle and line profile and the expression for ηij to the escape probability averaged over the line profile. In order to quickly evaluate the integrals in the above expressions, they are implemented using a Padé-approximation which is accurate to better than 0.1% for the whole opacity range used in the models.
The new approach, which is similar to other 1+1D disk models (e.g. Gorti & Hollenbach 2004; Woods & Willacy 2009; Woitke et al. 2009) has the advantage of including the detailed continuum radiation field from the Monte-Carlo calculation for the radiative pumping of the molecules. Another advantage is that it avoids the iteration over the whole structure in order to solve the thermal-balance problem. This cuts down the calculation time of a single disk model by an order of magnitude down to of order 2 h on a standard desktop computer. The accuracy of a similar approach has been tested by Kamp et al. (2010) who find very small differences between this approach and a full radiative transfer calculation.
Appendix A.3: Raytracing
The raytracing to obtain spectral cubes of the line images has been extended by the contribution of scattered continuum photons to the source function. Also, we have implemented a step-size adjustment along the rays, which avoids that the raytracer takes too small steps in regions where the line does not intersect with the frequency of the current channel due to the velocity profile. This method is similar to the technique implemented in RadLite (Pontoppidan et al. 2009) and speeds up the raytracing considerably.
As an additional test for the raytracing to those reported in Bruderer et al. (2012), we have calculated the emission of a completely optically thin line from a molecule that is only abundant in the inner disk with strong velocity gradients. In this situation, the velocity integrated flux in a beam much larger than the disk can be calculated analytically by summing up the contribution of all cells. We have compared the results of the raytracer with the analytical results and find agreement to within a few percent, independent of the inclination of the disk. We note this is a meaningful benchmark test, as strong velocity gradients in the inner disk require an accurate step-size adjustment along the ray in order not to miss narrow lines (Pontoppidan et al. 2009).
Appendix A.4: Thermal balance
Several small changes have been implemented into the thermal balance calculation:
Line heating/cooling
In order to also account for atomic heating through absorption of UV/optical photons followed by radiative and collisional decay, we have implemented larger model atoms into the non-LTE calculation. Table A.1 provides a list of the implemented atoms and the spectroscopic and collisional rates used. Collisional coefficients with electrons have mostly been taken from the Chianti database (v7.0, Dere et al. 1997). Collisional rates with atomic or molecular hydrogen are missing for Mg ii, Si ii, S ii and Fe ii. For Si ii and Fe ii we use estimated collisional rates by Sternberg & Dalgarno (1995), which however only connect the fine structure levels within the electronic ground state.
The molecular coolants considered in the non-LTE calculation are 12CO, 13CO, C18O, OH, H2O, CN and HCN. For the isotope ratios, we take 12C/13C = 70, 16O/18O = 560 and 18O/17O = 3.2 (Wilson & Rood 1994).
Molecular data has been taken from the LAMDA database (Schöier et al. 2005) except for 12CO, where also ro-vibrational levels are accounted for. The ro-vibrational collisional rates are obtained using the approach by Chandra & Sharma (2001), using the current rates from the LAMDA database for the vibrational ground state.
Considered atomic lines.
Pumping of atomic oxygen by OH photodissociation
We now also account for the population of the 1D levels of atomic oxygen by the photodissociation of OH, 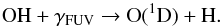 (A.6)Following van Dishoeck & Dalgarno (1984), we assume that ~50% of OH photodissociations lead to O(1D).
(A.6)Following van Dishoeck & Dalgarno (1984), we assume that ~50% of OH photodissociations lead to O(1D).
H 2 heating/cooling
X-ray heating through H2 ionization (Glassgold & Langer 1973; Meijerink & Spaans 2005) is now also accounted for. For the H2 heating and cooling, we use a model with 15 vibrational levels including the effects of fluorescence and excited formation similar to Sternberg & Dalgarno (1995). Since the previously used rates by Röllig et al. 2006 are fits to this small model, the heating/cooling rates of the two approaches agree very well, except for the case of high temperatures where the 15 level model can cool more efficiently than the two level approach since higher vibrational levels are excited (see Röllig et al. 2006).
Appendix A.5: Chemistry
The chemical network is taken consistently with Bruderer et al. (2012), except that we use the H2 formation rate by Cazaux & Tielens (2004, 2010). An additional reaction for the hydrogen loss of a hydrogenated PAH by a photoreaction, 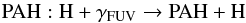 (A.7)is added. It is set to a rate of 10-8G0 s-1, with G0 the FUV field in units of the interstellar radiation field (Le Page et al. 2001).
(A.7)is added. It is set to a rate of 10-8G0 s-1, with G0 the FUV field in units of the interstellar radiation field (Le Page et al. 2001).
To solve for the steady-state abundances, we use an improved version of our globally convergent Newton-Raphson solver (Bruderer et al. 2012). In case this method fails to converge, we use a time-dependent solver. Instead of the DVODE package (Brown et al. 1989), we use the LIMEX package (Ehrig et al. 1999) which was found to be more robust.
Appendix A.6: Testing
As a comparison, we have rerun the representative model of HD 100546 in Bruderer et al. (2012) using the updated model. Line fluxes of both models together with observed line fluxes (Sturm et al. 2010) are given in Fig. A.2. While the atomic fine structure lines of C, C+ and O agree to within 20% between the models, the mid-J and high-J lines of CO show differences of up to a factor of two due to changes in the thermal balance. However, all conclusion made in Bruderer et al. (2012) remain unchanged. As pointed out by Bruderer et al. (2012), the mid-J and high-J CO lines are particularly sensitive on the gas temperature.
Appendix B: Intensity and flux conversions
The conversion between intensity in units of Kelvin (Tν) and flux (Fν) requires the knowledge of the telescope beam. Assuming a Gaussian beam with full width at halve maximum of θFWHM, the solid angle of the beam is  (B.1)thus, the conversion between Tν and Fν is
(B.1)thus, the conversion between Tν and Fν is 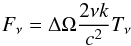 (B.2)in units, this is
(B.2)in units, this is 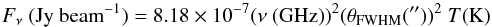 (B.3)for frequency/velocity integrated intensities it is
(B.3)for frequency/velocity integrated intensities it is 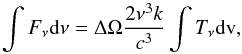 (B.4)where dν/ν = dv/c has been used. Thus
(B.4)where dν/ν = dv/c has been used. Thus 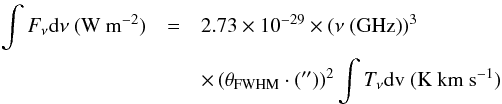 (B.5)
(B.5)
Appendix C: Effect of different Rgap and Rcav
 |
Fig. C.1 The representative model with inner disk and dust gap from 10 AU to 45 AU compared to a model with a dust gap from 10 AU to 22.5 AU. Integrated intensities of 12CO 3 − 2 and C18O 3 − 2 inside the gap (r = 16.25 AU) and in the outer disk (r = 100 AU) are shown. |
 |
Fig. C.2 The representative model with inner disk and dust gap from 10 AU to 45 AU compared to a model with a dust gap from 1 AU to 45 AU. Integrated intensities of 12CO 3 − 2 and C18O 3 − 2 inside the gap (r = 28 AU) and in the outer disk (r = 100 AU) are shown. |
 |
Fig. D.1 Integrated intensities of 12CO 3 − 2 at the center of the gap (r = 28 AU) and in the outer disk (r = 100 AU) for different X-ray luminosities (LX), stellar bolometric luminosities (Lbol) and effective temperatures (Teff). The considered range of the X-ray spectrum is given in brackets (either 0.1−10 keV or 1−100 keV). Note that the lines in the left panel lie ontop of each other. |
In order to study the effect of a different cavity size (Rcav in Fig. 1a) and extent of the inner disk (Rgap in Fig. 1a), we have calculated the representative model also with a dust gap extending from 1 AU to 45 AU (Rgap = 1 AU instead of 10 AU) and 10 AU to 22.5 AU (Rcav = 22.5 AU, instead of 45 AU). The resulting integrated intensities in the gap and outer disk are shown Figs. C.1 and C.2 in the same way as Fig. 12. In Fig. C.1 we present the integrated intensity in the center of the smaller cavity, at 16.25 AU (see Sect. 6.1.1).
Models with a smaller cavity radius (smaller Rcav) result in similar integrated intensities at a given radius inside the cavity, with differences <40%. This results from the fact that a point at a certain radius is much more affected by positions at smaller radii than at larger radii, because of the stellar heating and photodissociating radiation coming from inside. We conclude that calculations with smaller cavities are necessary for a detailed modeling, but the trends found from the 45 AU gap also hold for smaller gaps.
Models with a smaller inner disk (smaller Rgap) yield almost same integrated intensity profile inside the cavity, because the inner wall of the inner disk absorbs the stellar heating and photodissociating FUV radiation. This can be seen in Fig. 4d, showing the local FUV radiation. We conclude that the size of the inner disk is not a key parameter, as long as its inner wall can shield the stellar radiation.
Appendix D: Dependence on X-rays
The effect of X-ray radiation on the CO integrated intensity mainly depends on the X-ray luminosity (LX) compared to the FUV luminosity (LFUV). Figure D.1 shows the 12CO 3 − 2 and C18O 3 − 2 integrated intensity for models with dusty inner disk present and Lbol = 10 L⊙, Teff = 10 000 K or Lbol = 1 L⊙, Teff = 6000 K. The latter is the model with the highest LX/LFUV ~ 1 in our grid. However, even this model only shows a change of the 12CO integrated intensity in the gap with the X-ray luminosity, if the amount of gas in the cavity is low (δgas ≲ 10-5). This is because the heating of the upper layers in the gap is dominated by different effects (Sect. 3.1), while deeper in the disk, shielding by the inner disk is sufficient to render X-ray heating less important. The effect of X-rays does not change if the energy range of the thermal spectra is shifted to 0.1−10 keV instead of 1−100 keV. The rare isotopologue C18O shows the same dependence on the X-rays as 12CO. Stellar X-rays are thus not an important parameter for the low-J CO lines.
Acknowledgments
I am grateful to Ewine van Dishoeck, Gregory Herczeg, Til Birnstiel, Cornelius Dullemond, Davide Fedele, Nienke van der Marel, Geoff Mathews, and the anonymous referee for stimulating discussions. I thank Ruud Visser for providing the routines to calculate PAH opacities. I acknowledge a stipend by the Max Planck Society.
References
- Acke, B., & van den Ancker, M. E. 2006, A&A, 449, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aikawa, Y., & Nomura, H. 2006, ApJ, 642, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, R. D., Clarke, C. J., & Pringle, J. E. 2006, MNRAS, 369, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J. 2011, ARA&A, 49, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Avrett, E. H., & Hummer, D. G. 1965, MNRAS, 130, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Bally, J., & Scoville, N. Z. 1982, ApJ, 255, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010, A&A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Ormel, C. W., & Dullemond, C. P. 2011, A&A, 525, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Andrews, S. M., & Ercolano, B. 2012a, A&A, 544, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012b, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bjorkman, J. E., & Wood, K. 2001, ApJ, 554, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Brittain, S. D., Simon, T., Najita, J. R., & Rettig, T. W. 2007, ApJ, 659, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, P. N., Byrne, G. D., & Hindmarsh, A. C. 1989, SIAM J. Sci. Stat. Comput., 10, 1038 [Google Scholar]
- Brown, J. M., Blake, G. A., Dullemond, C. P., et al. 2007, ApJ, 664, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., Blake, G. A., Qi, C., Dullemond, C. P., & Wilner, D. J. 2008, ApJ, 675, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., Blake, G. A., Qi, C., et al. 2009, ApJ, 704, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., Herczeg, G. J., Pontoppidan, K. M., & van Dishoeck, E. F. 2012, ApJ, 744, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Bruderer, S., van Dishoeck, E. F., Doty, S. D., & Herczeg, G. J. 2012, A&A, 541, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calvet, N., D’Alessio, P., Hartmann, L., et al. 2002, ApJ, 568, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., D’Alessio, P., Watson, D. M., et al. 2005, ApJ, 630, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Casassus, S., van der Plas, G. M S. P., et al. 2013, Nature, 493, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., & Tielens, A. G. G. M. 2004, ApJ, 604, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., & Tielens, A. G. G. M. 2010, ApJ, 715, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Chandra, S., & Sharma, A. K. 2001, A&A, 376, 356 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cieza, L. A., Schreiber, M. R., Romero, G. A., et al. 2010, ApJ, 712, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Cieza, L. A., Schreiber, M. R., Romero, G. A., et al. 2012, ApJ, 750, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, C. J., Gendrin, A., & Sotomayor, M. 2001, MNRAS, 328, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Cleeves, L. I., Bergin, E. A., Bethell, T. J., et al. 2011, ApJ, 743, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T., & Sicilia-Aguilar, A. 2011, ApJ, 732, 24 [NASA ADS] [CrossRef] [Google Scholar]
- D’Alessio, P., Hartmann, L., Calvet, N., et al. 2005, ApJ, 621, 461 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- D’Alessio, P., Calvet, N., Hartmann, L., Franco-Hernández, R., & Servín, H. 2006, ApJ, 638, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Dartois, E., Dutrey, A., & Guilloteau, S. 2003, A&A, 399, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Graauw, T., Helmich, F. P., Phillips, T. G., et al. 2010, A&A, 518, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dodson-Robinson, S. E., & Salyk, C. 2011, ApJ, 738, 131 [CrossRef] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ApJ, 598, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Bertoldi, F. 1996, ApJ, 468, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2005, A&A, 434, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Dutrey, A., Guilloteau, S., Piétu, V., et al. 2008, A&A, 490, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ehrig, R., Nowak, U., Oeverdieck, L., & Deuflhard, P. 1999, in High Performance Scientific and Engineering Computing, eds. H.-J. Bungartz, F. Durst, & Chr. Zenger, Notes in Computational Science and Engineering (Springer), 8, 233 [Google Scholar]
- Ercolano, B., Drake, J. J., Raymond, J. C., & Clarke, C. C. 2008, ApJ, 688, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Ercolano, B., Drake, J. J., & Clarke, C. J. 2009, A&A, 496, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espaillat, C., Calvet, N., D’Alessio, P., et al. 2007, ApJ, 670, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Espaillat, C., Calvet, N., Luhman, K. L., Muzerolle, J., & D’Alessio, P. 2008, ApJ, 682, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Espaillat, C., D’Alessio, P., Hernández, J., et al. 2010, ApJ, 717, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Espaillat, C., Ingleby, L., Hernández, J., et al. 2012, ApJ, 747, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Geers, V. C., Augereau, J., Pontoppidan, K. M., et al. 2006, A&A, 459, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geers, V. C., Pontoppidan, K. M., van Dishoeck, E. F., et al. 2007, A&A, 469, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glassgold, A. E., & Langer, W. D. 1973, ApJ, 179, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Glassgold, A. E., Najita, J., & Igea, J. 2004, ApJ, 615, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Gorti, U., & Hollenbach, D. 2004, ApJ, 613, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Gorti, U., & Hollenbach, D. 2009, ApJ, 690, 1539 [Google Scholar]
- Harries, T. J. 2011, MNRAS, 416, 1500 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Heinzeller, D., Nomura, H., Walsh, C., & Millar, T. J. 2011, ApJ, 731, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D., Johnstone, D., Lizano, S., & Shu, F. 1994, ApJ, 428, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Ilgner, M., & Nelson, R. P. 2006, A&A, 445, 223 [CrossRef] [EDP Sciences] [Google Scholar]
- Jonkheid, B., Faas, F. G. A., van Zadelhoff, G.-J., & van Dishoeck, E. F. 2004, A&A, 428, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jonkheid, B., Kamp, I., Augereau, J.-C., & van Dishoeck, E. F. 2006, A&A, 453, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jonkheid, B., Dullemond, C. P., Hogerheijde, M. R., & van Dishoeck, E. F. 2007, A&A, 463, 203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamp, I., & van Zadelhoff, G.-J. 2001, A&A, 373, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamp, I., Tilling, I., Woitke, P., Thi, W., & Hogerheijde, M. 2010, A&A, 510, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaufman, M. J., Wolfire, M. G., Hollenbach, D. J., & Luhman, M. L. 1999, ApJ, 527, 795 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., Del Zanna, G., Young, P. R., Dere, K. P., & Mason, H. E. 2012, ApJ, 744, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2001, ApJS, 132, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
- Lucy, L. B. 1999, A&A, 344, 282 [NASA ADS] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Lyo, A.-R., Ohashi, N., Qi, C., Wilner, D. J., & Su, Y.-N. 2011, AJ, 142, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Mathews, G. S., Williams, J. P., & Ménard, F. 2012, ApJ, 753, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Meijerink, R., & Spaans, M. 2005, A&A, 436, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merín, B., Brown, J. M., Oliveira, I., et al. 2010, ApJ, 718, 1200 [NASA ADS] [CrossRef] [Google Scholar]
- Min, M., Dullemond, C. P., Dominik, C., de Koter, A., & Hovenier, J. W. 2009, A&A, 497, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulders, G. D., Paardekooper, S.-J., Panić, O., et al. 2013, A&A, 557, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nomura, H., & Millar, T. J. 2005, A&A, 438, 923 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Benisty, M., & Birnstiel, T. 2012a, A&A, 545, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Birnstiel, T., Ricci, L., et al. 2012b, A&A, 538, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Ménard, F., Duchêne, G., & Bastien, P. 2006, A&A, 459, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Harries, T. J., Min, M., et al. 2009, A&A, 498, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pontoppidan, K. M., Blake, G. A., van Dishoeck, E. F., et al. 2008, ApJ, 684, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Pontoppidan, K. M., Meijerink, R., Dullemond, C. P., & Blake, G. A. 2009, ApJ, 704, 1482 [NASA ADS] [CrossRef] [Google Scholar]
- Ralchenko, Y. 2009, Phys. Scr. Volume T, 134, 014025 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T. P. 2010, A&A, 520, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röllig, M., Ossenkopf, V., Jeyakumar, S., Stutzki, J., & Sternberg, A. 2006, A&A, 451, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röllig, M., Abel, N. P., Bell, T., et al. 2007, A&A, 467, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romero, G. A., Schreiber, M. R., Cieza, L. A., et al. 2012, ApJ, 749, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Rosotti, G. P., Ercolano, B., Owen, J. E., & Armitage, P. J. 2013, MNRAS, 430, 1392 [NASA ADS] [CrossRef] [Google Scholar]
- Salyk, C., Blake, G. A., Boogert, A. C. A., & Brown, J. M. 2007, ApJ, 655, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Salyk, C., Blake, G. A., Boogert, A. C. A., & Brown, J. M. 2009, ApJ, 699, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Salyk, C., Blake, G. A., Boogert, A. C. A., & Brown, J. M. 2011, ApJ, 743, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Semenov, D., & Wiebe, D. 2011, ApJS, 196, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Dutkevitch, D., Strom, S. E., et al. 1990, AJ, 99, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Sternberg, A., & Dalgarno, A. 1989, ApJ, 338, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Sternberg, A., & Dalgarno, A. 1995, ApJS, 99, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Störzer, H., & Hollenbach, D. 2000, ApJ, 539, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Strom, K. M., Strom, S. E., Edwards, S., Cabrit, S., & Skrutskie, M. F. 1989, AJ, 97, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Sturm, B., Bouwman, J., Henning, T., et al. 2010, A&A, 518, L129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 722 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, N., van Dishoeck, E., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Dishoeck, E. F., & Dalgarno, A. 1984, ApJ, 277, 576 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., Jonkheid, B., & van Hemert, M. C. 2006, in Chemical Evolution of the Universe. Faraday Discussions, 133, 231 [Google Scholar]
- van Zadelhoff, G., van Dishoeck, E. F., Thi, W., & Blake, G. A. 2001, A&A, 377, 566 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Zadelhoff, G.-J., Aikawa, Y., Hogerheijde, M. R., & van Dishoeck, E. F. 2003, A&A, 397, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasyunin, A. I., Semenov, D., Henning, T., et al. 2008, ApJ, 672, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Visser, R., Geers, V. C., Dullemond, C. P., et al. 2007, A&A, 466, 229 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Visser, R., van Dishoeck, E. F., & Black, J. H. 2009, A&A, 503, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Visser, R., Doty, S. D., & van Dishoeck, E. F. 2011, A&A, 534, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Woitke, P., Kamp, I., & Thi, W. 2009, A&A, 501, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolf, S., & Voshchinnikov, N. V. 2004, Comput. Phys. Commun., 162, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Woodall, J., Agúndez, M., Markwick-Kemper, A. J., & Millar, T. J. 2007, A&A, 466, 1197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woods, P. M., & Willacy, K. 2009, ApJ, 693, 1360 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C. 2008, ARA&A, 46, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Nelson, R. P., Hartmann, L., Espaillat, C., & Calvet, N. 2011, ApJ, 729, 47 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Schematic view of the physical structure used in this work and definition of the main parameters. a) Surface density structure. b) Vertical density structure. |
| In the text | |
 |
Fig. 2 Dust and PAH opacities. Absorption (κ) and scattering (σ) mass coefficients are given by solid and dashed lines, respectively. |
| In the text | |
 |
Fig. 3 Surface density profiles of the observed transition disks (black lines; Andrews et al. 2011) compared to the model surface density profiles used in this work (red lines). Dotted lines indicate regions within the gap. The red and black dots show (Rc,Σc/e). |
| In the text | |
 |
Fig. 4 Physical conditions in a representative model (Table 1) with δgas = 10-2 and δdust = 10-5 (dusty inner disk present). Only regions with a gas density larger than 105 cm-3 are shown. The contour lines on the panels match to the lines on the color bars. The panels provide a) gas density structure; b) gas/dust mass ratio; c) calculation grid; d) FUV radiation field; e) visual extinction; f) abundance of PAHs; g) dust temperature; h) gas temperature; i) ratio of gas to dust temperature; j) H2 abundance; k) CO abundance; and l) O abundance. |
| In the text | |
 |
Fig. 5 H2 and CO abundance in the representative model (Table 1) with different gas content in the cavity (δgas = 1,10-4 and 10-6) and a dusty inner disk present (δdust = 10-5). Only regions with gas density larger than 105 cm-3 are shown. Upper panels: CO abundance. Lower panels: H2 abundance. |
| In the text | |
 |
Fig. 6 H2 and CO abundance of a representative model (Table 1) with dusty inner disk (δdust = 10-5) compared to a model without dusty inner disk (δdust = 10-10). Both models have δgas = 10-4. Upper panels: H2 abundance. Lower panels: CO abundance. |
| In the text | |
 |
Fig. 7 C and C+ abundance of the representative models (Table 1) with δgas = 10-6 and no dusty inner disk (δdust = 10-10) or δgas = 10-4,10-6 with dusty inner disk (δdust = 10-5). Upper panels: C+ abundance. Lower panels: C abundance. |
| In the text | |
 |
Fig. 8 Vertical column densities of the representative models (Table 1) a) H2; b) CO; c) neutral carbon, and d) ionized carbon. Different colors shows models with different values of δgas. Solid lines represent models with a dusty inner disk present (δdust = 10-5) and the dashed lines models without dusty inner disk (δdust = 10-10). |
| In the text | |
 |
Fig. 9 Continuum subtracted integrated line intensity as function of the radius for CO 3 − 2 and its isotopologues. The figure shows intensities derived from the representative models (Table 1). The vertical gray lines at 28 AU and 100 AU indicate the radii and which the intensities are provided in Figs. 12 and 15. |
| In the text | |
 |
Fig. 10 Surface of τ = 1 and line opacities of CO 3 − 2 and isotopologues for the representative model (Table 1) with δgas = 10-2 and a dusty inner disk present (δdust = 10-5). The vertical gray line at 28 AU shows the center of the gap. Upper panel: line center opacity depending on the radius. Lower panel: position of the τ = 1 surface for different radii. |
| In the text | |
 |
Fig. 11 Images of the integrated intensity (in K km s-1) of 12CO 3 − 2 from the series of representative models (Table 1). Models with δgas = 1,10-2,10-3 and 10-4 are shown. The inclination i = 30° and the black dashed lines show the size of the gap (10 < r < 45 AU). Red dashed lines show the radius where PAHs can survive in absence of UV shielding by a dusty inner disk (Sect. 3). Upper panels: models with a dusty inner disk present (δdust = 10-5). Lower panels: models without an inner disk (δdust = 10-10). |
| In the text | |
 |
Fig. 12 Integrated intensities of CO 3 − 2 and isotopologues at the center of the gap (r = 28 AU) and in the outer disk (r = 100 AU). The ALMA detection limit for a 5σ detection after 1 h on-source observation with a 0.1′′ beam (see Sect. 6) is given by the vertical dashed black line. Upper panels: models with a dusty inner disk (δdust = 10-5). Lower panels: models without inner disk (δdust = 10-10). |
| In the text | |
 |
Fig. 13 Beam convolved integrated intensities of CO 3 − 2 for different beam sizes. The representative model with a dusty inner disk present is shown. The disk is face on. Left panel: 12CO 3 − 2. Right panel: C18O 3 − 2. |
| In the text | |
 |
Fig. 14 Beam convolved images of the integrated intensity (in K km s-1) of 12CO 3 − 2 from a representative model (Table 1) with dusty inner disk present and δgas = 10-4 (Sect. 4). The inclination is i = 30° and the images are convolved to a Gaussian beam with FWHM 0.05′′, 0.1′′, 0.15′′ and 0.2′′. The black dashed lines indicate the size of the gap (r = 10 − 45 AU). |
| In the text | |
 |
Fig. 15 Integrated intensities of 12CO 3 − 2 (solid lines) and C18O 3 − 2 (dashed lines) at the center of the gap (r = 28 AU) and in the outer disk (r = 100 AU). The panels show the intensities for variations of one parameter (Rc, Lbol, Teff and the PAH abundance). If not varied, the parameters are set to the values of the representative models (Table 1: Rc = 50 AU, Lbol = 10 L⊙, Teff = 10 000 K and a PAH abundance of 10% the ISM abundance). |
| In the text | |
 |
Fig. 16 Integrated intensities of [C i] 3P |
| In the text | |
 |
Fig. 17 Beam convolved integrated intensities of [C ii] 2P |
| In the text | |
 |
Fig. 18 Beam convolved integrated intensities of [O i] 3P1 − 3P2 at 63 μm and 3P0 − 3P1 at 145 μm and for different beam sizes. The disk is face on and has a dusty inner disk present. |
| In the text | |
 |
Fig. 19 Images of the integrated intensity (in K km s-1) of CO isotopologues (12CO, 13CO, C17O, and 13C18O) from the series of representative models (Table 1) with dusty inner disk present (δdust = 10-5). Models with δgas = 1,10-1,10-2 and 10-3 are shown. The inclination i = 30° and the black dashed lines show the size of the gap (10 < r < 45 AU). The C18O images look similar to the C17O images and thus not shown. 1st row: 12CO 3 − 2. 2nd row: 13CO 3 − 2. 3rd row: C17O 3 − 2. 4th row: 13C18O 3 − 2. |
| In the text | |
 |
Fig. 20 Images of the integrated intensity (in K km s-1) of CO isotopologues (12CO, 13CO, C17O, and 13C18O) from the series of representative models (Table 1) without dusty inner disk (δdust = 10-10). Models with δgas = 1,10-1,10-2 and 10-3 are shown. The inclination i = 30° and the black dashed lines show the size of the gap (10 < r < 45 AU). The C18O images look similar to the C17O images and thus not shown. 1st row: 12CO 3 − 2. 2nd row: 13CO 3 − 2. 3rd row: C17O 3 − 2. 4th row: 13C18O 3 − 2. |
| In the text | |
 |
Fig. A.1 Disk midplane dust temperature for the disk benchmark problem proposed in Pinte et al. (2009) (τ = 105). The result obtained from our code is given in the red dashed line, the results by MCFost (Pinte et al. 2006) in black. |
| In the text | |
 |
Fig. A.2 Comparison of the model fluxes between the current model and the representative model of HD 100546 in Bruderer et al. (2012). |
| In the text | |
 |
Fig. C.1 The representative model with inner disk and dust gap from 10 AU to 45 AU compared to a model with a dust gap from 10 AU to 22.5 AU. Integrated intensities of 12CO 3 − 2 and C18O 3 − 2 inside the gap (r = 16.25 AU) and in the outer disk (r = 100 AU) are shown. |
| In the text | |
 |
Fig. C.2 The representative model with inner disk and dust gap from 10 AU to 45 AU compared to a model with a dust gap from 1 AU to 45 AU. Integrated intensities of 12CO 3 − 2 and C18O 3 − 2 inside the gap (r = 28 AU) and in the outer disk (r = 100 AU) are shown. |
| In the text | |
 |
Fig. D.1 Integrated intensities of 12CO 3 − 2 at the center of the gap (r = 28 AU) and in the outer disk (r = 100 AU) for different X-ray luminosities (LX), stellar bolometric luminosities (Lbol) and effective temperatures (Teff). The considered range of the X-ray spectrum is given in brackets (either 0.1−10 keV or 1−100 keV). Note that the lines in the left panel lie ontop of each other. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.