| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 22 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220090 | |
| Published online | 04 June 2013 | |
Cores, filaments, and bundles: hierarchical core formation in the L1495/B213 Taurus region⋆,⋆⋆
1 Observatorio Astronómico Nacional (IGN), Alfonso XII 3, 28014 Madrid, Spain
2 Institute for Astrophysics, University of Vienna, Türkenschanzstrasse 17, 1180 Vienna, Austria
e-mail: alvaro.hacar@univie.ac.at
3 Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, CA 91109, USA
4 University of Minnesota, 116 Church St SE, Minneapolis, MN 55414, USA
Received: 24 July 2012
Accepted: 8 March 2013
Context. Core condensation is a critical step in the star-formation process, but it is still poorly characterized observationally.
Aims. We have studied the 10 pc-long L1495/B213 complex in Taurus to investigate how dense cores have condensed out of the lower density cloud material.
Methods. We observed L1495/B213 in C18O(1−0), N2H+(1−0), and SO(JN = 32–21) with the 14 m FCRAO telescope, and complemented the data with dust continuum observations using APEX (870 μm) and IRAM 30 m (1200 μm).
Results. From the N2H+ emission, we identify 19 dense cores, some starless and some protostellar. They are not distributed uniformly, but tend to cluster with relative separations on the order of 0.25 pc. From the C18O emission, we identify multiple velocity components in the gas. We have characterized them by fitting Gaussians to the spectra and by studying the distribution of the fits in position–position–velocity space. In this space, the C18O components appear as velocity-coherent structures, and we identify them automatically using a dedicated algorithm (FIVE: Friends In VElocity). Using this algorithm, we identify 35 filamentary components with typical lengths of 0.5 pc, sonic internal velocity dispersions, and mass-per-unit length close to the stability threshold of isothermal cylinders at 10 K. Core formation seems to have occurred inside the filamentary components via fragmentation, with few fertile components with higher mass-per-unit length being responsible for most cores in the cloud. On large scales, the filamentary components appear grouped into families, which we refer to as bundles.
Conclusions. Core formation in L1495/B213 has proceeded by hierarchical fragmentation. The cloud fragmented first into several pc-scale regions. Each of these regions later fragmented into velocity-coherent filaments of about 0.5 pc in length. Finally, a small number of these filaments fragmented quasi-statically and produced the individual dense cores we see today.
Key words: ISM: clouds / ISM: kinematics and dynamics / ISM: molecules / ISM: structure / stars: formation / radio lines: ISM
Based on observations carried out with the FCRAO 14 m and IRAM 30 m telescopes. IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain). Also based on data acquired with the Atacama Pathfinder Experiment (APEX). APEX is a collaboration between the Max-Planck-Institut für Radioastronomie, the European Southern Observatory, and the Onsala Space Observatory (ESO projects 080.C-3054 and 083.C-0453).
The Gaussian fits results presented in Sect. 5 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/554/A55
© ESO, 2013
1. Introduction
Dense cores are the sites of individual or binary stellar birth (Benson & Myers 1989; di Francesco et al. 2007), and their condensation from the ambient cloud represents a critical step in the process of star formation. Core formation, however, appears as a bottleneck in the road from clouds to stars. At any given time, only a small fraction of the material in a cloud is in the form of dense cores (<10%, i.e., Enoch et al. 2007), and this apparent difficulty making dense cores is very likely connected to the low efficiency of the star-formation process (Evans 2008). Core formation, in addition, seems to play a key role in determining the mass of the final star, since the distribution of masses among starless cores in a cloud mimics the initial distribution of stellar masses (Motte et al. 1998; Alves et al. 2007). Core formation, therefore, represents a crucial gas transition by which a cloud selects a small fraction of its material to form the next generation of stars and leaves the rest as a sterile remnant to be dispersed into the more diffuse interstellar medium.
Despite its critical role in star formation, the process of core formation is still poorly understood. A number of condensation mechanisms have been proposed over the years, ranging from quasi-static contraction mediated by ambipolar-diffusion (Shu et al. 1987; Mouschovias & Ciolek 1999) to gravo-turbulent fragmentation driven by supersonic motions (Padoan et al. 2001; Klessen et al. 2005; Vázquez-Semadeni et al. 2005). Observations, however, do not clearly favor any single model, partly due to the intrinsic difficulty in measuring time scales of core evolution and magnetic field intensities, which are the main parameters that distinguish the different models (Ward-Thompson et al. 2007, for a review).
New approaches to studying core formation are needed, and a promising strategy is to analyze the velocity field of the gas in detail, comparing the internal motions of the dense cores with those of the surrounding low-density gas from which they have condensed. Following this approach, Hacar & Tafalla (2011) found that the gas surrounding the cores of the L1517 cloud is subsonic and quiescent, like the gas inside the dense cores, in contradiction to the predictions from models of gravo-turbulent fragmentation. More interestingly, the lower density gas in L1517 forms a network of filaments whose velocity fields are continuous and subsonic on scales of about 0.5 pc, which is significantly larger than the typical core size (≈0.1 pc). These so-called velocity-coherent filaments therefore seem to constitute the parent structures from which the cores form. The observed continuity between the large-scale velocity field of the filaments and the internal velocity gradients of the cores indicates that the transition between the two regimes involves very small kinematical changes, and in particular, an absence of shock compression.
The analysis of L1517 suggests that core formation in this Taurus cloud has occurred in two steps, with the velocity-coherent filaments forming first and the cores fragmenting later from the already quiescent filament gas. In this scenario, turbulent dissipation precedes core formation, and gravitational fragmentation of the filaments is the final step in the core-formation sequence.
Independent work using dust continuum data from the Herschel Space Observatory has revealed that filamentary structures in clouds are ubiquitous and that filament-based core formation is likely to be a widespread process in both low- and high-mass star-forming regions (André et al. 2010; Molinari et al. 2010; Arzoumanian et al. 2011). (See also Schneider & Elmegreen 1979; Johnstone & Bally 1999; Hartmann 2002; Myers 2009, for previous work emphasizing the importance of filaments in core formation.) Understanding core formation inside filaments has therefore become an urgent task, and kinematic information is an element needed to complete the picture of filament physics. For this reason, we have selected the most prominent filamentary region of the Taurus cloud, which consists of the B211, B213, B216, B217, and B218 dark patches (Barnard 1927) and ends in the L1495 cloud (Lynds 1962), and we have subjected it to observations similar to those used to study L1517.
Our cloud of study, which we refer to as L1495/B213 for brevity, appears in optical images as a several-degree-long filament first noticed by Barnard (1907), who incidentally used this and other Taurus filaments to argue that at least some dark objects result from obscuration by a physical substratum, and not from the mere absence of background stars as previously thought. Owing to its striking appearance, the L1495/B213 complex has been investigated and characterized by several authors over the years. Initial extinction maps were presented by Gaida et al. (1984) and Cernicharo et al. (1985) using optical data and, more recently, by Schmalzl et al. (2010) using deep NIR observations. The gas component of the cloud has been studied systematically in 13CO and C18O by Duvert et al. (1986), who noticed a complex velocity structure that was interpreted as resulting from colliding filaments. Additional large-scale maps of the region in CO isotopologues have been presented by Heyer et al. (1987), Mizuno et al. (1995), Onishi et al. (1996), and Goldsmith et al. (2008). Very recently, Palmeirim et al. (2013) have presented high dynamic-range Herschel images of the dust continuum emission.
Embedded in the relatively low-density CO-emitting gas of L1495/B213 lies a population of dense cores, which has been explored by Benson & Myers (1989) and Onishi et al. (2002) using NH3 and H13CO+ observations, respectively, with additional and more limited N2H+ observations presented by Tatematsu et al. (2004). Some of these dense cores are starless, while others are associated with young stellar objects (YSOs) of different ages. This population of YSOs has been the subject of a number of dedicated studies, most recently by Luhman et al. (2009) and Rebull et al. (2010), and by the dedicated outflow search from Davis et al. (2010).
The above observations, and additional work reviewed by Kenyon et al. (2008), show that the L1495/B213 complex has been and still is an active site of star formation in Taurus. In fact, all stages of the star-formation sequence can be found in the cloud, from starless cores that may have recently condensed, to Class 0 and Class I protostars with active outflows and signs of accretion, to classical and weak T Tauri stars in their path to the main sequence. This rich population of objects makes L1495/B213 an ideal laboratory to study core and star formation, with the additional advantage that the region has a well-defined filamentary geometry that simplifies its mapping.
2. Observations
The main dataset used in this paper consists of observations carried out with the FCRAO 14 m radio telescope during several sessions between March 2002 and November 2005. In each session, the telescope was equipped with the 32-pixel SEQUOIA focal-plane array receiver and the DCC autocorrelator, which allowed us to observe two different spectral lines simultaneously, either in the 85−100 GHz or the 100−115 GHz bands. As the two main lines of the project, N2H+(1−0) and C18O(1−0), could not be observed simultaneously, the L1495/B213 region was mapped twice. In one pass, N2H+(J = 1−0) and SO(JN = 32–21) were observed simultaneously, and in the other pass, C18O(J = 1−0) and C17O(J = 1−0) were observed. To achieve high velocity resolution, the DCC autocorrelator was configured to provide 1024 spectral channels with a spacing of 25 kHz, or approximately 0.07 km s-1. Rest frequencies are assumed to have the same values as in Hacar & Tafalla (2011).
All observations were done in on-the-fly mode with a common center at 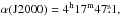 δ(J2000) = + 27°37′18′′ and covering the cloud with a mosaic of 10′ × 10′ fields. Position switching was used to subtract the sky and receiver contributions, and the reference position was located (+ 2300′′, − 4500′′) with respect to the map center. This position has a C18O(J = 1 − 0) peak intensity Tmb < 0.03 K averaged over the SEQUOIA footprint, as estimated from frequency-switched observations. This intensity is negligible compared to the typical on-source values, which are greater than 1 K.
δ(J2000) = + 27°37′18′′ and covering the cloud with a mosaic of 10′ × 10′ fields. Position switching was used to subtract the sky and receiver contributions, and the reference position was located (+ 2300′′, − 4500′′) with respect to the map center. This position has a C18O(J = 1 − 0) peak intensity Tmb < 0.03 K averaged over the SEQUOIA footprint, as estimated from frequency-switched observations. This intensity is negligible compared to the typical on-source values, which are greater than 1 K.
During the observations, calibration was done every ten minutes, and pointing corrections were determined every three hours from SiO maser observations, finding typical errors within 5′′ rms. According to FCRAO-provided information1, the beam efficiency of the telescope is approximately 0.5, and the FWHM beam size depends linearly on frequency, having a value of 56′′ at the lowest (N2H+) frequency and of 47′′ at the highest (C17O) frequency.
Data reduction consisted in the creation of Nyquist-sampled maps with the otftool program2, and resulted in data sets of more than 35 000 spectra for each of our four program lines. These spectra were later converted into the GILDAS/CLASS format3 for second-degree baseline subtraction and a spatial convolution with a Gaussian to eliminate residual noise. The final resolution of all the FCRAO data is 60′′, taking the off-line convolution into account, and the grid spacing is 30′′. With this sampling, the size of each molecular dataset is approximately 23 000 spectra.
Additional line observations of L1495/B213 were made using the IRAM 30 m telescope. These complementary data consisted of simultaneous N2H+(1−0) and C18O(2−1) spectra observed toward a selected group of positions to clarify the velocity structure of the gas. The observations were done in 2010 April and 2011 December using the EMIR heterodyne receiver in frequency switching mode. The backend was the VESPA autocorrelator configured to provide a velocity resolution of 0.06 km s-1. Sky calibration was carried out every 15 min, and pointing corrections every 2 h. Conversion to the mean brightness temperature scale was done using the facility-provided telescope efficiencies. The angular resolution of the observations was approximately 25′′ for N2H+(1−0) and 12′′ for C18O(2−1).
Dust continuum observations of selected parts of L1495/B213 were carried out at 1200 μm with the MAMBO-2 array on the IRAM 30 m telescope during several runs between 2003 December and 2009 November. The observations were done in on-the-fly mode with a scanning speed of 8′′ s-1, a wobbler period of 0.5 s, and wobbler throws between 50′′ and 70′′. Atmospheric calibration was carried out using data from sky dips every 1.5 h, and the absolute calibration was achieved using observations of CRL618. The data were reduced with the MOPSIC software using a method to recover extended emission consisting of ten iterations with a model source and subtraction of correlated noise.
Additional dust continuum observations of L1495/B213 were carried out at 870 μm with the LABOCA array on the APEX telescope in 2007 November and 2009 July. The observation consisted of two on-the-fly maps (2007 observations) and a mosaic of seven raster-spiral (quarter) maps Siringo et al. (2009, 2009 observations). Calibration was carried out using sky dips and observations of Mars and CRL618 about every two hours, and the reduction used the BOA software together with the method to recover extended emission presented by Belloche et al. (2011). An artistic rendition of these observations can be found in the ESO photo release eso12094.
3. Large-scale cloud properties from the integrated maps: evidence of sequential fragmentation
 |
Fig. 1 Integrated intensity maps of L1495/B213 in C18O(1−0) (top) and SO(JN = 32 − 21) (bottom). The offsets refer to the FCRAO map center at |
 |
Fig. 2 Top: integrated intensity map of L1495/B213 in N2H+(1−0) adding all hyperfine components. The white contour corresponds to 0.5 K km s-1. Central position and offsets are as in Fig. 1. First contour and contour interval are 0.5 K km s-1. Bottom: schematic view of the L1495/B213 complex indicating the regions defined in this paper, which approximately match those of Barnard (1927). The black solid line represents the lowest C18O(1−0) contour in Fig. 1 and delineates the boundary of the cloud. The red lines represent the N2H+(1−0) emission, which traces the dense cores, and the red labels identify the cores described in Sect. 4 and summarized in Table 2. The stars correspond to stellar objects from the survey of Rebull et al. (2010). Solid symbols represent the youngest objects (Class I and Flat), and open symbols represent evolved objects (Classes II and III). |
Figures 1 and 2 present integrated-intensity maps of L1495/B213 in C18O, SO, and N2H+. The different species provide complementary information on the gas conditions due to a combination of excitation and abundance effects. C18O is the most sensitive tracer of the low-density material in the cloud thanks to its lower critical density and relatively large abundance, although it disappears from the gas phase in dense, chemically evolved regions due to freeze out onto dust grains (Caselli et al. 1999; Bergin et al. 2002; Tafalla et al. 2002). The SO molecule, on the other hand, presents a higher critical density that makes it more selective of dense gas. Its abundance, however, is especially sensitive to the evolutionary state of the material, and is higher during the earliest phases of gas contraction (Tafalla et al. 2006; Hacar & Tafalla 2011). Finally, N2H+ is a tracer of dense, chemically evolved gas due to its abundance enhancement when CO freezes out, and thus highlights the population of dense cores in the cloud (see Bergin & Tafalla 2007, for a review on core chemistry).
As can be seen in Fig. 1, the C18O emission (top panel) traces a curved filamentary cloud over approximately 4°, or about 10 pc for our assumed distance of 140 pc (Elias 1978). This emission has a bright condensation towards the northern end that coincides with the location of the L1495 dark cloud and with one of the main groups of pre-main sequence stars in Taurus (Kenyon et al. 2008). From L1495, the emission extends first south and then southeast, and contains several elongated regions of enhanced intensity. Finally, it forks into two branches of relatively diffuse emission towards the east and the southeast.
Overall, the distribution of C18O emission matches the distribution of extinction derived by Schmalzl et al. (2010) from NIR data with an angular resolution similar to that of our FCRAO observations. It also approximately matches the LABOCA and MAMBO dust continuum maps presented in the next section. There are, however, significant departures between the C18O emission and both the dust extinction and emission maps. These departures coincide with the location of the dense cores that dominate the N2H+ emission, and they can be seen by comparing the maps of C18O and N2H+. Between Δα = 1000′′ and 3000′′, for example, there is a chain of several cores that is bright both in N2H+ and the dust continuum (next section), but that only presents weak and diffuse C18O emission in the map of Fig. 1. This anticorrelation between the C18O and N2H+ emissions is typical of regions of core formation, and it indicates that CO has depleted from the dense gas (Caselli et al. 1999; Bergin et al. 2002; Tafalla et al. 2002). While CO depletion is common in the inner part of dense cores, the region with the core chain in B213 is unusual in presenting depressed CO emission on a scale more than 0.5 pc in length.
Properties of the subregions in L1495/B213.
While the large-scale geometry of L1495/B213 suggests that the cloud is a single entity with a common physical origin, the internal structure of the gas presents strong evidence of fragmentation. This can be seen in the maps of Fig. 1, and it has already been noticed by Barnard from the study of the optical images, which lead to his subdivision of the cloud into distinct condensations (Barnard 1927). To better refer to the different parts of the cloud in our study, we have divided the mapped area into regions and labeled these regions following the original notation by Barnard as closely as possible. Barnard’s description, however, is only qualitative, and some parts of the cloud are not assigned to any of his condensations, so the correspondence between our regions and Barnard’s regions should only be considered approximate (see also Schmalzl et al. 2010, for a similar attempt to subdivide L1495/B213). The resulting cloud division is shown in the bottom panel of Fig. 2 using color-coded boxes superposed to the lowest C18O(1−0) contour from in Fig. 1.
Barnard’s division of the cloud was purely based on the appearance of the optical images, but is correlated with a number of independent cloud properties. One of these properties is the stellar population. In Fig. 2, we use stars to represent the stellar objects classified as “previously identified” or “most likely” (A+ rank) Taurus members by the Spitzer telescope survey of Rebull et al. (2010). Identifying the full stellar population of this Taurus region is still subject to debate, especially at the low-luminosity end of the distribution (e.g., Palau et al. 2012), and for this reason we have conservatively required that our candidates have an A+ rank in the notation of Rebull et al. (2010). To distinguish between the different stellar classes, we have used in Fig. 2 solid star symbols for the youngest objects (Class I and Flat, see Rebull et al. 2010) and open star symbols for the more evolved objects (Class II and III).
As can be seen, the stellar population of the cloud is not distributed uniformly over the different Barnard regions. Most YSOs are located in regions B7, B213, and B217, which together contain 51% of the cloud mass but have 88% of the stars (i.e., the other 49% of mass only contains 12% of the stars, Table 1). Even among these three regions, there are significant differences in the type of associated stellar objects. B7 and B217 contain twice as many evolved objects as young ones, while the B213 region contains the same number of young and evolved objects. These differences suggest that star formation has not occurred simultaneously in all the regions, but that different parts of the cloud have been forming stars at different rates.
Another property that correlates with the subdivision of the cloud in regions is the chemical composition of the gas. Comparing the intensities of C18O, SO, and N2H+ in Figs. 1 and 2, it is clear that the emission ratio for the different species changes between regions, even when taking the different excitation requirements of the tracers into account. The most striking contrast between regions occurs in the contiguous B211 and B213 regions. As mentioned before, the B213 region presents relatively weak C18O and SO emission, while being associated with bright N2H+. This is indicative of strong CO and SO depletion and suggests that the gas in B213 is chemically evolved and has condensed into several cores. These two properties are in good agreement with the finding that B213 has the highest fraction of young protostars.
In contrast to B213, the nearby B211 region presents very bright emission in both C18O and SO, together with intense dust millimeter continuum (see next section). Its N2H+ emission, however, is almost undetected by our observations, except for a single core (number 7 in the Fig. 2) that is not associated with the main part of the filament (see Fig. 4 below). This combination of bright C18O and SO together with weak N2H+ indicates that the gas in B211 has an unusually young chemical composition. Such chemical youth is again in good agreement with the lack of stellar population, which has already been used to argue that the B211 region is at a very early state of evolution (Goldsmith et al. 2008; Schmalzl et al. 2010).
While B211 presents the strongest evidence of chemical youth, B10 also seems to be relatively unevolved. This can be seen in Figs. 1 and 2, where B10 presents relatively bright SO emission, especially when compared to the C18O-brighter B7 region to its north. In contrast to B211, however, B10 is relatively weak in C18O and has a number of N2H+-bright dense cores, which suggests that some CO depletion has already taken place. B10 must therefore be somewhat more evolved than B211. Interestingly, while B10 has already formed several dense cores, none of them seems associated to any Class I or Flat objects in the catalog of Rebull et al. (2010).
In summary, the evolutionary state of the different Barnard regions is as follows. B211 appears to be the least evolved region due to its chemical composition, lack of protostars, and presence of a single (starless) core. B10 seems to follow in terms of evolution, since it has several dense cores, but only one is possibly associated with a YSO. B216 also appears to be at a similarly young stage, owing to its lack of protostars and cores, but its more diffuse nature makes its status less clear. Next in evolution comes B213, which has recently started forming stars and is doing so very actively. Next is B218, which has a number of starless cores, including the very young L1521E (Hirota et al. 2002; Tafalla & Santiago 2004), and has a very young stellar object. Finally, B7 and B217 have several Class I/Flat objects, but whose stellar population is dominated by more evolved objects. Among these two regions, B7 has the largest number of Class III objects (7 out of 25 YSOs), so it is likely to be more evolved than the rest.
While the differences in evolutionary stage between the parts of the L1495/B213 complex are clear, the assignment of relative ages is more uncertain. Overall, we can estimate that some parts of the cloud have been forming stars for at least 1−2 Myr. B7, for example, has seven Class II and Class III objects with ages in the range 1−6 Myr, according to the estimates by Bertout et al. (2007). B213 is associated with FS Tau B, with an estimated age of 2.5 Myr, and B217 contains FV Tau/c, which seems older than 1 Myr (Kraus & Hillenbrand 2009). At the other end of the scale, the B211 region, despite being more massive than B213 or B217, does seem not yet to have formed a single star. This means that the large-scale cloud, despite its striking appearance as a single 10 pc filament, has not fragmented as a single entity, but that different parsec-sized regions have followed different star-formation histories over the past 1−2 Myr.
Since the differences in stellar population are correlated with differences in the chemical composition of the gas (Table 1), and since this composition is very sensitive to the amount of time the gas has remained dense (e.g., Bergin & Tafalla 2007), it seems unlikely that regions with little or no star formation, like B211, have maintained with their current physical conditions for more than 1−2 Myr, while regions like B217 were forming stars. To appear chemically young, regions like B211 must have condensed more recently from less-dense cloud material than regions like B217. This suggests that the complex fragmentation of the cloud reflects a similarly complex pattern of assembling of the large-scale filament, by which evolved regions like B7 and B217 condensed and started to form stars first, while other regions like B211 seem to have only become dense very recently. As we will see below, this pattern of differential evolution has left an imprint in the large-scale pattern of gas velocities.
 |
Fig. 3 Expanded view of the B7-B10 region. C18O(1−0) emission in color and N2H+(1−0) emission in white contours (sum of all hyperfine components). First contour and contour interval are 0.5 K km s-1. Stars as in Fig. 2, and offsets refer to the FCRAO map center (see Sect. 2). |
 |
Fig. 4 Expanded view of the B211 region and the NW part of B213 (to better connect with the following figure). Top: C18O(1−0) and N2H+(1−0) maps as in Fig. 3. Bottom: 850 μm continuum map from LABOCA observations and N2H+(1−0) emission (contours). |
 |
Fig. 5 Expanded view of the B213 region. Top: C18O(1−0) and N2H+(1−0) maps as in Fig. 3. Bottom: 1200 μm continuum map from MAMBO observations and N2H+(1−0) emission (contours). |
 |
Fig. 6 Expanded view of the B218 region. Top: C18O(1−0) and N2H+(1−0) maps as in Fig. 3. Bottom: 850 μm continuum map from LABOCA observations and N2H+(1−0) emission (contours). |
4. Dense cores in L1495/B213
The maps in Figs. 1 and 2 are too large to reveal the details of the compact N2H+ emission and to allow a comparison with C18O. In Figs. 3−6 we zoom in towards the regions of bright N2H+ emission and superpose this emission (in white contours) on the emissions of C18O and the dust continuum if available (color).
As discussed before and now clearly seen in Figs. 3−6, the C18O emission systematically avoids the regions of brightest N2H+. This was attributed to CO depletion, a conclusion that we confirm from the good match between the N2H+ emission peaks and the peaks of the dust continuum. This match guarantees that the N2H+ peaks arise from true enhancements of the gas column density and rules out a possible explanation in terms of anomalous excitation of N2H+. Especially striking is the chain of four cores shown in both the B211 and B213 panels (towards the SW in the first one and towards the NE in the second one). This 0.5 pc-long chain is very prominent both in N2H+ in the dust continuum, but is practically invisible in C18O.
4.1. Core selection and physical properties
As a first step in our analysis of the core population in the L1495/B213 complex, we took a census of N2H+ condensations. Focusing on the N2H+ emission guarantees a homogeneous core census, since the continuum maps (the alternative in a search for cores) do not cover the full extent of the cloud. It does however lead our missing a small fraction of N2H+-poor condensations, such L1521E in B218, which are known to be at the earliest stages of evolution (Hirota et al. 2002; Tafalla & Santiago 2004).
To search for N2H+ condensations, we first identified all N2H+ peaks with intensity exceeding 1.2 K km s-1 and fitted them with 2D Gaussians. For that, we used the fitting algorithm of the MOPSIC program5, which determines automatically the position, size, and intensity of each emission peak. In regions where several cores overlap or are very close to each other, the fitting process was applied sequentially. In a first step, the brightest peaks were fitted and subtracted from the image. Then, a new search for peaks was carried out in the residual image, fitting additional Gaussians to peaks that still exceeded the intensity threshold. This process was repeated until no peaks brighter than the threshold remained.
Table 2 presents the results of our core search. In total, 19 N2H+ cores were identified in the region. This number probably represents a lower limit to the number of cores, because if we use an intensity threshold lower than the chosen 1.2 K km s-1, the core-finding algorithm identifies slightly more cores. Visual inspection of these weaker cores, however, shows that their determination is uncertain due to the presence of weak and extended N2H+ emission in several parts of the cloud. To guarantee that each of our selected cores corresponds to a well-defined emission peak, we preferred to use a conservative criterion based on a relatively high threshold. Our analysis, therefore, focuses on this set of the brightest dense cores of the cloud.
Dense cores in L1495/B213.
The results of our core search presented in Table 2 show that the L1495/B213 condensations have sizes and N2H+ intensities typical of the Taurus core population (Benson & Myers 1989; Caselli et al. 2002). Some of these cores are associated with embedded Class 0 and Class I objects and therefore must have already undergone gravitational collapse, while others are starless and likely represent prestellar condensations. A number of our N2H+-selected cores have counterparts in the catalog by Onishi et al. (2002), which is based on H13CO+ observations. Our core list, on the other hand, has very little overlap with the longer list of extinction-selected cores presented by Schmalzl et al. (2010). As can be seen in Table 2 of these authors, these extinction-selected cores have densities on the order of 104 cm-3, and are therefore likely to represent a population of condensations at an earlier state of contraction than our N2H+-selected cores.
4.2. Core clustering
As we saw in Fig. 2, the N2H+ cores in L1495/B213 are not uniformly distributed over the cloud, but seem to form small groups of a few objects each. A similar trend toward clustering, but in the lower density gas, was found by Schmalzl et al. (2010) using a two-point correlation analysis of the distribution of extinction peaks. In this section, we study the clustering of the N2H+ cores using the mean surface density of companions Σ(θ), which is equivalent to the two-point correlation function but more often used in studies of stellar clustering (e.g., Larson 1995, see also Simon 1997 for the simple relation between the two). Following Simon (1997), we measured for each core the angular separation to all the other cores in the cloud, and we binned the set of angular separations in logarithmic intervals with a step equal to a factor of 2. To convert this number of separations into Σ(θ), we divided the result by the area of the bin (which we assumed rectangular with a width of 100′′), and finally we normalized the value by the total number of cores in the cloud.
The resulting density of core companions in L1495/B213 is presented in Fig. 7. To compare it with the expectation from a truly uniform distribution of cores, we carried out a set of 100 Monte Carlo simulations. In each simulation, 19 different cores have been created with coordinates randomly distributed over a rectangle with dimensions 13 100′′ × 100′′, which is approximately the size of the C18O-emitting region in Fig. 1. Each of these sets of 19 cores has been treated like the original N2H+ data set, and has been used to calculate a separate mean surface density of core companions with the same code used for the data. The mean of the 100 Monte Carlo experiments is represented in Fig. 7 together with error bars indicating the rms value of the dispersion.
 |
Fig. 7 Mean density of companions for the N2H+ cores presented in Table 2. The red solid squares represent observations and the open black squares with error bars represent the prediction from a series of 100 Monte Carlo runs (see text). |
As can be seen from the figure, the N2H+ data and the Monte Carlo simulation agree within approximately 1-σ in the four largest bins, indicating that the distribution of cores with separations larger than about 700′′ (0.5 pc) is consistent with being spatially uniform. At shorter distances, however, the observed distribution of cores deviates from the prediction of the uniform model. This is especially striking for the second smallest bin, which is centered on core separations of 350′′ (0.25 pc). In this bin, the observed density of core companions exceeds the model prediction by a factor of three, indicating that our sample has three times more cores with separations of 2−3 core diameters than expected for a uniform distribution of objects. Whether a similar or smaller excess of cores occurs at smaller separations is unclear. The data in the first bin of Fig. 7 presents an excess that is not statistically significant, but our experiments with the core-finding algorithm show that this bin is prone to incompleteness due to our limited angular resolution and to confusion with extended emission. Higher quality data are required to analyze the behavior of the core distribution at distances of one or two core diameters.
The excess of cores with separations of about 0.25 pc is a strong indication that the conditions of core formation in L1495/B213 are not randomly distributed over the cloud. Some regions seem to be specially favorable to forming cores, and therefore give rise to multiple condensations in close proximity. These regions, however, cannot extend for much more than about 0.5 pc, since the mean surface density of core companions approximates a uniform distribution on scales of that size or larger. As we see below, this behavior of the distribution of cores can be understood if core formation occurs by the fragmentation of filamentary structures that have 0.5 pc or so in length, provided that the cloud is composed of a large number of filaments and that only some of them have conditions leading to core formation. The signature of core formation by fragmentation of 0.5 pc-long structures therefore seems imprinted in the distribution of core positions.
 |
Fig. 8 Central panel: FCRAO integrated intensity maps of the B211-B213 region in C18O(1−0) (gray scale and black contours) and N2H+(1−0) (red contours). Left and right panels: spectra from selected positions illustrating the complex velocity structure of the emission. The blue spectra correspond to C18O(2−1) and the red spectra correspond to the isolated (F1F = 01–12) component of N2H+(1−0) (multiplied by 3) observed simultaneously with the IRAM 30 m telescope. Note the presence of 5 different C18O peaks in panel 3. |
5. Velocity structure: evidence of multiple components
Even taking into account the large-scale fragmentation of the L1495/B213 complex discussed before, the maps of integrated emission and dust continuum give the impression that the material in L1495/B213 consists of a single filamentary structure. The molecular spectra, however, reveal a much more complex picture and show that the cloud contains multiple velocity components that often overlap in projection. This can be noticed from inspecting the FCRAO C18O(1−0) data, but it is better appreciated using a series of high S/N spectra taken using the IRAM 30 m telescope with the specific goal of characterizing the velocity structure of the cloud. Some of these spectra are shown in Fig. 8, which illustrates the kinematics of the gas in the vicinity of of the B213 region, the one with the most complex velocity pattern. Previous observations of this region had noticed two velocity components separated by more than 1 km s-1 (Heiles & Katz 1976; Clark et al. 1977; Duvert et al. 1986; Onishi et al. 1996; Li & Goldsmith 2012). Our high-sensitivity IRAM 30 m data reveal now that the kinematics of the region is more complex and that the number of C18O velocity peaks is higher and changes rapidly with position. Figure 8 shows how each of two previously known velocity components (near 5.3 and 6.7 km s-1, see panel 2), splits in some places into additional, well-separated components, like those illustrated in panel 4. A more extreme splitting occurs in the the vicinity of (− 100′′, 200′′), where the C18O spectrum presents five separate peaks (panel 3). Surprisingly, this region with multiple velocity peaks corresponds to a single emission maximum in both the continuum and the FCRAO C18 integrated intensity map.
The multiple velocity peaks in the C18O spectra of Fig. 8 seem to originate in true velocity components in the gas responsible for the emission. Self absorption could also create multiple velocity peaks in a spectrum by depressing the intensity at intermediate velocities, but this effect does not seem to not occur in the C18O data. The isolated component of N2H+(1−0) (F1F = 01 − 12), which is optically thin in 86% of our positions according to hyperfine-structure fits, always appears if detected at the velocity of one of the C18O components, and not between the two, as expected in the case of self absorption (e.g., Leung 1978). This is illustrated in panels 1, 2, and 4 of Fig. 8, where the isolated component of N2H+(1−0) is superposed in red on the multicomponent C18O spectrum from the same position. As can be seen, the N2H+ line is associated with one of the C18O peaks in a way that is inconsistent with a self-absorption origin of the C18O velocity peaks. (The lack of N2H+ in the other velocity component suggests it has a lower density or a lower N2H+ abundance.) At the extreme position with five components in the C18O spectrum (panel 3), no clear emission is seen in the isolated component of N2H+, but a nearby position less than 60′′ away presents an N2H+ spectrum with two weak components that coincide with the two reddest peaks of the two groups of C18O components. This again argues against self absorption being the cause of the multiple peaks seen in the C18O spectrum.
The multiplicity of velocity components in the C18O spectra presents a significant challenge for representing and analyzing the emission. Velocity structure in a cloud is commonly characterized using channel maps, in which the emission is integrated in narrow ranges of velocity that can be selected to highlight particular gas components. For the L1495/B213 complex, however, this approach fails because the components partially overlap in velocity (Fig. 8) and slightly change their velocity with position. A better approach to studying the velocity field is to search for the different velocity components directly in the spectra. Figure 8 shows that the velocity components are relatively symmetric when found in isolation or detected in N2H+, and this suggests that fitting multiple Gaussians to the emission can determine the main properties of each component, notably its average velocity and its velocity dispersion. Fitting an indeterminate number of Gaussians manually to each spectrum in a dataset that contains tens of thousands of spectra is highly impractical, so we have developed a semi-automatic procedure. Several tests suggested that the following steps provide a reasonable balance between automation and supervision.
-
1.
Divide the mapped area in fields of150′′ × 150′′, each containing 25 individual spectra.
-
2.
For each field, discard all spectra with no channel brighter than three times the typical rms (≈0.3 K). If less than three spectra are left in a given field, the field is discarded from the analysis.
-
3.
Average all accepted spectra in a field to obtain a high S/N template, which is inspected visually to determine how many components are needed to fit it (in cases of doubt, the individual spectra were inspected). To be considered real, a component needs to lie at least 0.25 km s-1 (3 channels) apart from the other components in the spectrum.
-
4.
Fit each spectrum in a field using the number of Gaussian components determined in the previous step. This is done using the MINIMIZE command of CLASS. The fit starts with an initial guess based on the average spectrum of the field, but the properties of each Gaussian component (intensity, central velocity, and dispersion) are left unconstrained and fitted automatically.
-
5.
Discard those fits whose intensity is lower than three times the rms in the spectrum.
With this procedure, it was possible to process the approximately 23 000 spectra of the FCRAO C18O(1−0) map reasonably quickly and fit a total of more than 11 000 Gaussian components with S/N equal to or larger than three. For the N2H+(1−0) data, the analysis was simpler, since no FCRAO spectrum showed two velocity components with high enough S/N to deserve a multi-Gaussian fit. We therefore applied a single-component hyperfine-structure fit (using the HFS option in CLASS) and again selected those fits as real that exceed three times the rms in the spectrum. Almost 400 N2H+ spectra were fitted this way6.
Since each Gaussian component is characterized by a position in the sky and a center velocity (plus a width), the most convenient way to explore the results of the multicomponent Gaussian fit to the data is by plotting the component line-center velocities in a cube of position–position–velocity (PPV) space. Such PPV space represents a subset of the gas phase space and allows visualizing structures that are spatially confused in the plane of the sky but separated in velocity. Figure 9 shows one such a PPV cube that covers approximately the same region as is presented in the integrated map of Fig. 8 and contains the result of our Gaussian fitting. Although undoubtedly complex, the distribution of points in PPV space shows clear signs of arising from an organized structure. Most points cluster in elongated groups that lie at different “heights” (velocities) and present smooth and often oscillatory patterns. These groups are associated with the different velocity components seen in the spectra, and their clean separation in the cube shows how working in PPV space can help disentangle the complex gas kinematics of the cloud.
The next step in our analysis requires a procedure for identifying and isolating the different components in the PPV cubes. By visually exploring those cubes, it is possible to identify several individual groups of points that form coherent structures and very likely correspond to physically distinct cloud components. It seems, however, preferable to have an objective algorithm that not only automatizes the selection, but also provides a quantitative measurement of the degree of correlation between points in PPV space.
 |
Fig. 9 Position–position–velocity cube showing the line-center velocities derived from the Gaussian fit to the C18O(1−0) and N2H+(1−0) spectra towards the B211-B213 region presented in Fig. 8. Semi-transparent points have intensities between 3 and 6 times rms and opaque points have intensities higher than or equal to 6 rms. |
6. Friends In VElocity (FIVE): an algorithm to identify velocity components
The problem of identifying velocity structures in a PPV cube like that of Fig. 9 has a number of similarities with the problem encountered in the field of cosmology when identifying groups of galaxies in a redshift survey. Redshift surveys provide catalogs in which each galaxy is characterized by two coordinates and a redshift (equivalent to our PPV data), and a search for galaxy groups involves identifying those subsets of galaxies that are strongly correlated in both position and redshift. One of the first and simplest algorithms for identifying galaxy groups in redshift surveys is the so-called friends-of-friends (FoF) method, initially presented by Huchra & Geller (1982) and still widely used (e.g., Berlind et al. 2006). This FoF algorithm starts by selecting a random galaxy in the catalog and searching the rest of the catalog for related galaxies (“friends”) using predetermined thresholds in both position and redshift. Each of the galaxies identified as a friend is added to the galaxy group, and a new search for friends is this time centered on the friend galaxies. The new finds (friends of friends) are added to the group, and the process is iterated until no more friends are found, at which point the group is considered complete. When this happens, a new unassigned galaxy is selected from the catalog and a new search for friends is started to identify a new galaxy group. The final product of the algorithm is a catalog of galaxy groups and a catalog of isolated galaxies not belonging to any group (see Fig. 1 in Huchra & Geller 1982, for a flow chart).
Applying the FoF technique to the line center velocity of the C18O components follows the spirit of the cosmology implementation, but requires a number of adjustments owing to the different nature of the emitting material. Each galaxy in a redshift survey is a discrete entity, physically separated from the rest (excluding mergers), and therefore represented well by a single point in PPV space. A velocity component in a C18O spectrum, on the other hand, represents a parcel of a fluid that extends over a large region of space and has no sharp boundaries. The C18O emission, in addition, has been mapped with Nyquist sampling and the data points form a dense grid, in contrast to the sparse sampling of a redshift survey data. These peculiarities of the C18O emission require modifying the standard FoF approach, in particular, to avoid a weakness of the method when applied to fluids, which we refer to as “fragility”. This fragility of the FoF method means that a single bad point (e.g., from a poor Gaussian fit) can potentially create an artificial bridge between two components that are otherwise disconnected in PPV space and that represent physically independent entities. While this is not likely to occur in redshift data because of their sparse nature, it is a real problem when dealing with the Nyquist-sampled and diffuse C18O emission. This fragility can lead, for example, to an absurd situation in which two distinct velocity components in a spectrum become connected by the FoF algorithm because each one is linked through several friends to a distant and weak point with an intermediate velocity, because of either due to a poor fit or a more complex velocity pattern.
To mitigate the fragility of the FoF algorithm, we need to combine the proximity concept of the standard FoF implementation with an additional constraint. One possibility is to use the intensity of the emission as an additional criterion to identify components. This approach seems the most natural extension of FoF when dealing with diffuse emission, since intensity itself (which is proportional to column density) is the criterion already used to define cloud components in velocity-insensitive datasets like continuum or integrated-intensity maps. By adding an intensity consideration to the FoF algorithm, our goal is to make it capable of recognizing that structures like the two long ridges separated by a deep emission valley represent different cloud components, even if the velocity of the gas in both ridges differs by less than the FoF-imposed threshold. Adding intensity weighting to the FoF algorithm however is a complex task. A number of geometrical and intensity considerations are needed, and the sophistication of models used to analyze intensity-only continuum data from the Herschel Space Observatory testifies to the needed level of complexity (e.g., Men’shchikov et al. 2012). To analyze our data, we chose a simplified method that merges the concepts of FoF and intensity weighting and that has been shown to work well in the PPV data set produced from our FCRAO observations. The main idea behind the method is that the emission intensity can be used to apply the FoF algorithm selectively in a top-down manner, starting from the brightest points in the map and working the way downwards in sensitivity. A cutoff that selects the brightest 50% points in the dataset is used to define the independent components in PPV space. This approach, which is illustrated in Fig. 10 with an idealized case, consists of the following three steps.
 |
Fig. 10 Schematic view of the 3 steps in the modified FoF method used to identify components in PPV space. To simplify the view, two projections of the PPV cube are presented. The left panels show the PP plane (integrated map) and the right panels show a projection on a PV plane. The black points represent all data with S/N ≥ 3. The green points in the first row of panels are those selected as significant to use in the first application of the FoF algorithm. The red and blue colors in the lower panels indicate positions belonging to each of the two structures identified by FoF as connected. The colored lines indicate the individual connection between points. Points are gradually assigned to the two velocity structures. The boxes illustrate the regions used to calculate the number of neighbor points and the velocity gradients for the FoF algorithm. |
-
1.
We first identify the most significant points in the PPV cube thatcan serve as seeds for the FoF algorithm. We do so by findingpositions that either have a S/N ≥ 3 in N2H+, or have both S/N ≥ 6 in C18O7 and more than half of the eight nearest neighbors in the 30′′ grid with S/N ≥ 6 and a difference in velocity equivalent to a gradient lower than 3 km s-1 pc-1. (A 3 km s-1 pc-1 threshold guarantees that no two points in the 30′′ differ in velocity by more than the typical nonthermal dispersion of the C18O(1−0) line, which is on the order of the sound speed, or 0.19 km s-1.) These criteria were found to select the ≈35% of points in the sample that lie in regions of homogeneous properties from which the different cloud components can be identified.
-
2.
Using the points selected in the first step, we run an FoF search using the C18O data with a box of 120′′ and the previous 3 km s-1 pc-1 velocity gradient threshold. The choice of the box size, which covers two layers of the 30′′ grid around the point, allows the algorithm to explore greater distances than simply the next neighbors, and provides insurance against small-scale drops in the intensity of the emission that could otherwise fragment the component. Once the FoF search has been completed, the cloud velocity components are defined as those groups of friends that are isolated from the rest and that contain a minimum number of eight members.
-
3.
The final step in the analysis consists of assigning the points with few neighboring friends and/or S/N less than six to the different cloud components defined in the previous step. For this, we relax the previous neighbor and S/N thresholds, and test each component point for new friends again using the 3 km s-1 pc-1 velocity gradient threshold. In line with the intensity-weighting scheme discussed before, this new search for friends is applied sequentially, advancing each cloud component by one step. When no new friends are found, the analysis is stopped and the remaining points (typically <20%) are considered as unassigned. Most of these points are low S/N data or points that belong to what appear to be separate cloud regions that did not have enough points in step 2 to qualify as a bona-fide component according to our definition.
All the above steps are carried out automatically using our new algorithm FIVE, which is programed using the R language (http://www.r-project.org/). More information on the algorithm and its implementation can be found in Hacar (2012). A series of tests to determine its success rate and to illustrate the choice of internal parameters are presented in Appendix A.
 |
Fig. 11 Analysis of the PPV cube of Fig. 9 using the FIVE algorithm. Top: seed points selected using the threshold values described in the text (color-coded green). Middle: points identified after a friends-of-friends search that starts with the seed points from the previous step. The color coding illustrates the different cloud components. Bottom: final assignment of points to the different cloud components (colored points). The black points represent unassigned points. |
7. The nature of the cloud components
7.1. Components as filaments
While Fig. 10 showed an idealized view of our FoF analysis, Fig. 11 presents the true result of applying the FIVE algorithm to the the PPV cube of data from the region previously shown in Fig. 9. There may be some ambiguity in the assignment of the weakest points to the different components, but the algorithm seems to identify as separate entities most structures in PPV space that visually appear as distinct components in the cube. Over the whole cloud, the FIVE algorithm identifies 35 different components, 17 of them in the region shown in Fig. 11. The main physical properties of these components are summarized in Table 3 and discussed in the rest of this section.
The most noticeable property of the L1495/B213 components is their filamentary geometry. This can be seen directly in the PPV cubes, where many of these components appear as long and twisted structures. It is, however, better appreciated using standard position–position maps. With these maps, we have determined for each component a principal axis by connecting the emission centroids of 90′′-long fragments with straight lines, as explained in more detail in Appendix B. These principal axes represent the backbones of the components, and they are shown in Fig. 12 superposed on the 250 μm dust continuum Herschel-SPIRE archive from the Gould Belt Survey (André et al. 2010; Palmeirim et al. 2013).
Main properties of the L1495/B213 cloud components.
The most striking aspect of Fig. 12 is the intricate pattern of intertwining filamentary components, especially towards the B211−B213 regions shown in detail in the figure inset. A multiplicity of components was of course expected from the multiple velocity peaks seen in the spectra of Fig. 8. The map of principal axes, however, shows that the components belong to a rather organized structure, despite their very different velocities. What at first sight seemed like a single 10 pc-long filamentary cloud now becomes a complex network of braided filaments.
Another remarkable aspect of Fig. 12 is how well the principal axes of the velocity components follow the 250 μm dust emission mapped with SPIRE. This is especially noticeable in the B211−213 region, where most of the components are located. It suggests that the cloud components traced by the combination of C18O and N2H+ emission correspond to the same material as traced by the SPIRE observations of the dust emission. Indeed, the mass estimated by Palmeirim et al. (2013) for the B211-213 region closely matches the mass estimated by our analysis (Table 1). The additional kinematic information provided by our line data show that the continuum-emitting material consists of multiple velocity components, and this multiplicity, as discussed in the next section, has important consequences when estimating the mass per unit length.
7.2. Statistics of filament properties
We start the analysis of the filaments using a statistical approach. Figure 13 presents a series of histograms showing how the most relevant properties are distributed among the 35 filaments identified by the FIVE algorithm. In agreement with the previous discussion, the histogram of aspect ratios (top left) shows a distribution significantly shifted from 1, with 75% of the components having an aspect ratio over 3. This high value provides a justification for our using the word “filament” to refer to most of the observed components.
The statistics of linear sizes is illustrated in the top right hand histogram of Fig. 13, which shows that despite a significant tail of high values, 60% of the cloud components lie in a relatively narrow peak between 0.2−0.6 pc in size8.
A related quantity is the mass per unit length, which is presented in the middle left hand histogram (Fig. 13c). This parameter has been calculated directly from the C18O emission assuming the standard C18O abundance of Frerking et al. (1982). To compensate for CO depletion, the contribution from positions with bright N2H+ emission (S/N ≥ 3) has been supplemented with a mass estimated using the N2H+ emission and assuming standard excitation and abundance values (Caselli et al. 2002; Tafalla et al. 2004). These N2H+-derived contributions increase the filament mass typically by 25% and never reach 50% of the C18O-derived mass. As the histogram shows, the mean mass per unit length of the components is about 15 M⊙ pc-1. This value is significantly lower than the ≈54 M⊙ pc-1 derived by Palmeirim et al. (2013) from their Herschel continuum data, but as mentioned before, this difference results from the fact that the continuum analysis associates all the mass to a single cloud component, while our line analysis shows that the mass is distributed among distinct velocity components.
Interestingly, the derived mean mass per unit length of 15 M⊙ pc-1 is very close to the equilibrium value for an isothermal cylinder in pressure equilibrium at 10 K (Stodólkiewicz 1963; Ostriker 1964). This property, and both the length and aspect ratio discussed before, make the L1495/B213 components very similar to the velocity-coherent filaments of the nearby L1517 cloud, also studied using C18O data. These L1517 filaments had aspect ratios of approximately 4, typical lengths of 0.5 pc, and mass per unit length in agreement with the prediction for a 10 K isothermal cylinder (Hacar & Tafalla 2011).
A notable difference with the L1517 filaments is the larger velocity dispersion of the gas in the L1495/B213 components. The middle right hand histogram in Fig. 13 shows the distribution of the nonthermal velocity dispersion normalized to the sound speed at 10 K, as calculated by taking the unweighted mean of the nonthermal linewidths in the individual Gaussian fits to the spectra. (The dispersion of the individual line center velocities presents similar behavior.) While the gas in the L1517 filaments was overwhelmingly subsonic (98% of the points) with a typical σNT/cs = 0.54 ± 0.19, the gas in L1495/B213 presents an approximately sonic dispersion of σNT/cs = 1.0 ± 0.2, although there is a ~15% minority of subsonic, L1517-like filaments. This higher value of the C18O nonthermal motions in L1495/B213 does not arise only from the action of the embedded protostars (whose effect is noticeable but local) and indicates that the gas in most L1495/B213 filaments is more turbulent, or has larger internal velocity gradients, than the gas in L1517. Even so, the estimated σNT/cs values indicate that the internal motions in the L1495/B213 filaments are at most mildly transonic, and therefore inconsistent with a possible picture of supersonic turbulence.
 |
Fig. 12 Location of the cloud components of L1495/B213 identified with the FIVE algorithm. Each component is represented by its central axis and has been color-coded for easier identification. The background gray-scale image is a SPIRE 250 μm continuum map from the Gould Belt Survey (André et al. 2010) that has been blanked out to match the coverage of our FCRAO data. |
Probably related to this larger C18O dispersion is an also larger dispersion of the nonthermal component of N2H+. The mean σNT/cs value for this species is 0.61 ± 0.17, compared to 0.36 ± 0.09 in L1517. Apart from this higher velocity dispersion, the behavior of the gas in the L1495/B213 filaments is very similar to L1517, as we discuss in the following section.
The final two histograms present the distribution of velocity gradients measured along the long axis of each filament (bottom panels of Fig. 13). The left histogram shows the distribution of global velocity gradients, which are determined by fitting the full set of LSR velocity values along the long axis with a single linear gradient. The right histogram (Fig. 13f) shows the distribution of local velocity gradients, which are determined using a similar method, but this time splitting the velocity data in 0.1 pc fragments and then taking the average of the fits. As can be seen, the mean value of the global gradients is close to 0.5 km s-1 pc-1, and the mean value of the local gradients is about 1 km s-1 pc-1. The higher value of the local gradients results from the presence of velocity oscillations inside the components, which average out when taking a global gradient. Similar behavior was seen in L1517.
 |
Fig. 13 Distribution of parameters in the 35 cloud components derived using the FIVE algorithm. a) Aspect ratio, b) length, c) mass per unit length, d) nonthermal velocity dispersion, e) global velocity gradients, f) local velocity gradients. |
7.3. Core formation in the L1495/B213 filaments
In Sect. 4 we identified 19 dense cores in the L1495/B213 complex based on their N2H+ emission. Now we study the relation between these dense cores and the 35 filamentary components identified from the C18O data. Table 3 shows the assignment of the cores to the different filaments based on the matching of the N2H+ and C18O emission in both position and velocity. Cores 2 and 5 were not assigned to any filament because their surrounding C18O emission did not meet the minimum number of points required for filament definition in the FIVE analysis. This lack of association seems a sensitivity problem and not an indication that these cores are peculiar, since a FIVE analysis using an S/N threshold of 2.5 (instead of the standard 3 value) identifies C18O filaments associated to these cores (but also suffers from confusion in different regions).
A notable aspect of the assignment of cores to filaments is that only 5 out of 19 cores can be classified as single, in the sense that they belong to filaments containing no other core. (To be conservative, unassigned cores 2 and 5 are treated as single.) This low number of single cores seems highly improbable, since there are almost twice as many filaments as cores. A Monte Carlo simulation indeed shows that the probability of having 5 or fewer single cores in the cloud is less than 1%, and therefore, that the observed distribution of cores among filaments does not arise from a process equivalent to throwing randomly 19 cores into 35 independent filaments. Core formation in L1495/B213, therefore, seems to have occurred in a nonrandom manner, with a small fraction of filaments forming multiple cores (“fertile” filaments) and the majority of the filaments remaining sterile.
The dichotomy between “fertile” and “sterile” filaments provides a simple explanation for our finding in Sect. 4 that there is an excess of cores with separations around 0.25 pc. This is so because if most of the cores in the cloud have formed inside a small number of fertile filaments, with each fertile filament generating more than one core, the resulting core population is expected to be distributed in small groups, and each core is expected to have a neighbor at a distance of about a fraction of the filament length. Since the median filament length is approximately 0.5 pc, the excess of cores should occur at separations around 0.25 pc, which is what is shown in Fig. 7.
The fertile/sterile dichotomy of filaments, together with the multiplicity of cores per fertile filament, points to a core formation mechanism that depends more on a global property of the filament than on a local event in its interior. To explore this possibility, we have compared the physical properties of the two filament populations using the data in Table 3. One noticeable trend is that fertile filaments have higher mass-per-unit length than sterile filaments: 24 vs. 10 M⊙ pc-1 when comparing the means and 18 vs. 9 M⊙ pc-1 when comparing the medians. Although the mass per unit length is undoubtedly an uncertain parameter due to its dependence on the C18O abundance, part of this uncertainty is mitigated by the relative nature of the comparison and by the fact that all cores have been analyzed in the same way. Interestingly, the data in Table 3 show that fertile filaments not only have higher mass per unit length, but that both their mean and their median values exceed 16 M⊙ pc-1, which is the equilibrium limit against fragmentation for an isothermal cylinder at 10 K (Stodólkiewicz 1963; Ostriker 1964). Sterile filaments, on the other hand, have on average a mass-per-unit length that is below the fragmentation limit and therefore should be gravitationally stable. If this is correct (and it should be tested with a more accurate mass estimate, preferably from continuum dust emission), it would suggest that core formation in the filaments of L1495/B213 simply depends on how much mass the filament has been able to accumulate. Most filaments do not seem to reach the fragmentation limit, and therefore fail to form cores, while a selected few do so and produce multiple condensations.
 |
Fig. 14 Velocity profiles of filaments with cores. Blue squares are C18O data and red triangles are N2H+ data. |
7.4. Velocity coherence of the filament gas
In L1517, Hacar & Tafalla (2011) found that the internal velocity field of the cores follows the large-scale velocity gradients seen in the filaments, suggesting that core formation has occurred inside the filaments with little external interaction (contradicting the expectation from some turbulent models, see Klessen et al. 2005). To explore this issue in L1495/B213, we present in Fig. 14 velocity profiles for all filaments containing dense cores. As can be seen, the gas in the dense cores of L1495/B213 presents large-scale velocity fields that follow the large-scale gradients of the lower-density material traced in C18O, in good agreement with the L1517 results. This suggests that the transition from cloud to core conditions in L1495/B213 has also proceeded without a significant change in the gas velocity field. Core formation, therefore, seems to have resulted from a quasi-static process that has not decoupled the kinematics of the dense gas from its surrounding material. Internal fragmentation of the filaments, and not collisions between gas flows, therefore seems the core-forming mechanism operating in L1495/B213.
Although the velocity field in the cores continues the motions of the surrounding material, and this suggests that no kinematic changes occur during core formation, the nonthermal velocity component of the N2H+ lines is on average almost half the C18O value. A similar difference was found in L1517, and could in principle result from a lower level of local random motions in the dense core material. This would suggest that turbulence has been dissipated during core formation. As argued for L1517, however, it is also possible that the velocity difference between C18O and N2H+ arises from a combination of large-scale gas motions and the fact that each molecule traces a different column of cloud gas. The N2H+ emission is very selective of the dense gas thanks to a combination of excitation and chemistry, and it only samples a small fraction of the gas along any line of sight (as illustrated by the sparse distribution of N2H+ emission in the maps of Fig. 2). The C18O emission, on the other hand, is sensitive to the extended and lower density cloud material owing to its close-to-thermal excitation and high abundance, and it samples a much higher column density of gas than N2H+. As seen in Fig. 14, all filaments present large-scale velocity gradients in the plane of the sky, making it likely that similar gradients occur along the line of sight. Thus, any C18O spectrum must contain the contribution from more parcels of gas moving at different velocities along the line of sight than the equivalent spectrum of N2H+, and this will undoubtedly cause a larger nonthermal component. This effect is confirmed by the recent numerical simulations of core-forming filaments by Smith et al. (2012).
The final characteristic of the velocity field that we investigate is the presence of large-scale organized patterns, often in the form of quasi-sinusoidal oscillations (see, e.g., filaments 32 and 34 in Fig. 14). These patterns, also seen in L1517, suggest that the velocity of the gas in the filaments can be correlated on scales as large as the filament length, or about 0.5 pc. Such a level of organization in the velocity field seems to deviate from the expectation that gas belongs to the turbulent cloud regime, which is characterized by a random pattern that follows a linewidth-size relation (Larson 1981). Because of that, the L1517 filaments were referred to as “velocity coherent,” extending the term proposed by Goodman et al. (1998) for scales of dense cores. As Fig. 14 shows, the same attribute of coherence now seems applicable to the L1495/B213 filaments, even if their nonthermal motions are close to the sound speed. The L1495/B213 filaments seem to have also decoupled from the general turbulent velocity field of the cloud and become separate entities with a coherent velocity field.
In L1517, some filaments presented a correlation between the oscillations of the velocity field and oscillations in the filament density, and from that, it was proposed that the oscillations represent core-forming streaming motions (Hacar & Tafalla 2011). The origin of the oscillations in L1495/B213 is less clear due to the more complex velocity patterns and the mix of cores at different stages of evolution (i.e, starless and protostellar) next to each other, which indicates that core formation in the L1495/B213 filaments cannot be treated with the simple perturbation formalism used in the case of L1517. Higher angular resolution observations of selected filaments are being planned to explore the possible connection between velocity oscillations and filament formation.
7.5. Filament bundles: a scenario of filament-forming fragmentation
The picture that emerges from the previous sections is one of hierarchical fragmentation. The L1495/B213 complex (~10 pc long) seems to have fragmented first into velocity-coherent filaments of about 0.5 pc in length. Then, some of these filaments have further fragmented into cores (<0.1 pc) in an almost quasi-static way. Our discussion so far has concentrated on the second level of fragmentation, the one that breaks up the velocity-coherent filaments into star-forming dense cores. This process is better constrained by the data because both the “before” (filament) and “after” (core) stages can be identified by a different molecular tracer. In this section we turn our attention to the first level of fragmentation, the one by which the large-scale cloud produces the velocity-coherent filaments, which unfortunately is less constrained by the data at hand.
A clue to a possible sequence of filament-forming fragmentation comes again from the spectra of the B211−B213 region shown in Fig. 8. As discussed before, these spectra reveal two families of velocity components, one near 5.4 km s-1 and the other near 7.0 km s-1. Each of these families further splits into two or three individual components, which according to our analysis, represent distinct velocity-coherent filaments. Panel 3 in Fig. 8 illustrates how the velocity differences between the components in each family are smaller than the differences between the families. This pattern suggests that there is some type of hierarchy in the gas velocity field, in the sense that the components are grouped into families, and that the filaments of a given family are more closely connected to each other than to filaments of other families.
The idea that filaments are grouped into families is reinforced by the analysis of the physical and chemical properties of the gas. Filaments with velocities close to VLSR = 5.4 km s-1 (blue-shifted group of components in Fig. 8) are associated with intense emission in C18O and SO, and at the same time have very weak N2H+ emission. As discussed in Sect. 3, these signatures indicate that the gas has an early-type composition, which is expected if the material has condensed recently from a more diffuse state. The group of components near VLSR = 7.0 km s-1, on the other hand, is associated with bright N2H+ emission and dense cores containing YSOs, which are signatures of more chemically evolved gas. The 5.4 and 7.0 km s-1 families of filaments, therefore, not only differ in their kinematics, but seem to be at different stages of evolution. This behavior strengthens the idea that there is a close connection between the filaments inside a given family, while there are noticeable differences between the families themselves.
 |
Fig. 15 Spatial distribution of the nine bundles of filaments identified by FIVE. The extent of each bundle is represented by a colored background, and the axis of the individual filaments are represented by red lines. The gray-scale background is the same SPIRE map as is shown in Fig. 12. |
To further explore the possibility that the filaments in the L1495/B213 complex are organized into families, e have again used the FIVE algorithm. This time, we have relaxed its parameters so that it can identify structures that are more loosely connected than the filaments themselves, but that are still noticeably distinct from each other. Motivated by the differences and similarities between the 5.4 and 7.0 km s-1 families, we have set the velocity gradient threshold required to define a “friend” to 5 km s-1 pc-1. Also, to favor structures larger than the filaments, we have required a minimum of 30 points to define a distinct component and use a box size of 180′′. The results of this search are shown in Fig. 15, where the different families of filaments are identified using different colors. As can be seen, the filaments in the L1495/B213 complex seem to belong to a small number of families, which from now on will be referred to as “bundles” because of their thread-like appearance. (The number of bundles may be smaller than the 9 shown in Fig. 15, since bundle 3 is likely connected to bundle 6 by low-level emission, Narayanan et al. 2008.)
While the search for families using the FIVE algorithm is strictly based on the kinematic properties of the gas, the resulting bundles shown in Fig. 15 reproduce remarkably well the division of the cloud into regions proposed by Barnard and illustrated in the bottom panel of Fig. 2. In Sect. 3, we saw that Barnard’s subdivision is not simply a morphological one, but that reflects a separation of the gas into regions that have had almost independent contraction histories. The similarity we find now between these Barnard regions and the velocity-defined bundles suggests that the two structures are either coincident or closely related, and therefore are likely to have a common origin. As discussed in Sect. 3, the different Barnard regions seem to have condensed from the diffuse gas on different time scales, indicating that a large-scale (pc-sized) fragmentation has occurred early on in the history of the cloud. If the velocity-defined bundles correspond to these fragments, bundle formation must be related to the assemblage of the large-scale filamentary cloud, and therefore must have preceded filament formation.
A piecewise formation picture of L1495/B213 seems at first to contradict the high degree of organization suggested by the single-filament appearance of the cloud on large (~10 pc) scales (e.g., Schmalzl et al. 2010; Palmeirim et al. 2013). This is however not necessarily so if the L1495/B213 complex was formed by the convergence of large-scale flows, a mechanism favored by a number of theoretical considerations and numerical simulations (e.g., Elmegreen 1993; Vázquez-Semadeni et al. 2006; Hennebelle et al. 2008; Heitsch et al. 2008). In this converging-flows scenario, it is unlikely that gas spread over 10 pc linear scales can synchronize its convergence without producing pc-scale irregularities. For example, perturbations in the gas velocity on the order of 10% can produce the observed differences in evolutionary state between regions over the expected 10−20 Myr accumulation time of the cloud (e.g., Bergin et al. 2004). Thus, although the 1−2 Myr differences in contraction time have had a notable influence on the fragmentation of the cloud into bundles of filaments, they still represent a small amount from the point of view of the full cloud formation process.
While the fragmentation of the cloud gas into families of filaments seems to arise from local differences in the time scale of gas concentration, the internal fragmentation of each family into a small group of velocity-coherent filaments seems to be intrinsic to the gas. Even B211, the youngest region of the cloud, consists of multiple velocity-coherent filaments despite not yet having formed stars or cores. This early appearance of the filaments in the gas suggests that their presence results from physical processes that took place at density regimes lower than those traced by our C18O data (approximately <104 cm-3). A number of instabilities are known to occur at those regimes (e.g., Heitsch et al. 2008) and may be responsible for this fragmentation, which has a typical scale length of 1.5−2 pc. Observations of lower density gas, such as those provided by the more abundant CO isotopes (Goldsmith et al. 2008), may hold the key to understand the origin of these velocity-coherent filaments.
8. Summary
We have studied the 10 pc-long L1495/B213 filamentary complex in Taurus with the goal of clarifying the process of dense core formation. Our data consists of Nyquist-sampled maps in lines of C18O, N2H+, and SO, together with partial mapping in the 870 μm and 1200 μm dust continuum. From the analysis of these data we have reached the following main conclusions.
Large-scale properties of L1495/B213. The L1495/B213 complex generally appears as a single large-scale filament, but differences across the complex in the YSO population and chemical composition suggest that the gas did not assemble all at once. Different regions, approximately coinciding with the condensations originally identified by Barnard from optical images, seem to have condensed on time scales that differ by up to 1−2 Myr (Sect. 3). Embedded in this molecular complex, there is a population of at least 19 dense cores, some of them starless and some of them protostellar. The cores are not distributed uniformly, but tend to cluster with favored separations on the order of 0.25 pc (Sect. 4).
Cloud velocity structure. The C18O spectra often present multiple peaks that indicate the existence of overlapping velocity components in the gas (Sect. 5). We fitted multiple Gaussians to the C18O spectra, and found that when the fit parameters are represented in position–position–velocity (PPV) space, the velocity components appear as coherent structures that are well-separated from each other (Sect. 5). To disentangle these components, we developed a new algorithm that identifies and extracts automatically structures in PPV space. The algorithm, named FIVE, uses a friends-of-friends approach similar to that often employed to identify clusters of galaxies in redshift surveys (Sect. 6). With its help, we identified 35 separate components in L1495/B213. These components are filamentary and tend to be aligned with the axis of the large-scale cloud. They have typical lengths of 0.5 pc, internal velocity dispersions close to the sound speed, and coherent velocity fields. They also have mass-per-unit lengths close to the fragmentation threshold of an isothermal cylinder at 10 K (Sect. 7.2).
Core formation. Despite the large number of filaments in L1495/B213, only a few of them have formed dense cores, and the distribution of cores among filaments does not seem to be random. A few “fertile” filaments are responsible for most cores in the cloud, and this suggests that core formation depends on an intrinsic property of each velocity-coherent filament, such as the mass per unit length (Sect. 7.3). Both fertile and sterile filaments present coherent, large-scale oscillations in their velocity field that suggest that they have decoupled from cloud-wide turbulent motions (Sect. 7.4). When a filament contains a core, the continuity between the velocity field of the core gas and that of the surrounding less dense material suggests that core formation occurs with little effect on the gas kinematics, in contradiction to the expectation from models of core formation by gas flow collisions (Sect. 7.4).
Hierarchical fragmentation. The 35 filaments of L1495/B213 seem to be grouped in nine different families, which we refer to as bundles. Filaments inside a given bundle have similar kinematics and chemical composition, suggesting that they have a common physical origin. This structuring of the gas into bundles, filaments, and cores suggests that fragmentation in the L1495/B213 complex has proceeded in a hierarchical manner. First, the cloud has fragmented into subregions (bundles) that coincide approximately with the condensations identified originally by Barnard. This large-scale fragmentation seems to have resulted from differences on the local time scale of gas condensation. At later times, the subregions have fragmented into velocity-coherent filaments that have typical sizes of 0.5 pc and velocity dispersions close to the sound speed. Finally, a small group of fertile velocity-coherent filaments have accumulated enough mass to fragment quasi-statically into individual dense cores (Sect. 7.5).
The intensity of the C18O(1−0) emission in positions with bright N2H+(1−0) lines (SNR ≥ 3) has been multiplied by 2 to compensate for the drop in C18O intensity due to freeze out, which is typically a factor of 2 (Tafalla et al. 2004).
Some of the longest components may result from the artificial merging of smaller units. Indeed, the longest component (number 20) often splits into two separate components when we run FIVE using slightly different thresholds for the FoF algorithm. Higher sensitivity data are required to solve this ambiguity.
Acknowledgments
We thank Mark Heyer for assistance during the FCRAO observations We thank Carlos De Breuck, Thomas Stanke, and Giorgio Siringo for assistance during the APEX observations, and Axel Weiss and Arnaud Belloche for help with the data reduction. We also thank Guillermo Quintana-Lacaci and the IRAM staff for help during the MAMBO observations. An anonymous referee provided a number of useful comments and suggestions that are greatly appreciated. This publication is supported by the Austrian Science Fund (FWF). This research made use of NASA’s Astrophysics Data System Bibliographic Services and the SIMBAD database, operated at the CDS, Strasbourg, France. M.T. acknowledges support by MINECO within the program CONSOLIDER INGENIO 2010, under grant “Molecular Astrophysics: The Herschel and ALMA era − ASTROMOL” (ref.: CSD2009-00038).
References
- Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Barnard, E. E. 1907, ApJ, 25, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Barnard, E. E. 1927, Catalogue of 349 dark objects in the sky (Chicago: University of Chicago Press) [Google Scholar]
- Belloche, A., Schuller, F., Parise, B., et al. 2011, A&A, 527, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benson, P. J., & Myers, P. C. 1989, ApJS, 71, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Alves, J., Huard, T., & Lada, C. J. 2002, ApJ, 570, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Hartmann, L. W., Raymond, J. C., & Ballesteros-Paredes, J. 2004, ApJ, 612, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Berlind, A. A., Frieman, J., Weinberg, D. H., et al. 2006, ApJS, 167, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bertout, C., Siess, L., & Cabrit, S. 2007, A&A, 473, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Benson, P. J., Myers, P. C., & Tafalla, M. 2002, ApJ, 572, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Bachiller, R., & Duvert, G. 1985, A&A, 149, 273 [NASA ADS] [Google Scholar]
- Clark, F. O., Giguere, P. T., & Crutcher, R. M. 1977, ApJ, 215, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, P. C., Glover, S. C. O., Klessen, R. S., & Bonnell, I. A. 2012, MNRAS, 424, 2599 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, C. J., Chrysostomou, A., Hatchell, J., et al. 2010, MNRAS, 405, 759 [NASA ADS] [Google Scholar]
- di Francesco, J., Evans, N. J., II, Caselli, P., et al. 2007, Protostars and Planets V, 17 [Google Scholar]
- Duvert, G., Cernicharo, J., & Baudry, A. 1986, A&A, 164, 349 [NASA ADS] [Google Scholar]
- Elias, J. H. 1978, ApJ, 224, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G. 1993, ApJ, 419, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Glenn, J., Evans, N. J., II, et al. 2007, ApJ, 666, 982 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. J., II 2008, Pathways Through an Eclectic Universe, eds. J. H. Knapen, T. J. Mahoney, & A. Vazdekis, ASP Conf. Ser., 390, 52 [Google Scholar]
- Frerking, M. A., Langer, W. D., & Wilson, R. W. 1982, ApJ, 262, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Gaida, M., Ungerechts, H., & Winnewisser, G. 1984, A&A, 137, 17 [NASA ADS] [Google Scholar]
- Goldsmith, P. F., Heyer, M., Narayanan, G., et al. 2008, ApJ, 680, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Barranco, J. A., Wilner, D. J., & Heyer, M. H. 1998, ApJ, 504, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Hacar, A. 2012, Ph.D. Thesis, Univ. Complutense, Madrid [Google Scholar]
- Hacar, A., & Tafalla, M. 2011, A&A, 533, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L. 2002, ApJ, 578, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., & Katz, G. 1976, AJ, 81, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Heitsch, F., Hartmann, L. W., Slyz, A. D., Devriendt, J. E. G., & Burkert, A. 2008, ApJ, 674, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M. H., Vrba, F. J., Snell, R. L., et al. 1987, ApJ, 321, 855 [Google Scholar]
- Hennebelle, P., Banerjee, R., Vázquez-Semadeni, E., Klessen, R. S., & Audit, E. 2008, A&A, 486, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirota, T., Ito, T., & Yamamoto, S. 2002, ApJ, 565, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Hirota, T., Maezawa, H., & Yamamoto, S. 2004, ApJ, 617, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J. P., & Geller, M. J. 1982, ApJ, 257, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Johnstone, D., & Bally, J. 1999, ApJ, 510, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., Gómez, M., & Whitney, B. A. 2008, Handbook of Star Forming Regions, ed. B. Reipurth, I, 405 [Google Scholar]
- Klessen, R. S., Ballesteros-Paredes, J., Vázquez-Semadeni, E., & Durán-Rojas, C. 2005, ApJ, 620, 786 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, A. L., & Hillenbrand, L. A. 2009, ApJ, 704, 531 [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1995, MNRAS, 272, 213 [NASA ADS] [Google Scholar]
- Leung, C. M. 1978, ApJ, 225, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Li, D., & Goldsmith, P. F. 2012, ApJ, 756, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Mamajek, E. E., Allen, P. R., & Cruz, K. L. 2009, ApJ, 703, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Lynds, B. T. 1962, ApJS, 7, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Men’shchikov, A., André, P., Didelon, P., et al. 2012, A&A, 542, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mizuno, A., Onishi, T., Yonekura, Y., et al. 1995, ApJ, 445, L161 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Andre, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] [Google Scholar]
- Mouschovias, T. C., & Ciolek, G. E. 1999, NATO ASIC Proc. 540: The Origin of Stars and Planetary Systems, 305 [Google Scholar]
- Myers, P. C. 2009, ApJ, 700, 1609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narayanan, G., Heyer, M. H., Brunt, C., et al. 2008, ApJS, 177, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Onishi, T., Mizuno, A., Kawamura, A., Ogawa, H., & Fukui, Y. 1996, ApJ, 465, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Onishi, T., Mizuno, A., Kawamura, A., Tachihara, K., & Fukui, Y. 2002, ApJ, 575, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Padoan, P., Juvela, M., Goodman, A. A., & Nordlund, Å. 2001, ApJ, 553, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Palau, A., de Gregorio-Monsalvo, I., Morata, Ò., et al. 2012, MNRAS, 424, 2778 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeirim, P., André, P., Kirk, J., et al. 2013, A&A, 550, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rebull, L. M., Padgett, D. L., McCabe, C.-E., et al. 2010, ApJS, 186, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Schmalzl, M., Kainulainen, J., Quanz, S. P., et al. 2010, ApJ, 725, 1327 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, S., & Elmegreen, B. G. 1979, ApJS, 41, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 [Google Scholar]
- Simon, M. 1997, ApJ, 482, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Siringo, G., Kreysa, E., Kovács, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, R. J., Shetty, R., Stutz, A. M., & Klessen, R. S. 2012, ApJ, 750, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Stodólkiewicz, J. S. 1963, Acta Astron., 13, 30 [NASA ADS] [Google Scholar]
- Tafalla, M., & Santiago, J. 2004, A&A, 414, L53 [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., Walmsley, C. M., & Comito, C. 2002, ApJ, 569, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., & Walmsley, C. M. 2004, A&A, 416, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tafalla, M., Santiago-García, J., Myers, P. C., et al. 2006, A&A, 455, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tatematsu, K., Umemoto, T., Kandori, R., & Sekimoto, Y. 2004, ApJ, 606, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni, E., Kim, J., Shadmehri, M., & Ballesteros-Paredes, J. 2005, ApJ, 618, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni, E., Ryu, D., Passot, T., González, R. F., & Gazol, A. 2006, ApJ, 643, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Ward-Thompson, D., André, P., Crutcher, R., et al. 2007, Protostars and Planets V, 33 [Google Scholar]
Appendix A: Testing and fine-tuning the FIVE algorithm
Our analysis of the L1495/B213 complex has used the Friends In VElocity (FIVE) algorithm to identify and extract individual gas components from the molecular line data. As mentioned in Sect. 6, this algorithm is based on the friends-of-friends method, which has a well-documented record of reliability in the analysis of redshift-survey data over the past three decades (Huchra & Geller 1982; Berlind et al. 2006). Its usa with molecular-line data, however, exceeds the range of previous applications, and for this reason, it is necessary to extend the algorithm testing using molecular-cloud conditions. In this appendix, we present a series of tests of the FIVE algorithm under conditions similar to those of the Taurus cloud to illustrate both the successes and limitations of the method.
The analysis of the FCRAO data from L1495/B213 already provides a number of opportunities to test FIVE, and different runs of the algorithm were carried out to determine how the choice of internal parameters (intensity threshold, maximum velocity gradient, etc.) affects the output results. It is more informative, however, to test FIVE using model data that have well-defined parameters, since this allows comparing the FIVE-derived solution with the original model input. Experience using the algorithm shows that most of its behavior can be reproduced with a model that consists of two filamentary cloud components. This model is simple enough to allow a systematic study of the dependence of the results on the choice of internal parameters, and thus determine the conditions under which the FIVE algorithm succeeds in separating cloud components, as well as the situations where the algorithm fails by either merging the components, fragmenting them artificially, or simply missing them due to low SNR.
The FIVE algorithm uses both velocity and spatial information to identify cloud components. The role of these two properties is almost orthogonal, in the sense that FIVE uses different internal parameters to determine the velocity and spatial structure of the gas. For this reason, in the following two sections we separately test the effect of velocity and space using two models: (i) two cloud components that overlap spatially but differ in velocity; and (ii) two cloud components that have the same velocity but differ in position.
 |
Fig. A.1 Analysis of a model consisting of two components that overlap in position but are separated in velocity by 1.25 times the linewidth. Top: position–position–velocity cube with the results of Gaussian fits to the spectra. Bottom: results from the FIVE analysis using the favored choice of internal parameters (see text). Compare with Fig. 11. |
Appendix A.1: Overlapping components of different velocities
The case of two components that overlap in space but have different central velocities captures a unique feature of FIVE, its ability to use velocity information to disentangle cloud structure confused in the plane of the sky. Our model for this case assumes that the cloud is made of two cylindrical gas components that resemble the velocity-coherent filaments of L1495/B213. Each component has a radial profile of column density parameterized with a Gaussian of 150′′ FWHM, and its length is 840′′, which are typical values of the C18O emission from L1495/B213 (Sect. 7.2). The emission from these two components was modeled with the CLASS program generating a series of synthetic spectra that have the same number of channels and velocity resolution as the FCRAO C18O(1−0) data. In each spectrum, the velocity components are represented by Gaussian line profiles that have an FWHM of 0.48 km s-1 (average C18O(1−0) linewidth) and a velocity separation that is kept as a free parameter to explore the level of success or failure of the FIVE analysis. To make the model more realistic, the intensity of the emission, which is 3 K in the filament axis, has been allowed to vary randomly by 20% (to simulate the observed non-uniform intensity of the data), and random noise has been added to each channel of the spectra assuming an rms level of 0.3 K (similar to the noise level of our FCRAO observations).
To simulate the reduction of real data, we have processed the model spectra following the same steps as with the observations. First, we fitted the spectra with two Gaussian components, determining the line center velocity of the components at each cloud position. These line center velocities have been used to generate PPV diagrams like the one shown in Fig. A.1, and they have been input to the FIVE algorithm to attempt recovering the original components. To explore the ability of FIVE recovering cloud components with different amounts of velocity overlap, we ran a series of models in which the components differ in velocity by 1.0, 1.25, 1.5 and 2.0 times the spectral line FWHM. For each case, we used different choices of the internal parameters of FIVE, such as the number of required neighbors, the intensity threshold to select points in the first search for friends, and the maximum velocity gradient allowed for defining friends (Sect. 6). If the FIVE algorithm was able to recover the original two components of the model, we classified the test as a success. If not, we classified it as a failure.
 |
Fig. A.2 “Traffic-light” diagram showing the rates of success and failure of the FIVE algorithm when disentangling a model cloud that consists of two components that overlap in position but differ in velocity. The diagram represents a matrix of pie charts, each of them showing the fraction of success (green) and failure (red) for 10 independent models with a given velocity difference between the components (in units of the spectral line FWHM, x-axis) and a maximum velocity gradient used in the definition of friend (y-axis). The horizontal box encloses the results for the favored gradient of 3 km s-1pc-1. (All models use a number of neighbors of 5 and an intensity threshold of 6 rms, as recommended by the results shown in Fig. A.3.) |
Figure A.2 presents a summary view of the test results with a “traffic light” diagram, which consists of a matrix of pie charts. Each pie chart shows the fraction of successes and failures for a series of ten independent tests of FIVE that combine a given value of the velocity separation between the filaments (in units of the line FWHM, x-axis) and a value of the maximum velocity gradient between the points used in the definition of friend (y-axis). Other internal parameters of FIVE, such as the intensity threshold and the number of points used in the definition of friend, have been kept fixed at the values used in the analysis of the real data, and which are recommended by the models without velocity structure discussed in the next section and to which they are more sensitive.
As can be seen in Fig. A.2, for a velocity separation between the components of 1.0 FWHM, no choice of the velocity gradient produces a reasonable (>50%) fraction of successes. This is not surprising, since at this level of proximity, the velocity components in the spectrum start to merge, and the Gaussian fitting algorithm often converges to a wrong result. At the other extreme of separations, velocity components differing by 1.5 FWHM (or more) are disentangled successfully by FIVE for any reasonable choice of the velocity gradient. This level of success demonstrates how FIVE can easily recognize cloud components that overlap in space but are separated in velocity by an amount large enough to produce a double-peaked profile in the spectrum.
The critical case in Fig. A.2 is that of velocity components separated by 1.25 FWHM (middle column of pie charts). In this case, the success rate of FIVE depends slightly on the choice of the velocity gradient, and is significantly lower (60%) for the lowest value of 1.5 km s-1 pc-1. Such a small velocity gradient makes FIVE prone to artificially fragmenting the components, since small errors in the velocity determination (due to the partial velocity overlap between components) may create gaps between sections of the same component that FIVE fails to recognize as connected. Although not seen in the simple two-component model of Fig. A.2, using a high value for the gradient, like 5 km s-1 pc-1, often leads to the opposite effect, the artificial merging of the two components that are close in velocity if the S/N is low. As a result, the best choice for the maximum velocity gradient used in the friend determination seems to be close to 3.0 km s-1 pc-1, which is the value we used in analyzing the real L1495/B213 data.
 |
Fig. A.3 “Traffic-light” diagrams for a model with two cloud components that have the same velocity but are separated in the plane of the sky. Left: rates of success (green) and failure (red) for a matrix of separation between components (in units of axial FWHM, x-axis) and number of neighbors used in the friend definition (y-axis) Righ: same as in left panel but for models of variable intensity threshold (in units of rms). The horizontal boxes enclose the results for the choice of parameters favored by our modeling. (All models assume a gradient of 3 km s-1 pc-1, as recommended by the results shown in Fig. A.2, and for each panel, the best choice of the other panel is used.) |
Appendix A.2: Non overlapping components of the same velocity
Our second set of models tests the ability of FIVE to separate cloud structure based on spatial information. These models assume that the cloud consists of two components that have the same radial velocity but are separated in the plane of the sky by an amount that we treat as a free parameter. These models are complementary to those of the previous section, and can be used to constrain a different set of internal parameters of FIVE, those that are related to spatial information, such as the number of points required to define a friend and the intensity threshold required to consider points in the search for friends.
For this second set of tests, we followed the same steps described in the previous section. First, we generated a series of model spectra using the CLASS program. For this, we assumed that each individual cloud component has the same physical dimensions, velocity structure, emerging intensity, and noise level as the components in the previous section. Then, we fitted Gaussians to the spectra, although this time we used single Gaussians because the two cloud components do not overlap in space, and the spectra consist of single peaks. Finally, we input the fit results into FIVE and compared the number and properties of the cloud components found by the algorithm with those originally put in the model. As before, we classified the result as a success if FIVE recovers the original structure. If not, we classified it as a failure.
Figure A.3 summarizes the results of our second set of models using again “traffic light” diagrams. As mentioned before, the models in this section mainly explore two parameters of FIVE, the number of points used in the definition of friends and the intensity threshold used for the selection of points. For this reason, Fig. A.3 consists of two panels, each one showing the success rate of one of the parameters when disentangling two components that are separated by a distance value given in terms of the filament width (FWHM).
As can be seen, no choice of parameters allows FIVE to disentangle filaments that are closer than 1.25 times the spatial width or less. This limiting value is higher than the 1.0 times the velocity linewidth found in the previous section, indicating that FIVE is not as sensitive when using spatial information as it is when using velocity data. The (slight) asymmetry between space and velocity likely arises from the simpler treatment by FIVE of the spatial information, which in turn results from the more complex nature of this parameter, which can vary in two dimensions, while the radial velocity has only one dimension to change.
Another result seen in Fig. A.3 is the success of FIVE to disentangle components that are separated by 2.0 FWHM (or more) in distance unless some of the internal parameters of the algorithm are set to extreme values (e.g., intensity threshold larger than 8 rms). This level of success indicates that FIVE can correctly reconstruct cloud structure that is well-separated in the plane of the sky, and that it only tends to fail when the two cloud components overlap in space.
Figure A.3 also indicates that the success rate of FIVE can be maximized by choosing appropriate values for both the number of neighbors and the intensity threshold used in the friend definition. As can be seen, a choice of five neighbors and a threshold equal to six times the intensity rms provides a high success rate even in the case of components separated by 1.5 FWHM. For this reason, the previous choice of values was used in the analysis of the L1495/B213 data. It is important to stress, however, that this parameter choice depends on the physical properties of the gas and the sampling and sensitivity of the observations. Different cloud conditions or a different type of observation may require using different parameter choices.
To finish our analysis, we study how the FIVE algorithm fails in the limiting case of components separated by 1.5 FWHM when its parameters have not been optimized. This is instructive because it shows the compromise that is often needed to determine the optimal value of a given parameter. As Fig. A.3 shows, in the case of a variable number of neighbors (left panel), a choice of five neighbors produces a higher rate of success than a choice of three or seven neighbors. This is because a choice of a too few neighbors, say thee, can lead to the erroneous merging of the components, since it becomes possible that a statistical fluctuation due to noise or variations in intensity affects a few positions that can find enough neighbors to create an artificial bridge between separated components. On the other hand, a choice of too many neighbors, say seven, can lead to the erroneous splitting of a single component. This is because a requirement of seven neighbors for the definition of a friend leaves too little room for possible noise effects. A statistical fluctuation that eliminates several of the eight possible nearest neighbors breaks the component in two and makes the algorithm fail.
A similar situation occurs with the choice of the intensity threshold, as shown in the right hand panel of Fig. A.3. Choosing too low a value (e.g. 4 rms) allows the low-intensity tails of the Gaussian distributions to merge, and this makes the algorithm fail to separate the two cloud components. Choosing too large a threshold (e.g. 8 rms), on the other hand, makes the algorithm sensitive to the loss of points in statistical fluctuations, and this leads again to artificial fragmentation. The optimal value of choice (threshold of 6 rms), therefore, represents a compromise between the two opposite trends of merging and fragmentation, and makes it possible to disentangle cloud components separated by 1.5 FWHM.
Appendix A.3: Summary: successes and limitations of FIVE
While our two-component cloud can only be considered a toy model, its analysis with FIVE presents remarkable similarities with the analysis of the real L1495/B213 data. This is likely a combination of the realistic emission parameters of the model and the fact that most problems analyzing of real data arise when dealing with pairs of components, especially when trying to separate them if they are close in velocity or position. Under these conditions, the previous tests show that FIVE can recognize components with an accuracy that approximates that of a human observer who has the patience of inspecting the individual spectra and who looks for connections between spectral features at different positions. Reproducing such human behavior was in fact the main goal when designing FIVE, given the large size of the L1495/B213 dataset and the need to automatize the velocity analysis.
The success of FIVE is remarkable in view of its simplified analysis, but is accompanied by important intrinsic limitations. As we have seen, FIVE cannot disentangle components that are blended either in position or velocity by amounts comparable to their spatial or velocity width, even if the blending occurs over a limited region in space. Improving on that limit may require a significantly different type of analysis. Like similar algorithms, FIVE has only a local view of the emission, and cannot take advantage of the information provided by the data on global scales to separate so far unresolvable components. Adding such a global view to FIVE not only requires a more sophisticated numerical scheme to combine local and global patterns, but an a priori understanding of the physical nature of the components themselves. This understanding, unfortunately, still eludes us today.
Appendix B: Principal axis determination of the velocity components
 |
Fig. B.1 Schematic view of the two-step process used to determine the principal axis of a filamentary velocity component. The gray-scale and contours represent the C18O(1−0) emission. The blue straight line is the first-step determination of the principal axis, and the red polygonal curve is the second-step determination of the axis. |
To analyze different properties of the filamentary velocity components identified with the FIVE algorithm, such as their spatial location and velocity field, it is convenient to determine an axis for each of them that follows the long dimension of the filament. We did this using the process illustrated in Fig. B.1, which consists of two steps. First, we fit a straight line to the distribution of all points identified by FIVE as belonging to the same velocity component, weighting each point by the intensity of the C18O(1−0) emission (in cases of suspected CO depletion, the C18O intensity has been corrected as described in Sect. 6). As a result of this step, we obtained a first approximation to the principal axis of each velocity component (blue line in Fig. B.1). Using this axis as a reference, we then divided the set of points into 90′′-long segments, and for each segment, we determined the emission centroid following the same wighting scheme as in the first step. Connecting the emission centroids with a polygonal curve, we defined the second and final approximation to the principal axis of each filament (red line in Fig. B.1).
All Tables
All Figures
 |
Fig. 1 Integrated intensity maps of L1495/B213 in C18O(1−0) (top) and SO(JN = 32 − 21) (bottom). The offsets refer to the FCRAO map center at |
| In the text | |
 |
Fig. 2 Top: integrated intensity map of L1495/B213 in N2H+(1−0) adding all hyperfine components. The white contour corresponds to 0.5 K km s-1. Central position and offsets are as in Fig. 1. First contour and contour interval are 0.5 K km s-1. Bottom: schematic view of the L1495/B213 complex indicating the regions defined in this paper, which approximately match those of Barnard (1927). The black solid line represents the lowest C18O(1−0) contour in Fig. 1 and delineates the boundary of the cloud. The red lines represent the N2H+(1−0) emission, which traces the dense cores, and the red labels identify the cores described in Sect. 4 and summarized in Table 2. The stars correspond to stellar objects from the survey of Rebull et al. (2010). Solid symbols represent the youngest objects (Class I and Flat), and open symbols represent evolved objects (Classes II and III). |
| In the text | |
 |
Fig. 3 Expanded view of the B7-B10 region. C18O(1−0) emission in color and N2H+(1−0) emission in white contours (sum of all hyperfine components). First contour and contour interval are 0.5 K km s-1. Stars as in Fig. 2, and offsets refer to the FCRAO map center (see Sect. 2). |
| In the text | |
 |
Fig. 4 Expanded view of the B211 region and the NW part of B213 (to better connect with the following figure). Top: C18O(1−0) and N2H+(1−0) maps as in Fig. 3. Bottom: 850 μm continuum map from LABOCA observations and N2H+(1−0) emission (contours). |
| In the text | |
 |
Fig. 5 Expanded view of the B213 region. Top: C18O(1−0) and N2H+(1−0) maps as in Fig. 3. Bottom: 1200 μm continuum map from MAMBO observations and N2H+(1−0) emission (contours). |
| In the text | |
 |
Fig. 6 Expanded view of the B218 region. Top: C18O(1−0) and N2H+(1−0) maps as in Fig. 3. Bottom: 850 μm continuum map from LABOCA observations and N2H+(1−0) emission (contours). |
| In the text | |
 |
Fig. 7 Mean density of companions for the N2H+ cores presented in Table 2. The red solid squares represent observations and the open black squares with error bars represent the prediction from a series of 100 Monte Carlo runs (see text). |
| In the text | |
 |
Fig. 8 Central panel: FCRAO integrated intensity maps of the B211-B213 region in C18O(1−0) (gray scale and black contours) and N2H+(1−0) (red contours). Left and right panels: spectra from selected positions illustrating the complex velocity structure of the emission. The blue spectra correspond to C18O(2−1) and the red spectra correspond to the isolated (F1F = 01–12) component of N2H+(1−0) (multiplied by 3) observed simultaneously with the IRAM 30 m telescope. Note the presence of 5 different C18O peaks in panel 3. |
| In the text | |
 |
Fig. 9 Position–position–velocity cube showing the line-center velocities derived from the Gaussian fit to the C18O(1−0) and N2H+(1−0) spectra towards the B211-B213 region presented in Fig. 8. Semi-transparent points have intensities between 3 and 6 times rms and opaque points have intensities higher than or equal to 6 rms. |
| In the text | |
 |
Fig. 10 Schematic view of the 3 steps in the modified FoF method used to identify components in PPV space. To simplify the view, two projections of the PPV cube are presented. The left panels show the PP plane (integrated map) and the right panels show a projection on a PV plane. The black points represent all data with S/N ≥ 3. The green points in the first row of panels are those selected as significant to use in the first application of the FoF algorithm. The red and blue colors in the lower panels indicate positions belonging to each of the two structures identified by FoF as connected. The colored lines indicate the individual connection between points. Points are gradually assigned to the two velocity structures. The boxes illustrate the regions used to calculate the number of neighbor points and the velocity gradients for the FoF algorithm. |
| In the text | |
 |
Fig. 11 Analysis of the PPV cube of Fig. 9 using the FIVE algorithm. Top: seed points selected using the threshold values described in the text (color-coded green). Middle: points identified after a friends-of-friends search that starts with the seed points from the previous step. The color coding illustrates the different cloud components. Bottom: final assignment of points to the different cloud components (colored points). The black points represent unassigned points. |
| In the text | |
 |
Fig. 12 Location of the cloud components of L1495/B213 identified with the FIVE algorithm. Each component is represented by its central axis and has been color-coded for easier identification. The background gray-scale image is a SPIRE 250 μm continuum map from the Gould Belt Survey (André et al. 2010) that has been blanked out to match the coverage of our FCRAO data. |
| In the text | |
 |
Fig. 13 Distribution of parameters in the 35 cloud components derived using the FIVE algorithm. a) Aspect ratio, b) length, c) mass per unit length, d) nonthermal velocity dispersion, e) global velocity gradients, f) local velocity gradients. |
| In the text | |
 |
Fig. 14 Velocity profiles of filaments with cores. Blue squares are C18O data and red triangles are N2H+ data. |
| In the text | |
 |
Fig. 15 Spatial distribution of the nine bundles of filaments identified by FIVE. The extent of each bundle is represented by a colored background, and the axis of the individual filaments are represented by red lines. The gray-scale background is the same SPIRE map as is shown in Fig. 12. |
| In the text | |
 |
Fig. A.1 Analysis of a model consisting of two components that overlap in position but are separated in velocity by 1.25 times the linewidth. Top: position–position–velocity cube with the results of Gaussian fits to the spectra. Bottom: results from the FIVE analysis using the favored choice of internal parameters (see text). Compare with Fig. 11. |
| In the text | |
 |
Fig. A.2 “Traffic-light” diagram showing the rates of success and failure of the FIVE algorithm when disentangling a model cloud that consists of two components that overlap in position but differ in velocity. The diagram represents a matrix of pie charts, each of them showing the fraction of success (green) and failure (red) for 10 independent models with a given velocity difference between the components (in units of the spectral line FWHM, x-axis) and a maximum velocity gradient used in the definition of friend (y-axis). The horizontal box encloses the results for the favored gradient of 3 km s-1pc-1. (All models use a number of neighbors of 5 and an intensity threshold of 6 rms, as recommended by the results shown in Fig. A.3.) |
| In the text | |
 |
Fig. A.3 “Traffic-light” diagrams for a model with two cloud components that have the same velocity but are separated in the plane of the sky. Left: rates of success (green) and failure (red) for a matrix of separation between components (in units of axial FWHM, x-axis) and number of neighbors used in the friend definition (y-axis) Righ: same as in left panel but for models of variable intensity threshold (in units of rms). The horizontal boxes enclose the results for the choice of parameters favored by our modeling. (All models assume a gradient of 3 km s-1 pc-1, as recommended by the results shown in Fig. A.2, and for each panel, the best choice of the other panel is used.) |
| In the text | |
 |
Fig. B.1 Schematic view of the two-step process used to determine the principal axis of a filamentary velocity component. The gray-scale and contours represent the C18O(1−0) emission. The blue straight line is the first-step determination of the principal axis, and the red polygonal curve is the second-step determination of the axis. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


