| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 17 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201220463 | |
| Published online | 07 May 2013 | |
The energy of waves in the photosphere and lower chromosphere
IV. Inversion results of Ca II H spectra⋆
1
Instituto de Astrofísica de Canarias (IAC),
C/ Via Lactéa, 38205
La Laguna ( Tenerife), Spain
2
Departamento de Astrofísica, Universidad de La
Laguna, 38206
La Laguna ( Tenerife), Spain
e-mail:
cbeck@iac.es
3
Kiepenheuer-Institut für Sonnenphysik (KIS),
Schöneckstr. 6, 79104
Freiburg,
Germany
e-mail:
rrezaei@kis.uni-freiburg.de
4
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam,
Germany
e-mail:
kgp@aip.de
Received: 28 September 2012
Accepted: 6 March 2013
Context. Most semi-empirical static one-dimensional (1D) models of the solar atmosphere in the magnetically quiet Sun (QS) predict an increase in temperature at chromospheric layers. Numerical simulations of the solar chromosphere with a variable degree of sophistication, i.e. from 1D to three-dimensional (3D) simulations; assuming local thermal equilibrium (LTE) or non-LTE (NLTE), on the other hand, only yielded an increase in the brightness temperature without any stationary increase in the gas temperature.
Aims. We investigate the thermal structure in the solar chromosphere as derived from an LTE inversion of observed Ca ii H spectra in QS and active regions (ARs).
Methods. We applied an inversion strategy based on the SIR (Stokes inversion by response functions) code to Ca ii H spectra to obtain 1D temperature stratifications. We investigated the temperature stratifications on differences between magnetic and field-free regions in the QS, and on differences between QS and ARs. We determined the energy content of individual calcium bright grains (BGs) as specific candidates of chromospheric heating events. We compared observed with synthetic NLTE spectra to estimate the significance of the LTE inversion results.
Results. The fluctuations of observed intensities yield a variable temperature structure with spatio-temporal rms fluctuations below 100 K in the photosphere and between 200 and 300 K in the QS chromosphere. The average temperature stratification in the QS does not exhibit a clear chromospheric temperature rise, unlike the AR case. We find a characteristic energy content of about 7 × 1018 J for BGs that repeat with a cadence of about 160 s. The precursors of BGs have a vertical extent of about 200 km and a horizontal extent of about 1 Mm. The comparison of observed with synthetic NLTE profiles partly confirms the results of the LTE inversion that the solar chromosphere in the QS oscillates between an atmosphere in radiative equilibrium and one with a moderate chromospheric temperature rise. Two-dimensional x − z temperature maps exhibit nearly horizontal canopy-like structures with an extent of a few Mm around photospheric magnetic field concentrations at a height of about 600 km.
Conclusions. The large difference between QS regions and ARs and the better match of AR and NLTE reference spectra suggest that magnetic heating processes are more important than commonly assumed. The temperature fluctuations in QS derived by the LTE inversion do not suffice on average to maintain a stationary chromospheric temperature rise. The spatially and vertically resolved information on the temperature structure allows one to investigate in detail the topology and evolution of the thermal structure in the lower solar atmosphere.
Key words: Sun: chromosphere / Sun: oscillations
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
The thermal structure of the solar chromosphere remains enigmatic and to a great extent unexplained more than a century after the first description of the existence of the chromosphere itself (Secchi 1860; Lockyer 1868). Nowadays, two competing views of the thermal structure exist, i.e. a static/stationary and a dynamical view.
The static view is expressed by a long series of one-dimensional (1D) thermal stratifications that reproduce observed spectra (e.g. Gingerich et al.1971; Holweger & Müller1974; Vernazza et al.1981; Fontenla et al.1993, 2006; see Rutten & Uitenbroek2012; and Rutten2012, for additional references). To produce emission in the line cores of chromospheric spectral lines, all of these 1D models require a reversal of the temperature gradient with height at some point. Their common feature, therefore, is the existence of a temperature minimum at a height of about 500 km above the photosphere, where the gas temperature starts to rise towards higher layers (e.g. Vernazza et al. 1976; Ulmschneider et al. 1978; Leenaarts et al. 2011). These 1D models with a temperature reversal faithfully reproduce observed (average) spectra to the most minute level, but all lack something: they provide a temperature stratification with height in the solar atmosphere, but they do not explain the reason for its shape.
The dynamical view of the solar chromosphere is newer than the static 1D models and has emerged thanks to the increase in the available computing power during the last two decades. Unlike the static models that were derived from observations, the dynamical approach usually goes the opposite way and tries to model the solar chromosphere from basic principles, i.e. numerical simulations that encompass the differential equations that govern the temporal evolution of material in the solar atmosphere (Nordlund 1982). One of the advantages of this forward modelling is that one only needs to decide what the relevant physical processes are that must be included in the set of differential equations. Whereas numerical simulations of the solar photosphere abound (e.g. Nordlund & Stein 1990; Steiner et al. 1998; Stein & Nordlund 1998; Steiner et al. 2008; Fabbian et al. 2010; Beeck et al. 2012), there are relatively few chromospheric simulations (Rammacher & Ulmschneider 1992; Carlsson & Stein 1997; Wedemeyer et al. 2004; Schaffenberger et al. 2006; Cuntz et al. 2007; Leenaarts et al. 2009).
One reason is the spatial, and especially the vertical extent of the simulation domain that has to reach a height of about 2 Mm to encompass the solar chromosphere with a sufficiently fine sampling on the order of a few tens of km. A second limitation is caused by the physical conditions in the upper solar atmosphere. The gas density in the solar photosphere is high enough that the assumption of local thermal equilibrium (LTE) is justified. In LTE, the available total energy is distributed over all available degrees of freedom by frequent collisions between particles such that each degree of freedom obtains a fully determined fraction of the total energy. The exact distribution depends solely on the physical laws holding in the material of interest. Assuming LTE, the values of several physical quantities such as population states, thermal motions, etc., are determined instantly as soon as a temperature value is given. Because of the decrease in the gas density with height in the gravitationally stratified solar atmosphere, the LTE condition breaks down when a sufficient number of collisions takes longer than the dynamical evolution of the physical quantities that can change by radiative processes for example (e.g. Carlsson 2007; Wedemeyer-Böhm & Carlsson 2011). A complete treatment of this regime in a non-LTE (NLTE) formalism still exceeds the computing power of even the most recent computer clusters (Auer & Mihalas 1969; Ayres & Wiedemann 1989; Rammacher & Cuntz 1991; Carlsson & Stein 1992, 1997; Uitenbroek 2000; Asensio Ramos et al. 2003; Leenaarts et al. 2007; Wedemeyer-Böhm & Carlsson 2011; Carlsson & Leenaarts 2012; Martínez-Sykora et al. 2012).
The dynamical numerical simulations of the solar chromosphere revealed a quite different thermal structure than the static 1D models. The brightness temperature at chromospheric layers tended to fluctuate strongly, leading to intermittent emission in the synthesized chromospheric spectra. The gas temperature, however, did not show any temperature reversal on a temporal average, contrary to most of the static 1D models (cf. Carlsson & Stein 1995, 1997; Kalkofen 2001, 2012). Thus, the average brightness and gas temperatures in such simulations differed significantly, while the average synthesized chromospheric line spectra corresponded to neither the average gas nor the average brightness temperature. This puzzling behaviour even raised the question of how to define a mean temperature at all under these conditions (Rammacher & Cuntz 2005; Uitenbroek & Criscuoli 2011). This point is actually more important than it seems at first glance because the static 1D models are based on the relation between brightness temperature (i.e. observed spectra) and gas temperature (i.e. model output). Questioning this relation between gas and brightness temperature, or the definition of temperature, leads directly to questioning the results of the static 1D models that provide an excellent fit to observed average spectra (Kalkofen 2012).
There are some common problems for both the static and the dynamical view of the solar chromosphere. One is the width of spectral lines synthesized from the simulations or models. Observed chromospheric spectral lines are usually found to be significantly broader than the synthetic lines, (far) in excess of the thermal line width for any reasonable temperature range. This behaviour shows up most prominently in off-limb observations (e.g. Beckers 1968; Beck & Rezaei 2011). Part of this excess in line width can be explained by the spatial resolution of the observations that represent a spatial average over solar structures with different physical properties, and especially different macroscopic mass flows with their related Doppler shifts. But the average of synthetic spectra from simulations with spatial grid sizes down to a few ten kms also lacks the observed line width, which indicates that some physical ingredient is missing in the simulations, or that their spatial sampling – despite being below the photon mean free-path length – still is insufficient to capture all of the dynamical evolution of small-scale mass flows for example. The line width in both static and dynamical models is, therefore, often adjusted ad-hoc by some additional broadening parameters (cf. Allende Prieto et al. 2004; Asplund et al. 2004, and references therein), usually labeled as macroturbulent and microturbulent velocities that represent spatially unresolved line-broadening mechanisms of unknown origin (e.g. Cram 1981; Rutten 2003).
A second problem is how to reconcile the temperature stratifications with the observations of molecular lines at chromospheric heights (Ayres & Testerman 1981). This problem affects the static more than the dynamical models, because in the former the location of the temperature reversal at low heights prevents any significant formation of molecules at layers above it (Ayres 1981, 2002; Kalkofen et al. 1999). A cool chromospheric part could also be included in static models by shifting the chromospheric temperature rise to higher layers (Ayres 2002; Ayres et al. 2006; Fontenla et al. 2007; Rezaei et al. 2008), but it was imposed in some sense as a post-facto crutch. In most numerical simulations, phases with a temperature that is sufficiently low to allow the formation of molecules were usually automatically present (Wedemeyer et al. 2004; Leenaarts et al. 2011).
A third problem is the discrepancy between observations in different spectral lines that yield seemingly contradictory results. Observations with the Solar Ultraviolet Measurement of Emitted Radiation (SUMER) instrument on-board the SOlar and Heliospheric Observatory (SOHO) satellite in ultraviolet (UV) lines revealed that all these lines are in permanent and ubiquitous emission with little intrinsic variation in quiet Sun (QS) regions of the solar surface (Carlsson et al. 1997). All these lines are classified as chromospheric. However, other chromospheric lines, especially Ca ii H and K in the near-UV, show large spatio-temporal fluctuations from reversal-free absorption profiles to moderate emission in the line cores (Liu & Smith 1972; Cram & Dame 1983; Rezaei et al. 2008; Beck et al. 2008). While the temporal evolution is naturally explained in dynamical simulations, persistent emission is only reproduced in static 1D models with a permanent chromospheric temperature rise.
The way to resolve this contradictory behaviour of observed spectral lines and to reconcile the conflicting views of the static and dynamical solar chromospheric models is not clear at present. There is one additional piece of information to be considered: the temperature in the solar photosphere is about 6000 K, while the ion and electron temperature in the solar corona exceeds one million K, where both results are undoubted. Thus, there has to exist a reversal of the temperature gradient at some height, but where exactly is unclear.
Magnetic fields could be a possible mediator between the two conflicting scenarios of the solar chromosphere. Firstly, magnetic fields have not been considered in all of the static nor in many of the dynamical models (but see also Martínez-Sykora et al. 2012; Khomenko & Collados 2012). Secondly, in QS conditions, concentrations of magnetic flux are theoretically expected to spread out from their confined diameter in the low photosphere to fill the full volume in the chromosphere. This structure of several expanding flux tubes automatically creates a dividing layer at some chromospheric height by the so-called magnetic canopy that separates field-free from magnetized plasma (Giovanelli 1980; Steiner et al. 1986; Solanki et al. 1991; Štěpán & Trujillo Bueno 2010; Nutto et al. 2012; Holzreuter & Solanki 2012), i.e. that separates a dynamical chromospheric regime below the canopy from a stationary one above it (as sketched for instance in Beck et al. 2008, their Fig. 22).
In this contribution, we investigate the spatio-temporal behaviour of the thermal structure in the solar chromosphere as derived from an inversion of Ca ii H spectra assuming LTE (Beck et al.2013; BE13). This study follows the approach of the static 1D models by deriving a gas temperature from an observed brightness temperature, but uses spatially resolved spectra that trace the dynamical properties of the solar chromosphere – as in the dynamical view of the chromosphere (see also Henriques 2012). We use observations of both QS and active regions (ARs) to investigate differences between these types of solar structures. The observations and the inversion scheme are described in detail in BE13; we refer the reader to this publication. We will only highlight some observational limitations that are relevant for the current contribution in Sect. 2. We then concentrate on the thermal structure of the chromosphere in QS and ARs in Sect. 3, both on average and spatially resolved. The findings are discussed in Sect. 4. Section 5 provides our conclusions. Appendix A discusses the possible amount of spectral broadening by different mechanisms acting on the observed spectra.
2. Relevant observational details
We use in total five different observations taken with the POlarimetric LIttrow Spectrograph (POLIS; Beck et al. 2005). POLIS delivered1 intensity spectra in Ca ii H at 396.85 nm together with spectropolarimetric data of the two Fe i lines at 630 nm. Two data sets were taken in QS regions, i.e. a time series of about one-hour duration and a large-area map (cf. Beck et al.2009, 2012; BE09 and BE12 in the following). The other three data sets are large-area maps of the active region NOAA 10978 (cf. Beck & Rammacher 2010; Bethge et al. 2012). The parameters most relevant in the present context are the slit width of 0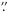 5, the step width in the case of spatial scanning of also 0
5, the step width in the case of spatial scanning of also 0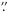 5, the temporal cadence of the time series of 21 secs, and the spatial sampling along the slit of 0
5, the temporal cadence of the time series of 21 secs, and the spatial sampling along the slit of 0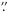 292 in the Ca ii H spectra. These values provide a pixel scale of 0
292 in the Ca ii H spectra. These values provide a pixel scale of 0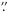 5 × 0
5 × 0 292 in the Ca spectra. The data were taken with real-time seeing correction by the Kiepenheuer-Institut adaptive optics system (von der Lühe et al. 2003) and have a seeing-limited spatial resolution of about 1′′, which roughly coincides with the sampling-limited resolution in the scanning direction.
292 in the Ca spectra. The data were taken with real-time seeing correction by the Kiepenheuer-Institut adaptive optics system (von der Lühe et al. 2003) and have a seeing-limited spatial resolution of about 1′′, which roughly coincides with the sampling-limited resolution in the scanning direction.
Besides the study of individual events in the time series (Sect. 3.5), the average of the statistics in all individual maps is always used to expand the statistical base.
 |
Fig. 1 Relative occurrence of temperatures in the QS. Top left: temperature vs. optical depth for the full FOV. The relative occurrence of a given temperature is indicated by the colour with the corresponding colour bar at top. Thick black line: original HSRA model. Dashed line: average temperature. The vertical dashed lines denote the layers of log τ for which the temperature histograms are shown in the rest of the panels. In the histograms, black/blue/red lines denote the full FOV/magnetic/field-free locations. |
3. Results of LTE inversion
The inversion setup for Ca ii H described in BE13 yields temperature stratifications for spatially resolved spectra. With the inversion results we now can investigate the statistics of the temperature distributions at different optical depth levels log τ, analogously to BE12, where the intensity distributions at different λ and the characteristic properties of different spatial samples in the observed field of view (FOV), i.e. field-free or magnetic regions, and the full FOV, were analyzed. The distinction between field-free and magnetic sample is made using the simultaneous polarimetric observations in the 630 nm channel of POLIS by setting a threshold in the observed polarization signal (cf. BE12).
3.1. Average temperature and temperature statistics in QS
Following the approach of BE12, we calculated the characteristics of the temperature distributions up to second order (mean, root-mean-squared (rms) fluctuation, skewness). The average value was subtracted each time before the calculation of the rms fluctuations. Figure 1 shows some of the statistics of temperature vs. optical depth for the maps taken in the QS. The upper-left panel shows the relative occurrence (denoted by the colour bar) of temperatures in the full FOV for each optical depth level. The three samples in the FOV (field-free, magnetic, full FOV) differed only slightly in this way of presentation, therefore only the latter is shown. The remaining panels show the histograms of temperature for all spatial samples at three optical depth levels of log τ = −0.6, −2.6, and − 4.6, respectively. The magnetic locations (blue lines) show a weak preference for slightly higher temperatures compared to the full FOV or the field-free locations. The average temperatures of all three samples do not show an indication of a chromospheric temperature rise as predicted, e.g. by the original Harvard Smithsonian Reference Atmosphere model (HSRA; Gingerich et al. 1971), e.g. compare the black-solid line (HSRA) and black-dotted line (⟨ T ⟩ in the full FOV) in the upper-left panel of Fig. 1.
The lower panel of Fig. 2 shows the variation of the rms fluctuations of temperature with optical depth and geometrical height. For the conversion from one to the other we used the tabulated relation given in the HSRA atmosphere model, not a derivation of the height scale from the inversion results themselves as in Puschmann et al. (2005, 2010). We note that in the derivation of the temperature statistics the individual temperature stratifications vs. optical depth were always used, and that the rms value will (slightly) underestimate the characteristic range of fluctuations in the case of asymmetric distributions (cf. Fig. 1). The geometrical heights in Fig. 2 only indicate a probable value for the average location of the formation heights. As in the analysis of the intensity statistics of Ca ii H and Ca ii IR spectra in BE12, we find that the rms fluctuations increase nearly monotonically in geometrical height, with a minimum of fluctuations near z ~ 100 km (corresponding to log τ ~ −1) caused by the temperature inversion of granules and inter-granular lanes (cf. Puschmann et al. 2003, 2005). The fluctuations stay below 100 K up to a height of 500 km, and reach only 200–300 K at 1000 km. The magnetic regions show slightly higher rms fluctuations at all heights and pass through the minimum of rms fluctuations lower in the atmosphere than the other two samples. This behaviour is presumably caused by the shift of the optical depth scale on magnetic locations. The maximal temperature variations (dotted lines in the lower panel of Fig. 2) reach about 1000 K at log τ ~ −4 (z ~ 700 km).
 |
Fig. 2 Bottom panel: rms fluctuations of temperature for the full FOV (black line), field-free locations (red line), and magnetic locations (blue line). The three dotted lines indicate the maximum deviation from the average temperature. The dashed line denotes the rms fluctuation in an AR map. Top panel: skewness of the temperature distributions. The vertical dotted line indicates z = 150 km. |
Beck et al. (2012; BE12) found a pronounced difference in the skewness of intensity distributions between field-free and magnetic locations, i.e. an increased skewness on magnetic locations at intermediate wavelengths between the line wing and the core, corresponding to formation heights of about z = 135−150 km. The upper panel of Fig. 2 shows that this also happens at about the same height in the case of the temperature retrieved by the inversion. A positive skewness indicates that temperature excursions towards values above the average are more frequent than those towards values below it. The skewness on magnetic locations increases strongly at lower optical depths of about log τ ~ −4 when compared with the other two samples. Again this could be caused by a shift of the optical depth scale on magnetic locations, but could also indicate that propagating waves turn into shock fronts at lower heights in the rarefied medium of magnetic flux concentrations than in the field-free surroundings.
 |
Fig. 3 Relative occurrence of temperatures in an AR. Dash-dotted line: average temperature in the AR. Dotted line: average temperature in QS. Thick black line: original HSRA model. |
3.2. Average temperature and temperature statistics in AR
One could argue that with the list of assumptions used in the inversion (LTE, unmodified HSRA density, lack of hydrostatic equilibrium, complete frequency redistribution), it would be impossible to obtain a chromospheric temperature rise in the inversion of spectra because the (partial) decoupling between temperature and emitted intensity that exists in NLTE would be needed. Figure 3 shows that this is not the case, but that a chromospheric temperature rise results also in LTE if input spectra different to those in QS are analyzed. Both the average temperature and the distribution of temperatures in the AR data cover the temperature rise in the original HSRA model (Fig. 3). The offset of the temperature stratifications in the optical depth scale – the HSRA temperature starts to rise at a larger height (log τ = −4) than the average AR temperature retrieved from the inversion (log τ ~ −3) – is presumably caused by the off-centre location of the AR (θ = 50°) and the related shift of the optical depth scale because of the inclined line of sight (LOS). We remark that the drop of temperature at the uppermost optical depth levels (log τ < −5.5) is purely artificial. It results from the need for a reduction of temperature at the uppermost atmosphere layers for generating double reversals in the Ca line core when using the LTE approximation. The rms fluctuation of the temperature in one of the AR maps is over-plotted in the bottom panel of Fig. 2. It reflects the intrinsically larger spatial variation of temperature in an AR compared to that in QS, but we note that the range goes up to beyond 1000 K rms, implying even larger maximal variations. Temperature fluctuations of this size are large enough to raise the temperature from an atmosphere in radiative equilibrium with about 4000 K in the chromosphere to the temperature values of commonly used atmospheric models such as the HSRA.
3.3. Correlation between intensity and temperature
In our inversion approach, each wavelength λ is attributed a corresponding value in τ, i.e. to adjust the intensity I(λ), the corresponding temperature T(τ) should be varied. The iterative inversion process, however, does not modify the temperature only at the given value of τ, but instead uses a fourth-order polynomial for modifying the full temperature stratification. In addition, when the radiative transfer equation through the model atmosphere is solved in the spectral synthesis, the temperature values of some extended optical depth ranges contribute to the intensity at one given wavelength. Therefore, the one-to-one correlation between a given wavelength and its attributed optical depth is partially broken up. Additionally, some solar surface structures such as (vertical) magnetic fields leave a signature in intensities, and hence temperature over some extended height/optical depth ranges.
To determine which layer in log τ corresponds to the intensity at a given wavelength, we calculated the linear correlation coefficient C (cf. Beck & Rammacher 2010) between intensity vs. wavelength and temperature vs. log τ. Figure 4 shows the result for the large-area scan on the disc centre. The correlation coefficient between intensity and temperature is similar to the intensity contribution function (e.g. Fig. 1 of BE09) in the line wing up to about 396.65 nm, with a single maximum of correlation between log τ ≈ −0.5 to − 1.5 that slowly moves to upper layers for wavelengths closer to the line core. Between 396.65 nm and 396.8 nm, the correlation coefficient shows a second, slightly weaker local maximum of correlation at about log τ ≈ −3.5. In the line-core region from 396.81 nm to 396.89 nm, two clear local maxima of correlation exist, where the upper one above log τ ≈ −4 corresponds to the intensity contribution function, whereas the origin of the lower one at log τ ≈ −1 is not immediately clear.
 |
Fig. 4 Correlation coefficient between intensity at a given wavelength I(λ) and temperature T(log τ). |
Figure 5 reveals that the maximum correlation between line-core intensity and temperature at low atmosphere layers is most likely caused by locations with large photospheric magnetic flux. A comparison between the line-core intensity Icore (lower-left panel in Fig. 5) as the most prominent tracer of photospheric magnetic flux and the temperature at optical depths of log τ = −0.9, −2.5, and −5.4 shows that the photospheric magnetic network can be identified at both log τ = −0.9 and − 5.4 (correlation coefficient with Icore of 0.50 and 0.85, respectively), but is completely inconspicuous at log τ = −2.5 (C = 0.08). This implies that vertical or only weakly inclined magnetic fields – characteristic of the magnetic network and isolated magnetic flux concentrations because of the buoyancy force – leave prominent signatures in temperature in at least two height ranges, i.e. at upper atmospheric layers above log τ = −4, and at lower atmospheric layers at about log τ ≈ −1. This is most likely the reason for the increased skewness in the magnetic sample at log τ ≈ −1.2 (z ~ 150 km) found in the previous section and in BE12: magnetic flux concentrations and their immediate surroundings appear brighter than the quiet inter-network (IN) at intermediate wavelengths, and hence have a slightly enhanced temperature at the corresponding atmospheric layers (cf. Sheminova et al. 2005; Sheminova 2012). This, however, does not explain why the intensity (temperature) is enhanced only at these wavelengths (heights), but not in between.
 |
Fig. 5 Comparison of line-core intensity (lower left) and temperature at log τ = −0.9 (lower right), − 2.5 (upper left), and − 5.4 (upper right). The correlation coefficient between Icore and T(τ) is denoted at the bottom of the temperature panels. |
3.4. Energy flux
3.4.1. Temperature rms fluctuations with height
To estimate the vertical energy flux, we determined the evolution of the energy content with height assuming that the energy balance is effected in the vertical direction in a gravitationally stratified atmosphere with radial energy transport at least up to the photosphere with its convective granulation. To separate the dynamical part of the energy balance from any possible static background caused by radiative equilibrium with the incoming photospheric continuum radiation, we converted the rms fluctuations of the temperature ΔTrms(τ) – instead of using the modulus of the temperature T(τ) – to the equivalent increase in internal energy using 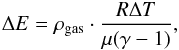 (1)where R = 8.31 J mol-1K-1, μ = 1.3 g mol-1 and γ = 5/3 are the gas constant, the specific mass and the adiabatic coefficient, respectively (cf. Eq. (4) of BE09). The tabulated values of the gas density ρgas in the HSRA model were used. With the relation between τ and geometrical height z tabulated in the HSRA model, this yields the (stationary) average variation of energy with height (top panel of Fig. 6).
(1)where R = 8.31 J mol-1K-1, μ = 1.3 g mol-1 and γ = 5/3 are the gas constant, the specific mass and the adiabatic coefficient, respectively (cf. Eq. (4) of BE09). The tabulated values of the gas density ρgas in the HSRA model were used. With the relation between τ and geometrical height z tabulated in the HSRA model, this yields the (stationary) average variation of energy with height (top panel of Fig. 6).
 |
Fig. 6 Variation of energy density with height. Top: energy density equivalents corresponding to velocity (red line with pluses), intensity (purple-dash-dotted line), and temperature rms fluctuations (black-solid line). The black-dashed line shows results for the temperature rms fluctuations when using the gas density in the original HSRA model. The blue line indicates the gas density in the modified HSRA model. Middle: energy gradient per km in height assuming a propagation with vac. The red line shows results from using a net cooling rate of 100 W g-1 (CL12). Bottom: radiative losses in the units used in CL12. |
The resulting volume energy density E/V can be compared with the result found in the first two papers of this series. The energy density derived from the direct conversion of intensity fluctuations to temperature (see BE12) lies slightly above the one derived from the temperature fluctuations in the inversion. The reason is that in the inversion the variation of intensity is implicitly converted to a temperature fluctuation over some optical depth ranges, whereas in the direct conversion from intensity to temperature all variation is attributed to a single optical depth point. This approach therefore leads to larger rms fluctuations than in the case of considering the radiative transport through the atmosphere. The energy density corresponding to the velocity rms (BE09) lies below that derived from intensity fluctuations by direct conversion or by inversion up to z ~ 1 Mm, but exceeds the others above that height. We note that all temperature fluctuations – when using ΔT without applying Eq. (1) – from either velocity, intensity, or the LTE inversion fall short of the energy required to lift an atmosphere in radiative equilibrium to the HSRA or any similar atmospheric model (~1000 K needed at z ~ 1 Mm, but ΔT is about 500 K at maximum, e.g. Fig. 2). If one assumes that the energy related to the temperature fluctuations is transported vertically by (acoustic) waves moving with a speed vac of about 6 km s-1 (cf. Sect. 3.5.5 below), the generic chromospheric energy requirement of about 4 kW m4 of Vernazza et al. (1976) corresponds to about 0.67 J m-3 (horizontal dotted line in the top panel of Fig. 6). The atmospheric energy content from all three approaches (velocity, intensity, LTE inversion) intersects with this requirement at a height of about 750 km, but drops rapidly below this value at higher atmospheric layers. The ratio of the generic energy flux of 4 kW m-2 and the energy density multiplied by a constant sound speed of 6 km s-1 is about ten at z ~ 1000 km and increases rapidly to a factor of several hundreds at higher layers.
The rapid drop of the energy density with height is caused by the exponentially decreasing gas density ρgas that is over-plotted in the top panel of Fig. 6. The increase in rms fluctuations with height is not able to compensate for the decrease in ρgas. We used two different gas densities for test purposes, on the one hand the tabulated values of the HSRA, 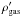 , and on the other hand the gas density ρ in the modified HSRA model that uses a linear extrapolation above log τ = −4. The differences between these two gas densities, however, do not significantly change the resulting energy density (compare the black-solid and black-dashed curves in the top panel of Fig. 6). There is, however, a height range from about z = 100 km to 250 km, where the energy of the temperature fluctuations from the LTE inversion stays roughly constant while the density reduces by a factor of two in the same height interval, similar to the height range of constant energy found for individual bright grains (see Fig. 10 below).
, and on the other hand the gas density ρ in the modified HSRA model that uses a linear extrapolation above log τ = −4. The differences between these two gas densities, however, do not significantly change the resulting energy density (compare the black-solid and black-dashed curves in the top panel of Fig. 6). There is, however, a height range from about z = 100 km to 250 km, where the energy of the temperature fluctuations from the LTE inversion stays roughly constant while the density reduces by a factor of two in the same height interval, similar to the height range of constant energy found for individual bright grains (see Fig. 10 below).
3.4.2. (Radiative) energy losses
The derivative of the energy content, again multiplied by vac, gives the energy losses with height (middle panel of Fig. 6). The region of roughly constant energy density can again be identified at about z ~ 200 km. Integrating the area of the energy gradient for all heights above 750 km that can be considered to contribute to the radiative losses in the Ca line core, i.e. the chromosphere, yields a value of about 3.5 kW m-2, which would match the generic chromospheric energy requirement. This would, however, imply that no energy is left for heating the layers above – such as the corona – since this amount of energy is assumed to be radiated away in all of the chromospheric spectral lines.
For comparison with the gradient of energy losses with height, we used the value of chromospheric radiative losses derived from a set of numerical simulations by Carlsson & Leenaarts (2012; CL12). Their Figs. 15 and 16 yield an average cooling rate of about 100 W g-1 in the chromosphere that can be converted to losses in energy density by a multiplication with the gas density as a function of height. The resulting energy gradient with height using a constant value of 100 W g-1 (red line in the middle panel of Fig. 6) is larger than our estimate (black line in the middle panel of Fig. 6) by a factor of about 2 to 3 between z ~ 200–300 km, and nearly identical above z ~ 800 km. This difference might be caused to some extent because we only considered rms fluctuations of temperature in the energy estimate, whereas the value of CL12 refers to all radiative losses, i.e. losses related to the modulus of temperature itself, not its variation. For a final comparison with CL12, we determined the energy loss rate per mass by dividing our energy gradient with height by the mass density (bottom panel in Fig. 6, compare with Fig. 16 of CL12). The global trend of an increase in radiative losses from the photosphere towards the chromosphere is identical in both estimates with the prediction of a maximum at about 1 Mm. Less pronounced local maxima at z ~ 800 and 1300 km appear in both estimates, albeit in the case of our estimate their significance is doubtful. In total, a roughly constant value of radiative losses of about 100–200 W g-1 in the lower chromosphere fits both our estimate and the one of CL12.
 |
Fig. 7 Residual of an energy input of 100 % at a height of 240 km (black-solid line). Top: linear scale. Bottom: logarithmic scale. The red pluses and blue diamonds give the corresponding values of FA12 for a high (case a) and low (case b) magnetic fill factor. The green asterisks give the values of ST08 for acoustic waves (case a), the orange triangles those of gravity waves (case b). The purple squares were taken from Felipe et al. (2011) and pertain to magneto-acoustic waves in a sunspot umbra. |
3.4.3. Residual energy content
Figure 7 shows the residual energy left at a given height when some amount of energy is dumped into the atmosphere at a height of z = 240 km. To clearly visualize the effect of the energy losses with height, we provide a linear and a logarithmic plot. The black curve corresponds to our result for the height variation of the internal energy density shown in the upper-left panel of Fig. 6, but normalized to the energy density at z = 240 km. With the strong gradient of energy with height, only 5% of the initial energy are left at a height of 500 km, similar to the reduction of wave energy by 80% at 400 km found in Cuntz et al. (2007). For comparison, we also over-plotted the relative energy fluxes in the numerical simulations of acoustic wave propagation of Fawzy et al. (2012; FA12; first and last column of their Table 3). Their wave energy at 600 km was normalized to the corresponding fraction of our curve at that height. We also read off the value of the energy fluxes for acoustic waves and gravity waves from Straus et al. (2008; ST08; their Fig. 3), both normalized to 100% at z = 250 km. As a last reference, the acoustic energy flux in a wave simulation inside a sunspot umbra from Felipe et al. (2011; their Fig. 16) is also overplotted.
A comparison of the various curves shows that our result on the variation of the energy density with height, which corresponds to the rms fluctuations of brightness temperature in the QS, matches best with all those derived for acoustic waves in a weakly magnetized plasma (case (a) of ST08 and case (b) of FA12). This implies that any gravity waves present in the atmosphere should have no signature in intensity spectra, and thus no signature in temperature, otherwise the inversion would have had to retrieve a significantly different slope of the energy density with height as given by case (b) of ST08.
3.5. Individual bright grains in the quiet Sun
Bright grains (BGs; see Rutten & Uitenbroek 1991) are one of the most prominent features in observations of the chromospheric Ca ii lines, independent on whether two-dimensional (2D) imaging data or spectroscopic data are used. They are transient, strong intensity brightenings in chromospheric layers that appear with a random spatial pattern, but a characteristic period of about three minutes. They are clearly related to some sort of energy transport towards and energy increase in the solar chromosphere (e.g. Carlsson & Stein1997; BE08). Carlsson & Stein (1997; CS97) studied the purely hydrodynamical case of BGs in numerical simulations and were able to show the photospheric origin of these features.
Following the general approach used throughout our series of papers, we will treat all BG events in our data in the same way without trying to distinguish between a possible acoustic or magnetic origin, which would be possible using the spectropolarimetric data in the photospheric Fe i lines at 630 nm. The simultaneous polarisation measurements (cf. BE08; their Fig. 4) showed a stable magnetic environment without clear indications of either magnetic flux emergence (e.g. Gömöry et al. 2010) or flux cancellation events (e.g. Bellot Rubio & Beck 2005).
To estimate the energy transport related to BGs, we studied the occurrence rate, spatial extension and energy content of individual BGs for an extrapolation of their total energy contribution to the chromospheric energy balance. We used the data of the time series taken at the disc centre (observation No. 2 in BE12) for that purpose. We define BGs as any temporally isolated temperature enhancement in the lower solar atmosphere, i.e. also below chromospheric layers.
3.5.1. Temporal frequency
To derive the characteristic occurrence frequency of BGs, we analyzed the temporal evolution of the temperature on the existence of local extrema, i.e. local temperature maxima. The top panel of Fig. 8 shows the temporal evolution of the temperature excursions around the mean value at log τ = −3.6 for one pixel along the slit as an example. The temporal evolution of the temperature is similar to the observed intensity at λ = 396.83 nm, which roughly forms at that optical depth (red-dash-dotted line). We then applied a method developed for finding polarisation lobes or local intensity reversals in line profiles (e.g. Beck 2006; Rezaei et al. 2008) to all pixels along the slit and all layers in log τ to find the locations of local maxima in the temperature excursions. To be counted as a local maxima, the value at a given instant of time has to be larger than the values on the two time steps before and after, i.e. it has to be the largest value in a range of ± 40 s. With this approach, the influence of noise on the determination is reduced. Given the typical duration and cadence of BGs (cf. Figs. 10 and 13 below), ± 40 s is a characteristic time span in which usually only a single BG happens. The temperature maps were filtered beforehand for all variations with periods above 7.5 min to suppress the long-term variation caused by the granular evolution. We implicitly identify in the following local temperature maxima with BGs.
 |
Fig. 8 Temporal occurrence frequency of BG events. Top: temporal evolution of temperature at log τ = −3.6 for one pixel along the slit. The red-dash-dotted line shows the intensity at λ = 396.83 nm in arbitrary units for comparison. The vertical dashed lines indicate local maxima. Middle: temporal average of number of maxima along the slit. The red-dash-dotted line shows the unsigned integrated Stokes V signal in arbitrary units. Bottom: average number of local maxima during 3150 s as a function of log τ. |
Along the slit, the number of maxima was comparable for all pixels, regardless if they were related to photospheric magnetic fields or not (middle panel of Fig. 8). We find only a weak dependence of the total number of maxima in the 3150 s duration of the time series on log τ, with a slight increase in the occurrence rate at upper atmospheric layers (bottom panel of Fig. 8). On average, we find about 20 maxima in temperature excursions at all slit positions and layers of log τ, which yields a characteristic cadence of about 160 s (cf. von Uexküll & Kneer 1995). The lack of variation with optical depth may seem puzzling at a first glance, given that solar oscillations are usually separated into photospheric 5-min and chromospheric 3-min oscillations, but ascribing any period to not necessarily repeated events can also be misleading. For instance, the three BGs traced in Figs. 10 and 13 below remain three events throughout all optical depth layers (see also Kalkofen et al. 2010; Stangalini & Moretti 2012).
The number of 20 events in 3150 s yields an occurrence rate of about 0.006 s-1, which is comparable to the values given in Tritschler et al. (2007; their Fig. 7, 0.0075 s-1 at maximum). We note that our rate is an upper limit for the occurrence of BGs because the simple identification method by local temperature maxima presumably has also counted some peaks that could result from observational effects such as residual image jitter rather than from physical processes in the solar atmosphere (cf. the top panel of Fig. 8 at t ~ 40 min). We repeated the determination of locations of local temperature maxima with a width of ± 4 time steps (≡±80 s) or after applying a running mean with a width of five time steps, which both yielded only about 15 maxima on average. The dependence of the number of maxima on optical depth did not change by the additional requirement/smoothing. When analysing the intensity variation with time for local maxima in a ± 40 s range (top panel of Fig. 8), three additional local maxima are found compared to the temperature curve. Thus, the most probable range for the number of temporally local intensity or temperature maxima, and hence BGs is from 15 to 22 in 3150 s (0.005–0.007 s-1).
The area fraction of BGs, i.e. the number of pixels along the slit that exhibit a temperature maximum at a given moment of time relative to the total number of pixels, is about 10%. A similar estimate can be made from Fig. 9 that shows about one BG of 1 Mm diameter in each 2D FOV of about 1 Mm × 10 Mm.
3.5.2. Horizontal spatial extent
To estimate the spatial extent of individual BGs, we used the fact that the time series on the disc centre (observation No. 2 in BE12) actually consists of 150 repeated scans of 4 steps with 0 5 step width each, even if only the single step of each scan that was co-spatial in 396 nm and 630 nm was investigated in detail. Figure 9 shows the temporal evolution of the H2V intensity in a 2D FOV of 1.45 Mm × 14.8 Mm over 651 s (≡31 repetitions of scanning the same area). The three consecutive brightenings of Fig. 10 are located at (x,y) ≈ (0−32,6) Mm. Several BGs can be identified throughout the FOV, but their full extent in most cases is only covered along the slit in y, whereas they are truncated in x when they were not almost centred inside the scanned area of 2′′ extent (e.g. the BG in the fourth repetition at y ~ 6 Mm in Fig. 9).
5 step width each, even if only the single step of each scan that was co-spatial in 396 nm and 630 nm was investigated in detail. Figure 9 shows the temporal evolution of the H2V intensity in a 2D FOV of 1.45 Mm × 14.8 Mm over 651 s (≡31 repetitions of scanning the same area). The three consecutive brightenings of Fig. 10 are located at (x,y) ≈ (0−32,6) Mm. Several BGs can be identified throughout the FOV, but their full extent in most cases is only covered along the slit in y, whereas they are truncated in x when they were not almost centred inside the scanned area of 2′′ extent (e.g. the BG in the fourth repetition at y ~ 6 Mm in Fig. 9).
 |
Fig. 9 Temporal evolution of the H2V intensity in a 2D FOV. The white vertical lines denote the area of one scan of about 1.5 Mm extent in x taken in about 21 s each. The short white bar at (x,y) ≈ (11,6) Mm indicates a length of 1 Mm. |
From the section of the FOV shown in Fig. 9, a roundish shape with an average diameter of about 1 Mm can be attributed to BGs. To improve the statistics, we manually identified about 100 BGs in the full FOV of all the time series. The BGs were required to be located outside of regions with strong polarisation signals and to be visible in at least three repetitions of scanning the same area. We then selected the BGs at the time of their largest brightness and took intensity cuts along the slit through their centres. We fit Gaussians to the intensity cuts to obtain the diameters of the BGs. The diameters ranged between 0.50 and 1.83 Mm, with an average diameter of 1.17 Mm. A set of about 30 BGs that appeared on locations with significant polarisation signals showed a slightly larger average diameter of 1.36 Mm. In the following we will thus assume a typical radius of 0.5 Mm for a single BG, which agrees well with the characteristic diameter of BGs of 1–2′′ found in Ca ii imaging data (e.g. Wöger et al. 2006; Wöger 2007; Tritschler et al. 2007).
 |
Fig. 10 Estimate of the energy content of individual BG events. Top panel: temperature enhancements (left column) and internal energy enhancements (right column) for a pixel with BG activity (bottom row) and a quiet reference pixel (top row). Bottom panel: average internal energy density for the active (black line) and the quiet pixel (red line) vs. geometrical height. The blue line shows their difference. |
3.5.3. Energy content
To determine the energy content of individual BGs, one needs to derive the temperature enhancement related to them. One additional problem here is to separate the temperature contribution of BGs from, e.g. the background (brightness) temperature that results from an atmosphere that is in radiative equilibrium with the incoming photospheric radiation. This background radiation needs not be constant throughout the FOV because photospheric magnetic fields or variations in the granular evolution can modify it. We therefore first determined a minimum-temperature stratification Tmin(τ,y) for each pixel along the slit defined by the lowest temperature at each layer of log τ attained on the pixel y during the one-hour time series. A subtraction of this minimal temperature from the temperature stratification on the pixel y at a given moment of time then yields only positive temperature fluctuations. These fluctuations represent the minimum amount of additional energy above the lowest energy state that the atmosphere exhibited during nearly one hour, without excluding that the lowest energetic state was energetically above radiative equilibrium.
 |
Fig. 11 Spatio-temporal occurrence of temperature maxima. Bottom row, left to right: intensity maps at λ = 396.724, 396.822, and 396.851 nm. The horizontal white/black bars mark the locations of the active/reference pixel used before. Middle row, left to right: energy density at heights of log τ = −1.6, −3.3, and − 4.6 at the time of temperature maxima. Top: complementary map of energy density on all other locations. |
To isolate the BG contribution to the energy and to remove any additional contribution from the background radiation, we first selected two different locations for comparison, i.e. one pixel with a significant activity in the form of a sequence of three prominent and well-defined BGs that appear consecutively, and one pixel that showed no clear BG or other activity (called “active” and “quiet” pixel in the following; both are marked in Fig. 11). The top panel of Fig. 10 shows the temperature fluctuations relative to Tmin(τ,y) for the two pixels over a period of 651 s, with the active pixel in the bottom row and the quiet reference pixel in the top row. The left column shows the temperature fluctuations ΔT and the right column the corresponding variations of the internal energy density ΔE that were calculated using Eq. (1). For the conversion to geometrical height, we assumed the tabulated relation between log τ and geometrical height z of the HRSA to be valid as a first order estimate also for individual spatially resolved temperature stratifications.
To determine the characteristic energy content of a BG, we averaged the value of ΔE for the two pixels over 651 s (bottom panel of Fig. 10). The difference between the two average values of ΔE reaches a maximum of 22.6 J m-3 at a height of about 250 km. There are several arguments for using the difference at about this height as the actual energy input of one BG. Around this height, the average energy density is nearly constant for the active pixel, whereas it drops steeply at higher atmosphere layers, indicating that the energy is inserted at low altitudes in the atmosphere. This is also evident from the temporal evolution of the temperature fluctuations, where the precursors of the BG appear first low in the atmosphere in each case and then propagate upwards. The temporal evolution of the temperature (upper panel of Fig. 10) also shows clearly the occurrence of three BGs during the time used for the average, which are caused by three short-lived (<100 s) events of energy input into the low atmosphere. The temporal fill factor – as estimated from the time intervals when the BGs can be clearly identified in the temperature variation in Fig. 10 – of all three BGs together in the time span considered is about 50%. The energy enhancement of a single BG should thus correspond to about twice the temporally average value, i.e. about 45 J m-3.
To improve the statistical base of the result and to ensure that it is not strongly biased by exactly the train of BGs and the reference pixel that we selected, we also calculated the statistics of BGs relative to non-BGs for the full FOV. To that extent, we used the mask of locations with local temperature maxima determined in Sect. 3.5.1. The internal energy density of all locations, where local temperature maxima at three different optical depths occurred, is shown in the middle panel of Fig. 11, whereas the top panel shows the complementary map of the energy density. The bottom panel shows the intensity at the wavelengths that were attributed to these optical depths. A comparison of the middle and upper panel reveals that the BGs with their apparent diameter of 1 Mm are usually only a part of a wave front that extends up to ten Mm (cf. von Uexküll & Kneer 1995) and induces temperature maxima along its full length. The temperature maxima mark the spines of intensity brightenings, with a similar rise and decay time of the individual BG events (top panel of Fig. 11). The temporal extent appears strongly compressed in the spatio-temporal map in comparison to the spatial extent.
To determine the maximum energy enhancement caused by a BG, we calculated the average value of the energy density for all temperature maxima and for the complementary sample, i.e. all points in time and space that did not correspond to a local temperature maximum. For the optical depth of log τ = −1.2 (≡148 km), BGs have an average energy density of 135 J m-3, whereas the corresponding value at log τ = −2.2 (≡244 km) is 124 J m-3. For the non-BG sample, the average energy density is 89 J m-3 and 80 J m-3, respectively. We excluded the location of the temperature maximum, and the immediately preceding and following time steps in the calculation of the average non-BG energy. The energy difference between BGs and non-BGs then is 46 J m-3 and 44 J m-3 at a height of 150 km and 250 km, respectively, matching the estimate above from individual BGs. We will use a characteristic enhancement of the internal energy density of 45 J m-3 for one BG in the following.
3.5.4. Vertical extent
To determine the vertical extent of BGs, in principle the curve of the energy difference between the quiet and the active pixel could be used (lower panel of Fig. 10), but we decided to use the temperature stratifications instead because of the larger amplitude of the temperature fluctuations. We converted the temperature stratifications at the onset of two BGs (indicated by the white vertical dotted lines in the lower left panel of Fig. 10) from optical depth to geometrical height (Fig. 12). The BGs at this stage of their evolution show up as Gaussian-like temperature bumps centred at about z ~ 300 km. The full-width at half-maximum (FWHM) of the temperature enhancements is about 200 km in height, which would correspond to half a period of a sinusoidal wave with 400 km wavelength (blue line in Fig. 12). Identifying BGs with acoustic waves with a period of 3 or 5 min and assuming propagation with sound speed (about 6 km s-1) would predict significantly larger wavelengths of 1 and 1.8 Mm instead. The propagation of BGs in the atmosphere is not purely vertical, but also has a horizontal component (cf. Figs. 9 and 11; some of the BGs move along the slit with time), which modifies the apparent vertical wavelength. The angle between local vertical and the wave propagation directions seems, however, to be small in most cases.
 |
Fig. 12 Temperature stratifications vs. geometrical height at the onset of two BGs corresponding to the vertical white-dotted lines in the top panel of Fig. 10. The horizontal dotted lines denote the FWHM of the BG events. The blue line shows a sine curve with a wavelength of 400 km for comparison. |
 |
Fig. 13 Vertical propagation speed of temperature perturbations. The background image shows the temperature variation of the active pixel of Fig. 10 vs. geometrical height. The three dotted lines trace the propagation of the perturbations with time. |
With the information on the vertical extent and the effective enhancement of the internal energy density, one can derive an estimate of the total energy of a BG by E = V·ΔE. For a single pixel of 0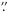 5 × 0
5 × 0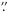 292 extent, assuming a vertical extent of 200 km, and using ΔE = 45 Jm-3, one obtains a total energy of the BG of 6.91 × 1017 J. Assuming a roundish structure with a radius of 0.5 Mm, the total energy of a BG is about 7.1 × 1018 J.
292 extent, assuming a vertical extent of 200 km, and using ΔE = 45 Jm-3, one obtains a total energy of the BG of 6.91 × 1017 J. Assuming a roundish structure with a radius of 0.5 Mm, the total energy of a BG is about 7.1 × 1018 J.
3.5.5. Vertical propagation speed
To estimate the vertical energy flux, the characteristic vertical propagation speed of BGs is needed. The LTE inversion provides the necessary information in form of temperature variations in optical depth. As before, we used the tabulated relation between τ and z of the HSRA model to convert from optical depth to a geometrical height scale. Figure 13 shows the resulting temperature fluctuations at the active pixel vs. geometrical height. The precursors of the BGs leave inclined traces in the lower part of the atmosphere up to about 600 km in height, whereas above this height the temperature enhancements are nearly vertical, i.e. seemingly affecting all higher layers at the same time. This presumably does not indicate that the propagation speed increases strongly, but rather that the relation between τ and z is not valid inside a shock front. Carlsson & Stein (1997; CS97) concluded from their 1D NLTE simulations that the emission in Ca ii H at maximal brightness of a BG stems from a height range of about z ~ 1 to 1.4 Mm, where the strongest contributions to the emergent intensity originate in shocks. For the lower part and the onset of the BGs, the propagation speed of the temperature perturbations can, however, be measured well (inclined dotted lines in Fig. 13). The corresponding slopes denote vertical propagation velocities of about 5.0, 6.3, and 6.7 km s-1, respectively, comparable to the sound speed (see also von Uexküll et al. 1983). We note that an estimate of the propagation speed and direction in all three spatial dimensions can be derived from an inversion of all steps of each repeated scan, dropping the restriction of using only the step that was co-spatial in the Ca ii H and 630 nm spectra.
The magnified view of Fig. 13 of the BG events allows one to estimate an additional characteristic, the typical duration. Above a height of 600 km, none of the BG events lasts longer than about 60 s from its onset to its subsequent complete disappearance.
3.5.6. Energy flux related to BGs
The temporal evolution of the intensity or temperature shows that the energy of BGs is removed by both propagation and radiation in a short time. There are, however, different ways to estimate the vertical energy flux per unit area. Using the energy content of a single BG of 6.91 × 1017 J per pixel of 0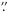 5 × 0
5 × 0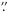 292 as estimated above, and assuming that all this energy disappears again before the onset of the next BG 160 secs later, yields an energy flux of 56.3 kW m-2, but without specifying into which spatial direction (or into which degree of freedom) the energy is dissipated or disappears. The average energy enhancement of 22.6 J m-3 of the active pixel relative to the quiet pixel (Fig. 10) yields an energy flux of 41.4 kW m-2 from both the influx and dissipation of the energy of three BGs in a time span of 651 s. Excluding a downward energy transport and otherwise equal probability for an energy transport to the remaining five possible spatial directions, the upwards vertical energy flux would be about (41.4−56.3)/5 ~ (8.3−11.3) kW m-2. This estimate uses the characteristic temporal evolution in the derivation, i.e. about 160 s cadence between BGs or three events in 651 s, respectively, and refers to the energy flux at a height between about 150 to 350 km.
292 as estimated above, and assuming that all this energy disappears again before the onset of the next BG 160 secs later, yields an energy flux of 56.3 kW m-2, but without specifying into which spatial direction (or into which degree of freedom) the energy is dissipated or disappears. The average energy enhancement of 22.6 J m-3 of the active pixel relative to the quiet pixel (Fig. 10) yields an energy flux of 41.4 kW m-2 from both the influx and dissipation of the energy of three BGs in a time span of 651 s. Excluding a downward energy transport and otherwise equal probability for an energy transport to the remaining five possible spatial directions, the upwards vertical energy flux would be about (41.4−56.3)/5 ~ (8.3−11.3) kW m-2. This estimate uses the characteristic temporal evolution in the derivation, i.e. about 160 s cadence between BGs or three events in 651 s, respectively, and refers to the energy flux at a height between about 150 to 350 km.
However, even if individual BGs induce a vertical energy flux of up to a few tens of kW m-2 in the low solar atmosphere (z < 400 km), it seems that at z ~ 1 Mm far less than 5% of the energy flux is left over (Fig. 7). We remark that in our case the underlying curve that predicts this behaviour is directly proportional to the temperature rms with height and the gas density (Eq. (1)). Modifications in the stratification of either of the two quantities, therefore, will change the residual energy as well.
 |
Fig. 14 Comparison of average observed and best-fit profiles with theoretical NLTE profiles. Bottom panel: spectra from a time series in the QS on disc centre. Top panel: spectra from an AR map off centre. Thick black line: average observed QS profile. Thin purple line: average best-fit QS profile. Blue line: LTE profile of modified HSRA. Red/orange lines: NLTE FAL-C/A profile. For the AR, average profiles of a plage area (blue-dotted line) and an umbra are over-plotted (orange-dash-dotted line). The vertical dotted line denotes the wavelength of intensity normalization. |
4. Discussion
The reliability of the results of our analysis depends to some extent on the LTE assumption taken. We return first to a discussion of observed and theoretical profiles that is partly independent of the (N)LTE question.
4.1. Comparison of average profiles and corresponding temperature stratifications
Figure 14 shows the average observed and best-fit profile in QS for our time series and for one of the AR maps, an average umbral and plage profile from the same AR map, the profile synthesized in LTE from the modified HSRA model without a temperature rise, and two profiles synthesized in NLTE from the FAL-A and FAL-C temperature stratifications (Fontenla et al. 2006) using the code of Uitenbroek (2001). The spectral sampling of the FAL NLTE profiles in the synthesis was 0.75 pm without any additional spectral degradation (cf. Appendix A). To facilitate an easier comparison of the variations in the line core in this figure, all profiles from the AR map were normalized to the same intensity at 396.9 nm.
Both NLTE FAL profiles exceed the observed emission peaks in the QS on the disc centre (lower panel of Fig. 14). The FAL-C profile exceeds even the emission in the QS region of the AR map (top panel). To exclude a possible influence of the large-scale averaging that could reduce the amplitude of the emission peaks through the presence of spatially/temporally varying Doppler shifts, we calculated a QS profile that was averaged only over 112 spectra, i.e. one slit position in the time series. This small-scale average QS profile showed a slightly increased amplitude of the H2V emission peak, but the change was minor and the intensity still fell far short of that in the NLTE FAL profiles. Both the observed and average best-fit profile, however, clearly exceed the profile corresponding to the modified HSRA atmosphere. Average profiles in the QS therefore fall between a profile from an atmosphere in radiative equilibrium and an atmosphere with a chromospheric temperature rise such as in FAL-C or FAL-A. For the case of the AR map, the profiles change significantly. The observed average QS profile has two clear emission peaks, and the average best-fit profile in the QS starts to resemble the NLTE FAL profiles. We remark that inside the AR map, the QS regions contain far more magnetic flux than found in the QS at disc centre, and furthermore that the AR observations were taken at a heliocentric angle of about 50°. The emission in average plage and umbra exceeds the FAL NLTE profiles by a factor of about two.
 |
Fig. 15 Comparison of temperature stratifications. Bottom: QS maps. Top: one of the AR maps. Thick black line: average QS temperature in the LTE fit. Blue line: modified HSRA model. Dashed line: original HSRA model. Red line: FAL-C. Orange line: FAL-A. For the AR, the average temperature stratification of a plage area (blue-dotted line) and of the umbra are over-plotted (orange-dash-dotted line). |
The corresponding temperature stratifications in Fig. 15 closely reflect the differences in the profiles themselves. The modified HSRA lies below the average temperature of the QS on the disc centre retrieved by the inversion, and the two FAL models above it, whereas the stratifications obtained by the inversion for a plage area inside the AR and the umbra of a sunspot follow to some extent the chromospheric temperature rise in the FAL models or the original HSRA model (top panel in Fig. 15).
The LTE assumption certainly has a tremendous effect on the retrieved temperature stratifications, but the main problem already consists in reconciling the observed average spectra in QS with those predicted by the NLTE FAL profiles (lower panel of Fig. 14). Appendix A discusses possible spectral broadening mechanisms that could reduce the amplitude of the emission peaks in observed spectra. We find that any reasonable instrumental broadening, or broadening by unresolved micro- and macroturbulent velocities with reasonable velocities (<10 km s-1) are insufficient to reduce the emission peaks from the NLTE FAL models enough to fully match the observed spectra, leaving as the only option a clear reduction of the chromospheric temperature (cf. Rezaei et al. 2008).
4.2. Difference between temperature stratifications in quiet Sun and active regions
Even if it is well known that the emission in the Ca ii H line core increases in the presence of (photospheric) magnetic fields (e.g. Simon & Leighton 1964; Linsky & Avrett 1970; Liu & Smith 1972; Dunn & Zirker 1973; Mattig & Kneer 1978; Schrijver et al. 1989; Rezaei et al. 2007), the difference between temperatures in QS and AR retrieved by the inversion is surprisingly large. The LTE approach used in the inversion retrieves temperature stratifications with a clear chromospheric rise in the AR, even though it supposedly underestimates the temperature. This underestimation comes with a caveat caused by a dichotomy in the (N)LTE problem. In the LTE assumption, (gas) temperature and intensity are directly coupled. When an increase in emission is not caused by an increase in the gas temperature but by NLTE effects on the emitted radiation field, the LTE inversion will still attribute it to a temperature change and will yield a gas temperature that is too high. When the emission is caused by an increase in the gas temperature, the LTE approach will yield a temperature that is too low, because it assumes that the corresponding energy will be evenly distributed over all degrees of freedom, whereas in NLTE a significant fraction can go into additional ionization or other energy sinks without increasing the emitted radiation.
For active regions, the temperature structure in the solar atmosphere seems to be more stable than in the QS. While umbral profiles, for example, show clear indications of upwards propagating wave patterns that produce shock waves in the chromosphere as they do in the QS (e.g. Lites 1986; Centeno et al. 2006; Felipe et al. 2010), Ca ii H spectra in umbrae never loose their emission peaks (Mattig & Kneer 1978; Kneer et al. 1981b,a; Rouppe van der Voort et al. 2003; Felipe et al. 2010), in contrast to QS profiles that oscillate between low or no emission and intensity reversals (e.g. Liu1974; Cram & Dame1983; Rezaei et al.2008; BE12). The strong variability in QS was also found in numerical simulations (CS97; Wedemeyer et al. 2004; Leenaarts et al. 2011), but the corresponding prediction for active regions or the interior of sunspots is still pending. Even if we cannot provide a conclusive proof, the results of our LTE inversion support a more stable gas temperature structure in active regions with a clear chromospheric temperature rise. This does not exclude that the line shape is caused by NLTE effects, but suggests that the underlying temperature stratification seems to be less influenced by temporal variations than in the QS.
The modulus of the difference between the QS and active regions, even in our LTE approach, indicates that heating processes related to strong magnetic fields are up to five times stronger than those related to acoustic waves in the QS: the spatial temperature rms in the AR is about five times larger than the spatial or temporal rms in the QS (Fig. 2) and the enhancement of the QS temperature stratification above the modified HSRA model (ΔT < 1000 K; Fig. 15) is roughly five times smaller than for the average plage (ΔT ~ 4000 K). Because in most of the studies of low chromospheric lines such as Ca ii H the presence of magnetic fields was neglected, their inclusion could be the turning point to reconcile the high variability of Ca ii H with the low variability of chromospheric lines observed by SUMER (Carlsson et al. 1997). We point out that these authors also found a permanent presence of emission in the SUMER lines in QS, in conflict to Ca ii H spectra in QS, but in full agreement with the behaviour of Ca ii H spectra in the umbra. This would fit with the assumption that the SUMER lines form in a magnetized atmosphere (like Ca ii H in the umbra) in QS, e.g. above a magnetic canopy with a strong damping of impinging acoustic oscillation, whereas Ca ii H forms below the canopy in QS (cf. Beck et al.2008; their Fig. 22). We note also that the same effect is suggested by the numerical simulations of FA12. The average temperature stratifications shown in their Fig. 6 do not exhibit a clear temperature reversal below a height of 1 Mm, and additionally show a strong increase in the temperature when the magnetic fill factor is increased by an order of magnitude, caused by the related reduction of the gas density in a partially evacuated magnetized plasma.
4.3. Energy content of bright grains and related energy flux
We estimated the energy content of the precursors of chromospheric bright grains. We find a spatial extent of about 1 Mm by 0.2 Mm in height, with an increase in the internal energy of about 45 J m-3 and a total energy of about 7 × 1018 J per event. The temperature enhancements propagate upwards with a speed of about 6 km s-1, comparable to the local sound speed (see also Worrall 2012). With the typical temporal cadence of 160 s for individual events, this yields a vertical energy flux of about 10 kW m-2 at a height of about 250 km. Some insecurity in this calculation arises from the characteristic cadence because it is sensitive to how local maxima are identified and counted. Our determination yields from 15 to 22 maxima in 3150 s, which gives roughly a 20% error in the energy flux. Our specific data is less suited for the determination of the occurrence rate of BGs than time series of intrinsically two-dimensional data. The number of about 10 kW m-2 falls in line with the energy fluxes between 3 to 12 kW m-2 at a height of about 250 km determined from velocity oscillations in, e.g. Bello González et al. (2009, 2010) or Malherbe et al. (2012; MA12). The latter authors also determined the total energy contained in what they call “acoustic events”, i.e. a phase of upwards directed energy transport that can cover a few wave trains and can last up to 10 min (cf. Fig. 9 of MA12). They found total energies of about 1.9 × 1019 J per acoustic event, which fits the example used in our Sect. 3.5 with three BGs of about 2.1 × 1019 J in total in 651 s.
Malherbe et al. (2012; MA12) found an occurence rate of acoustic events of about 5.7 × 10-16 s-1 m-2. With 20 temperature extrema in 3150 secs on each pixel of 0 3 × 0
3 × 0 5, and a spatial fill fraction of BGs of about 10 % along the slit, we obtain a rate of 8.3 × 10-15 s-1 m-2, or about 0.5 min-1 Mm-2, respectively. The difference between the two rates is about a factor of 15, where our rate should be larger by a factor of 3 to 5 because of the existence of multiple temperature maxima during an acoustic event as defined by MA12. The remaining difference could be caused by the lower spatial resolution of our data, where the area of BGs will be slightly overestimated because of the spatial smearing. The recently inaugurated 1.5-m GREGOR telescope (Schmidt et al. 2012) will offer the possibility to obtain high-resolution, high-cadence spectra of the Ca ii IR lines around 850 nm with the Gregor Fabry-Perót Interferometer (GFPI; e.g. Puschmann et al. 2012a,b,c) and of Ca ii H with the BLue Imaging Solar Spectrometer (BLISS; Puschmann et al. 2012c, 2013) in the near future.
5, and a spatial fill fraction of BGs of about 10 % along the slit, we obtain a rate of 8.3 × 10-15 s-1 m-2, or about 0.5 min-1 Mm-2, respectively. The difference between the two rates is about a factor of 15, where our rate should be larger by a factor of 3 to 5 because of the existence of multiple temperature maxima during an acoustic event as defined by MA12. The remaining difference could be caused by the lower spatial resolution of our data, where the area of BGs will be slightly overestimated because of the spatial smearing. The recently inaugurated 1.5-m GREGOR telescope (Schmidt et al. 2012) will offer the possibility to obtain high-resolution, high-cadence spectra of the Ca ii IR lines around 850 nm with the Gregor Fabry-Perót Interferometer (GFPI; e.g. Puschmann et al. 2012a,b,c) and of Ca ii H with the BLue Imaging Solar Spectrometer (BLISS; Puschmann et al. 2012c, 2013) in the near future.
 |
Fig. 16 Spatial temperature and velocity maps of the time series. Panel a) temporally averaged temperature ⟨ T ⟩ t vs. optical depth. Panel b) ⟨ T ⟩ t minus temporally and spatially averaged temperature stratification ⟨ T ⟩ vs. geometrical height. Panel c) temperature at one scan step minus ⟨ T ⟩ vs. geometrical height. The z-axis in the panels b) and c) is stretched by a factor of five relative to the x-axis. The black lines at the lower border of each panel denote the total circular polarisation along the slit in arbitrary units. The blue lines show one flux tube model of SO91. The orange/red/purple contours in panel b) mark temperature excesses of 50, 100 and 150 K, while in panel c) they denote temperature excesses of 100, 200 and 300 K. |
Photospheric energy fluxes in the range of a few kW m-2 would suffice to replenish the generic chromospheric energy requirement of 4 kW m-2, if – and only if – this amount of energy finally reached the chromosphere. The estimates of the energy losses with height, however, predict that less than 5% of an energy input at 250 km height reaches layers above 400 km. This suggests that the chromospheric radiative losses cannot be balanced by the energy of propagating waves or temperature perturbations despite a sufficiently large reservoir of mechanical energy in the photosphere (but see also Petrukhin et al. 2012). We note that the temperature stratifications and the rms temperature fluctuations retrieved by our inversion only predict on average a drastic loss of energy with height, but do not directly provide information about where the energy is going. To determine the exact fraction of the energy dissipated by radiation, thermal conduction, or changes of the ionization fraction requires a detailed study of individual events.
4.4. Visibility and extent of magnetic canopies in temperature maps
We have discussed the properties of chromospheric brightenings and the chromospheric thermal structure in the QS as a purely hydrodynamical phenomenon without considering the presence of magnetic fields. The simultaneous polarimetric observations of the 630 nm channel of POLIS, however, also provide information on polarisation signals, hence photospheric magnetic fields. We can thus investigate the influence of the magnetic topology on the thermal structure in the QS as well.
The typical behaviour of the Ca ii H line with its repeated change from reversal-free absorption to emission and vice versa in field-free regions, i.e. on locations that are polarisation-signal-free down to amplitudes of about 10-3 of Ic, and with a persistent stationary emission on locations with photospheric polarisation signal fits to the idea of magnetic field lines as a mediator between a stationary and transient emission pattern in Ca ii H. For photospheric magnetic flux concentrations, geometrical models can be constructed by setting field strength and total magnetic flux in the photosphere, and requiring (magneto-)hydrostatic pressure balance with their surroundings. This yields the classical expanding flux tubes whose diameter increases with height in the atmosphere (e.g. Solanki et al.1991; SO91). If the magnetic fields have a profound influence on the chromospheric temperature structure, they have to show up in the temperature stratifications retrieved by the inversion, regardless of the LTE – NLTE problem.
Figure 16 shows that this is clearly the case. Panel (a) shows the temporally averaged temperature stratifications along the slit vs. optical depth. The temporally averaged unsigned Stokes V signal is over-plotted as a black line as a reference of photospheric magnetic fields that were roughly persistent over the duration of the time series of about one hour. Already in the temporally averaged temperature, flux-tube-like features are found co-spatial to the largest values of | V |. To increase the visibility, and because the main effect of the magnetic fields is an increase in temperature relative to field-free surroundings, we subtracted the temporally and spatially averaged temperature stratification from the temporally averaged temperatures (panel b). In that case, temperature enhancements of +50, +100 and +150 K over the average temperature almost exclusively occur on locations of photospheric magnetic fields. For the two strong magnetic flux concentrations at x ~ 14.5 Mm and 35 Mm, the temperature enhancements at chromospheric layers above 500 km given by the +50 K contour form exactly the wine-glass shape predicted and used in many photospheric flux tube models (SO91; Pizzo et al. 1993; Gadun et al. 2001; Uitenbroek 2011; Khomenko & Collados 2012, their Fig. 10). In both cases, the temperature enhancements yield a nearly horizontal temperature canopy at a height of about 620 km that extends between 1 and 5 Mm horizontally away from the central axis (see also de la Cruz Rodríguez et al. 2013). The temperature enhancements delineate vertical structures at the end of the canopies.
The restricted horizontal extent of the temperature enhancements is better seen in panel (c) that shows the temperature stratifications for one step of the time series. Close to photospheric polarisation signals, the nearly horizontal canopies in temperature again appear prominently, especially from x ~ 6 to 16 Mm where three neighboring flux tubes create a continuous temperature canopy, but in-between separated flux tubes areas of several Mm extent with a strongly reduced temperature show up (x ~ 0−7 Mm, x ~ 23−33 Mm). In similar-sized areas, reversal-free Ca ii H spectra have already been found (Rezaei et al. 2008). In total, this implies that on the one hand magnetic canopies have a direct effect on the temperature stratification even in a single snapshot of the solar atmosphere, and on the other hand there are no clear indications for volume-filling magnetic fields in the formation height of Ca ii H in the temperature map of Fig. 16. The appearance changes a bit in the temperature map for the large-area scan at high layers (observation No. 1 of BE09, cf. Fig. 5).
Figure 16 clearly demonstrates that photospheric magnetic fields are a second acting agent for the chromospheric temperature structure in addition to the transient BGs. A more detailed study of the modification of the thermal structure at or close to the locations of photospheric magnetic fields is, however, beyond the scope of the present paper.
4.5. Applicability of LTE inversion
Because of the known problems of assuming LTE in an inversion of any chromospheric line, it might be worth noting a few examples where the LTE inversion still serves a purpose without any, or with only weak restrictions. We remark that primarily the modulus of the temperature derived from the LTE inversion has a high inaccuracy because of the missing instantaneous coupling between gas temperature and radiation field in NLTE conditions, and that the conversion from optical depth to geometrical height suffers from the lack of hydrostatical equilibrium. The second point could, however, be obtained post-facto with a presumably minor impact on the resulting synthetic spectra.
The detectability of canopies in temperature maps – that are implicitly assumed to correspond to the theoretically expected magnetic canopies – does depend only slightly on the modulus of temperature. Our results clearly show that the signature of the canopies can be detected in the surroundings of photospheric magnetic flux concentrations up to a few Mm (cf. Fig. 16). This is in contrast to the results of Judge et al. (2010) who found a strong confinement of intensity enhancements, and hence magnetic flux in the chromosphere. The mismatch of these two results shows that a quantitative in-depth analysis of spectra, even with the limiting LTE assumptions, is crucial for tracing the topology at chromospheric layers.
To estimate the energy of individual BGs, we used a height range, or equivalently, a wavelength region in the line wing, where NLTE effects can be assumed to play a minor role (z < 500 km). These results are thus rather robust and would presumably not change significantly when a different inversion method would be used. The advantage of the inversion of the Ca ii H spectra now is to provide on the one hand also a quantitative guess for the corresponding properties at the atmosphere layers above, which cannot be accessed by any photospheric line, and on the other hand to provide clear information on the temporal evolution, such as the vertical propagation speed (Fig. 13), or the exact propagation direction from combining horizontal motions in the 2D sections of the FOV (Fig. 9) with the vertical propagation speed.
5. Summary and conclusions
In an LTE inversion of Ca ii H spectra, we cannot retrieve an average chromospheric temperature rise in quiet Sun (QS) regions, whereas in active regions (ARs) we are able to. The difference between QS and ARs can be directly traced back to the observed input profiles themselves, independent of the LTE assumption in the inversion. We confirm the findings of BE12 of a layer at a height of about 150 km with an increased occurence of high-intensity, and hence high-temperature events near and in magnetic features. A comparison of line-core and line-wing images, and the correlation coefficient between intensities and temperature vs. optical depth suggests that the increased skewness of the intensity histograms on magnetic locations is caused by a direct signature of magnetic fields in temperature at two different atmosphere layers, i.e. both in the chromosphere and the mid photosphere. The magnetic network is inconspicuous at the layers in-between. The appearance of the network in the mid photosphere could be caused by the hot wall effect in combination with the shift of the optical depth scale inside magnetic fields (Spruit 1976), whereas the appearance in the chromosphere indicates an energy deposit instead.
The energy contained in the rms fluctuations of temperature and the large difference between QS and AR profiles and temperature stratifications indicate the importance of chromospheric heating processes related to the presence of magnetic fields. The physical processes that could yield this heating should be investigated in more detail in the future and included in the analysis of chromospheric lines. The temperature fluctuations in the QS fall short of the requirements needed to maintain a stationary chromospheric temperature rise.
The properties of individual (heating) events related to chromospheric bright grains (BGs) can be determined during all of their existence in the LTE inversion results, from the BG precursors in the photosphere to their culmination in the lower chromosphere. The mechanical energy content and the vertical energy flux in the photosphere would be sufficient to fulfill the generic chromospheric energy requirement of about 4 kW m-2, but only a fraction well below 5% of the mechanical energy reaches the chromosphere, falling far short of the generic requirement. The decrease in the internal energy density with height agrees with that expected for acoustic waves.
The topology of magnetic fields in the chromosphere is seemingly directly reflected in the temperature structure at layers above a height of 500 km also in an LTE analysis, as indicated by the appearance of canopy structures around magnetic field concentrations both in average and in instantaneous x − z temperature maps. With all of the shortcomings of the LTE approach, this quantitative analysis of large-scale data sets in a chromospheric spectral line provides a wealth of interesting features that can be used to address open questions in solar chromospheric physics of which this paper still has not covered all despite its extent.
Online material
Appendix A: Effects of spectral broadening
 |
Fig. A.1 Convolution of the FAL NLTE profiles with different spectral PSFs. Bottom: convolution of FAL-C with Gaussians of σ = 3.4 pm (blue line) and 9.4 pm (purple line). The black line shows the observed average QS profile. Left column: line wing. Right column: line core. Top: convolution of FAL-A with a wavelength-dependent Gaussian with σ between 3.4 and 9.4 pm. |
The effective spectral resolution of the POLIS spectrograph can lead to a loss in amplitude of the emission peaks by spectral smearing because of their small spectral extent. The default spectral resolution of POLIS is 220.000@400 nm (≡1.8 pm), but because of the on-chip binning by a factor of two, the resolution is sampling-limited to about 3.8 pm. Convolving an FTS (Kurucz et al. 1984) reference spectrum with the method of Allende Prieto et al. (2004) and Cabrera Solana et al. (2007) to match the observed average Ca profile yielded the need for a Gaussian with σ ~ 1.7 pm. We note that the FTS spectrum contains line broadening by macroturbulent velocities because of being a spatially averaged QS spectrum.
For an estimate of the maximal spectral smearing between the observed average QS profile and the FAL-C NLTE profile − synthesized without a macroturbulent velocity – by instrumental effects, we first convolved the FAL-C NLTE profile as reference by a Gaussian to match the shape and width of the line blends in the Ca line wing in the average observed spectrum. The lower-left panel of Fig. A.1 shows that this requires a value of σ of about 3.4 pm, which is in rough agreement with the prediction from the sampling limit. A convolution of the full spectrum with this value as an estimate of the instrumental and velocity broadening in the atmosphere reduces, however, the amplitude of the emission peaks of the FAL-C NLTE profile only slightly (lower-right panel of Fig. A.1). To force the emission peaks in the synthetic profile to a shape roughly resembling the observed profile requires a convolution of FAL-C with a Gaussian with σ = 9.4 pm. The line blends in the wing, however, clearly exclude such a large instrumental broadening because in the FAL-C NLTE profile convolved with σ = 9.4 pm (purple line) the blends are twice as broad and half as deep as in the observed spectrum (lower-left panel of Fig. A.1).
We then decided to try a wavelength-dependent width of the Gaussian used as spectral point spread function (PSF). The width
was set to 3.4 pm in the line wing up to λ = 396.75 nm, gradually increasing to 9.4 pm at λ = 396.85 nm, and reducing down to 3.4 pm again at λ = 396.94 nm. As it seemed impossible to match the FAL-C NLTE and the observed profile even with a large broadening in the very core, we applied this variable convolution to the FAL-A NLTE profile instead. The temperature stratification of FAL-A has a weaker chromospheric temperature rise than FAL-C (Fig. 15) and the corresponding NLTE profile differs significantly from FAL-C, especially in the residual line-core intensity (Fig. 14). The approach with the variable spectral PSF maintains the match in the line wing (upper-left panel of Fig. A.1) and leads to an acceptable agreement between the emission peaks of the convolved FAL-A NLTE profile and the observed spectrum (upper-right panel).
The wavelength-dependent Gaussian spectral PSF would correspond to a microturbulent velocity vmic that changes from 2.6 km s-1 in the photosphere to 7.1 km s-1 in the chromosphere. The NLTE synthesis already included a height-dependent microturbulent velocity of more than 5 km s-1 for log τ < −5.5. Thus, the effective microturbulent velocity necessary to match the averaged observed and the FAL-A NLTE profile should be nearly twice as large as the initial value of vmic, and has to be present already at lower layers of log τ ~ −3 to yield the correct shape of the H1V and H1R minima next to the emission peaks. We note that similar values of vmic would be also required to match the FTS atlas and the FAL-A NLTE profile, because the line shape in the FTS is similar to the average QS spectra shown here. Whether such a high value of vmic is reasonable for spectra at about 1′′ spatial resolution needs further investigation. Additionally, the increase in vmic at comparably low layers of log τ also already affects the Fe i line blend at 396.93 nm strongly, broadening it significantly beyond its width in observed spectra. Doubling vmic therefore seems not to be a valid option to match observed and theoretical NLTE profiles, leaving a reduction of temperature as the only option (cf. Rezaei et al. 2008).
Acknowledgments
The VTT is operated by the Kiepenheuer-Institut für Sonnenphysik (KIS) at the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias (IAC). The POLIS instrument has been a joint development of the High Altitude Observatory (Boulder, USA) and the KIS. C.B. acknowledges partial support by the Spanish Ministry of Science and Innovation through project AYA2010–18029 and JCI-2009-04504. R.R. acknowledges financial support by the DFG grant RE 3282/1-1. We thank H. Socas-Navarro and T. Carroll for helpful discussions.
References
- Allende Prieto, C., Asplund, M., & Fabiani Bendicho, P. 2004, A&A, 423, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asensio Ramos, A., Trujillo Bueno, J., Carlsson, M., & Cernicharo, J. 2003, ApJ, 588, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., Allen de Prieto, C., & Kiselman, D. 2004, A&A, 417, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Auer, L. H., & Mihalas, D. 1969, ApJ, 158, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Ayres, T. R. 1981, ApJ, 244, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Ayres, T. R. 2002, ApJ, 575, 1104 [NASA ADS] [CrossRef] [Google Scholar]
- Ayres, T. R., & Testerman, L. 1981, ApJ, 245, 1124 [NASA ADS] [CrossRef] [Google Scholar]
- Ayres, T. R., & Wiedemann, G. R. 1989, ApJ, 338, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Ayres, T. R., Plymate, C., & Keller, C. U. 2006, ApJS, 165, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, C. 2006, Ph.D. Thesis, Albert-Ludwigs-University, Freiburg, http://www.freidok.uni-freiburg.de/volltexte/2346/pdf/beck_christian_diss.pdf [Google Scholar]
- Beck, C. A. R., & Rammacher, W. 2010, A&A, 510, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C. A. R., & Rezaei, R. 2011, A&A, 531, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Schmidt, W., Kentischer, T., & Elmore, D. 2005, A&A, 437, 1159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Schmidt, W., Rezaei, R., & Rammacher, W. 2008, A&A, 479, 213 (BE08) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Khomenko, E., Rezaei, R., & Collados, M. 2009, A&A, 507, 453 (BE09) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Rezaei, R., & Puschmann, K. G. 2012, A&A, 544, A46 (BE12) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Rezaei, R., & Puschmann, K. G. 2013, A&A, 549, A24 (BE13) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beckers, J. M. 1968, Sol. Phys., 3, 367 [NASA ADS] [Google Scholar]
- Beeck, B., Collet, R., Steffen, M., et al. 2012, A&A, 539, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bello González, N., Flores Soriano, M., Kneer, F., & Okunev, O. 2009, A&A, 508, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bello González, N., Franz, M., Martínez Pillet, V., et al. 2010, ApJ, 723, L134 [NASA ADS] [CrossRef] [Google Scholar]
- Bellot Rubio, L., & Beck, C. 2005, ApJ, 626, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Bethge, C., Beck, C., Peter, H., & Lagg, A. 2012, A&A, 537, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabrera Solana, D., Bellot Rubio, L. R., Beck, C., & Del Toro Iniesta, J. C. 2007, A&A, 475, 1067 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlsson, M. 2007, in The Physics of Chromospheric Plasmas, eds. P. Heinzel, I. Dorotovič, & R. J. Rutten, ASP Conf. Ser., 368, 49 [Google Scholar]
- Carlsson, M., & Leenaarts, J. 2012, A&A, 539, A39 (CL12) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlsson, M., & Stein, R. F. 1992, ApJ, 397, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., & Stein, R. F. 1995, ApJ, 440, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., & Stein, R. F. 1997, ApJ, 481, 500 (CS97) [Google Scholar]
- Carlsson, M., Judge, P. G., & Wilhelm, K. 1997, ApJ, 486, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Centeno, R., Collados, M., & Trujillo Bueno, J. 2006, ApJ, 640, 1153 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cram, L. E. 1981, ApJ, 247, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Cram, L. E., & Dame, L. 1983, ApJ, 272, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Cuntz, M., Rammacher, W., & Musielak, Z. E. 2007, ApJ, 657, L57 [NASA ADS] [CrossRef] [Google Scholar]
- de la Cruz Rodríguez, J., De Pontieu, B., Carlsson, M., & Rouppe van der Voort, L. H. M. 2013, ApJ, 764, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Dunn, R. B., & Zirker, J. B. 1973, Sol. Phys., 33, 281 [NASA ADS] [Google Scholar]
- Fabbian, D., Khomenko, E., Moreno-Insertis, F., & Nordlund, Å. 2010, ApJ, 724, 1536 [NASA ADS] [CrossRef] [Google Scholar]
- Fawzy, D. E., Cuntz, M., & Rammacher, W. 2012, MNRAS, 426, 1916 (FA12) [NASA ADS] [CrossRef] [Google Scholar]
- Felipe, T., Khomenko, E., Collados, M., & Beck, C. 2010, ApJ, 722, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Felipe, T., Khomenko, E., & Collados, M. 2011, ApJ, 735, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Fontenla, J. M., Avrett, E. H., & Loeser, R. 1993, ApJ, 406, 319 (FAL93) [NASA ADS] [CrossRef] [Google Scholar]
- Fontenla, J. M., Avrett, E., Thuillier, G., & Harder, J. 2006, ApJ, 639, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Fontenla, J. M., Balasubramaniam, K. S., & Harder, J. 2007, in The Physics of Chromospheric Plasmas, eds. P. Heinzel, I. Dorotovič, & R. J. Rutten, ASP Conf. Ser., 368, 499 [Google Scholar]
- Gadun, A. S., Solanki, S. K., Sheminova, V. A., & Ploner, S. R. O. 2001, Sol. Phys., 203, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gingerich, O., Noyes, R. W., Kalkofen, W., & Cuny, Y. 1971, Sol. Phys., 18, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Giovanelli, R. G. 1980, Sol. Phys., 68, 49 [Google Scholar]
- Gömöry, P., Beck, C., Balthasar, H., et al. 2010, A&A, 511, A514 [Google Scholar]
- Henriques, V. M. J. 2012, A&A, 548, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holweger, H., & Müller, E. A. 1974, Sol. Phys., 39, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Holzreuter, R., & Solanki, S. K. 2012, A&A, 547, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Judge, P., Knölker, M., Schmidt, W., & Steiner, O. 2010, ApJ, 720, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Kalkofen, W. 2001, ApJ, 557, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Kalkofen, W. 2012, Sol. Phys., 276, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Kalkofen, W., Ulmschneider, P., & Avrett, E. H. 1999, ApJ, 521, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Kalkofen, W., Rossi, P., Bodo, G., & Massaglia, S. 2010, A&A, 520, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khomenko, E., & Collados, M. 2012, ApJ, 747, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Kneer, F., Mattig, W., Scharmer, G., et al. 1981a, Sol. Phys., 69, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Kneer, F., Mattig, W., & v. Uexkuell, M. 1981b, A&A, 102, 147 [NASA ADS] [Google Scholar]
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar flux atlas from 296 to 1300 nm (National Solar Observatory, Sunspot, NM) [Google Scholar]
- Leenaarts, J., Carlsson, M., Hansteen, V., & Rutten, R. J. 2007, A&A, 473, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leenaarts, J., Carlsson, M., Hansteen, V., & Rouppe van der Voort, L. 2009, ApJ, 694, L128 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., Carlsson, M., Hansteen, V., & Gudiksen, B. V. 2011, A&A, 530, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linsky, J. L., & Avrett, E. H. 1970, PASP, 82, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W. 1986, ApJ, 301, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, S.-Y. 1974, ApJ, 189, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, S.-Y., & Smith, E. V. P. 1972, Sol. Phys., 24, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Lockyer, J. N. 1868, Roy. Soc. London Proc. Ser. I, 17, 131 [Google Scholar]
- Malherbe, J.-M., Roudier, T., Rieutord, M., Berger, T., & Franck, Z. 2012, Sol. Phys., 278, 241 (MA12) [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Sykora, J., De Pontieu, B., & Hansteen, V. 2012, ApJ, 753, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Mattig, W., & Kneer, F. 1978, A&A, 65, 11 [NASA ADS] [Google Scholar]
- Nordlund, A. 1982, A&A, 107, 1 [NASA ADS] [Google Scholar]
- Nordlund, Å., & Stein, R. F. 1990, Comput. Phys. Comm., 59, 119 [Google Scholar]
- Nutto, C., Steiner, O., & Roth, M. 2012, A&A, 542, L30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrukhin, N. S., Pelinovsky, E. N., & Batsyna, E. K. 2012, Astron. Lett., 38, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Pizzo, V. J., MacGregor, K. B., & Kunasz, P. B. 1993, ApJ, 404, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Puschmann, K., Vázquez, M., Bonet, J. A., Ruiz Cobo, B., & Hanslmeier, A. 2003, A&A, 408, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puschmann, K. G., Ruiz Cobo, B., Vázquez, M., Bonet, J. A., & Hanslmeier, A. 2005, A&A, 441, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puschmann, K. G., Ruiz Cobo, B., & Martínez Pillet, V. 2010, ApJ, 720, 1417 [NASA ADS] [CrossRef] [Google Scholar]
- Puschmann, K., Denker, C., Kneer, F., et al. 2012a, AN, 333, 880 [Google Scholar]
- Puschmann, K. G., Balthasar, H., Bauer, S. M., et al. 2012b, in Magnetic fields from the photosphere to the corona, ed. T. R. Rimmele, A. Tritschler, F. Woeger, et al., ASP Conf. Ser., 463, 423 [Google Scholar]
- Puschmann, K. G., Balthasar, H., Beck, C., et al. 2012c, in Ground-based and Airborne Instrumentation for Astronomy IV, ed. I. S. MacLean, S.K. Ramsay, & H. Takami, SPIE Conf. Ser., 8446, 79 [Google Scholar]
- Puschmann, K. G., Denker, C., Balthasar, H., et al. 2013, Opt. Eng. 52, in press, Doi: 10.1117/1.OE.52.8.081606 [arXiv:1302.7157] [Google Scholar]
- Rammacher, W., & Cuntz, M. 1991, A&A, 250, 212 [NASA ADS] [Google Scholar]
- Rammacher, W., & Cuntz, M. 2005, A&A, 438, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rammacher, W., & Ulmschneider, P. 1992, A&A, 253, 586 [NASA ADS] [Google Scholar]
- Rezaei, R., Schlichenmaier, R., Beck, C. A. R., Bruls, J. H. M. J., & Schmidt, W. 2007, A&A, 466, 1131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rezaei, R., Bruls, J. H. M. J., Schmidt, W., et al. 2008, A&A, 484, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rouppe van der Voort, L. H. M., Rutten, R. J., Sütterlin, P., Sloover, P. J., & Krijger, J. M. 2003, A&A, 403, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rutten, R. J. 2003, Radiative Transfer in Stellar Atmospheres, Sterrekundig Instituut Utrecht [Google Scholar]
- Rutten, R. J. 2012, Roy. Soc. London Phil. Trans. Ser. A, 370, 3129 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. J., & Uitenbroek, H. 1991, Sol. Phys., 134, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. J., & Uitenbroek, H. 2012, A&A, 540, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaffenberger, W., Wedemeyer-Böhm, S., Steiner, O., & Freytag, B. 2006, in Solar MHD Theory and Observations: A High Spatial Resolution Perspective, eds. J. Leibacher, R. F. Stein, & H. Uitenbroek, ASP Conf. Ser., 354, 345 [Google Scholar]
- Schmidt, W., von der Lühe, O., Volkmer, R., et al. 2012, AN, 333, 796 [Google Scholar]
- Schrijver, C. J., Cote, J., Zwaan, C., & Saar, S. H. 1989, ApJ, 337, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Secchi, A. 1860, Astron. Nachr., 54, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Sheminova, V. A. 2012, Sol. Phys., 280, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Sheminova, V. A., Rutten, R. J., & Rouppevan der Voort, L. H. M. 2005, A&A, 437, 1069 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, G. W., & Leighton, R. B. 1964, ApJ, 140, 1120 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., Steiner, O., & Uitenbroek, H. 1991, A&A, 250, 220 (SO91) [NASA ADS] [Google Scholar]
- Spruit, H. C. 1976, Sol. Phys., 50, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Stangalini, M., & Moretti, P. F. 2012, Mem. Soc. Astron. It. Suppl., 19, 121 [Google Scholar]
- Stein, R. F., & Nordlund, A. 1998, ApJ, 499, 914 [Google Scholar]
- Steiner, O., Pneuman, G. W., & Stenflo, J. O. 1986, A&A, 170, 126 [NASA ADS] [Google Scholar]
- Steiner, O., Grossmann-Doerth, U., Knoelker, M., & Schuessler, M. 1998, ApJ, 495, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, O., Rezaei, R., Schaffenberger, W., & Wedemeyer-Böhm, S. 2008, ApJ, 680, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Štěpán, J., & Trujillo Bueno, J. 2010, ApJ, 711, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Straus, T., Fleck, B., Jefferies, S. M., et al. 2008, ApJ, 681, L125 (ST08) [Google Scholar]
- Tritschler, A., Schmidt, W., Uitenbroek, H., & Wedemeyer-Böhm, S. 2007, A&A, 462, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Uitenbroek, H. 2000, ApJ, 536, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Uitenbroek, H. 2001, ApJ, 557, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Uitenbroek, H. 2011, in Solar Polarization 6, eds. J. R. Kuhn, D. M. Harrington, H. Lin, et al., ASP Conf. Ser., 437, 439 [Google Scholar]
- Uitenbroek, H., & Criscuoli, S. 2011, ApJ, 736, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Ulmschneider, R., Schmitz, F., Kalkofen, W., & Bohn, H. U. 1978, A&A, 70, 487 [NASA ADS] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1976, ApJS, 30, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 (VAL81) [NASA ADS] [CrossRef] [Google Scholar]
- von der Lühe, O., Soltau, D., Berkefeld, T., & Schelenz, T. 2003, in Innovative Telescopes and Instrumentation for Solar Astrophysics, eds. S. L. Keil, & S. V. Avakyan, SPIE Conf. Ser., 4853, 187 [Google Scholar]
- von Uexküll, M., & Kneer, F. 1995, A&A, 294, 252 [NASA ADS] [Google Scholar]
- von Uexküll, M., Kneer, F., & Mattig, W. 1983, A&A, 123, 263 [NASA ADS] [Google Scholar]
- Wedemeyer, S., Freytag, B., Steffen, M., Ludwig, H.-G., & Holweger, H. 2004, A&A, 414, 1121 (WE04) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S., & Carlsson, M. 2011, A&A, 528, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wöger, F. 2007, Ph.D. Thesis, Albert-Ludwigs-University, Freiburg, http://www.freidok.uni-freiburg.de/volltexte/2933/ [Google Scholar]
- Wöger, F., Wedemeyer-Böhm, S., Schmidt, W., & von der Lühe, O. 2006, A&A, 459, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Worrall, G. 2012, Sol. Phys., 279, 43 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Relative occurrence of temperatures in the QS. Top left: temperature vs. optical depth for the full FOV. The relative occurrence of a given temperature is indicated by the colour with the corresponding colour bar at top. Thick black line: original HSRA model. Dashed line: average temperature. The vertical dashed lines denote the layers of log τ for which the temperature histograms are shown in the rest of the panels. In the histograms, black/blue/red lines denote the full FOV/magnetic/field-free locations. |
| In the text | |
 |
Fig. 2 Bottom panel: rms fluctuations of temperature for the full FOV (black line), field-free locations (red line), and magnetic locations (blue line). The three dotted lines indicate the maximum deviation from the average temperature. The dashed line denotes the rms fluctuation in an AR map. Top panel: skewness of the temperature distributions. The vertical dotted line indicates z = 150 km. |
| In the text | |
 |
Fig. 3 Relative occurrence of temperatures in an AR. Dash-dotted line: average temperature in the AR. Dotted line: average temperature in QS. Thick black line: original HSRA model. |
| In the text | |
 |
Fig. 4 Correlation coefficient between intensity at a given wavelength I(λ) and temperature T(log τ). |
| In the text | |
 |
Fig. 5 Comparison of line-core intensity (lower left) and temperature at log τ = −0.9 (lower right), − 2.5 (upper left), and − 5.4 (upper right). The correlation coefficient between Icore and T(τ) is denoted at the bottom of the temperature panels. |
| In the text | |
 |
Fig. 6 Variation of energy density with height. Top: energy density equivalents corresponding to velocity (red line with pluses), intensity (purple-dash-dotted line), and temperature rms fluctuations (black-solid line). The black-dashed line shows results for the temperature rms fluctuations when using the gas density in the original HSRA model. The blue line indicates the gas density in the modified HSRA model. Middle: energy gradient per km in height assuming a propagation with vac. The red line shows results from using a net cooling rate of 100 W g-1 (CL12). Bottom: radiative losses in the units used in CL12. |
| In the text | |
 |
Fig. 7 Residual of an energy input of 100 % at a height of 240 km (black-solid line). Top: linear scale. Bottom: logarithmic scale. The red pluses and blue diamonds give the corresponding values of FA12 for a high (case a) and low (case b) magnetic fill factor. The green asterisks give the values of ST08 for acoustic waves (case a), the orange triangles those of gravity waves (case b). The purple squares were taken from Felipe et al. (2011) and pertain to magneto-acoustic waves in a sunspot umbra. |
| In the text | |
 |
Fig. 8 Temporal occurrence frequency of BG events. Top: temporal evolution of temperature at log τ = −3.6 for one pixel along the slit. The red-dash-dotted line shows the intensity at λ = 396.83 nm in arbitrary units for comparison. The vertical dashed lines indicate local maxima. Middle: temporal average of number of maxima along the slit. The red-dash-dotted line shows the unsigned integrated Stokes V signal in arbitrary units. Bottom: average number of local maxima during 3150 s as a function of log τ. |
| In the text | |
 |
Fig. 9 Temporal evolution of the H2V intensity in a 2D FOV. The white vertical lines denote the area of one scan of about 1.5 Mm extent in x taken in about 21 s each. The short white bar at (x,y) ≈ (11,6) Mm indicates a length of 1 Mm. |
| In the text | |
 |
Fig. 10 Estimate of the energy content of individual BG events. Top panel: temperature enhancements (left column) and internal energy enhancements (right column) for a pixel with BG activity (bottom row) and a quiet reference pixel (top row). Bottom panel: average internal energy density for the active (black line) and the quiet pixel (red line) vs. geometrical height. The blue line shows their difference. |
| In the text | |
 |
Fig. 11 Spatio-temporal occurrence of temperature maxima. Bottom row, left to right: intensity maps at λ = 396.724, 396.822, and 396.851 nm. The horizontal white/black bars mark the locations of the active/reference pixel used before. Middle row, left to right: energy density at heights of log τ = −1.6, −3.3, and − 4.6 at the time of temperature maxima. Top: complementary map of energy density on all other locations. |
| In the text | |
 |
Fig. 12 Temperature stratifications vs. geometrical height at the onset of two BGs corresponding to the vertical white-dotted lines in the top panel of Fig. 10. The horizontal dotted lines denote the FWHM of the BG events. The blue line shows a sine curve with a wavelength of 400 km for comparison. |
| In the text | |
 |
Fig. 13 Vertical propagation speed of temperature perturbations. The background image shows the temperature variation of the active pixel of Fig. 10 vs. geometrical height. The three dotted lines trace the propagation of the perturbations with time. |
| In the text | |
 |
Fig. 14 Comparison of average observed and best-fit profiles with theoretical NLTE profiles. Bottom panel: spectra from a time series in the QS on disc centre. Top panel: spectra from an AR map off centre. Thick black line: average observed QS profile. Thin purple line: average best-fit QS profile. Blue line: LTE profile of modified HSRA. Red/orange lines: NLTE FAL-C/A profile. For the AR, average profiles of a plage area (blue-dotted line) and an umbra are over-plotted (orange-dash-dotted line). The vertical dotted line denotes the wavelength of intensity normalization. |
| In the text | |
 |
Fig. 15 Comparison of temperature stratifications. Bottom: QS maps. Top: one of the AR maps. Thick black line: average QS temperature in the LTE fit. Blue line: modified HSRA model. Dashed line: original HSRA model. Red line: FAL-C. Orange line: FAL-A. For the AR, the average temperature stratification of a plage area (blue-dotted line) and of the umbra are over-plotted (orange-dash-dotted line). |
| In the text | |
 |
Fig. 16 Spatial temperature and velocity maps of the time series. Panel a) temporally averaged temperature ⟨ T ⟩ t vs. optical depth. Panel b) ⟨ T ⟩ t minus temporally and spatially averaged temperature stratification ⟨ T ⟩ vs. geometrical height. Panel c) temperature at one scan step minus ⟨ T ⟩ vs. geometrical height. The z-axis in the panels b) and c) is stretched by a factor of five relative to the x-axis. The black lines at the lower border of each panel denote the total circular polarisation along the slit in arbitrary units. The blue lines show one flux tube model of SO91. The orange/red/purple contours in panel b) mark temperature excesses of 50, 100 and 150 K, while in panel c) they denote temperature excesses of 100, 200 and 300 K. |
| In the text | |
 |
Fig. A.1 Convolution of the FAL NLTE profiles with different spectral PSFs. Bottom: convolution of FAL-C with Gaussians of σ = 3.4 pm (blue line) and 9.4 pm (purple line). The black line shows the observed average QS profile. Left column: line wing. Right column: line core. Top: convolution of FAL-A with a wavelength-dependent Gaussian with σ between 3.4 and 9.4 pm. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


