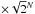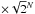| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 39 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201220374 | |
| Published online | 04 March 2013 | |
Mosaiced wide-field VLBI observations of the Lockman Hole/XMM⋆
1
Astronomisches Institut, Ruhr-Universität Bochum, Universitätsstr.
150,
44801
Bochum,
Germany
e-mail:
middelberg@astro.rub.de
2
ASTRON, Dwingeloo, The Netherlands
3
Australia Telescope National Facility, PO Box 76,
Epping
NSW
1710,
Australia
4
Max-Planck-Institut für Plasmaphysik, Boltzmannstrasse 2, 85478
Garching,
Germany
5
Max-Planck-Institut für Extraterrestrische Physik,
Giessenbachstrasse,
Garching,
Germany
6
Excellence Cluster “Universe”, Boltzmannstr. 2, 85748
Garching,
Germany
7
Curtin University of Technology, GPO BOX U1987, Perth, WA
6845,
Australia
8
National Radio Astronomy Observatory, PO Box 0, Socorro, NM
87801,
USA
9
Department of Physics, Durham University,
South Road, Durham, DH1
3LE, UK
Received:
12
September
2012
Accepted:
13
December
2012
Active galactic nuclei (AGN) play a decisive role in galaxy evolution, particularly so when they launch powerful jets, which reshape their surroundings. However, identifying them is difficult, since radio observations typically have a resolution between 1 arcsec and 10 arcsec, which is equally sensitive to radio emission from star-forming activity and from AGN. Very Long Baseline Interferometry (VLBI) observations allow only the most compact non-thermal emission to be filtered from radio survey data. The observational and computational demands to do this in large surveys have, until recently, been too high to make this practical. Only the recent advent of wide-field observing techniques have enabled such observations, and we here present the results of a survey of 217 radio sources in the Lockman Hole/XMM field. We describe in detail some new aspects of the calibration, including primary beam correction, multi-source self-calibration, and mosaicing. We detected 65 out of the 217 radio sources and were able to construct, for the first time, the source counts of VLBI-detected AGN. The source counts indicate that at least 15–25% of the sub-mJy radio sources are AGN-driven, consistent with recent findings using other AGN selection techniques. We have used optical, infrared and X-ray data to enhance our data set and to investigate the AGN hosts. We find that among the sources nearby enough to be resolved in the optical images, 88% (23/26) could be classified as early-type or bulge-dominated galaxies. While 50% of these sources are correctly represented by the SED of an early-type galaxy, the best fit for the remainder was obtained with a heavily extinct starburst template. However, this is due to a degeneracy in the fit, as such extinction in the templates is mimicking early-type objects. Our data suggest that the hosts of VLBI-detected sources are typically early-type or bulge-dominated galaxies.
Key words: techniques: interferometric / galaxies: active / galaxies: evolution
Tables 6, 7, and Figs. 21–24 are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
It has recently become clear that the formation and evolution of galaxies is significantly influenced by the presence of active galactic nuclei (AGN). The large amounts of radiation produced by AGN can heat the interstellar gas in galaxies so that star formation is slowed down (e.g., Di Matteo et al. 2005), but the ejecta from AGN can also compress interstellar gas and trigger star formation (e.g., Gaibler et al. 2012). It is therefore important to determine if an AGN is present or not, but this is a difficult undertaking. Unambiguous identifications of AGN are difficult to make, since the AGN can be shielded from our view at most wavelengths, and so a non-detection does not imply that an AGN is not present.
An exception is the radio regime. Even the most dust-rich galaxies are transparent at GHz frequencies, and so sensitive radio surveys of large portions of the sky have become an indispensable ingredient in the melting pot of contemporary extragalactic surveys. They provide information about thermal and non-thermal emission and kpc-scale morphology, and so yield clues about the stellar and accretion activity in galaxies. However, most galactic nuclei are unresolved at arcsec resolution, and so compact interferometer surveys have insufficient angular resolution to determine the emission process.
Fortunately, the Very Long Baseline Interferometry (VLBI) technique provides milli-arcsecond-scale resolution, so a detection implies that the emission comes from a very small volume, which in turn implies that the brightness temperatures of these regions must be high (of order 106 K). Such brightness temperatures generally can only be reached by AGN or extremely bright supernovae (Kewley et al. 2000), but at redshifts 0.1 the luminosity required for a detection can only be achieved by an AGN. In nearby objects, non-thermal sources such as supernova remnants can be bright enough for VLBI studies.
But VLBI observations traditionally target single, carefully selected objects, because of the computational challenges inherent in imaging larger fields (Garrett et al. 2005; Lenc et al. 2008), and because objects that provide detectable high brightness temperatures are sparsely distributed on the sky. Recent technical progress, however, has made it feasible to carry out the required calculations to image larger fields (Deller et al. 2007, 2011), and have facilitated bandwidth upgrades resulting in substantial sensitivity improvements. Therefore imaging wide fields with VLBI techniques has become feasible, and first exploratory projects have proven to be successful (Middelberg et al. 2011a; Morgan et al. 2011). VLBI observers finally have the chance to carry out surveys of large portions of the sky.
However, such experiments fell short of matching typical wide, deep radio surveys because they only used single pointings and required sources with substantial flux density in their fields to enable self-calibration of the data, required to reach the full sensitivity of the observations. We therefore embarked on a project to test the feasibility of surveying fields that are larger than a single pointing and that do not contain suitable in-beam calibrators. The Very Long Baseline Array (VLBA) was the instrument of choice, since it has equal antennas, which simplifies the calibration, and the antennas are small (25 m), which results in comparatively large primary fields of view.
This paper is structured as follows. Section 1.1 describes the selection of the target field; Sect. 2 describes the observations and Sect. 3 the calibration of the data, including several new aspects required in wide-field VLBI observations. Section 4 presents the imaging and image analysis and Sect. 5 contains an analysis of the results, detailing the fraction of detected sources, radio source counts, and properties of the host galaxies. Section 6 summarises these results, and Appendix A contains catalogues, contour plots and RGB images of the detected sources.
1.1. Field selection
Even though this project aimed at further developing VLBI survey techniques, care was taken to ensure an adequate interpretation of the results. Hence, to maximise the output of this project a field was selected based on (i) visibility; (ii) coverage at other wavelengths; and (iii) availability of calibrators, inside and outside the field (here a calibrator source is defined as any source with an arcsec-scale flux density of tens of mJy, as there is no available information as to whether that source would be sufficiently compact for VLBI observations). The candidates along with a few of their characteristics are shown in Table 1, ranked in descending order of suitability. The COSMOS area is quite far away from a listed source suitable for external calibration and there is no sufficiently strong source in the field; ATLAS/CDFS is very far south; Subaru/XMM is far south and has relatively shallow arcsec-resolution coverage; Lockman Hole/North does not have good coverage at other wavelengths and was deliberately chosen to avoid strong sources (i.e., potential calibrators); and the ELAIS fields have too shallow arcsec-resolution coverage.
Candidate field parameters.
Therefore the Lockman Hole/XMM field was targeted, at declination +57°. An overview of the radio observations is shown in Fig. 1. Complementary data include Giant Metrewave Radio Telescope 610 MHz data, providing spectral indices (or limits) for all sources; deep Spitzer/SWIRE data (Lonsdale et al. 2003); deep XMM-Newton data (Brunner et al. 2008); and optical coverage with the Large Binocular Telescope and the Subaru telescope (Barris et al. 2004; Rovilos et al. 2009; Fotopoulou et al. 2012). Furthermore, very deep 3.6 μm and 4.5 μm data from the Spitzer/SERVS mission (Mauduit et al. 2012), and very deep 250–500 μm data from the HERMES project will be available soon. These data are crucial for selecting galaxies with matching properties and to disentangle the contributions of AGN to the bolometric luminosity.
Only sources with integrated flux densities of more than 100 μJy were targeted in our observations, because it was expected that the noise in the combined VLBA images would reach around 20 μJy beam-1. Of the input sample, 496 sources met this criterion and were located within 20 arcmin of any of the pointing centres. However, after calibration only 217 were found to be potentially detectable, having VLA flux densities greater than 6 times the local noise level (see Sect. 5 for details). An overview of the 3 VLBA pointings, along with the location of target sources, is shown in Fig. 1, and a histogram of the source flux densities is shown in Fig. 2.
 |
Fig. 1 Overview of the Lockman Hole/XMM observations. Shown is the Spitzer 3.6 μm image as colour scale in the background. The three circles denote the FWHM of the VLBA antennas’ primary beams. The pointing coordinates have been taken from the VLA observations of this field reported in Ibar et al. (2009). It is also indicated which pointings have been observed in epochs A to D. Crosses indicate radio sources from Ibar et al. (2009) with a flux density of 100 μJy or more, and located within 20 arcmin of a pointing centre. |
2. Observations
The observations for this project were carried out with the VLBA at 1.382 GHz on 3 June
(epoch A), 4 July (epoch B), 16 July (epoch C) and 3 September (epoch D) of 2010. A
recording bit-rate of 512 Mbps was used, resulting in a bandwidth of 64 MHz in two
parallel-hand polarisations, yielding a nominal sensitivity of around
24 μJy beam-1 towards the pointing centre. The fringe-finder
4C 39.25 was observed every 2.5 h for data consistency checks, and the fields were observed
for 4.5 min, followed by a 1 min observation of the phase-referencing source
NVSS J105837+562811. The elapsed time of the observations was 12 h per epoch, resulting in a
total on-source time of around 326 baseline-hours per epoch. The VLBA observational status
summary1 predicts a baseline sensitivity of 3.3 mJy
in a 2 min observations with a recording rate of 256 Mbit, scaling to an image sensitivity
of 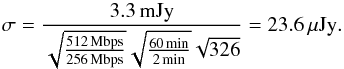 (1)A pre-production
version of VLBA-DiFX was used to correlate the data, using the new multi-field-centre mode.
A memory leak in an associated program (difx2fits, which converts the data from the internal
DiFX format to FITS-IDI) caused the loss of the first half of the data of the epoch A
observations, which was overwritten with the second half. This was only discovered after the
raw data had already been deleted, and a recorrelation was not possible. A reobservation of
epoch A was requested and granted (epoch D), so that one of the three pointings in the
Lockman Hole/XMM region now has deeper coverage than the other two. Correlation of the data
resulted in approximately 320 data sets per epoch, each with a spectral resolution of
500 kHz and 4 s integrations. Since the field of view of each data set is centred on the
known position of a VLA-detected source, the area to be imaged is relatively small, and
bandwidth and time smearing are not an issue (see Morgan et
al. 2011 for a detailed description of these effects). The data volume was around
1 GB per source, per epoch.
(1)A pre-production
version of VLBA-DiFX was used to correlate the data, using the new multi-field-centre mode.
A memory leak in an associated program (difx2fits, which converts the data from the internal
DiFX format to FITS-IDI) caused the loss of the first half of the data of the epoch A
observations, which was overwritten with the second half. This was only discovered after the
raw data had already been deleted, and a recorrelation was not possible. A reobservation of
epoch A was requested and granted (epoch D), so that one of the three pointings in the
Lockman Hole/XMM region now has deeper coverage than the other two. Correlation of the data
resulted in approximately 320 data sets per epoch, each with a spectral resolution of
500 kHz and 4 s integrations. Since the field of view of each data set is centred on the
known position of a VLA-detected source, the area to be imaged is relatively small, and
bandwidth and time smearing are not an issue (see Morgan et
al. 2011 for a detailed description of these effects). The data volume was around
1 GB per source, per epoch.
 |
Fig. 2 Distribution of VLA source flux densities in bins with edges at
100 μJy |
 |
Fig. 3 Contour plot of the radio source L0412 before (left) and after (right) multi-source self-calibration has been applied. Contours are drawn at 0.1 mJy × (1, 2, 4, ...). The S/N was improved from 72 to 115. The peak flux density has increased significantly, the noise has dropped, and image artefacts are much reduced. At low elevation, or when calibration is poorer, these effects will be more pronounced. |
3. Calibration
3.1. Standard steps
The calibration followed standard procedures used in phase-referenced VLBI observations, using the Astronomical Image Processing System (AIPS)2 with its Python interface, ParselTongue3 (Kettenis et al. 2006). Amplitude calibration was carried out using Tsys measurements and known gain curves. Fringe-fitting was carried out on the phase calibrator directly, to compensate for residual delays, without fringe-fitting the fringe finder (4C39.25) first, as would normally be done (a bug in the VLBA electronics causes unpredictable delay jumps in observations using a recording rate of 512 Mbps and 8 MHz IFs, and fringe finder observations are too infrequent to keep track of these jumps). However, the phase calibrator was bright enough to be detected separately in each IF channel during the 1 min scans, and so there was no need to use the fringe finder.
3.2. Multi-field self-calibration
After fringe fitting the delay and phase corrections were copied to the individual data files. In phase-referenced observations such as ours the signal-to-noise ratio (S/N) typically is limited by ionospheric and atmospheric turbulence between calibrator scans, and therefore purely phase-referenced images have reduced coherence. When the target is sufficiently strong, self-calibration can be used to improve coherence, but here the targets were too faint. However, the combined flux density of the strongest few targets would be sufficient to carry out phase self-calibration. This has already been pointed out by Garrett et al. (2004), but had never been demonstrated in practice. We describe here a simple procedure that implements multi-field self-calibration:
-
Phase-referenced images were made of all targets, and the imageswere searched for emission. Typically around30 sources were found with an S/N of more than 7,with the brightest reaching an S/N of almost 100. The data are latercombined using weights that are proportional to the square of theS/N. Hence a source with S/N = 10 contributes only 1/100 of the combined signal compared to a source with S/N = 100. Therefore only the brightest 10 sources or so were used in the following steps.
-
The individual data sets were divided by the CLEAN model obtained during imaging. This results in data sets each showing a 1 Jy point source in the field centre. It is worth noting that in this process the data weights are modified by the inverse square of the amplitude adjustment, and so this procedure conveniently takes care of proper weighting when the data are combined.
-
The source coordinates in the data set headers were set to the same value. Subsequently, the data were concatenated into a single data set. For each baseline, time, and frequency the combined data now contains multiple measurements of a point source.
-
Self-calibration was used with a 1 Jy point source model to improve the coherence of the combined data set. The phase corrections derived in this process were then copied to all original data sets, and improved images could be made.
The improvement attainable with this technique is illustrated in Fig. 3.
3.3. Mosaicing
After multi-field self-calibration, the calibration of each individual epoch was considered to be complete, and the data from the various epochs were combined to reach maximum sensitivity. Two effects needed to be calibrated before combining the data: a potential systematic astrometric offset, and the primary beam attenuation.
Astrometric offsets between the epochs arise from a number of effects. First, unmodelled propagation delays (e.g., due to tropospheric water vapour, or the ionosphere) will vary between epochs and lead to a different residual phase error at the target field. Second, any component of these unmodelled propagation effects that is constant over long timescales will introduce further errors that differ between epochs, since the separation between phase calibrator and target field changes between epochs. And third, the in-beam calibrators will all have modelled positions and structure that differ from their true properties due to the limited S/N during the initial image reconstruction and differential phase calibration effects across the target field. The necessary use of different sets of in-beam calibrators for multi-source selfcal in the different pointings will also introduce small errors between the epochs.
To measure and calibrate a potential systematic offset, we selected from epoch B a set of 18 sources that were also found in epochs A/D and C (but not all sources were present in all data epochs). These sources were imaged after multi-field self-calibration and the images were searched for the brightest pixels. The position differences relative to epoch B were calculated and the median used as the best approximation of a systematic offset between epochs A/C/D and B. The median offsets were found to be less than 1 mas in all cases, while the resolution of the images was around 10 mas × 8 mas. Correction of the offsets before the data were combined resulted in an increase of the peak flux densities of the calibrator sources of around 1%, compared to a trial run in which the data were combined without offset correction. The mean offsets of epochs A/C/D relative to B before and after correction are listed in Table 2.
Average position offsets relative to epoch B before and after position correction.
3.4. Primary beam corrections
The primary beam correction scheme used here has been described in detail in Middelberg et al. (2011a), who noted that the accuracy of the scheme was unknown, and they estimated its errors to be of the order of 10%. We present here the results of an experiment to improve the quality of the corrections and to assess their accuracy.
On 21 September 2011, a pattern of pointing positions around 3C 84 was observed with the VLBA at 1.382 GHz to measure the primary beam response of the antennas. The frequency setup was identical to the VLBA observations of the CDFS by Middelberg et al. (2011a) and the Lockman Hole/XMM.
 |
Fig. 4 Locations of the antenna pointing positions used to test the primary beam attenuation of the VLBA antennas, shown on top of an NVSS postage stamp. 3C 84, in the image centre, has always been used as the field centre in the correlation, so that it was seen by the antennas through the various parts of the primary beam power pattern, the FWHM of which is indicated by the circle. |
The pattern of pointings used for this experiment is shown in Fig. 4. The antennas were pointed towards each position for 1 min, except for the central pointing, which was observed five times for 1.5 min for amplitude reference. Correlation was performed using the true position of 3C 84 for all pointings, hence the amplitudes were only affected by primary beam effects. Initial amplitude calibration was carried out using Tsys measurements and known antenna gain curves. Fringe-fitting using the data from all pointings was used to correct phase and delay errors. The data from the central 1.5 min scan of 3C 84 was then imaged to obtain an approximate Stokes I model for further calibration. Amplitude self-calibration was subsequently carried out using this model to correct for residual amplitude variations and in particular to remove amplitude differences between RCP and LCP (assuming 3C 84 is circularly unpolarised at frequencies below 15 GHz, Homan & Wardle 2004). These corrections were then applied to the data from all pointing positions, so that amplitude variations should exclusively be caused by primary beam attenuation. Images were then made of all pointings and the flux densities of the brightest image pixels were extracted. Note that for an image of the pointing centred on the true position of 3C 84 only the centre scan was used to eliminate effects arising from a better (u,v) coverage for this pointing.
The uncorrected peak flux densities are shown in Fig. 5 as a function of distance to the 3C 84 position. Two models have been used to
reproduce these measurements: a Gaussian and an Airy disk. A Gaussian is a good
approximation to the inner portion of an antenna’s power pattern, and is conveniently
described by a single parameter: the full width at half maximum (FWHM). However, it does a
poor job near and beyond the first null of the antenna power pattern, and increasingly
deviates from this simple model. A relatively obvious starting point for an improved model
is the Airy disk, which essentially is a Bessel function. To first order an antenna can be
treated as a uniformly illuminated disk, the Fraunhofer diffraction pattern of which is
given by 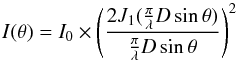 (2)where
J1(x) is the Bessel function of order one,
λ is the observing wavelength, D is the diameter of
the aperture, and θ is the direction in which the intensity is to be
calculated. Since only deviations from the on-axis sensitivity are to be calculated,
I0 can be set to one and ignored. Both the Gaussian and the
Airy disk model have been fitted to the data; in the case of the Gaussian the FWHM has
been allowed to vary and in the case of the Airy disk model the antenna diameter was
allowed to vary (and the wavelength was kept constant). Since the antenna feed horns may
illuminate a solid angle smaller or larger than that of the dish, the effective dish
diameter can differ slightly from the geometric aperture. It therefore is more appropriate
to solve for the effective dish diameter rather than for the observing wavelength. For the
observations presented here the centre observing wavelength was
λ = 0.21685 m.
(2)where
J1(x) is the Bessel function of order one,
λ is the observing wavelength, D is the diameter of
the aperture, and θ is the direction in which the intensity is to be
calculated. Since only deviations from the on-axis sensitivity are to be calculated,
I0 can be set to one and ignored. Both the Gaussian and the
Airy disk model have been fitted to the data; in the case of the Gaussian the FWHM has
been allowed to vary and in the case of the Airy disk model the antenna diameter was
allowed to vary (and the wavelength was kept constant). Since the antenna feed horns may
illuminate a solid angle smaller or larger than that of the dish, the effective dish
diameter can differ slightly from the geometric aperture. It therefore is more appropriate
to solve for the effective dish diameter rather than for the observing wavelength. For the
observations presented here the centre observing wavelength was
λ = 0.21685 m.
The best-fitting FWHM of the Gaussian model was found to be 29.13 arcmin, and the best-fitting antenna diameter for the Airy disk model was found to be D = 25.47 m. The antenna diameter is slightly larger than the geometric aperture, and this effect is likely to be caused by the shadowing of the main dish by the 4 m secondary reflector. This situation leads to the outer radii contributing more than would be the case for uniform illumination. A diameter of 25.47 m was subsequently used to correct for the primary beam attenuation, using the Airy disk model.
 |
Fig. 5 Peak flux densities of 3C 84 before and after primary beam correction. Left panel: peak amplitudes measured using the pointings in Fig. 4 as a function of distance to the true source position. Also shown are two fits to the data, one using a Gaussian (dashed line) and one using an Airy disk (solid line). The Airy disk performs slightly better. Right panel: peak amplitudes after applying the primary beam corrections using an Airy disk model fitted to the data in the left panel. The standard deviation of the measurements, normalised to their mean (shown as the solid line), is 0.039. |
Since the receivers of the VLBA antennas are not aligned with the optical axis of the system, but are mounted off-axis, the beam patterns for the two orthogonal polarisations are offset on the sky by approximately 5% of the primary beam FWHM (see Uson & Cotton 2008 and references therein for a detailed assessment of the effect at the VLA, which has similar antennas). This effect is called beam squint, and is important when measuring circular polarisation. In total intensity, however, the impact of beam squint is rather small, since RCP and LCP tend to average out. Nevertheless it was incorporated into the correction scheme here, using measurements of the squint carried out by R. Craig Walker (priv. comm., Table 3). These measurements were carried out at 1438 MHz, a few percent above the observing frequency used here. But beam squint is expected to be a fixed fraction of the primary beam width, and therefore the squint measurements were scaled linearly to the centre frequencies of the IFs used in our observations.
Beam squint parameters at 1.438 GHz for the VLBA antennas (C. Walker, priv. comm.).
The results of the improved primary beam correction scheme can be summarised as follows. After applying the corrections to the data, the quality of the corrections was measured as the standard deviation of the corrected peak flux densities, normalised to the average peak flux density of the images from all pointings. This value was found to be 0.039, which is better than estimated by Middelberg et al. (2011a), and comparable to the typical amplitude calibration error assigned to VLBI observations (Figs. 5 and 6). The squint correction can be illustrated by plotting the ratio of the RCP and LCP amplitudes (Fig. 7). Overall the measurements indicate that the primary beam correction scheme performs well and does not introduce significant systematic errors.
 |
Fig. 6 Visibility amplitudes before and after primary beam correction. Left panel: visibility amplitudes from all pointings on a few selected baselines before primary beam correction. The pointing centres are indicated at the bottom of the diagram. Shown is total intensity after averaging all frequencies and the two polarisations. Right panel: the same visibilities after primary beam correction. Whilst there are only small steps and discontinuities in the corrected visibilities (indicating that the correction scheme is working well), there are longer-term trends in the amplitudes, which may be attributed to the substantial structure of 3C 84, which was not modelled due to the poor (u,v) coverage of the data. The larger scatter during some pointings is a consequence of the reduced sensitivity towards directions well away from the pointing centre. |
3.5. Amplitude consistency between epochs
 |
Fig. 7 Illustration of the effects of beam squint and its correction. Left panel: the ratio of the RCP and LCP amplitudes on a few selected baselines before primary beam correction. The pointing centres are indicated at the bottom of the diagram. Deviations from unity are caused by the RCP and LCP beams pointed at different positions. Right panel: the same visibilities after primary beam correction. The differences have essentially be eliminated. |
 |
Fig. 8 Illustration of the amplitude consistency between epochs. Left panel: amplitudes of a sample of bright sources in epochs A/C/D as a function of the amplitude in epoch B. Right panel: the same diagram but amplitudes have been extracted from images with the same limited (u,v) coverage. |
The amplitude errors can be estimated by imaging a few bright sources from each epoch separately, and comparing the amplitudes between epochs. While this approach is susceptible to variability, however, selecting a sufficient number of sources (we use 18) is likely to be a robust estimator for the average amplitude error. Of this sample, 7 sources have been observed in two epochs only (e.g., in the overlap region between A/B, or B/C), 5 have been observed in three epochs (e.g., in A/D/B) and 6 in all four epochs. All sources were observed in epoch B (the one between A/D and C, see Fig. 1) to maximise the overlap. The brightest image pixel was extracted as a measure for the amplitude. All amplitudes from epochs A/C/D were then plotted against the amplitudes measured in epoch B (Fig. 8). The consistency of the amplitude calibration can be determined by calculating the median of the ratios of the amplitudes between epochs, and the standard deviation is a measure of the uncertainty when measuring individual flux densities (including the effects of variability). The median ratios of flux densities in the pairs A/B, C/B, and D/B were found to be 0.799, 0.955, and 0.990, respectively, and the standard deviations (i.e., errors for single measurements) were 0.100, 0.129, and 0.084. Epochs B/C/D therefore appear to be consistent within 1σ, whereas epoch A deviates by around 20%. One potential cause of this is the limited (u,v) coverage during epoch A (where half the data were lost post-correlation due to a software bug). The exercise was therefore repeated by limiting the (u,v) coverage in all epochs to the same extent, but the amplitude ratios and standard deviations were found not to have changed by much: the medians were determined for A/B, C/B, and D/B as 0.838, 0.989, 1.051, and the standard deviations 0.137, 0.143, and 0.078, respectively. Hence epoch A appears to yield consistently lower amplitudes by around 15% to 20%. However, epoch A contributed only 6 h of observing time out of a total of 42 h, therefore its contribution to the final sensitivity is only around 8%, and the final images will only marginally be affected by this systematic error.
From this exercise one can conclude that the scatter of amplitudes between epochs arising from amplitude calibration errors, combined with potential source variability, is of order 10%. This margin was used later in source extraction to determine the errors of the integrated flux densities.
4. Imaging and image analysis
Three types of images were made: naturally-weighted, untapered images, naturally-weighted images using a 10 Mλ taper, and uniformly-weighted, untapered images. Natural weighting was used for source detection, whereas uniform weighting was used to measure integrated flux densities.
An illustration of the sensitivity across the observed area is shown in Fig. 9. Measurements of the rms fluctuations in the naturally-weighted images were placed on a regular grid and then linearly interpolated across the image. The most sensitive region is slightly displaced from the centre of the field because the pointing at the north-east corner was observed twice, in epoch A and epoch D.
To search for emission, natural weighting with no tapering was used for maximum sensitivity. Because the extended VLA emission is potentially offset from the AGN, it was expected that in some cases the VLA position would be significantly offset from the VLBA core, so large images were made, covering 67.1 arcsec2. The pixel size for these images was 1 mas, and the median resolution was 11.7 × 9.4 mas2. Deconvolution using the CLEAN algorithm was stopped after the first negative model component.
Additionally, tapered images were made using a Gaussian taper falling to 30% at 10 Mλ. This enabled the pixel size to be increased to 2.5 mas to cover a larger area, at the expense of a 25% increase in image noise. Imaging a larger area was desirable for a small number of targets where the catalogued VLA position was significantly offset from the likely location of the nucleus. The median resolution was 21.7 × 19.9 mas2.
Finally, the detected sources were imaged using uniform weighting. In natural weighting, the distribution of the VLBA antennas causes the point spread function (the “dirty beam”) to exhibit a significant plateau around the main peak, as illustrated in Fig. 10. This plateau was found to increase the integrated flux density measurements, in particular at low S/N. Whilst deconvolution using the CLEAN algorithm in principle should separate the true emission from the dirty beam, we explored a variety of CLEANed images, and remains of the plateau were found in all. It was therefore decided that integrated flux densities would be measured from uniformly-weighted images, which do not exhibit similar artifacts. The pixel size for these images was 0.5 mas, and the median resolution was 7.4 × 5.5 mas2.
 |
Fig. 9 Sensitivity map of the VLBA observations. The rms noise of the individual images has
been placed on a grid and then linearly interpolated to fill the map. The colour bar
indicates Jy, and contours were drawn at |
 |
Fig. 10 Point spread functions using uniform (left panel) and natural (right panel) weighting. Contours are drawn at 10% × N (N = 0, 1, 2, ..., 9) of the peak. The plateau in the naturally-weighted image at the 30% level is obvious. |
4.1. Identifying detections
 |
Fig. 11 Histogram of the pixels in the image made from source L0211, which was not detected. The upper panel shows the histogram along with a model distribution calculated from the pixel’s σ, and vertical lines indicating the mean and ± 1σ, ± 3σ, and ± 5σ. The lower panel shows the residuals, normalised to the histogram. At the very low and very high end an excess of pixels can be clearly seen. |
A common practice in radio surveys is to treat pixels exceeding 5 times the local noise as a detection. Since the images are relatively large, however, there is a substantial chance of having random noise peaks exceeding this threshold. We estimate this chance as follows.
The number of independent resolution elements, N, can be estimated
following Eq. (3) in Hales et al. (2012):
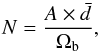 (3)where
A is the covered area,
(3)where
A is the covered area, 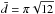 is a correction factor for the packing of the beams, and Ωb is the beam volume
according to
is a correction factor for the packing of the beams, and Ωb is the beam volume
according to 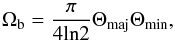 (4)with
Θmaj and Θmin the beam’s major and minor axes. Therefore, in this
case here, with
A = 8.1922 arcsec2 = 67.1 arcsec2:
(4)with
Θmaj and Θmin the beam’s major and minor axes. Therefore, in this
case here, with
A = 8.1922 arcsec2 = 67.1 arcsec2:
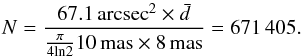 (5)If the image
noise is Gaussian, the number of beams exceeding 5σ, with
σ the standard deviation of the image pixels, is
(5)If the image
noise is Gaussian, the number of beams exceeding 5σ, with
σ the standard deviation of the image pixels, is
![\begin{equation} N_{+5}=N \times \left[1-{\rm erf}\left(5/\sqrt{2}\right)\right]/2 = 0.193. \end{equation}](/articles/aa/full_html/2013/03/aa20374-12/aa20374-12-eq77.png) (6)However, it
was found that N+5 was of the order of 1 to 3 and sometimes
was as high as 6. A typical pixel histogram clearly shows that the distribution of pixel
values is non-Gaussian at the edges (Fig. 11).
Exploring a number of different weighting schemes of the visibilities did not result in a
reduction of the effect. Furthermore, averaging all images, to investigate whether the
effect is a subtle structure present in all images, also did not result in conclusive
evidence. The cause of this non-Gaussian noise distribution therefore remains unknown.
(6)However, it
was found that N+5 was of the order of 1 to 3 and sometimes
was as high as 6. A typical pixel histogram clearly shows that the distribution of pixel
values is non-Gaussian at the edges (Fig. 11).
Exploring a number of different weighting schemes of the visibilities did not result in a
reduction of the effect. Furthermore, averaging all images, to investigate whether the
effect is a subtle structure present in all images, also did not result in conclusive
evidence. The cause of this non-Gaussian noise distribution therefore remains unknown.
An unwelcome consequence of this finding is that the presence of a 5σ peak in an image is inadequate for deciding if a source has been detected or not, and a 6σ threshold had to be used for identifying true emission.
In five cases, >6σ peaks were detected but deemed to be noise spikes since there was no coincidence with the VLA emission. Conversely, one has to conclude that a small number of the >6σ detections that coincide with VLA emission potentially are chance coincidences. This fraction can be estimated as follows.
The median of the separation between the VLBA-detected emission and the maximum of the
VLA emission is 133 mas, and in 88% of the cases the separation was smaller than 500 mas
(and in those cases where the separation was larger it was quite obvious that the VLA
position was not a good indicator of the AGN position anyway). The area covered by a
circle of 500 mas radius is only 1.2% of that in an image that is 8.2 arcsec on a side. If
one assumes that the number of >6σ peaks is of order 10, and if
these noise spikes are scattered randomly across the images, then the number of
6σ noise spike within 500 mas of the VLA position is, following a
binomial distribution: 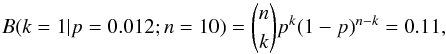 (7)i.e., less than 1. Since
the number of random >6σ noise peaks is likely to be smaller and
visual inspection of images helps to weed out chance coincidences, one can be reasonably
certain that no >6σ peak coincident with a VLA and SWIRE source is
due to noise.
(7)i.e., less than 1. Since
the number of random >6σ noise peaks is likely to be smaller and
visual inspection of images helps to weed out chance coincidences, one can be reasonably
certain that no >6σ peak coincident with a VLA and SWIRE source is
due to noise.
4.2. Synthesis with VLA and SWIRE data
For each of the 496 targeted sources, we generated a contour plot of the VLA emission superimposed on the 3.6 μm image from the SWIRE survey (Fig. 12). The SWIRE data from data release 3 were retrieved from the NASA/IPAC Infrared Science Archive4 and mosaiced using the Montage package5, and then a 30 × 30 arcsec2 cutout centred on each VLA position was extracted. Postage stamps from the VLA observations were provided by Ibar et al. (2009). Contours were drawn from the 2σ level, to accentuate faint emission, increasing by factors of 2. The two VLBA images for each source – untapered and tapered – were analysed and searched for emission. Along with these data a contour plot was produced of the untapered VLBA image, centred on the brightest image pixel, starting at 2σ and increasing by factors of two. These plots were used to associate catalogued radio components to radio sources, to identify the correct SWIRE counterparts to these sources and to check the plausibility of a VLBA detection. The three sources shown in Fig. 12 illustrate this process.
As noted in Sect. 1.1 and further discussed in Sect. 5, only sources with an integrated VLA flux density exceeding 6 times the noise in the VLBA images were deemed to be detectable, and after calibration only 217 sources were found to satisfy this criterion. Nevertheless, we inspected all 496 targeted sources, to ensure proper cross-identifications and to inspect the data for errors (such as the false >6σ peaks described in Sect. 4.1) and unexpected results. However, none of the remaining (496−217) = 279 sources with insufficient sensitivity in the VLBA data were found to yield a credible VLBA detection.
 |
Fig. 12 Example contour plots of the VLBA, VLA, and SWIRE data. The upper panel shows the logarithm of the SWIRE 3.6 μm emission as a pixel map, superimposed with contours of the VLA data of source L0034. Contours start at 2 times the local rms (as indicated in the plots) and increase by factors of 2. This object has four entries in the VLA catalogue: one, L0034, representing it as a source and three for its constituents, L0035, L0036, and L0037. Their locations are marked as labels in the image. Three black squares indicate (from large to small) (i) the regions imaged with the VLBA using a 10 Mλ taper; (ii) the region imaged using untapered data; and (iii) the region shown in the contour plot in the bottom panel. The maximum of the tapered VLBA data is marked with a cross, and the maximum of the untapered VLBA data is marked with an open circle. In this case, the maxima of the tapered and untapered VLBA images are not coincident, because the tapered image has reduced sensitivity. However, the maximum at full-resolution (6.2σ) coincides with a faint SWIRE source located between L0035 and L0036, indicating that this is the location of the AGN. Furthermore, the value of the tapered image exceeds 5σ at the location of the maximum of the untapered image, adding credibility to the detection. The bottom panel shows a contour map of a region 0.36 arcsec across, centred on the maximum of the untapered VLBA image. Contours start at 2 times the local rms (as indicated in the plots) and increase by factors of 2. |
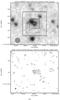 |
Fig. 12 continued. This plot shows data for source L0119. Three catalogued VLA components belong to this source. The detection at 24σ and cross-identification with a SWIRE source is unambiguous. |
 |
Fig. 12 continued. This plot shows data for source L0698, which has been grouped with source L0697. The maxima of the two VLBA images coincide neither with each other, nor with an infrared source, and therefore this source with a maximum of 5.2σ was deemed to be undetected. |
4.3. Flux density extraction
In radio astronomy, source flux densities are commonly measured by fitting 2D Gaussians to the image pixels. Whilst this method is suitable under well-constrained circumstances, it is known to yield inaccurate results when left unconstrained. For example, if the S/N of a source is below 10, then a 2D Gaussian is likely to overestimate the flux density. Also if a source has a non-Gaussian shape then the model is inappropriate and will yield incorrect results. In a recent publication, Hales et al. (2012) presented a source extraction program, BLOBCAT6, which uses the flood fill algorithm to measure the integrated flux density of sources. It takes proper account of the various biases involved and performs better than Gaussian fits when the source has low S/N or is irregularly shaped. It was therefore used to measure the flux densities of the VLBA-detected sources from uniformly-weighted images.
Two modifications to the default settings of BLOBCAT were made. First, a pixellation error of only 1% was assumed because of the significant oversampling of the point spread function (–ppe=0.01). Second, the error of the surface brightness in the images was assumed to be 10% (–pasbe=0.1), reflecting the amplitude calibration errors.
 |
Fig. 13 Fraction of VLBA-detected sources. Left panel: the fraction of
VLBA-detected sources as a function of flux density. Detectable sources have been
grouped into bins with limits
100 μJy |
5. Discussion
The primary result from the VLBA observations of the Lockman Hole/XMM is the detection or non-detection of a source, and its mas-scale flux density and morphology. Even though the initial sample consisted of 496 radio sources with S > 100 μJy, it was always clear that many would not be detectable with our observations, because the VLA had a 1σ sensitivity of 6 μJy beam-1, compared to a 1σ sensitivity of just under 20 μJy beam-1 of our VLBA data. For the subsequent analysis a sub-sample was selected based on whether sources would have been, in principle, detectable. The criterion we used was that the noise in the full-resolution, naturally-weighted image was smaller than 1/6 of the VLA peak flux density, because we used a 6σ threshold for source detection. Out of the original sample, 217 sources satisfied this criterion and were used for analysis. Out of these 217 detectable sources, 65 were deemed to be actually detected. Note that whilst naturally-weighted images were used to determine detections because of the higher sensitivity, flux densities were measured from uniformly-weighted images to reduce the effect of the plateau in the point spread function (see Sect. 4 and Fig. 10).
5.1. Fraction of detected sources
The fraction of VLBA-detected sources is an interesting quantity because it essentially gives us a lower limit on the number of radio-emitting AGN in the sample. Since our sample is large we can subdivide it and determine the detection fraction as a function of flux density. The results are shown in Fig. 13 and Table 4.
The fraction of VLBA-detected sources is obviously a function of sensitivity. Towards faint flux density levels, only sources that are increasingly compact can be detected, yet at some flux density level the detection fraction approaches completeness. One can estimate that level as follows. Around 90% of the targets have been observed with a sensitivity of 60 μJy/beam-1, allowing the detection of sources brighter than 360 μJy, when a 6σ cutoff is used. If one requires a minimum of 10% of that flux density to come from the core, providing emission for a VLBA detection, then sources brighter than 3.6 mJy can be detected across 90% of the area. In Fig. 13 (right panel), the nearest point is at 3.2 mJy, and the detection fraction is 60% (12 out of 20 sources).
Fraction of detected sources as a function of VLA flux density.
 |
Fig. 14 Ratio of the VLBA and VLA flux densities. Blue dots show the detectable sources, placed at 6 × rms/SVLA (where rms is the local noise level of the VLBA observations), and red dots with error bars detected sources. Out of the 65 detected sources, 6 exceed a ratio of 1.0 by more than 1σ, but only one source exceeds 1 + 3σ. |
5.2. Variability
For an unresolved radio source, the interferometric visibility amplitude is constant with baseline length; for resolved sources, it must generally decrease with baseline length (although constructive interference between separated, compact components can lead to local increases). When comparing VLBA baselines with lengths of hundreds to thousands of kilometres to VLA baselines with lengths of much less than 100 km, it can be safely assumed that the visibility amplitudes on longer baselines must be less than, or at most equal to, the visibility amplitudes on short baselines.
It is therefore a useful consistency check to compare the VLBA flux densities to the VLA flux densities. In Fig. 14 the ratios of the integrated VLBA flux densities to the integrated VLA flux densities are plotted for all detectable sources and the 65 detected ones. Out of the 65 detected targets, 6 have ratios that exceed 1.0 by more than the width of their error bars (1σ), in particular at low flux densities: L0231, L0578, L0593, L0648, L0997, and L1200. While it is clear that some sources might have flux density ratios in excess of 1 + σ by chance, one source (L0593) exceeds 1 + 3 σ, which is significant given our sample size. We interpret this result as source variability, for several reasons:
-
Although the variability of bright radio sources has longbeen studied, the variability of the mJy and sub-mJy ra-dio source population is poorly constrained. Carilliet al. (2003) found that the den-sity of variable sources in this flux density regime is less than5 × 10-3 arcmin-2.
-
The elapsed time between the VLA and VLBA observations is significant. Whilst the VLBA observations where carried out in July–September 2010, the VLA data were obtained between 2002 and 2005.
-
Faint sources are preferably detected if they are variable and in a state with high flux density, compared to their average flux density. Faint sources in a state with low flux density will be missed, and this is the reason why the fraction of sources with ratios greater than 1 increases towards fainter flux densities.
-
The VLA observations are sensitive to the combined emission from star formation and AGN, whereas the VLBA observations isolate the AGN emission. Hence the variability of the AGN is likely to be higher than determined by our observations, because only one of our two available flux density measurements (VLA and VLBA) is purely sensitive to the AGN emission.
The effect of interstellar scintillation on the source flux densities is difficult to estimate with our data, but is likely to be small. The galactic latitude of the Lockman Hole/XMM field is 53°, where, according to Walker (1998), sources (or parts thereof) are required to be smaller than around 6 μas (0.05 pc at z = 1) to show significant scintillation. Most of the VLBA-measured flux densities are lower than the VLA flux densities, implying that the sources are partly resolved between the length scales probed by the VLBA and VLA. We deem it safe to assume that most, if not all, of the sources had been resolved further, had the resolution of our observations been higher. Thus, whilst it is possible that small fractions of the flux density recovered by our VLBA observations originate in regions sufficiently small for scintillation, we do not expect it to have a significant effect.
5.3. Spectral index
A common method to classify radio sources into AGN and non-AGN is to use the spectral index, α, with S ∝ να. Sources with spectral indices larger than −0.3 (“flat” or “inverted”) or less than around −1.0 (“steep”) are typically classified as AGN, because flat and inverted spectral indices arise in compact, optically thick synchrotron emitters typical of AGN, whereas steep indices are attributed to optically thin emission from radio lobes, with a potentially aged particle population. Sources with α around −0.7 can not be classified based on spectral index alone, because both starburst galaxies and AGN can exhibit such values, which arises from synchrotron emission with a continuous injection of fresh particles (e.g., Pacholczyk 1970).
Whilst the histogram of the spectral indices of detectable sources is typical of the population found in sensitive, extragalactic radio surveys, the histogram of detected sources exhibits a prominent deficiency at low spectral indices. The lowest spectral index of any detected source is −0.88, whereas the distribution of detectable sources extends to well below −1.0. Almost all sources with α > 0.0 are detected, but no source with α < −0.9 is.
One might argue that this is a selection effect, which de-selects steep spectral indices, because they tend to have lower 1.4 GHz flux densities than flat- or inverted-spectrum sources (the spectral indices at our disposal were measured between 610 MHz and 1.4 GHz). However, we find only a mild correlation between the spectral index and the flux density, with a product-moment correlation coefficient of −0.02 (where +1 and −1 denote perfect linear correlation and anti-correlation). We therefore conclude that, whilst inverted spectra arise from compact synchrotron emission and therefore are likely to be detected, steep spectral indices arise from larger and therefore potentially older regions, which tend to be resolved out. What follows from this exercise is that at “normal” spectral indices of between −1.0 and −0.3 VLBI observations can cleanly separate the AGN from star-forming activity, whereas in the regime of α > −0.3 spectral index alone is already a good indicator for AGN.
 |
Fig. 15 A histogram of the spectral indices of detectable (blue bars) and detected (red bars) sources. |
5.4. Source counts
While radio source counts of VLBI-detected sources at flux density levels of above 100 mJy are in principle available from VLBI calibrator searches, counts of the mJy and sub-mJy population are currently unknown, because they would have required prohibitive amounts of observing time using conventional methods. The work presented here yielded the detection of only 65 sources in total (a number frequently found in a single bin in other source count studies), yet this is, to our knowledge, the first attempt to produce radio source counts of VLBI-detected sources in the mJy and sub-mJy regime.
It is worth noting that in this paper we do not construct radio source counts using VLBI flux densities, since such measurements would be plagued by tremendous resolution effects that would render the source counts useless. Instead, we use the VLBI observations to select a sub-sample of radio sources with very compact cores from the parent sample of known radio sources detected with the VLA, and then use the VLA flux densities of this sub-sample to construct the source counts.
When constructing source counts, two effects need to be taken into account. The first is a weighting factor arising from the varying sensitivity of the observations, i.e., for each source flux density one needs to determine over which area this source would have been detected. Since observations typically have significantly smaller areas with very high sensitivity than with lower sensitivity, this correction can have a large effect on the source counts if not carried out correctly. The second effect is resolution bias. Extended sources can remain undetected when they are close to the detection limit of the survey, and so the counts at low flux density levels will underestimate the true source counts. This effect depends on the resolution of the observations, and in our case is much smaller than the correction for effective area, of order below 10% (Ibar et al. 2009). Hence the number of sources in each bin needs to be corrected by 1 + c, where c is of order 0 to 0.1.
As a consistency check, we initially constructed the source counts from the VLA data
published by Ibar et al. (2009). From their
catalogue we have eliminated all entries marked as components (non-zero “m_Name” column).
Corrections for effective area and resolution were extracted from their Figs. 6 and 7,
from which we constructed look-up tables using Dexter7. Using the same bins as Ibar et al.
(2009) we determined 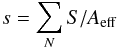 (8)for the
N sources in each bin, where Aeff was
determined from a look-up table. This procedure ensures proper weighting of all sources in
a bin. Each bin was then corrected for resolution bias by multiplying its value by
1 + c, where c is a value extracted from the other
look-up table. The bin values were then divided by the bin widths, and subsequently by the
geometric mean of the bin edges raised to the power of −2.5. Count errors of the
area-weighted counts in Eq. (8) were
estimated as
(8)for the
N sources in each bin, where Aeff was
determined from a look-up table. This procedure ensures proper weighting of all sources in
a bin. Each bin was then corrected for resolution bias by multiplying its value by
1 + c, where c is a value extracted from the other
look-up table. The bin values were then divided by the bin widths, and subsequently by the
geometric mean of the bin edges raised to the power of −2.5. Count errors of the
area-weighted counts in Eq. (8) were
estimated as 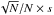 and then propagated through the
same steps as the counts themselves. This procedure resulted in identical counts as
published by Ibar et al. (2009), with the exception
of the two lowest bins, where we found agreement with previously published counts (Fig.
16). The reason for this discrepancy can in
principle arise from the way the effective area is dealt with. If one uses, e.g., the
lower edge of a bin to calculate the effective area for the entire bin, then one
underestimates the area over which a source would be detected, resulting in an
over-estimate of the source counts.
and then propagated through the
same steps as the counts themselves. This procedure resulted in identical counts as
published by Ibar et al. (2009), with the exception
of the two lowest bins, where we found agreement with previously published counts (Fig.
16). The reason for this discrepancy can in
principle arise from the way the effective area is dealt with. If one uses, e.g., the
lower edge of a bin to calculate the effective area for the entire bin, then one
underestimates the area over which a source would be detected, resulting in an
over-estimate of the source counts.
 |
Fig. 16 Source counts in the Lockman Hole/XMM field. Shown are the Euclidean-normalised source counts of the VLBA-detected sources, using their VLA flux densities (red line). Shown with black lines are source counts that would have been measured had the sensitivity of our observations been lower by factors of 1.1, 1.5, and 2.0. For comparison, we have plotted the source counts constructed from the Ibar et al. (2009) data using the same methods (blue line), the source counts as published by Ibar et al. (2009) (green line), and the data compilation from Hopkins et al. (2003) (light grey squares) along with their 6th order polynomial fit. |
We proceeded to calculate the source counts for the VLBA-detected sources only, using the same methods as for the VLA source counts. However, the determination of the effective area was different. Two corrections are needed to properly account for the effective area – one to determine over which area each source would in principle be detectable with the VLBA, another to determine the area over which this source would in principle be detectable with the VLA. The first correction was carried out as follows. For each source the area over which it could have been detected with the VLBA was determined using the sensitivity map shown in Fig. 9. The number of pixels with values smaller than 6 times the VLA source flux density was counted and multiplied with the pixel area. The second correction would have required knowledge of the rms distribution of the VLA observations, which was not available (the catalogue of Ibar et al. 2009 only lists peak-to-noise ratio, but neither peak nor noise is given). However, Fig. 6 in Ibar et al. (2009) indicates that for our weakest source greater than the lowest bin edge at 120 μJy, at S = 127 μJy, the area over which it was detectable is 94% of the entire observed area, and for stronger sources this percentage comes even closer to 100%. We therefore neglected this correction.
The source count bins were defined to begin at a total integrated flux density of 120 μJy and to increase by factors of two to 3.84 mJy. This resulted in a reasonably even distribution of the number of sources per bin. The source counts of all sources, the VLBA-detected sources, and the source counts by Hopkins et al. (2003) are shown in Fig. 16.
At the bright end of the distribution the source counts of VLBA-detected sources appear to be an extrapolation of the general radio source counts, indicating that this population is dominated by AGN. Between 1 mJy and 2 mJy there is a sharp drop, which is also visible in the percentage of detected sources in Fig. 13 (left panel). However, the counts of VLBA-detected sources exhibit a shoulder between 0.1 mJy and 1 mJy, and this shoulder is a lower limit on the number of radio-emitting AGN at sub-mJy flux density levels.
It is important to note here that this lower limit is subject to the sensitivity of the VLBA observations. At high flux densities a detection can be made even if only a small fraction of the radio flux density originates from the AGN, whereas at flux density levels near the detection limit only the most compact sources will be detected (see Fig. 14). Our counts near the VLBA detection limit therefore underestimate the “true” detection rate by a larger margin than at higher flux density levels. At higher sensitivity, the counts of VLBA-detected sources would rise towards the general radio source counts.
To illustrate this effect we have constructed source counts that would have been measured with lower sensitivity. We multiplied the sensitivity map in Fig. 9 by factors of 1.1, 1.5, and 2.0 and selected only those sources that would have been detected with this increased noise level. This was done by selecting sources with a peak flux density in the VLBA observations exceeding 6 times the modified noise. The source counts from this exercise are shown in Fig. 16 as black lines (solid, dashed, and dash-dotted). One can see that the source counts drop with decreasing sensitivity, as expected, because less sensitivity requires that only the most compact sources can be detected. Conversely, if one extrapolates this trend to higher sensitivity, one can conclude that the source counts of VLBA-detected sources are likely to be higher, above the red line, but below the general radio source counts.
We therefore conclude that at flux density levels of between 0.1 mJy and 1 mJy, at least 15% to 25% of the radio sources contain radio-emitting AGN. This finding adds new and independent support for the recently established picture that a substantial fraction of the sub-mJy radio populations is AGN-driven, rather than powered by star-forming activity. For example, Smolčić et al. (2008) classified radio sources from the COSMOS survey using optical colours and found that 50% to 60% of the sub-mJy radio sources contain AGN. In another study, Padovani et al. (2011) classified radio sources in the Chandra Deep Field South using Spitzer data, and found that 50% contained AGN. A recent compilation of studies investigating the AGN fraction of the sub-mJy radio source population can be found in Fig. 4 of Norris et al. (2011b).
Source counts of VLBA-detected sources.
 |
Fig. 17 The difference between the 1.4 GHz radio luminosity measured with the VLA, LVLA and measured with the VLBA, LVLBA, as a function of LVLBA. The solid line indicates the correlation as indicated in the text, and the dotted lines the error of the normalisation. |
5.5. The extended emission
As one can see in Fig. 14, the flux density recovered with the VLBA is in general less than the VLA flux density. Only a small part of this trend can be explained by variability, which can explain neither the large differences found in many sources, nor the majority of the VLBA non-detections. Moreover, Fig. 15 shows that the spectral indices of the VLA sources (extended) tend to be lower than those of the VLBA sources (compact), indicating that the nature of the compact emission is different than that of the extended emission. Here, we assume that the compact emission comes from the AGN, whereas the extended emission comes from star-formation, either circumnuclear, or from the host galaxy. In a recent study of radio-quiet (L ≲ 1024.5 W Hz-1) VLA sources in the Chandra Deep Field South (CDFS), Padovani et al. (2011) found, by comparing the luminosity functions of radio-quiet AGN, that the bulk of the their emission comes from star-formation processes and radio-loud AGN. Also Fig. 16 showed that the source counts of VLBA-detected and VLBA-undetected sources are significantly different, so it is safe to assume that the extended part of the emission traces star-formation, whereas the compact emission traces the AGN.
A sample of AGN where we can measure the host galaxy properties (star-formation rate) independently from the AGN emission provides us with the opportunity to test the co-evolution of the AGN and their hosts. There is observational evidence that some co-evolution between the AGN and the host galaxy exists (e.g., the M-σ relation, Ferrarese & Merritt 2000), and recent observations link host star formation rates to their AGN for different luminosities and redshifts (see Shao et al. 2010; Mullaney et al. 2012; Rovilos et al. 2012; Rosario et al. 2012, but also Page et al. 2012). In Fig. 17 we plot the difference between the VLA and the VLBA luminosities (see Sect. 5.6 and Table 7) as a function of VLBA luminosity for our sample. There are a number of sources for which the VLBA luminosity is higher than the VLA luminosity, and we assume that this is because of variability (see Sect. 5.2). These cases have been treated as follows: in cases where LVLA < LVLBA but LVLA + ΔLVLA > LVLBA − ΔLVLBA, we used LVLA + ΔLVLA − (LVLBA − ΔLVLBA) as an upper limit of the extended component. In cases where LVLA + ΔLVLA < LVLBA − ΔLVLBA, we assumed that the extended component of the radio emission seen by the VLA but resolved out by the VLBA was small. Since some extended emission is likely to be present, we adopted an upper limit of the extended component of 5% of the VLA luminosity.
One can see from Fig. 17 that there is a positive
correlation between the two luminosities, and applying the generalised Kendall’s
τ method using the ASURV package (Rev. 1.3, Lavalley et al. 1992), we find that the significance of the correlation
is at the 96.2% level. The solid and dotted lines correspond to the equation:
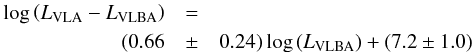 (9)(only
the standard deviation of the normalisation is shown in the dotted lines). If we ignore
the upper limits, the significance rises to 97%. However, one can also see that in a small
number of sources the extended luminosity is larger than
1024.5 W Hz-1, so there might be a contribution from the AGN
to the extended flux, from structures that are resolved out by the VLBA observations.
Ignoring those cases, the correlation becomes even more statistically significant, at the
99.81% and 99.98% levels, including and excluding upper limits, respectively.
(9)(only
the standard deviation of the normalisation is shown in the dotted lines). If we ignore
the upper limits, the significance rises to 97%. However, one can also see that in a small
number of sources the extended luminosity is larger than
1024.5 W Hz-1, so there might be a contribution from the AGN
to the extended flux, from structures that are resolved out by the VLBA observations.
Ignoring those cases, the correlation becomes even more statistically significant, at the
99.81% and 99.98% levels, including and excluding upper limits, respectively.
An issue that needs to be addressed is whether the correlation is driven by a redshift effect. It is known that the mean star-formation rate increases with redshift up to z ≈ 2 (see, e.g., Daddi et al. 2007; Elbaz et al. 2011), and also the VLBA luminosity can increase with redshift, because the survey is flux density-limited. Such an effect can mimic an AGN-host correlation (see Mullaney et al. 2012). As a test we determined the correlation in the flux density domain and found that after excluding the upper limits the correlation is at the 94.7% level, but its significance drops to 91.8% if we include the upper limits. We therefore claim that a tentative correlation exists. This tentative correlation shows that the most luminous VLBA AGN tend to have higher levels of star-forming activity, as predicted by the current standard cold-mode accretion model (Croton et al. 2006; Hardcastle et al. 2007).
5.6. Multi-wavelength properties of the detected sources.
In addition to the basic results from the VLBA survey, significantly more information can be gathered from the literature, to obtain flux densities at other wavebands. Therefore the VLA and VLBA observations were cross-matched to the publicly available multi-band photometry and photometric redshift catalogues of the Lockman Hole/XMM by Fotopoulou et al. (2012). In this catalogue the Large Binocular Telescope (LBT) images presented in Rovilos et al. (2009) were combined to create a new catalogue of optically and near-infrared detected sources in the field. In addition to the UBV bands this multi-wavelength photometry catalogue includes the PSF-homogenised fixed-aperture photometry from LBT Y and z-band observations, the Subaru R, Ic, z′ bands from Barris et al. (2004), the UKIDSS J and K bands, the 3.6 μm to 8.0 μm photometry from the Spitzer Wide-area Infrared Extragalactic survey (SWIRE, Lonsdale et al. 2003) and GALEX photometry. Except for the near-infrared data, all the other bands provide very sensitive data (see Table 2 of Fotopoulou et al. 2012 for the depth of the optical bands). The photometric redshift catalogue uses all the above-mentioned bands to produce accurate photometric redshifts for normal galaxies and for X-ray detected sources by using templates of normal galaxies and AGN hybrids, and luminosity and morphological priors to reduce the parameter space of possible redshift solutions (more details can be found in Fotopoulou et al. 2012).
 |
Fig. 18 VLBA-detected sources with optical counterparts (red circles). The multi-wavelength coverage of the field is also shown: Subaru Rc, Ic, z′ filters (image), LBT U and B filters (blue solid line), LBT VYz′ filters (blue dashed line), IRAC 3.6 μm and 5.8 μm (yellow solid line), IRAC 4.5 μm and 8 μm (yellow dashed line), SDSS (black dashed line), J and K UKIDSS filters (black solid lines). The black circle denotes the area observed by XMM-Newton. |
We cross-matched the catalogues8 to our data by visual inspection, and by overplotting the locations of the radio, Spitzer/IRAC, and optical positions to ensure that the emission originated from the same object in each case. Because of the depth of the available data and the highly accurate astrometry of the VLBA observations, we are confident that a simple match in coordinates provides the correct counterpart. It was found that the VLBA position and the optical position were in very good agreement. The mean separation between the two positions was 0.28 arcsec, with a maximum of 0.88 arcsec. In a first attempt, optical counterparts were searched using a 3 arcsec radius. All sources with separations of >1 arcsec between the radio and optical positions were found to be chance coincidences upon closer inspection of the images, and so a 1 arcsec search radius, followed by visual inspection, was adopted for cross-identification. Of our 65 VLBA-detected sources, 10 were located outside the region covered by the optical data, 47 had reliable optical counterparts (shown in Fig. 22), and 6 had either faint or uncatalogued counterparts, sometimes because of blending, or were overlapping with image artifacts such as diffraction spikes (L0199, L0251, L0386, L0506, L0708, L1148, see Fig. 23). The remaining 2 had no identifiable counterparts at all (L0194, L1364, see Fig. 24).
In two objects, L0506 and L1148 (Fig. 23), the position of the VLBA source is at the very edge of a clearly visible optical source, but a cross-identification with these objects was deemed unlikely. In L0506, a small extension to the optical source can be seen, indicating that two objects are blending and a reliable cross-identification can not be made. In L1148 both the VLA and the VLBA positions are offset from the foreground object by more than 1 arcsec. The nature of the three sources without any optical counterpart (Fig. 24) is puzzling. Radio sources with extremely faint or invisible optical or infrared counterparts have recently gained some attention (see, e.g., Higdon et al. 2005; Middelberg et al. 2011b; Norris et al. 2011a), and the speculation is that they are similar to high-redshift radio galaxies. But our data do not allow any further conclusions to be drawn.
Figure 19 presents the Rc band distribution of the optical counterparts as a function of the radio flux density. We also plot the line of log (S1.4/Rc) = 1.4 which, according to Padovani (2011), defines the maximum value of that ratio for star-forming galaxies and radio-quiet AGN. Whilst star-forming galaxies and radio-quiet AGN are most likely confined to the top-left corner, radio-loud AGN can in principle populate the entire diagram. We find that the majority of the sources are classified as radio-loud (33/47), while 11 out of the 47 are located on the line. Only 3 objects are classified as star-forming galaxies or radio-quiet AGN (but could in principle also be radio-loud AGN).
 |
Fig. 19 Rc magnitude vs. VLA flux density for the 47 sources with optical counterparts (for source L0953 the SDSS r magnitude was used). The majority of the population is classified as radio-loud. The limit for star-forming galaxies and radio-quiet AGN is given by the grey dashed line indicating log (SVLA/Rc) = 1.4, but radio-loud AGN can in principle populate the entire diagram. |
In Fig. 20, we plot the X-ray flux versus VLA flux density for the sources located in the area observed by XMM-Newton. The lines in the plot show the loci occupied by X-ray AGN (dash-dotted line), radio-quiet AGN (dotted line), star-forming objects (dashed line) and radio galaxies (solid line), as presented in Padovani (2011). Out of the 47 sources with optical counterparts 26 are inside the area observed by XMM-Newton, and only 10 are detected in the X-rays (Flim,0.5−2 keV = 1.9 × 10-16 erg/s/cm2). The low number of X-ray detected sources does not allow statistically meaningful conclusions to be drawn about the population. Nevertheless we can see that the X-ray sources are preferentially occupying the locus between star-forming and radio galaxies. We also include upper limits for the 16 sources inside the XMM-Newton area that fall below the X-ray flux limit. These sources show similar behaviour to the detected sample, with the majority occupying the area between star-forming and radio galaxies.
 |
Fig. 20 X-ray flux versus VLA flux density for the 26 sources inside the area covered by XMM-Newton. The lines denote the area occupied by X-ray AGN (dash-dotted line), radio-quiet AGN (dotted line), star-forming objects (dashed line) and radio galaxies (solid line), as presented in Padovani (2011). Upper limits are drawn for the 16 sources below the X-ray flux limit. |
In order to classify the sources and rank the reliability of each SED fit, colour images for all 55 sources with optical coverage were produced. In Figs. 22–24 we show the results of the best SED fits and photometric redshift computation. The following two subsections present the main result from this exercise.
5.6.1. Variety of radio source host galaxy morphologies
The host galaxies of the detected sources display a great variety in morphology. We have attempted to coarsely group them by visual appearance into 0 – point-like (as L0227); 1 – unresolved (as L0119); 2 – early type or bulge dominated (as L0449 and L0876, respectively); 3 – unclassified (as L0256) and 4 – spiral (as L1374, our only clear, though lopsided, spiral).
Sources in the “unresolved” or “unclassified” groups (coded 1 or 3, respectively) are unresolved, or barely larger than the point spread function. However, they are mostly very faint, so one cannot tell if the faint speck that is seen in an image is only the brightest part of a much larger object. In an expanding universe, the surface brightness of an object decreases with (1 + z)4, a situation known as the “Tolman effect” (Tolman 1930). Therefore extended but faint parts of objects quickly become very difficult to detect as their redshift increases. Some objects in this category could also reasonably be assigned to the “ellipticals” subset (L0423, L0997), but judging by the visual appearance this is a matter of taste.
The “bulge dominated’ group (coded 2) are mostly circular, extended objects with a more or less pronounced surface brightness gradient towards the edges. Some have clearly extended halos as one typically finds in cD galaxies (L0449, L0846), while others have less pronounced halos (L0535).
In total 21 sources (45%) were classified as unresolved/unclassified, 23 sources (49%) as bulge-dominated, 2 (4%) as point-like and 1 (2%) as a spiral. To determine if this is correlated with the selection of VLBA-detected sources we have selected a control sample of 66 VLBA-undetected radio sources that has a VLA flux density distribution similar to that of the VLBA-detected sources. Since most bright sources were detected, the control sample had a slight deficiency in bright sources and a slight overabundance of fainter sources. Out of the 66 sources in the control sample, only 36 had reliable counterparts, but these counterparts displayed a similar variety in host galaxy types. Since 22 out of the 25 morphologically classified objects are early-type objects, we can conclude that the VLBA radio sources are found in the expected hosts. This also agrees well with distribution of sources in the Rc vs. VLA flux density diagram in Fig. 19, where the majority of the sources are in the radio-loud regime.
5.6.2. The SED models of radio source host galaxies
Using the photometric redshift estimation code LePhare9, normal galaxy and AGN templates were fitted to the photometric points (see
Ilbert et al. 2009; Salvato et al. 2009, 2011 for
a detailed description of the fitting procedure). The normal galaxy templates include
extinction values of E(B − V) = 0.00,
0.05, 0.10–0.50 (in steps of 0.1, see Fotopoulou et al.
2012 for details). Spiral and starburst templates (Sb-SB3) include extinction
according to the Small Magellanic Cloud (SMC) law given in Prevot et al. (1984). This law is also used for the library of AGN
and hybrids. Bluer templates (SB4-SB11) include extinction laws from Calzetti et al. (2000) and a modified Calzetti law
(Ilbert et al. 2009), while templates redder
than Sb (ellipticals and S0) include no further extinction. In addition to the best
photometric redshift solution LePhare also provides the full probability distribution
function (PDFz), 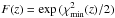 . This distribution
is calculated for a predefined redshift range
(0 < z < 7 for this
work) and is plotted as an inset in Fig. 22. In
general, a source with a broad PDFz does not have a well-constrained redshift solution.
. This distribution
is calculated for a predefined redshift range
(0 < z < 7 for this
work) and is plotted as an inset in Fig. 22. In
general, a source with a broad PDFz does not have a well-constrained redshift solution.
Clearly, the accuracy of the fit depends on the number, wavelength and depth of bands available (depending on the redshift of the source a band is more or less crucial to identify specific spectral features). The fit also depends on whether the source varied in flux (typical AGN behaviour) within the time scale of the observations, and on contamination of photometry from objects within the aperture used to compute the flux (in this case 3 arcsec diameter). We could not identify quantifiable criteria, such as number of available bands, or reduced χ2 of the fit, to judge the quality of the models. Instead, we rated the fits according to the following guidelines:
-
1: a bad fit due to a limited number of bands (less than 6) or because the source is at the border of the imaged field (see for example L0140).
-
2: a doubtful fit because the photometry is affected by blending with nearby objects (see for example L0352).
-
3: a potential AGN (doubtful fit): the lack of Xray information did not allow the use of proper template (see example L0227).
-
4: the optical photometry is not contaminated and the number of bands is sufficient.
We do not discuss here sources with a SED fit rated 1 and 2 for obvious reasons. Only two sources are rated 3 (L0227 and L1374), classified as potential AGN due to their morphological appearance and due to the typical power-law seen in the mid-infrared bands. These objects lie outside the XMM area and thus were treated as normal galaxies during the photometric redshift estimation. Following the definition of SEDs as in Fotopoulou et al. (2012) and Salvato et al. (2011) we classified the 30 sources with a good fit as follows: 11 present a typical SED of an early type galaxy, 6 are best modelled as spirals, and 12 are classified as starburst (either pure starburst or X-ray detected but still starburst dominated). Three of the 12 objects classified as starburst are clearly early-type objects by visual appearance. The erroneous SED fit is a clear and well-known case of degeneracy where a starburst template with heavy extinction (0.3, 0.35 and 0.4 of E(B − V), as visible in the plot of L0397 and L0911 and L1165) can mimic an early-type template (see also the discussion in Onodera et al. 2012). In the case of L0973 the image clearly indicates an early-type, and the best fit is obtained with the template of M 82. Unlike the other starburst templates that are theoretical, this one is empirical and already includes dust. For this reason we group this source with the 3 described above. For the remaining 8 sources fit by a starburst template the applied extinction is very high but we cannot be certain that they are early type because they are morphologically unresolved.
6. Conclusions
The main results from this work are summarised as follows:
-
VLBI observations of 217 sources have been carried out with the VLBA. Primary beam corrections have been developed and tested using dedicated observations, and a novel multi-source self-calibration scheme has improved the coherence of the data significantly. Data from overlapping pointings were added to improve the sensitivity in the overlap regions (mosaicing). Images were made of all targets, and 65 sources were detected, a fraction of 30%. Data from the literature were added for interpretation. VLBI observations with hundreds of pointings are now feasible and can be added to large surveys carried out at other wavelengths.
-
The VLBA-detected sources have larger spectral indices than the non-detected sources, which is consistent with their emission coming from more compact regions near the AGN. Above a spectral index of α = 0.0, almost all sources (14/17) are detected, confirming that spectral index is a strong selection criterion for radio AGN. Using the difference between the flux densities measured with the VLA and the VLBA as a measure for star forming activity, a positive correlation has been found between the star formation and AGN activity.
-
Source counts of VLBA-detected, faint radio sources are presented for the first time. They form a lower limit on the fraction of radio AGN among the radio source population. At the bright end of the distribution the counts line up with literature values, indicating that the majority of mJy sources is AGN-powered. At the sub-mJy level, the counts drop below the sub-mJy plateau seen at arcsec-scale resolution but seem to exhibit a similar flattening. A significant fraction of the sub-mJy, 15% to 25%, are AGN-driven. However, the high resolution of the VLBA observations implies that some AGN-driven radio sources are not detected, and so it is expected that the correct fraction of AGN-driven sources is higher.
-
Using literature data we discuss the multiwavelength properties of the counterparts to 47 of the 65 VLBA-detected radio sources. The morphologies of about 50% of the sources suggest the hosts to be early-type galaxies. For the rest of the sources the image quality and the redshift do not allow any assessment of the morphology. In many cases the best fit is obtained with the template of a heavily extinct starburst. This is a well-known case of degeneracy in SED fitting where these kinds of templates plus extinction mimic an early-type object. Globally, the typical hosts of VLBI sources are passive galaxies, in agreement with previous results.
With software correlators, accurate primary beam corrections and multi-source self-calibration, wide-field VLBA observations have become practical and versatile. The calibration strategies will certainly improve, and larger bandwidths of future instruments will make such observations easier because the instantaneous sensitivity increases.
The significance of wide-field VLBI observations has been acknowledged by NRAO in accepting a 276 h proposal for a sensitive survey of the 2 deg2 field of the COSMOS survey with the VLBA, to observe almost 3000 sub-mJy radio sources. This survey will greatly simplify the data analysis since it will result in a uniform sensitivity over a large region. Furthermore, a 200 h project has been accepted, aiming at carrying out snapshot observations of more than 10 000 FIRST sources over 100 deg2. The data from these two projects taken together, and adding statistics from all-sky surveys of VLBI calibrator sources, will allow a construction of the source counts of VLBI-detected sources from the Jy to the μJy regime.
Online material
Data of the 217 sources which were in principle detectable (SVLA > 6 × rms).
Multi-wavelength data for the VLBI-detected sources.
 |
Fig. 21 Contour plots of the VLBA images of the 65 detected sources. The plots show
regions of 216 mas × 216 mas, centred on the sources, except for the plot of
L0703, which shows a region of 360 mas × 360 mas. Black contours indicate the
full-resolution, naturally-weighted images, whereas grey, dashed contours indicate
images made with a 10 Mλ taper. The black and grey ellipses in
the lower left corners indicate the size and orientation of the restoring beams
used with full resolution and a 10 Mλ taper, respectively. In
both cases contours start at the 3 times the naturally-weighted image noise and
increase by factors of |
 |
Fig. 21 continued. |
 |
Fig. 21 continued. |
 |
Fig. 21 continued. |
 |
Fig. 21 continued. |
 |
Fig. 22 Left column: UV to mid-infrared SED fits. Black points: photometric observations, red line: best-fitting model, cyan line: stellar template, black line (where applicable): galaxy template of second photometric redshift solution. The inset shows the probability distribution function of the best-fit model. Right column: RGB cutouts made from Subaru RcIcz′ images, with a single VLA contour overlaid and the VLBA position indicated with red crosses. These images show regions 28.8 arcsec × 28.8 arcsec in size. |
 |
Fig. 22 continued. |
 |
Fig. 22 continued. |
 |
Fig. 22 continued. |
 |
Fig. 22 continued. |
 |
Fig. 22 continued. |
 |
Fig. 22 continued. |
 |
Fig. 22 continued. |
 |
Fig. 22 continued. |
 |
Fig. 22 continued. |
 |
Fig. 23 RGB images of sources with uncatalogued, blended, or otherwise unavailable counterparts, made using the same settings as used for Fig. 22. In L0199, L0251, L0386 and L0708 very faint, but uncatalogued counterparts can be seen in the images; in L0506 and L1148 the VLBA detection is offset from the foreground object by so much that an association was deemed unlikely. |
 |
Fig. 24 RGB images of sources with no visible counterparts, made using the same settings as used for Fig. 22. |
Updated versions of the catalogues are available at http://www.rzg.mpg.de/~sotiriaf/surveys/LH
Acknowledgments
This work made ample use of Topcat (Taylor 2005), written by Mark Taylor and available at http://www.star.bris.ac.uk/~mbt/topcat. We wish to thank its author for support and added features, which greatly simplified the data analysis presented here. We also acknowledge the authors of APLpy, an open-source plotting package for Python hosted at http://aplpy.github.com, with which many of the figures shown here were made. Finally we wish to thank the VLBA staff who greatly supported the experimental observations in this project, and who continue to do so. The National Radio Astronomy Observatory, which operates the VLBA, is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
References
- Barris, B. J., Tonry, J. L., Blondin, S., et al. 2004, ApJ, 602, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Brunner, H., Cappelluti, N., Hasinger, G., et al. 2008, A&A, 479, 283 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., Ivison, R. J., & Frail, D. A. 2003, ApJ, 590, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Ciliegi, P., McMahon, R. G., Miley, G., et al. 1999, MNRAS, 302, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Clopper, C., & Pearson, E. S. 1934, Biometrika, 26, 404 [CrossRef] [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A. T., Tingay, S. J., Bailes, M., & West, C. 2007, PASP, 119, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A. T., Brisken, W. F., Phillips, C. J., et al. 2011, PASP, 123, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Elbaz, D., Dickinson, M., Hwang, H. S., et al. 2011, A&A, 533, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Fotopoulou, S., Salvato, M., Hasinger, G., et al. 2012, ApJS, 198, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gaibler, V., Khochfar, S., Krause, M., & Silk, J. 2012, MNRAS, 3446 [Google Scholar]
- Garrett, M. A., Wrobel, J. M., & Morganti, R. 2004, in European VLBI Network on New Developments in VLBI Science and Technology, eds. R. Bachiller, F. Colomer, J.-F. Desmurs, & P. de Vicente, 35 [Google Scholar]
- Garrett, M. A., Wrobel, J. M., & Morganti, R. 2005, ApJ, 619, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Hales, C. A., Murphy, T., Curran, J. R., et al. 2012, MNRAS, 425, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Evans, D. A., & Croston, J. H. 2007, MNRAS, 376, 1849 [NASA ADS] [CrossRef] [Google Scholar]
- Higdon, J. L., Higdon, S. J. U., Weedman, D. W., et al. 2005, ApJ, 626, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D. C., & Wardle, J. F. C. 2004, ApJ, 602, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M., Afonso, J., Chan, B., et al. 2003, AJ, 125, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Ibar, E., Ivison, R. J., Biggs, A. D., et al. 2009, MNRAS, 397, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Kettenis, M., van Langevelde, H. J., Reynolds, C., & Cotton, B. 2006, in Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 497 [Google Scholar]
- Kewley, L. J., Heisler, C. A., Dopita, M. A., et al. 2000, ApJ, 530, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Lavalley, M. P., Isobe, T., & Feigelson, E. D. 1992, BAAS, 24, 839 [Google Scholar]
- Lenc, E., Garrett, M. A., Wucknitz, O., Anderson, J. M., & Tingay, S. J. 2008, ApJ, 673, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Lonsdale, C. J., Smith, H. E., Rowan-Robinson, M., et al. 2003, PASP, 115, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Mauduit, J.-C., Lacy, M., Farrah, D., et al. 2012, PASP, 124, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Middelberg, E., Deller, A., Morgan, J., et al. 2011a, A&A, 526, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Middelberg, E., Norris, R. P., Hales, C. A., et al. 2011b, A&A, 526, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morgan, J. S., Mantovani, F., Deller, A. T., et al. 2011, A&A, 526, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mullaney, J. R., Pannella, M., Daddi, E., et al. 2012, MNRAS, 419, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, R. P., Afonso, J., Appleton, P. N., et al. 2006, AJ, 132, 2409 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, R. P., Afonso, J., Cava, A., et al. 2011a, ApJ, 736, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, R. P., Hopkins, A. M., Afonso, J., et al. 2011b, PASA, 28, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Onodera, M., Renzini, A., Carollo, M., et al. 2012, ApJ, 755, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, F. N., & Morrison, G. E. 2008, AJ, 136, 1889 [NASA ADS] [CrossRef] [Google Scholar]
- Pacholczyk, A. G. 1970, Radio astrophysics. Nonthermal processes in galactic and extragalactic sources (Series of Books in Astronomy and Astrophysics, San Francisco: Freeman) [Google Scholar]
- Padovani, P. 2011, MNRAS, 411, 1547 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., Miller, N., Kellermann, K. I., et al. 2011, ApJ, 740, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Page, M. J., Symeonidis, M., Vieira, J. D., et al. 2012, Nature, 485, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Prevot, M. L., Lequeux, J., Prevot, L., Maurice, E., & Rocca-Volmerange, B. 1984, A&A, 132, 389 [NASA ADS] [Google Scholar]
- Rosario, D. J., Santini, P., Lutz, D., et al. 2012, A&A, 545, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rovilos, E., Burwitz, V., Szokoly, G., et al. 2009, A&A, 507, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rovilos, E., Comastri, A., Gilli, R., et al. 2012, A&A, 546, A58 [Google Scholar]
- Salvato, M., Hasinger, G., Ilbert, O., et al. 2009, ApJ, 690, 1250 [CrossRef] [Google Scholar]
- Salvato, M., Ilbert, O., Hasinger, G., et al. 2011, ApJ, 742, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Smolčić, V., Carilli, C. L., et al. 2007, ApJS, 172, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Shao, L., Lutz, D., Nordon, R., et al. 2010, A&A, 518, L26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simpson, C., Martínez-Sansigre, A., Rawlings, S., et al. 2006, MNRAS, 372, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Smolčić, V., Schinnerer, E., Scodeggio, M., et al. 2008, ApJS, 177, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 29 [Google Scholar]
- Tolman, R. C. 1930, Proceedings of the National Academy of Science, 16, 511 [Google Scholar]
- Uson, J. M., & Cotton, W. D. 2008, A&A, 486, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, M. A. 1998, MNRAS, 294, 307 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Average position offsets relative to epoch B before and after position correction.
Beam squint parameters at 1.438 GHz for the VLBA antennas (C. Walker, priv. comm.).
All Figures
 |
Fig. 1 Overview of the Lockman Hole/XMM observations. Shown is the Spitzer 3.6 μm image as colour scale in the background. The three circles denote the FWHM of the VLBA antennas’ primary beams. The pointing coordinates have been taken from the VLA observations of this field reported in Ibar et al. (2009). It is also indicated which pointings have been observed in epochs A to D. Crosses indicate radio sources from Ibar et al. (2009) with a flux density of 100 μJy or more, and located within 20 arcmin of a pointing centre. |
| In the text | |
 |
Fig. 2 Distribution of VLA source flux densities in bins with edges at
100 μJy |
| In the text | |
 |
Fig. 3 Contour plot of the radio source L0412 before (left) and after (right) multi-source self-calibration has been applied. Contours are drawn at 0.1 mJy × (1, 2, 4, ...). The S/N was improved from 72 to 115. The peak flux density has increased significantly, the noise has dropped, and image artefacts are much reduced. At low elevation, or when calibration is poorer, these effects will be more pronounced. |
| In the text | |
 |
Fig. 4 Locations of the antenna pointing positions used to test the primary beam attenuation of the VLBA antennas, shown on top of an NVSS postage stamp. 3C 84, in the image centre, has always been used as the field centre in the correlation, so that it was seen by the antennas through the various parts of the primary beam power pattern, the FWHM of which is indicated by the circle. |
| In the text | |
 |
Fig. 5 Peak flux densities of 3C 84 before and after primary beam correction. Left panel: peak amplitudes measured using the pointings in Fig. 4 as a function of distance to the true source position. Also shown are two fits to the data, one using a Gaussian (dashed line) and one using an Airy disk (solid line). The Airy disk performs slightly better. Right panel: peak amplitudes after applying the primary beam corrections using an Airy disk model fitted to the data in the left panel. The standard deviation of the measurements, normalised to their mean (shown as the solid line), is 0.039. |
| In the text | |
 |
Fig. 6 Visibility amplitudes before and after primary beam correction. Left panel: visibility amplitudes from all pointings on a few selected baselines before primary beam correction. The pointing centres are indicated at the bottom of the diagram. Shown is total intensity after averaging all frequencies and the two polarisations. Right panel: the same visibilities after primary beam correction. Whilst there are only small steps and discontinuities in the corrected visibilities (indicating that the correction scheme is working well), there are longer-term trends in the amplitudes, which may be attributed to the substantial structure of 3C 84, which was not modelled due to the poor (u,v) coverage of the data. The larger scatter during some pointings is a consequence of the reduced sensitivity towards directions well away from the pointing centre. |
| In the text | |
 |
Fig. 7 Illustration of the effects of beam squint and its correction. Left panel: the ratio of the RCP and LCP amplitudes on a few selected baselines before primary beam correction. The pointing centres are indicated at the bottom of the diagram. Deviations from unity are caused by the RCP and LCP beams pointed at different positions. Right panel: the same visibilities after primary beam correction. The differences have essentially be eliminated. |
| In the text | |
 |
Fig. 8 Illustration of the amplitude consistency between epochs. Left panel: amplitudes of a sample of bright sources in epochs A/C/D as a function of the amplitude in epoch B. Right panel: the same diagram but amplitudes have been extracted from images with the same limited (u,v) coverage. |
| In the text | |
 |
Fig. 9 Sensitivity map of the VLBA observations. The rms noise of the individual images has
been placed on a grid and then linearly interpolated to fill the map. The colour bar
indicates Jy, and contours were drawn at |
| In the text | |
 |
Fig. 10 Point spread functions using uniform (left panel) and natural (right panel) weighting. Contours are drawn at 10% × N (N = 0, 1, 2, ..., 9) of the peak. The plateau in the naturally-weighted image at the 30% level is obvious. |
| In the text | |
 |
Fig. 11 Histogram of the pixels in the image made from source L0211, which was not detected. The upper panel shows the histogram along with a model distribution calculated from the pixel’s σ, and vertical lines indicating the mean and ± 1σ, ± 3σ, and ± 5σ. The lower panel shows the residuals, normalised to the histogram. At the very low and very high end an excess of pixels can be clearly seen. |
| In the text | |
 |
Fig. 12 Example contour plots of the VLBA, VLA, and SWIRE data. The upper panel shows the logarithm of the SWIRE 3.6 μm emission as a pixel map, superimposed with contours of the VLA data of source L0034. Contours start at 2 times the local rms (as indicated in the plots) and increase by factors of 2. This object has four entries in the VLA catalogue: one, L0034, representing it as a source and three for its constituents, L0035, L0036, and L0037. Their locations are marked as labels in the image. Three black squares indicate (from large to small) (i) the regions imaged with the VLBA using a 10 Mλ taper; (ii) the region imaged using untapered data; and (iii) the region shown in the contour plot in the bottom panel. The maximum of the tapered VLBA data is marked with a cross, and the maximum of the untapered VLBA data is marked with an open circle. In this case, the maxima of the tapered and untapered VLBA images are not coincident, because the tapered image has reduced sensitivity. However, the maximum at full-resolution (6.2σ) coincides with a faint SWIRE source located between L0035 and L0036, indicating that this is the location of the AGN. Furthermore, the value of the tapered image exceeds 5σ at the location of the maximum of the untapered image, adding credibility to the detection. The bottom panel shows a contour map of a region 0.36 arcsec across, centred on the maximum of the untapered VLBA image. Contours start at 2 times the local rms (as indicated in the plots) and increase by factors of 2. |
| In the text | |
 |
Fig. 12 continued. This plot shows data for source L0119. Three catalogued VLA components belong to this source. The detection at 24σ and cross-identification with a SWIRE source is unambiguous. |
| In the text | |
 |
Fig. 12 continued. This plot shows data for source L0698, which has been grouped with source L0697. The maxima of the two VLBA images coincide neither with each other, nor with an infrared source, and therefore this source with a maximum of 5.2σ was deemed to be undetected. |
| In the text | |
 |
Fig. 13 Fraction of VLBA-detected sources. Left panel: the fraction of
VLBA-detected sources as a function of flux density. Detectable sources have been
grouped into bins with limits
100 μJy |
| In the text | |
 |
Fig. 14 Ratio of the VLBA and VLA flux densities. Blue dots show the detectable sources, placed at 6 × rms/SVLA (where rms is the local noise level of the VLBA observations), and red dots with error bars detected sources. Out of the 65 detected sources, 6 exceed a ratio of 1.0 by more than 1σ, but only one source exceeds 1 + 3σ. |
| In the text | |
 |
Fig. 15 A histogram of the spectral indices of detectable (blue bars) and detected (red bars) sources. |
| In the text | |
 |
Fig. 16 Source counts in the Lockman Hole/XMM field. Shown are the Euclidean-normalised source counts of the VLBA-detected sources, using their VLA flux densities (red line). Shown with black lines are source counts that would have been measured had the sensitivity of our observations been lower by factors of 1.1, 1.5, and 2.0. For comparison, we have plotted the source counts constructed from the Ibar et al. (2009) data using the same methods (blue line), the source counts as published by Ibar et al. (2009) (green line), and the data compilation from Hopkins et al. (2003) (light grey squares) along with their 6th order polynomial fit. |
| In the text | |
 |
Fig. 17 The difference between the 1.4 GHz radio luminosity measured with the VLA, LVLA and measured with the VLBA, LVLBA, as a function of LVLBA. The solid line indicates the correlation as indicated in the text, and the dotted lines the error of the normalisation. |
| In the text | |
 |
Fig. 18 VLBA-detected sources with optical counterparts (red circles). The multi-wavelength coverage of the field is also shown: Subaru Rc, Ic, z′ filters (image), LBT U and B filters (blue solid line), LBT VYz′ filters (blue dashed line), IRAC 3.6 μm and 5.8 μm (yellow solid line), IRAC 4.5 μm and 8 μm (yellow dashed line), SDSS (black dashed line), J and K UKIDSS filters (black solid lines). The black circle denotes the area observed by XMM-Newton. |
| In the text | |
 |
Fig. 19 Rc magnitude vs. VLA flux density for the 47 sources with optical counterparts (for source L0953 the SDSS r magnitude was used). The majority of the population is classified as radio-loud. The limit for star-forming galaxies and radio-quiet AGN is given by the grey dashed line indicating log (SVLA/Rc) = 1.4, but radio-loud AGN can in principle populate the entire diagram. |
| In the text | |
 |
Fig. 20 X-ray flux versus VLA flux density for the 26 sources inside the area covered by XMM-Newton. The lines denote the area occupied by X-ray AGN (dash-dotted line), radio-quiet AGN (dotted line), star-forming objects (dashed line) and radio galaxies (solid line), as presented in Padovani (2011). Upper limits are drawn for the 16 sources below the X-ray flux limit. |
| In the text | |
 |
Fig. 21 Contour plots of the VLBA images of the 65 detected sources. The plots show
regions of 216 mas × 216 mas, centred on the sources, except for the plot of
L0703, which shows a region of 360 mas × 360 mas. Black contours indicate the
full-resolution, naturally-weighted images, whereas grey, dashed contours indicate
images made with a 10 Mλ taper. The black and grey ellipses in
the lower left corners indicate the size and orientation of the restoring beams
used with full resolution and a 10 Mλ taper, respectively. In
both cases contours start at the 3 times the naturally-weighted image noise and
increase by factors of |
| In the text | |
 |
Fig. 21 continued. |
| In the text | |
 |
Fig. 21 continued. |
| In the text | |
 |
Fig. 21 continued. |
| In the text | |
 |
Fig. 21 continued. |
| In the text | |
 |
Fig. 22 Left column: UV to mid-infrared SED fits. Black points: photometric observations, red line: best-fitting model, cyan line: stellar template, black line (where applicable): galaxy template of second photometric redshift solution. The inset shows the probability distribution function of the best-fit model. Right column: RGB cutouts made from Subaru RcIcz′ images, with a single VLA contour overlaid and the VLBA position indicated with red crosses. These images show regions 28.8 arcsec × 28.8 arcsec in size. |
| In the text | |
 |
Fig. 22 continued. |
| In the text | |
 |
Fig. 22 continued. |
| In the text | |
 |
Fig. 22 continued. |
| In the text | |
 |
Fig. 22 continued. |
| In the text | |
 |
Fig. 22 continued. |
| In the text | |
 |
Fig. 22 continued. |
| In the text | |
 |
Fig. 22 continued. |
| In the text | |
 |
Fig. 22 continued. |
| In the text | |
 |
Fig. 22 continued. |
| In the text | |
 |
Fig. 23 RGB images of sources with uncatalogued, blended, or otherwise unavailable counterparts, made using the same settings as used for Fig. 22. In L0199, L0251, L0386 and L0708 very faint, but uncatalogued counterparts can be seen in the images; in L0506 and L1148 the VLBA detection is offset from the foreground object by so much that an association was deemed unlikely. |
| In the text | |
 |
Fig. 24 RGB images of sources with no visible counterparts, made using the same settings as used for Fig. 22. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.