| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 14 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201220133 | |
| Published online | 16 January 2013 | |
γ-ray DBSCAN: a clustering algorithm applied to Fermi-LAT γ-ray data
I. Detection performances with real and simulated data
1
ISDC, University of Geneva,
Chemin d’Ecogia 16,
1290
Versoix,
Switzerland
e-mail:
andrea.tramacere@unige.ch
2
Politecnico di Milano, Piazza L. da Vinci 32,
20133
Milano,
Italy
Received:
30
July
2012
Accepted:
30
September
2012
Context. The density based spatial clustering of applications with noise (DBSCAN) is a topometric algorithm used to cluster spatial data that are affected by background noise. For the first time, we propose this method to detect sources in γ-ray astrophysical images obtained from the Fermi-LAT data, where each point corresponds to the arrival direction of a photon.
Aims. We investigate the detection performance of the γ-ray DBSCAN in terms of detection efficiency and rejection of spurious clusters.
Methods. We used a parametric approach, exploring a large volume of the γ-ray DBSCAN parameter space. By means of simulated data we statistically characterized the γ-ray DBSCAN, finding signatures that distinguish purely random fields from fields with sources. We defined a significance level for the detected clusters and successfully tested this significance with our simulated data. We applied the method to real data and found an excellent agreement with the results obtained with simulated data.
Results.We find that the γ-ray DBSCAN can be successfully used in detecting clusters in γ-ray data. The significance returned by our algorithm is strongly correlated with that provided by the maximum likelihood analysis with standard Fermi-LAT software, and can be used to safely remove spurious clusters. The positional accuracy of the reconstructed cluster centroid compares to that returned by standard maximum likelihood analysis, allowing one to look for astrophysical counterparts in narrow regions, which minimizes the chance probability in the counterpart association.
Conclusions.We found that γ-ray DBSCAN is a powerful tool for detecting of clusters in γ-ray data. It can be used to look for both point-like sources and extended sources, and can be potentially applied to any astrophysical field related to detecting clusters in data. In a companion paper we will present the application of the γ-ray DBSCAN to the full Fermi-LAT sky, discussing the potential of the algorithm to discover new sources.
Key words: gamma rays: general / methods: statistical / methods: data analysis / methods: numerical
© ESO, 2013
1. Introduction
Modern γ-ray telescopes operating at energies above the MeV window provide event-resolved observational data. Each event (after the reconstruction process) is typically described by a tuple (i.e., an ordered list of elements) storing sky coordinates, arrival time, and energy. Discrete sources (either point-like or extended) are detected with various methods. Given the discrete topological nature of γ-ray images, methods based on cluster search, such as the minimum spanning three (MST; Campana et al. 2007, 2012), have successfully been used. One of the main advantages of topometric methods compared to methods using the spatial binning is to minimize the impact of the poor energy-dependent point spread function (PSF), typical of γ-ray telescopes, and to preserve the spatial information of each event. Moreover, these methods are able to detect sources compounded by a small amount of events, but they need to be fine-tuned to take the background properly into account. The problem of background rejection is the most penalizing feature of topometric methods. Therefore we here present for the first time a method based on the density based spatial clustering of applications with noise (DBSCAN) algorithm (Ester et al. 1996). The DBSCAN is a topometric algorithm used to cluster spatial data that are affected by background noise. Compared to other topometric methods, it has the advantage to embed the discrimination between signal (cluster) and background (noise) inside the algorithm itself, according to the local density of events within a typical scanning brush, i.e., within a given scanning area.
The aim of the present paper is to show the potential of the method, and its statistical characterization when applied to astrophysical γ-ray data. We applied this method to detect point-like sources in the Fermi-LAT data. We explored a large volume of the γ-ray DBSCAN parameter space by means of simulated data, and we provide a statistical characterization of the γ-ray DBSCAN, finding signatures that distinguish purely random fields from fields with sources. We defined a significance level for the detected clusters, and we successfully tested this significance with our simulated data. We applied the method to real Fermi-LAT γ-ray data and we found an excellent agreement with the results obtained with simulated data.
In a companion paper (Tramacere, in prep.), we will apply the method to the Fermi-LAT sky, investigating specific questions related to the Fermi-LAT response functions, showing the potential to the discovery new sources, in particular of small clusters located at high galactic latitude, or clusters on the Galactic plane that are affected by a strong background.
The paper is organized as follows. In Sect. 2 we describe the logic of the DBSCAN method and present the algorithm implemented to analyze γ-ray data, the γ-ray DBSCAN. In Sect. 3 we discuss some caveats regarding the application of the γ-ray DBSCAN algorithm to γ-ray data. In Sect. 4 we study the statistical properties of the γ-ray DBSCAN detection, using a simulated test field with only noise, and five simulated test fields with noise plus point-like sources. In Sect. 5 we evaluate the detection performance of the method in terms of positional accuracy, cluster reconstruction, and rejection of spurious clusters. In Sect. 6 we investigate the significance of the clusters and describe our algorithmic implementation. In Sect. 7 we finally use our method with real Fermi-LAT data, investigating the detection performance, and comparing the γ-ray DBSCAN clusters significance to that returned by the maximum likelihood method with standard Fermi-LAT software1. In Sect. 8, we present our conclusions and discuss future developments and applications.
2. The γ-ray DBSCAN algorithm
The DBSCAN (Ester et al. 1996) is a topometric algorithm used to cluster spatial data that are affected by background noise. Some modifications have been developed to adapt the original DBSCAN algorithm to our study. Our algorithm is mainly built upon the following criteria:
-
1.
In a list of photons D, where each element pi is a tuple storing positional sky coordinates, ρ(pk,pl) is the angular distance between two photons pk and pl.
-
2.
We iterate over the full photon list D. A seed cluster
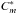 is built
when a minimum number of photons K + 1 is enclosed within a circle of
radius ε centered on pi.
is built
when a minimum number of photons K + 1 is enclosed within a circle of
radius ε centered on pi.
-
3.
For each photon
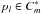 , we build
the photon list
, we build
the photon list 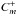 by
collecting all photons pk that meet the
condition
ρ(pl,pk) < ε,
and
by
collecting all photons pk that meet the
condition
ρ(pl,pk) < ε,
and 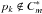 .
. -
4.
For each photon
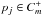 , if the
number of photons enclosed within a circle of radius ε centered on
pj is ≤K and
, if the
number of photons enclosed within a circle of radius ε centered on
pj is ≤K and
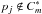 , then
pj will be attached to the final photon
list of the cluster without a recursive search for more neighbors, these points are
defined density-reachable.
, then
pj will be attached to the final photon
list of the cluster without a recursive search for more neighbors, these points are
defined density-reachable. -
5.
For each photon
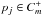 , if the
number of photons enclosed within a circle of radius ε centered on
pj is >K and
, if the
number of photons enclosed within a circle of radius ε centered on
pj is >K and
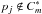 ,
pj is attached to the
,
pj is attached to the
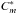 , and step
3 is repeated recursively.
, and step
3 is repeated recursively. -
6.
When both conditions at step 4 and 5 are false, the cluster Cm is built by joining the density-reachable events to those in the
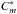 and in
the
and in
the 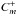 lists.
lists.
-
7.
The process starts again from step 1 searching for new clusters, skipping the events already flagged as noise or clusters, until all events in D are flagged as cluster, or noise, or density-reachable events.
-
8.
At the end of the process the full photon list will be partitioned as follows:
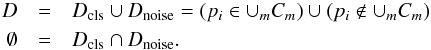 (1)
(1)
In this way high-density areas are classified as clusters (sources), conversely low-density areas are classified as noise (background). The recursive call of step 3 is not implemented in the original DBSCAN algorithm and represents a novelty. This new feature allows us to reconstruct clusters significantly larger than the ε radius, which makes it unlikely that a single clusters is fragmented into small satellite clusters. Moreover, it allows the possibility to reconstruct extended structures, in particular extended sources, or filamentary structures in the background.
After the clustering process, each photon in D will be described by a
tuple storingthe photon position (both in galactic and celestial coordinates), the photon
class type (noise or cluster), and the ID of the cluster
the photon belongs to. Each cluster Cm will be
described by a tuple storing the position of the centroid with his positional error, the
ellipse of the cluster containment, the cluster effective radius
(reff), and number of photons in the cluster
(Np). The ellipse of the cluster containment
is defined by major and minor semi-axis (σx and
σy) and the inclination angle
(σalpha) of the major semi-axis w.r.t. the latitudinal
coordinate (b or Dec). To evaluate the ellipse axis we use the principal
component analysis method (PCA; Jolliffe 1986). This
method uses the eigenvalue decomposition of the covariance matrix of the two position arrays
x and y. By definition, the square root of the first eigenvalue
will correspond to σx and the second to
σy. The axes represent the two orthogonal
directions of maximum variance of the cluster. The effective radius is defined as
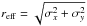 .
To find the centroid of the cluster and its uncertainty, we used a weighted average of the
position of each photon in Cm, as follows:
.
To find the centroid of the cluster and its uncertainty, we used a weighted average of the
position of each photon in Cm, as follows:
-
We define the first order centroid (Cave) as the average of the position ofeach cluster photon: Cave = (⟨x⟩, ⟨y ⟩).
-
We define the weight array, according to the distance between pk ∈ Cm and Cave: wk = 1/ρ(pk,Cave).
-
The cluster centroid Cctr will result from the average of the position of each cluster point weighted by wk.
-
The centroid position uncertainty (poserr) is determined by propagating the error on the weighted average of Cctr. We have numerically verified that poserr corresponds to a ≈95% positional uncertainty.
3. Caveat on the application to γ-ray data
The application of clustering methods, such as the γ-ray DBSCAN, leads to practical difficulties that are mostly related to the instrument PSF and to gradient and/or structures in the background. To deal with these problems without biasing the detection results, we recommend to apply some criteria that we discuss in the following.
We first comment on the PSF impact. The PSF imposes a limit on the capability of an instrument to resolve sources separated by a distance smaller than the PSF size. Sources with sizes smaller than the PSF are classified as point-like, otherwise they are classified as extended. Another complication is that the PSF often depends on the energy; in the case of Fermi-LAT, the 68% containment angle of the reconstructed incoming photon direction, for normal incidence photons, has a size of about 5 degrees at 100 MeV (Ackermann et al. 2012), and scales down to a few tenths of degree above the GeV energies2. The size of the PSF is strongly connected to the size ε of the γ-ray DBSCAN scanning brush. Indeed, if ε is much smaller than the PSF size, it might occur the risk to loose clusters characterized by small Np, or to fragment a cluster with large Np in smaller fake satellite clusters. We stress that the formation of satellite clusters is a very rare event, thanks to our recursive DBSCAN implementation, which we explain in Sect. 2. In contrast, if ε is much larger than the PSF, it is likely to build extended clusters contaminated by the background or by close sources.
A careful and self-consistent analysis of the effects of the energy dependence of the PSF, and in general of problems related to the Fermi-LAT response function, is beyond the scope of this paper, where we focus mostly on a statistical characterization of the method. These topics will be investigated in the companion paper (Tramacere, in prep.).
A second relevant problem, is the inhomogeneity of the background, which affects the choice of both ε and K. If the background is homogeneous over the entire field, the best choice of a single pair of values of ε and K guarantees a safe rejection of the background. Indeed, values of ε and K such that the average density of photons within ε is significantly higher than the average density of the background photons, make it unlikely that a cluster grows from a background fluctuation. Unfortunately, the γ-ray sky shows strong gradients of background, in particular at low galactic latitudes. To solve this problem, one could think to adapt the value of ε and K according to a local value of the background photon density. Since ε has a strong constraint imposed by the PSF, one should tune mainly the value of K. The drawback is that as we increase the value of K to compensate for the background, we decrease the capability to detect clusters with small Np. To overcome this difficulty, we adopted an alternative solution. We used a unique pair of values of ε and K for each field, where ε is mostly constrained by the PSF, and K by the field average background, and we take into account the background inhomogeneities by defining a significance level of the cluster, according to the signal-to-noise ratio (S/N; Li & Ma 1983), evaluated from the local background. This is explained in detail in Sect. 6. The capability to reject clusters according to a low significance level allows one to relax the constrain on ε and K, increasing the number of clusters detected, hence increasing the detection ratio, and at the same time allows one to reject spurious sources, because of the significance threshold. To avoid that the background is so high that the fluctuations in the background events can lead to densities comparable to those of weak sources, it’s recommended to apply a cut in energy, to make this possibility rare. To optimize the ratio between background and cluster events, we use a threshold energy of 3 GeV in the following, that mitigates the possible bias caused by the background fluctuations.
 |
Fig. 1 Photon map for the sky test field 1, with the result of the γ-ray DBSCAN detection for K = 5 and ε = 0.17 deg. The blue crosses refer to the simulated sources, the green boxes to 51 detected true clusters, and the red boxes to the 2 fake ones. The black dots represent the background events, the remaining colors indicate cluster events. |
4. Statistical properties of the γ-ray DBSCAN clusters
4.1. The test fields
In this section we study the statistical properties of the clusters, looking for signatures that characterize random Poissonian fields and fields with point-like sources. To accomplish this task we compare results obtained for a test field with only noise (random test field) and the five test fields with noise plus point-like sources (sky test fields 1–5).
As skytest fields we use the same fields as in Campana et al. (2012). Each of these five sky fields
covers a broad sky region with a galactic longitude extension of
80° < l < 170° and a galactic latitude extension of
40° < b < 65°. The γ-ray background was
simulated using the standard gtobssim3 tool, developed by the Fermi-LAT collaboration, simulating
both the Galactic and isotropic components for a two-year-long period, using a threshold
energy of 3 GeV for a total amount of 9322 photons. To this photon list we added 70
simulated sources: for each source, the number of photons was chosen from a probability
distribution given by a power-law with exponent 2 from a minimum value of 4 up to 40
photons, joined to a constant tail up of to 240 photons. The number of the sources is
similar to that reported in the Fermi-LAT Second Source Catalog (Nolan et al. 2012, 2FGL hereafter), in the same region
of the sky. The source events are spatially distributed with a bivariate Gaussian
probability density function (PDF) with 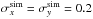 deg,
centered at the source location. Five simulated test fields were generated, adding the
simulated sources to the diffuse background. The only difference in the five realizations
is the source location, randomly chosen to have different brightness contrast between
sources and the background. The random test field covers the same area as
the sky test fields and a number of events equal to the sky
test field-1 (background and sources) for a total amount of 11 044 events.
deg,
centered at the source location. Five simulated test fields were generated, adding the
simulated sources to the diffuse background. The only difference in the five realizations
is the source location, randomly chosen to have different brightness contrast between
sources and the background. The random test field covers the same area as
the sky test fields and a number of events equal to the sky
test field-1 (background and sources) for a total amount of 11 044 events.
In Fig. 1 we show the photon map for the sky test field 1 and the result of the γ-ray DBSCAN detection for K = 5 and ε = 0.17 deg. We detect 51 true clusters, and only 2 fake ones. A cluster is defined as true if the position of the simulated source falls within a circle centered on the cluster centroid, with a radius equal to 2poserr.We call the remaining clusters fake. In Fig. 2, we show a close-up of two true clusters. The black ellipses correspond to the ellipses of the cluster containment, and the purple and orange thick points represent the cluster points, while the black thick dots represent the background.
4.2. Test strategy
We investigated the statistical properties of the γ-ray DBSCAN clusters, in particular signatures that distinguish purely random fields from fields with point-like sources, and their dependence on K and ε. To systematically investigate a broad volume of the parameter space, we used a parametric approach. We set the range of ε in [0.1 ÷ 0.50] deg. with a step of 0.01 deg, and the range of K in [2 ÷ 15], with a step of 1. The total amount of detection trials for each test field was 574. We collected the statistics of the trials and investigated the distribution of reff and Np, and their connection with ε and K, respectively.
 |
Fig. 2 Close-up of two true clusters reported in Fig. 1. The ellipses correspond to the ellipse of the cluster containment. The purple and orange points represent the cluster points, the black dots represent the background events, the blue crosses the position of the simulated sources, and green boxes the position of the cluster centroid. |
4.3. Statistics of reff and connection with ε
We started by investigating the distribution of the log (reff) values for the random and the sky test field 1. The distribution for the detections collected over the full K-ε parameter space (top left panel of Fig. 3) shows a symmetric shape well fitted by a Gaussian distribution (log-normal w.r.t. reff), with the mean value of ⟨log 10(reff)⟩ ≃ −0.45 (corresponding to ⟨reff⟩ ≃ 0.3 deg) and a dispersion of σlog 10(reff) ≃ 0.23.The log-normal distribution provides a reasonable description of the empirical distributions also for individual pairs of (K, ε) values. An example is given in panel c of Fig. 3 for K = 3, ε = 0.3 deg, where the best fit values are ⟨log 10(reff)⟩ ≃ −0.51, and σlog 10(reff) ≃ 0.16. We now investigate the empirical distribution of log 10(reff) for fields with point-like sources. In the right panel of Fig. 3, we show the case of the sky test field 1. The distributions of log 10(reff) are still described by a by a normal. For fake clusters (red dashed line) the best fit values of the mean (⟨log 10(reff)⟩ ≃ −0.46) and of the dispersion (σlog 10reff ≃ 0.24) are very similar to those found for the random test field. In contrast, the true cluster distribution (blue hatched histogram) is peaking around the value of log 10(reff) ≃ −0.67 deg, corresponding to reff ≃ 0.21 deg, very close to the value of the dispersion σsim = 0.20 deg, which was used to simulate the sources.Since the simulation parameter σsim reproduces the effect of the instrumental PSF, we observe that the typical size of the reconstructed clusters for non-random fields, is constrained by the PSF, suggesting that the empirical rule is to set the value of ε of about the PSF size.
To investigate the connection between ε and the PSF more accurately, we analyzed the statistical properties of the quantity reff/ε as a function of ε. For each value of ε, we determined the median, and the two-sided 1-σ confidence level (CL) interval around the median of the reff/ε distributions. In the left panel of Fig. 4 we plot the reff/ε median (blue solid circles) and 1-σ CL region as a function of ε for the random field. We note that the reff/ε trend is slightly increasing with ε, and that the 1-σ CL region is consistent with reff/ε = 1, but the upper boundary shows a systematic increase compared to the lower boundary for ε ≳ 0.30 deg. The trend for the true clusters in sky test field 1 (right panel Fig. 4), shows a different behavior. The median of reff/ε (red solid circles) is slightly decreasing with ε, showing that for trueclusters reff is not sensitive to the size of ε, being mostly constrained by the simulated PSF size. As expected, for the fake clusters (blue dashed line), the trend is almost identical to that of the clusters in the random field.
 |
Fig. 3 Panel a) distribution of the values of log 10reff for the random field case, for the full parameter space (black line) and fit by means of Gaussian distribution (blue line). Panel b) the same as in the top panel, for K = 3 and ε = 0.3 deg. Panel c) distribution of log 10reff for the sky test field 1, for fake clusters (red solid line), and true clusters (blue solid line, hatched histogram). The dashed lines represent the Gaussian best fit. |
 |
Fig. 4 Left panel: the reff/ε statistical distribution as a function of ε for the random field case. The blue solid circles represent the median, and the gray shaded area represents the 1-σ confidence level region, for each value of ε. Right panel: the same as in the bottom left panel for the sky test field 1. The red solid circles represent the median of the true clusters case, and the grey area the 1-σ confidence level region. The dashed line shows the 1-σ confidence level region, for the fake clusters. |
 |
Fig. 5 Left panels: the distribution of
Np for the random
test field for K = 2, ε = 0.20 deg (panel
a), red solid boxes). The empty blue bar line represents a Poissonian
best fit. Panel b) shows K = 2
ε = 0.30 deg (purple solid triangles). Panel c) shows
the full K-ε parameter space, the solid black line
represent a log-normal best fit. Right panels: panel c)
shows the distribution of |
 |
Fig. 6 Panel b) the Np statistical distribution as a function of K for the random field case. The blue solid circles represent the median and the gray shaded area represents the 1-σ confidence level region around the median for each value of K. The dashed black line represents the Np = K + 1 law. Panel e) same as in panel b) for the sky test field 1 case. Panel a) number of detected clusters for the random test field case (blue solid points) as a function of K, and best fit by means of a Poissonian survival function (red empty bars). Panel c) number of detected cluster for the sky test field 1 case (black solid points), for the fake clusters as a function of K, and best fit by means of a Poissonian survival function (red empty bars). Panel d) number of detected cluster for the sky test field 1 case (red solid boxes) for the true clusters as a function of K, and best fit by means of a Poissonian survival function (black empty boxes). |
4.4. Statistics of Np and connection with K
We now investigate the statistics of the distribution of the number of photons per
cluster. For random fields we expect that the number of photons in a
cluster follows a Poisson distribution. Indeed, for a generic two-dimensional Poisson
process, the probability to observe a number of events
(N(S) = j) enclosed by a surface
S is given by 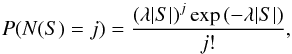 (2)where
λ is the average spatial density. Translating S in
terms of ε2, we can rewrite
(2)where
λ is the average spatial density. Translating S in
terms of ε2, we can rewrite 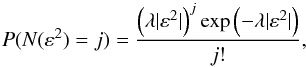 (3)from which it
follows that given the value of K and ε, the probability
to find a cluster as function of K and ε will be given
by
(3)from which it
follows that given the value of K and ε, the probability
to find a cluster as function of K and ε will be given
by 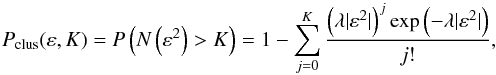 (4)that is the
Poissonian survival function. Owing to the logic of the DBSCAN clustering process, the
Poisson statistics cannot be extended from ε to
reff for any value of ε. Indeed, a cluster
is not a simple collection of points enclosed within a surface S, this
holds only within the ε-sized circle, the seed of the
cluster (C∗). If we consider the annulus defined between
ε and the cluster radius rclus, not all
points in the annulus will be cluster members, but only those that are at least density
reachable. This implies that we expect a deviation from the Poisson statistics, when
reff is significantly larger than ε, i.e.
ε ≳ 0.3 deg (according to the analysis presented in the previous
section). This expected deviation from the Poissonian statistics is confirmed by the plots
in the left panels of Fig. 5. In panel a we show the
distribution of Np for K = 2
and ε = 0.20 deg. We note that the Poisson distribution (Eq. (3)) gives a reasonable description of the
empirical distribution. In contrast, for ε = 0.30 deg (panel b) we
observe that the Poisson distribution shows stronger deviations, in particular for
K > 6. When we take into account the
Np distribution for the full parameter
space (panel c), the Possonian distribution is failing to provide a reasonable description
of the empirical distribution, whilst a log-normal distribution gives a good fit.
(4)that is the
Poissonian survival function. Owing to the logic of the DBSCAN clustering process, the
Poisson statistics cannot be extended from ε to
reff for any value of ε. Indeed, a cluster
is not a simple collection of points enclosed within a surface S, this
holds only within the ε-sized circle, the seed of the
cluster (C∗). If we consider the annulus defined between
ε and the cluster radius rclus, not all
points in the annulus will be cluster members, but only those that are at least density
reachable. This implies that we expect a deviation from the Poisson statistics, when
reff is significantly larger than ε, i.e.
ε ≳ 0.3 deg (according to the analysis presented in the previous
section). This expected deviation from the Poissonian statistics is confirmed by the plots
in the left panels of Fig. 5. In panel a we show the
distribution of Np for K = 2
and ε = 0.20 deg. We note that the Poisson distribution (Eq. (3)) gives a reasonable description of the
empirical distribution. In contrast, for ε = 0.30 deg (panel b) we
observe that the Poisson distribution shows stronger deviations, in particular for
K > 6. When we take into account the
Np distribution for the full parameter
space (panel c), the Possonian distribution is failing to provide a reasonable description
of the empirical distribution, whilst a log-normal distribution gives a good fit.
 |
Fig. 7 Isolevel maps for Dfake (panel a)), Dtrue (panel b)), Deff (panel c)), and Q (panel d)), for the sky test field 1. The white lines show isolevel = 0, the black lines show isolevel = 0.68, and the blue lines show isolevel = 0.95. |
The log-normal trend of Np is consistent
with the log-normal trend of the reff distribution. Since the
number of photons in a cluster will be approximatively
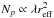 , we can write the
PDF of Np
, we can write the
PDF of Np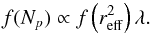 (5)To evaluate the
distribution of
(5)To evaluate the
distribution of 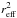 we can use
the standard transformation theory of random variables (RV; Papoulis 1965). It can be easily proved that for an RV X with a
log-normal distribution,
we can use
the standard transformation theory of random variables (RV; Papoulis 1965). It can be easily proved that for an RV X with a
log-normal distribution, 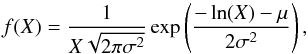 (6)the RV
Y = X2 will follow a log-normal
distribution given by
(6)the RV
Y = X2 will follow a log-normal
distribution given by 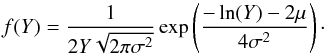 (7)Indeed, our
(7)Indeed, our
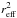 distribution,
for the random field (panel d, Fig. 5), is fitted by a log-normal distribution peaking at ≃0.03 deg2.
Hence, according to Eq. (5) we expect that
also f(Np) will follow a
log-normal distribution, when Np is not ruled
by a Poissonian statistics.
distribution,
for the random field (panel d, Fig. 5), is fitted by a log-normal distribution peaking at ≃0.03 deg2.
Hence, according to Eq. (5) we expect that
also f(Np) will follow a
log-normal distribution, when Np is not ruled
by a Poissonian statistics.
We verified that the same statistical trends describe the real sky fields. Panels e and f in Fig. 5 show the statistical distribution of Np for the sky test field 1. In agreement with the analysis for the random test field, we see that the fakeclusters (ε = 0.30 deg, panel e in Fig. 5) are described by a Possonian statistic, whilst the true clusters (panel f in Fig. 5) are better described by a log-normal distribution (red dashed line) than by a Poissonian distribution (solid black line). We also observe that the log-normal law reasonably describes the empirical distribution only for values of Np ≲ 50, but shows significant deviation in the tail, consistent with the statistics of our simulated source population.
To complete this statistical characterization, we investigated the distribution of the number of detected clusters as a function of the threshold K. According to Eq. (4), we expect that the number of detected clusters for a random field follows a Poisson survival distribution. Plot a of Fig. 6 confirms our hypothesis; indeed, the Poisson survival function provides a reasonable description of the empirical distribution. The same holds for fake clusters of the sky test field 1 (plot c Fig. 6). In contrast, for true clusters (panel d Fig. 6), the Poisson survival distribution is unable to reproduce the observed trend, consistently with the non-Poissonian statistic of the simulated clusters. Panels b and e of Fig. 6s show the 1–σ CL region for Np as a function of K. Both for random and sky field true clusters the lower boundary of the region is constrained by the equation y = K + 1, which is consistent with the γ-ray DBSCAN logic. In contrast, the upper boundary shows a different behavior. For the random field, the upper boundary deviates from the lower boundary, which is compatible with the fluctuations of the events around the ε circle, and ranges from about 8 to about 16. In contrast, for the true sky field the upper boundary is constrained by the statistics of the number of events in the simulated sources, and ranges from about 60 to 100.
5. Testing the detection performance with simulated γ-ray data
In this section we investigate the detection performance of the γ-ray DBSCAN. We first study the dependency of the detection efficiency on K and ε and their impact on the spurious ratio, and on the detection efficiency. Then, we investigate the capability of the algorithm to reconstruct the simulated clusters, and the positional accuracy of the reconstructed centroids. We test the detection performance of the γ-ray DBSCAN, using as benchmark the five sky test fields used in the previous section, exploring the same parameter space.
5.1. Detection efficiency and spurious ratio as a function of K and ε
To investigate the detection performance of the γ-ray DBSCAN, we ran for each of the five sky test fields and for each pair of values K, ε, a γ-ray DBSCAN detection. For each detection run, we built a cluster catalog. Starting from this, we built the corresponding candidate catalog. This is a list of sources built by taking into account two possible biases, the confusion and the multiple association, in detail:
-
A cluster is defined as true, i.e., with a possible counterpart, if theposition of the simulated source falls within a circle centered onthe cluster centroid, with a radius equal to 2poserr.
-
Two or more true clusters are defined as confused if they have the same counterpart
-
A true cluster has a multiple association if it has more than one counterpart.
We stress that the number of confused clusters is negligible, indeed, the average number of confused clusters per run is about 0.08, and no confused clusters are found for K > 4. Moreover, the average number of multiple associations per run is about 0.2.
The final candidate catalog will count a number of candidate sources Nsrc, each identified by a unique SRCID. The number of spurious sources will be Nfake = Nsrc − Ntrue. To characterize the performance, we define the following parameters:
-
the detection efficiency:
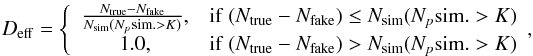 (8)where
Nsim(Npsim. > K)
is the number of simulated sources with a number of simulated events larger than
K
(8)where
Nsim(Npsim. > K)
is the number of simulated sources with a number of simulated events larger than
K -
the true detection ratio Dtrue = Ntrue/Nsrc
-
the spurious detection ratio Dfake = Nfake/Nsrc
-
the overall detection quality factor (Q), which takes into account the tradeoff between Deff and Dfake, defined as
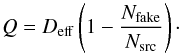 (9)
(9)
The Deff parameter shows the fraction of simulated clusters above the threshold Npsim = K detected by the method after subtracting the fake ones. Hence, it does not provide an indication of the spurious contamination. For this reason we introduced the Q parameter, which rescales the Deff according to the ratio between fake clusters, and found clusters Nsrc. We recall that according to the Deff definition in Eq. (8), it is possible to obtain values of Deff > 1.0. Assuming to have a simulated cluster where, for a given K and ε, the corresponding seed cluster has a size N∗ = Npsim. = K. If there are no background events within the circle of radius ε, this cluster will be rejected. If we have one or more background events contained within the circle of radius ε, i.e., N∗ > K, the cluster will be detected. For this reason, we then report a value of Deff = 1.0. The same applies to Q.
 |
Fig. 8 Panel a) red solid boxes show the mean positional error of the centroid for true clusters in sky test field 1 and the standard deviation (vertical error bar) vs. Np. The clusters are binned in Np, with the bin width indicated by the horizontal error bar. The black solid circles represent the corresponding trend for the distance between the cluster centroid and the simulated source position.Panel b) the distribution of the distance between the simulated source position and the cluster centroid, expressed in arcsec, for ε = 0.10 deg (black line), ε = 0.15 deg (blue line), and ε = 0.20 deg (red lines). Panel c) the cumulative distributions corresponding to panel b). |
Summary of the detections obtained for all the five sky fields for detections with a number of fake sources ≤6.
 |
Fig. 9 Top panel: the average number of photons associated to each clusters Np, and their dispersion (vertical bar) vs. the number of photons simulated (Np sim). The red points refer to the sub parameter space ε = 0.15 deg, and the solid blue circles to the ε = 0.20 deg subspace. The solid green lines represent the law Np = Np sim. The dashed lines represent the law Np = Np sim. ± 10. Bottom panel: the corresponding fractional deviation (Np − Npsim.)/Npsim. |
In Fig. 7 we summarize the detection runs for sky test field 1 for the full parameters space with K > 2. Panel a shows the isolevel map of the fake clusters detection ratio. The gradient in the isolevel map is quite sharp, and roughly half of the parameter space shows no fake clusters (white isolevel line). To have a better understanding of the impact of fake clusters, it’s interesting to compare the Dfake isolevel map to the Dtrue isolevel map (panel b Fig. 7). The map shows also in this case a sharp gradient, and the region with Dtrue > 0.95 overlaps the Dfake = 0 region. These two maps clearly show the region of the parameter space where the algorithm has the best performance, but the Dtrue and Dfake ratios do not provide information on the ratio between the number of true detected clusters and the number of simulated clusters. For this point more information is provided by the Deff isolevel map (panel c, Fig. 7). To focus on the “effective” volume of the parameter space, we hide the region where Deff < 0 with a white area. We note that the isolevel lines Deff = 0 and the isomap lines in the maximum gradient area show a positive correlation between K and ε, meaning that an increased value of ε requires an increased value of K to obtain a better background rejection. To evaluate the trade-off between Dtrue and Dfake better, we plot in panel d of Fig. 7 the isolevel map of Q. This plot shows that the area corresponding to Q > 0.95 is consistent with that found for Deff. In Table 1 we report the Deff values obtained for all five sky fields, for detections with a number of fake sources ≤6. The average values of true clusters ranges between 44 and 51, with the fake ones ranging between 1 and 3, and an average Deff between 0.96 and 1.0. This is a very promising result.
5.2. Cluster reconstruction and positional accuracy
The positional accuracy of the topometric methods, is probably the most important feature of this class of algorithms. In Sect. 2, we have described our weighting method to reconstruct the centroid of the cluster.
Panel a of Fig. 8 shows with red solid boxes the
mean positional error of the cluster centroids and the standard deviation (vertical error
bar) vs. Np, for the true
clusters of sky test field 1 with ε ≤ 30 deg.
The clusters are binned in Np, with the bin
width indicated by the horizontal error bar. As expected, the uncertainty on the
reconstructed cluster centroid is 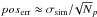 (solid red line). The
solid black circles represent the corresponding trend for the separation between the
simulated cluster position and the reconstructed cluster centroid. For
Np ≳ 30, the separation is below 2′. In
panel b of Fig. 8 we plot the distribution histogram
of the angular separation between the position of the simulated source and the position of
the cluster centroid. For the three cases of ε = 0.10 deg,
ε = 0.15 deg, and ε = 0.20 deg, the positional error
is below the 1.5′, for 68% of the sample.
(solid red line). The
solid black circles represent the corresponding trend for the separation between the
simulated cluster position and the reconstructed cluster centroid. For
Np ≳ 30, the separation is below 2′. In
panel b of Fig. 8 we plot the distribution histogram
of the angular separation between the position of the simulated source and the position of
the cluster centroid. For the three cases of ε = 0.10 deg,
ε = 0.15 deg, and ε = 0.20 deg, the positional error
is below the 1.5′, for 68% of the sample.
 |
Fig. 10 Left panel: the distribution (blue line) of the square of the significance for the fake clusters in sky test field 1 for the full K, ε parameter space compared to a χ2 distribution with one degree of freedom. Right panel: the spurious ratio Dfake for Scls > 4.0, the white line shows the isolevel Dfake = 0.0. |
In addition to positional accuracy, is also important to understand the capability of the γ-ray DBSCAN to reconstruct the simulated cluster in terms of number of photons. Indeed, this information gives an idea of the average number of background photons contaminating the reconstructed cluster. In the top left panel of Fig. 9, we show the scatter plot of Np vs. the number of simulated events (Np sim.). The solid points represent the average value of Np, for a given value of Np sim., and the error bar corresponds to the standard deviation. The solid green line represents Np = Np sim., and the dashed upper and lower lines represent Np = Np ± 10 sim. For ε = 0.15 deg and ε = 0.20 deg, the scatter is bounded by the dashed lines, showing that the highest excess in the Np is about 10 photons, independently of Np sim. For ε = 0.15 deg, the number of reconstructed photons systematically underestimates the simulated number, whilst the ε = 0.20 deg case does not shows this bias. It is possible to appreciate this effect better in the bottom left panel of Fig. 9, where we show the fractional reconstruction error (Np − Np sim.)/Np sim. vs. Np sim. The solid green line represents the 0 error, and the dashed lines represent the ± 20% boundaries.
The bias on Np for ε = 0.15 deg again shows the strong correlation between ε and the PSF radius. When ε is smaller than the σsim (that in our simulations reproduces the PSF effect), the number of reconstructed events Np is systematically smaller than Np sim., in contrast, when the ε radius matches the PSF radius size (ε = 0.20 deg), the bias disappears.
6. Cluster significance, background inhomogeneities, and rejection of spurious clusters
Even though we have identified the region of the K-ε parameter space where the detection efficiency is higher and the probability to detect fake clusters is lower, in the application to real data it is mandatory to provide a significance level that expresses the probability that a cluster is not originated in a background fluctuation. We propose a method derived from the Li & Ma (1983) approach, based on the evaluation of the S/N. A significance method based on the S/N fits the γ-ray DBSCAN implementation well, because the algorithm directly provides a partition of the photon list in cluster and noise events. Hence, for each cluster we can easily evaluate the S/N, knowing the exact nature of each event. The procedure to evaluate the significance is summarized by the following items:
 |
Fig. 11 Aitoff projection of the Fermi sky region. The purple boxes represent the γ-ray DBSCAN sources (K = 8,ε = 0.21 deg). The green crosses are the 2FGL sources with TS > 16, the red crosses those with TS ≤ 16. There are no fake sources, and the γ-ray DBSCAN finds all the sources with TS > 16, except one, enclosed by the red circle, whose center is positioned at the edge of the field. |
-
1.
For each cluster we define an annular region with an inner radius rin and an external radius rout.
-
2.
rinis set to an initial value of rin = 2reff, and is adaptively increased with a step of rin/10 for a maximum of 10 trials until at least the 95% of the cluster events are enclosed within rin.
-
3.
routis set to 3rin.
-
4.
We count all cluster events
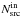 and the
background events
and the
background events 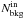 that are
enclosed within the circle with radius rin and are
centered on the cluster centroid.
that are
enclosed within the circle with radius rin and are
centered on the cluster centroid. -
5.
We determine the
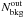 background
level, rescaling the number of background events in
rin < r < rout,
to a circle with radius rin.
background
level, rescaling the number of background events in
rin < r < rout,
to a circle with radius rin. -
6.
To evaluate possible gradients in the background, we select a region far enough from the cluster to properly sample the background level, and close enough to the cluster to measure a local background level. For this, we define the radius
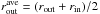 , and evaluate the
average background level (
, and evaluate the
average background level (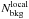 ) in a
circle of radius rin, centered on each point in
) in a
circle of radius rin, centered on each point in
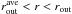 .
. -
7.
If no background points are found in
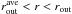 , we set
, we set
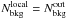 .
. -
8.
By comparing
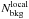 to
to
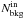 , we evaluate
the fraction of noise already resolved by the γ-ray
DBSCAN and evaluate the effective background level
, we evaluate
the fraction of noise already resolved by the γ-ray
DBSCAN and evaluate the effective background level
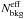 by correcting
by correcting
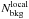 for
for
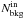 .
. -
9.
We evaluate the significance according to the Likelihood Ratio Test (LRT) method proposed by Li & Ma (1983):
![\begin{equation} S_{\rm cls}=\sqrt{2 \left( N^{\rm in}_{\rm src} \ln \left[ \frac{2 N^{\rm in}_{\rm src}}{N^{\rm in}_{\rm src}+N^{\rm eff}_{\rm bkg}} \right]+ N^{\rm eff}_{\rm bkg} \ln \left[ \frac{2N^{\rm in}_{\rm src}}{N^{\rm in}_{\rm src}+N^{\rm eff}_{\rm bkg}} \right ] \right)\cdot} \label{eq:signif} \end{equation}](/articles/aa/full_html/2013/01/aa20133-12/aa20133-12-eq167.png) (10)
(10)
Assuming
that a cluster is due to a background fluctuation, the variable
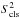 is expected to
follow a chi square distribution, with one degree of freedom
(χ(1)2). In the left panel of Fig. 10, we plot the distribution of
is expected to
follow a chi square distribution, with one degree of freedom
(χ(1)2). In the left panel of Fig. 10, we plot the distribution of 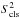 for the fake
clusters in sky test field 1 (blue histogram), compared to a
χ(1)2 distribution. The empirical distribution is well
described by the expected χ(1)2 distribution, proving that the
value of Scls can be used as the “significance” of the detected
cluster. A highly illustrating example of the power of Scls in
rejecting fake clusters is given by the plot in the right panel in Fig.
10, where we plot the
Dfake ratio isolevel map, applying the selection
Scls > 4.0. The fake ratio is 0 for
the parameter space with ε ≲ 0.25 deg. For 0.25 deg
≲ ε ≲ 0.35 deg, there are fluctuations showing
Dfake ≲ 0.05. The fake ratio shows a
significant increase only for ε ≳ 0.40 deg and K ≲ 8, but
we stress that in this region of the parameter space ε is more than twice
of the PSF size, hence this is a region of the parameter space that should not be used in
the detection with real data.
for the fake
clusters in sky test field 1 (blue histogram), compared to a
χ(1)2 distribution. The empirical distribution is well
described by the expected χ(1)2 distribution, proving that the
value of Scls can be used as the “significance” of the detected
cluster. A highly illustrating example of the power of Scls in
rejecting fake clusters is given by the plot in the right panel in Fig.
10, where we plot the
Dfake ratio isolevel map, applying the selection
Scls > 4.0. The fake ratio is 0 for
the parameter space with ε ≲ 0.25 deg. For 0.25 deg
≲ ε ≲ 0.35 deg, there are fluctuations showing
Dfake ≲ 0.05. The fake ratio shows a
significant increase only for ε ≳ 0.40 deg and K ≲ 8, but
we stress that in this region of the parameter space ε is more than twice
of the PSF size, hence this is a region of the parameter space that should not be used in
the detection with real data.
7. Application to real Fermi-LAT data
The last step in our investigation of the γ-ray DBSCAN is the application to real Fermi-LAT γ-ray data. We selected the same region of the sky as was used for the simulated test field ( 80° < l < 170°, and 40° < b < 65°) and extracted all the photons with energy E > 3 GeV. The photons are collected for the same time span of the 2FGL catalog. We repeated the detection test performed with simulated data (see Sects. 5 and 6), restricting the parameter space to 2 ≤ K ≤ 10 and 0.10 ≤ ε ≤ 0.30 deg.
To properly understand the detection performance, we need to take into account that the
2FGL catalog has been built using photons with an energy threshold of 100 MeV, whilst we
used a value of 3 GeV. A possibility is to select sources with a reported flux higher than
zero, in the 3–10 GeV band flux column of the 2FGL. This flux-based selection is not the
best way to study the detection performance of the γ-ray DBSCAN, indeed,
the flux does not contain an unambiguous relation with the significance of the detection for
that energy threshold. A more reliable criterion is to select the sources according to the
significance reported in the 2FGL. The 2FGL detection significance is given by the
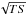 .
The TS is the test statistic defined as
TS = 2(log L(source) − log L(no source)),
where L is the likelihood of the data given the model with or without a
source present at a given position on the sky (Nolan et al.
2012). We applied a selection according to
.
The TS is the test statistic defined as
TS = 2(log L(source) − log L(no source)),
where L is the likelihood of the data given the model with or without a
source present at a given position on the sky (Nolan et al.
2012). We applied a selection according to 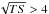 and refer to the corresponding
source list (counting 35 sources) as 2FGLTS>16.
and refer to the corresponding
source list (counting 35 sources) as 2FGLTS>16.
An example of the application of the γ-ray DBSCAN to real Fermi-LAT data is given in Fig. 11, where we report an Aitoff projection in galactic coordinates of the analyzed γ-ray sky region. The red crosses represent the 2FGL sources with TS < 16 in the 3–10 GeV band, and the green crosses represent those with TS ≥ 16. The purple boxes represent the γ-ray DBSCAN sources found for K = 8, ε = 0.21 deg. For this choice of parameters, we find no fake sources, and we find all sources with TS > 16, except for one that is enclosed by the red circle and is positioned at the edge of the sky region, with a galactic latitude l = 64.85 deg. In Table 2 we summarize the detection performance for detections with a number of fake sources ≤4. Values of true clusters range between 35 and 34, out of the 35 present in the 2FGLTS>16. The fake ones range between 1 and 4, and we obtain an average detection efficiency of Deff = 0.94.
In Fig. 12 we compare the localization performance of
the γ-ray DBSCAN algorithm with that returned by the likelihood analysis
implemented in the Fermi Science Tools. For each source in our
2FGLTS>16 list, associated to one or more γ-ray DBSCAN
clusters, we plot the the error on the position of the reconstructed cluster centroid and
its standard deviation (represented by the error bar) vs. the 95% positional uncertainty
reported in the 2FGL. We evaluate the 2FGL 95% positional uncertainty as
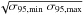 ,
where σ95,min and σ95,max are the
semimajor and semiminor axes of the 95% confidence source location region. The dashed red
line represents a linear best fit with a slope of ≃0.99 and an intercept of ≃9.53, showing
that the error on the position of the reconstructed cluster centroid, performed with a
threshold of 3 GeV, is of the same order of the 95% positional uncertainty reported in the
2FGL catalog, performed above 100 MeV.
,
where σ95,min and σ95,max are the
semimajor and semiminor axes of the 95% confidence source location region. The dashed red
line represents a linear best fit with a slope of ≃0.99 and an intercept of ≃9.53, showing
that the error on the position of the reconstructed cluster centroid, performed with a
threshold of 3 GeV, is of the same order of the 95% positional uncertainty reported in the
2FGL catalog, performed above 100 MeV.
To test the reliability of the significance Scls to reject spurious sources, we plot the Dfake and Deff based on the 2FGLTS>16 catalog in Fig. 13. Panels a and b correspond to no selection on Scls. Both the Dfake and the Deff trends are very similar to the case of the simulated sky. If we apply a significance cut of Scls > 2.0 (panels c,d), we observe that the spurious ratio is Dfake ≤ 0.05 for almost half of the parameter space (region to the right of the purple line). The more severe cut of Scls > 4.0 (panels d and e), removes all fake clusters for ε ≲ 0.20 deg, except two for ε ≲ 0.15 deg. Only for ε ≳ 0.25 deg, the Dfake ratio shows a significant increase, ranging from 0.05 up to ≃0.1. In agreement with our analysis on simulated data, the region of the parameter space where ε is comparable to the PSF size gives the better performance.
To have an additional confirmation about the robustness of our significance we plot in the
right panel of Fig. 14,
Scls vs. 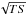 .
For each source in our 2FGLTS>16 list, associated to one or more
γ-ray DBSCAN cluster, we plot the
.
For each source in our 2FGLTS>16 list, associated to one or more
γ-ray DBSCAN cluster, we plot the 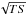 in the 3–10 GeV band vs. the average value of Scls and its
standard deviation (represented by the error bar). The average value of
Scls and its standard deviation are evaluated from the list of
all clusters associated to the same 2FGL source. The solid blue boxes represent the full
K, ε parameter space case, and the red solid circles
represent the ε = 0.10 deg case. The dashed black line represents a linear
best fit. The slope of the linear fit is ≃0.5. The strong correlation in the scatter plots
(r ≃ 0.98, for both data sets) proves that our significance
implementation is consistent with the
in the 3–10 GeV band vs. the average value of Scls and its
standard deviation (represented by the error bar). The average value of
Scls and its standard deviation are evaluated from the list of
all clusters associated to the same 2FGL source. The solid blue boxes represent the full
K, ε parameter space case, and the red solid circles
represent the ε = 0.10 deg case. The dashed black line represents a linear
best fit. The slope of the linear fit is ≃0.5. The strong correlation in the scatter plots
(r ≃ 0.98, for both data sets) proves that our significance
implementation is consistent with the 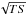 reported in the 2FGL, and the slope of the linear fit suggests that
reported in the 2FGL, and the slope of the linear fit suggests that
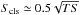 .
.
Summary of the detection performance for the real Fermi-LAT field for detections with a number of fake sources ≤4.
 |
Fig. 12 Scatter plot of the positional error of the γ-ray DBSCAN clusters vs. the positional error of the corresponding associated 2FGLTS>16 sources. For each 2FGLTS>16 source associated to one or more γ-ray DBSCAN clusters, we plot the error on the position of the reconstructed cluster centroid and its standard deviation (represented by the error bar). The dashed red line represents a linear best fit with a slope of ≃ 0.99 and an intercept of ≃ 9.53. |
 |
Fig. 13 Dfake (left panels) and Deff (right panels) for the real sky detections using the 2FGLTS>16 catalog. Panels a), b) no cut on Scls applied. Panels c), d) Scls > 2.0. Panels e), f) Scls > 4.0. |
 |
Fig. 14 Left panel: scatter plot of
Scls vs. |
8. Conclusions
For the first time, we have used the DBSCAN to detect sources in γ-ray astrophysical images. We implemented a new version of the DBSCAN, the γ-ray DBSCAN, which is optimized for the application to γ-ray astrophysical images with relevant background noise. Our γ-ray DBSCAN presents the novelty of recursive call of the DBSCAN algorithm, which allows an excellent reconstruction of the cluster with an effective background rejection. We tested the algorithm with a sample of simulated γ-ray Fermi-LAT fields to give a statistical characterization of the method and to benchmark the detection performance. The results, with the simulated γ-ray data, are summarized below.
-
The radius of the γ-ray DBSCAN scanning brush ε has a strong correlation with the instrumental PSF radius. We find that the typical size of the reconstructed true cluster is on the order of the simulated PSF size σsim, and that the precision of the reconstructed centroid is on the order of
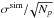 .
. -
The number of reconstructed events Np is ruled by the Poissonian statistics in the randomfields and for the fake clusters. In contrast, for true clusters, the statistics of Np is ruled by that of the simulated sources.
-
The fractional error on the reconstructed event number is about 20% for Npsim. ≲ 50, and is negligible for higher values, with best performance obtained when ε ≃ σsim.
-
We investigated the detection performance for a wide range of the K, ε parameter space and identified the region with the best performance in terms of detection efficiency, and spurious ratio.
-
We implemented an algorithm to estimate the S/N, able to deal with local background inhomogeneities and nearby sources contamination, and we successfully used the S/N estimate to determine the significance of the clusters, using the definition in Li & Ma (1983).
-
Our cluster significance, Scls, for random clusters follows the χ(1)2 statistics and can be used to reject spurious sources. The chance to find spurious sources for Scls > 4 is negligible. This means that our Scls is a robust and reliable tool to reject spurious sources, and that χ(1)2 statistics can be used to evaluate the probability of a cluster to be spurious.
We successfully applied the γ-ray DBSCAN to real
Fermi-LAT data. We found an excellent agreement with results from the
simulated fields. We tested our detection performance using the 2FGL source catalog with a
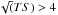 cut. The results, with the real
Fermi-LAT γ-ray data, are:
cut. The results, with the real
Fermi-LAT γ-ray data, are:
-
The error on the position of the reconstructed cluster centroid,performed with a threshold of 3 GeV, is on the same order as the 95%positional uncertainty reported in the 2FGL, performed above100 MeV.
-
We tested the γ-ray DBSCAN significance, finding that it is strongly correlated with the TS provided in the 2FGL. The significance cut allows one to safely remove spurious clusters.
-
The detection efficiency with real data is excellent, we are able to find all 35 sources with
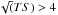 .
. -
When working with ε on the order of the instrumental PSF size, we obtain the best performance in terms of spurious rejection and detection efficiency,
In general, we find that the γ-ray DBSCAN is a very powerful detection method to find clusters in γ-ray images, corresponding to real sources. It has the great advantage to deal self-consistently with gradient in the background, providing an effective rejection of spurious clusters. Our implementation of the detection significance, in addition to the algorithm to evaluate local fluctuations in the background, allows one to apply a statistically significant selection, making the rejection of spurious sources even more effective.
In a companion paper (Tramacere, in prep.), we will a apply the method to the Fermi-LAT sky, showing the potential to discover new sources, in particular small clusters located at high galactic latitude, or clusters on the Galactic plane that are affected by a strong background. We will also investigate how to include the energy dependence of the PSF into the γ-ray DBSCAN algorithm, and how to improve the detection performance taking into account other Fermi-LAT calibration properties.
We remark that, since the γ-ray DBSCAN also provides density maps, it can potentially be used to detect large-scale
structures in the Galactic γ-ray background, providing patterns to compare to the interstellar gas distribution. We also stress that the applications of this method are not limited to γ-ray images, but can potentially be used for any application related to the detection of spatial, and/or spatio/temporal clusters.
Acknowledgments
We are grateful to E. Massaro, R. Campana and E. Bernieri for helpful comments and for providing us the simulated test fields. We are grateful to G. Tosti for helpful comments. We thank the anonymous referee for providing us with constructive comments and useful suggestions.
References
- Ackermann, M. Ajello, M. Albert, A. et al. (Fermi-LAT collaboration) 2012, ApJS, 203, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, R., Massaro, E., Gasparrini, D., Cutini, S., & Tramacere, A. 2007, MNRAS, 383, 1166 [Google Scholar]
- Campana, R., Massaro, E., Bernieri, E., Tinebra, F., & Tosti, G. 2012, submitted [Google Scholar]
- Ester, M., Kriegel, H., Sander, J., & Xu, X. 1996, In Proc. 2nd International Conference on Knowledge Discovery and Data Mining [Google Scholar]
- Jolliffe, I. T. 1986, Principal component analysis [Google Scholar]
- Li, T.-P., & Ma, Y.-Q. 1983, ApJ, 272, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Papoulis, A. 1965, Probability, Randon Variables and Stochastic Processes [Google Scholar]
All Tables
Summary of the detections obtained for all the five sky fields for detections with a number of fake sources ≤6.
Summary of the detection performance for the real Fermi-LAT field for detections with a number of fake sources ≤4.
All Figures
 |
Fig. 1 Photon map for the sky test field 1, with the result of the γ-ray DBSCAN detection for K = 5 and ε = 0.17 deg. The blue crosses refer to the simulated sources, the green boxes to 51 detected true clusters, and the red boxes to the 2 fake ones. The black dots represent the background events, the remaining colors indicate cluster events. |
| In the text | |
 |
Fig. 2 Close-up of two true clusters reported in Fig. 1. The ellipses correspond to the ellipse of the cluster containment. The purple and orange points represent the cluster points, the black dots represent the background events, the blue crosses the position of the simulated sources, and green boxes the position of the cluster centroid. |
| In the text | |
 |
Fig. 3 Panel a) distribution of the values of log 10reff for the random field case, for the full parameter space (black line) and fit by means of Gaussian distribution (blue line). Panel b) the same as in the top panel, for K = 3 and ε = 0.3 deg. Panel c) distribution of log 10reff for the sky test field 1, for fake clusters (red solid line), and true clusters (blue solid line, hatched histogram). The dashed lines represent the Gaussian best fit. |
| In the text | |
 |
Fig. 4 Left panel: the reff/ε statistical distribution as a function of ε for the random field case. The blue solid circles represent the median, and the gray shaded area represents the 1-σ confidence level region, for each value of ε. Right panel: the same as in the bottom left panel for the sky test field 1. The red solid circles represent the median of the true clusters case, and the grey area the 1-σ confidence level region. The dashed line shows the 1-σ confidence level region, for the fake clusters. |
| In the text | |
 |
Fig. 5 Left panels: the distribution of
Np for the random
test field for K = 2, ε = 0.20 deg (panel
a), red solid boxes). The empty blue bar line represents a Poissonian
best fit. Panel b) shows K = 2
ε = 0.30 deg (purple solid triangles). Panel c) shows
the full K-ε parameter space, the solid black line
represent a log-normal best fit. Right panels: panel c)
shows the distribution of |
| In the text | |
 |
Fig. 6 Panel b) the Np statistical distribution as a function of K for the random field case. The blue solid circles represent the median and the gray shaded area represents the 1-σ confidence level region around the median for each value of K. The dashed black line represents the Np = K + 1 law. Panel e) same as in panel b) for the sky test field 1 case. Panel a) number of detected clusters for the random test field case (blue solid points) as a function of K, and best fit by means of a Poissonian survival function (red empty bars). Panel c) number of detected cluster for the sky test field 1 case (black solid points), for the fake clusters as a function of K, and best fit by means of a Poissonian survival function (red empty bars). Panel d) number of detected cluster for the sky test field 1 case (red solid boxes) for the true clusters as a function of K, and best fit by means of a Poissonian survival function (black empty boxes). |
| In the text | |
 |
Fig. 7 Isolevel maps for Dfake (panel a)), Dtrue (panel b)), Deff (panel c)), and Q (panel d)), for the sky test field 1. The white lines show isolevel = 0, the black lines show isolevel = 0.68, and the blue lines show isolevel = 0.95. |
| In the text | |
 |
Fig. 8 Panel a) red solid boxes show the mean positional error of the centroid for true clusters in sky test field 1 and the standard deviation (vertical error bar) vs. Np. The clusters are binned in Np, with the bin width indicated by the horizontal error bar. The black solid circles represent the corresponding trend for the distance between the cluster centroid and the simulated source position.Panel b) the distribution of the distance between the simulated source position and the cluster centroid, expressed in arcsec, for ε = 0.10 deg (black line), ε = 0.15 deg (blue line), and ε = 0.20 deg (red lines). Panel c) the cumulative distributions corresponding to panel b). |
| In the text | |
 |
Fig. 9 Top panel: the average number of photons associated to each clusters Np, and their dispersion (vertical bar) vs. the number of photons simulated (Np sim). The red points refer to the sub parameter space ε = 0.15 deg, and the solid blue circles to the ε = 0.20 deg subspace. The solid green lines represent the law Np = Np sim. The dashed lines represent the law Np = Np sim. ± 10. Bottom panel: the corresponding fractional deviation (Np − Npsim.)/Npsim. |
| In the text | |
 |
Fig. 10 Left panel: the distribution (blue line) of the square of the significance for the fake clusters in sky test field 1 for the full K, ε parameter space compared to a χ2 distribution with one degree of freedom. Right panel: the spurious ratio Dfake for Scls > 4.0, the white line shows the isolevel Dfake = 0.0. |
| In the text | |
 |
Fig. 11 Aitoff projection of the Fermi sky region. The purple boxes represent the γ-ray DBSCAN sources (K = 8,ε = 0.21 deg). The green crosses are the 2FGL sources with TS > 16, the red crosses those with TS ≤ 16. There are no fake sources, and the γ-ray DBSCAN finds all the sources with TS > 16, except one, enclosed by the red circle, whose center is positioned at the edge of the field. |
| In the text | |
 |
Fig. 12 Scatter plot of the positional error of the γ-ray DBSCAN clusters vs. the positional error of the corresponding associated 2FGLTS>16 sources. For each 2FGLTS>16 source associated to one or more γ-ray DBSCAN clusters, we plot the error on the position of the reconstructed cluster centroid and its standard deviation (represented by the error bar). The dashed red line represents a linear best fit with a slope of ≃ 0.99 and an intercept of ≃ 9.53. |
| In the text | |
 |
Fig. 13 Dfake (left panels) and Deff (right panels) for the real sky detections using the 2FGLTS>16 catalog. Panels a), b) no cut on Scls applied. Panels c), d) Scls > 2.0. Panels e), f) Scls > 4.0. |
| In the text | |
 |
Fig. 14 Left panel: scatter plot of
Scls vs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


