| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 23 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201219144 | |
| Published online | 14 June 2012 | |
LABOCA 870 μm dust continuum mapping of selected infrared-dark cloud regions in the Galactic plane⋆
Department of Physics, PO Box 64, University of
Helsinki, 00014 Helsinki Finland
e-mail: oskari.miettinen@helsinki.fi
Received:
1
March
2012
Accepted:
5
April
2012
Context. Imaging surveys of dust emission at (sub)millimetre wavelengths provide a powerful tool for studying molecular clouds and the early stages of star formation.
Aims. Through submm dust continuum mapping, we attempt to search for genuine infrared-dark clouds (IRDCs) and precursors to massive stars and stellar clusters in the Galactic plane, and to determine their basic physical properties.
Methods. We have mapped four selected fields of about 0.°5×0.°5 that contain Spitzer 8-μm dark regions with LABOCA at 870 μm. Selected positions in the fields were observed in C17O(2−1) to obtain kinematic information. The obtained LABOCA maps are used in conjunction with the Spitzer IR images.
Results. The total number of clumps identified in this survey is 91, out of which 40 (44%) appear dark at 8 and 24 μm. The remaining clumps are associated with mid-IR emission. Seven clumps associated with extended 4.5 μm emission are candidate extended green objects (EGOs). Filamentary dust “ridges” were found towards the Spitzer bubbles N10/11 in one of our fields. The relative number of IR-dark and IR-bright clumps suggests that the duration of the former stage is about 1.6 × 105 yr. The mass distribution of the total sample of clumps, and that separately constructed for the IR-dark and IR-bright clumps, could be fitted at the high-mass end with the power-law function dN/dlog M ∝ M−Γ, where Γ ≃ 0.7...0.8. The C17O observation positions appear to be dominated by non-thermal motions, and the data also revealed some potential sites of strong CO depletion. In G11.36+0.80, which is the best example of a filamentary IRDC in our sample, the clumps appear to be gravitationally bound. The fragmentation of the filament can be understood in terms of a sausage-type fluid instability, in agreement with the results for other IRDCs. The fragmentation and the CO depletion timescales in G11.36 appear to be very similar to each other.
Conclusions. Many of the identified clumps are massive enough to allow high-mass star formation, and some of them already show clear signposts of that. In the N10/11 bubble environment, the morphology of the detected dust emission conforms to the triggered high-mass star formation in the system. The clump mass distributions are similar to those found for diffuse CO clumps, and can be explained by the action of supersonic turbulence. The formation of filamentary IRDCs might be caused by converging turbulent flows, and the same process may play a role in exciting the fluid perturbations responsible for the fragmentation of the clouds into clumps.
Key words: stars: formation / ISM: clouds / submillimeter: ISM
© ESO, 2012
1. Introduction
Understanding the origin of high-mass (M > 8 M⊙) stars, particularly the first steps in the formation process, is probably one of the greatest challenges of modern astrophysics. Since the discovery of the so-called infrared-dark clouds, or IRDCs (Pérault et al. 1996; Egan et al. 1998), ample evidence has been gathered concerning their important role in the earliest stages of Galactic high-mass star formation (e.g., Rathborne et al. 2006; Beuther & Steinacker 2007; Chambers et al. 2009; Battersby et al. 2010; Zhang et al. 2011, and many other works). In particular, studies of IRDCs have the potential to help understanding the inital conditions of high-mass star and stellar cluster formation, which is necessary to constrain, or even distinguish, between different theoretical views1.
Thermal dust continuum emission at far-infrared (FIR) and (sub)millimetre wavelengths provides a powerful observational tool to search and study the densest parts of IRDCs. Dust continuum imaging with bolometer cameras can be used to distinguish the real IRDCs, i.e., cold dense molecular clouds, from the minima in the Galactic mid-infrared (MIR) background radiation, which may look like candidate IRDCs (Wilcock et al. 2012). Optically thin dust emission also provides a probe of the basic physical properties of dense clouds, such as the column density of molecular hydrogen and the mass of the cloud. This information is needed to learn the physical conditions that prevail in the precursor regions of stellar clusters and high-mass stars.
In this paper, we present the results of our submm dust continuum observations at 870 μm of four selected regions in the Galactic plane, each of which contain IRDCs. Throughout the paper, we use the term “clump” to refer to sources whose typical radii, masses, and mean densities are ~0.2−1 pc, ~102−103 M⊙, and 103−104 mm-3, respectively (cf. Bergin & Tafalla 2007). The rest of the present paper is organised as follows. Observations and data reduction are described in Sect. 2. Observational results are presented in Sect. 3. Analysis and its results are presented in Sect. 4, and in Sect. 5 we discuss the obtained results. In Sect. 6, we summarise the results and draw our main conclusions.
2. Observations and data reduction
2.1. Archival data from the Spitzer Space Telescope
In this study, we used the Spitzer (Werner et al. 2004) IR data taken as part of the GLIMPSE (Benjamin et al. 2003; Churchwell et al. 2009) and MIPSGAL (Carey et al. 2009) Galactic plane surveys. The former survey employed the IRAC instrument operating at 3.6, 4.5, 5.8, and 8.0 μm (Fazio et al. 2004), whereas the latter one used the MIPS instrument at 24 and 70 μm (Rieke et al. 2004). The angular resolution of the Spitzer-IRAC instrument is 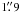 at 8 μm, and that of the MIPS instrument is 6″ at 24 μm. We note that we have used the data provided by both the GLIMPSE I and II surveys, which covered the nominal Galactic longitude ranges of 10° ≤ |l| ≤ 65° and |l| ≤ 10°, respectively. The data were retrieved from the Spitzer Science Archive2.
at 8 μm, and that of the MIPS instrument is 6″ at 24 μm. We note that we have used the data provided by both the GLIMPSE I and II surveys, which covered the nominal Galactic longitude ranges of 10° ≤ |l| ≤ 65° and |l| ≤ 10°, respectively. The data were retrieved from the Spitzer Science Archive2.
The 8 μm images of the Galactic plane are particularly useful for the search of candidate IRDCs. The GLIMPSE 8 μm band contains the UV-excited 7.7 and 8.6 μm PAH (polycyclic aromatic hydrocarbon) features (e.g., Draine 2003), which together with emission from warm interstellar dust yield a bright MIR background. High columns of cold dust in IRDCs cause them to appear as dark absorption features against this background radiation field.
2.2. LABOCA dust continuum mapping
As a starting point of our study we visually inspected the Spitzer-GLIMPSE 8-μm images of the Galactic plane, and chose four target fields that contain filamentary IR-dark features to be mapped in the submm dust continuum emission. Because IRDCs often exhibit filamentary shapes and are relatively devoid of (visible) star formation, the target sources of this study are likely to represent fairly typical IRDCs. The selected fields, which all belong to the first Galactic quadrant (0° < l < 90°), are listed in Table 1. These target fields were mapped with the Large APEX BOlometer CAmera (LABOCA; Siringo et al. 2009) on the 12-m Atacama Pathfinder EXperiment (APEX) telescope at Llano de Chajnantor in the Atacama desert of the Chilean Andes (Güsten et al. 2006)3. The LABOCA instrument is a multi-channel bolometer array, where 295 semiconducting composite bolometers are arranged in a series of nine concentric hexagons around a central channel. The system operates at a central frequency of 345 GHz (λ = 870 μm) with a bandwidth of about 60 GHz to match the corresponding atmospheric window. The nominal angular resolution of LABOCA is 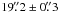 (half power beamwidth; HPBW), and its total field of view is
(half power beamwidth; HPBW), and its total field of view is 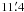 (about 0.09 pc and 3.3 pc at 1 kpc, respectively).
(about 0.09 pc and 3.3 pc at 1 kpc, respectively).
Our LABOCA observations took place on 19 May 2011, during the UTC time ranges of 03:17–06:20 and 07:54–10:50. The observing conditions were very good: the atmospheric zenith opacity, as determined using skydip measurements, was in the range τz = 0.10−0.12, and the amount of precipitable water vapour (PWV) was in the range 0.15–0.30 mm. The telescope focus and pointing were optimised and checked at regular intervals on the planets Saturn and Neptune, the Class 0 protostellar core IRAS 16293-2422, the ultracompact (UC) HII region G10.62-0.38, and the massive young stellar object (MYSO) G305.80-0.24 (B13134). The absolute calibration uncertainty is estimated to be about 10%.
The observations were performed using the on-the-fly (OTF) mapping mode, in which the telescope scanned continuously in right ascension (RA) along each row. We used a scanning speed of 3′ s-1 and step size 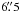 (~1/3 the beam HPBW) between RA subscans. The step size ≲1/3 × the beam HPBW is recommended to avoid beam broadening. The angular sizes of the maps are given in Col. (2) of Table 1 (sizes are in the range of ~0.23−0.30 deg2, with a total angular area of about 1 deg2). The target fields were mapped three to five times, with total on-source integration times in the range 49–79 min (Col. (4) of Table 1).
(~1/3 the beam HPBW) between RA subscans. The step size ≲1/3 × the beam HPBW is recommended to avoid beam broadening. The angular sizes of the maps are given in Col. (2) of Table 1 (sizes are in the range of ~0.23−0.30 deg2, with a total angular area of about 1 deg2). The target fields were mapped three to five times, with total on-source integration times in the range 49–79 min (Col. (4) of Table 1).
Data reduction was made with the CRUSH-2 (Comprehensive Reduction Utility for SHARC-2) (version 2.11-a1) software package4 (Kovács 2008). We used the pipeline iterations with the default reduction parameters, and also with specifying the “extended” option, which better preserves the extended structures. For G1.87-0.14, G2.11+0.00, and G13.22-0.06 (hereafter, G1.87, etc.), the “extended”-reduced maps were finally chosen for the analysis because fainter extended structures were clearly better recovered compared to the default reduction method. For G11.36, however, we adopted the map reduced with the default parameters because the clumpy structure of the filament became more clearly visible (Fig. 3). A slight beam-smoothing was applied in the reduction process, i.e., the maps were smoothed with a Gaussian kernel of the size 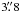 (full width at half maximum; FWHM). The instrument beam HPBW used by CRUSH-2 was
(full width at half maximum; FWHM). The instrument beam HPBW used by CRUSH-2 was 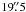 , and therefore the angular resolution of the final maps is
, and therefore the angular resolution of the final maps is 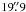 (~0.1 pc at 1 kpc). The gridding was performed with a cell size of 4″. The resulting 1σ rms noise levels in the final co-added maps are ~40−90 mJy beam-1 [Col. (5) of Table 1]. Assuming that the 870-μm dust opacity and the dust temperature are 1.38 cm2 g-1 and 15 K (see Sect. 4), the above surface-brightness sensitivity levels translate into 1σ H2 column-density detection thresholds of N(H2) ≃ 2.0−4.4 × 1021 mm-2. These correspond to visual extinction values of AV = N(H2)/0.94 × 1021 ≃ 2.1−4.7 mag (Bohlin et al. 1978)5. We note that employing the “extended” option in the reduction process leads to maps with a higher noise level than the values of ~30−50 mJy beam-1 resulting from the standard procedure (because large-scale emission is tried to be preserved). Therefore, the noise in the map of G11.36, which was reduced in the standard way, is clearly lower than in the other cases.
(~0.1 pc at 1 kpc). The gridding was performed with a cell size of 4″. The resulting 1σ rms noise levels in the final co-added maps are ~40−90 mJy beam-1 [Col. (5) of Table 1]. Assuming that the 870-μm dust opacity and the dust temperature are 1.38 cm2 g-1 and 15 K (see Sect. 4), the above surface-brightness sensitivity levels translate into 1σ H2 column-density detection thresholds of N(H2) ≃ 2.0−4.4 × 1021 mm-2. These correspond to visual extinction values of AV = N(H2)/0.94 × 1021 ≃ 2.1−4.7 mag (Bohlin et al. 1978)5. We note that employing the “extended” option in the reduction process leads to maps with a higher noise level than the values of ~30−50 mJy beam-1 resulting from the standard procedure (because large-scale emission is tried to be preserved). Therefore, the noise in the map of G11.36, which was reduced in the standard way, is clearly lower than in the other cases.
Target fields mapped with LABOCA.
2.3. C17O(2–1) line observations
From each target field, we selected seven to eight positions for single-pointing C17O(2−1) observations. These positions, which are listed in Table 2, were chosen from the Spitzer 8-μm images, and they correspond to (apparently) highly extincted parts along the filamentary structures near the map centres. The main purpose of these line observations was to obtain the cloud radial velocity, which is needed to determine the cloud kinematic distance (Sect. 4.1).
The C17O(2−1) observations at 224 714.199 MHz were carried out on 18, 22, and 26 May 2011 with APEX using the Swedish Heterodyne Facility Instrument (SHeFI; Belitsky et al. 2007; Vassilev et al. 2008a) [the heterodyne-part of the project 087.F-9315(A, B)]. As a frontend we used the APEX-1 receiver of the SHeFI (Vassilev et al. 2008b). The backend was the Fast Fourier Transfrom Spectrometer (FFTS; Klein et al. 2006) with a 1 GHz bandwidth divided into 8 192 channels. The resulting channel spacing is 122 kHz or 0.16 km s-1. The telescope beam size (HPBW) at the observing frequency is 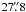 .
.
The observations were performed in the wobbler-switching mode with a 150″ azimuthal throw (symmetric offsets) and a chopping rate of 0.5 Hz (2 s wobbler period). Total (on+off) integration time was 5.6 min per position. The telescope pointing accuracy was checked by CO(2−1) cross maps of the carbon star RAFGL1922, and was found to be below ≲ 4″. The focus was checked by measurements on Saturn. Calibration was made by means of the chopper-wheel technique and the output intensity scale given by the system is 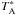 , which represents the antenna temperature corrected for the atmospheric attenuation. The observed intensities were converted to the main-beam brightness temperature scale by
, which represents the antenna temperature corrected for the atmospheric attenuation. The observed intensities were converted to the main-beam brightness temperature scale by 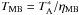 , where ηMB = 0.75 is the main-beam efficiency at the frequency used. The single-sideband system temperature, in units of TMB, was in the range 387−415 K. The absolute calibration uncertainty is estimated to be about 10%.
, where ηMB = 0.75 is the main-beam efficiency at the frequency used. The single-sideband system temperature, in units of TMB, was in the range 387−415 K. The absolute calibration uncertainty is estimated to be about 10%.
The spectra were reduced using the Fortran 90 version of the CLASS programme from the GILDAS software package6. The individual spectra were averaged and the resulting spectra were Hanning-smoothed to improve the signal-to-noise ratio of the data. A first- or third-order polynomial was applied to correct the baseline in the final spectra. The resulting 1σ rms noise levels are ~77−91 mK at the smoothed resolution (4 095 channels).
We note that the 17O nucleus has a nuclear spin of I = 5/2, so it has an electric quadrupole moment (−2.6 × 10-26 mm2). The latter couples to the electric-field gradient at the nucleus. This causes the rotational lines of C17O to have a hyperfine structure. The C17O(2−1) line is split into nine hyperfine (hf) components, which cover a velocity range of about 2.36 km s-1. We fitted this hf structure using “method hfs” of CLASS90 to derive the LSR velocity (vLSR) of the emission, and FWHM linewidth (Δv). The hf-line fitting can also be used to derive the line optical thickness, τ. However, in all spectra the hf components are blended, therefore the optical thickness could not be reliably determined. The rest frequencies and relative weights of the hf components were taken from Ladd et al. (1998; Table 6 therein).
Target positions of the C17O(2−1) observations in the equatorial J2000.0 system.
 |
Fig. 1 Left: LABOCA 870-μm map of G1.87-0.14. The image is shown with linear scaling, and the colour bar indicates the surface-brightness scale in Jy beam-1. The overlaid contours go from 0.27 Jy beam-1 (3σ) to 1.62 Jy beam-1, in steps of 3σ. Selected clumps are labelled with their designation (as listed in Table 3). The green plus signs indicate the positions of our C17O(2−1) observations (see Table 2). A scale bar indicating the 10 pc projected length is shown in the bottom left, with the assumption of a 10.57 kpc line-of-sight distance. The effective LABOCA beam of |
 |
Fig. 2 Same as Fig. 1 but towards G2.11+0.00. The overlaid LABOCA contours go from 0.18 Jy beam-1 (3σ) to 1.08 Jy beam-1, in steps of 3σ. A scale bar indicating the 5 pc projected length is shown in the bottom left, with the assumption of a 5.51 kpc line-of-sight distance. The clump SMM 5, which is associated with IRAS 17474-2704, lies at a distance of 7.40 kpc (see text). |
 |
Fig. 3 Same as Fig. 1 but towards G11.36+0.80. The obtained LABOCA map is zoomed-in towards the filamentary structure in the map centre because no submm dust emission was detected in other parts of the map. The overlaid LABOCA contours go from 0.12 Jy beam-1 (3σ) to 0.60 Jy beam-1, in steps of 3σ. Note that most of the line-observation target positions match the submm peak positions well. A scale bar indicating the 1 pc projected length is shown in the bottom left, with the assumption of a 3.27 kpc line-of-sight distance. |
 |
Fig. 4 Same as Fig. 1 but towards G13.22-0.06. The overlaid LABOCA contours go from 0.24 Jy beam-1 (3σ) to 1.44 Jy beam-1, in steps of 3σ. The field contains several clumps at different kinematic distances, and therefore only the angular scale bar is shown. The green circles in the Spitzer 8 μm image on the right panel indicate the positions and outer radii of the bubbles N10 and N11 from Churchwell et al. (2006; their Table 2). |
3. Observational results
3.1. LABOCA 870-μm maps
The obtained LABOCA maps are shown in Figs. 1–4. In the right panel of each figure, we show the Spitzer 8-μm image of the target field, overlaid with contours of the LABOCA submm dust emission.
As can be seen from the maps, the fields contain filamentary structures and clumps of different projected shapes. It can also be seen, especially towards the G1.87 and G2.11 fields, that not all 8-μm dark features are seen in submm emission. These may be structures whose column density is too low to be detected with the sensitivity limit of our data. On the other hand, as was pointed out by Wilcock et al. (2012), some of the 8-μm dark regions are not real dense clouds; they may just be dips in the MIR background that resemble the appearance of IRDCs.
We note that in the 0.23 degr2-sized G11.36 field, the filament in the map centre appeared to be the only submm-emitting object. Therefore, Fig. 3 shows only the zoomed-in view towards the filament.
3.2. Clump identification
To systematically identify the submm clumps from the LABOCA maps, we employed the commonly used two-dimensional clumpfind algorithm, clfind2d, developed by Williams et al. (1994). The algorithm requires two configuration parameters: i) the intensity threshold, i.e., the lowest contour level, which determines the minimum emission to be included into the clump; and ii) the contour level spacing, which determines the required “contrast” between two clumps to be considered as different objects. We set both of these parameters to the classical value of 3σ (~120−270 mJy beam-1), where the adopted 1σ sensitivity levels are given in Col. (5) of Table 1 (the value in parenthesis when the noise level varies across the map). Only clumps with peak flux densities greater than ~5σ were taken to be real. With these definitions, the number of clumps found by clfind2d are 40, 10, 7, and 34 in G1.87, G2.11, 11.36, and G13.22, respectively. This amounts to 91 identified clumps in this survey.
In each field, the clumps are called SMM 1, SMM 2, etc., in order of increasing right ascension. The J2000.0 coordinates of the peak 870 μm emission, peak surface brightnesses, integrated flux densities (within 3σ), and clump effective radii ( , where A is the projected area within the 3σ contour) are listed in Cols. (2)–(6) of Table 3. The quoted flux density uncertainties are based on the rms noise values and the 10% absolute calibration error. The clump effective radii listed in Table 3 are not corrected for beam size. Note that the clumps SMM 32 and 40 in G1.87, SMM 2 in G2.11, SMM 6 in G11.36, and SMM 1, 2, and 8 in G13.22 are only barely resolved because their sizes are only slightly larger than the beam. We also note that clump SMM 32 in G13.22 (Fig. 4) could be clearly resolved by eye into two “subclumps”, but they are treated as a single source by clfind2d with our settings.
, where A is the projected area within the 3σ contour) are listed in Cols. (2)–(6) of Table 3. The quoted flux density uncertainties are based on the rms noise values and the 10% absolute calibration error. The clump effective radii listed in Table 3 are not corrected for beam size. Note that the clumps SMM 32 and 40 in G1.87, SMM 2 in G2.11, SMM 6 in G11.36, and SMM 1, 2, and 8 in G13.22 are only barely resolved because their sizes are only slightly larger than the beam. We also note that clump SMM 32 in G13.22 (Fig. 4) could be clearly resolved by eye into two “subclumps”, but they are treated as a single source by clfind2d with our settings.
3.3. C17O(2–1) spectra
As shown by the green plus signs in Figs. 1–4, the selected C17O(2−1) observation target positions match the submm dust emission peaks very well only in G11.36. The target positions C and D in G1.87 are within the 3σ contour of SMM 35 (E is just outside). However, the target positions towards G2.11 do not have much, if any, associated dust emission (position D is an exception; it is coincident with SMM 2). Towards the G13.22 field the positions A, C, E, and F match the peak positions of SMM 18, 22, 23, and 27 quite well. The obtained C17O(2−1) spectra towards all target positions are shown in Figs. 5–8. Towards all fields, more than one velocity component is detected. This is unsurprising because we have observed along the Galactic midplane towards the inner Galaxy, where many molecular clouds along the line of sight can be expected. The fields G1.87, G2.11, and G13.22 show emission at negative and positive LSR velocities. Inspecting the longitude-velocity maps of CO by Dame et al. (2001), this can be expected at the Galactic longitudes in question. We note that the critical density of the C17O(2−1) transition is 9.5 × 103 mm-3 (assuming T = 15 K and using the data from the LAMDA molecular database7; Schöier et al. 2005), and therefore the line emission originates in dense gas.
Characteristics of the clumps identified from the LABOCA maps.
The C17O(2−1) line parameters are given in Table 4. The LSR velocities and FWHM linewidths derived from hf-structure fits are given in Cols. (2) and (3). The peak intensities derived through Gaussian fitting are listed in Col. (6), and in Col. (7) we give the integrated line intensities computed over the velocity range indicated in square brackets in the corresponding column. The uncertainties in the latter two parameters take into account the corresponding rms noise values and the 10% calibration uncertainty. For non-detections, we provide the 3σ upper limit to the line intensity in Col. (6). The other parameters listed in Table 4 are described below.
 |
Fig. 5 Smoothed C17O(2−1) spectra towards selected positions in G1.87-0.14. Most lines are seen at ~− 41 km s-1. Hyperfine-structure fits to the lines are overlaid in green. No line emission is detected towards position B, whereas two velocity components are seen towards positions C and F. |
 |
Fig. 6 Same as Fig. 5 but towards the selected positions in G2.11+0.00. Most detected lines are near ~16 km s-1. No lines were detected towards positions D, F, and G. Two velocity components are seen towards position C. |
 |
Fig. 7 Same as Fig. 5 but towards the selected positions in G11.36+0.80. We note that clear line emission at ~28 km s-1 is seen towards all positions. Two velocity components are detected towards positions A, B and F, but the secondary line is very weak in the former two cases. |
 |
Fig. 8 Same as Fig. 5 but towards the selected positions in G13.22-0.06. We note that clear line emission at ~37 km s-1 is seen towards all positions. Two velocity components are detected towards positions A–C and G. |
C17O(2−1) line parameters, column densities and fractional abundances, and CO depletion factors.
3.4. Clump associations
The Spitzer 8- and 24-μm images were visually inspected to see how the detected 870-μm clumps appear at these MIR wavelengths. The remarks concerning the 8/24 μm appearance of the clumps are given in the last column of Table 3. From the fields G1.87, G2.11, G11.36, and G13.22, we found 21, 5, 2, and 7 clumps that appear dark at both 8 and 24 μm (35 in total). The corresponding numbers of the clumps associated with either both 8 and 24 μm emission, or only with 24 μm emission, are 16, 3, 5, and 27 (51 in total). The type of this MIR emission was found to be either point sources, groups of point sources, extended, or diffuse-like. In addition, we found five clumps with an 8-μm point source near the submm peak position, which appear dark at 24 μm, however. If the 8-μm source were to be embedded within the clump, one would also expect to see emission at 24 μm (from warm dust). As noted in Table 3, these 8-μm sources have Spitzer-GLIMPSE [3.6]−[4.5] , [4.5]−[5.8] , and [4.5]−[8.0] colours of ≃ −0.03−0.80, 0.16−0.78, and 0.03−0.848. Because these colours are not sufficiently red for sources to be protostellar in nature, they are likely to be chance projections of foreground stars where the emission is primarily photospheric (cf. Gutermuth et al. 2008; Robitaille et al. 2008). For sources near the Galactic plane and/or at long distances from the Sun, the foreground-star population can be significant, and therefore five chance projections out of 91 clumps (5.5%) may not be surprising. We deal with these foreground contaminated clumps as IR-dark, although in some studies these cases are excluded from the source sample (for example, this was the case in the study by Chambers et al. (2009), who called these sources “blue cores”). This renders the total number of IR-dark clumps in our survey to be 40.
We used the SIMBAD Astronomical Database9 to search for possible source associations with our clumps. The resulting associations are given in Table 3, where we list the sources within about one beam size (~20″) from the LABOCA peak position.
In particular, 38 out of 91 clumps (42%) were found to be associated with 1.1-mm clumps from the Bolocam Galactic Plane Survey (BGPS; Rosolowsky et al. 2010; Aguirre et al. 2011)10. The BGPS survey, with an effective FWHM resolution of 33″, has detected and catalogued about 8400 clumps. Twenty-two clumps (24%) are associated with SCUBA submm clumps from Di Francesco et al. (2008). The SCUBA maps of Di Francesco et al. (2008) are composed of a so-called Fundamental Map Data Set at 850 and 450 μm (5061 objects), and an Extended Map Data Set at only 850 μm (6118 objects). Most of these associations (14 clumps) were found from the Extended Data Set (marked with “JCMTSE”), and eight sources have counterparts in the Fundamental Data Set (marked with “JCMTSF”). Thirteen clumps, or 14% of the sources, were found to be associated with IRDCs identified by Peretto & Fuller (2009)11; these are marked with “SDC” in Table 3.
Some other associations worth mentioning here are as follows. Four clumps were found to be associated with IRAS point sources: SMM 5 in G2.11 with IRAS 17474-2704, and the clumps SMM 8, 13, and 29 in G13.22 with IRAS 18112-1720, 18114-1718, and 18117-1738. The clumps SMM 35 and 40 in G1.87, SMM 4 in G11.36, and SMM 5, 15, and 17 in G13.22 are associated with YSO candidates from Robitaille et al. (2008). Moreover, SMM 24 in G13.22 is associated with a candidate AGB star from Robitaille et al. (2008). Two MIR bubbles from the Churchwell et al. (2006) catalogue, namely N10 and N11, are associated with the concentration of several clumps in G13.22 (see Figs. 4 and 13, and Sect. 5.1.2). Finally, we note that some of the clumps are associated with Class II methanol masers and UC HII regions, both of which are clear signposts of high-mass star formation. The diffuse/extended MIR emission seen towards some of the clumps is a typical characteristics of associated HII regions and photon-dominated regions (PDRs) surrounding them.
For G2.11-SMM 9, G13.22-SMM 2, G13.22-SMM 9, and G13.22-SMM 11, the clump appears to be partly associated (in projection) with diffuse- and/or somewhat extended MIR emission, and is partly IR dark. Especially in the N10/11 bubble environment, the clump classification into IR dark or IR bright was difficult because of the very bright and extended appearance of the region at 8 and 24 μm. We note that classifying clumps in the above four cases is a subjective process, influenced by the adopted colour scale of the 8- and 24-μm images.
4. Analysis and results
4.1. Kinematic distances
The distance to the source is an important parameter when its physical properties, such as mass, are to be determined. Because our sources belong to the first quadrant (0° ≤ l < 90°) in the inner Galaxy (i.e., inside the solar circle), each radial velocity corresponds to two kinematic-distance values along the line of sight. However, in the first Galactic quadrant, the radial velocity of the source increases as a function of distance up to the tangent point. At this point, the source’s velocity vector and the line of sight are aligned with each other, and the radial velocity has its maximum value. After passing the tangent point, the radial velocity starts to decrease as a function of distance, all the way down to negative values (Roman-Duval et al. 2009; Fig. 2 therein). In general, it is reasonable to assume, and often has been assumed, for sources associated with IRDCs, that they lie at the near distance, because in that case there is more background radiation against which to see the cloud in absorption.
To calculate the kinematic distances of G1.87, G2.11, and G11.36, we adopted the average C17O(2−1) radial velocities towards each field (using the velocities at which most lines were seen, and excluding the additional velocity components). The obtained average LSR velocities for G1.87, G2.11, and G11.36 are −41.5, 16.7 (from positions A and B), and 27.8 km s-1. The clump SMM 5 (IRAS 17474-2704) in G2.11 is an exception. Although it is near to our line observation positions in the plane of the sky, it has its peak Class II CH3OH maser emission at 63 km s-1 (Caswell et al. 1995). The OH and H2O masers towards this source also peak at comparable velocities (Forster & Caswell 1989). Therefore, we adopted a velocity of 63 km s-1 for G2.11-SMM 5.
The average C17O(2−1) LSR velocity for G13.22 is 35.9 km s-1. However, from the HCO+ and N2H+ survey of the BGPS 1.1-mm clumps by Schlingman et al. (2011), we obtained velocity information for the following clumps in G13.22: SMM 5, 10, 13, 17, 24, 25, 27, 28, 29, and 32. As shown in Fig. 4, the other clumps in G13.22 are seen in projection close to the above listed clumps. For example, the clumps near the bubbles N10/11, such as SMM 5 and 7, are likely physically connected, and SMM 31 is likely associated with SMM 28. Another example is SMM 26, which is likely a member of the filament connecting SMM 24 and 29. Therefore, we did not adopt our C17O-derived radial velocity for the field G13.22, but instead used the values from Schlingman et al. (2011). Sewilo et al. (2004), using the H110α and H2CO observations, were able to distinguish between the near and far distances of G13.22-SMM 29 (IRAS 18117-1738); H2CO absorption was seen between the source velocity and the velocity at the tangent point, placing the source at the far distance12.
We employed the rotation curve of the Galaxy by Reid et al. (2009), which is based on direct measurements of trigonometric parallaxes and the proper motions of masers in high-mass star-forming regions. The best-fit rotation parameters of Reid et al. (2009) are (Θ0, R0) = (254 km s-1, 8.4 kpc), where Θ0 is the orbital velocity of the Sun around the Galactic Centre, and R0 is the solar galactocentric distance. The resulting near and far kinematic distances, dnear and dfar, and the Galactocentric distances, RGC, are given in Table 5. Unless otherwise stated, the near distance was adopted. We note that RGC does not have a distance ambiguity. All other clumps in G13.22 for which we adopted the distances derived using the data from Schlingman et al. (2011) are listed in Col. (5) of Table 5. We note that our distances for the G13.22 clumps correspond to the values reported by Schlingman et al. (2011), who also used the Reid et al. (2009) rotation curve.
As discussed above, the negative radial velocity of G1.87 places it at the far distance. In principle, it could also belong to the near 3-kpc arm at d ~ 5 kpc (Dame & Thaddeus 2008; Green et al. 2011; Tackenberg et al. 2012), but the far solution is adopted in this work. Another noteworthy issue to raise is that our line observations were only made towards the filamentary structures near the map centres, and therefore the derived radial velocities may not apply for all clumps detected in the field. This may especially be the case towards G1.87, where many clumps are detected at low Galactic longitudes. Additional distance-uncertainty towards G1.87 is caused by the possible association of some of the clumps with the near 3-kpc arm. On the other hand, the field G11.36, where only one velocity-coherent filament is detected, can be considered to have the most reliable distance estimate among our target fields.
4.2. Temperatures
The dust and gas temperatures, Tdust and Tkin, are also essential knowledge when studying the physics and chemistry of molecular clumps. To our knowledge, for only one clump in our sample, namely SMM 5 in G13.22, the gas kinetic temperature measurement has been published. Pillai et al. (2007) derived the NH3 rotation temperature of Trot = 17.4 ± 1.3 K for SMM 5 (their source G13.18+0.06). Using the Trot−Tkin relationship from Tafalla et al. (2004), we obtain Tkin = 20.5 ± 1.7 K13. We note that at high densities of n(H2) ≳ 3 × 104 mm-3, where collisional coupling between the gas and dust becomes efficient, the gas and dust temperatures are expected to be similar, Tkin ≃ Tdust (e.g., Galli et al. 2002).
For those four clumps in our sample that are associated with IRAS point sources, we estimated the dust temperature to be the same as the 60/100-μm colour temperature defined by Henning et al. (1990) as ![\begin{equation} T_{\rm dust}\simeq T_{\rm c}\left(\frac{60}{100}\right)=96\left[(3+\beta)\ln \left(\frac{60}{100}\right)-\ln \left(\frac{S_{60}}{S_{100}}\right) \right]^{-1} \cdot \end{equation}](/articles/aa/full_html/2012/06/aa19144-12/aa19144-12-eq908.png) (1)In this formula, β is the dust emissivity index, and Sλ is the flux density at the wavelength λ. The value of β was set to be 1.8 to be consistent with the Ossenkopf & Henning (1994) dust model discussed in Sect. 4.3. For the IRAS sources 17474-2704, 18112-1720, 18114-1718, and 18117-1738, i.e., for the clumps G2.11-SMM 5, G13.22-SMM 8, G13.22-SMM 13, and G13.22-SMM 29, we derived the Tdust values of 30.0, 18.9, 35.5, and 18.9 K.
(1)In this formula, β is the dust emissivity index, and Sλ is the flux density at the wavelength λ. The value of β was set to be 1.8 to be consistent with the Ossenkopf & Henning (1994) dust model discussed in Sect. 4.3. For the IRAS sources 17474-2704, 18112-1720, 18114-1718, and 18117-1738, i.e., for the clumps G2.11-SMM 5, G13.22-SMM 8, G13.22-SMM 13, and G13.22-SMM 29, we derived the Tdust values of 30.0, 18.9, 35.5, and 18.9 K.
For the remaining 86 clumps we assumed the dust temperatures to be the following: 15 K for IR-dark clumps, 20 K for IR-bright clumps (8/24 μm emission), and 30 K for clumps associated with HII regions/radio sources. The choice of Tdust = 15 K or 20 K for most of our clumps is expected to be reasonable because previous molecular-line observations of clumps within IRDCs have shown the typical gas kinetic temperature to lie in the range Tkin ≈ 10−20 K (Carey et al. 1998; Teyssier et al. 2002; Sridharan et al. 2005; Pillai et al. 2006; Sakai et al. 2008; Zhang et al. 2011; Devine et al. 2011; Ragan et al. 2011). For comparison, in their study of a massive clump associated with an IRDC, Hennemann et al. (2009) derived the Tdust values of 22 K and 15 K for the clump’s substructures (“cores”) with and without 24-μm sources, respectively. Rathborne et al. (2010) also found that 24-μm bright clumps embedded in IRDCs are warmer than their 24-μm dark counterparts. The assumption of a slightly higher temperature of 30 K in clumps with embedded HII regions is supported by the 30-K temperature of the UC HII region G2.11-SMM 5 derived above, and also consistent with some other observational results (see, e.g., Sreenilayam & Fich 2011, and references therein).
Finally, we note that the BGPS 1.1-mm data available for 42% of our clumps could, in principle, be used to estimate the dust colour temperature. However, there are three factors that would hamper this analysis: i) the Bolocam 1.1-mm flux densities may be somewhat uncertain (due to spatial filtering and calibration issues), and should be multiplied by 1.5 ± 0.15 as recommended by Aguirre et al. (2011); ii) one should make assumptions about the value of β as above; and iii) the LABOCA and Bolocam wavelengths are quite close to each other (0.87 mm vs. 1.1 mm), and therefore the corresponding flux densities are comparable to each other. In addition, our LABOCA data should be smoothed to the 33″ BGPS resolution for a proper comparison. For these reasons, it seems justified to assume that the Tdust values are similar to those observed in some other sources of similar type.
4.3. Radii, masses, and H2 column and number densities
The linear clump effective radii (in pc) were derived from the angular radii and kinematic distances as Reff [pc] = Reff [rad] × d [pc] . The error in Reff was computed from the average value between the ± -distance errors quoted in Table 5.
The clump masses, M, over an effective area of radius Reff were estimated from the integrated 870-μm flux densities and using the standard optically thin dust emission formulation (see, e.g., Eq. (6) in Miettinen & Harju 2010; hereafter MH10). Following Hatchell et al. (2007), the peak surface brightness was used if it was higher than the integrated flux density (this was the case for G1.87-SMM 40, G2.11-SMM 2, G11.36-SMM 6, and G13.22-SMM 8; all but G2.11-SMM 2 are associated with previously known sources, and are therefore likely to be real). The distances and dust temperatures used were as explained above. The dust opacity per unit dust mass at 870 μm was taken to be κ870 = 1.38 mm2 g-1. This value was extrapolated from the Ossenkopf & Henning (1994) model describing graphite-silicate dust grains that have coagulated and accreted thin ice mantles over a period of 105 yr at a gas density of nH = n(H) + 2n(H2) ≃ 2n(H2) = 105 mm-3.14 In this model, the dust emissivity index is β ≃ 1.8, as determined from the slope between 350 and 1300 μm (κλ ∝ λ−β). For the average dust-to-gas mass ratio, Rd ≡ ⟨ Mdust/Mgas ⟩ , we adopted the canonical value 1/100 (Spitzer 1978). The uncertainty in mass was propagated from the uncertainties in flux density and source distance (the 1.7-K temperature error was also employed for G13.22-SMM 5).
The peak beam-averaged H2 column densities, N(H2), were computed from the peak surface brightnesses in a standard way (see, e.g., Eq. (8) in MH10). For this calculation we assumed a He/H abundance ratio of 0.1, which leads to the mean molecular weight per H2 molecule of μH2 = 2.8. Other parameters (Tdust, κ870, Rd) were the same as used in the mass calculation. The error in N(H2) is solely based on the uncertainty in the peak surface brightness (except for G13.22-SMM 5, where Tdust error was also used). The volume-averaged H2 number densities over Reff, ⟨ n(H2) ⟩ , were calculated using Eq. (7) of MH10, and the corresponding errors were propagated from those of M and Reff.
The values of the physical parameters derived above are listed in Cols. (6)–(9) of Table 3. Their distributions are shown in Fig. 9: panels a)–d) show the histograms of Reff, M, N(H2), and ⟨ n(H2) ⟩ , respectively. The parameters’ mean and median values are described in the figure caption.
 |
Fig. 9 Distributions of a) clump effective radii, b) masses, c) H2 column densities, and d) H2 number densities. Open histograms represent the IR-dark clumps, while shaded histograms represent the IR-bright clumps (those with 8/24 μm emission). The solid and dashed vertical lines indicate the average values for IR-dark and IR-bright clumps, respectively. The average (median) radii for IR-dark and IR-bright clumps are 1.19 (1.14) and 0.96 (0.87) pc, respectively. The average (median) mass of IR-dark clumps is 3079 (2108) M⊙, whereas that of IR-bright clumps is 1604 (804) M⊙. The mean H2 column density is 3.2 × 1022 mm-2 for both distributions (median values are 2.8 × 1022 and 2.1 × 1022 cm-2 for IR-dark and IR-bright clumps, respectively). The average (median) H2 number densities for IR-dark and IR-bright clumps are 7250 (6000) cm-3 and 6667 (6000) mm-3, respectively. |
4.4. Non-thermal velocity dispersion
The measured C17O(2−1) linewidths were used to calculate the non-thermal portion of the line-of-sight velocity dispersion, σNT (averaged over a 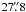 beam); see, e.g., Eq. (1) in Miettinen (2012, hereafter M12). We also computed the ratio σNT/cs, where
beam); see, e.g., Eq. (1) in Miettinen (2012, hereafter M12). We also computed the ratio σNT/cs, where 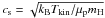 is the isothermal sound speed with kB the Boltzmann constant, μp = 2.33 the mean molecular weight per free particle for solar composition (He/H = 0.1), and mH the mass of the hydrogen atom. Some of our line observations are probing embedded YSOs, and Tkin = 20 K was accordingly assumed for these. For other positions, the value Tkin = 15 K was adopted. The values of σNT and σNT/cs are listed in Cols. (4) and (5) of Table 4. The uncertainties are based on the linewidth uncertainties. The vast majority of the positions show supersonic non-thermal motions (σNT > cs), which are presumably due to turbulence. This is a general observational feature of the interstellar molecular clouds (e.g., Larson 1981; McKee & Zweibel 1992; Heyer & Brunt 2004).
is the isothermal sound speed with kB the Boltzmann constant, μp = 2.33 the mean molecular weight per free particle for solar composition (He/H = 0.1), and mH the mass of the hydrogen atom. Some of our line observations are probing embedded YSOs, and Tkin = 20 K was accordingly assumed for these. For other positions, the value Tkin = 15 K was adopted. The values of σNT and σNT/cs are listed in Cols. (4) and (5) of Table 4. The uncertainties are based on the linewidth uncertainties. The vast majority of the positions show supersonic non-thermal motions (σNT > cs), which are presumably due to turbulence. This is a general observational feature of the interstellar molecular clouds (e.g., Larson 1981; McKee & Zweibel 1992; Heyer & Brunt 2004).
4.5. C17O column densities, fractional abundances, and CO depletion factors
The beam-averaged C17O column densities, N(C17O), were derived following the standard LTE analysis outlined, e.g., in the paper by M12 (Appendix A.3 therein). In brief, we have assumed optically thin line emission, and computed the N(C17O) values from the integrated line intensities. In the two cases where the detected line does not cover all the hf components (see Table 4), the column densities were scaled by the inverse of the relative line strength within the detected line. The C17O(2−1) transition was assumed to be thermalised at the gas temperature of the target position as seen in previous studies (e.g., Miettinen et al. 2011). Therefore, the line excitation temperature was adopted to be Tex = 15 K towards all the positions except those associated with MIR emission, where Tex = 20 K was used. We note that if Tex increases from 10 to 20 K, the column density decreases by a factor of 2.3 (or by a factor of 1.3 for Tex of 15–20 K). The errors in N(C17O) were propagated from those associated with the integrated intensity.
The fractional C17O abundances were computed by dividing the C17O column density by the H2 column density as x(C17O) = N(C17O)/N(H2). For this purpose, the N(H2) values were derived from the LABOCA maps smoothed to the 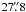 resolution of the line observations. The uncertainty in x(C17O) was derived from both the errors in the C17O and H2 column densities.
resolution of the line observations. The uncertainty in x(C17O) was derived from both the errors in the C17O and H2 column densities.
The CO depletion factors, fD, were also derived following the analysis in M12 (see Appendix A.4 and references therein). In summary, the Galactocentric distance of the source was first used to estimate the appropriate canonical (or undepleted) CO abundance. For example, the “field” RGC values shown in Table 5 lead to the CO abundances of x(CO) ≃ 1.5−2.2 × 10-4. We also employd the RGC-dependent [16O]/[18O] ratio, which is ≃ 166−345 for the “field” RGC values, and adopted the [18O]/[17O] ratio of 3.52. This way, we estimated the canonical C17O abundance and calculated the depletion factor as fD = x(C17O)can/x(C17O)obs. The fD uncertainty was propagated from that in the observed fractional abundance. The results of the calculations presented in this section are shown in Table 4 (the last three columns). We note that we only report the values of fD for the “main” velocity components, because the line profiles in these cases are more reliable than those of the additional velocity components. We also stress that the formal fD errors probably underestimate the true uncertainties by a factor of ≳ 2−3 because of the uncertainties in the assumptions used (Tex, oxygen-isotopic ratios, etc.). Therefore, some of the fD values might be significantly lower than reported here. In this regard, the apparent variation of fD between different sources might not be robust.
4.6. Analysis of the filamentary IRDC G11.36+0.80
The G11.36 cloud represents the best example of a filamentary IRDC in our survey. In addition, as demonstrated in Fig. 3, our C17O line observations probe the clumps along the filament. For these reasons, we will analyse the filament’s properties in more detail here.
The north-south oriented G11.36 filament has a total projected length of about 4.05′ or 3.85 pc, and its average radius is about 0.4 pc. By excluding the clumps SMM 6 and 7, which lie on the side of the filament, we can estimate the mass of the filament to be ~762 M⊙ as the sum of the clump masses within it. This results in a filament mass per unit length, or line mass, of Mline ~ 198 M⊙ pc-1. The average projected separation between the five clumps in the filament is about 0.9 pc.
As shown in Col. (5) of Table 4, the filament appears to be dominated by supersonic non-thermal motions (σNT/cs ≃ 1.5−3.7). Therefore, to examine the dynamical state of the filament, we calculated its virial mass per unit length as 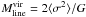 , where ⟨ σ2 ⟩ is the square of the total (thermal+non-thermal) velocity dispersion, i.e., the square of the effective sound speed (ceff), and G is the gravitational constant (Fiege & Pudritz 2000a). Assuming that the gas kinetic temperature is Tkin = 15 K, and using the average non-thermal velocity dispersion of 0.69 km s-1, we obtain ceff = 0.73 km s-1. Thus, we derive the values
, where ⟨ σ2 ⟩ is the square of the total (thermal+non-thermal) velocity dispersion, i.e., the square of the effective sound speed (ceff), and G is the gravitational constant (Fiege & Pudritz 2000a). Assuming that the gas kinetic temperature is Tkin = 15 K, and using the average non-thermal velocity dispersion of 0.69 km s-1, we obtain ceff = 0.73 km s-1. Thus, we derive the values 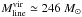 pc-1 and
pc-1 and 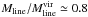 . This implies that G11.36 as a whole is close to virial equilibrium.
. This implies that G11.36 as a whole is close to virial equilibrium.
The magnetohydrodynamic sausage-type instability theory predicts that growing perturbations can fragment a self-gravitating fluid cylinder into successive condensations with almost periodic separations (e.g., Chandrasekhar & Fermi 1953; Nagasawa 1987; see also Jackson et al. 2010). This separation distance corresponds to the wavelength of the fastest growing mode, λmax = 2π/kmax (kmax is the wavenumber), which, in turn, is twice the wavelength of the axisymmetric perturbations to which the cylinder is unstable. Jackson et al. (2010) and M12 applied the sausage-type instability predictions about clump separations to the filamentary IRDCs “Nessie” Nebula and G304.74+01.32. Both studies found that the observed clump separations agree with theoretical predictions when non-thermal (turbulent) motions are taken into account. In this case, the fastest growing mode in an isothermal, infinitely long gas cylinder appears at 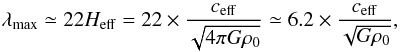 (2)where Heff is the effective radial scale height with ρ0 the central gas-mass density along the cylinder’s axis. If we compute ρ0 assuming that the central number density is 105 mm-3, which seems reasonable because even the volume-averaged densities are ~104 cm-3 (Table 3), we derive the values Heff ≃ 0.04 pc and λmax ≃ 0.9 pc. This excellently agrees with the observed average clump separation of ~0.9 pc. The cloud may therefore lie close to the plane of the sky. Moreover, the wavelength of the fastest growing perturbation appears to be approximately equal to the filament’s diameter of ~0.8 pc, in accordance with theory (Nakamura et al. 1993).
(2)where Heff is the effective radial scale height with ρ0 the central gas-mass density along the cylinder’s axis. If we compute ρ0 assuming that the central number density is 105 mm-3, which seems reasonable because even the volume-averaged densities are ~104 cm-3 (Table 3), we derive the values Heff ≃ 0.04 pc and λmax ≃ 0.9 pc. This excellently agrees with the observed average clump separation of ~0.9 pc. The cloud may therefore lie close to the plane of the sky. Moreover, the wavelength of the fastest growing perturbation appears to be approximately equal to the filament’s diameter of ~0.8 pc, in accordance with theory (Nakamura et al. 1993).
In this theoretical framework, the clump masses should be less than M ~ λmaxMline (see Jackson et al. 2010). Using either the observed line mass or the 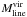 value, the predicted maximum mass is about 180 or 220 M⊙. The estimated clump masses in the filament are in the range ~101−192 M⊙, which conforms to the theoretical expectation. The fragmentation timescale for a filament of radius Rfil is expected to be comparable to its radial signal crossing time, τcross = Rfil/ ⟨ σ2 ⟩ 1/2 (see Eq. (26) in Fiege & Pudritz 2000b). For G11.36, this is estimated to be ~5.4 × 105 yr.
value, the predicted maximum mass is about 180 or 220 M⊙. The estimated clump masses in the filament are in the range ~101−192 M⊙, which conforms to the theoretical expectation. The fragmentation timescale for a filament of radius Rfil is expected to be comparable to its radial signal crossing time, τcross = Rfil/ ⟨ σ2 ⟩ 1/2 (see Eq. (26) in Fiege & Pudritz 2000b). For G11.36, this is estimated to be ~5.4 × 105 yr.
4.7. Virial analysis of the clumps in G11.36+0.80
We employed the C17O(2−1) linewidths and Eq. (3) in M12 to calculate the virial masses, Mvir, of the clumps in G11.36. It was assumed that the clumps have a density profile of the form n(r) ∝ r-1.6 found by, e.g., Beuther et al. (2002) for high-mass star-forming clumps. The corresponding virial parameters were derived following the definition of Bertoldi & McKee (1992), i.e., αvir = Mvir/M. If αvir = 1, the clump is in virial equilibrium, whereas the clumps with αvir ≤ 2 are taken to gravitationally bound. The derived values of Mvir and αvir are given in Table 6, and αvir is also plotted as a function of the clump mass in Fig. 10. The error in Mvir was propagated from those associated with Δv and Reff, whereas the error of αvir includes the uncertainties in both the mass values Mvir and M. Although the uncertainties are large, it seems that five out of seven clumps in G11.36 are gravitationally bound. The corresponding ratio is 4/5 when considering only the clumps in the filament We note that the submm peak of SMM 4 was missed by the line observations, position D being closest to it. Therefore, the virial parameter of SMM 4 should be interpreted with some caution.
Virial masses and parameters for the clumps in G11.36.
 |
Fig. 10 Virial parameter vs. mass for the clumps in G11.36. The dashed line indicates the virial-equilibrium limit of αvir = 1, and the dash-dotted line shows the limit of gravitational boundedness or αvir = 2. |
5. Discussion
5.1. The nature of the detected clumps
The sizes and masses of the clumps detected in this study indicate that they are the precursors/formation sites of stellar clusters and groups, rather than those of single stars or low-order multiples. Among our sample, 40 clumps are IR dark, and 51 clumps are IR bright, leading to a relative fractions of 44% and 56%. Some of the detected IR-dark clumps may represent the high-mass starless “cores” (HMSCs). However, it is fully possible that at least some of them do contain embedded YSOs, which are not bright enough to be detected with the present sensitivity, however. The clumps associated with point-like MIR emission at 8 and 24 μm, or only at 24 μm, are likely to host YSOs. The only exceptions may be the cases where the clump is partly IR-dark, and partly associated with extended MIR emission, possibly from the nearby sources as for the N10/11 bubble environment. For example, star-formation activity within a clump, such as mass accretion, heats the surrounding dust, causing it to emit the 24-μm IR radiation. Towards eight clumps, a group of 8-μm point sources is resolved. This indicates that the clumps were fragmented into smaller units, and the formation of a stellar group/cluster is taking place. For comparison, from their total sample of 190 clumps associated with IRDCs, Chambers et al. (2009) found that 98 (52%) contain 24-μm sources, a percentage similar to ours. Parsons et al. (2009) found that from their (sub)sample of 69 clumps within IRDCs, 48 (70%) were associated with embedded 24-μm source(s). More recently, Tackenberg et al. (2012) found that only ~23% of the clumps in their ATLASGAL-survey study showed no signs of IR emission.
The estimated masses of the detected IR-dark and IR-bright clumps lie in the ranges ~25−2 × 104 M⊙ and ~42−9.5 × 103 M⊙, respectively. The clump masses as a function of radius are plotted in Fig. 11. As can be seen, many of the clumps appear to lie above the mass-radius threshold for massive-star formation proposed by Kauffmann & Pillai (2010). In particular, 31 IR-dark clumps (~78%) lie on or above this threshold line, hence they are potential sites of future high-mass star formation. For example, Beuther et al. (2011) estimated that the initial mass of a clump has to be ~850 M⊙ if it is to form at least one 20 M⊙ star; similarly, a ~1900 M⊙ clump is needed to form a 40 M⊙ star. In this regard, our sample contains 28 (22) IR-dark clumps, which could be able to give birth to a 20 (40) M⊙ star.
Following Casoli et al. (1986; their Sect. 4.1), we can compute the IR luminosities, LIR, of the detected IRAS sources using the sources’ distances and flux densities at 12, 25, 60, and 100 μm. The obtained LIR values of IRAS 17474-2704, 18112-1720, 18114-1718, and 18117-1738 are 4.4 × 104, 1.3 × 104, 7.4 × 103, and 1.9 × 105 L⊙. These should be interpreted as lower limits to the bolometric luminosity, Lbol, because other wavelength data (e.g., near-IR and submm) were not employed. These high luminosities are indicative of massive-star formation in the corresponding clumps. The clump G2.11-SMM 5, associated with IRAS 17474-2704, also shows Class II CH3OH maser emission at 6.7 GHz (Caswell et al. 1995). Because this maser transition results from radiatively pumped population inversion by IR emission from warm dust, it can only occur near MYSOs (e.g., Cragg et al. 1992; Minier et al. 2003; Xu et al. 2008).
Krumholz & McKee (2008) showed that a clump’s mass surface density needs to be Σ ≳ 1 g cm-2 if heating is to prevent clump fragmentation into smaller units, and hence, enable high-mass star formation. In terms of H2 column density, this threshold is N(H2) = Σ/μH2mH ≃ 2.1 × 1023 mm-2. The estimated beam-averaged N(H2) values are all lower than this, but the (possible) substructure within the clumps, or dense cores, can have much higher column densities. Also, as discussed above, some of the clumps already show clear signposts of high-mass star formation.
 |
Fig. 11 Relation between mass and effective radius for the detected clumps. The IR-dark and IR-bright clumps have been plotted with open and filled circles, respectively. The dotted line represents the mass-radius threshold for massive-star formation proposed by Kauffmann & Pillai (2010), i.e., M(R) = 870 M⊙ × (R/ pc)1.33. |
5.1.1. Are there any EGOs?
A visual inspection of the Spitzer 4.5-μm images revealed somewhat extended emission associated with the clumps SMM 13, 17, 23, 25, 27, 29, and 32 in G13.22 (see Fig. 12). These type of sources are known as extended green objects (EGOs; Cyganowski et al. 2008) or “green fuzzies” (Chambers et al. 2009). The enhanced/extended 4.5-μm emission is believed to be mainly caused by shock-excited H2 lines and/or ro-vibrational lines of CO(ν = 1−0), implying the presence of outflow shocks in the source (Marston et al. 2004; Smith & Rosen 2005; Smith et al. 2006; Ybarra & Lada 2009; De Buizer & Vacca 2010). However, Takami et al. (2012) discussed the possibility that the dominant emission mechanism responsible for EGOs might be scattered continuum in outflow cavities. In any case, EGOs appear to be related to outflow activity. Finding EGOs among our sources is unsurprising, because they often appear to be associated with IRDCs and 6.7-GHz Class II CH3OH masers (Chen et al. 2010).
 |
Fig. 12 Spitzer-IRAC three-colour composite images towards EGO candidates in G13.22 overlaid with contours of LABOCA dust continuum emission. The 3.6, 4.5, and 8.0 μm emission is coded in blue, green, and red, respectively, and the colours are shown in linear scales. The contours are as in Fig. 4. Towards G13.22-SMM 13 (top left), the black circles indicate the positions of the 1.5-GHz VLA radio sources from Garwood et al. (1988), the diamond symbol shows the position of the 5-GHz VLA radio source from Becker et al. (1994), and the white cross shows the nominal catalogue position of IRAS 18114-1718. Towards G13.22-SMM 29 (middle right), the position of IRAS 18117-1738 is indicated by a black cross. The black circle towards G13.22-SMM 32 (bottom) denotes the 1.4-GHz radio source 181449-173243 from Condon et al. (1998). The white plus signs in the middle left and bottom panels represent the positions of our C17O observations. We note that in the bottom panel the linear scale bar corresponds to the line-of-sight distance of SMM 25. |
 |
Fig. 13 Spitzer-IRAC three-colour composite image towards the bubbles N10 and N11 overlaid with contours of LABOCA dust continuum emission. The 3.6, 4.5, and 8.0 μm emission is coded in blue, green, and red, respectively, and the colours are shown in linear scales. The contours are as in Fig. 4. The squares show the positions of the two 870-μm condensations found by Deharveng et al. (2010); their condensation 1 is associated with our clump SMM 5, and condensation 2 is associated with SMM 7. The circles show the positions of the candidate embedded MYSOs on the rims of N10 (Watson et al. 2008). The diamond symbols indicate the positions of the 6.7-GHz Class II methanol masers from Szymczak et al. (2002; right) and Pandian et al. (2008; left). |
5.1.2. The bubbles N10 and N11
A zoom-in view towards the N10/11 bubble environment in G13.22 is shown in Fig. 13. Our LABOCA clumps SMM 4, 5, 7, and 11 appear to form a  or ~9.1 pc long ridge between these two IR bubbles from Churchwell et al. (2006). Moreover, the clumps SMM 6 and 9 form a filamentary structure, extending perpendicularly to the southeast from the above mentioned ridge.
or ~9.1 pc long ridge between these two IR bubbles from Churchwell et al. (2006). Moreover, the clumps SMM 6 and 9 form a filamentary structure, extending perpendicularly to the southeast from the above mentioned ridge.
Churchwell et al. (2006) classified N10 and N11 as complete (or closed) bubbles, with N10 enclosing a star cluster (see also Watson et al. 2008; their Fig. 14). Moreover, the N10/11 system was classified as a bipolar bubble whose lobes are in contact. Both bubbles are coincident with HII regions (Deharveng et al. 2010 and references therein), and Watson et al. (2008) identified four possible ionising stars located inside N10 in projection. Watson et al. (2008) also identified four embedded candidate MYSOs on the rims of N10, and suggested that the bubble could be associated with triggered massive-star formation. The elongated dust emission morphology observed here is perhaps consistent with this scenario. The third observation noted by Watson et al. (2008) was that inside the 8-μm shell of N10, emission at both 24 μm and 20 mm peak at the same position, implying the presence of hot dust inside the HII region.
Deharveng et al. (2010) reported the detection of two LABOCA condensations on the border of N10. As shown in Fig. 13, the two condensations are coincident with our clumps SMM 5 and 7. As discussed by these authors, a Class II methanol maser associated with the edge of SMM 5 (their condensation 1) supports the scenario of triggered massive-star formation. Another CH3OH maser is seen close to the centre of N10 in projection (Pandian et al. 2008). Deharveng et al. (2010) also speculated that N10 could be in the process of opening, because of its elongated shape. They speculated that the observed bipolar morphology of the system might result from the expansion of an HII region simultaneously in two opposite directions through the edge of the cloud. The dust filament consisting of SMM 6 and 9 could perhaps be related to the bubble expansion. As already noted by Deharveng et al. (2010), N11 is not associated with significant LABOCA 870-μm emission.
5.2. Lifetime of massive IR-dark clumps
We can use the relative numbers of IR-dark and IR-bright clumps to estimate the statistical lifetime of the former stage. We avoid to use the term “starless” clump here, because some of the IR-dark clumps may well harbour faint YSOs, which cannot be detected with the current detection limit.
Following Chambers et al. (2009), we also adopted as a representative YSO lifetime the accretion timescale ~2 × 105 yr from Zinnecker & Yorke (2007). If we also assume that i) all our IR-bright clumps, including those that are only partly associated with diffuse-like emission, host YSOs, ii) the star-formation rate is constant as a function of time, and iii) the clump’s lifetime does not depend on its mass, we estimate the duration of the IR-dark phase of clump evolution to be τIR−dark ~ 40/51 × 2 × 105 ~ 1.6 × 105 yr. Concerning the third assumption, Clark et al. (2007) noted that the clumps of different mass are expected to have different lifetimes, because their free-fall timescales, τff ∝ 1/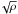 , can be different. They pointed out that this timescale problem may not be a problem if the studied clumps have roughly the same density, i.e., the same τff. The estimated average densities of our IR-dark and IR-bright clumps vary by factors of ~7 and 15, respectively, so their evolutionary rates can also vary. This makes our third assumption therefore fairly tentative.
, can be different. They pointed out that this timescale problem may not be a problem if the studied clumps have roughly the same density, i.e., the same τff. The estimated average densities of our IR-dark and IR-bright clumps vary by factors of ~7 and 15, respectively, so their evolutionary rates can also vary. This makes our third assumption therefore fairly tentative.
For comparison, Chambers et al. (2009), by considering only their quiescent (no embedded IR emission) and active (green fuzzies and 24 μm emission) sources (69 and 37 sources, respectively), estimated a factor of ~2 longer duration for the quiescent phase, i.e., ~3.7 × 105 yr. However, by comparing the relative numbers of their quiescent and 24-μm sources only (“intermediate cores”), 69/98 ≃ 0.7, the quiescent-phase timescale becomes ~1.4 × 105 yr, which is very similar to our estimate. Parsons et al. (2009), adopting the embedded YSO duration of 104−105 yr, deduced that the IR-dark phase of massive clumps lasts a few times 103−104 yr. With the aid of SiO spectral-line data, Russeil et al. (2010) estimated that the combined lifetime of starless clumps (no IR emission/high-velocity SiO emission) and IR-quiet MYSOs is ~1 × 104 + 6 × 104 = 7 × 104 yr in the NGC 6334/6357 complex, which is a factor of ~2 less than our τIR−dark value. Tackenberg et al. (2012) inferred the lifetime of massive IR-dark (“starless” in their nomenclature) clumps to be ~(6 ± 5) × 104 yr, the upper limit being roughly comparable to our estimate. We also note that in their Herschel/Hi-GAL study of IRDCs, Wilcock et al. (2012) inferred the lifetime ~2 × 105 yr for the IR-quiet phase, which is close to our estimate. We note that Wilcock et al. (2012) adopted the same YSO lifetime as we (~2 × 105 yr).
 |
Fig. 14 From left to right are shown the differential (dN/dlog M) clump mass distributions of the entire sample, IR-dark clumps, and IR-bright clumps. In all panels the mass bin size is Δlog (M/M⊙) ≃ 0.44. The error bars correspond to the standard Poisson |
Inspecting the diverse and somewhat heterogeneous lifetime estimates for IR-dark clumps, it seems that the true value is somewhere between ~104−105 yr, although values as low as <103 yr have also been proposed (Motte et al. 2007). Extremely short lifetimes of massive IR-dark clumps would mean, however, that it would be rather unlikely to see them in a large number in observational surveys.
5.3. Clump mass distribution
The clump mass distributions (CMDs) for the entire sample (composed of IR-dark and IR-bright clumps), and separately for the IR-dark and IR-bright clumps are shown in Fig. 14. The CMDs are plotted as dN/dlog M versus M, where the first term is approximated as the number of clumps in each bin divided by the logarithmic mass interval, i.e., ΔN/Δlog M. Following López et al. (2011), we kept the histogram bin size Δlog M at a constant value of about 0.44. The CMDs were fitted with power-laws of the form dN/dlog M ∝ M−Γ, with the slopes Γ = 0.8 ± 0.1, 0.7 ± 0.2, and 0.7 ± 0.1 for the entire sample, IR-dark clumps, and IR-bright clumps, respectively. The errors of the slopes were determined by considering only the statistical Poisson 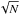 uncertainty of the data, and the mass uncertainties were not taken into account. The mass ranges used in the fits were ~2.4 × 103−1.8 × 104 M⊙ for the entire sample and IR-dark clumps, and ~1.5 × 103−1.1 × 104 M⊙ for the IR-bright clumps. Even the CMD slopes for the IR-dark and IR-bright clumps are similar, the CMDs themselves appear to be very different from each other; a two-sample Kolmogorov-Smirnov (K-S) test gives a probability of only 0.48% that they are drawn from the same underlying parent distribution. We note that the CMDs can also be expressed in the differential form of dN/dM ∝ M−α, where α = Γ + 1.
uncertainty of the data, and the mass uncertainties were not taken into account. The mass ranges used in the fits were ~2.4 × 103−1.8 × 104 M⊙ for the entire sample and IR-dark clumps, and ~1.5 × 103−1.1 × 104 M⊙ for the IR-bright clumps. Even the CMD slopes for the IR-dark and IR-bright clumps are similar, the CMDs themselves appear to be very different from each other; a two-sample Kolmogorov-Smirnov (K-S) test gives a probability of only 0.48% that they are drawn from the same underlying parent distribution. We note that the CMDs can also be expressed in the differential form of dN/dM ∝ M−α, where α = Γ + 1.
The clumps studied here lie at different distances, and the sensitivities of the four maps are also different (median being ~70 mJy beam-1). Therefore, the mass detection limit varies, and is not straightforward to determine. For example, at the median distance of our sources, ~4.4 kpc, a source of 1 Jy corresponds to a 15-K mass of ~225 M⊙. Our completeness limit is, however, likely to be at a much higher mass, as suggested by the apparent peak near ~2000 M⊙. Because our sample is very heterogeneous in nature, it is not ideal for the CMD study. However, it is interesting to compare the derived slopes with those from the literature.
The slope of the Salpeter (1955) initial mass function (IMF) is Γ = 1.35 or α = 2.35 for stars with masses in the range 0.4 M⊙ ≲ M ≲ 10 M⊙. Our slopes are clearly shallower than the Salpeter value. On the other hand, our results are similar to the CMDs of diffuse CO clumps, which are found to be well described by power-law forms with α between 1.6 and 1.8 (e.g., Stutzki & Güsten 1990; Kramer et al. 1998; Simon et al. 2001). These slopes also resemble those of stellar clusters’ mass function, implying that massive clumps are not the direct progenitors of individual stars, but will instead presumably fragment to form groups/clusters of stars (e.g., Elmegreen et al. 2000).
Rathborne et al. (2006) found a slope of α = 2.1 ± 0.4 above ~100 M⊙ for their sample of MSX 8-μm dark clumps, which is quite close to the Salpeter power-law IMF, but also consistent with our values within the error bars. Interestingly, a two-sample K-S test yields practically a zero probability (~10-12) that our IR-dark clump masses and those from Rathborne et al. (2006) are drawn from the common underlying distribution. We note that for this test the clump masses from Rathborne et al. (2006) were multiplied by 1.214 to be consistent with the dust model we have adopted (their 1.2-mm dust opacity of 1.0 mm2 g-1 was replaced by the value κ1.2 mm ≃ 0.82 mm2 g-1). Ragan et al. (2009) also built a CMD for their entire sample of IR-dark and IR-bright clumps (cf. left panel of our Fig. 14), and derived the slope α = 1.76 ± 0.05 (from 30 to 3000 M⊙), which is very similar to our corresponding value of 1.8 ± 0.1. Tackenberg et al. (2012) found a Salpeter-like slope of α = 2.2 for the CMD of candidate massive starless clumps. We note that Salpeter-like slopes have also been determined for the mass distributions of more evolved massive clumps (e.g., Reid & Wilson 2005; Beltrán et al. 2006; Bally et al. 2010), although the uncertainties are often too large to say whether they are actually flatter (or steeper) than the exact Salpeter slope. Indeed, in addition to our study, some authors have found the mass functions of evolved massive clumps to be similar to those of CO clumps (e.g., Beuther et al. 2011; López et al. 2011).
Mass distributions of whole IRDCs have also been studied by Simon et al. (2006), Marshall et al. (2009), and Peretto & Fuller (2010), who determined slopes of α = 1.97 ± 0.09, α = 1.75 ± 0.06, and α = 1.85 ± 0.07, respectively. These are also comparable to our results and to the CMD slopes of the CO clumps. Marshall et al. (2009) suggested that the similarity between the mass distributions of IRDCs and CO clumps perhaps indicates that IRDCs are the result of density fluctuations caused by interstellar turbulence. The analytical theory by Hennebelle & Chabrier (2008) is able to explain the flat mass spectra of CO clumps formed by supersonic turbulent flows. For large-scale turbulent flows, the slope of the CMD’s power-law tail is determined by the spectral index of the turbulent power spectrum. In our notation, the CMD slope Γ in the Hennebelle-Chabrier theory is given by Γ = 2 − n′/3, where n′ is the three-dimensional power-spectrum index of the logarithmic density field. As discussed by Hennebelle & Chabrier (2008), n′ appears to be ≃ 11/3, i.e., similar to the Kolmogorov power spectrum index 11/3 of the velocity field in incompressible turbulence. This leads to the value Γ ≃ 7/9 ≃ 0.8, which is remarkably close to the CMD slopes of CO clumps and the values derived in the present study.
5.4. The origin and hierarchical fragmentation of filamentary IRDCs
The formation of filamentary structures by colliding shock fronts is clearly seen in numerical simulations (e.g., Banerjee et al. 2006). Large-scale colliding supersonic turbulent flows offer an intriguing mechanism for the formation of filamentary IRDCs. As discussed in the previous section, the IRDCs’ mass functions can be understood in terms of turbulent flows. Moreover, Jiménez-Serra et al. (2010) found extended SiO emission along the filamentary IRDC G035.39-00.33, which might have been produced in shocks caused by converging flows. Hernandez & Tan (2011) and M12 found evidence that the surface pressure may play an important role in the dynamics of filamentary IRDCs. This could also be related to the cloud formation in gas overdensities resulting from colliding flows.
Although the formation of IRDCs could be caused by interstellar turbulent flows, their further fragmentation may have its origin in some other mechanism(s). As was shown in the present study, the fragmentation of the filamentary IRDC G11.36 into clumps can be explained by the sausage-type fluid instability. In an IRDC, this was first found to be the case in the Nessie Nebula by Jackson et al. (2010). More recently, M12 inferred that this is also the case in the filamentary IRDC G304.74+01.32. Hence, to our knowledge there are three different filamentary IRDCs where the predictions of the sausage-instability theory have been tested so far. In all cases, the theory and observations agree very well. One remarkable feature is that in all the three above mentioned cases the fragmentaion length scale corresponds to the wavelength of the fastest growing mode only when the non-thermal motions are taken into account. Non-thermal (“turbulent”) motions are therefore still important in the fragmentation process, at least on the scale of clumps. However, this can also continue in a hierarchical way down to the scale of cores, as found by Wang et al. (2011) in the massive IRDC clump G28.34+0.06-P1. A Jeans-type gravitational instability may start to dominate inside dense cores, i.e., cause them to fragment into still smaller condensations (cf. Miettinen et al. 2012).
5.5. CO depletion and its implications on the age of the G11.36+0.80 filament
The CO depletion factors we estimate towards 25 target positions lie in the range ~1.0 ± 0.2−20.7 ± 0.8. Some of the values are very high, given that the beam size 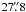 is probing the scale of clumps at the source distances. In contrast, using the same kind of APEX/C17O data as here, Miettinen et al. (2011) found depletion factors of only ~0.6−2.7 towards a sample of seven clumps in IRDCs and similar values of ~0.3−2.3 were found by M12 towards the clumps in the IRDC G304.74. On the other hand, Chen et al. (2011), who used 34″ C18O observations, reported fD values as high as ~19 in the IRDC G34.43+0.24, which resembles our highest fD values. Pillai et al. (2007) derived the CO depletion factor of 9.3 towards one of our clumps, namely G13.22-SMM 5 (their source G13.18+00.06).
is probing the scale of clumps at the source distances. In contrast, using the same kind of APEX/C17O data as here, Miettinen et al. (2011) found depletion factors of only ~0.6−2.7 towards a sample of seven clumps in IRDCs and similar values of ~0.3−2.3 were found by M12 towards the clumps in the IRDC G304.74. On the other hand, Chen et al. (2011), who used 34″ C18O observations, reported fD values as high as ~19 in the IRDC G34.43+0.24, which resembles our highest fD values. Pillai et al. (2007) derived the CO depletion factor of 9.3 towards one of our clumps, namely G13.22-SMM 5 (their source G13.18+00.06).
Some of the highest fD values in the present study are found towards the positions C, D, E, and F in the filamentary IRDC in G1.87, and position A in G13.22. These might be potential sites to search for high levels of molecular deuteration, since the depletion of CO plays a key role in the deuterium fractionation. Interestingly, the highest fD value of ~20.7 is seen towards the edge of G2.11-SMM 5 (position H). This raises the question whether the high depletion factor is the result of molecular freeze-out onto dust grains, or possibly due to photodissociation by FUV photons at the edge of the clump (Tielens & Hollenbach 1985; Visser et al. 2009). Photodissociation could also play a role in reducing the C17O abundance in some other positions of our line observations.
The fD values in the G11.36 filament (excluding positions F and G), where we best probe the submm peak positions among our sources, are ~1.6 ± 0.2−3.9 ± 0.6. This implies that non-negligible CO depletion might be present in some parts of the filament. Hernandez et al. (2011) inferred depletion factors of ~3−4 for the thinnest part of the filamentary IRDC G035.30-00.33, and used the CO depletion timescale to estimate the cloud’s age. Here, we do the same exercise for G11.36. The CO depletion timescale can be computed as the inverse of the freezing rate (Rawlings et al. 1992) as 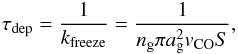 (3)where ng is the grain number density, ag is the average grain radius (
(3)where ng is the grain number density, ag is the average grain radius (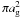 is the mean cross section of the dust grains, and
is the mean cross section of the dust grains, and  is the grain opacity), vCO is the thermal speed of the CO molecules, and S is their sticking coefficient. We can write the grain number density as ng = xgn(H2), where xg is the fractional grain abundance given by
is the grain opacity), vCO is the thermal speed of the CO molecules, and S is their sticking coefficient. We can write the grain number density as ng = xgn(H2), where xg is the fractional grain abundance given by 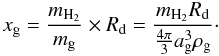 (4)In the above formula, mH2 is the H2 molecule’s mass, mg (ρg) is the mass (density) of the grain particle, and Rd = 1/100 is again the dust-to-gas mass ratio. By adopting the “standard” values ag = 0.1 μm and ρg = 3.0 g cm-3, we obtain xg = 2.7 × 10-12. The Maxwellian mean thermal speed of the CO molecules (mCO = 28mH) at Tkin = 15 K is vCO = (8 kBTkin/πmCO)1/2 ≃ 106 m s-1. Assuming that S = 1, i.e., that the CO molecules stick to the dust grains in each collision, we can write τdep ~ 4.4 × 109/n(H2) [mm-3] yr15. The volume-averaged density in the G11.36 clumps is ~104 mm-3 (Table 3), which gives τdep ~ 4.4 × 105 yr. Interestingly, this is very close to the estimated fragmentation timescale in G11.36 (~5.4 × 105 yr). The age of the filament may therefore be similar to its fragmentation time. In this case, the cloud’s fragmentation would have started at the same time as it was formed. Perhaps the cloud-forming flows also triggered the sausage-type fluid instability in the cloud.
(4)In the above formula, mH2 is the H2 molecule’s mass, mg (ρg) is the mass (density) of the grain particle, and Rd = 1/100 is again the dust-to-gas mass ratio. By adopting the “standard” values ag = 0.1 μm and ρg = 3.0 g cm-3, we obtain xg = 2.7 × 10-12. The Maxwellian mean thermal speed of the CO molecules (mCO = 28mH) at Tkin = 15 K is vCO = (8 kBTkin/πmCO)1/2 ≃ 106 m s-1. Assuming that S = 1, i.e., that the CO molecules stick to the dust grains in each collision, we can write τdep ~ 4.4 × 109/n(H2) [mm-3] yr15. The volume-averaged density in the G11.36 clumps is ~104 mm-3 (Table 3), which gives τdep ~ 4.4 × 105 yr. Interestingly, this is very close to the estimated fragmentation timescale in G11.36 (~5.4 × 105 yr). The age of the filament may therefore be similar to its fragmentation time. In this case, the cloud’s fragmentation would have started at the same time as it was formed. Perhaps the cloud-forming flows also triggered the sausage-type fluid instability in the cloud.
6. Summary and conclusions
Four selected regions in the Galactic plane, all containing IRDCs, were mapped with APEX/LABOCA at 870 μm. Moreover, selected positions in the fields were observed in C17O(2−1) with APEX. Our main results and conclusions can be summarised as follows:
-
1.
The total number of clumps identified in this survey is 91. Thenumber of Spitzer 8- and 24-μm dark clumps was estimated to be 40. The remaining 51 clumps were found to be associated with both 8 and 24 μm emission, or only with 24 μm emission (embedded point sources, group of point sources, diffuse/extended emission).
-
2.
Many of the clumps appear to be potential sites of (future) high-mass star formation, as implied by the comparison with the mass-radius threshold proposed by Kauffmann & Pillai (2010). Some of the clumps already show clear signposts of ongoing high-mass star formation, such as Class II CH3OH maser emission.
-
3.
Seven clumps show somewhat extended 4.5 μm emission, hence are classified as candidate EGOs.
-
4.
One of the mapped fields (G13.22) contains the Spitzer MIR-bubbles N10/11 found by Churchwell et al. (2006). The bubble region is believed to be associated with triggered massive-star formation, and the observed dust emission morphology might have been created by the bubble shell-cloud interaction process.
-
5.
The relative numbers of IR-dark and IR-bright clumps imply that the duration of the IR-dark stage is ~1.6 × 105 yr. Although this estimate is likely to suffer from the relatively low number statistics, it is comparable with some earlier lifetime estimates (Chambers et al. 2009; Wilcock et al. 2012). Surveys with more sources typically indicate shorter lifetimes for massive IR-dark clumps (e.g., Tackenberg et al. 2012).
-
6.
The clump mass distributions were constructed for the total clump sample, and for the IR-dark and IR-bright clumps separately. In all cases, the high-mass tail could be fitted with the power-law function of the form dN/dlog M ∝ M−Γ, with Γ ≃ 0.7...0.8. This is very similar to the mass functions found for the diffuse CO clumps, and can be understood in terms of supersonic-turbulence-induced cloud formation (Hennebelle & Chabrier 2008).
-
7.
The C17O observations revealed potential targets of strong CO depletion. In some cases, however, our line observations probe more dilute gas, where the low C17O abundances could be caused by photodissociation by FUV photons.
-
8.
The filamentary IRDC G11.36+0.80 was studied in more detail, because there our line observation positions matched the submm peak positions well. The filament’s fragmentation into clumps can be satisfactorily explained by a sausage-type fluid instability. In particular, the observed projected clump separations agree excellently with the theoretical prediction. This is consistent with the results for other IRDCs (Jackson et al. 2010; M12). Most clumps in the filament appear to be gravitationally bound, and the filament as a whole appers to be close to virial equilibrium. Interestingly, the estimated fragmentation timescale of the filament and the CO depletion timescale were inferred to be comparable to each other (~5 × 105 yr). The perturbations responsible for the filament fragmentation into clumps might have been excited by the cloud-forming process, i.e., by converging turbulent flows.
The observations presented here are not part of the APEX Telescope Large Area Survey of the GALaxy (ATLASGAL) conducted with the LABOCA array (Schuller et al. 2009; http://www.mpifr.de/div/atlasgal/index.html). However, the ATLASGAL survey covers the same regions we have mapped. At the time of writing, the ATLASGAL data were not yet released into the public domain. We note that ATLASGAL has the average 1σ rms of ~50 mJy beam-1 and the resolution of ~19 2.
2.
Grenoble Image and Line Data Analysis Software is provided and actively developed by IRAM, and is available at http://www.iram.fr/IRAMFR/GILDAS
From the GLIMPSE point source catalogue available at http://irsa.ipac.caltech.edu/
The IRDC catalogue of Peretto & Fuller (2009) is available at www.irdarkclouds.org/
Acknowledgments
I thank the anonymous referee for his/her constructive comments and suggestions. I am grateful to the staff at the APEX telescope for performing the service-mode observations presented in this paper. In particular, I would like to thank the APEX operator Felipe Mac-Auliffe for providing helpful information on the observations. The Academy of Finland is acknowledged for the financial support through grant 132291. This work is based in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with NASA. This research has made use of NASA’s Astrophysics Data System and the NASA/IPAC Infrared Science Archive, which is operated by the JPL, California Institute of Technology, under contract with the NASA. This research has also made use of the SIMBAD database, operated at CDS, Strasbourg, France.
References
- Aguirre, J. E., Ginsburg, A. G., Dunham, M. K., et al. 2011, ApJS, 192, 4 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Argon, A. L., Reid, M. J., & Menten, K. M. 2000, ApJS, 129, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Bally, J., Aguirre, J., Battersby, C., et al. 2010, ApJ, 721, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, R., Pudritz, R. E., & Anderson, D. W. 2006, MNRAS, 373, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Battersby, C., Bally, J., Jackson, J. M., et al. 2010, ApJ, 721, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Beaumont, C. N., & Williams, J. P. 2010, ApJ, 709, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, R. H., White, R. L., Helfand, D. J., & Zoonematkermani, S. 1994, ApJS, 91, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Belitsky, V., Lapkin, I., Vassilev, V., et al. 2007, in Proc. joint 32nd International Conference on Infrared Millimeter Waves and 15th International Conference on Terahertz Electronics, September 3–7 (Cardiff, Wales, UK: City Hall), 326 [Google Scholar]
- Beltrán, M. T., Brand, J., Cesaroni, R., et al. 2006, A&A, 447, 221 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2003, PASP, 115, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bertoldi, F., & McKee, C. F. 1992, ApJ, 395, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., & Steinacker, J. 2007, ApJ, 656, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Schilke, P., Menten, K. M., et al. 2002, ApJ, 566, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Linz, H., Henning, T., et al. 2011, A&A, 531, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Clark, F. O., Egan, M. P., et al. 1998, ApJ, 508, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Noriega-Crespo, A., Mizuno, D. R., et al. 2009, PASP, 121, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Casoli, F., Combes, F., Dupraz, C., et al. 1986, A&A, 169, 281 [NASA ADS] [Google Scholar]
- Caswell, J. L., Batchelor, R. A., Forster, J. R., & Wellington, K. J. 1983, Aust. J. Phys., 36, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Caswell, J. L., Vaile, R. A., Ellingsen, S. P., et al. 1995, MNRAS, 272, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, E. T., Jackson, J. M., Rathborne, J. M., & Simon, R. 2009, ApJS, 181, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S., & Fermi, E. 1953, ApJ, 118, 116 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chen, X., Shen, Z.-Q., Li, J.-J., et al. 2010, ApJ, 710, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H.-R., Liu, S.-Y., Su, Y.-N., & Wang, M.-Y. 2011, ApJ, 743, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Chini, R., Kruegel, E., & Wargau, W. 1987, A&A, 181, 378 [NASA ADS] [Google Scholar]
- Churchwell, E., Povich, M. S., Allen, D., et al. 2006, ApJ, 649, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Churchwell, E., Babler, B. L., Meade, M. R., et al. 2009, PASP, 121, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, P. C., Klessen, R. S., & Bonnell, I. A. 2007, MNRAS, 379, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Cragg, D. M., Johns, K. P., Godfrey, P. D., & Brown, R. D. 1992, MNRAS, 259, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog, II/246 [Google Scholar]
- Cyganowski, C. J., Whitney, B. A., Holden, E., et al. 2008, AJ, 136, 2391 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., & Thaddeus, P. 2008, ApJ, 683, L143 [NASA ADS] [CrossRef] [Google Scholar]
- De Buizer, J. M., & Vacca, W. D. 2010, AJ, 140, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Deharveng, L., Schuller, F., Anderson, L. D., et al. 2010, A&A, 523, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Devine, K. E., Chandler, C. J., Brogan, C., et al. 2011, ApJ, 733, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Di Francesco, J., Johnstone, D., Kirk, H., et al. 2008, ApJS, 175, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Egan, M. P., Shipman, R. F., Price, S. D., et al. 1998, ApJ, 494, L199 [NASA ADS] [CrossRef] [Google Scholar]
- Egan, M. P., Price, S. D., Moshir, M. M., et al. 2001, VizieR Online Data Catalog, V/107 [Google Scholar]
- Egan, M. P., Price, S. D., Kraemer, K. E., et al. 2003, VizieR Online Data Catalog, V/114 [Google Scholar]
- Elmegreen, B. G., Efremov, Y., Pudritz, R. E., & Zinnecker, H. 2000, in Protostars and Planets IV, ed. V. Mannings, A. P. Boss, & S. S. Russell (Tucson: Univ. of Arizona Press), 179 [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Fiege, J. D., & Pudritz, R. E. 2000a, MNRAS, 311, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Fiege, J. D., & Pudritz, R. E. 2000b, MNRAS, 311, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Forster, J. R., & Caswell, J. L. 1989, A&A, 213, 339 [NASA ADS] [Google Scholar]
- Forster, J. R., & Caswell, J. L. 2000, ApJ, 530, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, D., Walmsley, M., & Gonçalves, J. 2002, A&A, 394, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garwood, R. W., Perley, R. A., Dickey, J. M., & Murray, M. A. 1988, AJ, 96, 1655 [NASA ADS] [CrossRef] [Google Scholar]
- Green, J. A., Caswell, J. L., McClure-Griffiths, N. M., et al. 2011, ApJ, 733, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Gutermuth, R. A., Myers, P. C., Megeath, S. T., et al. 2008, ApJ, 674, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatchell, J., Fuller, G. A., Richer, J. S., et al. 2007, A&A, 468, 1009 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Chabrier, G. 2008, ApJ, 684, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Hennemann, M., Birkmann, S. M., Krause, O., et al. 2009, ApJ, 693, 1379 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, T., Pfau, W., & Altenhoff, W. J. 1990, A&A, 227, 542 [NASA ADS] [Google Scholar]
- Hernandez, A. K., & Tan, J. C. 2011, ApJ, 730, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Hernandez, A. K., Tan, J. C., Caselli, P., et al. 2011, ApJ, 738, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M. H., & Brunt, C. M. 2004, ApJ, 615, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. M., Finn, S. C., Chambers, E. T., et al. 2010, ApJ, 719, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Caselli, P., Tan, J. C., et al. 2010, MNRAS, 406, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, J., & Pillai, T. 2010, ApJ, 723, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, B., Philipp, S. D., Krämer, I., et al. 2006, A&A, 454, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovács, A. 2008, Proc. SPIE, 7020, 45 [NASA ADS] [Google Scholar]
- Kramer, C., Stutzki, J., Rohrig, R., & Corneliussen, U. 1998, A&A, 329, 249 [NASA ADS] [Google Scholar]
- Krumholz, M. R., & McKee, C. F. 2008, Nature, 451, 1082 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ladd, E. F., Fuller, G. A., & Deane, J. R. 1998, ApJ, 495, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- López, C., Bronfman, L., Nyman, L.-Å., et al. 2011, A&A, 534, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacLeod, G. C., van der Walt, D. J., North, A., et al. 1998, AJ, 116, 2936 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, D. J., Joncas, G., & Jones, A. P. 2009, ApJ, 706, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Marston, A. P., Reach, W. T., Noriega-Crespo, A., et al. 2004, ApJS, 154, 333 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Zweibel, E. G. 1992, ApJ, 399, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Miettinen, O. 2012, A&A, 540, A104 (M12) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miettinen, O., & Harju, J. 2010, A&A, 520, A102 (MH10) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miettinen, O., Hennemann, M., & Linz, H. 2011, A&A, 534, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miettinen, O., Harju, J., Haikala, L. K., & Juvela, M. 2012, A&A, 538, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minier, V., Ellingsen, S. P., Norris, R. P., & Booth, R. S. 2003, A&A, 403, 1095 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Bontemps, S., Schilke, P., et al. 2007, A&A, 476, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagasawa, M. 1987, Prog. Theor. Phys., 77, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, F., Hanawa, T., & Nakano, T. 1993, PASJ, 45, 551 [NASA ADS] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Pandian, J. D., Momjian, E., & Goldsmith, P. F. 2008, A&A, 486, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parsons, H., Thompson, M. A., & Chrysostomou, A. 2009, MNRAS, 399, 1506 [NASA ADS] [CrossRef] [Google Scholar]
- Pérault, M., Omont, A., Simon, G., et al. 1996, A&A, 315, L165 [Google Scholar]
- Peretto, N., & Fuller, G. A. 2009, A&A, 505, 405 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peretto, N., & Fuller, G. A. 2010, ApJ, 723, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Pillai, T., Wyrowski, F., Carey, S. J., et al. 2006, A&A, 450, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pillai, T., Wyrowski, F., Hatchell, J., et al. 2007, A&A, 467, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ragan, S. E., Bergin, E. A., & Gutermuth, R. A. 2009, ApJ, 698, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Ragan, S. E., Bergin, E. A., & Wilner, D. 2011, ApJ, 736, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Jackson, J. M., & Simon, R. 2006, ApJ, 641, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Jackson, J. M., Chambers, E. T., et al. 2010, ApJ, 715, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Rawlings, J. M. C., Hartquist, T. W., Menten, K. M., & Williams, D. A. 1992, MNRAS, 255, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. A., & Wilson, C. D. 2005, ApJ, 625, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Zheng, X. W., et al. 2009, ApJ, 700, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., Young, E. T., Engelbracht, C. W., et al. 2004, ApJS, 154, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T. P., Meade, M. R., Babler, B. L., et al. 2008, AJ, 136, 2413 [NASA ADS] [CrossRef] [Google Scholar]
- Roman-Duval, J., Jackson, J. M., Heyer, M., et al. 2009, ApJ, 699, 1153 [Google Scholar]
- Rosolowsky, E., Dunham, M. K., Ginsburg, A., et al. 2010, ApJS, 188, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Russeil, D. 2003, A&A, 397, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russeil, D., Zavagno, A., Motte, F., et al. 2010, A&A, 515, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakai, T., Sakai, N., Kamegai, K., et al. 2008, ApJ, 678, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Schlingman, W. M., Shirley, Y. L., Schenk, D. E., et al. 2011, ApJS, 195, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sewilo, M., Watson, C., Araya, E., et al. 2004, ApJS, 154, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, R., Jackson, J. M., Clemens, D. P., et al. 2001, ApJ, 551, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, R., Rathborne, J. M., Shah, R. Y., et al. 2006, ApJ, 653, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Siringo, G., Kreysa, E., Kovács, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, M. D., & Rosen, A. 2005, MNRAS, 357, 1370 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, H. A., Hora, J. L., Marengo, M., & Pipher, J. L. 2006, ApJ, 645, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L., Jr. 1978, Physical Processes in the Interstellar Medium (New York: Wiley Interscience) [Google Scholar]
- Sreenilayam, G., & Fich, M. 2011, AJ, 142, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Sridharan, T. K., Beuther, H., Saito, M., et al. 2005, ApJ, 634, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Stutzki, J., & Güsten, R. 1990, ApJ, 356, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Szymczak, M., Kus, A. J., Hrynek, G., et al. 2002, A&A, 392, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tackenberg, J., Beuther, H., Henning, T., et al. 2012, A&A, 540, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., & Walmsley, C. M. 2004, A&A, 416, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takami, M., Chen, H.-H., Karr, J. L., et al. 2012, ApJ, 748, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, D., Hennebelle, P., & Pérault, M. 2002, A&A, 382, 624 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, M. A., Hatchell, J., Walsh, A. J., et al. 2006, A&A, 453, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Urquhart, J. S., Hoare, M. G., Purcell, C. R., et al. 2009, A&A, 501, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vassilev, V., Meledin, D., Lapkin, I., et al. 2008a, A&A, 490, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vassilev, V., Henke, D., Lapkin, I., et al. 2008b, IEEE Microwave and Wireless Components Letters, 55, 18 [Google Scholar]
- Visser, R., van Dishoeck, E. F., & Black, J. H. 2009, A&A, 503, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, K., Zhang, Q., Wu, Y., & Zhang, H. 2011, ApJ, 735, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, C., Povich, M. S., Churchwell, E. B., et al. 2008, ApJ, 681, 1341 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [Google Scholar]
- White, R. L., Becker, R. H., & Helfand, D. J. 2005, AJ, 130, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Wilcock, L. A., Ward-Thompson, D., Kirk, J. M., et al. 2012, MNRAS, 2638 [Google Scholar]
- Williams, J. P., de Geus, E. J., & Blitz, L.1994, ApJ, 428, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Wink, J. E., Altenhoff, W. J., & Mezger, P. G. 1982, A&A, 108, 227 [NASA ADS] [Google Scholar]
- Xu, Y., Li, J. J., Hachisuka, K., et al. 2008, A&A, 485, 729 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ybarra, J. E., & Lada, E. A. 2009, ApJ, 695, L120 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, S. B., Yang, J., Xu, Y., et al. 2011, ApJS, 193, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Zinnecker, H., & Yorke, H. W. 2007, ARA&A, 45, 481 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
C17O(2−1) line parameters, column densities and fractional abundances, and CO depletion factors.
All Figures
 |
Fig. 1 Left: LABOCA 870-μm map of G1.87-0.14. The image is shown with linear scaling, and the colour bar indicates the surface-brightness scale in Jy beam-1. The overlaid contours go from 0.27 Jy beam-1 (3σ) to 1.62 Jy beam-1, in steps of 3σ. Selected clumps are labelled with their designation (as listed in Table 3). The green plus signs indicate the positions of our C17O(2−1) observations (see Table 2). A scale bar indicating the 10 pc projected length is shown in the bottom left, with the assumption of a 10.57 kpc line-of-sight distance. The effective LABOCA beam of |
| In the text | |
 |
Fig. 2 Same as Fig. 1 but towards G2.11+0.00. The overlaid LABOCA contours go from 0.18 Jy beam-1 (3σ) to 1.08 Jy beam-1, in steps of 3σ. A scale bar indicating the 5 pc projected length is shown in the bottom left, with the assumption of a 5.51 kpc line-of-sight distance. The clump SMM 5, which is associated with IRAS 17474-2704, lies at a distance of 7.40 kpc (see text). |
| In the text | |
 |
Fig. 3 Same as Fig. 1 but towards G11.36+0.80. The obtained LABOCA map is zoomed-in towards the filamentary structure in the map centre because no submm dust emission was detected in other parts of the map. The overlaid LABOCA contours go from 0.12 Jy beam-1 (3σ) to 0.60 Jy beam-1, in steps of 3σ. Note that most of the line-observation target positions match the submm peak positions well. A scale bar indicating the 1 pc projected length is shown in the bottom left, with the assumption of a 3.27 kpc line-of-sight distance. |
| In the text | |
 |
Fig. 4 Same as Fig. 1 but towards G13.22-0.06. The overlaid LABOCA contours go from 0.24 Jy beam-1 (3σ) to 1.44 Jy beam-1, in steps of 3σ. The field contains several clumps at different kinematic distances, and therefore only the angular scale bar is shown. The green circles in the Spitzer 8 μm image on the right panel indicate the positions and outer radii of the bubbles N10 and N11 from Churchwell et al. (2006; their Table 2). |
| In the text | |
 |
Fig. 5 Smoothed C17O(2−1) spectra towards selected positions in G1.87-0.14. Most lines are seen at ~− 41 km s-1. Hyperfine-structure fits to the lines are overlaid in green. No line emission is detected towards position B, whereas two velocity components are seen towards positions C and F. |
| In the text | |
 |
Fig. 6 Same as Fig. 5 but towards the selected positions in G2.11+0.00. Most detected lines are near ~16 km s-1. No lines were detected towards positions D, F, and G. Two velocity components are seen towards position C. |
| In the text | |
 |
Fig. 7 Same as Fig. 5 but towards the selected positions in G11.36+0.80. We note that clear line emission at ~28 km s-1 is seen towards all positions. Two velocity components are detected towards positions A, B and F, but the secondary line is very weak in the former two cases. |
| In the text | |
 |
Fig. 8 Same as Fig. 5 but towards the selected positions in G13.22-0.06. We note that clear line emission at ~37 km s-1 is seen towards all positions. Two velocity components are detected towards positions A–C and G. |
| In the text | |
 |
Fig. 9 Distributions of a) clump effective radii, b) masses, c) H2 column densities, and d) H2 number densities. Open histograms represent the IR-dark clumps, while shaded histograms represent the IR-bright clumps (those with 8/24 μm emission). The solid and dashed vertical lines indicate the average values for IR-dark and IR-bright clumps, respectively. The average (median) radii for IR-dark and IR-bright clumps are 1.19 (1.14) and 0.96 (0.87) pc, respectively. The average (median) mass of IR-dark clumps is 3079 (2108) M⊙, whereas that of IR-bright clumps is 1604 (804) M⊙. The mean H2 column density is 3.2 × 1022 mm-2 for both distributions (median values are 2.8 × 1022 and 2.1 × 1022 cm-2 for IR-dark and IR-bright clumps, respectively). The average (median) H2 number densities for IR-dark and IR-bright clumps are 7250 (6000) cm-3 and 6667 (6000) mm-3, respectively. |
| In the text | |
 |
Fig. 10 Virial parameter vs. mass for the clumps in G11.36. The dashed line indicates the virial-equilibrium limit of αvir = 1, and the dash-dotted line shows the limit of gravitational boundedness or αvir = 2. |
| In the text | |
 |
Fig. 11 Relation between mass and effective radius for the detected clumps. The IR-dark and IR-bright clumps have been plotted with open and filled circles, respectively. The dotted line represents the mass-radius threshold for massive-star formation proposed by Kauffmann & Pillai (2010), i.e., M(R) = 870 M⊙ × (R/ pc)1.33. |
| In the text | |
 |
Fig. 12 Spitzer-IRAC three-colour composite images towards EGO candidates in G13.22 overlaid with contours of LABOCA dust continuum emission. The 3.6, 4.5, and 8.0 μm emission is coded in blue, green, and red, respectively, and the colours are shown in linear scales. The contours are as in Fig. 4. Towards G13.22-SMM 13 (top left), the black circles indicate the positions of the 1.5-GHz VLA radio sources from Garwood et al. (1988), the diamond symbol shows the position of the 5-GHz VLA radio source from Becker et al. (1994), and the white cross shows the nominal catalogue position of IRAS 18114-1718. Towards G13.22-SMM 29 (middle right), the position of IRAS 18117-1738 is indicated by a black cross. The black circle towards G13.22-SMM 32 (bottom) denotes the 1.4-GHz radio source 181449-173243 from Condon et al. (1998). The white plus signs in the middle left and bottom panels represent the positions of our C17O observations. We note that in the bottom panel the linear scale bar corresponds to the line-of-sight distance of SMM 25. |
| In the text | |
 |
Fig. 13 Spitzer-IRAC three-colour composite image towards the bubbles N10 and N11 overlaid with contours of LABOCA dust continuum emission. The 3.6, 4.5, and 8.0 μm emission is coded in blue, green, and red, respectively, and the colours are shown in linear scales. The contours are as in Fig. 4. The squares show the positions of the two 870-μm condensations found by Deharveng et al. (2010); their condensation 1 is associated with our clump SMM 5, and condensation 2 is associated with SMM 7. The circles show the positions of the candidate embedded MYSOs on the rims of N10 (Watson et al. 2008). The diamond symbols indicate the positions of the 6.7-GHz Class II methanol masers from Szymczak et al. (2002; right) and Pandian et al. (2008; left). |
| In the text | |
 |
Fig. 14 From left to right are shown the differential (dN/dlog M) clump mass distributions of the entire sample, IR-dark clumps, and IR-bright clumps. In all panels the mass bin size is Δlog (M/M⊙) ≃ 0.44. The error bars correspond to the standard Poisson |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


