| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201118153 | |
| Published online | 24 April 2012 | |
Temperature and kinematics of protoclusters with intermediate and high-mass stars: the case of IRAS 05345+3157
1 INAF – Osservatorio Astrofisico di Arcetri, L.go E. Fermi 5, 50125 Firenze, Italy
e-mail: fontani@arcetri.astro.it
2 School of Physics and Astrophysics, University of Leeds, Leeds, LS2 9JT, UK
3 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street MS78, Cambridge, MA 02138, USA
4 INAF – Istituto di Radioastronomia, via P. Gobetti 101, 40129 Bologna, Italy
5 INAF-Istituto di Astrofisica e Planetologia Spaziali, via Fosso del Cavaliare 100, 00133 Roma, Italy
6 Institut de Ciències de l’Espai (CSIC-IEEC), Campus UAB-Facultat de Ciències, Torre C5-parell 2, 08193 Bellaterra, Spain
Received: 26 September 2011
Accepted: 13 March 2012
Context. Improving our understanding of the complex star formation process in clusters requires studies of star-forming clouds to search for dependencies of the physical properties on environmental variables, such as overall density, stellar crowding and feedback from massive (proto-)stars.
Aims. We aim to map at small spatial scales the temperature and the velocity field in the protocluster associated with IRAS 05345+3157, which contains both intermediate-/high-mass protostellar candidates and starless condensations, and is thus an excellent location to investigate the role of massive protostars on protocluster evolution.
Methods. We observed the ammonia (1, 1) and (2, 2) inversion transitions with the VLA. Ammonia is the best thermometer for dense and cold gas, and the observed transitions have critical densities able to trace the kinematics of the intracluster gaseous medium.
Results. The ammonia emission is extended and distributed in two filamentary structures. The starless condensations are colder than the star-forming cores, but the gas temperature across the whole protocluster is higher (by a factor of 1.3−1.5) than that measured typically in both infrared dark clouds and low-mass protoclusters. The non-thermal contribution to the observed line broadening is at least a factor of 2 larger than the expected thermal broadening even in starless condensations, contrary to the close-to-thermal line widths measured in low-mass quiescent dense cores. The NH3/N2H+ abundance ratio is greatly enhanced (a factor of 10) in the pre-stellar core candidates, probably due to freeze-out of most molecular species heavier than He.
Conclusions. The more massive and evolved objects likely play a dominant role in the physical properties and kinematics of the protocluster. The high level of turbulence and the fact that the measured core masses are larger than the expected thermal Jeans masses indicate that turbulence likely was an important factor in the initial fragmentation of the parental clump and can provide support against further fragmentation of the cores.
Key words: stars: formation / radio lines: ISM / ISM: individual objects: IRAS 05345+3157 / ISM: kinematics and dynamics / ISM: molecules
© ESO, 2012
1. Introduction
Most stars form in clusters in the densest portions of giant molecular clouds, but the initial conditions of the star formation process in clusters are still poorly understood. Studies have unveiled the physical and chemical properties of isolated low-mass pre-stellar cores, i.e. starless condensations on the verge of gravitational collapse, in nearby low-mass star-forming regions. These works show that pre-stellar cores have dense (n ~ 105−106 cm-3) and cold (T ~ 10 K) nuclei, and that their internal motions are thermally dominated, as demonstrated by their close-to-thermal line widths, even when observed at low angular resolution (see Bergin & Tafalla 2007, for a review). One as yet poorly investigated major issue is if, and how, the environment influences the physical and chemical properties of these pre-stellar cores. In clusters containing several forming stars in a small area (≤0.1 pc), turbulence, relative motions, and interactions with nearby forming (proto-)stars can in principle affect the less evolved condensations (Ward-Thompson et al. 2007). Such interaction is expected to be very important in clusters containing intermediate- and high-mass protostars or newly formed massive stars, given the typical energetic feedback provided by these objects (powerful outflows, strong winds, UV radiation, expanding Hii regions). There is also vigorous theoretical debate on how star formation proceeds in clustered regions. Specifically: is the local kinematics of the gas dominated by feedback from protostellar outflows of already-forming, generally low-mass stars (Nakamura & Li 2007) or by feedback from high-mass stars? To what extent does turbulence regulate the star formation rate? Can a model of star formation starting from quiescent starless cores be applied to clustered regions (McKee & Tan 2003)? To put constraints on theoretical models it is crucial to determine the kinematics and the physical properties of starless cores in clustered environments, especially those containing sources of very energetic feedback.
An observational effort in this direction has started, but it is mostly concentrated on nearby low-mass star-forming regions like Ophiuchus (see e.g. André et al. 2007; Friesen et al. 2009), Perseus (Foster et al. 2009) and the Pipe Nebula (Rathborne et al. 2008; Forbrich et al. 2009). Foster et al. (2009) and Friesen et al. (2009) show that cores within low-mass star-forming clusters have typically higher kinetic temperatures (~15 K) than low-mass isolated ones (10 K). On the other hand, the kinematics seems to be dominated by thermal motions like in more isolated cores, even though the external environment is turbulent (André et al. 2007; Rathborne et al. 2008). Few works have been performed towards protoclusters forming intermediate- and high-mass stars to date (Palau et al. 2007a,b; Leurini et al. 2007; Pillai et al. 2011), due to the fact that the typically large distances ( ≥ 0.5 − 1 kpc) of high-mass star-forming regions make the study of clustered environments challenging.
The target of the present paper is a well-studied protocluster embedded in a massive (180 M⊙) pc-scale clump (Fontani et al. 2006; Klein et al. 2005). The protocluster harbours intermediate- to high-mass protostellar objects and starless condensations (Fontani et al. 2008; Fontani et al. 2009, hereafter Paper I and Paper II, respectively), and is located at a distance of 1.8 kpc, ~1′ north-east from the IRAS source 05345+3157 associated with a rich cluster of infrared sources (Varricatt et al. 2010). Hereafter, the protocluster will be called I05345. One can summarise the main findings of the previous observations as follows (as general reference, see Fig. 1):
-
at a resolution of ~3′′, the millimetre continuum reveals three dusty cores, C1 − C3. C1 is then resolved into two peaks, C1-a and C1-b, down to
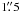 resolution (Paper I, Paper II);
resolution (Paper I, Paper II); -
both C1-a and C1-b are associated with infrared emission and are believed to harbour intermediate- to high-mass protostars, with C1-b being the most massive and associated with a hot core, unlike C1-a; in Paper II we wrongly claimed that C1-b is likely associated with 3.6 cm-continuum emission (Molinari et al. 2002) due to an error in the coordinates of the peak. The radio continuum emission is instead more likely associated with C2, and it can be due either to a radio jet or to a deeply embedded Hii region. In either case, C2 harbours a very young intermediate- or high-mass object; C3 is also associated with both dense gas and an infrared source, but its nature is less clear (Paper I, Varricatt et al. 2010; Lee et al. 2011);
-
an extended gaseous emission detected in N2H+ (1 − 0) with the PdBI encompasses all continuum cores and reveal additional condensations (Paper I, Paper II);
-
two of these condensations, called N and S, were also detected in emission lines of N2D+ but not in the mm- and IR-continuum. Based on the chemistry and on the lack of infrared emission, N and S are probably starless and in the pre-stellar phase (Paper I);
-
a widespread CO outflow likely driven by C1-b and/or C1-a interacts with the starless condensations (Paper II).
These features make this protocluster an excellent location to investigate if and how starless cores are influenced by the feedback from forming intermediate- to high-mass stars. In this paper we present new VLA high-angular resolution observations of the (1, 1) and (2, 2) inversion transitions of NH3 towards I05345, focusing mainly on the kinetic temperature and the kinematics of the dense gas. NH3 is the ideal thermometer because it is known to be a tracer of relatively dense gas and to be present in the gas phase even in regions where CO and other C-bearing species are frozen onto dust grains, and the NH3 (2, 2) to (1, 1) line ratio is sensitive to temperature. Also, the critical density of both transitions (about 104 cm-3) allows us to investigate the kinematics of the gaseous envelope in which the dense protocluster cores are embedded.
In Sect. 2 we outline the details of the VLA observations and data reduction. Section 3 presents the immediate observational results and the method used to derive the physical parameters from NH3, while in Sect. 4 we show the maps of these parameters. In Sect. 5 we discuss some aspects of the chemistry and the implications of this work in the context of the protocluster formation problem. A summary and the main conclusions are given in Sect. 6.
2. Observations and data reduction
The NRAO Very Large Array (VLA)1 ammonia observations towards I05345 were performed on October 31 and November 2, 2009. As phase centre we used the nominal position of the sub-millimetre peak detected with the JCMT (Fontani et al. 2006), namely RA(J2000) = 05h37m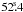 and Dec(J2000) = 32°00′06′′, which roughly corresponds to the position of C1. The local standard of rest velocity VLSR is − 18.4 km s-1. The NH3 (J, K) = (1, 1) and (2, 2) inversion transitions at 23.694496 and 23.722633 GHz, respectively, were observed simultaneously, using the 2-IF spectral line mode of the correlator, with 3.125 MHz bandwidths: the first IF covered the main line and the two innermost satellites of the (1, 1) transition, while the other IF was used to observe the (2, 2) line. Channel spacing was 24.414 kHz, correspoding to a spectral resolution of ~0.3 km s-1 at the frequency of the lines. The array was used in the most compact configuration (D), offering baselines from 35 m to 1 km. The primary beam was ~2′ at the line frequencies. The flux density scale was established by observing the standard primary calibrators 3C 286 and 3C 48, and the uncertainty is expected to be less than ~15%. Gain calibration was ensured by frequent observations of the compact quasar J0555+398. The quasar 3C 84 was used for passband calibration. Pointing corrections were derived from X-band observations of nearby quasars and applied online. The data were edited and calibrated following standard tasks and procedures of the Astronomical Image Processing System (AIPS). Imaging and deconvolution were performed using the IMAGR task, applying natural weighting to the visibilities. The resulting synthesised beam full widths at half-maximum are
and Dec(J2000) = 32°00′06′′, which roughly corresponds to the position of C1. The local standard of rest velocity VLSR is − 18.4 km s-1. The NH3 (J, K) = (1, 1) and (2, 2) inversion transitions at 23.694496 and 23.722633 GHz, respectively, were observed simultaneously, using the 2-IF spectral line mode of the correlator, with 3.125 MHz bandwidths: the first IF covered the main line and the two innermost satellites of the (1, 1) transition, while the other IF was used to observe the (2, 2) line. Channel spacing was 24.414 kHz, correspoding to a spectral resolution of ~0.3 km s-1 at the frequency of the lines. The array was used in the most compact configuration (D), offering baselines from 35 m to 1 km. The primary beam was ~2′ at the line frequencies. The flux density scale was established by observing the standard primary calibrators 3C 286 and 3C 48, and the uncertainty is expected to be less than ~15%. Gain calibration was ensured by frequent observations of the compact quasar J0555+398. The quasar 3C 84 was used for passband calibration. Pointing corrections were derived from X-band observations of nearby quasars and applied online. The data were edited and calibrated following standard tasks and procedures of the Astronomical Image Processing System (AIPS). Imaging and deconvolution were performed using the IMAGR task, applying natural weighting to the visibilities. The resulting synthesised beam full widths at half-maximum are 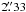 ×
× 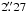 (position angle 92°) and
(position angle 92°) and 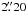 ×
× 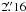 (position angle 90°) for the (1, 1) and (2, 2) lines, respectively. The noise level in each channel is about 1.4 mJy beam-1 and 1.5 mJy beam-1 for the (1, 1) and (2, 2) data, respectively.
(position angle 90°) for the (1, 1) and (2, 2) lines, respectively. The noise level in each channel is about 1.4 mJy beam-1 and 1.5 mJy beam-1 for the (1, 1) and (2, 2) data, respectively.
Calibrated channel maps and spectra were analysed using the GILDAS2 software developed at IRAM and the Observatoire de Grenoble.
3. Immediate results and derivation of physical parameters
 |
Fig. 1 Left panel: zero-th order moment map of the NH3 (1, 1) line obtained with the VLA towards I05345 (red contours). Contours start from the 6% of the maximum (0.039 Jy beam-1 km s-1), and are in steps of 10% of the maximum (0.065 Jy beam-1 km s-1). The integration velocity interval is −19.33 and − 16.24 km s-1, corresponding to the main group of hyperfine components. Contour levels start from the 3σ rms (~0.0012 Jy beam-1 km s-1), and are in steps of 3σ. The grey scale represents the 96 GHz continuum observed with the PdBI (first level is the 3σ rms = 0.004 Jy beam-1; step = 3σ rms), and the compact 3 millimetre continuum cores detected in Paper II are marked by crosses and labelled as C1-a, C1-b, C2 and C3. The two blue contours correspond to the 3σ level of the integrated emission of N2D+ (3−2) observed with the SMA (Paper I). The arrows identify the emission peaks of the ammonia cores A1 and A2 (this work). The star pinpoints the 3.6 cm continuum peak detected by Molinari et al. (2002). The dashed circle represents the VLA primary beam at ~22 GHz (~114′′). The ellipse in the bottom left corner shows the synthesised beam of the NH3 (1, 1) image. Right panel: spectra of the NH3 (1, 1) line towards the continuum cores C1-a, C1-b, C2 and C3, as well as the N2D+ condensations N and S, and the ammonia cores A1 and A2 (see left panel) in synthesised beam temperature units (Tsb). The spectra of C1-a and C1-b have been averaged over the 3σ rms contour level of the 284 GHz emission shown in Fig. 3 of Paper II, because these are resolved in that image only. For C2 and C3, we used the 225 GHz 3σ rms contour level shown in Fig. 1 of Paper I, because the 225 GHz image is less affected by the flux filtering problem. |
 |
Fig. 2 a) first-order moment map (colour scale) of the NH3 (1, 1) main group of hyperfine components. Same contour levels as in the left panel of Fig. 1 are shown. The synthesised beam of the NH3 (1, 1) VLA observations is shown in the bottom-left corner. The symbols have the same meaning as in Fig. 1; b) same as panel a) for the second-order moment. |
 |
Fig. 3 Same as Fig. 1 for the NH3 (2, 2) transition. In left panel, the NH3 (2, 2) line emission has been integrated over the velocity interval − 19.02 and − 16.55 km s-1. Contour levels start from the 6% of the maximum (~0.015 Jy beam-1 km s-1), and are in steps of 10%. |
3.1. Integrated intensity maps, moments and averaged spectra of NH3 (1, 1) and (2, 2)
In the left panel of Fig. 1 we show the zero-th order moment map of NH3 (1, 1) obtained towards I05345, by integrating over the main group of hyperfine components. The shape is irregular with a main central filamentary structure extended ≥ 80′′ in the NS direction, and a second clumpy filamentary-like structure to the NW having an arch-like shape (significance level from 6 to 9σ), oriented roughly in the NE-SW direction. The NH3 (1, 1) integrated emission traces an envelope that encompasses all the sources previously detected in the millimetre continuum and N2D+ (Fig. 1, we adopt the same nomenclature as in Paper II), in agreement with the relatively low critical density of the transition (~104 cm-3). The largest integrated intensity is detected towards the millimetre continuum cores, i.e. in the direction of active star formation (see Sect. 1).
Although it is difficult to identify separate cores given the complex emission shape, we point out two additional ammonia peaks labelled as A1 and A2, seen also in N2H+ (see Sect. 3.2). Both peaks are undetected in the infrared, as we will show in Sect. 3.2.1. A2 is in between the continuum sources C1 and C3 in the central filament and located close to a marginal detection in the millimetre continuum (Fig. 1) called C4 in Paper II. C4 is a marginal detection in the millimetre continuum, while A2 is a well defined ammonia condensation, and it does not peak exactly at the position of C4. Therefore we cannot be sure that the two cores are associated. Note that we did not include C4 in any of the figures to make them clearer.
Figure 2 shows the maps of the first- and second-order moments of the main group of hyperfine components of the (1, 1) line. The first-order moment (panel a) does not show very steep velocity gradients. The second-order moment (panel b) clearly shows an enhancement of the velocity dispersion towards the continuum cores, i.e. close to active star formation. There is also evidence of line broadening towards the arch-like NW filament, around 30′′ north of the continuum source C1, with values up to 1 km s-1 (corresponding to line widths of 2.35 km s-1). Both the velocity field and the velocity dispersion across I05345 will be examined more extensively in Sect. 4.
The NH3 (2, 2) zeroth order moment map is shown in the left panel of Fig. 3. The emission is more compact than that of the (1, 1) line, and arises mostly from the mm-continuum cores. Significant integrated emission is detected towards the starless cores S, N, A1 and A2. The arch-like filament to the NE is also clearly detected, but appears less extended than in the NH3 (1, 1) map. For this line we do not show the first and second order moment maps, which do not give any additional information with respect to that presented in Fig. 2.
Derived line parameters for the cores from the spectra integrated above the 3σ level.
In the right panels of Figs. 1 and 3 we show the spectra of NH3 (1, 1) and (2, 2), respectively, averaged over all identified cores. The contours used to extract the spectra are: the 3σ rms level of the 284 GHz continuum for C1-a and C1-b (Paper II); the 3σ rms level of the 225 GHz continuum for C2 and C3 (Paper I); the 3σ rms level of the N2D+ (3−2) integrated emission for N and S (Paper I). We used the 3σ rms level of the NH3 (2, 2) emission to extract the spectra of A1 and A2. Both lines are systematically broader towards the continuum cores, showing once again that the other cores are more quiescent.
The (1, 1) lines were fitted by taking into account their hyperfine structure using METHOD NH3 of the CLASS package3. For the (2, 2) transition, the hyperfine fitting procedure did not give good results because the magnetic hyperfine components of the main central line were not resolved (expected maximum separation of ~0.12 km s-1), and the inner satellites of the electric structure were not included in our observed bandwidth, so that we decided to fit the lines with single Gaussians.
The results are listed in Table 1. For each core, small differences are noticeable between Vpeak of the (1, 1) and (2, 2) lines beyond the indicated error margins (e.g., for C1, C1-b, and N), probably because of the different fit method that does not take into account the hyperfine structure for the (2, 2) line (see above). This could also explain the fact that Δv is found to be slightly but systematically smaller for the (1, 1) than for the (2, 2) line. However, in the protostellar cores this can have another origin: because the (2, 2) transition needs higher temperatures to be excited, it likely arises from gas closer to the forming protostars (as the integrated intensity maps in Figs. 1 and 3 suggest), and hence likely more turbulent.
3.2. Comparison with other tracers
3.2.1. Near- and mid-infrared continuum images
The two ammonia filaments shown in Fig. 1 are located about ~1′ north-east of the near-infrared cluster corresponding to the IRAS source, as it can be seen from the 2MASS (Ks-band) image (Fig. 4). Two of the four IRAC images (band central wavelengths 4.5 and 8 μm) of the region, taken with the Spitzer Space Telescope, are shown in Fig. 5. We do not show the 3.6 and 5.8 μm IRAC images because they are very similar to the 4.5 μm one. The star-forming cores C1-a, C1-b, C2 and C3 are all associated with mid-infrared emission, while the starless cores N, S, A1 and A2 lie in infrared-dark regions (see Figs. 4 and 5). In both the 2MASS and 4.5 μm image, we highlight the presence of a point-like source located approximately 15′′ north of C1-a (see yellow circle in Figs. 4 and 5), in between C1-a and the north-western filament, which seems placed at the centre of a region almost devoided of ammonia emission. We will discuss better this source and its possible influence in the surrounding gas in Sect. 4.1. The nature of the (near- to far-)infrared emission in I05345 will be discussed through deeper sensitivity and angular resolution images in a forthcoming paper (Fontani et al., in prep.).
 |
Fig. 4 2MASS Ks-band image of the region associated with IRAS 05345+3157 (colour scale). The white contour represents the 6% level of the maximum (~0.039 Jy beam-1 km s-1) of the NH3 (1, 1) zero-th order moment map. The yellow circle centred roughly at Dec +32°00′20′′ pinpoints the location of the 4.5 μm source discussed in the text (Sect. 3.2.1). The position error of the IRAS source is indicated by the grey ellipse. |
 |
Fig. 5 Mid-infrared emission observed towards I05345 with the Spitzer Space Telescope. The two colour images show the Spitzer IRAC bands centred at 4.5 (top panel) and 8 μm (bottom panel). The white contour indicates the ammonia (1, 1) emission and is the same as in Fig. 4. The yellow circle about 15′′ above C1-a pinpoints the location of the 4.5 μm source discussed in the text (as in Fig. 4), and the other symbols indicate the location of the cores as in Fig. 1. The two grey contours represent the 3σ level of the N2D+ (3−2) integrated emission, and are the same as the blue contours in Fig. 1. In each panel, The VLA synthesised beam is shown in the bottom-left corner. |
3.2.2. High density gas and outflow tracers
The ammonia emission is in very good agreement with that of N2H+ as can be seen in panel (a) of Fig. 6, where we superimpose the integrated intensity of the main group of hyperfine components of N2H+ (1−0) (Paper I) on the NH3 (1, 1) emission map shown in Fig. 1. Because the primary beam of the N2H+ map is smaller that that of the NH3 maps, the N2H+ emission looks less extended, but inside the PdBI primary beam (~48′′) the two tracers are almost coincident, although N2H+ (1−0) is expected to trace gas at slightly higher densities (ncrit ~ 105 cm-3). N2H+ (1−0) is clearly detected towards both A1 and A2 indicating that these are real physical structures, even though in Paper II we did not discuss them because they fall at the edge of the PdBI primary beam. A more exhaustive comparison between NH3 and N2H+ will be presented in Sect. 5.1.
In panel (b) of Fig. 6 we plot the overlay between the NH3 (1, 1) emission and the widespread outflow detected in 12CO and reported in Paper II. The internal part of the blue lobe of the outflow coincides spatially with the elongated mid-infrared emission detected west of C1-b (compare panel (b) of Figs. 6 with 5), suggesting that this emission could arise from the warm gas associated with the outflow.
CARMA CS (2–1) observations of the region (Lee et al. 2011) reveal seven emission peaks, which are plotted in panel (c) of Fig. 6. CS emission is detected towards C1, C3, A1, and close to the southern part of N. Cores C2, A2, S and N are not detected in CS. Because CS is well known to be highly depleted towards low-mass pre-stellar cores (e.g. Tafalla et al. 2002), the non detection in cores N and S could be due to molecular freeze-out, which would support the conclusions of Paper I and II that N and S are likely in the pre-stellar phase. Core A2, not detected in CS, marginally detected in the millimetre continuum (C4 in Paper II), and clearly detected only in the non-depleted species NH3 and N2H+, might be another very young protocluster member where CS is depleted like in the pre-stellar core candidates. On the other hand, the non-detection of core C2 is puzzling since this condensation likely harbours the most evolved (and maybe most massive) object of the protocluster.
 |
Fig. 6 Overlay between the NH3 (1, 1) integrated emission (grey contour, same level as in Figs. 4 and 5), and the integrated emission of three previously observed tracers. They are, from left to right: a) the main group of hyperfine components of N2H+ (1−0) observed with the PdBI (Paper I, blue contours. First level and step = 0.02 Jy beam-1); b) the 12CO integrated emission over the red and blue non-Gaussian wings derived from SMA + NRAO merged data (same contours as in Paper II); c) the CS (2−1) line emission peaks detected with CARMA (Lee et al. 2011, peak positions are taken from their Table 1). In each panel, black contours indicate the 3σ rms contour level of the N2D+ (3−2) emission, and crosses mark the peak position of the 3 mm continuum sources and of the ammonia cores as in Figs. 1 and 3. The ellipse in the bottom left corner and the dashed circle represent the synthesised beam and the primary beam, respectively, of the instrument used to observe the tracer superimposed on the ammonia emission: PdBI (left panel); SMA + NRAO (middle panel); CARMA (right panel). |
3.3. Derivation of physical parameters from ammonia
3.3.1. Rotation temperature and NH3 column density
From the averaged ammonia spectra shown in Figs. 1 and 3, fitted as explained in Sect. 3.1, we have derived several physical parameters. Rotation temperatures, Trot, and column densities, N(NH3), were calculated from the (2, 2)-to-(1, 1) line intensity ratio as described in Appendix A of Busquet et al. (2009). The method, based on Ho & Townes (1983), assumes that: (1) the inversion doublets constitute a two-level system; (2) the excitation temperature, Tex, and line widths at half maximum, ΔV, are the same for both transitions; (3) the physical conditions of the gas are homogeneous along the line-of-sight, so that if gradients are present, the derived parameters are average values along the line-of-sight. In the derivation of the parameters, we also assumed a unity filling factor. We stress that the Trot derived using the results of Gaussian fits for the (2, 2) transition (see Sect. 3.1) should differ only of 15% from the Trot that we would derive by fitting the hyperfine structure.
Trot and N(NH3) are given in Table 2. As expected, the coldest condensations are the pre-stellar core candidates N and S, with a Trot of 13 and ~16 K, respectively, while the continuum cores C1-a, C1-b, C2 and C3 have temperatures larger than 17 K. Because C1-b harbours a hot-core (detected in Paper II through CH3CN and OCS lines), the rotation temperature derived for this condensation is representative only of the lower-density envelope in which the hot-core is embedded. The source averaged ammonia column densities are different among the cores, going from ~4 × 1014 cm-2 for C1-b and C3 to ~1.3 × 1015 cm-2 for C2. We will come back over this point in Sect. 5.1. We stress that the uncertainties on the column densities given in Table 2, which are very small (less than 10%), do not take into account the error in the flux calibration, typically of about 10 − 15%. Therefore, an uncertainty of about 30% seems more realistic for N(NH3).
Physical parameters from ammonia for the cores.
3.3.2. Core gas masses
The gas mass can be estimated from the ammonia total column density from the relation: 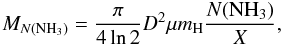 (1)where μ = 2.33 is the mean molecular weight, mH is the hydrogen mass, D is the linear diameter, N(NH3) is the ammonia total column density and X is the [NH3/H2] abundance ratio. We adopt a uniform density as zero-th order assumption (i.e. N(NH3) = n(NH3) × D) because we do not know the density profile of the condensations.
(1)where μ = 2.33 is the mean molecular weight, mH is the hydrogen mass, D is the linear diameter, N(NH3) is the ammonia total column density and X is the [NH3/H2] abundance ratio. We adopt a uniform density as zero-th order assumption (i.e. N(NH3) = n(NH3) × D) because we do not know the density profile of the condensations.
To have an estimate of the NH3 abundance in our region, we can use the H2 column densities computed in Paper II from the millimetre continuum emission (see Table 3 of Paper II): we recomputed the masses from the optically thin millimetre continuum emission using Eq. (1) of Paper II, assuming the temperatures derived from NH3 in this work (and a gas-to-dust ratio of 100). For C1-b, which harbours a hot-core, we have used both the ammonia temperature, representative of the lower-density envelope of the core, and that computed from the hot-core tracer CH3CN in Paper II (i.e. ~200 K). This implicitely assumes coupling between gas and dust, which seems reasonable at the densities of our cores ( ≥ 106 cm-3). We derive X ≃ 1 × 10-8 and X ≃ 0.85 × 10-8 for cores C1 and C2, respectively. In massive star-forming regions X is found to be of the order of 10-7 to 10-8 (Harju et al. 1993; Wu et al. 2006). We decided to adopt X = 10-8. As in Paper II, we do not consider the continuum sources close to or beyond the interferometer fields of view (namely C3 and C4). The various mass estimates are listed in Table 2. We point out that the dust masses derived from the millimetre continuum are affected by factors of uncertainty, which are difficult to quantify, especially the dust mass opacity coefficient and the gas-to-dust ratio (see e.g. Beuther et al. 2002), expected to introduce factors of 2 or more in the uncertainty of the dust mass, which hence also affect both the H2 column density and the NH3 abundance. Therefore, both the dust mass estimates given in Table 2 and the derived ammonia abundances must be regarded with caution.
4. Maps of the physical parameters
From the datacubes of both NH3 (1, 1) and (2, 2) we have extracted spectra on a grid of spacing 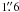 ×
× 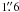 . These have been fitted as outlined in Sect. 3.1. From the fit results, we have derived maps of I05345 in several physical parameters, the discussion of which is the main subject of this section.
. These have been fitted as outlined in Sect. 3.1. From the fit results, we have derived maps of I05345 in several physical parameters, the discussion of which is the main subject of this section.
4.1. Velocity field
 |
Fig. 7 Map of the peak velocity of the NH3 (1, 1) (left panel) and (2, 2) (right panel) inversion transitions fitted as outlined in Sect. 3.1. Crosses indicate the emission peaks of cores C1-a, C1-b, C2, C3, and A2 (see Fig. 1). Solid contours mark the location of the N2D+ cores, (see Fig. 1). In both panels, the dotted contours range from − 19.5 to − 16.5 km s-1, in steps of 0.3 km s-1, and the ellipse in the bottom left corner shows the VLA synthesised beam. |
Maps of the peak velocity of NH3 (1, 1) and (2, 2) for the main filament are shown in Fig. 7. These maps are more accurate than that shown in panel a of Fig. 2 because they are based on the fitting method that takes into account the line hyperfine structure. However, both maps agree quite well with the first-order moment map. The maps in Fig. 7 have been made interpolating the input data points on a regular grid. Because of this method, we recommend to regard with caution regions containing several points with faint emission, namely along the external edge of the emission and in the southern portion of the main filament.
In Sect. 3.2.1 we have remarked the presence of an infrared source detected in both the 2MASS and the Spitzer-IRAC images (see Figs. 4 and 5), placed in between the main filament and the arch-like northern one at the centre of a region devoided of ammonia emission. Such a feature resembles the “hole” predicted by the model of Arce et al. (2011) for an expanding bubble (see their Fig. 5 and Sect. 3). In order to investigate this aspect in more detail, we computed position-velocity (p − v) plots along perpendicular cuts marked in the left panel of Fig. 8 centred on the infrared source. As seen in the figure, the two position-velocity diagrams show a U-like shape. In the Arce et al.’s model, an expanding shell would give a ring in the (p − v) plots (see their Fig. 5), while we only see the redshifted half of it. However, Arce et al. (2011) suggests that such a feature is consistent with a source driving the bubble slightly displaced towards the observer with respect to the surrounding molecular gas, so that we mainly see the gas, which is moving away from us. This suggests that the infrared source is sweeping out the surrounding material through its winds/radiation, with an expansion velocity (difference between the “tip” of the U-like feature and the “tails”) of about 1 km s-1 (see Fig. 8). In addition, the largest NH3 (1, 1) line width in the region is found very close to this infrared source (see Fig. 2, right panel), suggesting again the interaction of its winds/radiation with the dense surrounding gas. Thus, the more evolved members of the protocluster seem to be kinematically perturbing the starless cores, like condensation N. This finding raises further questions about interactions in protoclusters, such as to what extent are the physical (temperature and density), and chemical (C-bearing species, NH3/N2H+ ratio, deuterium fractionation, etc.) properties of starless cores affected by more evolved cluster members. Thus, the I05345 region harbours cores, which are eminently suitable for assessing the influence of formed stars on starless condensations.
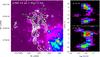 |
Fig. 8 a) NH3 (1, 1) integrated emission (white contours) overplotted on the 4.5 μm Spitzer IRAC emission. Contours start at 10% of the peak intensity, (39.03 Jy beam-1 m/s), and increase in steps of 15%. b) Position-velocity (p − v) plot of the NH3 (1, 1) emission along the cut at PA 70° and centred on (−5′′, 13 |
4.2. Temperature and column density
Following the procedure described in Sect. 3.3.1 we have derived rotation temperature and total ammonia column density across I05345. The results are shown in Fig. 9. We have excluded from the plots the arch-like filament, in which the (2, 2) transition as well as the satellites of the (1, 1) line are generally too faint to derive accurate fit results. In general we also excluded from the analysis the pixels for which the (2, 2) line is not detected at a ~4σ rms level, and we have used the same interpolation method as for Fig. 7, thus we recommend to regard with caution especially the values at the edge of the emission and towards N. In the left panel we see that Trot is mostly in between 15 and 20 K along the main filament, especially close to C1 (both C1-a and C1-b), C2 and C3, while it is lower (less than 15 K) towards N and in the eastern part of S.
Although the temperature map does not reveal big gradients, one can notice three temperature enhancements: (east of) C1-b, north-east of C2, and east of A2. The temperature enhancement in C1-b could be due to a combination of internal heating from the hot core (Paper II) as well as heating by the passage of the outflow, which seems to be launched around this position. The enhancement north-east of C2 could be due to either external heating by C2 (although this is not too likely because there is no clear heating associated with C2) or to the red lobe of the widespread CO outflow (see panel (b) in Fig. 6). However, because this temperature enhancement is found at the edge of the emission, where the errors on Trot are of 4−5 K, we cannot be sure that this is real. The enhancement east of A2 could be possibly tracing an embedded source, which would be related to the (faint) continuum emission detected at this position. Only high-sensitivity millimetre and infrared maps can help us to understand the nature of this temperature enhancement. Note that the average temperature of the plateau that surrounds the temperature enhancements east of C1-b and east of A2 is 15.8 K (with a 1σ rms of 1 K), i.e. significantly lower than the maxima measured (20 and 22 K, respectively). Therefore, the temperature enhancement proposed, except that north-east of C2, can be considered statistically significant.
In general, the measured temperatures across I05345 are higher than those derived towards infrared-dark clouds (IRDCs), believed to be the earliest phases of massive star and cluster formation, in which Trot is of the order of ~8−13 K (Ragan et al. 2011). They are also significantly higher than in clustered cores in low-mass star-forming regions such as Perseus (Schnee et al. 2009; Foster et al. 2009), where typical Trot from ~9 to ~15 K are measured. This indicates that the presence of already formed intermediate- and high-mass protostellar objects make the temperature of the dense gas systematically higher.
The ammonia column density is on average of the order of ~1015 cm-2 across the filament (right panel in Fig. 9), with the highest peak in between S and C2, and significant peaks towards C3, A2, south of N and east of C1-b.
 |
Fig. 9 Map of rotation temperature (Trot, left panel) and NH3 total column density (N(NH3), right panel) derived from the NH3 (2, 2)-to-(1, 1) ratio as described in Sect. 3.3.1. In left panel, contour levels (dotted lines) range from 11 K to 20 K in steps of 3 K, while they range from 4 × 1014 cm-2 to 3.2 × 1015 cm-2 in steps of 4 × 1014 cm-2 in the right panel. Crosses and solid contours indicate the millimetre continuum cores and the N2D+ cores, respectively, as in Figs. 1 and 3. In both panels, the ellipse in the bottom left corner shows the VLA synthesised beam. |
4.3. Non-thermal contribution to the velocity dispersion
Assuming the gas to be in Local Thermodynamic Equilibrium (LTE) so that Trot approximates the kinetic temperature, Tk, we can compute the non-thermal contribution to the observed velocity dispersion from the relation: 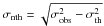 where σobs is the measured velocity dispersion of the core ( = Δv/(8ln2)1/2 for a Gaussian line profile with Δv the measured FWHM of the line) and σth is the thermal velocity disperion. For NH3, assuming a Maxwellian velocity distribution, σth can be approximated by
where σobs is the measured velocity dispersion of the core ( = Δv/(8ln2)1/2 for a Gaussian line profile with Δv the measured FWHM of the line) and σth is the thermal velocity disperion. For NH3, assuming a Maxwellian velocity distribution, σth can be approximated by 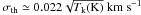 , with Tk = Trot. In Fig. 10 we plot both σnth and the ratio σnth/σth, derived from the NH3 (1, 1) lines. As expected, the non-thermal contribution to the line widths is more pronounced close to the centre of the star formation activity, especially towards C2 that likely harbours an Hii region, but also towards C1 and C3. For all these cores σnth exceeds σth of a factor larger than ~3.5. Towards N, S, A2 and the diffuse intracluster emission of the main filament, the ratio is mostly in between 2 and 3, suggesting that the gas is more quiescent here but still with a dominant non-thermal contibution. In particular, we highlight the clear drop in the ratio σnth/σth at the edge of core S, which resambles the sharp transition in the gas turbulence observed inside and out of the low-mass dense core Barnard 5 (Pineda et al. 2010).
, with Tk = Trot. In Fig. 10 we plot both σnth and the ratio σnth/σth, derived from the NH3 (1, 1) lines. As expected, the non-thermal contribution to the line widths is more pronounced close to the centre of the star formation activity, especially towards C2 that likely harbours an Hii region, but also towards C1 and C3. For all these cores σnth exceeds σth of a factor larger than ~3.5. Towards N, S, A2 and the diffuse intracluster emission of the main filament, the ratio is mostly in between 2 and 3, suggesting that the gas is more quiescent here but still with a dominant non-thermal contibution. In particular, we highlight the clear drop in the ratio σnth/σth at the edge of core S, which resambles the sharp transition in the gas turbulence observed inside and out of the low-mass dense core Barnard 5 (Pineda et al. 2010).
The plot is in agreement with the one made in Paper II from the N2H+ (1 − 0) line widths (see left panel of their Fig. 11) which, however, was limited to the central portion of the main filament. The increase in the σnth close to YSOs is found also in low-mass star-forming regions (see e.g. Pineda et al. 2011), but the difference here is more dramatic. André et al. (2007) and Foster et al. (2009) found that in the low-mass clustered cores embedded in Ophiuchus and Perseus σnth is comparable to or smaller than the thermal broadening, respectively, regardless of whether the cores are isolated, clustered, starless or star-forming. On the other hand, in the few examples of protoclusters that contain more massive objects, line widths comparable to those measured in I05345 have been found (e.g. Palau et al. 2007a; Busquet et al. 2010; Pillai et al. 2011).
These findings suggest that on the spatial scales resolved by us, i.e. ~0.02 pc, the non-thermal motions are dominant in protoclusters that contain intermediate- and high-mass objects, and the dissipation of turbulence does not seem to occur at these sub-pc scales. High levels of turbulence on small spatial scales can be due to the overall high pressure of the environment (McKee & Tan 2002) and/or to large amounts of energy and momentum injected locally in the environment by the most massive protocluster members. The presence of the widespread 12CO outflow, which covers a large portion of the dense gas and interacts with most of the condensations (see middle panel in Fig. 3) suggests that the turbulence-injected scenario is very likely for I05345.
 |
Fig. 10 Map of the non-thermal velocity dispersion (σnth, left panel) and ratio between non-thermal and thermal contribution to the observed velocity dispersion (σnth/σth, right panel). In the left panel, the contour levels (dotted contours) range from 0.2 to 0.6 km s-1, in steps of 0.1 km s-1, while in the right panel they range from 1 to 6, in steps of 1. Crosses and solid contours indicate the millimetre continuum cores and the N2D+ cores, respectively, as in Figs. 3 and 1. |
5. Discussion
5.1. NH3 and N2H+ relative abundance: an evolutionary tracer?
Unlike most of the C-bearing molecules, the nitrogen-bearing molecules NH3 and N2H+ do not suffer from depletion even at high-densities (i.e. in between ~105 and ~107 cm-3, e.g. Tafalla et al. 2002) and are therefore excellent tracers of dense gas. Studies in both low- and high-mass star-forming regions (Hotzel et al. 2004; Palau et al. 2007a) suggest that the abundance ratio of the two species in dense cores is sensitive to evolution during the pre-stellar phase and the very beginning of the protostellar phase, with the ratio NH3/N2H+ decreasing with time. Once CO is considerably desorbed from grain mantles by protostellar feedback (either by outflow passage or by an increase in temperature), N2H+ is progressively destroyed and the ratio increases again (Busquet et al. 2011). However, the underlying physical and chemical reasons for the high values of NH3/N2H+ ratio during the pre-stellar phase and its subsequent decrease have not been investigated yet.
To probe this intriguing chemical behaviour in the cores of I05345, we have extracted spectra of N2H+ (1 − 0)4 and derived N2H+ column densities following the method described in Paper I. We excluded C3 from the analysis because this is outside the primary beam of the N2H+ observations. In Table 3 we list the resulting column density ratio N(NH3)/N(N2H+). We find ratios from ~30 to ~80 in all the protostellar objects, ~60 and ~100 for A1 and A2, respectively, and ~400 and ~600 for the N2D+ condensations S and N, respectively. Because N and S are supposed to be pre-stellar, the relative abundance of NH3 to N2H+ seems greatly enhanced in pre-stellar cores (we point out that both A1 and A2 were close to the edge of the primary beam of the N2D+, and were undetected, with a N2D+ column density upper limit of ~5 × 1011 cm-2, corresponding to an upper limit on the N2D+-to-N2H+ column density ratio of ~0.01).
That the NH3-to-N2H+ relative abundance in the gas phase is somehow enhanced in quiescent cores was firstly found in the intermediate-/high-mass protocluster IRAS 20293+3952 by Palau et al. (2007a), in consistency with observations of low-mass star-forming regions (Hotzel et al. 2004; Friesen et al. 2010). In the low-mass regime, the NH3/N2H+ abundance ratio was also found to increase towards the centre of low-mass starless cores (e.g. Tafalla et al. 2002), which can be understood when freeze-out of species heavier than He becomes important (e.g. Flower et al. 2006; Aikawa et al. 2005). Depletion of heavy species like CO and other neutrals is also at the origin of the deuteration mechanism (see e.g. Millar et al. 1989), which could then explain the relation between high deuteration and high NH3/N2H+ abundance ratio. Given that no detailed explanation of the chemical processes driving the NH3/N2H+ increase can be found in the literature, we summarise the main passages in Appendix A, where we also present the predictions of a simple chemical model able to explain the observed NH3/N2H+ enhancement in dense cores characterised by high values of molecular depletion.
NH3-to-N2H+ column density ratio for the cores.
5.2. Implications for the formation of (proto-)clusters
An aspect with important implications for the formation of stellar clusters is how the observed separation between the members of a protocluster compares to typical fragmentation scale(s). A typical scale is the thermal Jeans length, which can be evaluated from the temperature according to the relation (Stahler & Palla 2005):
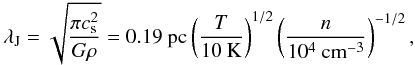 (2)where
(2)where 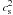 is the sound speed, and ρ and n are the mass density and volume number density, respectively. To compute a reasonable estimate of the Jeans length in I05345 we consider an interval of 15 − 20 K for the temperature. For the density, the average density of the clump in which I05345 is embedded is ~1 × 106 cm-3 (Fontani et al. 2006). With these values, we obtain a thermal Jeans length λJ ~ 0.023−0.027 pc, corresponding to angular scales of
is the sound speed, and ρ and n are the mass density and volume number density, respectively. To compute a reasonable estimate of the Jeans length in I05345 we consider an interval of 15 − 20 K for the temperature. For the density, the average density of the clump in which I05345 is embedded is ~1 × 106 cm-3 (Fontani et al. 2006). With these values, we obtain a thermal Jeans length λJ ~ 0.023−0.027 pc, corresponding to angular scales of 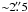 . The spatial resolution of our observations is barely sufficient to resolve these scales.
. The spatial resolution of our observations is barely sufficient to resolve these scales.
The average projected separation among the intensity peaks of the protocluster members within the central part of the main filament is 10′′ (see e.g. left panel in Fig. 1), larger than the expected thermal Jeans length. The two sources separated more than the Jeans length from any other cluster member are A2 and C3. However, it is still unclear which is the nature of these condensations and whether they are real protocluster members (especially C3, which is quite isolated from the rest). If we consider only the cores that almost certainly belong to the protocluster, namely C1-a, C1-b, C2, N and S, their projected separations are roughly consistent with thermal fragmentation. On the other hand, the masses are of one order of magnitude higher than the expected Jeans mass (see Table 2), 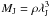 , estimated to be between ~0.1 and 0.18 M⊙.
, estimated to be between ~0.1 and 0.18 M⊙.
Zhang et al. (2009) found a similar result in the IRDC G28.34+0.06, with core separations comparable to the Jeans length and core masses larger than the Jeans masses, and concluded that non-thermal motions such as turbulence and/or magnetic fields can be dominant in the fragmentation of the IRDC. Similar findings have been found by Pillai et al. (2011), who derived that the fragmentation in two IRDCs cannot be explained by thermal fragmentation alone, but must include significant contributions from non-thermal motions. Because of the high non-thermal velocity dispersion measured (Sect. 4.3), a turbulent-driven fragmentation scenario or a significant contribution of magnetic fields can be applied to I05345 as well.
6. Summary and conclusions
We carried out VLA observations of the ammonia (1, 1) and (2, 2) inversion transitions towards the protocluster I05345. Ammonia is the best thermometer in dense gas and allows one to derive both temperature, column density and kinematics of the dense gas associated with the protocluster. The most direct results of this work are the following:
-
The ammonia emission is distributed in one main central filamentthat encompasses all the previously detected high density cores,and a secondary one to the NW of the protocluster centre.
-
The starless condensations have rotation temperatures of about 15 K, while the protostellar cores are hotter (Trot in between ~17 and 22 K). The temperature across I05345 is on average higher (roughly a factor ~1.3−1.5) than that measured in both low-mass protoclusters and IRDCs using the same diagnostics. We suggest that this is due to the feedback of the already formed intermediate- to high-mass protostellar objects both inside and outside the protocluster.
-
The non-thermal contribution to the observed line widths is significantly higher than the thermal broadening both in the starless (σnth/σth ≥ 2) and in the protostellar (σnth/σth ≥ 4) condensations. Specifically, the starless condensations are more turbulent than those observed in low-mass protoclusters (Ophiuchus and Perseus). Like the temperature enhancement, turbulence can be increased by the nearby massive protostars and/or surrounding more evolved stellar clusters.
-
The NH3-to-N2H+ column density ratio seems greatly enhanced in the pre-stellar core candidates N and S, which show NH3-to-N2H+ column density ratio a factor 10 larger than the others. Predictions of a chemical model show that this can be due to large freeze-out of molecular species heavier than He in dense cores.
-
By comparing the observed core masses and separations to the expected Jeans mass and Jeans length, we speculate that the turbulence played an important role in the initial fragmentation of the parent clump, confirming similar evidence found in IRDCs.
The GILDAS software is available at http://www.iram.fr/IRAMFR/GILDAS
This method assumes that all the hyperfine components have the same excitation temperature and width, and that their separation is fixed to the laboratory value. The method also provides an estimate of the optical depth of the line, based on the intensity ratio of the different hyperfine components. See the CLASS manual at http://iram.fr/IRAMFR/GILDAS/doc/html/class-html/class.html for details.
KInetic Database for Astrochemistry; http://kida.obs.u-bordeaux1.fr/
Acknowledgments
F.F. is grateful to R. Cesaroni for a careful reading of the manuscript and for providing useful comments and suggestions. A.P. is supported by the Spanish MICINN grant AYA2008-06189-C03 (co-funded with FEDER funds) and by a JAE-Doc CSIC fellowship co-funded with the European Social Fund. G.B. is funded by an Italian Space Agency (ASI) fellowship under contract number I/005/07/01. Many thanks to the anonymous referee for his/her useful comments and suggestions.
References
- Aikawa, Y., Herbst, E., Roberts, H., & Caselli, P. 2005, ApJ, 620, 330 [NASA ADS] [CrossRef] [Google Scholar]
- André, P., Belloche, A., Motte, F., & Peretto, N. 2007, A&A, 472, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arce, H. G., Borkin, M. A., Goodman, A. A., Pineda, J. E., & Beaumont, C. N. 2011, ApJ, 742, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Bachiller, R. 1996, ARA&A, 34, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Schilke, P., & Menten, K. M. 2002, ApJ, 566, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Thorwirth, S., Zhang, Q., et al. 2005, ApJ, 627, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Busquet, G. 2010, Ph.D. Thesis, University of Barcelona [Google Scholar]
- Busquet, G., Palau, A., Estalella, R., et al. 2009, A&A, 506, 1183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Busquet, G., Palau, A., Estalella, R., et al. 2010, A&A, 517, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Busquet, G., Estalella, R., Zhang, Q., et al. 2011, A&A, 525, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caselli, P. 2005, in Cores to Clusters: Star Formation with Next Generation Telescopes, ed. M. S. Nanda Kumar, M. Tafalla, & P. Caselli (New York: Springer), 47 [Google Scholar]
- Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Pineau Des Forêts, G., & Walmsley, C. M. 2006, A&A, 456, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontani, F., Caselli, P., Crapsi, A., et al. 2006, A&A, 460, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontani, F., Caselli, P., Bourke, T. L., Cesaroni, R., & Brand, J. 2008, A&A, 477, L45, Paper I [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontani, F., Zhang, Q., Caselli, P., & Bourke, T. L. 2009, A&A, 499, 233 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Forbrich, J., Lada, C. J., Muench, A. A., Alves, J., & Lombardi, M. 2009, ApJ, 704, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, J. B., Rosolowsky, E. W., Kauffmann, J., et al. 2009, ApJ, 696, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Friesen, R. K., Di Francesco, J., Shirley, Y. L., & Myers, P. C. 2009, ApJ, 697, 1457 [NASA ADS] [CrossRef] [Google Scholar]
- Friesen, R. K., Di Francesco, J., Shimajiri, Y., & Takakuwa, S. 2010, ApJ, 708, 1002 [NASA ADS] [CrossRef] [Google Scholar]
- Harju, J., Walmsley, C. M., & Wouterloot, J. G. A. 1993, A&AS, 98, 51 [NASA ADS] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 261, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Hily-Blant, P., Walmsley, M., Pineau Des Forêts, G., & Flower, D. 2010, A&A, 513, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ho, P. T. P., & Townes, C. H. 1983, ARA&A, 21, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Hotzel, S., Harju, J., & Walmsley, C. M. 2004, A&A, 415, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keto, E., & Caselli, P. 2010, MNRAS, 402, 1625 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, R., Posselt, B., Schreyer, K., Forbrich, J., & Henning, Th. 2005, ApJS, 161, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., & Mac Low, M.-M. 2009, in Structure Formation in Astrophysics, ed. G. Chabrier (Cambridge, UK: Cambridge University Press), 427 [Google Scholar]
- Lee, K. I., Looney, L. W., Klein, R., & Wang, S. 2011, MNRAS, 415, 2790 [NASA ADS] [CrossRef] [Google Scholar]
- Leurini, S., Beuther, H., Schilke, P., et al. 2007, A&A, 475, 925 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McKee, C. F., & Tan, J. C. 2002, Nature, 416, 59 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McKee, C. F., & Tan, J. C. 2003, ApJ, 585, 850 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Millar, T. J., Bennett, A., & Herbst, E. 1989, ApJ, 340, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Testi, L., Rodriguez, L. F., & Zhang, Q. 2002, ApJ, 570, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, M., & Li, Z.-Y. 2007, ApJ, 656, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Palau, A., Estalella, R., Ho, P. T. P., Beuther, H., & Beltrán, M. T. 2007a, A&A, 474, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palau, A., Estalella, R., Girart, J. M., et al. 2007b, A&A, 465, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peters, T., Banerjee, R., Klessen, R. S., & Mac Low, M.-M. 2011, ApJ, 729, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Pillai, T., Kauffmann, J., Wyrowski, F., et al. 2011, A&A, 530, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pineda, J. E., Goodman, A. A., Arce, H. G., et al. 2010, ApJ, 712, L116 [NASA ADS] [CrossRef] [Google Scholar]
- Pineda, J. E., Goodman, A. A., Arce, H. G., et al. 2011, ApJ, 739, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Ragan, S. E., Bergin, E. A., & Wilner, D. 2011, ApJ, 736, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Lada, C. J., Muench, A. A., Alves, J. F., & Lombardi, M. 2008, ApJS, 174, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, C. J., Greenberg, J. M., Schutte, W. A., & van Dishoeck, E. F. 2004, A&A, 415, 203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stahler, S. W., & Palla, F. 2005, The Formation of Stars, ed. S. W. Stahler, & F. Palla (Wiley-VCH), 865 [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., Walmsley, C. M., & Comito, C. 2002, ApJ, 569, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Schnee, S., Rosolowsky, E., Foster, J., Enoch, M., & Sargent, A. 2009, ApJ, 691, 1754 [NASA ADS] [CrossRef] [Google Scholar]
- Varricatt, W. P., Davis, C. J., Ramsay, S., & Todd, S. P. 2010, MNRAS, 404, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Walmsley, C. M., Flower, D. R., & Pineau des Forêts, G. 2004, 418, 1035 [Google Scholar]
- Wang, Y., Zhang, Q., Pillai, T., Wyrowski, F., & Wu, Y. 2008, ApJ, 672, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Ward-Thompson, D., André, P., & Crutcher, R. 2007, PPV Conf., 951, 33 [Google Scholar]
- Wu, Y., Zhang, Q., Yu, W., et al. 2006, A&A, 450, 607 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Q., Hunter, T. R., Brand, J., et al. 2005, ApJ, 625, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q., Wang, Y., Pillai, T., & Rathborne, J. 2009, ApJ, 696, 268 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: NH3/N2H+ abundance ratio
The NH3/N2H+ column density ratio has been found to significantly increase in starless cores, in particular in those with the highest N2D+ to N2H+ abundance ratio (Sect. 5.1). This trend is reminiscent of the NH3/N2H+ abundance increase towards the centre of low-mass starless cores (e.g. Tafalla et al. 2002), and can be understood in terms of freeze-out of species heavier than He (Flower et al. 2006; Aikawa et al. 2005). We present here the predictions of a chemical model, given that a detailed explanation of the chemical processes leading to the NH3/N2H+ increase is lacking in the literature.
The freeze-out time scale (tfreeze) is inversely proportional to the density and becomes shorter than any dynamical time scale if the volume density (nH) is larger than ~104 cm-3 (tfreeze ≃ 109/nH yr; e.g. Bergin & Tafalla 2007). Therefore, in regions with nH larger than a few times 104 cm-3, atomic and molecular species heavier than He becomes increasingly more depleted from the gas phase. In dark regions, this process is only counterbalanced by nonthermal desorption due to cosmic-rays impulsive heating of dust grains (e.g. Hasegawa & Herbst 1993) and to photodesorption caused by UV photons produced by the interaction of cosmic rays with H2 molecules (Shen et al. 2004; Keto & Caselli 2010). Non-thermal photodesorption however does not depend on volume density, so freeze-out will eventually win in the densest regions (nH > 106 cm-3) of starless cores.
Volatile elements such as H, D, and He are not affected by freeze-out. Actually, abundances of H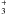 (and its deuterated forms), He+ and H+ increase towards dense regions, where neutral species such as O and CO (their main destruction partners) are mostly frozen onto dust grains (e.g. Walmsley et al. 2004). How does this affect the abundance of N2H+ and NH3? To answer this question, one needs to consider the main formation and destruction routes of these species.
(and its deuterated forms), He+ and H+ increase towards dense regions, where neutral species such as O and CO (their main destruction partners) are mostly frozen onto dust grains (e.g. Walmsley et al. 2004). How does this affect the abundance of N2H+ and NH3? To answer this question, one needs to consider the main formation and destruction routes of these species.
For this purpose, we used a reduced gas-phase chemical network extracted from KIDA5 and run models with different amounts of elemental freeze-out. The model includes H, He, O, C, N, S, Si, Fe and molecules up to 5 atoms in size. Initial conditions are based on standard low-metal elemental abundances (Table 1 of Caselli 2005), with all the elements in atomic form, except for hydrogen, which is all in H2. The adopted H2 volume density, extinction and gas temperature are 105 cm-3, 30 mag and 15 K, respectively. To study the effects of freeze-out, we varied the elemental abundance of all species heavier than He between a factor of 1 and 104. In Fig. A.1 (top panel), the fractional abundace with respect to total H nuclei of key species and (bottom panel) the NH3/N2H+ abundance ratio (RN) are plotted as a function of depletion factor (fD), together with the observed values from Table 3. Figure A.1 shows that RN first decreases with fD (when fD is between 1 and 7) and then constantly increases to values larger than 1000. The reason for this trend is due to the fact that N2H+ is directly linked to N2, given that its main formation route is 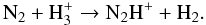 (A.1)On the other hand, the formation of NH3 depends on N+, which can be produced by reactions of N-bearing species such as N2, CN, and NH2 with He+:
(A.1)On the other hand, the formation of NH3 depends on N+, which can be produced by reactions of N-bearing species such as N2, CN, and NH2 with He+: 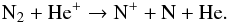 (A.2)
(A.2)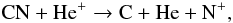 (A.3)
(A.3)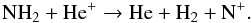 (A.4)Reactions (A.2), (A.3) and (A.4) are followed by successive hydrogen abstraction reactions with H2 until all nitrogen valence electrons are used:
(A.4)Reactions (A.2), (A.3) and (A.4) are followed by successive hydrogen abstraction reactions with H2 until all nitrogen valence electrons are used: 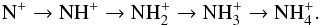 (A.5)Once ammonium (NH
(A.5)Once ammonium (NH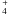 ) is formed, it dissociatively recombines with electrons, to form ammonia.
) is formed, it dissociatively recombines with electrons, to form ammonia.
 |
Fig. A.1 Top panel: fractional abundance of selected species as a function of depletion factor (see text for details). Note the sharp drop of N2 and the shallower drop of NH3 compared to N2H+. Bottom panel: NH3/N2H+ abundance ratio as a funciton of depletion factor. Horizontal lines are the observed values (see Table 3) for protostellar (continuous) and starless (dashed) cores. Note that although all protostellar cores are consistent with both low and large values of freeze-out, two of the starless cores can only be reproduce by values of depletion factor around 1000, similar to what measured in the core nucleus of L1544 (Caselli et al. 1999). |
Reaction (A.2) dominates in non-depleted conditions, whereas reactions (A.3) and (A.4) dominate at large values of fD, when the formation rate of N2 drops. In fact, N2 forms via two (relatively slow) neutral-neutral reactions (e.g. Hily-Blant et al. 2010): 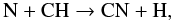 (A.6)
(A.6)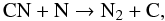 (A.7)so that an increase of fD affects the production rate of N2 more severely than the production rate of species formed via only one neutral-neutral reactions (e.g. CN, see reaction A.6). Moreover, as stated above, with the increase of fD, abundances of important destruction partners of N2 (H
(A.7)so that an increase of fD affects the production rate of N2 more severely than the production rate of species formed via only one neutral-neutral reactions (e.g. CN, see reaction A.6). Moreover, as stated above, with the increase of fD, abundances of important destruction partners of N2 (H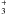 and He+) increases, further reducing the N2 abundance. This is evident in the upper panel of Fig. A.1, where N2 shows the steepest drop in abundance with fD.
and He+) increases, further reducing the N2 abundance. This is evident in the upper panel of Fig. A.1, where N2 shows the steepest drop in abundance with fD.
The N2H+ abundance increases between fD = 1 and 7, because the drop in N2 is counterbalanced by a drop in CO, the main destruction partner at moderate values of fD ( ≤ 10): 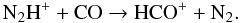 (A.8)At larger values of fD, dissociative recombination with electrons becomes the most important destruction route:
(A.8)At larger values of fD, dissociative recombination with electrons becomes the most important destruction route: 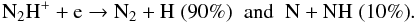 (A.9)Reaction (A.8) reforms N2, which can produce again N2H+ via reaction (A.1). Reaction (A.9) forms N2 in 90% of the cases. The other 10% of dissociative recombinations form NH, permanently removing N2 from the gas-phase.
(A.9)Reaction (A.8) reforms N2, which can produce again N2H+ via reaction (A.1). Reaction (A.9) forms N2 in 90% of the cases. The other 10% of dissociative recombinations form NH, permanently removing N2 from the gas-phase.
Destruction of NH3 happens via H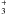 (at large fD) and H3O+ (at low fD):
(at large fD) and H3O+ (at low fD): 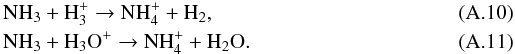 However, unlike N2H+, the destruction of NH3 at all values of fD reforms ammonium, the precursor of NH3. Therefore, the NH3 abundance drop follows the abundance of N+ precursors (see reactions A.2 − A.4). From Fig. A.1, it is evident that CN, NH2 and N (important for the formation of CN, see reaction A.6) all maintain large abundances until fD ~ 1000, whereas N2H+ shows a constant drop for fD > 10.
However, unlike N2H+, the destruction of NH3 at all values of fD reforms ammonium, the precursor of NH3. Therefore, the NH3 abundance drop follows the abundance of N+ precursors (see reactions A.2 − A.4). From Fig. A.1, it is evident that CN, NH2 and N (important for the formation of CN, see reaction A.6) all maintain large abundances until fD ~ 1000, whereas N2H+ shows a constant drop for fD > 10.
All Tables
Derived line parameters for the cores from the spectra integrated above the 3σ level.
All Figures
 |
Fig. 1 Left panel: zero-th order moment map of the NH3 (1, 1) line obtained with the VLA towards I05345 (red contours). Contours start from the 6% of the maximum (0.039 Jy beam-1 km s-1), and are in steps of 10% of the maximum (0.065 Jy beam-1 km s-1). The integration velocity interval is −19.33 and − 16.24 km s-1, corresponding to the main group of hyperfine components. Contour levels start from the 3σ rms (~0.0012 Jy beam-1 km s-1), and are in steps of 3σ. The grey scale represents the 96 GHz continuum observed with the PdBI (first level is the 3σ rms = 0.004 Jy beam-1; step = 3σ rms), and the compact 3 millimetre continuum cores detected in Paper II are marked by crosses and labelled as C1-a, C1-b, C2 and C3. The two blue contours correspond to the 3σ level of the integrated emission of N2D+ (3−2) observed with the SMA (Paper I). The arrows identify the emission peaks of the ammonia cores A1 and A2 (this work). The star pinpoints the 3.6 cm continuum peak detected by Molinari et al. (2002). The dashed circle represents the VLA primary beam at ~22 GHz (~114′′). The ellipse in the bottom left corner shows the synthesised beam of the NH3 (1, 1) image. Right panel: spectra of the NH3 (1, 1) line towards the continuum cores C1-a, C1-b, C2 and C3, as well as the N2D+ condensations N and S, and the ammonia cores A1 and A2 (see left panel) in synthesised beam temperature units (Tsb). The spectra of C1-a and C1-b have been averaged over the 3σ rms contour level of the 284 GHz emission shown in Fig. 3 of Paper II, because these are resolved in that image only. For C2 and C3, we used the 225 GHz 3σ rms contour level shown in Fig. 1 of Paper I, because the 225 GHz image is less affected by the flux filtering problem. |
| In the text | |
 |
Fig. 2 a) first-order moment map (colour scale) of the NH3 (1, 1) main group of hyperfine components. Same contour levels as in the left panel of Fig. 1 are shown. The synthesised beam of the NH3 (1, 1) VLA observations is shown in the bottom-left corner. The symbols have the same meaning as in Fig. 1; b) same as panel a) for the second-order moment. |
| In the text | |
 |
Fig. 3 Same as Fig. 1 for the NH3 (2, 2) transition. In left panel, the NH3 (2, 2) line emission has been integrated over the velocity interval − 19.02 and − 16.55 km s-1. Contour levels start from the 6% of the maximum (~0.015 Jy beam-1 km s-1), and are in steps of 10%. |
| In the text | |
 |
Fig. 4 2MASS Ks-band image of the region associated with IRAS 05345+3157 (colour scale). The white contour represents the 6% level of the maximum (~0.039 Jy beam-1 km s-1) of the NH3 (1, 1) zero-th order moment map. The yellow circle centred roughly at Dec +32°00′20′′ pinpoints the location of the 4.5 μm source discussed in the text (Sect. 3.2.1). The position error of the IRAS source is indicated by the grey ellipse. |
| In the text | |
 |
Fig. 5 Mid-infrared emission observed towards I05345 with the Spitzer Space Telescope. The two colour images show the Spitzer IRAC bands centred at 4.5 (top panel) and 8 μm (bottom panel). The white contour indicates the ammonia (1, 1) emission and is the same as in Fig. 4. The yellow circle about 15′′ above C1-a pinpoints the location of the 4.5 μm source discussed in the text (as in Fig. 4), and the other symbols indicate the location of the cores as in Fig. 1. The two grey contours represent the 3σ level of the N2D+ (3−2) integrated emission, and are the same as the blue contours in Fig. 1. In each panel, The VLA synthesised beam is shown in the bottom-left corner. |
| In the text | |
 |
Fig. 6 Overlay between the NH3 (1, 1) integrated emission (grey contour, same level as in Figs. 4 and 5), and the integrated emission of three previously observed tracers. They are, from left to right: a) the main group of hyperfine components of N2H+ (1−0) observed with the PdBI (Paper I, blue contours. First level and step = 0.02 Jy beam-1); b) the 12CO integrated emission over the red and blue non-Gaussian wings derived from SMA + NRAO merged data (same contours as in Paper II); c) the CS (2−1) line emission peaks detected with CARMA (Lee et al. 2011, peak positions are taken from their Table 1). In each panel, black contours indicate the 3σ rms contour level of the N2D+ (3−2) emission, and crosses mark the peak position of the 3 mm continuum sources and of the ammonia cores as in Figs. 1 and 3. The ellipse in the bottom left corner and the dashed circle represent the synthesised beam and the primary beam, respectively, of the instrument used to observe the tracer superimposed on the ammonia emission: PdBI (left panel); SMA + NRAO (middle panel); CARMA (right panel). |
| In the text | |
 |
Fig. 7 Map of the peak velocity of the NH3 (1, 1) (left panel) and (2, 2) (right panel) inversion transitions fitted as outlined in Sect. 3.1. Crosses indicate the emission peaks of cores C1-a, C1-b, C2, C3, and A2 (see Fig. 1). Solid contours mark the location of the N2D+ cores, (see Fig. 1). In both panels, the dotted contours range from − 19.5 to − 16.5 km s-1, in steps of 0.3 km s-1, and the ellipse in the bottom left corner shows the VLA synthesised beam. |
| In the text | |
 |
Fig. 8 a) NH3 (1, 1) integrated emission (white contours) overplotted on the 4.5 μm Spitzer IRAC emission. Contours start at 10% of the peak intensity, (39.03 Jy beam-1 m/s), and increase in steps of 15%. b) Position-velocity (p − v) plot of the NH3 (1, 1) emission along the cut at PA 70° and centred on (−5′′, 13 |
| In the text | |
 |
Fig. 9 Map of rotation temperature (Trot, left panel) and NH3 total column density (N(NH3), right panel) derived from the NH3 (2, 2)-to-(1, 1) ratio as described in Sect. 3.3.1. In left panel, contour levels (dotted lines) range from 11 K to 20 K in steps of 3 K, while they range from 4 × 1014 cm-2 to 3.2 × 1015 cm-2 in steps of 4 × 1014 cm-2 in the right panel. Crosses and solid contours indicate the millimetre continuum cores and the N2D+ cores, respectively, as in Figs. 1 and 3. In both panels, the ellipse in the bottom left corner shows the VLA synthesised beam. |
| In the text | |
 |
Fig. 10 Map of the non-thermal velocity dispersion (σnth, left panel) and ratio between non-thermal and thermal contribution to the observed velocity dispersion (σnth/σth, right panel). In the left panel, the contour levels (dotted contours) range from 0.2 to 0.6 km s-1, in steps of 0.1 km s-1, while in the right panel they range from 1 to 6, in steps of 1. Crosses and solid contours indicate the millimetre continuum cores and the N2D+ cores, respectively, as in Figs. 3 and 1. |
| In the text | |
 |
Fig. A.1 Top panel: fractional abundance of selected species as a function of depletion factor (see text for details). Note the sharp drop of N2 and the shallower drop of NH3 compared to N2H+. Bottom panel: NH3/N2H+ abundance ratio as a funciton of depletion factor. Horizontal lines are the observed values (see Table 3) for protostellar (continuous) and starless (dashed) cores. Note that although all protostellar cores are consistent with both low and large values of freeze-out, two of the starless cores can only be reproduce by values of depletion factor around 1000, similar to what measured in the core nucleus of L1544 (Caselli et al. 1999). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.