| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A110 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201015773 | |
| Published online | 03 August 2011 | |
Fast horizontal flows in a quiet sun MHD simulation and their spectroscopic signatures
Sterrekundig Instituut, Utrecht University,
Postbus 80 000,
3508 TA
Utrecht,
The Netherlands
e-mail: N.Vitas@uu.nl
Received: 17 September 2010
Accepted: 12 June 2011
Numerical simulations of solar surface convection have predicted the existence of supersonic horizontal flows in the photospheric granulation. Recently, the detection of such flows in data from the Hinode satellite was reported. We study supersonic granular flows in detail to understand their signatures in spectral lines and to test the observational detection method used to identify these flows in the Hinode observations. We perform time-dependent 3D radiative MHD numerical simulations and synthesize the Fe i 6302 Å spectral lines at the resolution of the Hinode data for different viewing angles covering the center-limb variation. There is very large variation in the detailed shape of the emergent line profiles depending on the viewing angle and the particular flow properties and orientation. At the full simulation resolution the supersonic flows can even produce distinct satellite lines. After smearing to the Hinode resolution sufficient signature of supersonic motion remains. Our analysis shows that the detection method used to analyze the Hinode data is indeed applicable. However, the detection is very sensitive to ad hoc parameter choices and can also misidentify supersonic flows.
Key words: convection / Sun: photosphere / line: formation / radiative transfer / Sun: granulation / hydrodynamics
© ESO, 2011
1. Introduction
Continuum images of the solar surface show a pattern of isolated bright cells called granules that are separated by dark intergranular lanes. The physics causing this pattern is well understood and has been successfully reproduced in highly realistic 3D hydrodynamical simulations (Stein & Nordlund 1998; Vögler & Schüssler 2003; Wedemeyer et al. 2004). A detailed review of solar granulation is given by Nordlund et al. (2009). In this paper we employ numerical MHD simulations to study high velocity flows and shocks in granular outflows and their observational signatures.
We briefly summarize the physics of solar granulation: bright granules are locations where hot, high-entropy and low density gas parcels reach a height at which the continuum opacity is sufficiently low to allow photons to escape. The temperature and entropy of the parcel are reduced by radiative losses in a thin layer at the solar surface. The parcel expands and reaches a characteristic surface granule size of around 1 Mm. The horizontally outflowing, radiatively cooled, dense material collides with neighboring granular flows and sinks in the dark intergranular lanes.
A closer look at particle trajectories within the parcel shows that, once at the surface, the particles continue to move upwards and penetrate into a stable layer (e.g., Fig. 18 of Stein & Nordlund 1998; and Fig. 8 of Cheung et al. 2007b). There the entropy temporarily increases due to a small amount of radiative heating from below. Finally, due to mass conservation and the horizontal pressure gradient, the flows diverge horizontally outwards. The particle trajectories in this overshooting zone differ depending on the individual initial velocity and location within the granule. In some cases the accelerated flows reach large horizontal velocities that occasionally become supersonic at the granular edges (Cattaneo et al. 1990; Malagoli et al. 1990; Stein & Nordlund 1998). Gas parcels that are located initially at the granule center have the longest trajectories and so are likely to reach the highest velocities (Stein & Nordlund 1998).
At disk center, Doppler measurements of supersonic horizontal flows in the granulation are not possible. Therefore Nesis et al. (1993) proposed to use line broadening as an indirect indicator of such flows. However, Solanki et al. (1996) compared the velocity field in 2D granulation simulations with synthesized line profiles and showed that, at disk center, other properties of the downflow lanes can cause comparable line broadening, and pointed out that unresolved vertical velocity gradients can also produce apparent line broadening. They concluded that all line widths observed by Nesis et al. (1993) can be attributed to limited resolution.
At the limb, the broadest profiles found by Solanki et al. (1996) were all associated with strong horizontal velocity gradients. However, the inverse was not true, as not all supersonic horizontal flows resulted in large line broadening. Solanki et al. (1996) and Gadun & Hanslmeier (2000) analyzed 2D granulation simulations and concluded that limb observations are more favorable than disk center observations for the detection of such fast horizontal flows. Rybák et al. (2004) performed spectroscopy with high angular resolution at a viewing angle corresponding to μ = 0.65, found shock signatures in spectral line widths, and presented the first observation of the time evolution of such a granular shock. In high-resolution data obtained with the IMaX instrument on the balloon-borne Sunrise telescope, Khomenko et al. (2010) observed line profiles with small FWHM at the granular edges. They compared the observations with results of magneto-convection simulations and concluded that the narrow profiles originate from regions where the granular flows bend.
Recently, Bellot Rubio (2009) detected granular shocks in spectra obtained with the SOT/SP instrument on Hinode (Suematsu et al. 2008). At its high-angular resolution, individual line profiles sometimes show shock signatures as considerable profile distortions, even as separate blue-wing satellite components. These high-quality observations motivated the present study in which we synthesize spectral line profiles from numerical simulations snapshots and compare them to the SP/SOT Hinode measurements of Bellot Rubio (2009).
2. Computational method
Model atmosphere.
We use snapshots from a time-dependent 3D radiative magnetohydrodynamics (MHD) simulation of the quiet sun. The simulation was performed with the MURaM (MPS/University of Chicago Radiative MHD) code (Vögler & Schüssler 2003; Vögler et al. 2005) that successfully has reproduced multiple phenomena in the solar photosphere (e.g. Schüssler & Vögler 2006; Vögler & Schüssler 2007; Cameron et al. 2007; Cheung et al. 2007a; Schüssler & Vögler 2008; Rempel et al. 2009; Cheung et al. 2010). The simulated box spans 6 Mm in the horizontal direction, evaluated at 288 grid points, and 1.4 Mm in the vertical axis with 100 grid points. The average unsigned magnetic flux at τ = 1 is 30 G with an exact balance of positive and negative polarities (i.e. the signed magnetic flux is 0 G). The lower boundary of the simulation domain is open for mass flows, while the upper boundary is closed with stress-free conditions for the horizontal velocities. The flow is stabilized numerically with an artificial viscosity and artificial thermal diffusivity that keep gradients resolved and prevent the buildup of spurious numerical oscillations (“ringing”). In order to reduce the effect of the closed upper boundary on the flow in the domain, the amplitude of the numerical diffusion coefficients is increased in the uppermost 200 km of the simulation domain and reaches an enhancement factor ≈ 5 directly at the upper boundary. Consequently, any upward travelling wave is dampened and the effect of artificial wave reflection is greatly reduced. More details on the boundary conditions and artificial diffusivities can be found in Vögler (2004). The snapshot from which our simulation was started is one of the snapshots chosen by Khomenko et al. (2005) in their study of quiet-sun Stokes diagnostics. We continued the simulation for approximately an hour of solar time. From this time sequence we extracted 20 snapshots at intervals of 3 min for further analysis.
Speed of sound.
The local sound speed is computed from the results of the simulation. Since MURaM takes partial ionization into account, we evaluate the sound speed, cs, from its general definition: 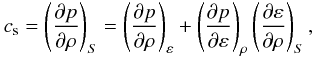 where p is the total gas pressure, ρ the density, ε the internal energy, and S the entropy. In the case of an isentropic process the last term is given by the first law of thermodynamics:
where p is the total gas pressure, ρ the density, ε the internal energy, and S the entropy. In the case of an isentropic process the last term is given by the first law of thermodynamics: 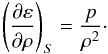 The partial derivatives of the pressure at constant density and internal energy are found from the precomputed tables of the equation of state p(ρ,ε) (see Vögler et al. 2005).
The partial derivatives of the pressure at constant density and internal energy are found from the precomputed tables of the equation of state p(ρ,ε) (see Vögler et al. 2005).
Skewing the snapshot.
Since we are interested in the properties of the snapshot at different viewing angles μ, where μ = cosθ with θ the angle between the line of sight (LOS) and the vertical, we skewed the snapshots to mimic the center-to-limb variation of the quiet sun at μ = 0.4 and 0.6. The periodic horizontal boundary conditions of the simulation enable evaluation along any LOS through the skewed snapshot. The skewing was done along the x-axis, in negative (towards the “left” limb) and positive (“right” limb) directions. The skewing method was adopted from Keller et al. (2004).
Line synthesis.
We assume local thermodynamic equilibrium (LTE) for the spectral line synthesis, employing the LILIA code of Socas-Navarro (2001). The one-dimensional spectral synthesis was done assuming that the columns of the simulation snapshot along the LOS are independent, each representing a one-dimensional model atmosphere. We so synthesized the two Fe i lines at 6301.5012 Å and 6302.4936 Å with a wavelength sampling of 12 mÅ. The atomic data for these lines were taken from Khomenko et al. (2005).
Image degradation.
To degrade the computed line profiles to the diffraction-limited angular resolution of the SOT on Hinode we adopt the ideal part of the empirical point spread function (PSF) of Wedemeyer-Böhm (2008). After the smearing, the computed intensities were resampled to the pixel size of 0.16 ″. It is important to note that, at disk center, roughly 6 × 6 simulation pixels correspond to one pixel in the SOT observations. Due to geometrical foreshortening, the number of simulation pixels per SOT pixel increases linearly with 1/μ and, at μ = 0.4, that number becomes as large as 90. In addition to that, the convolution with the PSF increases the number even further.
3. Velocity field
3.1. Statistics of supersonic events
We identified supersonic flows by comparing the magnitude of the velocity with the local sound speed at constant τ5000 surfaces in the simulation snapshots. The fraction of the surface occupied by supersonic flows, without distinguishing between different orientations, versus optical depth is shown in Fig. 1. It shows that shocks occur only rarely, less than 1.5% in any snapshots and at any optical depth in the plotted range. In the upper half of the range, that fraction is even smaller, exceeding 0.3% only occasionally as in the thick curve for snapshot S1. Projection of the horizontal supersonic flows in snapshot S1 to the horizontal plane occupies 2.5% of the surface, while projection of the vertical flows covers 1.6%. Projections of horizontal and vertical supersonic flows in snapshot S0 cover similar area of ~1%. Similar to that, Stein & Nordlund (1998) found: “the shocks at the edges of intergranular lanes are [... ] a rare occurance. At any one time, supersonic flow occurs in only ~3−4% of the surface”.
Figure 1 shows that the amount of supersonic events in our simulation varies with time. This is in qualitative agreement with the findings of Malagoli et al. (1990), who identified distinguishable episodes of increased supersonic occurrences in their less realistic simulations.
Furthermore, Fig. 1 suggests two different populations of supersonic cells: one below the surface (2 > log τ5000 > 1), and one roughly peaking at log τ5000 > −1. That finding is in agreement with results obtained by Gadun et al. (2000) in 2D simulations and by Stein & Nordlund (1998) in 3D.
 |
Fig. 1 The fraction of dx × dy × d(log τ) cells with supersonic flows versus optical depth for disk center viewing with μ = 1. Each curve represents one of the 20 analyzed snapshots. The supersonic flow may be in any direction. The thick solid curve corresponds to the snapshot with the largest abundance of supersonic flows (S1, lower row in Fig. 3), while the thick dashed curve corresponds to the initial snapshot (S0, upper row in Fig. 3). |
 |
Fig. 2 Two-dimensional histogram of the distribution of supersonic flows in optical depth and orientation (γ = 0° corresponds to an upflow, γ = 90° to a horizontal flow, and γ = 180° to a downflow). The histogram is made from all snapshots. The populations of the horizontal flows and the vertical flows are separated in height. The horizontal flows are found mainly above the surface; the vertical flows below it. |
The two-dimensional histogram in Fig. 2 shows the inclination angles γ of the supersonic flows versus optical depth for all snapshots. There are two distinct areas of increased occurence. The supersonic flows above the surface are predominantly horizontal with a slight tendency towards downflow, while the supersonic downflows are located in the layers just below the surface.
The largest Mach number of the predominantly horizontal supersonic flows is 1.37 and is reached at log τ5000 = −1. This is in a good agreement with Fig. 32 of Stein & Nordlund (1998).
3.2. Selection of events
In Fig. 3 we show the continuum intensity at 6300 Å, temperature, horizontal velocity and total magnetic field strength at the surface of constant optical depth log τ5000 = −1 for two snapshots. The upper row is taken from the initial snapshot which is characterized by a relatively small number of supersonic events in the photosphere (S0, thick dashed curve in Fig. 1). The lower row shows the snapshot with the largest abundance of supersonic flows (S1, thick solid curve in Fig. 1). The time separation between the two snapshots is only 6 minutes of solar time. Although that time is sufficient for the convective scenery to be largely changed, the magnetic field did not evolve as strongly.
The contours obtained by outlining the projection of the volume occupied by supersonic flows on a horizontal plane are overplotted on the continuum images. Different colors correspond to different inclination angles γ. The patches of horizontal supersonic flows occur above granular edges, whereas the vertical supersonic flows are located mainly in the downdrafts beneath the dark lanes.
The temperature maps in Fig. 3 show reversed granulation. This phenomenon has been studied extensively by Cheung et al. (2007b) as adiabatic heating at the granular edges. Superimposed on this pattern, the temperature maps in Fig. 3 show enhanced values at the locations where horizontal supersonic flows are present, indicating the presence of shock heating.
The horizontal velocity map (Fig. 3) shows “fountain-like” topology (Stein & Nordlund 1998). The horizontal velocity increases towards the granular edges, and vanishes at the very edge where the horizontal flows turn into downflows. The horizontal supersonic flows are not exclusively associated with large granules as it might be expected from a simple description of the solar granulation. Moreover, even in the large granules in our sample these flows do not occur symmetrically arround the granular rim, but only at a small fraction of the rim (Fig. 3).
Figure 3 also shows that large horizontal flows are generally not related to strong magnetic concentrations.
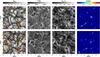 |
Fig. 3 Maps of the two snapshots analyzed in detail (top, S0; bottom, S1). From left to right: continuum intensity at 6300 Å, temperature, magnitude of the horizontal velocity in units of the local sound speed, and total magnetic field strength at the log τ5000 = −1 surface. Contours show the projection on the horizontal plane of cells containing supersonic flows (red specifies flows that are nearly horizontal 120° > γ > 60° and; yellow nearly vertical flows 180° > γ > 150° and 30° > γ > 0°; orange flows with inclinations 150° > γ > 120° and 60° > γ > 30°. The four numbered markers point to selected events discussed in detail in Sect. 3.2. |
We select four events of fast horizontal flow in snapshots S0 and S1 for a more detailed analysis. They are indicated by markers in Fig. 3. Vertical cross-sections through the temperature and velocity stratification for events 1, 2 and 4 are shown in Fig. 4, while Event 3 is studied in more detail in Fig. 6.
 |
Fig. 4 Vertical cross-section of temperature (gray scale) and velocity (arrows) for events 1 and 2 (upper panels) and 4 (lower panel) (cf. Fig. 3). Subsonic velocities are indicated by white arrows, red arrows correspond to supersonic velocities. White curves represent the log τ5000 = 0,−1 and −2 levels, respectively. |
 |
Fig. 5 Temporal evolution of the shock front in event 3 at a fixed geometrical height of ~100 km above the average log τ5000 = 0 level. From the bottom up, the curves represent time samples at 25 s intervals. The scale on the vertical axis is for snapshot S1 (thick curve). The range of the horizontal axis is same as in Fig. 6. Upper left panel: temperature deviation from the horizontal mean; upper right: horizontal velocity (positive along x); middle left: pressure deviation from the horizontal mean; middle right: entropy deviation from the horizontal mean in units of the universal gas constant; lower left: log τ5000; lower right: density deviation from the horizontal mean. |
Event 1 samples the edge of a small granule. The vertical cross-section in the first panel of Fig. 4 has an irregular shape with supersonic upward and downward flows close together. There is no clear shock front related to this event in the temperature distribution.
Event 2 (Fig. 4) is characterized by fast, mainly subsonic horizontal flows, containing only a few areas of supersonic velocities. An area of enhanced temperature is located at the front of the horizontal flow. It is a hot and coherent front where the velocities of a decaying shock have already dropped below the sound speed. The convection roll visible as a vortex flow in the vertical plane is very similar to the features analyzed by Steiner et al. (2010).
Event 3 is analyzed in Figs. 5 and 6. It is located at the edge of a large granule. The area contaning supersonic velocities is almost 1 Mm wide (extent of the red contour in Fig. 3) and extends over 300 km vertically (see Fig. 6). The time evolution of this event is shown in Fig. 5. Before the shock (bottom curve in the plot) the temperature at the granular edge is lower than at the center of the granule whereas the density increases towards the edge. This results in a pressure difference that accelerates the horizontal flow. In addition to that, the sound speed is locally reduced, and the flow reaches supersonic velocities. This leads to compression and a shock front. A well-defined shock front occurs in the temperature distribution (Fig. 3). It is also evident in the entropy in the middle right panel of Fig. 5. The subsequent upstream drift of the shock front can be traced in all six parameters shown in Fig. 5. When the velocity becomes subsonic, the temperature enhancement persists for some time, as in Event 2.
Finally, Event 4 is located in an area with supersonic flows on both sides of an intergranular lane which contains strong magnetic field (≈ 0.5 kG). This is the only case of supersonic horizontal flow close to a strong-field concentration in these snapshots. As shown in 2D simulations (Steiner et al. 1998), granular flows and magnetic flux concentrations can interact in a complex manner leading, for example, to the bending and displacement of flux sheets. Such flux sheet dynamics are also capable of triggering shocks, providing an alternative shock production mechanism in addition to purely hydrodynamic, fast granular flows.
Event 3 seems to be the best example of a shock produced by a granular outflow; we select it for further analysis in the next section.
4. Shock signatures in Fe I 6301.5 Å
4.1. At full resolution
Figures 6 and 7 show parameters of Event 3 at five viewing angles obtained by skewing snapshot S1 to μ = 0.6 and 0.4 towards the “left” and “right” limbs as described in Sect. 2.
The upper row of Fig. 6 shows cross-sections in the x−h plane, where h measures height along the LOS and x is the simulation coordinate specified in arcsec to show the foreshortening. The grey scale shows the temperature, the arrows the velocity with red specifying supersonic values. The second row shows x−λ spectrograms synthesized along the cross-sections, with line profiles along the six LOS’s indicated by color markers shown in the upper row of Fig. 7. Since the two lines behave so similarly, we only present results for Fe i 6301.5 Å in this paper. The stratification of the temperature and the velocity along the specified LOS’s are plotted in Fig. 7 (middle and bottom row, respectively). The third row of Fig. 6 shows the x−y maps of the emergent continuum intensity.
4.1.1. Disk center
The velocity field in the shock is largely horizontal and has a negligible effect on the emergent line profiles (central columns of Figs. 6 and 7).
The pale-blue LOS defined in Fig. 6 cuts through the supersonic flow, the green and yellow LOS’s cut through the hot shock front. The corresponding line profiles are slightly red shifted due to the flow turning downward.
The continuum intensity map (Fig. 6, center, bottom) is mainly determined by the deformation of the optical depth unity surface (specified with the white solid curve in the top row Fig. 6) due to the formation of the horizontal roll at the bottom edge of the shock. A dark stripe is clearly seen behind the shock where the optical depth unity surface is slightly elevated into higher and cooler layers as the density is locally increased. Similar dark zones are visible behind several of the other shock fronts in the simulated time sequence. The horizontal vortex tubes corresponding to bright granular edges were recently found in an MHD simulation analyzed in detail by Steiner et al. (2010). In IMaX/Sunrise observations they apear as a leading bright rim and following dark zone. The observed vortex tubes move toward the center of a granule, consistent with the upstream drift of a shock front we found in Fig. 5.
4.1.2. Away from disk center
Away from disk center, the velocity in the shock front is increasingly aligned with the LOS, and discrete features from Doppler shifts appear in the synthesized line profiles. These become quite complex as seen in the spectrograms (Fig. 6) and the individual profiles (Fig. 7).
As the different LOS’s at a given μ at one limb sample the flow and shock front at varying heights, the profile asymmetries caused by the Doppler shifts appear at different positions in the line profile. Where large velocities along the LOS combine with a local temperature enhancement, the line profiles extended strongly in one of the wings, or become even double-peaked with clearly visible satellites. Such satellites can appear in either wing depending on how the LOS samples the shock. An example can be seen at the “left” limb (μ = 0.4) in the red and purple profiles where satellites appear in opposite wings. The LOS represented by the purple markers samples the shock at roughly log τ = −2, and the fast flow towards the observer broadens the blue wing. Along the LOS represented by the red markers the blueshift in the line profile is invisible because the shock sits below the log τ = 1 surface. The redshift observed in this line profile is actually caused by the horizontal flow towards the intergranular lane seen at the righthand side of the top center μ = 1 panel of Fig. 6.
 |
Fig. 6 Top row: vertical cross-section through event 3. Subsonic velocities are indicated by white arrows, whereas red arrows correspond to supersonic velocities. The temperature distribution is shown as a background in gray-scale. White curves represent the log τ5000 = 1,−1 and −2 levels, respectively. Middle row: spectrogram of Fe i 6301.5 and 6302.5 Å synthesized from the cross-section; bottom row: continuum intensity maps of the area of the flow. The white markers specify the location of the vertical cross-section in the top panels. The five columns correspond to the five viewing angles specifed at the top. The h coordinate is measured along the line of sight (LOS). The x coordinate is the horizontal simulation coordinate in the center-to-limb plane containing the LOS, not the projected skewed coordinate. The projected extent in arcsec x′ is added underneath. The color markers specify six LOS’s shown in detail in Fig. 7. The box in the bottom row specifies the size of a SP/SOT pixel. |
 |
Fig. 7 Profiles of the Fe i 6301.5 Å line computed for six LOS’s corresponding to the colors (purple, blue, pale-blue, green, yellow, red) indicated in Fig. 6 for every μ (top row). Temperature and velocity distributions along these LOS’s are shown in the middle and the bottom rows. Positive velocities correspond to motions away from the observer. The line profiles are normalized to the quiet-sun continuum at disk center. |
 |
Fig. 8 Response function of intensity to temperature variation computed for Fe i 6301.5 Å at μ = 0.4 at opposite limbs. It is computed for the LOS that cuts through the center of the shock at the two disk locations (pale blue, first and fifth column of Figs. 6 and 7). Corresponding line profiles (dashed line) are overplotted in an arbitrary and inverted intensity scale. |
The flow directions in the shock also have a strong effect on the line profiles. The nearly horizontal motions in the shock at μ = 1 lead to a clear separation of the core and the satellite when viewed head-on (“left” limb) and to profile smearing when viewed from the other side (“right” limb).
In Event 3 the fast flow is seen moving towards the observer at the “left” limb and the LOS cuts through the upper layers of the adjacent, centerward granule and through the intergranular lane.
At the “right” limb, where the fast flow is seen moving away from the observer, the LOS cuts through the granular material behind the shock that has a locally increased opacity (cf., Fig. 5). As a consequence, at the “left” limb the hot shock front appears slightly narrower and higher up in the corresponding optical depth scale (compare the humps at the “left” and “right” limb in the temperature panels in Fig. 7).
Figure 8 shows response functions of the emergent intensity to temperature perturbations computed following Ruiz Cobo & del Toro Iniesta (1994) and Cabrera Solana et al. (2005) at the “left” and “right” limb in order to estimate where the line asymmetries are formed along the LOS. They are computed for the pale-blue LOS that cuts through the center of the shock at both limbs. At the “left” limb, the line has a blue-wing satellite with very localized temperature contribution which comes from the granular side of the shock where the temperature decreases with optical depth and the velocity along the LOS drops from 5 to 0 km s-1. In contrast, at the “right” limb the extended red wing is formed in the layers where both temperature and velocity increase with optical depth, with the velocity ranging from nearly zero to supersonic values.
At the “left” limb, the temperature and source function increase with height in this region (Fig. 7), producing a reversal in the blue wing of the line and a full separation of the satellite component. In contrast, along the LOS at the “right” limb, due to the higher opacity, the shock front is shifted to slightly deeper layers and extends over a wider range in optical depth. The majority of these profiles do not show intensity reversals, as the temperature decreases monotonically with height in the regions of largest response in the wing.
The corresponding line profiles synthesized for the other three events show similar asymmetries.
4.2. At Hinode resolution
 |
Fig. 9 Profiles of Fe i 6301.5 Å computed for four events (see Fig. 3) after the images at every wavelength were degraded to the resolution of the SP/SOT Hinode. Rows from top to bottom correspond to Events 1−4, respectively. Columns correspond to five locations of the snapshot on the solar disk. We also the wavelength axis in terms of corresponding Doppler shifts. |
The line profiles are computed from the skewed snapshot. As the field of view is foreshortened away from disk center, we expand it to a square by replicating the 2D images in the limb direction at every wavelength. The images are then smeared to the angular resolution of the SP/SOT and resampled at the SP/SOT pixel size. The full width at half maximum of the PSF of SOT is 0.32″, while the pixel size is 0.16 × 0.16″. After the spatial smearing and resampling, the profiles are also smeared to the SP/SOT spectral resolution and resampled at the wavelength step of this instrument. The SP/SOT instrument records spectra with a resolution of 30 mÅ and a spectral sampling of 21.5 mÅ.
The large asymmetries seen in the high-resolution profiles vanish in the degraded ones. In Fig. 9 a selection of emergent profiles for the 4 events is shown for the five viewing angles. The third row of Fig. 9 corresponds to the top row of Fig. 7. For each event, Fig. 9 plots the line profile for the central pixel and for the 8 surrounding pixels.
In all 4 events the disk-center profiles are only slightly broadened and/or shifted in comparison to their full-resolution counterparts. Away from disk center, the profiles of Events 1 and 2 are somewhat broadened but no clear satellites are visible at μ = 0.4 or μ = 0.6.
Event 3, identified as a supersonic flow with a well developed shock front, only shows the presence of the blue wing satellite when it is observed at μ = 0.4 at the “left” limb. The profiles at the same μ at the “right” limb show only a hint of the second component, but the line in the central pixel corresponding to the shock area is redshifted as a whole.
Event 4 shows profile deformations in both line wings at both limbs. This event exhibits fast horizontal granular flows hitting the intergranular lane from opposite sides, causing two distinct components in the emerging line profiles.
4.2.1. Azimuthal dependence
Figure 6 shows how the line profile for Event 3, in the full spectral and spatial resolution, changes at the two limbs depending on whether the shock front is seen head-on (“left” limb) or from the other side (“right”). Thus, the orientation of the flow in the shock relative to the LOS determines the size and shape of the emergent profile. This projection effect will also affect the signature of the shock for different azimuth angles of the LOS (ϕ), which is defined here as having ϕ = 0 for the “left” limb with counter-clockwise rotation around the z axis of the snapshot seen from the top. To simulate this effect, the snapshot S1 was first rotated at disk center by multiples of 45° and then skewed to μ = 0.4 to position the simulation box at 8 different limb locations1. The line profiles computed and degraded for every location are shown in Fig. 10.
The shock front is curved and is seen nearly head-on for azimuth values between ϕ = 0° and 45°. At ϕ = 0° two separate components are clearly seen, one at the rest wavelength and the other shifted towards the blue by ≈7 km s-1. In contrast to that, at ϕ = 45° the line is broadened, entirely shifted to the blue, but no satellite component is present. Towards ϕ = 180° where the shock is seen from the other side, the line core exhibits a red shift, whereas the asymmetry in the blue wing (satellite component or extended wing) diminishes. At ϕ = 180° the profile is very broad with an extended red wing. Rotation from ϕ = 180° to ϕ = 360° shows the same change in the opposite direction.
 |
Fig. 10 Line profiles of Fe i 6301.5 Å computed for Event 3 at μ = 0.4 for eight azimuth values ϕ. All profiles are normalized to their local continuum. The vertical line indicates the rest wavelength of the spectral line. |
4.2.2. Line asymmetries and shifts
The contours in the first row of Fig. 11 show projections of volumes occupied by horizontal supersonic flows to the plane perpendicular to the LOS at every μ. Flows moving away from the observer are specified in red and flows moving towards the observer in blue. The projected area increases from ~2.5% at disk center to ~3.5% at μ = 0.4.
Bellot Rubio (2009) searched for signatures of these flows in several parameters infered from the observed lines. He analyzed continuum intensity, equivalent width, full width at half maximum, line core velocity and used, in particular, bisector velocities Vbi to detect supersonic events2. In an empirical way, Bellot Rubio estimated that the value Vbi = ±2.6 km s-1 at the 70% intensity level represents an optimal threshold for the detection of supersonic flows. Using that criterion, he found that 0.3% of the field of view at μ = 0.55 is covered by pixels with profiles showing Vbi < −2.6 km s-1, while pixels with Vbi > 2.6 km s-1 occur very rarely. The negative velocities are observed at the edges of large granules, whereas the positive ones are observed “almost exclusively in intergranular lanes”.
To test the robustness of the criterion and the chosen threshold, we measured Vbi of the profiles synthesized from snapshot S1 and degraded to the SP/SOT Hinode resolution, again for our five viewing angles. For the rest wavelength we adopt the value that we used to synthesize the profiles (6301.5012 Å). The detection results are plotted over the continuum intensity maps in the second row of Fig. 11. Pixels with Vbi < −2.6 km s-1 and Vbi > 2.6 km s-1 are indicated with blue and red contours, respectively.
In contrast to Bellot Rubio’s identification of predominantly negative bisector velocities above the threshold, events with both positive and negative velocities are similarly abundant in the synthetic observations. Event 3 is detected at the “right” limb where the flow is moving away from the observer (red contour), while it is invisible at the opposite limb. The line profiles in the supersonic flow of Event 4 show bisector velocities above the threshold at both limbs. At the “right” limb the flow is towards the observer (blue contour), and at the “left” limb it moves away from the observer (red contour). In addition to these two events, another small supersonic flow is correctly identified at the “right” limb at both μ = 0.6 and 0.4, while all other supersonic flows remain undetected. Apart from these detections, there are few wrongly-identified pixels, all with negative bisector velocities.
Therefore, the fraction of pixels correctly detected as supersonic varies significantly with the viewing angle. For example, at μ = 0.6 at the “left” limb, the method detects horizontal supersonic flows moving away from the observer in ~0.6% of the area (red contour), in comparison to ~1.4% found in the simulation. At μ = 0.6 at the “right” limb, the detected area of the supersonic flows moving away (~1.3%) agrees well with the area found in the simulation.
Bellot Rubio speculated that the difference in the number of identified flows with positive and negative bisector velocities and the presence of satellites in the blue wings exclusively may be due to the flows at the far side of the granules occuring below the optical depth unity surface. However, our analysis shows that supersonic horizontal flows do produce observable asymmetries in both line wings, i.e., at both disk-center and limb side of a granule. Another reason for the unequal abundance of detected supersonic flows moving in opposite directions in the observations of Bellot Rubio (2009) may be presence of an offset in the rest wavelength determined as the location of the minimum of the average line profile over the entire field of view. To estimate the influence of such an offset, we apply artificial shifts to our adopted rest wavelength.
The third and fourth row of Fig. 11 show results after the rest wavelength has been shifted toward the red by Δλ = 5 mÅ and 10 mÅ, corresponding to Doppler velocities of 240 m/s and 480 m/s, respectively. The detection of supersonic events changes significantly. As expected, the number of pixels exhibiting Vbi < −2.6 km s-1 increases, while the number of pixels with Vbi > +2.6 km s-1 decreases. Events 3 and 4 are clearly detected as fast flows moving towards the observer, whereas the contours identifying motions away from the observer are strongly reduced. At the “left” limb, Event 4 disappears, whereas Event 3 appears. Hence, the precise determination of the reference wavelenght is very important for the correct detection of supersonic horizontal flows.
Finally, to estimate how the detection of the flows depends on the chosen value of the threshold, we reduce that value from 2.6 km s-1 to 2.0 km s-1 in steps of 0.2 km s-1. Obviously, the number of pixels identified as supersonic increases with decrease of the threshold causing a clear detection of Events 3 and 4 at both limbs. However, the area of pixels misidentified as supersonic also increases. This result supports empirically determined threshold of Bellot Rubio (2009).
4.3. Line broadening
Nesis et al. (1992) argued that the spectral line broadening they observed at disk center in the dark intergranular lanes was evidence of post-shock turbulence caused by supersonic horizontal flows. Solanki et al. (1996) made a comparative study using 2D granulation simulation. They found that even without supersonic horizontal flows a significant line broadening was observed in the synthetic spectral lines that were smeared to mimic observations. They showed that, at disk center, both, horizontal gradients in the vertical and horizontal velocity at the full resolution are able to reproduce the broadened line profiles after smearing. They concluded that the broadened profiles observed in the dark lanes by Nesis et al. (1992) were not necessarily an indication of supersonic flows, whereas the observations in Nesis et al. (1993) of line broadened profiles at the edges of granules, between the granule and the intergranular lane, were more likely due to turbulence caused by supersonic flows.
 |
Fig. 11 Continuum intensity map computed from snapshot S1 at μ = 0.4 and 0.6 at the “left” limb, at disk center, and at μ = 0.6 and 0.4 at the “right” limb (from left to right). Away from disk center, the foreshortened maps are replicated to fill a square. First row: contours show projection of volumes with supersonic horizontal flows to the plane perpendicular to the line of sight. Flows moving towards the observer are specified in blue; flows moving away from the observer in red. Second row: supersonic flows detected as pixels with bisector velocity smaller than −2.6 km s-1 (blue contours) and larger than 2.6 km s-1 (red). The zero wavelength for the bisector measurement is the laboratory wavelength of the Fe i 6301.5012 Å line. Third and fourth row: the zero wavelength is shifted by 5 and 10 mÅ towards the red, respectively. In the bottom three rows, the zero wavelength is the laboratory wavelength for all panels, but the threshold for the determination of supersonic flows varies: ±2.4 km s-1 (fifth row), ±2.2 km s-1 (sixth) and ±2.0 km s-1 (seventh). |
Keller (2006) suggested a simple mechanism able to produce broadened line profiles at the edge of granules with no additional turbulence needed. We perform the computation for Fe i 6301.5 Å, the less-magnetic of the two iron lines and illustrate the result in Fig. 12. The normalized continuum intensity along a spatial direction is compared to the variation in FWHM of the unsmeared and smeared profiles in the upper panel. As a smearing function we employ again the PSF of the SOT onboard Hinode. We find enhanced line broadening at locations of steep intensity gradients, for example, at x = 4.4 Mm and 5.4 Mm.
To demonstrate the effect of the smearing on the FWHM, we alter the line profiles to artificially keep the FWHM constant throughout the sample. In the lower panel of Fig. 12, we show that even in that simple case, when the profiles have the same FWHM and differ only in Doppler velocity and intensity, the smearing produces line broadening, especially at locations of steepest continuum intensity gradient, as seen at x = 0.6 Mm and x = 4.4 Mm. Line broadening is therefore not a reliable indicator for supersonic horizontal flows.
5. Discussion and conclusions
Although the large asymmetries in the computed Fe i 6301.5 Å profiles are smeared out almost completely at the SP/SOT Hinode resolution at μ = 0.4 and 0.6, various line-profile deformations remain visible, even with a few discernable satellites in the blue wing (Fig. 9). This is in good agreement with the measurements of Bellot Rubio (2009) who identified satellite components of the Fe i 6301.5 Å line exclusively in the blue wing of the observed profiles. In addition, we find extended red wings corresponding to the supersonic flows moving away from the observer at the limb side of granules.
Bellot Rubio (2009) defined an empirical criterion for automatic detection of supersonic horizontal flows through bisector measurements, setting a treshold of 2.6 km s-1 for the absolute bisector velocity at 70% of the line intensity to indicate such flows. Our analysis shows that his method of detection is generally applicable and supports his conclusion that this ±2.6 km s-1 threshold is rather conservative. However, we note that the bisector velocity analysis can be used to identify only a certain class of horizontal supersonic flows as was already pointed out by Solanki et al. (1996). Only large volumes with directionally coherent supersonic flows can be unambiguously detected. Furthermore, the LOS has to be sufficiently aligned with the flow. This alignment obviously depends on the azimuthal direction of the flow and the heliocentric angle. The number of pixels detected as supersonic is also critically sensitive to ad hoc parameter choices. For a lower threshold value we indeed obtain more supersonic flow detections, but with an increasing fraction of false identifications. In addition, this supersonic flow detection method critically depends on a precise wavelength calibration.
In our simulation, at disk center, projection of the supersonic horizontal flows covers ~2.6% of the surface. The surface coverage increases limbward, in snaphsot S1 it reaches ~3.5%. Using the bisector velocity analysis, Bellot Rubio (2009) identified supersonic flows in 0.3% of the field of view. The difference between this number and the abundance of the flows found in the simulation of Stein & Nordlund (1998) has been attributed by him to the projection effects. In Sect. 4.2.2 we simulated the measurements of Bellot Rubio (2009). The results of this simulation show that the fraction of correctly identified supersonic pixels depends on the viewing angle, threshold used, and the position of the reference wavelength. This fraction can vary from almost zero (e.g., first column, second row of Fig. 11) to more than one (e.g., fourth column, third row of Fig. 11).
However, our analysis is based on 20 simulation snapshots covering in total an area ~10 times smaller than the area observed by Bellot Rubio (2009). It would be necessary to employ much larger number of snapshots to quantify the fraction of supersonic pixels that can be detected by Bellot Rubio’s method. Without such a quantification we cannot rule out an additional mechanism able to accelerate the flows to supersonic velocities. One possible mechanism that is not present in our simulation and can trigger supersonic flows is magnetic flux emergence as shown by Cheung et al. (2007a) in their large-scale simulation. Bellot Rubio has considered the possibility that a similar mechanism can operate on small-scales as well, but no clear evidence was found in the observations. The next step consists in simulating flux emergence at granular scales, studying how it affects the dynamics of horizontal granular outflows, and synthesizing the corresponding observational signatures.
 |
Fig. 12 Continuum intensity at 6300 Å and FWHM of the Fe i 6301.5 Å line along a spatial cut of a simulation snapshot. Upper panel: the black curve shows the normalized continuum intensity along the spatial cut at the full resolution of the snapshot. The red curve shows the FWHM of the spectral line profile derived from the simulation at the same spatial location and the blue curve, the FWHM of the spectral lines after smearing. All curves are normalized to their mean values. Lower panel: the black curve shows the normalized continuum intensity along the spatial cut at the full resolution of the snapshot. To demonstrate the influence of the smearing of the snapshot on the FWHM of the spectral line, we carry out a thought experiment and artificially fix the FWHM at each spatial location to a single value (red line) by stretching/compressing the spectral lines. The blue line, showing the FWHM obtained after smearing, still show a large variation. This demonstrates that the detection of an enlarged FWHM is not necessarily an indicator for supersonic flows, but can be an artifact introduced by the smearing. |
The bisector velocity is the wavelength distance between the bisector of a line and its rest wavelength at a given fraction of the line intensity (cf. Grossmann-Doerth 1994). Note that the bisector velocity does not say anything about line asymmetry with respect to the line core, but only with respect to the rest wavelength. For example, if the radial velocity is constant with height, the spectral line will be shifted by the value of the bisector velocity, but relative to the line core, it will remain symmetric.
Acknowledgments
We thank to R. J. Rutten for carefully reading the manuscript and making numerous comments and suggestions that significantly improved it. We thank J. de la Cruz Rodríguez, L. Bellot Rubio, R. Keppens and R. F. Stein for useful discussions. We also thank S. Wedenmeyer-Böhm for making available the point spread function of the SOT on Hinode, E. Khomenko for providing the initial snapshot of our simulation, and H. Socas-Navarro for the opportunity to run the simulations on the LaPalma Supercomputer. The authors thankfully acknowledge the technical expertise and assistance provided by the Spanish Supercomputing Network (Red Española de Supercomputación), as well as the computer resources used: the LaPalma Supercomputer, located at the Instituto de Astrofísica de Canarias. This research is supported by a Marie Curie Early Stage Research Training Fellowship of the EC’s Sixth Framework Programme under contract number MEST-CT-2005-020395. This research has made use of NASA’s Astrophysics Data System.
References
- Bellot Rubio, L. R. 2009, ApJ, 700, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera Solana, D., Bellot Rubio, L. R., & del Toro Iniesta, J. C. 2005, A&A, 439, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cameron, R., Schüssler, M., Vögler, A., & Zakharov, V. 2007, A&A, 474, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cattaneo, F., Hurlburt, N. E., & Toomre, J. 1990, ApJ, 349, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Cheung, M. C. M., Schüssler, M., & Moreno-Insertis, F. 2007a, A&A, 467, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cheung, M. C. M., Schüssler, M., & Moreno-Insertis, F. 2007b, A&A, 461, 1163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cheung, M. C. M., Rempel, M., Title, A. M., & Schüssler, M. 2010, ApJ, 720, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Gadun, A. S., & Hanslmeier, A. 2000, Kinematika i Fizika Nebesnykh Tel, 16, 130 [NASA ADS] [Google Scholar]
- Gadun, A. S., Hanslmeier, A., Pikalov, K. N., et al. 2000, A&AS, 146, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grossmann-Doerth, U. 1994, A&A, 285, 1012 [NASA ADS] [Google Scholar]
- Keller, C. U. 2006, in Solar MHD Theory and Observations: A High Spatial Resolution Perspective, ed. J. Leibacher, R. F. Stein, & H. Uitenbroek, ASP Conf. Ser., 354, 3 [Google Scholar]
- Keller, C. U., Schüssler, M., Vögler, A., & Zakharov, V. 2004, ApJ, 607, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Khomenko, E. V., Shelyag, S., Solanki, S. K., & Vögler, A. 2005, A&A, 442, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khomenko, E., Martínez Pillet, V., Solanki, S. K., et al. 2010, ApJ, 723, L159 [NASA ADS] [CrossRef] [Google Scholar]
- Malagoli, A., Cattaneo, F., & Brummell, N. H. 1990, ApJ, 361, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Nesis, A., Bogdan, T. J., Cattaneo, F., et al. 1992, ApJ, 399, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Nesis, A., Hanslmeier, A., Hammer, R., et al. 1993, A&A, 279, 599 [NASA ADS] [Google Scholar]
- Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys., 6, 2 [Google Scholar]
- Rempel, M., Schüssler, M., Cameron, R. H., & Knölker, M. 2009, Science, 325, 171 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ruiz Cobo, B., & del Toro Iniesta, J. C. 1994, A&A, 283, 129 [NASA ADS] [Google Scholar]
- Rybák, J., Wöhl, H., Kučera, A., Hanslmeier, A., & Steiner, O. 2004, A&A, 420, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schüssler, M., & Vögler, A. 2006, ApJ, 641, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Schüssler, M., & Vögler, A. 2008, A&A, 481, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Socas-Navarro, H. 2001, in Advanced Solar Polarimetry – Theory, Observation, and Instrumentation, ed. M. Sigwarth, ASP Conf. Ser., 236, 487 [Google Scholar]
- Solanki, S. K., Rueedi, I., Bianda, M., & Steffen, M. 1996, A&A, 308, 623 [NASA ADS] [Google Scholar]
- Stein, R. F., & Nordlund, A. 1998, ApJ, 499, 914 [Google Scholar]
- Steiner, O., Grossmann-Doerth, U., Knoelker, M., & Schuessler, M. 1998, ApJ, 495, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, O., Franz, M., Bello González, N., et al. 2010, ApJ, 723, L180 [NASA ADS] [CrossRef] [Google Scholar]
- Suematsu, Y., Tsuneta, S., Ichimoto, K., et al. 2008, Sol. Phys., 249, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Vögler, A. 2004, Three-dimensional simulations of magneto-convection in the solar photosphere, Ph.D. Thesis, University of Göttingen [Google Scholar]
- Vögler, A., & Schüssler, M. 2003, Astron. Nachr., 324, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Vögler, A., & Schüssler, M. 2007, A&A, 465, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer, S., Freytag, B., Steffen, M., Ludwig, H., & Holweger, H. 2004, A&A, 414, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S. 2008, A&A, 487, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 The fraction of dx × dy × d(log τ) cells with supersonic flows versus optical depth for disk center viewing with μ = 1. Each curve represents one of the 20 analyzed snapshots. The supersonic flow may be in any direction. The thick solid curve corresponds to the snapshot with the largest abundance of supersonic flows (S1, lower row in Fig. 3), while the thick dashed curve corresponds to the initial snapshot (S0, upper row in Fig. 3). |
| In the text | |
 |
Fig. 2 Two-dimensional histogram of the distribution of supersonic flows in optical depth and orientation (γ = 0° corresponds to an upflow, γ = 90° to a horizontal flow, and γ = 180° to a downflow). The histogram is made from all snapshots. The populations of the horizontal flows and the vertical flows are separated in height. The horizontal flows are found mainly above the surface; the vertical flows below it. |
| In the text | |
 |
Fig. 3 Maps of the two snapshots analyzed in detail (top, S0; bottom, S1). From left to right: continuum intensity at 6300 Å, temperature, magnitude of the horizontal velocity in units of the local sound speed, and total magnetic field strength at the log τ5000 = −1 surface. Contours show the projection on the horizontal plane of cells containing supersonic flows (red specifies flows that are nearly horizontal 120° > γ > 60° and; yellow nearly vertical flows 180° > γ > 150° and 30° > γ > 0°; orange flows with inclinations 150° > γ > 120° and 60° > γ > 30°. The four numbered markers point to selected events discussed in detail in Sect. 3.2. |
| In the text | |
 |
Fig. 4 Vertical cross-section of temperature (gray scale) and velocity (arrows) for events 1 and 2 (upper panels) and 4 (lower panel) (cf. Fig. 3). Subsonic velocities are indicated by white arrows, red arrows correspond to supersonic velocities. White curves represent the log τ5000 = 0,−1 and −2 levels, respectively. |
| In the text | |
 |
Fig. 5 Temporal evolution of the shock front in event 3 at a fixed geometrical height of ~100 km above the average log τ5000 = 0 level. From the bottom up, the curves represent time samples at 25 s intervals. The scale on the vertical axis is for snapshot S1 (thick curve). The range of the horizontal axis is same as in Fig. 6. Upper left panel: temperature deviation from the horizontal mean; upper right: horizontal velocity (positive along x); middle left: pressure deviation from the horizontal mean; middle right: entropy deviation from the horizontal mean in units of the universal gas constant; lower left: log τ5000; lower right: density deviation from the horizontal mean. |
| In the text | |
 |
Fig. 6 Top row: vertical cross-section through event 3. Subsonic velocities are indicated by white arrows, whereas red arrows correspond to supersonic velocities. The temperature distribution is shown as a background in gray-scale. White curves represent the log τ5000 = 1,−1 and −2 levels, respectively. Middle row: spectrogram of Fe i 6301.5 and 6302.5 Å synthesized from the cross-section; bottom row: continuum intensity maps of the area of the flow. The white markers specify the location of the vertical cross-section in the top panels. The five columns correspond to the five viewing angles specifed at the top. The h coordinate is measured along the line of sight (LOS). The x coordinate is the horizontal simulation coordinate in the center-to-limb plane containing the LOS, not the projected skewed coordinate. The projected extent in arcsec x′ is added underneath. The color markers specify six LOS’s shown in detail in Fig. 7. The box in the bottom row specifies the size of a SP/SOT pixel. |
| In the text | |
 |
Fig. 7 Profiles of the Fe i 6301.5 Å line computed for six LOS’s corresponding to the colors (purple, blue, pale-blue, green, yellow, red) indicated in Fig. 6 for every μ (top row). Temperature and velocity distributions along these LOS’s are shown in the middle and the bottom rows. Positive velocities correspond to motions away from the observer. The line profiles are normalized to the quiet-sun continuum at disk center. |
| In the text | |
 |
Fig. 8 Response function of intensity to temperature variation computed for Fe i 6301.5 Å at μ = 0.4 at opposite limbs. It is computed for the LOS that cuts through the center of the shock at the two disk locations (pale blue, first and fifth column of Figs. 6 and 7). Corresponding line profiles (dashed line) are overplotted in an arbitrary and inverted intensity scale. |
| In the text | |
 |
Fig. 9 Profiles of Fe i 6301.5 Å computed for four events (see Fig. 3) after the images at every wavelength were degraded to the resolution of the SP/SOT Hinode. Rows from top to bottom correspond to Events 1−4, respectively. Columns correspond to five locations of the snapshot on the solar disk. We also the wavelength axis in terms of corresponding Doppler shifts. |
| In the text | |
 |
Fig. 10 Line profiles of Fe i 6301.5 Å computed for Event 3 at μ = 0.4 for eight azimuth values ϕ. All profiles are normalized to their local continuum. The vertical line indicates the rest wavelength of the spectral line. |
| In the text | |
 |
Fig. 11 Continuum intensity map computed from snapshot S1 at μ = 0.4 and 0.6 at the “left” limb, at disk center, and at μ = 0.6 and 0.4 at the “right” limb (from left to right). Away from disk center, the foreshortened maps are replicated to fill a square. First row: contours show projection of volumes with supersonic horizontal flows to the plane perpendicular to the line of sight. Flows moving towards the observer are specified in blue; flows moving away from the observer in red. Second row: supersonic flows detected as pixels with bisector velocity smaller than −2.6 km s-1 (blue contours) and larger than 2.6 km s-1 (red). The zero wavelength for the bisector measurement is the laboratory wavelength of the Fe i 6301.5012 Å line. Third and fourth row: the zero wavelength is shifted by 5 and 10 mÅ towards the red, respectively. In the bottom three rows, the zero wavelength is the laboratory wavelength for all panels, but the threshold for the determination of supersonic flows varies: ±2.4 km s-1 (fifth row), ±2.2 km s-1 (sixth) and ±2.0 km s-1 (seventh). |
| In the text | |
 |
Fig. 12 Continuum intensity at 6300 Å and FWHM of the Fe i 6301.5 Å line along a spatial cut of a simulation snapshot. Upper panel: the black curve shows the normalized continuum intensity along the spatial cut at the full resolution of the snapshot. The red curve shows the FWHM of the spectral line profile derived from the simulation at the same spatial location and the blue curve, the FWHM of the spectral lines after smearing. All curves are normalized to their mean values. Lower panel: the black curve shows the normalized continuum intensity along the spatial cut at the full resolution of the snapshot. To demonstrate the influence of the smearing of the snapshot on the FWHM of the spectral line, we carry out a thought experiment and artificially fix the FWHM at each spatial location to a single value (red line) by stretching/compressing the spectral lines. The blue line, showing the FWHM obtained after smearing, still show a large variation. This demonstrates that the detection of an enlarged FWHM is not necessarily an indicator for supersonic flows, but can be an artifact introduced by the smearing. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


