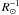| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 13 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201015507 | |
| Published online | 25 November 2010 | |
Three-dimensional hydrodynamical simulations of red giant stars: semi-global models for interpreting interferometric observations
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Str. 1, Postfach
1317,
85741
Garching b. München,
Germany
e-mail: chiavass@mpa-garching.mpg.de
Received:
30
July
2010
Accepted:
9
September
2010
Context. Theoretical predictions from models of red giant branch stars are a valuable tool for various applications in astrophysics ranging from galactic chemical evolution to studies of exoplanetary systems.
Aims. We use the radiative transfer code Optim3D and realistic 3D radiative-hydrodynamical (RHD) surface convection simulations of red giants to explore the impact of granulation on interferometric observables. We assess how 3D simulations of surface convection can be validated against observations.
Methods. We computed intensity maps for the 3D simulation snapshots in two filters, the optical at 5000 ± 300 Å and the K band 2.14 ± 0.26 μm FLUOR filter, corresponding to the wavelength-range of instruments mounted on the CHARA interferometer. From the intensity maps, we constructed images of the stellar disks and account for center-to-limb variations. We then derived interferometric visibility amplitudes and phases. We study their behavior with position angle and wavelength, and compare them with CHARA observations of the red giant star HD 214868.
Results. We provide average limb darkening coefficients for different metallicities and wavelengths ranges. We explain prospects for detecting and characterizing granulation and center-to-limb variations of red giant stars with today’s interferometers. Regarding interferometric observables, we find that the effect of convective-related surface structures depends on metallicity and surface gravity. We provide theoretical closure-phases that should be incorporated into the analysis of red giant planet companion closure phase signals. We estimate 3D − 1D corrections to stellar radii determination: 3D models are ~3.5% smaller to ~1% larger in the optical than 1D, and roughly 0.5 to 1.5% smaller in the infrared. Even if these corrections are small, they are needed to properly set the zero point of effective temperature scale derived by interferometry and to strengthen the confidence of existing red giant catalogs of calibrating stars for interferometry. Finally, we show that our RHD simulations provide an excellent fit to the red giant HD 214868 even though more observations are needed at higher spatial frequencies and shorter wavelength.
Key words: stars: horizontal-branch / stars: atmospheres / hydrodynamics / radiative transfer / techniques: interferometric / stars: individual: HD 214868
© ESO, 2010
1. Introduction
Red giant branch stars have evolved from the main sequence and are powered by hydrogen burning in a thin shell surrounding their helium core. Their masses are typically less than ~2.0 M⊙ (Salaris et al. 2002), their effective temperatures range from ~4000 to ~5100 K depending on metallicity, their surface gravities from ~3.5 to ~1.0 in log g (Hekker & Meléndez 2007), and their radii from ~3 to ~70 R⊙ (van Belle et al. 1999; Baines et al. 2010). Determine the fundamental parameters of red giant stars is very important in astrophysics: (i) red giant stars will be used as tracers of the morphology and evolution of the Galaxy in the framework of the Gaia mission (Perryman et al. 2001; Lindegren et al. 2008), because they are intrinsically bright and thus can probe regions obscured by interstellar extinction; (ii) they are extensively used for spectroscopic elemental abundance analyses of distant stellar populations (e.g. McWilliam et al. 1995; Ryan et al. 1996; Fulbright 2000); (iii) they are relatively easy targets in open (Yong et al. 2005; Carney et al. 2005) and globular clusters (see Gratton et al. 2004, for a review) and can be used for a number of purposes, including measuring Galactic metallicity gradients; (iv) red giant stars have been included in planet search surveys (Sato et al. 2005; Döllinger et al. 2007; Johnson et al. 2008).
Three-dimensional hydrodynamical modeling of convection of stellar surfaces has been already extensively employed to study the effects of photospheric inhomogeneities and velocity fields on the formation of spectral lines in a number of cases, including the Sun, dwarfs, and subgiants (e.g. Asplund et al. 1999; Asplund & García Pérez 2001; Asplund et al. 2009; Caffau et al. 2010; Behara et al. 2010; Sbordone et al. 2010) and red giants (e.g. Collet et al. 2007, 2009; Wende et al. 2009; Kučinskas et al. 2009). Such simulations are paramount for an accurate quantitative analysis of observed data. These studies provide valuable information to properly understand astrophysical processes such as stellar nucleosynthesis, internal mixing mechanisms in stars, and Galactic chemical evolution.
Simulations of red giant stars used in this work.
In this work, we present interferometric predictions obtained from three-dimensional surface convection simulations of red giant stars with different effective temperatures, surface gravities, and metallicities.
2. Surface convection simulations and radiative transfer calculations
2.1. Radiative-hydrodynamical simulations of red giant stars
We adopt here time-dependent, three-dimensional (3D), radiative-hydrodynamical (RHD) surface convection simulations of red giant stars generated by Collet et al. (2007) and Collet et al. (2009) with the Stein & Nordlund (1998) code and with the Stagger-Code1 respectively. In these simulations, the equations of conservation of mass, momentum, and energy are solved for representative rectangular volumes located across the stars’ optical surfaces. Heat losses and gains due to radiation are accounted for by solving the 3D radiative transfer equation in the local thermodynamic equilibrium (LTE) approximation. The simulations employ realistic input physics: the equation of state is an updated version of the one by Mihalas et al. (1988). Continuous and line opacities are taken from Gustafsson et al. (1975); Kurucz (1992, 1993). The simulation domains are chosen large enough to cover at least ten pressure scale heights vertically and to allow for about ten granules to develop at the surface; they are periodic horizontally, while their top and bottom boundaries are left open. The parameters of the adopted simulations are given in Table 1. For all simulations, we assume a solar chemical composition from Grevesse & Sauval (1998) but with all metal abundances scaled proportionally to the desired iron abundance. The simulations assume a constant gravitational acceleration parallel to the vertical axis; hence, there is a degeneracy between stellar mass and radius (g ∝ M/R2). Nonetheless, in the present work, we assume for each simulation a mass of 0.8 M⊙ – typical of red giants with stellar parameters like the ones considered here – to estimate the spatial frequency scale in Sect. 5.
2.2. Post processing radiative transfer code
We used the 3D pure-LTE radiative transfer code Optim3D (Chiavassa et al. 2009) to compute intensity maps from the snapshots of the RHD simulations listed in Table 1. The code takes into account the Doppler shifts due to convective motions. The radiative transfer equation is solved monochromatically using extinction pre-tabulated coefficients as a function of temperature, density, and wavelength. The lookup tables were computed for the same chemical compositions as the RHD simulations using the same extensive atomic and molecular opacity data as the latest generation of MARCS models (Gustafsson et al. 2008). We assumed a zero micro-turbulence since the velocity fields inherent in 3D models are expected to self-consistently and adequately account for non-thermal Doppler broadening of spectral lines (Asplund 2000). The temperature and density ranges spanned by the tables are optimized for the values encountered in the RHD simulations.
Optim3D computes the emerging intensities for vertical rays cast through the computational box, for all required wavelengths, with the method described by Chiavassa et al. (2009). The procedure is repeated after tilting the computational box by an angle θ with respect to the line of sight (vertical axis) and rotating it azimuthally by an angle φ. The final result is a spatially resolved intensity spectrum at different angles. This implementation of Optim3D enables radiative transfer calculations with RHD simulations either in the star-in-a-box configuration (e.g. Chiavassa et al. 2009) or in the box-in-a-star configuration (this work).
3. Sphere tiling: from local images to a semi-global intensity maps
In this Section, we aim to obtain an image of the stellar disk as a nearby observer would see it as required to extract the interferometric observables.
The computational domain of each simulation represents only a small portion of the stellar surface (see Sect. 2.1). To overcome this limitation, and at the same time account for limb darkening effects, we computed surface intensity maps for different inclinations with respect to the vertical (θ-angles) and for representative series of simulation snapshots2 and used them to tile a spherical surface. The actual value of the θ-angle used to generate each map depended on the position (longitude and latitude) of the tile on the sphere and was determined by computing the angular distance of the tile from the center of the stellar disk (0° in longitude and latitude on the sphere). For practical reasons, we actually computed intensity maps for a set of 15 predefined values of μ ≡ cos(θ) = [ 1.000, 0.989, 0.978, 0.946, 0.913, 0.861, 0.809, 0.739, 0.669, 0.584, 0.500, 0.404, 0.309, 0.206, 0.104] (Fig. 1) and interpolated linearly in between them. Mapping onto a spherical surface induces distortions especially at high latitudes and longitudes; we accounted for that by appropriately cropping the square-shaped intensity maps when defining the spherical tiles.
 |
Fig. 1 Intensity maps in the optical top-hat filter of Fig. 3 for the simulation with log g = 1.6 and [Fe/H ] = −3.0 (Table 1) with μ = 1.00, 0.81, 0.58, and 0.40. The intensities typically ranges from 3 × 104 to 1.2 × 106 erg cm-2 s-1 Å-1. |
In addition, we took into consideration statistical tile-to-tile fluctuations in the number of granules and in their shape and size and computed intensity maps by selecting snapshots at random from each simulation’s time-series. This random selection process also avoided that the assumption of periodic boundary conditions resulted in a tiled spherical surface globally displaying an artifactual periodic granulation pattern. Based on the stellar radii estimates given in Table 1 and on the sizes of the simulations’ domains, we required 14 to 23 tiles to cover half a great circle from side to side on the sphere, depending on the surface gravity of the models (log g = 1.6 and 2.2, respectively). The adopted number of μ-angles for the pre-computed intensity maps is therefore is large enough to ensure an accurate representation of the center-to-limb variations for the present work. To produce the final stellar disk images, we performed an orthographic projection of the tiled spheres on a plane perpendicular to the line-of-sight (θ = 0°). The orthographic projection returned images of the globes in which distortions are greatest toward the rim of the hemisphere where distances are compressed. The sketch in Fig. 2 outlines our method we used to tile spherical surfaces and constructing the synthetic stellar disk images.
 |
Fig. 2 Toy model representing our method used to tile spherical surfaces and constructing the synthetic stellar disk images. |
For the computation of the interferometric observables, we consider two spectral bands: (i) in the optical between 4700 and 5300 Å and (ii) in the infrared at 2.14 ± 0.26 μm FLUOR filter, Fig. 3. These wavelength intervals have been chosen because they correspond to the range of instruments mounted on CHARA interferometer (ten Brummelaar et al. 2005). These telescopes are particularly suited to observations of red giant stars because of its long baselines that allow resolution of objects with small apparent diameters. The resulting intensity maps reported are normalized to the filter transmission as: 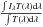 where Iλ is the intensity and
where Iλ is the intensity and  is the transmission curve of the filter at a certain wavelength. The spectra in Fig. 3 were computed along rays of four μ-angles [0.88, 0.65, 0.55, 0.34] and four φ-angles [0°, 90°, 180°, 270°], after which we performed a disk integration and a temporal average over all selected snapshots.
is the transmission curve of the filter at a certain wavelength. The spectra in Fig. 3 were computed along rays of four μ-angles [0.88, 0.65, 0.55, 0.34] and four φ-angles [0°, 90°, 180°, 270°], after which we performed a disk integration and a temporal average over all selected snapshots.
 |
Fig. 3 Left panel: synthetic spectra for different 3D model red giant atmospheres in the wavelength range 4700−5300 Å. The intensity maps corresponding to this filter have been computed assuming a top-hat filter (dashed line). This wavelength range corresponds to the VEGA instrument (Mourard et al. 2009) mounted on CHARA with a spectral resolution λ/Δλ = 5000. From the bottom: the black curve refers to the simulation with log g = 2.2 and [Fe/H ] = 0.0 and no offset applied, the red curve to log g = 2.2 and [Fe/H ] = −1.0 with an offset of 1, the green curve to log g = 2.2 and [Fe/H ] = −2.0 with an offset of 2, the light blue curve to log g = 2.2 and [Fe/H ] = −3.0 with an offset of 3, and the dark blue curve log g = 1.6 and [Fe/H ] = −3.0 with an offset of 4 (see Table 1). Right panel: transmission curve (dashed line) of the FLUOR (2.14 ± 0.26 μm) filter (Mérand et al. 2006) mounted on CHARA. Colors and offsets are the same as in left panel. |
 |
Fig. 4 Synthetic stellar disk images of the simulation with [Fe/H ] = −3.0 and log g = 1.6 (Table 1). The intensity range is 5.0 × 103−2.1 × 106 erg cm-2 s-1 Å-1 for the optical filter and 5.0 × 103−1.1 × 105 erg cm-2 s-1 Å-1 for the FLUOR filter. |
4. Three-dimensional limb darkening coefficients
In this Section we derive average center-to-limb intensity profiles with their limb darkening (LD) laws for the simulations in Table 1. Figure 4 shows the resulting synthetic stellar disk images for the [Fe/H ] = −3.0 and log g = 1.6 simulation in both filters of Fig. 3. The surface of the simulated giants stars appear irregular, permeated with structures. The center-to-limb variations are visible in both images, but are more pronounced in the optical filter. This is due to the integrated extinction by atomic and molecular lines in the upper layers which is more important in the optical range than in the FLUOR filter: this difference further increases for metal-poor models (see Fig. 3).
We then derived azimuthally averaged intensity profiles for every synthetic stellar disk image from the simulations, with two examples shown in Fig. 5. The profiles were constructed using rings regularly spaced in μ = cos(θ) for μ ≤ 1 (i.e. r/R ⋆ ≤ 1), with θ the angle between the line of sight and the radial direction. The parameter μ is related to the impact parameter r/R ⋆ through 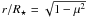 , where R ⋆ is the stellar radius reported in Table 1. We ensure a good characterization of the intensity towards the limb using 285 rings, which is half size in pixels of the images of Fig. 4. The standard deviation of the average intensity, σI(μ), was computed within each ring. As for the images in Fig. 4, the center-to-limb variations is steeper in the case of the optical filter. Moreover, the fluctuations are stronger in the optical case with values up to 20% with respect to the average (Fig. 5).
, where R ⋆ is the stellar radius reported in Table 1. We ensure a good characterization of the intensity towards the limb using 285 rings, which is half size in pixels of the images of Fig. 4. The standard deviation of the average intensity, σI(μ), was computed within each ring. As for the images in Fig. 4, the center-to-limb variations is steeper in the case of the optical filter. Moreover, the fluctuations are stronger in the optical case with values up to 20% with respect to the average (Fig. 5).
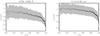 |
Fig. 5 Radially averaged intensity profiles (black line) derived from the synthetic stellar disk images of Fig. 4 and corresponding to RHD simulation with [Fe/H ] = −3.0 and log g = 1.6. The dashed gray areas denote the one sigma spatial fluctuations with respect to the averaged intensity profile. The intensity is normalized to the mean intensity at disk center and the radius is normalized to the radius given in Table 1. |
We used these averaged profiles to determine LD laws for the simulations. For this purpose, we fitted the azimuthally averaged intensities determined from the simulations with a polynomial LD law of the form 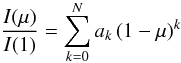 (1)as in Chiavassa et al. (2009), where I(μ) is the intensity, ak the LD coefficients, and N + 1 their number. We fitted all the azimuthally averaged profiles using this law and weighting the fit by 1/σI(μ). We varied the order N of the polynomial LD laws and found that N = 2 in practice already gave an optimal fit, with the N = 3 solution providing only minor and altogether negligible improvements to the χ2 minimization. At the same time, we would like to stress that using fewer terms in Eq. (1) (e.g. a simple power law) does not provide a good representation of the azimuthally averaged profiles and we therefore discourage this practice. In Table 2 we listed the LD coefficients ak for each simulation and for both filters considered in the present work.
(1)as in Chiavassa et al. (2009), where I(μ) is the intensity, ak the LD coefficients, and N + 1 their number. We fitted all the azimuthally averaged profiles using this law and weighting the fit by 1/σI(μ). We varied the order N of the polynomial LD laws and found that N = 2 in practice already gave an optimal fit, with the N = 3 solution providing only minor and altogether negligible improvements to the χ2 minimization. At the same time, we would like to stress that using fewer terms in Eq. (1) (e.g. a simple power law) does not provide a good representation of the azimuthally averaged profiles and we therefore discourage this practice. In Table 2 we listed the LD coefficients ak for each simulation and for both filters considered in the present work.
We have also computed classical 1D, LTE, plane-parallel, hydrostatic marcs model atmospheres (Gustafsson et al. 1975; Asplund et al. 1997) with identical stellar parameters, input data, and chemical compositions as the 3D simulations of Table 1. With Optim3D, we computed the emerging intensities for the same regularly spaced 285 μ-values used to get the azimuthally averaged intensity profiles from the synthetic stellar disk images and for the wavelength range spanned by both filters, assuming a micro-turbulent broadening of 2 kms-1. For each μ-value, we integrated the monochromatic intensities over the filters’ ranges to obtain a 1D intensity profile. Figure 6 illustrates the comparison between the average intensity profile from a 3D simulation, together with its LD fit, compared to a 1D model profile. The latter displays large differences with respect to 3D profile. Moreover, full LD (I(μ)/I(1) = μ) and partial LD (I(μ)/I(1) = 0.5·μ) profiles largely diverge from both 1D and 3D profiles. The effects on diameter determination from these visibility curves are analyzed in Sect. 5.2.
 |
Fig. 6 LD fits (red dashed line) obtained using the Eq. (1) with N = 2 for the RHD azimuthally average intensity profile (solid line) of two simulations of Table 1. The dotted line is the intensity profile computed with the 1D model having identical stellar parameters, input data, and chemical compositions as the 3D simulation. A full LD (dash-dotted line), a partial LD (triple dot-dashed line) are also shown. |
5. Interferometric predictions: departure from spherical symmetry
We derive the interferometric observables to determine the impact of the limb darkening and granulation pattern on visibility curves and closure phases, using the same method described in Chiavassa et al. (2009). For each synthetic stellar disk image, we calculated the discrete complex Fourier transform z. The visibility, vis, is defined as the modulus | z | , of the Fourier transform normalized by the value of the modulus at the origin of the frequency plane, | z0 | , with the phase tanϕ = ℑ(z)/ℜ(z), where ℑ(z) and ℜ(z) are the imaginary and real parts of the complex number z, respectively. We introduced also a theoretical spatial frequency scale expressed in units of inverse solar radii (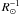 ). The conversion between spatial frequencies expressed in the latter scale and in the more usual scale of 1/″ is given by:
). The conversion between spatial frequencies expressed in the latter scale and in the more usual scale of 1/″ is given by: ![\begin{equation} \label{eqvis1} \nu~\left[\frac{1}{\arcsec}\right]=\nu~\left[\frac{1}{{R}_\odot^{-1}}\right]\times d~[{\rm pc}]\times 214.9 \end{equation}](/articles/aa/full_html/2010/16/aa15507-10/aa15507-10-eq86.png) (2)where ν is the spatial frequency, 214.9 is the astronomical unit expressed in solar radii, and d is the distance of the observed star. Also useful is the following relation
(2)where ν is the spatial frequency, 214.9 is the astronomical unit expressed in solar radii, and d is the distance of the observed star. Also useful is the following relation 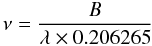 (3)where ν is the spatial frequency in arcsec-1 at the observed wavelength λ in μm for the baseline B of an interferometer in meters.
(3)where ν is the spatial frequency in arcsec-1 at the observed wavelength λ in μm for the baseline B of an interferometer in meters.
5.1. Visibility curves
 |
Fig. 7 Top row: visibility curves from the RHD simulation with [Fe/H ] = −3.0 and log g = 1.6 in the optical (left column) and infrared (right column) filters. The visibilities are computed for 36 different azimuth angles 5° apart (thin gray lines). The dotted line is an uniform disk scaled to match the same radius, i.e. the first null in visibility curve. The visibilities are displayed only longward of the first null visibility point (see text). A logarithm scale is used on y-axis. Bottom row: visibility fluctuations with respect to the average value as a function of spatial frequencies. |
The first null point of the visibility curve is mostly sensitive to the radial extension of the observed object (e.g. Quirrenbach 2001, and Chiavassa et al.2010 for an application to RHD simulations). In fact, the radius of Table 1 can be estimated using ![$R_\star[{R}_\odot]=\frac{\Theta[{R}_\odot]}{2}=\frac{1.22}{2\cdot\nu[{R}_\odot^{-1}]}$](/articles/aa/full_html/2010/16/aa15507-10/aa15507-10-eq94.png) , where
, where ![$\nu[{R}_\odot^{-1}]$](/articles/aa/full_html/2010/16/aa15507-10/aa15507-10-eq95.png) is the spatial frequency corresponding to the first null point and Θ the angular diameter. This formula is related to the resolving power of a telescope. Our predictions concerning the first lobe of the visibility curves, however, cannot be used to fit the observed data because of the geometrical limitations of our models. In our spherical tiling model, based on box-in-a-star simulations, the stellar radius is effectively a free-parameter. Only 3D simulations in the star-in-a-box configuration can be strictly used for this purpose (Chiavassa et al. 2009). On the other hand, the first null point and the second lobe of the visibility curves are sensitive to the limb darkening (Hanbury Brown et al. 1974). These frequency points are then crucial to test RHD simulations against observations to recover the information on the temperature stratification in the external layers of the star.
is the spatial frequency corresponding to the first null point and Θ the angular diameter. This formula is related to the resolving power of a telescope. Our predictions concerning the first lobe of the visibility curves, however, cannot be used to fit the observed data because of the geometrical limitations of our models. In our spherical tiling model, based on box-in-a-star simulations, the stellar radius is effectively a free-parameter. Only 3D simulations in the star-in-a-box configuration can be strictly used for this purpose (Chiavassa et al. 2009). On the other hand, the first null point and the second lobe of the visibility curves are sensitive to the limb darkening (Hanbury Brown et al. 1974). These frequency points are then crucial to test RHD simulations against observations to recover the information on the temperature stratification in the external layers of the star.
 |
Fig. 8 Top left panel: synthetic stellar disk image in the FLUOR filter for the simulation with [Fe/H ] = −3.0 and log g = 1.6 tiled using only one intensity map at different μ-angles (see text for details). The granulation pattern is continuous. The intensity range is [5000, 0.11 × 106] erg cm-2 s-1 Å-1. Top right panel: synthetic stellar disk image in the same filter and using the same intensity map but flipping the y-axis every second tile to remove the periodicity at the side of each box. Bottom panel: ratio of the fluctuations of the synthetic visibility curves derived from the above images: σref/visref refers to top left panel and σshuffle/visshuffle to top right panel. |
Figure 7 (top panels) shows the visibility curves computed for 36 different cuts through the centers of the stellar disk images in Fig. 4. This is equivalent to generating different realizations of the stellar disk images with intensity maps computed for different sets of randomly selected snapshots. The comparison with the uniform disk visibility in top left panel of Fig. 7 shows that the synthetic visibilities deviate greatly from circular symmetry and they are systematically lower than the uniform disk model at the leftmost spatial frequencies shown in the plot. This is due to a the limb darkening effect already visible in Fig. 4. Moreover, bottom panels of Fig. 7 shows the one σ visibility fluctuations, F, with respect to the average value 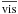 (
(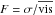 ): the dispersion clearly increases with spatial frequency. On the top of the second lobe, which is easy to reach both in the optical and in the FLUOR filters with CHARA of a typical red giants, the fluctuations are about 2% (optical) and 0.3% (FLUOR). In fact, the effect of line blanketing in FLUOR filter (Fig. 4, right panel) is less important than the in the optical case and the image seems closer to a uniform disk.
): the dispersion clearly increases with spatial frequency. On the top of the second lobe, which is easy to reach both in the optical and in the FLUOR filters with CHARA of a typical red giants, the fluctuations are about 2% (optical) and 0.3% (FLUOR). In fact, the effect of line blanketing in FLUOR filter (Fig. 4, right panel) is less important than the in the optical case and the image seems closer to a uniform disk.
In addition to this, the synthetic visibilities of the simulation at log g = 1.6 and [Fe/H ] = −3.0 show, in the optical filter, the largest deviation from UD in the range 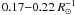 . This is due to the small scale structure on the model stellar disk shown in Chiavassa et al. (2010). This frequency range corresponds to surface structures of 2.27−2.94 R⊙ or 1500−2200 Mm, approximatively the size of one of the granules as shown in Fig. 1.
. This is due to the small scale structure on the model stellar disk shown in Chiavassa et al. (2010). This frequency range corresponds to surface structures of 2.27−2.94 R⊙ or 1500−2200 Mm, approximatively the size of one of the granules as shown in Fig. 1.
Observing red giant stars at high spatial resolution is thus crucial for two reasons, at least:
-
1.
to further test the limb darkening predicted by our RHDsimulations. For this purpose, it would be worthy searching forangular visibility variations, observing with the same telescopeconfiguration (covering spatial frequencies higher than the firstlobe) and using the Earth rotation in order to span multipleposition angles. Assuming measurement errors below 2%, forvisibilities of ~10%, one night would be enough. For comparison, theinstrumental error of VEGA on CHARA is ~1% (Mourardet al. 2009);
-
2.
to characterize the granulation pattern. This requires observations at very high spatial frequencies that may be possible only in the optical range. In fact, considering that the maximum baseline of CHARA is 331 m (ten Brummelaar et al. 2005), for a red giant with an apparent radius of 2.7 mas (e.g. HD 214868 Baines et al. 2010), a baseline of ~270 (1200) meters is necessary to probe the seventh lobe at 0.5 (2.14) μm.
Our method of constructing realizations of red giant stellar disk images (Sect. 3) inevitably introduces some discontinuities between neighbouring tiles by randomly selecting temporal snapshots and by cropping intensity maps at high latitudes and longitudes. We checked whether these artifacts produce significant fluctuations in the theoretical visibility curves. These discontinuities in the granulation pattern stem from using random snapshots of the simulation sequences. We explored the impact of such discontinuities at the edges of neighbouring tiles by constructing two mock stellar disk images (Fig. 8). To generate the first image, we tiled a sphere with intensity maps computed for one single simulation snapshot: in this case, the continuity of the granulation pattern is ensured by the the periodic horizontal boundary conditions of the simulation. For the second image, we used the same intensity map as for the previous case but flipping the y-axis every second tile: in this way, we generated a granulation pattern that is statistically similar to the one in the first image in terms of fine spatial structures but at the same time has discontinuities at the boundaries between tiles (top right panel). We then computed the visibility curves for 36 different angles 5° apart and derived the visibility fluctuations (Fig. 8, bottom panel). Both in the optical and in the FLUOR filter, the visibility fluctuations caused by the disentangled periodicity at the sides of each boxes have a contribution about two orders of magnitude smaller than the signal observed in Fig. 7. We conclude that our approach to constructing the orthographic projection with random snapshots less of an effect on the visibility curves than the signal due to the inhomogeneities of the stellar surface.
In relatively large filters, such as FLUOR, several spatial frequencies are simultaneously observed by the interferometer. This effect is called bandwidth smearing. Kervella et al. (2003a,b) show that this effect is negligible for squared visibilities larger than 40% but it is important spatial frequencies close to the first minimum of the visibility function. To account for this effect, Wittkowski et al. (2004) proposed to compute averaged squared visibility amplitudes, ⟨vis2⟩, as 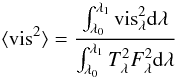 (4)where vis
(4)where vis is the squared visibility at wavelength λ, λ0 and λ1 are the filter wavelength limits, Tλ is the transmission curve of the filter and Fλ is the flux at wavelength λ (see Fig. 3).
is the squared visibility at wavelength λ, λ0 and λ1 are the filter wavelength limits, Tλ is the transmission curve of the filter and Fλ is the flux at wavelength λ (see Fig. 3).
In our case, first we generated a synthetic stellar disk image at every wavelength and then we computed the visibility curves 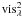 for 36 different cuts through the centers of the stellar disk images. Then we applied Eq. (4) to obtain the averaged squared visibilities and finally we derived the visibility fluctuations with respect to the average values. Figure 9 shows that there is not a clear difference between the visibility fluctuations computed with and without taking into account the bandwidth smearing effect.
for 36 different cuts through the centers of the stellar disk images. Then we applied Eq. (4) to obtain the averaged squared visibilities and finally we derived the visibility fluctuations with respect to the average values. Figure 9 shows that there is not a clear difference between the visibility fluctuations computed with and without taking into account the bandwidth smearing effect.
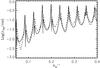 |
Fig. 9 Visibility fluctuations with respect to the average value as a function of spatial frequencies for the RHD simulation with [Fe/H ] = 0.0 and log g = 2.2 in the FLUOR filter. The dashed line corresponds to fluctuations of visibility computed taking into account the bandwidth smearing effect (see text and Eq. (4)) while the solid line to fluctuations of visibility computed without bandwidth smearing. |
 |
Fig. 10 Top and central rows: synthetic stellar disk images in the optical filter for the four simulations of Table 1 having log g = 2.2. The intensity range is [5000, 1.5 × 106] erg cm-2 s-1 Å-1 for [Fe/H ] = 0.0 and −1.0; [5000, 2.0 × 106] erg cm-2 s-1 Å-1 for [Fe/H ] = −2.0 and −3.0. Bottom panel: fluctuations of the synthetic visibility curves derived from the above images. The colors have the same meaning as in Fig. 3. We dropped the first lobe of the visibility curves as in Fig. 7. |
 |
Fig. 11 Visibility curves computed with Eq. (5) for and angular diameter of 2 mas and for the 3D (solid line), 1D (dotted line), and fully limb darkening (dash-dotted line) intensity profiles of Fig. 6. In top panels, the dotted and solid lines are almost overlying, while in bottom left panel the dotted line is almost overlying the dash-dotted one. A logarithm scale is used on y-axis. Synthetic visibilities in these plots are not realistic near the nulls but are intended only for model-to-model comparison. |
The simulations of Collet et al. (2007) showed that the predicted characteristic size of granules decreases with the metallicity of the star. Therefore, we focus now on the simulations of Table 1 with the same surface gravity, log g = 2.2, and different [Fe/H] and effective temperature. We considered only the optical filter that show larger (and thus easier to detect) visibility fluctuations. Figure 10 displays the synthetic stellar disk images and the visibility fluctuations derived from the visibility curves. The solar metallicity simulation has almost systematically smaller fluctuations (except for the 3rd lobe at 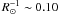 ) at all frequencies until
) at all frequencies until 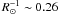 (i.e. the 6th lobe, that is close to the baseline extension limit of CHARA interferometer for a 2.7 mas star). The difference between [Fe/H ] = 0.0 (black curve) and [Fe/H ] = −3.0 (light blue curve) is about 1% (same order of the instrumental error of VEGA) on the top of the second lobe (
(i.e. the 6th lobe, that is close to the baseline extension limit of CHARA interferometer for a 2.7 mas star). The difference between [Fe/H ] = 0.0 (black curve) and [Fe/H ] = −3.0 (light blue curve) is about 1% (same order of the instrumental error of VEGA) on the top of the second lobe (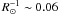 ) with peaks of about 1.2−1.7% at
) with peaks of about 1.2−1.7% at 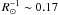 and 0.20, respectively. We emphasize that it is possible to study the metallicity dependence on visibility curves to characterize the granulation pattern of red giant stars. It is however important to carefully consider specific instrumental effects that could affect the visibility fluctuations. This can be already done with present day interferometers in addition to image reconstruction (Berger et al. 2010; Malbet et al. 2010) which eventually will be able to measure the size of granules directly.
and 0.20, respectively. We emphasize that it is possible to study the metallicity dependence on visibility curves to characterize the granulation pattern of red giant stars. It is however important to carefully consider specific instrumental effects that could affect the visibility fluctuations. This can be already done with present day interferometers in addition to image reconstruction (Berger et al. 2010; Malbet et al. 2010) which eventually will be able to measure the size of granules directly.
5.2. Estimation of diameter correction: 1D versus 3D models
Interferometric data are often fitted with a simple uniform disk model that, although unphysical, has the advantage of immediately telling if a star is resolved, after which limb darkening corrections are applied. Thus, to estimate the angular diameter from measured visibilities it is necessary to know the intensity distribution of the stellar disk and, for this purpose, parametric (e.g. full or partial limb darkened) or photospheric one dimensional models (e.g. MARCS) models are used.
We used the intensity profiles obtained from 3D and 1D models (see Sect. 4 and Fig. 6) to estimate the correction on the uniform disk diameter determination. We derived the visibility law Vλ(B,Θ) from the intensity profile I(λ,μ) using the Hankel integral: 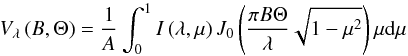 (5)where λ is the wavelength in meters (in this case the central wavelength of the filters in Fig. 3), B is the baseline in meters, Θ is an arbitrary angular diameter in radians (we assume 2 mas), J0 the zeroth order of the Bessel function, μ = cos(θ) as defined in Sect. 4, and A the normalization factor:
(5)where λ is the wavelength in meters (in this case the central wavelength of the filters in Fig. 3), B is the baseline in meters, Θ is an arbitrary angular diameter in radians (we assume 2 mas), J0 the zeroth order of the Bessel function, μ = cos(θ) as defined in Sect. 4, and A the normalization factor: 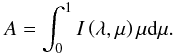 (6)Figure 11 shows the visibilities computed from the intensity profiles of Fig. 6. For typical red giant stars having 4600 ≲ Teff ≲ 5100 K (compare with Table 1) differences in angular diameters vary from ~−3.5% to ~1% in the optical, and are roughly in the range between −0.5 and −1.5% in the infrared (Table 3), the corresponding change in effective temperature being
(6)Figure 11 shows the visibilities computed from the intensity profiles of Fig. 6. For typical red giant stars having 4600 ≲ Teff ≲ 5100 K (compare with Table 1) differences in angular diameters vary from ~−3.5% to ~1% in the optical, and are roughly in the range between −0.5 and −1.5% in the infrared (Table 3), the corresponding change in effective temperature being 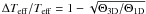 . These corrections depend on wavelength, the deviations being moderately stronger in the optical than in the infrared. Differences between the 1D and the mean 3D atmospheric structures and inhomogeneities of red giant stars have been already studied by means of 3D hydrodynamical simulations (Collet et al. 2007). These differences have a significant effects on the predicted strengths of spectral lines as well as on the center-to-limb profiles. As a consequence, when using LD laws obtained from 1D models (e.g. Claret 2000) to determine angular diameters from observed data, one must take into account that 3D models usually predict a lower center-to-limb variations with respect to 1D, thus implying smaller radii and moderately hotter effective temperatures.
. These corrections depend on wavelength, the deviations being moderately stronger in the optical than in the infrared. Differences between the 1D and the mean 3D atmospheric structures and inhomogeneities of red giant stars have been already studied by means of 3D hydrodynamical simulations (Collet et al. 2007). These differences have a significant effects on the predicted strengths of spectral lines as well as on the center-to-limb profiles. As a consequence, when using LD laws obtained from 1D models (e.g. Claret 2000) to determine angular diameters from observed data, one must take into account that 3D models usually predict a lower center-to-limb variations with respect to 1D, thus implying smaller radii and moderately hotter effective temperatures.
While the impact of the corrections in Table 3 is usually not dramatic, they are not negligible to properly set the zero point of the effective temperature scale derived by mean of this fundamental method. In particular, when future long baseline interferometers working in the optical will be able to (partly) resolve (very) metal-poor stars, it will be fundamental to take those corrections into account for a correct derivation of their diameters. Moreover, the model dependence on the diameter determination has also an impact on the reliability of the existing catalogs of calibrator stars for interferometry that are based on red giants with similar parameters to those studied in this work. In fact, the formal high accuracy reached on diameter determination (a fraction of 1%, Mérand et al. 2010) is based only on 1D models, while we show that the correction reported in Table 3 can have a sizeable impact.
Our results in Table 3 are in qualitative agreement with those obtained by Allend Prieto et al. (2002), Aufdenberg et al. (2005) and Bigot et al. (2006) for dwarf stars, though the lower surface gravity of red giants might also play a role, since the size of surface related convective structures is roughly inversely proportional to the gravity. As we already discussed, the size of these inhomogeneities have an impact on the average intensity profile and thus on the interferometric observables.
These corrections could also be relevant in explaining some discrepancies known in literature, which involve the comparison with interferometric angular diameters. For example, in the library of stellar spectra assembled by Cohen et al. (1999), absolute spectrophotometry has the tendency to return angular diameters systematically smaller by a few percent with respect to interferometry. Smaller angular diameters for cool giants would also explain the dichotomy reported by Alonso et al. (1994) when trying to set on the same scale Teff derived for hot and cool stars from interferometry with those determined from the Infrared Flux Method. Recent revision of the latter technique support in fact hotter effective temperatures also for dwarfs and subgiants (Casagrande et al. 2006, 2010) and the extension to giants is currently under way (Casagrande et al., in prep.). Smaller limb-darkened angular diameters (i.e. hotter effective temperatures) would also reduce the discrepancy recently noticed by Baines et al. (2010) when comparing interferometric with spectroscopic Teff of giants. Thus, it is important to keep in mind that even when interferometry is used to derive effective temperatures in the most fundamental way, there is a non negligible – and still partly unexplored – model dependence in the correction from uniform to limb-darkened disks. We remark that our results are currently limited to a rather small range in effective temperatures and gravities and to this respect, 3D models will also give an important contribution to set the effective temperature scale on a physically sounder base.
5.3. Closure phases
One can use closure phase between three telescopes, as the sum of all phase differences removes the atmospheric contribution, leaving the phase information of the object visibility unaltered (e.g. Monnier 2007). The closure phase thus offers an important complementary piece of information, revealing asymmetries and inhomogeneities of stellar disk images.
 |
Fig. 12 Scatter plot of closure phases of 2000 random baseline triangles for RHD simulation with [Fe/H ] = −3.0 and log g = 1.6 with a maximum linear extension of ~510 m at 0.5 μm and ~2200 m at 2.14 μm and for a star at 100 pc. The extension of the baselines has been expressed in |
 |
Fig. 13 Comparison of the RHD simulation with [Fe/H ] = 0. and log g = 2.2 (Table 1) to the observations (red dots) of the giant HD 214868 (Baines et al. 2010). The solid thick line corresponds to the best fit (reduced χ2 = 0.59) visibility curve, the dashed line is the uniform disk (2.721 mas with reduced χ2 = 0.72) model introduced by Baines et al.. The visibility curve from RHD simulation never goes to zero due to the bandwidth smearing effect. A logarithm scale is used on y-axis. |
The characterization of the closure phase, together with the limb darkening behavior (see Sect. 4), is important for two more reasons in red giant stars. First, Renard et al. (2008) demonstrated that closure phases provide the differential planet to star contrast ratio as a function of wavelength. When observing a star with a faint companion, their fringe patterns add up incoherently and the presence of a planet causes a slight decrease in the phase changes and, consequently, the closure phases. This difference can be measured with a temporal survey and should be corrected with the intrinsic closure phases of the parental star. Second, van Belle (2008) provided a technique based on closure phases to determine the orbital plane position angle of a planet transiting in front of the star as well as the planet’s radius using the high-precision multi-telescope beam combiner MIRC (Monnier et al. 2006) on CHARA. Also in this case, theoretical predictions of the closure phases of the parental stars are crucial.
6. Comparison with the interferometric observations of HD 214868
In this section, we compare our RHD simulations to the giant HD 214868 (K2 III, Teff = 4440 ± 70, log g = 2.1 ± 0.2 and [Fe/H] = −0.18 ± 0.50 dex; Baines et al. 2010). This star has been chosen because it has been observed up to the second lobe with CHARA in a filter centered at ~2.15 μm and sensitive to the range 1.00−2.50 μm (McAlister et al. 2005), which is close to FLUOR filter. For this purpose, we chose the model of Table 1 having the closest parameters (i.e. Teff = 4697 ± 18, [Fe/H ] = 0.0, and log g = 2.2) and compared our synthetic visibilities in the FLUOR filter to the observations (Fig. 13). The absolute model dimensions have been scaled to match the interferometric observation in the first lobe. However, as already mentioned in Sect. 5, the information about the radius cannot be retrieved because of the limitations in the method we use to construct the stellar disk images. We therefore concentrate on the visibility data points in the second lobe (i.e. where the limb darkening effects are important; Hanbury Brown et al. 1974). A Levenberg-Marquardt least-squares minimization returns reduced χ2 = 0.59 for the best RHD synthetic visibility, all RHD visibilities falling in the range [0.59, 0.66]. Formally, the RHD simulation shows an improvement over parametric model (uniform disk model has reduced χ2 = 0.72) for the interpretation of these interferometric observations, though it must be noted that observed points in Fig. 13 fall at baselines where 3D and uniform disk models nearly overlap. A more uniform sampling (e.g. close to the first null point) will be very valuable to further test our simulation. For the sake of completeness, we also remark that the simulation used in this specific exercise is not tailored exactly to the stellar parameters of the studied star, and improvements along this direction are still possible.
7. Conclusions
In this work, we provided a set of interferometric predictions from our RHD simulations of red giant stars that will be tested against observations with today interferometers like CHARA. Red giant stars are ideal targets for interferometers because they are numerous and have large angular diameters as well as bright infrared apparent magnitudes.
We derived average center-to-limb intensity profiles from the synthetic stellar disk images based on RHD simulations and computed limb darkening coefficients in the optical as well as in the infrared. The predicted center-to-limb variations of 3D simulations can be tested against observations: the visibilities and the closure phases show evident departures from from circular symmetry, which are due to inhomogeneities on the stellar surface. We emphasize that red giant stars should be observed at high spatial frequencies, to characterize the granulation pattern, and in particular in the optical range where the visibility fluctuations are larger. In addition to this, it would be valuable to couple the observations in the optical and in the infrared to test models predictions for limb darkening. We counted at least 58 red giants stars using the stellar diameters catalog of Lafrasse et al. (2010) with stellar parameters corresponding to our simulations, an apparent diameter larger than 2 mas in the visible and V magnitude lower than 6 (the current magnitude limit of VEGA is 7, Mourard et al. 2009). We provided also a first comparison with the red giant star HD 214868 showing that our RHD simulations returns a better fit with respect to simple parametric uniform disk models. More observations along this direction will provide useful information not only on red giants, but also on our RHD models. This will include the center-to-limb variation, which carry the information on the temperature stratification in the stellar atmosphere, and the characterization of the granulation pattern in terms of size and contrast with varying metallicity and effective temperature. Moreover, the study of the closure phases behavior will help to recover the physical parameters of possible hot Jupiters around red giant stars.
Interferometry is advantageous in that it provides the ability to directly measure stellar angular diameters. We found that, for typical red giant stars studied in this work, differences in angular diameters using 3D or 1D limb darkening laws vary from ~−3.5% to ~1% in the optical, and are roughly in the range between −0.5 and −1.5% in the infrared, with 3D models returning in general smaller angular diameters with respect to 1D, thus implying moderately hotter effective temperatures. The impact of these corrections is not dramatic, but they are not negligible to correctly set the zero point of the effective temperature scale derived by means of this fundamental method, in particular, for future observations of metal-poor stars. Moreover, the model dependence on the diameter determination has also an impact on the reliability of the existing catalogs of calibrator stars for interferometry that are based on giants with parameters similar to those covered in this work. We emphasize that even when interferometry is used to derive effective temperatures in the most fundamental way, there is a non-negligible and still partly unexplored model dependence.
Acknowledgments
We thank the Rechenzentrum Garching (RZG) for providing some of the computational resources necessary for this work.
References
- Allende Prieto, C., Asplund, M., García López, R. J., & Lambert, D. L. 2002, ApJ, 567, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1994, A&A, 282, 684 [NASA ADS] [Google Scholar]
- Asplund, M. 2000, A&A, 359, 755 [NASA ADS] [Google Scholar]
- Asplund, M., & García Pérez, A. E. 2001, A&A, 372, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Gustafsson, B., Kiselman, D., & Eriksson, K. 1997, A&A, 318, 521 [NASA ADS] [Google Scholar]
- Asplund, M., Nordlund, Å., Trampedach, R., & Stein, R. F. 1999, A&A, 346, L17 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Aufdenberg, J. P., Ludwig, H., & Kervella, P. 2005, ApJ, 633, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Baines, E. K., Döllinger, M. P., Cusano, F., et al. 2010, ApJ, 710, 1365 [NASA ADS] [CrossRef] [Google Scholar]
- Behara, N. T., Bonifacio, P., Ludwig, H., et al. 2010, A&A, 513, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berger, J.-P., Malbet, F., Baron, F., et al. 2010, A&A Rev., submitted [Google Scholar]
- Bigot, L., Kervella, P., Thévenin, F., & Ségransan, D. 2006, A&A, 446, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Ludwig, H., Steffen, M., Freytag, B., & Bonifacio, P. 2010, Sol. Phys., 66 [Google Scholar]
- Carney, B. W., Yong, D., Teixera de Almeida, M. L., & Seitzer, P. 2005, AJ, 130, 1111 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Portinari, L., & Flynn, C. 2006, MNRAS, 373, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiavassa, A., Plez, B., Josselin, E., & Freytag, B. 2009, A&A, 506, 1351 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Chiavassa, A., Haubois, X., Young, J. S., et al. 2010, A&A, 515, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Cohen, M., Walker, R. G., Carter, B., et al. 1999, AJ, 117, 1864 [NASA ADS] [CrossRef] [Google Scholar]
- Collet, R., Asplund, M., & Trampedach, R. 2007, A&A, 469, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collet, R., Nordlund, Å., Asplund, M., Hayek, W., & Trampedach, R. 2009, Mem. Soc. Astron. Ital., 80, 719 [Google Scholar]
- Döllinger, M. P., Hatzes, A. P., Pasquini, L., et al. 2007, A&A, 472, 649 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fulbright, J. P. 2000, AJ, 120, 1841 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Bell, R. A., Eriksson, K., & Nordlund, A. 1975, A&A, 42, 407 [NASA ADS] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanbury Brown, R., Davis, J., Lake, R. J. W., & Thompson, R. J. 1974, MNRAS, 167, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Hekker, S., & Meléndez, J. 2007, A&A, 475, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, J. A., Marcy, G. W., Fischer, D. A., et al. 2008, ApJ, 675, 784 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Thévenin, F., Morel, P., Bordé, P., & Di Folco, E. 2003a, A&A, 408, 681 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Thévenin, F., Ségransan, D., et al. 2003b, A&A, 404, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. 1993, Opacities for Stellar Atmospheres (Cambridge, Mass.: SAO), CD-ROMs, 2 [Google Scholar]
- Kurucz, R. L. 1992, Rev. Mexicana Astron. Astrofis., 23, 181 [Google Scholar]
- Kučinskas, A., Ludwig, H., Caffau, E., & Steffen, M. 2009, Mem. Soc. Astron. Ital., 80, 723 [Google Scholar]
- Lafrasse, S., Mella, G., Bonneau, D., et al. 2010, VizieR Online Data Catalog, 2300, [Google Scholar]
- Lindegren, L., Babusiaux, C., Bailer-Jones, C., et al. 2008, in A Giant Step: from Milli- to Micro-arcsecond Astrometry, ed. W. J. Jin, I. Platais, & M. A. C. Perryman (Cambridge: Cambridge University Press), IAU Symp., 248, 217 [Google Scholar]
- Malbet, F., Cotton, W., Duvert, G., et al. 2010, SPIE, 7734, 77342N [CrossRef] [Google Scholar]
- McAlister, H. A., ten Brummelaar, T. A., Gies, D. R., et al. 2005, ApJ, 628, 439 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., Preston, G. W., Sneden, C., & Searle, L. 1995, AJ, 109, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- Mérand, A., Coudé du Foresto, V., Kellerer, A., et al. 2006, in SPIE Conf. Ser., 6268 [Google Scholar]
- Mérand, A., Kervella, P., Barban, C., et al. 2010, A&A, 517, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mihalas, D., Dappen, W., & Hummer, D. G. 1988, ApJ, 331, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D. 2007, New Astron. Rev., 51, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Pedretti, E., Thureau, N., et al. 2006, in SPIE Conf. Ser., 6268 [Google Scholar]
- Mourard, D., Clausse, J. M., Marcotto, A., et al. 2009, A&A, 508, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quirrenbach, A. 2001, ARA&A, 39, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Renard, S., Absil, O., Berger, J., et al. 2008, in SPIE Conf. Ser., 7013 [Google Scholar]
- Ryan, S. G., Norris, J. E., & Beers, T. C. 1996, ApJ, 471, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Cassisi, S., & Weiss, A. 2002, PASP, 114, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, B., Fischer, D. A., Henry, G. W., et al. 2005, ApJ, 633, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Sbordone, L., Bonifacio, P., Caffau, E., et al. 2010, A&A, 522, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stein, R. F., & Nordlund, A. 1998, ApJ, 499, 914 [Google Scholar]
- ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G. T. 2008, PASP, 120, 617 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G. T., Lane, B. F., Thompson, R. R., et al. 1999, AJ, 117, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Wende, S., Reiners, A., & Ludwig, H. 2009, A&A, 508, 1429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittkowski, M., Aufdenberg, J. P., & Kervella, P. 2004, A&A, 413, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yong, D., Carney, B. W., & Teixera de Almeida, M. L. 2005, AJ, 130, 597 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Intensity maps in the optical top-hat filter of Fig. 3 for the simulation with log g = 1.6 and [Fe/H ] = −3.0 (Table 1) with μ = 1.00, 0.81, 0.58, and 0.40. The intensities typically ranges from 3 × 104 to 1.2 × 106 erg cm-2 s-1 Å-1. |
| In the text | |
 |
Fig. 2 Toy model representing our method used to tile spherical surfaces and constructing the synthetic stellar disk images. |
| In the text | |
 |
Fig. 3 Left panel: synthetic spectra for different 3D model red giant atmospheres in the wavelength range 4700−5300 Å. The intensity maps corresponding to this filter have been computed assuming a top-hat filter (dashed line). This wavelength range corresponds to the VEGA instrument (Mourard et al. 2009) mounted on CHARA with a spectral resolution λ/Δλ = 5000. From the bottom: the black curve refers to the simulation with log g = 2.2 and [Fe/H ] = 0.0 and no offset applied, the red curve to log g = 2.2 and [Fe/H ] = −1.0 with an offset of 1, the green curve to log g = 2.2 and [Fe/H ] = −2.0 with an offset of 2, the light blue curve to log g = 2.2 and [Fe/H ] = −3.0 with an offset of 3, and the dark blue curve log g = 1.6 and [Fe/H ] = −3.0 with an offset of 4 (see Table 1). Right panel: transmission curve (dashed line) of the FLUOR (2.14 ± 0.26 μm) filter (Mérand et al. 2006) mounted on CHARA. Colors and offsets are the same as in left panel. |
| In the text | |
 |
Fig. 4 Synthetic stellar disk images of the simulation with [Fe/H ] = −3.0 and log g = 1.6 (Table 1). The intensity range is 5.0 × 103−2.1 × 106 erg cm-2 s-1 Å-1 for the optical filter and 5.0 × 103−1.1 × 105 erg cm-2 s-1 Å-1 for the FLUOR filter. |
| In the text | |
 |
Fig. 5 Radially averaged intensity profiles (black line) derived from the synthetic stellar disk images of Fig. 4 and corresponding to RHD simulation with [Fe/H ] = −3.0 and log g = 1.6. The dashed gray areas denote the one sigma spatial fluctuations with respect to the averaged intensity profile. The intensity is normalized to the mean intensity at disk center and the radius is normalized to the radius given in Table 1. |
| In the text | |
 |
Fig. 6 LD fits (red dashed line) obtained using the Eq. (1) with N = 2 for the RHD azimuthally average intensity profile (solid line) of two simulations of Table 1. The dotted line is the intensity profile computed with the 1D model having identical stellar parameters, input data, and chemical compositions as the 3D simulation. A full LD (dash-dotted line), a partial LD (triple dot-dashed line) are also shown. |
| In the text | |
 |
Fig. 7 Top row: visibility curves from the RHD simulation with [Fe/H ] = −3.0 and log g = 1.6 in the optical (left column) and infrared (right column) filters. The visibilities are computed for 36 different azimuth angles 5° apart (thin gray lines). The dotted line is an uniform disk scaled to match the same radius, i.e. the first null in visibility curve. The visibilities are displayed only longward of the first null visibility point (see text). A logarithm scale is used on y-axis. Bottom row: visibility fluctuations with respect to the average value as a function of spatial frequencies. |
| In the text | |
 |
Fig. 8 Top left panel: synthetic stellar disk image in the FLUOR filter for the simulation with [Fe/H ] = −3.0 and log g = 1.6 tiled using only one intensity map at different μ-angles (see text for details). The granulation pattern is continuous. The intensity range is [5000, 0.11 × 106] erg cm-2 s-1 Å-1. Top right panel: synthetic stellar disk image in the same filter and using the same intensity map but flipping the y-axis every second tile to remove the periodicity at the side of each box. Bottom panel: ratio of the fluctuations of the synthetic visibility curves derived from the above images: σref/visref refers to top left panel and σshuffle/visshuffle to top right panel. |
| In the text | |
 |
Fig. 9 Visibility fluctuations with respect to the average value as a function of spatial frequencies for the RHD simulation with [Fe/H ] = 0.0 and log g = 2.2 in the FLUOR filter. The dashed line corresponds to fluctuations of visibility computed taking into account the bandwidth smearing effect (see text and Eq. (4)) while the solid line to fluctuations of visibility computed without bandwidth smearing. |
| In the text | |
 |
Fig. 10 Top and central rows: synthetic stellar disk images in the optical filter for the four simulations of Table 1 having log g = 2.2. The intensity range is [5000, 1.5 × 106] erg cm-2 s-1 Å-1 for [Fe/H ] = 0.0 and −1.0; [5000, 2.0 × 106] erg cm-2 s-1 Å-1 for [Fe/H ] = −2.0 and −3.0. Bottom panel: fluctuations of the synthetic visibility curves derived from the above images. The colors have the same meaning as in Fig. 3. We dropped the first lobe of the visibility curves as in Fig. 7. |
| In the text | |
 |
Fig. 11 Visibility curves computed with Eq. (5) for and angular diameter of 2 mas and for the 3D (solid line), 1D (dotted line), and fully limb darkening (dash-dotted line) intensity profiles of Fig. 6. In top panels, the dotted and solid lines are almost overlying, while in bottom left panel the dotted line is almost overlying the dash-dotted one. A logarithm scale is used on y-axis. Synthetic visibilities in these plots are not realistic near the nulls but are intended only for model-to-model comparison. |
| In the text | |
 |
Fig. 12 Scatter plot of closure phases of 2000 random baseline triangles for RHD simulation with [Fe/H ] = −3.0 and log g = 1.6 with a maximum linear extension of ~510 m at 0.5 μm and ~2200 m at 2.14 μm and for a star at 100 pc. The extension of the baselines has been expressed in |
| In the text | |
 |
Fig. 13 Comparison of the RHD simulation with [Fe/H ] = 0. and log g = 2.2 (Table 1) to the observations (red dots) of the giant HD 214868 (Baines et al. 2010). The solid thick line corresponds to the best fit (reduced χ2 = 0.59) visibility curve, the dashed line is the uniform disk (2.721 mas with reduced χ2 = 0.72) model introduced by Baines et al.. The visibility curve from RHD simulation never goes to zero due to the bandwidth smearing effect. A logarithm scale is used on y-axis. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.