| Issue |
A&A
Volume 699, July 2025
|
|
|---|---|---|
| Article Number | A320 | |
| Number of page(s) | 17 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202451292 | |
| Published online | 16 July 2025 | |
The diverse physical origins of stars in the dynamically hot bulge: CALIFA versus IllustrisTNG
1
Shanghai Astronomical Observatory, Chinese Academy of Sciences,
80 Nandan Road,
Shanghai
200030,
China
2
School of Astronomy and Space Sciences, University of Chinese Academy of Sciences,
No. 19A Yuquan Road,
Beijing
100049,
PR
China
3
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg,
Germany
4
Department of Astronomy, Xiamen University, Xiamen,
Fujian
361005,
China
5
Kavli Institute for Astronomy and Astrophysics, Peking University,
Beijing
100871,
China
6
Instituto de Astrofísica de Canarias, Calle Via Láctea s/n,
38200
La Laguna, Tenerife,
Spain
7
Depto. Astrofísica, Universidad de La Laguna, Calle Astrofísico Francisco Sánchez s/n,
38206
La Laguna, Tenerife,
Spain
★ Corresponding authors: zhangle@shao.ac.cn; lzhu@shao.ac.cn
Received:
28
June
2024
Accepted:
9
December
2024
We compare the internal stellar structures of central galaxies in the TNG50 and TNG100 simulations and field galaxies in the CALIFA survey. The luminosity fractions of the dynamically cold, warm, and hot components in both TNG50 and TNG100 galaxies exhibit general consistency with those observed in CALIFA galaxies. For example, they all exhibit a minimum luminosity fraction (fhot ~ 0.18) of the dynamically hot component in galaxies with stellar masses of M* ~ 1–2 × 1010 M⊙, and the morphology of each orbital component in the TNG50 and TNG100 galaxies closely resembles that found in the CALIFA galaxies. We therefore used the simulations to quantify the physical origins of the different components, focusing on the dynamically hot component in TNG50. We identify three primary regimes and thus physical processes: (1) in low-mass galaxies (M* ≲ 1010 M⊙) that have not experienced major mergers, stars are born with a wide range of circularity distributions and have remained relatively unchanged until the present day. Consequently, hot stars in such galaxies at redshift z = 0 are predominantly born hot. (2) In higher-mass galaxies (M* ≳ 1010 M⊙) lacking major mergers, most stars are initially born cold but are subsequently heated through secular evolution. (3) In galaxies across the entire mass range, mergers, if they occurred, significantly increased the hot orbital fraction. As a result, the dynamically hot bulge within Re of present-day galaxies does not indicate their past merger histories; instead, the hot stars in the outer regions are mostly heated or accreted by mergers, thus indicating galaxy merger history. Massive galaxies are initially born with cold, rotationally supported structures, consistent with recent observations from the James Webb Space Telescope (JWST) regarding high-redshift galaxies.
Key words: methods: numerical / galaxies: evolution / galaxies: general / galaxies: kinematics and dynamics
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Galaxies consist of various structural components, including thin disks, thick disks, classical bulges, pseudo-bulges, and stellar halos, each of which serves as a historical record of their formation and assembly. Stars in thin disks form and remain in quiescent environments. However, the formation of bulges involves several proposed mechanisms: (1) stars may be heated from rotation-supported structures through mergers with other galaxies (e.g., Davies & Illingworth 1983; Quinn et al. 1993) or via secular evolution (e.g., Jenkins & Binney 1990; Aumer et al. 2016); (2) bulges could also arise from the compact and rapid formation of central gaseous clumps carried by filaments and gas-rich mergers or form from violent disk instability, especially during high redshift periods (e.g., Elmegreen et al. 2008; Lapiner et al. 2023); (3) stars in non-circular orbits might originate, in part, from the accretion of satellite galaxies (e.g., Gómez et al. 2017; Read et al. 2008). Galaxies do not exist in isolation; their formation and evolution are intertwined with larger-scale environments. Therefore, interactions with other galaxies and mergers can profoundly affect or even determine the distribution of stellar orbits in galaxies. This is particularly evident in the case of stars that make up stellar halos in the Milky Way (MW) (Helmi et al. 2018).
Modern hydrodynamical cosmological simulations, such as IllustrisTNG1 and EAGLE2, have demonstrated the ability to generate a variety of galaxy types. These simulations offer a unique opportunity to quantitatively investigate the origins of different galaxy structures within a cosmic volume. In cosmological simulations, galaxies exhibit diverse merger histories. Major mergers, if experienced by a galaxy, have the potential to disrupt disks and lead to substantial growth in bulges and halos (Sotillo-Ramos et al. 2022; Zhu et al. 2022b; Pulsoni et al. 2021; Lagos et al. 2018). However, intriguingly, there are galaxies dominated by bulges that appear to have been minimally affected by mergers since z ~ 2 (Du et al. 2021), suggesting alternative pathways for bulge growth. The secular evolution (Seidel et al. 2015) and the dissolution of the bar by the infalling gas might play an important role in the formation of the bulge (Bournaud & Combes 2002; Bournaud et al. 2005; Du et al. 2017; Guo et al. 2020; Li et al. 2023). Disk heating by secular evolution plays a significant role in creating the dynamically hot bulge in half of the quiescent elliptical galaxies in TNG50 (Park et al. 2022) and in MW-like galaxies from the Auriga simulation (Fragkoudi et al. 2020). However, in some other zoom-in MW-like simulations (Yu et al. 2023; Bird et al. 2013; Stinson et al. 2013), their structures, including thin disks, thick disks, and dynamically hot bulges, evolve in a manner that aligns with their formation at birth. Bulges are formed by stars born dynamically hot; neither merger nor secular evolution plays a significant role in their formation. The formation of bulges might depend on the galaxy formation model, such as feedback process (Obreja et al. 2013), as well as the galaxy stellar mass, on which merger frequency and bar frequency strongly depend. The relative contributions of these diverse physical processes to the formation of bulges in a representative sample of galaxies, spanning the Hubble sequence and a broad range of masses, have yet to be quantified.
On the one hand, simulations require calibration against actual observed galaxies. However, the task of comparing galaxy structures derived from observations with those from simulations is not straightforward. In the simulations mentioned earlier, the definitions of structures such as disks, bulges, and halos are typically dynamic and can vary between different studies. Conversely, in the case of real galaxies, morphological decomposition techniques, such as the bulge-disk decomposition, have been extensively employed, yielding invaluable insights over the past decades. However, it is important to note that these methods are subject to significant uncertainties, which makes them challenging to compare fairly with the simulation results. It is only through the establishment of systematic and well-defined methodologies for comparing observed and simulated galaxies that substantial progress in this field can be achieved.
The Milky Way stands as the only real galaxy amenable to dynamic decomposition in a manner comparable to simulations, mainly due to the availability of 6D phase-space information for its stars, as gleaned from observations (e.g., recently Helmi et al. 2018; Belokurov et al. 2018). Over the past decade, integral field unit (IFU) spectroscopy surveys, including SAURON (Davies et al. 2001), SAMI (Croom et al. 2012), CALIFA (Sánchez et al. 2012), MaNGA (Bundy et al. 2014), have provided stellar kinematic maps for thousands of galaxies. With an orbit superposition model Schwarzschild (1979) for IFU data, insights into the internal distribution of stellar orbits become possible for nearby galaxies, with some approximations. The method (van den Bosch et al. 2008) has been widely applied to large galaxies samples observed by SAURON (Cappellari 2016), CALIFA (Zhu et al. 2018c), MaNGA (Jin et al. 2020), SAMI (Santucci et al. 2022) and MUSE (Ding et al. 2023; Zhu et al. 2022b; Poci et al. 2021). Recently, the code has been made publicly available (Thater et al. 2022) and has been enhanced to explicitly incorporate the galactic bar (Tahmasebzadeh et al. 2021, 2022, 2024). Despite the capability of deriving stellar orbit distributions through the orbit-superposition method, it is important to note that these distributions have limited accuracy, with certain fine-scale structures remaining undetermined. In the case of the CALIFA sample, each of the 300 galaxies has been coarsely divided into dynamically cold, warm, hot, and counter-rotating (CR) components, with the luminosity fractions and morphological characteristics of each component quantified (Zhu et al. 2018a). The precision and uncertainty of these results have been thoroughly tested and understood. The dynamically cold and hot +CR components can be roughly linked to the photo-metrically defined thin disk and bulge, respectively. The warm component could be a mixture of thick disk and pseudo-bulge (Zhu et al. 2018a). The CR component sometimes constructs a CR disk, but such cases are rare and are not statistically important in the CALIFA sample.
In this study, our objective is to bridge the gap between observations and simulations. To achieve this, we adopt a consistent methodology to define cold, warm, hot, and CR components for both TNG50 and TNG100 galaxies of IllustrisTNG suites, mirroring the approach used for CALIFA galaxies. We then establish a benchmark for the simulations by directly comparing the luminosity fractions and morphological properties of these components with those observed in CALIFA galaxies. Subsequently, we trace the formation of these components, with a particular emphasis on understanding the nature of the dynamically hot bulge component in TNG50 galaxies across the Hubble sequence and within a broad mass range.
The paper is organized in the following way: we introduce the observations and simulations in Section 2, describe the method in Section 3, compare the TNG50, TNG100, and CALIFA galaxies in Section 4, quantify the formation of different structures in TNG50 in Section 5. We discuss our results in Section 6 and conclude in Section 7.
2 Observations and simulations
The CALIFA survey encompasses galaxies of all morphological types across the Hubble diagram, exhibiting a diverse range of kinematic properties, from dispersion-dominated elliptical galaxies to rotation-dominated disk galaxies (Sánchez et al. 2012; Falcón-Barroso et al. 2017). Notably, all CALIFA galaxies are situated in the field, and the CALIFA mother sample is considered to be representative of galaxies in the nearby universe within the stellar mass range of 108.7 M⊙ to 1011.9 M⊙. More than 95% of the galaxies in the mother sample are in the mass ranges of 109.7 M⊙ to 1011.4 M⊙ where the selection function is well defined (Walcher et al. 2014).
The CALIFA Data Release 2 (DR2) has made available data for 300 galaxies selected from the CALIFA mother sample, with 260 of them being isolated and devoid of kinematic biases introduced by dust lanes. A uniform application of the triaxial orbit-superposition Schwarzschild method (e.g., Schwarzschild 1979; Van Den Bosch et al. 2008) is employed for each of the 260 galaxies (Zhu et al. 2018c). This method yielded the stellar orbit distribution within the effective radius Re, presented as a probability density distribution of orbits within Re with respect to circularity λz. Based on the model, each galaxy is dynamically decomposed into four components: the cold (λz > 0.8), warm (0.25 < λz < 0.8), hot (|λz| < 0.25), and counter-rotating (λz < −0.25) component. The luminosity fraction of each of these components as a function of stellar mass is determined.
The result represents an observationally determined orbit distribution for galaxies in the nearby universe after sample corrections are applied to ensure a volume-average representation. To quantify morphological properties, the 3D density distribution of each component, constructed using orbits from the model, is projected onto the observational plane with an edge-on view (Zhu et al. 2018a). The combination of luminosity fractions and morphological properties of these four dynamical components provides a comprehensive description of galaxy structures, enabling direct comparisons with many galaxies in cosmological simulations.
2.1 IllustrisTNG simulations and TNG50
Among the various cosmological hydrodynamical simulations on galaxy formation and evolution, IllustrisTNG simulations (hereafter TNG, Springel et al. 2018; Marinacci et al. 2018; Naiman et al. 2018; Pillepich et al. 2018a; Nelson et al. 2018) have emerged as a major success in replicating a wide range of observational findings (Nelson et al. 2019). These accomplishments encompass several key areas, including the galaxy mass-size relation at 0 < z < 2 (Genel et al. 2018), the dimensions and heights of gaseous and stellar disks (Pillepich et al. 2019), galaxy colors, the stellar mass-age/metallicity relationship at z ~ 0, which are consistent with SDSS results (Nelson et al. 2018), resolved star formation in star-forming galaxies (Nelson et al. 2021), and the ability to accurately model the characteristics of stellar orbit distributions in the CALIFA survey (Xu et al. 2019) and the kinematics of early-type galaxies, in line with ATLAS-3D, MaNGA, and SAMI data (Pulsoni et al. 2020).
We refer the reader to the methodological papers by Weinberger et al. 2017; Pillepich et al. 2018b for a complete understanding of the numerical and physical models implemented in the TNG simulations. The suite comprises three flagship simulations: TNG50, TNG100, and TNG300, each corresponding to different cosmological volumes of (50 Mpc)3, (100 Mpc)3, and (300 Mpc)3, with associated stellar particle resolutions of 8.5 × 104 M⊙, 1.4 × 106 M⊙, and 1.1 × 107 M⊙, respectively (Nelson et al. 2019).
The luminosity fractions of the cold, warm, and hot components in TNG100 galaxies closely align with those of CALIFA galaxies within the stellar mass range of M* = 109.7−1011.4 M⊙ (Xu et al. 2019). However, the enhanced resolution of TNG50 significantly improves its capacity to resolve galactic structures, particularly within the inner 1 kpc region and the thin disk.
 |
Fig. 1 Stellar mass versus Re. CALIFA (left lower), TNG50 (middle) and TNG100 (right) samples are shown for comparison. The galaxies are color-coded by their sSFR, as indicated by the colorbar. The upper panels show the whole sample of central galaxies in the TNG50 and TNG100 selected from the mass-size plane. The bottom panels show samples that matched the CALIFA in mass, size, and sSFR. |
2.2 Galaxy samples selected from TNG100 and TNG50
We selected simulated galaxies based on their galaxy stellar mass, and the comparison between observations and simulations mainly concentrates on stars within one effective radius Re of galaxies, aligning with the typical data coverage of most CALIFA galaxies. The Re of CALIFA galaxies is defined as the half-light semi-major axis measured from the r-band images. For the TNG galaxies, we define galaxy stellar mass as the total mass of all stars that are gravitationally bound to a galaxy according to the Subfind algorithm. We adopt a similar approach as that of CALIFA galaxies to calculate Re by first randomly projecting the particles to the 2D observational plane and then selecting the 2D elliptical radius that covers half of the total r-band luminosity.
To mirror the characteristics of the CALIFA sample in Zhu et al. (2018c), our selection criteria encompass galaxies at z = 0 (snapshot 99) that (1) are central galaxies; (2) are not in the midst of a merger event; (3) possess stellar masses within the range of M* ∈ [109, 1012] M⊙ for TNG50 and M* ∈ [109.7, 1012] M⊙ for TNG100; (4) Re > 1 kpc for TNG50 and Re > 2 kpc for TNG100. We include lower-mass galaxies from TNG50 with their structures well-resolved with higher-mass and spatial resolution. The TNG50 sample we select covers the mass range of the full sample of the CALIFA galaxies. Consequently, our analysis encompasses 1838 galaxies from TNG50 and 5356 galaxies from TNG100, spanning various morphological types. For a fair comparison, we further compose a sample from TNG50 and TNG100 to match the CALIFA galaxies in M*, Re, and specific star formation rate (sSFR). We take the three TNG50 counterparts and five TNG100 counterparts for each CALIFA galaxy with the smallest differences in M*, Re and SSFR (only galaxies with M* ≥ 109.7 M⊙ are included for TNG100). This results in 281 TNG50 galaxies and 891 TNG100 galaxies selected out; a large fraction of them are selected more than once; we count them repeatedly to keep the whole sample representative of CALIFA.
In Fig. 1, we present the CALIFA, TNG50, and TNG100 samples in the space of stellar mass vs. Re, color-coded by the sSFR. The galaxies from CALIFA and TNG50 show broad consistency in the distribution of mass, size, and sSFR. The passive population in TNG100 with sSFR < 12.5 does not exist in the CALIFA sample. There are a limited number of galaxies with stellar masses M* ≥ 1011 M⊙ in TNG50, which potentially might introduce some statistical biases.
Within the framework of this study, we specifically compared galactic structures in the CALIFA, TNG100, and TNG50 galaxies, including the luminosity fractions and morphological properties of each orbital component. In addition, we traced the formation of these structures using the TNG50 simulation.
 |
Fig. 2 Stellar orbit distribution of TNG50 galaxy. The orbits are represented as the probability density distribution in the phase space of circularity λz vs. radius r. On the left, we use the λz and r calculated from instantaneous positions and velocities of the stellar particles. On the right, we use the orbital λz and r obtained through a phase-space averaging approach, where particles with similar energy and angular momentum are grouped. Dashed lines are used to demarcate the boundaries separating the cold (λz > 0.8), warm (0.25 < λz < 0.8), hot (|λz| < 0.25), and counter-rotating (CR) (λz < −0.25) components based on circularity. |
3 Methodology
3.1 Orbital structure decomposition
The stellar orbit distributions of CALIFA galaxies, as determined through the orbit-superposition method, are described as the probability density distribution of the stellar orbits in the phase space of the time-averaged radius r versus the circularity λz. In this context, λz≡Jz/Jmax(Eb) of an orbit represents the angular momentum around the short axis Jz normalized by the maximum angular momentum achievable by a circular orbit with the same binding energy, denoted as Jmax(Eb). Both r and Jz of an orbit are average values of a sample of particles sampled with an equal time step along the orbital trajectory. From a simulated galaxy, the 6D phase-space information of stellar particles provides us with instantaneous data at a given snapshot. However, it is crucial to note that particles moving in a specific orbit do not conserve their radius and also angular momentum in triaxial systems. To directly compare with the output of the orbit-superposition model, we employ an approximate method to calculate r and λz for the orbits on which the stellar particles move. We achieve this through phase-space averaging, as follows: we categorize all particles within a simulated galaxy into bins within a 3D grid defined by angular momentum Jz, total angular momentum J, and bounding energy Eb. This categorization is made under the assumption that particles occupying the same bin follow similar orbits, albeit in a different phase space. We then compute the average values of r and λz for the particles within each bin, considering these values as the orbital r and λz of these particles.
In Fig. 2, we present the stellar orbit distribution of a TNG50 galaxy. The left panel shows the instantaneous r versus circularity λz, while the right panel displays the phase-space-averaged r versus circularity λz. In principle, box orbits exhibit circularity λz ~ 0, and particles sampled from a box orbit can encompass a wide range of instantaneous λz, extending even to λz ~ 1, Consequently, these particles may introduce contamination in the cold disk component if using the instantaneous λz. When considering the phase-space-averaged λz, the distribution of particles from box orbits narrows more closely around zero, although not precisely at λz = 0. This reduces the contamination of box orbit particles to the dynamically cold component.
Using the stellar orbit distribution based on phase-space averaged λz, we classify each galaxy into four distinct dynamical components: cold (λz ≥ 0.8), warm (0.25 ≤ λz ≤ 0.8), hot (|λz| ≤ 0.25), and counter-rotating (CR) components (λz ≤ −0.25). For a direct comparison with the CALIFA galaxies, we restrict our analysis to particles within Re, which aligns with the spatial coverage of the CALIFA data.
The stellar orbit using phase-space-averaged r and λz is shown to work well in representing cold, warm, and hot components similar to those using time-averaged values (Zhu et al. 2022a, 2018c). In addition, when evaluating the performance of the orbit superposition model against simulations, the ground truth of the simulations is described in the phase-space-averaged r and λz, and the luminosity fractions of various components derived from the orbit superposition model are consistent with the ground truth (Zhu et al. 2018b,c). Therefore, we think it is fair to compare the phase-space-averaged stellar orbit distributions of simulated galaxies with those of CALIFA galaxies obtained from the orbit superposition model.
The cold and hot +CR components are the main ingredients of the morphologically defined thin disk and bulge, respectively, while the warm component could be a mixture of thick disk and pseudo-bulge (Zhu et al. 2018a). Our definition of cold, warm, and hot +CR components within 1 Re is statistically consistent with the cold disk, warm disk, and bulge identified by the automated Gaussian Mixture Models (auto-GMM in Du et al. 2019), while the hot + CR component in the outer regions roughly corresponds to their halo. The bar or pseudobulge is not well separated in Du et al. (2019) and may be included mostly in the warm disk component.
3.2 Description of morphology
In the case of CALIFA galaxies, the 3D density distribution of each component is reconstructed using particles sampled from the corresponding orbits; subsequently, these distributions are projected in an edge-on fashion onto the 2D observational plane. In line with this approach, we reconstruct the edge-on surface brightness of each component using the same method for the TNG galaxies, with one case shown in Fig. 3. We then describe the morphology of each component using two key parameters: intrinsic flattening qRe and the Sérsic index n, obtained precisely in the same way as defined for the CALIFA galaxies in Zhu et al. (2018a).
The qRe of each component is calculated using only the stellar particles within r < Re:
![$\[q_{R_e}=\sqrt{\left(\sum_i L_i z_i^2\right) /\left(\sum_i L_i x_i^2\right)},\]$](/articles/aa/full_html/2025/07/aa51292-24/aa51292-24-eq1.png) (1)
(1)
where Li is the r-band luminosity, xi and zi are particle positions along the long and short axis of that component, respectively.
to the projected edge-on surface brightness (SB) along the major axis of each component, with two free parameters, the effective surface density Σe and Sérsic index n. As shown in Fig. 3, our Sérsic profile fittings align closely with the simulated profile, demonstrating a good match.
 |
Fig. 3 Illustrative example of morphology of various orbital components. The panels from left to right represent the entire galaxy, followed by the cold, warm, and hot components, respectively. In the top panel, we observe the edge-on surface brightness, while the bottom panel exhibits the surface brightness along the major axis. The latter is given in red and is fitted by a Sérsic profile (black). |
3.3 In situ and ex situ stars
In the TNG simulations, the identification of halos, subhalos, and fundamental galaxy properties is based on the Friends-of-Friends (FoF) and SUBFIND algorithms (Springel et al. 2001; Dolag et al. 2009). To comprehensively trace the histories of galaxies in the simulations, we employ merger trees constructed by the SUBLINK-GAL code, primarily based on the baryonic components of subhaloes (Rodriguez-Gomez et al. 2015). In this algorithm, each galaxy is assigned a unique descendant. It allows us to identify, for each galaxy, its “mergers” – that is, secondary galaxies with well-defined “infall” times that eventually merge with it and do not exist as individually identified SUBFIND objects after the “coalescence.” Additionally, for any given galaxy at a specific time, we can also identify its “satellites,” which are galaxies with well-defined “infall” times or orbits that orbit around it, potentially merging in the future.
Thanks to the merger trees, we can distinguish between two categories of stars: in situ and ex situ stars (Rodriguez-Gomez et al. 2019; Pillepich et al. 2018b). Stars in a galaxy at z = 0 are classified as in situ if they originated from a progenitor belonging to the galaxy’s primary progenitor branch. In contrast, stars are labeled ex situ if they form outside the galaxy and subsequently accreted. Ex situ stars are predominantly composed of stellar particles stripped from satellites and accreted into the galaxy. These stars are primarily the result of mergers with other objects that have already merged at the time of examination. However, a portion of ex situ stars may also arise from the stripping of orbiting satellites that have not yet been destroyed.
Throughout the paper, we define the merger mass ratio M*,sat/M*,main,z=0 by the stellar mass of the satellite at its peak over the stellar mass of the main progenitor at z = 0, and we define mergers with mass ratios of > 1:3, 1:3–1:10, and <1 : 10 as major, minor, and mini mergers, respectively. This suggests that significant mergers take place at a later stage, resulting in the influx of a substantial number of ex situ stars. These mergers strongly influence the pre-existing disks, while earlier mergers, which occur at a formative stage, have minimal impact on the disks that develop subsequently.
3.4 The circularity of in situ stars at birth
In the TNG50 simulation, we can determine the circularity of in situ stars at the time of their formation. To achieve this, we rely on the “ParticleIDs” catalog, which provides a unique ID for each star or wind particle and remains constant throughout the simulation. For each in situ stellar particle, we backtrack its formation by using the “ParticleIDs.” We pinpoint the snapshot in which it first appears as a star and subsequently calculate its phase-space-averaged circularity λz at this specific snapshot, considering this value as the particle’s orbital circularity at birth.
Note that we did not manage to identify the birth snapshot for all in situ particles. This inability to pinpoint the exact birth snapshot can be attributed to the intricacies of the SUBFIND algorithm. However, the results are not significantly affected by this limitation, as the number of particles for which we cannot determine the birth snapshot is not more than 1% of the total in situ stars.
 |
Fig. 4 Comparison of luminosity fractions of four orbital components at z ~ 0. All samples shown in Fig. 1 are included. The trend across the four panels each represents the luminosity fraction of the cold, warm, hot, and CR components as functions of stellar mass. Each red solid curves represent the CALIFA galaxies from Zhu et al. (2018c), and the associated error bars represent the 1σ uncertainties. The black and blue curves represent the mean values of luminosity fraction as a function of stellar mass for TNG50 and TNG100 galaxies, respectively. The solid lines are for the whole sample and the dashed lines for the sample matched CALIFA in mass, size, and sSFR. The shaded areas represent the corresponding 1σ scatters, indicating that 68% of the galaxies fall within these regions. Both TNG50 and TNG100 broadly replicate the luminosity fractions of the four components and their dependence on stellar mass, as observed in the CALIFA galaxies. |
4 Comparison between observations and simulations
4.1 Luminosity fractions of four orbital components
With the orbital decomposition, we can directly compare the internal orbital structures of observed galaxies to their simulated counterparts. In Fig. 4, we show the luminosity fractions of the cold, warm, hot, and CR components as functions of stellar mass for the TNG50, TNG100, and CALIFA galaxies. The luminosity fractions of different orbital components from CALIFA galaxies are also consistent with those obtained from SAMI (Santucci et al. 2022) and MaNGA (Jin et al. 2020) galaxies that we do not show here. For TNG50 and TNG100 galaxies, we show the results from the whole sample and the sample rigorously matched to CALIFA galaxies in mass, size, and sSFR: there is no noticeable difference between the two samples.
The luminosity fractions of the four components and their dependence on stellar mass exhibit broad consistency among TNG50, TNG100, and CALIFA, particularly within the intermediate mass range of M* ∈ [1010, 1011] M⊙. In both TNG and CALIFA galaxies, the luminosity fraction of the cold component peaks at M* ~ 1–2 × 1010 M⊙, and decreases at lower and higher-mass ranges, with the fractions of the hot and CR components increasing. However, the luminosity fraction of the warm component remains largely unaffected, remaining relatively constant in galaxies with stellar masses M* ≲ 1011 M⊙ but declining in the most massive galaxies. The consensus among the three datasets suggests that: (1) the TNG model effectively replicates the kinematics of actual galaxies; and (2) the kinematics portrayed by the TNG model remain consistent across varying resolutions, indicating resilience to resolution effects.
However, there are some noticeable differences between CALIFA and TNG galaxies at the low and high ends of the mass range. In galaxies with M* ≤ 1010 M⊙, the luminosity fraction of the cold component (fcold) is slightly higher in TNG50 than in CALIFA (0.25 in TNG50 vs. 0.19 in CALIFA), while fhot and fCR are slightly lower. It is important to note that the CALIFA sample is not complete and the data quality is relatively low at M* < 109.7 M⊙, due to the limited spectral resolution, which could contribute to this offset.
At the high-mass end, with M* ≥ 2 × 1011 M⊙, TNG50 and TNG100 galaxies exhibit lower fractions of the hot component and higher fractions of the warm components compared to CALIFA galaxies (fhot: 0.34 in TNG vs. 0.50 in CALIFA; fwarm: 0.43/0.37 in TNG50/100 vs. 0.27 in CALIFA). This discrepancy might be partly caused by the approximations involved in obtaining circularity λz by phase-space averaging, as described in Section 3. Massive elliptical galaxies are dominated by box orbits with λz ~ 0, and their instantaneous λz have a wide distribution. Phase-space averaging can somewhat narrow the λz distribution, but it may still categorize some particles on dynamically hot orbits as warm or CR components due to method imperfections. These biases in classifying hot, warm, and CR orbits may be present in all galaxies but are most pronounced in the most massive galaxies dominated by hot orbits.
The variation of orbit components shown above is consistent with the findings reported in Liang et al. (2024) that galaxies with MW mass (M* ~1010.5 M⊙) have the thinnest disks settled. This marks the point where TNG50 galaxies undergo, on average, a morphological transformation from irregular or clumpy disk-like systems to symmetric Hubble-type systems on the main sequence at z ~ 1 (Varma et al. 2022). This transformation results in an increase in density within the central region of 1 kpc, mainly compose of hot orbits due to the central truncation of the dynamically cold disk (Du et al. 2020).
 |
Fig. 5 Intrinsic flattening of samples as functions of stellar mass M*. The three columns, from left to right, represent the cold, warm, and hot components, respectively. Line styles and colors are same as Fig. 4. |
4.2 Morphology of four orbital components
We further compared the morphology of the orbital components between the TNG50, TNG100, and CALIFA galaxies. As described in Section 3, we defined two parameters to describe the morphology: the intrinsic flattening qRe calculated within Re and the Sérsic index n. Both parameters were calculated for the TNG galaxies exactly the same way as for the CALIFA galaxies (Zhu et al. 2018a).
4.2.1 Intrinsic flattening
In Fig. 5, we show the intrinsic flattening qRe of the cold, warm, and hot+CR components as functions of stellar mass for TNG50, TNG100, and CALIFA galaxies. Generally, the dynamically hotter components appear to be rounder, as indicated by higher values of qRe, compared to the cold component. This trend is observed in both CALIFA and TNG galaxies, and it is expected from the correlation of galactic dynamics and morphology (Zhu et al. 2018c). For TNG50 and TNG100, we show the results of the whole sample and the matched sample, respectively. The results of the two samples are almost identical.
In CALIFA, the intrinsic flattening qRe of the cold and warm components does not show a significant dependence on the galaxy’s stellar mass, with median values of approximately 0.3 and 0.5, respectively. However, the hot component appears to be rounder in more massive galaxies, with qRe increasing from ~0.6 for galaxies with stellar masses around M* ~109−1010 M⊙ to ~0.8 with M* ~ 1011 M⊙.
For the cold and warm components, both TNG50 and TNG100 galaxies exhibit good consistency with the CALIFA galaxies in terms of their flattening characteristics and show no significant dependence on galaxy mass. However, the hot components in TNG50 and TNG100 have qRe ~ 0.9 with no apparent dependence on the galaxy mass. This suggests that the hot components in the TNG simulations are generally rounder than the hot components in CALIFA, particularly in galaxies with stellar masses below M* < 1010 M⊙.
4.2.2 Sérsic Index
In Fig. 6, we show the Sérsic index n of the cold, warm, and hot+CR components as functions of the galaxies’ stellar mass for the TNG50, TNG100, and CALIFA galaxies.
In CALIFA galaxies, the cold component has a relatively constant Sérsic index of n ~ 0.5, throughout the stellar mass range. However, the warm and hot components are more spatially concentrated in more massive galaxies. For galaxies with M* ~109−1010 M⊙, n is ~1 for the warm and hot components, while increasing to ~2 and ~3, separately, for galaxies with M* ~ 1011 M⊙. Still, the samples matched to CALIFA galaxies show a similar trend to the whole sample of galaxies, for both TNG50 and TNG100.
In TNG50 and TNG100, the cold component shows good consistency with CALIFA galaxies, with similar Sérsic index values and no apparent dependence on stellar mass. On the other hand, both the warm and the hot components exhibit a similar trend of increasing n with galaxy stellar mass, which is consistent with CALIFA galaxies. However, the values of n for the warm and hot components in the TNG simulations are smaller than those in CALIFA galaxies. The warm and hot components in the TNG galaxies are not as centrally concentrated as those in the CALIFA galaxies, consistent with the conclusion of Du et al. (2020). Despite the morphology of CALIFA galaxies not being perfectly consistent with TNG simulations, the characteristics of the four kinematic components of observed galaxies are broadly reproduced in the simulations.
 |
Fig. 6 Sérsic index n of samples as functions of stellar mass M*. Line styles and colors are same as Fig. 5. |
5 The physical origins of different components
Given the consistency of internal structures of CALIFA and TNG50 galaxies as shown in the last section. Here we trace the formation of different orbital components, especially the dynamically hot+CR bulge component, using the TNG50 simulation.
5.1 Illustration of three typical cases
In Fig. 7, we illustrate three typical pathways of galaxy structure evolution for galaxies with different stellar masses and merger histories. As described before, we define the merger mass ratio M*,sat/M*,main,z=0 by the stellar mass of the satellite at its peak over the stellar mass of the main progenitor at z = 0, and we define mergers with mass ratios of >1:3, 1:3–1:10, and <1:10 as major, minor, and mini mergers, respectively.
In the left column, we show a low-mass galaxy M* = 5.7 × 109 M⊙ with no major mergers. This galaxy, characterized by a gas-rich environment, exhibits a stable star formation rate over cosmic time. Stars born in different periods were in different dynamical status: (1) stars born on predominantly hot orbits in the early universe (t ≲ 3 Gyr), displaying a wide distribution of λz at birth; (2) stars born in colder orbits at 3 Gyr ≲ t ≲ 8 Gyr, but still with some stars born on warm and hot orbits; (3) only in the recent universe (t ≳ 8 Gyr), stars that are overwhelmingly born on cold orbits. The present-day λz distribution of the stars at z = 0 generally conserves their λz distribution at birth. The λz distribution of the main progenitor remains largely unchanged. As a result, the dynamically hot bulge in this galaxy at z = 0 is born hot mostly in the early and intermediate universe.
In the middle column, we show a galaxy with a higher-mass M* = 1.3 × 1011 M⊙ and still without major mergers, the most massive satellite merged contributing ≤ 0.01 of the current stellar mass of the galaxy. This galaxy has a starburst in the early universe (t ~ 2 Gyr), with most stars born on cold orbits and a small fraction of stars born in warm/hot orbits; the star formation rate drops rapidly after that and it keeps star forming for a long term (2 ≲ t ≲ 8) with stars predominantly form in cold orbits; the star formation quenched at t ~ 9 Gyr in this galaxy. Despite the absence of major mergers, stars in the inner regions (r < Re) of this galaxy are gradually heated at the epoch of t ~ 5–7 Gyr, forming a dynamically warm/hot bulge. No significant mergers or external disturbances are detected during the period. The stars that have been heated are spatially concentrated in the inner regions and mostly form in the early starburst. Stars in the outer regions (Re < r < 5Re), also form later, maintain a dynamically cold disk until z = 0.
In the right column, we show a massive galaxy (M* = 2.6 × 1011 M⊙) that experienced a major merger with a mass ratio of 1:3 at cosmic time t ~ 6 Gyr. Before the major merger, most stars in this galaxy form in dynamically cold orbits. The merger dramatically reshaped the galaxy, heating all stars that form before the merger. A sudden transition in the circularity distribution occurs during the merger, affecting stars in all regions. After the merger, stars in the inner region r < Re remain hot until z = 0, while new stars reform a cold disk in the outer regions Re < r < 5Re. The cold disk form after the merger gradually gets warm over the past ~3 Gyr, probably due to gas removal and tidal heating by a cluster. One consequence of the major merger is the absence of old stars on cold orbits, and thus the stellar age distribution of the cold disk can serve as an indicator of the epoch of the last massive merger (Zhu et al. 2022b).
In summary, the dynamically hot stars within 1 Re of these galaxies have diverse origins. In low-mass galaxies without a significant merger, the hot stars at z = 0 are predominantly born on hot orbits and have largely preserved their original kinematics. In contrast, in high-mass galaxies, most stars initially form on cold orbits and later heated to hotter orbits. This heating can be attributed to secular evolution or merger events, depending on the galaxy’s merger history. Notably, secular evolution heats stars in the inner region, while major mergers create hot stars across the whole galaxy.
5.2 The dynamical heating as a function of stellar mass
In the above cases, we have seen that stars may be significantly heated after birth. We statistically analyze the dynamical heating that occurred in TNG50 central galaxies in a wide range of stellar masses by classifying them into four mass bins with intervals of M* = 109.5, 1010, 1010.5, 1011, 1011.5 M⊙. For galaxies at z = 0, we separate in situ and ex situ stars, and for in situ stars, we trace their formation history and find their orbital circularity at birth, as described in Section 3.
In Fig. 8, we show the circularity distribution of in situ and ex situ stars in present-day galaxies at z = 0, as well as the birth circularity distribution of the in situ stars, for all TNG50 central galaxies. Galaxies in different stellar mass bins are shown from left to right. The stars in the inner (r < Re) and outer regions (Re < r < 5Re) are depicted in the top and bottom panels, respectively, to show the different effects of dynamical heating on the inner and outer regions of galaxies.
For the inner regions (r < Re), stars in lower-mass galaxies (M* < 1010 M⊙) are born with a wide distribution of λz, and keep the distribution almost unchanged until z = 0. On the other hand, stars in higher-mass galaxies (M* > 1010 M⊙) are born on dynamically colder orbits with a pronounced peak at λz ~ 1; these stars undergo significant heating and become dynamically hot by z = 0, with the heating more important in more massive galaxies. In the most massive galaxies, the in situ stars at z = 0 have a circularity distribution centralized around λz ~ 0, similar to that of ex situ stars. The ex situ stars in the z = 0 galaxies are mostly dynamically hot but only contribute a significant fraction of stars in the most massive galaxies.
In the outer regions (Re < r < 5Re), in situ stars are predominantly born on dynamically cold orbits across all mass bins. These stars experience only marginal heating until z = 0. Even in the most massive galaxies, the in situ stars at z = 0 remain significantly colder than the ex situ stars.
To further understand the role of mergers in dynamical heating, for galaxies in each mass bin, we further separate them into three categories based on their merger histories: galaxies with at least one major merger with mass ratio >1:3 (27 galaxies in our sample), at least one minor merger with mass ratio 1:3–1:10 (246) or only mini mergers with a mass ratio of < 1 : 10 (1565).
In Fig. 9, we show the stars in the inner regions (r < Re) for galaxies in different stellar mass bins from left to right, and with different merger histories from top to bottom. In lower-mass galaxies, the circularity distribution of the in situ star remains almost unchanged in galaxies with quiescent merger history, while noticeably heated in galaxies with major mergers; mergers play a significant role in heating stars. In higher-mass galaxies, stars in all galaxies are substantially heated, irrespective of their merger histories. In the most massive galaxies, even galaxies that have not experienced any mergers above 1:10, the in situ stars at z = 0 are dynamically hot, with circularity distribution centered at λ ~ 0, similar to the ex situ stars. This suggests that in massive galaxies, stars in the inner Re, if not heated by mergers, are anyway heated by secular evolution. The heating processes occur universally for all galaxies in the inner regions, and thus the dynamically hot bulge in the inner Re is not a good indicator of merger history.
In Fig. 10, we show a similar figure for stars in the outer regions (Re < r < 5Re). In galaxies in all massive bins, the in situ stars in the outer regions remain dynamically cold until z = 0 if they do not experience significant mergers or only characterizemini mergers; they are only heated in galaxies that experienced massive mergers. The ex situ stars in the outer regions are also dynamically hot. The dynamically hot stars in the outer regions are mainly produced by mergers, either accreted or heated. This suggests that to understand a galaxy’s merger history, observational data should cover its outer regions.
 |
Fig. 7 Three typical cases of galaxy structure evolution. For each galaxy, we present the star formation history and its kinematics in the top three rows: (1) star formation history: the star formation rate as a function of cosmic time; (2) the birth circularity distribution within 5Re for stars forming at different cosmic epochs; (3) the present day (z = 0) circularity distribution within 5Re for stars born at different cosmic epochs. In the subsequent three rows, we show the mass assembly history of the main progenitor; (4) the red solid and dotted curves represent the baryonic and stellar mass evolution of the main progenitor over cosmic time, and the blue lines represent those of secondary galaxies that merged with the main progenitor. The vertical dashed lines indicate the time of mergers, if any; (5) circularity distribution of stars at r < Re of the main progenitor at different cosmic epochs; (6) circularity distribution of stars at Re < r < 5Re of the main progenitor. Left: in the left panel, we show a low-mass galaxy (M* = 109.76 M⊙) that has not experienced any major mergers. Stars in this galaxy form in a relatively warm state, and their circularity distribution at birth remains largely unchanged until the present day. There is no significant change in the stellar circularity distribution in the main progenitor over time. Middle: in the middle panel, we show a high-mass galaxy (M* = 1011.12 M⊙) that also lacks major mergers, with the most significant merger having a mass ratio M*,sat/M*,main,z=0 ≤ 0.01). The majority of stars in this galaxy are born in a dynamically cold state. However, stars born during the star formation peak at t ~ 2 Gyr and become dynamically warm/hot by z = 0. The circularity distribution of stars in the main progenitor within r < Re gradually transitions from dynamically cold to dynamically hot, while the stars at Re < r < 5Re remain dynamically cold. Right: in the right panel, we show a high-mass galaxy (M* = 1011.41 M⊙) that experienced a major merger with (M*,sat/M*,main,z=0 ~ 0.2). Most stars in this galaxy are born in a cold state, and stars born before the merger event are warm/hot at z = 0. The circularity distribution of stars in the main progenitor, both in the central and outer regions, has undergone dramatic changes due to the merger. |
 |
Fig. 8 Comparison of circularity distribution at z = 0 and at birth. All central galaxies in TNG50 are included. The columns from left to right represent galaxies with increasing stellar masses, and the top and bottom rows represent stellar particles in the inner Re and in the outer regions Re < r < 5Re, respectively. Within each panel, the solid black and green curve represent the present-day circularity distribution at z = 0 for in situ and ex situ stars, respectively, while the dashed black curve represents the birth circularity distribution of in situ stars. The shaded areas indicate the 1σ scatters among galaxies in each bin. Combining in situ and ex situ stars results in the overall present-day circularity distribution of stars in galaxies at z = 0. In lower-mass galaxies, the in situ stars at z = 0 maintain a circularity distribution similar to their birth conditions, with little or no significant heating across the whole galaxy. In higher-mass galaxies, the in situ stars are mostly born on cold orbits with peaking λz ~ 1. The stars in the inner Re have much lower λz at z = 0 compared to their condition at birth, indicating that significant heating occurred in the inner regions. The stars in the outer regions Re < r < 5Re have circularity distributions at z = 0 similar to those at birth. |
5.3 Quantifying the diverse origins of hot bulge
We have learned that stars of a galaxy form dynamically in distinct ways and are heated by various physical processes, depending on the galaxy’s mass and merger history. Here we focus on quantifying the physical origins of the dynamically hot component in galaxies at z = 0. We trace the formation history of each star in the dynamically hot component and characterise its origin as in situ born cold, born warm, born hot, or ex situ. Again, the birth circularity of in situ stars is found at the snapshot where the star particle first appeared.
In Fig. 11, we show the overall luminosity fraction of the hot component within Re as a function of stellar mass, for the TNG50 and CALIFA galaxies, the same as that shown in Fig. 4. We further show the luminosity fraction of the hot stars originating in situ as born cold, born warm, born hot, and ex situ. In lower-mass galaxies (M* ≲ 1010 M⊙), a significant fraction of hot stars are born hot and remain hot until today. In galaxies with M* ≳ 1010 M⊙, the fraction of stars born hot decreases, and the fraction of stars born cold/warm but heated increases with galaxy stellar mass. Only in galaxies with M* ≳ 5 × 1010 M⊙, the contribution of ex situ stars becomes more and more important. The combination of these three physical origins results in the U-shaped profile of the overall hot orbit fraction as a function of galaxy stellar mass.
We further separate galaxies into three groups based on their merger histories: those that experienced >1 : 3 major mergers, 1:10–1:3 minor mergers, and those only with <1 : 10 mini mergers, and check the origin of hot stars in both the inner (r < Re) and outer regions (Re < r < 5Re), as shown in Fig. 12. For stars in the inner regions (r < Re), the hot orbit fraction as a function of galaxy stellar mass exhibits a similar U-shaped pattern across galaxies with different merger histories. The hot orbit fraction is consistently higher in galaxies with more major mergers, primarily due to the significant contribution of hot stars directly accreted from mergers. The stars born cold but heated show a similar profile of increasing with increasing stellar mass; the inner regions of galaxies are anyway heated by secular evolution, if not by mergers.
In summary, the dynamically hot component in the inner Re of present-day galaxies has various physical origins, in terms of galaxy stellar mass and merger history. The combination of these physical processes results in the U-shaped profile of the hot orbit fraction in the inner Re as a function of stellar mass, similar to what is observed. The dynamically hot bulge in the inner Re is thus not a good indicator of the galaxy merger history.
In contrast, in the outer regions (Re < r < 5Re), galaxies with major mergers have significantly higher fractions of a hot component than those with quiescent merger histories, and the hot stars are either accreted or heated by the mergers. The dynamically hot stars in the outer regions Re < r < 5Re can be used to indicate the galaxy merger history. This is consistent with previous studies (Zhu et al. 2022a) showing that a hot inner stellar halo, defined by dynamically hot stars (λz < 0.5) at r > 3.5 kpc, is a strong indicator of galaxies’ total ex situ stellar mass.
 |
Fig. 9 Comparison of circularity distribution within Re at z = 0 and at birth. Line styles and colors are akin to the top panel of Fig. 8. Galaxies are categorized into three rows based on their merger histories. From top to bottom, they are galaxies with at least one major merger (mass ratio larger than 1:3), galaxies experienced mergers with ratios between 1:3 and 1:10, and galaxies have not experienced any mergers with a mass ratio larger than 1:10. In lower-mass galaxies, the in situ stars are born with a wide distribution of circularity; they are significantly heated in galaxies with major mergers and keep almost unchanged in galaxies with quiescent merger history. In higher-mass galaxies, the in situ stars are mostly born cold, especially in galaxies that have not experienced major mergers; all in situ stars at r < Re are significantly heated, resulting in similar circularity distributions at z = 0 irrespective of the merger history. |
5.4 The evolution of galaxy structures with redshift
A galaxy is assembled by all the stars that form and by all the dynamical processes that occur in the past. In this section, we further show how the accumulation of the physical processes we analyze causes the evolution of galaxy structures over time. We first calculate the mass fraction of the cold, warm, hot, and CR components within Re as a function of the galaxy stellar mass for all galaxies at z = 0, similar to Fig. 4, but with mass fractions instead of luminosity fractions used here to enable a direct comparison with their progenitors. Then for each galaxy, we find their main progenitor galaxy at z = 0.5, z = 1.0, and z = 2.0, and calculate the mass fraction of the four components also within Re measured at z = 0.
In Fig. 13, we show the mass fraction of cold, warm, hot+CR components as a function of stellar mass, from top to bottom, together with those in their main progenitors at different redshifts. And from left to right, we show all galaxies, galaxies with major mergers (>1:3), galaxies with minor mergers (1:10–1:3), and those without any mergers (<1:10).
In general, lower-mass galaxies at M* ≲ 2 × 1010 M⊙ are dynamically hotter in the past, with a lower fraction of cold orbits in their progenitors at higher redshift. This is consistent with the case of the low-mass galaxy we show in Section 5.1, whose stars are born hotter in the high redshift and colder in the low redshift. The stars remain as they are born in the cosmic timescale. Dynamical heating does not play a major role in these galaxies. In contrast, the higher-mass galaxies M* ≳ 2 × 1010 M⊙ are dynamically colder in the past, with a higher fraction of cold orbits in their progenitors at higher redshifts. In these massive galaxies, stars are born mostly in cold orbits in all cosmic epochs, and they become more and more heated with time, either by secular heating or mergers.
The structure evolution is different in galaxies with different merger histories, as expected. The number of galaxies with major mergers (mass ratio >1:3) that happened in a certain cosmic epoch is small, so the curves in the second column of Fig. 13 are stochastic. However, in general, galaxies in this group across all mass ranges once have higher cold-disk fractions in the past than today; they are dynamically hotter at z = 0 caused by major mergers accumulating across the lifetime. For galaxies with quiescent merger histories (mass ratio <1:10), their structure evolution is not significantly altered by mergers. Thus, the low-mass galaxies smoothly change from hot to cold, and the high-mass galaxies change from cold to hot from high to low redshift. Galaxies with minor mergers (mass ratio 1:3–1:10) experienced structure evolution between the above two groups.
The structure assembly of the entire galaxy sample statistically aligns with the group of galaxies without any mergers, albeit with a slightly different peak galaxy mass exhibiting the maximum cold orbit fraction at z = 0. This is expected in low-mass galaxies with low merger frequencies. The merger frequency is higher in higher-mass galaxies, and mergers create significant hot orbits in the most massive galaxies; however, when accumulated with lifetime, secular heating can anyway heat the disk within Re in the absence of mergers, leading to a statistically similar evolution of orbital structures in galaxies without mergers at the high-mass end. Note that we are only considering stars within Re here, if we consider all stars including those in the outer regions, the structure evolution should be different for the massive galaxies with or without mergers.
The structure evolution of massive galaxies shown here is consistent with that found from the EAGLE simulations (Santucci et al. 2024), and also with the direct observations at high redshift. The compact star-forming galaxies presenting SFR = 100–200 M⊙ yr−1 observed at high redshifts are mostly rotational-supported, and they are supposed to be the progenitors of quiescent galaxies in the local universe (Wisnioski et al. 2018; Van Dokkum et al. 2015; Barro et al. 2013, 2015). ETGs at z ~ 1 are also found to be more rotation-supported than their local counterparts (Bezanson et al. 2018; D’Eugenio et al. 2024; Stott et al. 2016; Förster Schreiber et al. 2018).
 |
Fig. 10 Comparison of circularity distribution in the outer regions at z = 0 and at birth. All panels are similar to Fig. 9, though stars at Re < r < 5Re are included in this figure. For galaxies in all mass bins, the stars in the outer regions are born cold, especially colder in galaxies with quiescent merger history in which they keep almost unchanged until z = 0; the stars are significantly heated in galaxies that have experienced more mergers. |
 |
Fig. 11 Origin of dynamically hot orbits as a function of stellar mass. All central galaxies in TNG50 are encompassed. The solid black curve depicts the overall luminosity fraction of hot orbits in galaxies at z = 0, consistent with the CALIFA galaxies from observations (red dashed). The blue, yellow, and red curves indicate the contribution from in situ stars born cold, warm, and hot, respectively. The dashed curve represents the contribution of ex situ stars. The shadow areas are the 1σ scatter of galaxies in each mass bin. |
 |
Fig. 12 Origin of dynamically hot orbits with merger history categorization. Line styles and colors are akin to Fig. 11. From left to right rows are all central galaxies in TNG50, galaxies with major mergers (mass ratio > 1 : 3), galaxies with minor mergers (mass ratio 1:3–1:10), and galaxies without any mergers with mass ratio >1:10. The stars in the inner regions (r < Re) and the outer regions (Re < r < 5Re) are shown at the top and bottom, respectively. In each panel, the solid black curve depicts the overall luminosity fraction of hot orbits in galaxies at z = 0, and the blue, yellow, and red curves indicate the contribution from in situ stars born cold, warm, and hot, respectively, the dashed curve represents the contribution of ex situ stars. The dynamically hot stars in the inner regions (r < Re) originate from a combination of different physical processes, and significant hot stars are produced in galaxies even without any mergers. In contrast, hot stars in the outer regions (Re < r < 5 Re) are primarily a product of mergers, either accreted or heated through merger processes. |
 |
Fig. 13 The evolution of galaxy orbital composition with redshift. The columns from left to right are all galaxies, galaxies with major mergers (mass ratio > 1:3), galaxies with minor mergers (mass ratios between 1:10–1:3), and galaxies with negligible mergers or no mergers (mass ratio < 1:10). The rows from top to bottom represent the mass fractions of cold, warm, hot+CR components as functions of the galaxy’s stellar mass within Re. In each panel, the solid, dashed, dash-dotted, and dotted curves represent galaxies at z = 0, and their progenitors at z = 0.5, z = 1, and z = 2, respectively. |
6 Discussion
6.1 Limitations in observations and simulations
The comparison between the stellar orbit distributions in TNG100, TNG50, and CALIFA galaxies provides valuable insights, and it is crucial to consider certain factors when inter-preting the differences. Given the resolution and scale of our samples, the most statistically robust comparison emerges within the intermediate mass range M* ∈ [1010, 1011] M⊙, where the three datasets exhibit strong consistency in the luminosity fractions of the four orbital components. The TNG model adeptly replicates the dynamics of the real universe and remains largely unaffected by resolution disparities.
In low-mass galaxies with M* ≲ 1010 M⊙, TNG50 galaxies exhibit a higher cold-disk fraction compared to CALIFA. However, it is important to note limitations in CALIFA’s kinematic maps for galaxies in this mass range. Some CALIFA galaxies have limited spatial bins in their kinematic maps, and the spectral resolution of CALIFA may not be sufficient to fully resolve the velocity dispersion of these galaxies (Falcón-Barroso et al. 2017), although the peculiar high-dispersion data point is carefully excluded (Zhu et al. 2018c). This limitation could introduce biases in the kinematic maps, potentially impacting the comparison with TNG50. Therefore, before definitive conclusions are drawn, further confirmation from IFU data with robust kinematics is necessary for low-mass galaxies.
For the most massive galaxies with M* ≳ 2 × 1011 M⊙, TNG simulations suggest more warm and fewer hot orbits compared to CALIFA. This discrepancy is attributed to the orbit classification method used in the simulations. For the simulated galaxies, we employ phase-space averaging rather than precise orbit integration to construct the circularity of orbits for stellar particles (Sect. 3.1). Although this method is effective in narrowing down the circularity distribution of particles in highly radial orbits, it is not perfect. Some particles in highly radial orbits may still exhibit relatively large λz after phase space averaging, leading to being classified as warm or CR components. The most massive galaxies, dominated by highly radial orbits, are particularly affected by this issue.
The morphologies of the cold, warm, and hot + CR components in TNG50 and TNG100 galaxies are generally consistent with those of CALIFA galaxies, except for a notable difference in the concentration of warm and hot components. This deviation is associated with a known limitation in TNG50, where the simulation struggles to accurately capture the dense inner regions of quenched spheroidal galaxies (Zanisi et al. 2021).
We find a good consistency between the CALIFA and TNG galaxies of a U-shaped profile of the hot orbit fraction as a function of stellar mass, with a minimum at M* ~ 1–2 × 1010 M⊙. This indicates that both the observations and the simulations support the diverse origins of the dynamically hot bulges in different galaxies across a wide mass range. Such U-shaped profiles are also found in EAGLE (Santucci et al. 2024). For galaxies with or without mergers, we presume a similar diverse origin of hot orbits in EAGLE.
However, it is not guaranteed that the physical origins we find in the TNG simulations all truly occur in real galaxies. The formation of dynamically hot bulges is still highly degenerate in simulations with complicated feedback models and dynamical processes. Taking MW-like galaxies (galaxies with M* ~ 5 × 1010 M⊙) as an example, the formation of dynamically hot bulges are different in different simulations. In TNG50, we find that stars are mostly born cold in MW-like galaxies, and they are heated mostly by secular evolution to form a dynamical hot bulge (like the second case in Fig. 7). In FIRE-2 with strong stellar feedback, stars form in a bursty phase at high redshift, and they remain unchanged and form the dynamically hot bulge at z = 0 (Yu et al. 2021). In Auriga, secular heating by the bar is also an important process in heating the stars and creating an in situ bulge for MW-like galaxies if no significant mergers. It is hard for us to constrain the formation of bulges further with the luminosity fractions measured from observations; the chemodynamical properties of the stars in the bulge might help.
6.2 Dynamical heating in secular evolution
We find that stars in the inner regions (r < Re) of massive galaxies with M* ≳ 1010 M⊙ are universally heated in all galaxies, irrespective of their merger histories, with small scatters, as shown in Fig. 9.
We consider secular evolution to play a dominant role in producing dynamically hot bulges in massive galaxies that do not experience massive mergers with a mass ratio >1 : 10. The merger mass ratio is defined by the stellar mass of the two progenitor galaxies. We might miss some mergers with dark galaxies (with very few or no stars) or galaxy interactions, which can also heat the stellar disk of the main progenitor galaxy. However, heating by mergers should have a stronger or at least similar impact on the outer disk (see Sect. 5.1). However, the outer disks of these galaxies remain cold, as shown in Fig. 10. Such mergers with dark galaxies should not be a major reason for the heating of the inner regions either. For similar reasons, interactions with other galaxies, such as fly-by, cannot be a major reason either.
Such secular evolution is found for the formation of massive quiescent galaxies in TNG50 (Park et al. 2022); half of such galaxies at z = 0 are rapidly quenched at higher redshift while still disk-like, and they become more elliptical mostly by disk heating but still maintain some degree of rotation at z = 0. This is consistent with what we find that only the inner regions of galaxies are significantly heated by secular evolution, not the outer regions. Park et al. (2022) also find that quenching and morphological transformation are largely decoupled in these galaxies; the morphological transformation appears to be not directly correlated with the feedback processes.
In our analysis, secular evolution has occurred in almost all massive galaxies without major mergers, irrespective of their star formation history. In Fig. 14, we show all massive galaxies (M* ≥ 1010.5) that have only experienced mini mergers with the merger mass ratio <1:10. We take the luminosity fraction of hot orbits born cold to represent stars heated by secular evolution fhot,secular–heated because mergers do not play a significant role in heating the cold orbits in these galaxies. As shown in Fig. 14, the luminosity fraction of stars heated by secular evolution fhot,secular–heated is correlated with the quench time of the galaxy, with the Pearson’s correlation coefficient r = −0.726, stronger than the correlation between fhot,secular–heated and the age of the stars that have been heated. Although some star-forming galaxies have a high fraction of stars heated through secular evolution, the disks of early quenched galaxies are more inclined to be heated. One possible explanation is that the rapid depletion of gas by supermassive black holes (SMBHs) (Varma et al. 2022) in the central region reduces the stability of the stellar disk, making it more susceptible to bar heating (Grand et al. 2016) or interactions with flyby galaxies. Furthermore, Walters et al. (2021) suggests that the accretion history of SMBHs can indicate rapid core growth: galaxies with higher SMBH accretion rates exhibit faster increases in core density. The processes of quenching and disk heating might be decoupled, although the timing of quenching can influence subsequent transformations.
The heating by secular evolution might be correlated with the onset of bars in the simulation, caused by either internal instability or external interactions. There is a high fraction of barred galaxies in massive galaxies of TNG and EAGLE, which could be as high as fbar ~ 70% in galaxies with M* ~ 1011 M⊙ (Roshan et al. 2021), although it could be much lower (with fbar ~ 30%) with different selection criteria (Zhao et al. 2020). Some barred galaxies undergo episodes of bar creation, destruction, and regeneration in cosmological simulations (Cavanagh et al. 2022), thus the bar heating might be even more common than the fraction of barred galaxies found at z = 0. Bars expel angular momentum to dark matter in resonances (Athanassoula 2005), as well as contribute to the development of boxy/peanut-shaped bulges (Athanassoula 2016; Anderson et al. 2024). The latest study in Lu et al. (2025) shows that TNG produces bars reasonably well, though there may be somewhat more numerous short bars in TNG50 than observed (see also Frankel et al. 2022). It is noticed that the growth of bars drives the decrease of the overall rotation of disk galaxies, which partially contributes to the dynamical heating in the secular evolution in our study.
Due to the limited resolution of the simulations and different mass resolutions of stellar and dark matter particles, stars in simulation could be spuriously heated by numerical reasons Ludlow et al. (2023). In our analysis, hot stars in the low-mass galaxies are mostly born hot, and spurious heating should not be a major factor in their origins. But stars in massive galaxies are mostly born cold and heated later. To check the importance of spurious heating, we still focus on massive galaxies with M* ≳ 3 × 1010 M⊙ with extremely clear merger histories that have only experienced mergers with the ratio <1:10; mergers do not play a significant role in heating, but their inner regions are still gradually heated.
According to the analysis in Ludlow et al. (2023), spurious heating mainly takes place in the galaxy center and mainly influences galaxies in low-mass halos. Above a halo mass of a few ×1011 M⊙ the global galaxy structure and kinematic quantities within Re are largely unbiased by spurious heating. Since spurious heating becomes insignificant only when the number of enclosed particles reaches a minimum threshold, most TNG50 galaxies with M* ≳ 1010.5 M⊙ (halo mass > 1012 M⊙) should be safe at the radius enclosing 25 percent of the stellar mass (R25). We compare the prevalence of heating within r < R25 and R25 < r < Re in galaxies with M* ≳ 1010.5 M⊙ that have experienced only minor or no mergers (mass ratio <1:10). As shown in Fig. 15, the fraction of hot stars forming in cold regions is similar for r < R25 and R25 < r < Re. Although quantifying the contribution of spurious heating to the heating of stars in these regions remains challenging, it is unlikely that it is the dominant process.
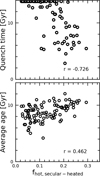 |
Fig. 14 Influence of starforming history on secular heating. The two panels are luminosity fraction of hot orbits heated by secular evolution fhot,secular–heated vs. the cosmic time when the galaxy quenched (upper panel), and vs. the average stellar age of this group of stars (lower panel). All TNG50 massive galaxies (stellar mass M* ≥ 1010.5 M⊙) with quiescent histories (merger ratio of <1:10) are included. For galaxies that are still with star formation at z = 0, we set quench time to be the age of the universe (13.8 Gyr). The Pearson correlation coefficients of the two panels are labeled. Galaxies quenched at an earlier stage are more significantly heated by secular processes, while the average ages of their stars exhibit a weaker correlation. |
7 Conclusions
In this study, we select a comparative sample of galaxies from the IllustrisTNG simulations (TNG50 and TNG100) that is akin to the CALIFA sample, which in turn comprises 260 field galaxies in the local universe, with a stellar mass range of M* ∈ [109, 1012] M⊙. As shown in Sect. 2.1, the simulated samples encompass central galaxies at z = 0, with stellar mass ranging M* ∈ [109.7, 1012] M⊙ for TNG100 and M* ∈ [109, 1012] M⊙ for TNG50. We begin by decomposing the simulated galaxies into four stellar orbital components – cold, warm, hot, and counter-rotating components – based on the stellar circularity distribution of each galaxy, in a way comparable, but not identical, to what is done for CALIFA galaxies with the orbit-superposition method in Zhu et al. (2018c). We can hence directly compare the luminosity fractions and morphological properties of each orbital component in CALIFA and TNG galaxies to assess the realism of the simulated galaxies and to gain insights from the simulations about the origin of such components.
Our analysis reveals a broad consistency between the galaxies observed in CALIFA and those simulated within TNG (see Figs. 4–6). Such an agreement supports the usage of the TNG50 output to trace the stars in the present-day galaxies back to their circularity at birth and to quantify the physical origins of stars in different components; hence, statistically. In this paper, we focus especially on the dynamically hot bulge in the present-day galaxies.
The direct comparison between CALIFA and the TNG50/TNG100 galaxies reveals several key findings:
Both TNG100 and TNG50 reproduce the typical, that is average luminosity fractions of the cold, warm, hot, and counter-rotating components seen in CALIFA galaxies across the stellar mass range of M* = 109−1012 M⊙ (Fig. 4). They have a maximum (minimum) cold (hot) orbit fraction at the stellar mass M* = 1–2 × 1010 M⊙, whereby the cold orbit fraction decreases and the hot orbit fraction increases in galaxies with lower and higher-mass. Despite the different underlying resolutions, the TNG100 and TNG50 simulations demonstrate notable consistency with each other;
TNG100 and TNG50 galaxies broadly reproduce the morphological properties of each component found in the CALIFA galaxies (Fig. 5). The intrinsic flattening within Re remains nearly constant for each component, with values ~0.3, 0.5, 0.9 for the cold, warm, and hot components, respectively, in both CALIFA and TNG galaxies. However, it should be noted that the hot components in TNG galaxies do not exhibit the systematic flattening seen in lower-mass (M* ≲ 1010 M⊙) CALIFA galaxies;
The Sérsic index of the cold components can be less than 1 for all galaxies, while those of the warm and hot components increase from low to high-mass galaxies (Fig. 6). However, the Sérsic indices of warm and hot components in TNG galaxies are systematically lower than those in CALIFA, that is, the dynamically warm and hot components in TNG galaxies are not compact enough compared to observations.
By tracing back the formation histories of galaxies in TNG50, we find the following.
Stars on dynamically hot orbits within the inner Re exhibit varied origins depending on the stellar masses and merger histories of galaxies. In contrast, stars in outer regions (r > Re) are predominantly born on cold orbits and are subsequently heated by mergers. One direct consequence is that the hot orbit fraction in the inner Re of current galaxies does not strongly correlate with their merger histories, while the hot orbit fraction in the outer regions serves as a reliable indicator of merger history, consistent with previous studies (Zhu et al. 2022a; Du et al. 2021);
There are three main regimes and physical origins contributing to the hot orbits in the inner Re of galaxies (Fig. 7): (1) in the lower-mass galaxies (109 < M* ≲ 1010 M⊙) without significant mergers, hot stars are primarily born on hot orbits: stars in the inner Re are born with a wide distribution of λz, and generally preserve their λz distribution until z = 0; (2) in the higher-mass galaxies (M* ≳ 1010 M⊙) without significant mergers, stars are mainly born on cold orbits but undergo prolonged secular heating over cosmic time; (3) mergers significantly increase the hot orbit fraction across all studied mass ranges through the heating of previously cold disks, the accretion of stars from the merging galaxy, and triggering star formation in dynamically hot orbits during the mergers if gas-rich;
The combination of the three physical origins effectively explains the peak in the cold orbit fraction and the dip in the hot orbit fraction in galaxies with M* ~ 1–2 × 1010 M⊙. In lower-mass galaxies, the increase in hot orbit fraction is due to a higher proportion of stars born on hot orbits. In higher-mass galaxies, the rise in the hot orbit fraction results from increased heating through secular evolution or mergers, along with a higher fraction of ex situ stars that are mostly in dynamically hot orbits;
Secular heating plays a statistically important role in creating dynamically hot stars in the inner Re for massive galaxies (M* ≳ 1010 M⊙). For these galaxies with quiescent merger histories, all stars are born on cold orbits but are significantly heated until z = 0, although the circularity λz distribution is not centered exactly at λz = 0, slightly different from the resulting λz distribution from major mergers. Massive galaxies are mostly born cold and are commonly heated by a long-term secular process, consistent with the early onset of bar, as observed by JWST in galaxies at z > 1 (Guo et al. 2023; Tsukui et al. 2024; Le Conte et al. 2024).
In conclusion, according to the TNG simulations, the assembly histories of orbital structures differ markedly in low- and high-mass galaxies. Lower-mass galaxies are predominantly hot in the past and have become more disk-dominated at lower redshifts. In contrast, massive galaxies have been statistically more disk-dominated and rotation-supported in the past, aligning with observational results (Kartaltepe et al. 2023; Bezanson et al. 2018; D’Eugenio et al. 2024).
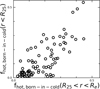 |
Fig. 15 Luminosity fractions of hot stars with cold origins at different radius. We show hereby R25<r<Re (x-axis) vs. r<R25 (y-axis), for the massive galaxies (stellar mass M* ≥ 1010.5 M⊙) with quiescent histories (merger ratio of <1:10). The sample is same as Fig. 14. Secular heating exerts a similar effect on orbits for R25<r<Re and r<R25, indicating that spurious heating does not play a major role. |
Acknowledgements
This work is supported by the Max-Planck Partner’s group led by L.Z. and A.P. L.Z. acknowledges the support of the CAS Project for Young Scientists in Basic Research under grant No. YSBR-062 and the National Key R&D Program of China No. 2022YFF0503403. M.D. acknowledges the support by the Fundamental Research Funds for the Central Universities (No. 20720230015), the Natural Science Foundation of Xiamen, China (No. 3502Z202372006), and the Science Fund for Creative Research Groups of the National Natural Science Foundation (NSFC) of China (No. 12221003). J.F-B acknowledges the support from PID2022-140869NB-100 granted from the Spanish Ministry of Science and Innovation.
References
- Anderson, S. R., Gough-Kelly, S., Debattista, V. P., et al. 2024, MNRAS, 527, 2919 [Google Scholar]
- Athanassoula, E. 2005, Ann. N. Y. Acad. Sci., 1045, 168 [Google Scholar]
- Athanassoula, E. 2016, in Galactic Bulges (Springer), 391 [Google Scholar]
- Aumer, M., Binney, J., & Schönrich, R. 2016, MNRAS, 462, 1697 [NASA ADS] [CrossRef] [Google Scholar]
- Barro, G., Faber, S., Pérez-González, P. G., et al. 2013, ApJ, 765, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Barro, G., Trump, J., Koo, D. C., et al. 2015, in American Astronomical Society Meeting Abstracts #225, 111 [Google Scholar]
- Belokurov, V., Erkal, D., Evans, N. W., Koposov, S. E., & Deason, A. J. 2018, MNRAS, 478, 611 [Google Scholar]
- Bezanson, R., van der Wel, A., Pacifici, C., et al. 2018, ApJ, 858, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Bird, J. C., Kazantzidis, S., Weinberg, D. H., et al. 2013, ApJ, 773, 43 [Google Scholar]
- Bournaud, F., & Combes, F. 2002, A&A, 392, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bournaud, F., Combes, F., & Semelin, B. 2005, MNRAS, 364, L18 [Google Scholar]
- Bundy, K., Bershady, M. A., Law, D. R., et al. 2014, ApJ, 798, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2016, ARA&A, 54, 597 [Google Scholar]
- Cavanagh, M. K., Bekki, K., Groves, B. A., & Pfeffer, J. 2022, MNRAS, 510, 5164 [Google Scholar]
- Croom, S. M., Lawrence, J. S., Bland-Hawthorn, J., et al. 2012, MNRAS, 421, 872 [NASA ADS] [Google Scholar]
- Davies, R. L., & Illingworth, G. 1983, ApJ, 266, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. L., Kuntschner, H., Emsellem, E., et al. 2001, ApJ, 548, L33 [Google Scholar]
- Ding, Y., Zhu, L., van de Ven, G., et al. 2023, A&A, 672, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dolag, K., Borgani, S., Murante, G., & Springel, V. 2009, MNRAS, 399, 497 [Google Scholar]
- Du, M., Shen, J., Debattista, V. P., & de Lorenzo-Cáceres, A. 2017, ApJ, 836, 181 [Google Scholar]
- Du, M., Ho, L. C., Zhao, D., et al. 2019, ApJ, 884, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Du, M., Ho, L. C., Debattista, V. P., et al. 2020, ApJ, 895, 139 [CrossRef] [Google Scholar]
- Du, M., Ho, L. C., Debattista, V. P., et al. 2021, ApJ, 919, 135 [NASA ADS] [CrossRef] [Google Scholar]
- D’Eugenio, F., Pérez-González, P. G., Maiolino, R., et al. 2024, Nat. Astron., 8, 1443 [CrossRef] [Google Scholar]
- Elmegreen, B. G., Bournaud, F., & Elmegreen, D. M. 2008, ApJ, 688, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Falcón-Barroso, J., Lyubenova, M., Van De Ven, G., et al. 2017, A&A, 597, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Förster Schreiber, N. M., Wilman, D., Wisnioski, E. S., et al. 2018, The Messenger, 174, 28 [Google Scholar]
- Fragkoudi, F., Grand, R. J. J., Pakmor, R., et al. 2020, MNRAS, 494, 5936 [Google Scholar]
- Frankel, N., Pillepich, A., Rix, H.-W., et al. 2022, ApJ, 940, 61 [CrossRef] [Google Scholar]
- Genel, S., Nelson, D., Pillepich, A., et al. 2018, MNRAS, 474, 3976 [Google Scholar]
- Gómez, F. A., Grand, R. J. J., Monachesi, A., et al. 2017, MNRAS, 472, 3722 [CrossRef] [Google Scholar]
- Grand, R. J., Springel, V., Gómez, F. A., et al. 2016, MNRAS, 459, 199 [Google Scholar]
- Guo, M., Du, M., Ho, L. C., Debattista, V. P., & Zhao, D. 2020, ApJ, 888, 65 [Google Scholar]
- Guo, Y., Jogee, S., Finkelstein, S. L., et al. 2023, ApJ, 945, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [Google Scholar]
- Jenkins, A., & Binney, J. 1990, MNRAS, 245, 305 [NASA ADS] [Google Scholar]
- Jin, Y., Zhu, L., Long, R. J., et al. 2020, MNRAS, 491, 1690 [NASA ADS] [Google Scholar]
- Kartaltepe, J. S., Rose, C., Vanderhoof, B. N., et al. 2023, ApJ, 946, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Lagos, C. d. P., Stevens, A. R. H., Bower, R. G., et al. 2018, MNRAS, 473, 4956 [Google Scholar]
- Lapiner, S., Dekel, A., Freundlich, J., et al. 2023, MNRAS, 522, 4515 [NASA ADS] [CrossRef] [Google Scholar]
- Le Conte, Z. A., Gadotti, D. A., Ferreira, L., et al. 2024, MNRAS, 530, 1984 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z., Du, M., Debattista, V. P., et al. 2023, ApJ, 958, 77 [Google Scholar]
- Liang, J., Jiang, F., Mo, H., et al. 2024, MNRAS, submitted [arXiv:2403.14749] [Google Scholar]
- Lu, S., Du, M., & Debattista, V. P. 2025, A&A, 697, A236 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ludlow, A. D., Fall, S. M., Wilkinson, M. J., Schaye, J., & Obreschkow, D. 2023, MNRAS, 525, 5614 [NASA ADS] [CrossRef] [Google Scholar]
- Marinacci, F., Vogelsberger, M., Pakmor, R., et al. 2018, MNRAS, 480, 5113 [NASA ADS] [Google Scholar]
- Naiman, J. P., Pillepich, A., Springel, V., et al. 2018, MNRAS, 477, 1206 [Google Scholar]
- Nelson, D., Pillepich, A., Springel, V., et al. 2018, MNRAS, 475, 624 [Google Scholar]
- Nelson, D., Springel, V., Pillepich, A., et al. 2019, Computat. Astrophys. Cosmol., 6, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, E. J., Tacchella, S., Diemer, B., et al. 2021, MNRAS, 508, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Obreja, A., Domínguez-Tenreiro, R., Brook, C., et al. 2013, ApJ, 763, 26 [Google Scholar]
- Park, M., Tacchella, S., Nelson, E. J., et al. 2022, MNRAS, 515, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Pillepich, A., Nelson, D., Hernquist, L., et al. 2018a, MNRAS, 475, 648 [Google Scholar]
- Pillepich, A., Springel, V., Nelson, D., et al. 2018b, MNRAS, 473, 4077 [Google Scholar]
- Pillepich, A., Nelson, D., Springel, V., et al. 2019, MNRAS, 490, 3196 [Google Scholar]
- Poci, A., McDermid, R. M., Lyubenova, M., et al. 2021, A&A, 647, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pulsoni, C., Gerhard, O., Arnaboldi, M., et al. 2020, A&A, 641, A60 [EDP Sciences] [Google Scholar]
- Pulsoni, C., Gerhard, O., Arnaboldi, M., et al. 2021, A&A, 647, A95 [EDP Sciences] [Google Scholar]
- Quinn, P. J., Hernquist, L., & Fullagar, D. P. 1993, ApJ, 403, 74 [Google Scholar]
- Read, J. I., Lake, G., Agertz, O., & Debattista, V. P. 2008, MNRAS, 389, 1041 [Google Scholar]
- Rodriguez-Gomez, V., Genel, S., Vogelsberger, M., et al. 2015, MNRAS, 449, 49 [Google Scholar]
- Rodriguez-Gomez, V., Snyder, G. F., Lotz, J. M., et al. 2019, MNRAS, 483, 4140 [NASA ADS] [CrossRef] [Google Scholar]
- Roshan, M., Ghafourian, N., Kashfi, T., et al. 2021, MNRAS, 508, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S., Kennicutt, R., De Paz, A. G., et al. 2012, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santucci, G., Brough, S., van de Sande, J., et al. 2022, ApJ, 930, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Santucci, G., Lagos, C. D. P., Harborne, K. E., et al. 2024, MNRAS, 528, 2326 [Google Scholar]
- Schwarzschild, M. 1979, ApJ, 232, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Seidel, M. K., Cacho, R., Ruiz-Lara, T., et al. 2015, MNRAS, 446, 2837 [Google Scholar]
- Sotillo-Ramos, D., Pillepich, A., Donnari, M., et al. 2022, MNRAS, 516, 5404 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Tormen, G., & Kauffmann, G. 2001, MNRAS, 328, 726 [Google Scholar]
- Springel, V., Pakmor, R., Pillepich, A., et al. 2018, MNRAS, 475, 676 [Google Scholar]
- Stinson, G. S., Bovy, J., Rix, H.-W., et al. 2013, MNRAS, 436, 625 [Google Scholar]
- Stott, J. P., Swinbank, A., Johnson, H. L., et al. 2016, MNRAS, 457, 1888 [Google Scholar]
- Tahmasebzadeh, B., Zhu, L., Shen, J., Gerhard, O., & Qin, Y. 2021, MNRAS, 508, 6209 [NASA ADS] [CrossRef] [Google Scholar]
- Tahmasebzadeh, B., Zhu, L., Shen, J., Gerhard, O., & van de Ven, G. 2022, ApJ, 941, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Tahmasebzadeh, B., Zhu, L., Shen, J., et al. 2024, MNRAS, 534, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Thater, S., Jethwa, P., Tahmasebzadeh, B., et al. 2022, A&A, 667, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsukui, T., Wisnioski, E., Bland-Hawthorn, J., et al. 2024, MNRAS, 527, 8941 [Google Scholar]
- Van Den Bosch, R., Van De Ven, G., Verolme, E., Cappellari, M., & De Zeeuw, P. 2008, MNRAS, 385, 647 [Google Scholar]
- van den Bosch, R. C. E., van de Ven, G., Verolme, E. K., Cappellari, M., & de Zeeuw, P. T. 2008, MNRAS, 385, 647 [Google Scholar]
- Van Dokkum, P. G., Nelson, E. J., Franx, M., et al. 2015, ApJ, 813, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Varma, S., Huertas-Company, M., Pillepich, A., et al. 2022, MNRAS, 509, 2654 [NASA ADS] [Google Scholar]
- Walcher, C., Wisotzki, L., Bekeraité, S., et al. 2014, A&A, 569, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walters, D., Woo, J., Ellison, S. L., & Hani, M. H. 2021, MNRAS, 504, 1677 [Google Scholar]
- Weinberger, R., Springel, V., Hernquist, L., et al. 2017, MNRAS, 465, 3291 [Google Scholar]
- Wisnioski, E., Mendel, J., Schreiber, N. F., et al. 2018, ApJ, 855, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, D., Zhu, L., Grand, R., et al. 2019, MNRAS, 489, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, S., Bullock, J. S., Klein, C., et al. 2021, MNRAS, 505, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, S., Bullock, J. S., Gurvich, A. B., et al. 2023, MNRAS, 523, 6220 [NASA ADS] [CrossRef] [Google Scholar]
- Zanisi, L., Huertas-Company, M., Lanusse, F., et al. 2021, MNRAS, 501, 4359 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, D., Du, M., Ho, L. C., Debattista, V. P., & Shi, J. 2020, ApJ, 904, 170 [Google Scholar]
- Zhu, L., van de Ven, G., Méndez-Abreu, J., & Obreja, A. 2018a, MNRAS, 479, 945 [Google Scholar]
- Zhu, L., van den Bosch, R., van de Ven, G., et al. 2018b, MNRAS, 473, 3000 [Google Scholar]
- Zhu, L., Ven, G. v. d., Bosch, R. v. d., et al. 2018c, Nat. Astron., 2, 233 [Google Scholar]
- Zhu, L., Pillepich, A., van de Ven, G., et al. 2022a, A&A, 660, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhu, L., van de Ven, G., Leaman, R., et al. 2022b, A&A, 664, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Stellar mass versus Re. CALIFA (left lower), TNG50 (middle) and TNG100 (right) samples are shown for comparison. The galaxies are color-coded by their sSFR, as indicated by the colorbar. The upper panels show the whole sample of central galaxies in the TNG50 and TNG100 selected from the mass-size plane. The bottom panels show samples that matched the CALIFA in mass, size, and sSFR. |
| In the text | |
 |
Fig. 2 Stellar orbit distribution of TNG50 galaxy. The orbits are represented as the probability density distribution in the phase space of circularity λz vs. radius r. On the left, we use the λz and r calculated from instantaneous positions and velocities of the stellar particles. On the right, we use the orbital λz and r obtained through a phase-space averaging approach, where particles with similar energy and angular momentum are grouped. Dashed lines are used to demarcate the boundaries separating the cold (λz > 0.8), warm (0.25 < λz < 0.8), hot (|λz| < 0.25), and counter-rotating (CR) (λz < −0.25) components based on circularity. |
| In the text | |
 |
Fig. 3 Illustrative example of morphology of various orbital components. The panels from left to right represent the entire galaxy, followed by the cold, warm, and hot components, respectively. In the top panel, we observe the edge-on surface brightness, while the bottom panel exhibits the surface brightness along the major axis. The latter is given in red and is fitted by a Sérsic profile (black). |
| In the text | |
 |
Fig. 4 Comparison of luminosity fractions of four orbital components at z ~ 0. All samples shown in Fig. 1 are included. The trend across the four panels each represents the luminosity fraction of the cold, warm, hot, and CR components as functions of stellar mass. Each red solid curves represent the CALIFA galaxies from Zhu et al. (2018c), and the associated error bars represent the 1σ uncertainties. The black and blue curves represent the mean values of luminosity fraction as a function of stellar mass for TNG50 and TNG100 galaxies, respectively. The solid lines are for the whole sample and the dashed lines for the sample matched CALIFA in mass, size, and sSFR. The shaded areas represent the corresponding 1σ scatters, indicating that 68% of the galaxies fall within these regions. Both TNG50 and TNG100 broadly replicate the luminosity fractions of the four components and their dependence on stellar mass, as observed in the CALIFA galaxies. |
| In the text | |
 |
Fig. 5 Intrinsic flattening of samples as functions of stellar mass M*. The three columns, from left to right, represent the cold, warm, and hot components, respectively. Line styles and colors are same as Fig. 4. |
| In the text | |
 |
Fig. 6 Sérsic index n of samples as functions of stellar mass M*. Line styles and colors are same as Fig. 5. |
| In the text | |
 |
Fig. 7 Three typical cases of galaxy structure evolution. For each galaxy, we present the star formation history and its kinematics in the top three rows: (1) star formation history: the star formation rate as a function of cosmic time; (2) the birth circularity distribution within 5Re for stars forming at different cosmic epochs; (3) the present day (z = 0) circularity distribution within 5Re for stars born at different cosmic epochs. In the subsequent three rows, we show the mass assembly history of the main progenitor; (4) the red solid and dotted curves represent the baryonic and stellar mass evolution of the main progenitor over cosmic time, and the blue lines represent those of secondary galaxies that merged with the main progenitor. The vertical dashed lines indicate the time of mergers, if any; (5) circularity distribution of stars at r < Re of the main progenitor at different cosmic epochs; (6) circularity distribution of stars at Re < r < 5Re of the main progenitor. Left: in the left panel, we show a low-mass galaxy (M* = 109.76 M⊙) that has not experienced any major mergers. Stars in this galaxy form in a relatively warm state, and their circularity distribution at birth remains largely unchanged until the present day. There is no significant change in the stellar circularity distribution in the main progenitor over time. Middle: in the middle panel, we show a high-mass galaxy (M* = 1011.12 M⊙) that also lacks major mergers, with the most significant merger having a mass ratio M*,sat/M*,main,z=0 ≤ 0.01). The majority of stars in this galaxy are born in a dynamically cold state. However, stars born during the star formation peak at t ~ 2 Gyr and become dynamically warm/hot by z = 0. The circularity distribution of stars in the main progenitor within r < Re gradually transitions from dynamically cold to dynamically hot, while the stars at Re < r < 5Re remain dynamically cold. Right: in the right panel, we show a high-mass galaxy (M* = 1011.41 M⊙) that experienced a major merger with (M*,sat/M*,main,z=0 ~ 0.2). Most stars in this galaxy are born in a cold state, and stars born before the merger event are warm/hot at z = 0. The circularity distribution of stars in the main progenitor, both in the central and outer regions, has undergone dramatic changes due to the merger. |
| In the text | |
 |
Fig. 8 Comparison of circularity distribution at z = 0 and at birth. All central galaxies in TNG50 are included. The columns from left to right represent galaxies with increasing stellar masses, and the top and bottom rows represent stellar particles in the inner Re and in the outer regions Re < r < 5Re, respectively. Within each panel, the solid black and green curve represent the present-day circularity distribution at z = 0 for in situ and ex situ stars, respectively, while the dashed black curve represents the birth circularity distribution of in situ stars. The shaded areas indicate the 1σ scatters among galaxies in each bin. Combining in situ and ex situ stars results in the overall present-day circularity distribution of stars in galaxies at z = 0. In lower-mass galaxies, the in situ stars at z = 0 maintain a circularity distribution similar to their birth conditions, with little or no significant heating across the whole galaxy. In higher-mass galaxies, the in situ stars are mostly born on cold orbits with peaking λz ~ 1. The stars in the inner Re have much lower λz at z = 0 compared to their condition at birth, indicating that significant heating occurred in the inner regions. The stars in the outer regions Re < r < 5Re have circularity distributions at z = 0 similar to those at birth. |
| In the text | |
 |
Fig. 9 Comparison of circularity distribution within Re at z = 0 and at birth. Line styles and colors are akin to the top panel of Fig. 8. Galaxies are categorized into three rows based on their merger histories. From top to bottom, they are galaxies with at least one major merger (mass ratio larger than 1:3), galaxies experienced mergers with ratios between 1:3 and 1:10, and galaxies have not experienced any mergers with a mass ratio larger than 1:10. In lower-mass galaxies, the in situ stars are born with a wide distribution of circularity; they are significantly heated in galaxies with major mergers and keep almost unchanged in galaxies with quiescent merger history. In higher-mass galaxies, the in situ stars are mostly born cold, especially in galaxies that have not experienced major mergers; all in situ stars at r < Re are significantly heated, resulting in similar circularity distributions at z = 0 irrespective of the merger history. |
| In the text | |
 |
Fig. 10 Comparison of circularity distribution in the outer regions at z = 0 and at birth. All panels are similar to Fig. 9, though stars at Re < r < 5Re are included in this figure. For galaxies in all mass bins, the stars in the outer regions are born cold, especially colder in galaxies with quiescent merger history in which they keep almost unchanged until z = 0; the stars are significantly heated in galaxies that have experienced more mergers. |
| In the text | |
 |
Fig. 11 Origin of dynamically hot orbits as a function of stellar mass. All central galaxies in TNG50 are encompassed. The solid black curve depicts the overall luminosity fraction of hot orbits in galaxies at z = 0, consistent with the CALIFA galaxies from observations (red dashed). The blue, yellow, and red curves indicate the contribution from in situ stars born cold, warm, and hot, respectively. The dashed curve represents the contribution of ex situ stars. The shadow areas are the 1σ scatter of galaxies in each mass bin. |
| In the text | |
 |
Fig. 12 Origin of dynamically hot orbits with merger history categorization. Line styles and colors are akin to Fig. 11. From left to right rows are all central galaxies in TNG50, galaxies with major mergers (mass ratio > 1 : 3), galaxies with minor mergers (mass ratio 1:3–1:10), and galaxies without any mergers with mass ratio >1:10. The stars in the inner regions (r < Re) and the outer regions (Re < r < 5Re) are shown at the top and bottom, respectively. In each panel, the solid black curve depicts the overall luminosity fraction of hot orbits in galaxies at z = 0, and the blue, yellow, and red curves indicate the contribution from in situ stars born cold, warm, and hot, respectively, the dashed curve represents the contribution of ex situ stars. The dynamically hot stars in the inner regions (r < Re) originate from a combination of different physical processes, and significant hot stars are produced in galaxies even without any mergers. In contrast, hot stars in the outer regions (Re < r < 5 Re) are primarily a product of mergers, either accreted or heated through merger processes. |
| In the text | |
 |
Fig. 13 The evolution of galaxy orbital composition with redshift. The columns from left to right are all galaxies, galaxies with major mergers (mass ratio > 1:3), galaxies with minor mergers (mass ratios between 1:10–1:3), and galaxies with negligible mergers or no mergers (mass ratio < 1:10). The rows from top to bottom represent the mass fractions of cold, warm, hot+CR components as functions of the galaxy’s stellar mass within Re. In each panel, the solid, dashed, dash-dotted, and dotted curves represent galaxies at z = 0, and their progenitors at z = 0.5, z = 1, and z = 2, respectively. |
| In the text | |
 |
Fig. 14 Influence of starforming history on secular heating. The two panels are luminosity fraction of hot orbits heated by secular evolution fhot,secular–heated vs. the cosmic time when the galaxy quenched (upper panel), and vs. the average stellar age of this group of stars (lower panel). All TNG50 massive galaxies (stellar mass M* ≥ 1010.5 M⊙) with quiescent histories (merger ratio of <1:10) are included. For galaxies that are still with star formation at z = 0, we set quench time to be the age of the universe (13.8 Gyr). The Pearson correlation coefficients of the two panels are labeled. Galaxies quenched at an earlier stage are more significantly heated by secular processes, while the average ages of their stars exhibit a weaker correlation. |
| In the text | |
 |
Fig. 15 Luminosity fractions of hot stars with cold origins at different radius. We show hereby R25<r<Re (x-axis) vs. r<R25 (y-axis), for the massive galaxies (stellar mass M* ≥ 1010.5 M⊙) with quiescent histories (merger ratio of <1:10). The sample is same as Fig. 14. Secular heating exerts a similar effect on orbits for R25<r<Re and r<R25, indicating that spurious heating does not play a major role. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\[\Sigma(r)=\Sigma_e 10^{-b_n\left(\left(r / r_s\right)^{1 / n}-1\right)},\]$](/articles/aa/full_html/2025/07/aa51292-24/aa51292-24-eq2.png)