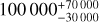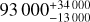EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 697 (May 2025) A&A, 697 (2025) A14 Full HTML
Euclid on Sky
Open Access
Issue
A&A
Volume 697, May 2025
Euclid on Sky
Article Number A14
Number of page(s) 16
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202451868
Published online 30 April 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Strong gravitational lensing by massive galaxies offers a plethora of applications in both cosmology and astrophysics. Some notable examples include measuring the total mass of lens galaxies within the Einstein radius and disentangling the contributions from visible and dark matter components (e.g. Auger et al. 2009). When coupled with deep spectroscopic observations, it enables the placement of constraints on the stellar initial mass function of lens galaxies (e.g. Ferreras et al. 2010; Dutton & Treu 2014; Sonnenfeld et al. 2019). Thanks to the lensing magnification, strong gravitational lensing serves as a natural telescope to study lensed sources otherwise too faint or angularly too small to be detected (e.g. Hezaveh et al. 2013), and even to map their velocity field with unprecedented spatial resolution (e.g. Paraficz et al. 2018). Studying small-scale distortions of lensed images or arcs allows us to infer the presence of low-mass dark halos either in the lens or along the line of sight up to the source redshift, and in turn to study the properties of dark matter (e.g. Vegetti et al. 2010; O’Riordan et al. 2023; Gilman et al. 2024). Moreover, when the lensed source is time-variable, such as a quasar or a supernova, strong lensing offers an independent way of measuring the expansion rate of the Universe, H0 (Refsdal 1964; Wong et al. 2020; Shajib et al. 2023; Grillo et al. 2024; Pascale et al. 2025).

Lastly, the measurement of weak lensing shear from strong lensing images has been proposed as a potential cosmological probe (Birrer et al. 2017, 2018). A minimal model for the shear that is non-degenerate with lens model parameters was derived by Fleury et al. (2021), and this quantity was shown to be measurable in mock imaging data by Hogg et al. (2023). For high-precision cosmological constraints, however, a Euclid-sized dataset of O(105) strong lenses will be required.

Galaxy-scale strong lensing events are rare, with about one object out of thousands showing lensing features (Oguri & Marshall 2010; Collett 2015). In addition, these systems are small in angular terms, spanning between tenths of an arcsecond to a few arcseconds on the sky, and the lensed images of the sources (arcs, rings, and multiple point sources) are often hidden in the glare of the foreground lensing galaxy. Because lenses are rare, compact, and low-contrast objects, they are best discovered in deep, sharp, wide-field surveys. Euclid is exactly that (Euclid Collaboration: Mellier et al. 2025), and is the focus of the present work. In fact, lensed quasi-stellar object candidates have already been proposed from Euclid observations (Cuillandre et al. 2025b).

However, even with high-quality Euclid data, finding lenses remains challenging, not only because of the intrinsic rarity of strong lensing, but also because other non-lensing objects mimic the morphology of lenses (e.g. ring galaxies, galaxy mergers, spiral galaxies, or even random alignments). So far, the best methods for discovering lenses involve various flavours of con-volutional neural networks (see Petrillo et al. 2019; Jacobs et al. 2019; Stein et al. 2022; Savary et al. 2022; Rojas et al. 2022, to cite just a few) and, more recently, transformer networks (Thuruthipilly et al. 2022; Grespan et al. 2024; González et al. 2025). These networks require training sets that match the instrumental and astrophysical properties of the data very closely. Since we do not possess enough strong lens observations to constitute a training set, they have to be simulated, and the effectiveness of simulations in emulating nature is limited.

Machine learning methods are effective at finding lenses, but they are limited in terms of purity and false-positive rates. When false-positive rates are below 1%, such methods are useful for pre-selecting candidates from parent samples of tens or even hundreds of millions of galaxies (Cañameras et al. 2024). However, as the true – and poorly known – prevalence of lenses on the plane of the sky is very low, even a 1% false-positive rate can result in samples dominated by contaminants and unconvincing candidates. This is known as the base rate fallacy. As a result, human visual inspection is almost always necessary to fine-tune the network selection, although humans themselves sometimes have difficulty deciding on the validity of a lens candidate. This is especially true for small-Einstein-radius lenses.

Human visual inspection is useful on its own as a lens finding method but is limited by the volume of data that can be inspected by a team of experts in a reasonable amount of time. However, it has the advantage that it can pick up unusual lensing configurations (e.g. Keeton et al. 2000; Orban de Xivry & Marshall 2009; Collett & Bacon 2016) that, by definition, do not appear in large numbers in simulated training sets. It is also the only way to evaluate the prevalence of lenses on the plane of the sky and therefore the expected surface density of lensing systems for a given instrument, depth, spatial resolution, and wavelength. This has been attempted a few times in the past, for example in Hubble Space Telescope imaging (e.g. Faure et al. 2008; Pawase et al. 2014; Garvin et al. 2022). Rojas et al. (2023) also evaluated the performance of visual inspection with simulated data.

In the Early Release Observations (ERO) Lens Search Experiment (ELSE), we carried out a blind visual search of galaxy-scale strong lensing systems using some of the first data from the European Space Agency (ESA) satellite Euclid (Euclid Collaboration: Scaramella et al. 2022; Euclid Collaboration: Mellier et al. 2025). We focused on the Euclid ERO imaging of the Perseus galaxy cluster (Cuillandre et al. 2025a), and the only selection criterion for the extended sources to be inspected was a magnitude cut. Our search is therefore one of the broadest visual searches carried out so far in terms of pre-selection. The goals were: (1) to evaluate the performance of the Euclid telescope at finding galaxy-scale lenses; (2) to study the prevalence of strong lenses found by humans in Euclid; (3) to test the efficiency of human experts at finding lenses; and (4) to optimise future visual inspections that will be performed on lens candidates found by the automatic pipeline in Euclid.

The humans involved in this exercise are all lensing experts but were limited in number (41 exactly). Our work therefore contrasts with more intensive citizen science searches involving much larger numbers of humans but spanning a much smaller range in terms of expertise (Marshall et al. 2015; More et al. 2016).

Finally, assuming subtraction of the lens light, Euclid is predicted to find 170000 lenses in its six-year main survey (Collett 2015). We tested that prediction in this work, with the caveat that we did not perform any subtraction of the lens light. Thus, our results represent a lower bound in this regard.

We introduce the Euclid ERO observations of the Perseus cluster in Sect. 2. We then explain the methodology of the visual inspections in Sect. 3, along with the visualisation tools used. Afterwards, we report the results from the visual inspection in Sect. 4 and present the sample of lens candidates and some initial modelling in Sect. 5. In Sect. 6 we then compare the sample against the literature and estimate the number of lenses that will be discovered in the Euclid Wide Survey (EWS). We conclude in Sect. 7.

thumbnail Fig. 1

9″.9 × 9″..9 VIS cutouts of galaxies randomly selected across different IE bins, ranging from the brightest galaxies with IE < 16 (leftmost) down to very faint systems with 24.5 < IE < 25 (rightmost). The blue arrow represents the magnitude cut used to select our parent sample.

2 Data

The Euclid ERO programme (Euclid Early Release Observations 2024) targeted the Perseus galaxy cluster, obtaining very deep data of the central region of the cluster in 0.7 deg2, in the broad optical filter IE from the visible imager (VIS) instrument (Euclid Collaboration: Cropper et al. 2025), and the three broad filters YE, JE, and HE in the near-infrared from the Near-Infrared Spectrometer and Photometer (NISP) instrument (Euclid Collaboration: Jahnke et al. 2025).

These data were collected during the Euclid performance verification phase in September 2023 (Cuillandre et al. 2025a). All Euclid science observations adhere to a reference observing sequences (ROSs; Euclid Collaboration: Scaramella et al. 2022), which consists of four dithered exposures lasting 566 seconds each in the IE filter, and four dithered exposures of 87.2 seconds each in the YE, JE, and HE filters. Four ROSs were obtained for this field, with a total integration time of 7456.0 seconds in the IE filter and 1392.2 seconds in the YE, JE, and HE filters, achieving a depth 0.75 magnitudes deeper than that of the EWS, which relies on a single ROS (Euclid Collaboration: Scaramella et al. 2022). Therefore, these exceptional data reach a point-source depth of Ie = 27.3 (Ye, Je, He = 24.9) at 10 σ, with a 0″.16 (0″.48) full width at half maximum, and a surface brightness limit of 30.1 (29.2) mag arcsec−2. We refer the reader to Cuillandre et al. (2025a) for more details on the data reduction.

The astrometrically and photometrically calibrated imaging stacks across all four Euclid bands are accompanied by catalogues for compact sources produced using the tool SourceExtractor (Bertin & Arnouts 1996) on the ‘flattened’ stack, that is, with the low spatial frequencies removed (sky background and any Galactic cirrus or nebulae). Multi-wavelength catalogues including VIS, NISP, and ground-based Canada-France-Hawaii Telescope MegaCam photometry have been provided in Cuillandre et al. (2025b). After star–galaxy separation and limiting the analysis to sources with Ie < 23, we ended up with a parent sample of 12 086 objects, which was later used in the visual classification procedure. As shown in Fig. 1, the adopted magnitude cut is justified by the fact that sources at fainter magnitudes are compact and featureless. For the experiment, cutouts in the four Euclid bands of 9″.9 × 9″.9 (i.e. 99 × 99 pixels and 33 × 33 pixels in the VIS and NISP bands, respectively) were created using the flattened stacks.

3 Method

3.1 The visualisation tools

We used the visualisation tools prepared by Acevedo Barroso et al. (2025) to carry out the visual inspection1. The tools are based on the visualisation tools used in Savary et al. (2022) and Rojas et al. (2022), but re-implemented in the Qt 6 framework with extended functionality targeting the requirements of the Euclid ERO data. The two applications correspond to a mosaic viewer and a one-by-one sequential viewer, both presented in Fig. 2. The mosaic viewer displays rectangular mosaics of objects for the user to inspect. Then, the user is tasked with clicking on objects that show any signs of lensing. Additionally, the user is allowed to mark objects as ‘interesting, but not a lens’. This is exemplified in the left panel of Fig. 2. By contrast, the one-by-one sequential tool displays one object at the time and the user is tasked with classifying it into one of the following non-overlapping categories:

  • ‘A’ indicates a sure lens: it shows clear lensing features and no additional information is needed.

  • ‘B’ indicates a probable lens: it shows lensing features but additional information is required to verify it as a definite lens.

  • ‘C’ indicates a possible lens: it shows lensing features, but they can be explained without resorting to gravitational lensing.

  • ‘X’ indicates it is definitively not a lens.

  • ‘Interesting’ indicates it is definitively not a lens but is interesting in some other way.

The grades A, B, and C are deemed as positive grades, whereas X and Interesting are deemed as negative. The one-by-one sequential tool is shown in the right panel of Fig. 2. Both tools allow the users to change the colour map used for the monochromatic images, as well as the function used to scale the pixel intensities. For every object to inspect, the tools generate three high-contrast images:

  • a monochromatic IE image at the VIS resolution of 0″.1 pixel−1;

  • a red-green-blue (RGB) composite image using the HE, YE, and IE bands, at the NISP resolution of 0″.3 pixel−1;

  • an RGB composite image using the HE, JE, and YE bands, at the NISP resolution of 0″.3 pixel−1.

Before creating the composite images, we re-projected the IE band data from the sky-coordinate system and resolution of the VIS instrument to the corresponding ones in the NISP instrument. This aligns the images and corrects for the different pixel scales between instruments. The experts were required to use the monochromatic high-resolution IE band, and the HE YE IE composite. The HE JE YE composite is not shown by default in the tools, but it is also available. Additionally, the users also have access to the individual NISP bands when using the one-by-one sequential tool. This is shown in Fig. 2.

thumbnail Fig. 2

Visualisation tools used for the visual inspection. Left panel: mosaic tool showing 12 sources in a 3 × 4 rectangular grid. The first object of the second row is marked as a lens candidate, whereas the second object of the third row is marked as interesting. Right panel: one-by-one sequential tool showing an object graded as C. Both tools show a monochromatic high-resolution IE band image, an HE YE IE RGB composite image, and a HE JE YE RGB composite image (in the second row for the one-by-one sequential tool). Both RGB composite images are at the NISP resolution. The one-by-one sequential tool also shows, in its first row, the three NISP bands: YE, JE, and HE. Users are only required to inspect the high-resolution IE monochromatic image and the HE YE IE composite image.

3.2 The visual inspections

To make better use of the large number of strong lensing experts available for the visual inspection, we split the 41 experts into two non-overlapping teams. This allowed us to try different visual inspection schemes while still retaining enough experts per team for the classifications not to be dominated by noise. Team 1 comprises 22 experts, and Team 2 comprises 19. Both teams inspect the 12 086 cutouts described in Sect. 2, along with six extra cutouts of simulated lenses produced following the prescription of Euclid Consortium, Metcalf et al. (in prep). The introduction of simulated mocks tests the ability of the experts to identify lenses, and serves as a sanity check of their performance. The experts are not informed about the mocks in order to avoid any biases. The six simulated lenses can be seen in Fig. 3. Both teams are given two weeks per stage. There is no communication either between or within the teams, and their results are not combined until after the visual inspections are completed.

Both teams followed a two-stage approach. First, they focused on cleaning the parent sample of obvious non-lens contaminants. Then, they inspected the remaining sources in detail and settled on a final classification following the grades introduced in Sect. 3.1.

Team 1 first inspects the entire parent sample using the mosaic tool. This corresponds to 12 092 cutouts after adding the mock lenses. The experts were allowed to change the number of sources per page shown in the mosaic, with most experts observing between 20 and 42 sources per mosaic page. Afterwards, Team 1 reinspected all the objects selected in the first stage using the one-by-one sequential tool and assigning detailed classifications.

Simultaneously, Team 2 is further divided into three groups: two groups comprising six experts each and one group comprising seven. Each group inspects one third of the sources using the one-by-one sequential tool, while focusing on rejecting obvious contaminants. During the first stage, no detailed classification is required. Subsequently, all the selected sources are reinspected by Team 2 as a whole, using again the one-by-one sequential tool but assigning detailed classifications.

Afterwards, we aggregated the final classifications of each team independently. The output is a single final classification per team for every source. Thus, if more than half of the experts voted negatively, then the source was classified as a non-lens; otherwise, we classified it as the majority vote between A, B, and C. In the case of a tie between A and B, or A and C, A took precedence. This prioritisation reflects the expectation that experts will only vote for A if they are confident about the presence of lensing features. If there is a tie between B and C, we favoured C to minimise noise in the final B sample. In the event of a tie among all three positive classes, B was preferred.

thumbnail Fig. 3

Six simulated lenses as seen in the visualisation tools. The left side of each panel corresponds to the high-resolution IE band data, and the right to the HE YE IE composite image. The letter at the upper-left corner of each panel corresponds to the final joint grade given in the visual inspection.

4 Visual inspection

The experts are anonymised at every stage of the analysis to avoid biasing the visual inspection results. We refer to the experts only by their expert ID, for example, ‘expert number 12’.

4.1 Team 1

The first stage of the visual inspection was completed by 20 out of the 22 experts that registered for Team 1. Figure 4 presents the number of lens candidates selected by each expert. We note that expert number 1 selected 15 σ more sources for reinspection when compared to the mean and standard deviation of the other experts from Team 1, which selected 106 ± 100 sources for reinspection. Figure 5 presents the distribution of votes with and without expert number 1. We observe that the number of sources selected only by a single expert drops by half when excluding the outlier expert. Consequently, we removed the classifications from expert number 1. This provided us with a generous selection for the second stage, in which we included every source chosen by any of the remaining experts, while also keeping the sample reasonably small. The total number of sources selected for inspection in stage 2 was 1233.

The second stage was completed by 17 out of the 22 experts. Figure A.1 presents the number of votes per grade per expert. Similarly, Table 1 presents the average number of votes per grade for every stage that used the one-by-one sequential tool. Both Fig. A.1 and Table 1 show that the experts of Team 1 were conservative when assigning the highest grade, A. This trend, however, was not the case for grades B and C, for which multiple experts assigned hundreds of votes in the 1233 sample. This indicates confusion among some experts for what constitutes a lens when the lensing features are not strikingly obvious. However, the experts with a large number of positive classifications were still a minority. Ultimately, the behaviour of all experts during the second stage was deemed acceptable and none of classifications were removed.

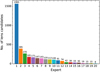thumbnail Fig. 4

Number of candidates selected in the first stage for reinspection by Team 1 using the mosaic tool. The experts were anonymised, and the expert IDs correspond only to the first stage of the visual inspection.

4.2 Team 2

The first round of visual inspection was completed by 16 out of 19 experts involved in Team 2. The distribution among groups was as follows: five experts from both the first and second group, and another six from the third group. Figure A.2 and Table 1 summarise the behaviour of the experts during the inspection. The grades A and B were given to only a small number of sources and the overall proportion of positive votes was low. This is consistent with the task of removing the contaminants, which was the goal for stage 1. The visual inspection results are presented in Fig. 6. We discarded all the sources with a negative majority vote, except those that got at least one vote for A or B. This amounted to 691 sources for reinspection in stage 2.

The second stage of Team 2 was completed by 17 experts out of the 19 who registered. The grading behaviour of the experts is presented in Fig. A.3. A few of the experts gave a large number of positive grades, one grading positively 673 out of the 691. Still, most of the experts reserved the grades A and B for the few best candidates, and thus, we did not remove any experts. This is justified by the aggregation method introduced in Sect. 3.2, which relies on a majority vote to assign final grades.

thumbnail Fig. 5

Distribution of the number of positive votes for Team 1 before and after removing the outlier expert. Most of the sources received only one vote, and no object was selected by all the experts.
Table 1

Average number of votes per grade per expert for the inspections using the one-by-one sequential tool.

4.3 Time cost of the inspections

It took the experts of Team 1 between 1h 15m and 5h 15m to inspect the whole parent sample using the mosaic tool, with the median time being 2 h 45 m. By contrast, it took the experts from Team 2 between 1h30m to 3h30m with a median time of 2 h 15 m to inspect one third of the parent sample, but using the one-by-one sequential tool. The median time per source was 0.8 s and 2.0 s for Teams 1 and 2, respectively.

For the second stage, Team 1 experts took between 30 m and 3 h 30 m. The median time was 1 h 30 m, equivalent to 4.4 s per source. Finally, Team 2 experts took between 15 m and 2h, and the median was 45 m, which corresponds to 4.0 s per source. Overall, the time taken per source during the second stage was consistent for both teams. Given the filtering of the sample during the first stage, the time taken per source in the second stage corresponds more closely to the real time that a visual inspection would take on a preselected sample, for example the output of a convolutional neural network.

5 Results

5.1 The visual inspection candidates

We computed three grades for each source: two individual grades from Team 1 and Team 2 plus a final joint grade. The final grade of each team is determined by applying the scheme presented in Sect. 3.2 to their respective set of votes. The joint final grade is determined the same way but using the votes of both teams together in the computation, with the exception of sources that were rejected by one of the teams during the first stage. In that case, we added two negative votes to the classifications of the other team and calculated the final joint classification using the 19 votes.

Overall, we obtain three grade A, 13 grade B, and 52 grade C lens candidates from the final joint grades. We present a summary of the number of candidates per team in Fig. 7. Furthermore, we show the grade A and B candidates in Fig. 8, along with their three final grades: the final grade from Team 1, the final grade from Team 2, and the final joint grade (in yellow, cyan, and red, respectively). The grade C candidates, along with the sources selected by either team but rejected from the joint sample, are presented in a Zenodo appendix. We note that Team 1 found almost double the amount of grade A and grade B candidates, but about the same number of grade C candidates as Team 2. Moreover, all the candidates selected by Team 1 but rejected from the final sample were also rejected by Team 2 during the first stage. By contrast, most of the sources selected by Team 2 but rejected from the final sample were also rejected by Team 1 during the second stage. This suggests that using the one-by-one sequential tool to filter out the obvious non-lenses, as Team 2 did during the first stage, is in fact a more aggressive filter than using the mosaic tool to preselect candidates.

5.2 Modelling of the lens candidates

We further assessed the validity of the 16 grade A and B candidates by modelling the lens galaxy light and mass distribution, and surface brightness distribution of the lensed source. We did this using the pronto software (Vegetti & Koopmans 2009; Rybak et al. 2015a,b; Rizzo et al. 2018; Ritondale et al. 2019; Powell et al. 2021). We used a singular isothermal ellipsoid (SIE) density profile to describe the mass distribution of the galaxy, a composite of three Sérsic profiles for the lens galaxy light, and a pixelated, free-form reconstruction of the source surface brightness distribution. The parameters for the lens light and mass models are found through a non-linear optimisation using MultiNest (Feroz et al. 2009). For each set of light and mass parameters, the surface brightness distribution of the source is solved for linearly, up to some regularisation condition, which, in this case, penalises large gradients in the source. The strength of this regularisation is itself a non-linear parameter. The full model has 23 free parameters.

We used a circular mask centred on the lensing galaxy and large enough to enclose what are assumed to be lensed images. We also used the positions of these assumed lensed images as an input to the optimisation scheme. After selecting two, three, or four positions in the image plane, the non-linear optimiser will only accept models where these image plane positions have a root mean square separation in the source plane below some tolerance, in this case 1 arcsec. This removes the need to fine-tune the initial modelling conditions, since only combinations of lens parameters that focus the source are accepted. The large tolerance of 1 arcsec also prevents the subjective choice of image positions from placing strict restrictions on the model.

After the optimisation, we checked each model against three criteria to determine if its data are well described by a strong lensing model. These criteria are:

  1. Is there an SIE critical curve that can enclose or exclude the right number of bright components in the image plane?

  2. Is the centroid of this critical curve consistent with that of the light profile?

  3. Is the reconstructed source surface brightness distribution consistent with a compact, focused object, inside a caustic?

Given the small sample size, the evaluation of these criteria is done in a qualitative basis through the visual inspection of the models (see Appendix B). A systematic and quantitative assessment requires evaluating these criteria against realistic simulations where the ground-truth is known, which is beyond the scope of this work.

Five of the 16 grade A and B candidates are found to have valid lens models according to the criteria above. Six candidates cannot be determined as lenses with the available data, and a final five candidates do not have valid lens models. For the five valid candidates, we measure Einstein radii in the range 0″.68–1″.24. The result for one valid candidate is shown, as an example, in Fig. 9; the rest are shown in Appendix B. The results of the visual inspection and modelling are summarized in Table 2.

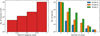thumbnail Fig. 6

Results from Team 2 during the first stage. Left: histogram of the ratio of negative votes versus the total number of classifications for the source. The sources with a ratio of negative votes lower than 0.5 were selected for stage 2. Right: total number of sources that received a given number of votes for a given classification. Most of the sources had zero votes for A, B, and C. All sources with at least one vote for A or B were also selected for stage 2.
thumbnail Fig. 7

Distribution of final grades for each team and for the joint classification.

6 Discussion

6.1 The lens candidates in the literature

We crossmatched the sky coordinates of the 68 lens candidates against the Strong Lens Database (SLED; Vernardos et al., in prep.), a database of gravitational lenses, lens candidates, and known contaminants, encompassing more than 20000 entries. We found no matches between our sample and the database. Furthermore, the database indicates that there have been no lens searches in the area, since the closest match is more than 6° away. This is expected given that the Perseus cluster is near the Galactic plane, and thus, is not generally targeted by large-scale optical galaxy surveys.

Nonetheless, Li et al. (2024) have performed a lens search in some of the ERO fields, including the Perseus cluster, in order to test the lens detection algorithm to be used by the Chinese Space Station Telescope (CSST) team. For that purpose, they used the high-resolution media images published by ESA2. They found four lens candidates in the Perseus cluster and reported the pixel coordinates in the TIFF image. Three of those candidates are included in our parent sample and were selected by Team 1 for reinspection in the second stage. However, all of them were rejected in the second stage. A smaller committee of experts inspected the fourth candidate and ultimately rejected it. Thus, we believe that none of the Li et al. (2024) candidates in the Perseus cluster are lenses. The lack of real lenses in their sample is likely a consequence of using the lower-resolution TIFF images and the fact that their model was not trained to detect lenses in Euclid data. Therefore, the false positives in the Perseus cluster do not necessarily reflect on the potential performance of the algorithm in CSST data.

thumbnail Fig. 8

Mosaic of the grade A and B lens candidates from the visual inspection. For each candidate we show the high-resolution IE band cutout in the left panel, and the lower-resolution HE YE IE composite image in the right panel. The final grades by Team 1, Team 2, and the final joint grade are shown in yellow, cyan, and red, respectively. No grade is shown if one of the sources was rejected by a team during the first stage of the visual inspection. The green borders highlight candidates with valid models, and red borders candidates rejected due to the modelling.

6.2 The expected prevalence of ELSE lenses

Collett (2015, C15 hereafter) forecasts that 15 000 deg2 of Euclid imaging should contain 170000 strong gravitational lenses. Naively scaling down to the 0.7 deg2 Perseus field gives an expectation of eight galaxy-galaxy lenses, of which six should have IE < 23. We have three grade A and 13 grade B candidates, of which five have a valid lens model, and six are indeterminate. Despite the small number statistics, it is clear that our results and the C15 forecasts are broadly consistent. As well as the Poisson noise, our limited understanding of the discovery selection function, and the lack of spectroscopic redshift confirmation of our candidates makes it impossible to precisely compare our absolute number of lenses with the forecast population.

The median Einstein radius forecast in C15 is 0″.65, whereas the smallest Einstein radius of the five lenses with valid models in Sect. 5.2 is 0″.68. This tension is alleviated somewhat by accounting for the fact we only look at lenses with Ie < 23: by excluding the faintest lenses we prefer higher-mass or lower-redshift lenses, both of which result in larger Einstein radii. After applying this cut, the forecast median Einstein radius increases to 0″.75. Figure 10 shows the expected number of lenses in 0.7 deg2 of Euclid data, their Einstein radius distribution, and the Einstein radius distribution of successfully modelled ELSE candidates. The C15 forecasts assumed that the lens galaxy light would be subtracted, which is very helpful for finding small-Einstein-radius lenses: we have not done this. In future work, we will calibrate this selection function using simulations (Rojas et al., in prep.); in this study we used a toy model to estimate it. We assumed that the shape of the underlying Einstein radius population follows the Euclid forecasts of C15, and that the visual inspection introduced a selection function in the form of a step function, we detect every lens above a threshold Einstein radius (θmin) and none below this threshold. Using Bayes’ theorem, we infer P(θmin) given that we discovered five lenses and the lowest Einstein radius is in the range 0″.65–0″.70.

We used a Monte Carlo simulation to draw many realisations of five Einstein radii but varied the discovery threshold, assuming a uniform prior on the discovery threshold, θmin. We find that the threshold is 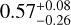0.57−0.26+0.08$0.57_{ - 0.26}^{ + 0.08}$ arcsec at 68% confidence. This corresponds to a forecast total population of 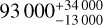93000−13 000+34 000$93\,000_{ - 13000}^{ + 34\,000} $ lenses in the full Euclid dataset that are discoverable with visual inspection without lens light subtraction and with lens IE < 23. Moreover, scaling down the area to 0.7 deg2 the forecast predicts approximately five lenses, coinciding with the five lens candidates with good models.

Table 2

Grade A and B candidates with magnitude, modelling status, and Einstein radii when available.

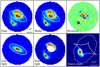thumbnail Fig. 9

Modelling results for one of the five valid candidates, EUCL J031741.85+412702.8. The six panels show, from left to right, top to bottom: the VIS cutout data, masked to a circle around the object; the model lens light and lensed source light distributions, convolved with the point spread function model; the normalised residuals on a colour scale between −3 σ and 3 σ; the lens light only; the lensed source light only, with the brightest parts of the lens light masked; and the reconstructed source plane model. The solid and dashed white ellipses in the image plane are the tangential and radial critical curves, with the corresponding caustics shown in the source plane. The image plane frames all have the same scale, as indicated in the first frame.
thumbnail Fig. 10

Comparison of the number of lenses and their Einstein radius distribution of successfully modelled ELSE candidates (blue histogram), and the forecasts of Collett (2015) rescaled to 0.7 deg2 (dotted black line). The dotted black line is a prediction, not a fit. The orange ‘cutoff’ line is a modification of the Collett (2015) forecasts to account for the selection function arising from our methodology missing small-Einstein-radius lenses.

6.3 The prevalence of ELSE lenses

We extrapolated the five lens candidates with valid lens models found in the ERO Perseus field to the entire EWS. For this, we made three key assumptions:

  1. We have found all the discoverable lenses with IE < 23 within the ERO Perseus field.

  2. The average number density of sources with IE < 23 in the EWS is the same as in the ERO Perseus field: ~ 17 000 extended sources per deg23.

  3. The likelihood that a given source within the EWS exhibits lensing features mirrors that of the sources within the parent sample.

We defined a lens as discoverable if it can be identified via expert visual inspection and a valid lens model can be found for it. This assumption means that, in fact, we are mostly estimating the prevalence of larger Einstein radius lenses, which are easier to model and experts will identify more easily. However, small-Einstein-radius lenses can still be identified if the source is bright and the geometry of the lensed images is particularly evident; for example, the mock lens in the bottom right panel of Fig. 3, which has an Einstein radius of 0″.49, but also a typical quad geometry, was still graded A by the experts. Furthermore, given the increased depth of the ERO Perseus field data compared to the EWS (0.75 magnitudes), we simulated cutouts for the 16 lens candidates with the typical S/N of the EWS. We observe that the lensing features are still visible and clearly identifiable in the shallower cutouts. Consequently, we assumed that they would had been identified in the shallower EWS.

Under the key assumptions above, the prevalence of ELSE lenses in the EWS can be estimated as follows. The likelihood P(k) of finding k lenses among n trialled sources is given by the hypergeometric distribution 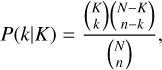P(k∣K)=(Kk)(N−Kn−k)(Nn),$P(k\mid K) = {{\left( \matrix{ K \cr k \cr} \right)\left( \matrix{ N - K \cr n - k \cr} \right)} \over {\left( \matrix{ N \cr n \cr} \right)}},$(1)

where K and N are the total numbers of lenses and sources in the EWS. Using the second assumption, we estimate the total number of extended sources with IE < 23 in the 14 000 deg2 of the EWS to be N = 242 000 000. The number of trialled sources was n = 12 086, and the number of discoverable lenses was k = 5. We could then compute the posterior probability, P(K), using Bayes’ theorem (i.e. P(K|k) ∝ P(k|K)P(K)). We assumed that the prior probability of K, P(K), is such that the ratio K/N is distributed uniformly in log-space between 10−10 and unity. Overall, we expect 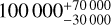100 000−30 000+70 000$100\,000_{ - 30\,000}^{ + 70\,000}$ ELSE-type lenses in the entire EWS. The posterior distribution P(K) is presented in Fig. 11, with the 68% confidence interval highlighted in light blue. Figure 11 also shows in orange the forecast of C15 as described in the previous section, which lies inside the confidence range of our estimate, showing a good agreement between the forecast and our estimate.

thumbnail Fig. 11

Posterior probability density distribution of our estimation of the number of ELSE lenses in the EWS. The blue-shaded region marks the 68% confidence interval of our estimation: 100 000−30 000+70 000$100\,000_{ - 30\,000}^{ + 70\,000}$ ELSE lenses in the EWS. The orange-shaded region marks the 68% confidence interval of the Collett (2015) forecast after applying our selection function: 93000−13 000+34 000$93\,000_{ - 13\,000}^{ + 34\,000}$.

7 Conclusions

In this work, we have investigated the performance of the Euclid telescope for detecting galaxy-scale gravitational lenses. We employed 41 experts to carry out a blind visual search for lenses in the Euclid ERO data of the Perseus cluster. The search yielded 3 grade A and 13 grade B lens candidates.

We modelled the 16 candidates to test whether the observed VIS images are consistent with a single background galaxy lensed by a simple, plausible lens. We have obtained convincing models for five of the candidates. Modelling for six of the candidates produced inconclusive results, whilst five of the visual inspection candidates are definitively non-lenses according to our modelling.

We extrapolated the five candidates with valid lens models to the entire EWS and estimated the number of lenses in it that are discoverable with visual inspection and can be confirmed through modelling of the VIS data. This extrapolation yields 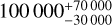100 000−30 000+70 000$100\,000_{ - 30\,000}^{ + 70\,000}$ lenses in the full EWS. This is broadly consistent with the 170 000 forecast by C15.

Even though our magnitude cut of IE < 23 effectively removes many of the small-Einstein-radius objects, the distribution of Einstein radii in our modelled sample is still on the higher side when compared to C15, indicating that we are either unable to identify small-Einstein-radius systems in the visual inspections or unable to model them under our simplifying assumptions. Assuming a step function cutoff in Einstein radius, we inferred the cutoff point to be 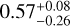0.57−0.26+0.08$0.57_{ - 0.26}^{ + 0.08}$ arcsec; below this, our methodology is likely missing most of the lens candidates. Convolving our inferred cutoff with the Collett (2015) Euclid population, we now predict that 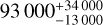93000−13 000+34 000$93\,000_{ - 13\,000}^{ + 34\,000}$ galaxy-scale lenses will be detected in the whole EWS (assuming that the same visual inspection discovery and modelling methodology are performed on the entire dataset). Down-scaling to the 0.7 deg2 visually inspected in this work gives approximately five lenses, which is in perfect accordance with the five lens candidates with valid models.

This sample represents the first gravitational lenses reported in this patch of the sky, and some of the first lenses discovered with Euclid data. There is tentative evidence that we are missing small-Einstein-radius lenses, so future work will be necessary to develop identification techniques targeting small-Einstein-radius lens candidates. There are also substantial challenges in how we scale up from this field to the full dataset: blind visual inspection of 14 000 deg2 is implausible. Neural networks and citizen science are both likely to be needed to reduce the sample to a manageable size.

Even without spectroscopic confirmation of our candidates, our simple lens modelling provides compelling evidence that at least five of them are indeed strong gravitational lenses. These results are hugely promising for the future of strong lensing science with Euclid. Forecasts and early data both now point to the discovery of 105 or more gravitational lenses in the full Euclid dataset.

Data availability

Supplementary materials showing the lens candidates discovered in the search but not included in the main sample are available on Zenodo, at https://zenodo.org/records/14946028

Acknowledgements

This work has made use of the Early Release Observations (ERO) data from the Euclid mission of the European Space Agency (ESA), 2024, https://doi.org/10.57780/esa-qmocze3. The Euclid Consortium acknowledges the European Space Agency and a number of agencies and institutes that have supported the development of Euclid, in particular the Agenzia Spaziale Italiana, the Austrian Forschungsförderungsgesellschaft funded through BMK, the Belgian Science Policy, the Canadian Euclid Consortium, the Deutsches Zentrum für Luft- und Raumfahrt, the DTU Space and the Niels Bohr Institute in Denmark, the French Centre National d’Etudes Spatiales, the Fundação para a Ciência e a Tecnologia, the Hungarian Academy of Sciences, the Ministerio de Ciencia, Innovación y Universidades, the National Aeronautics and Space Administration, the National Astronomical Observatory of Japan, the Netherlandse Onderzoekschool Voor Astronomie, the Norwegian Space Agency, the Research Council of Finland, the Romanian Space Agency, the State Secretariat for Education, Research, and Innovation (SERI) at the Swiss Space Office (SSO), and the United Kingdom Space Agency. A complete and detailed list is available on the Euclid web site (www.euclid-ec.org). J. A. A. B., B. C., and F. C. acknowledge support from the Swiss National Science Foundation (SNSF). C. O’R thanks the Max Planck Society for support through a Max Planck Lise Meitner Group. C. T. and V. B. acknowledge the INAF grant 2022 LEMON. T. E. C. is funded by a Royal Society University Research Fellowship. S. H. S. thanks the Max Planck Society for support through the Max Planck Fellowship. This research is supported in part by the Excellence Cluster ORIGINS which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (LensEra: grant agreement No. 945536 and LENSNOVA: grant agreement No. 771776).

Appendix A Expert classifications in visual inspections

We show in this appendix the detailed classifications given by the experts when using the one-by-one sequential tool.

thumbnail Fig. A.1

Classifications given by Team 1 during the second stage of the visual inspection. Each expert inspected 1221 sources and assigned the grades introduced in Sect. 3.1. Negative grades (X) were not included, for the sake of simplicity. The expert IDs correspond only to the second stage.
thumbnail Fig. A.2

Classifications given by Team 2 during the first stage of the visual inspection. Each expert inspected about 4030 sources and assigned the grades introduced in Sect. 3.1. Negative grades (X) were not included, for the sake of simplicity. The expert IDs correspond only to the first stage.
thumbnail Fig. A.3

Classifications given by Team 2 during the second stage of the visual inspection. Each expert inspected 691 sources and assigned the grades introduced in Sect. 3.1. Negative grades (X) were not included, for the sake of simplicity. The expert numbers correspond only to the second stage.

Appendix B Modelling results

The results of modelling all 16 grade A and B candidates are shown in Figs. B.1 to B.3.

thumbnail Fig. B.1

Modelling results for all five of the candidates that have valid lens models. Panels (A): VIS cutout data, masked to a circle around the object. Panels (B): Model lens light and lensed source light distributions, convolved with the point spread function model. Panels (C): Normalised residuals on a colour scale between −3 σ and 3 σ. Panels (D): Lens light only. Panels (E): Lensed source light only, with the brightest parts of the lens light masked. Panels (F): Reconstructed source plane model. The solid and dashed white ellipses in the image planes are the tangential and radial critical curves, with the corresponding caustics shown in the source plane. The image plane frames all have the same scale, which is indicated in the first frame.
thumbnail Fig. B.2

Modelling results for the six candidates for which we cannot determine their lensing status by modelling the current data. Mosaics follow the same layout as Fig. B.1.
thumbnail Fig. B.3

Modelling results for the five candidates that do not have valid lens models. Mosaics follow the same layout as Fig. B.1.

References

  1. Acevedo Barroso, J. A., Clément, B., Courbin, F., et al. 2025, A&A submitted [arXiv:2503.10610] [Google Scholar]
  2. Auger, M. W., Treu, T., Bolton, A. S., et al. 2009, ApJ, 705, 1099 [Google Scholar]
  3. Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Birrer, S., Welschen, C., Amara, A., & Refregier, A. 2017, J. Cosmology Astropart. Phys., 2017, 049 [Google Scholar]
  5. Birrer, S., Refregier, A., & Amara, A. 2018, ApJ, 852, L14 [Google Scholar]
  6. Cañameras, R., Schuldt, S., Shu, Y., et al. 2024, A&A, 692, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Collett, T. E. 2015, ApJ, 811, 20 [NASA ADS] [CrossRef] [Google Scholar]
  8. Collett, T. E., & Bacon, D. J. 2016, MNRAS, 456, 2210 [CrossRef] [Google Scholar]
  9. Cuillandre, J.-C., Bertin, E., Bolzonella, M., et al. 2025a, A&A, 697, A6 (Euclid on Sky SI) [Google Scholar]
  10. Cuillandre, J.-C., Bolzonella, M., Boselli, A., et al. 2025b, A&A, 697, A11 (Euclid on Sky SI) [Google Scholar]
  11. Dutton, A. A., & Treu, T. 2014, MNRAS, 438, 3594 [NASA ADS] [CrossRef] [Google Scholar]
  12. Euclid Collaboration (Scaramella, R., et al.) 2022, A&A, 662, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Euclid Collaboration (Cropper, M. S., et al.) 2025, A&A, 697, A2 (Euclid on Sky SI) [Google Scholar]
  14. Euclid Collaboration (Jahnke, K., et al.) 2025, A&A, 697, A3 (Euclid on Sky SI) [Google Scholar]
  15. Euclid Collaboration (Mellier, Y., et al.) 2025, A&A, 697, A1 (Euclid on Sky SI) [Google Scholar]
  16. Euclid Early Release Observations 2024, https://doi.org/10.57780/esa-qmocze3 [Google Scholar]
  17. Faure, C., Kneib, J.-P., Covone, G., et al. 2008, ApJS, 176, 19 [NASA ADS] [CrossRef] [Google Scholar]
  18. Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
  19. Ferreras, I., Saha, P., Leier, D., Courbin, F., & Falco, E. E. 2010, MNRAS, 409, L30 [NASA ADS] [CrossRef] [Google Scholar]
  20. Fleury, P., Larena, J., & Uzan, J.-P. 2021, J. Cosmology Astropart. Phys., 2021, 024 [Google Scholar]
  21. Garvin, E. O., Kruk, S., Cornen, C., et al. 2022, A&A, 667, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Gilman, D., Birrer, S., Nierenberg, A., & Oh, M. S. H. 2024, MNRAS, 533, 1687 [Google Scholar]
  23. González, J., Holloway, P., Collett, T., et al. 2025, arXiv e-prints [arXiv:2501.15679] [Google Scholar]
  24. Grespan, M., Thuruthipilly, H., Pollo, A., et al. 2024, A&A, 688, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Grillo, C., Pagano, L., Rosati, P., & Suyu, S. H. 2024, A&A, 684, L23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Hezaveh, Y. D., Marrone, D. P., Fassnacht, C. D., et al. 2013, ApJ, 767, 132 [NASA ADS] [CrossRef] [Google Scholar]
  27. Hogg, N. B., Fleury, P., Larena, J., & Martinelli, M. 2023, MNRAS, 520, 5982 [Google Scholar]
  28. Jacobs, C., Collett, T., Glazebrook, K., et al. 2019, ApJS, 243, 17 [Google Scholar]
  29. Keeton, C. R., Mao, S., & Witt, H. J. 2000, ApJ, 537, 697 [NASA ADS] [CrossRef] [Google Scholar]
  30. Li, X., Sun, R., Lv, J., et al. 2024, AJ, 167, 264 [Google Scholar]
  31. Marshall, P. J., Lintott, C. J., & Fletcher, L. N. 2015, ARA&A, 53, 247 [NASA ADS] [CrossRef] [Google Scholar]
  32. More, A., Verma, A., Marshall, P. J., et al. 2016, MNRAS, 455, 1191 [NASA ADS] [CrossRef] [Google Scholar]
  33. Oguri, M., & Marshall, P. J. 2010, MNRAS, 405, 2579 [NASA ADS] [Google Scholar]
  34. Orban de Xivry, G., & Marshall, P. 2009, MNRAS, 399, 2 [Google Scholar]
  35. O’Riordan, C. M., Despali, G., Vegetti, S., Lovell, M. R., & Moliné, Á. 2023, MNRAS, 521, 2342 [CrossRef] [Google Scholar]
  36. Paraficz, D., Rybak, M., McKean, J. P., et al. 2018, A&A, 613, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Pascale, M., Frye, B. L., Pierel, J. D. R., et al. 2025, ApJ, 979, 13 [Google Scholar]
  38. Pawase, R. S., Courbin, F., Faure, C., Kokotanekova, R., & Meylan, G. 2014, MNRAS, 439, 3392 [NASA ADS] [CrossRef] [Google Scholar]
  39. Petrillo, C. E., Tortora, C., Chatterjee, S., et al. 2019, MNRAS, 482, 807 [NASA ADS] [Google Scholar]
  40. Powell, D., Vegetti, S., McKean, J. P., et al. 2021, MNRAS, 501, 515 [Google Scholar]
  41. Refsdal, S. 1964, MNRAS, 128, 307 [NASA ADS] [CrossRef] [Google Scholar]
  42. Ritondale, E., Vegetti, S., Despali, G., et al. 2019, MNRAS, 485, 2179 [Google Scholar]
  43. Rizzo, F., Vegetti, S., Fraternali, F., & Di Teodoro, E. 2018, MNRAS, 481, 5606 [Google Scholar]
  44. Rojas, K., Savary, E., Clément, B., et al. 2022, A&A, 668, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Rojas, K., Collett, T. E., Ballard, D., et al. 2023, MNRAS, 523, 4413 [NASA ADS] [CrossRef] [Google Scholar]
  46. Rybak, M., McKean, J. P., Vegetti, S., Andreani, P., & White, S. D. M. 2015a, MNRAS, 451, L40 [Google Scholar]
  47. Rybak, M., Vegetti, S., McKean, J. P., Andreani, P., & White, S. D. M. 2015b, MNRAS, 453, L26 [NASA ADS] [CrossRef] [Google Scholar]
  48. Savary, E., Rojas, K., Maus, M., et al. 2022, A&A, 666, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Shajib, A. J., Mozumdar, P., Chen, G. C. F., et al. 2023, A&A, 673, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Sonnenfeld, A., Jaelani, A. T., Chan, J., et al. 2019, A&A, 630, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Stein, G., Blaum, J., Harrington, P., Medan, T., & Lukić, Z. 2022, ApJ, 932, 107 [NASA ADS] [CrossRef] [Google Scholar]
  52. Thuruthipilly, H., Zadrozny, A., Pollo, A., & Biesiada, M. 2022, A&A, 664, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Vegetti, S., & Koopmans, L. V. E. 2009, MNRAS, 392, 945 [Google Scholar]
  54. Vegetti, S., Koopmans, L. V. E., Bolton, A., Treu, T., & Gavazzi, R. 2010, MNRAS, 408, 1969 [Google Scholar]
  55. Wong, K. C., Suyu, S. H., Chen, G. C. F., et al. 2020, MNRAS, 498, 1420 [Google Scholar]
1

The version used for this work is available at https://github.com/ClarkGuilty/Qt-stamp-visualizer/tree/ERO_edition

3

About 5% of sources are cluster members and they occlude about 5% of the sky. In terms of number of sources, the effect of the cluster balances out.

All Tables

Table 1

Average number of votes per grade per expert for the inspections using the one-by-one sequential tool.

In the text
Table 2

Grade A and B candidates with magnitude, modelling status, and Einstein radii when available.

In the text

All Figures

thumbnail Fig. 1

9″.9 × 9″..9 VIS cutouts of galaxies randomly selected across different IE bins, ranging from the brightest galaxies with IE < 16 (leftmost) down to very faint systems with 24.5 < IE < 25 (rightmost). The blue arrow represents the magnitude cut used to select our parent sample.
In the text
thumbnail Fig. 2

Visualisation tools used for the visual inspection. Left panel: mosaic tool showing 12 sources in a 3 × 4 rectangular grid. The first object of the second row is marked as a lens candidate, whereas the second object of the third row is marked as interesting. Right panel: one-by-one sequential tool showing an object graded as C. Both tools show a monochromatic high-resolution IE band image, an HE YE IE RGB composite image, and a HE JE YE RGB composite image (in the second row for the one-by-one sequential tool). Both RGB composite images are at the NISP resolution. The one-by-one sequential tool also shows, in its first row, the three NISP bands: YE, JE, and HE. Users are only required to inspect the high-resolution IE monochromatic image and the HE YE IE composite image.
In the text
thumbnail Fig. 3

Six simulated lenses as seen in the visualisation tools. The left side of each panel corresponds to the high-resolution IE band data, and the right to the HE YE IE composite image. The letter at the upper-left corner of each panel corresponds to the final joint grade given in the visual inspection.
In the text
thumbnail Fig. 4

Number of candidates selected in the first stage for reinspection by Team 1 using the mosaic tool. The experts were anonymised, and the expert IDs correspond only to the first stage of the visual inspection.
In the text
thumbnail Fig. 5

Distribution of the number of positive votes for Team 1 before and after removing the outlier expert. Most of the sources received only one vote, and no object was selected by all the experts.
In the text
thumbnail Fig. 6

Results from Team 2 during the first stage. Left: histogram of the ratio of negative votes versus the total number of classifications for the source. The sources with a ratio of negative votes lower than 0.5 were selected for stage 2. Right: total number of sources that received a given number of votes for a given classification. Most of the sources had zero votes for A, B, and C. All sources with at least one vote for A or B were also selected for stage 2.
In the text
thumbnail Fig. 7

Distribution of final grades for each team and for the joint classification.
In the text
thumbnail Fig. 8

Mosaic of the grade A and B lens candidates from the visual inspection. For each candidate we show the high-resolution IE band cutout in the left panel, and the lower-resolution HE YE IE composite image in the right panel. The final grades by Team 1, Team 2, and the final joint grade are shown in yellow, cyan, and red, respectively. No grade is shown if one of the sources was rejected by a team during the first stage of the visual inspection. The green borders highlight candidates with valid models, and red borders candidates rejected due to the modelling.
In the text
thumbnail Fig. 9

Modelling results for one of the five valid candidates, EUCL J031741.85+412702.8. The six panels show, from left to right, top to bottom: the VIS cutout data, masked to a circle around the object; the model lens light and lensed source light distributions, convolved with the point spread function model; the normalised residuals on a colour scale between −3 σ and 3 σ; the lens light only; the lensed source light only, with the brightest parts of the lens light masked; and the reconstructed source plane model. The solid and dashed white ellipses in the image plane are the tangential and radial critical curves, with the corresponding caustics shown in the source plane. The image plane frames all have the same scale, as indicated in the first frame.
In the text
thumbnail Fig. 10

Comparison of the number of lenses and their Einstein radius distribution of successfully modelled ELSE candidates (blue histogram), and the forecasts of Collett (2015) rescaled to 0.7 deg2 (dotted black line). The dotted black line is a prediction, not a fit. The orange ‘cutoff’ line is a modification of the Collett (2015) forecasts to account for the selection function arising from our methodology missing small-Einstein-radius lenses.
In the text
thumbnail Fig. 11

Posterior probability density distribution of our estimation of the number of ELSE lenses in the EWS. The blue-shaded region marks the 68% confidence interval of our estimation: 100 000−30 000+70 000$100\,000_{ - 30\,000}^{ + 70\,000}$ ELSE lenses in the EWS. The orange-shaded region marks the 68% confidence interval of the Collett (2015) forecast after applying our selection function: 93000−13 000+34 000$93\,000_{ - 13\,000}^{ + 34\,000}$.
In the text
thumbnail Fig. A.1

Classifications given by Team 1 during the second stage of the visual inspection. Each expert inspected 1221 sources and assigned the grades introduced in Sect. 3.1. Negative grades (X) were not included, for the sake of simplicity. The expert IDs correspond only to the second stage.
In the text
thumbnail Fig. A.2

Classifications given by Team 2 during the first stage of the visual inspection. Each expert inspected about 4030 sources and assigned the grades introduced in Sect. 3.1. Negative grades (X) were not included, for the sake of simplicity. The expert IDs correspond only to the first stage.
In the text
thumbnail Fig. A.3

Classifications given by Team 2 during the second stage of the visual inspection. Each expert inspected 691 sources and assigned the grades introduced in Sect. 3.1. Negative grades (X) were not included, for the sake of simplicity. The expert numbers correspond only to the second stage.
In the text
thumbnail Fig. B.1

Modelling results for all five of the candidates that have valid lens models. Panels (A): VIS cutout data, masked to a circle around the object. Panels (B): Model lens light and lensed source light distributions, convolved with the point spread function model. Panels (C): Normalised residuals on a colour scale between −3 σ and 3 σ. Panels (D): Lens light only. Panels (E): Lensed source light only, with the brightest parts of the lens light masked. Panels (F): Reconstructed source plane model. The solid and dashed white ellipses in the image planes are the tangential and radial critical curves, with the corresponding caustics shown in the source plane. The image plane frames all have the same scale, which is indicated in the first frame.
In the text
thumbnail Fig. B.2

Modelling results for the six candidates for which we cannot determine their lensing status by modelling the current data. Mosaics follow the same layout as Fig. B.1.
In the text
thumbnail Fig. B.3

Modelling results for the five candidates that do not have valid lens models. Mosaics follow the same layout as Fig. B.1.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.