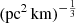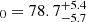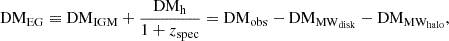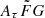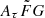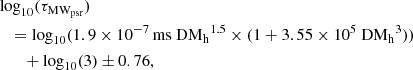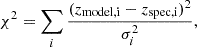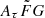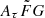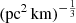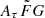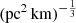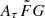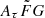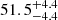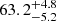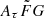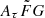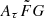| Issue |
A&A
Volume 693, January 2025
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 13 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202450823 | |
| Published online | 03 January 2025 | |
Constraining the Hubble constant with scattering in host galaxies of fast radio bursts
1
Department of Physics, National Chung Hsing University, 145, Xingda Road, Taichung 40227 Taiwan, ROC
2
Institute of Astronomy, National Tsing Hua University, 101, Section 2. Kuang-Fu Road, Hsinchu 30013, Taiwan ROC
3
Department of Physics, National Tsing Hua University, 101, Section 2. Kuang-Fu Road, Hsinchu 30013 Taiwan, ROC
4
Research School of Astronomy and Astrophysics, The Australian National University, Canberra, ACT 2611 Australia
5
Centre for Astrophysics and Supercomputing, Swinburne University of Technology, P.O. Box 218 Hawthorn, VIC 3122 Australia
6
OzGrav: The Australian Research Council Centre of Excellence for Gravitational Wave Discovery, Hawthorn, VIC 3122 Australia
7
ASTRO3D: The Australian Research Council Centre of Excellence for All-sky Astrophysics in 3D, ACT 2611, Australia
8
Sabancı University, Faculty of Engineering and Natural Sciences, 34956 Istanbul, Turkey
⋆ Corresponding author; tetsuya@phys.nchu.edu.tw
Received:
22
May
2024
Accepted:
21
October
2024
Aims. Measuring the Hubble constant (H0) is one of the most important missions in astronomy. Nevertheless, recent studies exhibit differences between the employed methods.
Methods. Fast radio bursts (FRBs) are coherent radio transients with large dispersion measures (DM) with a duration of millisecondsḊMIGM, the free electron column density along a line of sight in the intergalactic medium (IGM), could open a new avenue for probing H0. However, it has been challenging to separate DM contributions from different components (i.e., the IGM and the host galaxy plasma), and this hampers the accurate measurements of DMIGM and hence H0. We adopted a method to overcome this problem by using the temporal scattering of the FRB pulses due to the propagation effect through the host galaxy plasma (scattering time). The scattering-inferred DM in a host galaxy improves the estimate of DMIGM, which in turn leads to a better constraint on H0. In previous studies, a certain value or distribution has conventionally been assumed of the dispersion measure in host galaxies (DMh). We compared this method with ours by generating 100 mock FRBs, and we found that our method reduces the systematic (statistical) error of H0 by 9.1% (1%) compared to the previous method.
Results. We applied our method to 30 localized FRB sources with both scattering and spectroscopic redshift measurements to constrain H0. Our result is H0 = 74−7.2+7.5 km s−1 Mpc−1, where the central value prefers the value obtained from local measurements over the cosmic microwave background. We also measured DMh with a median value of 103−48+68 pc cm−3.
Conclusions. The DMh had to be assumed in previous works to derive DMIGM. Scattering enables us to measure DMIGM without assuming DMh to constrain H0. The reduction in systematic error is comparable to the Hubble tension (∼10%). Combined with the fact that more localized FRBs will become available, our result indicates that our method can be used to address the Hubble tension using future FRB samples.
Key words: scattering / intergalactic medium / cosmological parameters
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The expansion rate of the Universe is one of the most fundamental physical parameters in astrophysics. The Hubble constant, H0, describes the relative expansion rate of the Universe. H0 has been measured so far with different methods, such as the cosmic microwave background (CMB) (e.g., Planck Collaboration VI 2020) and local distance ladders (e.g., Riess et al. 2022). However, there is a difference of 4 to 6σ between the two methods, namely the CMB and the local distance ladder (e.g. Verde et al. 2019; Di Valentino et al. 2021; Riess et al. 2021; Hu & Wang 2023). The recent estimate of H0 from the CMB by the Planck Collaboration is 67.4 ± 0.5 km s−1 Mpc−1 (Planck Collaboration VI 2020), while the local distance ladder method by the Supernova H0 for the Equation of State (SH0ES) team yielded H0 = 73.0 ± 1.0 km s−1 Mpc−1 (Riess et al. 2022). One possible solution to the Hubble tension might be so-called early dark energy, which introduces an additional energy density to the early Universe (e.g., Hill & Baxter 2018), although the difference might be explained by observational systematics (e.g., Mörtsell et al. 2022).
Fast radio bursts (FRBs) are enigmatic coherent radio flashes that occur at cosmological distances (z ≳ 0.05; e.g., Lorimer et al. 2024; Bailes 2022; Petroff et al. 2019). They are characterized by a brief duration of approximately 1 ms and their exceptional brightness (e.g., Lorimer et al. 2007). The dispersion measure (DM) is a unique observable of FRBs. It represents a free electron density along the line of sight to an FRB. The definition of the DM is DM ≡∫neds, where ne is the electron number density, and ds is the distance segment along the line of sight. The DM is proportional to the amount of plasma along a line of sight between an FRB source and an observer. Therefore, it can be used as an indicator of the redshift and distance to the FRB (Lorimer et al. 2007). The FRBs are critically important for addressing the issues of missing baryons (e.g., Macquart et al. 2020) and the equation of state of dark energy (e.g., Zhou et al. 2014). This made them a significant focus for further research. We rather focus on the Hubble tension in this particular paper because the existing difference between well-established methods (i.e., ∼10% systematics), including the CMB and the local distance ladder, underscores the importance of adding a new independent method to the comparison. The FRB method would be useful if it could achieve an accuracy better than ∼10% by mitigating the potential systematics in the method in the sense that it can distinguish between the H0 values derived from the CMB and local distance ladder methods. Our primary focus is on leveraging the DM of FRBs as a unique distance indicator to derive H0.
The observed DM (DMobs) can be separated into three main components. One component is DMMW, which is the DM contributed by Milky Way interstellar medium (ISM) and halo. Another is DMh, which is the DM in a galaxy hosting one FRB source (FRB host galaxy). The other is DMIGM, which is the DM in the intergalactic medium (IGM) between the Milky Way and a host galaxy,
where zspec is the spectroscopic redshift of the host galaxy. The DMh is divided by 1 + zspec to convert it into the observer’s frame, and the DM is given in units of pc cm−3. The DMMW can be divided into two components, the disk and the halo (DMMWdisk and DMMWhalo, respectively),
According to Eq. 9 in Zhou et al. (2014), the cosmic average of DMIGM is proportional to H0. The main focus of Zhou et al. (2014) was to discuss a constraint on the w parameter for the equation of state of dark energy with FRBs. In this work, we implement their formalization (their Eq. 9) in our analysis, combined with scattering, to measure H0. Therefore, H0 can be constrained with DMIGM. To derive DMIGM, DMh has to be subtracted from DMobs. However, in previous works (e.g., Hagstotz et al. 2022; Zhao et al. 2022), a certain distribution of DMh was assumed for all FRB samples to calculate DMIGM (see Sect. 6.2 for details). Therefore, there might be unknown systematic uncertainties in DMh and DMIGM in previous works.
The scattering time (τ) is the pulse-broadening effect of radio pulses, including pulsars and FRBs, due to the propagation through the plasma. The scattering time becomes longer when a radio pulse propagates in a larger amount of plasma with turbulence, and the scattering tail (Petroff et al. 2019) becomes more significant. The scattering time has a minimal impact on the pulse-broadening effect in the Milky May and IGM (e.g., Cordes et al. 2022). Therefore, we assumed that scattering only occurs within a host galaxy. The scattering time is a similar quantity as the DMh in the sense that both increase with increasing amount of plasma in a host galaxy. Therefore, the scattering time has information on DMh and is proportional to the square of DMh (Cordes et al. 2022). The DMh can be measured based on the observed scattering. This approach is free of the potential systematics involved in the assumption on DMh, that is, either a fixed value of DMh or a fixed shape of the distribution. This marks a novel application of the scattering time in determining DMh, and it might improve the method employed to measure H0. We focus on the capability of this approach using scattering to constrain H0, while Cordes et al. (2022) used it to constrain the fraction of baryons in the IGM.
Throughout this paper, we assume the Planck 2018 results implemented in Astropy (Planck Collaboration VI 2020), that is, a Λ cold dark matter cosmology with (Ωm, Ωb) = (0.31, 0.049).
2. Method
We provide an overview of the method for constraining H0 with DM and scattering. We followed the formalization presented in Cordes et al. (2022). Cordes et al. (2022) constrained the fraction of baryons in the intergalactic space with a given H0. We instead focus on how accurately H0 can be constrained under their formalization. The scattering time (τ) was used to measure a probability density function (PDF) of DMh, where the PDF is described as a function of two parameters: DMh and 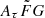 . These two parameters are discussed in detail in Sect. 2.1. The integration of the PDF over all possible ranges of the two parameters (Cordes et al. 2022) was computed as a function of the redshift to derive the PDF of redshift. Using the 50th percentile of the PDF of the redshift, we can then determine a modeled redshift (zmodel) that is derived by using DM and τ. zmodel can be optimized to the observed redshift (zspec) by changing H0. The best-fit zmodel provides us with the measurement of H0.
. These two parameters are discussed in detail in Sect. 2.1. The integration of the PDF over all possible ranges of the two parameters (Cordes et al. 2022) was computed as a function of the redshift to derive the PDF of redshift. Using the 50th percentile of the PDF of the redshift, we can then determine a modeled redshift (zmodel) that is derived by using DM and τ. zmodel can be optimized to the observed redshift (zspec) by changing H0. The best-fit zmodel provides us with the measurement of H0.
2.1. Measuring DMh
We adopted this equation to describe the rest-frame τrest as a function of DMh,
where vrest is the rest-frame frequency in units of GHz. The quantity Cτ = 0.48 ms (Cordes et al. 2022) is a numerical constant. To account for how empirical estimates for the scattering time are related to the e−1 time, Cordes et al. (2022) introduced a dimensionless factor Aτ. 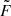 (pc2 km)−1/3 is a parameter that characterizes density fluctuations. G is a dimensionless geometric factor. While the three parameters Aτ,
(pc2 km)−1/3 is a parameter that characterizes density fluctuations. G is a dimensionless geometric factor. While the three parameters Aτ, 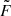 , and G have different physical meanings, they appear in the formalization as a product. Therefore, we treated the product
, and G have different physical meanings, they appear in the formalization as a product. Therefore, we treated the product 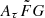 as a single parameter. The prior assumption on the
as a single parameter. The prior assumption on the 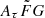 range is from 0.001 to 10 (pc2 km)
range is from 0.001 to 10 (pc2 km)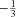 (Cordes et al. 2022).
(Cordes et al. 2022).
Two parameters, DMh (pc cm−3) and 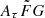 (ϕ)
(ϕ) 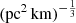 , are used to describe the PDF of DMh (Cordes et al. 2022):
, are used to describe the PDF of DMh (Cordes et al. 2022):
In Eq. (4), there are two terms on the right side: the first term uses DM, and the second term uses τ. The first term, fDMh, is expressed as
fDMh is determined using the PDF of DMIGM (fDMIGM), where DM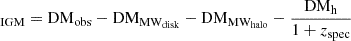 . The uncertainty of DMMW can be accounted for by introducing prior PDFs of DMMWdisk and DMMWhalo in Eq. (5). We assumed a flat PDF for DMMWdisk centered at the mean value derived from the NE2001 (Cordes & Lazio 2002) with ±20% deviations (Cordes et al. 2022). A flat PDF of
. The uncertainty of DMMW can be accounted for by introducing prior PDFs of DMMWdisk and DMMWhalo in Eq. (5). We assumed a flat PDF for DMMWdisk centered at the mean value derived from the NE2001 (Cordes & Lazio 2002) with ±20% deviations (Cordes et al. 2022). A flat PDF of 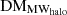 was assumed. It ranged from 25 to 80 pc cm−3 (Prochaska & Neeleman 2018; Shull & Danforth 2018; Prochaska & Zheng 2019; Yamasaki & Totani 2020). We used a log-normal distribution to characterize fDMIGM (Cordes et al. 2022). The log-normal in the form, N(μ, σ), is a function of the following parameters:
was assumed. It ranged from 25 to 80 pc cm−3 (Prochaska & Neeleman 2018; Shull & Danforth 2018; Prochaska & Zheng 2019; Yamasaki & Totani 2020). We used a log-normal distribution to characterize fDMIGM (Cordes et al. 2022). The log-normal in the form, N(μ, σ), is a function of the following parameters:
with the cosmic variance of DMIGM (σDMIGM). σDMIGM is described as follows:
where DMc is a constant, that is, DMc = 50 pc cm−3 (McQuinn 2014), and 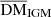 is the cosmic average of DM in the nonuniform intergalactic medium. The
is the cosmic average of DM in the nonuniform intergalactic medium. The 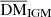 is described as follows:
is described as follows:
for a flat ΛCDM Universe. The proton mass is mp = 1.67 × 10−27 kg, and 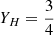 and
and 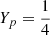 are the mass fractions of hydrogen and helium, respectively (Zhou et al. 2014). The fraction of baryons in the IGM is fIGM = 0.85 ± 0.05 (Cordes et al. 2022). The matter and baryon density are Ωm and Ωb (Zhou et al. 2014), respectively. For the cosmological parameters, we used the Planck 2018 results implemented in Astropy (Planck Collaboration VI 2020).
are the mass fractions of hydrogen and helium, respectively (Zhou et al. 2014). The fraction of baryons in the IGM is fIGM = 0.85 ± 0.05 (Cordes et al. 2022). The matter and baryon density are Ωm and Ωb (Zhou et al. 2014), respectively. For the cosmological parameters, we used the Planck 2018 results implemented in Astropy (Planck Collaboration VI 2020).
In the second term of Eq. (4), fτ is the PDF of 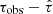 , where τobs is the observed scattering, and
, where τobs is the observed scattering, and 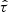 is the theoretical value of the scattering.
is the theoretical value of the scattering. 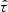 is described as follows:
is described as follows:
where Cτ = 0.48 ms (Cordes et al. 2022). The observed frequency vobs is given in units of GHz, and ϕ is the 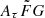 parameter (Cordes et al. 2022).
parameter (Cordes et al. 2022).
A Gaussian function was assumed to express 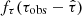 (Fig. 1 top). In the Gaussian function, the mean value was 0, and the observed error in the scattering (στ) was adopted as the standard deviation. However, some FRBs only have upper limits of the scattering. In these cases, we assumed a flat PDF of
(Fig. 1 top). In the Gaussian function, the mean value was 0, and the observed error in the scattering (στ) was adopted as the standard deviation. However, some FRBs only have upper limits of the scattering. In these cases, we assumed a flat PDF of 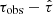 (Fig. 1 bottom). We adopted 3στ as the upper bound of the flat PDF.
(Fig. 1 bottom). We adopted 3στ as the upper bound of the flat PDF.
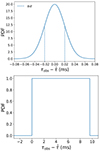 |
Fig. 1. PDF of |
To visualize Eq. (4), we show the PDF of DMh as a function of DMh and 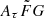 in the top panels of Fig. 2, where H0 = 74.3 km s−1 Mpc−1 was assumed. By integrating
in the top panels of Fig. 2, where H0 = 74.3 km s−1 Mpc−1 was assumed. By integrating 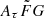 from 0.001 to 10
from 0.001 to 10 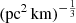 , we present the PDF of DMhin the bottom panels of Fig. 2.
, we present the PDF of DMhin the bottom panels of Fig. 2.
 |
Fig. 2. Two examples of the PDF in our observational samples. Top left panel: Three-dimensional image of fDMh for FRB 20181112A (see Sect. 4 and Table 1 for details). The x-axis is the DMh parameter from 20 to 600 pc cm−3. The y-axis is the |
FRB samples.
2.2. Redshift PDF
We used the following equation to calculate the redshift PDF (fz) with the parameters of DMobs and τobs:
where the integration range of DMh was [20, 1600] pc cm−3 (Cordes et al. 2022). In Eq. (11), we calculate the integration of all possible DMh and 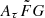 , which provided us with fz.
, which provided us with fz.
To demonstrate fz, we show examples of nine FRBs assuming H0 = 74.3 km s−1 Mpc−1 in Fig. 3. Following Cordes et al. (2022), we present two prior assumptions on the 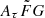 range in this work: narrow [0.5, 2] and wide [0.001, 10]
range in this work: narrow [0.5, 2] and wide [0.001, 10] 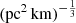 . The possible impact on the H0 measurement with different prior assumptions on the
. The possible impact on the H0 measurement with different prior assumptions on the 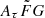 parameter is discussed in Sects. 3 and 5. Throughout the paper, we present the results assuming the wide range of
parameter is discussed in Sects. 3 and 5. Throughout the paper, we present the results assuming the wide range of ![$ A_{\tau} \tilde{F} G =[0.001, 10] $](/articles/aa/full_html/2025/01/aa50823-24/aa50823-24-eq82.gif)
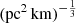 as a fiducial model unless otherwise mentioned.
as a fiducial model unless otherwise mentioned.
 |
Fig. 3. Nine examples representing the PDFs of redshift (z). These were randomly selected from our FRB samples (see Sect. 4 and Table 1 for details). H0 = 74.3 km s−1 Mpc−1 and DMh = [20, 1600] pc cm−3 were adopted. In each panel, we present PDFs based on two different ranges of |
2.3. Optimize H0
We chose the 50 percentile of fz to define the modeled redshift (zmodel). By letting H0 be a parameter (Eq. 9), zmodel is a function of H0. To optimize H0, we compared zmodel and zspec, and we adjusted H0 so that these two quantities became consistent within their errors, that is, zmodel = zspec. In Fig. 4, we show how zmodel depends on H0.
 |
Fig. 4. Observed redshift (zspec) vs. modeled redshift (zmodel) to optimize H0. To demonstrate how zmodel depends on H0, we present three values of H0, 60, 68, and 80 km s−1 Mpc−1, in the different panels. We used 30 FRBs (see Sect. 4 and Table 1 for details) with DMh = [20, 1600] pc cm−3 and |
We only changed H0 in Fig. 4 to demonstrate how this method works using 30 FRB samples (see Sect. 4 and Table 1 for details). However, H0 degenerates with fIGM in Eq. (9) because the observational error of fIGM is ∼6% (e.g., Li et al. 2019; Cordes et al. 2022). Therefore, we present two cases of (i) fIGM × H0 as a single parameter in Eq. (9) and (ii) H0 alone for a given fIGM and its error in Sect. 5.
3. Simulation using mock FRB samples
3.1. Our method using scattering
Before we applied our method to the observed data, we demonstrate how accurate our measurements are compared with a previous method via simulations. Our aim is a prediction based on a reasonable sample size that can be achieved in the near future. With future instruments such as the CHIME Outrigger (Mena-Parra et al. 2022) and BURSTT (Lin et al. 2022; Ho et al. 2023), it would be feasible to identify 100 FRB host galaxies. Moreover, James et al. (2022) predicted that a sample of approximately 100 FRBs with spectroscopic redshifts would be sufficient to distinguish the ∼10% systematic discrepancies of the Hubble tension between the distance ladder and CMB methods. Therefore, we followed James et al. (2022) to decide the sample size of the mock data. We generated 100 mock FRBs as follows. First, we randomly selected redshift values for 100 mock FRBs from the CHIME FRB catalog (CHIME/FRB Collaboration 2021) based on the DM-derived redshift in Hashimoto et al. (2022) to create mock redshifts, zmock. Then, we randomly sampled NE2001 values for 100 FRBs from the same catalog to create mock DMMWdisk values (DMMWdisk, mock). The adopted value of the mock DMMWhalo (DMMWhalo, mock) is 52.5 pc cm−3. Using zmock, we calculated DMIGM based on Eq. (9) assuming H0 = 68 km s−1 Mpc−1 and fIGM = 0.85, where the line-of-sight fluctuation of DMIGM was taken into account based on Eq. (8) to create mock DMIGM values (DMIGM, mock). Figure 5 illustrates the generation of 100 DMIGM, mock.
 |
Fig. 5. DMIGM, mock as a function of zmock. The red dots represent DMIGM, mock generated by using Eq. (8) at each zmock, taking the line-of-sight fluctuation of DMIGM into account. For a given zmock, we randomly selected one mock data point (red dot) from the blue dots. We iterated this process 100 times at the different zmock, generating 100 mock FRB data. |
In general, DMh is highly uncertain because DMobs is an integrated quantity along a line of sight to an FRB, and hence, it is hard to separate between DMh and DMIGM without using scattering. For instance, Macquart et al. (2020) assumed DMh = 50 pc cm−3 in their analysis. In contrast, Rafiei-Ravandi et al. (2021) conducted a cross-correlation analysis between CHIME FRB samples and galaxy catalogs to conclude that DMh is about 400 pc cm−3, statistically. An even larger average DMh might be suggested by a population-model approach (e.g., Wang & van Leeuwen 2024). These works highlight the significant uncertainty of the typical value of DMh, ranging from ∼50 to ∼400 pc cm−3. To generate mock FRBs, we assumed a normal distribution with a mean of 200 pc cm−3 and a standard deviation of 50 pc cm−3 to create mock DMh values (DMh, mock).
Subsequently, using Eq. (1), we derived 100 mock DMobs values (DMobs, mock) from the zmock, DMIGM, mock, DMMW, mock, and DMh, mock. The mock scattering times (τmock) at the host frame 1 GHz for the 100 mock FRBs were determined using DMh, mock with 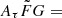 1
1 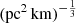 and v = 1 GHz from Eq. (3). τmock at the observer’s frame (τmock, obs) was calculated by dividing τmock by a (1 + zmock)3 factor, assuming ν−4 dependence of τ and a time-dilation factor of (1 + z). The mock error in scattering (στ,mock) was simulated based on the median value of the fractional errors of τobs in Table 1 (i.e., στ,mock = 5.2%). In summary, we generated 100 mock FRBs including zmock, DMIGM, mock, DMMW, mock, DMh, mock, DMobs, mock, τmock, obs, and στ,mock.
and v = 1 GHz from Eq. (3). τmock at the observer’s frame (τmock, obs) was calculated by dividing τmock by a (1 + zmock)3 factor, assuming ν−4 dependence of τ and a time-dilation factor of (1 + z). The mock error in scattering (στ,mock) was simulated based on the median value of the fractional errors of τobs in Table 1 (i.e., στ,mock = 5.2%). In summary, we generated 100 mock FRBs including zmock, DMIGM, mock, DMMW, mock, DMh, mock, DMobs, mock, τmock, obs, and στ,mock.
Figure 6 displays the PDF of H0 × fIGM and H0 derived by applying our method to the 100 mock FRBs. The result is H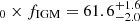 km s−1 Mpc−1. This value corresponds to H
km s−1 Mpc−1. This value corresponds to H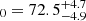 km s−1 Mpc−1, where we assumed fIGM = 0.85 taking the ±0.05 error of fIGM (Cordes et al. 2022) into account. This reconstructed H0 is consistent with the assumption made in the simulation, that is, H0 = 68.0 km s−1 Mpc−1 within the statistical error.
km s−1 Mpc−1, where we assumed fIGM = 0.85 taking the ±0.05 error of fIGM (Cordes et al. 2022) into account. This reconstructed H0 is consistent with the assumption made in the simulation, that is, H0 = 68.0 km s−1 Mpc−1 within the statistical error.
 |
Fig. 6. Simulation results using our method with mock FRB samples. Top panel: PDF of H0 × fIGM derived by using the 100 mock FRBs and our method with scattering (blue curve). The vertical dashed blue lines correspond to 84.2 and 15.8 percentiles (±σ) of the PDF. Bottom panel: PDF of H0 by changing the scale from H0 × fIGM (top panel) to H0. To generate the mock data, we assumed H0 = 68.0 km s−1 Mpc−1, which is shown by the solid vertical black line. The vertical dashed blue lines are the positive and negative standard deviations of H0 after taking the fIGM error into account, where the fIGM error is ±0.05 (Cordes et al. 2022). |
3.2. Prior assumptions on the 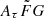 range in our method
range in our method
In Eq. (11), the prior assumption on the 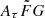 range needs to be specified. Following Cordes et al. (2022), we briefly present how the narrow and wide
range needs to be specified. Following Cordes et al. (2022), we briefly present how the narrow and wide 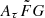 ranges affect the H0 measurements based on the 100 FRB mock data. We applied the method described in Sect. 2 to the 100 mock data, assuming
ranges affect the H0 measurements based on the 100 FRB mock data. We applied the method described in Sect. 2 to the 100 mock data, assuming 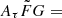 [0.5, 2] and [0.001, 10]
[0.5, 2] and [0.001, 10] 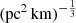 . For a given value of fIGM = 0.85 ± 0.05, the derived H0 are 70.6
. For a given value of fIGM = 0.85 ± 0.05, the derived H0 are 70.6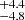 and 72.5
and 72.5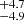 km s−1 Mpc−1 for
km s−1 Mpc−1 for 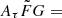 [0.5, 2] and [0.001, 10]
[0.5, 2] and [0.001, 10] 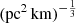 , respectively. These reconstructed H0 values are consistent with the assumption on H0 = 68 km s−1 Mpc−1 within the errors. This is probably because
, respectively. These reconstructed H0 values are consistent with the assumption on H0 = 68 km s−1 Mpc−1 within the errors. This is probably because 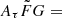 1
1 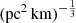 was adopted when the mock FRBs were generated (Sect. 3.1), and the two
was adopted when the mock FRBs were generated (Sect. 3.1), and the two 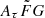 ranges cover this initial assumption reasonably well. Therefore, in this ideal case, no significant systematics due to the prior
ranges cover this initial assumption reasonably well. Therefore, in this ideal case, no significant systematics due to the prior 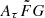 assumption are expected. However, this might not be the case when observed data are used to constrain H0 because the physically reasonable range of
assumption are expected. However, this might not be the case when observed data are used to constrain H0 because the physically reasonable range of 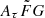 is yet to be ascertained (Cordes et al. 2022). A further discussion of using observed data is described in Sect. 6.3.
is yet to be ascertained (Cordes et al. 2022). A further discussion of using observed data is described in Sect. 6.3.
3.3. Previous FRB method assuming DMh
For a comparison, we tested a previous method without τmock, obs, assuming DMh = 50 pc cm−3 to calculate DMIGM. In this previous method, DMIGM was calculated solely based on Eq. (1) for the same 100 FRB mock samples as were used for our method above. The top panel of Fig. 7 illustrates the resulting DMIGM as a function of zmock. We fit Eq. (9) to the mock data by changing H0 as a fitting parameter. The derived PDFs of H0 × fIGM and H0 are shown in the middle and bottom panels of Fig. 7, respectively. The result is H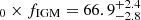 km s−1 Mpc−1. This value corresponds to H
km s−1 Mpc−1. This value corresponds to H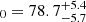 km s−1 Mpc−1, where we assumed fIGM = 0.85 taking the ±0.05 error of fIGM into account. This reconstructed H0 significantly deviates from the assumed value of H0 = 68.0 km s−1 Mpc−1 in the simulation.
km s−1 Mpc−1, where we assumed fIGM = 0.85 taking the ±0.05 error of fIGM into account. This reconstructed H0 significantly deviates from the assumed value of H0 = 68.0 km s−1 Mpc−1 in the simulation.
 |
Fig. 7. Simulation results using the previous method with mock FRB samples. Top panel: DMIGM, mock as a function of zmock. The blue dots with error bars show 100 mock FRB data, where DMIGM, mock is calculated by the previous method, assuming DMh = 50 pc cm−3. We fit Eq. (9) to the mock FRB data with a free parameter of H0. The best-fit function is shown by the solid black line, where H |
3.4. Comparison between our method and the previous FRB method
Fig. 8 summarizes the systematic difference between the previous method and our method. In Fig. 8, we note that the reconstructed H0 value with our method is consistent with the assumed value of H0 = 68 km s−1 Mpc−1 within an uncertainty of 1σ. The 1σ error is presented by the dashed vertical orange lines in Fig. 8, where the assumed value (solid vertical black line) is within this error. Therefore, the reconstructed H0 with our method does not deviate in a statistically significant way from the assumed value. The apparent offset between our method and the assumed value in Fig. 8 would be due to the statistical fluctuation owing to the random process in generating the mock FRB data. The systematic errors of H0 are 15.7% and 6.6% for the previous method and our method, respectively. This corresponds to a reduction of the systematic error by 9.1%. By adopting our method, the statistical error slightly decreases from 3.9% to 2.9%, which corresponds to a reduction of 1%. This small reduction is probably due to a systematic effect, where the intrinsic variation in DMh contaminates the DMIGM variation in the previous method, while our method reduces this contamination by measuring the individual DMh from scattering. Notably, the reduction in the systematic error is closely aligned with the systematics of the Hubble tension, that is, an ∼10% systematic uncertainty. This highlights the potential of our method to address the Hubble tension using forthcoming FRB datasets.
 |
Fig. 8. PDFs of H0 derived by our method (orange) with positive and negative standard deviations (orange vertical dashed lines) and the previous method (blue) with positive and negative standard deviations (vertical dashed blue lines), using the same 100 mock FRB data. The vertical black line indicates H0 = 68.0 km s−1 Mpc−1, which was assumed when we generated the 100 mock FRBs. |
4. Selection criteria for the observed FRB samples
In the previous section, we applied our method to the simulated mock FRB samples to demonstrate how our method works compared with the previous method. In this section, we apply our method as described in Sect. 2 to 30 localized FRBs, which are shown in Table 1. In our method, we require localized FRBs with measurements of the spectroscopic redshift. Although more than 700 FRBs have been detected so far1, only ∼40 of them are localized to host galaxies (e.g., Bhandari et al. 2022; Law et al. 2024). Additionally, our method requires information about the scattering time, which meant that we were left with 37 data sets to work with. According to Cordes et al. (2022), the reasonable range of the 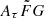 parameter is smaller than 10
parameter is smaller than 10 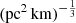 . The PDF of the
. The PDF of the 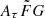 parameter can be computed by integrating Eq. (4) (the top panels of Fig. 2) over DMh. We found that the PDFs of the
parameter can be computed by integrating Eq. (4) (the top panels of Fig. 2) over DMh. We found that the PDFs of the 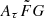 parameter peak beyond 10
parameter peak beyond 10 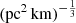 for four FRB samples, that is, FRBs 20191228A, 20210405I, 20210410D, and 20220912A. Their PDFs of the
for four FRB samples, that is, FRBs 20191228A, 20210405I, 20210410D, and 20220912A. Their PDFs of the 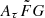 parameter are mostly distributed at
parameter are mostly distributed at 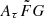 > 10
> 10 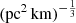 . The range of the peaks is
. The range of the peaks is ![$ A_{\tau} \tilde{F} G = [10,1000]\,(\mathrm{pc}^2\,\mathrm{km})^{-\frac{1}{3}} $](/articles/aa/full_html/2025/01/aa50823-24/aa50823-24-eq117.gif) for these four samples. Therefore, we excluded these four FRBs from our samples as outliers in the
for these four samples. Therefore, we excluded these four FRBs from our samples as outliers in the 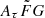 parameter.
parameter.
We also excluded three FRB samples that had negative DMIGM as follows. The extragalactic component of the dispersion measure (DMEG) is described as
where DMMWhalo = 52.5 pc cm−3, and DMMWdisk was adopted from the NE2001 model. Here, certain values were used for DMMWhalo and DMMWdisk for the sample selection alone. The PDFs of DMMWhalo and DMMWdisk were taken into account in our method (Sect. 2) to constrain H0. We found that DMEG of FRB 20200120E and 20220319D are negative, indicating a negative DMIGM. The DMEG of FRB 20181030A is 9.93 pc cm−3. This value is lower than the lower bound of the prior assumption on DMh ( = 20 pc cm−3) adopted in this work, following Cordes et al. (2022). These three FRBs correspond to negative DMIGM. Therefore, we also excluded these three FRBs from our analysis. We excluded 7 of the 37 data sets, and the remaining 30 FRB samples were used in this work. Table 2 lists the 7 FRBs we excluded from our samples. In Fig. 9, we compare the scattering time at the rest-frame 1 GHz and DMEG for the 30 FRB samples, along with 5 samples out of 7 excluded samples. We only show 5 excluded samples because 2 of the 7 have a negative DMEG. These 5 excluded samples are close to or above the model line of 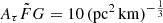 (solid green line in Fig. 9). The empirical relation between the scattering at the rest-frame 1 GHz and DMh expected from Galactic pulsar observations is described as
(solid green line in Fig. 9). The empirical relation between the scattering at the rest-frame 1 GHz and DMh expected from Galactic pulsar observations is described as
 |
Fig. 9. Scattering time vs. DMEG or DMh. The x-axis is the DMEG from Eq. (12) in the log scale for the FRB samples (black dots), and it shows DMh for the empirical relation based on Galactic pulsars (shaded blue region) and the |
FRB samples that we excluded from our analysis either because of (i) outliers in the 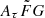 parameter space or because (ii) the DMEG is negative.
parameter space or because (ii) the DMEG is negative.
DMh and zmodel computed for the FRB samples.
(Cordes et al. 2022), which is shown as the shaded blue region in Fig. 9. The term of log10(3) represents a scaling factor for taking the spherical wavefront difference between pulsars in the Milky Way and FRBs in host galaxies in the extragalactic Universe into account.
5. Results for the observed FRB samples
As described in Sect. 2.3, we treated fIGM × H0 as a single parameter to fit zmodel to zspec. The top panel of Fig. 10 shows the χ2 of the fitting as a function of fIGM × H0,
 |
Fig. 10. The results using our method with observed FRB samples. Top panel: χ2 described by Eq. (14) as a function of fIGM × H0 using the 30 FRB samples and our method. The black line indicates the χ2 values derived by changing fIGM × H0. The blue line is the best-fit polynomial function to χ2. Middle panel: PDF of fIGM × H0 from the χ2 (top panel). The vertical dashed black lines correspond to the 84.2 and 15.8 percentiles (±σ) of the PDF. Bottom panel: PDF of H0 by changing the scale from H0 × fIGM (middle panel) to H0 for a given fIGM = 0.85 ± 0.05. The solid vertical line indicates the peak of the PDF, and the dashed vertical lines indicate the uncertainty range of H0 after taking the 0.05 error of fIGM into account. The orange area indicates the CMB measurement of H0 (e.g., Planck Collaboration VI 2020). The blue area shows the measurement by local distance ladders (e.g., Riess et al. 2022). |
where σi is the error of zmodel of the ith FRB sample. We calculated the PDF of fIGM × H0 assuming PDF ∝exp(−χ2/2). The result is shown in the middle panel of Fig. 10 with prior assumptions on DMh = [20, 1600] pc cm−3, and ![$ A_{\tau} \tilde{F} G = [0.001,10] $](/articles/aa/full_html/2025/01/aa50823-24/aa50823-24-eq157.gif)
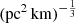 . The best-fit result is
. The best-fit result is 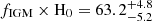 km s−1 Mpc−1. Given fIGM = 0.85 ± 0.05 (Cordes et al. 2022), the best-fit result corresponds to
km s−1 Mpc−1. Given fIGM = 0.85 ± 0.05 (Cordes et al. 2022), the best-fit result corresponds to 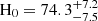 km s−1 Mpc−1, where the uncertainty of fIGM was taken into account (bottom panel of Fig. 10). The median value of DMh in our analysis is DMh
km s−1 Mpc−1, where the uncertainty of fIGM was taken into account (bottom panel of Fig. 10). The median value of DMh in our analysis is DMh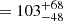 pc cm−3 (see also Table 3 and Fig. 11). These errors were determined by calculating the median of the DMh errors.
pc cm−3 (see also Table 3 and Fig. 11). These errors were determined by calculating the median of the DMh errors.
6. Discussion
6.1. Comparison with the CMB and local distance ladders
Our measurement of the Hubble constant is H0 = 74.3−7.5+7.2 km s−1 Mpc−1 using scattering. The central value of this measurement prefers the measurement from the local distance ladder (H0 = 73.0 ± 1.0 km s−1 Mpc−1; Riess et al. 2022) than the CMB (H0 = 67.7 ± 0.4 km s−1 Mpc−1; Planck Collaboration VI 2020). However, our measurement is still consistent with these two methods within the 1σ error. To address the Hubble tension with FRBs, both statistical and systematic errors have to be reduced in the future, as discussed in the following sections.
6.2. Comparison with the other FRB methods
Recently, some papers reported H0 values that were constrained by FRBs, and the methods differed from ours. Hagstotz et al. (2022) assumed a normal distribution of DMh with μ= 100 pc cm−3 and σ= 50 pc cm−3. They derived H0 = 62.3 ± 9.1 km s−1 Mpc−1 using the DMIGM–z relation with nine localized FRB samples. They assumed fIGM = 0.84, where the difference from our assumption, fIGM = 0.85, is negligibly small compared to the uncertainty of H0. James et al. (2022) combined FRB population models and the DMEG-z relation, which were parameterized by seven quantities for fitting, including μ and σ of the lognormal distribution of DMh and H0. They fit the model to the 76 FRB data obtained from The Commensal Real-time The Australian Square Kilometre Array Pathfinder Fast Transients Coherent (CRACO) survey (16 localized and 60 unlocalized), where the best-fit model indicates 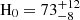 km s−1 Mpc−1,
km s−1 Mpc−1, 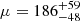 pc cm−3, and σ = 3.5 pc cm−3. They assumed fIGM = 0.844. Zhao et al. (2022) used a Bayesian framework to estimate H
pc cm−3, and σ = 3.5 pc cm−3. They assumed fIGM = 0.844. Zhao et al. (2022) used a Bayesian framework to estimate H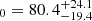 km s−1 Mpc−1 with 12 unlocalized FRB samples with a prior assumption on a lognormal distribution of DMh with μ = 68 pc cm−3 and σ = 0.88 pc cm−3. The samples were collected from FRBs detected with the Australian Square Kilometre Array Pathfinder (ASKAP). These previous works assumed a certain shape of the DMh distribution, that is, a lognormal distribution or a normal distribution. Our method is free of this assumption. The scattering is used to derive the individual DMh and DMIGM in the samples.
km s−1 Mpc−1 with 12 unlocalized FRB samples with a prior assumption on a lognormal distribution of DMh with μ = 68 pc cm−3 and σ = 0.88 pc cm−3. The samples were collected from FRBs detected with the Australian Square Kilometre Array Pathfinder (ASKAP). These previous works assumed a certain shape of the DMh distribution, that is, a lognormal distribution or a normal distribution. Our method is free of this assumption. The scattering is used to derive the individual DMh and DMIGM in the samples.
Our result is 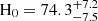 km s−1 Mpc−1 (Sect. 5), which is consistent with H0 in these previous works within the statistical errors. In the previous method, however, there might be significant unknown systematics in the assumption on DMh as we demonstrated in Sect. 3. Depending on the different assumptions on DMh, the central values of derived H0 systematically differ in the previous works mentioned above. This possible systematics is still smaller than the large statistical error based on the current FRB samples. However, the possible systematics would be problematic in the future when the statistical uncertainty is significantly reduced by large FRB samples. In contrast to previous studies, our method can minimize these systematics using the scattering time to derive the individual DMh rather than assuming a certain DMh distribution.
km s−1 Mpc−1 (Sect. 5), which is consistent with H0 in these previous works within the statistical errors. In the previous method, however, there might be significant unknown systematics in the assumption on DMh as we demonstrated in Sect. 3. Depending on the different assumptions on DMh, the central values of derived H0 systematically differ in the previous works mentioned above. This possible systematics is still smaller than the large statistical error based on the current FRB samples. However, the possible systematics would be problematic in the future when the statistical uncertainty is significantly reduced by large FRB samples. In contrast to previous studies, our method can minimize these systematics using the scattering time to derive the individual DMh rather than assuming a certain DMh distribution.
6.3. Prior assumption on the 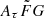 parameter range
parameter range
Our simulation described in Sect. 3.2 suggests that the prior assumption on the 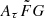 range does not significantly impact the best-fit result of H0, as far as the prior covers the true
range does not significantly impact the best-fit result of H0, as far as the prior covers the true 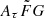 value. However, this might not be the case when observed data are used because the true
value. However, this might not be the case when observed data are used because the true 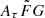 distribution is unknown (Cordes et al. 2022).
distribution is unknown (Cordes et al. 2022).
We compared results based on the observed data, assuming narrow and wide ranges of ![$ A_{\tau} \tilde{F} G =[0.5,2] $](/articles/aa/full_html/2025/01/aa50823-24/aa50823-24-eq170.gif) and [0.001, 10]
and [0.001, 10] 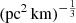 , respectively. Figure 12 shows a comparison between the narrow and wide ranges of
, respectively. Figure 12 shows a comparison between the narrow and wide ranges of 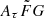 in zmodel versus zspec. The figure includes our 30 FRB samples, where we fixed the value of fIGM × H0 = 63.2 km s−1 Mpc−1 to highlight the difference between the
in zmodel versus zspec. The figure includes our 30 FRB samples, where we fixed the value of fIGM × H0 = 63.2 km s−1 Mpc−1 to highlight the difference between the 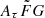 ranges. χ2 is 75.1 for the narrow range, and 37.9 is for the wide range. We found that zmodel with
ranges. χ2 is 75.1 for the narrow range, and 37.9 is for the wide range. We found that zmodel with ![$ A_{\tau} \tilde{F} G =[0.5,2] $](/articles/aa/full_html/2025/01/aa50823-24/aa50823-24-eq174.gif)
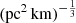 are systematically lower than that with
are systematically lower than that with ![$ A_{\tau} \tilde{F} G =[0.001,10] $](/articles/aa/full_html/2025/01/aa50823-24/aa50823-24-eq176.gif)
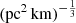 , indicating that the different prior assumptions on
, indicating that the different prior assumptions on 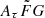 systematically affect the H0 measurement. To demonstrate this point, we present the best-fit zmodel to zspec for two cases of the
systematically affect the H0 measurement. To demonstrate this point, we present the best-fit zmodel to zspec for two cases of the 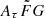 ranges by optimizing fIGM × H0 in the top panel of Fig. 13. The best-fit fIGM × H0 (and χ2) are
ranges by optimizing fIGM × H0 in the top panel of Fig. 13. The best-fit fIGM × H0 (and χ2) are 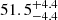 km s−1 Mpc−1 (58) and
km s−1 Mpc−1 (58) and 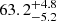 km s−1 Mpc−1 (37.9) for the narrow and wide ranges, respectively (middle panel of Fig. 13). Given a fixed value of fIGM = 0.85 ± 0.05, these correspond to
km s−1 Mpc−1 (37.9) for the narrow and wide ranges, respectively (middle panel of Fig. 13). Given a fixed value of fIGM = 0.85 ± 0.05, these correspond to 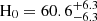 km s−1 Mpc−1 and
km s−1 Mpc−1 and 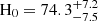 km s−1 Mpc−1 for the narrow and wide
km s−1 Mpc−1 for the narrow and wide 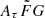 ranges, respectively (bottom panel of Fig. 13)
ranges, respectively (bottom panel of Fig. 13)
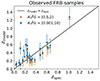 |
Fig. 12. zmodel vs. zobs, comparing two prior assumptions on the |
 |
Fig. 13. Comparison of results across different |
The χ2 value is higher for the narrow 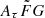 range, suggesting a worse fit to the observed data with
range, suggesting a worse fit to the observed data with ![$ A_{\tau} \tilde{F} G =[0.5,2] $](/articles/aa/full_html/2025/01/aa50823-24/aa50823-24-eq198.gif)
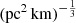 . This might suggest that the narrow range does not fully cover the true
. This might suggest that the narrow range does not fully cover the true 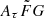 distribution in the FRB samples. The narrow-range model therefore does not fit the observed data well. In contrast, the wide
distribution in the FRB samples. The narrow-range model therefore does not fit the observed data well. In contrast, the wide 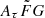 range is expected to perform better because its coverage in the
range is expected to perform better because its coverage in the 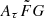 parameter space is better. We speculate that the wide
parameter space is better. We speculate that the wide 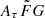 range covers the true
range covers the true 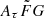 distribution better, and it would be closer to the ideal situation of our simulation without significant systematics (Sect. 3.2) than the narrow
distribution better, and it would be closer to the ideal situation of our simulation without significant systematics (Sect. 3.2) than the narrow 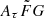 range. In this sense, the wide
range. In this sense, the wide 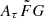 range would be preferable in our analysis.
range would be preferable in our analysis.
Detailed investigations of the 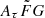 impact on figm × H0 have to be made and the optimal range of
impact on figm × H0 have to be made and the optimal range of 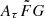 must be determined before our method can address the Hubble tension properly. Physically motivated constraints of the
must be determined before our method can address the Hubble tension properly. Physically motivated constraints of the 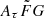 parameter would also play an important role in searching for the optimal
parameter would also play an important role in searching for the optimal 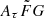 range. We leave these points as future work because we focused on proposing a method for constraining H0 with the scattering rather than emphasizing the current accuracy in this paper.
range. We leave these points as future work because we focused on proposing a method for constraining H0 with the scattering rather than emphasizing the current accuracy in this paper.
6.4. Future FRB samples
Currently, the number of localized FRBs is limited to ∼40 (e.g., Bhandari et al. 2022; Law et al. 2024). About 100 localized FRBs would be sufficient to clarify the Hubble tension with an uncertainty of ∼2.5 km s−1 Mpc−1 (James et al. 2022). More FRBs will be localized with scattering measurements with future instruments, including the CHIME outrigger (Mena-Parra et al. 2022), the Deep Synoptic Array-110, ASKAP, and the Bustling Universe Radio Survey Telescope in Taiwan (BURSTT) (Lin et al. 2022; Ho et al. 2023). BURSTT can localize ∼100 FRBs per year (Lin et al. 2022) to identify host galaxies with scattering measurements. Unlocalized FRBs can be used to derive the redshift statistically to further increase the samples (e.g., Zhao et al. 2022). Therefore, our method can be tested with better statistics in the near future.
7. Conclusions
A significant difference of 4 to 6 sigma exists in determining the Hubble constant (H0) for two distinct methods, the cosmic microwave background (CMB) and the local distance ladders. This difference is most likely caused by unknown systematic errors. Therefore, devising an independent method for measuring H0 is the most important mission for addressing this unresolved puzzle. The FRBs offer a unique observable, DMIGM, which is a new distance indicator to derive H0. We summarize the result of this work below.
-
DMh had to be assumed in previous works to derive DMIGM. The scattering enabled us to measure DMIGM with a parameter that combined a pulse profile, density fluctuations, and the geometry of a scattering screen (
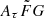 parameter). We used this parameterization for 30 FRBs with scattering measurements to model the redshifts, and we compared them with the observed redshifts (spectroscopic redshifts) to constrain H0.
parameter). We used this parameterization for 30 FRBs with scattering measurements to model the redshifts, and we compared them with the observed redshifts (spectroscopic redshifts) to constrain H0. -
We demonstrated that our method reduces the systematic error of H0 by 9.1% compared to the previous method, and the statistical error is reduced by 1%. The reduction in systematic error is comparable to the Hubble tension (∼10%), indicating that our method can address the Hubble tension using future FRB samples.
-
We measured a Hubble constant of H0 = 74.3−7.5+7.2 km s−1 Mpc−1 with our method using scattering. The central value of this result prefers the measurement from the local distance ladder (H0 = 73.0 ± 1.0 km s−1 Mpc−1; Riess et al. 2022) over the CMB (H0 = 67.7 ± 0.4 km s−1 Mpc−1; Planck Collaboration VI 2020). However, our measurement is still consistent with the two methods within an error of 1σ.
We described two future directions to reduce the error in our measurement. The first direction is to use more localized FRBs with scattering measurements, which are to be detected with future instruments, including BURSTT (Lin et al. 2022). BURSTT is the Taiwanese radio array, which can localize ∼100 FRBs per year to identify host galaxies with scattering (Lin et al. 2022). The second direction is to statistically treat unlocalized FRBs to further increase the samples (e.g., Zhao et al. 2022).
Acknowledgments
We would like to express our deepest appreciation to the anonymous referee for the comprehensive and thoughtful review of our manuscript. Their detailed examination and insightful suggestions have played a crucial role in refining our work, and the constructive feedback has greatly enhanced the overall quality and clarity of the paper. T-CY is grateful to Ms. Poya Wang for insightful discussions. T-CY is also grateful to Dr. Shotaro Yamasaki for insightful discussions. TG acknowledges the support of the National Science and Technology Council of Taiwan through grants 108-2628-M-007-004-MY3, 111-2112-M-007-021, and 112-2123-M-001-004-. TH acknowledges the support of the National Science and Technology Council of Taiwan through grants 110-2112-M-005-013-MY3, 110-2112-M-007-034-, 113-2112-M-005-009-MY3, and 113-2123-M-001-008-. We acknowledge the use of the CHIME/FRB Public Database, provided at https://www.chime-frb.ca/ by the CHIME/FRB Collaboration. This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2018).
References
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bailes, M. 2022, Science, 378, abj3043 [NASA ADS] [CrossRef] [Google Scholar]
- Bannister, K. W., Deller, A. T., Phillips, C., et al. 2019, Science, 365, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Bhandari, S., Kumar, P., Shannon, R. M., & Macquart, J. P. 2019, ATel, 12940, 1 [NASA ADS] [Google Scholar]
- Bhandari, S., Bannister, K. W., Lenc, E., et al. 2020, ApJ, 901, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Bhandari, S., Heintz, K. E., Aggarwal, K., et al. 2022, AJ, 163, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Bhandari, S., Gordon, A. C., Scott, D. R., et al. 2023, ApJ, 948, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Caleb, M., Driessen, L. N., Gordon, A. C., et al. 2023, MNRAS, 524, 2064 [NASA ADS] [CrossRef] [Google Scholar]
- Cassanelli, T., Leung, C., Sanghavi, P., et al. 2023, ArXiv e-prints [arXiv:2307.09502] [Google Scholar]
- Chawla, P., Andersen, B. C., Bhardwaj, M., et al. 2020, ApJ, 896, L41 [NASA ADS] [CrossRef] [Google Scholar]
- CHIME/FRB Collaboration (Andersen, B. C., et al.) 2019, ApJ, 885, L24 [Google Scholar]
- CHIME/FRB Collaboration (Amiri, M., et al.) 2021, ApJS, 257, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Cho, H., Macquart, J.-P., Shannon, R. M., et al. 2020, ApJ, 891, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Connor, L., Ravi, V., Catha, M., et al. 2023, ApJ, 949, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002, ArXiv e-prints [arXiv:astro-ph/0207156] [Google Scholar]
- Cordes, J. M., Ocker, S. K., & Chatterjee, S. 2022, ApJ, 931, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Day, C. K., Deller, A. T., Shannon, R. M., et al. 2020, MNRAS, 497, 3335 [NASA ADS] [CrossRef] [Google Scholar]
- Di Valentino, E., Mena, O., Pan, S., et al. 2021, Class. Quant. Grav., 38, 153001 [NASA ADS] [CrossRef] [Google Scholar]
- Driessen, L. N., Barr, E. D., Buckley, D. A. H., et al. 2024, MNRAS, 527, 3659 [Google Scholar]
- Hagstotz, S., Reischke, R., & Lilow, R. 2022, MNRAS, 511, 662 [CrossRef] [Google Scholar]
- Hashimoto, T., Goto, T., Chen, B. H., et al. 2022, MNRAS, 511, 1961 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, J. C., & Baxter, E. J. 2018, JCAP, 2018, 037 [CrossRef] [Google Scholar]
- Ho, S. C. C., Hashimoto, T., Goto, T., et al. 2023, ApJ, 950, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, J.-P., & Wang, F.-Y. 2023, Universe, 9, 94 [CrossRef] [Google Scholar]
- James, C. W., Ghosh, E. M., Prochaska, J. X., et al. 2022, MNRAS, 516, 4862 [NASA ADS] [CrossRef] [Google Scholar]
- Josephy, A., Chawla, P., Fonseca, E., et al. 2019, ApJ, 882, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., Day, C. K., Shannon, R. M., et al. 2020, ATel, 13694, 1 [NASA ADS] [Google Scholar]
- Kumar, P., Shannon, R. M., Moss, V., Qiu, H., & Bhandari, S. 2021, ATel, 14502, 1 [NASA ADS] [Google Scholar]
- Law, C. J., Butler, B. J., Prochaska, J. X., et al. 2020, ApJ, 899, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Law, C. J., Sharma, K., Ravi, V., et al. 2024, ApJ, 967, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, K.-G., Khrykin, I. S., Simha, S., et al. 2023, ApJ, 954, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z., Gao, H., Wei, J.-J., et al. 2019, ApJ, 876, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, H. H., Lin, K. Y., Li, C. T., et al. 2022, PASP, 134, 094106 [NASA ADS] [CrossRef] [Google Scholar]
- Lorimer, D. R., Bailes, M., McLaughlin, M. A., Narkevic, D. J., & Crawford, F. 2007, Science, 318, 777 [Google Scholar]
- Lorimer, D. R., McLaughlin, M. A., & Bailes, M. 2024, Ap&SS, 369, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Macquart, J.-P., Prochaska, J. X., McQuinn, M., et al. 2020, Nature, 581, 391 [Google Scholar]
- McQuinn, M. 2014, ApJ, 780, L33 [Google Scholar]
- Mena-Parra, J., Leung, C., Cary, S., et al. 2022, AJ, 163, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Mörtsell, E., Goobar, A., Johansson, J., & Dhawan, S. 2022, ApJ, 935, 58 [CrossRef] [Google Scholar]
- Nimmo, K., Hessels, J. W. T., Kirsten, F., et al. 2022, Nat. Astron., 6, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Niu, M., Kasai, A., Tanuma, M., et al. 2022, Sci. Adv., 8, eabi6375 [CrossRef] [Google Scholar]
- Petroff, E., Hessels, J. W. T., & Lorimer, D. R. 2019, A&ARv, 27, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Price, D. C., Foster, G., Geyer, M., et al. 2019, MNRAS, 486, 3636 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., & Neeleman, M. 2018, MNRAS, 474, 318 [CrossRef] [Google Scholar]
- Prochaska, J. X., & Zheng, Y. 2019, MNRAS, 485, 648 [NASA ADS] [Google Scholar]
- Prochaska, J. X., Macquart, J.-P., McQuinn, M., et al. 2019, Science, 366, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Qiu, H., Shannon, R. M., Farah, W., et al. 2020, MNRAS, 497, 1382 [Google Scholar]
- Rafiei-Ravandi, M., Smith, K. M., Li, D., et al. 2021, ApJ, 922, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Ravi, V., Catha, M., D’Addario, L., et al. 2019, Nature, 572, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Ravi, V., Law, C. J., Li, D., et al. 2022, MNRAS, 513, 982 [CrossRef] [Google Scholar]
- Ravi, V., Catha, M., Chen, G., et al. 2023a, ArXiv e-prints [arXiv:2301.01000] [Google Scholar]
- Ravi, V., Catha, M., Chen, G., et al. 2023b, ApJ, 949, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2021, ApJ, 908, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Yuan, W., Macri, L. M., et al. 2022, ApJ, 934, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Ryder, S. D., Bannister, K. W., Bhandari, S., et al. 2023, Science, 382, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Sammons, M. W., Deller, A. T., Glowacki, M., et al. 2023, MNRAS, 525, 5653 [NASA ADS] [CrossRef] [Google Scholar]
- Shannon, R. M., Bannister, K. W., Bera, A., et al. 2023, arXiv e-prints [arXiv:2408.02083] [Google Scholar]
- Shull, J. M., & Danforth, C. W. 2018, ApJ, 852, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Simha, S., Lee, K.-G., Prochaska, J. X., et al. 2023, ApJ, 954, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Spitler, L. G., Cordes, J. M., Hessels, J. W. T., et al. 2014, ApJ, 790, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Tendulkar, S. P., Bassa, C. G., Cordes, J. M., et al. 2017, ApJ, 834, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Verde, L., Treu, T., & Riess, A. G. 2019, Nat. Astron., 3, 891 [Google Scholar]
- Wang, Y., & van Leeuwen, J. 2024, A&A, 690, A377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yamasaki, S., & Totani, T. 2020, ApJ, 888, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, Z. W., Zhang, J. G., Li, Y., Zhang, J. F., & Zhang, X. 2022, ArXiv e-prints [arXiv:2212.13433] [Google Scholar]
- Zhou, B., Li, X., Wang, T., Fan, Y. Z., & Wei, D. M. 2014, Phys. Rev. D, 89, 107303 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
FRB samples that we excluded from our analysis either because of (i) outliers in the 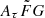 parameter space or because (ii) the DMEG is negative.
parameter space or because (ii) the DMEG is negative.
All Figures
 |
Fig. 1. PDF of |
| In the text | |
 |
Fig. 2. Two examples of the PDF in our observational samples. Top left panel: Three-dimensional image of fDMh for FRB 20181112A (see Sect. 4 and Table 1 for details). The x-axis is the DMh parameter from 20 to 600 pc cm−3. The y-axis is the |
| In the text | |
 |
Fig. 3. Nine examples representing the PDFs of redshift (z). These were randomly selected from our FRB samples (see Sect. 4 and Table 1 for details). H0 = 74.3 km s−1 Mpc−1 and DMh = [20, 1600] pc cm−3 were adopted. In each panel, we present PDFs based on two different ranges of |
| In the text | |
 |
Fig. 4. Observed redshift (zspec) vs. modeled redshift (zmodel) to optimize H0. To demonstrate how zmodel depends on H0, we present three values of H0, 60, 68, and 80 km s−1 Mpc−1, in the different panels. We used 30 FRBs (see Sect. 4 and Table 1 for details) with DMh = [20, 1600] pc cm−3 and |
| In the text | |
 |
Fig. 5. DMIGM, mock as a function of zmock. The red dots represent DMIGM, mock generated by using Eq. (8) at each zmock, taking the line-of-sight fluctuation of DMIGM into account. For a given zmock, we randomly selected one mock data point (red dot) from the blue dots. We iterated this process 100 times at the different zmock, generating 100 mock FRB data. |
| In the text | |
 |
Fig. 6. Simulation results using our method with mock FRB samples. Top panel: PDF of H0 × fIGM derived by using the 100 mock FRBs and our method with scattering (blue curve). The vertical dashed blue lines correspond to 84.2 and 15.8 percentiles (±σ) of the PDF. Bottom panel: PDF of H0 by changing the scale from H0 × fIGM (top panel) to H0. To generate the mock data, we assumed H0 = 68.0 km s−1 Mpc−1, which is shown by the solid vertical black line. The vertical dashed blue lines are the positive and negative standard deviations of H0 after taking the fIGM error into account, where the fIGM error is ±0.05 (Cordes et al. 2022). |
| In the text | |
 |
Fig. 7. Simulation results using the previous method with mock FRB samples. Top panel: DMIGM, mock as a function of zmock. The blue dots with error bars show 100 mock FRB data, where DMIGM, mock is calculated by the previous method, assuming DMh = 50 pc cm−3. We fit Eq. (9) to the mock FRB data with a free parameter of H0. The best-fit function is shown by the solid black line, where H |
| In the text | |
 |
Fig. 8. PDFs of H0 derived by our method (orange) with positive and negative standard deviations (orange vertical dashed lines) and the previous method (blue) with positive and negative standard deviations (vertical dashed blue lines), using the same 100 mock FRB data. The vertical black line indicates H0 = 68.0 km s−1 Mpc−1, which was assumed when we generated the 100 mock FRBs. |
| In the text | |
 |
Fig. 9. Scattering time vs. DMEG or DMh. The x-axis is the DMEG from Eq. (12) in the log scale for the FRB samples (black dots), and it shows DMh for the empirical relation based on Galactic pulsars (shaded blue region) and the |
| In the text | |
 |
Fig. 10. The results using our method with observed FRB samples. Top panel: χ2 described by Eq. (14) as a function of fIGM × H0 using the 30 FRB samples and our method. The black line indicates the χ2 values derived by changing fIGM × H0. The blue line is the best-fit polynomial function to χ2. Middle panel: PDF of fIGM × H0 from the χ2 (top panel). The vertical dashed black lines correspond to the 84.2 and 15.8 percentiles (±σ) of the PDF. Bottom panel: PDF of H0 by changing the scale from H0 × fIGM (middle panel) to H0 for a given fIGM = 0.85 ± 0.05. The solid vertical line indicates the peak of the PDF, and the dashed vertical lines indicate the uncertainty range of H0 after taking the 0.05 error of fIGM into account. The orange area indicates the CMB measurement of H0 (e.g., Planck Collaboration VI 2020). The blue area shows the measurement by local distance ladders (e.g., Riess et al. 2022). |
| In the text | |
 |
Fig. 11. Histogram of DMh derived by using scattering (see also Table 3). |
| In the text | |
 |
Fig. 12. zmodel vs. zobs, comparing two prior assumptions on the |
| In the text | |
 |
Fig. 13. Comparison of results across different |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



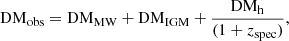
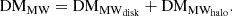
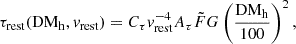
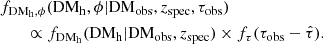
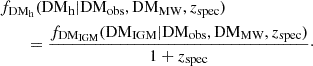
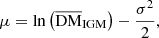
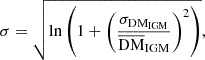
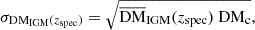
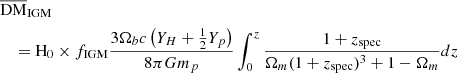
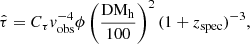
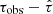
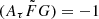
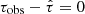
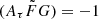
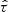
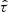
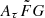
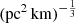
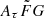
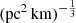
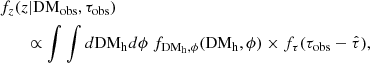
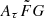
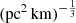
![$ A_{\tau} \tilde{F} G = [0.001,10] $](/articles/aa/full_html/2025/01/aa50823-24/aa50823-24-eq86.gif)