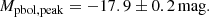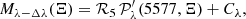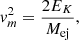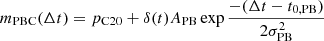| Issue |
A&A
Volume 693, January 2025
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 23 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202346313 | |
| Published online | 23 December 2024 | |
SN 2019odp – A massive oxygen-rich Type Ib supernova
1
Department of Astronomy, The Oskar Klein Centre, Stockholm University, AlbaNova, 10691 Stockholm, Sweden
2
Technische Universität München, TUM School of Natural Sciences, Physik-Department, James-Franck-Straße 1, 85748 Garching, Germany
3
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild Straße 1, 85748 Garching, Germany
4
Department of Physics, The Oskar Klein Center, Stockholm University, AlbaNova, 10691 Stockholm, Sweden
5
School of Physics and Astronomy, University of Minnesota, Minneapolis, Minnesota 55455, USA
6
Department of Astronomy, University of Maryland, College Park, MD 20742, USA
7
Division of Physics, Mathematics and Astronomy, California Institute of Technology, Pasadena, CA 91125, USA
8
Max-Planck-Institut für extraterrestrische Physik, Gießenbachstraße 1, D-85748 Garching, Germany
9
Department of Particle Physics and Astrophysics, Weizmann Institute of Science, 234 Herzl St, 76100 Rehovot, Israel
10
IPAC, California Institute of Technology, 1200 E. California Blvd, Pasadena CA 91125, USA
11
Caltech Optical Observatories, California Institute of Technology, Pasadena, CA 91125, USA
12
Université Clermont Auvergne, CNRS/IN2P3, LPC, F-63000 Clermont-Ferrand, France
⋆ Corresponding author; tassilo.schweyer@astro.su.se
Received:
3
March
2023
Accepted:
3
October
2024
Aims. Stripped envelope (SE) supernovae are explosions of stars that have somehow lost most of their outer envelopes. We present the discovery and analyse the observations of the Type Ib supernova 2019odp (a.k.a. ZTF19abqwtfu) covering epochs within days of the explosion to late nebular phases at 360 d post-explosion.
Methods. Our observations include an extensive set of photometric observations and low- to medium-resolution spectroscopic observations, both covering the complete observable time range. We analysed the data using analytic models for the recombination cooling emission of the early excess emission and the diffusion of the peak light curve. We expanded on existing methods to derive oxygen mass estimates from nebular phase spectroscopy, and briefly discuss progenitor models based on this analysis.
Results. Our spectroscopic observations confirm the presence of He in the supernova ejecta and we thus (re)classify SN 2019odp as a Type Ib supernova. From the pseudo-bolometric light curve, we estimate a high ejecta mass of Mej ∼ 4 − 7 M⊙. The high ejecta mass, large nebular [O I]/[Ca II] line flux ratio (1.2 − 1.9), and an oxygen mass above ⪆0.5 M⊙ point towards a progenitor with a pre-explosion mass higher than 18 M⊙. Whereas a majority of analysed SE supernovae in the literature seem to have low ejecta masses, indicating stripping in a binary star system, SN 2019odp instead has parameters that are consistent with an origin in a single massive star. The compact nature of the progenitor (≲10 R⊙) suggests that a Wolf-Rayet star is the progenitor.
Key words: supernovae: general / supernovae: individual: SN 2019odp
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Supernovae are luminous transients marking the end of the life cycles of certain stars. The traditional supernova classification scheme (Filippenko 1997) is based on the presence or absence of spectral features close to peak brightness. If no hydrogen lines are present, they are classified as Type I supernovae. The presence of helium distinguishes helium-rich Type Ib supernovae from helium-poor Type Ic supernovae. Based on the high expansion velocities, broad-lined Type Ic (Type Ic-BL) supernovae can be distinguished. Type Ib and Ic supernovae are often considered together, since their estimated explosion parameters overlap (Lyman et al. 2016), but the actual connection to progenitors and explosion mechanisms are still under debate (Modjaz et al. 2019). There also exist transitional transients that change their type over time, motivating additional classification schemes (Prentice & Mazzali 2017; Williamson et al. 2019).
For Type Ibc supernovae, the progenitor stars have to lose their outer envelope, stripping away most of the hydrogen or helium. The exact mechanisms are still under debate, but one possible progenitor channel is single massive stars that eject their outer atmosphere in strong stellar winds (Puls et al. 2008; Woosley et al. 1993). One key issue here is that only the most massive stars (MZAMS ≳ 40 M⊙) are able to strip their hydrogen envelope completely by this mechanism. Alternatively, the evolution in a binary system could transfer the outer envelope to the companion star (e.g., Tauris et al. 2015). Direct detections of progenitors for Type Ib supernovae are still rare, with iPTF13bvn (Fremling et al. 2016) and SN 2019yvr (Kilpatrick et al. 2021) being examples, but Yoon et al. (2012) argue that the existing data on progenitor luminosities are not constraining for the binary versus single massive star question. A monotonically increasing tracer for the zero-age main sequence (ZAMS) mass is the oxygen mass (Laplace et al. 2021), which may be estimated using nebular phase spectra (e.g., Jerkstrand et al. 2014).
Observations shortly after first light can also yield valuable information about shock cooling, recombination effects, and nickel mixing, which can be used to constrain aspects of the outer structure of the progenitor. After a short (∼hours) shock-breakout flash in the ultra-violet (UV) and X-ray, such as that seen in SN 2008D (Modjaz et al. 2009; Chevalier & Fransson 2008), follows the ‘shock cooling envelope’ (SCE) emission, which can be seen as an early excess or plateau before the main peak for stripped envelope supernovae, as was discussed in connection with the Type Ib supernovae SN 2008D and SN 1999ex (Stritzinger et al. 2002). For Type IIb supernovae, this has been seen in a number of objects, with SN 2011dh (Arcavi et al. 2011; Ergon et al. 2015), SN 2016gkg (Bersten et al. 2018), and SN 2017jgh (Armstrong et al. 2021) being well-studied examples. However, despite more and more transients being discovered at ever earlier times thanks to large-area high-cadence survey programmes (Bruch et al. 2021), not all supernovae show these cooling features early on, and iPTF13bvn for example showed no signs of any early excess.
In this paper, we present and discuss SN 2019odp and attempt to infer some clues about the progenitor based on observations from very early to very late times. We reclassify SN 2019odp as a Type Ib supernova instead of a Type Ic-BL supernova. From the light curve, we deduce a large ejecta mass and a compact progenitor. The nebular spectra allow us to put strict limits on the oxygen mass.
The paper is structured as follows. In Sect. 2.1, we outline the initial discovery. In Sect. 2, we present the photometric and spectroscopic observations of the supernova, and we discuss the evolution of observables in Sect. 3. In Sect. 4, we apply semi-analytical models to estimate physical parameters, such as the ejecta mass, progenitor radius, and oxygen mass. Finally, in Sect. 5 we discuss these properties in the context of different progenitor scenarios and summarise our findings.
We use the following unless otherwise specified: the supernova phase is in observer-frame days relative to the g-band peak, all quantities have been corrected for the estimated line-of-sight Milky Way extinction (see Sect. 3.1), all magnitudes are given in the AB magnitude system, and error bars denote 1σ uncertainties.
2. Observations and data reduction
2.1. Discovery and initial classification
The transient SN 2019odp (ZTF19abqwtfu) was discovered as part of the Zwicky Transient Facility survey (ZTF; Bellm et al. 2019b; Graham et al. 2019) and was first reported to the Transient Name Server (TNS1) by Nordin et al. (2019). The discovery was made on August 21 2019 (MJD = 58 716.38) in the r band with a magnitude of 18.7. The previous epoch on August 18 2019 (MJD = 58 713.44) shows a 2σ flux excess in the i band with a magnitude of 20.9. The last non-detection was on August 17 2019 (MJD = 58 712.48) in the g band. We define the explosion epoch, texpl, to be at MJD 58 714.5 ± 2 – the centre point between the last non-detection and the first significant (> 3σ) detection.
We estimated the g-band peak epoch, tgpeak, using the interpolated g-band light curve (see Sect. 2.4) to be at MJD = 58 734 ± 1 days. We specify the phase, Δtgpeak, relative to this g-band peak epoch in the rest of the paper.
The transient is located at a right ascension of 23:07:19.090 (h:m:s) and declination of +13:51:21.42 (°:′:″; J2000.0) in the spiral galaxy UGC 12373 (see Fig. 1). The transient is located approximately 25″ from the core of the galaxy, corresponding to a projected separation of around 8 kpc. Adopting the H I based redshift of z = 0.01435 from Schneider et al. (1990), we used the derived Hubble flow distance of D = 64 ± 5 Mpc and distance modulus of μ = 34.0 ± 0.2 mag from the NASA/IPAC Extragalactic Database (NED)2.
 |
Fig. 1. Stacked r′-band GROND image using images taken between +29d and +79d showing the field of the supernova. The supernova is marked with the two red markers. The transient is located approximately 25″ from the core of the galaxy, corresponding to a projected separation of around 8 kpc. The bottom left of the image shows a saturated star with heavy blooming. |
On August 23 2019, (MJD = 58 718.2) SN 2019odp was classified as a Type Ic-BL supernova by Brennan et al. (2019) as part of the ePESSTO+ survey (Smartt et al. 2015). However, based on further observations, we reclassify it as a Type Ib supernova in Sect. 3.7.1.
2.2. Photometry
Follow-up photometry in the g, r, and i bands was obtained using the ZTF camera (Dekany et al. 2020) mounted on the Palomar 48-inch telescope (P48) as part of the ZTF survey (Bellm et al. 2019a,b). The obtained data were processed using the ZTF pipeline (Masci et al. 2019), which detrends the images and does PSF-matching image-subtraction against stacked template images and automatic photometric calibration against field stars using the Pan-STARRS 1 (PS1; Chambers et al. 2016) survey catalogue. We used ztflc3 to perform forced photometry for all epochs. Based on this photometry, we see no outbursts before the main explosion; however, we notice a small plateau before the main peak (see Fig. 2).
 |
Fig. 2. Photometric evolution of SN 2019odp around the discovery epoch. The light curve is given in flux units to show the pre-discovery upper limits on the same scale. The different colours denote the different bands. The zero flux level is denoted by a dashed line. The faintly overlaid light curves are light curve realisations drawn from the conditioned Gaussian process interpolation kernel (see Sect. 2.4 for a detailed description). For illustration purposes, they are drawn beyond their validity time range (turning into a extrapolation). The light curves have not been corrected for extinction. The times of spectroscopic observations are marked in the top bar by vertical lines. |
In addition, we obtained manually triggered observations in the u, g, r, and i bands using the Spectral Energy Distribution Machine (SEDM; Blagorodnova et al. 2018) Rainbow Camera mounted on the Palomar 60-inch telescope (P60). The obtained data were automatically processed using the SEDM-RC pipeline (Fremling et al. 2016).
We also obtained some post-peak follow-up photometry in the g′r′i′z′JHKs bands using the Gamma-ray Burst Optical/Near-infrared Detector (GROND; Greiner et al. 2008) mounted on the MPG 2.2 m telescope located at the ESO La Silla observatory. The data were reduced using a pyraf/IRAF-based4 pipeline (Krühler et al. 2008). For the near-infrared (NIR) bands, aperture photometry was performed. The g′r′i′z′ bands were calibrated against the Sloan Digital Sky Survey Data Release 15 catalogue (SDSS DR15; Aguado et al. 2019) and the NIR JHKS bands were calibrated against the Two Micron All Sky Survey catalogue (2MASS; Skrutskie et al. 2006). The GROND NIR Vega magnitudes were converted to AB magnitudes using Blanton & Roweis (2007).
Late-time optical photometry in the g, r, and i bands were obtained using the Alhambra Faint Object Spectrograph and Camera instrument (ALFOSC) mounted on the Nordic Optical Telescope (NOT). The observations were reduced using the PyNOT5 pipeline. We then performed image subtraction using hotpants (Becker 2015) against matching PS1 images as a template. Resampling of the template image to the same pixel scale as the science images was performed using SWarp (Bertin et al. 2002). Aperture photometry was then performed on the difference image using photutils (Bradley et al. 2021).
To extend the wavelength coverage to the UV, we utilised the 30 cm UV Optical Telescope (UVOT; Roming et al. 2005) on board the Neil Gehrels Swift Observatory (Gehrels et al. 2004). We retrieved science-ready data from the Swift archive6. We first co-added all sky exposures for a given epoch and filter using uvotimsum in HEAsoft7 version 6.26.1. Afterwards, we measured the brightness of SN 2019odp with the Swift tool uvotsource. The source aperture had a radius of 3″, while the background region had a significantly larger radius. The photometry was calibrated with the latest calibration files from September 2020 and converted to the AB system using Breeveld et al. (2011).
The combined light curve is shown in Fig. 3 and a list of photometric measurements is provided in Table E.1. For the first 70 days, the light curve has an average cadence of 2 days in the g band (no gap larger than 4 days), 1 day in the r band (no gap larger than 5 days), and 3 days in the i band (no gap larger than 7 days).
 |
Fig. 3. Photometric evolution of SN 2019odp in the ugriz′J bands using the combined photometry dataset. The colour denotes the band and the different markers denote the source instrument. The faintly overlaid light curves are light curve realisations drawn from the conditioned Gaussian process interpolation kernel (see Sect. 2.4 for a detailed description). The light curves have not been corrected for extinction. The times of spectroscopic observations are marked in the top bar by vertical lines. |
2.3. Spectroscopy
The first spectrum was obtained on August 21 2019 – less than a day after the discovery – using the SEDM Integral Field Unit (SEDM IFU; Blagorodnova et al. 2018). The observations were reduced using the pysedm package (Rigault et al. 2019).
We obtained further follow-up spectroscopy using the SEDM and the NOT ALFOSC spectrograph. In addition, we obtained one pre-peak spectrum using the Double Spectrograph (DBSP; Oke & Gunn 1982) mounted on the Palomar 200-inch telescope (P200). In total, we obtained 8 spectra before the peak, and 30 spectra in total. This also includes the public NTT classification spectrum from Brennan et al. (2019) under the ePESSTO programme.
We also obtained two high signal-to-noise (S/N) late-time spectra using the Low Resolution Imaging Spectrograph (LRIS; Oke et al. 1995) mounted on the Keck 1 telescope. The LRIS observations were reduced using the fully automated pipeline by Perley (2019).
All spectra were absolute flux-calibrated using synthetic r-band photometry, derived using the speclite8 package, against the interpolated light curve dataset (see Sect. 2.4).
We show the spectral sequence split into the early phase (Fig. 4), photospheric phase (Fig. 5), pre-nebular phase (Fig. 6), and nebular phase (Fig. 7). The full log of spectroscopic observations can be found in Table E.2. The observation epochs are also indicated in the upper part of the light curve figure (Fig. 3). The final reduced and flux-calibrated spectra are available on WISeREP9 (Yaron & Gal-Yam 2012).
 |
Fig. 4. Spectral sequence of obtained spectra from discovery to before peak. The observation phase of each spectrum is denoted on the right of each spectrum. Rest wavelengths of strong He I features have been marked in green, and the positions of Balmer lines are denoted in blue. A Telluric absorption feature has been denoted with a shaded region and a ⊕ symbol. |
 |
Fig. 5. Spectral sequence of obtained spectra around the photospheric phase. The notation is the same as in Fig. 4, but here we have also marked the wavelengths of several intermediate-mass elements. |
 |
Fig. 6. Spectral sequence of obtained spectra in the pre-nebular phase. The notation is the same as in Fig. 4, but here we have also marked the wavelengths of several intermediate-mass elements. |
 |
Fig. 7. Spectral sequence of SN 2019odp in the nebular phase. We have marked several of the O I lines as well as some Ca II lines. |
2.4. Light curve interpolation and parameter estimation
For SN 2019odp and the comparison sample (see Sect. 3.2), we performed light curve dataset combination, interpolation, and fitting using the same framework. For each transient, we performed the following procedure. First, we pre-processed the individual instrument light curves by transforming all photometry to the AB system and correcting for the extinction with instrument-specific coefficients (see Sect. 3.1 for SN 2019odp and Sect. 3.2 for the values used for the comparison sample). We used Gaussian process interpolation (see Görtler et al. 2019 for a review) to produce per-band light curves combining the different photometric datasets from the different instruments. Simultaneously, we estimated empirical light curve observables, such as the late-time decline rate and peak time, by fitting empirical model functions to the light curves. This was done by using them as the mean function in the Gaussian process. These photometric model functions are described in Appendix B.
We used the dynesty dynamic nested sampler (Speagle 2020; Skilling 2004, 2006; Higson et al. 2019) to estimate the posterior distribution of the model parameters as well as the amplitude and length-scale parameters of the Gaussian process Matérn-3/2 kernel. When more than one photometric instrument (with a nominally similar photometric filter system) and overlapping observations were available, we also included an offset parameter in the parameter estimation. The offsets are stated relative to the photometric instrument with the best coverage (for instance, ZTF in the case of SN 2019odp). Additional photometric observables, such as the peak magnitude, Mmax, the light curve rise parameter, Δm−10, or the light curve decline parameter, Δm15, were estimated by Monte Carlo sampling the derived Gaussian process function.
3. Analysis
3.1. Extinction
Based on the dust maps by Schlafly & Finkbeiner (2011), we can estimate the Milky Way extinction, E(B − V), at the position of the transient to be in the range from 0.14 to 0.20 mag. For analysis requiring extinction-corrected values, we propagated the uncertainty using Monte Carlo methods. We assume no host extinction based on the lack of any visible sodium absorption features. In addition, we have compared the colours against the intrinsic colour templates at +10 d from Stritzinger et al. (2018) and notice that our supernova has bluer g − r and g − i colours than any supernova class in that study. Comparing our light curve against the light curves of the sample supernovae that the Stritzinger colour templates are based on, we notice that SN 2019odp is bluer at virtually any time. This further strengthens our assumption of no host galaxy extinction for this event.
We used the computed Ax/E(B − V) values for the different filters from Schlafly & Finkbeiner (2011) for RV = 3.1 for all photometric extinction corrections. We used the extinction (Barbary 2016) Python implementation of the Cardelli et al. (1989) extinction law to extinction-correct all spectra.
3.2. Comparison datasets
We have compared the properties of SN 2019odp against a selected sample of well-observed objects from the literature that are prototypes for the different supernova classes: SN 1998bw (Ic-BL) and SN iPTF13bvn (Ib). We also included SN 2002ap (Ic-BL), since it has the same peak brightness and might be a more suitable comparison object for Type Ic-BL supernovae than the much brighter SN 1998bw. We also included SN 2008D (Ib), since it was a very close match spectroscopically and showed a somewhat similar unusual behaviour right after discovery. The adopted supernova parameters for the comparison objects are presented in Table 1.
Adopted parameters for the comparison objects.
For SN 1998bw, we used the UBVRI light curves compiled by Clocchiatti et al. (2011). For iPTF13bvn, we used the gri light curve by Fremling et al. (2016) with additional U-band UVOT photometry points from Brown et al. (2014). For SN 2008D, we used the BVg′r′ light curves from Bianco et al. (2014) and the UVOT U-band light curve from Brown et al. (2014). For SN 2002ap, we used the UBVRI light curves compiled by Foley et al. (2003). Where necessary, we converted the magnitudes from Vega to AB magnitudes and we used the same interpolation procedure as is described in Sect. 2.4.
3.3. Photometric evolution
In this section, we compare the photometric evolution of SN 2019odp with our previously introduced comparison supernovae. A light curve comparison is shown in Fig. 8. We estimated the light curve parameters using the method described in Sect. 2.4 that uses the empirical photometric models described in Appendix B. The resulting parameter estimates for the light curve observables, which we discuss below, are summarised in Table 2.
Basic light curve observables extracted for SN 2019odp and the comparison objects.
 |
Fig. 8. Comparison of the evolution of the absolute light curves in g/V (panel A, left) and r/R (panel B, middle) bands between SN 2019odp and selected comparison objects. In addition, the pseudo-bolometric light curve derived using the Lyman method is shown (panel C, right). In the pseudo-bolometric light curve (panel C), the error bars around the peak represent the combined error from the distance uncertainty, extinction uncertainty, and the scatter from the Lyman relation. The interpolated light curves for each supernova have been placed over the observed datapoints in the same colour. These were used to derive the pseudo-bolometric light curves in the right panel. The bottom left corners of panels A and B zoom in on the very early evolution. |
Zooming in on the time period around the discovery (Fig. 2) shows that the initial light curve evolution for SN 2019odp is more consistent with a plateau than with an exponential rise. This behaviour is seen in both the g and r bands (i-band data has too low cadence). Comparing the absolute r- and g-band light curves between SN 2019odp and SN 2008D (see inset in Fig. 8), which is another supernova that showed signs of an early plateau or a shock cooling peak, the bump appears at roughly the same relative phase and is marginally fainter in SN 2019odp than in SN 2008D (when taking distance uncertainty into account, the difference is not statistically significant). This in stark contrast to iPTF13bvn, which shows no early feature down to a limit several magnitudes deeper. We estimate the absolute plateau magnitude for SN 2019odp to be  mag in the g band and
mag in the g band and  mag in the r band. For SN 2019odp, this is about 1.9 mag fainter than the peak magnitude, while for SN 2008D the difference is only about 1 mag, and for iPTF13bvn the difference is more than 2 mag in the g band and more than 3 mag in r band.
mag in the r band. For SN 2019odp, this is about 1.9 mag fainter than the peak magnitude, while for SN 2008D the difference is only about 1 mag, and for iPTF13bvn the difference is more than 2 mag in the g band and more than 3 mag in r band.
Following the plateau, SN 2019odp rises to the main peak in 14 − 15 days in the g band, 17 − 21 days in the r band, and 17 − 21 days in the i band (measured as time between the first data point ≥3σ above the plateau level and peak). The light curve rise timescale, τrise (see Appendix B for the definition), is also much longer in all bands for SN 2019odp than in any of the comparison objects, except perhaps SN 2008D. The light curve for SN 2019odp peaks at an absolute magnitude of ∼ − 18 mag in the gri bands (see Table 2 for the exact values for each band). This is towards the brighter end of the luminosity distribution previously established for Type Ib supernovae (Taddia et al. 2015), but within the bulk of the distribution for Type Ic-BL supernovae (Taddia et al. 2019). In the r band, the supernova shows a rather flat peak at an apparent magnitude of 15.9 that is at least 7 days in duration. This is not clearly seen in the g or the i bands (limited by the sampling period at peak). The main peak is several days wider in all bands compared to the light curves of iPTF13bvn and SN 2008D and more closely resembles the width of SN 1998bw. The light curve width can be an indicator of a higher ejecta mass (e.g., Karamehmetoglu et al. 2023), as is discussed in more detail in Sect. 4.1.1. This difference is most pronounced in the r and i bands. The peak width, σ, of the fitted Gaussian is given in Table 2.
The late-time linear-slope decline parameter, β (see Appendix B for the definition), in all bands is significantly slower for SN 2019odp than for the comparison objects. The measured linear slopes are provided in Table 2. This can also be an indicator of a large ejecta mass.
3.4. Colour evolution
During the very early ≳2-day plateau-phase, both the g − r colours (shown in the upper panel of Fig. 9) and the r − i colours (shown in Fig. 9, lower panel) are bluer than for any of the comparison objects. The g − r colour stays constant during this phase, showing no bump, unlike all of the comparison objects. Afterwards, the g − r colour of SN 2019odp evolves to a redder colour, but this evolution happens later and is slower than in the comparison objects. It gets redder until it meets the colour light curve of iPTF13bvn at around 25 days post-peak and afterwards follows the same evolution. The r − i colour shows an early time valley around 10 days before peak, which is unseen or much weaker in the comparison objects before becoming redder again and joining the evolution of the other supernovae (which mostly stay constant after 40 days post-peak).
 |
Fig. 9. Colour evolution of SN 2019odp and the comparison objects. The top panel shows the g − r colour (or corresponding Johnson colour). The lower panel shows the r − i colour (or corresponding Johnson colour). For each transient, we sampled 1000 realisations of the supernova light curve from the interpolation kernel. For SN 2019odp, we also included synthetic photometry based on the observed spectra as a consistency check (using the same filter curve as for the photometric dataset). They are denoted with black crosses. |
The initial U − r colour evolution of SN 2019odp matches that of iPTF13bvn. However, at around −5 days for iPTF13bvn, the U − r colour quickly starts to get redder, while SN 2019odp only starts getting redder after the peak. Due to the limited U-band observations, the exact inflection point is not known. One interesting observation is that while SN 2019odp has bluer colours in all other colour indices, this is not true in the U − r colour, where SN 2008D starts almost 1 magnitude bluer and monotonically gets redder.
3.5. Blackbody evolution
We can estimate blackbody parameters using the interpolated photometry datasets for all supernovae in the comparison sample (Sect. 2.4). We used the gri bands when they were available and the closest matches in wavelength if they were not. The detailed description of the method can be found in Appendix D. Whereas the emission from these supernovae is not really a blackbody (see the spectral sequences in Fig. 4 and Fig. 5), the derived blackbody parameters are suitable mainly for a rough qualitative comparison between the objects. The time evolution of the photospheric temperature and radius is shown in Fig. 10.
 |
Fig. 10. Time evolution of the inferred blackbody parameters from the photometry for SN 2019odp and selected comparison objects. We chose the closest matching filter sets for all transients and performed our own fitting for all objects. The error bars contain all uncertainties including the distance and extinction uncertainties. The upper panel shows the temperature time evolution and the lower panel the photospheric radius time evolution. |
Initially, SN 2019odp is both hotter and the initial photospheric radius is smaller than for any of the comparison objects. This is most likely an underestimate of the true photospheric temperature (and at the same time a slight overestimate of the radius), since the blue part of the spectral energy distribution (SED) seems to be suppressed (only considering the ri bands yields a closer match to the full grizJH photometry modelling for the time-period post-peak when it is available). Roughly 20 days after the peak, the temperature evolution for SN 2019odp joins that of most other supernovae in the comparison sample. SN 2019odp shows a larger peak photospheric radius compared to all comparison transients except SN 1998bw.
3.6. Pseudo-bolometric light curve
Using the photometric datasets (Sect. 2.4) for SN 2019odp and the comparison sample, we computed pseudo-bolometric light curves with the Lyman et al. (2014) method using the g and r bands (or closely corresponding bands for some of the comparison transients). Based on a sample of well-observed stripped envelope supernovae, Lyman et al. (2014) has calculated bolometric correction factors for multiple pairs of photometric bands. Using the provided polynomial fits to the sample, we can apply the derived corrections to our supernova:
where M is the absolute magnitude, m is the extinction-corrected apparent magnitude, Dm is the distance modulus in magnitudes, BC is the bolometric correction, and ci are the polynomial fit parameters from Lyman et al. (2014) for the g − r band pair. Pseudo-bolometric refers to the neglect of any UV contribution, which we deem to be more uncertain. This means that the derived pseudo-bolometric luminosities constitute only a lower limit.
The derived pseudo-bolometric light curves are shown in the right panel of Fig. 8. We first estimated the peak epoch of the pseudo-bolometric light curve by sampling the interpolated light curve (excluding any uncertainties that affect the light curve globally) in a 10-day window around the g-band peak epoch and then selecting the time of the brightest point for each sampled light curve. We estimated the peak magnitude by sampling the interpolated light curve at the peak epoch (including global uncertainties), which yields
We converted the absolute pseudo-bolometric magnitudes to luminosities using the bolometric luminosity of the Sun, Lbol, ⊙ = 3.828 × 1033 erg s−1, and Mbol, ⊙ = 4.74 mag, to get
This is well in line with peak pseudo-bolometric luminosities seen previously for Type Ib supernovae (Lyman et al. 2016) or Type Ic-BL supernovae (Taddia et al. 2019). As one would expect based on the photometric comparison (see Sect. 3.3), the pseudo-bolometric main peak is also wider than for most of the comparison objects (see right panel in Fig. 8). The total integrated radiated luminosity (radiated energy) is
We also measured the duration of the early plateau to be in the range of 2 to 5 days. Using direct integration of the photometric measurements in the ZTF gri bands, we estimated the plateau pseudo-bolometric luminosity to be
which corresponds to Mplateau, pbol ≃ −14.6 mag.
3.7. Spectroscopic evolution
We present the early spectral evolution between discovery and peak in Fig. 4. The first spectrum, taken 16.8 days before peak, is mostly blue and featureless with some suppression of the blue side of the spectrum. The second spectrum, taken one day later, is dominated by a staircase-shaped continuum that has flat regions in the ranges of 5570−6670 Å and 7050−9000 Å with some narrow emission lines that we identify as host galaxy contamination. While the first spectrum of the sequence might be explained by a single (partially absorbed) blackbody, the later spectra clearly show signs of emission or absorption lines.
The first identifiable line features are seen in the spectrum at a phase of −12 days. We can identify two P-Cygni features that we associate with He I λλ5876,6678 and possibly He I λ4471 at roughly 14 000 km s−1 and with blueshifted emission peaks. We investigate the velocity evolution of the helium feature in more detail in Sect. 3.7.2.
Post-peak, the lines gain in strength, the helium P-Cygni features become much more pronounced, and additional lines such as the various forbidden calcium lines become visible. The spectral evolution in the photospheric phase is shown in Fig. 5. A feature that is possibly associated with Mg I] λ4571 becomes more obvious. At around 5000 Å, a feature becomes visible, which could be [O III] λλ4959,5007. This line was first identified by Lunnan et al. (2016) in super-luminous supernovae (SLSNe) and is seen in SLSN model spectra by Jerkstrand et al. (2017). We can identify similar features in the comparison between Type Ib supernovae SN 2008D and iPTF13bvn, which suggests that this may not be an uncommon feature for Type Ib supernovae. However, both helium and iron have lines quite close in wavelength to those features as well.
We show the pre-nebular phase covering from +42d to +104d post-peak in Fig. 6. The calcium NIR triplet Ca II λλ8498,8542,8662 becomes the strongest emission feature in the spectrum, with some oxygen recombination features, such as O I λ7774, also being quite pronounced. The helium features, He I λλ6678,7065, become less noticeable due to overlap with the broad oxygen doublet [O I] λλ6300,6364 and the calcium doublet [Ca II] λλ7291,7324.
We show the nebular phase spectra from +101d to +348d post-peak in Fig. 7. The most conspicuous emission features are the [O I] λλ 6300,6364 complex and the [Ca II] λλ7292,7324 and Ca II λλ8493,8542,8662 lines. In the spectra, there are also oxygen recombination lines visible at O I λλ7772,7774,7775, and O I λ8446 and another feature at 9264 Å. The oxygen lines show substantial structure, which complicates the measurements. The Mg I] λ4571 and Mg I] λ5167 lines become more pronounced. There is a quite pronounced Na I D line visible, which slowly replaces the He I λ5876 feature.
The late-time Keck spectrum (+348d) is dominated by the [O I] λλ6300,6364 complex, by [Ca II] λλ7292,7324, and a little bit of emission of Mg I] λ4571. All other previously mentioned emission lines have vanished at this epoch.
One can use the oxygen-to-calcium abundance ratio as a diagnostic of the core mass (Fransson & Chevalier 1989), since while oxygen monotonically increases with increasing core mass, calcium does not (Limongi & Chieffi 2003). The [O I] to [Ca II] line-flux ratio is often used as a proxy for the abundance ratio (Fang et al. 2019). Using integration, we estimated the ratio for SN 2019odp to be in the range of 1.2–1.9, increasing towards the last spectroscopic epoch. This means that this transient belongs to the class of calcium-poor (or oxygen-rich) supernovae (Prentice et al. 2022) and is likely to have a more massive progenitor. However, as Fransson & Chevalier (1989) have already pointed out, it is only a very crude estimator at best, since a given abundance ratio does not translate into a unique line-flux ratio, but is strongly influenced by mixing and also evolves over time.
3.7.1. Classification
As was mentioned in Sect. 2.1, SN 2019odp was initially classified as a Type Ic-BL supernova by Brennan et al. (2019). When comparing the early spectra obtained shortly after discovery against Type Ib (iPTF13bvn) and Type Ic-BL (SN 1998bw) supernovae (Fig. 11, left panel), it indeed seems quite suggestive to classify this supernova as a Type Ic-BL due to the overall structure of the continuum and the absence of obvious identifiable lines. Comparing against typical supernova databases used for classifications such as SNID (Blondin & Tonry 2007) supports this conclusion. However, later spectra (Fig. 11, right panel) showed the presence of lines with much smaller line widths than are typically associated with Type Ic-BL supernovae as well as the presence of helium lines (see Figs. 5 and 6), which clearly show that this is a Type Ib supernova.
 |
Fig. 11. Comparison of spectra of SN 2019odp before peak (left panel) and after peak (right panel) against selected comparison objects. The phases with respect to the respective g/V-band peak epochs are denoted in the legend. Telluric absorptions have been marked and masked, and the spectra have been corrected for host extinction. At the early phase, the spectrum of SN 2019odp (the NTT classification spectrum) looks very much like the Type Ic-BL SN 1998bw (shown in red, Patat et al. 2001), and not at all like the typical Type Ib iPTF13bvn (shown in blue, Fremling et al. 2016). This is the reason for the initial classification on TNS as a Type Ic-BL supernova. However it looks quite similar to the Type Ib SN 2008D (shown in orange, Shivvers et al. 2019; Modjaz et al. 2014), which has earlier observations than iPTF13bvn. At later phases (right panel), SN 2019odp is instead similar to typical Type Ib supernovae such as iPTF13bvn, showing narrower lines and clear helium features, as opposed to SN 1998bw. In fact, the most similar object might be the Type Ib SN 2008D. Some of the spectra suffer from host contamination. |
Using our own classification database and code10, we searched for other supernovae that were a close spectral match for the early pre-peak spectra and found that the Type Ib SN 2008D is a quite good match (Fig. 11, left panel) as well. This suggests that this lack of features at early phases of the supernova is not completely unseen for Type Ib supernovae and additional care should be taken when classifying transients at very early phases.
It is not obvious if the lack of helium lines and the broad spectral shape at early phases is due to very high velocities or due to other effects. Modjaz et al. (2016) argue that the lack of observed helium lines in Type Ic-BL supernovae cannot solely be explained by the helium lines being smeared out by the high velocities in the ejecta. Further transitional objects, such as SN 2016coi (Yamanaka et al. 2017; Prentice et al. 2018), have been discovered that show helium lines initially, but evolve to more closely resemble Type Ic-BL supernovae later on. This is the inverse to what is seen in SN 2008D and in SN 2019odp, where initially there were no visible helium lines, but they appeared later on. SN 2017ens (Chen et al. 2018) is another supernova that shows characteristics of a Type Ic-BL supernova early on, but then changes its class to a Type IIn supernova. On the other hand, there are normal Type Ib supernovae, such as iPTF13bvn, that have been discovered at similarly early phases and that show no hints of broad lines. Bengyat & Gal-Yam (2022) argue for a split in the Type Ib class, which might explain these different behaviours.
3.7.2. Helium velocity evolution
We estimated the helium line velocities as the absorption minima of the P-Cygni features of the individual helium lines. We used the nested sampler dynesty to fit the following P-Cygni model function, Mλ, to the individual helium features:
where Cλ is the linear continuum function, 𝒢λ is the (normalised) Gaussian function, E is the amplitude of the emission feature, A is the amplitude of the absorption feature, Λ is the rest-wavelength of the feature, ΔA, E are the velocity-offsets of the absorption and emission peak, respectively, and, σA, E are the widths of the absorption or emission Gaussians. The measured velocity evolutions for SN 2019odp and the comparison Type Ib supernovae are shown in Fig. 12.
 |
Fig. 12. Velocity evolution of the He I lines in SN 2019odp and the comparison Type Ib supernovae. |
We estimated the He Iλ 5876 line velocity at the peak by fitting the following exponential model to the individual velocity estimates using a GP kernel as a likelihood function:
where v0, t0, and α are free parameters (within reasonably chosen priors). We only included significant measurements in the time range from −15.5 d to 30 d. Our estimate for the absorption velocity at the peak is thus
4. Modelling
4.1. Photospheric phase
In Sect. 4.1.1, we model the diffusion part of the light curve, while in Sect. 4.2 we focus on the earliest part of the light curve. Section 4.3 includes detailed modelling of the nebular spectra.
4.1.1. Arnett modelling results
Using the Arnett (1982, hereafter A82) models, which we summarise in Sect. A, we estimated the supernova parameters using the light curve diffusion peak. As the input, we used the pseudo-bolometric light curves derived in Sect. 3.6 and the Bayesian parameter estimation algorithm described in Sect. A.2. We considered both the canonical A82-c model (c for compact), which assumes a small initial radius (R0 ≪ 1000 R⊙) described in Sect. A, and the A82-e model (e for extended) for a large initial radius, which is described in Sect. A.1. As a cross-check of the overall method, we also performed the same procedure for the comparison object iPTF13bvn.
We summarise the parameter estimation results in Table 3 and also include parameter estimates taken from the literature for iPTF13bvn. The high nickel mass (MNi ∼ 0.25 M⊙), ejecta mass (Mej ∼ 5 M⊙), and kinetic energy (EK ∼ 6 × 1051 erg) of SN 2019odp point towards a very energetic explosion of a massive star. Compared to other samples of Type Ib supernovae, such as Taddia et al. (2018) or Lyman et al. (2016), SN 2019odp is near the edge of the distribution, but there are objects in these samples that have similar ejecta masses and nickel masses. The inferred kinetic energy (EK ∼ 6 × 1051 erg) is significantly higher than for most other Type Ib supernovae, with a few exceptions (with SN 2008D being in a similar range), and is more comparable to values seen in Type Ic-BL supernovae. While the A82-e model does not place a strict constraint on the initial radius, R0, it does indicate a more compact progenitor. We investigate the progenitor radius further in the context of shock cooling models in Sect. 4.2.
Supernova parameter estimates for different pseudo-bolometric light curve models.
For comparison purposes, we also calculated the ejecta mass and kinetic energy under the (often used) assumption of vsc = vph(tpeak) (Lyman et al. 2016; Wheeler et al. 2015) instead of the method based on Dessart et al. (2016), which is described in more detail in Sect. A. This yields a lower ejecta mass of ∼4.2 M⊙ and a kinetic energy of ∼3.8 × 1051 erg. We note that this energy also exceeds the values commonly derived in theoretical works for neutrino-driven explosions, which do not exceed an explosion energy of ∼2 × 1051 erg (Ertl et al. 2020).
4.2. Early plateau
As was noted in Sect. 3.3, the first few observations show an excess or plateau rather than a smoothly rising light curve. Other supernovae that have shown an early excess or light curve ‘bump’ include the Type Ib XRF-SN 2008D, the Type Ic-BL GRB-SN 2006aj, and the Type IIb SN 2016gkg (Tartaglia et al. 2017; Arcavi et al. 2017). Common features among these three are blue colours, strong UV emission, high colour temperatures (Tcolor ≳ 12 000 K) that decrease right from discovery, and the early excess being shaped like an additional (usually smaller) early peak in the light curve. While SN 2019odp does show a very blue colour (Sect. 3.4; Fig. 9) and high temperatures early on (Sect. 3.5; Fig. 10), it shows neither strong UV emission initially (the U − r colour in fact gets bluer instead of redder) nor a similar initial light curve (no early peak, but an actual plateau; Sect. 3.3).
One commonly invoked scenario to explain this early excess is shock cooling emission (Chevalier & Fransson 2008; Arcavi et al. 2017). Several (semi-)analytical shock cooling emission models have been developed to explore the UV/optical light curve (Nakar & Sari 2010; Rabinak & Waxman 2011; Piro et al. 2021). As the shock cools, at some point the temperature will drop below the recombination temperature of the shocked material (Dessart et al. 2011; Rabinak & Waxman 2011) and then the luminosity will start to plateau until the radioactive energy input becomes significant (Piro & Nakar 2013). Since we do not see any excess UV emission in SN 2019odp and the luminosity plateaued right after discovery, we conclude that in this scenario we have missed the shock cooling emission itself and are only seeing emission from the recombination phase. Based on the numerically recalibrated shock model by Nakar & Sari (2010), Piro & Nakar (2013) use the plateau luminosity and explosion parameters to estimate the progenitor radius, R0. We solved Eq. (5) from Piro & Nakar (2013) for R0:
Piro & Nakar (2013) predicted a plateau following the shock cooling emission peak based on a diffusion wave travelling inwards in the expanding supernova ejecta. The predicted start of the plateau after the explosion for a < 10 R⊙ progenitor and the estimated explosion parameters in Sect. 4.1.1 is between 20 hours and 4 days – both of which fit easily in the observation gap before first light. Using the estimated plateau luminosity (Sect. 3.6; Eq. (5)), we used Eq. (9) to estimate the progenitor radius to be 0.6 − 1.4 R⊙. This is comparable to the estimate of R0 ≈ 2 R⊙ for SN 2008D by Rabinak & Waxman (2011). This value is also compatible with the upper limit of 18 R⊙ (Table 3) derived using the large-radius formulation of the Arnett equation (Sect. A.1).
Another possible scenario for this early emission is imperfect mixing of the nickel throughout the ejecta (Yoon et al. 2019). Depending on the mixing fraction, they argue that different light curve plateaus or ‘pre-bumps’ are possible. A lack of nickel in the outer part of the ejecta would also be consistent with the helium absorption lines only becoming visible later on (Sect. 3.7) due to the lack of non-thermal excitation of the helium by the nickel decays (Lucy 1991). Taddia et al. (2015) explore plateau duration, luminosity, and the magnitude difference with the peak (ΔM ≡ Mplat − Mpeak) using a small grid of hydrodynamical models. While the inferred ejecta mass and energy for SN 2019odp (Sect. 4.1.1) fall outside the model grid, the observed plateau duration of 2 − 5 d, plateau luminosity, log Lplateau = 41.3 [log(erg s−1)], and magnitude difference, ΔM ≈ 3.3 mag (Sect. 3.6), fall well into the range of values seen in their model grid. Extrapolating the trend seen for the ejecta mass and nickel mixing beyond the model grid suggests that very low nickel mixing scenarios are not an obvious candidate, since both low nickel mixing and high ejecta mass increase the duration of the plateau.
4.3. Constraining the oxygen mass from nebular spectra
Nebular spectra provide important diagnostics as they allow one to peer into the optically thin ejecta (Fransson & Chevalier 1989). Some observable parameters of supernova progenitors, such as the oxygen mass, provide information on the initial stellar mass, which in turn can constrain the possible progenitor channels (Houck & Fransson 1996; Uomoto 1986; Li & McCray 1992). One technique to estimate the ZAMS mass of the progenitor is to use the oxygen mass as a proxy, as it has good sensitivity to the pre-explosion mass in stellar evolution models (Limongi & Chieffi 2003; Heger & Woosley 2010; Hirschi et al. 2005). A method of estimating an upper limit on the oxygen mass is described in Jerkstrand et al. (2014) based on measured nebular spectroscopy. For this, we integrated the flux in a 100 Å window around the [O I] λ5577 line and the [O I] λλ6300,6364 lines11, while subtracting a background baseline. Based on the line ratio, we estimate a temperature in the range from 3888 K to 4600 K and an oxygen mass in the range from 4.5 M⊙ to 6 M⊙. We show some comparison values from the literature in Table 4, where one can see that in the context of Type Ib supernovae SN 2019odp is in the very high range of estimated oxygen masses. Values seen in Type IIb supernovae are typically also much smaller, but some extreme cases of Type Ic supernovae, in particular SN 2011bm (Valenti et al. 2012), which was deduced to be an explosion of a very massive star, have been reported to show even higher oxygen masses.
Oxygen mass estimates for stripped envelope supernovae from the literature.
Most of the oxygen masses in the literature (Table 4) were obtained using the method from Uomoto (1986) and assuming a temperature in the range of 3000 − 4500 K as well as local thermodynamic equilibrium (LTE) conditions. If we do the same for SN 2019odp (for T = 3888 K), we get an minimum oxygen mass of ∼5 M⊙. This would be an uncomfortably large fraction of the estimated ejecta mass.
Therefore, we expanded on the method used in Jerkstrand et al. (2014) to take into account deviation from LTE as well. We first describe the analytic models that we use in Sect. 4.3.1, and in Sect. 4.3.2 we describe the fitting method employed to actually apply the improved model. In Sect. 4.3.3, we describe the results of this methodology.
4.3.1. Constraining the oxygen mass from nebular spectra: Model description
The most important oxygen emission lines for this are the [O I] λλ6300,6364 doublet lines as well as the [O I] λ 5577 line. We used the total line luminosity, Lλ(Nu, βλ), where βλ is the Sobolev escape probability and Nu is the total number of ions in the excited state, u, assuming the Sobolev approximation and uniform density defined in Jerkstrand (2017, their Eq. (34)).
A difference in our method is that we treated the two [O I] λλ6300,6364 doublet lines separately. Since both share the same source state and only differ in the split ground state (which is in LTE), they only differ by the radiative decay rate, A, as well as in the escape probability, β. We assume that all oxygen line emission comes from the same environmental conditions, and thus we can state the [O I] λ 6364 optical depth in terms of the [O I] λ 6300 optical depth (Elmhamdi 2011; Li & McCray 1992):
Since we fitted both lines of the doublet simultaneously, we can use the amplitude ratio between the two lines to constrain the optical depth of both lines. This replaces the fixed assumption of β6300, 6364 ≈ 0.5 in Jerkstrand et al. (2014). We specified all optical depths in relation to the [O I] λ 6300 optical depth: τ ≡ τ6300.
The Sobolev escape probability, β, in terms of the optical depth, τ, was defined as follows (Jerkstrand 2017; Li & McCray 1992):
We assumed the first excited state, u1, to be in LTE and used the Saha equation (as it is defined shortly before Eq. (42) in Jerkstrand 2017) to approximate the state number, Nu1. In the case of state u2, we allowed this population number to fall below the LTE estimate (N2LTE → d2N2LTE, where d2 is the LTE departure coefficient). Temperatures in the emission regions in the nebular phase are typically assumed to be below 5000 K in the high-density regime (Elmhamdi et al. 2004; Sollerman et al. 1998), but we adopted a more conservative prior range of 1000 − 8000 K, since it is difficult to define any particular cut-off point for the temperature.
We approximated the partition function with the statistical weight, gg, of the ground state and stated the equation in terms of the oxygen mass, MOI, using N = MOI μ−1mp−1 and the O I λ 6300 and O I λ 6364 line luminosity as
where  , μ = 16 is the mean atomic weight of oxygen, mp is the mass of the proton, Aλ is the radiative decay rate of the transition, gu is the statistical weight of the upper state, and gg is the statistical weight of the lower state (values for physical constants can be found in Table 5).
, μ = 16 is the mean atomic weight of oxygen, mp is the mass of the proton, Aλ is the radiative decay rate of the transition, gu is the statistical weight of the upper state, and gg is the statistical weight of the lower state (values for physical constants can be found in Table 5).
Physical constants used in the oxygen analysis.
If we assume the first excited state, u1, to be in LTE, we can state the optical depth of [O I] λ 5577 relative to the [O I] λ 6300 optical depth:
where d2 is the NLTE deviation fraction for the second excited state, u2, and ΔE2 → 1 = E2 − E1. In Jerkstrand et al. (2014), the analog for this is the assumed ratio of β5577/β6300, 6364 ≈ 1.5. The LTE departure coefficient denotes by how much the number density of the u2 state falls below the LTE estimate. Jerkstrand et al. (2014) find a range for d2 of 0.8 to 0.3 over the time range of 250 to 450 days post-explosion from their modelling efforts for Type IIP supernovae. We adopted a conservative range of 0.1 − 1.0 as our prior for d2.
Combined with Eq. (11), we can calculate β5577(d2, T, τ) and state the [O I] λ 5577 line luminosity as follows (based on Jerkstrand et al. 2014, their Eq. (2)):
with the physical constants given in Table 5.
Based on the observed line luminosities L5577, L6300, L6364, one can then use Eqs. (15) and (12) to constrain MOI, T, d2, and τ. With fewer input parameters than output parameters, some of the parameters are degenerate, which is why the priors have to be carefully considered. The fitting method is described in Sect. 4.3.2.
4.3.2. Constraining the oxygen mass from nebular spectra: Fitting method
While our oxygen estimation method improves upon Jerkstrand et al. (2014), it requires the disentangling of the flux from the [O I] λ 6300 and the [O I] λ 6364 lines, which overlap due to the large velocities present in supernovae. This means we have to make assumptions about the line profile function, 𝒫. To make this whole process more tractable, we split the problem into two parts. First, we estimated the line fluxes, {F}, for the three relevant oxygen lines using empirical models for the spectral line profiles. Then, we used the model described in Sect. 4.3.1 to derive the physical parameters of the model from the line fluxes.
We used the nested sampler dynesty to fit the parameter vector, Ξ. Since in the early nebular spectra the O I λ7774 recombination line is still present, we used this line to estimate the line profile of the forbidden oxygen lines for those epochs. We projected a section around the O I λ7774 line into velocity space, normalised it, and then used it as an empirical line profile function, 𝒫λ. For the last (+348 d) spectrum, the recombination line was no longer visible and we used a parametric Gaussian as the line profile function instead:
To this central line profile function, 𝒫, we added a thick shell function, 𝒮, to model any additional emission in the outer regions of the supernova ejecta, since the simple Gaussian does not capture all of the flux of the line complex:
where F are the line fluxes. The line profile function for the thick shell is approximated by an elongated Gaussian function:
where λc is the centre position, λs is the elongation width (corresponding to the inner cut-off velocity of the shell), σ is the Gaussian width (corresponding to the width of the shell), and k is the numerically derived normalisation constant.
We segmented the spectra into two spectral regions: the [O I] λ 5577 region and the [O I] λλ 6300,6364 region. These line profile functions were then (re)projected onto the observed wavelength grid around the [O I] λ 5577 region and the [O I] λλ 6300,6364 regions. We allowed for a global wavelength offset, Δλ. For the [O I] λλ 6300,6364 region, we have the following model spectral flux function:
with ℛ6 ≡ F6364/F6300, which is constrained to the range between what is fully optically thin (ℛ6 = 1/3) and fully optically thick (ℛ6 = 1). For the [O I] λ 5577 region, we have the following model spectral flux function:
with ℛ5 ≡ F5577/F6300. For each region, we assumed a separate linear continuum:
where λRC is the centre of the region (5577 Å and 6330 Å, respectively).
We marginalised over all nuisance parameters to yield a three-dimensional posterior distribution, which only contains the three line fluxes, F5577, F6300, and F6364. Next, we calculated the mean and covariance matrix of this three-dimensional posterior distribution, which was then used as an input for the second stage of the analysis.
For the second stage Bayesian model, the parameter vector, θ, only consists of a few parameters: the oxygen mass, MOI, temperature, T, optical depth, τ, distance, D, and LTE departure coefficient, d2. We used the nested sampler dynesty to estimate the posterior distribution using the priors given in Table 6 and the line fluxes measured in the previous stage. In each iteration of the sampler, we did the following (using the parameter vector, θ, as an input):
Priors for the second stage of the oxygen mass estimation fit.
-
Calculate the line luminosities, L6300 and L6364, using Eq. (12) and the oxygen mass, MOI, temperature, T, and optical depth, τ, as inputs from the parameter vector.
-
Calculate the optical depth ratio, τ5577/τ, using Eq. (13), which depends on the LTE departure coefficient, d2, and temperature, T.
-
Calculate the luminosity, L5577, using Eq. (15), which depends on L6300, d2, T, and τ.
-
Convert the line luminosities to line fluxes using the distance, D.
-
Calculate the log likelihood using a Gaussian multivariate and the derived mean and covariance matrix from the previous stage.
As the number of output parameters is actually larger than the number of input parameters and the main goal of the study is to constrain the oxygen mass of the supernova, we marginalised over all parameters except for the oxygen mass. This allowed us to take into consideration any prior information for these parameters, without having to assume specific values.
We applied this methodology to the three early-to-late nebular phase spectra (+128 d, +138 d, and +348 d) for SN 2019odp. The estimated line luminosities from the spectral line fitting are summarised in Table 7 and the detailed fitting results (spectral line fits) can be found in Appendix C.2. The used models for spectral fitting are also outlined in Table 7. For the +348 d spectrum, the [O I] λ 5577 line was not detected, and thus the line luminosity should be taken as an upper limit. Using the measured line luminosities, we estimated the physical parameters.
Inferred line luminosities for the nebular phase spectra obtained.
4.3.3. Constraining the oxygen mass from nebular spectra: Results
The resulting posterior distributions for the +138 d and +348 d spectra are shown in Fig. 13.
 |
Fig. 13. Scatter plot of the marginalised posterior distribution showing the oxygen mass as a function of the temperature for the last two observed spectra (the left-most trace corresponds to the very late time spectrum at +348 d). The colour denotes the LTE departure coefficient. The estimated value range for the LTE departure coefficient from the O I λ 7774 recombination line (Sect. C.1) is marked in the colour bar. One can see that the earlier spectrum provides a lower mass constraint, while the late one does not. |
While the distribution is fairly broad, we can state without any additional constraints:
The lower limit on the oxygen mass corresponds to the high-temperature end of our prior. The LTE departure coefficient, d2, of 0.1 corresponds to an electron number density, ne, of around 107 cm−3 (Maeda et al. 2007). While Eq. (23) corresponds to a strict upper limit on the oxygen mass, it is only a strict limit on the light-emitting neutral oxygen mass and not on the total oxygen mass.
To further constrain the oxygen mass, one can try to roughly estimate the electron density (and thus LTE deviation) in the oxygen zone based on the observed O I λ 7774 recombination line, which we do in Sect. C.1. The recombination line analysis points to an LTE deviation, d2, in the range of 0.6 to 0.72 (or even higher in the case in which the oxygen zone is clumpy), which thus points towards an oxygen mass of
However, the analysis for this is less rigorous, which is why we have also kept the assumption-free limit. One caveat to this is that the emission for the recombination line does not necessarily have to come from the same zone in the ejecta as the forbidden line emission (although in the spectra used for this analysis the spectral shape of the forbidden and recombination line match fairly well).
4.3.4. Constraining the oxygen mass from nebular spectra: Zero-age main sequence mass estimate
In this section, we try to put the constraints we derived on the oxygen mass from the nebular spectroscopy in context with some stellar evolution models from the literature, since the ultimate goal is to derive ZAMS mass estimates for the progenitor star. We have selected five different studies to highlight the complexity and range of results depending on methodology and assumptions, and we discuss these in conjunction with our derived properties for SN 2019odp. As was outlined in Sect. 1, there are two primary progenitor channels to consider: single massive star and binary stars. Several model grids for both progenitor channels are summarised in Fig. 14, showing the well-known monotonic evolution of ejected oxygen mass versus ZAMS mass, with both oxygen mass lower limits and the upper limit derived in Sect. 4.3.3 marked using dashed lines. Aside from consistency with the oxygen mass estimates, we also require that the models be roughly consistent with our estimates for the ejecta mass (Sect. 4.1.1) and be mostly stripped of the hydrogen layers in the explosion (Sect. 3.7 and Sect. 3.7.1). The models that are not consistent with these observables are shown using unfilled circles or squares in Fig. 14 for completeness.
 |
Fig. 14. Relation between the supernova ejecta oxygen yield and the ZAMS mass of different stellar evolution and supernova explosion models. The lower dashed line denotes the constraint-free lower limit on the oxygen mass (Eq. (22)), while the upper dashed line denotes the minimum oxygen mass assuming the NLTE conditions derived from the recombination line analysis (Eq. (24)). Binary evolution models are shown using circles and single massive star models are denoted by square markers. Models inconsistent with the estimated ejecta mass or not fully stripped of hydrogen are shown using unfilled symbols. |
As can be seen in Fig. 14, there is a considerable spread in the ZAMS mass to oxygen mass relation (whereas the positive correlation is common to all model grids). This can be attributed to the differing assumptions between the different model grids and the general complexity of stellar evolution and supernova explosion physics. We thus estimate ZAMS mass ranges for each model grid separately and try to provide an extrapolated lower limit on the ZAMS mass in case the model grid contains no models that are massive enough. This is summarised in Table 8 for both of the derived lower limits on the oxygen mass for SN 2019odp. Despite the above-mentioned shortcomings, we can use this discussion to constrain the ZAMS mass based on our measurements. In the binary scenario, we are restricted to a range above 17 − 38 M⊙ for the strictest limit on the oxygen mass. For the minrecMOI(T) = 2.1 M⊙ limit, Fig. 14 shows that only very massive stars are feasible. For the single massive star scenario, the range permitted by our strictest oxygen mass is larger with 12 − 60 M⊙, but for single star models we can also exclude models below a ZAMS mass of ∼40 M⊙, since this is currently believed to be the threshold to fully strip the hydrogen in this scenario. The single mass models from Dessart et al. (2011) can fulfil our strictest oxygen limit, but again only very massive stars are compatible with our highest limit on the ejected oxygen mass. All evidence thus points to SN 2019odp being the explosion of a massive star. We emphasise that although a binary scenario is not ruled out, SN 2019odp is a stripped envelope supernova with observables consistent with a massive single progenitor star.
ZAMS mass estimates using different model grids.
5. Summary and conclusions
We have presented photometric and spectroscopic observations of the Type Ib SN 2019odp. Below, we list some of the main conclusions based on our analysis of these observations.
-
Based on the identification of helium absorption features in spectroscopic observations near the peak, we have reclassified SN 2019odp as a Type Ib supernova (Sect. 3.7.1). The pre-peak spectra, however, bear great spectral similarity to Type Ic-BL supernovae as well as other transitional supernovae (SN 2008D, SN 2016coi, and SN 2017ens). This may suggest a common scenario for all these supernovae early on.
-
Using optical photometric observations, we have constructed a (pseudo-)bolometric light curve (Sect. 3.6) and estimated the peak luminosity to be
 (Mqbol ≃ −17.9 mag). This corresponds to the bright end of the distribution for Type Ib supernovae and the faint end of the distribution for Type Ic-BL supernovae.
(Mqbol ≃ −17.9 mag). This corresponds to the bright end of the distribution for Type Ib supernovae and the faint end of the distribution for Type Ic-BL supernovae. -
Using analytic bolometric light curve models, we estimate the SN 2019odp ejecta mass to be 5.4 ± 1.5 M⊙, with a nickel yield of 0.25 ± 0.04 M⊙ and a kinetic energy of 6.4 ± 1.5 × 1051 erg (Sect. 4.1.1). These values are at the extreme end of values for Type Ib supernovae and more in line with values typically seen in Type Ic-BL supernovae.
-
We identify the presence of a pronounced plateau in the early light curve that is 2 − 5 d in duration (Sect. 3.3) and
 in luminosity (Sect. 3.6). Using analytic shock cooling models, we identify this plateau as the recombination plateau following an undetected shock breakout (Sect. 4.2). Based on this, we estimate the progenitor radius to be ∼1 R⊙. Alternatively, the plateau may also be explained by insufficient nickel mixing during the explosion (Sect. 4.2).
in luminosity (Sect. 3.6). Using analytic shock cooling models, we identify this plateau as the recombination plateau following an undetected shock breakout (Sect. 4.2). Based on this, we estimate the progenitor radius to be ∼1 R⊙. Alternatively, the plateau may also be explained by insufficient nickel mixing during the explosion (Sect. 4.2). -
We expand upon existing methods for estimating oxygen masses from nebular spectra and describe both the improved model (Sect. 4.3.1) as well as the full Bayesian fitting methodology (Sect. 4.3.2). Using this new method, we derive a strict range of MO, strict = 0.5 − 5 M⊙ for SN 2019odp (Sect. 4.3.3). Based on studies on single massive star evolution, this points to a ZAMS mass of at least 40 − 60 M⊙ for binary star evolution to a ZAMS mass of at least 17 − 38 M⊙ (Sect. 4.3.4). If one takes into account further information from the analysis of oxygen recombination lines (Sect. C.1), one can further constrain the oxygen mass range, MO, rec = 2.1 − 5 M⊙. In that case, low-mass binary models can be excluded and only binary models more massive than MZAMS ≈ 35 M⊙ are consistent.
-
Many observational sample papers (Lyman et al. 2014; Taddia et al. 2018; Barbarino et al. 2021) have found relatively low ejecta masses for Type Ibc supernovae, which in combination with stellar evolution models hint at low ZAMS masses, and therefore binary progenitors for those objects. For SN 2019odp, we have deduced both a high ejecta mass from the diffusion phase light curve and a large mass of ejected oxygen from the nebular spectrum analysis, which is compatible with a single massive scenario. Thus, whereas we cannot rule out binary evolution for this supernova, SN 2019odp is one of the few stripped envelope supernovae for which such a scenario does not seem to be required. The existence of such objects is of importance for understanding the fate of the most massive stars.
Data availability
The final reduced and flux-calibrated spectra are available on WISeREP (see https://wiserep.weizmann.ac.il/) (Yaron & Gal-Yam 2012).
The code and (most) data reduction inputs are available at https://gitlab.com/welterde/ccsn-sn2019odp (with a snapshot archived on Zenodo at https://zenodo.org/record/7568627).
The data reduction products and data reduction diagnostics are available on Zenodo at https://zenodo.org/record/7554926.
This adopts the following cosmology parameters: H0 = 67.8 km s−1 Mpc−1, Ωmatter = 0.308, and Ωvacuum = 0.692. We used the value for the peculiar velocities that include the Virgo, great attractor, and Shapley supercluster velocity fields from NED. (Mould et al. 2000).
https://github.com/MickaelRigault/ztflc by M. Rigault.
https://github.com/jkrogager/PyNOT by Jens-Kristian Krogager.
Arnett (1980) calculate ζ2 ≡ IK/IM for uniform and different exponential density distributions. Liu et al. (2018) provides analytic expressions for broken power-law distributions.
This pregeneration step is purely for performance reasons, since the Gaussian process step is quite expensive. We chose a large enough number of realisations for us to be able to replace the call to the Gaussian Process sampler function inside the likelihood function with a random choice of one such realisation without affecting the resulting posterior distribution
Acknowledgments
We thank Jakob Nordin and the anonymous referee for comments. Based on observations obtained with the Samuel Oschin Telescope 48-inch and the 60-inch Telescope at the Palomar Observatory as part of the Zwicky Transient Facility project. ZTF is supported by the National Science Foundation under Grant No. AST-1440341 and a collaboration including Caltech, IPAC, the Weizmann Institute of Science, the Oskar Klein Center at Stockholm University, the University of Maryland, the University of Washington, Deutsches Elektronen-Synchrotron and Humboldt University, Los Alamos National Laboratories, the TANGO Consortium of Taiwan, the University of Wisconsin at Milwaukee, and Lawrence Berkeley National Laboratories. Operations are conducted by COO, IPAC, and UW. SED Machine is based upon work supported by the National Science Foundation under Grant No. 1106171. This work was supported by the GROWTH project (Kasliwal et al. 2019) funded by the National Science Foundation under Grant No 1545949. Part of the funding for GROND (both hardware as well as personnel) was generously granted from the Leibniz-Prize to Prof. G. Hasinger (DFG grant HA 1850/28-1). Based on observations made with the Nordic Optical Telescope, owned in collaboration by the University of Turku and Aarhus University, and operated jointly by Aarhus University, the University of Turku and the University of Oslo, representing Denmark, Finland and Norway, the University of Iceland and Stockholm University at the Observatorio del Roque de los Muchachos, La Palma, Spain, of the Instituto de Astrofisica de Canarias. Some of the data presented here were obtained in part with ALFOSC, which is provided by the Instituto de Astrofisica de Andalucia (IAA) under a joint agreement with the University of Copenhagen and NOT. Some of the data presented herein were obtained at the W. M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W. M. Keck Foundation. M. W. Coughlin acknowledges support from the National Science Foundation with grant numbers PHY-2010970 and OAC-2117997. P. Rosnet acknowledges the support received from the Agence Nationale de la Recherche of the French government through the program ANR-21-CE31-0016-03. This research has made use of the NASA/IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has made use of NASA’s Astrophysics Data System. The acknowledgements were compiled using the Astronomy Acknowledgement Generator. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France. This research made use of Astroquery (Ginsburg et al. 2019). This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2018, 2013). PyRAF is a product of the Space Telescope Science Institute, which is operated by AURA for NASA. This research made use of APLpy, an open-source plotting package for Python hosted at http://aplpy.github.com. This research made use of SciPy (Virtanen et al. 2020). This research made use of NumPy (Harris et al. 2020). IRAF is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under cooperative agreement with the National Science Foundation (Tody 1993). This research made use of matplotlib, a Python library for publication quality graphics (Hunter 2007). This work made use of the IPython package (Pérez & Granger 2007). We acknowledge the use of public data from the Swift data archive.
References
- Aguado, D. S., Ahumada, R., Almeida, A., et al. 2019, ApJS, 240, 23 [Google Scholar]
- Arcavi, I. 2022, ApJ, 937, 75 [CrossRef] [Google Scholar]
- Arcavi, I., Gal-Yam, A., Yaron, O., et al. 2011, ApJ, 742, L18 [Google Scholar]
- Arcavi, I., Hosseinzadeh, G., Brown, P. J., et al. 2017, ApJ, 837, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Armstrong, P., Tucker, B. E., Rest, A., et al. 2021, MNRAS, 507, 3125 [Google Scholar]
- Arnett, W. D. 1980, ApJ, 237, 541 [Google Scholar]
- Arnett, W. D. 1982, ApJ, 253, 785 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Barbarino, C., Sollerman, J., Taddia, F., et al. 2021, A&A, 651, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barbary, K. 2016, extinction v0.3.0, https://doi.org/10.5281/zenodo.804967 [Google Scholar]
- Becker, A. 2015, Astrophysics Source Code Library [record ascl:1504.004] [Google Scholar]
- Bellm, E. C., Kulkarni, S. R., Barlow, T., et al. 2019a, PASP, 131, 068003 [Google Scholar]
- Bellm, E. C., Kulkarni, S. R., Graham, M. J., et al. 2019b, PASP, 131, 018002 [Google Scholar]
- Bengyat, O., & Gal-Yam, A. 2022, ApJ, 930, 31 [CrossRef] [Google Scholar]
- Bersten, M. C., Benvenuto, O. G., Folatelli, G., et al. 2014, AJ, 148, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Bersten, M. C., Folatelli, G., García, F., et al. 2018, Nature, 554, 497 [Google Scholar]
- Bertin, E., Mellier, Y., Radovich, M., et al. 2002, ASP Conf. Ser., 281, 228 [Google Scholar]
- Bianco, F. B., Modjaz, M., Hicken, M., et al. 2014, ApJS, 213, 19 [Google Scholar]
- Blagorodnova, N., Neill, J. D., Walters, R., et al. 2018, PASP, 130, 035003 [Google Scholar]
- Blanton, M. R., & Roweis, S. 2007, AJ, 133, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, S., & Tonry, J. L. 2007, ApJ, 666, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Bradley, L., Sipöcz, B., Robitaille, T., et al. 2021, astropy/photutils: 1.2.0, https://doi.org/10.5281/zenodo.5525286 [Google Scholar]
- Breeveld, A. A., Landsman, W., Holland, S. T., et al. 2011, Am. Inst. Phys. Conf. Ser., 1358, 373 [NASA ADS] [Google Scholar]
- Brennan, S., Fraser, M., Ihanec, N., Gromadzki, M., & Yaron, O. 2019, Transient Name Server Classification Report 2019-1595, 1 [Google Scholar]
- Brown, P. J., Breeveld, A. A., Holland, S., Kuin, P., & Pritchard, T. 2014, Ap&SS, 354, 89 [Google Scholar]
- Bruch, R. J., Gal-Yam, A., Schulze, S., et al. 2021, ApJ, 912, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, ArXiv e-prints [arXiv:1612.05560] [Google Scholar]
- Chatzopoulos, E., Wheeler, J. C., & Vinko, J. 2012, ApJ, 746, 121 [Google Scholar]
- Chen, T. W., Inserra, C., Fraser, M., et al. 2018, ApJ, 867, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Fransson, C. 2008, ApJ, 683, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Clocchiatti, A., Suntzeff, N. B., Covarrubias, R., & Candia, P. 2011, AJ, 141, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Contardo, G., Leibundgut, B., & Vacca, W. D. 2000, A&A, 359, 876 [NASA ADS] [Google Scholar]
- Das, K. K., Kasliwal, M. M., Fremling, C., et al. 2023, ApJ, 959, 12 [CrossRef] [Google Scholar]
- Das, K. K., Kasliwal, M. M., Sollerman, J., et al. 2024, ApJ, 972, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Dekany, R., Smith, R. M., Riddle, R., et al. 2020, PASP, 132, 038001 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Hillier, D. J., Livne, E., et al. 2011, MNRAS, 414, 2985 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Hillier, D. J., Woosley, S., et al. 2016, MNRAS, 458, 1618 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Yoon, S.-C., Aguilera-Dena, D. R., & Langer, N. 2020, A&A, 642, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elmhamdi, A. 2011, Acta Astron., 61, 179 [NASA ADS] [Google Scholar]
- Elmhamdi, A., Danziger, I. J., Cappellaro, E., et al. 2004, A&A, 426, 963 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ergon, M., Jerkstrand, A., Sollerman, J., et al. 2015, A&A, 580, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ertl, T., Woosley, S. E., Sukhbold, T., & Janka, H. T. 2020, ApJ, 890, 51 [CrossRef] [Google Scholar]
- Fang, Q., Maeda, K., Kuncarayakti, H., Sun, F., & Gal-Yam, A. 2019, Nat. Astron., 3, 434 [Google Scholar]
- Filippenko, A. V. 1997, ARA&A, 35, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J., Papenkova, M. S., Swift, B. J., et al. 2003, PASP, 115, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Fransson, C., & Chevalier, R. A. 1989, ApJ, 343, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Fremling, C., Sollerman, J., Taddia, F., et al. 2016, A&A, 593, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [Google Scholar]
- Ginsburg, A., Sipőcz, B. M., Brasseur, C. E., et al. 2019, AJ, 157, 98 [Google Scholar]
- Görtler, J., Kehlbeck, R., & Deussen, O. 2019, Distill, https://distill.pub/2019/visual-exploration-gaussian-processes [Google Scholar]
- Graham, M. J., Kulkarni, S. R., Bellm, E. C., et al. 2019, PASP, 131, 078001 [Google Scholar]
- Greiner, J., Bornemann, W., Clemens, C., et al. 2008, PASP, 120, 405 [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., & Woosley, S. E. 2010, ApJ, 724, 341 [Google Scholar]
- Higson, E., Handley, W., Hobson, M., & Lasenby, A. 2019, Stat. Comput., 29, 891 [Google Scholar]
- Hirschi, R., Meynet, G., & Maeder, A. 2005, A&A, 433, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Houck, J. C., & Fransson, C. 1996, ApJ, 456, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jerkstrand, A. 2017, in Handbook of Supernovae, ed. A. W. Alsabti, & P. Murdin, 795 [CrossRef] [Google Scholar]
- Jerkstrand, A., Smartt, S. J., Fraser, M., et al. 2014, MNRAS, 439, 3694 [Google Scholar]
- Jerkstrand, A., Ergon, M., Smartt, S. J., et al. 2015, A&A, 573, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jerkstrand, A., Smartt, S. J., Inserra, C., et al. 2017, ApJ, 835, 13 [Google Scholar]
- Karamehmetoglu, E., Sollerman, J., Taddia, F., et al. 2023, A&A, 678, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kasliwal, M. M., Cannella, C., Bagdasaryan, A., et al. 2019, PASP, 131, 038003 [NASA ADS] [CrossRef] [Google Scholar]
- Khatami, D. K., & Kasen, D. N. 2019, ApJ, 878, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Kilpatrick, C. D., Drout, M. R., Auchettl, K., et al. 2021, MNRAS, 504, 2073 [CrossRef] [Google Scholar]
- Kramida, A., Ralchenko, Yu., Reader, J., & NIST ASD Team 2017, in NIST Atomic Spectra Database (ver. 5.9) (Gaithersburg, MD: National Institute of Standards and Technology), https://physics.nist.gov/asd [Google Scholar]
- Krühler, T., Küpcü Yoldaş, A., Greiner, J., et al. 2008, ApJ, 685, 376 [Google Scholar]
- Kumar, B., Singh, A., Sahu, D. K., & Anupama, G. C. 2022, ApJ, 927, 61 [CrossRef] [Google Scholar]
- Kuncarayakti, H., Maeda, K., Bersten, M. C., et al. 2015, A&A, 579, A95 [CrossRef] [EDP Sciences] [Google Scholar]
- Laplace, E., Justham, S., Renzo, M., et al. 2021, A&A, 656, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, H., & McCray, R. 1992, ApJ, 387, 309 [CrossRef] [Google Scholar]
- Limongi, M., & Chieffi, A. 2003, ApJ, 592, 404 [CrossRef] [Google Scholar]
- Liu, L.-D., Zhang, B., Wang, L.-J., & Dai, Z.-G. 2018, ApJ, 868, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1991, ApJ, 383, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Lunnan, R., Chornock, R., Berger, E., et al. 2016, ApJ, 831, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Lyman, J. D., Bersier, D., & James, P. A. 2014, MNRAS, 437, 3848 [Google Scholar]
- Lyman, J. D., Bersier, D., James, P. A., et al. 2016, MNRAS, 457, 328 [Google Scholar]
- Maeda, K., Tanaka, M., Nomoto, K., et al. 2007, ApJ, 666, 1069 [NASA ADS] [CrossRef] [Google Scholar]
- Masci, F. J., Laher, R. R., Rusholme, B., et al. 2019, PASP, 131, 018003 [Google Scholar]
- Mazzali, P. A., Nomoto, K., Patat, F., & Maeda, K. 2001, ApJ, 559, 1047 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzali, P. A., Deng, J., Maeda, K., et al. 2002, ApJ, 572, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Medler, K., Mazzali, P. A., Teffs, J., et al. 2022, MNRAS, 513, 5540 [NASA ADS] [CrossRef] [Google Scholar]
- Modjaz, M., Li, W., Butler, N., et al. 2009, ApJ, 702, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Modjaz, M., Blondin, S., Kirshner, R. P., et al. 2014, AJ, 147, 99 [Google Scholar]
- Modjaz, M., Liu, Y. Q., Bianco, F. B., & Graur, O. 2016, ApJ, 832, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Modjaz, M., Gutiérrez, C. P., & Arcavi, I. 2019, Nat. Astron., 3, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Mould, J. R., Huchra, J. P., Freedman, W. L., et al. 2000, ApJ, 529, 786 [Google Scholar]
- Nadyozhin, D. K. 1994, ApJS, 92, 527 [Google Scholar]
- Nakar, E., & Sari, R. 2010, ApJ, 725, 904 [NASA ADS] [CrossRef] [Google Scholar]
- National Optical Astronomy Observatories 1999, Astrophysics Source Code Library [record ascl:9911.002] [Google Scholar]
- Nordin, J., Brinnel, V., Giomi, M., et al. 2019, Transient Name Server Discovery Report, 2019–1585, 1 [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1982, PASP, 94, 586 [Google Scholar]
- Oke, J. B., Cohen, J. G., Carr, M., et al. 1995, PASP, 107, 375 [Google Scholar]
- Patat, F., Cappellaro, E., Danziger, J., et al. 2001, ApJ, 555, 900 [Google Scholar]
- Pérez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
- Perley, D. A. 2019, PASP, 131, 084503 [Google Scholar]
- Piro, A. L., & Nakar, E. 2013, ApJ, 769, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., Haynie, A., & Yao, Y. 2021, ApJ, 909, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Prentice, S. J., & Mazzali, P. A. 2017, MNRAS, 469, 2672 [Google Scholar]
- Prentice, S. J., Ashall, C., Mazzali, P. A., et al. 2018, MNRAS, 478, 4162 [NASA ADS] [CrossRef] [Google Scholar]
- Prentice, S. J., Maguire, K., Siebenaler, L., & Jerkstrand, A. 2022, MNRAS, 514, 5686 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Rabinak, I., & Waxman, E. 2011, ApJ, 728, 63 [Google Scholar]
- Rigault, M., Neill, J. D., Blagorodnova, N., et al. 2019, A&A, 627, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [Google Scholar]
- Sahu, D. K., Gurugubelli, U. K., Anupama, G. C., & Nomoto, K. 2011, MNRAS, 413, 2583 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Schneider, S. E., Thuan, T. X., Magri, C., & Wadiak, J. E. 1990, ApJS, 72, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Science Software Branch at STScI 2012, Astrophysics Source Code Library [record ascl:1207.011] [Google Scholar]
- Shivvers, I., Filippenko, A. V., Silverman, J. M., et al. 2019, MNRAS, 482, 1545 [Google Scholar]
- Skilling, J. 2004, Am. Inst. Phys. Conf. Ser., 735, 395 [NASA ADS] [Google Scholar]
- Skilling, J. 2006, Bayesian Anal., 1, 833 [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J., Valenti, S., Fraser, M., et al. 2015, A&A, 579, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soderberg, A. M., Berger, E., Page, K. L., et al. 2008, Nature, 453, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Soffitta, P., Feroci, M., Piro, L., et al. 1998, IAU Circ., 6884, 1 [NASA ADS] [Google Scholar]
- Sollerman, J., Leibundgut, B., & Spyromilio, J. 1998, A&A, 337, 207 [NASA ADS] [Google Scholar]
- Speagle, J. S. 2020, MNRAS, 493, 3132 [Google Scholar]
- Stritzinger, M., Hamuy, M., Suntzeff, N. B., et al. 2002, AJ, 124, 2100 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M., Mazzali, P., Phillips, M. M., et al. 2009, ApJ, 696, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M. D., Taddia, F., Burns, C. R., et al. 2018, A&A, 609, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taddia, F., Sollerman, J., Leloudas, G., et al. 2015, A&A, 574, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taddia, F., Stritzinger, M. D., Bersten, M., et al. 2018, A&A, 609, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taddia, F., Sollerman, J., Fremling, C., et al. 2019, A&A, 621, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takada-Hidai, M., Aoki, W., & Zhao, G. 2002, PASJ, 54, 899 [NASA ADS] [Google Scholar]
- Tartaglia, L., Fraser, M., Sand, D. J., et al. 2017, ApJ, 836, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., Langer, N., & Podsiadlowski, P. 2015, MNRAS, 451, 2123 [NASA ADS] [CrossRef] [Google Scholar]
- Tody, D. 1993, ASP Conf. Ser., 52, 173 [NASA ADS] [Google Scholar]
- Uomoto, A. 1986, ApJ, 310, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, S., Taubenberger, S., Pastorello, A., et al. 2012, ApJ, 749, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Wheeler, J. C., Johnson, V., & Clocchiatti, A. 2015, MNRAS, 450, 1295 [Google Scholar]
- Williamson, M., Modjaz, M., & Bianco, F. B. 2019, ApJ, 880, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Langer, N., & Weaver, T. A. 1993, ApJ, 411, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Wygoda, N., Elbaz, Y., & Katz, B. 2019, MNRAS, 484, 3941 [Google Scholar]
- Yamanaka, M., Nakaoka, T., Tanaka, M., et al. 2017, ApJ, 837, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Yaron, O., & Gal-Yam, A. 2012, PASP, 124, 668 [Google Scholar]
- Yoon, S. C., Gräfener, G., Vink, J. S., Kozyreva, A., & Izzard, R. G. 2012, A&A, 544, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., Chun, W., Tolstov, A., Blinnikov, S., & Dessart, L. 2019, ApJ, 872, 174 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Arnett model description
The most used analytic model for estimating ejecta properties for supernovae from the light curve peak is the Arnett (1982; hereafter A82) model. The model is based on the following assumptions:
-
Homologous expansion of the ejecta:
-
The ejecta is a radiation-dominated gas
-
The diffusion approximation applies
-
The opacity κopt is constant throughout the ejecta and also constant in time
-
Spherical symmetry
-
Volume emission of radioactive decay energy is proportional to the radiation energy per unit volume. In this case the radioactive decay energy refers to the 56Ni and 56Co decays.
Apart from these assumptions further approximations can be made, such as the commonly used approximation that the initial radius R(t = 0) is small and thus R(t)≃vsc t.
Using the formalism from Khatami & Kasen (2019, their eq. 1112) we can state the luminosity as follows:
where τm is the diffusion timescale and Qdep(t) is the time-dependent heating term.
The diffusion timescale relates to the ejecta mass and scale-velocity vsc in the following way (Arnett 1982, eqs. 18 and 22):
where Mej is the ejecta mass, β is a density-profile integration constant and κopt is the opacity.
Since the scale velocity is not a quantity that can be measured directly we need to find some proxy for it. We can use the ‘representative’ mean expansion rate vm from Dessart et al. (2016) (which corresponds to < v2> in Arnett (1980)):
where EK is the total kinetic energy of the explosion.
We use Arnett (1980), their Eq. 31) to relate the mean expansion rate to the scale velocity:
where ζ is a density-profile dependent integration constant13.
We use the following relation between He Iλ 5876 line velocity vabs (see Sect. 3.7.2) and the mean expansion rate vm from Dessart et al. (2016), their sec. 5.3):
we estimate the expansion rate of SN 2019odp at light curve peak to be vm = 10912 ± 1435 km s−1.
Thus the ejecta mass and kinetic energy can be given in terms of the mean expansion rate vm:
Assuming a power-law density profile (with a limited range of the power-law index around uniform density) we approximate β/ζ as a constant value (17.8 for this paper14), and adopt a mean opacity κopt = 0.07 cm2g−1.
We use the formalism for the heating function from Wygoda et al. (2019) for the radioactive decay heating of 56Ni and 56Co (their Eqs. 11 and 12):
where ϵNi is the specific heating rate for 56Ni decay, ϵCo, γ is the gamma-ray specific heating rate for 56Co decay, ϵCo, e+ is the positron specific heating rate for 56Co decay, τNi, Co are the decay timescales (Nadyozhin 1994). The used physical constants for the heating function(s) are summarised in Table A.1. The total heating function is given by:
Nuclear decay constants used in the radioactive decay chain heating function.
A.1. Arnett model: Large initial radius variant
While the A82 model as previously described assumes the initial radius R0 to be negligible (R0 ≪ 1000 R⊙) one can relax this assumption.
For this we introduce an additional timescale:
and then following the approach from Chatzopoulos et al. (2012) (but using the more generalised notation from before) we get the following function for the luminosity:
A.2. Photometric fitting framework
Based on the observed photometric evolution of the supernovae we want to use a Bayesian framework to estimate the parameters of the models discussed in Sect. A. We use the combined and interpolated photometric dataset described in Sect. 2.4 as input. We use the Python nested sampling framework dynesty to both estimate the posterior as well as the evidence of the model under consideration. The methodology propagates all the correlated uncertainties (extinction, distance, Lyman bolometric correction factor) into the derived posterior.
We pregenerate 12000 realisations of the bolometric light curve based on the following algorithm15:
-
We sample Nt = 50 uniform times (𝒰(tmin, tmax)) from the temporal validity range of the underlying interpolated light curves (to ensure we are only interpolating them and not extrapolating).
-
We create a pseudo-bolometric light curve realisation by sampling the Gaussian process of the combined light curves (see Sect. 2.4) and then applying the bolometric method to convert the apparent magnitudes into pseudo-bolometric magnitudes (see Sect. 3.6).
-
Next we sample from each of the uncertainty distributions of the correlated uncertainties mentioned before and apply the offset to the whole realisation of the bolometric light curve (since we assume them to be the same for each point in the light curve).
In the actual likelihood function we then randomly select one of those light curve realisations IX in each iteration and calculate the model magnitudes M based on the given parameter vector θ for the iteration. The likelihood is then given as
Using this method we can assure that all correlated uncertainties and the uncertainty from the Gaussian-process interpolation step are correctly propagated.
The used priors for the model are shown in Table A.2. Since the model does not contain any treatment for gamma-ray leakage we restrict the fitting range to roughly the diffusion timescale. The resulting parameter estimates for SN 2019odp and the comparison objects for all models are shown in Table 3 (we also include literature values where available as a consistency check).
Priors for the small R0 Arnett model fit.
Appendix B: Photometric models
Used photometric models per supernova and band.
In this section we describe the used analytic photometry light curve models and priors for the models. We use different models depending on the light curve coverage and the shape of the early excess (if there was one detected) with the decision being specific to the photometric band. The assignment of photometric model to a given transient and band is listed in Table B.1. All analytic functions use the phase relative to the prior peak estimate: Δt ≡ t − tpeak.
Our (complex) light curve models are based on the light curve model by Contardo et al. (2000) (hereafter C20):
where Δt is the phase relative to the main peak prior time, δ(t) is the explosion scaling function, α is the linear intercept, β is the linear slope, ADF is the amplitude of the main diffusion peak Gaussian, t0, DF is the phase offset of the main diffusion peak Gaussian and σDF is the width of the Gaussian. The rise scaling function is given as
where t0, rise is the phase offset of the rise scaling function, τrise is the rise timescale.
We derive two modified light curve models from the C20 depending on the shape of the early excess:
-
The ‘plateau-contardo’ model adds a smoothing function g(t) to interpolate between the plateau magnitude mplat and the mC20 function:
This introduces three additional parameters to the C20 model that we allow to vary in a reasonable range: plateau magnitude mplat, plateau end time t0, plat and the smoothing timescale τsmooth.
-
The ‘prebump-contardo’ model adds a secondary Gaussian peak at a peak relative to the main peak:
This introduces three additional parameters to the model: pre-bump amplitude APB, pre-bump width σPB and centre time of the pre-bump t0, PB.
If the data only covers a small time range before/after peak we use a linear model instead:
Appendix C: Oxygen mass modelling
C.1. NLTE deviation factor
The LTE departure coefficient is defined as follows:
We estimate the sensitivity to deviations from LTE conditions by running the fitting procedure for a spectrum multiple times in a sequence where we vary the allowed maximum LTE departure coefficient d2 from 0.01 to 1.0 (where 1.0 means LTE conditions). The resulting change due to the change of the LTE departure can be seen in Fig. C.1.
 |
Fig. C.1. Sensitivity of the oxygen mass percentiles as a function of the minimum LTE departure coefficient d2. |
We get a rough estimate for the LTE departure coefficient d2 by estimating the electron density ne from the O I λ 7774 recombination line and using the following relation:
which we got by dividing Eq. 2 from Houck & Fransson (1996) by Eq. 2 from Jerkstrand et al. (2015). To approximate the electron density we use the oxygen recombination lines that are visible in the earlier spectra. We can use the following relation from Jerkstrand et al. (2015) to relate the line luminosity to the electron density (their Eq. 3):
where Vcore is the line width, t is the time since explosion, Ψ is the fraction of electrons provided by oxygen initiations and fO is the oxygen zone filling factor.
We assume Ψ to be of order unity (from Jerkstrand et al. 2015). We estimate Vcore from the measured Gaussian line width. Since αeff depends on the temperature, we use the values from Jerkstrand et al. (2015), their sect. C.1) for three different temperatures. Using α(T = 2500 K) = 2.8 × 10−13 cm3 s−1, α(T = 5000 K) = 1.6 × 10−13 cm3 s−1 and α(T = 7500 K) = 1.1 × 10−13 cm3 s−1 and a crudely estimated line luminosity of L ≃ 27 ⋅ 1038 erg s−1 as well as the line width estimated velocity of 2464 km s−1 (both from the +158 d Keck spectrum) we estimate  to be 2.2 ⋅ 108 cm−3 (2500 K), 2.9 ⋅ 108 cm−3 (5000 K) and 3.5 ⋅ 108 cm−3 (7500 K). This is in line to the values seen in Jerkstrand et al. (2015). Using Eq. C.2 we get a range of 0.6 to 0.72 for LTE departure coefficient d2 for an assumed zone filling factor of one. Higher filling factors would yield even higher values. However the recombination lines can be emitted from higher density regions than the nebular lines we are using in the main analysis and are thus not really suitable for quantitative analysis and we thus do not use this estimated d2 value/range in our main analysis.
to be 2.2 ⋅ 108 cm−3 (2500 K), 2.9 ⋅ 108 cm−3 (5000 K) and 3.5 ⋅ 108 cm−3 (7500 K). This is in line to the values seen in Jerkstrand et al. (2015). Using Eq. C.2 we get a range of 0.6 to 0.72 for LTE departure coefficient d2 for an assumed zone filling factor of one. Higher filling factors would yield even higher values. However the recombination lines can be emitted from higher density regions than the nebular lines we are using in the main analysis and are thus not really suitable for quantitative analysis and we thus do not use this estimated d2 value/range in our main analysis.
C.2. Spectral fitting results
In this section we show the best fit results from the spectral line profile models. In Figs. C.2, C.3, and Fig. C.4 we show the relevant spectral fitting regions with model spectra drawn from the posterior distribution overplotted. The corresponding corner plots visualising the posterior distributions (as well as the trace files) can be found on Zenodo at https://zenodo.org/record/7554926.
 |
Fig. C.2. NOT/ALFOSC spectrum at 128 days post-peak with model spectra drawn from the posterior distribution of the model overlaid in grey. |
 |
Fig. C.3. Early Keck/LRIS spectrum at 138 days post-peak with model spectra drawn from the posterior distribution of the model overlaid in grey. |
 |
Fig. C.4. Late Keck/LRIS spectrum at 358 days post-peak with model spectra drawn from the posterior distribution of the model overlaid in grey. |
Appendix D: Photometric blackbody fitting
We use the interpolated and pre-processed light curve constructed by the method described in Sect. 2.4. We construct the time grid to perform the fitting by selecting all observations between the first time all selected filter bands had at least one detection and the peak and then selecting all days post-peak that had at least one observation. This ensures we are only interpolating the light curve and never have to rely on extrapolating it (which is highly uncertain at the very early epochs).
For each time on the time grid we estimate the extinction-corrected magnitude in all filter bands. Next we fit a three-parameter Bayesian model to these observations: temperature log T, radius log R and the distance D. We follow the suggestion by Arcavi (2022) and use a log-uniform prior for the temperature (although we use nested sampling instead of MCMC). The distance is a nuisance parameter, which is constrained by the redshift uncertainty. In the likelihood function we generate a blackbody SED using the temperature and radius. We then perform synthetic photometry using the corresponding filter curves to compare to the light curve. We perform the posterior calculation using the nested sampling code dynesty.
D.1. Validation
We compare the resulting temperature and radius between three different filter combinations: gri, ri and rizJH. The comparison is shown in Fig. D.1. We only have a full spectral coverage from optical to NIR between 40 and 80 days.
 |
Fig. D.1. Comparison between three filter sets. |
Appendix E: Observation logs
A partial listing of the forced photometry dataset is given in Table E.1 with the full dataset available on Zenodo at https://zenodo.org/record/7554926. The used photometric filters, reference systems and calibration sources are described in Table E.3. The observation log of the spectroscopic observations is given in Table E.2.
Full forced photometry dataset obtained for SN 2019odp.
Observation log of the spectroscopic observations.
Facilities used for photometric follow-up observations as well as their respective native filter systems and calibration sources.
All Tables
Basic light curve observables extracted for SN 2019odp and the comparison objects.
Supernova parameter estimates for different pseudo-bolometric light curve models.
Facilities used for photometric follow-up observations as well as their respective native filter systems and calibration sources.
All Figures
 |
Fig. 1. Stacked r′-band GROND image using images taken between +29d and +79d showing the field of the supernova. The supernova is marked with the two red markers. The transient is located approximately 25″ from the core of the galaxy, corresponding to a projected separation of around 8 kpc. The bottom left of the image shows a saturated star with heavy blooming. |
| In the text | |
 |
Fig. 2. Photometric evolution of SN 2019odp around the discovery epoch. The light curve is given in flux units to show the pre-discovery upper limits on the same scale. The different colours denote the different bands. The zero flux level is denoted by a dashed line. The faintly overlaid light curves are light curve realisations drawn from the conditioned Gaussian process interpolation kernel (see Sect. 2.4 for a detailed description). For illustration purposes, they are drawn beyond their validity time range (turning into a extrapolation). The light curves have not been corrected for extinction. The times of spectroscopic observations are marked in the top bar by vertical lines. |
| In the text | |
 |
Fig. 3. Photometric evolution of SN 2019odp in the ugriz′J bands using the combined photometry dataset. The colour denotes the band and the different markers denote the source instrument. The faintly overlaid light curves are light curve realisations drawn from the conditioned Gaussian process interpolation kernel (see Sect. 2.4 for a detailed description). The light curves have not been corrected for extinction. The times of spectroscopic observations are marked in the top bar by vertical lines. |
| In the text | |
 |
Fig. 4. Spectral sequence of obtained spectra from discovery to before peak. The observation phase of each spectrum is denoted on the right of each spectrum. Rest wavelengths of strong He I features have been marked in green, and the positions of Balmer lines are denoted in blue. A Telluric absorption feature has been denoted with a shaded region and a ⊕ symbol. |
| In the text | |
 |
Fig. 5. Spectral sequence of obtained spectra around the photospheric phase. The notation is the same as in Fig. 4, but here we have also marked the wavelengths of several intermediate-mass elements. |
| In the text | |
 |
Fig. 6. Spectral sequence of obtained spectra in the pre-nebular phase. The notation is the same as in Fig. 4, but here we have also marked the wavelengths of several intermediate-mass elements. |
| In the text | |
 |
Fig. 7. Spectral sequence of SN 2019odp in the nebular phase. We have marked several of the O I lines as well as some Ca II lines. |
| In the text | |
 |
Fig. 8. Comparison of the evolution of the absolute light curves in g/V (panel A, left) and r/R (panel B, middle) bands between SN 2019odp and selected comparison objects. In addition, the pseudo-bolometric light curve derived using the Lyman method is shown (panel C, right). In the pseudo-bolometric light curve (panel C), the error bars around the peak represent the combined error from the distance uncertainty, extinction uncertainty, and the scatter from the Lyman relation. The interpolated light curves for each supernova have been placed over the observed datapoints in the same colour. These were used to derive the pseudo-bolometric light curves in the right panel. The bottom left corners of panels A and B zoom in on the very early evolution. |
| In the text | |
 |
Fig. 9. Colour evolution of SN 2019odp and the comparison objects. The top panel shows the g − r colour (or corresponding Johnson colour). The lower panel shows the r − i colour (or corresponding Johnson colour). For each transient, we sampled 1000 realisations of the supernova light curve from the interpolation kernel. For SN 2019odp, we also included synthetic photometry based on the observed spectra as a consistency check (using the same filter curve as for the photometric dataset). They are denoted with black crosses. |
| In the text | |
 |
Fig. 10. Time evolution of the inferred blackbody parameters from the photometry for SN 2019odp and selected comparison objects. We chose the closest matching filter sets for all transients and performed our own fitting for all objects. The error bars contain all uncertainties including the distance and extinction uncertainties. The upper panel shows the temperature time evolution and the lower panel the photospheric radius time evolution. |
| In the text | |
 |
Fig. 11. Comparison of spectra of SN 2019odp before peak (left panel) and after peak (right panel) against selected comparison objects. The phases with respect to the respective g/V-band peak epochs are denoted in the legend. Telluric absorptions have been marked and masked, and the spectra have been corrected for host extinction. At the early phase, the spectrum of SN 2019odp (the NTT classification spectrum) looks very much like the Type Ic-BL SN 1998bw (shown in red, Patat et al. 2001), and not at all like the typical Type Ib iPTF13bvn (shown in blue, Fremling et al. 2016). This is the reason for the initial classification on TNS as a Type Ic-BL supernova. However it looks quite similar to the Type Ib SN 2008D (shown in orange, Shivvers et al. 2019; Modjaz et al. 2014), which has earlier observations than iPTF13bvn. At later phases (right panel), SN 2019odp is instead similar to typical Type Ib supernovae such as iPTF13bvn, showing narrower lines and clear helium features, as opposed to SN 1998bw. In fact, the most similar object might be the Type Ib SN 2008D. Some of the spectra suffer from host contamination. |
| In the text | |
 |
Fig. 12. Velocity evolution of the He I lines in SN 2019odp and the comparison Type Ib supernovae. |
| In the text | |
 |
Fig. 13. Scatter plot of the marginalised posterior distribution showing the oxygen mass as a function of the temperature for the last two observed spectra (the left-most trace corresponds to the very late time spectrum at +348 d). The colour denotes the LTE departure coefficient. The estimated value range for the LTE departure coefficient from the O I λ 7774 recombination line (Sect. C.1) is marked in the colour bar. One can see that the earlier spectrum provides a lower mass constraint, while the late one does not. |
| In the text | |
 |
Fig. 14. Relation between the supernova ejecta oxygen yield and the ZAMS mass of different stellar evolution and supernova explosion models. The lower dashed line denotes the constraint-free lower limit on the oxygen mass (Eq. (22)), while the upper dashed line denotes the minimum oxygen mass assuming the NLTE conditions derived from the recombination line analysis (Eq. (24)). Binary evolution models are shown using circles and single massive star models are denoted by square markers. Models inconsistent with the estimated ejecta mass or not fully stripped of hydrogen are shown using unfilled symbols. |
| In the text | |
 |
Fig. C.1. Sensitivity of the oxygen mass percentiles as a function of the minimum LTE departure coefficient d2. |
| In the text | |
 |
Fig. C.2. NOT/ALFOSC spectrum at 128 days post-peak with model spectra drawn from the posterior distribution of the model overlaid in grey. |
| In the text | |
 |
Fig. C.3. Early Keck/LRIS spectrum at 138 days post-peak with model spectra drawn from the posterior distribution of the model overlaid in grey. |
| In the text | |
 |
Fig. C.4. Late Keck/LRIS spectrum at 358 days post-peak with model spectra drawn from the posterior distribution of the model overlaid in grey. |
| In the text | |
 |
Fig. D.1. Comparison between three filter sets. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.