| Issue |
A&A
Volume 687, July 2024
|
|
|---|---|---|
| Article Number | A296 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202450015 | |
| Published online | 26 July 2024 | |
A multi-grain multi-layer astrochemical model with variable desorption energy for surface species
Engineering Research Institute ‘Ventspils International Radio Astronomy Center’ of Ventspils University of Applied Sciences,
Inženieru 101,
Ventspils
3601,
Latvia
e-mail: juris.kalvans@venta.lv
Received:
18
March
2024
Accepted:
19
May
2024
Context. Interstellar surface chemistry is a complex process that occurs in icy layers that have accumulated onto grains of different sizes. The efficiency of the surface processes often depends on the immediate environment of the adsorbed molecules.
Aims. We investigated how gas-grain chemistry changes when the surface molecule binding energy is modified, depending on the properties of the surface.
Methods. In a gas-grain astrochemical model, molecular binding energy gradually changes for three different environments –(1) the bare grain surface, (2) polar water-dominated ices, and (3) weakly polar carbon monoxide-dominated ices. In addition to diffusion, evaporation, and chemical desorption, photodesorption was also made binding energy-dependent, in line with experimental results. These phenomena occur in a collapsing prestellar core model that considers five grain sizes with ices arranged into four layers.
Results. Variable desorption energy moderately affects gas-grain chemistry. Bare-grain effects slow down ice accumulation, while easier diffusion of molecules on weakly polar ices promotes the production of carbon dioxide. Efficient chemical desorption from bare grains significantly delays the appearance of the first ice monolayer.
Conclusions. The combination of multiple aspects of grain surface chemistry creates a gas-ice balance that is different from simpler models. The composition of the interstellar ices is regulated by several binding-energy dependent desorption mechanisms. Their actions overlap in time and space, explaining the similar proportions of major ice components (water and carbon oxides) observed in all directions.
Key words: astrochemistry / molecular processes / methods: numerical / stars: formation / ISM: clouds / dust, extinction
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
During the last decade, theoretical astrochemists have expanded gas-grain models with additional phases of solid matter. These include molecules residing either on grains of different sizes or in bulk-ice ice layers. The new phases, dynamical evolution of clouds, and detailed microscopic phenomena allow one to paint a new picture about chemical processes in interstellar and circumstellar ices. The microscopic phenomena most notably include efficient chemical desorption (ejection of products from a grain to the gas phase after an exothermic surface reaction) and the molecular desorption (binding) energy that varies depending on its surrounding environment. The above ingredients have never been combined in a single model, which means current astrochemical models may be missing key processes that regulate ice formation and distribution between solid phases.
‘Multi-grain’ models consider surface chemistry on grains with an assortment of sizes. Acharyya et al. (2011) found that the smallest grains, having the largest overall surface, accumulate most of the ice (by default, here we consider the MRN grain size distribution of Mathis et al. 1977, Ice accumulation onto small grains is amplified by an expansion of the surface area with grain growth, which is most pronounced for the small grains. Pauly & Garrod (2016), Ge et al. (2016), Iqbal & Wakelam (2018), and Chen et al. (2018) consider basic aspects for multi-grain models, such as the effect of the number of grain size bins, the applicability of the rate-equation method, effects of differential grain temperature, and ice accumulation. Several papers focus on the efficiency of cosmic-ray induced desorption for grains of different sizes (Zhao et al. 2018; Sipilä et al. 2020; Kalvāns & Kalnin 2022). Some of these indicate that ices cannot efficiently accumulate on the smallest grains (Silsbee et al. 2021; Rawlings 2022). Some of the multi-grain models have been applied in further astrochemical studies (Pauly & Garrod 2018; Gavino et al. 2021). The chemical effect for the multi-grain approach is that surface processes occur slightly differently for each grain size, owing to their physical differences, such as the temperature and the number of surface adsorption sites.
Compared to multi-grain models, ‘multi-layer’ models have undergone significant evolution. They consider at least two layers of the icy mantle that cover grain surfaces (Hasegawa & Herbst 1993b), both of which may be chemically active (Kalvāns & Shmeld 2010). Current models resolve separate monolayers (MLs; Taquet et al. 2012) or up to six chemically active ice layers (Furuya et al. 2017) with limited-diffusion approaches for binary bulk-ice reactions (Chang & Herbst 2014). The mere existence of subsurface ice is a significant development because it is isolated from most of the desorption mechanisms acting on the exposed surface molecules. Chemically active bulk ice allows for different molecule synthesis paths, for example, in CO- and H2O-dominated environments (Chang & Herbst 2016). Moreover, multi-layer models allow one to regulate evaporation from ices in protostellar envelopes, either via layer-by-layer removal (Taquet et al. 2014) or by allowing for hyper-volatile molecules to diffuse out of the mantle first (Garrod 2013a). With hyper-volatiles here we understand icy species with desorption energies ED below about 1300 K, such as H2, N2, O2, CO, and CH4 (energies of molecular-level phenomena are expressed in terms of E/kB per single molecule or atom).
Astrophysical importance for ‘variable molecular desorption energy’ ED for icy surfaces with a polar (primarily, H2O) and weakly polar (CO and other hyper-volatiles) composition was noted early by Tielens & Hagen (1982), Leger (1983), Sandford & Allamandola (1988), and Bergin et al. (1995). The latter authors included this effect in an astrochemical model, albeit not in a self-consistent manner (Bergin & Langer 1997). Compared to hyper-volatile ices, a surface covered with H2O allows for binding via dipole-dipole and dipole-induced dipole interactions, as well as the strong hydrogen bonds. Besides desorption, such bonding affects also mobility of the surface species, and thus, their reactivity. Further exploration of the idea of variable ED has been limited. The main effects for grains covered by hyper-volatile ices are easier desorption ices and a faster diffusion of molecules and atoms, facilitating chemical reactions (He et al. 2016; Garrod et al. 2022).
Molecule adhesion to the ‘refractory bare grains’ differs from that of ices. An aspect of the variable-ED approach is differentiating between the bare and ice-covered surfaces. The binding energies to materials similar to interstellar grains are known for a limited number of species (e.g. Vidali et al. 1991). Dual (bare grain and ice) ED have been used by Chang et al. (2007), Taquet et al. (2014), and Hocuk & Cazaux (2015). Unlike multi-layer and multi-grain models, all variable ED chemical effects are much less understood with no dedicated studies.
The aim of this study is to combine the above phenomena within a single model that produces reasonable results, namely, ice composition, and deduce if variable ED has astrochemically significant effects. The necessary tasks include:
developing an integrated multi-grain multi-layer array system for chemical species, grain, and ice parameters;
adapting or creating descriptions of the microscopic processes, notably, variable ED; the descriptions should allow for simple inclusion in other astrochemical codes;
investigating the significance of variable ED in modelling results;
exploring effects that arise from phenomena that have not yet been combined together in astrochemical models.
Reproducing the proportions of major species observed in interstellar ices has been possible with simpler codes (Ruffle & Herbst 2001; Garrod & Pauly 2011), which may have deterred the need for more complex models. The latter two tasks involve limited parameter space analysis and will allow us to understand the gas-grain physico-chemical interplay in dense cloud cores with the updated code. This analysis is essential before further exploration of ice chemistry can occur with the new model.
2 Methodology
The model was developed on the basis of the modified rate-equation code with multi-layer ice chemistry Alchemic-Venta of Kalvāns (2021), the default reference. Some multi-grain aspects have been tested by Kalvāns & Silsbee (2022). The chemical model is set in a gas parcel in a low-mass contracting prestellar dark molecular core. Below, we describe the complete model with all functionalities enabled, referenced to as Model full in Sect. 3. Table 1 gives a list of variables and abbreviations used throughout the paper.
2.1 Chemical model
Table 2 lists the initial chemical abundances, used at the start of the simulation. The cosmic-ray ionisation rate ζ was calculated following Padovani et al. (2009), with model ‘High’ spectra from Ivlev et al. (2015) and depends on hydrogen column density NH. The ζ value obtained this way is rather high for the 10−17…10−16 values typically applied in astrochemistry, hence we divide it by 4π with the justification that our typical low-mass cloud core is located far from the Galactic centre and is shielded by a parent giant molecular complex. In other words, it can be said that spatially one steradian of the core is exposed to full interstellar cosmic-ray intensity. The intensity of cosmic-ray induced photons depends on ζ and was calculated with Eq. (2) of Kalvāns & Kalnin (2019). The cloud is irradiated by normal interstellar radiation intensity with G0 of 1.7×108, s−1cm−2, attenuated the cloud’s matter with NH/AV = 2.2×1021 cm−2 (Zuo et al. 2021). Gas temperature Tgas was calculated according to Eq.(2) of Kalvāns (2021). Because this equation works only when the interstellar extinction AV is below or similar to 40 mag, Tgas was coupled to dust temperature at higher extinctions.
Neutral molecules adsorb onto grain surfaces, forming an ice layer. The sticking coefficient was taken to be unity for heavy species and calculated according to Thi et al. (2010) for the light species H and H2. The size of a ‘cubic average’ molecule was assumed to be 0.32 nm. When the ice thickness b exceeds 1 ML, excess icy molecules are moved to bulk-ice and are sequentially ordered in three subsurface ice layers. All layers are chemically active. Icy species can be destroyed via photodissociation by interstellar and cosmic-ray induced UV photons at a rate that is equal to 0.3 times their gas-phase photodissociation rate (Kalvāns 2018; Terwisscha van Scheltinga et al. 2022). The surface diffusion energy Ediff was taken to be 0.50ED. Reactions with activation barriers proceed either by hopping across the barrier or via quantum tunnelling that is possible for H and H2 (Hasegawa & Herbst 1993a). Chemical reaction rate coefficients were adjusted for reaction-diffusion competition (Garrod & Pauly 2011). Bulk-ice molecules react with other molecules in the same layer with an approach that assumes that they are frozen in place with a bulk-ice binding (absorption) energy equal to 3ED (Kalvāns 2015a). Similar methods for bulk-ice chemistry have recently gained traction (Shingledecker et al. 2019; Jin & Garrod 2020).
The model considers several desorption mechanisms, with the simplest being evaporation, which is most important for H2. Pantaleone et al. (2021) present a credible evidence that the reaction heat of the common H+H reaction on grains may induce desorption of an adjacent hyper-volatile icy molecule. This indirect reactive desorption mechanism was included in our model with the help of Eq.(16) of Kalvāns (2015a) and an efficiency parameter of ϵ = 0.001 desorbed molecules per H+H reaction act (Duley &Williams 1993; Willacy et al. 1994, see also Takahashi & Williams 2000).
For desorption via cosmic-ray induced whole-grain heating (Hasegawa & Herbst 1993a), a law that assumes similar heating frequencies for grains of different sizes is used by Kalvāns & Silsbee (2022). Here we improved this law according to the exhaustive new data from Kalvāns & Kalnin (2022). Namely, the cosmic-ray induced heating frequency fCRD is now proportional to the inverse square root of the grain radius a, in addition to its dependence to NH,
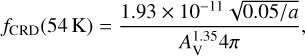 (1)
(1)
where a is expressed in μm. The cooling time for the grains was taken to be similar to the characteristic sublimation time of CO (Hasegawa & Herbst 1993a) that is 0.002 s for a temperature of 54 K in our model. Like ζ, fCRD was also divided by 4π. Photodesorption and desorption of chemical reaction products are described separately in Sects. 2.6 and 2.7.
The chemistry in ice layers was explicitly considered so that the model calculates molecular abundances for each ice layer on each grain type. The actual reaction network includes multiple similar lists of molecular processes for each grain type and ice layer.
Symbols and abbreviations used repeatedly.
Initial chemical abundances relative to the total hydrogen.
2.2 Reactions network
We employ UDfA Rate12 chemical network (McElroy et al. 2013) for the gas phase and a reduced OSU database for surface reactions (Garrod et al. 2008). Following Vasyunin et al. (2017), we added gas-phase complex organic molecule (COM) reactions to balance the alcohol-aldehyde chemistry (Table 3). The variable-ED approach results in generally lower molecular binding energies and more rapid diffusion of surface species that may overproduce CO hydrogenation products. To address this, higher, original OSU database activation energy barrier EA of 2500 K was returned for the CO + H surface reaction. Additionally, three ‘unproductive‘, H2-producing hydrogenation reactions of intermediate CO hydrogenation products were added, all with branching probabilities of 0.5, as suggested by Minissale et al. (2016b). The latter reactions supplement similar additions to Alchemic-Venta in Tables 4 and 6 of Kalvāns (2015b). Table 3 summarises these changes to the network.
To reduce the overall number of species and reactions, phosphorus compounds with two or more C atoms were removed. These species are irrelevant to the overall chemistry, because of the low abundance of P, and their low abundance, even relative to simpler P species. Network reduction ensured a smooth operation of the code and reduced computing time at a little cost to the scientific output, since we do not study the chemistry of phosphorus.
Additions to thereaction network.
Dust grain radius a and the number density relative to H atoms.
2.3 Grain physics
We divided the MRN grain size distribution in five bins with logarithmic spacing. It is a compromise that allows for modelling multi-grain surface chemistry in significant detail, while not making the model overly complex. The number of the grain size bins has a limited effect on modelling results (Iqbal & Wakelam 2018), while five bins have been used also by other authors (Acharyya et al. 2011; Pauly & Garrod 2016; Sipilä et al. 2020). Table 4 shows the assumed grain sizes and abundances.
Moreover, here we assumed grains that have already undergone processing in a star-forming region, thus the grains have a carbonaceous coating, not unlike interplanetary dust particles (Flynn 2020). While such a choice may be physically justified, in our model it has the benefit of bare surface being significantly different from water-dominated ices. This means that the effects of an ED that differs for bare and ice-covered grains can be more pronounced (Sect. 2.5). A second consequence of the processed-grain assumption is that the smallest grains must have been depleted by sticking to larger grains (Silsbee et al. 2020); thus we adopted the sizes and relative abundances of grains from Sipilä et al. (2020). Exclusion of the small grains reduces the average temperature and reactivity of the surface species that results, for example, in lower abundances of CO2 ice [see also Iqbal & Wakelam 2018). Therefore, the grain size distribution is another aspect that regulates the calculated composition of ices, in addition to the existence of active or passive bulk ice, the Ediff/ED ratio, reaction activation barriers, and selective desorption mechanisms. A benefit for our model is that the exclusion of the small grains allows for adequate operation of the modified rate-equation procedure of the ALCHEMIC code (Semenov et al. 2010).
For calculating the cosmic-ray-induced whole-grain heating rate (see above), Kalvāns & Kalnin (2022) considered refractory grains consisting of 40% amorphous carbon and 60% silicates by mass. The resulting grain density was 2.6 g cm−3. The grain mass obtained with this density constitutes 0.4% of the gas mass, in contrast to 0.5% for distributions that include smaller grains, such as Acharyya et al. (2011). We did not consider loss of grain mass; instead the small grains are stuck on the large grains, in effect, increasing their abundance. To account for the mass gap, the Sipilä et al. (2020) grain abundances were multiplied by a factor of 1.25. An additional 0.8% of the cloud mass are in elements heavier than He (‘metals’) that constitute icy mantles in freeze-out conditions (Table 2). Grains grow as the icy mantles accumulate and increase in thickness. The temperature of the dust grains Td was calculated with the method given by Hocuk et al. (2017, for a = 0.1 μ m grains], and attributed to different grain sizes following Pauly & Garrod (2016), that is Td∝a−1/6.
2.4 Variable desorption energy
For a surface molecule, ED determines the possibility for desorption. At the low temperatures of molecular clouds, even limited alterations in ED can determine, if a molecule evaporates or stays on the surface in a given environment. In the case of dense cloud cores, where all species can freeze, except for hydrogen and helium, changes in Ediff (a function of ED) are more important, since it determines the rate of surface diffusion and thus, chemical reactions. The synthesis of CO2 ice is a prominent example, with a rate determined by the most mobile of its parent species, CO, that can react with O or OH, both practically immobile at 10 K, to produce CO2. In the process of a dense core gravitationally contracting, becoming darker and colder, CO becomes immobile, too. The longer CO remains mobile, thanks to a lower Ediff on CO-dominated ices, the longer CO2 synthesis is possible. The same effect affects the surface synthesis of some COMs (Vasyunin & Herbst 2013). Therefore, variable ED for surface species affects the abundances of major as well as minor icy species.
Our task here was to describe ED as a function of the ice composition, that is, how desorption energy for a molecule surrounded by polar species (ED,pol) changes when the same molecule is embedded in a non-polar environment (ED,np). In interstellar ices, these two environments are water and the hyper-volatile molecules, respectively. Of ED measurements and calculations made over the years, we were interested in those that correlate ED,pol and ED,np for the same species. Such measurements are possible only for volatile molecules that evaporate first. Probably the most relevant molecule is CO that is sufficiently abundant to make up the hyper-volatile component (Sandford & Allamandola 1988; Tielens et al. 1991). While it is clear that the actual ED includes a range of values, depending on the properties of individual adsorption sites and the orientation of the molecule (He et al. 2018; Grassi et al. 2020), here we employ single-value ED for a species in a given icy phase, a standard practice in astrochemistry.
Desorption energy for CO in watery ices is considered to be 1150 K (Collings et al. 2004; Noble et al. 2012; Penteado et al. 2017) or 1300 K (Wakelam et al. 2017; Das et al. 2018). In a pure-ice CO matrix, ED,np,CO of CO was measured to be 954 K by Shinoda (1969), while more recent measurements give values of 855, 858, 866, and 899 K (Öberg et al. 2005; Acharyya et al. 2007; Fayolle et al. 2016; Martín-Doménech et al. 2014, respectively). Another molecule for which data are available is molecular nitrogen. In a H2O matrix, ED,pol, N2 is in the range of 810 –1400 K (Wakelam et al. 2017; Das et al. 2018; Penteado et al. 2017). For non-polar environments, ED,np, N2, measurements for N2 matrices produce values of 779 and 790 K (Fayolle et al. 2016; Öberg et al. 2005, respectively). These laboratory and simulation results yield a wide-ranged ED,np/ED,pol ratio of 0.56...0.98 and average value of 0.8. The values of ED,pol and ED,np clearly differ and do not overlap. The ED,np/ED,pol ratio is similar for CO and N2, justifying an unified approach for variable ED.
The procedure in our model for calculating ED for species in ices was as follows.
The original, or default ED values correspond to water surface, ED,pol. These were adopted from the OSU surface network, replaced by those of Wakelam et al. (2017), where possible. An exception was made for the volatile CO, N2, and CH4 molecules, whose ED,pol were adopted from Penteado et al. (2017). The values of ED,pol correspond to a matrix (surface) consisting of a pure water with ED,pol,H2O =5600 K. First, the model obtains the weighed average ĒD,pol for the whole ice phase in consideration (one of the four layers on one of the five types of the grains), taking into account all icy species in that phase,
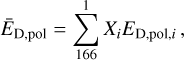 (2)
(2)
where Xi is the fractional abundance of the ith species in the icy phase, while 166 is the number of unique icy species. Then we calculate ED,np/ED,pol with
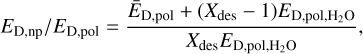 (3)
(3)
and the final desorption energy for species A, ED,A, used for calculating desorption and surface diffusion rates is
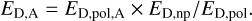 (4)
(4)
There certainly are other possible fitting functions for adjusting species’ ED in accordance with the environment it resides in. Eq. (3) depends only on a single fitting parameter Xdes, and allows for mimicking the ED changes for CO and N2. The value of Xdes was taken to be 4.00, corresponding to ED,np/ED,pol ≈ 0.8 in accordance with the experimental measurements. For CO, ED,CO decreases from 1150 K in a H2O matrix environment to 922 K in a pure CO matrix, while for N2 ED,N2 the respective values are 990 and 786 K. In modelled multi-layer ices, where Eq. (3) operates, the extreme values are never reached and the ED,np/ED,pol lies in between 0.8 and 1. Equation (3) was not applied in cases when a molecule’s ED,pol,A was already lower than the average ED,pol in the ice layer. To avoid discontinuities in modelled abundances, variable ED was applied proportionally to ice thickness, from 0 MLs with no effect, when the icy molecules barely interact, to full effect at 2 MLs and above, when most of the icy molecules primarily interact with neighbouring adsorbed species, instead of the refractory grain surface.
Summarising, Eqs. (2)–(4) present a simple approach for calculating ED for a molecule in ice with changing composition and, thus, changing average desorption energy of species in this icy phase. In practice, ED,np/ED,pol is determined by a few species that dominate a given ice phase at a given time step. Most often these are H2O, CO, CO2, N2, and CH3OH. Equation 4 was used to calculate ED for all icy species. Because the composition is different for each icy phase, ED,np/ED,pol was also different for each layer in each grain size bin.
Variable ice ED, calculated from the abundance of H2, has also been employed by Garrod et al. (2022). They do not apparently base their approach on experimental or theoretical data. Within our model, H2 is among the species considered in ĒD,pol and the abundance of the surface H2 itself is regulated with the help of the encounter desorption (Hincelin et al. 2015).
Derivation of the H-bond rule: selected molecular ED on carbonaceous and icy surfaces.
2.5 Desorption energy on bare grains
As stated in Sect. 2.3, our bare grains have a carbonaceous coating. A few other studies have struggled to obtain an assortment of ED,bare for molecules on carbon because only limited experimental data are available. Cuppen & Herbst (2007) developed such a list for water chemistry that has been updated by Cazaux et al. (2010). Similar lists were compiled by Hocuk & Cazaux (2015) and Minissale et al. (2016a); however the latter studies less rigidly stuck to carbon and included ED values from experiments with silicate or other materials, instead of using estimates for carbon.
The above-mentioned authors employed small reaction networks. Our task here was to derive a generalised approach with which the differences in ED,pol on ices and ED,bare on carbonaceous grains can be attributed to a variety of species. Table 5 summarises data from studies that have ED,pol and ED,bare based on similar considerations. A striking feature, apparent in the compiled data, is the low ED,bare values for species that are able to form hydrogen bonds. Experiments using highly oriented pyrolytic graphite (HOPG) surface show also a lower bare surface ED for isolated H-bond forming molecules (Minissale & Dulieu 2014; Doronin et al. 2015; Chaabouni et al. 2018). Another issue is variation of the desorption energies for volatile species from H to O2, with no clear pattern.
Table 5 allowed us to derive the general approach on devising ED,bare: subtracting hydrogen bond energy from ED,pol. It gives also an indication on the values that need to be subtracted, which are about ≥2000 K for molecules containing O –H bonds and ≈3000 K for molecules containing two O –H bonds. Naturally, these are lower than the often used hydrogen bond energy of about 2800 K because, in absence of the H-bonds, other types of molecule-surface bonding are formed instead.
For consistency, we extrapolated the lack of the hydrogen bonds on bare grains, or ‘the H-bond rule’ for other molecules containing electronegative atoms associated with H capable of hydrogen bonding, such as nitrogen or halogens. Such a need is underlined by the study of Kakkenpara Suresh et al. (2024), who emphasise the importance of the H-bonds for ammonia in circumstellar ices. The qualitative task was now to choose the types of H-bonds that can make a difference in the grain-ice interface. The quantitative task was to evaluate the differences ED,pol-ED,bare for the chosen types of H-bonds.
One has to keep in mind that the carbonaceous grain surface likely is irregular, seeded with heteroatoms with undivided electron pairs and even an occasional H atom attached to an electronegative atom, such as C in sp hybridisation. In other words, the carbonaceous surface itself sports some components for weak hydrogen bond formation. From this aspect we infer that only the molecules that can serve as both electron and proton donors, and are able to form the strongest H-bonds can make a difference in the transition from bare surface to icy mantles.
The energy of the OH⋯O bond in water has been studied most extensively (e.g. Tomoda & Kimura 1983; Ahirwar et al. 2022) with dimer dissociation energies usually in the range of 2300 –3300 K (Walrafen 2004; Kikuta et al. 2008; Spanu et al. 2008; Sterpone et al. 2008). These results allow the effective binding energy difference caused by H-bonding ED,pol –ED,bare to be estimated with an accuracy of about 500 to 1000 K. Organic molecules, for example, alcohols and carboxylic acids are also capable of forming hydrogen bonds via the oxygen atom. Their dissociation energy is in the same range (Andersen et al. 2015). Taking into account the data from Table 5, it seems reasonable to assume ED,pol-ED,bare = 2000 K for OH⋯O bonds. It is encouraging that a 2000 K H-bond energy value is also close to the ED difference for CH2OH and CH3O obtained by Garrod et al. (2008) via completely different considerations.
The Cuppen & Herbst (2007) and Cazaux et al. (2010) ED compilations indicate that the ability of a molecule to form double H-bonds for H2O and H2O2 does not translate into an ED,pol-ED,bare twice as high. Here, we take this factor to be 1.5 so that ED,pol-ED,bare = 3000 K for water and hydrogen peroxide.
In the case of ammonia, NH⋯N hydrogen bonds are only about half as strong. However, the OH⋯N bond energy is similar or even higher than that of OH⋯O, with dissociation energies of about 3800 K (Yeo & Ford 1994; Kikuta et al. 2008; Ahirwar et al. 2021). Their strength decreases if functional groups are attached to the nitrogen atom (Boryskina et al. 2007; Vallet & Masella 2015). The case of ammonia is further complicated by its protonation in water, not explicitly considered here. As a first approximation, we assumed that ED,pol-ED,bare = 3000, K for ammonia and 1500 K for other compounds containing the N-H bond.
For hydrogen halogenides HF and HCl, dissociation energies for H-bonds with water are about 4300 K and 2700 K by Alkorta & Legon (2023). For hydrogen cyanide, the same authors provide an average value of 2400 K. In line of the above considerations, we assumed ED,pol –ED,bare 3000; 2000, and 1500 K for HF, HCl, and HCN, respectively. The latter value was attributed also to the related HNC, HNO, and a few other similar molecules.
The ED,pol – ED,bare values assumed above are only educated guesses. However, they provide a systemic approach for the bare grain ED,bare that leaves room for improvements with new data. Table 6 summarises the hydrogen bond rule applied in this study. The values provided in the table are exact only for completely bare grains, and their effect is reduced proportionally to ice coverage on grains, until the H-bond rule disappears completely. It occurs, when the formal ice thickness reaches 2 MLs, and mobility or evaporation can no longer be affected by molecular interactions with the surface of the refractory grains. This means, for example, that a 1 ML coverage, the ED,pol-ED,bare values are only half of their values given in Table 6. Therefore, during the accumulation of the first two ice MLs on a grain with a given size, the H-bond rule for bare grains was gradually replaced by the variable ED approach designed for icy environments in Sect. 2.4.
Two MLs as the final threshold for conversion from bare grain effects to the variable ED in ices was chosen because at 1 ML, all molecules are still affected by their attachment to the bare grain surface, and the effects of the latter cannot be discarded yet. Moreover, the higher 2 ML threshold allowed us to account for some clustering of molecules on bare grain surface (Garrod 2013b), where diffusion, reactions, and desorption on patches of the bare surface are still possible, even when the nominal ice thickness exceeds 1 ML.
H-bond rule: assumed ED,pol-ED,bare for surface species in the model.
2.6 Photodesorption
Photodesorption yield Ypd, molecules per UV photon, has now been measured in a number of experiments. Molecular dynamics simulations reveal that it involves photon absorption at different ice layer depths, followed by direct desorption or photodissociation with trapping, recombination, or desorption of products, and ‘kicking out’ neighbours by excited molecules (Andersson et al. 2006; Arasa et al. 2015; van Hemert et al. 2015). The resulting desorption of intact molecules or their fragments depends on surface type (volatile or non-volatile ices, or bare grain, Bertin et al. 2012; Potapov et al. 2019), composition of icy mixtures (Bertin et al. 2016; Carrascosa et al. 2019), possibility for co-desorption (Bertin et al. 2013), as well as the spectrum of the incident radiation (Fayolle et al. 2011). Experiments show that Ypd depends on ice temperature (Muñoz Caro et al. 2010; Muñoz Caro et al. 2016), deposition angle (González Díaz et al. 2019), and ice thickness (Öberg et al. 2009b; Sie et al. 2022). Possible presence of atmospheric gases has to be addressed, while a number of the experiments irradiate their astrophysical ice analogues by photons with energies below 10 –11 eV. This can be a deficiency because important absorption bands may lie at higher energies (Chen et al. 2014; Martín-Doménech et al. 2015; Paardekooper et al. 2016). The missing wavelengths may induce more efficient desorption as in the case of N2, or raise the proportion of dissociative desorption, thus reducing the effective Ypd for intact molecules at full λ range.
Several issues become also important, when the experimentally obtained Ypd are applied in astrochemical models. First, two types of UV radiation are present –interstellar and cosmic-ray induced photons. Some studies differentiate between the two (Fayolle et al. 2011); the difference is usually within a factor of 2. Second, dissociated fragments may recombine or react with other surface species and undergo chemical desorption (Sect. 2.7), enhancing the effective yield. This effect is more pronounced for complex molecules that are more easily dissociated.
Considering the above, we compiled set of reliable Ypd data, shown in Fig. 1. We used Ypd values for the interstellar radiation field whenever possible because the interstellar photons determine the formation epoch for ices. Moreover, we opted for sources that consider the full 7 –13.6 eV range of UV photons in molecular clouds. Only values for desorption of intact molecules were used because any dissociation fragments have a considerable probability of chemical desorption. Based on the experience from Kalvāns (2015a), temperature and spectral influence were considered to be of minor importance and were ignored. Photodesorption from subsurface layers was addressed by allowing photodesorption for molecule depth from up to 4 ice MLs (Andersson & van Dishoeck 2008).
Carbon monoxide CO photodesorption is, perhaps, the most studied and we had the luxury for obtaining an average desorption yield Ypd≈ 10−2 value from several experimental reports. A number of papers have studied also the photodesorption of water H2O (e.g. Öberg et al. 2009a; Cruz-Diaz et al. 2018; Bulak et al. 2023), and carbon dioxide CO2, while only Fillion et al. (2014, 2022) considered desorption by photons above 11 eV. Ammonia NH3 was not included because no ice desorption data were found for photons with energies exceeding 10.9 eV (Martín-Doménech et al. 2018). Molecular oxygen O2 largely desorbs via dissociation, and its yield for intact molecules is uncertain (Fayolle et al. 2013). Importantly, usable data are available for some COMs. Their intact molecule Ypd is low and chemical desorption of dissociated fragments is the main ejection pathway (Cruz-Diaz et al. 2016; Bulak et al. 2020).
An empirical relation that connects the selected measurements is
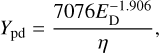 (5)
where η is unity for simple molecules with number of atoms Nat<5 and η = 10Nat−4.2 for complex molecules with Nat of 5 or more atoms.
(5)
where η is unity for simple molecules with number of atoms Nat<5 and η = 10Nat−4.2 for complex molecules with Nat of 5 or more atoms.
ED is expressed in K. This equation is illustrated with Fig. 1. An exception, where Eq. (5) was not applied, was created for the diatomic mono-elemental molecules H2, N2, and O2 that have low yields from pure ices and more efficiently are removed via co-desorption (Fayolle et al. 2013). A fixed value Ypd = 0.0055 was applied for these molecules (Bertin et al. 2013). We note that because the molecular ED varies, photodesorption yields typically are lower by about a factor of 0.8 for hyper-volatile molecules and higher for less-volatile ices. In the important and extreme case of water on bare grains (ED,bare,H2O = 2600 K), its Ypd,bare,H2O = 0.002. Such an significanTLY elevated yield is nonetheless in agreement with experimental data that indicate total (intact and dissociative) Ypd,bare,H2O of up to 0.5 (Potapov et al. 2019).
 |
Fig. 1 ED-dependent photodesorption yield of icy molecules. The line connects data points calculated with Eq. (5), while dots indicate experimental data with references in parentheses: 1 –Bertin et al. (2013), 2 –Fayolle et al. (2011), 3 –Fayolle et al. (2013), 4 –Muñoz Caro et al. (2016), 5 –Dupuy et al. (2017a), 6 –Dupuy et al. (2017b), 7 –Fillion et al. (2014), 8 –Féraud et al. (2019), 9 –Basalgète et al. (2021), 10 –Bertin et al. (2016), 11 –Fillion et al. (2022). |
2.7 Chemical desorption
Highly efficient chemical desorption of exothermic surface reaction products has been explored experimentally during the last decade (Chaabouni et al. 2012, see also Cazaux et al. 2010). Desorption probability of this process can be up to 90% (for the OH + H reaction on a silicate surface) and has been quantified and parameterised in further experiments and theoretical works (Dulieu et al. 2013; Minissale & Dulieu 2014; Minissale et al. 2016a; Fredon et al. 2017; Oba et al. 2018; Pantaleone et al. 2020; Molpeceres et al. 2023). This mechanism is especially important for H2O that forms via two-step hydrogenation on grain surfaces. Thanks to hydrogenation-dehydrogenation cycles, chemical desorption is also relevant for CO (Minissale et al. 2016b).
Because chemical desorption is effective for water-forming reactions on bare grains, it significantly affects the onset of the first ice layer formation. This aspect cannot be ignored in chemical modelling focussing on interstellar ices. Thus, we replaced the ‘reactive desorption’ of Garrod et al. (2006), previously applied in the Alchemic-Venta model, with the ‘chemical desorption’ method by Minissale et al. (2016a). The variable ED approach naturally produces different chemical desorption results for different types of surfaces –bare grains, polar, and hyper-volatile ices. To account for the less-effective desorption from ices observed in experiments, the chemical desorption efficiency (fraction of desorbed molecules) fCD was modified by a factor of 0.5 for reactions on grains with ice thickness exceeding 1 ML. Table 7 compares experimental fCD values to those used in our model. The application of the chemical desorption in concert with variable ED is what allowed for a realistic and effectual representation of this mechanism.
2.8 Collapsing prestellar core macrophysical model
We considered a single point located at the centre of a spherical interstellar molecular core. The cloud model is relatively simple and follows the approach of previous studies. It consisted of two main parts. First, the central density n0 of the core was calculated according to a free-fall collapse scenario (Brown et al. 1988). Hydrodynamical simulations (e.g. Pavlyuchenkov & Zhilkin 2013; Pavlyuchenkov et al. 2015) indicate that actual core collapse can be a few times longer than the free-fall time; thus we delayed the contraction rate by a factor of 0.5. The initial conditions were nH = 2000 cm−3 and NH = 1.1×1021,cm−2, corresponding to initial interstellar extinction AV = 0.5. Second, for each integration step, the spherical (1D) density distribution in the core was obtained with Eq. (1) of Kalvāns (2021). This time, core mass was maintained at 2 M⊙. Core collapse lasts for 1.55 Myr until a final density of 1×107, cm−3 is reached. At this point, the freeze-out is effectively over and ice composition does not change any more. Figure 2 shows the evolution of the physical conditions at the centre of the core.
In the first Results Sect. 3.1 we explored variable ED effects in pseudo time-dependent Model const of a stable, dark molecular core, with the collapsing core feature switched off. For chemical relaxation, both models were preceded by a 1 Myr long diffuse cloud period, with hydrogen numerical density nH = 2000 cm−3 and interstellar extinction AV =0.5 mag.
Chemical desorption efficiency as calculated in model for watery ices and bare grains, compared to experimental results.
3 Results
Section 2 includes a number of assumptions about desorption energy on interstellar grain surfaces. These assumptions may be closer or farther from reality, however, it is clear that molecule diffusion, evaporation, photodesorption, chemical desorption, and desorption by the H+H surface reaction all depend on ED to some extent. In turn, ED is subject to change in different surroundings. Our aim was to clarify if this latter dependence is astrochemically significant and deduce its overall character. To do this, we primarily explored results with a model with a complete set of the simulated processes, as described in Sect. 2 (Model full). For illustrating the significance of one or more processes, limited functionality models were used. Table 8 shows that four functionalities of Model full were switched off or reduced to rudimentary values: the cloud’s macrophysical evolution, the variable-ED approach, chemical desorption, and photodesorption. For context with other models considering multi-grain or bulk-ice chemistry, our Table 8 can be compared with Tables 1 and 3 of Pauly & Garrod (2016) and Tables 1 and 7 of Garrod et al. (2022).
We start the description of the results with pseudo-time dependent dense core Models const and const_noEd (Sect. 3.1), continue by describing the results of Model full and comparing them to Model noEd, where the ED variability is disabled (Sect. 3.2) and conclude by discussing the importance of photo- and chemical desorption (Sect. 3.3).
 |
Fig. 2 Density, extinction, dust and gas temperature, and grain size evolution in the model. For the latter two graphs, thicker curves are for larger grains. |
 |
Fig. 3 Grain size and temperature in pseudo time-dependent cold core Model const. Thicker curves are for larger grains; a is the refractory grain radius (constant), while ice mantle thickness b varies with time. |
3.1 Cold core model
As an initial test case, we present the basic chemical results for a dense, cold, dark core with constant ‘classical’ physical conditions of nH = 2×104cm−3 and AV =10 mag. This Model const was run for an integration time t =1.0 Myr. During the first few hundred kyr, grain growth occurs up to an ice thickness of 78 MLs on the smallest grains and 66 MLs on the largest grains. Figure 3 shows the change in grain sizes along with the accompanying changes in their temperatures. Gas temperature is constant at Tgas = 8.9 K, while the cosmic-ray ionisation rate ζ = 3.2×10−17 (Sect. 2.1).
Figure 4 shows that the abundances of major gaseous species differ little between Models const and const_noEd with and without the variable-ED approach, respectively. The easier desorption facilitated by variable ED is visible in slightly higher gas-phase abundances. The changes are most pronounced for species that are formed via multiple steps on grain surfaces, such as methanol CH3OH and hydrogen peroxide H2O2. Nevertheless, the two simulations produce gas abundances that agree within a factor of 2 for most species and time periods.
Figure 5 shows calculated abundances, relative to water ice, for major icy species for cold core simulations with and without variable ED. In Model const, 90% freeze-out is reached at 0.45 Myr that is later probably by 0.1 Myr or more, relative to comparable multi-grain models (Pauly & Garrod 2016; Sipilä et al. 2020). Differences in the freeze-out times are primarily caused by the consideration or non-consideration of the bulk ice that isolates majority of the icy species from most desorption mechanisms, and by the efficient chemical desorption that acts as delaying function. 99% freeze-out is reached at 0.74 Myr. For Model const_Ed without differing ED on bare grains and weakly polar ices, the 90% freeze-out is earlier only by about 0.02 Myr.
A characteristic feature is the low abundance of CO2 ice for most of the time. The ice ratio CO2:H2O≈20...30 is often observed to be similar to that of CO:H2O (McClure et al. 2023) but here reaches only 8% at 90% freeze-out and 16% at 99% freeze-out conditions. However, ice CO2:H2O continues growing to 23% at 1 Myr thanks to CO2 photoproduction via bulk-ice reactions at the expense of H2O and CO. The cold core model, with its high initial NH and AV, is more of a testbed calculation, not able to closely represent real-life scenarios. Underproduction of CO2 is a typical feature in such models (see Ruffle & Herbst 2001; Bredehöft 2020). The similarity between the abundances of the major icy species in Models const and const_noEd indicates that chemistry under rapid freeze-out conditions is regulated mostly by the abundantly adsorbing surface reactants and little affected by ED variability.
For a review of similar results, albeit without chemical desorption, we refer to Pauly & Garrod (2016), who also employed a model that considers bulk ice and included a breakdown of ice composition on five grain sizes in their discussion of modelling results. Because we considered larger grains with accordingly lower temperatures, their 5G_T8 models are most relevant. The main difference between our model and that of Pauly & Garrod (2016) is that we consider chemical processing of the bulk ice that slowly elevates the abundance of CO2 ice. Moreover, our model overproduces methanol CH3OH ice, while their model tends to overproduce methane CH4 ice, which apparently can be caused by differences in reaction networks.
Model functionalities and their basic ice chemistry results.
 |
Fig. 4 Calculated gas-phase chemical abundances in the cold core model. Panel a: relative abundances of major gas-phase species. Panel b: gas-phase abundances for important molecules that mostly originate from grain surfaces. In both panels, solid lines are for Model const with variable ED, while dotted lines are for Model const_noEd with an unchanging ED. |
 |
Fig. 5 Calculated chemical abundances of icy species in cold core model. Panel a: abundances, relative to those of the H2O ice of major icy molecules. The black curve is the average ice thickness |
 |
Fig. 6 Overall chemical results for prestellar core Model full with variable ED and other features enabled. Panel a: abundance of the primary gaseous species relative to that of H2. Panel b: species that are abundant in ices; solid lines are for the gas phase, while dashed lines are for solid phase abundances, relative to H2. Panel c: percentage, relative to H2O ice, for major icy molecules. The black curve is the average ice thickness |
 |
Fig. 7 Variable-ED induced changes in the translucent cloud. Comparison between Models full (solid lines) and noEd (dotted lines) for selected species including those with gas-phase abundances most affected by ED changes via the H-bond rule: inorganic in a, carbon chains in b, and another organics in c. d shows the growth of the ice mantles on the grains, with thinner lines indicating smaller grains. The changes are caused by a lack of strong H bonding on bare grains in Model full. |
3.2 General results
As a context for the discussion that follows, in Figure 6 we show the general chemical results –abundances of major species –for the prestellar core model. With regard to evolution of ices, three periods can be discerned. First is the translucent cloud, dominated by gaseous atomic species and CO, while ice thickness remains below 1 ML. This period lasts for ≈1.2 Myr, until NH exceeds 104 cm−3 and AV≈1.8, mag. Second is the ice formation period, when the core contraction becomes increasingly rapid and up to 99% of the metals are accreted onto grains at t=1.5 Myr, nH=3×105 cm−3 and AV =14 mag. Third, during the remaining 25 kyr density increases thirtyfold (with a presumed further collapse towards the first core) with little change in the composition of ices. This period is of limited interest for this study. We continue by describing the translucent and ice formation periods in more detail.
3.2.1 The sub-ML regime in translucent cloud
Adsorbed molecules with average ice thickness below 1 ML likely are present in diffuse and translucent molecular envelopes and thus form a part of sight-lines towards prestellar cores. In Model full, this is the period when the H-bond ED rule of the bare grains is in effect (Sect. 2.5). The lack of the hydrogen bonding for surface species does not lower their ED and Ediff to significantly promote evaporation or diffusion across the grains (Table 6). However, it is sufficient to elevate chemical desorption and photodesorption yields (Sects. 2.6 and 2.7).
Surface chemistry in the translucent cloud is regulated by an interplay between accretion and desorption. Accreted molecules can be desorbed directly by photodesorption or dissociated into fragments. Chemical radicals created on the surface or accreted from the gas react and the product molecules can be desorbed via chemical desorption. Figure 7 shows that two groups of surface-origin species can be discerned, whose gas abundance is regulated by desorption. First, species like H2O, NH3, CH4, CO2, CH3OH reach high gas-phase abundances relative to H2 (n/n(H2)) in excess of 10−9, thanks to photodesorption and rather high surface abundances of >10−8. Second, a variety of species have highly efficient chemical desorption that, in combination with surface photodissociation, increase gas-phase n/n(H2) to 10−12 and above. These include, for example, hydrogen peroxide H2O2 that is subject to a strong H-bond rule (Table 6) and whose abundance changes by about an order of magnitude between Models full and noEd.
In absolute numbers, most of the COMs have gas-phase n/n(H2) below 10−13 during the translucent period. However, for methanol and a few related compounds, such as CH3O, abundances exceed 10−12 and thus the effect of the lack of H bonds on bare-grains could be observed. Figure 7 shows that formaldehyde H2CO that has also effective chemical desorption. Its ED is unaffected by the H-bond rule that means it has similar translucent cloud abundances for Models full and noEd. The abundance of CH3OH and CH3O is higher by a factor of ≈5 in Model full relative to Model noEd; for H2O2 and O2H this factor is 6...10. These factors become lower as time goes by because with the accumulation of ice, the importance of the H-bond rule decreases.
Lack of the H bonds on bare grains has a significant effect on overall ice abundances in the sub-ML regime. The release of more H2O, CO2, and NH3 to the gas phase in Model full results in lower by a factor of 2...3 adsorbed species’ abundances in the variable ED model. Overall, the H-bond rule delays the formation of the first ice monolayer by 40 kyr for the smallest and 67 kyr for the largest grains. This delay has an inverse effect on H2O and CO2, for which the gas-phase abundances are lower by a factor of 2 because there are less of these molecules on the surface, available for photodesorption. In turn and to a similar extent, a lower gas-phase H2O abundance positively affects the abundance of carbon chains because H2O interferes with carbon-chain gas-phase production by reducing the abundance of their building blocks, such as CH, as illustrated with panel b of Fig. 7. The increase in carbon chain abundance by about a factor of two may not be high but its significance lies in that virtually all unsaturated chains are affected by it.
 |
Fig. 8 Variable-ED induced changes during ice formation epoch: calculated n/n(H2) for species ending up with a high ice abundance. Solid and dashed lines are for the Model full gas phase and solid species, respectively. Dotted and dash-dotted lines are for gas and solids in Model noEd, respectively. |
3.2.2 Ice formation epoch
The ice formation period is when most of the ice mass is being accreted onto grains and the ice acquires its initial composition. If the ice is not destroyed (e.g. by falling into the protostar), this composition can be further modified by heating or photoprocessing. Ice formation is characterised by initial formation of a 1 ML thick H2O-CO2 layer at the end of the translucent cloud period. It is followed by further accumulation of H2O and CO2. When Td drops below 12 K and CO becomes immobile, CO2 surface synthesis stalls (Pauly & Garrod 2016) and CO ice accumulates more rapidly, eventually overtaking CO2 but not H2O.
In Model full, a lower (typically by about 10%, i.e. ED,np/ED,pol≈0.9) varying ED has two counteracting effects on the abundance of the major icy species, compared to Model noEd with unchanging ED. First, a lower Ediff for surface CO allows it to remain mobile for longer in Model full and thus produce more CO2 in reactions with O and OH. This effect becomes visible when Td drops below 14 K. Second, lower ED,CO allows for a more efficient desorption of CO, retaining it longer in the gas-phase. As a result, CO accretes later at lower Td and produces less CO2. The balance of these two effects depends on the evolution of the modelled cloud and the choice of model parameters, such as the efficiency of the various desorption mechanisms, grain size distribution, Td of grains of different sizes, and, in our model, also the variable ED approach. Table 8 shows that Model full has a CO2 ice abundance higher by a factor of 1.4 than Model noEd, that is, CO2 production at lower grain temperatures has been more significant.
The overall effect of the addition of the varying ED in the model during the freeze-out stage is higher gas-phase abundances for most species, typically elevated by a factor of 1.5...2 (abundance ratio Model full/noEd). This occurs thanks to the more efficient chemical and photodesorption. Figure 8 demonstrates several general variable-ED effects that affect major icy species.
First, the period between 1.19 and 1.26 Myr differs most because the first ice MLs have formed in Model noEd but not on the grains of Model full. The synthesis of H2O, NH3, CO2, and CH3OH depends on intermediate radical species with hydrogen bonds (OH, NH, NH2, CH2OH). The non-existence of strong H-bonds on bare surface and the resulting efficient chemical desorption (Table 7) is what delays the accumulation of the ice layer in Model full.
Second, the lower overall ED in ices continues to heighten fCD and Ypd for the remainder of cloud evolution, ensuring higher gas-phase abundances for CO, CO2, N2, and CH4 in Model full. A ED,CH4 lowered by about 100 K means that desorption by the H+H surface reaction heat works on methane in Model full but not in Model noEd.
The third effect is chemistry in bulk-ices, the primary place of synthesis for hydrogen peroxide H2O2 and contributes also to the formation of CO2. Bulk-ice synthesis becomes possible only when >1 MLs of ice have formed. It switches on rapidly and has an immediate effect on H2O2 abundances in ice. H2O2 appears also in the gas because our model allows for photodesorption of bulk ice equal to up to 3 MLs, in addition to 1 surface ML (see Sect. 2.6).
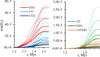 |
Fig. 9 Evolution of the relative abundances for major icy species on grain populations with different sizes. Thicker lines are for larger grains. |
3.2.3 Distribution of ices
During the ≈50 kyr after the ice formation epoch, residual gas molecules continue to be depleted onto grains. No equilibrium is established because gas density continues to increase rapidly. The final ice composition significantly differs between separate grain size populations. Figure 9 shows that all grains achieve a similar ice thickness in the range of 70...75 MLs. Notably, at the end of the simulation with variable ED, the smallest grains carry 59% of all CO2 and 40% of CO ice, while other icy species are more evenly distributed between all grain size bins. These results can be explained primarily by the higher temperature of the small grains that make CO2 surface synthesis faster and possible for a longer time in cloud evolution. Because a single CO2 molecule is formed instead of two molecules of H2O and CO, ice layer on small-grains is not the thickest (72 MLs at t = 1.55 Myr). Concentration of CO2 on smaller grains occurs also in other multi-grain models (Pauly & Garrod 2016; Iqbal & Wakelam 2018).
Figure 10 illustrates the proportions of the major icy species in the grain size bins at simulation end time t=1.55 Myr. The smallest 0.037 μm grains carry the highest amount of ice –37% of all molecules, compared to only 9% on the largest 0.232 μm grains. Unlike other simulations, especially two-phase models without bulk-ice (Iqbal & Wakelam 2018; Sipilä et al. 2020), cosmic-ray induced desorption has no major effects on the distribution of ices between grains of different sizes.
3.3 Effects of ED
Photodesorption and chemical desorption (Sects. 2.6 and 2.7) are two mechanisms whose yields quantitatively depend on ED and are calculated separately for each surface molecule in each of the five grain size bins in the programme. Thus, fCD and Ypd change along with ED, whose variation is described in Sects. 2.4 and 2.5. In other words, chemical desorption and photodesorption are the instruments that help communicate ED variations to the gas-ice balance. The efficiency of these mechanisms is anchored in experimental data and often is about an order higher than the safe assumptions applied in astrochemical models during preceding decades.
For comparison with Model full, we ran simulations with the following changes:
Model noPD, where the ED-dependent photodesorption yield was replaced with a single constant value Ypd = 0.001 for all species;
Model noCD, where the ED-dependent chemical desorption efficiency was replaced with constant 3% of all the surface reaction products going to the gas phase (fCD = 0.03; a simplified version of the reactive desorption by Garrod et al. 2006). This fCD is still significantly higher than that used by Garrod et al. (2022).
The above means that in Models noPD and noCD, photo- or chemical desorption are not disabled, only significantly reduced for simple icy molecules. The fixed fCD and Ypd values are close to previously commonly used desorption parameters. For complex molecules with high ED and high number of atoms, these fixed desorption efficiencies are actually higher, when compared to the fully ED-dependent Model full. This is why Model noCD shows a peak gas-phase methanol abundance of 1.5 × 10−8 relative to H2, four times higher than that of Model full (Fig. 11).
In Model noPD, the first ice ML is formed at 1.19 Myr on the smallest grains and 1.23 Myr on the largest grains, compared to 1.23...1.24 Myr for Model full. Such a moderately earlier ice layer formation is associated with build-up of solid CO2 and H2O ices that have translucent stage abundances higher by factors of 3 and 2 relative to Model full, respectively, thanks to their lower Ypd on bare grains. Because CO2 formation occurs mostly on the smallest grains because of their higher Td, the first ice layer on the small grains in Model noPD forms 40 kyr earlier than in Model full. For other grain size bins this difference is 16 kyr. Thanks to this advantage, the smallest grains grow the thickest ice, 77 MLs, compared to 65..70 MLs for other grain size bins in Model noPD. Once the first layer has formed, ice mass in Model full catches up with Model noPD within 0.2 Myr because accretion dominates over desorption in the dense core. Table 8 shows that the effect of our ED-dependent photodesorption approach is moderate, with H2O:CO:CO2:CH3OH:NH3 final ice abundance ratio being 100:60:39:10:3 in Model noPD and 100:63:34:10:3 in Model full.
Figure 11 shows that changes introduced by chemical desorption are more pronounced than those of photodesorption. The first ice ML in Model noCD forms already at t = 1.03, Myr and on the largest, not smallest grains that is the case in other models. Such a reverse trend can be explained by more efficient hydrogenation of surface O on the lower-temperature large grains along with the fact that H2O synthesis rate is not diminished by an efficient chemical desorption in Model noCD. The abundance of atomic H on grains is in the vicinity of 10−12 for all grain size bins in most models. Consequently, the small 0.037 μm grains achieve their first ice ML only at 1.08 Myr and grow the thinnest ice layer of 66 MLs, while for other grain size bins the end thickness is similar at 72...75 MLs.
The rapid ice accumulation in Model noCD means that the first ice ML forms already at AV = 1.1 mag. In Model full this happens only at AV =1.8 mag. Observable water ice first appears at 3.2 mag extinction along the line-of-sight (Whittet et al. 2001). Our model is too simple to discern, which of the two mechanisms –the high-efficiency chemical desorption (Minissale et al. 2016a) or the low-efficiency reactive desorption (Garrod et al. 2006) –is more consistent with observations because it depends on a number of factors, such as the history of the cloud, its density, geometry, irradiation intensity, and lifetime of the translucent and dark core stages (see Hocuk et al. 2016).
The earlier ice accumulation in Model noCD starts at Td in the range of 12...16 K (a degree higher than in Model full) and at about 1.5 times higher interstellar irradiation. Both of these aspects promote surface oxidation of CO, resulting in higher initial CO2 ice abundances. At later and colder stages, rapid surface synthesis of H2O wins the competition for surface O and OH because of the inefficiency of the chemical desorption of OH and H2O in hydrogenation reactions in Model noCD.
Oxygen chemistry in Model noCD is notably changed by the appearance of surface O2. The early accumulation of O atoms on relatively warm grains in combination with inefficient hydrogenation allows them to combine with the newly formed O2 mostly remaining on the surface (see also Pauly & Garrod 2016). Oxygen ice takes up 3.4% of all oxygen budget, an order of magnitude higher than in Model full. Abundant O2, together with a 60% higher abundance of H2O2, reduces the abundance of water ice by one fifth. This reduction consequently increases the ratios of carbon oxide ices relative to H2O. The absolute abundances of CO and CO2 have changed only within 7% relative to Model full.
The H2O:CO:CO2:CH3OH:NH3:O2 final ice abundance ratio in Model noCD is 100:73:44:10:7:5. This ratio and Fig. 11 reveals another important result –the lack of an effective chemical desorption allows for the formation of ammonia ice with H2O:NH3 ratios closer to the ≈10% value indicated by observations (Boogert et al. 2011). Thus, our results predict that the chemical desorption efficiency of nitrogen hydrogenation products NH, NH2, and NH3 should be about an order of magnitude lower than indicated by the method of Minissale et al. (2016a).
Chemical desorption has also a significant effect in the pseudo-time dependent model const, where, when the Minissale et al. (2016a) chemical desorption is replaced with fCD = 3, the first full ice ML forms already at t =2 kyr, while 90% freeze-out is reached about 0.1 Myr earlier.
As far as we know, this is the first published study of a multi-grain astrochemical model considering chemical desorption based on Minissale et al. (2016a). While there are a few other such ‘firsts’, combining multiple grain size bins with chemical desorption is important. In multi-grain models, grain surface area is higher by about a factor of two, allowing for an earlier accretion of ices. This means accretion at higher gas temperatures of around 20 K, with higher thermal velocities that make accretion even more rapid. Small grains increase their surface area with each adsorbed ice ML, leading to a possibility of a runaway freeze-out. When the chemical desorption is added, it delays the formation of the first ice ML on the bare grain, where it is most effective. Further ice growth continues to be hampered because tens of per cent of hydrogenation reaction products going to the gas phase. Therefore, for multi-grain models considering bulk-ice (meaning that a major part of ice is isolated from desorption) and efficient chemical desorption, a completely different gas-grain dynamics occurs, producing results that can be superficially similar to those of much simpler models.
 |
Fig. 10 Distribution of major icy species in different grain size bins, indicated by their size (nm) at final time t = 1.55 Myr. The four ice layers are numbered: layer (1) is the surface, while layer (4) is adjacent to the refractory grain core. Species within a single layer are intermixed, they are shown separately here to illustrate their proportions within the layer. Although thickness is similar for all bulk-ice layers for a given grain size, the species in the outer layers are more abundant because the grain has grown. This effect is more pronounced for the smallest grains. Most of the ‘other’ molecules are NH3 and also CH4. |
 |
Fig. 11 Ice growth and chemical desorption. This is a comparison of abundances between Model full gas (solid lines) and icy (dashed lines) species with those of Model noCD (dotted and dash-dotted lines for gas and ices, respectively). In the ice thickness plot, thicker lines are for larger grains, according to Table 4. |
4 Summary and conclusions
The inclusion of the variable ED has mostly insignificant chemical effects in the rapid ice accretion regime of the cold core and a moderate effect in the contracting core model full. A few species, such as H2O2, CH3OH have their gas-phase abundances elevated by up to an order of magnitude, while the abundances of the whole carbon chain compound class have become lower by about a factor of 2. The first ice ML appears 56 kyr earlier than in the model noEd without variable ED. A higher abundance of CO2 is the main effect on ice composition. Such changes are comparable with those introduced by the multi-grain or multi-layer approaches (Acharyya et al. 2011; Vasyunin & Herbst 2013). Thus, variable ED is among necessary steps for accurate astrochemical modelling. In this study it has been implemented in a rather careful manner with ED,np/ED,pol=0.8, compared to Bergin & Langer (1997), who took ED,np/ED,pol = 0.56.
The inclusion of the chemical desorption (Minissale et al. 2016a) in the multi-grain multi-layer gas-surface chemical model turned out to be of major importance. In effect, chemical desorption decreases the rate of icy molecule synthesis, delaying the formation of the first ice ML by almost 0.2 Myr, as demonstrated by the comparison of Models full and noCD in Sect. 3.3. This aspect is not readily apparent in pseudo-time dependent models, such as Vasyunin et al. (2017) and Rawlings & Williams (2021), and has been largely missed so far.
Variable ED has its most visible effect on the abundances of major icy species by increasing the amount of CO2 at the expense of CO and H2O. The final calculated relative ice abundances H2O:CO:CO2 were 100:63:34, in agreement with heavily shielded dense cores (Whittet et al. 2011; Boogert et al. 2013). The removal of ED-dependence for one or two molecular-level processes does not change the approximate calculated ice abundance ratio for water and carbon oxides. It indicates a resilience in the modelling results in the sense that they do not depend on a few sensible parameters. The H2O:CO:CO2 ice abundance ratio is determined by the partial combination of co-adsorbing atomic O and CO into CO2 ices (Ruffle & Herbst 2001).
A mechanism that regulates the balance between water and carbon oxide ices has been sought by several studies (Nejad & Williams 1992; Bergin et al. 1995; Ruffle & Herbst 2001; Roberts et al. 2007; Kalvāns 2015a). In this study, such a mechanism is chemical desorption, photodesorption, and desorption by H+H surface reactions, all together. Their general effect is ensuring co-adsorption of some atomic O and CO onto grains sufficiently warm for their partial conversion into CO2 ices (Garrod & Pauly 2011). If one of the desorption mechanisms is ineffective in a given cloud core, others can partially offset it, retaining the characteristic H2O >[CO≈ CO2] ice abundance sequence (cf. Figs. 8 and 11). The latter aspect explains the ubiquity of the H2O:CO:CO2 ice ratio observations (Gibb et al. 2004; Whittet et al. 2007). Our model is unable to explain a separate problem –the relatively low depletion of CO in interstellar clouds (Leger 1983; Leger et al. 1985; Whittet et al. 2010). Other mechanisms that can contribute to the balance between water and carbon oxides are photodesorption by infrared photons (Williams et al. 1992; Dzegilenko & Herbst 1995; Santos et al. 2023) and cosmic-ray induced desorption (Sect. 2.1) that does not have a great effect in our model. Grain size distribution plays a role, with smaller grains being warmer and more efficient at producing CO2 ice.
The abundance of solid CH3OH, in combination with desorption facilitated by lower ED, is sufficient to explain its observed gas-phase abundance in dark cores (Bacmann et al. 2012; Cernicharo et al. 2012). This is not true for most other COMs, probably due to a limited reaction network. Regarding NH3, underproduction of ammonia in Model full might be explained by an over-effective chemical desorption of hydrogen nitrides (corroborated by Sipilä et al. 2019). The chemistry of COMs and nitrogen both merit detailed investigation with this model.
Summarising, the model combines ten gradual steps in theoretical (surface) astrochemistry: (1) several grain size bins, (2) bulk ice that is (3) chemically active and (4) consists of several separate layers, experiment-based estimates for (5) chemical and (6) photodesorption, updated estimates for (7) cosmic-ray induced desorption and (8) desorption by surface H atom combination reaction heat, (9) a general approach for adjusting ED on bare grains and (10) a method for estimating ED in weakly polar icy environment. While any one of these features may not contribute much and its method can be improved, all together they bring new understanding on how interstellar grain surface chemistry operates, as indicated by the previous studies that have investigated many of these features separately (Sect. 1). Features (6), (9), and (10) are described in a novel way in this study. The above-discussed delay in ice formation occurs because of combining features (5) and (9). The production of CO2 ice is positively affected by (1), (3), and (10), and negatively by (5), (6), (8), and (9).
Acknowledgements
This research is funded by the Latvian Science Council grant ‘Desorption of icy molecules in the interstellar medium (DIMD)’, project no. lzp-2021/1-0076. J.K. thanks Ventspils City Council for support. This research has made use of NASA’s Astrophysics Data System. We thank the anonymous referee for necessary improvements.
References
- Acharyya, K., Fuchs, G. W., Fraser, H. J., van Dishoeck, E. F., & Linnartz, H. 2007, AAP, 466, 1005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acharyya, K., Hassel, G. E., & Herbst, E. 2011, APJ, 732, 73 [CrossRef] [Google Scholar]
- Ahirwar, M. B., Patkar, D., Yadav, I., & Deshmukh, M. M. 2021, Phys. Chem. Chem. Phys., 23, 17224 [NASA ADS] [CrossRef] [Google Scholar]
- Ahirwar, M. B., Gurav, N. D., Gadre, S. R., & Deshmukh, M. M. 2022, Phys. Chem. Chem. Phys., 24, 15462 [CrossRef] [Google Scholar]
- Alkorta, I., & Legon, A. 2023, JPCA, 127, 4715 [NASA ADS] [CrossRef] [Google Scholar]
- Andersen, J., Heimdal, J., & Wugt Larsen, R. 2015, Phys. Chem. Chem. Phys., 17, 23761 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, S., & van Dishoeck, E. F. 2008, AAP, 491, 907 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andersson, S., Al-Halabi, A., Kroes, G.-J., & van Dishoeck, E. F. 2006, JCP, 124, 064715 [Google Scholar]
- Arasa, C., Koning, J., Kroes, G.-J., Walsh, C., & van Dishoeck, E. F. 2015, AAP, 575, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacmann, A., Taquet, V., Faure, A., Kahane, C., & Ceccarelli, C. 2012, AAP, 541, A12 [Google Scholar]
- Basalgète, R., Ocaña, A. J., Féraud, G., et al. 2021, APJ, 922, 213 [CrossRef] [Google Scholar]
- Bergin, E. A., & Langer, W. D. 1997, APJ, 486, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Langer, W. D., & Goldsmith, P. F. 1995, APJ, 441, 222 [CrossRef] [Google Scholar]
- Bertin, M., Fayolle, E. C., Romanzin, C., et al. 2012, Phys. Chem. Chem. Phys., 14, 9929 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, M., Fayolle, E. C., Romanzin, C., et al. 2013, APJ, 779, 120 [CrossRef] [Google Scholar]
- Bertin, M., Romanzin, C., Doronin, M., et al. 2016, APJ, 817, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Boogert, A. C. A., Huard, T. L., Cook, A. M., et al. 2011, APJ, 729, 92 [CrossRef] [Google Scholar]
- Boogert, A. C. A., Chiar, J. E., Knez, C., et al. 2013, APJ, 777, 73 [CrossRef] [Google Scholar]
- Boryskina, O. P., Bolbukh, T. V., Semenov, M. A., Gasan, A. I., & Maleev, V. Y. 2007, J. Mol. Struct., 827, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bredehöft, J. H. 2020, Front. Astron. Space Sci., 7, 33 [CrossRef] [Google Scholar]
- Brown, P. D., Charnley, S. B., & Millar, T. J. 1988, MNRAS, 231, 409 [Google Scholar]
- Bulak, M., Paardekooper, D. M., Fedoseev, G., & Linnartz, H. 2020, AAP, 636, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bulak, M., Paardekooper, D. M., Fedoseev, G., Samarth, P., & Linnartz, H. 2023, AAP, 677, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrascosa, H., Hsiao, L. C., Sie, N. E., Muñoz Caro, G. M., & Chen, Y. J. 2019, MNRAS, 486, 1985 [CrossRef] [Google Scholar]
- Cazaux, S., Cobut, V., Marseille, M., Spaans, M., & Caselli, P. 2010, AAP, 522, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Marcelino, N., Roueff, E., et al. 2012, APJ, 759, L43 [CrossRef] [Google Scholar]
- Chaabouni, H., Minissale, M., Manicò`, G., et al. 2012, JCP, 137, 234706 [Google Scholar]
- Chaabouni, H., Diana, S., Nguyen, T., & Dulieu, F. 2018, AAP, 612, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chang, Q., & Herbst, E. 2014, APJ, 787, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, Q., & Herbst, E. 2016, APJ, 819, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, Q., Cuppen, H. M., & Herbst, E. 2007, AAP, 469, 973 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Y. J., Chuang, K. J., Muñoz Caro, G. M., et al. 2014, APJ, 781, 15 [Google Scholar]
- Chen, L.-F., Chang, Q., & Xi, H.-W. 2018, MNRAS, 479, 2988 [NASA ADS] [CrossRef] [Google Scholar]
- Collings, M. P., Anderson, M. A., Chen, R., et al. 2004, MNRAS, 354, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Cruz-Diaz, G. A., Martín-Doménech, R., Muñoz Caro, G. M., & Chen, Y. J. 2016, AAP, 592, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cruz-Diaz, G. A., Martín-Doménech, R., Moreno, E., Muñoz Caro, G. M., & Chen, Y.-J. 2018, MNRAS, 474, 3080 [Google Scholar]
- Cuppen, H. M., & Herbst, E. 2007, APJ, 668, 294 [CrossRef] [Google Scholar]
- Das, A., Sil, M., Gorai, P., Chakrabarti, S. K., & Loison, J. C. 2018, APJS, 237, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Doronin, M., Bertin, M., Michaut, X., Philippe, L., & Fillion, J. H. 2015, JCP, 143, 084703 [Google Scholar]
- Duley, W. W., & Williams, D. A. 1993, MNRAS, 260, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Dulieu, F., Congiu, E., Noble, J., et al. 2013, Sci. Rep., 3, 1338 [Google Scholar]
- Dupuy, R., Bertin, M., Féraud,G., et al. 2017a, AAP, 603, A61 [CrossRef] [EDP Sciences] [Google Scholar]
- Dupuy, R., Féraud, G., Bertin, M., et al. 2017b, AAP, 606, A9 [Google Scholar]
- Dzegilenko, F., & Herbst, E. 1995, APJ, 443, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Fayolle, E. C., Bertin, M., Romanzin, C., et al. 2011, APJ, 739, L36 [CrossRef] [Google Scholar]
- Fayolle, E. C., Bertin, M., Romanzin, C., et al. 2013, AAP, 556, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fayolle, E. C., Balfe, J., Loomis, R., et al. 2016, APJ, 816, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Féraud, G., Bertin, M., Romanzin, C., et al. 2019, ACS Earth Space Chem., 3, 1135 [Google Scholar]
- Fillion, J.-H., Fayolle, E. C., Michaut, X., et al. 2014, Faraday Discuss., 168, 533 [Google Scholar]
- Fillion, J.-H., Dupuy, R., Féraud, G., et al. 2022, ACS Earth Space Chem., 6, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Flynn, G. J. 2020, in, Oxford Research Encyclopedia of Planetary Science, Oxford University Press, 143 [Google Scholar]
- Fredon, A., Lamberts, T., & Cuppen, H. M. 2017, APJ, 849, 125 [CrossRef] [Google Scholar]
- Furuya, K., Drozdovskaya, M. N., Visser, R., et al. 2017, AAP, 599, A40 [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T. 2013a, APJ, 765, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T. 2013b, APJ, 778, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T., & Herbst, E. 2006, AAP, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., & Pauly, T. 2011, APJ, 735, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R., Park, I. H., Caselli, P., & Herbst, E. 2006, Faraday Discuss., 133, 51 [Google Scholar]
- Garrod, R. T., Weaver, S. L. W., & Herbst, E. 2008, APJ, 682, 283 [CrossRef] [Google Scholar]
- Garrod, R. T., Jin, M., Matis, K. A., et al. 2022, APJS, 259, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gavino, S., Dutrey, A., Wakelam, V., et al. 2021, AAP, 654, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ge, J. X., He, J. H., & Li, A. 2016, MNRAS, 460, L50 [NASA ADS] [CrossRef] [Google Scholar]
- Gibb, E. L., Whittet, D. C. B., Boogert, A. C. A., & Tielens, A. G. G. M. 2004, APJS, 151, 35 [CrossRef] [Google Scholar]
- González Díaz, C., Carrascosa de Lucas, H., Aparicio, S., et al. 2019, MNRAS, 486, 5519 [CrossRef] [Google Scholar]
- Grassi, T., Bovino, S., Caselli, P., et al. 2020, AAP, 643, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993a, MNRAS, 261, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993b, MNRAS, 263, 589 [Google Scholar]
- He, J., Acharyya, K., & Vidali, G. 2016, APJ, 825, 89 [NASA ADS] [CrossRef] [Google Scholar]
- He, J., Emtiaz, S., & Vidali, G. 2018, APJ, 863, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Hincelin, U., Chang, Q., & Herbst, E. 2015, AAP, 574, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hocuk, S., & Cazaux, S. 2015, AAP, 576, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hocuk, S., Cazaux, S., Spaans, M., & Caselli, P. 2016, MNRAS, 456, 2586 [Google Scholar]
- Hocuk, S., Szűcs, L., Caselli, P., et al. 2017, AAP, 604, A58 [CrossRef] [EDP Sciences] [Google Scholar]
- Iqbal, W., & Wakelam, V. 2018, AAP, 615, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivlev, A. V., Padovani, M., Galli, D., & Caselli, P. 2015, APJ, 812, 135 [CrossRef] [Google Scholar]
- Jin, M., & Garrod, R. T. 2020, APJS, 249, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, D. G., Blitz, M. A., & Seakins, P. W. 2000, Phys. Chem. Chem. Phys., 2, 2549 [NASA ADS] [CrossRef] [Google Scholar]
- Kakkenpara Suresh, S., Dulieu, F., Vitorino, J., & Caselli, P. 2024, AAP, 682, A163 [CrossRef] [EDP Sciences] [Google Scholar]
- Kalvāns,J. 2015a, APJ, 803, 52 [CrossRef] [Google Scholar]
- Kalvāns, J. 2015b, APJ, 806, 196 [CrossRef] [Google Scholar]
- Kalvāns, J. 2018, MNRAS, 478, 2753 [CrossRef] [Google Scholar]
- Kalvāns, J. 2021, APJ, 910, 54 [CrossRef] [Google Scholar]
- Kalvāns, J., & Kalnin, J. R. 2019, MNRAS, 486, 2050 [CrossRef] [Google Scholar]
- Kalvāns, J., & Kalnin, J. R. 2022, APJS, 263, 5 [CrossRef] [Google Scholar]
- Kalvāns, J., & Shmeld, I. 2010, AAP, 521, A37 [CrossRef] [EDP Sciences] [Google Scholar]
- Kalvāns, J., & Silsbee, K. 2022, MNRAS, 515, 785 [CrossRef] [Google Scholar]
- Kikuta, Y., Ishimoto, T., & Nagashima, U. 2008, Chem. Phys., 354, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Leger, A. 1983, AAP, 123, 271 [NASA ADS] [Google Scholar]
- Leger, A., Jura, M., & Omont, A. 1985, AAP, 144, 147 [NASA ADS] [Google Scholar]
- Martín-Doménech, R., Muñoz Caro, G. M., Bueno, J., & Goesmann, F. 2014, AAP, 564, A8 [CrossRef] [EDP Sciences] [Google Scholar]
- Martín-Doménech, R., Manzano-Santamaría, J., Muñoz Caro, G. M., et al. 2015, AAP, 584, A14 [CrossRef] [EDP Sciences] [Google Scholar]
- Martín-Doménech, R., Cruz-Díaz, G. A., & Muñoz Caro, G. M. 2018, MNRAS, 473, 2575 [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, APJ, 217, 425 [Google Scholar]
- McClure, M. K., Rocha, W. R. M., Pontoppidan, K. M., et al. 2023, Nat. Astron., 7, 431 [NASA ADS] [CrossRef] [Google Scholar]
- McElroy, D., Walsh, C., Markwick, A. J., et al. 2013, AAP, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minissale, M., & Dulieu, F. 2014, JCP, 141, 014304 [Google Scholar]
- Minissale, M., Dulieu, F., Cazaux, S., & Hocuk, S. 2016a, AAP, 585, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minissale, M., Moudens, A., Baouche, S., Chaabouni, H., & Dulieu, F. 2016b, MNRAS, 458, 2953 [Google Scholar]
- Molpeceres, G., Zaverkin, V., Furuya, K., Aikawa, Y., & Kästner, J. 2023, AAP, 673, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muñoz Caro, G. M., Jiménez-Escobar, A., Martín-Gago, J. Á., et al. 2010, AAP, 522, A108 [CrossRef] [EDP Sciences] [Google Scholar]
- Muñoz Caro, G. M., Chen, Y. J., Aparicio, S., et al. 2016, AAP, 589, A19 [CrossRef] [EDP Sciences] [Google Scholar]
- Nejad, L. A. M., & Williams, D. A. 1992, MNRAS, 255, 441 [NASA ADS] [Google Scholar]
- Noble, J. A., Congiu, E., Dulieu, F., & Fraser, H. J. 2012, MNRAS, 421, 768 [NASA ADS] [Google Scholar]
- Oba, Y., Tomaru, T., Lamberts, T., Kouchi, A., & Watanabe, N. 2018, Nat. Astron., 2, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., van Broekhuizen, F., Fraser, H. J., et al. 2005, APJ, 621, L33 [CrossRef] [Google Scholar]
- Öberg, K. I., Linnartz, H., Visser, R., & van Dishoeck, E. F. 2009a, APJ, 693, 1209 [CrossRef] [Google Scholar]
- Öberg, K. I., van Dishoeck, E. F., & Linnartz, H. 2009b, AAP, 496, 281 [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, D. M., Fedoseev, G., Riedo, A., & Linnartz, H. 2016, AAP, 596, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padovani, M., Galli, D., & Glassgold, A. E. 2009, AAP, 501, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pantaleone, S., Enrique-Romero, J., Ceccarelli, C., et al. 2020, APJ, 897, 56 [CrossRef] [Google Scholar]
- Pantaleone, S., Enrique-Romero, J., Ceccarelli, C., et al. 2021, APJ, 917, 49 [CrossRef] [Google Scholar]
- Pauly, T., & Garrod, R. T. 2016, APJ, 817, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Pauly, T., & Garrod, R. T. 2018, APJ, 854, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlyuchenkov, Y. N., & Zhilkin, A. G. 2013, Astron. Rep., 57, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlyuchenkov, Y. N., Zhilkin, A. G., Vorobyov, E. I., & Fateeva, A. M. 2015, Astron. Rep., 59, 133 [CrossRef] [Google Scholar]
- Penteado, E. M., Walsh, C., & Cuppen, H. M. 2017, APJ, 844, 71 [CrossRef] [Google Scholar]
- Potapov, A., Jäger, C., & Henning, T. 2019, APJ, 880, 12 [CrossRef] [Google Scholar]
- Rawlings, J. M. C. 2022, MNRAS, 517, 3804 [CrossRef] [Google Scholar]
- Rawlings, J. M. C., & Williams, D. A. 2021, MNRAS, 500, 5117 [Google Scholar]
- Roberts, J. F., Rawlings, J. M. C., Viti, S., & Williams, D. A. 2007, MNRAS, 382, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffle, D. P., & Herbst, E. 2001, MNRAS, 324, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Sandford, S. A., & Allamandola, L. J. 1988, ICARUS, 76, 201 [CrossRef] [Google Scholar]
- Santos, J. C., Chuang, K. J., Schrauwen, J. G. M., et al. 2023, AAP, 672, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Semenov, D., Hersant, F., Wakelam, V., et al. 2010, AAP, 522, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shingledecker, C. N., Vasyunin, A., Herbst, E., & Caselli, P. 2019, APJ, 876, 140 [CrossRef] [Google Scholar]
- Shinoda, T. 1969, Bull. Chem. Soc. Japan, 42, 2815 [CrossRef] [Google Scholar]
- Sie, N.-E., Cho, Y.-T., Huang, C.-H., et al. 2022, APJ, 938, 48 [CrossRef] [Google Scholar]
- Silsbee, K., Ivlev, A. V., Sipilä, O., Caselli, P., & Zhao, B. 2020, AAP, 641, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silsbee, K., Caselli, P., & Ivlev, A. V. 2021, MNRAS, 507, 6205 [NASA ADS] [CrossRef] [Google Scholar]
- Sipilä, O., Caselli, P., Redaelli, E., Juvela, M., & Bizzocchi, L. 2019, MNRAS, 487, 1269 [Google Scholar]
- Sipilä, O., Zhao, B., & Caselli, P. 2020, AAP, 640, A94 [CrossRef] [EDP Sciences] [Google Scholar]
- Spanu, L., Sterpone, F., Ferraro, L., Sorella, S., & Guidoni, L. 2008, Amer. Phys. Soc., 2008 APS March Meeting, Q26.006 [Google Scholar]
- Sterpone, F.,Spanu, L.,Ferraro, L.,Sorella, S., & Guidoni, L.2008, arXiv eprints [arXiv:0806.4169] [Google Scholar]
- Takahashi, J., & Williams, D. A. 2000, MNRAS, 314, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Taquet, V., Ceccarelli, C., & Kahane, C. 2012, AAP, 538, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taquet, V., Charnley, S. B., & Sipilä, O. 2014, APJ, 791, 1 [CrossRef] [Google Scholar]
- Terwisscha van Scheltinga, J., Ligterink, N. F. W., Bosman, A. D., Hogerheijde, M. R., & Linnartz, H. 2022, AAP, 666, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thi, W.-F., Woitke, P., & Kamp, I. 2010, MNRAS, 407, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., & Hagen, W. 1982, AAP, 114, 245 [NASA ADS] [Google Scholar]
- Tielens, A. G. G. M., Tokunaga, A. T., Geballe, T. R., & Baas, F. 1991, APJ, 381, 181 [CrossRef] [Google Scholar]
- Tomoda, S., & Kimura, K. 1983, Chem. Phys. Lett., 102, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Vallet, V., & Masella, M. 2015, Chem. Phys. Lett., 618, 168 [NASA ADS] [CrossRef] [Google Scholar]
- van Hemert, M. C., Takahashi, J., & van Dishoeck, E. F. 2015, JPCA, 119, 6354 [NASA ADS] [CrossRef] [Google Scholar]
- Vasyunin, A. I., & Herbst, E. 2013, APJ, 762, 86 [CrossRef] [Google Scholar]
- Vasyunin, A. I., Caselli, P., Dulieu, F., & Jiménez-Serra, I. 2017, APJ, 842, 33 [CrossRef] [Google Scholar]
- Vidali, G., Ihm, G., Kim, H.-Y., & Cole, M. W. 1991, Surf. Sci. Rep., 12, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Loison, J. C., Mereau, R., & Ruaud, M. 2017, Mol. Astrophys., 6, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Walrafen, G. E. 2004, in, AIP Conf Ser., 716, Portable Synchrotron Light Sources and Advanced Applications: International Symposium on Portable Synchrotron Light Sources and Advanced Applications, eds. H. Yamada, N. Mochizuki-Oda, & M. Sasaki, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B., Gerakines, P. A., Hough, J. H., & Shenoy, S. S. 2001, APJ, 547, 872 [CrossRef] [Google Scholar]
- Whittet, D. C. B., Shenoy, S. S., Bergin, E. A., et al. 2007, APJ, 655, 332 [CrossRef] [Google Scholar]
- Whittet, D. C. B., Goldsmith, P. F., & Pineda, J. L. 2010, APJ, 720, 259 [CrossRef] [Google Scholar]
- Whittet, D. C. B., Cook, A. M., Herbst, E., Chiar, J. E., & Shenoy, S. S. 2011, APJ, 742, 28 [CrossRef] [Google Scholar]
- Willacy, K., Williams, D. A., & Duley, W. W. 1994, MNRAS, 267, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, D. A., Hartquist, T. W., & Whittet, D. C. B. 1992, MNRAS, 258, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Yeo, G. A., & Ford, T. A. 1994, Spectrochim. Acta A: Mol. Spectrosc., 50, 5 [Google Scholar]
- Zhao, B., Caselli, P., & Li, Z.-Y. 2018, MNRAS, 478, 2723 [Google Scholar]
- Zuo, W., Li, A., & Zhao, G. 2021, APJS, 252, 22 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Derivation of the H-bond rule: selected molecular ED on carbonaceous and icy surfaces.
Chemical desorption efficiency as calculated in model for watery ices and bare grains, compared to experimental results.
All Figures
 |
Fig. 1 ED-dependent photodesorption yield of icy molecules. The line connects data points calculated with Eq. (5), while dots indicate experimental data with references in parentheses: 1 –Bertin et al. (2013), 2 –Fayolle et al. (2011), 3 –Fayolle et al. (2013), 4 –Muñoz Caro et al. (2016), 5 –Dupuy et al. (2017a), 6 –Dupuy et al. (2017b), 7 –Fillion et al. (2014), 8 –Féraud et al. (2019), 9 –Basalgète et al. (2021), 10 –Bertin et al. (2016), 11 –Fillion et al. (2022). |
| In the text | |
 |
Fig. 2 Density, extinction, dust and gas temperature, and grain size evolution in the model. For the latter two graphs, thicker curves are for larger grains. |
| In the text | |
 |
Fig. 3 Grain size and temperature in pseudo time-dependent cold core Model const. Thicker curves are for larger grains; a is the refractory grain radius (constant), while ice mantle thickness b varies with time. |
| In the text | |
 |
Fig. 4 Calculated gas-phase chemical abundances in the cold core model. Panel a: relative abundances of major gas-phase species. Panel b: gas-phase abundances for important molecules that mostly originate from grain surfaces. In both panels, solid lines are for Model const with variable ED, while dotted lines are for Model const_noEd with an unchanging ED. |
| In the text | |
 |
Fig. 5 Calculated chemical abundances of icy species in cold core model. Panel a: abundances, relative to those of the H2O ice of major icy molecules. The black curve is the average ice thickness |
| In the text | |
 |
Fig. 6 Overall chemical results for prestellar core Model full with variable ED and other features enabled. Panel a: abundance of the primary gaseous species relative to that of H2. Panel b: species that are abundant in ices; solid lines are for the gas phase, while dashed lines are for solid phase abundances, relative to H2. Panel c: percentage, relative to H2O ice, for major icy molecules. The black curve is the average ice thickness |
| In the text | |
 |
Fig. 7 Variable-ED induced changes in the translucent cloud. Comparison between Models full (solid lines) and noEd (dotted lines) for selected species including those with gas-phase abundances most affected by ED changes via the H-bond rule: inorganic in a, carbon chains in b, and another organics in c. d shows the growth of the ice mantles on the grains, with thinner lines indicating smaller grains. The changes are caused by a lack of strong H bonding on bare grains in Model full. |
| In the text | |
 |
Fig. 8 Variable-ED induced changes during ice formation epoch: calculated n/n(H2) for species ending up with a high ice abundance. Solid and dashed lines are for the Model full gas phase and solid species, respectively. Dotted and dash-dotted lines are for gas and solids in Model noEd, respectively. |
| In the text | |
 |
Fig. 9 Evolution of the relative abundances for major icy species on grain populations with different sizes. Thicker lines are for larger grains. |
| In the text | |
 |
Fig. 10 Distribution of major icy species in different grain size bins, indicated by their size (nm) at final time t = 1.55 Myr. The four ice layers are numbered: layer (1) is the surface, while layer (4) is adjacent to the refractory grain core. Species within a single layer are intermixed, they are shown separately here to illustrate their proportions within the layer. Although thickness is similar for all bulk-ice layers for a given grain size, the species in the outer layers are more abundant because the grain has grown. This effect is more pronounced for the smallest grains. Most of the ‘other’ molecules are NH3 and also CH4. |
| In the text | |
 |
Fig. 11 Ice growth and chemical desorption. This is a comparison of abundances between Model full gas (solid lines) and icy (dashed lines) species with those of Model noCD (dotted and dash-dotted lines for gas and ices, respectively). In the ice thickness plot, thicker lines are for larger grains, according to Table 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.