| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | A255 | |
| Number of page(s) | 37 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202449148 | |
| Published online | 20 June 2024 | |
Bias versus variance when fitting multi-species molecular lines with a non-LTE radiative transfer model
Application to the estimation of the gas temperature and volume density
1
Université de Toulon, Aix Marseille Univ, CNRS, IM2NP,
Toulon,
France
e-mail: antoine.roueff@univ-tln.fr
2
IRAM,
300 rue de la Piscine,
38406
Saint-Martin-d’Hères,
France
3
LERMA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités,
75014
Paris,
France
4
Instituto de Física Fundamental (CSIC).
Calle Serrano 121,
28006,
Madrid,
Spain
5
National Radio Astronomy Observatory,
520 Edgemont Road,
Charlottesville,
VA
22903,
USA
6
Laboratoire d’Astrophysique de Bordeaux, Univ. Bordeaux, CNRS, B18N,
Allée Geoffroy Saint-Hilaire,
33615
Pessac,
France
7
Univ. Grenoble Alpes, Inria, CNRS, Grenoble INP, GIPSA-Lab,
Grenoble
38000,
France
8
Chalmers University of Technology, Department of Space, Earth and Environment,
412 93
Gothenburg,
Sweden
9
Univ. Lille, CNRS, Centrale Lille,
UMR 9189 - CRIStAL,
59651
Villeneuve d’Ascq,
France
10
LERMA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités,
92190
Meudon,
France
11
Institut de Recherche en Astrophysique et Planétologie (IRAP), Université Paul Sabatier,
Toulouse cedex 4,
France
12
Instituto de Astrofísica, Pontificia Universidad Católica de Chile,
Av. Vicuña Mackenna 4860,
7820436 Macul, Santiago,
Chile
13
Laboratoire de Physique de l’Ecole normale supérieure, ENS, Université PSL, CNRS, Sorbonne Université, Université de Paris, Sorbonne Paris Cité,
Paris,
France
14
Jet Propulsion Laboratory, California Institute of Technology,
4800 Oak Grove Drive,
Pasadena,
CA
91109,
USA
15
Department of Earth, Environment, and Physics, Worcester State University,
Worcester,
MA
01602,
USA
16
Harvard-Smithsonian Center for Astrophysics,
60 Garden Street,
Cambridge,
MA,
02138,
USA
17
School of Physics and Astronomy, Cardiff University,
Queen’s buildings,
Cardiff
CF24 3AA,
UK
Received:
2
January
2024
Accepted:
19
February
2024
Context. Robust radiative transfer techniques are requisite for efficiently extracting the physical and chemical information from molecular rotational lines.
Aims. We study several hypotheses that enable robust estimations of the column densities and physical conditions when fitting one or two transitions per molecular species. We study the extent to which simplifying assumptions aimed at reducing the complexity of the problem introduce estimation biases and how to detect them.
Methods. We focus on the CO and HCO+ isotopologues and analyze maps of a 50 square arcminutes field. We used the RADEX escape probability model to solve the statistical equilibrium equations and compute the emerging line profiles, assuming that all species coexist. Depending on the considered set of species, we also fixed the abundance ratio between some species and explored different values. We proposed a maximum likelihood estimator to infer the physical conditions and considered the effect of both the thermal noise and calibration uncertainty. We analyzed any potential biases induced by model misspecifications by comparing the results on the actual data for several sets of species and confirmed with Monte Carlo simulations. The variance of the estimations and the efficiency of the estimator were studied based on the Cramér-Rao lower bound.
Results. Column densities can be estimated with 30% accuracy, while the best estimations of the volume density are found to be within a factor of two. Under the chosen model framework, the peak 12CO (1 – 0) is useful for constraining the kinetic temperature. The thermal pressure is better and more robustly estimated than the volume density and kinetic temperature separately. Analyzing CO and HCO+ isotopologues and fitting the full line profile are recommended practices with respect to detecting possible biases.
Conclusions. Combining a non-local thermodynamic equilibrium model with a rigorous analysis of the accuracy allows us to obtain an efficient estimator and identify where the model is misspecified. We note that other combinations of molecular lines could be studied in the future.
Key words: line: profiles / radiative transfer / methods: data analysis / methods: statistical / ISM: clouds / ISM: general
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Recent progress in developing receiver and backend technologies has now made it possible for a significant proportion of a giant molecular cloud to be imaged with enough sensitivity to simultaneously map dozens of molecular lines. Nishimura et al. (2017) and Watanabe et al. (2017) observed the W3(OH) and W 51 molecular clouds with the Nobeyama 45m telescope over a significant fraction of the 87–112 GHz spectral range, while Barnes et al. (2020) studied the W49N massive star-forming region with the IRAM 30m telescope in two spectral ranges: 86.1–99.9 GHz and 101.8–115.6 GHz. We studied the Orion B star-forming cloud with the IRAM 30 m telescope within the framework of the project named Outstanding Radio-Imaging of OrioN-B (ORION-B, PI: Jérôme Pety & Maryvonne Gerin). The resulting data cube covers 13 × 18 pc on the sky and a bandwidth of 40 GHz at a typical resolution of 50 mpc and 0.6 km s−1 and at a typical sensitivity of 0.1 K in the main beam temperature scale, as described by Pety et al. (2017) in their discussion of results from a subset of 5.6 × 7.5 pc. These scales are derived assuming a distance to the Orion B cloud of 400 pc, as discussed in Pety et al. (2017) and confirmed by more recent analyses based on Gaia distances who found a distance between 397 and 410 pc (Zucker et al. 2021; Cao et al. 2023). Extracting physical information from such large spectroscopic datasets requires the use of robust and fast radiative transfer methods that can be applied with limited human supervision. Large imaging datasets with thousands of pixels usually include bright spectral lines in a specific spectral range, for instance, the 3 mm spectral window. The number of mapped lines for a given species is then usually limited to one. Extracting quantitative information therefore represents a different challenge as compared to studies of specific objects where several transitions of a few molecular species can be obtained on a restricted field of view. For this reason, and because the method is simple and fast, the local thermodynamic equilibrium (LTE) framework is often used to provide estimations of molecular column densities and excitation temperature over the covered large scale maps. As shown by Roueff et al. (2021), this simple hypothesis may lead to bias in the derived parameters as the excitation temperatures of the three main CO isotopologues are different, the excitation temperature of 12CO being typically twice as large as that of 13CO and C18O. In general, the excitation temperature of the three CO isotopologues are different with Tex(12CO) ≥ Tex(13CO) ≥ Tex(C18O). If it is not taken properly into account, this difference may induce significant errors in the derivation of molecular column densities and relative abundances.
Furthermore, the hypothesis that the level populations of the considered species are at thermal equilibrium is often proven to be invalid because the volume densities are too low for collisions to be fully effective in balancing the populations of the energy levels (see, e.g., Shirley 2015). Non-LTE excitation and radiative transfer models have thus been developed for decades to analyze the molecular line emission and have been widely used in different contexts, most often by adding a priori information on some properties of the considered source (e.g., its structure) to limit the parameter space that is meant to be explored. When studying a specific object, an analytical model of the geometry, density structure, and velocity field of the object is often specified. The information in the line intensities is then used to fit the velocity field, volume density, temperature structure, and the molecular column densities. Additional hypotheses on the temperature can also be made, either by using additional information (e.g., the kinetic temperature equal to the dust temperature) or by fixing the kinetic temperature to some given value. For instance, Tafalla et al. (2021) used an isothermal model with simple parametric laws for the variation of the density, velocity dispersion, and molecular abundances as a function of the position to analyze their survey of the Perseus molecular cloud. Outputs of thermo-chemical models such as the Meudon PDR code (Le Petit et al. 2006) can also be used as inputs for radiative transfer calculations. Using the volume density, kinetic temperature, and relative abundances of CS and CO isotopologues from a plane-parallel PDR model of the Horsehead nebula, Goicoechea et al. (2006) computed the expected molecular emission in an edge-on cloud with a nonlocal and non-LTE Monte Carlo radiative transfer model, and set the derived constraints on the sulfur abundance. These examples show that this approach works well for known sources with many observations across a broad range of wavelengths accessible because it requires substantial a priori information.
For sources with less available information, especially when a simple geometry cannot be specified, fitting molecular line emission may lead to ambiguities and uncertainties in the derived parameters. In their analysis of the (1 − 0) lines of 12CO, 13CO, and C18O in the Orion A molecular cloud, Castets et al. (1990) showed that the correlation between the estimated kinetic temperature and the volume density may lead to ambiguities and large uncertainties in these parameters. For this particular cloud, using the peak 12CO intensity as a constraint for the kinetic temperature offers relatively poor results because different values of the kinetic temperature ought to be used for the different CO isotopologues. Castets et al. (1990) assumed that these different values of the kinetic temperature are spatially uniform across the cloud and deduced them from observations of the ammonia inversion lines towards small sub-regions of the map. Hence, these examples show that even with a non-LTE model, the inversion of the radiative transfer equation is not solely based on the information provided by the considered molecular lines; rather, it makes use of additional a priori information, which may be derived from the analysis of additional datasets or from a geometric or theoretical model. The uncertainties on the derived parameters are then more difficult to evaluate as they depend both on the quality of the data and the quality of the model, including the additional a priori assumptions.
The question of accuracy of the retrieval of physical conditions from a set of observed noisy lines was discussed by Tunnard & Greve (2016) for the observations of CO or HCN lines in distant galaxies. In this study, the authors used relatively optimistic observation conditions with a noise level set either to 0 or to 10% of the line intensity. They showed that the accuracy of the estimated parameters (density, temperature, and pressure) is not better than half a dex (i.e., a factor of three) and that using isotopologue lines helps to increase the accuracy of the retrieval. For the considered species and lines, they show that better results are obtained when the isotopologue abundance ratio is not fixed because introducing a fixed value may bias the results and lead to satisfactory fits even though the fitted parameters have significant offsets from their true values. Tunnard & Greve (2016) analyzed CO and HCN separately and did not attempt to combine the information from these two species.
To study the bias in the gas column density determination based on CO (1 − 0) rotational line emission, Teng et al. (2023) discussed how the (1 − 0), (2 − 1), and (3 − 2) CO isotopologue emission, and the CO column density in three nearby galaxies depend on the physical conditions. Using a large grid of RADEX models, they derived (for each pixel) the volume density, kinetic temperature, CO column density per unit line width, and the isotopic ratio between 12CO and 13CO and between 13CO and C18O. An additional constraint on the path length along the line of sight was added to remove models with low volume density and very large CO column densities. In these models, the CO abundance relative to H2 is fixed. The fitted results are used to estimate the H2 column density from the CO column density and the conversion factor between the 12CO (1 − 0) intensity and the H2 column density for each pixel. They showed that the variations of this conversion factor are mainly related to variations of the CO optical depth and secondly to variations of the kinetic temperature. The necessity to constrain the length along the line of sight illustrates once again the presence of ambiguities in the derivation of the physical conditions and the possibility of non physical results. An anti-correlation between the volume density and kinetic temperature is clearly seen in their likelihood distributions.
As in the case of LTE models, non-LTE models may also suffer from bias induced by a priori information, but such effects are not sufficiently documented in studies of non-LTE radiative transfer modeling. The present paper focuses on the quantitative uncertainties obtained for the volume density and kinetic temperature derived for the Horsehead nebula, when analyzing the 3 mm spectrum of the different isotopologues of CO and HCO+. As shown by Bron et al. (2018) the combination of the (1 − 0) lines of the three main CO isotopologues and of HCO+ is sufficient to identify the different regimes of volume density and FUV illumination across the mapped area. It is now necessary to transform this qualitative study into quantitative maps of physical parameters, using non-LTE radiative transfer models.
Non-LTE models can be developed for different source geometries. The simplest formulation, which is implemented in local escape probability codes such as RADEX (van der Tak et al. 2007), uses a uniform 1D source description. It solves the combined radiative transfer and molecular excitation in a local way, where local means that molecules interact with the local radiation field and are fully decoupled from other radiation emission along any other position of the cloud. The emergent radiation results from the combination of all locally produced photons. More sophisticated radiative transfer codes can treat the non-local interaction between the excitation of molecular levels at a given position of the cloud and the radiation field from any other cloud position. for instance the MOLPOP-CEP code (Asensio Ramos & Elitzur 2018) or codes based on Monte Carlo methods (Bernes 1979; Goicoechea et al. 2006; Brinch & Hogerheijde 2010). These more sophisticated models naturally take into account the presence of density, kinetic temperature, or relative abundance gradients along the line of sight. Such nonlocal methods are however more complicated to implement, they are numerically heavier, and they require more a priori information about the structure of the considered cloud. They provide more accurate results than non-LTE local models, especially in the case when radiative effects become dominant; for instance, in the case of the radiative transport of optically thick lines in a medium where the volume density is much lower than the critical density.
The article is organized as follows. Section 2 presents the tools that will be used in this paper: the RADEX radiative transfer code, the Cramér-Rao bound (CRB) used to infer a reference precision, and a maximum likelihood estimator used to fit simultaneously several lines for each line of sight. After a succinct presentation of the data, Sect. 3 offers a comparison of the estimated parameters when fitting the data under different assumptions. We discuss the tradeoff between variance and bias on two experiments in Sect. 4. Section 5 presents a parametric study of the achievable precision on the column densities, kinetic temperature, volume density, and thermal pressure. Section 6 discusses the best strategy to maximize the precision without biasing the results. Appendices A and B present details about the computation of the Cramér-Rao bound and the maximum likelihood estimator. Appendices C and D show supplemental figures related to the discussion in Sects. 3 and 5.
2 Methods
This section introduces the astrophysical framework (the non-LTE escape probability radiative transfer code RADEX and the associated concept of critical density) and the statistical method (the Cramér-Rao bound and our maximum likelihood fitter) used throughout this paper.
2.1 RADEX:A non-LTE radiative transfer model to estimate the gas volume density and kinetic temperature
The non-LTE radiative transfer code RADEX (van der Tak et al. 2007) uses an escape probability formalism to compute the emerging radiation from an homogeneous medium of simple geometry. In this article, we use the uniform sphere geometry. Below, we clarify the associated notations and equations for a single species.
As recalled recently in Roueff et al. (2021), the brightness temperature, s, at observed frequency v around the rest frequency of a line (vl) can be written as
![$s(v) = \left\{ {J\left( {{T_{{\rm{ex }},l}},{v_l}} \right) - J\left( {{T_{{\rm{CMB}}}},v} \right)} \right\}\left[ {1 - \exp \left( { - {\Psi _l}(v)} \right)} \right].$](/articles/aa/full_html/2024/06/aa49148-24/aa49148-24-eq1.png) (1)
(1)
In this equation
-
where B(T, v) is the spectral distribution of the radiation of a blackbody at temperature, T, and h, k are the Planck and Boltzmann constants, respectively.
As we assume that the only background source of emission is the cosmic microwave background (CMB), we compute J at its temperature (TCMB = 2.73 K).
-
Tex,l is the excitation temperature related to the ratio of the population in the upper (nup) and lower (nlow) levels of the line, l,
![${{{n_{{\rm{up }}}}} \over {{n_{{\rm{low }}}}}} = {{{g_{{\rm{up }}}}} \over {{g_{{\rm{low }}}}}}\exp \left[ { - {{h{v_l}} \over {k{T_{{\rm{ex}},l}}}}} \right].$](/articles/aa/full_html/2024/06/aa49148-24/aa49148-24-eq3.png) (3)
(3)The population of the different energy levels is locally computed by solving the statistical balance between radiative and collisional excitation and de-excitation of the important energy levels. Table 1 lists the origin of the collisional coefficients used in this article.
-
The term [1 − exp(−Ψ(v))] in Eq. (1) represents the emission (or absorption) by the emitting (or absorbing) medium along the line of sight (LoS). The function Ψ is the opacity profile that corresponds to the integrated opacity through the whole slab. The RADEX code computes the radiative transfer assuming that the opacity profile has a rectangular shape with a specified full width at half maximum (FWHM). To be able to fit the line profiles, we assume that each line l is described by a Gaussian profile
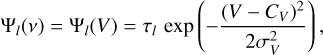 (4)
(4)where τl is the line opacity computed by RADEX, CV and σV are the systemic velocity and the velocity dispersion of the source along the studied LoS. In this equation, the velocity and frequency are related by the Doppler formula expressed in the radio convention as
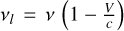 . The FWHM used by RADEX is related to σV through
. The FWHM used by RADEX is related to σV through
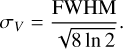 (5)
(5)The difference between the integrated opacities of the rectangular and Gaussian profiles is small, using
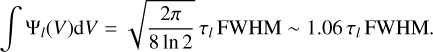 (6)
(6)Furthermore, assuming that J(TCMB, v) = J(TCMB, vl) for v close to
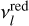 , Eq. (1) can be simplified as
, Eq. (1) can be simplified as
![$s(V) = \left\{ {J\left( {{T_{{\rm{ex }},l}},{v_l}} \right) - J\left( {{T_{{\rm{CMB}}}},{v_l}} \right)} \right\}\left[ {1 - \exp \left( { - {\Psi _l}(V)} \right)} \right].$](/articles/aa/full_html/2024/06/aa49148-24/aa49148-24-eq9.png) (7)
(7)The physical conditions are thus characterized by five unknown parameters: the kinetic temperature, Tkin, the volume density,
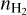 , the column density, N, of the considered species, the velocity dispersion, σV, and the mean velocity, CV, along the considered LoS. The emerging spectrum is computed through Eqs. (4) and (7), where the excitation temperature, Tex,l, and opacity, τl, are computed with the RADEX code. RADEX uses {Tkin,
, the column density, N, of the considered species, the velocity dispersion, σV, and the mean velocity, CV, along the considered LoS. The emerging spectrum is computed through Eqs. (4) and (7), where the excitation temperature, Tex,l, and opacity, τl, are computed with the RADEX code. RADEX uses {Tkin, 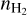 , N, FWHM} as input parameters plus two additional parameters that we fixed as follows.
, N, FWHM} as input parameters plus two additional parameters that we fixed as follows. -
The ortho-to-para ratio (OPR) of the molecular hydrogen is defined as
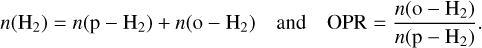 (8)
(8)Introducing the numerical values of the level energies of molecular hydrogen, we obtain the thermal equilibrium value as
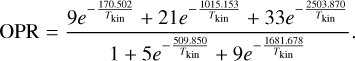 (9)
(9)This equation assumes that the H2 level population is at thermal equilibrium and that Tkin < 500 K.
-
The electron density n(e−) is derived from the gas volume density with
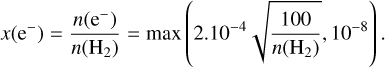 (10)
(10)This formula takes into account the decrease of the ionization as a function of density due to recombination. It includes a lower limit consistent with chemical model predictions in dense and dark regions (Bron et al. 2021).
Inelastic collisions with electrons contribute to the excitation of molecular rotational levels as long as the electron fraction remains higher than the ratio of the downward collision rates with H2 and with electrons. For HcO+, collisions with electrons will be effective for an electron fraction larger than about 3 × 10−5 at a kinetic temperature of 30 K. With the adopted scaling law (Eq. (10)) this corresponds to densities lower than ~4000 cm−3. For CO, only collisions with neutral species are included, because collisions with electrons are only efficient compared to collisions with H2 or helium for high dipole molecules like HCO+ or HCN at the typical electron fractions found in GMCs (Liszt 2012; Goldsmith & Kauffmann 2017; Santa-Maria et al. 2023).
Origin of the collision coefficients used in this article.
2.2 The notion of critical density to help with the interpretation of the results
The critical density is the volume density at which (de-) excitations by collisions equal radiative (de-)excitations. It is thus a crucial characteristic of each line, which allows us to assess the typical density above which the LTE regime is reached. As both collisional and radiative excitation processes contribute, the critical density is usually defined in the context of an optically thin line, 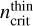 , and then modified to take into account radiative excitation (Shirley 2015). The effective critical density
, and then modified to take into account radiative excitation (Shirley 2015). The effective critical density 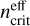 , including line trapping effects, can be calculated for each line with
, including line trapping effects, can be calculated for each line with
![$n_{{\rm{crit }}}^{{\rm{eff }}} = n_{{\rm{crit }}}^{{\rm{thin }}}\beta \quad {\rm{ where }}\quad \beta = {{1.5} \over \tau }\left[ {1 - {2 \over {{\tau ^2}}} + \left( {{2 \over \tau } + {2 \over {{\tau ^2}}}} \right){e^{ - \tau }}} \right]{\rm{. }}$](/articles/aa/full_html/2024/06/aa49148-24/aa49148-24-eq17.png) (11)
(11)
The value 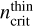 is computed as the sum of the Einstein coefficients, A, divided by the sum of collisional de-excitation rates. The parameter β is the average escape probability in the case of a uniform sphere (the default case in RADEX, see van der Tak et al. 2007).
is computed as the sum of the Einstein coefficients, A, divided by the sum of collisional de-excitation rates. The parameter β is the average escape probability in the case of a uniform sphere (the default case in RADEX, see van der Tak et al. 2007).
2.3 The Cramér-Rao bound to provide a reference precision
Once the physical model and its associated assumptions are clearly stated, the Cramér-Rao bound delivers a lower bound of the variance of the estimation of each fitted parameter. This means that all the information will have been extracted from the data when we find an unbiased estimator of any given physical parameter whose variance is equal to the Cramér-Rao bound.
Based on a physical model and the associated assumptions, one can calculate the Fisher matrix (defined in Eq. (A.6)) and then numerically compute its inverse to get the Cramér-Rao bound matrix
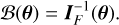 (12)
(12)
Noting θ1, θ2, … the unknown parameters of the problem, the ith diagonal term of the CRB matrix provides a lower bound on any unbiased estimator 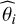 of θi (see, e.g., Roueff et al. 2021, for an example)
of θi (see, e.g., Roueff et al. 2021, for an example)
![${\mathop{\rm var}} \left( {{{\hat \theta }_i}} \right) \ge {[{\cal B}({\bf{\theta }})]_{ii}}.$](/articles/aa/full_html/2024/06/aa49148-24/aa49148-24-eq21.png) (13)
(13)
Thus, ![${{\cal B}^{1/2}}\left( {{\theta _i}} \right) = \sqrt {{{[{\cal B}(\theta )]}_{ii}}} $](/articles/aa/full_html/2024/06/aa49148-24/aa49148-24-eq22.png) is equivalent to a standard deviation, which can be interpreted as a precision of reference for each physical environments (e.g., diffuse gas, dense core, etc.) which takes into account the statistics of the noise that disturbs the observation. The CRB is a local property. For example, for a Gaussian noise, the CRB is the curvature of the negative log-likelihood (NLL) at its minimum. Thus, the CRB is useful as a first guess of the precision that can be expected, but it is not sensitive to the presence of other local minima, which may induce “abnormal” estimations in low signal-to-noise ratio (S/N) cases (Garthwaite et al. 1995).
is equivalent to a standard deviation, which can be interpreted as a precision of reference for each physical environments (e.g., diffuse gas, dense core, etc.) which takes into account the statistics of the noise that disturbs the observation. The CRB is a local property. For example, for a Gaussian noise, the CRB is the curvature of the negative log-likelihood (NLL) at its minimum. Thus, the CRB is useful as a first guess of the precision that can be expected, but it is not sensitive to the presence of other local minima, which may induce “abnormal” estimations in low signal-to-noise ratio (S/N) cases (Garthwaite et al. 1995).
Appendix A details the computation of the Fisher matrix for our use of the RADEX model, when the unknown parameters are ![$\theta = \left[ {\log {T_{{\rm{kin}}}},\log {n_{{{\rm{H}}_2}}},\log N,{\sigma _V},{C_V}} \right]$](/articles/aa/full_html/2024/06/aa49148-24/aa49148-24-eq23.png) . Section 5 analyzes the evolution of
. Section 5 analyzes the evolution of 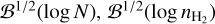 and ℬ1/2(Tkin) as a function of the volume density and the column density, while the other parameters remain fixed. As the thermal pressure may be better constrained than the volume density or kinetic temperature, it is useful to also compute the Cramér-Rao bound for the thermal pressure. Formally, since log
and ℬ1/2(Tkin) as a function of the volume density and the column density, while the other parameters remain fixed. As the thermal pressure may be better constrained than the volume density or kinetic temperature, it is useful to also compute the Cramér-Rao bound for the thermal pressure. Formally, since log 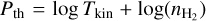 , one simply has
, one simply has
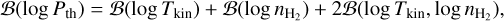 (14)
(14)
where 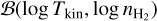 is the off-diagonal term of the CRB matrix. This term can be interpreted as the covariance between the log Tkin and log
is the off-diagonal term of the CRB matrix. This term can be interpreted as the covariance between the log Tkin and log 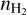 estimations.
estimations.
2.4 A maximum likelihood estimator to fit the data
In addition to the RADEX and noise models, we need an algorithm to fit the data and deliver the associated estimation 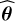 of the physical parameters θ. Each pixel is fitted independently from all the other ones. We will classically fit the observed data x by looking for the estimated
of the physical parameters θ. Each pixel is fitted independently from all the other ones. We will classically fit the observed data x by looking for the estimated 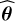 that maximizes the log-likelihood function
that maximizes the log-likelihood function
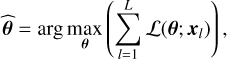 (15)
(15)
where l is the line index of the L observed lines. For a given pixel, our algorithm can be decomposed in four steps, as described below.
Signal detection and estimation of the centroid velocity. We first compute the noise level of the spectrum in channels devoid of signal. Then, we detect the presence of a peak in the intensity for each analyzed line. The initial centroid velocity for all the lines is estimated as the peak location on the summation of 13CO and C18O line spectra. This is a tradeoff between fully optically thin lines, and one with high S/N. We then decide whether the pixel of the image is further fitted. Since all species are assumed to share the same centroid velocity, we only require that more than half of the lines are detected. For example, for the set 𝒮 {C18O, H13CO+}, we only require that both C18O lines are detected.
Initialization of the fit estimation. We initialize the estimation of the other physical parameters on the point that minimizes the negative log-likelihood (NLL) on a grid that regularly samples the fitted parameters. Here it is crucial to take into account the a priori constraints that are assumed, for instance, the same kinetic temperature and volume density (see Appendix B.2 for details). This step yields an initial estimation of all parameters θ. It may also induce some implicit a priori information depending on the chosen grid boundaries.
Maximization of the likelihood. We then refine our initial estimation with a standard iterative gradient descent. The iterator is stopped when one of the following conditions is achieved: 1) The difference of NLL between two consecutive iterations is smaller than 10−6; or 2) the number of iterations reaches 30; or 3) the NLL minimum does not decrease for five consecutive iterations. This may happen because of numerical instability.
Estimation of the confidence interval. Once the physical parameters have been obtained, we compute the Cramér-Rao bound for each parameter 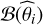 to provide a reference interval of confidence. Although we replaced θi by
to provide a reference interval of confidence. Although we replaced θi by 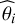 , this interval of confidence remains mostly valid as long as the model is valid, and as soon as the estimator is efficient (i.e., it is unbiased and the variance is equal to the Cramér-Rao bound).
, this interval of confidence remains mostly valid as long as the model is valid, and as soon as the estimator is efficient (i.e., it is unbiased and the variance is equal to the Cramér-Rao bound).
Additional implementation details about these implementations are provided in Appendix B.
Properties of the observed lines.
3 Quantifying the variability of the estimation of physical parameters on actual data
In this prototype study, we used the RADEX model to fit the spectra of a combination of the (1 − 0) and (2 − 1) transitions for some of the following species: 12CO, 13CO, C18O, HCO+, and H13CO+. Table 2 lists the properties of each line (frequency, upper energy level and Einstein coefficient) as well as the properties of the observed spectra (spectral spacing and thermal noise). The studied field of view covers about 50 square arcminutes towards the Horsehead Pillar at the South West of Orion B, which is illuminated by the σ-Ori star.
3.1 Data
3.1.1 Acquisition and data reduction
The data were obtained at the IRAM 30m telescope. The (1 − 0) lines were acquired in 2013-2020 in the context of the ORION-B large program (Pety et al. 2022; Gerin et al. 2023), using a combination of the EMIR receivers and FTS spectrometers. The (2 − 1) lines towards the Horsehead pillar were acquired in 2006 (PI: N. Peretto) using the ABCD generation of receivers and the VESPA auto-correlator. They have been first presented and used in Roueff et al. (2021).
The data reduction is described in Pety et al. (2017) and Roueff et al. (2021). It uses the standard methods provided by the GILDAS1/CLASS software. The data cubes were gridded on the same astrometric grid. They were smoothed to the lowest achieved angular resolution (i.e., 31″) in order to ease the multi-line fit towards the same LoS without having to take care of different angular resolutions. The velocity spacings are listed in Table 2. We used two velocity spacings (0.1 and 0.5 km s−1) depending on the native spectral resolution of the spectrometer used for each line.
3.1.2 Presentation of the data
Figure 1 summarizes the data with a combination of images of the peak and integrated intensities as well as percentiles of the line intensities as a function of the velocity among the considered pixels. The spatial shape of the Horsehead pillar varies with the species. The 12CO (1 − 0) line is detected towards most of the field of view, while the rarer CO isotopologues better show the spine of the Horsehead. The H13CO+ (1 − 0) line is mainly detected towards the two known dense cores of the Horsehead (e.g. Ward-Thompson et al. 2006). Table 3 lists the specified locations on the image. The two crosses show the positions of these two dense cores. The position of the western dense core is the Horsehead dense core position defined in Pety et al. (2007) and extensively studied in the framework of the Horse-head WHISPER project (see, e.g., Guzmán et al. 2014). The cross for the eastern dense core points towards the local maximum of the H13CO+ (1 − 0) line emission. The HCO+ (1 − 0) line exhibits a mixed behavior with some filamentary structure embedded in more diffuse emission that has a similar shape as the 12CO (1 − 0) line.
The line profiles mostly show a main velocity component centered near VLSR ~ 10.5 km s−1. The 12CO, HCO+, and H13CO+ (1 − 0) lines exhibit a second velocity component or wing around VLSR ~ 13.0 km s−1. As the presence of a single velocity component is required to be consistent with the hypothesis that the lines are emitted by the same layer of molecular gas along the LoS, we only concentrate on the 10.5 km s−1 velocity component. Moreover this 10.5 km s−1-velocity component is clearly detected for all the lines.
The 13CO (2 − 1) and C18O (2 − 1) lines have similar properties as their (1 − 0) transitions regarding their spatial and spectral shapes, but with minor differences due to excitation effects. Finally, most of the observed lines have high S/N with the noteworthy exception of H13CO+ (1 − 0).
 |
Fig. 1 Presentation of the data towards the Horsehead pillar. Left and middle panels: spatial distribution of the peak intensity and of the integrated intensity. The used projection is the Azimuthal one, centered on RA= 05h40m54.27s, Dec= −02°28′00.00″ in the ICRS frame, and with a position angle of 14°. The two crosses show the positions of the two dense cores whose coordinates are in Table 3. The black dot shows the position of the line of sight studied in more detailed in Sect. 4. Right panel: the green, blue, and red spectra show the spectra of percentiles at 10, 50, and 90%, respectively, computed over the associated field of view. |
3.2 Fitting assumptions
3.2.1 Simplifying physical and chemical assumptions
As detailed in Sect. 2.1, the considered non-LTE model is characterized by five unknown parameters (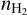 , Tkin, N, σV and CV) per modeled species. The purpose of this article is to analyze the possibility of estimating those parameters as a function of the LoS from observations of few lines (1 or 2), from several species. We consider here different sets of species containing from one to three species among: 12CO, 13CO, C18O, HCO+, and H13CO+. Since the number of unknown parameters is too large compared to the available data, assumptions are required in order to reduce the number of unknowns with respect to the number of fitted lines. Table 4 lists the cases considered in this section. For all species sets, we assume that the gas emitting the different lines share the same kinetic temperature, volume density, centroid velocity and velocity dispersion. In other words, we assume that their emissions come from the same gas cell in the cloud. We also often assume that at least one of the column density ratios is known and thus fixed. We thus have between 5 and 6 unknowns. The first five ones are the kinetic temperature, volume density, centroid velocity and velocity dispersion, and the column density of either 13CO or C18O. For some sets, the sixth unknown is either the
, Tkin, N, σV and CV) per modeled species. The purpose of this article is to analyze the possibility of estimating those parameters as a function of the LoS from observations of few lines (1 or 2), from several species. We consider here different sets of species containing from one to three species among: 12CO, 13CO, C18O, HCO+, and H13CO+. Since the number of unknown parameters is too large compared to the available data, assumptions are required in order to reduce the number of unknowns with respect to the number of fitted lines. Table 4 lists the cases considered in this section. For all species sets, we assume that the gas emitting the different lines share the same kinetic temperature, volume density, centroid velocity and velocity dispersion. In other words, we assume that their emissions come from the same gas cell in the cloud. We also often assume that at least one of the column density ratios is known and thus fixed. We thus have between 5 and 6 unknowns. The first five ones are the kinetic temperature, volume density, centroid velocity and velocity dispersion, and the column density of either 13CO or C18O. For some sets, the sixth unknown is either the 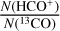 or the
or the 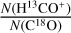 relative abundance.
relative abundance.
Considering a single species with two lines, for instance, the 13CO or C18O isotopologues, allows us to get an idea of their column densities without the assumption of co-location. For sets containing two species, we associate species that share a good probability of being emitted from similar regions: 𝒮{13CO, HCO+} for diffuse regions, 𝒮{13CO, C18O} for denser filaments, and 𝒮 {C18O, H13CO+} for dense cores. We add the12 CO peak value to check its influence.
The (1 − 0) lines of the HCO+ isotopologues have higher critical densities than the CO isotopologues’ ground-state transitions because the dipole moments of these molecular ions is much larger than the ones of neutral species (Shirley 2015). These lines may thus bring additional information towards the two dense cores of the Horsehead pillar. We use the two main isotopologues to assess the impact of their different optical depths and S/Ns.
Since this paper focuses on a region with 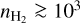 cm−3, we only use the spectrum of 12CO at its peak value. Indeed, the line profile delivered by the non-LTE model with a simple Gaussian opacity profile does not suitably describe the profile of extremely optically thick lines such as 12CO (1 − 0) (Leung & Liszt 1976).
cm−3, we only use the spectrum of 12CO at its peak value. Indeed, the line profile delivered by the non-LTE model with a simple Gaussian opacity profile does not suitably describe the profile of extremely optically thick lines such as 12CO (1 − 0) (Leung & Liszt 1976).
We add a 𝒜 symbol in the set name when we fix the relative abundance. In this case, the relative abundance is defined by using the typical isotopic ratios for Orion 12C/13C = 63, 16O/18O = 510, N(13CO)/N(H2)=2.3 × 10−6 and N(HCO+)/N(H2)=3 × 10−9 (Gerin et al. 2019; Roueff et al. 2021, and references therein).
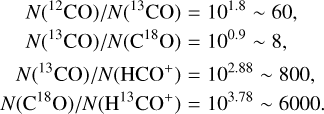 (16)
(16)
We also varied the last three abundance ratios by ±0.3 dex in order to assess the impact of variations of the assumed chemistry. These cases are marked with the 𝒜★ symbol.
Sets of species, the assumed chemistry, the number of available lines, and the number of unknown parameters.
3.2.2 Noise model
The data are affected by thermal noise and calibration uncertainty. We thus use the following model of data
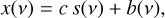 (17)
(17)
where x is the observed data, s the source intensity, b is the thermal noise, and c represents the calibration uncertainty. We assume that b and c are independent random variables with normal distribution: 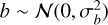 and
and 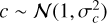 (see Einig et al. 2023, for more details).
(see Einig et al. 2023, for more details).
The standard deviations associated to the calibration uncertainty are fixed as
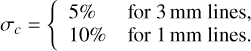 (18)
(18)
The median values of the thermal standard deviation measured on the data are listed in Table 2.
3.2.3 Choice of likelihood and S/N saturation
When quantifying the theoretical precision of estimations (see Sect. 5), we take into account both the thermal noise and calibration uncertainty. However, we neglect the calibration uncertainty and we instead set the S/N to a maximum value of 10, when fitting the data with the maximum likelihood estimator.
On one hand, including the multiplicative factor in the estimation leads to fits where the potential shortcomings of the physical assumptions are incorrectly attributed to calibration errors, because the fit then cares too much about the shape of the spectra, and too little about its amplitude. This is counterproductive for real data analysis. We thus choose the standard negative likelihood when fitting data (x), i.e.,
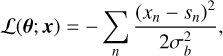 (19)
(19)
where sn is a sampled version of Eq. (7) and thus is a function of the unknown parameters. On the other hand, we artificially set σb such that the S/N, defined as
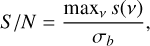 (20)
(20)
has a maximum value of 10. This artificial saturation is required to ensure that lines with a S/N between 3 and 10 (e.g., H13CO+ (1 − 0)) have a non negligible weight compared to lines with S/N of 100 (e.g., the 13CO lines). The value of 10 also ensures that calibration errors that are lower than 10% are considered as noise, and contribute to the error budget together with the additive noise.
3.3 Results
We systematically check here the stability of the fitted parameters as a function of the set of species fitted and the associated a priori hypotheses. In the following figures, we select one parameter at a time. We look at chemical (column densities and relative abundances, i.e., ratios of column densities) and physical (kinetic temperature, volume density, and thermal pressure) parameters. We focus on reliable estimations defined as
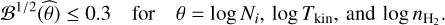 (21)
(21)
For each parameter, we present two figures: 1) the maps of the fitted parameter on the Horsehead pillar data for different sets of species and/or a priori (e.g., the top of Fig. 2); 2) joint histograms of this parameter estimations. The bottom of Fig. 2 compares the estimations of N(13CO) obtained for 7 different sets of species and/or a priori defined in Table 4: 𝒮{13CO)}, 𝒮{13CO, HCO+; 𝒜}, 𝒮{13CO, HCO+;𝒜*}, 𝒮{13CO, C18O; 𝒜}, 𝒮{13CO, C18O; 𝒜*}, 𝒮{12CO, 13CO, HCO+} and 𝒮{12CO, 13CO, C18O}. There are 21 pairs for 7 different fits. The figure thus appears as a lower triangle of size 6 × 6. For conciseness sake, we only show in the main paper these two kinds of figures for the case of the column density of 13CO. For the other parameters, we put these figures in Appendix C, and we synthesize the joint histograms by their distance in log-space to the line of slope 1. More precisely, we compute the mean and the standard deviation of 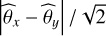 , where θx and θy are the estimated parameters plotted along the x and y axes of the histograms. We present these values in a tabular way where we put in the same lower triangle the values of the mean and standard deviation, color-coded by the root mean square error,
, where θx and θy are the estimated parameters plotted along the x and y axes of the histograms. We present these values in a tabular way where we put in the same lower triangle the values of the mean and standard deviation, color-coded by the root mean square error, 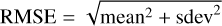 . Figure 3 shows the associated “tables” for N(13CO), N(C18O), N(HCO+), and N(H13CO+), Tkin, and
. Figure 3 shows the associated “tables” for N(13CO), N(C18O), N(HCO+), and N(H13CO+), Tkin, and 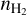 . A non zero mean indicates a systematic shift compared to the line of slope 1, while a large standard deviation indicates a large dispersion of the distances to the line whose slope is the mean, and a large RMSE a large dispersion of the distances to the line of slope 1. Quantitatively the values can also be interpreted with the help of Table 8. Values of ±0.1, ±0.3, and ±0.6 correspond to multiplicative uncertainty of the order of 20%, a factor 2, and 4 respectively.
. A non zero mean indicates a systematic shift compared to the line of slope 1, while a large standard deviation indicates a large dispersion of the distances to the line whose slope is the mean, and a large RMSE a large dispersion of the distances to the line of slope 1. Quantitatively the values can also be interpreted with the help of Table 8. Values of ±0.1, ±0.3, and ±0.6 correspond to multiplicative uncertainty of the order of 20%, a factor 2, and 4 respectively.
3.3.1 One detailed case: The column density of 13CO
The top of Fig. 2 shows the maps of the column densities of 13CO fitted on the Horsehead pillar under different hypotheses. In this case, almost all pixels deliver a column density with a good CRB reference precision whatever the set of species and of a priori used during the fit. However, the shape of the maps of the column density varies depending on the chosen set of lines. If we take the case where we only fit the 13CO lines as reference (panel a), we see different behaviors. First, adding the C18O lines increases N(13CO) towards the two dense cores or the surrounding filaments depending on the assumed chemistry. Second, adding the HCO+ lines decreases N(13CO) towards the dense core in the Horsehead throat but increases it towards the dense core on the top of the head. The effect is more or less pronounced depending on the assumed chemistry. Third, adding the peak temperature of the 12CO (1 − 0) line regularizes the overall shape of the column density map.
These trends are quantitatively confirmed by the joint histograms shown in the bottom of Fig. 2. The most consistent values of the column densities are obtained in the cases 𝒮{13CO, HCO+; 𝒜} and 𝒮{13CO, HCO+; 𝒜★} where only the assumed chemistry is changed. This is followed by the pairs (𝒮{12CO, 13CO, C18O} and 𝒮{12CO, 13CO, HCO+}), and (𝒮{13CO} and 𝒮{13CO, HCO+, 𝒜}). The less consistent values. of the column densities are obtained for the pairs (𝒮{13CO, C18O; 𝒜} and 𝒮{13CO, C18O; 𝒜★}).
Overall, the column densities of 13CO are defined within a typical multiplicative accuracy of 30%. Adding C18O (resp. HCO+) gives more weight to the dense cores (resp. more diffuse envelope) when fitting the column density of 13CO.
3.3.2 Column densities and relative abundances
The top row of Fig. 3 and the associated figures in Appendix C synthesize the results on column densities. The column densities of C18O are mostly consistent within 15%. That is a factor ~ 2 better than 13CO. Accordingly, the maps of N(C18O) show spatial variations that are similar in all tested cases (see Fig. C.1). The noteworthy exception are the couples (𝒮{13CO, C18O; 𝒜} and 𝒮{13CO, C18O; 𝒜★}), probably because the column density of C18O is sensitive to the choice of the N(13CO)/N(C18O) abundance ratio.
The column densities of HCO+ and H13CO+ are more scattered and biased depending on the fitted case. The worst case is N(H13CO+) because the associated line has the lowest S/N of all. But N(HCO+) also shows a large scatter. We relate this to a possible evolution of the HCO+ chemistry between dense cores and more diffuse gas, implying an evolution of its relative abundance.
Figure 4 illustrates the stability of the relative abundances depending on the case. The relative abundance of C18O and 13CO is pretty insensitive to the presence or absence of the peak intensity of the 12CO (1 − 0) line during the fit. In contrast, the relative abundances of (13CO and HCO+) or (C18O and H13CO+) are sensitive (both in bias and scatter) to the presence or absence of the peak intensity of the 12CO (1 − 0) line. This may be due to the fact that the peak intensity mostly constrains the kinetic temperature. As the CO isotopologue line intensities are mostly sensitive to the thermal pressure in the considered parameter space, the constraint on the temperature has an effect on the volume density determination. With their high dipole moment (thus higher critical densities) the HCO+ isotopologue excitation is sensitive to the volume density.
3.3.3 Kinetic temperature
The determination of the kinetic temperature presents large variations depending on the chosen set of lines. As shown in Fig. C.3, using both the (1 − 0) and (2 − 1) lines of 13CO and C18O enables a correct determination of the kinetic temperature in the high column density filament. In addition, the choice of the fixed relative abundance between these species has little impact on the Tkin estimation. In contrast, the same set of lines leads to unrealistic high values of Tkin outside the filament. The combination of either 13CO and HCO+ or C18O and H13CO+ performs poorly. The determination of the kinetic temperature is sensitive to the assumption made on the relative abundances. The Tkin estimations seem to be biased as the correlation with the determinations from 13CO and C18O shows some scatter and presents a significant offset.
Adding 12CO to the set of lines improves the Tkin estimation because this sets an upper limit to the value of Tkin of about 30 K. The resulting temperature maps are more extended and present smooth variations. The two sets perform about equally well and lead to similar estimations across the map with no systematic difference. However, using the peak of the 12CO (1 − 0) emission introduces a bias in the estimation as this line is produced in the external regions of the considered sight-line, where the kinetic temperature may not be representative of the conditions along the full LoS.
 |
Fig. 2 Comparison of the estimated column density of 13CO on the Horsehead pillar data for different sets of species and/or a priori. In all cases Tkin, |
 |
Fig. 3 Mean and standard deviation of the distance in log-space between the estimations (i.e., |
3.3.4 Volume density
The volume density is the most difficult parameter to estimate. The scatter can reach a factor of ten and different sets of lines can lead to determinations with a systematic offset of up to 0.5 dex, a factor of three. In the high column density regions, the sets combining C18O and H13CO+ perform well, but the absolute value of the volume density scales with the fixed relatives abundance. Indeed, the determination are well correlated but offset from each other by 0.34 dex, which corresponds to the change in the fixed relative abundances. A similar effect is seen for the sets combining 13CO and HCO+, which leads to well correlated but offsets density estimations. For pixels where both sets can be used and the hypotheses on abundances are consistent, it is encouraging to see that 13CO and HCO+, and C18O and H13CO+ lead to similar estimations of the volume density with no significant offset, even if a significant scatter of about 0.2 dex remains.
The estimations of the volume density made from the sets combining CO isotopologues only, seem to reach a maximum value near 104.3 cm−3 (see Fig. C.4). This may be related to the limited range of kinetic temperature and the lower critical density of the considered CO isotopologue transitions as compared with those of the high dipole moment species HCO+ and H13CO+.
 |
Fig. 4 Maps and joint histograms of relative abundances for log {N(13CO)/N(HCO+)} (left), log {N(13CO)/N(C18O)} (middle), and log {N(C18O)/N(H13CO+)} (right). The layout of the figure is similar to Fig. 2. |
3.3.5 Thermal pressure
The estimation of the thermal pressure is more accurate and less biased than that of Tkin and 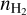 separately (see Fig. C.5). In particular the hypothesis on relative abundance has little impact on the estimation of the thermal pressure, while we have seen that it has a strong influence on the volume density. Estimations made with or without 12CO are consistent in most cases. The thermal pressure for the pixels associated with dense cores where C18O and H13CO+ are detected with high S/N is somewhat higher when using C18O and H13CO+ only as compared with sets including 12CO but the effect is small. The better accuracy of the thermal pressure estimations can be understood by looking at the shape of the NLL function in the (
separately (see Fig. C.5). In particular the hypothesis on relative abundance has little impact on the estimation of the thermal pressure, while we have seen that it has a strong influence on the volume density. Estimations made with or without 12CO are consistent in most cases. The thermal pressure for the pixels associated with dense cores where C18O and H13CO+ are detected with high S/N is somewhat higher when using C18O and H13CO+ only as compared with sets including 12CO but the effect is small. The better accuracy of the thermal pressure estimations can be understood by looking at the shape of the NLL function in the (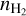 , Tkin) parameter space. This is discussed in Sect. 4.
, Tkin) parameter space. This is discussed in Sect. 4.
3.4 Intermediate summary
In this section, we have systematically compared the results of line fits with the RADEX non-LTE radiative transfer model, on the same dataset with the same fitting algorithm. The main difference between the different experiments has been the number and the set of fitted lines. The fitted parameters have been the column densities of the 13CO and HCO+ isotopologues, and the associated kinetic temperature and volume density. We have also studied the derived relative abundances and thermal pressure.
This systematic comparison emphasizes the potential variability of the estimated parameters depending on the chosen set of fitted species and lines. The joint histograms of the same fitted parameters as a function of the fitting assumptions show not only important scatter around the line of slope 1 but also biases with respect to this line. The maps of fitted parameters show regular patterns, suggesting that the noise level is not the cause of the found variations. The volume density is the least accurate estimated parameter, followed by the kinetic temperature. The thermal pressure estimates are more accurate than the volume density and kinetic temperature. The column densities and, above all, the ratio of column densities are the most accurate fitted parameters.
We do not address here whether the quality of the fit allows us to define which set of species and associated assumptions best fits the data for two reasons. First, we here explore the impact of the typical analysis of line data where the best solution is selected by minimizing the negative log-likelihood of the fit for a fixed set of species. Second, fitting a subset of lines necessarily leads to smaller χ2, but this does not imply that estimations are better. Third, comparing the quality of fit performed with different numbers of unknown parameters requires more advanced statistical tools than just the χ2 value to select the “best” estimations. For instance, when the abundance are estimated instead of being fixed, the χ2 is necessarily smaller, but this does not imply that the estimation is better, notably because of the induced estimation variance. This topic will be studied in a future paper.
Input physical parameters for the two experiments
Line characteristics for experiment #1.
Line characteristics for experiment #2.
4 On the importance of prior assumptions on the bias-variance tradeoff
In the previous section, we tried to estimate the gas volume density and kinetic temperature in addition to the molecular column densities, when fitting different combinations of the CO and HCO+ main isotopologue lines together. This requires some additional a priori knowledge linking the parameters so that the number of unknowns becomes smaller than the number of constraints, and the associated confidence interval become “reasonably” small. In particular, we make the hypothesis that the same region along the LoS dominates the emission of all lines, with a unique volume density and kinetic temperature. We also make chemical assumptions in the form of fixed relative abundances. However, a priori knowledge may turn into estimation biases if the assumptions happen to be incorrect. This problem is the well-known variance vs. bias tradeoff. In this section, we will study this tradeoff on simulated data in order to identify potential sources of bias.
4.1 Description of the experiments and associated line characteristics
To do this, we choose input physical conditions based on the estimations computed in Sect. 3 on actual data towards the Horsehead nebula. We choose a pixel at the edge of the central dense core (black point in Fig. 1), for which the fit on actual data shows different values of kinetic temperature and volume density, depending on the set of species studied. In particular, analyzing just the 13CO and C18O lines provides nonphysical solutions (large kinetic temperature and small volume density compared to standard dense core values). Meaningful values for kinetic temperature and volume density are only obtained when adding different species.
Table 5 lists the parameters for two experiments sampling typical conditions for this pixel. In experiment #1, the gas is warm (~27 K) and moderately dense (~4.5 × 103 cm−3). In experiment #2, the gas is colder (~22 K) and denser (~4.5 × 104 cm−3). Tables 6 and 7 list the characteristics of the lines for experiment #1 and #2, respectively. In this section, calibration errors and thermal noise are treated as follows. On one hand, when generating the spectra, we use the model described in Sect. 3 to simulate data with calibration errors and thermal noise. We directly use a thermal noise level that will give a maximum S/N value of 10, except for the low S/N line H13CO+. On the other hand, when fitting the spectra, we use the likelihood that only takes into account the additive noise as in the fit of the actual data in Sect. 3. As explained there, this allows the low S/N lines to contribute to the fit.
Figure 5 compares the associated typical profiles of the spectra. For each experiment, we have computed 200 Monte-Carlo realizations with white Gaussian drawings for the thermal noise and calibration error. We fitted the obtained spectra with the maximum likelihood estimator described in Sect. 2.4. We thus sample the probability distribution function of the fitted parameters.
In experiment #1, the peak S/N of H13CO+ (1 − 0) is low (~1.5) and this line has a probability of detection of 63%, whereas all the lines are detected in experiment #2, i.e., the peak S/N ≳ 5.
The 12CO (1 − 0) line has a large opacity (τ > 50) in both experiments and its excitation temperature is equal to the kinetic temperature. This can be understood as a consequence of the significantly large volume density of the gas with respect to the line’s effective critical density. Very large opacities deliver flat-top line profiles that are not found in actual observations of 12CO (1 − 0) lines in interstellar clouds. The absence of flat topped 12CO profiles shows that even 12CO probes into the cloud instead of just its surface because of the large velocity gradients along the LoS. This example shows that just fitting the integrated line emission is not sufficient. Estimating the goodness of fit requires a comparison between the modeled and measured line profiles. For this reason, we only used the peak emission of the 12CO (1 − 0) line, but we did fit the whole profile for the other species, including 13CO and C18O.
The 13CO and C18O lines have different excitation regimes depending on the experiment. In experiment #2, where the volume density is one order of magnitude larger than the (thin and effective) critical densities, both the (1 − 0) and (2 − 1) lines are close to the local thermodynamic equilibrium (LTE), i.e., their excitation temperature is close to the kinetic temperature. However, in experiment #1, where the volume density is of the same order of magnitude as the (thin and effective) critical densities, only the 13CO (1 − 0) line is close to LTE. The 13CO and C18O (2 − 1) lines are sub-thermally excited, and the C18O (1 − 0) line is supra-thermally excited. Such a regime of suprathermal excitation of the low- J CO lines has already been pointed out by Leung & Liszt (1976). The HCO+ and H13CO+ (1 − 0) lines are sub-thermally excited in both experiments.
The C18O (1 − 0) and (2 − 1) lines, as well as the H13CO+ (1 − 0) line, are optically thin in both experiments. The 13CO lines have similar opacities (1 and 3 – 4 for the (1 − 0) and (2 − 1) lines) in both experiments. The opacity of the HCO+ (1 − 0) line is three times larger in experiment #1 than in experiment #2 where the lowest energy levels are much less populated because the density is higher.
 |
Fig. 5 Comparison of the ideal (in red) line profiles with noisy (in blue) ones for experiment #1 and #2 (see Table 5). In the legends, c is the estimated calibration factor (see Eq. (17)). |
4.2 Structure of the figures
Figures 6 to 8 show the comparison between the Cramér-Rao bound reference precision and the parameters fitted on Monte-Carlo drawings of noisy RADEX models for experiments #1 and #2. In the three figures, the top row describes the RADEX input parameters. The next rows show the results obtained when fitting different sets of lines. We first show the results when the assumptions are consistent between the model used to generate the data and the fitted spectra. We then show the results when these fitting assumptions are “biased” (e.g., simplified) with respect to the (true) generative models. In these cases, the bottom row lists the values of the parameters of the generative models, which are modified compared to the top row, i.e., these changes are ignored when fitting the spectra.
The first column describes the set of lines used and the kind of assumptions made (biased or unbiased) during the fits. The next two columns then compare the estimated column densities for both experiments. The estimated column densities are shown as scatter plots, except for the second row of Fig. 6 where only one species is fitted. In this specific case, we compare the histogram from the Monte-Carlo experiment (in green) with the normal density of an unbiased efficient estimator (i.e., with a mean equal to the true input value, and a variance equal to the CRB of log N) in red. The last two columns show the scatter plots of the estimated kinetic temperature and volume density.
In these figures, the green dots correspond to the estimated parameters obtained on the 200 independent realizations of the Monte-Carlo experiments. The red ellipse is a confidence region centered on the true parameters. Its size and orientation is computed from the Cramér-Rao bound matrix. The percentage of realizations that lie in this confidence ellipse is mentioned in the legend of the graph. Any unbiased efficient estimator will deliver 99% ± 1% of its estimations inside the confidence ellipse.
When the temperature and volume density vary among the species, the red cross indicates the true values for 13CO and/or C18O, and the black cross indicates the true values for the other species (12CO or HCO+). This allows us to visualize the effect of the biased a priori knowledge on the fit. The axes and associated uncertainties are computed on the logarithm of the estimated parameters. In Figs. 7 and 8, where the abundance ratios of the column densities is assumed fixed during the fit, the estimated values lie on a straight lines, and the confidence ellipses become straight lines as well. In other words, the estimation of these column densities are perfectly correlated, as expected.
The Tkin vs. 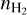 scatter plots are overlaid on the variations of the negative log-likelihood as a function of Tkin and
scatter plots are overlaid on the variations of the negative log-likelihood as a function of Tkin and 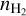 . In all generality, the negative log-likelihood variations lie in a space of dimension larger than two (the true value of estimated parameters). However, as explained in Appendix B.2, the variations of the negative log-likelihood can be projected on the 2D sub-space for the couple of parameters (Tkin,
. In all generality, the negative log-likelihood variations lie in a space of dimension larger than two (the true value of estimated parameters). However, as explained in Appendix B.2, the variations of the negative log-likelihood can be projected on the 2D sub-space for the couple of parameters (Tkin, 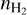 ) because the maximum likelihood estimator assumes that all species have the same Tkin and
) because the maximum likelihood estimator assumes that all species have the same Tkin and 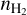 . The images thus show the projection of the 4D matrix of negative log-likelihood onto the plane (
. The images thus show the projection of the 4D matrix of negative log-likelihood onto the plane (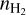 , Tkin) by choosing the column density (N) and velocity dispersion (σV) that maximize it for each value of (
, Tkin) by choosing the column density (N) and velocity dispersion (σV) that maximize it for each value of (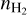 , Tkin).
, Tkin).
This projection of the negative log-likelihood is shown for the ideal realization of the RADEX model without Gaussian noise. While the shape of the negative log-likelihood varies slightly with the noise realization, its minimum location that yields the values of the estimated parameters may change drastically depending on the specific noise realization. This explains why the estimated parameters shown as green dots explore the blue valleys in these images. Finally, the effective critical densities of the different lines are overlaid as dotted vertical lines.
 |
Fig. 6 Comparison of the performances of our maximum likelihood estimator for the estimation of the column densities (Cols. #2 and #3) and the couple (Tkin, |
 |
Fig. 7 Same as Fig. 6 except that 1) the couple of species used to estimate the parameters are 13CO and HCO+, and 2) the biases on the RADEX model are imposed on the HCO+ species. |
 |
Fig. 8 Same as Fig. 6 except that 1) the couple of species used to estimate the parameters are C18O and H13CO+, and 2) the RADEX model are not biased. |
4.3 Results for the column densities
Figures 6 to 8 show that the column densities are derived with a low variance (high certainty). Biased hypotheses on kinetic temperature and volume densities do not influence the column density values much. In contrast, biased hypotheses on abundance ratios bias the derived column densities.
For most of the cases, more than 95% of the estimated column densities (13CO, C18O, HCO+, or H13CO+) are in the confidence ellipse, illustrating the good performance of the Maximum Likelihood Estimator (MLE). The variance on the column density reduces as the number of assumptions implemented in the estimator increases. For some scenario (e.g., first row of Fig. 6, experiment #2), enforcing the volume density to be smaller than 106.5 cm−3 provides column density estimations with smaller variance than the one predicted by the CRB.
The effects of biased assumptions depend on the case. On one hand, assuming a too low kinetic temperature or a too high volume density for 12CO does slightly bias the estimated column densities of 13CO and C18O (fifth row of Fig. 6), but they remain inside the CRB ellipses. Similarly, assuming an incorrect abundance ratio for N(12CO)/N(13CO) does not impact the values of the column densities of 13CO or C18O much. This is probably due to the fact that only the peak intensity of the 12CO (1 − 0) line is used to constrain the kinetic temperature. On the other hand, assuming an abundance ratio for N(13CO)/N(HCO+) twice as low as the true values artificially increases the column density of 13CO and decreases the column density of HCO+. The bias introduced on N(13CO) is smaller than the one on N(HCO+).
4.4 Results for the kinetic temperature and the volume density
The situation for the physical conditions (the kinetic temperature and volume density) is different. In this section, we first compare the shape of the negative log-likelihood as a function of the kinetic temperature and volume density in the different cases. We then analyze the variances and biases of these parameters for the two experiments separately.
4.4.1 Shape of the negative log-likelihood image
The shape of the NLL significantly depends on the combination of lines/species used, in particular on their effective critical densities. When fitting only the CO isotopologue lines (Fig. 6), the minimum of the NLL has the shape of a valley at approximately constant thermal pressure 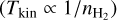 below a density of ~ 104 cm−3 and constant temperature above this density. When fitting 𝒮{13CO, HCO+} (Fig. 7), the shape of the NLL minimum (blue) region is more complex. For experiment #1, where the modeled gas has Tkin = 27.1 K and
below a density of ~ 104 cm−3 and constant temperature above this density. When fitting 𝒮{13CO, HCO+} (Fig. 7), the shape of the NLL minimum (blue) region is more complex. For experiment #1, where the modeled gas has Tkin = 27.1 K and 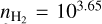 cm−3 (i.e., a thermal pressure of ~1.2 × 105 K cm−3), it is bounded at an approximately low constant temperature of ~ 15 K and at an approximately constant pressure of ~ 2 × 105 K cm−3. However, the chance of getting a second local NLL minimum at a
cm−3 (i.e., a thermal pressure of ~1.2 × 105 K cm−3), it is bounded at an approximately low constant temperature of ~ 15 K and at an approximately constant pressure of ~ 2 × 105 K cm−3. However, the chance of getting a second local NLL minimum at a 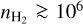 cm−3 exists and it increases in experiment #2, where the modeled gas has Tkin = 22.1 K and
cm−3 exists and it increases in experiment #2, where the modeled gas has Tkin = 22.1 K and 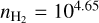 cm−3 (i.e., a thermal pressure of ~ 106 K cm−3). This implies that some ambiguity between a low and a high volume density solution can occur. The shape is qualitatively similar for 𝒮{C18O, H13CO+}. However, many estimations are localized on the second local maxima in experiment #2 because the two local maxima gets closer to each other compared to experiment #1 (see Cols. 3 and 4 of Fig. 8).
cm−3 (i.e., a thermal pressure of ~ 106 K cm−3). This implies that some ambiguity between a low and a high volume density solution can occur. The shape is qualitatively similar for 𝒮{C18O, H13CO+}. However, many estimations are localized on the second local maxima in experiment #2 because the two local maxima gets closer to each other compared to experiment #1 (see Cols. 3 and 4 of Fig. 8).
4.4.2 Experiment #1
The maximum likelihood estimator (MLE) only becomes efficient (most of the dots gather inside the CRB ellipse) and the variation of the estimation decreases quickly when relevant information is delivered by adding lines.
In Fig. 6, the confidence ellipse for 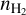 covers 2 orders of magnitude when studying 𝒮 {13CO}, one order of magnitude when studying 𝒮{13CO, C18O}, and a factor 1.9 when studying 𝒮{12CO, 13CO, C18O}. The confidence ellipse for Tkin covers about 1 order of magnitude when studying either 𝒮{13CO} or 𝒮{13CO, C18O}, and a factor 1.4 when studying 𝒮{12CO, 13CO, C18O}. Adding the information about the peak temperature of a very optically thick line at LTE as 12CO (1 − 0) allows us to constrain the temperature.
covers 2 orders of magnitude when studying 𝒮 {13CO}, one order of magnitude when studying 𝒮{13CO, C18O}, and a factor 1.9 when studying 𝒮{12CO, 13CO, C18O}. The confidence ellipse for Tkin covers about 1 order of magnitude when studying either 𝒮{13CO} or 𝒮{13CO, C18O}, and a factor 1.4 when studying 𝒮{12CO, 13CO, C18O}. Adding the information about the peak temperature of a very optically thick line at LTE as 12CO (1 − 0) allows us to constrain the temperature.
A combination of optically thick and thin lines improves the determination of the density by an order of magnitude (case 𝒮{13CO, C18O}). But the volume density only becomes well constrained at the same time as the temperature when adding the fit of the 12CO (1 − 0) peak temperature. Figure 7 indicates that the fitting of 𝒮{13CO, HCO+} delivers small uncertainty intervals compared to, e.g., the fitting of 𝒮{13CO, C18O}. Increased precision here is not a question of the S/N, as the S/N of C18O is higher than that of HCO+, but of difference in the critical density. Indeed, the effective critical density of the HCO+ (1 − 0) line is more than one order of magnitude greater than those for the two 13CO lines (see vertical lines).
Having lines of different critical densities is, however, not always sufficient. In Fig. 8, the uncertainties of the kinetic temperature and volume density are about one order of magnitude each when fitting 𝒮{C18O, H13CO+} whose critical densities differ by more than one order of magnitude. In this case, all lines are optically thin, implying a degeneracy between temperature and density, the pressure being relatively well constrained. We verified that the 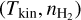 degeneracy remains when increasing the S/N of the H13CO+ line by decreasing the noise level σb by a factor 10.
degeneracy remains when increasing the S/N of the H13CO+ line by decreasing the noise level σb by a factor 10.
Assuming that the spatial portion of the LoS that dominates the emission of the lines is identical for the 12CO line and its rare isotopologues slightly biases the estimation to high kinetic temperatures and low volume densities (row 4 of Fig. 6). This confirms that the kinetic temperature is above all constrained by the peak temperature of the 12CO (1 − 0) line. In the test where the generative model assumes that the HCO+ line emission comes from gas at a slightly different temperature and volume density than the gas producing the 13CO emission (2nd row of Fig. 7), the kinetic temperature becomes highly biased. As we know that dense cores and filaments are surrounded by a more diffuse, lower density and warmer envelope, a multi-layer model could be more suited in this case. This will be the subject of another article.
Assuming an N(13CO)/N(HCO+) abundance ratio lower than reality by a factor 2 positively biases the estimated volume density by a factor 2 as shown in the fourth row of Fig. 7. The main difference with the impact of biases on the column densities is that a majority of the estimations lies outside the CRB ellipses.
4.4.3 Experiment #2
Several significant differences exist between Experiment #1 and Experiment #2. While the accuracy of the temperature increases significantly when adding the constraint from the 12CO (1 − 0) peak temperature, no information on the volume density can be recovered in experiment #2, when using only the CO isotopologue lines. The CRB interval of confidence for 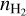 covers the full range of explored densities. This is due to the fact that all lines get close to the LTE state (see the excitation temperature in Table 7) where only the kinetic temperature determines the excitation of the species.
covers the full range of explored densities. This is due to the fact that all lines get close to the LTE state (see the excitation temperature in Table 7) where only the kinetic temperature determines the excitation of the species.
The fifth column of Fig. 7 shows that improving the 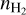 estimation requires us to analyze a line or species with a higher effective critical density than the considered CO isotopologue lines. But here again, this is only true when some of the fitted lines are optically thin and others are optically thick in order to lift the degeneracy between kinetic temperature (kinetic energy of collisions) and volume density (number of collisions) during the excitation of the species. Moreover, Fig. 8 shows that there exist ambiguities between the two local minima of the NLL at the true volume density of the generative model or at a much higher density value.
estimation requires us to analyze a line or species with a higher effective critical density than the considered CO isotopologue lines. But here again, this is only true when some of the fitted lines are optically thin and others are optically thick in order to lift the degeneracy between kinetic temperature (kinetic energy of collisions) and volume density (number of collisions) during the excitation of the species. Moreover, Fig. 8 shows that there exist ambiguities between the two local minima of the NLL at the true volume density of the generative model or at a much higher density value.
Just like experiment #1, an underestimation of the a priori knowledge on the abundance ratio between 13CO and 12CO leads to an overestimation of 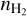 , but the induced bias, which can be observed in the fourth row of Fig. 6, is much more important here: almost a factor 10. Not only is the volume density biased, but even worse, the observed variance is small. This means that the observer obtains a region with low spatial variance for the estimated parameters when the maximum likelihood estimator is applied to several pixels, thus giving an incorrect impression of the robustness of the results. Such an example shows that a physical or chemical misspecification in the hypotheses of the model used to fit the data can lead to incorrect estimates of the fitted parameters, most notably the kinetic temperature and/or the volume density.
, but the induced bias, which can be observed in the fourth row of Fig. 6, is much more important here: almost a factor 10. Not only is the volume density biased, but even worse, the observed variance is small. This means that the observer obtains a region with low spatial variance for the estimated parameters when the maximum likelihood estimator is applied to several pixels, thus giving an incorrect impression of the robustness of the results. Such an example shows that a physical or chemical misspecification in the hypotheses of the model used to fit the data can lead to incorrect estimates of the fitted parameters, most notably the kinetic temperature and/or the volume density.
One possible explanation of this bias is that since 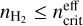 , the non-LTE excitation model feeds the line upper level with more collisions to compensate for the underestimation of N(HCO+) in order to produce a sufficiently bright HCO+ (1 − 0) line.
, the non-LTE excitation model feeds the line upper level with more collisions to compensate for the underestimation of N(HCO+) in order to produce a sufficiently bright HCO+ (1 − 0) line.
4.5 Intermediate summary
We have studied the estimation of the column densities, kinetic temperatures, and volume densities when fitting different combinations of the CO and HCO+ isotopologue lines with the RADEX escape probability model, on two example lines of sight. While the Cramér-Rao bound is a lower limit for the variance of any unbiased estimator, we here confirm that this lower limit can be reached by a “standard” maximum likelihood estimator, provided that the assumptions used during the fitting process are consistent (i.e., unbiased) with respect to reality (generative model).
Estimations of the column density are efficient on the considered examples, even when the uncertainty (CRB) on 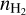 or Tkin are large. This means that the escape probability models provide robust estimations of column densities allowing for the production of maps in a wide variety of situations, which can be quantitatively characterized a priori with ℬ1/2(log N) < 0.1. Assuming an incorrect abundance ratio for, e.g., N(13CO)/N(HCO+) biases the estimation of log(N(HCO+)) more than the estimation of log(N(13CO)).
or Tkin are large. This means that the escape probability models provide robust estimations of column densities allowing for the production of maps in a wide variety of situations, which can be quantitatively characterized a priori with ℬ1/2(log N) < 0.1. Assuming an incorrect abundance ratio for, e.g., N(13CO)/N(HCO+) biases the estimation of log(N(HCO+)) more than the estimation of log(N(13CO)).
Likewise, we confirm that CRB precisions for the volume density and kinetic temperature can be achieved by a “standard” maximum likelihood estimator when ℬ1/2(log Tkin) < 0.1, and 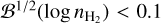 . A good estimation of the kinetic temperature and volume density requires a combination of high-enough S/N lines of different opacities (thick and thin) and effective critic. al densities. On one hand, this is delivered by the fit of 𝒮{12CO, 13CO, C18O} in experiment #1, where
. A good estimation of the kinetic temperature and volume density requires a combination of high-enough S/N lines of different opacities (thick and thin) and effective critic. al densities. On one hand, this is delivered by the fit of 𝒮{12CO, 13CO, C18O} in experiment #1, where 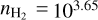 cm−3 and Tkin = 27.1 K. In this case, a perfect knowledge of N(12CO)/N(13CO) is not required, but an incorrect assumption about the gas temperature that emits the 12CO line biases both the kinetic temperature and the volume density. This is consistent with the fact that the 12CO peak is mostly useful to regularize the estim} ation of Tkin. On the other hand, fitting 𝒮{12CO, 13CO, C18O} in experiment #2, where
cm−3 and Tkin = 27.1 K. In this case, a perfect knowledge of N(12CO)/N(13CO) is not required, but an incorrect assumption about the gas temperature that emits the 12CO line biases both the kinetic temperature and the volume density. This is consistent with the fact that the 12CO peak is mostly useful to regularize the estim} ation of Tkin. On the other hand, fitting 𝒮{12CO, 13CO, C18O} in experiment #2, where 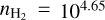 cm−3 and Tkin = 22.1 K, fails to constrain the volume density, in agreement with the fact that the low-J lines of the CO isotopologues have almost reached LTE.
cm−3 and Tkin = 22.1 K, fails to constrain the volume density, in agreement with the fact that the low-J lines of the CO isotopologues have almost reached LTE.
Fitting a set of lines that have different critical densities enlarges the range of (Tkin, 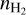 ) values for which the kinetic temperature and volume density can be estimated as long as some of the lines are optically thin and others optically thick. An incorrect assumption on the abundance ratio between 13CO and HCO+ biases the estimation of the temperature and density because the corresponding (1 − 0) lines have different effective critical densities.
) values for which the kinetic temperature and volume density can be estimated as long as some of the lines are optically thin and others optically thick. An incorrect assumption on the abundance ratio between 13CO and HCO+ biases the estimation of the temperature and density because the corresponding (1 − 0) lines have different effective critical densities.
5 Parametric study of the reference precisions on the column densities, kinetic temperature, volume density and thermal pressure
The Cramér-Rao bound gives the reference precision that can be achieved by an unbiased and efficient estimator for a given physical model (here RADEX) and observational setup (combination of lines and noise levels). In the previous section, we studied two specific combinations of physical conditions for a molecular cloud. We now extend this quantitative study to a large domain of physical conditions that can be constrained with a suitable precision for different combinations of species, associated lines, and a priori knowledge linking them.
We will restrict the combination of species to the CO and HCO+ main isotopologues and the combination of lines to the (1 − 0) transition for all species, plus the (2 − 1) transition for the 13CO and C18O species. In more details, we will study the information that can be extracted in the following sets of observations: 1) We analyze in depth the simplest case, i.e., when only the (1 − 0) and (2 − 1) lines of 13CO are available. 2) We then quantify the gain in precision when adding the same lines of the rarer C18O isotopologue. 3) We also compare the benefits of two different combinations of one CO isotopologue with one isotopologue of HCO+. We will combine C18O and H13CO+ that are easy to observe in dense cores, but also 13CO and H12CO+ that are better suited to probe the lower volume density envelope. 4) We quantify the gain in precision when adding the constraint from the peak temperature of the 12CO (1 − 0) lines to the previous combinations of species and lines. 5) We then quantify the loss of information when only the lowest J line of 13CO and C18O are available. This is of particular interest for the ORION-B project that mapped a large fraction of the Orion B cloud between 70 and 116 GHz. 6) We finally check the potential advantage of fixing the relative abundances.
For these studies, we will explore the variations of the precision in the two-dimensional space: column density of molecular hydrogen (1020 ≤ N(H2) ≤ 1024 cm−2) vs. its volume density 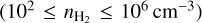 . The other parameters to generate the model and compute the CRB are as follows.
. The other parameters to generate the model and compute the CRB are as follows.
Physical parameters. A kinetic temperature of 22 K, a velocity dispersion of 0.32 km s−1, and a centroid velocity of 0 km s−1.
Chemical abundances. We use those defined in Eq. (16) in Sect. 3, plus the following 13CO abundance relative to molecular hydrogen
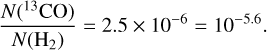 (22)
(22)
The range of studied column densities for the different species has been adapted so that it fits the range of molecular hydrogen column densities, given the chosen relative abundances.
5.1 Typical figure layout
The first column of Fig. 9, as well as Figs. 11–13 compare the CRB reference precisions when combining different low-J lines of different species. This precision is plotted for different values of column densities (y-axes) and volume densities (x-axes). The values of the parameters that are fixed when generating the RADEX spectra are listed in the bottom row. The reference precision depends on the a priori assumptions that are taken into account by the estimator. These are listed in the second row from the top. From top to bottom, the panels show the precisions on the species column densities, and gas kinetic temperature, volume density, and thermal pressure.
For any parameter x, ℬ1/2(log x) is equal to the standard deviation of any unbiased and efficient estimators of log x. Table 8 lists the relationship between ℬ1/2(log x) and the associated relative interval of confidence on x and the adopted color code. We are going from a ± 1σ interval to a multiplicative factor interval of [10−σ, 10+σ]. A ± 1σ value of 0.03 gives a relative confidence interval of the same order of magnitude as the calibration error (5-10%). A ± 1σ value of 0.1 corresponds to a multiplicative uncertainty of the order of 20%. This is considered a good precision for the column density and kinetic temperature. Values of 0.3 and 0.6 for ± 1σ give a precision within a factor of 2 and 4, respectively. Getting a reliable estimate of the volume density at this precision level would already be a great achievement. Values of 1 and 2 for ± 1σ deliver an uncertainty that covers between two and four orders of magnitude. The associated parameters are too uncertain to be useful.
In order to emphasize these different ranges of relative precisions, the maps of ℬ1/2(log x) are systematically color-coded throughout the paper as follows: green means good to excellent relative precisions, yellow and orange standard relative precisions, and red to pink poor relative precisions. The grey color is used to indicate the parameter space where the precision is so low that we consider that the lines deliver no information on the considered parameter.
5.2 A simple case:13 CO (1-0) and (2-1)
Figure 9 compares the CRB reference precisions with the main characteristics of the (1 − 0) and (2 − 1) lines for 13CO. The precisions depend much on the considered physical parameter.
5.2.1 Precision of the column density
The column density is the easiest parameter to estimate. It can be estimated within a factor of two for a large variety of column and volume densities. However the range of column densities with a good precision decreases from three orders of magnitude at low volume density to 0.5 order of magnitude at high volume density.
A precision better than 25% can only be reached for volume densities lower than 5 × 103 cm−3 and a column density between 1021.5 and 1022.5cm−2. The latter conditions imply τ(1−0) < 10, τ(2−1) > 1, and 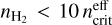 for the two lines. The influence of the opacity can be interpreted as a trade-off between having a sufficiently high S/N while avoiding a loss of information on the column density because the line intensities saturate. The influence of
for the two lines. The influence of the opacity can be interpreted as a trade-off between having a sufficiently high S/N while avoiding a loss of information on the column density because the line intensities saturate. The influence of 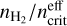 is more complex but can be related to the radiative pumping effect at high column densities and low volume densities.
is more complex but can be related to the radiative pumping effect at high column densities and low volume densities.
 |
Fig. 9 Comparison of the CRB reference precisions (left column) on the column density, kinetic temperature, volume density, and thermal pressure, when fitting the 13CO (1 − 0) and 13CO (2 − 1) lines, with these lines main characteristics (right column): S/Ns, opacities, ratios of the volume density to the effective critical densities, and ratios of the excitation temperature over the kinetic temperature. The blue and red curves show the results for the (1 − 0) and (2 − 1) lines, respectively. The values of the parameters that are fixed when generating the RADEX spectra are listed in the bottom row. The a priori knowledge that are used when computing the CRB precisions are listed in the second row. |
5.2.2 Precision on the kinetic temperature
The kinetic temperature can be estimated within a factor of two in a narrower range of conditions that typically spans one order of magnitude for the column density around N(H2) = 1022.3 cm−2 when the volume density is larger than the optically thin critical density ~ 103 cm−3.
A precision better than 25% can only be reached in a different parameter space from the one that maximimizes the precision on the column density. It corresponds to a column density 1022.1 < N(H2) < 1022.6 cm−2 for 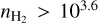 cm−3. This implies similar conditions for the line opacities (τ(1−0) < 10, τ(2-1) > 1), but a different condition on the line critical density
cm−3. This implies similar conditions for the line opacities (τ(1−0) < 10, τ(2-1) > 1), but a different condition on the line critical density 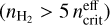 .
.
For high opacity, Eq. (1) simplifies at its peak value to s ≃ J(Tex) − J(TCMB). Moreover, when 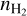 is sufficiently above
is sufficiently above 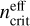 , the local thermodynamic equilibrium is reached, and Tex = Tkin for both lines. It thus makes sense that the estimation of Tkin can be accurate when these conditions are met. It is counterintuitive that the precision decreases when the 13CO column density increases above 1017cm−2 and
, the local thermodynamic equilibrium is reached, and Tex = Tkin for both lines. It thus makes sense that the estimation of Tkin can be accurate when these conditions are met. It is counterintuitive that the precision decreases when the 13CO column density increases above 1017cm−2 and 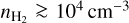 cm−3. Indeed, the approximation s ≃ J(Tkin) − J(TCMB) is expected to be valid under these conditions, and the gas is expected to be at local thermodynamic equilibrium.
cm−3. Indeed, the approximation s ≃ J(Tkin) − J(TCMB) is expected to be valid under these conditions, and the gas is expected to be at local thermodynamic equilibrium.
To understand this phenomenon, we compare in Fig. 10 the spectra of the lines for the (1 − 0) to (4 − 3) transitions of 13CO for two different pairs of 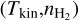 values, (22 K, 105 cm−3) and (60 K, 101.65 cm−3), and logarithms of the column densities that differ by the precision we aim for, i.e., 0.1: N(13CO) = 1018 cm−2 or 1017.9 cm−2. The (1 − 0) and (2 − 1) line have similar profiles within the calibration uncertainty for these two sets of conditions, implying uncertain kinetic temperatures and column densities. An ambiguity therefore remains between a high density, low kinetic temperature case, and a low density, high kinetic temperature case, even for a large molecular column density2. Table 9 lists the main parameters of the lines shown in Fig. 10. It shows that only Tex are significantly different between the blue and red profiles, and LTE is not reached for the red profiles.
values, (22 K, 105 cm−3) and (60 K, 101.65 cm−3), and logarithms of the column densities that differ by the precision we aim for, i.e., 0.1: N(13CO) = 1018 cm−2 or 1017.9 cm−2. The (1 − 0) and (2 − 1) line have similar profiles within the calibration uncertainty for these two sets of conditions, implying uncertain kinetic temperatures and column densities. An ambiguity therefore remains between a high density, low kinetic temperature case, and a low density, high kinetic temperature case, even for a large molecular column density2. Table 9 lists the main parameters of the lines shown in Fig. 10. It shows that only Tex are significantly different between the blue and red profiles, and LTE is not reached for the red profiles.
This example shows the power of the Cramér-Rao bound. It quantifies the precision that any unbiased efficient estimator will reach for a given model, independent on the physical insight we can have. Indeed, assuming that the peak temperature of the spectra is a good approximation of the kinetic temperature for optically thick lines is an a priori knowledge that would change the model of Eq. (1), and thus the CRB computation. When the RADEX model is used for fitting noisy data without this a priori knowledge, the precision on the kinetic temperature and column density decreases significantly. Two other possibilities to increase the precision would be to average many observations of the (1 − 0) or (2 − 1) lines to decrease the noise level and the uncertainty of the calibration or to add the observations of the (3 − 2) or (4 − 3) lines with enough S/N because their profiles are much more sensitive to the variations of the physical conditions. A gain of a factor 10 on the precision of the estimation of σb is approximately required to gain the same factor on the estimation of the kinetic temperature. Adding lines is thus a better strategy than increasing the integration time because the required integration time to actually detect a new line is often significantly lower than the additional time needed to improve the S/N and calibration uncertainty on an already detected line.
 |
Fig. 10 Comparison of the spectral shape of the (1 − 0) (top) to (4 − 3) (bottom) lines of 13CO for two different combinations of kinetic temperature, volume density, and column density. The plain blue and dashed red histograms show the spectra for (22 K, 105 cm−3,1018 cm−2) and (60 K, 101.65 cm−3, 1017.9 cm−2), respectively. The lines share the same centroid velocity CV = 0 km s−1 and velocity dispersion σV = 0.32 km s−1. The two sets of physical conditions deliver degenerate spectral profiles within the noise level for the (1 − 0) and (2 − 1) lines. Additional information, e.g., the (3 − 2) or (4 − 3) lines, is needed to lift this degeneracy. |
5.2.3 Precision of the volume density or thermal pressure
The precision of the volume density is at best a factor of 4 for a small region around 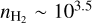 cm−3 and N(H2) ~ 1022 cm−2. As expected, when Tex ≃ Tkin, the local thermal equilibrium is reached, and the line loses any sensitivity to the volume density. When
cm−3 and N(H2) ~ 1022 cm−2. As expected, when Tex ≃ Tkin, the local thermal equilibrium is reached, and the line loses any sensitivity to the volume density. When 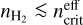 , the line becomes sensitive either to the volume density or to the thermal pressure. It is well known that when the lines become optically thin, the excitation is controlled by the product of the volume density and kinetic temperature, namely, the thermal pressure. The independent determination of the volume density and the kinetic temperature is difficult (the shape of their CRB are similar at low densities), while the thermal pressure can be determined to within a factor of two. It can therefore be interesting to derive thermal pressure maps of molecular clouds, which can be compared with maps of the magnetic or turbulent pressure.
, the line becomes sensitive either to the volume density or to the thermal pressure. It is well known that when the lines become optically thin, the excitation is controlled by the product of the volume density and kinetic temperature, namely, the thermal pressure. The independent determination of the volume density and the kinetic temperature is difficult (the shape of their CRB are similar at low densities), while the thermal pressure can be determined to within a factor of two. It can therefore be interesting to derive thermal pressure maps of molecular clouds, which can be compared with maps of the magnetic or turbulent pressure.
5.2.4 Effective critical density versus excitation temperature
While the ratios of the volume density to the effective critical density show similar behaviors for the (1 − 0) and (2 − 1) lines, the ratios of the line excitation temperatures to the gas kinetic temperature behave quite differently for 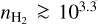 cm−3 and N(H2) ≤ 1022 cm−2. In this region Tex(1 − 0) ≳ Tkin. This is the sign that the J = 1 energy level becomes super-thermally excited. While this inversion of population effect is moderate, it happens in a region of (Tkin,
cm−3 and N(H2) ≤ 1022 cm−2. In this region Tex(1 − 0) ≳ Tkin. This is the sign that the J = 1 energy level becomes super-thermally excited. While this inversion of population effect is moderate, it happens in a region of (Tkin, 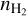 ) that is well represented in the Horsehead pillar.
) that is well represented in the Horsehead pillar.
5.3 One or two CO isotopologues
Figure 11 compares the precision that can be reached when studying either a single CO isotopologue (either 13CO or C18O) or their combinations. In all three cases we use their (1 − 0) and/or (2 − 1) lines, but we make no assumption on their abundances.
The two first columns compare the cases when using the two lines of either 13CO or C18O. As C18O and 13CO have similar values of Eup, vl and A (see Table 2), the shapes of the CRB variations in the N(H2), 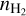 space are similar, but the results for the reference precisions with C18O are vertically shifted by the fixed abundance ratio N(13CO)/N(C18O) = 100.9 with respect to the reference precisions with 13CO. For a given N(H2) column density and noise level, this makes two major differences. First, the C18O lines will have lower S/N. This difference will only have an impact when the S/N becomes lower than 10 as this is our noise saturation level. Second, the C18O lines will often be optically thin when the 13CO lines will have a higher opacity, approaching the optically thick regime. These two effects imply that the C18O lines will be more suited to constrain gas with larger column densities than the 13CO lines for the same velocity dispersion.
space are similar, but the results for the reference precisions with C18O are vertically shifted by the fixed abundance ratio N(13CO)/N(C18O) = 100.9 with respect to the reference precisions with 13CO. For a given N(H2) column density and noise level, this makes two major differences. First, the C18O lines will have lower S/N. This difference will only have an impact when the S/N becomes lower than 10 as this is our noise saturation level. Second, the C18O lines will often be optically thin when the 13CO lines will have a higher opacity, approaching the optically thick regime. These two effects imply that the C18O lines will be more suited to constrain gas with larger column densities than the 13CO lines for the same velocity dispersion.
When we assume that the emission of 13CO and C18O is produced in gas with the same 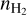 , Tkin, and velocity dispersion, the combinations of different opacities and S/Ns for the same rotational transition of two isotopologues will considerably modify the shape of the precision in the N(H2) vs.
, Tkin, and velocity dispersion, the combinations of different opacities and S/Ns for the same rotational transition of two isotopologues will considerably modify the shape of the precision in the N(H2) vs. 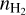 space. This corresponds to the physical situation where 13CO and C18O are co-located spatially. The last column of Fig. 11 shows the CRB reference precisions when using both isotopologues together.
space. This corresponds to the physical situation where 13CO and C18O are co-located spatially. The last column of Fig. 11 shows the CRB reference precisions when using both isotopologues together.
The most spectacular change on precision happens for the kinetic temperature. The low precision for Tkin at N(H2) ≃ 1023.6 cm−2 and 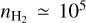 cm−3 is now replaced by an excellent precision. Adding an isotopologue therefore helps to resolve the ambiguity between low density-high temperature and high density-low temperature gas as discussed above. As the C18O lines have smaller opacities than the 13CO ones, the associated effective critical densities
cm−3 is now replaced by an excellent precision. Adding an isotopologue therefore helps to resolve the ambiguity between low density-high temperature and high density-low temperature gas as discussed above. As the C18O lines have smaller opacities than the 13CO ones, the associated effective critical densities 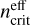 are closer to the optically thin critical densities, and we can expect that
are closer to the optically thin critical densities, and we can expect that 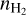 is more precisely estimated. Indeed, the best precision achieved on
is more precisely estimated. Indeed, the best precision achieved on 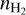 increased by a factor 2.
increased by a factor 2.
 |
Fig. 11 Comparison of the CRB precisions when combining the first two J transitions of one or two CO isotopologues. These reference precisions are plotted for different values of column densities (y-axes) and volume densities (x-axes). The values of the parameters that are fixed when generating the RADEX spectra are listed in the bottom row. The precision depends on the a priori knowledges that are taken into account by the estimator. These are listed in the second row. The first two columns show the precisions for a single CO isotopologue (13CO or C18O, while the last column shows the precisions when studying the 13CO and C18O isotopologues simultaneously. From top to bottom, the panels show the precisions on the 13CO and C18O column densities, kinetic temperature, volume density, and thermal pressure. The CRB precisions are color coded as listed in Table 8. |
 |
Fig. 12 Comparison of the CRB reference precisions for different combinations of two species and all their available lines. The layout of this figure is identical to Fig. 11, except for the combination of studied lines: the first column shows the precision when the (1 − 0) and (2 − 1) lines of the 13CO and C18O isotopologues are used. The last two columns study a combination of the one CO isotopologue with one HCO+ isotopologue: 13CO and H12CO+ on the second column and C18O and H13CO+ on the third column. |
5.4 Two CO isotopologues versus one CO plus one HCO+ isotopologues
Figure 12 compares the CRB reference precisions when studying two molecular species among four. The first column shows the precision for the two low-J lines of 13CO and C18O, while the last two columns combines the two low-J lines of one of the CO isotopologues with the (1 − 0) line of one of the HCO+ isotopologues.
As the effective critical density, 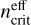 , of HCO+ (resp. H13CO+) is significantly larger than the one of 13CO (resp. C18O, see Table 6), we expect a significant gain in precision for
, of HCO+ (resp. H13CO+) is significantly larger than the one of 13CO (resp. C18O, see Table 6), we expect a significant gain in precision for 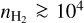 cm−3 compared to the estimations using only the 13CO and C18O lines. This is indeed the case for N(H2) column densities above 1021.1 cm−2 and below 1022.6 cm−2 for the 𝒮{13CO, HCO+} set of species, and for N(H2) column densities above 1022.2 cm−2 for the 𝒮{C18O, H13CO+} set. This is due to the lower abundance of C18O and H13CO+ that turns into lower opacities, and thus a greater sensitivity to physical conditions at large column densities. For the 𝒮{13CO, HCO+} set of species, the precision for the kinetic temperature, volume density and pressure is now reasonable for almost all the space of covered N(H2),
cm−3 compared to the estimations using only the 13CO and C18O lines. This is indeed the case for N(H2) column densities above 1021.1 cm−2 and below 1022.6 cm−2 for the 𝒮{13CO, HCO+} set of species, and for N(H2) column densities above 1022.2 cm−2 for the 𝒮{C18O, H13CO+} set. This is due to the lower abundance of C18O and H13CO+ that turns into lower opacities, and thus a greater sensitivity to physical conditions at large column densities. For the 𝒮{13CO, HCO+} set of species, the precision for the kinetic temperature, volume density and pressure is now reasonable for almost all the space of covered N(H2), 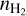 values. A precision better than 25% seems reachable for the conditions encountered in the Horsehead nebula, which corresponds to
values. A precision better than 25% seems reachable for the conditions encountered in the Horsehead nebula, which corresponds to 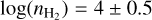 cm−3 and Tkin ∊ [15, 40] K as shown in Fig.16.
cm−3 and Tkin ∊ [15, 40] K as shown in Fig.16.
5.5 Adding the constraint from the 12CO (1–0) peak temperature
Figure 13 compares the same combinations of species (𝒮{13CO, C18O} or 𝒮{13CO, HCO+}) and their associated available transitions with the additional information coming from the peak temperature (line temperature at the velocity channel that maximizes the intensity) of the 12CO (1 − 0) line.
As expected by the fact that the 12CO (1 − 0) line is highly optically thick, this additional constraint enables one to reach an estimation of Tkin within 10% for almost all the covered space of physical conditions. Adding this constraint also has a significant impact on the 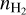 accuracy for the 𝒮{13CO, C18O} set. The impact remains modest for the other set, 𝒮{13CO, HCO+}.
accuracy for the 𝒮{13CO, C18O} set. The impact remains modest for the other set, 𝒮{13CO, HCO+}.
5.6 Only using the (1−0) lines
Roueff et al. (2021) showed in the LTE framework that using the two lowest J transition for 13CO or C18O considerably increases the space of N(H2), 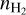 values for which the CRB reference precision is reasonable. We find a similar effect when only studying 13CO or C18O alone or even their combination. However this result is linked to the association of species (13CO and C18O) having similar collisional and radiative rate coefficients. We here consider the benefit of using only the (1 − 0) lines or both the (1 − 0) and (2 − 1) lines of 13CO and C18O when studying the associations with one of the isotopologues of HCO+ that have a much higher dipole moment, and thus different radiative rate coefficients.
values for which the CRB reference precision is reasonable. We find a similar effect when only studying 13CO or C18O alone or even their combination. However this result is linked to the association of species (13CO and C18O) having similar collisional and radiative rate coefficients. We here consider the benefit of using only the (1 − 0) lines or both the (1 − 0) and (2 − 1) lines of 13CO and C18O when studying the associations with one of the isotopologues of HCO+ that have a much higher dipole moment, and thus different radiative rate coefficients.
Columns 1 and 2 (resp. 4 and 5) of Fig. 14 allow us to quantify the benefit of using the (1 − 0) and (2 − 1) lines over only using the (1 − 0) line for the 𝒮{C18O, H13CO+} (resp. 𝒮{12CO, 13CO, HCO+}) set. In contrast with the cases using only the CO isotopologues, the loss of precision remains weak when combining a ground state transition from a CO isotopologue with the same line from an HCO+ isotopologue. The region of N(H2), 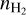 values for which the CRB stays relatively constant only slightly decreases. This suggests that getting several low-J lines of selected species with 1) different excitation requirements and 2) a sufficiently well understood chemistry, would be a good surrogate to observations of higher J transitions of the same species, which lie in atmospheric windows that require more stringent weather conditions to get good observations.
values for which the CRB stays relatively constant only slightly decreases. This suggests that getting several low-J lines of selected species with 1) different excitation requirements and 2) a sufficiently well understood chemistry, would be a good surrogate to observations of higher J transitions of the same species, which lie in atmospheric windows that require more stringent weather conditions to get good observations.
 |
Fig. 13 Comparison of the CRB reference precisions for all the available lines of different combinations of two species, plus the constraint from 12CO (1 − 0) peak temperature. The reminder of the layout is identical to Fig. 12. |
5.7 Fixing the relative abundances of the CO and HCO+ isotopologues
Up to now, we only studied cases where the relative abundance of the CO and HCO+ isotopologues have been unconstrained. We finally study the impact of fixing the abundance of either 13CO/HCO+ or C18O/H13CO+ on the CRB reference precision. Columns #2 and #3 (resp. #5 and #6) of Fig. 14 allow us to quantify the benefit of fixing the relative abundances at constant number of transitions for the 𝒮{C18O, H13CO+} (resp. 𝒮{12CO, 13CO, HCO+}) set. The increase of precision is important for the column densities as expected because information on the abundances has been added and we thus have two measurements at different opacities of the same quantity (the column density). However, the increase of the precision is also obvious for kinetic temperature, volume density, and thermal pressure, in the case of the 𝒮{C18O, H13CO+} set. For the 𝒮{12CO, 13CO, HCO+} case, only the volume density and thermal pressure show an increased precision as the kinetic temperature is mostly constrained by the 12CO (1 − 0) peak intensity. However, these gains in precision require an accurate a priori on the abundance ratio. Otherwise it induces biases as shown in Sect. 4. Leaving the relative abundance as free as possible is thus a better solution as long as their knowledges is imprecise.
6 Astrophysical consequences and perspectives
In the previous sections we have analyzed the accuracy that can be achieved on the column density and physical conditions, depending on the choice of considered spectral lines, the S/N, and domain of parameters. Figures 15 and 16 summarize the fits obtained on molecular maps of the Horsehead nebula, in the framework of a single emitting layer with uniform physical conditions and fixed or free relative abundances. Three sets of molecular lines are used: 13CO and HCO+, 13CO and C18O, and C18O and H13CO+. The first one is adapted to more diffuse lines of sight, while the third one is more suited to denser ones. Each set of estimations has been performed with or without the additional constraint from the peak 12CO intensity. The used abundance ratio values, when fixed, are the ones listed in Eq. (16).
6.1 Column density
The temperature information brought by the 12CO (1 − 0) peak intensity is essential to keep the kinetic temperature in an acceptable range, below 100 K. However this constraint may bias the results on column densities in the presence of a temperature gradient along the LoS. As the temperature probed by the12 CO (1 − 0) line corresponds to the outer layers where the line is emitted, it may be invalid for the deeper and more shielded layers.
A comparison of the middle column of rows a and c in Fig. 15 shows that the 13CO and C18O column densities derived with or without using the 12CO peak temperature agree well with each other. This suggests that this bias is acceptable for the CO isotopologues. The flattening of the N(C18O) vs. N(13CO) histogram for low values may reflect the effect of noise in the relatively faint C18O lines since a positive fluctuation of the noise may lead to an apparently stronger line given the relatively low line intensity in these regions, ≤ 0.5 Kkm s−1.
The situation is more complex for the high dipole moment species HCO+ and H13CO+. For both species, the scatter is quite large reaching about 0.5 dex or a factor of three. The flattening of the relation at low column densities in the case of N(HCO+) vs. N(C18O), and the presence of high HCO+ column density pixels for moderate values of N(13CO) in the case of N(HCO+) vs. N(13CO), probably indicate a bias induced by our hypotheses in addition to the effect of noise. For instance, in regions with relatively faint 13CO emission, the hypothesis of optically thick12 CO (1 − 0) emission may not be fully valid leading to a bias in the assumed kinetic temperature. When the 13CO (1 − 0) line is not fully optically thick, its peak temperature is expected to be lower than the kinetic temperature, which implies that the kinetic temperature could be biased towards somewhat lower values.
An independent result is that the H13CO+ column densities derived without fixing the abundance ratio are somewhat higher (by a factor of about two) than when fixing it. The scatter thus probably indicates real variation of the relative abundances of these two species.
 |
Fig. 14 Comparison of the CRB reference precisions when using either only (1 − 0) lines or adding the (2 − 1) lines for 13CO and C18O and influence of the a priori on the abundance ratio. |
6.2 Kinetic temperature
The effect of the assumptions used to derive the kinetic temperature is clearly seen in rows b and c of Fig. 16. Without the information from 12CO(1 − 0), the fitted physical conditions are tightly correlated. This reflects the shape of the log-likelihood function shown in Fig. 6 to 8. Indeed the strong degeneracy between a low density/high temperature and high density/low temperature models implies that the derived parameters explore the valley of low negative log-likelihood in the (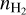 ,Tkin) space, depending on the line intensities, line profiles, and noise level of each pixel.
,Tkin) space, depending on the line intensities, line profiles, and noise level of each pixel.
The situation is slightly better when combining the (1 − 0) and (2 − 1) lines of both 13CO and C18O because the lower opacity of the C18O lines as compared to 13CO implies a higher sensitivity of the level population to the H2 density up to the C18O (2 − 1) critical density of ~ 104 cm−3.
The combination of C18O and H13CO+ data also leads to an exploration of the shape of the log-likelihood function by the different pixels. The results towards dense core pixels reach 106cm−3, a somewhat unrealistically high value at the spatial scale probed by the studied observations, 0.05–0.1 pc. Since these pixels have high C18O column densities and a good CRB, this incorrect result suggests a model mismatch, or an impossibility to separate the different minima of the negative log-likelihood function.
When the kinetic temperature is constrained by the 12CO peak temperature, the range of derived temperatures and densities becomes smaller and more consistent between the different ensembles of molecular lines. However, the small scatter of the kinetic temperature map may be directly related to the hypotheses (single layer, use of 12CO) and may not reflect the real physical conditions.
 |
Fig. 15 Comparison of the column density and physical conditions obtained towards the Horsehead nebula using different sets of molecular lines. The red contour delineates the pixels associated with dense cores and where H13CO+ (1 − 0) is detected at the 3σ level. When abundances or abundance ratios are fixed, the values are given in Eq. (16). Only estimations with a good reference precision (CRB) have been kept (see Eq. (21)). |
6.3 Volume density
The bias and variance analyses presented in Sects. 4 and 5 have shown that it is difficult to obtain a good precision on molecular gas density because 1) of degeneracies between the volume density, the kinetic temperature, and the column densities, or 2) of the potential presence of more than one local minimum in the log-likelihood function. These degeneracies are clearly seen in the plots displaying the variation of the derived column densities as a function of the density when 12CO (1 − 0) is not used (see Figs. 15d and e). The anti-correlation between the density and column density when using the 13CO and HCO+ lines seems nonphysical, as high column density regions are usually associated with high density regions. The lower density pixels appear to have a high kinetic temperature, a consequence of the degeneracy between the density and kinetic temperature. The same behavior is seen for the two other sets of lines, with densities shifted towards somewhat higher values as these sets of lines include transitions with higher effective critical densities than the first set of lines.
Adding a constraint on the kinetic temperature from 12CO breaks the degeneracy. The derived densities occupy a rather narrow range of values, between ~ 3 × 103 cm−3 and ~ 3 × 104 cm−3 for all sets of lines. There is no difference in the volume density between the pixels associated with the dense cores (defined as regions with strong H13CO+ emission) and pixels elsewhere in the map, while it would have been expected that the density increases in the dense cores.
When looking at the volume density maps displayed in Fig. C.4 more differences appear. Using the 12CO peak temperature is essential for the first set of lines as the kinetic temperatures (and densities) become too high (resp. low) without this constraint. The combination of 13CO and C18O lines performs quite well without 12CO in the high column density region of the horsehead neck, but many pixels remain with nonphysical estimations. For these two sets of lines, using 12CO without adding a constraint on the relative abundances appears to be the best choice. Because the H13CO+(1 − 0) emission is only detected in restricted areas, the different hypotheses have a strong impact on the derived parameters as some hypotheses allow for the use of pixels with marginal detections while others do not. Fixing the relative abundances between C18O and H13CO+ allows us to obtain reasonable values for the density and kinetic temperature in the H13CO+ cores with a good CRB. This avoids the risk of biasing the temperature by using a temperature probe associated with the cloud envelope. However, the analysis is limited to the small set of pixels with a good S/N detection of H13CO+(1 − 0).
 |
Fig. 17 Methodological and astrophysical summary. |
6.4 Pressure
Although the estimations of density and temperature may be biased, the estimation of the thermal pressure is expected to be more accurate as the minimum of the negative log-likelihood function is nearly coincident with the locus of constant thermal pressure. Nevertheless, a detailed analysis of the accuracy of the pressure determination remains necessary, as the different degeneracies described above still play a role. In addition, the determination of the thermal pressure results from a fit of the molecular line emission under some hypotheses (e.g., uniform medium, co-localized molecular species, etc). Therefore, it is recommended to clearly describe the assumptions leading to the estimation of the parameters of interest as different sets of hypotheses may lead to different values. Overall, the CO isotopologue lines can be used to obtain rather good estimations of the thermal pressure, an interesting quantity for the energy budget of molecular gas when all hypotheses are clearly stated as recommended above.
6.5 Generalization
From the analysis of the Horsehead nebula, we can draw some recommendations for the analysis of the selected molecular emission lines: low J lines of the CO and HCO+ isotopologues using radiative transfer models of a uniform cloud. Figure 17 summarizes these recommendations. These lines are among the strongest seen in Galactic molecular clouds and nearby galaxies. It is therefore interesting to optimize their analysis and extract most of information from such observations.
In many conditions, even the excitation of the CO isotopologues departs from the local thermodynamic equilibrium (see Fig. D.1), and a non-LTE model like RADEX should be preferred for the analysis of the molecular line emission. However, it is important that the hypotheses involved in the non-LTE calculations are clearly spelled out.
The determination of column densities is accurate for 13CO and C18O. It does not need additional hypotheses than the presence of all species in the same volume. Column densities for the higher dipole moment species HCO+ and H13CO+ are more sensitive to the set of hypotheses as these species are sub-thermally excited in most of the explored parameter space, hence their emission is sensitive to the physical conditions. The lower S/N of the faint emission lines also implies a lower accuracy of the determined parameters.
The determination of the molecular hydrogen volume density and kinetic temperature is more difficult to achieve with a good precision. As discussed in Sect. 4.4.3, because of the strong degeneracy between the density and kinetic temperature in determining the CO isotopologue excitation, an independent constraint on the kinetic temperature is needed. Using the peak value of the 12CO (1 − 0) line works well for that purposes and allows us to at least partially break the degeneracy. This constraint is useful for the determination of the kinetic temperature but ambiguities may remain for the molecular hydrogen density. Given the achievable S/N and calibration accuracy, different physical conditions may lead to very similar emerging spectra as illustrated in Fig. 10 and discussed in Sect. 5.2. Adding a line from a high dipole moment species is useful for constraining the volume density, provided the line is observed with a good S/N and this species abundance relative to that of one CO isotopologue can be used to constrain the fit. Otherwise, adding another line is less beneficial because of the degeneracy between density and column density. An error in fixing the relative abundance of the high dipole moment species relative to the CO isotopologue leads to a bias in the derivation of the density but this bias remains tolerable when compared to the uncertainties when only one CO isotopologue is used.
Using different molecular lines from different species brings more constraints for deriving the physical conditions and column densities, at the expense of the need for a strong hypothesis: the presence of all species within the same volume of gas with uniform conditions. Such a strong hypothesis may be far from the reality of interstellar clouds which exhibit gradients of density, temperature and molecular abundances across their volumes. In particular, towards lines of sight where dense cores are present, the range of physical conditions is broad and the uniform cloud hypothesis is expected to lead to poor results. One example of such poor results is the determination of the kinetic temperature using the 12CO (1 − 0) line which does not differentiate pixels within dense cores from pixels outside cores. In fact, it is known from more detailed analyses that the kinetic temperature decreases from the extended molecular cloud envelopes to cores (e.g., Hocuk et al. 2017; Rodríguez-Baras et al. 2021). Instead of uniform models, more sophisticated geometrical layouts are needed for specific environments. For instance, dense cores that are embedded in filaments, and in the molecular gas envelope clearly need a multi-layer model, in which a cold and dense region is surrounded by a warmer and more diffuse envelope. This will be the subject of another paper. Another case which would deserve a multi-layer model could be a dense, non edge-on, UV illuminated photodissociation region (PDR) where a strong temperature gradient is present due to the attenuation of the UV radiation when entering the molecular gas. Such PDRs often have a nearly isobaric equation of state (e.g., Hernández-Vera et al. 2023, for the Horsehead nebula), hence an isobaric model would be better suited than a uniform model with a single density and temperature value.
For all cases, having a temperature probe independent of the lines used for the column density and volume density estimations has been shown to be useful for breaking the degeneracies in the excitation conditions. The peak temperature of the 12CO (1 − 0) line is adequate for the bulk of the molecular emission, but overestimates the temperature of the dense and shielded regions. In these regions, the ratio of the (1, 1) and (2, 2) inversion lines of NH3 near 23 GHz is known to perform well as a temperature probe (Maret et al. 2009), but getting such data requires combining observations from different telescopes. Efforts should be made to find another, easily accessible, temperature probe based on molecular lines, that could be used in the analysis of well shielded regions. Hacar et al. (2020) proposed to use the ratio of the HCN and HNC intensities to probe the kinetic temperature between about 15 and 60 K. However in their extensive analysis of the Orion B cloud, Santa-Maria et al. (2023) showed that the HCN/HNC ratio is more sensitive to the radiation field than to the kinetic temperature. Another possibility to probe the kinetic temperature of shielded regions could be using the dust temperature, but this also requires observations over a wide range of wavelengths to break the degeneracy between the dust temperature and column density. Rodríguez-Baras et al. (2021) have used radiative transfer calculations and showed that the difference between the kinetic temperature and the dust temperature remains lower than 1 K along lines of sight with an extinction larger than 8 magnitudes (4 mag on each side from the cloud edge) for the conditions corresponding to the sources probed in the GEMS IRAM large program, dense cores with an external FUV radiation field between 5 and 60 times the Inter-Stellar Radiation Field and a thermal pressure of 5 × 105 Kcm−3). Further studies over a wider parameter space and including the comparison of the predicted dust temperature and its estimation from the fit of the spectral energy distribution are needed to establish the conditions where the dust temperature is a good proxy of the kinetic temperature, and thus the bias which could be introduced by this hypothesis.
7 Conclusion
In this article, we study the fit of multi-species molecular lines with a non-LTE radiative transfer model and we propose a method to test the derived results, including the possibility of identifying potential model misspecifications. Figure 17 summarizes our main recommendations and their implications for further studies. We list a few general points below.
While LTE models are simple to run and interpret, the excitation of CO isotopologues does not always reach this limit and non-LTE models should be preferred, especially when the analysis of CO isotopologue lines is combined with lines from higher dipole moment species.
It is important to take into account the S/N of the transition studied, including the thermal noise and calibration uncertainties, when fitting radiative transfer models to observed molecular emission. This can be done for instance by limiting the S/N ratio of the strongest lines to mimic the effect of calibration uncertainties.
When fitting radiative transfer models to observations, it is important to consider the information from the full line profile and not just from the integrated intensity, because this allows us to consider the broadening of the line profile when the opacity increases.
Because different physical conditions may produce very similar line profiles for some transitions, it is important to account for such potential degeneracies when exploring the parameter space.
Combining molecular species with different excitation requirements, for instance, high dipole (high critical density) and low dipole moment species (low critical density), allows for the degeneracy in the physical condition parameter space to be broken, provided the relative abundances of the considered species are known from independent observations or from models.
The escape probability model is adequate for studying large scale molecular line maps. For detailed studies of specific objects of known geometry, more sophisticated models may be required to better take into account the radiative coupling along the line of sight.
Based on the precision analysis, we make the following additional recommendations.
To increase the precision of the estimations, it is more interesting to combine lines with different excitation requirements than to increase the S/N ratio of a targeted spectral line. This is because the needed integration time to detect a new line if often significantly lower than the additional time needed to improve the S/N ratio on an already detected line.
With the availability of broad band receivers, combining lines from different species accessible with the same receiver usually allows for a more efficient use of the observing time than accessing lines from different energy levels, which often require stringent weather conditions to get good observations.
The thermal pressure of the emitting medium is often determined with a better precision than the kinetic temperature of volume density taken separately. It can therefore be interesting to derive thermal pressure maps of molecular clouds, which can be compared with maps of the magnetic or turbulent pressure.
This work is focused on the combination of CO and HCO+ isotopologue lines. Other high-dipole moment species could be considered in the future. For instance, CS, CN, HNC or N2H+ have bright lines that are easily detectable in large scale maps of molecular clouds. While this study is also focused on a single homogeneous layer, it is clear that this hypothesis is not fully suited to lines of sight towards dense cores. In a following paper, we will study a multi-layer model and compare its performances with the homogeneous model.
Acknowledgements
This work is based on observations carried out under project numbers 019-13, 022-14, 145-14, 122-15, 018-16, and finally the large program number 124-16 with the IRAM 30m telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain). This work was supported by the French Agence Nationale de la Recherche through the DAOISM grant ANR-21-CE31-0010, and by the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP, co-funded by CEA and CNES. This project has received financial support from the CNRS through the MITI interdisciplinary programs. JRG and MGSM thank the Spanish MCINN for funding support under grant PID2019-106110G-100. Part of the research was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration (80NM0018D0004). D.C.L. was supported by USRA through a grant for SOFIA Program 09-0015. This research has made use of spectroscopic and collisional data from the EMAA (https://emaa.osug.fr and https://dx.doi.org/10.17178/EMAA) and LAMDA (https://home.strw.leidenuniv.nl/~moldata/) databases. EMAA is supported by the Observatoire des Sciences de l'Univers de Grenoble (OSUG). The LAMDA database is supported by the Netherlands Organization for Scientific Research (NWO), the Netherlands Research School for Astronomy (NOVA), and the Swedish Research Council.
Appendix A Fisher information matrix
To compute Cramér-Rao bound associated to the unknown parameters θ, we need to calculate the Fisher matrix of the L observed lines x1:L = {x1…, xL}. Nevertheless, since the noise on the different lines are statistically independent, the Fisher matrix of x1:L is simply the sum of the Fisher matrix of each line
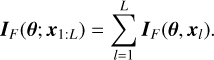 (A.1)
(A.1)
Below we detail the calculation of the Fisher matrix for a single line and the vector of unknown parameter is simply θ = [log 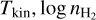 , log N, σV, CV]. The generalization of these computations to the case where we also fit the logarithm of some of the column densities; for instance, θ = [log Tkin, log
, log N, σV, CV]. The generalization of these computations to the case where we also fit the logarithm of some of the column densities; for instance, θ = [log Tkin, log 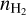 , log N(13CO), log N(C18O), σV, CV], is straightforward. For didactic reasons, the presentation is organized in two parts. In Sect. A.1, the multiplicative noise is omitted. It is taken into account in Sect. A.2.
, log N(13CO), log N(C18O), σV, CV], is straightforward. For didactic reasons, the presentation is organized in two parts. In Sect. A.1, the multiplicative noise is omitted. It is taken into account in Sect. A.2.
Appendix A.1 Case without multiplicative noise
In this section, we assume only additive noise:
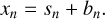 (A.2)
(A.2)
where bn is a white Gaussian noise with variance 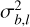 and sn is a sampled version of Eq. (7):
and sn is a sampled version of Eq. (7):
![${s_n} = \left\{ {J\left( {{T_{{\rm{ex}},l}},{v_l}} \right) - J\left( {{T_{{\rm{CMB}}}},{v_l}} \right)} \right\}\left[ {1 - \exp \left( { - {\Psi _n}} \right)} \right].$](/articles/aa/full_html/2024/06/aa49148-24/aa49148-24-eq133.png) (A.3)
(A.3)
Thus, Ψn is a sampled version of Eq. (4):
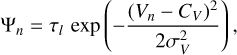 (A.4)
(A.4)
where Vn is the velocity at channel n. Assuming that the noise is white, the log-likelihood of the sampled observation at line l is
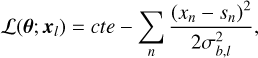 (A.5)
(A.5)
and the Fisher matrix IF (see Stoica & Moses 2005) is
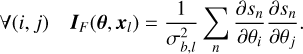 (A.6)
(A.6)
Thus, to get IF(θ, xl), we simply need to evaluate the gradient 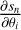 , where θi is the ith component of θ. This is done in the following.
, where θi is the ith component of θ. This is done in the following.
Appendix A.1.1 Calculation of 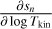
Moreover, based on Eq. (A.3), we have
![$\eqalign{ & {{\partial {s_n}} \over {\partial {T_{{\rm{kin}}}}}} = {{\partial J\left( {{T_{{\rm{ex}},ll}},{v_l}} \right)} \over {\partial {T_{{\rm{ex}},l}}}}{{\partial {T_{{\rm{e}},l}}} \over {\partial {T_{{\rm{kin}}}}}}\left[ {1 - \exp \left( { - {\Psi _n}} \right)} \right] \cr & & + \left\{ {J\left( {{T_{{\rm{ex}},l}},{v_l}} \right) - J\left( {{T_{{\rm{CMB}}}},{v_l}} \right)} \right\}{{\partial {\Psi _n}} \over {\partial {T_{{\rm{kin}}}}}}\exp \left( { - {\Psi _n}} \right). \cr} $](/articles/aa/full_html/2024/06/aa49148-24/aa49148-24-eq140.png) (A 8)
(A 8)
In practice, we numerically estimated 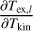 with a finite difference technique using RADEX with a step of Tkin/1024.
with a finite difference technique using RADEX with a step of Tkin/1024.
Appendix A.1.2 Calculation of 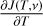
Appendix A.1.3 Calculation of 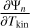
where the term 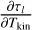 is also numerically estimated with finite difference as in Eq (A 8)
is also numerically estimated with finite difference as in Eq (A 8)
Appendix A.1.4 Calculation of 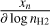 and
and 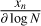
The calculation of 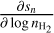 and
and 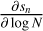 are straightforward adaptations from
are straightforward adaptations from 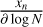 . We only need to specify that the finite difference technique is applied for both log
. We only need to specify that the finite difference technique is applied for both log 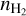 and log N with a step of 0 001
and log N with a step of 0 001
Appendix A.1.5 Calculation of 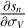
we need to detail the calculation of 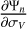 .
.
Appendix A.1.6 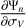
Based on Eq. (A.4), one has
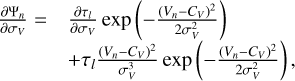 (A.14)
(A.14)
where the term 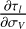 is numerically estimated with a finite difference technique with a step of FWHM/128.
is numerically estimated with a finite difference technique with a step of FWHM/128.
Appendix A.1.7 Gradient calculation along ∆V
Appendix A.1.8 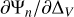
Based on Eq. (A.4), one has
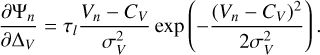 (A.16)
(A.16)
Appendix A.2 Case with multiplicative noise
Let us now take into account the multiplicative noise
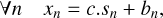 (A. 17)
(A. 17)
where in addition of bn, one has 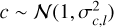 , which is assumed independent bn. The column vector x = [x1, x2, …]T is the sum of two Gaussian random vectors, thus it remains a Gaussian vector. Its mean is s = [s1 s2, …]T and it is straightforward to show that is covariance matrix is
, which is assumed independent bn. The column vector x = [x1, x2, …]T is the sum of two Gaussian random vectors, thus it remains a Gaussian vector. Its mean is s = [s1 s2, …]T and it is straightforward to show that is covariance matrix is
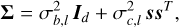 (A.18)
(A.18)
where Id is the identity matrix. The log-likelihood of x is
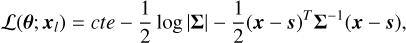 (A.19)
(A.19)
which leads, after tedious but straightforward calculations, to
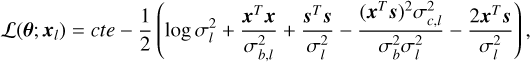 (A.20)
(A.20)
where 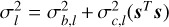 . The Slepian-Bang formula Stoica & Moses (2005) gives us the following relations,
. The Slepian-Bang formula Stoica & Moses (2005) gives us the following relations,
![${\left[ {{{\bf{I}}_F}} \right]_{ij}} = {{\partial {{\bf{s}}^T}} \over {\partial {\theta _i}}}{{\bf{\Sigma }}^{ - 1}}{{\partial {\bf{s}}} \over {\partial {\theta _j}}} + {1 \over 2}{\mathop{\rm tr}\nolimits} \left( {{{\bf{\Sigma }}^{ - 1}}{{\partial {\bf{\Sigma }}} \over {\partial {\theta _i}}}{{\bf{\Sigma }}^{ - 1}}{{\partial {\bf{\Sigma }}} \over {\partial {\theta _j}}}} \right),$](/articles/aa/full_html/2024/06/aa49148-24/aa49148-24-eq170.png) (A.21)
(A.21)
which leads, after tedious but straightforward calculations to
![$\eqalign{ & {\left[ {{{\bf{I}}_F}} \right]_{ij}} = \left( {{{\sigma _l^2 + \sigma _{c,l}^4\left( {{s^T}s} \right)} \over {\sigma _{b,l}^2\sigma _l^2}}} \right)\left( {{{\partial {s^T}} \over {\partial {\theta _i}}}{{\partial s} \over {\partial {\theta _j}}}} \right) \cr & & + \left( {{{\sigma _{b,l}^2,\sigma _{c,l}^4 - \sigma _{c,l}^6\left( {{s^T}s} \right)} \over {\sigma _{b,l}^2\sigma _l^4}} - {{\sigma _{c,l}^2} \over {\sigma _{b,l}^2\sigma _l^2}}} \right)\left( {{s^T}{{\partial s} \over {\partial {\theta _i}}}} \right)\left( {{s^T}{{\partial s} \over {\partial {\theta _j}}}} \right). \cr} $](/articles/aa/full_html/2024/06/aa49148-24/aa49148-24-eq171.png) (A.22)
(A.22)
Appendix B Details on the used maximum likelihood estimator
The following subsections provide details on the implementation of the maximum likelihood estimator we use in this article. We first explain how we localize and detect the Gaussian opacity profile (Eq. (4)) on high S/N and optically thin lines. This allows us to provide an initial estimation of the centroid velocity. We then discuss 1) the initialization of the other parameters and 2) the iterative algorithm to refine their estimation.
Appendix B.1 Signal detection and initial estimation of the centroid velocity
We start by computing the noise standard deviation on baseline channels by using the range of channels that are devoid of signal on the studied field of view. These channels can be selected manually from raw data (see the right part of Fig. 1). We then estimate the centroid velocity CV. To do this, we first increase the S/N by adding all the lines from C18O and 13CO after resampling them on the same velocity grid. Although the 12CO (1 − 0) line is bright, its high opacity makes it mostly sensitive to the kinematics of surface of the cloud instead of the bulk of the flow. On the opposite, the S/N on HCO+ and H13CO+ is significantly lower, which make them useless to estimate centroid velocity. We then apply a matched filter by convolving the summed spectra with a Gaussian shape of FWHM = 0.35 km/s. This shape corresponds to an optically thin approximation of a line. Selecting the velocity where the intensity of the filtered signal is maximum thus delivers an initial estimation of the centroid velocity CV for all the lines.
Minimum and maximum parameter bounds, where estimations are saturated to prevent RADEX from crashing
Afterwards, we additionally check the presence of the velocity component in a majority of the studied lines. More precisely, the pixel is further processed only when more than half of the lines are detected. Else, the estimated parameters are nullified. To do this, we integrate the profile within a velocity interval of 1 km s−1 centered on the estimated centroid velocity, CV. The line is considered detected when the signal is larger than 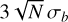 , where N is the number of velocity channels in 1 km s−1, and σb the associated noise standard deviation.
, where N is the number of velocity channels in 1 km s−1, and σb the associated noise standard deviation.
Appendix B.2 Initializing the fit estimation
The signal detection step provides an initial estimate of the centroid velocity for all the lines. In order to initialize the other parameters, we compute the negative log-likelihood (NLL) on a fixed grid of models computed with RADEX. This grid sample the parameter space in logarithmic steps for all parameters whose range of plausible values cover at least one order of magnitude. In practice, only the velocity dispersion is sampled linearly. In details,
The velocity dispersion, FWHM, is sampled linearly between 0.25 and 2 km s−1 in steps of 0.05 km s−1.
The kinetic temperature, Tkin, is sampled between 4 and 113 K in logarithmic steps of 0.05.
The H2 volume density, n(H2) is sampled between 102 and 1065 cm−3 in logarithmic steps of 0.1.
N(13CO) is sampled between 1013 and 1018 cm−2 in logarithmic steps of 0.05.
The column densities of 12CO, C18O, HCO+, and H13CO+ are sampled with the same grid as 13CO, shifted to take into account the relative abundances defined in Eq. (16).
Using this grid, for each species, we thus get a 4D tensor of negative log-likelihood (NLL) values. The way we explore this tensor, depends on the a priori information that are available. For instance, let us consider the 𝒮{13CO, HCO+} estimation problem (see Table 4). We need to estimate the column density of these two species independently with the constraint that the triplet (Tkin, 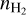 , σV) is identical for all species. On the other hand, with 𝒮{13CO, HCO+; 𝒜}, the situation is slightly different since we need to impose the abundance ratio between 13CO and HCO+ . Adapting the implemented estimator to every possible a priori knowledge is thus required. At the end of this process, we get an initial estimation noted θ(0).
, σV) is identical for all species. On the other hand, with 𝒮{13CO, HCO+; 𝒜}, the situation is slightly different since we need to impose the abundance ratio between 13CO and HCO+ . Adapting the implemented estimator to every possible a priori knowledge is thus required. At the end of this process, we get an initial estimation noted θ(0).
Appendix B.3 Iterative gradient descent
To refine our estimation of the negative log-likelihood, we use the following iterative estimation in which the Hessian is the Fisher matrix starting from θ(0)
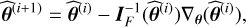 (B.1)
(B.1)
where i is the ith iteration, IF (θ) is the Fisher matrix as a function of θ, and ∇θ(θ) is the gradient of the negative log-likelihood
![$\forall j\quad {\left[ {{\nabla _{\bf{\theta }}}({\bf{\theta }})} \right]_j} = \sum\limits_{l = 1}^L {{1 \over {\sigma _{b,l}^2}}} \sum\limits_{n = 1}^K {{{\partial {s_{n,l}}} \over {\partial {\theta _j}}}} \left( {{s_{n,l}} - {x_{n,l}}} \right),$](/articles/aa/full_html/2024/06/aa49148-24/aa49148-24-eq176.png) (B.2)
(B.2)
where j is the index of the estimated parameter. The inversion of Fisher matrix in Eq. (B.1) may be numerically unstable. When the ratio between the highest and the smallest eigenvalue is higher than 109, we use the Moore Penrose pseudo-inverse instead of the inverse in Eq. (B.1).
Furthermore, when Eq. (B.1) would lead to parameters out of the initial grid, we saturate these parameters to prevent RADEX from crashing (see Table B.1). For example, we impose 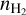 to be smaller than 106.5cm−3. While a volume density at 106.5 cm−3 cannot be trusted in this case, the column density may still be reliable. These conditions add some a priori knowledge that is not available in the computation of the Cramér-Rao bound.
to be smaller than 106.5cm−3. While a volume density at 106.5 cm−3 cannot be trusted in this case, the column density may still be reliable. These conditions add some a priori knowledge that is not available in the computation of the Cramér-Rao bound.
Appendix C Supplemental figures on data fit
Appendix D Supplemental figure for the parametric study of the reference precisions
Figure D.1 shows the main characteristics (signal-to-noise ratios, opacities, ratios of the volume density to the effective critical densities, and ratios of the excitation temperature over the kinetic temperature) of all the lines used in this paper for the same range of volume and column densities.
 |
Fig. D.1 Line main characteristics: S/Ns, opacities, ratios of the volume density to the effective critical densities, and ratios of the excitation and kinetic temperatures. The blue and red curves show the results for the (1 − 0) and (2 − 1) lines, respectively. The values of the parameters that are fixed when generating the RADEX spectra are listed in the bottom row, except for the abundances that are given in Eq. (16). |
References
- Asensio Ramos, A., & Elitzur, M. 2018, A&A, 616, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, A. T., Kauffmann, J., Bigiel, F., et al. 2020, MNRAS, 497, 1972 [NASA ADS] [CrossRef] [Google Scholar]
- Bernes, C. 1979, A&A, 73, 67 [NASA ADS] [Google Scholar]
- Brinch, C., & Hogerheijde, M. R. 2010, A&A, 523, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bron, E., Daudon, C., Pety, J., et al. 2018, A&A, 610, A12 [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Bron, E., Roueff, E., Gerin, M., et al. 2021, A&A, 645, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cao, Z., Jiang, B., Zhao, H., & Sun, M. 2023, ApJ, 945, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Castets, A., Duvert, G., Dutrey, A., et al. 1990, A&A, 234, 469 [NASA ADS] [Google Scholar]
- Denis-Alpizar, O., Stoecklin, T., Dutrey, A., & Guilloteau, S. 2020, MNRAS, 497, 4276 [Google Scholar]
- Einig, L., Pety, J., Roueff, A., et al. 2023, A&A, 677, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuente, A., Garcia-Burillo, S., Usero, A., et al. 2008, A&A, 492, 675 [CrossRef] [EDP Sciences] [Google Scholar]
- Garthwaite, P. H., Jolliffe, I. T., & Jones, B. 1995, Statistical Inference (London: Prentice Hall Europe) [Google Scholar]
- Gerin, M., Liszt, H., Neufeld, D., et al. 2019, A&A, 622, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., Pety, J., Roueff, A., Bron, E., & Orion-B Team. 2023, in Physics and Chemistry of Star Formation: The Dynamical ISM Across Time and Spatial Scales, 230 [Google Scholar]
- Goicoechea, J. R., Pety, J., Gerin, M., et al. 2006, A&A, 456, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F., & Kauffmann, J. 2017, ApJ, 841, 25 [Google Scholar]
- Guzmán, V. V., Pety, J., Gratier, P., et al. 2014, Faraday Discuss., 168, 103 [Google Scholar]
- Hacar, A., Bosman, A. D., & van Dishoeck, E. F. 2020, A&A, 635, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernández-Vera, C., Guzmán, V. V., Goicoechea, J. R., et al. 2023, A&A, 677, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hocuk, S., Szucs, L., Caselli, P., et al. 2017, A&A, 604, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Leung, C. M., & Liszt, H. S. 1976, ApJ, 208, 732 [CrossRef] [Google Scholar]
- Liszt, H. S. 2012, A&A, 538, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maret, S., Faure, A., Scifoni, E., & Wiesenfeld, L. 2009, MNRAS, 399, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [Google Scholar]
- Nishimura, Y., Watanabe, Y., Harada, N., et al. 2017, ApJ, 848, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Pety, J. 2005, in SF2A-2005: Semaine de l’Astrophysique Francaise, eds. F. Casoli, T. Contini, J. M. Hameury, & L. Pagani, 721 [Google Scholar]
- Pety, J., Goicoechea, J. R., Hily-Blant, P., Gerin, M., & Teyssier, D. 2007, A&A, 464, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J., Guzmán, V. V., Orkisz, J. H., et al. 2017, A&A, 599, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J., Gerin, M., Bron, E., et al. 2022, in Eur. Phys. J. Web Conf. 265, 00048 [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez-Baras, M., Fuente, A., Riviére-Marichalar, P., et al. 2021, A&A, 648, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roueff, A., Gerin, M., Gratier, P., et al. 2021, A&A, 645, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santa-Maria, M. G., Goicoechea, J. R., Pety, J., et al. 2023, A&A, 679, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shirley, Y. L. 2015, PASP, 127, 299 [Google Scholar]
- Stoica, P., & Moses, R. 2005, Spectral Analysis of Signals (New Jersey: Prentice Hall) [Google Scholar]
- Tafalla, M., Usero, A., & Hacar, A. 2021, A&A, 646, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teng, Y.-H., Sandstrom, K. M., Sun, J., et al. 2023, ApJ, 950, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Tunnard, R., & Greve, T. R. 2016, ApJ, 819, 161 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ward-Thompson, D., Nutter, D., Bontemps, S., Whitworth, A., & Attwood, R. 2006, MNRAS, 369, 1201 [CrossRef] [Google Scholar]
- Watanabe, Y., Nishimura, Y., Harada, N., et al. 2017, ApJ, 845, 116 [Google Scholar]
- Yang, B., Stancil, P. C., Balakrishnan, N., & Forrey, R. C. 2010, ApJ, 718, 1062 [Google Scholar]
- Zucker, C., Goodman, A., Alves, J., et al. 2021, ApJ, 919, 35 [NASA ADS] [CrossRef] [Google Scholar]
See http://www.iram.fr/IRAMFR/GILDAS for more information about the GILDAS software (Pety 2005).
All Tables
Sets of species, the assumed chemistry, the number of available lines, and the number of unknown parameters.
Minimum and maximum parameter bounds, where estimations are saturated to prevent RADEX from crashing
All Figures
 |
Fig. 1 Presentation of the data towards the Horsehead pillar. Left and middle panels: spatial distribution of the peak intensity and of the integrated intensity. The used projection is the Azimuthal one, centered on RA= 05h40m54.27s, Dec= −02°28′00.00″ in the ICRS frame, and with a position angle of 14°. The two crosses show the positions of the two dense cores whose coordinates are in Table 3. The black dot shows the position of the line of sight studied in more detailed in Sect. 4. Right panel: the green, blue, and red spectra show the spectra of percentiles at 10, 50, and 90%, respectively, computed over the associated field of view. |
| In the text | |
 |
Fig. 2 Comparison of the estimated column density of 13CO on the Horsehead pillar data for different sets of species and/or a priori. In all cases Tkin, |
| In the text | |
 |
Fig. 3 Mean and standard deviation of the distance in log-space between the estimations (i.e., |
| In the text | |
 |
Fig. 4 Maps and joint histograms of relative abundances for log {N(13CO)/N(HCO+)} (left), log {N(13CO)/N(C18O)} (middle), and log {N(C18O)/N(H13CO+)} (right). The layout of the figure is similar to Fig. 2. |
| In the text | |
 |
Fig. 5 Comparison of the ideal (in red) line profiles with noisy (in blue) ones for experiment #1 and #2 (see Table 5). In the legends, c is the estimated calibration factor (see Eq. (17)). |
| In the text | |
 |
Fig. 6 Comparison of the performances of our maximum likelihood estimator for the estimation of the column densities (Cols. #2 and #3) and the couple (Tkin, |
| In the text | |
 |
Fig. 7 Same as Fig. 6 except that 1) the couple of species used to estimate the parameters are 13CO and HCO+, and 2) the biases on the RADEX model are imposed on the HCO+ species. |
| In the text | |
 |
Fig. 8 Same as Fig. 6 except that 1) the couple of species used to estimate the parameters are C18O and H13CO+, and 2) the RADEX model are not biased. |
| In the text | |
 |
Fig. 9 Comparison of the CRB reference precisions (left column) on the column density, kinetic temperature, volume density, and thermal pressure, when fitting the 13CO (1 − 0) and 13CO (2 − 1) lines, with these lines main characteristics (right column): S/Ns, opacities, ratios of the volume density to the effective critical densities, and ratios of the excitation temperature over the kinetic temperature. The blue and red curves show the results for the (1 − 0) and (2 − 1) lines, respectively. The values of the parameters that are fixed when generating the RADEX spectra are listed in the bottom row. The a priori knowledge that are used when computing the CRB precisions are listed in the second row. |
| In the text | |
 |
Fig. 10 Comparison of the spectral shape of the (1 − 0) (top) to (4 − 3) (bottom) lines of 13CO for two different combinations of kinetic temperature, volume density, and column density. The plain blue and dashed red histograms show the spectra for (22 K, 105 cm−3,1018 cm−2) and (60 K, 101.65 cm−3, 1017.9 cm−2), respectively. The lines share the same centroid velocity CV = 0 km s−1 and velocity dispersion σV = 0.32 km s−1. The two sets of physical conditions deliver degenerate spectral profiles within the noise level for the (1 − 0) and (2 − 1) lines. Additional information, e.g., the (3 − 2) or (4 − 3) lines, is needed to lift this degeneracy. |
| In the text | |
 |
Fig. 11 Comparison of the CRB precisions when combining the first two J transitions of one or two CO isotopologues. These reference precisions are plotted for different values of column densities (y-axes) and volume densities (x-axes). The values of the parameters that are fixed when generating the RADEX spectra are listed in the bottom row. The precision depends on the a priori knowledges that are taken into account by the estimator. These are listed in the second row. The first two columns show the precisions for a single CO isotopologue (13CO or C18O, while the last column shows the precisions when studying the 13CO and C18O isotopologues simultaneously. From top to bottom, the panels show the precisions on the 13CO and C18O column densities, kinetic temperature, volume density, and thermal pressure. The CRB precisions are color coded as listed in Table 8. |
| In the text | |
 |
Fig. 12 Comparison of the CRB reference precisions for different combinations of two species and all their available lines. The layout of this figure is identical to Fig. 11, except for the combination of studied lines: the first column shows the precision when the (1 − 0) and (2 − 1) lines of the 13CO and C18O isotopologues are used. The last two columns study a combination of the one CO isotopologue with one HCO+ isotopologue: 13CO and H12CO+ on the second column and C18O and H13CO+ on the third column. |
| In the text | |
 |
Fig. 13 Comparison of the CRB reference precisions for all the available lines of different combinations of two species, plus the constraint from 12CO (1 − 0) peak temperature. The reminder of the layout is identical to Fig. 12. |
| In the text | |
 |
Fig. 14 Comparison of the CRB reference precisions when using either only (1 − 0) lines or adding the (2 − 1) lines for 13CO and C18O and influence of the a priori on the abundance ratio. |
| In the text | |
 |
Fig. 15 Comparison of the column density and physical conditions obtained towards the Horsehead nebula using different sets of molecular lines. The red contour delineates the pixels associated with dense cores and where H13CO+ (1 − 0) is detected at the 3σ level. When abundances or abundance ratios are fixed, the values are given in Eq. (16). Only estimations with a good reference precision (CRB) have been kept (see Eq. (21)). |
| In the text | |
 |
Fig. 16 Continuation of Fig. 15 showing the |
| In the text | |
 |
Fig. 17 Methodological and astrophysical summary. |
| In the text | |
 |
Fig. C.1 Same as Fig. 2 but for N(C18O). |
| In the text | |
 |
Fig. C.2 Same as Fig. 2 but for N(HCO+) (left) and N(H13CO+) (right). |
| In the text | |
 |
Fig. C.3 Same as Fig. 2 but for Tkin. |
| In the text | |
 |
Fig. C.4 Same as Fig. 2 but for |
| In the text | |
 |
Fig. C.5 Same as Fig. 2 but for Pth. |
| In the text | |
 |
Fig. D.1 Line main characteristics: S/Ns, opacities, ratios of the volume density to the effective critical densities, and ratios of the excitation and kinetic temperatures. The blue and red curves show the results for the (1 − 0) and (2 − 1) lines, respectively. The values of the parameters that are fixed when generating the RADEX spectra are listed in the bottom row, except for the abundances that are given in Eq. (16). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



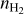
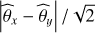
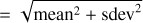
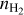
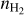
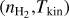
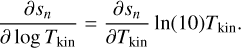
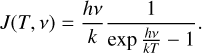
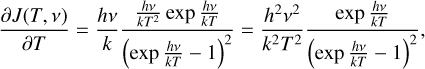
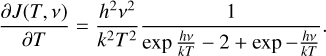
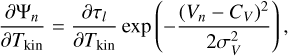
![$\eqalign{ & {{\partial {s_n}} \over {\partial {\sigma _V}}} = {{\partial J\left( {{T_{{\rm{ex}},l}},{v_l}} \right)} \over {\partial {T_{{\rm{ex}},l}}}}{{\partial {T_{{\rm{ex}},l}}} \over {\partial {\sigma _V}}}\left[ {1 - \exp \left( { - {\Psi _n}} \right)} \right] \cr & & + \left\{ {J\left( {{T_{{\rm{ex}},l}},{v_l}} \right) - J\left( {{T_{{\rm{CMB}}}},{v_l}} \right)} \right\}{{\partial {\Psi _n}} \over {\partial {\sigma _V}}}\exp \left( { - {\Psi _n}} \right), \cr} $](/articles/aa/full_html/2024/06/aa49148-24/aa49148-24-eq156.png)