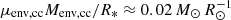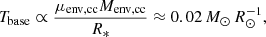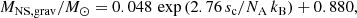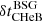| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 26 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202347854 | |
| Published online | 28 May 2024 | |
Pre-supernova evolution and final fate of stellar mergers and accretors of binary mass transfer⋆
1
Heidelberger Institut für Theoretische Studien, Schloss-Wolfsbrunnenweg 35, 69118 Heidelberg, Germany
e-mail: fabian.schneider@h-its.org
2
Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg, Mönchhofstr. 12-14, 69120 Heidelberg, Germany
3
University of Oxford, St Edmund Hall, Oxford OX1 4AR, UK
Received:
31
August
2023
Accepted:
21
February
2024
The majority of massive stars are expected to exchange mass or merge with a companion during their lives. This immediately implies that most supernovae (SNe) are from such post-mass-exchange objects. Here, we explore how mass accretion and merging affect the pre-SN structures of stars and their final fates. To this end, we modelled these complex processes by rapid mass accretion onto stars of different evolutionary stages and followed their evolution up to iron core collapse. We used the stellar evolution code MESA and inferred the outcome of core-collapse using a neutrino-driven SN model. Our models cover initial masses from 11 to 70 M⊙ and the accreted mass ranges from 10−200% of the initial mass. All models are non-rotating and for solar metallicity. The rapid accretion model offers a systematic way to approach the landscape of mass accretion and stellar mergers. It is naturally limited in scope and serves as a clean zeroth order baseline for these processes. We find that mass accretion, in particular onto post-main-sequence (post-MS) stars, can lead to a long-lived blue supergiant (BSG) phase during which stars burn helium in their cores. In comparison to genuine single stars, post-MS accretors have small core-to-total mass ratios, regardless of whether they end their lives as BSGs or cool supergiants (CSGs), and they can have genuinely different pre-SN core structures. As in single and binary-stripped stars, we find black-hole (BH) formation for the same characteristic CO core masses MCO of ≈7 M⊙ and ≳13 M⊙. In models with the largest mass accretion, the BH formation landscape as a function of MCO is shifted by about 0.5 M⊙ to lower masses, that is, such accretors are more difficult to explode. We find a tight relation between our neutron-star (NS) masses and the central entropy of the pre-SN models in all accretors and single stars, suggesting a universal relation that is independent of the evolutionary history of stars. Post-MS accretors explode both as BSGs and CSGs, and we show how to understand their pre-SN locations in the Hertzsprung-Russell (HR) diagram. Accretors exploding as CSGs can have much higher envelope masses than single stars. Some BSGs that avoid the luminous-blue-variable (LBV) regime in the HR diagram are predicted to collapse into BHs of up to 50 M⊙, while others explode in SNe and eject up to 40 M⊙, greatly exceeding ejecta masses from single stars. Both the BH and SN ejecta masses increase to about 80 M⊙ in our models when allowing for multiple mergers, for example, in initial triple-star systems, and they can be even higher at lower metallicities. Such high BH masses may fall into the pair-instability-SN mass gap and could help explain binary BH mergers involving very massive BHs as observed in GW190521. We further find that some of the BSG models explode as LBVs, which may lead to interacting SNe and possibly even superluminous SNe.
Key words: binaries: general / stars: black holes / stars: evolution / stars: massive / stars: neutron / supernovae: general
Full Table A.1 is available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/686/A45
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Most massive stars are born in binary, triple, and other multiple-star systems (e.g. Kobulnicky & Fryer 2007; Mason et al. 2009; Sana et al. 2012, 2013, 2014; Chini et al. 2012; Kobulnicky et al. 2014; Moe & Di Stefano 2017; Offner et al. 2023). For example, almost all O-type stars are found in binary systems and the triple and higher-order multiple-star fraction of these stars even exceeds 50% (e.g. Sana et al. 2014; Moe & Di Stefano 2017; Offner et al. 2023). As a consequence, the majority of massive stars exchange mass with a companion at some point in their evolution, that is also most supernovae (SNe) are from stars that evolved through past mass exchange with a companion (e.g. Podsiadlowski et al. 1992; Sana et al. 2012; Moe & Di Stefano 2017). In about 40–50% of the cases, mass exchange proceeds via stable Roche-lobe overflow (RLOF), but it can also lead to stellar mergers in about 20–30% and common-envelope phases in 10–20% of cases1 (see e.g. Sana et al. 2012; Schneider et al. 2015; Stegmann et al. 2022; Henneco et al. 2024).
During stable mass transfer and in common-envelope events, stars lose their hydrogen-rich envelopes. These binary-stripped stars develop distinctly different pre-SN core structures compared to single stars, affecting their final fate (e.g. Timmes et al. 1996; Wellstein & Langer 1999; Brown et al. 2001; Podsiadlowski et al. 2004; Woosley 2019; Ertl et al. 2020; Schneider et al. 2021, 2023; Laplace et al. 2021; Aguilera-Dena et al. 2023). For example, they explode in SN Ib/c and the inherently different pre-SN core structures result in neutron-star (NS) formation over a much larger initial mass range than in genuine single stars; they also explode with higher explosion energies, on average, resulting in larger nickel yields and faster NS kicks (Schneider et al. 2021); the systematically higher nickel yields are confirmed by observations (e.g. Anderson 2019; Meza & Anderson 2020). Moreover, their chemical yields differ from those of single stars (Farmer et al. 2021, 2023), and they may produce black holes (BHs) of universal masses of about 9 M⊙ and ≳16 M⊙ over a large range of metallicities (Schneider et al. 2023). The first hints for the existence of such universal BH masses may have been found in the chirp and BH mass distributions of binary BH mergers observed by gravitational-wave detectors (e.g. Tiwari & Fairhurst 2021; Abbott et al. 2023a; Tiwari 2022; Edelman et al. 2023).
Compared to the situation of binary-stripped stars, less is known about the pre-SN core structures and the final fates of the accretors of mass transfer and stellar mergers. It is estimated that about half of all Type II SNe are from such accretors in binary systems, with mergers being the dominant contribution (e.g. Zapartas et al. 2019). Main-sequence (MS) accretors likely rejuvenate and adjust their structure to the new mass such that they continue their evolution similar to that of single stars (e.g. Hellings 1983; Braun & Langer 1995; Dray & Tout 2007; Schneider et al. 2016, 2019, 2020). In contrast, post-MS accretors can become core-helium-burning blue supergiants (BSGs) and explode as such stars (Hellings 1983, 1984; Podsiadlowski & Joss 1989; Podsiadlowski et al. 1990; Claeys et al. 2011; Vanbeveren et al. 2013; Justham et al. 2014; Menon & Heger 2017; Menon et al. 2023). They may, however, also evolve and explode as cool supergiants (CSGs)2, but with different core masses than what is expected from single CSGs (e.g. Zapartas et al. 2021).
The well-studied SN 1987A was from a BSG that is likely the result of a merger (see e.g. reviews by Podsiadlowski 1992, 2017a and some of the latest models for SN 1987A by Menon & Heger 2017; Urushibata et al. 2018; Menon et al. 2019). More massive BSGs from stellar mergers have further been suggested to explode as luminous blue variables (LBVs) in interacting and possibly superluminous SNe (Justham et al. 2014), and hydrogen-rich, pair-instability SNe (PISNe; Vigna-Gómez et al. 2019). Furthermore, very massive merged stars with cores not massive enough for electron-positron pair production but large envelope masses might form BHs with masses in the pair-instability mass gap (e.g. Di Carlo et al. 2020; Renzo et al. 2020a; Costa et al. 2022; Ballone et al. 2023).
In this paper, we systematically model the response of stars to rapid mass accretion on a thermal timescale in an attempt to approximate the complex physics occurring in accretors of stable RLOF in semi-detached binaries and stellar mergers. We follow the evolution of these models until the onset of core collapse to understand how such accretion events may modify the core structures and hence affect the final fates and SN explosions of these stars. While our models are simplified and, for example, do not take into account rotation and the complex mixing in stellar mergers, they nevertheless allow us to study the resulting structures of mass accretors in a uniform and controlled way. In light of these approximations, we caution the reader when using these models. To explore the outcome of core collapse, we use the pre-SN stellar structures of our accretor models as input to the neutrino-driven SN model of Müller et al. (2016). We describe how we model accretors in the stellar evolution code MESA (Paxton et al. 2011, 2013, 2015, 2018, 2019) and explain the coupling to the SN code in Sect. 2. We present our results on the pre-SN evolution and core structures of the accretors at core collapse in Sect. 3. In Sect. 4, we show our findings on the final fates of accretors with a focus on their explodability, compact-remnant, and SN-ejecta masses, and pre-SN locations in the Hertzsprung-Russell (HR) diagram. Further explosion properties will be presented in a forthcoming publication (Schneider et al., in prep.). We discuss our results concerning model simplifications and uncertainties, and wider implications, for example, on the maximum BH and SN-ejecta masses from accretors at solar metallicity in Sect. 5. A summary of our main findings is given in Sect. 6.
2. Methods
The stellar models were computed with revision 10398 of the Modules-for-Experiments-in-Stellar-Astrophysics (MESA) software package (Paxton et al. 2011, 2013, 2015, 2018, 2019). We used the same basic MESA setup as in Schneider et al. (2021) and briefly summarise it in Sect. 2.1. In Sect. 2.2, we explain how we model binary-star accretion. For comparison of these accretion models with genuine single stars, we employ the single-star models of Schneider et al. (2021). In Sect. 2.3, we briefly describe how we coupled our models to a SN code to study their final fates and possible SN explosions. An overview of all models and key properties discussed in this work are provided in Table A.1. MESA inlists and other settings required to reproduce our models are published online on Zenodo3.
2.1. Stellar-model physics
All models were non-rotating and had the initial chemical composition of Asplund et al. (2009), that is an initial hydrogen mass fraction of X = 0.7155, helium mass fraction of Y = 0.2703, and metallicity of Z = 0.0142. Convection was described by mixing-length theory (Henyey et al. 1965) and we used a mixing-length parameter of αmlt = 1.8. The Ledoux criterion was applied and semi-convection was treated with an efficiency factor of αsc = 0.1. We enabled MESA’s MLT++ scheme that boosts convective energy transport in some stellar envelopes. Convective-boundary mixing was only applied to convective cores during hydrogen and helium burning, and was included via so-called “step overshooting” of 0.2 pressure-scale height. We used the stellar-wind prescription of Schneider et al. (2021) that closely follows MESA’s “Dutch” scheme. Cool-star winds followed Nieuwenhuijzen & de Jager (1990), while hot-star winds applied the Vink et al. (2000, 2001) rates. For Wolf–Rayet (WR) stars, we followed Nugis & Lamers (2000). The metallicity scaling of the cool-star and WR winds were as in Mauron & Josselin (2011) and Vink & de Koter (2005), respectively. No additional wind-mass loss was applied to luminous blue variables (LBVs). However, we mark models that spend more than 104 yr on the cool side of the diagonal S Doradus instability strip in the Hertzsprung-Russell (HR) diagram (Smith et al. 2004) and/or at effective temperatures Teff < 12 500 K while exceeding a luminosity of log L/L⊙ = 5.5 (i.e. connecting the hot-part of S Doradus instability strip with the absence of red supergiants (RSGs) of log L/L⊙ ≳ 5.5 at Teff = 12 500 K, Davies et al. 2018); such stars likely experience significant mass loss possibly leading to the removal of the entire hydrogen-rich envelope. Nuclear burning was implemented via the approx21_cr60_plus_co56.net reaction network. While this network properly reflects energy production by nuclear burning, it cannot follow accurately the electron fraction or proton-to-neutron ratio because of, for example, missing weak reactions. Reaction rates themselves were from the JINA REACLIB database V2.2 (Cyburt et al. 2010) and, for example, the important 12C(α, γ)16O reaction rate was taken from Xu et al. (2013).
2.2. Binary-star accretion models
2.2.1. Model assumptions
Mass transfer by stable RLOF in semi-detached binaries and stellar mergers are events during which the masses of stars increase rapidly. Hence, to zeroth order, these processes may be viewed as accretion events where one star, called accretor from hereon, effectively gains mass. The accretion timescales during these events cover the entire spectrum from dynamic-timescale accretion in stellar mergers to thermal- and nuclear-timescale accretion in binary mass transfer. In stable Case A RLOF in semi-detached binaries, most mass is often accreted on a thermal timescale (e.g. Wellstein et al. 2001), but this can vary from case to case. In our accretion models, we accreted a certain fraction of the initial mass of a star, facc ≡ ΔMacc/Mini, on the momentary thermal timescale of the accretor, that is at a rate of
where L, R, and M are the momentary luminosity, radius, and mass of the accretor, respectively, τKH is the Kelvin-Helmholtz timescale and G is the gravitational constant. The chemical composition of the accreted mass was always the same as that on the surface of the accretor.
We computed models for accretion fractions facc of 10%, 25%, 50%, 75%, 100%, 150%, and 200%. The latter two fractions are not achievable by stellar mergers in isolated binary evolution but can be achieved by stable RLOF4. In stellar mergers, facc > 1 may be possible in triple systems and dense stellar clusters (see Sect. 5.4 for further discussion). To better distinguish these cases visually, we show the facc = 150% and 200% models in blue colour in the rest of the paper. All other accretion fractions are possible in both stable binary mass transfer and stellar mergers.
As with envelope stripping by RLOF (e.g. Schneider et al. 2021), the future evolution of stars depends critically on the exact evolutionary moment when the matter is accreted. In analogy to envelope stripping, we use the terms Cases A–C, but now applied to the evolutionary stage of the accretor. Hence, Cases A–C refer to stars that accrete mass when they burn hydrogen in their cores, have finished core hydrogen burning but have not started core helium burning yet, and have finished core helium burning, respectively. We have defined the end of core helium burning as that point in evolution when the central hydrogen mass fraction drops below 10−6. We also distinguish between “early” and “late” Cases A and B. In our case, early and late Case A accretion refer to when the central hydrogen mass fraction of the accretor drops below 0.35 and 0.05, respectively. In Case B accretors, early means that the accretor has just left the main sequence while late is when the accretor has developed a convective envelope and is shortly before core helium ignition.
2.2.2. Model limitations
The simple accretion models cannot reproduce all the important physics of binary mass transfer and stellar mergers, and only account for one such phase while several mass-accretion and mass-loss episodes are possible in general (see also Schneider et al. 2021). Nevertheless, applying such models allows us to understand and study the resulting stellar structures in a uniform and controlled way, and our models offer a zeroth-order approximation to these complex physical processes. We mention some limitations of our approach here and further discuss them in Sect. 5.
Our models are non-rotating while in particular accretors of binary mass transfer are likely spun up to near critical surface rotation (see e.g. Langer 2012). Such rapid rotation can induce mixing of chemical elements and angular momentum that we do not take into account. The mixing can enlarge the cores of MS accretors and thereby affect the core structure at the pre-SN stage. Moreover, rotation changes the mass-loss history of stars.
Multi-dimensional hydrodynamic simulations show that mixing also occurs in stellar mergers (e.g. Lombardi et al. 2002; Ivanova et al. 2002; Glebbeek et al. 2013; Schneider et al. 2019). It can enlarge the effective core sizes in mergers of two MS stars increasing the effect of rejuvenation but can also lead to smaller cores in mergers with post-MS stars. Moreover, nuclear-processed core material of the two stars may be mixed in the outer layers of the merger remnant, which we do not take into account. Consequently, our models cannot reproduce the chemical surface enrichment observed in such simulations (cf. Lombardi et al. 2002; Ivanova 2002; Glebbeek et al. 2013). Our accretion models also neglect strong magnetic fields that may be generated in the merging process and that can affect the evolution of merged stars, for example, via internal angular-momentum transport and magnetic braking (Schneider et al. 2019, 2020).
Lastly, our models cannot reproduce the surface chemical abundances expected for products of binary mass transfer and stellar mergers. For example, they do not show the nitrogen and helium enrichment from accreting nuclear-processed material during the later accretion phases in stable binary mass transfer (see e.g. review by Langer 2012). In some of our models, stellar winds have removed parts of the stellar envelope such that helium-rich layers are visible at the surface. In these cases, we then accrete helium-enriched material.
2.3. Semi-analytic supernova model
Pre-SN stellar structures were analysed with the semi-analytic, parametric-SN code of Müller et al. (2016) once the MESA models reached an iron-core infall velocity of 950 km s−1. The code explores the explodability of pre-SN stellar models within the framework of neutrino-driven SNe and takes into account the entire interior structure of our models at core collapse. It predicts SN properties such as explosion energy, synthesised nickel masses, compact remnant masses, and NS kick velocities. We applied the same calibrations of this neutrino-driven-explosion model as in Schneider et al. (2021), that is an average explosion energy of Type IIP SNe from single-star models of 0.69 ± 0.17 B and a NS kick-velocity distribution that is in agreement with the Maxwellian with σ = 265 km s−1 of Hobbs et al. (2005). The maximum, gravitational NS mass is chosen to be 2 M⊙.
We classify SN explosions as SN IIb if the mass of the hydrogen-rich envelope is smaller than 1 M⊙ following Sravan et al. (2019). The mass of the hydrogen-rich envelope is defined as the layer with a hydrogen mass fraction XH > 0.01 and a helium mass fraction XHe > 0.1. If the hydrogen mass in the SN ejecta is smaller than 0.1 M⊙ (Hachinger et al. 2012), we say that the SN is of Type Ib/c. We do not distinguish between SN Ib and SN Ic in this work. In all other cases with more hydrogen and larger hydrogen-rich envelopes, we define the SN to be of Type II.
3. Pre-supernova evolution and structure
Rapid accretion of mass can change the stellar structure in such a way that the accretors (merged stars) spend most of their core-helium-burning lifetime and immediate pre-SN evolution as BSGs (e.g. Hellings 1983; Podsiadlowski & Joss 1989; Podsiadlowski et al. 1990; Braun & Langer 1995; Claeys et al. 2011; Vanbeveren et al. 2013; Justham et al. 2014; Menon & Heger 2017; Urushibata et al. 2018). We describe the occurrence and structure of such BSGs in Sect. 3.1. A star’s final fate is mostly determined already by the end of core helium burning and depends on the then CO core mass 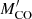 and central carbon mass fraction XC (Chieffi & Limongi 2020; Patton & Sukhbold 2020; Schneider et al. 2021). In our models, the CO core masses at the end of core helium burning are almost identical to those at core collapse, MCO. We show how core masses such as MCO and the important central carbon mass fraction XC are affected by mass accretion in Sects. 3.2 and 3.3, respectively, before presenting the structures of our models at core collapse in Sect. 3.4.
and central carbon mass fraction XC (Chieffi & Limongi 2020; Patton & Sukhbold 2020; Schneider et al. 2021). In our models, the CO core masses at the end of core helium burning are almost identical to those at core collapse, MCO. We show how core masses such as MCO and the important central carbon mass fraction XC are affected by mass accretion in Sects. 3.2 and 3.3, respectively, before presenting the structures of our models at core collapse in Sect. 3.4.
3.1. Blue supergiants
In Fig. 1, we show an exemplary Hertzsprung-Russell (HR) diagram with initial 13 M⊙ stars accreting mass shortly after finishing core hydrogen burning (early Case B5). We find three qualitatively different outcomes of mass accretion: the accretor burns helium in its core (i) as a CSG (facc = 0.10, 0.25), (ii) as a BSG but explodes as a CSG (facc = 0.50) and (iii) as a BSG and explodes as a BSG (facc ≥ 0.75). Here, we define BSGs as supergiants with effective temperatures of log Teff/K > 3.9 while CSGs are cooler than that. When burning helium in the core as a BSG, stars do so for a nuclear timescale, that is for several 105 − 106 yr (see Figs. A.3 and A.4, and Table A.1), and we refer to them as long-lived BSGs6. The required amount of accreted mass to turn stars into BSGs depends on the mass and evolutionary stage of the accretors. For example, none of our early Case A accretors turn into BSGs and only one model does so in late Case A accretion (facc = 0.25; Fig. A.1). Most of the Case A models fully rejuvenate and the accretors continue their evolution similarly to single stars with a higher mass (see below for more details on the rejuvenation). In late Case B accretion, the models with facc = 1.0, 1.5, and 2.0 are BSGs during core helium burning and also explode as BSGs, while this only occurs for facc = 1.5 and 2.0 in the Case C accretors (Fig. A.2). In general, we find that the more evolved the stars are, the more mass needs to be accreted to turn them into BSGs.
 |
Fig. 1. Hertzspung-Russell diagram with initial 13 M⊙ stars accreting a fraction facc of their initial mass (colour coded) shortly after they finished core hydrogen burning (early Case B). The dotted parts of the tracks show the accretion phase and the dashed grey evolutionary track is for a single star. Plus symbols are added every 2 × 105 yr after finishing core hydrogen burning to indicate in which region of the HR diagram stars burn helium in the core. The observationally inferred maximum luminosity of RSGs of log L/L⊙ = 5.5 (Davies et al. 2018) is shown by a dotted black line. Explosion sites are indicated as well as the likely SN type. The grey bands show the hot and cool part of the S Doradus instability strip (Smith et al. 2004). For facc ≳ 0.50, the models burn helium as a BSG and for facc ≳ 0.75 they also explode as a BSG. |
We have not considered the mixing of helium-rich material out of the core into the envelope. It is well known that the dredge-up of helium favours the occurrence of BSG structures (Barkat & Wheeler 1988; Saio et al. 1988). Therefore, in the context of a stellar merger, the combination of the addition of matter to the envelope and the dredge-up of part of the helium-rich core, which increases the helium abundance in the evelope, but also further decreases the core to total mass ratio, is particularly favourable for producing BSGs (e.g. Hillebrandt & Meyer 1989; Podsiadlowski et al. 1990, 1992; Ivanova & Podsiadlowski 2002; Menon & Heger 2017; Podsiadlowski 2017b). The more recent, systematic study of such mergers by Menon & Heger (2017) also shows that the ultimate SN explosions resulting from such mergers can reproduce the properties of peculiar SNe, such as SN 1987A, much better than single BSG progenitors (Menon et al. 2019). Similarly, merger products also better reproduce the observed population of BSGs (Bernini-Peron et al. 2023; Menon et al. 2023). Since we do not include these dredge-up effects, this means that the accretion thresholds for BSG formation mentioned above are upper limits when compared to actual stellar mergers. Interior mixing from stellar mergers also affects Case A mergers, which is not accounted for in our models either but, for example, can further enhance complex morphologies in star clusters above and around the MS turn-off region (see e.g. Wang et al. 2020). In Cases B and C accretors of binary mass transfer, such mixing is not expected to occur, and the extra mixing and growth of the convective core in Case A accretors is covered by our models. We show an overview of our accretor model grid in Fig. A.3 that illustrates and summarises which of our models evolve and end their lives as CSGs and BSGs. For further, general considerations of stellar structures that may spend time as a BSG, see for example Schootemeijer et al. (2019), Farrell et al. (2022) and Sibony et al. (2023).
The interior structures of the long-lived BSGs are characterised by hydrogen shell burning driving a large convective region (Fig. 2). This occurs if the accreted mass is so large that the temperature at the base of the hydrogen-rich envelope becomes high enough to drive convection by large nuclear energy generation from hydrogen shell burning (cf. Sect. 4.1). For facc = 0.1, the accretion modifies the temperature stratification at the base of the hydrogen-rich envelope such that hydrogen shell burning is pushed to lower mass coordinates but does not turn convective (Fig. 2a). Contrarily, for facc = 1.0, shell burning becomes convective (Fig. 2b). The structure of such BSGs may be viewed as that of a (relatively) unevolved MS star on top of a helium star. In this picture, the convective hydrogen-burning shell corresponds to the core of the MS star. This analogous picture also explains intuitively why the envelope of such BSGs remains radiative and why the extent of the convective hydrogen-burning shell decreases during core helium burning7 (Fig. 2b).
 |
Fig. 2. Kippenhahn diagrams with initial 13 M⊙ early Case B systems accreting (a) 10% and (b) 100% of their initial mass. The moment of mass accretion is indicated by an arrow. Energy generation by nuclear burning, ϵnuc, and loss by neutrinos, ϵν, are colour-coded. The right y-axes show the mass fractions of carbon, XC, and oxygen, XO, in the centre of the stars. Carbon starts being produced when core helium burning begins. The grey hatched areas show convective regions, purple hatchings are for convective overshooting, yellow stands for thermohaline mixing and brown is for semi-convection. The dotted blue lines show where the hydrogen mass fraction drops below 0.5, that is they trace the helium core mass. Hydrogen shell burning in the facc = 0.1 model is radiative and the star evolves into a CSG. In the facc = 1.0 model, hydrogen shell burning proceeds convectively and the star evolves as a BSG (cf. Fig. 1). |
To further illustrate the structural differences between stars evolving through a long-lived BSG phase and those becoming CSGs, we compare in Fig. 3 the interior nuclear burning at the end of core oxygen burning of an initially 20 M⊙ single star and two early Case B accretors with initial masses of 20 M⊙ and 23 M⊙, and accretion fractions of facc = 0.1 and facc = 1.0, respectively. All models have similar CO core masses of MCO = 5.62 M⊙, 5.64 M⊙, and 5.89 M⊙, respectively, but evolve differently. In particular, the accretor model with facc = 1.0 evolves as a long-lived BSG while the other two models become CSGs. The largely different hydrogen-shell burning in the BSG facc = 1.0 accretor is visible (cf. Fig. 2) as well as markedly different strengths, mass coordinates, and extensions in mass of the nuclear reaction rates due to carbon and neon burning (helium burning is also different). Carbon and neon burning are particularly important for the final core structures (see also Sect. 3.3). As is shown later, such differences can distinguish between successful SN explosions or direct collapse into a BH.
 |
Fig. 3. TULIPS diagram (Laplace 2022) of the nuclear energy generation rate ϵnuc at the end of core oxygen burning (central oxygen mass fraction < 10−4). Shown are the interiors of a single star of Mini = 20 M⊙ (bottom), an early Case B accretor model of Mini = 20 M⊙ and facc = 0.1 (top left), and an early Case B accretor model of Mini = 23 M⊙ and facc = 1.0 (top right). The three models have a similar CO core masses of MCO = 5.62 M⊙, 5.64 M⊙, and 5.89 M⊙, respectively. The facc = 0.1 accretor model is a CSG while the facc = 1.0 model is a BSG, which can be recognised by the strong hydrogen-shell burning that drives a thick convection zone (not indicated here for clarity, but cf. Figs. 2 and A.5). |
Whether Case A accretors can become long-lived BSGs depends on whether they adjust their interior structure to the new mass, that is whether they rejuvenate. If an accreting MS star fully rejuvenates, the convective core will have the same size as that of a single star with the same mass. This means that also the helium core masses at the terminal-age main sequence (TAMS) will be the same and thus also the average helium mass fraction ⟨Y⟩. The relative deviation of ⟨Y⟩ at the TAMS between our Case A accretors and genuine single stars shows that early Case A accretors (almost) fully rejuvenate for accretion fractions larger than ≈10% (Fig. 4a). The same is true for late Case A accretors for facc ≳ 25% (Fig. 4b). These findings and in particular that late Case A accretors need to accrete more mass than early Case A accretors to fully rejuvenate agree qualitatively with the results of Braun & Langer (1995). As explained by Braun & Langer (1995), semi-convection regulates whether a convective core can grow and mix through chemical gradients upon mass accretion. The chemical gradients are steeper at a later MS phase such that more accretion is needed to allow semi-convection to mix through the gradient and the convective core to grow to a value found in genuine single stars of the same mass. Compared to the models of Braun & Langer (1995), semi-convection with αsc = 0.1 is much more efficient in our models such that most of them tend to fully rejuvenate. According to Schootemeijer et al. (2019), semi-convection may even be more efficient than assumed here such that all Case A accretors would fully rejuvenate.
 |
Fig. 4. Rejuvenation of early (panel a) and late (panel b) Case A accretors. The rejuvenation is quantified as the difference of the average helium mass fraction ⟨Y⟩ of the accretors at the terminal-age main sequence (TAMS) relative to that of single stars. The relative differences are plotted as a function of mass at the TAMS, MTAMS. Negative differences mean that the accretors have burnt less hydrogen into helium compared to single stars, that is they have less massive convective cores. This is a sign that accretors did not (fully) adjust their structure to the new total mass after accretion, that is they did not (fully) rejuvenate. |
In our models, not all Case A accretors fully rejuvenate (Fig. 4). However, this does not automatically mean that they can also burn helium in their cores as BSGs. To evolve into long-lived BSGs, they must also reach conditions to drive convective hydrogen shell burning. The initially 13 M⊙ late Case A accretor with facc = 0.25 does not fully rejuvenate (Fig. 4b) and has accreted sufficient mass such that it becomes a BSG during core helium burning (Fig. A.1b). Contrarily, the facc = 0.10 model also does not fully rejuvenate but accretes too little mass to develop convective hydrogen shell burning (Fig. A.1b).
3.2. Helium core, carbon-oxygen core, and final stellar masses
In the evolution of stars, the core mass plays an important role. Here, we concentrate on the helium and carbon-oxygen (CO) core masses MHe and MCO, respectively, that are mostly set by the extent of convection during core hydrogen and helium burning. Both core masses can vary during the evolution (e.g. due to shell burning or dredge-ups) and we measure them at the onset of core collapse in this work. We define MHe as the mass coordinate where the hydrogen mass fraction XH drops below < 10−5 while MCO is defined by the helium mass fraction XHe becoming smaller than 0.5.
In Fig. 5, we show MCO as a function of initial mass Mini for single stars and Cases A–C accretors. The trends for the helium core masses are qualitatively similar to those of the CO core masses and are therefore not shown in the main text but only in Fig. A.6. Most of our Case A accretors fully adjust their interior structures to the new mass and then continue the evolution as if they were born with that high mass, that is most of them fully rejuvenate (see Fig. 4 and Sect. 3.1). This is exemplified by the increasing helium and CO core masses at constant initial mass and increasing accretion fractions. The rejuvenation can even be seen more directly in Fig. 6, where we plot the masses of stars at core collapse, Mfinal, as a function of MCO. Case A accretors mostly follow the trend of single stars, that is they produce the same core mass for a given total final mass, except for the models that do not fully rejuvenate and have higher final masses (cf. Fig. 4). This deviation from the single-star final masses is larger in the late than the early Case A models. In particular, some non-rejuvenating, late Case A accretors (partly) burn helium in their cores as BSGs and not CSGs (Braun & Langer 1995). In turn, they avoid the stronger CSG wind mass loss and retain higher final masses at core collapse.
 |
Fig. 5. CO core masses MCO at core collapse as a function of the initial mass Mini for Case A (panel a), Case B (panel b), and Case C (panel c) accretors. Colours show the accretion fraction facc of the models, and single stars are shown in blue squares for comparison in panel a. Panels b and c show the difference in MCO relative to the corresponding single-star core masses. To guide the eye, data points for facc = 0.1 (mostly CSGs) and 2.0 (BSGs) are connected by dashed lines and highlighted. |
Some Case A accretor models with facc ≳ 0.75 at MCO > 20 M⊙ appear to be offset to higher MCO relative to the single stars (Figs. 5a and 6a). These models are so massive after accretion that their strong winds erode their envelopes and the final mass is the same as the CO core mass. At MCO > 10 M⊙, winds have removed most of the hydrogen-rich envelope, explaining the almost linear relation of single stars and Case A accretors in Fig. 6a.
 |
Fig. 6. Similar to Fig. 5 but showing the final masses of stars as a function of the CO core mass MCO at core collapse. In all three panels, single-star models are plotted as blue squares. We further indicate models that experience SN fallback by grey squares while crosses mark those models that should have experienced enhanced LBV-like mass loss, which is not accounted for in our models (see Sect. 2.1). The dotted black line is a one-to-one relation. |
Cases B and C accretors cannot rejuvenate as is visible by the relative difference of their helium and CO core masses in comparison to single stars (Figs. 5b and A.6b). We find that they differ at most by an order of 𝒪(10%). This immediately implies that – when comparing to single stars – such accretors roughly keep their core masses constant while mass is mostly added to their envelopes. One may thus expect that, to zeroth order, the cores of such accretors evolve similarly to core collapse as those of the corresponding single stars with the same initial mass. This expectation is met in accretors of binary mass transfer but not in fully realistic stellar mergers. In the latter, parts of the core are mixed into the envelope of the merged star, which reduces the core mass. This effect is not covered by our models (see Sect. 2.2.2), that is the core masses of our Cases B and C accretors are upper limits in comparison to what is expected from fully realistic stellar mergers.
In Case B accretors, the CSG and BSG sequences can be distinguished in Figs. 5b and A.6b: models with facc = 0.1 are generally CSGs while those with facc = 2.0 always become BSGs (see Fig. A.3 for a detailed overview of which minimum accretion fractions are required in our models to turn accretors into BSGs). Post-accretion CSGs hardly deviate from the core masses of the single stars while the BSGs deviate by a few tens of percent in MHe and MCO; they follow the indicated trend for facc = 2.0. For Mini ≲ 15 M⊙, the Case B accretors have helium and CO core masses at core collapse that are larger than those of single stars while they are smaller for Mini ≳ 15 M⊙8. For all initial masses, the convective cores of accretors at the beginning of core helium burning are less massive than those of single stars and the location of the hydrogen-burning shell is at lower mass coordinates (i.e. smaller MHe at this time in evolution as can be seen in Fig. 2). Because of the hydrogen shell burning, the helium core and with it the convective core grow in mass. In Case B accretors, the convective core grows relatively more in less massive stars. For example, for Mini ≳ 30 M⊙, the convective core masses remain almost constant during core helium burning (Fig. A.5) while they grow significantly for Mini ≲ 15 M⊙ (Fig. 2).
In Case C accretors, there is not enough remaining time before core collapse for hydrogen and helium shell burning to add significantly to MHe and MCO. This is indeed borne out by the helium core masses being almost unchanged (they change by an order of 𝒪(1%)) regardless of whether stars evolve as CSGs or BSGs (Fig. A.6c). The picture is seemingly different for the CO core masses at Mini ≳ 20 M⊙ that can exceed the single-star MCO by an order of 𝒪(10%). This increase is not caused by helium shell burning but by a brief revival of core helium burning9 because of the mass accretion (see also Sect. 3.3). The nuclear burning drives a transient convective core that mixes in fresh helium fuel, thereby leading to more massive MCO. For Mini ≲ 20 M⊙, we do not find such a strong revival of core helium burning and MCO does not grow as much.
The final masses of rejuvenated Case A accretors closely follow those of single stars of the same CO core mass, which is not the case in non-rejuvenating Case A and most Case B accretors (Fig. 6). In the latter cases, stars retain more mass and we find final stellar masses of up to 100 − 200 M⊙ in our models. So while MHe and MCO change at most by some tens of percent in comparison to single stars, the final core-to-stellar mass ratios can be reduced by up to an order of magnitude: Cases A and B accretors have comparably small cores for their total stellar mass.
As mentioned in Sect. 2, our models do not account for LBV-like mass loss. Even disregarding all models that likely experience significant LBV mass loss (marked by crosses in Fig. 6), Case B accretors have the largest final stellar masses, followed by Cases C and A accretors (and single stars). Case C accretors generally have smaller final masses than Case B accretors for the following reasons. Firstly, when accretion starts, Case C models have been subject to strong wind mass loss on the RGB branch while Case B accretors can avoid this entirely as BSGs and thus reach larger final masses. Secondly, even if Case B accretors do not evolve through a long-lived BSG phase but also become CSGs, they have smaller helium and CO core masses than Case C accretors and single stars. As we will subsequently show, the luminosity of CSGs scales with their core mass such that Case C accretors and single stars have stronger wind mass loss and smaller final masses because of their higher luminosities. We further discuss the final stellar masses in relation to BH and SN-ejecta masses in Sect. 4.2.
3.3. Central carbon abundance after core helium burning
As explained above, the central carbon mass fraction XC after core helium burning is an important parameter that sets the initial conditions for the later nuclear-burning stages and thereby the pre-SN core structure. It is determined by helium burning that proceeds in two steps. First, the triple-α reaction produces 12C. Second, once α-particles become rarer and 12C nuclei have been formed, the 12C(α, γ)16O nuclear reaction eventually becomes dominant and consumes 12C to its final abundance XC (see e.g. Langer 1989; Woosley et al. 1993; Brown et al. 2001; Chieffi & Limongi 2020; Sukhbold & Adams 2020; Laplace et al. 2021, and Figs. 2 and A.5). How much carbon is depleted depends on the central density10, that is the (core) mass of the star, and how much the convective core grows during helium burning, which can mix in fresh α-particles that are then captured onto 12C to produce 16O.
We show the carbon mass fraction XC at the end of core helium burning of our models as a function of the CO core mass in Fig. 7 (a similar diagram as a function of the initial mass can be found in Fig. A.7). As discussed in Sect. 3.2, most Case A accretors fully rejuvenate and adjust their interior structure to the new total mass such that they have the same XC as in single stars of the same MCO (Fig. 7a). We also find again that those Case A accretors, which spend most of their time burning helium in their cores as BSGs, deviate from the single-star trend and deplete relatively more 12C. The reason is the same as in Case B accretors discussed next.
 |
Fig. 7. Similar to Fig. 5 but showing the central carbon mass fraction at the end of core helium burning XC as a function of the CO core mass MCO. |
In Case B accretors, we find that the CSG and BSG sequences differ considerably in XC (Fig. 7b). The post-accretion BSG models roughly follow the facc = 2.0 models and end core helium burning with less carbon than single stars while the CSG models follow the single-star trends. We find that Case B accretors with MCO ≲ 15 M⊙ (Mini ≲ 40 M⊙) can have up to 80% less carbon in their cores than single stars while this is < 10% for MCO ≳ 15 M⊙.
The differences are due to different growths of the convective cores during helium burning. At Mini = 13 M⊙ (Fig. 2), the convective core driven by helium burning still grows considerably more in mass in the facc = 1.0 model after reaching a maximum carbon mass fraction of ≈0.55 than in the facc = 0.1 model. The larger core growth during this phase mixes more α-particles into the convective core and the 12C(α, γ)16O nuclear reaction thus burns more 12C into 16O. The facc = 1.0 model then ends core helium burning with XC ≈ 0.13 while the facc = 0.1 model has a larger abundance of XC ≈ 0.30 (Fig. 2). For a higher initial mass of 30 M⊙, the convective cores in the facc = 0.1 and facc = 1.0 models grow similarly after reaching the maximum core carbon mass fraction of ≈0.55 (Fig. A.5). Consequently, similar amounts of α-particles are mixed into the convectively helium-burning cores such that both models reach similar final core carbon mass fractions of about 0.2.
The carbon mass fractions XC of the facc = 2.0 early Case B accretors never reach the same values in single stars as a function of the CO core mass (Fig. 7b) while they are the same as in single stars as a function of initial mass for Mini ≳ 35 M⊙ (Fig. A.7b). At first sight, this may sound contradictory but it is not. The accretor models follow a different MCO − Mini relation than single stars. For Mini > 15 M⊙, they have ≈20% smaller CO cores than single stars of the same initial mass (Fig. 5b). Generally, XC drops with increasing MCO and Mini (Figs. 7 and A.7). At the same initial mass, both single stars and Case B accretors have the same XC. Translating into a XC − MCO relation, the XC of the accretor models are then compared to those of single stars of ≈20% smaller MCO, that is higher XC.
In Case C accretors, we find XC values reduced by ≈70% for 7 ≲ MCO/M⊙ ≲ 25 and facc ≳ 0.1 (Fig. 7c). In these models, accretion increases the star’s central temperature. Helium burning is revived and drives a transient convective core that mixes in fresh helium fuel. As 12C(α, γ)16O is the dominant reaction in these models at this moment of evolution, significantly more carbon is converted into oxygen compared to the equivalent single-star models. Once core helium burning ceases entirely, XC is reduced to 4−6%. In the other models with different MCO, this mechanism does not operate and XC remains close to that found in the corresponding single-star models.
As explained above, fully realistic Cases B and C stellar mergers have smaller cores than in our accretion models. The same mechanism of mixing fresh helium into the helium-burning core will also operate in such stars. Hence, we expect that also such stars show different XC branches depending on whether the merged star becomes a long-lived BSG or evolves into a CSG.
3.4. Pre-SN stellar structure
The different starting conditions for the later nuclear-burning stages, that is MCO and XC (see Sects. 3.2 and 3.3), can lead to inherently different core structures during the advanced burning stages and at core collapse. We summarise the pre-SN stellar structures of our models by their iron core mass, MFe, the central specific entropy, sc, and the so-called compactness parameter,
which is the ratio of a mass coordinate M and the radius at this location R(M) (O’Connor & Ott 2011). Usually, M = 2.5 M⊙, and ξ2.5 ≳ 0.45 indicates that stars are unable to explode in SNe and form BHs (e.g. O’Connor & Ott 2011; Ugliano et al. 2012; Sukhbold & Woosley 2014; Ertl et al. 2016; Sukhbold et al. 2016; Müller et al. 2016; Chieffi & Limongi 2020; Patton & Sukhbold 2020; Schneider et al. 2021, 2023). MFe, sc and ξ2.5 are closely related and they provide similar insights into the pre-SN structure (see also Fryer 2014; Schneider et al. 2021; Takahashi et al. 2023; Temaj et al. 2024). For example, the effective Chandrasekhar mass that an iron core approaches when it starts to collapse is a function of the electron fraction Ye and electronic entropy se, c (the average electronic entropy is roughly ⟨se, c⟩≈⟨sc⟩/3 but depends on each case; see e.g. Baron & Cooperstein 1990; Timmes et al. 1996),
This relation directly links sc to MFe at core collapse and sc is further a measure of the mass-radius relation of the iron core, that is it relates to ξ2.5 (Schneider et al. 2021). Also, the gravitational binding energy of the material exterior of the iron core could have been used as a summary proxy of the structure of stars at core collapse (e.g. Sukhbold & Woosley 2014; Temaj et al. 2024). All of these quantities follow similar trends such as peaks and troughs at the same Mini and MCO.
The evolution of massive stars beyond core helium burning is driven by thermal neutrino losses and the delicate balance between these losses, energy gain from nuclear burning, and energy release and consumption from changes in the gravitational potential of stars. For example, the central carbon abundance XC at the end of core helium burning generally decreases with increasing MCO (Fig. 7). With fewer carbon atoms available for carbon burning, there is a critical MCO beyond which energy loss from neutrinos overcomes energy generation from core carbon burning. Consequently, the carbon burning proceeds no longer under convective but radiative conditions, the evolution speeds up and the stellar cores at core collapse become more compact, reach higher MFe and have larger entropy. With further increasing MCO, the next nuclear burning stages ignite more quickly after the beginning of core carbon burning, become more vigorous and reduce ξ2.5, MFe and sc at core collapse. For an even higher MCO, neon burning also becomes neutrino dominated, turns radiative and again leads to increased ξ2.5, MFe and sc at core collapse (e.g. Patton & Sukhbold 2020; Sukhbold & Adams 2020; Schneider et al. 2021, 2023; Laplace et al., in prep.).
This sequence of changes in the nuclear burning conditions in the deep interior of stars leads to peaks and troughs in ξ2.5, MFe and sc at core collapse with MCO (Fig. 8). In our single-star models, a peak in ξ2.5, MFe and sc is found at MCO ≈ 7 M⊙ and they increase and reach generally high values for MCO ≳ 13 M⊙. We find an indistinguishable ξ2.5, MFe and sc landscape with MCO compared to single stars in our Case A accretors (Figs. 8a, d, g); even in the non-rejuvenated Case A systems, there is no obviously deviating trend. We attribute the latter to the fact that also the non-rejuvenated Case A accretors show the same relation between XC and MCO as the single stars (Fig. 7a).
 |
Fig. 8. Core compactness ξ2.5 (panels a–c), iron core mass MFe (panels d–f), and central specific entropy sc (panels g–i) as a function of the CO core mass MCO at core collapse. As in other figures, we distinguish between Cases A–C accretors, and colour-code the mass accretion fraction facc. Accretion fractions of 25%, 75%, and 200% are connected by dashed lines to better visualise trends and systematic shifts. |
In the Case B accretors, the ξ2.5, MFe, and sc landscapes are qualitatively similar to those of single stars but we find a systematic shift of the peaks and troughs to lower MCO (Figs. 8b, e, h). The magnitude of the shift depends on the amount of accreted mass. For facc = 2.0, the compactness peak is shifted by about 0.5 M⊙ to a lower MCO of ≈6.5 M⊙ and the second major increase of compactness is shifted by about 1 M⊙ to MCO ≈ 12 M⊙. In these models, the carbon abundance at the end of core helium burning is reduced (Fig. 7) such that core carbon and core neon burning become neutrino dominated at slightly lower MCO. This finding is analogous but in the opposite direction to binary-stripped stars where the removal of the hydrogen-rich envelope results in a larger XC at the end of core helium burning and thus in a systematic shift of the compactness landscape to higher MCO (Woosley 2019; Schneider et al. 2021, 2023; Laplace et al. 2021). In the example in Fig. 3, the accretor model with facc = 1.0 falls into the shifted compactness peak for such models (ξ = 0.63) while the single star and facc = 0.1 accretor have rather low compactness parameters of 0.24 and 0.12, respectively. This illustrates further that accretor models can achieve inherently different core structures compared to single stars despite similar CO core masses.
The relation of ξ2.5, MFe, and sc as a function of MCO in Case C accretors is qualitatively different from those of the single stars and Cases A and B accretors at MCO ≳ 5 M⊙ (Figs. 8c, f, i). The much reduced XC in these models (Fig. 7c) results in a shortened core-carbon-burning phase and generally larger ξ2.5, MFe, and sc at MCO ≳ 5 M⊙ compared to the single-star models. The first compactness peak occurs at lower MCO and is broadened with respect to that of the single stars and we find a dependence on the amount of accreted mass. The compactness peak at MCO ≈ 7 M⊙ is broadened the most for facc = 0.25 while it is broadened to a lesser extent for higher accretion fractions. Because of this, the second major increase in compactness is pushed to MCO ≈ 18 M⊙ in the facc = 0.25 models and to MCO ≈ 14 M⊙ for facc = 2.0. The facc = 0.1 models, where we found no clear trend in the reduction of XC (Fig. 7c), also seem to show no clear trend in ξ2.5, MFe, and sc.
The mixing of core material into the envelope in fully realistic stellar mergers may affect both the envelope and the pre-SN core structures. However, the qualitative trends of ξ2.5, MFe, and sc with MCO are expected to be similar. We expect fully realistic mergers that end their lives as CSGs (BSGs) to follow similar relations of ξ2.5, MFe, and sc with MCO as is found in pre-SN CSGs (BSGs) from our accretors. However, the mapping of MCO to Mini will differ and, as explained above, which facc thresholds result in long-lived BSGs from Cases B and C stellar mergers and hence which mergers correspond to the most strongly shifted ξ2.5, MFe, and sc curves.
4. Final fate and SN explosions
Applying the SN code of Müller et al. (2016) to our models at core collapse (Sect. 2), we find that a compactness threshold of ξ2.5 < 0.44 for successful SN explosions agrees with the model of Müller et al. (2016) in more than 95% of cases. Similarly, the two-parameter explodability criterion of Ertl et al. (2016), μ4 < k1M4μ4 + k2 with constants k1 = 0.200 and k2 = 0.072 (see Schneider et al. 2023), agrees in 89% of cases. In the Ertl et al. (2016) criterion, μ4 = dm/dr is the radial mass derivative in units of M⊙/1000 km and M4 the mass in M⊙ at a specific entropy of s = 4. In particular, all explodability criteria predict BH formation in the compactness peak at MCO ≈ 7 M⊙ and generally also for high compactness at MCO ≳ 13 M⊙. The ξ2.5-landscape found in this work is thus a good proxy for whether stars may explode in neutrino-driven SNe11 (see also the review by Heger et al. 2023). This agrees with the expectation that stars with high compactness, large iron core mass and high gravitational binding energy exterior to the iron core are more prone to collapsing into BHs (see e.g. Sukhbold & Woosley 2014; Heger et al. 2023). It is important to note, however, that there are core-collapse simulations that show shock revival in stars with high core compactness (see e.g. Ott et al. 2018; Burrows et al. 2020; Chan et al. 2018, 2020; Kuroda et al. 2018; Couch et al. 2020; Powell & Müller 2020), but this does not immediately imply a successful SN explosion (Heger et al. 2023).
We first present the pre-SN locations of our models in the HR diagram in Sect. 4.1. Thereafter, we show the resulting compact remnant and SN ejecta masses using the SN model of Müller et al. (2016) in Sect. 4.2.
4.1. Pre-SN locations in the HR diagram
We show the pre-SN locations of all our models in the HR diagram in Fig. 9. Because we do not apply LBV-like mass loss, our models at log L/L⊙ ≳ 5.5 do not lose large fractions of their envelopes and do not become WR stars. Moreover, we do not model stars with initial masses < 13 M⊙, which explains the lowest pre-SN luminosity of log L/L⊙ ≈ 4.7.
 |
Fig. 9. Pre-SN locations of the Cases A–C accretors in the HR diagram. The dotted line at log L/L⊙ = 5.5 (Davies et al. 2018) is the maximum luminosity of RSGs and the grey shaded regions indicate the hot and cool parts of the S Doradus instability strip. The dashed line is the Humphreys–Davidson limit (Humphreys & Davidson 1979). The dark-grey boxes indicate the locations of the RSG N6946-BH that likely collapsed into a BH without a bright SN (Gerke et al. 2015; Adams et al. 2017a,b; Basinger et al. 2021), and the BSG progenitor of SN 1987A (Woosley 1988). The grey evolutionary tracks are single-star models with the masses given by the labels. |
The single-star models reach core collapse at the same sites in the HR diagram as the Case A accretors, and are not shown for clarity (Fig. 9a). Both reach core collapse along a well-defined branch in the HR diagram. Moreover, also those Cases B and C accretors that have no thick hydrogen-burning shell at core collapse follow the same branch. The cores of these pre-SN stars after core helium burning evolve independently from the envelope because of a drop in pressure by many orders of magnitude at the core–envelope boundary. The photon luminosity is produced by nuclear burning which takes place in and near the core, that is these stars follow a core-mass–luminosity relation (Fig. 10a). The long-lived BSGs with their thick hydrogen-burning shell do not follow such a relation as shown below. For the core mass, we take MCO at core collapse but using MHe gives a similar result. For comparison, we show the fit function log L/L⊙ = 4.372 + 1.268log MCO/M⊙ from Temaj et al. (2024) in Fig. 10a. This function has been obtained by fitting the pre-SN luminosities of single stars with different convective core overshooting parameters. It also represents well the pre-SN luminosities of Cases A–C accretors that do not explode as BSGs. The luminosities of the CSG Cases C and B accretors fit well up to MCO ≈ 10 M⊙ and for larger MCO the slope of the relation steepens slightly from 1.268 to ≈1.350 (Fig. 10a).
 |
Fig. 10. Core-mass–luminosity relation (panel a) and the relationship between the effective temperature and the average hydrogen mass fraction in the envelope (panel b) of single stars and Cases A–C accretors at core collapse. In the core-mass–luminosity relation, only CSG Cases B and C accretors are shown as the BSG accretors with their thick hydrogen-burning shell follow a different mass-luminosity relation (see main text and Fig. 11). The dashed black curve in panel a is the fit of the core-mass–luminosity relation from Temaj et al. (2024). |
The effective temperature of CSGs (i.e. the Hayashi line) is set by opacity and also the convective mixing-length efficiency, αMLT. With an increasing mass of stars, more and more of the hydrogen-rich envelope is lost, and stars become hotter and appear as BSGs until they are eventually hot helium stars. We find a close relationship between the effective temperature of single stars and Cases A–C accretors at core collapse and the average hydrogen mass fraction in their envelope, ⟨Xenv⟩cc at effective temperatures larger than those of CSGs (i.e. log Teff, cc/K ≳ 3.9) and for ⟨Xenv⟩cc ≲ 0.5 (Fig. 10b). As expected, stars with lower hydrogen content in their envelopes have a hotter effective temperature. Together with the core-mass–luminosity relation, this explains the location of pre-SN single stars, the Case A accretors and some Cases B and C accretors in the HR diagram. The effective temperatures of BSGs with a thick hydrogen-burning shell and stars on the Hayashi line do not depend on ⟨Xenv⟩cc.
Our models develop high compactness at MCO ≈ 7 M⊙ and MCO ≳ 13 M⊙ (Figs. 8a, d) that results in BH formation (see also Sect. 4.2). Because of the core mass-luminosity relation, this translates into luminosities of log L/L⊙ ≈ 5.4 and log L/L⊙ ≳ 5.8 where BHs are formed by stars that avoided the aforementioned BSG phase caused by the thick convective hydrogen burning shell. To date, N6946-BH is the only star known that may have collapsed into a BH without giving rise to a SN12 (Gerke et al. 2015; Adams et al. 2017a,b; Basinger et al. 2021). Interestingly, its location in the HR diagram seems to agree with where we predict BH formation from the compactness peak (Fig. 9; see also Sukhbold & Adams 2020). Progenitors of SN IIP are observed up to luminosities of log L/L⊙ ≈ 5.1 (Smartt 2015), but these luminosities remain uncertain (see e.g. Davies et al. 2018; Davies & Beasor 2020; Temaj et al. 2024 and also the vastly different luminosities of log L/L⊙ = 4.74 ± 0.07 and log L/L⊙ = 5.1 ± 0.2 inferred for the progenitor of SN 2023ixf by Kilpatrick et al. 2023; Jencson et al. 2023, respectively).
The long-lived BSG structures in some of the Cases B and C accretors are characterised by a thick convective shell driven by hydrogen burning and we describe it in Sect. 3.1 as if a main sequence star with a convective core was added on top of a helium star. The surface photon luminosity of these stars is primarily given by the luminosity produced by hydrogen shell burning such that they follow an envelope mass-luminosity relation and no longer a core-mass–luminosity relation (Fig. 11a). The mass-luminosity exponent is larger at low (Menv, cc ≲ 30 M⊙) and smaller at high envelope masses (Menv, cc ≲ 80 M⊙) than the value of 1.60 found by fitting the entire mass range.
 |
Fig. 11. Envelope mass-luminosity relation (panel a) and H-envelope base temperature-effective temperature relation (panel b) for Case B accretors. Single stars are shown for comparison and models with an average hydrogen mass fraction in their envelopes of ⟨Xenv⟩cc < 0.4 are marked. These stars may appear as BSGs at core collapse but their hot Teff, cc is due to the low hydrogen content in their envelopes and not due to a thick convective hydrogen burning shell. Power-law fits are added and the dotted lines in panel b indicate log Teff, cc/K = 3.9 and the transition base temperature at |
Convection during hydrogen burning occurs if the produced energy is so large that it cannot be transported away by photons (Kippenhahn & Weigert 1994). In general, energy generation by nuclear burning has a very strong temperature sensitivity and this tends to increase for isotopes with higher nucleon numbers13. Convective hydrogen shell burning is thus expected to happen if the temperature at the base of the envelope exceeds a certain threshold. From homology relations of main sequence stars, one finds that the central temperature scales as Tc ∝ μM/R, where μ is the mean molecular weight, M the total mass of a star and R the radius. Within this analogy, the temperature at the base of the hydrogen-rich envelope then scales as Tbase ∝ μenvMenv/Renv. The helium core of such stars has a negligible radius (𝒪(1 R⊙)) compared to the envelope (𝒪(10 − 100 R⊙)) such that Renv can be approximated by the radius of the entire star, R*. Indeed, the pre-SN stars with thick convective hydrogen shell burning follow a close relation in the Teff–Tbase diagram (Fig. 11b). Beyond the critical value of
stars have a hot enough Tbase such that hydrogen shell burning is convective and the stars reach core collapse as BSGs with effective temperatures exceeding log Teff, cc/K ≈ 3.9.
We also find high compactness in Cases B and C accretors for MCO ≈ 7 M⊙ and MCO ≳ 13 M⊙ that leads to BH formation and no SN explosion (Figs. 8 and 12). In the HR diagram, BH formation occurs close to the hot side of the S Doradus instability strip because of the compactness peak at MCO ≈ 7 M⊙ and at cooler effective temperatures and larger luminosities because of high compactness at MCO ≳ 13 M⊙ (Figs. 9b, c). Hence, some of our accretor models may explode in SNe while appearing as LBVs and they may have experienced significant mass loss before their SN. Other models in a very similar location in the HR diagram may just collapse into BHs but also these stars could have experienced significant mass loss before their collapse. Accretor models that are too hot to enter the LBV regime in the HR diagram are all predicted to explode in SNe.
 |
Fig. 12. Black-hole and neutron-star masses of Case A (panels a, d), Case B (panels b, e), and Case C (panels d, f) accretors as a function of the final CO core mass MCO. The bottom row is a zoom into the NS-mass regime. The NS and BH masses of the single-star models are shown for comparison and accretor models with facc = 0.25, 0.75, and 2.00 are connected by lines to guide the eye. Systems likely experiencing SN fallback are marked by grey boxes and models that should have experienced LBV-like mass loss are indicated by crosses (cf. Sect. 2.1). |
While our models generally predict exploding BSGs in a region of the BSG progenitor of SN 1987A, a Case C model is required to explain this particular object (see e.g. Podsiadlowski 1992, 2017a; Menon & Heger 2017; Urushibata et al. 2018). None of our current Case C accretors reproduce its location in the HR diagram (Fig. 9c), but these models do not dredge up core material and mix it throughout the envelope (see Sect. 2.2). Models including such mixing can explain the BSG location and further observed characteristics (see discussion in Sect. 5). Moreover, all our long-lived BSG accretors are likely systematically biased to too-cold effective temperatures compared to what is expected from fully realistic mergers because of this missing mixing of core material into the envelope.
4.2. Compact-remnant and SN-ejecta masses
We show the gravitational NS and BH masses in Fig. 12. The NS masses appear uncorrelated with the amount of accreted mass and the mass-accretion Cases A–C. Generally, the NS masses are on average more massive in stars with larger CO core masses, and the largest NS masses are found at CO core masses close to regions of the highest compactness (Figs. 12d–f), where the models are on the brink of not to result in a successful neutrino-driven explosion.
As shown by Temaj et al. (2024) for single stars with different degrees of convective boundary mixing, the NS masses follow a tight relation with the central specific entropy sc of the SN progenitors. We find a similar relation in our models and the exponential best fit of Temaj et al. (2024),
also fits our data well despite the different evolutionary histories of their and our models (Fig. 13). In particular, the neutron star mass–entropy relation is the same in our Cases A–C accretors. Both studies apply the same SN code of Müller et al. (2016), where shock reversal and hence SN explosions are triggered outside the iron core near a mass coordinate of M4, that is within the oxygen shell (cf. Fig. A.1 in Schneider et al. 2021). Hence, the resulting NS masses are directly proportional to M4 and thus MFe. Because MFe and sc are closely related (see Eq. (3) and Fig. 8), it is not surprising that we find a strong correlation between MNS, grav and sc, but it could not be foreseen that this relation is so tight and does not carry information on the evolutionary history of the stars (Fig. 13). It thus seems that sc is a good indicator of that mass coordinate at which neutrino-driven SNe within the model of Müller et al. (2016) are launched. Whether such a connection is more general and can also be made in other neutrino-driven SN models remains unclear and warrants further investigation.
 |
Fig. 13. Gravitational neutron star mass MNS, grav as a function of the central specific entropy sc of the progenitor stars for Case A (panel a), Case B (panel b), and Case C (panel c) accretion. The dashed black line is the exponential fit to the neutron star masses of single stars computed for different convective boundary mixing found by Temaj et al. (2024). |
The BH masses (Figs. 12a–c) are closely linked to the final stellar masses (Fig. 6), that is to the mass loss history of stars. Because of rejuvenation, most Case A accretors evolve as single stars of higher initial masses and thus collapse to BHs of similar mass for the same MCO. Only the non-rejuvenating accretors have smaller cores compared to their total mass and lose less mass, thus forming more massive BHs (Fig. 12a). In Cases B and C accretors and regardless of whether stars explode as red or blue supergiants, we find that all BH masses are larger than those of single stars with the same MCO because of the larger final stellar masses (Figs. 12b, c; see also Sect. 3.2). The compactness peak at MCO ≈ 7 M⊙ results in BH formation and this island of BH formation is shifted by about 0.5 M⊙ to lower MCO in Case B models that accreted enough mass to evolve through a long-lived BSG phase (Fig. 12b; cf. Sect. 3.4). The generally higher compactness at core collapse in Case C accretors is reflected by BH formation over a larger MCO range compared to Case B accretors (for example at MCO ≈ 10 M⊙, some Case C accretors collapse into BHs while this is not the case in the Case B models). Neglecting enhanced mass loss in massive CSGs and LBVs, BH masses are in the range of 12.5 − 50 M⊙, 15 − 190 M⊙, and 15 − 150 M⊙ in our Case A accretors and single stars, Case B accretors, and Case C accretors, respectively. The minimum BH masses (≈12.5 M⊙) are for stars in the compactness peak.
The SN-ejecta masses (Fig. 14) are similar to those of BHs (Fig. 12): if a star does not collapse into a BH, it explodes and ejects a mass that we assume is given by the final total stellar mass minus the (baryonic) mass of the formed NS. Stars in our models explode and eject significant mass for MCO ≲ 13 M⊙ and outside the compactness peak at MCO ≈ 7 M⊙ (Fig. 14). Fully rejuvenating Case A accretors eject the same mass as single stars of the same MCO while the non-rejuvenating models retain higher final mass and eject correspondingly more mass in their SN explosions (Fig. 14a). The ejecta masses of Cases B and C accretors scale directly with the amount of accreted mass and greatly exceed those of single stars (Figs. 14b, c). While single stars eject 8.6 − 14.0 M⊙, the ejecta masses reach values of up to 30 M⊙, 100 M⊙, and 70 M⊙ in our (non-rejuvenated) Cases A–C accretors, respectively.
 |
Fig. 14. Same as Figs. 6 and 12 but showing the SN ejecta mass Mej. Models marked by crosses (i.e. also those with the highest SN ejecta mass) are expected to have experienced LBV-like mass loss such that these ejecta masses are upper limits. |
As with the final masses (Fig. 6), some BH and SN ejecta masses (Figs. 12 and 14, respectively) are rather upper limits because of unaccounted for mass loss. For example, no RSG has been observed today at log L/L⊙ ≳ 5.5 (Davies et al. 2018) and this might be because of enhanced mass loss in such luminous RSGs that erode the hydrogen-rich envelope and turn stars into hotter, for example WR, stars. Similarly, eruptive mass loss, for example, because of envelope instabilities in LBVs may result in the loss of the entire hydrogen-rich envelope. Typical averaged LBV mass-loss rates at log L/L⊙ ≳ 6.0 are 10−4 M⊙ yr−1 (Smith 2014), suggesting that such LBVs would lose 1 M⊙ within 104 yr. We identify all models that would be subject to such LBV-like mass loss for longer than this time, that is those models that likely lose more than 1 M⊙ before core collapse. For example, none of our initially 13 M⊙ early Case B models are expected to be subject to such enhanced mass loss (e.g. Fig. 1) while some of the initially 30 M⊙ models are (e.g. Fig. 15).
 |
Fig. 15. Same as Fig. 1 but for the initial 30 M⊙ stars. The dashed black line is the Humphreys–Davidson limit (Humphreys & Davidson 1979). Cross symbols indicate models that may experience enhanced, LBV-like mass loss and may thus rather explode at hotter effective temperatures as stripped-envelope SNe of Type Ib/c. Plus symbols are separated by Δt = 5 × 104 yr. |
The initially 30 M⊙ early Case B accretors burn helium in their cores as BSGs for facc ≳ 0.50 and otherwise as CSGs (Fig. 15). Only the facc = 1.0 and 2.0 models enter the LBV instability regime for less than 104 yr and are thus probably not much affected by LBV-like mass loss. The other models may encounter enhanced mass loss as an LBV star just before the SN explosion. Models with facc = 0.50 and 0.75 explode in the S Dor instability strip and may be LBV SN progenitors. The models evolving into CSGs (including the initially 30 M⊙ single star) are expected to lose significant mass that we do not account for in our models. They may even lose their entire hydrogen-rich envelope and then rather explode as a stripped-envelope SN (SN Ib/c).
To better understand the possible maximum BH and SN ejecta masses of our models, we show them as a function of the maximum time spent in the LBV region of the HR diagram in Fig. 16. Models indicated by the grey-shaded areas are the same as those marked by cross symbols throughout this paper, that is for which considerable mass loss is expected. Generally, the maximum BH masses are larger than the SN ejecta masses and, if a single-star model evolves into the LBV region in the HR diagram, it spends most of its core-helium burning in these locations (i.e. > 105 yr). Considering 104 yr as the limiting time a star can spend as an LBV in the HR diagram before it loses considerable fractions of its mass, we find maximum BH (SN ejecta) masses of about 13, 50, and 77 M⊙ (12, 37, and 84 M⊙) for our single stars and accretors with facc ≤ 1.0 (e.g. mergers in isolated binary stars) and facc ≤ 2.0 (e.g. allowing also for repeated mergers in triples), respectively. These values reduce to 13, 36, and 36 M⊙ (11, 32, and 42 M⊙) for models that avoid the LBV region in the HR diagram altogether – they can thus be considered lower limits. Neglecting LBV-like mass loss, we find maximum BH (SN ejecta) masses of 47, 112, and 190 M⊙ (14, 62, and 98 M⊙), respectively.
 |
Fig. 16. Maximum BH and SN ejecta mass of single stars and accretors with facc ≤ 1.0 and facc ≤ 2.0 as a function of the maximum time spent in the LBV region of the HR diagram. The grey-shaded region indicates models for which we expect significant LBV-like mass loss such that the maximum BH and SN ejecta masses should be considered upper limits. |
The exact BH and ejecta masses depend on a multitude of modelling uncertainties and the limitations of our models to fully represent mass gainers of binary mass transfer and stellar mergers (see discussion in Sect. 5.1). However, regardless of the uncertainties and limitations, accretors of binary mass transfer and stellar mergers lead to a much larger range of BH and SN ejecta masses that single stars can only reproduce at much lower metallicities (cf. Sect. 5.3).
5. Discussion
5.1. Main model uncertainties and limitations
Our effective merger and binary mass-transfer prescription of accreting certain fractions facc of the initial mass of stars over the accretor’s thermal timescale (see Sect. 2.2) is simplified and cannot fully catch the complex physics of these phases (see Sect. 2.2.2). In the following, we discuss how our assumptions of the chemical composition of the accreted mass, the absence of mixing of parts of the helium core in mergers and the dynamic mass loss in mergers affect our results. We also touch upon the role of wind mass loss, rotation of our accretors, possible magnetic fields produced in stellar mergers, and multiple and extended mass exchange episodes in binary stars. Moreover, we discuss to which extent the findings from our solar-metallicity models can be generalised to accretors of other metallicities. The role of semi-convection is discussed already in Sect. 3.1. As discussed in the following and mentioned previously, our assumptions for the merger models are such that one should expect to find a higher fraction of post-merger BSGs than what is predicted by our models (i.e. BSG solutions occur at lower facc than predicted by our current models).
5.1.1. Chemical composition of accreted mass
We assume that the accreted mass has a chemical composition of that of the surface of the accretor, that is almost the primordial chemical composition of our models. However, the accreted material is certainly enriched in helium in stellar mergers and possibly also during binary mass-transfer events. In Cases B and C accretors, a larger mean molecular weight in the accreted material will increase the temperature at the base of the hydrogen-rich envelope, Tbase ∝ μenvMenv/R*; this might also occur in Case A accretors that do not fully rejuvenate. Hence, we expect to find BSGs for smaller facc compared to our current models such that more models evolve as BSGs and less as CSGs (cf. Eq. (4)). The BSGs themselves will then have a higher luminosity and cooler effective temperature because the luminosities and effective temperatures of the BSGs mostly depend on the hydrogen-rich envelopes which evolve analogously to main-sequence stars (Sects. 3.1 and 4.1). In RSGs, the larger mean molecular weight of accreted mass decreases the opacity and thereby increases the effective temperature according to the new location of the Hayashi line in the HR diagram (Hayashi & Hoshi 1961). If enough helium-rich material is accreted, such stars may no longer look like RSGs but more like yellow super- and hypergiants, and show a clear surface helium and nitrogen enrichment.
5.1.2. Core mixing in stellar mergers and SN 1987A
In all stellar mergers (i.e. Cases A–C), parts of the helium-enriched core of the more evolved star can be dredged up and replenished by hydrogen-rich material (see e.g. Podsiadlowski 1992; Ivanova et al. 2002; Ivanova & Podsiadlowski 2002; Podsiadlowski et al. 2007; Glebbeek et al. 2013; Menon & Heger 2017; Schneider et al. 2019). This mechanism may operate during the dynamic merger phase but also during the later thermal relaxation of the merger product (see also Schneider et al. 2020). In Case A mergers, the mixing can prolong the core hydrogen burning phase and thereby extend the MS turn-off to cooler temperatures and larger luminosities. In Cases B and C mergers, the partial mixing of the helium core out into the envelope has two main consequences: (i) the helium core becomes effectively less massive and the envelope correspondingly more massive, and (ii) the dredged-up helium results in a higher mean molecular weight of the envelope. The effect of the larger mean molecular weight in the envelope is already discussed above, and the smaller helium core mass and larger envelope mass effectively have similar consequences as an increased mean molecular weight. Because of a larger Menv, Tbase ∝ μenvMenv/R* is hotter and stars more easily become BSGs. Moreover, a larger Menv also increases the star’s luminosity and effective temperature (see Sect. 4.1). This will also affect the structures of stars at core collapse and their explodability, and can lead to vastly different outcomes of core collapse because of the non-monotonic relation of various interior properties (e.g. compactness and central entropy) with the stellar core mass.
In models for the progenitor of SN 1987A (see e.g. Hillebrandt & Meyer 1989; Podsiadlowski et al. 1990; Podsiadlowski 1992, 2017b; Menon & Heger 2017), the dredge-up of helium-rich material from the core of the more evolved star is required to explain observations for two main reasons. First, the triple-ring nebula is enriched in helium and nitrogen, that is by-products of hydrogen burning (e.g. Arnett et al. 1989; Lundqvist & Fransson 1996). Second, the expansion timescale of the rings surrounding SN 1987A is only about 20 000 yr (e.g. Burrows et al. 1995), that is the proposed merger must have occurred after core-helium burning as a Case C system. The mixing of helium-rich material into the envelope of the merged star helps the progenitor models to become a BSG (see the discussion in Sect. 3.1). Indeed, we do not find BSGs from Case C accretors with facc ≤ 1.0 that can explain the position of SN 1987A’s progenitor in the HR diagram (see e.g. Fig. 9). Most recently, this has again been demonstrated by the merger models of Menon & Heger (2017) and Urushibata et al. (2018) that show a good match to the BSG progenitor of SN 1987A. Such models can then also reproduce the light curve of SN 1987A, along with other peculiar Type II SNe (Menon et al. 2019). Moreover, Case B mergers with similar physics can also explain several properties of observed BSGs (Menon et al. 2023).
5.1.3. Mass loss via binary mass transfer and mergers
We do not take into account mass loss from non-conservative binary mass transfer or dynamic stellar mergers. In this regard, our accretion fractions are “effective” fractions of how much mass is truly accreted by stars. Hence, mass loss is only relevant when linking our different accretion scenarios to the initial binary-star configurations. Binary mass transfer can be fully conservative for Case A systems but also almost entirely non-conservative when the donor star is more evolved (e.g. Podsiadlowski et al. 1992; Pols 1994; Wellstein et al. 2001; de Mink et al. 2007; Henneco et al. 2024). In stellar mergers, Glebbeek et al. (2013) find that up to ten percent of the total binary mass is dynamically ejected and the ejection fraction depends on the binary mass ratio q = M2/M1, fej ≈ 0.3q/(1 + q)2 (M1 > M2). The authors conduct head-on collisions where the ejection fraction depends strongly on the exact collision setup (e.g. collision energy and impact parameter, see also Freitag & Benz 2005) and similar mergers in binary systems on Keplerian orbits find lower ejection fractions of less than one percent (Schneider et al. 2019). In general, the mass loss fraction depends on the evolutionary state of the merging stars, and mergers of more evolved stars lead to higher mass loss because their binding energies are lower. While mergers of two main-sequence stars may eject less than one percent of their total mass (e.g. Schneider et al. 2019), mergers of giant stars may proceed more like traditional common-envelope phases and could lead to full envelope ejection, that is ejection fractions of 50% and higher (e.g. Moreno et al. 2022). The triple-ring nebula of SN 1987A is an example of left-over debris from a stellar merger (see e.g. Morris & Podsiadlowski 2007, 2009).
5.1.4. Mass loss via winds and LBV-like outflows
Stellar wind mass-loss rates are still substantially uncertain (easily by a factor of 2−3 depending on the stellar type, see e.g. Smith 2014). In Case A accretors, wind mass loss directly influences the core evolution and stars adjust their structure to the modified total mass. In Case C accretors, the core and envelope are already decoupled such that mass loss mainly reduces the envelope mass and leaves the further core evolution untouched. This is not true for Case B accretors where a reduced envelope mass can still affect the further core evolution. With a lower envelope mass (i.e. higher mass loss), BSG formation becomes more difficult as discussed in Sects. 5.1.1 and 5.1.2 and some initial BSGs might evolve to the red giant branch when hydrogen shell burning turns radiative.
In our hydrogen-rich accretors, WR wind mass loss is negligible, and the wind mass loss applied to hot (Teff ≥ 11 000 K) and cool (Teff ≤ 10 000 K) stars mostly affects our results. The applied cool wind mass loss is generally higher than that applied to our hot stars such that models that remain hot for most of their evolution lose considerably less mass than models that evolve into CSGs. Hence, models that end as CSGs tend to be more affected by uncertainties in the applied wind mass-loss rates than those that end as BSGs. Smith (2014) suggest that the mass-loss rates as applied in our models are an overestimate. If true, our models would lose less mass and could result in higher SN ejecta masses and more massive BHs.
In massive stars, winds are mostly line-driven and therefore scale with metallicity. This is likely not true for LBV-like winds and eruptions. These have been suggested to be connected to helium opacity in the outer envelopes of massive stars (Jiang et al. 2018; Grassitelli et al. 2021) and such a mechanism would operate at all metallicities (albeit less severely at lower metallicity with generally lower opacity and luminosity-to-mass ratios). This seems to be confirmed observationally: Davies et al. (2018) find that their re-evaluated Humphreys–Davidson limit for cool supergiants is the same in the Milky Way, LMC, and SMC, and LBVs have been found in low-metallicity galaxies (e.g. SMC; Humphreys & Davidson 1994; Weis & Bomans 2020). So while line-driven winds of hot and cool stars become less strong at lower metallicity, LBV-like mass loss might be always present. This is particularly relevant for our massive accretors that evolve through or close to the S Dor instability strip and that may lose a significant fraction of their hydrogen-rich envelopes.
Our models employ MESA’s MLT++ scheme. Switching this off, stars would develop more strongly inflated envelopes and would more easily evolve into the LBV region in the HR diagram. This could potentially lead to enhanced mass loss.
5.1.5. Rotation
Accretors of binary mass transfer can be easily spun up to critical rotation if tides are not efficient enough to slow them down (see e.g. de Mink et al. 2013). Merger products may also show unusual rotation velocities. Traditionally, it is assumed that such stars would rotate critically because of the large amount of angular momentum in the pre-merger binary orbit. However, Schneider et al. (2019, 2020) have shown that merged stars may actually spin slowly. They attribute this to the efficient coupling of the merged star to a toroidal accretion structure right after the merger that could transport away angular momentum and to an unusual moment of inertia of the merged star right after the coalescence that does not allow the merged star to gain high spin angular momentum as a solid body rotator. The merger of two stars gives birth to a new, more massive star and this situation might be comparable to the star-formation process. Also, most young massive stars do not seem to rotate unusually rapidly (e.g. Dufton et al. 2013; Ramírez-Agudelo et al. 2013, 2015) and this may well apply to merger products. Moreover, merged stars could lose angular momentum in a variety of ways, for example, through magnetic braking and mass ejection episodes (see below and also Schneider et al. 2020). In lower-mass blue straggler stars originating from collisions of stars, slow rotation seems to be favored over rapid rotation (e.g. Leonard & Livio 1995; Sills et al. 2005; Ferraro et al. 2023), further supporting our hypothesis that merged massive stars may actually not rotate rapidly.
While most of the above is true for MS stars and hence Case A accretors, less is known for Cases B and C accretors. The larger binary orbits of such systems imply an overall larger orbital angular momentum which could enhance the likelihood of obtaining more rapidly rotating Cases B and C accretors than those from Case A accretion. However, as shown by Urushibata et al. (2018), most of the available angular momentum of their merger models must be lost by some mechanism such that the merged star can become massive enough to explain the BSG progenitor of SN 1987A. This would also speak in favour of a mechanism that can efficiently remove angular momentum from Cases B and C mergers.
Our models are for non-rotating stars. While this assumption may be adequate for some of our accretors as described above, some will certainly rotate rapidly. Rotation could lead to enhanced mass loss, internal mixing, reduced ejecta masses and spin up of the remnants. As discussed in Sect. 5.1.4, the enhanced mass loss makes BSG formation more difficult. The additional mixing of chemical elements has the opposite effect and enhances the likelihood of BSG formation because it likely mixes helium-enriched material out into the envelope.
5.1.6. Magnetic fields
Observationally, strong, large-scale surface magnetic fields are observed in about 5−10% of massive stars (e.g. Donati & Landstreet 2009; Wade et al. 2014; Ferrario et al. 2015; Fossati et al. 2015; Schöller et al. 2017; Grunhut et al. 2017). It has been shown that such magnetic fields can be produced in the merger of two stars (Schneider et al. 2019). In stars accreting mass by binary mass transfer, strong, large-scale magnetic fields are probably not being produced (Langer 2014; Schneider et al. 2016) as exemplified by the absence of detected magnetic fields in Be stars of which at least some are expected to be post-mass-transfer accretors (e.g. Wade et al. 2014; Neiner et al. 2015). Hence, only the accretor models representing stellar mergers may lack physics ingredients to account for the effects of magnetic fields.
The magnetic fields in merger products can influence the further evolution in various ways (see e.g. Meynet et al. 2011; Potter et al. 2012; Petermann et al. 2015; Petit et al. 2017; Quentin & Tout 2018; Keszthelyi et al. 2019; Schneider et al. 2020). Most importantly, magnetic fields may effectively reduce wind mass loss by confinement, lead to enhanced angular momentum transport in the stellar interior, inhibit convective boundary mixing, and magnetic braking can spin stars down. The reduced mass loss and, in particular, the inhibition of convection can make it more likely that merged stars evolve as BSGs (Petermann et al. 2015). Given that our accretor models are non-rotating, they may be viewed as models with extremely efficient magnetic braking.
5.1.7. Multiple and extended binary mass-transfer phases
In the evolution of binary stars, there can be multiple phases of mass exchange with a companion before a star reaches core collapse. Each phase can leave its characteristic fingerprint on the final stellar structure and may influence the outcome of core collapse. For example, a star that accreted mass in the first mass-transfer episode may be stripped off its envelope in a second mass-transfer phase. For example, Renzo et al. (2023) modelled a rejuvenated former accretor that evolves into a supergiant with a reduced envelope binding energy because of the past mass accretion. The supergiant then engulfs a companion and initiates a common-envelope phase whose outcome may now be affected by the previous mass accretion. Similarly, previous mass exchange in a binary can affect the structures of pre-merger stars (see e.g. Menon et al. 2023). Such additional mass-exchange phases are not covered by our models. They may affect the accretor models representing mass gainers of binary mass transfer and stellar mergers (the pre-merger stars may have already evolved through a phase of binary mass transfer).
As detailed in Sect. 2.2, our models accrete mass on a thermal timescale but this timescale can be much longer, for example on a nuclear timescale in case of accretion from an MS donor star (classical Case A binary systems, not to be confused with a Case A accretor). In such systems, we expect continued rejuvenation. The evolution of such systems can differ from our models, most notably by the chemical composition and specific angular momentum of the accreted matter. Also in the case of stellar mergers, there can be a preceding mass-transfer episode that modifies the structures of the pre-merger stars and then gives rise to a different merger outcome. Such effects are not accounted for in our models.
5.2. Metallicity
Our models are for the solar metallicity of Asplund et al. (2009) and we now discuss to which degree our results can be generalised to other metallicities Z. While the quantitative results will differ for models of another metallicity, the qualitative picture should remain the same. For example, the general landscape of ξ2.5, MFe, and sc with MCO in binary-stripped stars is robust for a large range of metallicities (Schneider et al. 2023) and we expect the same outcome for accretors of binary mass transfer and stellar mergers. Similarly, long-lived BSGs may form from merging at various metallicities. These stars will always lose the least mass in stellar winds, hence they will produce the most massive BHs and the largest SN ejecta masses for a given Z. As such they could naturally explain some high-mass BHs in the observed population of binary BH mergers (Abbott et al. 2023b,a). Furthermore, the accretor models may always have larger final masses than single stars of the same Z and larger envelope-to-core-mass ratios.
The metallicity enters stellar evolution mainly through the opacity of the stellar matter and the strength of line-driven stellar winds. At lower metallicities, stars are more compact and have weaker winds. This leads to the general picture that wind mass loss is most important for the evolution of single stars at high Z while rotation and rotationally induced mixing become more important at low Z where less angular momentum is lost through winds. As discussed in Sect. 5.1.4, weaker winds at lower Z increase the likelihood of the formation of long-lived BSGs (and vice versa at higher Z with stronger winds). Because of the increased importance of rotation at low Z, our accretor models for mass gainers of binary mass transfer become less and less applicable because they are for non-rotating stars. This may not apply to stellar mergers as discussed in Sect. 5.1.5.
5.3. Maximum BH and SN ejecta mass
The maximum BH and SN ejecta masses are both closely connected to the maximum final mass of our models and thus to wind mass loss (Sects. 3.2 and 4.2). Wind mass-loss rates of CSGs and WR stars are stronger than those of stars on the main sequence (e.g. Smith 2014). Hence, stars that undergo core helium burning as BSGs can avoid the strong CSG and WR winds, and, if they are also not subject to LBV-like mass loss, they will retain the highest mass. A natural way to obtain such stars is by stellar mergers as shown here14 (see also Justham et al. 2014).
Our models are for solar-like metallicity. Even when assuming that the entire hydrogen-rich envelope is lost when stars enter the LBV region in the HR diagram, we find BHs and SN ejecta masses of almost 40 M⊙ and 35 M⊙, respectively, from stellar mergers in binaries (i.e. facc ≤ 1.0). These numbers go up to about 50 M⊙ and 40 M⊙, respectively, when assuming that LBV-like mass loss can be neglected for stars spending less than 104 yr in the LBV region of the HR diagram. At lower metallicities, the final and thus also the BH and SN ejecta masses of all our models would be even larger.
Already at solar metallicity and for rather conservative assumptions on LBV-like mass loss, we predict BH masses that may populate the so-called PISN BH mass gap at about 45 − 130 M⊙ (Woosley et al. 2002; Woosley 2017; Farmer et al. 2019, 2020; Marchant & Moriya 2020; Renzo et al. 2020b; Farag et al. 2022). Avoiding the pair instability in merger models that become BSGs is possible because such stars have relatively small cores and large envelope masses. For example, an initially 27 M⊙ star turns into a BSG upon accreting with facc = 1.0 as an early Case B system and has a CO core mass of MCO ≈ 6.5 M⊙ at core collapse. This MCO places the star in the compactness peak and a BH of MBH, grav ≈ 50 M⊙ forms in our models (it spends some 9000 yr as an LBV in the HR diagram). Such a core mass is far from the ≳35 M⊙ required to trigger a PISN. In the event of multiple and/or repeated mergers (e.g. facc = 2.0, see Sect. 5.4), the final BH mass even reaches 80 M⊙ in our models (in this case, the model evolves for ≈4500 yr as an LBV in the HR diagram).
With the observation of the binary BH merger GW190521 with component masses of ≈85 M⊙ and ≈66 M⊙ (Abbott et al. 2020a,b), two BHs in the PISN BH mass gap have been observed. This raises the question of how such massive BHs can form. Unless we neglect LBV-like mass loss in our models and/or consider mergers with facc > 1.0, we do not predict the existence of such massive BHs at solar-like metallicity. A lower metallicity and/or mergers with facc > 1.0 are required. This is generally consistent with other studies involving the merger of massive stars to obtain BSGs that avoid significant mass loss and retain a large final mass to produce BHs in the PISN mass gap (e.g. Di Carlo et al. 2019; Renzo et al. 2020a; Costa et al. 2022; Ballone et al. 2023). As noted by Renzo et al. (2020a), however, the maximum possible BH mass depends crucially on how strong the LBV-like wind mass loss is and whether the merged stars can retain their large hydrogen mass. As shown here, some BH-forming, merged BSGs may be able to avoid the LBV regime, but their total mass is limited by the fact that these stars have to have CO core masses which fall into the compactness peak where we anticipate BH formation. Hence, even at lower metallicity, it seems that multiple and/or repeated mergers are required to obtain BHs of ≳66 − 85 M⊙ when assuming that LBV-like mass loss can erode most of the hydrogen-rich envelope of stars.
The maximum SN ejecta mass in our models is closely related to the maximum BH mass if we assume that models lose almost their entire envelope by LBV-like mass loss. In this case, the most massive BH forms from a Case B accretor with a core mass falling into the compactness peak while the SN with the largest ejecta mass is a model that has a core just a little bit less massive such that it does not reach high core compactness and explodes in a SN. Consequently, we predict that the maximum SN ejecta mass is a little bit less massive than the most massive BH (cf. Fig. 16). Our accretors with high SN ejecta mass explode as Type II SNe. Observationally, Hamuy (2003) report SN ejecta masses in the range 14 − 56 M⊙ for SN IIP, and SN ejecta masses of 10 − 60 M⊙ are reported for long-rising SN 1987A-like Type II SNe (Taddia et al. 2016; Pumo et al. 2023). In our models at solar metallicity, single stars have SN ejecta masses of ≲15 M⊙ and can thus not account for the observed large SN ejecta masses (see also Zapartas et al. 2021). Contrarily, the accretor models can have larger final stellar masses and thus better match these observations.
5.4. Formation channels for facc > 1 mergers
In the following, we denote the primary star in a binary system as the initially more massive and thus more evolved star at the beginning of the first phase of binary mass exchange (stable mass transfer or stellar merger). In a merger, it is expected that its core forms the core of the merger remnant because it is denser and less buoyant15. In this picture, the less massive secondary star accretes onto the more massive primary star and facc ≤ 1 in our models of standard stellar mergers in isolated binary stars.
In binary mass transfer, facc > 1 is possible, because now the initially less massive secondary accretes mass from the initially more massive primary. In most cases, the accretor will be a main sequence star (accretor). Cases B and C accretors, that is accreting post-main sequence stars, are only possible in binaries with initial mass ratios close to one because the post-main sequence lifetime is short compared to that of the main sequence. Hence, Cases B and C accretors are also only possible up to facc ≈ 1 in the first mass transfer phase of binary stars.
Triples and other multiples are common among massive stars (> 50% of all systems, see e.g. Sana et al. 2014; Moe & Di Stefano 2017; Offner et al. 2023). In triples and higher order multiples, mergers with facc > 1 are possible. For example, the initially most massive star could merge with a close binary system whose individual masses do not exceed the mass of the primary but its total mass does, possibly leading to Cases A–C mergers with facc > 1.0. Similarly, initial hierarchical triple and/or multiple systems can be rendered unstable if, for example, mass transfer in a close binary leads to orbital widening (see e.g. merger model in an initial triple for the formation of η Car, Hirai et al. 2021). Furthermore, Justham et al. (2014) estimate that 10% of early Case B mergers might later accrete additional mass from an outer tertiary companion, effectively leading to accretors with facc > 1.0.
In star clusters and other dense stellar systems, repeated mergers of stars are possible on a short timescale (e.g. Portegies Zwart & McMillan 2002; Portegies Zwart et al. 2004; Mapelli 2016; Gieles et al. 2018; Di Carlo et al. 2019, 2020). This mechanism can easily explain effective accretion fractions of facc > 1.0 and even facc > 2.0 that are not covered here. Such mergers have in fact been invoked to explain how BHs may populate the PISN mass gap (e.g. Di Carlo et al. 2019, 2020) and they can also form in sequential mergers in triples and higher-order multiples (Vigna-Gómez et al. 2021).
6. Summary and conclusions
Envelope stripping because of binary mass exchange is known to affect the structures of stars at core collapse and generally allows stars to explode in SNe over a larger initial mass range than what is expected from single stars (Timmes et al. 1996; Wellstein & Langer 1999; Brown et al. 2001; Podsiadlowski et al. 2004; Woosley 2019; Ertl et al. 2020; Schneider et al. 2021, 2023; Laplace et al. 2021). In this work, we have explored how mass accretion as such in stable Roche-lobe overflow or in a stellar merger affects the further evolution of stars and the stellar structures just prior to core collapse. To this end, we assume that stars accrete a fraction facc of their initial mass on a thermal timescale at various points in their evolution. Our main findings can be summarised as follows.
-
Beyond certain accretion thresholds and regardless of when stars accrete mass in their evolution, they can evolve through a long-lived BSG phase during which they burn helium in their cores. Some also reach core collapse as BSGs and thereby avoid the CSG phase altogether. The BSG phase is related to a thick, convective, hydrogen-burning shell in stars with a sufficiently large envelope mass compared to their core mass such that hydrogen-shell burning becomes convective.
-
The accretion thresholds depend on when stars accrete mass in their evolution, the initial mass, and also the amount of mixing of core material into the envelope (the latter is only relevant for stellar mergers and has not been considered here). Most of our Case A accretors fully rejuvenate such that they evolve just as single stars of higher mass. At low accretion fractions, however, for which stars do not fully rejuvenate, we also find long-lived BSG phases. Generally, the more evolved the post-main-sequence accretors are, the more mass they need to accrete to become long-lived BSGs.
-
At core collapse, all (non-rejuvenated) accretors have a core size within 10–20% of that of single stars of the original initial mass but a possibly much higher envelope mass. Because of the larger envelope mass, accretors end core helium burning with a lower central carbon abundance than genuine single stars. These fewer carbon atoms change the burning episodes beyond core-helium burning and generally lead to pre-SN structures that are more difficult to explode than those of single stars with the same final core mass. This is the opposite trend of what is found in binary-stripped stars.
-
The final masses of non-rejuvenated Case A, and all Cases B and C accretors are larger than those of single stars, with those of Case B accretors being the largest. In particular, accretors that evolve through a long-lived BSG phase can avoid the higher wind mass-loss rates as CSGs and thereby retain the most mass.
-
We find that the central entropy is a particularly useful summary quantity of the pre-SN structures because it directly links to the effective Chandrasekhar mass at which core collapse occurs and contains information on the mass-radius relation of the inner core region. For these reasons, we prefer this quantity over the often-used compactness parameter.
-
The trend of central entropy (and compactness) at core collapse with the CO core mass MCO is qualitatively similar to that found in single and binary-stripped stars: there are two main characteristic MCO of about 7 M⊙ and 13 M⊙ at which we find high central entropy and compactness. These core masses are linked to central carbon and neon burning becoming radiative as a consequence of a low carbon abundance after core-helium burning. While the overall trend is shifted to larger MCO in binary-stripped stars, it is shifted to lower MCO in (non-rejuvenated) accretors. Stars that evolve through a long-lived BSG phase show the largest shift towards lower MCO of about 0.5 M⊙.
-
When analysing our pre-SN interior structures with the neutrino-driven SN model of Müller et al. (2016), we find that the explodability closely follows the trend of central entropy with core mass. We find BH formation for the high central entropy models with MCO of ≈7 M⊙ and ≳13 M⊙, successful SN explosions with NS formation for MCO ≲ 7 M⊙, and partial fallback SNe with likely BH formation in some models with MCO ≈ 7 − 13 M⊙.
-
The positions in the HR diagram of accretors that do not reach core collapse in the long-lived BSG phase, are in the same region as those of single stars. Because of the island of BH formation at MCO ≈ 7 M⊙, accretors ending their lives as CSGs collapse into BHs at luminosities of log L/L⊙ ≈ 5.4, the same luminosity as in BH-forming CSGs from genuine single stars. Accretors with MCO ≈ 7 M⊙ that end their lives as BSGs and collapse into BHs, populate a region along the hot side of the S Dor instability strip.
-
Some of the accretors evolving as BSGs explode inside the S Dor instability strip, that is our models predict that some LBVs may be SN progenitors. If the SN explodes into recently ejected material from an LBV eruption, interacting and possibly superluminous SNe seem possible.
-
In all of our accretor models, we find a tight relation between their central entropy at core collapse and the resulting NS mass. A similar relation has already been found in single stars with varying degrees of convective boundary mixing (Temaj et al. 2024) and the very same relation also fits our models.
-
Because accretors evolving and ending their lives as BSGs have high final stellar masses, they can also result in large BH and SN ejecta masses. Accounting only for models that likely do not experience strong LBV-like mass loss and restricting facc to values of ≤1 (i.e. values achievable by stellar mergers in binary stars), we find maximum BH and SN ejecta masses of up to 50 M⊙ and 40 M⊙, respectively. The ejecta masses greatly exceed those from genuine single stars. Allowing for repeated and/or multiple mergers (i.e. facc > 1), both masses increase to about 80 M⊙. This could potentially result in BH masses from stars at solar metallicity that fall into the PISN mass gap.
We have shown here that accretor models approximating mass gainers in binary mass transfer and products of stellar mergers reach core collapse with interior structures that can be profoundly different from single stars. While our models cannot fully account for the complex physics of binary mass transfer and stellar mergers, they serve as a zeroth-order baseline. To obtain a more complete picture of stellar mergers and specifically the mixing in such events, further detailed multi-dimensional, hydrodynamic simulations and a systematic exploration of the relevant parameter space are warranted. This will be explored in upcoming work. We have focussed on the core structures at core collapse, the explodability of models, and their final BH and SN ejecta masses. In a forthcoming publication (Schneider et al., in prep.), we will present further explosion properties and implications for the zoo of SN transients.
Because of overshooting, the models studied here show no drastic second dredge-up. Thus, the larger MHe and MCO of the accretors compared to single stars are not related to a second dredge-up in the single stars which is naturally absent in BSG accretors without a deep convective envelope (cf. Podsiadlowski et al. 2004).
The triple-α reaction is proportional to the third power of the α-particle number density while the 12C(α, γ)16O reaction scales linearly with this density. More massive stars have denser cores such that the latter reaction becomes dominant earlier during helium burning than in lower-mass stars, and more carbon is depleted and converted into oxygen.
After submission of this work, new JWST observations revealed an infrared source at the location of N6946-BH that, for example, could be the dust enshrouded missing RSG or dust debris from a failed SN (Beasor et al. 2024; Kochanek et al. 2024). Hence, only future observations will finally clarify whether this RSG indeed collapsed into a BH or not.
In hydrogen burning via the CNO cycle, the energy generation rate ϵCNO scales with T13…23 for T = 10…50 × 106 K (Kippenhahn & Weigert 1994).
It is also possible to tune the physics of stars to obtain core-helium-burning BSGs from single stars as explored in detail when trying to understand the BSG progenitor of SN 1987A (see e.g. the review in Sect. 3 of Podsiadlowski 1992). Vink et al. (2021) show that this is also possible for stars with initial masses of 90 − 100 M⊙. In many cases, however, the choice of physics might be in tension with other observations of stars (e.g. unusually little or no convective boundary mixing).
In almost equal-mass merger, however, the core of the secondary often forms the core of the merger product (see e.g. Glebbeek et al. 2013; Schneider et al. 2019).
Acknowledgments
We thank the reviewer for their careful reading of our manuscript and helpful and constructive comments. The authors acknowledge support by the Klaus Tschira Foundation. This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement No. 945806) and is supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC 2181/1-390900948 (the Heidelberg STRUCTURES Excellence Cluster). This research made use of NumPy (Oliphant 2006), SciPy (Virtanen et al. 2020), Matplotlib (Hunter 2007) and Jupyter Notebooks (Kluyver et al. 2016).
References
- Abbott, R., Abbott, T. D., Abraham, S., et al. 2020a, Phys. Rev. Lett., 125, 101102 [Google Scholar]
- Abbott, R., Abbott, T. D., Abraham, S., et al. 2020b, ApJ, 900, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, R., Abbott, T. D., Acernese, F., et al. (LIGO Scientific Collaboration, Virgo Collaboration, and KAGRA Collaboration) 2023a, Phys. Rev. X, 13, 011048 [NASA ADS] [Google Scholar]
- Abbott, R., Abbott, T. D., Acernese, F., et al. (LIGO Scientific Collaboration, Virgo Collaboration, and KAGRA Collaboration) 2023b, Phys. Rev. X, 13, 041039 [Google Scholar]
- Adams, S. M., Kochanek, C. S., Gerke, J. R., Stanek, K. Z., & Dai, X. 2017a, MNRAS, 468, 4968 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, S. M., Kochanek, C. S., Gerke, J. R., & Stanek, K. Z. 2017b, MNRAS, 469, 1445 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilera-Dena, D. R., Müller, B., Antoniadis, J., et al. 2023, A&A, 671, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, J. P. 2019, A&A, 628, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnett, W. D., Bahcall, J. N., Kirshner, R. P., & Woosley, S. E. 1989, ARA&A, 27, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Ballone, A., Costa, G., Mapelli, M., et al. 2023, MNRAS, 519, 5191 [NASA ADS] [CrossRef] [Google Scholar]
- Barkat, Z., & Wheeler, J. C. 1988, ApJ, 332, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Baron, E., & Cooperstein, J. 1990, ApJ, 353, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Basinger, C. M., Kochanek, C. S., Adams, S. M., Dai, X., & Stanek, K. Z. 2021, MNRAS, 508, 1156 [NASA ADS] [CrossRef] [Google Scholar]
- Beasor, E. R., Hosseinzadeh, G., Smith, N., et al. 2024, ApJ, 964, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Bernini-Peron, M., Marcolino, W. L. F., Sander, A. A. C., et al. 2023, A&A, 677, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braun, H., & Langer, N. 1995, A&A, 297, 483 [NASA ADS] [Google Scholar]
- Brown, G. E., Heger, A., Langer, N., et al. 2001, New Astron., 6, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, C. J., Krist, J., Hester, J. J., et al. 1995, ApJ, 452, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Radice, D., Vartanyan, D., et al. 2020, MNRAS, 491, 2715 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, C., Müller, B., Heger, A., Pakmor, R., & Springel, V. 2018, ApJ, 852, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, C., Müller, B., & Heger, A. 2020, MNRAS, 495, 3751 [NASA ADS] [CrossRef] [Google Scholar]
- Chieffi, A., & Limongi, M. 2020, ApJ, 890, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Chini, R., Hoffmeister, V. H., Nasseri, A., Stahl, O., & Zinnecker, H. 2012, MNRAS, 424, 1925 [Google Scholar]
- Claeys, J. S. W., de Mink, S. E., Pols, O. R., Eldridge, J. J., & Baes, M. 2011, A&A, 528, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Costa, G., Ballone, A., Mapelli, M., & Bressan, A. 2022, MNRAS, 516, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Couch, S. M., Warren, M. L., & O’Connor, E. P. 2020, ApJ, 890, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, B., & Beasor, E. R. 2020, MNRAS, 493, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, B., Crowther, P. A., & Beasor, E. R. 2018, MNRAS, 478, 3138 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Pols, O. R., & Hilditch, R. W. 2007, A&A, 467, 1181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [Google Scholar]
- Di Carlo, U. N., Giacobbo, N., Mapelli, M., et al. 2019, MNRAS, 487, 2947 [NASA ADS] [CrossRef] [Google Scholar]
- Di Carlo, U. N., Mapelli, M., Bouffanais, Y., et al. 2020, MNRAS, 497, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., & Landstreet, J. D. 2009, ARA&A, 47, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Dray, L. M., & Tout, C. A. 2007, MNRAS, 376, 61 [Google Scholar]
- Dufton, P. L., Langer, N., Dunstall, P. R., et al. 2013, A&A, 550, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edelman, B., Farr, B., & Doctor, Z. 2023, ApJ, 946, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Ertl, T., Janka, H.-T., Woosley, S. E., Sukhbold, T., & Ugliano, M. 2016, ApJ, 818, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Ertl, T., Woosley, S. E., Sukhbold, T., & Janka, H. T. 2020, ApJ, 890, 51 [CrossRef] [Google Scholar]
- Farag, E., Renzo, M., Farmer, R., Chidester, M. T., & Timmes, F. X. 2022, ApJ, 937, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Farmer, R., Renzo, M., de Mink, S. E., Marchant, P., & Justham, S. 2019, ApJ, 887, 53 [Google Scholar]
- Farmer, R., Renzo, M., de Mink, S. E., Fishbach, M., & Justham, S. 2020, ApJ, 902, L36 [CrossRef] [Google Scholar]
- Farmer, R., Laplace, E., de Mink, S. E., & Justham, S. 2021, ApJ, 923, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Farmer, R., Laplace, E., Ma, J.-Z., de Mink, S. E., & Justham, S. 2023, ApJ, 948, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Farrell, E., Groh, J. H., Meynet, G., & Eldridge, J. J. 2022, MNRAS, 512, 4116 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrario, L., Melatos, A., & Zrake, J. 2015, Space Sci. Rev., 191, 77 [CrossRef] [Google Scholar]
- Ferraro, F. R., Mucciarelli, A., Lanzoni, B., et al. 2023, Nat. Commun., 14, 2584 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., Castro, N., Schöller, M., et al. 2015, A&A, 582, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freitag, M., & Benz, W. 2005, MNRAS, 358, 1133 [Google Scholar]
- Fryer, C. 2014, Proceedings of Frontier Research in Astrophysics (FRAPWS2014) held 26–31 May, 4 [Google Scholar]
- Gerke, J. R., Kochanek, C. S., & Stanek, K. Z. 2015, MNRAS, 450, 3289 [Google Scholar]
- Gieles, M., Charbonnel, C., Krause, M. G. H., et al. 2018, MNRAS, 478, 2461 [Google Scholar]
- Glebbeek, E., Gaburov, E., Portegies Zwart, S., & Pols, O. R. 2013, MNRAS, 434, 3497 [NASA ADS] [CrossRef] [Google Scholar]
- Grassitelli, L., Langer, N., Mackey, J., et al. 2021, A&A, 647, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grunhut, J. H., Wade, G. A., Neiner, C., et al. 2017, MNRAS, 465, 2432 [NASA ADS] [CrossRef] [Google Scholar]
- Hachinger, S., Mazzali, P. A., Taubenberger, S., et al. 2012, MNRAS, 422, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M. 2003, ApJ, 582, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C., & Hoshi, R. 1961, PASJ, 13, 442 [Google Scholar]
- Heger, A., Müller, B., & Mandel, I. 2023, in Black Holes as the End State of Stellar Evolution: Theory and Simulations, ed. Z. Haima, 61 [Google Scholar]
- Hellings, P. 1983, Ap&SS, 96, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Hellings, P. 1984, Ap&SS, 104, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Henneco, J., Schneider, F. R. N., & Laplace, E. 2024, A&A, 682, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henyey, L., Vardya, M. S., & Bodenheimer, P. 1965, ApJ, 142, 841 [Google Scholar]
- Hillebrandt, W., & Meyer, F. 1989, A&A, 219, L3 [NASA ADS] [Google Scholar]
- Hirai, R., Podsiadlowski, P., Owocki, S. P., Schneider, F. R. N., & Smith, N. 2021, MNRAS, 503, 4276 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974 [Google Scholar]
- Humphreys, R. M., & Davidson, K. 1979, ApJ, 232, 409 [Google Scholar]
- Humphreys, R. M., & Davidson, K. 1994, PASP, 106, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N. 2002, PhD Thesis, University of Oxford, UK [Google Scholar]
- Ivanova, N., & Podsiadlowski, P. 2002, Ap&SS, 281, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Podsiadlowski, P., & Spruit, H. 2002, MNRAS, 334, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Jencson, J. E., Pearson, J., Beasor, E. R., et al. 2023, ApJ, 952, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, Y.-F., Cantiello, M., Bildsten, L., et al. 2018, Nature, 561, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Justham, S., Podsiadlowski, P., & Vink, J. S. 2014, ApJ, 796, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Keszthelyi, Z., Meynet, G., Georgy, C., et al. 2019, MNRAS, 485, 5843 [NASA ADS] [CrossRef] [Google Scholar]
- Kilpatrick, C. D., Foley, R. J., Jacobson-Galán, W. V., et al. 2023, ApJ, 952, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1994, Stellar Structure and Evolution (New York: Springer-Verlag) [Google Scholar]
- Kluyver, T., Ragan-Kelley, B., Pérez, F., et al. 2016, in Positioning and Power in Academic Publishing: Players, Agents and Agendas, eds. F. Loizides, & B. Schmidt (IOS Press), 87 [Google Scholar]
- Kobulnicky, H. A., & Fryer, C. L. 2007, ApJ, 670, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., Kiminki, D. C., Lundquist, M. J., et al. 2014, ApJS, 213, 34 [Google Scholar]
- Kochanek, C. S., Neustadt, J. M. M., & Stanek, K. Z. 2024, ApJ, 962, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Kuroda, T., Kotake, K., Takiwaki, T., & Thielemann, F.-K. 2018, MNRAS, 477, L80 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N. 1989, A&A, 210, 93 [NASA ADS] [Google Scholar]
- Langer, N. 2012, ARA&A, 50, 107 [CrossRef] [Google Scholar]
- Langer, N. 2014, IAU Symp., 302, 1 [NASA ADS] [Google Scholar]
- Laplace, E. 2022, Astron. Comput., 38, 100516 [NASA ADS] [CrossRef] [Google Scholar]
- Laplace, E., Justham, S., Renzo, M., et al. 2021, A&A, 656, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leonard, P. J. T., & Livio, M. 1995, ApJ, 447, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, J. C., Warren, J. S., Rasio, F. A., Sills, A., & Warren, A. R. 2002, ApJ, 568, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Lundqvist, P., & Fransson, C. 1996, ApJ, 464, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Mapelli, M. 2016, MNRAS, 459, 3432 [NASA ADS] [CrossRef] [Google Scholar]
- Marchant, P., & Moriya, T. J. 2020, A&A, 640, L18 [EDP Sciences] [Google Scholar]
- Mason, B. D., Hartkopf, W. I., Gies, D. R., Henry, T. J., & Helsel, J. W. 2009, AJ, 137, 3358 [Google Scholar]
- Mauron, N., & Josselin, E. 2011, A&A, 526, A156 [CrossRef] [EDP Sciences] [Google Scholar]
- Menon, A., & Heger, A. 2017, MNRAS, 469, 4649 [NASA ADS] [Google Scholar]
- Menon, A., Utrobin, V., & Heger, A. 2019, MNRAS, 482, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Menon, A., Ercolino, A., Urbaneja, M. A., et al. 2023, arXiv e-prints [arXiv:2311.05581] [Google Scholar]
- Meynet, G., Eggenberger, P., & Maeder, A. 2011, A&A, 525, L11 [CrossRef] [EDP Sciences] [Google Scholar]
- Meza, N., & Anderson, J. P. 2020, A&A, 641, A177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moe, M., & Di Stefano, R. 2017, ApJS, 230, 15 [Google Scholar]
- Moreno, M. M., Schneider, F. R. N., Röpke, F. K., et al. 2022, A&A, 667, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morris, T., & Podsiadlowski, P. 2007, Science, 315, 1103 [Google Scholar]
- Morris, T., & Podsiadlowski, P. 2009, MNRAS, 399, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, B., Heger, A., Liptai, D., & Cameron, J. B. 2016, MNRAS, 460, 742 [Google Scholar]
- Neiner, C., Mathis, S., Alecian, E., et al. 2015, in Polarimetry, eds. K. N. Nagendra, S. Bagnulo, R. Centeno, & M. J. Martínez González, 305, 61 [NASA ADS] [Google Scholar]
- Nieuwenhuijzen, H., & de Jager, C. 1990, A&A, 231, 134 [NASA ADS] [Google Scholar]
- Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS] [Google Scholar]
- O’Connor, E., & Ott, C. D. 2011, ApJ, 730, 70 [Google Scholar]
- Offner, S. S. R., Moe, M., Kratter, K. M., et al. 2023, in Protostars and Planets VII, eds. S. Inutsuka, Y. Aikawa, T. Muto, K. Tomida, & M. Tamura, ASP Conf. Ser., 534, 275 [NASA ADS] [Google Scholar]
- Oliphant, T. E. 2006, A Guide to NumPy (USA: Trelgol Publishing), 1 [Google Scholar]
- Ott, C. D., Roberts, L. F., da Silva Schneider, A., et al. 2018, ApJ, 855, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Patton, R. A., & Sukhbold, T. 2020, MNRAS, 499, 2803 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Petermann, I., Langer, N., Castro, N., & Fossati, L. 2015, A&A, 584, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petit, V., Keszthelyi, Z., MacInnis, R., et al. 2017, MNRAS, 466, 1052 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P. 1992, PASP, 104, 717 [CrossRef] [Google Scholar]
- Podsiadlowski, P. 2017a, in Handbook of Supernovae, eds. A. W. Alsabti, & P. Murdin, 635 [CrossRef] [Google Scholar]
- Podsiadlowski, P. 2017b, arXiv e-prints [arXiv:1702.03973] [Google Scholar]
- Podsiadlowski, P., & Joss, P. C. 1989, Nature, 338, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Joss, P. C., & Rappaport, S. 1990, A&A, 227, L9 [NASA ADS] [Google Scholar]
- Podsiadlowski, P., Joss, P. C., & Hsu, J. J. L. 1992, ApJ, 391, 246 [Google Scholar]
- Podsiadlowski, P., Langer, N., Poelarends, A. J. T., et al. 2004, ApJ, 612, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Morris, T. S., & Ivanova, N. 2007, AIP Conf. Ser., 937, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R. 1994, A&A, 290, 119 [Google Scholar]
- Portegies Zwart, S. F., & McMillan, S. L. W. 2002, ApJ, 576, 899 [Google Scholar]
- Portegies Zwart, S. F., Baumgardt, H., Hut, P., Makino, J., & McMillan, S. L. W. 2004, Nature, 428, 724 [Google Scholar]
- Potter, A. T., Chitre, S. M., & Tout, C. A. 2012, MNRAS, 424, 2358 [NASA ADS] [CrossRef] [Google Scholar]
- Powell, J., & Müller, B. 2020, MNRAS, 494, 4665 [NASA ADS] [CrossRef] [Google Scholar]
- Pumo, M. L., Cosentino, S. P., Pastorello, A., et al. 2023, MNRAS, 521, 4801 [CrossRef] [Google Scholar]
- Quentin, L. G., & Tout, C. A. 2018, MNRAS, 477, 2298 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez-Agudelo, O. H., Simón-Díaz, S., Sana, H., et al. 2013, A&A, 560, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez-Agudelo, O. H., Sana, H., de Mink, S. E., et al. 2015, A&A, 580, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renzo, M., Cantiello, M., Metzger, B. D., & Jiang, Y. F. 2020a, ApJ, 904, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Renzo, M., Farmer, R. J., Justham, S., et al. 2020b, MNRAS, 493, 4333 [NASA ADS] [CrossRef] [Google Scholar]
- Renzo, M., Zapartas, E., Justham, S., et al. 2023, ApJ, 942, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., Kato, M., & Nomoto, K. 1988, ApJ, 331, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sana, H., Le Bouquin, J. B., Lacour, S., et al. 2014, ApJS, 215, 15 [Google Scholar]
- Schneider, F. R. N., Izzard, R. G., Langer, N., & de Mink, S. E. 2015, ApJ, 805, 20 [Google Scholar]
- Schneider, F. R. N., Podsiadlowski, P., Langer, N., Castro, N., & Fossati, L. 2016, MNRAS, 457, 2355 [Google Scholar]
- Schneider, F. R. N., Ohlmann, S. T., Podsiadlowski, P., et al. 2019, Nature, 574, 211 [Google Scholar]
- Schneider, F. R. N., Ohlmann, S. T., Podsiadlowski, P., et al. 2020, MNRAS, 495, 2796 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, F. R. N., Podsiadlowski, P., & Müller, B. 2021, A&A, 645, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, F. R. N., Podsiadlowski, P., & Laplace, E. 2023, ApJ, 950, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Schöller, M., Hubrig, S., Fossati, L., et al. 2017, A&A, 599, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schootemeijer, A., Langer, N., Grin, N. J., & Wang, C. 2019, A&A, 625, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sibony, Y., Georgy, C., Ekström, S., & Meynet, G. 2023, A&A, 680, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sills, A., Adams, T., & Davies, M. B. 2005, MNRAS, 358, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J. 2015, PASA, 32, e016 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N. 2014, ARA&A, 52, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Vink, J. S., & de Koter, A. 2004, ApJ, 615, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Sravan, N., Marchant, P., & Kalogera, V. 2019, ApJ, 885, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Stegmann, J., Antonini, F., & Moe, M. 2022, MNRAS, 516, 1406 [NASA ADS] [CrossRef] [Google Scholar]
- Sukhbold, T., & Adams, S. 2020, MNRAS, 492, 2578 [Google Scholar]
- Sukhbold, T., & Woosley, S. E. 2014, ApJ, 783, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Sukhbold, T., Ertl, T., Woosley, S. E., Brown, J. M., & Janka, H.-T. 2016, ApJ, 821, 38 [Google Scholar]
- Taddia, F., Sollerman, J., Fremling, C., et al. 2016, A&A, 588, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takahashi, K., Takiwaki, T., & Yoshida, T. 2023, ApJ, 945, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Temaj, D., Schneider, F. R. N., Laplace, E., Wei, D., & Podsiadlowski, P. 2024, A&A, 682, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1996, ApJ, 457, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Tiwari, V. 2022, ApJ, 928, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Tiwari, V., & Fairhurst, S. 2021, ApJ, 913, L19 [CrossRef] [Google Scholar]
- Ugliano, M., Janka, H.-T., Marek, A., & Arcones, A. 2012, ApJ, 757, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Urushibata, T., Takahashi, K., Umeda, H., & Yoshida, T. 2018, MNRAS, 473, L101 [CrossRef] [Google Scholar]
- Vanbeveren, D., Mennekens, N., Van Rensbergen, W., & De Loore, C. 2013, A&A, 552, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vigna-Gómez, A., Justham, S., Mandel, I., de Mink, S. E., & Podsiadlowski, P. 2019, ApJ, 876, L29 [CrossRef] [Google Scholar]
- Vigna-Gómez, A., Toonen, S., Ramirez-Ruiz, E., et al. 2021, ApJ, 907, L19 [Google Scholar]
- Vink, J. S., & de Koter, A. 2005, A&A, 442, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., Higgins, E. R., Sander, A. A. C., & Sabhahit, G. N. 2021, MNRAS, 504, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Meth., 17, 261 [Google Scholar]
- Wade, G. A., Grunhut, J., Alecian, E., et al. 2014, IAU Symp., 302, 265 [Google Scholar]
- Wang, C., Langer, N., Schootemeijer, A., et al. 2020, ApJ, 888, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Weis, K., & Bomans, D. J. 2020, Galaxies, 8, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Wellstein, S., & Langer, N. 1999, A&A, 350, 148 [NASA ADS] [Google Scholar]
- Wellstein, S., Langer, N., & Braun, H. 2001, A&A, 369, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woosley, S. E. 1988, ApJ, 330, 218 [Google Scholar]
- Woosley, S. E. 2017, ApJ, 836, 244 [Google Scholar]
- Woosley, S. E. 2019, ApJ, 878, 49 [Google Scholar]
- Woosley, S. E., Langer, N., & Weaver, T. A. 1993, ApJ, 411, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y., Takahashi, K., Goriely, S., et al. 2013, Nucl. Phys. A, 918, 61 [Google Scholar]
- Zapartas, E., de Mink, S. E., Justham, S., et al. 2019, A&A, 631, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zapartas, E., de Mink, S. E., Justham, S., et al. 2021, A&A, 645, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Supplemental information
Complementary HR diagrams to Fig. 1 of accreting stars with an initial mass of 13 M⊙ for early and late Case A, and late Case B and Case C are shown in Figs. A.1 and A.2, respectively. An overview of the final fates of the models in our grid is provided in Fig. A.3. An additional Kippenhahn diagram for initially 30 M⊙ accretors can be found in Fig. A.5. The helium core masses and central carbon mass fractions after core-helium burning are shown in Figs. A.6 and A.7 as a function of initial mass. A table with key properties of all our accretor models is provided in Tab. A.1.
 |
Fig. A.1. Same as Fig. 1 but for early (panel a) and late (panel b) Case A accretors initially with 13 M⊙. |
 |
Fig. A.2. Same as Fig. 1 but for late Case B (panel a) and Case C (panel b) accretors initially with 13 M⊙. |
 |
Fig. A.3. Endstages of the accretor models as BSGs and CSGs in the grid spanned by the initial mass Mini and the accretion fraction facc. Supergiants that are hot (blue; BSGs) because of a high surface helium mass fraction (⟨Xenv⟩cc < 0.5) are shown separately. Cross symbols indicate models that burn helium in their cores for more than 0.2 Myr at effective temperatures of log Teff/K < 3.9, that is as BSGs, and the three panels are for Case A, B, and C accretors. Early Case A and-B accretors are offset to lower values along their respective facc indicated by the dotted black lines while late Case A and-B models are offset to slightly higher values. This overview of the model grid visually underlines two key results presented in Sect. 3. Firstly, there are models that burn helium in their cores as BSGs but explode as CSGs while other models also explode as BSGs and never become CSGs because of the accretion. Secondly, the need for larger facc in more evolved pre-accretors to turn them into long-lived BSGs is illustrated clearly. The threshold facc values to turn stars into long-lived BSGs is significantly lower in merger models that also account for mixing of core material into the envelope such that the values here should be understood as upper limits. |
 |
Fig. A.4. Similar to Fig. A.3, but showing the time |
 |
Fig. A.5. Same as Fig. 2 but for initially 30 M⊙ stars accreting (a) 10% and (b) 100% of their initial mass as early Case B systems. |
Properties of the single and accretor models.
All Tables
All Figures
 |
Fig. 1. Hertzspung-Russell diagram with initial 13 M⊙ stars accreting a fraction facc of their initial mass (colour coded) shortly after they finished core hydrogen burning (early Case B). The dotted parts of the tracks show the accretion phase and the dashed grey evolutionary track is for a single star. Plus symbols are added every 2 × 105 yr after finishing core hydrogen burning to indicate in which region of the HR diagram stars burn helium in the core. The observationally inferred maximum luminosity of RSGs of log L/L⊙ = 5.5 (Davies et al. 2018) is shown by a dotted black line. Explosion sites are indicated as well as the likely SN type. The grey bands show the hot and cool part of the S Doradus instability strip (Smith et al. 2004). For facc ≳ 0.50, the models burn helium as a BSG and for facc ≳ 0.75 they also explode as a BSG. |
| In the text | |
 |
Fig. 2. Kippenhahn diagrams with initial 13 M⊙ early Case B systems accreting (a) 10% and (b) 100% of their initial mass. The moment of mass accretion is indicated by an arrow. Energy generation by nuclear burning, ϵnuc, and loss by neutrinos, ϵν, are colour-coded. The right y-axes show the mass fractions of carbon, XC, and oxygen, XO, in the centre of the stars. Carbon starts being produced when core helium burning begins. The grey hatched areas show convective regions, purple hatchings are for convective overshooting, yellow stands for thermohaline mixing and brown is for semi-convection. The dotted blue lines show where the hydrogen mass fraction drops below 0.5, that is they trace the helium core mass. Hydrogen shell burning in the facc = 0.1 model is radiative and the star evolves into a CSG. In the facc = 1.0 model, hydrogen shell burning proceeds convectively and the star evolves as a BSG (cf. Fig. 1). |
| In the text | |
 |
Fig. 3. TULIPS diagram (Laplace 2022) of the nuclear energy generation rate ϵnuc at the end of core oxygen burning (central oxygen mass fraction < 10−4). Shown are the interiors of a single star of Mini = 20 M⊙ (bottom), an early Case B accretor model of Mini = 20 M⊙ and facc = 0.1 (top left), and an early Case B accretor model of Mini = 23 M⊙ and facc = 1.0 (top right). The three models have a similar CO core masses of MCO = 5.62 M⊙, 5.64 M⊙, and 5.89 M⊙, respectively. The facc = 0.1 accretor model is a CSG while the facc = 1.0 model is a BSG, which can be recognised by the strong hydrogen-shell burning that drives a thick convection zone (not indicated here for clarity, but cf. Figs. 2 and A.5). |
| In the text | |
 |
Fig. 4. Rejuvenation of early (panel a) and late (panel b) Case A accretors. The rejuvenation is quantified as the difference of the average helium mass fraction ⟨Y⟩ of the accretors at the terminal-age main sequence (TAMS) relative to that of single stars. The relative differences are plotted as a function of mass at the TAMS, MTAMS. Negative differences mean that the accretors have burnt less hydrogen into helium compared to single stars, that is they have less massive convective cores. This is a sign that accretors did not (fully) adjust their structure to the new total mass after accretion, that is they did not (fully) rejuvenate. |
| In the text | |
 |
Fig. 5. CO core masses MCO at core collapse as a function of the initial mass Mini for Case A (panel a), Case B (panel b), and Case C (panel c) accretors. Colours show the accretion fraction facc of the models, and single stars are shown in blue squares for comparison in panel a. Panels b and c show the difference in MCO relative to the corresponding single-star core masses. To guide the eye, data points for facc = 0.1 (mostly CSGs) and 2.0 (BSGs) are connected by dashed lines and highlighted. |
| In the text | |
 |
Fig. 6. Similar to Fig. 5 but showing the final masses of stars as a function of the CO core mass MCO at core collapse. In all three panels, single-star models are plotted as blue squares. We further indicate models that experience SN fallback by grey squares while crosses mark those models that should have experienced enhanced LBV-like mass loss, which is not accounted for in our models (see Sect. 2.1). The dotted black line is a one-to-one relation. |
| In the text | |
 |
Fig. 7. Similar to Fig. 5 but showing the central carbon mass fraction at the end of core helium burning XC as a function of the CO core mass MCO. |
| In the text | |
 |
Fig. 8. Core compactness ξ2.5 (panels a–c), iron core mass MFe (panels d–f), and central specific entropy sc (panels g–i) as a function of the CO core mass MCO at core collapse. As in other figures, we distinguish between Cases A–C accretors, and colour-code the mass accretion fraction facc. Accretion fractions of 25%, 75%, and 200% are connected by dashed lines to better visualise trends and systematic shifts. |
| In the text | |
 |
Fig. 9. Pre-SN locations of the Cases A–C accretors in the HR diagram. The dotted line at log L/L⊙ = 5.5 (Davies et al. 2018) is the maximum luminosity of RSGs and the grey shaded regions indicate the hot and cool parts of the S Doradus instability strip. The dashed line is the Humphreys–Davidson limit (Humphreys & Davidson 1979). The dark-grey boxes indicate the locations of the RSG N6946-BH that likely collapsed into a BH without a bright SN (Gerke et al. 2015; Adams et al. 2017a,b; Basinger et al. 2021), and the BSG progenitor of SN 1987A (Woosley 1988). The grey evolutionary tracks are single-star models with the masses given by the labels. |
| In the text | |
 |
Fig. 10. Core-mass–luminosity relation (panel a) and the relationship between the effective temperature and the average hydrogen mass fraction in the envelope (panel b) of single stars and Cases A–C accretors at core collapse. In the core-mass–luminosity relation, only CSG Cases B and C accretors are shown as the BSG accretors with their thick hydrogen-burning shell follow a different mass-luminosity relation (see main text and Fig. 11). The dashed black curve in panel a is the fit of the core-mass–luminosity relation from Temaj et al. (2024). |
| In the text | |
 |
Fig. 11. Envelope mass-luminosity relation (panel a) and H-envelope base temperature-effective temperature relation (panel b) for Case B accretors. Single stars are shown for comparison and models with an average hydrogen mass fraction in their envelopes of ⟨Xenv⟩cc < 0.4 are marked. These stars may appear as BSGs at core collapse but their hot Teff, cc is due to the low hydrogen content in their envelopes and not due to a thick convective hydrogen burning shell. Power-law fits are added and the dotted lines in panel b indicate log Teff, cc/K = 3.9 and the transition base temperature at |
| In the text | |
 |
Fig. 12. Black-hole and neutron-star masses of Case A (panels a, d), Case B (panels b, e), and Case C (panels d, f) accretors as a function of the final CO core mass MCO. The bottom row is a zoom into the NS-mass regime. The NS and BH masses of the single-star models are shown for comparison and accretor models with facc = 0.25, 0.75, and 2.00 are connected by lines to guide the eye. Systems likely experiencing SN fallback are marked by grey boxes and models that should have experienced LBV-like mass loss are indicated by crosses (cf. Sect. 2.1). |
| In the text | |
 |
Fig. 13. Gravitational neutron star mass MNS, grav as a function of the central specific entropy sc of the progenitor stars for Case A (panel a), Case B (panel b), and Case C (panel c) accretion. The dashed black line is the exponential fit to the neutron star masses of single stars computed for different convective boundary mixing found by Temaj et al. (2024). |
| In the text | |
 |
Fig. 14. Same as Figs. 6 and 12 but showing the SN ejecta mass Mej. Models marked by crosses (i.e. also those with the highest SN ejecta mass) are expected to have experienced LBV-like mass loss such that these ejecta masses are upper limits. |
| In the text | |
 |
Fig. 15. Same as Fig. 1 but for the initial 30 M⊙ stars. The dashed black line is the Humphreys–Davidson limit (Humphreys & Davidson 1979). Cross symbols indicate models that may experience enhanced, LBV-like mass loss and may thus rather explode at hotter effective temperatures as stripped-envelope SNe of Type Ib/c. Plus symbols are separated by Δt = 5 × 104 yr. |
| In the text | |
 |
Fig. 16. Maximum BH and SN ejecta mass of single stars and accretors with facc ≤ 1.0 and facc ≤ 2.0 as a function of the maximum time spent in the LBV region of the HR diagram. The grey-shaded region indicates models for which we expect significant LBV-like mass loss such that the maximum BH and SN ejecta masses should be considered upper limits. |
| In the text | |
 |
Fig. A.1. Same as Fig. 1 but for early (panel a) and late (panel b) Case A accretors initially with 13 M⊙. |
| In the text | |
 |
Fig. A.2. Same as Fig. 1 but for late Case B (panel a) and Case C (panel b) accretors initially with 13 M⊙. |
| In the text | |
 |
Fig. A.3. Endstages of the accretor models as BSGs and CSGs in the grid spanned by the initial mass Mini and the accretion fraction facc. Supergiants that are hot (blue; BSGs) because of a high surface helium mass fraction (⟨Xenv⟩cc < 0.5) are shown separately. Cross symbols indicate models that burn helium in their cores for more than 0.2 Myr at effective temperatures of log Teff/K < 3.9, that is as BSGs, and the three panels are for Case A, B, and C accretors. Early Case A and-B accretors are offset to lower values along their respective facc indicated by the dotted black lines while late Case A and-B models are offset to slightly higher values. This overview of the model grid visually underlines two key results presented in Sect. 3. Firstly, there are models that burn helium in their cores as BSGs but explode as CSGs while other models also explode as BSGs and never become CSGs because of the accretion. Secondly, the need for larger facc in more evolved pre-accretors to turn them into long-lived BSGs is illustrated clearly. The threshold facc values to turn stars into long-lived BSGs is significantly lower in merger models that also account for mixing of core material into the envelope such that the values here should be understood as upper limits. |
| In the text | |
 |
Fig. A.4. Similar to Fig. A.3, but showing the time |
| In the text | |
 |
Fig. A.5. Same as Fig. 2 but for initially 30 M⊙ stars accreting (a) 10% and (b) 100% of their initial mass as early Case B systems. |
| In the text | |
 |
Fig. A.6. Same as Fig. 5 but for the helium core masses MHe. |
| In the text | |
 |
Fig. A.7. Same as Fig. 7 but as a function of the initial mass Mini. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



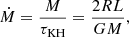
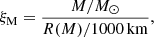
![$$ \begin{aligned} M_{\rm Ch} \approx 1.457\,M_\odot \,\left(\frac{Y_{\rm e}}{0.5}\right)^2 \left[1 + \left(\frac{s_{\rm e,c}}{\pi Y_{\rm e} k_{\rm B} N_{\rm A}}\right)^2\right]. \end{aligned} $$](/articles/aa/full_html/2024/06/aa47854-23/aa47854-23-eq4.gif)