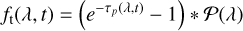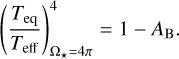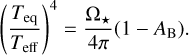| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 19 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202348107 | |
| Published online | 07 March 2024 | |
The elusive atmosphere of WASP–12 b
High-resolution transmission spectroscopy with CARMENES
1
Thüringer Landessternwarte Tautenburg,
Sternwarte 5,
07778
Tautenburg,
Germany
e-mail: sczesla@tls-tautenburg.de
2
Instituto de Astrofísica de Andalucía (IAA-CSIC),
Glorieta de la Astronomía s/n,
18008
Granada,
Spain
3
Universitäts-Sternwarte, Ludwig-Maximilians-Universität München,
Scheinerstrasse 1,
81679
München,
Germany
4
Exzellenzcluster Origins,
Boltzmannstrasse 2,
85748
Garching,
Germany
5
Institut für Astrophysik und Geophysik, Georg-August-Universität Göttingen,
Friedrich-Hund-Platz 1,
37077
Göttingen,
Germany
6
Instituto de Astrofísica de Canarias,
c/ Vía Láctea s/n,
38205
La Laguna,
Tenerife,
Spain
7
Departamento de Astrofísica, Universidad de La Laguna,
38206
Tenerife,
Spain
8
Centro de Astrobiología (CSIC-INTA), ESAC,
Camino bajo del castillo s/n,
28692
Villanueva de la Cañada,
Madrid,
Spain
9
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg,
Germany
10
Landessternwarte, Zentrum für Astronomie der Universität Heidelberg,
Königstuhl 12,
69117
Heidelberg,
Germany
11
Department of Astronomy, University of Science and Technology of China,
Hefei
230026,
PR China
12
Centro Astronómico Hispano en Andalucía, Observatorio de Calar Alto,
Sierra de los Filabres,
04550
Gérgal,
Almería,
Spain
13
Departamento de Física de la Tierra y Astrofísica and IPARCOS-UCM (Instituto de Física de Partículas y del Cosmos de la UCM), Facultad de Ciencias Físicas, Universidad Complutense de Madrid,
28040
Madrid,
Spain
14
Institut de Ciències de l’Espai (ICE, CSIC),
Campus UAB, c/ de Can Magrans s/n,
08193
Bellaterra,
Barcelona,
Spain
15
Institut d’Estudis Espacials de Catalunya (IEEC),
08034
Barcelona,
Spain
16
Hamburger Sternwarte, Universität Hamburg,
Gojenbergsweg 112,
21029
Hamburg,
Germany
Received:
28
September
2023
Accepted:
26
December
2023
To date, the hot Jupiter WASP–12 b has been the only planet with confirmed orbital decay. The late F-type host star has been hypothesized to be surrounded by a large structure of circumstellar material evaporated from the planet. We obtained two high-resolution spectral transit time series with CARMENES and extensively searched for absorption signals by the atomic species Na, H, Ca, and He using transmission spectroscopy, thereby covering the He I λ10833 Å triplet with high resolution for the first time. We apply SYSREM for atomic line transmission spectroscopy, introduce the technique of signal protection to improve the results for individual absorption lines, and compare the outcomes to those of established methods. No transmission signals were detected and the most stringent upper limits as of yet were derived for the individual indicators. Nonetheless, we found variation in the stellar Hα and He I λ10833 Å lines, the origin of which remains uncertain but is unlikely to be activity. To constrain the enigmatic activity state of WASP–12, we analyzed XMM-Newton X-ray data and found the star to be moderately active at most. We deduced an upper limit for the X-ray luminosity and the irradiating X-ray and extreme ultraviolet (XUV) flux of WASP–12 b. Based on the XUV flux upper limit and the lack of the He I λ10833 Å signal, our hydrodynamic models slightly favor a moderately irradiated planet with a thermospheric temperature of ≲12 000 K, and a conservative upper limit of ≲4 × 1012 g s−1 on the mass-loss rate. Our study does not provide evidence for an extended planetary atmosphere or absorption by circumstellar material close to the planetary orbit.
Key words: techniques: radial velocities / planets and satellites: atmospheres / planets and satellites: individual: WASP-12 / X-rays: stars
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The hot Jupiter WASP–12 b orbits its late F-type host star every 1.09 d at a separation of 0.024 au (Hebb et al. 2009), corresponding to a mere 3.1 stellar radii. The WASP–12 planetary system is a member of a larger hierarchical triplet, including an additional M-dwarf binary at a projected separation of about 1 arcsec, which consists of almost identical stars (Bergfors et al. 2013; Bechter et al. 2014). WASP–12 stands out as the only known planetary system that shows transit timing variations, widely accepted to originate from planetary orbital decay caused by tidal interactions (Bailey & Goodman 2019; Yee et al. 2020; Turner et al. 2021; Wong et al. 2022; Bai et al. 2022). As another promising candidate for orbital decay, WASP–4 b has been identified only recently (Harre et al. 2023). The geometric white-light albedo of the planet is very low (Ageom < 0.064, Bell et al. 2017). The thermally dominated phase curve of WASP–12 b observed by the Transiting Exoplanet Survey Satellite (TESS) satellite shows a marginal eastward offset, indicative of a superrotating equatorial wind (Wong et al. 2022). The photometry also shows a large contrast between day and night sides. No significant variability was found in the TESS photometry (Owens et al. 2021; Wong et al. 2022).
The activity state of WASP–12 remains enigmatic. On the one hand, the star shows an unexpectedly low spectroscopic v sin i value (Table 1; Fukuda 1982; Albrecht et al. 2012) and unusually dark cores in the chromospherically sensitive Mg II and Ca II lines (Haswell et al. 2012; Fossati et al. 2013), which may point to an extremely low activity level. On the other hand, Haswell et al. (2012) also report a likely flaring event, and the sky-projections of the planetary orbit normal and the stellar spin axis are misaligned by 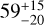 deg (Albrecht et al. 2012), so that a projection effect is a plausible explanation for the low v sin i value. The exceptionally low flux in the cores of the chromo-spheric lines of WASP–12 may be explained by absorption in a very extended structure of circumstellar material originating from the planet (Haswell et al. 2012), which may be a phenomenon also occurring in other planetary systems with close-in planets (Fossati et al. 2013). The one-dimensional atmospheric simulations by Salz et al. (2016b,a) yield a mass-loss rate of 4 × 1011 g s−1 for WASP–12b, which is about an order of magnitude higher than the value adopted by Haswell et al. (2012) and in that sense consistent with the formation of an extended planetary-fed structure. The three-dimensional gas-dynamical modeling by Bisikalo et al. (2013, 2015) indicates that the material mainly escapes in the form of two streams across the first and second Lagrange points. Finally, the 3D hydrodynamic simulations by Debrecht et al. (2018) also show the formation of a two-streamed outflow morphology along with the development of an extended circumstellar torus, which reaches sufficient densities to affect strong spectral lines such as the Hα line and potentially the He I λ10833Å triplet on the timescale of only a few years. Altogether, it appears that WASP–12 is unlikely to be extremely inactive.
deg (Albrecht et al. 2012), so that a projection effect is a plausible explanation for the low v sin i value. The exceptionally low flux in the cores of the chromo-spheric lines of WASP–12 may be explained by absorption in a very extended structure of circumstellar material originating from the planet (Haswell et al. 2012), which may be a phenomenon also occurring in other planetary systems with close-in planets (Fossati et al. 2013). The one-dimensional atmospheric simulations by Salz et al. (2016b,a) yield a mass-loss rate of 4 × 1011 g s−1 for WASP–12b, which is about an order of magnitude higher than the value adopted by Haswell et al. (2012) and in that sense consistent with the formation of an extended planetary-fed structure. The three-dimensional gas-dynamical modeling by Bisikalo et al. (2013, 2015) indicates that the material mainly escapes in the form of two streams across the first and second Lagrange points. Finally, the 3D hydrodynamic simulations by Debrecht et al. (2018) also show the formation of a two-streamed outflow morphology along with the development of an extended circumstellar torus, which reaches sufficient densities to affect strong spectral lines such as the Hα line and potentially the He I λ10833Å triplet on the timescale of only a few years. Altogether, it appears that WASP–12 is unlikely to be extremely inactive.
Its unusual properties have made WASP–12 b a coveted target with studies for emission and transmission spectroscopy. While the emission of WASP–12 b has been analyzed in some detail, many aspects of its (dayside) atmospheric structure remain under discussion. In particular, it is debated if and to what extent the carbon-to-oxygen ratio is elevated and if a thermal inversion layer exists as one expects in planets such as WASP–12b (Madhusudhan et al. 2011; Stevenson et al. 2014a; Line et al. 2014; Oreshenko et al. 2017; Himes & Harrington 2022).
Likewise, numerous studies of the transmission spectrum exist. Fossati et al. (2010b), Haswell et al. (2012), and Nichols et al. (2015) present near-ultraviolet transmission spectroscopy of a total of six primary transits of WASP-12 b observed with the Cosmic Origins Spectrograph (COS) onboard the Hubble Space Telescope. These data reveal excess in-transit absorption (Nichols et al. 2015) with increased transit depths observed in resonance lines of various metals (Fossati et al. 2010b). The near-ultraviolet transit observations show variability and are indicative of an extended atmospheric structure overfilling the planetary Roche lobe (Haswell et al. 2012).
Sing et al. (2013) study the transmission spectrum of WASP-12 in the 2900–10 300 Å range at low spectral resolution. They find their transmission spectrum to show a Rayleigh scattering slope while being otherwise devoid of any strong molecular or atomic absorption features. Specifically, the authors report non-detections of Na, K, Hα, and Hβ using 30 Å-wide resolution elements, and conclude that, if present at all, such features must be confined to a narrow core region. Indeed, Burton et al. (2015) and Bai et al. (2022) find a tentative detection of excess intransit absorption in the Na I D lines in the spectra of WASP–12, and Jensen et al. (2018) describe pronounced excess transit absorption in the Na ID and Hα lines of WASP–12 observed at moderately high spectral resolution (R ≈ 15 000) but with non-continuous temporal sampling, possibly extending into the preand post-transit phases. Kreidberg & Oklopčič (2018) analyze data obtained by the Wide Field Camera 3 onboard the Hubble Space Telescope and report the non-detection of He I λ10833 Å absorption, however, at low spectral resolution. Analyzing the transmission spectrum up to 5 µm, Stevenson et al. (2014b) report features likely attributable to molecular absorption and Kreidberg et al. (2015) detect water in the transmission spectrum of WASP–12 b. The atmosphere of WASP–12 b is thought to have a cloud deck, which attenuates spectral features from the underlying atmosphere (Wakeford et al. 2017), which can explain the apparent lack of strong atmospheric signals.
Relevant system parameters of WASP-12.
2 Observations
We obtained two spectral transit time series of WASP–12 with CARMENES1 (Quirrenbach et al. 2018). The CARMENES spectrograph has two channels, namely VIS and NIR, that cover the wavelength ranges 0.52–0.96 µm and 0.96–1.71 µm, respectively. The spectral resolutions are 94 600 in the VIS channel and 80 400 in the NIR channel.
Our two observing runs commenced on 18 December 2019 20:04 and 17 November 2020 22:00 (UTC), which we refer to as night 1 and night 2 in the following. A total of 22 and 21 spectra with individual exposure times of 15 min where obtained during our runs. The data were reduced using the caracal pipeline (CARMENES Reduction And CALibration; Zechmeister et al. 2014; Caballero et al. 2016) and a telluric correction was subsequently performed using the molecfit package (Smette et al. 2015; Kausch et al. 2015). Figure 1 shows the evolution of airmass and signal-to-noise ratio (S/N) per pixel in the order covering the Hα line along with the transit contact points.
2.1 Systemic velocity
To determine the systemic radial velocity, γ, of the system, we first obtained master spectra for the individual spectral orders of the CARMENES VIS channel. To that end, we carried out the barycentric correction for the telluric-corrected spectra and obtained the pixel-wise median spectrum. The thus obtained master order spectra were then compared to a synthetic PHOENIX spectrum computed for Teff = 6200 Κ and log g = 4.5 (Husser et al. 2013). The comparison was done by a fit in which we considered a free normalization by a quadratic polynomial, the coefficients of which were treated as nuisance parameters, and a free parameter for the systemic radial velocity (RV). We then calculated the median value and the median deviation about the median as a robust estimator of the standard deviation (Hampel 1974; Rousseeuw & Croux 1993; Czesla et al. 2018), which we subsequently divided by the square root of the number of orders to get the error of the mean. In Table 1, we list the thus obtained best-fit value for the systemic velocity. Our result of 19.46 + 0.02 km s−1 is well consistent yet more precise than the value of 20.6 ± 1.4 km s−1 reported by Gaia DR3.
2.2 Roche geometry
WASP–12 b is so close to its host star that tidal forces become significant. The combined gravitational and centrifugal forces on test masses in the rotating frame of two orbiting bodies is described by the Roche potential (e.g., Hilditch 2001, and Appendix D). In Fig. 2, we show a pole-on view (i.e., the line-of-sight is along the normal of the orbital plane) of WASP–12 b’s geometry, indicating the equipotential surfaces defining the Roche lobe and the planetary body, which both assume typical drop-like shapes. While the deviation from the spherical shape is strongest in the substellar direction, also the polar and side radii of the drop differ slightly (e.g., Haswell et al. 2012). As photometric transit measurements are primarily sensitive to the fractional area covered by the occulting planet, we interpret the planetary radius, RP, given in Table 1 as the radius of a circular disk with the same area as the projection of the drop-like planetary body during conjunction. Modeling the latter as an ellipse, we obtain the potential level defining the planetary surface by the condition of equal area (see, e.g., Delrez et al. 2016)
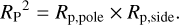 (1)
(1)
This criterion yields the following values for the radii in the sub-stellar, polar, and side directions: Rp,Subsoiar = 2.18 RJup, Rp,pole = 1.86 RJup, and Rp,side = 1.91 RJup. The corresponding radii of the Roche lobe read RRl,subsolar = 3.29 Rjup, RRl,pole = 2.12 RJup, and RRl,side = 2.21 RJup. The planetary body fills 59% of its Roche lobe volume.
 |
Fig. 1 Evolution of airmass and S/N in night 1 (solid) and night 2 (dotted). Dotted vertical lines indicate the four contact points of the transit. |
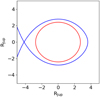 |
Fig. 2 Pole-on view of the Roche geometry of WASP–12 b. The host star is to the left. The equipotential surfaces of the Roche lobe (blue) and planetary surface (red) are indicated. |
2.3 Transit timing
Nights 1 and 2 covered the transits with epochs no. 2319 and 2626 with respect to the ephemerides given by Turner et al. (2021, Table 1). While the change in orbital period predicted by the orbital decay model is only about –0.2 s per epoch, the difference in the transit times obtained using the constant period and orbital decay ephemerides accumulates to between one and two minutes at these epochs. A two minute timing error amounts to a RV shift of 1.9 km s−1 in the planetary rest frame during the center of the transit and, thus, transmission spectrum, if not accounted for. Throughout the paper, we adopt the orbital decay ephemerides published by Turner et al. (2021). The more recent quadratic ephemerides provided by Wong et al. (2022) and Bai et al. (2022) yield consistent transit times, which differ by only a few seconds for our events.
Orbital motion causes an acceleration of 15.9 m s−2 of the planet along the line-of-sight direction during the central transit phase. For individual exposure times of 900 s, this results in a change of 14.3 km s−1 in the orbital planetary RV during every single exposure. Using the formulation given by Czesla et al. (2022), we treated the broadening effect of this phase smearing on the transmission spectrum by adopting an effective instrumental resolution of 30 000, which is appropriate for both channels of CARMENES, because the smearing dominates the line broadening.
2.4 X-ray observations with XMM-Newton
We observed WASP–12 with XMM-Newton on 14 September 2019 (PI: Sanz-Forcada). Our 9 ks exposure with the combined EPIC detectors only gave a poor S/N = 1.3 detection (Sanz-Forcada et al., in prep.). The large stellar distance implies a canonical interstellar medium H I absorption column of ≈2 × 1021 cm−2. We performed a spectral fit to the source, forcing a “solar” coronal temperature of log T(K) = 6.3, which yields an upper limit of 6 × 1028 erg s−1 in the X-ray (5–100 Å) band. The relatively low ratio of X-ray to bolometric luminosity, log LX/Lbol < −5.4, indicates that the star is of moderate activity at most, consistent with observations of the Ca II lines. The resulting upper limit of 4.5 × 1029 erg s−1 on the extreme ultraviolet (EUV, 100–920 Å) stellar flux was calculated with a coronal plasma model extrapolated to the temperatures of the transition region as outlined by Sanz-Forcada et al. (2011). While X-ray-EUV scaling relations such as those by Chadney et al. (2015), King et al. (2018), Johnstone et al. (2021), or, in fact, Sanz-Forcada et al. (2011) themselves may provide slightly different estimates, we emphasize that the main source of uncertainty is the poor X-ray photon statistics.
3 Analysis and results
In the following, we study the use of SYSREM in atomic line spectroscopy (Sect. 3.1) and apply the technique to WASP–12 (Sect. 3.2). We then analyze spectral changes in the stellar reference frame (Sect. 3.3) and examine interstellar absorption (Sect. 3.4).
3.1 Atomic line transmission spectroscopy with SYSREM
The observed spectra contain the stellar and planetary signals as well as a number of confounding components. The most important of these in ground-based transmission spectroscopy are the presence of potentially variable telluric absorption and emission lines as well as interstellar absorption lines. Additionally, stellar line profile variations such as those caused by activity and rotation may exist.
3.1.1 Representation of time series measurements
When a spectral time series is observed with a telescope, measurements of the specific flux from some solid angle in the sky are obtained in N time intervals, [ti, ti + Δti], and M wavelength bins, [λj,λj + Δλj]. For the purpose of the following discussion, we assume that the specific flux, ℱT(λ, t), collected from the direction of the transiting planetary system can be modeled by the following expression
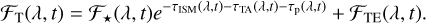 (2)
(2)
Here ℱ★(λ, t) is the disk-integrated stellar flux scaled by distance, τISM(λ, t) is the optical depth of the interstellar medium, τTA(λ, t) is the optical depth of telluric absorption, τp(λ, t) is the optical depth of the planetary atmosphere in front of the stellar disk, and ℱTE(λ, t) represents the flux of telluric emission features observed in the direction of the target. The optical depth of the planetary atmosphere τp(λ, t) is often only larger than zero during the optical transit, but examples of prolonged or early starting atmospheric transits are known (e.g., Cauley et al. 2015; Nortmann et al. 2018; Czesla et al. 2022; Zhang et al. 2023). Equation (2) remains an approximation at least because the planetary opaque disk blocks out some light and the absorption by the planetary atmosphere is a local phenomenon, as it does not act upon the disk-integrated spectrum (e.g., Dethier & Bourrier 2023). If spaceborne observatories such as the Hubble Space Telescope are used, the telluric absorption term in Eq. (2) vanishes (i.e., τTA(λ, t) = 0). Yet, emission terms such as those attributable to geocoronal emission lines may remain significant. We assume that the telescope system and data reduction can be represented by the function I
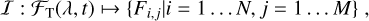 (3)
(3)
where the Fi,j are normally distributed random variables with expected values given by
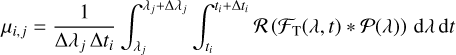 (4)
(4)
and standard deviations denoted by σij. The * symbol implies convolution with the instrumental profile, Ƥ(λ), and the function ℛ summarizes the spectral response of the instrumental system and data reduction process.
Actual measurements are considered to be realizations, fi,j, of the random variables Fi,j. A time series observation may be represented by N × M matrices
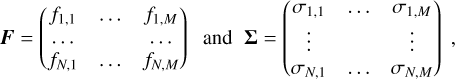 (5)
(5)
where the rows of F are the observed spectra and Σ holds the uncertainties.
While the relative RV shifts of the spectral components included in Eq. (2) are defined by their physical origin, their absolute shifts and to some extent their time evolution are determined by the reference frame with respect to which the spectra are given. The most relevant reference frames for our purpose are the observer’s reference frame (OF), the barycentric reference frame (BF), the stellar reference frame (SF), and the planetary reference frame (PF). Observations are naturally obtained in the OF, although the data reduction pipeline of the spectrograph may already apply a transformation during the extraction of the one-dimensional spectra from the raw frames. The telluric absorption and emission lines remain stationary in the OF of a ground-based observatory (at least to within about 20 m s−1, Caccin et al. 1985), but their strengths are usually time dependent.
Transformations of the matrices F and Σ between reference frames can be obtained by applying appropriate Doppler shifts to the individual rows. For example, we denote by
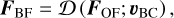 (6)
(6)
a transformation of the matrix FOF from the OF into the BF by applying the appropriate barycentric correction, vi,BC, to the ith row of FOF; the corrections for all rows are given by the vector vBC = (v1,BC … VN,BC).
3.1.2 The SYSREM algorithm
The SYSREM algorithm was described by Tamuz et al. (2005). It can be applied to matrices of the form
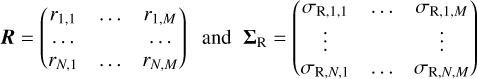 (7)
(7)
where R contains the input data and ΣR the standard deviations, σr,i,j, of the associated uncertainties. SYSREM defines a mapping, S, from R and ΣR to a model, M,
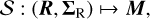 (8)
(8)
which approximates the input data. The model is the outer product of two (column) vectors a = (a1,…,aN) and c = (c1,…, cM)
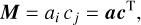 (9)
(9)
the elements of which are defined by the condition that the quantity
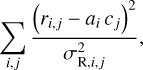 (10)
(10)
is minimized. The input data matrix is then updated by subtracting the model
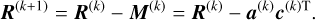 (11)
(11)
As the SYSREM algorithm is typically applied iteratively, we follow Tamuz et al. (2005) and use the superscript (k) to denote the number of iterations and understand that R(0) = R. From Eq. (11), it follows that after k iterations
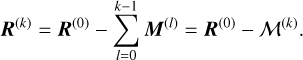 (12)
(12)
We call ℳ(k) the cumulative model and refer to the rows of R(k) as residual spectra.
In the analysis of spectral time series with SYSREM, one possibility is to use the individual spectra (or sections thereof) in the OF as rows of the data matrix, that is, R(0) = FOF and ΣR = ΣOF. Intuitively, the first SYSREM model (M(0), Eq. (9)) then consists of a kind of average spectrum, c(0), with individual scaling factors, a , to best match the observations. Such a model mainly reproduces components with stationary wavelengths and variable strength, but does not efficiently reproduce components, shifting fast through the spectra. Therefore, the suitability of the reference frames for the analysis is largely determined by the ensuing wavelength shifts of the individual components in Eq. (2).
For close-in planets, orbital motion can produce strong RV variations of the planetary component with regard to the stellar and telluric spectral components, which are crucial to distinguish planetary signals from other effects. During our two individual observing runs targeted at WASP-12, the barycentric correction changes by ≲0.5 km s−1 and the stellar reflex motion produces a Doppler shift of ≲0.3 km s−1. In contrast, the RV induced by the planetary orbital motion changes by about 160 km s−1.
3.1.3 Deriving the observable transmission spectrum
the observable transmission spectrum, which is the planetary component in Eq. (2) with unity subtracted, broadened by the instrumental profile. Our problem is to define an estimator for the observable transmission spectrum. This estimator should have favorable properties such as being unbiased.
Based on R(k) and ΣR, expressed in any reference frame, average residual spectra, b = (b1, …, bM), can be constructed by defining a function B such that
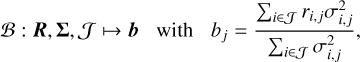 (14)
(14)
where ℑ is the set of indices of the rows considered in the averaging. Thus, for example, B(FOF, ΣOF, ℑ) is the error-weighted, bin-wise averaged observed spectrum over the indices ℑ in the OF.
Assume, we start the SYSREM iteration with the observed spectral time series expressed in a hypothetical reference frame, XF, in which all but the planetary signal can be assumed to be stationary (R = FXF and ΣR = ΣXF). As an idealization, we may then assume that after a sufficient number, ks, of SYSREM iterations, all spectral components in Eq. (2) but the fast-shifting planetary signal are reproduced by the model so that the expected value of the cumulative model becomes
![$E\left[ {{{\cal M}^{\left( {{k_s}} \right)}}} \right] = E\left[ {{\cal I}\left( {{{\cal F}_ \star }(\lambda ,t){e^{ - {\tau _{{\rm{ISM}}}}(\lambda ,t) - {\tau _{{\rm{TA}}}}(\lambda ,t)}} + {{\cal F}_{{\rm{TE}}}}(\lambda ,t)} \right)} \right].$](/articles/aa/full_html/2024/03/aa48107-23/aa48107-23-eq18.png) (15)
(15)
Subtracting the cumulative model from the observations gives the matrix 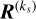 with expected value
with expected value
![$\matrix{ {E\left[ {{{\bf{R}}^{\left( {{k_s}} \right)}}} \right] = E\left[ {{\bf{F}} - {{\cal M}^{\left( {{k_s}} \right)}}} \right] = } \hfill \cr {E[{\cal I}\left( {{{\cal F}_ \star }(\lambda ,t){e^{ - {\tau _{{\rm{ISM}}}}(\lambda ,t) - {\tau _{{\rm{TA}}}}(\lambda ,t)}}\left( {{e^{ - {\tau _{\rm{P}}}(\lambda ,t)}} - 1} \right)} \right].} \hfill \cr } $](/articles/aa/full_html/2024/03/aa48107-23/aa48107-23-eq20.png) (16)
(16)
If Jin denotes the set of in-transit indices,
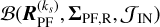 (17)
(17)
is the average in-transit residual spectrum in the PF, which is an estimator of the observable transmission spectrum averaged over the in-transit period. It is, however, not generally an unbiased estimator of ft(λ, t). Only if the factor 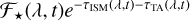 is unity, implying a flat stellar spectrum and a continuum normalization, the estimator is unbiased. The basic problem here is that the basic SYSREM operation is a subtraction, while the planetary atmospheric absorption component is a multiplicative factor acting upon the underlying continuum.
is unity, implying a flat stellar spectrum and a continuum normalization, the estimator is unbiased. The basic problem here is that the basic SYSREM operation is a subtraction, while the planetary atmospheric absorption component is a multiplicative factor acting upon the underlying continuum.
Assuming that no telluric emission is present (ℱTE(λ, t)) = 0), a more general, ideally unbiased estimator can be constructed if we divide by the cumulative model
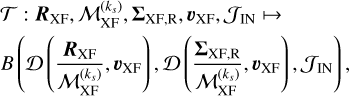 (18)
(18)
where the matrix division is to be understood element-wise and uXF denotes the velocities required to transform the matrices into the planetary frame. In words, evaluating the estimator T requires that we (i) apply SYSREM for ks iterations, (ii) divide the input matrices element-wise by the cumulative model, (iii) transform the matrices into the planetary frame, and (iv) compute the average residual spectrum including the desired set of spectra. Ideally, the expected value of the estimate, τj, for the jth spectral bin is given by
![$E\left[ {{\tau _j}} \right] = {1 \over {\Delta {\lambda _j}}}\mathop \smallint \limits_{{\lambda _j}}^{{\lambda _j} + \Delta {\lambda _i}} \left( {{e^{ - {\tau _p}(\lambda )}} - 1} \right)*(\lambda ){\rm{d}}\lambda ,$](/articles/aa/full_html/2024/03/aa48107-23/aa48107-23-eq24.png) (19)
(19)
making T a good estimator of the observable transmission spectrum. This implicitly assumes that convolution is distributive over multiplication so that we may write
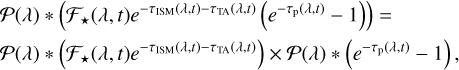 (20)
(20)
which is not the case, but a reasonable approximation in our problem (see Appendix B). The methodology represented by Eq. (18) is essentially that used by Gibson et al. (2020), who correctly asserted that it “preserves the relative depths of the planet’s transmission spectrum” without giving, however, a more detailed explanation of this statement. The technique has since been regularly applied in the literature (e.g., Merritt et al. 2020; Yan et al. 2020; Cont et al. 2022; Gibson et al. 2022).
3.1.4 Signal protection via error adjustment
The assertion of Eq. (19) depends on more idealizations than the distributivity of convolution. In particular, the SYSREM model may also be expected to pick up on the fast shifting planetary signal although not as efficiently as on more stationary components (e.g., Brogi & Line 2019; Gibson et al. 2022). A simulation with a simplified though realistic setting readily demonstrates how the SYSREM model starts to reproduce the shifting absorption signal as the number of iterations is increased. For the simulation, we adopt the temporal and spectral sampling of the Hα line region obtained during our night 1 CARMENES observations of WASP–12. We then simulate synthetic spectra by using a mock stellar Hα line, modeled as a Gaussian centered at 6565.058 Å with a full width at half maximum (FWHM) of 2 Å and a depth of 0.9, and subsequently inject a planetary absorption signal at the nominal radial velocity of the planetary orbital motion. The latter signal is modeled by a Gaussian with a constant equivalent width (EW) of 20 mÅ during the transit and a FWHM of 0.15 Å. We include in our simulation the shifts caused by the stellar orbital motion and the barycentric motion of WASP–12 in the OF and add Gaussian noise to simulate a S/N of 100 per spectral bin. The thus obtained mock spectral time series are represented by the matrices FM,OF and ΣMOF, which we use as the input for the SYSREM algorithm. After applying SYSREM for k times, we obtain the average in-transit transmission spectrum using Eq. (18) and determine the wavelength, width, and depth of the resulting signal by fitting a Gaussian. Additionally, a free continuum offset is included in the fit, which is treated as a nuisance. By repeating this experiment 1000 times, we find the expected values and standard deviations for the parameters, which we list in Table 2. The upper section of Table 2 clearly shows that the EW of the remaining signal in the reconstructed transmission spectrum decreases as the number of SYSREM iterations increases. It should also be noted, however, that the width and location of the signal, as obtained by the Gaussian fit, remain intact.
If the planetary orbital velocity is known with sufficient accuracy, also the likely wavelength of a potential planetary atmospheric absorption signal can be derived. In this case, the signal can be “protected from the model” by modifying the uncertainties used by SYSREM in signal protection (SP) regions. To prevent the SYSREM model from picking up on the signal, we strongly increase the uncertainties of the spectral bins in a region centered on the nominal location of the planetary signal for all in-transit spectra, making them infinite for practical purposes. We here use a region with a total width of ±6 resolution elements. The relevant section of the resulting modified uncertainty matrix, ΣM,OF,SP, is shown in Fig. 3, where we used an arbitrary, large value of 103 (i.e., a S/N of 10−3 per spectral bin) for the uncertainty in the SP regions. We emphasize, however, that to evaluate 𝒯 (Eq. (18)) the original uncertainties should be used irrespectively. Increased uncertainties in Eq. (18) may be used to mask specific spectral regions, which is regularly done, but not our goal here. The effect of SP on our mock problem is demonstrated in the second half of Table 2, which shows that the characteristics of the input signal can be recovered for all tested numbers of SYSREM iterations.
The details of the optimal SP procedure depend on the observation. If, for example, a prolonged transit is expected, it may be useful to also include out-of-transit spectra in the SP. As a note of caution, we emphasize that neither the target signal nor any other nuisance signal such as telluric lines or variations caused by stellar activity are included in the model in spectral sections covered by SP regions. If the SP regions are arranged such that specific wavelength intervals are always excluded from the modeling, the model remains unconstrained for these wavelength regions. In our mock setting (Fig. 3), the same spectral range is covered by at most three SP regions in consecutive observations. This form of SP is, therefore, suitable for fast moving, narrow signals, but not for the analysis of chemical species, such as many molecules, exhibiting a dense population of features.
Parameters of the planetary signal.
3.1.5 Overfitting
The SYSREM model has M + N free parameters per iteration (Sect. 3.1.2). After k SYSREM iterations, a total of k × (M + N) best-fit parameter values have been estimated. Fitting a model with a large number of parameters can lead to overfitting, which means that the model starts to reproduce not only the signal but also the random noise structure of the data. As a demonstration of the effect, we generated 30 mock observations à 200 data points, all independent realizations of a standard normal distribution with zero mean, and applied SYSREM to these data, which of course contain no signal.
In Fig. 4, we show the standard deviation of the residuals as a function of the number, k,of SYSREM iterations
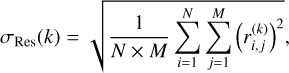 (21)
(21)
where 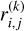 denotes the residual after k iterations. The initial model, prior to the first iteration, is taken to be zero in all points, which is correct by construction and any subsequent iteration overfits the data more severely. As the number of iterations increases, the standard deviation of the residuals decreases. Simultaneously, the standard deviation of the model rises, which incorporates the noise (Fig. 4). Assuming that any of k iterations removes M + N degrees of freedom from the sum of squares of the residuals, as is usual in linear regression problems (e.g., Darlington & Hayes 2016), a model for the evolution of the standard deviation may be written as
denotes the residual after k iterations. The initial model, prior to the first iteration, is taken to be zero in all points, which is correct by construction and any subsequent iteration overfits the data more severely. As the number of iterations increases, the standard deviation of the residuals decreases. Simultaneously, the standard deviation of the model rises, which incorporates the noise (Fig. 4). Assuming that any of k iterations removes M + N degrees of freedom from the sum of squares of the residuals, as is usual in linear regression problems (e.g., Darlington & Hayes 2016), a model for the evolution of the standard deviation may be written as
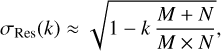 (22)
(22)
which is a useful expression only as long as the argument of the square root remains positive. As shown in Fig. 4, this model approximately describes the empirical result obtained for the standard deviation though the latter drop faster, which would yield a reduced χ2 value smaller than one, again consistent with overfitting.
Over a large range of SYSREM iterations, the evolution in the standard deviation of residuals is approximately linear. By carrying out sufficiently many of them, the residuals can be diminished to essentially any level. While overfitting may not be an actual problem in many applications, it is a problem if the magnitude of the residuals is critical for the result as, for instance, when the residuals are used to estimate upper limits.
 |
Fig. 3 Section of mock uncertainty matrix, Σm,o.f,sp, showing the effect of SP. Dark regions indicate increased uncertainties. |
 |
Fig. 4 Standard deviation of residuals as a function of the number of SYSREM iteration in the application to white noise (solid blue), the approximation based on the degrees of freedom (green dotted), and the standard deviation of the cumulative model (dotted red). |
 |
Fig. 5 Transmission spectra of the Na I D2 (top), Hα (middle), and He I λ 10833 Å triplet lines (bottom) obtained using SYSREM (solid black) and a conventional approach (dashed red, Sect. 3.2.3). The night 2 spectra are shifted by 0.05. The dotted vertical line indicates the nominal wavelength of the line (the center of the stronger doublet in the case of the He I λ 10833 Å triplet). |
3.2 Transmission spectroscopy of WASP–12
In the following, we apply the technique described in Sect. 3.1 to our CARMENES data of WASP012. In particular, we study the Na I D1,2, Hα, Ca IRT, and He I λ 10833 Å lines.
To obtain the transmission spectra in the PF, we evaluate the estimator 𝒯 (Eq. (18)), after 1,2,3,5 and 10 SYSREM iterations, using the OF for the SYSREM input matrices. As in-transit spectra, we adopt the observations with the running numbers 6–14 for night 1 and 5–13 for night 2 (see Appendix A). As examples, we show the thus obtained estimates of the transmission spectra for the Na I D2, Hα, and the He I λ 10833 Å triplet lines in Fig. 5 along with transmission spectra obtained using a more conventional methodology (Sect. 3.2.3). Based on the transmission spectra, we calculate the EW of the signal in regions with a width of one, two, and eight times the expected FWHM of a narrow absorption signal (see Sect. 2.3) both with and without applying SP.
To obtain the standard deviation of the EW estimate under the hypothesis that no planetary absorption signal exists, we carry out a bootstrap analysis. To that end, we shuffle the residual spectra obtained after the application of SYSREM in the OF by randomly (and with replacement) drawing rows from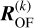 to destroy the temporal order of the series. We then proceed to transform into the PF, obtain the averaged in-transit spectrum, and calculate the EW. The distribution of the EW is found by repetition of these steps and can be used to estimate the significance of the actually found value or upper limits in the case of a non-detection.
to destroy the temporal order of the series. We then proceed to transform into the PF, obtain the averaged in-transit spectrum, and calculate the EW. The distribution of the EW is found by repetition of these steps and can be used to estimate the significance of the actually found value or upper limits in the case of a non-detection.
EW of Hα as a function of SYSREM iterations and absorption band widths.
3.2.1 Hα line
We first turn to the Hα line. In Table 3, we report the derived 95% confidence level upper limits for the line as a function of the number of SYSREM iterations and the width of the respective interval, centered on the nominal wavelength of the Hα line. Signal protection was applied. The SP regions were centered on the changing nominal orbital velocity of the Hα line, covering a range of ±15 km s−1, which roughly corresponds to the orbital RV shift per observation. This range covers three times the FWHM of a phase-smeared, narrow planetary signal. Switching off SP only marginally affects the numbers. The upper limit and standard deviation of the transmission spectrum decreases as the number of SYSREM iterations increases, which we attribute to overfitting (Sect. 3.1.5). To estimate the influence on the upper limit, we take advantage of the approximately linear evolution of the noise standard deviation observed in Sect. 3.1.5 by fitting the evolution of upper limits and standard deviations as function of SYSREM iteration for all considered band widths with a linear model. We then evaluate this model at the hypothetical point of zero iterations. The result is given in the bottom row of Table 3, where 0* indicates the reconstruction, and we consider this the best estimate of the upper limit. The reconstructed values are similar to those obtained after the first iteration, indicating that the outcome is not strongly affected by one iteration and that result may be used as an appropriate estimate for the upper limit and standard deviation, if a single iteration is suitable to appropriately model the observation in the first place (see Sect. 3.2.2 for a counterexample).
 |
Fig. 6 Average spectrum of WASP–12 during night 1 and 2 in the SF before correction for telluric absorption lines. Dotted vertical lines indicate the nominal wavelengths of the lines of the He I λ10833 Å triplet. Marks at the bottom indicate the nominal wavelengths of the four OH emission lines and the strongest water line during night 1. |
3.2.2 He I λ 10833 Å line
The He I λ 10833 Å lines are strongly affected by variable telluric emission lines (e.g., Nortmann et al. 2018; Czesla et al. 2022). This is also clearly visible in Fig. 6, where we show the night-averaged spectra for nights 1 and 2 around the He I λ10833Å lines in the SF. The spectra show strong OH doublets close to the He I λ 10833 Å triplet (Czesla et al. 2022), which would reach peak heights of about three and five in units of normalized flux for nights 1 and 2. Additionally, a prominent water absorption line is present. All telluric lines shift in the figure owing to the choice of reference system. Curiously, the stronger blended doublet of the He I λ10833 Å triplet appears to be deeper in night 1, which is discussed further in Sect. 3.3.2.
In Fig. 7, we show the transmission spectrum in the PF as obtained after one, three, and five SYSREM iterations both with and without applying SP. After one iteration, the impact of the OH emission lines is clearly seen, as they shift through the spectrum in the PF. After three and five iterations, the relics are removed in the night 1 transmission spectra. For the night 2 data, we find a marked difference between the transmission spectra obtained with and without SP. In particular, the former show strong relics (in apparent absorption) of the OH lines within a range compatible with the width of the adopted SP region, while the latter do not. This is clearly a consequence of the SP not selectively shielding the planetary signal but also the underlying OH lines, which are not correctly interpolated by the SYSREM model.
In Table 4, we show the bootstrap-derived upper limits for possible absorption in the He I λ 10833 Å lines, obtained without applying SP. After one and possibly also after two iterations, the values strongly decrease indicating that the overfitting regime had not yet been reached and real spectral structure such as the OH lines were still incorporated into the model. Therefore, we adopted only the values obtained after three or more iterations in our linear reconstruction (Sect. 3.2).
3.2.3 Comparison with conventional approach
The conventional approach to obtain planetary transmission spectra of atomic lines does not involve SYSREM, but relies on a comparison of spectra taken during the event with those before and after (e.g., Wyttenbach et al. 2015). Typically, a reference out-of-transit spectrum, ƒOOT, is obtained by averaging spectra taken before and after the transit, which do supposedly not contain the planetary signal. Residual spectra are then obtained by dividing the observed spectra by ƒOOT in the SF or BF. These residual spectra are subsequently shifted into the PF. Averaging them over some time interval of interest such as the transit yields the associated transmission spectrum. Regions strongly contaminated by stellar, telluric, or instrumental signals can be masked in the process, which of course leads to a loss of the masked signal.
To compare our results, we also show transmission spectra obtained by this conventional approach in Fig. 5. In the case of the He I λ 10833 Å lines, masking regions with a total width of four times the instrumental FWHM were placed on the four offending OH lines at vacuum rest wavelengths of 10 832.412 Å, 10 832.103 Å, 10 834.338 Å, and 10 834.241 Å (Oliva et al. 2015; Czesla et al. 2022), with the final mask being the union of the individual ones.
The resulting transmission spectra are very similar. In most instances, structure on the scale of the instrumental resolution is reproduced. This indicates that the conventional reference spectrum and the model constructed by SYSREM bear strong similarity. For the Na I D2 line (top panel in Fig. 5), we did not mask the telluric emission. The fast RV change of the planetary signal obviously helps to smear this out in the conventional analysis. For the Hα line transmission spectrum, some difference on a larger scale is visible particularly for the night 1 transmission spectra. We speculate that this is caused by variation in the broad core region of the Hα line during the transit, which is not accounted for in the conventional approach, but incorporated into the SYSREM model. Also the transmission spectra of the He I λ10833Å lines show rather insignificant differences given the noise. This clearly shows that the modeling results obtained by SYSREM, here after three iterations, are at least on a par with that produced by complete masking of the region.
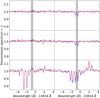 |
Fig. 7 Transmission spectra after one (bottom row), three (middle row), and five (top row) SYSREM iterations for night 1 (left column) and night 2 (right column) with SP (solid blue) and without (dashed red). The gray shade indicates the width of the SP region. |
 |
Fig. 8 Light curves of the Hα and Ca IIIRT lines in the stellar frame. Top: Hα light curves (1.5 Å passband) normalized by the mean of the night 1 light curve. Bottom: as top but for 0.5 Å passband centered on bluest component of the Ca II IRT. |
3.3 Hα, Ca II IRT, and He I λ 10833Å line variation in the stellar frame
Our night 1 and 2 observing runs both last for approximately six hours, which are separated by 335 days. Therefore, stellar spectral changes on the hour and year timescale can be examined. Variability in the stellar spectrum of WASP–12 may potentially be caused by magnetic activity or changes in absorption by circumstellar material such as a giant atmosphere or toruslike structure (Fossati et al. 2013; Haswell et al. 2012; Debrecht et al. 2018).The Hα and He I λ10833 Å triplet lines are potentially sensitive to both of these effects.
3.3.1 The Hα and Ca II IRT lines
In Fig. 8, we show the Hα and Ca II IRT line light curves during the two observing nights. For the Hα line, the light curves were obtained by integrating the flux density in a 1.5 Å wide band centered on the nominal wavelength of the Hα line in the SF. The light curve was normalized by the mean of integrals of the flux density in two reference bands (6550–6555 Å and 6578–6583 Å), and, finally, the night 1 and 2 light curves were divided by the mean of the night 1 light curve. For the Ca II IRT line, a 0.5 Å wide band was adopted. Uncertainties were estimated from the data using the βσ estimator (Czesla et al. 2018). No clear flaring can be discerned in the light curves. During night 1, the Hα light curve shows more short-term variation primarily before the egress and conspicuous drops close to the in-and egress phases, which are, however, not reproduced in night 2. This shape is independent of whether the telluric correction is used. As also the night 1 S/N is lowest before egress (Fig. 1), we consider it unlikely that the variation is astrophysical in origin. The night 2 light curve shows a systematic rise, indicative of a continuous fill-in of the Hα line center, which is not observed during night 1. We approximated the Hα light curves by a linear model and used a bootstrap analysis to show that the null hypothesis of a constant light curve can confidently be rejected (p-value 5 × 10−5) for the night 2 light curve, while the night 1 light curve is consistent with being constant. If anything, the corresponding Ca II IRT light curve shows a decline, which is, however, not highly significant (p-value 4.6%).
To get a better view of the actual spectral changes, we now compare the spectra of night 1 and 2 directly. In night 1, we obtained one more spectrum and the observing run commenced at slightly earlier orbital phase (e.g., Fig. 1). To compare the spectral evolution between the two nights at similar orbital phases, we, therefore, discard the first spectrum of night 1 and compare the remaining spectra. The maximum thus obtained orbital phase offset between the night 1 and 2 observations is 5.7 × 10−3 or 9 min. Dividing the night 2 by the night 1 spectra, we obtain the ratios shown in Fig. 9. The most pronounced differences can be distinguished in the vicinity of the core of the Hα line in the SF after the nominal fourth contact, which provides a useful but not necessarily physically meaningful temporal subdivision of the time series in this context. The ratios indicate a fill-in of the Hα line core in night 2 compared to night 1, consistent with the light curve (Fig. 8). In Fig. 10, we show the mean post-transit spectral ratio, which clearly displays the night 2 fill-in. A Gaussian fit of the feature yields an EW of 37 ± 7 mÅ, a FWHM of 0.45 ± 0.13 Å or 21 ± 6 km s−1, and a RV shift of −4.4 ± 1.5 km s−1.
A possible explanation for the differences in the core of the Hα line may arise from a change in the level of stellar magnetic activity between night 1 and night 2 as well as during the night 2 observing run itself. Examples of Hα line variability tantamount to our observation have been reported for M dwarfs, which show comparable and larger long-term variations in the Hα EW (Fuhrmeister et al. 2023). Rotational modulation in the Hα line with an EW amplitude of about ±20 mÅ was also observed in the active K-dwarf HD 189733 (Kohl et al. 2018) and the fast-rotating, active G2 dwarf V 889 Her shows an amplitude of about ±50 mÅ (Frasca et al. 2010). Yet, rotational modulation appears to be an unlikely cause for the observed Hα line variations as WASP–12 shows almost no spectroscopic rotational broadening, which is required to produce rotational modulation irrespective of projection effects. Also the Ca II IRT line provides no evidence for a change in activity.
A second conceivable explanation may be Hα line contamination from the M-dwarf binary companion, however, we argue that this is unlikely. Firstly, the M dwarf binary is significantly fainter than the primary. Bechter et al. (2014) derived a spectral type of M3V for them, but the Gaia (Gaia Collaboration 2023) upward revision of the distance estimate (Table 1) suggests a slightly earlier spectral type of M1V and an effective temperature of about 3600 K (Kraus & Hillenbrand 2007). We consulted synthetic PHOENIX spectra calculated by Husser et al. (2013) to compare the flux densities of the primary and the secondary. In the core of the Hα line, we find a ratio of 33, and a ratio of 90 in the close-by pseudo-continuum. The observed contrast is further enhanced by their separation of 1″ which puts the binary beyond the acceptance angle of the 1.5″ diameter fiber feeding CARMENES (Quirrenbach et al. 2018). Although the seeing disks may show some overlap with the fiber pointed at the primary, M1V type dwarfs show essentially no photospheric Hα line. As activity and contamination appear unlikely, the variation probably originates in the WASP–12 system itself.
A third explanation for the observed differences may be artifacts from the data taking or reduction. As WASP–12 is a relatively faint target, the S/N of individual spectra remains moderate (Fig. 1). During night 1, the S/N is systemically lower in the first half of the night. In such cases, and in particular in the deep trough of the Hα line, the relative contribution of the background increases, so that small errors in its estimation may produce spurious changes in the line depth. However, neither the light curve of the Hα nor the Ca II IRT lines (Fig. 8) show structure reminiscent of the night 1 step in S/N. Moreover, the observed systematic evolution in the line profile presumably took place during night 2 when the S/N and, thus, signal level were more stable. While this does not rule out such a scenario, it does not appear a likely explanation. Finally, the variation may be caused by variable atmospheric absorption further discussed in Sect. 4.3.
 |
Fig. 9 Ratio of night 2 and 1 spectra in the SF as a function of time from transit center. Horizontal dotted lines indicate the first to fourth contact, the dash-dotted vertical line denotes the nominal position of the Hα line, and the dashed diagonal line shows the orbital velocity track of the planet. |
 |
Fig. 10 Average post-transit ratio of night 2 and night 1 spectra around the Hα line (blue) along with best-fit Gaussian model (red solid). |
 |
Fig. 11 Average Na I D2 lines of WASP–12 in nights 1 and 2. The average wavelengths of the telluric line are indicated by vertical lines. |
3.3.2 The He I λ10833 Å lines
For the He I λ10833 Å triplet lines, changes in the SF are more challenging to quantify because of the strong telluric contamination as demonstrated by the night-averaged He I λ10833 Å spectra of WASP–12 shown in Fig. 6. Nonetheless, the same figures readily demonstrates that also the He I λ10833 Å line core in the night 2 spectrum appears to show a fill-in with respect to the night 1 spectrum. We argue that this is likely not spurious, because in night 1, the strong OH line doublet located redward of the He I λ10833 Å lines is much closer to the actual He I λ10833 Å line. If anything, it tends to add contaminating flux in the He I λ10833 Å core and not subtract any. Likewise, any potential water-line contamination would tend to be deeper in night 2 (Fig. 6) besides from taken care of by the telluric correction. The difference amounts to about 10 mÅ at slightly above instrumental width. Although we consider an actual change in the He I λ10833 Å line core likely, which shows the same trend as that observed in the Hα line core, the numbers are unreliable owing to the contamination.
3.4 Interstellar absorption in the Na I D lines
The Na I D lines of WASP–12 are affected by interstellar and possibly circumstellar absorption (Fossati et al. 2013). Additionally, our CARMENES observations show telluric emission. In Fig. 11 the average spectra of the Na I D2 line of WASP012 during night 1 and 2 are shown. The impact of telluric emission is particularly pronounced during night 2, where it occurs close to the line core. Clearly, the lower envelope of the two average spectra shown in Fig. 11, which we call the minimum master spectrum, ƒmima(λ), represents a better approximation of the true stellar line profile than any of the individual spectra.
By investigating the Ca II H and K as well as the Na I D lines of similarly distant early-type stars at lines of sight close to WASP–12, Fossati et al. (2013) identified at least two discernible absorption components attributable to interstellar material, which are mainly blue shifted with regard to the spectrum of WASP–12. To verify and examine the presence of interstellar absorption components in our spectra of WASP–12, we used the minimum master spectrum of the Na I D lines obtained above and assumed that the stellar Na I D lines are intrinsically symmetric. This premise is backed by synthetic PHOENIX spectra (Husser et al. 2013), but factors such as stellar activity are not accounted for in these models. We reflected the minimum master spectrum at the nominal wavelengths of the Na I D lines (Fig. 12, upper panel) and used the reflection as an estimate of the unabsorbed stellar spectrum. The lower panel of Fig. 12 shows the ratio of the original and reflected minimum master spectrum, which clearly shows the effect of interstellar absorption. This technique remains insensitive to absorption in the line center and symmetric absorption in both wings of the Na I D lines.
We modeled the absorption in the blue flank between velocity offsets of −2.5 km s−1 and −35 km s−1 (indicated by shades in the figure) using a two-component model for the wavelength-dependent optical depth, τ(λ), of the absorbers. The latter are parameterized as (e.g., Axner et al. 2004)
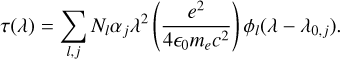 (23)
(23)
Here, the index l ∈ {r, b} denotes the two Gaussian components, which we dub blue (b) and red (r) to be consistent with Fossati et al. (2013), and the index j ∈ 1,2 the individual sodium D1 and D2 lines with reference wavelengths λo,j, Nj is the column density of absorbing particles, αj is the oscillator strength of the respective line, e is the electric charge, ϵ0 is the vacuum permittivity, me denotes the electron mass, and c is the speed of light. The profile functions φl are assumed to be Gaussian. The free parameters of our model are the column densities, Nl, the widths of the Gaussian profile functions, and their offset from the line centers. The fit is carried out for both lines simultaneously.
In Table 5, we give our best-fit parameters with error derived using the jackknife method (e.g., Efron & Stein 1981) along with the values reported by Fossati et al. (2013) for the line of sight toward HD 257926, a star at a sky-projected separation angle of about 16′ and, therefore, with a similar line of sight. The EW and column density derived for the blue absorption component are consistent within the error margin. Our best-fit values for the FWHM and RV are somewhat smaller, which may be attributed to a true difference in absorption between the lines of sights of WASP–12 and HD 257926, or plausibly, our continuum estimation method of reflecting the spectrum. The latter can also explain the differences in the value determined for the red component, which we find to be considerably weaker than reported by Fossati et al. (2013). This component is located closer to the Na I D line center and, thus, the reflection axis of the spectrum, which explains our likely spurious finding of a weaker component.
 |
Fig. 12 Properties of the Na I D lines of WASP–12. Top panel: Na I D2 line of WASP–12 (solid blue) along with spectrum reflected at nominal wavelength of the line (red dashed). Bottom panel: ratio between original and reflected spectrum for Na I D1 and Na I D2 lines (solid magenta and black) along with best-fit model (dashed magenta and black). The green shade indicates the considered fit range. |
Best-fit parameters of Na I D ISM absorption components in WASP–12 and values derived by Fossati et al. (2013).
4 Discussion
4.1 SYSREM for individual line transmission spectroscopy
In Sect. 3.2.3, we already showed that comparable results can be obtained with SYSREM, used as described in Sect. 3.1, and a more conventional approach to transmission spectroscopy at least in the case of our data. In the following, we compare the approaches on a more conceptional level.
In both approaches, the handling of the residual spectra is identical once obtained, but the construction of the reference differs. In Sect. 3.1, the SYSREM model assumes a role comparable to the out-of-transit reference spectrum by which the spectra are divided to produce residuals in the conventional approach. If used as described in Sect. 3.1, at least two differences between these models stand out: (i) the SYSREM algorithm can incorporate the information of all spectra into the model, as opposed to being limited to out-of-transit spectra and (ii) for each spectrum an individual reference spectrum is constructed by SYSREM.
One advantage of using all spectra in the modeling is that the model has better leverage on approximately stationary though time-dependent effects such as telluric absorption and emission lines as well as stellar activity. A case in point is our analysis of the transmission signal of the He I λ10833 Å signal (Sect. 3.2.2), which demonstrates that the strong OH lines are handled satisfactorily after a few SYSREM iterations. Likewise, we found that the correction of telluric absorption lines was not critical for our results. However, the model also gains leverage in the actual signal of interest, which, at least for isolated spectral lines, may be countered by shielding the signal using signal protection (Sect. 3.1.4). The application of SYSREM is advantageous in situations where time-variable effects such as telluric emission lines are strong, which complicates the construction of a suitable reference spectrum. Notably, useful results could be obtained in our case without carrying out a telluric correction or the masking of other contaminants.
4.2 Comparison to previous tentative detections or non-detections
Kreidberg & Oklopčić (2018) report a non-detection of He I λ10833 Å absorption in WASP–12. In particular, they find the transit depth to be (insignificantly) elevated by (49 ± 143) × 10−6, in a 70 Å wide band centered on the nominal wavelength of the He I λ10833 Å triplet. This corresponds to an EW of 4 ± 10 mÅ, which is consistent with our more stringent upper
Burton et al. (2015) find a tentative detection of absorption in the Na I D lines at a level of 0.15 ± 0.03% across2 Å wide intervals, which corresponds to an EW of 3 ± 0.6 mÅ per line, assuming that both lines contribute equally. Given that 2 Å correspond to about 10 times the FWHM of a narrow signal in the Na I D lines at our effective spectral resolution, the result is consistent with our upper limit (Table 6) insofar as we cannot rule out a broad signal with this EW. However, if the signal EW is more concentrated on the line core region, we can give more stringent upper limits.
4.3 Absorption by a heterogeneous torus
In their analysis of the Na I D and Hα lines of WASP–12 b, Jensen et al. (2018) find excess absorption at levels of 52.6 mÅ and 64.9 mÅ, respectively, measured across 2 Å wide regions. The signals reach depths of about 6% in the Hα and 3% in the Na I D lines and both signals are blueshifted by about −9 km s−1 in the SF, though the authors caution that their methodology may not be well suited to provide accurate atmospheric shifts. The width of the signal is consistent with their spectral resolution of 15 000, that is, around 20 km s−1. The absorption signals studied by Jensen et al. (2018) appear to be modulated on the timescale of the planetary orbital period. According to these authors, this can be understood in the light of evidence for a possibly asymmetric circumstellar torus or disk-like structure in the WASP–12 system, ultimately formed by material originating from the planet (e.g., Lai et al. 2010; Li et al. 2010; Haswell et al. 2012).
In our analysis, we found no evidence for Hα absorbing material with a steady-state velocity structure, moving along with the planetary body in the PF (Table 3). If hypothetical excess absorption were caused by an extended structure producing a very prolonged transit, as suggested by Jensen et al. (2018) for WASP–12 and recently observed in the case of HAT–P–32b (Zhang et al. 2023), our temporal baseline may not be long enough to cover the event in its entirety. However, while this is also the case for the CARMENES data of HAT–P–32 b analyzed by Czesla et al. (2022), significant variation in the Hα and He I λ10833 Å lines is detected nonetheless. Also the UV transits studied by Fossati et al. (2010a), Haswell et al. (2012), Nichols et al. (2015), despite showing evidence for prolonged and potentially variable UV transits, are consistent with the bulk of absorption occurring during the optical transit. A signal may of course still be present in WASP–12, but too weak to be detected by us.
The temporal evolution of the Hα line in the SF is different in night 1 and night 2. In particular, a slightly blue-shifted fill-in with an EW of about 37 mÅ develops toward the end of our night 2 run. The signal width of about 21 km s−1 is clearly above our instrumental resolution. The width, shift, and strength of this signal are compatible with that observed by Jensen et al. (2018), accounting for the differences in spectral resolution. However, our signal was extracted by comparing spectra obtained during the same planetary orbital phases. Assuming optically thin conditions, the observed variation would require a column density difference on the order of 1011 cm−2 between the post-transit phases of night 2 and night 1 and, likewise, during the approximately 1.5 h post-transit phase of night 2 (cf. Eq. (23)).
In Fig. 13, we show a hypothetical Hα absorption line profile of a homogeneous torus of material at the planetary distance, covering the entire star. Assuming that the material moves with Keplerian speeds strongly broadens the line. Due to the circular shape of the star, more material absorbs close to the center of the stellar disk where its vertical is longer and the material has zero line-of-sight velocity. This gives the profile its almost semicircular shape, typical of rotational line profiles. While details such as limb-darkening were not accounted for and the Hα line absorption profile was assumed to be narrow at the instrumental resolution, this hypothetical line profile is in any case much broader than the observed spectral change between night 1 and 2. Any heterogeneity in the torus, which would cause time-dependent absorption, would also be subject to Keplerian motion and, thus, likely produce significant Doppler shifts in the SF. At the planetary distance, the Keplerian RV of the material changes at a rate of about 15 m s−2 or 54 km s−1 h−1 during the transit. We do not see evidence for a significant change in the RV shift of the signal in the SF. Therefore, the signal can hardly be caused by a change in column density of torus material, moving on a Keplerian orbit at an orbital separation similar to that of the planetary body. If one attributes the observed −4.4 km s−1 blueshift of the signal to Keplerian orbital motion during ingress, an orbit with a radius of about 0.15 au is required. A change in column density of material farther out in the system, where Keplerian speeds are lower seems a possible explanation for the observation. Alternatively, different atmospheric geometries may produce narrower absorption profiles.
 |
Fig. 13 Hypothetical Hα absorption line profile caused by a homogeneous torus at the planetary orbital separation, covering the entire stellar disk. |
4.4 Interpretation of the He I λ10833 Å upper limit
With WASP–12 b filling 59% of its Roche lobe volume (Sect. 2.2), there remains little room for an upper atmosphere within it. This is thought to make Roche-lobe overflow the dominant mass-loss mechanism in WASP–12 b. In the Roche-lobe overflow scenario, energy deposited by optical and infrared light drives the denser, lower atmosphere across the Roche lobe boundary (e.g., Koskinen et al. 2022; Huang et al. 2023), and the atmospheric density and velocity at this surface determine the mass-loss rate (Koskinen et al. 2022). Assuming an isothermal atmosphere for WASP–12 b with the effective planetary temperature (Table 1), we solved the hypsometric equation (e.g., Koskinen et al. 2022) on the terminator. Assuming a pressure of one bar at the optical radius, we found that the atmosphere reaches the Roche lobe at the terminator at a pressure level of about 10−9 bar. Therefore, the incoming XUV radiation is mainly absorbed at or above the Roche lobe, where it continues to play a crucial role in the structure of the unbound gas outflow (e.g., Huang et al. 2023).
To interpret our upper limits on the He I λ10833 Å absorption, we employed the spherically symmetric hydrodynamic model presented by Lampón et al. (2020). The latter is a variation of the isothermal Parker wind approach (Parker 1958) with the speed of sound being held constant throughout the thermosphere. The two main steps in the modeling are the solution of the hydrodynamical equations and the computation of the population of the He (23S) excited state in non-local ther-modynamic equilibrium (NLTE), which causes the planetary He I λ10833 Å absorption. Its free parameters are the temperature, the hydrogen-to-helium number ratio, and the mass-loss rate; for details, we refer to Lampón et al. (2020). Although the actual mass-loss mechanism of WASP–12 b may be unrelated to the XUV irradiation, mass continuity combined with our ad hoc treatment of the mass-loss rate render the model applicable to simulate the atmosphere from the thermobase outward, where the He I λ10833 Å triplet is produced.
In Fig. 14, we show the Roche potential in the vicinity of WASP–12 b evaluated in the orbital plane along the line connecting the star and the planet as well as toward the side. The latter represents an outward radial direction from the planetary terminator. While the potential to the side only marginally differs from that of an isolated point mass, the stellar pull and tidal forces strongly affect it in the direction of the star. To approximate the effect of the modified potential on our modeling, and, in particular, the result of the lower potential barrier on the mass-loss rate at the substellar point, we set up a terminator and a substellar-point model, differing in the adopted value of the planetary mass and radius. Specifically, we used the nominal mass of 1.46 MJup (Table 1) to represent the conditions along the terminator and an effective substellar planetary mass, Mp.eff, of 0.66 MJup and a radius of 2.18 RJup to approximate the conditions at the substellar point. This effective mass is defined by the condition that the potential difference between the planetary surface and the Roche lobe at the substellar point (i.e., the specific energy required to remove material from the planet) matches that of the Roche potential. A comprehensive treatment of the atmosphere would require the inclusion of the Roche potential and Coriolis forces in three dimensions (see Appendix D). Yet, for instance, the study by MacLeod & Oklopčić (2022) showed that spherical planetary wind solutions can still provide good approximations of the He I λ10833 Å transmission spectrum at least in scenarios with comparably weaker Roche effects.
Here, we follow a similar approach to Koskinen et al. (2022) and Huang et al. (2023), who found that substellar-point models give an upper limit for the mass-loss rate in planets undergoing Roche lobe overflow. As the level of irradiation of WASP–12 b remains uncertain, we look at two illustrative cases in some more detail, which we call the high and the moderate irradiation scenario. These are characterized by XUV fluxes of 318 000 erg cm−2 s−1 at the planetary orbit, corresponding to the nominal upper limit of the stellar XUV flux, and a factor of 100 less in the moderate scenario. We assume a hydrogen-to-helium number ratio of 99/1, which is in line with the trend found in other systems (Lampón et al. 2021b, 2023). Finally, a narrow Doppler profile with a FWHM of 0.3 Å, located at the center of the stronger doublet, is adopted to synthesize the absorption signal. The bulk of such a signal is contained within twice the FWHM of the smearing-corrected instrumental resolution. Therefore, we adopt an upper limit of 4 mÅ for the He I λ10833Å signal (Table 4). In Fig. 15, we show the distribution of the obtained EWs from our terminator simulations as a function of temperature and mass-loss rate for the high irradiation scenario and indicate the combinations of mass-loss rate and temperature consistent with our measurements for both the terminator and substellar-point models. As we expect the true absorption to be better described by a weighted average of these models, the borders of these regions outline the extremes of the expectable mass-loss rate as a function of temperature. In both models, the peak of the metastable helium concentration is found within or close to the Roche lobe (Fig. 16), indicating a rather compact thermosphere, which may, therefore, plausibly still be adequately described by a one-dimensional model.Clearly, the admissible mass-loss rates for the substellar model are significantly higher than those for the terminator model.
To narrow down the likely location of WASP–12 b in the diagram of Fig. 15, plausible values for the thermospheric temperature and the mass-loss rate are needed. To that end, we put the planet into the context of the sample study by Lampón et al. (2023). In the high-flux scenario, the XUV irradiation level of WASP–12 b is situated between those of WASP–76 b and HAT–P–32b (Table 7), which puts WASP–12 b in the recombination-limited escape regime, characterized by a largely ionized thermosphere (Lampón et al. 2021a). For WASP076b and HAT–P–32 b temperatures of about 12 000 K and mass-loss rates in the range of 1012 gs−1 to 1013 gs−1 were found. At 12000 K, we find limits of 8 × 1011 gs−1 and 4 × 1012 gs−1 for the upper limit of the mass-loss rate. The conservative upper limit is, thus, given by the higher value, while lower values may be expected depending on the contribution of the terminator region to the atmospheric absorption. A key difference between WASP–12 b and both WASP–76 b and HAT–P–32 b lies in the higher gravitational potential of WASP–12 b, which may contribute to the conspicuous lack of a He I λ10833 Å signal in WASP–12 b.
In the moderate irradiation scenario, the irradiating XUV flux of WASP–12 b becomes comparable to that of HD 209458 b. For such moderately irradiated planets, thermospheric temperature correlates with gravitational potential (Salz et al. 2016a; Lampón et al. 2023). The latter is situated between those of HD 209458 b and HD 189733 b, which is, however, more strongly irradiated (Table 7). Using these as bounding cases yields a temperature estimate in the range of 7500–12 500 K. Adopting a plausible temperature estimate of 10 000 K, we find upper limits of 1012 g s−1 for the terminator model to be consistent with our non-detection of He I λ10833 Å absorption. In the substellar-point model, the lower gravitational potential well leads to a faster outflow of gas, which produces stronger adiabatic cooling. Under such conditions, we expect a lower value of around 7000 K for the maximum temperature, which yields a mass-loss rate of about 4 × 1012 g s−1.
In particular, in the case of the moderate irradiation scenario, the excited He I λ10833 Å atmosphere maybe be rather extended at the terminator so that geometrical effects caused by the partial overlap with the stellar disk and of course the limitations of a one-dimensional representation can become relevant. However, such a large extent may be unrealistic because the flow is confined by other factors. Using a two-dimensional model, Dwivedi et al. (2019) found that strong stellar winds induce a lateral ionopause boundary for which they estimated altitudes between two and four planetary radii at the terminator and no significant confinement at the substellar point. To evaluate the effect of such a confinement in our results, we took into account the ionopause by truncating the atmosphere as demonstrated by Lampón et al. (2023). We found that the mass-loss rates are similar or lower at any given temperature, so that our upper limits on the mass-loss rates remain valid even in a strong stellar wind environment.
While we cannot rule out either irradiation scenario, the combination of the derived upper limit on the He I λ10833 Å EW in transmission and our models for atmospheric absorption slightly favors the moderate irradiation scenario as outlined above, with mass-loss rates of ≲4 × 1012 g s−1 for the substellar-point model, which is consistent with the results of Dwivedi et al. (2019), who estimated a mass-loss rate of 1012 gs−1 based on Mg II absorption from WASP–12 b. We caution, however, that there are many assumptions in our analysis by necessity.
 |
Fig. 14 Roche potential around WASP–12 b evaluated in the orbital plane toward the star (blue) and toward the side (red) along with the potential of a point mass (black dashed). The substellar radius and the height of the Roche lobe at the substellar point are indicated. The acceleration caused by gravitational and centrifugal forces in the respective directions is given by the derivative of the potential. |
 |
Fig. 15 Modeled EW of the He I λ10833 Å signal as a function of temperature and mass-loss rate at the terminator for the high irradiation scenario. The admissible region is indicated by connected blue circles. Similarly, admissible regions are indicated for the moderate irradiation scenario (white, F/100) and the substellar-point model in Roche-lobe overflow (RLO, triangles). |
 |
Fig. 16 Density of excited helium as a function of distance for the high-irradiation scenario and various thermospheric temperatures for the terminator (solid) and substellar-point models (dashed); RP is taken to be 1.91 RJup for the plot. |
Gravitational potential in Jovian units, XUV irradiation at planetary separation (5–920 Å, see Sect. 2.4), and derived thermospheric temperature range for relevant systems from Lampón et al. (2023).
 |
Fig. 17 Absorption EW in the Na I D2 line as a function of the fractional atmospheric coverage fraction per scale height, ΔA, for a sample of planets along with WASP–12 b (data adopted from Wyttenbach et al. 2015; Seidel et al. 2019; Casasayas-Barris et al. 2019; Chen et al. 2020b,a; Cabot et al. 2020; Langeveld et al. 2022; Rahmati et al. 2022). |
4.5 The lack of Na I D absorption
The cores of the Na I D doublet lines belong to the most sensitive atomic tracers of the atmosphere (e.g., Brown 2001). In our analysis of WASP–12 b, we only find upper limits for their strength. As shown in Sect. 4.4, the gravitational potential of WASP–12 b at the terminator is almost that of a point mass. Using petitRadtrans (Mollière et al. 2019), we calculated synthetic transmission spectra for an isothermal hydrogen-helium plus sodium atmosphere with a mean molecular weight of 2.3 and sodium mass fractions of up to 10−3 (i.e., about 30 time the solar value). These simulations predict EWs of ≤1 mÅ for the cores of the Na I D lines in the transmission spectrum if the atmosphere is truncated at 10−9 bar, where it reaches the Roche lobe (Sect. 4.4). Extending it beyond that up to 10−12 bar, the EWs become about 20% larger. Any of these values are consistent with our upper limit of about 2 mÅ (Table 6), together with the presumed presence of a cloud deck on WASP–12 b (Wakeford et al. 2017), which would tend to further decrease the absorption signal.
In Fig. 17, we put our upper limit into the context of previous detections. In particular, we show the EW of the core of the Na I D2 line as a function of the fractional atmospheric coverage fraction per scale height (Rahmati et al. 2022)
 (24)
(24)
where H is the atmospheric scale height, for which we obtained a value of 880 km at the terminator of WASP–12 b. The cited measurements suggest a trend, which is, however, not (yet) overly significant (Person’s correlation coefficient has a value of 0.82 with a p-value of 2.4%). While the Na I D absorption in WASP–12 b may still be small in the context of the existing sample, an unusually high value can be ruled out.
5 Conclusion
We analyzed two high-resolution spectral time series of WASP–12 b obtained with CARMENES about one year apart. Both series cover about six hours and are approximately centered on the optical transit. Our data contain the He I λ10833 Å triplet lines with high resolution for the first time and simultaneously provide continuous coverage of the Hα lines. The spectrum of WASP–12 shows strong interstellar features in the Na I D lines, the strengths of which we found to be consistent with previous measurements along a close-by line of sight.
The in-transit transmission spectrum of WASP–12 b was obtained with the help of the SYSREM algorithm and the technique of signal protection. We found SYSREM to be well suited to carry out atomic line transmission spectroscopy in planets showing sufficiently large orbital radial velocity variation. A comparison with a conventional approach showed comparable results. The obtained transmission spectrum is devoid of all tested atomic features in the PF to within our sensitivity limits. This result is consistent with the non-detections by Sing et al. (2013), but based on considerably higher spectral resolution, which specifically adds sensitivity to the line cores. The upper limit on the planetary Na I D features is consistent with predictions by isothermal atmospheric models and previous measurements in other similar systems. The cores of the He and the He I λ10833 Å lines of the system show variations between night 1 and 2 in the SF, primarily after the optical transit. The characteristics of this variation are difficult to explain by a heterogeneous torus of material at the planetary orbital separation or by stellar activity. We speculate that a change in column density of Hα absorbing material farther out in the system might cause the observed behavior. This does not exclude a large structure fed by planetary material similar to the one recently observed in the HAT–P–32 system (Zhang et al. 2023), but only that the observed changes between night 1 and 2 are unlikely to be caused by it.
Our analysis of XMM-Newton observations of WASP–12 yields a marginal detection of X-rays from the system, which we interpreted as an upper limit. Combining this upper limit with the absence of a He I λ10833 Å absorption signal and models of the upper planetary atmosphere slightly favors a moderate irradiation level for the planet, with a thermospheric temperature of 12000 K, and a conservative upper limit of ≲4 × 1012 g s−1 on the mass-loss rate, consistent with previous estimates based on Mg II absorption (Dwivedi et al. 2019). We caution, however, that this result relies on a number of assumptions. Overall, our results provide no evidence against the hypothesis that WASP–12 is, indeed, a very inactive, slowly rotating star. Although the state of WASP–12 b’s elusive atmosphere remains enigmatic, we put more stringent limits on it.
Acknowledgements
CARMENES is an instrument at the Centro Astronómico Hispano en Andalucía (CAHA) at Calar Alto (Almería, Spain), operated jointly by the Junta de Andalucía and the Instituto de Astrofísica de Andalucía (CSIC). The authors wish to express their sincere thanks to all members of the Calar Alto staff for their expert support of the instrument and telescope operation. CARMENES was funded by the Max-Planck-Gesellschaft (MPG), the Consejo Superior de Investigaciones Científicas (CSIC), the Ministerio de Economía y Competitividad (MINECO) and the European Regional Development Fund (ERDF) through projects FICTS-2011-02, ICTS-2017-07-CAHA-4, and CAHA16-CE-3978, and the members of the CARMENES Consortium (Max-Planck-Institut für Astronomie, Instituto de Astrofísica de Andalucía, Landessternwarte Königstuhl, Institut de Ciències de l’Espai, Institut für Astrophysik Göttingen, Universidad Complutense de Madrid, Thüringer Landessternwarte Tautenburg, Instituto de Astrofísica de Canarias, Hamburger Sternwarte, Centro de Astrobiología and Centro Astronómico Hispano-Alemán), with additional contributions by the MINECO, the Deutsche Forschungsge-meinschaft (DFG) through the Major Research Instrumentation Programme and Research Unit FOR2544 “Blue Planets around Red Stars”, the Klaus Tschira Stiftung, the states of Baden-Württemberg and Niedersachsen, and by the Junta de Andalucía. We acknowledge financial support from the Agencia Estatal de Investigación (AEI/10.13039/501100011033) of the Ministerio de Ciencia e Innovación and the ERDF “A way of making Europe” through projects PID2021-125627OB-C31, PID2019-110689RB-I00, PID2019-109522GB-C5[1:4], and the Centre of Excellence “Severo Ochoa” and “María de Maeztu” awards to the Instituto de Astrofísica de Canarias (CEX2019-000920-S), Instituto de Astrofísica de Andalucía (CEX2021-001131-S) and Institut de Ciències de l’Espai (CEX2020-001058-M). This work was also funded by the Generalitat de Catalunya/CERCA programme, the LMU Munich Astrophysics Fraunhofer and Schwarzschild Postdoctoral Fellowship, and the DFG through projects 390783311 (under Germany’s Excellence Strategy EXC 2094) and 314665159, and priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets” (CZ 222/5-1, CZ 222/3-1).
Observation log of night 1a.
Appendix A Observation log
Observation log for our CARMENES observations of WASP-12b. The numbers refer to the VIS channel spectra. The values for the corresponding NIR channel observations differ only slightly.
Appendix B Convolution and multiplication
Multiplication and convolution cannot generally be exchanged, but the error incurred by it may be acceptable nonetheless. Let us assume there are two functions F(λ) and g(λ) and a profile function 𝒫(λ). We know the results of 𝒫(λ) * (F(λ) g(λ)) and 𝒫(λ) * F(λ) and need to calculate 𝒫(λ) * g(λ). Potential other methods notwithstanding, this would be a simple matter if we could write 𝒫(λ) * (F(λ) g(λ)) = (𝒫(λ) * F(λ)) × (𝒫(λ) * g(λ)), that is, if convolution were (left) distributive over multiplication, which is, unfortunately, not the case. To estimate the magnitude of the deviation
 (B.1)
(B.1)
incurred by the assumption, we need to specify the functions.
To get a handle on our problem, we assume that all functions are Gaussian. With 𝒩(µ, σ) denoting the density of the normal distribution with mean µ and standard deviation σ, we specify
 (B.2)
(B.2)
Here, dF and dg parametrize the depths of the Gaussians. With this choice, an analytic though rather convoluted form for the expression in Eq. B.1 can be derived using, for instance, the computer algebra system maxima2. In our experiment, we adopt the specific values σ0 = 0.032 Å, dF = 0.9, σF = 0.85 Å, µF = 6564 Å, dg = 10−3, and σg = σ0. The standard deviation of the profile function, σ0, is compatible with the instrumental resolution around the Hα line, which is represented by the function F(λ), while g(λ) models a hypothetical planetary absorption signal, for which we assume a depth of 10−3. In Fig. B.1, we show the deviation caused by assuming distributivity of convolution over multiplication (Eq. B.1) for various placements of the absorption signal within the trough. In all tested cases, the difference is about two orders of magnitude smaller than the absorption signal, which we intend to recover. Therefore, at least in this case, we consider the approximation justifiable.
 |
Fig. B.1 Error as defined by Eq. B.1 incurred by assuming distributivity of convolution over multiplication. |
Appendix C Planetary equilibrium temperature
A formula for the planetary equilibrium temperature, Teq, valid for close-in planets, where the usual assumption of a small ratio between the stellar radius, R★, and the semi-major axis, a, is no longer accurate is given by
 (C.1)
(C.1)
where Teff is the stellar effective temperature and AB the planetary Bond albedo. As shown below, Eq. C.1 still requires a ⪢ RP. For R★ ≪a, Eq. C.1 readily reduces to the usual expression by a Taylor expansion of the square root
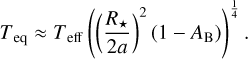 (C.2)
(C.2)
A derivation of Eq. C.1 can be formulated on the grounds of geometrical arguments. The planetary equilibrium temperature is defined by the condition that the rate of radiative energy absorbed by the (spherical) planet,  , from the star is balanced by the energy homogeneously re-radiated from its surface into space via thermal back-body emission,
, from the star is balanced by the energy homogeneously re-radiated from its surface into space via thermal back-body emission, 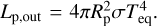 If the planet has non-zero bond albedo, only a fraction of the available incoming radiation, Lp,in, is absorbed so that
If the planet has non-zero bond albedo, only a fraction of the available incoming radiation, Lp,in, is absorbed so that 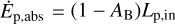 .
.
In the hypothetical case of a “star” covering the entire sky (Ω★ = 4π), radiative equilibrium demands
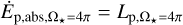 (C.3)
(C.3)
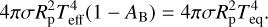 (C.4)
(C.4)
For a perfect black body (AB = 0), the effective and equilibrium temperatures are equal. If the solid angle subtended by the star is reduced, the amount of radiation absorbed by the spherical planet decreases in proportion so that
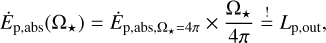 (C.6)
(C.6)
Now, the solid angle subtended by a spherical star with radius R★, viewed from a point at a distance a from its center, is that of a cone with half opening angle θ = arcsin (R★ a−1), which is given by
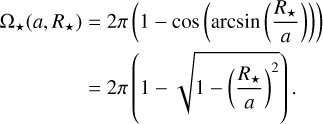 (C.8)
(C.8)
Substituting Eq. C.8 into Eq. C.7 yields Eq. C.1. In the latter substitution, we implicitly assumed that Eq. C.8 holds for every point on the planetary surface, which implies RP ≪a.
Appendix D The Roche potential
For the star placed at the origin of a right-handed coordinate system, corotating with the orbital motion of a planet located at (a, 0,0), the Roche potential, ϕr, is given by (e.g., Hilditch 2001)
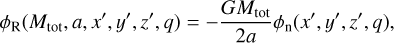 (D.1)
(D.1)
where the total mass, Mtot, is M★ + Mp, the mass ratio, q, is given by  , G is the gravitational constant, and the dimension-less coordinates x′, y′, and z′ are obtained through scaling by the orbital separation
, G is the gravitational constant, and the dimension-less coordinates x′, y′, and z′ are obtained through scaling by the orbital separation
 (D.2)
(D.2)
The dimensionless distances from the star and planet,  , are given by
, are given by
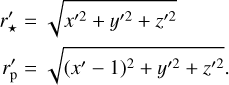 (D.3)
(D.3)
Finally, the dimensionless Roche potential ϕn has the form
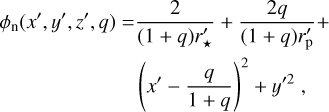 (D.4)
(D.4)
which completes the specification of Eq. D.1. As the coordinate system rotates, moving matter is additionally subject to Corio-lis forces, which cannot be represented by a scalar potential. For small mass ratios q ≪ 1 and small planets, the Roche potential in the vicinity of the planet  reduces to the usual expression of a point mass
reduces to the usual expression of a point mass
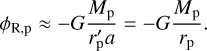 (D.5)
(D.5)
References
- Albrecht, S., Winn, J. N., Johnson, J. A., et al. 2012, ApJ, 757, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Axner, O., Gustafsson, J., Omenetto, N., & Winefordner, J. D. 2004, Spectrochimica Acta, 59, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, L., Gu, S., Wang, X., et al. 2022, MNRAS, 512, 3113 [NASA ADS] [CrossRef] [Google Scholar]
- Bailey, A., & Goodman, J. 2019, MNRAS, 482, 1872 [NASA ADS] [CrossRef] [Google Scholar]
- Bechter, E. B., Crepp, J. R., Ngo, H., et al. 2014, ApJ, 788, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, T. J., Nikolov, N., Cowan, N. B., et al. 2017, ApJ, 847, L2 [Google Scholar]
- Bergfors, C., Brandner, W., Daemgen, S., et al. 2013, MNRAS, 428, 182 [Google Scholar]
- Bisikalo, D., Kaygorodov, P., Ionov, D., et al. 2013, ApJ, 764, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Bisikalo, D. V., Kaigorodov, P. V., & Konstantinova, N. I. 2015, Astron. Rep., 59, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Brogi, M., & Line, M. R. 2019, AJ, 157, 114 [Google Scholar]
- Brown, T. M. 2001, ApJ, 553, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Burton, J. R., Watson, C. A., Rodríguez-Gil, P., et al. 2015, MNRAS, 446, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero, J. A., Guàrdia, J., López del Fresno, M., et al. 2016, SPIE Conf. Ser., 9910, 99100E [Google Scholar]
- Cabot, S. H. C., Madhusudhan, N., Welbanks, L., Piette, A., & Gandhi, S. 2020, MNRAS, 494, 363 [Google Scholar]
- Caccin, B., Cavallini, F., Ceppatelli, G., Righini, A., & Sambuco, A. M. 1985, A&A, 149, 357 [NASA ADS] [Google Scholar]
- Casasayas-Barris, N., Pallé, E., Yan, F., et al. 2019, A&A, 628, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cauley, P. W., Redfield, S., Jensen, A. G., et al. 2015, ApJ, 810, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Chadney, J. M., Galand, M., Unruh, Y. C., Koskinen, T. T., & Sanz-Forcada, J. 2015, Icarus, 250, 357 [Google Scholar]
- Chen, G., Casasayas-Barris, N., Pallé, E., et al. 2020a, A&A, 642, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, G., Casasayas-Barris, N., Pallé, E., et al. 2020b, A&A, 635, A171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cont, D., Yan, F., Reiners, A., et al. 2022, A&A, 668, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Czesla, S., Molle, T., & Schmitt, J. H. M. M. 2018, A&A, 609, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Czesla, S., Lampón, M., Sanz-Forcada, J., et al. 2022, A&A, 657, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Darlington, R., & Hayes, A. 2016, Regression Analysis and Linear Models: Concepts, Applications, and Implementation, Methodology in the Social Sciences (New York: Guilford Publications) [Google Scholar]
- Debrecht, A., Carroll-Nellenback, J., Frank, A., et al. 2018, MNRAS, 478, 2592 [NASA ADS] [CrossRef] [Google Scholar]
- Delrez, L., Santerne, A., Almenara, J. M., et al. 2016, MNRAS, 458, 4025 [NASA ADS] [CrossRef] [Google Scholar]
- Dethier, W., & Bourrier, V. 2023, A&A, 674, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dwivedi, N. K., Khodachenko, M. L., Shaikhislamov, I. F., et al. 2019, MNRAS, 487, 4208 [CrossRef] [Google Scholar]
- Efron, B., & Stein, C. 1981, Ann. Statist., 9, 586 [CrossRef] [MathSciNet] [Google Scholar]
- Fossati, L., Bagnulo, S., Elmasli, A., et al. 2010a, ApJ, 720, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., Haswell, C. A., Froning, C. S., et al. 2010b, ApJ, 714, L222 [Google Scholar]
- Fossati, L., Ayres, T. R., Haswell, C. A., et al. 2013, ApJ, 766, L20 [Google Scholar]
- Frasca, A., Biazzo, K., Kovári, Z., Marilli, E., & Çakirli, Ö. 2010, A&A, 518, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmeister, B., Czesla, S., Perdelwitz, V., et al. 2023, A&A, 670, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fukuda, I. 1982, PASP, 94, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gibson, N. P., Merritt, S., Nugroho, S. K., et al. 2020, MNRAS, 493, 2215 [Google Scholar]
- Gibson, N. P., Nugroho, S. K., Lothringer, J., Maguire, C., & Sing, D. K. 2022, MNRAS, 512, 4618 [NASA ADS] [CrossRef] [Google Scholar]
- Hampel, F. R. 1974, J. Am. Statist. Assoc., 69, 383 [CrossRef] [Google Scholar]
- Harre, J. V., Smith, A. M. S., Barros, S. C. C., et al. 2023, A&A, 669, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haswell, C. A., Fossati, L., Ayres, T., et al. 2012, ApJ, 760, 79 [Google Scholar]
- Hebb, L., Collier-Cameron, A., Loeillet, B., et al. 2009, ApJ, 693, 1920 [Google Scholar]
- Hilditch, R. W. 2001, An Introduction to Close Binary Stars (Cambridge: Cambridge University Press), 392 [Google Scholar]
- Himes, M. D., & Harrington, J. 2022, ApJ, 931, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, C., Koskinen, T., Lavvas, P., & Fossati, L. 2023, ApJ, 951, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jensen, A. G., Cauley, P. W., Redfield, S., Cochran, W. D., & Endl, M. 2018, AJ, 156, 154 [Google Scholar]
- Johnstone, C. P., Bartel, M., & Güdel, M. 2021, A&A, 649, A96 [EDP Sciences] [Google Scholar]
- Kausch, W., Noll, S., Smette, A., et al. 2015, A&A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- King, G. W., Wheatley, P. J., Salz, M., et al. 2018, MNRAS, 478, 1193 [NASA ADS] [Google Scholar]
- Knutson, H. A., Howard, A. W., & Isaacson, H. 2010, ApJ, 720, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Kohl, S., Salz, M., Czesla, S., & Schmitt, J. H. M. M. 2018, A&A, 619, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koskinen, T. T., Lavvas, P., Huang, C., et al. 2022, ApJ, 929, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, A. L., & Hillenbrand, L. A. 2007, AJ, 134, 2340 [NASA ADS] [CrossRef] [Google Scholar]
- Kreidberg, L., & Oklopcic, A. 2018, Res. Notes Am. Astron. Soc., 2, 44 [Google Scholar]
- Kreidberg, L., Line, M. R., Bean, J. L., et al. 2015, ApJ, 814, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, D., Helling, C., & van den Heuvel, E. P. J. 2010, ApJ, 721, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Lampón, M., López-Puertas, M., Lara, L. M., et al. 2020, A&A, 636, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lampón, M., López-Puertas, M., Czesla, S., et al. 2021a, A&A, 648, L7 [CrossRef] [EDP Sciences] [Google Scholar]
- Lampón, M., López-Puertas, M., Sanz-Forcada, J., et al. 2021b, A&A, 647, A129 [EDP Sciences] [Google Scholar]
- Lampón, M., López-Puertas, M., Sanz-Forcada, J., et al. 2023, A&A, 673, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langeveld, A. B., Madhusudhan, N., & Cabot, S. H. C. 2022, MNRAS, 514, 5192 [NASA ADS] [CrossRef] [Google Scholar]
- Li, S.-L., Miller, N., Lin, D. N. C., & Fortney, J. J. 2010, Nature, 463, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Line, M. R., Knutson, H., Wolf, A. S., & Yung, Y. L. 2014, ApJ, 783, 70 [Google Scholar]
- MacLeod, M., & Oklopcic, A. 2022, ApJ, 926, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N., Harrington, J., Stevenson, K. B., et al. 2011, Nature, 469, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, S. R., Gibson, N. P., Nugroho, S. K., et al. 2020, A&A, 636, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mollière, P., Wardenier, J. P., van Boekel, R., et al. 2019, A&A, 627, A67 [Google Scholar]
- Nichols, J. D., Wynn, G. A., Goad, M., et al. 2015, ApJ, 803, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Nortmann, L., Pallé, E., Salz, M., et al. 2018, Science, 362, 1388 [Google Scholar]
- Oliva, E., Origlia, L., Scuderi, S., et al. 2015, A&A, 581, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oreshenko, M., Lavie, B., Grimm, S. L., et al. 2017, ApJ, 847, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Owens, N., de Mooij, E. J. W., Watson, C. A., & Hooton, M. J. 2021, MNRAS, 503, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Quirrenbach, A., Amado, P. J., Ribas, I., et al. 2018, SPIE Conf. Ser., 10702, 107020W [Google Scholar]
- Rahmati, H., Czesla, S., Khalafinejad, S., & Mollière, P. 2022, A&A, 668, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rousseeuw, P. J., & Croux, C. 1993, J. Am. Statist. Assoc., 88, 1273 [CrossRef] [Google Scholar]
- Salz, M., Czesla, S., Schneider, P. C., & Schmitt, J. H. M. M. 2016a, A&A, 586, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salz, M., Schneider, P. C., Czesla, S., & Schmitt, J. H. M. M. 2016b, A&A, 585, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanz-Forcada, J., Micela, G., Ribas, I., et al. 2011, A&A, 532, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seidel, J. V., Ehrenreich, D., Wyttenbach, A., et al. 2019, A&A, 623, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sing, D. K., Lecavelier des Etangs, A., Fortney, J. J., et al. 2013, MNRAS, 436, 2956 [NASA ADS] [CrossRef] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J., Wheatley, P. J., & Sams, G. 2007, MNRAS, 379, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Stassun, K. G., Collins, K. A., & Gaudi, B. S. 2017, AJ, 153, 136 [Google Scholar]
- Stevenson, K. B., Bean, J. L., Madhusudhan, N., & Harrington, J. 2014a, ApJ, 791, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Stevenson, K. B., Bean, J. L., Seifahrt, A., et al. 2014b, AJ, 147, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Tamuz, O., Mazeh, T., & Zucker, S. 2005, MNRAS, 356, 1466 [Google Scholar]
- Turner, J. D., Ridden-Harper, A., & Jayawardhana, R. 2021, AJ, 161, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Wakeford, H. R., Visscher, C., Lewis, N. K., et al. 2017, MNRAS, 464, 4247 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, I., Shporer, A., Vissapragada, S., et al. 2022, AJ, 163, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Wyttenbach, A., Ehrenreich, D., Lovis, C., Udry, S., & Pepe, F. 2015, A&A, 577, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, F., Pallé, E., Reiners, A., et al. 2020, A&A, 640, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yee, S. W., Winn, J. N., Knutson, H. A., et al. 2020, ApJ, 888, L5 [Google Scholar]
- Zechmeister, M., Anglada-Escudé, G., & Reiners, A. 2014, A&A, 561, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Z., Morley, C. V., Gully-Santiago, M., et al. 2023, Sci. Adv., 9, eadf8736 [Google Scholar]
All Tables
Best-fit parameters of Na I D ISM absorption components in WASP–12 and values derived by Fossati et al. (2013).
Gravitational potential in Jovian units, XUV irradiation at planetary separation (5–920 Å, see Sect. 2.4), and derived thermospheric temperature range for relevant systems from Lampón et al. (2023).
All Figures
 |
Fig. 1 Evolution of airmass and S/N in night 1 (solid) and night 2 (dotted). Dotted vertical lines indicate the four contact points of the transit. |
| In the text | |
 |
Fig. 2 Pole-on view of the Roche geometry of WASP–12 b. The host star is to the left. The equipotential surfaces of the Roche lobe (blue) and planetary surface (red) are indicated. |
| In the text | |
 |
Fig. 3 Section of mock uncertainty matrix, Σm,o.f,sp, showing the effect of SP. Dark regions indicate increased uncertainties. |
| In the text | |
 |
Fig. 4 Standard deviation of residuals as a function of the number of SYSREM iteration in the application to white noise (solid blue), the approximation based on the degrees of freedom (green dotted), and the standard deviation of the cumulative model (dotted red). |
| In the text | |
 |
Fig. 5 Transmission spectra of the Na I D2 (top), Hα (middle), and He I λ 10833 Å triplet lines (bottom) obtained using SYSREM (solid black) and a conventional approach (dashed red, Sect. 3.2.3). The night 2 spectra are shifted by 0.05. The dotted vertical line indicates the nominal wavelength of the line (the center of the stronger doublet in the case of the He I λ 10833 Å triplet). |
| In the text | |
 |
Fig. 6 Average spectrum of WASP–12 during night 1 and 2 in the SF before correction for telluric absorption lines. Dotted vertical lines indicate the nominal wavelengths of the lines of the He I λ10833 Å triplet. Marks at the bottom indicate the nominal wavelengths of the four OH emission lines and the strongest water line during night 1. |
| In the text | |
 |
Fig. 7 Transmission spectra after one (bottom row), three (middle row), and five (top row) SYSREM iterations for night 1 (left column) and night 2 (right column) with SP (solid blue) and without (dashed red). The gray shade indicates the width of the SP region. |
| In the text | |
 |
Fig. 8 Light curves of the Hα and Ca IIIRT lines in the stellar frame. Top: Hα light curves (1.5 Å passband) normalized by the mean of the night 1 light curve. Bottom: as top but for 0.5 Å passband centered on bluest component of the Ca II IRT. |
| In the text | |
 |
Fig. 9 Ratio of night 2 and 1 spectra in the SF as a function of time from transit center. Horizontal dotted lines indicate the first to fourth contact, the dash-dotted vertical line denotes the nominal position of the Hα line, and the dashed diagonal line shows the orbital velocity track of the planet. |
| In the text | |
 |
Fig. 10 Average post-transit ratio of night 2 and night 1 spectra around the Hα line (blue) along with best-fit Gaussian model (red solid). |
| In the text | |
 |
Fig. 11 Average Na I D2 lines of WASP–12 in nights 1 and 2. The average wavelengths of the telluric line are indicated by vertical lines. |
| In the text | |
 |
Fig. 12 Properties of the Na I D lines of WASP–12. Top panel: Na I D2 line of WASP–12 (solid blue) along with spectrum reflected at nominal wavelength of the line (red dashed). Bottom panel: ratio between original and reflected spectrum for Na I D1 and Na I D2 lines (solid magenta and black) along with best-fit model (dashed magenta and black). The green shade indicates the considered fit range. |
| In the text | |
 |
Fig. 13 Hypothetical Hα absorption line profile caused by a homogeneous torus at the planetary orbital separation, covering the entire stellar disk. |
| In the text | |
 |
Fig. 14 Roche potential around WASP–12 b evaluated in the orbital plane toward the star (blue) and toward the side (red) along with the potential of a point mass (black dashed). The substellar radius and the height of the Roche lobe at the substellar point are indicated. The acceleration caused by gravitational and centrifugal forces in the respective directions is given by the derivative of the potential. |
| In the text | |
 |
Fig. 15 Modeled EW of the He I λ10833 Å signal as a function of temperature and mass-loss rate at the terminator for the high irradiation scenario. The admissible region is indicated by connected blue circles. Similarly, admissible regions are indicated for the moderate irradiation scenario (white, F/100) and the substellar-point model in Roche-lobe overflow (RLO, triangles). |
| In the text | |
 |
Fig. 16 Density of excited helium as a function of distance for the high-irradiation scenario and various thermospheric temperatures for the terminator (solid) and substellar-point models (dashed); RP is taken to be 1.91 RJup for the plot. |
| In the text | |
 |
Fig. 17 Absorption EW in the Na I D2 line as a function of the fractional atmospheric coverage fraction per scale height, ΔA, for a sample of planets along with WASP–12 b (data adopted from Wyttenbach et al. 2015; Seidel et al. 2019; Casasayas-Barris et al. 2019; Chen et al. 2020b,a; Cabot et al. 2020; Langeveld et al. 2022; Rahmati et al. 2022). |
| In the text | |
 |
Fig. B.1 Error as defined by Eq. B.1 incurred by assuming distributivity of convolution over multiplication. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.