| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 22 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202347463 | |
| Published online | 05 December 2023 | |
The miniJPAS and J-NEP surveys: Identification and characterization of the Lyα emitter population and the Lyα luminosity function at redshift 2.05 < z < 3.75
1
Observatori Astronòmic de la Universitat de València, Ed. Instituts d’Investigació, Parc Científic. C/ Catedrático José Beltrán, n2, 46980 Paterna, Valencia, Spain
e-mail: alberto.torralba@uv.es
2
Departament d’Astronomia i Astrofísica, Universitat de València, 46100 Burjassot, Spain
3
Department of Astronomy, MongManWai Building, Tsinghua University, Beijing 100084, PR China
4
Dipartimento di Fisica “G. Occhialini”, Università degli Studi di Milano-Bicocca, Università degli Studi di Milano-Bicocca, Piazza della Scienza 3, 20126 Milano, Italy
5
INFN, Sezione di Milano-Bicocca, Piazza della Scienza 3, 20126 Milano, Italy
6
Instituto de Física de Cantabria (CSIC-UC), Avda. Los Castros s/n, 39005 Santander, Spain
7
Unidad Asociada “Grupo de Astrofísica Extragaláctica y Cosmología”, IFCA-CSIC/Universitat de València, València, Spain
8
Donostia International Physics Center, Paseo Manuel de Lardizabal, 4, 20018 Donostia-San Sebastián (Gipuzkoa), Spain
9
IKERBASQUE, Basque Foundation for Science, 48013 Bilbao, Spain
10
Instituto de Astrofísica de Andalucía – CSIC, Apdo 3004, 18080 Granada, Spain
11
Centro de Estudios de Física del Cosmos de Aragón (CEFCA), Plaza San Juan 1, 44001 Teruel, Spain
12
Departamento de Física Matemática, Instituto de Física, Universidade de Saõ Paulo, Rua do Matão 1371, CEP 05508-090, São Paulo, Brazil
13
Observatório Nacional, Rua General é Cristino 77, São Cristóvão, 20921-400 Rio de Janeiro, RJ, Brazil
14
Instituto de Física, Universidade Federal da Bahia, 40210-340 Salvador, BA, Brazil
15
Departamento de Astronomia, Instituto de Astronomia, Geofísica e Ciências Atmosféricas, Universidade de São Paulo, Sáo Paulo, Brazil
16
Instruments4, 4121 Pembury Place, La Canada Flintridge, CA, 91011 California, USA
Received:
14
July
2023
Accepted:
8
October
2023
We present the Lyman-α (Lyα) luminosity function (LF) at 2.05 < z < 3.75, estimated from a sample of 67 Lyα-emitter (LAE) candidates in the Javalambre Physics of the Accelerating Universe Astronomical Survey (J-PAS) pathfinder surveys: miniJPAS and J-NEP. These two surveys cover a total effective area of ∼1.14 deg2 with 54 narrow band (NB) filters (FWHM ∼ 145 Å) across the optical range, with typical limiting magnitudes of ∼23. This set of NBs allowed us to probe Lyα emission in a wide and continuous range of redshifts. We developed a method for detecting Lyα emission for the estimation of the Lyα LF using the whole J-PAS filter set. We tested this method by applying it to the miniJPAS and J-NEP data. In order to compute the corrections needed to estimate the Lyα LF and to test the performance of the candidate selection method, we built mock catalogs. These include representative populations of LAEs at 1.9 < z < 4.5 as well as their expected contaminants, namely low-z galaxies and z < 2 quasi-stellar objects (QSOs). We show that our method is able to provide the Lyα LF at the intermediate-bright range of luminosity (43.5 ≲ log10(LLyα/erg s−1) ≲ 44.5) combining both miniJPAS and J-NEP. The photometric information provided by these surveys suggests that our samples are dominated by bright, Lyα-emitting active galactic nuclei (i.e., AGNs). At log10(LLyα/erg s−1) < 44.5, we fit our Lyα LF to a power law with a slope of A = 0.70 ± 0.25. We also fit a Schechter function to our data, obtaining the following: log10(Φ∗/Mpc−3) = −6.30−0.70+0.48, log10(L∗/erg s−1) = 44.85−0.32+0.50, and α = −1.65−0.27+0.29. Overall, our results confirm the presence of an AGN component at the bright end of the Lyα LF. In particular, we find no significant contribution of star-forming LAEs to the Lyα LF at log10(LLyα/erg s−1) > 43.5. This work serves as a proof of concept for the results that can be obtained with the upcoming data releases of the J-PAS survey.
Key words: methods: observational / quasars: emission lines / galaxies: luminosity function / mass function / galaxies: high-redshift / line: identification
Note to the reader: the HTML version contained an incorrect mathematical sign in a formula of the Abstract. It was corrected on 12 December 2023.
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The Lyman-α (Lyα) emission line (λ0 = 1215.67 Å) is among the brightest lines in the UV spectrum of astrophysical sources (Partridge & Peebles 1967; Pritchet 1994; Vanden Berk et al. 2001; Nakajima et al. 2018). Due to its intrinsic strength, Lyα constitutes a fundamental probe for the high-z Universe, allowing us to identify very faint objects at the optical and near-infrared, sometimes even without an explicit detection of the continuum (e.g., Bacon et al. 2015). The Lyα line can be seen redshifted into the optical range at z ∼ 2 − 7. Several works have searched for Lyα emission in this range, using blind spectroscopy (e.g., Martin & Sawicki 2004; Cassata et al. 2011, 2015; Song et al. 2014; McCarron et al. 2022; Liu et al. 2022b), using narrow band (NB) imaging (e.g., Cowie & Hu 1998; Hu et al. 1998; Gronwall et al. 2007; Ouchi et al. 2008; Ciardullo et al. 2012; Yamada et al. 2012; Shibuya et al. 2012; Matthee et al. 2015; Santos et al. 2016, 2021; Konno et al. 2018; Ono et al. 2021), and using integral field unit spectroscopy (e.g., Blanc et al. 2011; Adams et al. 2011; Bacon et al. 2015; Karman et al. 2015; Drake et al. 2017).
One of the main drivers of Lyα surveys is to measure the Lyα luminosity function (LF) over a specific redshift interval. The LF is a statistical measurement of the abundance of Lyα emitters (LAEs), defined as the number density of LAEs per unit comoving volume as a function of the Lyα luminosity (LLyα). Many works have managed to estimate the Lyα LF for different redshift ranges (e.g., Konno et al. 2016; Sobral et al. 2018; Spinoso et al. 2020; Zhang et al. 2021; Liu et al. 2022b). Generally, the observed LAE population is divided into two main kinds of sources: quasi-stellar objects (QSOs) with an active galactic nucleus (AGN) and star-forming galaxies (SFGs). It was found that the population that dominates the low luminosity regime of the Lyα LF (log10(LLyα/erg s−1) ≲ 43.5) is that of SFGs (e.g., Guaita et al. 2011; Drake et al. 2017). These objects are typically low-mass galaxies with a high star formation rate, low dust content, small rest-frame half-light radius, and, in general, faint emission lines except for Lyα (see e.g., Arrabal Haro et al. 2020; Santos et al. 2020). In SFGs, Lyα emission is produced through recombination processes in the inter-stellar medium (ISM), which is heated by recent star formation events (e.g., Charlot & Fall 1993; Pritchet 1994; Arrabal Haro et al. 2020). Meanwhile the brightest part of the LF (log10(LLyα/erg s−1) ≳ 43.5) is mainly populated by QSOs, where the recombination processes are triggered by the action of the AGN (e.g., Calhau et al. 2020).
Identifying the LAEs’ population and characterizing its luminosity census is a crucial step in order to understand a multitude of processes in the high-z Universe. SFG LAEs are thought to be analogous to the progenitors of many galaxies that we observe in the nearby Universe, for this reason they provide useful insight into early phases of galaxy evolution (e.g., Gawiser et al. 2007; Ouchi et al. 2010). Furthermore, at high-z, these objects constitute a probe of high-z galaxy clustering and the large structure formation history (e.g., Guaita et al. 2010; Khostovan et al. 2019). On the other hand, the characterization of the galactic features of LAEs are key to understanding processes such as the AGN fueling and feedback and their effects on star formation (e.g., Bridge et al. 2013). In addition, through the study of the fraction of ionizing photons in the ISM of LAEs, it is possible to measure the ionization state of the high-z Universe, shortly after the cosmic epoch of reionization (EoR, z ∼ 6–7; see e.g., Bouwens et al. 2012; Nakajima & Ouchi 2014; Jaskot & Oey 2014).
The evolution of the Lyα LF with redshift is another interesting topic. Past studies have claimed that the SFG Lyα LF grows substantially from z ∼ 0.3 up to z ∼ 2–3 and remains broadly constant up to z ∼ 6–7. At higher redshift, the SFG Lyα LF shows a strong evolution, resulting in a decrease in the observed number density of LAEs. This is generally interpreted as an indirect probe of the Universe’s reionization progress, since the higher fraction of neutral hydrogen would efficiently absorb Lyα radiation, hindering the detectability of z ∼ 6–7 SFG LAEs (e.g., Malhotra & Rhoads 2004; Kashikawa et al. 2006; Clément et al. 2012; Dijkstra 2016; Ning et al. 2022). On the other hand, the Lyα LF of QSOs shows an evolution compatible with the progress of AGN activity through cosmic history (see e.g., Hasinger et al. 2005; Miyaji et al. 2015; Sobral et al. 2018).
Many works in the last decade have sought to estimate the Lyα LF at different luminosity regimes. The works of Konno et al. (2016), Sobral et al. (2017, 2018), estimated the Lyα LF at various redshifts in the faint and intermediate regime using deep NB imaging. In all of these works, it was found that the LF deviates from a Schechter function (Schechter 1976) to a power-law-like shape for 43.5 ≲ log10(LLyα/erg s−1) ≲ 44.5. The analysis of the X-ray counterparts in Ouchi et al. (2008), Konno et al. (2016), and Sobral et al. (2018) revealed that essentially every LAE with log10(LLyα/erg s−1) > 43.5 is associated with X-ray emission, which is typically interpreted as a signature of AGN activity.
More recently, a few works have explored the brightest end of the Lyα LF. In Spinoso et al. (2020), the Lyα LF was built from ∼103 deg2 of data from the Javalambre-Photometric Local Universe Survey (J-PLUS; Cenarro et al. 2019), at four redshifts defined by four NB filters (z = 2.24, 2.38, 2.54, and 3.23) and focusing on the bright regime of log10(LLyα/erg s−1) ≳ 44.5. On the other hand, Zhang et al. (2021) combined the spectroscopic data from the Hobby-Eberly Telescope Dark Energy Experiment (HETDEX; Gebhardt et al. 2021) with the r-band images of Subaru/HSC to obtain the Lyα LF, covering ∼11.4 deg2 of sky at 2 < z < 3. Later, Liu et al. (2022b) obtained analogous results for the Lyα AGN LF from the spectroscopic QSO sample of HETDEX, over 30.61 deg2. The latter work showed great agreement with the J-PLUS LF Schechter fit, while covering a wider range of luminosity (42.3 ≲ log10(LLyα/erg s−1) ≲ 45.9). While the LAEs sample of Zhang et al. (2021) relies on the r-band detection of HSC, in Liu et al. (2022b), the selection was made using purely HETDEX blind spectroscopy, allowing for a more complete sample over a broader area to be obtained. Overall, the Lyα LF at the full range of luminosity (41 ≲ log10(LLyα/erg s−1) ≲ 46) can be well fit by a double Schechter curve, making the contributions of both SFG as well as AGN populations evident (e.g., Zhang et al. 2021; Spinoso et al. 2020).
For this work, we developed a method for detecting Lyα emission in the photometric data of multi-NB surveys such as the Javalambre-Physics of the Accelerating Universe Astronomical Survey (J-PAS1; Benitez et al. 2014) and its pathfinder surveys, namely miniJPAS (Bonoli et al. 2021) and J-NEP (Hernán-Caballero et al. 2023). More specifically, we developed our method on the already observed fields of miniJPAS and J-NEP, in order to pave the way for the upcoming J-PAS survey. Multi-NB photometric surveys such as J-PAS allow one to perform blind searches of LAEs at various redshifts over a wide field of observations, with a more efficient selection function than typical spectroscopic surveys (e.g., Zhang et al. 2021; Liu et al. 2022b). Furthermore, the availability of a photospectrum (λ ∼ 3750–9000 Å) for each source in the survey catalog can be used for contaminant identification.
We characterized the performance of our selection method by building mock-survey data and we ultimately built the Lyα LF at 2.05 < z < 3.75 in the medium-bright luminosity range (43.5 ≲ log10(LLyα/erg s−1) ≲ 45). This range is still poorly constrained by photometric surveys, due to the small areas probed and the limited number of NBs used (e.g., Konno et al. 2016; Sobral et al. 2017, 2018; Matthee et al. 2017; Spinoso et al. 2020). At the same time, Lyα is an excellent tracer for z > 2 AGNs due to its intrinsic brightness. The estimation of the Lyα LF is motivated by the need to constrain the evolution of the AGN population across cosmic time. For instance, the role played by AGNs at the EoR is still debated. While some works point out that AGNs could be a significant source to the ionizing photon budget (e.g., Giallongo et al. 2015; Dayal et al. 2020), others conclude that AGNs could only make a marginal contribution, in favor of star formation activity (e.g., Qin et al. 2017; Hassan et al. 2018). At lower redshifts, being able to trace the fraction of active galaxies as well as the AGN luminosity distribution is useful to shed light on processes such as AGN-driven feedback and its effect on the host galaxy (e.g., Brownson et al. 2019; Mezcua et al. 2019; Jin et al. 2023) or the build-up of scaling relations between active super-massive black holes and their host galaxies (see e.g., Reines & Volonteri 2015, for a review). Therefore, developing reliable methods to estimate the Lyα LF allows systematic studies of AGN populations since the EoR down to cosmic noon (z ∼ 2). Furthermore, optical multi-NB surveys offer the possibility to perform these analyses in a tomographic fashion across redshift.
This paper is structured as follows. In Sect. 2 we describe the observations used to obtain the scientific results of this work. In Sect. 3 we define the procedure to build mock catalogs that mimic the observations, which we use to assess the performance of our method. In Sect. 4 we explain our LAE candidate selection method and the procedure used to estimate the Lyα LF, and we present the LAE catalog for miniJPAS and J-NEP. In Sect. 5 we present the Lyα LF in different intervals of redshift and estimate the QSO/SFG ratio of our candidates. Finally, Sect. 6 summarizes the content of this work.
Throughout this work we use a ΛCDM cosmology as described by PLANCK18 (Planck Collaboration VI 2020), with ΩΛ = 0.69, ΩM = 0.31, and H0 = 67.7 km s−1 Mpc−1, unless specified otherwise. All of the magnitudes are given in the AB system (Oke & Gunn 1983).
2. Observations
2.1. J-PAS: Javalambre-Physics of the Accelerating Universe Astronomical Survey
J-PAS is a ground-based survey that will be performed by the JST/T250 telescope at the Javalambre Astrophysical Observatory at Teruel (Spain). It is planned to observe ∼8500 deg2 of the northern sky via narrow-band imaging with the JPCam instrument. The JPCam is a 1.2 Gpixel multi-CCD camera composed of an array of 14 CCDs, with a field of view of ∼4.2 deg2 (see Taylor et al. 2014; Marín-Franch et al. 2017).
In the context of this work, the most relevant feature of J-PAS is its filter-set. This set is composed of 54 narrow bands with FWHM of ∼145 Å, covering the optical range of the electromagnetic spectrum. In addition, this filter-set features two medium bands, respectively at the blue and red ends of the optical range, and four broad bands (BBs) equivalent to those used by the SDSS survey: u, g, r and i (York et al. 2000). These technical features make J-PAS particularly suitable to detect line emitters (e.g., Martínez-Solaeche et al. 2021, 2022; Iglesias-Páramo et al. 2022). Indeed, the NB set provides a wide and continuous coverage of the optical range (∼3500–10 000 Å), allowing the development of algorithms for photometric source identification (e.g., Baqui et al. 2021; González Delgado et al. 2021), and precise determination of photometric redshifts (Hernán-Caballero et al. 2021; Laur et al. 2022). The same filter set was used by the pathfinder surveys miniJPAS and J-NEP.
2.2. The pathfinder surveys of J-PAS: miniJPAS and J-NEP
The miniJPAS survey (Bonoli et al. 2021) is a scientific project designed to pave the ground for J-PAS data analysis. The observations of miniJPAS were carried out between May and September 2018 using the JPAS-Pathfinder camera mounted in the JST/T250. The JPAS-Pathfinder camera is an instrument composed of one single CCD with an effective field of view of 0.27 deg2. The miniJPAS data cover a total of ∼1 deg2 (effective area after masking 0.895 deg2) of the AEGIS field (Davis et al. 2007), in the northern galactic hemisphere. This field is covered by miniJPAS in 4 pointings (AEGIS001–AEGIS004). AEGIS is a widely studied region of the sky, located within the Extended Groth Strip, for which a plethora of multiband and spectroscopic observations are available in the literature. For instance, the entirety of the miniJPAS area is covered by the Sloan Digital Sky Survey (SDSS; Blanton et al. 2017), granting spectroscopic counterparts to many sources in the miniJPAS catalogs. The outcome of miniJPAS serves as a demonstration of the potential of J-PAS and allows us to make a forecast about the results that will be possible to achieve once the survey delivers the first set of data.
J-NEP (for Javalambre North Ecliptic Pole) is the second data release obtained using the JST/T250 and the Pathfinder camera, covering the James Webb Space Telescope North Ecliptic Pole Time-Domain Field (JWST-TDF; Jansen & Windhorst 2018). This survey was carried out in a single pointing, with an effective area of ∼0.24 deg2 (Hernán-Caballero et al. 2023). The JWST-TDF will be covered by JWST via a dedicated program in the near future. J-NEP has slightly longer exposure times than miniJPAS, reaching deeper magnitudes.
In Table 1, we list the limiting 5σ magnitudes of both surveys for all relevant filters for this work. We use 20 NBs to probe for Lyα emission covering a redshift range of z = 2.05–3.75, the choice of this range is discussed in Sect. 4.3. The number in the J-PAS NB names makes reference to the approximate pivot wavelength (λpivot) in nanometers.
Limit 5σ magnitudes of the BBs and NBs used to select LAEs.
Throughout this work we use the dual mode catalogs of miniJPAS and J-NEP described in Bonoli et al. (2021) and Hernán-Caballero et al. (2023), respectively. These catalogs are generated using the “dual mode” of the SExtractor code (Bertin & Arnouts 1996). In this operating mode, SExtractor performs a first source-detection on a specific band (r for J-PAS, since this is the deepest among the BBs). Then, the positions of these r-band detected sources is used to perform forced-photometry in the images obtained with all the remaining filters. We use the 3″ forced aperture photometry fluxes and magnitudes. The PSF FWHM of the miniJPAS and J-NEP images varies in the range 0.6–2″. The total effective area, after masking, combining miniJPAS and J-NEP is 1.14 deg2.
3. Mock catalogs
Given our wavelength coverage (3700 Å–5700 Å) our sample is prone to be contaminated by sources with prominent emission lines other than Lyα, such as C IV (λ 1549 Å), C III] (λ 1908 Å), Mg II (λ 2799 Å) and Si IV (λ 1397 Å) AGN lines; and galactic emission lines associated to star formation at low-z such as Hβ (λ 4861 Å), [O III] (λλ 4959, 5007 Å) and [O II] (λλ 3727, 3729 Å). We have designed mock catalogs of LAEs and its main contaminants in order to estimate completeness and purity of our selection methodology as well as the uncertainty on our measured Lyα LF.
3.1. Characterization of the photometry flux uncertainties
The first step in building the mock catalogs is to characterize the photometric uncertainty distribution of the survey we want to emulate. We assume that the distribution of measured magnitude errors (σ[m]) in each observed pointing can be modeled as a simple exponential:
We perform a fit for the parameters A, B and C for every NB in every pointing of miniJPAS and J-NEP. Following this fit, we add Gaussian uncertainties in magnitude to our mock objects in order to mimic the JPAS-Pathfinder observations. Next, all magnitudes are converted to fluxes (fλ). The bands with a flux below the 5σ limiting flux of that band 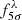 , are assigned an error equal to
, are assigned an error equal to 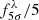 . The reason for this is that assuming Gaussian magnitude uncertainties is only valid for m ≲ m5σ, as some parts of many of the synthetic spectra have fluxes compatible with zero, and the Gaussian approximation of the magnitude errors is no longer valid due to the logarithmic nature of the magnitude system. A few examples of these fits can be found in Fig. 1. We generate five versions of our mocks, each one with the uncertainty distribution corresponding to each field of miniJPAS and J-NEP.
. The reason for this is that assuming Gaussian magnitude uncertainties is only valid for m ≲ m5σ, as some parts of many of the synthetic spectra have fluxes compatible with zero, and the Gaussian approximation of the magnitude errors is no longer valid due to the logarithmic nature of the magnitude system. A few examples of these fits can be found in Fig. 1. We generate five versions of our mocks, each one with the uncertainty distribution corresponding to each field of miniJPAS and J-NEP.
 |
Fig. 1. Exponential fits of magnitude errors according to Eq. (1). For brevity, we show the magnitudes of 4 NBs and 2 BBs (colored dots) of J-NEP and their corresponding fits (dashed black lines). We get highly similar results for every filter in J-NEP and all pointings of miniJPAS. |
3.2. Star-forming galaxy mock
In order to reproduce the population of SFGs, we generate a set of synthetic spectra of galaxies. We use the stellar population models from Bruzual & Charlot (2003), where the stellar continuum of a galaxy is described by three parameters: metallicity, age and extinction (MET, AGE and EXT, respectively). In order to generate a realistic LAEs population, we start from a sample of 397 spectra of LAEs at 2 < z < 5 from the VIMOS VLT Deep Survey (VVDS) and VIMOS Ultra-Deep Survey (VUDS; Cassata et al. 2011, 2015). We convert all the spectra to the rest-frame, using the spectroscopic redshifts, then stack them to obtain a composite spectrum. We fit the stacked spectrum to a grid of templates in MET, AGE and EXT using a Markov chain Monte Carlo (MCMC) algorithm2. The positions of the walkers in the final steps of the chain in the parameter space describe a disperse distribution of the most likely combinations of MET, AGE and EXT to reproduce the continuum of a SFG LAE. First we use the triplets of parameters sampled from this distribution to interpolate the Bruzual & Charlot (2003) templates and generate the normalized spectral continua of our mock catalog of SFG LAEs.
In a second step, we add the Lyα emission lines to the spectra, following the expected distributions for LLyα and equivalent width. We sample values of LLyα from the best Schechter fit in Sobral et al. (2018): log10(Φ*/Mpc−3) = − 3.45, log10(L*/erg s−1) = 42.93, α = −1.93. The Lyα LF has been proven to show little variation with redshift at z = 2.5–7 (Sobral et al. 2017, 2018; Drake et al. 2017; Ouchi et al. 2020). In Appendix C we discuss the effect of assuming this prior LF at z = 2–2.5. We sample values of Lyα EW0 from an exponential distribution,
where N0 is a normalizing factor and α = 129 Å (see Zheng et al. 2014; Santos et al. 2020; Kerutt et al. 2022). The fluxes of each object are rescaled applying a multiplicative factor so that the integrated line flux FLyα and the observed equivalent width (EW) follow the definition:
where 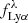 and
and 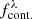 are the flux densities of the Lyα line and the continuum, respectively. The approximation at the rightmost part of Eq. (3) assumes a flat continuum over the width of the emission line. The relation between the observed EW and the rest-frame equivalent width is EW = EW0 ⋅ (1 + z). The redshift values are sampled from a distribution within z ∈ [1.9, 4.5] such as the number density per unit volume is constant. Finally, the Lyα line is added as a gaussian profile with σ = 5 Å (see e.g., Gurung-López et al. 2022; McCarron et al. 2022; Davis et al. 2023) and the adequate integrated flux to match the required LLyα.
are the flux densities of the Lyα line and the continuum, respectively. The approximation at the rightmost part of Eq. (3) assumes a flat continuum over the width of the emission line. The relation between the observed EW and the rest-frame equivalent width is EW = EW0 ⋅ (1 + z). The redshift values are sampled from a distribution within z ∈ [1.9, 4.5] such as the number density per unit volume is constant. Finally, the Lyα line is added as a gaussian profile with σ = 5 Å (see e.g., Gurung-López et al. 2022; McCarron et al. 2022; Davis et al. 2023) and the adequate integrated flux to match the required LLyα.
The result is a sample of synthetic spectra of SFG LAEs at 2 < z < 4 that mimics the Lyα LF measured by Sobral et al. (2018) over 400 deg2. All these spectra are convolved with the transmission curves of the J-PAS filters in order to obtain a mock catalog of fluxes. Then, the uncertainties are added as detailed in Sect. 3.1.
3.3. QSO mock
For the construction of our QSO mock we follow a very similar procedure to that used in Queiroz et al. 2023. In their work, they provide mock catalogs of QSOs (0 < z < 4.2), morphologically point-like galaxies and stars for miniJPAS, based on the SDSS DR12Q Superset (Pâris et al. 2017). We build a new QSO mock catalog following Queiroz et al. (2023) instead of using the already available mock for various reasons. In the first place, our mock needs to accurately represent the LLyα distribution of the QSO population at z > 2. Secondly, we add the flux uncertainties according to Eq. (1) in order to be consistent with the rest of the populations in our mocks. Finally, we need to substantially increase the size of the mock sample in order to obtain significant statistics, as explained below.
Our aim is to generate a set of QSOs with redshifts z = 0–4.5. For this, we use spectra from the SDSS DR16Q Superset (Lyke et al. 2020). We select all sources with good median signal-to-noise over all pixels (SN_MEDIAN_ALL > 0), so we can neglect the errors of the spectroscopy when performing the synthetic photometry; no redshift warning flags (ZWARNING = 0); and classified as QSO by the SDSS pipeline (IS_QSO_FINAL = 1). We sample values of z and r magnitude from the 2D PLE+LEDE model in Palanque-Delabrouille et al. (2016). This model predicts the number counts of detected QSOs in a photometric survey as a function of magnitude and redshift per unit area. We compute the total number of objects to include in the mock by integrating the Palanque-Delabrouille et al. (2016) model over an area of 400 deg2. For QSOs with log10(LLyα/erg s−1) > 44, due to the exponential drop of sources at this luminosity, we use a 10 times bigger area for better statistics. For each pair of values (z, r), a source is selected randomly from the SDSS DR16Q within a redshift interval smaller than 0.06, then the spectral flux is corrected by a multiplicative factor in order to match the sampled value of r.
As shown in the top panel of Fig. 2, the resulting QSO mock yields a 2 < z < 4 distribution in line with a Schechter function for Lyα line luminosity. The depth of SDSS is lower than that of miniJPAS and J-NEP, and their catalog is only complete up to r ∼ 20.5. Hence, to obtain sources up to r = 24, we need to largely correct some objects under the assumption of a weak dependecy of the QSO properties with luminosity (for a similar procedure and discussion see Abramo et al. 2012; Queiroz et al. 2023). The bottom panel of Fig. 2 shows that the distribution of LLyα of the QSO mock extrapolates reasonably at r ≳ 22, far out of the range of SDSS.
 |
Fig. 2. Basic properties of the QSO mock. Top: output Lyα LF of the QSO mock at z > 2. The measurement of the Lyα line can often be affected by the presence of the N V line, for this reason we also show the Lyα+N V LF. The bias correction in the LLyα measurement caused by N V is addressed in Sect. 4.2. We compare with the fits for the QSO Lyα LF in Spinoso et al. (2020) and Zhang et al. (2021), using a Schechter and a double power-law, respectively. Bottom: LLyα as a function of r magnitude for the sources in the QSO mock (orange) and the QSOs of SDSS DR16Q with a LLyαS/N > 5 (blue). The contour lines mark the regions containing the 68% and 95% of the objects. |
3.4. Low-z galaxy mock
As stated at the beginning of Sect. 3, a significant part of the contaminants are expected to be low-z galaxies (z ∼ 0–1) with prominent emission lines, especially at the faintest regime of the Lyα LF. To reproduce this population, we generate a synthetic miniJPAS observation, analogous to that designed by Izquierdo-Villalba et al. (2019) for the J-PLUS survey. In our case, the mock-observation is built over a total area of 3 deg2, by employing the L-Galaxies semi-analytic model (Guo et al. 2011; Henriques et al. 2015) to predict the continuum features of galaxies over the halos of the Millennium N-body dark matter simulation (Springel et al. 2005), selecting the line of sight oriented at RA = 58.9 deg, Dec = 56.3 deg. This simulated observation directly produces synthetic photometry of all the 60 miniJPAS filters for a catalog of 144 183 galaxies with magnitude r < 24 and z < 4 (∼90% of which are at z < 1). For simplicity, hereafter we refer to this mock-observation as “lightcone.”
The nebular emission lines of the galaxies in the lightcone are computed using the method of Orsi et al. (2014), which employs the Levesque et al. (2010) model for H II regions in order to compute the output line fluxes of simulated galaxy spectra. Several emission lines are considered, including the potential interlopers of a LAEs sample (e.g., Hβ, [O III] and [O II], as stated in Sect. 3). These line fluxes are corrected with an empirical dust attenuation model in order to reproduce the Hα, Hβ, [O II] and [O III] luminosity functions from several observations. This dust model performs well for almost every galactic line for a wide range of redshift. However, as discussed in Izquierdo-Villalba et al. (2019), this dust model tends to overcorrect the line flux in the case of [O II] for z ≤ 0.5, the interval in which this line has particular relevance for our work. In order to avoid underestimating the fraction of contaminants, we remove the dust attenuation coefficient from the [O II] lines in our mock for z < 0.5. By doing so, the [O II] LF is better reproduced in the lightcone, for this specific redshift interval.
4. Methods
In this section, we describe our methods to obtain a LAE sample in miniJPAS and J-NEP and estimate the Lyα LF. The parameters used in this pipeline were chosen to optimize the selection of LAEs, after extensive testing using the mocks described in Sect. 3. In this section we also characterize the candidate sample obtained from the observations and provide the catalog of LAEs.
4.1. Candidate selection method
In this subsection, we describe the procedure we use to select sources from the miniJPAS and J-NEP catalogs, and classify them as LAEs. In the first place, in Sect. 4.1.1 we define a parent sample from which to perform the selection. Second, in Sect. 4.1.2 we explain how the continuum flux is computed. Finally, in Sect. 4.1.3 we enumerate the criteria for selecting candidates based on NB flux excess with respect to the continuum.
4.1.1. Parent sample
Our LAE candidate selection is based on the dual mode catalogs of miniJPAS and the J-NEP field (see Sect. 2.2). We remove every source flagged by the catalog masks. The masks cover the window frames, artifacts, bright stars and objects near them. We also remove objects marked with SExtractor photometry flags. After this first cut, we are left with a total of 63 923 objects: 46 477 in miniJPAS and 17 446 in J-NEP.
We continue the preliminary cuts by requiring 17 ≤ r ≤ 24. Sources fainter than this threshold may have very low signal-to-noise to be classified reliably; r ∼ 24 is the 5σ detection limit for miniJPAS and J-NEP (see Table 1). On the other hand, we expect the number of LAEs at z ≥ 2 with magnitudes brighter than r = 17 to be very low (see Fig. 2). At these bright magnitudes, the number counts will be dominated by stars (see, e.g., Fig. 18 of Bonoli et al. 2021). For this reason, we remove these bright sources which are very likely to be stars. In any case, the exact value for this bright cut is somehow arbitrary.
Objects showing significant proper motion or parallax are likely to be stars. We remove these objects making use of the cross-match tables of the miniJPAS and J-NEP dual mode catalogs with the Gaia survey Early Data Release 3 (EDR3; Gaia Collaboration 2021). Among all the non-flagged sources in the miniJPAS and J-NEP dual catalogs, only 2739 (4.3%) have a counterpart in Gaia EDR3. In the spectroscopic follow up program of Spinoso et al. (2020), it was found that stars constituted a non-negligible part of the NB emitters sample from J-PLUS. Therefore, we remove secure stars following Spinoso et al. (2020), imposing
where σpmdec, σpmra and σμ are the relative errors of the proper motion in declination and right ascension and parallax, respectively.
After these cuts the dual-mode catalogs we are left with 36 026 sources in total (28 447 in miniJPAS and 7549 in J-NEP). This constitutes our starting sample for the selection of LAE candidates.
4.1.2. Continuum estimation
In order to find emission lines within the sources of the miniJPAS and J-NEP catalogs, we look for NBs with a reliable flux excess with respect to the continuum flux at the central wavelength of those NBs. The continuum flux density can be estimated using the information from the filters near the narrow band of interest. In particular, for a given NB filter n, we compute the continuum estimate 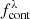 by considering an equal number k of NBs both at bluer and redder wavelengths than n. We obtain
by considering an equal number k of NBs both at bluer and redder wavelengths than n. We obtain 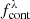 as the weighted average of this set of 2k NBs, after excluding the two NBs directly adjacent to n, on each side. The reason for excluding these two NBs is that emission lines can be broad enough to be detected in more than one NB at a time, as in many cases of QSO’s Lyα lines (see e.g., Greig et al. 2016). Narrow emission lines can also contribute to more than one NB due to the overlap of the transmission curves of the J-PAS filters.
as the weighted average of this set of 2k NBs, after excluding the two NBs directly adjacent to n, on each side. The reason for excluding these two NBs is that emission lines can be broad enough to be detected in more than one NB at a time, as in many cases of QSO’s Lyα lines (see e.g., Greig et al. 2016). Narrow emission lines can also contribute to more than one NB due to the overlap of the transmission curves of the J-PAS filters.
We chose to set k = 6, so that our 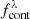 estimate is based on 12 NBs. With this number of NBs, we cover the widest wavelength range possible without contamination of other luminous lines near Lyα (O VI+Lyβ and C IV). We highlight that the seven NBs at the bluest-end of the miniJPAS filter set do not have enough NBs on their bluer side. In these cases we still use the same computation described before, but only with the available filters; this leads to a bias in the line luminosity estimation that will be corrected later on, as detailed in Sect. 4.2.
estimate is based on 12 NBs. With this number of NBs, we cover the widest wavelength range possible without contamination of other luminous lines near Lyα (O VI+Lyβ and C IV). We highlight that the seven NBs at the bluest-end of the miniJPAS filter set do not have enough NBs on their bluer side. In these cases we still use the same computation described before, but only with the available filters; this leads to a bias in the line luminosity estimation that will be corrected later on, as detailed in Sect. 4.2.
We note that by estimating 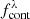 as the average flux around the wavelength of the emission line we are implicitly assuming that the continuum has an antisymmetric shape with respect to that wavelength. However, at bluer wavelengths than the observed λLyα the effect of the Lyman-alpha forest comes into play. The Lyα forest is a series of absorption lines caused by the scattering of the Lyα photons by neutral hydrogen in the inter-galactic medium (IGM; see e.g., Weinberg et al. 2003; Gurung-López et al. 2020). The Lyα forest cannot be resolved through NB photometry, but its overall effect is a significant attenuation of the measured flux in a given band. The effective transmission of the IGM due to the Lyα forest can be approximated with an exponential law,
as the average flux around the wavelength of the emission line we are implicitly assuming that the continuum has an antisymmetric shape with respect to that wavelength. However, at bluer wavelengths than the observed λLyα the effect of the Lyman-alpha forest comes into play. The Lyα forest is a series of absorption lines caused by the scattering of the Lyα photons by neutral hydrogen in the inter-galactic medium (IGM; see e.g., Weinberg et al. 2003; Gurung-López et al. 2020). The Lyα forest cannot be resolved through NB photometry, but its overall effect is a significant attenuation of the measured flux in a given band. The effective transmission of the IGM due to the Lyα forest can be approximated with an exponential law,
with a = −0.001845 and b = 3.924, as found by Faucher-Giguère et al. (2008). Having this in mind, we can compensate the attenuation due to the Lyα forest on our continuum estimate. We do this for each of the NBs i which are at bluer wavelengths than n. In particular, we divide the flux fi by the IGM transmission computed at the central wavelength of the ith NB (λi). That is: ti = TIGM(λi). Then, the continuum flux density is estimated as
where 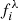 is the flux of the ith NB, σi its associated uncertainty and i ∈ [n−k−1, …, n−2, n+2, …, n+k+1].
is the flux of the ith NB, σi its associated uncertainty and i ∈ [n−k−1, …, n−2, n+2, …, n+k+1].
Correcting for the average IGM transmission allows us to both: (i) improve our continuum estimate and reduce the bias on our Lyα luminosity estimate and (ii) discard low-z contaminants from our selection. Indeed, the latter do not suffer from the Lyα forest effect, therefore our correction produces an artificial over-estimation of their continua. This translates into an under-estimate of their measured EW, pushing these sources out of our selection cut.
4.1.3. LAE candidate selection criteria
After the estimation of the continuum for every source at the central wavelength of every NB, we check every filter for a reliable excess that is compatible with a Lyα emission line. The criteria of this selection are the following:
3σ flux excess. The NB flux density, 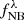 , must show an excess with respect to the continuum
, must show an excess with respect to the continuum 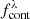 larger than a 3σ confidence interval (see e.g., Bunker et al. 1995; Fujita et al. 2003; Sobral et al. 2009; Bayliss et al. 2011). That is:
larger than a 3σ confidence interval (see e.g., Bunker et al. 1995; Fujita et al. 2003; Sobral et al. 2009; Bayliss et al. 2011). That is:
where σNB and σcont are the uncertainties of the NB and continuum fluxes. When multiple NBs satisfy this condition in one source (either in adjacent or noncontiguous NBs), we consider as a candidate Lyα emission only the NB with the highest measured flux. We adopt this criterion under the assumption that Lyα is the most luminous line in the optical range for z > 2 QSOs, and the only relevant line in the case of SFGs. Then, we assign a redshift zNB assuming λpivot of the detection NB as the observed Lyα wavelength.
Minimum S/N. In addition to the NB-excess significance, we impose a minimum signal-to-noise ratio of S/N > 6 for the NB where we identified the line detection. This ensures that the photometry in the selected filter is clean and reliable. Lowering this threshold significantly increases the number of spurious detections due to random fluctuations of the photometric fluxes.
EW0 cut. Lyα has a large intrinsic EW0 in comparison to other galactic emission lines (Vanden Berk et al. 2001; Nakajima et al. 2018). Many past works have imposed a minimum EW0 in order to reduce the number of contaminants (e.g., Fujita et al. 2003; Gronwall et al. 2007; Ouchi et al. 2008; Santos et al. 2016; Sobral et al. 2018; Spinoso et al. 2020). Following these approaches, we impose: EW0> 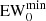 . From the definition of EW we can derive
. From the definition of EW we can derive
where zNB is the Lyα redshift associated with the selected NB. We choose a cut at 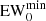 = 30 Å. Lowering the value of
= 30 Å. Lowering the value of 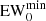 significantly increases contamination without a meaningful increase in completeness.
significantly increases contamination without a meaningful increase in completeness.
Multiple line combinations. Some sources of our catalog show multiple NB excesses compatible with emission lines. The ratios between the observed wavelengths of the multiple lines in a given source can be used to identify contaminants or to confirm true positive LAE detections. Indeed, SFG LAEs are not expected to show relevant line emission features other than Lyα in the rest-frame UV (Nakajima et al. 2018). On the other hand, QSOs are likely to present extra emission lines which can only appear in specific combinations. After the Lyα line search, we check for other NBs with 5σ significant excesses, with an observed equivalent width EWobs > 100 Å. For the detection of these additional lines we estimate the spectral continuum without applying the IGM correction, which is only correct assuming the position of a Lyα line. In particular, we check if these additional flux excesses are compatible with the most prominent QSO lines: O VI, Si IV, C IV, C III] or Mg II (see, e.g., Matthee et al. 2017; Spinoso et al. 2020). The sources showing multiple NB excesses which do not follow a compatible QSO emission pattern are discarded from our LAE candidate sample.
Color cuts. In most cases, the continuum of both QSO and SFG LAEs can be well fitted by a power law (Vanden Berk et al. 2001; Nakajima et al. 2018). Therefore, as shown in Fig. 3, both classes of LAEs are likely to present bluer broad-band colors than the low-z galaxy contaminants. This allows us to define a set of color cuts to remove part of these contaminants. We keep only sources with r − i < 0.6 ∧ g − r < 0.6 when selecting candidates with zLyα < 3. At zLyα > 3 the Lyα forest affects the flux of the g band and this propagates into the expected colors. The color cut at zLyα > 3 is defined as r − i < 0.6 ∧ g − r < 1.5. However, if a source has multiple line detection compatible with QSO lines, this color cut does not apply and the object is classified as a true QSO LAE.
 |
Fig. 3. Color distributions of the selected candidates in our mock before applying the color cut. The objects in the shaded area are removed from the sample after applying the cut. Through these BB color cuts we remove objects showing significant red colors, which are likely to be nearby galaxies. |
4.2. Lyα luminosity estimation
The flux of a NB selected as a Lyα emission-line candidate contains the contribution of both the line flux and the continuum. Therefore, we estimate the Lyα integrated flux as:
This equation implicitly assumes that the NB transmission curve can be reasonably approximated by a squared top-hat filter (as in the case of the J-PAS NBs, see Bonoli et al. 2021). Then, the Lyα luminosity is obtained as
where dL is the luminosity distance corresponding to the Lyα redshift associated to the wavelength of the detection NB, according to our cosmology.
There are several factors that can affect the estimation of LLyα: the variable width of the Lyα line, the uncertain position of the line center with respect to the NB transmission boundaries, the chosen photometric aperture and the uncertainty on the continuum estimate, among others. In addition to that, QSOs often show rather strong N V emission lines (λ 1240 Å) that contaminate the Lyα measurement. While in most spectroscopic surveys it is possible to resolve the Lyα and N V line profiles separately, both lines cannot be disentangled with NB imaging, thus N V significantly affects the Lyα flux measurement in QSOs. As a consequence, our NB-estimated Lyα line flux actually includes the sum of both contributions: FLyα+N V. We account for these biases on our measured LLyα by computing the median offset between the estimated and real values for our mock LAEs (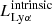 ), as a function of LLyα,
), as a function of LLyα,
This bias is computed in bins of log10(LLyα/erg s−1) and subtracted from the LLyα measurement. Figure 4 shows the measured log10(LLyα/erg s−1) distribution from the mock as a function of the intrinsic luminosity. Since there is no clear way to systematically disentangle QSOs from SFG LAEs in our sample, we apply the same correction indistinctly.
 |
Fig. 4. Contours showing the areas encompassing the 68% and 95% of the LAEs in the mock showing the retrieved (observed) Lyα luminosity as a function of the real value in the catalog. The dotted and solid line contours show the values of LLyα before and after applying the bias subtraction, respectively (see Sect. 4.2). Black dots represent the observational candidates from miniJPAS with a spectroscopic counterpart (see Sect. 4.8). |
4.3. Purity and completeness
We compute the purity P of our mock sample as
and the completeness C as
where TP, FP and FN are the number of true positive, false positive and false negative detections, respectively. After applying the selection method to our mocks, we can estimate the purity and completeness curves of the selected sample for each filter, and for the whole set as a function of LLyα.
In Fig. 5 we show the purity (top panel) and completeness (bottom panel) of our selection method as a function of the Lyα luminosity for the whole sample (r < 24, 2.05 < z < 3.75). We also show the purity and completeness for the 6 bins of redshift used to compute the Lyα LFs. The redshift intervals are composed of groups of 5 NBs, as listed in Table 2. All the redshift bins exhibit a similar behavior: the completeness increases with LLyα, reaching values of ≳75% for log10(LLyα/erg s−1) ≥ 44 for 2 ≲ z ≲ 3.3, and for log10(LLyα/erg s−1) ≥ 44.5 at 3.1 ≤ z ≤ 3.8. The sample purity also increases with LLyα for all redshift bins, with a slight decline for the brightest luminosity in some intervals (see Fig. 5, top panel). The drop in purity at the bright end can be explained by the overestimation of the line luminosity of the contaminants (for example, a C IV emitter at z = 1.7 with log10(LC IV/erg s−1) = 44 will appear to have log10(LC IV/erg s−1) = 44.4 if we assume its redshift to be z = 2.5). This effect is increased by the rather high uncertainties on the line flux measurements in combination with the Eddington bias (Eddington 1913). Interestingly, for z ≳ 2.8 the estimated purity reaches values very close to 1 for the brightest Lyα luminosity. This can be explained by the fact that the potential contaminants in this luminosity regime are QSOs with z > 2 for which the selected feature is the C IV. We note that most of these sources are classified as LAEs at their correct redshift by our selection pipeline.
 |
Fig. 5. Purity and completeness as a function of LLyα of the full retrieved sample at 2.05 < z < 3.75. We show the values of purity and completeness for the whole redshift range in black solid lines, and for each redshift interval used in colored solid lines. We represent an additional redshift interval to show the trend beyond the redshift range probed by this work (dashed line). |
Groups of NBs used in this work for the computation of the Lyα LF, their associated redshift coverage of Lyα, and the comoving volume of the Universe sampled by those redshift intervals for an area of 1.14 deg2.
4.4. 2D purity and number counts correction maps
We apply our selection method (see Sect. 4.1) to the mock in order to characterize its performance as a function of r magnitude and measured LLyα, in terms of purity and number count correction. We build 2D maps of these two quantities over a grid of (r, log10(LLyα/erg s−1)) values, that will be used in the Lyα LF computation.
As a first step, we compute the purity (P2D) of the sample in bins of (Δr, Δlog10LLyα), according to Eq. (12). We consider as true positives the objects detected inside a given interval of (Δr, Δlog10LLyα) with a minimum Lyα EW0 = 30 Å, whose redshift measurement is correct within a confidence interval of Δz = 0.123. As a second step, we define the number counts correction (w2D) as the ratio between the number of eligible LAEs inside a given interval of r and log10(LLyα/erg s−1) and the number of true positives retrieved by the selection inside that interval. This number-counts correction can be seen as the inverse of the completeness as a function of measured LLyα, defined in Eq. (13). Due to the uncertainties on the estimation of LLyα, some bins of this map contain values below 1, meaning that in some regimes we might get a larger number of true positives than the intrinsic number of LAEs.
We show an example of these correction maps in Appendix B. In general terms, the purity of the sample increases with LLyα and r. This is because for a fixed value of LLyα, fainter magnitudes mean larger equivalent widths and therefore, our selection method is more successful in retrieving true LAEs at these regimes. For the brightest magnitudes the purity increases again due to the low relative errors of the photometry, which allow to reliably discern between true positives and contaminants.
4.5. Computation of the Lyα luminosity function
We compute our Lyα LF through several realizations in order to take into account the various sources of uncertainty and variability. At each realization, we perturb the estimated values of LLyα assuming Gaussian errors. Then, every selected LAE candidate is included in the current subsample with a probability based on the 2D purity, that is inferred from the r magnitude and the perturbed log10(LLyα/erg s−1; see Sect. 4.4). For the candidate j, let us define pj as
where ξj is a random number drawn from a uniform distribution in the interval ξj ∈ [0, 1].
Next, each source is weighted with a value wj, computed as
where w2D is the number count correction (as defined in Sect. 4.4) and Cint the intrinsic completeness of the survey. The value of Cint is computed for point-like and extended sources separately in miniJPAS (see Bonoli et al. 2021). This process is done equivalently for J-NEP (see Hernán-Caballero et al. 2023). We assign every LAE candidate a value of Cint using the miniJPAS and J-NEP completeness curves, in terms of r magnitude and the field in which the object was detected. Our target population are LAEs at z > 2, these objects are expected to appear point-like in the BB images of miniJPAS and J-NEP. Hence, we use the intrinsic completeness curves for point-like objects.
Each NB can probe Ly[[INLINE403]] in an effective range of redshift equal to (λNB ± 0.5 ⋅ FWHMNB)/λ0 − 1. The volume (V) considered for the LF is the comoving volume comprised between those redshifts in the survey area, according to our cosmology. Given that the number count of candidates is not large enough to accurately estimate the LF at each NB independently, we combine several NBs to build the LF. The associated redshift range of each group of NBs goes from the minimum z of the bluest filter to the maximum z of the reddest. Adjacent miniJPAS NBs show significant overlap (∼45 Å). As explained in Sect. 4.1.3, in case of multiple line detections in adjacent NBs, we assign the Lyα line to the NB with the highest measured flux. Therefore, the effective volume probed by a single NB in the wavelengths of the overlaps is halved.
The ith iteration of the LF Φi is computed as follows:
where the sum extends to all the objects with a perturbed LLyα falling inside a given luminosity bin. After performing 1000 realizations, our final LF (Φ) is built with the median values of Φi for each luminosity bin.
For estimating the Φ uncertainties we have to take into account the contribution of: (i) the spatial variance of the candidates in the surveyed area (commonly referred to as “cosmic variance”), (ii) the uncertainty of LLyα estimation and (iii) the shot noise of the candidate sample. In order to estimate the contribution of (i), we divide our candidate sample in five subsamples. First, we split the miniJPAS footprint in four regions of equal angular area. Then, the candidates are assigned to four different subsamples according to the split region they belong. The fifth subsample is that of the J-NEP candidates. After that, we perform 1000 realizations of Φi, each time using the candidates of five random subsamples with repetition. On each realization, we resample the candidates of each subsample using the bootstrap technique and we also perturb LLyα as explained above. The final uncertainties on our LFs are inferred via the 16th and 84th percentiles of the Φi distribution.
4.6. Lyα emitters candidate sample
The result of the preliminary selection is a sample of 135 candidates (38, 19, 22, 14 and 34 in AEGIS001, AEGIS002, AEGIS003, AEGIS004 and J-NEP, respectively) with redshifts between 2.05 and 3.75. Eight of these selected candidates were removed immediately after a first visual inspection, because their NB images were clearly affected by cosmic rays or artifacts, leaving a sample of 127 candidates.
In Fig. 6 we show examples of miniJPAS and J-NEP sources in order to illustrate the populations retrieved by our selection method. The five objects on the left Cols. (1–5) are examples of genuine QSO LAEs. Three of them have SDSS/HETDEX spectroscopic confirmation. Candidates 1–4 have secondary QSO line detections that support the Lyα redshift estimation (see Sect. 4.1.3). Candidate 5 lacks spectroscopical confirmation or other QSO line detection, however, through visual inspection we determined the presence of spectral features consistent with QSO emission lines, given the estimated Lyα redshift (O VI+Ly[[INLINE427]], Si IV+O IV, C IV). Candidates 6–9 are examples of QSO contaminants selected because of their strong C IV or C III] emission. In the particular case of candidate 9, our method detects a secondary line consistent with Mg II, given that the selected NB is spectroscopically identified as C III] at z = 1.03. Hence, candidate 9 is effectively not selected by our pipeline. Finally, candidate 10 is an example of a contaminant [O II] emitter. A visual inspection reveals that this candidate shows a relevant feature consistent with H[[INLINE429]] and [O III] emission lines, if we assume the selected NB is [O II] at z = 0.54. Moreover, candidate 10 shows significant emission at bluer wavelengths than its strong emission line at λobs ≈ 5800 Å. Therefore, it is unlikely that this line is Lyα, due to the absence of the expected decrease in flux due to the Lyα forest, and beyond the Lyman limit break at λ0 < 912 Å (λobs ≪ 5800 Å for the assumed Lyα redshift of zLyα = 3.69; see the photometric drop at λobs < 4200 Å in the photospectrum of candidate 3, in the central left panel of Fig. 6).
 |
Fig. 6. Examples of miniJPAS and J-NEP LAE candidates. We show the fluxes of the 56 narrow medium (colored circles) and broad bands (colored squares) of the J-PAS filter set. The NB selected as Lyα by our pipeline is marked with a red dashed line. The detected secondary QSO lines are marked with green dashed lines (see Sect. 4.1.3). Spectroscopically or visually identified emission lines of the objects are shown with a gray dotted line. We also show the images of each source in r and the selected NB. The spectra of the SDSS DR16 (HETDEX) counterparts are shown in gray (orange) when available. The five objects in the left column are examples of LAEs identified by our method. The right column show five examples of possible contaminants. |
4.7. Sample contamination
As discussed in Sect. 3, we expect the interlopers of our selection to be mainly low-z galaxies and z < 2 QSOs. Through the analysis of the selected sample in our mock, we can describe the predicted populations of contaminants.
Due to its typically high intrinsic luminosity, the C IV line is the QSO feature that mainly contributes to the contamination of our samples (see Vanden Berk et al. 2001), followed by C III], and in a lesser amount, Mg II and O VI. This can be clearly seen in Fig. 7, which presents the number of objects in the mock classified as LAEs by our method, as a function of the rest-frame wavelength of the selected feature. This is in line with the results of the spectroscopic follow-up presented in Spinoso et al. (2020), which show that C IV is the main source of contamination for samples of bright, NB-selected, LAE candidates. The contaminants whose NB wavelength does not correspond to any relevant QSO spectral feature are selected because of the scatter of NB fluxes due to random fluctuations. This causes either: (i) the flux of a NB to incidentally exceed our 3σ detection limit or (ii) produce an under-estimation of the continuum.
 |
Fig. 7. Rest-frame wavelength of the selected features in the QSO and low-z galaxy mock. The rest-frame wavelength is computed as λ0 = λNB/(1 + z), where λNB is the central wavelength of the selected NB and z the true redshift of the mock object. |
Regarding low-z galaxy interlopers, Fig. 7 shows that several galaxies are selected as LAE candidates at a redshift which is not associated to any specific emission line, with the exception of a small peak at the [O II] wavelength. Therefore, most of the low-z galaxy contamination can be explained as false line detections caused by noise. On the other hand, many candidates in our observational sample might show extended BB emission, which classifies them as low-z galaxies. These wrongly selected candidates can be easily removed via a posterior visual inspection (see Sect. 4.11).
4.8. Spectroscopic counterparts
We cross-match the miniJPAS and J-NEP catalogs with the spectroscopic catalogs of SDSS DR16 and HETDEX in order to characterize our candidate sample.
4.8.1. Cross-match with SDSS DR16
We cross-match with the SDSS DR16 source catalog (Lyke et al. 2020), using a search radius of 1.5″ among the whole catalog of miniJPAS. As a result, 32 (17 with log10(LLyα/erg s−1) > 44) sources are identified as QSO LAEs by SDSS (i.e., sources with redshift in the range zspec = 2.1–4, no redshift warnings and a significant Lyα measurement). Among these 32 sources, 17 are selected by our method (53%), and 13 out of 17 (76.5%) within the ones with log10(LLyα/erg s−1) > 44. This retrieval rate is in agreement with the completeness estimated by our mock (see Fig. 5), considering the statistical uncertainties and cosmic variance.
4.8.2. Cross-match with HETDEX Public Source Catalog 1
We also cross-match the miniJPAS catalog with the HETDEX Public Source Catalog 1 (Mentuch Cooper et al. 2023). This catalog contains the spectra of 232 650 sources observed by the HETDEX program (Gebhardt et al. 2021) over 25 deg2. The footprint of the HETDEX catalog partly overlaps with miniJPAS. We find 158 objects within a radius of 1.5″ of any miniJPAS source with a reliable spectroscopic redshift measure according to the HETDEX catalog (z_hetdex_conf > 0.9). Among these objects, 22 are labeled as AGNs by HETDEX and 12 have zspec > 2. Within our selection, 10 objects have a HETDEX identification: 9 AGNs and one [O II] emitter. Finally, 5 of the 9 spectroscopically confirmed AGNs have z > 2 and clear Lyα emission line measurements. This numbers translate into a ∼(41 ± 22)% recovery rate of AGNs with z > 2, and a purity of ∼(56 ± 30)%.
Moreover, the cross-match with HETDEX reveals the presence of 17 SFG LAEs (z_hetdex_conf > 0.9) in the dual mode catalogs of miniJPAS. However, none of them is detected in our sample. This is because all these SFG LAEs are too faint both in Lyα luminosity and r magnitude to be selected by our method. Indeed, they all show log10(LLyα/erg s−1) ≲ 43.2 and rSDSS magnitudes close or below the miniJPAS nominal depth (see Table 1). Hence, the signal-to-noise of these sources photometry is overall too low for them to be detected by our selection pipeline.
4.8.3. Spectroscopic characterization of the LAE candidate sample
Within our candidate subsample, we find an SDSS counterpart for 41 out of 127 LAE candidates, all of which are identified as QSOs at any redshift by SDSS. Figure 8 (upper panel) shows the spectroscopic redshift of those candidates with an SDSS or HETDEX counterpart, confirming that z < 2 AGN emitting C IV or C III] (misclassified as Lyα) are the main source of contamination for our pipeline results. There are no spectroscopically confirmed contaminants at zLyα ≥ 3, which is in line with the high-purity we estimate for our samples at these high redshifts (Fig. 5). In the bottom panel of Fig. 8 we show the offsets between the NB Lyα redshift of our candidates and the SDSS spectroscopic redshift. For LAEs at z ∼ 2, the observed Lyα wavelength could lay slightly below the lower limits of our survey. In some of those cases, we still detect the redmost part of the line, often affected by the N V flux. For this reason, we notice a small bias in the measured redshift for LAEs with zspec ≲ 2.1 (see the bottom panel of Fig. 8). At higher redshifts, zNB is a good estimator within the interval of confidence given by the width of the NBs. The mean offset of zNB with respect to zspec is |Δz|≈0.013, about a 20% of the zNB uncertainty.
 |
Fig. 8. Comparison between the NB and spectroscopic redshifts of the candidates. Top: retrieved Lyα redshift of the candidates with SDSS or HETDEX spectrum. The straight lines represent the redshift at which the most common QSO contaminant lines are selected as Lyα. Bottom: difference between the NB Lyα redshift of the good candidates and the spectroscopic redshifts given by SDSS or HETDEX. The error bars show the redshift interval covered by the width of the NB in which the candidate is selected. |
In Fig. 4 we show the comparison between the measured and spectroscopic log10(LLyα/erg s−1) from SDSS DR16Q, compared to mock distributions. This figure shows that the estimation of log10(LLyα/erg s−1) in the spectroscopic subsample of our candidates is consistent with the results in the mock.
4.9. Photometric redshifts
The miniJPAS and J-NEP dual-mode catalogs provide accurate photometric redshifts for galaxies in the interval z = 0–1.5 (Hernán-Caballero et al. 2021, 2023). These photo-z have been obtained using a template-fitting method which employs a sample of 50 galaxy templates. Figure 9 shows the photo-z of the LAE candidates as compared to the redshifts obtained from the NB central wavelengths, assuming that the detected line of a candidate is Lyα. From this figure it is not evident any clear pattern which may help to identify a systematic source of contamination; this is in agreement with the results of the contamination analysis of the mocks, that predicts a rather flat distribution in the selected rest-frame wavelengths of the galactic contaminants, with a small peak in the [O II] line (Fig. 7). On the other hand, the current photo-z code does not account for QSOs, hence they are not useful to confirm QSO LAEs or contaminants; most of the sources with zphot = 1.5 are likely to be QSOs with bad fit of the photo-z. For the same reason, the photo-z values exhibit arbitrary correspondence with the redshifts of our candidates having spectroscopic counterparts. (green filled circles in Fig. 9). Analogously, the photo-z are not useful to confirm SFG LAEs because their redshift (z > 2) is far out of the working range of the miniJPAS photo-z code.
 |
Fig. 9. Retrieved Lyα redshift of the candidates as compared to the miniJPAS photometric redshifts (Hernán-Caballero et al. 2021). We show spectroscopically confirmed LAEs (green filled circles) and contaminants (red empty circles), objects with extended morphology (morph_star_prob < 0.1; blue empty squares), and sources without any spectral or morphology identification (gray crosses). The dashed lines mark the confusion between Lyα and typical galactic emission lines. |
4.10. Morphology cut
We notice that some of our candidates have visually evident extended emission in their BB images. The population of LAEs at z > 2 is expected to appear point-like given the expected observed size of either high-z QSOs or SFG LAEs, and the average PSF of miniJPAS and J-NEP. Hence, the candidates clearly showing BB extended morphologies are very likely to be low-z contaminants. In order to remove this kind of objects from the Lyα LF estimation, we make use of the star-galaxy estimator morph_prob_star (López-Sanjuan et al. 2019), available in the miniJPAS and J-NEP catalogs. We only keep objects with morph_prob_star > 0.1. With this cut we remove 36 extended objects (28.3% of the selected sample), leaving a sample of 91 LAE candidates. To perform such morphology cut in the mock sample is not possible due to the lack of photometric images for the mock sources. However, the corrections for the Lyα LF can be recomputed taking into account the morphology cut, and other posterior catalog cuts (see Sect. 4.11).
On the other hand, LAEs often present NB extended emission in the Lyα observed wavelength (see, e.g., Haardt & Madau 1996; Borisova et al. 2016; Arrigoni Battaia et al. 2016) – not to be confused with extended BB continuum emission. The recent work of Rahna et al. (2022) presented the Lyα extended emission of two miniJPAS QSOs showing double-core Lyα emission (z = 3.218, 3.287); both objects are detected by our pipeline and included in our catalog.
4.11. Visual inspection
We perform a visual inspection of the images and photospectra of the 127 initial candidates. We identify 39 objects in our sample as nearby galaxies either by their extended BB morphology or by their spectral features (e.g., emission lines not detected by our method, the presence of a 4000 Å break etc.), 36 of which are already systematically removed by a cut in morph_prob_star > 0.1 (see Sect. 4.10). Another 21 objects are clearly identified as contaminant QSOs at z < 2. Finally, 32 objects are visually classified as secure QSOs with Lyα emission. The remaining 35 objects do not have a secure classification due to having very noisy continua and/or unclear BB images. We remove the visually confirmed contaminants, leaving a sample of 67 objects. The visual inspection of the candidates is aided by the spectroscopic counterparts of SDSS and HETDEX (Sect. 4.8).
After removing the visually selected contaminants, the purity of the final sample increases. Our mock selection predicts number counts of 53, 23, 59 and 4 deg−2 for QSO LAEs, contaminant QSOs, low-z galaxies and SFG LAEs, respectively, in the effective area of miniJPAS and J-NEP. Hence, we conclude that after a visual inspection, we are able to remove ∼80% of the QSO contaminants and ∼58% of the low-z galactic contaminants. The 35 unidentified objects are consistent with the remaining ∼42% galaxies and the visually unidentified LAEs predicted by our mock selection. These purity estimates are reasonable within the sampling error of our method. We recompute the 2D purity and number count (see Sect. 4.4) of the remaining sample assuming the above fractions of removed galaxy and QSO contaminants. We highlight that the Lyα LFs we present in Sect. 5.2 are estimated using the sample of 67 candidates obtained after our visual inspection of the photospectra and NB images.
4.12. miniJPAS and J-NEP LAEs catalog
In Table 3 we show the number of candidates after applying every cut described in Sect. 4.1.3. The last three columns of this table display the number of candidates in three relevant subsamples for this work with, respectively: 127, 91 and 67 candidates. The first subsample is the direct result of applying the selection method to the miniJPAS and J-NEP catalogs, before the morphology cut. This first subsample will be used throughout Sect. 5 to compare with the mock results. The second subsample, composed of 91 candidates, is obtained after applying the morphology cut to the previous one. In Table A.1 we provide the catalog of sources in this subsample. Finally, we obtain the third subsample of 67 candidates, after performing a cross-match with available spectroscopic surveys and a visual inspection for further contamination removal. Nonetheless, in future J-PAS observations the available spectroscopic data can be limited. Also the volume of data can be large enough to make a visual inspection of all the candidates not feasible. The sample presented in Table A.1 could therefore be intended as representative of what can be statistically obtained from any J-PAS dataset.
5. Results and discussion
In this section, we describe the relevant features of the LAE candidate sample and we present the Lyα LF. We also fit our Lyα LF to a Schechter function and a power-law and give an estimation of the AGN/SFG fraction as a function of Lyα luminosity. Finally, we discuss the expected performance of the method described through this work in future data releases of J-PAS.
5.1. EW0 distribution
We obtain the rest-frame Lyα EW from the measured FLyα, following Eq. (3). As stated in Sect. 4.1.3, one of the criteria of our candidates selection is a cut in Lyα EW0 > 30 Å. However, the additional conditions on the NB-photometry S/N and on the line-excess significance (see Sect. 4.1.3) can override the condition on EW0, effectively forcing a higher EW0 limit (especially for faint sources and shallow NBs).
The distribution of EW0 retrieved from our 127 candidates sample (before applying the morphology cut, in order to match the mock; see Sect. 4.12) is shown in Fig. 10. The miniJPAS and J-NEP Lyα EW0 distribution (orange dashed line) is in good agreement with the one resulting from applying our selection pipeline to our mock data (gray dashed line).
 |
Fig. 10. Distribution of Lyα EW0 of the candidate sample of miniJPAS and J-NEP. We compare the whole sample of candidates retrieved by our method in the mock (gray, dashed histogram) and in the observational data (orange, dashed histogram). We also compare the distribution of Lyα EW0 for the mock subsample of true-positive LAEs (solid, black histogram) and the visually inspected subsample of miniJPAS and J-NEP (solid, red histogram) as defined in Sect. 4.11. For |
Figure 10 also shows that the selected objects with  , are likely to be genuine LAEs, as the distribution of mock-LAEs (black solid line) becomes closely comparable to the whole mock sample. Moreover, the EW0 distribution of the selected LAEs in our mock is remarkably close to that of the observational sources visually classified as LAEs. Our retrieved Lyα EW0 distribution is also compatible with the determinations of Spinoso et al. (2020) and Liu et al. (2022a) for Lyα lines of QSOs with z ∼ 2–3.5. All of our candidates are inside the range EW0 = 30–400 Å except for one candidate with an extremely large EW0 of 2379 ± 278 Å. However, this candidate has r = 23.8, very close to the detection limit and the estimation of its continuum flux under the Lyα line is likely to be underestimated (and its error overestimated). Furthermore, despite being in our selection, the purity assigned to this candidate by our method is P2D = 0, making it irrelevant for the Lyα LF estimation.
, are likely to be genuine LAEs, as the distribution of mock-LAEs (black solid line) becomes closely comparable to the whole mock sample. Moreover, the EW0 distribution of the selected LAEs in our mock is remarkably close to that of the observational sources visually classified as LAEs. Our retrieved Lyα EW0 distribution is also compatible with the determinations of Spinoso et al. (2020) and Liu et al. (2022a) for Lyα lines of QSOs with z ∼ 2–3.5. All of our candidates are inside the range EW0 = 30–400 Å except for one candidate with an extremely large EW0 of 2379 ± 278 Å. However, this candidate has r = 23.8, very close to the detection limit and the estimation of its continuum flux under the Lyα line is likely to be underestimated (and its error overestimated). Furthermore, despite being in our selection, the purity assigned to this candidate by our method is P2D = 0, making it irrelevant for the Lyα LF estimation.
5.2. Lyα Luminosity Functions
We compute the Lyα LF for every redshift interval listed in Table 2 through the procedure explained in Sect. 4.5. We use the candidate sample of 67 objects obtained after the visual inspection (see Sect. 4.11). Using this configuration, the full redshift range at which we probe the Lyα LF is 2.05 < z < 3.75. For z ≳ 3.8, the available QSO data in the SDSS DR16 starts to become scarce, thus limiting the effectiveness of our mock to compute the LF corrections (see Sect. 3.3). Furthermore, the completeness of our sample drops drastically for z ≳ 3.5 (see Fig. 5). With the miniJPAS and J-NEP dataset we are able to estimate the Lyα LF in the intermediate luminosity regime (43.5 ≳ log10(LLyα/erg s−1) ≲ 44.5). This is the regime where the contribution of Lyα emitting AGN begins to produce a clear deviation from a Schechter exponential decay of the Lyα LF (see e.g., Konno et al. 2016; Sobral et al. 2018; Zhang et al. 2021). Our analysis at the faint end of the LF is limited by the depth of miniJPAS and J-NEP (i.e., r ∼ 24 at 5σ), while at the bright end (log10(LLyα/erg s−1) ∼ 45) our results are limited by low number counts and cosmic variance. In this regime, the determinations of Zhang et al. (2021) and Liu et al. (2022b) present an exponential decay.
As we explained in Sect. 4.11, we confidently remove ∼75% and ∼100% of the contaminants coming from low-z galaxies and QSOs, respectively. For the estimation of the Lyα LFs, we remove the securely identified contaminants from the candidate sample, and correct the 2D purity estimates according to the fraction of contaminants withdrawn after visual inspection.
5.2.1. Evolution of the Lyα LF with redshift
We stress that the necessity to group NBs in order to increase the number counts in each z bin is only due to the small area surveyed by miniJPAS. On the other hand, we expect that our method will be able to produce a reliable LF determination for each NB as soon as a wide-enough area of the J-PAS survey will be observed. This upcoming possibility will allow to study the Lyα LF evolution with an unprecedented redshift detail. Therefore, the results presented in the following may be regarded as a proof of concept for these kind of tomographic analysis of the Lyα LF (further discussion in Sect. 5.4).
In Fig. 11 we show the Lyα luminosity functions for different bins of redshift, ranging from z = 2.05 to z = 3.75. We compare our Lyα LF estimates to previous determinations in the literature. Several works explore the faint and intermediate regime of the Lyα LF (43.3 < log10(LLyα/erg s−1) < 44), at the transition between the population of SFG and AGN LAEs (Ouchi et al. 2008; Blanc et al. 2011; Konno et al. 2016; Sobral et al. 2017; Matthee et al. 2017). Our measurements of the Lyα LF at every redshift interval is compatible with all of these works.
 |
Fig. 11. Lyα LFs for six intervals in redshift. We show the full redshift range power-law fit for reference (dashed red line). The redshift bins showed in this figure overlap and are therefore correlated. The Lyα LF shows no significant evolution with redshift within the given uncertainties. |
Our data do not show evidence of evolution with redshift of the Lyα LF within the given uncertainties. In Fig. 12 we show the integral in the range 43.6 < log10(LLyα/erg s−1) < 44.8 of the Lyα LFs estimated for each of the six intervals in redshift. The integral is computed as the sum of the LF bins multiplied by the width of the bins.
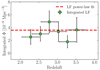 |
Fig. 12. Integrated LFs in 43.6 < log10(LLyα/erg s−1) < 44.8 in the six intervals of redshift shown in Fig. 11. The chosen LLyα interval is that where all six realizations of the Lyα LF are well defined. The horizontal error bars represent the width of the redshift interval. The dashed red line represents the integral of the best power-law fit presented in Sect. 5.2.2. |
We also estimate the Lyα LF in the full redshift range covered by our selection. Figure 13 shows the Lyα LF computed through the usual procedure (see Sect. 4.5) but using all the realizations of the LF of every redshift bin. We compare our results to three past realizations of the Lyα LF which cover similar redshift ranges (i.e., Blanc et al. 2011; Zhang et al. 2021; Liu et al. 2022b).
 |
Fig. 13. Lyα LF over the whole 2.05 < z < 3.75 range (red squares and black error bars), obtained by combining data from all the NBs we employ. Our estimation covers the intermediate regime of the Lyα LF, where the transition between the SFG and the QSO populations is expected. |
5.2.2. Schechter function and power-law fits
We use an MCMC algorithm in order to constrain the three parameters of a Schechter function,
namely: the normalization Φ*, the characteristic Lyα luminosity L* and the faint-end slope α. As already discussed in Sect. 5.2, our ability to reliably sample the bright end of the Lyα LF is limited by the surveyed area. Our data can measure the Lyα LF up to log10(LC IV/erg s−1) ∼ 44.5. Past works have shown that at higher luminosity than this, the Lyα LF shows significant deviations from a simple power-law, either in the form of a Schechter exponential decay, or a “broken power law” (see Spinoso et al. 2020; Zhang et al. 2021; Liu et al. 2022b). Due to this limitation, we use a gaussian with μ = 44.65 and σ = 0.7 as prior distribution for L*, based on the results of Spinoso et al. (2020) and Zhang et al. (2021). We use wide, flat priors for the parameters Φ* and α. We obtain a best fitting Schechter function with 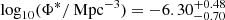 ,
, 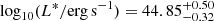 and
and 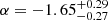 . Our constraints on the Schechter parameters are compatible within 1σ to those found by Spinoso et al. (2020; see Table 4). Our results are as well compatible within 1σ with the analog values obtained by Zhang et al. (2021) fitting the AGN Lyα LF to a double power-law (DPL). In left panel of Fig. 14 we show our Schechter fit and compare it to the fits in Spinoso et al. (2020) for four NBs of J-PLUS.
. Our constraints on the Schechter parameters are compatible within 1σ to those found by Spinoso et al. (2020; see Table 4). Our results are as well compatible within 1σ with the analog values obtained by Zhang et al. (2021) fitting the AGN Lyα LF to a double power-law (DPL). In left panel of Fig. 14 we show our Schechter fit and compare it to the fits in Spinoso et al. (2020) for four NBs of J-PLUS.
 |
Fig. 14. Schechter and power-law fits of the 2.05 < z < 3.75 Lyα LF. Left panel: Schechter best fit and 1σ confidence region for the fit of the full z range of this work (blue solid line and shaded area). We compare our result with the Schechter fits in Spinoso et al. (2020) for 4 NBs of J-PLUS. Our Schechter fit is in line with the fits in Spinoso et al. (2020) for z = 2.2, 2.5 and 3.2 at the faintest bins of our LF. We advise some caution when considering our results at the brightest luminosity (i.e., log10(LLyα/erg s−1) > 45.5). Indeed our results in this regime are limited by our survey area. Right panel: power-law fit to our Lyα LF at log10(LLyα/erg s−1) < 45.5. The bins of the LF represented with empty squares are not used in this fit in particular. We compare to the power-law fits in Matthee et al. (2017), Sobral et al. (2018) in the same LLyα regime. The shaded blue area marks the 1σ confidence region. Our constraint on the power-law slope A for the faint-end of the AGN Lyα LF is consistent with the other realizations shown in this plot within a 1σ confidence interval. |
Fit parameters obtained for the QSO/AGN Lyα LF in the literature.
The LF estimated by our data in the full redshift range is better described by a power-law. This can be interpreted as our data representing the faint-end of a Schechter function for the QSO/AGN component of the global Lyα LF4. We fit our Lyα LF for log10(LLyα/erg s−1) < 45.5 to a power-law of the form:
We obtain the following results for the power-law fit: 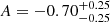 ,
, 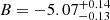 . Past works that have fitted a power law in the same regime of the AGN Lyα LF, obtaining: A = −0.74 ± 0.17, Matthee et al. (2017); and A = −0.75 ± 0.17, Sobral et al. (2018). Our estimation of the power-law slope A, is consistent with these past realizations.
. Past works that have fitted a power law in the same regime of the AGN Lyα LF, obtaining: A = −0.74 ± 0.17, Matthee et al. (2017); and A = −0.75 ± 0.17, Sobral et al. (2018). Our estimation of the power-law slope A, is consistent with these past realizations.
5.3. QSO/AGN fraction
Figure 15 shows the fraction of AGN within the sample of sources with r < 23 extracted from our mock data (blue solid line). At log10(LLyα/erg s−1) ≳ 43.75 the fraction of AGN is greater than ∼90%. This is in line with past works which analyzed high-z samples of bright LAEs and found that the AGN fraction approaches to 100% at log10(LLyα/erg s−1) ≳ 44 (e.g., Matthee et al. 2017; Wold et al. 2014; Sobral et al. 2018; Calhau et al. 2020). By considering the depth of the miniJPAS and J-NEP observations, we conclude that our analysis can primarily focus on the luminosity range log10(LLyα/erg s−1) > 43, where the class of AGN is expected to be numerically dominant. Hence, if we assume that our power-law fit (see Sect. 5.2.2) describes a regime of the Lyα LF populated entirely by QSOs, we can compute the intrinsic QSO fraction assuming that the SFG population is well described by the Lyα LF presented in Sobral et al. (2018), which is measured in the range 42.5 < log10(LLyα/erg s−1) < 44 using a sample of ∼3700 LAEs showing no X-ray emission. This result is shown as the green solid line in Fig. 15. The estimated intrinsic QSO fraction drops faster than the fraction in our candidate sample at log10(LLyα/erg s−1) ∼ 43.75. This happens because SFGs typically have fainter continua, thus their detection is limited by the magnitude cut of our selection pipeline (r = 24).
 |
Fig. 15. Fraction of QSOs in the candidate sample from the mock at 2.05 < z < 3.75. We represent our estimation of the QSO fraction (green solid line and green shaded area for 1σ uncertainty) based on the power-law fit to our Lyα LF and the SFG Lyα LF of Sobral et al. (2018). We also show the QSO fraction extracted from our mocks (blue solid line). We compare our results to previous realizations from past works. |
Nevertheless, our results can also populate the intermediate luminosity regime of 43.5 ≲ log10(LLyα/erg s−1) ≲ 44.5 which, to date, it is yet relatively unexplored (see e.g., Zhang et al. 2021; Liu et al. 2022b). At this “intermediate” luminosity, bright SFG LAEs may still produce some minor contribution to the Lyα LF. Consequently, we can speculate that our candidate samples contain a small fraction of SFGs. Nevertheless, systematic spectroscopic confirmation of our selected sources would be necessary to draw a definitive conclusion about this point.
5.4. Expected results in J-PAS
With the eventual release of the full J-PAS dataset, there will be a significantly larger source catalog available with very similar features to the one of miniJPAS and J-NEP. Therefore, an analogous method to the one described in this work could be applied to the complete J-PAS dataset to build the Lyα LF. The target depth for J-PAS is expected to be slightly shallower than miniJPAS and J-NEP, yet a much larger dataset will allow to describe the SFG-AGN transition of the Lyα LF with better statistics. As to the bright end, in this work we are limited by the intrinsic scarcity of extremely bright objects in Lyα. In other words, due to the small area sampled by miniJPAS and J-NEP, our LF at log10(LLyα/erg s−1) > 44.5 is dominated by shot noise and cosmic variance. On the other hand, a larger dataset will allow to estimate the Lyα LF for every individual NB of the filter set. This has the potential to provide a precise and tomographic analysis of the Lyα LF evolution with redshift.
Our work provides the means to infer the expected results for the first hundreds of square degrees of observed J-PAS data. By integrating the power-law fit of our Lyα LF (see Sect. 5.2.2), we obtain a predicted number count of 72 ± 25 deg−2 of LAEs in the range 43.5 < log10(LLyα/erg s−1) < 44.5 at 2.05 < z < 3.75. The mean recovery rate of our method in this range is C ∼ 60%. This results translate into ∼4300 recovered LAEs for the first 100 deg2, and ∼3.7 × 105 in the full 8500 deg2 expected at the completion of the J-PAS survey. On the other hand, our work cannot reliably provide a direct estimate for the number count of objects with log10(LLyα/erg s−1) > 44.5. Therefore, for the analysis of the Lyα LF bright end, we integrate the best Schechter fit of Spinoso et al. (2020). At this bright regime, the exponential decay component of the Schechter function dominates, rapidly decreasing the number of available candidates with increasing LLyα. The predicted number count of QSOs with Lyα emission is ∼24.5 deg−2 for log10(LLyα/erg s−1) > 44.5 and ∼1.7 deg−2 for log10(LLyα/erg s−1) > 45. We define the upper limit  as the maximum Lyα luminosity for which the predicted average number of candidates with
as the maximum Lyα luminosity for which the predicted average number of candidates with  in a given survey area is > 1 (at 2.05 < z < 3.75). For 1 deg2, this limit is
in a given survey area is > 1 (at 2.05 < z < 3.75). For 1 deg2, this limit is 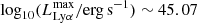 , consistent with our candidate sample. This limit increases to
, consistent with our candidate sample. This limit increases to 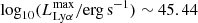 over 100 deg2,
over 100 deg2, 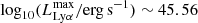 over 1000 deg2, and
over 1000 deg2, and 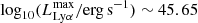 over 8500 deg2. At this bright-end regime, the estimated completeness of our method is C ≳ 80% (see Sect. 4.3).
over 8500 deg2. At this bright-end regime, the estimated completeness of our method is C ≳ 80% (see Sect. 4.3).
Furthermore, as stated before, an increase in the volume of data will allow to measure the Lyα LF in smaller bins of redshift. For example, with the release of the first 100 deg2 of J-PAS, it will be possible to estimate the Lyα LF for each individual NB up to z ∼ 4 (in intervals of Δz ∼ 0.12) with 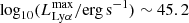 (
(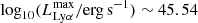 for 8500 deg2). This will provide a remarkable measurement of the Lyα LF evolution with redshift.
for 8500 deg2). This will provide a remarkable measurement of the Lyα LF evolution with redshift.
6. Summary
For this work we developed a method to detect sources with Lyα emission within the J-PAS filter system, and applied it to the J-PAS pathfinder surveys – miniJPAS and J-NEP – in order to estimate the Lyα LF in the redshift range 2.05 < z < 3.75. We summarize our main results below.
First, we built a mock catalog of LAEs and their contaminants in order to test and calibrate the accuracy of our LAE selection method, as well as to compute the corrections needed to estimate the Lyα LF. The mock is composed of four populations: (i) QSOs with z > 2, which are potential LAE candidates; (ii) QSO interlopers, that is, z < 2 QSOs detected via strong emission lines that are different from Lyα; (iii) SFG LAEs at z > 2; and (iv) low-z galaxies (0 < z < 2). By studying the performance of our selection method on our mock, we were able to build 2D maps of purity and number count corrections in terms of the LLyα- and r-band magnitude (see Fig. B.1). These 2D maps were used in order to compute the corrections for the Lyα LF estimate.
Our method retrieved a sample of 127 LAE candidates with 2.05 < z < 3.75. From our mock, we show that our sample is > 75% complete and > 60% pure at log10(LLyα/erg s−1) ≳ 43.75. This sample was obtained from a total effective area of ∼1.14 deg2. Through a visual inspection of the NB images and photospectra, we confirm 32 candidates as QSO LAEs, 39 as low-z galaxies, and 21 as QSOs with z < 2. The remaining 35 candidates are left with no visual classification.
Using the data from our LAE candidate sample (32 visually confirmed QSO LAEs and 35 candidates with no clear visual identification), we were able to determine the Lyα LF in the intermediate-bright luminosity range (43.5 ≲ log10(LLyα/erg s−1) ≲ 45). At the faint end of this regime, we are limited by the depth of our survey (r ∼ 24 at 5σ), while at the brightest end we are limited by the survey area.
We fit Schechter function and power-law models to our estimated Lyα LF in the whole redshift range used in this work: 2.05 < z < 3.75. The resulting Schechter parameters are as follows: 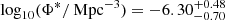 ,
,  , and
, and  . The LF at log10(LLyα/erg s−1) < 44.5 is fitted to a power law of the form A · (log10(LLyα/erg s−1) − 4.35) + B with
. The LF at log10(LLyα/erg s−1) < 44.5 is fitted to a power law of the form A · (log10(LLyα/erg s−1) − 4.35) + B with 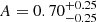 and
and 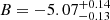 . These parameters are compatible with previous results and show the potential of our method when the larger survey area of J-PAS will be available.
. These parameters are compatible with previous results and show the potential of our method when the larger survey area of J-PAS will be available.
Finally, we give predictions about the performance of the method in the eventual release of the J-PAS data. With the completion of the first hundreds of square degrees of J-PAS, it will already be possible to resolve the Lyα LF in redshift bins of Δz = 0.12 in the luminosity interval 43.5 ≲ log10(LLyα/erg s−1) ≲ 45. This achievement will allow the evolution of the Lyα AGN LF to be studied with redshift with unprecedented precision.
For the fit we use the Python package emcee (Foreman-Mackey et al. 2013).
Acknowledgments
We thank the anonymous scientific referee for their useful comments that have helped to refine the final version of the manuscript. We thank Mirjana Pović for insightful discussion on the results of this work. This work has been funded by project PID2019-109592GBI00/AEI/10.13039/501100011033 from the Spanish Ministerio de Ciencia e Innovación (MCIN)-Agencia Estatal de Investigación, by the Project of Excellence Prometeo/2020/085 from the Conselleria d’Innovació Universitats, Ciència i Societat Digital de la Generalitat Valenciana. The authors acknowledge the financial support from the MCIN with funding from the European Union NextGenerationEU and Generalitat Valenciana in the call Programa de Planes Complementarios de I+D+i (PRTR 2022). Project (VAL-JPAS), reference ASFAE/2022/025. D.S. acknowledges funding from National Key R&D Program of China (grant no. 2018YFA0404503), the National Science Foundation of China (grant no. 12073014), the science research grants from the China Manned Space Project with no. CMS-CSST2021-A05 and Tsinghua University Initiative Scientific Research Program (no. 20223080023). R.G.D. acknowledges financial support from the grant CEX2021-001131-S funded by MCIN/AEI/10.13039/501100011033 and PID2019-109067-GB100. I.M. acknowledges financial support from the Severo Ochoa grant CEX2021-001131-S funded by MCIN/AEI/10.13039/501100011033 and PID2019-106027GB-C41. This work is based on observations made with the JST250 telescope and PathFinder camera for Mini J-PAS project at the Observatorio Astrofísico de Javalambre, in Teruel, owned, managed and operated by the Centro de Estudios de Física del Cosmos de Aragón. We acknowledge the OAJ Data Processing and Archiving Unit (UPAD) for reducing and calibrating the OAJ data used in this work. Funding for the J-PAS Project has been provided by the Governments of Spain and Aragón through the Fondo de Inversión de Teruel, European FEDER funding and the Spanish Ministry of Science, Innovation and Universities, and by the Brazilian agencies FINEP, FAPESP, FAPERJ and by the National Observatory of Brazil. Additional funding was also provided by the Tartu Observatory and by the J-PAS Chinese Astronomical Consortium. Funding for the Sloan Digital Sky Survey V has been provided by the Alfred P. Sloan Foundation, the Heising-Simons Foundation, the National Science Foundation, and the Participating Institutions. SDSS acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org. SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration, including the Carnegie Institution for Science, Chilean National Time Allocation Committee (CNTAC) ratified researchers, the Gotham Participation Group, Harvard University, Heidelberg University, The Johns Hopkins University, L’Ecole polytechnique fédérale de Lausanne (EPFL), Leibniz-Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Extraterrestrische Physik (MPE), Nanjing University, National Astronomical Observatories of China (NAOC), New Mexico State University, The Ohio State University, Pennsylvania State University, Smithsonian Astrophysical Observatory, Space Telescope Science Institute (STScI), the Stellar Astrophysics Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Illinois at Urbana-Champaign, University of Toronto, University of Utah, University of Virginia, Yale University, and Yunnan University. HETDEX is led by the University of Texas at Austin McDonald Observatory and Department of Astronomy with participation from the Ludwig-Maximilians-Universität München, Max-Planck-Institut für Extraterrestrische Physik (MPE), Leibniz-Institut für Astrophysik Potsdam (AIP), Texas A&M University, Pennsylvania State University, Institut für Astrophysik Göttingen, The University of Oxford, Max-Planck-Institut für Astrophysik (MPA), The University of Tokyo and Missouri University of Science and Technology. Observations for HETDEX were obtained with the Hobby-Eberly Telescope (HET), which is a joint project of the University of Texas at Austin, the Pennsylvania State University, Ludwig-Maximilians-Universität München, and Georg-August-Universität Göttingen. The HET is named in honor of its principal benefactors, William P. Hobby and Robert E. Eberly. The Visible Integral-field Replicable Unit Spectrograph (VIRUS) was used for HETDEX observations. VIRUS is a joint project of the University of Texas at Austin, Leibniz-Institut für Astrophysik Potsdam (AIP), Texas A&M University, Max-Planck-Institut fürExtraterrestrische Physik (MPE), Ludwig-Maximilians-Universität München, Pennsylvania State University, Institut für Astrophysik Göttingen, University of Oxford, and the Max-Planck-Institut fur Astrophysik (MPA). Funding for HETDEX has been provided by the partner institutions, the National Science Foundation, the State of Texas, the US Air Force, and by generous support from private individuals and foundations.
References
- Abramo, L. R., Strauss, M. A., Lima, M., et al. 2012, MNRAS, 423, 3251 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, J. J., Blanc, G. A., Hill, G. J., et al. 2011, ApJS, 192, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Arrabal Haro, P., Rodríguez Espinosa, J. M., Muñoz-Tuñón, C., et al. 2020, MNRAS, 495, 1807 [NASA ADS] [CrossRef] [Google Scholar]
- Arrigoni Battaia, F., Hennawi, J. F., Cantalupo, S., & Prochaska, J. X. 2016, ApJ, 829, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Bacon, R., Brinchmann, J., Richard, J., et al. 2015, A&A, 575, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baqui, P. O., Marra, V., Casarini, L., et al. 2021, A&A, 645, A87 [EDP Sciences] [Google Scholar]
- Bayliss, K. D., McMahon, R. G., Venemans, B. P., Ryan-Weber, E. V., & Lewis, J. R. 2011, MNRAS, 413, 2883 [NASA ADS] [CrossRef] [Google Scholar]
- Benitez, N., Dupke, R., Moles, M., et al. 2014, ArXiv e-prints [arXiv:1403.5237] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanc, G. A., Adams, J. J., Gebhardt, K., et al. 2011, ApJ, 736, 31 [CrossRef] [Google Scholar]
- Blanton, M. R., Bershady, M. A., Abolfathi, B., et al. 2017, AJ, 154, 28 [Google Scholar]
- Bonoli, S., Marín-Franch, A., Varela, J., et al. 2021, A&A, 653, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borisova, E., Cantalupo, S., Lilly, S. J., et al. 2016, ApJ, 831, 39 [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2012, ApJ, 752, L5 [Google Scholar]
- Bridge, C. R., Blain, A., Borys, C. J. K., et al. 2013, ApJ, 769, 91 [Google Scholar]
- Brownson, S., Maiolino, R., Tazzari, M., Carniani, S., & Henden, N. 2019, MNRAS, 490, 5134 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Bunker, A. J., Warren, S. J., Hewett, P. C., & Clements, D. L. 1995, MNRAS, 273, 513 [Google Scholar]
- Calhau, J., Sobral, D., Santos, S., et al. 2020, MNRAS, 493, 3341 [Google Scholar]
- Cassata, P., Le Fèvre, O., Garilli, B., et al. 2011, A&A, 525, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassata, P., Tasca, L. A. M., Le Fèvre, O., et al. 2015, A&A, 573, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cenarro, A. J., Moles, M., Cristóbal-Hornillos, D., et al. 2019, A&A, 622, A176 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charlot, S., & Fall, S. M. 1993, ApJ, 415, 580 [Google Scholar]
- Ciardullo, R., Gronwall, C., Wolf, C., et al. 2012, ApJ, 744, 110 [CrossRef] [Google Scholar]
- Clément, B., Cuby, J. G., Courbin, F., et al. 2012, A&A, 538, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowie, L. L., & Hu, E. M. 1998, AJ, 115, 1319 [Google Scholar]
- Davis, M., Guhathakurta, P., Konidaris, N. P., et al. 2007, ApJ, 660, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, D., Gebhardt, K., Cooper, E. M., et al. 2023, ApJ, 946, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Dayal, P., Volonteri, M., Choudhury, T. R., et al. 2020, MNRAS, 495, 3065 [Google Scholar]
- Dijkstra, M. 2016, Astrophys. Space Sci. Lib., 423, 145 [CrossRef] [Google Scholar]
- Drake, A. B., Garel, T., Wisotzki, L., et al. 2017, A&A, 608, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eddington, A. S. 1913, MNRAS, 73, 359 [Google Scholar]
- Faucher-Giguère, C.-A., Prochaska, J. X., Lidz, A., Hernquist, L., & Zaldarriaga, M. 2008, ApJ, 681, 831 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Fujita, S. S., Ajiki, M., Shioya, Y., et al. 2003, AJ, 125, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gawiser, E., Francke, H., Lai, K., et al. 2007, ApJ, 671, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Mentuch Cooper, E., Ciardullo, R., et al. 2021, ApJ, 923, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Giallongo, E., Grazian, A., Fiore, F., et al. 2015, A&A, 578, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González Delgado, R. M., Díaz-García, L. A., de Amorim, A., et al. 2021, A&A, 649, A79 [Google Scholar]
- Greig, B., Mesinger, A., McGreer, I. D., Gallerani, S., & Haiman, Z. 2016, MNRAS, 466, 1814 [Google Scholar]
- Gronwall, C., Ciardullo, R., Hickey, T., et al. 2007, ApJ, 667, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Guaita, L., Gawiser, E., Padilla, N., et al. 2010, ApJ, 714, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Guaita, L., Acquaviva, V., Padilla, N., et al. 2011, ApJ, 733, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., White, S., Boylan-Kolchin, M., et al. 2011, MNRAS, 413, 101 [Google Scholar]
- Gurung-López, S., Orsi, Á. A., Bonoli, S., et al. 2020, MNRAS, 491, 3266 [Google Scholar]
- Gurung-López, S., Gronke, M., Saito, S., Bonoli, S., & Orsi, Á. A. 2022, MNRAS, 510, 4525 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Madau, P. 1996, ApJ, 461, 20 [Google Scholar]
- Hasinger, G., Miyaji, T., & Schmidt, M. 2005, A&A, 441, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hassan, S., Davé, R., Mitra, S., et al. 2018, MNRAS, 473, 227 [Google Scholar]
- Henriques, B. M. B., White, S. D. M., Thomas, P. A., et al. 2015, MNRAS, 451, 2663 [Google Scholar]
- Hernán-Caballero, A., Varela, J., López-Sanjuan, C., et al. 2021, A&A, 654, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernán-Caballero, A., Willmer, C. N. A., Varela, J., et al. 2023, A&A, 671, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hu, E. M., Cowie, L. L., & McMahon, R. G. 1998, ApJ, 502, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias-Páramo, J., Arroyo, A., Kehrig, C., et al. 2022, A&A, 665, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izquierdo-Villalba, D., Angulo, R. E., Orsi, A., et al. 2019, A&A, 631, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jansen, R. A., & Windhorst, R. A. 2018, PASP, 130, 124001 [CrossRef] [Google Scholar]
- Jaskot, A. E., & Oey, M. S. 2014, ApJ, 791, L19 [Google Scholar]
- Jin, S., Wang, J., Kong, M. Z., et al. 2023, ApJ, 950, 16 [CrossRef] [Google Scholar]
- Karman, W., Caputi, K. I., Grillo, C., et al. 2015, A&A, 574, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kashikawa, N., Shimasaku, K., Malkan, M. A., et al. 2006, ApJ, 648, 7 [Google Scholar]
- Kerutt, J., Wisotzki, L., Verhamme, A., et al. 2022, A&A, 659, A183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khostovan, A. A., Sobral, D., Mobasher, B., et al. 2019, MNRAS, 489, 555 [Google Scholar]
- Konno, A., Ouchi, M., Nakajima, K., et al. 2016, ApJ, 823, 20 [Google Scholar]
- Konno, A., Ouchi, M., Shibuya, T., et al. 2018, PASJ, 70, S16 [Google Scholar]
- Laur, J., Tempel, E., Tamm, A., et al. 2022, A&A, 668, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levesque, E. M., Kewley, L. J., & Larson, K. L. 2010, AJ, 139, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, C., Gebhardt, K., Cooper, E. M., et al. 2022a, ApJS, 261, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, C., Gebhardt, K., Cooper, E. M., et al. 2022b, ApJ, 935, 132 [CrossRef] [Google Scholar]
- López-Sanjuan, C., Vázquez Ramió, H., Varela, J., et al. 2019, A&A, 622, A177 [Google Scholar]
- Lyke, B. W., Higley, A. N., McLane, J. N., et al. 2020, ApJS, 250, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, S., & Rhoads, J. E. 2004, ApJ, 617, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Marín-Franch, A., Taylor, K., Santoro, F. G., et al. 2017, in Highlights on Spanish Astrophysics IX, eds. S. Arribas, A. Alonso-Herrero, F. Figueras, C. Hernández-Monteagudo, A. Sánchez-Lavega, & S. Pérez-Hoyos, 670 [Google Scholar]
- Martin, C. L., & Sawicki, M. 2004, ApJ, 603, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Solaeche, G., González Delgado, R. M., García-Benito, R., et al. 2021, A&A, 647, A158 [EDP Sciences] [Google Scholar]
- Martínez-Solaeche, G., González Delgado, R. M., García-Benito, R., et al. 2022, A&A, 661, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matthee, J., Sobral, D., Santos, S., et al. 2015, MNRAS, 451, 400 [Google Scholar]
- Matthee, J., Sobral, D., Best, P., et al. 2017, MNRAS, 471, 629 [NASA ADS] [CrossRef] [Google Scholar]
- McCarron, A. P., Finkelstein, S. L., Chavez Ortiz, O. A., et al. 2022, ApJ, 936, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Mentuch Cooper, E., Gebhardt, K., Davis, D., et al. 2023, ApJ, 943, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Mezcua, M., Suh, H., & Civano, F. 2019, MNRAS, 488, 685 [Google Scholar]
- Miyaji, T., Hasinger, G., Salvato, M., et al. 2015, ApJ, 804, 104 [Google Scholar]
- Nakajima, K., & Ouchi, M. 2014, MNRAS, 442, 900 [Google Scholar]
- Nakajima, K., Fletcher, T., Ellis, R. S., Robertson, B. E., & Iwata, I. 2018, MNRAS, 477, 2098 [NASA ADS] [CrossRef] [Google Scholar]
- Ning, Y., Jiang, L., Zheng, Z.-Y., & Wu, J. 2022, ApJ, 926, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Ono, Y., Itoh, R., Shibuya, T., et al. 2021, ApJ, 911, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Orsi, Á., Padilla, N., Groves, B., et al. 2014, MNRAS, 443, 799 [Google Scholar]
- Ouchi, M., Shimasaku, K., Akiyama, M., et al. 2008, ApJS, 176, 301 [Google Scholar]
- Ouchi, M., Shimasaku, K., Furusawa, H., et al. 2010, ApJ, 723, 869 [Google Scholar]
- Ouchi, M., Ono, Y., & Shibuya, T. 2020, ARA&A, 58, 617 [Google Scholar]
- Palanque-Delabrouille, N., Magneville, C., Yèche, C., et al. 2016, A&A, 587, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pâris, I., Petitjean, P., Ross, N. P., et al. 2017, A&A, 597, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Partridge, R. B., & Peebles, P. J. E. 1967, ApJ, 147, 868 [Google Scholar]
- Planck Collaboration VI 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pritchet, C. J. 1994, PASP, 106, 1052 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, Y., Mutch, S. J., Poole, G. B., et al. 2017, MNRAS, 472, 2009 [NASA ADS] [CrossRef] [Google Scholar]
- Queiroz, C., Abramo, L. R., Rodrigues, N. V. N., et al. 2023, MNRAS, 520, 3476 [Google Scholar]
- Rahna, P. T., Zheng, Z. Y., Chies-Santos, A. L., et al. 2022, A&A, 668, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reines, A. E., & Volonteri, M. 2015, ApJ, 813, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, S., Sobral, D., & Matthee, J. 2016, MNRAS, 463, 1678 [Google Scholar]
- Santos, S., Sobral, D., Matthee, J., et al. 2020, MNRAS, 493, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, S., Sobral, D., Butterworth, J., et al. 2021, MNRAS, 505, 1117 [CrossRef] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Shibuya, T., Kashikawa, N., Ota, K., et al. 2012, ApJ, 752, 114 [Google Scholar]
- Sobral, D., Best, P. N., Geach, J. E., et al. 2009, MNRAS, 398, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Matthee, J., Best, P., et al. 2017, MNRAS, 466, 1242 [Google Scholar]
- Sobral, D., Santos, S., Matthee, J., et al. 2018, MNRAS, 476, 4725 [Google Scholar]
- Song, M., Finkelstein, S. L., Gebhardt, K., et al. 2014, ApJ, 791, 3 [Google Scholar]
- Spinoso, D., Orsi, A., López-Sanjuan, C., et al. 2020, A&A, 643, A149 [EDP Sciences] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [Google Scholar]
- Taylor, K., Marín-Franch, A., Laporte, R., et al. 2014, J. Astron. Instrum., 3, 1350010 [Google Scholar]
- Vanden Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [Google Scholar]
- Weinberg, D. H., Davé, R., Katz, N., & Kollmeier, J. A. 2003, AIP Conf. Ser., 666, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Wold, I. G. B., Barger, A. J., & Cowie, L. L. 2014, ApJ, 783, 119 [Google Scholar]
- Yamada, T., Nakamura, Y., Matsuda, Y., et al. 2012, AJ, 143, 79 [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 1579 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Ouchi, M., Gebhardt, K., et al. 2021, ApJ, 922, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, Z.-Y., Wang, J.-X., Malhotra, S., et al. 2014, MNRAS, 439, 1101 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Candidates catalog
Table A.1 lists the 91 candidates selected by our method as LAEs, containing only the sources with morph_prob_star < 0.1, as explained in Sect. 4.10. This entire catalog is representative of what can be directly obtained of any J-PAS dataset. The sources used in the Lyα LF estimation are marked in blue. As explained in Sect. 4.11, the subsample of objects used for the Lyα LF are chosen after a visual inspection and cross-matches with SDSS DR16 and HETDEX Source Catalog 1.
Catalog of sources selected as LAEs.
The description of each column is the following:
-
Field: The subfield of miniJPAS or J-NEP in which the source was detected by SExtractor.
-
tile_id: The ID identifying the selection tile of miniJPAS or J-NEP.
-
number: Unique ID of each object within each tile in the dual-mode catalogs of miniJPAS or J-NEP.
-
RA, DEC: Right ascension and declination.
-
zNB: Lyα redshift of the central wavelength of the line detection. The provided error is inferred from the FWHM of the NB.
-
Selected NB: Name of the NB of the Lyα line detection.
-
SDSS spCL, SDSS zspec: Spectroscopic class and redshift of the counterpart in SDSS DR16.
-
HETDEX spCl, HETDEX zspec: Spectroscopic class and redshift of the counterpart in HETDEX Source Catalog 1.
-
VI class: Class assigned in the visual inspection (see Sect. 4.11)
-
log10LLyα: Estimated Lyα luminosity.
-
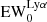 : Estimated rest-frame EW of the Lyα line.
: Estimated rest-frame EW of the Lyα line. -
P2D: Purity extracted from the 2D correction maps according to the source LLyα and r magnitude (see Sect. 4.4). This value can be seen as the probability of each source to be a true positive LAE.
Appendix B: 2D purity and number count corrections
In Fig. B.1 we show example representations of the 2D correction maps described in Sect. 4.4, for 2.3 < z < 2.8. These maps are computed for every redshift interval used in this work, for every field of miniJPAS and J-NEP. The non-colored regions in Fig. B.1 correspond to combinations of parameters incompatible with the LAEs of our mock, thus the candidates laying in this areas of the 2D map are assigned P2D = w2D = 0.
 |
Fig. B.1. 2D maps of the purity and number count correction for the four miniJPAS fields and J-NEP in the redshift interval z = 2.3–2.8. The maps are computed for every field in miniJPAS and J-NEP and every interval of redshift used in this work, only one z interval is shown for brevity. The black squares and error bars represent the LAE candidates of each field in the chosen interval of redshift. |
Appendix C: Purity calibration
As introduced in Sect. 3, the corrections of our LF are likely to be biased by the underlying luminosity distribution we impose to our mock data. The number count correction estimate does not depend on the parameter space distribution of the mocks, as it is only a measure on how likely is to select a source as a function of its intrinsic LLyα and EW. Nonetheless, the purity estimate is strongly dependent on the relative abundances of the objects from the target population in relation to that of the contaminants.
To check the robustness of our corrections in the QSO regime, we alter the purity estimate by introducing a factor ρ to the true positive count. We recalculate the 2D purity as
and compute the Lyα LF of miniJPAS and J-NEP, using this new definition of the purity, for different values of ρ. Since the effect of increasing or decreasing the value of ρ is equivalent to increasing or decreasing the mock QSO number density, this procedure tests the effect of underestimating and overestimating the purity of our selected sample. We estimate the Lyα LF for different values of ρ using the whole selected sample of 127 candidates (see Sec. 4.6). The upper panel of Fig. C.1 shows the recomputed LFs for different values of ρ (as detailed by the plot label). Solid lines show the resulting LLyα distribution of our QSO mock, for each ρ value. The comparison between the different LF realizations (colored squares and error-bars) show that the change produced onto the LF by varying ρ is small, especially when compared to the 1σ uncertainties for the ρ = 1 realization (black error bars). In addition, the value of ρ that produces an input LF comparable to the estimated is close to ρ ∼ 1. With the eventual release of larger catalog of J-PAS, it will be possible to accurately calibrate the purity of the LAE candidate sample.
 |
Fig. C.1. Effects of varying the sample purity on the estimated Lyα LF. Top: Colored squares show different realizations of our Lyα LF in the range z = 2.0 − 3.8, obtained after scaling the number of true positives in the purity computation by a factor ρ = 0.1, 0.5, 1.0, 1.5, 2.0. We also show the mock QSO LF for each ρ (solid lines). We show the uncertainties of the LF with ρ = 1. The variation of the LF is inside the 1σ errors for all the shown values of ρ. Bottom: Estimated purity for the different values of ρ. |
As already discussed in Sect. 5.3, our LAE candidate sample is expected to be vastly dominated by AGN. Consequently, any change in the prior LF used for the construction of the SFG mock produces a minimum change onto our final results. Although we predict a nonzero contribution of SFG in our sample, the observational data are insufficient for calibrating the purity at the SFG regime (log10(LLyα/erg s−1) ≲ 43.5) with the current selection method.
All Tables
Groups of NBs used in this work for the computation of the Lyα LF, their associated redshift coverage of Lyα, and the comoving volume of the Universe sampled by those redshift intervals for an area of 1.14 deg2.
All Figures
 |
Fig. 1. Exponential fits of magnitude errors according to Eq. (1). For brevity, we show the magnitudes of 4 NBs and 2 BBs (colored dots) of J-NEP and their corresponding fits (dashed black lines). We get highly similar results for every filter in J-NEP and all pointings of miniJPAS. |
| In the text | |
 |
Fig. 2. Basic properties of the QSO mock. Top: output Lyα LF of the QSO mock at z > 2. The measurement of the Lyα line can often be affected by the presence of the N V line, for this reason we also show the Lyα+N V LF. The bias correction in the LLyα measurement caused by N V is addressed in Sect. 4.2. We compare with the fits for the QSO Lyα LF in Spinoso et al. (2020) and Zhang et al. (2021), using a Schechter and a double power-law, respectively. Bottom: LLyα as a function of r magnitude for the sources in the QSO mock (orange) and the QSOs of SDSS DR16Q with a LLyαS/N > 5 (blue). The contour lines mark the regions containing the 68% and 95% of the objects. |
| In the text | |
 |
Fig. 3. Color distributions of the selected candidates in our mock before applying the color cut. The objects in the shaded area are removed from the sample after applying the cut. Through these BB color cuts we remove objects showing significant red colors, which are likely to be nearby galaxies. |
| In the text | |
 |
Fig. 4. Contours showing the areas encompassing the 68% and 95% of the LAEs in the mock showing the retrieved (observed) Lyα luminosity as a function of the real value in the catalog. The dotted and solid line contours show the values of LLyα before and after applying the bias subtraction, respectively (see Sect. 4.2). Black dots represent the observational candidates from miniJPAS with a spectroscopic counterpart (see Sect. 4.8). |
| In the text | |
 |
Fig. 5. Purity and completeness as a function of LLyα of the full retrieved sample at 2.05 < z < 3.75. We show the values of purity and completeness for the whole redshift range in black solid lines, and for each redshift interval used in colored solid lines. We represent an additional redshift interval to show the trend beyond the redshift range probed by this work (dashed line). |
| In the text | |
 |
Fig. 6. Examples of miniJPAS and J-NEP LAE candidates. We show the fluxes of the 56 narrow medium (colored circles) and broad bands (colored squares) of the J-PAS filter set. The NB selected as Lyα by our pipeline is marked with a red dashed line. The detected secondary QSO lines are marked with green dashed lines (see Sect. 4.1.3). Spectroscopically or visually identified emission lines of the objects are shown with a gray dotted line. We also show the images of each source in r and the selected NB. The spectra of the SDSS DR16 (HETDEX) counterparts are shown in gray (orange) when available. The five objects in the left column are examples of LAEs identified by our method. The right column show five examples of possible contaminants. |
| In the text | |
 |
Fig. 7. Rest-frame wavelength of the selected features in the QSO and low-z galaxy mock. The rest-frame wavelength is computed as λ0 = λNB/(1 + z), where λNB is the central wavelength of the selected NB and z the true redshift of the mock object. |
| In the text | |
 |
Fig. 8. Comparison between the NB and spectroscopic redshifts of the candidates. Top: retrieved Lyα redshift of the candidates with SDSS or HETDEX spectrum. The straight lines represent the redshift at which the most common QSO contaminant lines are selected as Lyα. Bottom: difference between the NB Lyα redshift of the good candidates and the spectroscopic redshifts given by SDSS or HETDEX. The error bars show the redshift interval covered by the width of the NB in which the candidate is selected. |
| In the text | |
 |
Fig. 9. Retrieved Lyα redshift of the candidates as compared to the miniJPAS photometric redshifts (Hernán-Caballero et al. 2021). We show spectroscopically confirmed LAEs (green filled circles) and contaminants (red empty circles), objects with extended morphology (morph_star_prob < 0.1; blue empty squares), and sources without any spectral or morphology identification (gray crosses). The dashed lines mark the confusion between Lyα and typical galactic emission lines. |
| In the text | |
 |
Fig. 10. Distribution of Lyα EW0 of the candidate sample of miniJPAS and J-NEP. We compare the whole sample of candidates retrieved by our method in the mock (gray, dashed histogram) and in the observational data (orange, dashed histogram). We also compare the distribution of Lyα EW0 for the mock subsample of true-positive LAEs (solid, black histogram) and the visually inspected subsample of miniJPAS and J-NEP (solid, red histogram) as defined in Sect. 4.11. For |
| In the text | |
 |
Fig. 11. Lyα LFs for six intervals in redshift. We show the full redshift range power-law fit for reference (dashed red line). The redshift bins showed in this figure overlap and are therefore correlated. The Lyα LF shows no significant evolution with redshift within the given uncertainties. |
| In the text | |
 |
Fig. 12. Integrated LFs in 43.6 < log10(LLyα/erg s−1) < 44.8 in the six intervals of redshift shown in Fig. 11. The chosen LLyα interval is that where all six realizations of the Lyα LF are well defined. The horizontal error bars represent the width of the redshift interval. The dashed red line represents the integral of the best power-law fit presented in Sect. 5.2.2. |
| In the text | |
 |
Fig. 13. Lyα LF over the whole 2.05 < z < 3.75 range (red squares and black error bars), obtained by combining data from all the NBs we employ. Our estimation covers the intermediate regime of the Lyα LF, where the transition between the SFG and the QSO populations is expected. |
| In the text | |
 |
Fig. 14. Schechter and power-law fits of the 2.05 < z < 3.75 Lyα LF. Left panel: Schechter best fit and 1σ confidence region for the fit of the full z range of this work (blue solid line and shaded area). We compare our result with the Schechter fits in Spinoso et al. (2020) for 4 NBs of J-PLUS. Our Schechter fit is in line with the fits in Spinoso et al. (2020) for z = 2.2, 2.5 and 3.2 at the faintest bins of our LF. We advise some caution when considering our results at the brightest luminosity (i.e., log10(LLyα/erg s−1) > 45.5). Indeed our results in this regime are limited by our survey area. Right panel: power-law fit to our Lyα LF at log10(LLyα/erg s−1) < 45.5. The bins of the LF represented with empty squares are not used in this fit in particular. We compare to the power-law fits in Matthee et al. (2017), Sobral et al. (2018) in the same LLyα regime. The shaded blue area marks the 1σ confidence region. Our constraint on the power-law slope A for the faint-end of the AGN Lyα LF is consistent with the other realizations shown in this plot within a 1σ confidence interval. |
| In the text | |
 |
Fig. 15. Fraction of QSOs in the candidate sample from the mock at 2.05 < z < 3.75. We represent our estimation of the QSO fraction (green solid line and green shaded area for 1σ uncertainty) based on the power-law fit to our Lyα LF and the SFG Lyα LF of Sobral et al. (2018). We also show the QSO fraction extracted from our mocks (blue solid line). We compare our results to previous realizations from past works. |
| In the text | |
 |
Fig. B.1. 2D maps of the purity and number count correction for the four miniJPAS fields and J-NEP in the redshift interval z = 2.3–2.8. The maps are computed for every field in miniJPAS and J-NEP and every interval of redshift used in this work, only one z interval is shown for brevity. The black squares and error bars represent the LAE candidates of each field in the chosen interval of redshift. |
| In the text | |
 |
Fig. C.1. Effects of varying the sample purity on the estimated Lyα LF. Top: Colored squares show different realizations of our Lyα LF in the range z = 2.0 − 3.8, obtained after scaling the number of true positives in the purity computation by a factor ρ = 0.1, 0.5, 1.0, 1.5, 2.0. We also show the mock QSO LF for each ρ (solid lines). We show the uncertainties of the LF with ρ = 1. The variation of the LF is inside the 1σ errors for all the shown values of ρ. Bottom: Estimated purity for the different values of ρ. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \sigma [m] = A \cdot \exp \left[B \cdot m + C\right]. \end{aligned} $$](/articles/aa/full_html/2023/12/aa47463-23/aa47463-23-eq4.gif)
![$$ \begin{aligned} N[\mathrm{EW}_0]=N_0\cdot \exp [\mathrm{EW}_0/\alpha ], \end{aligned} $$](/articles/aa/full_html/2023/12/aa47463-23/aa47463-23-eq7.gif)
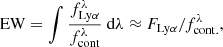
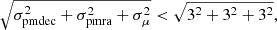
![$$ \begin{aligned} T_\mathrm{IGM} \,[\lambda _\mathrm{obs} ]= {\left\{ \begin{array}{ll} \exp \left[{a\cdot \left(\frac{\lambda _\mathrm{obs} }{\lambda _{\mathrm{Ly} \alpha }}\right)^b}\right],&\lambda _\mathrm{obs} \le \lambda _{\mathrm{Ly} \alpha }\\ 1,&\lambda _\mathrm{obs} >\lambda _{\mathrm{Ly} \alpha } \end{array}\right.}, \end{aligned} $$](/articles/aa/full_html/2023/12/aa47463-23/aa47463-23-eq16.gif)
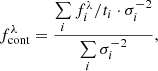
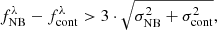
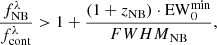
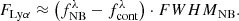
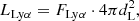
![$$ \begin{aligned} \Delta \log _{10} L = \mathrm{median} [\log _{10}L_{\mathrm{Ly} \alpha } - \log _{10}L_{\mathrm{Ly} \alpha }^\mathrm{intrinsic}].\end{aligned} $$](/articles/aa/full_html/2023/12/aa47463-23/aa47463-23-eq29.gif)
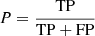

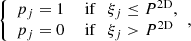
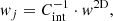
![$$ \begin{aligned} \Phi _i\left[\log _{10}L_{\mathrm{Ly} \alpha }\right] = \frac{\sum \limits _j p_j \cdot { w}_j}{V\cdot \Delta \log _{10}L_{\mathrm{Ly} \alpha }}, \end{aligned} $$](/articles/aa/full_html/2023/12/aa47463-23/aa47463-23-eq34.gif)
![$ \log_{10}[\mathrm{EW}_0^{\mathrm{Ly\alpha}}/{\AA}] > 2 $](/articles/aa/full_html/2023/12/aa47463-23/aa47463-23-eq35.gif)
![$$ \begin{aligned} \Phi [L]\mathrm{d} \left(\log _{10} L\right)=\log 10\cdot \Phi ^*\cdot \left(\frac{L}{L^*}\right)^{\alpha + 1}\cdot \mathrm{e} ^{-L/L^*}\mathrm{d} \left(\log _{10} L\right), \end{aligned} $$](/articles/aa/full_html/2023/12/aa47463-23/aa47463-23-eq37.gif)
![$$ \begin{aligned}&\log _{10}\Phi _\text{PL}[\log _{10}(L_{\mathrm{Ly} \alpha } / \mathrm{erg}\,\mathrm{s}^{-1})]=A\cdot (\log _{10}(L_{\mathrm{Ly} \alpha } / \mathrm{erg}\,\mathrm{s}^{-1}) - 43.5) + B. \end{aligned} $$](/articles/aa/full_html/2023/12/aa47463-23/aa47463-23-eq55.gif)