EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 679 (November 2023) A&A, 679 (2023) A91 Full HTML
Open Access
Issue
A&A
Volume 679, November 2023
Article Number A91
Number of page(s) 15
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202347418
Published online 15 November 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The baryon cycle, which includes processes such as the infall of neutral, pristine gas onto galaxies and their subsequent chemical enrichment with dust and metals, is one of the fundamental drivers of galaxy formation and evolution (Tinsley 1980; Dayal & Ferrara 2018; Maiolino & Mannucci 2019; Péroux & Howk 2020). In particular, dust serves as a catalyst for the production of molecular hydrogen, H2, on the surfaces of its grains (Hollenbach & Salpeter 1971; Black & van Dishoeck 1987), an important prerequisite for star formation. The fraction of dust to the overall gas and metal abundances is governed by the most predominant dust production channels, in addition to the efficiency of grain growth in the interstellar medium (ISM) or potential supernova dust destruction or condensation scenarios (Draine 2003; Dunne et al. 2003; Mattsson et al. 2012; Dwek 2016; Schneider et al. 2016; De Vis et al. 2021).

Long-duration gamma-ray bursts (GRBs) offer unique insights into the dust and metal abundances of the ISM in their star-forming host galaxies (Savaglio et al. 2003; Jakobsson et al. 2004; Fynbo et al. 2006; Prochaska et al. 2007). Since most GRBs are associated with the death of massive stars (e.g., Woosley & Bloom 2006), they are linked to active star formation and thereby provide a reliable probe of star-forming galaxies through most of cosmic time (Jakobsson et al. 2006b; Kistler et al. 2009; Robertson & Ellis 2012; Tanvir et al. 2012; Greiner et al. 2015; Perley et al. 2016; Ghirlanda & Salvaterra 2022). Moreover, GRBs are some of the most energetic, brightest cosmological sources known (Gehrels et al. 2009; Malesani et al. 2023), which enables detailed studies of the ISM in their host galaxies based on absorption-line spectroscopy, even out to z ≳ 6 (Kawai et al. 2006; Hartoog et al. 2015; Saccardi et al. 2023). While recent observations of nearby GRBs connected to dynamical merger origins challenge this picture (Rastinejad et al. 2022; Levan et al. 2023) and current evidence seems to point to a potential “metallicity bias” that limits the production of GRBs in metal-rich environments at z ≲ 2 (Levesque et al. 2010; Japelj et al. 2016; Palmerio et al. 2019; Graham et al. 2019; Björnsson 2019), these effects are arguably small in the high-redshift universe.

Due to their physical origin, most GRBs trace the central, dense star-forming regions of their host galaxies, showing high neutral hydrogen (H I) column densities of NHI ≥ 1020.3 cm−2 (Vreeswijk et al. 2004; Jakobsson et al. 2006a; Fynbo et al. 2009; Tanvir et al. 2019; Selsing et al. 2019), known as damped Lyman-α absorbers (DLAs; Wolfe et al. 2005). Furthermore, they enable studies of the molecular gas phase (Prochaska et al. 2009; Krühler et al. 2013; Friis et al. 2015; Bolmer et al. 2019; Heintz et al. 2019a,b) and the dust-rich environments (Zafar et al. 2012; Fynbo et al. 2014; Heintz et al. 2017, 2019c; Zafar & Møller 2019) of their host galaxies, which are much less frequently probed with absorbers in quasar sightlines (though do appear to be more common in dusty, gas- or molecular-rich sightlines; Heintz et al. 2018; Ranjan et al. 2020; Krogager et al., in prep.). This is due to the typical higher impact parameters of quasar absorbers (Péroux et al. 2011; Krogager et al. 2012, 2017; Christensen et al. 2014; Rahmani et al. 2016; Rhodin et al. 2018), which mostly probe the extended neutral gas reservoirs rather than the star-forming ISM (Neeleman et al. 2019; Heintz et al. 2021). Using GRBs as probes thus provides valuable insights into the dust and chemical abundances, in particular the dust-to-gas (DTG) and dust-to-metal (DTM) ratios, of the star-forming ISM of high-redshift galaxies.

Here we present new measurements and comprehensive analyses of the metal abundance and dust content of three GRB systems at z > 2, studied through the absorption-line spectroscopy of their bright optical/near-infrared afterglow. To complement these measurements, we further compiled all GRB afterglows at z ≳ 2 observed with intermediate- to high-resolution spectrographs for which similar measurements can be obtained, to provide the most comprehensive study to date of the metallicity and dust content of GRB-selected star-forming galaxies through cosmic time.

The paper is structured as follows. In Sect. 2 we present the observations of the three new GRBs and describe the overall sample compilation. In Sect. 3 we detail the derivation of the metal abundances, the visual extinction, the dust-corrected metallicities, and the DTG and DTM ratios for each GRB. In Sect. 4 we present our results and quantify the evolutionary trends of these properties with redshift and metallicity. Finally, in Sect. 5 we discuss and conclude on our work, with a particular emphasis on the implications of our results for galaxy evolution studies at high redshifts.

Throughout the paper we assume the concordance Λ cold dark matter cosmological model with Ωm = 0.315, ΩΛ = 0.685, and H0 = 67.4 km s−1 Mpc−1 (Planck Collaboration VI 2020). We derive relative abundances of specific elements X and Y using the solar abundances as reference, [X/Y] = log(NX/NY)−log(NX/NY)⊙, assuming the solar chemical abundances from Asplund et al. (2021) based on the recommendations by Lodders et al. (2009). Unless indicated otherwise, all uncertainties are given at the 1σ confidence level throughout the paper.

2. Observations and sample compilation

In this work we present measurements of the metal abundance and dust content in the sightlines of three new GRBs, GRBs 190106A, 190919B, and 191011A, observed as part of the European Southern Observatory (ESO) Very Large Telescope (VLT) STARGATE ToO program (PI: N. R. Tanvir). Furthermore, we compiled all the GRB afterglows known to date that match a few predefined criteria, as detailed below. The large majority of the GRB afterglows in this work have been observed with the ESO VLT/X-shooter spectrograph (Vernet et al. 2011) as part of the XS-GRB survey program (PI: J. Fynbo; Selsing et al. 2019; Bolmer et al. 2019). Our compiled sample also includes eight bursts observed with the higher-resolution Ultraviolet and Visual Echelle Spectrograph (UVES) on the VLT (six out of eight; Dekker et al. 2000) and the Echellette Spectrograph and Imager (ESI) on Keck (two out eight; Sheinis et al. 2002). For this work, we required that the GRB afterglow was observed with intermediate- (ℛ = 7000) to high-resolution (ℛ > 40 000) spectrographs to ensure the robustness of the metal abundance measurements. We additionally imposed that at least the wavelength regions of the redshifted transitions of the refractory element Fe II and the volatile elements S II or Zn II are covered and that the signal-to-noise ratio (S/N) is S/N > 3 per resolution element in the regions surrounding these transitions. This is to further optimize the column density measurements of these transitions and to ensure that we cover at least one heavily depleted and one volatile element to compute the dust-corrected gas-phase metallicities and the dust depletions in GRB-selected galaxies.

2.1. ESO-VLT/X-shooter observations

GRBs 190106A and 191011A were initially detected with the Neil GehrelsSwift Observatory (Swift hereafter; Gehrels et al. 2004), as reported by Sonbas et al. (2019) and Laha et al. (2019), respectively. GRB 190919B was detected with INTEGRAL (Winkler et al. 2003) as reported by Mereghetti et al. (2019). Following the detection of the optical counterpart, we obtained ultraviolet to near-infrared (300–2500 nm) spectroscopy of the GRB afterglows with the X-shooter spectrograph (Vernet et al. 2011) mounted on the ESO/VLT Unit Telescope 2 (in 2019). The observations were carried out 11 h (GRB 190106A), 4.87 h (GRB 190919B), and 23.3 min (GRB 191011A, using the rapid-response mode) after trigger. Each observation covered the ultraviolet to near-infrared simultaneously using the UVB, VIS, and NIR arms of the VLT/X-shooter with slit-widths of 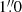1 . ″ 0 $ 1{{\overset{\prime\prime}{.}}}0 $ (UVB) and 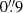0 . ″ 9 $ 0{{\overset{\prime\prime}{.}}}9 $ (VIS, NIR) and nominal spectral resolutions of ℛ = λ/#x0394;λ = 5400 (UVB), 8900 (VIS), and 5600 (NIR). The delivered spectral resolution are in most observations superior to the nominal, since the seeing full width at half maximum is considerably smaller than the slit width (Selsing et al. 2019).

The spectroscopic data were reduced and processed following a similar approach as described in Selsing et al. (2019). We used version v. 3.5.3 of the ESO X-shooter pipeline (Modigliani et al. 2010). The flux-calibrated 1D spectra were moved to the vacuum-heliocentric system in the process and corrected for Galactic extinction along the line of sight using the values from Schlafly & Finkbeiner (2011).

2.2. Sample compilation

In addition to these bursts, we compiled all GRB afterglow measurements from the literature following our criteria outlined above. This includes measurements from the pre-X-shooter era of the GRBs 000926, 030226, 050730, 050820A, 050922C, 071031, 080413A, and 081008 (Savaglio et al. 2003; Shin et al. 2006; Prochaska et al. 2007; Piranomonte et al. 2008; Ledoux et al. 2009; D’Elia et al. 2011; Wiseman et al. 2017; Zafar & Møller 2019). Furthermore, we considered all the GRBs observed as part of the XS-GRB legacy survey. Specifically, we adopted the column density and metallicity measurements from Bolmer et al. (2019), which includes GRB 090809A up to GRB 170202A. Beyond this, the GRB afterglows in our sample were all observed with the VLT/X-shooter as part of the STARGATE program (PI: N.R. Tanvir). In addition to the three bursts presented above, we further included GRBs 181020A, 190114A, and 210905A. GRBs 181020A and 190114A have already been presented in Heintz et al. (2019a), but we re-derived their basic properties for consistency and homogeneity with the rest of the sample and additionally included the new metallicity measurements for GRB 210905A from Saccardi et al. (2023). We note that GRB 180325A has been observed with X-shooter as part of the STARGATE program as well (Zafar et al. 2018a). However, since the relevant metal line transitions are all heavily saturated, hindering robust metallicity and depletion measurements, we excluded this burst from the sample. The full GRB afterglow sample comprises 36 bursts; their physical properties are summarized in Table 1.

Table 1.

Overview of the absorption-derived GRB host galaxy ISM properties.

3. Methods and analysis

3.1. Metal abundances

To model the absorption lines of the three new GRBs 190106A, 190919B, and 191011A considered here, we used the Python module VoigtFit (Krogager 2018). This code takes the observed spectra as input, convolves the Voigt-profiles to match the delivered spectral resolution, and provides the best-fit column density N and broadening parameter b for each transition separately for each of the identified velocity components. We modeled and tied b and the velocity structure for all the low-ionization transitions, based on the assumption that they physically trace the bulk of the neutral gas (e.g., Prochaska & Wolfe 1997), that is, NFeII = NFe. This is physically motivated since the ionization potentials of the neutral ions considered here are below that of hydrogen (13.6 eV) and so will predominantly be in the singly ionized state in the neutral gas phase. Furthermore, these absorption-line abundances have been found to not be influenced by photoionization from the GRB prompt emission since they typically probe gas in the ISM on kpc scales away from the GRB progenitor (Vreeswijk et al. 2007; Prochaska et al. 2007, 2008; Ledoux et al. 2009; Heintz et al. 2018).

The absorption-line spectra and the best-fit models are shown in Appendix A. To determine the gas-phase metallicity, [X/H] = log(NX/NH)−log(NX/NH)⊙, for each burst, we first fit the H I column density based on the broad damped Lyman-α absorption trough. Then, we relied primarily on the volatile elements Zn or S to determine the metal abundances. To infer the overall dust depletion level, quantified via [Zn/Fe] = log(NZn/NFe)−log(NZn/NFe)⊙ (see, e.g., De Cia et al. 2018), we either derived it directly from the measured abundances or, if Zn was inaccessible, we determined the expected [Zn/Fe]exp following the relations from De Cia et al. (2018) as described below. The derived H I column densities, [X/H] and [Zn/Fe] for each of the bursts in the full sample are summarized in Table 1.

3.2. Dust-corrected metallicities

Due to the mild and strong dust depletion of volatile and refractory elements, respectively, a significant fraction of the metals will be missing from the observed gas-phase abundances, [X/H]obs. To gauge the actual metal abundance of the GRB host galaxies we therefore needed to take the metals in both the dust and gas phases into account. The model for the expected relative abundances can be expressed as

[ X / H ] exp = δ X + [ M / H ] tot = A 2 X + B 2 X × [ Zn / Fe ] + [ M / H ] tot , $$ \begin{aligned} \mathrm{[X/H]_{\rm exp}} = \delta _{\rm X} + \mathrm{[M/H]_{tot}} = A2_{\rm X} + B2_{\rm X} \times \mathrm{[Zn/Fe]} + \mathrm{[M/H]_{tot}} ,\end{aligned} $$(1)

where δX is the dust depletion of element X (see, e.g., De Cia et al. 2016; Konstantopoulou et al. 2022) and A2X and B2X are empirically computed linear depletion parameters, here taken from Konstantopoulou et al. (2023; see also De Cia et al. 2016). For all cases, δX ≤ 0, with more negative values indicating higher depletion levels. For each source, we can thus derive the total, dust-corrected metallicity [M/H]tot and the overall strength of dust depletion, [Zn/Fe]fit, by performing a fit minimizing the difference between the observed relative abundances [X/H]obs and the relative abundances [X/H]exp given by Eq. (1).

To sample the posterior distribution of the best fit parameters, we used the implementation of a dynamical nested sampling algorithm provided by the dynesty package (Skilling 2004; Higson et al. 2018; Speagle 2020). This type of sampling algorithm has the benefits of focused Bayesian posterior estimation as performed by Markov chain Monte Carlo samplers while retaining the ability to determine marginal likelihoods for model comparison like other Nested Sampling algorithms. We used a uniform prior between 0 < [Zn/Fe] < 1.7 for the depletion strength parameter, where the upper limit is motivated by the strongest levels of depletion in Galactic sightlines presented by Jenkins (2009). For the dust-corrected metallicity, we also used a uniform prior but allowed it to run from [M/H]tot = −3.0 to 1.0, which encompasses all known Milky Way (MW) sightlines and high-z GRB absorption systems. As expected, the dust-corrected metallicities are overall higher than the metallicities inferred using Zn, S, or Si as tracers. For GRBs 190106A, 190919B, and 191011A, we derive dust-corrected gas-phase metallicities of [M/H]tot = −0.40 ± 0.10, −1.25 ± 0.15, and −0.63 ± 0.08, respectively. The dust-corrected metallicities reported in Bolmer et al. (2019) were computed following a similar approach, and the pre-X-shooter GRB sample were reanalyzed to compute dust-corrected metallicities following De Cia et al. (2018). The full sample covers a large range in metallicities of [M/H]tot = −2.3 to 0.2 (i.e., 0.5%–150% solar abundances).

3.3. Line-of-sight visual extinction

To determine the total integrated amount of dust in the GRB host-galaxy sightline, we modeled the extinction of the observed afterglow spectral energy distribution (SED; e.g., Watson et al. 2006; Schady et al. 2010; Zafar et al. 2011, 2018b; Greiner et al. 2011; Covino et al. 2013). Since the optical afterglows of GRBs follow an underlying smooth, temporally varying power law (Sari et al. 1998), it is possible to very accurately measure the visual extinction AV and the total-to-selective extinction RV. In contrast, the dust in DLAs in quasar sightlines are more difficult to disentangle due to the potential additional extinction of the background quasar spectrum and the uncertainties in functional shape. Following Heintz et al. (2019b), we adopted from the Swift X-Ray Telescope (XRT) repository1 the X-ray spectral slope in photon units, #x0393;, as derived from the Swift/XRT afterglow spectrum as prior for the intrinsic spectral slope converted to a function of wavelength as Fλ = F0λ#x0393; − #x0394;β − 3 and allowed the synchrotron cooling spectral break, #x0394;β, to take a value of #x0394;β = 0.0 or 0.5 (Sari et al. 1998).

We modeled the observed, dust-extinguished afterglow as 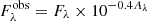F λ obs = F λ × 10 −0.4 A λ $ F^{\rm obs}_\lambda = F_\lambda \times 10^{-0.4 A_\lambda} $ where Aλ is the extinction as a function of wavelength. To determine the visual extinction AV for three new GRBs, we assumed the average Small Magellanic Cloud (SMC) extinction law (as parametrized by Gordon et al. 2003) due to the lack of any evidence for the rare 2175 Å extinction bump or an unusual steep (or flat) reddening curve in this sample (see also Appendix A). This is also in line with past GRB observations (Savaglio & Fall 2004; Perley et al. 2008; Kann et al. 2006, 2010; Friis et al. 2015; Zafar et al. 2018b; Corre et al. 2018), where the 2175 Å dust bump is only observed in a handful of cases (Zafar et al. 2012, 2018a; Heintz et al. 2019c). More exotic extinction curves have also been seen, either being extremely steep, as in the case of GRB 140506A (Fynbo et al. 2014; Heintz et al. 2017), or in a few bursts that show more flat, “gray” dust distributions (e.g., Stratta et al. 2004, 2005; Perley et al. 2008). However, in the majority of cases, an SMC-like extinction curves appear to be the most prevalent considering GRBs with spectral coverage from X-rays to the ultraviolet and near-infrared (Zafar et al. 2018b).

We normalized the intrinsic afterglow spectrum to the flux level in the NIR arm around the wavelength region of the typical K-band (∼2 μm). We fixed the redshift to zGRB and thereby only fit for AV for each case. We derive AV = 0.83 ± 0.03, < 0.03 (3σ), and 0.48 ± 0.13 mag for GRBs 190106A, 190919B, and 191011A, respectively. The spectra and best-fit extinction curve models are shown in Appendix A and the results are summarized for the full sample in Table 1.

4. Results and interpretations

4.1. Dust-corrected metallicity evolution with redshift

In Fig. 1 we present the redshift evolution of the dust-corrected metallicities measured for the 36 GRBs in our sample, spanning zGRB = 1.7 − 6.3. We performed a linear fit of the data, including the errors on [M/H]tot, from which we find [M/H]tot(z) = (−0.21 ± 0.04)z − (0.47 ± 0.14). This slope is slightly steeper and the intercept at z = 0 higher than inferred previously for GRBs, and implies a significant evolution compared to previous results (Cucchiara et al. 2015). Their work did not consider the dust-corrected metallicities, however, which would explain the offset in the intercept. The evolution of [M/H]tot with redshift is observed to be even steeper for DLAs in quasar sightlines (De Cia et al. 2016, 2018), with a slope of −0.32 ± 0.04 as inferred from the dust-corrected metallicities of their large sample. The observed lower intercept of the quasar-DLA relation (De Cia et al. 2018) is also expected since GRB-selected samples are weighted toward more metal-rich galaxies compared to quasar DLAs due to their lower impact parameters (Fynbo et al. 2008; Arabsalmani et al. 2015). We caution that our inferred metallicity evolution with redshift is largely driven by the high-redshift points at z ≳ 5, which is still sparsely populated and may be subject to a more severe selection bias as they will appear optically “dark” (e.g., Fynbo et al. 2001).

thumbnail Fig. 1.

Dust-corrected metallicity [M/H]tot as a function redshift for the GRB-selected galaxies. The small red data points show individual measurements, and the large red hexagons represent the H I-weighted means with redshift, where the error bars denote the redshift interval and 1σ dispersion, respectively. The best-fit relation [M/H]tot(z) = (−0.21 ± 0.04)z − (0.47 ± 0.14) is shown as the solid black line, with the dark- and light-shaded gray regions indicating the 1 and 2σ confidence intervals. For comparison, we overplot the average dust-corrected metallicities of MW, LMC, and SMC sightlines and predictions from the compiled set of simulations from Yates et al. (2021b): the DM and MM from the L-Galaxies simulations (Henriques et al. 2020; Yates et al. 2021a), the EAGLE simulations (Crain et al. 2015; Schaye et al. 2015), and the IllustrisTNG-100 (Pillepich et al. 2018; Springel et al. 2018). Generally, all observations and simulations seem to find similar slopes of #x0394;log(O/H)/#x0394;z ≈ 0.1 − 0.3. However, only the L-Galaxies simulations are able to reproduce the lower average metallicities inferred from the GRB sightlines.

To account for the low-metallicity GRB systems that carry less gas in our analysis, we derived the average H I-weighted metallicities, ⟨[M/H]⟩HI, defined as

⟨ [ M / H ] ⟩ HI = ∑ ( 10 [ M / H ] tot × N HI ) ∑ N HI $$ \begin{aligned} \langle \mathrm{[M/H]}\rangle _{\rm HI} = \frac{\sum (10^\mathrm{[M/H]_{tot}} \times N_{\rm HI})}{\sum N_{\rm HI}} \end{aligned} $$(2)

and shown in Fig. 1. The error bars on z represent the span on the redshift range and the standard deviation on ⟨[M/H]⟩HI. We divided the sample into larger redshift bins at higher redshifts, considering points at z = 1.7 − 2.2, z = 2.2 − 2.8, z = 2.8 − 3.5, z = 3.5 − 4.5, and z = 4.5 − 6.3, respectively, to account for the sparser number of sources in our sample at early cosmic epochs.

To put our results into context, we compared our measurements to recent simulations mapping the chemical enrichment and the metal mass density in galaxies across cosmic time. In particular, we adopted the “default model” (DM) and the “modified model” (MM) from the L-Galaxies simulations (Henriques et al. 2020; Yates et al. 2021a), the EAGLE simulations (Crain et al. 2015; Schaye et al. 2015), and the IllustrisTNG-100 (Pillepich et al. 2018; Springel et al. 2018), as compiled and described in detail by Yates et al. (2021b). While all simulations seem to find slopes for the redshift evolution of [M/H]tot(z) in agreement with our measurements, the EAGLE and TNG-100 simulations return a higher normalization, in particular at z ≳ 5. This could be due to an over-production or over-retention of metals inside galaxies in these particular simulations, which could indicate that EAGLE and TNG-100 contain an overabundance of massive galaxies. Overall, the L-Galaxies MM galaxy evolution models seem to best reproduce the data, with near-solar metallicity at z ∼ 0 and reaching [M/H]tot = −2 at z ≳ 5. These lower cosmic metallicities are achieved in L-Galaxies MM through highly efficient removal of metal-rich material from galaxies by supernova-driven galactic winds (see Yates et al. 2021a). We also note the particular metal-poor GRB system GRB 050730 with [M/H]tot = −2.31 ± 0.18 at z = 3.969, which neither of the models are able to reproduce and is also substantially offset from the underlying metallicity-evolution probed by the GRB sample. This is most likely related to the selection effects of the high-resolution VLT/UVES sample (Ledoux et al. 2009), but overall still imply that very metal-poor galaxies exist at z = 4. These observations thus provide new statistics on galaxy properties and their population scatter, which has to be considered in most recent simulation frameworks.

Furthermore, while GRBs do not have the same biases as emission-selected galaxies and thus provide a more complete census of star-forming galaxies at high-z (Fynbo et al. 2008), they may show an aversion to massive, metal-rich host galaxies at z < 2 (Perley et al. 2013; Schulze et al. 2015; Vergani et al. 2015, 2017; Japelj et al. 2016; Palmerio et al. 2019). This would explain the lower intercept at z = 0 of the GRB absorbers compared to simulations. However, this does not explain the offset at higher redshifts (z > 3), where GRBs are found to robustly trace the star-forming galaxy population. We also note that we observe a substantial scatter in the dust-corrected metallicities for a given redshift in the GRB sample, which is not recovered by any of the simulations. This observed scatter potentially seems to decrease with increasing redshift, though this may simply be due to lack of statistics.

While GRBs provide unique measures of the gas-phase metallicities in the ISM of galaxies out to high redshifts, other recent efforts to characterize the metallicities of galaxies out to and beyond z ≈ 4 have recently been carried out in emission as well (e.g., Sanders et al. 2020; Cullen et al. 2021; Heintz et al. 2022a; Curti et al. 2023). New approaches for deriving metallicities based on FIR line features such as [O III]−88 μm detectable by ALMA at the same epoch has also recently been established (e.g., Jones et al. 2020). However, these galaxies are luminosity-selected, and therefore represent only the most massive and metal-rich population of star-forming galaxies at these redshifts. Indeed, Cullen et al. (2021) find oxygen abundances in the range 12 + log(O/H) = 7.7 − 8.4 (i.e., [M/H] ≈ −0.80 to 0.0) for galaxies at z ≈ 3, which is systematically higher than the average GRB absorption-based metallicity at this redshift (likely related to their high stellar masses, M⋆ > 108.5 M⊙). Similarly, Jones et al. (2020) derive oxygen abundances in the range 12 + log(O/H) = 7.5 − 8.2 (i.e., [M/H] = −1.2 to −0.5) for galaxies at z ≳ 7, representing only the top 15% most metal-rich GRB host galaxies at these redshifts. Moreover, metallicity measurements from nebular emission lines, such as those taken by Cullen et al. (2021), are strongly dependent on the strong-line diagnostics used (Kewley & Ellison 2008), and generally only represent the metals in H II regions, which may be a poor reflection of the abundances in the more diffuse ISM. Further comparing the redshift evolution of luminosity-selected galaxies, we find that the evolution inferred for GRBs is slightly steeper than the slope #x0394;log(O/H)/#x0394;z ≈ −0.11 ± 0.02 measured by Sanders et al. (2021) from the MOSDEF galaxy survey, which is also consistent with the results of Jones et al. (2020) from z ≈ 0 − 8. This discrepancy (at 2σ confidence) can potentially be due to the different galaxy luminosity distributions and mass ranges probed with either approach or attributed to the different evolution of the stellar and gas-phase metallicities in galaxies (e.g., Yates et al. 2021b; Fraser-McKelvie et al. 2022) or total integrated versus line-of-sight effects (e.g., Arabsalmani et al. 2023).

4.2. The evolution of the dust-to-metal ratio

One way of inferring the DTM ratio in the GRB sightlines is by using the direct measurements of NHI and [M/H]tot to trace the equivalent metal column density, log NM = log NHI + [M/H]tot, and the visual extinction AV, which traces the total integrated dust column in the line of sight. This is presented in Fig. 2. Overall, we observe a substantial scatter with respect to a constant DTM ratio (dashed curve), with an average value in the GRB sample of DTMSED = log AV − (log NHI + [M/H]tot) = 4 × 10−22 mag cm2. This is consistent with previous GRB measurements (e.g., Zafar & Watson 2013; Wiseman et al. 2017; Zafar & Møller 2019), and slightly lower than the DTM measured for the MW, DTMGal = 4.5 × 10−22 mag cm2 (Watson 2011), though still consistent within the uncertainties. Notably, AV does not seem to decrease significantly below log NHI + [M/H]tot < 20.0, which might suggest that a non-negligible fraction of the dust in the line of sight is not associated with the neutral gas phase and instead might originate in the more ionized medium.

thumbnail Fig. 2.

AV vs. the equivalent metal column density, log NHI + [M/H]tot, i.e., the DTM ratio. The red symbols show the GRB sample; the triangles denote 1σ upper limits. The dashed and dotted lines represent the average MW ratio and the scatter (Watson 2011). GRB sightlines probe a large range in DTM ratios, with an average around the Galactic mean value.

Furthermore, we can infer the mass of the elements Xi in the dust phase relative to the total metal mass in the line of sight, the DTM mass ratio, based on the total, dust-corrected metallicity and depletion level inferred for each GRB host galaxy. Following the approach described in Konstantopoulou et al. (2023), we derive

DTM mass = M dust M metals = ∑ X i ( 1 − 10 δ X i ) 10 ( [ X i / H ] ⊙ + [ M / H ] tot ) W X i ∑ X i 10 ( [ X i / H ] ⊙ + [ M / H ] tot ) W X i , $$ \begin{aligned} \mathrm{DTM_{mass}} = \frac{M_{\rm dust}}{M_{\rm metals}} = \frac{\sum _{\mathrm{X}_i}(1{-}10^{\delta _{\mathrm{X}_i}})10^{([\mathrm{X}_i/\mathrm{H}]_\odot + [\mathrm{M/H}]_{\rm tot})} W_{\mathrm{X}_i}}{\sum _{\mathrm{X}_i} 10^\mathrm{([\mathrm{X}_i/\mathrm{H}]_\odot + \mathrm{[M/H]}_{\rm tot})} W_{\mathrm{X}_i}} ,\end{aligned} $$(3)

where δXi is the dust depletion of each element X (see also De Cia et al. 2016; Konstantopoulou et al. 2022), WXi the atomic weight, and 10([Xi/H]⊙ + [M/H]tot) represents the total metal column of each element X. It is evident that the dust-corrected metallicity [M/H]tot cancels out such that the DTMmass ratio is independent of the overall metallicity of the system. While only a subset of all the expected metals in the dust and gas phases are measured, we calculated the total contribution from each element based on the overall depletion level [Zn/Fe]. We derived the depletion for each element X from the empirical relations, δX = A2X + B2X × [Zn/Fe], assuming the empirical depletion coefficients A2X and B2X from Konstantopoulou et al. (2022). The resulting DTMmass ratios span 0.03 ± 0.01 (GRB 071031) to 0.41 ± 0.05 (GRB 190106A), generally lower than the Galactic average of DTM = 0.45, as listed in Table 2.

Table 2.

Depletion-derived DTM and DTG mass ratios.

In Fig. 3 we show the evolution of the DTM ratio as a function of redshift, both considering the DTM derived from the visual extinction AV and the total metal column density, DTMSED, and the depletion-derived DTMmass. We observe no clear evolution of DTMSED with redshift, with a Pearson correlation coefficient of r = −0.01, and the sample overall shows a large scatter. This is consistent with earlier results using GRB and quasar absorbers to probe DTMSED (Zafar & Watson 2013). The depletion-derived DTMmass shows a mild evolution with redshift consistent with simulations (e.g., Li et al. 2019), with a best-fit DTM = (− 0.03 ± 0.01)×z + 0.35 ± 0.05, and a Pearson r coefficient of r = −0.34. The GRB-selected galaxies further show systematically lower DTMmass than the MW, Lyman-break galaxies at z ≈ 3 (Shapley et al. 2020), and are on average also more dust deficient than the SMC and Large Magellanic Cloud (LMC; Konstantopoulou et al. 2023). Previous studies of the DTM ratios of high-redshift galaxies using GRB absorbers reached similar conclusions, though based on a different parametrization of the DTM relative to the MW average (De Cia et al. 2013; Wiseman et al. 2017).

thumbnail Fig. 3.

SED-derived DTM ratio, DTMSED = log AV − (log NHI + [M/H]tot) (top), and depletion-derived DTMmass ratio (bottom) as a function of redshift. Red dots (measurements) and triangles (1σ upper limits) denote the GRB host-galaxy absorbers. Gray symbols show the equivalent values for the MW, LMC, and SMC. The Pearson correlation coefficients, r, are marked for each data set. We observe no clear evolution of DTMSED with redshift but do see a mild evolution of DTMmass; the best-fit relation is shown as the solid black line, and the dark- and light-shaded gray regions indicate the 1 and 2σ confidence intervals.

In Fig. 4 we now consider the evolution of the DTM ratio as a function of the total dust-corrected metallicity, again using both the extinction and depletion-derived expressions for the DTM. We observe a large scatter in the relation with DTMSED, but find evidence for a potential mild anticorrelation with increasing metallicity with r = −0.41. On the contrary, we observe a significant correlation with r = 0.68 of DTMmass with increasing metallicity, with a best-fit relation of DTMmass = (0.11 ± 0.03)×[M/H]tot + (0.37 ± 0.04). This suggests that galaxies with metallicities relative to solar of 10% to 1% will have DTMmass ratios that are ≈60% to ≈30% of the Galactic average. This is in good qualitative agreement with predictions from some simulations (Vijayan et al. 2019; Hou et al. 2019; Graziani et al. 2020). However, GRB hosts do suggest more efficient dust production at low metallicities above z ∼ 2 than is found in simulations such as L-Galaxies MM (see Fig. 4 and Yates et al., in prep.). This is likely due to inefficient grain growth (or other production mechanisms) at high redshift in such simulations, although biases in observational samples could also play a role (see further discussion in Sect. 4.4). We also caution that absorbing gas is a mix of clouds with different chemical properties, and this complexity might be difficult to take into account in the simulations.

thumbnail Fig. 4.

SED-derived DTM ratio, DTMSED = log AV − (log NHI + [M/H]tot) (top), and depletion-derived DTMmass ratio (bottom) as a function of dust-corrected metallicity [M/H]tot. The symbol notation follows Fig. 3. Median relations at five discrete redshifts are also shown from the L-Galaxies MM simulation (Yates et al., in prep.). We observe a potential anticorrelation of DTMSED with metallicity and a stronger, positive correlation of DTMmass with increasing metallicity.

The discrepancy between the metallicity evolution of DTMSED and DTMmass might originate from the distinct dust phases probed by these two approaches. Dust depletion (and thus DTMmass) traces the amount of dust in the warm neutral medium in the GRB host galaxy ISM or circumgalactic medium (CGM) and is less sensitive to clumps of dense cold gas, in particular if rich in carbonaceous grains (Konstantopoulou et al. 2023). AV on the other hand probes the integrated extinction along the line of sight and is therefore less sensitive to more diffuse and dust-poor regions in the GRB host galaxy, as well as the presence of large grains that may produce gray extinction. Based on our results, there is evidence for DTMmass to be more tightly linked to the total metallicity of the star-forming host galaxy. The evolution with redshift is thus likely just a consequence of the DTM–[M/H]tot relation and the overall chemical enrichment of star-forming galaxies with redshift. We caution that our result on the tentative anticorrelation of DTMSED with metallicity is likely nonphysical as dust growth in the ISM is generally expected to result in an increasing DTM with metallicity. If no ISM dust growth is considered, such that the dust would purely originate from stellar sources, the DTM should be constant but not decrease with metallicity (Mattsson et al. 2014).

4.3. The evolution of the dust-to-gas ratio

The H I column densities and visual extinction, AV, measured directly in the GRB sightlines provide an independent measure of the DTG ratio, DTGSED = AV/NHI, in high-redshift galaxies. In Fig. 5 we show the distribution of AV and NHI observed for the GRB sample. For comparison, the average DTGSED ratios from specific Galactic sightlines and toward the SMC bar, the mean LMC and the LMC2 supershell from Gordon et al. (2003) are shown as well. We find that the majority of the GRB sightlines probe DTG ratios lower than observed in these local galaxies, and measure an average value (AV/NHI)GRB = 8.95 × 10−23 mag cm2. This is consistent with previous estimates of high-z GRB (Schady et al. 2010; Zafar et al. 2011) and general quasar DLA (Vladilo et al. 2008; Khare et al. 2012) sightlines. We note that the molecular hydrogen gas fraction is ≈5% at maximum in the GRB absorption systems (Bolmer et al. 2019; Heintz et al. 2019a), and is therefore negligible in the derivation of the DTG.

thumbnail Fig. 5.

Visual extinction (AV) vs. H I column density (NHI), i.e., the DTG ratio. The symbol notation follows Fig. 3. For comparison are overplotted the average DTG ratios from specific sightlines in the Local Group (MW, LMC, LMC2, and SMC) from Gordon et al. (2003). GRBs typically probe sightlines with lower AV for a given NHI than the local galaxies.

Similar to DTMmass, we can also infer the mass of an element X in the dust phase relative to the total gas mass, the DTG mass ratio, DTGmass, here based on Eq. (3) as

DTG mass = M dust M gas = DTM × 10 [ M / H ] tot × Z ⊙ , $$ \begin{aligned} \mathrm{DTG_{mass}} = \frac{M_{\rm dust}}{M_{\rm gas}} = \mathrm{DTM} \times 10^\mathrm{[M/H]_{\rm tot}} \times Z_\odot ,\end{aligned} $$(4)

where [M/H]tot is again the total dust-corrected metallicity and Z⊙ = 0.0139 is the solar metallicity by mass (Asplund et al. 2021). The derived DTGmass ratios span 10−5 − 2 × 10−3 as summarized in Table 2.

To explore the cause of the low relative DTG content in the GRB sightlines, we first examined the evolution of the DTG as a function of redshift in Fig. 6. Here, we again considered the DTG ratios calculated both from the SED fit of the dust extinction DTGSED and the depletion-derived DTGmass. We observe a tendency for a decreasing DTG as a function of redshift in both parameterizations, albeit with a large scatter. This implies that the difference in the SED- and dust-depletion-based DTM is likely not due to the differences in how the dust is probed. Notably, the bulk of the GRB-selected galaxies at z > 2 have DTGmass measurements below the MW average, reaching three orders of magnitudes lower at DTG = DTGmass = 3.5 × 10−6 (GRB 050730; see also Wiseman et al. 2017).

thumbnail Fig. 6.

SED-derived DTG ratio, DTGSED = AV/NHI (top), and depletion-derived DTGmass (bottom) as a function of redshift. The symbol notation follows Fig. 3. For comparison we mark the DTG ratios of the MW, LMC, and SMC. The GRB sightlines through high-redshift galaxies typically probe lower DTG content than inferred from these local galaxies.

In Fig. 7 we further examine the evolution of the DTG as a function of metallicity. Here we also plot the DTG ratios measured for the MW, SMC, and LMC. We find strong correlations between the DTG ratios inferred both from the dust extinction and from the depletion-derived mass ratio, with best-fit relations

log DTG SED = ( 0.89 ± 0.07 ) × [ M / H ] tot − ( 21.61 ± 0.08 ) mag cm − 2 , $$ \begin{aligned} \log \mathrm{DTG}_{\rm SED} = (0.89\pm 0.07)\times \mathrm{[M/H]_{tot}} - (21.61\pm 0.08)\, \mathrm{mag\,cm^{-2}} ,\end{aligned} $$(5)

thumbnail Fig. 7.

SED-derived DTG ratio, DTGSED = AV/NHI (top), and depletion-derived DTGmass (bottom) as a function of dust-corrected metallicity, [M/H]tot. The symbol notation follows Fig. 3. We find strong correlations between the DTG inferred both from the SED (top panel) and from depletion (bottom panel) with the metallicity. In the bottom panel we also show the predictions from the Simba simulation at z ∼ 0 − 6 (dotted blue line; Li et al. 2019) and the L-Galaxies MM simulation at z ∼ 2 − 6 (dashed lines; Yates et al., in prep.). The dashed orange line is the limit at which all metals are incorporated into grains (DTM = 1).

assuming the DTG ratio described by AV/NHI, with a Pearson correlation coefficient of r = 0.58, and

log DTG mass = ( 0.92 ± 0.06 ) × [ M / H ] tot − ( 2.81 ± 0.08 ) , $$ \begin{aligned} \log \mathrm{DTG_{mass}} = (0.92\pm 0.06)\times \mathrm{[M/H]_{tot}} - (2.81\pm 0.08) ,\end{aligned} $$(6)

assuming DTGmass measured from the depletion level, with a correlation coefficient of r = 0.97. These relations are in good agreement with the measurements of the DTG ratios in the MW, SMC, and LMC, populating the high-metallicity end. Notably, GRB 141028A have a DTGSED ratio of AV/NHI ≳ 5 × 10−22 mag cm2, exceeding the average MW DTG ratio of 4.5 × 10−22 mag cm2 (Watson 2011), but at substantially lower metallicities of −1.62 ± 0.28. On the other hand, the depletion-derived DTGmass is observed to follow a tight correlation with the dust-corrected metallicity [M/H]tot. This suggests that for some particular sightlines like in GRBs 141028A, the extinction in the line of sight caused by dust grains are substantially larger than predicted from the overall depletion strength (see also Savaglio & Fall 2004; Wiseman et al. 2017; Bolmer et al. 2019; Konstantopoulou et al. 2022). This could potentially indicate that a dominant contribution from dust grains probed via the extinction are not recovered in the depletion analysis. Potential causes of the discrepancy are that a substantial amount of dust in this system is either confined in clumps of cold neutral medium or in intervening systems along the line of sight.

We further compared our relations to the predictions by Li et al. (2019) based on the Simba cosmological hydrodynamic galaxy formation simulation and the L-Galaxies simulations by Yates et al. (in prep.). Although L-Galaxies MM matches the GRB relation well for systems below z ∼ 3, both simulations find steeper slopes for the metallicity evolution of the DTG than observed in the higher-redshift GRB sightlines. This could potentially indicate a more efficient dust production in the low-metallicity regime probed by these high-redshift sightlines than what is currently prescribed in the simulations, as also indicated previously by the excess DTMmass ratios. Additionally, we caution that Popping & Péroux (2022) demonstrated a large variety in the predictions from a number of semi-analytical and hydro-dynamical models and thereby also how accurately they able to reproduce the observed DTG and DTM ratios.

4.4. Quantifying the dust bias in our sample

Since this analysis is based on GRB afterglows observed with medium to high-resolution spectroscopy, we might be biased against the most metal- or dust-rich sightlines that obscure the afterglow light below the detection threshold (Ledoux et al. 2009). To investigate whether our parent sample is subject to this bias, we compared the AV distribution to that of the more unbiased photometric GRB sample presented by Covino et al. (2013), limited to z > 1.7. Following Heintz et al. (2019a), we normalized the two distributions by the number of bursts at AV < 0.1 mag (assuming that the spectroscopic sample is at least complete to this limit) and then computed the detection probability, fdet, of the fraction of GRBs in the spectroscopic sample versus that of the unbiased sample at the given range in AV (see Fig. 8). We find that the spectroscopic sample is complete up to AV = 0.3 mag (i.e., fdet = 1), but that we are only recovering 25% of the expected GRB sightlines at AV = 0.3 − 1.0 mag (fdet = 0.25). At AV > 1 mag, the spectroscopic sample is only 7% complete and even less at larger visual extinctions.

thumbnail Fig. 8.

Dust-corrected metallicity as a function of H I column density. The red dots again represent the main GRB sample but here are size-coded as a function of the SED-derived AV. The gray-shaded regions represent increasing AV, marked for each region, assuming the constant DTMSED ratio derived in this work of log AV − [log NHI + [M/H]tot]= − 21.4. The estimated detection probability for GRBs in each of these AV ranges is marked as well (see Sect. 4.4 for further details).

An additional complication might be introduced via our selection. For instance, since we required a detection of at least a set of metal lines at 3σ, this will inherently disfavor low-metallicity systems, albeit less severely the potentially dust-extinguished sightlines due to the broader spectral continuum range observed. This might partly alleviate the tension of our observations with the simulations in the low-metallicity regimes of the DTG and DTM mass ratios (Figs. 4 and 7), and potentially indicate even steeper correlations with metallicity.

Conservatively, we can thus only conclude that the relations derived here are representative of the moderately extinguished (AV ≲ 0.3 mag) GRB host-galaxy population, and may deviate at larger dust columns. We note, however, that the large majority of the GRB population in complete samples of GRBs has AV < 1 mag, and there is no clear evidence that we are missing the most dust-obscured bursts at z > 2 (Krühler et al. 2011, 2012). Nevertheless, while this potential dust obscuration bias may limit the number of the most dust- and metal-rich GRBs in the spectroscopic sample, the inferred trends of the relative DTM and DTG ratios are likely still valid. The main advantage of using GRBs as cosmic probes, lie in the high-z, low-metallicity regime, which is more difficult and time consuming to probe with direct emission-based surveys.

5. Summary and future outlook

In this work we have presented the most comprehensive analysis to date of the chemical enrichment and the evolution of dust and metals in the ISM of star-forming galaxies at z = 1.7 − 6.3 that host GRBs. We have compiled all GRB afterglow spectra observed over more than two decades (2000 − 2021) that have sufficient spectral resolutions (ℛ > 7000) and signal-to-noise ratios (S/N > 3) per resolution bin to enable robust measurements of the element abundances in the GRB lines of sight. GRBs are particularly efficient and relatively unbiased tracers of dense star-forming regions and thereby provide a unique view into the star-forming ISM properties of high-redshift galaxies in absorption that are otherwise difficult to probe in emission.

We find that the GRB-selected, star-forming galaxies had metallicities, corrected for the abundance of elements in the dust phase, that were on average evolving as a function of redshift following [M/H]tot(z) = (−0.21 ± 0.04)z − (0.47 ± 0.14). These galaxies revealed a slower gradual metal buildup compared to DLAs in quasar sightlines (De Cia et al. 2018), which traces the neutral gas on larger scales around galaxies. Our observations further exhibited a large scatter in the dust-corrected metallicities at a given redshift, which is not captured in most state-of-the-art galaxy evolution simulations, although there is overall agreement with the chemical enrichment as a function of cosmic time. The largest observational uncertainty in this relation is reflected by the sparser population of GRB afterglows detected at the highest redshifts, z ≳ 5. This particular population of GRBs may also be subject to a more severe selection bias than at lower redshifts since they will appear optically dark.

Based on our observations, we further derived the redshift and metallicity evolution of the DTG and DTM ratios in GRB-selected, star-forming galaxies at z > 2. Previously, the far-infrared emission of galaxies has been used to determine the mass and temperature of the dust in the ISM (e.g., Draine & Li 2007). These dust mass estimates have commonly been used to infer the total gas or ISM mass of high-redshift galaxies (e.g., Magdis et al. 2012; Scoville et al. 2016) but typically assuming average MW DTG ratios or conversion factors. However, they might be systematically underestimated if the fraction of dust relative to the total gas and metal abundance in the high-redshift, metal-poor regimes of galaxies changes substantially. Indeed, in this work we observe that all the z ≳ 2 GRB-selected galaxies probe sightlines with lower DTM and DTG ratio values compared to the Galactic average. In particular, we find that the average DTM mass ratios at z ≈ 2 and z ≈ 6 were 0.3 and 0.15, respectively, two to three times lower than what is observed in the MW. Similarly, the average gas-to-dust mass ratio is ≈150 for the MW, where, for comparison, we observe sightlines reaching gas-to-dust mass ratios of ≈105 at z ≳ 3 or metallicities [M/H]tot < −1.5 (i.e., 3% solar).

The DTM and DTG mass ratios derived here do not rely on any conversion factors and thus provide an accurate measure of the relative mass fractions of gas, dust, and metals along the GRB line of sight. However, since GRBs only probe narrow pencil-beam sightlines through their host galaxies, the total integrated dust and metal abundances are difficult to determine without knowing the size and morphology of the systems. For example, the distribution of dust, metals, and gas within the galaxy ISM may impact the measured DTM and DTG ratios along a single line of sight. In spatially resolved observations, the DTG mass ratio has been found to vary as a function of hydrogen surface density (Clark et al. 2023) and metallicity (Solís-Castillo & Albrecht 2020), with variations of over an order of magnitude within a single galaxy. A similar variation is also seen as a function of radius in galaxy evolution simulations out to 4 − 5 Re (Yates et al., in prep.). The DTM mass ratio is similarly observed to vary within galaxies as a function of metallicity (Chiang et al. 2018), irrespective of the αCO conversion factor applied. The average DTM and DTG mass ratios measured along single sightlines in absorption may thus be weighted differently to the average properties probed in emission. For example, this would likely be more biased toward the higher-metallicity and higher-surface-density regions of a galaxy, which have higher DTM and DTG mass ratios. It is also important to consider differences in the gas and dust radial profiles, with the former generally extending out to larger radii by up to 50–100% (Thomas et al. 2004). This could dilute the DTG and DTM ratios measured along GRB sightlines, although this is not supported by simulations, which predict systematically lower DTG and DTM mass ratios than what is measured along GRB sightlines (e.g., Figs. 4 and 7). Some additional caveats of directly mapping the GRB results to simulations and emission-selected galaxy studies include the physical environments of the GRBs, such as the ionization state and density of the gas.

Despite the expected differences between absorption and emission probes, the GRB absorption approach has proven to be extremely effective in determining the [C I]-to-H2 conversion factor in high-redshift, low-metallicity galaxies (Heintz & Watson 2020), which is otherwise difficult to constrain (Bolatto et al. 2013), and even provides novel constraints on the H I gas masses of galaxies at z > 2 (Heintz et al. 2021, 2022b). This would suggest that GRBs are able to probe galaxy average properties in the radial direction, albeit only along a single sightline. The DTM and DTG mass abundance ratios derived here therefore likely enable more accurate determinations of the total gas or ISM masses of high-redshift galaxies, based on the dust masses inferred from the far-infrared dust continuum emission of independent galaxy samples.

In the near future, this field is certain to rapidly advance with the new spectroscopic observations of high-redshift galaxies with the James Webb Space Telescope (JWST). Gas-phase metallicities of galaxies have already been measured using temperature-sensitive diagnostics up to z ≈ 9 in emission (Heintz et al. 2022a; Curti et al. 2023; Nakajima et al. 2023; Sanders et al. 2023) and have even been approximately inferred through strong-line diagnostics at z > 10 (Bunker et al. 2023; Hsiao & Coe 2023; Heintz et al. 2023b). The unique synergy between JWST and the Atacama Large Millimetre/submillimetre Array (ALMA) further enables direct DTM and DTG mass ratio measurements of galaxies well into the epoch of reionization at z > 6 (Heintz et al. 2023a). Characterizing the host galaxies of GRBs in emission with similar observations would be the natural next step, solidifying the link between galaxy properties derived in absorption and emission.

Acknowledgments

First and foremost, we would like to thank all the astronomers around the globe that have been on duty throughout the years, tirelessly following up GRBs, which resulted in this exquisite GRB spectroscopic afterglow legacy sample. K.E.H. acknowledges support from the Carlsberg Foundation Reintegration Fellowship Grant CF21-0103. The Cosmic Dawn Center (DAWN) is funded by the Danish National Research Foundation under grant No. 140. A.D.C. and C.K. acknowledge support by the Swiss National Science Foundation under grant 185692. AR acknowledges support from the INAF project Premiale Supporto Arizona & Italia. A.S. and S.D.V. acknowledge support from CNES and DIM-ACAV+. G.S. acknowledges the support by the State of Hesse within the Research Cluster ELEMENTS (Project ID 500/10.006) Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere.

References

  1. Arabsalmani, M., Møller, P., Fynbo, J. P. U., et al. 2015, MNRAS, 446, 990 [NASA ADS] [CrossRef] [Google Scholar]
  2. Arabsalmani, M., Garratt-Smithson, L., Wijers, N., et al. 2023, ApJ, 952, 67 [NASA ADS] [CrossRef] [Google Scholar]
  3. Asplund, M., Amarsi, A. M., & Grevesse, N. 2021, A&A, 653, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Björnsson, G. 2019, ApJ, 887, 219 [CrossRef] [Google Scholar]
  5. Black, J. H., & van Dishoeck, E. F. 1987, ApJ, 322, 412 [Google Scholar]
  6. Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [CrossRef] [Google Scholar]
  7. Bolmer, J., Ledoux, C., Wiseman, P., et al. 2019, A&A, 623, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bunker, A. J., Saxena, A., Cameron, A. J., et al. 2023, A&A, 677, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Chiang, I.-D., Sandstrom, K. M., Chastenet, J., et al. 2018, ApJ, 865, 117 [NASA ADS] [CrossRef] [Google Scholar]
  10. Christensen, L., Møller, P., Fynbo, J. P. U., & Zafar, T. 2014, MNRAS, 445, 225 [NASA ADS] [CrossRef] [Google Scholar]
  11. Clark, C. J. R., Roman-Duval, J. C., Gordon, K. D., et al. 2023, ApJ, 946, 42 [NASA ADS] [CrossRef] [Google Scholar]
  12. Corre, D., Buat, V., Basa, S., et al. 2018, A&A, 617, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Covino, S., Melandri, A., Salvaterra, R., et al. 2013, MNRAS, 432, 1231 [NASA ADS] [CrossRef] [Google Scholar]
  14. Crain, R. A., Schaye, J., Bower, R. G., et al. 2015, MNRAS, 450, 1937 [NASA ADS] [CrossRef] [Google Scholar]
  15. Cucchiara, A., Fumagalli, M., Rafelski, M., et al. 2015, ApJ, 804, 51 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cullen, F., Shapley, A. E., McLure, R. J., et al. 2021, MNRAS, 505, 903 [CrossRef] [Google Scholar]
  17. Curti, M., D’Eugenio, F., Carniani, S., et al. 2023, MNRAS, 518, 425 [Google Scholar]
  18. Dayal, P., & Ferrara, A. 2018, Phys. Rep., 780, 1 [Google Scholar]
  19. De Cia, A., Ledoux, C., Savaglio, S., Schady, P., & Vreeswijk, P. M. 2013, A&A, 560, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. De Cia, A., Ledoux, C., Mattsson, L., et al. 2016, A&A, 596, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. De Cia, A., Ledoux, C., Petitjean, P., & Savaglio, S. 2018, A&A, 611, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, SPIE Conf. Ser., 4008, 534 [Google Scholar]
  23. D’Elia, V., Fynbo, J. P. U., Covino, S., et al. 2010, A&A, 523, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. D’Elia, V., Campana, S., Covino, S., et al. 2011, MNRAS, 418, 680 [CrossRef] [Google Scholar]
  25. D’Elia, V., Fynbo, J. P. U., Goldoni, P., et al. 2014, A&A, 564, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. de Ugarte Postigo, A., Thöne, C. C., Bolmer, J., et al. 2018, A&A, 620, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. De Vis, P., Maddox, S. J., Gomez, H. L., Jones, A. P., & Dunne, L. 2021, MNRAS, 505, 3228 [NASA ADS] [CrossRef] [Google Scholar]
  28. Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
  29. Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [CrossRef] [Google Scholar]
  30. Dunne, L., Eales, S., Ivison, R., Morgan, H., & Edmunds, M. 2003, Nature, 424, 285 [NASA ADS] [CrossRef] [Google Scholar]
  31. Dwek, E. 2016, ApJ, 825, 136 [NASA ADS] [CrossRef] [Google Scholar]
  32. Fraser-McKelvie, A., Cortese, L., Groves, B., et al. 2022, MNRAS, 510, 320 [Google Scholar]
  33. Friis, M., De Cia, A., Krühler, T., et al. 2015, MNRAS, 451, 167 [NASA ADS] [CrossRef] [Google Scholar]
  34. Fynbo, J. U., Jensen, B. L., Gorosabel, J., et al. 2001, A&A, 369, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Fynbo, J. P. U., Starling, R. L. C., Ledoux, C., et al. 2006, A&A, 451, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Fynbo, J. P. U., Prochaska, J. X., Sommer-Larsen, J., Dessauges-Zavadsky, M., & Møller, P. 2008, ApJ, 683, 321 [NASA ADS] [CrossRef] [Google Scholar]
  37. Fynbo, J. P. U., Jakobsson, P., Prochaska, J. X., et al. 2009, ApJS, 185, 526 [NASA ADS] [CrossRef] [Google Scholar]
  38. Fynbo, J. P. U., Krühler, T., Leighly, K., et al. 2014, A&A, 572, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [Google Scholar]
  40. Gehrels, N., Ramirez-Ruiz, E., & Fox, D. B. 2009, ARA&A, 47, 567 [NASA ADS] [CrossRef] [Google Scholar]
  41. Ghirlanda, G., & Salvaterra, R. 2022, ApJ, 932, 10 [NASA ADS] [CrossRef] [Google Scholar]
  42. Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279 [NASA ADS] [CrossRef] [Google Scholar]
  43. Graham, J. F., Schady, P., & Fruchter, A. S. 2019, ApJ, in press [arXiv:1904.02673] [Google Scholar]
  44. Graziani, L., Schneider, R., Ginolfi, M., et al. 2020, MNRAS, 494, 1071 [NASA ADS] [CrossRef] [Google Scholar]
  45. Greiner, J., Krühler, T., Klose, S., et al. 2011, A&A, 526, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Greiner, J., Fox, D. B., Schady, P., et al. 2015, ApJ, 809, 76 [NASA ADS] [CrossRef] [Google Scholar]
  47. Hartoog, O. E., Malesani, D., Fynbo, J. P. U., et al. 2015, A&A, 580, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Heintz, K. E., & Watson, D. 2020, ApJ, 889, L7 [Google Scholar]
  49. Heintz, K. E., Fynbo, J. P. U., Jakobsson, P., et al. 2017, A&A, 601, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Heintz, K. E., Fynbo, J. P. U., Ledoux, C., et al. 2018, A&A, 615, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Heintz, K. E., Bolmer, J., Ledoux, C., et al. 2019a, A&A, 629, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Heintz, K. E., Ledoux, C., Fynbo, J. P. U., et al. 2019b, A&A, 621, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Heintz, K. E., Zafar, T., De Cia, A., et al. 2019c, MNRAS, 486, 2063 [NASA ADS] [CrossRef] [Google Scholar]
  54. Heintz, K. E., Watson, D., Oesch, P. A., Narayanan, D., & Madden, S. C. 2021, ApJ, 922, 147 [NASA ADS] [CrossRef] [Google Scholar]
  55. Heintz, K. E., Brammer, G. B., Giménez-Arteaga, C., et al. 2022a, arXiv e-prints [arXiv:2212.02890] [Google Scholar]
  56. Heintz, K. E., Oesch, P. A., Aravena, M., et al. 2022b, ApJ, 934, L27 [NASA ADS] [CrossRef] [Google Scholar]
  57. Heintz, K. E., Giménez-Arteaga, C., Fujimoto, S., et al. 2023a, ApJ, 944, L30 [NASA ADS] [CrossRef] [Google Scholar]
  58. Heintz, K. E., Watson, D., Brammer, G., et al. 2023b, arXiv e-prints [arXiv:2306.00647] [Google Scholar]
  59. Henriques, B. M. B., Yates, R. M., Fu, J., et al. 2020, MNRAS, 491, 5795 [NASA ADS] [CrossRef] [Google Scholar]
  60. Higson, E., Handley, W., Hobson, M., & Lasenby, A. 2018, Stat. Comput., 29, 891 [Google Scholar]
  61. Hollenbach, D., & Salpeter, E. E. 1971, ApJ, 163, 155 [NASA ADS] [CrossRef] [Google Scholar]
  62. Hou, K.-C., Aoyama, S., Hirashita, H., Nagamine, K., & Shimizu, I. 2019, MNRAS, 485, 1727 [NASA ADS] [CrossRef] [Google Scholar]
  63. Hsiao, T. Y.-Y., Coe, D., Abdurro’uf, et al. 2023, ApJ, 949, L34 [NASA ADS] [CrossRef] [Google Scholar]
  64. Jakobsson, P., Hjorth, J., Fynbo, J. P. U., et al. 2004, A&A, 427, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Jakobsson, P., Fynbo, J. P. U., Ledoux, C., et al. 2006a, A&A, 460, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Jakobsson, P., Levan, A., Fynbo, J. P. U., et al. 2006b, A&A, 447, 897 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Japelj, J., Vergani, S. D., Salvaterra, R., et al. 2016, A&A, 590, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Jenkins, E. B. 2009, ApJ, 700, 1299 [Google Scholar]
  69. Jones, T., Sanders, R., Roberts-Borsani, G., et al. 2020, ApJ, 903, 150 [CrossRef] [Google Scholar]
  70. Kann, D. A., Klose, S., & Zeh, A. 2006, ApJ, 641, 993 [NASA ADS] [CrossRef] [Google Scholar]
  71. Kann, D. A., Klose, S., Zhang, B., et al. 2010, ApJ, 720, 1513 [Google Scholar]
  72. Kawai, N., Kosugi, G., Aoki, K., et al. 2006, Nature, 440, 184 [NASA ADS] [CrossRef] [Google Scholar]
  73. Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [Google Scholar]
  74. Khare, P., Vanden Berk, D., York, D. G., Lundgren, B., & Kulkarni, V. P. 2012, MNRAS, 419, 1028 [NASA ADS] [CrossRef] [Google Scholar]
  75. Kistler, M. D., Yüksel, H., Beacom, J. F., Hopkins, A. M., & Wyithe, J. S. B. 2009, ApJ, 705, L104 [Google Scholar]
  76. Konstantopoulou, C., De Cia, A., Krogager, J.-K., et al. 2022, A&A, 666, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Konstantopoulou, C., De Cia, A., Ledoux, C., et al. 2023, A&A, submitted [Google Scholar]
  78. Krogager, J. K. 2018, arXiv e-prints [arXiv:1803.01187] [Google Scholar]
  79. Krogager, J. K., Fynbo, J. P. U., Møller, P., et al. 2012, MNRAS, 424, L1 [NASA ADS] [CrossRef] [Google Scholar]
  80. Krogager, J. K., Møller, P., Fynbo, J. P. U., & Noterdaeme, P. 2017, MNRAS, 469, 2959 [NASA ADS] [CrossRef] [Google Scholar]
  81. Krühler, T., Greiner, J., Schady, P., et al. 2011, A&A, 534, A108 [CrossRef] [EDP Sciences] [Google Scholar]
  82. Krühler, T., Fynbo, J. P. U., Geier, S., et al. 2012, A&A, 546, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Krühler, T., Ledoux, C., Fynbo, J. P. U., et al. 2013, A&A, 557, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Laha, S. L., Gronwall, C., Gropp, J. D., et al. 2019, GRB Coordinates Network, 25988, 1 [NASA ADS] [Google Scholar]
  85. Ledoux, C., Vreeswijk, P. M., Smette, A., et al. 2009, A&A, 506, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Levan, A. J., Malesani, D. B., Gompertz, B. P., et al. 2023, Nat. Astron., 7, 976 [NASA ADS] [CrossRef] [Google Scholar]
  87. Levesque, E. M., Kewley, L. J., Berger, E., & Zahid, H. J. 2010, AJ, 140, 1557 [NASA ADS] [CrossRef] [Google Scholar]
  88. Li, Q., Narayanan, D., & Davé, R. 2019, MNRAS, 490, 1425 [CrossRef] [Google Scholar]
  89. Lodders, K., Palme, H., & Gail, H. P. 2009, Landolt Börnstein, 4B, 712 [Google Scholar]
  90. Magdis, G. E., Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]
  91. Maiolino, R., & Mannucci, F. 2019, A&ARv, 27, 3 [Google Scholar]
  92. Malesani, D. B., Levan, A. J., Izzo, L., et al. 2023, A&A, submitted [arXiv:2302.07891] [Google Scholar]
  93. Mattsson, L., Andersen, A. C., & Munkhammar, J. D. 2012, MNRAS, 423, 26 [CrossRef] [Google Scholar]
  94. Mattsson, L., De Cia, A., Andersen, A. C., & Zafar, T. 2014, MNRAS, 440, 1562 [NASA ADS] [CrossRef] [Google Scholar]
  95. Mereghetti, S., Gotz, D., Ferrigno, C., et al. 2019, GRB Coordinates Network, 25788, 1 [NASA ADS] [Google Scholar]
  96. Modigliani, A., Goldoni, P., Royer, F., et al. 2010, SPIE Conf. Ser., 7737, 773728 [Google Scholar]
  97. Nakajima, K., Ouchi, M., Isobe, Y., et al. 2023, ApJS, accepted [arXiv:2301.12825] [Google Scholar]
  98. Neeleman, M., Kanekar, N., Prochaska, J. X., Rafelski, M. A., & Carilli, C. L. 2019, ApJ, 870, L19 [NASA ADS] [CrossRef] [Google Scholar]
  99. Palmerio, J. T., Vergani, S. D., Salvaterra, R., et al. 2019, A&A, 623, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Perley, D. A., Bloom, J. S., Butler, N. R., et al. 2008, ApJ, 672, 449 [CrossRef] [Google Scholar]
  101. Perley, D. A., Levan, A. J., Tanvir, N. R., et al. 2013, ApJ, 778, 128 [Google Scholar]
  102. Perley, D. A., Tanvir, N. R., Hjorth, J., et al. 2016, ApJ, 817, 8 [Google Scholar]
  103. Péroux, C., & Howk, J. C. 2020, ARA&A, 58, 363 [CrossRef] [Google Scholar]
  104. Péroux, C., Bouché, N., Kulkarni, V. P., York, D. G., & Vladilo, G. 2011, MNRAS, 410, 2237 [CrossRef] [Google Scholar]
  105. Pillepich, A., Springel, V., Nelson, D., et al. 2018, MNRAS, 473, 4077 [Google Scholar]
  106. Piranomonte, S., Ward, P. A., Fiore, F., et al. 2008, A&A, 492, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  107. Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  108. Popping, G., & Péroux, C. 2022, MNRAS, 513, 1531 [CrossRef] [Google Scholar]
  109. Prochaska, J. X., & Wolfe, A. M. 1997, ApJ, 487, 73 [NASA ADS] [CrossRef] [Google Scholar]
  110. Prochaska, J. X., Chen, H.-W., Dessauges-Zavadsky, M., & Bloom, J. S. 2007, ApJ, 666, 267 [NASA ADS] [CrossRef] [Google Scholar]
  111. Prochaska, J. X., Dessauges-Zavadsky, M., Ramirez-Ruiz, E., & Chen, H.-W. 2008, ApJ, 685, 344 [Google Scholar]
  112. Prochaska, J. X., Sheffer, Y., Perley, D. A., et al. 2009, ApJ, 691, L27 [NASA ADS] [CrossRef] [Google Scholar]
  113. Pugliese, G., Saccardi, A., D’Elia, V., et al. 2023, A&A, submitted [Google Scholar]
  114. Rahmani, H., Péroux, C., Turnshek, D. A., et al. 2016, MNRAS, 463, 980 [NASA ADS] [CrossRef] [Google Scholar]
  115. Ranjan, A., Noterdaeme, P., Krogager, J. K., et al. 2020, A&A, 633, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  116. Rastinejad, J. C., Gompertz, B. P., Levan, A. J., et al. 2022, Nature, 612, 223 [NASA ADS] [CrossRef] [Google Scholar]
  117. Rhodin, N. H. P., Christensen, L., Møller, P., Zafar, T., & Fynbo, J. P. U. 2018, A&A, 618, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  118. Robertson, B. E., & Ellis, R. S. 2012, ApJ, 744, 95 [Google Scholar]
  119. Saccardi, A., Vergani, S. D., De Cia, A., et al. 2023, A&A, 671, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  120. Sanders, R. L., Shapley, A. E., Reddy, N. A., et al. 2020, MNRAS, 491, 1427 [NASA ADS] [CrossRef] [Google Scholar]
  121. Sanders, R. L., Shapley, A. E., Jones, T., et al. 2021, ApJ, 914, 19 [CrossRef] [Google Scholar]
  122. Sanders, R. L., Shapley, A. E., Jones, T., et al. 2023, ApJ, 942, 24 [NASA ADS] [CrossRef] [Google Scholar]
  123. Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [Google Scholar]
  124. Savaglio, S., & Fall, S. M. 2004, ApJ, 614, 293 [CrossRef] [Google Scholar]
  125. Savaglio, S., Fall, S. M., & Fiore, F. 2003, ApJ, 585, 638 [NASA ADS] [CrossRef] [Google Scholar]
  126. Schady, P., Page, M. J., Oates, S. R., et al. 2010, MNRAS, 401, 2773 [NASA ADS] [CrossRef] [Google Scholar]
  127. Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
  128. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
  129. Schneider, R., Hunt, L., & Valiante, R. 2016, MNRAS, 457, 1842 [NASA ADS] [CrossRef] [Google Scholar]
  130. Schulze, S., Chapman, R., Hjorth, J., et al. 2015, ApJ, 808, 73 [NASA ADS] [CrossRef] [Google Scholar]
  131. Scoville, N., Sheth, K., Aussel, H., et al. 2016, ApJ, 820, 83 [Google Scholar]
  132. Selsing, J., Malesani, D., Goldoni, P., et al. 2019, A&A, 623, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  133. Shapley, A. E., Cullen, F., Dunlop, J. S., et al. 2020, ApJ, 903, L16 [NASA ADS] [CrossRef] [Google Scholar]
  134. Sheinis, A. I., Bolte, M., Epps, H. W., et al. 2002, PASP, 114, 851 [Google Scholar]
  135. Shin, M.-S., Berger, E., Penprase, B. E., et al. 2006, arXiv e-prints [arXiv:astro-ph/0608327] [Google Scholar]
  136. Skilling, J. 2004, AIP Conf. Ser., 735, 395 [Google Scholar]
  137. Solís-Castillo, B., & Albrecht, M. 2020, IAU Symp., 341, 78 [Google Scholar]
  138. Sonbas, E., Barthelmy, S. D., Beardmore, A. P., et al. 2019, GRB Coordinates Network, 23615, 1 [NASA ADS] [Google Scholar]
  139. Sparre, M., Hartoog, O. E., Krühler, T., et al. 2014, ApJ, 785, 150 [NASA ADS] [CrossRef] [Google Scholar]
  140. Speagle, J. S. 2020, MNRAS, 493, 3132 [Google Scholar]
  141. Springel, V., Pakmor, R., Pillepich, A., et al. 2018, MNRAS, 475, 676 [Google Scholar]
  142. Stratta, G., Fiore, F., Antonelli, L. A., Piro, L., & De Pasquale, M. 2004, ApJ, 608, 846 [Google Scholar]
  143. Stratta, G., Perna, R., Lazzati, D., et al. 2005, A&A, 441, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  144. Tanvir, N. R., Levan, A. J., Fruchter, A. S., et al. 2012, ApJ, 754, 46 [Google Scholar]
  145. Tanvir, N. R., Fynbo, J. P. U., de Ugarte Postigo, A., et al. 2019, MNRAS, 483, 5380 [Google Scholar]
  146. Thomas, H. C., Alexander, P., Clemens, M. S., et al. 2004, MNRAS, 351, 362 [NASA ADS] [CrossRef] [Google Scholar]
  147. Thöne, C. C., Fynbo, J. P. U., Goldoni, P., et al. 2013, MNRAS, 428, 3590 [CrossRef] [Google Scholar]
  148. Tinsley, B. M. 1980, Fund. Cosmic Phys., 5, 287 [Google Scholar]
  149. Vergani, S. D., Salvaterra, R., Japelj, J., et al. 2015, A&A, 581, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  150. Vergani, S. D., Palmerio, J., Salvaterra, R., et al. 2017, A&A, 599, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  151. Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  152. Vijayan, A. P., Clay, S. J., Thomas, P. A., et al. 2019, MNRAS, 489, 4072 [NASA ADS] [CrossRef] [Google Scholar]
  153. Vladilo, G., Prochaska, J. X., & Wolfe, A. M. 2008, A&A, 478, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  154. Vreeswijk, P. M., Ellison, S. L., Ledoux, C., et al. 2004, A&A, 419, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  155. Vreeswijk, P. M., Ledoux, C., Smette, A., et al. 2007, A&A, 468, 83 [CrossRef] [EDP Sciences] [Google Scholar]
  156. Watson, D. 2011, A&A, 533, A16 [CrossRef] [EDP Sciences] [Google Scholar]
  157. Watson, D., Fynbo, J. P. U., Ledoux, C., et al. 2006, ApJ, 652, 1011 [NASA ADS] [CrossRef] [Google Scholar]
  158. Winkler, C., Courvoisier, T. J. L., Di Cocco, G., et al. 2003, A&A, 411, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  159. Wiseman, P., Schady, P., Bolmer, J., et al. 2017, A&A, 599, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  160. Wolfe, A. M., Gawiser, E., & Prochaska, J. X. 2005, ARA&A, 43, 861 [NASA ADS] [CrossRef] [Google Scholar]
  161. Woosley, S. E., & Bloom, J. S. 2006, ARA&A, 44, 507 [Google Scholar]
  162. Yates, R. M., Henriques, B. M. B., Fu, J., et al. 2021a, MNRAS, 503, 4474 [NASA ADS] [CrossRef] [Google Scholar]
  163. Yates, R. M., Péroux, C., & Nelson, D. 2021b, MNRAS, 508, 3535 [NASA ADS] [CrossRef] [Google Scholar]
  164. Zafar, T., & Møller, P. 2019, MNRAS, 482, 2731 [Google Scholar]
  165. Zafar, T., & Watson, D. 2013, A&A, 560, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  166. Zafar, T., Watson, D., Fynbo, J. P. U., et al. 2011, A&A, 532, A143 [CrossRef] [EDP Sciences] [Google Scholar]
  167. Zafar, T., Watson, D., Elíasdóttir, Á., et al. 2012, ApJ, 753, 82 [NASA ADS] [CrossRef] [Google Scholar]
  168. Zafar, T., Heintz, K. E., Fynbo, J. P. U., et al. 2018a, ApJ, 860, L21 [NASA ADS] [CrossRef] [Google Scholar]
  169. Zafar, T., Watson, D., Møller, P., et al. 2018b, MNRAS, 479, 1542 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Column densities and visual extinctions of new GRB afterglows

Here we present the measurements and detail the derivations of the metal abundances and line-of-sight visual extinction for the three new GRBs examined in this work: GRBs 190106A, 190919B, and 191011A.

A.1. GRB 190106A

To determine the metallicity of GRB 190106A, we first measured the H I column density based on the broad Lyman-α transition using VoigtFit. The VLT/X-shooter afterglow spectrum and the best-fit model with log(NHI/cm−2) = 21.00 ± 0.04 is shown in Fig. A.1. Then, we derived the metal abundances of each element X by modeling the absorption-line profiles of the low-ionization metal transitions as outlined in Sect. 3. GRB 190106A shows multiple velocity components as displayed in Fig. A.2, but we report only the sum for the Zn and Fe transitions in Table 1 for the metallicity and depletion measurements. The spectroscopic redshift of the strongest low-ionization component that we considered as the redshift of the GRB is zGRB = 1.8599.

thumbnail Fig. A.1.

VLT/X-shooter GRB afterglow spectrum of GRB 190106A. The normalized 1D spectrum is shown in black, with the associated error spectrum shown by the gray region. The best-fit damped Lyman-α profile with log(NHI/cm−2) = 21.00 ± 0.04 is shown in red.

thumbnail Fig. A.2.

Metal absorption-line modeling of GRB 190106A. The normalized VLT/X-shooter spectrum is shown in black, with the best-fit Voigt profiles to each of the line transitions and velocity components (marked in blue) shown by the red curves. At the top of each panel are shown the residual plots.

Following the description in Sect. 3.3, we determined the visual extinction along the line of sight to GRB 190106A using the X-ray derived photon index, #x0393; = 1.90, as prior on the intrinsic GRB afterglow power-law slope, Fλ = F0λ#x0393; − #x0394;β − 3. We find that the spectral synchrotron cooling break is consistent with #x0394; = 0.5, meaning the intrinsic spectral Fλ power law becomes β = −1.60. Modeling the observed afterglow spectrum with an SMC extinction curve parametrization from Gordon et al. (2003), yields AV = 0.27 ± 0.03 mag (see Fig. A.3).

thumbnail Fig. A.3.

Visual extinction, AV, of GRB 190106A. The extracted 1D VLT/X-shooter GRB afterglow spectrum is shown in black, the intrinsic power-law shape derived from the Swift/XRT photon index in blue, and the best-fit model with AV = 0.27 ± 0.03 mag (assuming an SMC extinction curve) in red.

A.2. GRB 190919B

Following the same procedure as in Sect. A.1 but for GRB 190919B, we derive a best-fit H I column density of log(NHI/cm−2) = 21.49 ± 0.03 as shown in Fig. A.4. We determined the metal abundances from the single absorption component detected in the afterglow spectrum at zGRB = 3.2241, as reported in Table 1 and shown in Fig. A.5. The XRT photon index #x0393; = 2.10 represents an intrinsic optical/near-infrared power-law slope of β = −1.40, which yields a visual extinction of AV < 0.03 mag (at 1σ; see Fig. A.6).

thumbnail Fig. A.4.

Same as Fig. A.1 but for GRB 190919B, with a best-fit log(NHI/cm−2) = 21.49 ± 0.03.

thumbnail Fig. A.5.

Same as Fig. A.2 but for GRB 190919B.

thumbnail Fig. A.6.

Same as Fig. A.3 but for GRB 190919B, with a constraint on AV < 0.03 mag (1σ).

GRB 191011A

For GRB 191011A, we computed an H I column density of log(NHI/cm−2) = 21.65 ± 0.08 as shown in Fig. A.7. We determined the metal abundances from the sum of the velocity components detected in the afterglow spectrum, with the redshift of the strongest component being zGRB = 1.7204, as reported in Table 1 and shown in Fig. A.8. The XRT photon index #x0393; = 1.89 represents an intrinsic optical/near-infrared power-law slope of β = −1.61, which yields a visual extinction of AV < 0.43 ± 0.03 mag (see Fig. A.9).

thumbnail Fig. A.7.

Same as Fig. A.1 but for GRB 191011A, with a best-fit log(NHI/cm−2) = 21.49 ± 0.03.

thumbnail Fig. A.8.

Same as Fig. A.2 but for GRB 191011A.

thumbnail Fig. A.9.

Same as Fig. A.3 but for GRB 191011A, with a best-fit of AV = 0.43 ± 0.03 mag.

All Tables

Table 1.

Overview of the absorption-derived GRB host galaxy ISM properties.

In the text
Table 2.

Depletion-derived DTM and DTG mass ratios.

In the text

All Figures

thumbnail Fig. 1.

Dust-corrected metallicity [M/H]tot as a function redshift for the GRB-selected galaxies. The small red data points show individual measurements, and the large red hexagons represent the H I-weighted means with redshift, where the error bars denote the redshift interval and 1σ dispersion, respectively. The best-fit relation [M/H]tot(z) = (−0.21 ± 0.04)z − (0.47 ± 0.14) is shown as the solid black line, with the dark- and light-shaded gray regions indicating the 1 and 2σ confidence intervals. For comparison, we overplot the average dust-corrected metallicities of MW, LMC, and SMC sightlines and predictions from the compiled set of simulations from Yates et al. (2021b): the DM and MM from the L-Galaxies simulations (Henriques et al. 2020; Yates et al. 2021a), the EAGLE simulations (Crain et al. 2015; Schaye et al. 2015), and the IllustrisTNG-100 (Pillepich et al. 2018; Springel et al. 2018). Generally, all observations and simulations seem to find similar slopes of #x0394;log(O/H)/#x0394;z ≈ 0.1 − 0.3. However, only the L-Galaxies simulations are able to reproduce the lower average metallicities inferred from the GRB sightlines.
In the text
thumbnail Fig. 2.

AV vs. the equivalent metal column density, log NHI + [M/H]tot, i.e., the DTM ratio. The red symbols show the GRB sample; the triangles denote 1σ upper limits. The dashed and dotted lines represent the average MW ratio and the scatter (Watson 2011). GRB sightlines probe a large range in DTM ratios, with an average around the Galactic mean value.
In the text
thumbnail Fig. 3.

SED-derived DTM ratio, DTMSED = log AV − (log NHI + [M/H]tot) (top), and depletion-derived DTMmass ratio (bottom) as a function of redshift. Red dots (measurements) and triangles (1σ upper limits) denote the GRB host-galaxy absorbers. Gray symbols show the equivalent values for the MW, LMC, and SMC. The Pearson correlation coefficients, r, are marked for each data set. We observe no clear evolution of DTMSED with redshift but do see a mild evolution of DTMmass; the best-fit relation is shown as the solid black line, and the dark- and light-shaded gray regions indicate the 1 and 2σ confidence intervals.
In the text
thumbnail Fig. 4.

SED-derived DTM ratio, DTMSED = log AV − (log NHI + [M/H]tot) (top), and depletion-derived DTMmass ratio (bottom) as a function of dust-corrected metallicity [M/H]tot. The symbol notation follows Fig. 3. Median relations at five discrete redshifts are also shown from the L-Galaxies MM simulation (Yates et al., in prep.). We observe a potential anticorrelation of DTMSED with metallicity and a stronger, positive correlation of DTMmass with increasing metallicity.
In the text
thumbnail Fig. 5.

Visual extinction (AV) vs. H I column density (NHI), i.e., the DTG ratio. The symbol notation follows Fig. 3. For comparison are overplotted the average DTG ratios from specific sightlines in the Local Group (MW, LMC, LMC2, and SMC) from Gordon et al. (2003). GRBs typically probe sightlines with lower AV for a given NHI than the local galaxies.
In the text
thumbnail Fig. 6.

SED-derived DTG ratio, DTGSED = AV/NHI (top), and depletion-derived DTGmass (bottom) as a function of redshift. The symbol notation follows Fig. 3. For comparison we mark the DTG ratios of the MW, LMC, and SMC. The GRB sightlines through high-redshift galaxies typically probe lower DTG content than inferred from these local galaxies.
In the text
thumbnail Fig. 7.

SED-derived DTG ratio, DTGSED = AV/NHI (top), and depletion-derived DTGmass (bottom) as a function of dust-corrected metallicity, [M/H]tot. The symbol notation follows Fig. 3. We find strong correlations between the DTG inferred both from the SED (top panel) and from depletion (bottom panel) with the metallicity. In the bottom panel we also show the predictions from the Simba simulation at z ∼ 0 − 6 (dotted blue line; Li et al. 2019) and the L-Galaxies MM simulation at z ∼ 2 − 6 (dashed lines; Yates et al., in prep.). The dashed orange line is the limit at which all metals are incorporated into grains (DTM = 1).
In the text
thumbnail Fig. 8.

Dust-corrected metallicity as a function of H I column density. The red dots again represent the main GRB sample but here are size-coded as a function of the SED-derived AV. The gray-shaded regions represent increasing AV, marked for each region, assuming the constant DTMSED ratio derived in this work of log AV − [log NHI + [M/H]tot]= − 21.4. The estimated detection probability for GRBs in each of these AV ranges is marked as well (see Sect. 4.4 for further details).
In the text
thumbnail Fig. A.1.

VLT/X-shooter GRB afterglow spectrum of GRB 190106A. The normalized 1D spectrum is shown in black, with the associated error spectrum shown by the gray region. The best-fit damped Lyman-α profile with log(NHI/cm−2) = 21.00 ± 0.04 is shown in red.
In the text
thumbnail Fig. A.2.

Metal absorption-line modeling of GRB 190106A. The normalized VLT/X-shooter spectrum is shown in black, with the best-fit Voigt profiles to each of the line transitions and velocity components (marked in blue) shown by the red curves. At the top of each panel are shown the residual plots.
In the text
thumbnail Fig. A.3.

Visual extinction, AV, of GRB 190106A. The extracted 1D VLT/X-shooter GRB afterglow spectrum is shown in black, the intrinsic power-law shape derived from the Swift/XRT photon index in blue, and the best-fit model with AV = 0.27 ± 0.03 mag (assuming an SMC extinction curve) in red.
In the text
thumbnail Fig. A.4.

Same as Fig. A.1 but for GRB 190919B, with a best-fit log(NHI/cm−2) = 21.49 ± 0.03.
In the text
thumbnail Fig. A.5.

Same as Fig. A.2 but for GRB 190919B.
In the text
thumbnail Fig. A.6.

Same as Fig. A.3 but for GRB 190919B, with a constraint on AV < 0.03 mag (1σ).
In the text
thumbnail Fig. A.7.

Same as Fig. A.1 but for GRB 191011A, with a best-fit log(NHI/cm−2) = 21.49 ± 0.03.
In the text
thumbnail Fig. A.8.

Same as Fig. A.2 but for GRB 191011A.
In the text
thumbnail Fig. A.9.

Same as Fig. A.3 but for GRB 191011A, with a best-fit of AV = 0.43 ± 0.03 mag.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.